Симплексный метод для чайников: Симплексный метод для чайников примеры. Пример
Симплекс метод решения задач линейного программирования и его свойства — Задачи линейного программирования (ЗЛП) в экономике
Добрый день. Мы продолжаем знакомство с курсом «Экономико-математическое моделирование». Сегодня у нас десятый урок. Тема урока: Симплекс метод решения задач линейного программирования и графическое решение задач линейного программирования на примере задачи максимизации прибыли при ограничении на ресурсы. Содержание данного урока. Мы рассмотрим симплекс метод решения задач линейного программирования и рассмотрим пример, который решается с помощью метода графического программирования, как всегда, заключение и литература в конце урока. Итак, симплекс метод решения задач линейного программирования, как общий метод решения любой задачи линейного программирования. То есть любую задачу линейного программирования можно свести к следующей стандартной нормализованной форме. Целевая функция, мы не умаляя общности, будем считать, что эта целевая функция подлежит минимизации. Еще раз напоминаю, что здесь идет речь о скалярном произведении заданного вектора c, c1, c2… и так далее cn и искомого вектора x1, x2… и так далее xn. То есть скалярное произведение— это есть линейная суперпозиция c1×x1, c2×x2…и так далее cn×xn. Вот в сокращенной такой форме эта линейная комбинация записывается через два таких вектора в виде их скалярного произведения. Ограничения. Ограничения здесь задаются с помощью двух таких систем: равенства и неравенства. Равенство — это матрица A размерности m×n, действует на вектор x, получаем вектор размерности m, и он равняется вектору размерности nb. Вектор b задан, m×n элементов матрицы А также заданы. Ну и естественные ограничения, как правило, они требуются во всех, практически во всех задачах экономического характера — неотрицательность искомых управляющих переменных. Математически x больше или равно нулевому вектору. То есть каждая компонента вектора x, xi≥0. C, еще раз повторяю. — m-мерный вектор, а b — n-мерный вектор.
Еще раз напоминаю, что здесь идет речь о скалярном произведении заданного вектора c, c1, c2… и так далее cn и искомого вектора x1, x2… и так далее xn. То есть скалярное произведение— это есть линейная суперпозиция c1×x1, c2×x2…и так далее cn×xn. Вот в сокращенной такой форме эта линейная комбинация записывается через два таких вектора в виде их скалярного произведения. Ограничения. Ограничения здесь задаются с помощью двух таких систем: равенства и неравенства. Равенство — это матрица A размерности m×n, действует на вектор x, получаем вектор размерности m, и он равняется вектору размерности nb. Вектор b задан, m×n элементов матрицы А также заданы. Ну и естественные ограничения, как правило, они требуются во всех, практически во всех задачах экономического характера — неотрицательность искомых управляющих переменных. Математически x больше или равно нулевому вектору. То есть каждая компонента вектора x, xi≥0. C, еще раз повторяю. — m-мерный вектор, а b — n-мерный вектор. Причем m, естественно, должно быть меньше, чем n, иначе задача будет бессмысленна, с точки зрения постановки ее, как задачи на xm. Итак, рассматриваем вот эти ограничения типа равенств. Их m штук. Решаем эту систему из m уравнений, относительно m базовых переменных, выразив их через оставшиеся n-m свободных переменных. Не умаляя общности, мы будем считать, что первые m переменных (x1, x2 и так далее xn) могут быть выбраны в качестве базовых. А остальные переменные, начиная с xn+1 до xn, являются, в данном случае свободными переменными. Итак выражаем их через систему базовых переменных, получаем вот — систему два вот с такими коэффициентами: β — свободный член и коэффициенты α с соответствующими индексами, которые фиксируют и номер уравнения, и номер тех свободных переменных, в качестве множителя перед которыми они стоят. Если положить все свободные переменные равные нулю, то есть xm+1, xm+2… и так далее равные нулю, то получаем решение этой системы: x1=β1, x2=β2 … и так далее βm.
Причем m, естественно, должно быть меньше, чем n, иначе задача будет бессмысленна, с точки зрения постановки ее, как задачи на xm. Итак, рассматриваем вот эти ограничения типа равенств. Их m штук. Решаем эту систему из m уравнений, относительно m базовых переменных, выразив их через оставшиеся n-m свободных переменных. Не умаляя общности, мы будем считать, что первые m переменных (x1, x2 и так далее xn) могут быть выбраны в качестве базовых. А остальные переменные, начиная с xn+1 до xn, являются, в данном случае свободными переменными. Итак выражаем их через систему базовых переменных, получаем вот — систему два вот с такими коэффициентами: β — свободный член и коэффициенты α с соответствующими индексами, которые фиксируют и номер уравнения, и номер тех свободных переменных, в качестве множителя перед которыми они стоят. Если положить все свободные переменные равные нулю, то есть xm+1, xm+2… и так далее равные нулю, то получаем решение этой системы: x1=β1, x2=β2 … и так далее βm. Если все βi, i от 1 до m равны, больше или равны 0 — неотрицательны, тогда полученные решения, неотрицательные, которые требуются по требованиям исходной задачи, условиям исходной задачи, — удовлетворяет всем требованиям этой задачи. И такая точка называется угловой точкой. Еще раз повторяю, угловой точкой это будет x1=0, x2=0, и так далее xn0 равное соответственно, β, а все остальные нули, начиная с xn+1. В теории линейных задач линейного программирования доказывается, что если задача 1 разрешима, то решение задачи 1 достигается в одной из таких вот угловых точек, где часть переменных равна нулю, а оставшаяся часть базовых переменных является неотрицательными числами. Выразим целевую функцию задачи 1 через свободные переменные для угловой точки, полученной угловой точки x1=0 и так далее xn0T, где нуль показывает начальную точку, угловую, из которой мы будем стартовать. Тогда целевая функция будет выражаться через свободные переменные, переменные m+1 с индексами от m+1 до n, поскольку мы все базовые переменные выражаем через свободные.
Если все βi, i от 1 до m равны, больше или равны 0 — неотрицательны, тогда полученные решения, неотрицательные, которые требуются по требованиям исходной задачи, условиям исходной задачи, — удовлетворяет всем требованиям этой задачи. И такая точка называется угловой точкой. Еще раз повторяю, угловой точкой это будет x1=0, x2=0, и так далее xn0 равное соответственно, β, а все остальные нули, начиная с xn+1. В теории линейных задач линейного программирования доказывается, что если задача 1 разрешима, то решение задачи 1 достигается в одной из таких вот угловых точек, где часть переменных равна нулю, а оставшаяся часть базовых переменных является неотрицательными числами. Выразим целевую функцию задачи 1 через свободные переменные для угловой точки, полученной угловой точки x1=0 и так далее xn0T, где нуль показывает начальную точку, угловую, из которой мы будем стартовать. Тогда целевая функция будет выражаться через свободные переменные, переменные m+1 с индексами от m+1 до n, поскольку мы все базовые переменные выражаем через свободные. Если все коэффициенты bi больше нуля, смотрим выражение 3 в правой части. То тогда найденная угловая точка является решением задачи 1, и минимум вот этой целевой функции равен тогда, когда свободные переменные равны нулю, позиционные переменные и в этом случае, он равен p0— свободному члену, стоящему в правой части равенства 3. Если хотя бы одни pi перед тем индексом i, мы его обозначили i0, отрицательно, и при этом для всех отрицательных pi среди коэффициентов α, стоящих исходно в равенстве 2, имеется хотя бы один положительный коэффициент αi1 i0, то существует угловая точка, и мы сейчас скажем, как к ней перейти, в которой значение функций меньше, чем значение предыдущей угловой точки. Еще раз напоминаю, что у нас цель минимизировать целевую функцию. То есть, чем меньше, тем лучше. Для перехода от угловой точки, начальной точки x0 к одной из угловых точек x1, следующей угловой точке, реализуем следующий алгоритм. Найдем значение k по базисной переменной, базовой, можно говорить переменной из условия, что мы рассматриваем отношение вот этих свободных членов в равенстве 2, в системе равенств 2: βi/αi i0 по всем тем I, αi i0, которые положительные.
Если все коэффициенты bi больше нуля, смотрим выражение 3 в правой части. То тогда найденная угловая точка является решением задачи 1, и минимум вот этой целевой функции равен тогда, когда свободные переменные равны нулю, позиционные переменные и в этом случае, он равен p0— свободному члену, стоящему в правой части равенства 3. Если хотя бы одни pi перед тем индексом i, мы его обозначили i0, отрицательно, и при этом для всех отрицательных pi среди коэффициентов α, стоящих исходно в равенстве 2, имеется хотя бы один положительный коэффициент αi1 i0, то существует угловая точка, и мы сейчас скажем, как к ней перейти, в которой значение функций меньше, чем значение предыдущей угловой точки. Еще раз напоминаю, что у нас цель минимизировать целевую функцию. То есть, чем меньше, тем лучше. Для перехода от угловой точки, начальной точки x0 к одной из угловых точек x1, следующей угловой точке, реализуем следующий алгоритм. Найдем значение k по базисной переменной, базовой, можно говорить переменной из условия, что мы рассматриваем отношение вот этих свободных членов в равенстве 2, в системе равенств 2: βi/αi i0 по всем тем I, αi i0, которые положительные. Обозначим этот индекс i, который дает этот минимум через k, и тогда справедливо следующее утверждение, что базисное решение x1, которое получается путем замены базисной переменной xk на переменную xi0, то есть xi0, — это есть свободная переменная, она из свободных перемещается в базисную, а базисная xk перемещается в свободные переменные, то в такой точке x1 значение целевой функции будет меньше, чем в начальной точке x0. То есть будем двигаться при реализации такого алгоритма от одной угловой точки к другой, уменьшая значение целевой функции до тех пор, пока не дойдем до решения. Итак, базисному решению x1 соответствует набор свободных переменных, которые вот записаны в качестве набора 4. И таким образом, переход от угловой точки x0 к угловой точке x1 осуществляется путем взаимной замены двух переменных xk и xi0, входящих в число базисных и свободных переменных. А именно, свободная переменная xi0 переходит в число базисных переменных, а базисная переменная xk переходит в число свободных переменных.
Обозначим этот индекс i, который дает этот минимум через k, и тогда справедливо следующее утверждение, что базисное решение x1, которое получается путем замены базисной переменной xk на переменную xi0, то есть xi0, — это есть свободная переменная, она из свободных перемещается в базисную, а базисная xk перемещается в свободные переменные, то в такой точке x1 значение целевой функции будет меньше, чем в начальной точке x0. То есть будем двигаться при реализации такого алгоритма от одной угловой точки к другой, уменьшая значение целевой функции до тех пор, пока не дойдем до решения. Итак, базисному решению x1 соответствует набор свободных переменных, которые вот записаны в качестве набора 4. И таким образом, переход от угловой точки x0 к угловой точке x1 осуществляется путем взаимной замены двух переменных xk и xi0, входящих в число базисных и свободных переменных. А именно, свободная переменная xi0 переходит в число базисных переменных, а базисная переменная xk переходит в число свободных переменных. То есть одна только замена, одной переменной из базисной в свободную. и наоборот. Повторяя указанный переход от одной угловой точки к другой с последовательным уменьшением значения целевой функции, приходим к ситуации, когда для получения новой угловой точки будут выполнены условия, представленные на слайде условия 1. И тем самым будет получено решение основной задачи. Можно задать такой естественный вроде вопрос: а почему не перебрать все возможные угловые точки, сравнить значение целевых функций в этих угловых точках, и выбрать ту, в качестве…, оно и будет решение, где значение целевой функции минимально. Дело в том, что если число переменных в исходной задаче несколько десятков, а на практике, в экономике, как правило, это будет не только десятков, а и сотен, и тысяч может быть переменных. В этом случае, такого рода задачи не поддаются решениям даже на суперкомпьютере. Поскольку число и объем вычислений растет по факториалу так, что оно становится она неподъемна даже для суперкомпьютера.
То есть одна только замена, одной переменной из базисной в свободную. и наоборот. Повторяя указанный переход от одной угловой точки к другой с последовательным уменьшением значения целевой функции, приходим к ситуации, когда для получения новой угловой точки будут выполнены условия, представленные на слайде условия 1. И тем самым будет получено решение основной задачи. Можно задать такой естественный вроде вопрос: а почему не перебрать все возможные угловые точки, сравнить значение целевых функций в этих угловых точках, и выбрать ту, в качестве…, оно и будет решение, где значение целевой функции минимально. Дело в том, что если число переменных в исходной задаче несколько десятков, а на практике, в экономике, как правило, это будет не только десятков, а и сотен, и тысяч может быть переменных. В этом случае, такого рода задачи не поддаются решениям даже на суперкомпьютере. Поскольку число и объем вычислений растет по факториалу так, что оно становится она неподъемна даже для суперкомпьютера. Поэтому и был предложен и изобретен метод, симплекс метод, который дает возможность не перебирать все угловые точки, а двигаться по тем угловым точкам на каждом шаге, значение которых, в которых значение целевой функции будет монотонно убывать. И это сокращает на огромное число порядков число вычислений и делает их возможным даже на простом ноутбуке, с числом переменных, доходящем до сотен. Рассмотрим конкретный пример задачи линейного программирования с помощью симплекс метода. Здесь целевая функция, как вы видите, есть функция шести переменных: x1, x2 и так далее x6. Наложено 4 ограничения типа, то есть m=4, n=6. Ну и естественно ограничение неотрицательности всех переменных x1, x2 и так далее xn. В задачах экономики, как правило, это— объемы выпускаемой продукции, и поэтому они неотрицательны. Выберем в качестве базисных переменных 4 переменные, это: x2, x4, x5 и x6. Система 2 для выбранных набора базисных переменных имеет вид, вот записано в виде 4 равенств через базисные переменные x2, x4, x5 и x6, и свободные переменные — x1 и x3.
Поэтому и был предложен и изобретен метод, симплекс метод, который дает возможность не перебирать все угловые точки, а двигаться по тем угловым точкам на каждом шаге, значение которых, в которых значение целевой функции будет монотонно убывать. И это сокращает на огромное число порядков число вычислений и делает их возможным даже на простом ноутбуке, с числом переменных, доходящем до сотен. Рассмотрим конкретный пример задачи линейного программирования с помощью симплекс метода. Здесь целевая функция, как вы видите, есть функция шести переменных: x1, x2 и так далее x6. Наложено 4 ограничения типа, то есть m=4, n=6. Ну и естественно ограничение неотрицательности всех переменных x1, x2 и так далее xn. В задачах экономики, как правило, это— объемы выпускаемой продукции, и поэтому они неотрицательны. Выберем в качестве базисных переменных 4 переменные, это: x2, x4, x5 и x6. Система 2 для выбранных набора базисных переменных имеет вид, вот записано в виде 4 равенств через базисные переменные x2, x4, x5 и x6, и свободные переменные — x1 и x3. Таким образом, если бы мы положим x1 и x3 равным нулю, мы получаем значения базисных переменных положительные: 40, 20, 10 и 30, соответственно, для x2, x4, x5 и x6. То есть, x0 — вот такая точка является угловой. Выразим целевые функции задачи 5 через свободные переменные. Получается вот такое выражение: 880-7×1-14×3 (восемьсот восемьдесят минус семь икс один минус четырнадцать умножить на икс три). К сожалению, коэффициент, стоящий перед свободными переменными отрицательный. Поэтому необходимо делать вот эти переборы последовательные. Возьмем для замены x3, номер K равный шестой переменной, то есть заменим x3 из свободных переменных вместо шестой, x6, которая является базовой переменной, первой, в первом выборе. Теперь x6 станет свободной переменной. Получаем систему равенств, выражая через свободные переменные x1 и x6 базовые переменные x2, x4, x5 и x3. И тем самым x1 получаем, новую угловую точку, которая стоит внизу этого слайда, значение координат этой точки. Подсчитываем значение целевой функции этой точки.
Таким образом, если бы мы положим x1 и x3 равным нулю, мы получаем значения базисных переменных положительные: 40, 20, 10 и 30, соответственно, для x2, x4, x5 и x6. То есть, x0 — вот такая точка является угловой. Выразим целевые функции задачи 5 через свободные переменные. Получается вот такое выражение: 880-7×1-14×3 (восемьсот восемьдесят минус семь икс один минус четырнадцать умножить на икс три). К сожалению, коэффициент, стоящий перед свободными переменными отрицательный. Поэтому необходимо делать вот эти переборы последовательные. Возьмем для замены x3, номер K равный шестой переменной, то есть заменим x3 из свободных переменных вместо шестой, x6, которая является базовой переменной, первой, в первом выборе. Теперь x6 станет свободной переменной. Получаем систему равенств, выражая через свободные переменные x1 и x6 базовые переменные x2, x4, x5 и x3. И тем самым x1 получаем, новую угловую точку, которая стоит внизу этого слайда, значение координат этой точки. Подсчитываем значение целевой функции этой точки. Как вы видите, в этой угловой точке уже 460, оно уменьшилось почти в два раза. Итак, заменяем номер x1 на x2, решаем вот ту экстремальную задачу, которая была на предыдущем слайде, на предыдущих слайдах. Получаем систему равенств относительно теперь базовых переменных x1, x3, x4, x5. Свободные переменные у нас x2, x6, вторая и шестая по нумерации, и получаем новую угловую точку, 10, 0, 30, 40, 50, 0. То есть значения нулей — это вторая и шестая свободные переменные. Значение целевой функции стало 390, в этой угловой точке, когда мы полагаем x2 и x6 нули. Оба коэффициента перед свободной переменной в этом выражении положительны. Тем самым полученная угловая точка является решением задачи. И минимальное значение целевой функции равно390. Меньше этого значения целевой функции нет. В условиях тех ограничений, которые у нас имеются в исходной постановке задачи. Задача решена. Итак, на десятом уроке дана постановка задач линейного программирования в экономике представлен общий метод решения задач линейного программирования —симплекс метод, приведен пример решения задач линейного программирования с помощью симплекс метода.
Как вы видите, в этой угловой точке уже 460, оно уменьшилось почти в два раза. Итак, заменяем номер x1 на x2, решаем вот ту экстремальную задачу, которая была на предыдущем слайде, на предыдущих слайдах. Получаем систему равенств относительно теперь базовых переменных x1, x3, x4, x5. Свободные переменные у нас x2, x6, вторая и шестая по нумерации, и получаем новую угловую точку, 10, 0, 30, 40, 50, 0. То есть значения нулей — это вторая и шестая свободные переменные. Значение целевой функции стало 390, в этой угловой точке, когда мы полагаем x2 и x6 нули. Оба коэффициента перед свободной переменной в этом выражении положительны. Тем самым полученная угловая точка является решением задачи. И минимальное значение целевой функции равно390. Меньше этого значения целевой функции нет. В условиях тех ограничений, которые у нас имеются в исходной постановке задачи. Задача решена. Итак, на десятом уроке дана постановка задач линейного программирования в экономике представлен общий метод решения задач линейного программирования —симплекс метод, приведен пример решения задач линейного программирования с помощью симплекс метода. Спасибо за внимание.
Спасибо за внимание.
Образование
….. Представлены курсы видео лекций по следующим разделам математики.
…….. Линейная алгебра — 4 лекции………………………….. Линейное программирование — 3 лекции.
…….. Дифференциальное исчисление — 9 лекций…… Интегральное исчисление — 9 лекций.
…….. Теория вероятностей — 8 лекций…………………….. Эконометрика — 3 лекции.
….. Это лекции для чайников! Раньше чайниками называли начинающих горнолыжников. Они вели себя непредсказуемо: могли неожиданно врезаться в дерево или внезапно упасть в самом неподходящем месте. А перед объективом они позировали с вытянутой вверх рукой: ну чайник и чайник! Позже понятие чайника расширили: появились книжки под названием «…для чайников», а в Интернете прижилось новое понятие «ячайник». В данном контексте чайник не обидное прозвище, а просто означает, что изучение соответствующего раздела математики начинается с нуля!
 …. Лекционный материал изложен на доступном для начинающих уровне. Нажимаем на соответствующую пиктограмму с кратким названием соответствующей лекции и слушаем!
…. Лекционный материал изложен на доступном для начинающих уровне. Нажимаем на соответствующую пиктограмму с кратким названием соответствующей лекции и слушаем!Все видео лекции являются дополнением к факультативному курсу лекций,
и их следует рассматривать только как руководство к решению задач.
….. В экономике часто встречаются ситуации, когда требуется достичь определенной цели при ограниченных ресурсах. Математическая модель таких задач связана с нахождением наибольшего или наименьшего значения целевой функции, зависящей от многих показателей различных видов деятельности, при определенных ограничительных соотношениях. Если целевая функция и ограничительные соотношения — линейные, то это задача линейного программирования.
….. В случае двух переменных для решения задачи линейного программирования можно использовать геометрический метод. В остальных случаях применяется симплекс-метод. Важный частный случай задачи линейного программирования — транспортная задача. Для ее решения успешно используется метод потенциалов.
Важный частный случай задачи линейного программирования — транспортная задача. Для ее решения успешно используется метод потенциалов.
….. Если вы приступили к прослушиванию лекций по дифференциальному исчислению, то первая сессия успешно сдана и вы поняли, что на лекциях надо внимать преподавателю, а не спать, спрятавшись за портфелем.
….. Усаживайтесь перед экраном компьютера и внимательно слушайте. Останавливайте лекцию в любом месте, тренируйтесь находить производную на бумаге. Сходить на дискотеку вы сможете в другое время. А прослушав лекции до конца, вы удивите преподавателя легкостью, с которой находите производную сложной функции.
….. Изучение интегрального исчисления нельзя начинать с нуля. Вы были чайниками при изучении пределов и производных. Поздравляю, теперь вы больше не чайник, а грамотный студент!
….. Лекции излагаются на доступном уровне. Например, после первой лекции вы удивите преподавателя легкостью, с которой заменяете переменную в неопределенном интеграле!
….. Цель настоящих лекций — помочь в изучении факультативного курса эконометрики.
….. Многие студенты чувствуют себя неуверенно в прослушанных математических курсах, поэтому до минимума сокращен математический материал. Особый упор сделан на сущность эконометрики, чтобы студенты могли, например, описать регрессионные результаты словесно с использованием терминологии, понятной неспециалисту.
….. Представлены контрольные работы, которые предлагались студентам 1-го и 2-го курсов вечернего и заочного отделений общетехнических и экономических (менеджмент, мировая экономика, экономика по отраслям и т.
Вариант задания определяется по последней цифре шифра (номера зачетной книжки) студента.
решаем слау легко. Методы исключения гаусса
Пусть дана система , ∆≠0. (1)Метод Гаусса – это метод последовательного исключения неизвестных.
Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей , из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. Рассмотрим одну из вычислительных схем. Эта схема называется схемой единственного деления. Итак, рассмотрим эту схему. Пусть a 11 ≠0 (ведущий элемент) разделим на a 11 первое уравнение. Получим
Пользуясь уравнением (2), легко исключить неизвестные x 1 из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x 1), то есть на первом шаге получим
.

Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.
Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x 2 (шаг 2).
(3)
Таким образом, на первом этапе мы получим треугольную систему (3). Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения x n , x n -1 , …, x 1 .
Обозначим полученное решение за x 0 . Тогда разность ε=b-A·x 0 называется невязкой .
Если ε=0, то найденное решение x 0 является верным.
Вычисления по методу Гаусса выполняются в два этапа:
- Первый этап называется прямым ходом метода.
 На первом этапе исходную систему преобразуют к треугольному виду.
На первом этапе исходную систему преобразуют к треугольному виду. - Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.
Назначение метода Гаусса
Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.Виды метода Гаусса
- Классический метод Гаусса;
- Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k -ом шаге ведущим элементом оказывался наибольший по модулю элемент k -го столбца.
- Метод Жордано-Гаусса;
 В методе Гаусса направление поиска решения происходит по столбцам (преобразование к системе с треугольной матрицей).
В методе Гаусса направление поиска решения происходит по столбцам (преобразование к системе с треугольной матрицей). Пример решения методом Гаусса
Решим систему:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Из 1-ой строки выражаем x 3:
Из 2-ой строки выражаем x 2:
Из 3-ой строки выражаем x 1:
Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x 1 | x 2 | x 3 | B |
| 1 / 1 = 1 | 2 / 1 = 2 | -2 / 1 = -2 | 1 / 1 = 1 |
Разрешающий элемент равен (3).

На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
| x 1 | x 2 | x 3 | B |
| 0 / 3 = 0 | 3 / 3 = 1 | 1 / 3 = 0.33 | 4 / 3 = 1.33 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
Ответ : x 1 = 1, x 2 = 1, x 3 = 1
Реализация метода Гаусса
Метод Гаусса реализован на многих языках программирования, в частности: Pascal, C++, php, Delphi , а также имеется реализация метода Гаусса в онлайн режиме .Использование метода Гаусса
Применение метода Гаусса в теории игр
В теории игр при отыскании максиминной оптимальной стратегии игрока составляется система уравнений, которая решается методом Гаусса.Применение метода Гаусса при решении дифференциальных уравнений
Для поиска частного решения дифференциального уравнения сначала находят производные соответствующей степени для записанного частного решения (y=f(A,B,C,D)), которые подставляют в исходное уравнение. Далее, чтобы найти переменные A,B,C,D составляется система уравнений, которая решается методом Гаусса.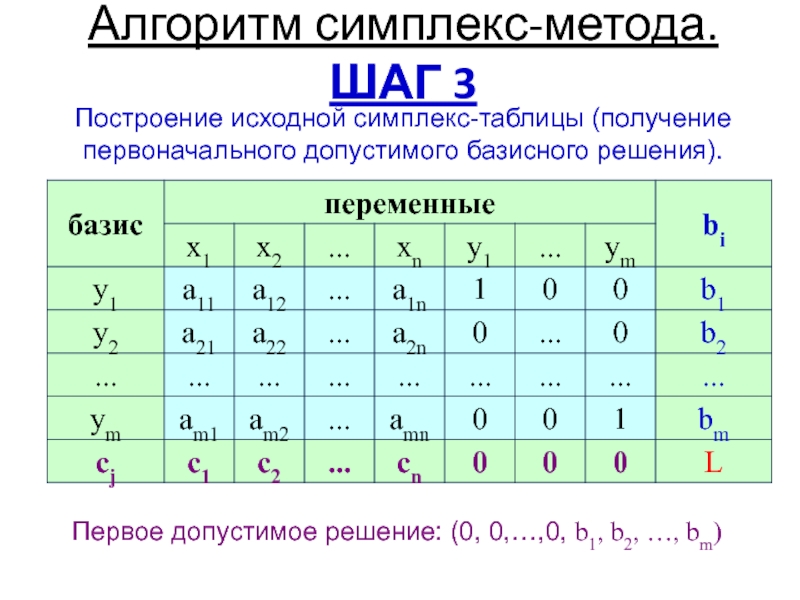
Применение метода Жордано-Гаусса в линейном программировании
В линейном программировании, в частности в симплекс-методе для преобразования симплексной таблицы на каждой итерации используется правило прямоугольника, в котором используется метод Жордано-Гаусса.Рассмотрим один из самых распространенных методов решения систем линейных алгебраических уравнений — метод Гаусса. Этот метод (который называют также методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Вычисления с помощью метода Гаусса состоят из двух основных этапов, называемых прямым ходом и обратным ходом (обратной подстановкой). Прямой ход метода Гаусса заключается в последовательном исключении неизвестных из системы (5.1) для преобразования ее к эквивалентной системе с верхней треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода.
1. Схема единственного деления.
Рассмотрим сначала простейший вариант метода Гаусса, называемый схемой единственного деления.
Прямой ход состоит из шагов исключения.
1-й шаг. Целью этого шага является исключение неизвестного из уравнений с номерами Предположим, что коэффициент Будем называть его главным (или ведущим) элементом 1-го шага.
Найдем величины
называемые множителями 1-ю шага. Вычтем последовательно из второго, третьего, уравнений системы (5.1) первое уравнение, умноженное соответственно на Это позволит обратить в
нуль коэффициенты при во всех уравнениях, кроме первого. В результате получим эквивалентную систему
в которой вычисляются по формулам
2-й шаг. Целью этого шага является исключение неизвестного из уравнений с номерами Пусть где — коэффициент, называемый главным (или ведущим) элементом шага. Вычислим множители 2-го шага
и вычтем последовательно из третьего, четвертого, уравнений системы (5.30) второе уравнение, умноженное соответственно на . В результате получим систему
Здесь коэффициенты вычисляются по формулам
Аналогично проводятся остальные шаги. Опишем очередной шаг.
Опишем очередной шаг.
k-й шаг. В предположении, что главный (ведущий) элемент шага отличен от нуля, вычислим множители шага
и вычтем последовательно из уравнений полученной на предыдущем шаге системы уравнение, умноженное соответственно на
После шага исключения получим систему уравнений
матрица которой является верхней треугольной. На этом вычисления прямого хода заканчиваются.
Обратный ход. Из последнего уравнения системы (5.33) находим Подставляя найденное значение в предпоследнее уравнение, получим Осуществляя обратную подстановку, далее последовательно находим Вычисления неизвестных здесь проводятся по формулам
Трудоемкость метода. Оценим число арифметических операций, необходимых для реализации схемы единственного деления.
Вычисления 1-го шага исключения по формулам (5.29), (5.31) требуют выполнения деления, умножений и вычитаний, т. е. общее число арифметических операций составляет Аналогично, на шаге требуется операций, а на шаге — операций.
Подсчитаем теперь приближенно общее число арифметических операций прямого хода, считая размерность системы достаточно большой:
Как нетрудно видеть, для реализации обратного хода по формулам (5.34) нужно всего операций, что при больших пренебрежимо мало по сравнению с числом операций прямого хода.
Таким образом, для реализации метода Гаусса требуется примерно арифметических операций, причем подавляющее число этих действий совершается на этапе прямого хода.
Пример 5.7. Методом Гаусса решим систему
Прямой ход. 1-й шаг. Вычислим множители Вычитая из второго, третьего и четвертого уравнений системы (5.35) первое уравнение, умноженное на соответственно получим
2-й шаг. Вычислим множители Вычитая из третьего и четвертого уравнений системы (5.36) второе уравнение, умноженное на соответственно, приходим к системе
3-й шаг. Вычисляя множитель и вычитая из четвертого уравнения системы (5.37) третье уравнение, умноженное на приводим систему к треугольному виду:
Обратный ход. Из последнего уравнения системы находим Подставляя значение в третье уравнение, находим
Из последнего уравнения системы находим Подставляя значение в третье уравнение, находим
Результаты вычислений можно свести в следующую таблицу.
Таблица 5.2 (см. скан)
Необходимость выбора главных элементов. Заметим, что вычисление множителей, а также обратная подстановка требуют деления на главные элементы Поэтому если один из главных элементов сказывается равным нулю, то схема единственного деления не может быть реализована. Здравый смысл подсказывает, что и в ситуации, когда все главные элементы отличны от нуля, но среди них есть близкие к нулю, возможен неконтролируемый рост погрешности.
Пример 5.8. Используя метод Гаусса, решим систему уравнений
на -разрядной десятичной ЭВМ.
Прямой ход. 1-й шаг. Вычисляем множители и преобразуем систему к виду
Все вычисления на этом шаге выполняются без округлений.
2-й шаг. После вычисления множителя последнее уравнение системы должно быть преобразовано к виду где Однако на используемой ЭВМ будет получено уравнение
Действительно, коэффициент определяется точно, так как при его вычислении не возникает чисел, мантиссы которых имеют более 6 разрядов. В то же время при вычислении умножение коэффициента 3.0001 на дает 7-разрядное число 105003.5, после округления которого до 6 разрядов получится 105004. Вычисление 62) завершается выполнением операции вычитания: . После округления последнего числа до 6 разрядов мантиссы приходим к уравнению (5.41).
В то же время при вычислении умножение коэффициента 3.0001 на дает 7-разрядное число 105003.5, после округления которого до 6 разрядов получится 105004. Вычисление 62) завершается выполнением операции вычитания: . После округления последнего числа до 6 разрядов мантиссы приходим к уравнению (5.41).
Обратный ход. Из уравнения (5.41) находим и 1.00001. Сравнение с истинным значением показывает, что эта величина получена с очень высокой для используемой ЭВМ точностью. Дальнейшие вычисления дают
После округления имеем .
Как нетрудно видеть, найденные значения неизвестных имеют мало общего с истинными значениями решения
В чем же причина появления такой значительной погрешности? Говорить о накоплении ошибок округления не приходится, так как всего было выполнено 28 арифметических операций и лишь в 4 случаях потребовалось округление. Предположение о плохой обусловленности системы не подтверждается; вычисление дает значение и 100.
В действительности причина состоит в использовании на шаге малого ведущего элемента Следствием этого стало появление большого
множителя и существенное возрастание коэффициента в последнем уравнении системы.
Таким образом, изложенный выше вариант метода Гаусса (схема единственного деления) оказался некорректным и, следовательно, непригодным для вычислений на ЭВМ. Этот метод может привести к аварийному останову (если при некотором и вычисления по нему могут оказаться неустойчивыми.
2. Метод Гаусса с выбором главного элемента по столбцу (схема частичного выбора).
Описание метода. На шаге прямого хода коэффициенты уравнений системы с номерами преобразуются по формулам
Интуитивно ясно, что во избежание сильного роста коэффициентов системы и связанных с этим ошибок нельзя допускать появления больших множителей
В методе Гаусса с выбором главного элемента по столбцу гарантируется, что для всех к Отличие этого варианта метода Гаусса от схемы единственного деления заключается в том, что на шаге исключения в качестве главного элемента выбирают максимальный по модулю коэффициент а. при неизвестной в уравнениях с номерами Затем соответствующее выбранному коэффициенту уравнение с номером меняют местами с уравнением системы для того, чтобы главный элемент занял место коэффициента
После этой перестановки исключение неизвестного производят, как в схеме единственного деления.
Пример 5.9. Решим систему уравнений (5.39) методом Гаусса с выбором главного элемента по столбцу на -разрядной десятичной ЭВМ.
Прямой ход. 1-й шаг. Максимальный в первом столбце элемент матрицы находится в первой строке, поэтому перестановка уравнений не нужна. Здесь 1-й шаг проводится точно так же, как и в примере 5.8.
2-й шаг. Среди элементов матрицы системы (5.40) максимальный принадлежит третьему уравнению. Меняя местами второе и третье уравнения, получим систему
После вычисления последнее уравнение системы преобразуется к виду
Обратный ход. Из последнего уравнения находим Далее, имеем В данном случае ответ получился точным.
Заметим, что дополнительная работа по выбору главных элементов в схеме частичного выбора требует порядка действий, что практически не влияет на общую трудоемкость метода.
Вычислительная устойчивость схемы частичного выбора. Детальное исследование метода Гаусса показывает, что действительной причиной неустойчивости схемы единственного деления является возможность неограниченного роста элементов промежуточных матриц в процессе прямого хода. Так как на шаге схемы частичного выбора 1, то для вычисленных по формулам (5.42) элементов справедлива оценка Следовательно, максимальное по модулю значение элементов матрицы возрастает на одном шаге не более чем в 2 раза и в самом неблагоприятном случае шаг прямого хода даст коэффициент роста
Так как на шаге схемы частичного выбора 1, то для вычисленных по формулам (5.42) элементов справедлива оценка Следовательно, максимальное по модулю значение элементов матрицы возрастает на одном шаге не более чем в 2 раза и в самом неблагоприятном случае шаг прямого хода даст коэффициент роста
Гарантия ограниченности роста элементов матрицы делает схему частичного выбора вычислительно устойчивой. Более того, для нее оказывается справедливой следующая оценка погрешности:
Здесь вычисленное на ЭВМ решение системы; его относительная погрешность; число обусловленности матрицы ем — машинное эпсилон; наконец, причем некоторая медленно растущая функция, зависящая от порядка системы (типа степенной функции с небольшим показателем), коэффициент роста.
Наличие в оценке (5.43) множителя указывает на то, что при большом схема частичного выбора может оказаться плохо обусловленной и возможна существенная потеря точности. Однако практика матричных вычислений показывает, что существенный рост элементов матрицы происходит крайне редко. В подавляющем большинстве случаев действительное значение коэффициента роста не превышает 8-10. Если система хорошо обусловлена, то погрешность вычисленного решения оказывается, как правило, малой.
В подавляющем большинстве случаев действительное значение коэффициента роста не превышает 8-10. Если система хорошо обусловлена, то погрешность вычисленного решения оказывается, как правило, малой.
Иногда для проверки качества приближенного решения х
вычисляют невязку и о степени близости приближенного решения к точному пытаются судить по тому, насколько мала невязка. Этот метод ненадежен по отношению к схеме частичного выбора, так как известно, что она гарантированно дает малые невдэки. Более точно это утверждение можно сформулировать так: справедлива оценка
где то же, что и в оценке (5.43). Заметим, что в неравенство (5.44) не входит число обусловленности.
3. Метод Гаусса с выборок главного элемента по всей матрице (схема полного выбора).
В этой схеме допускается нарушение естественного порядка исключения неизвестных.
На 1-м шаге метода среди элементов определяют максимальный по модулю элемент Первое уравнение системы и уравнение с номером меняют местами. Далее стандартным образом производят исключение неизвестного х, из всех уравнений, кроме первого. (что значительно меньше соответствующего значения для схемы частичного выбора). Подчеркнем, что до сих пор еще не найдено матрицы, для которой полный выбор дал бы значение Таким образом, для хорошо обусловленных систем этот вариант метода Гаусса является хорошо обусловленным.
Далее стандартным образом производят исключение неизвестного х, из всех уравнений, кроме первого. (что значительно меньше соответствующего значения для схемы частичного выбора). Подчеркнем, что до сих пор еще не найдено матрицы, для которой полный выбор дал бы значение Таким образом, для хорошо обусловленных систем этот вариант метода Гаусса является хорошо обусловленным.
Однако гарантия хорошей обусловленности достигается здесь ценой значительных затрат на выбор главных элементов. Для этого дополнительно к арифметических действий требуется произвести примерно операций сравнения, что может ощутимо замедлить процесс решения задачи на ЭВМ. Поэтому в большинстве случаев на практике предпочтение отдается все же схеме частичного выбора. Как уже отмечено, ситуации, когда при использовании этого варианта метода Гаусса происходит существенный рост элементов, встречаются чрезвычайно редко. Более того, эти ситуации могут быть легко выявлены с помощью заложенных в современных программах эффективных методов слежения за ростом элементов матриц.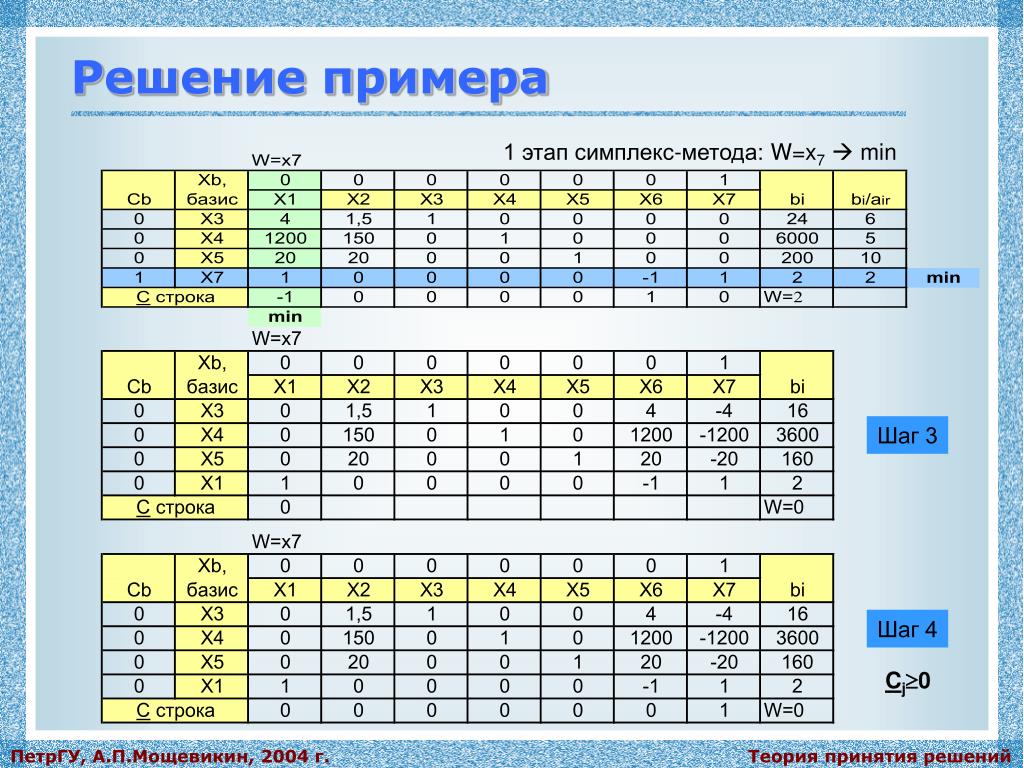
4. Случаи, когда выбор главных элементов не нужен.
Известно, что для некоторых классов матриц при использовании схемы единственного деления главные элементы гарантированно располагаются на главной диагонали и потому применять частичный выбор нет необходимости. Так, например, обстоит дело для систем с положительно определенными матрицами, а также с матрицами, обладающими следующим свойством диагонального преобладания:
Матрицы, удовлетворяющие условию (5.45), таковы, что в каждой из строк модуль элемента расположенного на главной диагонали, больше суммы модулей всех остальных элементов строки.
5. Масштабирование.
Перед началом решения целесообразно масштабировать систему так, чтобы ее коэффициенты были величинами порядка единицы.
Существуют два естественных способа масштабирования системы Первый заключается в умножении каждого из уравнений на некоторый масштабирующий множитель Второй состоит в умножении на масштабирующий множитель каждого столбца матрицы, что соответствует замене переменных (фактически — это замена единиц измерения). В реальных ситуациях чаще всего масштабирование может быть выполнено без существенных трудностей. Однако подчеркнем, что в общем случае удовлетворительного способа масштабирования пока не найдено.
В реальных ситуациях чаще всего масштабирование может быть выполнено без существенных трудностей. Однако подчеркнем, что в общем случае удовлетворительного способа масштабирования пока не найдено.
На практике масштабирование обычно производят с помощью деления каждого уравнения на его наибольший по модулю коэффициент. Это вполне удовлетворительный способ для большинства реально встречающихся задач.
Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Далее полезно изучить урок .
Метод
Гаусса – это просто! Почему?
Известный немецкий математик Иоганн
Карл Фридрих Гаусс еще при жизни получил
признание величайшего математика всех
времен, гения и даже прозвище «короля
математики». А
всё гениальное, как известно –
просто! Кстати,
на деньги попадают не только лохи, но
еще и гении – портрет Гаусса красовался
на купюре в 10 дойчмарок (до введения
евро), и до сих пор Гаусс загадочно
улыбается немцам с обычных почтовых
марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной ).
Метод
Гаусса – наиболее мощный и универсальный
инструмент для нахождения решениялюбой системы
линейных уравнений. Как мы помним, правило
Крамера и матричный метод непригодны
в тех случаях, когда система имеет
бесконечно много решений или несовместна.
А метод последовательного исключения
неизвестных в
любом случае приведет
нас к ответу! На данном уроке мы опять
рассмотрим метод Гаусса для случая №1
(единственное решение системы), под
ситуации пунктов №№2-3 отведена
статья. Замечу, что сам алгоритм метода во всех
трёх случаях работает одинаково.
Замечу, что сам алгоритм метода во всех
трёх случаях работает одинаково.
Вернемся к простейшей системе с урока Как решить систему линейных уравнений? и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы : . По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.
После
того, как расширенная матрица системы
записана, с ней необходимо выполнить
некоторые действия, которые также
называются элементарными
преобразованиями .
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .
4)
Строку матрицы можно умножить
(разделить) на
любое число, отличное
от нуля .
Рассмотрим, например, матрицу .
Здесь целесообразно первую строку
разделить на –3, а вторую строку –
умножить на 2: .
Данное действие очень полезно, поскольку
упрощает дальнейшие преобразования
матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .
На практике так подробно, конечно, не расписывают, а пишут короче: Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: »
«Сначала
первый столбец. Внизу мне нужно получить
ноль. Поэтому единицу вверху умножаю
на –2: ,
и ко второй строке прибавляю первую: 2
+ (–2) = 0. Записываю результат во вторую
строку: »
Записываю результат во вторую
строку: »
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ : рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя! Вернемся к нашей системе . Она практически разобрана по косточкам.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :
(1)
Ко второй строке прибавили первую
строку, умноженную на –2. И снова: почему
первую строку умножаем именно на –2?
Для того чтобы внизу получить ноль, а
значит, избавиться от одной переменной
во второй строке.
И снова: почему
первую строку умножаем именно на –2?
Для того чтобы внизу получить ноль, а
значит, избавиться от одной переменной
во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .
В результате элементарных преобразований получена эквивалентная исходной система уравнений:
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Рассмотрим
наиболее распространенную ситуацию,
когда методом Гаусса требуется решить
систему трёх линейных уравнений с тремя
неизвестными.
Пример 1
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы:
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число: Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
Теперь первая строка у нас останется неизменной до конца решения . Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:
Нули
получаем как раз с помощью «трудного»
преобразования. Сначала разбираемся
со второй строкой (2, –1, 3, 13). Что нужно
сделать, чтобы на первой позиции получить
ноль? Нужно ко
второй строке прибавить первую строку,
умноженную на –2 . Мысленно или на черновике умножаем
первую строку на –2: (–2, –4, 2, –18). И
последовательно проводим (опять же
мысленно или на черновике) сложение, ко
второй строке прибавляем первую строку,
уже умноженную на –2 :
Мысленно или на черновике умножаем
первую строку на –2: (–2, –4, 2, –18). И
последовательно проводим (опять же
мысленно или на черновике) сложение, ко
второй строке прибавляем первую строку,
уже умноженную на –2 :
Результат записываем во вторую строку:
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :
Результат записываем в третью строку:
На
практике эти действия обычно выполняются
устно и записываются в один шаг:
Не
нужно считать всё сразу и одновременно .
Порядок вычислений и «вписывания»
результатов последователен и
обычно такой: сначала переписываем
первую строку, и пыхтим себе потихонечку
– ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :
А
мысленный ход самих расчётов я уже
рассмотрел выше.
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
Для
этого к
третьей строке прибавляем вторую строку,
умноженную на –2 :
Попробуйте
разобрать это действие самостоятельно
– мысленно умножьте вторую строку на
–2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат:
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:
Ответ :
Как
уже неоднократно отмечалось, для любой
системы уравнений можно и нужно сделать
проверку найденного решения, благо, это
несложно и быстро.
Пример 2
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить систему линейных уравнений методом Гаусса
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь
слева вверху «минус один», что нас вполне
устроит. Кто хочет получить +1, может
выполнить дополнительное телодвижение:
умножить первую строку на –1 (сменить
у неё знак).
Кто хочет получить +1, может
выполнить дополнительное телодвижение:
умножить первую строку на –1 (сменить
у неё знак).
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем
обратный ход, в оформлении примеров
часто не переписывают саму систему, а
уравнения «берут прямо из приведенной
матрицы». Обратный ход, напоминаю,
работает, снизу вверх. Да тут подарок
получился:
Обратный ход, напоминаю,
работает, снизу вверх. Да тут подарок
получился:
Ответ : .
Пример 4
Решить систему линейных уравнений методом Гаусса
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
В последней части рассмотрим некоторые особенности алгоритма Гаусса. Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например: Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули: Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.
Вторая
особенность состоит вот в чём. Во всех
рассмотренных примерах на «ступеньки»
мы помещали либо –1, либо +1. Могут ли там
быть другие числа? В ряде случаев могут.
Рассмотрим систему: .
Могут ли там
быть другие числа? В ряде случаев могут.
Рассмотрим систему: .
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
Метод
Гаусса универсален, но есть одно
своеобразие. Уверенно научиться решать
системы другими методами (методом
Крамера, матричным методом) можно
буквально с первого раза – там очень
жесткий алгоритм. Но вот чтобы уверенно
себя чувствовать в методе Гаусса, следует
«набить руку», и прорешать хотя бы 5-10
десять систем. Поэтому поначалу возможны
путаница, ошибки в вычислениях, и в этом
нет ничего необычного или трагического.
Но вот чтобы уверенно
себя чувствовать в методе Гаусса, следует
«набить руку», и прорешать хотя бы 5-10
десять систем. Поэтому поначалу возможны
путаница, ошибки в вычислениях, и в этом
нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Желаю успехов!
Решения и ответы:
Пример
2: Решение : Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду.
Выполненные
элементарные преобразования: (1)
Ко второй строке прибавили первую
строку, умноженную на –2. К третьей
строке прибавили первую строку, умноженную
на –1. Внимание! Здесь
может возникнуть соблазн из третьей
строки вычесть первую, крайне не
рекомендую вычитать – сильно повышается
риск ошибки. Только складываем! (2)
У второй строки сменили знак (умножили
на –1). Вторую и третью строки поменяли
местами. Обратите
внимание ,
что на «ступеньках» нас устраивает не
только единица, но еще и –1, что даже
удобнее. (3)
К третьей строке прибавили вторую
строку, умноженную на 5. (4)
У второй строки сменили знак (умножили
на –1). Третью строку разделили на 14.
Обратный ход:
Ответ : .
Пример
4: Решение : Запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду:
Выполненные
преобразования: (1)
К первой строке прибавили вторую. Таким
образом, организована нужная единица
на левой верхней «ступеньке». (2)
Ко второй строке прибавили первую
строку, умноженную на 7. К третьей
строке прибавили первую строку, умноженную
на 6.
Таким
образом, организована нужная единица
на левой верхней «ступеньке». (2)
Ко второй строке прибавили первую
строку, умноженную на 7. К третьей
строке прибавили первую строку, умноженную
на 6.
Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы (3) К третьей строке прибавили вторую, умноженную на –1. (4) Ко второй строке прибавили третью, умноженную на –3. Нужная вещь на второй ступеньке получена . (5) К третьей строке прибавили вторую, умноженную на 6. (6) Вторую строку умножили на –1, третью строку разделили на -83.
Обратный ход:
Ответ :
Пример
5: Решение : Запишем
матрицу системы и с помощью элементарных
преобразований приведем ее к ступенчатому
виду:
Выполненные
преобразования: (1)
Первую и вторую строки поменяли
местами. (2)
Ко второй строке прибавили первую
строку, умноженную на –2. К третьей
строке прибавили первую строку, умноженную
на –2. К четвертой строке прибавили
первую строку, умноженную на –3. (3)
К третьей строке прибавили вторую,
умноженную на 4. К четвертой строке
прибавили вторую, умноженную на –1. (4)
У второй строки сменили знак. Четвертую
строку разделили на 3 и поместили вместо
третьей строки. (5)
К четвертой строке прибавили третью
строку, умноженную на –5.
(2)
Ко второй строке прибавили первую
строку, умноженную на –2. К третьей
строке прибавили первую строку, умноженную
на –2. К четвертой строке прибавили
первую строку, умноженную на –3. (3)
К третьей строке прибавили вторую,
умноженную на 4. К четвертой строке
прибавили вторую, умноженную на –1. (4)
У второй строки сменили знак. Четвертую
строку разделили на 3 и поместили вместо
третьей строки. (5)
К четвертой строке прибавили третью
строку, умноженную на –5.
Обратный ход:
Ответ :
Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что с помощью элементарных преобразований исходная система приводится к равносильной ей системе ступенчатого или треугольного вида, из которой последовательно, начиная с последних (по номеру), неизвестных находятся все остальные неизвестные. Дана система (1)
Начинаем
осуществлять прямой
ход . Считаем, что коэффициент а 11 ≠ 0;
если же это не так, меняем местами
уравнения.
Считаем, что коэффициент а 11 ≠ 0;
если же это не так, меняем местами
уравнения.
Первый
шаг состоит в том, чтобы исключить
неизвестное х 1
из всех уравнений, кроме первого. Для
этого ко второму уравнению прибавим
первое уравнение, умноженное на число
,
к третьему уравнению прибавим первое
уравнение, умноженное на число
,
и так далее до последнего уравнения.
После первого шага получим систему:
Полученная система равносильна исходной системе.
Вторым
шагом исключают неизвестное из всех
уравнений, кроме первого и второго. Для
этого повторяем все действия первого
шага для второго и последующих уравнений,
а именно: считаем, что коэффициент
≠ 0
и так далее. Если в результате преобразований
получается нулевое уравнение, то его
удаляют, если же получается несовместное
уравнение, то решение системы закончено
– она несовместна. Процесс исключения
неизвестных продолжаем до тех пор, пока
это возможно. Обозначим количество
уравнений, оставшихся после прямого
хода, через r . Это число равно рангу основной матрицы
системы и может быть меньше или равно n .
Рассмотрим оба случая.
Это число равно рангу основной матрицы
системы и может быть меньше или равно n .
Рассмотрим оба случая.
1) Если r = n
где с 11 ≠ 0, с 22 ≠ 0, …, с nn ≠ 0.
Обратным ходом , начиная с последнего уравнения, последовательно найдем значения x n , (где x n = ), x n – 1 , …, x 1 . В этом случае система линейных уравнений имеет единственное решение, то есть является определенной.
2) Если r n , то система после прямого хода принимает вид:
где с 11 ≠ 0, с 22 ≠ 0,
…, с rr ≠ 0.
Неизвестные x 1 , x 2 ,
…, x r ,
с которых начинаются уравнения, называются главными
неизвестными ,
а остальные x r + 1 , x r + 2 ,
…, x n – свободными .
В этом случае обратным ходом, начиная
с последнего уравнения, выражают главные
неизвестные через свободные неизвестные. Получают следующие равенства:
Получают следующие равенства:
x 1 = k 1, r + 1 x r + 1 + … + k 1, n x n + t 1 ,
x 2 = k 2, r + 1 x r + 1 + … + k 2, n x n + t 2 ,
……………………………………..
x r = k r , r + 1 x r + 1 + … + k r , n x n + t r .
Определение 6.10. Общим решением системы называется выражение главных неизвестных через свободные.
Если свободным неизвестным придать какие-нибудь числовые значения, то из общего решения получим значения главных неизвестных. Таким образом, получают частное решение системы. Из способа его получения следует, что система имеет более одного решения, то есть является неопределенной.
Пример 6.3. Решить методом Гаусса систему линейных уравнений:
Решение . Преобразования
с системой линейных удобнее производить
не с самими уравнениями, а с матрицей
их коэффициентов. Расширенная матрица
этой системы имеет вид: (А |B ) =
Преобразования
с системой линейных удобнее производить
не с самими уравнениями, а с матрицей
их коэффициентов. Расширенная матрица
этой системы имеет вид: (А |B ) =
.
Осуществляем
прямой ход. Первым шагом исключаем
неизвестное х 1
из всех уравнений, кроме первого. Так
как а 11 = 1 ≠ 0,
то переставлять уравнения местами не
нужно. Прибавим ко второму уравнению
системы первое уравнение, умноженное
на (–1), к третьему уравнению – первое,
умноженное на (–3). Получим после
преобразований следующую матрицу:
,
в которой элемент а 22 = 1.
Перестановка местами уравнений (первое
уравнение трогать не следует) не поможет,
поэтому переходим к следующему
неизвестному х 3
и исключаем его из всех уравнений, кроме
первого и второго. Для этого к третьему
уравнению прибавим второе, умноженное
на (–2) и вычеркнем получившееся нулевое
уравнение. После прямого хода получаем
следующую систему:
.
Прямой ход завершен. В этом случае n = 4, r = 2, r n
,
и, следовательно, система неопределенная. Главные неизвестные – это те неизвестные,
с которых начинаются уравнения, в нашем
случае это х 1
и х 3 .
Неизвестные х 2
и х 4
– свободные.
Главные неизвестные – это те неизвестные,
с которых начинаются уравнения, в нашем
случае это х 1
и х 3 .
Неизвестные х 2
и х 4
– свободные.
Обратным
ходом надо выразить главные неизвестные
через свободные. Для этого в столбцах,
содержащих ведущие элементы строк,
следует получить нули. Здесь это элемент а 13 .
Прибавим к первому уравнению, умноженному
на 2, второе и выпишем получившуюся
матрицу коэффициентов:
,
а затем и сами уравнения:
Из
этих уравнений получаем общее решение:
Найдем какое-нибудь частное решение; пусть х 2 = 3, х 4 = 1, тогда из общего решения получим значения х 1 = , и х 1 = –2. Таким образом, частное решение – вектор а = (, 3, –2, 1).
Ответ :
общее решение {(
, х 2 ,
, х 4)},
где х 2 , х 4 R;
частное решение, если х 2 = 3, х 4 = 1, то (, 3, –2, 1).
Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:
Он обладает рядом преимуществ по сравнению с другими методами:
- во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;
- во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;
- в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.
Краткий обзор статьи.
Сначала дадим необходимые определения и введем обозначения.
Далее опишем алгоритм метода Гаусса для простейшего случая, то есть, для систем линейных алгебраических уравнений, количество уравнений в которых совпадает с количеством неизвестных переменных и определитель основной матрицы системы не равен нулю. При решении таких систем уравнений наиболее отчетливо видна суть метода Гаусса, которая заключается в последовательном исключении неизвестных переменных. Поэтому метод Гаусса также называют методом последовательного исключения неизвестных. Покажем подробные решения нескольких примеров.
Поэтому метод Гаусса также называют методом последовательного исключения неизвестных. Покажем подробные решения нескольких примеров.
В заключении рассмотрим решение методом Гаусса систем линейных алгебраических уравнений, основная матрица которых либо прямоугольная, либо вырожденная. Решение таких систем имеет некоторые особенности, которые мы подробно разберем на примерах.
Навигация по странице.
Основные определения и обозначения.
Рассмотрим систему из p линейных уравнений с n неизвестными (p может быть равно n ):
Где — неизвестные переменные, — числа (действительные или комплексные), — свободные члены.
Если , то система линейных алгебраических уравнений называется однородной , в противном случае – неоднородной .
Совокупность значения неизвестных переменных , при которых все уравнения системы обращаются в тождества, называется решением СЛАУ .
Если существует хотя бы одно решение системы линейных алгебраических уравнений, то она называется совместной , в противном случае – несовместной .
Если СЛАУ имеет единственное решение, то она называется определенной . Если решений больше одного, то система называется неопределенной .
Говорят, что система записана в координатной форме , если она имеет вид
.
Эта система в матричной форме записи имеет вид , где — основная матрица СЛАУ, — матрица столбец неизвестных переменных, — матрица свободных членов.
Если к матрице А
добавить в качестве (n+1)-ого
столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т
, а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,
Квадратная матрица А называется вырожденной , если ее определитель равен нулю. Если , то матрица А называется невырожденной .
Следует оговорить следующий момент.
Если с системой линейных алгебраических уравнений произвести следующие действия
- поменять местами два уравнения,
- умножить обе части какого-либо уравнения на произвольное и отличное от нуля действительное (или комплексное) число k ,
- к обеим частям какого-либо уравнения прибавить соответствующие части другого уравнения, умноженные на произвольное число k ,
то получится эквивалентная система, которая имеет такие же решения (или также как и исходная не имеет решений).
Для расширенной матрицы системы линейных алгебраических уравнений эти действия будут означать проведение элементарных преобразований со строками:
- перестановку двух строк местами,
- умножение всех элементов какой-либо строки матрицы T на отличное от нуля число k ,
- прибавление к элементам какой-либо строки матрицы соответствующих элементов другой строки, умноженных на произвольное число k .
Теперь можно переходить к описанию метода Гаусса.
Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.
Как бы мы поступили в школе, если бы получили задание найти решение системы уравнений .
Некоторые сделали бы так.
Заметим, что прибавив к левой части второго уравнения левую часть первого, а к правой части — правую, можно избавиться от неизвестных переменных x 2 и x 3 и сразу найти x 1 :
Подставляем найденное значение x 1 =1 в первое и третье уравнение системы:
Если умножить обе части третьего уравнения системы на -1 и прибавить их к соответствующим частям первого уравнения, то мы избавимся от неизвестной переменной x 3 и сможем найти x 2 :
Подставляем полученное значение x 2 =2
в третье уравнение и находим оставшуюся неизвестную переменную x 3
:
Другие поступили бы иначе.
Разрешим первое уравнение системы относительно неизвестной переменной x 1
и подставим полученное выражение во второе и третье уравнение системы, чтобы исключить из них эту переменную:
Теперь разрешим второе уравнение системы относительно x 2
и подставим полученный результат в третье уравнение, чтобы исключить из него неизвестную переменную x 2
:
Из третьего уравнения системы видно, что x 3 =3 . Из второго уравнения находим , а из первого уравнения получаем .
Знакомые способы решения, не правда ли?
Самое интересное здесь то, что второй способ решения по сути и есть метод последовательного исключения неизвестных, то есть, метод Гаусса. Когда мы выражали неизвестные переменные (сначала x 1
, на следующем этапе x 2
) и подставляли их в остальные уравнения системы, мы тем самым исключали их. Исключение мы проводили до того момента, пока в последнем уравнении не осталась одна единственная неизвестная переменная. Процесс последовательного исключения неизвестных называется прямым ходом метода Гаусса . После завершения прямого хода у нас появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется обратным ходом метода Гаусса .
После завершения прямого хода у нас появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется обратным ходом метода Гаусса .
Следует заметить, что когда мы выражаем x 1 через x 2 и x 3 в первом уравнении, а затем подставляем полученное выражение во второе и третье уравнения, то к такому же результату приводят следующие действия:
Действительно, такая процедура также позволяет исключить неизвестную переменную x 1 из второго и третьего уравнений системы:
Нюансы с исключением неизвестных переменных по методу Гаусса возникают тогда, когда уравнения системы не содержат некоторых переменных.
Например, в СЛАУ в первом уравнении отсутствует неизвестная переменная x 1
(иными словами, коэффициент перед ней равен нулю). Поэтому мы не можем разрешить первое уравнение системы относительно x 1
, чтобы исключить эту неизвестную переменную из остальных уравнений. Выходом из этой ситуации является перестановка местами уравнений системы. Так как мы рассматриваем системы линейных уравнений, определители основных матриц которых отличны от нуля, то всегда существует уравнение, в котором присутствует нужная нам переменная, и мы это уравнение можем переставить на нужную нам позицию. Для нашего примера достаточно поменять местами первое и второе уравнения системы , дальше можно разрешить первое уравнение относительно x 1
и исключить ее из остальных уравнений системы (хотя во втором уравнении x 1
уже отсутствует).
Поэтому мы не можем разрешить первое уравнение системы относительно x 1
, чтобы исключить эту неизвестную переменную из остальных уравнений. Выходом из этой ситуации является перестановка местами уравнений системы. Так как мы рассматриваем системы линейных уравнений, определители основных матриц которых отличны от нуля, то всегда существует уравнение, в котором присутствует нужная нам переменная, и мы это уравнение можем переставить на нужную нам позицию. Для нашего примера достаточно поменять местами первое и второе уравнения системы , дальше можно разрешить первое уравнение относительно x 1
и исключить ее из остальных уравнений системы (хотя во втором уравнении x 1
уже отсутствует).
Надеемся, что суть Вы уловили.
Опишем алгоритм метода Гаусса.
Пусть нам требуется решить систему из n линейных алгебраических уравнений с n неизвестными переменными вида , и пусть определитель ее основной матрицы отличен от нуля.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1
из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому
уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
Исключим неизвестную переменную x 1
из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому
уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
где , а .
К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1 исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому
уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид
где , а . Таким образом, переменная x 2
исключена из всех уравнений, начиная с третьего.
Таким образом, переменная x 2
исключена из всех уравнений, начиная с третьего.
Далее приступаем к исключению неизвестной x 3
, при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как , с помощью полученного значения x n находим x n-1 из предпоследнего уравнения, и так далее, находим x 1 из первого уравнения.
Разберем алгоритм на примере.
Пример.
методом Гаусса.
Решение.
Коэффициент a 11 отличен от нуля, так что приступим к прямому ходу метода Гаусса, то есть, к исключению неизвестной переменной x 1 из всех уравнений системы, кроме первого. Для этого к левой и правой частям второго, третьего и четвертого уравнения прибавим левую и правую части первого уравнения, умноженные соответственно на , и :
Неизвестную переменную x 1
исключили, переходим к исключению x 2
. К левым и правым частям третьего и четвертого уравнений системы прибавляем левую и правую части второго уравнения, умноженные соответственно на и :
К левым и правым частям третьего и четвертого уравнений системы прибавляем левую и правую части второго уравнения, умноженные соответственно на и :
Для завершения прямого хода метода Гаусса нам осталось исключить неизвестную переменную x 3
из последнего уравнения системы. Прибавим к левой и правой частям четвертого уравнения соответственно левую и правую часть третьего уравнения, умноженную на :
Можно начинать обратный ход метода Гаусса.
Из последнего уравнения имеем ,
из третьего уравнения получаем ,
из второго ,
из первого .
Для проверки можно подставить полученные значения неизвестных переменных в исходную систему уравнений. Все уравнения обращаются в тождества, что говорит о том, что решение по методу Гаусса найдено верно.
Ответ:
А сейчас приведем решение этого же примера методом Гаусса в матричной форме записи.
Пример.
Найдите решение системы уравнений методом Гаусса.
Решение.
Расширенная матрица системы имеет вид . Сверху над каждым столбцом записаны неизвестные переменные, которым соответствуют элементы матрицы.
Сверху над каждым столбцом записаны неизвестные переменные, которым соответствуют элементы матрицы.
Прямой ход метода Гаусса здесь предполагает приведение расширенной матрицы системы к трапецеидальному виду с помощью элементарных преобразований. Этот процесс схож с исключением неизвестных переменных, которое мы проводили с системой в координатной форме. Сейчас Вы в этом убедитесь.
Преобразуем матрицу так, чтобы все элементы в первом столбце, начиная со второго, стали нулевыми. Для этого к элементам второй, третьей и четвертой строк прибавим соответствующие элементы первой строки умноженные на , и на соответственно:
Далее полученную матрицу преобразуем так, чтобы во втором столбце все элементы, начиная с третьего стали нулевыми. Это будет соответствовать исключению неизвестной переменной x 2 . Для этого к элементам третьей и четвертой строк прибавим соответствующие элементы первой строки матрицы, умноженные соответственно на и :
Осталось исключить неизвестную переменную x 3
из последнего уравнения системы. Для этого к элементам последней строки полученной матрицы прибавим соответствующие элементы предпоследней строки, умноженные на :
Для этого к элементам последней строки полученной матрицы прибавим соответствующие элементы предпоследней строки, умноженные на :
Следует отметить, что эта матрица соответствует системе линейных уравнений
которая была получена ранее после прямого хода.
Пришло время обратного хода. В матричной форме записи обратный ход метода Гаусса предполагает такое преобразование полученной матрицы, чтобы матрица, отмеченная на рисунке
стала диагональной, то есть, приняла вид
где — некоторые числа.
Эти преобразования аналогичны преобразованиям прямого хода метода Гаусса, но выполняются не от первой строки к последней, а от последней к первой.
Прибавим к элементам третьей, второй и первой строк соответствующие элементы последней строки, умноженные на , на и на соответственно:
Теперь прибавим к элементам второй и первой строк соответствующие элементы третьей строки, умноженные на и на соответственно:
На последнем шаге обратного хода метода Гаусса к элементам первой строки прибавляем соответствующие элементы второй строки, умноженные на :
Полученная матрица соответствует системе уравнений , откуда находим неизвестные переменные.
Ответ:
ОБРАТИТЕ ВНИМАНИЕ.
При использовании метода Гаусса для решения систем линейных алгебраических уравнений следует избегать приближенных вычислений, так как это может привести к абсолютно неверным результатам. Рекомендуем не округлять десятичные дроби. Лучше от десятичных дробей переходить к обыкновенным дробям.
Пример.
Решите систему из трех уравнений методом Гаусса .
Решение.
Отметим, что в этом примере неизвестные переменные имеют другое обозначение (не x 1 , x 2 , x 3 , а x, y, z ). Перейдем к обыкновенным дробям:
Исключим неизвестную x из второго и третьего уравнений системы:
В полученной системе во втором уравнении отсутствует неизвестная переменная y , а в третьем уравнении y присутствует, поэтому, переставим местами второе и третье уравнения:
На этом прямой ход метода Гаусса закончен (из третьего уравнения не нужно исключать y
, так как этой неизвестной переменной уже нет).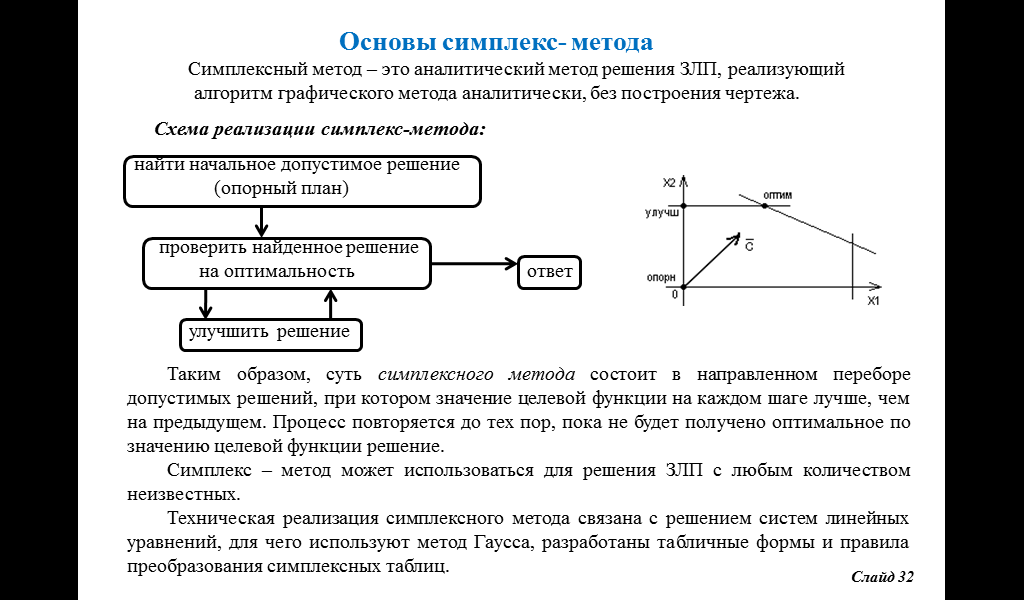
Приступаем к обратному ходу.
Из последнего уравнения находим ,
из предпоследнего
из первого уравнения имеем
Ответ:
X = 10, y = 5, z = -20 .
Решение систем линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных или основная матрица системы вырожденная, методом Гаусса.
Системы уравнений, основная матрица которых прямоугольная или квадратная вырожденная, могут не иметь решений, могут иметь единственное решение, а могут иметь бесконечное множество решений.
Сейчас мы разберемся, как метод Гаусса позволяет установить совместность или несовместность системы линейных уравнений, а в случае ее совместности определить все решения (или одно единственное решение).
В принципе процесс исключения неизвестных переменных в случае таких СЛАУ остается таким же. Однако следует подробно остановиться на некоторых ситуациях, которые могут возникнуть.
Переходим к самому важному этапу.
Итак, допустим, что система линейных алгебраических уравнений после завершения прямого хода метода Гаусса приняла вид и ни одно уравнение не свелось к (в этом случае мы бы сделали вывод о несовместности системы). Возникает логичный вопрос: «Что делать дальше»?
Выпишем неизвестные переменные, которые стоят на первом месте всех уравнений полученной системы:
В нашем примере это x 1
, x 4
и x 5
. В левых частях уравнений системы оставляем только те слагаемые, которые содержат выписанные неизвестные переменные x 1
, x 4
и x 5
, остальные слагаемые переносим в правую часть уравнений с противоположным знаком:
Придадим неизвестным переменным, которые находятся в правых частях уравнений, произвольные значения , где — произвольные числа:
После этого в правых частях всех уравнений нашей СЛАУ находятся числа и можно преступать к обратному ходу метода Гаусса.
Из последнего уравнений системы имеем , из предпоследнего уравнения находим , из первого уравнения получаем
Решением системы уравнений является совокупность значений неизвестных переменных
Придавая числам различные значения, мы будем получать различные решения системы уравнений. То есть, наша система уравнений имеет бесконечно много решений.
То есть, наша система уравнений имеет бесконечно много решений.
Ответ:
где — произвольные числа.
Для закрепления материала подробно разберем решения еще нескольких примеров.
Пример.
Решите однородную систему линейных алгебраических уравнений методом Гаусса.
Решение.
Исключим неизвестную переменную x из второго и третьего уравнений системы. Для этого к левой и правой части второго уравнения прибавим соответственно левую и правую части первого уравнения, умноженные на , а к левой и правой части третьего уравнения — левую и правую части первого уравнения, умноженные на :
Теперь исключим y
из третьего уравнения полученной системы уравнений:
Полученная СЛАУ равносильна системе .
Оставляем в левой части уравнений системы только слагаемые, содержащие неизвестные переменные x
и y
, а слагаемые с неизвестной переменной z
переносим в правую часть:
Что такое число неизвестных в метод гаусса.
 Метод гаусса для чайников: решаем слау легко
Метод гаусса для чайников: решаем слау легкоМетод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья . Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно.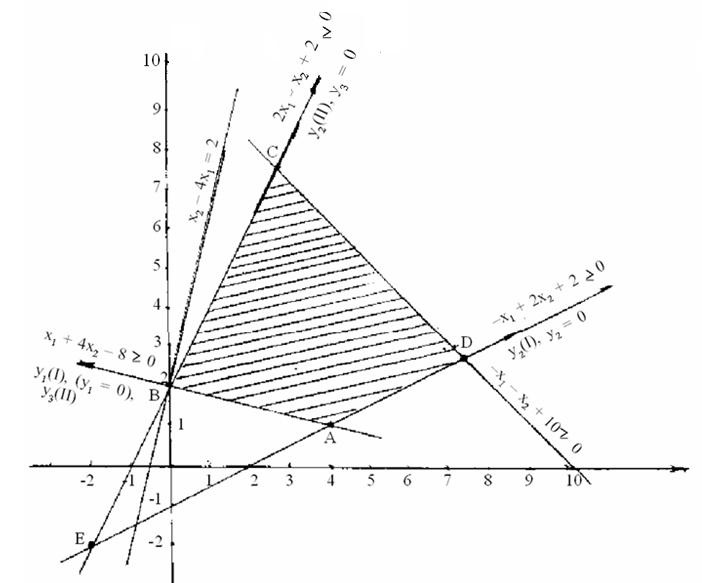 Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .
Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .
Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .
На практике так подробно, конечно, не расписывают, а пишут короче:
Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: »
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ : рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!
Вернемся к нашей системе . Она практически разобрана по косточкам.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :
(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .
Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .
В результате элементарных преобразований получена эквивалентная исходной система уравнений:
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример 1
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы:
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:
И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду.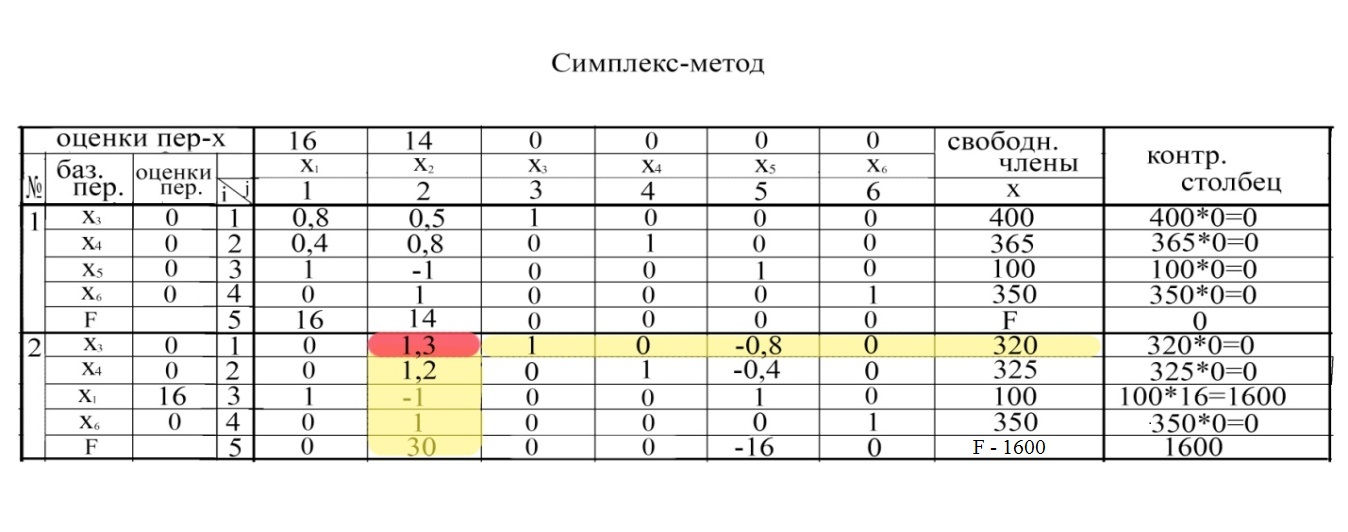 С чего начать действия?
С чего начать действия?
Сначала смотрим на левое верхнее число:
Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
Теперь первая строка у нас останется неизменной до конца решения . Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :
Результат записываем во вторую строку:
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :
Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :
Результат записываем в третью строку:
На практике эти действия обычно выполняются устно и записываются в один шаг:
Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО :
А мысленный ход самих расчётов я уже рассмотрел выше.
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :
Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:
Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат:
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:
Ответ :
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.
Пример 2
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить систему линейных уравнений методом Гаусса
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:
Ответ : .
Пример 4
Решить систему линейных уравнений методом Гаусса
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
В последней части рассмотрим некоторые особенности алгоритма Гаусса.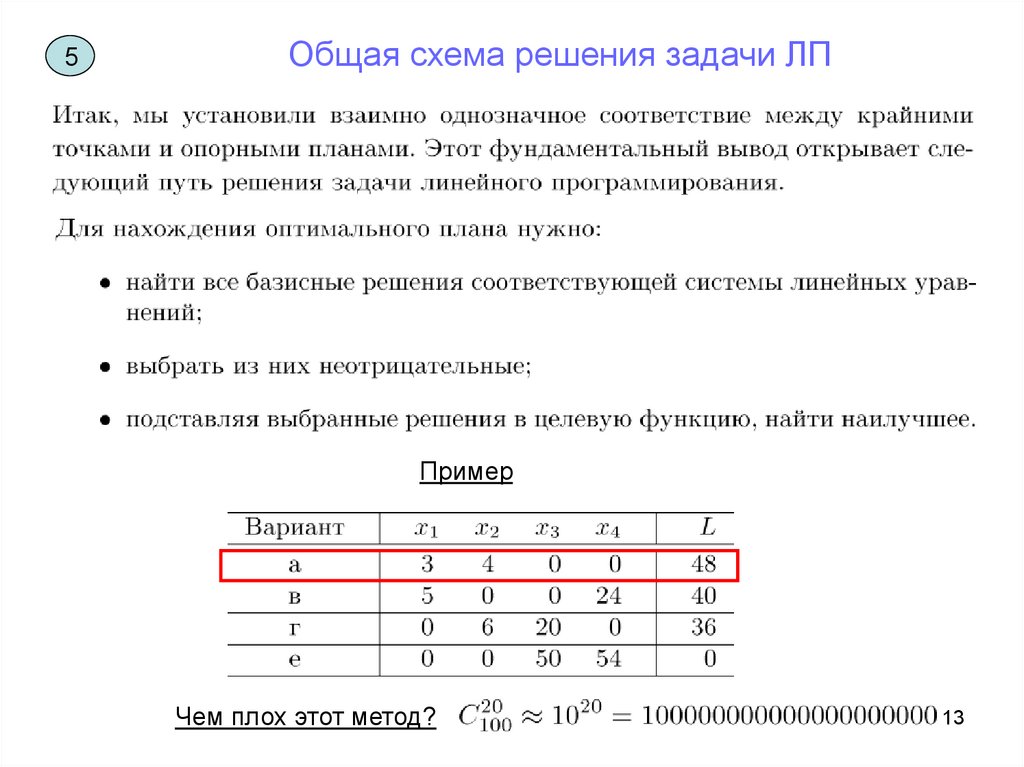
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:
Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:
Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.
Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Таким образом, мы получим нужные нули в первом столбце.
Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Желаю успехов!
Решения и ответы:
Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.
Обратный ход:
Ответ : .
Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.
Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы
Преобразования (3) и (4) будут направлены на получение нужной единицы
(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.
Обратный ход:
Решение систем линейных уравнений методом Гаусса. Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными
определитель основной матрицы которой отличен от нуля.
Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x 1 из всех уравнений системы, начиная со второго, далее исключается x 2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная x n . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .
Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменную x 1 из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на , и так далее, к n-ому уравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет вид
где , а .
К такому же результату мы бы пришли, если бы выразили x 1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x 1 исключена из всех уравнений, начиная со второго.
Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на , и так далее, к n-ому уравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет вид
где , а . Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем x n из последнего уравнения как , с помощью полученного значения x n находим x n-1 из предпоследнего уравнения, и так далее, находим x 1 из первого уравнения.
Пример.
Решите систему линейных уравнений методом Гаусса. .
Ответ:
x 1 = 4, x 2 = 0, x 3 = -1 .
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (бытьнесовместной ).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним,правило Крамера и матричный методнепригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений , который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы — матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) с троки матрицыможно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следуетудалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить .
4) строку матрицы можноумножить (разделить) на любое число,отличное от нуля.
5) к строке матрицы можноприбавить другую строку, умноженную на число , отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» — с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду:
элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»).
 Например, к такому виду:
Например, к такому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х 1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х 1 , стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х 1 не будут иметь коэффициент 0.
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х 2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х 2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х n . Для этого решаем элементарное уравнение А*х n = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
Обычно это можно сделать несколькими способами. Поступим так:
1 шаг . К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
2 шаг . Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг . Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг . К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг . Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23)
, и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23)
, и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x 3 = 1
x 2 = 3
x 1 + x 2 – x 3 = 1, следовательно x 1 + 3 – 1 = 1, x 1 = –1
Ответ 😡 1 = –1, x 2 = 3, x 3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0. 4 –0.6 0.6
4 –0.6 0.6
0 0.64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х 3 = 0,96 или приблизительно 1.
х 2 = 3 и х 1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор .
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Метод Гаусса был предложен известнейшим немецким математиком Карлом Фридрихом Гауссом (1777 — 1855) и является одним из наиболее универсальных методов решения СЛАУ. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении задачи, расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к ступенчатому виду. Далее последовательно находятся все неизвестные, начиная снизу вверх.
Принцип метода Гаусса
Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса, обратный — методом Гаусса-Жордана, который отличается от первого только последовательностью исключения переменных.
Метод Гаусса идеально подходит для решения систем содержащих больше трех линейных уравнений, для решения систем уравнений,
которые не являются квадратными (чего не скажешь про
метод Крамера и
матричный метод). То есть метод Гаусса — наиболее
универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет
бесконечно много решений или несовместна.
То есть метод Гаусса — наиболее
универсальный метод для нахождения решения любой системы линейных уравнений, он работает в случае, когда система имеет
бесконечно много решений или несовместна.
Примеры решения систем уравнений
Пример
Задание. Решить СЛАУ методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент равнялся 1 (это мы делаем для упрощения вычислений):
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на ):
От третьей строки отнимаем вторую, умноженную на 3:
Умножив третью строку на , получаем:
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент
, для этого от второй строки отнимем третью.
Начнем с элементов третьего столбца. Надо обнулить элемент
, для этого от второй строки отнимем третью.
Метод Гаусса – это метод последовательного исключения неизвестных.
Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей , из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. Рассмотрим одну из вычислительных схем. Эта схема называется схемой единственного деления. Итак, рассмотрим эту схему. Пусть a 11 ≠0 (ведущий элемент) разделим на a 11 первое уравнение. Получим
x 1 +a (1) 12 ·x 2 +…+a (1) 1n ·x n =b (1) 1 (2)
Пользуясь уравнением (2), легко исключить неизвестные x 1 из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x 1), то есть на первом шаге получим
.
Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.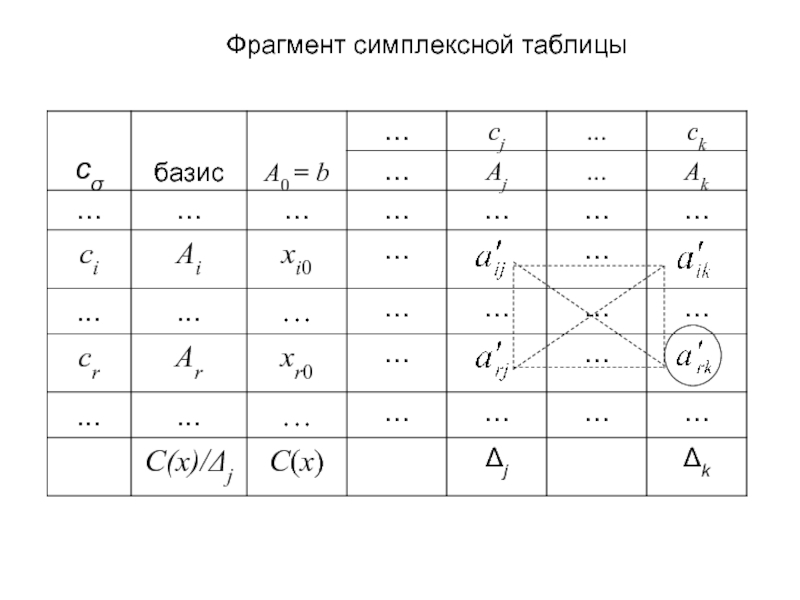
Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x 2 (шаг 2).
После n шагов вместо (1) получим равносильную систему
(3)
Таким образом, на первом этапе мы получим треугольную систему (3). Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения x n , x n -1 , …, x 1 .
Обозначим полученное решение за x 0 . Тогда разность ε=b-A·x 0 называется невязкой .
Если ε=0, то найденное решение x 0 является верным.
Вычисления по методу Гаусса выполняются в два этапа:
- Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду.
- Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.
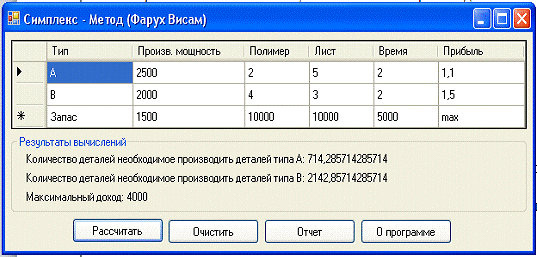
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.
Назначение метода Гаусса
Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.Виды метода Гаусса
- Классический метод Гаусса;
- Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k -ом шаге ведущим элементом оказывался наибольший по модулю элемент k -го столбца.
- Метод Жордано-Гаусса;

Проиллюстрируем отличие метода Жордано-Гаусса от метода Гаусса на примерах.
Пример решения методом Гаусса
Решим систему:
Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой
Из 1-ой строки выражаем x 3:
Из 2-ой строки выражаем x 2:
Из 3-ой строки выражаем x 1:
Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x 1 | x 2 | x 3 | B |
| 1 / 1 = 1 | 2 / 1 = 2 | -2 / 1 = -2 | 1 / 1 = 1 |
Разрешающий элемент равен (3).
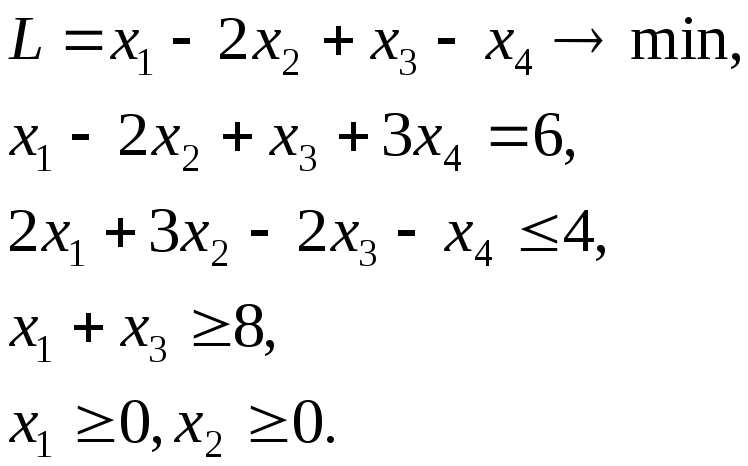
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
| x 1 | x 2 | x 3 | B |
| 0 / 3 = 0 | 3 / 3 = 1 | 1 / 3 = 0.33 | 4 / 3 = 1.33 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
Ответ : x 1 = 1, x 2 = 1, x 3 = 1
Реализация метода Гаусса
Метод Гаусса реализован на многих языках программирования, в частности: Pascal, C++, php, Delphi , а также имеется реализация метода Гаусса в онлайн режиме .Использование метода Гаусса
Применение метода Гаусса в теории игр
В теории игр при отыскании максиминной оптимальной стратегии игрока составляется система уравнений, которая решается методом Гаусса.Применение метода Гаусса при решении дифференциальных уравнений
Для поиска частного решения дифференциального уравнения сначала находят производные соответствующей степени для записанного частного решения (y=f(A,B,C,D)), которые подставляют в исходное уравнение. Далее, чтобы найти переменные A,B,C,D составляется система уравнений, которая решается методом Гаусса.
Применение метода Жордано-Гаусса в линейном программировании
В линейном программировании, в частности в симплекс-методе для преобразования симплексной таблицы на каждой итерации используется правило прямоугольника, в котором используется метод Жордано-Гаусса.Примеры
Пример №1 . Решить систему методом Гаусса:x 1 +2x 2 — 3x 3 + x 4 = -2
x 1 +2x 2 — x 3 + 2x 4 = 1
3x 1 -x 2 + 2x 3 + x 4 = 3
3x 1 +x 2 + x 3 + 3x 4 = 2
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Для удобства вычислений поменяем строки местами:
Из 1-ой строки выражаем x 4
Из 2-ой строки выражаем x 3
Из 3-ой строки выражаем x 2
Из 4-ой строки выражаем x 1
Пример №3 .
- Решить СЛАУ методом Жордано-Гаусса. Запишем систему в виде:
Разрешающий элемент равен (2.2). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
 x 1 = 1.00, x 2 = 1.00, x 3 = 1.00
x 1 = 1.00, x 2 = 1.00, x 3 = 1.00
Example1 - Систему линейных уравнений решить методом Гаусса
ПримерПосмотрите, как быстро можно определить, является ли система совместной
- Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку найденного решения: Решение
- Решить систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
Решение :xls - Решить систему линейных уравнений тремя способами: а) методом Гаусса последовательных исключений неизвестных; б) по формуле x = A -1 b с вычислением обратной матрицы A -1 ; в) по формулам Крамера.
Решение :xls - Решить методом Гаусса следующую вырожденную систему уравнений.
Скачать решение doc - Решите методом Гаусса систему линейных уравнений записанную в матричной форме:
7 8 -3 x 92
2 2 2 y = 30
-9 -10 5 z -114
Решение системы уравнений методом сложения
Решите 6x+5y=3, 3x+3y=4 систему уравнений методом сложения.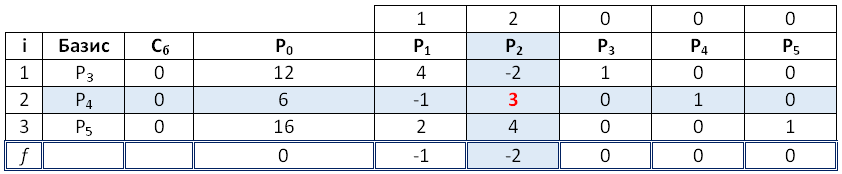
Решение.
6x+5y=3
3x+3y=4
Умножим второе уравнение на (-2).
6x+5y=3
-6x-6y=-8
============ (складываем)
-y=-5
Откуда y = 5
Находим x:
6x+5*5=3 или 6x=-22
Откуда x = -22/6 = -11/3
Пример №2
. Решение СЛАУ в матричной форме означает, что исходную запись системы необходимо привести к матричной (так называемая расширенная матрица). Покажем это на примере.
Запишем систему в виде расширенной матрицы:
Умножим 1-ую строку на (15). Умножим 2-ую строку на (-9). Добавим 2-ую строку к 1-ой:
Теперь исходную систему можно записать как:
x 3 = -21/(-21) = 1
x 2 = /15
x 1 = /3
Из 2-ой строки выражаем x 2:
Из 3-ой строки выражаем x 1:
Пример №3
. Решить систему методом Гаусса:
x 1 +2x 2 — 3x 3 + x 4 = -2
x 1 +2x 2 — x 3 + 2x 4 = 1
3x 1 -x 2 + 2x 3 + x 4 = 3
3x 1 +x 2 + x 3 + 3x 4 = 2
Решение:
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Добавим 2-ую строку к 1-ой
Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой
Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой
Для удобства вычислений поменяем строки местами:
Умножим 1-ую строку на (0). Добавим 2-ую строку к 1-ой
Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой
Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой
Из 1-ой строки выражаем x 4
Из 2-ой строки выражаем x 3
Из 3-ой строки выражаем x 2
Из 4-ой строки выражаем x 1
примеры решений. Применение метода Жордано-Гаусса в линейном программировании
Еще с начала XVI-XVIII веков математики усиленно начали изучать функции, благодаря которым так много в нашей жизни изменилось. Компьютерная техника без этих знаний просто не существовала бы. Для решения сложных задач, линейных уравнений и функций были созданы различные концепции, теоремы и методики решения.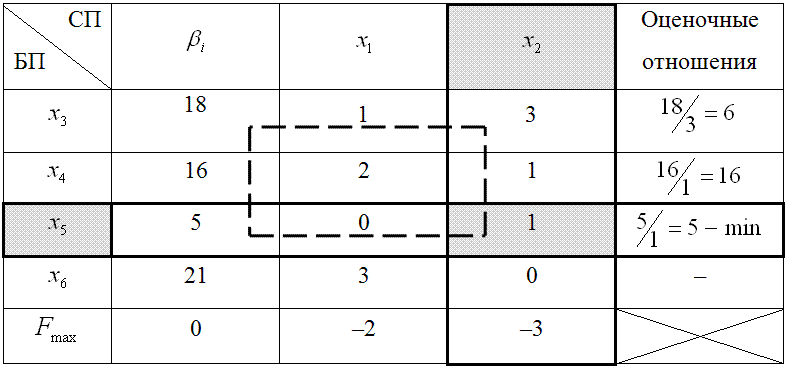 Одним из таких универсальных и рациональных способов и методик решения линейных уравнений и их систем стал и метод Гаусса. Матрицы, их ранг, детерминант — все можно посчитать, не используя сложных операций.
Одним из таких универсальных и рациональных способов и методик решения линейных уравнений и их систем стал и метод Гаусса. Матрицы, их ранг, детерминант — все можно посчитать, не используя сложных операций.
Что представляет собой СЛАУ
В математике существует понятие СЛАУ — система линейных алгебраических уравнений. Что же она собой представляет? Это набор из m уравнений с искомыми n неизвестными величинами, обычно обозначающимися как x, y, z, или x 1 , x 2 … x n, или другими символами. Решить методом Гаусса данную систему — означает найти все искомые неизвестные. Если система имеет одинаковое число неизвестных и уравнений, тогда она называется системой n-го порядка.
Наиболее популярные методы решения СЛАУ
В учебных заведениях среднего образования изучают различные методики решения таких систем. Чаще всего это простые уравнения, состоящие из двух неизвестных, поэтому любой существующий метод для поиска ответа на них не займет много времени. Это может быть как метод подстановки, когда из одного уравнения выводится другое и подставляется в изначальное. Или метод почленного вычитания и сложения. Но наиболее легким и универсальным считается метод Гаусса. Он дает возможность решать уравнения с любым количеством неизвестных. Почему именно эта методика считается рациональной? Все просто. Матричный способ хорош тем, что здесь не требуется по несколько раз переписывать ненужные символы в виде неизвестных, достаточно проделать арифметические операции над коэффициентами — и получится достоверный результат.
Или метод почленного вычитания и сложения. Но наиболее легким и универсальным считается метод Гаусса. Он дает возможность решать уравнения с любым количеством неизвестных. Почему именно эта методика считается рациональной? Все просто. Матричный способ хорош тем, что здесь не требуется по несколько раз переписывать ненужные символы в виде неизвестных, достаточно проделать арифметические операции над коэффициентами — и получится достоверный результат.
Где используются СЛАУ на практике
Решением СЛАУ являются точки пересечения прямых на графиках функций. В наш высокотехнологический компьютерный век людям, которые тесно связаны с разработкой игр и прочих программ, необходимо знать, как решать такие системы, что они представляют и как проверить правильность получившегося результата. Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики.
Критерий совместимости СЛАУ
Такую систему можно решить только в том случае, если она совместима. Для понятности представим СЛАУ в виде Ax=b. Она имеет решение, если rang(A) равняется rang(A,b). В этом случае (A,b) — это матрица расширенного вида, которую можно получить из матрицы А, переписав ее со свободными членами. Выходит, что решить линейные уравнения методом Гаусса достаточно легко.
Возможно, некоторые обозначения не совсем понятны, поэтому необходимо рассмотреть все на примере. Допустим, есть система: x+y=1; 2x-3y=6. Она состоит всего из двух уравнений, в которых 2 неизвестные. Система будет иметь решение только в том случае, если ранг ее матрицы будет равняться рангу расширенной матрицы. Что такое ранг? Это число независимых строк системы. В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=».
Почему СЛАУ можно представить в матричном виде
Исходя из критерия совместимости по доказанной теореме Кронекера-Капелли, систему линейных алгебраических уравнений можно представить в матричном виде. Применяя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ на всю систему. Если ранг обычной матрицы равняется рангу ее расширенной матрицы, но при этом меньше количества неизвестных, тогда система имеет бесконечное количество ответов.
Применяя каскадный метод Гаусса, можно решить матрицу и получить единственный достоверный ответ на всю систему. Если ранг обычной матрицы равняется рангу ее расширенной матрицы, но при этом меньше количества неизвестных, тогда система имеет бесконечное количество ответов.
Преобразования матриц
Прежде чем переходить к решению матриц, необходимо знать, какие действия можно проводить над их элементами. Существует несколько элементарных преобразований:
- Переписывая систему в матричный вид и осуществляя ее решение, можно умножать все элементы ряда на один и тот же коэффициент.
- Для того чтобы преобразовать матрицу в канонический вид, можно менять местами два параллельных ряда. Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся — нулями.
- Соответствующие элементы параллельных рядов матрицы можно прибавлять один к другому.
Метод Жордана-Гаусса
Суть решения систем линейных однородных и неоднородных уравнений методом Гаусса в том, чтобы постепенно исключить неизвестные. Допустим, у нас есть система из двух уравнений, в которых две неизвестные. Чтобы их найти, необходимо проверить систему на совместимость. Уравнение методом Гаусса решается очень просто. Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Допустим, у нас есть система из двух уравнений, в которых две неизвестные. Чтобы их найти, необходимо проверить систему на совместимость. Уравнение методом Гаусса решается очень просто. Необходимо выписать коэффициенты, находящиеся возле каждого неизвестного в матричный вид. Для решения системы понадобится выписать расширенную матрицу. Если одно из уравнений содержит меньшее количество неизвестных, тогда на место пропущенного элемента необходимо поставить «0». К матрице применяются все известные методы преобразования: умножение, деление на число, прибавление соответствующих элементов рядов друг к другу и другие. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Простой пример решения системы 2х2
Для начала возьмем простенькую систему алгебраических уравнений, в которой будет 2 неизвестных.
Перепишем ее в расширенную матрицу.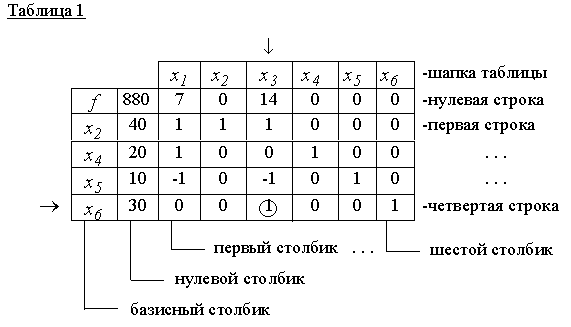
Чтобы решить данную систему линейных уравнений, требуется проделать всего две операции. Нам необходимо привести матрицу к каноническому виду, чтобы по главной диагонали стояли единицы. Так, переводя с матричного вида обратно в систему, мы получим уравнения: 1x+0y=b1 и 0x+1y=b2, где b1 и b2 — получившиеся ответы в процессе решения.
- Первое действие при решении расширенной матрицы будет таким: первый ряд необходимо умножить на -7 и прибавить соответственно отвечающие элементы ко второй строке, чтобы избавиться от одного неизвестного во втором уравнении.
- Так как решение уравнений методом Гаусса подразумевает приведение матрицы к каноническому виду, тогда необходимо и с первым уравнением проделать те же операции и убрать вторую переменную. Для этого вторую строку отнимаем от первой и получаем необходимый ответ — решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.

Как видим, наша система решена методом Жордана-Гаусса. Переписываем ее в необходимую форму: x=-5, y=7.
Пример решения СЛАУ 3х3
Предположим, что у нас есть более сложная система линейных уравнений. Метод Гаусса дает возможность высчитать ответ даже для самой, казалось бы, запутанной системы. Поэтому, чтобы более глубоко вникнуть в методику расчета, можно переходить к более сложному примеру с тремя неизвестными.
Как и в прежнем примере, переписываем систему в вид расширенной матрицы и начинаем приводить ее к каноническому виду.
Для решения этой системы понадобится произвести гораздо больше действий, чем в предыдущем примере.
- Сначала необходимо сделать в первом столбце один единичный элемент и остальные нули. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую — уже в измененном.
- Далее убираем эту же первую неизвестную из третьего уравнения.
 Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья — уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья — уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена. - Теперь необходимо проделать операции и над другими элементами рядов. Третье и четвертое действие можно объединить в одно. Нужно разделить вторую и третью строку на -1, чтобы избавиться от минусовых единиц по диагонали. Третью строку мы уже привели к необходимому виду.
- Дальше приведем к каноническому виду вторую строку. Для этого элементы третьего ряда умножаем на -3 и прибавляем их ко второй строчке матрицы. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
- Чтобы из второго элемента строки сделать 0, необходимо умножить третью строку на -3 и прибавить ее к первому ряду.

- Следующим решающим этапом будет прибавление к первой строке необходимые элементы второго ряда. Так мы получаем канонический вид матрицы, а, соответственно, и ответ.
Как видно, решение уравнений методом Гаусса довольно простое.
Пример решения системы уравнений 4х4
Некоторые более сложные системы уравнений можно решить методом Гаусса посредством компьютерных программ. Необходимо вбить в существующие пустые ячейки коэффициенты при неизвестных, и программа сама пошагово рассчитает необходимый результат, подробно описывая каждое действие.
Ниже описана пошаговая инструкция решения такого примера.
В первом действии в пустые ячейки вписываются свободные коэффициенты и числа при неизвестных. Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.
И производятся все необходимые арифметические операции, чтобы привести расширенную матрицу к каноническому виду. Необходимо понимать, что не всегда ответ на систему уравнений — это целые числа. Иногда решение может быть из дробных чисел.
Иногда решение может быть из дробных чисел.
Проверка правильности решения
Метод Жордана-Гаусса предусматривает проверку правильности результата. Для того чтобы узнать, правильно ли посчитаны коэффициенты, необходимо всего-навсего подставить результат в изначальную систему уравнений. Левая сторона уравнения должна соответствовать правой стороне, находящейся за знаком «равно». Если ответы не совпадают, тогда необходимо пересчитывать заново систему или попробовать применить к ней другой известный вам метод решения СЛАУ, такой как подстановка или почленное вычитание и сложение. Ведь математика — это наука, которая имеет огромное количество различных методик решения. Но помните: результат должен быть всегда один и тот же, независимо от того, какой метод решения вы использовали.
Метод Гаусса: наиболее часто встречающиеся ошибки при решении СЛАУ
Во время решения линейных систем уравнений чаще всего возникают такие ошибки, как неправильный перенос коэффициентов в матричный вид. Бывают системы, в которых отсутствуют в одном из уравнений некоторые неизвестные, тогда, перенося данные в расширенную матрицу, их можно потерять. В результате при решении данной системы результат может не соответствовать действительному.
Бывают системы, в которых отсутствуют в одном из уравнений некоторые неизвестные, тогда, перенося данные в расширенную матрицу, их можно потерять. В результате при решении данной системы результат может не соответствовать действительному.
Еще одной из главных ошибок может быть неправильное выписывание конечного результата. Нужно четко понимать, что первый коэффициент будет соответствовать первому неизвестному из системы, второй — второму, и так далее.
Метод Гаусса подробно описывает решение линейных уравнений. Благодаря ему легко произвести необходимые операции и найти верный результат. Кроме того, это универсальное средство для поиска достоверного ответа на уравнения любой сложности. Может быть, поэтому его так часто используют при решении СЛАУ.
1. Система линейных алгебраических уравнений
1.1 Понятие системы линейных алгебраических уравнений
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких переменных. Системой линейных алгебраических уравнений (далее – СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:
Системой линейных алгебраических уравнений (далее – СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:
где числа a ij называются коэффициентами системы, числа b i – свободными членами, a ij и b i (i=1,…, m; b=1,…, n) представляют собой некоторые известные числа, а x 1 ,…, x n – неизвестные. В обозначении коэффициентов a ij первый индекс i обозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент. Подлежат нахождению числа x n . Такую систему удобно записывать в компактной матричной форме: AX=B. Здесь А – матрица коэффициентов системы, называемая основной матрицей;
– вектор-столбец из неизвестных xj.– вектор-столбец из свободных членов bi.
Произведение матриц А*Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).
Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов
1. 2 Решение системы линейных алгебраических уравнений
2 Решение системы линейных алгебраических уравнений
Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений системы обращается в верное равенство.
Решением системы называется n значений неизвестных х1=c1, x2=c2,…, xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Однородная система всегда совместна, так как x1=x2=x3=…=xn=0 является решением системы. Это решение называется нулевым или тривиальным.
2. Метод исключения Гаусса
2.1 Сущность метода исключения Гаусса
Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.
1. Прямой ход.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним.
После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид:
,Коэффициенты aii называются главными (ведущими) элементами системы.
(если a11=0, переставим строки матрицы так, чтобы a 11 не был равен 0. Это всегда возможно, т. к. в противном случае матрица содержит нулевой столбец, ее определитель равен нулю и система несовместна).Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на
и сложим почленно со вторым уравнением системы (или из второго уравнения почленно вычтем первое, умноженное на ). Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы (или из третьего почленно вычтем первое, помноженное на ). Таким образом, последовательно умножаем первую строку на число и прибавляем к i -й строке, для i= 2, 3, …, n.Продолжая этот процесс, получим эквивалентную систему:
– новые значения коэффициентов при неизвестных и свободные члены в последних m-1 уравнениях системы, которые определяются формулами:
Таким образом, на первом шаге уничтожаются все коэффициенты, лежащие под первым ведущим элементом a 11
0, на втором шаге уничтожаются элементы, лежащие под вторым ведущим элементом а 22 (1) (если a 22 (1) 0) и т.д. Продолжая этот процесс и дальше, мы, наконец, на (m-1) шаге приведем исходную систему к треугольной системе.Если в процессе приведения системы к ступенчатому виду появятся нулевые уравнения, т.е. равенства вида 0=0, их отбрасывают. Если же появится уравнение вида
то это свидетельствует о несовместности системы.На этом прямой ход метода Гаусса заканчивается.
2. Обратный ход.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений.
Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (она в нем всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх.
Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Примечание: на практике удобнее работать не с системой, а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент a11 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на a11).
2.2 Примеры решения СЛАУ методом Гаусса
В данном разделе на трех различных примерах покажем, как методом Гаусса можно решить СЛАУ.
Пример 1. Решить СЛАУ 3-го порядка.
Обнулим коэффициенты при
во второй и третьей строчках. Для этого домножим их на 2/3 и 1 соответственно и сложим с первой строкой:Одним из простейших способов решения системы линейных уравнений является прием, основанный на вычислении определителей (правило Крамера ). Его преимущество состоит в том, что он позволяет сразу провести запись решения, особенно он удобен в тех случаях, когда коэффициенты системы являются не числами, а какими-то параметрами. Его недостаток – громоздкость вычислений в случае большого числа уравнений, к тому же правило Крамера непосредственно не применимо к системам, у которых число уравнений не совпадает с числом неизвестных. В таких случаях обычно применяют метод Гаусса .
Системы линейных уравнений, имеющие одно и то же множество решений, называются эквивалентными . Очевидно, что множество решений линейной системы не изменится, если какие-либо уравнения поменять местами, или умножить одно из уравнений на какое-либо ненулевое число, или если одно уравнение прибавить к другому.
Метод Гаусса (метод последовательного исключения неизвестных ) заключается в том, что с помощью элементарных преобразований система приводится к эквивалентной системе ступенчатого вида. Сначала с помощью 1-го уравнения исключается x 1 из всех последующих уравнений системы. Затем с помощью2-го уравнения исключается x 2 из 3-го и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса , продолжается до тех пор, пока в левой части последнего уравнения останется только одно неизвестное x n . После этого производится обратный ход метода Гаусса – решая последнее уравнение, находим x n ; после этого, используя это значение, из предпоследнего уравнения вычисляем x n –1 и т.д. Последним находим x 1 из первого уравнения.
Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицами их коэффициентов. Рассмотрим матрицу:
называемую расширенной матрицей системы, ибо в нее, кроме основной матрицы системы, включен столбец свободных членов. Метод Гаусса основан на приведении основной матрицы системы к треугольному виду (или трапециевидному виду в случае неквадратных систем) при помощи элементарных преобразованиях строк (!) расширенной матрицы системы.
Пример 5.1. Решить систему методом Гаусса:
Решение . Выпишем расширенную матрицу системы и, используя первую строку, после этого будем обнулять остальные элементы:
получим нули во 2-й, 3-й и 4-й строках первого столбца:
Теперь нужно чтобы все элементы во втором столбце ниже 2-й строки были равны нулю. Для этого можно умножить вторую строку на –4/7 и прибавить к 3-й строке. Однако чтобы не иметь дело с дробями, создадим единицу во 2-й строке второго столбца и только
Теперь, чтобы получить треугольную матрицу, нужно обнулить элемент четвертой строки 3-го столбца, для этого можно умножить третью строку на 8/54 и прибавить ее к четвертой. Однако чтобы не иметь дело с дробями поменяем местами 3-ю и 4-ю строки и 3-й и 4-й столбец и только после этого произведем обнуление указанного элемента. Заметим, что при перестановке столбцов меняются местами, соответствующие переменные и об этом нужно помнить; другие элементарные преобразования со столбцами (сложение и умножение на число) производить нельзя!
Последняя упрощенная матрица соответствует системе уравнений, эквивалентной исходной:
Отсюда, используя обратный ход метода Гаусса, найдем из четвертого уравнения x 3 = –1; из третьего x 4 = –2, из второго x 2 = 2 и из первого уравнения x 1 = 1. В матричном виде ответ записывается в виде
Мы рассмотрели случай, когда система является определенной, т.е. когда имеется только одно решение. Посмотрим, что получится, если система несовместна или неопределенна.
Пример 5.2. Исследовать систему методом Гаусса:
Решение . Выписываем и преобразуем расширенную матрицу системы
Записываем упрощенную систему уравнений:
Здесь, в последнем уравнении получилось, что 0=4, т.е. противоречие. Следовательно, система не имеет решения, т.е. она несовместна . à
Пример 5.3. Исследовать и решить систему методом Гаусса:
Решение . Выписываем и преобразуем расширенную матрицу системы:
В результате преобразований, в последней строке получились одни нули. Это означает, что число уравнений уменьшилось на единицу:
Таким образом, после упрощений осталось два уравнения, а неизвестных четыре, т.е. два неизвестных «лишних». Пусть «лишними», или, как говорят, свободными переменными , будут x 3 и x 4 . Тогда
Полагая x 3 = 2a и x 4 = b , получим x 2 = 1–a и x 1 = 2b –a ; или в матричном виде
Записанное подобным образом решение называется общим , поскольку, придавая параметрам a и b различные значения, можно описать все возможные решения системы. à
Пусть дана система , ∆≠0. (1)Метод Гаусса – это метод последовательного исключения неизвестных.
Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей , из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. Рассмотрим одну из вычислительных схем. Эта схема называется схемой единственного деления. Итак, рассмотрим эту схему. Пусть a 11 ≠0 (ведущий элемент) разделим на a 11 первое уравнение. Получим
(2)
Пользуясь уравнением (2), легко исключить неизвестные x 1 из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x 1), то есть на первом шаге получим
.
Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.
Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x 2 (шаг 2).
После n шагов вместо (1) получим равносильную систему
(3)
Таким образом, на первом этапе мы получим треугольную систему (3). Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения x n , x n -1 , …, x 1 .
Обозначим полученное решение за x 0 . Тогда разность ε=b-A·x 0 называется невязкой .
Если ε=0, то найденное решение x 0 является верным.
Вычисления по методу Гаусса выполняются в два этапа:
- Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду.
- Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.
Назначение метода Гаусса
Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.Виды метода Гаусса
- Классический метод Гаусса;
- Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k -ом шаге ведущим элементом оказывался наибольший по модулю элемент k -го столбца.
- Метод Жордано-Гаусса;
Проиллюстрируем отличие метода Жордано-Гаусса от метода Гаусса на примерах.
Пример решения методом Гаусса
Решим систему:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Из 1-ой строки выражаем x 3:
Из 2-ой строки выражаем x 2:
Из 3-ой строки выражаем x 1:
Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x 1 | x 2 | x 3 | B |
| 1 / 1 = 1 | 2 / 1 = 2 | -2 / 1 = -2 | 1 / 1 = 1 |
Разрешающий элемент равен (3).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
| x 1 | x 2 | x 3 | B |
| 0 / 3 = 0 | 3 / 3 = 1 | 1 / 3 = 0.33 | 4 / 3 = 1.33 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
Ответ : x 1 = 1, x 2 = 1, x 3 = 1
Реализация метода Гаусса
Метод Гаусса реализован на многих языках программирования, в частности: Pascal, C++, php, Delphi , а также имеется реализация метода Гаусса в онлайн режиме .Использование метода Гаусса
Применение метода Гаусса в теории игр
В теории игр при отыскании максиминной оптимальной стратегии игрока составляется система уравнений, которая решается методом Гаусса.Применение метода Гаусса при решении дифференциальных уравнений
Для поиска частного решения дифференциального уравнения сначала находят производные соответствующей степени для записанного частного решения (y=f(A,B,C,D)), которые подставляют в исходное уравнение. Далее, чтобы найти переменные A,B,C,D составляется система уравнений, которая решается методом Гаусса.Применение метода Жордано-Гаусса в линейном программировании
В линейном программировании, в частности в симплекс-методе для преобразования симплексной таблицы на каждой итерации используется правило прямоугольника, в котором используется метод Жордано-Гаусса.Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (бытьнесовместной ).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним,правило Крамера и матричный методнепригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений , который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы — матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) с троки матрицыможно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следуетудалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить .
4) строку матрицы можноумножить (разделить) на любое число,отличное от нуля.
5) к строке матрицы можноприбавить другую строку, умноженную на число , отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» — с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х 1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х 1 , стоящий в каждом уравнении, и умножаем на К. После этого из второго уравнения (коэффициенты при неизвестных и свободные члены) вычитаем первое. Получаем при х 1 во втором уравнении коэффициент 0. Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х 1 не будут иметь коэффициент 0.
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х 2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х 2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную х n . Для этого решаем элементарное уравнение А*х n = В. В примере, приведенном выше, х 3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной. Например, х 2 – 4 = 1, т.е. х 2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
1 шаг . К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
2 шаг . Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг . Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг . К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг . Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23) , и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x 3 = 1
x 2 = 3
x 1 + x 2 – x 3 = 1, следовательно x 1 + 3 – 1 = 1, x 1 = –1
Ответ 😡 1 = –1, x 2 = 3, x 3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.6875 –1.5625
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х 3 = 0,96 или приблизительно 1.
х 2 = 3 и х 1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор .
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Пример 2 В магазине продаются стереосистемы трех марок: марок A, B и C. Всего в месяц можно продать 100 стереосистем. Первое ограничение : a + b + c <= 100 ( Примечание <= означает меньше или равно.) Торговые марки A, B и C занимают, соответственно, 5, 4 и 4 кубических фута складских площадей, а максимальная доступная складская площадь составляет 480 кубических футов. Второе ограничение : 5a + 4b + 4c <= 480 Бренды A, B и C генерируют комиссионные с продаж в размере 40, 20 и 30 долларов соответственно, и 3200 долларов доступны для оплаты комиссионных с продаж. Третье ограничение : 40a + 20b + 30c <= 3200 Прибыль от продажи каждого бренда составляет 70, 210 и 140 долларов соответственно. Сколько стереосистем каждой марки нужно продать, чтобы максимизировать прибыль? Целевая функция : 70а + 210б + 140с | |||
| |||
Построить СИМПЛЕКСНУЮ ТАБЛИЦУ (таблицу).
| |||
Выбор ПОВОРОТНОЙ КОЛОННЫ.
| |||
| |||
Выбор ПОВОРОТНОГО ЭЛЕМЕНТА.
| |||
ПОВОРОТ вокруг выбранного элемента
| |||
Поворот вокруг выбранного элемента (продолжение…)
| |||
Поворот вокруг выбранного элемента (продолжение)..)
| |||
Мы уже закончили?
| |||
| Левая часть нижнего ряда не содержит отрицательных значений. Итак, мы закончили поворот. Напишем решение. | |||
Решение.
| |||
| Что означает это решение? Максимальная прибыль составляет 21 000 долларов США при продаже 100 систем марки B (без марок A или C). Мы игнорируем переменные резерва, за исключением M, но они полезны для определения другой информации, не описанной в этих разделах. | |||
Линейное программирование: пример симплекс-метода
В наименовании переменных внесены изменения, устанавливающие следующие соответствия:
- x становится X1
- г становится X2
Поскольку независимые условия всех ограничений положительны, никаких дальнейших действий не требуется. В противном случае было бы умножение на «-1» в обеих частях неравенства (заметим, что эта операция также влияет на тип ограничения).
Неравенства становятся уравнениями путем добавления запаса , избытка и искусственных переменных в виде следующей таблицы:
| Тип неравенства | Появляющаяся переменная |
| ≥ | — избыточный + искусственный |
| = | + искусственный |
| ≤ | + люфт |
В этом случае в каждое из ограничений типа ≤ вводится резервная переменная (X3, X4 и X5), для преобразования их в равенства, что приводит к системе линейных уравнений:
| 2·Х1 + Х2 + Х3 = 18 |
| 2·Х1 + 3·Х2 + Х4 = 42 |
| 3·Х1 + Х2 + Х5 = 24 |
Z — 3·X1 — 2·X2 — 0·X3 — 0·X4 — 0·X5 = 0
Исходная таблица симплекс-метода состоит из всех коэффициентов переменных решения исходной задачи и резерва, избыточных и искусственных переменных, добавленных на втором этапе (в столбцах, с P0 в качестве постоянного члена и Pi в качестве коэффициентов остальных переменных Xi) и ограничения (в строках). Столбец Cb содержит коэффициенты переменных, которые находятся в базе.
Первая строка состоит из коэффициентов целевой функции, а последняя строка содержит значение целевой функции и приведенных затрат Zj — Cj.
Последняя строка вычисляется следующим образом: Zj = Σ(Cbi·Pj) для i = 1..m, где если j = 0, то P0 = bi и C0 = 0, иначе Pj = aij. Хотя это первая таблица симплекс-метода и все Cb нулевые, поэтому расчет можно упростить, и к этому моменту Zj = -Cj.
| Таблица I .1-я итерация | |||||||
|---|---|---|---|---|---|---|---|
| 3 | 2 | 0 | 0 | 0 | |||
| Основание | Кб | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 |
| Р3 | 0 | 18 | 2 | 1 | 1 | 0 | 0 |
| Р4 | 0 | 42 | 2 | 3 | 0 | 1 | 0 |
| Р5 | 0 | 24 | 3 | 1 | 0 | 0 | 1 |
| З | 0 | -3 | -2 | 0 | 0 | 0 | |
Если целью является максимизация, когда в последней строке (строке индикатора) нет отрицательного значения между дисконтированными затратами (столбцы P1 ниже), достигается условие остановки.
В этом случае алгоритм достигает конца, так как возможности улучшения нет. Значение Z (столбец P0) является оптимальным решением задачи.
Другой возможный сценарий: все значения отрицательные или нулевые в столбце входных переменных базы. Это указывает на то, что проблема не ограничена и решение всегда будет улучшаться.
В противном случае последовательно выполняются следующие шаги.
Сначала определяется входная базовая переменная. Для этого выбирается столбец, значение которого в строке Z меньше всех отрицательных значений. В этом примере это будет переменная X1 (P1) с коэффициентом -3.
Если есть два или более одинаковых коэффициента, удовлетворяющих вышеуказанному условию (случай равенства), то выбрать базовую переменную.
Столбец входной базовой переменной называется сводным столбцом (выделен зеленым цветом).
После получения входной базовой переменной определяется выходная базовая переменная. Решение основано на простом вычислении: разделить каждый независимый член (столбец P0) между соответствующим значением в сводном столбце, если оба значения строго положительны (больше нуля). Выбирается строка, результатом которой является минимальный балл.
Если какое-либо значение меньше или равно нулю, это частное не будет выполнено.Если все значения опорного столбца удовлетворяют этому условию, то будет достигнуто условие остановки и задача имеет неограниченное решение (см. теорию симплекс-метода).
В этом примере: 18/2 [=9], 42/2 [=21] и 24/3 [=8]
Член опорного столбца, который привел к меньшему положительному частному в предыдущем делении, указывает строку резервной переменной, выходящую из базы. В данном примере это X5 (P5) с коэффициентом 3. Эта строка называется сводной строкой (зеленого цвета).
Если два или более частных удовлетворяют условию выбора (случай равенства), выбирается не эта базовая переменная (где это возможно).
Пересечение сводного столбца и сводной строки отмечает значение сводки , в этом примере 3.
Новые коэффициенты таблицы рассчитываются следующим образом:
Таким образом, сводная точка нормализуется (ее значение становится равным 1), а другие значения опорной колонки отменяются (аналогично методу Гаусса-Жордана).
Расчеты для строки P4 показаны ниже:
| Предыдущий ряд P4 | 42 | 2 | 3 | 0 | 1 | 0 |
| — | — | — | — | — | — | |
| Предыдущее значение в сводном столбце | 2 | 2 | 2 | 2 | 2 | 2 |
| х | х | х | х | х | х | |
| Новое значение в сводной строке | 8 | 1 | 1/3 | 0 | 0 | 1/3 |
| = | = | = | = | = | = | |
| Новый ряд P4 | 26 | 0 | 7/3 | 0 | 1 | -2/3 |
Таблица, соответствующая этой второй итерации:
| Таблица II .2-я итерация | |||||||
|---|---|---|---|---|---|---|---|
| 3 | 2 | 0 | 0 | 0 | |||
| Основание | Кб | Р0 | Р1 | Р2 | Р3 | Р4 | Р5 |
| Р3 | 0 | 2 | 0 | 1/3 | 1 | 0 | -2/3 |
| Р4 | 0 | 26 | 0 | 7/3 | 0 | 1 | -2/3 |
| Р1 | 3 | 8 | 1 | 1/3 | 0 | 0 | 1/3 |
| З | 24 | 0 | -1 | 0 | 0 | 1 | |
- 6.1. Входной базовой переменной является X2 (P2), так как это переменная, соответствующая столбцу, где коэффициент равен -1.
- 6.2. Для расчета выходной базовой переменной постоянные члены столбца P0) делятся на члены нового сводного столбца: 2 / 1/3 [= 6], 26 / 7/3 [= 78/7] и 8 / 1/. 3 [=24]. Поскольку меньшее положительное частное равно 6, выходная базовая переменная равна X3 (P3).
- 6.3.Новый стержень равен 1/3.
- 7. Обновление значений таблицы снова получается:
Таблица III. 3-я итерация 3 2 0 0 0 Основание Кб Р0 Р1 Р2 Р3 Р4 Р5 Р2 2 6 0 1 3 0 -2 Р4 0 12 0 0 -7 1 4 Р1 3 6 1 0 -1 0 1 З 30 0 0 3 0 -1
- 6.1. Входной базовой переменной является X5 (P5), так как это переменная, соответствующая столбцу, где коэффициент равен -1.
- 6.2. Чтобы вычислить выходную базовую переменную, постоянные члены (P0) делятся на члены нового сводного столбца: 6/(-2) [=-3] , 12/4 [=3] и 6/1 [= 6]. В этой итерации выходная базовая переменная равна X4 (P4).
- 6.3. Новый стержень 4.
- 7. Обновление значений таблицы снова получается:
Таблица IV. 4-я итерация 3 2 0 0 0 Основание Кб Р0 Р1 Р2 Р3 Р4 Р5 Р2 2 12 0 1 -1/2 1/2 0 Р5 0 3 0 0 -7/4 1/4 1 Р1 3 3 1 0 3/4 -1/4 0 З 33 0 0 5/4 1/4 0
Отмечено, что в последней строке все коэффициенты положительные, значит, условие остановки выполнено.
Оптимальное решение задается значением Z в столбце постоянных условий (столбец P0), в примере: 33. В том же столбце показана точка, в которой оно достигает, наблюдая за соответствующими строками входных переменных решения. : X1 = 3 и X2 = 12.
Отмена изменения имени дает x = 3 и y = 12.
Симплексный метод – обзор
Описанный выше (базовый) симплексный метод для двух факторов может быть обобщен на случай f с факторами.Хотя двумерный симплекс можно визуализировать геометрически, это уже невозможно для трехмерных и более мерных симплексов. Тем не менее, принцип остается точно таким же. При рассмотрении f факторов симплекс содержит f + 1 вершин или точек. После определения вершины, подлежащей отбраковке, координаты новой вершины получаются следующим образом. Координаты оставшихся f вершин суммируются для каждого фактора и делятся на f /2.Из полученных значений вычитаются координаты отвергнутой точки, что дает координаты новой вершины. Вышеприведенное является обобщением уравнений (4–5).
в векторной записи, при изучении F Факторы, F + 1 точки начального симплекса, B , N 1 , N 2 , …, N F -1 , и W можно представить векторами B , N 1 , N 2 , …, N F -1 и w , то есть b = [ x 1 b 2 b x 99754 x x FB ], N 1 = [ x 9095 9099 1n 1 995 9 , 2 N 9 N 1 9995, …, x FN 1 ], N N N 2 = [ x 1n 2 909 95 , x 2n 2 9 , …, 9995 FN 2 5 2 ], …, N F — 1 = [ 1 N F -1 -1 , 2 N 9 N F -1 9995, …, 9995 FN 9094 F -1 ], а Вт = [ x 1 w , x 2 w , …, x fw 9]. B и W — лучший и худший результаты соответственно. N 1 , N 2 , …, N f −1 не являются ни лучшими, ни худшими результатами. Затем центроид P 1 гиперпространства, оставшегося после удаления вершины, дающей наихудший ответ W , и представленный в виде вектора p 1 , определяется уравнением (6), и координаты новой вершины R 1 , представленные вектором r 1 , задаются уравнением (5).Кроме того, действуют те же правила, что приведены выше.
(6)p1=(n1+n2+…+nf−1+b)f=[(x1n1+x1n2+…+x1nf−1+x1b),(x2n1+x2n2+…+x2nf−1+x2b),…, (xfn1+xfn2+…+xfnf−1+xfb)]f
Линейное программирование | Brilliant Math & Science Wiki
Симплекс-алгоритм — это метод получения оптимального решения линейной системы ограничений при заданной линейной целевой функции. Он работает, начиная с основных вершин допустимой области, а затем итеративно перемещаясь к соседним вершинам, каждый раз улучшая решение, пока не будет найдено оптимальное решение.
Симплексный алгоритм состоит из множества шагов и правил, поэтому полезно понять логику этих шагов и правил на простом примере, прежде чем переходить к формальному алгоритму.
Учитывая систему ограничений
{2x+3y≤903x+2y≤120x≥0y≥0,\begin{случаи} \begin{выровнено} 2x+3y &\le 90\\ 3x+2y &\le 120\\ х & \ge 0 \\ у&\ге 0, \end{выровнено} \end{case}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧2x+3y3x+2yxy≤90≤120≥0≥0,
максимизировать целевую функцию
f(x,y)=7x+5y.f(x,y)=7x+5y.f(x,y)=7x+5y.
Симплекс-алгоритм начинается с преобразования ограничений и целевых функций в систему уравнений. Это делается путем введения новых переменных, называемых резервными переменными . Переменные резерва представляют собой положительную разницу, или резерва , между левой частью неравенства и правой частью этого неравенства.
Неравенство
2x+3y≤902x+3y \le 902x+3y≤90
становится
2x+3y+s1=90.2x+3y+s_1=90,2x+3y+s1=90.
Аналогично, неравенство
3x+2y≤1203x+2y \le 1203x+2y≤120
становится
3x+2y+s2=120,3x+2y+s_2 = 120,3x+2y+s2=120.
В дополнение к резервным переменным введена переменная zzz для представления значения целевой функции. Это дает уравнение
z-7x-5y=0.z-7x-5y=0.z-7x-5y=0.
Эти уравнения дают систему уравнений
{z-7x-5y=0(0)2x+3y+s1=90(1)3x+2y+s2=120.(2)\begin{случаи} \begin{массив}{cccccccccccc} z & — & 7x & — & 5y & & & & & & = & 0 && (0) \\ & & 2x & + & 3y & + & s_1 & & & = & 90 && (1) \\ & & 3x & + & 2y & & & + & s_2 & = & 120. && (2) \конец{массив} \end{case}⎩⎨⎧z−7x2x3x−++5y3y2y+s1+s2===0
- .(0)(1)(2)
В расширенной матричной форме это
. [1−7−50000231001120].(0)(1)(2)\влево[\begin{массив}{ccccc|c}
1 и -7 и -5 и 0 и 0 и 0 \\
0 и 2 и 3 и 1 и 0 и 90 \\
0 и 3 и 2 и 0 и 1 и 120
\end{массив}\right]. \qquad
\begin{array}{c} (0) \\ (1) \\ (2) \end{array}⎣⎡100−723−5320100010⎦⎤.(0) (1)(2)
Подразумевается, что все переменные в этой системе (включая s1,s_1,s1, s2,s_2,s2 и zzz) больше или равны 0. Переменные s1s_1s1 и s2s_2s2 имеют нулевые коэффициенты в строке ( 0)(0)(0) и называются базовыми переменными .Переменные xxx и yyy имеют ненулевые коэффициенты в строке (0)(0)(0) и называются неосновными переменными . В любой момент этого процесса базовое решение задается установкой неосновных переменных в 0. В настоящее время базовое решение
.x=0,y=0,s1=90,s2=120,z=0.x=0, \quad y=0, \quad s_1=90, \quad s_2=120, \quad z=0.x =0,y=0,s1=90,s2=120,z=0.
Подумайте, как повлияет увеличение значений неосновных переменных на значение z.з.з. Увеличение либо xxx, либо yyy приведет к увеличению zzz, поскольку xxx и yyy имеют отрицательные коэффициенты в строке (0).(0).(0). Таким образом, это не оптимальное решение.
Итерации симплексного алгоритма включают обмен базовыми и небазовыми переменными с помощью операций над строками матриц. На каждом этапе процесса небазовая переменная в строке (0)(0)(0) удаляется, в результате чего другая базовая переменная занимает ее место в качестве небазовой переменной. Это называется стержнем .
Предположим, что xxx нужно исключить из строки (0).(0).(0). Это можно сделать с помощью строки (1)(1)(1) или строки (2).(2).(2).
Случай 1. Исключение xxx в строке (0)(0)(0) со строкой (1)(1)(1),
[102127203150231001120].(0)12(1)(2)\left[\begin{array}{ccccc|c}
1 & 0 & \frac{21}{2} & \frac{7}{2} & 0 & 315 \\
0 и 2 и 3 и 1 и 0 и 90 \\
0 и 3 и 2 и 0 и 1 и 120
\end{массив}\right]. \qquad
\begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2) \end{array}⎣⎡1000232213227 10001315⎦⎤.(0)21(1)(2)
Во время этого разворота переменная xxx вошла в в качестве базовой переменной, а переменная s1s_1s1 оставила , чтобы стать небазовой переменной. Теперь исключите xxx в строке (2)(2)(2):
[10212720315023109000−52−321−15].(0)12(1)(2)12\left[\begin{array}{ccccc|c} 1 & 0 & \frac{21}{2} & \frac{7}{2} & 0 & 315 \\ 0 и 2 и 3 и 1 и 0 и 90 \\ 0 & 0 & -\frac{5}{2} & -\frac{3}{2} & 1 & -15 \end{массив}\right].\qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \end{array} ⎣⎡1000202213−25271−2300131590−15⎦⎤.(0)21(1)(2)21
Это дает основное решение
x=45,y=0,s1=0,s2=-15,z=315.x=45, \quad y=0, \quad s_1=0, \quad s_2=-15, \quad z=315 .x=45,y=0,s1=0,s2=-15,z=315.
Это решение невозможно, так как оно приводит к отрицательному значению одной из переменных.
Случай 2. Исключение xxx в строке (0)(0)(0) со строкой (2)(2)(2),
[10−130732800231001120].(0)12(1)(2)\влево[\begin{массив}{ccccc|c}
1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\
0 и 2 и 3 и 1 и 0 и 90 \\
0 и 3 и 2 и 0 и 1 и 120
\end{массив}\right]. \qquad
\begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2) \end{array}⎣⎡100023−3132 0103701280⎦⎤.(0)21(1)(2)
Во время этого разворота переменная xxx вошла в в качестве базовой переменной, а переменная s2s_2s2 оставила , чтобы стать небазовой переменной.Теперь исключите xxx в строке (1)(1)(1):
.[10−1307328000531−231003201120].(0)12(1)12(2)\left[\begin{array}{ccccc|c} 1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 и 3 и 2 и 0 и 1 и 120 \end{массив}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array} ⎣⎡100003−3135201037−32128010120⎦⎤.(0)21(1)21(2)
Это дает основное решение
х=40,у=0,s1=10,s2=0,z=280.x=40, \quad y=0, \quad s_1=10, \quad s_2=0, \quad z=280.x=40,y=0,s1=10,s2=0,z=280.
Такое решение возможно, но не оптимально, так как в строке (0).(0).(0) стоит отрицательный коэффициент. Это означает, что zzz можно увеличить еще больше, увеличив y.y.y. Для поиска оптимального решения потребуется еще один поворот.
Достаточно много работы, чтобы выполнить поворот только для того, чтобы обнаружить, что это дает неосуществимое решение. К счастью, можно предвидеть, какой поворот приведет к допустимому решению, наблюдая за отношением элемента в правой части расширенной матрицы к коэффициенту входной переменной.Рассмотрим yyy как входную переменную и рассчитаем эти отношения:
[10−1307328000531−231003201120].(0)12(1)12(2)\left[\begin{array}{ccccc|c} 1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\ 0 & 0 & {\ color {# D61F06} \ frac {5} {3}} & 1 & — \ frac {2} {3} & {\ color {# D61F06} 10} \\ 0 & 3 & {\color{#3D99F6}2} & 0 & 1 & {\color{#3D99F6}120} \end{массив}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array} ⎣⎡100003−3135201037−32128010120⎦⎤.(0)21(1)21(2)
Для ввода переменной y,y,y это соотношение равно 10÷53=610\div \frac{5}{3}=610÷35=6 для строки (1)(1)(1) и 1202=60 \frac{120}{2}=602120=60 для строки (2).(2).(2). Выбор строки, в которой минимизирует этого отношения, гарантирует, что поворот приведет к допустимому решению. Таким образом, строка (1)(1)(1) должна быть выбрана в качестве основной строки.
Удаление yyy в строке (0)(0)(0) со строкой (1)(1)(1),
[1001511528200531−231003201120].(0)12(1)12(2)\left[\begin{array}{ccccc|c} 1 & 0 & 0 & \frac{1}{5} & \frac{11}{5} & 282 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 и 3 и 2 и 0 и 1 и 120 \end{массив}\right].\qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array} ⎣⎡10000303525110511−32128210120⎦⎤.(0)21(1)21(2)
Затем исключить yyy в строке (2)(2)(2),
[1001511528200531−2310030−6595108].(0)12(1)12(2)12\left[\begin{array}{ccccc|c} 1 & 0 & 0 & \frac{1}{5} & \frac{11}{5} & 282 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 & 3 & 0 & -\frac{6}{5} & \frac{9}{5} & 108 \end{массив}\right].\qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2)\vphantom{\frac {1}{2}} \end{массив}⎣⎡1000030350511−56511−325928210108⎦⎤.(0)21( 1)21(2)21
Это дает основное решение
x=36,y=6,s1=0,s2=0,z=282.x=36, \quad y=6, \quad s_1=0, \quad s_2=0, \quad z=282.x =36,y=6,s1=0,s2=0,z=282.
Это решение должно быть оптимальным, поскольку любое увеличение неосновных переменных s1s_1s1 и s2s_2s2 вызовет уменьшение z.з.з. Таким образом, максимальное значение целевой функции равно
.f(36,6)=282. □f(36,6)=282.\ _\squareref(36,6)=282. □
Симплекс-алгоритм для задач минимизации работает путем преобразования задачи в задачу максимизации. Эта концепция, состоящая в том, что каждая задача максимизации имеет соответствующую задачу минимизации, формализована с помощью принципа двойственности фон Неймана.
Учитывая систему ограничений
{4x+3y+5z≥65x+3y+2z≥382x+3y+4z≥52x,y,z≥0,\begin{случаи}\begin{выровнены} 4x+3y+5z &\ge 65\\ х+3у+2г &\ге 38\\ 2x+3y+4z &\ge 52\\ х, у, z &\ge 0, \end{выровнено}\end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧4x+3y+5zx+3y+2z2x+3y+4zx,y,z≥65≥38≥52≥0,
свернуть функцию
f(x,y,z)=12x+3y+10z.f(x,y,z)=12x+3y+10z.f(x,y,z)=12x+3y+10z.
Эту задачу можно было бы представить в форме, показанной в приведенных выше примерах максимизации, но возникла бы проблема с поиском первого базового решения: установка x,x,x, y,y,y и z,z,z, переменные в 000 дали бы недопустимое решение с переменными резерва, принимающими отрицательные значения. Симплекс-алгоритм должен начинаться с допустимого решения, поэтому это не сработает. Метод Big-M предлагает обходной путь для этой проблемы, но есть гораздо более простой метод для решения этой проблемы.
«Дуал» этой задачи можно записать, переставив коэффициенты. Поместите коэффициенты ограничений в расширенную матрицу. Поместите коэффициенты целевой функции в нижнюю строку с 0 в правой части:
[435651323823452123100].\left[\begin{array}{ccc|c} \color{#20A900}4 & \color{#D61F06}3 & \color{#3D99F6}5 & \color{#EC7300}65 \\ \color{#20A900}1 & \color{#D61F06}3 & \color{#3D99F6}2 & \color{#EC7300}38 \\ \color{#20A900}2 & \color{#D61F06}3 & \color{#3D99F6}4 & \color{#EC7300}52 \\ \hline \color{#20A900}12 & \color{#D61F06}3 & \color{#3D99F6}10 & \color{#EC7300}0 \end{массив}\right].⎣⎢⎢⎡412123333524106538520⎦⎥⎥⎤.
Транспонировать элементы матрицы:
[412123333524106538520].\left[\begin{array}{ccc|c} \color{#20A900}4 & \color{#20A900}1 & \color{#20A900}2 & \color{#20A900}12 \\ \color{#D61F06}3 & \color{#D61F06}3 & \color{#D61F06}3 & \color{#D61F06}3 \\ \color{#3D99F6}5 & \color{#3D99F6}2 & \color{#3D99F6}4 & \color{#3D99F6}10 \\ \hline \color{#EC7300}65 & \color{#EC7300}38 & \color{#EC7300}52 & \color{#EC7300}0 \end{массив}\right].⎣⎢⎢⎡435651323823452123100⎦⎥⎥⎤.
Примечание: Заманчиво разделить 3 во второй строке этой матрицы, но это нарушит симметрию, необходимую для возврата к исходной задаче.
Это дает новую систему ограничений и целевую функцию, которая должна быть максимизирована: Учитывая систему ограничений
{4u+v+2w≤123u+3v+3w≤32u+3v+4w≤52u,v,w≥0,\begin{case}\begin{выровнено} 4u+v+2w &\le 12\\ 3u+3v+3w &\le 3\\ 2u+3v+4w &\le 52\\ u,v,w &\ge 0, \end{выровнено}\end{cases}⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧4u+v+2w3u+3v+3w2u+3v+4wu,v,w≤12≤3≤52≥0,
максимизировать функцию
г(и,в,ж)=65и+38в+52ж.g(u,v,w)=65u+38v+52w.g(u,v,w)=65u+38v+52w.
Теперь можно применить симплекс-алгоритм для поиска оптимального решения
[1−65−38−52000004121001203330103023400152].(0)(1)(2)(3)\left[\begin{array}{ccccccc|c} 1 и -65 и -38 и -52 и 0 и 0 и 0 и 0 \\ 0 и 4 и 1 и 2 и 1 и 0 и 0 и 12 \\ 0 и 3 и 3 и 3 и 0 и 1 и 0 и 3 \\ 0 и 2 и 3 и 4 и 0 и 0 и 1 и 52 \end{массив}\right]. \qquad \begin{массив}{c} (0) \\ (1) \\ (2) \\ (3) \end{массив}⎣⎢⎢⎡1000−65432−38133−5223401000010 0001012352⎦⎥⎥⎤.(0)(1)(2)(3)
Введите uuu со строкой (2)(2)(2):
[102713065306500−3−21−40801110130100120−2150].(0)12(1)(2)12(3)\left[\begin{array}{ccccccc|c} 1 & 0 & 27 & 13 & 0 & \frac{65}{3} & 0 & 65 \\ 0 и 0 и -3 и -2 и 1 и -4 и 0 и 8 \\ 0 & 1 & 1 & 1 & 0 & \frac{1}{3} & 0 & 1 \\ 0 и 0 и 1 и 2 и 0 и -2 и 1 и 50 \end{массив}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \\ (3) \end{массив}⎣⎢⎢⎡1000001027−31113−2120100365−431−20001658150⎦⎥⎥⎤.(0)21(1)(2)21(3)
Все коэффициенты в строке (0)(0)(0) положительны, так что это оптимальное решение. Максимальное значение в правом верхнем углу матрицы, 65,65,65, совпадает с минимальным значением исходной задачи. Однако переменные u, u, u, v, v, v и www не совпадают с переменными в исходной задаче. К счастью, значения переменных, которые минимизируют исходную задачу, соответствуют коэффициентам резервных переменных в строке (0).(0).(0).
[102713065306500−3−21−40801110130100120−2150].(0)12(1)(2)12(3)\влево[\begin{массив}{ccccccc|c} 1 & 0 & 27 & 13 & \color{#D61F06}0 & \color{#D61F06}\frac{65}{3} & \color{#D61F06}0 & 65 \\ 0 и 0 и -3 и -2 и 1 и -4 и 0 и 8 \\ 0 & 1 & 1 & 1 & 0 & \frac{1}{3} & 0 & 1 \\ 0 и 0 и 1 и 2 и 0 и -2 и 1 и 50 \end{массив}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \\ (3) \end{массив}⎣⎢⎢⎡1000001027−31113−2120100365−431−20001658150⎦⎥⎥⎤.(0)21(1)(2)21(3)
Таким образом, значения исходной задачи, минимизирующие целевую функцию, равны
х=0,у=653,г=0. □x=0, \quad y=\frac{65}{3}, \quad z=0.\ _\squarex=0,y=365,z=0. □
пример стандартного симплексного метода
|
|
|
| ||
| См. шаги 3,4,5 из . СИМПЛЕКСНЫЙ МЕТОД как вы обращаетесь с ИНДИКАТОРАМИ, СООТНОШЕНИЯ и ПОВОРОТКИ. |
|
|
|
|
|
|   |
| Все индикаторы {0, 0, | 49 16 | , 0, | 1 16 | и | 3 8 | } теперь равны нулю или больше («13» НЕ показатель). |
| Таким образом, как и в шаге 8 СИМПЛЕКСНОГО МЕТОДА, последняя таблица является ОКОНЧАТЕЛЬНОЙ ТАБЛИЦЕЙ. | ||||||
| Выполняются рядовые операции СИМПЛЕКСНОГО МЕТОДА. |
|
|
Что такое симплекс-метод?
Что означает симплекс-метод?
Симплекс-метод в математической оптимизации является хорошо известным алгоритмом, используемым для линейного программирования.Согласно журналу Computing in Science & Engineering, этот метод считается одним из 10 лучших алгоритмов, созданных в двадцатом веке.Симплекс-метод представляет собой организованную стратегию оценки вершин допустимой области. Это помогает определить оптимальное значение целевой функции.
Джордж Данциг разработал симплексный метод в 1946 году.
Этот метод также известен как симплексный алгоритм.
Techopedia объясняет симплекс-метод
Симплекс-метод используется для устранения проблем в линейном программировании.Он последовательно проверяет соседние вершины допустимого набора, чтобы убедиться, что в каждой новой вершине целевая функция увеличивается или не изменяется. В общем, симплекс-метод является чрезвычайно мощным, который обычно требует максимум от 2 до 3 млн итераций (здесь m обозначает диапазон ограничений равенства), и он сходится за ожидаемое полиномиальное время для конкретных распределений случайных входных данных.Симплекс-метод использует систематическую стратегию для создания и проверки возможных вершинных решений линейной программы.На каждой итерации он выбирает переменную, которая может внести наибольшие изменения в сторону минимального решения. Затем эта переменная заменяет одну из своих копеременных, которая наиболее резко ее ограничивает, тем самым сдвигая симплекс-метод к другой части набора решений и к окончательному решению.
Кроме того, симплекс-метод позволяет оценить, действительно ли не существует решения. Можно заметить, что алгоритм является жадным, поскольку он выбирает наилучший вариант на каждой итерации, не требуя информации от предыдущих или предстоящих итераций.
Иногда основную структуру данных, применяемую симплексным методом, называют словарем. Словари включают иллюстрацию набора уравнений, которые точно настроены на существующую основу. Словари можно использовать для интуитивного понимания того, почему все переменные входят в базис и покидают его.
Симплексная оптимизация числовых и категориальных входных данных на ранних стадиях разработки биопроцессов: тематические исследования в HT-хроматографии
Исследования развития биопроцессов часто включают исследование числовых и категориальных входных данных с помощью методов планирования экспериментов (DoE).Привлекательной альтернативой является развертывание совместимого с сеткой варианта Simplex, который, как было показано, быстро и последовательно дает оптимальные результаты. В этой работе метод сочетается с фиктивными переменными и применяется в трех тематических исследованиях, в которых пространства состоят как из категориальных, так и из числовых входных данных, что невозможно разрешить с помощью традиционных симплексных методов. В первом исследовании используются данные in silico и излагается методология фиктивных переменных. В последних двух используются экспериментальные данные хроматографических исследований, проведенных с использованием фильтровальных пластин и миниатюрных колонок с высокой пропускной способностью (HT).Растворенным веществом, представляющим интерес в первом случае, было моноклональное антитело, тогда как во втором имелось дело с разделением бинарной системы модельных белков. Реализованный подход предотвратил застревание симплекс-метода в локальных оптимумах из-за произвольной обработки категориальных входных данных и позволил одновременно оптимизировать числовые и категориальные, многоуровневые и/или дихотомические входные данные.

 На первом этапе исходную систему преобразуют к треугольному виду.
На первом этапе исходную систему преобразуют к треугольному виду. Например, к такому виду:
Например, к такому виду: x 1 = 1.00, x 2 = 1.00, x 3 = 1.00
x 1 = 1.00, x 2 = 1.00, x 3 = 1.00
 Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья — уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.
Для этого элементы первой строки умножаем на -2 и прибавляем их к третьему ряду. Теперь первая и вторая строки переписываются в изначальном виде, а третья — уже с изменениями. Как видно по результату, мы получили первую единицу в начале главной диагонали матрицы и остальные нули. Еще несколько действий, и система уравнений методом Гаусса будет достоверно решена.