С логарифмами: Действия с логарифмами. Постигаем азы!

Действия с логарифмами. Постигаем азы!

        На прошлом занятии мы познакомились с понятием логарифма и порешали несколько несложных примеров на определение и смысл логарифма. Для начального знакомства.)

        Теперь настал черёд более тесного знакомства с логарифмами и, соответственно, решения более серьёзных примеров. Начнём мы с ограничений в логарифмах.

 

Ограничения в логарифмах.

        Как и у любого математического понятия, у логарифма тоже есть свои свойства и фишки. Именно о них мы сейчас и будем разговаривать. И в первую очередь это ограничения в логарифмах. До сих пор мы с вами знали лишь два жёстких ограничения в математике:

        — нельзя делить на ноль;

        — нельзя извлекать корень чётной степени из отрицательного числа.

       

        С этого момента к этим двум добавляются дополнительные ограничения в логарифмах.

        Для начала запишем определение логарифма в самом общем виде. Через буквы.

        log_ab = c

        Напоминаю, что это равенство означает всего лишь решение показательного уравнения

        a^c = b.

        И всё.

        А теперь подумаем, любым ли числом может быть a? Пусть, к примеру, a = 1. Тогда получается забавная штука: единица в любой степени равна единице… И каким бы ни было число c, числа a и b останутся единичками. Та же самая история и с нулём. Не подходят эти числа в качестве основания…

        Отрицательные числа — очень вредные и капризные. В одну степень их можно возводить, а в другую — нельзя. Вот и поступили математики с ними, как со всеми капризными — вовсе исключили из рассмотрения.

        В результате у нас получилось такое ограничение на основание:

        a > 0,    a ≠ 1.

        А каким может быть число b? Давайте подумаем: если заведомо положительное основание a возвести любую степень c, то какое число мы в итоге получим? Верно, положительное число и получим!

        Отсюда ещё одно ограничение на аргумент логарифма:

        b > 0.

        Вот и все ограничения. Число c (значение логарифма) может быть совершенно любым.

        Конечно, при решении безобидных числовых примеров на логарифмы эти ограничения практически никак не сказываются. Зато когда столкнётесь с логарифмическими уравнениями и неравенствами, вы про эти ограничения ещё не раз вспомните! А если не вспомните, то я вам напомню. И буду напоминать при каждом удобном случае.) Ибо эти ограничения очень (!) важны при решении уравнений и неравенств. Про ОДЗ помните? Вот, то-то и оно…

 

Свойства логарифмов.

        Итак, с ограничениями на логарифмы разобрались. Пора переходить на следующий уровень и знакомиться со свойствами логарифмов. Вот они:

        

        Здесь всюду b>0 и c>0, а также a>0, a≠1.

        Вот такой вот джентльменский набор. Ни много ни мало.) Теперь кратенько пробежимся по каждому из этих свойств. Чтобы ясно было, откуда ноги растут, как говорится.)

        Начнём с первого свойства:

        

        Обычно это свойство именуют особо — основным логарифмическим тождеством. Откуда же оно берётся? Запишем снова уже до боли знакомое нам равенство:

        log_ab = c

        Из самого определения логарифма мы с вами знаем, что, если число а (основание) возвести в степень c (показатель), то получим число b:

        a^c = b

        А теперь подумаем, чему же равно у нас число c? Да вот же оно:

        с = log_ab

        Подставим это выражение в предыдущее равенство и получим как раз то, что нам и требуется:

        

        «И зачем нам такая странная перетасовка?» — спросите вы. А затем, что многоэтажное выражение превращается в элементарное b! Полезная формула.) Это единственная формула, где логарифм стоит в показателе степени.

        Следующая группа формул (2-3):

        

        Думаю, тут комментарии излишни. Всё прямо из определения логарифма следует.) И даже примеры разбирались. В предыдущем материале. Кому всё-таки непонятно, применяем старый добрый способ — словесную расшифровку. Проверено, помогает.)

 

        Переходим к следующей группе формул (4-5):

        

        Коротко эти формулы называются логарифм произведения и логарифм частного (дроби).

        А вот с их доказательствами вопрос похитрее будет.) Эти два свойства проистекают из обычного умножения и деления степеней с одинаковым основанием. Как именно? Мы с седьмого класса помним, что при перемножении двух степеней с одинаковым основанием показатели степеней складываются, а при делении — вычитаются:

           

        Для доказательства, например, четвёртой формулы (логарифм произведения) придётся ввести вспомогательные обозначения:

        m = log_a

b  

        и 

        n = log_ac.

        До конца доказывать эти две формулы я не буду. Как продолжить доказательство? Подставьте выражения для m и n в формулу умножения степеней и воспользуйтесь основным логарифмическим тождеством (формула №1). Попробуйте! Очень полезно.)

        Кстати, прошу обратить внимание: данные формулы справедливы только при одинаковых основаниях! Если основания разные, то, скорее всего, преобразования более мудрёные…

        Идём дальше. Следующая группа формул (6-7) — это формулы, позволяющие избавляться от степеней в аргументе или в основании логарифма:

        

        Смысл их тоже прост. Если аргумент логарифма возводится в степень, то показатель степени n можно вынести наружу и приписать перед логарифмом. То же самое происходит и тогда, когда в степень возводится основание логарифма, только показатель степени переворачивается. Эти две полезные формулы избавляют нас от степеней в аргументе/основании. Если это мешает, конечно. Это понятно.)

        Осталась последняя формула №8:

        

        Это — так называемая

формула перехода к новому основанию. Самая трудная для запоминания формула. Поэтому народ частенько и ленится её запоминать… А вы запомните. Не сочтите за труд.) Когда она применяется? А когда основания логарифмов — разные.) Скажем, в примере куча логарифмов по основанию 3 и затесался один логарифм по основанию 7. Его и менять надо. На тройку.) Мы с этой формулой крепко подружимся. И примеры тоже порешаем.) В соответствующем уроке.

        Вот такой вот перечень формул и свойств. Их вполне достаточно, чтобы уверенно решать примеры на логарифмы любого уровня сложности. Эти формулы нужно не просто помнить, но и уметь применять. Причём в обоих направлениях — как слева направо, так и справа налево.

        Ещё не помешало бы знать, что такое десятичный логарифм и что такое натуральный логарифм.

        Десятичный логарифм — это просто логарифм по основанию 10:

        log₁₀b = lg b

        В написании десятичного логарифма всего лишь пропадает буковка «о».

        Натуральный логарифм (хотя чего уж в нём такого натурального) — это логарифм по основанию e. Иррациональному числу «e».

        e = 2,71828182845…

        Что это за загадочное число, узнаете и поймёте, когда поступите в институт. В курсе матанализа.) В школьной математике это число практически не встречается, зато в высшей — сплошь и рядом.)

        Обозначается натуральный логарифм вот так:

        log_eb = ln b

        Логарифмы по этим основаниям хотя и имеют своё особое написание, но ни по определению, ни по свойствам ничем не отличаются от обычных логарифмов, скажем, по основанию два. Или три. И решаются точно так же.

        Итак, будем считать, что необходимая теоретическая база подготовлена. Переходим к практике.)

       

Начальный уровень. Немного формул. Немного дробей. Немного степеней.

        На этом уровне мы:

        — впрямую используем определение логарифма,

        — впрямую используем самые простые свойства логарифмов.

        Мыслей здесь особых не нужно. Главное — память и внимательность. Итак, читаем, смотрим, вникаем.

        Пример 1

        Вычислить:

        

        Решение примера вытекает непосредственно из определения и смысла логарифма. В какой степени 1/3 даёт 1/27? В кубе, конечно. То есть, в третьей степени.

        Ответ: 3.

 

        Следующий пример:

        Пример 2

        

        Всё то же самое, только дроби десятичные. Ну и что? Опять напрямую пользуемся определением логарифма: в какой степени 0,3 даст 0,09? В квадрате, разумеется! Или во второй степени. )

        Ответ: 2.

 

        И ещё один примерчик на дроби:

        Пример 3

        

        А вот тут некоторые могут и зависнуть. Почему? Потому что связь между 0,5 и 1/128 визуально просматривается плохо. Что делать?

        Что-что… Да к обычным дробям перейти! Вот вам и первый практический совет:

        Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.

         Этот приём, между прочим, работает не только в логарифмах, но и в других смежных темах — в показательных выражениях, в корнях.

        В нашем примере 0,5 = 5/10 = 1/2. Ну и как? Связь между 1/2 и 1/128 легче углядеть? Естественно! 1/128 — это 1/2 в седьмой степени.

        Ответ: 7

        Что? Забыли, что 128 — это 2 в седьмой степени? Срочно повторить степени!

 

        Следующий пример:

        Пример 4

        

        Прямое применение формулы разности логарифмов:

        

        И как вам? Оба логарифма по отдельности ровно не считаются, зато через формулу разности — отлично!

        Ответ: 1

       

        Ещё пример:

        Пример 5

        

        А вот здесь складывать по формуле нельзя: основания разные — тройка и двойка. А формула — штука жёсткая. Раз требуются одинаковые основания, значит, так и надо.

        Но тут ничего хитрого нет: оба логарифма считаются ровно.

        Ответ: 10.                     

        Не каждый, правда, догадается, что 243 — это 3 в пятой степени, а 32 — это 2 в пятой… Но тут дело уже не в логарифмах, дело в степенях!

        Вот вам и второй практический совет.

        Степени популярных чисел надо знать. В лицо!

        Конечно, возвести двойку в седьмую степень или тройку в пятую может каждый. Не в уме, так хотя бы на черновике. Но это умение слабо помогает в работе с логарифмами, да. А вот сообразить, какое число и в какой степени скрывается за числом 128 или 243 — это уже совсем другое дело. Почувствуйте разницу, что называется!

        Поскольку умение распознавать степени в лицо пригодится не только на этом уровне, но и на следующих, вот вам небольшое задание:

        Определить, какими степенями и каких чисел являются числа:

        4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.

        Ответы (вразброс, естественно):

        27²; 2¹⁰; 3⁶; 7²; 2⁶; 9²; 3⁴; 4³; 10²; 2⁵; 3⁵; 7³; 16²; 2⁷; 5³; 2⁸; 6²; 3³; 2⁹; 2⁴; 2²; 4⁵; 25²; 4⁴; 6³; 8²; 9³.

        Да-да! Не удивляйтесь, что ответов побольше, чем заданий. Например, 2⁸, 4⁴ и 16² — это всё 256.

        А теперь я настоятельно рекомендую взять любой учебник по школьной математике и порешать оттуда простейшие примеры на логарифмы. Порешали? Хоть что-то получилось? Тогда будем считать, что начальный уровень вы прошли. Переходим на следующий уровень.

 

Почти все формулы. Почти все степени. Поиск «братьев по степени».

        На этом уровне применяем почти все формулы работы с логарифмами. Кроме последней формулы перехода к новому основанию. А также закрепляем наши навыки работы со степенями.

        Поехали расширять наши возможности!

        Пример 6

        

        Вот тут прямое применение определения логарифма не годится: из четвёрки 128 простым возведением в степень никак не сделаешь. И формулы логарифмов непонятно как употреблять… Не беспокойтесь, сейчас всё получится.)  При маленьком условии, что вы узнали в лицо число 128. Да! Это 2 в седьмой степени! Так и запишем:

        log₄128 = log₄2⁷

        Вот и одна из формул (третья снизу) приходит на помощь. Та, где показатель степени ставится множителем перед логарифмом:

        log_axⁿ = n·log_ax

        Вот и выносим семёрку за наш логарифм. Пишем:

        log₄2⁷ = 7log₄2

        Что дальше? Дальше осталось вспомнить, что 4 = 2². Верно!

        7log₄2 = 7log₂²2

        Вот и ещё одна формулка в дело просится!) Вторая снизу, где в степень возводится основание логарифма. Только в этом случае при вынесении показателя наружу его надо перевернуть: 1/n.

        

        Записываем:

        

        Ответ: 3,5

        Вот так вот! А если бы мы не узнали в числе 128 степень двойки, то так и застряли бы на этом, в общем-то несложном примере…

                                           

        А теперь мы вплотную подошли к одному весьма и весьма полезному приёму в работе с логарифмическими и показательными выражениями. Приём этот называется «поиск братьев». Братьев по степени. И по разуму тоже.) Суть этого полезного приёма заключается в тщательном осмотре примера и распознавании одного и того же числа в разных степенях.

        Этот приём (шифровка одного и того же числа в разных степенях) — очень популярный приём в логарифмах! Да и в показательных уравнениях и неравенствах тоже. Например, числа 27 и 243 — родные братья! Да, 243 из 27 прямым возведением в натуральную степень никак не получить, но зато они — родня по тройке! Так как 27 = 3³, а 243 = 3⁵. В разобранном только что примере родственниками оказались 4 и 128. По числу 2. В общем, идея понятна, да?

        И зачем всё это нужно — распознавать степени и родственников? А затем, что примеры от этого проще становятся! И формулы свойств логарифмов сразу высвечиваются.) Особенно важно получить в примере одинаковые основания у логарифмов, ибо чем больше одинаковых значков в примере и меньше разных, тем лучше. И не нужно здесь применять формулу перехода к новому основанию: зачем же из пушки по воробьям палить.?)

 

        Следующий пример на братьев (или сестёр):

        Пример 7

        Вычислить:

        

        В примере стоит сумма логарифмов, но основания логарифмов разные — тройка и девятка. Стало быть, применять напролом формулу суммы логарифмов нельзя. Но! Первый логарифм уже считается ровно, получится просто тройка:

        log₃27 = log₃3³ = 3

        А со вторым логарифмом что? Из девятки 27 возведением в целую степень не получишь! Но зато 9 и 27 — родня! По тройке.) Самое время вспомнить, что:

        9 = 3²

        Что ж, поработаем отдельно со вторым логарифмом. Перейдём в основании от девятки к тройке. Поможет нам такое преобразование или нет — неизвестно. Но что-то делать всё-таки надо, правда? Итак, преобразовываем второй логарифм по второй (снизу) формуле — выносим степень из основания за логарифм:

        

        Осталось лишь сложить 3 (первый логарифм) и 3/2 (второй логарифм)

        Ответ: 4,5

 

        Так, с близкой роднёй разобрались. Идём дальше. Иногда пример может не соответствовать в точности формуле, а может быть лишь похожим на одну из формул. И наша задача — сначала преобразовать пример под ту или иную формулу. Как, например, этот:

        Пример 8

        

        Напоминаю, что запись lg означает просто логарифм по основанию 10. И всё.)

        Итак, основания логарифмов уже одинаковые — десятка. Ну прям напрашивается формула суммы логарифмов! А н-е-ет, не катит! Двойка во втором слагаемом всё портит. Коэффициент, понимаешь.) А формула применима только к чистым логарифмам, безо всяких коэффициентов. Но горевать рано! Мы эту двойку сейчас ликвидируем. Безопасно для примера.) Мы её внутрь логарифма загоним. Как? Всё по той же формуле логарифма от степени:

        log_axⁿ = n·log_ax

        Здесь как раз тот случай, когда формулу надо применять справа налево. Ни в одной другой теме школьной математики нельзя вот так красиво избавляться от мешающих коэффициентов, а в логарифмах — пожалуйста! Итак, избавляемся от двойки перед вторым логарифмом:

        2lg5 = lg5² = lg25

        Вот так. Осталось лишь сложить два логарифма по формуле логарифма произведения (опять же в применении справа налево). Вот и складываем:

        lg4 + lg25 = lg(4́·25) = lg100 = 2

        Напоминаю, что десятичные логарифмы формулу ничуть не портят, ибо они по своим свойствам ничем не отличаются от обычных!    

        Ответ: 2

        Вот вам и третий практический совет.

        Любую степень можно записать множителем перед логарифмом. И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.

       Ну что, вот и состоялась наше более близкое знакомство с логарифмами! Осталось теперь с ними крепко подружиться. На следующем уровне и в следующем уроке.)

        Традиционные примеры для самостоятельного решения.

        Вычислить:

        

        

        

        

        Ответы (вразнобой): 0; 1; 2; 3; 

Как решить логарифмическое уравнение: подробное объяснение

Как решить логарифмическое уравнение? Этим вопросом задаются многие школьники, особенно в преддверии сдачи ЕГЭ по математике. Ведь в задании С1 профильного ЕГЭ могут встретиться именно логарифмические уравнения.

Уравнение, в котором неизвестное находится внутри логарифмов, называется логарифмическим. Причем неизвестное может находится как в аргументе логарифма, так и в его основании.

Способов решения таких уравнений существует несколько. В этой статье мы разберем способ, который легко понять и запомнить.

1. Как решать уравнения с логарифмами: 2 способа с примерами
2. Пример решения логарифмического уравнения с разными основаниями
3. Пример решения логарифмического уравнения с переменными основаниями
4. Как сделать проверку – это важно

Как решать уравнения с логарифмами: 2 способа с примерами

Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.

При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!

Давайте посмотрим, как это работает на примере:

Воспользуемся определением логарифма и получим:

2х + 3 = 3²

Теперь перед нами простейшее уравнение, решить которое не составит труда:

2х + 3 = 9

2х = 6

х = 3

Сделаем проверку. Подставим найденный Х в исходное уравнение:Так как 3² = 9, то последнее выражение верно. Следовательно,  х = 3 является корнем уравнения.

Ответ: х = 3

Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании log_af(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.

Поэтому мы покажем еще один способ решения логарифмических уравнений.

Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:

Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.

Решим еще раз то же самое уравнение, но теперь этим способом:В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.

Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:То есть в нашем случае:Возьмем правую часть нашего уравнения и начнем ее преобразовывать:Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:

Воспользуемся этим свойством в нашем случае, получим:Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:

2х + 3 = 3²

2х + 3 = 9

2х = 6

х = 3

Ответ: х = 3

Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.

Разберем другой пример:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:После преобразования правой части наше уравнение принимает следующий вид:Теперь можно зачеркнуть логарифмы и тогда получим:Вспоминаем свойства степеней:

3х – 5 = 4

3х = 9

х = 3

Теперь делаем проверку:то последнее выражение верно. Следовательно,  х = 3 является корнем уравнения.

Ответ: х = 3

Еще один пример решения логарифмического уравнения:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями.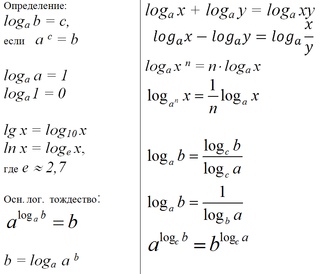 Воспользуемся свойством суммы логарифмов и получим:Теперь преобразуем правую часть уравнения:Выполнив преобразования правой и левой частей уравнения, мы получили:Теперь мы можем зачеркнуть логарифмы:

Решим данное квадратное уравнение, найдем дискриминант:

Сделаем проверку, подставим х₁ = 1 в исходное уравнение:Верно, следовательно, х₁ = 1 является корнем уравнения.

Теперь подставим х₂ = -5 в исходное уравнение:Так как аргумент логарифма должен быть положительным, выражение не является верным. Следовательно, х₂ = -5 – посторонний корень.

Ответ: х = 1

Пример решения логарифмического уравнения с разными основаниями

Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,

Правильно, нужно привести логарифмы в правой и левой части к одному основанию!

Итак, разберем наш пример:Преобразуем правую часть нашего уравнения:

Мы знаем, что 1/3 = 3^-1. Еще мы знаем свойство логарифма, а именно вынесение показателя степени из логарифма:Применяем эти знания и получаем:Но пока у нас есть знак «-» перед логарифмом в правой части уравнения, зачеркивать мы их не имеем права. Необходимо внести знак «-» в логарифмическое выражение. Для этого воспользуемся еще одним свойством логарифма:

Тогда получим:Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:Делаем проверку:Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:Верно, следовательно, х = 4 является корнем уравнения.

Ответ: х = 4.

Пример решения логарифмического уравнения с переменными основаниями

Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т.е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, log_x+1(х²+5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:

1. Аргумент логарифма должен быть больше ноля, следовательно:

2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:

Сведем все требования в систему:

Данную систему требований мы можем упростить. Смотрите х²+5х-5 больше ноля, при этом оно приравнивается к (х + 1)², которую в свою очередь так же больше ноля. Следовательно, требование х²+5х-5 > 0 выполняется автоматически и мы можем его не решать. Тогда наша система будет сведена к следующему:Перепишем нашу систему:Следовательно, наша система примет следующий вид:Теперь решаем наше уравнение:Справа у нас квадрат суммы:Данный корень удовлетворяет наши требования, так как 2 больше -1 и не равно 0. Следовательно, х = 2 – корень нашего уравнения.

Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:

Т.к. 3²=9, то  последнее выражение верно.

Ответ: х = 2

Как сделать проверку

Еще раз обращаем ваше внимание, что при решении логарифмических уравнений необходимо учитывать область допустимых значений. Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т.е. больше ноля.

Если наше уравнение имеет вид log_a (f(x)) = log_a (g(x)), то должны выполняться следующие ограничения:

После решения логарифмического уравнения нужно обязательно сделать проверку.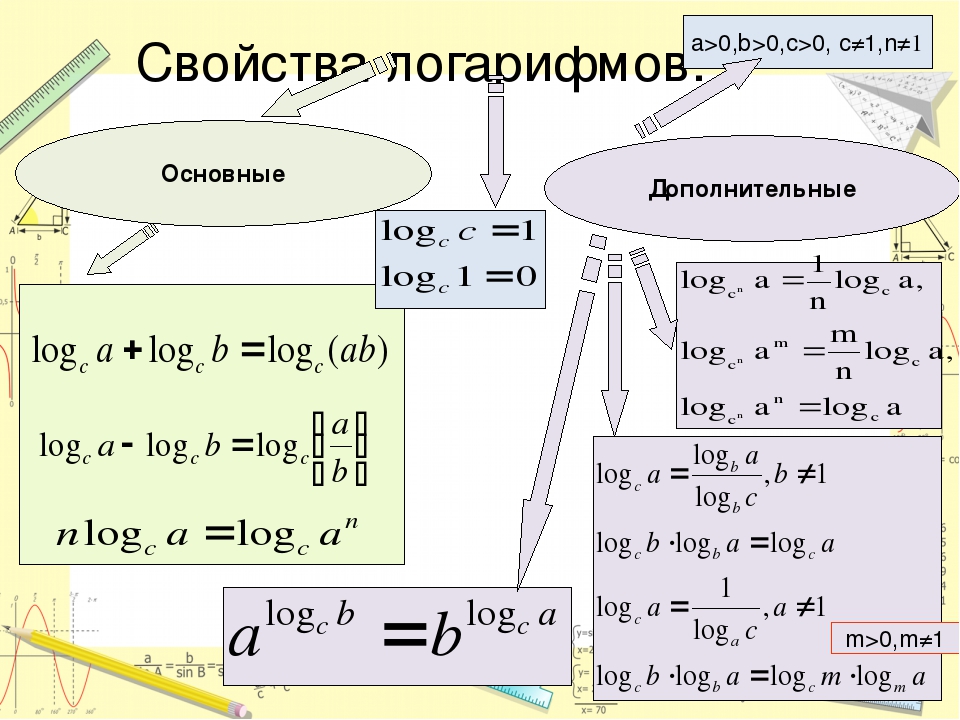 Для этого вам необходимо подставить получившееся значения в исходное уравнение и посчитать его. Времени это займет немного, зато позволит не записать в ответ посторонние корни. Ведь так обидно правильно решить уравнение и при этом неправильно записать ответ!

Итак, теперь вы знаете, как решить логарифмическое уравнение с помощью определения логарифма и с помощью преобразования уравнения, когда в обеих его частях стоят логарифмы с одинаковыми основаниями, которые мы можем «зачеркнуть». Отличное знание свойств логарифма, учет области определения, выполнение проверки – залог успеха при решении логарифмических уравнений.

Логарифмические уравнения — подготовка к ЕГЭ по Математике

Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.

.

При этом .

Обратим внимание на область допустимых значений логарифма:

.

Основное логарифмическое тождество:

,

.

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)

Формула перехода к новому основанию:

.

Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.

Все это пригодится нам в решении логарифмических уравнений.

Простейшие логарифмические уравнения

1. Решите уравнение:

Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.

Получаем:

Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при .

Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.

2. Решите уравнение:

В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.

Ответ: -124

3. Решите уравнение:

Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.

;

;

;

4. Решите уравнение:

Область допустимых значений: Значит,

Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом .

.

Ответ: 21.

5. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: –4.

Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.

6.Решите уравнение: .

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Запишем решение как цепочку равносильных переходов.

Ответ: 19.

7.Решите уравнение: .

Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.

ОДЗ:

Теперь можно «убрать» логарифмы.

— посторонний корень, поскольку должно выполняться условие .

Ответ:

8. Решите уравнение .

ОДЗ уравнения:

Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.

Вернемся к переменной х:

9.Решите уравнение:

Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.

Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.

«Отбрасываем» логарифмы.

Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену

Вернемся к переменной х. Получим:

. Мы нашли все корни исходного уравнения.

Ответ: .

Логарифмические уравнения могут встретиться вам и в задании №5 Профильного ЕГЭ по математике, и в задании №13. И если в задании №5 нужно решить простейшее уравнение, то в задаче 13 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.

Выражения с логарифмами — презентация онлайн

1. ПОВТОРЕНИЕ

Урок № 4
ПОВТОРЕНИЕ
Выражения с логарифмами
log a b
log – знак логарифма,
a – основание логарифма,
b – выражение под логарифмом
И не пытайся понять мою душу:
там такие, сударь ты мой, логарифмы!
Авессалом Подводный. Отдельные мысли
ОПРЕДЕЛЕНИЕ
log a b x ,
b 0
ax b
a 0
Теория
a 1
ОСНОВНОЕ
ЛОГАРИФМИЧЕСКОЕ
ТОЖДЕСТВО
a
loga b
b
ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
log 10 b lg b
log e b ln b
СВОЙСТВА ЛОГАРИФМОВ
1) log a 1 0 2) log a a 1
3) log a b log a c log a (bc)
b
4) log a b log a c log a
5) log a b r r log a b
c
log c b
1
1
6) log a k b log a b
7) log a b
8) log a b
k
log c a
log b a
a
logc b
b
logc a
=х
Устно
4 16
х
Логарифмом положительного числа b по основанию a, где
a 0 a 1
называется показатель степени в которую нужно возвести
a, чтобы получить b.
Устно
a
loga b
b
log a 1 0
a 1
Устно
0
логарифм единицы равен нулю
log a a 1
a a
1
логарифм a по основанию a равен единице
log 6 1
log
log 1/ 2
3
3
1
2
log 2, 4 1
Устно
log a (bc) log a b log a c
логарифм произведения
положительных множителей
равен сумме логарифмов
этих множителей
b
log a
c
log a b log a c
логарифм частного
положительных числителя и знаменателя
равен разности
логарифма числителя и логарифма знаменателя
Устно
Вычислите
Предложите,
как лучше запомнить данные две формулы?
Устно
log a b r log a b
r
логарифм степени равен
произведению
показателя степени
на логарифм основания
log a k
1
b log a b
k
Устно
Формулы приведения к новому основанию
log c b
log a b
log c a
1
log a b
log b a
Очень часто появляется необходимость
поменять местами a и b
основание и выражение под логарифмом
Устно
Письменно
В классе нечётные номера, дома – чётные.
1
6
2
7
3
4
5
8
9
Письменно
10
16
11
17
12
13
14
15
18
19
Письменно
20
21
Дополнительная задачка
Домашнее задание № 4
В классе нечётные номера, дома – чётные.
х 2 3х ax 2a 2 3a
0
( х 3)( х 3)
Дробь равна нулю,
если числитель равен нулю,
а знаменатель нулю не равен.
х 2 х(3 a) (2a 2 3a)
0
( х 3)( х 3)
х 2 х(3 a) (2a 2 3a) 0
( х 3)( х 3) 0
Уравнение будет иметь ровно один корень, если
1) дискриминант квадратного уравнения равен нулю и корни не
совпадают с числами 3 и -3;
2) дискриминант положителен и один из корней равен 3 или -3.
{
1) D=(3-a)²+4(2a²-3a)=0
-9+3(3-a)+2a²-3a≠0
-9-3(3-a)+2a²-3a≠0
{
2) D=(3-a)²+4(2a²-3a)>0
-9+3(3-a)+2a²-3a=0
-9-3(3-a)+2a²-3a=0
1
{
D=(3-a)²+4(2a²-3a)=0
-9+3(3-a)+2a²-3a≠0
-9-3(3-a)+2a²-3a≠0
2
{
D=(3-a)²+4(2a²-3a)>0
-9+3(3-a)+2a²-3a=0
-9-3(3-a)+2a²-3a=0
1 D=(3-a)²+4(2a²-3a)=0 -9+3(3-a)+2a²-3a≠0 -9-3(3-a)+2a²-3a≠0
9-6a+a²+8a²-12a=0
2a²-6a≠0
2a²≠18
9a²-18a+9=0 |:9
a≠0 a≠3
a≠-3 a≠3
a²-2a+1=0
(a-1)²=0
При a=1 уравнение имеет ровно одно решение.
a=1
2 D=(3-a)²+4(2a²-3a)>0
-9+3(3-a)+2a²-3a=0
-9-3(3-a)+2a²-3a=0
(a-1)²>0
a=0 a=3
a=-3 a=3
a≠1
При a=0 и a=-3 уравнение имеет ровно одно решение.
Ответ: при a=0, a=1, a=3 исходное уравнение
имеет ровно одно решение.

Уравнения с логарифмами. Логарифмические уравнения. Как решать логарифмические уравнения

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
• если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
3. Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
4. Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Заключительные видео из длинной серии уроков про решение логарифмических уравнений. В этот раз мы будем работать в первую очередь с ОДЗ логарифма — именно из-за неправильного учета (или вообще игнорирования) области определения возникает большинство ошибок при решении подобных задач.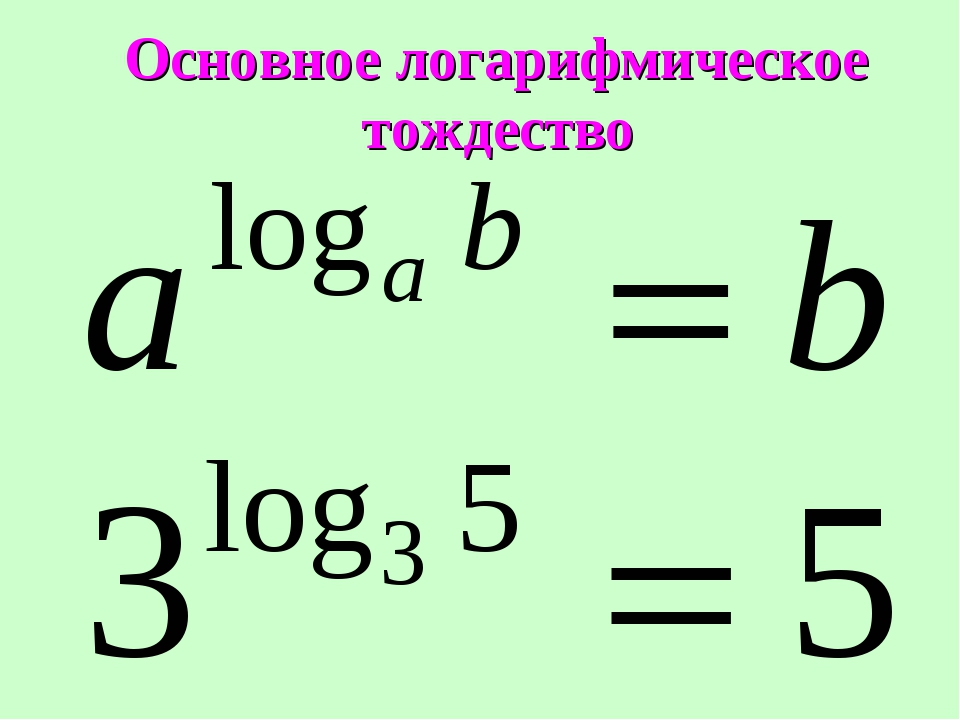

В этом коротком видеоуроке мы разберем применение формул сложения и вычитания логарифмов, а также разберемся с дробно-рациональными уравнениями, с которыми у многих учеников также возникают проблемы.

О чем пойдет речь? Главная формула, с которой я хотел бы разобраться, выглядит так:

log a (f g ) = log a f + log a g

Это стандартный переход от произведения к сумме логарифмов и обратно. Вы наверняка знаете эту формулу с самого начала изучения логарифмов. Однако тут есть одна заминка.

До тех пор, пока в виде переменных a , f и g выступают обычные числа, никаких проблем не возникает. Данная формула работает прекрасно.

Однако, как только вместоf и g появляются функции, возникает проблема расширения или сужения области определения в зависимости от того, в какую сторону преобразовывать. Судите сами: в логарифме, записанном слева, область определения следующая:

fg > 0

А вот в сумме, записанной справа, область определения уже несколько иная:

f > 0

g > 0

Данный набор требований является более жестким, чем исходный. В первом случае нас устроит вариант f 0 выполняется).

Итак, при переходе от левой конструкции к правой возникает сужение области определения. Если же сначала у нас была сумма, а мы переписываем ее в виде произведения, то происходит расширение области определения.

Другими словами, в первом случае мы могли потерять корни, а во втором — получить лишние. Это необходимо учитывать при решении реальных логарифмических уравнений.

Итак, первая задача:

[Подпись к рисунку]

Слева мы видим сумму логарифмов по одному и тому же основанию. Следовательно, эти логарифмы можно сложить:

[Подпись к рисунку]

Как видите, справа мы заменил ноль по формуле:

a = log b b a

Давайте еще немного преобразуем наше уравнение:

log 4 (x − 5) 2 = log 4 1

Перед нами каноническая форма логарифмического уравнения, мы можем зачеркнуть знак log и приравнять аргументы:

(x − 5) 2 = 1

|x − 5| = 1

Обратите внимание: откуда взялся модуль? Напомню, что корень из точного квадрата равен именно модулю:

[Подпись к рисунку]

Затем решаем классическое уравнение с модулем:

|f | = g (g > 0) ⇒f = ±g

x − 5 = ±1 ⇒x 1 = 5 − 1 = 4; x 2 = 5 + 1 = 6

Вот два кандидат на ответ. Являются ли они решением исходного логарифмического уравнения? Нет, ни в коем случае!

Оставить все просто так и записать ответ мы не имеем права. Взгляните на тот шаг, когда мы заменяем сумму логарифмов одним логарифмом от произведения аргументов. Проблема в том, что в исходных выражениях у нас стоят функции. Следовательно, следует потребовать:

х(х − 5) > 0; (х − 5)/х > 0.

Когда же мы преобразовали произведение, получив точный квадрат, требования изменились:

(x − 5) 2 > 0

Когда это требование выполняется? Да практически всегда! За исключением того случая, когда х − 5 = 0. Т.е. неравенство сведется к одной выколотой точке:

х − 5 ≠ 0 ⇒ х ≠ 5

Как видим, произошло расширение области определения, о чем мы и говорили в самом начале урока. Следовательно, могут возникнуть и лишние корни.

Как же не допустить возникновения этих лишних корней? Очень просто: смотрим на наши полученные корни и сравниваем их с областью определения исходного уравнения. Давайте посчитаем:

х (х − 5) > 0

Решать будем с помощью метода интервалов:

х (х − 5) = 0 ⇒ х = 0; х = 5

Отмечаем полученные числа на прямой. Все точки выколотые, потому что неравенство строгое. Берем любое число, больше 5 и подставляем:

[Подпись к рисунку]

На интересуют промежутки (−∞; 0) ∪ (5; ∞). Если мы отметим наши корни на отрезке, то увидим, что х = 4 нас не устраивает, потому что этот корень лежит за пределами области определения исходного логарифмического уравнения.

Возвращаемся к совокупности, вычеркиваем корень х = 4 и записываем ответ: х = 6. Это уже окончательный ответ к исходному логарифмическому уравнению. Все, задача решена.

Переходим ко второму логарифмическому уравнению:

[Подпись к рисунку]

Решаем его. Заметим, что первое слагаемое представляет собой дробь, а второе — ту же самую дробь, но перевернутую. Не пугайтесь выражения lgx — это просто десятичный логарифм, мы можем записать:

lgx = log 10 x

Поскольку перед нами две перевернутые дроби, предлагаю ввести новую переменную:

[Подпись к рисунку]

Следовательно, наше уравнение может быть переписано следующим образом:

t + 1/t = 2;

t + 1/t − 2 = 0;

(t 2 − 2t + 1)/t = 0;

(t − 1) 2 /t = 0.

Как видим, в числителе дроби стоит точный квадрат. Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля:

(t − 1) 2 = 0; t ≠ 0

Решаем первое уравнение:

t − 1 = 0;

t = 1.

Это значение удовлетворяет второму требованию. Следовательно, можно утверждать, что мы полностью решили наше уравнение, но только относительно переменной t . А теперь вспоминаем, что такое t :

[Подпись к рисунку]

Получили пропорцию:

lgx = 2 lgx + 1

2 lgx − lgx = −1

lgx = −1

Приводим это уравнение к канонической форме:

lgx = lg 10 −1

x = 10 −1 = 0,1

В итоге мы получили единственный корень, который, по идее, является решением исходного уравнения. Однако давайте все-таки подстрахуемся и выпишем область определения исходного уравнения:

[Подпись к рисунку]

Следовательно, наш корень удовлетворяет всем требованиям. Мы нашли решение исходного логарифмического уравнения. Ответ: x = 0,1. Задача решена.

Ключевой момент в сегодняшнем уроке один: при использовании формулы перехода от произведения к сумме и обратно обязательно учитывайте, что область определения может сужаться либо расширяться в зависимости от того, в какую сторону выполняется переход.

Как понять, что происходит: сужение или расширение? Очень просто. Если раньше функции были вместе, а теперь стали по отдельности, то произошло сужение области определения (потому что требований стало больше). Если же сначала функции стояли отдельно, а теперь — вместе, то происходит расширение области определения (на произведение накладывается меньше требований, чем на отдельные множители).

С учетом данного замечания хотел бы отметить, что второе логарифмическое уравнение вообще не требует данных преобразований, т. е. мы нигде не складываем и не перемножаем аргументы. Однако здесь я хотел бы обратить ваше внимание на другой замечательный прием, который позволяет существенно упростить решение. Речь идет о замене переменной.

Однако помните, что никакие замены не освобождает нас от области определения. Именно поэтому после того были найдены все корни, мы не поленились и вернулись к исходному уравнению, чтобы найти его ОДЗ.

Часто при замене переменной возникает обидная ошибка, когда ученики находят значение t и думают, что на этом решение закончено. Нет, ни в коем случае!

Когда вы нашли значение t , необходимо вернуться к исходному уравнению и посмотреть, что именно мы обозначали этой буквой. В результате нам предстоит решить еще одно уравнение, которое, впрочем, будет значительно проще исходного.

Именно в этом состоит смысл введения новой переменной. Мы разбиваем исходное уравнение на два промежуточных, каждое из которых решается существенно проще.

Как решать «вложенные» логарифмические уравнения

Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого логарифма. Оба уравнения мы будем решать с помощью канонической формы.

Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого. Оба уравнения мы будем решать с помощью канонической формы. Напомню, если у нас есть простейшее логарифмическое уравнение вида log a f (x ) = b , то для решения такого уравнения мы выполняем следующие шаги. В первую очередь, нам нужно заменить число b :

b = log a a b

Заметьте: a b — это аргумент. Точно так же в исходном уравнении аргументом является функция f (x ). Затем мы переписываем уравнение и получаем вот такую конструкцию:

log a f (x ) = log a a b

Уже затем мы можем выполнить третий шаг — избавится от знака логарифма и просто записать:

f (x ) = a b

В результате мы получим новое уравнение. При этом никаких ограничений на функцию f (x ) не накладывается. Например, на ее месте также может стоять логарифмическая функция. И тогда мы вновь получим логарифмическое уравнение, которое снова сведем к простейшему и решим через каноническую форму.

Впрочем, хватит лирики. Давайте решим настоящую задачу. Итак, задача № 1:

log 2 (1 + 3 log 2 x ) = 2

Как видим, перед нами простейшее логарифмическое уравнение. В роли f (x ) выступает конструкция 1 + 3 log 2 x , а в роли числа b выступает число 2 (в роли a также выступает двойка). Давайте перепишем эту двойку следующим образом:

Важно понимать, что первые две двойки пришли к нам из основания логарифма, т. е. если бы в исходном уравнении стояла 5, то мы бы получили, что 2 = log 5 5 2 . В общем, основание зависит исключительно от логарифма, который изначально дан в задаче. И в нашем случае это число 2.

Итак, переписываем наше логарифмическое уравнение с учетом того, что двойка, которая стоит справа, на самом деле тоже является логарифмом. Получим:

log 2 (1 + 3 log 2 x ) = log 2 4

Переходим к последнему шагу нашей схемы — избавляемся от канонической формы. Можно сказать, просто зачеркиваем знаки log. Однако с точки зрения математики «зачеркнуть log» невозможно — правильнее сказать, что мы просто просто приравниваем аргументы:

1 + 3 log 2 x = 4

Отсюда легко находится 3 log 2 x :

3 log 2 x = 3

log 2 x = 1

Мы вновь получили простейшее логарифмическое уравнение, давайте снова приведем его к канонической форме. Для этого нам необходимо провести следующие изменения:

1 = log 2 2 1 = log 2 2

Почему в основании именно двойка? Потому что в нашем каноническом уравнении слева стоит логарифм именно по основанию 2. Переписываем задачу с учетом этого факта:

log 2 x = log 2 2

Снова избавляемся от знака логарифма, т. е. просто приравниваем аргументы. Мы вправе это сделать, потому что основания одинаковые, и больше никаких дополнительных действий ни справа, ни слева не выполнялось:

Вот и все! Задача решена. Мы нашли решение логарифмического уравнения.

Обратите внимание! Хотя переменная х и стоит в аргументе (т. е. возникают требования к области определения), мы никаких дополнительных требований предъявлять не будем.

Как я уже говорил выше, данная проверка является избыточной, если переменная встречается лишь в одном аргументе лишь одного логарифма. В нашем случае х действительно стоит лишь в аргументе и лишь под одним знаком log. Следовательно, никаких дополнительных проверок выполнять не требуется.

Тем не менее, если вы не доверяете данному методу, то легко можете убедиться, что х = 2 действительно является корнем. Достаточно подставить это число в исходное уравнение.

Давайте перейдем ко второму уравнению, оно чуть интересней:

log 2 (log 1/2 (2x − 1) + log 2 4) = 1

Если обозначить выражение внутри большого логарифма функцией f (x ), получим простейшее логарифмическое уравнение, с которого мы начинали сегодняшний видеоурок. Следовательно, можно применить каноническую форму, для чего придется представить единицу в виде log 2 2 1 = log 2 2.

Переписываем наше большое уравнение:

log 2 (log 1/2 (2x − 1) + log 2 4) = log 2 2

Изваляемся от знака логарифма, приравнивая аргументы. Мы вправе это сделать, потому что и слева, и справа основания одинаковые. Кроме того, заметим, что log 2 4 = 2:

log 1/2 (2x − 1) + 2 = 2

log 1/2 (2x − 1) = 0

Перед нами снова простейшее логарифмическое уравнение вида log a f (x ) = b . Переходим к канонической форме, т. е. представляем ноль в виде log 1/2 (1/2)0 = log 1/2 1.

Переписываем наше уравнение и избавляемся от знака log, приравнивая аргументы:

log 1/2 (2x − 1) = log 1/2 1

2x − 1 = 1

Опять же мы сразу получили ответ. Никаких дополнительных проверок не требуется, потому что в исходном уравнении лишь один логарифм содержит функцию в аргументе.

Следовательно, никаких дополнительных проверок выполнять не требуется. Мы можем смело утверждать, что х = 1 является единственным корнем данного уравнения.

А вот если бы во втором логарифме вместо четверки стояла бы какая-то функция от х (либо 2х стояло бы не в аргументе, а в основании) — вот тогда потребовалось бы проверять область определения. Иначе велик шанс нарваться на лишние корни.

Откуда возникают такие лишние корни? Этот момент нужно очень четко понимать. Взгляните на исходные уравнения: везде функция х стоит под знаком логарифма. Следовательно, поскольку мы записали log 2 x , то автоматически выставляем требование х > 0. Иначе данная запись просто не имеет смысла.

Однако по мере решения логарифмического уравнения мы избавляемся от всех знаков log и получаем простенькие конструкции. Здесь уже никаких ограничений не выставляется, потому что линейная функция определена при любом значении х.

Именно эта проблема, когда итоговая функция определена везде и всегда, а исходная — отнюдь не везде и не всегда, и является причиной, по которой в решении логарифмических уравнениях очень часто возникают лишние корни.

Но повторю еще раз: такое происходить лишь в ситуации, когда функция стоит либо в нескольких логарифмах, либо в основании одного из них. В тех задачах, которые мы рассматриваем сегодня, проблем с расширением области определения в принципе не существует.

Случаи разного основания

Этот урок посвящен уже более сложным конструкциям. Логарифмы в сегодняшних уравнениях уже не будут решаться «напролом» — сначала потребуется выполнить некоторые преобразования.

Начинаем решение логарифмических уравнений с совершенно разными основаниями, которые не являются точными степенями друг друга. Пусть вас не пугают подобные задачи — решаются они ничуть не сложнее, чем самые простые конструкции, которые мы разбирали выше.

Но прежде, чем переходить непосредственно к задачам, напомню о формуле решения простейших логарифмических уравнений с помощью канонической формы. Рассмотрим задачу вот такого вида:

log a f (x ) = b

Важно, что функция f (x ) является именно функцией, а в роли чисел а и b должны выступать именно числа (без всяких переменных x ). Разумеется, буквально через минуту мы рассмотрим и такие случаи, когда вместо переменных а и b стоят функции, но сейчас не об этом.

Как мы помним, число b нужно заменить логарифмом по тому же самому основанию а, которое стоит слева. Это делается очень просто:

b = log a a b

Разумеется, под словом «любое число b » и «любое число а» подразумеваются такие значения, которые удовлетворяют области определения. В частности, в данном уравнении речь идет лишь основание a > 0 и a ≠ 1.

Однако данное требование выполняется автоматически, потому что в исходной задаче уже присутствует логарифм по основанию а — оно заведомо будет больше 0 и не равно 1. Поэтому продолжаем решение логарифмического уравнения:

log a f (x ) = log a a b

Подобная запись называется канонической формой. Ее удобство состоит в том, что мы сразу можем избавиться от знака log, приравняв аргументы:

f (x ) = a b

Именно этот прием мы сейчас будем использовать для решения логарифмических уравнений с переменным основанием. Итак, поехали!

log 2 (x 2 + 4x + 11) = log 0,5 0,125

Что дальше? Кто-то сейчас скажет, что нужно вычислить правый логарифм, либо свести их к одному основанию, либо что-то еще. И действительно, сейчас нужно привести оба основания к одному виду — либо 2, либо 0,5. Но давайте раз и навсегда усвоим следующее правило:

Если в логарифмическом уравнении присутствуют десятичные дроби, обязательно переведите эти дроби из десятичной записи в обычную. Такое преобразование может существенно упростить решение.

Подобный переход нужно выполнять сразу, еще до выполнения каких-либо действий и преобразований. Давайте посмотрим:

log 2 (x 2 + 4x + 11) = log 1 /2 1/8

Что нам дает такая запись? Мы можем 1/2 и 1/8 представить как степень с отрицательным показателем:

[Подпись к рисунку]

Перед нами каноническая форма. Приравниваем аргументы и получаем классическое квадратное уравнение:

x 2 + 4x + 11 = 8

x 2 + 4x + 3 = 0

Перед нами приведенное квадратное уравнение, которое легко решается с помощью формул Виета. Подобные выкладки в старших классах вы должны видеть буквально устно:

(х + 3)(х + 1) = 0

x 1 = −3

x 2 = −1

Вот и все! Исходное логарифмическое уравнение решено. Мы получили два корня.

Напомню, что определять область определения в данном случае не требуется, поскольку функция с переменной х присутствует лишь в одном аргументе. Поэтому область определения выполняется автоматически.

Итак, первое уравнение решено. Переходим ко второму:

log 0,5 (5x 2 + 9x + 2) = log 3 1/9

log 1/2 (5x 2 + 9x + 2) = log 3 9 −1

А теперь заметим, что аргумент первого логарифма тоже можно записать в виде степени с отрицательным показателем: 1/2 = 2 −1 . Затем можно вынести степени с обеих сторон уравнения и разделить все на −1:

[Подпись к рисунку]

И вот сейчас мы выполнили очень важный шаг в решении логарифмического уравнения. Возможно, кто-то что-то не заметил, поэтому давайте я поясню.

Взгляните на наше уравнение: и слева, и справа стоит знак log, но слева стоит логарифм по основанию 2, а справа стоит логарифм по основанию 3. Тройка не является целой степенью двойки и, наоборот: нельзя записать, что 2 — это 3 в целой степени.

Следовательно, это логарифмы с разными основаниями, которые не сводятся друг к другу простым вынесением степеней. Единственный путь решения таких задач — избавиться от одного из этих логарифмов. В данном случае, поскольку мы пока рассматриваем довольно простые задачи, логарифм справа просто сосчитался, и мы получили простейшее уравнение — именно такое, о котором мы говорили в самом начале сегодняшнего урока.

Давайте представим число 2, которое стоит справа в виде log 2 2 2 = log 2 4. А затем избавимся от знака логарифма, после чего у нас остается просто квадратное уравнение:

log 2 (5x 2 + 9x + 2) = log 2 4

5x 2 + 9x + 2 = 4

5x 2 + 9x − 2 = 0

Перед нами обычное квадратное уравнение, однако оно не является приведенным, потому что коэффициент при x 2 отличен от единицы. Следовательно, решать мы его будем с помощью дискриминанта:

D = 81 − 4 5 (−2) = 81 + 40 = 121

x 1 = (−9 + 11)/10 = 2/10 = 1/5

x 2 = (−9 − 11)/10 = −2

Вот и все! Мы нашли оба корня, а значит, получили решение исходного логарифмического уравнения. Ведь в исходной задачи функция с переменной х присутствует лишь в одном аргументе. Следовательно, никаких дополнительных проверок на область определения не требуется — оба корня, которые мы нашли, заведомо отвечают всем возможным ограничениям.

На этом можно было бы закончить сегодняшний видеоурок, но в заключении я хотел бы сказать еще раз: обязательно переводите все десятичные дроби в обычные при решении логарифмических уравнений. В большинстве случаев это существенно упрощает их решение.

Редко, очень редко попадаются задачи, в которых избавление от десятичных дробей лишь усложняет выкладки. Однако в таких уравнениях, как правило, изначально видно, что избавляться от десятичных дробей не надо.

В большинстве остальных случаев (особенно если вы только начинаете тренироваться в решении логарифмических уравнений) смело избавляйтесь от десятичных дробей и переводите их в обычные. Потому что практика показывает, что таким образом вы значительно упростите последующее решение и выкладки.

Тонкости и хитрости решения

Сегодня мы переходим к более сложным задачам и будем решать логарифмическое уравнение, в основании которого стоит не число, а функция.

И пусть даже эта функция линейна — в схему решения придется внести небольшие изменения, смысл которых сводится к дополнительным требованиям, накладываемым на область определения логарифма.

Сложные задачи

Этот урок будет довольно длинным. В нем мы разберем два довольно серьезных логарифмических уравнения, при решении которых многие ученики допускают ошибки. За свою практику работы репетитором по математике я постоянно сталкивался с двумя видами ошибок:

1. Возникновение лишних корней из-за расширения области определения логарифмов. Чтобы не допускать такие обидные ошибки, просто внимательно следите за каждым преобразованием;
2. Потери корней из-за того, что ученик забыл рассмотреть некоторые «тонкие» случаи — именно на таких ситуациях мы сегодня и сосредоточимся.

Это последний урок, посвященный логарифмическим уравнениям. Он будет длинным, мы разберем сложные логарифмические уравнения. Устраивайтесь поудобней, заварите себе чай, и мы начинаем.

Первое уравнение выглядит вполне стандартно:

log x + 1 (x − 0,5) = log x − 0,5 (x + 1)

Сразу заметим, что оба логарифма являются перевернутыми копиями друг друга. Вспоминаем замечательную формулу:

log a b = 1/log b a

Однако у этой формулы есть ряд ограничений, которые возникают в том случае, если вместо чисел а и b стоят функции от переменной х:

b > 0

1 ≠ a > 0

Эти требования накладываются на основание логарифма. С другой стороны, в дроби от нас требуется 1 ≠ a > 0, поскольку не только переменная a стоит в аргументе логарифма (следовательно, a > 0), но и сам логарифм находится в знаменателе дроби. Но log b 1 = 0, а знаменатель должен быть отличным от нуля, поэтому a ≠ 1.

Итак, ограничения на переменную a сохраняется. Но что происходит с переменной b ? С одной стороны, из основания следует b > 0, с другой — переменная b ≠ 1, потому что основание логарифма должно быть отлично от 1. Итого из правой части формулы следует, что 1 ≠ b > 0.

Но вот беда: второе требование (b ≠ 1) отсутствует в первом неравенстве, посвященном левому логарифму. Другими словами, при выполнении данного преобразования мы должны отдельно проверить , что аргумент b отличен от единицы!

Вот давайте и проверим. Применим нашу формулу:

[Подпись к рисунку]

1 ≠ х − 0,5 > 0; 1 ≠ х + 1 > 0

Вот мы и получили, что уже из исходного логарифмического уравнения следует, что и а, и b должны быть больше 0 и не равны 1. Значит, мы спокойно можем переворачивать логарифмическое уравнение:

Предлагаю ввести новую переменную:

log x + 1 (x − 0,5) = t

В этом случае наша конструкция перепишется следующим образом:

(t 2 − 1)/t = 0

Заметим, что в числителе у нас стоит разность квадратов. Раскрываем разность квадратов по формуле сокращенного умножения:

(t − 1)(t + 1)/t = 0

Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Но в числителе стоит произведение, поэтому приравниваем к нулю каждый множитель:

t 1 = 1;

t 2 = −1;

t ≠ 0.

Как видим, оба значения переменной t нас устраивают. Однако на этом решение не заканчивается, ведь нам требуется найти не t , а значение x . Возвращаемся к логарифму и получаем:

log x + 1 (x − 0,5) = 1;

log x + 1 (x − 0,5) = −1.

Давайте приведем каждое из этих уравнений к канонической форме:

log x + 1 (x − 0,5) = log x + 1 (x + 1) 1

log x + 1 (x − 0,5) = log x + 1 (x + 1) −1

Избавляемся от знака логарифма в первом случае и приравниваем аргументы:

х − 0,5 = х + 1;

х − х = 1 + 0,5;

Такое уравнение не имеет корней, следовательно, первое логарифмическое уравнение также не имеет корней. А вот со вторым уравнением все намного интересней:

(х − 0,5)/1 = 1/(х + 1)

Решаем пропорцию — получим:

(х − 0,5)(х + 1) = 1

Напоминаю, что при решении логарифмических уравнений гораздо удобней приводить все десятичные дроби обычные, поэтому давайте перепишем наше уравнение следующим образом:

(х − 1/2)(х + 1) = 1;

x 2 + x − 1/2x − 1/2 − 1 = 0;

x 2 + 1/2x − 3/2 = 0.

Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:

(х + 3/2) (х − 1) = 0;

x 1 = −1,5;

x 2 = 1.

Получили два корня — они являются кандидатами на решение исходного логарифмического уравнения. Для того чтобы понять, какие корни действительно пойдут в ответ, давайте вернемся к исходной задаче. Сейчас мы проверим каждый из наших корней на предмет соответствия области определения:

1,5 ≠ х > 0,5; 0 ≠ х > −1.

Эти требования равносильны двойному неравенству:

1 ≠ х > 0,5

Отсюда сразу видим, что корень х = −1,5 нас не устраивает, а вот х = 1 вполне устраивает. Поэтому х = 1 — окончательное решение логарифмического уравнения.

Переходим ко второй задаче:

log x 25 + log 125 x 5 = log 25 x 625

На первый взгляд может показаться, что у всех логарифмов разные основания и разные аргументы. Что делать с такими конструкциями? В первую очередь заметим, что числа 25, 5 и 625 — это степени 5:

25 = 5 2 ; 625 = 5 4

А теперь воспользуемся замечательным свойством логарифма. Дело в том, что можно выносить степени из аргумента в виде множителей:

log a b n = n ∙ log a b

На данное преобразование также накладываются ограничения в том случае, когда на месте b стоит функция. Но у нас b — это просто число, и никаких дополнительных ограничений не возникает. Перепишем наше уравнение:

2 ∙ log x 5 + log 125 x 5 = 4 ∙ log 25 x 5

Получили уравнение с тремя слагаемыми, содержащими знак log. Причем аргументы всех трех логарифмов равны.

Самое время перевернуть логарифмы, чтобы привести их к одному основанию — 5. Поскольку в роли переменной b выступает константа, никаких изменений области определения не возникает. Просто переписываем:

[Подпись к рисунку]

Как и предполагалось, в знаменателе «вылезли» одни и те же логарифмы. Предлагаю выполнить замену переменной:

log 5 x = t

В этом случае наше уравнение будет переписано следующим образом:

Выпишем числитель и раскроем скобки:

2 (t + 3) (t + 2) + t (t + 2) − 4t (t + 3) = 2 (t 2 + 5t + 6) + t 2 + 2t − 4t 2 − 12t = 2t 2 + 10t + 12 + t 2 + 2t − 4t 2 − 12t = −t 2 + 12

Возвращаемся к нашей дроби. Числитель должен быть равен нулю:

[Подпись к рисунку]

А знаменатель — отличен от нуля:

t ≠ 0; t ≠ −3; t ≠ −2

Последние требования выполняются автоматически, поскольку все они «завязаны» на целые числа, а все ответы — иррациональные.

Итак, дробно-рациональное уравнение решено, значения переменной t найдены. Возвращаемся к решению логарифмического уравнения и вспоминаем, что такое t :

[Подпись к рисунку]

Приводим это уравнение к канонической форме, получим число с иррациональной степенью. Пусть это вас не смущает — даже такие аргументы можно приравнять:

[Подпись к рисунку]

У нас получилось два корня. Точнее, два кандидата в ответы — проверим их на соответствие области определения. Поскольку в основании логарифма стоит переменная х, потребуем следующее:

1 ≠ х > 0;

С тем же успехом утверждаем, что х ≠ 1/125, иначе основание второго логарифма обратится в единицу. Наконец, х ≠ 1/25 для третьего логарифма.

Итого мы получили четыре ограничения:

1 ≠ х > 0; х ≠ 1/125; х ≠ 1/25

А теперь вопрос: удовлетворяют ли наши корни указанным требованиям? Конечно удовлетворяют! Потому что 5 в любой степени будет больше нуля, и требование х > 0 выполняется автоматически.

С другой стороны, 1 = 5 0 , 1/25 = 5 −2 , 1/125 = 5 −3 , а это значит, что данные ограничения для наших корней (у которых, напомню, в показателе стоит иррациональное число) также выполнены, и оба ответа являются решениями задачи.

Итак, мы получили окончательный ответ. Ключевых моментов в данной задаче два:

1. Будьте внимательны при перевороте логарифма, когда аргумент и основание меняются местами. Подобные преобразования накладывают лишние ограничения на область определения.
2. Не бойтесь преобразовывать логарифмы: их можно не только переворачивать, но и раскрывать по формуле суммы и вообще менять по любым формулам, которые вы изучали при решении логарифмических выражений. Однако при этом всегда помните: некоторые преобразования расширяют область определения, а некоторые — сужают.

Подготовка к итоговому тестированию по математике включает в себя важный раздел — «Логарифмы». Задания из этой темы обязательно содержатся в ЕГЭ. Опыт прошлых лет показывает, что логарифмические уравнения вызвали затруднения у многих школьников. Поэтому понимать, как найти правильный ответ, и оперативно справляться с ними должны учащиеся с различным уровнем подготовки.

Сдайте аттестационное испытание успешно с помощью образовательного портала «Школково»!

При подготовке к единому государственному экзамену выпускникам старших классов требуется достоверный источник, предоставляющий максимально полную и точную информацию для успешного решения тестовых задач. Однако учебник не всегда оказывается под рукой, а поиск необходимых правил и формул в Интернете зачастую требует времени.

Образовательный портал «Школково» позволяет заниматься подготовкой к ЕГЭ в любом месте в любое время. На нашем сайте предлагается наиболее удобный подход к повторению и усвоению большого количества информации по логарифмам, а также по с одним и несколькими неизвестными. Начните с легких уравнений. Если вы справились с ними без труда, переходите к более сложным. Если у вас возникли проблемы с решением определенного неравенства, вы можете добавить его в «Избранное», чтобы вернуться к нему позже.

Найти необходимые формулы для выполнения задачи, повторить частные случаи и способы вычисления корня стандартного логарифмического уравнения вы можете, заглянув в раздел «Теоретическая справка». Преподаватели «Школково» собрали, систематизировали и изложили все необходимые для успешной сдачи материалы в максимально простой и понятной форме.

Чтобы без затруднений справляться с заданиями любой сложности, на нашем портале вы можете ознакомиться с решением некоторых типовых логарифмических уравнений. Для этого перейдите в раздел «Каталоги». У нас представлено большое количество примеров, в том числе с уравнениями профильного уровня ЕГЭ по математике.

Воспользоваться нашим порталом могут учащиеся из школ по всей России. Для начала занятий просто зарегистрируйтесь в системе и приступайте к решению уравнений. Для закрепления результатов советуем возвращаться на сайт «Школково» ежедневно.

С уравнениями мы все знакомы с начальных классов. Еще там мы учились решать самые простые примеры, и надо признать, что они находят свое применение даже в высшей математике. С уравнениями все просто, в том числи и с квадратными. Если у вас проблемы с этой темой, настоятельно рекомендуем вам повторить ее.

Логарифмы вы, вероятно, тоже уже прошли. Тем не менее, считаем важным рассказать, что это для тех, кто еще не знает. Логарифм приравнивается к степени, в которую нужно возвести основание, чтобы получилось число, стоящее справа от знака логарифма. Приведем пример, исходя из которого, вам все станет ясно.

Если вы возведете 3 в четвертую степень получится 81. Теперь подставьте по аналогии числа, и поймете окончательно, как решаются логарифмы. Теперь осталось лишь совместить два рассмотренных понятия. Изначально ситуация кажется чрезвычайно сложной, но при ближайшем рассмотрении весе становится на свои места. Мы уверены, что после этой короткой статьи у вас не будет проблем в этой части ЕГЭ.

Сегодня выделяют множество способов решения подобных конструкций. Мы расскажем о самых простых, эффективных и наиболее применимых в случае заданий ЕГЭ. Решение логарифмических уравнений должно начинаться с самого простого примера. Простейшие логарифмические уравнения состоят из функции и одной переменной в ней.

Важно учесть, что x находится внутри аргумента. A и b должны быть числами. В таком случае вы можете попросту выразить функцию через число в степени. Выглядит это следующим образом.

Разумеется, решение логарифмического уравнения таким методом приведет вас к верному ответу. Ног проблема подавляющего большинства учеников в этом случае заключается в том, что они не понимают, что и откуда берется. В результате приходится мириться с ошибками и не получать желаемых баллов. Самой обидной ошибкой будет, если вы перепутаете буквы местами. Чтобы решить уравнение этим способом, нужно зазубрить эту стандартную школьную формулу, потому что понять ее сложно.

Чтобы было проще, можно прибегнуть к другому способу – канонической форме. Идея крайне проста. Снова обратите внимание на задачу. Помните, что буква a – число, а не функция или переменная. A не равно одному и больше нуля. На b никаких ограничений не действует. Теперь из всех формул вспоминаем одну. B можно выразить следующим образом.

Из этого следует, что все исходные уравнения с логарифмами можно представить в виде:

Теперь мы можем отбросить логарифмы. Получится простая конструкция, которую мы уже видели ранее.

Удобство данной формулы заключается в том, что ее можно применять в самых разных случаях, а не только для самых простых конструкций.

Не переживайте насчет ООФ!

Многие опытные математики заметят, что мы не уделили внимание области определения. Сводится правило к тому, что F(x) обязательно больше 0. Нет, мы не упустили этот момент. Сейчас мы говорим об еще одном серьезном преимуществе канонической формы.

Лишних корней здесь не возникнет. Если переменная будет встречаться лишь в одном месте, то область определения не является необходимостью. Она выполняется автоматически. Чтобы убедиться в данном суждении, займитесь решением нескольких простых примеров.

Как решать логарифмические уравнения с разными основаниями

Это уже сложные логарифмические уравнения, и подход к их решению должен быть особым. Здесь редко получается ограничиться пресловутой канонической формой. Начнем наш подробный рассказ. Мы имеем следующую конструкцию.

Обратите внимание на дробь. В ней находится логарифм. Если вы увидите такое в задании, стоит вспомнить один интересный прием.

Что это значит? Каждый логарифм можно представить в виде частного двух логарифмов с удобным основанием. И у данной формулы есть частный случай, который применим с этим примером (имеем ввиду, если c=b).

Именно такую дробь мы и видим в нашем примере. Таким образом.

По сути, перевернули дробь и получили более удобное выражение. Запомните этот алгоритм!

Теперь нужно, что логарифмическое уравнение не содержало разных оснований. Представим основание дробью.

В математике есть правило, исходя из которого, можно вынести степень из основания. Получается следующая конструкция.

Казалось бы, что мешает теперь превратить наше выражение в каноническую форму и элементарно решить ее? Не все так просто. Дробей перед логарифмом быть не должно. Исправляем эту ситуацию! Дробь разрешается выносить в качестве степени.

Соответственно.

Если основания одинаковые, мы можем убрать логарифмы и приравнять сами выражения. Так ситуация станет в разы проще, чем была. Останется элементарное уравнение, которое каждый из нас умел решать еще в 8 или даже в 7 классе. Расчеты вы сможете произвести сами.

Мы получили единственно верный корень этого логарифмического уравнения. Примеры решения логарифмического уравнения достаточно просты, не так ли? Теперь и у вас получится самостоятельно разобраться даже с самыми сложными задачами для подготовки и сдачи ЕГЭ.

Что в итоге?

В случае с любыми логарифмическими уравнениями мы исходим из одного очень важного правила. Необходимо действовать так, чтобы привести выражение к максимально простому виду. В таком случае у вас будет больше шансов не просто решить задание правильно, но еще и сделать это максимально простым и логичным путем. Именно так всегда действуют математики.

Настоятельно не рекомендуем вам искать сложных путей, особенно в этом случае. Запомните несколько простых правил, которые позволят преобразовать любое выражение. К примеру, привести два или три логарифма к одному основанию или вывести степень из основания и выиграть на этом.

Также стоит помнить о том, что в решении логарифмических уравнений необходимо постоянно тренироваться. Постепенно вы будете переходить ко все более сложным конструкциям, а это приведет вас к уверенному решению всех вариантов задач на ЕГЭ. Готовьтесь к экзаменам заблаговременно, и удачи вам!

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Задачи с логарифмами

Продолжаем рассматривать прикладные задачи, которые входят в состав ЕГЭ по математике. Если вы не читали статью «Задачи по физике. Это не страшно!», то советую с ней ознакомиться. В этой статье речь пойдёт о задачах, где используется понятие логарифма. Повторюсь, что в решении таких задач нет сложностей. Необходимо в данную в условии формулу подставить исходные величины. В данных задачах решение их сводится к решению логарифмического уравнения, либо неравенства.

Что необходимо знать о логарифме?

1. Основное логарифмическое тождество.

Определение: Логарифмом числа  a  по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a.

log_b a = x     b^x = a  

(a > 0, b > 0, b ≠ 1)

Например:

log₃ 9 = 2  так как  3² = 9

Основное логарифмическое тождество:

2. Как решенается простое логарифмическое уравнение.

3. Как решается  простое логарифмическое неравенство.

Рассмотрим задачи из открытого банка задач ЕГЭ по математике:

Ёмкость высоковольтного конденсатора в телевизоре C = 5∙10^-6 Ф. Параллельно с конденсатором подключен резистор с сопротивлением R = 2∙10 Ом. Во время работы телевизора напряжение на конденсаторе U₀ = 25 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за  время,   определяемое  выражением:

Определите (в киловольтах), наибольшее возможное напряжение на конденсаторе, если после выключения телевизора прошло не менее 46 с.   

Нам необходимо найти наибольшее возможное U на конденсаторе, при условии, что прошло не менее  46 секунд, то есть t ≥ 46.

Двойку представим в виде логарифма с основанием 2:

Знаки логарифмов мы можем снять, так как основания логарифмов в обеих частях равны. Знак неравенства не изменяется, так как основание логарифма больше единицы. Таким образом, далее будем неравенство:

Напряжение величина положительная, знак неравенства не меняется (при умножении частей неравенства на отрицательное число знак изменяется на противоположный):

Наибольшее возможное напряжение на конденсаторе 6,25 кВ.

Ответ: 6,25

Решить самостоятельно:

Посмотреть решение 

Для обогрева помещения, температура в котором равна Т_п = 20⁰С, через радиатор отопления, пропускают горячую воду температурой  Т_в = 100⁰С. Расход проходящей через трубу воды m = 0,2 кг/с. Проходя по трубе расстояние x (м), вода охлаждается до температуры Т⁰С, при чём

где с = 4200Дж/кг∙С — теплоемкость воды

γ = 42 Вт/м∙⁰С— коэффициент теплообмена

α = 1,4 — постоянная.

До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 28 м?

В данном случае необходимо решить уравнение:

Найдём Т,  подставив  все  известные значения:

Единицу представим в виде логарифма с основанием 1:

Так как основания логарифмов равны, то равны их подлогарифмические выражения:

Вода охладится до температуры 60 градусов Цельсия.

Ответ: 60

Решить самостоятельно:

Посмотреть решение 

Водолазный колокол, содержащий в начальный момент времени υ = 4 моля воздуха объемом V₁ = 15л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма V₂. Работа, совершаемая водой при сжатии воздуха, определяется выражением:

где α = 9,15— постоянная

Т = 300К— температура воздуха.

Какой объём V₂ (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10980 Дж.

В данной задаче необходимо найти V₂, подставив все известные значения в формулу:

В отличие от уже решённых задач, так можно использовать определение основного логарифмического тождества:

Воздух станет занимать 7,5 литра.

Ответ: 7,5

Решить самостоятельно:

Посмотреть решение 

Находящийся в воде водолазный колокол, содержащий υ = 6 моля  воздуха при давлении p₁ = 2,5 атмосферы, медленно опускают на дно водоема. При этом происходит изотермическое сжатие воздуха. Работа, совершаемая водой при сжатии воздуха, определяется выражением:

α = 5,75— постоянная — постоянная

Т = 300К — температура воздуха

p₁ (атм) — начальное давление 

p₂ (атм) — конечное давление воздуха в колоколе.

До какого наибольшего давления p₂ можно сжать воздух в колоколе, если при сжатии воздуха совершается работа не более чем 10350 Дж? Ответ приведите в атмосферах.          

Сказано, что «совершается работа не более, чем 10350 Дж», то есть максимальная работа, которая совершается при сжатии воздуха это 10350 Дж. Наибольшее давление будет достигнуто именно при максимальной работе, поэтому подставив все известные величины в выражение,  решим уравнение и найдём  p₂:

Используем понятие основного логарифмического тождества:

При заданных условиях воздух можно сжать до 5 атмосфер.

Ответ: 5

Решить самостоятельно:

Посмотреть решение 

Подведём итог:

1. Подставляем данные в условии величины в  формулу.

2. Внимательно вычисляем.

Если решаем уравнение, то используем определение основного логарифмического тождества. Либо свойство логарифма при решении уравнений (знаки логарифмов с одним основанием можно «снимать», то есть приравнивать подлогарифмические выражения).

Если решаем неравенство, то при снятии знаков логарифма обращаем внимание на его основание. Если оно принадлежит интервалу от 0 до 1, то знак неравенства меняем на противоположный. Если более единицы, то знак неравенства не изменяем.

Если вы не понимаете, когда составляется неравенство, а когда просто решается уравнение, то решайте уравнение, его решение и будет являться результатом.

На этом закончим.  Успехов вам!!! 

С уважением, Александр

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Уравнения с логарифмами | Логарифмы

Рассмотрим уравнения с логарифмами, для решения которых используется метод оценки.

При решении уравнений методом оценки сравнивают область значений каждой из функций, стоящих в разных частях уравнения. Если для уравнения

   

одновременно выполняются условия

   

   

то уравнение равносильно системе

   

Остаётся найти корни одного из уравнений системы и проверить, удовлетворяют ли они другому уравнению.

Примеры уравнений с логарифмами, решаемых методом оценки левой и правой части.

   

ОДЗ:

   

Под знаком логарифма стоит квадратичная функция

   

Её график — парабола ветвями вверх. Своё наименьшее значение функция принимает в вершине параболы

   

и оно равно

   

поэтому

   

Так как основание 2>1, логарифмическая функция

   

возрастает, следовательно, большему значению аргумента соответствует большее значение функции, то есть при x0=4 f(x) принимает своё наименьшее значение и оно равно

   

   

то есть

   

Левая часть уравнения — квадратичная функция, график — парабола ветвями вниз, в вершине достигает своего наибольшего значения:

   

   

   

то есть

   

   

   

Решаем второе уравнение:

   

   

   

Его единственный корень

   

является также корнем первого уравнения, а значит, исходное уравнение имеет единственный корень x=4.

Ответ: 4.

   

ОДЗ:

   

Так как

   

то

   

Так как 0,9<1 и функция

   

убывает, то

   

С другой стороны,

   

Следовательно, исходное уравнение равносильно системе

   

Решим второе уравнение:

   

   

Проверяем, удовлетворяют ли полученные корни первому уравнению.

При x=1

   

   

При x= -1

   

   

Следовательно, уравнение имеет один корень x=1.

Ответ: 1.

   

ОДЗ:

   

   

   

Следовательно, исходное уравнение равносильно системе

   

Решим первое уравнение:

   

   

   

Проверяем, является ли 0 корнем второго уравнения:

   

   

Следовательно, исходное уравнение имеет один корень x=0.

Ответ: 0.

Решение экспоненциальных уравнений с логарифмами

Purplemath

Большинство экспоненциальных уравнений не решаются точно; не будет возможности преобразовать основания в одинаковые, например преобразовать 4 и 8 в степени 2. При решении этих более сложных уравнений вам придется использовать логарифмы.

Логарифмирование позволит нам воспользоваться правилом журнала, которое гласит, что мощности внутри журнала могут быть перенесены вперед как множители.Взяв журнал экспоненты, мы можем затем переместить переменную (находящуюся в экспоненте, которая теперь находится внутри журнала) вперед, как множитель в журнале. Другими словами, правило журнала позволит нам переместить переменную обратно на землю, где мы сможем ее получить.

Например:

MathHelp.com

Если бы это уравнение попросило меня «Решить 2 ^x = 32», то найти решение было бы легко, потому что я мог бы преобразовать 32 в 2 ⁵ , установить равные показатели и решить для « x = 5».Но, в отличие от 32, 30 — это не степень двойки, поэтому я не могу установить степени, равные друг другу. Мне нужен другой способ получить x , потому что я не могу решить уравнение с переменной, плавающей там выше 2; Мне нужно, чтобы он вернулся на землю, где ему и место, где я смогу добраться до него. И мне придется использовать логарифмы, чтобы уменьшить эту переменную.

Имея дело с уравнениями, я могу делать с уравнением все, что захочу, при условии, что я делаю одно и то же с обеими сторонами.И, чтобы решить уравнение, я должен получить переменную отдельно от знака «равно»; чтобы изолировать переменную, я должен «отменить» все, что было сделано с переменной.

В этом случае переменная x помещена в показатель степени. Обратные (технически «обратные») экспоненты — это логарифмы, поэтому мне нужно отменить экспоненту, взяв логарифм обеих частей уравнения. Это полезно для меня из-за правила журнала, которое гласит, что показатели внутри журнала можно превратить в множители перед журналом:

Когда я беру логарифм обеих сторон уравнения, я могу использовать любой журнал, который мне нравится (логарифм по основанию 10, лог по основанию 2, натуральный логарифм и т. Д.), Но некоторые из них иногда более полезны, чем другие.Поскольку основание в уравнении «2 ^x = 30» равно «2», я мог бы попробовать использовать журнал с основанием 2:

Любой журнал базы журнала возвращает значение 1, поэтому журнал ₂ (2) = 1. Тогда:

x · журнал ₂ (2) = журнал ₂ (30)

x (1) = журнал ₂ (30)

x = бревно ₂ (30)

Если вас просят «найти решение», то приведенный выше ответ должен быть приемлемым.Однако это значение, хотя и является «точным», не будет очень полезным для задач со словами (или в «реальной жизни»), если вам нужно числовое приближение.

Но мы не можем вычислить это выражение в наших калькуляторах в его нынешнем виде. Во-первых, нам нужно применить формулу замены базы, чтобы преобразовать выражение во что-то в базе, понятное нашим калькуляторам; а именно, натуральный журнал или обычный журнал. Это преобразование выглядит так:

Напоминание: «ln» — это сокращение от «logarithmus naturalis», латинской версии того, что в английском языке стало «натуральным логарифмом».Аббревиатура произносится как «ell-enn» и пишется со строчной буквы «L», за которой следует строчная буква «N». В названии функции нет «я» («глаз»)!

Что бы произошло, если бы я просто использовал натуральный логарифм вместо логарифма по основанию два? Процесс был бы точно таким же, и конечный ответ был бы эквивалентным.

2 ^x = 30

ln (2 ^x ) = ln (30)

x · ln (2) = ln (30)

x = ln (30) / ln (2)

В любом случае, я получаю тот же ответ, но использование естественного журнала было проще и короче.

Примечание: я мог бы использовать общий журнал (base-10) вместо естественного (то есть base- e ) журнала и все равно получить то же значение (при оценке в калькуляторе).

---

Поскольку наука очень часто использует натуральный логарифм и поскольку это один из двух логарифмов, которые могут вычислять калькуляторы, я предпочитаю использовать натуральный логарифм обеих сторон при решении экспоненциальных уравнений. Это (как правило) не требуется, но часто более полезно, чем другие варианты.

---

• Решите 5

  ^x = 212. Дайте ответ в точной форме и в виде десятичного приближения с точностью до трех знаков.

Поскольку 212 не является степенью 5, мне придется использовать журналы для решения этого уравнения. Я мог бы взять логарифм по основанию 5 для каждой стороны, решить, а затем применить формулу изменения базы, но я думаю, что лучше просто использовать естественный логарифм в первую очередь:

5 ^x = 212

ln (5 ^x ) = ln (212)

x · ln (5) = ln (212)

x = ln (212) / ln (5)

…или около 3,328 с округлением до трех десятичных знаков.

---

Поскольку 52 — это не степень 10, мне придется использовать журналы, чтобы решить эту проблему. В данном конкретном случае, поскольку база равна 10 и поскольку на калькуляторе можно вести журналы по основанию 10, я буду использовать общий журнал вместо натурального журнала для решения этого конкретного уравнения:

10 ^{2 x} = 52

журнал (10 ^{2 x} ) = журнал (52)

2 x · журнал (10) = журнал (52)

2 x (1) = журнал (52)

2 x = журнал (52)

x = ^{журнал (52)} / ₂

…или около 0,858 с округлением до трех десятичных знаков.

---

Прежде чем я смогу начать смотреть на экспоненту, мне сначала нужно избавиться от 3, поэтому я разделю это, чтобы получить:

Поскольку

³⁵⁰ / ₃ не является степенью двойки, мне придется использовать журналы. В этом случае я буду использовать естественный журнал:

…или около 2,866 с округлением до трех десятичных знаков.

---

Примечание. Вы также можете решить указанную выше проблему, используя правила экспоненты, чтобы разделить мощность на 2:

2 ^{x +4} = (2 ^x ) (2 ⁴ ) = (2 ^x ) (16)

Затем разделите на 16 и упростите, чтобы получить:

(2 ^x ) (16) = 350/3 2 ^x = 350 / (3 · 16) = 175/24

Затем бревно с каждой стороны.Вы получите ответ в виде:

Когда вы оцените это, вы получите тот же десятичный эквивалент 2,866 в своем калькуляторе. Не стесняйтесь проявлять гибкость!

---

URL: https://www.purplemath.com/modules/simpexpo2.htm

логарифм | Правила, примеры и формулы

Логарифм , показатель степени или степень, до которой необходимо возвести основание, чтобы получить данное число.Выражаясь математически, x — это логарифм от n до основания b , если b ^x = n , и в этом случае записывается x = log _b n . Например, 2 ³ = 8; следовательно, 3 — это логарифм 8 с основанием 2, или 3 = log ₂ 8. Таким же образом, поскольку 10 ² = 100, тогда 2 = log ₁₀ 100. Логарифмы последнего вида (что То есть логарифмы с основанием 10) называются обычными, или бриггсовскими, логарифмами и записываются просто log n .

Логарифмы, изобретенные в 17 веке для ускорения вычислений, значительно сократили время, необходимое для умножения чисел на многозначные числа. Они были основой численной работы более 300 лет, пока совершенствование механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделало их устаревшими для крупномасштабных вычислений. Натуральный логарифм (с основанием e 2,71828 и записанным ln n ), тем не менее, продолжает оставаться одной из наиболее полезных функций в математике с приложениями к математическим моделям во всех физических и биологических науках.

Свойства логарифмов

Логарифмы

были быстро приняты учеными из-за различных полезных свойств, которые упростили долгие и утомительные вычисления. В частности, ученые могли найти произведение двух чисел m и n , просмотрев логарифм каждого числа в специальной таблице, сложив логарифмы вместе, а затем снова обратившись к таблице, чтобы найти число с вычисленным логарифмом (известным как его антилогарифм). Выраженное в виде десятичных логарифмов, это соотношение дается логарифмом m n = log m + log n .Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы вместе (5), а затем найдя его антилогарифм (100000) в таблице. Точно так же задачи деления преобразуются в задачи вычитания с логарифмами: log m / n = log m — log n . Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться в качестве основания, поскольку все его степени равны 1), как показано в таблице логарифмических законов.

В таблицы логарифмов обычно включались только логарифмы для чисел от 0 до 10. Чтобы получить логарифм некоторого числа за пределами этого диапазона, число сначала было записано в экспоненциальной форме как произведение его значащих цифр и его экспоненциальной степени — например, 358 будет записано как 3,58 × 10 ² , а 0,0046 будет можно записать как 4,6 × 10 ⁻³ . Тогда логарифм значащих цифр — десятичная дробь от 0 до 1, известная как мантисса, — будет найден в таблице.Например, чтобы найти логарифм 358, нужно найти log 3,58 ≅ 0,55388. Следовательно, журнал 358 = журнал 3,58 + журнал 100 = 0,55388 + 2 = 2,55388. В примере числа с отрицательной экспонентой, например 0,0046, можно найти log 4,6 0,66276. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = −2,33724.

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

История логарифмов

Изобретение логарифмов было предсказано сравнением арифметических и геометрических последовательностей.В геометрической последовательности каждый член образует постоянное отношение со своим последователем; Например, … 1/1000, 1/100, 1/10, 1, 10, 100, 1000… имеет общее отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как общая разница; Например, … −3, −2, −1, 0, 1, 2, 3… имеет общее различие 1. Обратите внимание, что геометрическая последовательность может быть записана в терминах ее общего отношения; для примера геометрической последовательности, приведенной выше: … 10 ⁻³ , 10 ⁻² , 10 ⁻¹ , 10 ⁰ , 10 ¹ , 10 ² , 10 ³ ….Умножение двух чисел в геометрической последовательности, скажем 1/10 и 100, равносильно сложению соответствующих показателей общего отношения, -1 и 2, чтобы получить 10 ¹ = 10. Таким образом, умножение преобразуется в сложение. Первоначальное сравнение двух серий, однако, не было основано на явном использовании экспоненциальной записи; это было более позднее развитие. В 1620 году швейцарский математик Йост Бурджи опубликовал в Праге первую таблицу, основанную на концепции взаимосвязи геометрической и арифметической последовательностей.

Шотландский математик Джон Напьер опубликовал свое открытие логарифмов в 1614 году. Его цель заключалась в том, чтобы помочь в умножении величин, которые тогда назывались синусами. Полный синус был величиной стороны прямоугольного треугольника с большой гипотенузой. (Первоначальная гипотенуза Нэпьера была 10 ⁷ ). Его определение было дано в терминах относительных скоростей.

Логарифм, следовательно, любого синуса — это число, очень точно выражающее линию, которая одинаково увеличивалась за определенное время, в то время как линия всего синуса пропорционально уменьшалась до этого синуса, причем оба движения равны по времени и начало одинаково сдвигается.

В сотрудничестве с английским математиком Генри Бриггсом Нэпьер привел свой логарифм в его современную форму. Для логарифма Напериана сравнение будет происходить между точками, движущимися по градуированной прямой, точка L (для логарифма) равномерно перемещается от минус бесконечности к плюс бесконечности, точка X (для синуса) движется от нуля до бесконечность со скоростью, пропорциональной ее расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице и их скорость в этот момент равна.Суть открытия Напьера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; то есть умножение и возведение в степень значений точки X соответствуют сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L, и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0.Это изменение привело к появлению бриггсовского, или обыкновенного, логарифма.

Нэпьер умер в 1617 году, и Бриггс продолжал работать в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанных с точностью до 14 знаков после запятой для чисел от 1 до 20 000 и от 90 000 до 100 000. В 1628 году голландский издатель Адриан Влак создал 10-местную таблицу для значений от 1 до 100 000, добавив недостающие 70 000 значений. И Бриггс, и Влакк занимались настройкой тригонометрических таблиц журнала. Такие ранние таблицы были либо с точностью до одной сотой градуса, либо до одной угловой минуты.В 18 веке таблицы публиковались с интервалом в 10 секунд, что было удобно для таблиц с семью знаками после запятой. Как правило, более мелкие интервалы требуются для вычисления логарифмических функций меньших чисел — например, при вычислении функций log sin x и log tan x .

Наличие логарифмов сильно повлияло на форму плоской и сферической тригонометрии. Процедуры тригонометрии были переработаны для создания формул, в которых все операции, зависящие от логарифмов, выполняются одновременно.Тогда обращение к таблицам состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.

Фрэнсис Дж. Мюррей

Узнайте больше в этих связанных статьях Britannica:

Алгебра — логарифмические функции

Показать мобильное уведомление Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 6-2: Логарифмические функции

В этом разделе нам нужно перейти к функциям логарифмирования.Это может быть непростая функция для построения графика сразу. Будет несколько других обозначений, к которым вы не привыкли, и некоторые свойства могут быть не такими интуитивно понятными. Однако не расстраивайтесь. Как только вы разберетесь с ними, вы обнаружите, что они на самом деле не так уж и плохи, и обычно требуется немного поработать с ними, чтобы разобраться в них.

Вот определение функции логарифма.

Если \ (b \) — любое число такое, что \ (b> 0 \) и \ (b \ ne 1 \) и \ (x> 0 \), то

\ [y = {\ log _b} x \ hspace {0.y} = x \) называется экспоненциальной формой .

Обратите внимание, что требование \ (x> 0 \) на самом деле является результатом того факта, что мы также требуем \ (b> 0 \). Если подумать, это будет иметь смысл. Мы возводим положительное число в степень, и поэтому результат не может быть чем-то другим, кроме другого положительного числа. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.

Теперь давайте обратимся к используемым здесь обозначениям, так как это обычно самое большое препятствие, которое студенты должны преодолеть, прежде чем начать понимать логарифмы.Во-первых, «журнал» функции — это просто три буквы, которые используются для обозначения того факта, что мы имеем дело с логарифмом. Они не переменные и не означают умножения. Они просто говорят нам, что мы имеем дело с логарифмом.

Далее, \ (b \), стоящий в нижнем индексе в части «журнала», указывает нам, что такое основание, поскольку это важная часть информации. Кроме того, несмотря на то, как это может выглядеть, в приведенной выше форме логарифма нет возведения в степень.x} \) в этой форме, но это не так. Похоже, что это могло быть именно так.

Важно, чтобы запись логарифмов была прямой, иначе вам будет очень трудно понять их и работать с ними.

Теперь давайте кратко рассмотрим, как мы вычисляем логарифмы.

Пример 1 Вычислите каждый из следующих логарифмов.

1. \ ({\ log _4} 16 \)
2. \ ({\ log _2} 16 \)
3. \ ({\ log _6} 216 \)
4. \ (\ displaystyle {\ log _5} \ frac {1} {{125}} \)
5. \ ({\ log _ {\ frac {1} {3}}} 81 \)
6. \ ({\ log _ {\ frac {3} {2}}} \ displaystyle \ frac {{27}} {8} \)

Показать все решения Скрыть все решения Показать обсуждение

Теперь реальность такова, что непосредственное вычисление логарифмов может быть очень сложным процессом даже для тех, кто действительно их понимает.Обычно гораздо проще сначала преобразовать форму логарифма в экспоненциальную форму. В такой форме мы обычно можем получить ответ довольно быстро.

a \ ({\ log _4} 16 \) Показать решение

Хорошо, мы действительно спрашиваем вот о чем.

\ [{\ log _4} 16 =? \]

Как было предложено выше, давайте преобразуем это в экспоненциальную форму.

\ [{\ log _4} 16 =? \ hspace {0,25 дюйма} \ Rightarrow {\ mbox {}} \ hspace {0.4} \), и т. Д. , пока вы не получите 16. В этом случае нам нужен показатель степени 4. Следовательно, значение этого логарифма равно

\ [{\ log _2} 16 = 4 \]

Прежде чем перейти к следующей части, обратите внимание, что их основа является очень важной частью обозначений. Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.

c \ ({\ log _6} 216 \) Показать решение

Мы сделаем это без каких-либо реальных объяснений, чтобы увидеть, насколько хорошо вы вычислили логарифмы.3}}} = \ frac {{27}} {8} \]

Надеюсь, теперь у вас есть представление о том, как вычислять логарифмы, и вы начинаете понимать систему обозначений. Однако есть еще несколько вычислений, которые мы хотим сделать, нам нужно ввести некоторые специальные логарифмы, которые появляются на очень регулярной основе. Это десятичный логарифм и натуральный логарифм . Вот определения и обозначения, которые мы будем использовать для этих двух логарифмов.

\ [\ begin {align *} & {\ mbox {десятичный логарифм:}} \ hspace {0.25 дюймов} \ log x = {\ log _ {10}} x \\ & {\ mbox {натуральный логарифм:}} \ hspace {0,25 дюйма} \ ln x = {\ log _ {\ bf {e}}} x \ конец {выравнивание *} \]

Итак, десятичный логарифм — это просто логарифм по основанию 10, за исключением того, что мы отбрасываем часть обозначения с основанием 10. Точно так же натуральный логарифм — это просто логарифм \ (\ bf {e} \) с другим обозначением, и где \ (\ bf {e} \) — это то же число, которое мы видели в предыдущем разделе, и определяется как \ ({\ bf {e}} = 2,718281828 \ ldots \).

Давайте взглянем на еще пару оценок.

Пример 2 Вычислите каждый из следующих логарифмов.

1. \ (\ лог 1000 \)
2. \ (\ log \ displaystyle \ frac {1} {{100}} \)
3. \ (\ ln \ displaystyle \ frac {1} {{\ bf {e}}} \)
4. \ (\ ln \ sqrt {\ bf {e}} \)
5. \ ({\ log _ {34}} 34 \)
6. \ ({\ log _8} 1 \)

Показать все решения Скрыть все решения Показать обсуждение

Для выполнения первых четырех оценок нам просто нужно запомнить, каковы их обозначения и какое основание подразумевается в этих обозначениях.0} = 1 \). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.

Итак, при вычислении логарифмов все, что мы действительно спрашиваем, — это какой показатель степени мы положили на основание, чтобы получить число в логарифме.

Теперь, прежде чем мы перейдем к некоторым свойствам логарифмов, давайте сначала сделаем пару быстрых графиков.

Пример 3 Нарисуйте график десятичного и натурального логарифма на одной и той же системе координат.Показать решение

В этом примере есть две точки. Во-первых, он познакомит нас с графиками двух логарифмов, которые мы, скорее всего, увидим в других классах. Кроме того, это даст нам некоторую практику использования нашего калькулятора для вычисления этих логарифмов, потому что на самом деле именно так нам нужно будет проводить большую часть этих вычислений.

Вот таблица значений двух логарифмов.

}} = 1.20

5512 \]

Итак, мы получили один и тот же ответ, несмотря на то, что дроби содержали разные ответы.

Это закон, тоже законы логарифмов

Его закон, так и законы логарифмов

Авторские права 20022020 Стэн Браун

Резюме: У вас проблемы с запоминанием законов логарифмов? Делать вы знаете, почему вы можете изменить log (x) + log (y) на другую форму, но не журнал (x + y)? Эта страница поможет вам разобраться в законах логарифмы.

См. Также: Все законы логарифмов текут прямо из законов экспонент . Если ты чувствуешь себя немного неустойчивый с законами экспонент, просмотрите их перед тем, как продолжить.

---

Логарифм? Что такое логарифм?

Логарифм — это просто показатель степени.

Чтобы быть конкретным, логарифм числа x по основанию b это просто показатель степени, который вы положили на b , чтобы получить результат равно x .Например, поскольку 5 = 25, мы знаем, что 2 ( степень) — это логарифм 25 с основанием 5. Символически, журнал ₅ (25) = 2.

В более общем смысле, если x = b ^y , то мы скажем, что y — это логарифм x с основанием b или основание — b логарифм x . В символах y = log _b ( x ), часто пишется без скобок, y = бревно _b x .Каждое экспоненциальное уравнение можно переписать в виде логарифмического уравнения: и наоборот, просто поменяв местами x и y этим способом.

Вы нечасто видите это слово, но можете также говорят, что x — это антилогарифм из y к база б . Логарифм — это показатель степени, а антилогарифм — результат возведения основания в этот показатель.

Еще один способ взглянуть на это: журнал _b x функция определяется как обратная b ^x функция.Эти два утверждения выражают это обратное соотношение, показывающее, как экспоненциальное уравнение эквивалентно логарифмическому уравнению:

x = b ^y такой же как y = бревно _b x

В любом уравнении x — антилогарифм и y — логарифм, по основанию b .

Пример 1: 1000 = 10 ³ то же, что и 3 = журнал ₁₀ 1000.Логарифм равен 3, а антилогарифм равен 1000.

Пример 2: журнал ₃ 81 =? та же как 3 ^? = 81. Неизвестный ? — логарифм, а 81 — антилогарифм.

Нельзя сказать слишком часто: логарифм — это не что иное, как показатель степени. Вы можете написать приведенное выше определение компактно, и показать журнал как экспоненту, подставив второе уравнение в первое, чтобы исключить y :

Прочтите это как логарифм x по основанию b — это экспонента, которую вы положили на b , чтобы получить в результате x .

Откуда взялись журналы?

Раньше карманные калькуляторы несколько десятилетий назад, но в Студенческие годы вот и возраст динозавровответ было просто. Вам нужны журналы для вычисления большинства мощностей и корней с честным точность; даже умножение и деление большинства чисел было проще с журналами. В каждой приличной книге по алгебре были страницы и страницы журнальных таблиц на спина.

Изобретение бревен в начале 1600-х годов послужило толчком для научных революция. Тогда ученые, особенно астрономы, тратили огромные суммы чисел на бумаге.Сокращая время, которое они тратили на арифметические, логарифмы эффективно давали им более продуктивную жизнь. Логарифмическая линейка, когда-то почти мультяшный товарный знак ученого, был не чем иным, как устройством, созданным для выполнения различных вычислений быстро, используя логарифмы. См. Eli Maors e: The Story of a Number для получения дополнительной информации. это.

Сегодня журналы больше не используются в рутинной обработке чисел. Но все же есть веские причины для их изучения.

Почему нам не все равно?

Почему мы вообще используем логарифмы? Я мог бы написать целую статью о них может быть когда-нибудь.Но сейчас. …

• Узнать количество платежей на заем или время для получения инвестиционная цель.
• Для моделирования многих природных процессов, особенно в живых системах. Мы воспринимаем громкость звука как логарифм реального звука. интенсивность, а дБ (децибелы) — логарифмическая шкала. Мы также воспринимаем яркость света как логарифм действительной световой энергии, и звездные величины измеряются в логарифмической шкале.
• Для измерения pH или кислотности химического раствора.PH — это отрицательный логарифм концентрации свободных ионы водорода.
• Для измерения силы землетрясений по шкале Рихтера.
• Для анализа экспоненциальных процессов. Поскольку функция журнала является обратной экспоненциальной функции, мы часто анализируем экспоненциальную кривую с помощью логарифмы. Нанесение набора измеренных точек на бревенчатый или полубортовый лист может легко выявить такие отношения. Применения включают охлаждение мертвого тела, рост бактерий, и распад радиоактивных изотопов.Распространение эпидемии среди населения часто следует за измененным логарифмическая кривая называется логистической.
• Для решения некоторых форм задач с площадью в исчислении. (Площадь под кривой 1/ x , между x = 1 и x = A , равна ln A .)
• Также в расчетах дифференциация сложного продукта становится намного проще, если вы сначала возьмете логарифм.

(Исторически основная причина преподавания журналы в начальной школе было для упрощения вычислений, потому что журнал умножения понижает его до прибавления, а журнал мощности выражение понижает его до умножения.Конечно, с повсеместной доступностью персональных вычислительных устройств, сложность вычислений больше не вызывает беспокойства, но в журналах все еще есть многие приложения сами по себе.)

---

Основные факты

Из определения бревна как инверсии экспоненциально, можно сразу получить некоторые основные факты. Например, если вы построите график y = 10 ^x (или экспоненту с любым другим положительным основанием), вы увидеть, что его диапазон положительный реал; поэтому область y = log x (по любому основанию) — положительные числа.В другом слова, вы не можете взять журнал 0 или журнал отрицательного числа.

(На самом деле, если вы хотите выйти за рамки реалов, вы можете взять журнал отрицательного числа. Этой технике обучают на многих курсах тригонометрии.)

логарифм 1, лог равен 1

\ (х \)	\ (\ журнал x \)	\ (\ ln x \)
\ (\ frac {1} {2} \)	-0.3010	-0,6931
1	0	0
2	0,3010	0,6931
3	0,4771	1.0986
4	0.r}} \ right) = r {\ log _b} x \) Если \ ({\ log _b} x = {\ log _b} y \), то \ (x = y \). Мы не будем ничего делать с последним свойством в этом разделе; это здесь только для полноты картины. Мы подробно рассмотрим это свойство в нескольких разделах. Первые два перечисленных здесь свойства могут поначалу немного сбивать с толку, поскольку с одной стороны у нас есть произведение или частное внутри логарифма, а с другой стороны — сумма или разность двух логарифмов.Нам просто нужно быть осторожными с этими свойствами и обязательно использовать их правильно. Также обратите внимание, что нет никаких правил, как разбить логарифм суммы или разности двух членов. Чтобы прояснить это, отметим следующее: \ [\ begin {align *} {\ log _b} \ left ({x + y} \ right) & \ ne {\ log _b} x + {\ log _b} y \\ {\ log _b} \ left ( {x — y} \ right) & \ ne {\ log _b} x — {\ log _b} y \ end {align *} \] Будьте осторожны с ними и не пытайтесь использовать их, поскольку они просто не соответствуют действительности. 5}} \ right) \] Теперь, когда мы это сделали, мы можем использовать свойство 7 для каждого из этих отдельных логарифмов, чтобы получить окончательный упрощенный ответ.{\ frac {1} {2}}} \] В этой форме мы видим, что у всего члена есть один показатель степени, поэтому мы позаботимся об этом в первую очередь. \ [\ ln \ sqrt {xy} = \ frac {1} {2} \ ln \ left ({xy} \ right) \] Теперь займемся продуктом. \ [\ ln \ sqrt {xy} = \ frac {1} {2} \ left ({\ ln x + \ ln y} \ right) \] Обратите внимание на круглые скобки в этом ответе. \ (\ Frac {1} {2} \) умножает исходный логарифм, поэтому ему также потребуется умножить весь «упрощенный» логарифм.2}} \ справа) \] Теперь мы подошли к сути этой проблемы. Второй логарифм настолько упрощен, насколько это возможно. Помните, что мы не можем разбить журнал суммы или разницы, и поэтому он не может быть разбит дальше. Кроме того, мы можем иметь дело с показателями, только если весь член возведен в степень. Тот факт, что обе части этого члена возведены в квадрат, не имеет значения. Это должен быть квадрат целого члена, как в первом логарифме. Итак, мы можем еще больше упростить первый логарифм, но второй логарифм упростить уже нельзя.2}} \ справа) \] Теперь нам нужно проработать несколько других примеров. Этот следующий набор примеров, вероятно, более важен, чем предыдущий. Мы будем проделывать такую ​​логарифмическую работу в нескольких разделах. Пример 5 Запишите каждое из следующих значений в виде одного логарифма с коэффициентом 1. \ (7 {\ log _ {12}} x + 2 {\ log _ {12}} y \) \ (3 \ логарифм х — 6 \ логарифм у \) \ (5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x \) Показать все решения Скрыть все решения Показать обсуждение Инструкция, требующая коэффициента 1, означает, что когда мы переходим к окончательному логарифму, перед логарифмом не должно быть числа. Также обратите внимание, что в этих примерах будут использоваться свойства 5–7, только мы будем использовать их в обратном порядке. У нас будут выражения, которые выглядят как правая часть свойства, и мы будем использовать свойство для записи, чтобы оно выглядело как левая часть свойства. a \ (7 {\ log _ {12}} x + 2 {\ log _ {12}} y \) Показать решение Первый шаг — избавиться от коэффициентов при логарифмах. Это будет использовать свойство 7 в обратном порядке.6}}}} \ справа) \] c \ (5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x \) Показать решение В этом случае у нас есть три термина, и ни одно из свойств не содержит трех терминов. Это не проблема. Давайте сначала позаботимся о коэффициентах, а заодно вычтем минус из двух последних членов. Причина этого станет очевидной на следующем шаге. \ [5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x = \ ln {\ left ({x + y} \ right) ^ 5} — \ left ({\ ln {y ^ 2} + \ ln {x ^ 8}} \ right) \] Теперь обратите внимание, что количество в скобках представляет собой сумму двух логарифмов и поэтому может быть объединено в один логарифм с произведением следующим образом: \ [5 \ ln \ left ({x + y} \ right) — 2 \ ln y — 8 \ ln x = \ ln {\ left ({x + y} \ right) ^ 5} — \ ln \ left ( {{y ^ 2} {x ^ 8}} \ right) \] Теперь у нас осталось два логарифма, и они представляют собой разность логарифмов, и поэтому мы можем записать это как единственный логарифм с частным.8}}}} \ справа) \] Последняя тема, которую нам нужно обсудить в этом разделе, — это изменение формулы базы . Большинство современных калькуляторов могут вычислять десятичные и натуральные логарифмы. Однако это все, так что же нам делать, если нам нужно вычислить еще один логарифм, что не может быть сделано легко, как мы это сделали в первом наборе примеров, которые мы рассмотрели? Для этого у нас есть изменение базовой формулы.Вот изменение базовой формулы. \ [{\ log _a} x = \ frac {{{{\ log} _b} x}} {{{{\ log} _b} a}} \] , где мы можем выбрать \ (b \) как угодно. Чтобы использовать это, чтобы помочь нам вычислить логарифмы, это обычно обычный или натуральный логарифм. Вот изменение базовой формулы с использованием как десятичного, так и натурального логарифма. \ [{\ log _a} x = \ frac {{\ log x}} {{\ log a}} \ hspace {0,25 дюйма} {\ log _a} x = \ frac {{\ ln x}} {{\ ln a}} \] Давайте посмотрим, как это работает, на примере.?} = 7 \] , и это не то, на что кто-то может ответить сразу. Если бы 7 была 5, или 25, или 125, и т. Д. . мы могли бы это сделать, но это не так. Следовательно, мы должны использовать замену базовой формулы. Теперь мы можем использовать любой из них, и мы получим тот же ответ. Итак, давайте воспользуемся обоими и проверим это. Начнем с десятичного логарифма изменения основания. \ [{\ log _5} 7 = \ frac {{\ log 7}} {{\ log 5}} = \ frac {{0.845098040014}} {{0.698970004336}} = 1.20 5512 \] Теперь давайте попробуем натуральный логарифм изменения основной формулы. \ [{\ log _5} 7 = \ frac {{\ ln 7}} {{\ ln 5}} = \ frac {{1.945906}} {{1.609437

Вы знаете, что значение нулевой степени равно 1: b 0 = 1. Измените это на логарифмическую форму с определением журналов, и у вас будет
	log b 1 = 0 для любого основания b
Точно так же вы знаете, что первая степень любого числа — это именно это число: b 1 = b .Опять же, переведите это в логарифмическую форму, и вы получите
	журнал b b = 1 для любой базы b

Пример 3: ln 1 = 0

Пример 4: журнал ₅ 5 = 1

Записать как обратное

Журнал — это показатель степени, потому что функция журнала — это обратная экспоненциальной функции. Обратная функция отменяет действие исходной функции.(Я не большой поклонник большинства применений термина «отмена» в математике, но он вписываются в эту ситуацию.)

Это означает, что если вы возьмете логарифм экспоненты (конечно, с той же базой), вы вернетесь туда, откуда начали:
	log b b x = x для любого основания b
Этот факт позволяет вычислять многие логарифмы без калькулятора.

Пример 5: журнал ₅ 125 = журнал ₅ (5) = 3

Пример 6: журнал ₁₀ 10 ^3,16 = 3,16

Пример 7: ln e ^{— k t /2} = — k t /2

Что такое ln?

В качестве основания логарифмов подходит любое положительное число, но две базы используются больше, чем любые другие:

основание из логарифмов	символ	имя
10	журнал (если основание не показано)	десятичный логарифм
e	пер.	натуральный логарифм, произносится как ell-enn или lahn

Натуральные бревна — это бревна и следуют тем же правилам, что и любой другой логарифм.Просто помните:
	ln x означает журнал e x

Почему base e? Что такого особенного в е? Большинство объяснений требует некоторого исчисления, например, что e ^x — единственная функция, которая является самостоятельной и его собственная производная, или что е имеет это красивое определение в условия факториалов:

е = 1/0! + 1/1! + 1/2! + 1/3! + …

В числовом выражении e около 2.7182818284. Его иррациональное (десятичное расширение никогда не заканчивается и никогда не повторяется), и на самом деле, как и π, его трансцендентный (ни одно полиномиальное уравнение с целыми коэффициентами не имеет π или e как корень.)

e (например, π) встречается во всевозможных маловероятные места, такие как вычисления сложных процентов. Для объяснения потребовалась бы книга, и к счастью, — это книга, Эли Маорс e: История одного Номер . Он также занимается историей логарифмов, и книга стоит взять из вашей библиотеки.

---

Объединение журналов с одной и той же базой

Через минуту посмотрите на различные комбинации. Но сначала ты может захотеть узнать общий принцип: журналов сокращают количество операций на один уровень. Журналы превращают умножение в сложение, деление на вычитание, показатель степени на умножение и радикальное разделение. Теперь давайте разберемся, почему, и рассмотрим несколько примеров.

Умножение чисел, складывание их логарифмов

Умножение двух выражений соответствует сложению их логарифмов.Можем ли мы понять это?

y у нас есть две степени одной и той же базы.Если степени равны, то и показатели степени также должны быть равны. Следовательно,

По компактному определению
	x = b log b x и y = b log b y
и, следовательно, замена на x и y ,
	x y = b log b x b log b y
Но когда вы умножаете две степени , вы добавляете их показатели.Таким образом, правая часть становится
	x y = b log b x + log b y
Теперь примените компактное определение к левой = стороны:
	b log b ( x y ) = x y
Объедините это с предыдущим уравнением, чтобы получить
	b журнал b ( x y ) = b журнал b x + журнал b y
	лог b ( x y ) = лог b x + лог b y

Итак, что в итоге? Умножая два числа и беря log — это то же самое, что брать их логи и добавлять.

Пример 8: журнал ₈ ( x ) + журнал ₈ ( x ) то же самое, что журнал ₈ ( x x ) или просто журнал ₈ ( x ).(Как вы увидите в следующем разделе, это может быть далее упрощено до 3log ₈ x .)

Пример 9: журнал ₁₀ (20) + журнал ₁₀ (50) = журнал ₁₀ (2050) = журнал ₁₀ (1000) = 3.

Показатель степени, умножить логарифм

Продолжая нашу тему логарифмов, снижая уровень операций, если у вас есть y -я степень числа и взять log, результат будет в y раз больше log числа.Вот почему, начиная с x ^y :

Если мощности 9090 равны и основания равны, экспоненты должны быть равны:

Начнем с компактного определения логарифма:
	x = b log b x
и поднимите обе стороны до y power:
	x y = ( b log b x ) y
Степень эквивалентна простому умножению экспонент.Упростите правую часть:
	x y = b ( y log b x )
Перепишите левую часть, используя компактное определение журнала:
	b log b ( x y ) = x y
(шрифт может быть трудночитаемым: это x до степени y слева и справа.) и объедините последние два уравнения:
	b log b ( x y ) = b ( y log b x )
	журнал b ( x y ) = y журнал b x

Пример 10: ln (2 ⁶ ) = 6 ln 2 (где ln означает log _e , естественное логарифм).

Пример 11: log ₅ (5 x ) не равно 2 журнала ₅ (5 x ). Будьте внимательны с порядком действий! 5 x равно 5 ( x ), а не (5 x ). log ₅ (5 x ) необходимо сначала разложить как бревно товара: журнал ₅ 5 + журнал ₅ ( x ). Тогда второй член может использовать правило мощности, журнал ₅ ( x ) = 2 журнала ₅ x .Первый член всего 1. Подводя итоги, журнал ₅ (5 x ) = 1 + 2 журнала ₅ x .

Возведение чисел в любую степень

Уловка для вычисления таких выражений, как 6,7 ^4,4 , заключается в использовать правило экспоненты и определение логарифма как обратного:

х = 6,7 ^4,4

журнал x = 4,4 (журнал 6,7) = около 3,634729132

x = 10 ^{3,63472 …} = около 4312,5

Здесь нет ничего особенного в журналах base-10.В расчет может быть также

х = 6,7 ^4,4

ln x = 4,4 (ln 6,7) = примерно 8,369 273116

x = e ^{8,36927 …} = около 4312,5

Это будет работать для любого положительного основания и любого реального показателя степени, поэтому например

х = π ^π

журнал x = π (журнал π) = примерно 1,561842388

x = 10 ^{1,5618 …} = около 36,46215961

Вы можете комбинировать это с умножение чисел = добавление правила логарифма к оцените возможности, которые слишком велики для вашего калькулятора.Например, что такое 671 ²¹⁷ ?

х = 671 ²¹⁷

журнал x = 217 (журнал 671) = около 613,3987869

Теперь разделите целую и дробную части логарифм.

журнал x = около 0,3987869 + 613

х = 10 ^{0,3987869 + 613}

х = 10 ^0,3987869 10 ⁶¹³

x = около 2,505 10 ⁶¹³

Для таких примеров вам действительно нужно использовать base-10 журналы.

Если основание отрицательное или показатель сложный, см. Силы и корни комплексного числа.

Разделить числа, вычесть их логарифмы

Так как деление противоположно умножению, а вычитание противоположность сложения, неудивительно, что деление двух выражения соответствует вычитанию их журналов. Пока мы могли пойти вернемся к компактному определению, его вероятно, проще использовать два предыдущих свойства.

Начнем с того, что 1/ y = y −1 (см. Определение отрицательных показателей):
	x / y = x (1/ y ) = x y −1
и возьмите бревно с обеих сторон:
	журнал b ( x / y ) = журнал b ( x y −1 )
Правая сторона — журнал продукта , которая становится суммой журналов:
	log b ( x / y ) = log b x + log b ( y −1 )
и второй член логарифм степени, которая становится (-1) умноженной на логарифм или просто минус логарифм:
	журнал b ( x / y ) = журнал b x — журнал b y

Словами, если разделить и взять журнал , это то же самое, что и вычитая отдельные журналы.

Пример 12: 67515 = 45, поэтому журнал ₁₀ 675 — журнал ₁₀ 15 = log ₁₀ 45. (Попробуйте на своем калькуляторе!)

Пример 13: журнал ( x y ) — журнал ( x y ) = журнал ( x y / x y ) = журнал ( x / y ) = log ( x ) — журнал ( y ).

---

Замена базы

Теперь у вас есть все необходимое для изменения логарифмов с единицы база к другому.Посмотрите еще раз на компакт уравнение, определяющее логарифм с основанием b :

Чтобы изменить журнал с базы b на другую базу (назовите его a ), вы хотите найти журнал a ( x ). Поскольку у вас уже есть x на одной стороне приведенного выше уравнения, кажется, что хорошее начало — взять основание — , бревно с обеих сторон:
	log a ( b log b x ) = log a x
Но левая часть этого уравнения — это просто журнал власти.Вы помните, что журнал ( x y ) — это просто log ( x ), умноженный на y . Таким образом, уравнение упрощается до
	(журнал a b ) (журнал b x ) = журнал a x

Обратите внимание, что журнал _a 9 b постоянный. Этот означает, что журналы всех чисел в данной базе a пропорционально логам тех же чисел в другой базе б , а константа пропорциональности log _a b равна журнал одной базы в другой базе.Если вы похожи на меня, у вас могут быть проблемы с запоминанием умножать или делить. Если да, просто выведите уравнение, как видите, занимает всего два шага.

В некоторых учебниках формула замены базы представлена ​​в виде дроби. Чтобы получить дробь из приведенного выше уравнения, просто разделите на коэффициент пропорциональности log a b :
	журнал b x = (журнал a x ) / (журнал a b )

Пример 14: журнал ₄ 16 = (журнал 16) / (журнал 4).(Вы можете проверить это на своем калькуляторе, так как вы знать журнал ₄ 16 должно быть равно 2.)

Пример 15: Большинство калькуляторов не могут строить графики y = бревно ₃ x напрямую. Но вы можете изменить базу на e и легко построить график y = (ln x ) (ln 3). (Вы могли одинаково хорошо используйте базу 10.)

Из приведенной выше формулы ведет интересный переулок. Замените x везде на a , это допустимо, поскольку формула верна для всех положительных значений a , b и x .Получаете
	лог b a = (лог a a ) / (лог a b )
Но лог a a (см. Журнал 1 выше), поэтому формула принимает вид
	журнал b a = 1 / (журнал a b )

Пример 16: журнал ₁₀ e = 1 / (ln 10).(Вы можете проверить это на своем калькуляторе.)

Пример 17: журнал ₁₂₅ 5 = 1 / (журнал ₅ 125). В этом легко убедиться: 5 ³ = 125, а 5 — кубический корень из 125. Следовательно, log ₁₂₅ 5 = 1/3 и log ₅ 125 = 3, и 1/3 действительно равно 1/3.

---

Сводка

Законы логарифмов были разбросаны по этому длинному страницу, поэтому было бы полезно собрать их в одном месте. Делать это еще более полезно, , связанный здесь также показаны законы экспонент.

Ради бога, не пытайтесь запомнить эту таблицу! Просто используйте это, чтобы подбросьте свою память по мере необходимости. Еще лучше, поскольку журнал является экспонентой, используйте законы экспонентов, чтобы повторно получить любую собственность логарифмов, которые вы могли забыть. Таким образом, вы действительно получите владение этим материалом, и вы будете чувствовать себя уверенно операции.

показателя степени	логарифма
(Все законы применяются для любых положительных значений a , b , x и y .)
x = b y такой же как y = бревно b x
b 0 = 1	журнал b 1 = 0
b 1 = b	журнал b b = 1
b (лог b x ) = x	бревно b b x = x
b x b y =	бревно b ( x y ) = бревно b x + лог b y
b 8 900 b y = b x — y	бревно b ( x / y ) = бревно b x — лог b y
( b 9 ) y = b x y	бревно b ( x y ) = y бревно b x
	(журнал a b ) (журнал b x ) = журнал a x
	журнал b x = журнал a x ) / (лог a b )
	лог b a = 1 / (лог a b )

Не проявляйте творчества! Большинство вариантов вышеизложенного недействительны.

Пример 18: журнал (5+ x ) не то же самое, что журнал 5 + журнал x . Как вы знаете, журнал 5 + журнал x = журнал (5 x ), а не журнал (5+ x ). Посмотрите внимательно на приведенную выше таблицу, и вы увидите что вы ничего не можете сделать, чтобы разделить журнал ( x + y ) или журнал ( x — y ).

Пример 19: (журнал x ) / (журнал y ) не то же самое, что журнал ( x / y ).В Фактически, когда вы делите два журнала на одну базу, вы обратная работа по формуле замены базы. Хотя это не часто полезно, (журнал x ) / (журнал y ) = журнал _y x . Только не пишите журнал ( x / y )!

Пример 20: (журнал 5) (журнал x ) не является то же, что и журнал (5 x ). Вы знаете, что журнал (5 x ) журнал 5 + журнал x . Ты действительно мало что можешь делать с произведением двух бревен, когда они имеют одинаковую основу.(Вы можете переписать продукт как журнал ( x ^{журнал 5} ), но это вряд ли попроще.)

См. Также: Объединение операций (распределительные законы)

---

Заключение

Ну вот и все: законы логарифмов демистифицировано! Общее правило состоит в том, что журналы просто отбрасывают операцию на один уровень вниз: показатели становятся множителями, деления становятся вычитания и так далее. Если вы когда-нибудь не уверены в операции, например как сменить базу, работа это с помощью определения журнала и применяя законы экспонент, и вы не ошибетесь.

Что нового

• 7 декабря 2020 г. :
• 20/23 октября 2020 : страница преобразована из HTM 4.01 в HTML 5 и заменил устаревшие теги на CSS. К этому примеру добавлено небольшое предзнаменование.
• 17 августа 2015 г. : перемещено с OakRoadSystems.com на BrownMath.com.
• (промежуточные изменения подавлены)
• 11 января 1998 г .: адаптировать эту статью для Интернета
• 22 декабря 1997 г .: Опубликовать в alt.algebra.help.

Использование логарифмов в реальном мире — лучшее объяснение

Логарифмы везде.Вы когда-нибудь использовали следующие фразы?

• 6 цифр
• Двузначные цифры
• По порядку величины
• Процентная ставка

Вы описываете числа в терминах степени 10, логарифма. А процентная ставка — это логарифм роста инвестиций.

Удивлены, что логарифмы так распространены? Я тоже. Большинство попыток Math In the Real World ™ указывают на логарифмы в какой-то загадочной формуле или делают вид, что мы геологи увлечены шкалой Рихтера.«Ученые заботятся о бревнах, и вы должны тоже. Кроме того, можете ли вы представить мир без цинка?»

Нет, нет, нет, нет, нет, нет! (Мама миа!)

Math выражает концепции с помощью таких обозначений, как «ln» или «log». Найти «математику в реальном мире» означает встретить идеи в жизни и увидеть, как они могут быть записаны с обозначениями. Не ищите буквальных символов! Когда вы в последний раз писали знак деления? Когда вы в последний раз нарезали еду?

Хорошо, хорошо, мы поняли: что такое логарифмы?

Логарифмы находят причину следствия, т.е.e вход для некоторого выхода

Обычный «эффект» — это рост чего-то, например, переход от \ $ 100 до \ $ 150 за 5 лет. Как это случилось? Мы не уверены, но логарифм находит возможную причину: постоянный возврат ln (150/100) / 5 = 8,1% будет учитывать это изменение. Возможно, это не настоящая причина (весь ли рост произошел в последний год?), Но это плавное среднее значение, которое мы можем сравнить с другими изменениями.

Кстати, понятие «причина и следствие» имеет нюансы.Почему 1000 больше 100?

• 100 — это 10, которые выросли сами по себе за 2 периода времени (10 долларов * 10 долларов)
• 1000 — 10, которые выросли сами по себе за 3 периода (10 * 10 * 10 $)

Мы можем думать о числах как о выходах (1000 — это «1000 выходов») и входах («Во сколько раз нужно вырасти 10, чтобы получить эти выходы?»). Итак,

  1000 выходов> 100 выходов
  

потому что

  3 входа> 2 входа
  

Или другими словами:

  журнал (1000)> журнал (100)
  

Почему это полезно?

Логарифмы помещают числа в удобную для человека шкалу.80 $ = количество молекул во Вселенной

Шкала от 0 до 80 перевела нас от одного объекта к количеству объектов во Вселенной. Не слишком потрепанный.

Логарифмы считают умножение как шаги

Логарифмы описывают изменения в терминах умножения: в приведенных выше примерах каждый шаг в 10 раз больше. С натуральным логарифмом каждый шаг в «е» (2,71828 …) раз больше.

Имея дело с серией умножений, логарифмы помогают «подсчитать» их, точно так же, как для нас считается сложение, когда добавляются эффекты.

Покажи мне математику

Время для мяса: посмотрим, где появятся логарифмы!

Шестизначная зарплата или двузначные расходы

Мы описываем числа с точки зрения их цифр, то есть сколько у них степеней десяти (десятки, сотни, тысячи, десятки тысяч и т. 5 $) и 100000 получаем результат из 6 цифр.Говорить о «6» вместо «Сто тысяч» — это суть логарифмов. Это дает приблизительное ощущение масштаба, не вдаваясь в детали.

Бонусный вопрос: как бы вы описали 500 000? Сказать «шестизначный» вводит в заблуждение, потому что шестизначное число часто означает что-то ближе к 100000. Подойдет ли «6.5 фигура»?

Не совсем. В нашей голове 6.5 означает «половину» между 6 и 7 цифрами, но это мышление сумматора. В логарифмах «.5» означает половину умножения, т.е..5 $ означает, что квадратный корень из 9 — 3 равен половине умножения, потому что он 1 к 3 и 3 к 9).

Взяв логарифм (500 000), мы получим 5,7, прибавим 1 к дополнительной цифре, и мы можем сказать, что «500 000 — это число из 6,7 цифр». Попробуйте здесь:

По порядку величины

Мы, фанаты, любим эту фразу. Это означает примерно «10-кратную разницу», но просто звучит круче, чем «на 1 цифру больше».

В компьютерах, где все считается битами (1 или 0), каждый бит имеет эффект удвоения (не 10x).16 $ ~ 65 536 раз больше памяти, которую можно адресовать.

Процентные ставки

Как определить темпы роста? Страна не намерена расти на 8,56% в год. Вы смотрите на ВВП в один год и на ВВП в следующий и берете логарифм, чтобы найти неявный темп роста , равный .

Две мои любимые интерпретации натурального логарифма (ln (x)), то есть натурального логарифма 1,5:

• Предполагая 100% рост, сколько времени вам нужно, чтобы достичь 1.5? (.405, меньше половины периода времени)
• Принимая 1 единицу времени, как быстро вам нужно вырасти до 1,5? (40,5% в год, непрерывно начисляется)

Логарифмы — это то, как мы определяем, насколько быстро мы растем.

Шкала измерения: Google PageRank

Google присваивает каждой странице в Интернете оценку (PageRank), которая является приблизительной мерой авторитета / важности. Это логарифмическая шкала, которая в моей голове означает «PageRank подсчитывает количество цифр в вашей оценке».4 $ = 10000).

Грубо говоря, у меня бывает около 7000 посещений в день. Используя свои математические вычисления, я могу предположить, что CNN получает около 7000 * 10 000 = 70 миллионов посещений в день. (Как я это сделал? В голове я думаю, что $ 7k * 10k = 70 * k * k = 70 * M $). У них может быть в несколько раз больше (100M, 200M), но, вероятно, не до 700M.

Google передает много информации с очень приблизительной шкалой (1-10).

Шкала измерения: Рихтер, децибел и т. Д.

Вздох. Мы находимся в типичном примере «логарифмов из реального мира»: шкале Рихтера и децибелах.Идея состоит в том, чтобы поместить события, которые могут сильно различаться (землетрясения), в единую шкалу с небольшим диапазоном (обычно от 1 до 10). Как и в случае с PageRank, каждое увеличение на 1 пункт означает 10-кратное повышение мощности. Самое сильное землетрясение, зарегистрированное людьми, составило 9,5 баллов; Удар на полуострове Юкатан, который, вероятно, привел к вымиранию динозавров, составил 13.

Децибелы аналогичны, но могут быть отрицательными. Звуки могут варьироваться от очень тихих (пиндроп) до очень громких (самолет), и наш мозг может все это обработать. На самом деле звук двигателя самолета в миллионы (миллиарды, триллионы) раз мощнее пиндропа, и неудобно иметь шкалу от 1 до миллиарда.Журналы хранят все в разумном масштабе.

Логарифмические графики

Вы часто будете видеть элементы, нанесенные на «логарифмическую шкалу». В моей голове это означает, что одна сторона считает «количество цифр» или «количество умножений», а не само значение. Опять же, это помогает отображать сильно различающиеся события по единой шкале (от 1 до 10, а не от 1 до миллиардов).

Закон Мура — отличный пример: мы удваиваем количество транзисторов каждые 18 месяцев (изображение любезно предоставлено Википедией).

Отличная особенность графиков в логарифмическом масштабе — экспоненциальные изменения (скорости процессора) отображаются в виде прямой линии. Рост в 10 раз в год означает, что вы неуклонно продвигаетесь по «цифровой» шкале.

Вперед и вверх

Если концепция хорошо известна, но не пользуется большой популярностью, это означает, что нам нужно развивать нашу интуицию. Найдите аналогии, которые работают, и не соглашайтесь на помойку из учебника. В голове:

• Логарифмы найдите основную причину эффекта (см. Рост, найдите процентную ставку)
• Они помогают подсчитывать умножения или числа с бонусом в виде частичного подсчета (500k — это 6.0 = 1?)
• Использование логарифмов в реальном мире
• Как думать экспонентами и логарифмами
• Понимание дискретного и непрерывного роста
• Что на самом деле означает показатель степени?
• Q: Почему е особенное? (2,718 …, а не 2, 3,7 или другое число?)

Логарифмические функции

Логарифмические функции — это инверсии экспоненциальных функций, и любая экспоненциальная функция может быть выражена в логарифмической форме. Точно так же все логарифмические функции можно переписать в экспоненциальной форме.Логарифмы действительно полезны, поскольку позволяют нам работать с очень большими числами, манипулируя числами гораздо более управляемого размера.

Если бы x = 2 ^y нужно было решить для y , чтобы его можно было записать в функциональной форме, необходимо было бы ввести новое слово или символ. Если x = 2 ^y , тогда y = (степень на базе 2), чтобы равняться x . Слово логарифм, сокращенно log, введено для удовлетворения этой потребности.

y = (мощность на базе 2) равняется x

Это уравнение переписывается как y = log ₂ x .

Это читается как « y равно логарифму x , основание 2» или « y равно логарифму, основание 2, x ».

Логарифмическая функция является функцией вида

, которое читается как « y равно журналу x , основание b » или « y равно журналу, основанию b , x .”

В обеих формах x > 0 и b > 0, b ≠ 1. Нет никаких ограничений для y .

Пример 1

Перепишите каждое экспоненциальное уравнение в его эквивалентной логарифмической форме. Решения следующие.

1. 5 ² = 25

Пример 2

Перепишите каждое логарифмическое уравнение в эквивалентной экспоненциальной форме.Решения следующие.

1. журнал ₆ 36 = 2

2. бревно _a м = p

Пример 3

По возможности решите следующие уравнения.

1. журнал ₇ 49 = y

3. журнал _y 8 = 3

4. журнал ₄ y = –2

5. журнал ₃ (–9) = y

5. Это невозможно, так как 3 ^y всегда будет положительным результатом.Напомним, что логарифмы имеют только положительную область значений; следовательно, –9 не входит в область логарифма.

Чаще всего при работе с логарифмами используются основания с основанием 10 и основанием и . (Буква e представляет собой иррациональное число, которое имеет множество применений в математике и естественных науках. Значение e составляет приблизительно 2,718281828…) Логическая основа 10, log ₁₀ , известна как десятичный логарифм и записывается как журнал, при этом база не записывается, но считается равной 10.Логарифм с основанием e , log _e , известен как натуральный логарифм и записывается как ln.

Пример 5

Найдите следующие логарифмы.

1. журнал 100

2. журнал 10,000

3. журнал 0,1

4. пер. и

5. пер. и ²

Логарифмические свойства

Логарифмические свойства Вернуться к содержанию

Числа и их применение — Урок 17

Обзор урока

Логарифм — это показатель степени.

Обратите внимание, что приведенное выше — это не определение , а просто краткое описание.

Так же, как вычитание является обратной операцией сложения, и извлечение квадратного корня является обратной операцией возведения в квадрат, возведение в степень и логарифмы — обратные операции. Нахождение бревна — операция, обратная поиску бревна, таково другое название возведения в степень. Однако исторически так и было сделано. как поиск по таблице.Некоторая история была приведена ранее и формальное определение повторяется ниже, на этот раз с ограничениями.

y = журнал b x тогда и только тогда, когда b y = x , где x > 0, b > 0 и b 1.

Как отмечалось выше, основание может быть любым положительным числом (кроме 1). Однако наиболее распространены два варианта: 10 и е = 2.718281828 …. Журналы по базе 10 часто называются , общие журналы , тогда как бревна к основанию и часто называют натуральными бревнами . Логи к базам 10 и е теперь оба являются стандартными для большинства калькуляторов. Часто при взятии бревна основание бывает произвольным и не требует будет уточнено. Однако в других случаях это необходимо и необходимо предполагаться или уточняться.

Только на уровне средней школы, log x последовательно означает log 10 x . В колледже, особенно по математике и физике, log x последовательно означает log e x . Популярная нотация (которую некоторые презирают): ln x означает журнал e x .

Для расчета журналов по другим базам, следует использовать изменение базового правила ниже (# 4). Это всего лишь умножение на константу (1 / log _a b ).

лог b ( xy ) = лог b x + лог b y . журнал b ( x / y ) = журнал b x — журнал b y . журнал b ( x n ) = n журнал b x . бревно b x = бревно a x / лог a b .

Все эти четыре основных свойства вытекают непосредственно из того факта, что журналы являются показателями. На словах первые три можно запомнить как: Журнал продукта равен сумме журналов факторов.Журнал частного равен разнице между бревнами. числителя и демонинатора. Журнал мощности равен мощности, умноженной на журнал основания.

Перечислены дополнительные свойства, некоторые очевидные, некоторые не столь очевидные. ниже для справки. Номер 6 называется взаимной собственностью .

журнал b 1 = 0. журнал b b = 1. журнал b b 2 = 2. журнал b b x = x . b бревно b x = x . лог a b = 1 / лог b a .

Изобретение бревен быстро последовало изобретение линейки слайдов.Правила слайдов упрощают умножение и деление путем преобразования этих операций в сложение и вычитание. Это делается путем размещения чисел на логарифмической шкале. Ниже приведены журналы некоторых небольших целых чисел.

n	журнал 10 n	журнал e n
1	0,000	0,000
2	0.301	0,693
3	0,477	1,099
4	0.602	1.386
5	0,699	1,609
6	0,778	1,792
7	0,845	1,946
8	0,903	2,079
9	0.954	2,197
10	1.000	2.303

Отсюда мы можем легко проверить такие свойства, как: log 10 = log 2 + log 5 и log 4 = 2 log 2. Это верно для любой базы. Фактически, полезный результат 10 ³ = 1000 1024 = 2 ¹⁰ можно легко увидеть как 10 журнал ₁₀ 2 3.

Приведенная ниже логарифмическая линейка представлена ​​в разобранном состоянии для облегчения резки.(Кроме того, если поместить его ниже, он будет внизу страницы 3 и будет пустым. бумага позади него.) Часть выше скользит в центре части ниже и должна распечатать, а затем вырезать в демонстрационных целях следующим образом.

1. Совместите левую 1 на шкале D с 2 на шкале C. Соблюдайте число выше 4 шкалы D по шкале C. Поскольку эти числа разложены в логорифмической шкале, вы показали, что журнал 2 + журнал 4 = журнал (2 × 4) = журнал 8.Обведите это 8.
2. Совместите правую 1 на шкале D с 4 на шкале C. Соблюдайте число под левым 1 по шкале C. Вы только что показали, что log 10 — log 4 = log 2.5. Обведите это 2.5.
3. Совместите шкалу D и шкалу A. Шкала A построена аналогично, за исключением присутствуют два цикла. Обратите внимание на число чуть выше 9 на шкале D. Вы только что показали, что 2 log 9 = log 9 ² = log 81. Обведите этот 81.
4. Посмотрите, как масштаб K можно использовать для кубирования объектов.
5. Обратите внимание, как шкалу CI также можно использовать для деления.
Обычно это курсор (исходное значение, не то, что мигает на экране компьютера) присутствует, что позволяет получить около трех десятичных знаков точности, отсюда и термин точность логарифмической линейки . Журналы используются в различных областях науки, некоторые из самых распространены: измерение громкости (децибелы), измерение силы землетрясения (Шкала Рихтера), радиоактивный распад и кислотность (pH = -log ₁₀ [H ⁺ ]).Они необходимы в математике для решения некоторых задач экспоненциального типа.

Ниже приводится интересная задача, связывающая квадратичную формулу: логарифмы и показатели вместе очень аккуратно.

журнал (2 x +2) + журнал x — журнал (12) = 0 Упростите логарифмы, объединив их.
журнал (2 x ² + 2 x ) — журнал (12) = 0
журнал (( 2x ² + 2x ) / 12) = 0
После деления на 2 возвести в степень обе стороны (основание b произвольно, так как это не было указано выше)!
( x ² + x ) / 6 = b ⁰
( x ² + x ) / 6 = 1
x ² + x = 6
x ² + x — 6 = 0
( x + 3) ( x — 2) = 0 x {-3, 2}

Пустое пространство, поэтому при печати с помощью Mozilla (ой, без полей) оно находится позади линейки.

Однако x -3 поскольку домен журнала — это только положительные числа. ( b ^x никогда не может быть отрицательным числом с b > 0).

В следующем примере (6.11 # 51) логарифмы объединяются с системами уравнений. Это также очень удобно ввести понятие подстановки, которое так полезно в исчислении.

журнал ₉ x + журнал _y 8 = 2.
журнал _x 9 + журнал ₈ y = 8/3.

Пусть u = log ₉ x и v = log ₈ y . По взаимному свойству выше, 1 / u = log _x 9 и 1 / v = log _y 8.

Теперь мы можем переписать наши уравнения как:

и + 1/ v = 2
1/ u + v = 8/3 Решение заменой, u = 2 — 1/ v , таким образом: 1 / (2 — 1/ против ) + против = 8/3.
3 (1 + 2 против -1) = 8 (2-1 / против )
6 v ² = 16 v — 8.
6 v ² — 16 v + 8 = 0.
3 v ² — 8 v + 4 = 0.
К этому мы применяем формулу корней квадратного уравнения и находим, что
v = (8 ± (64 — 48)) / 6.
= (8 ± 4) / 6 или 2, 2/3.
Таким образом, u = 3/2 или 1/2 или ( u , v ) = {(3/2, 2), (1/2, 2/3)}
Таким образом ( x , y ) = {(27, 64), (3, 4)} .