Решение задач симплекс методом примеры для чайников: Решение симплекс методом задачи ЛП: пример и алгоритм
Решение симплекс методом задачи ЛП: пример и алгоритм
Симплекс метод — это метод последовательного перехода от одного базисного решения (вершины многогранника решений) системы ограничений задачи линейного программирования к другому базисному решению до тех пор, пока функция цели не примет оптимального значения (максимума или минимума).
Симплекс метод был предложен американским математиком Р.Данцигом в 1947 году, с тех пор для нужд промышленности этим методом нередко решаются задачи линейного программирования с тысячами переменных и ограничений.
Перед тем, как перейти к алгоритму симплекс метода, несколько определений.
Всякое неотрицательное решение системы ограничений называется допустимым решением.
Пусть имеется система m ограничений с n переменными
(m n).
Допустимым базисным решением является решение, содержащее m неотрицательных основных (базисных) переменных и n — m неосновных. (небазисных, или свободных) переменных. Неосновные переменные в базисном решении равны нулю, основные же переменные, как правило, отличны от нуля, то есть являются положительными числами.
Любые m переменных системы m линейных уравнений с
n переменными называются основными, если определитель из коэффициентов при них
отличен от нуля. Тогда остальные
Алгоритм симплекс метода
- Шаг 1. Привести задачу линейного программирования к канонической форме. Для этого
перенести свободные члены в правые части (если среди этих свободных членов окажутся отрицательные,
то соответствующее уравнение или неравенство умножить на — 1) и в каждое ограничение
ввести дополнительные переменные
(со знаком «плюс», если в исходном неравенстве знак «меньше или равно», и со знаком «минус»,
если «больше или равно»).

- Шаг 2. Если в полученной системе m уравнений, то m переменных принять за основные, выразить основные переменные через неосновные и найти соответствующее базисное решение. Если найденное базисное решение окажется допустимым, перейти к допустимому базисному решению.
- Шаг 3. Выразить функцию цели через неосновные переменные допустимого базисного решения. Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с отрицательными (положительными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным — решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с отрицательными (положительными) коэффициентами, перейти к новому базисному решению.
- Шаг 4.
 Из неосновных
переменных, входящих в линейную форму с отрицательными
(положительными) коэффициентами, выбирают ту, которой соответствует наибольший
(по модулю) коэффициент,
и переводят её в основные. Переход к шагу 2.
Из неосновных
переменных, входящих в линейную форму с отрицательными
(положительными) коэффициентами, выбирают ту, которой соответствует наибольший
(по модулю) коэффициент,
и переводят её в основные. Переход к шагу 2.
- Если допустимое базисное решение даёт оптимум линейной формы (критерий оптимальности выполнен), а в выражении линейной формы через неосновные переменные отсутствует хотя бы одна из них, то полученное оптимальное решение — не единственное.
- Если в выражении линейной формы имеется неосновная переменная
с отрицательным коэффициентом в случае её максимизации (с положительным — в случае
минимизации), а во все уравнения системы ограничений этого шага указанная переменная
входит также с отрицательными коэффициентами или отсутствует, то линейная форма не ограничена
при данной системе ограничений. В этом случае её максимальное (минимальное)
значение записывают в виде .

Путём построения симплексных таблиц решить задачу линейного программирования намного проще, чем путём алгебраических преобразований, который показан в следующем параграфе. Симплексные таблицы очень наглядны. Существует несколько разновидностей правил работы с симплексными таблицами. Мы разберём правило, которое чаще всего называется правилом ведущего столбца и ведущей строки.
Будет нелишним открыть в новом окне пособие Действия с дробями: их, дробей в задачах на симплекс-метод, мягко говоря, хватает.
Пример. Найти максимум функции при ограничениях
Решение.
Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений
.
Это было сделано с соблюдением следующего правила: если в первоначальном ограничении
знак «меньше или равно», то добавочную переменную нужно прибавлять, а если «больше или равно», то
добавочную переменную нужно отнимать.
Введённые добавочные переменные принимаем за основные (базисные). Тогда и — неосновные (свободные) переменные.
Выразив основные (базисные) переменные через неосновные (свободные), получим
Функцию цели также выразим через неосновные (свободные) переменные:
Из коэффициентов при переменных (неизвестных) построим первую симплексную таблицу.
| Таблица 1 | ||||
| Базисные неизвестные | Свободные неизвестные | Вспомогательные коэффициенты | ||
| X1 | X2 | |||
| X3 | -2 | 1 | -2 | |
| X4 | -4 | -1 | -1 | |
| X5 | 2 | 1 | -1 | |
| X6 | 6 | 0 | 1 | |
| F | 0 | -1 | -2 | |
Последнюю строку таблицы, в которой записаны функция цели и коэффициенты при свободных
переменных в ней, будем называть в индексной строкой.
Полученное решение не оптимально, так как в индексной строке коэффициенты при свободных переменных отрицательны. То есть оптимальным будет то решение, в котором коэффициенты при свободных переменных в индексной строке будут больше или равны нулю.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей таблице найдём наибольшее (по модулю) из чисел и . Это число 2. Поэтому ведущий столбец — тот столбец, в котором записано
Для определения ведущей строки находим минимум отношений свободных членов к элементам ведущего столбца, причём если в числителе положительное число, а в знаменателе отрицательное, отношение считается равным бесконечности.
Итак,
.
Поэтому ведущая строка — та, в которой записано
Ведущим элементом, таким образом, является -2.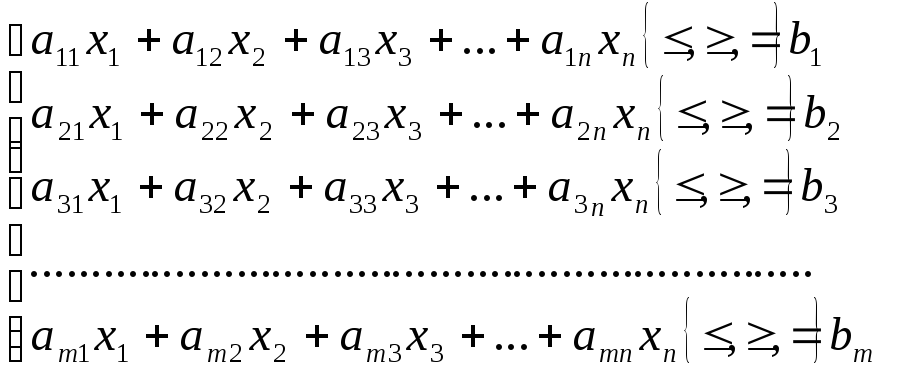
Составляем вторую симплексную таблицу.
Новый базисный элемент вписываем первой строкой, а столбец, в котором стояло , вписываем новую свободную переменную
Заполняем первую строку. Для этого все числа, стоящие в ведущей строке таблицы 1, делим на ведущий элемент и записываем в соответствующий столбец первой строки таблицы 2, кроме числа, стоящего в ведущем столбце, куда записывается величина, обратная ведущему элементу (то есть, единица, делённая на ведущий элемент).
Заполняем столбец вспомогательных коэффициентов. Для этого числа ведущего столбца таблицы 1, кроме ведущего элемента, записываем с противоположными знаками в графу вспомогательных коэффициентов таблицы 2.
| Таблица 2 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X1 | X3 | |||
| X2 | 1 | -1/2 | -1/2 | |
| X4 | -3 | -3/2 | -1/2 | 1 |
| X5 | 3 | 1/2 | -1/2 | 1 |
| X6 | 5 | 1/2 | 1/2 | -1 |
| F | 2 | -2 | -1 | 2 |
Кто ещё не открыл в новом окне пособие Действия с дробями,
может сделать это сейчас, поскольку самое время.
Для получения остальных строк таблицы 2 числа, уже стоящие в первой строке этой таблицы, умножаем на вспомогательный коэффициент, стоящий в заполняемой строке, и к результату прибавляем число из таблицы 1, стоящее в той же строке при соответствующей переменной.
Например, для получения свободного члена второй строки число 1 умножаем на 1 и прибавляем из таблицы 1 число -4. Получаем -3. Коэффициент при во второй строке находим так же: . Так как в предыдущей таблице отсутствует столбец с новой свободной переменной , то коэффициент второй строки в столбце новой свободной переменной будет (то есть из таблицы 1 прибавляем 0, так как в таблице 1 столбец с отсутствует).
Так же заполняется и индексная строка:
Полученное таким образом решение вновь не оптимально, так как в индексной строке
коэффициенты при свободных переменных вновь отрицательны.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к следующей симплексной таблице найдём наибольшее (по модулю) из чисел и , то есть, модулей коэффициентов в индексной строке. Это число 2. Поэтому ведущий столбец — тот столбец, в котором записано .
Для поиска ведущей строки найдём минимум отношений свободных членов к элементам ведущей строки. Получаем:
.
Следовательно, ведущая строка — та, в которой записано , а ведущим элементом является -3/2.
Составляем третью симплексную таблицу
Новую базисную переменную записываем первой строкой. В столбец, в котором было , вписываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
| Таблица 3 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X4 | X3 | |||
| X1 | 2 | -2/3 | 1/3 | |
| X2 | 2 | -1/3 | -1/3 | 1/2 |
| X5 | 2 | 1/3 | -2/3 | -1/2 |
| X6 | 4 | 1/3 | 1/3 | -1/2 |
| F | 6 | -4/3 | -1/3 | 2 |
Вычисление остальных строк на примере второй строки:
Полученное решение вновь не оптимальное, поскольку коэффициенты при свободных
неизвестных в индексной строке вновь отрицательные.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для перехода к четвёртой симплексной таблице найдём наибольшее из чисел и . Это число .
Следовательно, ведущий столбец — тот, в котором записано .
Для нахождения ведущей строки найдём минимум модулей отношений свободных членов к элементам ведущего столбца:
.
Поэтому ведущая строка — та, в которой записано , а ведущий элемент 1/3.
В четвёртой симплексной таблице новую базисную переменную записываем первой строкой. В столбец, где было , записываем новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
.
| Таблица 4 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X3 | |||
| X4 | 6 | 3 | -2 | |
| X1 | 6 | 2 | -1 | 2/3 |
| X2 | 4 | 1 | -1 | 1/3 |
| X6 | 2 | -1 | 1 | -1/3 |
| F | 14 | 4 | -3 | 4/3 |
Вычисление остальных строк на примере второй строки:
Полученное решение так же не оптимально, но оно уже лучше предыдущих, так как один
из коэффициентов при свободных переменных в индексной строке неотрицателено.
Для улучшения плана перейдём к следующей симплексной таблице.
Найдём наибольшее из чисел 4 и . Это число 4. Следовательно, ведущий столбец .
Для нахождения ведущей строки найдём
.
Следовательно, ведущая строка — та, в которой записано . Но и уже были вместе среди свободных переменных. Поэтому для перевода очередной переменной из свободных в базисные выбираем другой ведущий столбец — тот, в котором записано .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Для нахождения ведущей строки найдём
.
Следовательно, ключевая строка — та, в которой записано , а ведущий элемент 1.
В пятой симплексной таблице новую базисную переменную
записываем первой строкой.
В столбец, где было , записываем
новую свободную переменную .
Первая строка:
Вспомогательные коэффициенты:
.
| Таблица 5 | ||||
| Базисные неизвестные | Свободные члены | Свободные неизвестные | Вспомогательные коэффициенты | |
| X5 | X6 | |||
| X3 | 2 | -1 | 1 | |
| X4 | 10 | 2 | ||
| X1 | 8 | 1 | ||
| X2 | 6 | 1 | ||
| F | 20 | 1 | 3 | 3 |
Попробуем сразу узнать, не является ли решение оптимальным. Поэтому для остальных
строк вычислим только свободные члены (чтобы узнать значения базисных переменных при равенстве свободных
переменных нулю) и коэффициенты при свободных переменных в индексной строке.
Поэтому для остальных
строк вычислим только свободные члены (чтобы узнать значения базисных переменных при равенстве свободных
переменных нулю) и коэффициенты при свободных переменных в индексной строке.
Свободные члены:
— во второй строке ;
— в третьей строке ;
— в четвёртой строке .
Индексная строка:
Смотрим в симплексную таблицу 5. Видим, что получено оптимальное решение, так как коэффициенты при свободных неизвестных в индексной строке неотрицательны.
Ответ:
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс методом.
Решим алгебраическими преобразованиями тот же пример, что и в предыдущем параграфе.
Следует отметить, что при решении этой разновидностью симплекс метода лучше не записывать функцию
цели в виде ,
так как при этом легко запутаться в знаках. Но в этом случае пункт алгоритма, определяющий критерий
оптимальности, будет модифицирован следующим образом.
Но в этом случае пункт алгоритма, определяющий критерий
оптимальности, будет модифицирован следующим образом.
Если отыскивается максимум (минимум) линейной формы и в её выражении нет неосновных переменных с положительными (отрицательными) коэффициентами, то критерий оптимальности выполнен и полученное базисное решение является оптимальным — решение окончено. Если при нахождении максимума (минимума) линейной формы в её выражении имеется одна или несколько неосновных переменных с положительными (отрицательными) коэффициентами, перейти к новому базисному решению.
Пример. Найти максимум функции при ограничениях
Решение.
Шаг I. Вводим добавочные неотрицательные переменные и сводим данную систему неравенств к эквивалентной ей системе уравнений
.
Введённые добавочные переменные принимаем за основные, так как в этом случае базисное решение системы легко находится. Тогда и — неосновные переменные.
Выразив основные переменные через неосновные, получим
Следовательно, данному разбиению переменных на основные и неосновные соответствует базисное решение , которое является недопустимым (две переменные отрицательны), а поэтому оно не оптимальное. От этого базисного решения перейдём к улучшенному.
Чтобы решить, какую переменную следует перевести из неосновных в основные, рассмотрим любое из двух имеющихся уравнений последней системы с отрицательными свободными членами, например второе. Оно показывает, что в основные переменные можно перевести и , так как в этом уравнении они имеют положительные коэффициенты (следовательно, при их увеличении, а это произойдёт, если переведём любую из них в основные переменные, переменная увеличится).
Попробуем перевести в основные переменную . Чтобы установить, какую переменную следует перевести из основные в неосновные, найдём абсолютную величину наименьшего отношения свободных членов системы к коэффициентам при . Имеем . Оно получено из третьего уравнения, показывающего, что в неосновные нужно перевести переменную , которая в исходном базисном решении положительна. Следовательно, полученное базисное решение, как и исходное, содержит две отрицательные компоненты, т. е. при переходе к такому базисному решению улучшения не произойдёт.
Если же перевести в основные переменную , то наименьшее отношение свободных членов к коэффициентам при составит . Оно получено из первого уравнения, в котором свободный член отрицателен. Следовательно, переводя в основные, а в неосновные переменные, мы получим базисное решение, в котором число отрицательных компонент на единицу меньше, чем в исходном. Поэтому остановимся на этой возможности: переводим в основные, а в неосновные переменные. Поэтому в приведённой выше системе уравнений выделенным оказалось первое уравнение.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг II.
Основные переменные , неосновные переменные .
Выразим новые основные переменные через новые неосновные, начиная с выделенного на шаге I уравнения. В результате получим
Следовательно, имеем новое базисное решение , которое также является недопустимым, а поэтому не оптимальным. Но в нём, как мы и предвидели, только одна переменная отрицательна (а именно ).
От полученного базисного решения необходимо перейти к другому. Рассмотрим уравнение с отрицательным свободным членом, т. е. второе уравнение. Оно показывает, что в основные переменные можно перевести и . Переведём в основные переменные . Найдём наименьшее из абсолютных величин отношений свободных членов системы к коэффициентам при . Имеем . Значит, в неосновные переменные нужно перенести . Так как наименьшее отношение получено из второго уравнения, то его выделяем. В новом базисном решении уже не окажется отрицательных компонент, т. е. оно является допустимым.
В особых случаях решение завершается на II шаге: это, например, случаи, когда максимум целевой функции — бесконечность и когда система не имеет ни одного решения.
Шаг III.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Новое базисное решение имеет вид . Является ли оно оптимальным, можно установить, если выразить линейную форму через неосновные переменные рассматриваемого базисного решения. Сделав это, получим . Так как мы ищем максимум линейной формы, а нашли лишь одно допустимое решение, то продолжим перебор.
Переводим в число основных переменную , имеющую больший положительный коэффициент. Находим . Это наименьшее отношение получено из третьего уравнения системы, поэтому его выделяем. Оно показывает, что при переменная и поэтому перейдёт в число неосновных.
В некотором особом случае решение завершается на III шаге: это случай, когда оптимальное решение — не единственное.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Шаг IV.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Линейная форма, выраженная через те же неосновные переменные, примет вид . Продолжим перебор для поиска максимума.
Увеличение линейной формы возможно при переходе к новому базисному решению, в котором переменная является основной. Находим . Это наименьшее отношение получено из четвёртого уравнения системы и показывает, что при переменная и переходит в число неосновных.
Шаг V.
Основные переменные: , неосновные переменные: . Выразив основные переменные через неосновные, получим
Линейная форма, выраженная через неосновные переменные нового базисного решения, имеет вид . Критерий оптимальности для случая максимизации линейной формы выполнен. Следовательно, базисное решение является оптимальным, а максимум линейной формы
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Начало темы «Линейное программирование»
Продолжение темы «Линейное программирование»
Поделиться с друзьями
Симплекс-метод, примеры решения задач
Здесь приведено ручное (не апплетом) решение двух задач симплекс-методом (аналогичным решению апплетом) с подробными объяснениями для того, чтобы понять алгоритм решения задач симплекс-методом. Первая задача содержит знаки неравенства только » ≤ » (задача с начальным базисом), вторая может содержить знаки » ≥ «, » ≤ » или » = » (задача с искусственным базисом), они решаются по разному.
Симплекс-метод, решение задачи с начальным базисом
1)Симплекс-метод для задачи с начальным базисом (все знаки неравенств-ограничений » ≤ «).
Запишем задачу в канонической форме, т.е. ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные:
Эта система является системой с базисом (базис s1, s2, s3, каждая из них входит только в одно уравнение системы с коэффициентом 1), x1 и x2 — свободные переменные. Задачи, при решении которых применяется симплекс-метод, должны обладать следующими двумя свойствами: -система ограничений должна быть системой уравнений с базисом; -свободные члены всех уравнений в системе должны быть неотрицательны.
Полученная система — система с базисом и ее свободные члены неотрицательны, поэтому можно применить симплекс-метод. Составим первую симплекс-таблицу (Итерация 0) для решения задачи на симплекс-метод, т.е. таблицу коэффициентов целевой функции и системы уравнений при соответствующих переменных. Здесь «БП» означает столбец базисных переменных, «Решение» — столбец правых частей уравнений системы. Решение не является оптимальным, т.к. в z – строке есть отрицательные коэффициенты.
симплекс-метод итерация 0
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | -4 | -6 | 0 | 0 | 0 | 0 | — |
s1 | 2 | 1 | 1 | 0 | 0 | 64 | 64/1=64 |
s2 | 1 | 3 | 0 | 1 | 0 | 72 | 72/3=24 |
s3 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Для улучшения решения перейдем к следующей итерации симплекс-метода, получим следующую симплекс-таблицу. Для этого надо выбрать разрешающий столбец, т.е. переменную, которая войдет в базис на следующей итерации симплекс-метода. Он выбирается по наибольшему по модулю отрицательному коэффициенту в z-строке (в задаче на максимум) – в начальной итерации симплекс-метода это столбец x2 (коэффициент -6).
Затем выбирается разрешающая строка, т.е. переменная, которая выйдет из базиса на следующей итерации симплекс-метода. Она выбирается по наименьшему отношению столбца «Решение» к соответствующим положительным элементам разрешающего столбца (столбец «Отношение») – в начальной итерации это строка s3 (коэффициент 20).
Разрешающий элемент находится на пересечении разрешающего столбца и разрешающей строки, его ячейка выделена цветом, он равен 1. Следовательно, на следующей итерации симплекс-метода переменная x2 заменит в базисе s1. Заметим, что в z-строке отношение не ищется, там ставится прочерк » — «. В случае если есть одинаковые минимальные отношения, то выбирается любое из них. Если в разрешающем столбце все коэффициенты меньше или равны 0, то решение задачи бесконечно.
Заполним следующую таблицу «Итерация 1». Её мы получим из таблицы «Итерация 0». Цель дальнейших преобразований — превратить разрешающий столбец х2 в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов).
1)Вычисление строки х2 таблицы «Итерация 1». Сначала делим все члены разрешающей строки s3 таблицы «Итерация 0» на разрешающий элемент (он равен 1 в данном случае) этой таблицы, получим строку x2 в таблице «Итерации 1». Т.к. разрешающий элемент в данном случае равен 1, то строка s3 таблицы «Итерация 0» будет совпадать со строкой х2 таблицы «Итерация 1». Строку x2 таблицы «Итерации 1» мы получили 0 1 0 0 1 20, остальные строки таблицы «Итерация 1» будут получены из этой строки и строк таблицы «Итерация 0» следующим образом:
2) Вычисление z-строки таблицы «Итерация 1». На месте -6 в первой строке (z-строке) в столбце х2 таблицы «Итерация 0» должен быть 0 в первой строке таблицы «Итерация 1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1 0 0 1 20 умножим на 6, получим 0 6 0 0 6 120 и сложим эту строку с первой строкой (z — строкой) таблицы «Итерация 0» -4 -6 0 0 0 0, получим -4 0 0 0 6 120. В столбце x2 появился ноль 0, цель достигнута. Элементы разрешающего столбца х2 выделены красным цветом.
3) Вычисление строки s1 таблицы «Итерация 1». На месте 1 в s1 строке таблицы «Итерация 0» должен быть 0 в таблице «Итерация 1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1 0 0 1 20 умножим на -1, получим 0 -1 0 0 -1 -20 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 2 1 1 0 0 64, получим строку 2 0 1 0 -1 44. В столбце х2 получен необходимый 0.
4) Вычисление строки s2 таблицы «Итерация 1». На месте 3 в s2 строке таблицы «Итерация 0» должен быть 0 в таблице «Итерация 1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1 0 0 1 20 умножим на -3, получим 0 -3 0 0 -3 -60 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 1 3 0 1 0 72, получим строку 1 0 0 1 -3 12. В столбце х2 получен нужный 0. Столбец х2 в таблице «Итерация 1» стал единичным, он содержит одну 1 и остальные 0.
Строки таблицы «Итерация 1» получаем по следующему правилу:
Новая строка = Старая строка – (Коэффициент разрешающего столбца старой строки)*(Новая разрешающая строка).
Например для z-строки имеем:
Старая z-строка (-4 -6 0 0 0 0) -(-6)*Новая разрешающая строка -(0 -6 0 0 -6 -120) =Новая z-строка (-4 0 0 0 6 120).
Для следующих таблиц пересчет элементов таблицы делается аналогично, поэтому мы его опускаем.
симплекс-метод итерация 1
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | -4 | 0 | 0 | 0 | 6 | 120 | — |
s1 | 2 | 0 | 1 | 0 | -1 | 44 | 44/2=22 |
s2 | 1 | 0 | 0 | 1 | -3 | 12 | 12/1=12 |
x2 | 0 | 1 | 0 | 0 | 1 | 20 | — |
Разрешающий столбец х1, разрешающая строка s2, s2 выходит из базиса, х1 входит в базис. Совершенно аналогично получим остальные симплекс-таблицы, пока не будет получена таблица со всеми положительными коэффициентами в z-строке. Это признак оптимальной таблицы.
симплекс-метод итерация 2
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | 0 | 0 | 0 | 4 | -6 | 168 | — |
s1 | 0 | 0 | 1 | -2 | 5 | 20 | 20/5=4 |
x1 | 1 | 0 | 0 | 1 | -3 | 12 | — |
x2 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Разрешающий столбец s3, разрешающая строка s1, s1 выходит из базиса, s3 входит в базис.
симплекс-метод итерация 3
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | 0 | 0 | 6/5 | 8/5 | 0 | 192 | — |
s3 | 0 | 0 | 1/5 | -2/5 | 1 | 4 | — |
x1 | 1 | 0 | 3/5 | -1/5 | 0 | 24 | — |
x2 | 0 | 1 | -1/5 | 2/5 | 0 | 16 | — |
В z-строке все коэффициенты неотрицательны, следовательно, получено оптимальное решение x1 = 24, x2 = 16, zmax = 192.
Линейное программирование. Симплекс-метод | Решатель
Рассмотрим симплекс-метод для решения задач линейного программирования (ЛП). Он основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает.
Алгоритм симплекс-метода следующий:
- Исходную задачу переводим в канонический вид путем введения дополнительных переменных. Для неравенства вида ≤ дополнительные переменные вводят со знаком (+), если же вида ≥ то со знаком (—). В целевую функцию дополнительные переменные вводят с соответствующими знаками с коэффициентом, равным 0, т.к. целевая функция не должна при этом менять свой экономический смысл.
- Выписываются вектора Pi из коэффициентов при переменных и столбца свободных членов. Этим действием определяется количество единичных векторов. Правило – единичных векторов должно быть столько, сколько неравенств в системе ограничений.
- После этого исходные данные вводятся в симплекс-таблицу. В базис вносятся единичные вектора, и исключая их из базиса, находят оптимальное решение. Коэффициенты целевой функции записывают с противоположным знаком.
- Признак оптимальности для задачи ЛП – решение оптимально, если в f – строке все коэффициенты положительны. Правило нахождения разрешающего столбца – просматривается f – строка и среди ее отрицательных элементов выбирается наименьшее. Вектор Pi его содержащий становится разрешающим. Правило выбора разрешающего элемента – составляются отношения положительных элементов разрешающего столбца к элементам вектора Р0 и то число, которое дает наименьшее отношение становится разрешающим элементом, относительно которого будет произведен пересчет симплекс-таблицы. Строка, содержащая этот элемент называется разрешающей строкой. Если в разрешающем столбце нет положительных элементов, то задача не имеет решения. После определения разрешающего элемента переходят к пересчету новой симплекс – таблицы.
- Правила заполнения новой симплекс – таблицы. На месте разрешающего элемента проставляют единицу, а другие элементы полагают равными 0. Разрешающий вектор вносят в базис, из которого исключают соответствующий нулевой вектор, а остальные базисные вектора записывают без изменений. Элементы разрешающей строки делят на разрешающий элемент, а остальные элементы пересчитывают по правилу прямоугольников.
- Так поступают до тех пор, пока в f – строке все элементы не станут положительными.
Рассмотрим решение задачи с использованием рассмотренного выше алгоритма.
Дано:
Приводим задачу к каноническому виду:
Составляем вектора:
Заполняем симплекс – таблицу:
Правило прямоугольников:
Пересчитаем первый элемент вектора Р0, для чего составляем прямоугольник из чисел: и получаем: .
Аналогичные расчеты выполним для всех остальных элементов симплекс – таблицы:
В полученном плане f – строка содержит один отрицательный элемент – (-5/3), вектора P1. Он содержит в своем столбце единственный положительный элемент, который и будет разрешающим элементом. Сделаем пересчет таблицы относительно этого элемента:
Отсутствие отрицательных элементов в f – строке означает, что найден оптимальный план:
F* = 36/5, Х = (12/5, 14/5, 8, 0, 0).
Рекомендуемая литература
- Ашманов С. А. Линейное программирование, М: Наука, 1998г.,
- Вентцель Е.С. Исследование операций, М: Советское радио, 2001г.,
- Кузнецов Ю.Н., Кузубов В.И., Волошенко А.Б. Математическое программирование, М: Высшая школа, 1986г.
Решение линейного программирования на заказ
Заказать любые задания по этой дисциплине можно у нас на сайте. Прикрепить файлы и указать сроки можно на странице заказа.
Симплекс метод онлайн
Данный онлайн калькулятор решает задачу линейного программирования симплекс методом. Дается подробное решение с пояснениями. Для решения задачи линейного программирования задайте количество ограничений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить». Теоретическую часть смотрите в статье: Решение задачи линейного программирования. Симплекс метод.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Симплекс метод
Симплекс метод − это метод решения задачи линейного программирования (ЗЛП). Суть метода заключается в нахождении начального допустимого плана, и в последующем улучшении плана до достижения максимального (или минимального) значения целевой функции в данном выпуклом многогранном множестве или выяснения неразрешимости задачи. Подробнее в статье: Решение задачи линейного программирования. Симплекс метод.
Примеры решения ЗЛП симплекс методом
Пример 1. Решить следующую задачу линейного программирования:
Р е ш е н и е. Матрица коэффициентов системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1. Последние три векторы столбцы обазуют базис в трехмерном пространствое. Следовательно базисные переменные , а свободные переменные :
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . min(40:6, 28:2)=20/3 соответствует строке 1. Из базиса выходит вектор x3. Сделаем исключение Гаусса для столбца x2, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на -1/3, 1/6, 1/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-3), следовательно в базис входит вектор x1. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . min(44/3:11/3, 62/3:5/3)=4 соответствует строке 2. Из базиса выходит вектор x4. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 2. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 3, 4 со строкой 2, умноженной на 1/11, -5/11, 9/11, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Текущий опорный план является оптимальным, так как в строках 4 под переменными нет отрицательных элементов.
Решение можно записать так: .
Значение целевой функции в данной точке: F(X)=.
Пример 2. Найти максимум функции
при условиях
Р е ш е н и е. Матрица коэффициентов системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последняя строка — это целевая функция, умноженная на −1:
Базисные векторы x4, x3, следовательно, все элементы в столбцах x4, x3, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 3 со строкой 1, умноженной на 4. Обнулим все элементы столбца x3, кроме ведущего элемента. Для этого сложим строку 3 со строкой 2, умноженной на 1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательный элемент (-11), следовательно в базис входит вектор x2. Определяем, какой вектор выходит из базиса. Для этого вычисляем при . Все следовательно целевая функция неограничена сверху. Т.е. задача линейного программирования неразрешима.
Примеры решения ЗЛП методом искусственного базиса
Пример 1. Найти максимум функции
при условиях
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственное переменное, а в целевую функцию добавляем это переменное, умноженное на −M, где M, очень большое число:
Матрица коэффициентов системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
Базисные векторы следовательно, все элементы в столбцах ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-5), следовательно в базис входит вектор Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 3. Из базиса выходит вектор Сделаем исключение Гаусса для столбца учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строку 5 со строкой 3, умноженной на 1. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-3), следовательно в базис входит вектор Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 1. Из базиса выходит вектор x2. Сделаем исключение Гаусса для столбца x1, учитывая, что ведущий элемент соответствует строке 1. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 2, 3, 4 со строкой 1, умноженной на 3/2, -1/10, 3/2, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Данный опорный план не является оптимальным, так как в последней строке есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-13/2), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем при соответствует строке 3. Из базиса выходит вектор x5. Сделаем исключение Гаусса для столбца x3, учитывая, что ведущий элемент соответствует строке 3. Обнулим все элементы этого столбца, кроме ведущего элемента. Для этого сложим строки строки 1, 2, 4 со строкой 3, умноженной на 5/3, 25/9, 65/9, соответственно. Далее делим строку с ведущим элементом на ведущий элемент.
Симплекс таблица примет следующий вид:
Запишем текущий опорный план:
Текущий опорный план является оптимальным, так как в строках 4−5 под переменными нет отрицательных элементов.
Решение исходной задачи можно записать так:
| . |
Значение целевой функции в данной точке:
| . |
Пример 2. Найти оптимальный план задачи линейного программирования:
Р е ш е н и е. Так как количество базисных векторов должен быть 3, то добавляем искусственные переменные, а в целевую функцию добавляем эти переменные, умноженные на −M, где M, очень большое число:
Матрица коэффициентов системы уравнений имеет вид:
Правая часть ограничений системы уравнений имеет вид:
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов A. Последние две строки − это целевая функция, умноженная на −1 и разделенная на две части. Последняя строка − строка с исскуственными переменными:
Базисные векторы x4, x5, x6, следовательно, все элементы в столбцах x4, x5, x6, ниже горизонтальной линии должны быть нулевыми.
Обнулим все элементы столбца x4, кроме ведущего элемента. Для этого сложим строку 4 со строкой 1, умноженной на -1. Обнулим все элементы столбца x5, кроме ведущего элемента. Для этого сложим строку 5 со строкой 2, умноженной на -1. Обнулим все элементы столбца x6, кроме ведущего элемента. Для этого сложим строку 5 со строкой 3, умноженной на -1.
Симплекс таблица примет вид:
Запишем текущий опорный план:
В строке 5 элементы, соответствующие переменным x1, x2, x3, x4, x5, x6 неотрицательны, а число находящийся в пересечении данной строки и столбца x0 отрицательнo. Тогда исходная задача не имеет опорного плана. Следовательно она неразрешима.
Подробный разбор симплекс-метода / Хабр
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными $inline$b_i$inline$ умножаем на (-1).
- Если неравенство вида (≤), то к левой части добавляем $inline$s_i$inline$ – добавочную переменную, и получаем равенство.
- Если неравенство вида (≥), то из левой части вычитаем $inline$s_i$inline$, и получаем равенство.
- Делаем замену переменных:
- Если $inline$x_i ≤ 0$inline$, то $inline$x_i’= -x_i ≥ 0$inline$
- Если $inline$x_i$inline$ — любой, то $inline$x_i= x_i’ — x_i»$inline$, где $inline$x_i’, x_i»≥ 0$inline$
Замечание: Будем нумеровать $inline$s_i$inline$ по номеру неравенства, в которое мы его добавили.2 $inline$.
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит $inline$Х$inline$ (т.е. $inline$Х$inline$ – не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.
§4. Симплекс-метод
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции.T…$inline$, т.е. только одна координата вектора ненулевая и равна 1.
Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
- В первой строке указывают «наименование» всех переменных.
- В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
- В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
- Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
- Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.
Замечание: Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.
Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание: Коэффициенты в строке функционала берутся со знаком “-”.
Алгоритм симплекс-метода:
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
- Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
- Если задача на максимум – выбираем минимальный отрицательный.
Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.
Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
- Вектор правых частей почленно делится на ведущий столбец
- Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
Определение: Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.
Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение: Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
- Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
- Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка
Замечание: Преобразование такого вида направлено на введение выбранной переменной в базис, т.е. представление ведущего столбца в виде базисного вектора.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
1. Оптимальность
Условие оптимальности полученного решения:
- Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
- Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).
2. Неограниченность функционала
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Спасибо за внимание!
P.S.
Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.
Пример — Табличный симплекс метод
Необходимо решить задачу линейного программирования.
Целевая функция:
2x 1+5x2+3x3+8x4 →min
Ограничивающие условия:
3x1+6x2-4x3+x4≤12
4x1-13x2+10x3+5x4≥6
3x1+7x2+x3≥1
Приведем систему ограничений к каноническому виду, для этого необходимо перейти от неравенств к равенствам, с добавлением дополнительных переменных.
Так как наша задача – задача минимизации, то нам необходимо преобразовать ее к задаче на поиск максимума. Для этого изменим знаки коэффициентов целевой функции на противоположные. Элементы первого неравенства записываем без изменений, добавив в него дополнительную переменную x5 и изменив знак “≤” на “=”. Т. к. второе и третье неравенства имеют знаки “≥” необходимо поменять знаки их коэффициентов на противоположные и внести в них дополнительные переменные x6 и x7 соответственно. В результате получем эквивалентную задачу:
3x1+6x2-4x3+x4+x5=12
-4x1+13x2-10x3-5x4+x6=-6
-3x1-7x2-x3+x7=-1
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции с противоположным знаком.
x1 | x2 | x3 | x4 | Своб член | |
| F | 2 | 5 | 3 | 8 | 0 |
| X5 | 3 | 6 | -4 | 1 | 12 |
| X6 | -4 | 13 | -10 | -5 | -6 |
| X7 | -3 | -7 | -1 | 0 | -1 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю – это элемент: -6, он задает ведущую строку – X6. В этой строке так же находим максимальный по модулю отрицательный элемент: -10 он находится в столбце X3 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X1 | X2 | X6 | X4 | Своб член | |
| F | 0.8 | 8.9 | 0.3 | 6.5 | -1.8 |
| X5 | 4.6 | 0.8 | -0.4 | 3 | 14.4 |
| X3 | 0.4 | -1.3 | -0.1 | 0.5 | 0.6 |
| X7 | -2.6 | -8.3 | -0.1 | 0.5 | -0.4 |
В составленой нами таблице имеются отрицательные элементы в столбце свободных членов, находим среди них максимальный по модулю – это элемент: -0.4, он задает ведущую строку – X7. В этой строке так же находим максимальный по модулю отрицательный элемент: -8.3 он находится в столбце X2 который будет ведущим столбцом. Переменная в ведущей строке исключается из базиса, а переменная соответсвующая ведущему столцу включается в базис. Пересчитаем симплекс-таблицу:
| X1 | X7 | X6 | X4 | Своб член | |
| F | -1.988 | 1.072 | 0.193 | 7.036 | -2.229 |
| X5 | 4.349 | 0.096 | -0.41 | 3.048 | 14.361 |
| X3 | 0.807 | -0.157 | -0.084 | 0.422 | 0.663 |
| X2 | 0.313 | -0.12 | 0.012 | -0.06 | 0.048 |
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение.В строке F имеются отрицательные элементы, это означает что полученое решение не оптимально. Определим ведущий столбец. Для этого найдем в строке F максимальный по модулю отрицательный элемент – это -1.988 Ведущей строкой будет та для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X2, а ведущий элемент: 0.313.
| X2 | X7 | X6 | X4 | Своб член | |
| F | 6.351 | 0.31 | 0.269 | 6.655 | -1.924 |
| X5 | -13.895 | 1.763 | -0.577 | 3.882 | 13.694 |
| X3 | -2.578 | 0.152 | -0.115 | 0.577 | 0.539 |
| X1 | 3.195 | -0.383 | 0.038 | -0.192 | 0.153 |
Так как в строке F нет отрицательных элементов, то
найдено оптимальное решение. Так как исходной задачей был поиск минимума, то оптимальным решением будет свободный член строки F, взятый с противоположным знаком. F=1.924
при значениях переменных равных: x3=0.539, x1=0.153. Переменные x2 и x4 не входят в базис, поэтому x2=0 x4=0.
Решение задач симплекс методом. Пример работы программы
Решение задач симплекс методом. Пример работы программыРазработка сайтов и программного обеспечения, системное администрирование, обучение программированию и работе с СУБД MySQL
in englishГлавная → Проекты → Реализация метода искусственного базиса (М-метода) → Пример
Реализация симплекс-метода в случае произвольных свободных членов методом искусственного базиса (M-методом)
Исходные данные:
1.0*x1+ 1.0*x2 >= 4.01.0*x1+ 2.0*x2 >= 6.0
-1.0*x1+ 2.0*x2 1.0*x1+ 1.0*x2
F(x)= 1.0*x1+ 4.0*x2
Введем выравнивающие и искусственные переменные:
1.0*x1+ 1.0*x2 -1.0*x3 +1.0*y1 = 4.01.0*x1+ 2.0*x2 -1.0*x4 +1.0*y2 = 6.0
-1.0*x1+ 2.0*x2 +1.0*x5 = 12.0
1.0*x1+ 1.0*x2 +1.0*x6 = 12.0
F(x)= 1.0*x1+ 4.0*x2 — M*(y1 +y2) → max
Начнем решение задачи:
Шаг №1
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 | y1 | y2 | Оценка |
| y 1 | 4.0 | 1.0 | 1.0 | -1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 4.0 |
| y 2 | 6.0 | 1.0 | 2.0 | 0.0 | -1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 3.0 |
| x 5 | 12.0 | -1.0 | 2.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 6.0 |
| x 6 | 12.0 | 1.0 | 1.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 12.0 |
| F (x) | 0.0 | -1.0 | -4.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | max |
| M func | -10.0 | -2.0 | -3.0 | 1.0 | 1.0 | 0.0 | 0.0 | -1.0 | -1.0 | max |
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 | y1 | y2 |
| y 1 | 1.0 | 0.5 | 0.0 | -1.0 | 0.5 | 0.0 | 0.0 | 1.0 | -0.5 |
| x 2 | 3.0 | 0.5 | 1.0 | 0.0 | -0.5 | 0.0 | 0.0 | 0.0 | 0.5 |
| x 5 | 6.0 | -2.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | -1.0 |
| x 6 | 9.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 1.0 | 0.0 | -0.5 |
| F (x) | 12.0 | 1.0 | 0.0 | 0.0 | -2.0 | 0.0 | 0.0 | 0.0 | 2.0 |
| M func | -1.0 | -0.5 | 0.0 | 1.0 | -0.5 | 0.0 | 0.0 | -1.0 | 0.5 |
Шаг №2
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 | y1 | y2 | Оценка |
| y 1 | 1.0 | 0.5 | 0.0 | -1.0 | 0.5 | 0.0 | 0.0 | 1.0 | -0.5 | 2.0 |
| x 2 | 3.0 | 0.5 | 1.0 | 0.0 | -0.5 | 0.0 | 0.0 | 0.0 | 0.5 | 6.0 |
| x 5 | 6.0 | -2.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | 0.0 | -1.0 | беск |
| x 6 | 9.0 | 0.5 | 0.0 | 0.0 | 0.5 | 0.0 | 1.0 | 0.0 | -0.5 | 18.0 |
| F (x) | 12.0 | 1.0 | 0.0 | 0.0 | -2.0 | 0.0 | 0.0 | 0.0 | 2.0 | max |
| M func | -1.0 | -0.5 | 0.0 | 1.0 | -0.5 | 0.0 | 0.0 | -1.0 | 0.5 | max |
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 | y1 | y2 |
| x 1 | 2.0 | 1.0 | 0.0 | -2.0 | 1.0 | 0.0 | 0.0 | 2.0 | -1.0 |
| x 2 | 2.0 | 0.0 | 1.0 | 1.0 | -1.0 | 0.0 | 0.0 | -1.0 | 1.0 |
| x 5 | 10.0 | 0.0 | 0.0 | -4.0 | 3.0 | 1.0 | 0.0 | 4.0 | -3.0 |
| x 6 | 8.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | -1.0 | 0.0 |
| F (x) | 10.0 | 0.0 | 0.0 | 2.0 | -3.0 | 0.0 | 0.0 | -2.0 | 3.0 |
| M func | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
Шаг №3
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 | Оценка |
| x 1 | 2.0 | 1.0 | 0.0 | -2.0 | 1.0 | 0.0 | 0.0 | 2.0 |
| x 2 | 2.0 | 0.0 | 1.0 | 1.0 | -1.0 | 0.0 | 0.0 | беск |
| x 5 | 10.0 | 0.0 | 0.0 | -4.0 | 3.0 | 1.0 | 0.0 | 3.3 |
| x 6 | 8.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | беск |
| F (x) | 10.0 | 0.0 | 0.0 | 2.0 | -3.0 | 0.0 | 0.0 | max |
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 |
| x 4 | 2.0 | 1.0 | 0.0 | -2.0 | 1.0 | 0.0 | 0.0 |
| x 2 | 4.0 | 1.0 | 1.0 | -1.0 | 0.0 | 0.0 | 0.0 |
| x 5 | 4.0 | -3.0 | 0.0 | 2.0 | 0.0 | 1.0 | 0.0 |
| x 6 | 8.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| F (x) | 16.0 | 3.0 | 0.0 | -4.0 | 0.0 | 0.0 | 0.0 |
Шаг №4
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 | Оценка |
| x 4 | 2.0 | 1.0 | 0.0 | -2.0 | 1.0 | 0.0 | 0.0 | беск |
| x 2 | 4.0 | 1.0 | 1.0 | -1.0 | 0.0 | 0.0 | 0.0 | беск |
| x 5 | 4.0 | -3.0 | 0.0 | 2.0 | 0.0 | 1.0 | 0.0 | 2.0 |
| x 6 | 8.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 | 8.0 |
| F (x) | 16.0 | 3.0 | 0.0 | -4.0 | 0.0 | 0.0 | 0.0 | max |
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 |
| x 4 | 6.0 | -2.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 |
| x 2 | 6.0 | -0.5 | 1.0 | 0.0 | 0.0 | 0.5 | 0.0 |
| x 3 | 2.0 | -1.5 | 0.0 | 1.0 | 0.0 | 0.5 | 0.0 |
| x 6 | 6.0 | 1.5 | 0.0 | 0.0 | 0.0 | -0.5 | 1.0 |
| F (x) | 24.0 | -3.0 | 0.0 | 0.0 | 0.0 | 2.0 | 0.0 |
Шаг №5
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 | Оценка |
| x 4 | 6.0 | -2.0 | 0.0 | 0.0 | 1.0 | 1.0 | 0.0 | беск |
| x 2 | 6.0 | -0.5 | 1.0 | 0.0 | 0.0 | 0.5 | 0.0 | беск |
| x 3 | 2.0 | -1.5 | 0.0 | 1.0 | 0.0 | 0.5 | 0.0 | беск |
| x 6 | 6.0 | 1.5 | 0.0 | 0.0 | 0.0 | -0.5 | 1.0 | 4.0 |
| F (x) | 24.0 | -3.0 | 0.0 | 0.0 | 0.0 | 2.0 | 0.0 | max |
| Базис | Св.члены | x1 | x2 | x3 | x4 | x5 | x6 |
| x 4 | 14.0 | 0.0 | 0.0 | 0.0 | 1.0 | 0.3 | 1.3 |
| x 2 | 8.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.3 | 0.3 |
| x 3 | 8.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 1.0 |
| x 1 | 4.0 | 1.0 | 0.0 | 0.0 | 0.0 | -0.3 | 0.7 |
| F (x) | 36.0 | 0.0 | 0.0 | 0.0 | 0.0 | 1.0 | 2.0 |
Оптимальное решение найдено!
Реклама:
Метки: симплекс метод.
Комментарии:
имя:
e-mail (не публикуется):
комментарий:
| © Ткачев Филипп, 2005—2018 Программист, веб-разработка и прикладное ПО. Все права защищены. | |
4.2: Максимизация симплексным методом
В предыдущей главе мы использовали геометрический метод для решения задач линейного программирования, но геометрический подход не будет работать для задач, которые содержат более двух переменных. В реальных жизненных ситуациях задачи линейного программирования состоят буквально из тысяч переменных и решаются компьютерами. Мы можем решить эти задачи алгебраически, но это будет не очень эффективно. Предположим, нам поставили задачу с, скажем, 5 переменными и 10 ограничениями.Выбирая все комбинации пяти уравнений с пятью неизвестными, мы могли найти все угловые точки, проверить их на выполнимость и найти решение, если оно существует. Но проблема в том, что даже для задачи с таким небольшим количеством переменных мы получим более 250 угловых точек, и проверка каждой точки будет очень утомительной. Итак, нам нужен метод, который имеет систематический алгоритм и может быть запрограммирован для компьютера. Метод должен быть достаточно эффективным, чтобы нам не приходилось оценивать целевую функцию в каждой угловой точке.У нас есть как раз такой метод, и он называется симплексным методом .
Симплексный метод был разработан во время Второй мировой войны доктором Джорджем Данцигом. Его модели линейного программирования помогли союзным войскам с проблемами транспортировки и планирования. В 1979 году советский ученый Леонид Хачян разработал метод под названием эллипсоидный алгоритм, который должен был стать революционным, но, как оказалось, он не лучше симплексного метода. В 1984 году Нарендра Кармаркар, научный сотрудник AT&T Bell Laboratories, разработал алгоритм Кармаркара, который оказался в четыре раза быстрее симплексного метода для решения некоторых задач.Но симплексный метод по-прежнему лучше всего подходит для большинства задач.
В симплексном методе используется очень эффективный подход. Он не вычисляет значение целевой функции в каждой точке; вместо этого он начинается с угловой точки области допустимости, где все основные переменные равны нулю, а затем систематически перемещается от угловой точки к угловой точке, улучшая при этом значение целевой функции на каждом этапе. Процесс продолжается до тех пор, пока не будет найдено оптимальное решение.
Чтобы изучить симплекс-метод, мы попробуем довольно нестандартный подход. Сначала мы перечисляем алгоритм, а затем работаем над проблемой. Мы обосновываем аргументацию каждого шага в процессе. Тщательное обоснование выходит за рамки этого курса.
Начнем с примера, решенного в предыдущей главе графическим методом. Это даст нам некоторое представление о симплекс-методе и в то же время даст нам возможность сравнить несколько возможных решений, которые мы получили ранее с помощью графического метода.Но сначала перечислим алгоритм симплекс-метода.
Теперь мы используем симплексный метод для решения примера 3.1.1, геометрически решенного в разделе 3.1.
Пример \ (\ PageIndex {1} \)
Ники работает с неполным рабочим днем на двух работах: I и II. Она никогда не хочет работать больше 12 часов в неделю. Она определила, что на каждый час, который она работает в Задании I, ей нужно 2 часа времени на подготовку, и на каждый час, который она работает в Задании II, ей требуется один час времени на подготовку, и она не может потратить более 16 часов на подготовку.Если она зарабатывает 40 долларов в час на работе I и 30 долларов в час на работе II, сколько часов она должна работать в неделю на каждой работе, чтобы максимизировать свой доход?
Решение
При решении этой проблемы мы будем следовать алгоритму, указанному выше.
ШАГ 1. Устраните проблему. Напишите целевую функцию и ограничения.
Поскольку симплексный метод используется для задач, состоящих из многих переменных, нецелесообразно использовать переменные \ (x \), \ (y \), \ (z \) и т. Д.Мы используем символы \ (x_1 \), \ (x_2 \), \ (x_3 \) и так далее.
Пусть
- \ (x_1 \) = Количество часов в неделю Ники будет работать на работе I и
- \ (x_2 \) = Количество часов в неделю Ники будет работать на Работе II.
Обычно выбирают максимальную переменную как \ (Z \).
Задача формулируется так же, как и в предыдущей главе.
\ [\ begin {array} {ll}
\ textbf {Maximize} & \ mathrm {Z} = 40 \ mathrm {x} _ {1} +30 \ mathrm {x} _ {2} \\
\ textbf {При условии:} & \ mathrm {x} _ {1} + \ mathrm {x} _ {2} \ leq 12 \\
& 2 \ mathrm {x} _ {1} + \ mathrm {x} _ { 2} \ leq 16 \\
& \ mathrm {x} _ {1} \ geq 0; \ mathrm {x} _ {2} \ geq 0
\ end {array} \ nonumber \]
ШАГ 2.Преобразуйте неравенства в уравнения. Это делается путем добавления одной резервной переменной для каждого неравенства.
Например, чтобы преобразовать неравенство \ (x_1 + x_2 ≤ 12 \) в уравнение, мы добавляем неотрицательную переменную \ (y_1 \), и получаем
\ [x_1 + x_2 + y_1 = 12 \ nonumber \]
Здесь переменная \ (y_1 \) подбирает провисание и представляет величину, на которую \ (x_1 + x_2 \) отстает от 12. В этой задаче, если Ники работает менее 12 часов, скажем 10, то \ (y_1 \) равно 2.Позже, когда мы считываем окончательное решение из симплексной таблицы, значения переменных резервирования будут определять неиспользованные суммы.
Перепишем целевую функцию \ (Z = 40x_1 + 30x_2 \) как \ (- 40x_1 — 30x_2 + Z = 0 \).
После добавления переменных резервирования наша задача читает
\ [\ begin {array} {ll}
\ text {Целевая функция} & — 40x_1 — 30x_2 + Z = 0 \\
\ text {Подлежит ограничению:} & x_1 + x_2 + y_1 = 12 \\
& 2x_1 + x_2 + y_2 = 16 \\
& x1 ≥ 0; x2 ≥ 0
\ конец {массив} \ nonumber \]
ШАГ 3.Построить исходную симплексную таблицу . Каждое ограничение неравенства отображается в отдельной строке. (Ограничения неотрицательности не отображаются в виде строк в симплексной таблице , а не .) Запишите целевую функцию в нижней строке.
Теперь, когда неравенства преобразованы в уравнения, мы можем представить проблему в расширенной матрице, называемой исходной симплексной таблицей, следующим образом.
Здесь вертикальная линия отделяет левую часть уравнения от правой.Горизонтальная линия отделяет ограничения от целевой функции. Правая часть уравнения представлена столбцом C.
Читателю необходимо заметить, что последние четыре столбца этой матрицы выглядят как окончательная матрица для решения системы уравнений. Если мы произвольно выберем \ (x_1 = 0 \) и \ (x_2 = 0 \), мы получим
\ [\ left [\ begin {array} {ccccc}
y_ {1} & y_ {2} & Z & | & C \\
1 & 0 & 0 & | & 12 \\
0 & 1 & 0 & | & 16 \\
0 & 0 & 1 & | & 0
\ конец {массив} \ right] \ nonumber \]
, что означает
\ [y_1 = 12 \ quad y_2 = 16 \ quad Z = 0 \ nonumber \]
Решение, полученное путем произвольного присвоения значений некоторым переменным и последующего решения для остальных переменных, называется базовым решением , связанным с таблицей.Таким образом, приведенное выше решение является основным решением, связанным с исходной симплексной таблицей. Мы можем пометить базовую переменную решения справа от последнего столбца, как показано в таблице ниже.
ШАГ 4. Самая отрицательная запись в нижней строке определяет сводный столбец.
Самая отрицательная запись в нижней строке -40; поэтому столбец 1 идентифицируется.
Вопрос Почему мы выбираем наиболее отрицательную запись в нижней строке?
Ответ Самая отрицательная запись в нижней строке представляет собой наибольший коэффициент в целевой функции — коэффициент, вход которого будет увеличивать значение целевой функции быстрее всего.
Симплексный метод начинается в угловой точке, где все основные переменные, переменные с такими символами, как \ (x_1 \), \ (x_2 \), \ (x_3 \) и т. Д., Равны нулю. Затем он перемещается от угловой точки к соседней угловой точке, всегда увеличивая значение целевой функции. В случае целевой функции \ (Z = 40x_1 + 30x_2 \) имеет смысл увеличивать значение \ (x_1 \), а не \ (x_2 \). Переменная \ (x_1 \) представляет количество часов в неделю, которые Ники работает на Job I.Поскольку работа I платит 40 долларов в час, в то время как работа II платит только 30 долларов, переменная \ (x_1 \) увеличит целевую функцию на 40 долларов за единицу увеличения переменной \ (x_1 \).
ШАГ 5. Рассчитайте частные. Наименьшее частное определяет строку. Элемент на пересечении столбца, указанного на шаге 4, и строки, указанной на этом шаге, идентифицируется как опорный элемент.
Следуя алгоритму, чтобы вычислить частное, мы делим записи в крайнем правом столбце на записи в столбце 1, исключая запись в нижней строке.
Наименьшее из двух частных, 12 и 8, равно 8. Следовательно, строка 2 идентифицируется. Пересечение столбца 1 и строки 2 — это запись 2, которая была выделена. Это наш стержневой элемент.
Вопрос Почему мы находим частные и почему наименьшее частное определяет строку?
Ответ Когда мы выбираем наиболее отрицательную запись в нижней строке, мы пытаемся увеличить значение целевой функции, вводя переменную \ (x_1 \).Но мы не можем выбрать какое-либо значение для \ (x_1 \). Можем ли мы позволить \ (x_1 = 100 \)? Точно нет! Это потому, что Ники никогда не хочет работать более 12 часов на обеих работах вместе: \ (x_1 + x_2 ≤ 12 \). Можем ли мы позволить \ (x_1 = 12 \)? Опять же, ответ — нет, потому что время на подготовку к работе I в два раза больше времени, затрачиваемого на работу. Поскольку Ники никогда не хочет тратить на подготовку более 16 часов, максимальное время, которое она может работать, составляет 16 ÷ 2 = 8.
Теперь вы видите цель вычисления частных; использование частных для определения опорного элемента гарантирует, что мы не нарушаем ограничения.
Вопрос Почему мы идентифицируем элемент поворота?
Ответ Как мы упоминали ранее, симплекс-метод начинается с угловой точки, а затем переходит к следующей угловой точке, всегда улучшая значение целевой функции. Значение целевой функции улучшается за счет изменения количества единиц переменных. Мы можем добавить количество единиц одной переменной, отбрасывая единицы другой. Пивотинг позволяет нам это делать.
Переменная, единицы измерения которой добавляются, называется входной переменной , , а переменная, единицы измерения которой заменяются, называется исходящей переменной . Входящей переменной в приведенной выше таблице является \ (x_1 \), и она была идентифицирована самой отрицательной записью в нижней строке. Исходящая переменная \ (y_2 \) была идентифицирована наименьшим из всех частных.
ШАГ 6. Выполните поворот, чтобы обнулить все остальные записи в этом столбце.
В главе 2 мы использовали поворот, чтобы получить эшелонированную строку расширенной матрицы. Поворот — это процесс получения 1 в месте расположения сводного элемента с последующим обнулением всех остальных записей в этом столбце. Итак, теперь наша задача — сделать наш сводный элемент равным 1, разделив всю вторую строку на 2. Результат следует.
Чтобы получить ноль в первой записи над элементом поворота, мы умножаем вторую строку на -1 и прибавляем ее к строке 1. Получаем
Чтобы получить ноль в элементе ниже точки поворота, мы умножаем вторую строку на 40 и добавляем ее к последней строке.
Теперь мы определяем базовое решение, связанное с этой таблицей. Произвольно выбирая \ (x_2 = 0 \) и \ (y_2 = 0 \), мы получаем \ (x_1 = 8 \), \ (y_1 = 4 \) и \ (z = 320 \). Если мы напишем расширенную матрицу, левая часть которой представляет собой матрицу со столбцами, в которых одна единица и все остальные нули, мы получим следующую матрицу, указывающую то же самое.
\ [\ left [\ begin {array} {ccccc}
\ mathrm {x} _ {1} & \ mathrm {y} _1 & \ mathrm {Z} & | & \ mathrm {C} \\
0 & 1 & 0 & | & 4 \\
1 & 0 & 0 & | & 8 \\
0 & 0 & 1 & | & 320
\ end {array} \ right] \ nonumber \]
Мы можем переформулировать решение, связанное с этой матрицей, как \ (x_1 = 8 \), \ (x_2 = 0 \), \ (y_1 = 4 \), \ (y_2 = 0 \) и \ (z = 320 \) .На этом этапе игры говорится, что если Ники проработает 8 часов на Работе I и не будет часов на Работе II, ее прибыль Z составит 320 долларов. Напомним из примера 3.1.1 в разделе 3.1, что (8, 0) была одной из наших угловых точек. Здесь \ (y_1 = 4 \) и \ (y_2 = 0 \) означают, что у нее останется 4 часа рабочего времени и никакого времени на подготовку.
ШАГ 7. Когда в нижнем ряду больше нет отрицательных записей, мы закончили; в противном случае мы снова начинаем с шага 4.
Поскольку в нижнем ряду все еще есть отрицательная запись -10, нам нужно снова начать с шага 4.На этот раз мы не будем повторять детали каждого шага, вместо этого мы определим столбец и строку, которые дают нам сводный элемент, и выделим сводный элемент. Результат следующий.
Делаем опорный элемент 1, умножая строку 1 на 2, и получаем
Теперь, чтобы сделать все остальные записи в этом столбце нулями, мы сначала умножаем строку 1 на -1/2 и добавляем ее к строке 2, а затем умножаем строку 1 на 10 и добавляем ее к нижней строке.
У нас больше нет отрицательных записей в нижнем ряду, поэтому мы закончили.
Вопрос Почему мы закончили, если в нижней строке нет отрицательных записей?
Ответ Ответ находится в нижней строке. Нижняя строка соответствует уравнению:
\ [\ begin {array} {l}
0 x_ {1} +0 x_ {2} +20 y_ {1} +10 y_ {2} + Z = 400 \ quad \ text {или} \\
z = 400-20 лет 1-10 лет 2
\ end {array} \ nonumber \]
Поскольку все переменные неотрицательны, максимальное значение \ (Z \), которое когда-либо может быть достигнуто, равно 400, и это произойдет только тогда, когда \ (y_1 \) и \ (y_2 \) равны нулю.
ШАГ 8. Зачитай свои ответы.
Теперь мы зачитываем наши ответы, то есть определяем базовое решение, связанное с окончательной симплексной таблицей. Опять же, мы смотрим на столбцы, в которых есть 1, а все остальные записи — нули. Поскольку столбцы с метками \ (y_1 \) и \ (y_2 \) не являются такими столбцами, мы произвольно выбираем \ (y_1 = 0 \) и \ (y_2 = 0 \), и получаем
\ [\ left [\ begin {array} {ccccc}
\ mathrm {x} _ {1} & \ mathrm {x} _ {2} & \ mathrm {Z} & | & \ mathrm {C} \\
0 & 1 & 0 & | & 8 \\
1 & 0 & 0 & | & 4 \\
0 & 0 & 1 & | & 400
\ end {array} \ right] \ nonumber \]
Матрица читает \ (x_1 = 4 \), \ (x_2 = 8 \) и \ (z = 400 \).
Окончательное решение гласит, что если Ники проработает 4 часа на Работе I и 8 часов на Работе II, она максимизирует свой доход до 400 долларов. Поскольку обе переменные Slack равны нулю, это означает, что она израсходовала бы все рабочее время, а также время на подготовку, и ничего не останется.
3.3a. Решение стандартных задач максимизации с помощью симплекс-метода
В предыдущем разделе мы обнаружили, что графический метод решения задач линейного программирования, хотя и требует много времени, позволяет нам видеть области решения и определять угловые точки.Однако это невозможно при наличии нескольких переменных. Мы можем визуализировать до трех измерений, но даже это может быть сложно, когда есть множество ограничений.
Для решения задач линейного программирования, содержащих более двух переменных, математики разработали то, что теперь известно как симплекс-метод
. Это эффективный алгоритм (набор механических шагов), который «переключает» угловые точки, пока не найдет ту, которая максимизирует целевую функцию.Хотя это заманчиво, есть несколько вещей, на которые нам нужно обратить внимание, прежде чем использовать его.
Прежде чем приступить к математическим деталям, давайте рассмотрим пример задачи линейного программирования, для которой
подходит для симплекс-метода:
Пример 1
С помощью симплекс-метода можно решить следующую систему:
Цель Функция: P = 2 x + 3 y + z
При соблюдении ограничений:
3 x + 2 y ≤ 5
2 x + y — z ≤ 13
z ≤ 4
х, у, z≥0
Стандартная задача максимизации
С математической точки зрения, чтобы использовать симплексный метод для решения задачи линейного программирования, нам нужна стандартная задача максимизации:
- ,
- — целевая функция, а —
- одно или несколько ограничений в форме a 1 x 1 + a 2 x 2 +… a n x le n В
- Все числа a представляют собой действительные коэффициенты, а
- x число представляет соответствующие переменные.
- V — неотрицательное (0 или большее) действительное число
Наличие ограничений с верхними пределами должно иметь смысл, поскольку при максимизации количества у нас, вероятно, есть ограничения на то, что мы можем сделать. Если бы у нас не было ограничений, мы могли бы продолжать увеличивать, скажем, прибыль, бесконечно! Это противоречит тому, что мы знаем о реальном мире.
Чтобы использовать симплексный метод, технологически или вручную, мы должны настроить исходную симплексную таблицу
, которая представляет собой матрицу, содержащую информацию о задаче линейного программирования, которую мы хотим решить.
Во-первых, матрицы плохо справляются с неравенством. Во-первых, у матрицы нет простого способа отслеживать направление неравенства. Уже одно это препятствует использованию неравенств в матрицах. Как же нам этого избежать?
Рассмотрим следующую задачу линейного программирования
Развернуть:
P = 7 x + 12 y
При условии:
2 x + 3 y ≤ 6
3 x + 7 y ≤12
Поскольку мы знаем, что левые части обоих неравенств будут величинами, меньшими, чем соответствующие значения справа, мы можем быть уверены, что добавление «чего-то» к левой части сделает их в точности равными.То есть:
2 x + 3 y + s 1 = 6
3 x + 7 y + s 2 = 12
Например, предположим, что
x = 1, y = 1, тогда
2 + 3 + s 1 = 6 или s 1 = 1
3 + 7 + s 2 = 12 или s 2 = 2
Важно отметить, что эти две переменные, s 1 и s 2 , не обязательно одинаковы.Они просто действуют на неравенство, подбирая «слабину», которая не дает левой стороне выглядеть как правая. Следовательно, мы называем их резервными переменными . Это устраняет неравенство за нас. Поскольку расширенные матрицы содержат все переменные слева и константы справа, мы перепишем целевую функцию в соответствии с этим форматом:
–7 x — 12 y + P = 0
Теперь мы можем написать исходную систему уравнений :
| 2 x + 3 y + s 1 = 6 |
| 3 x + 7 y + s 2 = 12 |
| –7 x — 12 y + P = 0 |
Для этого нам потребуется матрица, которая может обрабатывать x , y , s 1 , s 2 и P .Мы разместим это в таком порядке. Наконец, симплексный метод требует, чтобы целевая функция была указана в нижней строке матрицы, чтобы мы имели:
Мы создали исходную симплексную таблицу . Обратите внимание, что горизонтальные и вертикальные линии используются просто для отделения коэффициентов ограничения от констант и коэффициентов целевой функции. Также обратите внимание, что столбцы переменных резервов вместе с выходными данными целевой функции образуют единичную матрицу.
Мы представим алгоритм решения, однако отметим, что он не совсем интуитивно понятен. Мы сосредоточимся на этом методе для одного примера, а затем перейдем к использованию технологий для выполнения процесса за нас.
1. Выберите столбец поворота
Сначала мы выбираем сводный столбец, который будет столбцом, содержащим наибольший отрицательный коэффициент в строке, содержащей целевую функцию. Обратите внимание, что наибольшее отрицательное число принадлежит члену, который больше всего влияет на целевую функцию.Это сделано намеренно, поскольку мы хотим сосредоточиться на значениях, которые делают вывод как можно большим.
Таким образом, наша точка поворота — это столбец и .
2. Выберите сводную строку
Сделайте это путем вычисления отношения каждой константы ограничения к соответствующему коэффициенту в сводном столбце — это называется тестовым соотношением . Выберите строку с наименьшим тестовым соотношением.
Сначала рассчитаем тестовые соотношения:
[латекс] \ displaystyle {\ left [\ matrix {{6 ÷ 3 = 2} \\ {12 ÷ 7≈1.7}} \ right]} [/ latex]
Поскольку тестовое соотношение для строки 2 меньше, мы выбираем ее в качестве сводной строки. Теперь значение в рамке называется нашей опорной точкой . Чтобы объяснить, почему мы это делаем, заметим, что 2 и 1.7 — это просто вертикальные пересечения двух неравенств. Мы выбираем меньшее, чтобы убедиться, что угловая точка находится в допустимой области:
3. Используя исключение Гаусса, удалите строки 1 и 3
Умножьте R2 на (1/7), чтобы преобразовать 7 в 1.
Затем используйте 1, чтобы удалить 3 в R1: -3R 2 + R 1 → R 1
И используйте 1, чтобы удалить -12 в R3: 12R 2 + R 3 → R 3
Получаем следующую матрицу (возможно, дроби)
Что мы сделали? Во-первых, мы максимально увеличили вклад 2-2 входного коэффициента значений
и в целевую функцию. Оптимизировали ли мы функцию? Не совсем так, поскольку мы все еще видим, что в первом столбце есть отрицательное значение.Это говорит нам, что все еще может вносить вклад в целевую функцию. Чтобы устранить это, мы сначала находим сводную строку, получая тестовые отношения:
[латекс] \ displaystyle {\ left [\ matrix {{5/7} & {0} & {1} & {- 3/7} & {0} & {|} {6/7} \\ {3 / 7} & {1} & {0} & {1/7} & {0} & {|} {12/7} \\ {- 13/7} & {0} & {0} & {12 / 7} & {1} & {|} {144/7}} \ right]} [/ latex]
[латекс] \ displaystyle {\ left [\ matrix {{(6/7) ÷ (5/7) ≈1.2} \\ {12 ÷ 3≈4}} \ right]} [/ latex]
Начиная с 1.2 <4, R1 - наша новая сводная строка.
Интересно, что это тестовое соотношение соответствует входному значению пересечения двух линий!
Аналогичным образом мы переходим к удалению всех неповоротных значений.
Умножьте R1 на (1 / 0,71), чтобы преобразовать 0,71 в 1.
Затем используйте 1, чтобы удалить 3 в R3: -3R 1 + R 2 → R 2
И используйте 1, чтобы удалить -12 в R3: 1.86R 1 + R 3 → R 3
Получаем следующую матрицу
[латекс] \ displaystyle {\ left [\ matrix {{1} & {0} & {7/5} & {- 3/5} & {0} & {|} {6/5} \\ {0 } & {1} & {- 3/5} & {2/5} & {0} & {|} {6/5} \\ {0} & {0} & {13/5} & {3 / 5} & {1} & {|} {114/5}} \ right]} [/ latex]
В строке целевой функции не осталось дополнительных отрицательных записей.Таким образом, мы имеем следующую матрицу:
[латекс] \ displaystyle {\ left [\ matrix {{1} & {0} & {7/5} & {- 3/5} & {0} & {|} {6/5} \\ {0 } & {1} & {- 3/5} & {2/5} & {0} & {|} {6/5} \\ {0} & {0} & {13/5} & {3 / 5} & {1} & {|} {114/5}} \ right]} [/ latex]
Таким образом, мы готовы читать решения.
4. Определите набор решений
Чтобы идентифицировать набор решений, мы сосредотачиваемся только на столбцах с ровно одной ненулевой записью — они называются базовыми переменными (столбцы с более чем одной ненулевой записью, таким образом, называются небазовыми переменными ) .
Мы замечаем, что оба столбца x any являются базовыми переменными. Нас действительно не волнуют переменные резервов, так же как мы игнорируем неравенство, когда находим пересечения. Теперь мы видим, что
[латекс] \ displaystyle {\ left [\ matrix {{1} & {0} & {7/5} & {- 3/5} & {0} & {|} {6/5} \\ {0 } & {1} & {- 3/5} & {2/5} & {0} & {|} {6/5} \\ {0} & {0} & {13/5} & {3 / 5} & {1} & {|} {114/5}} \ right]} [/ latex]
Установка переменных резерва на 0 дает:
x ≈ 1.2
y ≈ 1,2
P = 22,8
Таким образом, x = 1,2, y = 1,2, P = 22,8 — это решение задачи линейного программирования. То есть, входные данные x = 1,2 и y = 1,2 дадут максимальное значение целевой функции 22,8
.Хотя этот процесс несколько интуитивно понятен, за ним стоит больше, чем мы предполагаем. И вместо того, чтобы проходить эти изнурительные шаги до тошноты, мы позволим нашей технологии следовать этим шагам. Для этого нам понадобится специальная программа, которая будет распространяться в классе
.Для выполнения симплекс-метода с помощью графического калькулятора необходимы следующие программы:
- Поворот,
- Pivot1 и
- Симплекс
Pivot и Pivot1 напрямую не используются.Вместо этого программа Simplex обращается к этим двум приложениям, чтобы помочь ей с помощью довольно длинного и утомительного кода. Как работает код? Используя инструкции, он находит сводные столбцы, сводные строки, выполняет гауссовское исключение, проверяет наличие негативов в строке целевой функции и повторяет этот процесс по мере необходимости, пока все негативы не будут удалены.
Теперь, когда мы проиллюстрировали, что на самом деле симплекс-метод работает даже с двумя входными переменными, давайте покажем ситуацию, в которой этот метод особенно полезен.
Пример 2
Новая авиакомпания решила выйти на рынок. Он рассматривает возможность предложения рейсов из Феникса, штат Аризона, и первоначально хотел бы отправиться в три разных места: Сан-Диего, Сан-Франциско и Лас-Вегас. Расстояния каждого рейса туда и обратно, вылетающего из Феникса, составляют (приблизительно): 720 миль, 1500 миль и 1140 миль соответственно. Компания хотела бы использовать слоган: «Средняя цена за рейс никогда не превышает 200 долларов». Что касается затрат, ожидается, что полеты в Сан-Диего будут составлять около 10% от стоимости авиабилетов.Точно так же на Сан-Франциско будет приходиться 12%, а на Лас-Вегас — 14% авиаперевозок. Компания хочет, чтобы общая средняя стоимость не превышала 10% от заработанных авиабилетов. Недавнее исследование рынка позволяет компании сделать вывод, что она могла бы продать около 1900 билетов в Сан-Диего, 700 билетов в Сан-Франциско и 1000 билетов в Лас-Вегас. В этих условиях и при условии, что все проданные билеты являются рейсами в оба конца, какую сумму компания должна взимать за билет, чтобы максимизировать свой общий доход?
Решение
Мы хотим знать стоимость авиабилетов в каждый пункт назначения.Пусть,
x = цена билета в оба конца до Сан-Диего
y = цена билета в оба конца до Сан-Франциско
z = цена за билет в оба конца до Лас-Вегаса
Компания хочет максимизировать общий доход. Это основано на сумме количества проданных билетов, умноженной на цену за билет, которая составляет:
.R = 1900 x + 700 y + 1000 z
При соблюдении ограничений:
- Средняя цена за рейс не превышает 200 долларов США
- Средняя стоимость авиабилетов не более 10% от общей стоимости
Математически,
- Добавьте цены и разделите на 3
[latex] \ displaystyle \ frac {{{x} + {y} + {z}}} {{3}} \ le {200} [/ latex] - Или x + y + z ≤ 600
- Общий доход от продажи билетов в Сан-Диего составит 10% от этой суммы.То есть Стоимость = 0,10 (1900 x ) = 190 x . Точно так же имеем 0,12 (700 y ) = 84 y и 0,14 (1000 z ) = 140 z . Мы хотим, чтобы сумма этих затрат была меньше или равной 10% от общего дохода, что составляет 0,10 (1900 x + 700 y + 1000 z ) = 190 x + 70 y . + 100 z .
- 190 x + 84 y + 140 z ≤ 190 x + 70 y + 100 z
- или 14 y + 40 z ≤ 0
Поскольку оба ограничения имеют правильную форму, мы можем приступить к настройке исходной симплексной таблицы.В качестве примечания будьте очень осторожны при использовании симплексного метода, поскольку невыполненные требования делают полученные результаты недействительными.
Переписанная целевая функция:
–1900 x — 700 y — 1000 z + R = 0
И упрощенные ограничения:
x + y + z ≤ 600 (умножить обе стороны на 3)
14 y + 40 z ≤ 0
х, y≥0
Для каждого из двух ограничений потребуется переменная Slack, поэтому мы перепишем их следующим образом:
x + y + z + s 1 = 600
14 y + 40 z + s 2 = 0
У нас будут следующие столбцы переменных:
x , y , z, s 1 , s 2 , R и постоянный столбец, всего 7 столбцы.Всего у нас есть два ограничения и одна целевая функция для трех строк. Теперь напишем исходную симплексную таблицу:
[латекс] \ displaystyle {\ left [\ matrix {{1} & {1} & {1} & {1} & {0} & {0} & {|} {600} \\ {0} & { 14} & {40} & {0} & {1} & {0} & {|} {0} \\ {- 1900} & {- 700} & {- 1000} & {0} & {0} & {1} & {|} {0}} \ right]} [/ латекс]
Теперь таблица готова к решению с использованием Simplex.
Поворот по 1-му столбцу и 1-й строке. (Вы не можете делить на 0, чтобы получить сводную строку)
[латекс] \ displaystyle {\ left [\ matrix {{1} & {1} & {1} & {1} & {0} & {0} & {|} {600} \\ {0} & { 14} & {40} & {0} & {1} & {0} & {|} {0} \\ {0} & {1200} & {900} & {1900} & {0} & {1} & {|} {1140000}} \ right]} [/ латекс]
Поскольку базовым будет только столбец x , мы видим, что x = 600 — это решение.Поскольку y и z не являются базовыми переменными, мы устанавливаем y = z = 0. То есть они не способствуют максимизации дохода. Кроме того, R является активной переменной, поэтому мы видим, что R = 1 140 000 долларов США — это максимальный доход, который компания может получить с учетом ограничений. Им следует продавать билеты в Сан-Диего за 600 долларов и не продавать рейсы в другие города. Как нетрудно догадаться, компания, вероятно, немного ошеломлена. Мы рассмотрим это в следующем примере.
Интересно, что поездки в Сан-Диего сами по себе приносят наибольший доход, исходя из данных ограничений. Почему это? Если мы посмотрим на ограничения, мы увидим, что компания вполне уверена, что сможет продать 1900 рейсов в Сан-Диего. Компания также несколько озадачена тем, что предполагается продавать билеты по 600 долларов за штуку. На этом этапе он может решить добавить к модели некоторые дополнительные ограничения.
Пример 3
Предположим, что авиалайнер в Примере 2 решает, что он может взимать не более 150 долларов за билет до Сан-Диего, чтобы быть конкурентоспособным по сравнению с другими авиалайнерами, которые летают в тот же пункт назначения.Если предположить, что все остальные ограничения будут по-прежнему использоваться, как это повлияет на цены на билеты и максимальный доход?
Решение
Мы используем ту же исходную таблицу, но мы должны иметь дело со следующим новым ограничением:
x ≤ 150
Добавляя третью переменную slack, получаем
x + с 3 = 150
Это добавляет один столбец и одну строку в нашу таблицу:
[латекс] \ displaystyle {\ left [\ matrix {{1} & {1} & {1} & {1} & {0} & {0} & {0} & {|} {600} \\ { 0} & {14} & {40} & {0} & {1} & {0} & {0} & {|} {0} \\ {1} & {0} & {0} & {0} & {0} & {1} & {0} & {|} {150} \\ {- 1900} & {- 700} & {- 1000} & {0} & {0} & {0} & {1 } & {|} {0}} \ right]} [/ латекс]
Решение этого симплексом дает
[латекс] \ displaystyle {\ left [\ matrix {{0} & {0} & {- 13/7} & {1} & {- 1/14} & {- 1} & {0} & {| } {450} \\ {0} & {1} & {20/7} & {0} & {1/14} & {0} & {0} & {|} {0} \\ {1} & {0} & {0} & {0} & {0} & {1} & {0} & {|} {150} \\ {0} & {0} & {1000} & {0} & {50 } & {1900} & {1} & {|} {285000}} \ right]} [/ латекс]
Решение: x = 150, y = 0, z = 450 и R = 285000
Пример 4
Кейтеринговая компания приготовит обед к деловой встрече.Здесь подают бутерброды с ветчиной, легкие бутерброды с ветчиной и вегетарианские бутерброды. Сэндвич с ветчиной состоит из 1 порции овощей, 4 ломтиков ветчины, 1 ломтика сыра и 2 ломтиков хлеба. Легкий бутерброд с ветчиной состоит из 2 порций овощей, 2 ломтиков ветчины, 1 ломтика сыра и 2 ломтиков хлеба. Вегетарианский бутерброд состоит из 3 порций овощей, 2 ломтиков сыра и 2 ломтиков хлеба. Всего доступно 10 пакетов ветчины, в каждой по 40 ломтиков; Доступно 18 буханок хлеба, каждая по 14 ломтиков; Доступно 200 порций овощей и 15 пакетов сыра, по 60 ломтиков в каждом.Учитывая ресурсы, сколько бутербродов можно произвести, если цель состоит в том, чтобы максимально увеличить количество бутербродов?
Решение
Мы хотим увеличить количество бутербродов, поэтому давайте:
x = количество бутербродов с ветчиной
y = Количество легких бутербродов с ветчиной
z = количество вегетарианских бутербродов
Общее количество бутербродов равно
.S = x + y + z
Ограничения будут даны с учетом общего количества доступных ингредиентов.То есть у компании ограниченное количество ветчины, овощей, сыра и хлеба.
Всего у компании
10 (40) = 400 ломтиков ветчины, 18 (14) = 252 ломтика хлеба, 200 порций овощей и 15 (60) = 900 ломтиков сыра. Максимум, компания может использовать вышеуказанные суммы.
Есть два бутерброда с ветчиной: для первого требуется 4 ломтика ветчины, а для второго — только 2 на бутерброд. То есть 4 x + 2 y ≤ 400
То есть общее количество ломтиков ветчины не может превышать 400.
Для каждого бутерброда требуется 2 ломтика хлеба, поэтому 2 x + 2 y + 2 z ≤ 252
В бутербродах с ветчиной 1 и 2 порции овощей соответственно, а в вегетарианском бутерброде 3 порции овощей. Итак, 1 x + 2 y + 3 z ≤ 200
Для обоих бутербродов с ветчиной требуется один ломтик сыра, а для вегетарианского бутерброда — два ломтика сыра, поэтому 1 x + 1 y + 2 z ≤ 900 Ниже представлена законченная модель линейного программирования для этого примера.
| Развернуть: S = x + y + z |
| Субъект Кому: 4 x + 2 y ≤ 400 |
| 2 x + 2 y + 2 z ≤ 252 |
| x + 2 y + 3 z ≤ 200 |
| 1 x + 1 y + 2 z ≤ 900 |
| x, y, z≥0 |
Эти ограничения удовлетворяют требованиям симплекс-метода, поэтому продолжим.
Включая резервные переменные, получаем:
4 x + 2 y + 0 z + s 1 = 400
2 x + 2 y + 2 z + s 2 = 252
x + 2 y + 3 z + s 3 = 200
x + y + 2 z + s 4 = 900
— x — y — z + S = 0
Исходная симплексная таблица:
[латекс] \ displaystyle {\ left [\ matrix {{4} & {2} & {0} & {1} & {0} & {0} & {0} & {0} {|} & {400 } \\ {2} & {2} & {2} & {0} & {1} & {0} & {0} & {0} {|} & {252} \\ {1} & {2} & {3} & {0} & {0} & {1} & {0} & {0} {|} & {200} \\ {1} & {1} & {2} & {0} & { 0} & {0} & {1} & {0} {|} & {900} \\ {- 1} & {- 1} & {- 1} & {0} & {0} & {0} & {0} & {1} {|} & {0}} \ right]} [/ latex]
Поскольку наибольшее отрицательное число в нижней строке одинаково для трех столбцов, мы можем использовать любой столбец.Можно также использовать первый столбец. Наименьшее частное получается путем деления 4 на 400, так что строка 1 является сводным столбцом. Поворот на «4» в R1C1 дает доход.
[латекс] \ displaystyle {\ left [\ matrix {{1} & {1/2} & {0} & {1/4} & {0} & {0} & {0} & {0} {| } & {100} \\ {0} & {1} & {2} & {- 1/2} & {1} & {0} & {0} & {0} {|} & {52} \\ {0} & {3/2} & {3} & {- 1/4} & {0} & {1} & {0} & {0} {|} & {100} \\ {0} & { 1/2} & {2} & {- 1/4} & {0} & {0} & {1} & {0} {|} & {800} \\ {0} & {- 1/2} & {- 1} & {1/4} & {0} & {0} & {0} & {1} {|} & {100}} \ right]} [/ latex]
Примечание: мы увеличили S с 0 до 200, но у нас все еще есть отрицательный знак в нижней строке.Поскольку «-1» более отрицательно, чем «-1/2», мы будем вращаться по столбцу 3. После деления положительных чисел выше «-1» на константы мы получим наименьшее частное в строке 2. Вращаемся по «2». ”В выходах R2C3.
[латекс] \ displaystyle {\ left [\ matrix {{x} & {y} & {z} & {s1} & {s2} & {s3} & {s4} & {S} \\ {1} & {1/2} & {0} & {1/4} & {0} & {0} & {0} & {0} {|} & {100} \\ {0} & {1/2} & {1} & {- 1/4} & {1/2} & {0} & {0} & {0} {|} & {26} \\ {0} & {0} & {0} & { 1/2} & {- 3/2} & {1} & {0} & {0} {|} & {22} \\ {0} & {- 1/2} & {0} & {1 / 4} & {- 1} & {0} & {1} & {0} {|} & {748} \\ {0} & {0} & {0} & {1/2} & {0} & {0} & {0} & {1} {|} & {126}} \ right]} [/ latex]
Теперь у нас есть оптимальное решение
- x = 100 (базовая переменная в строке 1)
- y = 0 (небазовая переменная)
- z = 26 (основная переменная строка 2)
- s1 = 0 (небазовая переменная)
- s2 = 0 (небазовая переменная)
- s3 = 22 (основная переменная строка 3)
- s4 = 748 (основная переменная строка 4)
- S = 126 (основная переменная строка 5)
Конечно, нас действительно интересуют: x = 100, y = 0, z = 26, S = 126
Мы обнаружили, что необходимо приготовить 100 бутербродов с ветчиной, 26 вегетарианских бутербродов и 0 легких бутербродов с ветчиной, чтобы максимально увеличить общее количество приготовленных бутербродов.
Переменные резерва не важны в решении. Просто в достижении решения.
Дополнительные примеры см. В следующем разделе. Во многих задачах используются переменные с индексами, такие как x 1 , x 2 , x 3 и т. Д. Это особенно полезно, если у вас есть несколько переменных. Вы увидите это в следующих примерах.
Дополнительные ресурсы перечислены ниже:
Milos Podmanik, By the Numbers, «Решение стандартных задач максимизации с помощью симплекс-метода», лицензия CC BY-NC-SA 3.0 лицензия.
MathIsGreatFun, «MAT217 HW 2.2 # 1», под лицензией Standard YouTube.
MathIsGreatFun, «MAT217 2.2 # 2» под стандартной лицензией YouTube.
MathIsGreatFun, «MAT217 2.2 # 3» под стандартной лицензией YouTube.
MathIsGreatFun, «MATh317 2.2 # 4» под стандартной лицензией YouTube.
Линейное программирование: симплекс-метод
Линейное программирование: симплекс-методЗадача линейного программирования
Вот первая проблема, которая у нас была.
| Развернуть | -P | = | 40x 1 | + | 30x 2 | ||
|---|---|---|---|---|---|---|---|
| При условии: | х 1 | + | 2x 2 | ≤ | 16 | ||
| х 1 | + | х 2 | ≤ | 9 | |||
| 3x 1 | + | 2x 2 | ≤ | 24 | |||
| х 1 | , | х 2 | ≥ | 0 |
Исходная система
Исходная система находится путем преобразования ограничений ≤ в ограничения = путем добавления переменной запаса.
Это тот же шаг, что мы сделали в табличном методе.
| Развернуть | -P | = | 40x 1 | + | 30x 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| При условии: | х 1 | + | 2x 2 | + | с 1 | = | 16 | ||||||
| х 1 | + | х 2 | + | с 2 | = | 9 | |||||||
| 3x 1 | + | 2x 2 | + | с 3 | = | 24 | |||||||
| х 1 | , | х 2 | , | с 1 | , | с 2 | , | с 3 | ≥ | 0 |
Исходная таблица
Таблицы — это причудливые названия матриц.Сейчас мы преобразуем систему линейных уравнений в матрицы. Однако здесь есть еще одна уловка … мы перемещаем все переменные в левую часть, поэтому целевая функция становится -40x 1 — 30x 2 + P = 0. Мы также помещаем целевую функцию последней. в таблице и поместите над ней линию увеличения, чтобы отделить ее от ограничений.
| х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 0 | 0 | 0 | 16 | ||
| 1 | 1 | 0 | 1 | 0 | 0 | 9 | ||
| 3 | 2 | 0 | 0 | 1 | 0 | 24 | ||
| -40 | -30 | 0 | 0 | 0 | 1 | 0 |
Основные и неосновные переменные
В каждой строке таблицы будет базовая переменная, а целевая функция всегда будет базовой в нижней строке.
Каждая переменная соответствует столбцу в таблице. Если столбец очищен и в нем есть только один ненулевой элемент, то эта переменная является базовой. Если столбец не очищен и содержит более одного ненулевого элемента, эта переменная не является базовой, и значение этой переменной равно нулю.
Значения всех неосновных переменных (столбцы с более чем одним числом в них) равны нулю. В этой таблице это будет x 1 и x 2 .
Значения основных переменных находятся путем считывания решения из матрицы, которое получается путем удаления неосновных столбцов.
| с 1 | с 2 | с 3 | П | справа | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 16 | с 1 | = | 16 | |||
| 0 | 1 | 0 | 0 | 9 | с 2 | = | 9 | |||
| 0 | 0 | 1 | 0 | 24 | с 3 | = | 24 | |||
| 0 | 0 | 0 | 1 | 0 | -P | = | 0 |
Подведем итог тому, что у нас есть.
| Базовый | Неосновной |
|---|---|
| с 1 = 16, с 2 = 9, с 3 = 24, P = 0 | x 1 = 0, x 2 = 0 |
Связывание таблицы с таблицей
Напомним результаты, которые мы получили от табличного метода.
| Pt | х 1 | х 2 | с 1 | с 2 | с 3 | Возможно? | P = 40x 1 + 30x 2 |
|---|---|---|---|---|---|---|---|
| А | 0 | 0 | 16 | 9 | 24 | да | 0 |
| Б | 0 | 8 | 0 | 1 | 16 | да | 240 |
| С | 0 | 9 | -2 | 0 | 6 | № | НЕТ |
| Д | 0 | 12 | -8 | -3 | 0 | № | НЕТ |
| E | 16 | 0 | 0 | -7 | -24 | № | НЕТ |
| Ф. | 9 | 0 | 7 | 0 | -3 | № | НЕТ |
| г | 8 | 0 | 8 | 1 | 0 | да | 320 |
| H | 2 | 7 | 0 | 0 | 15 | да | 290 |
| I | 4 | 6 | 0 | –1 | 0 | № | НЕТ |
| Дж | 6 | 3 | 4 | 0 | 0 | да | 330 |
Если вы сравните значения, полученные при чтении таблицы, вы увидите, что мы находимся в точке A , где x 1 = 0 и x 2 = 0.
Определение основных переменных для каждой строки
В каждой строке таблицы будет одна переменная, которая является базовой для этой строки. Какую переменную можно определить довольно легко, не удаляя столбцы, соответствующие неосновным переменным.
Для столбцов, которые очищены и содержат только одну ненулевую запись, вы спускаетесь по столбцу, пока не найдете ненулевую запись. Каждый столбец будет иметь ненулевой элемент в отдельной строке. Переменная в этом столбце будет базовой переменной для строки с ненулевым элементом.
Это немного сбивает с толку, так что, возможно, это поможет.
- Столбец s 1 очищается, за исключением первой строки. Следовательно, s 1 — это базовая переменная в первой строке.
- Столбец s 2 очищен, за исключением второй строки. Следовательно, s 2 — это базовая переменная во второй строке.
- Столбец s 3 очищен, за исключением третьей строки. Следовательно, s 3 — это базовая переменная в третьей строке.
- Столбец P очищен, за исключением нижней строки. Следовательно, P является базовой переменной в нижней строке.
| Базовый | х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 1 | 2 | 1 | 0 | 0 | 0 | 16 | ||
| с 2 | 1 | 1 | 0 | 1 | 0 | 0 | 9 | ||
| с 3 | 3 | 2 | 0 | 0 | 1 | 0 | 24 | ||
| п | -40 | -30 | 0 | 0 | 0 | 1 | 0 |
Симплексный метод
Мы видели, что мы находимся на пересечении прямых x 1 = 0 и x 2 = 0.Это начало координат, а две неосновные переменные: x 1 и x 2 . Чтобы перемещаться по допустимой области, нам нужно переместиться с одной из линий x 1 = 0 или x 2 = 0 на одну из линий s 1 = 0, s 2 = 0, или s 3 = 0. Вопрос в том, в каком направлении двигаться?
Выбор поворотной колонны
Подумайте о целевой функции P = 40x 1 + 30x 2 . Для каждой единицы, которую мы перемещаем в направлении x 1 , мы получаем 40 в целевой функции.Для каждой единицы, которую мы перемещаем в направлении x 2 , мы получаем 30 в целевой функции. Подумайте об этом, так как за каждый шаг, который вы двигаетесь вправо (направление x 1 ), вы получаете 40 долларов, а за каждый шаг, который вы делаете (направление x 2 ), вы получаете 30 долларов.
Что бы вы предпочли? Надеюсь, ваш ответ — получать 40 долларов за каждый шаг. Если это не так, вы не очень хорошо поймете симплексный метод.
А теперь подумайте, как это 40 представлено в целевой функции таблицы.Когда мы поместили целевую функцию в таблицу, мы переместили переменные решения и их коэффициенты в левую часть и сделали их отрицательными. Следовательно, самое отрицательное число в нижней строке соответствует наиболее положительному коэффициенту целевой функции и указывает направление, в котором мы должны двигаться.
Сводный столбец — это столбец с наибольшим отрицательным числом в нижней строке. Если в нижнем ряду нет негативов, остановитесь, все готово.
Положительное значение в нижней строке таблицы будет соответствовать отрицательному коэффициенту в целевой функции, что означает, что движение в этом направлении фактически уменьшит значение цели. Это не то, что мы хотим делать, если хотим получить максимальное значение, поэтому мы останавливаемся, когда в нижней строке целевой функции больше нет отрицательных значений.
Мы выходим за линию, соответствующую неосновной переменной в сводном столбце. Это означает, что переменная выходит из набора базовых переменных и становится неосновной.
Поместите стрелку под сводную колонку.
Выбор поворотного ряда
Теперь, когда мы выбрали направление, нам нужно определить, как далеко мы должны двигаться в этом направлении. Помните, сейчас мы находимся в точке A и движемся в направлении x 1 или вправо. Это означает, что мы можем перейти к точкам E (16,0), F (9,0) или G (8,0).
- Точка E находится в точке (16,0) и является пересечением прямых x 2 = 0 и s 1 = 0.x 1 станет базовым, а s 1 станет неосновным. Значение x 1 изменится с x 1 = 0 на x 1 = 16, если мы переместимся в точку E .
- Точка F находится в точке (9,0) и является пересечением линий x 2 = 0 и s 2 = 0. x 1 станет базовой, а s 2 станет не базовой. Значение x 1 изменится с x 1 = 0 на x 1 = 9, если мы переместимся в точку F .
- Точка G находится в точке (8,0) и является пересечением прямых x 2 = 0 и s 3 = 0. x 1 станет базовой, а s 3 станет не базовой. Значение x 1 изменится с x 1 = 0 на x 1 = 8, если мы переместимся в точку G .
Давайте посмотрим, как мы можем узнать эту информацию из таблицы. Помните, мы пытаемся сделать это вообще без использования графика.
Сформируйте отношения между неотрицательными записями в правой части и положительными записями в сводном столбце для каждого из проблемных ограничений. Не найти отношения для целевой функции. Не находите соотношение, если элемент в сводном столбце отрицательный или нулевой, но найдите соотношение, если правая часть равна нулю.
| Базовый | х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | соотношение | ||
|---|---|---|---|---|---|---|---|---|---|---|
| с 1 | 1 | 2 | 1 | 0 | 0 | 0 | 16 | 16/1 = 16 | ||
| с 2 | 1 | 1 | 0 | 1 | 0 | 0 | 9 | 9/1 = 9 | ||
| с 3 | 3 | 2 | 0 | 0 | 1 | 0 | 24 | 24/3 = 8 | ||
| п | -40 | -30 | 0 | 0 | 0 | 1 | 0 | |||
| ↑ |
Вы бы посмотрели на эти отношения? 16, 9 и 8.И что еще лучше, 16 связано со строкой, где s 1 является базовым, 9 связано со строкой, где s 2 является базовым, а 8 связано со строкой, где s 3 является базовым.
Это означает, что мы можем сказать, насколько изменится x 1 , посмотрев на соотношение. Мы также можем сказать, к какой строке мы будем двигаться, посмотрев на переменную, которая является базовой для этой строки.
Какую строку выбрать? Ваша первая мысль может заключаться в том, что, поскольку мы получаем 40 долларов за каждую перемещаемую единицу, нам следует переместить как можно больше единиц.Если мы переместим 8 единиц, мы получим 40 × 8 = 320 долларов, если мы переместим 9 единиц, мы получим 40 × 9 = 360, а если мы переместим 16 единиц, мы получим 40 × 16 = 640 долларов. Есть одна очень большая проблема с это рассуждение, однако. Если мы переместимся больше чем на 8, мы выйдем из допустимой области. Следовательно, мы должны пройти как можно меньшее расстояние, чтобы оставаться в допустимой области.
Сводная строка — это строка с наименьшим неотрицательным коэффициентом. Если неотрицательных соотношений найти не удается, остановитесь, проблема не имеет решения.
Если одно из соотношений равно 0, это считается неотрицательным значением. Используй это.
Поместите стрелку рядом с наименьшим коэффициентом, чтобы указать строку поворота.
| Базовый | х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | соотношение | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| с 1 | 1 | 2 | 1 | 0 | 0 | 0 | 16 | 16/1 = 16 | |||
| с 2 | 1 | 1 | 0 | 1 | 0 | 0 | 9 | 9/1 = 9 | |||
| с 3 | 3 | 2 | 0 | 0 | 1 | 0 | 24 | 24/3 = 8 | ← | ||
| п | -40 | -30 | 0 | 0 | 0 | 1 | 0 | ||||
| ↑ |
Переменная, которая является базовой для строки сводки, будет выходить из набора основных.Он будет заменен переменной из сводного столбца, которая входит в набор основных переменных.
Пересечение сводной строки и сводного столбца называется сводным элементом. Обведите его.
вещей, которые мы можем сказать перед поворотом
Нам известно следующее.
- Целевая функция увеличивается на 40 для каждой единицы, которую мы перемещаем в направлении x 1 , и мы перемещаемся на 8 единиц. Это означает, что целевая функция увеличится на 40 × 8 = 320.Поскольку сейчас это 0, оно станет 320.
- Переменная x 1 заменяет s 3 в качестве базовой переменной в третьей строке. Остальные строки сохранят свои основные переменные.
- Сводная колонка будет очищена, за исключением сводного элемента, который станет 1.
- Строка поворота не изменится, кроме как путем деления, чтобы сделать элемент поворота равным 1. В этом случае мы разделим все на 3.
- Увеличение x 1 будет 8.
- Графически мы будем в точке G , где x 2 и s 3 не являются базовыми.
- Столбцы s 1 , s 2 и P останутся очищенными, а их базовые строки останутся прежними.
| Базовый | х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 1 | 0 | 0 | |||||
| с 2 | 0 | 0 | 1 | 0 | |||||
| x 1 | 1 | 2/3 | 0 | 0 | 1/3 | 0 | 8 | ||
| п | 0 | 0 | 0 | 1 | 320 |
Поворот!
Используйте операции со строками, чтобы очистить сводный столбец.То есть, когда вы закончите, единственной записью в сводном столбце будет элемент в 3-й строке, где находился сводный столбец.
| Базовый | х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 4/3 | 1 | 0 | -1/3 | 0 | 8 | ||
| с 2 | 0 | 1/3 | 0 | 1 | -1/3 | 0 | 1 | ||
| x 1 | 1 | 2/3 | 0 | 0 | 1/3 | 0 | 8 | ||
| п | 0 | -10/3 | 0 | 0 | 40/3 | 1 | 320 |
Интерпретация новой таблицы
На этот раз столбцы x 2 и s 3 не очищаются, поэтому они не являются базовыми и их значение равно 0.x 1 является базовым в третьей строке и имеет значение 8. s 1 является базовым в первой строке и его значение равно 8. s 2 является базовым во второй строке и его значение 1.
| Базовый | Неосновной |
|---|---|
| x 1 = 8, с 1 = 8, с 2 = 1, P = 320 | x 2 = 0, с 3 = 0 |
Сравните это с таблицей, которая была у нас ранее, и вы увидите, что мы действительно находимся в точке G .
| Pt | х 1 | х 2 | с 1 | с 2 | с 3 | Возможно? | P = 40x 1 + 30x 2 |
|---|---|---|---|---|---|---|---|
| г | 8 | 0 | 8 | 1 | 0 | да | 320 |
Повторение процесса
До тех пор, пока в нижней строке есть негативы, значение целевой функции можно увеличить, переместившись в новую точку.
Если вы посмотрите на целевую функцию, вы заметите, что есть только одно отрицательное значение, -10/3 в столбце x 2 . Это означает, что, двигаясь вверх (в направлении x 2 ), мы можем увеличить значение целевой функции. Мы будем двигаться от линии x 2 = 0, что означает, что мы будем двигаться по линии s 3 = 0. Где бы мы ни закончили, x 2 займет место этой базовой переменной. Если бы мы двинулись в направлении s 3 , это нанесло бы нам вред.
Как далеко мы можем продвинуться?
- Мы можем перейти к точке J , которая равна (6,3), поэтому увеличение x 2 будет 3. Эта точка находится на пересечении линий s 3 = 0 и s 1 = 0, поэтому s 1 станет неосновным и будет заменено на x 2 как базовое.
- Мы могли бы перейти к точке I , которая находится в точке (5,6), поэтому увеличение x 2 будет 6. Эта точка находится на пересечении прямых s 3 = 0 и s 2 = 0, поэтому s 2 станет неосновным и будет заменено на x 2 как базовое.
- Мы могли бы перейти к точке D , которая находится в точке (0,12), поэтому увеличение x 2 будет 12. Эта точка находится на пересечении линий s 3 = 0 и x 1 = 0, поэтому x 1 станет неосновным и будет заменено на x 2 как базовое.
Обратите внимание, что когда мы формируем отношения между неотрицательными элементами в правой части и положительными элементами в сводной строке, мы получаем 6, когда переходим к s 1 = 0 (точка I ), 3 когда мы переходим к s 2 = 0 (точка J ), и 12, когда мы перемещаемся к x 1 = 0 (точка D ).Мы еще раз выбираем наименьшее соотношение, чтобы оставаться в допустимом регионе.
| Базовый | х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | соотношение | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 4/3 | 1 | 0 | -1/3 | 0 | 8 | 8 / (4/3) = 6 | |||
| с 2 | 0 | 1/3 | 0 | 1 | -1/3 | 0 | 1 | 1 / (1/3) = 3 | ← | ||
| x 1 | 1 | 2/3 | 0 | 0 | 1/3 | 0 | 8 | 8 / (2/3) = 12 | |||
| п | 0 | -10/3 | 0 | 0 | 40/3 | 1 | 320 | ||||
| ↑ |
Вещи, которые мы можем сказать перед поворотом
Нам известно следующее.
- Целевая функция увеличивается на 10/3 для каждой единицы, которую мы перемещаем в направлении x 2 , и мы перемещаемся на 3 единицы. Это означает, что целевая функция увеличится на (10/3) × 3 = 10. Поскольку сейчас она 320, она станет 330.
- Переменная x 2 заменяет s 2 в качестве базовой переменной во второй строке. Остальные строки сохранят свои основные переменные.
- Сводной столбец станет очищенным, за исключением элемента сводной таблицы, который станет 1.
- Строка поворота не изменится, кроме как путем умножения, чтобы сделать элемент поворота равным 1. В этом случае мы умножим все на 3.
- Увеличение x 2 будет 3.
- Графически мы будем в точке J , где s 2 и s 3 не являются базовыми.
- Столбцы s 1 , x 1 и P останутся очищенными, а их базовые строки останутся прежними.
| Базовый | х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 0 | 1 | 0 | |||||
| x 2 | 0 | 1 | 0 | 3 | –1 | 0 | 3 | ||
| x 1 | 1 | 0 | 0 | 0 | |||||
| п | 0 | 0 | 0 | 1 | 330 |
Поворотный шарнир
Хорошо, теперь мы развернемся и найдем остальную информацию.
| Базовый | х 1 | х 2 | с 1 | с 2 | с 3 | П | справа | ||
|---|---|---|---|---|---|---|---|---|---|
| с 1 | 0 | 0 | 1 | -4 | 1 | 0 | 4 | ||
| x 2 | 0 | 1 | 0 | 3 | –1 | 0 | 3 | ||
| x 1 | 1 | 0 | 0 | -2 | 1 | 0 | 6 | ||
| п | 0 | 0 | 0 | 10 | 10 | 1 | 330 |
Интерпретация новой таблицы
На этот раз столбцы s 2 и s 3 не очищаются, поэтому они не являются базовыми и их значение равно 0.x 1 является базовым в третьей строке и его значение равно 6. s 1 является базовым в первой строке и его значение равно 4. x 2 является базовым во второй строке и его значение равно 3.
| Базовый | Неосновной |
|---|---|
| x 1 = 6, x 2 = 3, с 1 = 4, P = 330 | с 2 = 0, с 3 = 0 |
Сравните это с таблицей, которая была у нас ранее, и вы увидите, что мы действительно находимся в точке J .
| Pt | х 1 | х 2 | с 1 | с 2 | с 3 | Возможно? | P = 40x 1 + 30x 2 |
|---|---|---|---|---|---|---|---|
| Дж | 6 | 3 | 4 | 0 | 0 | да | 330 |
Готово!
Поскольку в нижней строке нет отрицательных значений, переход к другой точке приведет к снижению значения целевой функции, а не к его повышению.Поскольку мы пытаемся максимизировать значение целевой функции, это было бы контрпродуктивно. Мы останавливаемся, все готово.
Решение
Максимальное значение P равно 330, когда x 1 = 6 и x 2 = 3. Значения переменных резерва: s 1 = 4, s 2 = 0 и s 3 = 0.
Оптимизация
с помощью Python — Real Python
PuLP имеет более удобный API линейного программирования, чем SciPy. Вам не нужно математически модифицировать задачу или использовать векторы и матрицы.Все чище и менее подвержено ошибкам.
Теперь, когда вы импортировали PuLP, вы можете решить свои проблемы.
Пример 1
Теперь вы решите эту систему с помощью PuLP:
Первый шаг — инициализировать экземпляр LpProblem для представления вашей модели:
# Создать модель
model = LpProblem (name = "small-проблема", смысл = LpMaximize)
Параметр sense используется для выбора выполнения минимизации ( LpMinimize или 1 , значение по умолчанию) или максимизации ( LpMaximize или -1 ).Этот выбор повлияет на результат вашей проблемы.
Получив модель, вы можете определить переменные решения как экземпляры класса LpVariable :
# Инициализировать переменные решения
x = LpVariable (name = "x", lowBound = 0)
y = LpVariable (name = "y", lowBound = 0)
Необходимо указать нижнюю границу с lowBound = 0 , поскольку значение по умолчанию — отрицательная бесконечность. Параметр upBound определяет верхнюю границу, но вы можете опустить его здесь, потому что по умолчанию он равен положительной бесконечности.
Необязательный параметр cat определяет категорию переменной решения. Если вы работаете с непрерывными переменными, вы можете использовать значение по умолчанию «Непрерывный» .
Вы можете использовать переменные x и y для создания других объектов PuLP, которые представляют линейные выражения и ограничения:
>>> выражение = 2 * x + 4 * y
>>> тип (выражение)
<класс 'pulp.pulp.LpAffineExpression'>
>>> ограничение = 2 * x + 4 * y> = 8
>>> тип (ограничение)
<класс "мякоть.pulp.LpConstraint '>
Когда вы умножаете переменную решения на скаляр или строите линейную комбинацию нескольких переменных решения, вы получаете экземпляр pulp.LpAffineExpression , который представляет линейное выражение.
Точно так же вы можете комбинировать линейные выражения, переменные и скаляры с операторами == , <= или > = , чтобы получить экземпляры pulp.LpConstraint, которые представляют линейные ограничения вашей модели.
Примечание: Также возможно создавать ограничения с помощью расширенных методов сравнения .__ eq __ () , .__ le __ () и .__ ge __ () , которые определяют поведение операторов == , <= и > = .
Имея это в виду, следующим шагом будет создание ограничений и целевой функции, а также их присвоение вашей модели. Вам не нужно создавать списки или матрицы. Просто напишите выражения Python и используйте оператор + = , чтобы добавить их в модель:
# Добавить ограничения в модель
модель + = (2 * x + y <= 20, "красное_ограничение")
модель + = (4 * x - 5 * y> = -10, "blue_constraint")
модель + = (-x + 2 * y> = -2, "желтое_ограничение")
модель + = (-x + 5 * y == 15, "зеленое_ограничение")
В приведенном выше коде вы определяете кортежи, которые содержат ограничения и их имена. LpProblem позволяет добавлять ограничения в модель, определяя их как кортежи. Первый элемент - это экземпляр LpConstraint . Второй элемент - это удобочитаемое имя для этого ограничения.
Установка целевой функции очень похожа:
# Добавить в модель целевую функцию
obj_func = х + 2 * у
модель + = obj_func
В качестве альтернативы вы можете использовать более короткое обозначение:
# Добавить в модель целевую функцию
модель + = x + 2 * y
Теперь у вас добавлена целевая функция и определена модель.
Примечание: Вы можете добавить ограничение или цель к модели с помощью оператора + = , потому что его класс, LpProblem , реализует специальный метод .__ iadd __ () , который используется для определения поведения + = .
Для более крупных задач часто удобнее использовать lpSum () со списком или другой последовательностью, чем повторять оператор + . Например, вы можете добавить в модель целевую функцию с помощью этого оператора:
# Добавить в модель целевую функцию
модель + = lpSum ([x, 2 * y])
Дает тот же результат, что и предыдущий оператор.
Теперь вы можете увидеть полное определение этой модели:
>>> >>> модель
маленькая проблема:
МАКСИМАЛЬНО
1 * х + 2 * у + 0
ПРИ УСЛОВИИ
красное_ограничение: 2 x + y <= 20
blue_constraint: 4 x - 5 y> = -10
желтое_ограничение: - x + 2 y> = -2
зеленое_ограничение: - x + 5 y = 15
ПЕРЕМЕННЫЕ
x Непрерывный
y Непрерывный
Строковое представление модели содержит все соответствующие данные: переменные, ограничения, цель и их имена.
Наконец, вы готовы к решению проблемы.Вы можете сделать это, вызвав .solve () для вашего объекта модели. Если вы хотите использовать решатель по умолчанию (CBC), вам не нужно передавать аргументы:
# Решаем проблему
status = model.solve ()
.solve () вызывает базовый решатель, изменяет объект модели и возвращает целочисленный статус решения, который будет 1 , если будет найден оптимум. Остальные коды состояния см. В разделе LpStatus [] .
Вы можете получить результаты оптимизации как атрибуты модели . Функция value () и соответствующий метод .value () возвращают фактические значения атрибутов:
>>> print (f "status: {model.status}, {LpStatus [model.status]}")
статус: 1, Оптимальный
>>> print (f "objective: {model.objective.value ()}")
цель: 16.8181817
>>> для var в model.variables ():
... print (f "{var.name}: {var.значение()}")
...
х: 7.7272727
y: 4.5454545
>>> для имени, ограничения в model.constraints.items ():
... print (f "{имя}: {constraint.value ()}")
...
красное_ограничение: -9.999999939e-08
blue_constraint: 18.181818300000003
желтое_ограничение: 3.3636362999999996
green_constraint: -2.0000000233721948e-07)
model.objective содержит значение целевой функции, model.constraints содержит значения переменных резервирования, а объекты x и y имеют оптимальные значения переменных решения. model.variables () возвращает список с переменными решения:
>>> model.variables ()
[x, y]
>>> model.variables () [0] равно x
Правда
>>> model.variables () [1] равно y
Правда
Как видите, этот список содержит точные объекты, созданные с помощью конструктора LpVariable .
Результаты примерно такие же, как у SciPy.
Примечание: Будьте осторожны при использовании метода .solution () - меняет состояние объектов x и y !
Вы можете увидеть, какой решатель использовался, позвонив по номеру .solver :
>>> model.solver
<объект pulp.apis.coin_api.PULP_CBC_CMD по адресу 0x7f60aea19e50>
Выходные данные сообщают вам, что решателем является CBC. Вы не указали решатель, поэтому PuLP вызвал его по умолчанию.
Если вы хотите запустить другой решатель, вы можете указать его в качестве аргумента .решить () . Например, если вы хотите использовать GLPK и уже установили его, вы можете использовать solver = GLPK (msg = False) в последней строке. Имейте в виду, что вам также необходимо импортировать его:
Теперь, когда вы импортировали GLPK, вы можете использовать его внутри .solve () :
# Создать модель
model = LpProblem (name = "small-проблема", смысл = LpMaximize)
# Инициализировать переменные решения
x = LpVariable (name = "x", lowBound = 0)
y = LpVariable (name = "y", lowBound = 0)
# Добавляем ограничения в модель
модель + = (2 * x + y <= 20, "красное_ограничение")
модель + = (4 * x - 5 * y> = -10, "blue_constraint")
модель + = (-x + 2 * y> = -2, "желтое_ограничение")
модель + = (-x + 5 * y == 15, "зеленое_ограничение")
# Добавляем в модель целевую функцию
модель + = lpSum ([x, 2 * y])
# Решать проблему
статус = модель.решить (solver = GLPK (msg = False))
Параметр msg используется для отображения информации от решателя. msg = False отключает отображение этой информации. Если вы хотите включить информацию, просто опустите msg или установите msg = True .
Ваша модель определена и решена, поэтому вы можете проверить результаты так же, как и в предыдущем случае:
>>> >>> print (f "status: {model.status}, {LpStatus [model.статус]}")
статус: 1, Оптимальный
>>> print (f "objective: {model.objective.value ()}")
цель: 16.81817
>>> для var в model.variables ():
... print (f "{var.name}: {var.value ()}")
...
х: 7.72727
y: 4.54545
>>> для имени, ограничения в model.constraints.items ():
... print (f "{имя}: {constraint.value ()}")
...
красное_ограничение: -1.0000000000509601e-05
blue_constraint: 18.181830000000005
желтое_ограничение: 3.3636299999999997
зеленое_ограничение: -2.000000000279556e-05
Вы получили практически тот же результат с GLPK, что и с SciPy и CBC.
Давайте посмотрим, какой решатель использовался на этот раз:
>>> >>> model.solver
<объект pulp.apis.glpk_api.GLPK_CMD по адресу 0x7f60aeb04d50>
Как вы определили выше с помощью выделенного оператора model.solve (solver = GLPK (msg = False)) , решателем является GLPK.
Вы также можете использовать PuLP для решения задач линейного программирования со смешанными целыми числами. Чтобы определить целочисленную или двоичную переменную, просто передайте cat = "Integer" или cat = "Binary" в LpVariable .В остальном все осталось прежним:
# Создать модель
model = LpProblem (name = "small-проблема", смысл = LpMaximize)
# Инициализировать переменные решения: x - целое число, y - непрерывное
x = LpVariable (name = "x", lowBound = 0, cat = "Integer")
y = LpVariable (name = "y", lowBound = 0)
# Добавляем ограничения в модель
модель + = (2 * x + y <= 20, "красное_ограничение")
модель + = (4 * x - 5 * y> = -10, "blue_constraint")
модель + = (-x + 2 * y> = -2, "желтое_ограничение")
модель + = (-x + 5 * y == 15, "зеленое_ограничение")
# Добавляем в модель целевую функцию
модель + = lpSum ([x, 2 * y])
# Решать проблему
статус = модель.решать()
В этом примере у вас есть одна целочисленная переменная и вы получаете разные результаты, чем раньше:
>>> >>> print (f "status: {model.status}, {LpStatus [model.status]}")
статус: 1, Оптимальный
>>> print (f "objective: {model.objective.value ()}")
цель: 15,8
>>> для var в model.variables ():
... print (f "{var.name}: {var.value ()}")
...
х: 7.0
y: 4.4
>>> для имени, ограничения в model.constraints.items ():
... print (f "{имя}: {ограничение.значение()}")
...
красное_ограничение: -1.5999999999999996
blue_constraint: 16.0
желтое_ограничение: 3.8000000000000007
green_constraint: 0,0)
>>> model.solver
Теперь x - это целое число, как указано в модели. (Технически он содержит значение с плавающей запятой с нулем после десятичной точки.) Этот факт меняет все решение. Покажем это на графике:
Как видите, оптимальным решением является крайняя правая зеленая точка на сером фоне.Это возможное решение с наибольшими значениями x и y , что дает максимальное значение целевой функции.
ГЛПК может решить и такие задачи.
Пример 2
Теперь вы можете использовать PuLP для решения проблемы распределения ресурсов сверху:
Подход к определению и решению проблемы такой же, как в предыдущем примере:
# Определить модель
model = LpProblem (name = "распределение ресурсов", смысл = LpMaximize)
# Определить переменные решения
x = {i: LpVariable (name = f "x {i}", lowBound = 0) для i в диапазоне (1, 5)}
# Добавить ограничения
модель + = (lpSum (x.values ()) <= 50, "рабочая сила")
модель + = (3 * x [1] + 2 * x [2] + x [3] <= 100, "material_a")
модель + = (x [2] + 2 * x [3] + 3 * x [4] <= 90, "material_b")
# Ставим цель
модель + = 20 * x [1] + 12 * x [2] + 40 * x [3] + 25 * x [4]
# Решаем проблему оптимизации
status = model.solve ()
# Получите результаты
print (f "status: {model.status}, {LpStatus [model.status]}")
print (f "objective: {model.objective.value ()}")
для var в x.values ():
print (f "{var.name}: {var.value ()}")
для имени, ограничения в модели.constraints.items ():
print (f "{имя}: {constraint.value ()}")
В этом случае вы используете словарь x для хранения всех переменных решения. Этот подход удобен тем, что словари могут хранить имена или индексы переменных решения в качестве ключей и соответствующие объекты LpVariable в качестве значений. Также могут быть полезны списки или кортежи из экземпляров LpVariable .
Приведенный выше код дает следующий результат:
статус: 1, Оптимальный
цель: 1900 г.0
x1: 5,0
х2: 0,0
x3: 45,0
x4: 0,0
рабочая сила: 0,0
material_a: -40.0
material_b: 0,0
Как видите, решение согласуется с решением, полученным с помощью SciPy. Наиболее выгодное решение - производить 5,0 единиц первого продукта и 45,0 единиц третьего продукта в сутки.
Давайте сделаем эту задачу более сложной и интересной. Допустим, фабрика не может производить первую и третью продукцию параллельно из-за проблем с оборудованием. Какое решение в этом случае наиболее выгодно?
Теперь у вас есть еще одно логическое ограничение: если x ₁ положительно, то x должно быть равно нулю, и наоборот.Здесь очень полезны переменные двоичного решения. Вы будете использовать две двоичные переменные решения, y ₁ и y ₃, которые будут обозначать, генерируются ли вообще первый или третий продукты:
1model = LpProblem (name = "распределение ресурсов", смысл = LpMaximize)
2
3 # Определите переменные решения
4x = {i: LpVariable (name = f "x {i}", lowBound = 0) для i в диапазоне (1, 5)}
5y = {i: LpVariable (name = f "y {i}", cat = "Binary") для i в (1, 3)}
6
7 # Добавить ограничения
8model + = (lpSum (x.values ()) <= 50, "рабочая сила")
9модель + = (3 * x [1] + 2 * x [2] + x [3] <= 100, "material_a")
10модель + = (x [2] + 2 * x [3] + 3 * x [4] <= 90, "material_b")
11
12M = 100
13model + = (x [1] <= y [1] * M, "x1_constraint")
14model + = (x [3] <= y [3] * M, "x3_constraint")
15модель + = (y [1] + y [3] <= 1, "y_constraint")
16
17 # Установить цель
18модель + = 20 * x [1] + 12 * x [2] + 40 * x [3] + 25 * x [4]
19
20 # Решить проблему оптимизации
21status = model.solve ()
22
23print (f "status: {model.status}, {LpStatus [model.статус]}")
24print (f "objective: {model.objective.value ()}")
25
26 для var в model.variables ():
27 print (f "{var.name}: {var.value ()}")
28 год
29 для имени, ограничение в model.constraints.items ():
30 print (f "{name}: {constraint.value ()}")
Код очень похож на предыдущий пример, за исключением выделенных строк. Вот отличия:
Строка 5 определяет переменные двоичного решения
y [1]иy [3], содержащиеся в словареy.Строка 12 определяет произвольно большое число
M. Значение100в этом случае достаточно велико, потому что у вас не может быть более100единиц в день.Строка 13 говорит, что если
y [1]равно нулю, тоx [1]должно быть нулем, иначе это может быть любое неотрицательное число.Строка 14 говорит, что если
y [3]равно нулю, тоx [3]должно быть равно нулю, иначе это может быть любое неотрицательное число.Строка 15 говорит, что либо
y [1], либоy [3]равно нулю (или оба равны), поэтому либоx [1], либоx [3]также должны быть равны нулю.
Вот решение:
статус: 1, Оптимальный
цель: 1800.0
x1: 0,0
х2: 0,0
x3: 45,0
x4: 0,0
y1: 0,0
y3: 1.0
рабочая сила: -5.0
material_a: -55.0
material_b: 0,0
x1_constraint: 0.0
x3_constraint: -55.0
y_constraint: 0.0
Оказывается, оптимальный подход - исключить первый продукт и производить только третий.
Пример стандартного симплекс-метода
|
|
|
| ||
| См. Шаги 3,4,5 из . СИМПЛЕКСНЫЙ МЕТОД как вы работаете с ИНДИКАТОРАМИ, СООТНОШЕНИЯ и ПОВОРОТЫ. |
|
|
|
|
|
| и nbsp |
| Все индикаторы {0, 0, | 49 16 | , 0, | 1 16 | а также | 3 8 | } теперь равны нулю или больше («13» НЕ является индикатором). |
| Таким образом, как и на шаге 8 МЕТОДА SIMPLEX, последняя таблица является ЗАКЛЮЧИТЕЛЬНОЙ ТАБЛИЦЕЙ. | ||||||
| Выполняются строковые операции СИМПЛЕКСНОГО МЕТОДА. |
|
|
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
Simplex Method - обзор
7.1.3.1 Симплексный метод и методы внутренней точки
Симплексный алгоритм был введен Джорджем Б. Данцигом в 1947 году (Dantzig, 1990). Алгоритм обеспечивает систематическую процедуру для решения проблем LP, производя набор итераций путем построения допустимого решения в вершине допустимого пространства поиска (т. Е. Выпуклой области, ограниченной линейными ограничениями, выраженными в виде неравенств в математической модели, содержащей возможные значения для переменных решения), и итеративно перемещаясь по пути ребер пространства поиска, посещая и проверяя соседнюю вершину каждый раз с лучшим значением целевой функции (неубывающее значение для целей максимизации и уменьшающееся значение для целей минимизации), пока не будет найдена оптимальная точка, которая обычно находится в одной из вершин.
Типичная процедура симплексного алгоритма объясняется шаг за шагом следующим образом:
Шаг 1. Преобразование модели LP в стандартную форму.
Модель LP должна быть преобразована в стандартную форму, поскольку симплексный алгоритм работает с линейными программами в стандартной форме, которая является основным форматом для всех линейных программ. Эта форма необходима, поскольку она обеспечивает идеальную отправную точку для решения симплекс-метода. Стандартная форма отвечает трем основным требованиям; (1) он должен иметь максимальную целевую функцию, (2) все ограничения должны находиться в неравенстве «меньше или равно», и (3) все переменные должны быть неотрицательными.Эти требования могут быть удовлетворены путем преобразования данной модели LP (даже моделей минимизации) с использованием базовой алгебры и методов подстановки. Чтобы преобразовать LP с целевой функцией минимизации в LP с целевой функцией максимизации, левая и правая части целевой функции просто умножаются на -1. Линейные ограничения могут быть преобразованы из неравенства «больше или равно» в неравенство «меньше или равно» аналогично преобразованию целевой функции путем умножения обеих сторон неравенства на -1.
Шаг 2. Стандартная форма данной задачи LP преобразуется в каноническую симплексную таблицу путем введения переменных резервирования.
Ограничения неравенства преобразуются в ограничения равенства путем введения переменных резервов, которые будут иметь коэффициент +1 в стандартной форме LP. Симплексная таблица может быть создана после введения переменных резервирования. Эта процедура проиллюстрирована на рис. 7.1 в качестве примера. Каноническая симплексная таблица содержит коэффициенты, соответствующие целевой функции (в последней строке) и коэффициенты ограничений (во второй и третьей строках).Выполняются операции со строками в модели LP, и решение проверяется на оптимальность с помощью таблицы.
Рисунок 7.1. Симплексный метод.
Модель проверяется на оптимальное решение, которое существует в вершинах допустимой области, после построения таблицы. Если все значения в последней строке больше или равны нулю, это означает, что переменная достигла своего оптимального значения. В противном случае (если хотя бы одно значение меньше нуля) это означает, что оптимальность не была достигнута.В приведенной выше таблице показано, что оптимальное решение еще не достигнуто, однако можно получить базовое возможное решение, которое удовлетворяет исходной системе уравнений.
Шаг 3. Идентификация сводной переменной и создание новой таблицы.
Каждый шаг симплексной процедуры в основном управляет процессом перехода от базового допустимого решения к смежному базовому допустимому решению с помощью набора поворотных операций. Следовательно, генерируется последовательность улучшенных основных возможных решений с последовательно увеличивающимися значениями целевой функции до тех пор, пока не будет получено решение, которое максимизирует целевую функцию.На каждом шаге должна быть выбрана сводная переменная, чтобы создать новую таблицу, содержащую базовое возможное решение (в конечном итоге оптимальное решение), чтобы продолжить процесс.
Выбор поворотной переменной на каждом шаге основан на требовании, чтобы эта поворотная точка улучшала целевое значение. Переменная поворота выбирается при просмотре последней строки таблицы, столбец над наименьшим отрицательным значением в нижней строке (-8 в нашем примере) содержит переменную поворота (x 2 ).Чтобы определить, какая переменная будет поворотной, значения в правой части ограничений (12 и 9) делятся на соответствующие значения из выбранного столбца (12/2 = 6 и 9/1 = 9). Наименьшее неотрицательное значение (6 в нашем примере) указывает на опорное значение (2 в нашем примере).
После определения ключевой переменной и значения сводной таблицы можно построить новую симплексную таблицу, чтобы найти новое возможное оптимальное решение. С этой целью сводная переменная оптимизируется с помощью ряда операций со строками, в то время как остальная часть таблицы остается неизменной.Эти операции со строками включают:
- 1.
Переменная поворота преобразуется в единичное значение (значение 1) путем умножения строки, содержащей переменную поворота, на величину, обратную значению поворота. В приведенном выше примере значение переменной pivot изначально равно 2, поэтому вся строка умножается на 1/2.
- 2.
Остальные значения в столбце со значением единицы должны быть 0, так как переменная поворота (x 2 ) во втором ограничении пытается быть оптимизирована.Таким образом, значение переменной pivot в других равенствах преобразуется в 0 путем применения операций со строками.
- 3.
Операции со строками автоматически пересчитывают значения переменных в столбцах и строках, кроме сводного столбца и строки, чтобы сохранить эквивалентную таблицу. Эту операцию можно описать следующим уравнением:
Newtableauvalue = [(Negativeofthevalueinoldtableaupivotcolumn) × (valueinnewtableaupivotrow)] + (Oldtableauvalue)
Старая симплексная таблица:
Simplex tableau
с единицей измерения 2:Шаг 4.Проверка оптимальности.
Оптимальность, которую можно определить как нахождение оптимального решения с максимальным значением целевой функции, необходимо будет проверить после создания новой таблицы. Если все значения в последней строке больше или равны нулю, решение считается оптимальным. В противном случае процедура, описанная в шаге 3, повторяется для определения новой сводной переменной и построения новой симплексной таблицы. Процедура повторяется до тех пор, пока не будет достигнуто решение с максимальным значением целевой функции.Оптимальные значения переменных решения могут быть определены после того, как будет доказано, что таблица достигает оптимальности. Оптимальность может быть найдена путем различения основных и небазовых переменных. Базовая переменная имеет единственное значение 1 в своем столбце, а все остальные значения равны нулю, в противном случае переменная не является базовой. Оптимальное решение для небазовой переменной равно нулю, тогда как значение «b» , соответствующее строке, которая включает значение 1 базовой переменной, представляет собой оптимальное решение для этой переменной.
Если значение хотя бы одной из основных переменных в симплексной таблице равно нулю, такая ситуация называется вырождением, которое может привести к задержке решения практических задач при решении симплексным методом. Задержка - это ситуация, когда не может быть последовательно найдена сводная переменная для улучшения значения целевой функции, другими словами, не будет изменений в решении, даже если изменится набор основных переменных. Циклирование - еще одна нежелательная ситуация при решении задач оптимизации симплексным методом.Цикл относится к возможности того, что одни и те же значения базовых переменных впоследствии будут встречаться дважды, что означает, что операции поворота симплексного метода приведут к бесконечному циклу. В крупномасштабных приложениях вырождение является обычным явлением, и остановка может наблюдаться чаще, чем цикличность. Исследователи разработали новые правила поворота, чтобы избежать езды на велосипеде.
В практических приложениях симплекс-метод достаточно эффективен и гарантирует достижение глобального оптимума, если будут приняты особые меры предосторожности против езды на велосипеде.Основным недостатком симплекс-метода является то, что количество итераций увеличивается экспоненциально с увеличением количества переменных решения, что приводит к трудоемкой процедуре с чрезмерной вычислительной сложностью, особенно для задач среднего и крупного масштаба. Этот недостаток симплекс-метода привел к значительным усилиям по исследованию алгоритмов с большей вычислительной сложностью, пока не были разработаны методы внутренней точки с полиномиальным временем решения.
Методы внутренней точки представляют собой семейство алгоритмических методов, разработанных для решения задач LP (а также NLP) за полиномиальное время и привлекли значительное внимание исследователей, поскольку Кармаркар (1984) разработал алгоритм LP с полиномиальным временем, основанный на метод внутренней точки и доказал свою эффективность по сравнению с симплексным методом.У этих двух методов есть несколько общих стратегий. Однако методы внутренней точки быстро приближаются к оптимальному решению с меньшим количеством, но относительно дорогостоящих итераций, тогда как симплексный метод включает большее количество, но менее затратных итераций для приближения к оптимальному решению. По сути, методы внутренней точки сходятся к решению, проходящему через середину (внутреннюю или внешнюю) допустимой области, определяемой ограничениями задачи, а не через границу (или вокруг ее поверхности). Существует два основных алгоритма внутренней точки: метод прямой – двойственной внутренней точки и барьерный метод.


 Из неосновных
переменных, входящих в линейную форму с отрицательными
(положительными) коэффициентами, выбирают ту, которой соответствует наибольший
(по модулю) коэффициент,
и переводят её в основные. Переход к шагу 2.
Из неосновных
переменных, входящих в линейную форму с отрицательными
(положительными) коэффициентами, выбирают ту, которой соответствует наибольший
(по модулю) коэффициент,
и переводят её в основные. Переход к шагу 2.