Решение системных линейных уравнений: Решение систем линейных уравнений — как решать СЛАУ методами Гаусса, Крамера, подстановки и почленного сложения

Содержание

Решение систем линейных уравнений. Метод сложения

1. Неизвестная переменная x 1 вид — рецептивный лёгкое 2 Б. Дана система линейных уравнений. Найти переменную x.
2. Неизвестная переменная y 1 вид — рецептивный лёгкое 2 Б. Найти переменную y, если дана система линейных уравнений.
3. Система линейных уравнений 2 вид — интерпретация лёгкое 2 Б. Решение системы линейных уравнений методом сложения.
4.
Система линейных уравнений 		2 вид — интерпретация лёгкое 1 Б. Решение системы линейных уравнений методом сложения.
5.
Система линейных уравнений (одинаковые коэффициенты при y) 		2 вид — интерпретация среднее 4 Б. Решение системы линейных уравнений, у которых коэффициенты при y одинаковые.
6. Решение системы двух уравнений (обыкновенные дроби) 2 вид — интерпретация среднее 4 Б. Решение системы двух уравнений (обыкновенные дроби в результате).
7. Система двух линейных уравнений (одинаковые коэффициенты при x) 2 вид — интерпретация среднее 4 Б. Решение системы линейных уравнений, у которых коэффициенты при x одинаковые: вычитание уравнений.
8. Система линейных уравнений 2 вид — интерпретация среднее 4 Б.
 Решение системы линейных уравнений методом сложения.
9. Система линейных уравнений (смешанные числа и обыкновенные дроби) 2 вид — интерпретация среднее 4 Б. Решение системы уравнений (противоположные коэффициенты у разных переменных): умножение одного из уравнений на число.
10. Система линейных уравнений 2 вид — интерпретация среднее 1 Б. Решение системы линейных уравнений методом сложения.
11. Система линейных уравнений 2 вид — интерпретация среднее 4 Б. Решение системы линейных уравнений методом сложения.
12. Система линейных уравнений 2 вид — интерпретация среднее 4 Б. Решение системы уравнений: умножение обоих уравнений на число.
13.
 Система линейных уравнений, одно из которых целое по сути, но дробное по виду 2 вид — интерпретация среднее 4 Б. Решение системы линейных уравнений, одно из которых целое по сути, но дробное по виду.
14. Решение системы линейных уравнений 2 вид — интерпретация сложное 6 Б. Решение системы уравнений, коэффициенты одного из уравнений которой — обыкновенные дроби.
15. Система линейных уравнений (сумма дробей) 2 вид — интерпретация сложное 5 Б. Решение системы уравнений: умножение обоих уравнений на общие знаменатели дробей, избавление от дробей, вычитание уравнений.
16. Система двух уравнений 2 вид — интерпретация сложное 6 Б. Решение системы двух уравнений, применение основного свойства пропорции, сложение уравнений.

Решение системы линейных уравнений. Метод подстановки, сложения, графический. Особые случаи, тесты

Тестирование онлайн

  • Система линейных уравнений

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы.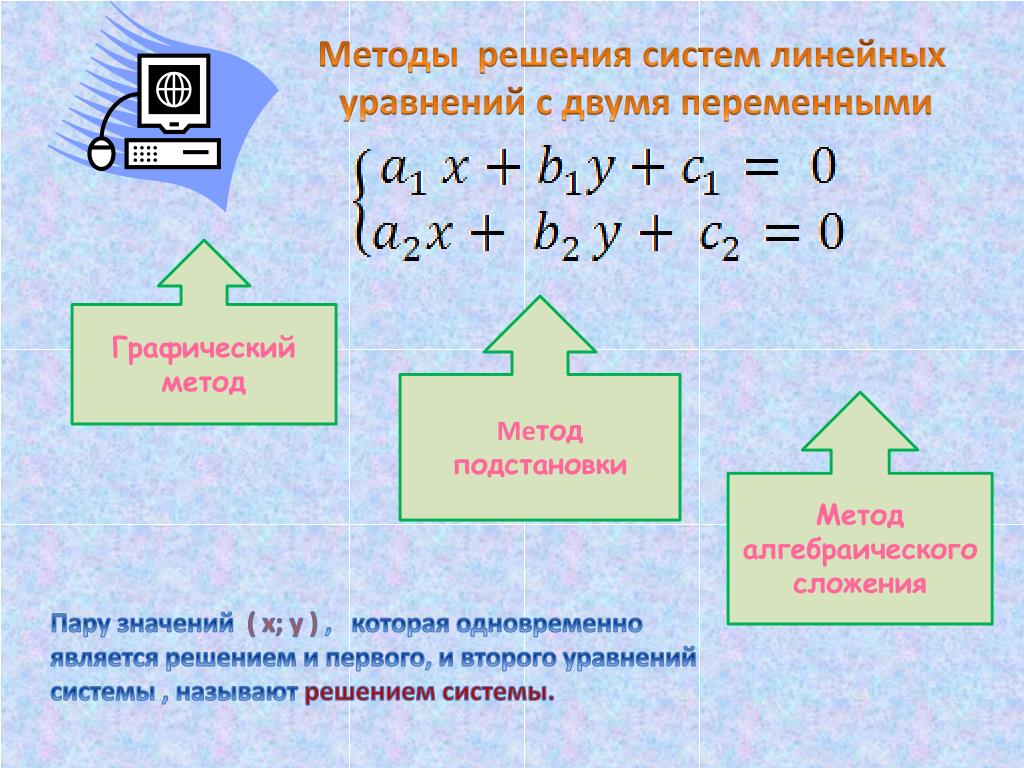 Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену , тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если , то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

Примеры решения систем методом подстановки

Рассмотрим конкретные примеры решения систем линейных уравнений методом подстановки.

   

В данном случае удобно из второго уравнения системы выразить x через y и подставить полученное выражение вместо x в первое уравнение:

   

Первое уравнение — уравнение с одной переменной y. Решаем его:

5(7-3y)-2y = -16

35-15y-2y= -16

-17y= -51

y=3.

Полученное значение y подставляем в выражение для x:

   

Ответ: (-2; 3).

   

В данной системе проще из первого уравнения выразить y через x и подставить полученное выражение вместо y во второе уравнение:

   

   

Второе уравнение — уравнение с одной переменной x. Решим его:

3x-4(-1,5-3,5x)=23

3x+6+14x=23

17x=17

x=1.

В выражение для y вместо x подставляем x=1 и находим y:

   

Ответ: (1; -5).

   

Здесь удобнее из второго уравнения выразить y через x (поскольку делить на 10 проще, чем на 4, -9 или 3):

   

   

Решаем первое уравнение:

4x-9(1,6-0,3x)= -1

4x-14,4+2,7x= -1

6,7x=13,4

x=2.

Подставляем x=2 и находим y:

   

Ответ: (2; 1).

   

Прежде чем применить метод подстановки, эту систему следует упростить. Обе части первого уравнения можно умножить на наименьший общий знаменатель, во втором уравнении раскрываем скобки и приводим подобные слагаемые:

   

   

Получили систему линейных уравнений с двумя переменными. Теперь применим подстановку. Удобно из второго уравнения выразить a через b:

   

   

Решаем первое уравнение системы:

3(21,5 + 2,5b) — 7b = 63

64,5+7,5b-7b=63

0,5b= -1,5

b= -3.

Осталось найти значение a:

   

Согласно правилам оформления, ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.

Ответ: (14; -3).

 

Выражая одну переменную через другую, иногда удобнее оставлять её с некоторым коэффициентом.

   

В данном случае удобно выразить y через x из второго уравнения. При этом лучше не делить обе части уравнения на 3, а оставить коэффициент 3 рядом с y, поскольку в первом уравнении 12y кратно 3:

   

   

9x-4(43-4x)=78

9x-172+16x=78

25x=250

x=10.

   

   

Ответ: (10;1).

 

Из всех способов решения систем уравнений метод подстановки в алгебре используется чаще других. С помощью этого метода могут быть решены не только системы линейных уравнений, но и системы уравнений других видов.

Урок 48. решение систем двух линейных уравнений с двумя неизвестными — Алгебра — 7 класс

Конспект урока

Алгебра

7 класс

Урок № 48

Решение систем двух линейных уравнений с двумя неизвестными

Перечень вопросов, рассматриваемых в теме:

  • Систематизация решений систем уравнений.
  • Использование отношений коэффициентов при решении систем уравнений.
  • Практическое применение теоремы.

Тезаурус:

Теорема.

Пусть дана система уравнений:

где все коэффициенты отличны от нуля.

Тогда система:

а) имеет единственное решение, если ;

б) не имеет решений, если ;

в) имеет бесконечно много решений, если , и при этом все решения можно записать в виде , где ─ любое число.

Основная литература:

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

Дополнительная литература:

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Решение систем двух линейных уравнений с двумя неизвестными.

Пусть дана система двух линейных уравнений с двумя неизвестными.

Перенеся все члены правых частей этих уравнений в левые части, и приведя подобные члены, получим равносильную данной систему вида:

где ─ некоторые числа.

Мы уже знаем, как решать такую систему, когда все коэффициенты при неизвестных отличны от нуля. Мы знаем так же, что если коэффициенты при неизвестных непропорциональны, то решение системы существует и единственно; если же коэффициенты при неизвестных системы пропорциональны, то либо решений бесконечно много, либо нет ни одного решения.

Нам остаётся рассмотреть те случаи, когда некоторые коэффициенты при неизвестных равны нулю. Рассмотрим это на характерных примерах.

Пример 1. Решим систему уравнений:

Второе уравнение этой системы имеет отличные от нуля коэффициенты при неизвестных, а первое уравнение имеет коэффициент при , отличный от нуля, и коэффициент при , равный нулю.

Эту систему проще решить методом подстановки. Найдем из первого уравнения:

И подставим его во второе. Получим:

Откуда

Таким образом, пара чисел есть единственное решение системы.

Пример 2. Решим систему уравнений:

Система есть частный случай системы , где

Единственным решением этой системы является пара чисел

Пример 3. Решим систему уравнений:

Из каждого уравнения системы получим

Так как систему мы рассматриваем как частный случай системы , где то система может быть записана так:

Здесь может быть любым числом, а .

Таким образом, решения системы записываются в виде пар чисел , где ─ любое число.

Пример 4. Решим систему уравнений

Эта система противоречива (не имеет решений), потому что не может одновременно равняться и 1, и .

Пример 5. Решим систему уравнений:

Если , то эта система противоречива, потому что никакая пара чисел не удовлетворяет второму уравнению системы

Если , то второе уравнение обращается в верное равенство при любых Остаётся только первое уравнение. Оно уже рассматривалось. Следовательно, все решения первого уравнения являются решениями системы.

О количестве решений системы двух уравнений первой степени с двумя неизвестными.

Теорема

Пусть дана система уравнений:

где все коэффициенты отличны от нуля.

Тогда система :

а) имеет единственное решение, если ;

б) не имеет решений, если ;

в) имеет бесконечно много решений, если , и при этом все решения можно записать в виде , где ─ любое число.

Доказательство.

Из первого уравнения системы получим, что:

. Подставив полученное выражение вместо во второе уравнение системы и учитывая, что получим уравнение:

Здесь возможны три случая.

  1. Если:

то уравнение имеет единственный корень, поэтому и система имеет единственное решение.

Так как и то условие можно записать в виде

  1. Если:

то уравнение не имеет корней и система не имеет решений.

Так как то условия можно записать в виде

  1. Если:

то уравнение имеет бесконечно много корней, поэтому и система имеет бесконечно много решений.

Так как то условия можно записать в виде

Итак:

если то система имеет единственное решение;

если то система не имеет решений;

если то система имеет бесконечно много решений, и эти решения задаются парами , где любое число.

Теорема доказана.

Пример 1. Определим число решений системы уравнений:

а) б) в)

Решение.

а) Так как выполняется условие , то система имеет единственное решение.

б) Так как выполняется условие , то система имеет бесконечно много решений.

в) Так как выполняется условие то система не имеет решений.

Ответ: а) единственное решение; б) бесконечно много решений; в) нет решений.

Пример 2. При каком значении система

не имеет решений?

Решение.

Система не имеет решений, если выполняется условие

. Условие выполняется лишь при При этом условие также выполняется. Следовательно, система не имеет решений при

Ответ: при

Пример 3. Существует ли значение , при котором система не имеет решений?

Решение.

Система не имеет решений, если выполняется условие . Условие выполняется лишь при При этом условие не выполняется. Следовательно, таких не существует.

Ответ: не существует.

Разбор решения заданий тренировочного модуля.

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.

Впишите пропущенные элементы при решении системы.

Задание:

Перенесем из первого уравнения в правую часть 4, получим

Найдем отношение коэффициентов при х и у в системе:

‑ так как отношения __ равны, значит, система имеет одно решение. Решим систему способом подстановки:

Ответ: ( ___; ___ ).

Решение.

Перенесем из первого уравнения в левую часть 4, получим:

Найдем отношение коэффициентов при х и у в системе:

‑ так как отношения не равны, значит, система имеет одно решение. Решим систему способом подстановки:

Ответ: (4; 16).

№2. Тип задания: восстановление последовательности элементов горизонтальное / вертикальное.

Задание:

Решите систему двух уравнений:

Варианты ответов:

Ответ: (1; 0).

Значит, система имеет единственное решение.

Так как отношение коэффициентов равно —

Значит, система имеет единственное решение.

Решение:

Так как отношение коэффициентов равно —

Значит, система имеет единственное решение.

Перенесем в первом уравнении из левой части в правую 4:

Ответ: (1; 0).

определение, история, применение систем линейных алгебраических уравнений на практике

Содержание:

Определение

Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

Решением системы уравнений называется упорядоченный набор чисел — значений неизвестных, при подстановке которых каждое уравнение системы обращается в верное равенство.

Определение

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

$$\left\{\begin{array}{l} a_{11} \cdot x_{1}+a_{12} \cdot x_{2}+\ldots+a_{1 n} \cdot x_{n}=b_{1} \\ a_{21} \cdot x_{1}+a_{22} \cdot x_{2}+\ldots+a_{2 n} \cdot x_{n}=b_{2} \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . {0}\right\}$ называется решением системы, если при подстановке в уравнения все уравнения превращаются в тождество.

История систем уравнений

Задачи, соответствующие современным задачам на составление и решение систем уравнений с несколькими неизвестными, встречаются еще в вавилонских и египетских рукописях II века до н.э., а также в трудах древнегреческих, индийских и китайских мудрецов. В китайском трактате «Математика в девяти книгах» словесно изложены правила решения систем уравнений, были замечены некоторые закономерности при решении.

Основные понятия и применения

Система может состоять из алгебраических уравнений, линейных алгебраических уравнений, нелинейных уравнений, дифференциальных уравнений.

Методы решения системы уравнений зависят от типа системы. Например, решения систем линейных алгебраических уравнений хорошо известны ( метод Крамера, метод Гаусса, матричный метод, метод итераций и т.д.). Для нелинейных же систем общего аналитического решения не найдено, они решаются разного рода численными методами. Аналогично дело обстоит и с системами дифференциальных уравнений.

Системы линейных уравнений широко используются в задачах экономики, физики, химии и других науках.

Решение систем линейных алгебраических уравнений — одна из основных задач вычислительной линейной алгебры. Хотя задача решения именно системы линейных уравнений сравнительно редко представляет самостоятельный интерес для прикладных задач, но от умения эффективно решать данные системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности — нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма.

Читать дальше: системы линейных алгебраических уравнений: основные понятия, виды.

Почему важно, что системы линейных уравнений решаются быстрее, чем множатся матрицы

В 1998, когда Google только появился, его киллер-фичей был патентованный алгоритм PageRank для сортировки результатов поиска по популярности. Описанный стэнфордскими аспирантами Брином и Пейджем в научной статье, он сводится к очень простой идее:

—где — множество входящих ссылок на страницу , — число исходящих ссылок на этой странице, а — число страниц в интернете. Таким образом выражает вероятность оказаться на странице при случайном брожении по интернету, когда с вероятностью мы переходим на следующую страницу по случайно выбранной исходящей ссылке, и с вероятностью — закрываем текущую страницу и открываем случайно выбранную.

Разработав PageRank и основав Google, Брин и Пейдж бросили аспирантуру — дальнейшие математические изыскания им уже не были интересны. Однако вычисление PageRank ставит нетривиальную математическую задачу: у нас есть система из линейных уравнений с неизвестными. В 1998 исчислялся в миллионах, сегодня — в миллиардах. Как решать систему уравнений с десятком миллиардов неизвестных?

Все мы учили в школе алгоритм исключения неизвестных по одной: подставим выражение для во все остальные уравнения, получим систему из уравнений с неизвестными, и так далее. Этот метод решения системы уравнений прост как пробка, но у него есть пара проблем:

Во-первых, подстановка одного выражения в одно уравнение — это умножений рациональных чисел. Значит, полное исключение одной неизвестной — это умножений, а всё решение целиком — это умножений. Когда исчисляется в миллиардах, то последовательных умножений займут дольше, чем остаётся существовать нашей планете до того, как Солнце расширится и поглотит её. Дольше где-то в десять тысяч раз.

К счастью, на каждую страницу в интернете ведут совсем немного входящих ссылок — не миллиард и даже не миллион. На популярную статью в Википедии могут ссылаться десятки тысяч страниц, на эту статью на Хабре — хорошо если десятки. Иными словами, почти все коэффициенты в системе уравнений интернета — нули. Каждый ненулевой коэффициент подвергнется умножениям при подстановке содержащего его уравнения во все остальные. Если обозначить число ненулевых коэффициентов как , то всё решение потребует умножений; в худшем случае , но в случае интернета , и для всех умножений хватит десятка-другого тысяч лет компьютерного времени. Если построить распределённую систему из миллиона-другого серверов, как у Google, то система уравнений интернета решится за неделю. До распространения криптовалют можно было с уверенностью сказать, что большая часть вычислительных ресурсов планеты идёт на решение систем уравнений.

Во-вторых, решение последнего уравнения будет результатом цепочки из умножений и сложений рациональных чисел. Нам либо потребуется битов для точного представления этого результата (и каждого из промежуточных), либо результат каждой операции придётся округлять до значащих битов. Накапливающиеся так ошибки округления способны исказить решение системы уравнений до неузнаваемости. Google может довольствоваться неточными значениями PageRank, но математикам нужны хоть какие-то гарантии точности — например, что в найденных значениях неизвестных будет по стольку же верных битов, как в коэффициентах системы.

Из школьного метода решения системы уравнений большего не выжать. Первокурсников учат более продвинутому матричному методу: систему PageRank можно записать в виде

или в ещё более общем виде: , и тогда вектор неизвестных выражается как . Иными словами, решение системы уравнений сводится к обращению матрицы коэффициентов и умножению обратной матрицы на вектор свободных членов.

Сам по себе матричный метод не даёт по сравнению со школьным ни большей скорости, ни большей точности: для обращения матриц тем способом, которому учат студентов, требуются всё те же умножений коэффициентов. За рамками вузовской программы, однако, существуют более эффективные методы: с 2005 известен вероятностный, а с 2019 — детерминированный алгоритм точного решения системы уравнений за перемножений матриц , и открытым остаётся вопрос об оптимальном алгоритме перемножения матриц. Лобовой способ («строка на столбец») требует умножений; алгоритм Штрассена (1969) —; алгоритм Копперсмита—Винограда (1987) —; его усовершенствования (последнее в 2020) — до . Поскольку для любого , то множитель не влияет на итоговую асимптотическую сложность решения системы уравнений; она получается равной асимптотической сложности умножения матриц. Само по себе умножение матриц — настолько часто встречающаяся практическая задача, что поиск для неё оптимального алгоритма интересовал всех и безотносительно решения систем уравнений: например, усовершенствование в 2020 позволило уменьшить степень асимптотической сложности меньше чем на 0.00001, и всё равно считается важным достижением. Равенство сложности решения системы уравнений, т.е. обращения матрицы, со сложностью умножения матриц — принималось как данность: оптимизация решения одной из этих задач казалась равносильной оптимизации решения второй.

Для практических целей алгоритм Копперсмита—Винограда, и тем более его усовершенствованные варианты, неприменимы: такие алгоритмы прозвали «галактическими», потому что вся Земля слишком мала для хранения матриц таких размеров, на которых эти алгоритмы дадут выигрыш в скорости по сравнению с более простыми. На практике самым важным оказывается частный случай, когда перемножаемые или обращаемые матрицы разрежены — почти все их элементы равны нулю, как и в матрице PageRank. Алгоритм умножения разреженных матриц, опубликованный в 2005, требует операций, и обгоняет Копперсмита—Винограда при ; а вот для обращения разреженных матриц не было известно более эффективных алгоритмов, чем для произвольных. Отчасти это связано с тем, что матрица, обратная разреженной, сама не будет разреженной, и на практике её будет просто негде сохранить.

Недавно на Хабре была опубликована заметка (с байками про рога и копыта, но без объяснения технической стороны вопроса) о том, что оба названных «психологических барьера» сломлены Сантошем Вемпалой и Ричардом Пенгом — парой математиков из Технологического института Джорджии, чья работа на ACM-SIAM Symposium on Discrete Algorithms в январе 2021 была признана лучшей из 637 поданных. Для системы уравнений с их алгоритм находит точное решение за операций, опережая степень асимптотической сложности умножения матриц на 0.04. Как мы помним, «школьный» метод исключения неизвестных по одной при условии приходит к ответу за операций, но не гарантирует точность найденных значений неизвестных. В основе нового алгоритма — вероятностный подход: значения неизвестных «угадываются», оценивается величина ошибки, и «угадывание» повторяется более прицельно. Таким образом, оценка сложности в относится к «наиболее вероятным» случаям, а не к худшим. Другое новшество в алгоритме — то, что на каждой итерации оцениваются сразу несколько случайных «догадок», что позволяет сократить общее число итераций и тем самым сдержать рост размера точных результатов.

Нужно понимать, что алгоритм Вемпалы и Пенга на одном из этапов пользуется алгоритмом Копперсмита—Винограда для умножения матриц — и поэтому новый алгоритм ещё более «галактический». Важность алгоритма Вемпалы и Пенга совсем не в практической применимости, а в доказательстве того, что сложность решения систем уравнений не ограничена сложностью умножения матриц, а значит, новые эффективные алгоритмы для решения разреженных систем уравнений стоит искать в других направлениях — и они гарантированно найдутся. Но ни новый алгоритм, ни другие математические достижения последнего полувека никак не повлияли на практически применимые способы решения систем уравнений: Google и все остальные так и продолжат пользоваться простым, быстрым и неточным итеративным способом.

Наши серверы можно использовать для любых вычислений.

Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!

решений линейного уравнения | Калькулятор

Решения линейного уравнения относятся к набору значений переменных в линейных уравнениях, дающих все возможные решения. Линейные уравнения включают неизвестные величины в виде одной или нескольких переменных для представления реальных задач. Это помогает легко узнать стоимость, пробег, скорость, расстояние и т. Д. Мы все используем линейные уравнения в нашей повседневной жизни, не зная об этом.

В этом уроке давайте подробно узнаем о решениях линейных уравнений, типах решений, способах их нахождения и т. д.

Каковы решения линейного уравнения?

Решения линейных уравнений — это точки, в которых линии или плоскости, представляющие линейные уравнения, пересекаются или встречаются друг с другом. Множество решений системы линейных уравнений — это множество значений переменных всех возможных решений. Например, при решении линейных уравнений можно визуализировать решение системы одновременных линейных уравнений, нарисовав 2 линейных графика и найдя точку их пересечения.

Красная линия представляет все решения уравнения 1, а синяя линия — решения уравнения 2. Пересечение в единственной точке (2,4) — это решение, удовлетворяющее обоим уравнениям.

Типы решений линейных уравнений

Система линейных уравнений может иметь 3 типа решений.

Уникальное решение системы линейных уравнений

Единственное решение линейного уравнения означает, что существует только одна точка, при подстановке которой L.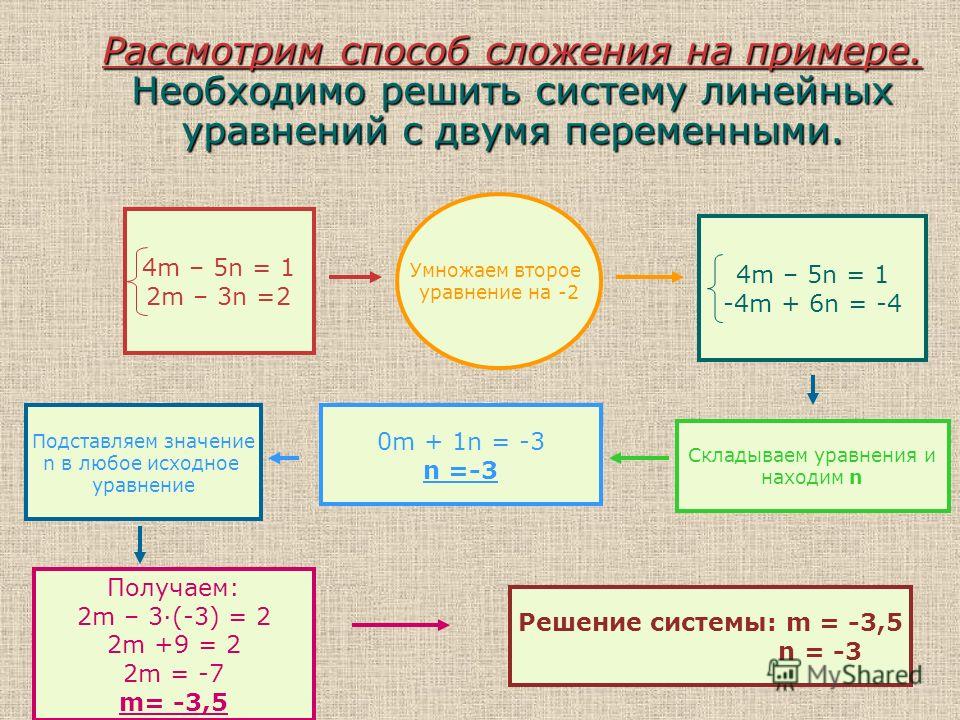 H.S и R.H.S уравнения становятся равными. Линейное уравнение с одной переменной всегда имеет единственное решение. Например, 3m = 6 имеет единственное решение m = 2, для которого L.H.S = R.H.S. Точно так же для одновременных линейных уравнений с двумя переменными единственным решением является упорядоченная пара (x, y), которая удовлетворяет обоим уравнениям.

Нет решения

Система линейных уравнений не имеет решения, если не существует точек, в которых прямые пересекаются друг с другом, или графики линейных уравнений параллельны.

Бесконечное множество решений

Система линейных уравнений имеет бесконечно много решений, если существует множество решений из бесконечных точек, для которых правая и левая стороны уравнения становятся равными, или на графике прямые линии перекрывают друг друга.

Как найти решение линейного уравнения?

Решения для линейных уравнений с одной переменной

Рассмотрим уравнение 2x + 4 = 8

  • Чтобы найти значение x, сначала удалим 4 из L. H.S, поэтому мы вычитаем 4 из обеих частей уравнения. 2x + 4 — 4 = 8 — 4
  • Просто. Теперь мы получаем, 2x = 4
  • Теперь нам нужно удалить 2 из L.H.S, чтобы получить x, поэтому мы делим уравнение на 2. 2x/2 = 4/2, x=2

Следовательно, решение уравнения 2x + 4 = 8 равно x=2.

Решения для линейных уравнений с двумя переменными

Для нахождения решений линейных уравнений с двумя переменными можно использовать следующие методы.

Метод замены

Рассмотрим следующую пару линейных уравнений, давайте решим следующие линейные уравнения.

х + у = 4 и х — у = 2

  • Преобразуем первое уравнение, чтобы выразить y через x следующим образом: x + y = 4, y = 4 — x
  • Теперь это выражение для у можно подставить во второе уравнение, так что у нас останется уравнение только относительно х: х — у = 2, х — 4 + х = 2, 2х = 6 х = 6/2, х = 3
  • Получив значение x, мы можем подставить его обратно в любое из двух уравнений, чтобы найти y. Подставим это в первое уравнение: x + y = 4 (3) + y = 4, y = 4 — 3 = 1, y = 1
  • Окончательное нетривиальное решение: x = 3, y = 1

Должно быть понятно, почему этот процесс называется замещением. Мы выражаем одну переменную через другую, используя одно из двух уравнений, и подставляем это выражение во второе уравнение.

Метод исключения

Рассмотрим следующую пару линейных уравнений:

2x + 3y — 11 = 0, 3x + 2y — 9 = 0

Коэффициенты x в двух уравнениях равны 2 и 3 соответственно.Умножим первое уравнение на 3, а второе уравнение на 2, чтобы коэффициенты при x в двух уравнениях стали равными:

  • 3 {2x + 3y — 11 = 0} 6x + 9y — 33 = 0
  • 2 {3x + 2y — 9 = 0} 6x + 4y — 18 = 0

Теперь вычтем два уравнения, это значит, что мы вычтем левые части двух уравнений, а правые части двух уравнений и равенство все равно сохранится.

6х + 9у — 33 = 0,6х + 4у — 18 = 0 0 + 5у — 15 = 0, 5у = ​​15, у = 3

Обратите внимание, что x исключается, и у нас остается уравнение только с y. Получив значение y, мы действуем, как и раньше, — подставляем его в любое из двух уравнений. Подставим это в первое уравнение:

2х + 3у — 11 = 0, 2х + 3 (3) — 11 = 0, 2х + 9 — 11 = 0\, 2х = 2, х = 1

Таким образом, нетривиальное решение: x = 1, y = 3

Графический метод

В качестве примера решим следующее линейное уравнение: x — y + 2 = 0, 2x + y — 5 = 0. Проведем соответствующие линии на тех же осях:

Точка пересечения (1,3), что означает, что x = 1, y = 3 является решением пары линейных уравнений, заданной (2).На самом деле, это единственное решение пары , так как две непараллельные прямые не могут пересекаться более чем в одной точке.

Важные примечания

Вы можете напрямую проверить типы решений, используя следующие условия:

  • Единственное решение (непротиворечивое и независимое) a1/a2 ≠ b1/b2
  • Нет решения (противоречивое и независимое) a1/a2 = b1/b2 ≠ c1/c2
  • Бесконечное множество решений (непротиворечивых и зависимых) a1/a2 = b1/b2 = c1/c2

Часто задаваемые вопросы о решениях линейных уравнений

Как решить систему линейных уравнений?

У нас есть разные методы решения системы линейных уравнений:

  • Графический метод
  • Метод замены
  • Метод перекрестного умножения
  • Метод исключения
  • Метод определителей

Что такое уникальное решение линейного уравнения?

Единственным решением системы линейных уравнений является упорядоченная пара или точка, которая делает равенство истинным в уравнении.

Что произойдет, если пара линейных уравнений непротиворечива?

Если пара линейных уравнений непротиворечива, то линии либо пересекаются, либо совпадают (накладываются) друг на друга.

Каковы 3 решения линейных уравнений?

Существует три способа решения систем линейных уравнений: подстановка, исключение и построение графика

Как найти решение линейной системы?

  • Сначала решите одно линейное уравнение относительно y через x.
  • Затем подставьте это выражение для y в другое линейное уравнение. Вы получите уравнение относительно x .

Линии пересекаются в нулевых точках.
Линии пересекаются ровно в одной точке.
Прямые пересекаются в бесконечном числе точек.

Как найти решение двух линейных уравнений?

Решение систем уравнений подстановкой

  • Решите одно из двух уравнений для одной из переменных относительно другой.
  • Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.

Как решать линейные уравнения с одной переменной?

  • Шаг 1: При необходимости упростите каждую сторону.
  • Шаг 2: Используйте доп./доп. Свойства, позволяющие переместить переменный термин в одну сторону, а все остальные термины — в другую.
  • Шаг 3: Используйте Множ./дел. …
  • Шаг 4: Проверьте свой ответ.

Сколько существует решений линейного уравнения 2x-5y=7?

В данном уравнении 2x – 5y = 7 для каждого значения x мы получаем соответствующее значение y и наоборот.Следовательно, линейное уравнение имеет бесконечно много решений.

Как найти упорядоченные парные решения линейных уравнений?

Чтобы выяснить, является ли упорядоченная пара решением уравнения, вы можете выполнить тест. Определите значение x в упорядоченной паре и подставьте его в уравнение. При упрощении, если полученное вами значение y совпадает со значением y в упорядоченной паре, то эта упорядоченная пара действительно является решением уравнения.

Как найти упорядоченное парное решение линейного уравнения с двумя переменными?

Чтобы убедиться, что упорядоченная пара является решением, подставьте соответствующие значения x и y в каждое уравнение, а затем упростите, чтобы увидеть, получите ли вы верное утверждение для обоих уравнений.

Системы линейных уравнений

 


Линейное уравнение — это уравнение для линии .

Линейное уравнение не всегда имеет форму y = 3,5 − 0,5x ,

Также может быть как y = 0,5(7 − x)

Или как у + 0,5х = 3,5

Или как y + 0,5x — 3,5 = 0 и больше.

(Примечание: это все одно и то же линейное уравнение!)

 

Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.

Пример: Вот два линейных уравнения:

Вместе они составляют систему линейных уравнений.

Можете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного. )

Давайте попробуем построить и решить реальный пример:

Пример: Вы против Лошади

Это гонка!

Вы можете пробежать 0,2 км каждую минуту.

Лошадь может бегать 0.5 км каждую минуту. Но чтобы оседлать лошадь, нужно 6 минут.

Как далеко ты уедешь, прежде чем тебя настигнет лошадь?

 

Мы можем составить два уравнения ( d = расстояние в км, t = время в минутах)

  • Каждую минуту вы бежите со скоростью 0,2 км, поэтому d = 0,2t
  • Лошадь бежит со скоростью 0,5 км в минуту, но мы уменьшаем ее время на 6: d = 0,5(t−6)

 

Итак, у нас есть система уравнений ( линейных ):

Решим на графике:

Видишь, как лошадь стартует через 6 минут, а потом бежит быстрее?

Кажется, тебя поймают через 10 минут… у вас всего 2 км.

В следующий раз беги быстрее.

Итак, теперь вы знаете, что такое система линейных уравнений.

Продолжаем узнавать о них больше….

Решение

Способов решения линейных уравнений может быть много!

Давайте посмотрим на другой пример:

Пример: Решите эти два уравнения:

На этом графике показаны два уравнения:

Наша задача — найти пересечение двух линий.

Ну, мы видим, где они пересекаются, так что это уже решено графически.

А теперь давайте решим ее по алгебре!

 

Хммм… как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:

х + у — (-3х + у) = 6 — 2

Теперь упростим:

х + у + 3х — у = 6 — 2

4x = 4

х = 1

Итак, теперь мы знаем, что линии пересекаются в точке x=1 .

И мы можем найти соответствующее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одно и то же значение при x=1). Используем первый (второй можете попробовать сами):

х + у = 6

1 + у = 6

г = 5

И решение:

х = 1 и у = 5

И график показывает, что мы правы!

Линейные уравнения

В линейных уравнениях допускаются только простые переменные. № x 2 , y 3 , √x и т. д. :


Линейный и нелинейный

Размеры

A Линейное уравнение может быть в двух измерениях …
(например, x и y )		  
… или в 3-х измерениях …
(делает самолет)		  
… или 4 размера …    
… или больше!    

Общие переменные

Чтобы уравнения «работали вместе», они используют одну или несколько переменных:

Система уравнений содержит два или более уравнений в одну или несколько переменных

Многие переменные

Итак, система уравнений может иметь много уравнений и много переменных.

Пример: 3 уравнения с 3 переменными

2x + и – 2з = 3
х – и – из = 0
х + и + 3з = 12

Может быть любая комбинация:

  • 2 уравнения с 3 переменными,
  • 6 уравнений с 4 переменными,
  • 9000 уравнений с 567 переменными,
  • и т.д.

Решения

Когда количество уравнений равно тому же , что и количество переменных, то вероятно будут решением. Не гарантировано, но вероятно.

На самом деле возможны только три случая:

  • Нет раствора
  • Один раствор
  • Бесконечное множество решений

Когда нет решения , уравнения называются «несовместимыми» .

Один или бесконечно много решений называются «непротиворечивыми»

Вот диаграмма для 2 уравнения с 2 переменными :

Независимый

«Независимый» означает, что каждое уравнение дает новую информацию.
В противном случае они «Зависимые» .

Также называется «линейная независимость» и «линейная зависимость».

Пример:

Эти уравнения «зависимы» , потому что они на самом деле то же самое уравнение , просто умноженное на 2.

Итак, второе уравнение не дало новой информации .

Где уравнения верны

Весь фокус в том, чтобы найти, где все уравнений верны одновременно .

Правда? Что это значит?

Пример: Вы против Лошади

Строка «you» истинна по всей своей длине (но больше нигде).

В любом месте этой строки d равно 0.2т

  • при t=5 и d=1 уравнение верно (d = 0,2t? Да, так как 1 = 0,2×5 верно)
  • при t=5 и d=3 уравнение неверно (верно ли d = 0,2t? Нет, так как 3 = 0,2×5 неверно )

Точно так же линия «лошадь» также истинна по всей своей длине (но больше нигде).

Но только в точке, где они пересекают (при t=10, d=2), оба истинны .

Значит, они должны быть верными одновременно …

… вот почему некоторые люди называют их «Одновременными линейными уравнениями»

Решить с помощью алгебры

Обычно для их решения используется алгебра.

Вот пример «Лошадь», решенный с помощью алгебры:

Пример: Вы против Лошади

Система уравнений:

В данном случае проще всего приравнять их друг к другу:

д = 0. 2t = 0,5(t−6)

 

Начните с :0,2t = 0,5(t − 6)

Расширение 0,5(t−6) :0,2t = 0,5t − 3

Вычесть 0,5t с обеих сторон: −0,3t = −3

Разделите обе части на -0,3 :t = -3/-0,3 = 10 минут

Теперь мы знаем , когда тебя поймают!

Зная t , мы можем вычислить d :d = 0,2t = 0,2×10 = 2 км

 

И наше решение:

t = 10 минут и d = 2 км

Алгебра против графиков

Зачем использовать алгебру, если графики так просты? Потому что:

Более 2 переменных не могут быть решены с помощью простого графика.

Итак, алгебра приходит на помощь двумя популярными методами:

  • Решение подстановкой
  • Решение методом исключения

Мы увидим каждый, с примерами в 2-х переменных и в 3-х переменных. Вот так…

Решение подстановкой

Вот шаги:

  • Напишите одно из уравнений в стиле «переменная =. ..»
  • Заменить (т.е. заменить) эту переменную в другом уравнении (уравнениях).
  • Решить другое уравнение(я)
  • (Повторите при необходимости)

Вот пример с 2 уравнения с 2 переменными :

Пример:

Мы можем начать с любого уравнения и любой переменной .

Используем второе уравнение и переменную «y» (выглядит простейшим уравнением).

 

Напишите одно из уравнений в стиле «переменная = …»:

Мы можем вычесть x из обеих частей x + y = 8, чтобы получить y = 8 − x . Теперь наши уравнения выглядят так:

 

Теперь замените «y» на «8 − x» в другом уравнении:

  • 3x + 2 (8 − x) = 19
  • у = 8 — х

 

Решите, используя обычные методы алгебры:

Расширить 2(8−x) :

  • 3x + 16 − 2x = 19
  • у = 8 — х

Тогда 3x−2x = x :

И, наконец, 19−16=3

 

Теперь, когда мы знаем, что такое x , мы можем представить это в уравнении y = 8 − x :

И ответ:

х = 3
у = 5

 

Примечание: поскольку является решением, уравнения «непротиворечивы»

 

Проверка: почему бы вам не проверить, работает ли x = 3 и y = 5 в обоих уравнениях?

 

Решение методом замены: 3 уравнения с 3 переменными

ОК! Давайте перейдем к более длинному примеру : 3 уравнения с 3 переменными .

Это не сложно сделать… просто это займет много времени !

Пример:

  • х + г = 6
  • г — 3г = 7
  • 2х + у + 3z = 15

Мы должны аккуратно выстроить переменные, иначе мы можем потерять представление о том, что мы делаем:

 

х     + из = 6      
  – 3 года + из = 7      
2x + и + 3з = 15      

 

Мы можем начать с любого уравнения и любой переменной. Давайте используем первое уравнение и переменную «x».

 

Запишите одно из уравнений в стиле «переменная =…»:

х         = 6 − я    
  – 3 года + из = 7      
2x + и + 3з = 15      

 

Теперь замените «x» на «6 − z» в других уравнениях:

(К счастью, есть только одно уравнение с x в нем)

  х         = 6 — я    
    – 3 года + из = 7      
2 (6-з) + и + 3з = 15      

 

Решите, используя обычные методы алгебры:

2(6−z) + y + 3z = 15 упрощается до y + z = 3 :

х         = 6 — я    
  – 3 года + из = 7      
    и + из = 3      

Хорошо. Мы добились некоторого прогресса, но еще не все.

 

Теперь повторите процесс , но только для двух последних уравнений.

 

Запишите одно из уравнений в стиле «переменная =…»:

Выберем последнее уравнение и переменную z:

х         = 6 — я    
  – 3 года + из = 7      
        з = 3 − у    

 

Теперь замените «z» на «3 − y» в другом уравнении:

х         = 6 — я    
  – 3 года + 3 − у = 7      
        из = 3 − у    

 

Решите, используя обычные методы алгебры:

−3y + (3−y) = 7 упрощается до −4y = 4 , или, другими словами, y = −1

х         = 6 — я    
    г     = −1      
        из = 3 − у    

Почти готово!

 

Зная, что y = −1 , мы можем вычислить, что z = 3−y = 4 :

х         = 6 — я    
    и     = −1      
        з = 4      

Зная, что z = 4 , мы можем вычислить, что x = 6−z = 2 :

х         = 2      
    и     = −1      
        из = 4      

 

И ответ:

х = 2
у = −1
z = 4

 

Проверка: пожалуйста, проверьте это сами.

Мы можем использовать этот метод для 4 или более уравнений и переменных… просто повторяйте одни и те же шаги снова и снова, пока не решите.

Вывод: Замена работает хорошо, но требует много времени.

 

Решение методом исключения

Ликвидация может быть быстрее… но должна быть аккуратной.

«Устранить» означает удалить : этот метод работает путем удаления переменных до тех пор, пока не останется только одна.

Идея в том, что мы можем смело :

  • умножить уравнение на константу (кроме нуля),
  • добавить (или вычесть) уравнение к другому уравнению

Как в этих примерах:

ПОЧЕМУ мы можем складывать уравнения друг с другом?

Представьте себе два очень простых уравнения:

х — 5 = 3
5 = 5

Мы можем добавить «5 = 5» к «x − 5 = 3»:

х — 5 + 5 = 3 + 5
х = 8

Попробуйте сами, но используйте 5 = 3+2 в качестве второго уравнения

Он по-прежнему будет работать нормально, потому что обе стороны равны (для этого и нужен =!)

 

Мы также можем поменять местами уравнения, чтобы первое могло стать вторым и т. д., если это поможет.

 

ОК, время для полного примера. Давайте используем 2 уравнения с 2 переменными пример из предыдущего:

Пример:

Очень важно поддерживать порядок:

3x + 2 года = 19      
х + и = 8      

 

Сейчас … наша цель исключить переменную из уравнения.

Сначала мы видим, что есть «2y» и «y», так что давайте поработаем над этим.

Умножить второе уравнение на 2:

3x + 2 года = 19      
2 х + 2 у = 16      

Вычесть второе уравнение из первого уравнения:

х     = 3      
2x + 2 года = 16      

Ура! Теперь мы знаем, что такое х!

 

Далее мы видим, что второе уравнение имеет «2x», поэтому давайте уменьшим его вдвое, а затем вычтем «x»:

Умножьте второе уравнение на ½ (т. е. разделить на 2):

х     = 3      
х + г = 8      

Вычесть первое уравнение из второго уравнения:

х     = 3      
    г = 5      

Готово!

И ответ:

х = 3 и у = 5

 

А вот и график:

Синяя линия показывает, где 3x + 2y = 19 верно

Красная линия показывает, где x + y = 8 верно

При x=3, y=5 (где линии пересекаются) они оба верны. Это и есть ответ.

Вот еще пример:

Пример:

  • 2х — у = 4
  • 6х — 3у = 3

Аккуратно разложить:

2x – и = 4      
6x – 3 года = 3      

Умножьте первое уравнение на 3:

6x – 3 года = 12      
6x – 3 года = 3      

Вычесть второе уравнение из первого уравнения:

0 – 0 = 9      
6x – 3 года = 3      

0 − 0 = 9 ???

Что здесь происходит?

 

Проще говоря, решения нет.

 

На самом деле это параллельные линии:  

И наконец:

Пример:

  • 2х — у = 4
  • 6х — 3у = 12

Аккуратно:

2x – и = 4      
6x – 3 года = 12      

Умножьте первое уравнение на 3:

6x – 3 года = 12      
6x – 3 года = 12      

Вычесть второе уравнение из первого уравнения:

0 – 0 = 0      
6x – 3 года = 3      

0 − 0 = 0

Ну, это действительно ПРАВДА! Ноль действительно равен нулю. ..

 

… потому что это одно и то же уравнение …

 

… так что существует бесконечное количество решений

Это одна и та же строка:  

Итак, мы рассмотрели пример каждого из трех возможных случаев:

  • Нет раствора
  • Один раствор
  • Бесконечное множество решений

Решение методом исключения: 3 уравнения с 3 переменными

Прежде чем мы начнем со следующего примера, давайте посмотрим на улучшенный способ выполнения действий.

Следуйте этому методу, и мы с меньшей вероятностью допустим ошибку.

Прежде всего, удалите переменные по порядку :

.
  • Сначала исключить x с (из уравнений 2 и 3, по порядку)
  • затем исключить y (из уравнения 3)

Вот как мы их устраняем:

Теперь у нас есть «форма треугольника»:

Теперь начните снизу и выполните резервное копирование (так называемая «обратная замена»)
(поместите z , чтобы найти y , затем z и y , чтобы найти x ):

И мы решили:

ТАКЖЕ, мы обнаружим, что легче выполнить некоторые расчеты в уме или на бумаге, чем всегда работать в рамках набора уравнений:

Пример:

  • х + у + г = 6
  • 2г + 5г = -4
  • 2x + 5y — z = 27

Аккуратно написано:

х + и + из = 6      
    2 года + 5з = −4      
2x + 5 лет – из = 27      

 

Во-первых, исключите x из второго и третьего уравнения.

Во втором уравнении нет x… переходим к третьему уравнению:

Вычтите 2 раза 1-е уравнение из 3-го уравнения (просто сделайте это в уме или на бумаге):

И получаем:

х + и + из = 6      
    2 года + 5з = −4      
    3 года – 3з = 15      

 

Затем исключите и из третьего уравнения.

Мы могли бы вычесть 1½ раза 2-е уравнение из 3-го уравнения (потому что 1½ умножить на 2 равно 3) …

… но мы можем избежать дробей , если мы:

  • умножить 3-е уравнение на 2 и
  • умножить второе уравнение на 3

и потом делаем вычитание… вот так:

И получаем:

х + и + из = 6      
    2 года + 5з = −4      
        з = −2      

Теперь у нас есть «треугольная форма»!

 

Теперь вернитесь снова «обратно-заменив»:

Мы знаем z , поэтому 2y+5z=−4 становится 2y−10=−4 , затем 2y=6 , поэтому y=3 :

х + и + из = 6      
    г     = 3      
        из = −2      

Тогда x+y+z=6 становится x+3−2=6 , поэтому x=6−3+2=5

х         = 5      
    и     = 3      
        из = −2      

 

И ответ:

х = 5
у = 3
z = −2

 

Чек: проверьте сами.

Общий совет

Как только вы привыкнете к методу исключения, он станет проще, чем замена, потому что вы просто выполняете шаги, и ответы появляются.

Но иногда Замена может дать более быстрый результат.

  • Замена часто проще для небольших случаев (например, 2 уравнения, а иногда и 3 уравнения)
  • Устранение проще для больших ящиков

И всегда стоит сначала просмотреть уравнения, чтобы увидеть, нет ли простого пути … так что опыт помогает.

 

11.1: Системы линейных уравнений — две переменные

Производитель скейтбордов представляет новую линейку досок. Производитель отслеживает свои затраты, которые представляют собой сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает на продаже своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов нужно произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы.

Введение в системы уравнений

Чтобы исследовать такие ситуации, как ситуация с производителем скейтборда, нам нужно признать, что мы имеем дело с более чем одной переменной и, вероятно, с более чем одним уравнением. Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.

В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

\[\begin{align*} 2x+y &= 15 \\ 3x–y &= 5 \end{align*}\]

Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. В этом примере упорядоченная пара \((4,7)\) является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует.

\[\begin{align*} 2(4)+(7) &=15 \text{ True} \\ 3(4)−(7) &= 5 \text{ True} \end{align*}\ ]

Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. Непротиворечивая система уравнений имеет хотя бы одно решение. Непротиворечивая система считается независимой системой , если она имеет единственное решение, как в примере, который мы только что рассмотрели. Две линии имеют разные наклоны и пересекаются в одной точке плоскости.Непротиворечивая система считается зависимой системой , если уравнения имеют одинаковый наклон и одинаковые и -перехваты. Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений.

Другим типом системы линейных уравнений является противоречивая система , в которой уравнения представляют две параллельные линии.Линии имеют одинаковый наклон и разные точки пересечения и . Нет общих точек для обеих прямых; следовательно, система не имеет решения.

ТИПЫ ЛИНЕЙНЫХ СИСТЕМ

Существует три типа систем линейных уравнений с двумя переменными и три типа решений.

  • Независимая система имеет ровно одну пару решений \((x,y)\). Точка пересечения двух прямых является единственным решением.
  • Несогласованная система не имеет решения.Обратите внимание, что две линии параллельны и никогда не пересекаются.
  • Зависимая система имеет бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.

На рисунке \(\PageIndex{2}\) сравниваются графические представления каждого типа системы.

Рисунок \(\PageIndex{2}\)

Для данной системы линейных уравнений и упорядоченной пары определите, является ли упорядоченная пара решением

  1. Подставьте упорядоченную пару в каждое уравнение в системе.
  2. Определить, верны ли утверждения в результате замены в обоих уравнениях; если да, то упорядоченная пара является решением.

Пример \(\PageIndex{1}\): определение того, является ли упорядоченная пара решением системы уравнений

Определить, является ли упорядоченная пара \((5,1)\) решением данной системы уравнений.

\[\begin{align*} x+3y &= 8 \\ 2x−9 &= y \end{align*}\]

Раствор

Подставьте упорядоченную пару \((5,1)\) в оба уравнения.

\[ \begin{align*} (5)+3(1) &= 8 \\ 8 &= 8 \text{ True} \\ 2(5)−9 &= (1) \\ 1 &= 1 \text{Истина} \end{align*}\]

Упорядоченная пара \((5,1)\) удовлетворяет обоим уравнениям, поэтому является решением системы.

Анализ

Мы можем ясно увидеть решение, построив график каждого уравнения. Поскольку решение представляет собой упорядоченную пару, удовлетворяющую обоим уравнениям, это точка на обеих прямых и, следовательно, точка пересечения двух прямых.См. рисунок \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\)

Упражнение \(\PageIndex{1}\)

Определите, является ли упорядоченная пара \((8,5)\) решением следующей системы.

\[\begin{align*} 5x−4y &= 20 \\ 2x+1 &= 3y \end{align*}\]

Ответить

Не решение.

Решение систем уравнений с помощью графика

Существует несколько методов решения систем линейных уравнений.Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, изобразив систему уравнений на одном и том же наборе осей.

Пример \(\PageIndex{2}\): решение системы уравнений с двумя переменными с помощью графика

Решите следующую систему уравнений с помощью графика. Определите тип системы.

\[\begin{align*} 2x+y &= −8 \\ x−y &= −1 \end{align*}\]

Раствор

Решите первое уравнение для \(y\).

\[\begin{align*} 2x+y &= −8 \\ y &= −2x−8 \end{align*}\]

Решите второе уравнение относительно \(y\).

\[\begin{align*} x−y &= −1 \\ y &= x+1 \end{align*}\]

Постройте график обоих уравнений на том же наборе осей, что и на рисунке \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\)

Линии пересекаются в точке \((−3,−2)\). Мы можем убедиться, что это решение системы, подставив упорядоченную пару в оба уравнения.

\[\begin{align*} 2(−3)+(−2) &= −8 \\ −8 &= −8 \text{ True} \\ (−3)−(−2) &= − 1 \\ −1 &= −1 \text{ True} \end{align*}\]

Решением системы является упорядоченная пара \((−3,−2)\), поэтому система независима.

Упражнение \(\PageIndex{2}\)

Решите следующую систему уравнений с помощью графика.

\[\begin{align*} 2x−5y &= −25 \\ −4x+5y &= 35 \end{align*}\]

Ответить

Решением системы является упорядоченная пара \((−5,3)\).

Рисунок \(\PageIndex{5}\)

Вопросы и ответы

Можно ли использовать графики, если система непоследовательна или зависима?

Да, в обоих случаях мы по-прежнему можем построить график системы, чтобы определить тип системы и решения. Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой.

Решение систем уравнений подстановкой

Решение линейной системы с двумя переменными с помощью графика хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод.Рассмотрим еще два метода решения системы линейных уравнений , которые являются более точными, чем построение графика. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение для решения второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.

Как: Для данной системы двух уравнений с двумя переменными решить ее методом подстановки.

  1. Решите одно из двух уравнений для одной из переменных относительно другой.
  2. Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.
  3. Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
  4. Проверьте решение обоих уравнений.

Пример \(\PageIndex{3}\): решение системы уравнений с двумя переменными путем замены

Решите следующую систему уравнений путем замены.

\[\begin{align*} −x+y &= −5 \\ ​​2x−5y &= 1 \end{align*}\]

Раствор

Сначала решим первое уравнение относительно \(y\).

\[\begin{align*} −x+y &=−5 \\ ​​y &= x−5 \end{align*}\]

Теперь мы можем подставить выражение \(x−5\) вместо \(y\) во втором уравнении.

\[\begin{align*} 2x−5y &= 1 \\ 2x−5(x−5) &= 1 \\ 2x−5x+25 &= 1 \\ −3x &= −24 \\ x & = 8 \конец{выравнивание*}\]

Теперь подставим \(x=8\) в первое уравнение и найдем \(y\).

\[\begin{align*} −(8)+y &= −5 \\ ​​y &= 3 \end{align*}\]

Наше решение: \((8,3)\).

Проверьте решение, подставив \((8,3)\) в оба уравнения.

\[\begin{align*} −x+y &= −5 \\ ​​−(8)+(3) &= −5 \text{ True} \\ 2x−5y &= 1 \\ 2(8) −5(3) &= 1 \text{ True} \end{align*}\]

Упражнение \(\PageIndex{3}\)

Решите следующую систему уравнений путем замены.

\[\begin{align*} x &= y+3 \\ 4 &= 3x−2y \end{align*}\]

Ответить

\((−2,−5)\)

Вопросы и ответы

Можно ли методом подстановки решить любую линейную систему с двумя переменными?

Да, но метод работает лучше всего, если одно из уравнений содержит коэффициент \(1\) или \(–1\), чтобы нам не приходилось иметь дело с дробями.

Решение систем уравнений с двумя переменными методом сложения

Третий метод решения систем линейных уравнений — метод сложения. В этом методе мы добавляем два слагаемых с одной и той же переменной, но с противоположными коэффициентами, так что сумма равна нулю. Конечно, не во всех системах два члена одной переменной имеют противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения путем умножения, чтобы исключить одну переменную путем сложения.

Как: Данную систему уравнений решить методом сложения.

  1. Напишите оба уравнения с x — и y -переменными слева от знака равенства и константами справа.
  2. Напишите одно уравнение над другим, выстраивая соответствующие переменные. Если одна из переменных в верхнем уравнении имеет противоположный коэффициент той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную.Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
  3. Решите полученное уравнение для оставшейся переменной.
  4. Подставьте это значение в одно из исходных уравнений и найдите вторую переменную.
  5. Проверьте решение, подставив значения в другое уравнение.

Пример \(\PageIndex{4}\): решение системы методом сложения

Решите данную систему уравнений сложением.

\[\begin{align*} x+2y &= −1 \\ −x+y &=3 \end{align*}\]

Раствор

Оба уравнения уже установлены равными константе. Обратите внимание, что коэффициент \(x\) во втором уравнении, \(–1\), противоположен коэффициенту \(x\) в первом уравнении, \(1\). Мы можем сложить два уравнения, чтобы исключить \(x\) без необходимости умножения на константу.

\[\begin{align*} x+2y &= -1 \\ \underline{-x+y}& = \underline{3} \\ 3y&= 2 \\ \end{align*}\]

Теперь, когда мы исключили \(x\), мы можем решить полученное уравнение относительно \(y\).

\[\begin{align*} 3y &= 2 \\ y &=\dfrac{2}{3} \end{align*}\]

Затем мы подставляем это значение для \(y\) в одно из исходных уравнений и находим \(x\).

\[\begin{align*} −x+y &= 3 \\ −x+\dfrac{2}{3} &= 3 \\ −x &= 3−\dfrac{2}{3} \\ − x &= \dfrac{7}{3} \\ x &= −\dfrac{7}{3} \end{align*}\]

Решением этой системы является \(\left(−\dfrac{7}{3},\dfrac{2}{3}\right)\).

Проверьте решение первого уравнения.

\[\begin{align*} x+2y &= −1 \\ \left(−\dfrac{7}{3}\right)+2\left(\dfrac{2}{3}\right) & = \\ −\dfrac{7}{3}+\dfrac{4}{3} &= −\dfrac{3}{3} \\ −1 &= −1 \;\;\;\;\; \;\;\; \text{True} \end{align*}\]

Анализ

Мы получаем важный взгляд на системы уравнений, глядя на графическое представление. См. рисунок \(\PageIndex{6}\), чтобы убедиться, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.

Рисунок \(\PageIndex{6}\)

Пример \(\PageIndex{5}\): использование метода сложения, когда требуется умножение одного уравнения

Решите данную систему уравнений методом сложения.

\[\begin{align*} 3x+5y &= −11 \\ x−2y &= 11 \end{align*}\]

Раствор

Добавление этих уравнений в представленном виде не приведет к удалению переменной. Однако мы видим, что в первом уравнении есть \(3x\), а во втором уравнении есть \(x\).Поэтому, если мы умножим второе уравнение на \(−3\), x -членов добавятся к нулю.

\[\begin{align*} x−2y &= 11 \\ −3(x−2y) &=−3(11) \;\;\;\;\;\;\;\; \text{Умножьте обе части на }−3. \\ −3x+6y &= −33 \;\;\;\;\;\;\;\;\; \text{Использовать свойство дистрибутива.} \end{align*}\]

Теперь добавим их.

\[\begin{align*} 3x+5y &= -11 \\ \underline{-3x+6y }& = \underline{-33} \\ 11y&= -44 \\ y&= -4 \end{align *}\]

На последнем этапе мы подставляем \(y=−4\) в одно из исходных уравнений и находим \(x\).

\[\begin{align*} 3x+5y &= −11 \\ 3x+5(−4) &= −11 \\ 3x−20 &= −11 \\ 3x &= 9 \\ x &= 3 \конец{выравнивание*}\]

Наше решение — упорядоченная пара \((3,−4)\). См. рисунок \(\PageIndex{7}\). Проверьте решение в исходном втором уравнении.

\[\begin{align*} x−2y &= 11 \\ (3)−2(−4) &= 3+8 \\ &= 11 \;\;\;\;\;\;\; \;\;\; \text{True} \end{align*}\]

Рисунок \(\PageIndex{7}\)

Упражнение \(\PageIndex{4}\)

Решите систему уравнений методом сложения.

\[\begin{align*} 2x−7y &= 2 \\ 3x+y &= −20 \end{align*}\]

Ответить

\((−6,−2)\)

Пример \(\PageIndex{6}\): использование метода сложения, когда требуется умножение обоих уравнений

Решите данную систему уравнений с двумя переменными методом сложения.

\[\begin{align*} 2x+3y &= −16 \\ 5x−10y &= 30 \end{align*}\]

Раствор

В одном уравнении \(2x\), а в другом \(5x\).Наименьшее общее кратное равно \(10x\), поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Удалим \(x\), умножив первое уравнение на \(−5\), а второе уравнение на \(2\).

\[\begin{align*} −5(2x+3y) &= −5(−16) \\ −10x−15y &= 80 \\ 2(5x−10y) &= 2(30) \\ 10x −20 лет &= 60 \end{align*}\]

Затем мы складываем два уравнения вместе.

\[\begin{align*} -10x-15y &= 80 \\ \underline{10x-20y}& = \underline{60} \\ -35y&= 140 \\ y&= -4 \end{align*} \]

Подставьте \(y=−4\) в исходное первое уравнение.

\[ \begin{align*} 2x+3(−4) &=−16 \\ 2x−12 &= −16 \\ 2x &= −4 \\ x &=−2 \end{align*}\ ]

Решение: \((−2,−4)\). Проверьте это в другом уравнении.

\[\begin{align*} 5x−10y &= 30 \\ 5(−2)−10(−4) &= 30 \\ −10+40 &= 30 \\30 &=30 \end{align *}\]

См. рисунок \(\PageIndex{8}\).

Рисунок \(\PageIndex{8}\)

Пример \(\PageIndex{7}\): использование метода сложения в системах уравнений, содержащих дроби

Решите данную систему уравнений с двумя переменными методом сложения.

\[ \begin{align*} \dfrac{x}{3}+\dfrac{y}{6} &= 3 \\ \dfrac{x}{2}−\dfrac{y}{4} &= 1 \конец{выравнивание*}\]

Раствор

Сначала очистите каждое уравнение дробей, умножив обе части уравнения на наименьший общий знаменатель.

\[\begin{align*} 6\left(\dfrac{x}{3}+\dfrac{y}{6}\right) &= 6(3) \\ 2x+y &= 18 \\ 4 \left(\dfrac{x}{2}−\dfrac{y}{4}\right) &= 4(1) \\ 2x−y &= 4 \end{align*}\]

Теперь умножьте второе уравнение на \(−1\), чтобы исключить x -переменную.

\[\begin{align*} −1(2x−y) &= −1(4) \\ −2x+y &= −4 \end{align*}\]

Сложите два уравнения, чтобы исключить переменную \(x\), и решите полученное уравнение.

\[\begin{align*} 2x+y &= 18 \\ −2x+y &= −4 \\ 2y &= 14 \\ y &=7 \end{align*}\]

Подставьте \(y=7\) в первое уравнение.

\[\begin{align*} 2x+(7) &= 18 \\ 2x &= 11 \\ x &= \dfrac{11}{2} \\ &= 7.5 \end{align*}\]

Решение: \(\left(\dfrac{11}{2},7\right)\).Проверьте это в другом уравнении.

\[\begin{align*} \dfrac{x}{2}-\dfrac{y}{4} &= 1 \\ \dfrac{\dfrac{11}{2}}{2}-\dfrac{ 7}{4} &=1 \\ \dfrac{11}{4}-\dfrac{7}{4} &=1 \\ \dfrac{4}{4} &=1 \end{align*}\ ]

Упражнение \(\PageIndex{5}\)

Решите систему уравнений методом сложения.

\[\begin{align*} 2x+3y &= 8 \\ 3x+5y &= 10 \end{align*}\]

Ответить

\((10,−4)\)

Идентификация несовместимых систем уравнений, содержащих две переменные

Теперь, когда у нас есть несколько методов решения систем уравнений, мы можем использовать методы для выявления несовместных систем. Напомним, что несогласованная система состоит из параллельных прямых, имеющих одинаковый наклон, но разные точки пересечения по оси y. Они никогда не пересекутся. При поиске решения несогласованной системы мы придем к ложному утверждению, например \(12=0\).

Пример \(\PageIndex{8}\): решение противоречивой системы уравнений

Решите следующую систему уравнений.

\[\begin{align*} x &= 9−2y \\ x+2y &= 13 \end{align*}\]

Раствор

Мы можем решить эту проблему двумя способами.Поскольку одно уравнение уже решено для \(x\), наиболее очевидным шагом является использование подстановки.

\[\begin{align*} x+2y &= 13 \\ (9−2y)+2y &= 13 \\ 9+0y &= 13 \\ 9 &= 13 \end{align*}\]

Ясно, что это утверждение является противоречием, потому что \(9≠13\). Следовательно, система не имеет решения.

Второй подход состоит в том, чтобы сначала манипулировать уравнениями так, чтобы они оба были в форме пересечения наклона. Поработаем с первым уравнением следующим образом.

\[\begin{align*} x &= 9−2y \\ 2y &= −x+9 \\ y &= −\dfrac{1}{2}x+\dfrac{9}{2} \end{ выровнять*}\]

Затем мы преобразуем второе уравнение, выраженное в форме пересечения наклона.

\[\begin{align*} x+2y &= 13 \\ 2y &= −x+13 \\ y &= −\dfrac{1}{2}x+\dfrac{13}{2} \end{ выровнять*}\]

Сравнивая уравнения, мы видим, что они имеют одинаковый наклон, но разные \(y\)-перехваты. Следовательно, прямые параллельны и не пересекаются.

\[\begin{align*} y &= −\dfrac{1}{2}x+\dfrac{9}{2} \\ y &= −\dfrac{1}{2}x+\dfrac{13} {2} \end{align*}\]

Анализ

Запись уравнений в форме пересечения наклона подтверждает, что система несовместима, потому что все линии в конечном итоге пересекутся, если они не параллельны.Параллельные линии никогда не пересекутся; таким образом, две прямые не имеют общих точек. Графики уравнений в этом примере показаны на рисунке \(\PageIndex{9}\).

Рисунок \(\PageIndex{9}\)

Упражнение \(\PageIndex{6}\)

Решите следующую систему уравнений с двумя переменными.

\[\begin{align*} 2y-2x &= 2 \\ 2y-2x &= 6 \end{align*}\]

Ответить

Нет решения. Это непоследовательная система.

Выражение решения системы зависимых уравнений с двумя переменными

Напомним, что зависимая система уравнений с двумя переменными — это система, в которой два уравнения представляют одну и ту же прямую. Зависимые системы имеют бесконечное число решений, потому что все точки на одной прямой находятся также и на другой прямой. После использования подстановки или сложения результирующее уравнение будет тождеством, например \(0=0\).

Пример \(\PageIndex{9}\): поиск решения зависимой системы линейных уравнений

Найдите решение системы уравнений методом сложения .

\[\begin{align*} x+3y &= 2 \\ 3x+9y &= 6 \end{align*}\]

Раствор

С помощью метода сложения мы хотим исключить одну из переменных, добавив уравнения. В этом случае давайте сосредоточимся на устранении \(x\). Если мы умножим обе части первого уравнения на \(−3\), то мы сможем исключить переменную x.

\[\begin{align*} x+3y &= 2 \\ (−3)(x+3y) &= (−3)(2) \\ −3x−9y &= −6 \end{align* }\]

Теперь добавим уравнения.

\[\begin{align*} -3x-9y &= -6 \\ \underline{+\space 3x+9y}& = \underline{6} \\ 0&= 0 \\ \end{align*}\ ]

Мы видим, что будет бесконечное количество решений, удовлетворяющих обоим уравнениям.

Анализ

Если бы мы переписали оба уравнения в форме пересечения наклона, мы могли бы знать, как будет выглядеть решение, прежде чем складывать. Давайте посмотрим, что происходит, когда мы преобразуем систему в форму пересечения наклона.

\[ \begin{align*} x+3y &= 2 \\ 3y &= −x+2 \\ y &= −\dfrac{1}{3}x+\dfrac{2}{3} \\ 3x +9y &= 6 \\ 9y &=−3x+6 \\ y &= −\dfrac{3}{9}x+\dfrac{6}{9} \\ y &= −\dfrac{1}{3 }x+\dfrac{2}{3} \end{align*}\]

См. рисунок \(\PageIndex{10}\). Обратите внимание, что результаты одинаковы. Общее решение системы: \(\left(x, −\dfrac{1}{3}x+\dfrac{2}{3}\right)\).

Рисунок \(\PageIndex{10}\)

Упражнение \(\PageIndex{7}\)

Решите следующую систему уравнений с двумя переменными.

\[\begin{align*} y−2x &= 5 \\ −3y+6x &= −15 \end{align*}\]

Ответить

Система зависима, поэтому существует бесконечное количество решений вида \((x,2x+5)\).

Использование систем уравнений для исследования прибыли

Используя то, что мы узнали о системах уравнений, мы можем вернуться к задаче о производстве скейтборда в начале раздела.Функция дохода производителя скейтборда — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением \(R=xp\), где \(x\)=количество и \(p\)=цена. Функция дохода показана оранжевым цветом на рисунке \(\PageIndex{11}\).

Функция затрат — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как арендная плата и заработная плата, и переменные затраты, такие как коммунальные услуги. Функция стоимости показана синим цветом на рисунке \(\PageIndex{11}\).Ось \(x\) представляет количество в сотнях единиц. Ось \(y\) представляет либо затраты, либо доход в сотнях долларов.

Рисунок \(\PageIndex{11}\)

Точка, в которой пересекаются две линии, называется точкой безубыточности. Из графика видно, что если произведено \(700\) единиц, то себестоимость составит \(3300$\), а выручка также составит \(3300$\). Другими словами, компания безубыточна, даже если она производит и продает \(700\) единиц. Они не зарабатывают и не теряют деньги.

Заштрихованная область справа от точки безубыточности представляет объемы, при которых компания получает прибыль.Заштрихованная область слева представляет объемы, по которым компания несет убытки. Функция прибыли представляет собой функцию дохода за вычетом функции затрат, записанную как \(P(x)=R(x)−C(x)\). Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.

Пример \(\PageIndex{10}\): нахождение точки безубыточности и функции прибыли с помощью подстановки

Учитывая функцию затрат \(C(x)=0,85x+35 000\) и функцию доходов \(R(x)=1.55x\), найти точку безубыточности и функцию прибыли.

Раствор

Напишите систему уравнений, используя \(y\), чтобы заменить запись функции.

\[\begin{align*} y &= 0,85x+35 000 \\ y &= 1,55x \end{align*}\]

Подставьте выражение \(0,85x+35 000\) из первого уравнения во второе уравнение и найдите \(x\).

\[\begin{align*} 0,85x+35 000 &= 1,55x \\ 35 000 &= 0,7x \\ 50 000 &= x \end{align*}\]

Затем мы подставляем \(x=50 000\) либо в функцию затрат, либо в функцию доходов.

\(1,55(50 000)=77 500\)

Точка безубыточности равна \((50,000,77,500)\).

Функция прибыли находится по формуле \(P(x)=R(x)−C(x)\).

\[\begin{align*} P(x) &= 1,55x−(0,85x+35 000) \\ &=0,7x−35 000 \end{align*}\]

Функция прибыли равна \(P(x)=0,7x−35 000\).

Анализ

Стоимость производства \(50 000\) единиц составляет \(77 500 долларов США\), а доход от продажи \(50 000\) единиц также составляет \(77 500 долларов США\).Чтобы получать прибыль, бизнес должен производить и продавать более \(50 000\) единиц. См. рисунок \(\PageIndex{12}\).

Рисунок \(\PageIndex{12}\)

Из графика на рисунке \(\PageIndex{13}\) видно, что функция прибыли имеет отрицательное значение до \(x=50 000\), когда график пересекает \ (х\)-ось. Затем график выходит на положительные \(y\)-значения и продолжается по этому пути, так как функция прибыли представляет собой прямую линию. Это показывает, что точка безубыточности для предприятий возникает, когда функция прибыли равна \(0\).Область слева от точки безубыточности представляет собой работу в убыток.

Рисунок \(\PageIndex{13}\)

Пример \(\PageIndex{11}\): запись и решение системы уравнений с двумя переменными

Стоимость билета в цирк составляет \($25. 00\) для детей и \($50.00\) для взрослых. В определенный день посещаемость цирка составляет \(2000\), а общий доход от продажи билетов составляет \(70000$\). Сколько детей и сколько взрослых купили билеты?

Раствор

Пусть \(с\) = количество детей и \(а\) = количество взрослых при исполнении служебных обязанностей.

Общее количество людей составляет \(2000\). Мы можем использовать это, чтобы написать уравнение для количества людей в цирке в тот день.

\(с+а=2000\)

Доход от всех детей можно найти, умножив \($25.00\) на количество детей, \(25c\). Доход от всех взрослых можно найти, умножив \($50.00\) на количество взрослых, \(50a\). Общий доход составляет \($70,000\). Мы можем использовать это, чтобы написать уравнение для дохода.

\(25с+50а=70 000\)

Теперь у нас есть система линейных уравнений с двумя переменными.

\(с+а=2000\)

\(25с+50а=70 000\)

В первом уравнении коэффициент обеих переменных равен \(1\). Мы можем быстро решить первое уравнение либо для \(с\), либо для \(а\). Мы будем решать для \(а\).

\[\begin{align*} c+a &= 2,000 \\ a &= 2,000−c \end{align*}\]

Подставьте выражение \(2,000−c\) во второе уравнение относительно a и найдите \(c\).

\[\begin{align*} 25c+50(2000−c) &= 70000 \\ 25c+100000−50c &= 70000 \\ −25c &= −30000 \\ c &= 1200 \end{align*} \]

Подставьте \(c=1,200\) в первое уравнение, чтобы найти \(a\).

\[\begin{align*} 1200+a &= 2000 \\ a &= 800 \end{align*}\]

Мы находим, что \(1200\) детей и \(800\) взрослых купили билеты в цирк в тот день.

Упражнение \(\PageIndex{8}\)

Билеты в цирк стоят \($4.00\) для детей и \($12.00\) для взрослых. Если было куплено \(1650\) талонов на питание на общую сумму \(14 200 долларов США\), сколько детей и сколько взрослых купили талоны на питание?

Ответить

\(700\) дети, \(950\) взрослые

СМИ

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с системами линейных уравнений.

Основные понятия
  • Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
  • Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. См. пример \(\PageIndex{1}\).
  • Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений и несовместные без решения.
  • Одним из методов решения системы линейных уравнений с двумя переменными является построение графика. В этом методе мы наносим уравнения на один и тот же набор осей. См. пример \(\PageIndex{2}\).
  • Другой метод решения системы линейных уравнений — подстановка. В этом методе мы находим одну переменную в одном уравнении и подставляем результат во второе уравнение. См. пример \(\PageIndex{3}\).
  • Третий метод решения системы линейных уравнений — сложение, в котором мы можем исключить переменную, добавляя противоположные коэффициенты соответствующих переменных. См. пример \(\PageIndex{4}\).
  • Часто бывает необходимо умножить одно или оба уравнения на константу, чтобы облегчить исключение переменной при сложении двух уравнений. См. Пример \(\PageIndex{5}\), Пример \(\PageIndex{6}\) и Пример \(\PageIndex{7}\).
  • Любой метод решения системы уравнений приводит к ложному утверждению для несовместимых систем, поскольку они состоят из параллельных линий, которые никогда не пересекаются. См. пример \(\PageIndex{8}\).
  • Решение системы зависимых уравнений всегда будет верным, поскольку оба уравнения описывают одну и ту же прямую. См. пример \(\PageIndex{9}\).
  • Системы уравнений можно использовать для решения реальных задач, включающих более одной переменной, например связанных с доходом, затратами и прибылью. См. пример \(\PageIndex{10}\) и пример \(\PageIndex{11}\).


Алгебра среднего уровня
Урок 19. Решение систем линейных уравнений
с двумя переменными

WTAMU > Виртуальная математическая лаборатория > Алгебра среднего уровня

Цели обучения

После завершения этого руководства вы сможете:
  1. Определите, является ли упорядоченная пара решением системы линейных уравнений в две переменные или нет.
  2. Решите систему линейных уравнений с двумя переменными с помощью графика.
  3. Решите систему линейных уравнений с двумя переменными заменой метод.
  4. Решить систему линейных уравнений с двумя переменными методом исключения метод.

Введение


В этом уроке мы будем специально рассматривать системы, которые имеют два уравнения и два неизвестных. Урок 20. Решение систем Линейный Уравнения с тремя переменными охватывают системы с тремя уравнения и три неизвестных. Мы рассмотрим их решение в трех разных способы: график, метод замещения и метод исключения. Это приведет нас к решению текстовых задач с системами, которые быть показано в Учебник 21: Системы линейных уравнений и задача Решение . Вот где мы получаем ответ на печально известный вопрос, когда мы будем использовать это? Но сначала мы должны научиться работать с системами в Общее. Вот почему мы используем общие переменные, такие как x и y . Если вы знаете, как это сделать в целом, то, когда у вас есть конкретная проблема что вы решаете, где переменные приобретают значение, например, время или Деньги (две вещи, которых нам всегда не хватает) вы будете готовы идти.   Итак, давайте посмотрим на системы в целом, чтобы подготовить нас к грядущим проблемам со словом из нас.

 

 

Учебник

 

Система линейных уравнений

Система линейных уравнений состоит из двух или более линейных уравнения, которые решаются одновременно.

В этом руководстве мы рассмотрим системы, которые иметь только два линейных уравнения и два неизвестных.




В общем случае решение системы с двумя переменными заказанный пара, которая делает ОБА уравнения истинными.

Другими словами, это место пересечения двух графиков, что у них есть в общем. Итак, если упорядоченная пара является решением одного уравнения, но не другое, то это НЕ решение системы.

Согласованная система — это система, в которой находится на хотя бы одно решение.

Несовместимая система — это система, в которой нет решения .

Уравнения системы зависимы если ВСЕ решения одного уравнения являются также решениями другого уравнения. В разное словами, они в конечном итоге будут одной и той же строкой .

Уравнения системы независимы , если они не делятся ВСЕ решения . Они могут иметь одну общую точку, но не все их.




Одно решение
Если система с двумя переменными имеет одно решение, то она заказанный пара, являющаяся решением ОБОИХ уравнений.   Другими словами, когда вы подставляете значения упорядоченной пары, это делает ОБА уравнения ИСТИННЫЙ.

Если вы получите одно решение для вашего окончательного ответа, эта система последовательная или непоследовательная?
Если вы сказали «последовательный», похлопайте себя по спине!

Если вы получите одно решение для своего окончательного ответа, уравнения зависимы или независимы?
Если вы сказали независимый, вы правы!

На приведенном ниже графике показана система двух уравнений и два неизвестных у которого есть одно решение:


Нет решения
Если две линии параллельны друг другу, они никогда не пересекаются. Это означает, что у них нет общих точек. В этом ситуация, у вас не было бы решения.

Если вы не получили решения для своего окончательного ответа, эта система последовательная или непоследовательная?
Если вы сказали непоследовательный, вы правы!

Если вы не получите решения для своего окончательного ответа, уравнения зависимы или независимы?
Если вы сказали независимый, вы правы!

На приведенном ниже графике показана система двух уравнений и два неизвестных не имеет решения:


Бесконечно Решения
Если две линии окажутся лежащими друг над другом, то Там есть бесконечное количество решений.   В этой ситуации они было бы в конечном итоге будет одна и та же строка, поэтому любое решение, которое будет работать в одном уравнение будет работать в другом.

Если вы получаете бесконечное количество решений для ваш окончательный ответ, я с эта система последовательная или непоследовательная?
Если вы сказали последовательно, вы правы!

Если вы получаете бесконечное количество решений для ваш окончательный ответ, будет уравнения зависимы или независимы?
Если вы сказали зависимый, вы правы!

На приведенном ниже графике показана система двух уравнений и два неизвестных имеющее бесконечное число решений:


Пример 1 : определить, является ли каждая упорядоченная пара решением из система.
(3, -1) и (0, 2)

Проверим упорядоченную пару (3, -1) в первой уравнение:



* Вставьте 3 для x и -1 для y

*Правдивое утверждение


Пока все хорошо, (3, -1) является решением проблемы первое уравнение x + y = 2.

Теперь проверим (3, -1) во втором уравнении:



* Вставьте 3 для x и -1 для y

*Правдивое утверждение


Эй, мы получили еще одно истинное утверждение, которое означает (3, -1) также решение второго уравнения х — у = 4.

Вот большой вопрос, является ли (3, -1) решением данная система?????
Поскольку это было решение ОБОИХ уравнений в системе, Затем это является решением общей системы.

Теперь подставим (0, 2) в первое уравнение:



*Подставьте 0 для x и 2 для y
*Истинное утверждение


Это истинное утверждение, поэтому (0, 2) является решением задачи первое уравнение х + у = 2.

Наконец, подставим (0,2) во второе уравнение:



*Подставьте 0 для x и 2 для y
*Ложное утверждение


На этот раз мы получили ложное заявление, вы знаете, что это означает. (0, 2) НЕ является решением второго уравнения x — y = 4.

Вот большой вопрос, является ли (0, 2) решением данная система?????
Так как это не было решением ОБОИХ уравнений в система, то это не решение всей системы.



Три способа Решение систем линейных уравнений
Уравнения с двумя переменными



Шаг 1: Нарисуйте первое уравнение.



Шаг 2: Нарисуйте второе уравнение на та же координата система как первая.


Вы рисуете второе уравнение так же, как и любое другое уравнение. Обратитесь к первому шагу, если вам нужно просмотреть различные способы график линия.

Разница здесь в том, что вы поставите его на тот же система координат как первый. Это как иметь две графические задачи в одной.


Шаг 3: Найдите решение.


Если две линии пересекаются в одном месте , то точка пересечение является решением системы.

Если две линии параллельны , то они никогда не пересекаются, поэтому нет нет решения.

Если две линии лежат друг над другом , то они та же строка , и у вас есть бесконечное количество решений. . В этом случае вы можете записать любое уравнение как решение указывать это одна и та же линия.


Шаг 4: Проверьте предложенный заказ парное решение в ОБА уравнения.


Предлагаемое решение можно подключить к ОБОИМ уравнения. Если это делает ОБА уравнения истинными, тогда у вас есть решение для система.

Если хотя бы одно из них окажется ложным, вам нужно идти вернуться и повторить проблема.



Пример 2 : Решите систему уравнений с помощью графика.




*Подставьте 0 для y для x -int
* x -intercept


Пересечение x равно (3, 0).

у — перехват



*Вставьте 0 для x для y -int
* y -intercept


Пересечение y равно (0, 3).

Найти другой решение, если x = 1.



*Вставьте 1 для x

Другое решение (1, 2).

Решения:

х г (х, у)
3 0 (3, 0)
0 3 (0, 3)
1 2 (1, 2)

Построение упорядоченных парных решений и рисование линия:






*Подставьте 0 для y для x -int
* x -intercept


Пересечение x равно (1, 0).

Y-точка пересечения



*Подставьте 0 для x для y -int

*Инверсия множ. на -1 это дел. по -1

* у -перехват


Пересечение y равно (0, -1).

Найти другой решение, если x = 2.



*Вставьте 2 для x
*Инверсия добавления 2 является вспомогательной. 2

*Инверсия множ. на -1 это деление по -1

 


Другое решение (2, 1).

Решения:  

х г (х, у)
1 0 (1, 0)
0 -1 (0, -1)
2 1 (2, 1)

Построение упорядоченных парных решений и рисование линия:



Мы должны спросить себя, есть ли место, где две линии пересекаются, и если да, то где?

Да, они пересекаются в (2, 1).



Вы обнаружите, что если вставить заказанную пару (2, 1) в ОБА уравнения исходной системы, что это решение ОБЕИХ из них.

Решение этой системы (2, 1).




Пример 3 : Решите систему уравнений с помощью графика.




*Подставьте 0 для y для x -int
* x -intercept


Пересечение x равно (5, 0).

у — перехват



*Подставьте 0 для x для y -int

* у -перехват


Пересечение y равно (0, 5).

Найти другой решение, если x = 1.



*Вставьте 1 для x
*Инверсия добавления 1 является вспомогательной. 1


Другое решение (1, 4).

Решения:

х г (х, у)
5 0 (5, 0)
0 5 (0, 5)
1 4 (1, 4)

Построение упорядоченных парных решений и рисование линия:





*Подставьте 0 для y для x -int
*Инверсия добавления 3 является вспомогательной. 3

*Инверсия множ. на -1 это дел. по -1

* х — перехват


Пересечение x равно (3, 0).

у — перехват



*Вставьте 0 для x для y -int
* y -intercept


Пересечение y равно (0, 3).

Найти другой решение, если x = 1.



*Вставьте 1 для x


Другое решение (1, 2).

Решения:

х г (х, у)
3 0 (3, 0)
0 3 (0, 3)
1 2 (1, 2)

Построение упорядоченных парных решений и рисование линия:



Мы должны спросить себя, есть ли место, где две линии пересекаются, и если да, то где?

Нет, они не пересекаются. Мы иметь два параллельных линии.



Нет заказанных пар для проверки.

Ответ — нет решения.



Решить методом подстановки

Шаг 1: При необходимости упростите.


Это включает удаление ( ) и удаление дробей.

Чтобы удалить ( ): просто используйте свойство дистрибутива.

Чтобы удалить дроби: так как дроби — это еще один способ написать деление, и обратным делением является умножение, вы удаляете дроби на умножение с обеих сторон ЖК-дисплеем всех ваших фракций.


Шаг 2. Решите одно уравнение для либо переменная.


Неважно, какое уравнение вы используете или какое переменная, которую вы выбираете решить для.

Вы хотите сделать это как можно проще.Если один уравнений уже решен для одной из переменных, то есть быстро и легко способ идти.

Если вам нужно найти переменную, попробуйте выбрать тот, у которого есть 1 в качестве коэффициента. Таким образом, когда вы идете, чтобы решить это, вы не будет делить на число и рисковать работать с дробная часть (фу!!).


Шаг 3: Замените то, что вы получаете шаг 2 в другое уравнение.


Вот почему он называется методом подстановки. Убедись в том, что вы подставляете выражение в ДРУГОЕ уравнение, то, которое вы не использовать на шаге 2.

Это даст вам одно уравнение с одним неизвестным.


Шаг 4. Решите для оставшаяся переменная.



Шаг 5. Решите для секунд Переменная.


Если вы найдете значение для переменной на шаге 4, значит два уравнения имеют одно решение.   Подставьте найденное значение в шаг 4 в любое из уравнений задачи и решить для другого Переменная.

Если ваша переменная выпадает и у вас FALSE заявление, значит ваш ответ не является решением.

Если ваша переменная выпадает и у вас ИСТИНА заявление, значит ваш ответ — бесконечные решения, которые были бы уравнением линия.


Шаг 6: Проверьте предложенный заказ парное решение в ОБА исходные уравнения.


Предлагаемое решение можно подключить к ОБОИМ уравнения. Если это делает ОБА уравнения верными, тогда у вас есть решение система.

Если хотя бы одно из них окажется ложным, вам нужно идти вернуться и повторить проблема.





Пример 4 : Решите систему уравнений подстановкой метод.


Оба эти уравнения уже упрощены. Нет нужды в работе сделать здесь.



Обратите внимание, что второе уравнение уже решено для y . Мы можем использовать его для этого шага.

Неважно, какое уравнение или какую переменную вы выбрать решение за. Но в ваших интересах, чтобы все было так просто, как возможный.

Решение второго уравнения для y :


*Решено для и



Подставьте выражение 2 x + 4 вместо y в первое уравнение и решите для x :
(когда вы подставляете такое выражение, это как если бы вы подставляли в число для вашей переменной) 



*Под. 2 x + 4 дюйма для г
*Расст. от -5 до (  )
*Объедините похожие термины

*Инверсия суб. 20 добавить 20

*Инверсия дел. на -7 мульт. по -7

 



Вставьте -5 для x в уравнение в шаг 2, чтобы найти значение y .



*Вставка -5 для x



Вы обнаружите, что если вы подключите заказанную пару (-5, -6) в ОБЕИХ уравнений исходной системы, что это решение ОБЕИХ их.

(-5, -6) — это решение для нашей системы.





Пример 5 : Решите систему уравнений подстановкой метод.


Оба эти уравнения уже упрощены. Нет нужды в работе сделать здесь.



На этот раз проблема не была нам так приятна, мы придется немного поработайте, чтобы решить одно уравнение для одной из наших переменных.

Неважно, какое уравнение или какую переменную вы выбрать решение за. Просто будь проще.

Так как x в первом уравнение имеет коэффициент 1, это означало бы, что нам не пришлось бы делить на номер решить для него и рискнуть работать с дробями (ФУТ!!) Самый простой путь здесь — решить первое уравнение для x , и мы определенно хотим пойти по легкому пути. Вы бы не были неправильный либо выбрать другое уравнение и/или решить для y, снова вы хотите чтобы это было как можно проще.

Решая первое уравнение для х получаем:



*Обратное значение вспомогательного. 2 у добавить 2 у

*Решено для x



Подставьте выражение 5 + 2 y  вместо x во второе уравнение и решите для y :
(когда вы подставляете такое выражение, это как если бы вы подставляли в число для вашей переменной) 



*Под. 5 + 2 и для x

*Переменная исключена И ложно


Минуточку, а куда делись наши переменная идет????

Как упоминалось выше, если ваша переменная выпадает, и вы иметь ЛОЖНОЕ утверждение, тогда решения нет. Если бы мы построили график этих двух, они будут параллельны друг другу.



Так как мы не получили значение для y , там тут нечего втыкать.



Нет заказанных пар для проверки.

Ответ — нет решения.



Решить методом исключения

Этот метод также известен как добавление или устранение добавлением метод.


Шаг 1: Упростите и поместите оба уравнения в виде A x + B y = C при необходимости.


Это включает удаление ( ) и удаление дробей.

Чтобы удалить ( ): просто используйте свойство дистрибутива.

Чтобы удалить дроби: так как дроби — это еще один способ написать деление, и обратным делением является умножение, вы удаляете дроби на умножение с обеих сторон ЖК-дисплеем всех ваших фракций.


Шаг 2: Умножьте одно или оба уравнения по числу это создаст противоположные коэффициенты для x или y , если это необходимо.


Забегая вперед, мы добавим эти два уравнения вместе . В этом процессе нам нужно убедиться, что одна из переменных вне, оставив нам одно уравнение и одно неизвестное. Единственный способ, которым мы можем гарантия, что если мы складываем противоположности . Сумма противоположности равно 0.

Если ни одна переменная не выпадет, то мы застряли с уравнение с два неизвестных неразрешима.

Неважно, какую переменную вы выберете для удаления вне. Вы хотите, чтобы это было как можно проще. Если переменная уже имеет противоположные коэффициенты, чем перейти к сложению двух уравнений вместе. Если это не так, вам нужно умножить одно или оба уравнения на число тот создаст противоположные коэффициенты в одной из ваших переменных.Ты может Думайте об этом как о ЖК-дисплее. Подумай, какой номер у оригинала коэффициенты оба входят и соответственно умножают каждое отдельное уравнение. Сделать убедитесь, что одна переменная положительна, а другая отрицательна, прежде чем вы добавлять.

Например, если у вас есть 2 x в одном уравнении и 3 x в другом уравнении, мы могли бы умножить первое уравнение на 3 и получаем 6 x и в второе уравнение на -2, чтобы получить -6 x . Так когда вы добавите эти два вместе, они выпадут.



Сложите два уравнения вместе.

Переменная с противоположными коэффициентами будет выпадать из этого шаг, и у вас останется одно уравнение с одним неизвестным.


Шаг 4: Найдите оставшуюся переменную.


Решите уравнение, найденное на шаге 3, для переменной что осталось.

Если вам нужен обзор, перейдите к учебнику . 7: Линейные уравнения с одной переменной.

Если обе переменные выпадают и у вас FALSE заявление, значит ваш ответ не является решением.

Если обе переменные выпадают и у вас есть ИСТИНА заявление, значит ваш ответ — бесконечные решения, которые были бы уравнением линия.


Шаг 5: Найдите вторую переменную.


Если вы найдете значение для переменной на шаге 4, значит два уравнения имеют одно решение.   Подставьте найденное значение в шаг 4 в любое из уравнений задачи и решить для другого Переменная.


Шаг 6: Проверьте предложенный заказ парное решение в ОБА исходные уравнения.


Предлагаемое решение можно подключить к ОБОИМ уравнения.Если это делает ОБА уравнения верными, тогда у вас есть решение система.

Если хотя бы одно из них окажется ложным, вам нужно идти вернуться и повторить проблема.




Пример 6 : Решить систему уравнений методом исключения метод.



Это уравнение полно этих неприятных дробей. Мы можем упростить оба уравнения путем умножения каждого отдельного на его ЖК-дисплей, точно так же, как вы можете сделать, когда вы работаете с одним уравнением. До тех пор, как вы сделайте то же самое с обеими частями уравнения, вы сохраните две стороны равны друг другу.

Умножив каждое уравнение на соответствующий ЖК-дисплей, мы получить:



*Множ. по ЖК 15

*мульт. по ЖК 6


 



Опять же, вы хотите сделать это так же просто, как возможный. Обратите внимание, как коэффициенты для обоих и равны 3. Мы должны быть противоположности, поэтому, если одна из них равна 3, а другая -3, Oни отменяли бы друг друга, когда мы собираемся добавить их.

Если бы мы сложили их вместе, как сейчас, мы бы закончить с одно уравнение и две переменные ничего бы не выпадало. И мы было бы не суметь ее решить.

Предлагаю умножить второе уравнение на -1, это будет создайте -3 перед x и мы имеют наши противоположности.

Обратите внимание, что мы могли бы так же легко умножить первый уравнение на -1 и не второй. В любом случае работа будет выполнена.

Умножая второе уравнение на -1 получаем:



*Множ. обе стороны 2-го уравнения. по -1

* и -х иметь напротив коэффициенты




*Обратите внимание, что и выбыл




*Инверсия множ.на 3 дел. по 3



Вы можете выбрать любое уравнение, используемое в этой задаче, чтобы подставьте найденное значение x .

Я решил подключить 11 для x к первое упрощенное уравнение (найденное на шаге 1) для нахождения y ценность.



*Вставка 11 для x

*Инверсия сложения 55 является вспомогательной.55

*Инверсия множ. на 3 дел. по 3

 



Вы обнаружите, что если подключить заказанную пару (11, -25/3) в ОБА уравнений исходной системы, что это решение ОБЕИХ их.

(11, -25/3) является решением для нашей системы.





Пример 7 : Решить систему уравнений методом исключения метод.



Эта задача уже упрощена.Тем не менее, второй уравнение не записывается в виде Ax + By = C. Другими словами, нам нужно написать в этой форме, так что все готово к работе, когда мы добавим два уравнения вместе.

Переписывая второе уравнение, получаем:



*Инверсия сложения 6 x является вспомогательной.6 x

*Все в ряд



Обратите внимание, что если мы умножим первое уравнение на 2, то Мы будем иметь a -6 x , что противоположно 6 x , найденному во втором уравнении.

Умножая первое уравнение на 2 получаем:


*Множ.1-е уравнение по 2

* x имеют противоположные коэффициенты



*Переменные исключены И истинны



Эй, куда делись наши переменные идти??

Как упоминалось выше, если переменная выпадает И мы иметь ИСТИННОЕ утверждение, тогда когда имеют бесконечное число решений. Они в конечном итоге та же линия.



Здесь нет значения для подстановки.



Здесь нет значения для подстановки.

Когда они окажутся одним и тем же уравнением, у вас будет бесконечное число решений.Вы можете записать свой ответ, написав либо уравнение, чтобы указать, что это одно и то же уравнение.

Ответ можно записать двумя способами: {( x , y )| 3 x — 2 y = 1} ИЛИ {( x , y ) | 4 у = 6 х — 2}.


 
Практические задачи

Это практические задачи, которые помогут вам следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как что-либо иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться Это. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.

Чтобы получить максимальную отдачу от них, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой проблемы . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

 

Практика Задача 1a: Решите систему, построив график.

 

 

 

Практика Задача 2а: Решить систему подстановкой метод.

 

 

Практика Задача 3а: Решить систему с помощью метод исключения.

 

 

 

Нужна дополнительная помощь по этим темам?


 


Последняя редакция Ким Сьюард от 10 июля 2011 г.
Авторское право на все содержимое (C) 2001–2011, WTAMU и Ким Сьюард. Все права защищены.

Системы линейных уравнений

В первой половине этого учебника мы будем в основном заниматься пониманием решений систем линейных уравнений.

Определение

Уравнение с неизвестными x,y,z,… называется линейным , если обе части уравнения представляют собой сумму (постоянных) кратных x,y,z,…, плюс необязательная константа.

Например,

3x+4y=2z-x-z=100

— это линейные уравнения, а

3x+yz=3sin(x)−cos(y)=2

нет.

Обычно мы переносим неизвестные в левую часть уравнения, а константы — в правую.

Система линейных уравнений представляет собой набор нескольких линейных уравнений, таких как

Ax+2y+3z=62x−3y+2z=143x+y−z=−2.(1.1.1)

Определение (наборы решений)
  • Решение системы уравнений представляет собой список чисел x,y,z,. .. которые делают все уравнения истинными одновременно.
  • Набор решений системы уравнений представляет собой совокупность всех решений.
  • Решить систему означает найти все решения с формулами, включающими некоторое количество параметров.

Система линейных уравнений может не иметь решения. Например, не существует чисел x и y, для которых одновременно верны следующие два уравнения:

Сх+2у=3х+2у=-3.

В этом случае набор решений пуст .Поскольку это довольно важное свойство системы уравнений, оно имеет собственное название.

Определение

Система уравнений называется несовместной , если она не имеет решений. Он называется последовательным иначе.

Решением системы уравнений с n переменными является список из n чисел. Например, (x,y,z)=(1,−2,3) является решением (1.1.1). Поскольку в этом тексте мы будем изучать решения систем уравнений, самое время закрепить наши представления о списках чисел.

Мы используем R для обозначения множества всех действительных чисел, т. е. числовой прямой. Он содержит такие числа, как 0,32,−π,104,…

.
Определение

Пусть n — целое положительное число. Определяем

Rn=все упорядоченные n-наборы вещественных чисел(x1,x2,x3,…,xn).

Набор из n действительных чисел называется точкой Rn.

Другими словами, Rn — это просто набор всех (упорядоченных) списков n действительных чисел. Через мгновение мы нарисуем Rn, но имейте в виду, что — это определение .Например, (0,32,−π) и (1,−2,3) являются точками R3.

Пример (числовая строка)

Когда n=1, мы просто возвращаем R: R1=R. Геометрически это числовая линия.

Пример (евклидова плоскость)

Когда n=2, мы можем думать о R2 как о плоскости xy. Мы можем это сделать, потому что каждая точка на плоскости может быть представлена ​​упорядоченной парой действительных чисел, а именно ее координатами x и y.

Пример (3-пробел)

Когда n=3, мы можем думать о R3 как о пространстве , в котором мы (кажется) живем.Мы можем сделать это, потому что каждая точка в пространстве может быть представлена ​​упорядоченной тройкой действительных чисел, а именно ее координатами x, y и z.

Так что же такое R4? или Р5? или Рн? Их труднее визуализировать, поэтому вам придется вернуться к определению: Rn — это множество всех упорядоченных n-кортежей действительных чисел (x1,x2,x3,…,xn).

Они по-прежнему являются «геометрическими» пространствами в том смысле, что наша интуиция относительно R2 и R3 часто распространяется на Rn.

Мы дадим определения и сформулируем теоремы, которые применимы к любому Rn, но мы будем рисовать только для R2 и R3.

Сила использования этих пространств заключается в способности маркировать различные интересующие объекты, такие как геометрические объекты и решения систем уравнений, точками Rn.

В приведенных выше примерах было полезно с психологической точки зрения заменить список из четырех чисел (представляющих транспортный поток) или 841 числа (представляющих QR-код) одним фрагментом данных: точкой в ​​некотором Rn. Это мощная концепция; начиная с раздела 2.2, мы почти исключительно будем записывать решения систем линейных уравнений таким образом.

Перед обсуждением того, как решить приведенную ниже систему линейных уравнений, полезно посмотреть на некоторые изображения того, как эти наборы решений выглядят геометрически.

Одно уравнение с двумя переменными

Рассмотрим линейное уравнение x+y=1. Мы можем переписать это как y=1−x, что определяет линию на плоскости: наклон равен −1, а точка пересечения с осью x равна 1.

Определение (линии)

Для наших целей линия — это луч, который является прямым и бесконечным в обоих направлениях.

Одно уравнение с тремя переменными

Рассмотрим линейное уравнение x+y+z=1. Это неявное уравнение для плоскости в пространстве.

Определение (плоскости)

Плоскость представляет собой плоский лист, бесконечный во всех направлениях.

Уравнение x+y+z+w=1 определяет «3-плоскость» в 4-пространстве, и, в более общем смысле, одно линейное уравнение с n переменными определяет «(n−1)-плоскость» в n-пространстве. . Мы уточним эти утверждения в разделе 2.7.

Два уравнения с двумя переменными

Теперь рассмотрим систему двух линейных уравнений

Сх-3у=-32х+у=8.

Каждое уравнение индивидуально определяет линию на плоскости, показанную ниже.

Решением системы обоих уравнений является пара чисел (x,y), которая делает оба уравнения истинными одновременно. Другими словами, это как точка, лежащая одновременно на обеих прямых. На картинке выше видно, что есть только одна точка пересечения прямых: следовательно, эта система имеет ровно одно решение.(Это решение (3,2), как может убедиться читатель.)

Обычно две линии на плоскости пересекаются в одной точке, но, конечно, это не всегда так. Рассмотрим теперь систему уравнений

Сх-3у=-3х-3у=3.

Они определяют параллельных линий на плоскости.

Тот факт, что линии не пересекаются, означает, что система уравнений не имеет решения. Конечно, это легко увидеть алгебраически: если x−3y=−3, то не может быть и так, что x−3y=3.

Есть еще одна возможность. Рассмотрим систему уравнений

Сх-3у=-32х-6у=-6.

Второе уравнение кратно первому, поэтому эти уравнения определяют ту же прямую на плоскости.

В этом случае существует бесконечно много решений системы уравнений.

Два уравнения с тремя переменными

Рассмотрим систему двух линейных уравнений

Вх+у+г=1х-г=0.

Каждое уравнение индивидуально определяет плоскость в пространстве.Решениями системы обоих уравнений являются точки, лежащие на обеих плоскостях. На картинке ниже мы видим, что плоскости пересекаются по прямой. В частности, эта система имеет бесконечно много решений.

Рисунок 21. Плоскости, определяемые уравнениями x+y+z=1 и x−z=0, пересекаются по красной линии, которая является набором решений системы обоих уравнений.

В общем случае решения системы уравнений с n переменными есть пересечение «(n−1)-плоскостей» в n-пространстве. Это всегда какое-то линейное пространство, как мы обсудим в разделе 2. 4.

Согласно этому определению, решение системы уравнений означает запись всех решений в терминах некоторого числа параметров. Мы дадим систематический способ сделать это в разделе 1.3; пока мы даем параметрические описания в примерах предыдущего пункта.

строк

Рассмотрим линейное уравнение x+y=1 из этого примера. В этом контексте мы называем x+y=1 неявным уравнением прямой. Мы можем записать ту же строку в параметрической форме следующим образом:

(x,y)=(t,1−t)для любого t∈R.

Это означает, что каждая точка на прямой имеет вид (t,1−t) для некоторого действительного числа t. В этом случае мы называем t параметром , поскольку он параметризует точек на линии.

Теперь рассмотрим систему двух линейных уравнений

Вх+у+г=1х-г=0

этого примера. В совокупности они образуют неявных уравнений для линии в R3. (Для определения линии в пространстве необходимы как минимум два уравнения. ) Эта линия также имеет параметрическую форму с одним параметром t:

(х, у, г) = (т, 1-2т, т).

Рисунок 24. Плоскости, определяемые уравнениями x+y+z=1 и x−z=0, пересекаются по желтой линии, которая параметризуется выражением (x,y,z)=(t,1−2t,t). Переместите ползунок, чтобы изменить параметризованную точку.

Обратите внимание, что в каждом случае параметр t позволяет нам использовать R для меток точек на линии. Однако ни одна из прямых не совпадает с числовой прямой R: действительно, каждая точка первой строки имеет две координаты, например точка (0,1), а каждая точка второй строки имеет три координаты, например (0,1 ,0).

Самолеты

Рассмотрим линейное уравнение x+y+z=1 из этого примера. Это неявное уравнение плоскости в пространстве. Эта плоскость имеет уравнение в параметрической форме : мы можем записать каждую точку на плоскости как

(x,y,z)=(1−t−w,t,w)для любого t,w∈R.

В этом случае нам нужны два параметра t и w для описания всех точек на плоскости.

Рисунок 26. Плоскость в R3 определяется уравнением x+y+z=1. Эта плоскость параметризуется двумя числами t,w; переместите ползунки, чтобы изменить параметризованную точку.

Обратите внимание, что параметры t,w позволяют нам использовать R2 для меток точек на плоскости. Однако эта плоскость , а не , как и плоскость R2: действительно, каждая точка на этой плоскости имеет три координаты, как и точка (0,0,1).

При наличии единственного решения, как в этом примере, нет необходимости использовать параметры для описания набора решений.

Как решить систему линейных уравнений

Линейное уравнение — это уравнение, отображающее линию.Система линейных уравнений состоит из двух или более линейных уравнений, сгруппированных вместе.

Для упрощения иллюстрации рассмотрим системы двух уравнений. Как следует из названия, есть две неизвестные переменные. Часто их обозначают буквами х и у . Если уравнения описывают какой-то процесс, буквы можно выбирать в зависимости от того, какую роль они играют. Например, d может обозначать расстояние, а t — время.

В этой статье мы научимся решать системы линейных уравнений двумя забавными способами.Но прежде чем мы начнем, давайте посмотрим, как мы получим конкретную систему, на примере из реальной жизни.

Получение системы

Мальчик садится на велосипед и едет в школу. Он проезжает 200 ярдов каждую минуту.

6 минут спустя его мать понимает, что ее сын забыл обед. Она садится на собственный велосипед и начинает преследовать мальчика. Она проезжает 500 ярдов каждую минуту (Она олимпийская чемпионка и золотая медалистка).

Мы хотим выяснить, сколько времени потребуется матери, чтобы догнать мальчика, и сколько ей нужно для этого проехать.

Поскольку мальчик проходит 200 ярдов каждую минуту, за t минут он пройдет 200 раз t ярдов, или 200t ярдов.

Его мать начинает кататься на велосипеде 6 минут позже, поэтому она едет (t — 6) минут. Поскольку она проходит 500 ярдов каждую минуту, за (t — 6) минут она проходит 500 умножить на (t — 6) ярдов, или 500 (t — 6) ярдов.

К тому времени, как она догоняет его, они оба преодолели одинаковое расстояние.Предположим, что это расстояние равно d .

Для мальчика имеем d = 200t , а для его матери имеем d = 500(t — 6) . Теперь у нас есть система из двух уравнений.

Система двух уравнений d=200t и d=500(t — 6)

Часто добавляется фигурная скобка, чтобы указать, что уравнения образуют систему.

Теперь давайте посмотрим, как мы можем решить эту систему.

Решение подстановкой

Первый метод, который мы рассмотрим, использует подстановку .

Здесь два неизвестных, d и t . Идея состоит в том, чтобы избавиться от одной переменной, выразив ее с помощью другой переменной.

Верхнее уравнение говорит нам, что d = 200t , поэтому давайте подставим 200t вместо d в нижнее уравнение. В результате мы имеем уравнение только с переменной t .

Уравнение с одной переменной 200t = 500(t — 6)

Сначала разложим правую часть: 500(t -6) = 500t — 500*6 = 500t — 3000 .

Затем упростим, переместив неизвестные элементы в одну сторону, а известные — в другую. Результат: 500т — 200т = 3000 .

Решение уравнения 300t = 3000 дает t = 10

Решение уравнения t дает нам t = 10 , или, поскольку мы измеряем время в минутах, t = 10 минут . Другими словами, мать догонит сына через 10 минут.

Вторая часть нашей задачи — выяснить, как далеко ей пришлось проехать на велосипеде, чтобы догнать его.

Чтобы ответить на этот вопрос, нам нужно найти d . Подстановка t = 10 в любое уравнение даст нам этот ответ.

Чтобы было проще, воспользуемся верхним уравнением: d = 200t = 200 * 10 = 2000 . Поскольку мы измеряем расстояние в ярдах, d = 2000 ярдов .

Давайте проверим ваши знания — попробуйте самостоятельно решить следующую систему:

В приведенной выше системе неизвестными переменными являются x и y .

Из верхнего уравнения мы знаем, что y = 2x .Подставив это в нижнее уравнение, мы получим 2(2x) = 3(x + 1) .

После расширения и упрощения мы получим 4x = 3x + 3 . Или х = 3 . Следовательно, у = 2 * 3 = 6 .

Решение с помощью графика

Второй метод, который мы рассмотрим, использует построение графика , , где мы находим решение системы уравнений, изображая их в виде графика.

Например, возьмем эту систему: y = 2x + 3 и y = 9 — x .

График каждого уравнения будет линией. Первый для y = 2x + 3 выглядит следующим образом: y = 9 — x

Эти две прямые пересекают ровно в одной точке. Эта точка является единственным решением обоих уравнений:

Графики y = 2x + 3 и y = 9 — x пересекаются в точке (2, 7)

Упорядоченная пара (2, 7) дает нам координаты нашей точки пересечения.Эта пара является решением системы. Подстановка x = 2 и y = 7 позволит нам убедиться в этом.

Что делать, если графики параллельны и вообще не пересекаются? Например:

Графики y = x — 1 и y = x — 3

Когда графики уравнений не пересекаются, это означает, что наша система не имеет решения. Попытка решить подстановкой докажет это.

Результатом x — 1 = x — 3 будет 0 = -2 , то есть всегда false .

Но что, если два одинаковых графика расположены непосредственно друг над другом?

Графики y = x — 2 и y = x — 2

В таких случаях существует бесконечное количество точек пересечения. Это означает, что наша система имеет бесконечное число решений. Использование метода подстановки докажет это.

Результатом x — 2 = x — 2 будет 0 = 0 , что всегда верно .

Больше практики

Попробуйте использовать методы подстановки и построения графиков для решения следующих систем.Эти методы дополняют друг друга и помогут вам закрепить свои знания.

Выбор конкретной переменной для замены должен облегчить поиск решения.

Попробуйте выразить x с двумя другими элементами в верхнем уравнении, затем подставьте результат в нижнее уравнение. Таким образом, вы избежите работы с дробями.

Давайте сделаем еще одно задание:

Теперь, когда вы достаточно знаете о подстановке и построении графиков, приступайте к решению других линейных уравнений.


Колледж Алгебра
Учебник 49: Решение систем
Линейные уравнения с двумя переменными

 

Цели обучения


После завершения этого руководства вы сможете:
  1. Знать, является ли упорядоченная пара решением системы линейные уравнения в две переменные или нет.
  2. Решить систему линейных уравнений с двумя переменными графически.
  3. Решить систему линейных уравнений с двумя переменными заменой метод.
  4. Решить систему линейных уравнений с двумя переменными устранением методом сложения.

Введение


В этом уроке мы будем специально рассматривать системы, которые имеют два уравнения и два неизвестных.Урок 50. Решение систем Линейный Уравнения с тремя переменными охватывают системы с тремя уравнения и три неизвестных. Мы рассмотрим их решение в трех разных способы: графически, методом подстановки и методом исключения добавление метод. Итак, давайте продолжим и посмотрим на эти системы.

 

 

Учебник

 

Система линейных уравнений

Система линейных уравнений состоит из двух или более линейных уравнения, которые решаются одновременно.

В этом руководстве мы рассмотрим системы, которые иметь только два линейных уравнения и два неизвестных.




В общем случае решение системы с двумя переменными заказанный пара, которая делает ОБА уравнения истинными.

Другими словами, это место пересечения двух графиков, что у них есть в общем.Итак, если упорядоченная пара является решением одного уравнения, но не другое, то это НЕ решение системы.

Согласованная система — это система, в которой находится на хотя бы одно решение.

Несовместимая система — это система, в которой нет решения .

Уравнения системы зависимы если ВСЕ решения одного уравнения являются также решениями другого уравнения.В разное словами, они в конечном итоге будут одной и той же строкой .

Уравнения системы независимы , если они не делятся ВСЕ решения . Они могут иметь одну общую точку, но не все их.




Одно решение
Если система с двумя переменными имеет одно решение, то она заказанный пара, являющаяся решением ОБОИХ уравнений.   Другими словами, когда вы подставляете значения упорядоченной пары, это делает ОБА уравнения ИСТИННЫЙ.

Если вы получите одно решение для вашего окончательного ответа, эта система последовательная или непоследовательная?
Если вы сказали «последовательный», похлопайте себя по спине!

Если вы получите одно решение для своего окончательного ответа, уравнения зависимы или независимы?
Если вы сказали независимый, вы правы!

На приведенном ниже графике показана система двух уравнений и два неизвестных у которого есть одно решение:


Нет решения
Если две линии параллельны друг другу, они никогда не пересекаются. Это означает, что у них нет общих точек. В этом ситуация, у вас не было бы решения.

Если вы не получили решения для своего окончательного ответа, эта система последовательная или непоследовательная?
Если вы сказали непоследовательный, вы правы!

Если вы не получите решения для своего окончательного ответа, уравнения зависимы или независимы?
Если вы сказали независимый, вы правы!

На приведенном ниже графике показана система двух уравнений и два неизвестных не имеет решения:


Бесконечно Решения
Если две линии окажутся лежащими друг над другом, то Там есть бесконечное количество решений.   В этой ситуации они было бы в конечном итоге будет одна и та же строка, поэтому любое решение, которое будет работать в одном уравнение будет работать в другом.

Если вы получаете бесконечное количество решений для ваш окончательный ответ, я с эта система последовательная или непоследовательная?
Если вы сказали последовательно, вы правы!

Если вы получаете бесконечное количество решений для ваш окончательный ответ, будет уравнения зависимы или независимы?
Если вы сказали зависимый, вы правы!

На приведенном ниже графике показана система двух уравнений и два неизвестных имеющее бесконечное число решений:




Пример 1 : определить, является ли каждая упорядоченная пара решением из система.
(3, 1) и (0, -1)

Проверим упорядоченную пару (3, 1) в первой уравнение:



*Вставьте 3 шт. для x и 1 шт. для y

*Правдивое утверждение


Пока все хорошо, (3, 1) является решением первого уравнение 2 x — 3 y = 3.

Теперь проверим (3, 1) во втором уравнении:



*Вставьте 3 шт. для x и 1 шт. для y

*Правдивое утверждение


Эй, мы получили еще одно истинное утверждение, которое означает (3, 1) также решение второго уравнения 4 x — 2 у = 10.

Вот большой вопрос, является ли (3, 1) решением проблемы данная система?????

Так как это было решение ОБОИХ уравнений в система, то она является решением общей системы.

Теперь подставим (0, -1) в первое уравнение:



*Подставьте 0 для x и -1 для y

*Правдивое утверждение


Это истинное утверждение, поэтому (0, -1) является решением первое уравнение 2 х — 3 у = 3.

Наконец, подставим (0, -1) во второе уравнение:



*Подставьте 0 для x и -1 для y

*Ложное утверждение


На этот раз мы получили ложное заявление, вы знаете, что это означает. (0, -1) НЕ является решением второго уравнения 4 x — 2 y = 10.

Вот большой вопрос, является ли (0, -1) решением данная система?????

Так как это не было решением ОБОИХ уравнений в система, то это не решение всей системы.

Три способа
Решение систем линейных
Уравнений с двумя переменными

 


Шаг 1: Нарисуйте первое уравнение.


Если в инструкции не сказано иначе, вы можете использовать любой «легитимный» способ графической линии. Если вам нужен обзор графических линий, не стесняйтесь вернуться к Уроку 27: Графические линии.

Шаг 2: Нарисуйте график второго уравнения на та же координата система как первая.


Вы рисуете второе уравнение так же, как и любое другое уравнение. Обратитесь к первому шагу, если вам нужно просмотреть, как график линия.

Разница здесь в том, что вы поставите его на тот же система координат как первый. Это как иметь две графические задачи в одной.


Шаг 3: Найдите решение.


Если две линии пересекаются в одном месте , то точка пересечение является решением системы.

Если две линии параллельны , то они никогда не пересекаются, поэтому нет нет решения.

Если две линии лежат друг над другом , то они та же строка и у вас есть бесконечное количество решений . В этом случае вы можете записать любое уравнение как решение указывать это одна и та же линия.


Шаг 4: проверьте предложенный заказ парное решение в ОБА уравнения.


Предлагаемое решение можно подключить к ОБОИМ уравнения.Если это делает ОБА уравнения истинными, тогда у вас есть решение для система.

Если хотя бы одно из них окажется ложным, вам нужно идти вернуться и повторить проблема.



Пример 2 : Решите систему уравнений с помощью графика.




*Подставьте 0 для y для x -int
* x -intercept


Пересечение по оси X равно (3, 0).

Y-точка пересечения



*Вставьте 0 для x для y -int
* y -intercept


Y-пересечение (0, 3).

Найти другой решение, положив х = 1.



*Вставьте 1 для x

Другое решение (1, 2).

Решения:

х г (х, у)
3 0 (3, 0)
0 3 (0, 3)
1 2 (1, 2)

Построение упорядоченных парных решений и рисование линия:






*Подставьте 0 для y для x -int
* x -intercept


Пересечение по оси X равно (1, 0).

Y-точка пересечения



*Подставьте 0 для x для y -int

*Инверсия множ. на -1 это дел. по -1

* у -перехват


Y-пересечение (0, -1).

Найти другой решение, если x = 2.



*Вставьте 2 для x
*Инверсия добавления 2 является вспомогательной. 2

*Инверсия множ. на -1 это деление по -1

 


Другое решение (2, 1).

Решения:


х г (х, у)
1 0 (1, 0)
0 -1 (0, -1)
2 1 (2, 1)

Построение упорядоченных парных решений и рисование линия:



Мы должны спросить себя, есть ли место, где две линии пересекаются, и если да, то где?

Да, они пересекаются в (2, 1).



Вы обнаружите, что если вставить заказанную пару (2, 1) в ОБА уравнения исходной системы, что это решение ОБЕИХ из них.

Решение этой системы (2, 1).




Пример 3 : Решите систему уравнений с помощью графика.




*Подставьте 0 для y для x -int
* x -intercept


Пересечение по оси x равно (5, 0).

Y-точка пересечения



*Подставьте 0 для x для y -int

* у -перехват


Y-пересечение (0, 5).

Найти другой решение, если x = 1.



*Вставьте 1 для x
*Инверсия добавления 1 является вспомогательной. 1


Другое решение (1, 4).

Решения:


х г (х, у)
5 0 (5, 0)
0 5 (0, 5)
1 4 (1, 4)

Построение упорядоченных парных решений и рисование линия:





*Подставьте 0 для y для x -int
*Инверсия добавления 3 является вспомогательной.3

*Инверсия множ. на -1 это дел. по -1

* х — перехват


Пересечение по оси X равно (3, 0).

Y-точка пересечения



*Вставьте 0 для x для y -int
* y -intercept


Y-пересечение (0, 3).

Найти другой решение, если x = 1.



*Вставьте 1 для x


Другое решение (1, 2).

Решения:


х г (х, у)
3 0 (3, 0)
0 3 (0, 3)
1 2 (1, 2)

Построение упорядоченных парных решений и рисование линия:



Мы должны спросить себя, есть ли место, где две линии пересекаются, и если да, то где?

Нет, они не пересекаются.Мы иметь два параллельных линии.



Нет заказанных пар для проверки.

Ответ — нет решения.


Решить методом подстановки

Шаг 1: При необходимости упростите.


Это включает удаление ( ) и удаление дробей.

Чтобы удалить ( ): просто используйте свойство дистрибутива.

Чтобы удалить дроби: так как дроби — это еще один способ написать деление, и обратным делением является умножение, вы удаляете дроби на умножение с обеих сторон ЖК-дисплеем всех ваших фракций.


Шаг 2. Решите один уравнение для любой переменной.


Неважно, какое уравнение вы используете или какое переменная, которую вы выбираете решить для.

Вы хотите сделать это как можно проще. Если один уравнений уже решен для одной из переменных, то есть быстро и легко способ идти.

Если вам нужно найти переменную, попробуйте выбрать тот, у которого есть 1 в качестве коэффициента. Таким образом, когда вы идете, чтобы решить это, вы не будет делить на число и рисковать работать с дробная часть (фу!!).


Шаг 3: Замените что вы получаете для шага 2 в другое уравнение.


Вот почему он называется методом подстановки. Убедись в том, что вы подставляете выражение в ДРУГОЕ уравнение, то, которое вы не используйте на шаге 2.

Это даст вам одно уравнение с одним неизвестным.


Шаг 4. Решите для оставшаяся переменная.


Решите уравнение, составленное на шаге 3 для переменной что осталось.

Если вам нужен обзор по решению линейных уравнений, почувствуйте бесплатно перейти к учебнику 14: Линейные уравнения в переменной.
 

Если ваша переменная выпадает и у вас FALSE заявление, значит ваш ответ не является решением.

Если ваша переменная выпадает и у вас ИСТИНА заявление, значит ваш ответ — бесконечные решения, которые были бы уравнением линия.


Шаг 5. Решите для вторая переменная.


Если вы придумаете значение переменной на шаге 4, значит два уравнения имеют одно решение.   Подставьте найденное значение в шаг 4 в любое из уравнений задачи и решить для другого Переменная.


Шаг 6. Проверьте предлагаемые упорядоченное парное решение в ОБОИХ исходных уравнениях.


Предлагаемое решение можно подключить к ОБОИМ уравнения.Если это делает ОБА уравнения верными, тогда у вас есть решение система.

Если хотя бы одно из них окажется ложным, вам нужно идти вернуться и повторить проблема.




Пример 4 : решить систему уравнений заменой метод:


Оба эти уравнения уже упрощены. Нет нужды в работе сделать здесь.



Неважно, какое уравнение или какую переменную вы выбрать решение за. Просто будь проще.

Поскольку разрешение x во втором уравнение имеет коэффициент 1, это означало бы, что нам не пришлось бы делить на номер решить для него и рискнуть работать с дробями (ЮК). Самый простой путь здесь — решить второе уравнение для x , и мы определенно хотим пойти по легкому пути.

Вы не ошибетесь, выбрав другой уравнение и/или решить для и , опять же, вы хотите сохранить его как просто насколько это возможно.

Решив второе уравнение для x мы получить:


*Второе уравнение решено для x



Подставим выражение y + 1 вместо x в первое уравнение и решим для y :
(когда вы подставляете такое выражение, это как если бы вы подставляли в число для вашей переменной) 



*Под. г + 1 дюйм для x
*Расст. от 3 до (  )
*Объедините похожие термины

*Инверсия сложения 3 является вспомогательной. 3



Вставьте 3 для и в уравнение в шаг 2, чтобы найти значение x .


*Вставка 3 для y



Вы обнаружите, что если вставить заказанную пару (4, 3) в ОБА уравнения исходной системы, что это решение ОБЕИХ из них.

(4, 3) — это решение для нашей системы.




Пример 5 : решить систему уравнений заменой метод:


Это уравнение полно этих неприятных дробей. Мы можем упростить оба уравнения путем умножения каждого отдельного на его ЖК-дисплей, точно так же, как вы можете сделать, когда вы работаете с одним уравнением.До тех пор, как вы сделайте то же самое с обеими частями уравнения, вы сохраните две стороны равны друг другу.

Умножив каждое уравнение на соответствующий ЖК-дисплей, мы получить:


*Множ. по ЖК 2

*мульт. по ЖК 2


 



Обратите внимание, что второе уравнение уже решено для y . Мы можем использовать его для этого шага.

Неважно, какое уравнение или какую переменную вы выбрать решение за. Но в ваших интересах, чтобы все было так просто, как возможный.

Решение второго уравнения для y :


*Решено для и



Подставьте выражение -3 x + 4 для y в первое уравнение и решить для x :
(когда вы подставляете такое выражение, это как если бы вы подставляли в число для вашей переменной) 



*Под.-3 х + 4 for y
*Переменная исключена И false


Минуточку, а куда делись наши переменная идет????

Как упоминалось выше, если ваша переменная выпадает, и вы иметь ЛОЖНОЕ утверждение, тогда решения нет. Если бы мы построили график этих двух, они будут параллельны друг другу.



Поскольку мы не получили значение для x , там тут нечего втыкать.



Нет заказанных пар для проверки.

Ответ — нет решения.




Пример 6 : решить систему уравнений заменой метод:


Оба эти уравнения уже упрощены. Нет нужды в работе сделать здесь.



Обратите внимание, что второе уравнение уже решено для y . Мы можем использовать его для этого шага.

Неважно, какое уравнение или какую переменную вы выбрать решение за. Но в ваших интересах, чтобы все было так просто, как возможный.

Решение второго уравнения для y :


*Решено для и



Подставим выражение 2 x — 4 для y в первое уравнение и решить для x :
(когда вы подставляете такое выражение, это как если бы вы подставляли в число для вашей переменной) 



*Под.2 x — 4 для y

*Переменная выпала И верно


Минуточку, а куда делись наши переменная идет????

Как упоминалось выше, если переменная выпадает И мы иметь ИСТИННОЕ утверждение, тогда когда имеют бесконечное число решений.Они в конечном итоге та же линия.



Поскольку мы не получили значение для x , там тут нечего втыкать.



Здесь нет значения для подстановки.

Когда они окажутся одним и тем же уравнением, у вас будет бесконечное число решений.Вы можете записать свой ответ, написав либо уравнение, чтобы указать, что это одно и то же уравнение.

Ответ можно записать двумя способами: {( x , y )| 2 x — y = 4} ИЛИ {( x , y ) | у = 2 х — 4}.


Решить путем исключения по Метод добавления


Шаг 1. Упростите и поместите оба уравнения в форму A x + B y = C, если это необходимо.


Это включает удаление ( ) и удаление дробей.

Чтобы удалить ( ): просто используйте свойство дистрибутива.

Чтобы удалить дроби: так как дроби — это еще один способ написать деление, и обратным делением является умножение, вы удаляете дроби на умножение с обеих сторон ЖК-дисплеем всех ваших фракций.


Шаг 2: Умножьте один или оба уравнения числом, которое создаст противоположные коэффициенты за либо x , либо y , если необходимо.


Забегая вперед, мы добавим эти два уравнения вместе . В этом процессе нам нужно убедиться, что одна из переменных вне, оставив нам одно уравнение и одно неизвестное.Единственный способ, которым мы можем гарантия, что если мы складываем противоположности . Сумма противоположности равно 0.

Если ни одна переменная не выпадет, то мы застряли с уравнение с два неизвестных неразрешима.

Неважно, какую переменную вы выберете для удаления вне. Вы хотите, чтобы это было как можно проще.Если переменная уже имеет противоположные коэффициенты, чем перейти к сложению двух уравнений вместе. Если это не так, вам нужно умножить одно или оба уравнения на число тот создаст противоположные коэффициенты в одной из ваших переменных. Ты может Думайте об этом как о ЖК-дисплее. Подумай, какой номер у оригинала коэффициенты оба входят и соответственно умножают каждое отдельное уравнение. Сделать убедитесь, что одна переменная положительна, а другая отрицательна, прежде чем вы добавлять.

Например, если у вас есть 2 x в одном уравнении и 3 x в другом уравнении, мы могли бы умножить первое уравнение на 3 и получаем 6 x и в второе уравнение на -2, чтобы получить -6 x . Так когда вы добавите эти два вместе, они выпадут.



Сложите два уравнения вместе.

Переменная с противоположными коэффициентами будет выпадать из этого шаг, и у вас останется одно уравнение с одним неизвестным.


Шаг 4: Решите, что осталось Переменная.


Решите уравнение, найденное в шаге 3, для переменной что осталось.

Если вам нужен обзор по решению линейных уравнений, почувствуйте бесплатно перейти к учебнику 14: Линейные уравнения в переменной.

Если обе переменные выпадают и у вас FALSE заявление, значит ваш ответ не является решением.

Если обе переменные выпадают и у вас есть ИСТИНА заявление, значит ваш ответ — бесконечные решения, которые были бы уравнением линия.


Шаг 5: Решение за секунду Переменная.


Если вы придумаете значение переменной на шаге 4, значит два уравнения имеют одно решение.   Подставьте найденное значение в шаг 4 в любое из уравнений задачи и решить для другого Переменная.


Шаг 6: Проверка предложенный упорядоченное парное решение в ОБОИХ исходных уравнениях.


Предлагаемое решение можно подключить к ОБОИМ уравнения.Если это делает ОБА уравнения верными, тогда у вас есть решение система.

Если хотя бы одно из них окажется ложным, вам нужно идти вернуться и повторить проблема.




Пример 7 : Решите систему уравнений с помощью устранение метод:



Это уравнение полно этих неприятных дробей. Мы можем упростить оба уравнения путем умножения каждого отдельного на его ЖК-дисплей, точно так же, как вы можете сделать, когда вы работаете с одним уравнением. До тех пор, как вы сделайте то же самое с обеими частями уравнения, вы сохраните две стороны равны друг другу.

Умножив каждое уравнение на соответствующий ЖК-дисплей, мы получить:



*Множ.по ЖК 6

*мульт. по ЖК 40


 



Опять же, вы хотите сделать это так же просто, как возможный.

Обратите внимание, как коэффициент на y в первом уравнение равно 2, а во втором уравнении — 5.Нам нужно иметь противоположности, так что если одна из них равна 10, а другая -10, они будут отменить друг друга, когда мы идем, чтобы добавить их. Если бы мы сложили их вместе в том виде, в котором они есть сейчас, мы получили бы одно уравнение и два переменные, ничего бы не выпало. И мы не смогли бы ее решить.

Итак, я предложил умножить первое уравнение на 5 и второй уравнение на -2, это создаст 10 и -10 перед y и у нас будут свои противоположности.

Умножение первого уравнения на 5 и второго уравнение на -2 получаем:


*Множ. обе стороны 1-го уравнения. по 5
*мульт. обе стороны 2-го уравнения. по -2

* и -х иметь напротив коэффициенты




*Обратите внимание, что и выбыл






Вы можете выбрать любое уравнение, используемое в этой задаче, чтобы подставьте найденное значение x .

Я решил подключить 10 для x к первое упрощенное уравнение (найденное на шаге 1) для нахождения y ценность.



*Подключить 10 для x

*Инверсия прибавления 30 является вспомогательной. 30

*Инверсия множ.на 2 дел. по 2

 



Вы обнаружите, что если подключить заказанную пару (10, 24) в ОБЕИХ уравнений исходной системы, что это решение ОБЕИХ их.

(10, 24) — это решение для нашей системы.




Пример 8 : Решите систему уравнений с помощью устранение метод:



Эта задача уже упрощена, однако вторая уравнение не пишется в виде А х + В у = С.Другими словами, нам нужно записать его в таком виде, чтобы все готов к работе, когда мы сложим два уравнения вместе.

Переписывая второе уравнение, получаем:



*Инверсия сложения x является вспомогательной. х

*Все выстроено



Обратите внимание, что x коэффициенты уже противоположности. y коэффициенты также противоположности в этом отношении.

Таким образом, нам не нужно умножать ни одно из уравнений на номер.




*Обратите внимание, что x и и оба выпали



Эй, куда делись наши переменные идти??

Как упоминалось выше, если переменная выпадает И мы иметь ИСТИННОЕ утверждение, тогда когда имеют бесконечное число решений.Они в конечном итоге та же линия.



Здесь нет значения для подстановки.



Здесь нет значения для подстановки.

Когда они окажутся одним и тем же уравнением, у вас будет бесконечное число решений.Вы можете записать свой ответ, написав либо уравнение, чтобы указать, что это одно и то же уравнение.

Ответ можно записать двумя способами: {( x , y )| x — y = 3} ИЛИ {( x , y ) | у = х — 3}.




Пример 9 : Решите систему уравнений с помощью устранение метод:



Оба эти уравнения уже упрощены и в правильная форма. Здесь не нужно делать никакой работы.



Опять же, вы хотите сделать это так же просто, как возможный.

Обратите внимание, как коэффициент на x в первом равен 5, а во втором равен 10. Нам нужно имеют противоположности, так что если одна из них равна -10, а другая 10, они будут отменить друг друга, когда мы идем, чтобы добавить их.Если бы мы сложили их вместе в том виде, в котором они есть сейчас, мы получили бы одно уравнение и два переменные, ничего бы не выпало. И мы не смогли бы ее решить.

Итак, я предложил умножить первое уравнение на -2, это создаст -10 и 10 перед x и у нас будут свои противоположности.

Умножив первое уравнение на -2, получим:


*Множ.обе стороны 1-го уравнения. по -2

* х и и -х имеют противоположные коэффициенты




*Обратите внимание, что x и и оба выпали



Минуточку, а куда делись наши переменная идет????

Как упоминалось выше, если ваша переменная выпадает, и вы иметь ЛОЖНОЕ утверждение, тогда решения нет. Если бы мы построили график этих двух, они будут параллельны друг другу.



Здесь нет значения для подстановки.



Здесь нет значения для подстановки.

Ответ — нет решения.


 

Практические задачи


Это тренировочные задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как и все в противном случае, если вы хотите добиться в этом успеха, вам нужно практиковаться. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.

Чтобы получить максимальную отдачу от них, вы должны решить проблему на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответа/обсуждения для этой проблемы .По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

Практические задачи 1a — 1c: Решите каждую систему с помощью замена или устранение методом добавления.

 

 

Практическая задача 2a:   Решите систему с помощью графика.

РубрикаРазное

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *