Решение систем линейных уравнений: Разбираемся в линейных уравнениях раз и навсегда
| 1. |
Неизвестная переменная x
Сложность: лёгкое |
2 |
| 2. |
Неизвестная переменная y
Сложность: лёгкое |
2 |
3.
|
Система линейных уравнений
Сложность: лёгкое |
2 |
| 4. |
Система линейных уравнений
Сложность: лёгкое |
1 |
5.
|
Система линейных уравнений (одинаковые коэффициенты при y)
|
4 |
| 6. |
Решение системы двух уравнений (обыкновенные дроби)
|
4 |
7.
|
Система двух линейных уравнений (одинаковые коэффициенты при x)
|
4 |
| 8. |
Система линейных уравнений
|
4 |
9.
|
Система линейных уравнений (смешанные числа и обыкновенные дроби)
|
4 |
| 10. | Сложность: среднее |
1 |
11. |
Система линейных уравнений
Сложность: среднее |
4 |
| 12. |
Система линейных уравнений
Сложность: среднее |
4 |
13.
|
Система линейных уравнений, одно из которых целое по сути, но дробное по виду
Сложность: среднее |
4 |
| 14. |
Решение системы линейных уравнений
Сложность: сложное |
6 |
15.
|
Система линейных уравнений (сумма дробей)
Сложность: сложное |
5 |
| 16. |
Система двух уравнений
Сложность: сложное |
6 |
Линейные уравнения, Системы линейных уравнений, Решения систем линейных уравнений, Метод Крамера
К решению систем линейных уравнений сводятся многочисленные задачи по математике. Рассмотрим постановку задачи.
Рассмотрим постановку задачи.
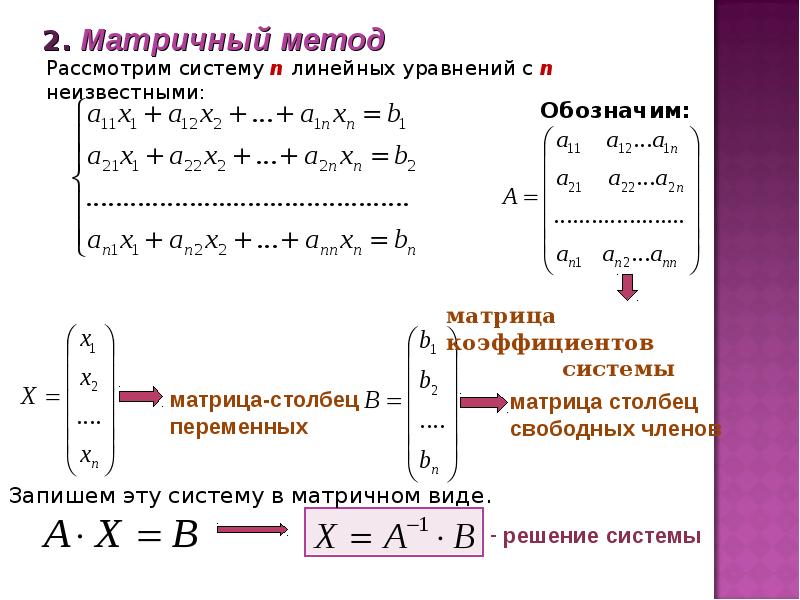
Дана система n алгебраических уравнений с n неизвестными:
Эту систему можно записать в матричном виде: А • X = В, где А — квадратная матрица коэффициентов, X — вектор-столбец неизвестных, В — вектор-столбец свободных членов.Численные методы решения систем линейных уравнений делятся на прямые и итерационные.
Прямые методы используют конечные соотношения для вычисления неизвестных. Эти методы сравнительно просты и пригодны для широкого класса систем.
Недостатки: требуют хранения в памяти ЭВМ сразу всей матрицы А. При больших порядках системы расходуется много места в памяти и накапливается вычислительная погрешность. Кроме того, существенно возрастает время вычисления вектора X. Поэтому прямые методы обычно применяют при небольших порядках системы (n < 200).
Примеры прямых методов решения систем линейных уравнений
Метод определителей Крамера, метод Гаусса. Первый из них применяется крайне редко, так как с ростом n алгоритм нахождения определителей резко возрастает.
Итерационные методы основаны на последовательных приближениях. Задается некоторое приближенное значение вектора Х — начальное приближение. Затем с помощью некоторого алгоритма проводится первый цикл вычислений — итерация, в результате которого получается новое приближение вектора Х. Итерации проводятся до получения решения с заданной точностью.
Алгоритм решения систем линейных уравнений здесь более сложен, чем у прямых методов. Не всегда выполняется условие сходимости. Однако в ряде случаев итерационные методы предпочтительнее. Они требуют хранения в памяти ЭВМ не всей матрицы A, а лишь нескольких векторов. Вычислительная погрешность практически не накапливается. Поэтому итерационные методы применимы и для больших порядков системы. Примеры — метод простой итерации и метод Зейделя.
Примеры работ
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
Механизм решения систем линейных алгебраических уравнений
10.08.2018
Данная статья является анонсом новой функциональности.
Не рекомендуется использовать содержание данной статьи для освоения новой функциональности.
Полное описание новой функциональности будет приведено в документации к соответствующей версии.
Полный список изменений в новой версии приводится в файле v8Update.htm.
Реализовано в версии 8.3.14.1565.
В сложных прикладных решениях 1С:Предприятия существует прикладной функционал расчета себестоимости товаров. Это достаточно сложная задача и мы решили сделать встроенный в платформу механизм, который будет максимально простым в использовании и, при этом, весьма производительным.
Проанализировав работу прикладных решений, мы пришли к выводу, что один из наиболее трудозатратных этапов представляет собой, по сути, решение системы линейных алгебраических уравнений (СЛУ). В результате в платформе, во встроенном языке, мы реализовали новый объект, позволяющий находить решение СЛУ.
В результате в платформе, во встроенном языке, мы реализовали новый объект, позволяющий находить решение СЛУ.
Существуют классические алгоритмы решения СЛУ, однако в платформе мы использовали собственный алгоритм с дополнительной оптимизацией. В случае разреженной матрицы СЛУ, что как раз соответствует задаче расчета себестоимости, наш алгоритм работает существенно быстрее классических алгоритмов. В случае плотной матрицы СЛУ он показывает результаты, близкие к классическим (гарантированно не хуже).
По нашим оценкам использование этого нового объекта в задаче расчета себестоимости позволит увеличить производительность в десятки раз.
Помимо этой задачи вы можете использовать новый объект и в других прикладных областях, которые автоматизируются решениями 1С:Предприятия:
- Задачи планирования;
- Взаиморасчеты между некоторым множеством юридических лиц, предприятий или отраслей;
- Балансовые модели;
- Прогнозирование;
- Задачи поиска экстремумов, в том числе условных экстремумов.

Задача решения системы линейных алгебраических уравнений
В общем виде система линейных алгебраических уравнений выглядит следующим образом:
где это известные коэффициенты уравнений.
Решение системы линейных уравнений заключается в нахождении таких значений , при которых все равенства выполняются.
Новый объект РасчетСистемЛинейныхУравнений
Объект РасчетСистемЛинейныхУравнений обладает рядом свойств, которые позволяют гибко настраивать необходимую точность решения через численные значения и количество итераций алгоритма. Кроме этого они позволяют устанавливать границу изменения алгоритма решения для получения оптимальной скорости вычислений.
Объект содержит конструктор и два метода:
- РассчитатьСистемыЛинейныхУравнений() — решает систему линейных уравнений и возвращает решение в виде объекта ТаблицаЗначений;
- ПолучитьКомпонентыСвязности() — находит компоненты связности и возвращает результат в виде объекта ТаблицаЗначений.
 Вы можете использовать этот метод для выделения нескольких подмножеств данных и распределённой работы с ними.
Вы можете использовать этот метод для выделения нескольких подмножеств данных и распределённой работы с ними.
Особенностью нового функционала является то, что он поддерживает параллельное использование вычислительных ресурсов. Вы можете регулировать количество используемых потоков вычисления. Функционал доступен на сервере, в толстом клиенте и в COM-соединении.
Схема использования механизма
Для решения системы линейных уравнений необходимо подготовить две таблицы с коэффициентами системы линейных уравнений – ИсточникДанныхУзлов и ИсточникДанныхСвязей. Эти таблицы могут быть объектами типа ТаблицаЗначений или РезультатЗапроса.
- ИсточникДанныхУзлов — должен содержать колонку с номерами уравнений и множество колонок, хранящих свободные коэффициенты уравнений;
- ИсточникДанныхСвязей — так же содержит колонку с номерами уравнений, колонку номеров переменных и множество колонок, хранящих коэффициенты, с которыми переменные входят в уравнения.

Далее нужно дать описание этих таблиц, выставив определенные свойства объекта РасчетСистемЛинейныхУравнений: КолонкаУравненияВУзлах, КолонкаУравненияВСвязях, КолонкаПеременныеВСвязях.
Следующим шагом является описание систем линейных уравнений, которые требуется решить. Для этого существует специальный объект ОписаниеСистемыЛинейныхУравнений. В нем нужно указать свойства КолонкаКоэффициентовВСвязях и КолонкаКоэффициентовВУзлах, соответствующие данной системе.
Полученные описания следует добавить в коллекцию ОписанияСистемЛинейныхУравнений (свойство ОписанияСистем объекта РасчетСистемЛинейныхУравнений). Для корректной работы нужно добавить в коллекцию как минимум одно ОписаниеСистемыЛинейныхУравнений.
Далее можно указать дополнительные (необязательные) свойства объекта РасчетСистемЛинейныхУравнений, которые позволяют тонко настроить механизм решения.
Финальный этап — вызов метода РассчитатьСистемыЛинейныхУравнений().
Отметим, что механизм позволяет рассчитывать сразу несколько систем линейных уравнений за один вызов метода РассчитатьСистемыЛинейныхУравнений().
Теги: 8.3.14 разработка
Рассказать друзьям:TensorFlow. Решение систем линейных уравнений
Библиотека TensorFlow широко известна, в основном, в контексте машинного обучения и нейронных сетей. Однако, TensorFlow изначально не является библиотекой машинного обучения в чистом виде, а позиционируется разработчиками, как библиотека для высокопроизводительных вычислений (high perfomance computing), а это значит, что область ее применения значительно шире. Итак, выступая на конференции с докладом о том, как мы применяли TensorFlow для задачи оценки показателей надежности, я получил вполне закономерный вопрос: «А можно ли использовать TF для решения систем уравнений?». Ответ, естественно, положительный, и в этой статье рассмотрим, как решать системы линейных алгебраических уравнений.
Ответ, естественно, положительный, и в этой статье рассмотрим, как решать системы линейных алгебраических уравнений.
Для систем линейных алгебраических уравнений TensorFLow содержит уже готовые методы в пакете tf.linalg. Непосредственно для решения систем линейных уравнений используется метод tf.linalg.solve.
Метод имеет следующую сигнатуру:
tf.linalg.solve(
matrix,
rhs,
adjoint=False,
name=None
)Где matrix — матрица коэффициентов левой части системы в формате тензора [..., M, M] (квадратная матрица), rhs — правая часть системы уравнений в формате тензора [..., M, K], adjoint — указывает на то, что матрица левой части является блочным сопряжением, Name — имя оператора в графе.
Пример решения
В качестве примера возьмем следующую систему линейных уравнений
\[
\begin{cases}
2x + 3y + z = 2 \\
3x + y + 2z = 7 \\
x + 2y + 3z = 3
\end{cases}
\]
Тогда матрица левой части системы уравнений (\(A\)) принимает вид:
\[
A = \begin{bmatrix}
2&3&1\\
3&1&2\\
1&2&3
\end{bmatrix}
\]
Правой части, соответственно:
\[B = \begin{bmatrix}
2\\
7\\
3
\end{bmatrix}
\]
Первым делом импортируем TensorFlow:
import tensorflow as tf
Далее создадим тензоры исходных данных. В нашем случае достаточно константных значений, однако, в общем случае это могут быть и переменные, и значения результатов других вычислений.
В нашем случае достаточно константных значений, однако, в общем случае это могут быть и переменные, и значения результатов других вычислений.
A = tf.constant([[2.0, 3.0, 1.0], [3.0, 1.0, 2.0], [1.0, 2.0, 3.0]]) B = tf.constant([[2.0, ], [7.0, ], [3.0, ]])
После создания тензоров с исходными данными применим функцию, предварительно создав сессию tensorflow.
Q = tf.linalg.solve(A, B) sess = tf.Session() print(sess.run(Q))
получим следующий вывод:
[[ 2. ] [-1.0000001] [ 1.0000001]]
Как видим, результаты соответствуют аналитическому решению.
Полный текст в формате jupyter notebook.
Решение системы линейных уравнений
Решение системы линейных уравнений
При помощи рассмотренного ранее инструмента Поиск решения можно также легко решать системы линейных равнений.Системой n линейных уравнений с m неизвестными называется система вида:
где: aij и bi (i = 1, … , m; b = 1, … , n) – некоторые известные числа, x1, … , xn – неизвестные.
В обозначении коэффициентов aij первый индекс i обозначает номер уравнения, а второй индекс j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных часто записывают в виде матрицы, которая называется матрицей системы:
Числа, стоящие в правых частях уравнений, b1, … , bm называются свободными членами.
Совокупность n чисел c1, … , cn называется решением данной системы уравнений, если каждое уравнение обращается в равенство после подстановки в него чисел c1, … , cn вместо соответствующих неизвестных x1, … , xn.
Наша задача найти решение системы. При этом могут возникнуть три ситуации:
При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений.
- И третий случай, когда система вообще не имеет решения.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Существуют различные способы нахождения решений системы:
- Матричный метод решения систем линейных уравнений.
- Метод Крамера.
- Метод Гаусса.
Создадим новый метод решения системы линейных уравнений, используя инструмент Поиск решения.
В качестве примера рассмотрим систему 3-х линейных уравнений с 3-мя неизвестными:
Коэффициенты при неизвестных и свободные члены запишем в виде таблицы:
В ячейках A7:C7 находятся будущие корни системы уравнений. Сначала присвоим им нулевые значения:
Сначала присвоим им нулевые значения:
В ячейку D2 запишем формулу для вычисления свободного члена первого уравнения =СУММПРОИЗВ($A$7:$C$7;A2:C2). Эта функция перемножает соответствующие элементы заданных массивов одинаковой размерности и возвращает сумму произведений. Затем сделаем автозаполнение формулы для двух других ячеек в столбце D:
Вот так выглядят наши таблички в режиме значений:
Наша задача добиться попарного совпадения значений в соседних ячейках столбцов D и E, изменяя значения в ячейках A7:C7. Для этого будем использовать Поиск решения (на вкладке Данные → в группе Анализ → кнопка Поиск решения):
В диалоговом окне
Поиск решения устанавливаем следующие параметры:- Установить целевую ячейку: тут должно быть пусто (стираем все значения, если они там были).

- Равной: значению: 0.
- Изменяя ячейки: $A$7:$C$7 (подбираем корни системы уравнений).
- Ограничения: $D$2:$D$4=$E$2:$E$4.
Нажимаем кнопку Выполнить:
Оставляем пункт Сохранить найденное решение → кнопка OK.
Теперь в ячейках A7, B7 и С7 будут записаны точные значения корней системы уравнений:
В противном случае в окне Результаты поиска решения получим сообщение Поиск не может найти подходящего решения:
Решение систем линейных уравнений
Напомним для начала определение решения системы линейных уравнений с двумя переменными.
В дальнейшем будем рассматривать системы из двух линейных уравнений с двумя переменными.
Рисунок 1.
Существуют три способа решения систем линейных уравнений: способ подстановки, способ сложения и графический способ. Рассмотрим его на следующем примере:
Рисунок 2.
Способ подстановки
Способ подстановки заключается в следующем: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
Рисунок 3.
Выразим из второго уравнения $y$ через $x$:
Подставим в первое уравнение, найдем $x$:
Найдем $y$:
Ответ: $(-2,\ 3)$
Способ сложения
Рассмотрим данный способ на примере:
Рисунок 4.
Умножим второе уравнение на $3$, получим:
Рисунок 5.
Теперь сложим оба уравнения между собой:
Найдем $y$ из второго уравнения:
Ответ: $(-2,\ 3)$
!!! Отметим, что в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении одна из переменных «исчезла».
Графический способ
Графический способ заключается в следующем: Оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
Рисунок 6.
Выразим из обоих уравнений $y$ через $x$:
Рисунок 7.
Изобразим оба графика на одной плоскости:
Рисунок 8.
Ответ: $(-2,\ 3)$
Пример решения систем линейных уравнений с двумя переменными
Пример 1
Решить систему уравнений тремя способами:
Рисунок 9.
Решение:
1) Способ подстановки.
Выразим $x$ через $y$:
\[x=y\]Подставим в второе уравнение, найдем $y$:
\[2y+3y=-5\] \[y=-1\]Найдем $x$:
\[x=-1\]Ответ: $(-1,-1)$
2) Способ сложения.
Умножим первое уравнение на $3$, получим:
Рисунок 10.
сложим оба уравнения между собой:
\[5x=-5\] \[x=-1\]Найдем $y$ из первого уравнения:
\[-1-y=0\] \[y=-1\]Ответ: $(-1,\ -1)$
3) Графический способ.
Выразим из обоих уравнений $y$ через $x$:
Рисунок 11.
Изобразим оба графика на одной плоскости:
Рисунок 12.
Ответ: $(-1,\ -1)$
Система линейных уравнений с двумя переменными. Методы решения систем уравнений.
Решением системы линейных уравнений двух переменных является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
Как можно решить систему уравнений с двумя переменными?
Системы уравнений с двумя переменными можно решить методом подстановки:
Системы уравнений с двумя переменными можно решить методом сложения:
Пример. Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).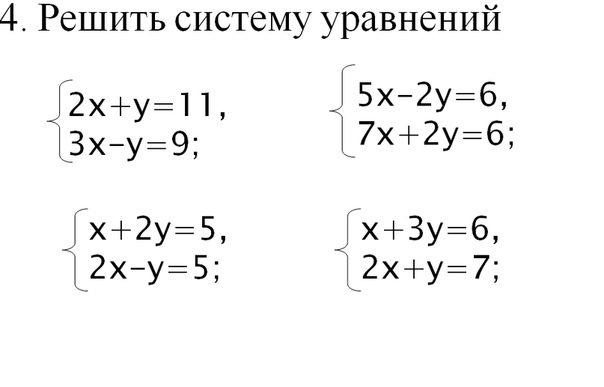
Решение:
Система уравнений состоящее из двух переменных должно удовлетворять всем решениям одновременно. Система линейных уравнений из двух переменных рассматривается одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, и это будет их решением, другие системы могут иметь бесконечное число решений. Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальное решение.
Выводы:
- Система линейных уравнений из двух переменных решается совместно методом подстановки или методом сложения.
- Чтобы найти решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям в системе одновременно.
- Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных.
- Решить систему уравнений это значит найти численное значение для каждой переменной в системе либо доказать что решений нет.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Метод исключения для решения линейных систем (Алгебра 1, Системы линейных уравнений и неравенств) — Mathplanet
Другой способ решения линейной системы — использовать метод исключения. В методе исключения вы либо складываете, либо вычитаете уравнения, чтобы получить уравнение с одной переменной.
Когда коэффициенты одной переменной противоположны, вы добавляете уравнения, чтобы исключить переменную, а когда коэффициенты одной переменной равны, вы вычитаете уравнения, чтобы исключить переменную.
Пример
$$ \ begin {matrix} 3y + 2x = 6 \\ 5y-2x = 10 \ end {matrix} $$
Мы можем исключить переменную x, добавив два уравнения.
$$ 3y + 2x = 6 $$
$$ \ underline {+ \: 5y-2x = 10} $$
$$ = 8лет \: \: \: \: \; \; \; \; = 16 $$
$$ \ begin {matrix} \: \: \: y \: \: \: \: \: \; \; \; \; \; = 2 \ end {matrix} $$
Теперь значение y можно подставить в любое из исходных уравнений, чтобы найти значение x
$$ 3y + 2x = 6 $$
$$ 3 \ cdot {\ color {зеленый} 2} + 2x = 6 $$
$$ 6 + 2x = 6 $$
$$ x = 0 $$
Решение линейной системы есть (0, 2).
Чтобы избежать ошибок, перед началом исключения убедитесь, что все одинаковые члены и знаки равенства находятся в одних и тех же столбцах.
Если у вас нет уравнений, в которых вы можете исключить переменную путем сложения или вычитания, вы можете непосредственно начать с умножения одного или обоих уравнений на константу, чтобы получить эквивалентную линейную систему, в которой вы можете исключить одну из переменных путем сложения. или вычитание.
Пример
$$ \ begin {matrix} 3x + y = 9 \\ 5x + 4y = 22 \ end {matrix} $$
Начните с умножения первого уравнения на -4 так, чтобы коэффициенты y были противоположны
$$ \ color {зеленый} {-4 \} \ cdot \ left (3x + y \ right) = 9 \ cdot {\ color {green} {-4} $$
$$ 5x + 4y = 22 $$
$$ — 12x-4y = -36 $$
$$ \ underline {+ 5x + 4y = 22} $$
$$ = — 7x \: \: \: \: \: \: \: \: \: \: = -14 $$
$$ \ begin {matrix} \: \: \; \: \: x \: \: \: \: \: \: \: \: \: \: \: = 2 \ end {matrix} $$
Подставьте x в любое из исходных уравнений, чтобы получить значение y
$$ 3x + y = 9 $$
$$ 3 \ cdot {\ color {зеленый} 2} + y = 9 $$
$$ 6 + y = 9 $$
$$ y = 3 $$
Решение линейной системы: (2, 3)
Видеоурок
Решите линейную систему методом исключения
$$ \ left \ {\ begin {matrix} 2y — 4x = 2 \\ y = -x + 4 \ end {matrix} \ right $$
4.2. Решение систем линейных уравнений с двумя переменными
Цели обучения
К концу этого раздела вы сможете:
- Определите, является ли упорядоченная пара решением системы уравнений
- Решите систему линейных уравнений, построив график
- Решите систему уравнений заменой
- Решите систему уравнений методом исключения
- Выберите наиболее удобный способ решения системы линейных уравнений
Прежде чем начать, пройдите тест на готовность.
- Для уравнения \ (y = \ frac {2} {3} x − 4 \),
ⓐ Является ли \ ((6,0) \) решением? Ⓑ Является ли \ ((- 3, −2) \) решением?
Если вы пропустили эту проблему, просмотрите [ссылка] . - Найдите наклон и пересечение y прямой \ (3x − y = 12 \).
Если вы пропустили эту проблему, просмотрите [ссылка] . - Найдите точки пересечения x- и y прямой \ (2x − 3y = 12 \).
Если вы пропустили эту проблему, просмотрите [ссылка] .
Определить, является ли упорядоченная пара решением системы уравнений
В разделе Решение линейных уравнений мы узнали, как решать линейные уравнения с одной переменной. Теперь мы будем работать с двумя или более линейными уравнениями, сгруппированными вместе, что известно как система линейных уравнений .
СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ
Когда два или более линейных уравнения сгруппированы вместе, они образуют систему линейных уравнений .
В этом разделе мы сосредоточим нашу работу на системах двух линейных уравнений с двумя неизвестными. Позже в этой главе мы решим более крупные системы уравнений.
Пример системы двух линейных уравнений показан ниже. Мы используем скобку, чтобы показать, что два уравнения сгруппированы вместе и образуют систему уравнений.
\ [\ left \ {\ begin {выровнено} 2x + y & = 7 \\ x − 2y & = 6 \ end {выровнено} \ right. \ nonumber \]
Линейное уравнение с двумя переменными, например \ (2x + y = 7 \), имеет бесконечное число решений.Его график представляет собой линию. Помните, что каждая точка на линии — это решение уравнения, а каждое решение уравнения — это точка на линии.
Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, которые являются решениями обоих уравнений. Другими словами, мы ищем упорядоченные пары \ ((x, y) \), которые делают оба уравнения истинными. Они называются решениями системы уравнений .
РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ
решений системы уравнений — это значения переменных, которые делают все уравнения истинными.Решение системы двух линейных уравнений представляется упорядоченной парой \ ((x, y) \).
Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение. Если упорядоченная пара делает оба уравнения истинными, это решение системы.
Пример \ (\ PageIndex {1} \)
Определите, является ли упорядоченная пара решением системы \ (\ left \ {\ begin {array} {l} x − y = −1 \\ 2x − y = −5 \ end {array} \ right.\).
ⓐ \ ((- 2, −1) \) ⓑ \ ((- 4, −3) \)
- Ответ
ⓐ
ⓑ
Пример \ (\ PageIndex {2} \)
Определите, является ли упорядоченная пара решением системы \ (\ left \ {\ begin {array} 3x + y = 0 \\ x + 2y = −5 \ end {array} \ right. \).
ⓐ \ ((1, −3) \) ⓑ \ ((0,0) \)
- Ответ
ⓐ да ⓑ нет
Пример \ (\ PageIndex {3} \)
Определите, является ли упорядоченная пара решением системы \ (\ left \ {\ begin {array} x − 3y = −8 \\ −3x − y = 4 \ end {array} \ right.\).
ⓐ \ ((2, −2) \) ⓑ \ ((- 2,2) \)
- Ответ
ⓐ нет ⓑ да
Решение системы линейных уравнений с помощью построения графиков
В этом разделе мы будем использовать три метода для решения системы линейных уравнений. Первый метод, который мы будем использовать, — это построение графиков.
График линейного уравнения представляет собой линию. Каждая точка на линии — это решение уравнения. Для системы двух уравнений мы построим график двумя линиями.Затем мы можем увидеть все точки, которые являются решениями каждого уравнения. И, обнаружив, что общего у линий, мы найдем решение системы.
Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, все числа являются решениями.
Точно так же, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий в одной плоскости, есть три возможных случая, как показано.
Рисунок \ (\ PageIndex {1} \)Каждый раз, когда мы демонстрируем новый метод, мы будем использовать его в той же системе линейных уравнений. В конце раздела вы решите, какой метод был наиболее удобным для решения этой системы.
Пример \ (\ PageIndex {4} \): как решить систему уравнений с помощью построения графиков
Решите систему, построив график \ (\ left \ {\ begin {array} {l} 2x + y = 7 \\ x − 2y = 6 \ end {array} \ right. \).
- Ответ
Пример \ (\ PageIndex {5} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} x − 3y = −3 \\ x + y = 5 \ end {array} \ right.\).
- Ответ
\ ((3,2) \)
Пример \ (\ PageIndex {6} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} −x + y = 1 \\ 3x + 2y = 12 \ end {array} \ right. \)
- Ответ
\ ((2,3) \)
Здесь показаны шаги, которые необходимо использовать для решения системы линейных уравнений с помощью построения графиков.
РЕШИТЕ СИСТЕМУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ ГРАФИКОВ.
- Изобразите первое уравнение.
- Постройте второе уравнение в той же прямоугольной системе координат.
- Определите, пересекаются ли линии, параллельны или совпадают.
- Определите решение системы.
- Если линии пересекаются, укажите точку пересечения. Это решение системы.
- Если линии параллельны, у системы нет решения.
- Если линии совпадают, система имеет бесконечное количество решений.
- Проверьте решение в обоих уравнениях.
В следующем примере мы сначала перепишем уравнения в форме углового пересечения, так как это упростит нам быстрое построение графика линий.
Пример \ (\ PageIndex {7} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} 3x + y = −1 \\ 2x + y = 0 \ end {array} \ right. \)
- Ответ
Мы решим оба этих уравнения относительно \ (y \), чтобы мы могли легко построить их график, используя их наклоны и \ (y \) — точки пересечения.
Пример \ (\ PageIndex {8} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} −x + y = 1 \\ 2x + y = 10 \ end {array} \ right. \).
- Ответ
\ ((3,4) \)
Пример \ (\ PageIndex {9} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} 2x + y = 6 \\ x + y = 1 \ end {array} \ right. \).
- Ответ
\ ((5, −4) \)
До сих пор во всех системах линейных уравнений линии пересекались и решение было одной точкой.В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, которая имеет бесконечное число решений.
Пример \ (\ PageIndex {10} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = \ tfrac {1} {2} x-3 \\ x-2y = 4 \ end {array} \ right. \ ).
- Ответ
Пример \ (\ PageIndex {11} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = — \ tfrac {1} {4} x + 2 \\ x + 4y = 4 \ end {array} \ right.\).
- Ответ
нет решения
Пример \ (\ PageIndex {12} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = 3x-1 \\ 6x-2y = 6 \ end {array} \ right. \).
- Ответ
нет решения
Иногда уравнения в системе представляют собой одну и ту же линию. Поскольку каждая точка на прямой делает оба уравнения истинными, существует бесконечно много упорядоченных пар, которые делают оба уравнения истинными.У системы бесконечно много решений.
Пример \ (\ PageIndex {13} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = 2x-3 \\ -6x + 3y = 9 \ end {array} \ right. \).
- Ответ
Если вы запишете второе уравнение в форме пересечения наклона, вы можете заметить, что уравнения имеют одинаковый наклон и одинаковое пересечение y .
Пример \ (\ PageIndex {14} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = -3x-6 \\ 6x + 2y = -12 \ end {array} \ right.\).
- Ответ
бесконечно много решений
Пример \ (\ PageIndex {15} \)
Решите систему, построив график: \ (\ left \ {\ begin {array} {l} y = \ tfrac {1} {2} x-4 \\ 2x-4y = 16 \ end {array} \ right. \ ).
- Ответ
бесконечно много решений
Когда мы нарисовали вторую линию в последнем примере, мы нарисовали ее прямо над первой линией.Мы говорим, что две строки совпадают с . Совпадающие линии имеют одинаковый наклон и точку пересечения y- .
СОВПАДАЮЩИЕ ЛИНИИ
Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения y- .
Каждая система уравнений в примере и примере имела две пересекающиеся линии. У каждой системы было одно решение.
В примере уравнения давали совпадающие линии, поэтому система имела бесконечно много решений.
Системы в этих трех примерах имели по крайней мере одно решение. Система уравнений, имеющая по крайней мере одно решение, называется согласованной системой .
Система с параллельными линиями, такая как Пример , не имеет решения. Мы называем такую систему уравнений несогласованной. Нет решения.
СОГЛАСОВАННЫЕ И НЕПОСРЕДСТВЕННЫЕ СИСТЕМЫ
Непротиворечивая система уравнений — это система уравнений, имеющая по крайней мере одно решение.
Непоследовательная система уравнений — это система уравнений, не имеющая решения.
Мы также классифицируем уравнения в системе уравнений, называя уравнения независимыми или зависимыми . Если два уравнения независимы, каждое из них имеет собственный набор решений. Пересекающиеся линии и параллельные линии независимы.
Если два уравнения являются зависимыми, все решения одного уравнения также являются решениями другого уравнения.Когда мы строим график двух зависимых уравнений, мы получаем совпадающие линии.
Подведем итог, посмотрев на графики трех типов систем. См. Ниже и таблицу .
| Строки | Пересечение | Параллельный | Совпадение |
|---|---|---|---|
| Количество решений | 1 балл | Нет решения | Бесконечно много |
| Согласованный / непоследовательный | Согласованный | Несоответствие | Согласованный |
| Зависимые / независимые | Независимая | Независимая | Зависимые |
Пример \ (\ PageIndex {16} \)
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
ⓐ \ (\ left \ {\ begin {array} {l} y = 3x − 1 \\ 6x − 2y = 12 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin {array} {l} 2x + y = −3 \\ x − 5y = 5 \ end {array} \ right. \)
- Ответ
ⓐ Сравним наклоны и пересечения двух линий.
\ (\ begin {array} {lll} {} & {} & {\ left \ {\ begin {array} {l} {y = 3x-1} \\ {6x − 2y = 12} \ end {массив } \ right.} \\ {} & {} & {y = 3x-1} \\ {\ text {Первое уравнение уже находится в форме пересечения наклона.}} & {} & {} \\ {\ text {Запишите второе уравнение в форме пересечения наклона.}} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {6x-2y = 12} \\ {} & {} & {- 2y = -6x + 12} \\ {} & { } & {\ frac {-2y} {- 2} = \ frac {-6x + 12} {- 2}} \\ {} & {} & {y = 3x-6} \\ {} & {y = 3x-1} & {y = 3x-6} \\ {} & {m = 3} & {m = 3} \\ {} & {b = -1} & {b = -6} \\ {\ text {Найдите наклон и точку пересечения каждой линии.}} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \ \ {} & {} & {} \\ {} & {\ text {Поскольку наклоны одинаковые, а точки пересечения y}} & {} \\ {} & {\ text {разные, линии параллельны.}} & {} \\ \ end {array} \)
ⓑ Мы сравним наклон и пересечения двух линий.
\ (\ begin {array} {lll} {} & {} & {} \\ {} & {\ left \ {\ begin {array} {l} 2x + y = -3 \\ x-5y = 5 \\ \ end {array} \ right.} & {} \\ {\ text {Запишите оба уравнения в форме углового пересечения.}} & {} & {} \\ {} & {} & {} \\ { } & {} & {} \\ {} & {} & {} \\ {} & {2x + y = -3} & {x-5y = 5} \\ {} & {y = -2x-3 } & {- 5y = -x + 5} \\ {} & {} & {\ frac {-5y} {- 5} = \ frac {-x + 5} {- 5}} \\ {} & { } & {y = \ frac {1} {5} -1} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {} & {} & {} \\ {\ text {Найдите наклон и точку пересечения каждой линии.}} & {} & {} \\ {} & {} & {} \\ {} & {y = -2x-3} & {y = \ frac {1} {5} -1} \\ {} & {m = -2} & {m = \ frac {1} {5}} \\ {} & {b = -3} & {b = -1} \\ {} & {} & {} \\ {} & {\ text {Поскольку уклоны разные, линии пересекаются.}} & {} \\ \ end {array} \)
Система уравнений, графики которой пересекаются, имеет одно решение, непротиворечива и независима.
Пример \ (\ PageIndex {17} \)
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
ⓐ \ (\ left \ {\ begin {array} {l} y = −2x − 4 \\ 4x + 2y = 9 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin {array } {l} 3x + 2y = 2 \\ 2x + y = 1 \ end {array} \ right. \)
- Ответ
ⓐ нет решения, непоследовательное, независимое ⓑ одно решение, последовательное, независимое
Пример \ (\ PageIndex {18} \)
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
ⓐ \ (\ left \ {\ begin {array} {l} y = \ frac {1} {3} x − 5 \\ x − 3y = 6 \ end {array} \ right.\) Ⓑ \ (\ left \ {\ begin {array} {l} x + 4y = 12 \\ −x + y = 3 \ end {array} \ right. \)
- Ответ
ⓐ нет решения, непоследовательное, независимое ⓑ одно решение, последовательное, независимое
Решение систем линейных уравнений с помощью графиков — хороший способ визуализировать типы решений, которые могут возникнуть. Однако во многих случаях решение системы с помощью построения графиков неудобно или неточно. Если графики выходят за пределы маленькой сетки с x и y как между \ (- 10 \), так и 10, построение линий может быть громоздким.И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения с графика.
Решите систему уравнений подстановкой
Теперь решим системы линейных уравнений методом подстановки.
Мы будем использовать ту же систему, которую мы использовали вначале для построения графиков.
\ [\ left \ {\ begin {array} {l} 2x + y = 7 \\ x − 2y = 6 \ end {array} \ right. \ nonumber \]
Сначала мы решим одно из уравнений относительно x или y .Мы можем выбрать любое уравнение и решить любую переменную, но мы постараемся сделать выбор, который упростит работу.
Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение с одной переменной — и мы знаем, как его решить!
После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и решим для другой переменной. Наконец, мы проверяем наше решение и убеждаемся, что оно выполняет оба уравнения.
Пример \ (\ PageIndex {20} \)
Решите систему заменой: \ (\ left \ {\ begin {array} {l} −2x + y = −11 \\ x + 3y = 9 \ end {array} \ right. \)
- Ответ
\ ((6,1) \)
Пример \ (\ PageIndex {21} \)
Решите систему заменой: \ (\ left \ {\ begin {array} {l} 2x + y = −1 \\ 4x + 3y = 3 \ end {array} \ right. \)
- Ответ
\ ((- 3,5) \)
РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ ПОДСТАВКОЙ.
- Решите одно из уравнений для любой переменной.
- Подставьте выражение из шага 1 в другое уравнение.
- Решите полученное уравнение.
- Подставьте решение шага 3 в любое из исходных уравнений, чтобы найти другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Будьте очень осторожны со знаками в следующем примере.
Пример \ (\ PageIndex {22} \)
Решите систему заменой: \ (\ left \ {\ begin {array} {l} 4x + 2y = 4 \\ 6x − y = 8 \ end {array} \ right. \)
- Ответ
Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение относительно y .
Пример \ (\ PageIndex {23} \)
Решите систему заменой: \ (\ left \ {\ begin {array} {l} x − 4y = −4 \\ −3x + 4y = 0 \ end {array} \ right.\)
- Ответ
\ ((2,32) \)
Пример \ (\ PageIndex {24} \)
Решите систему заменой: \ (\ left \ {\ begin {array} {l} 4x − y = 0 \\ 2x − 3y = 5 \ end {array} \ right. \)
- Ответ
\ ((- 12, −2) \)
Решите систему уравнений методом исключения
Мы решили системы линейных уравнений с помощью построения графиков и подстановки.Построение графиков хорошо работает, когда переменные коэффициенты малы, а решение имеет целочисленные значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решали систему с помощью подстановки, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добиться этого.
Метод исключения основан на добавочном свойстве равенства. Свойство сложения равенства говорит, что когда вы добавляете одинаковую величину к обеим сторонам уравнения, вы все равно получаете равенство. Мы расширим свойство сложения равенства, чтобы сказать, что когда вы добавляете равные количества к обеим сторонам уравнения, результаты равны.
Для любых выражений a, b, c, и d .
\ [\ begin {array} {ll} {\ text {if}} & {a = b} \\ {\ text {and}} & {c = d} \\ {\ text {then}} & { а + с = б + г.} \\ \ nonumber \ end {array} \]
Чтобы решить систему уравнений методом исключения, мы начнем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет легче всего устранить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
\ [\ left \ {\ begin {array} {l} 3x + y = 5 \\ \ underline {2x − y = 0} \ end {array} \ right.\ nonumber \]
\ [5x = 5 \ nonumber \]
и складываются с нулем, и мы получаем одно уравнение с одной переменной.
Давайте попробуем еще один:
\ [\ left \ {\ begin {array} x + 4y = 2 \\ 2x + 5y = −2 \ end {array} \ right. \ nonumber \]
На этот раз мы не видим переменную, которая может быть немедленно удалена, если мы добавим уравнения.
Но если мы умножим первое уравнение на \ (- 2 \), мы сделаем коэффициенты при x противоположными.Мы должны умножить каждый член в обеих частях уравнения на \ (- 2 \).
Затем перепишите систему уравнений.
Теперь мы видим, что коэффициенты членов x противоположны, поэтому x будет удалено, когда мы сложим эти два уравнения.
Как только мы получаем уравнение с одной переменной, мы его решаем. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную.И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы увидим, как использовать исключение для решения той же системы уравнений, которую мы решили с помощью построения графиков и подстановки.
Упражнение \ (\ PageIndex {26} \)
Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 3x + y = 5 \\ 2x − 3y = 7 \ end {array} \ right. \)
- Ответ
\ ((2, −1) \)
Упражнение \ (\ PageIndex {27} \)
Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 4x + y = −5 \\ −2x − 2y = −2 \ end {array} \ right.\)
- Ответ
\ ((- 2,3) \)
Шаги перечислены здесь для удобства.
РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ ПУТЕМ ИСКЛЮЧЕНИЯ.
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробными, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную исключить.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположными.
- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение из шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Теперь мы рассмотрим пример, в котором нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Упражнение \ (\ PageIndex {28} \)
Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 4x − 3y = 9 \\ 7x + 2y = −6 \ end {array} \ right. \)
- Ответ
В этом примере мы не можем умножить одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на разные константы, чтобы получить противоположности.
Упражнение \ (\ PageIndex {29} \)
Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 3x − 4y = −9 \\ 5x + 3y = 14 \ end {array} \ right.\)
- Ответ
\ ((1,3) \)
Упражнение \ (\ PageIndex {30} \)
Решите каждую систему методом исключения: \ (\ left \ {\ begin {array} {l} 7x + 8y = 4 \\ 3x − 5y = 27 \ end {array} \ right. \)
- Ответ
\ ((4, −3) \)
Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на ЖК-дисплей всех дробей в уравнении.
Упражнение \ (\ PageIndex {31} \)
Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} x + \ tfrac {1} {2} y = 6 \\ \ tfrac {3} {2} x + \ tfrac {2} { 3} y = \ tfrac {17} {2} \ end {array} \ right. \)
- Ответ
В этом примере в обоих уравнениях есть дроби. Нашим первым шагом будет умножение каждого уравнения на ЖК-дисплей всех дробей в уравнении, чтобы очистить дроби.
Упражнение \ (\ PageIndex {32} \)
Решите каждую систему методом исключения: \ (\ left \ {\ begin {array} {l} \ tfrac {1} {3} x− \ tfrac {1} {2} y = 1 \\ \ tfrac {3} { 4} x − y = \ tfrac {5} {2} \ end {array} \ right.\)
- Ответ
\ ((6,2) \)
Упражнение \ (\ PageIndex {33} \)
Решите каждую систему методом исключения: \ (\ left \ {\ begin {array} {l} x + \ tfrac {3} {5} y = — \ tfrac {1} {5} \\ — \ tfrac {1} { 2} x− \ tfrac {2} {3} y = \ tfrac {5} {6} \ end {array} \ right. \)
- Ответ
\ ((1, −2) \)
Когда мы решили систему с помощью построения графиков, мы увидели, что не все системы линейных уравнений имеют единственную упорядоченную пару в качестве решения.Когда два уравнения действительно представляли собой одну и ту же линию, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные линии, решения не было. Мы назвали это несовместимой системой.
То же самое и с заменой или исключением. Если уравнение в конце замены или исключения является истинным утверждением, у нас есть непротиворечивая, но зависимая система, а система уравнений имеет бесконечно много решений. Если уравнение в конце замены или исключения является ложным утверждением, мы имеем несовместимую систему и система уравнений не имеет решения.
Упражнение \ (\ PageIndex {34} \)
Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ y = 3− \ tfrac {3} {4} x \ end {array} \ right. \ )
- Ответ
\ (\ begin {array} {ll} {} & {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ y = 3− \ frac {3} {4} x \ end { array} \ right.} \\ {} & {} \\ {\ text {Запишите второе уравнение в стандартной форме.}} & {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ \ frac {3} {4} x + y = 3 \ end {array} \ right.} \\ {} & {} \\ {\ text {Очистите дроби, умножив} \\ \ text {второе уравнение на 4.}} & {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ 4 (\ frac {3} {4} x + y) = 4 (3) \ end {array} \ right. } \\ {} & {} \\ {\ text {Упростить.}} & {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ 3x + 4y = 12 \ end {array} \ верно. } \\ {} & {} \\ {\ text {Чтобы исключить переменную, мы умножаем второе уравнение} \\ \ text {на -1. Упростите и добавьте.}} & {\ Begin {array} {l} {\ left \ {\ begin {array} {l} 3x + 4y = 12 \\ \ underline {-3x-4y = -12} \ end { массив} \ право.} \\ {\ hspace {16mm} 0 = 0} \ end {array}} \\ \ end {array} \)
Это верное заявление. Уравнения непротиворечивы, но зависимы. Их графики будут одной линией. У системы бесконечно много решений.
После того, как мы очистили дроби во втором уравнении, заметили ли вы, что эти два уравнения совпадают? Это означает, что у нас есть совпадающие линии.
Упражнение \ (\ PageIndex {35} \)
Решите систему методом исключения: \ (\ left \ {\ begin {array} {l} 5x − 3y = 15 \\ 5y = −5 + \ tfrac {5} {3} x \ end {array} \ right.\)
- Ответ
бесконечно много решений
Упражнение \ (\ PageIndex {36} \)
Решите систему путем исключения: \ (\ left \ {\ begin {array} {l} x + 2y = 6 \\ y = — \ tfrac {1} {2} x + 3 \ end {array} \ right. \)
- Ответ
бесконечно много решений
Выберите наиболее удобный метод решения системы линейных уравнений
Когда вы решаете систему линейных уравнений в приложении, вам не сообщат, какой метод использовать.Вам нужно будет принять это решение самостоятельно. Так что вы захотите выбрать самый простой метод, который сводит к минимуму ваши шансы на ошибку.
\ [\ textbf {Выберите наиболее удобный метод для решения системы линейных уравнений} \\ \ begin {array} {lll} {\ underline {\ textbf {Graphing}}} & {\ underline {\ textbf {Substitution} }} & {\ underline {\ textbf {Исключение}}} \\ {\ text {Используется, когда вам нужно}} & {\ text {Используется, когда одно уравнение равно}} & {\ text {Используется, когда уравнения a} } \\ {\ text {картина ситуации.}} & {\ text {уже решено или может быть}} & {\ text {переустановить стандартную форму.}} \\ {\ text {}} & {\ text {легко решено для одного}} & {\ text {} } \\ {\ text {}} & {\ text {переменная.}} & {\ text {}} \\ \ end {array} \ nonumber \]
Пример \ (\ PageIndex {37} \)
Решите для каждой системы линейных уравнений, что удобнее решить: заменой или исключением. Поясните свой ответ.
ⓐ \ (\ left \ {\ begin {array} {l} 3x + 8y = 40 \\ 7x − 4y = −32 \ end {array} \ right.\) Ⓑ \ (\ left \ {\ begin {array} {l} 5x + 6y = 12 \\ y = \ tfrac {2} {3} x − 1 \ end {array} \ right. \)
- Ответ
ⓐ
\ [\ left \ {\ begin {array} {l} 3x + 8y = 40 \\ 7x − 4y = −32 \ end {array} \ right. \ Nonumber \]
Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.
ⓑ
\ [\ left \ {\ begin {array} {l} 5x + 6y = 12 \\ y = \ tfrac {2} {3} x − 1 \ end {array} \ right. \ Nonumber \]
Поскольку одно уравнение уже решено относительно y , использование подстановки будет наиболее удобным.
Пример \ (\ PageIndex {38} \)
Для каждой системы линейных уравнений решите, что удобнее будет решить заменой или исключением. Поясните свой ответ.
ⓐ \ (\ left \ {\ begin {array} {l} 4x − 5y = −32 \\ 3x + 2y = −1 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin { массив} {l} x = 2y − 1 \\ 3x − 5y = −7 \ end {array} \ right. \)
- Ответ
ⓐ Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.Ⓑ Поскольку одно уравнение уже решено для x , использование подстановки будет наиболее удобным.
Пример \ (\ PageIndex {39} \)
Для каждой системы линейных уравнений решите, что удобнее будет решить заменой или исключением. Поясните свой ответ.
ⓐ \ (\ left \ {\ begin {array} {l} y = 2x − 1 \\ 3x − 4y = −6 \ end {array} \ right. \) Ⓑ \ (\ left \ {\ begin {array } {l} 6x − 2y = 12 \\ 3x + 7y = −13 \ end {array} \ right. \)
- Ответ
ⓐ Поскольку одно уравнение уже решено относительно и , использование подстановки будет наиболее удобным.Ⓑ Поскольку оба уравнения имеют стандартную форму, использование исключения будет наиболее удобным.
Ключевые понятия
- Как решить систему линейных уравнений с помощью построения графиков.
- Изобразите первое уравнение.
- Постройте второе уравнение в той же прямоугольной системе координат.
- Определите, пересекаются ли линии, параллельны или совпадают.
- Определите решение системы.
Если линии пересекаются, укажите точку пересечения. Это решение системы.
Если линии параллельны, у системы нет решения.
Если линии совпадают, система имеет бесконечное количество решений. - Проверьте решение в обоих уравнениях.
- Как решить систему уравнений подстановкой.
- Решите одно из уравнений для любой переменной.
- Подставьте выражение из шага 1 в другое уравнение.
- Решите полученное уравнение.
- Подставьте решение шага 3 в любое из исходных уравнений, чтобы найти другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
- Как решить систему уравнений методом исключения.
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробными, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
Решите, какую переменную исключить.
Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположными. - Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение из шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений. \ [\ textbf {Выберите наиболее удобный метод для решения системы линейных уравнений} \\ \ begin {array} {lll} {\ underline {\ textbf {Graphing}}} & {\ underline {\ textbf {Substitution}} } & {\ underline {\ textbf {Устранение}}} \\ {\ text {}} & {\ text {Используется, когда одно уравнение равно}} & {\ text {}} \\ {\ text {Используется, когда вам нужно a}} & {\ text {уже решено или может быть}} & {\ text {Используйте, когда уравнения a}} \\ {\ text {изображение ситуации.}} & {\ text {легко решается для одного}} & {\ text {переустановить стандартную форму.}} \\ {\ text {}} & {\ text {variable.}} & {\ text {}} \\ \ конец {массив} \ nonumber \]
Глоссарий
- совпадающих линий
- Совпадающие линии имеют одинаковый наклон и одинаковое пересечение y .
- согласованные и несовместимые системы
- Согласованная система уравнений — это система уравнений, имеющая по крайней мере одно решение; Несогласованная система уравнений — это система уравнений, не имеющая решения.
- решения системы уравнений
- Решениями системы уравнений являются значения переменных, которые делают все уравнения истинными; Решение представлено упорядоченной парой (x, y). (x, y).
- система линейных уравнений
- Когда два или более линейных уравнения группируются вместе, они образуют систему линейных уравнений.
Решайте системы уравнений методом исключения — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решите систему уравнений методом исключения
- Решите приложения систем уравнений методом исключения
- Выберите наиболее удобный способ решения системы линейных уравнений
Мы решили системы линейных уравнений с помощью построения графиков и подстановки.Построение графиков хорошо работает, когда переменные коэффициенты малы, а решение имеет целочисленные значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решали систему с помощью подстановки, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добиться этого.
Решите систему уравнений методом исключения
Метод исключения основан на добавочном свойстве равенства. Свойство сложения равенства говорит, что когда вы добавляете одинаковую величину к обеим сторонам уравнения, вы все равно получаете равенство. Мы расширим свойство сложения равенства, чтобы сказать, что когда вы добавляете равные количества к обеим сторонам уравнения, результаты равны.
Для любых выражений a , b , c и d ,
Чтобы решить систему уравнений методом исключения, мы начнем с обоих уравнений в стандартной форме.Затем мы решаем, какую переменную будет легче всего устранить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
и складываются с нулем, и мы получаем одно уравнение с одной переменной.
Давайте попробуем еще один:
На этот раз мы не видим переменную, которая может быть немедленно удалена, если мы добавим уравнения.
Но если мы умножим первое уравнение на −2, мы сделаем коэффициенты при x противоположными. Мы должны умножить каждый член в обеих частях уравнения на −2.
Теперь мы видим, что коэффициенты членов x противоположны, поэтому x будет удалено, когда мы сложим эти два уравнения.
Сложите уравнения самостоятельно — результат должен быть −3 y = −6. И это кажется несложным, не так ли? Вот как бы это выглядело.
Сделаем еще один:
Не похоже, чтобы коэффициенты одной переменной были противоположными, умножая одно из уравнений на константу, если мы не используем дроби. Поэтому вместо этого нам придется умножить оба уравнения на константу.
Мы можем сделать коэффициенты x противоположными, если умножим первое уравнение на 3, а второе на −4, так что мы получим 12 x и −12 x .
Это дает нам два новых уравнения:
Когда мы складываем эти уравнения,
, x удаляются, и мы получаем −29 y = 58.
Как только мы получаем уравнение с одной переменной, мы его решаем. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы увидим, как использовать исключение для решения той же системы уравнений, которую мы решили с помощью построения графиков и подстановки.
Как решить систему уравнений методом исключения
Решите систему устранением.
Решите систему устранением.
Решите систему устранением.
Шаги перечислены ниже для удобства.
Как решить систему уравнений методом исключения.
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробными, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную исключить.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположными.
- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение из шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Сначала мы приведем пример, в котором мы можем сразу исключить одну переменную.
Решите систему устранением.
Решите систему устранением.
Решите систему устранением.
На (Рисунок) мы сможем сделать коэффициенты одной переменной противоположными, умножив одно уравнение на константу.
Решите систему устранением.
Решите систему устранением.
Решите систему устранением.
Теперь мы рассмотрим пример, в котором нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Решите систему устранением.
Решение
В этом примере мы не можем умножить одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на константу, чтобы получить противоположности.
Какие еще константы мы могли бы выбрать для исключения одной из переменных? Будет ли решение таким же?
Решите систему устранением.
Решите систему устранением.
Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на его ЖК-дисплей.
Решите систему устранением.
Решение
В этом примере в обоих уравнениях есть дроби. Нашим первым шагом будет умножение каждого уравнения на его ЖК-дисплей, чтобы очистить дроби.
Решите систему устранением.
Решите систему устранением.
В разделе «Решение систем уравнений с помощью графического представления» мы увидели, что не все системы линейных уравнений имеют единственную упорядоченную пару в качестве решения. Когда два уравнения действительно представляли собой одну и ту же линию, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные линии, решения не было. Мы назвали это несовместимой системой.
Решите систему устранением.
Решение
Это верное заявление. Уравнения непротиворечивы, но зависимы. Их графики будут одной линией. У системы бесконечно много решений.
После того, как мы очистили дроби во втором уравнении, заметили ли вы, что эти два уравнения совпадают? Это означает, что у нас есть совпадающие линии.
Решите систему устранением.
бесконечно много решений
Решите систему устранением.
бесконечно много решений
Решите систему устранением.
Решение
| Уравнения имеют стандартную форму. | |
| Умножьте второе уравнение на 3, чтобы исключить переменную. | |
| Упростить и сложить. |
Это утверждение не соответствует действительности. Уравнения несовместимы, поэтому их графики будут параллельными линиями.
В системе нет решения.
Решите систему устранением.
Решите систему устранением.
Практика ведет к совершенству
Решите систему уравнений методом исключения
В следующих упражнениях решите системы уравнений методом исключения.
бесконечно много решений
бесконечно много решений
бесконечно много решений
непоследовательно, нет решения
непоследовательно, нет решения
Решение приложений систем уравнений методом исключения
В следующих упражнениях переведите в систему уравнений и решите.
Сумма двух чисел равна 65. Их разница равна 25. Найдите числа.
Цифры 20 и 45.
Сумма двух чисел равна 37. Их разница равна 9. Найдите числа.
Сумма двух чисел равна −27. Их разница -59. Найдите числа.
Цифры 16 и −43.
Сумма двух чисел равна -45. Их разница -89. Найдите числа.
Андреа покупает новые рубашки и свитера.Она может купить 3 рубашки и 2 свитера за 114 фунтов стерлингов или 2 рубашки и 4 свитера за 164 евро. Сколько стоит рубашка? Сколько стоит свитер?
Рубашка стоит 16 фунтов, свитер — 33 евро.
Питер покупает канцелярские товары. Он может купить 3 пакета бумаги и 4 степлера за 40 фунтов стерлингов или 5 пакетов бумаги и 6 степлеров за 62 фунта стерлингов. Сколько стоит пачка бумаги? Сколько стоит степлер?
Общее количество натрия в 2 хот-догах и 3 стаканах творога составляет 4720 мг.Общее количество натрия в 5 хот-догах и 2 стаканах творога составляет 6300 мг. Сколько натрия в хот-доге? Сколько натрия в стакане творога?
В хот-доге 860 мг. В стакане творога 1000 мг.
Общее количество калорий в 2 хот-догах и 3 чашках творога составляет 960 калорий. Общее количество калорий в 5 хот-догах и 2 стаканах творога составляет 1190 калорий. Сколько калорий в хот-доге? Сколько калорий в стакане творога?
Выберите наиболее удобный метод решения системы линейных уравнений
В следующих упражнениях решите, что было бы удобнее решить систему уравнений путем подстановки или исключения.
ⓐ
ⓐ выбывание ⓑ замена
ⓐ
ⓐ
ⓐ замена ⓑ выбывание
ⓐ
Повседневная математика
Джози хочет приготовить 10 фунтов смеси для троп из орехов и изюма, и она хочет, чтобы общая стоимость смеси для трейлов составила 54 фунта стерлингов. Орехи стоят 6 фунтов за фунт, а изюм — 3 фунта за фунт. Решите систему, чтобы найти количество фунтов орехов и количество фунтов изюма, которые ей следует использовать.
Письменные упражнения
Решите систему
ⓐ путем замены
ⓑ путем построения графика
ⓒ Какой метод вы предпочитаете? Почему?
- ⓐ (8, 2)
- ⓑ
- ⓒ Ответы будут разными.
Решите систему
ⓐ путем замены
ⓑ путем построения графика
ⓒ Какой метод вы предпочитаете? Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Math Обзор решения систем линейных уравнений
Обзор
Системы линейных уравнений могут быть решены другими методами, кроме построения графиков, такими как подстановка и исключение. При решении методом исключения некоторые системы можно решить сложением, вычитанием и умножением.
Решение уравнений подстановкой
Некоторые системы линейных уравнений могут быть решены путем решения сначала для одной переменной, а затем подстановки этого значения в систему для решения для другой переменной.Предположим, что уравнения в системе имеют вид y = 2x и y = x +5. Оба уравнения системы уже были записаны через y. Затем подставьте значение 2x вместо y во втором уравнении, чтобы читать 2x = x +5. Вычтем x из обеих частей уравнения, так что 2x-x = x-x +5. Тогда x равно 5. Если y = 2 (5), то y равно 10 в первом уравнении. Во втором уравнении 10 = 5 +5. Упорядоченная пара, решающая систему, — это (5, 10).
Другой пример
Предположим, что уравнения в системе равны 2x + y = 5 и y = x -4.Второе уравнение записывается через y, поэтому его можно заменить как 2x + x -4 = 5 или 3x -4 = 5 или 3x -4 +4 = 5 +4 или 3x = 9. Разделив обе стороны на 3, 3x / 3 = 9/3 или x = 3. Следовательно, 6 + y = 5 и y = 3-4. Если y = 3-4, y равно -1 во втором уравнении. Переменная y также равна -1 в первом уравнении, так как 6-1 равно 5.
Решение систем методом исключения
При решении систем уравнений методом исключения оба уравнения в системе складываются. Уравнения сбалансированы таким образом, что исключена одна переменная.Два дополнительных шага выполняются перед тем, как значение одной переменной может быть заменено для решения другой. Подобные термины выровнены, так что можно исключить одну переменную. Всегда проверяйте значения переменных в обоих уравнениях, чтобы убедиться, что решение правильное, потому что оба уравнения в системе должны быть решены, чтобы решение было правильным. Предположим, что уравнения в системе следующие: x-2y = -19 и 5x + 2y = 1. Подобные члены уже выровнены, так что x + 5x + 2y -2y = -19 +1. Тогда 6x = -18, потому что значения y отменены.Значение 6x / 6 = -18/6 или x = -3. Затем подставьте -3 -2y = -19 или -2y = -16, или y = 8. Аналогично, 5 (-3) + 2 (8) = 1.
Другой пример использования умножения
Предположим, что уравнения имеют вид 2x + y = 3 и –x + 3y = -12. Несмотря на то, что одинаковые термины выровнены, одна переменная не может быть удалена за один шаг при добавлении уравнений. Обе части уравнения должны быть умножены на константу, прежде чем уравнения могут быть добавлены, так что 2 (-x + 3y = -12) равно -2x + 6y = -24.Комбинируя уравнения, получаем 2x-2x + y + 6y = 3-24. Тогда 7y = -21 или y = -3. Если 2x -3 равно 3, то 2x = 6 и x равно 3, а -3 + -9 = -12.
Заинтересованы в услугах репетиторства по математике? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.
SchoolTutoring Academy — ведущая компания в области образовательных услуг для школьников и школьников. Мы предлагаем учебные программы для учащихся K-12, AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и ученикам в Мэдисоне, Висконсин: посетите: Репетиторство в Мэдисоне, Висконсин
WTAMU > Виртуальная математическая лаборатория> Алгебра среднего уровня Цели обучения
Введение
Учебник
Нужна дополнительная помощь по этим темам? |
Системы уравнений с двумя переменными
Введение в системы уравнений
Система уравнений состоит из двух или более уравнений с двумя или более переменными, где любое решение должно одновременно удовлетворять всем уравнениям в системе.
Цели обучения
Объясните, какие системы уравнений могут представлять
Основные выводы
Ключевые моменты
- Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
- Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.
- Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных.
- Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара [латекс] (x, y) [/ latex], которая удовлетворяет каждому уравнению независимо. Графически решения — это точки пересечения линий.
Ключевые термины
- Система линейных уравнений : Набор из двух или более уравнений, состоящих из двух или более переменных, которые рассматриваются одновременно.
- зависимая система : система линейных уравнений, в которой два уравнения представляют
одну и ту же линию; существует бесконечное количество решений зависимой системы. - несовместимая система : Система линейных уравнений без общего решения, потому что они
представляют собой параллельные линии, которые не имеют общих точек или прямых. - независимая система : Система линейных уравнений с ровно одной парой решений [latex] (x, y) [/ latex].
Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям системы одновременно.Некоторые линейные системы могут не иметь решения, в то время как другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных. Даже в этом случае это не гарантирует уникального решения.
В этом разделе мы сосредоточимся в первую очередь на системах линейных уравнений, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными:
[латекс] 2x + y = 15 \ 3x — y = 5 [/ латекс]
Решение системы линейных уравнений с двумя переменными — это любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо.В этом примере упорядоченная пара (4, 7) является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
[латекс] 2 (4) + 7 = 15 \\ 3 (4) — 7 = 5 [/ латекс]
Оба эти утверждения верны, поэтому [latex] (4, 7) [/ latex] действительно является решением системы уравнений.
Обратите внимание, что система линейных уравнений может содержать более двух уравнений и более двух переменных.Например,
[латекс] 3x + 2y — z = 12 \\ x — 2y + 4z = -2 \\ -x + 12y -z = 0 [/ латекс]
— это система трех уравнений с тремя переменными [латекс] x, y, z [/ latex]. Решение системы выше дается
[латекс] x = 1 \ y = -2 \ z = — 2 [/ латекс]
, поскольку он делает все три уравнения действительными.
Типы линейных систем и их решения
В общем, линейная система может вести себя одним из трех возможных способов:
- В системе есть единственное уникальное решение.
- В системе нет решения .
- В системе есть бесконечно много решений .
Каждая из этих возможностей представляет собой определенный тип системы линейных уравнений с двумя переменными. Каждый из них может отображаться графически, как показано ниже. Обратите внимание, что решение системы линейных уравнений — это любая точка, в которой линии пересекаются.
Системы линейных уравнений: Графические представления трех типов систем.
Независимая система имеет ровно одну пару решений [latex] (x, y) [/ latex]. Точка пересечения двух линий — единственное решение.
Непоследовательная система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекутся.
У зависимой системы бесконечно много решений. Линии точно такие же, поэтому каждая пара координат на линии является решением обоих уравнений.
Графическое решение систем
Простой способ решить систему уравнений — это найти точку или точки пересечения уравнений.Это графический метод.
Цели обучения
Графическое решение системы уравнений с двумя переменными
Основные выводы
Ключевые моменты
- Чтобы решить систему уравнений графически, нарисуйте уравнения и укажите точки пересечения как решения. У системы уравнений может быть несколько решений.
- Система линейных уравнений будет иметь одну точку пересечения или одно решение.
- Чтобы построить график системы уравнений, записанных в стандартной форме, вы должны переписать уравнения в форме пересечения углов наклона.
Ключевые термины
- Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
- Графический метод : способ визуального поиска набора значений, который решает систему уравнений.
Система уравнений (также известная как одновременные уравнения) — это система уравнений с несколькими переменными, решаемая, когда значения всех переменных одновременно удовлетворяют всем уравнениям.Наиболее распространенные способы решения системы уравнений:
- Графический метод
- Метод замещения
- Метод исключения
Здесь мы обратимся к графическому методу.
Графическое решение систем
Некоторые системы имеют только один набор правильных ответов, в то время как другие имеют несколько наборов, которые удовлетворяют всем уравнениям. Графически показано, что набор уравнений, решенных только с одним набором ответов, будет иметь только одну точку пересечения, как показано ниже.Эта точка считается решением системы уравнений. В наборе линейных уравнений (например, на изображении ниже) есть только одно решение.
Система линейных уравнений с двумя переменными : Этот график показывает систему уравнений с двумя переменными и только одним набором ответов, который удовлетворяет обоим уравнениям.
Система с двумя наборами ответов, которые удовлетворяют обоим уравнениям, имеет две точки пересечения (таким образом, два решения системы), как показано на изображении ниже.
Система уравнений с несколькими ответами: Это пример системы уравнений, показанной графически, которая имеет два набора ответов, которые удовлетворяют обоим уравнениям в системе.
Преобразование в форму пересечения уклона
Прежде чем успешно решить систему графически, необходимо понять, как графически отображать уравнения, записанные в стандартной форме, или [latex] Ax + By = C [/ latex]. Вы всегда можете использовать графический калькулятор для графического представления уравнений, но полезно знать, как самостоятельно формулировать такие уравнения.
Для этого необходимо преобразовать уравнения в форму пересечения наклона или [латекс] y = mx + b [/ latex], где м = наклон и b = пересечение по оси y.
Лучший способ преобразовать уравнение в форму пересечения наклона — сначала выделить переменную y , а затем разделить правую часть на B , как показано ниже.
[латекс] \ begin {align} \ displaystyle Ax + By & = C \\ By & = — Ax + C \\ y & = \ frac {-Ax + C} {B} \\ y & = — \ frac {A} { B} x + \ frac {C} {B} \ end {align} [/ latex]
Теперь [latex] \ displaystyle — \ frac {A} {B} [/ latex] — это уклон м, и [latex] \ displaystyle \ frac {C} {B} [/ latex] — точка пересечения по оси Y б .
Определение решений на графике
После того, как вы преобразовали уравнения в форму с пересечением наклона, вы можете построить графики уравнений. Чтобы определить решения системы уравнений, определите точки пересечения между графическими уравнениями. Упорядоченная пара, которая представляет собой пересечение (я), представляет собой решение (я) системы уравнений.
Метод замены
Метод подстановки — это способ решения системы уравнений путем выражения уравнений только с помощью одной переменной.
Цели обучения
Решите системы уравнений с двумя переменными с помощью подстановки
Основные выводы
Ключевые моменты
- Система уравнений — это система уравнений, которая может быть решена с использованием определенного набора значений.
- Метод подстановки работает, выражая одну из переменных через другую, затем подставляя ее обратно в исходное уравнение и упрощая его.
- Очень важно проверить свою работу после того, как вы нашли набор значений для переменных.Сделайте это, подставив найденные вами значения обратно в исходные уравнения.
- Решение системы уравнений можно записать в виде упорядоченной пары ( x , y ).
Ключевые термины
- метод подстановки : Метод решения системы уравнений путем выражения уравнения только одной переменной
- Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Метод замены для решения систем уравнений — это способ упростить систему уравнений, выразив одну переменную через другую, тем самым удалив одну переменную из уравнения. Когда полученное упрощенное уравнение имеет только одну переменную, с которой можно работать, уравнение становится разрешимым.
Метод замещения состоит из следующих шагов:
- В первом уравнении решите одну из переменных через другие.
- Подставьте это выражение в остальные уравнения.
- Продолжайте, пока не сведете систему к одному линейному уравнению.
- Решите это уравнение, а затем выполняйте обратную замену, пока решение не будет найдено.
Решение методом подстановки
Попрактикуемся в этом, решив следующую систему уравнений:
[латекс] x-y = -1 [/ латекс]
[латекс] x + 2y = -4 [/ латекс]
Начнем с решения первого уравнения, чтобы выразить x через y .
[латекс] \ begin {align} \ displaystyle x-y & = — 1 \\ x & = y-1 \ end {align} [/ latex]
Затем мы заменим наше новое определение x во второе уравнение:
[латекс] \ displaystyle \ begin {align} x + 2y & = — 4 \\ (y-1) + 2y & = — 4 \ end {align} [/ latex]
Обратите внимание, что теперь это уравнение имеет только одну переменную (y). Затем мы можем упростить это уравнение и решить относительно y :
[латекс] \ displaystyle \ begin {align} (y-1) + 2y & = — 4 \\ 3y-1 & = — 4 \\ 3y & = — 3 \\ y & = — 1 \ end {align} [/ latex]
Теперь, когда мы знаем значение y , мы можем использовать его, чтобы найти значение другой переменной, x. Для этого подставьте значение y в первое уравнение и решите относительно x .
[латекс] \ displaystyle \ begin {align} x-y & = — 1 \\ x — (- 1) & = — 1 \\ x + 1 & = — 1 \\ x & = — 1-1 \\ x & = — 2 \ end {align} [/ latex]
Таким образом, решение системы: [latex] (- 2, -1) [/ latex], то есть точка, где две функции графически пересекаются. Проверьте решение, подставив значения в одно из уравнений.
[латекс] \ displaystyle \ begin {align} x-y & = — 1 \\ (- 2) — (- 1) & = — 1 \\ — 2 + 1 & = — 1 \\ — 1 & = — 1 \ end {align} [/ латекс]
Метод исключения
Метод исключения используется для исключения переменной, чтобы упростить поиск оставшейся переменной (переменных) в системе уравнений.
Цели обучения
Решите системы уравнений с двумя переменными методом исключения
Основные выводы
Ключевые моменты
- Этапы метода исключения следующие: (1) составить уравнения так, чтобы переменные выровнялись, (2) изменить одно уравнение, чтобы оба уравнения использовали согласованную переменную, которую можно исключить, (3) сложить уравнения, чтобы исключить переменную, (4) решить и (5) выполнить обратную замену для поиска другой переменной.
- Всегда проверяйте ответ.Это делается путем включения обоих значений в одно или оба исходных уравнения.
Ключевые термины
- метод исключения : процесс решения системы уравнений путем исключения одной переменной для более простого решения оставшейся переменной.
- Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Метод исключения для решения систем уравнений, также известный как исключение сложением , представляет собой способ исключения одной из переменных в системе, чтобы более просто оценить оставшуюся переменную.После успешного нахождения значений остальных переменных они подставляются в исходное уравнение, чтобы найти правильное значение для другой переменной.
Метод исключения состоит из следующих шагов:
- Перепишите уравнения так, чтобы переменные выровнялись.
- Измените одно уравнение так, чтобы оба уравнения имели переменную, которая компенсировалась бы при сложении уравнений.
- Добавьте уравнения и удалите переменную.
- Найдите оставшуюся переменную.
- Обратно подставить и решить для другой переменной.
Решение методом исключения
Метод исключения можно продемонстрировать на простом примере:
[латекс] \ displaystyle 4x + y = 8 \\ 2y + x = 9 [/ латекс]
Сначала выровняйте переменные, чтобы уравнения можно было легко сложить на более позднем этапе:
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ x + 2y & = 9 \ end {align} [/ latex]
Затем посмотрите, не настроены ли уже какие-либо переменные таким образом, что их сложение приведет к их исключению из системы.Если нет, умножьте одно уравнение на число, позволяющее компенсировать переменные. В этом примере переменную y можно исключить, если мы умножим верхнее уравнение на [латекс] -2 [/ латекс], а затем сложим уравнения.
Шаг умножения:
[латекс] \ displaystyle \ begin {align} -2 (4x + y & = 8) \\ x + 2y & = 9 \ end {align} [/ latex]
Результат:
[латекс] \ displaystyle \ begin {align} -8x-2y & = — 16 \\ x + 2y & = 9 \ end {align} [/ latex]
Теперь добавьте уравнения, чтобы исключить переменную y .
[латекс] \ displaystyle \ begin {align} -8x + x-2y + 2y & = — 16 + 9 \\ — 7x & = — 7 \ end {align} [/ latex]
Наконец, найдите переменную x .
[латекс] \ displaystyle \ begin {align} -7x & = — 7 \\ x & = \ frac {-7} {- 7} \\ x & = 1 \ end {align} [/ latex]
Затем вернитесь к одному из исходных уравнений и замените найденное нами значение на x . Проще всего выбрать простейшее уравнение, но подойдет любое уравнение.
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ 4 (1) + y & = 8 \\ 4 + y & = 8 \\ y & = 4 \ end {align} [/ latex]
Следовательно, решение уравнения (1,4).Всегда важно проверить ответ, подставив оба этих значения вместо соответствующих переменных в одно из уравнений.
[латекс] \ displaystyle \ begin {align} 4x + y & = 8 \\ 4 (1) + 4 & = 8 \\ 4 + 4 & = 8 \\ 8 & = 8 \ end {align} [/ latex]
Несогласованные и зависимые системы с двумя переменными
Для линейных уравнений с двумя переменными несовместные системы не имеют решений, а зависимые системы имеют бесконечно много решений.
Цели обучения
Объясните, когда системы уравнений с двумя переменными несовместимы или зависимы как графически, так и алгебраически.
Основные выводы
Ключевые моменты
- Графически уравнения в зависимой системе представляют собой одну и ту же линию. Уравнения в противоречивой системе представляют собой параллельные линии, которые никогда не пересекаются.
- Мы можем использовать методы решения систем уравнений для выявления зависимых и несовместимых систем: зависимые системы имеют бесконечное количество решений. Применение методов решения систем уравнений приведет к истинному тождеству, например [латекс] 0 = 0 [/ латекс].Несогласованные системы не имеют решений. Применение методов решения систем уравнений приведет к противоречию, например к утверждению [латекс] 0 = 1 [/ латекс].
Ключевые термины
- несовместимая система : Система линейных уравнений без общего решения, потому что они
представляют собой параллельные линии, у которых нет общих точек или прямых. - независимая система : Система линейных уравнений с ровно одной парой решений.
- зависимая система : система линейных уравнений, в которой два уравнения представляют
одну и ту же линию; существует бесконечное количество решений зависимой системы.
Напомним, что линейная система может вести себя одним из трех возможных способов:
- Система имеет единственное уникальное решение.
- В системе нет решения.
- В системе бесконечно много решений.
Также напомним, что каждая из этих возможностей соответствует типу системы линейных уравнений с двумя переменными. Независимая система уравнений имеет ровно одно решение [latex] (x, y) [/ latex]. Несогласованная система не имеет решения, а зависимая система имеет бесконечное количество решений.
В предыдущих модулях обсуждалось, как найти решение для независимой системы уравнений. Теперь мы сосредоточимся на выявлении зависимых и несовместимых систем линейных уравнений.
Зависимые системы
Уравнения линейной системы независимы , если ни одно из уравнений не может быть получено алгебраически из других. Когда уравнения независимы, каждое уравнение содержит новую информацию о переменных, и удаление любого из уравнений увеличивает размер набора решений.Системы, которые не являются независимыми, по определению являются зависимыми . Уравнения в зависимой системе могут выводиться друг из друга; они описывают одну и ту же линию. Они не добавляют новую информацию о переменных, и потеря уравнения из зависимой системы не изменяет размер набора решений.
Мы можем применять методы замены или исключения для решения систем уравнений, чтобы идентифицировать зависимые системы. Зависимые системы имеют бесконечное количество решений, потому что все точки на одной линии также находятся на другой линии.После использования замены или добавления результирующее уравнение будет идентичным, например [латекс] 0 = 0 [/ латекс].
Например, рассмотрим два уравнения
[латекс] 3x + 2y = 6 \ 6x + 4y = 12 [/ латекс]
Мы можем применить метод исключения для их оценки. Если бы мы умножили первое уравнение на коэффициент [латекс] -2 [/ латекс], мы получили бы:
[латекс] \ displaystyle \ begin {align} -2 (3x + 2y & = 6) \\ — 6x-4y & = — 12 \ end {align} [/ latex]
Добавление этого ко второму уравнению даст [латекс] 0 = 0 [/ латекс].Таким образом, две линии зависимы. Также обратите внимание, что это одно и то же уравнение, увеличенное в два раза; другими словами, второе уравнение может быть получено из первого.
На графике два уравнения дают идентичные линии, как показано ниже.
Зависимая система : Уравнения [латекс] 3x + 2y = 6 [/ latex] и [latex] 6x + 4y = 12 [/ latex] являются зависимыми, и при отображении на графике они образуют одну и ту же линию.
Обратите внимание, что существует бесконечное количество решений для зависимой системы, и эти решения относятся к общей линии.
Несогласованные системы
Линейная система непротиворечива, если у нее есть решение, и непоследовательна в противном случае. Напомним, что графическое представление несовместимой системы состоит из параллельных линий, которые имеют одинаковый наклон, но разные точки пересечения [latex] y [/ latex]. Они никогда не пересекутся.
Мы также можем применять методы решения систем уравнений для выявления несовместимых систем. Когда система несовместима, можно вывести противоречие из уравнений, например, утверждение [латекс] 0 = 1 [/ латекс].
Рассмотрим следующие два уравнения:
[латекс] 3x + 2y = 6 \ 3x + 2y = 12 [/ латекс]
Мы можем применить метод исключения, чтобы попытаться решить эту систему. Вычитая первое уравнение из второго, обе переменные удаляются, и мы получаем [латекс] 0 = 6 [/ латекс]. Это противоречие, и мы можем определить, что это несовместимая система. Графики этих уравнений на плоскости [latex] xy [/ latex] представляют собой пару параллельных линий.
Несогласованная система: Уравнения [латекс] 3x + 2y = 6 [/ latex] и [латекс] 3x + 2y = 12 [/ latex] несовместимы.
В общем случае несоответствия возникают, если левые части уравнений в системе линейно зависимы, а постоянные члены не удовлетворяют соотношению зависимости. Система уравнений, левые части которой линейно независимы, всегда непротиворечива.
Приложения систем уравнений
Системы уравнений могут использоваться для решения многих реальных задач, в которых несколько ограничений используются для одних и тех же переменных.
Цели обучения
Применение систем уравнений с двумя переменными к реальным примерам
Основные выводы
Ключевые моменты
- Если у вас есть проблема, которая включает несколько переменных, вы можете решить ее, создав систему уравнений.
- После определения переменных определите отношения между ними и запишите их в виде уравнений.
Ключевые термины
- Система уравнений : Набор уравнений с несколькими переменными, которые могут быть решены с использованием определенного набора значений.
Системы уравнений в реальном мире
Система уравнений, также известная как одновременные уравнения, представляет собой набор уравнений с несколькими переменными. Ответ на систему уравнений — это набор значений, который удовлетворяет всем уравнениям в системе, и таких ответов может быть много для любой данной системы.Ответы обычно записываются в виде упорядоченной пары: [латекс] \ left (x, y \ right) [/ latex]. Подходы к решению системы уравнений включают замену и исключение, а также графические методы.
Существует несколько практических приложений систем уравнений. Они подробно показаны ниже.
Планирование мероприятия
Система уравнений может использоваться для решения задачи планирования, где необходимо учитывать несколько ограничений:
Эмили устраивает большую вечеринку после школы.Принципал наложил два ограничения. Во-первых, общее количество людей (учителей и студентов, вместе взятых) должно составлять [латекс] 56 [/ латекс]. Во-вторых, на каждые семь учеников должен приходиться один учитель. Итак, сколько учеников и сколько учителей приглашено на вечеринку?
Во-первых, нам нужно идентифицировать и назвать наши переменные. В данном случае нашими переменными являются учителя и ученики. Количество учителей будет [latex] T [/ latex], а количество студентов будет [latex] S [/ latex].
Теперь нам нужно составить наши уравнения.Существует ограничение, ограничивающее общее количество людей [латекс] 56 [/ латекс], поэтому:
[латекс] T + S = 56 [/ латекс]
На каждые семь учеников должен приходиться один учитель, поэтому:
[латекс] \ frac {S} {7} = T [/ латекс]
Теперь у нас есть система уравнений, которую можно решить с помощью подстановки, исключения или графически. Решение системы: [латекс] S = 49 [/ латекс] и [латекс] T = 7 [/ латекс].
Поиск неизвестных величин
Этот следующий пример показывает, как системы уравнений используются для нахождения величин.
Группа студентов и учителей [латекс] 75 [/ латекс] в поле собирает сладкий картофель для нуждающихся. Кейси собирает в три раза больше сладкого картофеля, чем Дэвис, а затем, возвращаясь к машине, берет еще пять! Глядя на ее только что увеличившуюся кучу, Дэвис замечает: «Ух ты, у тебя [латекса] 29 [/ латекса] картофеля больше, чем у меня!» Сколько сладкого картофеля собрали Кейси и Дэвис каждый?
Чтобы решить, мы сначала определяем наши переменные. Количество сладкого картофеля, которое собирает Кейси, — [латекс] K [/ латекс], а количество сладкого картофеля, которое собирает Дэвис, — [латекс] D [/ латекс].
Теперь мы можем писать уравнения на основе ситуации:
[латекс] К-5 = 3D [/ латекс]
[латекс] D + 29 = K [/ латекс]
Отсюда замена, исключение или построение графика покажут, что [латекс] K = 41 [/ латекс] и [латекс] D = 12 [/ латекс].
Важно всегда проверять свои ответы. Хороший способ проверить решения системы уравнений — это посмотреть на функции графически, а затем увидеть, где пересекаются графики. Или вы можете подставить свои ответы в каждое уравнение и убедиться, что они приводят к точным решениям.
Другие приложения
Существует множество других приложений для систем уравнений, таких как определение того, какой ландшафтный дизайнер предлагает лучшее предложение, сколько разные операторы сотовой связи взимают плату за минуту, или сравнение информации о питании в рецептах.
Решение системы линейных уравнений с двумя переменными — концепция
Система линейных уравнений — это два или более уравнений, содержащих одни и те же переменные.Решения системы уравнений — это точка пересечения линий. Существует четыре метода решения систем линейных уравнений : построение графиков, подстановка, исключение и матрицы. Решение систем уравнений впервые появляется в алгебре I, но более сложные приложения встречаются в алгебре II.
Решение системы линейных уравнений с двумя переменными, поэтому, если вы помните, линейное уравнение — это в основном просто уравнение для линии, и когда мы решаем систему, мы смотрим на два уравнения, поэтому у нас есть две линии, и мы пытаемся выяснить, где пересекаются эти две линии, и если они вообще пересекаются, хорошо, значит, это может произойти тремя способами, хорошо? У нас есть две линии, которые могут пересекаться в одной точке, что означает, что у нас будет один ответ, который будет координатной точкой xy, скажем, 2, -4, что-то в этом роде.
Другая ситуация, которая может возникнуть, эти линии могут быть параллельны, что означает, что у них не будет никакого пересечения этих линий, у них не будет никакого решения, где эти две линии равны друг другу и, наконец, эти два уравнения может быть для одной и той же точной линии, что означает, что у нас будет бесконечное количество точек, лежащих на любой из этих линий, которые дадут нам решение, хорошо, и поэтому мы собираемся поговорить о каждой из этих .
Существует несколько различных способов решения этих проблем, вы можете решить их графически, и в Алгебре 2 мы обычно не делаем слишком много этого решения графически, в основном то, что вы делаете, — вы берете одну линию, которую вы строите, вы берете другую линию, которую вы строите это, и вы увидите, где они пересекаются, хорошо, поэтому мы знаем, как это сделать, но на самом деле это не даст нам математического ответа, мы не сможем найти эту точку, если наши графики не будут полностью точными, что своего рода трата времени, поэтому мы можем сделать это алгебраически, и в нашем распоряжении есть два способа: подстановка, когда мы решаем переменную и вставляем ее, или исключение, когда мы складываем или вычитаем два уравнения в надежде избавиться от одной из переменных so.
Системы линейных уравнений, в основном касающиеся того, как линии пересекаются или не пересекаются, и у нас есть несколько способов сделать это, а именно замена или исключение.


 Вы можете использовать этот метод для выделения нескольких подмножеств данных и распределённой работы с ними.
Вы можете использовать этот метод для выделения нескольких подмножеств данных и распределённой работы с ними.