Решение онлайн определитель: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.
Найти определитель матрицы — Онлайн калькулятор
Матрица представляет математический объект, который записан в виде таблицы элементов. Ее размер задается количеством столбцов и строк. В квадратной матрице число столбцов и строк одинаковое.
Чтобы найти определитель матрицы онлайн с помощью нашего сервиса, выберите необходимое число столбцов и строк. Затем введите значения в предназначенные для этого пустые поля и запустите расчет. Ответом будет найденный определитель (детерминант) — величина, которая может быть рассчитана и поставлена в однозначное соответствие квадратной матрице.
Определитель матрицы онлайн
Вычислить определитель матрицы онлайн понадобится студентам при решении задач по алгебре и высшей математике, научным сотрудникам для проверки правильности вычислений и сведения погрешностей к минимуму.
На нашем сайте вы можете посчитать определитель матрицы онлайн бесплатно.
- Для матриц порядка n=2 детерминант находится по формуле: Δ=a11*a22-a12*a21.
- Для матриц порядка n=3 детерминант находится с помощью алгебраического дополнения или методом Саррюса.
- При размерности матрицы больше трех она раскладывается на алгебраические дополнения, для которых рассчитываются свои детерминанты (миноры).
Вы сможете найти определитель матрицы с онлайн-калькулятором, что позволит проводить дальнейшие расчеты без ошибок и погрешностей. Это важно учитывать при разработке инструментов статистики в науке и технике, где точность вычислений имеет большое значение. Часто искомое значение определителя требуется как промежуточный результат для решения комплекса задач. В таком случае использование онлайн-калькулятора необходимо для экономии времени.
С помощью нашего сервиса легко осуществлять подготовку к занятиям.
Самостоятельно искать решение и сверятся с полученным детерминантом матрицы онлайн.
Найти определитель (детерминант) матрицы онлайн
При решении сложных систем уравнения большую роль играет определитель матрицы или детерминант матрицы. Это — важнейшая численная характеристика квадратной матрицы, используемая при решении многих задач. На вычислении определителя матрицы основан метод Крамера решения систем уравнений, он позволяет определять наличие и единственность решения систем уравнений. Обозначается определитель матрицы: det (A), |A|, или ∆(A). Определителем квадратной матрицы А размера n х n является число:
| det (A) = | Σ | (-1)N (α1,α2,…,αn)·aα11·aα22·…·aαnn |
| (α1,α2,…,αn) |
В данном выражении а1,а2,…
Свойства определителей:
- Определитель матрицы с двумя равными или пропорциональными строками (столбцами), с нулевой строкой (столбцом), с двумя или несколькими линейно зависимыми строками (столбцами) равняется нулю.
- Определитель единичной матрицы равняется единице: det (E) = 1.
- Определитель матрицы не меняется при транспонировании.
Способы вычисления определителя матрицы:
1. Значение определителя матрицы 1×1 равняется значению ее элемента:
∆ = |a11| = a11| ∆ = | = a11·a22 — a12·a21 |
3. Определитель матрицы 3×3 равен разности между суммой произведений элементов главной диагонали плюс произведение элементов лежащих на треугольниках, грань которых параллельна главной диагонали, и суммой произведений элементов побочной диагонали и элементов, лежащих на треугольниках с параллельной побочной диагонали гранью.
| ∆ = |
| = a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 — a12·a21·a33 |
Значение определителя матрицы 3-го порядка (3×3) можно рассчитать, используя правило Саррюса.
4. Определитель матрицы произвольного размера рассчитывается как сумма произведений элементов строки определителя на их алгебраические дополнения.
| n | |||
| det (A) = | Σ | aij·Aij | — разложение по i-той строке |
| j = 1 |
5. Определитель матрицы произвольного размера можно расчитать как суииу произведений элементов столбца определителя на их алгебраические дополнения:
| n | |||
| det (A) = | Σ | aij·Aij | — разложение по j-тому столбцу |
| i = 1 |
к. с увеличением размера матрицы расчеты становятся более сложными и громоздкими, что может привести к ошибке в ходе решения и окончательном ответе. С помощью онлайн калькулятора вы сможете произвести расчеты правильно и намного быстрей.| Размер матрицы: 2×23×34×45×56×67×7 Введите значения Матрицы: |
Калькулятор онлайн — Операции над матрицами: сложение, вычитание, умножение, деление, возведение в степень. Вычисление определителя матрицы, обратной матрицы, ранга матрицы
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Матрицы и операции над ними
Виды матриц
Определение 1.Матрицей размера \(m \times n \) называют прямоугольную числовую таблицу, состоящую из \(mn\) чисел, которые расположены в \(m\) строках и \(n\) столбцах.
Составляющие матрицу числа называют элементами этой матрицы.
Как правило, их обозначают строчной буквой с двумя индексами, например \(a_{ij}\), где \(i\) — номер строки ( \(i=\overline{1,m} \) ), \(j\) — номер столбца ( \(j=\overline{1,n} \) ), в которых расположен этот элемент.
Матрицу записывают так:
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} $$
Если по тексту ясно, в каких пределах изменяются индексы \(i\) и \(j\), то сокращённо матрицу можно записать так: \( \left(a_{ij} \right) \). Матрицу как единый объект обозначают прописной буквой: \(A\), \(B\) и т.д.
Элементами матриц могут быть не только действительные числа, но и комплексные, и даже другие математические объекты. Например, элементами матриц
могут быть многочлены или матрицы.
Матрицу называют матрицей-строкой, если матрица имеет размер \(1 \times n \), т.е. если у матрицы всего одна строка. Число элементов
в матрице-строке называют её длиной.
\(A=(a_1, \; …,\; a_n) \)
Матрицу называют матрицей-столбцом, если матрица имеет размер \(m \times 1 \), т.е. если у матрицы один столбец. Число элементов
в матрице-столбце называют её высотой.
\(A = \begin{pmatrix}
a_{1} \\
\vdots \\
a_{m} \\
\end{pmatrix} \)
Матрицу называют квадратной порядка \(n\), если \( m=n\), т.е. когда матрица имеет столько же столбцов, сколько и строк :
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{pmatrix} $$
а если \(m \neq n \) —
У квадратных матриц выделяют последовательности элементов \( a_{11}, \; a_{22}, \; …, \; a_{nn} \) — главную диагональ, и \( a_{n1}, \; a_{n-1,2}, \; …, \; a_{1n} \) — побочную диагональ. Элементы главной диагонали называют диагональными. Понятия диагонального элемента и главной диагонали распространяют и на прямоугольные матрицы.
Если в квадратной матрице порядка \(n\) все элементы, стоящие вне главной диагонали, равны нулю, т.е. если матрица имеет вид
$$ \begin{pmatrix}
a_{11} & 0 & \cdots & 0 \\
0 & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{pmatrix} $$,
то её называют диагональной к обозначают \( \text{diag} (a_{11}, \; …, \; a_{nn} ) \).
Если в диагональной матрице порядка \(n\) на
диагонали стоят единицы, то её называют единичной и обозначают обычно \(E\) :
$$ E = \begin{pmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1 \\
\end{pmatrix} $$,
Матрицу размера \(m \times n \), все элементы которой равны нулю, называют нулевой матрицей соответствующего размера и обозначают
буквой \(\Theta\) или цифрой 0.
Часто используют матрицы и других видов, например верхние треугольные матрицы
$$ \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{pmatrix} $$
у которых элементы, расположенные под главной диагональю, равны нулю, и нижние треугольные матрицы, у которых, наоборот,
элементы над главной диагональю равны нулю:
$$ \begin{pmatrix}
a_{11} & 0 & \cdots & 0 \\
a_{21} & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{pmatrix} $$
Ступенчатой матрицей (матрицей ступенчатого вида) называют матрицу размера \(m \times n \), если для любой её строки выполнено
следующее условие: под первым слева ненулевым элементом строки и предшествующими ему нулевыми элементами строки все элементы матрицы
равны нулю.
Следующие матрицы имеют ступенчатый вид:
\( \begin{pmatrix}
0 & 2 & 3 & 0 \\
0 & 0 & -1 & 1 \\
0 & 0 & 0 & 3 \\
\end{pmatrix} \)
\( \begin{pmatrix}
3 & 1 & 3 & 3 \\
0 & 0 & 2 & 1 \\
0 & 0 & 0 & 0 \\
\end{pmatrix} \)
\( \begin{pmatrix}
1 & 1 & 3 & 3 \\
0 & 3 & 0 & 1 \\
0 & 0 & 1 & -1 \\
\end{pmatrix} \)
Линейные операции над матрицами
Определение 2.
Две матрицы называют равными, если они имеют один и тот же размер и если у них совпадают соответствующие элементы.
Определение 3.
Суммой матриц \( A=(a_{ij}) \) и \( B=(b_{ij}) \) размера \(m \times n \) называют матрицу \( C=(c_{ij}) \) того же размера с элементами
\( c_{ij} = a_{ij} + b_{ij}, \; i=\overline{1,m} , \; j=\overline{1,n} \)
В подробной записи:
\( A+B = \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} + \)
\( \begin{pmatrix}
b_{11} & b_{12} & \cdots & b_{1n} \\
b_{21} & b_{22} & \cdots & b_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
b_{m1} & b_{m2} & \cdots & b_{mn} \\
\end{pmatrix} = \)
\( \begin{pmatrix}
a_{11}+b_{11} & a_{12}+b_{12} & \cdots & a_{1n}+b_{1n} \\
a_{21}+b_{21} & a_{22}+b_{22} & \cdots & a_{2n}+b_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1}+b_{m1} & a_{m2}+b_{m2} & \cdots & a_{mn}+b_{mn} \\
\end{pmatrix} = C \)
Сумма определена только для матриц одного размера.
Определение 4.
Произведением матрицы \( A=(a_{ij}) \) размера \(m \times n \) на число \( k \in \mathbb{R}\) называют матрицу
\( C=(c_{ij}) \) размера \(m \times n \) с элементами \( c_{ij} = k \cdot a_{ij} \).
Подробно это произведение выглядит так:
\( k \cdot \begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} \\
\end{pmatrix} = \)
\( \begin{pmatrix}
k \cdot a_{11} & k \cdot a_{12} & \cdots & k \cdot a_{1n} \\
k \cdot a_{21} & k \cdot a_{22} & \cdots & k \cdot a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
k \cdot a_{m1} & k \cdot a_{m2} & \cdots & k \cdot a_{mn} \\
\end{pmatrix} \)
Замечание. Операции сложения и умножения на число для матриц аналогичны одноименным операциям над векторами.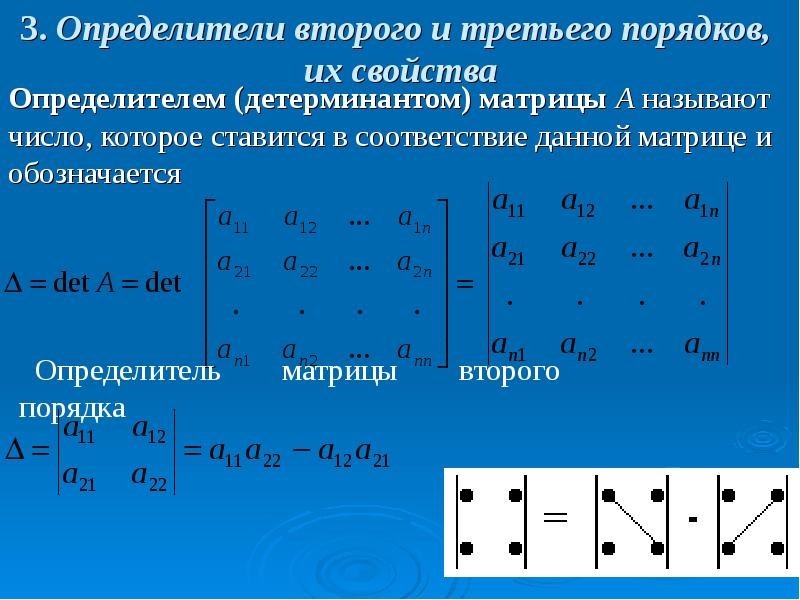
{n+m}\).
Элементарные преобразования матриц
Следующие три операции называют элементарными преобразованиями строк матрицы :1. Умножение строки матрицы на число не равное нулю.
2. Перестановка двух строк матрицы.
3. Суммирование одной строки с другой строкой, умноженной на число.
Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов.
Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование, которое преобразованную матрицу превращает в исходную.
Теорема. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду.
Определители
Определители n-го порядка
В теории определителей n-го порядка используются понятия перестановки, подстановки и их четности.
Всякое расположение чисел \( 1,\; 2,\; 3,\; …,\; n \) в определенном порядке называют перестановкой из \(n\) чисел.
Из \(n\) чисел можно образовать \(n!\) различных перестановок.
В общем случае перестановку записывают в виде матрицы-строки \( \alpha = (\alpha_1,\; \alpha_2,\; …,\; \alpha_n ) \)
Перестановку \( (1,\; 2,\; 3,\; …,\; n) \) называют нормальной.
Два числа \(\alpha_i\) и \(\alpha_j\) в перестановке \( \alpha = (\alpha_1,\; …,\; \alpha_n ) \) образуют инверсию,
если \(\alpha_j > \alpha_i \) но при этом \(\alpha_i\) стоит в перестановке правее \(\alpha_j\) (т.е. \(i>j\) ).
Общее количество инверсий в перестановке \(\alpha \) обозначают \( |\alpha | \), и если это число четное, то перестановку называют
четной, а если оно нечетное — нечетной.
Транспозицией перестановки называют такое её преобразование, при котором в ней меняются местами какие-либо два элемента,
а другие остаются на своих местах.
Теорема. Любая транспозиция меняет четность перестановки.
Из двух перестановок \( ( \alpha_1,\; …,\; \alpha_n ) \) и \( ( \beta_1,\; …,\; \beta_n ) \) одних и тех же чисел можно
составить новый объект
$$ \sigma = \begin{pmatrix}
\beta_1 & \beta_2 & \cdots & \beta_n \\
\alpha_1 & \alpha_2 & \cdots & \alpha_n \end{pmatrix} , \tag{1} $$
который называют подстановкой n-й степени.
Подстановку называют четной, если перестановки, из которых она состоит, имеют одинаковую четность, и нечетной в
противоположном случае.
Четность подстановки \( (1) \) совпадает с четностью числа \( |\beta|+|\alpha| \) — общего количества инверсий
в строках подстановки, которое обозначают \( |\sigma| \).
Транспозицией подстановки называют любую перестановку её столбцов. Поскольку транспозиция подстановки вызывает
транспозиции и в образующих её перестановках, то, согласно предыдущей теореме, очевидно, что транспозиция подстановки не меняет
её четность.
Каждая подстановка вида \( (1) \) задает взаимно однозначное отображение множества чисел \( 1,\; 2,\; 3,\; …,\; n \) на себя,
при котором \( \beta_1 \) отображается в \( \alpha_1 \; , \; \beta_2 \) — в \( \alpha_2\) и т.д.
В соответствии с интерпретацией подстановок как отображений две подстановки считают равными, если они отличаются только
порядком записи своих столбцов.
Например, подстановки
\( \begin{pmatrix}
1 & 3 & 4 & 2 \\
2 & 4 & 1 & 3 \\ \end{pmatrix}
\;\; и \;\;
\begin{pmatrix}
1 & 2 & 3 & 4 \\
2 & 3 & 4 & 1 \\ \end{pmatrix} \)
равны, так как вторая получается из первой перестановкой столбцов.
Соглашение о равенстве подстановок позволяет записать любую подстановку так, чтобы первая строка являлась нормальной перестановкой. Поэтому различных подстановок \(n\)-й степени имеется ровно \(n!\)
Определение.
{|\sigma|} a_{1\alpha_1} a_{2\alpha_2} … a_{n\alpha_n} \tag{3} $$
которая берется по всевозможным подстановкам вида
\( \sigma = \begin{pmatrix}
1 & 2 & \cdots & n \\
\alpha_1 & \alpha_2 & \cdots & \alpha_n \end{pmatrix} \)
Определитель матрицы \(A\) часто называют просто определителем, или детерминантом, и обозначают
\( \begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{vmatrix} \)
или \( \det A\), называя \(A\) матрицей этого определителя.
Свойства определителей
Поскольку определители соответствуют квадратным матрицам, в их теорию легко переносится матричная терминология
(порядок, элементы, строки, столбцы, диагональ, диагональные элементы, виды матриц и определителей,
транспонирование, элементарные преобразования строк и столбцов, линейные комбинации строк и столбцов
и др.
T \right| \)
Свойство 2. При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.
Свойство 3. Если все элементы \(j\)-го столбца определителя представлены в виде суммы двух слагаемых, то определитель равен
сумме двух определителей, у которых все столбцы, кроме \(j\)-го, такие же, как и в данном определителе, а \(j\)-й столбец
первого определителя состоит из первых слагаемых \(j\)-го столбца данного определителя, а второго — из вторых слагаемых :
\( \begin{vmatrix}
a_{11} & \cdots & \alpha_{1j} + \beta_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \alpha_{2j} + \beta_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \alpha_{nj} + \beta_{nj} & \cdots & a_{nn} \end{vmatrix} = \)
\( \begin{vmatrix}
a_{11} & \cdots & \alpha_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \alpha_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \alpha_{nj} & \cdots & a_{nn} \end{vmatrix} + \)
\( \begin{vmatrix}
a_{11} & \cdots & \beta_{1j} & \cdots & a_{1n} \\
a_{21} & \cdots & \beta_{2j} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots & \cdots \\
a_{n1} & \cdots & \beta_{nj} & \cdots & a_{nn} \end{vmatrix} \)
Аналогично для строки.
Свойство 4. Общий множитель элементов строки или столбца может быть вынесен за знак определителя.
Для умножения определителя на число достаточно умножить на это число элементы любой строки или любого столбца.
Свойство 5. Определитель равен нулю, если он имеет :
1) нулевую строку (столбец)
2) хотя бы две одинаковые строки (столбца)
3) хотя бы две строки (столбца), элементы которых пропорциональны
4) хотя бы одну строку (столбец), являющуюся линейной комбинацией других строк (столбцов).
Свойство 6. Определитель не изменится, если к любой его строке (столбцу) прибавить другую строку (столбцец), умноженную на число.
В матрице \(A\) вычеркнем \(i\)-ю строку и \(j\)-й столбец, в которых стоит элемент \(a_{ij}\). Из оставшихся элементов можно
составить новую квадратную матрицу (n-1)-го порядка, сдвинув строки и столбцы после вычеркивания.
Определитель построенной матрицы обозначают через \( M_{ij} \) и называют минором (матрицы \(A\) и её определителя
\(\Delta\) ), соответствующим элементу \(a_{ij}\).
{i+j} a_{ij} M_{ij} \tag{5} $$
( разложение по \(j\)-му столбцу )
Разложения по строке (4) и столбцу (5) дают правила, в соответствии с которыми определитель n-го порядка сводится к n
определителям (n-1)-го порядка, раскладывая которые получим n(n-1) определителей (n-2)-го порядка и т.д.
Эти вычисления получаются громоздкими, однако процесс упрощается, если среди элементов определителя имеется много нулей.
Целесообразно раскладывать определитель по тому ряду (строке, столбцу), в котором больше нулей.
Если же в этом смысле некоторые ряды одинаковы, то удобнее выбирать тот из них, в котором элементы имеют большие значения
по абсолютной величине, поскольку это упрощает выполнение арифметических вычислений.
Свойство 8. Определитель верхней (нижней) треугольной матрицы равен произведению элементов её главной диагонали,
т.е.
$$ \begin{vmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn} \\
\end{vmatrix} = $$
$$ \begin{vmatrix}
a_{11} & 0 & \cdots & 0 \\
a_{21} & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{vmatrix} = $$
$$ a_{11}a_{22}.
n a_{ii} $$
С помощью элементарных преобразований строк любая матрица приводится к ступенчатому виду. Квадратная матрица ступенчатого вида является частным случаем верхней треугольной матрицы, у которой диагональные элементы, начиная с некоторого, могут быть равны нулю. Определитель такой матрицы легко найти по свойству 8. В алгоритме приведения к ступенчатому виду используется перестановка строк, при которой определитель матрицы меняет знак. Изменение знака можно учесть, например, дополнительным умножением определителя или одной из строк на —1. Следовательно, квадратную матрицу всегда можно привести элементарными преобразованиями строк к верхнему треугольному виду с сохранением значения её определителя.
Свойство 9. Определитель произведения двух квадратных матриц A, B равен произведению их определителей, т.е. \( |АВ| = |A||B| \).
Свойство 10. Определитель обратной матрицы: \( \left| А^{-1} \right| = \frac{1}{|A|} \)
Свойство 11.
{1+3} a_{13} M_{13} = $$
$$ a_{11} \begin{vmatrix}
a_{22} & a_{23} \\
a_{32} & a_{33} \end{vmatrix}
— a_{12} \begin{vmatrix}
a_{21} & a_{23} \\
a_{31} & a_{33} \end{vmatrix}
+ a_{13} \begin{vmatrix}
a_{21} & a_{22} \\
a_{31} & a_{32} \end{vmatrix} = $$
$$ a_{11}a_{22}a_{33} — a_{11}a_{23}a_{32} — a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} — a_{13}a_{22}a_{31} $$
Чтобы запомнить, какие произведения элементов берутся со знаком \( «+» \), а какие со знаком \( «-» \) можно
использовать следующее правило треугольников.
Произведения элементов, стоящих на зелёных точках складываются, а на
синих — вычитаются :
Также для вычисления определителя 3-го порядка существует правило Саррюса.
Первый и второй столбцы матрицы записываются справа от основной матрицы.
Произведения элементов, стоящих на зелёных линиях складываются, а на
синих — вычитаются :
Обратная матрица и её свойства
Определение.
{-1}\), обратную к \(A\), фактически надо решить матричное уравнение \(AX=E\).
Отметим, что если над матрицей \(A\) выполняется какое-либо элементарное преобразование строк, то это же
преобразование осуществляется и над матрицей \(AX\), поскольку любое элементарное преобразование строк матрицы
эквивалентно умножению её слева на соответствующую матрицу специального вида. Таким образом, если в уравнении
\(AX=E\) над матрицами \(A\) и \(E\) одновременно выполнить какое-либо элементарное преобразование строк, т.е.
домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное
уравнение \(A_1X=B_1\). Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное
преобразование строк имеет обратное элементарное преобразование строк.
Последовательность элементарных преобразований строк надо подобрать так, чтобы на s-м шаге матрица \(A\)
превратилась в единичную матрицу.
В результате этих s шагов получается уравнение \(A_sX=B_s\), где \(A_s=E\), т.
{-1}\).
Ранг матрицы
Определение.Рангом матрицы называют число, которое равно максимальному порядку среди её ненулевых миноров.
Для ранга матрицы \(A\) используют обозначение \(\text{rang}A\).
Если квадратная матрица порядка n невырождена, то её ранг равен её порядку n : ненулевым является единственный
минор максимального порядка n, совпадающий с определителем матрицы.
В частности, ранг единичной матрицы \(E\) порядка n равен n.
Если квадратная матрица вырождена, то её ранг меньше её порядка : единственный минор максимального
порядка, равного порядку матрицы, является нулевым, и в этом случае ненулевые миноры имеют меньший порядок.
Ранг нулевой матрицы полагают равным нулю.
Ранг диагональной матрицы равен количеству её ненулевых диагональных элементов.
Непосредственно из определения ранга матрицы следует, что ранг имеет следующее свойство, полностью его
характеризующее.
T = \text{rang} A \)
Теорема. Ранг матрицы не меняется при элементарных преобразованиях её строк и столбцов.
Теорема о базисном миноре
Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.
Определение.
Минор \(M\) матрицы \(M\) называют базисным, если выполнены два условия:
1) он не равен нулю
2) его порядок равен рангу матрицы А
Матрица \(A\) может иметь несколько базисных миноров. Строки и столбцы матрицы \(A\), в которых расположен выбранный базисный минор, называют базисными.
Теорема о базисном миноре. Базисные строки (столбцы) матрицы \(A\), соответствующие любому её базисному минору \(M\), линейно независимы. Любые строки (столбцы) матрицы \(A\), не входящие в \(M\), являются линейными комбинациями базисных строк (столбцов).
Следствие. Для того чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы её
строки (столбцы) были линейно независимы.
Теорема. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).
Теорема. Для любой матрицы её ранг равен максимальному количеству её линейно независимых строк (столбцов).
Следствие. Для любой матрицы максимальное число линейно независимых строк равно максимальному числу линейно независимых столбцов.
Вычисление ранга матрицы
Метод окаймляющих миноров
Минор \(M’\) матрицы \(A\) называют окаймляющим для минора \(M\), если он получается из последнего
добавлением одной новой строки и одного нового столбца матрицы \(A\).
Ясно, что порядок окаймляющего минора \(M’\) на единицу больше, чем порядок минора \(M\).
Метод окаймляющих миноров позволяет найти один из базисных миноров матрицы и состоит в следующем.
Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы).
К очередному ненулевому минору
последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого
сделать нельзя, то последний ненулевой минор является базисным (что утверждает следующая ниже теорема). Этот
процесс рано или поздно закончится из-за ограниченных размеров матрицы.
Теорема. Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным.
Метод элементарных преобразований
При элементарных преобразованиях строк (столбцов) матрицы её ранг не меняется. С помощью этих преобразований можно так упростить матрицу, чтобы ранг новой матрицы легко вычислялся.
Например с помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду. Ранг
же ступенчатой матрицы равен количеству ненулевых строк. Базисным в ней является минор, расположенный на
пересечении ненулевых строк со столбцами, соответствующими первым слева ненулевым элементам в каждой из строк.
Действительно, этот минор ненулевой, так как соответствующая матрица является верхней треугольной, а любое его
окаймление содержит нулевую строку. Поэтому приведение матрицы к ступенчатому виду с помощью элементарных
преобразований строк позволяет вычислить ранг матрицы.
Приведенные два метода существенно отличаются друг от друга.
При нахождении ранга конкретной матрицы методом окаймляющих миноров может потребоваться большое количество
вычислений. Это связано с тем, что метод требует вычисления определителей, порядок которых может возрасти до
минимального из размеров матрицы. Однако в результате будет найден не только ранг матрицы, но и один из её
базисных миноров.
При нахождении ранга матрицы методом элементарных преобразований требуется гораздо меньше вычислений.
Причем разница в объемах вычислений возрастает с ростом размеров матрицы и усложнением её вида. Но этот метод
позволяет найти базисный минор лишь для матрицы ступенчатого вида, полученной в результате элементарных
преобразований.
Чтобы найти базисный минор исходной матрицы, нужны дополнительные вычисления с учетом уже
известного ранга матрицы.
Определитель 4 порядка. Калькулятор
Определители четвертого и старших порядков возможно вычислять по упрощенным схемам, которые заключаются в разложении по элементам строк или столбцов или сведении к треугольному виду. Оба метода для наглядности будут рассмотрены на матрицах 4-го порядка.
Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.
Пример 1. Вычислить определитель методом разложения.
Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются — выделено красным)
В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников
Найденные значения подставляем в выходной детерминант
Результат легко проверить с помощью матричного калькулятора YukhymCALC .
Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.
Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных
Результаты совпадают, следовательно вычисления проведены верно.
Пример 2. Вычислить определитель матрицы четвертого порядка.
Решение.
Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде
Далее переходим к отысканию определителей по правилу треугольников
Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем
Результат проверяем матричным калькулятором YukhymCALC .
Правильность расчетов подтверждается следующим рисунком
Метод возведения определителя к треугольному виду
Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.
Пример 3. Найти определитель матрицы сведением к треугольному виду
Решение.
Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим
Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем
Дальше целесообразнее от четвертой отнять удвоенную вторую строчку.
В результате элементарных преобразований определитель примет вид
Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе
По свойству, определитель треугольной матрицы равен произведению диагональных элементов.
По желанию можно проверить результат матричным калькулятором.
В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось.
Рассмотрим более сложный.
Пример 4.
Найти определитель матрицы 4-го порядка
Решение.
Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант
Для удобства вычислений, меняем третью строчку со вторым местами..
По свойству определителей любая замена строк местами ведет к изменению знака определителя.
Учитываем это в некотором множителе k=-1.
От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим
Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2.
Результат будет следующим
От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.
Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления
Проверка матричным калькулятором подтверждает правильность производимых вычислений.
Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений.
В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.
Как решить уравнение определителя онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только
возрастает. Определители играют большую роль в решении систем линейных уравнений и вычислить их можно только
для квадратной матрицы. Довольно часто для решения уравнений необходимо найти определитель второго и
третьего порядка. Под понятием найти определитель понимают найти число. Для его нахождения используют
формулы и алгоритмы. Чтобы понять логику записи определителей воспользуемся следующей схемой.
Возьмём
знакомую вам со школьной скамьи систему из двух уравнений с двумя неизвестными:
\[\left\{\begin{matrix} a_{11}x_1+a_{12}x_2=b_1\\ a_{21}x_1+a_{22}x_2=b_2 \end{matrix}\right.\]
Так же читайте нашу статью «Решить уравнение матрицы онлайн решателем»
Исходя из данной системы, в определитель запишем коэффициенты неизвестных для каждого уравнения:
\[\begin{vmatrix} a_{11} &a_{12}\\ a_{21} &a_{22} \end{vmatrix}\]
В такой вид преобразовалась наша исходная система, которую потом необходимо решить, оперируя основными методами решения квадратных матриц.
Допустим, нам необходимо вычислить определитель третьего порядка:
\[\begin{vmatrix} 0&1&-2\\ -1&2&3\\ 2&3&4 \end{vmatrix}\]
Руководствуясь правилом треугольников, получим:
\[\begin{vmatrix} 0&1&-2\\ -1&2&3\\ 2&3&4 \end{vmatrix}=0\cdot 2\cdot 4+1\cdot 3\cdot 2+(-2)\cdot (-1)\cdot 3-(-2)\cdot 2\cdot 2-1\cdot (-1)\cdot 4-0\cdot 3\cdot 3=24\]
Где можно решить уравнение определителя онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.
ru. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Калькулятор матриц. Решение матриц онлайн. Решение матричных уравнений
Решение матриц онлайн является одним из самых востребованных запросов в интернете среди студентов, причём сервисов, где можно решить онлайн матрицу, практически нет. И снова на помощь придёт многофункциональный математический калькулятор. В его арсенал входит калькулятор матриц онлайн, который выполняет все основные операции над матрицами!
Матрица — это совокупность значений, записанных в прямоугольную таблицу.
Каждый элемент матрицы имеет двойной порядковый номер в этой таблице, а именно номер столбца и номер строки. Размер матрицы определяется количеством строк и столбцов в таблице. Например, размер матрицы 3 на 5 значит, что она состоит из трёх строк и пяти столбцов.
Обратите внимание, 5 x 5 — это максимальный размер матрицы, которую может решить бесплатный калькулятор, предлагаемый на нашем сайте.
Как решать матрицы в онлайн калькуляторе
Чтобы вызвать калькулятор матриц, нажмите кнопку Matrix.
Кнопка, открывающая калькулятор матриц
Панель управления дополнится инструментами, с помощью которых выполняется решение матриц онлайн. Калькулятор позволяет выполнять следующие онлайн действия над матрицами: вычитание, сложение и умножение матриц, векторное произведение, решение матричных уравнений, транспонирование, нахождение обратной матрицы и вычисление определителя матрицы.
Кнопки калькулятора, выполняющие основные действия над матрицами
Помимо панели с кнопками онлайн калькулятор матриц содержит удобную форму для быстрого ввода выражения.
В левой и правой частях задаются матрицы, их размер выбирается из выпадающего списка. В середине выпадающее меню для выбора операции, которую нужно выполнить калькулятору с заданными матрицами. Другие возможности калькулятора можно посмотреть здесь Функции калькулятора.
Вычисление матриц онлайн с помощью формы быстрого ввода
Если элемент матрицы не указан, онлайн калькулятор подставляет значение «0».
Обратите внимание, при вызове меню решения матриц вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I», чтобы увидеть дисплей в полный размер.Вектор столбец
Матрица, состоящая только из одной строки или одного столбца, называется вектор-строкой или вектор-столбцом соответственно. В калькуляторе предусмотрены отдельные кнопки для ввода матрицы, число столбцов которой равно 1. Используйте эти клавиши, чтобы записать вектор-столбец из 3,4 или 5 строк соответственно.
Кнопки калькулятора для ввода вектора
(2, 6, 8)
Вектор-столбец из 3х строк
Квадратная матрица
Матрица называется квадратной, если число её строк равно числу столбцов.
Следует отметить, что только у квадратной матрицы может быть главная диагональ матрицы — линия, проходящая через элементы матрицы с одинаковыми индексами, начиная с ячейки первой строки первого столбца и заканчивая элементом, стоящем в последнем столбце последней строки.
Для быстрой записи квадратных матриц 2, 3 или 4-го порядка используйте специальные кнопки, которые предлагает калькулятор онлайн.
Кнопки калькулятора для ввода квадратных матриц
[[ 8, 4, 1, 8][ 7, 1, 8, 8][ 8, 4, 1, 6][ 4, 8, 3, 1]]
Пример квадратной матрицы 4 порядка
Квадратные матрицы, у которых все элементы, исключая элементы главной диагонали, равны нулю, называются диагональные матрицы. Симметричная матрица чисел представляет собой таблицу, в которой все элементы, симметричные относительно главной диагонали, равны.
[[ 1, 2, 8, 11][ 2, 3, 24, 5][ 8, 24, 6, 4][ 11, 5, 4, 9]]
Пример симметричной матрицы
Есть ещё такие виды матриц в математике.
Единичная матрица чисел — это таблица, в которой элементы главной диагонали равны единице, а все остальные элементы являются нулевыми.
[[ 1, 0, 0, 0][ 0, 1, 0, 0][ 0, 0, 1, 0][ 0, 0, 0, 1]]
Пример единичной матрицы
Таблица, у которой значение всех элементов равно 0, называется нулевая матрица.
[[ 0, 0, 0, 0][ 0, 0, 0, 0][ 0, 0, 0, 0][ 0, 0, 0, 0]]
Пример нулевой матрицы
Матрицы и действия над ними
Сложение и вычитание матриц онлайн
С помощью калькулятора можно произвести сложение матриц онлайн, а также найти разность матриц онлайн. Чтобы вычислить сумму матриц или найти их разность, выполняются соответствующие операции над их элементами. Например, найти сумму матриц значит определить такую матрицу, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц.
Найти сумму элементов матриц или их разность можно только в том случае, если исходные матрицы одинакового размера, т.
е. число их строк и столбцов соответственно равно. Вычитание и сложение матриц разного размера невозможно.
Для выполнения этих операций в калькуляторе используйте форму быстрого ввода или запишите выражение вручную.
Сложение матриц примеры
[[1, 2, 3][3, 1, 2][5, 0, 6]]+[[1, 2, 5][6, 3, 2][9, 9, 9]]
Сложение двух матриц
[[2, 7][4, 5]]+[[2, 10][6, 8]]
Сумма двух матриц
Векторное произведение матриц
Для выполнения этой операции используйте клавишу Cross Product.
(2, 6, 4)#(8, 2, 5)
Пример произведения векторов
Умножение матриц
Умножение матриц онлайн калькулятор производит с помощью клавиши Vector/Matrice-Multiplication.
Перемножение матриц возможно только в том случае, если количество столбцов одной матрицы равняется количеству строк другой. Чтобы матрицу умножить на число, нужно каждый элемент матрицы умножить на это число.
[[2, 8][4, 2]]*[[8, 8][7, 1]]
Умножение матриц пример
[[5, 6][7, 8]]*9
Умножение матрицы на число онлайн
Решение матричных уравнений
Эта функция калькулятора позволяет находить неизвестные матрицы, которые описаны уравнением зависимости одной матрицы от другой.
-1
Нахождение обратной матрицы пример
Нахождение определителя матрицы
В калькуляторе матриц нет специальной кнопки для того, чтобы найти определитель матрицы. Но вычислить его можно, написав в поле ввода специальную функцию — оператор det(Determinant).
det( [ [-2, 2, -3], [-1, 1, 3], [2, 0, -1] ] )
Пример, как найти определитель матрицы онлайн
Бесплатный калькулятор онлайн может не только решить онлайн матрицу, в его возможностях также: возведение в степень, калькулятор корней, тригонометрические функции, решение логарифмов и другие дополнительные функции.
Калькулятор Инструкция — обзор всех функций калькулятора и общее описание, как пользоваться калькулятором.
Решение высшей математики онлайн
‹— Назад С понятием определителя мы уже сталкивались при изучении векторного произведения в разделе 10.
Там были введены определители матриц второго и третьего порядка. В этом разделе мы дадим определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка . Такое рекуррентное определение и было использовано для введения определителя матрицы третьего порядка . Отметим также, что определитель существует только у квадратных матриц.Определитель квадратной матрицы будем обозначать или .
Легко проверить, что это определение для определителей второго и третьего порядка совпадает с данным ранее в разделе 10.
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка:
Замечание 14.
7 Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Рассмотрим некоторые свойства определителей, которые сформулируем в виде предложений.
Предложение 14.7 Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть .Ввиду ограниченности курса доказательства этих трех свойств мы опускаем.
Читатель может найти их в учебниках по линейной алгебре [3], [5] или же может без особых сложностей проверить их на матрицах второго и третьего порядков.
В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.
Доказательство.
Пусть — исходная матрица, — матрица, полученная из умножением первой строки на число : Тогда где — определитель матрицы, полученной из матрицы или, что то же самое, из матрицы вычеркиванием первой строки и -ого столбца.Вынесем множитель за знак суммы и получим
Пусть теперь матрица получается из матрицы умножением -ой строки на число . Поменяем местами первую и -ую строки в матрице и то же самое проделаем в матрице . Получим две новых матрицы и . По предложению 14.8| (14.10) |
Очевидно, что матрица получается из матрицы умножением первой строки на число . Как только что было доказано, . Таким образом, из второго равенства (14.10) находим , отсюда с помощью первого равенства (14.10) получаем .
Доказательство. Нулевую строку можно рассматривать как строку из единиц, умноженную на число ноль. По предложению 14.10 определитель такой матрицы равен нулю, умноженному на определитель матрицы, содержащей строку из единиц. Результат такого умножения всегда будет ноль.
Предложение 14.12 Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю. Доказательство. По предложению 14.10 определитель исходной матрицы равен числу , умноженному на определитель матрицы, у которой есть две одинаковые строки. По предложению 14.9 определитель последней матрицы равен нулю. Поэтому и определитель исходной матрицы равен нулю.
Доказательство. Пусть первая строка матрицы имеет вид . Тогда
Для случая утверждение доказано.
Пусть . Обозначим через , , матрицы , , и , в которых поменяли местами первую и -ую строки. По только что доказанному (для ) утверждению . По предложению 14.8 , , . Следовательно, . Умножив обе части последнего равенства на , получим требуемое утверждение.
Предложение 14.15 Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.
Доказательство. По предложению 14.13 определитель исходной матрицы равен сумме определителей матриц, в каждой из которых есть пропорциональные строки. По предложению 14.12 все эти определители равны нулю. Следовательно, и определитель исходной матрицы тоже равен нулю. Алгебраическое дополнение к элементу матрицы обозначается .
Пример 14.4 Пусть . Тогда Предложение 14.16 Разложение определителя по произвольной строке. Для определителя матрицы справедлива формула Доказательство. Если , положим . Пусть . Тогда -ую строку поменяем местами со строкой с номером . Определитель сменит знак. Затем строку с номером поменяем местами со строкой с номером . Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока -ая строка матрицы не станет первой строкой новой матрицы, которую мы обозначим .
Отметим, что в матрице , начиная со второй строки, стоят строки матрицы , причем порядок их следования не изменился.При переходе от матрицы к матрице определитель сменит знак раз (проверьте для случая ). Таким образом
| (14.11) |
Это соотношение верно и при . По определению 14.6 определителя, где — определитель матрицы, полученной из матрицы вычеркиванием первой строки и -ого столбца. Первая строка матрицы совпадает с -ой строкой матрицы , поэтому . Результат вычеркивания в матрице первой строки и -ого столбца будет таким же, как при вычеркивании в матрице -ой строки и -ого столбца. Поэтому , где — определитель матрицы, полученной при вычеркивании в матрице -ой строки и -ого столбца. Следовательно, В силу равенства (14.
11) получим По определению 14.7 алгебраического дополнения получим . Тогда из предыдущего равенства вытекает что и требовалось доказать. Пример 14.5 Вычислите .
Решение. Воспользуемся разложением по третьей строке, так выгоднее, поскольку в третьей строке два числа из трех — нули. Получим
Доказательство. Пусть — матрица, полученная из матрицы , в которой -ая строка заменена -ой строкой этой же матрицы, а сама -ая строка осталась без изменения. Таким образом, в матрице есть две одинаковые строки и в силу предложения 14.9 .
С другой стороны, используя разложение определителя по -ой строке (предложение 14.16), получим
где — алгебраическое дополнение к элементу .
Так как все строки матрицы , кроме -ой, совпадают со строками матрицы , то . Так как по построению матрицы , то Так как , то равенство (14.12) доказано. Предложение 14.18 Все свойства определителя, сформулированные для строк ( предложения 14.8-14.17), справедливы и для столбцов, в частности, справедливо разложение определителя по -ому столбцу
| (14.13) |
и равенство при . Доказательство. В силу предложения 14.6 определитель не меняется при транспонировании матрицы, а ее столбцы становятся строками транспонированной матрицы, для которой доказываемые свойства имеют место.
Доказательство. Воспользуемся индукцией по порядку матрицы.
Для : утверждение верно. Предположим, что доказываемое утверждение верно для матриц порядка . Покажем, что оно верно для матрицы порядка .Если — верхняя треугольная матрица, то используем разложение по первому столбцу (равенство (14.13) при ):
Справа стоит определитель треугольной марицы порядка . По предположению индукции этот определитель равен . Поэтому .
Если — нижняя треугольная матрицы, то нужно воспользоваться разложением по первой строке. В остальном рассуждения аналогичны.
Итак, утверждение верно для матрицы порядка . Предложение доказано.
Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений.
Алгоритм вычислений следующий.
Алгоритм создания нулей в столбце.
Пусть требуется вычислить определитель матрицы порядка . Если , то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель , будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрица имеет нулевой столбец и по предложениям 14.11, 14.18 ее определитель равен нулю.
Итак, считаем, что уже в исходной матрице . Первую строку оставляем без изменений. Прибавим ко второй строке первую строку, умноженную на число . Тогда первый элемент второй строки будет равен
Остальные элементы новой второй строки обозначим , . Определитель новой матрицы по предложению 14.14 равен .Первую строку умножим на число и прибавим к третьей.
Первый элемент новой третьей строки будет равен
Процесс получения нулей вместо первых элементов строк продолжим дальше. Наконец, первую строку умножим на число и прибавим к последней строке. В результате получается матрица, обозначим ее , которая имеет вид
причем . Для вычисления определителя матрицы используем разложение по первому столбцу Так как , то В правой части стоит определитель матрицы порядка . К нему применим тот же алгоритм, и вычисление определителя матрицы сведется к вычислению определителя матрицы порядка . Процесс повторяем до тех пор, пока не дойдем до определителя второго порядка, который вычисляется по определению.Если матрица не обладает какими-то специфическими свойствами, то заметно уменьшить объем вычислений по сравнению с предложенным алгоритмом не удается.
Еще одна хорошая сторона этого алгоритма — по нему легко составить программу для компьютера для вычисления определителей матриц больших порядков. В стандартных программах вычисления определителей используется этот алгоритм с не принципиальными изменениями, связанными с минимизацией влияния ошибок округления и погрешностей входных данных при вычислениях компьютера.
Решение. Первую строку оставляем без изменения. Ко второй строке прибавляем первую, умноженную на число :
Определитель не меняется. К третьей строке прибавляем первую, умноженную на число : Определитель не меняется. К четвертой строке прибавляем первую, умноженную на число : Определитель не меняется. В результате получаем По тому же алгоритму считаем определитель матрицы порядка 3, стоящий справа. Первую строку оставляем без изменений, ко второй строке прибавляем первую, умноженную на число : К третьей строке прибавляем первую, умноженную на число : В результате получаемОтвет.
.
Замечание 14.11 Внимательный читатель, наверное, отметил, что хотя при вычислениях использовались дроби, результат оказался целым числом. Действительно, используя свойства определителей и то, что исходные числа — целые, операций с дробями можно было бы избежать. Но в инженерной практике числа крайне редко бывают целыми. Поэтому, как правило, элементы определителя будут десятичными дробями и применять какие-то ухищрения для упрощения вычислений нецелесообразно.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Калькулятор определителя матрицы nxn
Как найти определитель матрицы?
Рассмотрим матрицу $ A = \ left [
\ begin {array} {cc}
а & б \\
CD \\
\ end {массив}
\ right] $ размером $ 2 \ times2 $.
Настоящее число
$$ \ left | \ begin {array} {cc}
а & б \\
CD \\
\ end {массив}
\ right | = ad-cb $$
— определитель матрицы $ A $. Точнее, чтобы найти определитель матрицы $ 2 \ times 2 $, нам нужно выполнить следующие шаги:
- Умножьте элемент в первой строке и первом столбце на элементы во второй строке и втором столбце;
- Умножить элемент в первой строке и втором столбце на элемент во второй строке и первом столбце;
- Определитель матрицы $ 2 \ times 2 $ — это разница между вторым и первым произведением.
Сначала выбираем строку в матрице. В каждой позиции в строке мы умножаем элемент на
его незначительный знак, умноженный на его позицию, и сложить все суммы для всей строки.Знаки позиции в матрице — плюс или минус в зависимости от позиции элемента. Например, знаки положения в матрице $ 3 \ times 3 $:
$$ \ left [
\ begin {array} {ccc}
+ & — & + \\
— & + & — \\
+ & — & + \\
\ end {массив}
\ right] $$
Это означает, что $$ \ begin {align} det (A) = | A | & = \ left |
\ begin {array} {ccc}
а & b & c \\
d & e & f \\
г & ч & я \\
\ end {массив}
\ право | \\ & = a \ left |
\ begin {array} {cc}
е & е \\
Привет \\
\ end {массив}
\ right | -b \ left |
\ begin {array} {cc}
д & е \\
г & я \\
\ end {массив}
\ right | + c \ left |
\ begin {array} {cc}
d & e \\
г & ч \\
\ end {массив}
\ right | \ end {align} $$
Если мы применим этот метод для вычисления определителя $ 4 \ times 4 $, мы получим
$$ \ begin {align} det (A) = | A | & = \ left |
\ begin {array} {cccc}
а & b & c & d \\
e & f & g & h \\
я & j & k & l \\
m & n & o & p \\
\ end {массив}
\ право |
\\ & = a \ left |
\ begin {array} {ccc}
f & g & h \\
j & k & l \\
n & o & p \\
\ end {массив}
\ right | -b \ left |
\ begin {array} {ccc}
e & g & h \\
я & к & л \\
м & о & п \\
\ end {массив}
\ right | + c \ left |
\ begin {array} {ccc}
e & f & h \\
я & j & l \\
m & n & p \\
\ end {массив}
\ right | -d \ left |
\ begin {array} {ccc}
e & f & g \\
я & j & k \\
м & н & о \\
\ end {массив}
\ право |
\ end {align} $$
Для каждого элемента исходной матрицы его минор является определителем $ 3 \ times 3 $.
Существует другой способ вычисления определителя $ 3 \ times 3 $, хорошо известный как правило Сарруса или схема Сарруса.
- Расширить определитель, переписав первые два столбца чисел:
- Сложите произведения красных диагоналей и вычтите произведения синих диагоналей, т. Е. $$ det (A) = aei + bfg + cdh-ceg-afh-bdi $$ Это правило можно запомнить, вспомнив о диагоналях расширенного определителя. читать диагонали означает плюс $ (aei + bfg + cdh) $, а синие диагонали означают минус $ (- ceg-afh-bdi) $.
Добро пожаловать в калькулятор определителя матрицы , где у вас будет возможность вычислить, ну, определители матрицы, используя простую в использовании формулу определителя для любой квадратной матрицы размером до 4×4. Кроме того, мы рассмотрим некоторые из основных свойств определителей , которые могут помочь в решении более крупных, таких как определитель матрицы 4×4.
« Что такое детерминант и почему меня это должно волновать? » Мы покажем вам определение детерминанта через некоторое время, но давайте просто скажем, что, помимо прочего, он чрезвычайно полезен при работе с системами уравнений. По сути, решение для решения системы трех уравнений аналогично тому, как найти определитель матрицы 3×3.
Убедили? Воодушевлены? В восторге? Тогда идем дальше, ладно?
Что такое определитель?
Почему бы нам не начать с , что представляет собой матрица ? Вы не поверите, но это не только классика научной фантастики 90-х.В математике это имя, которое мы даем массиву элементов (обычно чисел) с заданным количеством строк и столбцов . Пример матрицы
| А | = |
|
Как видите, числа заключены в две большие квадратные скобки: [ и ] .Также мы говорим, что, например, число 2 равно в ячейке во второй строке и втором столбце .
Определение определителя утверждает, что это число, полученное путем умножения и сложения ячеек квадратной матрицы в соответствии с заданным правилом . Давайте подробнее рассмотрим здесь несколько важных вещей.
- Как следует из определения определителя, нам нужна квадратная матрица , чтобы даже начать вычисления.Это означает, что мы можем найти определитель матрицы 2×2 или определитель матрицы 4×4, но не, например, чего-то похожего на приведенную выше
A, которая является матрицей 3×2 (три строки и два столбца); - Формула детерминанта для больших матриц становится довольно сложной . Количество его слагаемых равно количеству перестановок числа, являющегося стороной матрицы. Это означает, что определитель матрицы 2×2 имеет только два слагаемых, но для матриц 5×5 мы получаем 120 слагаемых;
- Есть способы упростить расчеты .Например, поиск определителя матрицы 4×4 можно превратить в задачу о том, как найти определитель матрицы 3×3. Мы рассмотрим некоторые из таких свойств определителей в разделе «Свойства определителей»; и
- Определитель матрицы ,
Aобозначается как| A |(просто замените квадратные скобки матрицы вертикальными линиями|) илиdet (A). Не путайте первое обозначение с абсолютным значением! В общем, определитель может быть отрицательным числом .
Итак, что такое определитель? Это число, мы многому научились. Но почему это полезно? Где это появляется?
Определитель матрицы — чрезвычайно полезный и часто используемый инструмент в линейной алгебре. Когда у нас есть матрица и мы хотим ее понять, определитель — это одно из первых, к чему мы обращаемся. Например, каждая система линейных уравнений может быть описана матрицей, и ее определители помогают нам найти решение, например, с помощью правила Крамера.Более того, когда мы используем матрицы для описания линейного преобразования, часто лучше всего диагонализовать их . Как мы это делаем? Конечно, с детерминантами. Наконец, нам обычно нужны собственные значения такого преобразования. Да, вы догадались — для этого , мы также используем определители .
Надеюсь, нам удалось убедить вас, что стоит изучить определение детерминанта. Но как это вычислить? Есть ли какая-нибудь короткая и понятная формула для определения детерминанта для повседневного использования?
Общая детерминантная формула
Прежде чем мы рассмотрим некоторые конкретные примеры, например, как найти определитель матрицы 3×3, давайте взглянем на чудовищность, которая составляет , общее определение определителя .
Пусть A будет квадратной матрицей размером n , где n — некоторое натуральное число. Обозначим ячейки A через i, j , где i — номер строки, а j — номер столбца. Тогда:
| A | = Σ (-1) sign (σ) Π a i, σ (i)
где,
-
Σ— некоторая из всех перестановок набора{1,2, ..., n}; и -
Πявляется произведениемi-s от1доn.
Красиво, не правда ли? Если перевести забавные символы в нечто более понятное, это означает примерно следующее:
Чтобы вычислить определитель, посмотрите на свою матрицу, возьмите n чисел, по одному из каждой строки и каждого столбца, и умножьте их вместе. Возьмите все такие пары n , иногда меняйте их знак и просуммируйте все это.
Не волнуйтесь, теперь, когда мы опубликовали это общее определение детерминанта, , мы больше не будем об этом думать .Мы будем придерживаться , простых случаев , где матрица не слишком велика, чтобы показать, что это на самом деле означает.
Определитель матрицы 2×2, 3×3 и 4×4
Размер имеет значение, как это часто бывает в жизни. В данном конкретном случае : чем меньше матрица, тем проще определить формулу . Для согласованности мы использовали те же обозначения, что и в калькуляторе определителя матрицы.
Если
| А | = |
|
, затем определитель A равен
| A | = a₁ * b₂ - a₂ * b₁ .
Обратите внимание, что это эквивалентно взятию числа одной из диагоналей квадратной матрицы (из верхнего левого угла в нижний правый) за вычетом другой (из верхнего правого угла в нижний левый).
Далее, если
| ⌈ | a₁ | b₁ | c₁ | ⌉ | ||
| В | = | | | a₂ | b₂ | c₂ | ｜ |
| ⌊ | a₃ | b₃ | c₃ | ⌋ |
, затем определитель B равен
| B | = a₁ * b₂ * c₃ + a₂ * b₃ * c₁ + a₃ * b₁ * c₂ - a₃ * b₂ * c₁ - a₁ * b₃ * c₂ - a₂ * b₁ * c₃ .
Здесь мы снова можем использовать диагонали, чтобы запомнить формулу. Чтобы это было ясно, давайте снова напишем две верхние строки под матрицей:
| | | a₁ | b₁ | c₁ | ｜ |
| | | a₂ | b₂ | c₂ | ｜ |
| | | a₃ | b₃ | c₃ | ｜ |
| a₁ | b₁ | c₁ | ||
| a₂ | b₂ | c₂ |
Теперь, как и в случае 2×2, начинается с диагонали исходной квадратной матрицы, которая идет от верхнего левого угла к нижнему правому — это первое слагаемое, a₁ * b₂ * c₃ .Затем мы возьмем всю эту диагональ и сдвинем ее на один шаг вниз , т.е. в каждом столбце возьмем элемент под тем, который мы взяли ранее. Здесь развернутый массив, который мы нарисовали выше, помогает нам увидеть, что это дает второе слагаемое, a₂ * b₃ * c₁ . Мы делаем это еще раз, чтобы получить a₃ * b₁ * c₂ и , на этом заканчиваются диагонали вниз-вправо и слагаемые, которые появляются со знаком плюс .
Затем, , мы переходим к другой диагонали исходной матрицы (от верхнего правого угла до нижнего левого) и получаем первое отрицательное слагаемое в формуле a₃ * b₂ * c₁ .Проделываем то же самое, что и раньше — перемещаем диагональ вниз на . Развернутая форма выше позволяет нам легко увидеть, что это дает два других отрицательных слагаемых: a₁ * b₃ * c₂ и a₂ * b₁ * c₃ .
Наконец, если
| С | = |
|
, то определитель такой матрицы 4×4 равен
| C | = a₁ * b₂ * c₃ * d₄ - a₂ * b₁ * c₃ * d₄ + a₃ * b₁ * c₂ * d₄ - a₁ * b₃ * c₂ * d₄ + a₂ * b₃ * c₁ * d₄ - a₃ * b₂ * c₁ * d₄ + a₃ * b₂ * c₄ * d₁ - a₂ * b₃ * c₄ * d₁ + a₄ * b₃ * c₂ * d₁ - a₃ * b₄ * c₂ * d₁ + a₂ * b₄ * c₃ * d₁ - a₄ * b₂ * c₃ * d₁ + a₄ * b₁ * c₃ * d₂ - a₁ * b₄ * c₃ * d₂ + a₃ * b₄ * c₁ * d₂ - a₄ * b₃ * c₁ * d₂ + a₁ * b₃ * c₄ * d₂ - a₃ * b₁ * c₄ * d₂ + a₂ * b₁ * c₄ * d₃ - a₁ * b₂ * c₄ * d₃ + a₄ * b₂ * c₁ * d₃ - a₂ * b₄ * c₁ * d₃ + a₁ * b₄ * c₂ * d₃ - a₄ * b₁ * c₂ * d₃ .
Уф, это был длинный, не так ли? Теперь вы можете видеть, что найти определитель матрицы 2×2 очень просто, и мы можем узнать, как найти определитель матрицы 3×3 за час или около того. Но — определитель матрицы 4×4 — это совершенно новая проблема . Не поймите нас неправильно, это вполне выполнимо, но кто будет платить нам за то время, которое мы потратили на вычисления, а затем на поиски, где мы взяли a вместо a₂ ?
Итак, как мы можем использовать здесь диагональный трюк? Ответ прост: у нас нет .К сожалению, это не работает для матриц от 4 и более.
« Итак, как я могу эффективно вычислить, что такое определитель 4х4? Или 5х5? » Ну, , как удобно с вашей стороны спросить! Мы покажем вам это в следующем разделе.
Свойства детерминантов
Теперь мы перечислим несколько важных свойств детерминантов , которые могут оказаться полезными. Мы начинаем с простых и выносим большие пушки в самом конце.
Определитель продукта является произведением определяющих факторов. Другими словами, если мы умножаем две квадратные матрицы и хотим найти определитель результата, то мы можем получить ответ, вычислив определители факторов и умножив их вместе.
Определитель матрицы равен определителю ее транспонирования. По сути, если вместо матрицы, с которой мы начали, мы «перевернем ее», так что ее первая строка будет первым столбцом, первый столбец будет первой строкой и т. Д. (Это называется транспонированием матрица ), то их определители будут одинаковыми.Например:
| | | 1 | 4 | -1 | ｜ | | | 1 | 0 | 6 | ｜ | |
| | | 0 | 2 | -3 | ｜ | = | | | 4 | 2 | 11 | ｜ |
| | | 6 | 11 | 5 | ｜ | | | -1 | -3 | 5 | ｜ |
- Если мы поменяем местами две строки или два столбца, определитель останется тем же, но с противоположным знаком. Это означает, что, например, если мы хотим знать, как найти определитель матрицы 3×3, то мы можем заменить, скажем, ее первый столбец третьим, чтобы получить то же число, но с другим знаком (см. пример ниже).
| | | 1 | 4 | -1 | ｜ | | | -1 | 4 | 1 | ｜ | ||
| | | 0 | 2 | -3 | ｜ | = | – | | | -3 | 2 | 0 | ｜ |
| | | 6 | 11 | 5 | ｜ | | | 5 | 11 | 6 | ｜ |
- Мы можем добавить любое ненулевое кратное от строки к некоторой другой строке (или столбцу к столбцу) и не изменять определитель .Это похоже на то, что мы делаем в методе исключения Гаусса, когда мы хотим найти эшелонированную форму строки системы уравнений, за исключением того, что здесь мы имели дело только со строками (которые соответствовали уравнениям). Это свойство означает, что если мы добавим, скажем, две копии первой строки ко второй, мы получим матрицу с тем же определителем. Например:
| | | 1 | 4 | -1 | ｜ | | | 1 | 4 | -1 | ｜ | |
| | | 0 | 2 | -3 | ｜ | = | | | 0 + 2 * 1 | 2 + 2 * 4 | -3 + 2 * (- 1) | ｜ |
| | | 6 | 11 | 5 | ｜ | | | 6 | 11 | 5 | ｜ |
что дает,
| | | 1 | 4 | -1 | ｜ | | | 1 | 4 | -1 | ｜ | |
| | | 0 | 2 | -3 | ｜ | = | | | 2 | 10 | -5 | ｜ |
| | | 6 | 11 | 5 | ｜ | | | 6 | 11 | 5 | ｜ |
- ( расширение Лапласа ) Помните вопрос « Что является определителем матрицы 5×5? » из приведенного выше раздела? Наконец, мы можем коснуться этой темы и представить мощный инструмент , который поможет нам с формулой детерминанта.
Пусть A будет квадратной матрицей размером n . Скажем, что j -я строка (или столбец) A имеет элементы a₁ , a₂ , …, aₙ . Обозначим через Aᵢ матрицу, полученную из A путем удаления всей строки и столбца, в которых у нас было aᵢ (тогда Aᵢ представляет собой квадратную матрицу размером n-1 ). Тогда
| A | = (-1) j + 1 * a₁ * | A₁ | + (-1) j + 2 * a₂ * | A₂ | +… + (-1) j + n * aₙ * | Aₙ |.
Вот это полезный инструмент, если мы когда-либо его видели. И пользоваться им довольно весело! Например, если нас спросят, как найти определитель матрицы 3×3, мы можем взять лист бумаги, выбрать, скажем, третью строку матрицы и с энтузиазмом написать:
| = | (-1) 3 + 1 * 6 * | + |
Чтобы прочитать всю эту теорию, должно быть, потребовались века, так почему бы нам наконец, , не взглянуть на пример ?
Пример: использование калькулятора определителя матрицы
Скажем, вы хотите вычислить определитель следующей матрицы :
| А | = |
|
Определитель матрицы 4х4 , а? Мы видели формулу определителя для одного в разделе «Определитель матрицы 2×2, 3×3 и 4×4», поэтому мы знаем, что будет не очень интересным , не так ли? Но с тех пор мы узнали некоторые свойства детерминантов, так почему бы нам не заставить работать в нашу пользу ?
Прежде чем мы это сделаем, давайте, , воспользуемся калькулятором определителя матрицы , чтобы увидеть, как наш инструмент упрощает такие проблемы.Прежде всего, мы имеем дело с матрицей 4×4, поэтому нам нужно сообщить об этом калькулятору , выбрав соответствующий вариант в « Размер матрицы ».
Это покажет нам пример такой матрицы с символической нотацией для ее элементов . Как мы видим, a₁ , b₁ , c₁ и d₁ обозначают числа в первой строке, поэтому давайте прокрутимся туда, где мы вводим данные, и загрузим калькулятор определителя матрицы тем, что мы имеем в нашем упражнении :
a₁ = 2 , b₁ = 5 , c₁ = 1 , d₁ = 3 .
Аналогично для остальных строк имеем:
a₂ = 4 , b₂ = 1 , c₂ = 7 , d₂ = 9 ,
a₃ = 6 , b₃ = 8 , c₃ = 3 , d₃ = 2 ,
a₄ = 7 , b₄ = 8 , c₄ = 1 , d₄ = 4 .
В тот момент, когда мы напишем последнее число, калькулятор определителя матрицы сотворит чудеса и выдаст ответ :
| A | = 630 .
Хорошо, теперь, когда у нас есть этот спойлер ответа, давайте посмотрим, , как мы можем получить этот ответ вручную . Очевидно, один из способов — просто использовать формулу детерминанта из 24 членов, но нам нужны дополнительные баллы для творчества, и мы хотим, чтобы использовал свойства детерминантов .
Мы будем использовать расширение Лапласа, но с умом. Мы выбираем произвольную строку или столбец, скажем, первую строку матрицы, и пытаемся немного упростить раскрытие.В конце концов, если мы сразу воспользуемся формулой, мы получим сумму четырех определителей 3×3. Не страшно, но и не здорово. Однако мы можем сделать что-нибудь сначала — использовать элементарные операции с столбцами .
В предыдущем разделе мы видели, что если мы добавим ненулевое кратное столбцу к другому столбцу, определитель останется прежним. Итак, , почему бы нам не добавить (-2) — кратное третьего столбца к первому ?
| | A | | = |
|
что дает,
| | A | | = |
|
И зачем мы это сделали? Напомним, что в разложении Лапласа слагаемые были такими: (-1) в некоторой степени, умноженной на элемент строки или столбца, который мы выбрали, умноженный на меньший определитель.Следовательно, если теперь развернуть | A | относительно первой строки, слагаемое, соответствующее первой ячейке в первой строке, будет равно (-1) в некоторой степени, умноженной на 0, умноженной на некоторый определитель. И это ноль , потому что все, умноженное на ноль, равно нулю.
Отлично, мы уменьшили количество слагаемых на одно! Так как насчет повторить процедуру и получить еще меньше ? Для этого мы хотим, чтобы в первой строке было больше нулей, поэтому давайте превратим 5 и 3 в 0 -s.Как и раньше, , мы добавляем к этим столбцам правое число, кратное третьему столбцу (с 1 ):
| | A | | = |
|
что дает,
| | A | | = |
|
Теперь это больше нравится! В этой форме, если мы используем разложение Лапласа для первой строки, мы получим только одно слагаемое, потому что три других будут в 0 раз больше, что составляет 0 .Если быть точным, получаем
| | A | | = | (-1) 1 + 3 * 1 * |
|
И мы хорошо знаем, как найти определитель матрицы 3×3, не так ли? Но помните, что , если вы хотите немного повеселиться, , вы можете снова использовать расширение Лапласа, чтобы получить определитель матрицы 2×2.В противном случае мы можем просто использовать формулу определителя и на основании приведенного выше получить:
| A | = (-1) ⁴ * (-10 * (- 7) * 1 + (-34) * (- 7) * 5 + (-12) * 0 * 5 - (-12) * (- 7) * 5 - (-10) * (- 7) * 3 - (-34) * 0 * 1) = 630 .
Ура, согласен с тем, что у нас было выше! Посмотрите, сколько времени может сэкономить калькулятор определителя матрицы? Вы знаете, сколько страниц нашей любимой книги мы могли прочитать за это время?
Калькулятор определителя матрицы
Калькулятор, приведенный в этом разделе, может использоваться для определения значения определителя матриц 2×2 и 3×3.
Помимо вышеперечисленного, если вам нужны какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
- 01
- Определитель двух векторов
- Определитель трех векторов
- Определитель матрицы
задачи на слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по скорости единицы
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Тригонометрические проблемы со словами
Проблемы со словами в процентах
Проблемы со словами в виде прибылей и убытков 9604 9602 Задачи
Задачи с десятичными словами
Задачи со словами на дроби
Задачи со словами на смешанные дроби
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейным неравенством
Задачи со словамиПроблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Теорема Пифагора Задачи со словами
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон 960 рациональных функций 9602 Область и диапазон 960 рациональных функций функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
с использованием длинного корня видение
L.Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Матричный определитель4×4
Калькулятор, представленный в этом разделе, может быть использован для нахождения определяющих значений матриц 4×4.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
- 01
задачи на слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по скорости единицы
задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Тригонометрические проблемы со словами
Проблемы со словами в процентах
Проблемы со словами в виде прибылей и убытков 9604 9602 Задачи
Задачи с десятичными словами
Задачи со словами на дроби
Задачи со словами на смешанные дроби
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейным неравенством
Задачи со словамиПроблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Теорема Пифагора Задачи со словами
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Область и диапазон 960 рациональных функций 9602 Область и диапазон 960 рациональных функций функции с отверстиями
График рациональных функций
График рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
с использованием длинного корня видение
L.Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 степени 256 на 17
Остаток при делении степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
1.Детерминанты
М. Борна
Прежде чем мы увидим, как использовать матрицу для решения системы одновременных уравнений, мы узнаем о детерминантах.
Определитель представляет собой квадратный массив чисел (записывается внутри пары вертикальных линий), что представляет собой определенную сумму продуктов.
Ниже приведен пример определителя 3 × 3 (у него 3 строки и 3 столбца).
`| (10,0, -3), (- 2, -4,1), (3,0,2) |`
Результатом умножения и последующего упрощения элементов определителя является одно число (скаляр , величина ).
Расчет определителя 2 × 2
В общем, мы находим значение определителя 2 × 2 с элементами a , b , c , d следующим образом:
`| (a, b), (c, d) | = ad-cb`
Умножаем диагонали (сначала верхний левый × нижний правый), затем вычитаем.
Пример 1
`| (4,1), (2,3) |`
`= 4xx3-2xx1`
`= 12-2`
`= 10`
Конечный результат — одно число .
Ниже мы увидим, как расширить определитель 3 × 3.
Использование определителей для решения систем уравнений
Мы можем решить систему уравнений, используя определители, но это становится очень утомительным для больших систем. Мы будем использовать только системы 2 × 2 и 3 × 3 с использованием определителей.
Правило Крамера
Решение ( x , y ) системы
`a_1x + b_1y = c_1`
`a_2x + b_2y = c_2`
можно найти с помощью определителей:
`x = | (c_1, b_1), (c_2, b_2) | / | (a_1, b_1), (a_2, b_2) |`
`y = | (a_1, c_1), (a_2, c_2) | / | (a_1, b_1), (a_2, b_2) |`
Пример 2
Решите систему, используя правило Крамера:
x — 3 y = 6
2 x + 3 y = 3
Ответ
Сначала мы определяем значения, которые нам понадобятся для правила Крамера:
a 1 = 1 б 1 = −3 с 1 = 6
а 2 = 2 б 2 = 3 с 2 = 3
`х = | (6, -3), (3,3) | / | (1, -3), (2,3) | = (18 + 9) / (3 + 6) = 3`
`y = | (1,6), (2,3) | / | (1, -3), (2,3) | = (3-12) / (3 + 6) = (- 9) / 9` = -1`
Итак, решение — `(3, -1)`.
Чек:
[1] `3 + 3 = 6` ОК
[2] `6 — 3 = 3` OK
3 × 3 ДетерминантыОпределитель 3 × 3
`| (a_1, b_1, c_1), (a_2, b_2, c_2), (a_3, b_3, c_3) |`
можно оценивать по-разному.
Мы будем использовать метод под названием «расширение по несовершеннолетним». Но сначала нам нужно определение.
Кофакторы
Определитель 2 × 2
`| (b_2, c_2), (b_3, c_3) |`
это называется кофактором из 1 для определителя 3 × 3:
`| (a_1, b_1, c_1), (a_2, b_2, c_2), (a_3, b_3, c_3) |`
Кофактор образован из элементов, которые не находятся в одной строке с a 1 и не в том же столбце, что и a 1 .
Аналогично определитель
`| (b_1, c_1), (b_3, c_3) |`
называется кофактором из a 2 . Он сформирован из элементы не в той же строке, что a 2 и не в том же столбце, что и a 2 .
Продолжаем узор для кофактора a 3 .
Расширение несовершеннолетними
Мы оцениваем наш определитель 3 × 3, используя разложение по минорам.Это включает в себя умножение элементов в первом столбце определителя на сомножителей этих элементов. Вычитаем средний продукт и добавляем конечный продукт.
`| (a_1, b_1, c_1), (a_2, b_2, c_2), (a_3, b_3, c_3) |` = a_1 | (b_2, c_2), (b_3, c_3) | « -a_2 | ( b_1, c_1), (b_3, c_3) | `+ a_3 | (b_1, c_1), (b_2, c_2) |`
Обратите внимание, , что мы работаем вниз по первому столбцу и умножаем его на сомножитель каждого элемента.
Пример 3
Оценить
`| (-2,3, -1), (5, -1,4), (4, -8,2) |`
(Вы можете изучить, о чем действительно спрашивает этот пример, в этом апплете трехмерных интерактивных систем уравнений.)
Ответ
`| (-2,3, -1), (5, -1,4), (4, -8,2) |` `= -2 | (-1,4), (- 8,2) | `-5 | (3, -1), (- 8,2) |` +4 | (3, -1), (- 1,4) | `
`= -2 [(- 1) (2) — (-8) (4)] — 5 [(3) (2)` `{: — (-8) (- 1)]` `+ 4 [ (3) (4) «{: — (-1) (- 1)]«
`= -2 (30) — 5 (-2) + 4 (11)`
`= -60 + 10 + 44`
`= -6`
Здесь мы расширяем на первый столбец . Мы можем выполнить расширение, используя первую строку, и получим тот же результат.
Правило Крамера для решения систем линейных уравнений 3 × 3
Мы можем решить общую систему уравнений,
a 1 x + b 1 y + c 1 z = d 1
a 2 x + b 2 y + c 2 z = d 2
a 3 x + b 3 y + c 3 z = d 3
с использованием определителей:
`x = | (d_1, b_1, c_1), (d_2, b_2, c_2), (d_3, b_3, c_3) | / Delta`
`y = | (a_1, d_1, c_1), (a_2, d_2, c_2), (a_3, d_3, c_3) | / Delta`
`z = | (a_1, b_1, d_1), (a_2, b_2, d_2), (a_3, b_3, d_3) | / Delta`
где
`Дельта = | (a_1, b_1, c_1), (a_2, b_2, c_2), (a_3, b_3, c_3) |`
Пример 4
Решите, используя правило Крамера:
2 x + 3 y + z = 2
— x + 2 y + 3 z = −1
−3 x — 3 y + z = 0
Ответ
`x = | (2,3,1), (- 1,2,3), (0, -3,1) | / Delta`
`y = | (2,2,1), (- 1, -1,3), (- 3,0,1) | / Delta`
`z = | (2,3,2), (- 1,2, -1), (- 3, -3,0) | / Delta`
где
`Дельта = | (2,3,1), (- 1,2,3), (- 3, -3,1) | « = 2 (11) +1 (6) -3 (7) « = 7`
Так
`x = (2 (11) +1 (6) +0) / 7 = 28/7 = 4`
`y = (2 (-1) +1 (2) -3 (7)) / 7` = -21 / 7« = -3`
`z = (2 (-3) +1 (6) -3 (-7)) / 7` = 21 / 7` = 3`
Проверочные решения:
[1] 2 (4) + 3 (-3) + 3 = 2 ОК
[2] — (4) + 2 (-3) + 3 (3) = -1 ОК
[3] −3 (4) — 3 (−3) + 3 = 0 ОК
Итак, решение — `(4, -3, 3)`.
Детерминантные упражнения
1. Оценить путем расширения несовершеннолетние:
`| (10,0, -3), (- 2, -4,1), (3,0,2) |`
Ответ
`| (10,0, -3), (- 2, -4,1), (3,0,2) | « = 10 | (-4,1), (0,2) | « — (- 2) | (0, -3), (0,2) | « +3 | (0, -3) , (- 4,1) | `
`= 10 [(- 4) (2) — (0) (1)]` + 2 [(0) (2) — (0) (- 3)] « + 3 [(0) (1 ) — (-4) (- 3)] `
`= 10 (-8) + 2 (0) + 3 (−12)`
`= −80 — 36`
`= −116`
2.Решите система с использованием определителей:
x + 3 y + z = 4
2 x — 6 y — 3 z = 10
4 x — 9 y + 3 z = 4
Ответ
`x = | (4,3,1), (10, -6, -3), (4, -9,3) | / Delta`
`y = | (1,4,1), (2,10, -3), (4,4,3) | / Delta`
где
`Дельта = | (1,3,1), (2, -6, -3), (4, -9,3) | `
`= 1 (−45) — 2 (18) + 4 (−3)`
`= −93`
Примечание: когда у нас есть x и y , мы можем найти z без использования правила Крамера.
Так
`x = (4 (-45) -10 (18) +4 (-3)) / — 93` = (- 372) / — 93« = 4`
`y = (1 (42) -2 (8) +4 (-22)) / — 93` = (- 62) / — 93« = 2 / 3`
Используя эти два результата, мы легко можем найти, что z = -2.
Проверка решения:
[1] `(4) + 3 (2/3) + -2 = 4`
[2] `2 (4) — 6 (2/3) — 3 (-2) = 10`
[3] `4 (4) — 9 (2/3) + 3 (-2) = 4`
Итак, решение — `(4, 2/3, -2)`.
Онлайн-калькулятор определителя — Solumaths
Описание:
Функция определителя вычисляет в режиме онлайн определитель векторов или определитель матрицы.
детерминантОписание:
Определитель Функция вычисляет определители в режиме онлайн. Калькулятор может рассчитать определитель двух векторов , определитель трех векторов или определитель матрицы.
В ортонормированной системе координат (O, `vec (i)`, `vec (j)`) вектор `vec (u)` имеет координаты (x, y) (`vec (i)`, `vec (j)`) вектор `vec (v)` имеет координаты (x ‘, y’).Определитель `vec (u)` et `vec (v)` равен число xx’-yy ‘.
Калькулятор может вычислять определители , давая точные результаты: для вычисления определителя (3, `1/2`) и (` 4/5`, 2) введите определитель (`[[3; 1/2]; [4/5; 2]]`), после расчета возвращается результат.
Калькулятор позволяет проводить символьные вычисления, возможно использование букв: до вычислить определитель двух векторов следующим образом: (a, b) et (3a, 2) введите определитель (`[[a; b]; [3a; 2]]`), после расчета возвращается результат.
Примечание: Когда определитель двух векторов равен нулю, два вектора коллинеарны.
В ортонормированной системе координат (O, `vec (i)`, `vec (j)`, `vec (k)`) вектор `vec (u)` имеет координаты (x, y, z) , вектор `vec (v)` имеет координаты (x ‘, y’, z ‘), вектор `vec (k)` имеет координаты (x’ ‘, y’ ‘, z’ ‘). Определитель векторов `vec (u)`, `vec (v)`, `vec (k)` равен числу xy’z » + x’y»z + x»yz’-xy » z’-x’yz » — x»y’z.
Чтобы вычислить определитель трех векторов , используйте следующий синтаксис: определитель (`[[3; 1; 0]; [3; 2; 1]; [4; 0; 7]]`).
Калькулятор определителя может использоваться с квадратными матрицами порядка n, он также может выполнять символьные вычисления. Чтобы вычислить определитель матрицы , используйте следующий синтаксис: определитель (`[[3; 1; 0]; [3; 2; 1]; [4; 1; 2]]`).
Функция определителя вычисляет в режиме онлайн определитель векторов или определитель матрицы.
Синтаксис:
определитель (матрица)Примеры:
определитель (`[[3; 1; 0]; [3; 2; 1]; [4; 1; 7]]`), возвращает 22 Рассчитать онлайн с определителем (определителем)Онлайн калькулятор для расчета определителя 5×5
Онлайн-калькулятор определителя 5×5
Онлайн-калькулятор вычисляет значение определителя матрицы 5×5 с разложением Лапласа в строке или столбце и алгоритмом Гаусса.
Определитель 5×5
det A = a11a12a13a14a15a21a22a23a24a25a31a32a33a34a35a41a42a43a44a45a51a52a53a54a55
Введите коэффициенты
Расчет значения определителя с разложением Лапласа
Вы можете выбрать строку или столбец, которые будут использоваться для расширения.
Расчет по алгоритму Гаусса
Примечание:
Если ведущие коэффициенты равны нулю, то столбцы или строки следует поменять местами соответственно, чтобы было возможно деление на ведущий коэффициент.Значение определителя является правильным, если после преобразований нижняя треугольная матрица равна нулю, а все элементы главной диагонали равны 1.
Объяснение методов
Теорема о разложении Лапласа
Теорема развития Лапласа предоставляет метод для вычисления определителя, в котором определитель разворачивается после строки или столбца. Размерность уменьшается и может быть уменьшена шаг за шагом до скаляра.
det A = & Sum; i = 1n-1i + j⋅aijdetAij (расширение в j-м столбце)
det A = & Sum; j = 1n-1i + j⋅aijdetAij (Разложение в i-й строке)
, где A ij , подматрица матрицы A, которая возникает при удалении i-й строки и j-го столбца.
Пример расширения Лапласа согласно первой строке матрицы 3×3.
det A = a11a12a13a21a22a23a31a32a33
Первый элемент задается коэффициентом a 11 и вспомогательным определителем, состоящим из элементов с зеленым фоном.
a11a12a13a21a22a23a31a32a33 => a11a22a23a32a33
Второй элемент задается коэффициентом a 12 и вспомогательным определителем, состоящим из элементов с зеленым фоном.
a11a12a13a21a22a23a31a32a33 => a12a21a23a31a33
Третий элемент задается множителем a 13 и вспомогательным определителем, состоящим из элементов с зеленым фоном.
a11a12a13a21a22a23a31a32a33 => a13a21a22a31a32
С тремя элементами определитель может быть записан как сумма определителей 2×2.
det A = a11a12a13a21a22a23a31a32a33 = a11a22a23a32a33-a12a21a23a31a33 + a13a21a22a31a32
Важно учитывать, что знаки элементов меняются следующим образом.
+ — + — + — + — +
Метод Гаусса
В методе Гаусса определитель преобразуется так, что элементы матрицы нижнего треугольника становятся нулевыми.