Решение методом обратной матрицы онлайн с решением: Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.

(2+1) = -1.

В результате вы получите матрицу дополнений, теперь транспонируйте ее. Транспонирование — это операция, симметричная относительно главной диагонали матрицы, столбцы и строки меняются местами. Таким образом, вы нашли присоединенную матрицу A*.

В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.

Определение 1

Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.

Пример 1

Найти решение системы n линейных уравнений с n неизвестными:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n

Матричный вид записи : А × X = B

где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.

X = x 1 x 2 ⋮ x n — столбец неизвестных,

B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.

Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1:

A — 1 × A × X = A — 1 × B .

Так как А — 1 × А = Е, то Е × X = А — 1 × В или X = А — 1 × В.

Замечание

Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю. Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А.

В том случае, если d e t A н е р а в е н н у л ю, у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.

Содержание

Пример решения системы линейных уравнений с помощью метода обратной матрицы

Пример 2

Решаем СЛАУ методом обратной матрицы:

2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2

Как решить?

Записываем систему в виде матричного уравнения А X = B , где

А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .

Выражаем из этого уравнения X:

Находим определитель матрицы А:

d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × (- 2) × 5 + 3 × (- 4) × 4 + 3 × (- 1) × 1 — 3 × (- 2) × 3 — — 1 × (- 4) × 5 — 2 × 4 — (- 1) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25

d e t А не равняется 0, следовательно для этой системы подходит метод решения обратной матрицей.

Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А:

А 11 = (- 1) (1 + 1) — 2 4 — 1 5 = — 10 + 4 = — 6 ,

А 12 = (- 1) 1 + 2 1 4 3 5 = — (5 — 12) = 7 ,

А 13 = (- 1) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,

А 21 = (- 1) 2 + 1 — 4 3 — 1 5 = — (- 20 + 3) = 17 ,

А 22 = (- 1) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,

А 23 = (- 1) 2 + 3 2 — 4 3 — 1 = — (- 2 + 12) = — 10 ,

А 31 = (- 1) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,

А 32 = (- 1) 3 + 2 2 3 1 4 = — (8 — 3) = — 5 ,

А 33 = (- 1) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .

Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А:

А * = — 6 7 5 17 1 — 10 — 10 — 5 0

Записываем обратную матрицу согласно формуле:

A — 1 = 1 d e t A (A *) T: А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,

Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:

X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1

Ответ : x 1 = — 1 ; x 2 = 0 ; x 3 = 1

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Эта тема является одной из самых ненавистных среди студентов. Хуже, наверное, только определители.

Фишка в том, что само понятие обратного элемента (и я сейчас не только о матрицах) отсылает нас к операции умножения. Даже в школьной программе умножение считается сложной операцией, а уж умножение матриц — вообще отдельная тема, которой у меня посвящён целый параграф и видеоурок.

Сегодня мы не будем вдаваться в подробности матричных вычислений. Просто вспомним: как обозначаются матрицы, как они умножаются и что из этого следует.

Повторение: умножение матриц

Прежде всего договоримся об обозначениях. Матрицей $A$ размера $\left[ m\times n \right]$ называется просто таблица из чисел, в которой ровно $m$ строк и $n$ столбцов:

\=\underbrace{\left[ \begin{matrix} {{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} \\ {{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} \\ … & … & … & … \\ {{a}_{m1}} & {{a}_{m2}} & … & {{a}_{mn}} \\\end{matrix} \right]}_{n}\]

Чтобы случайно не перепутать строки и столбцы местами (поверьте, на экзамене можно и единицу с двойкой перепутать — что уж говорить про какие-то там строки), просто взгляните на картинку:

Определение индексов для клеток матрицы

Что происходит? Если разместить стандартную систему координат $OXY$ в левом верхнем углу и направить оси так, чтобы они охватывали всю матрицу, то каждой клетке этой матрицы можно однозначно сопоставить координаты $\left(x;y \right)$ — это и будет номер строки и номер столбца.

Почему система координат размещена именно в левом верхнем углу? Да потому что именно оттуда мы начинаем читать любые тексты. Это очень просто запомнить.

А почему ось $x$ направлена именно вниз, а не вправо? Опять всё просто: возьмите стандартную систему координат (ось $x$ идёт вправо, ось $y$ — вверх) и поверните её так, чтобы она охватывала матрицу. Это поворот на 90 градусов по часовой стрелке — его результат мы и видим на картинке.

В общем, как определять индексы у элементов матрицы, мы разобрались. Теперь давайте разберёмся с умножением.

Определение. Матрицы $A=\left[ m\times n \right]$ и $B=\left[ n\times k \right]$, когда количество столбцов в первой совпадает с количеством строк во второй, называются согласованными.

Именно в таком порядке. Можно сумничать и сказать, мол, матрицы $A$ и $B$ образуют упорядоченную пару $\left(A;B \right)$: если они согласованы в таком порядке, то совершенно необязательно, что $B$ и $A$, т.

{n}{{{a}_{ik}}}\cdot {{b}_{kj}}\]

Другими словами: чтобы получить элемент ${{c}_{ij}}$ матрицы $C=A\cdot B$, нужно взять $i$-строку первой матрицы, $j$-й столбец второй матрицы, а затем попарно перемножить элементы из этой строки и столбца. Результаты сложить.

Да, вот такое суровое определение. Из него сразу следует несколько фактов:

Умножение матриц, вообще говоря, некоммутативно: $A\cdot B\ne B\cdot A$;
Однако умножение ассоциативно: $\left(A\cdot B \right)\cdot C=A\cdot \left(B\cdot C \right)$;

И даже дистрибутивно: $\left(A+B \right)\cdot C=A\cdot C+B\cdot C$;
И ещё раз дистрибутивно: $A\cdot \left(B+C \right)=A\cdot B+A\cdot C$.

Дистрибутивность умножения пришлось отдельно описывать для левого и правого множителя-суммы как раз из-за некоммутативности операции умножения.

Если всё же получается так, что $A\cdot B=B\cdot A$, такие матрицы называются перестановочными.

Среди всех матриц, которые там на что-то умножаются, есть особые — те, которые при умножении на любую матрицу $A$ снова дают $A$:

Определение.
{-1}}$. Тогда эта обратная матрица — единственная.
Доказательство. Пойдём от противного: пусть у матрицы $A$ есть хотя бы два экземпляра обратных —$B$ и $C$. Тогда, согласно определению, верны следующие равенства:
\[\begin{align} & A\cdot B=B\cdot A=E; \\ & A\cdot C=C\cdot A=E. \\ \end{align}\]
Из леммы 1 мы заключаем, что все четыре матрицы — $A$, $B$, $C$ и $E$ — являются квадратными одинакового порядка: $\left[ n\times n \right]$. Следовательно, определено произведение:
Поскольку умножение матриц ассоциативно (но не коммутативно!), мы можем записать:
\[\begin{align} & B\cdot A\cdot C=\left(B\cdot A \right)\cdot C=E\cdot C=C; \\ & B\cdot A\cdot C=B\cdot \left(A\cdot C \right)=B\cdot E=B; \\ & B\cdot A\cdot C=C=B\Rightarrow B=C. \\ \end{align}\]

Получили единственно возможный вариант: два экземпляра обратной матрицы равны. Лемма доказана.

Приведённые рассуждения почти дословно повторяют доказательство единственность обратного элемента для всех действительных чисел $b\ne 0$. {-1}} \right|\ne 0.\]

Вот и получается, что $\left| A \right|\ne 0$. Лемма доказана.

На самом деле это требование вполне логично. Сейчас мы разберём алгоритм нахождения обратной матрицы — и станет совершенно ясно, почему при нулевом определителе никакой обратной матрицы в принципе не может существовать.

Но для начала сформулируем «вспомогательное» определение:

Определение. Вырожденная матрица — это квадратная матрица размера $\left[ n\times n \right]$, чей определитель равен нулю.

Таким образом, мы можем утверждать, что всякая обратимая матрица является невырожденной.

Как найти обратную матрицу

Сейчас мы рассмотрим универсальный алгоритм нахождения обратных матриц. Вообще, существует два общепринятых алгоритма, и второй мы тоже сегодня рассмотрим.

Тот, который будет рассмотрен сейчас, очень эффективен для матриц размера $\left[ 2\times 2 \right]$ и — частично — размера $\left[ 3\times 3 \right]$. {t}}$, где $t$ — это (вот сейчас внимание!) сумма номеров всех выбранных строчек и столбцов. Это и будет алгебраическое дополнение.

Взгляните на третий шаг: там вообще-то сумма $2k$ слагаемых! Другое дело, что для $k=1$ мы получим лишь 2 слагаемых — это и будут те самые $i+j$ — «координаты» элемента ${{a}_{ij}}$, для которого мы ищем алгебраическое дополнение.

Таким образом сегодня мы используем слегка упрощённое определение. Но как мы увидим в дальнейшем, его окажется более чем достаточно. Куда важнее следующая штука:

Определение. Союзная матрица $S$ к квадратной матрице $A=\left[ n\times n \right]$ — это новая матрица размера $\left[ n\times n \right]$, которая получается из $A$ заменой ${{a}_{ij}}$ алгебраическими дополнениями ${{A}_{ij}}$:

\\Rightarrow S=\left[ \begin{matrix} {{A}_{11}} & {{A}_{12}} & … & {{A}_{1n}} \\ {{A}_{21}} & {{A}_{22}} & … & {{A}_{2n}} \\ … & … & … & … \\ {{A}_{n1}} & {{A}_{n2}} & . {T}}=\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]\]

Ну вот и всё. Задача решена.

Ответ. $\left[ \begin{array}{*{35}{r}} 2 & -1 \\ -5 & 3 \\\end{array} \right]$

Задача. Найдите обратную матрицу:

\[\left[ \begin{array}{*{35}{r}} 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end{array} \right]\]

Решение. Опять считаем определитель:

\[\begin{align} & \left| \begin{array}{*{35}{r}} 1 & -1 & 2 \\ 0 & 2 & -1 \\ 1 & 0 & 1 \\\end{array} \right|=\begin{matrix} \left(1\cdot 2\cdot 1+\left(-1 \right)\cdot \left(-1 \right)\cdot 1+2\cdot 0\cdot 0 \right)- \\ -\left(2\cdot 2\cdot 1+\left(-1 \right)\cdot 0\cdot 1+1\cdot \left(-1 \right)\cdot 0 \right) \\\end{matrix}= \\ & =\left(2+1+0 \right)-\left(4+0+0 \right)=-1\ne 0. \\ \end{align}\]

Определитель отличен от нуля — матрица обратима. А вот сейчас будет самая жесть: надо посчитать аж 9 (девять, мать их!) алгебраических дополнений. {-1}}=\frac{1}{-1}\cdot \left[ \begin{matrix} 2 & -1 & -2 \\ 1 & -1 & -1 \\ -3 & 1 & 2 \\\end{matrix} \right]=\left[ \begin{array}{*{35}{r}}-2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]\]

Ну и всё. Вот и ответ.

Ответ. $\left[ \begin{array}{*{35}{r}} -2 & -1 & 3 \\ 1 & 1 & -1 \\ 2 & 1 & -2 \\\end{array} \right]$

Как видите, в конце каждого примера мы выполняли проверку. В связи с этим важное замечание:

Не ленитесь выполнять проверку. Умножьте исходную матрицу на найденную обратную — должна получиться $E$.

Выполнить эту проверку намного проще и быстрее, чем искать ошибку в дальнейших вычислениях, когда, например, вы решаете матричное уравнение.

Альтернативный способ

Как я и говорил, теорема об обратной матрице прекрасно работает для размеров $\left[ 2\times 2 \right]$ и $\left[ 3\times 3 \right]$ (в последнем случае — уже не так уж и «прекрасно»), а вот для матриц больших размеров начинается прям печаль.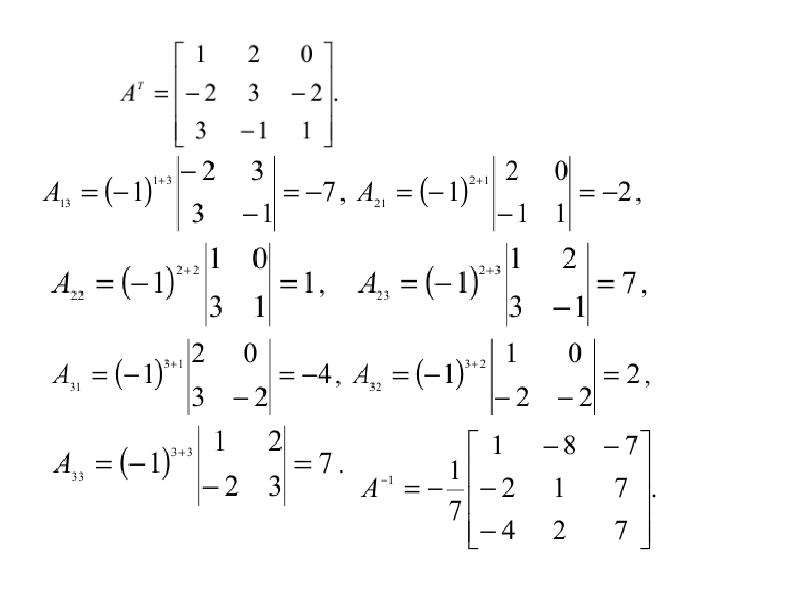

Но не переживайте: есть альтернативный алгоритм, с помощью которого можно невозмутимо найти обратную хоть для матрицы $\left[ 10\times 10 \right]$. Но, как это часто бывает, для рассмотрения этого алгоритма нам потребуется небольшая теоретическая вводная.

Элементарные преобразования

Среди всевозможных преобразований матрицы есть несколько особых — их называют элементарными. Таких преобразований ровно три:

Умножение. Можно взять $i$-ю строку (столбец) и умножить её на любое число $k\ne 0$;
Сложение. Прибавить к $i$-й строке (столбцу) любую другую $j$-ю строку (столбец), умноженную на любое число $k\ne 0$ (можно, конечно, и $k=0$, но какой в этом смысл? Ничего не изменится же).
Перестановка. Взять $i$-ю и $j$-ю строки (столбцы) и поменять местами.

Почему эти преобразования называются элементарными (для больших матриц они выглядят не такими уж элементарными) и почему их только три — эти вопросы выходят за рамки сегодняшнего урока. Поэтому не будем вдаваться в подробности.

Важно другое: все эти извращения нам предстоит выполнять над присоединённой матрицей. Да, да: вы не ослышались. Сейчас будет ещё одно определение — последнее в сегодняшнем уроке.

Присоединённая матрица

Наверняка в школе вы решали системы уравнений методом сложения. Ну, там, вычесть из одной строки другую, умножить какую-то строку на число — вот это вот всё.

Так вот: сейчас будет всё то же, но уже «по-взрослому». Готовы?

Определение. Пусть дана матрица $A=\left[ n\times n \right]$ и единичная матрица $E$ такого же размера $n$. Тогда присоединённая матрица $\left[ A\left| E \right. \right]$ — это новая матрица размера $\left[ n\times 2n \right]$, которая выглядит так:
\[\left[ A\left| E \right. \right]=\left[ \begin{array}{rrrr|rrrr}{{a}_{11}} & {{a}_{12}} & … & {{a}_{1n}} & 1 & 0 & … & 0 \\{{a}_{21}} & {{a}_{22}} & … & {{a}_{2n}} & 0 & 1 & . {-1}}\]

Вот так всё просто! Короче говоря, алгоритм нахождения обратной матрицы выглядит так:

Записать присоединённую матрицу $\left[ A\left| E \right. \right]$;
Выполнять элементарные преобразования строк до тех пор, пока права вместо $A$ не появится $E$;
Разумеется, слева тоже что-то появится — некая матрица $B$. Это и будет обратная;
PROFIT!:)

Конечно, сказать намного проще, чем сделать. Поэтому давайте рассмотрим парочку примеров: для размеров $\left[ 3\times 3 \right]$ и $\left[ 4\times 4 \right]$.

Задача. Найдите обратную матрицу:
\[\left[ \begin{array}{*{35}{r}} 1 & 5 & 1 \\ 3 & 2 & 1 \\ 6 & -2 & 1 \\\end{array} \right]\]
Решение. Составляем присоединённую матрицу:
\[\left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end{array} \right]\]
Поскольку последний столбец исходной матрицы заполнен единицами, вычтем первую строку из остальных:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 3 & 2 & 1 & 0 & 1 & 0 \\ 6 & -2 & 1 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \downarrow \\ -1 \\ -1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end{array} \right] \\ \end{align}\]
Больше единиц нет, кроме первой строки. Но её мы не трогаем, иначе в третьем столбце начнут «размножаться» только что убранные единицы.
Зато можем вычесть вторую строку дважды из последней — получим единицу в левом нижнем углу:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 5 & -7 & 0 & -1 & 0 & 1 \\\end{array} \right]\begin{matrix} \ \\ \downarrow \\ -2 \\\end{matrix}\to \\ & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right] \\ \end{align}\]
Теперь можно вычесть последнюю строку из первой и дважды из второй — таким образом мы «занулим» первый столбец:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 1 & 5 & 1 & 1 & 0 & 0 \\ 2 & -3 & 0 & -1 & 1 & 0 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -1 \\ -2 \\ \uparrow \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right] \\ \end{align}\]
Умножим вторую строку на −1, а затем вычтем её 6 раз из первой и прибавим 1 раз к последней:
\[\begin{align} & \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & -1 & 0 & -3 & 5 & -2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} \ \\ \left| \cdot \left(-1 \right) \right. \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 6 & 1 & 0 & 2 & -1 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & -1 & 0 & 1 & -2 & 1 \\\end{array} \right]\begin{matrix} -6 \\ \updownarrow \\ +1 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrr|rrr} 0 & 0 & 1 & -18 & 32 & -13 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 1 & 0 & 0 & 4 & -7 & 3 \\\end{array} \right] \\ \end{align}\]
Осталось лишь поменять местами строки 1 и 3:
\[\left[ \begin{array}{rrr|rrr} 1 & 0 & 0 & 4 & -7 & 3 \\ 0 & 1 & 0 & 3 & -5 & 2 \\ 0 & 0 & 1 & -18 & 32 & -13 \\\end{array} \right]\]
Готово! Справа — искомая обратная матрица.
Ответ. $\left[ \begin{array}{*{35}{r}}4 & -7 & 3 \\ 3 & -5 & 2 \\ -18 & 32 & -13 \\\end{array} \right]$
Задача. Найдите обратную матрицу:
\[\left[ \begin{matrix} 1 & 4 & 2 & 3 \\ 1 & -2 & 1 & -2 \\ 1 & -1 & 1 & 1 \\ 0 & -10 & -2 & -5 \\\end{matrix} \right]\]
Решение. Снова составляем присоединённую:
\[\left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\]
Немного позалимаем, попечалимся от того, сколько сейчас придётся считать… и начнём считать. Для начала «обнулим» первый столбец, вычитая строку 1 из строк 2 и 3:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 1 & -2 & 1 & -2 & 0 & 1 & 0 & 0 \\ 1 & -1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \downarrow \\ -1 \\ -1 \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right] \\ \end{align}\]
Наблюдаем слишком много «минусов» в строках 2—4. Умножим все три строки на −1, а затем «выжжем» третий столбец, вычитая строку 3 из остальных:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & -6 & -1 & -5 & -1 & 1 & 0 & 0 \\ 0 & -5 & -1 & -2 & -1 & 0 & 1 & 0 \\ 0 & -10 & -2 & -5 & 0 & 0 & 0 & 1 \\\end{array} \right]\begin{matrix} \ \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\ \left| \cdot \left(-1 \right) \right. \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 4 & 2 & 3 & 1 & 0 & 0 & 0 \\ 0 & 6 & 1 & 5 & 1 & -1 & 0 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 10 & 2 & 5 & 0 & 0 & 0 & -1 \\\end{array} \right]\begin{matrix} -2 \\ -1 \\ \updownarrow \\ -2 \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
Теперь самое время «поджарить» последний столбец исходной матрицы: вычитаем строку 4 из остальных:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & -1 & -1 & 0 & 2 & 0 \\ 0 & 1 & 0 & 3 & 0 & -1 & 1 & 0 \\ 0 & 5 & 1 & 2 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right]\begin{matrix} +1 \\ -3 \\ -2 \\ \uparrow \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
Финальный бросок: «выжигаем» второй столбец, вычитая строку 2 из строки 1 и 3:
\[\begin{align} & \left[ \begin{array}{rrrr|rrrr} 1 & -6 & 0 & 0 & -3 & 0 & 4 & -1 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 5 & 1 & 0 & 5 & 0 & -5 & 2 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right]\begin{matrix} 6 \\ \updownarrow \\ -5 \\ \ \\\end{matrix}\to \\ & \to \left[ \begin{array}{rrrr|rrrr} 1 & 0 & 0 & 0 & 33 & -6 & -26 & -17 \\ 0 & 1 & 0 & 0 & 6 & -1 & -5 & 3 \\ 0 & 0 & 1 & 0 & -25 & 5 & 20 & -13 \\ 0 & 0 & 0 & 1 & -2 & 0 & 2 & -1 \\\end{array} \right] \\ \end{align}\]
И снова слева единичная матрица, значит справа — обратная. 🙂
Ответ. $\left[ \begin{matrix} 33 & -6 & -26 & 17 \\ 6 & -1 & -5 & 3 \\ -25 & 5 & 20 & -13 \\ -2 & 0 & 2 & -1 \\\end{matrix} \right]$

Ну вот и всё. Проверку сделайте сами — мне в лом.:)

www.сайт позволяет найти обратную матрицу онлайн . Сайт производит вычисление обратной матрицы онлайн . За неколько секунд сервер выдаст точное решение. Обратной матрицей будет являться такая матрица , умножение исходной матрицы на которую дает единичную матрицу , при условии, что определитель начальной матрицы не равен нулю, иначе обратной матрицы для нее не существует. В задачах, когда вычисляем обратную матрицу онлайн , необходимо, чтобы определитель матрицы был отличным от нуля, иначе www.сайт выдаст соответствующее сообщение о невозможности вычислить обратную матрицу онлайн . Такую матрицу еще называют вырожденной. Найти обратную матрицу в режиме онлайн можно только для квадратной матрицы . Операция нахождения обратной матрицы онлайн сводится к вычислению определителя матрицы , затем составляется промежуточная матрица по известному правилу, и в завершении операции — умножения найденного ранее определителя на транспонированную промежуточную матрицу . Точного результата от определения обратной матрицы онлайн можно добиться, изучив теорию по этому курсу. Данная операция занимает особое место в теории матриц и линейной алгебры, позволяет решать системы линейных уравнений, так называемым, матричным методом. Задача по нахождению обратной матрицы онлайн встречается уже в начале изучения высшей математики и присутствует почти в каждой математической дисциплине как базовое понятие алгебры, являясь математическим инструментом в прикладных задачах. www.сайт находит обратную матрицу заданной размерности в режиме онлайн мгновенно. Вычисление обратной матрицы онлайн при заданной её размерности — это нахождение матрицы той же размерности в числовом ее значении, а также в символьном, найденного по правилу вычисления обратной матрицы . Нахождение обратной матрицы онлайн широко распространено в теории матриц . Результат нахождения обратной матрицы онлайн используется при решении линейной системы уравнений матричным методом. Если определитель матрицы будет равен нулю, то обратной матрицы , для которой найден нулевой определитель, не существует. Для того, чтобы вычислить обратную матрицу или найти сразу для нескольких матриц соответствующие им обратные , необходимо затратить не мало времени и усилий, в то время как наш сервер в считанные секунды найдет обратную матрицу онлайн . При этом ответ по нахождению обратной матрицы будет правильным и с достаточной точностью, даже если числа при нахождении обратной матрицы онлайн будут иррациональными. На сайте www.сайт допускаются символьные записи в элементах матриц , то есть обратная матрица онлайн может быть представлена в общем символьном виде при вычислении обратной матрицы онлайн . Полезно проверить ответ, полученный при решении задачи по нахождению обратной матрицы онлайн , используя сайт www.сайт . При совершении операции вычисления обратной матрицы онлайн необходимо быть внимательным и предельно сосредоточенным при решении данной задачи. В свою очередь наш сайт поможет Вам проверить своё решение на тему обратная матрица онлайн . Если у Вас нет времени на долгие проверки решенных задач, то www.сайт безусловно будет являться удобным инструментом для проверки при нахождении и вычислении обратной матрицы онлайн .

Как правило, обратные операции используются для упрощения сложных алгебраических выражений. Например, если в задаче присутствует операция деления на дробь, можно заменить ее операцией умножения на обратную дробь, что является обратной операцией. Более того, матрицы делить нельзя, поэтому нужно умножать на обратную матрицу. Вычислять матрицу, обратную матрице размером 3х3, довольно утомительно, но нужно уметь делать это вручную. Также обратную величину можно найти с помощью хорошего графического калькулятора.

Шаги

С помощью присоединенной матрицы

Транспонируйте исходную матрицу. Транспонирование – это замена строк на столбцы относительно главной диагонали матрицы, то есть нужно поменять местами элементы (i,j) и (j,i). При этом элементы главной диагонали (начинается в верхнем левом углу и заканчивается в нижнем правом углу) не меняются.

Чтобы поменять строки на столбцы, запишите элементы первой строки в первом столбце, элементы второй строки во втором столбце, а элементы третьей строки в третьем столбце. Порядок изменения положения элементов показан на рисунке, на котором соответствующие элементы обведены цветными кружками.

Найдите определить каждой матрицы размером 2х2. Каждый элемент любой матрицы, включая транспонированную, связан с соответствующей матрицей 2х2. Чтобы найти матрицу 2х2, которая соответствует определенному элементу, зачеркните строку и столбец, в которых находится данный элемент, то есть нужно зачеркнуть пять элементов исходной матрицы 3х3. Незачеркнутыми останутся четыре элемента, которые являются элементами соответствующей матрицы 2х2.

Например, чтобы найти матрицу 2х2 для элемента, который расположен на пересечении второй строки и первого столбца, зачеркните пять элементов, которые находятся во второй строке и первом столбце. Оставшиеся четыре элемента являются элементами соответствующей матрицы 2х2.
Найдите определитель каждой матрицы 2х2. Для этого произведение элементов второстепенной диагонали вычтите из произведения элементов главной диагонали (смотрите рисунок).
Подробную информацию о матрицах 2х2, соответствующих определенным элементам матрицы 3х3, можно найти в интернете.

Создайте матрицу кофакторов. Результаты, полученные ранее, запишите в виде новой матрицы кофакторов. Для этого найденный определитель каждой матрицы 2х2 напишите там, где располагался соответствующий элемент матрицы 3х3. Например, если рассматривается матрица 2х2 для элемента (1,1), ее определитель запишите в позиции (1,1). Затем поменяйте знаки соответствующих элементов согласно определенной схеме, которая показана на рисунке.

Схема изменения знаков: знак первого элемента первой строки не меняется; знак второго элемента первой строки меняется на противоположный; знак третьего элемента первой строки не меняется и так далее построчно. Обратите внимание, что знаки «+» и «-», которые показаны на схеме (смотрите рисунок), не свидетельствуют о том, что соответствующий элемент будет положительным или отрицательным. В данном случае знак «+» говорит о том, что знак элемента не меняется, а знак «-» свидетельствует об изменении знака элемента.
Подробную информацию о матрицах кофакторов можно найти в интернете.
Так вы найдете присоединенную матрицу исходной матрицы. Иногда ее называют комплексно-сопряженной матрицей. Такая матрица обозначается как adj(M).

Разделите каждый элемент присоединенной матрицы на определитель. Определитель матрицы М был вычислен в самом начале, чтобы проверить, что обратная матрица существует. Теперь разделите каждый элемент присоединенной матрицы на этот определитель. Результат каждой операции деления запишите там, где находится соответствующий элемент. Так вы найдете матрицу, обратную исходной.

Определитель матрицы, которая показана на рисунке, равен 1. Таким образом, здесь присоединенная матрица является обратной матрицей (потому что при делении любого числа на 1 оно не меняется).
В некоторых источниках операция деления заменяется операцией умножения на 1/det(М). При этом конечный результат не меняется.

Запишите обратную матрицу. Запишите элементы, расположенные на правой половине большой матрицы, в виде отдельной матрицы, которая является обратной матрицей.

С помощью калькулятора

Выберите калькулятор, который работает с матрицами. С помощью простых калькуляторов нельзя найти обратную матрицу, но это можно сделать на хорошем графическом калькуляторе, таком как Texas Instruments TI-83 или TI-86.

Введите исходную матрицу в память калькулятора. Для этого нажмите кнопку Matrix (Матрица), если она есть. В случае калькулятора Texas Instruments, возможно, понадобится нажать кнопки 2 nd и Matrix.

Выберите меню Edit (Редактирование). Сделайте это с помощью кнопок со стрелками или соответствующей функциональной кнопки, которая находится в верхней части клавиатуры калькулятора (расположение кнопки зависит от модели калькулятора).

Введите обозначение матрицы. Большинство графических калькуляторов умеет работать с 3-10 матрицами, которые можно обозначить буквами А-J. Как правило, просто выберите [A], чтобы обозначить исходную матрицу. Затем нажмите кнопку Enter (Ввод).

Введите размер матрицы. В данной статье говорится о матрицах 3х3. Но графические калькуляторы умеют работать с матрицами больших размеров. Введите количество строк, нажмите кнопку Enter, затем введите количество столбцов и еще раз нажмите кнопку Enter.

Введите каждый элемент матрицы. На экране калькулятора отобразится матрица. Если ранее в калькулятор уже вводилась матрица, она появится на экране. Курсор выделит первый элемент матрицы. Введите значение первого элемента и нажмите Enter. Курсор автоматически переместится к следующему элементу матрицы.

Метод обратной матрицы и как найти обратную матрицу

Решать систему линейных уравнений с помощью обратной матрицы («найти обратную матрицу») — это не самый удобный способ, но он существует. Нахождение обратной матрицы применимо, если определитель, будучи составлен из коэффициентов при переменных, 0.

Для примера возьмем опять же знакомую нам систему:

Запишем эту систему в матричной форме

A * X = B

Будем искать матицу A¹, обратную к матрице А, с помощью
метода Гаусса

Для этого запишем расширенную матрицу, в которой слева будет находиться наша исходная
матрица А, а справа — единичная.

Используя метод Гаусса, постепенно приведем нашу исходную к единичной матрице. Это
преобразование применим ко всей расширенной матрице.

После приведения левой части расширенной матрицы к единичной, справа окажется матрица,
обратная к нашей исходной, а проследить последовательность приведения левой части расширенной
матрицы к единичной нам помогут серые выделенные элементы.

Рассмотрим столбец 1.

Преобразования матрицы удобнее производить в целых числах, для этого следует прибавить
соответствующие элементы строки 1 к элементам строки 2:

Прибавим соответствующие элементы строки 1 к элементам строки 2, помножив их на -3.

Это приведет к тому, что в левой части расширенной матрицы, все элементы расположенные ниже
главной диагонали = 0.

Проведем аналогичные преобразования, но уже применительно к элементам матрицы,
расположенными выше главной диагонали.

Рассмотрим столбец 2.

Разделим элементы строки 2 на -30.

Прибавим к элементам строки 1 соответствующие элементы строки 2, помноженные на -13.

Элементы строки 1 разделим на -1.

Запишем обратную матрицу.

Теперь вернемся к уравнению, записанному нами в матричной форме.

A * X = B

Умножим обе части уравнения на A¹

Произведение исходной матрицы на обратную дает единичную матрицу,
т.е. A¹ * A = Е, следовательно

X = A¹ * B

Ответ :

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Нахождение обратной матрицы 2 на 2. Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы

Похожие на обратные по многим свойствам.

Энциклопедичный YouTube

1 / 5

✪ Как находить обратную матрицу — bezbotvy

✪ Обратная матрица (2 способа нахождения)

✪ Обратная матрица #1

✪ 2015-01-28. {-1}b} . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Способы нахождения обратной матрицы

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы

Метод Гаусса-Жордана

Возьмём две матрицы: саму A и единичную E . Приведём матрицу A к единичной матрице методом Гаусса-Жордана применяя преобразования по строкам (можно также применять преобразования и по столбцам, но не в перемешку). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A −1 .

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ i {\displaystyle \Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

Λ 1 ⋅ ⋯ ⋅ Λ n ⋅ A = Λ A = E ⇒ Λ = A − 1 {\displaystyle \Lambda _{1}\cdot \dots \cdot \Lambda _{n}\cdot A=\Lambda A=E\Rightarrow \Lambda =A^{-1}} .

{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}

где adj (A) {\displaystyle {\mbox{adj}}(A)} — присоединенная матрица ;

Сложность алгоритма зависит от сложности алгоритма расчета определителя O det и равна O(n²)·O det .

Использование LU/LUP-разложения

Матричное уравнение A X = I n {\displaystyle AX=I_{n}} для обратной матрицы X {\displaystyle X} можно рассматривать как совокупность n {\displaystyle n} систем вида A x = b {\displaystyle Ax=b} . Обозначим i {\displaystyle i} -ый столбец матрицы X {\displaystyle X} через X i {\displaystyle X_{i}} ; тогда A X i = e i {\displaystyle AX_{i}=e_{i}} , i = 1 , … , n {\displaystyle i=1,\ldots ,n} ,поскольку i {\displaystyle i} -м столбцом матрицы I n {\displaystyle I_{n}} является единичный вектор e i {\displaystyle e_{i}} . другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³) . {-1}={\frac {1}{\det(\mathbf {A})}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}\,\,\,d&\!\!-b\\-c&\,a\\\end{bmatrix}}.}

Обращение матрицы 2х2 возможно только при условии, что a d − b c = det A ≠ 0 {\displaystyle ad-bc=\det A\neq 0} .

Пусть дана квадратная матрица . Требуется найти обратную матрицу.

Первый способ. В теореме 4.1 существования и единственности обратной матрицы указан один из способов ее нахождения.

1. Вычислить определитель данной матрицы. Если, то обратной матрицы не существует (матрицавырожденная).

2. Составить матрицу из алгебраических дополненийэлементов матрицы.

3. Транспонируя матрицу , получить присоединенную матрицу.

4. Найти обратную матрицу (4.1), разделив все элементы присоединенной матрицы на определитель

Второй способ. Для нахождения обратной матрицы можно использовать элементарные преобразования.

1. Составить блочную матрицу , приписав к данной матрицеединичную матрицу того же порядка.

2. При помощи элементарных преобразований, выполняемых над строками матрицы , привести ее левый блокк простейшему виду. При этом блочная матрица приводится к виду, где- квадратная матрица, полученная в результате преобразований из единичной матрицы.

3. Если , то блокравен обратной матрице, т.е.. Если, то матрицане имеет обратной.

В самом деле, при помощи элементарных преобразований строк матрицы можно привести ее левый блокк упрощенному виду(см. рис. 1.5). При этом блочная матрицапреобразуется к виду, где- элементарная матрица, удовлетворяющая равенству. Если матрицаневырожденная, то согласно п.2 замечаний 3.3 ее упрощенный вид совпадает с единичной матрицей. Тогда из равенстваследует, что. Если же матрицавырожденная, то ее упрощенный видотличается от единичной матрицы, а матрицане имеет обратной.

11. Матричные уравнения и их решение. Матричная форма записи СЛАУ. Матричный способ (метод обратной матрицы) решения СЛАУ и условия его применимости.

Матричными уравнениями называются уравнения вида: A*X=C; X*A=C; A*X*B=C где матрица А,В,С известны,матрица Х не известна, если матрицы А и В не вырождены, то решения исходных матриц запишется в соответственном виде: Х=А -1 *С; Х=С*А -1 ; Х=А -1 *С*В -1 Матричная форма записи систем линейных алгебраических уравнений. С каждой СЛАУ можно связать несколько матриц; более того – саму СЛАУ можно записать в виде матричного уравнения. Для СЛАУ (1) рассмотрим такие матрицы:

Матрица A называется матрицей системы . Элементы данной матрицы представляют собой коэффициенты заданной СЛАУ.

Матрица A˜ называется расширенной матрицей системы . Её получают добавлением к матрице системы столбца, содержащего свободные члены b1,b2,…,bm. Обычно этот столбец отделяют вертикальной чертой, – для наглядности.

Матрица-столбец B называется матрицей свободных членов , а матрица-столбец X – матрицей неизвестных .

Используя введённые выше обозначения, СЛАУ (1) можно записать в форме матричного уравнения: A⋅X=B.

Примечание

Матрицы, связанные с системой, можно записать различными способами: всё зависит от порядка следования переменных и уравнений рассматриваемой СЛАУ. Но в любом случае порядок следования неизвестных в каждом уравнении заданной СЛАУ должен быть одинаков.

Матричный метод подходит для решения СЛАУ, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы отличен от нуля. Если система содержит больше трех уравнений, то нахождение обратной матрицы требует значительных вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса .

12. Однородные СЛАУ, условия существования их ненулевых решений. Свойства частных решений однородных СЛАУ.

Линейное уравнение называется однородным, если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:

13 .Понятие линейной независимости и зависимости частных решений однородной СЛАУ. Фундаментальная система решений (ФСР) и её нахождение. Представление общего решения однородной СЛАУ через ФСР.

Система функций y 1 (x ), y 2 (x ), …, y n (x ) называется линейно зависимой на интервале (a , b ), если существует набор постоянных коэффициентов , не равных нулю одновременно, таких, что линейная комбинация этих функций тождественно равна нулю на (a , b ): для . Если равенство для возможно только при , система функций y 1 (x ), y 2 (x ), …, y n (x ) называется линейно независимой на интервале (a , b ). Другими словами, функции y 1 (x ), y 2 (x ), …, y n (x ) линейно зависимы на интервале (a , b ), если существует равная нулю на (a , b ) их нетривиальная линейная комбинация. Функции y 1 (x ),y 2 (x ), …, y n (x ) линейно независимы на интервале (a , b ), если только тривиальная их линейная комбинация тождественно равна нулю на (a , b ).

Фундаментальной системой решений (ФСР) однородной СЛАУ называется базис этой системы столбцов.

Количество элементов в ФСР равно количеству неизвестных системы минус ранг матрицы системы. Любое решение исходной системы есть линейная комбинация решений ФСР.

Теорема

Общее решение неоднородной СЛАУ равно сумме частного решения неоднородной СЛАУ и общего решения соответствующей однородной СЛАУ.

1 . Если столбцы — решения однородной системы уравнений, то любая их линейная комбинациятакже является решением однородной системы.

В самом деле, из равенств следует, что

т.е. линейная комбинация решений является решением однородной системы.

2. Если ранг матрицы однородной системы равен , то система имеетлинейно независимых решений.

Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений, придавая свободным переменным следующиестандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):

которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последнихстроках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен. Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).

Любая совокупность линейно независимых решенийоднородной системы называетсяфундаментальной системой (совокупностью) решений .

14 Минор -ого порядка, базисный минор, ранг матрицы. Вычисление ранга матрицы.

Минором порядка k матрицы А называется детерминант некоторой ее квадратной подматрицы порядка k.

В матрице А размеров m x n минор порядка r называется базисным, если он отличен от нуля, а все миноры большего порядка, если они существуют, равны нулю.

Столбцы и строки матрицы А, на пересечении которых стоит базисный минор, называются базисными столбцами и строками А.

Теорема 1. (О ранге матрицы). У любой матрицы минорный ранг равен строчному рангу и равен столбцовому рангу.

Теорема 2.(О базисном миноре). Каждый столбец матрицы раскладывается в линейную комбинацию ее базисных столбцов.

Рангом матрицы (или минорным рангом) называется порядок базисного минора или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Ранг нулевой матрицы по определению считают 0.

Отметим два очевидных свойства минорного ранга.

1) Ранг матрицы не меняется при транспонировании, так как при транспонировании матрицы все ее подматрицы транспонируются и миноры не меняются.

2) Если А’-подматрица матрицы А, то ранг А’ не превосходит ранга А, так как ненулевой минор, входящий в А’, входит и в А.

15. Понятие -мерного арифметического вектора. Равенство векторов. Действия над векторами (сложение, вычитание, умножение на число, умножение на матрицу). Линейная комбинация векторов.

Упорядоченная совокупность n действительных или комплексных чисел называется n-мерным вектором . Числа называются координатами вектора .

Два (ненулевых) вектора a и b равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными. Во всех остальных случаях векторы не равны.

Сложение векторов. Для сложения векторов есть два способа. 1. Правило параллелограмма. Чтобы сложить векторы и, помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторови.

2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и . По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Вычитание векторов. Вектор направлен противоположно вектору. Длины векторовиравны. Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины. Он сонаправлен с вектором, если k больше нуля, и направлен противоположно, если k меньше нуля.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними. Если векторы перпендикулярны, их скалярное произведение равно нулю. А вот так скалярное произведение выражается через координаты векторов и .

Линейная комбинация векторов

Линейной комбинацией векторов называют вектор

где — коэффициенты линейной комбинации. Если комбинация называется тривиальной, если — нетривиальной.

16 .Скалярное произведение арифметических векторов. Длина вектора и угол между векторами. Понятие ортогональности векторов.

Скалярным произведением векторов а и в называется число,

Скалярное произведение используется для вычисления:1)нахождения угла между ними;2)нахождение проекции векторов;3)вычисление длины вектора;4)условия перпендикулярности векторов.

Длиной отрезка АВ называют расстоянием между точками А иВ. Угол между векторами А и В называют угол α=(а,в) ,0≤ α ≤П. На который необходимо повернуть 1 вектор,чтоб его направления совпало с другим вектором. При условии,что их начала совпадут.

Ортом а называется вектор а имеющий единичную длину и направления а.

17. Система векторов и её линейная комбинация. Понятие линейной зависимости и независимости системы векторов. Теорема о необходимом и достаточном условиях линейной зависимости системы векторов.

Система векторов a1,a2,…,an называется линейно зависимой, если существуют числа λ1,λ2,…,λnтакие, что хотя бы одно из них отлично от нуля и λ1a1+λ2a2+…+λnan=0. В противном случае система называется линейно независимой.

Два вектора a1 и a2 называются коллинеарными если их направления совпадают или противоположны.

Три вектора a1,a2 и a3 называются компланарными если они параллельны некоторой плоскости.

Геометрические критерии линейной зависимости:

а) система {a1,a2} линейно зависима в том и только том случае, когда векторы a1 и a2 коллинеарны.

б) система {a1,a2,a3} линейно зависима в том и только том случае, когда векторы a1,a2 и a3компланарны.

теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)

Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.

Следствие.1. Система векторов векторного пространства является линейно независимой тогда и только тогда, когда ни один из векторов системы линейно не выражается через другие вектора этой системы.2. Система векторов, содержащая нулевой вектор или два равных вектора, является линейно зависимой.

Обратная матрица для данной это такая матрица, умножение исходной на которую дает единичную матрицу: Обязательным и достаточным условием наличия обратной матрицы является неравенство нулю детерминанта исходной (что в свою очередь подразумевает, что матрица должна быть квадратная). Если же определитель матрицы равняется нулю, то ее называют вырожденной и такая матрица не имеет обратной. В высшей математике обратные матрицы имеют важное значение и применяются для решения ряда задач. Например, на нахождении обратной матрицы построен матричный метод решения систем уравнений. Наш сервис сайт позволяет вычислять обратную матрицу онлайн двумя методами: методом Гаусса-Жордана и с помощью матрицы алгебраических дополнений. Прервый подразумевает большое количество элементарных преобразований внутри матрицы, второй — вычисление детерминанта и алгебраических дополнений ко всем элементам. Для вычисления определителя матрицы онлайн вы можете воспользоваться другим нашим сервисом — Вычисление детерминанта матрицы онлайн

Найти обратную матрицу на сайт

сайт позволяет находить обратную матрицу онлайн быстро и бесплатно. На сайте произвордятся вычисления нашим сервисом и выдается результат с подробным решением по нахождению обратной матрицы . Сервер всегда выдает только точный и верный ответ. В задачах по определению обратной матрицы онлайн , необходимо, чтобы определитель матрицы был отличным от нуля, иначе сайт сообщит о невозможности найти обратную матрицу ввиду равенства нулю определителя исходной матрицы. Задача по нахождению обратной матрицы встречается во многих разделах математики, являясь одним из самых базовых понятий алгебры и математическим инструментом в прикладных задачах. Самостоятельное определение обратной матрицы требует значительных усилий, много времени, вычислений и большой внимательности, чтобы не допустить описку или мелкую ошибку в вычислениях. Поэтому наш сервис по нахождению обратной матрицы онлайн значительно облегчит вам задачу и станет незаменимым инструментом для решения математических задач. Даже если вы находите обратную матрицу самостоятельно, мы рекомендуем проверить ваше решение на нашем сервере. Ввведите вашу исходную матрицу у нас на Вычисление обратной матрицы онлайн и сверьте ваш ответ. Наша система никогда не ошибается и находит обратную матрицу заданной размерности в режиме онлайн мгновенно! На сайте сайт допускаются символьные записи в элементах матриц , в этом случае обратная матрица онлайн будет представлена в общем символьном виде.

Шаги

С помощью присоединенной матрицы

Чтобы поменять строки на столбцы, запишите элементы первой строки в первом столбце, элементы второй строки во втором столбце, а элементы третьей строки в третьем столбце. Порядок изменения положения элементов показан на рисунке, на котором соответствующие элементы обведены цветными кружками.

Например, чтобы найти матрицу 2х2 для элемента, который расположен на пересечении второй строки и первого столбца, зачеркните пять элементов, которые находятся во второй строке и первом столбце. Оставшиеся четыре элемента являются элементами соответствующей матрицы 2х2.
Найдите определитель каждой матрицы 2х2. Для этого произведение элементов второстепенной диагонали вычтите из произведения элементов главной диагонали (смотрите рисунок).
Подробную информацию о матрицах 2х2, соответствующих определенным элементам матрицы 3х3, можно найти в интернете.

Схема изменения знаков: знак первого элемента первой строки не меняется; знак второго элемента первой строки меняется на противоположный; знак третьего элемента первой строки не меняется и так далее построчно. Обратите внимание, что знаки «+» и «-», которые показаны на схеме (смотрите рисунок), не свидетельствуют о том, что соответствующий элемент будет положительным или отрицательным. В данном случае знак «+» говорит о том, что знак элемента не меняется, а знак «-» свидетельствует об изменении знака элемента.
Подробную информацию о матрицах кофакторов можно найти в интернете.
Так вы найдете присоединенную матрицу исходной матрицы. Иногда ее называют комплексно-сопряженной матрицей. Такая матрица обозначается как adj(M).

Определитель матрицы, которая показана на рисунке, равен 1. Таким образом, здесь присоединенная матрица является обратной матрицей (потому что при делении любого числа на 1 оно не меняется).
В некоторых источниках операция деления заменяется операцией умножения на 1/det(М). При этом конечный результат не меняется.

Нахождение обратной матрицы.

В этой статье разберемся с понятием обратной матрицы, ее свойствами и способами нахождения. Подробно остановимся на решении примеров, в которых требуется построить обратную матрицу для заданной.

Навигация по странице.

Обратная матрица — определение.

Нахождение обратной матрицы с помощью матрицы из алгебраических дополнений.

Свойства обратной матрицы.

Нахождение обратной матрицы методом Гаусса-Жордана.

Нахождение элементов обратной матрицы с помощью решения соответствующих систем линейных алгебраических уравнений.

Обратная матрица — определение.

Понятие обратной матрицы вводится лишь для квадратных матриц, определитель которых отличен от нуля, то есть для невырожденных квадратных матриц.

Определение.

Матрица называется обратной для матрицы , определитель которой отличен от нуля , если справедливы равенства , где E – единичная матрица порядка n на n .

Нахождение обратной матрицы с помощью матрицы из алгебраических дополнений.

Как же находить обратную матрицу для данной?

Во-первых, нам потребуются понятия транспонированной матрицы , минора матрицы и алгебраического дополнения элемента матрицы.

Определение.

Минор k-ого порядка матрицы A порядка m на n – это определитель матрицы порядка k на k , которая получается из элементов матрицы А , находящихся в выбранныхk строках и k столбцах. (k не превосходит наименьшего из чисел m или n ).

Минор (n-1)-ого порядка, который составляется из элементов всех строк, кроме i-ой , и всех столбцов, кроме j-ого , квадратной матрицы А порядка n на n обозначим как .

Иными словами, минор получается из квадратной матрицы А порядка n на n вычеркиванием элементов i-ой строки и j-ого столбца.

Для примера запишем, минор 2-ого порядка, который получаетсся из матрицы выбором элементов ее второй, третьей строк и первого, третьего столбцов . Также покажем минор, который получается из матрицы вычеркиванием второй строки и третьего столбца . Проиллюстрируем построение этих миноров: и .

Определение.

Алгебраическим дополнением элемента квадратной матрицы называют минор (n-1)-ого порядка, который получается из матрицы А , вычеркиванием элементов ее i-ой строки и j-ого столбца, умноженный на .

Алгебраическое дополнение элемента обозначается как . Таким обрзом, .

Например, для матрицы алгебраическое дополнение элемента есть .

Во-вторых, нам пригодятся два свойства определителя, которые мы разобрали в разделевычисление определителя матрицы :

На основании этих свойств определителя, определения операции умножения матрицы на число и понятия обратной матрицы справедливо равенство , где — транспонированная матрица, элементами которой являются алгебраические дополнения .

Матрица действительно является обратной для матрицы А , так как выполняются равенства . Покажем это

Составим алгоритм нахождения обратной матрицы с использованием равенства .

Разберем алгоритм нахождения обратной матрицы на примере.

Пример.

Дана матрица . Найдите обратную матрицу.

Решение.

Вычислим определитель матрицы А , разложив его по элементам третьего столбца:

Определитель отличен от нуля, так что матрица А обратима.

Найдем матрицу из алгебраических дополнений:

Поэтому

Выполним транспонирование матрицы из алгебраических дополнений:

Теперь находим обратную матрицу как :

Проверяем полученный результат:

Равенства выполняются, следовательно, обратная матрица найдена верно.

Свойства обратной матрицы.

Понятие обратной матрицы, равенство , определения операций над матрицами и свойства определителя матрицы позволяют обосновать следующие свойства обратной матрицы :

Рассмотрим еще один способ нахождения обратной матрицы для квадратной матрицы А порядка n на n .

Этот метод основан на решении n систем линейных неоднородных алгебраических уравнений с n неизвестными. Неизвестными переменными в этих системах уравнений являются элементы обратной матрицы.

Идея очень проста. Обозначим обратную матрицу как X , то есть, . Так как по определению обратной матрицы , то

Приравнивая соответствующие элементы по столбцам, получим n систем линейных уравнений

Решаем их любым способом и из найденных значений составляем обратную матрицу.

Разберем этот метод на примере.

Пример.

Дана матрица . Найдите обратную матрицу.

Решение.

Примем . Равенство дает нам три системы линейных неоднородных алгебраических уравнений:

Не будем расписывать решение этих систем, при необходимости обращайтесь к разделурешение систем линейных алгебраических уравнений .

Из первой системы уравнений имеем , из второй — , из третьей — . Следовательно, искомая обратная матрица имеет вид . Рекомендуем сделать проверку, чтобы убедиться в правильности результата.

Подведем итог.

Мы рассмотрели понятие обратной матрицы, ее свойства и три метода ее нахождения.

Пример решений методом обратной матрицы

Задание 1. Решить СЛАУ методом обратной матрицы. 2 x 1 + 3x 2 + 3x 3 + x 4 = 1 3 x 1 + 5x 2 + 3x 3 + 2x 4 = 2 5 x 1 + 7x 2 + 6x 3 + 2x 4 = 3 4 x 1 + 4x 2 + 3x 3 + x 4 = 4

Начало формы

Конец формы

Решение . Запишем матрицу в виде: Вектор B: B T = (1,2,3,4) Главный определитель Минор для (1,1): = 5 (6 1-3 2)-7 (3 1-3 2)+4 (3 2-6 2) = -3 Минор для (2,1): = 3 (6 1-3 2)-7 (3 1-3 1)+4 (3 2-6 1) = 0 Минор для (3,1): = 3 (3 1-3 2)-5 (3 1-3 1)+4 (3 2-3 1) = 3 Минор для (4,1): = 3 (3 2-6 2)-5 (3 2-6 1)+7 (3 2-3 1) = 3 Определитель минора ∆ = 2 (-3)-3 0+5 3-4 3 = -3

Транспонированная матрица Алгебраические дополнения ∆ 1,1 = 5 (6 1-2 3)-3 (7 1-2 4)+2 (7 3-6 4) = -3 ∆ 1,2 = -3 (6 1-2 3)-3 (7 1-2 4)+1 (7 3-6 4) = 0 ∆ 1,3 = 3 (3 1-2 3)-3 (5 1-2 4)+1 (5 3-3 4) = 3 ∆ 1,4 = -3 (3 2-2 6)-3 (5 2-2 7)+1 (5 6-3 7) = -3 ∆ 2,1 = -3 (6 1-2 3)-3 (5 1-2 4)+2 (5 3-6 4) = 9 ∆ 2,2 = 2 (6 1-2 3)-3 (5 1-2 4)+1 (5 3-6 4) = 0 ∆ 2,3 = -2 (3 1-2 3)-3 (3 1-2 4)+1 (3 3-3 4) = -6 ∆ 2,4 = 2 (3 2-2 6)-3 (3 2-2 5)+1 (3 6-3 5) = 3 ∆ 3,1 = 3 (7 1-2 4)-5 (5 1-2 4)+2 (5 4-7 4) = -4 ∆ 3,2 = -2 (7 1-2 4)-3 (5 1-2 4)+1 (5 4-7 4) = 1 ∆ 3,3 = 2 (5 1-2 4)-3 (3 1-2 4)+1 (3 4-5 4) = 1 ∆ 3,4 = -2 (5 2-2 7)-3 (3 2-2 5)+1 (3 7-5 5) = 0 ∆ 4,1 = -3 (7 3-6 4)-5 (5 3-6 4)+3 (5 4-7 4) = -12 ∆ 4,2 = 2 (7 3-6 4)-3 (5 3-6 4)+3 (5 4-7 4) = -3 ∆ 4,3 = -2 (5 3-3 4)-3 (3 3-3 4)+3 (3 4-5 4) = 9 ∆ 4,4 = 2 (5 6-3 7)-3 (3 6-3 5)+3 (3 7-5 5) = -3 Обратная матрица Вектор результатов X X = A -1 ∙ B X T = (2,-1,-0. 33,1) x 1 = 2 x 2 = -1 x 3 = -0.33 x 4 = 1

см. также решений СЛАУ методом обратной матрицы online. Для этого введите свои данные и получите решение с подробными комментариями.

Задание 2 . Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения. Решение :xml :xls

Пример 2 . Записать систему уравнений в матричной форме и решить с помощью обратной матрицы. Решение :xml :xls

Пример . Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера ; 2) записать систему в матричной форме и решить ее средствами матричного исчисления. Методические рекомендации . После решения методом Крамера, найдите кнопку «Решение методом обратной матрицы для исходных данных». Вы получите соответствующее решение. Таким образом, данные вновь заполнять не придется. Решение . Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B — матрицу-столбец свободных членов:

Вектор B: B T =(4,-3,-3) С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B. Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А -1 . Умножив обе части уравнения на А -1 , получим: А -1 *А*Х = А -1 *B, А -1 *А=Е. Это равенство называется матричной записью решения системы линейных уравнений . Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А -1 . Система будет иметь решение, если определитель матрицы A отличен от нуля. Найдем главный определитель. ∆=-1 (-2 (-1)-1 1)-3 (3 (-1)-1 0)+2 (3 1-(-2 0))=14 Итак, определитель 14 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения. Пусть имеем невырожденную матрицу А:

Вычисляем алгебраические дополнения.

∆ 1,1 =(-2 (-1)-1 1)=1

∆ 1,2 =-(3 (-1)-0 1)=3

∆ 1,3 =(3 1-0 (-2))=3

∆ 2,1 =-(3 (-1)-1 2)=5

∆ 2,2 =(-1 (-1)-0 2)=1

∆ 2,3 =-(-1 1-0 3)=1

∆ 3,1 =(3 1-(-2 2))=7

∆ 3,2 =-(-1 1-3 2)=7

X T =(-1,1,2) x 1 = -14 / 14 =-1 x 2 = 14 / 14 =1 x 3 = 28 / 14 =2 Проверка . -1 -1+3 1+0 2=4 3 -1+-2 1+1 2=-3 2 -1+1 1+-1 2=-3 doc :xml :xls Ответ: -1,1,2.

Решение задач №3 Найти решение СЛАУ. | Vseznayka

Доброго времени суток. Сегодня возьмёмся за объёмную, но не менее интересную задачу. А именно поиск решения системы линейных алгебраических уравнений (СЛАУ) методом обратной матрицы. Для тех, кто знает как это делать и желает лишь убедиться в правильности своих мыслей, полное решение будет в конце статьи. Запишем систему:

Исходная система.

Система четвёртого порядка. Решение будет довольно не маленькое. Запишем формулу для вычисления системы уравнений методом обратной матрицы.

Формула для нахождения полного решения.

Где А» в минус первой степени:

Обратная матрица.

«А*» это матрица алгебраических элементов для основной матрицы. Буква «Т» обозначает транспонирование. То есть транспонирование матрицы состоящей из алгебраических дополнений. «det(A)» — определитель матрицы «А».

Как все догадались «А» в минус первой степени это и есть обратная матрица составленная из коэффициентов основной матрицы системы. «В» матрица столбца свободных элементов (те, что после равенства). «Х» матрица неизвестных, то есть тех что необходимо найти. Продемонстрируем:

Иначе говоря, если перемножить матрица «А» на матрицу «Х», мы получим матрицу «В», получится исходная система что записана в самом начале. Для того, чтобы убедиться в том, что СЛАУ можно решать методом обратной матрицы, нужно убедиться в невырожденности матрицы составленной из коэффициентов при неизвестных, то есть определитель должен быть отличен от нуля. Выполним проверку.

Вычисление определителя составленного из коэффициентов при неизвестных.

Стоит прокомментировать последовательность действий. Для удобства обнулили все элементы второго столбца начиная со второй строки, чтобы в дальнейшем сделать разложение матрицы по первой строке и второму столбцу. Умножили первую строку на минус один и потом сложив её с второй и четвёртой строками поочерёдно. Далее выполнили разложение по первой строке и второму столбцу. Получили определитель третьего порядка, после проделали подобные действия что и делали ранее, только по первому столбцу и первой строке. В конечном итоге получен определитель основной матрицы равный 135, он отличен от нуля, значит матрица невырожденная. Решать систему методом обратной матрицы можно. Продолжим.

На следующем этапе необходимо найти алгебраическое дополнение для каждого элемента основной матрицы. Запишем формулу нахождения алгебраического дополнения.

Формула нахождения алгебраического дополнения.

Используя её найдём 16 алгебраических дополнений.

Найдя все алгебраические дополнения используем формулу для нахождения обратной матрицы.

Обратная матрица.

Найдём все неизвестные по самой начальной формуле. Умножим обратную матрицу на столбец свободных элементов.

Выполнение перемножения обратной матрицы на столбец свободных членов.

В конце всё идеально сократилось, что говорит о правильности вычислений. Запишем конечный ответ в виде системы:

Ответ.

Подведём итоги. Решение СЛАУ методом обратной матрицы крайне долгое, много расчётов выходит. В следующий раз попробуем решить эту же систему другим способом. В этом случае можно будет точно сказать, на сколько данный метод дольше и сложнее относительно другого. Спасибо за внимание.

Полное решение:

Другие темы:

Калькулятор обратной матрицы — eMathHelp

Калькулятор найдет обратную (если она существует) квадратную матрицу, используя метод исключения Гаусса или метод сопряжения, с показанными шагами. {-1}$$$ с помощью Гаусса — Ликвидация Иордании.

Решение

Чтобы найти обратную матрицу, дополните ее единичной матрицей и выполните операции со строками, пытаясь сделать единичную матрицу слева. Тогда справа будет обратная матрица.

Итак, дополним матрицу единичной матрицей:

$$$\left[\begin{array}{cc|cc}2 & 1 & 1 & 0\\1 & 3 & 0 & 1\end{array }\right]$$$

Разделить строку $$$1$$$ на $$$2$$$: $$$R_{1} = \frac{R_{1}}{2}$$$.

$$$\left[\begin{array}{cc|cc}1 & \frac{1}{2} & \frac{1}{2} & 0\\1 & 3 & 0 & 1\end {array}\right]$$$

Вычесть строку $$$1$$$ из строки $$$2$$$: $$$R_{2} = R_{2} — R_{1}$$$.

$$$\left[\begin{array}{cc|cc}1 & \frac{1}{2} & \frac{1}{2} & 0\\0 & \frac{5}{2} } & — \frac{1}{2} & 1\end{массив}\right]$$$

Умножить строку $$$2$$$ на $$$\frac{2}{5}$$$: $$$R_{2} = \frac{2 R_{2}}{5}$$$.

$$$\left[\begin{array}{cc|cc}1 & \frac{1}{2} & \frac{1}{2} & 0\\0 & 1 & — \frac{1 }{5} & \frac{2}{5}\end{array}\right]$$$

Вычесть строку $$$2$$$, умноженную на $$$\frac{1}{2}$$$ из строки $$$1$$$: $$$R_{1} = R_{1} — \frac{R_{2}}{2}$$$.

$$$\left[\begin{array}{cc|cc}1 & 0 & \frac{3}{5} & — \frac{1}{5}\\0 & 1 & — \frac{ 1}{5} & \frac{2}{5}\end{array}\right]$$$

Готово. Слева — единичная матрица. Справа — обратная матрица.

Ответить

Обратная матрица: $$$\left[\begin{array}{cc}\frac{3}{5} & — \frac{1}{5}\\- \frac{1}{5} & \frac{2}{5}\end{массив}\right] = \left[\begin{массив}{cc}0,6 и -0.2\\-0,2 и 0,4\конец{массив}\справа].$$$A

Найдите обратную матрицу с помощью пошагового решения математических задач

В этом разделе мультипликативные элементы идентичности и мультипликативные обратные вводятся и используются для решения матричных уравнений. Это приводит к другому метод решения систем уравнений.

МАТРИЦЫ ИДЕНТИЧНОСТИ Свойство идентичности действительных чисел говорит, что a * I = a и I * a = a для любого действительного числа a. Если должно быть мультипликативный единичная матрица I такая, что:

AI = A и IA = A,

для любой матрицы A, то A и I должны быть квадратными матрицами одинакового размера. В противном случае было бы невозможно найти оба продукта. Например, пусть А матрица 2 X 2 и пусть

представляют собой единичную матрицу 2 X 2. Чтобы найти I, используйте тот факт, что IA = A, или

Перемножив две матрицы в левой части этого уравнения и установив элементов матрицы произведения, равных соответствующим элементам A, дает следующая система уравнений с переменными x11, x12, x21 и x22

Обратите внимание, что на самом деле это две системы уравнений с двумя переменными.Используйте один из методы предыдущей главы, чтобы найти решение этой системы: x11 = 1, x12 = x21 = 0 и X22 = 1. Из решения системы 2 X 2 единичная матрица

Убедитесь, что при таком определении I оба Al = A и IA = A.

Пример 1 ПРОВЕРКА СВОЙСТВА ИДЕНТИЧНОСТИ

Пусть

Убедитесь, что MI = M и IM = M

Матрица идентичности 2 X 2, найденная выше, предлагает следующее обобщение:

n x n МАТРИЦА ИДЕНТИЧНОСТИ

Для любого значения n существует единичная матрица размера n X n, имеющая l вниз по диагонали и 0 в другом месте. (-1).(-1). Этот матрица должна удовлетворять утверждениям

Мультипликативная обратная матрица может быть найдена с помощью преобразования строки матрицы, приведенные в предыдущем уроке и повторенные здесь для удобство.

ПРЕОБРАЗОВАНИЕ СТРОК МАТРИЦЫ

Преобразования строк матрицы:

перестановка любых двух строк матрицы местами;
умножение элементов любой строки матрицы на одинаковые ненулевой скаляр k; и

добавление нескольких элементов одной строки к элементам другого ряда.(-1) = 1 или

Путем умножения матриц,

Приравнивание соответствующих элементов дает систему уравнений

Поскольку уравнения (1) и (3) включают только x и z, а уравнения (2) и (4) включают только y и w, эти четыре уравнения приводят к двум системам уравнений,

2x + 4z = 1
x-z=0

2y + 4w = 0
y-w=1.

Запись двух систем в виде расширенных матриц дает

Каждая из этих систем может быть решена методом Гаусса-Жордана.Однако, поскольку элементы слева от вертикальной черты идентичны, две системы могут объединить в одну расширенную матрицу

и решить одновременно следующим образом. Поменяйте местами две строки, чтобы получить 1 в верхний левый угол.

Умножьте первую строку на -2 и прибавьте результаты ко второй строке, чтобы получить

Теперь, чтобы получить I во второй строке во втором столбце, умножьте второе ряд на 1/6.

Наконец, добавьте вторую строку к первой строке, чтобы получить 0 во втором столбце. выше 1.(-1) — это просто обозначение обратной матрицы A.

Калькулятор обратной матрицы — Онлайн калькулятор обратной матрицы

Калькулятор обратной матрицы вычисляет значение обратной матрицы для заданной матрицы. Предположим, мы умножаем матрицу на заданную матрицу, и произведение является мультипликативным тождеством. Тогда такая матрица называется обратной к данной матрице.

Что такое калькулятор обратной матрицы?

Калькулятор обратной матрицы — это онлайн-инструмент, который помогает вычислить обратную матрицу для заданной матрицы 2 × 2.Если определитель матрицы равен 0, то матрица, обратная такой, не может существовать. Чтобы использовать этот калькулятор обратной матрицы , введите значения в поля ввода.

Калькулятор обратной матрицы

*Используйте только до 3 цифр.

Как использовать калькулятор обратной матрицы?

Чтобы найти обратную матрицу с помощью онлайн-калькулятора обратной матрицы, выполните следующие действия:

Шаг 1: Перейдите к онлайн-калькулятору обратной матрицы Cuemath.
Шаг 1: Введите значение матрицы в соответствующие поля ввода калькулятора обратной матрицы.
Шаг 2: Нажмите кнопку «Вычислить» , чтобы найти результирующую обратную матрицу.
Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает калькулятор обратной матрицы?

Предположим, у нас есть матрица, заданная A.Обратное значение обозначим A ^-1 . Когда эти две матрицы перемножаются, мы получаем мультипликативное тождество. Таким образом, AA ^-1 = I. Чтобы существовала обратная матрица, ее определитель не должен быть равен 0. Кроме того, матрица должна быть квадратной матрицей. Шаги для вычисления обратной матрицы 2 × 2 следующие:

Шаг 1: Найдите определитель данной матрицы.
Шаг 2: Найдите матрицу кофакторов.
Шаг 3: Найдите транспонированную матрицу кофакторов.Это также известно как сопряжение матрицы.
Шаг 4: Разделите сопряженную матрицу, полученную на шаге 3, на определитель из шага 1. Это даст обратную матрицу.

В дополнение к шагам, упомянутым выше, можно использовать следующую формулу для нахождения обратной матрицы 2 × 2.

A = $\begin{bmatrix} a & b\\ c & d \end{bmatrix}$

A ^-1 = $\frac{1}{\begin{vmatrix} A \end{vmatrix}}adjA$

A ^-1 = $\frac{1}{ad — bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix}$

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.С Cuemath находите решения простыми и легкими шагами.

Забронируйте бесплатный пробный урок

Решенные примеры на обратной матрице

Пример 1: Найдите обратную матрицу A = $\begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}$ и проверьте ее с помощью калькулятора обратной матрицы.

Решение:

Дано: A = $\begin{bmatrix} 1 и 2\\ 3 и 4 \end{bmatrix}$

A ^-1 = $\frac{1}{ad — bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix}$

A ^-1 = $\frac{1}{4 — 6}\begin{bmatrix} 4 & -2\\ -3 & 1 \end{bmatrix}$

A ^-1 = $\begin{bmatrix} -2 & 1\\ 1. 5 & -0,5 \end{bmatrix}$

Пример 2: Найдите обратную матрицу A = $\begin{bmatrix} -10 & 4\\ 3 & -1 \end{bmatrix}$ и проверьте ее с помощью калькулятора обратной матрицы.

Решение:

Дано: A = $\begin{bmatrix} -10 и 4\\ 3 & -1 \end{bmatrix}$

A ^-1 = $\frac{1}{ad — bc}\begin{bmatrix} d & -b\\ -c & a \end{bmatrix}$

A ^-1 = $\frac{1}{10 — 12}\begin{bmatrix} -1 & -4\\ -3 & -10 \end{bmatrix}$

А ^-1 = $\begin{bmatrix} 0.5 и 2\\ 1,5 и 5 \end{bmatrix}$

Точно так же вы можете попробовать калькулятор обратной матрицы и найти обратную для заданных матриц:

А = $\begin{bmatrix} 5 и 10\\ 15 и 20 \end{bmatrix}$
B = $\begin{bmatrix} 18 и 21\\ 7 и 3 \end{bmatrix}$

☛ Математические калькуляторы:

матричный калькулятор | Калькулятор комплексных матричных решений

Введение в матричный калькулятор

Матричный калькулятор — это удобный инструмент, специально разработанный для студентов и преподавателей всех направлений. Он разработан с максимальным вниманием к деталям, поэтому вы можете без проблем использовать его во всех современных браузерах.

Онлайн-калькулятор матриц позволяет рассчитать значения матрицы 2×2, матрицы 3×3, матрицы 4×4 и так далее. Это полезно, если вы работаете с матрицами и хотите попробовать кое-что самостоятельно. Вы можете рассчитать матрицы с помощью калькулятора метода исключения Гаусса Джордана и всех возможных методов решения, доступных для матриц

Что такое матричный калькулятор?

Матричный математический калькулятор очень полезен во многих аспектах математики.Он используется в различных функциях, таких как определение площади данного участка, измерение двусторонней формы или ее окружности, а также в других, таких как нахождение разницы между двумя числами.

Почти все наши математические знания получены из использования матриц и функций и других аспектов теории чисел и комбинаций.

Зачем использовать матричный калькулятор?

Калькуляторы матричных решений

обычно используются для решения системных уравнений, которые чрезвычайно трудно решить вручную. Чтобы выполнить матричный расчет, вам необходимо ввести ряд величин, которые должны идеально сочетаться друг с другом.

Полученное значение затем сравнивается со всеми ранее сгенерированными значениями и отмечаются все несоответствия. Это может занять очень много времени и утомительно, особенно при работе с огромными объемами данных. Тем не менее, матричные калькуляторы были разработаны, чтобы облегчить пользователям эту задачу за счет автоматизации процесса. Процессы автоматизированы для каждого матричного метода. Например, вы можете выполнять транспонирование и инверсию матриц с помощью калькулятора транспонирования матриц и калькулятора инверсии матриц

Преимущества использования калькулятора матриц

Калькулятор сложения и вычитания матриц помогает решать матрицы онлайн, что ускоряет процесс обучения.Онлайн-калькуляторы — лучший способ научиться чему-то во время практики. Кроме того, он также имеет много других преимуществ, таких как:

Его можно использовать для решения множества сложных математических задач. Некоторым людям может быть интересно использовать его в возможных областях математики, таких как инженерия и геология.
Его также можно использовать для поиска ответа на любое уравнение, включая гипотезу Римана.
Также может использоваться в методе решения квадратного уравнения и некоторых других методах, где значение может быть определено в некоторой точке уравнения.
Это один из самых ценных инструментов для изучения математики в старших классах и колледжах.
Он также часто используется персоналом финансовой помощи при принятии решений о финансовой помощи для студентов.
Преимущество использования матричного калькулятора заключается в том, что он позволяет учащимся рассчитать общую стоимость своего образования, включая плату за обучение, книги, расходные материалы и другие необходимые расходы. Затем он разбивает эти категории, чтобы учащиеся могли точно видеть, какой будет их счет каждый месяц.

Как найти матричный калькулятор?

Матричный калькулятор — это онлайн-инструмент, который вы можете найти в Интернете. Вы можете найти наш калькулятор решателя матриц в Google или любой другой поисковой системе. Например, если вы хотите найти недействительность матрицы, вы можете ввести калькулятор недействительности матрицы или напрямую ввести Matrix-calculators.com в браузере мобильного или настольного компьютера, чтобы получить прямой доступ к этому калькулятору.

Как пользоваться матричным калькулятором?

Чтобы использовать матричный калькулятор, выполните следующие действия.

Шаг 1 : Перейдите к онлайн-калькулятору матриц.

Шаг 2 : Теперь введите значение 2 x 2 или 3 x 3 в поля ввода матрицы и выберите требуемую операцию из раскрывающегося списка.

Шаг 3 : После добавления значений нажмите кнопку «Рассчитать», чтобы найти результирующую матрицу.

Шаг 4 : Найдя ответ, нажмите кнопку «Сброс», чтобы очистить предыдущее поле и ввести новое значение.

Не забудьте использовать другие наши инструменты для матриц, которые очень важны для матричных задач, такие как калькулятор матрицы собственных значений и калькулятор матрицы LU-декомпозиции. Мы надеемся, что вам понравился наш калькулятор и различные инструменты для работы с матрицами, добавленные для вашего удобства.

Джеймс Джонсон — Последнее обновление: 25 сентября 2021 г.

Метод обратной матрицы — Бесплатная помощь по математике

Система решения линейных уравнений: (урок 5 из 5)

Метод обратной матрицы

Предположим, вам дано уравнение с одной переменной, например, $4x = 10$.потом вы найдете значение $x$, которое решает это уравнение, умножив уравнение, обратное 4: $\color{blue}{\frac14} \cdot 4x = \color{blue}{\frac14} \cdot 10$, поэтому решение будет $x = 2,5$.

Иногда мы можем сделать что-то очень похожее на решение систем линейных уравнения; в этом случае мы будем использовать обратную матрицу коэффициентов. Но сначала мы должны проверить, что эта инверсия существует! Условия существования матрицы, обратной матрице коэффициентов, такие же, как при использовании Правило Крамера, то есть

1. В системе должно быть одинаковое количество уравнения как переменные, то есть матрица коэффициентов системы должна быть квадратный.

2. Определитель матрица коэффициентов должна быть отличной от нуля. Причина, конечно, в том, что обратная матрицы существует именно тогда, когда ее определитель отличен от нуля.

3. Чтобы использовать этот метод, следуйте шаги продемонстрированы на следующей системе:

$$ \begin{выровнено} -х + 3у + г &= 1 \\ 2х + 5у &= 3\\ 3x + у — 2z &= -2 \end{выровнено} $$

Шаг 1: Перепишите систему, используя умножение матриц:

$$ \left ( {\ begin {массив} {* {20} {c}} — 1\\ 2\\ 3 \end{массив}\begin{массив}{*{20}{c}} 3\\ 5\\ 1 \end{массив}\begin{массив}{*{20}{c}} 1\\ 0\\ — 2 \end{массив}} \right)\left( {\begin{массив}{*{20}{c}} Икс\\ у\\ г \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} 1\\ 3\\ — 2 \end{массив}} \right) $$

и записав матрицу коэффициентов как A, мы имеем

$$ А \ влево ( {\ begin {массив} {* {20} {c}} Икс\\ у\\ г \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} 1\\ 3\\ — 2 \end{массив}} \right) $$

Шаг 2: Найдите обратную матрицу коэффициентов A. { — 1}}\left( {\begin{массив}{*{20}{c}} 1\\ 3\\ {- 2} \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} { — \фракция{{10}}{9}}\\ {\ гидроразрыва {4} {9}} \\ { — \фракция{{13}}{9}} \end{массив}\begin{массив}{*{20}{c}} {\ гидроразрыва {7} {9}} \\ { — \фракция{1}{9}}\\ {\ гидроразрыва {{10}} {9}} \end{массив}\begin{массив}{*{20}{c}} { — \фракция{5}{9}}\\ {\ гидроразрыва {2} {9}} \\ { — \фракция{{11}}{9}} \end{массив}} \right)\left( {\begin{массив}{*{20}{c}} 1\\ 3\\ {- 2} \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} {21}\\ {- 3}\\ {39} \end{массив}} \right) $$

и так решение

$$ \left ( {\ begin {массив} {* {20} {c}} Икс\\ у\\ г \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} {21}\\ {- 3}\\ {39} \end{массив}} \right) $$

Система линейных уравнений и обращение матриц

Этот учебный объект JavaScript E-labs предназначен для поиска решения систем линейных уравнений до трех уравнений с тремя неизвестными. Это также позволяет нам найти обратную матрицу.
Другие учебные объекты JavaScript для принятия решений из этой серии относятся к различным областям применения в разделе МЕНЮ на этой странице.
При вводе данных для перехода от ячейки к ячейке в матрице данных используйте клавишу Tab , а не клавиши со стрелками или клавиши ввода.
Инструкции и приложения:

Неизвестные имена переменных: X1, X2, X3,..и X10, в зависимости от того, есть ли у вас одно уравнение, два уравнения или три уравнения с одной неизвестной, двумя неизвестными или тремя неизвестными переменными соответственно.
Начиная с левого верхнего угла, замените столько нулей в матрице данных коэффициентами неизвестных переменных в уравнениях вместе с их правыми значениями, сколько необходимо. Матрица коэффициентов должна представлять собой квадратную матрицу, расположенную в верхнем левом углу матрицы данных, поэтому не оставляйте пустых строк между ними.
JavaScript основан на операциях строки Gauss-Jordan (GJ). Требование для операций GJ состоит в том, что первый элемент в матрице коэффициентов должен быть ненулевым. Поэтому сначала введите коэффициент всех уравнений, имеющих ненулевой коэффициент X1; затем введите все остальные уравнения. То есть любое уравнение с нулевыми коэффициентами для X1 должно стоять в конце таблицы ввода данных.
Численный пример 1. Рассмотрим следующую систему уравнений:
Х2 + Х3 = 5
3Х1 + Х3 = 6
-Х1 + Х2 = 1
Матрица коэффициентов переменных:
0    1    1
3    0    1
-1    1    0
Первая запись первого столбца равна нулю, хотя в нем всегда есть хотя бы один ненулевой элемент.Следовательно, мы должны перестроить систему уравнений таким образом, чтобы любое уравнение с нулевым коэффициентом X1 оказалось среди последнего набора уравнений. То есть, рассматривая эквивалентную систему уравнений:
3Х1 + Х3 = 6
-Х1 + Х2 = 1
Х2 + Х3 = 5
Решите эту эквивалентную систему уравнений, введя ее коэффициент и значения RHS в таблицу ввода данных, затем нажмите кнопку «Рассчитать». Выходом является решение: X1 = 1, X2 = 2 и X3 = 3, что можно проверить подстановками.
Нахождение обратной матрицы с помощью System of Equations Solver: Чтобы найти обратную квадратную матрицу размера n, решите n систем уравнений с единичным вектором в правой части. Следующий числовой пример иллюстрирует этот процесс:
Численный пример 2. Предположим, мы хотим найти обратную (A ^-1 ) следующую матрицу (если она существует) A:
В общем, чтобы найти A ^-1 , столбец за столбцом, решите n систем уравнений, имеющих матрицу коэффициентов A, но с n различными векторами идентичности в качестве их значения RHS.
Для этого числового примера мы должны решить следующие две системы уравнений:
2Х1 + Х1 = 1
Х1 — Х2 = 0
и
2Х1 + Х1 = 0
Х1 — Х2 = 1
Обратите внимание, что коэффициенты переменных X1 и X2 являются матрицей A в обеих системах уравнений, однако RHS являются двумя единичными векторами в n = 2-мерном пространстве.
Решения первой и второй систем уравнений в соответствии с вышеуказанной инструкцией дают первый и второй столбцы матрицы A ^-1.
Чтобы найти первый столбец A ^-1, решите:
2Х1 + Х1 = 1
Х1 — Х2 = 0
Это дает X1 = 1/3, X2 = 1/3. Чтобы найти второй столбец A ^-1, решите:
2Х1 + Х1 = 0
Х1 — Х2 = 1
Это дает X1 = 1/3, X2 = -2/3. Следовательно, A ^-1 p равно
1/3 1/3
А ^-1 =
1/3 -2/3
Примечание: Матрица, имеющая обратную, называется невырожденной или обратимой.Матрица называется вырожденной, если она не имеет обратной. Например, следующая матрица является сингулярной:
1    6    4
2    4   -1
-1    2    5
Поэтому при применении описанной выше процедуры обращения матрицы, если матрица вырожденная, то по крайней мере из систем уравнений не имеет решения.
Для редактирования ваших данных, включая добавление/изменение/удаление, вам не нужно нажимать на кнопку «очистить», а заново вводить свои данные заново.Вы можете просто добавить, изменить число на другое в той же ячейке или удалить число из ячейки, установив его значение равным нулю. После редактирования нажмите кнопку «Рассчитать».
Это полезно, например. найти обратную матрицу A _10×10, где мы должны изменить только значения RHS.
Для расширенного редактирования или использования JavaScript для нового набора данных используйте кнопку «Очистить».

Для получения технических подробностей вернитесь к:
тем по линейной алгебре.
Пожалуйста, отправьте ваши комментарии по адресу:
Профессор Хоссейн Аршам

МЕНЮ

Заявление об авторских правах. Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Руководством по добросовестному использованию образовательных мультимедиа от 1996 г. разрешено только в некоммерческих целях и в учебных целях.
Этот сайт может быть переведен и/или зеркально отображен в неизменном виде (включая эти уведомления) на любом сервере с общедоступным доступом. Все файлы доступны по адресу http://home.ubalt.edu/ntsbarsh/Business-stat для зеркалирования.
Пожалуйста, пришлите мне по электронной почте ваши комментарии, предложения и проблемы. Спасибо.
Вернуться к:
Домашняя страница доктора Аршама

ЕОФ: 1994-2015 гг.

Вычисление обратной матрицы с использованием продуктов семейства TI-Nspire™.

Управляйте настройками файлов cookie

Вы можете контролировать свои предпочтения относительно того, как мы используем файлы cookie для сбора и использования информации, когда вы находитесь на веб-сайтах TI, настраивая статус этих категорий.

Категория	Описание	Разрешить
Аналитические и эксплуатационные файлы cookie	Эти файлы cookie, в том числе файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI, а также отслеживать, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, упрощая поиск информации на сайте).
Рекламные и маркетинговые файлы cookie	Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах.Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламу, чтобы она лучше соответствовала вашим интересам, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы.
Функциональные файлы cookie	Эти файлы cookie помогают определить, кто вы, и хранить информацию о вашей деятельности и учетной записи для предоставления расширенных функций, включая более персонализированный и актуальный опыт на наших сайтах. РубрикаРазное Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Найти: Рубрики Биосфера Глобальное потепление Защита биосферы Климат Климатические пояса Обитатели океанов Океан Полезно знать Потепление Природа Разное Человек и природа Экология Экология России 2019 © Все права защищены. Карта сайта

		1/3	1/3
А ^-1	=
		1/3	-2/3

Решение методом обратной матрицы онлайн с решением: Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.

Пример решения системы линейных уравнений с помощью метода обратной матрицы

Повторение: умножение матриц

Как найти обратную матрицу

Альтернативный способ

Элементарные преобразования

Присоединённая матрица

Шаги

С помощью присоединенной матрицы

С помощью калькулятора

Метод обратной матрицы и как найти обратную матрицу

Нахождение обратной матрицы 2 на 2. Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы

Энциклопедичный YouTube

Способы нахождения обратной матрицы

Точные (прямые) методы

Метод Гаусса-Жордана

Использование LU/LUP-разложения

Найти обратную матрицу на сайт

Шаги

С помощью присоединенной матрицы

Решение задач №3 Найти решение СЛАУ. | Vseznayka

Калькулятор обратной матрицы — eMathHelp

Решение

Ответить

Найдите обратную матрицу с помощью пошагового решения математических задач

Калькулятор обратной матрицы — Онлайн калькулятор обратной матрицы

Что такое калькулятор обратной матрицы?

Калькулятор обратной матрицы

Как использовать калькулятор обратной матрицы?

Как работает калькулятор обратной матрицы?

Решенные примеры на обратной матрице

матричный калькулятор | Калькулятор комплексных матричных решений

Введение в матричный калькулятор

Что такое матричный калькулятор?

Зачем использовать матричный калькулятор?

Преимущества использования калькулятора матриц

Как найти матричный калькулятор?

Как пользоваться матричным калькулятором?

Метод обратной матрицы — Бесплатная помощь по математике

Метод обратной матрицы

Система линейных уравнений и обращение матриц

Вычисление обратной матрицы с использованием продуктов семейства TI-Nspire™.

Управляйте настройками файлов cookie

Добавить комментарий Отменить ответ