Производственная функция в экономике это – Производственная функция

Производственная функция

Производственная функция – зависимость объемов производства от количества и качества имеющихся производственных факторов, выраженная с помощью математической модели. Производственная функция дает возможность выявить оптимальный размер издержек, необходимых для производства некоторой порции товаров. При этом функция всегда предназначается для конкретной технологии – интеграция новых разработок влечет необходимость пересмотра зависимости.

 

Производственная функция: общий вид и свойства

 

Для производственных функций характерны следующие свойства:

 

• Повышение объемов выпуска за счет одного производственного фактора всегда предельно (пример – в одном помещении может работать ограниченное число специалистов).

 

• Производственные факторы бывают взаимозаменяемыми (человеческие ресурсы заменяются роботами) и взаимодополняемыми (работники нуждаются в инструментах и станках).

 

В общем виде производственная функция выглядит так:

 

Q = f (K, M, L, T, N),

 

где под К понимается капитал (имеющиеся станки), L – человеческие ресурсы, M – траты на сырье и полуфабрикаты, Т – применяемые в производстве технологии, N – предпринимательский талант. Q – объем производства, который зависит от всех вышеперечисленных переменных.

 

Производственная функция: виды

 

Особой популярностью пользуются два вида производственных функций: двухфакторная модель и функция Кобба-Дугласа.

 

Двухфакторная модель рассматривает зависимость объемов выпуска от таких факторов, как издержки на труд и капитал. Соответственно, функция имеет сокращенный вид:

 

Q = f (L, K)

 

Для анализа с помощью этого метода часто используются изокванты – прямые, соединяющие все возможные точки сочетаний факторов, позволяющих производить конкретный объем продукции. В результате график, по оси абсцисс которого указываются затраты на труд, по оси ординат – капитал, превращается в карту изоквант, являющуюся графическим выражением производственной двухфакторной модели.

 

Карта обладает такими свойствами:

 

• Чем дальше изокванта располагается от нулевой точки, тем больше объем выпуска.

 

• Если изокванта имеет нисходящий вид, значит, уменьшение использования капитала вызовет повышение издержек на оплату труда при необходимости сохранить объемы выпуска прежними.

 

• Форма изокванты зависит от возможности заменить капитал дополнительной единицей труда. Количество капитала, необходимое для замещения дополнительной единицы труда, носит название предельная норма замещения.

 

Функция Кобба-Дугласа предполагает зависимость объема производства от тех же факторов – капитала и затрат на труд. Однако формула имеет несколько иной вид:

 

Y = AKaLb

 

где

а, b – это постоянные значения (константы). Если сумма констант равна единице, говорят о постоянном эффекте масштаба. Важно отметить, что постоянные а и b могут принимать только положительные значения.

                                                                                             

Формула Кобба-Дугласа может корректироваться при необходимости учесть дополнительные факторы. Например, если нужно включить в расчет земельные ресурсы, добавляется одна переменная N и одна константа y. Формула обретает вид:

 

Y = AKaLbNy

 

Нестандартные изокванты

 

Изокванты могут иметь нестандартные конфигурации:

 

• При совершенной взаимозаменяемости ресурсов. Тогда объем может быть получен за счет использования лишь одного фактора: труда или капитала.

 

 

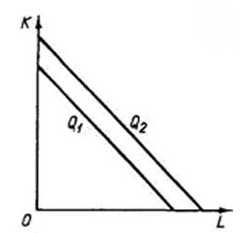
• При фиксированной структуре. Для выпуска требуемого объема продукции необходимо задействовать оба ресурса, притом в фиксированных пропорциях.

 

 

• При возможности действовать несколькими методами.

 

 

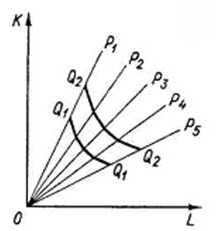
По мере движения от P1 к P5 предельная норма замещения снижается. Подобные карты изоквант активно используются при линейном программировании.

 

• При несовершенной замещаемости. Предполагается, что замена одного фактора другим возможна в некоторых пределах, однако, полное замещение недопустимо (либо нецелесообразно в экономическом плане).

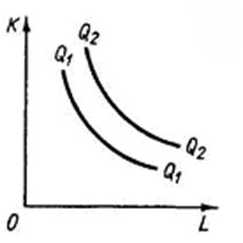
utmagazine.ru

Производственная функция

Производственная функция

Соотношение между вводимыми факторами и итоговым выходом продукции описывается производственной функцией. Она является исходным пунктом в микроэкономических расчетах фирмы, позволяет найти оптимальный вариант ис­пользования производственных возможностей.

Производственная функция показывает возможный максимальный выпуск продукции (Q) при определенном сочетании производственных факторов и избранной технологии.

Для каждой технологии производства существует своя особая функция. В наиболее общем виде она записывается:

,

где Q – объем производства,

K –капитал

L- труд

M – природные ресурсы

Рис. 1 Производственная функция

Производственная функция характеризуется определенными свойствами:

1. Существует предел для роста объема производства, который может быть достигнут за счет увеличения объема использования одного фактора при условии, что другие факторы производства не меняются. Данное свойство получило название закона убывающей производительности фактора производства. Он действует в краткосрочном периоде.

2. Существует определенная взаимодополняемость факторов производства, но без сокращения производства возможна и определенная взаимозаменяемость этих факторов.

3. Изменения в использовании факторов производства более эластичны на продолжительном отрезке времени, чем за короткий период.

Производственная функция может рассматриваться как однофакторная и многофакторная. Однофакторная полагает, что при прочих равных условиях, изменяется только фактор производства. Многофакторная предполагает изменение всех факторов производства.

Для краткосрочного периода используется однофакторная, а для долгосрочного – многофакторная.

Краткосрочный период – это такой период, в течение которого хотя бы один фактор остаётся неизменным.

Долгосрочный период – это период времени, в течение которого все факторы производства изменяются.

При анализе производства используются такие понятия как общий продукт (ТР) – объём товаров и услуг, произведенных за определённый период времени.

Средний продукт (АР) характеризует количество продукции, приходящейся на единицу используемого фактора производства. Он характеризует производительность фактора производства и рассчитывается по формуле:

Предельный продукт (МР) — дополнительная продукция, произведенная дополнительной единицей фактора производства. МР характеризует производительность дополнительно нанятой единицы фактора производства.

Таблица 1 — Результаты производства в краткосрочном периоде

Затраты капитала (К)	Затраты труда (L)	Объем производства (ТР)	Средний продукт труда (АР)	Предельный продукт труда (МР)
10	0	0	—	—
10	1	10	10	10
10	2	30	15	20
10	3	60	20	30
10	4	80	20	20
10	5	95	19	15
10	6	106	18	13
10	7	112	16	4
10	8	112	14	0
10	9	108	12	-4
10	10	100	10	-8

Анализ данных таблицы 1 позволяет выявить ряд закономерностей поведения общего, среднего и предельного продукта. В точке максимума общего продукта (ТР) предельный продукт (МР) равен 0. Если при росте объема используемого в производстве труда предельный продукт труда больше среднего, то значение среднего продукта растет и это свидетельствует о том, что отношение труда к капиталу далеко от оптимального и часть оборудования не используется в силу нехватки труда. Если при росте объема труда предельный продукт труда меньше среднего продукта, то средний продукт труда будет уменьшаться.

Закон замещения факторов производства.

Равновесное положение фирмы

Один и тот же максимальный объем производства фирмы можно обеспечить за счет разного сочетания факторов производства. Это обусловлено способностью одного ресурса вытесняться другим без ущерба для результатов производства. Такая способность называется взаимозаменяемостью факторов производства.

Так, если объемы ресурса труда увеличиваются, то использование капитала может уменьшаться. В этом случае мы прибегаем к трудоемкому варианту производства. Если, напротив, возрастает объем используемого капитала, а труд вытесняется, то речь идет о капиталоемком варианте производства. Скажем, вино можно произвести трудоемким ручным способом или капиталоемким способом с применением машинного оборудования для выжимки винограда.

Технология производства фирмы — это способ соединения факторов производства для выпуска продукции, основанный на определенном уровне знаний. По мере развития технологий фирма в состоянии получить такой же или больший объем выпуска при неизменном наборе производственных факторов.

Количественное соотношение взаимозаменяемых факторов позволяет оценить коэффициент, называемый предельной технологической нормой замещения (MRTS).

Предельная норма технологического замещения труда капиталом представляет собой величину, на которую можно сократить капитал за счет использования дополнительной единицы труда без изменения объема выпуска. Математиче­ски это можно выразить так:

MRTS_LK = — dK / dL = —ΔK / ΔL

где ΔK — изменение величины используемого капитала;

ΔL изменение трудозатрат на одну единицу продукции.

Рассмотрим вариант расчетов производственной функции и замещения факторов производства для гипотетической фирмы X.

Предположим, что данная фирма может изменять объемы производственных факторов, труд и капитал от 1 до 5 единиц. Изменения объемов выпуска, связанные с этим, могут быть представлены в виде таблицы, которая носит название «Производственная сетка» (табл. 2).

Таблица 2

Производственная сетка фирмы Х

Затраты капитала	Затраты труда
	1	2	3	4	5
1	20	40	55	65	75
2	40	60	75	85	90
3	55	75	90	100	105
4	65	85	100	110	115
5	75	90	105	115	120

Для каждой комбинации основных факторов мы определили максимально возможный выпуск продукции, т. е. значения производственной функции. Обратим внимание на тот факт, что, скажем, объем выпуска в 75 единиц достигается при четырех различных комбинациях труда и капитала, объем в 90 единиц — при трех комбинациях, 100 — при двух и т. д.

Представив производственную сетку графически, мы получим кривые, которые являются еще одним вариантом модели производственной функции, ранее зафиксированной в виде алгебраической формулы. Для этого мы соединим точки, которые соответствуют сочетаниям труда и капитала, позволяющим получить один и тот же объем выпуска (рис. 1).

K

Q = 90

Q = 75

Q = 55

0 L

Рис. 1. Карта изоквант.

Созданная графическая модель называется изоквантной. Набор изоквант — картой изоквант.

Итак, изокванта — это кривая, каждая точка которой со­ответствует сочетаниям производственных факторов, обеспе­чивающим определенный максимальный объем выпуска про­дукции фирмы.

Для того чтобы получить один и тот же объем выпуска, мы можем сочетать факторы, двигаясь в поиске вариантов вдоль изокванты. Движение по изокванте вверх означает, что фирма отдает предпочтение капиталоемкому производству, увеличивая количество станков, мощность электродвигате­лей, число компьютеров и т. п. Движение вниз отражает предпочтение фирмы в пользу трудоемкого производства.

Выбор фирмы в пользу трудоемкого или капиталоемкого варианта производственного процесса зависит от условий предпринимательства: общей суммы денежного капитала, ко­торым располагает фирма, соотношения цен на факторы про­изводства, производительности факторов и так далее.

Если D — денежный капитал; Р_K — цена на капитал; Р_L —цена на труд, то количество факторов, которое может приоб­рести фирма, полностью расходовав денежный капитал, К – количество капитала, L – количество труда, бу­дет определяться формулой:

D = P_KK + P_LL

Это уравнение прямой, все точки которой соответствуют полному использованию денежного капитала фирмы. Такая кривая называется изокостой или бюджетной линией.

K

A

Е

K₀

Q₃

Q₂

Q₁

0 L₀ B L

Рис. 2. Равновесие производителя.

На рис. 2 мы совместили линию бюджетного ограниче­ния фирмы, изокосту (АВ) с картой изоквант, т. е. набором альтернатив производственной функции (Q₁, Q₂, Q₃), чтобы показать точку равновесия производителя (Е).

Равновесие производителя — это такое положение фир­мы, для которого характерно полное использование денежно­го капитала и при этом достижение максимально возможно­го для данного количества ресурсов объема выпуска.

В точке Е изокванта и изокоста имеют равный угол накло­на, величину которого определяет показатель предельной нормы технологического замещения (MRTS).

Динамика показателя MRTS (он возрастает при движении вверх вдоль изокванты) показывает, что существуют пределы взаимозамещения факторов, связанные с тем, что эффектив­ность использования производственных факторов ограниче­на. Чем большее количество труда используется для вытес­нения капитала из производственного процесса, тем меньше производительность труда. Аналогичным образом замещение труда все большим количеством капитала снижает отдачу по­следнего.

Производство требует сбалансированного сочетания обо­их производственных факторов для наилучшего их использо­вания. Предпринимательская фирма готова заменить один фактор на другой при условии выигрыша или, по меньшей мере, равенства потери и выигрыша в производительности.

Но на рынке факторов важно учитывать не только их производительность, но и цены на них.

Наилучший вариант использования денежного капитала фирмы, или положение равновесия производителя, подчиня­ется следующему критерию: положение равновесия произво­дителя достигается, когда предельная норма технологическо­го замещения факторов производства равна соотношению цен на эти факторы. Алгебраически это можно выразить так:

—P_L /P_K = —dK / dL = MRTS

где P_L,,P_K — цены на труд и капитал; dK,dL — изменение ко­личества капитала и труда; MTRS — предельная норма техно­логического замещения.

Анализ технологических аспектов производства фирмы, максимизирующей прибыль, представляет интерес лишь с точки зрения достижения наилучших конечных результатов, т. е. продукта. Ведь вложения в ресурсы для предпринимателя являются только издержками, которые необходимо нести, чтобы получить продукт, реализуемый на рынке и принося­щий доход. Затраты приходится сопоставлять с результатом. Показатели результата, или продукта, приобретают поэтому особое значение.

6

studfiles.net

§4. Производственная функция, ее экономическое содержание

В реальной жизни в пределах используемой технологии предприниматель стремится найти наилучшее сочетание факторов производства (труд, земля, капитал) с тем, чтобы добиться наибольшего выхода продукции. Отношение между любым набором факторов производства и максимально возможным объемом продукции, производимой из этого набора факторов, характеризует производственную функцию. Производственная функцияописывает технологическую зависимость между затратами ресурсов и выпуском продукции. Она всегда строится для определенной технологической структуры. Улучшение технологии, увеличивающее максимально достигаемый объем выпускаемой продукции при любой комбинации факторов, всегда находит отражение в новой производственной функции. Производственную функцию можно использовать, чтобы определить минимальное количество затрат, необходимых для производства любого данного объема товаров.

Если весь набор факторов производства и ресурсов представить как затраты труда, материалов и капитала, производственная функция может быть описана следующим образом:

Q = f ( L, K, M ),

где Q — максимальный объем продукции, производимой при данной технологии и данном соотношении труда (L), капитала (К), материалов (М).

Производственная функция характеризует зависимость физического объема производства от количества используемых факторов производства. Хотя производственные функции различны для разных видов производств, все они обладают общими свойствами.

Существует предел для увеличения объема производства, которое может быть достигнуто увеличением затрат одного ресурса при прочих равных условиях. Предполагается, например, что на фабрике при данном количестве станков и производственных помещений существует предел увеличения производства посредством привлечения большого количества рабочих. Прирост производства, который может быть достигнут от прироста рабочих, очевидно, будет приближаться к нулю. Действительно, можно достигнуть такой точки, когда каждый новый рабочий на фабрике будет способствовать скорее сокращению, а не увеличению выпуска продукции! Это может произойти, если рабочий не будет обеспечен оборудованием для работы, и его присутствие будет мешать работе других рабочих и снижать их эффективность.

Существует определенная взаимная дополняемость (комплементарность) факторов производства, но без сокращения объема производства возможна и определенная взаимозаменяемость этих факторов. Работники выполняют свою работу более эффективно, если они снабжены всеми необходимыми инструментами. Точно так же инструменты могут оказаться бесполезными в том случае, если работники не будут обладать необходимой для их применения квалификацией. Тем не менее в производстве возможно заменить один ресурс на другой. Для получения данного урожая определенный размер посевной площади может быть обработан множеством рабочих вручную без применения химических удобрений и пестицидов. Этот же участок для производства такого же урожая может быть обработан лишь несколькими рабочими, использующими сложные машины, различные удобрения и пестициды.

Для анализа используется производственная функция, называемая функцией Кобба — Дугласа:

Q = k · Ka · Lb,

где Q — максимальный объем продукта при заданных факторах производства;

K, L – соответственно, затраты капитала, труда;

k — коэффициент пропорциональности или масштабности;

a, b — коэффициенты эластичности объема производства, соответственно, по капиталу, труду или коэффициенты прироста Q, приходящиеся на 1 % прироста соответствующего фактора:

a +b = 1.

Изменение капитала и труда может происходить в обратном направлении. Если количество капитала (применяемого оборудования) увеличивается, то, следовательно, применение живого труда уменьшается. При этом возрастание одного фактора и уменьшение другого происходит таким образом, что общий объем производства остается на прежнем уровне.

Эту зависимость можно представить графически с использованием изокванты. Изокванта — это кривая, отражающая все различные варианты комбинаций ресурсов, которые могут быть использованы для производства данного объема продукции (см. рис. 3).

Р и с. 3. Производственная функция Кобба — Дугласа

С увеличением объемов используемых факторов возникает возможность выпуска большего объема продукции. Изокванта, отражающая производство большего объема продукта (Q₂=300), будет расположена правее и выше предыдущей изокванты (Q₁=200).

Количество использованных факторов К и L может одновременно меняться, соответственно, будет уменьшаться или увеличиваться объем продукта. Следовательно, может возникнуть множество изоквант, соответствующих разным объемам продукции, которые образуют карту изоквант.

Крутизна наклона изокванты характеризуется предельной нормой технологического замещения (MRTS). Предельная норма технологического замещения измеряется отношением изменения фактора K к изменению фактора L. Поскольку замена факторов проис-ходит в обратном отношении, то математическое выражение MRTS берется со знаком минус.

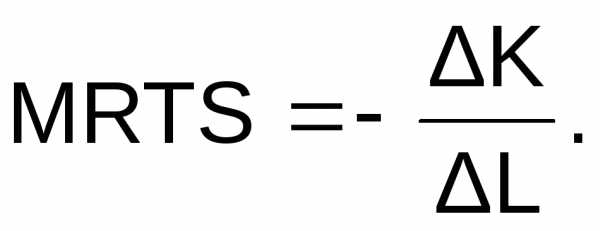
Если мы возьмем какую-либо точку на изокванте, например A, и проведем к ней касательную NM, то тангенс угла ее наклона даст нам значение MRTS (рис. 4).

MRTS = tg a .

Р и с. 4. Динамика предельной нормы технологического замещения

Можно отметить, что в верхней части изокванты угол наклона будет достаточно велик: изменение фактора L на единицу требует значительных изменений фактора K, поэтому в этой части кривой значение MRTS будет велико. По мере движения вниз по изокванте значение предельной нормы технологического замещения будет постепенно убывать, это означает, что для увеличения фактора L на единицу требуется незначительное уменьшение фактора K.

Производственные функции могут иметь разные области использования: для решения задач анализа и планирования, а также прогнозирования. Принцип «затраты-выпуск» может быть использован для описания взаимосвязей между используемыми объемами ресурсов в течение года на отдельном предприятии и годовым выпуском его продукции. В роли производственной системы здесь выступает отдельная фирма, и мы имеем микроэкономическую производственную функцию. В роли производственной системы может выступать отрасль или межотраслевой производственный комплекс. Макроэкономические производственные функции показывают связь обобщающего показателя выпуска с общими затратами ресурсов в экономике.

studfiles.net

Вопрос 3. Производственная функция и ее виды.

а) производство с одним переменным фактором;

б) производство с двумя переменными факторами.

В условиях современного общества ни один человек не может потреблять только то, что он сам производит. Каждый индивид выступает на рынке в двух ролях: как потребитель и как производитель. Без постоянного производства благ не было бы потребления. На известный вопрос «Что производить?» отвечают потребители на рынке, «голосуя» содержимым своего кошелька за те товары, которые им действительно нужны. На вопрос «Как произвести?» должны ответить те фирмы, которые производят товары на рынок.

В экономике присутствует два вида благ: потребительские блага и факторы производства (ресурсы) – это блага, необходимые для организации процесса производства

Hеоклассическая теория традиционно к факторам производства относила капитал, землю и рабочую силу.

В 70-е годы XIX столетия Альфредом Маршаллом был выделен четвертый фактор производства – организация. Далее, Йозефом Шумпетером этот фактор был назван предпринимательством.

Таким образом, производство представляет собой процесс соединения таких факторов как капитал, труд, земля и предпринимательство с целью получения новых благ и услуг, необходимых потребителям.

Для организации производственного процесса необходимые факторы производства должны присутствовать в определенном количестве.

Зависимость максимального объема производимого продукта от затрат используемых факторов называется производственной функцией:

Q = f(K, L, M),

где Q — максимальный объем продукта, который возможно произвести при заданной технологии и определенных факторах производства; K — затраты капитала; L — затраты труда; M — затраты сырья, материалов.

Для укрупненного анализа и прогнозирования используется производственная функция, называемая функцией Кобба-Дугласа:

Q = k · K· L· M,

где Q — максимальный объем продукта при заданных факторах производства; K, L, M — соответственно затраты капитала, труда, материалов; k — коэффициент пропорциональности, или масштабности; , , , — показатели эластичности объема производства соответственно по капиталу, труду и материалам, или коэффициенты прироста Q, приходящиеся на 1% прироста соответствующего фактора:

+ + = 1

Несмотря на то, что для производства конкретного продукта требуется сочетание разных факторов, производственная функция обладает рядом общих свойств:

1. факторы производства являются взаимодополняющими. Это означает, что данный процесс производства возможен только при наборе определенных факторов. Отсутствие одного из перечисленных факторов сделает невозможным производство запланированного продукта.

2. существует определенная взаимозаменяемость факторов. В процессе производства один фактор может быть заменен в определенной пропорции другим. Взаимозаменяемость не означает возможности полного исключения из производственного процесса какого-либо фактора.

Принято рассматривать 2 разновидности производственной функции: с одним переменным фактором и с двумя переменными факторами.

а) производство с одним переменным фактором;

Допустим, что в самом общем виде производственная функция с одним переменным фактором имеет вид:

Q = f(x,y),

где y — const, x — величина переменного фактора.

Для того чтобы отразить влияние переменного фактора на про­изводство, вводятся понятия совокупного (общего), среднего и пре­дельного продукта.

Совокупный продукт (TP) — это количество эко­номического блага, произведенное с использованием некоторого ко­личества переменного фактора. Это общее количество произведенного продукта изменяется по мере увеличения использования переменного фактора.

Средний продукт (AP)(средняя производительность ресурса) — это отношение общего продукта к количеству использованного в производстве переменного фактора:

AP =^TP/_x .

Предельный продукт (MP) (предельная производительность ресурса) обычно определя­ется как прирост совокупного продукта, полученный в резуль­тате бесконечно малого приращения количества использованного переменного фактора:

MP =^TP/_x .

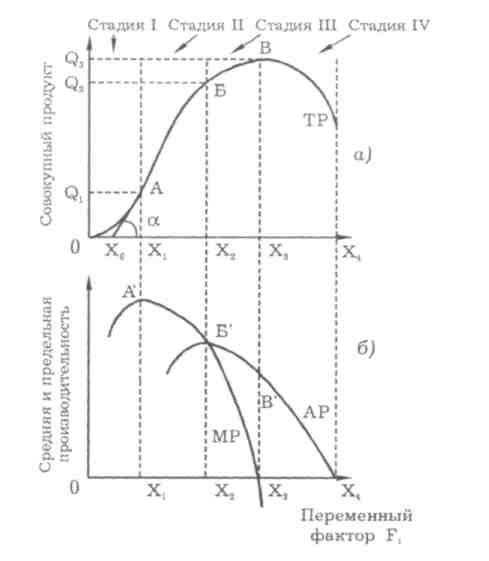
На графике изображено соотношение MP, AP и TP.

Совокупный продукт (Q) сростом использования в производ­стве переменного фактора (х) будет увеличиваться, однако этот рост имеет определенные пределы в рамках заданной технологии. На первой стадии производства (ОА) увеличение затрат труда способствует все более полному исполь­зованию капитала: предельная и общая производительность труда растут. Это выражается в росте предельного и среднего продукта, при этом MP > АР. В точке А’ предельный продукт достигает своего максимума. На второй стадии (AБ) величина пре­дельного продукта уменьшается и в точке Б’ становится равной среднему продукту (MP = АР). Если на первой стадии (0A) сово­купный продукт возрастает медленнее, чем использованное количе­ство переменного фактора, то на второй стадии (АБ) совокупный про­дукт растет быстрее, чем использованное количество переменного фактора (рис. 5—1а). На третьей стадии производства (БВ) MP < АР, в результате чего совокупный продукт растет медленнее затрат переменного фактора и, наконец, наступает четвертая стадия (пос­ле точки В), когда MP < 0. В результате прирост переменного фак­тора х приводит к уменьшению выпуска совокупной продукции. В этом и заключается закон убывающей предельной производительности. Он утверждает, что с ростом исполь­зования какого-либо производственного фактора (при неизменнос­ти остальных) рано или поздно достигается такая точка, в которой дополнительное применение переменного фактора ведет к снижению относительного и далее абсолютного объемов выпуска продукции.

б) производство с двумя переменными факторами.

Допустим, что в самом общем виде производственная функция с двумя переменными факторами имеет вид:

Q = f(x,y),

где x и y — величины переменного фактора.

Как правило, рассматривается 2 одновременно и взаимодополняемых и взаимозаменяемых фактора: труд и капитал.

Эту функцию можно представить графически с использованием изокванты :

Изокванта, или кривая равного продукта, отражает все возможные комбинации двух факторов, которые могут быть использованы для производства определенного объема продукта.

С увеличением объемов используемых переменных факторов, возникает возможность выпуска большего объема продукции. Изокванта, отражающая производство большего объема продукта, будет расположена правее и выше предыдущей изокванты.

Количество использованных факторов x и y может постоянно меняться, соответственно будет уменьшаться или увеличиваться максимальный выпуск продукта. Следовательно, может возникнуть множество изоквант, соответствующих разным объемам выпускаемой продукции, которые образуют карту изоквант.

Изокванты являются подобием кривых безразличия с той лишь разницей, что они отражают ситуацию не в сфере потребления, а в сфере производства. То есть изокванты обладают свойствами, близкими кривым безразличия.

Отрицательный наклон изоквант объясняется тем, что увеличение использования одного фактора при определенном объеме выпуска продукта всегда будет сопровождаться уменьшением количества другого фактора.

Так же как кривые безразличия, расположенные на разном расстоянии от начала координат, характеризуют разный уровень полезности для потребителя, так и изокванты дают информацию о разных уровнях выхода продукции.

Проблему заменяемости одного фактора другим можно решить, рассчитав предельную норму технологического замещения (MRTS_xy или MRTS_LK).

Предельная норма технологического замещения измеряется соотношением изменения фактора y к изменению фактора x. Поскольку замена факторов происходит в обратном отношении, то математическое выражение показателя MRTS_x,y берется со знаком минус:

MRTS_x,y = 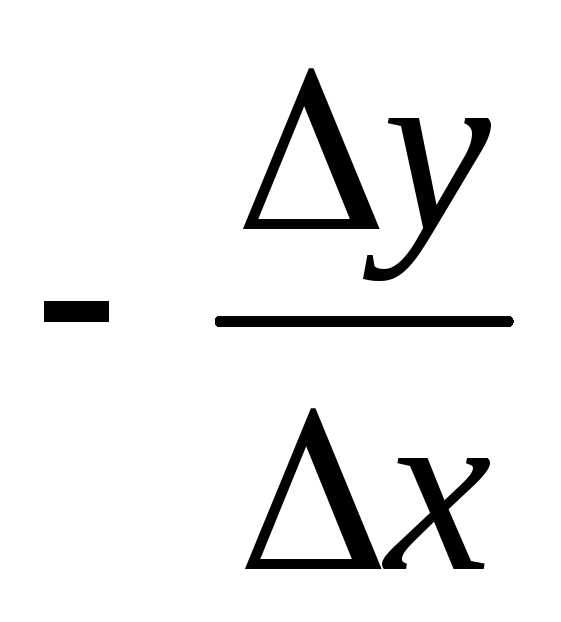илиMRTS_LK=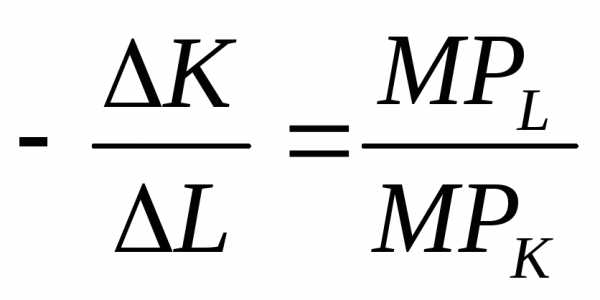

Если мы возьмем какую-либо точку на изокванте, например, точку A и проведем к ней касательную KM, то тангенс угла даст нам значение MRTS_x,y:

MRTS_x,y = tg .

Можно отметить, что в верхней части изокванты угол будет достаточно велик, что говорит о том, что для изменения фактора x на единицу требуются значительные изменения фактора y. Следовательно, в этой части кривой значение MRTS_x,y будет велико.

По мере движения вниз по изокванте значение предельной нормы технологического замещения будет постепенно убывать. Это означает, что для увеличения фактора x на единицу потребуется незначительное уменьшение фактора y.

В реальных производственных процессах встречается два исключительных случая в конфигурации изоквант:

• Это ситуация, когда два переменных фактора идеально взаимозаменяемы, При полной заменяемости факторов производства MRTS_x,y = const. Подобную ситуацию можно представить при возможности полной автоматизации производства. Тогда в точке A весь процесс производства будет состоять из затрат капитала. В точке B все машины будут заменены рабочими руками, а в точках C и D капитал и труд будут дополнять друг друга.

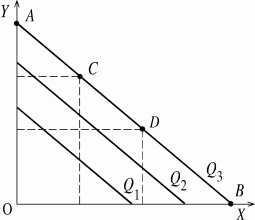
• В ситуации с жесткой дополняемостью факторов предельная норма технологического замещения будет равна 0 (MRTS_x,y = 0). Если мы возьмем современный таксопарк с постоянным количеством машин (y₁), для работы на которых необходимо определенное количество водителей (x₁), то можно сказать, что количество обслуживаемых пассажиров в течение суток не увеличится, если мы увеличим численность водительского состава до x₂, x₃, … x_n. Объем производимого продукта увеличится с Q₁ до Q₂ только в том случае, если увеличится количество используемых машин в таксопарке и численность водителей.

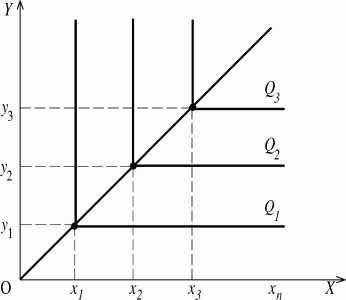
Каждый производитель, приобретая факторы для организации производства, имеет определенные ограничения в средствах.

Предположим, что в качестве переменных факторов выступают труд (фактор x) и капитал (фактор y). Они имеют определенные цены, которые на период анализа остаются постоянными (P_x, P_y — const).

Производитель может приобретать необходимые факторы в определенном сочетании, которое не выходит за рамки его бюджетных возможностей. Тогда его затраты на приобретение фактора x составят P_x · x, фактора y соответственно — P_y · y. Общие затраты (C) составят:

C = P_x · X + P_y · Y или .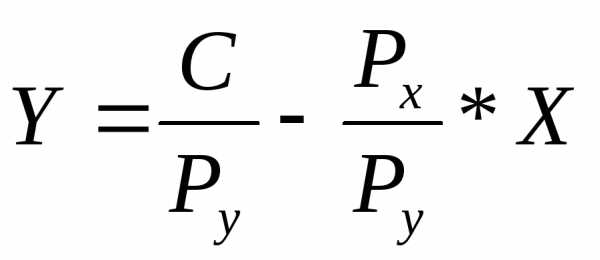

Для труда и капитала:

или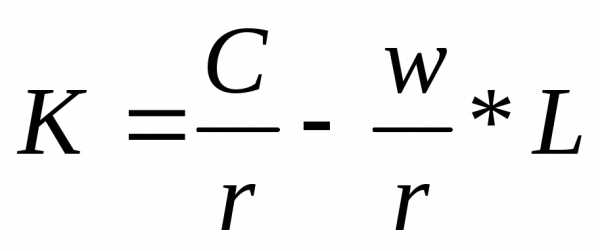

Графическое изображение функции затрат (С) называется изокостой (прямой равных издержек, т.е. это все комбинации ресурсов, использование которых ведет к одинаковым затратам, израсходованным на производство). Строится данная прямая по двум точкам аналогично бюджетной линии (в равновесии потребителя).

Наклон данной прямой определяется:

С увеличением средств на приобретение переменных факторов, то есть с уменьшением бюджетных ограничений, линия изокосты будет сдвигаться вправо и вверх:

C₁ = P_x · X₁ + P_y · Y₁ .

Графически изокосты выглядят так же, как бюджетная линия потребителя. При неизменных ценах изокосты представляют собой прямые параллельные линии с отрицательным углом наклона. Чем больше бюджетные возможности производителя, тем дальше от начала координат отстоит изокоста.

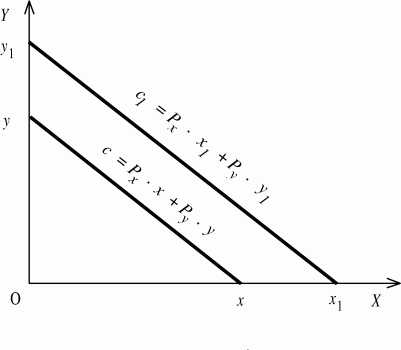
График изокосты в случае уменьшения цены на фактор x переместится по оси абсцисс из точки x₁ в x₂ в соответствии с увеличением применения этого фактора в процессе производства (рис. а).

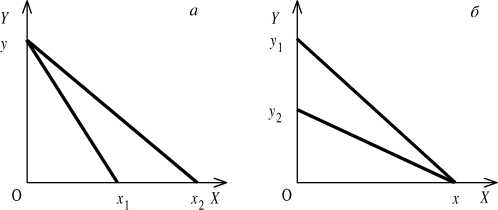
А в случае увеличения цены на фактор y производитель сможет меньшее количество этого фактора привлечь в производство. График изокосты по оси ординат переместится из точки y₁ в y₂.

Имея возможности производства (изокванты) и бюджетные ограничения производителя (изокосты), можно определить равновесие. Для этого совместим карту изоквант с изокостой. Та изокванта, по отношению к которой изокоста займет положение касательной, определит наибольший объем производства, при заданных бюджетных возможностях. Точка касания изокванты изокостой будет точкой наиболее рационального поведения производителя.

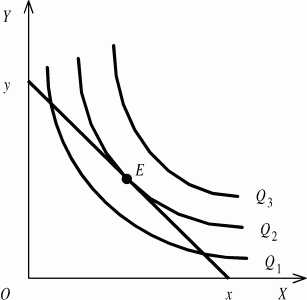
При анализе изокванты мы выяснили, что ее наклон в какой-либо точке определяется углом наклона касательной, или нормой технологического замещения:

MRTS_x,y =

Изокоста в точке E совпадает с касательной. Наклон изокосты, как мы определили ранее, равен угловому коэффициенту 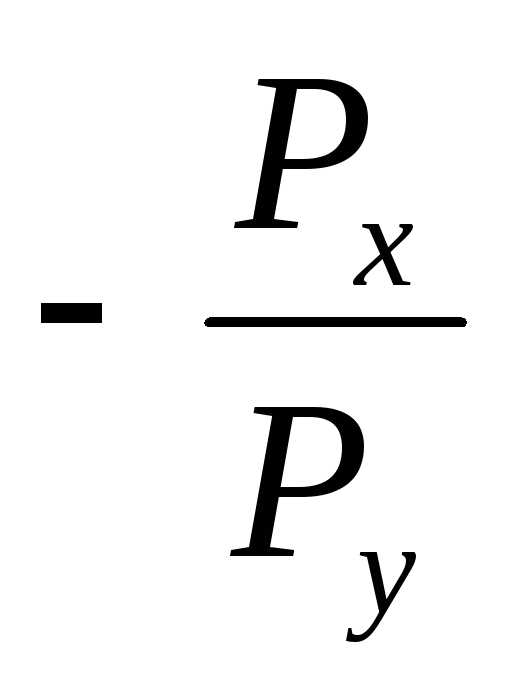. Исходя из этого, можно определитьточку равновесия потребителя как равенство соотношений между ценами на факторы производства и изменением этих факторов.

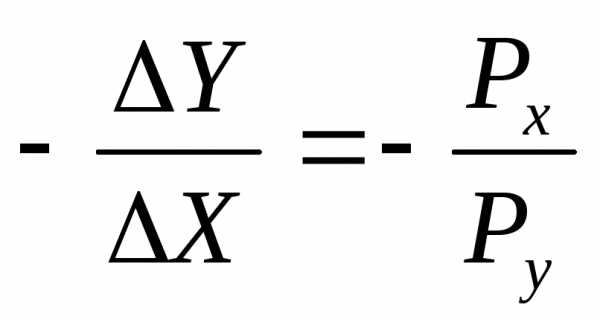или

Приведя данное равенство к показателям предельного продукта переменного фактора производства, в данном случае это MP_x и MP_y, получим:

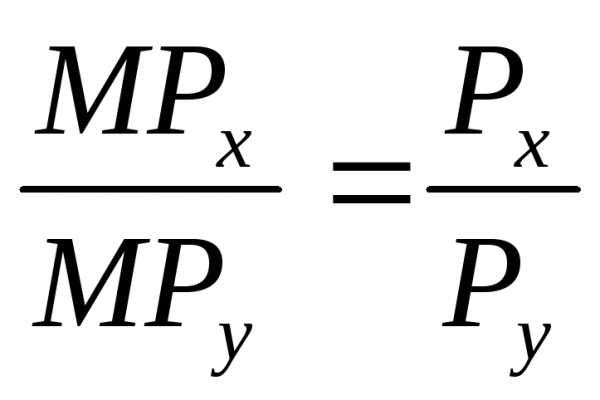или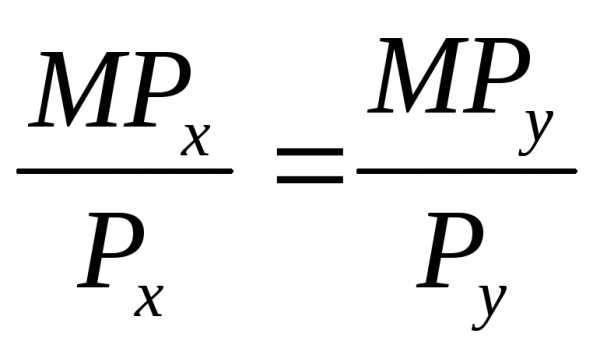

Это равновесие производителя или правило наименьших издержек.

Для труда и капитала равновесие производителя будет выглядеть следующим образом:

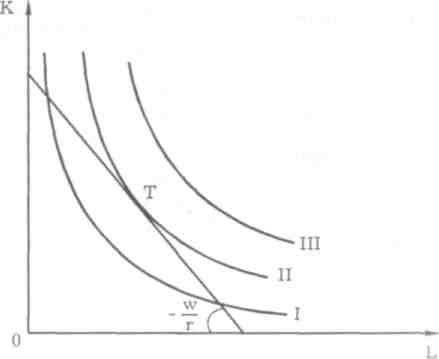
Предположим, что цены ресурсов остаются неизменными, тогда как бюджет производителя постоянно растет. Соединив точки пересечения изоквант с изокостами, мы получим линию OS — «путь развития» (аналогичную линии уровня жизни в теории поведения потребителя). Эта линия показывает темпы рос­та соотношения между факторами в процессе расширения произ­водства. На рисунке, например, труд в ходе развития производст­ва используется в большей мере, чем капитал. Форма кривой «путь развития» зависит, во-первых, от формы изоквант и, во-вторых, от цен на ресурсы (соотношение между которыми определяет наклон изокост). Линия «путь развития» может быть прямой или кривой, исходящей из начала координат.

Если расстояния между изоквантами уменьшаются, это свидетельствует о том, что существует возрастающая экономия от масштаба, т. е. увеличение выпуска достигается при относительной экономии ресурсов. И фирме необходимо наращивать объем производства, так как это приводит к относительной экономии имеющихся ресур­сов.

0 L

Если расстояния между изокванта­ми увеличиваются, это свидетельствует об убывающей экономии от масштаба. Убывающая экономия от масштаба свидетельствует о том, что минимально эффективный размер предприятия уже достигнут и дальнейшее наращивание производства нецелесообразно.

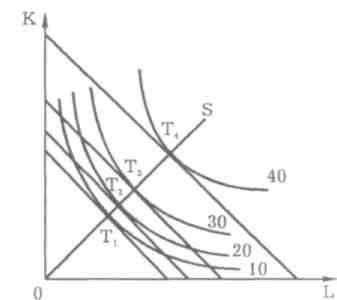
В случае, когда увеличение производства требует пропорцио­нального увеличения ресурсов, говорят о постоянной экономии от масштаба.

K

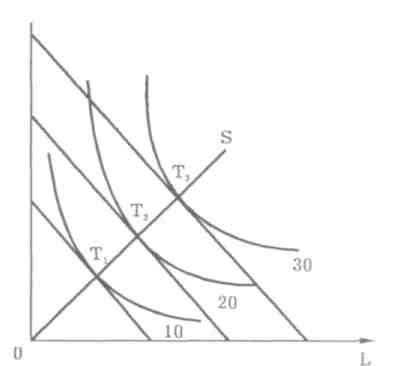
Таким образом, анализ выпуска с помощью изоквант позволяет определить техническую эффективность производства. Пересечение изоквант с изокостой позволяет определить не только технологическую, но и экономическую эффективность, т. е. выбрать технологию (трудо-или капиталосберегающую, энерго- или материалосберегающую и т. д.), позволяющую обеспечить максимальный выпуск продукции при тех денежных средствах, которыми располагает производи­тель для организации производства.

studfiles.net

34. Производство и производственная функция. Графическое отображение производственной функции.

Производство – любая деятельность по использованию экономических ресурсов, включая самого человек, для получения как осязаемых, так и неосязаемых благ.

В качестве образца теоретического подхода к производству берут теорию материального производства.

Под материальным производством понимают процесс трансформации экономических ресурсов в продукт.

Фонды предприятия:

1. Производственные фонды.

а) Основные: здания, сооружения, машины, оборудование.

б) Оборотные: производственные запасы, незавершенная продукция, расходы будущего производства.

2. Фонды обращения: готовая продукция, денежные средства в расчетах, денежные средства на расчете.

3. Фонды непроизводственного назначения: жилье, столовая, медицинский пункт.

Взаимосвязь между вводимыми факторами производства, процессом производства и итоговым выпуском продукции описывается при помощи производственной функции.

Производственная функция – зависимость между набором факторов производства и максимально возможным объемом продукции, производимым из этого набора.

Производственные функции бывают двухфакторные и трёхфакторные.

Производственная функция Кобба-Дугласа (трёхфакторная производственная функция)

Q =В · К^а1 · L^а2 · M^а3, где:

Q – объем производства (выпуска)

L, K, М – объемы приложенного труда и капитала

M – объем сырья и материалов

B, a – коэффициенты производствам (определяются статистикой)

Во-первых, производственная функция показывает максимальное количество товара, которое может быть произведено при различных сочетаниях факторов производства. Во-вторых, производственная функция показывает альтернативные возможности, при которых различные комбинации факторов обеспечивают один и тот же объем выпуска продукции.

Производственная функция строится под определенную технологию. Изменение технологии отображается с помощью новой производственной функции.

Существует предел для увеличения объема производства, который может быть достигнут при увеличении затрат одного фактора при прочих равных условиях.

Между факторами производства существуют как определенная взаимная дополняемость (комплиментарность), так и определенная их взаимозаменяемость.

Изоквантойназывают кривую, на которой расположены все сочетаниявводимыхфакторов производства, использование которых обеспечивает одинаковый объем выпуска продукции.

Эффект масштаба.

Расширение производства возможно двумя путями:

1) за счет применения новых технологий (интенсивный путь)

2) расширение применения всех ресурсов (экстенсивный путь)

Эффект масштаба – соотношение между относительным изменениемвеличины затрат факторов производства и относительным изменением объема выпускаемой продукции.

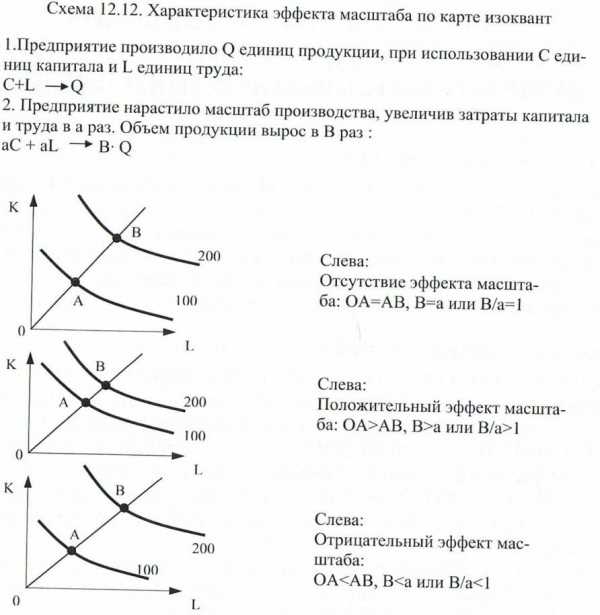
Предприятие производило Q единиц продукции при использовании C ед. капитала и L ед. труда. С+LQ.

Предприятие нарастило масштаб производства, увеличение затраты капитала и труда в a раз. Объем продукции вырос вВ раз aC+aLBQ.

Положительный эффект масштаба (OA>AB, B>a или B/a>1) – объемвыпуска увеличивается в больше пропорции, чем затраты факторов.

Постоянный эффект масштаба или отсутствие (OA=AB, B=a или B/a=1) – объем выпуска увеличивается в той же пропорции, что и затраты факторов.

Отрицательный эффект масштаба (OA<AB, B<a или B/a<1) – объем выпуска увеличивается в меньшей пропорции, чем затраты факторов.

Взаимосвязь между изменением масштаба производства и соответствующим изменением в объеме выпуска продукции называется отдачей от масштаба.

studfiles.net

2. Производственная функция и ее характеристики

2.1 Производственная функция, технология

Производственная функция – это зависимость между количеством и структурой использованных ресурсов (L-труд, K- капитал) и максимально возможным количеством продукции (Q), который фирма способна произвести в течение определенного периода времени.

Производственная функция характеризует данную технологию. Совершенствование технологии, которое обеспечивает новый достигнутый объем выпускаемой продукции при любой комбинации факторов отражается новой производственной функцией.

Набор факторов производства или ресурсов можно представить как затраты труда, капитала(орудия труда и материалы), тогда производственная функция может быть описана следующим образом:

Q = f (L, K),

где Q — максимальный объем продукции, производимый при данной технологии и данном соотношении труда — L, капитала — К.

2.2.Свойства производственной функции

Все производственные функции обладают общими свойствами:

Существуют границы роста объема производства, который может быть достигнут увеличением затрат одного ресурса при неизменных других ресурсах.

Возможна определенная взаимная дополняемость (комплементарность) факторов производства, но без уменьшения объема производства, возможна и определенная взаимозаменяемость этих факторов.

Изменения в применении факторов производства более эластичны на продолжительном отрезке времени, чем в течение короткого периода в деятельности фирмы.

Короткий период времени — это период производства, в течение которого все ресурсы за исключением одного являются неизменными, тогда весь прирост объема производства связан с приростом использования именно данного фактора.

Долгосрочный период времени — это период, в течение которого производитель может изменить все факторы производства данной продукции. В теории продолжительный период времени рассматривают как последовательно сменяющие друг друга короткие периоды.

Совокупный продукт переменного фактора производства (ТР)- это количество продукции, производимой при определенном количестве этого фактора и при прочих неизменных факторах производства.

Средний продукт переменного фактора производства — это отношение совокупного продукта переменного фактора к использованному количеству этого фактора. Например, средний продукт труда AP_(L) — это совокупный продукт труда ТР(_L), деленный на количество часов труда (L):

Представленная величина представляет собой производительность труда или величину выпуска продукции за каждый час труда.

Средний продукт капитала:

Предельный продукт переменного фактора производства — это изменение совокупного продукта этого фактора (например, ТР_L ) при изменении на единицу используемого фактора (например, фактор труд (L) меняется на единицу, а капитал не меняется).

,

где F фактор производства (L или K).

Закон убывающей отдачи (предельной производительности факторов производства):

В условиях осуществления производственной деятельности фир­ма должна использовать основные факторы производства в опреде­ленной пропорции между постоянными и переменными ресурсами. Если предприятие увеличивает только количество переменных фак­торов без изменения постоянного фактора, то в этом случае вступает в действие закон убывающей отдачи.

Закон убывающей предельной производительности факторов производства гласит, что если фирма наращивает объем исполь­зования только некоторых или одного из факторов производства, то прирост выпуска, приносимый дополнительными объемами этих факторов, в конце концов, начнет снижаться.

В соответствии с законом, непрерывное увеличение использо­вания одного переменного ресурса в сочетании с неизменным ко­личеством других ресурсов на определенном этапе приведет к пре­кращению роста отдачи, а затем и ее снижению. Следует отметить, что достаточно часто действие закона предполагает постоянство технологического уровня производства, и поэтому переход к более прогрессивной технологии может повысить отдачу независимо от соотношения постоянных и переменных факторов.

Рассмотрим следующий пример. Как на предприятии изменится отдача от переменного фактора в краткосрочном периоде, если часть ресурсов или факторов производства остается постоянной. В крат­косрочном периоде предприятие не в состоянии ввести новые цеха, установить новое оборудование и т. д.

Допустим, что предприятие в своей деятельности использует только один переменный ресурс — труд, отдачей которого является производительность. Необходимо определить, как будут изменяться издержки фирмы при постепенном увеличении переменного ресурса (количества рабочих).

В небольшом цехе на 3 единицы оборудования один рабочий де­лает за смену 5 изделий. С привлечением второго рабочего вдвоем они сделают за смену 12 изделий, третьим — 20, с четвертым — 25, с пятым — тоже 25, с шестым — 20. Присоединение второго рабочего дает прирост 7 единиц, третьего — 8 единиц, четвертого — 5 единиц, пятого — прироста не дает вовсе. Таким образом, уже с четвертой единицы переменного фактора фиксируем убывающую отдачу. То же наблюдаем в случае со средней величиной произведенной продукции. Один рабочий — 5 изделий, два — по 6, три — по 6,7, четыре — по 6,2, пять — по 5, шесть — 3,3. Возникает вопрос, почему так резко падает отдача? Потому что при тех же производственных мощностях (три станка) пятый и шестой рабочие уже не просто лишние, они мешают рациональному производственному процессу.

Таблица 5.3

Количество рабочих (L)	Общая производительность (TP)	Предельная производительность (MP)	Средняя производительность (АР)
1	5	5	5
2	12	7	6
3	20	8	67
4	25	—	6,2
5	25	5	5
6	20	0	3,3

Запишем приведенные данные в табл. 5.3 и построим соответ­ствующие графики 5.6 и 5.7.

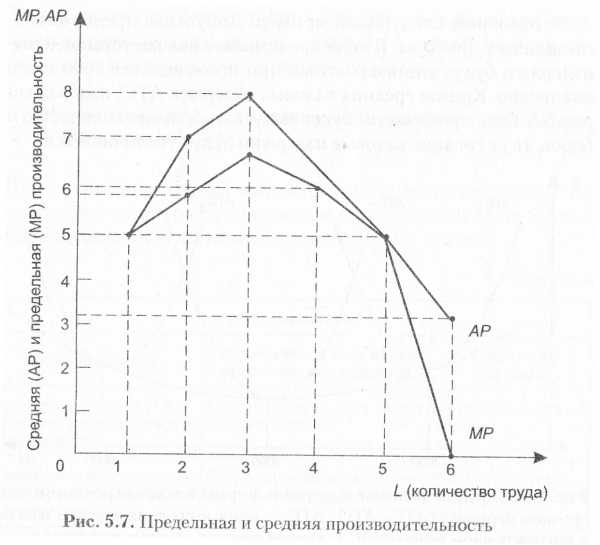
Данные таблицы и графики, построенные по ним, свидетельству­ют о том, что начиная с определенного момента, и общая, и предель­ная, и средняя производительности убывают. В этом проявляется сущность закона убывающей отдачи.

Эффект масштаба

Устранить действие закона убывающей отдачи можно, если фир­ма откроет дополнительные производства, то есть будут введены в действие новые производственные мощности. По сути, произойдет наращивание производственного потенциала — постоянного ресурса (долгосрочный период)

В долгосрочном периоде использование факторов производства (L и K) необходимо рассматривать как переменные. Это связано с тем, что фирма может активно изменять привлекаемые производственные ресурсы. В дан­ном случае все издержки предприятия будут выступать в качестве переменных.

Зависимость между увеличением факторов производства и объемом выпуска характеризуется эффектом масштаба:

Эффект масштаба
Состояние отдачи	Соотношение темпов объема производства и издержек	Состояние издержек
Возрастающая отдача от мас­штаба (положительный эф­фект масштаба)	Объем производства растет быстрее издержек	Средние издержки падают
Убывающая отдача от масшта­ба (отрицательный эффект масштаба)	Объем производства растет медленнее издержек	Средние издержки возрастают
Постоянная отдача от мас­штаба	Объем производства и из­держки растут одинаковыми темпами	Средние издержки не изменяются

Эффект масштаба будет положительным, если при увеличении объемов производства средние валовые издержки уменьшаются, и отрицательным — если они увеличиваются.

Анализ издержек фирмы в краткосрочном и долгосрочном пе­риодах является необходимым, но не достаточным условием при планировании выпуска продукции на ближайшее время и перспек­тиву. Минимизация издержек — это не самоцель, а лишь средство повышения прибыли или сокращения убытков, а в конечном сче­те — обеспечения стабильности и устойчивости положения фирмы в условиях рынка.

Таким образом, если в краткосрочном периоде для фирмы важно найти оптимальное соотношение факторов производства (K ,L), то в долгосрочном периоде фирмой решается задача выбора необходимого масштаба деятельности фирмы.

studfiles.net

2. Производственная функция. Свойства производственной функции

Для организации любого производственного процесса необхо­димы факторы производства.

Будем считать, что выпуск продукции Q произведен при ис­пользовании только двух факторов производства — труда L и ка­питала К. В общем виде производственная функция (1) имеет вид:

147

Q = f(L, К)

где f — форма производственной функции.

Производственная функция описывает технологическую вза­имосвязь между объемом выпускаемой продукции и произведен­ными затратами — затратами факторов производства, а также зависимость между затратами. В функции находит отражение максимальный объем продукции, который достигается при каж­дой комбинации факторов, то есть в определении производствен­ной функции максимизация продукции решена технически. Если в качестве независимых переменных выступают величины зат­рат, то производственную функцию называют функцией выпус­ка, если же фиксирована величина выпуска, то производствен­ная функция является функцией затрат.

При любой комбинации факторов можно достичь нескольких объемов выпуска в зависимости от эффективности организации производства. Если технология становится более прогрессивной, то фирма может увеличивать объем производства при фиксиро­ванном наборе производственных факторов. Производственная функция предполагает, что фирма использует каждое сочетание факторов с максимальной эффективностью. Если используются п факторов производства, то производственная функция в общей форме имеет вид:

Q = f{F₁ F₂, …, F_n),

где F₁, F₂, …, F_n — использованные факторы производства.

Если фиксирована величина выпуска, то производственная функция является функцией затрат и тогда затраты любого фак­тора F_h можно выразить как функцию всех остальных затрат:

где ф — форма функции.

Для укрупненного анализа и прогнозирования используется производственная функция Кобба-Дугласа (Впервые производственная функция была построена в 1928 году для обрабатывающей промышленности США за период 1899—1922 годы и носит имя её авторов Ч. Кобба и П. Дугласа.):

где Q — максимальный объем продукта при заданных факторах производства;

L, К — затраты труда, капитала;

k — коэффициент пропорциональности, или масштабности;

α, β — коэффициенты эластичности объема производства, со­ответственно, по труду и капиталу или коэффициенты прироста Q, приходящиеся на 1% прироста соответствующего фактора.

Названные коэффициенты в сумме измеряют совокупное про­центное изменение выпуска при данном процентном изменении затрат труда и капитала. Если а + Р = 1, то объём выпуска возрастает ровно на столько, на сколько увеличиваются затраты тру­да, капитала и материалов, имеет место постоянная отдача от масштаба, и функция Кобба-Дугласа в таком случае является однородной. Если (а + Р) > 1, то предприятием будет получена экономия от масштаба, свидетельствующая о том, что эффектив­ность факторов производства повышается в условиях техниче­ского прогресса. Если (а+Р) < 1, будет иметь место убывающая отдача от масштаба производства.

Свойства производственной функции

1. Факторы производства являются взаимодополняющими. Для производства любого продукта используется определенный набор факторов, отсутствие хотя бы одного из них делает производство невозможным. Это значит, что производственная функция превращается в нуль, когда один из факторов равен нулю:

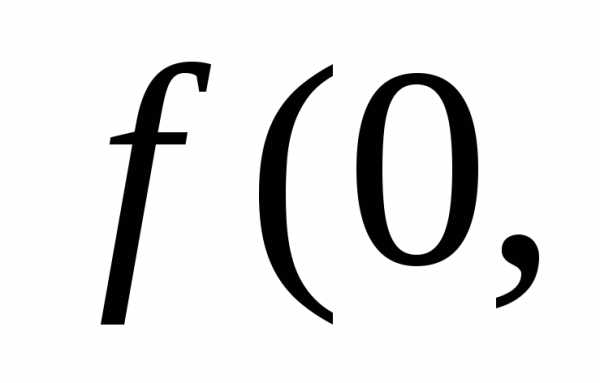^{К) = f(L, K) = 0.}

Кроме того, существует взаимозаменяемость факторов в оп­ределенной пропорции, которая обусловлена не только специфи­кой потребностей и конструктивных особенностей изделия, но и ограниченностью ресурсов, с одной стороны, и эффективностью их использования, с другой. Взаимозаменяемость не означает возможности полного исключения из производственного процес­са какого-либо фактора, так как в любом случае необходима зем­ля, на которой будет организован процесс производства, обору­дование и труд работников.

2. Аддитивность отражает тот факт, что объединение двух групп факторов (L₁, K₁) и (L₂, K₂) дает, по крайней мере, такой же объем продукции, как и при раздельном использовании этих двух групп факторов:

3. Делимость означает, что любой производственный процесс может осуществляться в сокращенных масштабах. Например, при уменьшении числа рабочих и объема капитала вдвое выпуск продукции сократится не более чем на половину:

Данное положение не применимо на малых предприятиях, где производственная деятельность при уменьшающихся масш­табах либо невозможна, либо неэффективна. Но такое свойство характерно для производственной функции на уровне отрасли или народного хозяйства. Так, если в отрасли уменьшится заня­тость и объем капитала на 10%, то это может означать остановку части предприятий при неизменности условий работы на всех остальных.

Для исследования влияния факторов на объем выпуска ис­пользуются понятия краткосрочного и долгосрочного периода, а все факторы производства делятся на переменные и постоянные. Краткосрочный период — период, в течение которого хотя бы один фактор остается неизменным. Долгосрочный период — пе­риод, в течение которого могут быть изменены все факторы про­изводства. Переменные факторы — это ресурсы, количества ко­торых могут быть изменены в рамках краткосрочного периода. Постоянные факторы — это ресурсы, количества которых не могут быть изменены в рамках краткосрочного периода.

Следует подчеркнуть, что хотя определения краткосрочного и долгосрочного периодов связаны со временем, их экономическое содержание обусловлено не временем, а реальными изменения­ми структуры производства. Поэтому в силу технологических особенностей разных производств временные рамки краткосроч­ного или долгосрочного периодов для каждого из них могут зна­чительно различаться.

studfiles.net