Производная от десятичного логарифма: Производная логарифма (logx)’
Таблица производных логарифм по основанию x. Формулы и примеры производной логарифма. Производная логарифма модуля x
При дифференцировании показательно степенной функции или громоздких дробных выражений удобно пользоваться логарифмической производной. В этой статье мы рассмотрим примеры ее применения с подробными решениями.
Дальнейшее изложение подразумевает умение пользоваться таблицей производных , правилами дифференцирования и знание формулы производной сложной функции .
Вывод формулы логарифмической производной.
Сначала производим логарифмирование по основанию e
, упрощаем вид функции, используя свойства логарифма, и далее находим производную неявно заданной функции:
Для примера найдем производную показательно степенной функции x в степени x .
Логарифмирование дает . По свойствам логарифма . Дифференцирование обеих частей равенства приводит к результату:
Ответ: .
Этот же пример можно решить и без использования логарифмической производной.
Пример.
Найти производную функции .
Решение.
В этом примере функция представляет собой дробь и ее производную можно искать с использованием правил дифференцирования. Но в силу громоздкости выражения это потребует множества преобразований. В таких случаях разумнее использовать формулу логарифмической производной . Почему? Вы сейчас поймете.
Найдем сначала . В преобразованиях будем использовать свойства логарифма (логарифм дроби равен разности логарифмов, а логарифм произведения равен сумме логарифмов, и еще степень у выражения под знаком логарифма можно вынести как коэффициент перед логарифмом):
Эти преобразования привели нас к достаточно простому выражению, производная которого легко находится:
Подставляем полученный результат в формулу логарифмической производной и получаем ответ:
Для закрепления материала приведем еще пару примеров без подробных объяснений.
Пример.
Найдите производную показательно степенной функции
Производная натурального логарифма от x равна единице, деленной на x:
(1) (ln
x)′ = .
Производная логарифма по основанию a равна единице, деленной на переменную x, умноженную на натуральный логарифм от a
:
Доказательство
Пусть есть некоторое положительное число, не равное единице. Рассмотрим функцию, зависящую от переменной x
,
которая является логарифмом по основанию :
.
Эта функция определена при .
Найдем ее производную по переменной x
.
По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам нужно знать следующие факты:
А) Свойства логарифма . Нам понадобятся следующие формулы:
(4) ;
(6) ;
Б) Непрерывность логарифма и свойство пределов для непрерывной функции:
(7) .

Здесь — некоторая функция, у которой существует предел и этот предел положителен.
В) Значение второго замечательного предела:
(8) .
Применяем эти факты к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим свойства (4) и (5).
.
Воспользуемся свойством (7) и вторым замечательным пределом (8):
.
И, наконец, применим свойство (6):
.
Логарифм по основанию e
.
Тогда ;
.
Тем самым мы получили формулу (2) производной логарифма.
Производная натурального логарифма
Еще раз выпишем формулу производной логарифма по основанию a
:
.
Эта формула имеет наиболее простой вид для натурального логарифма, для которого ,
.
Тогда
(1) .
Из-за такой простоты, натуральный логарифм очень широко используется в математическом анализе и в других разделах математики, связанных с дифференциальным исчислением. Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):
Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):
Производную логарифма по основанию можно найти из формулы (1), если вынести постоянную за знак дифференцирования:
.
Другие способы доказательство производной логарифма
Здесь мы предполагаем, что нам известна формула производной экспоненты:
(9) .
Тогда мы можем вывести формулу производной натурального логарифма, учитывая, что логарифм является обратной функцией к экспоненте.
Докажем формулу производной натурального логарифма, применив формулу производной обратной функции :
.
В нашем случае .
Обратной функцией к натуральному логарифму является экспонента:
.
Ее производная определяется по формуле (9). Переменные можно обозначить любой буквой. В формуле (9), заменим переменную x на y:
.
.
Тогда
.
Формула доказана.
Теперь докажем формулу производной натурального логарифма с помощью правила дифференцирования сложной функции . Поскольку функции и являются обратными друг к другу, то
Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x
:
(10) .
Производная от икса равна единице:
.
Применяем правило дифференцирования сложной функции :
.
Здесь .
Подставим в (10):
.
Отсюда
.
Пример
Найти производные от ln 2x, ln 3x и ln nx .
Решение
Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции
Итак, ищем производную от функции
y = ln nx .
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции ,
зависящей от переменной :
;
2) Функции ,
зависящей от переменной :
.
Тогда исходная функция составлена из функций и :
.
Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
Применяем формулу производной сложной функции .
.
Здесь мы подставили .
Итак, мы нашли:
(11) .
Мы видим, что производная не зависит от n
.
Этот результат вполне естественен, если преобразовать исходную функцию, применяя формулу логарифма от произведения:
.
— это постоянная. Ее производная равна нулю. Тогда по правилу дифференцирования суммы имеем:
.
Ответ
; ; .
Производная логарифма модуля x
Найдем производную от еще одной очень важной функции — натурального логарифма от модуля x
:
(12) .
Рассмотрим случай .
Тогда и функция имеет вид:
.
Ее производная определяется по формуле (1):
Теперь рассмотрим случай .
Тогда и функция имеет вид:
,
где .
Но производную этой функции мы также нашли в приведенном выше примере. Она не зависит от n
и равна
.
Тогда
.
Объединяем эти два случая в одну формулу:
.
Соответственно, для логарифма по основанию a
,
имеем:
.
Производные высших порядков натурального логарифма
Рассмотрим функцию
.
Мы нашли ее производную первого порядка:
(13) .
Найдем производную второго порядка:
.
Найдем производную третьего порядка:
.
Найдем производную четвертого порядка:
.
Можно заметить, что производная n-го порядка имеет вид:
Докажем это методом математической индукции.
Доказательство
Подставим в формулу (14) значение n = 1:
.
Поскольку ,
то при n = 1 ,
формула (14) справедлива.
Предположим, что формула (14) выполняется при n = k . Докажем, что из этого следует, что формула справедлива при n = k + 1 .
Действительно, при n = k
имеем:
.
Дифференцируем по переменной x
:
.
Итак, мы получили:
.
Эта формула совпадает с формулой (14) при n = k + 1 .
Таким образом, из предположения, что формула (14) справедлива при n = k
следует, что формула (14) справедлива при n = k + 1 .
Поэтому формула (14), для производной n-го порядка, справедлива для любых n .
Производные высших порядков логарифма по основанию a
Чтобы найти производную n-го порядка от логарифма по основанию a
,
нужно выразить его через натуральный логарифм:
.
Применяя формулу (14), находим n-ю производную:
.
Вам кажется, что до экзамена еще много времени? Это месяц? Два? Год? Практика показывает, что ученик лучше всего справляется с экзаменом в том случае, если начал готовиться к нему заблаговременно. В ЕГЭ немало сложных заданий, который стоят на пути школьника и будущего абитуриента к высшим баллам. Эти преграды нужно научиться преодолевать, к тому же, делать это несложно. Вам необходимо понять принцип работы с различными заданиями из билетов. Тогда и с новыми не возникнет проблем.
Логарифмы на первый взгляд кажутся невероятно сложными, но при детальном разборе ситуация значительно упрощается. Если вы хотите сдать ЕГЭ на высший балл, вам стоит разобраться в рассматриваемом понятии, что мы и предлагаем сделать в этой статье.
Для начала разделим эти определения. Что такое логарифм (log)? Это показатель степени, в которую надо возвести основание, чтобы получить указанное число. Если непонятно, разберем элементарный пример.
В этом случае основание, стоящее внизу, необходимо возвести во вторую степень, чтобы получить число 4.
Теперь разберемся со вторым понятием. Производная функции в любом виде называется понятие, характеризующее изменение функции в приведенной точке. Впрочем, это школьная программа, и если вы испытываете проблемы с данными понятиями по отдельности, стоит повторить тему.
Производная логарифма
В задания ЕГЭ по этой теме можно привести несколько задач в качестве примера. Для начала самая простая логарифмическая производная. Необходимо найти производную следующей функции.
Нам нужно найти следующую производную
Существует специальная формула.
В этом случае x=u, log3x=v. Подставляем значения из нашей функции в формулу.
Производная x будет равняться единице. С логарифмом немного труднее. Но принцип вы поймете, если просто подставите значения. Напомним, что производной lg x называется производная десятичного логарифма, а производная ln х — это производная от натурального логорифма (по основанию e).
Теперь просто подставьте полученные значения в формулу. Попробуйте сами, далее сверим ответ.
В чем здесь может быть проблема для некоторых? Мы ввели понятие натурального логарифма. Расскажем о нем, а заодно разберемся, как решать задачи с ним. Ничего сложного вы не увидите, особенно, когда поймете принцип его работы. К нему вам стоит привыкнуть, так как он нередко используется в математике (в высших учебных заведениях тем более).
Производная натурального логарифма
По своей сути, это производная логарифма по основанию e (это иррациональное число, которое равняется примерно 2,7). На деле ln очень прост, поэтому часто используется в математике в целом. Собственно, решение задачи с ним тоже не станет проблемой. Стоит запомнить, что производная от натурального логарифма по основанию е будет равно единице поделенной на x. Самым показательным будет решение следующего примера.
Собственно, решение задачи с ним тоже не станет проблемой. Стоит запомнить, что производная от натурального логарифма по основанию е будет равно единице поделенной на x. Самым показательным будет решение следующего примера.
Представим ее как сложную функцию, состоящую из двух простых.
Достаточно преобразовать
Ищем производную от u по x
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Специфика работы с логарифмами в задаче B15
Вообще говоря, для решения задачи B15 с логарифмом надо знать две формулы:
Первая формула — классическая производная натурального логарифма, вторая — производная сложной функции. Обратите внимание: в числителе стоит число k, это не опечатка.
Добавьте к этим формулам стандартные правила вычисления производных — и задача B15 решена:
(f ± g) ’ = f ’ ± g ’;
(c · f) ’ = c · f ’, c ∈ R.
В настоящих задачах логарифмы никогда не встречаются сами по себе. Поэтому обязательно приводите всю производную к общему знаменателю. Почему это важно, узнаете из примеров.
Почему это важно, узнаете из примеров.
Задача. Найдите наименьшее значение функции на отрезке [0,5; 4]:
y = 2x2 − 4 ln x + 5
Находим производную:
Выясняем, когда производная равна к нулю. Дробь равна нулю, когда ее числитель равен нулю. Имеем:
4(x2 − 1) = 0;
x2 = 1;
x = ±1.
Корень x = −1 не принадлежит отрезку [0,5; 4], поэтому нас интересует только x = 1. Кроме того, рассмотрим концы отрезка — числа 0,5 и 4. Итого три числа: 0,5; 1; 4. Поскольку требуется найти наименьшее значение функции, подставляем эти числа в исходную функцию:
y (0,5) = 2 · 0,52 − 4 ln 0,5 + 5 = 0,5 − 4 ln 0,5 + 5 = 5,5 − 4 ln 0,5;
y (1) = 2 · 12 − 4 ln 1 + 5 = 2 − 0 + 5 = 7;
y (4) = 2 · 42 − 4 ln 4 + 5 = 32 − 4 ln 4 + 5 = 37 − 4 ln 4.
В общем, выбирать особо не из чего. Ответ: 7. Потому что числа 5,5 − 4ln 0,5и 37 − 4ln 4 иррациональны, их нельзя записать в виде конечной десятичной дроби.
Задача. Найдите точку минимума функции:
y = 2x − 5 ln (x − 7) + 3
Снова считаем производную:
Под логарифмом стоит линейная функция y = x − 7. Коэффициент при переменной x равен k = 1, поэтому в числителе никаких дополнительных множителей не возникнет — только множитель 5, который стоит перед логарифмом.
Поскольку требуется найти точку минимума, считаем нули числителя и знаменателя:
2x − 19 ⇒ x = 19 : 2 = 9,5;
x − 7 = 0 ⇒ x = 7.
Отмечаем эти точки на прямой, расставляем знаки производной между точками:
Итак, в точке x = 9,5 производная меняет знак с минуса на плюс, если считать слева — направо, в направлении стрелки. Это и есть точка минимума.
Задача. Найдите наибольшее значение функции на отрезке [−1,5; 1]:
y = 3 ln (x + 2) − 3x + 10
Считаем производную:
Находим нули числителя:
−3x − 3 = 0;
x = −1.
Нули знаменателя нас не интересуют, поскольку требуется найти значение функции. А когда знаменатель равен нулю, значение функции не определено.
А когда знаменатель равен нулю, значение функции не определено.
Поскольку корень x = −1 ∈ [−1,5; 1], получаем три точки: −1,5; −1; 1. Подставляем их в исходную функцию:
y (−1,5) = 3 ln (−1,5 + 2) − 3 · (−1,5) + 10 = 3 ln 0,5 + 14,5;
y (−1) = 3 ln (−1 + 2) − 3 · (−1) + 10 = 3 ln 1 + 13 = 0 + 13 = 13;
y (1) = 3 ln (1 + 2) − 3 · 1 + 10 = 3 ln 3 + 7.
Понятно, что числа 3 ln 0,5 + 14,5и 3 ln 3 + 7 нельзя записать в ответ. Остается только число 13 — это и будет наибольшее значение.
Вынесение степени за знак логарифма
Еще одна полезная фишка, которая избавит вас от сложных производных:
ln (f (x))k = k · ln f (x)
Обратите внимание: в первом случае внутри логарифма стоит степень, для которой потребуется производная сложной функции. Во втором случае все намного проще, поскольку чаще всего f (x) — это обычная линейная функция.
Этот прием часто встречается в задачах на вычисление максимального и минимального значения. В задачах на точки экстремума его почти не применяют. Прежде чем решать такую задачу, обязательно найдите ОДЗ логарифма. Если забыли, что это такое, см. «Что такое логарифм».
Прежде чем решать такую задачу, обязательно найдите ОДЗ логарифма. Если забыли, что это такое, см. «Что такое логарифм».
Задача. Найдите наименьшее значение функции на отрезке [−4; 1]:
y = 5x − ln (x + 5)5
Итак, область допустимых значений логарифма — аргумент должен быть больше нуля. Имеем:
(x + 5)5 > 0;
x + 5 > 0;
x > −5;
x ∈ (−5; +∞).
Теперь решаем задачу. Сначала немного преобразуем исходное выражение:
y = 5x − 5 ln (x + 5)
Это и есть вынесение степени за знак логарифма. Считаем производную:
Дальше все стандартно. Нас интересует значение функции, поэтому приравниваем числитель к нулю:
5x + 20 = 0;
x = −4.
Полученное число x = −4 ∈ [−4; 1] совпадает с концом отрезка, поэтому кандидатов на наименьшее значение всего два: −4 и 1. Оба числа подходят по ОДЗ. Поскольку требуется найти наименьшее значение, подставляем эти числа в исходную функцию:
y (−4) = 5 · (−4) − 5 · ln (−4 + 5) = −20 − 5 · ln 1 = −20;
y (1) = 5 · 1 − 5 · ln (1 + 5) = 5 − 5 ln 6.
Второе число — точно не ответ, поскольку его нельзя представить в виде десятичного числа. Значит, наименьшее значение функции равно −20.
Задача. Найдите точку максимума функции:
y = 18 ln x − x2 + 5
ОДЗ логарифма: x > 0 ⇒ x ∈ (0; +∞). Считаем производную:
Поскольку требуется найти точку максимума, нас интересует и числитель, и знаменатель. Приравниваем их к нулю:
2 · (9 − x2) = 0 ⇒ x2 = 9 ⇒ x = ±3 — числитель;
x = 0 — знаменатель.
Получили три точки. Отмечаем эти точки и знаки производной на числовой прямой:
Требуется найти точку максимума — там, где плюс меняется на минус. Таких точек две: x = −3и x = 3. Но вспомним ОДЗ: x ∈ (0; +∞). Значит, точка x = −3 не подходит. Остается точка x = 3 — это и будет ответ.
Смотрите также:
- Показательные функции в задаче B15
- Задача B15: частный случай при работе с квадратичной функцией
- Решение ЕГЭ-2011: вариант 1, часть B
- Как решать задачи B15 без производных
- Как быстро запомнить таблицу синусов и косинусов
- ЕГЭ 2022, задание 6.
 Касательная к графику функции
Касательная к графику функции
Десятичный логарифм: как рассчитывается?
Степень отдельно взятого числа называется математическим термином, придуманным несколько столетий назад. В геометрии и алгебре встречается два варианта – десятичные и натуральные логарифмы. Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.
Особенности и важные признаки
На данный момент различают десять известных математических качеств. Самыми распространенными и востребованными из них являются:
- Подкоренной log, разделенный на величину корня, всегда такой же, как и десятичный логарифм √.
- Произведение log всегда равно сумме производителя.
- Lg = величине степени, перемноженной на число, которое в нее возводится.
- Если от log делимого отнять делитель, получится lg частного.
Кроме того, есть уравнение, основанное на главном тождестве (считается ключевым), переход к обновленному основанию и несколько второстепенных формул.
Вычисление десятичного логарифма — довольно специфическая задача, поэтому к интегрированию свойств в решение необходимо подходить осторожно и регулярно проверять свои действия и последовательность. Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.
Разновидности математического термина
Главные отличия математического числа «спрятаны» в основании (a). Если оно имеет показатель 10, то это десятичный log. В обратном случае «a» преобразуется в «у» и обладает трансцендентными и иррациональными признаками. Также стоит отметить, что натуральная величина рассчитывается специальным уравнением, где доказательством становится теория, изучаемая за пределами школьной программы старших классов.
Логарифмы десятичного типа получили широкое применение при вычислении сложных формул. Составлены целые таблицы, облегчающие расчеты и наглядно показывающие процесс решения задачи. При этом перед непосредственным переходом к делу нужно возвести log в стандартный вид. К тому же в каждом магазине школьных принадлежностей можно найти специальную линейку с нанесенной шкалой, помогающей решить уравнение любой сложности. Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.
К тому же в каждом магазине школьных принадлежностей можно найти специальную линейку с нанесенной шкалой, помогающей решить уравнение любой сложности. Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.
Два вида формулы
Все типы и разновидности задач на вычисление ответа, имеющие в условии термин log, обладают отдельным названием и строгим математическим устройством. Показательное уравнение является практически точной копией логарифмических расчетов, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированное число, помогающее быстрее разобраться в условии, а второй заменяет log на обыкновенную степень. При этом вычисления с применением последней формулы должны включать в себя переменное значение.
Разница и терминология
Оба главных показателя обладают собственными особенностями, отличающими числа друг от друга:
- Десятичный логарифм.
 Важная деталь числа – обязательное наличие основания. Стандартный вариант величины равен 10. Маркируется последовательностью – log x или lg x.
Важная деталь числа – обязательное наличие основания. Стандартный вариант величины равен 10. Маркируется последовательностью – log x или lg x. - Натуральный. Если его основанием является знак «e», представляющий собой константу, идентичную строго рассчитанному уравнению, где n стремительно движется к бесконечности, то приблизительный размер числа в цифровом эквиваленте составляет 2.72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, – ln x.
- Разные. Кроме основных логарифмов встречаются шестнадцатиричные и двоичные виды (основание 16 и 2 соответственно). Есть еще сложнейший вариант с базовым показателем 64, подпадающий под систематизированное управление адаптивного типа, с геометрической точностью производящее расчет итогового результата.
Терминология включает в себя следующие величины, входящие в алгебраическую задачу:
- значение;
- аргумент;
- основание.
Вычисление log числа
Есть три способа быстро и в устной форме сделать все необходимые расчеты по нахождению интересующего результата с обязательным правильным итогом решения. Изначально приближаем десятичный логарифм к своему порядку (научная запись числа в степени). Каждую положительную величину можно задать уравнением, где она будет равен мантиссе (цифра от 1 до 9), перемноженной на десятку в n-й степени. Такой вариант подсчета создан на основе двух математических фактов:
Изначально приближаем десятичный логарифм к своему порядку (научная запись числа в степени). Каждую положительную величину можно задать уравнением, где она будет равен мантиссе (цифра от 1 до 9), перемноженной на десятку в n-й степени. Такой вариант подсчета создан на основе двух математических фактов:
- произведение и сумма log всегда имеют одинаковый показатель;
- логарифм, взятый из числа от одного до десяти, не может превышать величину в 1 пункт.
- Если ошибка в вычислении все-таки происходит, то она никогда не бывает меньше одного в сторону вычитания.
- Точность повышается, если учесть, что lg с основанием три имеет итоговый результат – пять десятых от единицы. Поэтому любое математическое значение больше 3 автоматически добавляет к ответу один пункт.
- Практически идеальная точность достигается, если под рукой есть специализированная таблица, которую можно легко применять в своих оценочных действиях. С ее помощью можно выяснить, чему равен десятичный логарифм до десятых процентов от оригинального числа.

История вещественного log
Шестнадцатый век остро испытывал потребности в более сложных исчислениях, чем было известно науке того времени. Особенно это касалось деления и умножения многозначных цифр с большой последовательностью, в том числе дробей. В конце второй половины эпохи сразу несколько умов пришли к выводу о сложении чисел с помощью таблицы, которая сопоставляла две прогрессии: арифметическую и геометрическую. При этом все базовые расчеты должны были упираться в последнюю величину. Таким же образом ученые интегрировали и вычитание.
Первое упоминание об lg состоялось в 1614 году. Это сделал любитель-математик по фамилии Непер. Стоит отметить, что, несмотря на огромную популяризацию полученных результатов, в формуле была сделана ошибка из-за незнаний некоторых определений, появившихся позже. Она начиналась с шестого знака показателя. Наиболее близки к пониманию логарифма были братья Бернулли, а дебютное узаконивание произошло в восемнадцатом столетии Эйлером. Он же и распространил функцию в область образования.
Он же и распространил функцию в область образования.
История комплексного log
Дебютные попытки интегрировать lg в широкие массы делали на заре 18-го века Бернулли и Лейбниц. Но целостных теоретических выкладок они так и не сумели составить. По этому поводу велась целая дискуссия, но точного определения числу не присваивали. Позже диалог возобновился, но уже между Эйлером и Даламбером. Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.
Таблицы
Свойства числа указывают на то, что многозначные цифры можно не перемножать, а найти их log и сложить посредством специализированных таблиц.
Особенно ценным этот показатель стал для астрономов, которые вынуждены работать с большим набором последовательностей. 2
2
Наибольшее и наименьшее значение логарифмической функции. Задание В15
В этой статье мы рассмотрим решение двух примеров, которые на первый взгляд очень похожи, а на второй принципиально отличаются друг от друга.
Итак.
Пример 1
Найдите наибольшее значение функции на отрезке .
Чтобы найти наибольшее значение функции, нам надо найти ее производную, затем приравнять производную к нулю, определить ее знаки и выяснить поведение функции на отрезке.
В этом примере под знаком логарифма стоит выражение в пятой, то есть в нечетной степени. Если мы возводим отрицательное число в нечетную степень, то в результате получаем отрицательное число. Поскольку выражение по знаком логарифма должно быть больше нуля, следовательно, и отсюда .
Упростим функцию: вынесем показатель степени за знак логарифма. Получим .
Найдем производную функции. (Не забываем, что мы, строго говоря, имеем дело со сложной функцией.)
(Не забываем, что мы, строго говоря, имеем дело со сложной функцией.)
Найдем нули производной:
Определим знаки производной: (учитываем, что )
И, соответственно, поведение функции:
В точке производная меняет знак с «+» на «-«, следовательно, это точка максимума функции. Точка -4 принадлежит заданному отрезку:
Следовательно, в точке функция принимает наибольшее значение на отрезке .
Найдем значение функции при :
Ответ: 20.
Замечание. Так как при решений заданий В-части в ответе должно получиться целое число или конечная десятичная дробь, а натуральный логарифм при рациональном аргументе принимает такие значения только в том случае, если его аргументом является число 1, то мы могли бы сразу сказать, что , т.к. . Но это для тех, кому трудно освоить алгоритм нахождения наибольшего или наименьшего значения функции на отрезке.
Пример 2.
Найдите точку максимума функции
В этом примере под знаком логарифма стоит выражение в квадрате. Выражение в четной степени больше нуля, если основание степени не равно нулю, поэтому область допустимых значений этой функции . Если бы мы решили вынести показатель степени за знак логарифма, то получили бы такое выражение:
При вынесении четной степени не забываем ставить модуль! Если бы мы забыли поставить знак модуля, то сузили бы область определения функции.
Далее, чтобы взять производную, нам пришлось бы раскрыть модуль, а для этого рассмотреть два промежутка: и . Но поскольку в школе практически не рассматривают нахождение производной от функции с модулем, мы не будем выносить показатель степени за знак производной, а найдем производную сложной функции:
Найдем нули производной:
В точке -4 производная не определена, но меняет знак.
Исследуем знаки производной:
В точке производная равна нулю и меняет знак с «+» на «-«, следовательно, это точка максимума функции.
Ответ: -5
Вероятно, Ваш браузер не поддерживается. Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Firefox
И.В. Фельдман, репетитор по математике.
Десятичные и натуральные логарифмы: определения, свойства и примеры
п.1. Десятичный логарифм и его свойства
Логарифмы чисел по основанию 10 называют десятичными.
Для десятичных логарифмов принято специальное обозначение: \begin{gather*} \log_{10}x\overset{def}{=}\lg x \end{gather*}
Основание десятичных логарифмов \(10\gt 1\), поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).
Но у десятичных логарифмов есть также целых ряд дополнительных свойств, благодаря которым в докомпьютерную эпоху они широко использовались для трудоемких вычислений. Роль калькулятора тогда выполняли логарифмическая таблица и логарифмическая линейка.
Целая часть десятичного логарифма \([\lg x]\) называется характеристикой, а дробная часть \(\left\{\lg x\right\}\) – мантиссой. n\)
n\)
характеристика равна порядку числа \([\lg b]=n\), мантисса \(\left\{\lg b\right\}=\lg a\)
О стандартном виде числа, см. §41 справочника для 8 класса.
Например:
| Число b | Стандартный вид | Характеристика | Мантисса b | Унифицированная запись | Логарифм числа \(\lg b\) |
| 420 | 4,2·102 | 2 | 0,623 | 2,623 | 2,623 |
| 42 | 4,2·101 | 1 | 0,623 | 1,623 | 1,623 |
| 4,2 | 4,2 | 2 | 0 | 0,623 | 0,623 |
| 0,42 | 4,2·10–1 | –1 | 0,623 | \(\overline{1},623\) | –0,377 |
| 0,042 | 4,2·10–2 | –2 | 0,623 | \(\overline{2},623\) | –1,377 |
\(\lg 4,2\approx 0. 623\)
623\)
Если использовать унифицированную запись, как в представленной таблице, то мантисса всегда лежит в промежутке \(0\lt \lg a\lt 1\). У чисел, отличающихся только порядком, мантисса одинакова. Можно составить таблицы мантисс и пользоваться ими для умножения и деления, «разбавляя» их несложным сложением и вычитанием целых характеристик по необходимости.
Первые таблицы логарифмов были изданы в 1617 году оксфордским математиком Бригсом. Таблицы пересчитывались, дополнялись и переиздавались вплоть до 70-х гг. ХХ века, когда на столах стали появляться калькуляторы.
Таблицы Брадиса, которыми по традиции пользуются наши школьники с 1921 года, издаются до сих пор и постепенно перекочевывают в Интернет.
Непосредственная связь десятичных логарифмов с десятичной системой исчисления делает их удобным инструментом для оценки порядка числа и сравнения чисел.
В практике приближенных вычислений используется следующая оценочная таблица:
\(\lg 1\)
\(\lg 2\)
\(\lg 3\)
\(\lg 4\)
\(\lg 5\)
\(\lg 8\)
Относительная погрешность этих приближений (кроме \(\lg 3)\) \(\delta\sim 0,5\text{%}\)
Например:
Сравним \(\log_23\) и \(log_58\)
Сравнивая с помощью оценки, получаем: \begin{gather*} \log_23=\frac{\lg 3}{\lg 2}\approx\frac{0,5}{0,3}=\frac53,\ \ \log_58=\frac{\lg 8}{\lg 5}\approx\frac{0,9}{0,7}=\frac97\\ \frac{35}{21}\gt \frac{27}{21}\Rightarrow \frac53\gt \frac97\Rightarrow\log_23\gt\log_58 \end{gather*}
п.
 3}{3}\)
3}{3}\)Логарифм. Примеры
Логарифмом числа b по основанию a обозначают выражение . Вычислить логарифм значит найти такой степень x (),при котором выполняется равенство
Основные свойства логарифма
Приведенные свойства необходимо знать, поскольку, на их основе решаются практически все задачи и примеры связаны с логарифмами. Остальные экзотических свойств можно вывести путем математических манипуляций с данными формулами
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
При вычислениях формулы суммы и разности логарифмов (3,4 ) встречаются довольно часто. Остальные несколько сложные, но в ряде задач являются незаменимыми для упрощения сложных выражений и вычисления их значений.
Распространены случаи логарифмов
Одними из распространенных логарифмов такие в которых основание ровное десять, экспоненте или двойке.
Логарифм по основанию десять принято называть десятичным логарифмом и упрощенно обозначать lg(x).
Из записи видно, что основы в записи не пишут. Для примера
Натуральный логарифм – это логарифм у которого за основу экспонента ( обозначают ln(x)).
Экспонента равна 2,718281828…. Чтобы запомнить экспоненту можете изучить правило: экспонента равна 2,7 и два раза год рождения Льва Николаевича Толстого. Зная это правило будете знать и точное значение экспоненты, и дату рождения Льва Толстого.
И еще один важный логарифм по основанию два обозначают
Производная от логарифм функции равна единице разделенной на переменную
Интеграл или первообразная логарифма определяется зависимостью
Приведенного материала Вам достаточно, чтобы решать широкий класс задач связанных с логарифмами и логарифмирования. Для усвоения материала приведу лишь несколько распространенных примеров из школьной программы и ВУЗов.
Примеры на логарифмы
Прологарифмировать выражения
Пример 1. 2 (а>0,с>0).
2 (а>0,с>0).
По свойствам 3,5 вычисляем
2.
По свойству разницы логарифмов имеем
3.
Используя свойства 3,5 находим
4. где .
На вид сложное выражение с использованием ряда правил упрощается к виду
——————————————
Нахождение значений логарифмов
Пример 2. Найти х, если
Решение. Для вычисления применим до последнего слагаемого 5 и 13 свойства
Подставляем в запись и скорбим
Поскольку основания равные, то приравниваем выражения
——————————————
Пример 3. Пусть задано значение логарифмов
Вычислить log[a](x), если
Решение: Прологарифмируем переменную, чтобы расписать логарифм через сумму слагаемых
——————————————
На этом знакомство с логарифмами и их свойствами только начинается. Упражняйтесь в вычислениях, обогащайте практические навыки — полученные знания Вам скоро понадобятся для решения логарифмических уравнений. Изучив основные методы решения таких уравнений мы расширим Ваши знания для другой не менее важной теме — логарифмические неравенства …
Изучив основные методы решения таких уравнений мы расширим Ваши знания для другой не менее важной теме — логарифмические неравенства …
Теперь рассмотрим логарифмическую функцию с произвольным основанием и получим формулу для ее производной.
Итак, возьмем логарифмическую функцию \(y = {\log _a}x,\), где основание \(a\) больше нуля и не равно \(1:\) \(a \gt 0\ ), \(а \ne 1\). Согласно определению производной, мы даем приращение \(\Delta x \gt 0\) независимой переменной \(x\), предполагая, что \(x + \Delta x \gt 0\). Логарифмическая функция будет увеличиваться соответственно на значение \(\Delta y\), где
\[\Delta y = {\log _a}\left( {x + \Delta x} \right) — {\log _a}x.\]
Разделить обе стороны на \(\Delta x:\)
\[\frac{{\Delta y}}{{\Delta x}} = \frac{1}{{\Delta x}}\left[ {{{\log }_a}\left( {x + \ Delta x} \right) — {{\log }_a}x} \right] = \frac{1}{{\Delta x}}{\log _a}\frac{{x + \Delta x}}{x } = \frac{1}{{\Delta x}}{\log _a}\left( {1 + \frac{{\Delta x}}{x}} \right). 2} — 2x} \right)\]
2} — 2x} \right)\]
Пример 5
\[y = \frac{1}{{\ln x}}\]
Пример 6
\[y = \ln \left( {\sin x} \right)\]
Пример 1.\prime = \frac{1}{{\sin x}} \cdot \cos x = \frac{{\cos x}}{{\sin x}} = \cot x.\]
Дополнительные проблемы см. на стр. 2.
Исчисление I. Производные экспоненциальной и логарифмической функций
Показать мобильное уведомление Показать все примечания Скрыть все примечания Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. {\ln x}}}} = \frac{1} {Икс}\]
{\ln x}}}} = \frac{1} {Икс}\]
Последний шаг просто использует тот факт, что две функции являются обратными друг другу.
Все вместе дает
\[\ frac{d}{{dx}}\left( {\ln x} \right) = \frac{1}{x}\hspace{0,5in}x > 0\]Обратите внимание, что нам нужно потребовать, чтобы \(x > 0\), так как это требуется для логарифма и, следовательно, также должно требоваться для его производной. Можно также показать, что
\[\frac{d}{{dx}}\left( {\ln \left| x \right|} \right) = \frac{1}{x}\hspace{0.5in}x \ne 0\]Используя это все, что нам нужно избегать, это \(x = 0\).
В этом случае, в отличие от экспоненциальной функции, мы действительно можем найти производную функции общего логарифма.Все, что нам нужно, это производная от натурального логарифма, которую мы только что нашли, и замена формулы основания. Используя формулу замены основания, мы можем записать общий логарифм как
. \[{\log _a}x = \frac{{\ln x}}{{\ln a}}\] Дифференциация тогда довольно проста. т} \]
т} \]
Объект когда-нибудь перестает двигаться?
Показать решениеСначала нам понадобится производная.т} = 0\]
Теперь мы знаем, что экспоненциальные функции никогда не равны нулю, поэтому она будет равна нулю только при \(t = — 1\). Итак, если мы собираемся допустить отрицательные значения \(t\), то объект перестанет двигаться один раз в \(t = — 1\). Если мы не собираемся допускать отрицательных значений \(t\), то объект никогда не перестанет двигаться.
Прежде чем перейти к следующему разделу, нам нужно вернуться к паре производных, чтобы убедиться, что мы их не путаем.x}\ln a & \hspace{0.5in}{\mbox{Производная экспоненциальной функции}}\end{массив}\]
Важно отметить, что в правиле Степени показатель степени ДОЛЖЕН быть константой, а основание ДОЛЖНО быть переменной, в то время как для производной экспоненциальной функции требуется прямо противоположное. Для экспоненциальной функции показатель степени ДОЛЖЕН быть переменной, а основание ДОЛЖНО быть константой.
Легко зациклиться на одной из этих формул и просто использовать ее для обеих.Мы также даже не говорили о том, что делать, если и показатель степени, и основание включают переменные. Мы увидим эту ситуацию в следующем разделе.
5. Производная логарифмической функции
М. Борна
Сначала посмотрим на график логарифмической функции с основанием e , то есть:
f ( x ) = log e ( x ) (обычно пишется «ln x »).
Тангенс при x = 2 включен в график.
Наклон касательной y = ln x при `x = 2` составляет `1/2`. (Мы можем наблюдать это на графике, глядя на соотношение рост/рост).
Если у = ln х ,
| `х` | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| наклон графика | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
| `1/x` | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
Мы видим, что наклон графика для каждого значения x равен `1/x`. Это работает для любого положительного значения x (конечно, у нас не может быть логарифма отрицательного числа).
Это работает для любого положительного значения x (конечно, у нас не может быть логарифма отрицательного числа).
Если бы мы сделали еще много примеров, мы могли бы заключить, что производная логарифмической функции y = ln x равна
`dy/dx = 1/x`
Примечание 1: На самом деле этот результат исходит из первых принципов.
Примечание 2: Мы используем логарифмы с основанием e . Если вам нужно напоминание о функциях журнала, ознакомьтесь с базой журнала и ранее.
Производная логарифмической функции
y = ln xПроизводная логарифмической функции y = ln x определяется как:
`d/(dx)(ln\ x)=1/x`
Вы увидите, что это написано и несколькими другими способами. Следующие эквивалентны:
`d/(dx)log_ex=1/x`
Если y = ln x , то `(dy)/(dx)=1/x`
Теперь мы покажем, откуда взялась формула для производной `log_e x`, используя первые принципы. {1″/»t}` приближается к значению `e~~2,71828`.)
{1″/»t}` приближается к значению `e~~2,71828`.)
Я буду писать `log(x)` в значении `log_e(x) = ln(x)`, чтобы его было легче читать.
У нас есть `f(x) = log(x)`, поэтому производная будет равна:
`(df)/(dx) = lim_{h->0}(log(x+h)-log(x))/h `
Теперь вершина нашей дроби равна
.`log(x+h)-log(x)` `= log((x+h)/x)` `= log(1 + h/x)`.
Чтобы упростить алгебру, мы теперь заменяем `t=h/x`, и это дает нам `h = xt`.{1″/»т})`
`= 1/x log(e)`
`= 1/x`
Наконечник
Для некоторых задач мы можем использовать законы логарифмирования, чтобы упростить наше логарифмическое выражение перед его дифференцированием.
Пример 1
Найдите производную числа
у = пер 2 х
Ответить
Используем логарифмический закон:
журнал аб = журнал а + журнал б
Мы можем написать наш вопрос как:
у = пер 2 х = пер 2 + пер х
Теперь производная константы равна 0, поэтому
`d/(dx)ln\ 2=0`
Итак, у нас осталось (из нашей формулы выше)
`d/(dx)(ln\ x)=1/x`
Окончательный ответ:
`(dy)/(dx)=1/x`
Из следующего графика видно, что наклон y = ln 2 x (кривая зеленого цвета, касательная пурпурного цвета) такой же, как наклон y = ln x (кривая серого цвета, касательная выделена серым пунктиром) в точке x = 2.
Пример 2
Найдите производную числа
y = ln x 2
Ответить
Используем логарифмический закон:
логарифм a n = n логарифм a
Таким образом, мы можем записать вопрос как
.y = ln x 2 = 2 ln x
Производная будет просто в 2 раза больше производной ln x .2) на самом деле имеет 2 «руки», одну с отрицательной стороны и одну с положительной. На приведенном выше графике для простоты показано только положительное плечо.
Производная от
y = ln u (где u является функцией x )К сожалению, мы можем использовать законы логарифмирования только в ограниченном числе типов вопросов на дифференциацию логарифмов.
Чаще всего нам нужно найти производную логарифма некоторой функции x . Например, нам может понадобиться найти производную от y = 2 ln (3 x 2 − 1).
Например, нам может понадобиться найти производную от y = 2 ln (3 x 2 − 1).
Для решения таких задач нам понадобится следующая формула.
Если
у = пер у
и u есть некоторая функция x , тогда:
`(dy)/(dx)=(u’)/u`
, где u’ является производным от u
Другой способ написать это
`(dy)/(dx)=1/u(du)/(dx)`
Вы также можете увидеть следующую форму.Это означает то же самое.
Если
y = ln f ( х ),
, то производная от y определяется как:
`(dy)/(dx)=(f'(x))/(f(x)`
Пример 3
Найдите производную из
y = 2 ln (3 x 2 − 1).
2+1)`
Дифференцирование логарифмических функций с основанием, отличным от
eЕсли
u = f ( x ) является функцией x ,
и
y = log b u — логарифм с основанием b ,
, то мы можем получить производную логарифмической функции с основанием b , используя:
`(dy)/(dx)=(log_be)(u’)/u`
где
`u’` является производным от u
log b e — константа.См. изменение базового правила, чтобы узнать, как вычислить такие константы на вашем калькуляторе.)
Примечание 1: Эта формула получена из первых принципов.
Примечание 2: Если мы выберем e в качестве базы, то производная от ln u , где u является функцией x , просто дает нам нашу формулу выше:
`(dy)/(dx)=(u’)/u`
[Вспомним, что журнал e e = 1.
]
[См. главу об экспоненциальных и логарифмических функциях base e , если вам нужно освежить в памяти все это.]
Пример 6
Найдите производную y = логарифм 2 6 x .
Ответить
Мы начнем с использования следующего правила журнала, чтобы упростить наш вопрос:
журнал аб = журнал а + журнал б
Мы можем написать наш вопрос как:
y = логарифм 2 6 x = логарифм 2 6 + логарифм 2 x
Первый член, log 2 6, является константой, поэтому его производная равна 0.
Производная второго члена по нашей формуле выглядит следующим образом:
`(dy)/(dx)=(log_2e) (1/x)=(log_2e)/x`
Верхний член, log 2 e , является константой. 3-x`
3-x`
`x ≠ ±sqrt(0.5)`,
`х ≠ 0`
ПРИМЕЧАНИЕ. Нам нужно быть осторожными с доменом этого решения, так как оно верно только для определенных значений. х .
График y = ln(2 x 3 − x ) 2 (который имеет степень 2 ) определен для всех x
, кроме3` ± квадрат (0,5), 0`
Его график выглядит следующим образом:
График y = 2 ln(2 x 3 − x ), однако (у него впереди 2 × ) определен только для более ограниченного домен (поскольку у нас не может быть логарифма отрицательного номер.)
Таким образом, мы можем иметь только x в диапазоне `-sqrt 0,5 sqrt0,5.`
Итак, когда мы находим дифференцирование логарифма с помощью
указанный выше, мы должны быть осторожны, чтобы домен
заданы функция и область определения производной. 2`
2`
3.х(х\ раскладушка\ х+ln(sin х))`
График функции в упражнении 5 весьма интересен:
График y = (sin x ) x .
Производные логарифмических функций — Задача 3
Чтобы найти производную других логарифмических функций, необходимо использовать формулу замены основания: log a (x)= ln(x)/ln(a). При этом вы можете вывести логарифмические функции с любым основанием.Например, если f(x)=log 3 (x), то f(x)=ln(x)/ln(3). Поскольку ln(3) является константой, вы можете вывести ее так же, как и любую другую естественную логарифмическую функцию; f'(x)=(1/ln(3))*1/x=1/(ln(3)*x). Помните, что если база не указана, log(x) имеет базу 10.
Итак, мы поговорили о производной от натурального логарифма. Мы еще не говорили о производных других логарифмов.Поэтому я хочу поговорить об этом прямо сейчас. Прежде всего, напомним, что производная натурального логарифма равна 1 по x.
Мы еще не говорили о производных других логарифмов.Поэтому я хочу поговорить об этом прямо сейчас. Прежде всего, напомним, что производная натурального логарифма равна 1 по x.
Чтобы получить производные от других логарифмов, я воспользуюсь формулой замены основания. Логарифмическая база a для x равна lnx над lna. Конечно можно поменять на любую другую базу, но я поменяю натуральный бревно, т.к. у меня есть вот такая формула.
Итак, если бы я хотел дифференцировать журнал какой-то другой базы a, я бы сначала изменил его в эту форму; Производная по x от lnx по lna.Заметим, что это деление на lna — это просто умножение lna на 1. Это константа, так что ее можно вытащить. 1 над lna, умноженной на производную от lnx. Конечно, это просто 1 больше х. Итак, 1 на lna умножить на 1 на x. Это производная логарифмической базы a от x. Итак, давайте попробуем это на примере.
Если у равно логарифмическому основанию 5 числа х, какова производная? Dy/dx является производной логарифмической базы 5 от x. Согласно этой формуле, это 1 больше натурального логарифма основания, 5, умноженное на 1 больше x.Итак, 1 на ln5 умножить на 1 на x.
Согласно этой формуле, это 1 больше натурального логарифма основания, 5, умноженное на 1 больше x.Итак, 1 на ln5 умножить на 1 на x.
Немного более сложный пример. Найдем производную от 100 минус 3 log x. Помните, когда вы видите журнал, а база не записана, предполагается, что это общий журнал, поэтому журнал основан на 10.
Это производная от 100 минус 3 log x. Я могу использовать правило суммы и постоянное множественное правило. Я буду использовать оба одновременно. Это производная от 100 минус 3 умноженная на производную от log x.
Теперь 100, это просто константа, ее производная будет равна 0.У меня в 3 раза больше производной логарифмической базы 10 от x. Это будет 1 на ln из 10, умноженное на 1 на x. Так что мой ответ упрощается до -3 на ln 10. Это константа, умноженная на 1 на x. Это производная от y равна 100 минус 3 log x.
Решение производной ln(x) — видео и стенограмма урока
Шаги решения
Мы хотим найти производную ln( x ). Производная от ln( x ) равна 1/ x и на самом деле является хорошо известной производной, которую чаще всего запоминают.Однако всегда полезно знать, откуда берется эта формула, поэтому давайте взглянем на шаги, чтобы найти эту производную.
Производная от ln( x ) равна 1/ x и на самом деле является хорошо известной производной, которую чаще всего запоминают.Однако всегда полезно знать, откуда берется эта формула, поэтому давайте взглянем на шаги, чтобы найти эту производную.
Чтобы найти производную от ln( x ), первое, что мы делаем, это пусть y = ln( x ). Затем мы используем определение логарифма, чтобы записать y = ln( x ) в логарифмической форме. Определение логарифмов гласит, что y = log b ( x ) эквивалентно b y = x .Следовательно, по определению логарифмов и тому факту, что ln( x ) является логарифмом с основанием e , мы имеем, что y = ln( x ) эквивалентно e y = х .
Хорошо, еще несколько шагов, и у нас будет формула! Следующее, что мы хотим сделать, это рассматривать х как функцию х , и взять производную каждой части уравнения относительно х . Мы используем цепное правило в левой части уравнения, чтобы найти производную. Цепное правило — это правило, которое мы используем для получения производной от композиции функций, и оно имеет две формы.
Мы используем цепное правило в левой части уравнения, чтобы найти производную. Цепное правило — это правило, которое мы используем для получения производной от композиции функций, и оно имеет две формы.
левая сторона уравнения составляет е y , где y — это функция x , так что если мы выпустим F ( x ) = E x и г ( x ) = y , затем f ( г ( x )) = e y .Поскольку производная от e к переменной (например, e x ) совпадает с исходной, производная от f'(g(x)) равна e y . Следовательно, по цепному правилу производная e y равна e y dy / dx . Справа у нас есть производная от x , которая равна 1.
Имеем ( e y ) dy / dx = 1. Теперь вспомните, что e y = x . Мы собираемся использовать этот факт, чтобы подставить x в наше уравнение для e y .
Теперь вспомните, что e y = x . Мы собираемся использовать этот факт, чтобы подставить x в наше уравнение для e y .
Это дает нам уравнение ( x ) dy / dx = 1. Теперь мы подходим очень близко! Вы так же взволнованы, как и я? Мы можем разделить обе части этого уравнения на x , чтобы получить dy / dx = 1/ x .И последнее, что нужно вспомнить, что y = ln( x ) и подставить это в наше уравнение для y .
Та-да! Теперь мы видим, что d / dx ln( x ) = 1/ x , и теперь мы знаем, почему эта формула для производной ln( x ) верна. Итак, каково наше решение? Производная от ln( x ) равна 1/ x .
Логарифм — Энциклопедия Нового Света7. Каждая галочка на осях равна единице.
 Логарифмы всех оснований проходят через точку (1, 0), потому что любое число в степени 0 равно 1, и через точки ( b, 1) по основанию b, , потому что любое число в степени 1 является собой. Кривые приближаются к оси y, но не достигают ее из-за сингулярности логарифма при x = 0.
Логарифмы всех оснований проходят через точку (1, 0), потому что любое число в степени 0 равно 1, и через точки ( b, 1) по основанию b, , потому что любое число в степени 1 является собой. Кривые приближаются к оси y, но не достигают ее из-за сингулярности логарифма при x = 0.В математике логарифм (или log ) числа x по основанию b представляет собой степень (n) , в которую нужно возвести основание b , чтобы получить число x x x .Например, логарифм 1000 по основанию 10 — это число 3, потому что 10, возведенное в степень 3, равно 1000. Или логарифм 81 по основанию 3 равен 4, потому что 3, возведенное в степень 4, равно 81. .
В общих чертах, если x = b n , то логарифм x по основанию b обычно записывается как
- logb(x)=n.{\displaystyle \log _{b}(x)=n.\,}
(Значение b не должно быть ни 0, ни корнем из 1. {4}=3\умножить на 3\умножить на 3\умножить на 3=81\,}
{4}=3\умножить на 3\умножить на 3\умножить на 3=81\,}
В логарифмическом выражении это можно записать как
- log3(81)=4{\displaystyle \log _{3}(81)=4\,}
Другими словами, логарифм числа 81 по основанию 3 равен 4; или логарифмическая база-3 из 81 равна 4.
Наиболее широко используемыми основаниями логарифмов являются 10, математическая константа e (приблизительно равна 2,71828) и 2. Термин десятичный логарифм используется, когда основание равно 10; термин натуральный логарифм используется, когда основание равно e.
Метод логарифмов упрощает некоторые расчеты и используется для выражения различных величин в науке. Например, до появления калькуляторов и компьютеров метод логарифмов был очень полезен для развития астрономии, навигации и геодезии. Числовые последовательности, записанные в логарифмическом масштабе, продолжают использоваться учеными в различных дисциплинах. Примеры логарифмических шкал включают шкалу рН для измерения кислотности (или основности) в химии; шкала Рихтера для измерения интенсивности землетрясений; и шкала, выражающая видимую величину звезд, для обозначения их яркости. {н}}.
{н}}.
История
Метод логарифмов был впервые публично изложен в 1614 году в книге под названием Mirifici Logarithmorum Canonis Descriptio, Джоном Нейпиром, [1] бароном Мерчистона в Шотландии. (Юст Бюрги независимо открыл логарифмы, но опубликовал свое открытие только через четыре года после Напьера.)
Этот метод способствовал развитию науки, и особенно астрономии, делая возможными некоторые сложные вычисления.До появления калькуляторов и компьютеров он постоянно использовался в геодезии, навигации и других областях практической математики. Он вытеснил более сложный метод протезирования, который основывался на тригонометрических тождествах как на быстром методе вычисления продуктов. Помимо полезности в вычислениях, логарифмы также занимают важное место в высшей теоретической математике.
Сначала Нейпир назвал логарифмы «искусственными числами», а антилогарифмы — «натуральными числами».Позже он образовал слово логарифм для обозначения числа, обозначающего отношение: λόγος (логос) означает пропорцию, а ἀριθμός (арифмос) означает число. Нейпир выбрал это, потому что разница двух логарифмов определяет отношение чисел, которые они обозначают, так что арифметический ряд логарифмов соответствует геометрическому ряду чисел Термин «антилогарифм» был введен в конце семнадцатого века и, хотя никогда широко не использовался в математике, сохранялся в сборниках таблиц до тех пор, пока они вышли из употребления.
Нейпир выбрал это, потому что разница двух логарифмов определяет отношение чисел, которые они обозначают, так что арифметический ряд логарифмов соответствует геометрическому ряду чисел Термин «антилогарифм» был введен в конце семнадцатого века и, хотя никогда широко не использовался в математике, сохранялся в сборниках таблиц до тех пор, пока они вышли из употребления.
Нейпир не использовал основание, как мы теперь это понимаем, но его логарифмы были с точностью до коэффициента масштабирования эффективным основанием 1/ e . В целях интерполяции и простоты вычислений полезно сделать отношение х в геометрическом ряду близким к 1. Нейпир выбрал х = 1 — 10 −7 = 0,999999 (Бюрги выбрал х = 1 + 10 −4 = 1,0001). В исходных логарифмах Нейпира не log 1 = 0, а log 10 7 = 0.Таким образом, если N — число, а L — его логарифм, вычисленный Нейпиром, N = 10 7 (1 − 10 −7 ) L . С (1 — 10 -7 ) 10 7 7 составляет примерно 1/ E, Это составляет л /10 7 /10 7 Примерно равны логите 1/ E N /10 7 . [2]
С (1 — 10 -7 ) 10 7 7 составляет примерно 1/ E, Это составляет л /10 7 /10 7 Примерно равны логите 1/ E N /10 7 . [2]
Таблицы логарифмов
Часть таблицы десятичных логарифмов двадцатого века в справочнике Абрамовица и Стегуна.До появления компьютеров и калькуляторов использование логарифмов означало использование таблиц логарифмов, которые приходилось создавать вручную. Логарифмы по основанию 10 полезны в вычислениях, когда электронные средства недоступны.
В 1617 году Генри Бриггс опубликовал первую часть своей собственной таблицы десятичных логарифмов, содержащей логарифмы всех целых чисел от 1000 до восьми знаков после запятой. Этому он последовал в 1624 году, выпустив свою книгу Arithmetica Logarithmica, , содержащую логарифмы всех целых чисел от 1 до 20 000 и от 90 000 до 100 000 до четырнадцати знаков после запятой, а также ученое введение, в котором были рассмотрены теория и использование логарифмов. полностью разработан.
полностью разработан.
Интервал от 20 000 до 90 000 заполнил голландский математик Адриан Влак; но в его таблице, появившейся в 1628 г., логарифмы давались только до десяти знаков после запятой. Позже было обнаружено, что таблица Влака содержит 603 ошибки, но «это нельзя считать большим числом, если учесть, что таблица была результатом первоначального расчета и что более 2 100 000 печатных цифр могут быть ошибочными». [3] Издание работы Влака, содержащее множество исправлений, было выпущено в Лейпциге в 1794 году под названием Thesaurus Logarithmorum Completus Юрия Веги.
Семизначная таблица Франсуа Калле (Париж, 1795 г.) вместо того, чтобы остановиться на 100 000, давала восьмизначные логарифмы чисел от 100 000 до 108 000, чтобы уменьшить ошибки интерполяции, которые были наибольшими в начале стола; и это дополнение обычно включалось в таблицы на семь мест. Единственное важное опубликованное расширение таблицы Влака было сделано г-ном Сангом 1871 г. , чья таблица содержала семизначные логарифмы всех чисел ниже 200 000.
, чья таблица содержала семизначные логарифмы всех чисел ниже 200 000.
Бриггс и Влак также опубликовали оригинальные таблицы логарифмов тригонометрических функций.
Помимо таблиц, упомянутых выше, большая коллекция под названием Tables du Cadastre была создана под руководством Гаспара де Прони по оригинальному расчету под эгидой французского республиканского правительства 1700-х годов. Эта работа, содержащая логарифмы всех чисел от 100 000 до девятнадцати разрядов и чисел от 100 000 до 200 000 до двадцати четырех разрядов, существует только в рукописи «в семнадцати огромных фолиантах» в Парижской обсерватории.Он был начат в 1792 году; и «все расчеты, которые для обеспечения большей точности были выполнены в двух экземплярах, а две рукописи впоследствии тщательно сопоставлены, были выполнены за короткий промежуток времени в два года». [4] Кубическую интерполяцию можно использовать для нахождения логарифма любого числа с аналогичной точностью.
Логарифм как функция
Функция log b (x) зависит как от b , так и от x, , но термин логарифмическая функция (или логарифмическая функция ) в стандартной форме относится к функции log b (x) , в котором основание b фиксировано и поэтому единственным аргументом является x. Таким образом, существует одна функция логарифма для каждого значения основания b (которое должно быть положительным и должно отличаться от 1).
С этой точки зрения функция логарифма по основанию b является обратной функцией экспоненциальной функции b x . Слово «логарифм» часто используется для обозначения самой функции логарифмирования, а также для конкретных значений этой функции.
Таким образом, существует одна функция логарифма для каждого значения основания b (которое должно быть положительным и должно отличаться от 1).
С этой точки зрения функция логарифма по основанию b является обратной функцией экспоненциальной функции b x . Слово «логарифм» часто используется для обозначения самой функции логарифмирования, а также для конкретных значений этой функции.
Графическая интерпретация
Натуральный логарифм от до представляет собой площадь под кривой y = 1/ x между значениями 1 x и a .
Иррациональность
Для целых чисел b и x > 1 число log b (x) является иррациональным (то есть не является частным двух целых чисел), если либо b , либо x 9 главный фактор, которого нет у другого. В некоторых случаях этот факт можно доказать очень быстро: например, если бы log 2 3 было рациональным, то log 2 3 = n / m для некоторых натуральных чисел n и m , что означает 2 n = 3 m . Но это последнее тождество невозможно, так как 2 n четно, а 3 m нечетно. Известны гораздо более сильные результаты. См. теорему Линдеманна – Вейерштрасса.
Но это последнее тождество невозможно, так как 2 n четно, а 3 m нечетно. Известны гораздо более сильные результаты. См. теорему Линдеманна – Вейерштрасса.
Целые и нецелые показатели степени
Если n является положительным целым числом, то b n означает произведение n множителей, равных b:
- б × б × ⋯ × б⏟n. {\ displaystyle \ underbrace {b \ times b \ times \ cdots \ times b} _ {n}.}
Однако, если b — положительное действительное число, не равное 1, это определение можно распространить на любое действительное число n в поле (см. возведение в степень). Точно так же функция логарифма может быть определена для любого положительного действительного числа. Для каждого положительного основания b , не равного 1, существует одна логарифмическая функция и одна экспоненциальная функция, которые являются обратными друг другу.
Логарифмы могут сократить операции умножения до сложения, деления до вычитания, возведения в степень до умножения и корней до деления.Поэтому логарифмы полезны для облегчения выполнения длительных числовых операций, и до появления электронных компьютеров они широко использовались для этой цели в таких областях, как астрономия, инженерия, навигация и картография. Они обладают важными математическими свойствами и до сих пор широко используются.
Основания
Наиболее широко используемыми основаниями для логарифмов являются 10, математическая константа e ≈ 2,71828… и 2. Когда «лог» пишется без основания ( b отсутствует в журнале b ), намерение обычно может определяться из контекста:
- Натуральный логарифм (log e , ln, log или Ln) в математическом анализе
- Десятичный логарифм (log 10 или просто log) в машиностроении и когда таблицы логарифмов используются для упрощения ручных вычислений
- Двоичный логарифм (log 2 ) в теории информации и музыкальных интервалах
- Неопределенный логарифм, когда основание не имеет значения, например, в теории сложности при описании асимптотического поведения алгоритмов в большой записи O.

Во избежание путаницы лучше указать базу, если есть вероятность неправильного толкования.
Другие обозначения
Обозначение «ln (x) » неизменно означает log e (x) , то есть натуральный логарифм x, , но подразумеваемая база для «log (x) » зависит от дисциплины. :
- Математики обычно понимают как «ln (x) «, так и «log (x) » как log e (x) и пишут «log 10 (x) «, когда основание -10 логарифм x предназначен.
- Многие инженеры, биологи, астрономы и некоторые другие пишут только «ln (x) » или «log e (x) », когда имеют в виду натуральный логарифм x , и берут « log (x) » означает log 10 (x) или, иногда в контексте вычислений, log 2 (x) .
- На большинстве калькуляторов кнопка LOG имеет вид log 10 (x) , а LN — log e (x) .

- В наиболее часто используемых языках программирования, включая C, C++, Java, Fortran, Ruby и BASIC, функция «log» возвращает натуральный логарифм. Функция с основанием 10, если она доступна, обычно имеет вид «log10».
- Некоторые используют Log (x) (заглавная L ) для обозначения log 10 (x) , а log (x) со строчными буквами 52 909 909 8 для l означают l е (х) .
- Обозначение Log (x) также используется математиками для обозначения главной ветви функции (натурального) логарифма.
- В некоторых европейских странах часто используется обозначение b log (x) вместо log b (x) .
Этот хаос исторически возник из-за того факта, что натуральный логарифм имеет хорошие математические свойства (например, его производная равна 1/ x и имеет простое определение), в то время как логарифмы с основанием 10 или десятичные логарифмы были более удобны для ускорения вычислений (когда они использовались для этой цели). Таким образом, натуральные логарифмы широко использовались только в таких областях, как исчисление, в то время как десятичные логарифмы широко использовались в других местах.
Таким образом, натуральные логарифмы широко использовались только в таких областях, как исчисление, в то время как десятичные логарифмы широко использовались в других местах.
Еще в 1984 году Пол Халмос в своей «автоматографии» Я хочу стать математиком выразил презрение к тому, что он считал детским обозначением «ln», которое, по его словам, никогда не использовал ни один математик. (На самом деле это обозначение было изобретено в 1893 году Ирвингом Стрингемом, профессором математики в Беркли.) С 2005 года многие математики приняли обозначение «ln», но большинство используют «log.»
В информатике логарифм по основанию 2 иногда записывается как lg (x) , чтобы избежать путаницы. Это использование было предложено Эдвардом Рейнгольдом и популяризировано Дональдом Кнутом. Однако в русскоязычной литературе для логарифма по основанию 10 обычно используется обозначение lg (x) , так что даже такое использование не лишено опасностей. [5] В немецком языке lg (x) также обозначает логарифм по основанию 10, в то время как иногда ld (x) или lb (x) используется для логарифма по основанию 2. [2]
[2]
Смена базы
Хотя существует несколько полезных тождеств, наиболее важное для использования калькулятора позволяет находить логарифмы с основанием, отличным от встроенного в калькулятор (обычно log e и log 10 ). Чтобы найти логарифм с основанием b, , используя любое другое основание k:
- logb(x)=logk(x)logk(b).{\displaystyle \log _{b}(x)={\frac {\log _{k}(x)}{\log _ {k}(b)}}.}
Более того, из этого результата следует, что все функции логарифмирования (независимо от основания) подобны друг другу.Итак, чтобы рассчитать журнал с основанием 2 числа 16 с помощью вашего калькулятора:
- log2(16)=log(16)log(2).{\displaystyle \log_{2}(16)={\frac {\log(16)}{\log(2)}} .}
Использование логарифмов
Логарифмы полезны при решении уравнений, в которых показатели степени неизвестны. У них простые производные, поэтому их часто используют при решении интегралов. Логарифм — одна из трех тесно связанных функций. В уравнении b n = x, b можно определить с помощью радикалов, n с помощью логарифмов, а x с помощью экспонент.См. Логарифмические тождества для нескольких правил, управляющих логарифмическими функциями. Для обсуждения некоторых дополнительных аспектов логарифмов см. дополнительные разделы по логарифмам.
Логарифм — одна из трех тесно связанных функций. В уравнении b n = x, b можно определить с помощью радикалов, n с помощью логарифмов, а x с помощью экспонент.См. Логарифмические тождества для нескольких правил, управляющих логарифмическими функциями. Для обсуждения некоторых дополнительных аспектов логарифмов см. дополнительные разделы по логарифмам.
Наука и техника
Различные величины в науке выражаются в виде логарифмов других величин.
- Отрицательное значение логарифма по основанию 10 используется в химии, где оно выражает концентрацию ионов гидроксония (H 3 O + , форма H + принимает в воде) в единицах измерения, известных как pH .Концентрация ионов гидроксония в нейтральной воде составляет 10 -7 моль/л при 25 °C, следовательно, pH равен 7.
- 10 логарифмов отношений, таких как уровни мощности и уровни напряжения.
 Он в основном используется в телекоммуникациях, электронике и акустике. Он используется отчасти потому, что ухо логарифмически реагирует на акустическую мощность. Bel назван в честь пионера телекоммуникаций Александра Грэма Белла. децибел (дБ), равный 0.1 бел, используется чаще. непер — аналогичная единица, в которой используется натуральный логарифм отношения.
Он в основном используется в телекоммуникациях, электронике и акустике. Он используется отчасти потому, что ухо логарифмически реагирует на акустическую мощность. Bel назван в честь пионера телекоммуникаций Александра Грэма Белла. децибел (дБ), равный 0.1 бел, используется чаще. непер — аналогичная единица, в которой используется натуральный логарифм отношения.
- Шкала Рихтера измеряет интенсивность землетрясений по десятичной логарифмической шкале.
- В спектрометрии и оптике единица измерения оптической плотности, используемая для измерения оптической плотности, эквивалентна −1 Б.
- В психофизике закон Вебера-Фехнера предлагает логарифмическую зависимость между стимулом и ощущением.
- В информатике логарифмы часто появляются в пределах вычислительной сложности. Например, для сортировки N элементов с помощью сравнения может потребоваться время, пропорциональное N log N .
 {b}) = б \ журнал (а)}
{b}) = б \ журнал (а)}ab {\ displaystyle \! \, {\ sqrt [{b}] {a}}} А / б {\ Displaystyle \! \, А / б} log(ab)=log(a)b{\displaystyle \!\,\log({\sqrt[{b}]{a}})={\frac {\log(a)}{b} }} Эти отношения сделали такие операции с двумя числами намного быстрее, и правильное использование логарифмов было важным навыком до того, как стали доступны калькуляторы умножения.
Уравнение log(ab)=log(a)+log(b){\displaystyle \log(ab)=\log(a)+\log(b)} является фундаментальным (из него фактически следует другое три отношения в поле), потому что он описывает изоморфизм между аддитивной группой и мультипликативной группой поля.
Чтобы умножить два числа, нужно найти логарифмы обоих чисел в таблице десятичных логарифмов, сложить их, а затем найти результат в таблице, чтобы найти произведение. Это быстрее, чем умножать их вручную, при условии, что в результате требуется более двух знаков после запятой.
 Таблица, необходимая для получения точности до семи знаков после запятой, могла уместиться в большой книге, а таблица для девяти знаков после запятой занимала несколько полок.
Таблица, необходимая для получения точности до семи знаков после запятой, могла уместиться в большой книге, а таблица для девяти знаков после запятой занимала несколько полок.Открытие логарифмов незадолго до эпохи Ньютона оказало влияние на научный мир, которое можно сравнить с изобретением компьютера в двадцатом веке, потому что многие расчеты, которые были слишком трудоемкими, стали возможными.
Когда в восемнадцатом веке был изобретен хронометр, логарифмы позволили свести все расчеты, необходимые для астрономической навигации, к простым сложениям, что ускорило процесс на один или два порядка.Таблицы логарифмов с пятью десятичными знаками плюс логарифмы тригонометрических функций было достаточно для большинства астрономических навигационных вычислений, и эти таблицы умещались в небольшой книге.
Чтобы вычислить степени или корни числа, десятичный логарифм этого числа искали и умножали или делили на основание. Интерполяция может быть использована для еще более высокой точности.
 Логарифмические правила использовали логарифмы для более быстрого выполнения тех же операций, но с гораздо меньшей точностью, чем при использовании таблиц.Другие инструменты для выполнения умножения до изобретения калькулятора включают кости Нейпира и механические калькуляторы: см. Историю вычислительного оборудования.
Логарифмические правила использовали логарифмы для более быстрого выполнения тех же операций, но с гораздо меньшей точностью, чем при использовании таблиц.Другие инструменты для выполнения умножения до изобретения калькулятора включают кости Нейпира и механические калькуляторы: см. Историю вычислительного оборудования.Исчисление
Производная функции натурального логарифма равна
- ddxln(x)=1x.{\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}.} (Доказательство показано ниже.)
Применяя правило смены основания, производная для других оснований равна
- ddxlogb(x)=ddxln(x)ln(b)=1xln(b)=logb(e)x.{\ displaystyle {\ frac {d} {dx}} \ log _ {b} (x) = {\ frac {d} {dx}} {\ frac {\ ln (x)} {\ ln (b)} } = {\ frac {1} {x \ ln (b)}} = {\ frac {\ log _ {b} (e)} {x}}.}
Первопроизводная логарифма равна
- ∫logb(x)dx=xlogb(x)−xln(b)+C=xlogb(xe)+C.{\displaystyle \int \log _{b}(x)\,dx= х \ log _ {b} (x) — {\ frac {x} {\ ln (b)}} + C = x \ log _ {b} \ left ({\ frac {x} {e}} \ right )+C.
 }
}
См. также: таблица пределов логарифмических функций, список интегралов логарифмических функций.
Доказательство производной
Производная функции натурального логарифма легко находится по правилу обратной функции. Поскольку функция, обратная логарифму, является показательной функцией, мы имеем пер ‘ (х) = 1 ехр ‘ (пер (х)) {\ displaystyle \ ln ‘(x) = {\ frac {1} {\ exp ‘(\ln(x))}}}. Поскольку производная экспоненциальной функции сама по себе, правая часть уравнения упрощается до 1exp(ln(x))=1x{\displaystyle {\frac {1}{\exp(\ln(x))}} = {\ frac {1} {x}}}, экспоненциальное сокращение логарифма.
Компьютеры
При рассмотрении компьютеров обычным случаем является то, что аргумент и результат функции ln(x){\displaystyle \ln(x)} являются некоторой формой данных с плавающей запятой. Обратите внимание, что в большинстве компьютерных языков для этой функции используется log(x){\displaystyle \log(x)}, тогда как log10(x){\displaystyle \log _{10}(x)} обычно обозначается как log10(x) .

Поскольку аргумент представляет собой число с плавающей запятой, полезно учитывать следующее:
Значение x с плавающей запятой представлено мантиссой m и показателем степени n для формирования
х=m2n.{п}.\,}
Поэтому
пер (х) = пер (м) + п пер (2). {\ Displaystyle \ пер (х) = \ пер (м) + п \ пер (2). \,}
Таким образом, вместо вычисления пер(х){\displaystyle \ln(x)} мы вычисляем пер(м){\displaystyle \ln(m)} для некоторого m такого, что 1≤m<2{\displaystyle 1\leq м<2}. Наличие m {\ displaystyle m} в этом диапазоне означает, что значение всегда находится в диапазоне 0 ≤ u <. 13{\displaystyle 0\leq u<{\frac {1}{3}}}. Некоторые машины используют мантисса в диапазоне 0.5≤m<1{\displaystyle 0,5\leq m<1}, и в этом случае значение u будет находиться в диапазоне −13
Обобщения
Обыкновенный логарифм положительных вещественных чисел обобщается на отрицательные и комплексные аргументы, хотя это многозначная функция, которая нуждается в разрезе ветви, оканчивающейся в точке ветвления в 0, чтобы сделать обычную функцию или главную ветвь.
 Логарифмом (по основанию e ) комплексного числа z является комплексное число ln(| z |) + i arg (z) , где | из | — модуль z, arg (z) — аргумент, а i — мнимая единица.
Логарифмом (по основанию e ) комплексного числа z является комплексное число ln(| z |) + i arg (z) , где | из | — модуль z, arg (z) — аргумент, а i — мнимая единица.Дискретный логарифм является родственным понятием в теории конечных групп. Он включает в себя решение уравнения b n = x, , где b и x — элементы группы, а n — целое число, указывающее степень в групповой операции. Считается, что для некоторых конечных групп дискретный логарифм вычислить очень сложно, тогда как дискретные экспоненты вычислить довольно легко. Эта асимметрия имеет приложения в криптографии с открытым ключом.
Логарифм матрицы является обратным значением экспоненциальной матрицы.
A двойной логарифм , пер (пер (х)) {\ Displaystyle \ пер (\ пер (х))}, является обратной функцией двойной экспоненциальной функции. Суперлогарифм или гиперлогарифм является обратной функцией суперэкспоненциальной функции.
 Суперлогарифм х растет еще медленнее, чем двойной логарифм для больших х .
Суперлогарифм х растет еще медленнее, чем двойной логарифм для больших х .Для каждого положительного b , отличного от 1, функция log b (x) является изоморфизмом группы положительных действительных чисел при умножении в группу (всех) действительных чисел при сложении.Это единственные такие изоморфизмы, которые непрерывны. Функция логарифма может быть расширена до меры Хаара в топологической группе положительных действительных чисел при умножении.
Примечания
- ↑ Джеймс Миллс Пирс, Элементы логарифмов с объяснением трех- и четырехместных таблиц логарифмических и тригонометрических функций (1873).
- ↑ 2.0 2.1 Math Forum, Logarithms: History and Use Проверено 20 ноября 2018 г.
- ↑ Институт актуариев Великобритании, Журнал Института актуариев и журнала Assurance Magazine, 1873, Vol. 17 (Забытые книги, 2018 г., 978-0366971244).
- ↑ Чарльз Найт, English Cyclopaedia, Biography, Vol.
 IV., статья «Прони».
IV., статья «Прони». - ↑ MathWorld, Логарифм. Проверено 20 ноября 2018 г.
Ссылки
Ссылки ISBN поддерживают NWE за счет реферальных сборов
- Великобритания Институт актуариев, Журнал Института актуариев и журнал Assurance Magazine, 1873, Vol.17 . Забытые книги, 2018. 978-0366971244
- Найт, Чарльз. The English Cyclopaedia, Vol. 4 . Забытые книги, 2012.
- Пирс, Джеймс Миллс. Элементы логарифмов с объяснением трех- и четырехместных таблиц логарифмических и тригонометрических функций . Андезит Пресс, 2015. ISBN 978-1297495465
- Пшеворска-Ролевич, Д. Логарифмы и антилогарифмы: подход к алгебраическому анализу с приложением Збигнева Биндермана (Математика и ее приложения) .Нью-Йорк, штат Нью-Йорк: Springer, 1998. ISBN 07
- 741.
. - РЭА. Math Made Nice & Easy #2: Проценты, экспоненты, радикалы, логарифмы и основы алгебры (Math Made Nice & Easy) . Пискатауэй, Нью-Джерси: Ассоциация исследований и образования, 1999.
 ISBN 0878
ISBN 08780.
- Риффель, Генри, Роберт Грин, Холбрук Хортон и Эдвард Мессал. Математика на работе . Нью-Йорк, штат Нью-Йорк: Industrial Press, Inc., 1999. ISBN 0831130830.
Внешние ссылки
Все ссылки получены 20 ноября 2018 г.
Кредиты
Энциклопедия Нового Света писатели и редакторы переписали и дополнили статью Википедии в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с надлежащим указанием авторства. Упоминание должно осуществляться в соответствии с условиями этой лицензии, которая может ссылаться как на авторов New World Encyclopedia , так и на самоотверженных добровольных участников Фонда Викимедиа.Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в New World Encyclopedia :
Примечание.
 На использование отдельных изображений, лицензированных отдельно, могут распространяться некоторые ограничения.
На использование отдельных изображений, лицензированных отдельно, могут распространяться некоторые ограничения.%PDF-1.4 5 0 объект > эндообъект 8 0 объект (I. Числа, точки, линии и кривые) эндообъект 9 0 объект > эндообъект 12 0 объект (1.Что такое число?) эндообъект 13 0 объект > эндообъект 16 0 объект (Еще одна причина верить в 2) эндообъект 17 0 объект > эндообъект 20 0 объект (Почему действительные числа называются действительными?) эндообъект 21 0 объект > эндообъект 24 0 объект (Упражнения) эндообъект 25 0 объект > эндообъект 28 0 объект (2. Действительная числовая линия и интервалы) эндообъект 29 0 объект > эндообъект 32 0 объект (2.1. Интервалы) эндообъект 33 0 объект > эндообъект 36 0 объект (2.2. Установить обозначение) эндообъект 37 0 объект > эндообъект 40 0 объект (Упражнения) эндообъект 41 0 объект > эндообъект 44 0 объект (3. Наборы точек на плоскости) эндообъект 45 0 объект > эндообъект 48 0 объект (3.1. Декартовы координаты) эндообъект 49 0 объект > эндообъект 52 0 объект (3.
. 2. Наборы)
эндообъект
53 0 объект
>
эндообъект
56 0 объект
(3.3. Линии)
эндообъект
57 0 объект
>
эндообъект
60 0 объект
(Упражнения)
эндообъект
61 0 объект
>
эндообъект
64 0 объект
(4. Функции)
эндообъект
65 0 объект
>
эндообъект
68 0 объект
(4.1. Пример: найти область определения и диапазон f\(x\) = 1/x2)
эндообъект
69 0 объект
>
эндообъект
72 0 объект
(4.2. Функции в «реальной жизни»)
эндообъект
73 0 объект
>
эндообъект
76 0 объект
(5. График функции)
эндообъект
77 0 объект
>
эндообъект
80 0 объект
(5.1.Свойство вертикальной линии )
эндообъект
81 0 объект
>
эндообъект
84 0 объект
(5.2. Пример)
эндообъект
85 0 объект
>
эндообъект
88 0 объект
(6. Обратные функции и неявные функции)
эндообъект
89 0 объект
>
эндообъект
92 0 объект
(6.1. Пример)
эндообъект
93 0 объект
>
эндообъект
96 0 объект
(6.2. Другой пример: область определения неявно определенной функции)
эндообъект
97 0 объект
>
эндообъект
100 0 объект
(6.3. Пример: само по себе уравнение не определяет функцию)
эндообъект
101 0 объект
>
эндообъект
104 0 объект
(6.
2. Наборы)
эндообъект
53 0 объект
>
эндообъект
56 0 объект
(3.3. Линии)
эндообъект
57 0 объект
>
эндообъект
60 0 объект
(Упражнения)
эндообъект
61 0 объект
>
эндообъект
64 0 объект
(4. Функции)
эндообъект
65 0 объект
>
эндообъект
68 0 объект
(4.1. Пример: найти область определения и диапазон f\(x\) = 1/x2)
эндообъект
69 0 объект
>
эндообъект
72 0 объект
(4.2. Функции в «реальной жизни»)
эндообъект
73 0 объект
>
эндообъект
76 0 объект
(5. График функции)
эндообъект
77 0 объект
>
эндообъект
80 0 объект
(5.1.Свойство вертикальной линии )
эндообъект
81 0 объект
>
эндообъект
84 0 объект
(5.2. Пример)
эндообъект
85 0 объект
>
эндообъект
88 0 объект
(6. Обратные функции и неявные функции)
эндообъект
89 0 объект
>
эндообъект
92 0 объект
(6.1. Пример)
эндообъект
93 0 объект
>
эндообъект
96 0 объект
(6.2. Другой пример: область определения неявно определенной функции)
эндообъект
97 0 объект
>
эндообъект
100 0 объект
(6.3. Пример: само по себе уравнение не определяет функцию)
эндообъект
101 0 объект
>
эндообъект
104 0 объект
(6. 4. Зачем использовать неявные функции?)
эндообъект
105 0 объект
>
эндообъект
108 0 объект
(6.5. Обратные функции)
эндообъект
109 0 объект
>
эндообъект
112 0 объект
(6.6. Примеры)
эндообъект
113 0 объект
>
эндообъект
116 0 объект
(6.7. Обратные тригонометрические функции)
эндообъект
117 0 объект
>
эндообъект
120 0 объект
(Упражнения)
эндообъект
121 0 объект
>
эндообъект
124 0 объект
(II. Производные \(1\))
эндообъект
125 0 объект
>
эндообъект
128 0 объект
(7. Касательная к кривой)
эндообъект
129 0 объект
>
эндообъект
132 0 объект
(8. Пример — касательная к параболе)
эндообъект
133 0 объект
>
эндообъект
136 0 объект
(9. Мгновенная скорость)
эндообъект
137 0 объект
>
эндообъект
140 0 объект
(10.Скорость изменения)
эндообъект
141 0 объект
>
эндообъект
144 0 объект
(Упражнения)
эндообъект
145 0 объект
>
эндообъект
148 0 объект
(III. Пределы и непрерывные функции)
эндообъект
149 0 объект
>
эндообъект
152 0 объект
(11. Неформальное определение пределов)
эндообъект
153 0 объект
>
эндообъект
156 0 объект
(11.
4. Зачем использовать неявные функции?)
эндообъект
105 0 объект
>
эндообъект
108 0 объект
(6.5. Обратные функции)
эндообъект
109 0 объект
>
эндообъект
112 0 объект
(6.6. Примеры)
эндообъект
113 0 объект
>
эндообъект
116 0 объект
(6.7. Обратные тригонометрические функции)
эндообъект
117 0 объект
>
эндообъект
120 0 объект
(Упражнения)
эндообъект
121 0 объект
>
эндообъект
124 0 объект
(II. Производные \(1\))
эндообъект
125 0 объект
>
эндообъект
128 0 объект
(7. Касательная к кривой)
эндообъект
129 0 объект
>
эндообъект
132 0 объект
(8. Пример — касательная к параболе)
эндообъект
133 0 объект
>
эндообъект
136 0 объект
(9. Мгновенная скорость)
эндообъект
137 0 объект
>
эндообъект
140 0 объект
(10.Скорость изменения)
эндообъект
141 0 объект
>
эндообъект
144 0 объект
(Упражнения)
эндообъект
145 0 объект
>
эндообъект
148 0 объект
(III. Пределы и непрерывные функции)
эндообъект
149 0 объект
>
эндообъект
152 0 объект
(11. Неформальное определение пределов)
эндообъект
153 0 объект
>
эндообъект
156 0 объект
(11. 1. Пример)
эндообъект
157 0 объект
>
эндообъект
160 0 объект
(11.2. Пример: подстановка чисел для угадывания предела)
эндообъект
161 0 объект
>
эндообъект
164 0 объект
(11.3. Пример: подстановка чисел может привести к неправильному ответу)
эндообъект
165 0 объект
>
эндообъект
168 0 объект
(Упражнение)
эндообъект
169 0 объект
>
эндообъект
172 0 объект
(12.Формальное, авторитетное определение предела)
эндообъект
173 0 объект
>
эндообъект
176 0 объект
(12.1. Покажите, что limx33x+2=11 )
эндообъект
177 0 объект
>
эндообъект
180 0 объект
(12.2. Покажите, что limx1x2 = 1)
эндообъект
181 0 объект
>
эндообъект
184 0 объект
(12.3. Покажите, что limx41/x = 1/4)
эндообъект
185 0 объект
>
эндообъект
188 0 объект
(Упражнения)
эндообъект
189 0 объект
>
эндообъект
192 0 объект
(13. Вариации на предельную тему)
эндообъект
193 0 объект
>
эндообъект
196 0 объект
(13.1. Левый и правый пределы)
эндообъект
197 0 объект
>
эндообъект
200 0 объект
(13.2.Пределы на бесконечности. )
эндообъект
201 0 объект
>
эндообъект
204 0 объект
(13.
1. Пример)
эндообъект
157 0 объект
>
эндообъект
160 0 объект
(11.2. Пример: подстановка чисел для угадывания предела)
эндообъект
161 0 объект
>
эндообъект
164 0 объект
(11.3. Пример: подстановка чисел может привести к неправильному ответу)
эндообъект
165 0 объект
>
эндообъект
168 0 объект
(Упражнение)
эндообъект
169 0 объект
>
эндообъект
172 0 объект
(12.Формальное, авторитетное определение предела)
эндообъект
173 0 объект
>
эндообъект
176 0 объект
(12.1. Покажите, что limx33x+2=11 )
эндообъект
177 0 объект
>
эндообъект
180 0 объект
(12.2. Покажите, что limx1x2 = 1)
эндообъект
181 0 объект
>
эндообъект
184 0 объект
(12.3. Покажите, что limx41/x = 1/4)
эндообъект
185 0 объект
>
эндообъект
188 0 объект
(Упражнения)
эндообъект
189 0 объект
>
эндообъект
192 0 объект
(13. Вариации на предельную тему)
эндообъект
193 0 объект
>
эндообъект
196 0 объект
(13.1. Левый и правый пределы)
эндообъект
197 0 объект
>
эндообъект
200 0 объект
(13.2.Пределы на бесконечности. )
эндообъект
201 0 объект
>
эндообъект
204 0 объект
(13. 3. Пример — предел 1/x)
эндообъект
205 0 объект
>
эндообъект
208 0 объект
(13.4. Пример. Предел 1/x \(снова\))
эндообъект
209 0 объект
>
эндообъект
212 0 объект
(14. Свойства предела)
эндообъект
213 0 объект
>
эндообъект
216 0 объект
(15. Примеры предельных вычислений)
эндообъект
217 0 объект
>
эндообъект
220 0 объект
(15.1. Найти limx2x2)
эндообъект
221 0 объект
>
эндообъект
224 0 объект
(15.2. Попробуйте примеры 11.2 и 11.3, используя свойства limit)
эндообъект
225 0 объект
>
эндообъект
228 0 объект
(15.3. Пример — Найти limx2x )
эндообъект
229 0 объект
>
эндообъект
232 0 объект
(15.4. Пример. Найти limx2x )
эндообъект
233 0 объект
>
эндообъект
236 0 объект
(15.5. Пример. Производная x при x=2.)
эндообъект
237 0 объект
>
эндообъект
240 0 объект
(15.6. Предел по x рациональных функций)
эндообъект
241 0 объект
>
эндообъект
244 0 объект
(15.7. Другой пример с рациональной функцией)
эндообъект
245 0 объект
>
эндообъект
248 0 объект
(16. Когда пределов не существует)
эндообъект
249 0 объект
>
эндообъект
252 0 объект
(16.
3. Пример — предел 1/x)
эндообъект
205 0 объект
>
эндообъект
208 0 объект
(13.4. Пример. Предел 1/x \(снова\))
эндообъект
209 0 объект
>
эндообъект
212 0 объект
(14. Свойства предела)
эндообъект
213 0 объект
>
эндообъект
216 0 объект
(15. Примеры предельных вычислений)
эндообъект
217 0 объект
>
эндообъект
220 0 объект
(15.1. Найти limx2x2)
эндообъект
221 0 объект
>
эндообъект
224 0 объект
(15.2. Попробуйте примеры 11.2 и 11.3, используя свойства limit)
эндообъект
225 0 объект
>
эндообъект
228 0 объект
(15.3. Пример — Найти limx2x )
эндообъект
229 0 объект
>
эндообъект
232 0 объект
(15.4. Пример. Найти limx2x )
эндообъект
233 0 объект
>
эндообъект
236 0 объект
(15.5. Пример. Производная x при x=2.)
эндообъект
237 0 объект
>
эндообъект
240 0 объект
(15.6. Предел по x рациональных функций)
эндообъект
241 0 объект
>
эндообъект
244 0 объект
(15.7. Другой пример с рациональной функцией)
эндообъект
245 0 объект
>
эндообъект
248 0 объект
(16. Когда пределов не существует)
эндообъект
249 0 объект
>
эндообъект
252 0 объект
(16. 1. Знаковая функция вблизи x=0 )
эндообъект
253 0 объект
>
эндообъект
256 0 объект
(16.2. Пример обратного синуса)
эндообъект
257 0 объект
>
эндообъект
260 0 объект
(16.3. Попытка деления на ноль с использованием предела)
эндообъект
261 0 объект
>
эндообъект
264 0 объект
(16.4. Использование свойств лимита, чтобы показать, что лимит не существует)
эндообъект
265 0 объект
>
эндообъект
268 0 объект
(16.5. Ограничения на \040, которых не существует)
эндообъект
269 0 объект
>
эндообъект
272 0 объект
(17. Что в имени?)
эндообъект
273 0 объект
>
эндообъект
276 0 объект
(18. Пределы и неравенства)
эндообъект
277 0 объект
>
эндообъект
280 0 объект
(18.1. Бутерброд с обратным косинусом)
эндообъект
281 0 объект
>
эндообъект
284 0 объект
(19.Непрерывность)
эндообъект
285 0 объект
>
эндообъект
288 0 объект
(19.1. Многочлены непрерывны)
эндообъект
289 0 объект
>
эндообъект
292 0 объект
(19.2. Рациональные функции непрерывны)
эндообъект
293 0 объект
>
эндообъект
296 0 объект
(19.3. Некоторые разрывные функции)
эндообъект
297 0 объект
>
эндообъект
300 0 объект
(19.
1. Знаковая функция вблизи x=0 )
эндообъект
253 0 объект
>
эндообъект
256 0 объект
(16.2. Пример обратного синуса)
эндообъект
257 0 объект
>
эндообъект
260 0 объект
(16.3. Попытка деления на ноль с использованием предела)
эндообъект
261 0 объект
>
эндообъект
264 0 объект
(16.4. Использование свойств лимита, чтобы показать, что лимит не существует)
эндообъект
265 0 объект
>
эндообъект
268 0 объект
(16.5. Ограничения на \040, которых не существует)
эндообъект
269 0 объект
>
эндообъект
272 0 объект
(17. Что в имени?)
эндообъект
273 0 объект
>
эндообъект
276 0 объект
(18. Пределы и неравенства)
эндообъект
277 0 объект
>
эндообъект
280 0 объект
(18.1. Бутерброд с обратным косинусом)
эндообъект
281 0 объект
>
эндообъект
284 0 объект
(19.Непрерывность)
эндообъект
285 0 объект
>
эндообъект
288 0 объект
(19.1. Многочлены непрерывны)
эндообъект
289 0 объект
>
эндообъект
292 0 объект
(19.2. Рациональные функции непрерывны)
эндообъект
293 0 объект
>
эндообъект
296 0 объект
(19.3. Некоторые разрывные функции)
эндообъект
297 0 объект
>
эндообъект
300 0 объект
(19. 4. Как сделать функции разрывными)
эндообъект
301 0 объект
>
эндообъект
304 0 объект
(19.5. Бутерброд в галстуке-бабочке)
эндообъект
305 0 объект
>
эндообъект
308 0 объект
(20. Замена в лимитах)
эндообъект
309 0 объект
>
эндообъект
312 0 объект
(20.1. Вычислить limx3x3-3×2+2)
эндообъект
313 0 объект
>
эндообъект
316 0 объект
(Упражнения)
эндообъект
317 0 объект
>
эндообъект
320 0 объект
(21. Два предела в тригонометрии)
эндообъект
321 0 объект
>
эндообъект
324 0 объект
(Упражнения)
эндообъект
325 0 объект
>
эндообъект
328 0 объект
(IV. Производные \(2\))
эндообъект
329 0 объект
>
эндообъект
332 0 объект
(22. Определение производных)
эндообъект
333 0 объект
>
эндообъект
336 0 объект
(22.1. Другие обозначения)
эндообъект
337 0 объект
>
эндообъект
340 0 объект
(23. Прямое вычисление производных)
эндообъект
341 0 объект
>
эндообъект
344 0 объект
(23.1. Пример. Производная от f\(x\)=x2 есть f’\(x\) = 2x)
эндообъект
345 0 объект
>
эндообъект
348 0 объект
(23.2. Производная от g\(x\) = x равна g’\(x\)=1 )
эндообъект
349 0 объект
>
эндообъект
352 0 объект
(23.
4. Как сделать функции разрывными)
эндообъект
301 0 объект
>
эндообъект
304 0 объект
(19.5. Бутерброд в галстуке-бабочке)
эндообъект
305 0 объект
>
эндообъект
308 0 объект
(20. Замена в лимитах)
эндообъект
309 0 объект
>
эндообъект
312 0 объект
(20.1. Вычислить limx3x3-3×2+2)
эндообъект
313 0 объект
>
эндообъект
316 0 объект
(Упражнения)
эндообъект
317 0 объект
>
эндообъект
320 0 объект
(21. Два предела в тригонометрии)
эндообъект
321 0 объект
>
эндообъект
324 0 объект
(Упражнения)
эндообъект
325 0 объект
>
эндообъект
328 0 объект
(IV. Производные \(2\))
эндообъект
329 0 объект
>
эндообъект
332 0 объект
(22. Определение производных)
эндообъект
333 0 объект
>
эндообъект
336 0 объект
(22.1. Другие обозначения)
эндообъект
337 0 объект
>
эндообъект
340 0 объект
(23. Прямое вычисление производных)
эндообъект
341 0 объект
>
эндообъект
344 0 объект
(23.1. Пример. Производная от f\(x\)=x2 есть f’\(x\) = 2x)
эндообъект
345 0 объект
>
эндообъект
348 0 объект
(23.2. Производная от g\(x\) = x равна g’\(x\)=1 )
эндообъект
349 0 объект
>
эндообъект
352 0 объект
(23. 3. Производная любой постоянной функции равна нулю)
эндообъект
353 0 объект
>
эндообъект
356 0 объект
(23.4. Производная xn для n=1, 2, 3, \203 )
эндообъект
357 0 объект
>
эндообъект
360 0 объект
(23.5. Дифференцируемое подразумевает непрерывное)
эндообъект
361 0 объект
>
эндообъект
364 0 объект
(23.6. Некоторые недифференцируемые функции)
эндообъект
365 0 объект
>
эндообъект
368 0 объект
(Упражнения)
эндообъект
369 0 объект
>
эндообъект
372 0 объект
(24.Правила дифференциации)
эндообъект
373 0 объект
>
эндообъект
376 0 объект
(24.1. Правила суммы, произведения и частного)
эндообъект
377 0 объект
>
эндообъект
380 0 объект
(24.2. Доказательство правила сумм)
эндообъект
381 0 объект
>
эндообъект
384 0 объект
(24.3. Доказательство правила продукта)
эндообъект
385 0 объект
>
эндообъект
388 0 объект
(24.4. Доказательство частного правила)
эндообъект
389 0 объект
>
эндообъект
392 0 объект
(24.5. Более короткий, но не совсем совершенный вывод частного правила)
эндообъект
393 0 объект
>
эндообъект
396 0 объект
(24.
3. Производная любой постоянной функции равна нулю)
эндообъект
353 0 объект
>
эндообъект
356 0 объект
(23.4. Производная xn для n=1, 2, 3, \203 )
эндообъект
357 0 объект
>
эндообъект
360 0 объект
(23.5. Дифференцируемое подразумевает непрерывное)
эндообъект
361 0 объект
>
эндообъект
364 0 объект
(23.6. Некоторые недифференцируемые функции)
эндообъект
365 0 объект
>
эндообъект
368 0 объект
(Упражнения)
эндообъект
369 0 объект
>
эндообъект
372 0 объект
(24.Правила дифференциации)
эндообъект
373 0 объект
>
эндообъект
376 0 объект
(24.1. Правила суммы, произведения и частного)
эндообъект
377 0 объект
>
эндообъект
380 0 объект
(24.2. Доказательство правила сумм)
эндообъект
381 0 объект
>
эндообъект
384 0 объект
(24.3. Доказательство правила продукта)
эндообъект
385 0 объект
>
эндообъект
388 0 объект
(24.4. Доказательство частного правила)
эндообъект
389 0 объект
>
эндообъект
392 0 объект
(24.5. Более короткий, но не совсем совершенный вывод частного правила)
эндообъект
393 0 объект
>
эндообъект
396 0 объект
(24. 6. Дифференцирование постоянного кратного функции )
эндообъект
397 0 объект
>
эндообъект
400 0 объект
(24.7. Изображение правила продукта)
эндообъект
401 0 объект
>
эндообъект
404 0 объект
(25. Дифференцирующие степени функций)
эндообъект
405 0 объект
>
эндообъект
408 0 объект
(25.1. Правило произведения с более чем одним фактором)
эндообъект
409 0 объект
>
эндообъект
412 0 объект
(25.2. Правило мощности)
эндообъект
413 0 объект
>
эндообъект
416 0 объект
(25.3. Правило степени для отрицательных целых показателей)
эндообъект
417 0 объект
>
эндообъект
420 0 объект
(25.4. Степенное правило для рациональных показателей)
эндообъект
421 0 объект
>
эндообъект
424 0 объект
(25.5. Производная xn для целого числа n)
эндообъект
425 0 объект
>
эндообъект
428 0 объект
(25.6. Пример — дифференцировать многочлен)
эндообъект
429 0 объект
>
эндообъект
432 0 объект
(25.7. Пример — дифференцировать рациональную функцию)
эндообъект
433 0 объект
>
эндообъект
436 0 объект
(25.8. Производная квадратного корня)
эндообъект
437 0 объект
>
эндообъект
440 0 объект
(Упражнения)
эндообъект
441 0 объект
>
эндообъект
444 0 объект
(26.
6. Дифференцирование постоянного кратного функции )
эндообъект
397 0 объект
>
эндообъект
400 0 объект
(24.7. Изображение правила продукта)
эндообъект
401 0 объект
>
эндообъект
404 0 объект
(25. Дифференцирующие степени функций)
эндообъект
405 0 объект
>
эндообъект
408 0 объект
(25.1. Правило произведения с более чем одним фактором)
эндообъект
409 0 объект
>
эндообъект
412 0 объект
(25.2. Правило мощности)
эндообъект
413 0 объект
>
эндообъект
416 0 объект
(25.3. Правило степени для отрицательных целых показателей)
эндообъект
417 0 объект
>
эндообъект
420 0 объект
(25.4. Степенное правило для рациональных показателей)
эндообъект
421 0 объект
>
эндообъект
424 0 объект
(25.5. Производная xn для целого числа n)
эндообъект
425 0 объект
>
эндообъект
428 0 объект
(25.6. Пример — дифференцировать многочлен)
эндообъект
429 0 объект
>
эндообъект
432 0 объект
(25.7. Пример — дифференцировать рациональную функцию)
эндообъект
433 0 объект
>
эндообъект
436 0 объект
(25.8. Производная квадратного корня)
эндообъект
437 0 объект
>
эндообъект
440 0 объект
(Упражнения)
эндообъект
441 0 объект
>
эндообъект
444 0 объект
(26. Высшие производные)
эндообъект
445 0 объект
>
эндообъект
448 0 объект
(26.1. Производная есть функция)
эндообъект
449 0 объект
>
эндообъект
452 0 объект
(26.2. Обозначение оператора)
эндообъект
453 0 объект
>
эндообъект
456 0 объект
(Упражнения)
эндообъект
457 0 объект
>
эндообъект
460 0 объект
(27.Дифференциация тригонометрических функций)
эндообъект
461 0 объект
>
эндообъект
464 0 объект
(Упражнения)
эндообъект
465 0 объект
>
эндообъект
468 0 объект
(28. Цепное правило)
эндообъект
469 0 объект
>
эндообъект
472 0 объект
(28.1. Композиция функций)
эндообъект
473 0 объект
>
эндообъект
476 0 объект
(28.2. Реальный пример)
эндообъект
477 0 объект
>
эндообъект
480 0 объект
(28.3. Формулировка цепного правила)
эндообъект
481 0 объект
>
эндообъект
484 0 объект
(28.4. Первый пример)
эндообъект
485 0 объект
>
эндообъект
488 0 объект
(28.5. Пример, где вам действительно нужно цепное правило)
эндообъект
489 0 объект
>
эндообъект
492 0 объект
(28.6. Правило силы и правило цепи)
эндообъект
493 0 объект
>
эндообъект
496 0 объект
(28.
Высшие производные)
эндообъект
445 0 объект
>
эндообъект
448 0 объект
(26.1. Производная есть функция)
эндообъект
449 0 объект
>
эндообъект
452 0 объект
(26.2. Обозначение оператора)
эндообъект
453 0 объект
>
эндообъект
456 0 объект
(Упражнения)
эндообъект
457 0 объект
>
эндообъект
460 0 объект
(27.Дифференциация тригонометрических функций)
эндообъект
461 0 объект
>
эндообъект
464 0 объект
(Упражнения)
эндообъект
465 0 объект
>
эндообъект
468 0 объект
(28. Цепное правило)
эндообъект
469 0 объект
>
эндообъект
472 0 объект
(28.1. Композиция функций)
эндообъект
473 0 объект
>
эндообъект
476 0 объект
(28.2. Реальный пример)
эндообъект
477 0 объект
>
эндообъект
480 0 объект
(28.3. Формулировка цепного правила)
эндообъект
481 0 объект
>
эндообъект
484 0 объект
(28.4. Первый пример)
эндообъект
485 0 объект
>
эндообъект
488 0 объект
(28.5. Пример, где вам действительно нужно цепное правило)
эндообъект
489 0 объект
>
эндообъект
492 0 объект
(28.6. Правило силы и правило цепи)
эндообъект
493 0 объект
>
эндообъект
496 0 объект
(28. 7. Объем растущей дрожжевой клетки)
эндообъект
497 0 объект
>
эндообъект
500 0 объект
(28.8. Более сложный пример)
эндообъект
501 0 объект
>
эндообъект
504 0 объект
(28.9. Цепное правило и составление более двух функций)
эндообъект
505 0 объект
>
эндообъект
508 0 объект
(Упражнения)
эндообъект
509 0 объект
>
эндообъект
512 0 объект
(29. Неявное дифференцирование)
эндообъект
513 0 объект
>
эндообъект
516 0 объект
(29.1. Рецепт)
эндообъект
517 0 объект
>
эндообъект
520 0 объект
(29.2. Работа с уравнениями вида F1\(x,y\) = F2\(x, y\))
эндообъект
521 0 объект
>
эндообъект
524 0 объект
(29.3. Пример. Производная от [4]1-x4)
эндообъект
525 0 объект
>
эндообъект
528 0 объект
(29.4. Другой пример)
эндообъект
529 0 объект
>
эндообъект
532 0 объект
(29.5. Производные арксинуса и арктангенса)
эндообъект
533 0 объект
>
эндообъект
536 0 объект
(Упражнения на неявное дифференцирование)
эндообъект
537 0 объект
>
эндообъект
540 0 объект
(Упражнения на скорость изменения)
эндообъект
541 0 объект
>
эндообъект
544 0 объект
(V.
7. Объем растущей дрожжевой клетки)
эндообъект
497 0 объект
>
эндообъект
500 0 объект
(28.8. Более сложный пример)
эндообъект
501 0 объект
>
эндообъект
504 0 объект
(28.9. Цепное правило и составление более двух функций)
эндообъект
505 0 объект
>
эндообъект
508 0 объект
(Упражнения)
эндообъект
509 0 объект
>
эндообъект
512 0 объект
(29. Неявное дифференцирование)
эндообъект
513 0 объект
>
эндообъект
516 0 объект
(29.1. Рецепт)
эндообъект
517 0 объект
>
эндообъект
520 0 объект
(29.2. Работа с уравнениями вида F1\(x,y\) = F2\(x, y\))
эндообъект
521 0 объект
>
эндообъект
524 0 объект
(29.3. Пример. Производная от [4]1-x4)
эндообъект
525 0 объект
>
эндообъект
528 0 объект
(29.4. Другой пример)
эндообъект
529 0 объект
>
эндообъект
532 0 объект
(29.5. Производные арксинуса и арктангенса)
эндообъект
533 0 объект
>
эндообъект
536 0 объект
(Упражнения на неявное дифференцирование)
эндообъект
537 0 объект
>
эндообъект
540 0 объект
(Упражнения на скорость изменения)
эндообъект
541 0 объект
>
эндообъект
544 0 объект
(V. Набросок графа и проблемы максимума и минимума)
эндообъект
545 0 объект
>
эндообъект
548 0 объект
(30.Касательные и нормальные линии к графику)
эндообъект
549 0 объект
>
эндообъект
552 0 объект
(31. Теорема о промежуточном значении)
эндообъект
553 0 объект
>
эндообъект
556 0 объект
(Пример — Квадратный корень из 2)
эндообъект
557 0 объект
>
эндообъект
560 0 объект
(Пример — Уравнение +sin=2)
эндообъект
561 0 объект
>
эндообъект
564 0 объект
(Пример — Решение 1/x=0)
эндообъект
565 0 объект
>
эндообъект
568 0 объект
(32. Нахождение смены знака функции)
эндообъект
569 0 объект
>
эндообъект
572 0 объект
(32.1. Пример)
эндообъект
573 0 объект
>
эндообъект
576 0 объект
(33. Возрастающие и убывающие функции)
эндообъект
577 0 объект
>
эндообъект
580 0 объект
(34.Примеры)
эндообъект
581 0 объект
>
эндообъект
584 0 объект
(34.1. Пример: парабола y=x2)
эндообъект
585 0 объект
>
эндообъект
588 0 объект
(34.2. Пример: гипербола \040y=1/x )
эндообъект
589 0 объект
>
эндообъект
592 0 объект
(34.3.
Набросок графа и проблемы максимума и минимума)
эндообъект
545 0 объект
>
эндообъект
548 0 объект
(30.Касательные и нормальные линии к графику)
эндообъект
549 0 объект
>
эндообъект
552 0 объект
(31. Теорема о промежуточном значении)
эндообъект
553 0 объект
>
эндообъект
556 0 объект
(Пример — Квадратный корень из 2)
эндообъект
557 0 объект
>
эндообъект
560 0 объект
(Пример — Уравнение +sin=2)
эндообъект
561 0 объект
>
эндообъект
564 0 объект
(Пример — Решение 1/x=0)
эндообъект
565 0 объект
>
эндообъект
568 0 объект
(32. Нахождение смены знака функции)
эндообъект
569 0 объект
>
эндообъект
572 0 объект
(32.1. Пример)
эндообъект
573 0 объект
>
эндообъект
576 0 объект
(33. Возрастающие и убывающие функции)
эндообъект
577 0 объект
>
эндообъект
580 0 объект
(34.Примеры)
эндообъект
581 0 объект
>
эндообъект
584 0 объект
(34.1. Пример: парабола y=x2)
эндообъект
585 0 объект
>
эндообъект
588 0 объект
(34.2. Пример: гипербола \040y=1/x )
эндообъект
589 0 объект
>
эндообъект
592 0 объект
(34.3. График кубической функции)
эндообъект
593 0 объект
>
эндообъект
596 0 объект
(34.4. Функция, тангенс которой бесконечно часто поворачивается вверх и вниз вблизи начала координат)
эндообъект
597 0 объект
>
эндообъект
600 0 объект
(35. Максимумы и минимумы)
эндообъект
601 0 объект
>
эндообъект
604 0 объект
(35.1. Где найти локальные максимумы и минимумы)
эндообъект
605 0 объект
>
эндообъект
608 0 объект
(35.2. Как определить, является ли стационарная точка максимумом, минимумом или ни тем, ни другим)
эндообъект
609 0 объект
>
эндообъект
612 0 объект
(35.3. Пример — локальные максимумы и минимумы f\(x\) = x3-x)
эндообъект
613 0 объект
>
эндообъект
616 0 объект
(35.4. Стационарная точка, не являющаяся ни максимумом, ни минимумом)
эндообъект
617 0 объект
>
эндообъект
620 0 объект
(36. Всегда ли должен быть максимум?)
эндообъект
621 0 объект
>
эндообъект
624 0 объект
(37. Примеры — функции с максимумами и минимумами и без них)
эндообъект
625 0 объект
>
эндообъект
628 0 объект
(38. Общий способ построения графика функции)
эндообъект
629 0 объект
>
эндообъект
632 0 объект
(38.
График кубической функции)
эндообъект
593 0 объект
>
эндообъект
596 0 объект
(34.4. Функция, тангенс которой бесконечно часто поворачивается вверх и вниз вблизи начала координат)
эндообъект
597 0 объект
>
эндообъект
600 0 объект
(35. Максимумы и минимумы)
эндообъект
601 0 объект
>
эндообъект
604 0 объект
(35.1. Где найти локальные максимумы и минимумы)
эндообъект
605 0 объект
>
эндообъект
608 0 объект
(35.2. Как определить, является ли стационарная точка максимумом, минимумом или ни тем, ни другим)
эндообъект
609 0 объект
>
эндообъект
612 0 объект
(35.3. Пример — локальные максимумы и минимумы f\(x\) = x3-x)
эндообъект
613 0 объект
>
эндообъект
616 0 объект
(35.4. Стационарная точка, не являющаяся ни максимумом, ни минимумом)
эндообъект
617 0 объект
>
эндообъект
620 0 объект
(36. Всегда ли должен быть максимум?)
эндообъект
621 0 объект
>
эндообъект
624 0 объект
(37. Примеры — функции с максимумами и минимумами и без них)
эндообъект
625 0 объект
>
эндообъект
628 0 объект
(38. Общий способ построения графика функции)
эндообъект
629 0 объект
>
эндообъект
632 0 объект
(38. 1. Пример — график рациональной функции)
эндообъект
633 0 объект
>
эндообъект
636 0 объект
(39. Выпуклость, вогнутость и вторая производная)
эндообъект
637 0 объект
>
эндообъект
640 0 объект
(39.1. Пример — кубическая функция f\(x\) = x3-x)
эндообъект
641 0 объект
>
эндообъект
644 0 объект
(39.2. Тест второй производной)
эндообъект
645 0 объект
>
эндообъект
648 0 объект
(39.3. Пример — снова эта кубическая функция)
эндообъект
649 0 объект
>
эндообъект
652 0 объект
(39.4. Когда критерий второй производной не работает)
эндообъект
653 0 объект
>
эндообъект
656 0 объект
(40.Доказательства некоторых теорем)
эндообъект
657 0 объект
>
эндообъект
660 0 объект
(40.1. Доказательство теоремы о среднем значении)
эндообъект
661 0 объект
>
эндообъект
664 0 объект
(40.2. Доказательство теоремы 33.1)
эндообъект
665 0 объект
>
эндообъект
668 0 объект
(40.3. Доказательство теоремы 33.2)
эндообъект
669 0 объект
>
эндообъект
672 0 объект
(Упражнения)
эндообъект
673 0 объект
>
эндообъект
676 0 объект
(41. Проблемы оптимизации)
эндообъект
677 0 объект
>
эндообъект
680 0 объект
(41.
1. Пример — график рациональной функции)
эндообъект
633 0 объект
>
эндообъект
636 0 объект
(39. Выпуклость, вогнутость и вторая производная)
эндообъект
637 0 объект
>
эндообъект
640 0 объект
(39.1. Пример — кубическая функция f\(x\) = x3-x)
эндообъект
641 0 объект
>
эндообъект
644 0 объект
(39.2. Тест второй производной)
эндообъект
645 0 объект
>
эндообъект
648 0 объект
(39.3. Пример — снова эта кубическая функция)
эндообъект
649 0 объект
>
эндообъект
652 0 объект
(39.4. Когда критерий второй производной не работает)
эндообъект
653 0 объект
>
эндообъект
656 0 объект
(40.Доказательства некоторых теорем)
эндообъект
657 0 объект
>
эндообъект
660 0 объект
(40.1. Доказательство теоремы о среднем значении)
эндообъект
661 0 объект
>
эндообъект
664 0 объект
(40.2. Доказательство теоремы 33.1)
эндообъект
665 0 объект
>
эндообъект
668 0 объект
(40.3. Доказательство теоремы 33.2)
эндообъект
669 0 объект
>
эндообъект
672 0 объект
(Упражнения)
эндообъект
673 0 объект
>
эндообъект
676 0 объект
(41. Проблемы оптимизации)
эндообъект
677 0 объект
>
эндообъект
680 0 объект
(41. 1. Пример. Прямоугольник с наибольшей площадью и заданным периметром)
эндообъект
681 0 объект
>
эндообъект
684 0 объект
(41.2. Упражнения)
эндообъект
685 0 объект
>
эндообъект
688 0 объект
(VI. Экспоненты и логарифмы)
эндообъект
689 0 объект
>
эндообъект
692 0 объект
(42. Экспоненты)
эндообъект
693 0 объект
>
эндообъект
696 0 объект
(42.1. Проблема со степенями отрицательных чисел)
эндообъект
697 0 объект
>
эндообъект
700 0 объект
(43. Логарифмы)
эндообъект
701 0 объект
>
эндообъект
704 0 объект
(44. Свойства логарифмов)
эндообъект
705 0 объект
>
эндообъект
708 0 объект
(45. Графики показательных функций и логарифмов)
эндообъект
709 0 объект
>
эндообъект
712 0 объект
(46. Производная от ax и определение e)
эндообъект
713 0 объект
>
эндообъект
716 0 объект
(47.Производные логарифмов)
эндообъект
717 0 объект
>
эндообъект
720 0 объект
(48. Пределы, включающие экспоненты и логарифмы)
эндообъект
721 0 объект
>
эндообъект
724 0 объект
(49. Экспоненциальный рост и распад)
эндообъект
725 0 объект
>
эндообъект
728 0 объект
(49.
1. Пример. Прямоугольник с наибольшей площадью и заданным периметром)
эндообъект
681 0 объект
>
эндообъект
684 0 объект
(41.2. Упражнения)
эндообъект
685 0 объект
>
эндообъект
688 0 объект
(VI. Экспоненты и логарифмы)
эндообъект
689 0 объект
>
эндообъект
692 0 объект
(42. Экспоненты)
эндообъект
693 0 объект
>
эндообъект
696 0 объект
(42.1. Проблема со степенями отрицательных чисел)
эндообъект
697 0 объект
>
эндообъект
700 0 объект
(43. Логарифмы)
эндообъект
701 0 объект
>
эндообъект
704 0 объект
(44. Свойства логарифмов)
эндообъект
705 0 объект
>
эндообъект
708 0 объект
(45. Графики показательных функций и логарифмов)
эндообъект
709 0 объект
>
эндообъект
712 0 объект
(46. Производная от ax и определение e)
эндообъект
713 0 объект
>
эндообъект
716 0 объект
(47.Производные логарифмов)
эндообъект
717 0 объект
>
эндообъект
720 0 объект
(48. Пределы, включающие экспоненты и логарифмы)
эндообъект
721 0 объект
>
эндообъект
724 0 объект
(49. Экспоненциальный рост и распад)
эндообъект
725 0 объект
>
эндообъект
728 0 объект
(49. 1. Перерыв и удвоение времени)
эндообъект
729 0 объект
>
эндообъект
732 0 объект
(49.2. Определение X0 и k)
эндообъект
733 0 объект
>
эндообъект
736 0 объект
(Упражнения)
эндообъект
737 0 объект
>
эндообъект
740 0 объект
(VII. Интеграл)
эндообъект
741 0 объект
>
эндообъект
744 0 объект
(50. Площадь под графиком)
эндообъект
745 0 объект
>
эндообъект
748 0 объект
(51.Когда f меняет знак)
эндообъект
749 0 объект
>
эндообъект
752 0 объект
(52. Основная теорема исчисления)
эндообъект
753 0 объект
>
эндообъект
756 0 объект
(52.1. Терминология)
эндообъект
757 0 объект
>
эндообъект
760 0 объект
(Упражнения)
эндообъект
761 0 объект
>
эндообъект
764 0 объект
(53. Неопределенный интеграл)
эндообъект
765 0 объект
>
эндообъект
768 0 объект
(53.1. Вы всегда можете проверить ответ)
эндообъект
769 0 объект
>
эндообъект
772 0 объект
(53.2. О «+C»)
эндообъект
773 0 объект
>
эндообъект
776 0 объект
(53.3. Стандартные интегралы)
эндообъект
777 0 объект
>
эндообъект
780 0 объект
(54.Свойства интеграла)
эндообъект
781 0 объект
>
эндообъект
784 0 объект
(55.
1. Перерыв и удвоение времени)
эндообъект
729 0 объект
>
эндообъект
732 0 объект
(49.2. Определение X0 и k)
эндообъект
733 0 объект
>
эндообъект
736 0 объект
(Упражнения)
эндообъект
737 0 объект
>
эндообъект
740 0 объект
(VII. Интеграл)
эндообъект
741 0 объект
>
эндообъект
744 0 объект
(50. Площадь под графиком)
эндообъект
745 0 объект
>
эндообъект
748 0 объект
(51.Когда f меняет знак)
эндообъект
749 0 объект
>
эндообъект
752 0 объект
(52. Основная теорема исчисления)
эндообъект
753 0 объект
>
эндообъект
756 0 объект
(52.1. Терминология)
эндообъект
757 0 объект
>
эндообъект
760 0 объект
(Упражнения)
эндообъект
761 0 объект
>
эндообъект
764 0 объект
(53. Неопределенный интеграл)
эндообъект
765 0 объект
>
эндообъект
768 0 объект
(53.1. Вы всегда можете проверить ответ)
эндообъект
769 0 объект
>
эндообъект
772 0 объект
(53.2. О «+C»)
эндообъект
773 0 объект
>
эндообъект
776 0 объект
(53.3. Стандартные интегралы)
эндообъект
777 0 объект
>
эндообъект
780 0 объект
(54.Свойства интеграла)
эндообъект
781 0 объект
>
эндообъект
784 0 объект
(55. Определенный интеграл как функция его границ интегрирования)
эндообъект
785 0 объект
>
эндообъект
788 0 объект
(56. Метод замены)
эндообъект
789 0 объект
>
эндообъект
792 0 объект
(56.1. Пример)
эндообъект
793 0 объект
>
эндообъект
796 0 объект
(56.2. Обозначение Лейбница для замены)
эндообъект
797 0 объект
>
эндообъект
800 0 объект
(56.3. Замена определенных интегралов)
эндообъект
801 0 объект
>
эндообъект
804 0 объект
(56.4. Пример замены в определенном интеграле)
эндообъект
805 0 объект
>
эндообъект
808 0 объект
(Упражнения)
эндообъект
809 0 объект
>
эндообъект
812 0 объект
(VIII.Приложения интеграла)
эндообъект
813 0 объект
>
эндообъект
816 0 объект
(57. Области между графиками)
эндообъект
817 0 объект
>
эндообъект
820 0 объект
(Упражнения)
эндообъект
821 0 объект
>
эндообъект
824 0 объект
(58. Принцип Кавальери и объемы твердых тел)
эндообъект
825 0 объект
>
эндообъект
828 0 объект
(58.1. Пример — Объем пирамиды)
эндообъект
829 0 объект
>
эндообъект
832 0 объект
(58.2. Общий случай)
эндообъект
833 0 объект
>
эндообъект
836 0 объект
(58.
Определенный интеграл как функция его границ интегрирования)
эндообъект
785 0 объект
>
эндообъект
788 0 объект
(56. Метод замены)
эндообъект
789 0 объект
>
эндообъект
792 0 объект
(56.1. Пример)
эндообъект
793 0 объект
>
эндообъект
796 0 объект
(56.2. Обозначение Лейбница для замены)
эндообъект
797 0 объект
>
эндообъект
800 0 объект
(56.3. Замена определенных интегралов)
эндообъект
801 0 объект
>
эндообъект
804 0 объект
(56.4. Пример замены в определенном интеграле)
эндообъект
805 0 объект
>
эндообъект
808 0 объект
(Упражнения)
эндообъект
809 0 объект
>
эндообъект
812 0 объект
(VIII.Приложения интеграла)
эндообъект
813 0 объект
>
эндообъект
816 0 объект
(57. Области между графиками)
эндообъект
817 0 объект
>
эндообъект
820 0 объект
(Упражнения)
эндообъект
821 0 объект
>
эндообъект
824 0 объект
(58. Принцип Кавальери и объемы твердых тел)
эндообъект
825 0 объект
>
эндообъект
828 0 объект
(58.1. Пример — Объем пирамиды)
эндообъект
829 0 объект
>
эндообъект
832 0 объект
(58.2. Общий случай)
эндообъект
833 0 объект
>
эндообъект
836 0 объект
(58. 3. Принцип Кавальери)
эндообъект
837 0 объект
>
эндообъект
840 0 объект
(58.4. Тела вращения)
эндообъект
841 0 объект
>
эндообъект
844 0 объект
(59.Примеры объемов тел вращения)
эндообъект
845 0 объект
>
эндообъект
848 0 объект
(59.1. Задача 1: Вращение R вокруг оси Y)
эндообъект
849 0 объект
>
эндообъект
852 0 объект
(59.2. Задача 2. Вращение R вокруг линии x=-1)
эндообъект
853 0 объект
>
эндообъект
856 0 объект
(59.3. Задача 3: вращать R вокруг линии y=2)
эндообъект
857 0 объект
>
эндообъект
860 0 объект
(60. Объемы по цилиндрическим оболочкам)
эндообъект
861 0 объект
>
эндообъект
864 0 объект
(60.1. Пример. Твердое тело, полученное вращением R вокруг оси y, снова)
эндообъект
865 0 объект
>
эндообъект
868 0 объект
(Упражнения)
эндообъект
869 0 объект
>
эндообъект
872 0 объект
(61.Расстояние от скорости, скорость от ускорения)
эндообъект
873 0 объект
>
эндообъект
876 0 объект
(61.1. Движение по линии)
эндообъект
877 0 объект
>
эндообъект
880 0 объект
(61.2. Скорость от ускорения)
эндообъект
881 0 объект
>
эндообъект
884 0 объект
(61.
3. Принцип Кавальери)
эндообъект
837 0 объект
>
эндообъект
840 0 объект
(58.4. Тела вращения)
эндообъект
841 0 объект
>
эндообъект
844 0 объект
(59.Примеры объемов тел вращения)
эндообъект
845 0 объект
>
эндообъект
848 0 объект
(59.1. Задача 1: Вращение R вокруг оси Y)
эндообъект
849 0 объект
>
эндообъект
852 0 объект
(59.2. Задача 2. Вращение R вокруг линии x=-1)
эндообъект
853 0 объект
>
эндообъект
856 0 объект
(59.3. Задача 3: вращать R вокруг линии y=2)
эндообъект
857 0 объект
>
эндообъект
860 0 объект
(60. Объемы по цилиндрическим оболочкам)
эндообъект
861 0 объект
>
эндообъект
864 0 объект
(60.1. Пример. Твердое тело, полученное вращением R вокруг оси y, снова)
эндообъект
865 0 объект
>
эндообъект
868 0 объект
(Упражнения)
эндообъект
869 0 объект
>
эндообъект
872 0 объект
(61.Расстояние от скорости, скорость от ускорения)
эндообъект
873 0 объект
>
эндообъект
876 0 объект
(61.1. Движение по линии)
эндообъект
877 0 объект
>
эндообъект
880 0 объект
(61.2. Скорость от ускорения)
эндообъект
881 0 объект
>
эндообъект
884 0 объект
(61. 3. Свободное падение в постоянном гравитационном поле)
эндообъект
885 0 объект
>
эндообъект
888 0 объект
(61.4. Движение на плоскости — параметрические кривые)
эндообъект
889 0 объект
>
эндообъект
892 0 объект
(61.5. Скорость тела, движущегося в плоскости)
эндообъект
893 0 объект
>
эндообъект
896 0 объект
(61.6. Пример — два движения по кругу из \24761.4)
эндообъект
897 0 объект
>
эндообъект
900 0 объект
(62. Длина кривой)
эндообъект
901 0 объект
>
эндообъект
904 0 объект
(62.1. Длина параметрической кривой)
эндообъект
905 0 объект
>
эндообъект
908 0 объект
(62.2. Длина графика функции)
эндообъект
909 0 объект
>
эндообъект
912 0 объект
(62.3. Примеры вычисления длины)
эндообъект
913 0 объект
>
эндообъект
916 0 объект
(63. Работа силы)
эндообъект
917 0 объект
>
эндообъект
920 0 объект
(63.1. Работа как интеграл)
эндообъект
921 0 объект
>
эндообъект
924 0 объект
(63.m*;lsdf=4X%rz-cuSŽc%]ՕdZspokeYokt[H
/ ILɹ9h ‘
)c+0m$QW
конечный поток
эндообъект
930 0 объект > эндообъект
933 0 объект > эндообъект
934 0 объект > эндообъект
931 0 объект >
/ProcSet [ /PDF /текст ]
>> эндообъект
947 0 объект >
ручей
xڥVKFWP>ev0@rZ;T\*T> 4Z
3. Свободное падение в постоянном гравитационном поле)
эндообъект
885 0 объект
>
эндообъект
888 0 объект
(61.4. Движение на плоскости — параметрические кривые)
эндообъект
889 0 объект
>
эндообъект
892 0 объект
(61.5. Скорость тела, движущегося в плоскости)
эндообъект
893 0 объект
>
эндообъект
896 0 объект
(61.6. Пример — два движения по кругу из \24761.4)
эндообъект
897 0 объект
>
эндообъект
900 0 объект
(62. Длина кривой)
эндообъект
901 0 объект
>
эндообъект
904 0 объект
(62.1. Длина параметрической кривой)
эндообъект
905 0 объект
>
эндообъект
908 0 объект
(62.2. Длина графика функции)
эндообъект
909 0 объект
>
эндообъект
912 0 объект
(62.3. Примеры вычисления длины)
эндообъект
913 0 объект
>
эндообъект
916 0 объект
(63. Работа силы)
эндообъект
917 0 объект
>
эндообъект
920 0 объект
(63.1. Работа как интеграл)
эндообъект
921 0 объект
>
эндообъект
924 0 объект
(63.m*;lsdf=4X%rz-cuSŽc%]ՕdZspokeYokt[H
/ ILɹ9h ‘
)c+0m$QW
конечный поток
эндообъект
930 0 объект > эндообъект
933 0 объект > эндообъект
934 0 объект > эндообъект
931 0 объект >
/ProcSet [ /PDF /текст ]
>> эндообъект
947 0 объект >
ручей
xڥVKFWP>ev0@rZ;T\*T> 4Z


 Касательная к графику функции
Касательная к графику функции Важная деталь числа – обязательное наличие основания. Стандартный вариант величины равен 10. Маркируется последовательностью – log x или lg x.
Важная деталь числа – обязательное наличие основания. Стандартный вариант величины равен 10. Маркируется последовательностью – log x или lg x.
 2+1)`
2+1)` ]
]

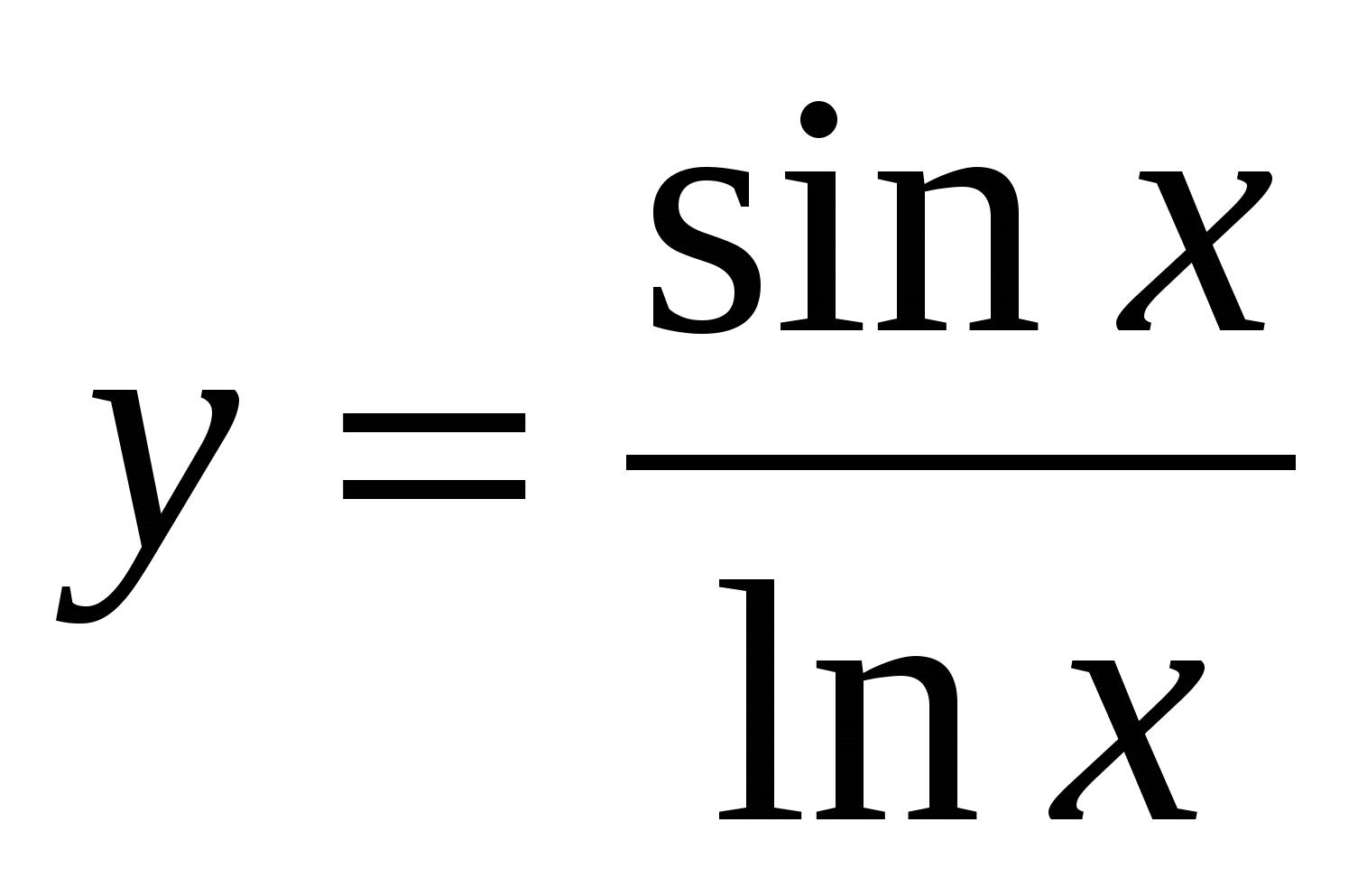 Он в основном используется в телекоммуникациях, электронике и акустике. Он используется отчасти потому, что ухо логарифмически реагирует на акустическую мощность. Bel назван в честь пионера телекоммуникаций Александра Грэма Белла. децибел (дБ), равный 0.1 бел, используется чаще. непер — аналогичная единица, в которой используется натуральный логарифм отношения.
Он в основном используется в телекоммуникациях, электронике и акустике. Он используется отчасти потому, что ухо логарифмически реагирует на акустическую мощность. Bel назван в честь пионера телекоммуникаций Александра Грэма Белла. децибел (дБ), равный 0.1 бел, используется чаще. непер — аналогичная единица, в которой используется натуральный логарифм отношения. Таблица, необходимая для получения точности до семи знаков после запятой, могла уместиться в большой книге, а таблица для девяти знаков после запятой занимала несколько полок.
Таблица, необходимая для получения точности до семи знаков после запятой, могла уместиться в большой книге, а таблица для девяти знаков после запятой занимала несколько полок. Логарифмические правила использовали логарифмы для более быстрого выполнения тех же операций, но с гораздо меньшей точностью, чем при использовании таблиц.Другие инструменты для выполнения умножения до изобретения калькулятора включают кости Нейпира и механические калькуляторы: см. Историю вычислительного оборудования.
Логарифмические правила использовали логарифмы для более быстрого выполнения тех же операций, но с гораздо меньшей точностью, чем при использовании таблиц.Другие инструменты для выполнения умножения до изобретения калькулятора включают кости Нейпира и механические калькуляторы: см. Историю вычислительного оборудования. }
}
 Логарифмом (по основанию e ) комплексного числа z является комплексное число ln(| z |) + i arg (z) , где | из | — модуль z, arg (z) — аргумент, а i — мнимая единица.
Логарифмом (по основанию e ) комплексного числа z является комплексное число ln(| z |) + i arg (z) , где | из | — модуль z, arg (z) — аргумент, а i — мнимая единица. Суперлогарифм х растет еще медленнее, чем двойной логарифм для больших х .
Суперлогарифм х растет еще медленнее, чем двойной логарифм для больших х . IV., статья «Прони».
IV., статья «Прони». ISBN 0878
ISBN 0878 2. Наборы)
эндообъект
53 0 объект
>
эндообъект
56 0 объект
(3.3. Линии)
эндообъект
57 0 объект
>
эндообъект
60 0 объект
(Упражнения)
эндообъект
61 0 объект
>
эндообъект
64 0 объект
(4. Функции)
эндообъект
65 0 объект
>
эндообъект
68 0 объект
(4.1. Пример: найти область определения и диапазон f\(x\) = 1/x2)
эндообъект
69 0 объект
>
эндообъект
72 0 объект
(4.2. Функции в «реальной жизни»)
эндообъект
73 0 объект
>
эндообъект
76 0 объект
(5. График функции)
эндообъект
77 0 объект
>
эндообъект
80 0 объект
(5.1.Свойство вертикальной линии )
эндообъект
81 0 объект
>
эндообъект
84 0 объект
(5.2. Пример)
эндообъект
85 0 объект
>
эндообъект
88 0 объект
(6. Обратные функции и неявные функции)
эндообъект
89 0 объект
>
эндообъект
92 0 объект
(6.1. Пример)
эндообъект
93 0 объект
>
эндообъект
96 0 объект
(6.2. Другой пример: область определения неявно определенной функции)
эндообъект
97 0 объект
>
эндообъект
100 0 объект
(6.3. Пример: само по себе уравнение не определяет функцию)
эндообъект
101 0 объект
>
эндообъект
104 0 объект
(6.
2. Наборы)
эндообъект
53 0 объект
>
эндообъект
56 0 объект
(3.3. Линии)
эндообъект
57 0 объект
>
эндообъект
60 0 объект
(Упражнения)
эндообъект
61 0 объект
>
эндообъект
64 0 объект
(4. Функции)
эндообъект
65 0 объект
>
эндообъект
68 0 объект
(4.1. Пример: найти область определения и диапазон f\(x\) = 1/x2)
эндообъект
69 0 объект
>
эндообъект
72 0 объект
(4.2. Функции в «реальной жизни»)
эндообъект
73 0 объект
>
эндообъект
76 0 объект
(5. График функции)
эндообъект
77 0 объект
>
эндообъект
80 0 объект
(5.1.Свойство вертикальной линии )
эндообъект
81 0 объект
>
эндообъект
84 0 объект
(5.2. Пример)
эндообъект
85 0 объект
>
эндообъект
88 0 объект
(6. Обратные функции и неявные функции)
эндообъект
89 0 объект
>
эндообъект
92 0 объект
(6.1. Пример)
эндообъект
93 0 объект
>
эндообъект
96 0 объект
(6.2. Другой пример: область определения неявно определенной функции)
эндообъект
97 0 объект
>
эндообъект
100 0 объект
(6.3. Пример: само по себе уравнение не определяет функцию)
эндообъект
101 0 объект
>
эндообъект
104 0 объект
(6. 4. Зачем использовать неявные функции?)
эндообъект
105 0 объект
>
эндообъект
108 0 объект
(6.5. Обратные функции)
эндообъект
109 0 объект
>
эндообъект
112 0 объект
(6.6. Примеры)
эндообъект
113 0 объект
>
эндообъект
116 0 объект
(6.7. Обратные тригонометрические функции)
эндообъект
117 0 объект
>
эндообъект
120 0 объект
(Упражнения)
эндообъект
121 0 объект
>
эндообъект
124 0 объект
(II. Производные \(1\))
эндообъект
125 0 объект
>
эндообъект
128 0 объект
(7. Касательная к кривой)
эндообъект
129 0 объект
>
эндообъект
132 0 объект
(8. Пример — касательная к параболе)
эндообъект
133 0 объект
>
эндообъект
136 0 объект
(9. Мгновенная скорость)
эндообъект
137 0 объект
>
эндообъект
140 0 объект
(10.Скорость изменения)
эндообъект
141 0 объект
>
эндообъект
144 0 объект
(Упражнения)
эндообъект
145 0 объект
>
эндообъект
148 0 объект
(III. Пределы и непрерывные функции)
эндообъект
149 0 объект
>
эндообъект
152 0 объект
(11. Неформальное определение пределов)
эндообъект
153 0 объект
>
эндообъект
156 0 объект
(11.
4. Зачем использовать неявные функции?)
эндообъект
105 0 объект
>
эндообъект
108 0 объект
(6.5. Обратные функции)
эндообъект
109 0 объект
>
эндообъект
112 0 объект
(6.6. Примеры)
эндообъект
113 0 объект
>
эндообъект
116 0 объект
(6.7. Обратные тригонометрические функции)
эндообъект
117 0 объект
>
эндообъект
120 0 объект
(Упражнения)
эндообъект
121 0 объект
>
эндообъект
124 0 объект
(II. Производные \(1\))
эндообъект
125 0 объект
>
эндообъект
128 0 объект
(7. Касательная к кривой)
эндообъект
129 0 объект
>
эндообъект
132 0 объект
(8. Пример — касательная к параболе)
эндообъект
133 0 объект
>
эндообъект
136 0 объект
(9. Мгновенная скорость)
эндообъект
137 0 объект
>
эндообъект
140 0 объект
(10.Скорость изменения)
эндообъект
141 0 объект
>
эндообъект
144 0 объект
(Упражнения)
эндообъект
145 0 объект
>
эндообъект
148 0 объект
(III. Пределы и непрерывные функции)
эндообъект
149 0 объект
>
эндообъект
152 0 объект
(11. Неформальное определение пределов)
эндообъект
153 0 объект
>
эндообъект
156 0 объект
(11. 1. Пример)
эндообъект
157 0 объект
>
эндообъект
160 0 объект
(11.2. Пример: подстановка чисел для угадывания предела)
эндообъект
161 0 объект
>
эндообъект
164 0 объект
(11.3. Пример: подстановка чисел может привести к неправильному ответу)
эндообъект
165 0 объект
>
эндообъект
168 0 объект
(Упражнение)
эндообъект
169 0 объект
>
эндообъект
172 0 объект
(12.Формальное, авторитетное определение предела)
эндообъект
173 0 объект
>
эндообъект
176 0 объект
(12.1. Покажите, что limx33x+2=11 )
эндообъект
177 0 объект
>
эндообъект
180 0 объект
(12.2. Покажите, что limx1x2 = 1)
эндообъект
181 0 объект
>
эндообъект
184 0 объект
(12.3. Покажите, что limx41/x = 1/4)
эндообъект
185 0 объект
>
эндообъект
188 0 объект
(Упражнения)
эндообъект
189 0 объект
>
эндообъект
192 0 объект
(13. Вариации на предельную тему)
эндообъект
193 0 объект
>
эндообъект
196 0 объект
(13.1. Левый и правый пределы)
эндообъект
197 0 объект
>
эндообъект
200 0 объект
(13.2.Пределы на бесконечности. )
эндообъект
201 0 объект
>
эндообъект
204 0 объект
(13.
1. Пример)
эндообъект
157 0 объект
>
эндообъект
160 0 объект
(11.2. Пример: подстановка чисел для угадывания предела)
эндообъект
161 0 объект
>
эндообъект
164 0 объект
(11.3. Пример: подстановка чисел может привести к неправильному ответу)
эндообъект
165 0 объект
>
эндообъект
168 0 объект
(Упражнение)
эндообъект
169 0 объект
>
эндообъект
172 0 объект
(12.Формальное, авторитетное определение предела)
эндообъект
173 0 объект
>
эндообъект
176 0 объект
(12.1. Покажите, что limx33x+2=11 )
эндообъект
177 0 объект
>
эндообъект
180 0 объект
(12.2. Покажите, что limx1x2 = 1)
эндообъект
181 0 объект
>
эндообъект
184 0 объект
(12.3. Покажите, что limx41/x = 1/4)
эндообъект
185 0 объект
>
эндообъект
188 0 объект
(Упражнения)
эндообъект
189 0 объект
>
эндообъект
192 0 объект
(13. Вариации на предельную тему)
эндообъект
193 0 объект
>
эндообъект
196 0 объект
(13.1. Левый и правый пределы)
эндообъект
197 0 объект
>
эндообъект
200 0 объект
(13.2.Пределы на бесконечности. )
эндообъект
201 0 объект
>
эндообъект
204 0 объект
(13. 3. Пример — предел 1/x)
эндообъект
205 0 объект
>
эндообъект
208 0 объект
(13.4. Пример. Предел 1/x \(снова\))
эндообъект
209 0 объект
>
эндообъект
212 0 объект
(14. Свойства предела)
эндообъект
213 0 объект
>
эндообъект
216 0 объект
(15. Примеры предельных вычислений)
эндообъект
217 0 объект
>
эндообъект
220 0 объект
(15.1. Найти limx2x2)
эндообъект
221 0 объект
>
эндообъект
224 0 объект
(15.2. Попробуйте примеры 11.2 и 11.3, используя свойства limit)
эндообъект
225 0 объект
>
эндообъект
228 0 объект
(15.3. Пример — Найти limx2x )
эндообъект
229 0 объект
>
эндообъект
232 0 объект
(15.4. Пример. Найти limx2x )
эндообъект
233 0 объект
>
эндообъект
236 0 объект
(15.5. Пример. Производная x при x=2.)
эндообъект
237 0 объект
>
эндообъект
240 0 объект
(15.6. Предел по x рациональных функций)
эндообъект
241 0 объект
>
эндообъект
244 0 объект
(15.7. Другой пример с рациональной функцией)
эндообъект
245 0 объект
>
эндообъект
248 0 объект
(16. Когда пределов не существует)
эндообъект
249 0 объект
>
эндообъект
252 0 объект
(16.
3. Пример — предел 1/x)
эндообъект
205 0 объект
>
эндообъект
208 0 объект
(13.4. Пример. Предел 1/x \(снова\))
эндообъект
209 0 объект
>
эндообъект
212 0 объект
(14. Свойства предела)
эндообъект
213 0 объект
>
эндообъект
216 0 объект
(15. Примеры предельных вычислений)
эндообъект
217 0 объект
>
эндообъект
220 0 объект
(15.1. Найти limx2x2)
эндообъект
221 0 объект
>
эндообъект
224 0 объект
(15.2. Попробуйте примеры 11.2 и 11.3, используя свойства limit)
эндообъект
225 0 объект
>
эндообъект
228 0 объект
(15.3. Пример — Найти limx2x )
эндообъект
229 0 объект
>
эндообъект
232 0 объект
(15.4. Пример. Найти limx2x )
эндообъект
233 0 объект
>
эндообъект
236 0 объект
(15.5. Пример. Производная x при x=2.)
эндообъект
237 0 объект
>
эндообъект
240 0 объект
(15.6. Предел по x рациональных функций)
эндообъект
241 0 объект
>
эндообъект
244 0 объект
(15.7. Другой пример с рациональной функцией)
эндообъект
245 0 объект
>
эндообъект
248 0 объект
(16. Когда пределов не существует)
эндообъект
249 0 объект
>
эндообъект
252 0 объект
(16. 1. Знаковая функция вблизи x=0 )
эндообъект
253 0 объект
>
эндообъект
256 0 объект
(16.2. Пример обратного синуса)
эндообъект
257 0 объект
>
эндообъект
260 0 объект
(16.3. Попытка деления на ноль с использованием предела)
эндообъект
261 0 объект
>
эндообъект
264 0 объект
(16.4. Использование свойств лимита, чтобы показать, что лимит не существует)
эндообъект
265 0 объект
>
эндообъект
268 0 объект
(16.5. Ограничения на \040, которых не существует)
эндообъект
269 0 объект
>
эндообъект
272 0 объект
(17. Что в имени?)
эндообъект
273 0 объект
>
эндообъект
276 0 объект
(18. Пределы и неравенства)
эндообъект
277 0 объект
>
эндообъект
280 0 объект
(18.1. Бутерброд с обратным косинусом)
эндообъект
281 0 объект
>
эндообъект
284 0 объект
(19.Непрерывность)
эндообъект
285 0 объект
>
эндообъект
288 0 объект
(19.1. Многочлены непрерывны)
эндообъект
289 0 объект
>
эндообъект
292 0 объект
(19.2. Рациональные функции непрерывны)
эндообъект
293 0 объект
>
эндообъект
296 0 объект
(19.3. Некоторые разрывные функции)
эндообъект
297 0 объект
>
эндообъект
300 0 объект
(19.
1. Знаковая функция вблизи x=0 )
эндообъект
253 0 объект
>
эндообъект
256 0 объект
(16.2. Пример обратного синуса)
эндообъект
257 0 объект
>
эндообъект
260 0 объект
(16.3. Попытка деления на ноль с использованием предела)
эндообъект
261 0 объект
>
эндообъект
264 0 объект
(16.4. Использование свойств лимита, чтобы показать, что лимит не существует)
эндообъект
265 0 объект
>
эндообъект
268 0 объект
(16.5. Ограничения на \040, которых не существует)
эндообъект
269 0 объект
>
эндообъект
272 0 объект
(17. Что в имени?)
эндообъект
273 0 объект
>
эндообъект
276 0 объект
(18. Пределы и неравенства)
эндообъект
277 0 объект
>
эндообъект
280 0 объект
(18.1. Бутерброд с обратным косинусом)
эндообъект
281 0 объект
>
эндообъект
284 0 объект
(19.Непрерывность)
эндообъект
285 0 объект
>
эндообъект
288 0 объект
(19.1. Многочлены непрерывны)
эндообъект
289 0 объект
>
эндообъект
292 0 объект
(19.2. Рациональные функции непрерывны)
эндообъект
293 0 объект
>
эндообъект
296 0 объект
(19.3. Некоторые разрывные функции)
эндообъект
297 0 объект
>
эндообъект
300 0 объект
(19. 4. Как сделать функции разрывными)
эндообъект
301 0 объект
>
эндообъект
304 0 объект
(19.5. Бутерброд в галстуке-бабочке)
эндообъект
305 0 объект
>
эндообъект
308 0 объект
(20. Замена в лимитах)
эндообъект
309 0 объект
>
эндообъект
312 0 объект
(20.1. Вычислить limx3x3-3×2+2)
эндообъект
313 0 объект
>
эндообъект
316 0 объект
(Упражнения)
эндообъект
317 0 объект
>
эндообъект
320 0 объект
(21. Два предела в тригонометрии)
эндообъект
321 0 объект
>
эндообъект
324 0 объект
(Упражнения)
эндообъект
325 0 объект
>
эндообъект
328 0 объект
(IV. Производные \(2\))
эндообъект
329 0 объект
>
эндообъект
332 0 объект
(22. Определение производных)
эндообъект
333 0 объект
>
эндообъект
336 0 объект
(22.1. Другие обозначения)
эндообъект
337 0 объект
>
эндообъект
340 0 объект
(23. Прямое вычисление производных)
эндообъект
341 0 объект
>
эндообъект
344 0 объект
(23.1. Пример. Производная от f\(x\)=x2 есть f’\(x\) = 2x)
эндообъект
345 0 объект
>
эндообъект
348 0 объект
(23.2. Производная от g\(x\) = x равна g’\(x\)=1 )
эндообъект
349 0 объект
>
эндообъект
352 0 объект
(23.
4. Как сделать функции разрывными)
эндообъект
301 0 объект
>
эндообъект
304 0 объект
(19.5. Бутерброд в галстуке-бабочке)
эндообъект
305 0 объект
>
эндообъект
308 0 объект
(20. Замена в лимитах)
эндообъект
309 0 объект
>
эндообъект
312 0 объект
(20.1. Вычислить limx3x3-3×2+2)
эндообъект
313 0 объект
>
эндообъект
316 0 объект
(Упражнения)
эндообъект
317 0 объект
>
эндообъект
320 0 объект
(21. Два предела в тригонометрии)
эндообъект
321 0 объект
>
эндообъект
324 0 объект
(Упражнения)
эндообъект
325 0 объект
>
эндообъект
328 0 объект
(IV. Производные \(2\))
эндообъект
329 0 объект
>
эндообъект
332 0 объект
(22. Определение производных)
эндообъект
333 0 объект
>
эндообъект
336 0 объект
(22.1. Другие обозначения)
эндообъект
337 0 объект
>
эндообъект
340 0 объект
(23. Прямое вычисление производных)
эндообъект
341 0 объект
>
эндообъект
344 0 объект
(23.1. Пример. Производная от f\(x\)=x2 есть f’\(x\) = 2x)
эндообъект
345 0 объект
>
эндообъект
348 0 объект
(23.2. Производная от g\(x\) = x равна g’\(x\)=1 )
эндообъект
349 0 объект
>
эндообъект
352 0 объект
(23. 3. Производная любой постоянной функции равна нулю)
эндообъект
353 0 объект
>
эндообъект
356 0 объект
(23.4. Производная xn для n=1, 2, 3, \203 )
эндообъект
357 0 объект
>
эндообъект
360 0 объект
(23.5. Дифференцируемое подразумевает непрерывное)
эндообъект
361 0 объект
>
эндообъект
364 0 объект
(23.6. Некоторые недифференцируемые функции)
эндообъект
365 0 объект
>
эндообъект
368 0 объект
(Упражнения)
эндообъект
369 0 объект
>
эндообъект
372 0 объект
(24.Правила дифференциации)
эндообъект
373 0 объект
>
эндообъект
376 0 объект
(24.1. Правила суммы, произведения и частного)
эндообъект
377 0 объект
>
эндообъект
380 0 объект
(24.2. Доказательство правила сумм)
эндообъект
381 0 объект
>
эндообъект
384 0 объект
(24.3. Доказательство правила продукта)
эндообъект
385 0 объект
>
эндообъект
388 0 объект
(24.4. Доказательство частного правила)
эндообъект
389 0 объект
>
эндообъект
392 0 объект
(24.5. Более короткий, но не совсем совершенный вывод частного правила)
эндообъект
393 0 объект
>
эндообъект
396 0 объект
(24.
3. Производная любой постоянной функции равна нулю)
эндообъект
353 0 объект
>
эндообъект
356 0 объект
(23.4. Производная xn для n=1, 2, 3, \203 )
эндообъект
357 0 объект
>
эндообъект
360 0 объект
(23.5. Дифференцируемое подразумевает непрерывное)
эндообъект
361 0 объект
>
эндообъект
364 0 объект
(23.6. Некоторые недифференцируемые функции)
эндообъект
365 0 объект
>
эндообъект
368 0 объект
(Упражнения)
эндообъект
369 0 объект
>
эндообъект
372 0 объект
(24.Правила дифференциации)
эндообъект
373 0 объект
>
эндообъект
376 0 объект
(24.1. Правила суммы, произведения и частного)
эндообъект
377 0 объект
>
эндообъект
380 0 объект
(24.2. Доказательство правила сумм)
эндообъект
381 0 объект
>
эндообъект
384 0 объект
(24.3. Доказательство правила продукта)
эндообъект
385 0 объект
>
эндообъект
388 0 объект
(24.4. Доказательство частного правила)
эндообъект
389 0 объект
>
эндообъект
392 0 объект
(24.5. Более короткий, но не совсем совершенный вывод частного правила)
эндообъект
393 0 объект
>
эндообъект
396 0 объект
(24.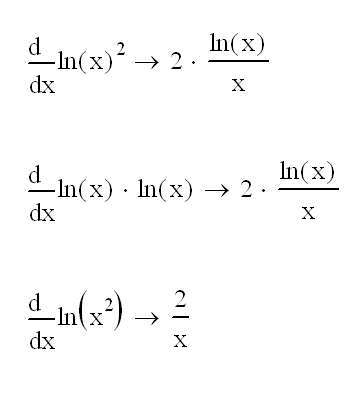 6. Дифференцирование постоянного кратного функции )
эндообъект
397 0 объект
>
эндообъект
400 0 объект
(24.7. Изображение правила продукта)
эндообъект
401 0 объект
>
эндообъект
404 0 объект
(25. Дифференцирующие степени функций)
эндообъект
405 0 объект
>
эндообъект
408 0 объект
(25.1. Правило произведения с более чем одним фактором)
эндообъект
409 0 объект
>
эндообъект
412 0 объект
(25.2. Правило мощности)
эндообъект
413 0 объект
>
эндообъект
416 0 объект
(25.3. Правило степени для отрицательных целых показателей)
эндообъект
417 0 объект
>
эндообъект
420 0 объект
(25.4. Степенное правило для рациональных показателей)
эндообъект
421 0 объект
>
эндообъект
424 0 объект
(25.5. Производная xn для целого числа n)
эндообъект
425 0 объект
>
эндообъект
428 0 объект
(25.6. Пример — дифференцировать многочлен)
эндообъект
429 0 объект
>
эндообъект
432 0 объект
(25.7. Пример — дифференцировать рациональную функцию)
эндообъект
433 0 объект
>
эндообъект
436 0 объект
(25.8. Производная квадратного корня)
эндообъект
437 0 объект
>
эндообъект
440 0 объект
(Упражнения)
эндообъект
441 0 объект
>
эндообъект
444 0 объект
(26.
6. Дифференцирование постоянного кратного функции )
эндообъект
397 0 объект
>
эндообъект
400 0 объект
(24.7. Изображение правила продукта)
эндообъект
401 0 объект
>
эндообъект
404 0 объект
(25. Дифференцирующие степени функций)
эндообъект
405 0 объект
>
эндообъект
408 0 объект
(25.1. Правило произведения с более чем одним фактором)
эндообъект
409 0 объект
>
эндообъект
412 0 объект
(25.2. Правило мощности)
эндообъект
413 0 объект
>
эндообъект
416 0 объект
(25.3. Правило степени для отрицательных целых показателей)
эндообъект
417 0 объект
>
эндообъект
420 0 объект
(25.4. Степенное правило для рациональных показателей)
эндообъект
421 0 объект
>
эндообъект
424 0 объект
(25.5. Производная xn для целого числа n)
эндообъект
425 0 объект
>
эндообъект
428 0 объект
(25.6. Пример — дифференцировать многочлен)
эндообъект
429 0 объект
>
эндообъект
432 0 объект
(25.7. Пример — дифференцировать рациональную функцию)
эндообъект
433 0 объект
>
эндообъект
436 0 объект
(25.8. Производная квадратного корня)
эндообъект
437 0 объект
>
эндообъект
440 0 объект
(Упражнения)
эндообъект
441 0 объект
>
эндообъект
444 0 объект
(26. Высшие производные)
эндообъект
445 0 объект
>
эндообъект
448 0 объект
(26.1. Производная есть функция)
эндообъект
449 0 объект
>
эндообъект
452 0 объект
(26.2. Обозначение оператора)
эндообъект
453 0 объект
>
эндообъект
456 0 объект
(Упражнения)
эндообъект
457 0 объект
>
эндообъект
460 0 объект
(27.Дифференциация тригонометрических функций)
эндообъект
461 0 объект
>
эндообъект
464 0 объект
(Упражнения)
эндообъект
465 0 объект
>
эндообъект
468 0 объект
(28. Цепное правило)
эндообъект
469 0 объект
>
эндообъект
472 0 объект
(28.1. Композиция функций)
эндообъект
473 0 объект
>
эндообъект
476 0 объект
(28.2. Реальный пример)
эндообъект
477 0 объект
>
эндообъект
480 0 объект
(28.3. Формулировка цепного правила)
эндообъект
481 0 объект
>
эндообъект
484 0 объект
(28.4. Первый пример)
эндообъект
485 0 объект
>
эндообъект
488 0 объект
(28.5. Пример, где вам действительно нужно цепное правило)
эндообъект
489 0 объект
>
эндообъект
492 0 объект
(28.6. Правило силы и правило цепи)
эндообъект
493 0 объект
>
эндообъект
496 0 объект
(28.
Высшие производные)
эндообъект
445 0 объект
>
эндообъект
448 0 объект
(26.1. Производная есть функция)
эндообъект
449 0 объект
>
эндообъект
452 0 объект
(26.2. Обозначение оператора)
эндообъект
453 0 объект
>
эндообъект
456 0 объект
(Упражнения)
эндообъект
457 0 объект
>
эндообъект
460 0 объект
(27.Дифференциация тригонометрических функций)
эндообъект
461 0 объект
>
эндообъект
464 0 объект
(Упражнения)
эндообъект
465 0 объект
>
эндообъект
468 0 объект
(28. Цепное правило)
эндообъект
469 0 объект
>
эндообъект
472 0 объект
(28.1. Композиция функций)
эндообъект
473 0 объект
>
эндообъект
476 0 объект
(28.2. Реальный пример)
эндообъект
477 0 объект
>
эндообъект
480 0 объект
(28.3. Формулировка цепного правила)
эндообъект
481 0 объект
>
эндообъект
484 0 объект
(28.4. Первый пример)
эндообъект
485 0 объект
>
эндообъект
488 0 объект
(28.5. Пример, где вам действительно нужно цепное правило)
эндообъект
489 0 объект
>
эндообъект
492 0 объект
(28.6. Правило силы и правило цепи)
эндообъект
493 0 объект
>
эндообъект
496 0 объект
(28. 7. Объем растущей дрожжевой клетки)
эндообъект
497 0 объект
>
эндообъект
500 0 объект
(28.8. Более сложный пример)
эндообъект
501 0 объект
>
эндообъект
504 0 объект
(28.9. Цепное правило и составление более двух функций)
эндообъект
505 0 объект
>
эндообъект
508 0 объект
(Упражнения)
эндообъект
509 0 объект
>
эндообъект
512 0 объект
(29. Неявное дифференцирование)
эндообъект
513 0 объект
>
эндообъект
516 0 объект
(29.1. Рецепт)
эндообъект
517 0 объект
>
эндообъект
520 0 объект
(29.2. Работа с уравнениями вида F1\(x,y\) = F2\(x, y\))
эндообъект
521 0 объект
>
эндообъект
524 0 объект
(29.3. Пример. Производная от [4]1-x4)
эндообъект
525 0 объект
>
эндообъект
528 0 объект
(29.4. Другой пример)
эндообъект
529 0 объект
>
эндообъект
532 0 объект
(29.5. Производные арксинуса и арктангенса)
эндообъект
533 0 объект
>
эндообъект
536 0 объект
(Упражнения на неявное дифференцирование)
эндообъект
537 0 объект
>
эндообъект
540 0 объект
(Упражнения на скорость изменения)
эндообъект
541 0 объект
>
эндообъект
544 0 объект
(V.
7. Объем растущей дрожжевой клетки)
эндообъект
497 0 объект
>
эндообъект
500 0 объект
(28.8. Более сложный пример)
эндообъект
501 0 объект
>
эндообъект
504 0 объект
(28.9. Цепное правило и составление более двух функций)
эндообъект
505 0 объект
>
эндообъект
508 0 объект
(Упражнения)
эндообъект
509 0 объект
>
эндообъект
512 0 объект
(29. Неявное дифференцирование)
эндообъект
513 0 объект
>
эндообъект
516 0 объект
(29.1. Рецепт)
эндообъект
517 0 объект
>
эндообъект
520 0 объект
(29.2. Работа с уравнениями вида F1\(x,y\) = F2\(x, y\))
эндообъект
521 0 объект
>
эндообъект
524 0 объект
(29.3. Пример. Производная от [4]1-x4)
эндообъект
525 0 объект
>
эндообъект
528 0 объект
(29.4. Другой пример)
эндообъект
529 0 объект
>
эндообъект
532 0 объект
(29.5. Производные арксинуса и арктангенса)
эндообъект
533 0 объект
>
эндообъект
536 0 объект
(Упражнения на неявное дифференцирование)
эндообъект
537 0 объект
>
эндообъект
540 0 объект
(Упражнения на скорость изменения)
эндообъект
541 0 объект
>
эндообъект
544 0 объект
(V. Набросок графа и проблемы максимума и минимума)
эндообъект
545 0 объект
>
эндообъект
548 0 объект
(30.Касательные и нормальные линии к графику)
эндообъект
549 0 объект
>
эндообъект
552 0 объект
(31. Теорема о промежуточном значении)
эндообъект
553 0 объект
>
эндообъект
556 0 объект
(Пример — Квадратный корень из 2)
эндообъект
557 0 объект
>
эндообъект
560 0 объект
(Пример — Уравнение +sin=2)
эндообъект
561 0 объект
>
эндообъект
564 0 объект
(Пример — Решение 1/x=0)
эндообъект
565 0 объект
>
эндообъект
568 0 объект
(32. Нахождение смены знака функции)
эндообъект
569 0 объект
>
эндообъект
572 0 объект
(32.1. Пример)
эндообъект
573 0 объект
>
эндообъект
576 0 объект
(33. Возрастающие и убывающие функции)
эндообъект
577 0 объект
>
эндообъект
580 0 объект
(34.Примеры)
эндообъект
581 0 объект
>
эндообъект
584 0 объект
(34.1. Пример: парабола y=x2)
эндообъект
585 0 объект
>
эндообъект
588 0 объект
(34.2. Пример: гипербола \040y=1/x )
эндообъект
589 0 объект
>
эндообъект
592 0 объект
(34.3.
Набросок графа и проблемы максимума и минимума)
эндообъект
545 0 объект
>
эндообъект
548 0 объект
(30.Касательные и нормальные линии к графику)
эндообъект
549 0 объект
>
эндообъект
552 0 объект
(31. Теорема о промежуточном значении)
эндообъект
553 0 объект
>
эндообъект
556 0 объект
(Пример — Квадратный корень из 2)
эндообъект
557 0 объект
>
эндообъект
560 0 объект
(Пример — Уравнение +sin=2)
эндообъект
561 0 объект
>
эндообъект
564 0 объект
(Пример — Решение 1/x=0)
эндообъект
565 0 объект
>
эндообъект
568 0 объект
(32. Нахождение смены знака функции)
эндообъект
569 0 объект
>
эндообъект
572 0 объект
(32.1. Пример)
эндообъект
573 0 объект
>
эндообъект
576 0 объект
(33. Возрастающие и убывающие функции)
эндообъект
577 0 объект
>
эндообъект
580 0 объект
(34.Примеры)
эндообъект
581 0 объект
>
эндообъект
584 0 объект
(34.1. Пример: парабола y=x2)
эндообъект
585 0 объект
>
эндообъект
588 0 объект
(34.2. Пример: гипербола \040y=1/x )
эндообъект
589 0 объект
>
эндообъект
592 0 объект
(34.3. График кубической функции)
эндообъект
593 0 объект
>
эндообъект
596 0 объект
(34.4. Функция, тангенс которой бесконечно часто поворачивается вверх и вниз вблизи начала координат)
эндообъект
597 0 объект
>
эндообъект
600 0 объект
(35. Максимумы и минимумы)
эндообъект
601 0 объект
>
эндообъект
604 0 объект
(35.1. Где найти локальные максимумы и минимумы)
эндообъект
605 0 объект
>
эндообъект
608 0 объект
(35.2. Как определить, является ли стационарная точка максимумом, минимумом или ни тем, ни другим)
эндообъект
609 0 объект
>
эндообъект
612 0 объект
(35.3. Пример — локальные максимумы и минимумы f\(x\) = x3-x)
эндообъект
613 0 объект
>
эндообъект
616 0 объект
(35.4. Стационарная точка, не являющаяся ни максимумом, ни минимумом)
эндообъект
617 0 объект
>
эндообъект
620 0 объект
(36. Всегда ли должен быть максимум?)
эндообъект
621 0 объект
>
эндообъект
624 0 объект
(37. Примеры — функции с максимумами и минимумами и без них)
эндообъект
625 0 объект
>
эндообъект
628 0 объект
(38. Общий способ построения графика функции)
эндообъект
629 0 объект
>
эндообъект
632 0 объект
(38.
График кубической функции)
эндообъект
593 0 объект
>
эндообъект
596 0 объект
(34.4. Функция, тангенс которой бесконечно часто поворачивается вверх и вниз вблизи начала координат)
эндообъект
597 0 объект
>
эндообъект
600 0 объект
(35. Максимумы и минимумы)
эндообъект
601 0 объект
>
эндообъект
604 0 объект
(35.1. Где найти локальные максимумы и минимумы)
эндообъект
605 0 объект
>
эндообъект
608 0 объект
(35.2. Как определить, является ли стационарная точка максимумом, минимумом или ни тем, ни другим)
эндообъект
609 0 объект
>
эндообъект
612 0 объект
(35.3. Пример — локальные максимумы и минимумы f\(x\) = x3-x)
эндообъект
613 0 объект
>
эндообъект
616 0 объект
(35.4. Стационарная точка, не являющаяся ни максимумом, ни минимумом)
эндообъект
617 0 объект
>
эндообъект
620 0 объект
(36. Всегда ли должен быть максимум?)
эндообъект
621 0 объект
>
эндообъект
624 0 объект
(37. Примеры — функции с максимумами и минимумами и без них)
эндообъект
625 0 объект
>
эндообъект
628 0 объект
(38. Общий способ построения графика функции)
эндообъект
629 0 объект
>
эндообъект
632 0 объект
(38. 1. Пример — график рациональной функции)
эндообъект
633 0 объект
>
эндообъект
636 0 объект
(39. Выпуклость, вогнутость и вторая производная)
эндообъект
637 0 объект
>
эндообъект
640 0 объект
(39.1. Пример — кубическая функция f\(x\) = x3-x)
эндообъект
641 0 объект
>
эндообъект
644 0 объект
(39.2. Тест второй производной)
эндообъект
645 0 объект
>
эндообъект
648 0 объект
(39.3. Пример — снова эта кубическая функция)
эндообъект
649 0 объект
>
эндообъект
652 0 объект
(39.4. Когда критерий второй производной не работает)
эндообъект
653 0 объект
>
эндообъект
656 0 объект
(40.Доказательства некоторых теорем)
эндообъект
657 0 объект
>
эндообъект
660 0 объект
(40.1. Доказательство теоремы о среднем значении)
эндообъект
661 0 объект
>
эндообъект
664 0 объект
(40.2. Доказательство теоремы 33.1)
эндообъект
665 0 объект
>
эндообъект
668 0 объект
(40.3. Доказательство теоремы 33.2)
эндообъект
669 0 объект
>
эндообъект
672 0 объект
(Упражнения)
эндообъект
673 0 объект
>
эндообъект
676 0 объект
(41. Проблемы оптимизации)
эндообъект
677 0 объект
>
эндообъект
680 0 объект
(41.
1. Пример — график рациональной функции)
эндообъект
633 0 объект
>
эндообъект
636 0 объект
(39. Выпуклость, вогнутость и вторая производная)
эндообъект
637 0 объект
>
эндообъект
640 0 объект
(39.1. Пример — кубическая функция f\(x\) = x3-x)
эндообъект
641 0 объект
>
эндообъект
644 0 объект
(39.2. Тест второй производной)
эндообъект
645 0 объект
>
эндообъект
648 0 объект
(39.3. Пример — снова эта кубическая функция)
эндообъект
649 0 объект
>
эндообъект
652 0 объект
(39.4. Когда критерий второй производной не работает)
эндообъект
653 0 объект
>
эндообъект
656 0 объект
(40.Доказательства некоторых теорем)
эндообъект
657 0 объект
>
эндообъект
660 0 объект
(40.1. Доказательство теоремы о среднем значении)
эндообъект
661 0 объект
>
эндообъект
664 0 объект
(40.2. Доказательство теоремы 33.1)
эндообъект
665 0 объект
>
эндообъект
668 0 объект
(40.3. Доказательство теоремы 33.2)
эндообъект
669 0 объект
>
эндообъект
672 0 объект
(Упражнения)
эндообъект
673 0 объект
>
эндообъект
676 0 объект
(41. Проблемы оптимизации)
эндообъект
677 0 объект
>
эндообъект
680 0 объект
(41. 1. Пример. Прямоугольник с наибольшей площадью и заданным периметром)
эндообъект
681 0 объект
>
эндообъект
684 0 объект
(41.2. Упражнения)
эндообъект
685 0 объект
>
эндообъект
688 0 объект
(VI. Экспоненты и логарифмы)
эндообъект
689 0 объект
>
эндообъект
692 0 объект
(42. Экспоненты)
эндообъект
693 0 объект
>
эндообъект
696 0 объект
(42.1. Проблема со степенями отрицательных чисел)
эндообъект
697 0 объект
>
эндообъект
700 0 объект
(43. Логарифмы)
эндообъект
701 0 объект
>
эндообъект
704 0 объект
(44. Свойства логарифмов)
эндообъект
705 0 объект
>
эндообъект
708 0 объект
(45. Графики показательных функций и логарифмов)
эндообъект
709 0 объект
>
эндообъект
712 0 объект
(46. Производная от ax и определение e)
эндообъект
713 0 объект
>
эндообъект
716 0 объект
(47.Производные логарифмов)
эндообъект
717 0 объект
>
эндообъект
720 0 объект
(48. Пределы, включающие экспоненты и логарифмы)
эндообъект
721 0 объект
>
эндообъект
724 0 объект
(49. Экспоненциальный рост и распад)
эндообъект
725 0 объект
>
эндообъект
728 0 объект
(49.
1. Пример. Прямоугольник с наибольшей площадью и заданным периметром)
эндообъект
681 0 объект
>
эндообъект
684 0 объект
(41.2. Упражнения)
эндообъект
685 0 объект
>
эндообъект
688 0 объект
(VI. Экспоненты и логарифмы)
эндообъект
689 0 объект
>
эндообъект
692 0 объект
(42. Экспоненты)
эндообъект
693 0 объект
>
эндообъект
696 0 объект
(42.1. Проблема со степенями отрицательных чисел)
эндообъект
697 0 объект
>
эндообъект
700 0 объект
(43. Логарифмы)
эндообъект
701 0 объект
>
эндообъект
704 0 объект
(44. Свойства логарифмов)
эндообъект
705 0 объект
>
эндообъект
708 0 объект
(45. Графики показательных функций и логарифмов)
эндообъект
709 0 объект
>
эндообъект
712 0 объект
(46. Производная от ax и определение e)
эндообъект
713 0 объект
>
эндообъект
716 0 объект
(47.Производные логарифмов)
эндообъект
717 0 объект
>
эндообъект
720 0 объект
(48. Пределы, включающие экспоненты и логарифмы)
эндообъект
721 0 объект
>
эндообъект
724 0 объект
(49. Экспоненциальный рост и распад)
эндообъект
725 0 объект
>
эндообъект
728 0 объект
(49. 1. Перерыв и удвоение времени)
эндообъект
729 0 объект
>
эндообъект
732 0 объект
(49.2. Определение X0 и k)
эндообъект
733 0 объект
>
эндообъект
736 0 объект
(Упражнения)
эндообъект
737 0 объект
>
эндообъект
740 0 объект
(VII. Интеграл)
эндообъект
741 0 объект
>
эндообъект
744 0 объект
(50. Площадь под графиком)
эндообъект
745 0 объект
>
эндообъект
748 0 объект
(51.Когда f меняет знак)
эндообъект
749 0 объект
>
эндообъект
752 0 объект
(52. Основная теорема исчисления)
эндообъект
753 0 объект
>
эндообъект
756 0 объект
(52.1. Терминология)
эндообъект
757 0 объект
>
эндообъект
760 0 объект
(Упражнения)
эндообъект
761 0 объект
>
эндообъект
764 0 объект
(53. Неопределенный интеграл)
эндообъект
765 0 объект
>
эндообъект
768 0 объект
(53.1. Вы всегда можете проверить ответ)
эндообъект
769 0 объект
>
эндообъект
772 0 объект
(53.2. О «+C»)
эндообъект
773 0 объект
>
эндообъект
776 0 объект
(53.3. Стандартные интегралы)
эндообъект
777 0 объект
>
эндообъект
780 0 объект
(54.Свойства интеграла)
эндообъект
781 0 объект
>
эндообъект
784 0 объект
(55.
1. Перерыв и удвоение времени)
эндообъект
729 0 объект
>
эндообъект
732 0 объект
(49.2. Определение X0 и k)
эндообъект
733 0 объект
>
эндообъект
736 0 объект
(Упражнения)
эндообъект
737 0 объект
>
эндообъект
740 0 объект
(VII. Интеграл)
эндообъект
741 0 объект
>
эндообъект
744 0 объект
(50. Площадь под графиком)
эндообъект
745 0 объект
>
эндообъект
748 0 объект
(51.Когда f меняет знак)
эндообъект
749 0 объект
>
эндообъект
752 0 объект
(52. Основная теорема исчисления)
эндообъект
753 0 объект
>
эндообъект
756 0 объект
(52.1. Терминология)
эндообъект
757 0 объект
>
эндообъект
760 0 объект
(Упражнения)
эндообъект
761 0 объект
>
эндообъект
764 0 объект
(53. Неопределенный интеграл)
эндообъект
765 0 объект
>
эндообъект
768 0 объект
(53.1. Вы всегда можете проверить ответ)
эндообъект
769 0 объект
>
эндообъект
772 0 объект
(53.2. О «+C»)
эндообъект
773 0 объект
>
эндообъект
776 0 объект
(53.3. Стандартные интегралы)
эндообъект
777 0 объект
>
эндообъект
780 0 объект
(54.Свойства интеграла)
эндообъект
781 0 объект
>
эндообъект
784 0 объект
(55. Определенный интеграл как функция его границ интегрирования)
эндообъект
785 0 объект
>
эндообъект
788 0 объект
(56. Метод замены)
эндообъект
789 0 объект
>
эндообъект
792 0 объект
(56.1. Пример)
эндообъект
793 0 объект
>
эндообъект
796 0 объект
(56.2. Обозначение Лейбница для замены)
эндообъект
797 0 объект
>
эндообъект
800 0 объект
(56.3. Замена определенных интегралов)
эндообъект
801 0 объект
>
эндообъект
804 0 объект
(56.4. Пример замены в определенном интеграле)
эндообъект
805 0 объект
>
эндообъект
808 0 объект
(Упражнения)
эндообъект
809 0 объект
>
эндообъект
812 0 объект
(VIII.Приложения интеграла)
эндообъект
813 0 объект
>
эндообъект
816 0 объект
(57. Области между графиками)
эндообъект
817 0 объект
>
эндообъект
820 0 объект
(Упражнения)
эндообъект
821 0 объект
>
эндообъект
824 0 объект
(58. Принцип Кавальери и объемы твердых тел)
эндообъект
825 0 объект
>
эндообъект
828 0 объект
(58.1. Пример — Объем пирамиды)
эндообъект
829 0 объект
>
эндообъект
832 0 объект
(58.2. Общий случай)
эндообъект
833 0 объект
>
эндообъект
836 0 объект
(58.
Определенный интеграл как функция его границ интегрирования)
эндообъект
785 0 объект
>
эндообъект
788 0 объект
(56. Метод замены)
эндообъект
789 0 объект
>
эндообъект
792 0 объект
(56.1. Пример)
эндообъект
793 0 объект
>
эндообъект
796 0 объект
(56.2. Обозначение Лейбница для замены)
эндообъект
797 0 объект
>
эндообъект
800 0 объект
(56.3. Замена определенных интегралов)
эндообъект
801 0 объект
>
эндообъект
804 0 объект
(56.4. Пример замены в определенном интеграле)
эндообъект
805 0 объект
>
эндообъект
808 0 объект
(Упражнения)
эндообъект
809 0 объект
>
эндообъект
812 0 объект
(VIII.Приложения интеграла)
эндообъект
813 0 объект
>
эндообъект
816 0 объект
(57. Области между графиками)
эндообъект
817 0 объект
>
эндообъект
820 0 объект
(Упражнения)
эндообъект
821 0 объект
>
эндообъект
824 0 объект
(58. Принцип Кавальери и объемы твердых тел)
эндообъект
825 0 объект
>
эндообъект
828 0 объект
(58.1. Пример — Объем пирамиды)
эндообъект
829 0 объект
>
эндообъект
832 0 объект
(58.2. Общий случай)
эндообъект
833 0 объект
>
эндообъект
836 0 объект
(58. 3. Принцип Кавальери)
эндообъект
837 0 объект
>
эндообъект
840 0 объект
(58.4. Тела вращения)
эндообъект
841 0 объект
>
эндообъект
844 0 объект
(59.Примеры объемов тел вращения)
эндообъект
845 0 объект
>
эндообъект
848 0 объект
(59.1. Задача 1: Вращение R вокруг оси Y)
эндообъект
849 0 объект
>
эндообъект
852 0 объект
(59.2. Задача 2. Вращение R вокруг линии x=-1)
эндообъект
853 0 объект
>
эндообъект
856 0 объект
(59.3. Задача 3: вращать R вокруг линии y=2)
эндообъект
857 0 объект
>
эндообъект
860 0 объект
(60. Объемы по цилиндрическим оболочкам)
эндообъект
861 0 объект
>
эндообъект
864 0 объект
(60.1. Пример. Твердое тело, полученное вращением R вокруг оси y, снова)
эндообъект
865 0 объект
>
эндообъект
868 0 объект
(Упражнения)
эндообъект
869 0 объект
>
эндообъект
872 0 объект
(61.Расстояние от скорости, скорость от ускорения)
эндообъект
873 0 объект
>
эндообъект
876 0 объект
(61.1. Движение по линии)
эндообъект
877 0 объект
>
эндообъект
880 0 объект
(61.2. Скорость от ускорения)
эндообъект
881 0 объект
>
эндообъект
884 0 объект
(61.
3. Принцип Кавальери)
эндообъект
837 0 объект
>
эндообъект
840 0 объект
(58.4. Тела вращения)
эндообъект
841 0 объект
>
эндообъект
844 0 объект
(59.Примеры объемов тел вращения)
эндообъект
845 0 объект
>
эндообъект
848 0 объект
(59.1. Задача 1: Вращение R вокруг оси Y)
эндообъект
849 0 объект
>
эндообъект
852 0 объект
(59.2. Задача 2. Вращение R вокруг линии x=-1)
эндообъект
853 0 объект
>
эндообъект
856 0 объект
(59.3. Задача 3: вращать R вокруг линии y=2)
эндообъект
857 0 объект
>
эндообъект
860 0 объект
(60. Объемы по цилиндрическим оболочкам)
эндообъект
861 0 объект
>
эндообъект
864 0 объект
(60.1. Пример. Твердое тело, полученное вращением R вокруг оси y, снова)
эндообъект
865 0 объект
>
эндообъект
868 0 объект
(Упражнения)
эндообъект
869 0 объект
>
эндообъект
872 0 объект
(61.Расстояние от скорости, скорость от ускорения)
эндообъект
873 0 объект
>
эндообъект
876 0 объект
(61.1. Движение по линии)
эндообъект
877 0 объект
>
эндообъект
880 0 объект
(61.2. Скорость от ускорения)
эндообъект
881 0 объект
>
эндообъект
884 0 объект
(61. 3. Свободное падение в постоянном гравитационном поле)
эндообъект
885 0 объект
>
эндообъект
888 0 объект
(61.4. Движение на плоскости — параметрические кривые)
эндообъект
889 0 объект
>
эндообъект
892 0 объект
(61.5. Скорость тела, движущегося в плоскости)
эндообъект
893 0 объект
>
эндообъект
896 0 объект
(61.6. Пример — два движения по кругу из \24761.4)
эндообъект
897 0 объект
>
эндообъект
900 0 объект
(62. Длина кривой)
эндообъект
901 0 объект
>
эндообъект
904 0 объект
(62.1. Длина параметрической кривой)
эндообъект
905 0 объект
>
эндообъект
908 0 объект
(62.2. Длина графика функции)
эндообъект
909 0 объект
>
эндообъект
912 0 объект
(62.3. Примеры вычисления длины)
эндообъект
913 0 объект
>
эндообъект
916 0 объект
(63. Работа силы)
эндообъект
917 0 объект
>
эндообъект
920 0 объект
(63.1. Работа как интеграл)
эндообъект
921 0 объект
>
эндообъект
924 0 объект
(63.m*;lsdf=4X%rz-cuSŽc%]ՕdZspokeYokt[H
/ ILɹ9h ‘
)c+0m$QW
конечный поток
эндообъект
930 0 объект > эндообъект
933 0 объект > эндообъект
934 0 объект > эндообъект
931 0 объект >
/ProcSet [ /PDF /текст ]
>> эндообъект
947 0 объект >
ручей
xڥVKFWP>ev0@rZ;T\*T> 4Z
3. Свободное падение в постоянном гравитационном поле)
эндообъект
885 0 объект
>
эндообъект
888 0 объект
(61.4. Движение на плоскости — параметрические кривые)
эндообъект
889 0 объект
>
эндообъект
892 0 объект
(61.5. Скорость тела, движущегося в плоскости)
эндообъект
893 0 объект
>
эндообъект
896 0 объект
(61.6. Пример — два движения по кругу из \24761.4)
эндообъект
897 0 объект
>
эндообъект
900 0 объект
(62. Длина кривой)
эндообъект
901 0 объект
>
эндообъект
904 0 объект
(62.1. Длина параметрической кривой)
эндообъект
905 0 объект
>
эндообъект
908 0 объект
(62.2. Длина графика функции)
эндообъект
909 0 объект
>
эндообъект
912 0 объект
(62.3. Примеры вычисления длины)
эндообъект
913 0 объект
>
эндообъект
916 0 объект
(63. Работа силы)
эндообъект
917 0 объект
>
эндообъект
920 0 объект
(63.1. Работа как интеграл)
эндообъект
921 0 объект
>
эндообъект
924 0 объект
(63.m*;lsdf=4X%rz-cuSŽc%]ՕdZspokeYokt[H
/ ILɹ9h ‘
)c+0m$QW
конечный поток
эндообъект
930 0 объект > эндообъект
933 0 объект > эндообъект
934 0 объект > эндообъект
931 0 объект >
/ProcSet [ /PDF /текст ]
>> эндообъект
947 0 объект >
ручей
xڥVKFWP>ev0@rZ;T\*T> 4Z