Приведите пример конечного множества чисел бесконечного множества чисел: Приведите пример: А) конечного множества чисел; Б) бесконечного множества чисел.

Содержание

О бесконечных множествах

Вадим Дунаев

Раздел из книги «Занимательная математика. Множества и отношения»

Профессор. Теория множеств создавалась как инструмент для выяснения устройства бесконечных совокупностей объектов. Бесконечность всегда привлекала внимание людей. Термином “бесконечность” сначала обозначали все, что было невозможно сосчитать или перечислить. Бесконечное — это что-то запредельное, невообразимо большое или, напротив, чрезвычайно малое, к чему можно стремиться сколь угодно долго, но достичь которого невозможно. Приведите, пожалуйста, пример бесконечного объекта.

Простак. Первое, что приходит мне на ум, — вселенная, состоящая из бесчисленного количества звезд, атомов и других частиц.

Зануда. Множество целых чисел бесконечно: какое бы число мы ни взяли, всегда можно перейти к следующему, прибавив к предыдущему 1. Таким образом, мы никогда не сможем сказать “вот, все целые числа перечислены и других целых чисел больше нет”.

Профессор. На каком основании Вы, Простак, считаете вселенную бесконечной? В действительности Вы и никто другой не знаете, какая она, — бесконечная или конечная. Муравью килограммовый камень кажется бесконечно тяжелым. Число 2¹⁰⁰ настолько огромно, что простой перебор всех целых чисел, не превышающих его, с помощью самого современного компьютера потребует невообразимо много сроков жизни самого компьютера. Тем не менее, количество таких чисел конечно. Это означает, что процесс их пересчета когда-нибудь да закончится. Мы называем вселенную бесконечной, имея в виду лишь ее очень большие размеры, а также то, что никто из людей никогда не достигал ее границ. А вот множество всех целых чисел в самом деле бесконечно. Иначе говоря, мы доподлинно знаем, что оно бесконечно, поскольку таковым по определению оно создано нашим разумом. Для обозначения бесконечно большого количества в математике используют специальный символ

, а для бесконечно малого — 1/.

Однако и 1/ это не числа, а просто символы, поскольку они не подчиняется обычным правилам арифметики. Так, 2, 100, , т.е. арифметические операции над бесконечно большим количеством оставляют это количество бесконечно большим.

С античных времен бесконечное множество рассматривали как совокупность объектов, данную не в завершенном виде, а как постоянно формирующуюся. По заданному правилу эту совокупность можно было дополнить новыми объектами когда угодно. Так, множество целых чисел считалось существующим не

актуально, в готовом или завершенном виде, а существующим только потенциально. Его можно было постоянно пополнять новыми членами, но этот процесс никогда не мог быть завершен. Такой взгляд на бесконечные множества существовал вплоть до начала 1870-х годов, когда Георг Кантор стал рассматривать бесконечные множества как данные актуально. В результате он показал, что одни бесконечные множества могут включать в себя другие, т.

е. что бесконечные множества можно сравнивать в количественном отношении подобно конечным множествам.

Сравнение бесконечных множеств

Профессор. Конечные множества можно сравнить в количественном отношении (хотя бы принципиально, если не практически) так: сначала подсчитать количество элементов в каждом из них, а затем сравнить полученные числа. Для бесконечных множеств данный способ не годится, поскольку подсчет количества их элементов никогда не закончится или, лучше сказать, не завершится какими-то числами, которые можно сравнивать. Тем не менее, интуиция подсказывает нам, что одни из бесконечных множеств могут быть больше других. Попробуйте сравнить бесконечные множества всех натуральных и четных натуральных чисел.

Простак. Натуральные числа это 1, 2, 3, …. Каждое второе из них — четное. Очевидно, что четных чисел меньше в два раза, хотя и тех, и других бесконечно много.

Зануда. Странно все это. С одной стороны, оба множества бесконечны и не имеют количественной характеристики, а с другой — одно из них больше другого, и даже видно, во сколько раз.

Профессор. Похоже, вы оба согласны, что бесконечные множества можно сравнивать. Однако результат сравнения, полученный Простаком, оказался неверным. В действительности четных натуральных чисел столько же, сколько и всех натуральных чисел. Прежде чем разобраться с этой задачей, попробуйте решить более простую. Пусть имеются конечные множества болтов и гаек. Как определить без подсчета, равны ли их количества?

Простак. Я бы стал навинчивать гайки на болты или просто выкладывать пары болт-гайка. Если бы для каждого болта нашлась бы своя гайка, то количества болтов и гаек равны, а в противном случае — нет. Таким образом, я решил задачу, не выясняя, сколько именно было гаек и болтов.

Профессор. Прекрасно. Воспользуемся Вашим методом применительно к бесконечным множествам чисел.

Простак. Идея метода состоит в сопоставлении друг другу элементов различных множеств. Выпишем ряд натуральных чисел, а под ним — ряд натуральных четных чисел:

1, 2 , 3, 4, 5, 6, … — натуральные числа;

2, 4, 6, 8, 10, 12, … — четные натуральные числа.

Не трудно заметить, что каждому натуральному числу однозначно соответствует некоторое четное натуральное число. Так, натуральному числу n соответствует четное натуральное число 2n. И наоборот, каждому четному натуральному числу k однозначно соответствует натуральное число k/2. Выходит, можно образовать пары из элементов рассматриваемых множеств так, что ни один элемент какого-то из двух множеств не окажется без пары. Следовательно, множества натуральных и четных натуральных чисел равночисленны, если позволительно так сказать.

Профессор. Вы прекрасно справились с данной задачей. Поскольку количество элементов бесконечного множества не может быть выражено каким-либо числом, то говорят не о количестве, а о мощности множества. Для конечных множеств понятия их количества и мощности совпадают. Итак, только что установлено, что множества всех натуральных чисел и четных натуральных чисел равномощны. Очевидно, что аналогичным способом можно доказать, что равномощны множества натуральных и нечетных натуральных чисел.

Зануда. Я вынужден согласиться с приведенным доказательством равномощности рассматриваемых множеств, хотя результат не согласуется с интуицией, которая говорит нам, что множество натуральных чисел состоит из четных и нечетных натуральных чисел, взятых вместе. Таким образом, мы видим, что нарушается принцип, что целое больше своей части.

Профессор. Это один из примеров того, что иногда математика позволяет выяснить нечто, не подвластное нашей интуиции. Соотношения, выполняющиеся для конечных множеств, могут не выполняться применительно к бесконечным множествам. Бесконечность имеет особые свойства, которых нет в конечном. Так в чем же состоит метод, с помощью которого мы устанавливаем равномощность или неравномощность множеств?

Зануда. Как мы видели, суть метода состоит в попытке установить соответствие между элементами сравниваемых множеств. Это соответствие должно быть взаимно однозначным, чтобы множества были равномощными. Иначе говоря, каждому элементу одного множества должен соответствовать некоторый единственный элемент другого множества, и наоборот.

Профессор. Вы верно выразили суть метода сравнения множеств по их мощности. Теперь вы сможете сравнить множества натуральных и целых чисел. Попробуйте сделать это.

Простак. Целые числа это натуральные числа плюс те же натуральные числа, но со знаком “минус”, и еще 0. Иначе говоря, целые числа можно представить рядом: …-3, -2, -1, 0, 1, 2, 3, …. Очевидно, что множество целых чисел содержит в качестве своего подмножества все натуральные числа. Однако это еще не основание говорить о том, что данные множества неравномощны. Попробуем установить взаимно однозначное соответствие между ними, для чего выпишем ряды чисел один под другим:

… -3, -2, -1, 0, 1, 2, 3, …

… 1, 2, 3,…

Однако из данной записи не очевидно, как следует образовывать пары чисел из двух рядов и возможно ли это в принципе. Здесь надо подумать.

Зануда. Давайте упорядочим целые числа иначе: 0, 1, -1, 2, -2, 3, -3, …; натуральные числа оставим в их естественном порядке. Расположим ряды этих чисел один под другим:

0, 1, -1, 2, -2, 3, -3, …— целые числа;

1, 2, 3, 4, 5, 6, 7, … — натуральные числа.

Нетрудно заметить, что n-е по порядку целое число (обозначим его через z_n) можно вычислить по следующей формуле:

z_n = n/2, если n четное;

z_n= — (n-1)/2, если n нечетное.

С другой стороны, для каждого целого числа z можно однозначно указать его номер (натуральное число):

n= 2z, если z > 0;

n = 2z+1, если z0.

Таким образом, между целыми и натуральными числами установлено взаимно однозначное соответствие: каждому натуральному числу однозначно сопоставляется некоторое единственное целое число и, наоборот, каждому целому числу однозначно соответствует некоторое единственное натуральное число. Следовательно, натуральных чисел не меньше, но и не больше, чем целых, а значит их множества равномощны.

Профессор. Хорошее решение, приводящее к правильному результату.

Итак, мы только что убедились, что множества всех натуральных, только четных натуральных, только нечетных натуральных и целых чисел равномощны. При этом равномощность множеств определяется как существование взаимно однозначного соответствия между элементами данных множеств. Замечу, что кажущаяся парадоксальность полученных результатов имеет своей причиной рассмотрение бесконечных множеств как актуально данных в своем завершенном виде. Такой подход к бесконечным множествам был выполнен Кантором преднамеренно, хотя еще Галилео Галлией указывал, что он приведет к необходимости признать, что четных чисел столько же, сколько четных и нечетных вместе, а это по мнению подавляющего большинства его современников и предшественников считалось абсурдным.

Для бесконечных множеств такое утверждение, как “часть меньше целого” перестает быть верным. Это заметил еще древнегреческий математик Зенон, рассматривая следующее обстоятельство. Пусть дан треугольник АВС, в котором отрезок В’C’ параллелен основанию ВС и соединяет середины сторон, выходящих из вершины А.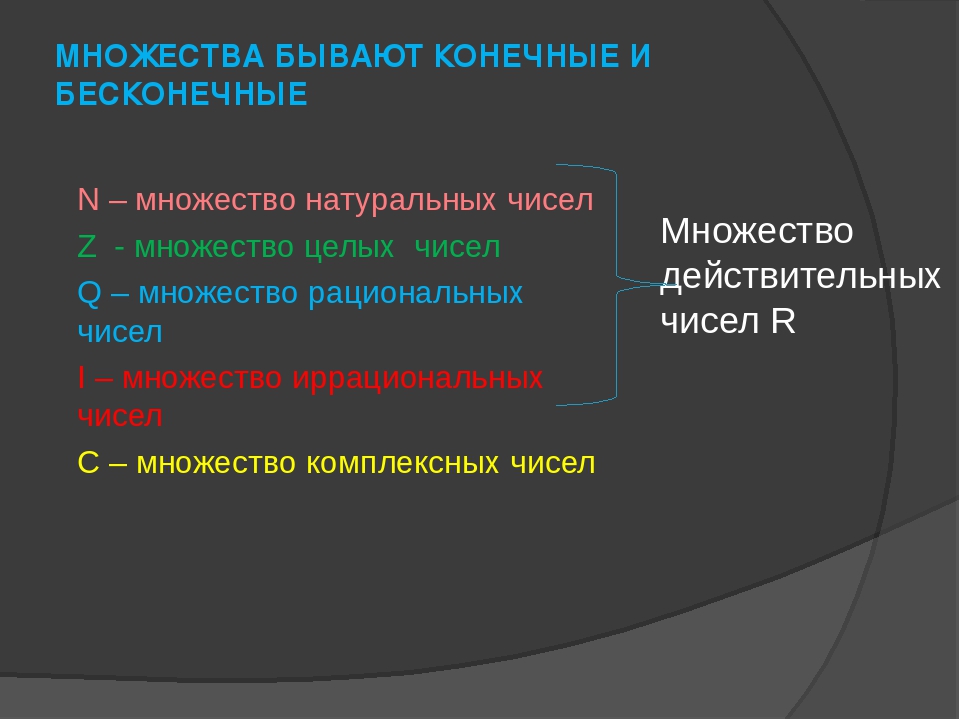 Спроектируем из этой вершины на ВС все точки отрезка В’C’. Тогда каждой точке отрезка В’C’ будет соответствовать некоторая точка основания ВС и, наоборот, каждой точке основания треугольника будет соответствовать какая-то точка отрезка В’C’. Например, точке X’ будет соответствовать точка X, а точке X — точка X ’. Следовательно, на отрезке В’C’, параллельном и равном отрезку ВА’ (А’ — середина основания ВС), размещается столько же точек, сколько и на вдвое большем отрезке ВС. При этом Зенон не знал, что аналогичный парадокс возникает при сравнении бесконечных подмножеств множества целых чисел.

На отрезке В’C’ размещается столько же точек, сколько на вдвое большем отрезке ВС

А теперь рассмотрим множество рациональных чисел, т.е. целых и дробей. Рациональное число, как известно, можно представить как частное от деления двух целых чисел. Особенность множества рациональных чисел состоит в том, что между любыми соседними целыми числами находится бесконечно много рациональных чисел. Например, между 0 и 1 находятся дроби 1/2, 1/3, 1/4, 1/5, … . Возникает подозрение, что рациональных чисел больше, чем целых: целых бесконечно много, а между любыми соседними целыми находится тоже бесконечно много чисел. Получается бесконечное множество, составленное из бесконечных множеств, что, согласитесь, представляется более сложным, чем множество натуральных чисел. Однако, как показал Кантор в 1874г., рациональных чисел столько же, сколько и натуральных. Трудность, с которой он столкнулся, заключалась в поиске способа нумерации рациональных чисел. Кантор расположил рациональные числа не в один ряд, а в бесконечной квадратной таблице, т.е. в бесконечно много рядов. Далее оставалось только найти зигзагообразный путь обхода всех чисел, позволяющий последовательно пронумеровать каждое из них.

Всякое множество, элементы которого можно взаимно однозначно сопоставить натуральным числам, Кантор назвал счетным. Другими словами, элементы счетного множества можно пересчитывать.

Метод доказательства счетности рациональных чисел

Зануда. А существуют ли несчетные множества, элементы которых пересчитать нельзя?

Профессор. Да, существуют. Например, множество всех действительных чисел, содержащее кроме рациональных еще и иррациональные числа (например, , ), несчетно. Множество действительных чисел находится во взаимно однозначном соответствии с множеством точек прямой. Обратите внимание, что множество рациональных чисел значительно “плотнее” множества целых чисел (между любыми соседними целыми числами располагается бесконечное множество рациональных чисел), но тем не менее оба эти множества равномощны. Плотность же множества действительных чисел существенно больше, и пересчитывать их нельзя. Последнее означает, что не существует взаимно однозначного соответствия между множествами действительных и натуральных чисел.

Простак. Мне трудно поверить в это. Что же может помешать нам последовательно, без пропусков, перебирать действительные числа, приписывая им натуральные номера?

Зануда. Сначала всем нам было трудно поверить, что натуральных чисел столько же, сколько целых и даже рациональных, а теперь трудно поверить, что есть множество, для нумерации элементов которого натуральных чисел просто не хватит. Но ведь именно последнее лучше всего согласуется с нашей интуицией. Воистину, наш разум способен сначала из сложного сделать простое, чтобы потом снова все усложнить! Вы хотите сказать, профессор, что нельзя придумать способ нумерации действительных чисел?

Профессор. Именно так!. Рассмотрим идею доказательства этого утверждения, придуманного Кантором. Сначала он предположил, что взаимно однозначное соответствие между натуральными и действительными числами существует. Затем он показал, что данное предположение приводит к противоречию и, следовательно, взаимно однозначное соответствие между натуральными и действительными числами невозможно. Таким образом, Кантор использовал метод доказательства от противного.

Доказательство можно заметно упростить, рассматривая только подмножество всех действительных чисел, заключенных между 0 и 1. Если уж это бесконечное подмножество окажется больше множества всех натуральных чисел, то все множество действительных чисел и подавно больше его.

Итак, предположим, что действительные числа в промежутке между 0 и 1 могут быть пронумерованы без повторов и пропусков натуральными числами. Другими словами, мы допускаем гипотезу, что все действительные числа, расположенные между 0 и 1, могут быть поставлены во взаимно однозначное соответствие с множеством натуральных чисел. Это означает, что мы можем составить некий бесконечный перечень действительных чисел, каждое из которых можно представить в виде бесконечной десятичной дроби.

Всякое действительное число можно представить бесконечной десятичной дробью. Такие бесконечные десятичные дроби, как 0.5000…, представим в виде эквивалентной бесконечной дроби 0.4999…. Перечень всех десятичных дробей, представляющих все действительные числа в промежутке от 0 до 1, может быть любым с точки зрения их порядка. Просто представим мысленно этот список: бесконечное количество различных бесконечно длинных десятичных представлений действительных чисел от 0 до 1. Каким бы ни был этот список, пронумеруем его элементами натуральными числами без пропусков и повторений. Перечень или, другими словами, список это — последовательность элементов, которым можно сопоставить натуральные числа: первому в списке элементу сопоставим 1, второму — 2 и т.д.

Теперь задача состоит в том, чтобы построить такую десятичную дробь, которой нет в указанном списке. Если нам это удастся, то тем самым мы докажем, что наш первоначальный перечень всех действительных чисел от 0 до 1 не полон и, следовательно, его нумерация не является нумерацией всех десятичных дробей от 0 до 1. Разумеется, мы можем пополнить начальный перечень вновь сконструированным числом. Однако ничто не мешает нам повторить аналогичные рассуждения, с помощью которых мы создадим еще одно новое действительное число, которого раньше не было в списке, и так далее. Итог будет один — список нумерованных действительных чисел всегда не полон. А это означает, что наша нумерация относится не к тому объекту, для которого она предназначалась изначально. Иначе говоря, наша нумерация нумерует не все действительные числа от 0 до 1 и, следовательно, она не является нумерацией этого подмножества действительных чисел. Так как это положение вещей будет сохраняться при сколь угодно долгом пополнении первоначального списка вновь созданными действительными числами, то мы должны признать, согласно Кантору, что нумерации действительных чисел просто не существует. Такова идея доказательства.

Зануда. Уважаемый профессор, если я Вас правильно понял, получается следующее. Сначала мы предполагаем, что множество действительных чисел можно представить в виде перечня всех его элементов, пусть даже бесконечного. Само понятие перечня предполагает некоторую, хотя бы произвольную, упорядоченность его элементов. Так, перечень создается из элементов любого множества следующим образом: сначала как-то выбирается первый элемент, затем второй и, далее, все остальные. Коль скоро мы можем сделать это, то можем и пронумеровать элементы этого списка натуральными числами 1, 2, 3,… . Таким образом, гипотеза о возможности нумерации действительных чисел уже провозглашена. Далее Вы, профессор, вместе с Кантором, говорите, что любая нумерация этого множества таковой не является по той простой причине, что само множество не соответствует своему определению, т.е. не является множеством всех действительных чисел в промежутке от 0 до 1. Ведь Вы говорите, что можете построить число, не входящее в исходный перечень. На этом основании Вы заключаете, что нумерация действительных чисел невозможна.

Профессор. Вы верно поняли мысль Кантора, которую я намерен лишь только растолковать, не претендуя ни на что большее. Давайте теперь рассмотрим ее техническую сторону. Это интересно как феномен изобретательской деятельности человека.

Итак, мы должны построить новое число, которого не было в первоначальном списке. Это число должно отличаться по крайней мере одним десятичным знаком (цифрой в одном из разрядов) от каждого из действительных чисел в списке. Вместе с тем, оно должно быть действительным числом, расположенным между 0 и 1.

Пусть имеется бесконечный перечень бесконечных десятичных представлений действительных чисел от 0 до 1. В этом перечне такие бесконечные десятичные дроби, как 0.5000…, представим в виде эквивалентной бесконечной дроби 0.4999….. Для построения нового числа, не входящего в указанный перечень, выполним следующие действия:

1. Берем первое число в исходном перечне. Первую десятичную цифру в новом числе определяем так:

· Если первая цифра десятичного представления рассматриваемого числа из перечня равна 1, то пишем 9 на первом месте после разделительной точки;

· Если первая цифра десятичного представления рассматриваемого числа не равна 1, то пишем 1 на первом месте после разделительной точки.

2. Берем второе число в исходном перечне и определяем вторую цифру в новом числе:

· Если вторая цифра десятичного представления рассматриваемого числа равна 1, то пишем 9 на первом месте после разделительной точки;

· Если вторая цифра десятичного представления рассматриваемого числа не равна 1, то пишем 1 на втором месте после разделительной точки.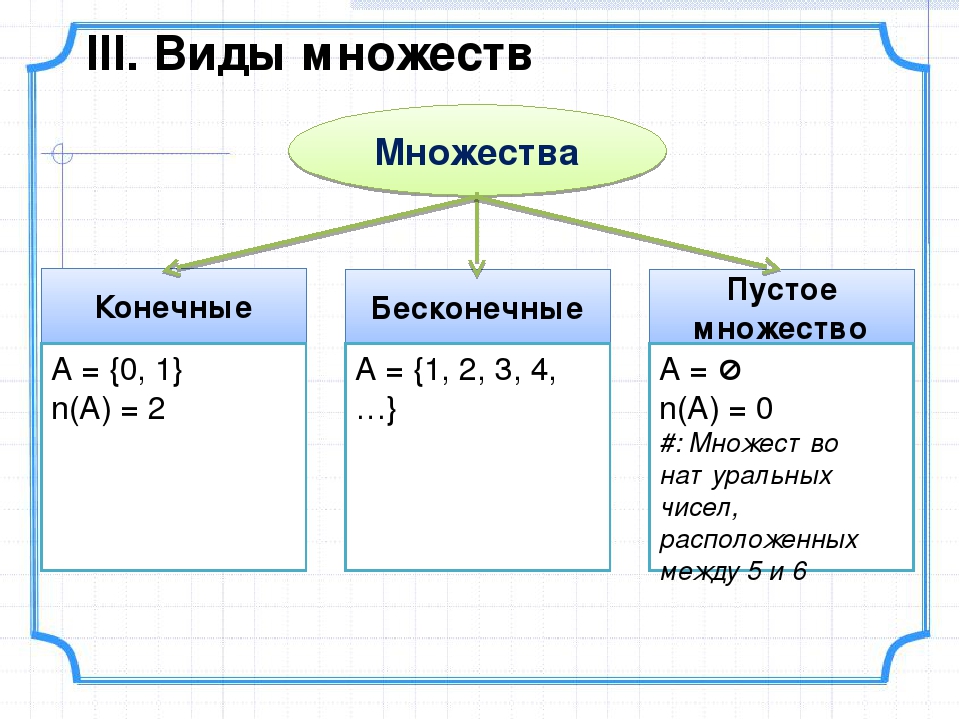

3. Построение нового числа продолжается путем изменения n-ой цифры n-го числа в исходном списке аналогичным образом:

· Если n-я цифра десятичного представления рассматриваемого числа равна 1, то пишем 9 на n-м месте после разделительной точки;

· Если n-я цифра десятичного представления рассматриваемого числа не равна 1, то пишем 1 на n-м месте после разделительной точки.

Новое число будет отличаться по крайней мере одним десятичным знаком от каждого действительного числа в исходном перечне и, вместе с тем, оно будет действительным числом, расположенным в промежутке от 0 до 1. Таким образом, предположение, что действительные числа можно взаимно однозначно сопоставить с натуральными числами, приводит к противоречию, а потому должно быть отброшено. Обратите внимание, что при доказательстве мы просматривали цифры чисел в перечне по диагонали. Поэтому метод, которым был получен данный результат, называют диагональным.

Диагональный метод доказательства того, что множество действительных чисел несчетно

Множество всех подмножеств данного множества

Профессор. Ранее мы рассматривали операции (объединение, пересечение, вычитание), с помощью которых можно было из одних множеств получать другие множества (см. разд. 3.2). Новые множества могут быть построены и другими средствами. Так, мы можем рассмотреть множество, составленное из всех подмножеств данного множества. Пусть, например, дано множество из трех элементов. Тогда множество всех его подмножеств (обозначим его как ) состоит из восьми элементов:

— само множество ,

Ø — пустое множество

}

Обратите внимание, что элементами множества являются множества. Если множество состоит из n элементов, то множество всех его подмножеств состоит из элементов. Если обозначить количество элементов множества как ||, то. В частности пустое множество не имеет элементов (|Ø|=0), поэтому . Я надеюсь, что вы понимаете, в чем состоит различие между и .

Очевидно, что множество всех подмножеств конечного множества всегда больше данного множества: . А выполняется ли это неравенство в случае бесконечных множеств?

Зануда. Сразу и не скажешь. Надо проверить, возможно ли взаимно однозначное соответствие между множествами и . Но как его построить?

Простак. Но быть может следует попытаться доказать неравенство методом от противного, чтобы не заниматься взаимно однозначным соответствием в явной форме?

Профессор. Это хорошая идея. Попробуйте реализовать ее.

Простак. Пусть это сделает Зануда со всей присущей ему тщательностью.

Зануда. Хорошо, я попытаюсь. Итак, теорему сформулируем следующим образом: любое множество неравномощно множеству всех его подмножеств.

Доказывать будем методом от противного, т.е. предположим, что равномощно множеству . Но это означает, что существует взаимно однозначное соответствие между элементами множества и элементами множества . Здесь я позволю себе ввести несложные символические обозначения. Пусть — указанное взаимно однозначное соответствие; — подмножество множества , которое соответствие сопоставляет элементу . Надеюсь понятно, что .

Очевидно, что каким бы ни было взаимно однозначное соответствие , для любого элемента возможны два варианта:

q — элемент принадлежит сопоставляемому множеству;

q — элемент не принадлежит сопоставляемому множеству

Вот здесь начинается самое интересное. Рассмотрим подмножество множества всех тех элементов , для которых . Не исключено, что множество пусто, но это не имеет значения. Так как соответствие взаимно однозначно, то существует элемент , для которого . Спрашивается, что имеет место: или ?

Соответствие f cопоставляет элементу x множества А некоторое его подмножество S

Допустим сначала, что . Но тогда , а и, следовательно, . Получаем противоречие. Предположим обратное: . Но тогда и опять получаем противоречие. Другими словами, с одной стороны , а с другой — . Данное противоречие мы получили в предположении, что множества и равномощны. Отсюда следует, что предположение было неверным. Значит, множества и не равномощны. На этом доказательство заканчивается.

Простак. Как только Зануда ввел в рассмотрение подмножество из всех таких элементов, что , я сразу понял, что следует ожидать противоречия. Это подмножество определяется таким же способом, как и множество гетерологических прилагательных, или множество тех, кого должен брить брадобрей. Только в данном случае противоречивость такого множества сыграла нам наруку, а не просто обескуражило.

Профессор. Как мы уже знаем, множества натуральных, целых и рациональных чисел счетны, а множество действительных чисел — нет. Теперь мы узнали, что множество всех подмножеств данного множества больше последнего. Например, множество всех подмножеств натуральных чисел больше множества всех рациональных чисел.

Прямая и плоскость

Профессор. Мы знаем со времен Рене Декарта, привнесшего числа и алгебру в геометрию, что каждой точке прямой можно сопоставить число — координату этой точки. Пусть дан отрезок прямой, левому концу которого приписано число 0, а правому — 1. Внутренним точкам данного отрезка взаимно однозначно сопоставлены числа в промежутке от 0 до 1 в их естественном порядке. Но какие числа? Хватит ли для этой цели только рациональных чисел (т.е. дробей)?

Простак. Любой отрезок прямой состоит и бесконечного количества точек. Точка не имеет протяженности. Если бы мы взяли лишь конечное их количество на отрезке прямой, то между ними образовались бы промежутки. С увеличением количества точек ширина промежутков между ними уменьшалась бы, но оставаясь все же больше нуля. Но тогда возможен случай, когда два отрезка пересекаются не в точке а в промежутке, что противоречит аксиоме евклидовой геометрии, согласно которой две пересекающиеся прямые имеют одну и только одну общую точку.

При недостаточной плотности точек пересекающиеся отрезки могут не иметь общей точки

Зануда. То, что точек в отрезке конечной длины бесконечно много, и так понятно.

Простак. А я и не собирался это доказывать. Просто я хотел наглядно показать, что может быть, если множество точек не достаточно плотно.

Зануда. Физическая линия как след, оставленный карандашом, под лупой с достаточным увеличением предстанет как набор дискретных пятен. Математическая же линия и под микроскопом любой силы будет выглядеть так же, как и без него. Впрочем, математическую линию мы видим не глазами, а умом. Плотность точек на ней столь велика, что между ними нет никаких промежутков. Не пойму, куда ты клонишь?

Простак. Минуточку терпения, Зануда. Допустим теперь, что каждой точке отрезка прямой можно взаимно однозначно сопоставить рациональные числа из подмножества, например, от 0 до 1. Возьмем два таких отрезка и используем их в качестве катетов прямоугольного треугольника. Заметьте, что концевые точки гипотенузы являются одновременно и концевыми точками катетов, на которые гипотенуза опирается. Другими словами, вершины треугольника это общие точки гипотенузы и смежных с ней катетов. Мы не можем удалить концевую точку ни гипотенузы, ни катета, ибо вершина треугольника это по определению точка пересечения сторон треугольника. Длины катетов равны 1, а гипотенуза, согласно теореме Пифагора, имеет длину . Это число, сопоставленное концевой точке гипотенузы не является рациональным, т.е. оно не может быть получено делением одного целого числа на другое целое число. Следовательно, рациональных чисел недостаточно, чтобы их можно было поставить во взаимно однозначное соответствие с точками отрезка прямой.

Рациональных чисел недостаточно, чтобы их можно было поставить во взаимно однозначное соответствие с точками отрезка прямой

Профессор. Будем считать Ваши рассуждения, Простак, не строгим доказательством, а проясняющими существо дела. Итак, точек на прямой больше, чем рациональных чисел. В действительности их столько же, сколько действительных чисел — рациональных и иррациональных вместе взятых. Это означает, что меду этими двумя множествами существует взаимно однозначное соответствие.

Говорят, что множества точек прямой (вообще любой линии) и действительных чисел образуют континуум — бесконечную и непрерывную совокупность. Между любыми двумя сколь угодно близкими точками линии находится бесконечно много точек, а между любыми двумя действительными числами находится бесконечно много действительных чисел.

А что вы скажете о возможности взаимно однозначного соответствия между множествами всех точек прямой и плоскости, например, между точками отрезка единичной длины и квадрата со стороной, равной 1?

Простак. Мне кажется, что в данном случае взаимно однозначного соответствия быть не может, поскольку точек в квадрате явно больше, чем на прямой. Можно представить себе квадрат как бесконечно много отрезков параллельных прямых, расположенных одна подле другой и покрывающих всю его площадь. При этом мощность множества таких отрезков должна быть такой же, как и мощность множества точек любого из них. А эта мощность, как нам уже известно, равна мощности множества всех действительных чисел.

Зануда. Ааналогия с покрытием квадрата очень узкими полосами лишь делает наглядными трудности построения или хотя бы выяснения возможности взаимно однозначного соответствия между точками квадрата и отрезка прямой. Интуиция подсказывает мне, что Простак скорее прав, чем не прав. Однако, имея дело с бесконечными множествами, мы должны быть готовы ко всему.

Профессор. Оказывается точки квадрата можно отобразить на точки отрезка прямой взаимно однозначным образом. Когда Кантор доказал это в 1877г. , то сам был чрезвычайно удивлен полученным результатом: “Я вижу это, но никак не могу этому поверить!” Для большинства математиков это было настоящей сенсацией, а немецкий математик Л. Кронекер вообще не принял его. Кронекер известен очень высокими требованиями к строгости определений математических объектов. Считая, что “Бог создал целые числа, а все остальное — дело рук человеческих”, он, в частности, не признавал существования иррациональных чисел. Так, число он представлял бесконечной суммой рациональных чисел 1 – 1/3 + 13 – 1/7 +…

Я лишь кратко поясню идею доказательства Кантора возможности взаимно однозначного соответствия между точками плоскости и прямой. Каждая точка плоскости представляется парой чисел — координатами , которые можно представить бесконечными десятичными дробями. Эти две дроби комбинируются по определенному правилу, чтобы получить одну дробь, которая сопоставляется с точкой на прямой. Данная процедура обратима и, следовательно, она устанавливает взаимно однозначное соответствие между точками плоскости и прямой.

Комбинация двух десятичных дробей, представляющих точку на плоскости, производится следующим образом. Цифры дроби последовательно разбиваются на группы. Каждая цифра, кроме 0, начинает новую группу. Бесконечная дробь, соответствующая точке на прямой, составляется из полученных групп цифр: первая группа из числа , первая группа из числе , вторая группа из числа , вторая группа из числа и так далее.

Установка взаимно однозначного соответствия между точками плоскости и прямой

Парадоксы бесконечности

Рука дающего не оскудеет

Профессор. Представим себе мешок с бесконечным количеством шаров, пронумерованных натуральными числами. В течение одной минуты шары вынимаются из мешка и возвращаются обратно по следующему алгоритму:

1. За одну минуту до окончания данного алгоритма из мешка вынимается шар с номером 1.

2. Через 1/2 минуты после шага 1 из мешка вынимаются шары с номерами 2 и 3, а шар 1 возвращается в мешок.

3. Через 1/4 минуты после шага 2 из мешка вынимаются шары с номерами 4, 5, 6, 7, а шары 2 и 3 возвращаются.

^4.Через 1/8 минуты после шага 3 из мешка вынимаются шары с номерами 8, 9,…, 15, а шары 4, 5,6, 7 возвращаются. Следующие шаги данного алгоритма выполняются аналогичным образом.

Не трудно заметить, что в каждый момент из мешка извлекается в два раза больше шаров, чем возвращается назад. Сколько шаров окажется вне мешка ровно через минуту после начала работы описанного алгоритма?

В каждый момент из мешка извлекается вдвое больше шаров, чем возвращается обратно

Зануда. На первом шагу, в самом начале минуты, вне мешка был один шар. На втором шагу, через 1/2 минуты, — 2 шара, на третьем, еще через 1/4 минуты, — 4 шара. На n-м шагу, через 1/2^n-1минуты после предыдущего шага или за это же время до окончания минутного срока, вне мешка будет 2^n-1 шара.

Очевидно, что необходимо сначала определить, сколько шагов будет сделано в течение всей минуты.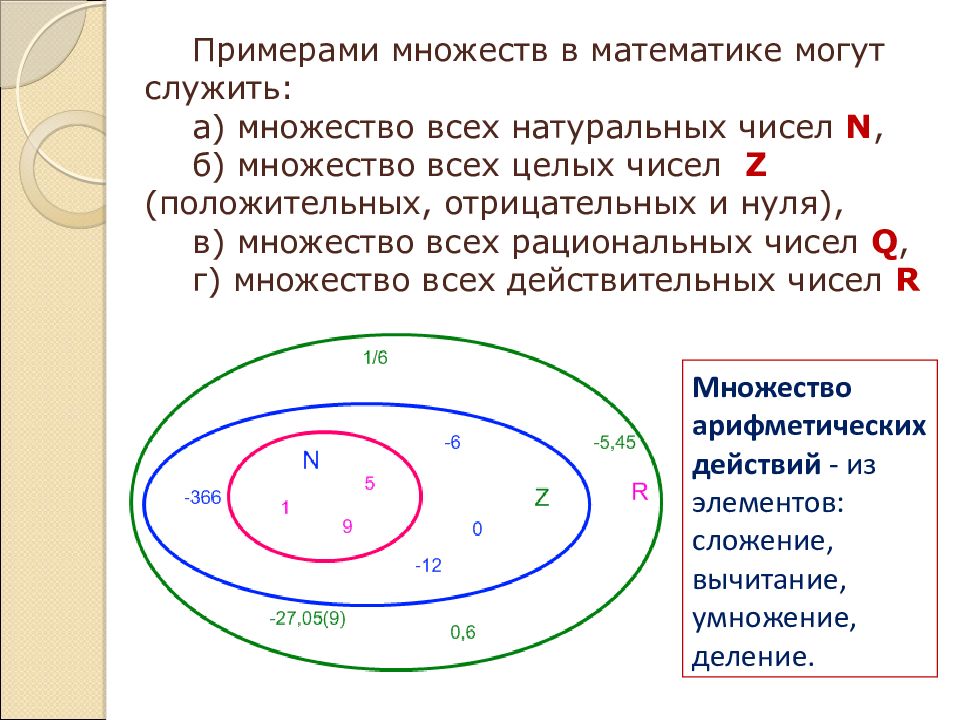 Первый шаг был сделан в начале минуты, второй — через 1/2 (т.е. 1/2¹ ) минуты, третий — через 1/2¹ + 1/2²после начала, четвертый — через 1/2¹ + 1/2² + 1/2³, n-й шаг был сделан через 1/2¹ + 1/2² + 1/2³ + … + 1/2^n-1 минуты. Очевидно, что количество шагов n, выполненное за одну минуту, можно найти из уравнения:

1/2¹ + 1/2² + 1/2³ + … + 1/2^n-1 = 1

Правда, я не знаю, как его решить, но это, я думаю, трудность технического характера, которую можно преодолеть с помощью, например, математического справочника.

Простак. Давайте попробуем составить другое уравнение. А именно, попытаемся определить, сколько времени еще осталось до истечения минуты на n-м шаге алгоритма. На первом шаге остается еще целая минута, на втором — 1/2 = 1/2¹ минуты, т.к. этот шаг был сделан через полминуты после начала работы. На третьем шаге оставалось 1/4 = 1/2² минуты, а на n-м шаге — 1/2^n-1минуты. Чтобы определить номер шага, на котором минута будет полностью исчерпана, достаточно решить очень простое уравнение:

1/2^n-1 = 0

Теперь мы хорошо видим, что ни при каком конечном числе n это равенство не выполняется точно, но в то же время замечаем, что с ростом n левая его часть очень быстро приближается к 0. Можно сказать, что при n→∞ величина 1/2^n-1 равна нулю со сколь угодно большой точностью. Например, на 10-м шаге работы алгоритма до окончания минуты останется меньше 0.12 секунды, а на 25-м шаге — меньше 0.000004 секунды. Это я подсчитал с помощью калькулятора.

Зануда. Но, насколько я помню, в задаче спрашивалось, сколько шаров окажется вне мешка ровно через минуту. На n-м шаге работы алгоритма это количество, как мы уже видели, равно 2^n-1. Минута будет исчерпана при n→∞ и, следовательно, вне мешка окажется бесконечно много шаров.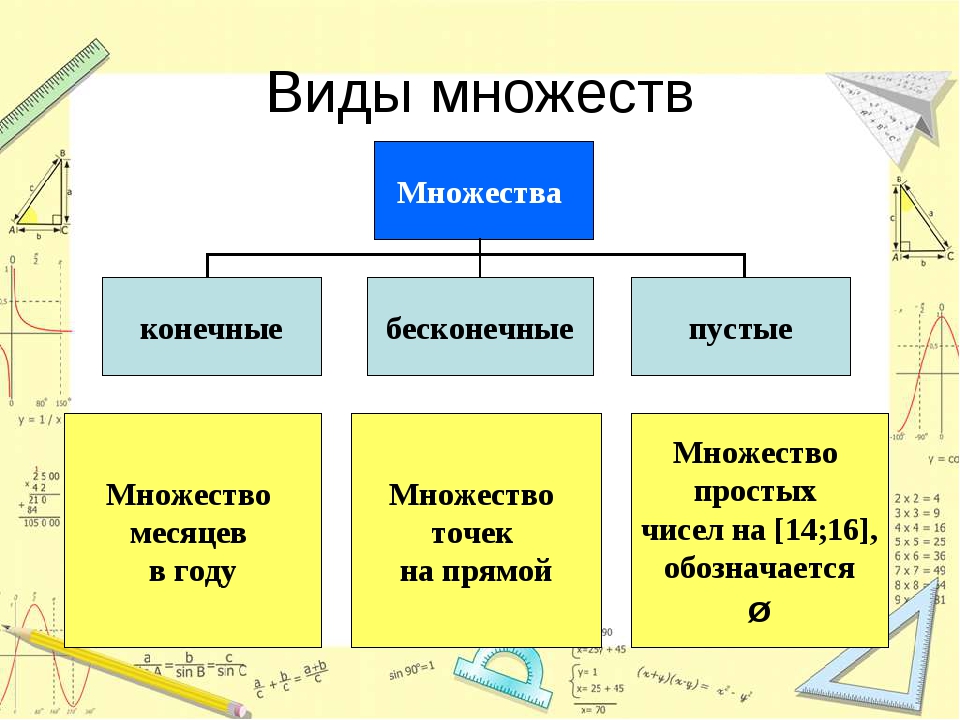

Простак. Но ведь и в мешке будет также бесконечно много шаров.

Зануда. А почему это тебя удивляет? Нас же теперь не шокирует тот факт, что если из множества всех целых чисел удалить все только четные числа, коих бесконечно много, то оставшихся чисел также будет бесконечно много.

Простак. Я не это имел ввиду, просто неудачно выразился. Меня удивляет, что по истечении минуты любой конкретный шар окажется в мешке, не смотря на то, что вне мешка будет бесконечно много шаров. Например, где окажется k-й шар в момент истечения минуты?

В момент, сколь угодно близкий к завершению минуты, шары 1, 2, 3 и так далее до, возможно, какого-то k-го шара уже будут в мешке. Особым является момент извлечения-возвращения шаров. Рассмотрим его подробнее.

Можно заметить, что на n-м шаге работы алгоритма из мешка извлекаются шары с номерами:

2ⁿ, 2ⁿ+ 1, …, 2ⁿ⁺¹-1,

а назад возвращаются (если n >1) шары с номерами:

2^n-1, 2^n-1+ 1, …, 2ⁿ— 1.

Для любого номера k найдется шаг n алгоритма такой, что

2^n-1k 2ⁿ— 1

и, следовательно, на этом шаге k-й шар окажется в мешке. Это произойдет до истечения минуты или в момент, сколь угодно близкий к ее окончанию. Таким образом, получается, что любой конкретный шар (с любым заданным номером) к моменту окончания минуты будет в мешке.

Зануда. Однако к этому же моменту, как мы убедились чуть ранее, вне мешка будут находиться бесконечно много шаров. Парадокс!

Профессор. Вы оба рассуждали довольно разумно, но упустили из виду важное обстоятельство, что и привело к противоречию. Обратите внимание, что алгоритм, состоящий из бесконечного количества извлечений-возвращений шаров, привязанных к моментам времени внутри минуты, не определен для последнего момента этой минуты. Данный алгоритм состоит из бесконечного количества шагов, но продолжительность его работы меньше одной минуты. Действительно, время работы алгоритма определяется суммой бесконечного количества временных интервалов между его шагами — 1/2¹ + 1/2² + 1/2³ + … + 1/2^n-1 + …. Для любого, сколь угодно большого числа шагов эта сумма меньше 1. Эту единицу можно рассматривать лишь как тот предел, к которому сумма постоянно приближается с добавлением каждого нового члена, но ни при каком конечном числе всех членов не достигает его. Последний момент минуты не принадлежит временному интервалу работы алгоритма, на котором он определен, а значит, мы не можем сказать, что он сотворит в этот момент.

Простак. Тем не менее мы можем предсказать, что будет в момент, сколь угодно близкий к концу минуты.

Профессор. Разумеется, поскольку для такого момента всегда найдется интервал, концы которого привязаны к двум смежным шагам алгоритма, содержащий этот момент.

Простак. Но как Вы объясните следующее обстоятельство. С одной стороны, алгоритм выполняет бесконечное количество шагов, т.е. никогда не завершает своей работы. С другой стороны, длительность его работы не может превысить одной минуты. Что же мы будем реально наблюдать в момент окончания минуты и далее? С одной стороны, спустя минуту и сколько угодно времени алгоритм должен продолжать работу, так как в противном случае он не содержал бы бесконечное количество шагов. Но, с другой стороны, он не определен на интервале времени, начинающемся с конца рассматриваемой минуты. Словом, я не могу представить себе эту противоречивую ситуацию.

Профессор. Противоречивую ситуацию всегда трудно себе представить наглядно, на то она и противоречивая. Поэтому математики и считают противоречивые объекты несуществующими.

Представьте себе некий алгоритм, который, согласно своему определению, что-то делает только по пятницам. А вас интересует, что он делает в остальные дни недели. Правомерно ли это? Думаю, что нет. Этот гипотетический алгоритм работает бесконечно долго, если считать, что время никогда не остановится и пятницы будут следовать друг за другом через каждую неделю. Однако для наблюдателя, переживающего сейчас, например, понедельник данный алгоритм просто ничего не делает, ожидая очередной пятницы. Если вы скажете, что такое ожидание входит в определение алгоритма и тем самым является его деятельностью, то тогда я скажу, что алгоритм приостановился на неделю.

— 1.

Практическая работа № 1. Способы задания множеств

Вопросы к работе

1. Какие множества называются конечными, какие бесконечными, какие пустыми? Приведите примеры конечных, бесконечных, пустых множеств.

2. Что значит задать множество?

3. Что значит задать множество пересечением элементов? Когда это можно сделать? Приведите пример множеств, заданных пересечением элементов.

4. Что значит задать множество указанием характеристического свойства элементов? Приведите примеры множеств, заданных указанием характеристического свойства элементов.

5. Дайте определение характеристического свойства элементов множества.

Образцы решения заданий

Пример 1. Задать с помощью характеристического свойства элементов множество всех положительных чисел.

Ответ: .

Пример 2. Задать перечислением элементов множества, заданные указанием характеристического свойства элементов:

. Ответ: М = {1; 2; 3; 4}.

Пример 3. Указать стандартное обозначение множества М и изобразить его на числовой прямой:

Упражнения

Приведите примеры множеств, составленных из объектов следующих видов:

а) неодушевленных предметов;

б) животных;

в) растений;

г) геометрических фигур;

д) населенных пунктов;

е) водоемов;

ж) политических деятелей.

2. Назовите элементы, принадлежащие множеству:

а) студентов вашей группы;

б) предметов, изучаемых в I семестре вашей специальности;

в) всех частей света;

г) субъектов федерации, входящих в Российскую Федерацию.

3. Пусть А – множество многоугольников. Принадлежат ли этому множеству:

а) восьмиугольник;

б) параллелограмм;

в) отрезок;

г) параллелепипед;

д) круг;

е) полукруг?

4. Множество С состоит из квадрата, круга и треугольника. Принадлежит ли этому множеству диагональ квадрата?

5. Прочитайте запись и укажите, какие из указанных высказываний истина, а какие ложь:

а) 270 N; ж) -3 Z;

б) 0 N; з) Q;

в) –3 N; и) R;

г) 1 Q; к) sin 2,3 R;

д) –7 N; л) tg R.

е) 22 N;

6. Пусть Е – множество европейских государств, А – множество азиатских государств. Какие из следующих высказываний истина, а какие – ложь?

а) Франция Е; з) Волга Е;

б) Испания Е; и) Нигерия А;

в) Монголия А; к) Гималаи А;

г) Индия А; л) Япония А;

д) Ирак Е; м) Альпы Е;

е) Турция А; н) Швеция А.

ж) Байкал А;

7. Запишите перечислением элементов следующие множества:

а) А – множество нечетных чисел на отрезке [1; 15];

б) В – множество натуральных чисел, меньших 8;

в) С – множество натуральных чисел, больших 10, но меньших 12;

г) D – множество двузначных чисел, делящихся на 10;

д) Е – множество натуральных делителей числа 18;

е) F – множество чисел, модуль которых равен .

8. Запишите перечислением элементов следующие множества:

а) множество различных букв в слове «головоломка»;

б) множества цифр числа 134433154.

9. Изобразите на числовой прямой множество решений неравенства с одним неизвестным x:

а) x > 5,3;

б) x ≤ –3,8;

в) – 4,5 ≤ x < 4;

г) 2,7 ≤ x ≤ 9.

10. Выясните, множество решений какого неравенства изображено на числовой прямой в каждом случае:

Индивидуальное задание

Прочитайте следующие записи и перечислите элементы каждого из множеств:

1. а) А = {x | x N , -2 ≤ x ≤ 5};

б) В = {х | x Z , | x | < 3};

в) С = {х | x N , 2х2 + 5х –3 = 0}.

2. а) А = {х | x Q , 3х2 = 9};

б) В = {х | x Z, x – 3 = (х + 2) · 4х};

в) С = {х | x N ,–3 ≤ х < 1}.

3. а) А = {х | x Z, | x | = 4};

б) В = {х | x N , –2 < х ≤ 5};

в) С = {х | x Q , x 2 + 3х + 4 = 0}.

4. а) А = {х | x Z, –2 ≤ x ≤ 3};

б) В = {х | x N , (5х + 6)(х – 4) ≤ 0};

в) С = {х | x N , |x| = 7}.

5. а) А = {х | x N , | х | ≤ 5};

б) В = {х | х Z , 2х – 3 = 5х + 7};

в) С = {х | х Z, –1 ≤ х ≤ 3}.

6. а) А = {х | х N, х ≤ 4};

б) В = {х | х Z, (х + 1)(–х – 3) > 0};

в) С = {х | х N, | х | = 5}.

7. а) А = {х | х N , -3 ≤ x ≤ 2};

б) В = {х | х Z , | х | < 3};

в) С = {х | х N, 3х2 + 5х – 2 = 0}.

8. а) А = {х | х Z, | х | ≤ 4};

б) В = {х | х N , (х + 1)(2х + 5) < 0};

в) С = {х | х N , –7 ≤ х ≤ 4}.

9. а) А = {х | х N , 3 = (5х + 2) х};

б) В = {х | х Z , | х | < 2};

в) С = {х | х N, –5 ≤ х < 4}.

10. а) А = {х | х Z , –1 ≤ х < 3};

б) В = {х | х Z , | х | ≤ 3},

в) С = {х | х N, 4х 2+ 4х – 3 = 0}.

Найти множество решений следующих уравнений и неравенств, изобразить это множество на числовой прямой:

Задания для самоконтроля

1) Найдите длину каждого из следующих множеств и назовите их элементы:

а) {а}; б) {{а}}; в) ; г) {}; д) {{ a; b }, { а }}; е) {{ a; b; c}, а };
ж) {{ а }, а, }.

2) Из каких элементов состоят следующие множества:

а) множество трехзначных чисел, составленных с помощью цифр 1 и 3;

б) множество трехзначных чисел, составленных с помощью цифр 1, 3, 5, причем так, что никакие две цифры не встречаются дважды;

в) множество трехзначных чисел, составленных из цифр 1, 3, 5 так, что любые две соседние цифры различны;

г) множество трехзначных чисел, сумма цифр которых равна 5.

3) Задайте перечислением элементов множество делителей числа 36. Можно ли задать таким образом множество кратных чисел числу 36?

Множества чисел и примеры числовых множеств

Множества чисел бывают конечными или бесконечными и их принято обозначать большими буквами A, B, …, а их элементы – маленькими буквами, например, x, y, z,….

Что такое множество чисел

Определение

Термин множества чисел можно описать, как совокупность, объединение, набор некоторых объектов произвольной природы – элементы множества. Например, множество книг в библиотеке, множество студентов факультета, множество парных чисел, множество точек заданного отрезка и т. п.

Если элемент принадлежит множеству , тогда пишут , если же элемент не принадлежит множеству , тогда пишут, что или .

Множества, в которых нет ни одного элемента, называется пустым множеством и обозначается .

Рассмотрим несколько важных операций:

1. Два множества и называются равными (обозначают ), если они состоят из одинаковых элементов.

2. Множество называется подмножным множеством , если каждый элемент множества есть элементом множества .

Это обозначается так: и читается содержится в или в находится . Очевидно, что пустое множество входит в любое множество .

Например, если множество состоит из элементов обозначают:

= {}), а в = {} тогда .

3. Множества элементов , которые принадлежат множеству или множеству , или и , называется объединением этих множеств и обозначается .

4. Множества элементов , которые принадлежат двум множествам и называется пересечением множеств и и обозначается

Если, например, и – это множества точек, что принадлежат двум фигурам соответственно, тогда схематически на рис. 1 изображены их объединения в случаях а) и б). На рис. 2 изображено пересечение множеств и .

Рис. 1

Рис. 2

5. Разницей множеств A и называется множество , что содержит те элементы , которые не есть элементами множества (см. рис. 3).

Рис. 3

Виды чисел

Существует 7 видов чисел:

1. Натуральные – ;

2. натуральные числа, в которые включается нуль – ;

3. целые числа – ;

а) целые положительные числа – ;

б) целые отрицательные числа – ;

4. рациональные числа – ;

5. иррациональные числа

6. Действительные числа – ;

7. Комплексные числа – .

Рассмотрим каждый вид числа более подробно:

1. Натуральные числа всегда используются при естественном счёте или перечислении предметов, вернее при их нумерации, то есть “первый”, “второй”, “третий”. Описывается множество натуральных чисел так:

= {1, 2, 3, …, }.

2. Натуральные числа, в которые включён нуль используются для обозначения количества предметов:

= {0, 1, 2, 3, …}

3. Целые числа – это числа, в которые входят натуральные числа с положительным и отрицательным знаками:

а) целые положительные числа (обозначаются ) и пишутся: {1, 2, 3, …};

б) целые отрицательные числа (обозначаются ) и пишутся: {…, -3, -2, -1};

= {…, -3, -2, -1, 0, 1, 2, 3, …}.

4. Рациональные числа – числа, которые представляются в виде обыкновенной дроби , где и – целые числа, а . Рациональные числа обозначаются латинской большой буквой :

= {}. Если переводить в десятичную дробь, тогда рациональное число может представляться конечной и бесконечной дробью.

5. Иррациональные числа – вещественное число, которое не рациональное и не может представляться в виде десятичной дроби.

6 Действительные числа или вещественные – это числа, в которых объединяются рациональные и иррациональные числа ().

7. Комплексные числа – это числа, в которых содержится – мнимая единица:

= { и }.

Нужна работа? Есть решение!

Более 70 000 экспертов: преподавателей и доцентов вузов готовы помочь вам в написании работы прямо сейчас.

Подробнее Гарантии Отзывы

Примеры решения задач

Пример 1

Задача

Записать множество , если , причём = {2, 4, 6, 8, 10, 12}, = {3, 6, 9, 12}.

Решение

есть не что иное, как объединение множеств и , то есть, множество будет состоять из элементов, принадлежащих как множеству , так и множеству : = {2, 3, 4, 6, 8, 9, 10, 12}.

Ответ

Множество состоит из элементов, которые принадлежат двум множествам и .

Пример 2

Задача

Все студенты курса изучают разные иностранные языки. Значит, из них, 91 студент изучает английский язык, ещё 96 студентов изучают немецкий язык, 94 студента изучают исключительно французский язык, 36 студентов изучают не только английский, но и немецкий языки, ещё 32 студента изучают английский и французский языки, а 10 студентов занимаются изучением всех языков без исключения.

Вопрос: сколько студентов занимаются изучением немецкого и французского языков, если всего на курсе по списку 189 студентов?

Решение

Итак, для начала введём обозначения:

– множество всех студентов, которые находятся на данном курсе;

– множество студентов, которые изучают только английский язык;

– множество студентов, которые занимаются изучением немецкого языка;

– множество студентов, изучающих исключительно французский язык;

– множество студентов, которые изучают, как английский, так и немецкий язык;

– множество студентов, изучающие английский и французский языки;

– множество студентов, которіе изучают немецкий и французский язіки;

– множество студентов, которые изучают абсолютно все языки;

– количество элементов множества .

По условию задачи:

Найдём – количество студентов, которые изучают немецкий и французский языки. Согласно вышеописанному обозначению, у нас получается:

, , , .

Из методов включения и исключения следует, что

Ответ

студента занимаются изучением немецкого и французского языков.

Множества чисел и примеры числовых множеств обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

В чем отличие конечных множеств от бесконечных.

Подпишитесь на бесплатную рассылку видео-курсов:

Конечное и бесконечное множества. Под множеством понимают совокупность объектов любой природы, обладающих некоторым общим свойством. Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно. Рассмотрим для примера два каких-либо множества M и N и поставим вопрос о том, одинаково или нет количество элементов в этих множествах. Если множество M конечно, то количество его элементов характеризуется некоторым натуральным числом — числом его элементов. В этом случае для сравнения количества элементов множеств M и N достаточно сосчитать число элементов в M, число элементов в N и сравнить полученные числа. Естественно также считать, что если одно из множеств M и N конечно, а другое бесконечно, то бесконечное множество содержит больше элементов, чем конечное. Конечные множества разделяются на счетные и несчетные. Если элементы бесконечного множества можно пронумеровать с помощью натурального ряда чисел, то оно называется счетным и несчетным в противном случае. Так множество четных чисел — счетное, множество действительных чисел — несчетное. Конечные и счетные множества называются дискретными множествами. Множество, не содержащее ни одного элемента, называется пустым. Однако, если оба множества M и N бесконечны, то путь простого счета элементов ничего не дает. Всякое бесконечное множество M содержит счетное множество N притом что M\N есть бесконечное множество Всякое бесконечное множество M содержит подмножество N M причем M\N есть бесконечное множество. Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым. Например: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д. Теорема Кантора-Бернштейна: Если из двух множеств M и N каждое эквивалентно части другого то эти два множества эквивалентны между собой.

6 класс. Математика. Никольский. Учебник. Ответы к стр. 47

Целые числа

Отрицательные целые числа

Ответы к стр. 47

202. Как называют числа, расположенные в ряду целых чисел:
а) справа от нуля; б) слева от нуля.

а) числа расположенные в ряду целых чисел справа от нуля называют натуральными или целыми положительными;

б) числа расположенные в ряду целых чисел слева от нуля называют целыми отрицательными.

203. Является ли число 0: а) положительным; б) отрицательным.

а) нет;
б) нет.

204. Прочитайте числа +2, -3, 0, +7, -9.
а) Какие из этих чисел расположены в ряду целых чисел справа от нуля; слева от нуля?
б) Какие из этих чисел являются положительными; отрицательными.

Плюс два, минус три, нуль, плюс семь, минус девять.

а) Числа расположенные в ряду целых чисел справа от нуля называют натуральными или целыми положительными. Числа расположенные в ряду целых чисел слева от нуля называют целыми отрицательными.
Справа от нуля расположены числа: +2; +7
Слева от нуля расположены числа: -3; -9.

б) положительные: +2, +7;
отрицательные: -3, -9.

205. Прочитайте записи и объясните их смысл:
Москва -2°, Калуга -8°, Тверь +3°.

Москва минус два градуса, Калуга минус восемь градусов, Тверь плюс три градуса.
В Москве 2 градуса мороза, в Калуге 8 градусов мороза, в Твери 3 градуса тепла.

206. Используя знаки «+» и «-», запишите:
а) 3° тепла; б) 4° тепла; в) 6° тепла;
г) 2° мороза; д) 5° ниже нуля; е) 1° холода.

На уличном термометре числа выше нуля читаются как градусы тепла (перед ними ставится знак «+»), а числа ниже нуля – как градусы мороза (перед ними ставится знак «-»).
а) +3°; б) +4°; в) +6°;
г) −2°; д) −5°; е) −1°.

207. Приведите пример:
а) конечного множества чисел;
б) бесконечного множества чисел.

а) числа от 0 до 100 или от −100 до 100 или от -100 до 0;
б) числа от 100 и больше или положительные или отрицательные.

Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.

Математика. 6 класс

Понравилось? Оцени!

Урок алгебры в 8 классе по теме «Множества. Элементы множеств» УМК А.Г. Мерзляк

Тема: Множество и его элементы. Урок № 51 13.01.2020

Деятельностная цель: формирование у учащихся умений реализации новых способов действия.
Содержательная цель: расширение понятийной базы за счет включения в нее новых элементов: множество, элементы множества, одноэлементное множество, равные множества, характеристическое свойство, пустое множество.

Планируемые результаты

Предметные: Формировать умение описывать понятие множества, элемента множества, задавать конечные множества, распознавать равные множества.

Метапредметные

Личностные: Формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.

Регулятивные — понимают причины своего неуспеха и находят способы выхода из этой ситуации.

Познавательные — делают предположения об информации, которая нужна для решения учебной задачи.

Коммуникативные — умеют критично относиться к своему мнению

ХОД УРОКА

1. Мотивация (самоопределение) к учебной деятельности.

Организация уч-ся, проверка готовности к уроку. Просмотр первого слайда презентации.

Учитель: Каким общим словом можно назвать предметы, изображенные на картинках?

(Ответы учащихся).

Сегодня на уроке мы познакомимся с понятием, которое характеризует общие свойства объектов.

2. Актуализация и фиксирование индивидуального затруднения в пробном действии.

А) Решите уравнения:

1) 5(х — 3) +2 = 3х + 4 + 2х – 17 (решений множество)

2) х(х + 2)(х — 4) = 0 (3 решения )

3) 5х + 15 = 0 (1 решение)

4) ( нет решений)

Б) Можете ли вы назвать количество девочек вашего класса, которым исполнилось 13 лет?

А количество мальчиков? Можете ли вы назвать количество учеников вашего класса, которым исполнилось 15 лет?

В) Назовите учеников школы, которые младше 17 лет.

3. Выявление места и причины затруднений.

Скажите, просто или сложно было вам находить ответы на мои вопросы? А всегда ли ответы были односложными?

4. Построение проекта выхода из затруднения (цель, тема, план, сроки, способ, средство).

Сегодня на уроке мы начнем изучение темы, которая называется «Множества и его элементы»

Сформулируйте цели урока….

Чтобы усвоение нового материала было успешным, вы будете работать с учебником на стр. 105, вести записи в тетрадях.

(Читают учебник по цепочке.)

Запись в тетради:

I. Обозначение множеств: А, В, С, М, Н ….

II. Элементы множества:

III. Способы задания множеств: 1) перечислением всех его элементов; 2) указанием характеристического свойства.

IV. Равные множества: множества, состоящие из одних и тех же элементов;

V. Количество элементов множеств: а) бесконечное множества; б) конечные множества

VI. Пустое множество:

5. Реализация построенного проекта

I. Приведите примеры конечного множества; бесконечного множества.

II. Приведите примеры равных множеств .

III. Приведите примеры пустого множества.

6. Первичное закрепление с проговариванием во внешней речи.

Работа с учебником: № 426 а) б) в) г)

№ 428; 1) да; 2) нет; 3) да; 4) нет; 5) нет; 6) да;

7. Самостоятельная работа с самопроверкой по эталону

№ 430 1) 2) 3) м, а, т, е, и, к 4) 5

№ 433 1) 2) 1- Джамалунгма; 3) 4) одна

8. Включение в систему знаний повторение.

№ 436: Всего – 42; красных – 14; синих – 16; зеленые — остальные

Решение: 42- 14-16 = 12. Р(зел.)=

9. Рефлексия УД на уроке (Слайд 16)

Назовите общие элементы этих множеств.
Какие элементы множества А не принадлежат множеству В?
Какие элементы множества В не принадлежат множеству А?
Назовите элементы, которые входят хотя бы в одно из данных множеств.

Домашнее задание: п. 13, № 427, 432

В 70-х годах ХIX века немецкий математик Г. Кантор создал новую область математики — теорию бесконечных множеств. Через несколько десятилетий почти вся математика была перестроена на теоретико-множественной основе.

Мы только начинаем знакомиться с множествами. (Слайд 3)

Множество — неопределяемое понятие в математике. С неопределяемыми понятиями мы уже встречались, например, в геометрии (прямая и точка). Множество можно представить себе как совокупность некоторых элементов.

Например, можно говорить о множестве цветов, которые растут на клумбе около нашей школы. Или о множестве точек на плоскости. Элементы множества могут быть любыми!

(Слайд 4)

Рассмотрим множество, которое состоит из чисел 1, 2, 3, 4, 5. Обозначим это множество А. Используется такая запись: А={1, 2, 3, 4, 5}. Число 1 — элемент данного множества. Можно сказать и так: «1 принадлежит множеству А». Есть специальный значок принадлежности: 1А Тот факт, что, скажем, число 7 не принадлежит множеству А, записываем следующим образом: 7А.

Говоря о множестве А, мы просто перечисляли его элементы. Иногда это отнимает много времени. Иногда вообще такое перечисление невозможно.

Рассмотрим множество всех положительных чисел. Пусть это множество В. С одной стороны, мы не в состоянии перечислить все элементы множества В, их бесконечно много, но, с другой стороны, мы понимаем, о каком множестве идет речь: с положительными числами мы хорошо знакомы — это числа, которые больше нуля. Записываем данное множество так: В={x|x>0}.

(Слайд 5 )

Дополнительные вопросы. Существует ли в этом множестве наибольший элемент? Приведите примеры элементов этого множества, которые меньше 1; 0,1; 0,01; 0,001. Существует ли наименьший элемент этого множества? Будет ли принадлежать этому множеству число 0?

На этом примере показано, что мы можем задать множество, описав самое важное свойство его элементов (оно называется характеристическим свойством множества). По этому свойству можно точно понять, из каких элементов состоит данное множество. Если нам удается это свойство сформулировать, то не нужно тратить время на перечисление элементов множества. Указав множество цветов, растущих на школьной клумбе, мы не обязаны перечислять все цветы. Мы только указали, где они находятся.

Таким образом, множества могут быть заданы по-разному. Самое главное, чтобы было понятно, какие именно элементы принадлежат данному множеству, а какие не принадлежат. Элементы могут быть любые, их порядок не важен. (Слайд 6)

Если два множества состоят из одних и тех же элементов, мы их считаем равными. Пусть множество М состоит из элементов: квадрат, трапеция, пятиугольник, круг, треугольник. Множество Р: круг, квадрат, треугольник, пятиугольник, трапеция. Будут ли множества М и Р равны? Ответ поясните.

Отметим, что здесь мы обсуждаем множество именно как математическое понятие. Но ведь в нашем обычной речи тоже встречается слово «множество»! Важно их не перепутать. «Математическое» множество вовсе не обязано состоять из большого количества элементов. Множество может содержать и всего один элемент. Например, пусть множество D состоит из моей птицы Чир. И даже может быть так, что в множестве вообще нет никаких элементов!

(Слайд 7)

Множество, в котором нет ни одного элемента, называется пустым множеством. Обозначение: . Например, множество говорящих рыб — пустое. Пустым будет множество корней уравнения 0х=3. Или, например, множество параллелограммов, в которых все углы острые.

О некоторых множествах трудно сразу сказать, пусты ли они или нет. Например, знаменитая проблема Ферма была решена только в 90-х годах ХХ века: было доказано, что не существует натуральных чисел n, больших двух, при которых уравнение xⁿ+yⁿ=zⁿ имеет целочисленные положительные решения, то есть множество таких n пусто.

Приведите сами примеры различных пустых множеств.

Среди всех множеств выделяют конечные множества и бесконечные. (Слайд 8)

В конечном множестве число его элементов всегда можно выразить определенным числом (иногда, правда, это число не так-то просто найти).

Приведем несколько примеров.

Множество из 4 элементов: M={a;b;c;d}
Множество цифр. Это множество из 10 элементов (назовите их!).
Множество букв русского алфавита. Сколько в нем элементов?
Множество всех тигров, живущих на Земле. К сожалению, тигров на Земле осталось очень мало. Экологи постоянно следят за их численностью. (Слайд 9)

Рассмотрим множество, состоящее из гласных букв. Сколько в нем элементов?

Будет ли это множество равно множеству, состоящему из цифр?

А в некоторых случаях даже представить себе конечность множества нелегко. Вычислительная техника стремительно развивается. Компьютер отвечает на наши повседневные вопросы очень быстро, иногда нам кажется, что мгновенно. И действительно, объем информации, которую может обрабатывать современный компьютер, громадно. Однако и возможности компьютера ограничены, то есть конечны. В начале ХХI века стали заметны серьезные проблемы. Оказалось, что есть несколько принципиальных (непреодолимых) барьеров: атомная структура вещества, ограничение скорости света, туннельный эффект и проблема отвода тепла (перегрев процессора). Современный процессор по своим размерам постепенно приближается к атому! Но меньше атома процессор быть уже не сможет. А сейчас самая передовая технология дает отличие от размеров атома всего на три порядка! По прогнозам ученых, к 2017 году при аналогичных методах развития наступит предел — процессор уже нельзя сделать меньше.

Перед человечеством встали задачи, которые можно решить с помощью существующих компьютеров только теоретически. В реальности на их решение потребуется время, сравнимое со временем существования Вселенной [3].

Математики и другие ученые предлагают ответы на то, как обойти эти барьеры и ищут новые решения.

В истории математики было много случаев, когда вновь созданная теория воспринималась сначала слишком искусственной, а потом приобретала важнейшее практическое значение. Так было и с теорией бесконечных множеств. А сейчас теория множеств — это «каркас современной математики, она не всегда хорошо видна, но обеспечивает прочность всей конструкции» [4]. (Слайд 10)

Бесконечные множества. В них количество элементов выразить конечным числом невозможно.

Примеры бесконечных множеств:

Множество всех положительных чисел.
Множество всех точек на прямой.
Множество всех треугольников.
Множество всех фигур на плоскости. (Слайд 11)

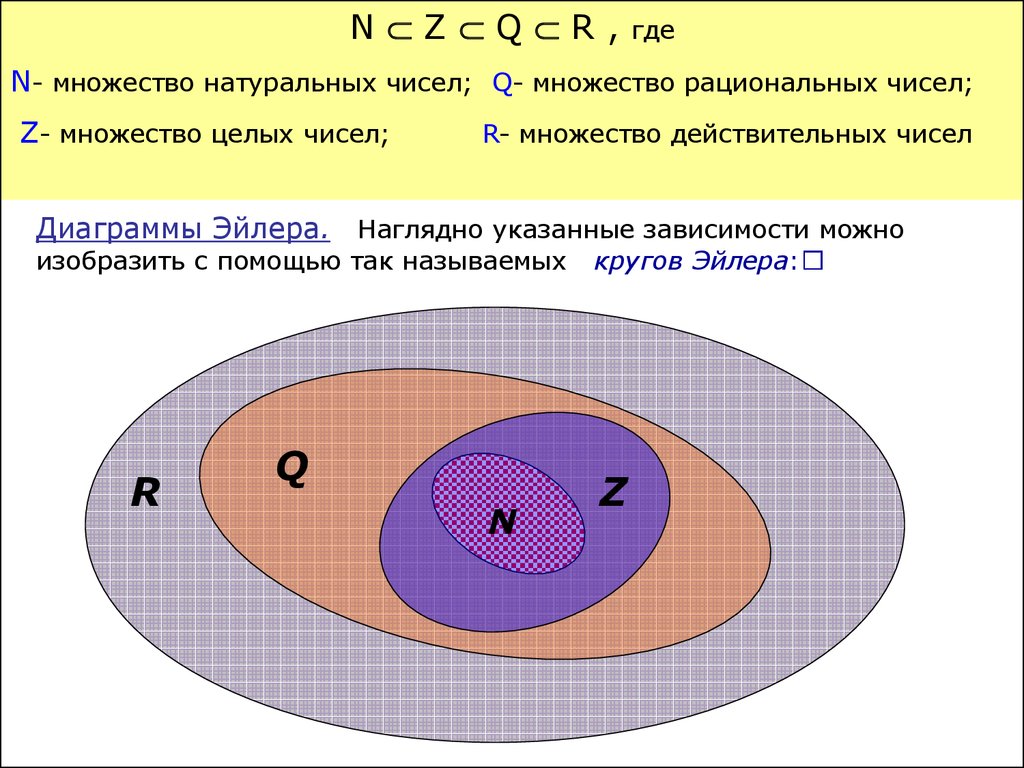
Нам уже известны самые важные числовые множества: N, Z, Q, R. Мы знаем, что натуральные числа — часть целых, целые числа составляют часть рациональных, рациональные — часть действительных. Как называются действительные числа, которые не рациональны?

Пусть даны числа 28; -15; 0,9; .

Запишите для каждого числа, принадлежит ли оно множествам N, Z, Q, R.

Попробуйте привести примеры множеств из геометрии, которые можно было бы проиллюстрировать аналогичной диаграммой (см. слайд: одно множество — часть другого).

(Слайд 12)

Мы уже знакомы с понятием «числовые промежутки». Это тоже множества.

Рассмотрим некоторые из них . Назовите несколько чисел, принадлежащих промежутку (5;8). Принадлежит ли этому промежутку число 8? Число 7,999? А можно ли назвать число из этого промежутка, которое больше 7,999? Есть ли на промежутке (5;8) самое большое число? Самое маленькое число?

Как вы думаете, сколько всего действительных чисел на промежутке (5;8)? Сколько на нем целых чисел? Назовите их.

Аналогичные вопросы можно рассмотреть для промежутков [5;8], [5;8).

В мире бесконечного мы встречаем много удивительного. Например, мы рассмотрели совсем небольшие, казалось бы, промежутки, а действительных чисел на них бесконечно много! Вспомним известный нам график — гиперболу. Что удивительного в гиперболе? А то, что она, приближаясь к осям координат, никогда не пересекает их. Но становится к ним все ближе и ближе! Как это возможно? Математики на это дали ответ (правда, далеко не сразу). Можно сравнить это настойчивое стремление с тем, как человек все время стремится к идеалу, но никогда его не достигает, а стремиться нужно!

Другой удивительный пример из мира бесконечного. Мы привыкли к тому, что часть всегда меньше целого. А с бесконечными множествами иногда получаем другую картину. Рассмотрим натуральные числа и четные числа. Казалось бы, раз четные числа — это только часть натуральных, то четных должно быть меньше. А получается, что их столько же, сколько и натуральных!

(Слайд 13)

Допустим, что в фантастической гостинице (аналогичный пример приведен в [1]) бесконечно много номеров, все они заняты гостями из разных галактик — значит, этих гостей столько же, сколько номеров, то есть столько же, сколько натуральных чисел. И приезжает еще много гостей, нужно их разместить. А ведь все номера заняты, что же делать? Директор очень вежливо просит прежних постояльцев перейти в другие номера: если у прежнего гостя был номер 1, то этот гость переходит в номер 2, номер 2 — в номер 4, то есть все прежние номера меняются на номера, в два раза большие. Тогда освобождаются все нечетные номера! И их бесконечно много! Гостиница готова к приему новых туристов. А в четных номерах живут постояльцы, которых столько же, сколько натуральных чисел. С другой стороны, если новые туристы быстро уедут, то прежние могут вернуться в свои номера. И тогда получается, что четные числа благополучно «размещаются» по номерам 1,2,3:. Таким образом, мы установили взаимно однозначное соответствие между множеством натуральных чисел и множеством четных чисел. Четных чисел и натуральных — одинаковое количество.

(Слайд 14)

Похожим образом можно показать, что количество точек на промежутке (5; 8) такое же, что и на всей прямой. Изменим форму промежутка так, чтобы получилась дуга, полуокружность (но без граничных точек А и В) — эта дуга изображена на слайде. Пусть О — центр окружности, АВ — диаметр. Нашу прямую (обозначим ее СD) расположим так, чтобы она была параллельна АВ. Из точки О можно провести бесконечно много прямых, которые будут пересекать дугу, и при этом каждая из этих прямых пересечет нашу прямую СD. Можно представить себе, что каждая точка дуги «переезжает» в точку на прямой CD (по прямой, идущей из т. О и пересекающей СD — пути «переезда» изображены на слайде стрелками). И наоборот: для каждой точки прямой СD есть соответствующая на дуге. Таким образом, точек на дуге и на всей прямой — одинаковое количество, а, значит, оно будет одинаковым и для промежутка, и для прямой.

Дополнительные вопросы.

Почему нужно было расположить прямую CD параллельно АВ? Укажите прямую, которая пройдет через точку О, но не пересечет дугу. Не забудьте, что мы рассматриваем дугу без концов!

Более трудный вопрос. Можно ли аналогичным образом устроить «переезд» точек для [5; 8], [5; 8)? Замечаем, что «мешают» граничные точки. С теми ребятами, кого заинтересует эта задача, мы обсудим ее на факультативном занятии.

Для всех множеств (и конечных, и бесконечных), мы должны научиться определять, какие элементы принадлежат данному множеству, а какие нет.

(Слайд 15)

Рассмотрим два множества, А и В. Пусть множество А состоит из параллелограмма, трапеции, треугольника, квадрата. Множество В состоит из круга, квадрата, треугольника, пятиугольника, трапеции.

Назовите общие элементы этих множеств.
Какие элементы множества А не принадлежат множеству В?
Какие элементы множества В не принадлежат множеству А?
Назовите элементы, которые входят хотя бы в одно из данных множеств. (Слайд 16)

Итак, мы познакомились с понятием множества, говорили об элементах множества. Узнали, что есть пустое множество. Множества бывают конечные и бесконечные. На следующих уроках мы узнаем о том, что с множествами можно производить некоторые действия (как и с числами — этим они немножко похожи друг на друга). Будем и дальше изучать множества! Они нам помогут лучше разобраться с другими задачами.

Скачано с www.znanio.ru

5.01 О границах числовых множеств

Множество, элементами которого являются вещественные числа, будем называть числовым. Если множество состоит из конечного числа элементов, то его называют конечным, в противном случае – бесконечным.

Определение. Числовое множество называется ограниченным сверху, если существует такое вещественное число , что для любого элемента из множества выполняется неравенство . Число называется верхней границей .

Определение. Если существует такое число , что все элементы множества удовлетворяют неравенству , то множество называется ограниченным снизу, а число – его нижней границей.

Определение. Числовое множество называется ограниченным, если оно ограничено сверху и снизу, т. е. если для всех выполняется неравенство .

Если – верхняя, а – нижняя границы множества , то числа и тоже будут соответственно верхней и нижней границами этого множества. Следовательно, всякое ограниченное множество имеет бесконечно много верхних и нижних границ.

Определение. Наименьшая из всех верхних границ множества называется точной верхней границей этого множества (обозначается ). Наибольшая из всех нижних границ называется точной нижней границей этого множества (обозначается ).

Точная верхняя и точная нижняя границы могут как принадлежать данному множеству, так и не принадлежать ему.

Если не ограничено сверху, то пишут , если снизу, то .

На вопрос о том, всегда ли у ограниченного множества существуют точные границы, отвечает следующая теорема.

Теорема. Всякое непустое ограниченное сверху множество имеет точную верхнюю границу, а всякое непустое ограниченное снизу множество имеет точную нижнюю границу.

Пример 1. Даны множества , и . Указать их точные границы.

Решение. – бесконечное, ограниченное снизу множество. Числа – его нижние границы, а . Сверху это множество не ограничено, т. е. . Множество – бесконечное ограниченное множество, т. е. оно ограничено и сверху, и снизу, его точные границы: , , – бесконечное множество, не ограниченное как сверху, так и снизу.

Любое конечное множество ограничено, так как среди его элементов всегда найдутся наибольшее и наименьшее числа, которые и будут точными границами. Обратное утверждение неверно, т. е. из ограниченности множества не следует его конечность, как это видно на примере множества .

Пример 2. Числовое множество состоит из всех чисел, для которых . Какие числа будут его границами?

Решение. Неравенство равносильно двойному неравенству , откуда видно, что число 3 и всякое большее число будет верхней границей, а число –3 и всякое меньшее число – его нижней границей. , .

Пример 3. Числовое множество состоит из чисел, удовлетворяющих условию . Укажите наименьшее число , удовлетворяющее неравенству для всех из данного множества. Какими границами для этого множества будут числа и ?

Решение. Так как равносильно неравенству , то за нужно взять такое положительное число, чтобы неравенства: и выполнялись одновременно. Это, очевидно, будет при , равном наибольшей из абсолютных величин чисел и , то есть при , при этом , a – верхняя (не точная) граница , точной верхней границей является .

Вопросы для самопроверки.

1. Приведите примеры ограниченных бесконечных множеств. Существуют ли конечные неограниченные множества?

2. Приведите примеры множеств, которым принадлежат их точные границы и множеств, которым не принадлежат их точные границы.

3. Приведите пример множества, которому принадлежит его точная нижняя граница, а точная верхняя не принадлежит.

< Предыдущая		Следующая >

Конечные и бесконечные множества — объяснение, свойства и решаемый пример

В математической теории множеств конечное множество определяется как множество, которое имеет конечное число элементов. Другими словами, конечный набор — это набор, который вы в принципе можете посчитать и закончить подсчет. Например, {1,3,5,7} — это конечный набор из четырех элементов. Элемент в конечном множестве — натуральное число, т.е. неотрицательное целое число. Множество S называется конечным, если существует биекция f: S = {1, ……, n} для натурального числа n.Пустое множество {} также считается конечным. Итак, S — конечное множество, если S допускает биекцию с некоторым множеством натуральных чисел вида {| x | <п}.

Мощность конечного набора

Мощность конечного набора равна n (A) = a, здесь a представляет количество элементов набора A.

Принимая во внимание, что мощность набора A всех английских алфавитов равна 26 , поскольку количество элементов (алфавитов) равно 26. Итак, n (A) = 26.

Это показывает, что вы можете перечислить все элементы конечного набора и записать их в фигурные скобки или в виде списка.Иногда количество факторов может быть слишком большим, но каким-то образом они исчисляемы или имеют начальную и конечную точку. Тогда этот тип множества называется непустым конечным множеством. Количество элементов обозначается n (A), и если n (A) — натуральное число, то только это конечное множество.

Является ли пустой набор конечным набором?

Пустой набор — это набор, в котором нет элементов. Он представлен как {}, что показывает, что в данном наборе нет элемента. Мощность пустого набора равна 0 (нулю), поскольку количество элементов равно нулю.

A = {} или n (A) = 0.

Конечное множество — это множество со счетными элементами. Как в пустом наборе есть нулевые элементы, так и в нем есть определенное количество элементов.

Следовательно, пустое множество — это конечное множество с нулевой мощностью.

Что такое бесконечный набор?

Набор, который не является конечным, бесконечен. Если количество элементов неисчислимо, то оно также называется бесконечным множеством. В отличие от конечных множеств, мы не можем легко представить бесконечное множество в форме реестра, поскольку его элементы не ограничены.Итак, точки используются для описания бесконечности множества.

Свойства бесконечного множества

Объединение двух бесконечных множеств всегда бесконечно.
Набор мощности бесконечного набора бесконечен.
Надмножество бесконечного множества также бесконечно.

Примеры бесконечного множества

Набор всех целых чисел счетно бесконечен, даже если он является правильным подмножеством целых чисел. Множество всех счетно рациональных чисел также является счетно бесконечным множеством, поскольку существует взаимно однозначное соответствие множеству целых чисел.

Набор всех действительных чисел бесконечно бесконечен. Кроме того, множество иррациональных чисел бесконечно.

Графическое представление конечных и бесконечных множеств

(изображение будет скоро загружено)

Здесь

A = {1,2,3,4,5}.

B = {1,2,6,7,8}.

AUB = {1,2,3,4,5,6,7,8}.

A∩B = {1,2}.

И A, и B являются конечными множествами, поскольку они имеют ограниченное количество элементов, поэтому AUB и A∩B также конечны.

Решенный пример

Q1.Какие из следующих множеств конечны или бесконечны?

Множество месяцев в году.
{1,3,5,… ..}.

Ответ: 1. Набор месяцев можно представить как A = {январь, февраль, март, апр, май, июль, август, сентябрь, октябрь, ноябрь, декабрь}. Он образует набор счетных элементов с количеством элементов = 12. Следовательно, это конечное множество.

2. Набор {1,3,5,…} содержит все натуральные числа, но не содержит конечных точек. Это делает его несчетным множеством, а значит, и бесконечным множеством.

2 кв. Какова мощность бесконечных множеств?

Ответ: Мощность множества выражается как n (A) = x, где x — количество элементов в множестве A.

Количество элементов в бесконечном множестве не ограничено, поэтому мощность бесконечного множества n (A) = бесконечность.

Конечные множества — определение и примеры

Математика неполная без чисел. Следовательно, важно развить правильное понимание чисел. Наборы могут помочь нам в этом.Бесконечный список чисел в математике можно классифицировать с помощью наборов.

В этом разделе мы будем развивать понимание конечных множеств .

Проще говоря, конечные множества определяются как:

Конечные множества — это наборы, содержащие счетные или конечные числа или элементы. Их еще называют счетными множествами.

В этом разделе конечных множеств мы рассмотрим следующие темы:

Что такое конечное множество?
Как доказать, что множество конечно?
Свойства конечных множеств.
Примеры
Практические задачи

Что такое конечное множество?

В реальной жизни все можно количественно оценить как исчисляемое или неисчислимое. Счетные элементы классифицируются как «конечные», тогда как бесчисленные элементы называются «бесконечными». Конечное множество состоит из счетных чисел.

Мы можем перефразировать это утверждение, объявив, что все предметы или элементы, которые можно подсчитать, конечны, в то время как те предметы или элементы, которые нельзя подсчитать, бесконечны.Возьмем два примера: корзина яблок и звезды во Вселенной. В этих примерах вы можете легко сосчитать яблоки в корзине, но невозможно даже сосчитать все звезды во Вселенной. Таким образом, яблоки в корзине можно отнести к категории конечных, а звезды Вселенной — бесконечным.

Математика — это вселенная чисел. С неограниченным числом, превышающим до бесконечности, нам нужно научиться классифицировать их как конечные или бесконечные, чтобы упростить мир вокруг нас.Эта классификация может помочь отличить конечное от бесконечного и рациональное от иррационального и может быть достигнута с помощью множеств.

В общих чертах, мы можем определить набор как группу или набор чисел, заключенных и содержащихся в двух скобках. Когда содержащиеся предметы можно легко подсчитать, набор будет классифицирован как конечный набор.

Теперь давайте посмотрим, как мы можем уведомить конечное множество.

Обозначение конечного множества:

Если «A» представляет собой систему счисления с начальной и конечной точкой, то все элементы в A могут быть подсчитаны и могут быть классифицированы с использованием конечного набора.

Обозначения конечных множеств такие же, как и у любого другого множества. Рассмотрим ту же систему счисления A, содержащую конечные или счетные элементы. Числа в этом наборе, хотя они могут быть 100 или миллиардом, если они имеют конечную точку, будут классифицированы в конечном наборе. Чтобы открыть и закрыть конечное множество, используются фигурные скобки {}. Система счисления A может иметь следующие обозначения:

A = {числа в системе счисления A}

Все счетные элементы будут включены в конечный набор и будут иметь такие же обозначения, как показано выше.Если у нас в руках более одного конечного набора, мы можем уведомить каждый набор независимо, дав им отдельные и отличные обозначения. Например, используя указанную выше систему счисления A, мы также можем обозначить это следующим образом:

Система счисления = {числа в системе счисления A}

или

X = {числа в системе счисления A}

Итак, вы можете использовать фразу, слово или даже букву для обозначения конечного множества.

Давайте рассмотрим несколько примеров для дальнейшего понимания концепции конечного множества.

Пример 1

P = {1,2,3,4,5,… .., 10}

X = {x: x целое число и 2

алфавитов = {A, B, C, …… .., Z}

Набор основных номеров до 10 = {2,3,5,7}

Пример 2

Определите, являются ли следующие наборы конечными или нет:

(i) Персиковые сады в стране.

(ii) Люди, живущие в городе

(iii) Люди, живущие в мире.

Решение

Мы решим этот пример, имея в виду концепцию счетного и несчетного.

(i) Общее количество персиковых садов в стране можно легко подсчитать, и да, его можно классифицировать как конечное множество. Обозначения будут примерно такими:

Peach Orchards = {no. персиковых садов за городом}

(ii) Общее количество людей, живущих в городе, можно легко подсчитать и записать. Следовательно, это может быть классифицировано в конечное множество и может иметь следующие обозначения:

жителей города = {количество жителей города}

(iii) Общее количество людей, живущих на Земле, не может быть подсчитано, поскольку это число колеблется с каждой секундой, и невозможно отследить эти числа вплоть до последнего.Следовательно, население мира не может быть классифицировано как конечное множество.

Как доказать, что множество конечно?

Набор может считаться конечным набором только в том случае, если он содержит в себе счетные элементы. Чтобы доказать, что данное множество является конечным, мы рассмотрим систему счисления.

Сама математика — это огромное царство чисел. Но чтобы доказать, является ли данный набор конечным набором или нет, мы рассмотрим фундаментальный набор натуральных чисел.Набор натуральных чисел — это набор, который начинается с 1 и не имеет ограниченного конца, как и числовой счет. Фактически, это может длиться до миллиардов и даже триллионов. Итак, чтобы доказать, является ли набор конечным набором или нет, мы сравним его с набором натуральных чисел.

Рассмотрим набор натуральных чисел, как показано ниже:

N = {1,2,3, ……………., K}

Теперь давайте рассмотрим множество A, которое нужно доказать, конечно или нет.

Один из простых способов получить ответ — сравнить множество A с множеством N.

Если набор A действительно лежит в наборе натуральных чисел N, то набор может быть объявлен как конечный набор.

С математической точки зрения это можно сформулировать так:

N = {1,2,3, ……………., K}

A = {x, y, z, …………… .., n}

If, x ϵ k и y ϵ k, а также x ϵ k

Or, n k

Тогда можно сказать, что множество A действительно принадлежит множеству натуральных чисел N, и, следовательно, множество A является конечным множеством.

Давайте решим несколько примеров, чтобы лучше понять эту концепцию.

Пример 3

Докажите, что множество X = {4,5,8,12} является конечным множеством.

Решение

Чтобы доказать, что множество X является конечным множеством, давайте рассмотрим набор натуральных чисел, который выглядит следующим образом:

N = {1,2,3,4,5,6,7,8,9,10,11,12, ………., N}

Теперь сравним два набора N и X, и давайте сравним каждый элемент X с набором натуральных чисел N.

Мы видим следующие результаты:

1-й элемент набора X = 4 ϵ N

2-й элемент комплекта X = 5 ϵ N

3-й элемент комплекта X = 8 ϵ N

4-й элемент набора X = 12 ϵ N

Поскольку все элементы множества X на самом деле являются натуральными числами и имеют конечную точку, множество X является конечным множеством.

Пример 4

Проверить, является ли множество S = {x: x простым числом, а 2

Решение

Чтобы проверить, является ли набор конечным или нет, мы сначала преобразуем его в разрешимый набор.

Очевидно, что множество S содержит простые числа, а диапазон этих первичных чисел составляет от 2 до 17.

Итак, множество S можно записать как:

S = {3,5,7,11,13}

Чтобы проверить, является ли множество S конечным множеством или нет, мы сравним его элементы с множеством натуральных чисел N.

N = {1,2,3,4,5,6,7,8,9,10,11,12,13, …………., K}

А теперь сравним эти элементы.

1-й элемент комплекта S = 3 ϵ k

2-й элемент комплекта S = 5 ϵ k

3-й элемент комплекта S = 7 ϵ k

4-й элемент набора S = 11 ϵ k

5-й элемент набора S = 13 ϵ k

Поскольку все эти элементы множества S фактически принадлежат множеству натуральных чисел и имеют конечную точку, множество S может быть определено как конечное множество.

Свойства конечного множества

Конечное множество, безусловно, уникальное и содержит счетные и реальные предметы.Эти наборы помогают нам классифицировать и различать исчисляемые и бесчисленные предметы. Подчеркивая важность конечных множеств и то, как они помогают упростить математику, мы рассмотрим некоторые важные свойства конечных множеств, чтобы развить полное и глубокое понимание конечных множеств.

1. Подмножество конечного множества:

Подмножество конечного набора всегда будет конечным набором.

Эту концепцию можно понять, поняв идею подмножеств.Подмножество — это в основном дочерний набор, который содержит некоторые элементы родительского набора. Придерживаясь этого утверждения, мы можем утверждать, что каждое конечное множество, содержащее натуральные числа, на самом деле является подмножеством множества натуральных чисел.

Подмножество конечного набора всегда будет конечным набором, что можно понять с помощью следующих утверждений.

Рассмотрим любое конечное множество A, содержащее n конечных элементов. Поскольку набор является конечным, он обязательно должен содержать натуральные числа.

Теперь рассмотрим набор a , который является подмножеством набора A и содержит (n-1) или (n-2) элементов. Поскольку этот набор a происходит из набора A, который содержал натуральные числа, набор a также будет иметь натуральные числа.

Следовательно, мы можем заявить, что подмножество и набора A также является конечным набором.

Давайте рассмотрим эту концепцию лучше на примерах.

Пример 5

Рассмотрим множество S = {1,2,3,4}, которое является конечным множеством.Докажите, что подмножество s = {1,2} также является конечным множеством.

Решение

Набор S = {1,2,3,4} состоит из 4 элементов, и все эти элементы являются натуральными числами.

Теперь рассмотрим подмножество s = {1,2}.

Поскольку 1-й элемент s является натуральным числом, а 2-й элемент также является натуральным числом, подмножество s также является конечным множеством.

2. Союз конечных множеств:

Объединение двух или более конечных наборов всегда будет конечным набором.

Объединение наборов фактически определяется как совместное соединение 2 или более наборов. Объединение 2 или более наборов содержит все элементы, содержащиеся в объединяемых наборах.

Объединение двух или более конечных множеств всегда будет конечным множеством, что можно понять, поскольку объединяемые множества являются конечными множествами. Следовательно, они будут содержать натуральные числа, поэтому их совместное множество, которое содержит все элементы объединяемых конечных множеств, также будет содержать конечные и натуральные числа и, следовательно, также будет конечным множеством.

Мы можем лучше понять эту концепцию на примере.

Пример 6

Рассмотрим 2 конечных множества A = {1,3,5} и B = {2,4,6}. Докажите, что это объединение также является конечным множеством.

Решение

Два набора A и B являются конечными наборами, и оба содержат натуральные числа.

Их союз можно выразить как:

A U B = {1,3,5} U {2,4,6}

A U B = Z = {1,2,3,4,5,6}

Итак, множество Z, которое указывает на объединение A и B, содержит одни и те же элементы из конечных множеств, и все эти элементы на самом деле являются натуральными числами.Следовательно, объединение множеств A и B также является конечным множеством.

3. Силовой набор конечного набора:

Набор мощности конечного набора всегда является конечным набором.

Набор степеней любого набора можно найти, увеличив степень двойки на общее количество элементов в конечном наборе.

Чтобы доказать, что набор степеней конечного набора также является конечным набором, давайте рассмотрим следующий пример:

Пример 7

Докажите, что набор степеней конечного множества S = {1,2,3,4} также является конечным множеством.4

Силовой комплект S = 16

Поскольку 16 — натуральное число, набор степеней конечного множества также является конечным множеством.

Итак, это вся информация о конечных множествах, необходимая для входа в мир множеств в математике. Чтобы еще больше укрепить понимание и концепцию конечного множества, рассмотрите следующие практические задачи.

Практические задачи

Проверьте, являются ли следующие наборы конечными наборами:

(i) A = {1,6,8,33456} (ii) B = {x: x — нечетное число и 3

Укажите, являются ли следующие наборы конечными наборами:

(i) Персиковые сады мира.

(ii) Волосы на голове человека.

(iii) Чипы в коробке Pringles.

Докажите, что подмножество множества A = {55,77,88,99} является конечным множеством.
Докажите, что объединение множеств X = {2,4,6,8} и Y = {3,6,9,12} является конечным множеством.
Докажите, что набор степеней S = {10,20,30,40,50,60,70} является конечным набором.

Ответы

(i) Конечное (ii) Не конечное множество.
(i) Конечное (ii) Не конечное множество (iii) Конечное
конечный
конечный
конечный

Предыдущий урок | Главная страница | Следующий урок

Бесконечные множества — определение и примеры

В математике мы используем наборы для классификации чисел или предметов.Мы можем в общих чертах разделить множества на два основных сегмента: конечные и бесконечные множества.

На предыдущем уроке мы классифицировали счетные предметы и достигли этого с помощью конечных множеств. Но что, если поставленные перед нами предметы или числа не подлежат исчислению? Ответ будет гораздо проще, если мы познакомимся с концепцией бесконечных множеств.

В этой статье объясняется Infinite Sets , чтобы вы могли понять их и знать, где их использовать .

Бесконечные наборы — это наборы, содержащие бесчисленное или бесконечное количество элементов.Бесконечные множества также называют несчетными множествами.

В этой статье мы рассмотрим следующие темы:

Что такое бесконечное множество?
Как доказать, что множество бесконечно?
Свойства бесконечных множеств.
Примеры
Практические задачи

Это также поможет вам лучше понять бесконечные наборы, если вы думаете, что вам нужно быстро освежить в памяти следующее:

Что такое бесконечный набор?

«Что такое бесконечное множество?» — это частый вопрос, который задают новые энтузиасты математики, и он применим в реальных сценариях.Но мы не можем сосчитать все в реальной жизни, поэтому мы классифицируем эти бесчисленные предметы и числа, используя бесконечные множества. Что вам нужно помнить, так это то, что элементы бесконечного множества не имеют конечной точки.

Есть множество примеров бесконечных наборов и предметов вокруг нас: звезды в полуночном небе, капли воды и миллионы клеток в человеческом теле. Но в математике идеальным примером бесконечного множества является набор натуральных чисел. Набор натуральных чисел неограничен и не имеет конца.Следовательно, для бесконечных множеств применяются одни и те же критерии классификации.

Еще нужно помнить, что математика — это не только определенные системы счисления. Графически мы можем построить максимум 2 или 3 оси, и, используя тот же график, существуют бесчисленные или бесконечные точки, которые могут быть объявлены как бесконечные множества.

Точно так же линейный сегмент может выглядеть как прямая линия с некоторой определенной величиной, но бесконечные точки соединяются, образуя линейный сегмент на микроскопическом уровне. Эти бесконечные точки также являются примерами бесконечных множеств.

В отличие от конечных множеств, бесконечное множество не требует определенного начала. Набор целых чисел — хороший пример. Рассмотрим следующий набор целых чисел Z:

Z = {…, -2, -1, 0, 1, 2,…}

Обозначение бесконечного множества:

Обозначение бесконечного множества аналогично любому другому множеству с числами и элементами, заключенными в фигурные скобки {}. Однако мы можем отличить бесконечные множества от конечных, используя эллипсы (…)

Эллипсы указывают, что набор не имеет конечной точки или что набор содержит неограниченное или бесконечное количество элементов.Мы также можем представить бесконечные множества, используя любую букву, слово или даже фразу.

Рассмотрим бесконечную систему счисления A. Эта система счисления A может иметь следующие обозначения.

A = {1, 2, 3,…}

Мы упоминали ранее, что можем также представлять бесконечные множества любой буквой, словом или фразой. Таким образом, одна и та же система счисления A может иметь следующие обозначения:

Система счисления = {1, 2, 3,…}

или

X = {1, 2, 3,…}

Еще несколько примеров бесконечных множеств приведены ниже:

Целые числа = {0, 1, 2, 3,…}

X = {x: x является целым числом и -4

E = {2, 4, 6,…, 2n}

здесь «n» означает любое число.

Вот некоторые примеры бесконечных множеств:

Пример 1

Определите, являются ли следующие наборы бесконечными.

(i) Отрезки прямых на плоскости.

(ii) Кратное 3.

(iii) Факторы 45.

Решение

(i) В плоскости может существовать бесконечное количество отрезков в разных направлениях. Следовательно, множество отрезков на плоскости — бесконечное множество. Он будет иметь следующее обозначение:

Сегментов линии на плоскости = {1, 2, 3,…, n}

Где «n» может быть любым целым числом.

(ii) Так как в вопросе не дается конечный предел для кратных 3, следовательно, кратные 3 также являются бесконечным множеством. Он будет иметь следующее обозначение:

, кратное 3 = {3, 6, 9,…, 3n}

Где «n» может быть любым целым числом.

(iii) Разложив 45 на множители, мы получим числа 1, 3, 5, 9 и 45 как множители. Поскольку общее количество этих факторов ограничено, то есть 5, 45 не бесконечный набор.

Как доказать бесконечность множества?

Чтобы доказать бесконечность множества, проверим его мощность.Как обсуждалось в уроке о конечных наборах, мощность указывается общим количеством элементов набора. Однако бесконечные множества содержат неограниченное количество элементов, что означает, что их мощность не является определенным числом и обозначается aleph-null (ℵ0).

Еще одним уникальным фактором бесконечных множеств является то, что они не могут иметь взаимно однозначного соответствия или взаимно однозначного отношения с любым эталонным множеством.

Давайте оценим это дальше. Рассмотрим эталонный набор R, который приведен ниже:

R = {1, 2, 3,…}

Теперь рассмотрим бесконечное множество A:

A = {0, 1, 2,…}

Оба набора R и A имеют неограниченное количество элементов, поэтому их количество элементов не определено и может быть названо aleph-null (ℵ0).Более того, окончание обоих наборов R и A невозможно предсказать, потому что мы не можем сформировать взаимно однозначное отношение между двумя наборами. Следовательно, множества R и A — бесконечные множества.

Следующие теоремы также могут помочь нам доказать, что множество бесконечно:

Теорема 1:

Пусть A и B два набора. Если A — бесконечное множество и A ≅ B, то B также бесконечное множество.

В этой теореме множества A и B примерно равны друг другу.

Пример 2

Если A — бесконечное множество и A = {5, 10, 15,…, 35,…}, тогда докажите, что B также бесконечное множество, учитывая, что B = {5, 10, 15,…, 50,…} .

Решение

Этот пример может быть решен в свете приведенной выше теоремы.

Согласно теореме 1:

A ≅ B

Теперь сравним два набора:

{5, 10, 15,…, 35,…} ≅ {5, 10, 15,…, 50,…}

Оба набора примерно равны из-за схожих элементов, которые они разделяют, но оба обладают мощностью aleph-null (ℵ0).

Поскольку множество A — бесконечное множество, значит, множество B также бесконечное множество.

Теорема 2:

Пусть A и B два набора.Если A — бесконечное множество и A ⊆ B, то B также бесконечное множество.

В этой теореме набор B является подмножеством мощности множества A.

Пример 3

Если A — бесконечное множество и A = {1, 3, 5,…}, то докажите, что B также бесконечное множество, учитывая, что B = {3, 5,…}.

Решение

Для решения этого примера воспользуемся теоремой 2.

Согласно теореме 2:

A ⊆ B

{1, 3, 5,…} ⊆ {3, 5,…}

Ясно, что множество A является бесконечным множеством, а множество B является подмножеством мощности множества A; следовательно, множество B также является бесконечным.

Свойства бесконечных множеств

Бесконечные множества решают дилемму сортировки бесчисленных элементов математики. Хотя бесконечные множества классифицируют более половины области математики, все же необходимо оценить некоторые свойства бесконечных множеств, чтобы упростить вычисления с участием бесконечных множеств. Эти свойства также помогут нам в понимании бесконечных множеств.

1. Союз бесконечных множеств

Объединение двух или более бесконечных множеств всегда будет бесконечным.

Объединение наборов — это способ объединить два или более наборов в один набор. Объединение наборов показывает объединенные элементы, которые содержались во всех наборах по отдельности.

Объединение двух или более бесконечных множеств всегда будет бесконечным, поскольку объединяемые множества содержат неограниченное количество элементов. В результате их совместный набор также будет содержать неограниченное количество элементов.

Мы можем лучше понять это свойство на примере.

Пример 4:

Рассмотрим два набора X = {2, 4, 6,…} и Y = {1, 3, 5,…}.Докажите, что их объединение тоже бесконечное множество.

Решение

Два набора, X и Y, бесконечны, поскольку оба содержат неограниченное количество элементов.

Мы можем выразить их союз как:

X U Y = {2, 4, 6,…} U {1, 3, 5,…}

X U Y = {1, 2, 3, 4, 5, 6,…}

Поскольку и X, и Y являются бесконечными множествами и имеют мощность aleph-null (ℵ0), их объединение также бесконечно и имеет мощность aleph-null (ℵ0).

2. Набор мощности бесконечного набора

Набор мощности бесконечного множества всегда бесконечен.∞ $

| P (A) | = ∞

Следовательно, доказано, что набор степеней бесконечного множества бесконечен.

3. Расширение бесконечного множества
Надмножество бесконечного множества всегда бесконечно.
Набор A является надмножеством другого набора B, если все элементы B присутствуют в A. Обозначение надмножества показано ниже:
A ⊃ B
Рассмотрим множество A, которое является бесконечным множеством. Его надмножество также будет бесконечным, поскольку оно также будет содержать неограниченное количество элементов.
Давайте рассмотрим следующий пример, чтобы понять это свойство.
Пример 6
Докажите, что надмножество S = {1, 2, 3,…} бесконечного множества T = {1, 3,…} также является бесконечным множеством.
Решение
Множество T — бесконечное множество, а его расширенное множество — S.
Согласно вышеуказанной собственности:
A ⊃ B
А,
{1, 2, 3,…} ⊃ {1, 3,…}
Итак, это доказывает, что надмножество S также является бесконечным.
Чтобы еще больше укрепить понимание и концепцию бесконечного множества, рассмотрите следующие практические задачи.
Практические задачи
Проверьте, какой из следующих наборов бесконечен:
(i) Кратное 100.
(ii) Коэффициенты 225.
Если A бесконечное множество и A = {22, 44, 66,…, 100} и B = {22, 44,…, 100}, докажите, что B также бесконечное множество.
Если A бесконечное множество и A = {100, 105, 110,…} и B = {100,…}, докажите, что B также бесконечное множество.
Выясните, является ли объединение двух бесконечных множеств X = {3, 6, 9,…} и Y = {7, 14, 28,…} бесконечным.
Определите, бесконечны ли следующие параметры мощности:
(i) A = {3, 4, 6,…}
(ii) B = {4, 5, 7, 8}
Ответы
(i) Бесконечное (ii) Не бесконечное
бесконечный
бесконечный
бесконечный
(i) Бесконечное (ii) Не бесконечное
Предыдущий урок | Главная страница | Следующий урок
Бесконечные множества и мощности — математика LibreTexts
Думая о том, как сопоставить натуральные числа с целыми числами, я вижу, как четные натуральные числа могут использоваться для положительных целых чисел, например:
\ [2 \ rightarrow 1 \ qquad \ qquad 4 \ rightarrow 2 \ qquad \ qquad 6 \ rightarrow 3 \ qquad \ qquad 8 \ rightarrow 4 \ qquad \ mbox {и т. Д.by} f (n) = \ frac {n} {2}. \]
Однако я понимаю, что нулю потребуется прообраз, поэтому я могу немного настроить функцию:
\ [2 \ rightarrow 0 \ qquad \ qquad 4 \ rightarrow 1 \ qquad \ qquad 6 \ rightarrow 2 \ qquad \ qquad 8 \ rightarrow 3 \ qquad \ mbox {и т. д. by} f (n) = \ frac {n-2} {2}. \]
Это позаботится натуральных чисел и ноль.
Для отрицательных целых чисел мне нужно использовать нечетные натуральные числа, чтобы получить:
\ [1 \ rightarrow -1 \ qquad \ qquad 3 \ rightarrow -2 \ qquad \ qquad 5 \ rightarrow -3 \ qquad \ qquad \ qquad 7 \ rightarrow -4 \ qquad \ mbox {и т. Д.}. \]
Теперь мне нужно придумать функцию для выполнения этого сопоставления с отрицательными целыми числами, и, немного подумав, я пришел к \ (f (n) = — \ frac {n + 1} {2} . \)
Их нужно будет объединить в кусочную функцию, с одной частью, если \ (n \) четно, и другой частью, если \ (n \) нечетно.
Определите \ (f: \ mathbb {N} \ to \ mathbb {Z} \) как \ (f (n) = \ begin {cases} \ frac {n-2} {2} & \ text {if} n \ mbox {четно} \\ — \ frac {n + 1} {2} & \ text {if} n \ mbox {нечетно} \ end {cases} \)
\ (f \) четко определено:
Случай 1: \ (n \) четно.\ (f (n) = \ frac {n-2} {2} \) и поскольку \ (n \) четное, \ (n = 2k \) для некоторого целого числа \ (k \) по определению четного.
Теперь \ (f (n) = \ frac {2k-2} {2} = k-1 \). Поскольку целые числа замкнуты при вычитании, \ (k-1 \ in \ mathbb {Z} \), поэтому \ (f (n) \ in \ mathbb {Z}. \)
Случай 2: \ (n \) нечетный . \ (f (n) = — \ frac {n + 1} {2} \) и поскольку \ (n \) нечетно, \ (n = 2j + 1 \) для некоторого целого числа \ (j \) по определению странно.
Теперь \ (f (n) = — \ frac {2j + 1 + 1} {2} = — j-1 \). Поскольку целые числа замкнуты относительно сложения и умножения, \ (- j-1 \ in \ mathbb {Z} \), поэтому \ (f (n) \ in \ mathbb {Z}.\)
По свойству четности \ (n \) должно быть четным или нечетным, поэтому мы показали для всех натуральных чисел \ (n \), \ (f (n) \ in \ mathbb {Z}, \ ), таким образом, \ (f \) определено корректно.
\ (f \) взаимно однозначно:
Пусть \ (f (x_1) = f (x_2) \ mbox {для некоторых} x_1, x_2 \ in \ mathbb {N}. \) Поскольку \ (f (x_1) = f (x_2) \), \ (f (x_1) \ mbox {и} f (x_2) \) либо неотрицательны, либо отрицательны. Если они неотрицательны, то \ (x_1 \ mbox {и} x_2 \) четные, а если отрицательные, то \ (x_1 \ mbox {и} x_2 \) нечетные.
Случай 1: \ (f (x_1) \ mbox {и} f (x_2) \) неотрицательны, \ (x_1 \ mbox {и} x_2 \) четны. \ (\ frac {x_1-2} {2} = \ frac {x_2-2} {2}. \) Тогда \ (x_1-2 = x_2-2, \ mbox {so} x_1 = x_2 \) (по алгебре ).
Случай 2: \ (f (x_1) \ mbox {и} f (x_2) \) отрицательны, \ (x_1 \ mbox {и} x_2 \) нечетны. \ (- \ frac {x_1 + 1} {2} = — \ frac {x_2 + 1} {2}. \) Тогда \ (x_1 + 1 = x_2 + 1, \ mbox {so} x_1 = x_2 \) ( по алгебре).
В обоих случаях, если \ (f (x_1) = f (x_2) \ mbox {then} x_1 = x_2 \) и, следовательно, по определению один-к-одному, \ (f \) взаимно однозначно .+ \). Таким образом, \ (n \ in \ mathbb {N}. \)
\ (f (n) = f (2y + 2) = \ frac {2y + 2-2} {2} = y. \)
Случай 2 : \ (Y \) отрицательно; примечание: \ (n \) нечетно. Выберите \ (n = -2y-1 \). Поскольку целые числа замкнуты относительно вычитания и умножения, \ (- 2y-1 \) является целым числом. Кроме того, поскольку \ (y <0, \ qquad \ qquad -2y> 0, \ qquad \ qquad -2y-1> -1. \) Наименьшее нечетное целое число больше \ (- 1 \) равно \ (1 \) , Таким образом, \ (n \ in \ mathbb {N}. \)
\ (f (n) = f (-2y-1) = — \ frac {-2y-1 + 1} {2} = \ frac {2y } {2} = y. \)
По свойству трихотомии \ (y \) должно быть неотрицательным или отрицательным, поэтому мы показали, что для произвольного элемента \ (y, \) области домена существует элемент в \ (\ mathbb {N} \), изображение которого — y, и поэтому, по определению on, \ (f \) находится на.
Поскольку \ (f \) является четко определенной, взаимно однозначной функцией на функцию, мы продемонстрировали взаимно однозначное соответствие от \ (\ mathbb {N} \ mbox {к} \ mathbb {Z }. \) Таким образом, \ (| \ mathbb {N} | = | \ mathbb {Z} | \) и, следовательно, множество целых чисел \ (\ mathbb {Z}, \) счетно.
Мощность | Конечные множества | Бесконечные наборы
Здесь нам нужно поговорить о мощности набора, которая в основном является размером набора. Мощность множества обозначается $ | A | $. Сначала обсудим мощность для конечных множеств и потом поговорим о бесконечных множествах.
Рассмотрим набор $ A $. Если $ A $ имеет только конечное число элементов, его мощность равна просто количество элементов в $ A $. Например, если $ A = \ {2,4,6,8,10 \} $, то $ | A | = 5 $. Перед обсуждением бесконечных множеств, что является основным обсуждением в этом разделе, мы хотели бы поговорить об очень Полезное правило: принцип включения-исключения . Для двух конечных множеств $ A $ и $ B $ имеем $$ | A \ чашка B | = | A | + | B | — | A \ cap B |. $$ Чтобы убедиться в этом, обратите внимание, что когда мы складываем $ | A | $ и $ | B | $, мы дважды подсчитываем элементы в $ | A \ cap B | $, таким образом, вычитая его из $ | A | + | B | $, мы получаем количество элементов в $ | A \ cup B | $, (можно см. рисунок 1.n \ left | A_i \ right | — \ sum_ {i \> \> \> \> \> \> + \ sum_ {i

Пример
На вечеринке,
есть люди за 10 долларов в белых рубашках и за 8 долларов за людей в красных рубашках;
$ 4 $ у людей черные туфли и белые рубашки;
$ 3 $ у людей черные туфли и красные рубашки;
Общее количество людей в белых или красных рубашках или черных туфлях составляет 21 доллар.
У скольких людей есть черные туфли?
Решение
Пусть $ W $, $ R $ и $ B $ будут количеством людей в белых рубашках, красных рубашках и черных туфлях. соответственно.Затем, вот краткое изложение доступной информации: $$ | W | = 10 $$ $$ | R | = 8 $$ $$ | W \ cap B | = 4 $$ $$ | R \ cap B | = 3 $$ $$ | W \ чашка B \ чашка R | = 21. $$ Также разумно предположить, что $ W $ и $ R $ не пересекаются, $ | W \ cap R | = 0 $. Таким образом, применяя принцип включения-исключения получаем
$ $ $
$ | W \ чашка R \ чашка B | $ = 21
$ = | W | + | R | + | B | — | W \ cap R | — | W \ cap B | — | R \ cap B | + | W \ cap R \ cap B |
$ = 10 + 8 + | B | -0-4-3 + 0 $.

Таким образом $$ | B | = 10. $$
Обратите внимание, что другой способ решить эту проблему — использовать диаграмму Венна, как показано на рисунке 1.11.
Рис.1.11 — Диаграмма включения-исключения Венна.

Бесконечные наборы:
Что, если $ A $ — бесконечное множество? Оказывается, нам нужно различать два типа бесконечных множеств: где один тип значительно «крупнее» другого.В частности, один вид называется счетным , в то время как другой называется бесчисленное . Такие множества, как $ \ mathbb {N} $ и $ \ mathbb {Z} $, называются счетными, но «большие» наборы, такие как $ \ mathbb {R} $, называются несчетными. Разница между двумя типами заключается в что вы можете перечислить элементы счетного множества $ A $, т.е. вы можете написать $ A = \ {a_1, a_2, \ cdots \} $, но вы не можете перечислить элементы в бесчисленном множестве. Например, вы можете написать
$ \ mathbb {N} = \ {1,2,3, \ cdots \} $,
$ \ mathbb {Z} = \ {0,1, -1,2, -2,3, -3, \ cdots \} $.
Тот факт, что вы можете перечислить элементы счетно бесконечного набора, означает, что набор может быть сопоставлен один к одному. соответствие с натуральными числами $ \ mathbb {N} $. С другой стороны, вы не можете перечислить элементы в $ \ mathbb {R} $, так что это бесчисленное множество. Если быть точным, вот определение.
Определение
Set $ A $ называется счетным, если выполняется одно из следующих утверждений.
, если это конечное множество, $ \ mid A \ mid
его можно поставить во взаимно однозначное соответствие с натуральными числами $ \ mathbb {N} $, в которых В этом случае множество называется счетно бесконечным.
Набор называется несчетным, если он не счетный.
Вот простой совет, чтобы решить, является ли набор счетным или нет. Что касается прикладной вероятности обеспокоен, этого руководства должно быть достаточно для большинства случаев.
$ \ mathbb {N}, \ mathbb {Z}, \ mathbb {Q} $ и любые их подмножества счетны.
Любой набор, содержащий интервал на действительной прямой, такой как $ [a, b], (a, b], [a, b), $ или $ (a, b) $, где $ a
Приведенного выше правила обычно достаточно для целей этой книги.Однако, чтобы аргументировать Более конкретно, здесь мы приводим некоторые полезные результаты, которые помогают нам доказать, является ли множество счетным или нет. Если доказательства вас меньше интересуют, вы можете их пропустить.

Теорема
Любое подмножество счетного множества счетно.
Любое надмножество неисчислимого множества неисчислимо.
Доказательство
Интуиция, лежащая в основе этой теоремы, такова: если множество счетно, то любое «меньшее» множество также должно быть счетным, поэтому подмножество счетного множества также должно быть счетным.Предоставлять доказательство, мы можем рассуждать следующим образом.
Пусть $ A $ счетное множество и $ B \ subset A $. Если $ A $ — конечное множество, то $ | B | \ leq | A |
Вторая часть теоремы может быть доказана с использованием первой части. Предположим, что $ B $ несчетное число. Если $ B \ subset A $ и $ A $ счетно, то по первой части теоремы $ B $ также является счетным множество, противоречие.

Теорема
Если $ A_1, A_2, \ cdots $ — это список счетных множеств, то множество $ \ bigcup_ {i} A_i = A_1 \ cup A_2 \ cup A_3 \ cdots $ также счетно.
Proof
Достаточно создать список элементов в $ \ bigcup_ {i} A_i $. Поскольку каждый $ A_i $ счетен, мы можем перечислите его элементы: $ A_i = \ {a_ {i1}, a_ {i2}, \ cdots \} $. Таким образом, мы имеем
$ A_1 = \ {a_ {11}, a_ {12}, \ cdots \} $,
$ A_2 = \ {a_ {21}, a_ {22}, \ cdots \} $,
$ A_3 = \ {a_ {31}, a_ {32}, \ cdots \} $,
…
Теперь нам нужно составить список, содержащий все перечисленные выше списки. Сделать это можно разными способами.Один из способов сделать это — использовать порядок, показанный на рис. 1.12, чтобы составить список. Здесь мы можем написать $$ \ bigcup_ {i} A_i = \ {a_ {11}, a_ {12}, a_ {21}, a_ {31}, a_ {22}, a_ {13}, a_ {14}, \ cdots \} \ hspace {100pt} (1.1) $$ Рис.1.12 — Порядок составления списка.
Мы смогли создать список, содержащий все элементы в $ \ bigcup_ {i} A_i $, так что это множество счетно.

Теорема
Если $ A $ и $ B $ счетны, то $ A \ times B $ также счетно.
Доказательство
Доказательство этой теоремы очень похоже на предыдущую теорему.Поскольку $ A $ и $ B $ являются счетно, мы можем написать $$ A = \ {a_1, a_2, a_3, \ cdots \}, $$ $$ B = \ {b_1, b_2, b_3, \ cdots \}. $$ Теперь мы создаем список, содержащий все элементы в $ A \ times B = \ {(a_i, b_j) | i, j = 1,2,3, \ cdots \} $. Идея точно такая же, как и раньше. На рисунке 1.13 показан один из возможных вариантов заказа.
Рис.1.13 — Порядок составления списка.
Приведенные выше аргументы можно повторить для любого набора $ C $ в виде $$ C = \ bigcup_i \ bigcup_j \ {a_ {ij} \}, $$ где индексы $ i $ и $ j $ принадлежат некоторым счетным множествам.Таким образом, любое множество в этой форме счетно. Например, следствием этого является счетность множества рациональных чисел $ \ mathbb {Q} $. Это потому, что мы можем написать $$ \ mathbb {Q} = \ bigcup_ {i \ in \ mathbb {Z}} \ bigcup_ {j \ in \ mathbb {N}} \ {\ frac {i} {j} \}. $$
Приведенные выше теоремы подтверждают, что такие множества, как $ \ mathbb {N}, \ mathbb {Z}, \ mathbb {Q} $ и их подмножества счетны. Однако, как мы упоминали, интервалы в $ \ mathbb {R} $ неисчислимы. Таким образом, вы никогда не сможете предоставить список в виде $ \ {a_1, a_2, a_3, \ cdots \} $, содержащий все элементы, скажем, в $ [0,1] $.Этот факт можно доказать с помощью так называемого диагонального аргумента, и мы опускаем доказательство здесь, поскольку оно не является важным для остальной части книги.
конечных и бесконечных множеств — учебный материал для IIT JEE

Определение конечного множества
Как следует из названия, конечный набор — это набор, имеющий конечное или счетное количество элементов.
Пример
Это набор всех английских алфавитов.
Как мы можем посчитать количество элементов здесь, так это конечный набор.
Мощность конечного множества
Мощность конечного набора равна n (A) = a, где a представляет количество элементов набора A.
Как на картинке выше, количество элементов этого набора равно 26, так как количество элементов равно 26.
Итак, n (A) = 26.
Это показывает, что если вы можете перечислить все элементы набора и записать их в фигурных скобках или вы можете сказать, что в форме списка, они называются конечными наборами.
Иногда может случиться так, что количество элементов очень велико, но где-то оно счетно или имеет начальную и конечную точки, тогда это непустой конечный набор . Здесь мы обозначаем количество элементов с помощью n (A), и если n (A) — натуральное число, то можно сказать, что это конечное множество.
Свойства конечных множеств
Подмножество конечного множества всегда конечно.
Объединение двух конечных множеств конечно.
Набор мощности конечного множества конечно.
Давайте посмотрим на примере
A = {1, 2, 3, 4}
B = {2, 4, 6, 8}
C = {2, 3}
Здесь все A, B и C — конечные множества, поскольку количество элементов ограничено и счетно.
C⊂A, то есть C является подмножеством A, поскольку все элементы множества C присутствуют в множестве A. Таким образом, подмножество конечного множества всегда конечно.
A B — это {1, 2, 3, 4, 6, 8}, поэтому объединение двух конечных множеств также конечно.
Количество элементов набора мощности набора равно 2 ⁿ, поэтому количество элементов набора мощности набора A равно 2 ⁵ = 32, поскольку количество элементов набора A равно 5. показывает, что набор мощности конечного множества конечно.
Пример
Z = {количество людей, проживающих в европе}
В этом примере сложно посчитать количество людей, проживающих в Европе, но это где-то натуральное число.Итак, это непустое конечное множество.
Конечное множество может быть представлено последовательно,
N — это набор натуральных чисел меньше n, поэтому мощность множества N равна n.
N = {1, 2, 3,…, n}
Y = y ₁, y2,…, n
Y = {y: y ₁ ∈N, y ₁ ≤i≤n}, где i — целые числа от 1 до n.
Примеры конечных множеств
R = {фиолетовый, индиго, синий, зеленый, желтый, оранжевый, красный}
п (R) = 7
N = {25, 26, 27,…, 100}
п (N) = 76
D = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}
п (D) = 7
Все вышеперечисленное — примеры конечных множеств, потому что количество элементов в них счетно.И их мощность — натуральное число.

Пусто Установить конечный набор?
Чтобы понять ответ на этот вопрос, сначала нам нужно понять значение пустого множества.
Пустой набор — Пустой набор — это набор, в котором нет элементов. Его можно представить как {}, что показывает, что в наборе нет элемента.
Мощность пустого набора равна 0 (нулю), то есть количество элементов равно нулю.
A = {} или ∅ (phi)
п (А) = 0
Конечное множество — это множество со счетным числом элементов, и поскольку пустое множество имеет нулевой элемент, значит, это определенное количество элементов.
Пустое множество — это конечное множество с нулевой мощностью .
Определение бесконечных множеств
Набор, который не является конечным набором, называется бесконечным набором . Или, если вы не можете подсчитать количество элементов определенного набора, это называется бесконечным набором.
Поскольку мы представляем конечное множество в форме списка, мы не можем легко представить бесконечное множество в форме списка, поскольку его элементы не ограничены, поэтому мы используем три точки (эллипсы) для представления бесконечности набора.
Пример
Как в примере выше,
N — это набор всех натуральных чисел, начиная с нуля. Его количество элементов не исчисляемо, поэтому мы используем три точки, чтобы обозначить его бесконечность.
Z — это набор всех целых чисел, так как его элементы также неисчислимы, поэтому мы используем три точки на обеих сторонах для бесконечности отрицательных и положительных целых чисел.
Важно отметить, что наборы должны иметь некоторую четко определенную структуру или шаблон, тогда только мы можем записать их в форме списка, поэтому невозможно записать все бесконечные множества в форме списка.
Поскольку мы не можем записать набор действительных чисел в форме реестра, так как нет правильной структуры этих чисел.
Мощность бесконечных множеств
Мощность набора равна n (A) = x, где x — количество элементов набора A.
Поскольку количество элементов в бесконечном множестве неограниченно, мощность бесконечного множества равна n (A) = ∞, т.е. бесконечна.

Свойства бесконечных множеств
Объединение двух бесконечных множеств бесконечно
Набор мощности бесконечного набора бесконечен
Супер набор бесконечного набора тоже бесконечен
Поскольку количество элементов бесконечного набора неограниченно, его набор мощности и надмножества также должны быть бесконечными.
Примеры бесконечных множеств
Вт = {1, 2, 3, 4,…}
Что означают равные множества в математике?
В математике мы называем число равным другому, если они точно такие же. Аналогично в наборах мы сказали , что два набора равны, если все элементы совпадают. Порядок элементов и повторение элементов значения не имеют.
Здесь набор A и набор B — это равные наборы, поскольку там элементы в точности совпадают.и там количество элементов тоже такое же.
Пример
A = {5, 6, 7, 8}
B = {6, 8, 5, 7}
C = {5, 5, 6, 6, 7, 7, 8, 8}
Здесь все три набора, набор A, набор B и набор C равны, так как там элементы одинаковы по несущественности порядка и повторения.
В чем разница между конечным и бесконечным множествами?
Разница между конечным и бесконечным множествами следующая:
Наборы могут быть равными, только если есть одинаковые элементы, поэтому набор может быть равен, только если это конечный набор.А если набор бесконечен, мы не можем сравнивать элементы наборов.
№
Очки
Конечные наборы
Бесконечные наборы
1
Определение
Набор является конечным набором, если он пуст или содержит ограниченное количество элементов.
Множество, которое не является конечным множеством, является бесконечным множеством.
2
Количество элементов
Счетное количество элементов.
Бесчисленное количество элементов.
3
Непрерывность
Запускается и тоже останавливается.
Он не имеет конца ни в начале, ни в конце, или может иметь непрерывность с обеих сторон.
4
Мощность
n (A) = n, n — количество элементов.
n (A) = ∞, бесконечно, поскольку количество элементов неисчислимо.
5
Союз
Объединение двух конечных множеств конечно.
Союз двух бесконечных множеств бесконечен.
6
Силовой агрегат
Мощность конечного множества конечна.
Мощность набора бесконечного набора бесконечна.
7
Форма реестра
Может быть легко представлен в форме реестра.
Все наборы не могут быть показаны в форме списка, поэтому мы используем три точки для представления бесконечности.
8
Пример
A = {2, 4, 6, 8}
X = {2, 4, 6, 8,…}
Набор четных чисел меньше 9.
Набор всех четных чисел.

Как определить, является ли набор конечным или бесконечным?
Как мы знаем, множество конечно, если у него есть как начальная, так и конечная точки, но набор называется бесконечным, если у него нет конца ни с одной стороны, ни с обеих сторон.
Очки для определения набора как конечного или бесконечного:
Если у набора есть начальная точка и конечная точка , тогда он конечен, но если у него нет начальной или конечной точки, то он бесконечен.
Если набор имеет ограниченное количество элементов , тогда он конечен, но если его количество элементов неограниченно, то оно бесконечно.
Что такое конечное или бесконечное?
Давайте попробуем определить, является ли множество конечным или бесконечным с их элементами.
№
Пример
Конечное или бесконечное
Почему?
1
А = {5,10,15,20}
Конечная
Этот набор имеет как начальную, так и конечную точки, а количество его элементов ограничено.
2
B = {5, 10, 15, 20,…}
бесконечный
Этот набор имеет начальную, но не конечную точку. Поскольку числа, кратные 5, не могут быть исчислены.
3
C = {…, -2, -1, 0, 1, 2,…}
бесконечный
У этого набора нет ни начальной, ни даже конечной точки, поэтому количество его элементов неисчислимо.
4
D = {x: x W и 0
Конечная
Это набор целых чисел от 0 до 10. Таким образом, количество элементов ограничено.
5
E = {x: x∈R и x-2 = 10}
Конечная
Это набор действительных чисел, элементами которого являются те, где x-2 = 10.Поскольку набор действительных чисел бесконечен, но здесь знак равенства делает его конечным.
6
F = {x: x∈R и x + 4> 12}
бесконечный
Здесь элементы этого набора: x + 4 — это любое значение больше 12. Поскольку набор действительных чисел бесконечен, конечной точки этого набора нет.

Графическое представление конечных и бесконечных множеств
Здесь, на картинке выше,
H = {a, s, h, e, d}
T = {a, s, t, i, l}
HUT = {a, s, h, e, d, t, i, l}
H∩T = {a, s}
И H, и T — конечные множества, поскольку они имеют ограниченное количество элементов.
n (H) = 5 и n (T) = 5
HUT и H∩T также конечны.
Это показывает, что мы можем легко представить конечные множества с помощью диаграммы Венна.
Объединение двух конечных множеств конечно.
Пересечение двух конечных множеств также конечно.
Но трудно представить бесконечное множество с помощью диаграммы Венна, поскольку оно имеет неограниченное количество элементов и не может быть ограничено кругом для представления.
Другие чтения
Конечные и бесконечные множества
Кардинальные числа
Литература к занятию 3 — (продолжение)
Наборы и целые числа
В предыдущая сессия, мы показали тесную взаимосвязь между концепцией индивидуального соответствие и представление о количестве элементов в наборе, называется мощностью множества.(См. Подсчет насекомых в Сессии 1.) Здесь мы формализуем эти отношения между наборами и целыми числами.
Наборы номеров: Набор натуральных чисел (или , считая числа ) — это набор N = {1, 2, 3,…}.
Набор целых чисел — это набор Вт = {0, 1, 2, 3, …}.
Кардинальное число набора : Количество элементов в наборе — Кардинальный номер этого набора.
Обозначение: Если набор A эквивалентен набор {1, 2, 3,…, N }, пишем n ( A ) = N и произнесите «The количество элементов комплекта A это N .”
Кроме того, n (Ø) = 0. кардинальное число для пустого множества равно нулю.
Пример: Пусть C = {#, $, %, &}. Показать n ( C ) = 4.
# $ % &
| | | |
1 2 3 4
Следовательно, C эквивалентен {1, 2, 3, 4} и n ( C ) = 4, поскольку соответствие 1-1 может быть установлен между C и {1, 2, 3, 4}.
Пример: Для M = {красный, синий, зеленый, желтый, оранжевый}, n ( M ) = 5.
Читается символ « n ( M ) = 5», «Кардинальное число набора M равно 5.”
Найдите время, чтобы установить соответствие 1-1 между M и {1, 2, 3, 4, 5}.
Пример: Для T = {2, 4, 6, 8, 10, 12, 14, 16}, n ( T ) = 8 .
На листе бумаги установите соответствие 1-1 между T и {1, 2, 3, 4, 5, 6, 7, 8}.
Пример: В этом на картинке кружки представляют собой наборы A и В . Точки внутри элементы наборов. Нам нужно убедиться, что мы смотрим на весь круг, даже если круги перекрываются.

n ( A ) = 5 n ( B ) = 8
Дополнительные примечания: Не отдадим точные определения терминов конечное и бесконечное .

РубрикаРазное

$ \| W \ чашка R \ чашка B \|	$ = 21
	$ = \| W \| + \| R \| + \| B \| — \| W \ cap R \| — \| W \ cap B \| — \| R \ cap B \| + \| W \ cap R \ cap B \|
	$ = 10 + 8 + \| B \| -0-4-3 + 0 $.

№	Очки	Конечные наборы	Бесконечные наборы
1	Определение	Набор является конечным набором, если он пуст или содержит ограниченное количество элементов.	Множество, которое не является конечным множеством, является бесконечным множеством.
2	Количество элементов	Счетное количество элементов.	Бесчисленное количество элементов.
3	Непрерывность	Запускается и тоже останавливается.	Он не имеет конца ни в начале, ни в конце, или может иметь непрерывность с обеих сторон.
4	Мощность	n (A) = n, n — количество элементов.	n (A) = ∞, бесконечно, поскольку количество элементов неисчислимо.
5	Союз	Объединение двух конечных множеств конечно.	Союз двух бесконечных множеств бесконечен.
6	Силовой агрегат	Мощность конечного множества конечна.	Мощность набора бесконечного набора бесконечна.
7	Форма реестра	Может быть легко представлен в форме реестра.	Все наборы не могут быть показаны в форме списка, поэтому мы используем три точки для представления бесконечности.
8	Пример	A = {2, 4, 6, 8}	X = {2, 4, 6, 8,…}
8	Пример	Набор четных чисел меньше 9.	Набор всех четных чисел.

№	Пример	Конечное или бесконечное	Почему?
1	А = {5,10,15,20}	Конечная	Этот набор имеет как начальную, так и конечную точки, а количество его элементов ограничено.
2	B = {5, 10, 15, 20,…}	бесконечный	Этот набор имеет начальную, но не конечную точку. Поскольку числа, кратные 5, не могут быть исчислены.
3	C = {…, -2, -1, 0, 1, 2,…}	бесконечный	У этого набора нет ни начальной, ни даже конечной точки, поэтому количество его элементов неисчислимо.
4	D = {x: x W и 0	Конечная	Это набор целых чисел от 0 до 10. Таким образом, количество элементов ограничено.
5	E = {x: x∈R и x-2 = 10}	Конечная	Это набор действительных чисел, элементами которого являются те, где x-2 = 10.Поскольку набор действительных чисел бесконечен, но здесь знак равенства делает его конечным.
6	F = {x: x∈R и x + 4> 12}	бесконечный	Здесь элементы этого набора: x + 4 — это любое значение больше 12. Поскольку набор действительных чисел бесконечен, конечной точки этого набора нет.

Приведите пример конечного множества чисел бесконечного множества чисел: Приведите пример: А) конечного множества чисел; Б) бесконечного множества чисел.

О бесконечных множествах

Вадим Дунаев

Раздел из книги «Занимательная математика. Множества и отношения»

Сравнение бесконечных множеств

Множество всех подмножеств данного множества

Прямая и плоскость

Парадоксы бесконечности

Рука дающего не оскудеет

— 1.

Множества чисел и примеры числовых множеств

Что такое множество чисел

Виды чисел

Примеры решения задач

В чем отличие конечных множеств от бесконечных.

6 класс. Математика. Никольский. Учебник. Ответы к стр. 47

Целые числа

Урок алгебры в 8 классе по теме «Множества. Элементы множеств» УМК А.Г. Мерзляк

5.01 О границах числовых множеств

Конечные и бесконечные множества — объяснение, свойства и решаемый пример

Мощность конечного набора

Является ли пустой набор конечным набором?

Что такое бесконечный набор?

Свойства бесконечного множества

Примеры бесконечного множества

Графическое представление конечных и бесконечных множеств

Решенный пример

Конечные множества — определение и примеры

Бесконечные множества — определение и примеры

Бесконечные множества и мощности — математика LibreTexts

Мощность | Конечные множества | Бесконечные наборы

конечных и бесконечных множеств — учебный материал для IIT JEE

Кардинальные числа

Добавить комментарий Отменить ответ