Примеры разности множеств: Страница не найдена — ПриМат

Страница не найдена — ПриМат

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2),

свойства, формулы включений и исключений, примеры

Пересечение множеств

Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:

$$ A \cap B = \{x|x \in \Bbb A и x \in \Bbb B \} $$

Если множества не пересекаются, то $A \cap B = \varnothing $ — пустое множество в пересечении. Если $B \subseteq A$ — подмножество, то $A \cap B = B$ – пересечением будет меньшее множество из двух.

Например:

Если A = {1;3;5;9}, Β = {3;7;11}, то $A \cap B$ = {3;5}.

Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A \cap B$ = {f|f-квадрат}.

Если A = $\{n|n⋮3, n \in \Bbb N \}$ — натуральные числа, кратные 3, B = $\{n|n⋮5, n \in \Bbb N \}$ — натуральные числа, кратные 5, то $A \cap B = {n|n⋮15, n \in \Bbb N}$ — натуральные числа, кратные 15.

Если A = {a│a-слон}, B = {a|a-птица}, то $A \cap B = \varnothing$.

Объединение множеств

Объединением – множеств A и B называют множество, содержащее те и только те элементы, которые входят хотя бы в одно из множеств, A или B:

$$ A \cup B = \{ x|x \in \Bbb A или x \in \Bbb B \} $$

Если $B \subseteq A$ — подмножество, то $A \cap B = A$ – объединением будет большее множество из двух.

Например:

Если A = {1;3;5;9}, Β = {3;7;11}, то $A \cup B$ = {1;3;5;7;9;11}. 2-4 = 0, x \in \Bbb R\}, B = \{x|x+3 = 2, x \in \Bbb R \}, то A \cup$ B = {-2;-1;2}

Если $A = \{n│n \in \Bbb Z \}$- все целые числа, $B = \{x|x = \frac{a}{b}, a \in \Bbb Z, b \in \Bbb N \}$ — все дроби, то $A \cup B = \{x│x \in \Bbb Q\}$ — множество рациональных чисел. Заметим, что в данном случае $A \subset B$.

Универсум и отрицание

Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.

В литературе универсум обозначают U.

На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:

Примеры универсумов:

При рассмотрении целочисленных задач, универсум – это множество целых чисел.

При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.

При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.

Отрицание (абсолютное дополнение) множества A — множество всех элементов универсума, не принадлежащих A:

$$ \bar{A} = \{x|x \notin A \} $$

Читается «не A».

У отрицания есть любопытное свойство: $\bar{\bar{Α}} = Α $(два раза «нет» — это «да»).

Например:

Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $\bar{A} = \{1;2;6;7\}$

Если U = $\{x|x \in \Bbb R\}$ — все действительные числа, A = $\{x|x \gt 0, x \in \Bbb R \}$ — все положительные действительные числа, то $ \bar{A} = \{x|x \le 0, x \in \Bbb R\}$.

Свойства операций пересечения и объединения

Коммутативность

Ассоциативность

$(A \cap B) \cap C = A \cap (B \cap C)$

$ (A \cup B) \cup C = A \cup ( B \cup C) $

Дистрибутивность

$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$

$ (A \cap B) \cup C = (A \cup C) \cap (B \cup C) $

Идемпотентность

Взаимодействие с отрицанием, пустым множеством и универсумом

$A \cap \bar{A} = \varnothing $

$A \cap U = A$

$A \cap \varnothing = \varnothing$

$A \cup \bar{A} = U $

$A \cup U = U$

$A \cup \varnothing = A$

Законы де Моргана

$ \overline{(A \cap B)} = \bar{A} \cup \bar{B} $

$ \overline{(A \cup B)} = \bar{A} \cap \bar{B} $

Закон поглощения

$ (A \cup B) \cap A = A $

$ (A \cap B) \cup A = A $

Разность множеств

Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:

$$ A\B = \{x|x \in \Bbb A , x \notin B\} $$

Читается «A без B».

На диаграммах Эйлера разности для пересекающихся множеств выглядят так:

Получается, что отрицание – частный случай разности: $ \bar{A} = \{x|x \in \Bbb U, x \notin A \} $= U\A

«Не A» — это «универсум без A».

Формулы включений и исключений

Рассмотрим два конечных пересекающихся множества A и B.

Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A \cap B)$.

Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A \cup B)$?

Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:

$$n(A \cup B) = n(A)+ n(B)-n(A \cap B)$$

Выведем аналогичную формулу для трёх пересекающихся конечных множеств.

Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.

е. отнять сумму $(n(A \cap B)+n(A \cap C)+n(B \cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A \cap B \cap C)$; значит, его нужно «вернуть».

Получаем:

$$ n(A \cup B \cup C) = n(A)+ n(B)+n(C)- $$

$$ -(n(A \cap B)+n(A \cap C)+n(B \cap C) )+n(A \cap B \cap C) $$

Примеры

Пример 1. Найдите пересечение данных множеств:

а) A = {0;5;8;10},

B = {3;6;8;9}

$б) A = \{x|x \lt 3, x \in \Bbb R\}, $

$ B = \{x|x \gt 1, x \in \Bbb R\} $

$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb R\}$ — отрезок

$в) A = \{x|x \lt 3, x \in \Bbb R\}, $

$ B = \{x|x \gt 1, x \in \Bbb N\} $

$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb N \} или A \cap B = \{2\}$ — одна точка

г) A = {f|f-правильный многоугольник},

B = {f|f-четырехугольник}

$A \cap B = \{f|f-квадрат\}$

Пример 2. Найдите объединение данных множеств:

а) A = {0;5;8;10}, B = {3;6;8;9}

$A \cup B$ = {0;3;5;6;8;9;10}

б) A = {1;2}, B = {1;2;3;4}

$A \subset B$ – строгое подмножество

$A \cup B $ = B = {1;2;3;4}

$в) A = \{x|x \lt 1, x \in \Bbb R\}, B = \{x|x \gt 1,x \in \Bbb R\} $

$A \cup B = \{x|x \neq 1, x \in \Bbb R \}$

$г) A = \{n│n⋮3, n \in \Bbb Z\}, B = \{n|n⋮9,n \in \Bbb N\} $

$B \subset A$ — строгое подмножество

$ A \cup B = A = \{n│n⋮3, n \in \Bbb Z\} $

Пример 3. Найдите отрицание данного множества на данном универсуме:

а) U = {1;2;3;4;5}, A = {2;3}

б) U = $\{x│x \in \Bbb Q \}$, A = $\{ \frac{4}{5}, \frac{7}{8} \}$

$ \bar{A} = \{x|x \neq \frac{4}{5}, x \neq \frac{7}{8}, x \in \Bbb Q\} $

$в) U = \{x│x \in \Bbb R\}, A = \{x|x \ge 2, x \in \Bbb R\} $

$\bar{A} = \{x|x \lt 2, x \in \Bbb R\}$

Пример 4. Найдите обе разности данных множеств:

а) A = {0;1;2;3;4}, B = {2;4}

A\B = {0;1;3}, $B\A = \{∅\}$

б) A = {0;1;3}, B = {2;4;6}

A\B = {0;1;3}, B\A = {2;4;6}

$в) A = \{x|x \gt 1, x \in \Bbb R\}, $

$ B = \{x|x \lt 3, x \in \Bbb R\} $

A\B $ = \{x|x \ge 3, x \in \Bbb R\}$

B\A $ = \{x|x \le 1,x \in \Bbb R\} $

$ г*) A = \{(x,y)|x \gt 0, x \in \Bbb R, y \in \Bbb R\} $

$ B = \{(x,y)|x \le 5, x \in \Bbb R, y \in \Bbb R\} $

A\B $ = \{(x,y)|x \gt 5, x \in \Bbb R, y \in \Bbb R\} $

B\A $ = \{(x,y)|x \le 0, x \in \Bbb R, y \in \Bbb R\} $

Пример 5. Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?

n(U) = 100

n(A) = 28, n(B) = 30, n(C) = 42

$ n(A \cap B) = 8, n(B \cap C) = 5, n(A \cap C) = 10 $

$n(A \cap B \cap C) = 3$

Всего программистов:

$ n(A \cup B \cup C) = n(A)+n(B)+n(C)- $

$ (n(A \cap B)+n(B \cap C)+n(A \cap C) )+n(A \cap B \cap C) $

$n(A \cup B \cup C) = 28+30+42-(8+5+10)+3 = 100-23+3 = 80$

Число не умеющих программировать:

$n(U)-n(A \cup B \cup C) = 100-80 = 20$

Ответ: 20 человек

4.1.3. Операции над множествами

Глава 4. Комбинаторика

4.1.

4.

1.3.

Рассмотрим некоторое множество E, которое будем называть основным, и не будем интересоваться его природой. Будем считать, что все множества, которые рассматриваются в данном пункте, являются подмножествами основного множества.

Аналогично определяется пересечение и объединение любого числа множеств.

Для удобства множества изображают в виде кругов, а основное множество в виде прямоугольника, их содержащего. Такие рисунки называются диаграммами Эйлера–Венна.

Модель 4.1. Множества на плоскости

Пример 1

Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}. Найти и

= {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19}, = {1, 3, 5, 7, 9}.

Пример 2

Пусть A = [−2; 1] и B = (0; 3). Найти и

= [−2; 3), = (0; 1].

Например,

Следует заметить, что мощность объединения и пересечения двух конечных множеств связаны следующим соотношением:

(здесь мощность множества A обозначена как |A|).

Для бесконечных множеств это равенство неверно. Если хотя бы одно из множеств A и B бесконечно, то мощность объединения

Пусть теперь A и B − некоторые множества в основном множестве E.

Кратко это можно записать так:

Очевидно, что для любого

Пример 3

Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}. Найти A \ B и B \ A.

A \ B = {2, 4, 6, 8}. B \ A = {11, 13, 17, 19}.

Для любых двух множеств A и B основного множества E справедливы законы де Моргана.

Законы де Моргана можно проиллюстрировать при помощи диаграмм Эйлера–Венна.



Операции над множествами — Visual Basic

• 000Z» data-article-date-source=»ms.date»>07/20/2015
• Чтение занимает 2 мин

В этой статье

Операции над множествами в LINQ — это операции запросов, результирующие наборы которых основываются на наличии или отсутствии эквивалентных элементов в одной или другой коллекции (или наборе).Set operations in LINQ refer to query operations that produce a result set that is based on the presence or absence of equivalent elements within the same or separate collections (or sets).

Методы стандартных операторов запросов, которые выполняют операции над множествами, перечислены в следующем разделе.The standard query operator methods that perform set operations are listed in the following section.

МетодыMethods

Имя методаMethod Name	ОписаниеDescription	Синтаксис выражения запроса Visual BasicVisual Basic Query Expression Syntax	Дополнительные сведенияMore Information
DistinctDistinct	Удаляет повторяющиеся значения из коллекции. Removes duplicate values from a collection.	Distinct	Enumerable.Distinct Queryable.Distinct
ИсключенияExcept	Возвращает разность множеств, т. е. элементы одной коллекции, которые отсутствуют во второй.Returns the set difference, which means the elements of one collection that do not appear in a second collection.	Не применяетсяNot applicable.	Enumerable.Except Queryable.Except
ПересечениеIntersect	Возвращает пересечение множеств, т. е. элементы, присутствующие в каждой из двух коллекций.Returns the set intersection, which means elements that appear in each of two collections.	Не применяетсяNot applicable.	Enumerable.Intersect Queryable.Intersect
ОбъединениеUnion	Возвращает объединение множеств, т. е. уникальные элементы, присутствующие в одной из двух коллекций.Returns the set union, which means unique elements that appear in either of two collections.	Не применяетсяNot applicable.	Enumerable.Union Queryable.Union

Сравнение операций над множествамиComparison of Set Operations

DistinctDistinct

На следующем рисунке показано поведение метода Enumerable.Distinct применительно к последовательности символов.The following illustration depicts the behavior of the Enumerable.Distinct method on a sequence of characters. Возвращаемая последовательность содержит уникальные элементы из входной последовательности.The returned sequence contains the unique elements from the input sequence.

ИсключенияExcept

На следующем рисунке показано поведение Enumerable.Except.The following illustration depicts the behavior of Enumerable.Except. Возвращаемая последовательность содержит только те элементы из первой входной последовательности, которых нет во второй.The returned sequence contains only the elements from the first input sequence that are not in the second input sequence.

ПересечениеIntersect

На следующем рисунке показано поведение Enumerable.Intersect.The following illustration depicts the behavior of Enumerable.Intersect. Возвращаемая последовательность содержит элементы, общие для обеих входных последовательностей.The returned sequence contains the elements that are common to both of the input sequences.

ОбъединениеUnion

На следующем рисунке показана операция объединения двух последовательностей символов.The following illustration depicts a union operation on two sequences of characters. Возвращаемая последовательность содержит уникальные элементы из обеих входных последовательностей.The returned sequence contains the unique elements from both input sequences.

Пример синтаксиса выражения запросаQuery Expression Syntax Example

В следующем примере Distinct предложение в запросе LINQ используется для возврата уникальных чисел из списка целых чисел.The following example uses the Distinct clause in a LINQ query to return the unique numbers from a list of integers.

Dim classGrades = New System.Collections.Generic.List(Of Integer) From {63, 68, 71, 75, 68, 92, 75}

Dim distinctQuery = From grade In classGrades
                    Select grade Distinct

Dim sb As New System.Text.StringBuilder("The distinct grades are: ")
For Each number As Integer In distinctQuery
    sb.Append(number & " ")
Next

' Display the results.
MsgBox(sb.ToString())

' This code produces the following output:

' The distinct grades are: 63 68 71 75 92 

См. также разделSee also

Python и теория множеств / Хабр

В Python есть очень полезный тип данных для работы с множествами – это set. Об этом типе данных, примерах использования, и небольшой выдержке из теории множеств пойдёт речь далее.

Следует сразу сделать оговорку, что эта статья ни в коем случае не претендует на какую-либо математическую строгость и полноту, скорее это попытка доступно продемонстрировать примеры использования множеств в языке программирования Python.

Множество

Множество – это математический объект, являющийся набором, совокупностью, собранием каких-либо объектов, которые называются элементами этого множества. Или другими словами:

Множество – это не более чем неупорядоченная коллекция уникальных элементов.

Что значит неупорядоченная? Это значит, что два множества эквивалентны, если содержат одинаковые элементы.

Элементы множества должны быть уникальными, множество не может содержать одинаковых элементов. Добавление элементов, которые уже есть в множестве, не изменяет это множество.

Множества, состоящие из конечного числа элементов, называются конечными, а остальные множества – бесконечными. Конечное множество, как следует из названия, можно задать перечислением его элементов. Так как темой этой статьи является практическое использование множеств в Python, то я предлагаю сосредоточиться на конечных множествах.

Множества в Python

Множество в Python можно создать несколькими способами. Самый простой – это задать множество перечислением его элементов в фигурных скобках:

fruits = {"banana", "apple", "orange"}

Единственное ограничение, что таким образом нельзя создать пустое множество. Вместо этого будет создан пустой словарь:

wrong_empty_set = {}
print(type(wrong_empty_set))

# Вывод
<class "dict">

Для создания пустого множества нужно непосредственно использовать set():

correct_empty_set = set()
print(type(correct_empty_set))

# Вывод
<class "set">

Также в set() можно передать какой-либо объект, по которому можно проитерироваться (Iterable):

color_list = ["red", "green", "green", "blue", "purple", "purple"]
color_set = set(color_list)
print(color_set)

# Вывод (порядок может быть другим):
{"red", "purple", "blue", "green"}

Ещё одна возможность создания множества – это использование set comprehension. Это специальная синтаксическая конструкция языка, которую иногда называют абстракцией множества по аналогии с list comprehension (Списковое включение).

numbers = [1, 2, 2, 2, 3, 3, 4, 4, 5, 6]

# Единственное отличие со списковыми включениями - это
# использование фигурных скобок вместо квадратных
even_numbers = {
    number for number in numbers
    if number % 2 == 0
}
print(even_numbers)

# Вывод (порядок может быть другим):
{2, 4, 6}

Хешируемые объекты

Существует ограничение, что элементами множества (как и ключами словарей) в Python могут быть только так называемые хешируемые (Hashable) объекты. Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.

# Множество кортежей (tuple)
records = {
    ("Москва", 17_200_000), 
    ("Санкт-Петербург", 5_400_000), 
    ("Новосибирск", 1_600_000),
    ("Москва", 17_200_000),
}

for city, population in records:
    print(city)

# Вывод (порядок может быть другим):
Москва
Новосибирск
Санкт-Петербург

Объекты пользовательских классов являются хешируемыми по умолчанию. Но практического смысла чаще всего в этом мало из-за того, что сравнение таких объектов выполняется по их адресу в памяти, т.е. невозможно создать два «равных» объекта.

class City:
    def __init__(self, name: str):
        self.name = name

    def __repr__(self) -> str:
        """ Определим метод __repr__ для наглядности следующих примеров
        """
        return f'City("{self.name}")'

print(City("Moscow") == City("Moscow"))

# Вывод:
False

cities = {City("Moscow"), City("Moscow")}
print(cities)

# Вывод
{City("Moscow"), City("Moscow")}

Скорее всего мы предполагаем, что объекты City("Moscow") должны быть равными, и следовательно в множестве cities должен находиться один объект.
Этого можно добиться, если определить семантику равенства для объектов класса City:

class City:
    def __init__(self, name: str):
        # Атрибут name не должен изменяться, пока объект существует
        # Для простоты пометим этот атрибут как внутренний
        self._name = name

    def __hash__(self) -> int:
        """ Хеш от объекта
        """
        return hash((self._name, self.__class__))

    def __eq__(self, other) -> bool:
        """ Определяем семантику равентсва (оператор ==)
        """
        if not isinstance(other, self.__class__):
            return False
        return self._name == other._name

    def __repr__(self) -> str:
        """ Определим метод __repr__ для наглядности следующих примеров
        """
        return f'City("{self._name}")'

Чтобы протокол хеширования работал без явных и неявных логических ошибок, должны выполняться следующие условия:

• Хеш объекта не должен изменяться, пока этот объект существует
• Равные объекты должны возвращать одинаковый хеш

moscow = City("Moscow")
moscow_again = City("Moscow")

print(moscow == moscow_again and hash(moscow) == hash(moscow_again))
# Вывод:
True

# Теперь множество городов работает более логично и интуитивно
cities = {City("Moscow"), City("Kazan"), City("Moscow")}
print(cities)

# Вывод (порядок может быть другим):
{City("Kazan"), City("Moscow")}

Свойства множеств

Тип set в Python является подтипом Collection (про коллекции), из данного факта есть три важных следствия:

• Определена операция проверки принадлежности элемента множеству
• Можно получить количество элементов в множестве
• Множества являются iterable-объектами

Принадлежность множеству

Проверить принадлежит ли какой-либо объект множеству можно с помощью оператора in. Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за O(1) с теми же оговорками, которые существуют для хеш-таблиц.

tremendously_huge_set = {"red", "green", "blue"}

if "green" in tremendously_huge_set:
    print("Green is there!")
else:
    print("Unfortunately, there is no green...")

# Вывод:
Green is there!

if "purple" in tremendously_huge_set:
    print("Purple is there!")
else:
    print("Unfortunately, there is no purple...")

# Вывод:
Unfortunately, there is no purple...

Мощность множества

Мощность множества – это характеристика множества, которая для конечных множеств просто означает количество элементов в данном множестве. Для бесконечных множеств всё несколько сложнее.

even_numbers = {i for i in range(100) if i % 2 == 0}

# Мощность множества
cardinality = len(even_numbers)
print(cardinality)

# Вывод:
50

Перебор элементов множества

Как уже было отмечено выше, множества поддерживают протокол итераторов, таким образом любое множество можно использовать там, где ожидается iterable-объект.

colors = {"red", "green", "blue"}

# Элементы множества можно перебрать с помощью цикла for
for color in colors:
    print(color)

# Вывод (порядок может быть другим):
red
green
blue

# Множества можно использовать там, где ожидается iterable-объект
color_counter = dict.fromkeys(colors, 1)
print(color_counter)

# Вывод (порядок может быть другим):
{"green": 1, "red": 1, "blue": 1}

Отношения между множествами

Между множествами существуют несколько видов отношений, или другими словами взаимосвязей. Давайте рассмотрим возможные отношения между множествами в этом разделе.

Равные множества

Тут всё довольно просто – два множества называются равными, если они состоят из одних и тех же элементов. Как следует из определения множества, порядок этих элементов не важен.

my_fruits = {"banana", "apple", "orange", "orange"}
your_fruits = {"apple", "apple", "banana", "orange", "orange"}
print(my_fruits == your_fruits)

# Вывод:
True

Непересекающиеся множества

Если два множества не имеют общих элементов, то говорят, что эти множества не пересекаются. Или другими словами, пересечение этих множеств является пустым множеством.

even_numbers = {i for i in range(10) if i % 2 == 0}
odd_numbers = {i for i in range(10) if i % 2 == 1}

# Очевидно, что множества чётных и нечётных чисел не пересекаются
if even_numbers.isdisjoint(odd_numbers):
    print("Множества не пересекаются!")

# Вывод:
Множества не пересекаются!

Подмножество и надмножество

Подмножество множества S – это такое множество, каждый элемент которого является также и элементом множества S. Множество S в свою очередь является надмножеством исходного множества.

# Множество чисел Фибоначчи меньших 100
fibonacci_numbers = {0, 1, 2, 3, 34, 5, 8, 13, 21, 55, 89}

# Множество натуральных чисел меньших 100
natural_numbers = set(range(100))

# Множество чисел Фибоначчи является подмножеством множества 
# натуральных чисел
if fibonacci_numbers.issubset(natural_numbers):
    print("Подмножество!")

# Вывод:
Подмножество!

# В свою очередь множество натуральных чисел является
# надмножеством множества чисел Фибоначчи
if natural_numbers. issuperset(fibonacci_numbers):
    print("Надмножество!")

# Вывод:
Надмножество!

Пустое множество является подмножеством абсолютно любого множества.

empty = set()

# Методы issubset и issuperset могут принимать любой iterable-объект
print(
    empty.issubset(range(100))
    and empty.issubset(["red", "green", "blue"])
    and empty.issubset(set())
)

# Вывод:
True

Само множество является подмножеством самого себя.

natural_numbers = set(range(100))

if natural_numbers.issubset(natural_numbers):
    print("Подмножество!")

# Вывод:
Подмножество!

Операции над множествами

Рассмотрим основные операции, опредяляемые над множествами.

Объединение множеств

Объединение множеств – это множество, которое содержит все элементы исходных множеств. В Python есть несколько способов объединить множества, давайте рассмотрим их на примерах.

my_fruits = {"apple", "orange"}
your_fruits = {"orange", "banana", "pear"}

# Для объединения множеств можно использовать оператор `|`,
# оба операнда должны быть объектами типа set
our_fruits = my_fruits | your_fruits
print(our_fruits)

# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}

# Также можно использовать ментод union. 
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)

# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}

Добавление элементов в множество

Добавление элементов в множество можно рассматривать как частный случай объединения множеств за тем исключением, что добавление элементов изменяет исходное множество, а не создает новый объект. Добавление одного элемента в множество работает за O(1).

colors = {"red", "green", "blue"}

# Метод add добаляет новый элемент в множество
colors.add("purple")
# Добавление элемента, который уже есть в множестве, не изменяет
# это множество
colors.add("red")
print(colors)

# Вывод (порядок может быть другим):
{"red", "green", "blue", "purple"}

# Метод update принимает iterable-объект (список, словарь, генератор и т.п.)
# и добавляет все элементы в множество
numbers = {1, 2, 3}
numbers. update(i**2 for i in [1, 2, 3])
print(numbers)

# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}

Пересечение множеств

Пересечение множеств – это множество, в котором находятся только те элементы, которые принадлежат исходным множествам одновременно.

def is_prime(number: int) -> bool:
    """ Возвращает True, если number - это простое число
    """
    assert number > 1
    return all(number % i for i in range(2, int(number**0.5) + 1))

def is_fibonacci(number: int) -> bool:
    """ Возвращает True, если number - это число Фибоначчи
    """
    assert number > 1
    a, b = 0, 1
    while a + b < number:
        a, b = b, a + b
    return a + b == number

# Множество простых чисел до 100
primes = set(filter(is_prime, range(2, 101)))

# Множество чисел Фибоначчи до 100
fibonacci = set(filter(is_fibonacci, range(2, 101)))

# Множество простых чисел до 100, которые одновременно являются
# числами Фибоначчи
prime_fibonacci = primes. intersection(fibonacci)

# Или используя оператор `&`, который определён для множеств
prime_fibonacci = fibonacci & primes

print(prime_fibonacci)

# Вывод (порядок может быть другим):
{2, 3, 5, 13, 89}

При использовании оператора & необходимо, чтобы оба операнда были объектами типа set. Метод intersection, в свою очередь, принимает любой iterable-объект. Если необходимо изменить исходное множество, а не возращать новое, то можно использовать метод intersection_update, который работает подобно методу intersection, но изменяет исходный объект-множество.

Разность множеств

Разность двух множеств – это множество, в которое входят все элементы первого множества, не входящие во второе множество.

i_know: set = {"Python", "Go", "Java"}
you_know: dict = {
    "Go": 0.4, 
    "C++": 0.6, 
    "Rust": 0.2, 
    "Java": 0.9
}

# Обратите внимание, что оператор `-` работает только
# для объектов типа set
you_know_but_i_dont = set(you_know) - i_know
print(you_know_but_i_dont)

# Вывод (порядок может быть другим):
{"Rust", "C++"}

# Метод difference может работать с любым iterable-объектом,
# каким является dict, например
i_know_but_you_dont = i_know. difference(you_know)
print(i_know_but_you_dont)

# Вывод:
{"Python"}

Удаление элементов из множества

Удаление элемента из множества можно рассматривать как частный случай разности, где удаляемый элемент – это одноэлементное множество. Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность O(1).

fruits = {"apple", "orange", "banana"}

# Удаление элемента из множества. Если удаляемого элемента
# нет в множестве, то ничего не происходит
fruits.discard("orange")
fruits.discard("pineapple")
print(fruits)

# Вывод (порядок может быть другим):
{"apple", "banana"}

# Метод remove работает аналогично discard, но генерирует исключение,
# если удаляемого элемента нет в множестве
fruits.remove("pineapple")  # KeyError: "pineapple"

Также у множеств есть метод differenсe_update, который принимает iterable-объект и удаляет из исходного множества все элементы iterable-объекта. , также существует два специальных метода – symmetric_difference и symmetric_difference_update. Оба этих метода принимают iterable-объект в качестве аргумента, отличие же состоит в том, что symmetric_difference возвращает новый объект-множество, в то время как symmetric_difference_update изменяет исходное множество.

non_positive = {-3, -2, -1, 0}
non_negative = range(4)

non_zero = non_positive.symmetric_difference(non_negative)
print(non_zero)

# Вывод (порядок может быть другим):
{-1, -2, -3, 1, 2, 3}

# Метод symmetric_difference_update изменяет исходное множество
colors = {"red", "green", "blue"}
colors.symmetric_difference_update(["green", "blue", "yellow"])
print(colors)

# Вывод (порядок может быть другим):
{"red", "yellow"}

Заключение

Я надеюсь, мне удалось показать, что Python имеет очень удобные встроенные средства для работы с множествами. На практике это часто позволяет сократить количество кода, сделать его выразительнее и легче для восприятия, а следовательно и более поддерживаемым. Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.

Полезные ссылки

Множества (Статья на Википедии)
Документация по типу set
Iterable-объекты (Глоссарий Python)
Hashable-объекты (Глоссарий Python)
Sets in Python
Set Theory: the Method To Database Madness

Разность множеств. Разность двух множеств

                                     

ⓘ Разность множеств

Разность двух множеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно разность множеств A {\displaystyle A} и B {\displaystyle B} обозначается как A ∖ B {\displaystyle A\setminus B}, но иногда можно встретить обозначение A − B {\displaystyle A-B} и A ∼ B {\displaystyle A\sim B}.

Пусть A {\displaystyle A} и B {\displaystyle B} — два указанных в определении множества, тогда их разность определяется на теоретико-множественном языке:

A ∖ B = { x ∈ A ∣ x ∉ B }. {\displaystyle A\setminus B=\{x\in A\mid x\not \in B\}.}

Это множество часто называют дополнением множества B {\displaystyle B} до множества A {\displaystyle A}. только когда множество В полностью принадлежит множеству А

Обычно предполагается, что рассматриваются подмножества одного и того же множества, которое, в этом случае называют универсумом, скажем, X {\displaystyle X}. Тогда можно рассматривать вместе с каждым множеством A ⊂ X {\displaystyle A\subset X} и его относительное дополнение X ∖ A {\displaystyle X\setminus A}, при обозначении которого часто опускается значок универсума: ∖ A {\displaystyle \setminus A} ; при этом говорится, что ∖ A {\displaystyle \setminus A} — просто дополнение множества без указания, дополнением до чего является данное множество.

С учётом данного замечания, оказывается, что A ∖ B = A ∩ ∖ B {\displaystyle A\setminus B=A\cap \setminus B}, то есть дополнение множества B {\displaystyle B} до множества A {\displaystyle A} есть пересечение множества A {\displaystyle A} и дополнения множества B {\displaystyle B}. {\complement }}, ∁ X A {\displaystyle \complement _{X}A} или если опустить универсальное множество ∁ A {\displaystyle \complement A}, A ¯ {\displaystyle {\overline {A}}}, A ′ {\displaystyle A}.

Операция разности множеств не является по определению симметричной по отношению ко входящим в неё множествам. Симметричный вариант теоретико-множественной разности двух множеств описывается понятием симметрической разности.

НОУ ИНТУИТ | Лекция | Теория множеств

Аннотация: Приводятся начальные сведения о множествах и основные понятия подмножества, мощности, булеана. Даются возможные способы представления множеств. Рассматриваются операции над множествами, такие как объединение, пересечение, разность, симметрическая разность и дополнение

Начальные сведения о множествах

Одним из основных исходных понятий математики является понятие множества и его элементов. Основатель теории множеств Кантор дал такую трактовку: «Под множеством понимают объединение в одно общее объектов, хорошо различимых нашей интуицией или нашей мыслью».

Понятие множества как и любое другое исходное понятие не имеет строгого математически точного описания. Можно дать следующее определение.

» Множество — это совокупность определенных различаемых объектов, причем таких, что для каждого можно установить, принадлежит этот объект данному множеству или нет.»

Как правило, элементы множества обозначаются маленькими буквами, а сами множества — большими. Принадлежность элемента множеству обозначается так: , где знак является стилизацией первой буквы греческого слова (есть, быть), знак непринадлежности — .

Множества могут быть конечными, бесконечными и пустыми. Множество, содержащее конечное число элементов, называется конечным. Если множество не содержит ни одного элемента, то оно называется пустым и обозначается . Например:

— множество студентов потока 99ПС — конечное множество ;

— множество звезд во Вселенной — бесконечное множество ;

— множество студентов потока 98СП, хорошо знающих три иностранных языка (японский, китайский и французский), видимо, пустое множество.

Множество называют подмножеством множества (обозначается ), если всякий элемент множества является элементом множества : ( рис. 1.1).

Рис. 1.1.

При этом говорят, что содержит , или покрывает . Невключение подмножества в множество обозначается так: .

Множества и равны ( ) тогда и только тогда, когда , и , т. е. элементы множеств и совпадают.

Множество называется собственным подмножеством множества , если , а . Обозначается так: .

Например: .

Мощностью конечного множества называется число его элементов. Обозначается . Например, , .

Принято считать, что пустое множество является подмножеством любого множества. Множество может обладать иерархической структурой. В этом случае говорят о семействе множества или булеане.

Семейством множества или булеаном является множество, элементами которого являются всевозможные подмножества множества .

Например,

В общем случае мощность булеана .

Универсальным множеством называется множество всех рассматриваемых в данной задаче элементов.

Способы задания множеств

Множества могут быть заданы списком, порождающей процедурой, арифметическими операциями, описанием свойств элементов или графическим представлением.

1. Задание множеств списком предполагает перечисление элементов. Например, множество состоит из букв или множество включает цифры .

   Пример: .

2. Задание множеств порождающей процедурой или арифметическими операциями означает описание характеристических свойств элементов множества: , т. е. множество содержит такие элементы , которые обладают свойством .

   Например:

3. Задание множества описанием свойств элементов: например, — это множество чисел, являющихся степенями двойки.

   К описанию свойств естественно предъявить требования точности и недвусмысленности. Так, » множество всех хороших песен 2003 года» каждый составит по-разному. Надежным способом однозначного задания множества является использование разрешающей процедуры, которая для любого объекта устанавливает, обладает ли он данным свойством и соответственно является ли элементом рассматриваемого множества.

   Например, — множество успевающих студентов. Разрешающей процедурой включения в множество является отсутствие неудовлетворительных оценок в последней сессии.

4. Графическое задание множеств происходит с помощью диаграмм Эйлера-Венна. Замкнутая линия-круг Эйлера — ограничивает множество, а рамка — универсальное пространство ( рис. 1.2). Заданы два множества: и . Если элементов множеств немного, то они могут на диаграмме указываться явно.

   
   Рис. 1.2.

Дополнение и разница наборов

Литература к занятию 5 — (продолжение)

Дополнение и разница множеств

Помните, что мы часто работать с определенным набором объектов при решении задач или обсуждение вопросов. Мы назвали этот набор объектов a универсальный набор или вселенная. Например, в приведенной выше задаче ввода универсальный набор может быть либо набором всех долларов США, либо набором 836 долларов Сэм изначально имел на текущем счете.

Комплектация набора: The дополнение набора, обозначенное А ‘, это множество всех элементов в данном универсальном множестве U чего нет в А .

В обозначениях производителей установок: A ‘= { x ∈ U : х ∉ A }.

Диаграмма Венна для комплектация набора A есть показано ниже, где заштрихованная область представляет А ‘.

Пример: Для вводной пример на предыдущей странице, пусть универсальный набор U будет Сэмом за 836 долларов имеет на текущем счете и пусть A быть набором 429 долларов чека. Дополнение набора — это набор из 407 долларов, оставшихся на текущем счете.

Пример: Пусть U = {1, 2, 3, 4, 5, 6} и A = {1, 3, 5}. Затем A ‘ = {2, 4, 6}.

Пример: U ‘ знак равно ∅ В дополнением вселенной является пустое множество.

Пример: ∅ ‘ знак равно U Дополнением к пустому множеству является универсальное множество.

комплект Разница: Модель относительное дополнение или разница наборов наборов A и B , обозначается A — B , это набор всех элементы в A , которые отсутствует в B .

В обозначении конструктора множеств А — B = { x ∈ U : х ∈ A и х ∉ B } = A ∩ B ‘.

Диаграмма Венна для заданной разности множеств A и B показаны ниже.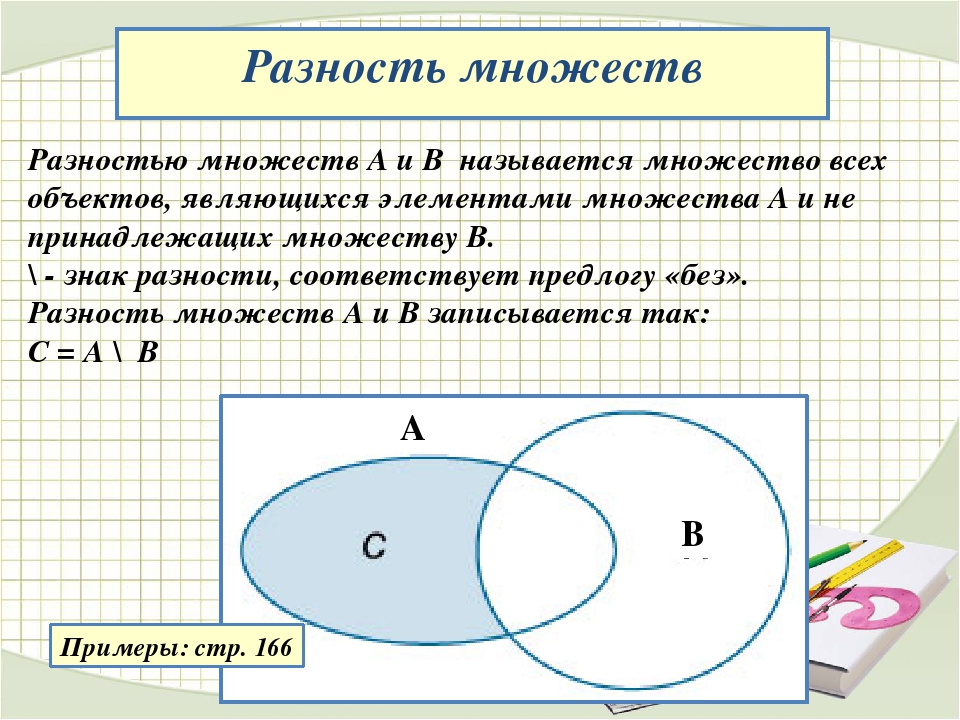 где заштрихованная область представляет А — В .

Пример: Для вводной пример на предыдущей странице, пусть универсальный набор U быть набором всех Долларов США, давай установим A быть набором из 836 долларов, который Сэм изначально имел на текущем счете, и пусть B будет набором 429 долларов чека. Тогда установленная разница A и B будет 407 долларов остающийся на текущем счете.

Пример: Пусть A = { a, b, c, d } и B = { b, д, д} . потом А — B = { a, c } и B — A = { e }.

Пример: Пусть G = { t, a, n } и H = { n, а, т }.Тогда G — H = ∅.

Как нам определить вычитание целых чисел?

в вводный пример на на предыдущей странице этого раздела, оставшийся баланс составлял разница между мощностями наборов для текущий счет и чек. Это также работает для третьего пример (выше) где

n ( G ) — n ( H ) = 3 — 3 = 0 = n (∅).

Но во втором примере (выше) разница между мощностями не дает ожидаемый результат, например,

n ( A ) — n ( B ) = 4 — 3 = 1 ≠ 2 = n ( A — В ).

В таком случае, B не является частью А . Это приводит к определение набора для вычитания целых чисел, указанных на Следующая страница.

Возврат на домашнюю страницу Пейля | Миннесота Государственный университет Мурхед | Математика Отдел

В чем разница двух множеств в теории множеств?

Разница между двумя наборами: A — B — это набор всех элементов A , которые не являются элементами B .Операция разности, наряду с объединением и пересечением, является важной и фундаментальной операцией теории множеств.

Описание разницы

Вычитание одного числа из другого можно рассматривать по-разному. Одна из моделей, помогающих понять эту концепцию, называется выносной моделью вычитания. В этом случае задача 5 — 2 = 3 будет продемонстрирована, если начать с пяти объектов, удалить два из них и посчитать, что осталось три.Подобно тому, как мы находим разницу между двумя числами, мы можем найти разницу между двумя наборами.

Пример

Мы рассмотрим пример различия наборов. Чтобы увидеть, как разница двух наборов образует новый набор, давайте рассмотрим наборы A = {1, 2, 3, 4, 5} и B = {3, 4, 5, 6, 7, 8} . Чтобы найти разницу A — B этих двух наборов, мы начнем с записи всех элементов A , а затем уберем каждый элемент A , который также является элементом B .Поскольку A разделяет элементы 3, 4 и 5 с B , это дает нам установленную разницу A — B = {1, 2}.

Порядок важен

Так же, как различия 4–7 и 7–4 дают нам разные ответы, мы должны быть осторожны с порядком, в котором мы вычисляем разницу наборов. Используя технический термин из математики, мы бы сказали, что установленная операция разности не коммутативна. Это означает, что в общем случае мы не можем изменить порядок разницы двух наборов и ожидать того же результата.Точнее можно сказать, что для всех наборов A, и B , A — B не равно B — A .

Чтобы убедиться в этом, вернитесь к приведенному выше примеру. Мы подсчитали, что для наборов A = {1, 2, 3, 4, 5} и B = {3, 4, 5, 6, 7, 8}, разница A — B = {1, 2}. Чтобы сравнить это с B — A, , мы начнем с элементов B , которые являются 3, 4, 5, 6, 7, 8, а затем удалим 3, 4 и 5, потому что они вместе с A .Результат: B — A = {6, 7, 8}. Этот пример ясно показывает нам, что A — B не равно B — A .

Дополнение

Одно различие достаточно важно, чтобы иметь собственное особое имя и символ. Это называется дополнением и используется для разницы наборов, когда первый набор является универсальным. Дополнение A задается выражением U — A . Это относится к набору всех элементов универсального набора, которые не являются элементами A .Поскольку понятно, что набор элементов, из которых мы можем выбирать, взят из универсального набора, мы можем просто сказать, что дополнение A — это набор, состоящий из элементов, которые не являются элементами A .

Дополнение набора относительно универсального набора, с которым мы работаем. При A = {1, 2, 3} и U = {1, 2, 3, 4, 5} дополнение к A равно {4, 5}. Если наш универсальный набор отличается, скажем, U = {-3, -2, 0, 1, 2, 3}, то дополнение к A {-3, -2, -1, 0}.Обязательно обращайте внимание на то, какой универсальный набор используется.

Обозначение дополнения

Слово «дополнение» начинается с буквы C, и поэтому оно используется в обозначениях. Дополнение набора A записывается как A ^C . Таким образом, мы можем выразить определение дополнения в символах как: A ^C = U — A .

Другой способ, который обычно используется для обозначения дополнения набора, включает апостроф и записывается как A ‘.

Другие идентичности, связанные с различиями и дополнениями

Существует множество наборов идентичностей, в которых используются операции различия и дополнения. Некоторые тождества сочетают в себе другие операции над множеством, такие как пересечение и объединение. Некоторые из наиболее важных излагаются ниже. Для всех наборов A, , B, и D мы имеем:

• A — A = ∅
• A — ∅ = A
• ∅ — A =
∅
• A — U = ∅
• ( A ^C ) ^C = A
• Закон ДеМоргана I: ( A ∩ B ) ^C = A ^C ∪ B ^C
• Закон ДеМоргана II: ( A ∪ B ) ^C = A ^C ∩ B ^C

Установить операции | Союз | Пересечение | Дополнение | Разница | Взаимоисключающие | Перегородки | Закон Де Моргана | Распределительный закон

---

1.

2.2 Настройка операций

Объединение двух наборов — это набор, содержащий все элементы, которые находятся в $ A $ или в $ B $ (возможно, оба). Например, $ \ {1,2 \} \ cup \ {2,3 \} = \ {1,2,3 \} $. Таким образом, мы можем написать $ x \ in (A \ cup B) $ тогда и только тогда, когда $ (x \ in A) $ или $ (x \ in B) $. Обратите внимание, что $ A \ cup B = B \ cup A $. На рисунке 1.4, объединение множеств $ A $ и $ B $ показано заштрихованной областью на диаграмме Венна.

Рис.1.4 — Заштрихованная область показывает набор $ B \ cup A $.{n} A_i. $$ Например, если $ A_1 = \ {a, b, c \}, A_2 = \ {c, h \}, A_3 = \ {a, d \} $, то $ \ bigcup_ {i} A_i = A_1 \ cup A_2 \ cup A_3 = \ {a, b, c, h, d \} $. Аналогичным образом мы можем определить объединение бесконечного множества множеств $ A_1 \ чашка A_2 \ чашка A_3 \ чашка \ cdots $.

Пересечение двух множеств $ A $ и $ B $, обозначенное $ A \ cap B $, состоит из всех элементов которые оба находятся в $ A $ $ \ underline {\ textrm {и}} $ $ B $. Например, $ \ {1,2 \} \ cap \ {2,3 \} = \ {2 \} $. На рисунке 1.5 пересечение множеств $ A $ и $ B $ показано заштрихованной областью с использованием диаграммы Венна.c $.

Рис.1.8 — Заштрихованная область показывает набор $ A-B $.

Два набора $ A $ и $ B $ являются взаимоисключающими или непересекающимися , если у них нет общих элементы; т.е. их пересечение — это пустое множество, $ A \ cap B = \ emptyset $. В общем, несколько наборов называются непересекающимися, если они попарно не пересекаются, т. е. никакие два из них не имеют общих элементов. На рис. 1.9 показаны три непересекающихся множества.

Рис.1.9 — Множества $ A, B, $ и $ C $ не пересекаются.

Если нашим образцом является земная поверхность, мы могли бы разделить ее на разные континенты. Точно так же страна может быть разделена на разные провинции. В общем, набор непустых множества $ A_1, A_2, \ cdots $ — это разбиение множества $ A $, если они не пересекаются и их объединение равно $ A $. c = \ {3,4,5,6 \} \ cap \ {1,3,6 \} = \ {3,6 \}.$

У нас есть $$ A \ cap (B \ cup C) = \ {1,2 \} \ cap \ {1,2,4,5,6 \} = \ {1,2 \}, $$, что является такой же как $$ (A \ cap B) \ cup (A \ cap C) = \ {2 \} \ cup \ {1 \} = \ {1,2 \}. $$

---

Декартово произведение двух наборов $ A $ и $ B $, записанное как $ A \ times B $, представляет собой набор, содержащий упорядоченных пары из $ A $ и $ B $. То есть, если $ C = A \ times B $, то каждый элемент $ C $ имеет форму $ (x, y) $, где $ x \ in A $ и $ y \ in B $: $$ A \ times B = \ {(x, y) | x \ in A \ textrm {и} y \ in B \}.$$ Например, если $ A = \ {1,2,3 \} $ и $ B = \ {H, T \} $, то $$ A \ times B = \ {(1, H), (1, T), (2, H), (2, T), (3, H), (3, T) \}. $$ Обратите внимание, что здесь пары упорядочены, например, $ (1, H) \ neq (H, 1) $. Таким образом, $ A \ times B $ равно , а не . то же, что и $ B \ times A $.

Если у вас есть два конечных множества $ A $ и $ B $, где $ A $ содержит $ M $ элементов, а $ B $ — $ N $ элементов, то $ A \ times B $ имеет $ M \ times N $ элементов. Это правило называется принципом умножения и очень полезно при подсчете количество элементов в наборах.Количество элементов в наборе обозначается $ | A | $, поэтому здесь мы пишем $ | A | = M, | B | = N $ и $ | A \ times B | = MN $. В приведенном выше примере $ | A | = 3, | B | = 2 $, поэтому $ | A \ times B | = 3 \ times 2 = 6 $. Аналогичным образом мы можем определить декартово произведение $ n $ множеств $ A_1, A_2, \ cdots, A_n $ как $$ A_1 \ times A_2 \ times A_3 \ times \ cdots \ times A_n = \ {(x_1, x_2, \ cdots, x_n) | x_1 \ в A_1 \ textrm {и} x_2 \ in A_2 \ textrm {и} \ cdots x_n \ in A_n \}. $$ Принцип умножения утверждает, что для конечных множеств $ A_1, A_2, \ cdots, A_n $, если $$ | A_1 | = M_1, | A_2 | = M_2, \ cdots, | A_n | = M_n, $$, затем $$ \ mid A_1 \ times A_2 \ times A_3 \ times \ cdots \ times A_n \ mid = M_1 \ times M_2 \ раз M_3 \ раз \ cdots \ times M_n.3 = \ mathbb {R} \ times \ mathbb {R} \ times \ mathbb {R} $ и так далее.

---

Разница комплектов

Этот урок объяснит, как найти разницу наборов. Начнем с определения. Определение:

Для данного набора A и набора B разница набора набора B и набора A является набором всех элементов в A, но не в B.

Мы можем записать A — B

Пример # 1.

Внимательно посмотрите на рисунок выше. Элементы в A только — это b, d, e и g.

Следовательно, A — B = {b, d, e, g}

Обратите внимание, что хотя элементы a, f, c находятся в A, мы не включили их в A — B, потому что мы не должны ничего брать из набора B

Иногда, вместо того, чтобы смотреть на диаграммы Венна, может быть проще записать элементы обоих наборов.

Затем выделим жирным шрифтом элементы, которые находятся в A, но не в B.

A = { b , d , e , g , a, f, c}

B = {k, h, u, a, f, c}

Пример №2.

Пусть A = {1 апельсин, 1 ананас, 1 банан, 1 яблоко}

Пусть B = {1 апельсин, 1 абрикос , 1 ананас, 1 банан, 1 манго , 1 яблоко, 1 киви }

Найдите B — A

Обратите внимание, что на этот раз вы ищете все, что видите в B только

Элементы, которые только в B, показаны ниже жирным шрифтом.

B — A = {1 абрикос, 1 манго, 1 киви}

Пример №3.

Найдите A — B

B = {1, 2, 4, 6}

A = {1, 2, 4, 6, 7 , 8 , 9 }

Что я вижу в A, которых нет в B, — это 7, 8 и 9

A — B = {7, 8, 9}

Пример № 4.

Найти B — A

A = {x / x — число больше 6 и меньше 10}

B = {x / x — положительное число меньше 15}

A = {7, 8 , 9} и B = { 1 , 2 , 3 , 4 , 5 , 6 , 7, 8, 9, 10 , 11 , 12 , 13 , 14 }

Все, что вы видите жирным шрифтом выше, относится только к B.

B — A = {1, 2, 3, 4, 5, 6, 10, 11, 12, 13, 14}

На графике ниже показана заштрихованная область для A — B и B — A

На этом урок о разнице наборов заканчивается.

Тест на разницу наборов, чтобы узнать, насколько хорошо вы усвоили этот урок.

Набор «Python

» | разница () — GeeksforGeeks

Набор Python | разница ()

Разница между двумя наборами в Python равна разнице между количеством элементов в двух наборах. Функция difference () возвращает набор, который представляет собой разницу между двумя наборами. Попробуем выяснить, в чем будет разница между двумя наборами A и B. Тогда (набор A — набор B) будут элементы, присутствующие в наборе A, но не в B, и (набор B — набор A) будут присутствующими элементами в наборе B, но не в наборе A.
Пример:

установить A = {10, 20, 30, 40, 80}
установить B = {100, 30, 80, 40, 60}

установить A - установить B = {10, 20}
установить B - установить A = {100, 60}

Пояснение: A - B равно элементам, присутствующим в A, но не в B
             B - A равно элементам, присутствующим в B, но не в A
 

Давайте посмотрим на диаграмму Венна следующей функции разностного набора.

Синтаксис:

  set_A.difference (set_B)  для (A - B)
  набор _B.разница (set_A)  для (B - A)
 

В этой программе мы попытаемся выяснить разницу между двумя наборами set_A и set_B, в обе стороны:

A = { 10 , 20 , 30 , 40 , 80 } B = { 100 , 30 , 30 80 , 40 , 60 } печать (A.разница (B)) печать (B.difference (A))

Выход:

{10, 20}
{100, 60}
 

Мы также можем использовать оператор -, чтобы найти разницу между двумя наборами.

A = { 10 , 20 , 30 , 40 80801 B = { 100 , 30 , 80 , 40 , 60 } печать (A - B) печать (B - A)

Выход:

{10, 20}
{100, 60}
 

Если у нас есть равные наборы, он вернет нулевой набор.

A = { 10 , 20 , 30 , 40 80801 B = { 10 , 20 , 30 , 40 , 80 , 100 2 5 00 печать 00 (A - B)

Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.

Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS . И чтобы начать свое путешествие по машинному обучению, присоединитесь к Машинное обучение - курс базового уровня

Python Метод Set difference () с примерами

Метод difference () в Python возвращает разницу между двумя заданными наборами. Допустим, у нас есть два набора A и B, разница между A и B обозначена A-B, и он содержит элементы, которые находятся в наборе A, но в наборе B.

Как рассчитывается разница между двумя наборами?

Допустим, у нас есть два набора X и Y следующим образом:
X = {«привет», 2, 5}
Y = {2, 9, «пока»}

Разница между двумя наборами обозначается знаком -.

Элементы, которые находятся в наборе X, но отсутствуют в наборе Y
X-Y = {«привет», 5}

Элементы, которые находятся в наборе Y, но отсутствуют в наборе X
Y-X = {9, «пока»}

Синтаксис метода Python Set difference ()

 Разница по оси X (Y) 

Это эквивалент X-Y.

Параметры: Этот метод принимает Set как параметр.
Возвращаемое значение: Возвращает набор, который является разницей между двумя наборами. Например, X.difference (Y) вернет Set, который содержит элементы, которые находятся в Set X, но отсутствуют в Set Y.

Пример метода Python Set difference ()

В следующем примере у нас есть два набора X и Y. Мы находим разницу между X и Y и Y и X с помощью метода difference ().

 # Set X
X = {"привет", 9, 10, "привет"}

# Установить Y
Y = {9, "привет", 6, "BeginnersBook"}

# Эквивалентно X - Y
print ("X-Y это:", X.разница (Y))

# Эквивалент Y - X
print ("YX is:", Y.difference (X)) 

Выход:

Разница между используемыми наборами - Оператор

Мы можем использовать оператор - для множеств. Это работает так же, как и метод difference (). Давайте возьмем тот же пример, который мы видели выше, с использованием оператора -.

 # Set X
X = {"привет", 9, 10, "привет"}

# Установить Y
Y = {9, "привет", 6, "BeginnersBook"}

# Эквивалентно X.difference (Y)
print ("X-Y:", X-Y)

# Эквивалентно Y.разница (X)
print ("Y-X:", Y-X) 

Выход:

 X-Y: {10, 'привет'}
Y-X - это: {'BeginnersBook', 6} 

Как видите, результат такой же.

операций установки

операций установки

• объединение двух наборов - это набор, содержащий все элементы из обоих этих наборов.
  • Написано \ (A \ cup B \) и определено \ [A \ чашка B = \ {x \ mid x \ in A \ vee x \ in B \} \,. \]
  • Например, \ [\ {1,2,3,4 \} \ cup \ {3,4,5,6 \} = \ {1,2,3,4,5,6 \} \, \\ \ mathbf {R} = \ mathbf {Q} \ cup \ overline {\ mathbf {Q}} \ ,.\]
• Пересечение двух наборов - это набор, содержащий элементы, которые находятся в обоих этих наборах.
  • Написано \ (A \ cap B \) и определено \ [A \ cap B = \ {x \ mid x \ in A \ wedge x \ in B \} \, \\ \ mathbf {Q} \ cap \ overline {\ mathbf {Q}} = \ emptyset \,. \]
  • Например, \ [\ {1,2,3,4 \} \ cap \ {3,4,5,6 \} = \ {3,4 \} \,. \]
• Разница между двумя наборами - это набор значений в одном, но не в другом: \ [A-B = \ {x \ mid x \ in A \ text {и} x \ notin B \} \ ,.\]
  • Например, \ [\ {1,2,3,4 \} - \ {3,4,5,6 \} = \ {1,2 \} \, \\ \ overline {\ mathbf {Q}} = \ mathbf {R} - \ mathbf {Q} \,. \]
  • Также иногда пишется \ (A \ setminus B \).
• Теорема: Для любых множеств \ (| A-B | \ le | A | \).

  Доказательство: Предположим, что нет, что \ (| A-B |> | A | \). Тогда должен быть элемент \ (x \) с \ (x \ in (A-B) \), но \ (x \ notin A \). Таким образом, \ (A-B \ not \ substeq A \).

  Но из определения разницы множеств мы видим, что \ [A-B = \ {x \ mid x \ in A \ text {и} x \ notin B \} \ substeq \ {x \ mid x \ in A \} = A \ ,.\] Противоречие, поэтому \ (| A-B | \ le | A | \). ∎

• С подобными доказательствами мы могли бы доказать следующее:

  Теорема: Для любых множеств \ (| A \ cap B | \ le | A | \) и \ (| A \ cap B | \ le | B | \).

  Теорема: Для любых множеств \ (| A \ cup B | \ ge | A | \) и \ (| A \ cup B | \ ge | B | \).

• При выполнении операций над наборами нам часто требуется определить универсальный набор , \ (U \).
  • Как и область для квантификаторов, это набор всех возможных значений, с которыми мы работаем.
  • Часто не определяется явно, но подразумевается в зависимости от рассматриваемой проблемы.
  • например когда мы работаем с действительными числами, возможно, \ (U = \ mathbf {R} \).
• Дополнение набора \ (S \) записывается \ (\ overline {S} \) и представляет собой набор всех значений , а не в \ (S \): \ [\ overline {S} = \ {x \ mid x \ notin S \} = U-S \,. \]
  • Стандартные обозначения иррациональных чисел теперь должны иметь большой смысл: с универсальным набором \ (\ mathbf {R} \) иррациональные числа (\ (\ overline {\ mathbf {Q}} \)) являются дополнением к рациональные числа (\ (\ mathbf {Q} \)).
• Теорема: Для любого набора \ (S \ cap \ overline {S} = \ emptyset \).

  Доказательство: Предположим от противного, что существует элемент \ (x \ in S \ cap \ overline {S} \). Тогда по определению операторов \ [ х \ в S \ cap \ overline {S} \\ x \ in S \ wedge x \ in \ overline {S} \\ x \ in S \ wedge x \ notin {S} \ ,. \] Это противоречие, поэтому мы должны иметь \ (S \ cap \ overline {S} = \ emptyset \). ∎

• Обратите внимание на сходство между соответствующим набором и логическими операторами: \ (\ vee, \ cup \) и \ (\ wedge, \ cap \) и \ (\ overline {\ mbox {S}}, \ neg \).
  • Это нечто большее, чем похожие символы.
• Вот некоторые важные идентификационные данные:

  Имя	Идентификатор
  Идентификатор	\ (A \ cap {U} = A \\ A \ cup \ emptyset = A \)
  Domination	\ (A \ cup {U} = {U} \\ A \ cap \ emptyset = \ emptyset \)
  Идемпотент	\ (A \ cap A = A \\ A \ cup A = A \)
  Двойное отрицание	\ (\ overline {(\ overline {A})} = A \)
  Коммутативный	\ (A \ cup B = B \ cup A \\ A \ cap B = B \ cap A \)
  Ассоциативный	\ ((A \ cup B) \ cup C = A \ cup (B \ cup C) \\ (A \ cap B) \ cap C = A \ cap (B \ cap C) \)
  Распределительный	\ (A \ cup (B \ cap C) = (A \ cup B) \ cap (A \ cup C) \\ A \ cap (B \ cup C) = (A \ cap B) \ чашка (A \ cap B) \)
  Закон Де Моргана	\ (\ overline {A \ cap B} = \ overline {A} \ cup \ overline {B} \\\ overline {A \ cup B } = \ overline {A} \ cap \ overline {B} \)
  Поглощение	\ (A \ cup (A \ cap B) = A \\ A \ cap (A \ cup B) = A \)
  Отрицание	\ (A \ cup \ overline {A} = {U} \\ A \ cap \ overline {A} = \ emptyset \)

• Знакомо? Это таблица логических эквивалентностей, в которой произведен некоторый поиск и замена.
• В качестве примера мы можем доказать один из законов Де Моргана (книга доказывает другой).
  • Мы будем осторожны с этим и будем манипулировать нотацией построителя множеств.

  Теорема: Для любых множеств \ (\ overline {A \ cup B} = \ overline {A} \ cap \ overline {B} \).

  Проба: По определению заданных операций, \ [\ begin {align *} \ overline {A \ cup B} & = \ {x \ mid x \ notin (A \ cup B) \} \\ & = \ {x \ mid \ neg (x \ in (A \ cup B)) \} \\ & = \ {x \ mid \ neg (x \ in A \ vee x \ in B) \} \\ & = \ {x \ mid \ neg (x \ in A) \ wedge \ neg (x \ in B) \} \\ & = \ {x \ mid x \ in \ overline {A} \ wedge x \ in \ overline {B}) \} \\ & = \ {x \ mid x \ in (\ overline {A} \ cap \ overline {B})) \} \\ & = \ overline {A} \ cap \ overline {B} \ ,.\ quad {} ∎ \ конец {выравнивание *} \]

  • Могли быть и менее формальные доказательства. (См. Раздел 2.2, пример 10.)
  • Это тот случай, когда, вероятно, проще быть более формальным: так больно записывать все детали в предложениях, что семь шагов в этом доказательстве легче читать. (См. Также пример 10 в примере.)
• Это доказательство может дать намек на то, почему таблицы эквивалентностей и наборов идентичностей так похожи.
  • Для любой одной из операций над наборами мы можем расширить его до нотации построителя наборов, а затем использовать логические эквиваленты для управления условиями.
  • Поскольку мы проделываем те же манипуляции, мы получили те же самые таблицы.
  • Будьте осторожны при выполнении других операций. То, что это сработало, не означает, что вы можете предполагать, что все одинаково. Нет никакой логической версии установленной разницы или установленной версии исключающего или (по крайней мере, насколько мы определили).

• Теорема: Для любых множеств \ (A-B = A \ cap \ overline {B} \).

  Менее формальное доказательство: Набор \ (A-B \) - это значения из \ (A \) с удаленными значениями из \ (B \).

  Набор \ (\ overline {B} \) - это набор всех значений, не входящих в \ (B \). Таким образом, пересечение с \ (\ overline {B} \) приводит к тому, что остаются только значения, не входящие в \ (B \). То есть \ (A \ cap \ overline {B} \) - это \ (A \) со всеми удаленными значениями из \ (B \). Таким образом, мы видим, что эти наборы содержат одни и те же элементы. ∎

  Более формальное доказательство: По определению множества операций, \ [\ begin {align *} А-Б & = \ {x \ mid x \ in A \ клин x \ notin B \} \\ & = \ {x \ mid x \ in A \ клин x \ in \ overline {B} \} \\ & = \ {x \ mid x \ in (A \ cap \ overline {B}) \} \\ & = A \ cap \ overline {B} \ ,.\ quad {} ∎ \ конец {выравнивание *} \]

• Я думаю, что любое из этих доказательств является действительным.
  • «Менее формальная» версия должна быть написана достаточно тщательно, чтобы убедить читателя (или TA в вашем случае).
  • «Более формальная» версия содержит больше шагов и не учитывает интуитивную причину (которая может помочь вам на самом деле вспомнить, почему).
• Мы можем использовать тождества множеств, чтобы доказать другие факты о множествах. Например:

  Теорема: \ (A- (B \ cup C) = (A-B) \ cap (A-C) \).

  Доказательство: Для множеств \ (A, B, C \) из приведенной выше теоремы имеем \ [\ begin {align *} A- (B \ чашка C) & = A \ cap \ overline {B \ cup C} \\ & = A \ cap \ overline {B} \ cap \ overline {C} \\ & = A \ cap \ overline {B} \ cap A \ cap \ overline {C} \\ & = (A-B) \ cap (A-C) \,. \ Quad {} ∎ \ конец {выравнивание *} \]

• Эти тождества должны убедить вас, что порядок объединений и пересечений не имеет значения (так же, как сложение, умножение, соединение и дизъюнкция: все они коммутативные операции).
  • Итак, мы можем написать их несколько без скобок, как с сложением / умножением / соединением / дизъюнкцией: \ [A \ чашка B \ чашка C \ чашка D \ ,, \\ A \ cap B \ cap C \ cap D \,. \]
• Если нам нужно выполнить объединение / пересечение множества вещей, иногда используется такое обозначение, как суммирование.