Пример решения совместной системы – 1. —
Вопрос 43. Система линейных уравнений, однородная и неоднородная система, решение системы, совместная и несовместная система, эквивалентные системы
Системой линейных алгебраических уравнений с неизвестными называется система уравнений вида
Числа называются коэффициентами системы; — свободными членами, — неизвестными. Количество уравнений в системе может быть меньше, больше или равно числу неизвестных.
Система называется однородной, если все свободные члены равны нулю; в противном случае она называется неоднородной.
Решением системы называется упорядоченная совокупность чисел такая, что после замены неизвестных соответственно числами каждое уравнение системы превращается в верное числовое равенство.
Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется
Две системы уравнений называются эквивалентными, если множество их решений совпадают
Вопрос 44. Матрица системы линейных уравнений, матричная форма записи системы
Исходную Системой линейных алгебраических уравнений можно записать в матричном виде:
,
где матрица называется матрицей системы, это матрица, составленная из коэффициентов при неизвестных; — вектором-столбцом неизвестных, — вектором-столбцом правых частей или свободных коэффициентов.
Вопрос 45. Правило Крамера
Системой однородных линейных уравнений называется система вида
Ясно, что в этой случае , т.к. все элементы одного из столбцов в этих определителях равны нулю.
Так как неизвестные находятся по формулам , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.
Вопрос 46. Минор к-ого порядка, ранг матрицы, базисный минор
Определитель, который образован элементами матрицы, стоящими на пересечении произвольно выбранных k строк и k столбцов, называется минором k-го порядкаэтой матрицы ( при этом минор 1-го порядка – это произвольный элемент данной матрицы).
Рангом матрицыназывается наивысший порядок ее миноров, отличных от нуля (ранг нулевой матрицы полагается равным нулю). Ранг матрицы А обозначается символомr(А).
Всякий неравный нулю минор, порядок которого равен рангу матрицы, называется ее базисным минором.
Вопрос 47. Элементарные преобразования над матрицами
Элементарными преобразованиями матрицы называются следующие 4 операции:
перестановка двух строк (столбцов)
умножение строки (столбца) на число, неравное нулю
прибавление к строке (столбцу) другой строки ( другого столбца), умноженной (умноженного) на любое число
отбрасывание нулевой строки (нулевого столбца)
Ранг матрицы не меняется при ее элементарных преобразованиях.
Вопрос 49. Теорема Кронекера-Капелли
Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.
Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Решить систему —
это значит выяснить, совместна она или
несовместна. Если система совместна,
найти ее
Вопрос 50. Условия существования ненулевого решения у однородной системы mхn и системы nхn
Условия существования ненулевого решения у однородной системы mхn:однородная система mхn имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных.
Условия существования ненулевого решения у однородной системы nхn:однородная система nхn имеет ненулевое решение тогда и только тогда, когда определитель системы равен нулю.
Вопрос 51. Изображение на числовой оси множеств действительных чисел, заданных равенством и неравенством
52. Модуль действительного числа и его свойства
Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = — х.
INCLUDEPICTURE «http://school.xvatit.com/images/f/f3/14-06-125.jpg» \* MERGEFORMATINET
1. |а| 0.
2.|аb| =|a| |b|.
INCLUDEPICTURE «http://school.xvatit.com/images/b/b2/14-06-127.jpg» \* MERGEFORMATINET
53. Геометрический смысл модуля числа и модуля разности двух чисел
Геометрический смысл – расстояние от точки с координатой Х на числовой прямой до начала координат.
Модуль разности – расстояние между соответствующими точками на числовой прямой.
54. Определение функции, определение графика функции
Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
График функции — понятие в математике, которое даёт представление о геометрическом образе функции.
В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией: точка располагается (или находится) на графике функции тогда и только тогда, когда INCLUDEPICTURE «http://upload.wikimedia.org/math/7/c/1/7c1c9491ba7c6e8d6d2cfa82e39b22ca.png» \* MERGEFORMATINET
studfiles.net
3.3. Общее, базисное и частное решение систем линейных алгебраических уравнений.
Пусть переменныхназываются основными (или базисными), если определитель матрицы из коэффициентов при них (т.е. базисный минор) отличен от нуля. Остальныепеременных называются неосновными (или свободными). Каждому разбиению переменных на основные и неосновные соответствует одно базисное решение, а число способов разбиения не превосходит числа сочетанийто и базисных решений имеется не более
Совместная система линейных уравнений спеременнымиимеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее
Достоинства метода Гаусса по сравнению с другими:
— менее трудоемкий метод;
— позволяет однозначно установить, совместна система или нет и в случае совместности найти ее решение;
— дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.
Рассмотрим пример. Найти решение системы линейных алгебраических уравнений
Составим расширенную матрицу по данной системе
поменяем местами первую и вторую строку
умножим первую строку на и сложим со второй строкой; умножим первую строку наи сложим с третьей строкой
умножим вторую строку на и сложим с третьей строкой
последняя строка вычеркивается, так как все ее элементы равны нулю
Ранг основной матрицы ранг расширенной матрицыследовательно, система совместна. Число строк в основной матрицечисло столбцов в основной матрицеследовательно, система имеет множество решений.
Выявим базисные переменные
следовательно, базисные переменные, тогда
3.4. Однородные системы линейных алгебраических уравнений
Система линейных уравнений спеременными называетсясистемой линейных однородных уравнений, если все их свободные члены равны нулю.
Системы линейных однородных уравнений:
Система линейных однородных уравнений всегда совместна, так как имеет, по крайней мере, нулевое решение
Если в однородной системе а ее определитель отличен от нуля, то такая система имеет только нулевое решение.
Система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при
Рассмотрим пример. Найти решение системы линейных алгебраических уравнений
Составим по данной системе расширенную матрицу
поменяем местами первую и третью строки
умножим первую строку на и сложим со второй строкой, а затем с третьей строкой, получим
умножим вторую строку на и сложим с третьей строкой
разделим последнюю строку на
Таким образом, ранг расширенной матрицы и ранг основной матрицы равны следовательно, система совместна. Число строк в основной матрице равно 3, а число столбцов равно 4, т.е. решений множество. Определим базисные переменные
базисные переменные.
Перейдем от матрицы к системе, выразим переменные через другие переменные
Контрольные вопросы
Сформулировать теорему Кронекера – Капелли.
Сформулировать Метод Гаусса решения систем m линейных уравнений с n неизвестными.
Дать определение базисному решению систем линейных алгебраических уравнений.
Какие системы линейных алгебраических уравнений называют однородными?
Лекция №4. Векторы
4.1. Векторы в науке и технике. Понятие вектора. Координаты вектора.
4.2. Линейные операции над векторами.
4.3. Декартова система координат. Базис векторного пространства.
4.4. Скалярное произведение векторов, основные свойства и выражение в координатной форме.
4.5. Векторное произведение векторов. Основные свойства векторного произведения векторов и выражение в координатной форме.
4.6. Применение векторного произведения векторов к решению задач.
4.7. Смешанное произведение векторов. Основные свойства смешанного произведения векторов и выражение в координатной форме.
4.8. Применение смешанного произведения векторов к решению задач.
Векторы в науке и технике. Понятие вектора. Координаты вектора
В физике и математике вектор – это величина, которая характеризуется численным значением и направлением. В физике встречается немало важных величин, которые характеризуются направлением. Например, сила, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Их можно противопоставить другим величинам, таким как масса, объем, давление, температура, плотность, которые можно описать обычным числом и называются они скалярными величинами.
Векторная запись используется при работе с величинами, которые невозможно задать полностью с помощью обычных чисел. Например, необходимо описать положение предмета, но полностью определить местоположение предмета невозможно, пока не будет известно направление, в котором он находится. Таким образом, местонахождение предмета характеризуется численным значением (расстоянием в километрах) и направлением.
При изучении и расчете цепей переменного тока удобно пользоваться векторными диаграммами, на которых синусоидальные напряжения и токи условно изображают с помощью векторов. Применение этих диаграмм упрощает изучение и расчет цепей и вносит наглядность в рассматриваемые соотношения.
Вектором на плоскости называется направленный отрезок с начальной точкой и конечной точкойкоторый можно перемещать параллельно самому себе.
Рис. 1
Вектор на плоскости
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос. При параллельном переносе точки смещаются по параллельным или совпадающим прямым на одно и тоже расстояние.
Нулевой вектор – точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Абсолютной величиной или модулем вектора называется длина отрезка, изображающего вектор. Другими словами длина вектора есть расстояние между началом и концом вектора
Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых. Нулевой вектор коллинеарен любому вектору. Если векторы иколлинеарны и их лучи сонаправлены, то векторыиназываютсонаправленными. Обозначают Если векторыиколлинеарны, а их лучи не являются сонаправленными, то векторы называютпротивоположно направленными. Обозначают Нулевой вектор условились считать сонаправленным с любым вектором.
Рис.2
Коллинеарные вектора
Свойство коллинеарных векторов.
Если векторы иколлинеарны и, то существует числотакое, что. Причем, еслито векторыисонаправленные, еслито противоположно направленные.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Признак компланарности трех векторов.
Если вектор можно разложить по векторами, т.е. представить в виде, где-некоторые числа, то векторы-компланарны.
Рис.3
Компланарные вектора
, где ;
, где
, где
studfiles.net
2.3.6. Примеры решения задач по теме «Системы уравнений общего вида. Мет
Задача 1.
Указать базисный минор матрицы
Указание
Определите вначале ранг матрицы А, а затем найдите ненулевой минор, порядок которого равен R(A).
Решение
Определим R(A). Вторая и четвертая строки А равны, поэтому после вычитания из 4-й строки 2-й получаем:
Вычислим минор полученной матрицы, составленный из первых трех столбцов:
Таким образом, найден минор максимально возможного (3-го) порядка, не равный нулю. Следовательно, ранг матрицы А равен рангу преобразованной матрицы, то есть равен 3, а рассмотренный минор является базисным.
Ответ:
Задача 2.
Определить количество решений системы линейных уравнений
.
Указание
Сравните ранги матрицы системы и расширенной матрицы.
Решение
Сравним ранги матрицы системы
И расширенной матрицы
.
Для удобства вычислений будем искать ранг матрицы А1, отделив ее последний столбец вертикальной чертой. Тогда столбцы, стоящие слева от черты, образуют матрицу А, и мы одновременно найдем ранги обеих матриц.
А1 ~ .
Вычтем из второй строки удвоенную первую, а из третьей – первую, умноженную на 3:
А1 ~ ~ .
Таким образом, R(A) = 2, a R(A1) = 3, следовательно, система не имеет решений.
Ответ: система несовместна.
Задача 3.
Найти общее решение линейной системы
.
Указание
Убедившись в том, что система совместна, определите базисные и свободные неизвестные и выразите базисные неизвестные через свободные.
Решение
Найдем R(A) и R(A1):
Итак, R = R(A) = R(A1) = 2, а число неизвестных П = 5. Следовательно, R < N, и система имеет бесконечно много решений (совместна, но не определена).
Число базисных неизвестных равно R, то есть двум. Выберем в качестве базисных неизвестных Х1 и Х2, коэффициенты при которых входят в базисный минор преобразованной матрицы А: .
Соответственно Х3, Х4, Х5 – свободные неизвестные.
Запишем систему, равносильную исходной, коэффициентами в которой являются элементы полученной матрицы:
И выразим базисные неизвестные через свободные:
.
Получено общее решение системы. Одно из частных решений можно найти, положив все свободные неизвестные равными нулю: Х3 = Х4 = Х5 = 0. Тогда
Ответ:
Задача 4.
Найти общее решение системы, выразив в ответе первые неизвестные через последние:
Указание
Приведите расширенную матрицу к виду
Решение
Минор, состоящий из первых трех столбцов полученной матрицы,
Поэтому R(A) = R(A1) = 3, выбранный минор является базисным, а Х1, Х2, Х3, коэффициенты при которых составляют базисный минор, – базисными неизвестными. Тогда свободное неизвестное – Х4, и система, равносильная исходной, имеет вид:
Откуда
Ответ:
Задача 5.
Найти фундаментальную систему решений однородной линейной системы
Указание
Количество решений, образующих фундаментальную систему, равно числу
Свободных неизвестных. Задайте свободным неизвестным значения 1,0,0; 0,1,0; 0,0,1 и вычислите соответствующие значения базисных неизвестных.
Решение
Количество решений, образующих фундаментальную систему, равно числу Свободных неизвестных. |
Матрица А1 отличается от матрицы А только добавлением нулевого столбца свободных членов, поэтому все ее ненулевые миноры являются минорами матрицы А, то есть R(A) = R(A1). Найдем R(A):
Выберем в качестве базисного минора
Значит, R(A) = 2. Пусть Х4, Х5 – базисные неизвестные, Х1, Х2, Х3 – свободные неизвестные. Запишем для них новую систему:
Откуда
Фундаментальная система решений состоит из трех столбцов. Рассмотрим три набора значений свободных неизвестных:
1) Х1 = 1, Х2 = Х3 = 0.
Тогда Х4 = -0,2, Х5 = 1,2, и решение можно записать в виде столбца
2) Х1 = 0, Х2 = 1, Х3 = 0.
При этом Х4 = 1,2, Х5 = 3,8, и следующее решение системы имеет вид
3) Х1 = Х2 = 0, Х3 = 1. Отсюда Х4 = -0,8, Х5 = -0,2, и последний столбец
Фундаментальная система решений, построенная при таком выборе свободных неизвестных, называется Нормальной. Поскольку столбцы свободных неизвестных , , линейно независимы, это гарантирует линейную независимость решений Х1, Х2, Х3. |
Итак, в качестве фундаментальной системы решений можно выбрать
При этом любое решение данной системы имеет вид: Х = с1Х1 + С2Х2 + С3Х3, где С1, С2, С3 – произвольные постоянные. Эта формула задает общее решение системы.
Ответ:
Задача 6.
Составить однородную систему из двух уравнений, для которой столбцы
Образуют фундаментальную систему решений.
Указание
Пусть искомая система имеет вид:
Подставьте вместо Х1, …, Х5 элементы столбцов Х1, Х2, Х3 и решите полученную систему уравнений для коэффициентов Aij.
Решение
Существует бесконечно много систем однородных линейных уравнений, для каждой из которых фундаментальная система решений имеет указанный вид. Число уравнений в таких системах может быть различным. При этом можно указать их наименьшее требуемое количество, а увеличивать их число можно неограниченно. |
Определим вначале, из какого наименьшего числа уравнений может состоять такая система.
Число элементов каждого столбца равно пяти, следовательно, в системе пять неизвестных (П = 5). Количество столбцов, составляющих фундаментальную систему, равно трем, то есть N – R = 3, поэтому R = 5 – 3 = 2. Значит, матрица А должна иметь по крайней мере 2 строки. Следовательно, система уравнений с заданной фундаментальной системой решений может состоять из двух и более уравнений.
Пусть искомая система имеет вид:
Подставим вместо Х1, …, Х5 элементы столбцов Х1, Х2, Х3. Получим:
Разобьем полученные 6 уравнений на две системы, одна из которых содержит A1I, а вторая – A2I:
Найдем какое-либо частное решение этой системы. Приведем ее матрицу к треугольному виду:
Откуда
Следовательно,
Выберем А14 = А15 = 4, тогда А11 = 0, А12 = 8, А13 = -4.
2) Так же выглядит общее решение системы для A2I:
Выберем свободные неизвестные так, чтобы получить решение, линейно независимое с предыдущим.
Пусть А24 = 4, А25 = 0, тогда А21 = 5, А22 = 5, А23 = -3.
Итак, используя найденные значения коэффициентов, можно составить линейную однородную систему:
Фундаментальная система решений которой имеет вид, приведенный в условии задачи.
Ответ:
Задача 7.
Найти общее решение неоднородной линейной системы
С помощью фундаментальной системы решений соответствующей однородной системы.
Указание
Убедитесь в том, что система совместна. Затем составьте соответствующую однородную систему и найдите для нее фундаментальную систему решений. Далее используйте то, что общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы.
Решение
Убедимся в том, что система совместна:
Итак, R(A) = R(A1) = 2 – система совместна.
Составим по преобразованной матрице однородную систему:
И найдем для нее фундаментальную систему решений:
Фундаментальная система решений может быть выбрана так:
Общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы. |
Теперь найдем какое-нибудь частное решение неоднородной системы
Положим Х3 = Х4 = Х5 = 0, тогда . Следовательно,
и общее решение системы имеет вид:
Х = с1Х1 + С2Х2 + С3Х3 + Хчастн, где С1, С2, С3 – произвольные постоянные.
Ответ:
Задача 8.
Решить систему методом Гаусса:
.
Указание
Поменяйте местами 1-е и 2-е уравнения, чтобы в первом уравнении коэффициент при Х равнялся единице, а затем исключите Х из второго и третьего уравнений.
Решение
Метод Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Для удобства его применения поменяем местами 1-е и
2-е уравнения, чтобы в первом уравнении коэффициент при Х равнялся единице:
Теперь исключим Х из второго и третьего уравнений. Для этого вычтем из второго уравнения первое, умноженное на 3, а из третьего – первое, умноженное на 2:
Далее можно легко исключить Z из третьего уравнения, если прибавить к нему второе:
Из последнего уравнения получаем, что У = 0. Подставляя это значение в первое и второе уравнения, находим остальные неизвестные: Z = 3, Х = 1.
Ответ: Х = 1, У = 0, Z = 3.
При применении метода Гаусса совсем не обязательно приводить систему к «классическому» треугольному виду: . Достаточно, чтобы матрица коэффициентов, например, системы трех уравнений с тремя неизвестными содержала два нуля в одном столбце и одновременно два нуля в одной строке, причем один из нулей стоял на пересечении этих строки и столбца. |
Задача 9.
Решить систему методом Гаусса:
Указание
Исключите Х2 из 2-го и 4-го уравнений, используя 1-е уравнение, а затем вычтите из 3-го уравнения 2-е, чтобы исключить Х3.
Решение
Исключим Х2 из 2-го и 4-го уравнений. Для этого из 2-го уравнения вычтем 1-е, а к 4-му прибавим 1-е, умноженное на 2:
Вычтем из 3-го уравнения 2-е, чтобы исключить Х3:
Теперь вычтем из 4-го уравнения удвоенное 3-е:
Из последнего уравнения находим . Тогда из 3-го уравнения Х1 = 0, из 2-го , из 1-го Х2 = 2.
Ответ:
| < Предыдущая | Следующая > |
|---|
matica.org.ua
§ 3. Системы линейных уравнений
Литература: (1, с. 18-34; 2, с. 82-100; 3, с. 286-275)
Основные понятия
Системой линейных уравнений называется совокупность рассматриваемых совместно нескольких линейных уравнений.
В системе может быть любое число уравнений с любым числом неизвестных.
Решением системы уравнений называется совокупность значений неизвестных, удовлетворяющая всем уравнениям системы, то есть обращающая их в тождества.
Система, имеющая решение, называется совместной, в противном случае – несовместной.
Для решения системы применяют различные методы.
Решение систем
 линейных уравнений с
линейных уравнений с неизвестными
неизвестными
Пусть (число уравнений равно числу неизвестных).
Метод Крамера
Рассмотрим решение системы трёх линейных уравнений с тремя неизвестными:
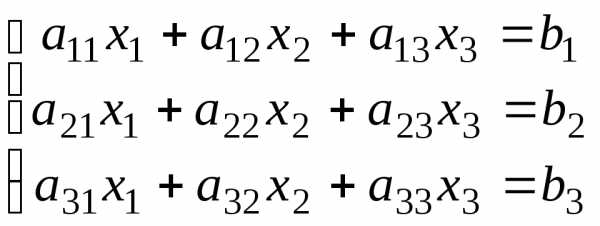 (7)
(7)
Для нахождения
неизвестных 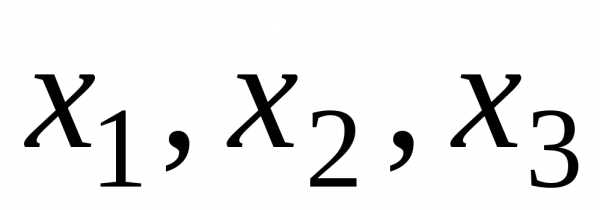 применим формулу Крамера:
применим формулу Крамера:
(8)
где  — определитель системы, элементы которого
есть коэффициенты при неизвестных:
— определитель системы, элементы которого
есть коэффициенты при неизвестных:
 .
.
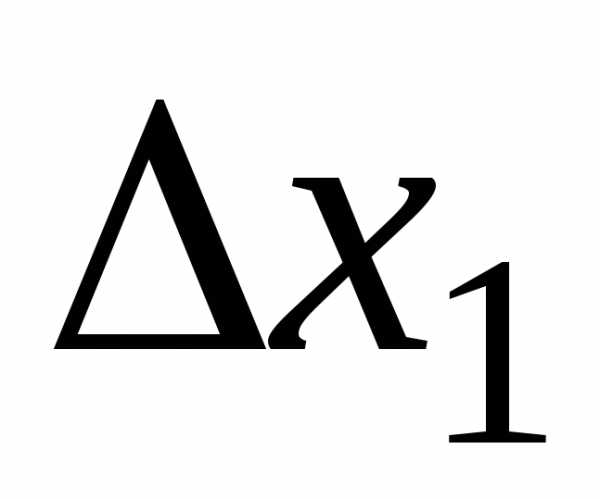 получается путём
замены первого столбца определителя
получается путём
замены первого столбца определителя  столбцом свободных членов:
столбцом свободных членов:
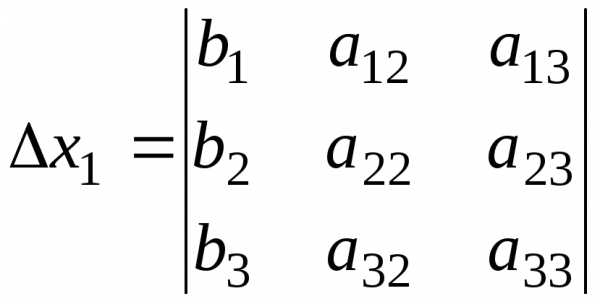 .
.
Аналогично:
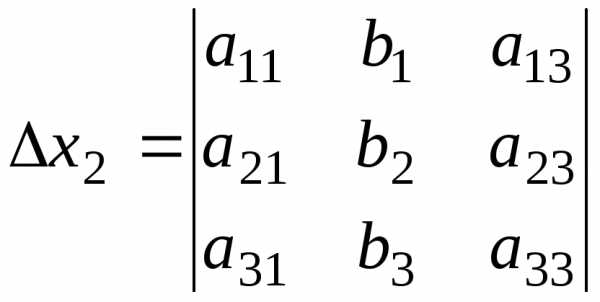 ;
;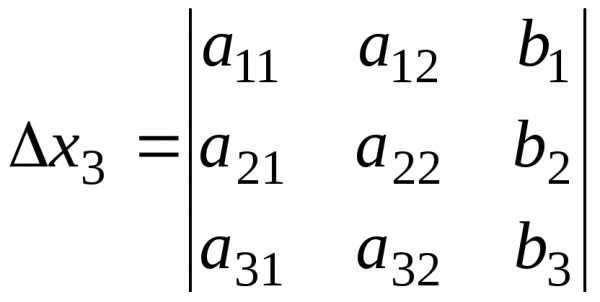 .
.
Пример 1. Решить систему по формуле Крамера:
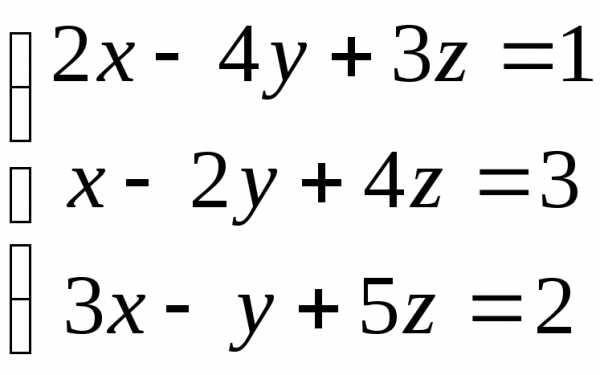 .
.
Решение: Воспользуемся формулами (8):
;
;
;
;
Тогда
Ответ: 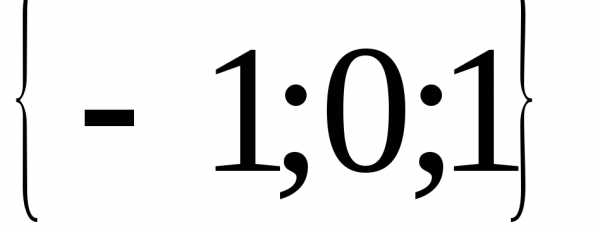 .
.
Для любой системы 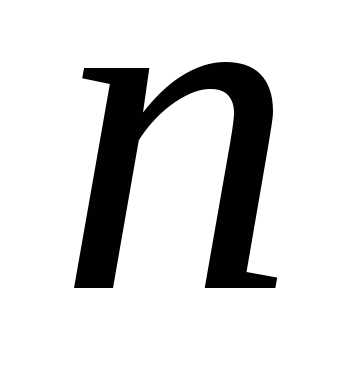 линейных уравнений с
линейных уравнений с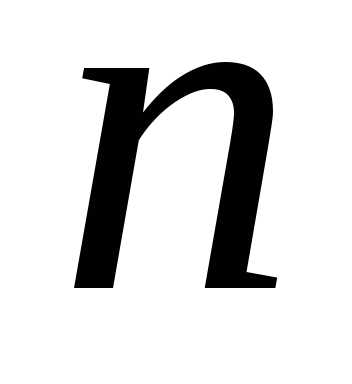 неизвестными можно утверждать:
неизвестными можно утверждать:
Если определить системы
 ,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.
,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.Если
 ,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, еслиили не иметь их, если хотя бы один из
определителейне равен нулю.
,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, еслиили не иметь их, если хотя бы один из
определителейне равен нулю.
Матричный способ решения
Рассмотрим решение системы (7) трёх линейных уравнений с тремя неизвестными матричным способом.
Используя правила умножения матриц, данную систему уравнений можно записать в виде: , где
.
Пусть матрица  невырожденная, т.е..
Умножая обе части матричного уравнения
слева на матрицу
невырожденная, т.е..
Умножая обе части матричного уравнения
слева на матрицу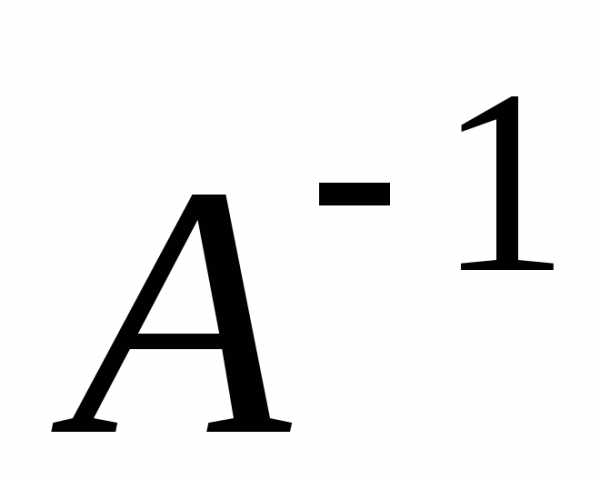 ,
обратную матрице
,
обратную матрице ,
получим:.
,
получим:.
Учитывая, что , имеем
(9)
Пример 2. Решить систему матричным способом:
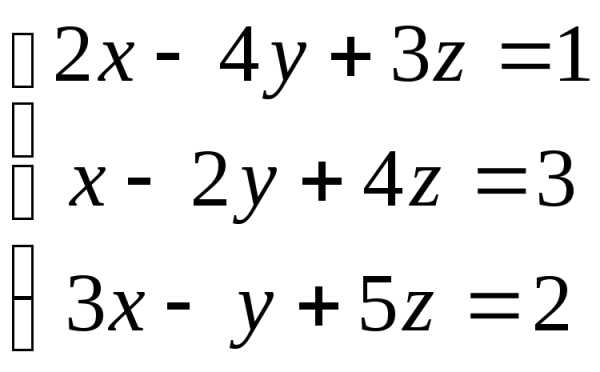 .
.
Решение: Введём матрицы:
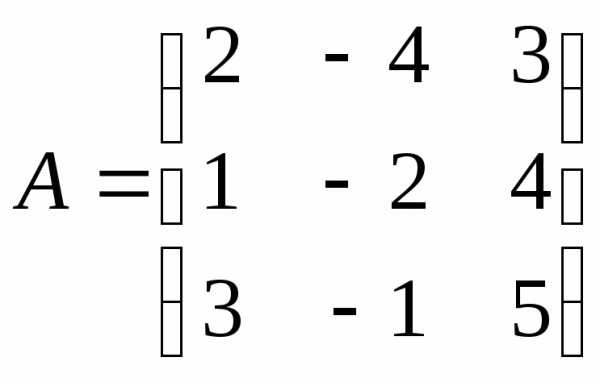 —
из коэффициентов при неизвестных;
—
из коэффициентов при неизвестных;
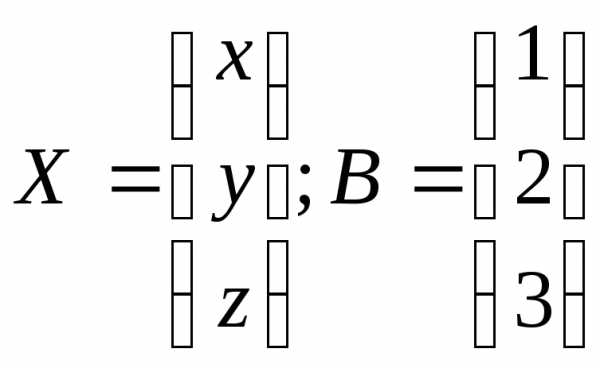 —
столбец свободных членов.
—
столбец свободных членов.
Тогда систему можно записать матричным уравнением: .
Воспользуемся
формулой (9). Найдём обратную матрицу 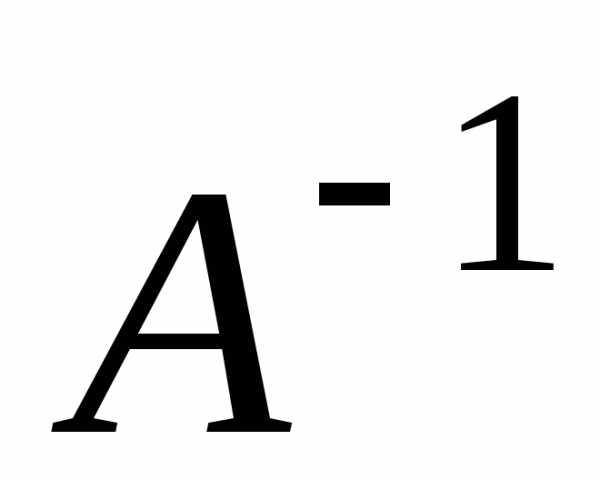 по формуле (6):
по формуле (6):
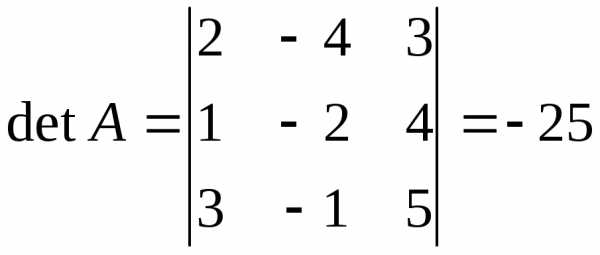 ;
;
Тогда
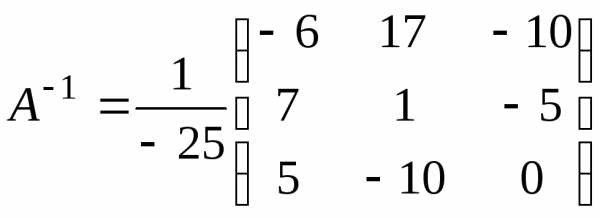 .
.
Следовательно,
Получили:
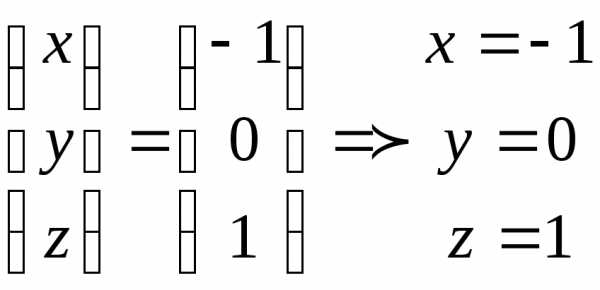 .
.
Ответ: 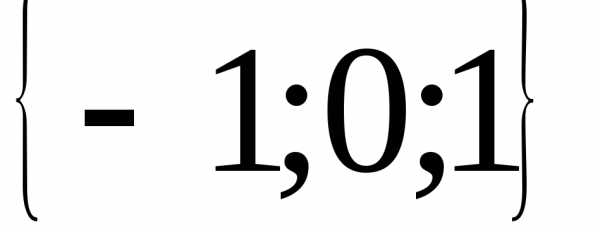 .
.
Метод последовательного исключения неизвестных (метод Гаусса)
Основная идея применяемого метода заключается в последовательном исключении неизвестных. Поясним смысл этого метода на системе трёх уравнений с тремя неизвестными:
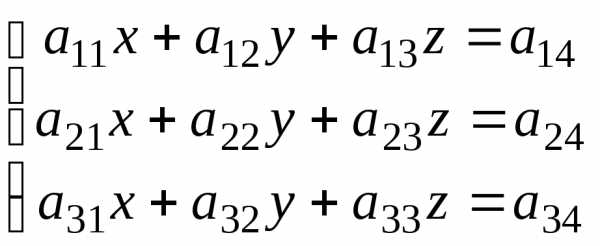 .
. 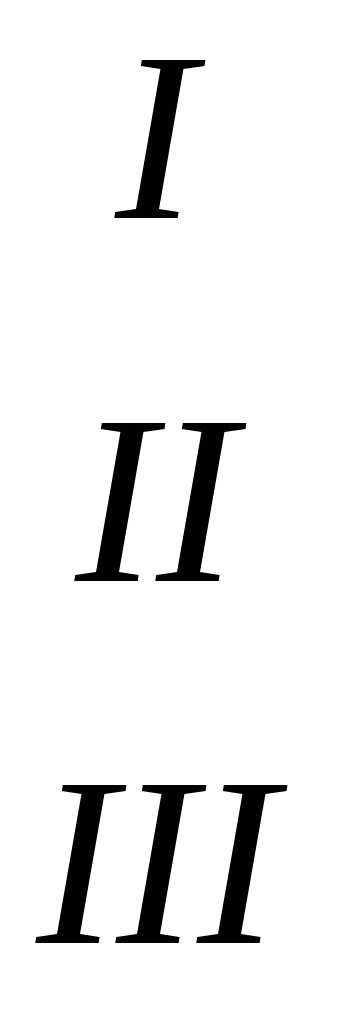
Допустим, что 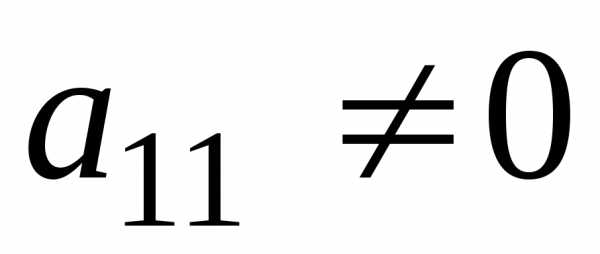 (если
(если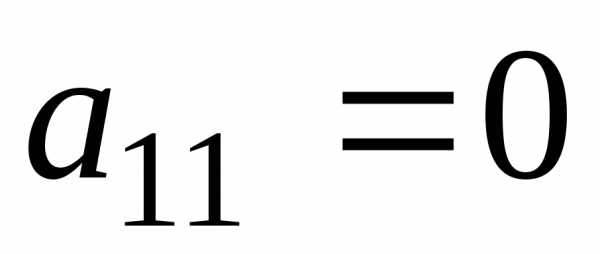 ,
то изменим порядок уравнений, выбрав
первым уравнением то, в котором коэффициент
при
,
то изменим порядок уравнений, выбрав
первым уравнением то, в котором коэффициент
при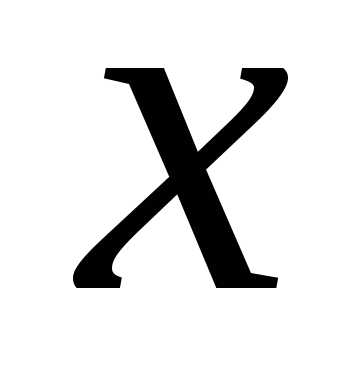 не равен нулю).
не равен нулю).
Первый шаг: а) делим
уравнение 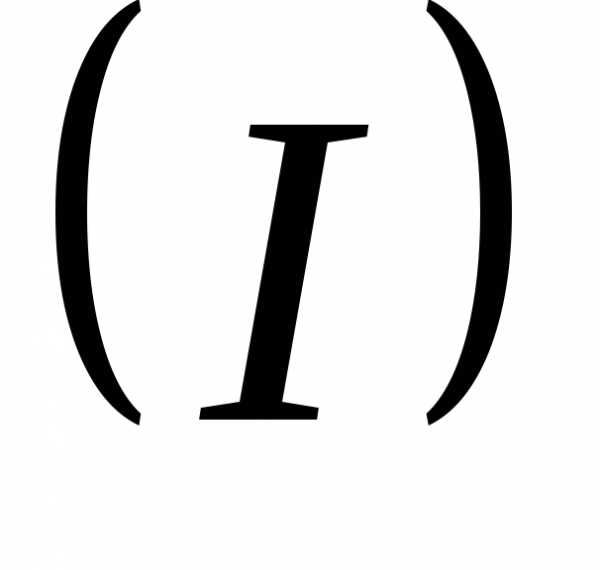 на
на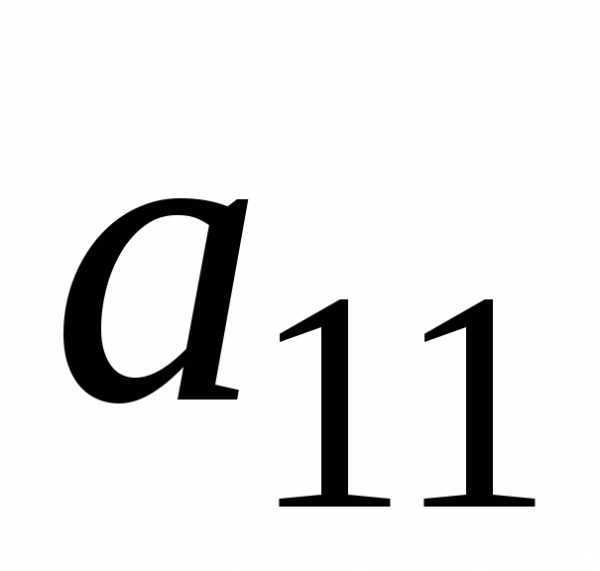 ;
б) умножаем полученное уравнение на
;
б) умножаем полученное уравнение на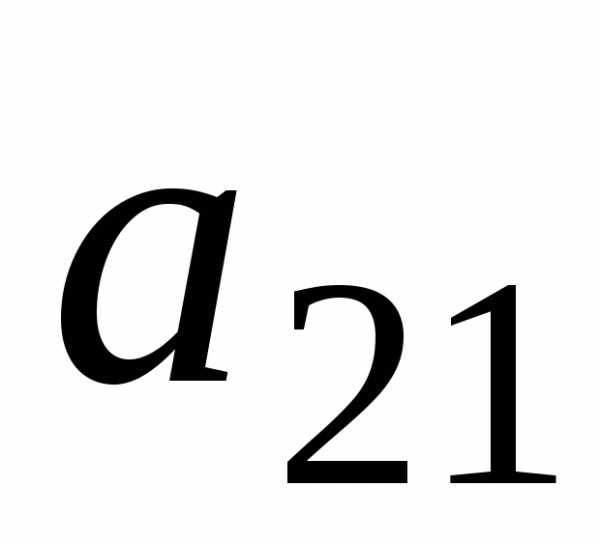 и вычитаем из
и вычитаем из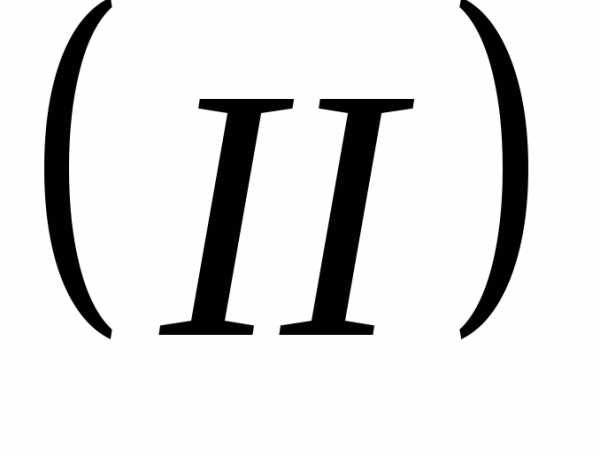 ;
в) затем полученное умножаем на
;
в) затем полученное умножаем на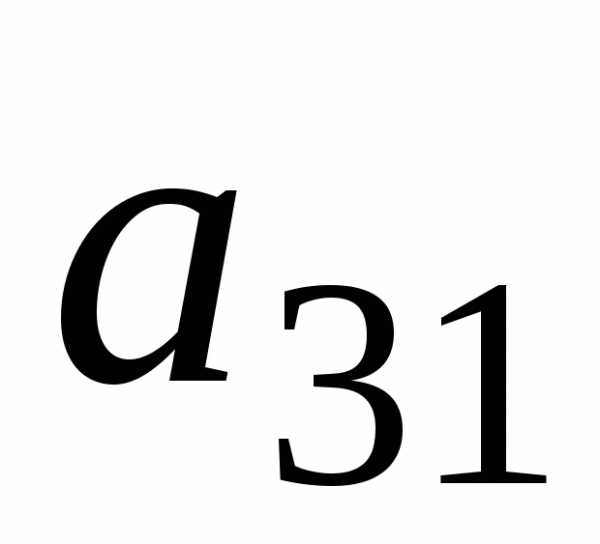 и вычитаем из
и вычитаем из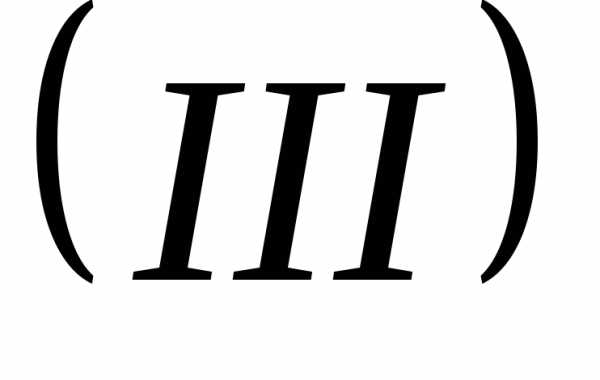 .
В результате первого шага будем иметь
систему:
.
В результате первого шага будем иметь
систему:
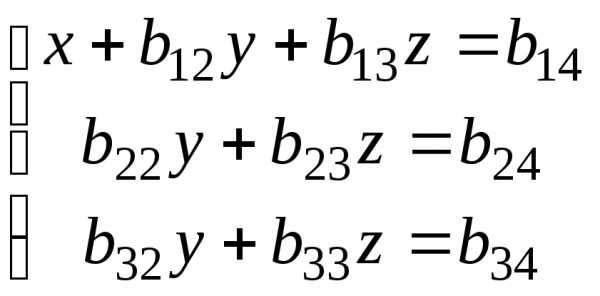

причём
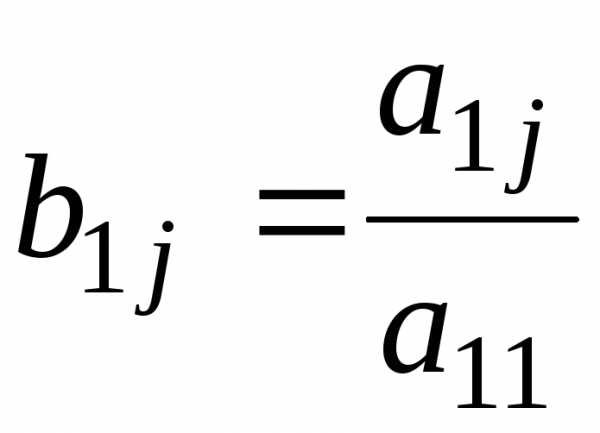 ,
,
Второй шаг: поступаем
с уравнением 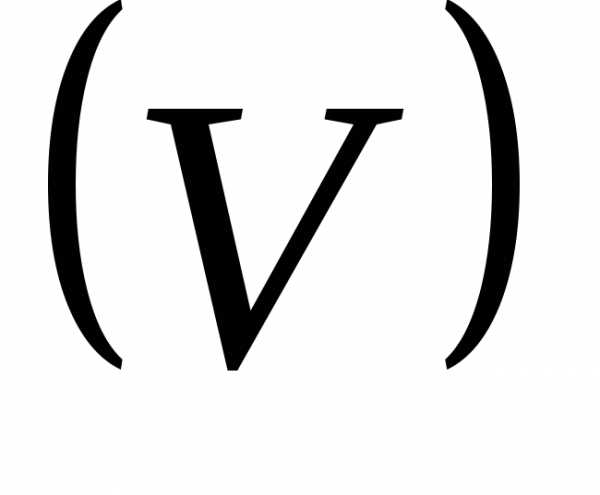 и
и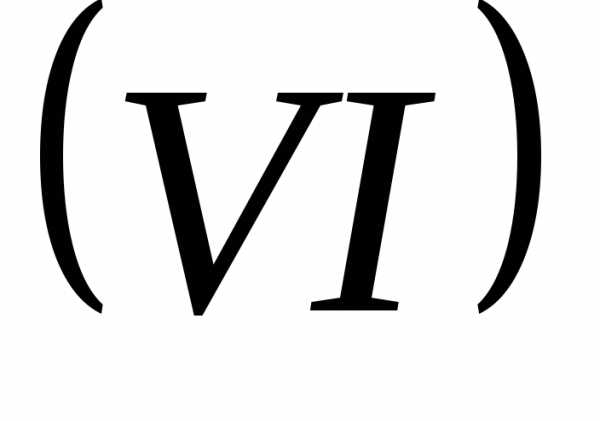 точно так же, как с уравнениями.
точно так же, как с уравнениями.
В итоге исходная система преобразуется к так называемому ступенчатому виду:
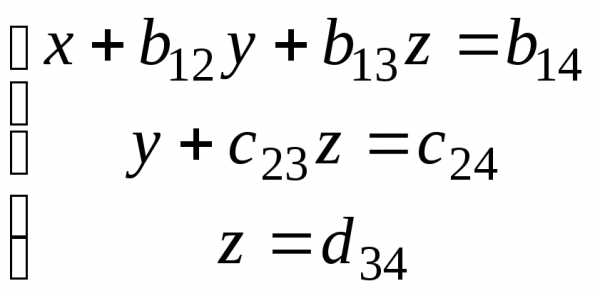
Из преобразованной системы все неизвестные определяются последовательно без труда.
Замечание. Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а матрицу из коэффициентов, при неизвестных, и свободных членов.
Пример 3. Решить методом Гаусса систему:
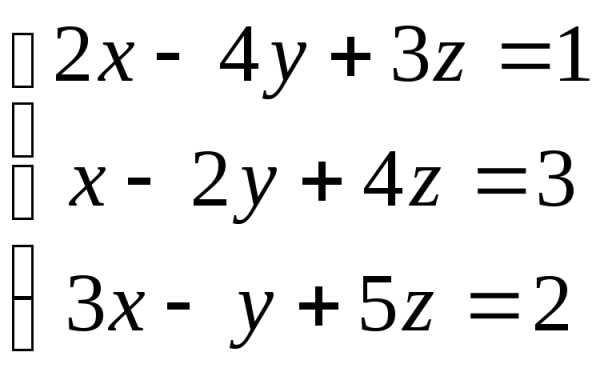 .
.
Переход от одной матрицы к другой будем записывать при помощи знака эквивалентности ~.
 ~
~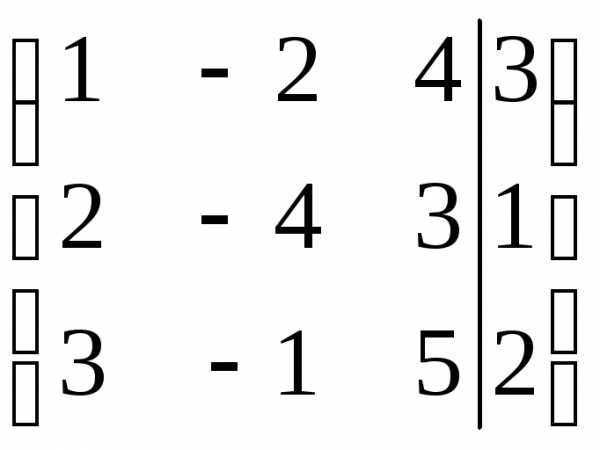 ~
~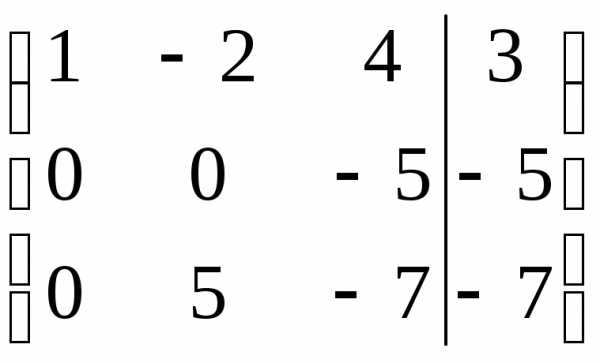 ~
~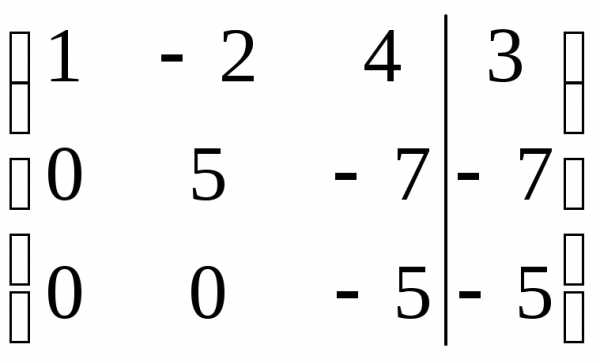 ~
~
~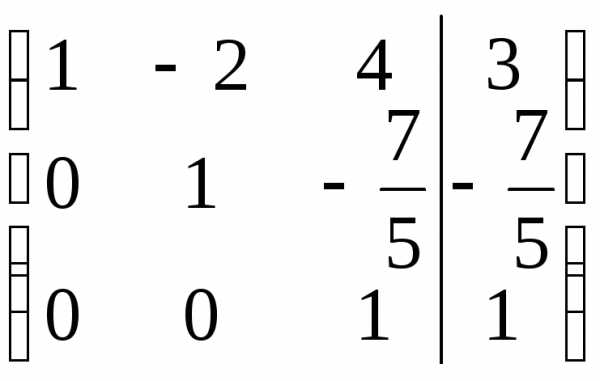 .
.
По полученной матрице выписываем преобразованную систему:
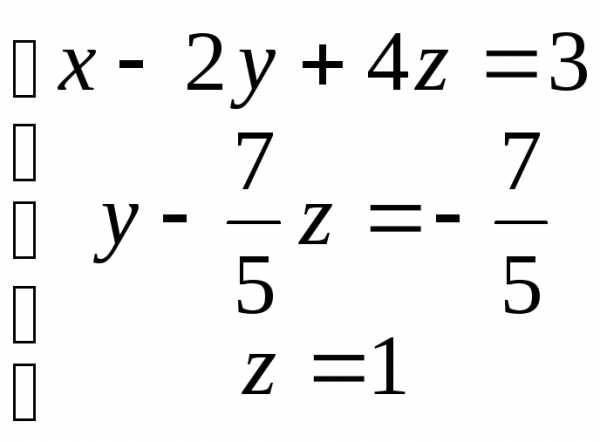 .
.
Тогда
Ответ: 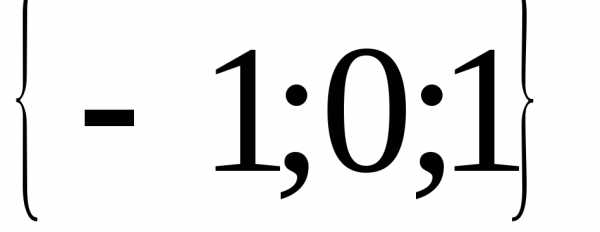 .
.
Замечание: Если
система имеет единственное решение, то
ступенчатая система приводится к
треугольной, то есть к такой, в которой
последнее уравнение будет содержать
одно неизвестное. В случае неопределённой
системы, то есть такой, в которой число
неизвестных больше числа линейно
независимых уравнений, треугольной
системы не будет, так как последнее
уравнение будет содержать более одного
неизвестного (система имеет бесчисленное
множество решений). Когда же система
несовместна, то, после приведения её к
ступенчатому виду, она будет содержать
хотя бы одно  значение вида
значение вида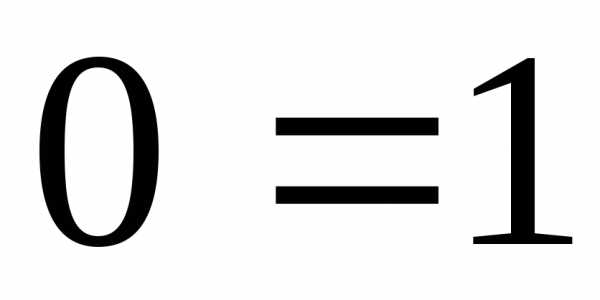 ,
то есть уравнение, в котором все
неизвестные имеют нулевые коэффициенты,
а правая часть отлична от нуля (система
решений не имеет). Метод Гаусса применим
к произвольной системе линейных уравнений
(при любых
,
то есть уравнение, в котором все
неизвестные имеют нулевые коэффициенты,
а правая часть отлична от нуля (система
решений не имеет). Метод Гаусса применим
к произвольной системе линейных уравнений
(при любых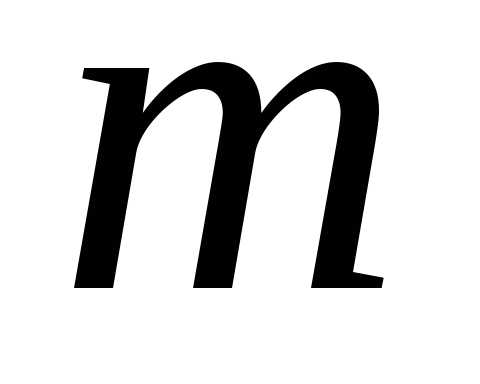 и
и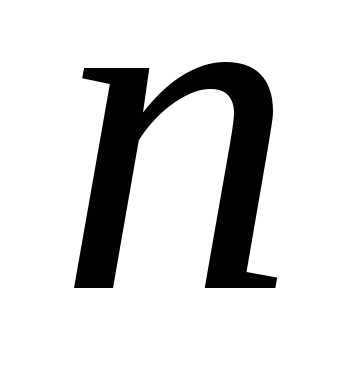 ).
).
Теорема существования решения системы линейных уравнений
При решении системы линейных уравнений методом гаусса ответ на вопрос, совместна или несовместна данная система может быть дан лишь в конце вычислений. Однако часто бывает важно решить вопрос о совместности или несовместности системы уравнений, не находя самих решений. Ответ на этот вопрос даёт следующая теорема Кронекера-Капелли.
Пусть дана система 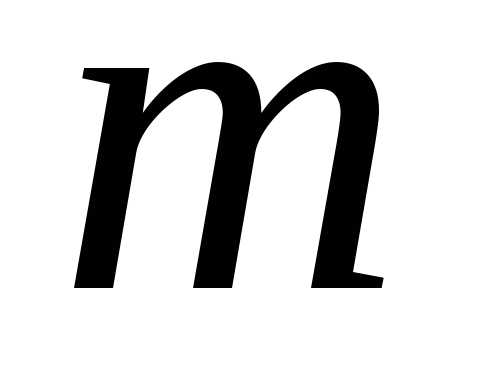 линейных уравнений с
линейных уравнений с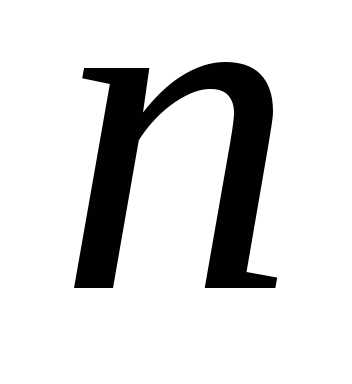 неизвестными:
неизвестными:
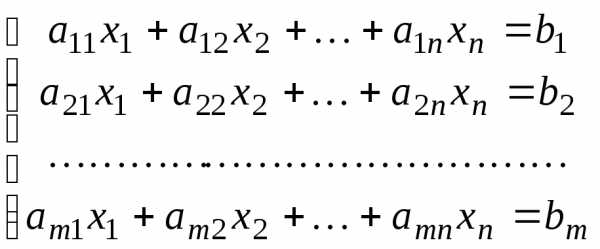 (10)
(10)
Для того, чтобы система (10) была совместной, необходимо и достаточно чтобы ранг матрицы системы
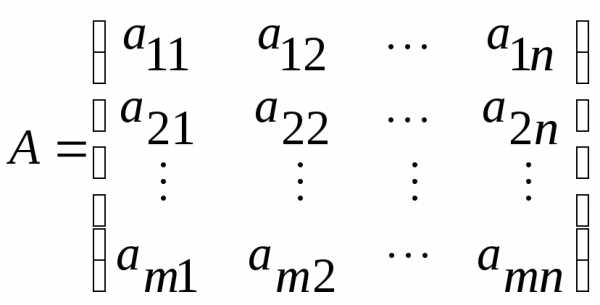 .
.
был равен рангу её расширенной матрицы
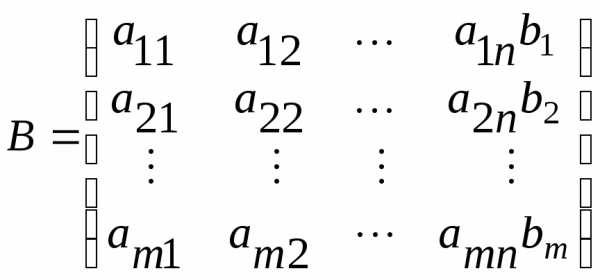 .
.
Причём, если , то система (10) имеет единственное решение; если же, то система имеет бесчисленное множество решений.
Линейная, однородная система
 уравнений с
уравнений с неизвестными
неизвестными
Рассмотрим однородную систему (все свободные члены равны нулю) линейных уравнений:
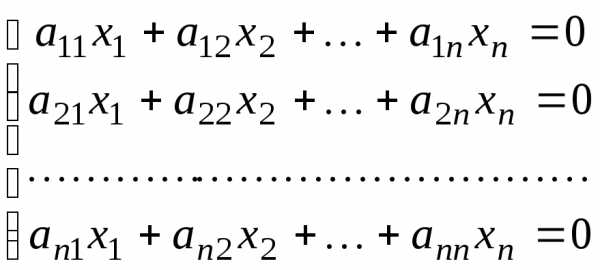 .
.
Эта система всегда совместна, так как она имеет нулевое решение .
В следующей теореме даны условия, при которых система имеет также решения, отличные от нулевого.
Терема. Для того,
чтобы однородная система линейчатых
уравнений имела нулевое решение,
необходимо и достаточно, чтобы её
определитель  был равен нулю:
был равен нулю:
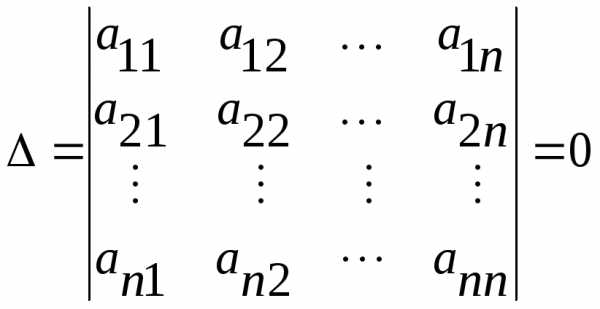 .
.
Таким образом,
если 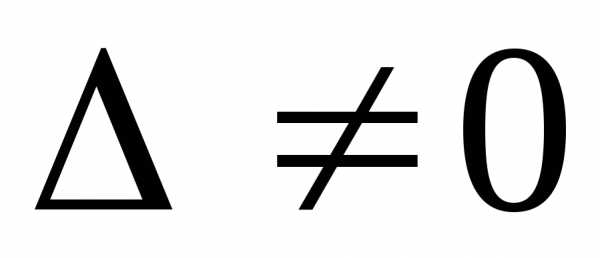 ,
то решение- единственное. Если
,
то решение- единственное. Если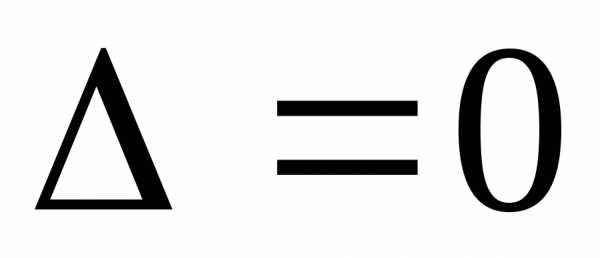 ,
то существует бесконечноё множество
других ненулевых решений. Укажем один
из способов отыскания решений для
однородной системы трёх линейных
уравнений с тремя неизвестными в случае
,
то существует бесконечноё множество
других ненулевых решений. Укажем один
из способов отыскания решений для
однородной системы трёх линейных
уравнений с тремя неизвестными в случае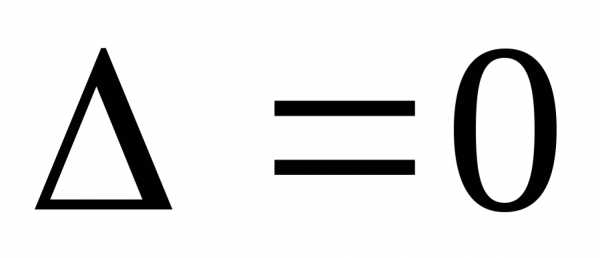 .
.
Можно доказать,
что если 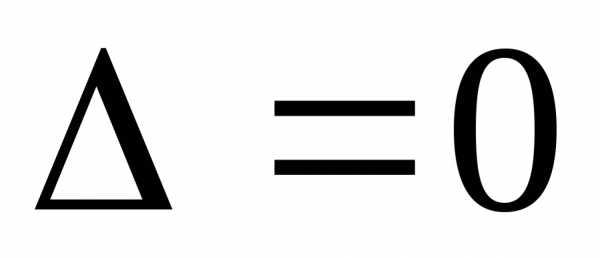 ,
а первое и второе уравнения непропорциональны
(линейно независимы), то третье уравнение
есть следствие первых двух. Решение
однородной системы трёх уравнений с
тремя неизвестными сводится к решению
двух уравнений с тремя неизвестными.
Появляется так называемое свободное
неизвестное, которому можно придавать
произвольные значения.
,
а первое и второе уравнения непропорциональны
(линейно независимы), то третье уравнение
есть следствие первых двух. Решение
однородной системы трёх уравнений с
тремя неизвестными сводится к решению
двух уравнений с тремя неизвестными.
Появляется так называемое свободное
неизвестное, которому можно придавать
произвольные значения.
Пример 4. Найти все решения системы:
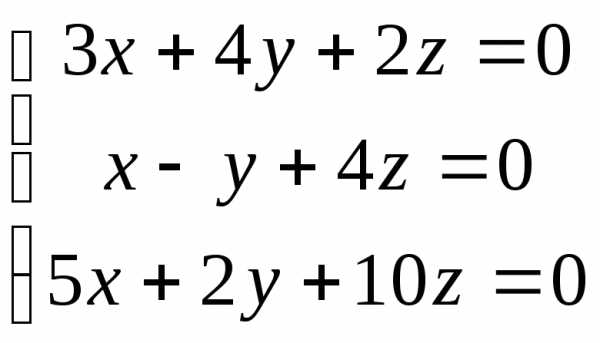 .
.
Решение. Определитель этой системы
.
Поэтому система имеет нулевые решения. Можно заметить, что первые два уравнения, например, непропорциональны, следовательно, они линейно независимые. Третье является следствием первых двух (получается, если к первому уравнению прибавить удвоенное второе). Отбросив его, получим систему двух уравнений с тремя неизвестными:
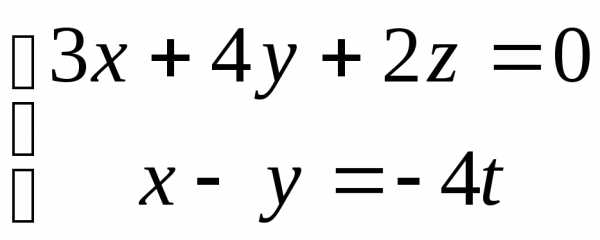 .
.
Полагая, например, 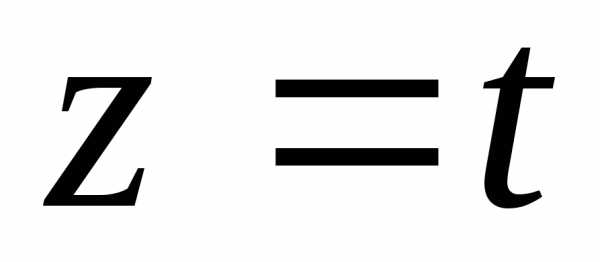 ,
получим
,
получим
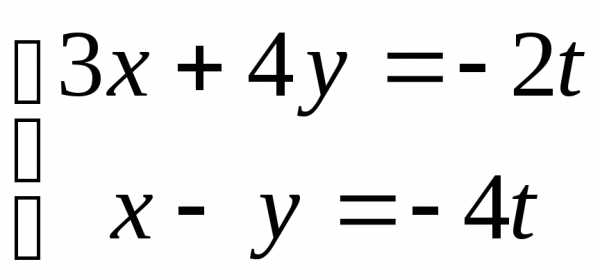 .
.
Решая систему двух
линейных уравнений, выразим 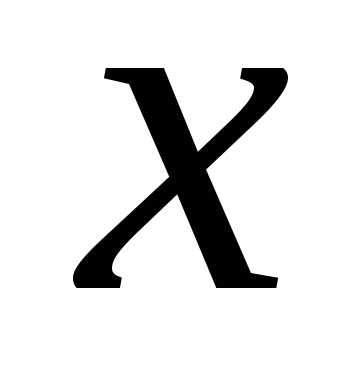 ичерез
ичерез :
: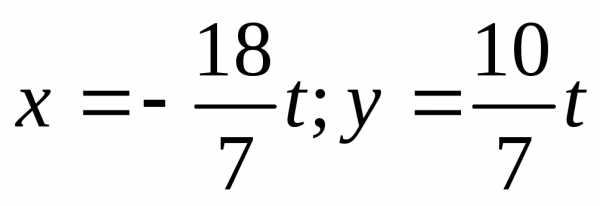 .
Следовательно, решение системы можно
записать в виде:,
где
.
Следовательно, решение системы можно
записать в виде:,
где — произвольное число.
— произвольное число.
Пример 5. Найти все решения системы:
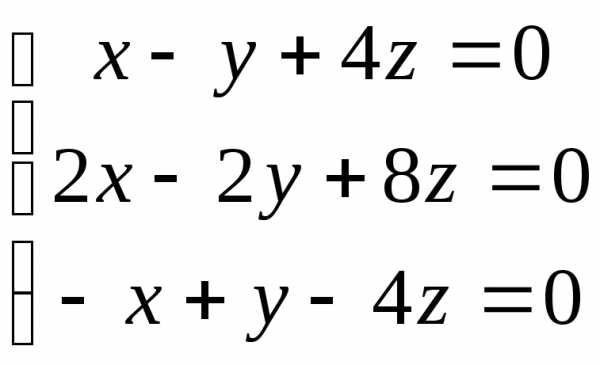 .
.
Решение. Нетрудно
видеть, что в данной системе только одно
независимое уравнение (два других ему
пропорциональны). Система из трёх
уравнений с тремя неизвестными свелась
к одному уравнению с тремя неизвестными.
Появляются два свободных неизвестных.
Найдя, например, из первого уравнения
при произвольных и
и ,
получим решения данной системы. Общих
вид решения можно записать,
где
,
получим решения данной системы. Общих
вид решения можно записать,
где и
и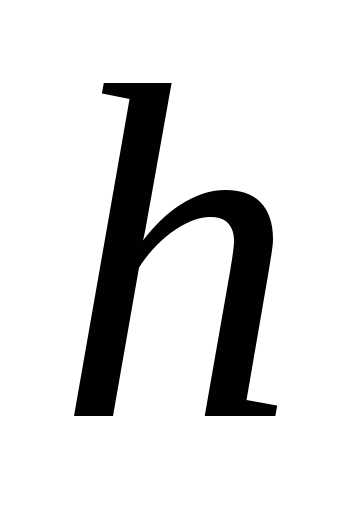 — произвольные числа.
— произвольные числа.
Вопросы для самопроверки
Сформулируйте
правило Крамера для решения системы 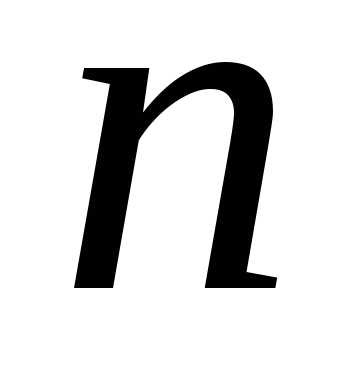 линейных уравнений с
линейных уравнений с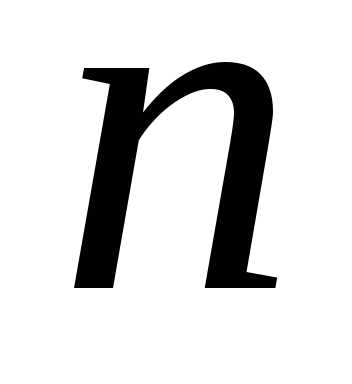 неизвестными.
неизвестными.
В чём сущность матричного способа решения систем?
В чём заключается метод Гаусса решения системы линейных уравнений?
Сформулируйте теорему Кронекера-Капелли.
Сформулируйте необходимое и достаточноё условие существования ненулевых решений однородной системы линейных уравнений.
Примеры для самостоятельного решения
Найдите все решения систем:
1. 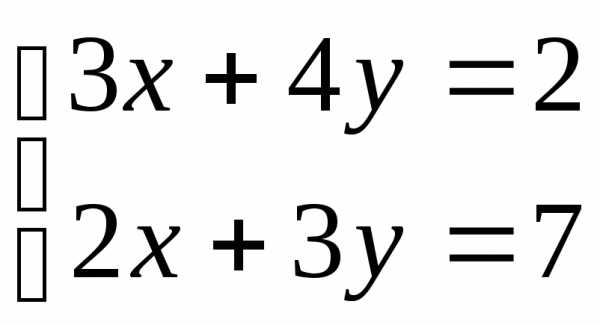 ; 2.
; 2.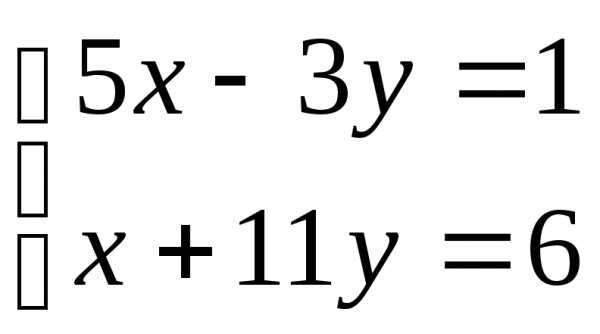 ;
;
3. 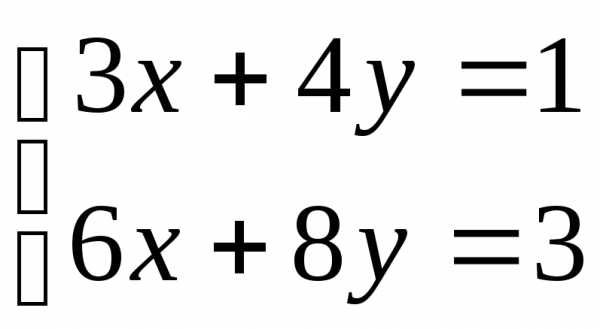 ; 4.
; 4.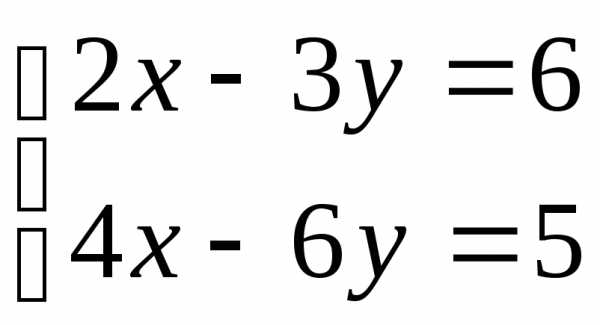 ;
;
5. 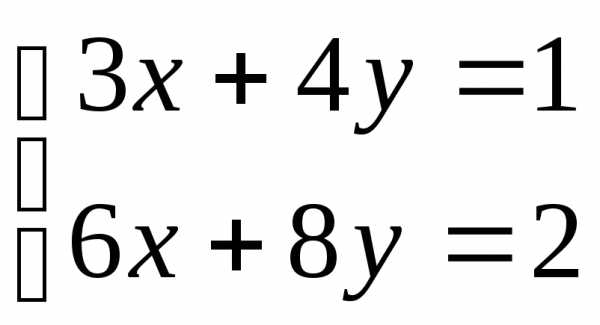 ; 6.
; 6.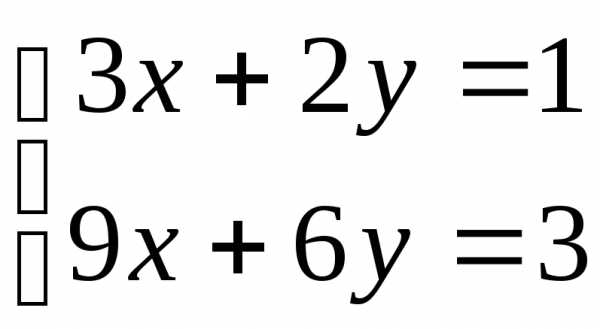 ;
;
7. 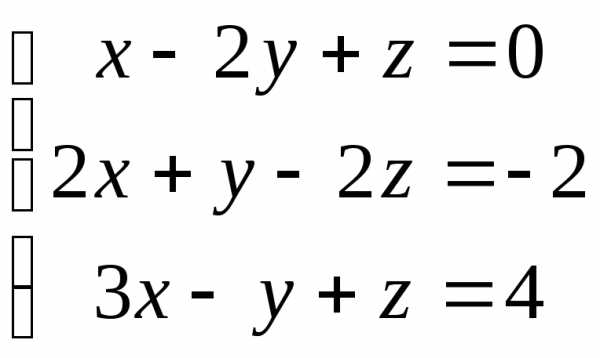 ; 8.
; 8.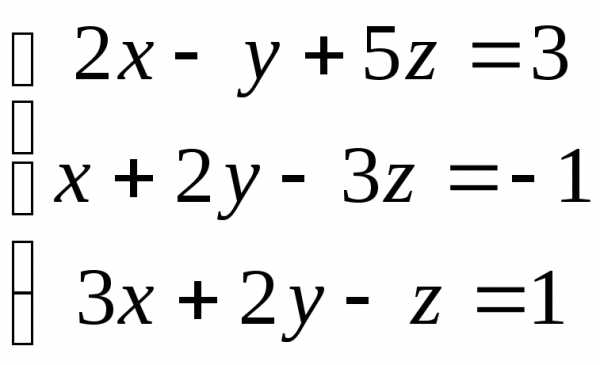 ;
;
9. 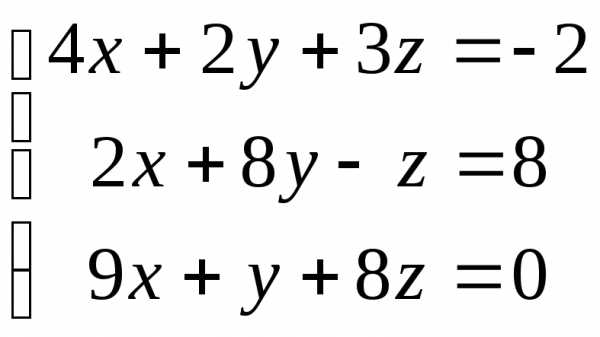 ; 10.
; 10.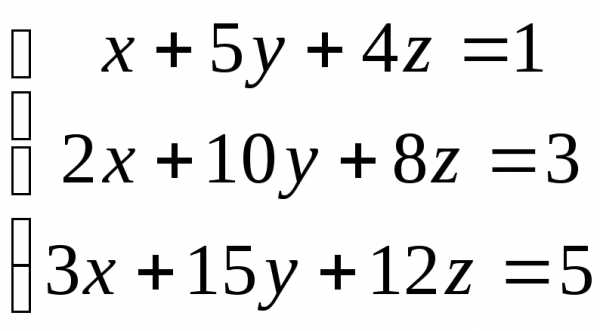 ;
;
11. 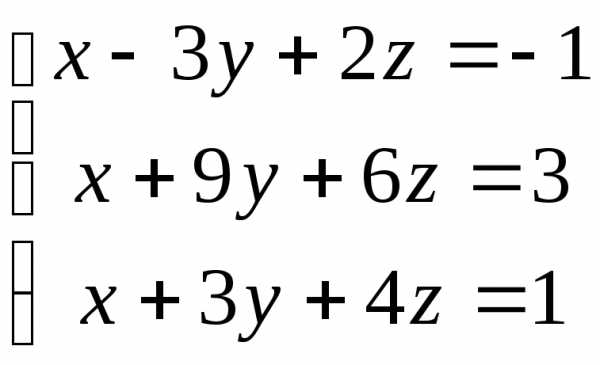 ; 12.
; 12.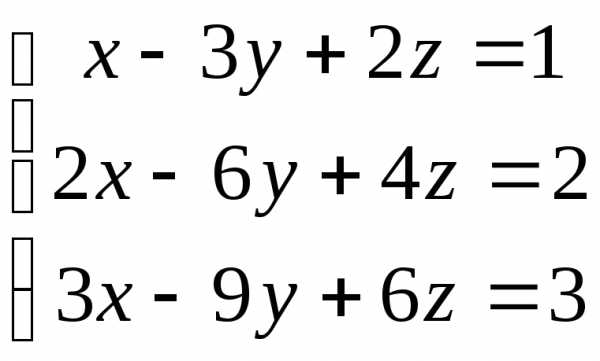 ;
;
13. 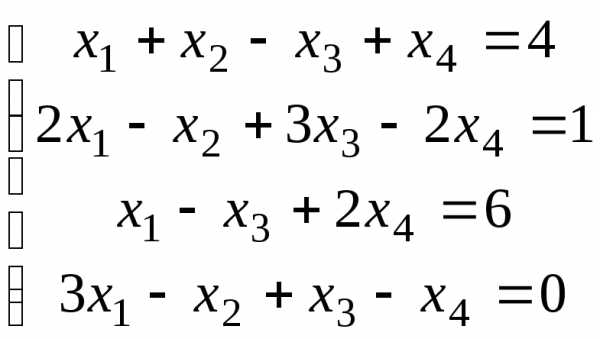 ;
14.
;
14. 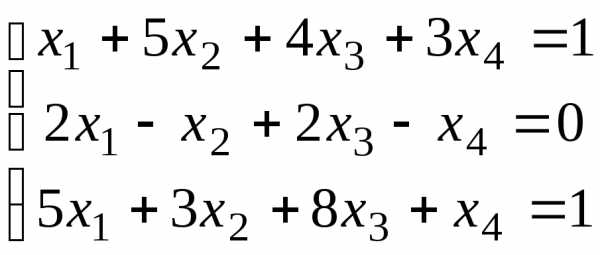 ;
;
15. .
Определите, при
каких значениях  и
и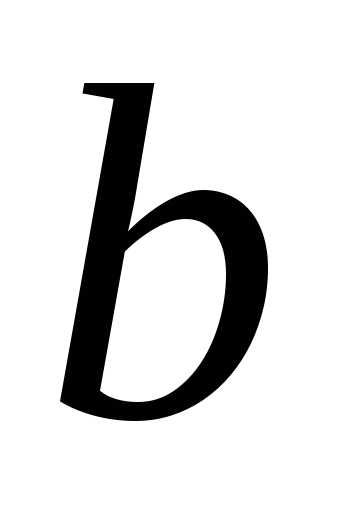 система уравнений
система уравнений
а) имеет единственное решение;
б) не имеет решения;
в) имеет бесконечно много решений.
16. 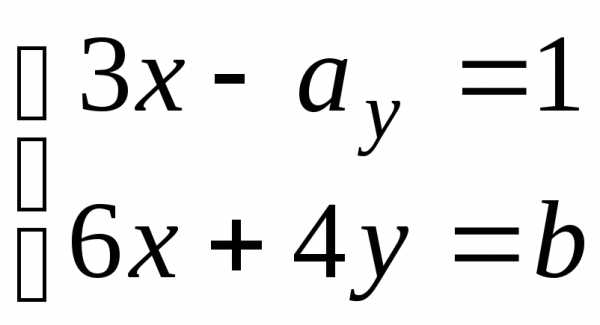 ; 17.
; 17.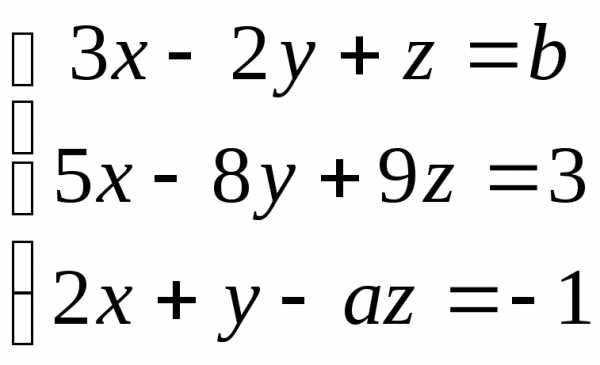 ;
;
Найти все решения следующих однородных систем:
18. 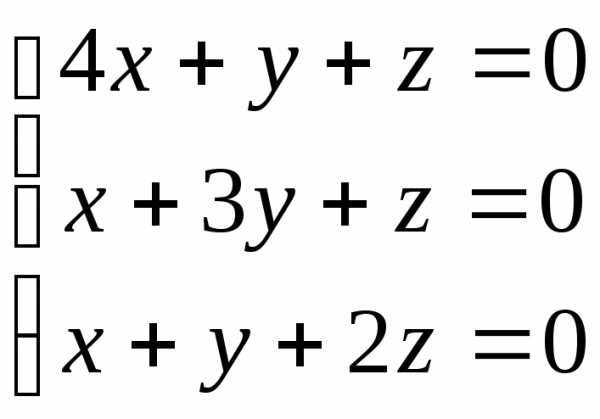 ; 19.
; 19.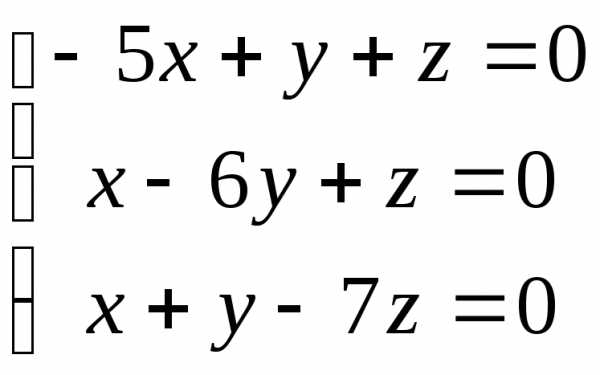 ;
;
20. 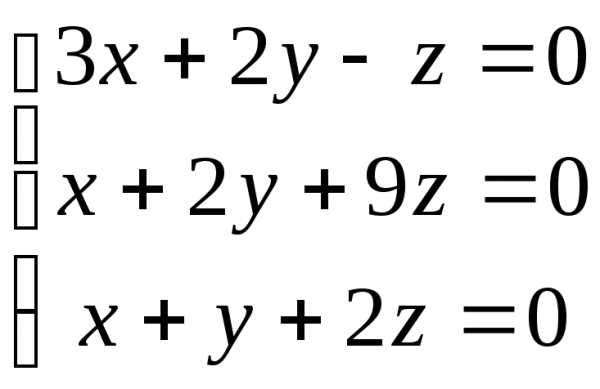 ; 21.
; 21.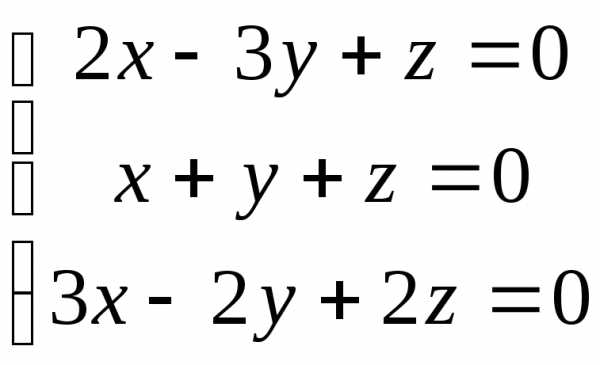 ;
;
22. 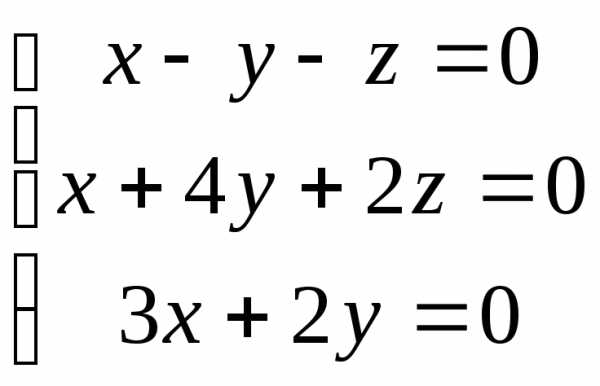 ; 23.
; 23.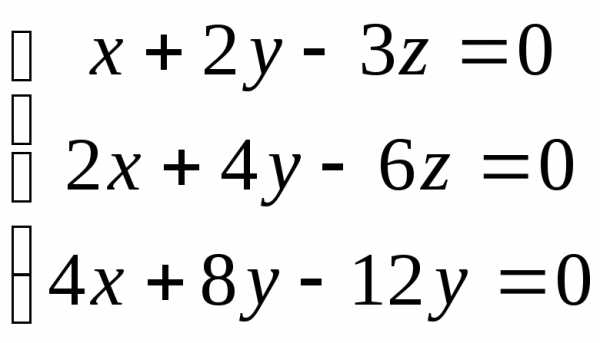 ;
;
Ответы к примерам
1.
; 2.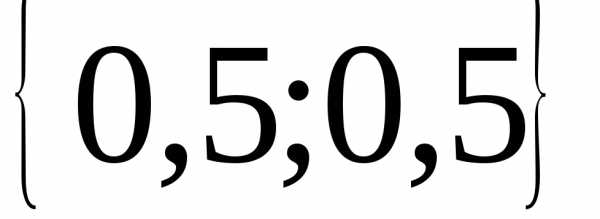 ; 3.
Ǿ; 4. Ǿ;
; 3.
Ǿ; 4. Ǿ;
5. 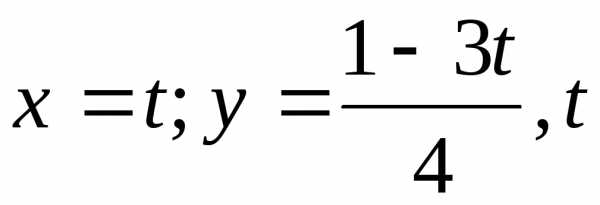 — произвольное число.
— произвольное число.
6.
,
где — произвольное число.
— произвольное число.
7. 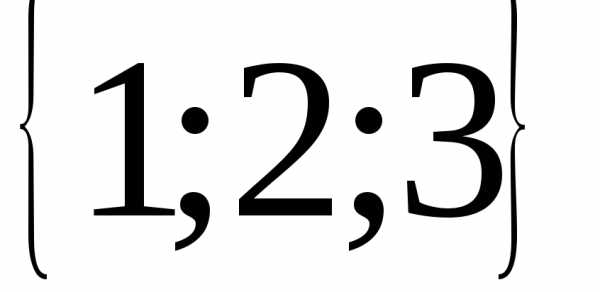 ; 8.
; 8.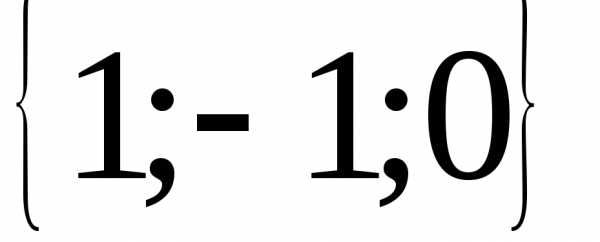 ; 9.
Ǿ; 10. Ǿ;
; 9.
Ǿ; 10. Ǿ;
11.
,
где — произвольное число.
— произвольное число.
12.
,
где и
и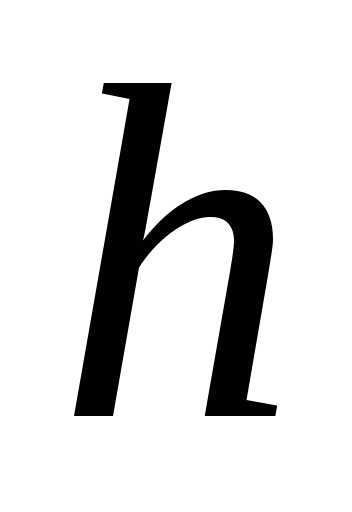 — произвольные числа.
— произвольные числа.
13. 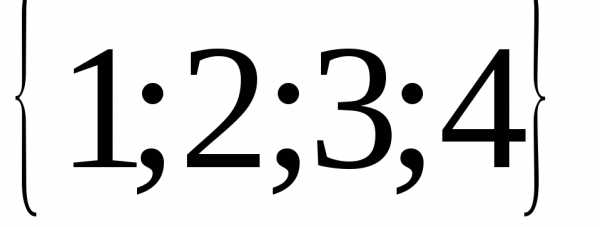 ; 14.
; 14.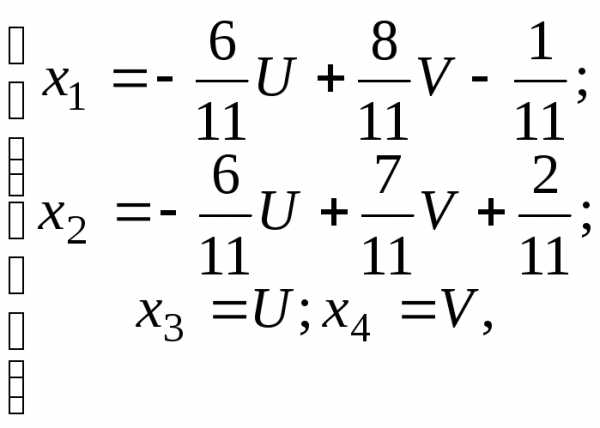 где
где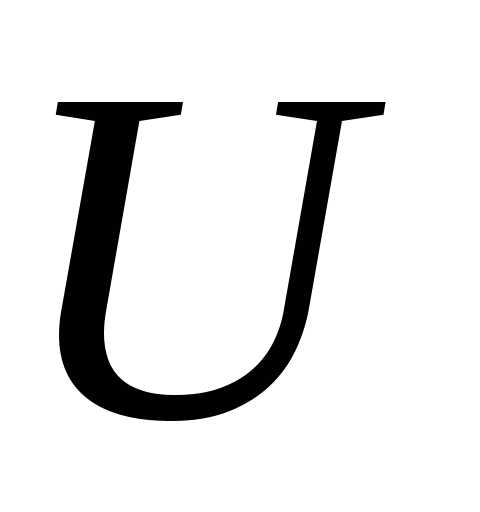 и
и — произвольные числа.
— произвольные числа.
15. Ǿ; 16. а) 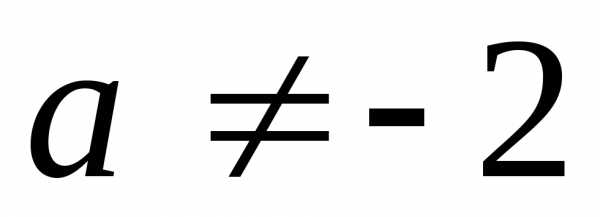 ;
б);
в).
;
б);
в).
17. а) 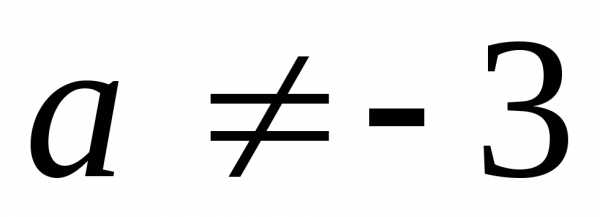 ;
б)
;
б)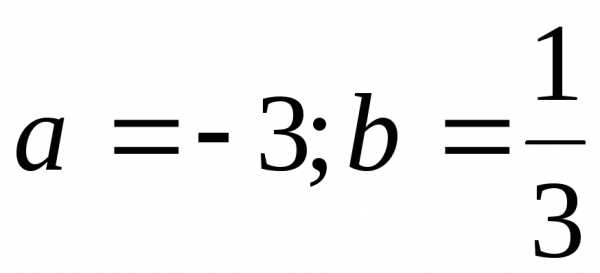 ;
в)
;
в)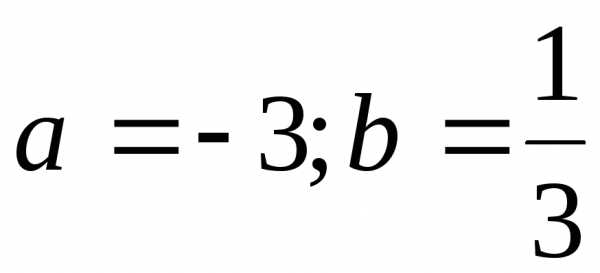 ;
;
18. 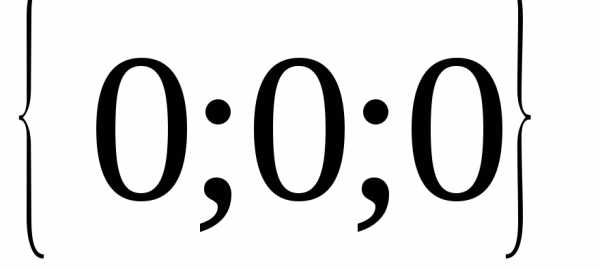 ; 19.
; 19.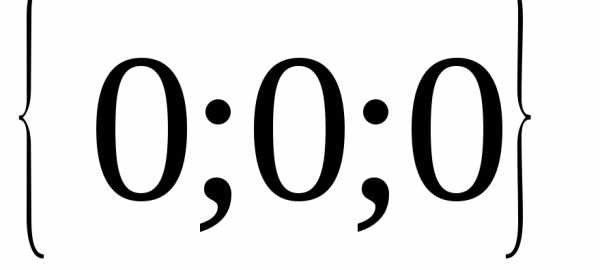 ; 20.,
где
; 20.,
где — произвольное число.
— произвольное число.
21.
,
где — произвольное число.
— произвольное число.
22.
,
где — произвольное число.
— произвольное число.
23.
,
где и
и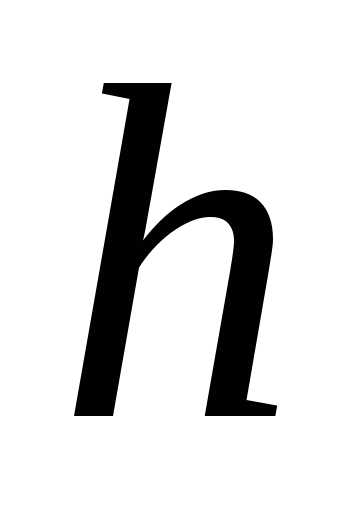 — произвольные числа.
— произвольные числа.
studfiles.net
29. Неоднородные системы линейных уравнений. Свойства их решений. Построение общего решения нслу.
Структура общего решения неоднородной системы уравнений
Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.
Рассмотрим неоднородную систему и соответствующую ей однородную систему. Между решениями этих систем имеются связи, выражающиеся следующими свойствами.
Свойства решений неоднородной системы уравнений
1. Разность двух решений инеоднородной системы есть решение однородной системы.
Действительно, из равенств иследует, что.
2. Пусть — решение неоднородной системы. Тогда любое решениенеоднородной системы можно представить в виде
, где — решение однородной системы.
В самом деле, для любого решения неоднородной системы разностьпо свойству 1 является решением однородной системы, т.е.— решение однородной системы.
Теорема 5.4 о структуре общего решения неоднородной системы.
Пусть — решение неоднородной системы, а— фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец
при любых значениях [i]произвольных постоянных является решением неоднородной системы, и, наоборот, для каждого решенияэтой системы найдутся такие значения произвольных постоянных, при которых это решениеудовлетворяет равенству (5.15).[/i]
Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.
Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.
Алгоритм решения неоднородной системы уравнений
1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).
6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.
7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательностандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.
8. Записать общее решение неоднородной системы по формуле (5.15).
Замечания 5.4
1. Используя фундаментальную матрицу однородной системы, решение неоднородной системыможно представить в виде
где — частное решение неоднородной системы, а— столбец произвольных постоянных.
2. Если базисный минор матрицы расположен в левом верхнем углу (в первыхстроках и первыхстолбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы
Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбецявляется частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде
где — столбец произвольных постоянных. Полученную формулу можно считатьвторым способом решения неоднородной системы.
Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы
Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:
Переменные — базисные, а— свободные.
6. Полагая , получаем частное решение неоднородной системы.
7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):
8. Записываем по формуле (5.15) общее решение неоднородной системы
Искомая структура множества решений найдена
Получим формулу общего решения вторым способом, используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:
Записываем частное решение неоднородной системы
и составляем фундаментальную матрицу:
По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):
которое совпадает с ранее полученным.
studfiles.net
Примеры систем линейных уравнений: метод решения
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.

Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.
Решить систему уравнений — это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:

Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:

Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.

Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.

Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
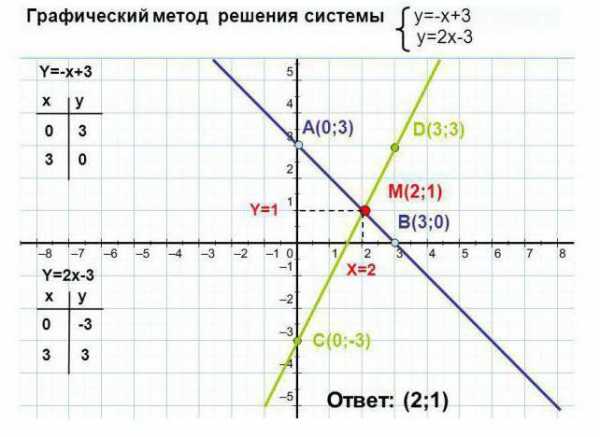
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
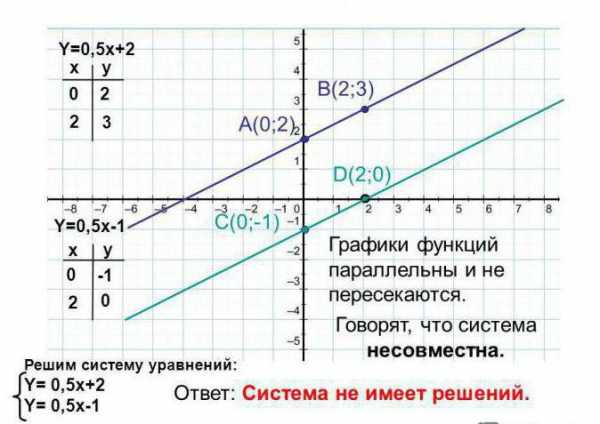
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.
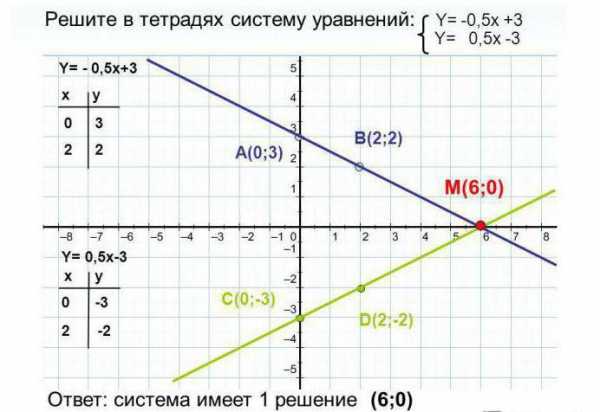
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. Матрица вида n*m имеет n — строк и m — столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K-1= 1 / |K|, где K-1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a1b2c3 + a1b3c2 + a3b1c2 + a2b3c1 + a2b1c3 + a3b2c1. Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.

В примере anm — коэффициенты уравнений, матрица — вектор xn — переменные, а bn — свободные члены.

Далее необходимо найти обратную матрицу и умножить на нее исходную. Найти значения переменных в полученной единичной матрицы легко выполнимая задача.

Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:

Как видно из примера, на шаге (3) было получено два уравнения 3x3-2x4=11 и 3x3+2x4=7. Решение любого из уравнений позволит узнать одну из переменных xn.

Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:
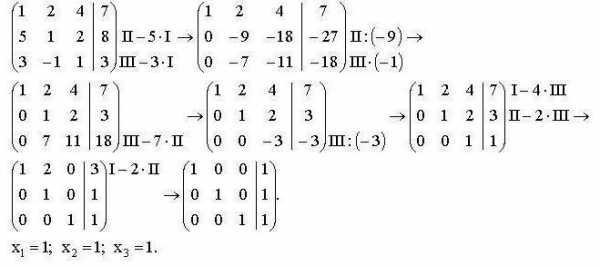
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. Вертикальная черта отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
fb.ru
Фундаментальная система решений
Рассмотрим систему однородных линейных алгебраических уравнений.
(1)
Выпишем матрицу A
Определение 1.
Минор матрицы называется базисным , если он неравен 0, и окаймляющие его миноры либо все равны 0, либо совсем отсутствуют.
Теорема о базисном миноре.
Столбцы матрицы, пересекающие главный минор линейно независимы; Всякий столбец через них линейно выражается.
Определение 2.
Всякая максимальная линейно независимая система решений однородной системы уравнений (1), называется фундаментальной системой решений (ФСР).
Теорема:
Если ранг r , матрицы из коэффициентов системы линейных однородных уравнений (1), меньше m, то всякая ФСР системы (1) состоит из n-r решений.
Пример №1.
Дана однородная система линейных алгебраических уравнений
.
Найти ФСР и общее решение системы.
1.Составим матрицу системы.
2. Легко показать, что ранг матрицы A=2, значит ФСР состоит из трех решений (5-2=3).
3. В матрице A возьмем базисный минор (минор второго порядка):
.
4. Отбрасываем последние уравнения системы , а неизвестные ,
считаем «свободными» и переносим их в правую часть уравнений.
Получим:
. (2)
5. Ищем первое базисное решение X , для этого положим , тогда получим систему:
(3)
Определителем матрицы системы является базисный минор, он отличен от 0, значит система (3) имеет единственное решение: .
Таким образом
= .
6. Полагая в системе (2), находимто есть, вторым базисным решением является столбец:
.
7. Полагая: , получаем —
.
8. Итак, ФСР получена; построенная таким образом ФСР называется нормальной.
9. Столбцы образующие ФСР линейно независимы, так как свободные неизвестные были выброшены так, что выделенный минор третьего порядка отличен от 0;
10.Теперь выпишем общее решение исходной однородной системы линейных алгебраических уравнений.
,
.
Неоднородная система линейных алгебраических уравнений
(1)
Общее решение неоднородной системы линейных алгебраических уравнений (1) имеет вид:
(2)
где – какое-либо решение системы (1).
общее решение соответствующей однородной системы, для которой – ФСР.
Пример №2.
Дана неоднородная система линейных алгебраических уравнений:
Доказать, что это система совместна и найти ее общее решение.
Решение:
Легко показать, что rang Ᾱ = rang A
Рассмотрим соответствующую однородную систему уравнений, эта система из примера №1. Её ФСР и общее решение найдены. Выделим в матрицу Ᾱ базисный минор, стоящий на пересечении первых двух строк со вторым и третьим столбцами. Тогда последовательность уравнений системы есть следствие двух первых уравнений системы, а неизвестные можно считать «свободными», поэтому исходная система эквивалентна системе:
Решив её, находим единственное решение:
Найдено частное решение данной неоднородной системы.
.
Общее решение исходной неоднородной системы получим с помощью формулы (2).
= или
Это решение можно было бы получить методом исключения неизвестных. ФСР определяется неоднозначно, но число элементов в ФСР всегда равно .
studfiles.net

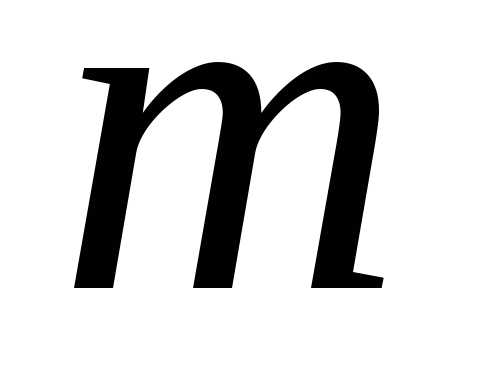 линейных уравнений с
линейных уравнений с неизвестными
неизвестными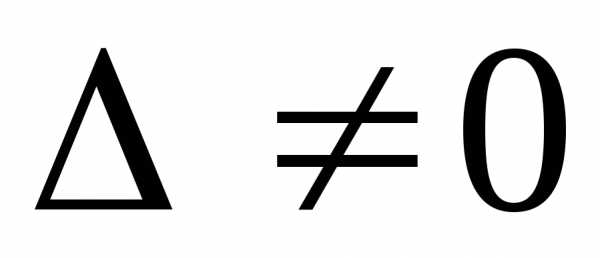 ,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.
,
то система имеет единственное решение,
которое может быть найдено по формулам
Крамера.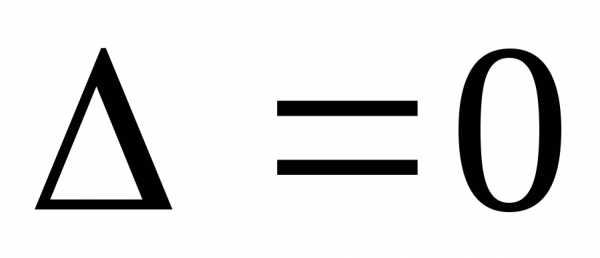 ,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, еслиили не иметь их, если хотя бы один из
определителейне равен нулю.
,
то правило Крамера неприменимо. В этом
случае система может иметь бесчисленное
множество решений, еслиили не иметь их, если хотя бы один из
определителейне равен нулю.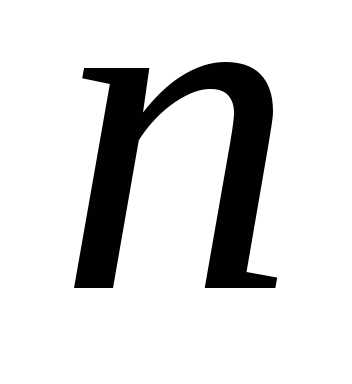 уравнений с
уравнений с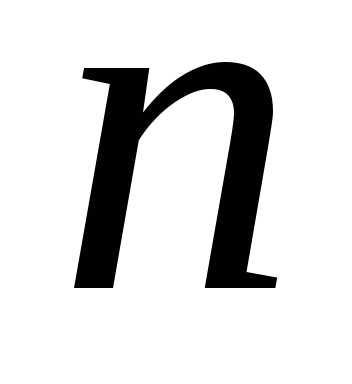 неизвестными
неизвестными