При управлении запасами на основе модели eoq регулируемым параметром: Ваш браузер не поддерживается
Управление активами организации.Тест Синергия — решенные тесты Синергия, тест Синергия,бизнес практикум Синергия
Сдано на 70баллов в 2017г.! Верно 21 из 30 Скриншот с отметкой прилагается к работе. Ответы выделены цветом в Worde.
На случай невозврата дебиторской задолженности предприятие формирует …
резервный фонд
резерв под обесценение материальных ценностей
резерв по сомнительным долгам
резерв предстоящих расходов
Ужесточение кредитной политики компании может привести …
к замедлению поступления денежных средств
к увеличению денежных средств на расчетном счете
к снижению объемов продаж
Инструментом оперативного управления денежными потоками предприятия является …
кредитный план
бюджет доходов и расходов
бюджет движения денежных средств
платежный календарь
резерв предстоящих расходов
Максимальный размер резерва по сомнительным долгам не должен превышать … выручки от продаж отчетного периода
15 %
20 %
10 %
5 %
При управлении запасами на основе модели EOQ регулируемым параметром является …
время ожидания заказа
максимальный уровень запасов
размер заказа
Замена первоначального обязательства другим между теми же лицами, но предусматривающего иной способ исполнения – это …
взаимозачет
факторинг
новация
отступное
К долгосрочным мерам сокращения оттока денежных средств можно отнести …
продажу или сдачу в аренду внеоборотных активов
привлечение внешних источников краткосрочного финансирования
сокращение инвестиционной программы
дополнительную эмиссию акций и облигаций
Такая форма финансовой отчетности, как является основной для анализа денежных потоков
бухгалтерский баланс хз
отчет об изменениях капитала
отчет о Движении денежных средств
… создаются для обеспечения независимости деятельности организации в пиковые моменты операционного и производственного цикла
Запасы готовой продукции
Сезонные запасы
Запасы сырья и материалов
К краткосрочным мерам сокращения оттока денежных средств можно отнести …
реструктуризацию дебиторской задолженности
сокращение затрат
привлечение внешних источников краткосрочного финансирования
использование предоплаты
Эквиваленты денежных средств — это .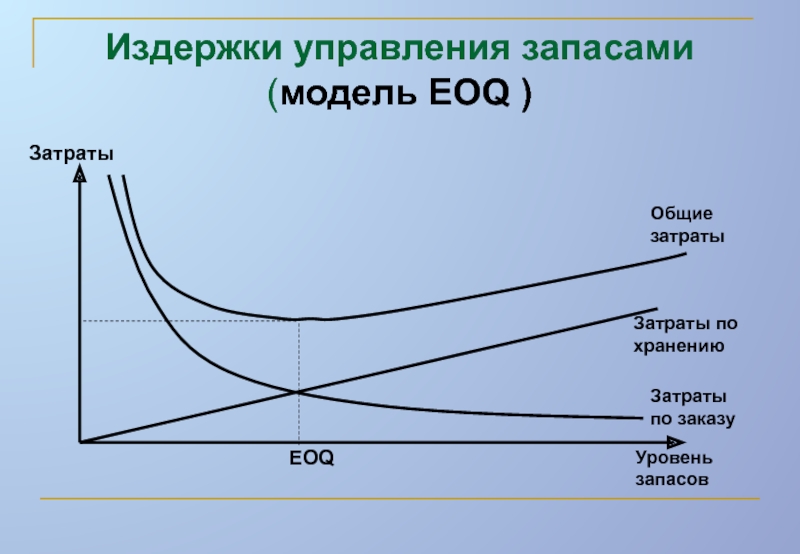 ..
..
высоколиквидные финансовые вложения
уставный капитал
кредиторская задолженность
К способам снижения рисков невозврата дебиторской задолженности относят …
хеджирование
лимитирование
диверсификацию
резервирование
Чистый оборотный капитал определяется …
разницей текущих активов и пассивов
суммой текущих активов и пассивов
суммой краткосрочной и долгосрочной кредиторской задолженности
суммой активов и дебиторской задолженностью
Снижение показателя чистой прибыли …
приводит к увеличению остатка денежных средств
не связано напрямую с показателями денежных средств
приводит снижению оборотных активов
Эффект финансового рычага связан с рассмотрением соотношений …
постоянных и переменных затрат
собственных и заемных средств
прибылей и убытков
доходов и расходов
График предельной стоимости капитала . ..
..
не имеет очевидной тенденции
является убывающим
является возрастащим
Сценарный анализ — это анализ риска, при котором …
результат наиболее вероятного варианта сравнивается с наиболее и с наименее благоприятными вариантами
результат наиболее вероятного варианта сравнивается с множеством случайно выбранных вариантов
Дивиденд — это способ получения дохода по.
облигациям
акциям
чекам
При политике поддержания дебиторской задолженности на низком уровне …
возможна потеря потенциальных клиентов
возможно уменьшение притока денежных средств
возможно увеличение конкурентоспособности компании
Нераспределенная прибыль — это прибыль,…
оставшаяся после выплаты дивидендов
оставшаяся после начисления дивидендов и формирования фондов и резервов
начисленная в виде дивидендов, но не полученная акционерами
не использованная для начисления дивидендов
Коэффициент накопления запасов > 1 свидетельствует о .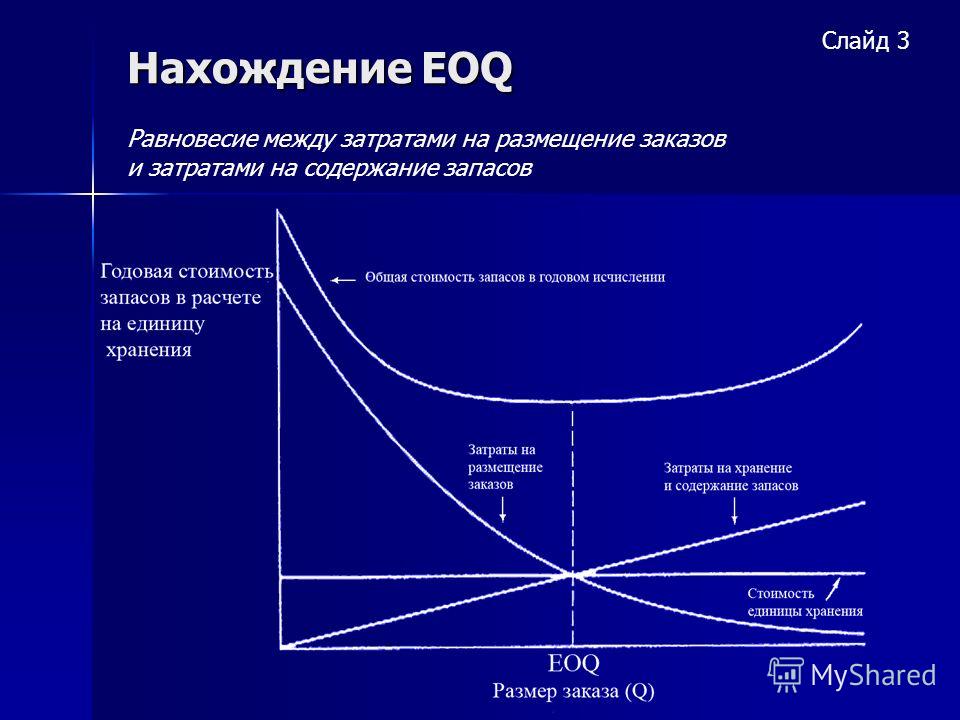
наличие проблем со сбытом
затоваривании складов готовой продукции
наличии сверхнормативных запасов сырья и материалов
оптимальном использовании запасов сырья и материалов
… — это специальный фонд денежных средств, образованный согласно уставу акционерного общества, формируемый за счет отчислений из прибыли и предназначенный для внутреннего страхования рисков
Фонд накопления
Фонд потребления
Добавочный капитал
Резервный фонд
При формировании дивидендной политики необходимо обеспечить …
приоритет интересов собственников
приоритет интересов менеджмента организации
рациональнее сочетание интересов собственников и менеджмента
Неверно, что … входит в состав добавочного капитала
эмиссионный доход
положительные курсовые разницы по вкладам в уставный капитал в иностранной валюте
поступления от дополнительной эмиссии акций
сумма дооценки основных средств
Получение организацией убытка в отчетном периоде при неизменных остальных показателях в финансовой отчетности . ..
..
снижает показатель фондоотдачи
снижает величину чистых активов
увеличивает активы предприятия
увеличивает финансовую устойчивость
… — это наименее ликвидная часть оборотного капитала организации
Незавершенное производство
Производственные запасы
Краткосрочные финансовые вложения
Неверно, что … относится к методам оптимизации дефицитного денежного потока
ускорение инкассации дебиторской задолженности
частичная или полная предоплата за произведенную продукцию
досрочное погашение долгосрочных кредитов
увеличение размера скидок за наличный расчет
При прочих равных условиях рост средневзвешенной стоимости капитала …
приводит к снижению стоимости фирмы
приводит к росту стоимости фирмы
не влияет на стоимость фирмы
Оптимальный уровень денежных средств организации при прогнозируемом характере денежных поступлений и выплат определяется с помощью модели …
Гордона
Баумоля
Цена капитала организации — это. ..
..
сумма уплаченных процентов по кредитам
сумма средств, которая показывает стоимость использования данного объема финансовых ресурсов
выраженная в процентах плата за использование определенного объема финансовых ресурсов
отношение суммы привлеченных ресурсов к сумме расходов за их привлечение
Управление активами и пассивами организации — МФПУ Синергия (МФПА) — Вопросы тестов онлайн — Каталог тестов
Снижение показателя чистой прибыли …
приводит к увеличению остатка денежных средств
не связано напрямую с показателями денежных средств
приводит снижению оборотных активов
приводит к снижению остатка денежных средств НЕ верный
… подход к управлению оборотными активами предусматривает минимизацию всех форм резервов
Агрессивный
Консервативный
Умеренный
К проблемам, связанным с избыточными запасами, относится …
упущенная выгода из-за недовыпуска готовой продукции
рост количества неликвидных запасов
срыв производственной программы нарушение
ритмичности производстваэ
Неверно, что . .. относится к методам оптимизации дефицитного денежного потока
.. относится к методам оптимизации дефицитного денежного потока
досрочное погашение долгосрочных кредитов
увеличение размера скидок за наличный расчет
частичная или полная предоплата за произведенную продукцию
ускорение инкассации дебиторской задолженности
При политике поддержания дебиторской задолженности на низком уровне … возможна потеря потенциальных клиентов
возможно уменьшение притока денежных средств
возможно увеличение конкурентоспособности компании
Финансирование оборотных средств преимущественно за счет собственного капитала приводит …
к недоиспользованию эффекта финансового рычага
к риску неэффективного использования собственных средств
к увеличению прибыли
к снижению финансовой устойчивости
… создаются для обеспечения текущей сбытовой деятельности
Запасы сырья и материалов
Сезонные запасы
Запасы готовой продукции
Увеличение скорости оборота дебиторской задолженности . .. операционного цикла
.. операционного цикла
не оказывает никакого влияния на длительность
приводит к увеличению длительности
приводит к уменьшению длительности
К краткосрочным мерам сокращения оттока денежных средств можно отнести …
реструктуризацию дебиторской задолженности
сокращение затрат
использование предоплаты
Неверно, что… относится к методам оптимизации избыточного денежного потока
формирование портфеля финансовых инвестиций
ускорение периода разработки и реализации инвестиционных проектов
диверсификация операционной деятельности
использование современных форм рефинансирования дебиторской задолженности
Потребность во внеоборотных активах покрывается … собственным капиталом и долгосрочными кредитами и займами собственным капиталом долгосрочными кредитами и займами уставным капиталом
Замедление оборачиваемости запасов .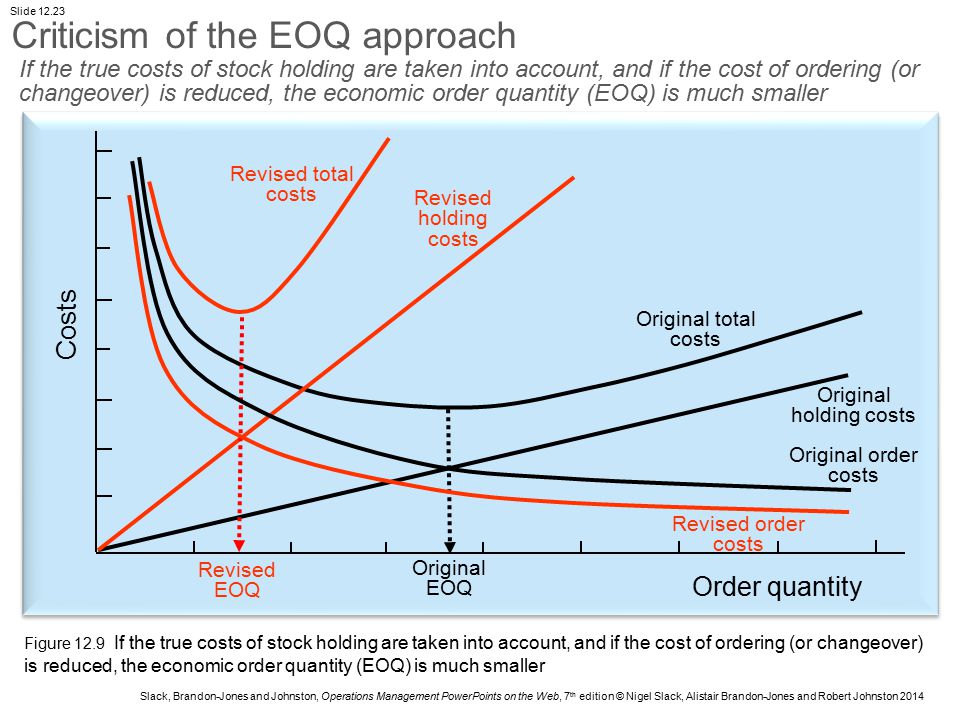 .. финансового цикла приводит к уменьшению длительности не оказывает никакого влияния на длительность приводит к увеличению длительности
.. финансового цикла приводит к уменьшению длительности не оказывает никакого влияния на длительность приводит к увеличению длительности
Период оборота дебиторской задолженности определяется как отношение … величины средней дебиторской задолженности к количеству дней в периоде количества дней в периоде к коэффициенту оборачиваемости дебиторской задолженности количества дней в периоде к величине средней дебиторской задолженности коэффициента оборачиваемости дебиторской задолженности к количеству дней в периоде
Замена первоначального обязательства другим между теми же лицами, но предусматривающего иной способ исполнения — это …
взаимозачет
факторинг
новация
отступное
Ужесточение кредитной политики компании может привести …
к замедлению поступления денежных средств
к увеличению денежных средств на расчетном счете
к снижению объемов продаж
К долгосрочным мерам сокращения оттока денежных средств можно отнести . ..
..
продажу или сдачу в аренду внеоборотных активов
привлечение внешних источников краткосрочного финансирования
сокращение инвестиционной программы
дополнительную эмиссию акций и облигаций
Консервативный подход к управлению оборотными активами характеризуется … большими запасами
низким удельным весом оборотных средств в активах
низкой оборачиваемостью
высокой дебиторской задолженностью
К способам снижения рисков невозврата дебиторской задолженности относят …
хеджирование
лимитирование
диверсификацию
резервирование
… подход к управлению оборотными активами обеспечивает оптимальное сочетание риска и эффективности использования
Умеренный
Консервативный
Агрессивный
Неверно, что внеоборотные активы…
подвержены потерям от инфляции
обладают слабой ликвидностью
подвержены моральному износу
плохо поддаются оперативному управлению
Чистый оборотный капитал определяется . ..
..
разницей текущих активов и пассивов суммой текущих активов и пассивов
суммой краткосрочной и долгосрочной кредиторской задолженности
суммой активов и дебиторской задолженностью
При управлении запасами на основе модели EOQ регулируемым параметром является …
время расходования запасов время ожидания заказа максимальный уровень запасов размер заказа
… — это наименее ликвидная часть оборотного капитала организации
Незавершенное производство
Краткосрочные финансовые вложения
Запасы готовой продукции Производственные запасы
… создаются для обеспечения независимости деятельности организации в пиковые моменты операционного и производственного цикла
Запасы готовой продукции
Сезонные запасы
Запасы сырья и материалов
Неиспользование избытка свободных денежных средств непосредственно приводит…
к снижению доходности организации
к снижению финансовой устойчивости
к снижению ликвидности
к повышению величины амортизационных отчислений
Источниками формирования оборотных активов организации являются . ..
..
собственный капитал и долгосрочные кредиты
собственный капитал, долгосрочные и краткосрочные кредиты
собственный капитал, краткосрочные кредиты банков и кредиторская задолженность
уставный капитал, добавочный капитал, краткосрочные кредиты банков и кредиторская задолженность
На случай невозврата дебиторской задолженности предприятие формирует … резервный фонд
резерв под обесценение материальных ценностей резерв по сомнительным долгам резерв предстоящих расходов
Максимальный размер резерва по сомнительным долгам не должен превышать… выручки от продаж отчетного периода
15%
20%
10%
5%
Финансовый менеджмент — МФПУ Синергия (МФПА) — Вопросы тестов онлайн — Каталог тестов
1. Схема простых процентов в сравнении со схемой сложных процентов
a. всегда выгоднее для кредитора
b. более выгодна для кредитора в случае долгосрочной финансовой операции
c. более выгодна для получателя средств
более выгодна для получателя средств
2. Эффект финансового рычага определяет … рациональность привлечения заемного капитала структуру финансового результата структуру затрат на производство и реализацию продукции отношение оборотных активов к краткосрочным пассивам
3. Под понятием финансовая устойчивость понимается степень обеспеченности организации собственными оборотными средствами и денежными активами, необходимыми для обеспечения платежеспособности
4. финансовая устойчивость — это наличие у организации собственного капитала независимость организации от внешних источников финансирования степень обеспеченности организации собственными оборотными средствами и денежными активами, необходимыми для обеспечения платежеспособности зависимость организации от конъюнктуры рынков
5. анализ изучает структуру средств предприятия и их источники Факторный Вертикальный Горизонтальный Трендовый
6. Модель Миллера-Орра предполагает создание страхового остатка денежных средств
7. относят к объектам управления финансовой деятельностью организации: денежные потоки финансовые результаты маркетинговые исследования финансовые риски
относят к объектам управления финансовой деятельностью организации: денежные потоки финансовые результаты маркетинговые исследования финансовые риски
8. При управлении запасами на основе модели EOQ регулируемым параметром является … время ожидания заказа время расходования запасов максимальный уровень запасов размер заказа
9. Показатель, отражающий величину ставки дисконтирования, при которой доходы по проекту равны инвестиционным затратам, – это
10. Метод чистой приведенной стоимости используется для … прогнозирования возможного банкротства организации оценки эффективности инвестиционных проектов анализа оборачиваемости собственного капитала оценки фондоотдачи
11. Операционный цикл – это период полного оборота всей суммы оборотных активов, в процессе которого происходит смена их видов
12. Дисконтирование денежных средств – это процесс … приведения будущей стоимости денег к их настоящей (текущей) стоимости расчета расходов на осуществление проекта приведения настоящей (текущей) стоимости денег к их будущей стоимости оценки эффективности инвестиционного проекта
13. Размер ежегодных отчислений в резервный фонд (капитал) определяется в … Гражданском кодексе РФ учетной политике уставе общества Федеральном законе «Об акционерных обществах»
Размер ежегодных отчислений в резервный фонд (капитал) определяется в … Гражданском кодексе РФ учетной политике уставе общества Федеральном законе «Об акционерных обществах»
14. При управлении запасами на основе модели АВС все виды сырья и материалов делятся … на очень дефицитные, менее дефицитные и доступные в любое время в соответствии с ассортиментом готовой продукции на очень дорогие, менее дорогие и малоценные
15. Выплату минимального стабильного размера дивидендов с надбавкой в различные периоды предполагает … дивидендная политика агрессивная консервативная умеренная
16. Цена капитала организации – это … выраженная в процентах плата за использование определенного объема финансовых ресурсов сумма уплаченных процентов по кредитам сумма средств, которая показывает стоимость использования данного объема финансовых ресурсов отношение суммы привлеченных ресурсов к сумме расходов за их привлечение
17. Финансовая стратегия не должна обеспечивать повышение рыночной стоимости организации снижение инвестиционной привлекательности организации укрепление имиджа организации во внешней среде финансовую устойчивость организации
18. Показатель, характеризующий использование предприятием заемных средств, которые оказывают влияние на изменение коэффициента рентабельности собственного капитала, эффект финансового левериджа
Показатель, характеризующий использование предприятием заемных средств, которые оказывают влияние на изменение коэффициента рентабельности собственного капитала, эффект финансового левериджа
Производственный рычаг это показатель, характеризующий использование
Эффект финансового рычага заключается в использовании
19. Основным направлением сокращения «омертвленного» капитала выступает Оптимизация запасов и незавершенного производства Минимизация остатков средств на расчетном счете и кассовой наличности Увеличение высокодоходной части фондового портфеля Сокращение низкодоходной части фондового портфеля
20. Наблюдение за состоянием и развитием бизнеса контрагентов и конкурентов по определенным направлениям с целью совершенствования деятельности собственного предприятия называется бенчмаркингом
21. Резервный фонд — это специальный фонд денежных средств, образованный согласно уставу акционерного общества, формируемый за счет отчислений из прибыли и предназначенный для внутреннего страхования рисков
22. Схема простых процентов в сравнении со схемой сложных процентов … более выгодна для получателя средств в случае краткосрочной финансовой операции более выгодна для кредитора в случае долгосрочной финансовой операции более выгодна для кредитора в случае краткосрочной финансовой операции всегда выгоднее для кредитора
Схема простых процентов в сравнении со схемой сложных процентов … более выгодна для получателя средств в случае краткосрочной финансовой операции более выгодна для кредитора в случае долгосрочной финансовой операции более выгодна для кредитора в случае краткосрочной финансовой операции всегда выгоднее для кредитора
23. Коэффициент обеспеченности запасов собственными оборотными средствами рассчитывается как отношение … запасов к величине собственных средств собственных средств к величине запасов собственных оборотных средств к величине запасов запасов к величине собственных оборотных средств
24. специальные бюджеты: Бюджет доходов и расходов Бюджет производственных расходов Бюджет коммерческих расходов Кредитный план
25. При формировании дивидендной политики необходимо обеспечить … рациональное сочетание интересов собственников и менеджмента приоритет интересов менеджмента организации приоритет интересов собственников
26. С позиции сторонников традиционного подхода к управлению капиталом привлечение заемного капитала … как правило, никак не влияет на величину WACC как правило, влияет на величину WACC в сторону уменьшения может влиять на величину WACC как в сторону увеличения, так и уменьшения как правило, влияет на величину WACC в сторону увеличения
27. средства резервного капитала предназначены для
средства резервного капитала предназначены для
предназначены средства резервного капитала начисления дивидендов выкупа собственных акций погашения облигаций общества покрытия убытков
28. К недостаткам проведения IPO можно отнести … открытость отсутствие долгового бремени, обретение рыночной стоимости, обеспечение повышенной ликвидности акций
29. Схема начисления простых процентов предполагает … начисление процентов на общую базу с учетом исходной величины денежных средств и капитализированных процентов многократное начисление процентов на всю сумму вклада неизменность базы, с которой происходит начисление однократное начисление процентов на всю сумму вклада
Экономичный объем заказа (EOQ) | Inc.com
Экономическое количество заказа (EOQ) — это количество единиц, которое компания должна добавить в запасы с каждым заказом, чтобы минимизировать общие затраты на инвентаризацию, такие как затраты на хранение, затраты на заказ и затраты на дефицит. EOQ используется как часть системы непрерывного обзора запасов, в которой уровень запасов отслеживается постоянно, и фиксированное количество заказывается каждый раз, когда уровень запасов достигает определенной точки повторного заказа. EOQ предоставляет модель для расчета подходящей точки повторного заказа и оптимального количества повторного заказа, чтобы обеспечить мгновенное пополнение запасов без дефицита.Это может быть ценным инструментом для владельцев малого бизнеса, которым необходимо принимать решения о том, сколько запасов держать под рукой, сколько товаров заказывать каждый раз и как часто менять заказ, чтобы нести минимально возможные затраты.
EOQ предоставляет модель для расчета подходящей точки повторного заказа и оптимального количества повторного заказа, чтобы обеспечить мгновенное пополнение запасов без дефицита.Это может быть ценным инструментом для владельцев малого бизнеса, которым необходимо принимать решения о том, сколько запасов держать под рукой, сколько товаров заказывать каждый раз и как часто менять заказ, чтобы нести минимально возможные затраты.
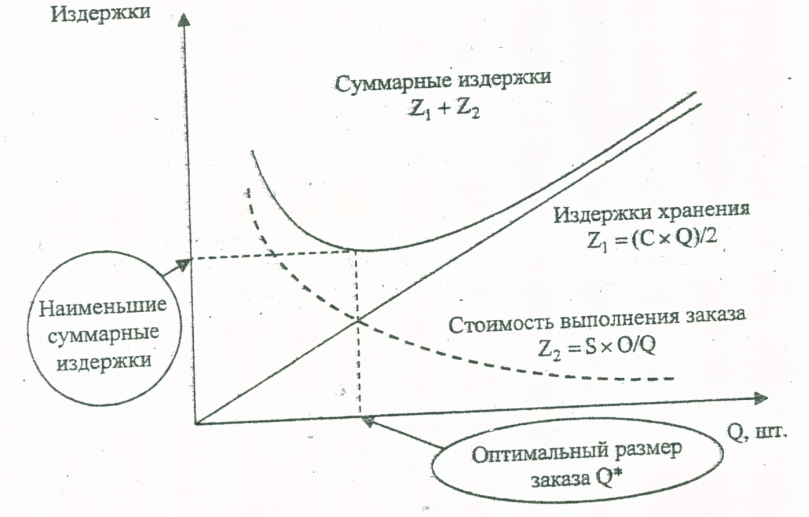
Модель EOQ предполагает, что спрос постоянен и что запасы истощаются с фиксированной скоростью, пока не достигнут нуля. В этот момент прибывает определенное количество предметов, чтобы вернуть инвентарь на начальный уровень. Поскольку модель предполагает мгновенное пополнение запасов, не возникает дефицита запасов или связанных с этим затрат.Следовательно, стоимость инвентаря в модели EOQ включает компромисс между затратами на хранение инвентаря (стоимостью хранения, а также стоимостью привязки капитала к инвентарю вместо его инвестирования или использования для других целей) и стоимостью заказа (любой сборы, связанные с размещением заказов, например стоимость доставки). Одновременный заказ большой суммы увеличит затраты малого бизнеса на хранение, в то время как выполнение более частых заказов меньшего количества товаров снизит затраты на хранение, но увеличит стоимость заказа.Модель EOQ находит количество, которое минимизирует сумму этих затрат.
Одновременный заказ большой суммы увеличит затраты малого бизнеса на хранение, в то время как выполнение более частых заказов меньшего количества товаров снизит затраты на хранение, но увеличит стоимость заказа.Модель EOQ находит количество, которое минимизирует сумму этих затрат.
Основное соотношение EOQ показано ниже. Давайте посмотрим на это, предполагая, что у нас есть маляр, использующий 3500 галлонов краски в год, платя 5 долларов за галлон, фиксированную плату в размере 15 долларов каждый раз, когда он / она заказывает, и стоимость запасов на галлон в среднем составляет 3 доллара за галлон в год.
Соотношение: TC = PD + HQ / 2 + SD / Q ‘¦, где
- TC — это общая годовая стоимость инвентаря, которую необходимо рассчитать.
- P — цена за уплаченную единицу продукции, предположим, что 5 долларов за единицу.
- D — общее количество единиц, приобретенных за год, предположим, что 3500 единиц.
- H — это стоимость владения на единицу в год — предположим, 3 доллара на единицу в год.

- Q — это количество, заказываемое каждый раз при размещении заказа — изначально предполагается 350 галлонов на заказ.
- S — это фиксированная стоимость каждого заказа (предположим, 15 долларов США за заказ).
Рассчитав TC с этими значениями, мы получаем общую стоимость запасов в 18 175 долларов за год. Обратите внимание, что основной переменной в этом уравнении является заказываемое количество Q.Художник может решить купить меньшее количество. Если он или она сделает это, большее количество заказов будет означать более фиксированные расходы на заказ (представленные буквой S), потому что больше заказов будет обработано, но более низкие сборы за хранение (представлены буквой H): потребуется меньше места для хранения краски и меньше связанных денег. в краске. Предполагая, что маляр покупает за раз 200 галлонов вместо 350, TC упадет до 18 063 доллара в год, что даст экономию 112 долларов в год. Ободренный этим, художник снижает количество покупок до 150 за раз. Но сейчас результаты неутешительны. Общие затраты сейчас составляют 18 075 долларов. Где найти оптимальное количество покупок?
Но сейчас результаты неутешительны. Общие затраты сейчас составляют 18 075 долларов. Где найти оптимальное количество покупок?
Формула EOQ дает ответ. Идеальное количество заказа достигается, когда две части основного отношения (показанного выше) — «HQ / 2» и «SD / Q» — равны. Мы можем рассчитать объем заказа следующим образом: Умножьте общую сумму единиц на фиксированные затраты на заказ (3500–15 долларов США) и получите 52 500 единиц; умножьте это число на 2 и получите 105000. Разделите это число на стоимость владения (3 доллара) и получите 35000.Извлеките квадратный корень из этого и получите 187. Тогда это число будет Q.
На следующем шаге HQ / 2 преобразуется в 281, а SD / Q также будет равно 281. Используя 187 для Q в основном соотношении, мы получаем общая годовая стоимость товарно-материальных запасов составляет 18 061 доллар США, что является самой низкой возможной стоимостью с учетом единицы и ценовых факторов, показанных в приведенном выше примере.
Таким образом, EOQ определяется по формуле: EOQ = квадратный корень из 2DS / H. Число, которое мы получаем, в данном случае 187, разделенное на 3500 единиц, предполагает, что художник должен покупать краску 19 раз в год, покупая за один раз 187 галлонов.
Число, которое мы получаем, в данном случае 187, разделенное на 3500 единиц, предполагает, что художник должен покупать краску 19 раз в год, покупая за один раз 187 галлонов.
EOQ иногда изменяется в результате оптовых скидок, предлагаемых некоторыми поставщиками в качестве стимула для клиентов, которые размещают более крупные заказы. Например, определенный поставщик может взимать 20 долларов за единицу при заказе менее 100 единиц и только 18 долларов за единицу при заказе более 100 единиц. Чтобы определить, имеет ли смысл воспользоваться скидкой за количество при повторном заказе запасов, владелец малого бизнеса должен вычислить EOQ по формуле (Q = квадратный корень из 2DS / H), вычислить общую стоимость запасов для EOQ и для всех точек ценового разрыва над ним, а затем выберите количество заказа, обеспечивающее минимальную общую стоимость.
Например, скажем, маляр может заказать 200 галлонов или больше по цене 4,75 доллара за галлон, при этом все остальные факторы в расчетах остаются прежними.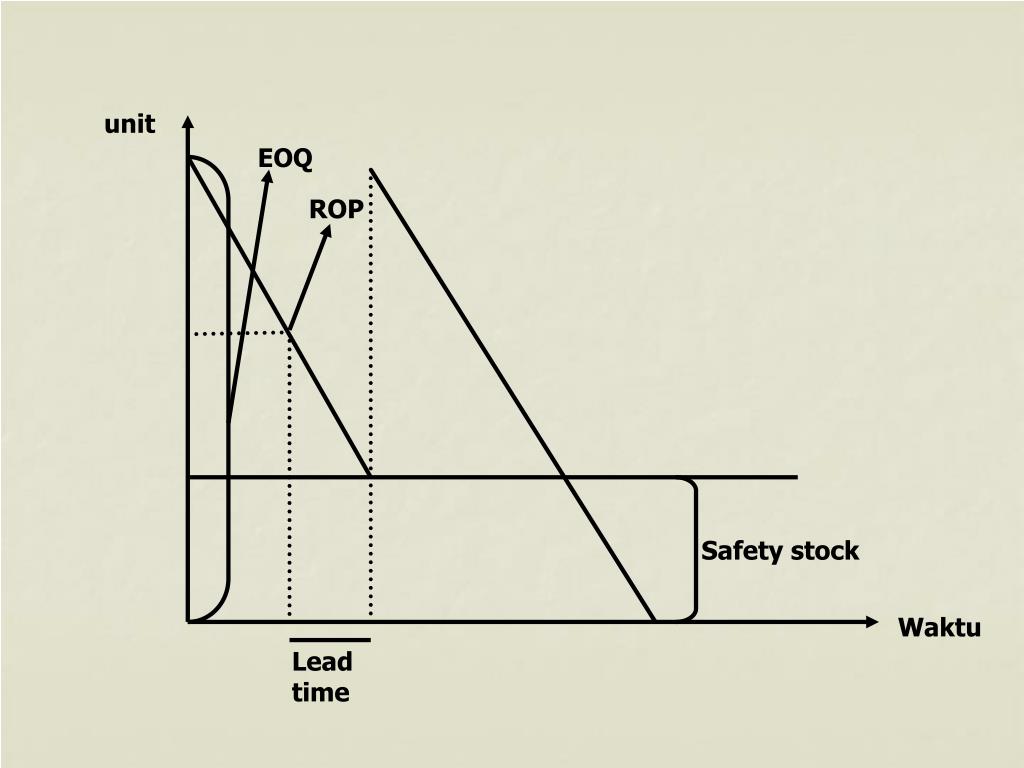 Он должен сравнить общие затраты на использование этого подхода с общими затратами согласно EOQ. Используя формулу общей стоимости, описанную выше, художник найдет TC = PD + HQ / 2 + SD / Q = (5 — 3500) + (3 à — 187) / 2 + (15 à — 3500) / 187 = 18 061 доллар. для EOQ. Заказ большего количества и получение скидки приведет к общей стоимости (4.75 Ö 3500) + (3 Ö 200) / 2 + (15 Ö 3500) / 200 = 17 187 долларов. Другими словами, маляр может сэкономить 875 долларов в год, воспользовавшись снижением цен и сделав 17,5 заказов в год по 200 единиц каждый.
Он должен сравнить общие затраты на использование этого подхода с общими затратами согласно EOQ. Используя формулу общей стоимости, описанную выше, художник найдет TC = PD + HQ / 2 + SD / Q = (5 — 3500) + (3 à — 187) / 2 + (15 à — 3500) / 187 = 18 061 доллар. для EOQ. Заказ большего количества и получение скидки приведет к общей стоимости (4.75 Ö 3500) + (3 Ö 200) / 2 + (15 Ö 3500) / 200 = 17 187 долларов. Другими словами, маляр может сэкономить 875 долларов в год, воспользовавшись снижением цен и сделав 17,5 заказов в год по 200 единиц каждый.
Расчеты EOQ редко бывают такими простыми, как показывает этот пример. Здесь цель состоит в том, чтобы объяснить основной принцип формулы. Малый бизнес с большим и часто меняющимся товарным запасом может быть хорошо обслужен поиском программного обеспечения для инвентаризации, которое более комплексно применяет концепцию EOQ к реальным ситуациям, чтобы помочь принимать решения о покупке более динамично.
БИБЛИОГРАФИЯ
«Бухгалтерское программное обеспечение».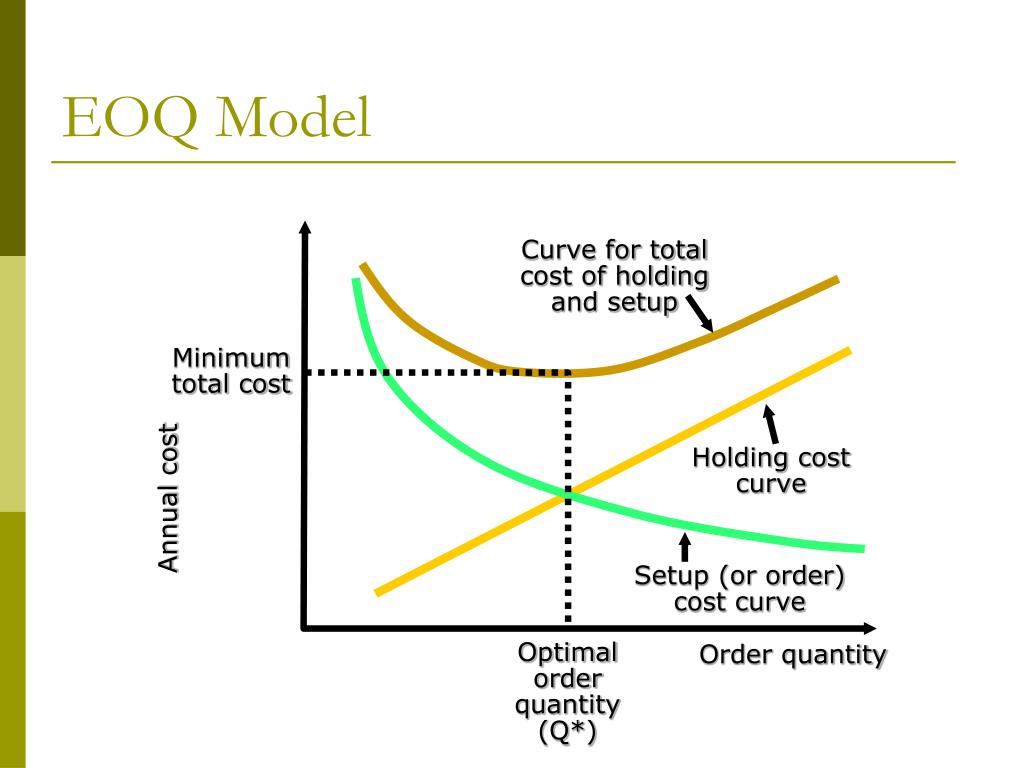 Финансовый директор . Октябрь 2002 г.
Финансовый директор . Октябрь 2002 г.
Балакришнан, Антарам, Майкл С. Пэнгберн и Юфимия Ставрулаки. «Сложите их высоко, пусть летят». Управленческая наука . Май 2004г.
Парк Кхуджа, Мутаз и Сунгжуне. «Оптимальный размер партии при постоянном снижении цен». Омега . Декабрь 2003 г.
Пясецки, Дэйв. «Оптимизация количества экономических заказов». Решения IIE .Январь 2001г.
Ван, Кунг-Дженг, Хуэй-Мин Ви, Шин-Фэн Гао и Шен-Лянь Чунг. «Производство и управление запасами с хаотическим спросом». Омега . Апрель 2005 г.
Вулси, Роберт Э.Д. и Рут Маурер. Управление запасами (для людей, которые действительно должны это делать) . Lionheart Publishing, март 2001 г.
Подходит ли модель экономического заказа (EOQ) для вашей организации?
Автор Jing Chen (на фото)
Консультант по цепочке поставок, Tata Consultancy Services
Хорошо известная модель экономического количества заказов (EOQ) предполагает, что спрос и стоимость заказа постоянны во времени, и для каждого доставленного заказа нет времени выполнения заказа. (Харрис, 1913). Цель модели EOQ — помочь производителю определить наилучший размер заказа, который мог бы минимизировать общую стоимость хранения запасов и стоимость заказа. Однако в действительности спрос и время выполнения заказа не постоянны.
(Харрис, 1913). Цель модели EOQ — помочь производителю определить наилучший размер заказа, который мог бы минимизировать общую стоимость хранения запасов и стоимость заказа. Однако в действительности спрос и время выполнения заказа не постоянны.
Это означает, что производитель не может предсказать точный размер заказа, чтобы удовлетворить будущие потребности; кроме того, неясна дата, когда производитель получит свои заказы. Чтобы предотвратить высокую стоимость потери деловой репутации, производителям рекомендуется размещать заказы большего размера.Таким образом, фактический оптимальный размер заказа будет больше, чем реальный объем заказа с экономической точки зрения. Более высокий уровень запасов обеспечивает более высокий уровень доступности продукта и лучшее обслуживание клиентов; однако это увеличивает средний уровень запасов и увеличивает затраты на хранение запасов. Это приводит к проблемам с точки зрения потери стоимости, поскольку некоторые продукты, такие как пищевые продукты с более короткими сроками хранения, склонны к более быстрому порче и устареванию. Следовательно, модель EOQ неадекватна и не должна использоваться в качестве универсального решения для управления запасами.
Следовательно, модель EOQ неадекватна и не должна использоваться в качестве универсального решения для управления запасами.
Woolsey (1988) уже подверг критике традиционную модель EOQ как нереалистичную, поскольку допущения этой модели не логичны в современном цифровом мире. Модель была создана и преподается учеными, у которых, по словам Вулси, мало реального опыта ведения бизнеса. Более того, модель слишком проста для объяснения и манипулирования. Из-за нереалистичных предположений Вулси также заявил, что модель слишком проста в использовании и расчетах. В качестве примера возьмем параметр «C» стоимости товара в долларах за единицу.Вулси утверждал, что реальная компания обычно принимает во внимание систему учета затрат при расчете стоимости заказа на единицу, поскольку значение стоимости (размеры партии) будет другим при использовании другого метода учета затрат. Кроме того, он также утверждал, что себестоимость должна использоваться как ее приведенная стоимость с поправкой на инфляцию; в противном случае стоимость не будет точной в некоторых странах с высоким уровнем инфляции.
На мой взгляд, это обычная проблема в реальности, поскольку она обычно усложняет для компаний точное определение их стоимости за заказ и затрат на транспортировку за единицу, а также обычно включает в себя гораздо более подробные затраты, такие как время, заказ. затраты на обработку, транспортировку и т. д., стоимость которых может быть значительной. Вдобавок, согласно Танелю (2012), модель EOQ очень нечувствительна к ошибкам, генерируемым такими параметрами, потому что они приглушены в функции квадратного корня формулы EOQ. Следовательно, объем заказа, полученный с помощью модели EOQ, может быть далек от реального оптимизированного объема заказа.
Хотя каждый параметр в модели EOQ может содержать ошибки в действительности, модель все еще применима для некоторых отраслей, таких как продукты, которые имеют более стабильный спрос в течение года, большой объем запасов, а также постоянный и повторяющийся шаблон заказа склад.Это особенно применимо для распределительных центров с закупкой на склад и производителей продукции на склад, где время выполнения заказа является относительно менее чувствительным фактором. Кроме того, это помогает компании (особенно мелким) поддерживать достаточный уровень запасов, чтобы соответствовать требованиям клиентов. В целом, модель обеспечивает базовую линию количества заказа и точки повторного заказа, что помогает компании сбалансировать процесс пополнения запасов и предлагать более качественное обслуживание клиентов, обеспечивая доступность запасов.
Кроме того, это помогает компании (особенно мелким) поддерживать достаточный уровень запасов, чтобы соответствовать требованиям клиентов. В целом, модель обеспечивает базовую линию количества заказа и точки повторного заказа, что помогает компании сбалансировать процесс пополнения запасов и предлагать более качественное обслуживание клиентов, обеспечивая доступность запасов.
Библиография
Харрис, Ф. У. (1913). Сколько деталей делать за один раз. Завод, Журнал Менеджмента, 10 (2), 135-136.
Танель Т. (20 июня 2012 г.). Как снова сделать EOQ актуальным. Получено 24 сентября 2013 г. у руководителя цепочки поставок и спроса: http://www.sdcexec.com/article/10732246/how-to-make-eoq-relevant-again
.Вулси, Г. (1988). Реквием по EOQ: передовица. Журнал управления производством и запасами, 68-72.
ПОДРОБНЕЕ ПО ЭТОЙ ТЕМЕ
- 9 сентября 2020 г.
 Превратите хороший прогноз спроса в оптимальный план инвентаризации
Превратите хороший прогноз спроса в оптимальный план инвентаризации - 19 октября 2020 г. Маркировка даты: шанс предотвратить образование пищевых отходов
- 24 сентября 2021 г. цепочка поставок нуждается в цифровой трансформации
- 20 октября 2021 г. Магазины без выходных — естественное развитие сектора розничной торговли, но требуются инвестиции в технологии
- 26 сентября 2018 г. Инвентаризация с помощью ERP в бизнесе 4.0 окружающая среда
- 6 июля 2020 г. Вернуться к жизни, вернуться к реальности? Ключевые моменты, которые следует учитывать при составлении плана возврата в офис
- 26 июня 2019 г.
 Упаковка пищевых отходов
Упаковка пищевых отходов - 12 апреля 2021 г. Контроль затрат на маркировку и художественное оформление
- 18 октября 2018 г. Управление сезонными запасами — Планирование для Хэллоуин
Inventory Control
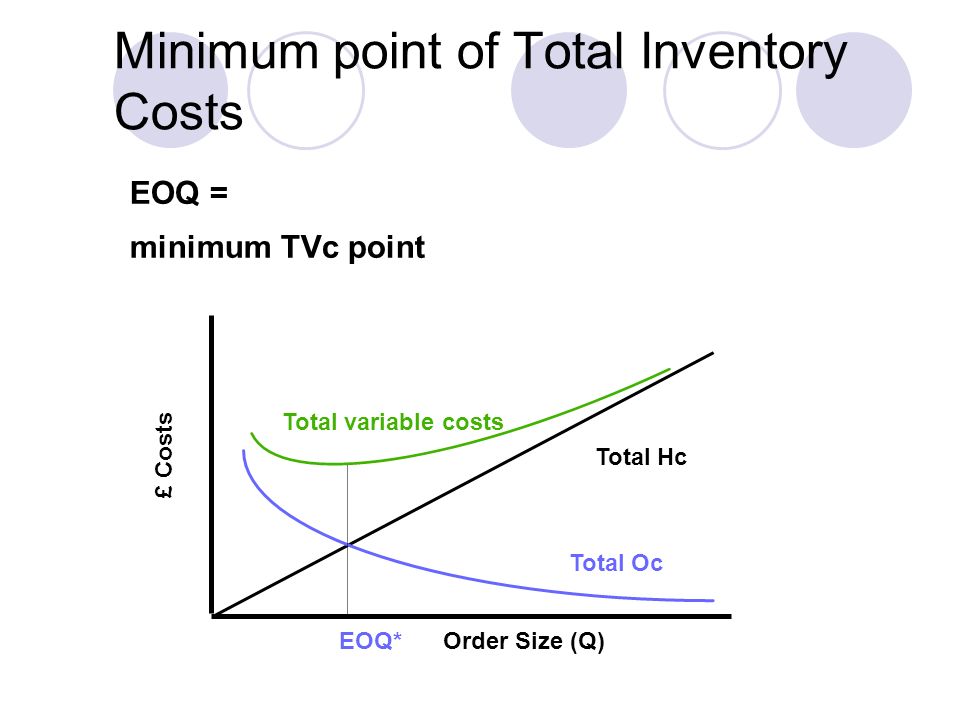
Этот сайт является частью JavaScript E-labs обучающих объектов для принятия решений.Другой JavaScript в этой серии подразделяется на разные области приложения в МЕНЮ раздел на этой странице.Управление запасами связано с минимизацией общей стоимости запасов. В Великобритании часто используется термин «складской контроль». Три основных фактора Процессом принятия решений по управлению запасами являются:
- Стоимость владения акциями (например, на основе процентной ставки).
- Стоимость оформления заказа (эл.g.
 , для запасов сырья) или
наладочная стоимость производства.
, для запасов сырья) или
наладочная стоимость производства. - Стоимость недостачи, то есть то, что теряется, если запаса недостаточно для удовлетворить все потребности.
Классификация ABC ABC система классификации предназначена для группировки товаров в соответствии с годовым объемом продаж, в попытке определить небольшое количество элементов, на которые приходится большая часть объема продаж, и это самые важные из них, которые нужно контролировать эффективное управление запасами.
Точка заказа: Уровень запасов R в который размещается, где R = D.L, D = уровень спроса (период спроса (день, неделя и т. д.), а L = время выполнения заказа.
Страховой запас: Остаточный запас между
время размещения заказа и получение нового запаса. Если есть
недостаточно запасов, тогда может возникнуть нехватка.
Если есть
недостаточно запасов, тогда может возникнуть нехватка.
Страховой запас — это защита от исчерпания запасов.Это дополнительный инвентарь, чтобы позаботиться о неожиданных событиях. Его часто называют буферным запасом. Отсутствие инвентаря называется дефицитом.
Расчет модели количественной скидки Шагов:
- Вычислить EOQ для каждой цены со скидкой.
- Находится ли вычисленный EOQ в диапазоне скидки?
- Если нет, используйте наименьшее стоимостное количество в диапазоне скидки.
- Вычислить общую стоимость для EOQ или наименьшего стоимостного количества в диапазоне скидки.
- Выберите количество с наименьшей общей стоимостью, включая стоимость купленные товары.
Следующий код JavaScript вычисляет оптимальные значения для решения переменные, основанные на имеющейся в настоящее время информации о вышеуказанных факторах.
Введите необходимую информацию и нажмите кнопку Рассчитать .
При вводе данных для перехода от ячейки к ячейке в матрице данных используйте Клавиша Tab не стрелка или клавиши ввода.
МЕНЮ:
- The Классическая модель
- Нехватка Разрешенная модель
- Производство и модель потребления
- Производство и потребление с моделью дефицита
- EOQ с нехваткой и временем выполнения заказа
- Классификация ABC
- Управление запасами с неопределенным спросом
Симметрия | Бесплатный полнотекстовый | Новая модель для определения EOQ при изменении ценовых параметров и времени повторного заказа
1.Введение
Устойчивые бизнес-решения требуют учета широкого спектра факторов и методологий [1,2,3,4]. Поэтому был предложен ряд моделей для эффективного управления запасами. В 1913 году Харрис представил экономическую концепцию количества заказов для решения этой проблемы в форме статической формулы (и начал применять статические модели управления запасами). Однако типичные модели статического экономического количества заказов (EOQ) [5,6] не удовлетворяют практикующих специалистов из-за их неспособности учитывать изменение потребительского спроса, требующего постоянных заказов в равные периоды времени [7].Непредсказуемые и постоянно меняющиеся потребности, влияющие на размер и частоту заказов, приводят к ситуациям, в которых классические модели управления запасами становятся непригодными для решения практических задач управления запасами и мотивируют поиск новых или модифицированных альтернатив. В последнее десятилетие мы наблюдаем повышенный научный интерес к решению этой проблемы. Во-первых, Сана [8] предложил модель EOQ для скоропортящихся товаров, реагирующую на изменения розничных цен, хотя практическая реализация ограничена пренебрежением минимизирующим эффектом отрицательной степенной функции цены, которая порождает высокую чувствительность потребительского спроса.Позже Dobson et al. [9] предположили, что скоропортящиеся товары, уровень спроса которых линейно убывает в зависимости от возраста продуктов, действуют аналогично нескоропортящимся товарам с удельной стоимостью хранения, равной отношению маржи вклада к сроку службы.
Однако типичные модели статического экономического количества заказов (EOQ) [5,6] не удовлетворяют практикующих специалистов из-за их неспособности учитывать изменение потребительского спроса, требующего постоянных заказов в равные периоды времени [7].Непредсказуемые и постоянно меняющиеся потребности, влияющие на размер и частоту заказов, приводят к ситуациям, в которых классические модели управления запасами становятся непригодными для решения практических задач управления запасами и мотивируют поиск новых или модифицированных альтернатив. В последнее десятилетие мы наблюдаем повышенный научный интерес к решению этой проблемы. Во-первых, Сана [8] предложил модель EOQ для скоропортящихся товаров, реагирующую на изменения розничных цен, хотя практическая реализация ограничена пренебрежением минимизирующим эффектом отрицательной степенной функции цены, которая порождает высокую чувствительность потребительского спроса.Позже Dobson et al. [9] предположили, что скоропортящиеся товары, уровень спроса которых линейно убывает в зависимости от возраста продуктов, действуют аналогично нескоропортящимся товарам с удельной стоимостью хранения, равной отношению маржи вклада к сроку службы. В своей модели они получают традиционные нижние и верхние границы, подобные количеству нескоропортящихся заказов (EOQ), для длины цикла и прибыли и показывают, что они приводят к почти оптимальным результатам для типичных примеров, таких как продукты питания. Zeng et al.[10] формулируют расширение модели Вильсона, варьируя количество заказов и различные периоды заказа. Их модель дает существенный экономический эффект, когда отмечается существенное изменение потребительского спроса и (или) должен быть обеспечен длительный период планирования логистического процесса. Традиционные модели управления запасами с неопределенным спросом, такие как вариации формулировки Харриса [11, 12,13], уравнения на основе уравнения Маркова [14,15] и формулировка Уилсона [16,17,18,19] предназначены для минимизации ожидаемых затрат на пополнение запасов и дефицит запасов.Они полагают, что полное удовлетворение неопределенного и трудно предсказуемого спроса слишком дорого или даже невозможно. Все эти модели разработаны в соответствии с принципом постоянного количества заказа, где размер следующего заказа основан на цели минимизировать все затраты на управление запасами компании.
В своей модели они получают традиционные нижние и верхние границы, подобные количеству нескоропортящихся заказов (EOQ), для длины цикла и прибыли и показывают, что они приводят к почти оптимальным результатам для типичных примеров, таких как продукты питания. Zeng et al.[10] формулируют расширение модели Вильсона, варьируя количество заказов и различные периоды заказа. Их модель дает существенный экономический эффект, когда отмечается существенное изменение потребительского спроса и (или) должен быть обеспечен длительный период планирования логистического процесса. Традиционные модели управления запасами с неопределенным спросом, такие как вариации формулировки Харриса [11, 12,13], уравнения на основе уравнения Маркова [14,15] и формулировка Уилсона [16,17,18,19] предназначены для минимизации ожидаемых затрат на пополнение запасов и дефицит запасов.Они полагают, что полное удовлетворение неопределенного и трудно предсказуемого спроса слишком дорого или даже невозможно. Все эти модели разработаны в соответствии с принципом постоянного количества заказа, где размер следующего заказа основан на цели минимизировать все затраты на управление запасами компании. Проблема количества экономических заказов (EOQ) хорошо известна и широко обсуждалась в научной литературе [20,21,22,23,24]. Определение EOQ имеет особое значение в торговле и розничной торговле.Оптимальный план заказов позволяет компаниям добиться бесперебойной работы и конкурентного преимущества [25,26,27]. В контексте устойчивого экономического роста модели EOQ, предполагающие устойчивый спрос на скоропортящиеся потребительские товары, подходят для определения размера партии [28,29,30]. Было проведено исследование EOQ применительно к кредитному рынку [31] и оптимизации динамического размера запасов в среде Logistic 4.0 для управления материальными потоками высокоскоростного поезда [32]. Однако колебания спроса и времени выполнения заказа не были приняты во внимание.Действительно, такие колебания становятся более важными во время сбоев в цепочках поставок (например, из-за пандемических событий). Возникновение торговых барьеров требует от ритейлеров пересмотреть оптимальный размер лота.
Проблема количества экономических заказов (EOQ) хорошо известна и широко обсуждалась в научной литературе [20,21,22,23,24]. Определение EOQ имеет особое значение в торговле и розничной торговле.Оптимальный план заказов позволяет компаниям добиться бесперебойной работы и конкурентного преимущества [25,26,27]. В контексте устойчивого экономического роста модели EOQ, предполагающие устойчивый спрос на скоропортящиеся потребительские товары, подходят для определения размера партии [28,29,30]. Было проведено исследование EOQ применительно к кредитному рынку [31] и оптимизации динамического размера запасов в среде Logistic 4.0 для управления материальными потоками высокоскоростного поезда [32]. Однако колебания спроса и времени выполнения заказа не были приняты во внимание.Действительно, такие колебания становятся более важными во время сбоев в цепочках поставок (например, из-за пандемических событий). Возникновение торговых барьеров требует от ритейлеров пересмотреть оптимальный размер лота. Эта проблема усугубляется колебаниями рыночных цен на отдельные товары. Действительно, кризис влияет на поведение потребителей и спрос на определенные товары [33,34,35]. Изменения спроса отражаются в ценах на продаваемые в розницу продукты [36,37]. Следовательно, необходимо корректировать решения по заказу и хранению товаров.Даже если не столкнуться с серьезным кризисом, со временем происходят изменения в ценах как на розничном рынке, так и на стоимости хранения. Таким образом, очевидна математическая модель, способная определить оптимальное экономичное количество заказа при изменении времени повторного заказа и ценовых параметров. Несмотря на то, что был предложен широкий спектр моделей для определения размеров партии (таблица 1), ни одна из них не способна справиться с изменяющимся количеством запасов в зависимости от изменяющейся цены и времени повторного заказа. В данной статье представлена модель для определения оптимального размера партии. с колебаниями цены, основанными на классической формулировке Вильсона после расширений Слесаренко и Несторенко [49] и Зенг и др.
Эта проблема усугубляется колебаниями рыночных цен на отдельные товары. Действительно, кризис влияет на поведение потребителей и спрос на определенные товары [33,34,35]. Изменения спроса отражаются в ценах на продаваемые в розницу продукты [36,37]. Следовательно, необходимо корректировать решения по заказу и хранению товаров.Даже если не столкнуться с серьезным кризисом, со временем происходят изменения в ценах как на розничном рынке, так и на стоимости хранения. Таким образом, очевидна математическая модель, способная определить оптимальное экономичное количество заказа при изменении времени повторного заказа и ценовых параметров. Несмотря на то, что был предложен широкий спектр моделей для определения размеров партии (таблица 1), ни одна из них не способна справиться с изменяющимся количеством запасов в зависимости от изменяющейся цены и времени повторного заказа. В данной статье представлена модель для определения оптимального размера партии. с колебаниями цены, основанными на классической формулировке Вильсона после расширений Слесаренко и Несторенко [49] и Зенг и др. [10]. Предлагаемая модель оптимизирует дисконтированные затраты на все заказы, а не затраты на один заказ. Из-за этого фундаментального различия наша модель больше подходит для принятия экономических решений и обеспечивает симметрию в процессе принятия решений. Представляя практическое применение моделей с различными параметрами, мы также показываем, как эта модель работает в реальных ситуациях.
[10]. Предлагаемая модель оптимизирует дисконтированные затраты на все заказы, а не затраты на один заказ. Из-за этого фундаментального различия наша модель больше подходит для принятия экономических решений и обеспечивает симметрию в процессе принятия решений. Представляя практическое применение моделей с различными параметрами, мы также показываем, как эта модель работает в реальных ситуациях.2. Предлагаемая модель управления партиями с параметрами затрат, зависящими от времени.
Управление запасами понимается как определение оптимальных контролируемых параметров (время между поставками ts (время установки) и q (количество или оптимальный размер заказа)) логистики. процессы, при которых минимальные общие затраты (TC) на закупку, доставку и хранение товаров достигаются за определенный плановый интервал времени [0, T].Если неконтролируемые параметры логистического процесса (закупочная цена p, стоимость доставки cs, (установка стоимости) суточный спрос μ и дневная процентная ставка i (r = i / 100%) известны и постоянны на протяжении всего интервала планирования, то это Проблема может быть решена с помощью экономико-математической модели Вильсона EOQ (Economic Order Quantity):TC (ts) = pD + csTts + 12чДц
(1)
где D — спрос за период (временной интервал) [0, T] (D = μT), а ch — стоимость хранения единицы товара в день (стоимость хранения).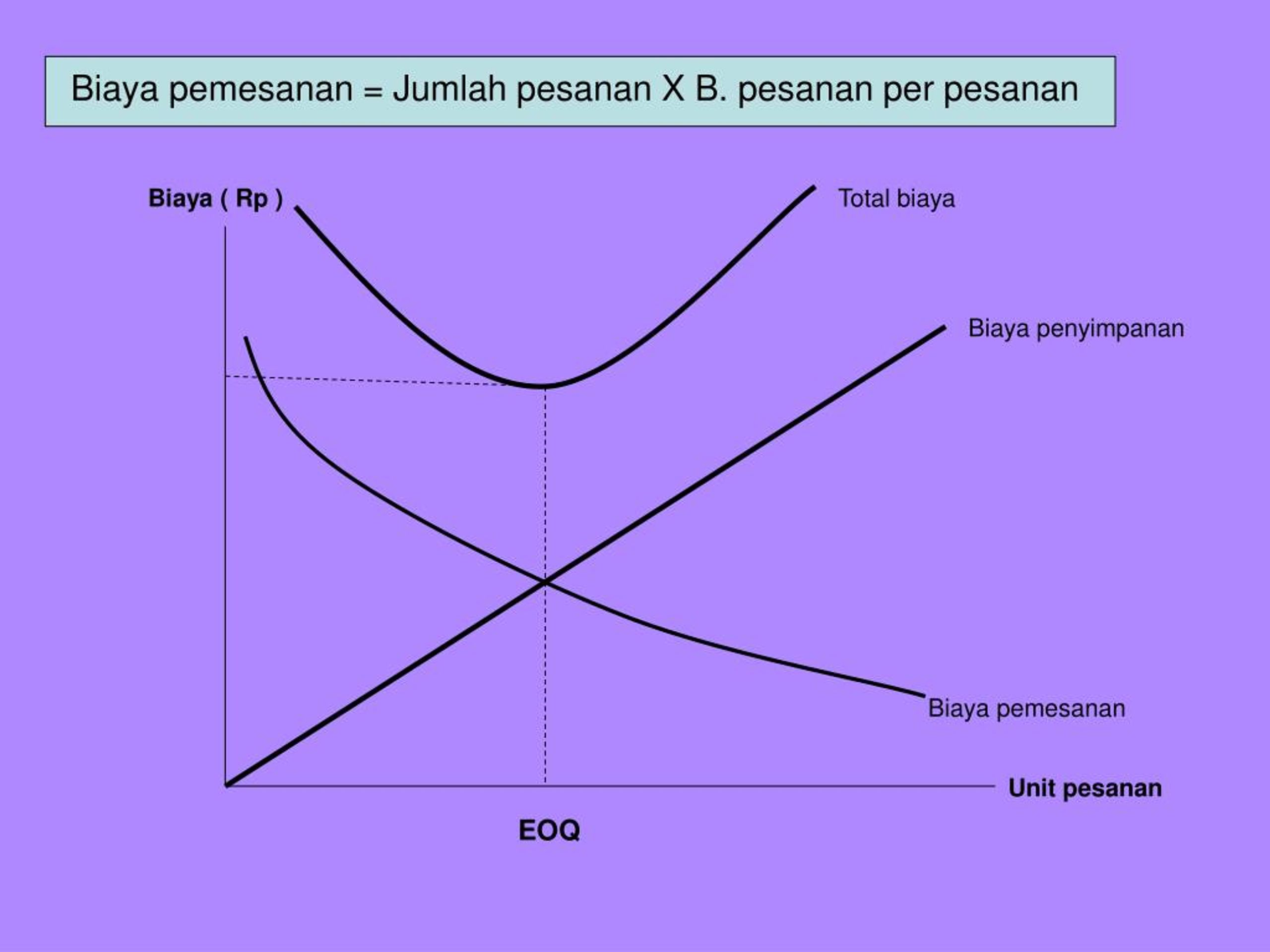 Оптимальное время между поставками (tso) и оптимальное количество заказа (qo) находятся по формуле Вильсона: Слесаренко и Несторенко [49], а также Несторенко и др. [50] предложили модифицированную модель EOQ:
Оптимальное время между поставками (tso) и оптимальное количество заказа (qo) находятся по формуле Вильсона: Слесаренко и Несторенко [49], а также Несторенко и др. [50] предложили модифицированную модель EOQ:TC (ts) = (cs + pμts) (1 + r) ts ((1 + r) T − 1) (1 + r) ts − 1
(4)
Оптимальное время между поставками находится по следующей формуле:Формула совпадает с формулой Вильсона (2), если стоимость хранения выражается в процентах от цены за единицу (ch = pμ).
При изменении параметров логистического процесса оптимальное решение пересчитывается по формуле Вильсона (5) с учетом изменений.На основании имеющейся информации можно строить прогнозы дальнейших экономических процессов поведения. Использование этой информации в экономико-математических моделях приводит к повышению их адекватности и точности.
Zeng et al. [10] предложены модели управления запасами, позволяющие определять оптимальные значения параметров в случае, когда известно, что суточный спрос имеет линейный тренд (μ (t) = μ + ωt, t∈ [0, T]).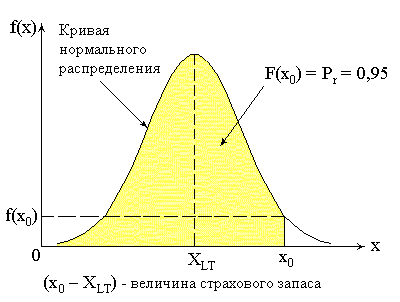 Чтобы найти эти параметры, необходимо использовать формулу Вильсона (5), заменив постоянное значение дневного спроса μ на среднее арифметическое дневного спроса μ¯ за период планирования [0, T] (μ¯ = μ + 0.5ωT).
Чтобы найти эти параметры, необходимо использовать формулу Вильсона (5), заменив постоянное значение дневного спроса μ на среднее арифметическое дневного спроса μ¯ за период планирования [0, T] (μ¯ = μ + 0.5ωT).Далее строятся экономико-математические модели управления запасами, которые позволяют определять значения оптимальных контролируемых параметров в случае, когда известно, что неконтролируемые параметры затрат (стоимость доставки и / или цена) имеют однородные относительные тенденции (cs (t) = cs (1 + ρc) t, p (t) = p (1 + ρp) t, t∈ [0, T]).
Модель 1.Модель управления запасами с одновременным равнопроцентным изменением затрат на доставку и цен (инфляционная модель).
В модели EOQ параметры неконтролируемых затрат, такие как стоимость доставки (cs = const) и цена (p = const) за период [0, T], будут заменены предположением, что стоимость доставки и цена одновременно изменяются равномерно с одинаковым процентным изменением (cs (t) = cs (1 + ρ) t, p (t) = p (1 + ρ) t, t∈ [0, T]). Это инфляционный процесс, когда ρ> 0, и дефляционный, когда ρ <0.
Это инфляционный процесс, когда ρ> 0, и дефляционный, когда ρ <0.
TC (ts) = (cs + pμts) (1 + r) nts + (cs (1 + ρ) ts + p (1 + ρ) tsμts) (1 + r) (n − 1) ts + ⋯ + (cs (1 + ρ) (n − 1) ts + p (1 + ρ) (n − 1) tsμts) (1 + r) ts
.(6)
где n — количество поставок партий товаров за период [0, T] (n = T / ts).Заменив его, получаем следующее:(1 + r) jts = eln (1 + r) jts, (1 + ρ) jts = eln (1 + ρ) jts, j = 1, n¯
После выполнения арифметических преобразований получаем следующее:TC (ts) = (cs + pμts) eln (1 + r) T (1 + e (ln (1 + ρ) −ln (1 + r)) ts + ⋯ + e (n − 1) (ln (1+ ρ) −ln (1 + r)) ts)
(7)
Используя формулу суммы первых членов геометрической прогрессии, мы получаем формулу общих затрат:TC (ts) = (cs + pμts) (eln (1 + r) −ln (1 + ρ)) T − 1) eln (1 + ρ) Te (ln (1 + r) −ln (1 + ρ) ) тс − 1
(8)
Минимальная общая стоимость получается следующим образом:dTC (ts) dts = pμ (e (ln (1 + r) −ln (1 + ρ)) T − 1) eln (1 + ρ) Te (ln (1 + r) −ln (1 + ρ)) ts − 1− (ln (1 + r) −ln (1 + ρ)) (cs + pμts) e (ln (1 + r) −ln (1 + ρ)) ts (e (ln (1 + r) −ln (1 + ρ)) T − 1) eln (1 + ρ) T (e (ln (1 + r) −ln (1 + ρ)) ts − 1) 2 = 0
.
(9)
После преобразований уравнение выглядит следующим образом:е (ln (1 + r) −ln (1 + ρ)) ts − 1 = (ln (1 + r) −ln (1 + ρ)) (cspμ + ts)
(10)
Оптимальное время между доставками партий товаров tso находится из решения нелинейного уравнения (10).Чтобы найти приближенное решение уравнения (10), мы используем первые три члена ряда Маклорена [51] разложения функции y = ex≈1 + x + 0,5×2 и первый член ряда Маклорена разложения функции y = ln (1 + r) ≈r.tso = ts = 2cs (r − ρ) pμ
(11)
Следовательно, для определения оптимального времени между доставками партий товаров tso можно использовать формулу Вильсона (5), заменив r разностью r — ρ.
Пусть α = ln (1 + ρ) / ln (1 + r) ≈ρ / r.Тогда уравнение (11) можно записать следующим образом: Зависимость оптимального времени между доставками партий товаров tso от α показана на рисунке 1. При α≥αmax = 1 − tw2T2 необходимо закупить в объеме qo = μT и доставить товар один раз за весь период планирования логистического процесса. При α≤αmin = 1 − tw2 необходимо ежедневно покупать и доставлять товары в количестве qo = μ. При αmin <α <αmax необходимо закупить и доставить товар за tso = tw1 − α дней и в объеме qo = μtw1 − α = qw1 − α.Изменение зависимости общих затрат TC (ts, α) от времени между доставками партий товаров ts для различных значений α, а также зависимости минимальных общих затрат TC (tso, α) от оптимального времени между доставками партий товаров tso для различных значений α (черная линия и черные квадраты) показаны на рисунке 2. Примечание: если определить значения контролируемых параметров в момент i (i = 1,2,3…) принятия решения - делая по формуле Вильсона (5), получаем одинаковое время между доставками, равное tw:
При α≤αmin = 1 − tw2 необходимо ежедневно покупать и доставлять товары в количестве qo = μ. При αmin <α <αmax необходимо закупить и доставить товар за tso = tw1 − α дней и в объеме qo = μtw1 − α = qw1 − α.Изменение зависимости общих затрат TC (ts, α) от времени между доставками партий товаров ts для различных значений α, а также зависимости минимальных общих затрат TC (tso, α) от оптимального времени между доставками партий товаров tso для различных значений α (черная линия и черные квадраты) показаны на рисунке 2. Примечание: если определить значения контролируемых параметров в момент i (i = 1,2,3…) принятия решения - делая по формуле Вильсона (5), получаем одинаковое время между доставками, равное tw:tsi = 2cs (1 + ρ) tsirp (1 + ρ) tsiμ = 2csrpμ = tw, i = 1,2,3…
(13)
Этот вариант принятия решения не является оптимальным (отличается от (11)).Результат использования этой опции для различных значений α (белые квадраты) также показан на Рисунке 2 Модель 2.
Модель управления запасами с процентным изменением стоимости доставки.
В модели EOQ предположение о постоянстве стоимости доставки неконтролируемого параметра (cs = const) в течение периода [0, T] заменено предположением, в котором стоимость доставки изменяется равномерно в соответствии с закономерностью cs (t) = cs (1 + ρc) t, t∈ [0, T]. Если ρc> 0, увеличивается стоимость доставки; если ρc <0, то уменьшение происходит.
Тогда логистический процесс закупки, доставки и хранения товаров с постоянным временем между доставками можно описать следующей формулой:TC (ts) = (cs + pμts) (1 + r) nts + (cs (1 + ρc) ts + pμts) (1 + r) (n − 1) ts + ⋯ + (cs (1 + ρc) (n− 1) ts + pμts) (1 + r) ts
(14)
где n — количество доставок партий товаров за период [0, T] (n = T / ts). Заменяя его, получаем:(1 + r) jts = eln (1 + r) jts, (1 + ρc) jts = eln (1 + ρc) jts, j = 1, n¯
После выполнения арифметических преобразований получаем следующее:TC (ts) = eln (1 + r) T (cs (1 + e (ln (1 + ρc) −ln (1 + r)) ts + ⋯ + e (n − 1) (ln (1 + ρc) — ln (1 + r)) ts) + pμts (1 + e − ln (1 + r) ts + ⋯ + e − ln (1 + r) (n − 1) ts))
.
(15)
Используя формулу суммы первых членов геометрической прогрессии, мы получаем формулу общих затрат:TC (ts) = cse (ln (1 + r) −ln (1 + ρc)) ts (eln (1 + r) T − eln (1 + ρc) T) e (ln (1 + r) −ln ( 1 + ρc)) ts − 1 + pμtseln (1 + r) ts (eln (1 + r) T − 1) eln (1 + r) ts − 1
.(16)
Минимальные общие затраты следующие:dTC (ts) dts = pμeln (1 + r) ts (eln (1 + r) T − 1) eln (1 + r) ts − 1 − ln (1 + r) pμtseln (1 + r)) ts (eln (1 + r) T − 1) (eln (1 + r) ts − 1) 2 − cs (ln (1 + r) −ln (1 + ρc)) e (ln (1 + r) −ln (1 + ρc)) ts (eln (1 + r) T − eln (1 + ρc) T) (e (ln (1 + r) −ln (1 + ρc)) ts − 1) 2 = 0
(17)
После преобразований уравнение выглядит следующим образом:eln (1 + r) ts − 1 − ln (1 + r) ts = cspμ (ln (1 + r) −ln (1 + ρc)) (eln (1 + r) ts − 1) 2eln (1 + ρc ) (e (ln (1 + r) −ln (1 + ρc)) ts − 1) 2 (eln (1 + r) T − eln (1 + ρc) T) (eln (1 + r) T − 1 )
(18)
В модели 2 оптимальное время между доставками партий товаров tso также находится из решения нелинейного уравнения (18). Чтобы найти приближенное решение уравнения (18), мы используем первые три члена ряда Маклорена разложения функции y = ex≈1 + x + 0,5×2 и первый член ряда Маклорена разложения функции y = ln (1 + r) ≈r.
Чтобы найти приближенное решение уравнения (18), мы используем первые три члена ряда Маклорена разложения функции y = ex≈1 + x + 0,5×2 и первый член ряда Маклорена разложения функции y = ln (1 + r) ≈r.tso = ts = 2cs (1 + ρc) 12Trpμ
(19)
Следовательно, для определения оптимального времени между поставками партий товаров tso можно использовать формулу Вильсона (5), заменив постоянное значение стоимости доставки cs на среднее геометрическое значение стоимости доставки cs¯ за период планирования [0, T] (cs¯ = cscs (1 + ρc) T = cs (1 + ρc) 12T).Пусть αc = ln (1 + ρc) / ln (1 + r); то уравнение (20) можно представить в таком виде: Зависимость оптимального времени между доставками партий товаров tso от αc представлена на рисунке 3. Изменение зависимости общих затрат TC (ts, αc) от времени между доставками партий товаров ts для различных значений αc, а также зависимость минимальных общих затрат TC (tso, αc) от оптимального времени между доставками партий товаров tso для различных значений αc (черная линия и черные квадраты). показано на рисунке 4.Модель 3.
показано на рисунке 4.Модель 3. Модель управления запасами с процентным изменением цены товаров.
В модели EOQ предположение о постоянстве неконтролируемого параметра цены товара (p = const) в течение периода [0, T] заменяется предположением, что цена товара изменяется равномерно в соответствии с порядком что p (t) = cp (1 + ρp) t, t∈ [0, T]). Если ρp> 0, происходит рост цен на товары, а если ρp <0 - снижение.
Для построения модели 3 мы будем использовать результаты построения модели 1 (8) и модели 2 (16).Мы представляем изменение (увеличение / уменьшение) цены как комбинацию двух процессов — изменение (увеличение / уменьшение) цены и стоимости доставки (модель 1) и одновременное изменение (уменьшение / увеличение) стоимости доставки ( модель 2) столько же раз. Изменение цены и стоимости доставки, согласно модели 1, приведет к замене ln (1 + r) на ln (1 + r) −ln (1 + ρp) в формуле (16) и будет умножено на eln (1 + ρp) Т. Для компенсации изменения стоимости доставки по модели 2 делаем замену 1 + ρc = 1 / (1 + ρp):TC (ts) = cseln (1 + r) ts (eln (1 + r) T − 1) eln (1 + r) ts − 1 + pμtse (ln (1 + r) −ln (1 + ρp)) ts (e (ln (1 + r) −ln (1 + ρp)) T − 1) eln (1 + ρp) Te (ln (1 + r) −ln (1 + ρp)) ts − 1
(22)
Минимальная общая стоимость определяется следующим образом:dTC (ts) dts = −csln (1 + r) eln (1 + r) ts (eln (1 + r) T − 1) (eln (1 + r) ts − 1) 2 + pμe (ln (1+ r) −ln (1 + ρp)) ts (e (ln (1 + r) −ln (1 + ρp)) T − 1) eln (1 + ρp) Te (ln (1 + r) −ln (1 + ρp)) ts − 1 − pμts (ln (1 + r) −ln (1 + ρp)) e (ln (1 + r) −ln (1 + ρp)) ts (e (ln (1 + r) −ln (1 + ρp)) T − 1) eln (1 + ρp) T (e (ln (1 + r) −ln (1 + ρp)) ts − 1) 2 = 0
.
(23)
После преобразований уравнение выглядит следующим образом:e (ln (1 + r) −ln (1 + ρp)) ts − 1− (ln (1 + r) −ln (1 + ρp)) ts = cspμln (1 + r) eln (1 + ρp) ts (e (ln (1 + r) −ln (1 + ρp)) ts − 1) 2 (eln (1 + r) T − 1) (eln (1 + r) ts − 1) 2 (e (ln ( 1 + r) −ln (1 + ρp)) T − 1) eln (1 + ρp) T
(24)
Повторяем ранее упомянутую процедуру: оптимальное время между доставками партий товаров tso находится из решения нелинейного уравнения (24).Чтобы найти приближенное решение уравнения (24), мы используем первые три члена ряда Маклорена разложения функции y = ex≈1 + x + 0,5×2 и первый член ряда Маклорена разложения функции y = ln (1 + r) ≈r.ts = 2cs (r − ρp) pe12ln (1 + ρp) Tμ
(25)
Следовательно, для определения оптимального времени между поставками партий товаров tso можно использовать формулу Вильсона (5), заменив r на разность r − ρ, а постоянное значение цены товара p на среднее геометрическое значение цены товаров p¯ на плановый период [0, T] (p¯ = pp (1 + ρp) T = p (1 + ρp) 12T).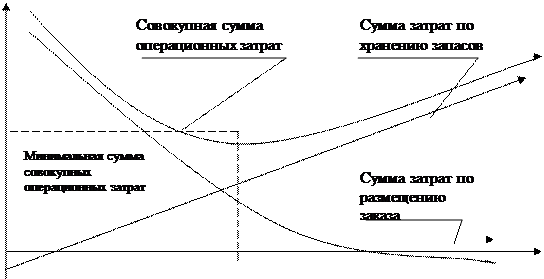
tso = tw (1 + ρp) 14T1 − αp
(26)
илиtso = tw (1 + r) 14αpT1 − αp
(27)
Зависимость оптимального времени между доставками партий товаров tso от αc представлена на рисунке 5. Изменение зависимости общих затрат TC (ts, αp) от времени между доставками партий товаров ts для различных значений αp как а также зависимость минимальных общих затрат TC (tso, αp) от оптимального времени между доставками партий товаров tso для различных значений αp (черная линия и черные квадраты) показаны на рисунке 6. Модель 4.Модель управления запасами с разным процентным изменением цены товаров.
В модели EOQ предположение о постоянстве неконтролируемого параметра цены товара (p = const) в течение периода [0, T] заменяется предположением, что цена товара изменяется равномерно в соответствии с порядком что p (t) = cp (1 + ρp) t, t∈ [0, T]). Если ρp> 0, происходит рост цен на товары, а если ρp <0 - снижение.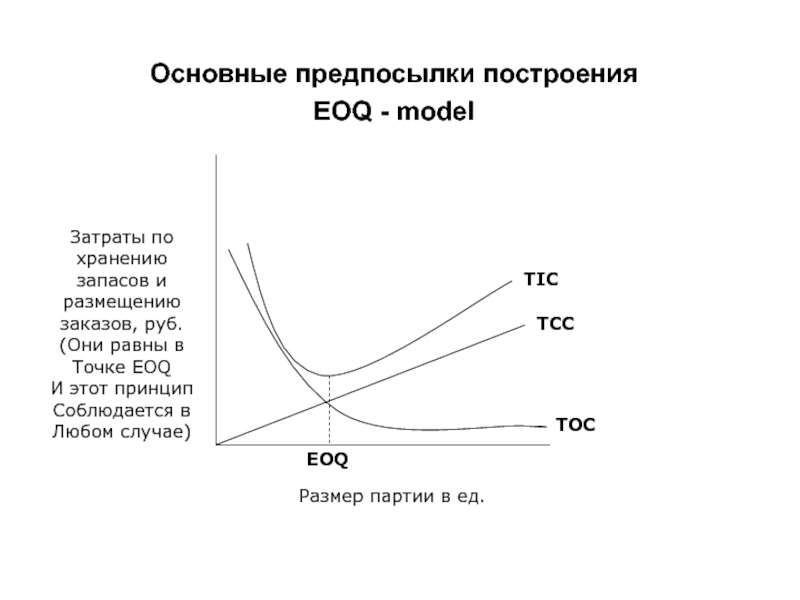
TC (ts) = cse (ln (1 + r) −ln (1 + ρc)) ts (e (ln (1 + r) −ln (1 + ρc)) T − 1) eln (1 + ρc) Te (ln (1 + r) −ln (1 + ρc)) ts − 1 + pμtse (ln (1 + r) −ln (1 + ρp)) ts (e (ln (1 + r) −ln (1+ ρp)) T − 1) eln (1 + ρp) Te (ln (1 + r) −ln (1 + ρp)) ts − 1
(28)
Минимальные общие затраты находятся следующим образом:dTC (ts) dts = pμe (ln (1 + r) −ln (1 + ρp)) ts (e (ln (1 + r) −ln (1 + ρp)) T − 1) eln (1 + ρp) Te (ln (1 + r) −ln (1 + ρp)) ts − 1 − cs (ln (1 + r) −ln (1 + ρc)) e (ln (1 + r) −ln (1 + ρc )) ts (e (ln (1 + r) −ln (1 + ρc)) T − 1) eln (1 + ρc) T (e (ln (1 + r) −ln (1 + ρc)) ts− 1) 2pμts (ln (1 + r) −ln (1 + ρp)) e (ln (1 + r) −ln (1 + ρp)) ts (e (ln (1 + r) −ln (1 + ρp )) T − 1) eln (1 + ρp) T (e (ln (1 + r) −ln (1 + ρp)) ts − 1) 2 = 0
(29)
После преобразований уравнение выглядит следующим образом:e (ln (1 + r) −ln (1 + ρp)) ts − 1− (ln (1 + r) −ln (1 + ρp)) ts = Cspμ (ln (1 + r) −ln (1+ ρc)) e (ln (1 + ρp) −ln (1 + ρc)) ts (e (ln (1 + r) −ln (1 + ρp)) ts − 1) 2 (eln (1 + r) T −eln (1 + ρc) T) (e (ln (1 + r) −ln (1 + ρc)) ts − 1) 2 (eln (1 + r) T − eln (ρp) T)
(30)
Оптимальное время между доставками партий товаров tso находится из решения нелинейного уравнения (30).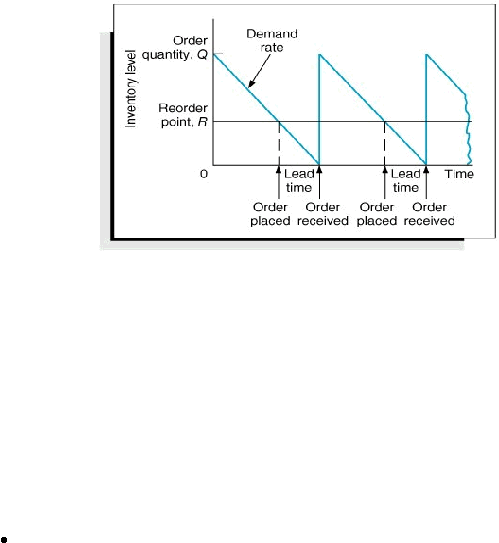 Чтобы найти приближенное решение уравнения (30), мы используем первые три члена ряда Маклорена разложения функции y = ex≈1 + x + 0,5×2 и первый член ряда Маклорена разложения функции y = ln (1 + r) ≈r.
Чтобы найти приближенное решение уравнения (30), мы используем первые три члена ряда Маклорена разложения функции y = ex≈1 + x + 0,5×2 и первый член ряда Маклорена разложения функции y = ln (1 + r) ≈r.tso = ts = 2cs (1 + ρc) 12T (r − ρp) p (1 + ρp) 12Tμ
(31)
Следовательно, для определения оптимального времени между поставками партий товаров tso можно использовать формулу Вильсона (5), заменив r на разность r − ρ, а постоянное значение цены товара p на среднее геометрическое значение цены товаров p¯ на плановый период [0, T] (p¯ = pp (1 + ρp) T = p (1 + ρp) 12T) и постоянное значение цены продукта cs на основе среднего геометрического значения цены продукта cs¯ на период планирования [0, T] (cs¯ = cscs (1 + ρc) T = cs (1 + ρc) 12T).
Пусть αp = ln (1 + ρp) / ln (1 + r) и αc = ln (1 + ρc) / ln (1 + r); то уравнение (31) можно представить следующим образом:tso = (1 + ρc) 14T (1 + ρp) 14Ttw1 − αp
(32)
илиtso = (1 + r) 14 (αc − αp) Ttw1 − αp
(33)
Зависимость оптимального времени между доставками партий товаров tso от αc и αp представлена на рисунке 7. Изменение зависимости полных затрат TC (ts, αc = −3, αp) с уменьшением стоимости доставки (αc = −3) от времени между доставками партий товаров ts при различных значениях αp, а также зависимости минимальных общих затрат TC (tso, αc = −3, αp) от оптимального времени между доставками грузов товаров tso для различных значений αp (черная линия и черные квадраты) показаны на рисунке 8.Изменение зависимости общих затрат TC (ts, αc = 0, αp) при постоянной стоимости доставки (αc = 0) от времени между доставками партий товаров ts для различных значений αp, а также зависимость минимальной суммы затраты TC (tso, αc = 0, αp) от оптимального времени между поставками партий товаров tso для различных значений αp (черная линия и черные квадраты) показаны на рисунке 6. Изменение зависимости общих затрат TC (ts , Αc = 3, αp) с увеличением стоимости доставки (αc = 3) от времени между доставками партий товаров ts для различных значений αp, а также зависимость минимальных суммарных затрат TC (tso, αc = 3, αp) об оптимальном времени между доставками партий товаров tso для различных значений αp (черная линия и черные квадраты) показаны на рисунке 9.
Изменение зависимости полных затрат TC (ts, αc = −3, αp) с уменьшением стоимости доставки (αc = −3) от времени между доставками партий товаров ts при различных значениях αp, а также зависимости минимальных общих затрат TC (tso, αc = −3, αp) от оптимального времени между доставками грузов товаров tso для различных значений αp (черная линия и черные квадраты) показаны на рисунке 8.Изменение зависимости общих затрат TC (ts, αc = 0, αp) при постоянной стоимости доставки (αc = 0) от времени между доставками партий товаров ts для различных значений αp, а также зависимость минимальной суммы затраты TC (tso, αc = 0, αp) от оптимального времени между поставками партий товаров tso для различных значений αp (черная линия и черные квадраты) показаны на рисунке 6. Изменение зависимости общих затрат TC (ts , Αc = 3, αp) с увеличением стоимости доставки (αc = 3) от времени между доставками партий товаров ts для различных значений αp, а также зависимость минимальных суммарных затрат TC (tso, αc = 3, αp) об оптимальном времени между доставками партий товаров tso для различных значений αp (черная линия и черные квадраты) показаны на рисунке 9.
Модель 4 является обобщением моделей 1–3:
для αc = αp получаем модель 1;
при αp = 0 получаем модель 2; и
для αc = 0 получаем модель 3.
Далее мы приводим несколько примеров различий, возникающих при использовании моделей 1–4 и модифицированной модели EOQ.
3. Эмпирическая иллюстрация
Модель 1
Если в начале периода [0, T], неконтролируемые параметры логистического процесса, такие как T = 400 дней, r = 0.001, и μ = 25 единиц / день известны, и стоимость доставки и цена увеличиваются одинаково в течение периода [0, T] с ρ = 0,00075, тогда картина роста будет cs (t) = 400 ∗ 1.00075t, p (t) = 20 ∗ 1.00075t, t∈ [0, T] (α = 0,75).
При использовании модели EOQ, без учета увеличения стоимости доставки и цен, время между доставками будет следующим:tw = 2 ∗ 4000.001 ∗ 20 ∗ 25 = 40 дней
Общие затраты на покупку, доставку и хранение в течение 400 дней составляют: TCw = (400 + 20 * 25 * 40) * 1. 001400+ (400 * 1.0007540 + 20 * 1.0007540 * 25 * 40) * 1.001360 + ⋯ + (400 * 1.00075360 + 20 * 1.00075360 * 25 * 40) * 1.00140 = 290911
001400+ (400 * 1.0007540 + 20 * 1.0007540 * 25 * 40) * 1.001360 + ⋯ + (400 * 1.00075360 + 20 * 1.00075360 * 25 * 40) * 1.00140 = 290911
TCo = (400 + 20 * 25 * 80) * 1.001400 + (400 * 1.0007580 + 20 * 1.0007580 * 25 * 80) * 1.001320 + ⋯ + (400 * 1.00075320 + 20 * 1.00075320 * 25 * 80) * 1.00180 = 289600 евро
Экономия будет следующей:ΔTC = 290911−289600 = 1311
евроЕсли стоимость доставки и цена уменьшатся одинаково в течение периода [0, T] при ρ = −0.003 картина роста имеет следующий вид: cs (t) = 400 ∗ 0,997t, p (t) = 20 ∗ 0,997t, t∈ [0, T] (α = −3).
При использовании модели EOQ, без учета снижения стоимости доставки и цен, время между доставками будет tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1,001400 + (400 * 0,99740 + 20 * 0,99740 * 25 * 40) * 1,001360 + ⋯ + (400 * 0,997360 + 20 * 0,997360 * 25 * 40) * 1,00140 = 164156 евро
При применении модели 1 время между доставками находится по формуле (12): Общие затраты на закупку, доставку и хранение в течение 400 дней составляют: TCo = (400 + 20 * 25 * 20) * 1.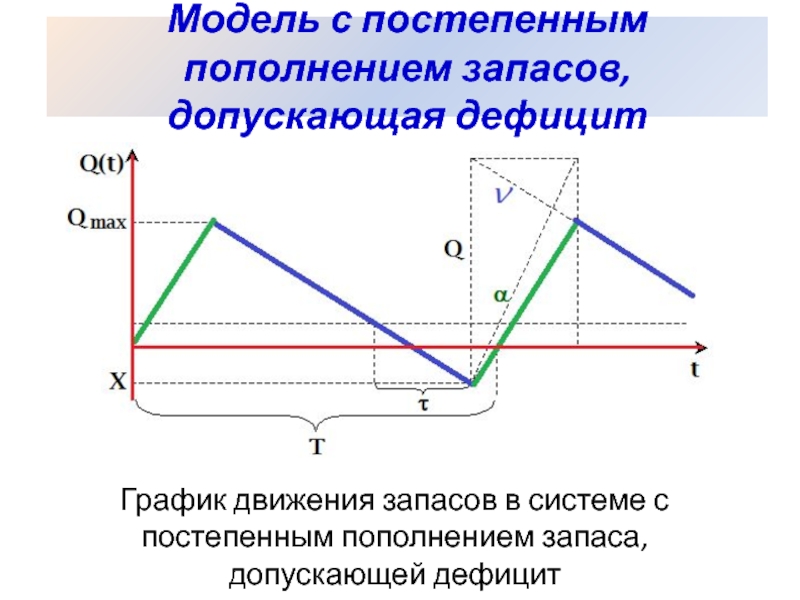 001400+ (400 * 0,99720 + 20 * 0,99720 * 25 * 20) * 1,001380 + ⋯ + (400 * 0,997380 + 20 * 0,997380 * 25 * 20) * 1,00120 = 160934
001400+ (400 * 0,99720 + 20 * 0,99720 * 25 * 20) * 1,001380 + ⋯ + (400 * 0,997380 + 20 * 0,997380 * 25 * 20) * 1,00120 = 160934
ΔTC = 164156−160934 = 3222
евроМодель 2
Если в начале периода [0, T] известны неконтролируемые параметры логистического процесса, такие как T = 400 дней, r = 0,001, μ = 25 единиц / день и p = 20 евро / единица и стоимость доставки увеличивается в течение периода [0, T] с ρ = 0,00075, тогда картина роста будет cs (t) = 400 ∗ 1.0023t, t∈ [0, T] (αc = 2,3).
При использовании модели EOQ, без учета увеличения стоимости доставки, время между доставками будет tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1,001400 + (400 * 1,002240 + 20 * 25 * 40) * 1,001360 + ⋯ + (400 * 1,0022360 + 20 * 25 * 40) * 1,00140 = 258365
евро При применении модели 2 время между поставками находится по формуле (20): tso = 1. 0023100 ∗ 40 = 50 дней
0023100 ∗ 40 = 50 дней
TCo = (400 + 20 * 25 * 50) * 1.001400+ (400 * 1,002250 + 20 * 25 * 50) * 1,001350 + ⋯ + (400 * 1,0022320 + 20 * 25 * 50) * 1,00150 = 258068
евро Экономия будет следующей:ΔTC = 258365−258068 = 297EUR
Если стоимость доставки уменьшается в течение периода [0, T] с ρc = −0,0018, картина роста имеет вид cs (t) = 400 ∗ 0,9982t, t∈ [0, T] (αc = −1,8) .
При использовании модели EOQ, без учета снижения стоимости доставки, время между доставками будет tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1.001400+ (400 * 0,998240 + 20 * 25 * 40) * 1,001360 + ⋯ + (400 * 0,9982360 + 20 * 25 * 40) * 1,00140 = 254627
евро При применении модели 2 время между поставками находится по формуле (20):tso = 0,9982100 ∗ 40 = 33 дня
Общие затраты на покупку, доставку и хранение в течение 400 дней составляют:TCo = (400 + 20 * 25 * 33) * 1,001400 + (400 * 0,998233 + 20 * 25 * 33) * 1,001367 + ⋯ + (400 * 0,9982367 + 20 * 25 * 33) * 1,00133 = 254513
евро Экономия будет следующей: ΔTC = 254627−254513 = 114 евро.
Модель 3
Если в начале периода [0, T] неконтролируемые параметры логистического процесса, такие как T = 400 дней, r = 0.001, μ = 25 единиц / день и cs = 25EUR известны, и если цена увеличивается в течение периода [0, T] с ρp = 0,000786, то картина роста будет p (t) = 20 ∗ 1.000786t, t∈ [0, T] (αp = 0,786).
При использовании модели EOQ без учета увеличения цены время между поставками будет tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1.001400 + (400 + 20 * 1.00078640 * 25 * 40) * 1.001360 + ⋯ + (400 + 20 * 1.000786360 * 25 * 40) * 1.00140 = 292146
евро При применении модели 3 время между поставками находится по формуле (26):tso = 401.0007861001−0,786 = 80 суток
Общие затраты на покупку, доставку и хранение в течение 400 дней составляют: TCo = (400 + 20 * 25 * 80) * 1,001400 + (400 + 20 * 1,00078680 * 25 * 80) * 1,001320 + ⋯ + (400 + 20 * 1. 000786320 * 25 * 80) * 1,00180 = 290915
000786320 * 25 * 80) * 1,00180 = 290915
ΔTC = 292146−290915 = 1331
евроЕсли цена снижается в течение периода [0, T] с ρp = −0,003, модель роста имеет вид p (t) = 20 ∗ 0,997t, t∈ [0, T] (αp = −3).
В модели EOQ, без учета снижения цен, время между поставками будет tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1,001400 + (400 + 20 * 0,99740 * 25 * 40) * 1,001360 + ⋯ + (400 + 20 * 0,997360 * 25 * 40) * 1,00140 = 165954
евро При применении модели 3 время между поставками находится по формуле (26):tso = 400.9971001 + 3 = 25 дней
Общие затраты на покупку, доставку и хранение в течение 400 дней составляют:TCo = (400 + 20 * 25 * 25) * 1,001400 + (400 + 20 * 0,99725 * 25 * 25) * 1,001375 + ⋯ + (400 + 20 * 0,997375 * 25 * 25) * 1,00125 = 164244
евро Экономия будет следующей:ΔTC = 165954−164244 = 1730
евроМодель 4
Если в начале периода [0, T] неконтролируемые параметры логистического процесса, такие как T = 400 дней, r = 0. 001, и μ = 25 единиц / день известны, а стоимость доставки и рост цены в период [0, T] с ρc = 0,003, ρp = 0,00075, то модель роста будет cs (t) = 400 ∗ 1.003t, p (t) = 20 ∗ 1.00075t, t∈ [0, T] (αc = 3, αp = 0,75).
001, и μ = 25 единиц / день известны, а стоимость доставки и рост цены в период [0, T] с ρc = 0,003, ρp = 0,00075, то модель роста будет cs (t) = 400 ∗ 1.003t, p (t) = 20 ∗ 1.00075t, t∈ [0, T] (αc = 3, αp = 0,75).
При использовании модели EOQ, без учета увеличения стоимости доставки и цен, время между доставками будет tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1,001400 + (400 * 1,00340 + 20 * 1.0007540 * 25 * 40) * 1,001360 + ⋯ + (400 * 1,003360 + 20 * 1,00075360 * 25 * 40) * 1,00140 = 294083
евро При применении модели 4 время между поставками находится по формуле (32):tso = 1.0031001.00075100401−0.75 = 100 дней
Общие затраты на покупку, доставку и хранение в течение 400 дней составляют:TC0 = (400 + 20 * 25 * 100) * 1.001400 + (400 * 1.003100 + 20 * 1.00075100 * 25 * 80) * 1.001300 + ⋯ + (400 * 1.003300 + 20 * 1.00075300 * 25 * 80) * 1.001100 = 2
евро
Экономия будет следующей:ΔTC = 294083−2
= 3335
евро Если стоимость доставки уменьшается и цена увеличивается в течение периода [0, T] с ρc = −0.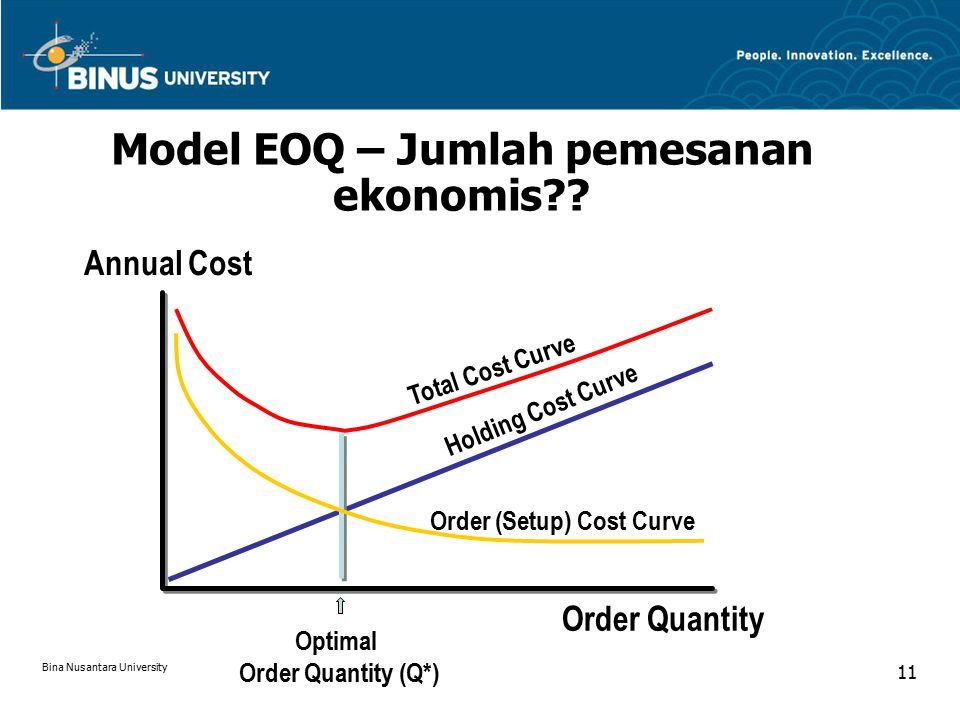 0039, ρp = 0,00075, картина роста имеет вид cs (t) = 400 ∗ 0,9961t, p (t) = 20 ∗ 1.00075t, t∈ [0, T] (αc = −3,9, αp = 0,75).
0039, ρp = 0,00075, картина роста имеет вид cs (t) = 400 ∗ 0,9961t, p (t) = 20 ∗ 1.00075t, t∈ [0, T] (αc = −3,9, αp = 0,75).
При использовании модели EOQ, без учета снижения затрат на доставку и повышения цен, время между доставками составит tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1,001400 + (400 * 0,996140 + 20 * 1,0007540 * 25 * 40) * 1,001360 + ⋯ + (400 * 0,9961360 + 20 * 1,00075360 * 25 * 40) * 1,00140 = 288180 евро
При применении модели 4 время между поставками находится по формуле (32):tso = 0.99611001,00075100401−0,75 = 50 дней
Общие затраты на покупку, доставку и хранение в течение 400 дней составляют:TCo = (400 + 20 * 25 * 50) * 1,001400 + (400 * 0,996150 + 20 * 1,0007550 * 25 * 50) * 1,001350 + ⋯ + (400 * 0,9961350 + 20 * 1,00075350 * 25 * 50) * 1,00150 = 288015 евро
Экономия будет следующей:ΔTC = 288180−288015 = 165
евро Если стоимость доставки увеличивается и цена снижается в течение периода [0, T] с ρc = 0,002, ρp = −0,003, картина роста имеет вид cs (t) = 400 ∗ 1,002t, p (t) = 20 ∗ 0.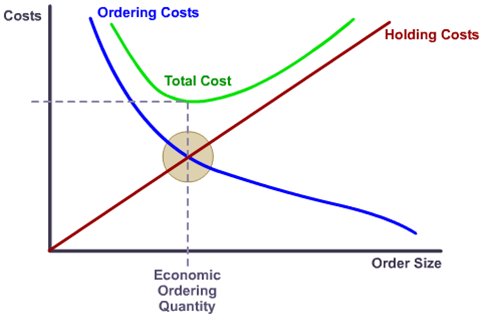 997t, t∈ [0, T] (αc = 2, αp = −3).
997t, t∈ [0, T] (αc = 2, αp = −3).
При использовании модели EOQ без учета увеличения стоимости доставки и снижения цены время между доставками составит tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1,001400 + (400 * 1,00240 + 20 * 0,99740 * 25 * 40) * 1,001360 + ⋯ + (400 * 1,002360 + 20 * 0,997360 * 25 * 40) * 1,00140 = 168249 евро
При применении модели 4 время между поставками находится по формуле (32):tso = 1.0021000.997100401 + 3 = 33 дня
Общие затраты на покупку, доставку и хранение в течение 400 дней составляют:TC0 = (400 + 20 * 25 * 33) * 1,001400 + (400 * 1,00233 + 20 * 0,99733 * 25 * 33) * 1,001367 + ⋯ + (400 * 1,002367 + 20 * 0,997367 * 25 * 33) * 1,00133 = 167620 евро
Экономия будет следующей:ΔTC = 168249−167620 = 629
евро Если в начале периода [0, T] известны неконтролируемые параметры логистического процесса, такие как T = 400 дней, r = 0,001 и μ = 25 единиц / день и стоимость доставки и цена снижаются в течение период [0, T] с ρc = −0. 001, ρp = −0,003, то картина роста будет: cs (t) = 400 ∗ 0,999t, p (t) = 20 ∗ 0,997t, t∈ [0, T] (αc = −1, αp = — 3).
001, ρp = −0,003, то картина роста будет: cs (t) = 400 ∗ 0,999t, p (t) = 20 ∗ 0,997t, t∈ [0, T] (αc = −1, αp = — 3).
При использовании модели EOQ, без учета снижения стоимости доставки и цен, время между доставками будет tw = 40 дней.
Общие затраты на закупку, доставку и хранение в течение 400 дней составляют:TCw = (400 + 20 * 25 * 40) * 1,001400 + (400 * 0,99940 + 20 * 0,99740 * 25 * 40) * 1,001360 + ⋯ + (400 * 0,999360 + 20 * 0,997360 * 25 * 40) * 1,00140 = 165335 евро
При применении модели 4 время между поставками находится по формуле (32):tso = 0.9991000.997100401 + 3 = 25 дней
Общие затраты на покупку, доставку и хранение в течение 400 дней составляют:TCo = (400 + 20 * 25 * 25) * 1,001400 + (400 * 0,99925 + 20 * 0,99725 * 25 * 25) * 1,001375 + ⋯ + (400 * 0,999375 + 20 * 0,997375 * 25 * 25) * 1,00125 = 163141 евро
Экономия будет следующей:ΔTC = 165335−163141 = 2194
евро 9-я Международная финансовая конференция прошла 28-29 октября 2021 года в SDMIMD (виртуальная модель). Техническая сессия, проведенная г-ном Бхаратрамом, Lokkur Finvestt Pvt Ltd, Бангалор, была посвящена факторам, влияющим на рынок капитала. С прощальной речью выступила г-жа Раджни Такур, главный экономист RBL Bank Ltd, Мумбаи.Она представила взгляд на текущее состояние финансовых рынков и обсудила, как глобальная пандемия повлияла на экономику в целом и на функционирование финансовых рынков. Она подчеркнула, что основы экономики начали восстанавливаться, и то же самое отразилось на показателях финансовых рынков Индии. |
(PDF) Оценка объема экономического заказа с переменными параметрами (пример из Украины)
Science Research 2017; 5 (1): 1-5 5
Ссылки
[1] Altintas, N. ; Erhun, F .; Таюр, С. (2008) Количественные скидки
; Erhun, F .; Таюр, С. (2008) Количественные скидки
при неопределенности спроса. Наука управления. 54 (4):
777–792. DOI: 10.1287 / mnsc.1070.0829.
[2] Уилсон Р. Х. (1943) Научная процедура контроля запасов.
Harvard Business Review. (13): 116—128.
[3] Миротин Л. Б., Ташбаев И. Е. (2002) Системный анализ в логистике
. Москва: Экзаменационное издательство.
[4] Халаван Л. (2007) Критерии логистической эффективности.Журнал
Дистрибьюция и логистика. 4 (11): с. 8–14.
[5] Таюр, С. (2000). Улучшение производственной деятельности и точное определение сроков выполнения заказа
на заводе по производству ламината. Интерфейсы. 30 (5), с. 1–15.
[6] Зипкин PH (2000) Основы управления запасами,
Бостон: McGraw Hill, ISBN 0-256-11379-3
[7] Малакути, Б. (2013) Операционные и производственные системы с
множественными Цели. Джон Вили и сыновья.
[8] Стивенсон В.(2009) Операционный менеджмент. 10-е изд. — 581.
10-е изд. — 581.
[9] Харви М. Вагнер и Томсон М. Уитин (1958) Динамическая
версия экономической модели размера лота / Management Science,
Vol. 5, стр. 89–96.
[10] Кэплин А. и Лихи Дж. (2010). Экономическая теория и
Мир практики: празднование (S, s) модели. The
Journal of Economic Perspectives, 24 (1), p.183-202.
[11] Триппи, Р., Левин, Д.(1974) Формулировка приведенной стоимости
классической проблемы количества экономического порядка, Решение
Sciences, 5 (1), стр. 30-35. URL: http: //www.sigma-
research.com/misc/A%20Present%20Value%20Formulation%
20of% 20the% 20Classical% 20EOQ% 20Problem.htm
[12] Adesso Solutions. 2005. Меч обоюдоострый. Автобус. Кредит
107 (9), п. 56–59.
[13] Давыдич Ю. О. (2010). Разбивка графика Руху
сельскохозяйственных предприятий при организации вантажных перевозок.
Харьков: ХУМГ. — 346 с.
[14] Монк Э. и Вагнер Б.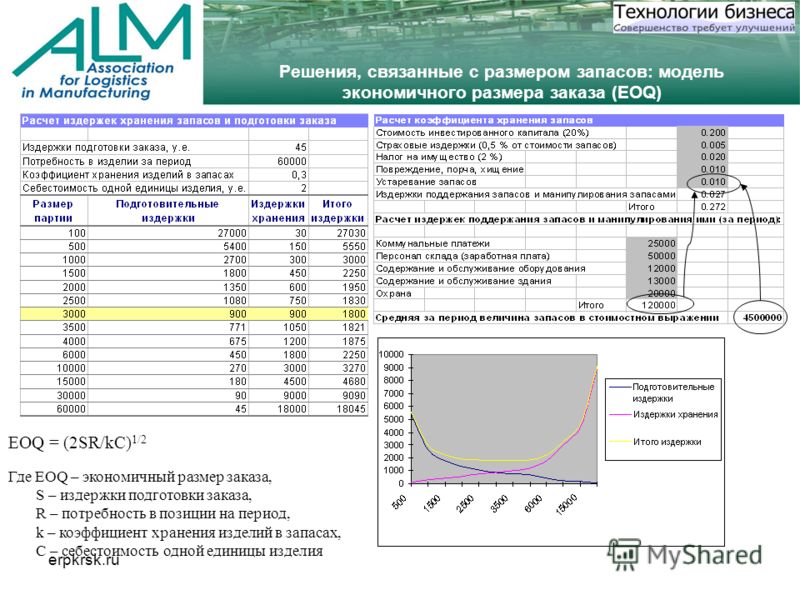 (2006) Концепции на предприятии
(2006) Концепции на предприятии
Планирование ресурсов. Канада: Технология курса Thomson.
[15] Erhun, F., & Tayur, S. (2003). Оптимизация в масштабе всего предприятия
общей конечной стоимости в продуктовом розничном магазине. Операционные исследования,
51 (3), 343-353.
[16] Галкин А. Куш Ю., Доля В. (2014) Несколько логистических цепочек
Услуги перевозки приближаются к одной транспортной компании.
Журнал L ‘Association 1901 «SEPIKE». № 4. с. 86-90.
[17] Раштон А., Краучер П. и Бейкер П. (2010). Справочник
по логистике и управлению распределением. Лондон: Коган Пейдж.
[18] Григоров М., Гаврилов Э., Григорова Т. & Доля, В. (2006),
Прогнозирование проектных характеристик конструкции и
эксплуатации автомобильных дорог: Монография. Надднепряночка,
Херсон, Украина.
[19] Рональд Х.Баллоу, Шривастава С. (2007) Бизнес-логистика:
Управление цепочками поставок. Pearson Education
[20] Джонсон Дж. И Джонсон Дж. (1999), Современная логистика.
И Джонсон Дж. (1999), Современная логистика.
Верхняя Сэдл-Ривер, Нью-Джерси: Prentice Hall.
[21] Филина-Давидович, Л., & Постан, М. (2016). Оптимальный складской учет
для скоропортящихся продуктов за дополнительную плату
для уменьшения порчи. ЛогФорум, 12.
[22] Литомин И., Толмачев И., Галкин А. (2016). Использование распределительного центра
в распределительной системе Украины.
Транспортные исследовательские процедуры, 16, стр. 313-322.
[23] Вакуленко К., Галкин А., Куш Эв., Пруненко Д., Бибик Н.
Доля В., (2016) Логистический подход к оборотному капиталу
менеджмент / Logistyka I jakość. Procesy doskonalące
zarządzenie: Monografia // Lublin: Wydział Ekonomiczny
Uniwersytetu Marii Curie-Skłodowskiej.- п. 442-455.
[24] Каннан Д., Ходаверди Р., Олфат Л., Джафариан А. и Диабат,
А. (2013). Интегрированное нечеткое многокритериальное принятие решений Метод
и подход многоцелевого программирования для
выбора поставщиков и распределения заказов в зеленой цепочке поставок.
Журнал чистого производства, 47, 355-367.
[25] Цинь З. и Кар С. (2013). Задача однократной инвентаризации
в условиях неопределенности.Прикладная математика и
Вычисления, 219 (18), с. 9630-9638.
[26] Саркар Б. и Мун И. (2014). Повышение качества, снижение затрат на установку на
и переменные затраты на невыполненный заказ при несовершенном производственном процессе
. Международный производственный журнал
Экономика, 155, стр. 204-213.
Биография
Андрей Галкин в настоящее время преподает курс
«Транспортные системы и логистика» (TSL) по тел.
О.Харьковский национальный университет им. М. Бекетова
Городское хозяйство (НУУЭ). В 2015 году защитил кандидатскую диссертацию
в НУУЭ кафедры ТСЛ
за разработку теории и
практики управления логистикой транспортных услуг, которые
заключаются в рассмотрении параметров нескольких материальных потоков в
с определением количества и соотношение собственных и арендованных автомобилей.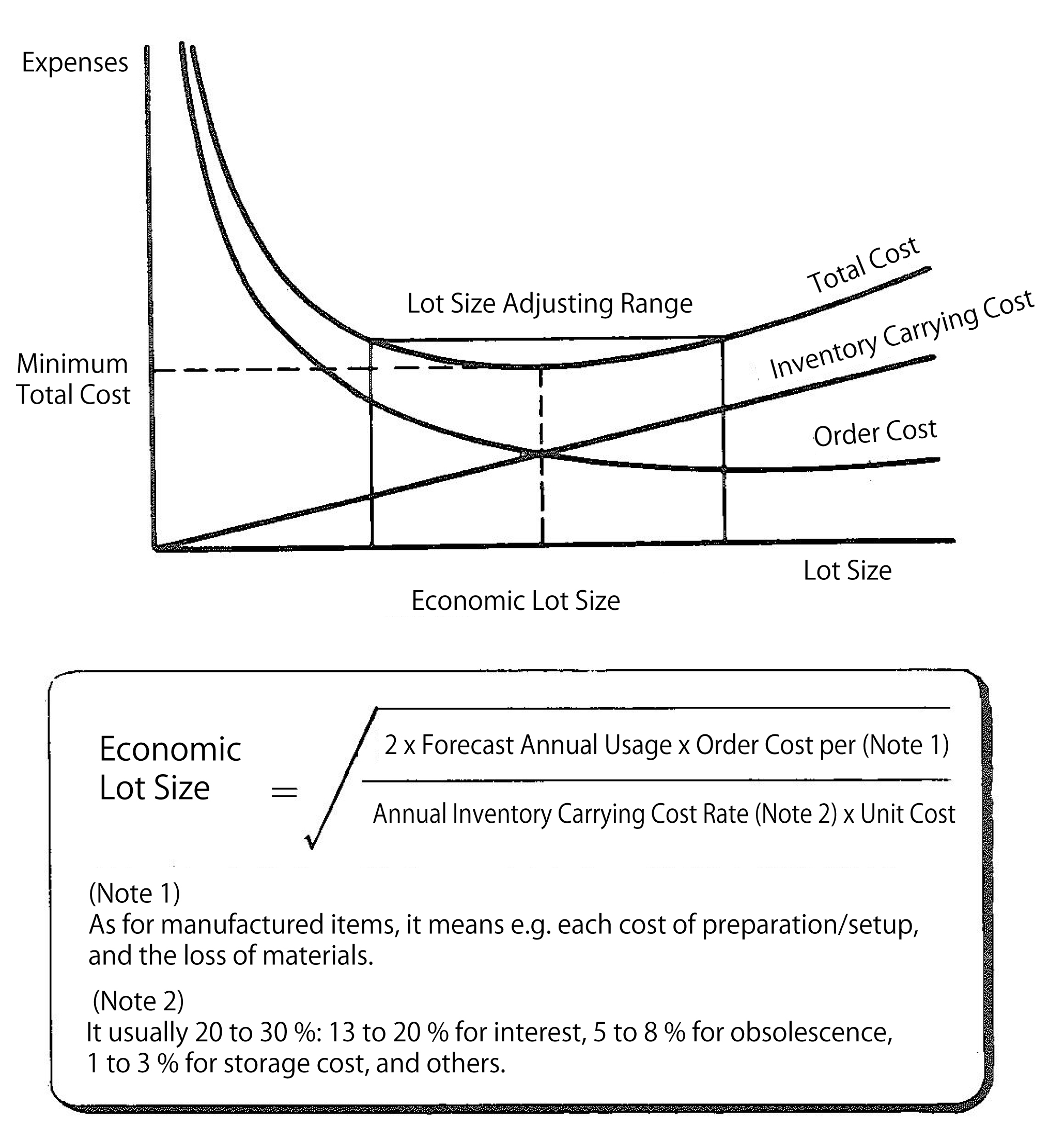 Он
Он
подробно интересуется логистикой и коммуникациями с потребителями,
человеческий фактор в логистике и его применение для проектирования городской сети
.
Формула и справочник по экономичному количеству для заказа
Что такое EOQ?
EOQ расшифровывается как экономичный объем заказа. Это измерение, используемое в области операций, логистики и управления поставками. По сути, EOQ — это инструмент, используемый для определения объема и частоты заказов, необходимых для удовлетворения заданного уровня спроса при минимизации затрат на заказ.
Важность EOQ
Объем экономического заказа — это контрольная точка, призванная помочь компаниям минимизировать затраты на заказ и хранение запасов. -прогресс, а готовая продукция а.Стоимость заказа товарно-материальных запасов снижается с увеличением объема заказа из-за закупок за счет экономии от масштаба Экономия от масштаба Экономия от масштаба относится к преимуществу затрат, которое испытывает фирма при увеличении уровня выпуска.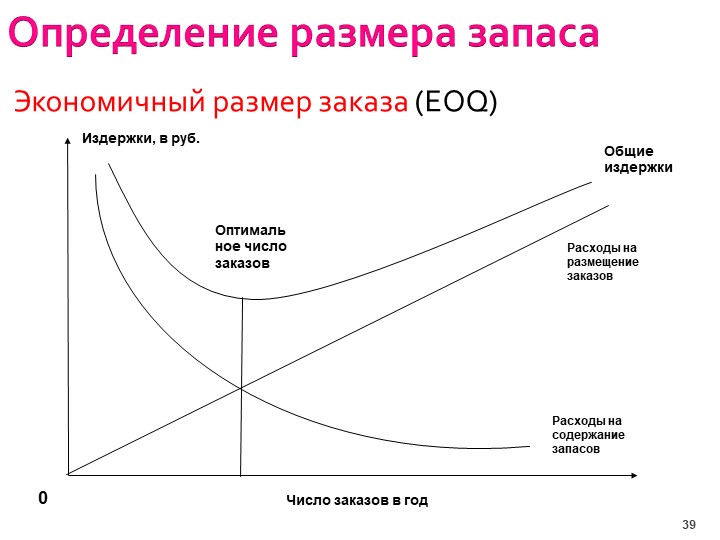 Преимущество возникает из-за. Однако по мере увеличения размера запасов возрастает стоимость их хранения. EOQ — это именно та точка, которая минимизирует обе эти обратно пропорционально связанные затраты.
Преимущество возникает из-за. Однако по мере увеличения размера запасов возрастает стоимость их хранения. EOQ — это именно та точка, которая минимизирует обе эти обратно пропорционально связанные затраты.
Формула EOQ
Формула экономического количества заказа рассчитывается путем минимизации общей стоимости заказа путем установки производной первого порядка равной нулю.Компоненты формулы, составляющие общую стоимость заказа, — это стоимость хранения запасов и стоимость заказа этих запасов. Ключевые обозначения для понимания формулы EOQ:
Компоненты формулы EOQ:
D : Требуемое годовое количество
Q : Объем на заказ
S : Стоимость заказа (Фиксированная стоимость)
C : Стоимость единицы (переменная стоимость)
H : Стоимость владения (переменная стоимость)
i : Стоимость обслуживания (процентная ставка)
Стоимость заказа
Число заказов, которые происходят ежегодно, можно найти, разделив годовой спрос на объем заказа. Формулу можно представить в виде:
Формулу можно представить в виде:
Для каждого заказа с фиксированной стоимостью, не зависящей от количества единиц S, годовая стоимость заказа определяется путем умножения количества заказов на эту фиксированную стоимость. Это выражается как:
Стоимость хранения
Хранение запасов часто связано с собственными затратами. Эти затраты могут быть в форме прямых затрат, понесенных при финансировании хранения указанных запасов, или альтернативных затрат. Альтернативные затраты. Альтернативные затраты — одна из ключевых концепций в изучении экономики и преобладающая во всех процессах принятия решений.Провести инвентаризацию вместо того, чтобы вкладывать деньги в другое место. Таким образом, стоимость владения на единицу часто выражается как стоимость единицы, умноженная на процентную ставку, выраженную следующим образом:
H = iC При условии, что спрос постоянен, количество видно, что запасы истощаются с постоянной скоростью с течением времени. Когда запасы достигают нуля, заказ размещается и пополняет запасы, как показано:
Когда запасы достигают нуля, заказ размещается и пополняет запасы, как показано:
Таким образом, стоимость хранения запасов рассчитывается путем нахождения суммарного произведения запасов в любой момент и стоимости удержания за Блок.Это выражается следующим образом:
Общая стоимость и экономическое количество заказа
Суммирование двух затрат дает общую годовую стоимость заказов. Чтобы найти оптимальное количество, которое минимизирует эти затраты, общие годовые затраты дифференцируются относительно Q. Это показано следующим образом:
Пример
Например, компания сталкивается с годовой спрос 2000 единиц.Это обходится компании в 1000 долларов за каждый размещенный заказ и 250 долларов за единицу продукта. Стоимость его переноски составляет 10% от стоимости единицы. Какое количество экономичного заказа?
Переменные можно расположить следующим образом:
Стоимость каждого значения Q отображается как:
Скачать бесплатный шаблон
Введите свое имя и отправьте электронное письмо в форму ниже и загрузите бесплатный шаблон прямо сейчас!
Шаблон количества экономического заказа
Загрузите бесплатный шаблон Excel, чтобы углубить свои знания в области финансов!Другие ресурсы
CFI призван помочь вам расширить свои знания, повысить свои навыки финансового аналитика и продвинуться по карьерной лестнице.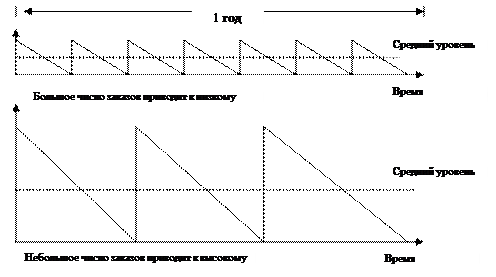

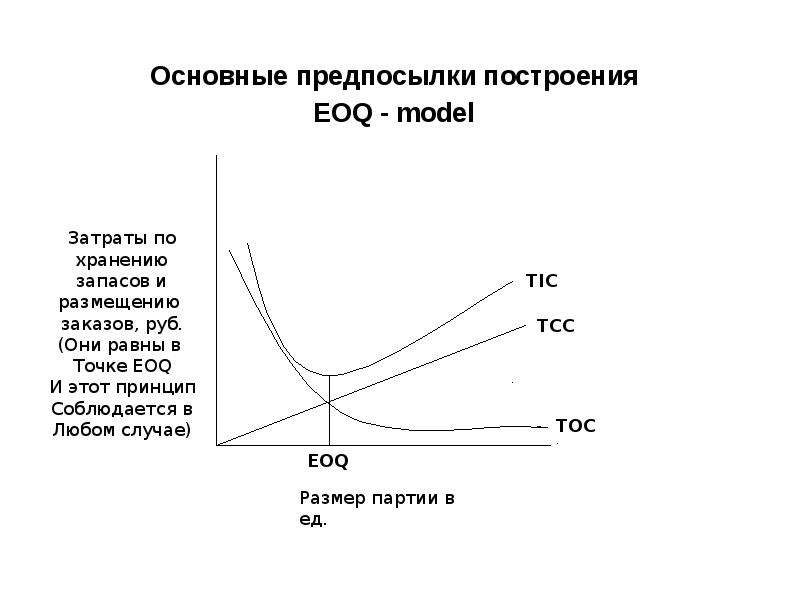
 Превратите хороший прогноз спроса в оптимальный план инвентаризации
Превратите хороший прогноз спроса в оптимальный план инвентаризации Упаковка пищевых отходов
Упаковка пищевых отходов , для запасов сырья) или
наладочная стоимость производства.
, для запасов сырья) или
наладочная стоимость производства.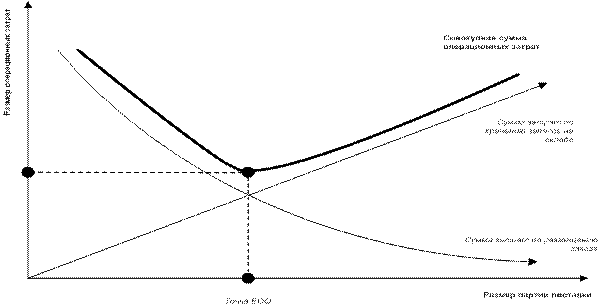 Конференцию открыл Шри.Ф. Р. Сингви, совместный управляющий директор Sansera Engineering Ltd Bengaluru, который также выступил с основным докладом. Во время основного выступления он подчеркнул важность наличия ликвидных активов для роста и поддержки бизнеса. Ликвидность гарантирует, что предприятия поддерживают адекватные денежные потоки и защищены от капризов изменений макроэкономических факторов. Он также коснулся того, как процесс автоматизации с помощью ИИ (искусственного интеллекта) и машинного обучения (машинного обучения) меняет ландшафт финансовой функции и бизнеса в целом.Доктор Н. Р. Парасураман, директор SDMIMD, выпустил материалы конференции в виде компакт-диска. В своем выступлении он остановился на последних событиях в сфере корпоративных финансов и финансовых рынков. Ранее д-р М. Срайрам, доцент по финансам, SDMIMD и председатель конференции приветствовали собрание и представили тему конференции на 2021 год.
Конференцию открыл Шри.Ф. Р. Сингви, совместный управляющий директор Sansera Engineering Ltd Bengaluru, который также выступил с основным докладом. Во время основного выступления он подчеркнул важность наличия ликвидных активов для роста и поддержки бизнеса. Ликвидность гарантирует, что предприятия поддерживают адекватные денежные потоки и защищены от капризов изменений макроэкономических факторов. Он также коснулся того, как процесс автоматизации с помощью ИИ (искусственного интеллекта) и машинного обучения (машинного обучения) меняет ландшафт финансовой функции и бизнеса в целом.Доктор Н. Р. Парасураман, директор SDMIMD, выпустил материалы конференции в виде компакт-диска. В своем выступлении он остановился на последних событиях в сфере корпоративных финансов и финансовых рынков. Ранее д-р М. Срайрам, доцент по финансам, SDMIMD и председатель конференции приветствовали собрание и представили тему конференции на 2021 год. Он также проинформировал аудиторию о различных аспектах, которые необходимо изучить, прежде чем делать какие-либо инвестиции. Г-н Якоб Томас, менеджер по доставке, TCS Ltd, Германия, рассказал о цепочке блоков и криптовалюте. В его докладе были затронуты нюансы технологии блокчейн и ее применения в различных аспектах управления. Было представлено около 50 научных работ, которые были представлены участниками из Индии и из-за рубежа.
Он также проинформировал аудиторию о различных аспектах, которые необходимо изучить, прежде чем делать какие-либо инвестиции. Г-н Якоб Томас, менеджер по доставке, TCS Ltd, Германия, рассказал о цепочке блоков и криптовалюте. В его докладе были затронуты нюансы технологии блокчейн и ее применения в различных аспектах управления. Было представлено около 50 научных работ, которые были представлены участниками из Индии и из-за рубежа.