Потенцирование логарифмов – Потенцирование | Логарифмы
Потенцирование | Логарифмы
Потенцирование — это действие, заключающееся в нахождении числа по данному логарифму через логарифмы других чисел (нем. potenzieren — возводить в степень, от Potenz — степень).
При решении уравнений потенцированием выражения преобразовывают с помощью свойств логарифмов, приводя их к виду
либо к виду
Схематически логарифмическое уравнение, решаемое потенцированием, можно представить приблизительно так:
Решение начинаем с нахождения ОДЗ:
Затем преобразовываем выражение: число перед логарифмом вносим в показатель степени выражения, стоящего под знаком логарифма, а отдельно стоящее число представляем в виде логарифма по тому же основанию, что и остальные логарифмы:
От суммы логарифмов переходим к логарифму произведения, от разности — к логарифму частного:
Теперь приравниваем выражения, стоящие под знаками логарифмов
и решаем алгебраическое уравнение.
Рассмотрим примеры решения логарифмических уравнений потенцированием.
ОДЗ:
(меньше меньшего).
От суммы логарифмов переходим к логарифму произведения:
По определению логарифма
Первый корень не входит в ОДЗ.
Ответ: -1.
ОДЗ:
Число 2 вносим в показатель степени выражения, стоящего под знаком логарифма. Единицу представляем в виде логарифма по основанию 3
(-x)²=x². От суммы логарифмов переходим к логарифму произведения
Так как равны логарифмы с одинаковыми основаниями, можем приравнять выражения, стоящие под знаками логарифмов:
Первый корень не входит в ОДЗ.
Ответ: -3.
ОДЗ:
Единицу представляем в виде логарифма по основанию 3:
От разности логарифмов переходим к логарифму частного:
Приравниваем выражения, стоящие под знаками логарифмов:
Можно применить основное свойство пропорции:
Первый корень не входит в ОДЗ.
Ответ: 3.
Потенцирование (математика) — это… Что такое Потенцирование (математика)?
- Потенцирование (математика)
Число ab называется степенью с основанием a и показателем b.
Число с называется n-ной степенью числа а, если .
Свойства:
- anam = an + m
- , n>m.
Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.
не определёнПо определению,
См. корень степени q
Пусть .
В школе действительную функцию вводят, используя тот факт, что между любыми двумя рациональными числами существует иррациональное, а между любыми двумя иррациональными — рациональное. Тогда , где p < q, | p − q | < ε, где ε — погрешность вычисления. Таким образом, для любого иррационального числа r подбираются два рациональных p и q с необходимой степенью точности и любое число между ap и aq принимается за ответ.
Другой подход основан на теории рядов и логарифмов. (см. определение комплексной степени)
Потенцирование
Потенцирование — это нахождение числа по известному значению его логарифма, то есть решение уравнения:
Из определения логарифма вытекает, что x = ab. Таким образом, потенцирование означает возведение основания логарифма в степень, равную значению логарифма. Например, если десятичный логарифм числа равен L, то искомое число равно 10L.
Определим некоторые функции:
теперь для вычисления az можно использовать свойства степеней и логарифмов:
Степень как функция
Поскольку в выражении xy принимает участие две переменных, то его можно рассматривать как:
См. также
Ссылки
- А. Б. Будак, Б. М. Щедрин «Элементарная математика» — Подготовка к вступительным экзаменам в МГУ
Wikimedia Foundation. 2010.
- Потенциан
- Потери НАТО в Афганистане
Смотреть что такое «Потенцирование (математика)» в других словарях:
Потенцирование (Математика) — Потенцирование (в математике) ( de. Potenzieren, от Potenz степень) действие, заключающееся в нахождении числа по данному логарифму. Другими словами, это действие, обратное логарифмированию … Википедия
Возведение в степень
Показатель степени — Число ab называется степенью с основанием a и показателем b. Содержание 1 Натуральная степень 2 Целая степень 3 Рациональная степень … Википедия
Логарифм — График двоичного логарифма Логарифм числа … Википедия
Псевдонаука — (от греч. ψευδής «ложный» + наука; синоним лженаука, близкие по значению термины: паранаука, квазинаука[1], альтернативная наука, неакадемическая наука) деятельность[2] или учение[2], осознанно или неосознанно имитирующие науку … Википедия
Логарифмическая линейка — Логарифмическая линейка, Счётная линейка аналоговое вычислительное устройство, позволяющее выполнять несколько математических операций, в том числе умножение и деление чисел, возведение в степень (чаще всего в квадрат и куб) и вычисление… … Википедия
Десятичные логарифмы — Рис. 1. Графики логарифмических функций Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: . Из определения следует, что записи и ax = b равносильны. Пример … Википедия
Логарифмическая таблица — Рис. 1. Графики логарифмических функций Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: . Из определения следует, что записи и ax = b равносильны. Пример … Википедия
Логарифмическая функция — Рис. 1. Графики логарифмических функций Логарифм числа b по основанию a определяется как показатель степени, в которую надо возвести число a, чтобы получить число b. Обозначение: . Из определения следует, что записи и ax = b равносильны. Пример … Википедия
dic.academic.ru
Урок-лекция по теме «Логарифмические уравнения. Основные методы их решения»
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
В моём календарно-тематическом планировании на тему “Логарифмические уравнения” отводится 3 часа. Я их разбиваю следующим образом:
1 возможный вариант:
1 урок — лекция “Логарифмические уравнения. Основные методы их решения”. В конце лекции задаю блок уравнений обязательного уровня.
2 урок – решение уравнений различного типа и сложности (это зависит от уровня математической подготовки класса, использую индивидуальный подход).
3 урок – решение уравнений и зачётная работа с само- и взаимопроверкой, а также проверкой учителем.
2 возможный вариант:
1 урок — лекция “Логарифмические уравнения. Основные методы их решения”, но только два метода – на основании определения и потенцирования. Решение уравнений на применение этих методов.
2 урок – лекция “Логарифмические уравнения. Основные методы их решения”, два других метода – подстановки и логарифмирования. Решение уравнений на применение этих методов.
3 урок – решение уравнений и зачётная работа с само- и взаимопроверкой, а также проверкой учителем.
Вариант подачи темы зависит от подготовленности класса.
1 урок
Лекция “Логарифмические уравнения. Основные методы их решения”.
Слайд 1.
Эпиграфом своей сегодняшней лекции я привожу слова Ричарда Олдингтона (1892 – 1962гг., английский поэт, прозаик, критик): “Ничему тому, что важно знать, научить нельзя, — всё, что может сделать учитель, это указать дорожки”.
Слайд 2.
А так же – русскую народную пословицу: “Кто говорит – тот сеет, кто слушает – тот собирает”.
В самом начале моей лекции я хотела бы обратить ваше внимание на следующее. При решении логарифмических уравнений применяют преобразования, которые не приводят к потере корней, но могут привести к приобретению посторонних корней. Поэтому проверка каждого из полученных корней обязательна, если нет уверенности в равносильности уравнений. Здесь возможны два подхода:
Проверка путём подстановки полученных решений в исходное уравнение.
Нахождение области допустимых значений уравнения (ОДЗ). Тогда корнями могут быть только те числа, которые принадлежат этой области.
В своей лекции я буду использовать оба этих подхода, а ваше право уже самим выбирать, какой лично вам больше нравится. Следует отметить, что при решении логарифмических неравенств возможен только один из них: ОДЗ!
Основные методы решения логарифмических уравнений.
Слайд 3.
Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.
Решение логарифмических уравнений на основании определения логарифма.
Определение логарифма: Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b. Т. е.
Таким образом, применяя его к нашей теме, мы получим следующее:
при этом
Пример 1:
Число 16 удовлетворяет ОДЗ, значит 16 – корень исходного уравнения.
Ответ: 16.
Слайд 4.
Пример 2:
Проверка: — верно, значит число 4 – корень исходного уравнения.
Ответ: 4.
Пример 3:
По определению логарифма значит
Ответ:
Слайд 5.
А сейчас мы рассмотрим пример, в котором в основании логарифма уже не число, а выражение, содержащее переменную. Т. е. уравнение будет иметь вид при этом Хочу отметить особо, что рассуждения НЕ ИЗМЕНИЛИСЬ!
Пример 4:
ОДЗ:.
С учётом ОДЗ получим, что решением данного уравнения является число 2.
Ответ: 2.
Как мы видим, наличие выражения с переменной в основании влияет лишь на ОДЗ, а не на ход рассуждений. Кроме того, данное уравнение можно решать, не прибегая к нахождению ОДЗ, а просто в конце выполнить проверку.
Метод потенцирования.
Слайд 6.
Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их.
, где
Пример 5:
Проверка:
— верно.
— не верно.
Значит, только число 1 является решением исходного уравнения.
Ответ:1.
Слайд 7.
Если же в основании – выражение с переменной, то рассуждения не меняем! В этом случае уравнение будет иметь вид
, где
И пример такого уравнения можно разобрать на предыдущем примере 5.
Пример 6:
Проверка:
— верно.
— не верно.
Значит, только число 1 является решением исходного уравнения.
Ответ:1.
ОДЗ для данного уравнения выглядит следующим образом:
Мы видим, что в этом уравнении рациональнее выполнить проверку, а не искать ОДЗ. Но ещё раз повторюсь, что при решении неравенств ОДЗ находить придётся ОБЯЗАТЕЛЬНО.
Рассмотрим пример, который, на первый взгляд, не может относиться к данному типу уравнений.
Слайд 8.
Пример7:
Сделаем замену , получим воспользовавшись свойством логарифма (сумма логарифмов равна логарифму произведения подлогарифмических выражений: ), получим уравнение которое в свою очередь замечательно решается методом потенцирования, т.е. А это линейное уравнение, решив которое, получим
Проверка: — верно.
Ответ: 0.
Замечу, что часто перед применением какого-либо метода решений, необходимо преобразовать уравнение, применив различные свойства логарифмов. Предыдущий пример, тому подтверждение.
Метод подстановки.
Слайд 9.
Данный метод мы достаточно часто встречаем в математике, вспомните тригонометрические или показательные уравнения. Поэтому применение его при решении логарифмических уравнений я вам покажу на примере.
Пример 8: .
В этом уравнении рациональней найти ОДЗ:
Пусть , тогда уравнение примет вид
,
Значит или . А это уравнения, которые мы решим, используя определение: 1)
2)
Мы видим, что оба корня удовлетворяют ОДЗ, значит оба числа являются решениями исходного уравнения.
Ответ:
Слайд 10.
Если в основании логарифма лежит выражение с переменной, то уравнение в общем виде будет выглядеть следующим образом:
, где
И опять, вы сами выбираете: ОДЗ или проверка.
Пример 9: .
ОДЗ:
Приведём логарифмы к одному основанию – 7, пользуясь свойством перехода к новому основанию , получим:
, выполним подстановку , получим уравнение
,
Значит,
Оба числа удовлетворяют ОДЗ.
Ответ:
Метод логарифмирования.
Слайд 11.
Данный метод является “обратным” методу потенцирования, т. е. мы от уравнения без логарифмов переходим к уравнению, их содержащему.
, при этом
Этот метод обычно используется, если в уравнении есть показательные функции, логарифмы – в показателе. Рассмотрим этот метод на примере.
Пример 10:
ОДЗ:
Прологарифмируем обе части уравнения по основанию 3:
а теперь воспользуемся свойством логарифмов , получим
Выполним подстановку , получим уравнение
Значит,
Оба числа удовлетворяют ОДЗ.
Ответ: 3, 27.
Этот пример показывает, что при решении логарифмических уравнений, возможна комбинация нескольких методов. А значит необходимо уметь пользоваться каждым из них. Научиться этому – теперь ваша задача.
Слайд 12.
Итак, сегодня мы с вами рассмотрели основные методы решения логарифмических уравнений:
- На основании определения логарифма.
- Метод потенцирования.
- Метод постановки.
- Метод логарифмирования.
Главным, по моему мнению, является метод, основанный на определении логарифма. Практически в каждом их других методов происходит “выход” на него. Кроме того, на примерах мы увидели, что все методы взаимосвязаны, в “чистом” виде при решении уравнений не используется ни один из них. Поэтому вам необходимо уметь пользоваться КАЖДЫМ!
Для отработки навыков решения логарифмических уравнений, я вам предлагаю следующее домашнее задание. Уравнения являются базовыми, т. е. решать их должен уметь решать каждый. Отмечу, что подборка сделана из открытого банка заданий для экзамена по математике ЕГЭ http://mathege.ru .
Замечание: домашнее задание распечатано на листах для каждого ученика.
Слайд 13.
2, 3 урок
Решение задач по теме “Логарифмические уравнения”. Зачёт.
Уравнения (примерные, зависит от математической подготовки учащихся).
Подборка уравнений к уроку, зачёту проводится на сайтах www.fipi.ru , http://mathege.ru , http://mathus.ru/ , http://reshuege.ru/ , http://www.math.md/school/praktikum/logr/logr.html (Виртуальная школа юного математика).
Тест к зачёту.
urok.1sept.ru
Конспект занятия по дисциплине Математика на тему логарифмирование и потенцирование
Урок 19
ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ ВЫРАЖЕНИЙ
Цели:
дидактическая:
повторение, систематизация и обобщение знаний;
закрепление умений решать практические задачи по теме;
воспитательная:
развивающая:
развитие логического мышления алгоритмической культуры;
развитие умения доказывать свои умозаключения, анализировать ответы друг друга;
продолжить формировать умение правильно воспринимать и активно запоминать новую информацию.
Тип урока: комбинированный урок
Методическое обеспечение: учебники, план-конспект урока, карточки.
Ход урока:
1. Организационный момент
Перед началом урока преподаватель проводит проверку подготовленности кабинета к занятию.
Приветствие обучающихся, определение отсутствующих, заполнение группового журнала. Сообщается тема и цель урока.
2. Повторение ранее изученного материала
3. Изучение нового материала
ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
1. Проверка домашнего задания, работа у доски над затруднительными моментами.
2. Дайте определение понятию логарифм.
Логарифм числа b по основанию а – это показатель степени, в которую нужно возвести число а, чтобы получить число b.
3. Приведите пример записи логарифма. Что означает эта запись?
3. Для того, чтобы проверить уровень усвоения материала, предлагается решить некоторые задания. На доске таблица, которую необходимо заполнить, указав решение примера и номер свойства из ранее записанного конспекта урока.
Пример
Решение. Ответ
Номер свойства
1
3
2
5
3
4
4
1
2
5
0
1
7
5
5, 1
8
6
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА
Логарифмирование – это нахождение логарифмов заданных чисел или выражений.
Пример: Найдем логарифм
Решение.
Последовательно воспользуемся сразу всеми тремя основными свойствами логарифмов, которые изложены выше (логарифм произведения, логарифм частного и логарифм степени):
Логарифмирование – это преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных.
Необходимо четко различать сумму логарифмов lga+lgb и логарифм суммы lg(a+b). Сумма логарифмов равна логарифму произведения, а для логарифма суммы формулы нет.
Пример. Дано , где a>0, b>0, c>0. Найти lg x.
Решение. Логарифмируя, получим:
Потенцирование – это преобразование, обратное логарифмированию.
Потенцировать – значит освобождаться от знаков логарифмов в процессе решения логарифмического выражения.
При решении уравнений потенцированием выражения преобразовывают с помощью свойств логарифмов, приводя их к виду
либо к виду
Например, надо решить уравнение log2 3x = log2 9.
Убираем знаки логарифмов – то есть потенцируем:
3х = 9.
В результате получаем простое уравнение, которое решается за несколько секунд:
х = 9 : 3 = 3.
Но потенцирование не сводится к простому и произвольному убиранию значков логарифмов. Для этого в обоих частях уравнения как минимум должно быть одинаковое значение основания (в нашем случае это основание 2).
Потенциирование применяется при решении логарифмических уравнений, с которыми мы познакомимся на следующем занятии.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
Прологорифмируйте выражение по основанию 10 при условии, что все переменные положительные:
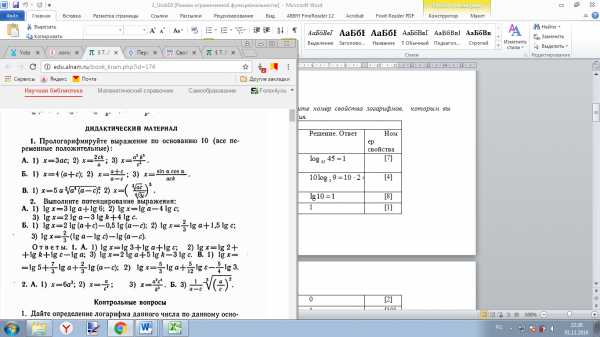
Выполните потенцирование выражения:
Группа разбивается на подгруппы по два-три человека. Каждая подгруппа составляет один пример для логарифмирования, передает его соседней подгруппе для решения. После чего подгруппы решают пример и передают его следующей подгруппе для решения. В итоге каждая подгруппа должна выставить оценку своим одногруппникам, решившим составленное выражение.
ДОМАШНЯЯ РАБОТА
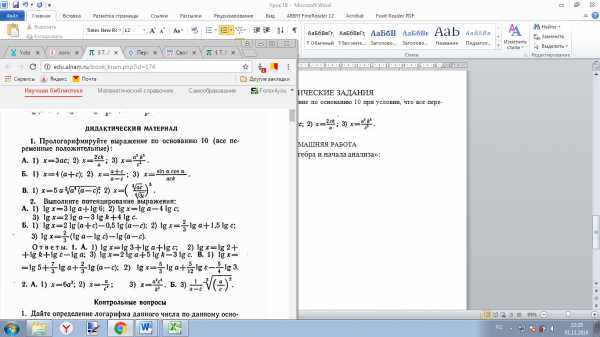
Прологорифмируйте выражение по основанию 10 при условии, что все переменные положительные:

Выполните потенцирование выражения:

infourok.ru
Конспект урока. Потенцирование логарифмических уравнений. 11 класс
«Решение логарифмических уравнений методом потенцирования»
Цели урока:
Образовательная— отработать навыки решения логарифмических уравнений методом потенцирования
Развивающая–применять методпотенцирования к решению уравнений; способствовать развитию математического кругозора, математического мышления.
Воспитательная— содействовать воспитанию интереса к логарифмическим уравнениям, воспитывать чувства коллективизма, самоконтроля, ответственности и уверенности в себе.
Тип урока:урок решения задач
Оборудование:презентация, мультимедиа проектор +компьютер, доска, мел
Применяемы методы: использование ИКТ, интерактивные методы.
Формирование ключевых компетенций: коммуникативных, учебно-познавательных.
План урока
Организационная часть.
Повторение теоретической части. (Фронтальный опрос)
Устная работа
Работа по вариантам, с программированными заданиями.
Разноуровневая самостоятельная работа с последующей проверкой.
Разгрузка –математический кроссворд.
Подведение итогов
Домашнее задание.
Ход урока.
Организационная часть.
Учитель входит в класс, здоровается, проверяет готовность к уроку. Знакомит обучающихся с темой, целями урока.
Мотивация темы: Тема «Логарифмические уравнения» очень важна для успешной сдачи письменного экзамена.
Актуализация знаний.
Начинается опрос. Ответы отображаются на слайде 1.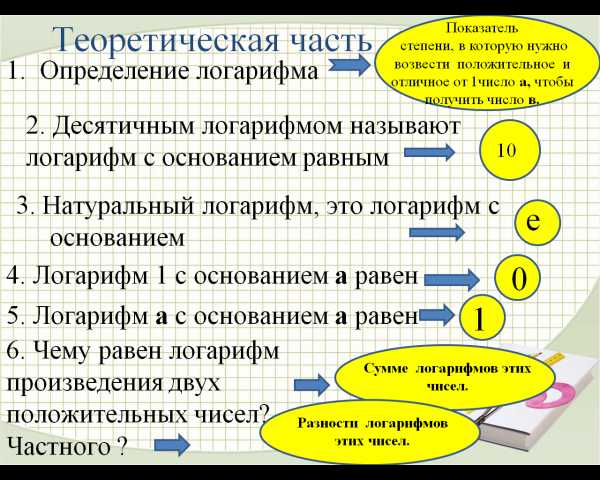
Далее предлагается выполнить устно по цепочке задания, отображдённые на слайдах 2, 3.По мере ответов зарполняются слайды Слайд 2.

Слайд 3

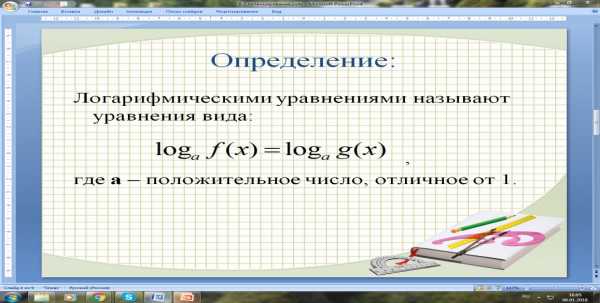
Затем, вопрос какие уравнения называют логарифмическими?
На слайде 4 отображается ответ Слайд 4
Появляется слайд 5, который заполняется в ходе беседы с обучающимися.
Какие методы решения логарифмических уравнений существуют? Слайд 5

Основан на использовании графических иллюстраций или каких либо свойств функции.
Он основан на теореме Слайд 6

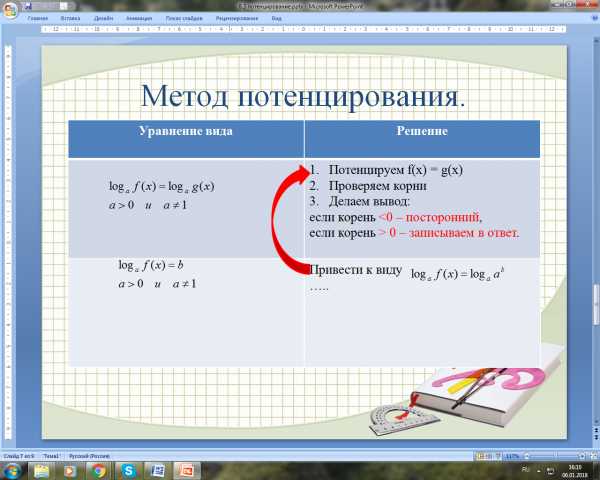
Слайд7.
Устная работа
Какая из формулировок не правильная? Почему? Слайд 8.
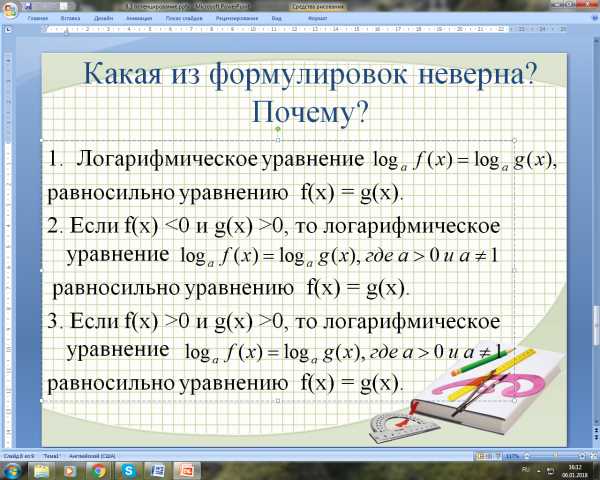
Предлагается ряд примеров, на которые устно дают ответы (примеры отображены на слайде 9) .

Ответы: 1) 4; 2) 3; 3) 9; 4) 10; 5) 0,25; 6) 18.
Работа по вариантам. Необходимо решить уравнение и выбрать правильный ответ. У доски работают трое, в итоге появляется определенный набор цифр.
V. Разноуровневая самостоятельная работа с последующей проверкой.
Предлагается оценить свои возможности и выбрать уровень заданий. На решение отводиться 6 -7 минут. После чего меняются тетрадями, и проверяют друг у друга
Разгрузка –математический кроссворд.На слайде появляется кроссворд, необходимо вписать математические термины по горизонтали.
Подсказка – ответы на вопросы.
Определение логарифма.
Находится при решение уравнений.
Изображение функции.
Есть у степени и у логарифма.
Тема нашего урока.
Сумма логарифмов равна…
Логарифмическая…
у =
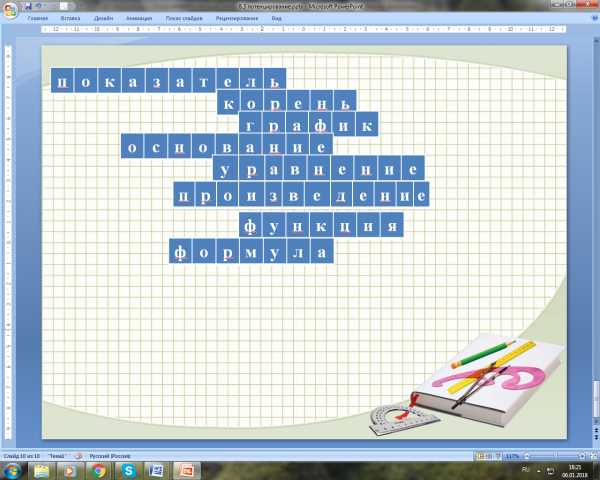
Подведение итогов урока.
Что нового вы узнали сегодня на уроке?
Чему вы научились сегодня на уроке?
Что на уроке вы сегодня повторили?
Что на уроке вы сегодня закрепили?
Домашнее задание
п.8.3 № 8,14 (а;в), 8.17 (а;б)
infourok.ru
Логарифмы | Все о логарифмах
Рассмотрим примеры логарифмических уравнений, сводящихся к уравнениям, решаемых методом логарифмирования. (далее…)
Как можно преобразовать выражение вида «с в степени логарифм»? Это зависит от основания степени и основания логарифма. (далее…)
Как преобразовать выражение, в котором квадрат логарифма стоит в показателе степени? (далее…)
Логарифмирование — действие, заключающееся в нахождении логарифма числа или выражения.
Логарифмирование является одним из двух действий, обратных возведению в степень. Если (далее…)
Потенцирование — это действие, заключающееся в нахождении числа по данному логарифму через логарифмы других чисел (нем. potenzieren — возводить в степень, от Potenz — степень).
При решении уравнений потенцированием выражения преобразовывают с помощью свойств логарифмов, приводя их к виду
либо к виду
(далее…)
Замена переменной в логарифмических уравнениях в ряде случаев позволяет упростить решение. Самый распространённый пример введения вспомогательной переменной — логарифмические уравнения, сводящиеся к квадратным — мы уже рассмотрели.
Замена переменной в уравнении, содержащем логарифмы в знаменателе, даёт возможность от логарифмического уравнения перейти к дробному рациональному. (далее…)
Взаимно обратные логарифмы — это логарифмы, произведение которых равно единице. В обратных логарифмах основание и выражение под знаком логарифма меняются местами:
и
(далее…)
www.logarifmy.ru
Подготовка к ЕГЭ по математике (видео). Уроки 29-31. Логарифм. Свойства логарифмов. Логарифмирование и потенцирование
Вашему вниманию предлагается видеокурс «Подготовка к ЕГЭ по математике. Базовый и продвинутый уровни». Содержание курса соответствует программам подготовительных курсов на базе высших учебных заведений.
Видеокурс поможет Вам не только подготовиться к успешной сдаче ЕГЭ, но и к продолжению обучения в ВУЗе.
Урок №29. Логарифм числа. Основное логарифмическое тождество
Содержание урока №29:
1. Определение логарифма.
2. Основное логарифмическое тождество.
3. Домашнее задание: https://drive.google.com/open?id=0BwZ—SEjA4BAVm13N3RqZFBFeEE&pageId=111461369108681513628
https://drive.google.com/open?id=0BwZ—SEjA4BAUTB0UThCdUpfUG8&pageId=111461369108681513628
Ответы к ДЗ: https://drive.google.com/open?id=0BwZ—SEjA4BATlJvRllxVVZRcWc&pageId=111461369108681513628
Урок №30. Свойства логарифмов. Решение упражнений
Содержание урока №30:
1. Свойства логарифмов.
3. Домашнее задание: https://drive.google.com/open?id=0BwZ—SEjA4BAZzJlNHpKUTFualU&pageId=111461369108681513628
Ответы к ДЗ: https://drive.google.com/open?id=0BwZ—SEjA4BATlJvRllxVVZRcWc&pageId=111461369108681513628
Урок №31. Логарифмирование и потенцирование
Содержание урока №31:
1. Логарифмирование.
2. Потенцирование.
3. Домашнее задание: https://drive.google.com/open?id=0BwZ—SEjA4BASzlaQ0VRQ3JZSm8&pageId=111461369108681513628
https://drive.google.com/open?id=0BwZ—SEjA4BAaWdVd2ppQXhjUlk&pageId=111461369108681513628
Ответы к ДЗ: https://drive.google.com/open?id=0BwZ—SEjA4BASnlRSFZiWFgxMU0&pageId=111461369108681513628
Смотрите все уроки видеокурса подряд: https://www.youtube.com/playlist?list=PLk91qesJngSI7sHLvugEqFr7TceS0bFzO
math-helper.ru
