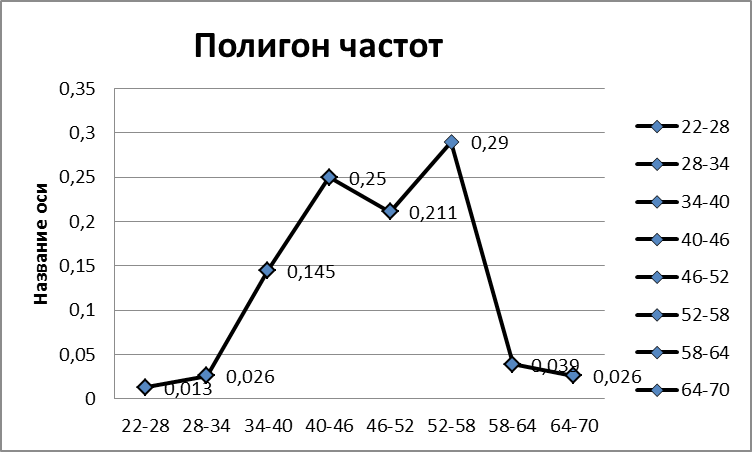
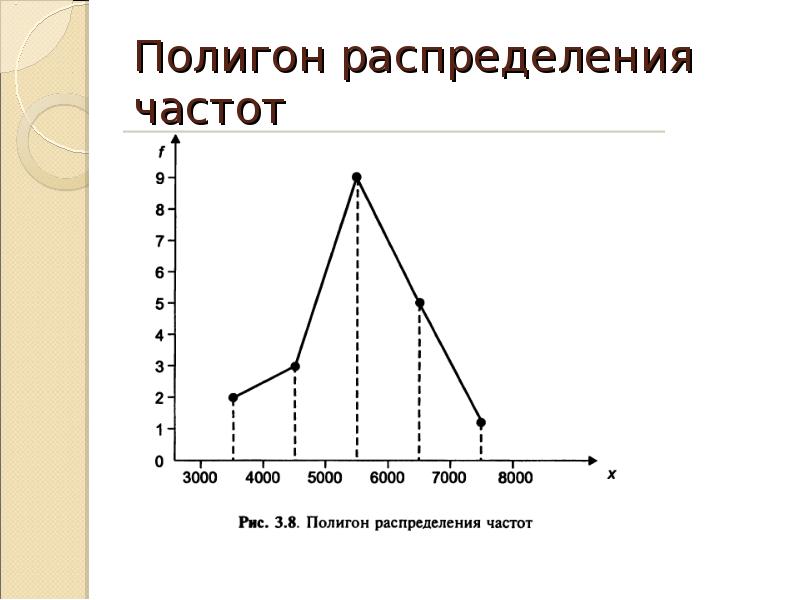
Построить полигон частот онлайн: Полигон и гистограмма частот и частостей (относительных частот). Кумулятивная кривая (кумулята). Огива. Теория вероятностей и математическая статистика
Полигон и гистограмма частот и частостей (относительных частот). Кумулятивная кривая (кумулята). Огива. Теория вероятностей и математическая статистика
Для наглядности строят различные графики статистического распределения, и, в частности, полигон и гистограмму.
Полигон
Полигоном частот называют ломаную, отрезки которой соединяют точки . Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты . Такие точки соединяют отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пример 1
Построить полигон частот и полигон относительных частот (частостей):
| 2 | 7 | 8 | 15 | 16 | 17 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим относительные частоты (частости):
| Относительные частоты, | ||
| 2 | 15 |  075 075
|
| 7 | 35 | 0.175 |
| 8 | 64 | 0.320 |
| 15 | 55 | 0.275 |
| 16 | 21 | 0.105 |
| 17 | 10 | 0.050 |
| Итого | 200 | 1.000 |
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального статистического распределения целесообразно построить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты (в случае равных интервалов) должны быть пропорциональны частотам. При построении гистограммы с неравными интервалами по оси ординат наносят не частоты, а плотность частоты . Это необходимо сделать для устранения влияния величины интервала на распределение и иметь возможность сравнивать частоты.
В случае построения гистограммы относительных частот (гистограммы частостей) высоты в случае равных интегралов должны быть пропорциональны относительной частоте , а в случае неравных интервалов высота равна плотности относительной частоты .
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пример 2
Построить гистограмму частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму частот (случай неравных интервалов).
| 2-4 | 4-8 | 8-13 | 13-15 | 15-17 | 17-20 | |
| 15 | 35 | 64 | 21 | 10 |
Решение
Вычислим плотности частоты:
| Интервалы, | Длина интервала, | Плотность частоты, | |
| 2 – 4 | 15 | 2 |
7. |
| 4 – 8 | 35 | 4 | 8.750 |
| 8 – 13 | 64 | 5 | 12.800 |
| 13 – 15 | 55 | 2 | 27.500 |
| 15 – 17 | 21 | 2 | 10.500 |
| 17 – 20 | 10 | 3 |
3. 333 333
|
| Итого | 200 | — | — |
Гистограмма частот
Кроме этой задачи на другой странице сайта есть пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов.
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.
Пример 4
Построить кумулятивную кривую:
| 2 | 8 | 11 | 14 | 17 | ||
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим накопленные частоты:
| Накопленные частоты, | ||
| 2 | 15 | 15 |
| 7 | 35 | 50 |
| 8 | 64 | 114 |
| 15 | 55 | 169 |
| 16 | 21 | 190 |
| 17 | 10 | 200 |
| Итого | 200 | — |
Кумулятивная кривая
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
25 лет я занимаюсь решением задач и потратил на это кучу времени. Вы можете освободить свое, стоит только обратиться за помощью.
онлайн гистограмма
Калькулятор строит гистограмму.
Количество групп можно определять по формуле Стерджесса, а можно и задавать вручную.
Работает калькулятор довольно просто — вам нужно ввести входные данные, сейчас перед вами уже есть данные вместе с графиком — это все нужно очистить, так как сделано для иллюстрации работы калькулятора. Вам нужно ввести свои данные, также нужно выбрать способ разбиения на группы, после чего калькулятор построит вам гистограмму.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Построить полигон частот по данному распределению выборки онлайн
Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдалось п1 раз, х2 – п2 раз, хк – пк раз и — объем выборки. Наблюдаемые значения х1 называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.
Число наблюдений варианты называют частотой, а ее отношение к объему выборки — относительной частотой .
Определение. Статистическим (эмпирическим) законом распределения выборки, или просто статистическим распределением выборки называют последовательность вариант и соответствующих им частот пiили относительных частот .
Статистическое распределение выборки удобно представлять в форме таблицы распределения частот, называемой статистическим дискретным рядом распределения:
(сумма всех частот равна объему выборки )
или в виде таблицы распределения относительных частот:
(сумма всех относительных частот равна единице ).
Пример 1. При измерениях в однородных группах обследуемых получены следующие выборки: 71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72, 72, 74, 72, 73, 72,74 (частота пульса). Составить по этим результатам статистический ряд распределения частот и относительных частот.
2) Объем выборки: п = 2 + 4 + 8 + 2 + 4 = 20. Найдем относительные частоты, для чего разделим частоты на объем выборки :
Найдем относительные частоты, для чего разделим частоты на объем выборки :
;
Полигоном частот называют ломаную, отрезки, которой соединяют точки Для построения полигона частот на оси абсцисс откладывают варианты х2, а на оси ординат – соответствующие им частоты пi. Точки соединяют отрезками и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки . Для построения полигона относительных частот на оси абсцисс откладывают варианты хi, а на оси ординат соответствующие им частоты wi. Точки соединяют отрезками и получают полигон относительных частот
Пример 2. Постройте полигон частот и полигон относительных частот по данным примера 1.
Решение: Используя дискретный статистический ряд распределения, составленный в примере 1 построим полигон частот и полигон относительных частот:
Статистическим дискретным рядом (или эмпирической функцией распределения) обычно пользуются в том случае, когда отличных друг от друга вариант в выборке не слишком много, или тогда, когда дискретность по тем или иным причинам существенна для исследователя.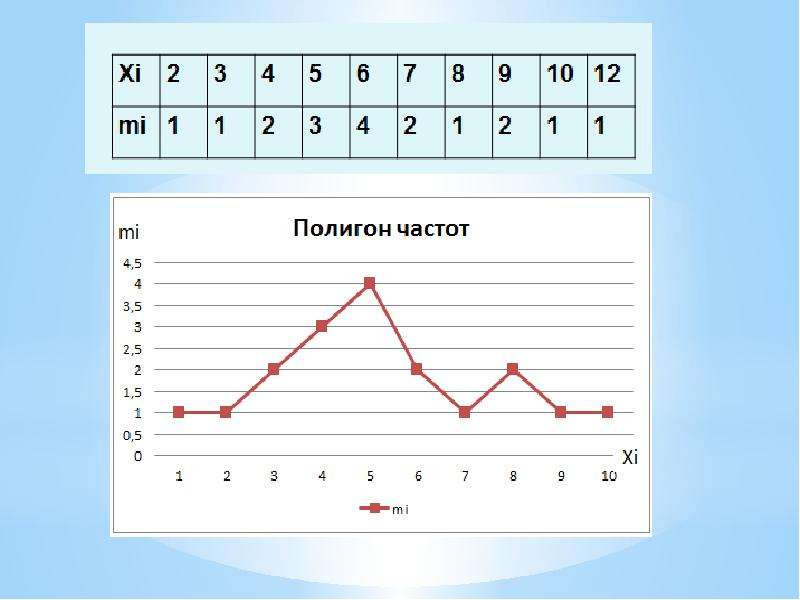 Если же интерисующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно ( или невозможно) учитывать, то варианты группируются в интервалы.
Если же интерисующий нас признак генеральной совокупности Х распределен непрерывно или его дискретность нецелесообразно ( или невозможно) учитывать, то варианты группируются в интервалы.
Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
2. k-число групп
3. (формула Стерджеса)
5.
Полученную группировку удобно представить в форме частотной таблицы, которая носит название статистический интервальный ряд распределения:
Исследовать сходимость ряда примеры с решением
Непрерывный интервальный ряд распределения. Гистограмма
1. Непрерывный интервальный ряд распределения. Гистограмма. Практическое применение.
Подготовили: Чагай Н. 319 “А”,Мендихан А. 319 “Б”
2. Введение
Статистический ряд распределения — этоупорядоченное количественное
распределение единиц совокупности на
однородные группы по варьирующему
(атрибутивному или количественному)
признаку.

Вариационными называются ряды
распределения, построенные по
количественному признаку, т.е. признаку,
имеющему числовое выражение.
3. Интервальный вариационный ряд
Интервальный вариационный ряд распределения(ИВРР) — это ряд распределения, в котором
группировочный признак, составляющий основание
группировки, может принимать в интервале любые
значения, отличающиеся друг от друга на сколь
угодно малую величину.
ИВР используют:
1. При непрерывной вариации признака ,
2. В тех ситуациях, когда исследуемая величина
принимает слишком много различных значений.
4. Как построить ИВР
• Для исследования ИВР определяетсяинтервал, в пределах которого варьируются
значения, затем данный интервал делится
на частичные интервалы, и по каждому
интервалу подсчитываются частоты –
количество вариант, которые в него
попали.
5. Последовательность шагов:
1. Построить ранжированный ряд2.
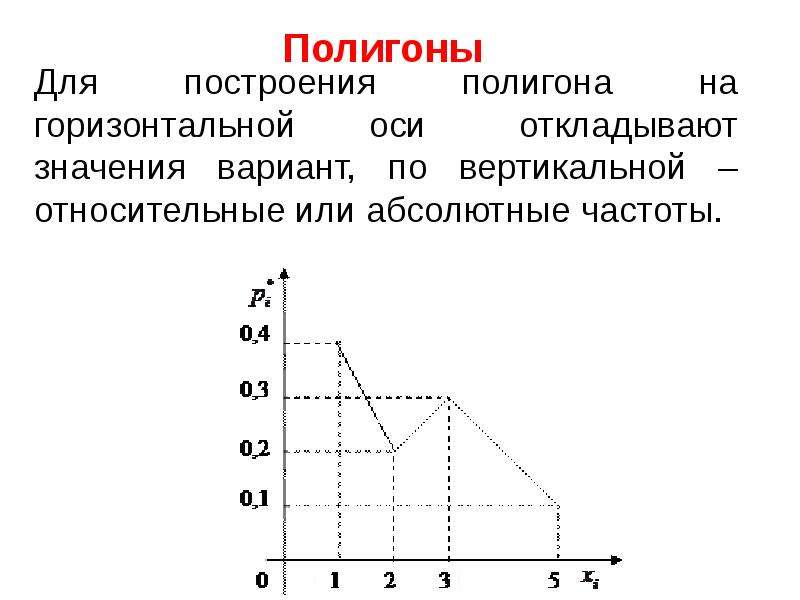 Вычислим размах вариации (R):
Вычислим размах вариации (R):общий интервал
6. Последовательность шагов:
3. Общий интервал нужно разбить на частичныеинтервалы. Для определения их количества
существует формула Стерджеса:
• lg n – десятичный логарифм от объёма выборки,
• к – оптимальное количество интервалов, при этом
результат округляют до ближайшего левого целого
значения.
7. Последовательность шагов:
• Длины частичных интервалов могут бытьразличны, для их определения
используется следующая формула:
i=R/k
• R – размах вариации
• к – число интервалов
8. Гистограмма
• Гистограмма относительных частот –это фигура, состоящая из прямоугольников,
ширина которых равна длинам частичных
интервалов, а высота – относительным
частотам:
9. Полигон
• полигон относительных частот – этоломаная, соединяющая соседние точки
середины интервалов
10. Пример
11. Практическое применение
Представление данных в виде гистограммы
Чтобы создать гистограмму, сделайте следующее:
-
Введите данные в электронную таблицу.

-
Выделите данные.
-
В зависимости от используемой версии Excel выполните одно из указанных ниже действий.
-
Excel 2016: на вкладке Вставка щелкните значок Вставить гистограмму или линейчатую диаграмму, а затем выберите нужный тип гистограммы.
-
Excel 2013: на вкладке Вставка щелкните значок Вставить гистограмму, а затем выберите нужный тип гистограммы.
-
Excel 2010 и Excel 2007: на вкладке Вставка щелкните значок Гистограмма, а затем выберите нужный тип гистограммы.

Вы можете при необходимости отформатировать диаграмму. Ниже описаны некоторые варианты.
Примечание: Перед применением форматирования нужно щелкнуть диаграмму.
-
Чтобы изменить макет диаграммы, щелкните Конструктор > Макет диаграммы и выберите макет.
-
Чтобы изменить стиль диаграммы, щелкните Конструктор > Стили диаграмм и выберите стиль.
-
Чтобы применить другой стиль фигуры, щелкните Формат > Стили фигур и выберите стиль.
Примечание: Стили фигур отличаются от стилей диаграмм. Стиль фигуры — это форматирование, применяемое к границе диаграммы, а стиль диаграммы — это форматирование, которое применяется ко всей диаграмме.

-
Чтобы применить различные эффекты, выберите Формат > Эффекты фигуры и выберите нужный вариант, например Рельеф или Свечение, и его параметры.
-
Чтобы применить тему, щелкните Разметка страницы > Темы и выберите тему.
-
Чтобы изменить форматирование определенного компонента диаграммы (например, вертикальной оси (значений), горизонтальной оси (категорий) или области диаграммы), щелкните Формат, выберите компонент в раскрывающемся списке Элементы диаграммы, щелкните Формат выделенного фрагментаи внесите необходимые изменения. Повторите это действие для каждого компонента, который вы хотите изменить.

Примечание: Если вы хорошо знакомы с диаграммами, вы также можете щелкнуть правой кнопкой мыши определенную область на диаграмме и выбрать параметр форматирования.
-
Чтобы создать гистограмму, сделайте следующее:
-
В окне сообщения выберите Вставка > Диаграмма.
-
В диалоговом окне Вставка диаграммы щелкните Гистограмма, выберите нужный тип гистограммы и нажмите кнопку ОК.
В разделенном окне откроется лист Excel с примером данных.
-
Замените их собственными данными.
Примечание: Если на диаграмме не отображаются данные листа, перетащите вертикальные линии вниз до последней строки таблицы.

-
При необходимости вы можете сохранить лист:
-
Щелкните значок Измените данные Microsoft Excel на панели быстрого доступа.
Лист откроется в Excel.
-
Сохраните лист.
Совет: Чтобы повторно открыть лист, щелкните Конструктор > Изменить данные и выберите нужный вариант.
Вы можете при необходимости отформатировать диаграмму. Ниже описаны некоторые варианты.
Примечание: Перед применением форматирования нужно щелкнуть диаграмму.
-
Чтобы изменить макет диаграммы, щелкните Конструктор > Макет диаграммы и выберите макет.

-
Чтобы изменить стиль диаграммы, щелкните Конструктор > Стили диаграмм и выберите стиль.
-
Чтобы применить другой стиль фигуры, щелкните Формат > Стили фигур и выберите стиль.
Примечание: Стили фигур отличаются от стилей диаграмм. Стиль фигуры — это форматирование, применяемое к границе диаграммы, а стиль диаграммы — это форматирование, которое применяется ко всей диаграмме.
-
Чтобы применить различные эффекты, выберите Формат > Эффекты фигуры и выберите нужный вариант, например Рельеф или Свечение, и его параметры.
-
Чтобы изменить форматирование определенного компонента диаграммы (например, вертикальной оси (значений), горизонтальной оси (категорий) или области диаграммы), щелкните Формат, выберите компонент в раскрывающемся списке Элементы диаграммы, щелкните Формат выделенного фрагментаи внесите необходимые изменения.
 Повторите это действие для каждого компонента, который вы хотите изменить.
Повторите это действие для каждого компонента, который вы хотите изменить.Примечание: Если вы хорошо знакомы с диаграммами, вы также можете щелкнуть правой кнопкой мыши определенную область на диаграмме и выбрать параметр форматирования.
-
Построение вариационного ряда
Министерство образования и науки РФ
Государственное образовательное учреждение
Высшего профессионального образования
«Алтайская государственная педагогическая академия»
Институт физико-математического образования
«Построение вариационного ряда»
Реферат
Выполнил: студент
4 курса, 372группы
Сорокин А. Б.
Б.
Барнаул 2010
Оглавление:
Вариационным ряд. 3
Дискретный вариационный ряд. 3
Интервальный вариационный ряд. 3
Частота. 3
Формула Стерджеса. 3
Обобщающие количественные показатели. 3
Средняя арифметическая. 4
Медиана. 4
Мода. 4
Размах вариации. 4
Дисперсия. 5
5
Стандартное отклонение. 5
Коэффициент вариации. 5
Пример 1. 6
Пример 2. 6
Пример 3. 6
Пример 4. 7
Пример 5. 8
Пример 6. 8
Пример 7. 10
Пример 8. 11
Пример 9. 12
Пример 10. 13
Список используемых источников: 15
Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им частотами или частостями
В зависимости от вида вариации может быть дискретным или интервальным. Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и интервальным, если варианты могут отличаться один от другого на сколь угодно малую величину. Интервалы в ряду могут быть как равными, так и неравными. Это зависит от характера статистических данных и задач исследования.
Определение числа интервалов (m) проводится согласно формуле Стерджеса m=1+3,322
lg n, а величина интервала xmax,xmin-наибольшее
и наименьшее значение признака соответственно.
Каждой варианте Xi соответствует частота Ni, т.е. величина, показывающая сколько раз данное значение варианты встречается в ряду. При построении вариационного ряда можно использовать не частоты, а частости Qi, которые вычисляются как отношения соответствующих частот к объему всей совокупности.
Qi = Ni/Сумма (Ni). Частости могут быть выражены в относительных числах (дроби) или в процентах.
Обобщающие количественные показатели (характеристики) в исследовании: вскрывают общие свойства имеющейся совокупности статистических данных; показывают тенденцию развития явления или процесса; нивелируют случайные индивидуальные отклонения изучаемого признака у некоторых объектов; позволяют сравнивать вариационные ряды; используются во всех разделах математической статистики при более сложном и полном анализе данных.
Средняя арифметическая: ,
где — объем совокупности значений в ряду
ni – частота варианты в ряду
xi – варианты с порядковым номером i
k – число вариант в ряду
При расчете средней арифметической в интервальном ряду за
значение варианты принимается середина интервала. Середина интервала вычисляется как среднее арифметическое его границ.
Середина интервала вычисляется как среднее арифметическое его границ.
Медиана (Ме) Срединное значение варьирующего признака в упорядоченном (ранжированном) ряду. Применяется в случаях, когда совокупность статистических данных неоднородна (асимметрична), поскольку Ме менее чувствительна к средним значениям ряда, чем средняя арифметическая.
Мода (Мо) Наиболее часто встречающаяся в ряду варианта. В интервальном вариационном ряду определяется модальный интервал. Мо используется для характеристики среднего уровня в неоднородных совокупностях, как и медиана.
Размах вариации (R) — разность максимального и минимального значений периода в вариационном ряду.
R=xmax-xmin
Зависит от случайных колебаний выборки, т.е. для вычисления R используются лишь крайние значения варианты.
Дисперсия — представляет собой среднюю
арифметическую квадратов отклонений всех вариант от их средней арифметической.
где
xi – варианты с порядковым номером i
– среднее арифметическое
k – число вариант в ряду
ni – частость ( частота) с порядковым номером i
Стандартное отклонение (среднее квадратическое отклонение) — квадратный корень из дисперсии. Используется исследователями чаще, чем дисперсия, так как вычисляется в тех же единицах измерения, что и варианты.
Коэффициент вариации (V) Относительный показатель рассеяния значений варианты. Достоинства: позволяет сравнивать вариацию одного и того же признака в разных совокупностях; позволяет выявить степень различия одного и того же признака у одной и той же группы объектов в разное время; сопоставить вариацию значений разных признаков у одной и той же группы объектов.
()
Если коэффициент вариации
признака, принимающего только положительные значения, высок ( например, более
100%), то, как правило, это свидетельствует о неоднородности значений признака.
Пример 1: α частицы, достигающие счетчика в некотором опыте, образуют следующую выборку:
|
хi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
mi |
21 |
81 |
156 |
200 |
195 |
152 |
97 |
54 |
26 |
11 |
7 |
Найдите выборочную
среднюю, моду и медиану для числа α — частиц, достигающих
счетчика.
=
Mo=3
Me=5
Пример 2:Измерение веса (в кг.) 100 телят совхоза «Луч» дало следующие результаты:
|
Вес |
154-158 |
158-162 |
162-166 |
166-170 |
170-174 |
174-178 |
178-182 |
|
Число телят |
10 |
14 |
26 |
28 |
12 |
8 |
2 |
Найдите выборочную среднюю и выборочное среднее квадратическое
отклонение веса телят.
Решение. В качестве хi примем середины интервалов и найдем выборочную среднюю веса телят.
=0,01·(156∙10+160∙14+164∙26+168∙28+172·12+176·8+180·2)=166 (кг.)
Вычислим теперь выборочную дисперсию:
S2=0,01·((-10)2·10+(-6)2·14+(-2)2·26+22·28+62·12+102·8+142·2)=33,44
и, извлекая из полученного числа корень квадратный, находим среднее квадратическое отклонение:
S=5,78 (кг.)
Пример 3: Имеются данные о количестве студентов в 30 группах физико-математического факультета:
|
26 |
25 |
25 |
26 |
25 |
23 |
|
23 |
24 |
19 |
23 |
20 |
19 |
|
22 |
24 |
24 |
23 |
20 |
23 |
|
24 |
19 |
21 |
18 |
21 |
18 |
|
20 |
18 |
18 |
21 |
15 |
15 |
Найти вариационный ряд количества студентов в
группах и размах варьирования. Построить полигон частот.
Построить полигон частот.
Решение. Записывая исходные данные в порядке возрастания, составим вариационный ряд:
|
хi |
15 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
mi |
2 |
4 |
2 |
4 |
3 |
1 |
5 |
4 |
3 |
2 |
Размах варьирования R=xmax-xmin=26-15=11
Для построения полигона частот
обозначим на оси абсцисс возможные значения признака, а на оси ординат
соответствующие частоты mi и полученные точки соединим
отрезками.
Пример 4: Школьникам предлагалось разгадать несколько числовых закономерностей и вписать в пропуски недостающие числа. Оценка осуществлялась по количеству правильно решенных задач и дала следующие результаты:
|
Кол-во баллов |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Кол-во школьников |
2 |
3 |
2 |
4 |
12 |
10 |
8 |
9 |
Составить статистическое
распределение количества школьников по количеству набранных баллов и построить
полигон относительных частот.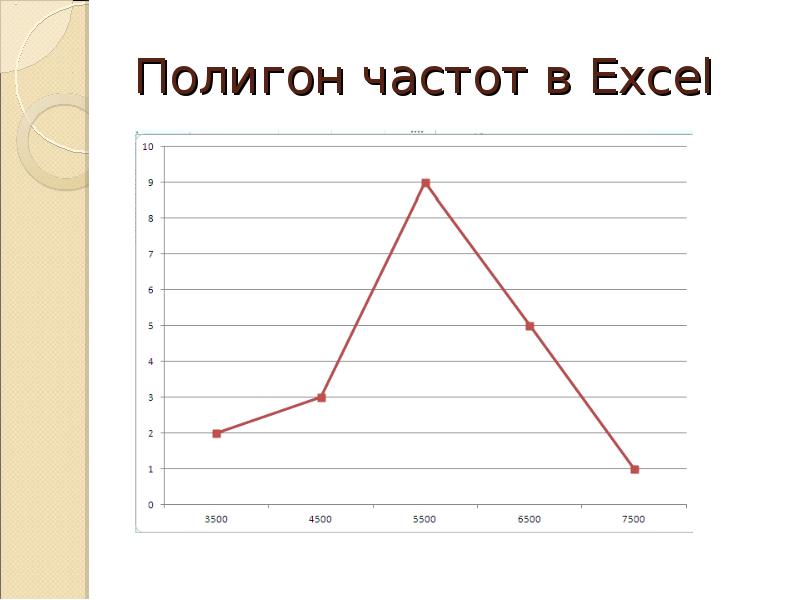
Решение. Пусть Х={количество набранных баллов}, a f = {относительные частоты}. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:
|
X |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
f |
0,04 |
0,06 |
0,04 |
0,08 |
0,24 |
0,2 |
0,16 |
0,18 |
Чтобы построить полигон относительных частот,
отложим на оси абсцисс значения X, а
на оси ординат — относительные частоты f. После этого
последовательно соединим полученные точки отрезками.
После этого
последовательно соединим полученные точки отрезками.
Пример 5: Распределение рабочих цеха по проценту выполнения норм выработки выглядит следующим образом:
|
% выполнения норм |
50 — 70 |
70 — 90 |
90 — 110 |
110 — 130 |
130 — 150 |
150 — 170 |
|
Число рабочих |
20 |
25 |
35 |
30 |
20 |
10 |
Найдите средний процент выполнения норм выработки
рабочими цеха.
Решение.
Пример 6: Над случайной величиной X проведено 100 независимых испытаний, в результате чего получена выборка.
|
1.49 |
1.44 |
1.68 |
1.19 |
3,93 |
2,34 |
7,08 |
1,56 |
0,46 |
1,14 |
|
0,60 |
3,58 |
1,32 |
2. |
4,32 |
0,78 |
1,63 |
2,13 |
2,22 |
3,36 |
|
1.26 |
0,89 |
2,35 |
1,59 |
2,38 |
0,80 |
1,23 |
0,78 |
1,65 |
0,95 |
|
0,34 |
0,64 |
0,26 |
3,05 |
0,68 |
0,96 |
0,69 |
1,77 |
1,02 |
1,07 |
|
0,69 |
2,02 |
3,42 |
4,35 |
2,66 |
1 |
1,85 |
3,25 |
0,93 |
1,44 |
|
1,63 |
3. |
1,16 |
1,44 |
0.45 |
2,41 |
0,87 |
0,81 |
2,85 |
1.94 |
|
1,25 |
1,90 |
0,72 |
2.05 |
2,38 |
1.80 |
2,88 |
2,02 |
1,26 |
1,11 |
|
0,54 |
0,94 |
1,71 . |
1,52 |
1,38 |
1,32 |
1,01 |
0,79 |
1,71 |
0,99 |
|
0.78 |
0,99 |
1,60 |
2.07 |
2,11 |
1.47 |
0.84 |
1,95 |
0,28 |
2,36 |
|
2,01 |
1,51 |
0,95 |
3,17 |
1,08 |
1,09 |
2. |
1,88 |
2,64 |
4,80. |
Требуется составить интервальный вариационный ряд и построить гистограмму относительных частот.
Решение. Количество интервалов разбиения считаем по формуле Стерджесса
m=1+3,322·lg n=1+6,664≈8
Минимальное значение элемента выборки 0,26. Максимальное 7,08. Для удобства разбиения выберем интервал (0; 7,2) с шагом разбиения
|
Интервал |
Абсолютная частота |
Относительная частота |
Середина интервала |
|
(0;0. |
21 |
0.21 |
0.45 |
|
(0.9; 1.8) |
41.5 |
0.415 |
1.35 |
|
(1.8; 2.7) |
23.5 |
0.235 |
2.25 |
|
(2.7; 3.6) |
9 |
0. |
3.15 |
|
(3.6; 4.5) |
3 |
0.03 |
4.05 |
|
(4.5; 5.4) |
1 |
0.01 |
4.95 |
|
(5.4; 6.3) |
0 |
0.00 |
5.85 |
|
(6. |
1 |
0.01 |
6.75 |
Пример 7: Суммарное число набранных баллов в соревнованиях:
|
Кол-во баллов |
49-52 |
52-55 |
55-58 |
58-61 |
61-64 |
64-67 |
67-70 |
|
Кол-во участников |
3 |
6 |
11 |
19 |
30 |
21 |
10 |
Построить гистограмму относительных
частот.
Решение. Пусть Х={количество набранных баллов}, a f = {относительные частоты}. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:
|
X |
49-52 |
52-55 |
55-58 |
58-61 |
61-64 |
64-67 |
67-70 |
|
f |
0,03 |
0,06 |
0,11 |
0,19 |
0,3 |
0,21 |
0,1 |
Пример 8: Горизонтальное отклонение от цели (м) для 200 испытаний ракет:
|
Границы интервалов |
-40– -30 |
-30– -20 |
-20– -10 |
-10– 0 |
0 – 10 |
|
Частоты |
7 |
11 |
15 |
24 |
49 |
|
Границы интервалов |
10–20 |
20–30 |
30–40 |
40–50 |
50–60 |
|
Частоты |
41 |
26 |
17 |
7 |
3 |
Найдите выборочную
среднюю и выборочное среднее квадратическое отклонение от цели.
Решение. В качестве хi примем середины интервалов и найдем выборочную среднее отклонение пули.
=8,6
Вычислим теперь выборочную дисперсию:
377,04
и, извлекая из полученного числа корень квадратный, находим среднее квадратическое отклонение:
S=19,42
Пример 9:Дан дискретный ряд распределения 50 рабочих механического цеха по тарифному разряду
|
Тарифный разряд хi |
1 |
2 |
3 |
4 |
5 |
6 |
|
Частота(кол-во рабочих) ni |
2 |
3 |
6 |
8 |
22 |
9 |
Построить полигон распределения по
данным таблицы и найти выборочную
среднюю.
Решение. Пусть Х={количество тарифных разрядов}, a f = {относительные частоты}. Тогда статистическое распределение выборки можно представить в виде следующей таблицы:
|
X |
1 |
2 |
3 |
4 |
5 |
6 |
|
f |
0,04 |
0,06 |
0,12 |
0,16 |
0,44 |
0,18 |
Чтобы построить полигон относительных частот,
отложим на оси абсцисс значения X, а
на оси ординат — относительные частоты f. После этого
последовательно соединим полученные точки отрезками.
После этого
последовательно соединим полученные точки отрезками.
Пример 10: X-число сделок на фондовой бирже за квартал; N=400 (инвесторов)
|
xi |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ni |
146 |
97 |
73 |
34 |
23 |
10 |
6 |
3 |
4 |
2 |
2 |
1) Построить полигон
2) Найти числовые характеристики вариационного ряда
а) Среднюю арифметическую
б) Дисперсию
в) Среднее квадратическое отклонение
г) Коэффициент вариации
Решение. 1)
1)
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
f |
0,365 |
0,2425 |
0,1825 |
0,085 |
0,0575 |
0,025 |
0,015 |
0,0075 |
0,01 |
0,005 |
0,005 |
3) а)
4) б)
в)
г)
1. Борисенко О. В.
Теория вероятностей и математическая статистика: Учебное – методическое
пособие. – Барнаул: Изд-во БГПУ. – 50 с.
Борисенко О. В.
Теория вероятностей и математическая статистика: Учебное – методическое
пособие. – Барнаул: Изд-во БГПУ. – 50 с.
2. Вуколов Э. А. Сборник задач по математике для вузов. В 4 частях. Ч. 4: Учебное пособие для вузов / Под общ. Ред. А. В. Ефимома и А. С. Поспелова. – 3-е изд. Перераб. И доп. – М.: Издательство Физико-математической литературы, 2003. – 432 с.
как построить, гистограмма частот для выборки
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
ОпределениеПолигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),. .., (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
.., (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(W_i=\frac{n_i}n\)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
ОпределениеГистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
\(\frac{n_ih}h=n_i\)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Многоугольник частот — Обзор, Как создать в Excel, пример
Что такое многоугольник частот?
Полигон частот — это визуальное представление распределения. Инструмент визуализации используется для понимания формы распределения. По сути, полигон частот указывает количество вхождений для каждого отдельного класса в наборе данных. Кроме того, график может использоваться для отображения кумулятивного распределения частот. Кумулятивное распределение частот. Кумулятивное распределение частот представляет собой форму распределения частот, которая представляет собой сумму класса и всех классов ниже него..
Кумулятивное распределение частот представляет собой форму распределения частот, которая представляет собой сумму класса и всех классов ниже него..
Полигон частот представляет собой кривую, построенную по осям x и y. По оси X представлены значения в наборе данных, а по оси Y — количество вхождений каждой отдельной категории.
Полигон частот может служить альтернативой гистограммеГистограммаГистограмма используется для суммирования дискретных или непрерывных данных. Другими словами, гистограмма обеспечивает визуальную интерпретацию числовых данных, показывая количество точек данных, попадающих в указанный диапазон значений (называемых «бинами»).Гистограмма похожа на вертикальную гистограмму. Тем не менее, гистограмма. Оба визуальных представления прекрасно отражают форму распределения. Однако, в отличие от гистограммы, полигон частот можно легко использовать для сравнения нескольких распределений на одном графике. В некоторых случаях можно одновременно использовать гистограмму и полигон частот, чтобы получить более точное представление о форме распределения.
Как создать полигон частот в Excel?
Excel может быть удобным и простым инструментом для создания полигона частот распределения.Полигон частот можно создать, выполнив следующие шаги:
- Определите классы в наборе данных, задав нижний и верхний пределы каждого класса и расположив их в одном столбце.
- Определите средние точки каждого класса. Средние точки можно найти по следующей формуле:
Средняя точка = (Нижний предел + Верхний предел) / 2
Идентифицированные средние точки должны располагаться в отдельном столбце.
- Рассчитайте частоты для каждого класса и расположите их в отдельной колонке.
- Чтобы гарантировать, что наш граф действительно является многоугольником (т. е. граф имеет замкнутую форму), мы должны включить первый и последний класс с нулевыми частотами.
- Выделите столбец, содержащий средние точки для каждого класса, и столбец, содержащий частоты.

- Выберите Вставить -> Графики -> Вставить разброс -> Разброс с прямыми линиями .
Пример многоугольника частот
Вы финансовый аналитикЧем занимается финансовый аналитикЧем занимается финансовый аналитик? Собирайте данные, систематизируйте информацию, анализируйте результаты, составляйте прогнозы и прогнозы, рекомендации, модели Excel, отчеты в розничном бизнесе.Вы готовите отчет о текущем финансовом состоянии компании. В одной части отчета описывается управление кредиторской задолженностью компании. Кредиторская задолженность. Кредиторская задолженность — это обязательство, возникающее, когда организация получает товары или услуги от своих поставщиков в кредит. Кредиторская задолженность есть. Вы получаете данные, определяющие, сколько дней требуется для расчета по каждому счету.
Вам необходимо создать полигон частот, который будет отражать распределение кредиторской задолженности. Используя данные из таблицы выше, давайте создадим полигон частот:
Используя данные из таблицы выше, давайте создадим полигон частот:
1. Классы в наборе данных перечислены в первом столбце таблицы выше.
2. Средние точки для каждого класса можно рассчитать следующим образом: ) / 2 = 4
Середина (5-7) = (5 + 7) / 2 = 6
Середина (7-9) = (7 + 9) / 2 = 8
3 .Частоты для каждого класса перечислены во втором столбце таблицы выше.
4. Чтобы наш график имел замкнутую форму, необходимо определить первый и последний класс с нулевыми частотами. Первый класс — нулевые дни с нулевой частотой. Последний класс — 10-12 дней (он должен показывать такой же спред, как и другие классы) и нулевая частота.
5. Таблица ввода для создания полигона частот представлена ниже:
- Выберите столбцы Mid-Point и Frequency .Затем выберите Insert -> Charts -> Insert Scatter -> Scatter with Straight Lines .
 Полигон частот должен выглядеть так, как показано на графике вверху этой статьи.
Полигон частот должен выглядеть так, как показано на графике вверху этой статьи.
Дополнительные ресурсы
CFI является официальным поставщиком глобального финансового моделирования и аналитика оценки (FMVA)™. помочь вам обрести уверенность, которая вам нужна в вашей финансовой карьере.Зарегистрируйтесь сегодня! программа сертификации, разработанная, чтобы помочь каждому стать финансовым аналитиком мирового уровня. Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI:
- Основные понятия статистики в финансахОсновные понятия статистики в финансахПолное понимание статистики крайне важно, чтобы помочь нам лучше понять финансы. Кроме того, концепции статистики могут помочь инвесторам отслеживать
- Ожидаемое значениеОжидаемое значениеОжидаемое значение (также известное как EV, ожидание, среднее или среднее значение) представляет собой долгосрочное среднее значение случайных величин.
 Ожидаемое значение также указывает
Ожидаемое значение также указывает - Распределение ПуассонаРаспределение ПуассонаРаспределение Пуассона — это инструмент, используемый в статистике теории вероятностей для прогнозирования величины отклонения от известной средней частоты возникновения в пределах
- Правило общей вероятностиПравило общей вероятностиПравило общей вероятности (также известное как закон полной вероятности) является основным правилом в статистике, относящимся к условным и предельным
Создайте полигон частот в SAS
Недавно меня спросили, как создать полигон частот в SAS.Полигон частот является альтернативой гистограмме, которая показывает аналогичную информацию о распределении одномерных данных. Это кусочно-линейная кривая, образованная соединением средних точек вершин бункеров. На графике справа показаны гистограмма и полигон частот для тех же данных. В этой статье показано, как создать полигон частот в SAS.
На практике полигоны частот используются не так часто, как гистограммы, но они являются полезным педагогическим инструментом для обучения основам оценки плотности. Гистограмма — это оценка плотности одномерных данных, но это столбчатая диаграмма. Соответственно, он выглядит иначе, чем кривые оценки плотности, такие как параметрические плотности и оценки ядерной плотности.
Полигон частот показывает ту же информацию, что и гистограмма, но отображает информацию в виде линейного графика. Таким образом, вам будет легче сравнивать кривую многоугольника частоты и другие кривые оценки плотности.
Гистограмма — это оценка плотности одномерных данных, но это столбчатая диаграмма. Соответственно, он выглядит иначе, чем кривые оценки плотности, такие как параметрические плотности и оценки ядерной плотности.
Полигон частот показывает ту же информацию, что и гистограмма, но отображает информацию в виде линейного графика. Таким образом, вам будет легче сравнивать кривую многоугольника частоты и другие кривые оценки плотности.
Полигон частот также является хорошим способом представить идеи, лежащие в основе кумулятивного распределения.Оживой называется график кумулятивной суммы вертикальных координат полигона частот. Ожив аппроксимирует кумулятивное распределение таким же образом, как полигон частот аппроксимирует плотность.
Создайте полигон частот в SAS
Вы можете использовать процедуру UNIVARIATE в SAS для создания точек для многоугольника частот.
Вы можете использовать параметр OUTHIST=, чтобы указать набор данных, содержащий количество для каждого столбца гистограммы. Средние точки интервалов гистограммы содержатся в переменной _MIDPT_. Количество в каждой ячейке равно
содержится в переменной _COUNT_.
Средние точки интервалов гистограммы содержатся в переменной _MIDPT_. Количество в каждой ячейке равно
содержится в переменной _COUNT_.
Если вам не нравится ширина столбцов гистограммы по умолчанию, вы можете использовать параметр MIDPOINTS=, чтобы задать собственный набор средних точек. Например, следующие операторы создают гистограмму для переменной EngineSize в наборе данных Sashelp.Cars. Вы можете использовать оператор SERIES в PROC SGPLOT для создания линейного графика, отображающего вертикальную высоту каждого столбца гистограммы, следующим образом:
proc univariate data=sashelp.автомобили (держать = EngineSize);
вар Размер двигателя;
гистограмма / outhist = сетка OutHist vscale = количество
средние точки = (от 1,4 до 8,4 на 0,4); /* используйте опцию midpoints=, чтобы указать средние точки */
бегать;
/* опционально, распечатать данные OutHist */
/* proc print data=OutHist; бегать; */
заголовок «Полигон частот»;
данные proc sgplot = OutHist;
серия x=_MIDPT_ y=_COUNT_ / маркеры;
значения сетки по оси y=(от 0 до 80 на 20) label="Count" offsetmin=0;
значения сетки по оси x = (от 1,4 до 8,4 на 0,4) label="Объем двигателя (л)";
бегать; |
Показан полигон частот. Как и гистограмма, форма полигона частот зависит от
Ширина бункера и положение якоря. Вы можете изменить эти значения, используя параметр MIDPOINTS=.
Как и гистограмма, форма полигона частот зависит от
Ширина бункера и положение якоря. Вы можете изменить эти значения, используя параметр MIDPOINTS=.
Наложение полигона частот и оценки плотности ядра
Как я упоминал ранее, преимущество полигона частот в том, что он кривая, а не гистограмма. Таким образом, его легче сравнивать с другими кривыми оценки плотности. В PROC UNIVARIATE вы можете использовать опцию KERNEL для наложения кривой плотности ядра на гистограмму.Вы можете использовать параметр OUTKERNEL= для записи оценки плотности ядра в набор данных. Затем вы можете наложить и сравнить кривую частоты (грубая оценка на основе гистограммы) и оценку плотности ядра следующим образом:
proc univariate data=sashelp.cars(keep=EngineSize);
вар Размер двигателя;
гистограмма / outhist = сетка OutHist vscale = количество
внешнее ядро = OutKer
средние точки = (от 1,4 до 8,4 на 0,4); /* используйте опцию midpoints=, чтобы указать средние точки */
или выберите «Гистограмма моментов»;
бегать;
плотность данных; /* объединяем оценки */
установить OutHist OutKer(rename=(_Count_=KerCount));
бегать;
заголовок «Оценка полигона частот и плотности ядра»;
данные proc sgplot = Плотность;
серия x=_MIDPT_ y=_COUNT_ / legendlabel="Полигон частоты";
series x=_VALUE_ y=KerCount / legendlabel="Оценка плотности ядра";
yaxis offsetmin=0 значения сетки=(от 0 до 80 на 20) label="Расчетное количество";
xaxis label="Объем двигателя (л)";
бегать; |
Как показано на графике, оценка плотности ядра представляет собой более сглаженную версию многоугольника частот.
Резюме
В этой статье показано, как создать график полигона частот в SAS. Многоугольник частот представляет собой кусочно-линейную кривую, образованную путем соединения средних точек вершин столбцов гистограммы. Полигон частот представляет собой кривую, поэтому его легче сравнивать с другими параметрическими или непараметрическими оценки плотности.
Последнее замечание: мне не нравится название «полигон частот». Многоугольник представляет собой 90 165 замкнутую 90 166 плоскую область, образованную путем соединения набора точек, а затем соединения первой и последней точек.Оценка плотности в этой статье не является закрытой. Я бы предпочел такие термины, как «полилиния частоты» или «кривая частоты», но «полигон», кажется, является стандартным термином, который появляется во вводных учебниках по статистике.
2.2.1: Полигоны частот и графики временных рядов
Полигоны частот
Частотные полигоны аналогичны линейным графикам, и точно так же, как линейные графики делают непрерывные данные визуально простыми для интерпретации, то же самое можно сказать и о частотных полигонах. Чтобы построить многоугольник частот, сначала проверьте данные и выберите количество интервалов или интервалов классов, которые будут использоваться на осях x и y . После выбора соответствующих диапазонов начните рисовать точки данных. После того, как все точки нанесены, нарисуйте отрезки, чтобы соединить их.
Чтобы построить многоугольник частот, сначала проверьте данные и выберите количество интервалов или интервалов классов, которые будут использоваться на осях x и y . После выбора соответствующих диапазонов начните рисовать точки данных. После того, как все точки нанесены, нарисуйте отрезки, чтобы соединить их.
. Вы можете создать многоугольник частот из сгруппированного распределения частот, используя средние точки класса для значений оси 90 165 x 90 166. Полигоны частот «привязаны» к оси x с обоих концов, как вы можете видеть ниже.
Пример \(\PageIndex{4}\)
Полигон частот был построен на основе приведенной ниже таблицы частот.
| Нижняя граница | Верхняя граница | Частота | Суммарная частота |
|---|---|---|---|
| 49,5 | 59. 5 5 | 5 | 5 |
| 59,5 | 69,5 | 10 | 15 |
| 69,5 | 79,5 | 30 | 45 |
| 79,5 | 89,5 | 40 | 85 |
| 89,5 | 99.5 | 15 | 100 |
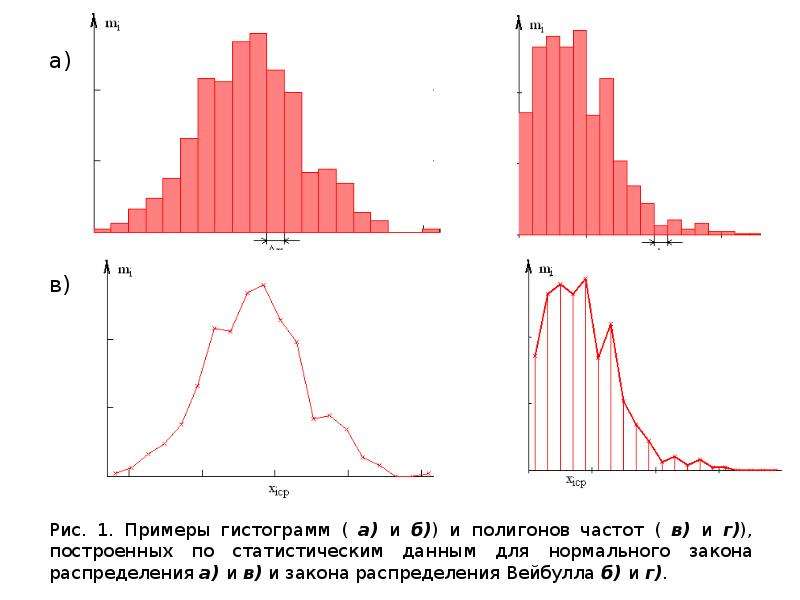
Первая метка на оси x равна 44,5. Это представляет собой интервал от 39,5 до 49,5. Поскольку наименьший результат теста равен 54,5, этот интервал используется только для того, чтобы график касался оси x . Точка с номером 54,5 представляет собой следующий интервал или первый «настоящий» интервал из таблицы и содержит пять баллов. Это рассуждение проводится для каждого из оставшихся интервалов с точкой 104.5, представляющий интервал от 99,5 до 109,5. Опять же, этот интервал не содержит данных и используется только для того, чтобы график касался оси x . Глядя на график, мы говорим, что это распределение искажено, потому что одна сторона графика не отражает другую сторону.
Упражнение \(\PageIndex{4}\)
Постройте частотный полигон возрастов президентов США на момент инаугурации, показанный в табл.
| Возраст при инаугурации | Частота |
|---|---|
41. 5–46,5 5–46,5 | 4 |
| 46,5–51,5 | 11 |
| 51,5–56,5 | 14 |
| 56,5–61,5 | 9 |
| 61,5–66,5 | 4 |
| 66,5–71,5 | 2 |
Ответить
Первая метка на оси x — 39.Это представляет собой интервал от 36,5 до 41,5. Поскольку нет возрастов меньше 41,5 лет, этот интервал используется только для того, чтобы график касался оси x . Точка с номером 44 представляет собой следующий интервал или первый «реальный» интервал из таблицы и содержит четыре балла. Это рассуждение применяется для каждого из оставшихся интервалов с точкой 74, представляющей интервал от 71,5 до 76,5. Опять же, этот интервал не содержит данных и используется только для того, чтобы график касался оси x .Глядя на график, мы говорим, что это распределение искажено, потому что одна сторона графика не отражает другую сторону.
Это рассуждение применяется для каждого из оставшихся интервалов с точкой 74, представляющей интервал от 71,5 до 76,5. Опять же, этот интервал не содержит данных и используется только для того, чтобы график касался оси x .Глядя на график, мы говорим, что это распределение искажено, потому что одна сторона графика не отражает другую сторону.
.
Рисунок \(\PageIndex{5}\).
Полигоны частот полезны для сравнения распределений. Это достигается путем наложения полигонов частот, нарисованных для разных наборов данных.
Пример \(\PageIndex{5}\)
Мы построим полигон частот наложения, сравнивая баллы из Примера с итоговой числовой оценкой учащихся.
| Нижняя граница | Верхняя граница | Частота | Суммарная частота |
|---|---|---|---|
| 49,5 | 59,5 | 5 | 5 |
| 59,5 | 69. 5 5 | 10 | 15 |
| 69,5 | 79,5 | 30 | 45 |
| 79,5 | 89,5 | 40 | 85 |
| 89,5 | 99,5 | 15 | 100 |
| Нижняя граница | Верхняя граница | Частота | Суммарная частота |
|---|---|---|---|
49.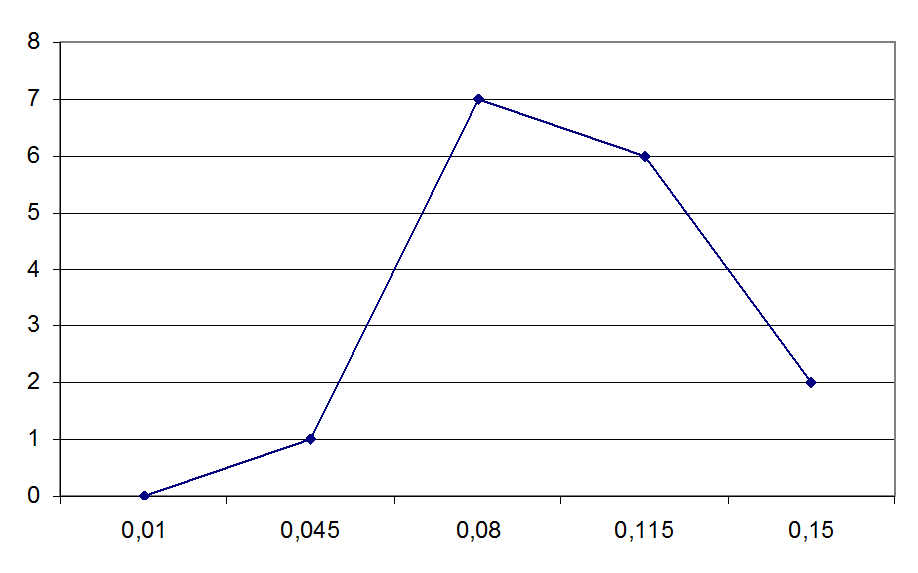 5 5 | 59,5 | 10 | 10 |
| 59,5 | 69,5 | 10 | 20 |
| 69,5 | 79,5 | 30 | 50 |
| 79,5 | 89,5 | 45 | 95 |
| 89.5 | 99,5 | 5 | 100 |

Предположим, мы хотим изучить температурный диапазон региона за целый месяц. Каждый день в полдень мы отмечаем температуру и записываем это в журнал. С этими данными можно проводить различные статистические исследования. Мы могли бы найти среднюю или медианную температуру за месяц. Мы могли бы построить гистограмму, отображающую количество дней, в течение которых температура достигает определенного диапазона значений.Однако все эти методы игнорируют часть собранных нами данных.
Одной из характеристик данных, которую мы, возможно, захотим рассмотреть, является время. Поскольку каждая дата связана с показаниями температуры за день, нам не нужно думать о данных как о случайных. Вместо этого мы можем использовать указанное время, чтобы установить хронологический порядок данных. График, который распознает этот порядок и отображает изменение температуры в течение месяца, называется графиком временных рядов.
Построение графика временных рядов
Чтобы построить график временных рядов, мы должны просмотреть обе части нашего парного набора данных . Начнем со стандартной декартовой системы координат. Горизонтальная ось используется для отображения приращений даты или времени, а вертикальная ось используется для отображения значений измеряемой переменной. Делая это, мы делаем так, чтобы каждая точка на графике соответствовала дате и измеренному количеству. Точки на графике обычно соединяются прямыми линиями в том порядке, в котором они встречаются.
Начнем со стандартной декартовой системы координат. Горизонтальная ось используется для отображения приращений даты или времени, а вертикальная ось используется для отображения значений измеряемой переменной. Делая это, мы делаем так, чтобы каждая точка на графике соответствовала дате и измеренному количеству. Точки на графике обычно соединяются прямыми линиями в том порядке, в котором они встречаются.
Пример \(\PageIndex{6}\)
Следующие данные показывают годовой индекс потребительских цен за каждый месяц в течение десяти лет.Постройте график временных рядов только для данных годового индекса потребительских цен.
| Год | Январь | Февраль | Март | Апрель | Май | Июн | июль |
|---|---|---|---|---|---|---|---|
| 2003 | 181. 7 7 | 183,1 | 184,2 | 183,8 | 183,5 | 183,7 | 183,9 |
| 2004 | 185,2 | 186,2 | 187,4 | 188,0 | 189,1 | 189,7 | 189,4 |
| 2005 | 190.7 | 191,8 | 193,3 | 194,6 | 194,4 | 194,5 | 195,4 |
| 2006 | 198,3 | 198,7 | 199,8 | 201,5 | 202,5 | 202,9 | 203,5 |
| 2007 | 202. 416 416 | 203.499 | 205,352 | 206,686 | 207,949 | 208.352 | 208,299 |
| 2008 | 211.080 | 211,693 | 213,528 | 214.823 | 216,632 | 218,815 | 219,964 |
| 2009 | 211.143 | 212,193 | 212.709 | 213.240 | 213,856 | 215,693 | 215,351 |
| 2010 | 216,687 | 216,741 | 217,631 | 218. 009 009 | 218,178 | 217,965 | 218.011 |
| 2011 | 220.223 | 221,309 | 223,467 | 224,906 | 225,964 | 225,722 | 225,922 |
| 2012 | 226,665 | 227,663 | 229,392 | 230.085 | 229,815 | 229.478 | 229,104 |
| Год | Август | Сентябрь | Октябрь | ноябрь | Декабрь | Годовой |
|---|---|---|---|---|---|---|
| 2003 | 184. 6 6 | 185,2 | 185,0 | 184,5 | 184,3 | 184,0 |
| 2004 | 189,5 | 189,9 | 190,9 | 191,0 | 190,3 | 188,9 |
| 2005 | 196,4 | 198.8 | 199,2 | 197,6 | 196,8 | 195,3 |
| 2006 | 203,9 | 202,9 | 201,8 | 201,5 | 201,8 | 201,6 |
| 2007 | 207,917 | 208. 490 490 | 208.936 | 210,177 | 210.036 | 207,342 |
| 2008 | 219.086 | 218.783 | 216,573 | 212.425 | 210.228 | 215.303 |
| 2009 | 215.834 | 215,969 | 216.177 | 216.330 | 215,949 | 214,537 |
| 2010 | 218. 312 312 | 218.439 | 218.711 | 218.803 | 219,179 | 218.056 |
| 2011 | 226,545 | 226.889 | 226.421 | 226.230 | 225,672 | 224,939 |
| 2012 | 230.379 | 231.407 | 231,317 | 230.221 | 229.601 | 229,594 |
Ответить
Рисунок \(\PageIndex{7}\).
Упражнение \(\PageIndex{5}\)
Следующая таблица является частью набора данных с сайта www.worldbank.org. Используйте таблицу, чтобы построить график временных рядов выбросов CO 2 для США.
| Украина | Соединенное Королевство | США | |
|---|---|---|---|
| 2003 | 352 259 | 540 640 | 5 681 664 |
| 2004 | 343 121 | 540 409 | 5 790 761 |
| 2005 | 339 029 | 541 990 | 5 826 394 |
| 2006 | 327 797 | 542 045 | 5 737 615 |
| 2007 | 328 357 | 528 631 | 5 828 697 |
| 2008 | 323 657 | 522 247 | 5 656 839 |
| 2009 | 272 176 | 474 579 | 5 299 563 |

Использование графика временных рядов
Графики временных рядов являются важными инструментами в различных приложениях статистики. При записи значений одной и той же переменной в течение длительного периода времени иногда бывает трудно различить какую-либо тенденцию или закономерность. Однако, когда одни и те же точки данных отображаются графически, некоторые функции выделяются. Графики временных рядов позволяют легко определить тенденции.
Обзор
Гистограмма представляет собой графическую версию частотного распределения.График состоит из полос одинаковой ширины, расположенных рядом друг с другом. Горизонтальная шкала представляет классы значений количественных данных, а вертикальная шкала представляет частоты. Высота столбиков соответствует частотным значениям. Гистограммы обычно используются для больших непрерывных наборов количественных данных. Частотный полигон можно использовать вместо гистограммы при графическом отображении больших наборов данных с повторяющимися точками данных. Данные обычно идут по оси x , а частота отображается на оси y . Графики временных рядов могут быть полезны при просмотре больших объемов данных для одной переменной за определенный период времени.
Данные обычно идут по оси x , а частота отображается на оси y . Графики временных рядов могут быть полезны при просмотре больших объемов данных для одной переменной за определенный период времени.
Каталожные номера
- Данные о ежегодных убийствах в Детройте, 1961–1973 гг., из книги Ганста и Мейсона «Регрессионный анализ и его применение», Марсель Деккер
- «Хронология: Путеводитель по президентам США: информация о месте рождения каждого президента, политической партии, сроке полномочий и многом другом». Scholastic, 2013. Доступно на сайте www.scholastic.com/teachers/a…-us-presidents (по состоянию на 3 апреля 2013 г.).
- «Президенты». Монстр фактов. Pearson Education, 2007. Доступно на сайте http://www.factmonster.com/ipka/A01
.html (по состоянию на 3 апреля 2013 г.). - «Статистика продовольственной безопасности». Продовольственная и сельскохозяйственная организация Объединенных Наций.
 Доступно на сайте http://www.fao.org/economic/ess/ess-fs/en/ (по состоянию на 3 апреля 2013 г.).
Доступно на сайте http://www.fao.org/economic/ess/ess-fs/en/ (по состоянию на 3 апреля 2013 г.). - «Индекс потребительских цен». Министерство труда США: Бюро статистики труда.Доступно в Интернете по адресу http://data.bls.gov/pdq/SurveyOutputServlet (по состоянию на 3 апреля 2013 г.).
- «Выбросы CO2 (кт)». The World Bank, 2013. Доступно на сайте http://databank.worldbank.org/data/home.aspx (по состоянию на 3 апреля 2013 г.).
- «Данные временного ряда рождений». Главное регистрационное управление Шотландии, 2013 г. Доступно на сайте www.gro-scotland.gov.uk/stati…me-series.html (по состоянию на 3 апреля 2013 г.).
- «Демография: Дети в возрасте до 5 лет с недостаточным весом.Индексмунди. Доступно на сайте http://www.indexmundi.com/g/r.aspx?t=50&v=2224&aml=en (по состоянию на 3 апреля 2013 г.).
- Ганст, Ричард, Роберт Мейсон. Регрессионный анализ и его применение: подход, ориентированный на данные . CRC Press: 1980.

- «Избыточный вес и ожирение: факты ожирения взрослых». Центры по контролю и профилактике заболеваний. Доступно на сайте http://www.cdc.gov/obesity/data/adult.html (по состоянию на 13 сентября 2013 г.).
- Частота
- количество раз, когда значение данных встречается
- Гистограмма
- графическое представление в форме \(x-y\) распределения данных в наборе данных; \(x\) представляет данные, а \(y\) представляет частоту или относительную частоту.Граф состоит из смежных прямоугольников.
- Относительная частота
- отношение количества раз, когда значение данных встречается в наборе всех результатов, к количеству всех результатов
Авторы и авторство
Барбара Илловски и Сьюзан Дин (Колледж Де Анза) со многими другими авторами. Контент, созданный OpenStax College, находится под лицензией Creative Commons Attribution License 4.0.Загрузите бесплатно по адресу http://cnx.
 org/contents/30189442-699…[email protected].
org/contents/30189442-699…[email protected].
График Ogive / полигон кумулятивной частоты в простых шагах
Описательная статистика > График Огива
Что такое Оживальный график?
Ожив ( oh-jive ), иногда называемый кумулятивным многоугольником частот, представляет собой тип многоугольника частот, который показывает кумулятивные частоты. Другими словами, совокупные проценты добавляются к графику слева направо.
Оживальный график отображает кумулятивную частоту по оси ординат и границы классов по оси абсцисс.Это очень похоже на гистограмму, только вместо прямоугольников оживальная маркировка имеет одну точку, где должен быть правый верхний угол прямоугольника. Обычно проще построить такой график из таблицы частот.
Посмотрите видео с примером того, как сделать оживальную диаграмму вручную:
com/embed/3VRFJ2udt7A» title=»YouTube video player» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Видео не видно? Кликните сюда.
Как нарисовать график Ожив
Пример вопроса: Нарисуйте график Оживе для следующего набора данных:
2, 7, 3, 8, 3, 15, 19, 16, 17, 13, 29, 20, 21, 21, 22, 25, 31, 51, 55, 55, 57, 58, 56, 57, 58.
Шаг 1: Создайте таблицу относительных частот на основе данных. В первом столбце указаны ограничения класса, во втором столбце — частота (количество), а в третьем столбце — относительная частота (частота класса / общее количество элементов):
Если вы не знаете, как создать свой класс ограничения (также называемые корзинами), посмотрите видео внизу этой статьи или см. Что такое корзина в статистике?
Шаг 2: Добавьте четвертый столбец и просуммируйте (суммируйте) частоты в столбце 2, спускаясь сверху вниз. Например, вторая запись — это сумма первой и второй строк в столбце частоты (5 + 5 = 10), а третья запись — это сумма первой, второй и третьей строк в частотном столбце ( 5 + 5 + 6 = 16):
Например, вторая запись — это сумма первой и второй строк в столбце частоты (5 + 5 = 10), а третья запись — это сумма первой, второй и третьей строк в частотном столбце ( 5 + 5 + 6 = 16):
Шаг 3: Добавьте пятый столбец и просуммируйте относительных частот из столбца 3. Если вы сделаете этот шаг правильно, ваши значения должны составить до 100% (или 1 как десятичный):
Шаг 4: Нарисуйте декартову плоскость (график xy) с накопленной относительной частотой в процентах по оси y (от 0 до 100% или в виде десятичной дроби от 0 до 1).Отметьте ось x границами класса.
Шаг 5: Нанесите точки. Примечание : Каждая точка должна быть нанесена на верхнюю границу границы класса. Например, если ваша первая граница класса находится в диапазоне от 0 до 10, точка должна быть нанесена на 10.
Шаг 6: Соедините точки прямыми линиями. ожив — это одна непрерывная линия, состоящая из нескольких более мелких линий, соединяющих пары точек, идущих слева направо.
Готовый график для этого примера данных:
Совет : Видео о том, как создать границы классов:
Видео не видно? Кликните сюда.
Ссылки
Агрести А. (1990) Категориальный анализ данных. Джон Уайли и сыновья, Нью-Йорк.
Левин, Д. (2014). Даже вы можете изучить статистику и аналитику: простое для понимания руководство по статистике и аналитике, 3-е издание. Пирсон ФТ Пресс
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице Facebook .
Полигоны частоты статистики: TutorTeddy.com
Задать любой вопрос по статистике/вероятности/математике
ДОБРО ПОЖАЛОВАТЬ на Tutorteddy.com. Это НАСТОЯЩИЙ сайт, предназначенный для помощи студентам в курсах статистики. Мы функционируем как онлайн-репетитор по статистике так же, как класс статистики. онлайн-помощь по статистике предоставляется студентам, исследователям и т. д. Наши эксперты помогут вам изучить статистику, а также дадут рекомендации по выполнению домашних заданий и заданий. Статистическая справка , предоставленная нами, поможет вам более точно изучить предмет.
График распределения: многоугольники частот
Цели:
- Полигоны частот — создание и интерпретация.
- Совокупные полигоны частот — создание и интерпретация.
- Наложенные полигоны частот — создание и интерпретация.
полигонов частот:
Графическое отображение таблицы частот также может быть реализовано с помощью полигона частот. Для создания полигона частот интервалы помечаются на оси X, а ось Y представляет собой высоту точки в середине интервала. Затем точки соединяются, соединяются с осью X, и таким образом формируется многоугольник.Итак, многоугольник частот — это график, который получается путем соединения средних точек интервалов. Мы также можем создать полигон частот из гистограммы. Если соединить средние верхние точки столбцов гистограммы, образуется полигон частот.
Для создания полигона частот интервалы помечаются на оси X, а ось Y представляет собой высоту точки в середине интервала. Затем точки соединяются, соединяются с осью X, и таким образом формируется многоугольник.Итак, многоугольник частот — это график, который получается путем соединения средних точек интервалов. Мы также можем создать полигон частот из гистограммы. Если соединить средние верхние точки столбцов гистограммы, образуется полигон частот.
Полигон частот и гистограмма служат той же цели. Однако первый полезен при сравнении разных наборов данных. В дополнение к этому полигон частот может использоваться для отображения кумулятивных частотных распределений.
Как создать полигон частот?
Как уже упоминалось, гистограмму можно использовать для построения полигона частот .На оси X представлены оценки набора данных, а на оси Y — частота для каждого из классов. Теперь отметьте средние верхние точки каждого столбца созданной гистограммы для каждого интервала класса. Обычно для маркировки используется точка. Теперь соедините все точки прямыми линиями и соедините их с осью X с обеих сторон. Для создания полигона частот без гистограммы вам просто нужно учитывать середину интервалов классов, чтобы она соответствовала частотам. Затем соедините точки, как указано выше.
Обычно для маркировки используется точка. Теперь соедините все точки прямыми линиями и соедините их с осью X с обеих сторон. Для создания полигона частот без гистограммы вам просто нужно учитывать середину интервалов классов, чтобы она соответствовала частотам. Затем соедините точки, как указано выше.
Следующая таблица представляет собой таблицу частоты оценок, полученных 50 учащимися на предтестовом экзамене.
Таблица 1. Частота Распределение оценок, полученных 50 студентами на предтестовом экзамене.
Границы класса | Частота | Суммарная частота (меньше типа) |
30.5-40,5 | 1 | 1 |
40,5-50,5 | 14 | 20 |
50. | 20 | 40 |
60,5-70,5 | 7 | 47 |
70.5-80,5 | 3 | 50 |
Всего | 50 |
Метки оси X являются серединами интервалов классов.Таким образом, первая метка на оси X будет 35,5, следующая 45,5, затем 55,5, 65,5 и, наконец, 75,5. Затем учитываются соответствующие частоты для создания полигона частот. Форму распределения можно определить по созданному полигону частот. Полигон частот показан на следующем рисунке.
Затем учитываются соответствующие частоты для создания полигона частот. Форму распределения можно определить по созданному полигону частот. Полигон частот показан на следующем рисунке.
Рис. 1: Полигон частот распределения оценок, полученных 50 учащимися на предтестовом экзамене.
Из приведенного выше рисунка видно, что кривая асимметрична и наклонена вправо.
Совокупный полигон частоты:
Совокупный полигон частот подобен полигону частот. Разница в том, что при создании полигона кумулятивных частот мы учитываем кумулятивные частоты, а не фактические частоты. Совокупная частота меньшего типа получается путем добавления частоты каждого интервала класса к сумме всех частот в нижних интервалах. В таблице 1, например, кумулятивная частота для интервала класса 30.5-40,5 равно 6, так как сумма всех частот в нижних интервалах равна 0. Опять же, совокупная частота для интервала классов 40,5-50,5 равна 20, поскольку сумма всех частот в нижних интервалах равна 14, т. е. 6+14= 20, поэтому для следующего интервала будет 6+14+20=40 и так далее.
е. 6+14= 20, поэтому для следующего интервала будет 6+14+20=40 и так далее.
Ниже приведен совокупный многоугольник частот
Рис. 2: Совокупный многоугольник частот оценок, полученных 50 учащимися на предтестовом экзамене.
Наложенный полигон частот:
Также для сравнения распределений различных наборов данных можно использовать полигон частот .В этом случае полигоны частот разных данных наносятся на один и тот же график. Сказанное выше можно пояснить с помощью иллюстраций.
Ниже приведен пример игральных костей, в которых распределение наблюдаемых частот и распределение ожидаемых частот сравниваются для разных результатов двух игральных костей. Кривые частот двух распределений используются для сравнения.
Рис. 3: Наложенный полигон частот распределения бросков двух игральных костей
Наблюдаемая кривая перекрывает ожидаемую кривую.Ожидаемая кривая гладкая, а наблюдаемая кривая не гладкая.
Кроме того, на этом же графике можно отобразить полигон кумулятивной частоты. На следующем рисунке показан такой график. Оценки двух работ сравниваются по совокупному полигону частот .
На следующем рисунке показан такой график. Оценки двух работ сравниваются по совокупному полигону частот .
Рис. 4: Наложенный полигон кумулятивной частоты
Рис. 5: Частотный полигон на гистограмме
Статистическая помощь и Онлайн-справка по статистике , предоставляемая нами, таким образом, поможет вам научиться правильному использованию и различным аспектам статистики.
Гистограммы, частотные полигоны и графики временных рядов — вводная статистика
OpenStaxCollege
[латексная страница]
Для большей части работы в этой книге вы будете использовать гистограмму для отображения данных. Одним из преимуществ гистограммы является то, что она может легко отображать большие наборы данных. Эмпирическое правило заключается в использовании гистограммы, когда набор данных состоит из 100 или более значений.
Гистограмма состоит из смежных (примыкающих) прямоугольников. Он имеет как горизонтальную ось, так и вертикальную ось. Горизонтальная ось помечена тем, что представляют данные (например, расстояние от вашего дома до школы). Вертикальная ось отмечена либо частотой, либо относительной частотой (или частотой в процентах, либо вероятностью). График будет иметь одинаковую форму с любой меткой. Гистограмма (как и stemplot) может дать вам форму данных, центр и разброс данных.
Он имеет как горизонтальную ось, так и вертикальную ось. Горизонтальная ось помечена тем, что представляют данные (например, расстояние от вашего дома до школы). Вертикальная ось отмечена либо частотой, либо относительной частотой (или частотой в процентах, либо вероятностью). График будет иметь одинаковую форму с любой меткой. Гистограмма (как и stemplot) может дать вам форму данных, центр и разброс данных.
Относительная частота равна частоте наблюдаемого значения данных, деленной на общее количество значений данных в выборке.(Помните, частота определяется как количество раз, когда появляется ответ.) Если:
- f = частота
- n = общее количество значений данных (или сумма отдельных частот) и
- RF = относительная частота,
тогда:
\(\text{RF}=\frac{f}{n}\)
Например, если трое учащихся в классе английского языка г-на Ахава из 40 человек получили от 90% до 100%, то –> f = 3, n = 40 и RF = \(\frac{f}{n}\) = \(\frac{3}{40}\) = 0. 075. 7,5 % учащихся получили 90–100 %. 90–100% — количественные показатели.
075. 7,5 % учащихся получили 90–100 %. 90–100% — количественные показатели.
Чтобы построить гистограмму , сначала решите, сколько баров или интервалов , также называемых классами, представляют данные. Многие гистограммы для наглядности состоят из 5–15 столбцов или классов. Необходимо выбрать количество баров. Выберите начальную точку для первого интервала меньше наименьшего значения данных. Удобная начальная точка — это более низкое значение, выполненное с точностью до одного десятичного знака больше, чем значение с наибольшим количеством десятичных знаков.Например, если значение с наибольшим количеством знаков после запятой равно 6,1 и это наименьшее значение, удобной отправной точкой будет 6,05 (6,1 – 0,05 = 6,05). Мы говорим, что 6.05 имеет большую точность. Если значение с наибольшим количеством знаков после запятой равно 2,23, а наименьшее значение равно 1,5, удобной отправной точкой является 1,495 (1,5 – 0,005 = 1,495). Если значение с наибольшим количеством знаков после запятой равно 3,234, а наименьшее значение равно 1,0, удобной отправной точкой является 0,9995 (1,0 – 0,0005 = 0,9995). Если все данные являются целыми числами, а наименьшее значение равно двум, то удобной отправной точкой будет 1.5 (2 – 0,5 = 1,5). Кроме того, когда начальная точка и другие границы переносятся на один дополнительный десятичный знак, никакое значение данных не попадает на границу. Следующие два примера подробно описывают, как построить гистограмму, используя непрерывные данные, и как создать гистограмму, используя дискретные данные.
Если значение с наибольшим количеством знаков после запятой равно 3,234, а наименьшее значение равно 1,0, удобной отправной точкой является 0,9995 (1,0 – 0,0005 = 0,9995). Если все данные являются целыми числами, а наименьшее значение равно двум, то удобной отправной точкой будет 1.5 (2 – 0,5 = 1,5). Кроме того, когда начальная точка и другие границы переносятся на один дополнительный десятичный знак, никакое значение данных не попадает на границу. Следующие два примера подробно описывают, как построить гистограмму, используя непрерывные данные, и как создать гистограмму, используя дискретные данные.
Следующие данные представляют собой рост (в дюймах с точностью до полдюйма) 100 мужчин-полупрофессиональных футболистов. Высота непрерывных данных , так как высота измеряется.
60; 60,5; 61; 61; 61,5
63,5; 63,5; 63,5
64; 64; 64; 64; 64; 64; 64; 64,5; 64,5; 64,5; 64,5; 64,5; 64,5; 64,5; 64,5
66; 66; 66; 66; 66; 66; 66; 66; 66; 66; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 66,5; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5; 67,5
68; 68; 69; 69; 69; 69; 69; 69; 69; 69; 69; 69; 69,5; 69,5; 69,5; 69,5; 69,5
70; 70; 70; 70; 70; 70; 70. 5; 70,5; 70,5; 71; 71; 71
5; 70,5; 70,5; 71; 71; 71
72; 72; 72; 72,5; 72,5; 73; 73,5
74
Наименьшее значение данных равно 60. Поскольку данные с наибольшим количеством десятичных разрядов имеют один десятичный знак (например, 61,5), мы хотим, чтобы наша начальная точка имела два десятичных разряда. Поскольку числа 0,5, 0,05, 0,005 и т. д. являются удобными числами, используйте 0,05 и вычтите его из 60, наименьшего значения, для удобной отправной точки.
60 – 0,05 = 59,95, что точнее, чем, скажем, 61,5 на один десятичный знак.Таким образом, отправной точкой является 59,95.
Наибольшее значение равно 74, поэтому 74 + 0,05 = 74,05 является конечным значением.
Затем вычислите ширину каждого бара или интервала класса. Чтобы рассчитать эту ширину, вычтите начальную точку из конечного значения и разделите на количество полос (вы должны выбрать желаемое количество полос). Предположим, вы выбрали восемь тактов.
\(\frac{74.05-59.95}{8}=1.76\)
ПРИМЕЧАНИЕ
Мы округлим до двух и сделаем каждую полосу или интервал класса шириной в две единицы.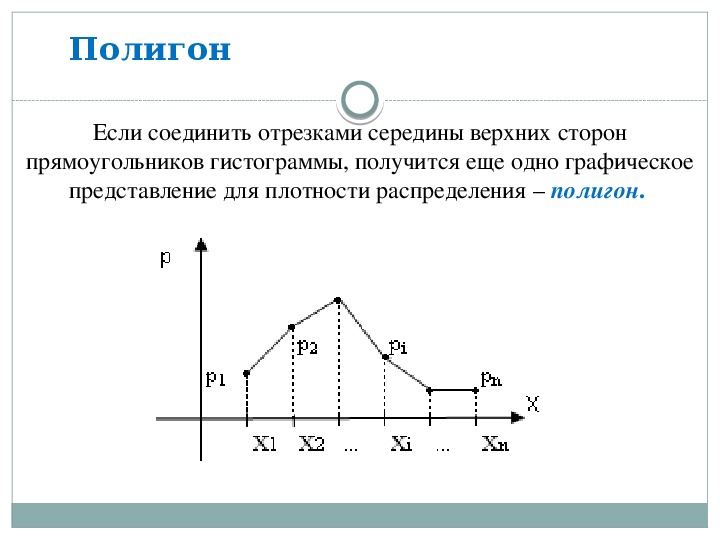 Округление до двух — это один из способов предотвратить попадание значения на границу. Округление до следующего числа часто необходимо, даже если это противоречит стандартным правилам округления. В этом примере также будет работать использование ширины 1,76. Рекомендации, которым следуют некоторые для ширины столбца или интервала класса, заключаются в том, чтобы взять квадратный корень из числа значений данных, а затем, при необходимости, округлить до ближайшего целого числа. Например, если имеется 150 значений данных, возьмите квадратный корень из 150 и округлите до 12 тактов или интервалов.
Округление до двух — это один из способов предотвратить попадание значения на границу. Округление до следующего числа часто необходимо, даже если это противоречит стандартным правилам округления. В этом примере также будет работать использование ширины 1,76. Рекомендации, которым следуют некоторые для ширины столбца или интервала класса, заключаются в том, чтобы взять квадратный корень из числа значений данных, а затем, при необходимости, округлить до ближайшего целого числа. Например, если имеется 150 значений данных, возьмите квадратный корень из 150 и округлите до 12 тактов или интервалов.
Границы:
- 59,95
- 59,95 + 2 = 61,95
- 61,95 + 2 = 63,95
- 63,95 + 2 = 65,95
- 65,95 + 2 = 67,95
- 67,95 + 2 = 69,95
- 69,95 + 2 = 71,95
- 71,95 + 2 = 73,95
- 73,95 + 2 = 75,95
Высота от 60 до 61,5 дюйма находится в интервале 59,95–61,95. Высоты 63,5 находятся в интервале 61,95–63,95. Рост от 64 до 64.5 находятся в интервале 63,95–65,95. Высоты от 66 до 67,5 находятся в интервале 65,95–67,95. Высоты от 68 до 69,5 находятся в интервале 67,95–69,95. Высоты с 70 по 71 находятся в интервале 69,95–71,95. Высоты от 72 до 73,5 находятся в интервале 71,95–73,95. Высота 74 находится в интервале 73,95–75,95.
Рост от 64 до 64.5 находятся в интервале 63,95–65,95. Высоты от 66 до 67,5 находятся в интервале 65,95–67,95. Высоты от 68 до 69,5 находятся в интервале 67,95–69,95. Высоты с 70 по 71 находятся в интервале 69,95–71,95. Высоты от 72 до 73,5 находятся в интервале 71,95–73,95. Высота 74 находится в интервале 73,95–75,95.
Следующая гистограмма отображает высоты по оси x и относительную частоту по оси y .
Попробуйте
Ниже приведены данные о размерах обуви 50 студентов мужского пола.Размеры являются непрерывными данными, поскольку измеряется размер обуви. Постройте гистограмму и рассчитайте ширину каждого бара или интервала класса. Предположим, вы выбрали шесть тактов.
9; 9; 9,5; 9,5; 10; 10; 10; 10; 10; 10; 10,5; 10,5; 10,5; 10,5; 10,5; 10,5; 10,5; 10,5
11; 11; 11; 11; 11; 11; 11; 11; 11; 11; 11; 11; 11; 11,5; 11,5; 11,5; 11,5; 11,5; 11,5; 11,5
12; 12; 12; 12; 12; 12; 12; 12,5; 12,5; 12,5; 12,5; 14
Наименьшее значение: 9
Наибольшее значение: 14
Удобное начальное значение: 9 – 0. 05 = 8,95
05 = 8,95
Удобное конечное значение: 14 + 0,05 = 14,05
\(\frac{14.05-8.95}{6}=0.85\)
В расчетах предлагается использовать 0,85 в качестве ширины каждой полосы или интервала класса. Также можно использовать интервал шириной, равной единице.
Следующие данные представляют собой количество книг, купленных 50 студентами-заочниками колледжа ABC. Количество книг дискретных данных , так как книги подсчитываются.
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1
2; 2; 2; 2; 2; 2; 2; 2; 2; 2
3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3
4; 4; 4; 4; 4; 4
5; 5; 5; 5; 5
6; 6
Одиннадцать студентов покупают одну книгу.Десять студентов покупают две книги. Шестнадцать студентов покупают три книги. Шесть студентов покупают четыре книги. Пять студентов покупают пять книг. Два студента покупают шесть книг.
Поскольку данные представляют собой целые числа, вычтите 0,5 из 1, наименьшего значения данных, и прибавьте 0,5 к 6, наибольшему значению данных.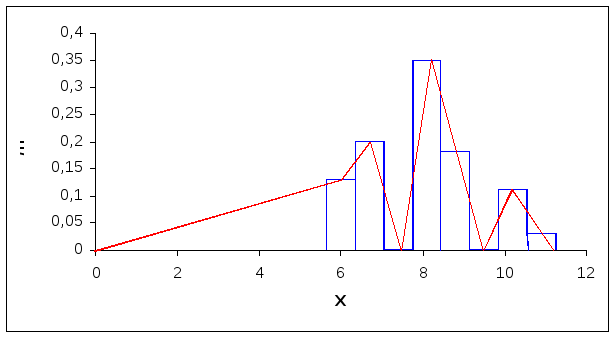 Тогда начальная точка равна 0,5, а конечное значение равно 6,5.
Тогда начальная точка равна 0,5, а конечное значение равно 6,5.
Затем вычислите ширину каждого бара или интервала класса. Если данные дискретны и различных значений не слишком много, наиболее удобна ширина, при которой значения данных помещаются в середину столбца или интервала класса.Поскольку данные состоят из чисел 1, 2, 3, 4, 5, 6, а начальная точка равна 0,5, ширина единицы помещает 1 в середину интервала от 0,5 до 1,5, а 2 в середину интервала. интервал от 1,5 до 2,5, 3 в середине интервала от 2,5 до 3,5, 4 в середине интервала от _______ до _______, 5 в середине интервала от _______ до _______ и _______ в середина интервала с _______ по _______ .
- от 3,5 до 4,5
- 4.от 5 до 5,5
- 6
- от 5,5 до 6,5
Рассчитайте количество баров следующим образом:
\(\frac{6.5-0.5}{\mathrm{количество баров}}=1\)
, где 1 — ширина полосы. Следовательно, баров = 6.
Следующая гистограмма отображает количество книг по оси x и частоту по оси y .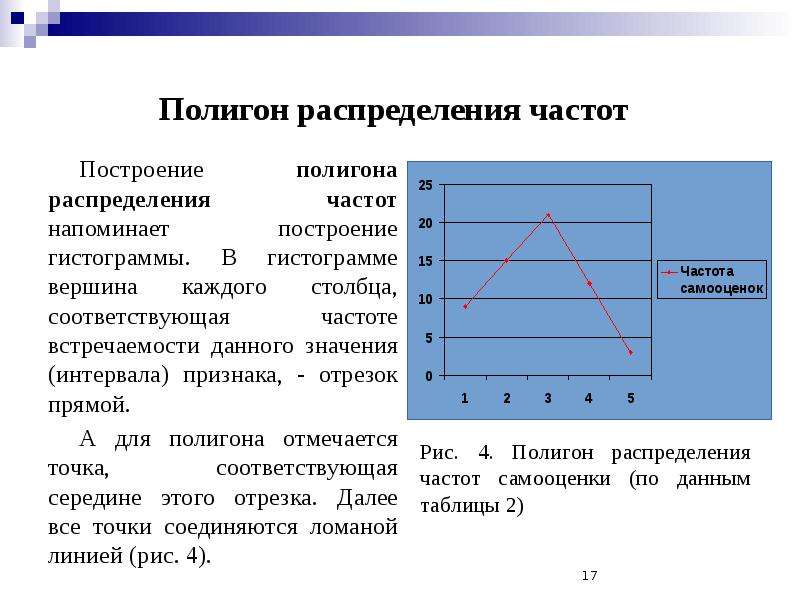
Перейти на [ссылка]. Существуют инструкции калькулятора для ввода данных и создания индивидуальной гистограммы.Создайте гистограмму для [ссылка].
- Нажмите Y=. Нажмите CLEAR, чтобы удалить все уравнения.
- Нажмите STAT 1:EDIT. Если в L1 есть данные, наведите стрелку вверх на имя L1, нажмите CLEAR, а затем стрелку вниз. При необходимости сделайте то же самое для L2.
- В L1 введите 1, 2, 3, 4, 5, 6.
- В L2 введите 11, 10, 16, 6, 5, 2.
- Нажмите ОКНО. Установите Xmin = 0,5, Xscl = (6,5 – 0,5)/6, Ymin = –1, Ymax = 20, Yscl = 1, Xres = 1.
- Нажмите 2 и Y=. Начните с нажатия 4:Plotsoff ENTER.
- Нажмите 2 и Y=. Нажмите 1:График 1. Нажмите Ввод. Стрелка вниз к ТИП. Стрелка к картинке 3 rd (гистограмма). Нажмите Ввод.
- Стрелка вниз к Xlist: введите L1 (2 и 1). Стрелка вниз к частоте. Введите L2 (2 и 2).
- Нажмите ГРАФИК.
- Используйте клавишу TRACE и клавиши со стрелками для просмотра гистограммы.

Попробуйте
Следующие данные представляют собой количество видов спорта, которыми занимаются 50 студентов-спортсменов. Количество видов спорта является дискретными данными, поскольку виды спорта подсчитываются.
1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1
2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2
3; 3; 3; 3; 3; 3; 3; 3
20 студентов-спортсменов занимаются одним видом спорта. 22 студента-спортсмена занимаются двумя видами спорта. Восемь студентов-спортсменов занимаются тремя видами спорта.
Заполните пропуски в следующем предложении. Поскольку данные состоят из чисел 1, 2, 3, а начальная точка равна 0,5, ширина, равная единице, помещает 1 в середину интервала 0.5 до _____, 2 в середине интервала от _____ до _____ и 3 в середине интервала от _____ до _____.
1,5
от 1,5 до 2,5
от 2,5 до 3,5
Используя этот набор данных, постройте гистограмму.
| Количество часов, проведенных моими одноклассниками за видеоиграми по выходным | ||||
|---|---|---|---|---|
| 9,95 | 10 | 2,25 | 16,75 | 0 |
| 19.5 | 22,5 | 7,5 | 15 | 12,75 |
| 5,5 | 11 | 10 | 20,75 | 17,5 |
| 23 | 21,9 | 24 | 23,75 | 18 |
| 20 | 15 | 22,9 | 18,8 | 20,5 |
Некоторые значения в этом наборе данных попадают в границы интервалов классов. Значение считается в интервале класса, если оно попадает на левую границу, но не попадает на правую границу.Разные исследователи могут строить гистограммы для одних и тех же данных по-разному. Существует несколько правильных способов построения гистограммы.
Попробуйте
Следующие данные представляют количество сотрудников в различных ресторанах Нью-Йорка. Используя эти данные, создайте гистограмму.
Используя эти данные, создайте гистограмму.
22351526402818202534322134402038и 28
Используйте 10–19 в качестве первого интервала.
Пересчитайте деньги (купюры и сдачу) в кармане или кошельке. Ваш инструктор запишет суммы.Как класс, постройте гистограмму, отображающую данные. Обсудите, сколько интервалов вы считаете уместным. Вы можете поэкспериментировать с количеством интервалов.
Частотные полигоны аналогичны линейным графикам, и точно так же, как линейные графики делают непрерывные данные визуально простыми для интерпретации, то же самое можно сказать и о частотных полигонах.
Чтобы построить многоугольник частот, сначала проверьте данные и выберите количество интервалов или интервалов классов, которые будут использоваться на осях x и y .После выбора соответствующих диапазонов начните рисовать точки данных. После того, как все точки нанесены, нарисуйте отрезки, чтобы соединить их.
Полигон частот был построен на основе приведенной ниже таблицы частот.
| Частотное распределение итоговых результатов тестов по исчислению | |||
|---|---|---|---|
| Нижняя граница | Верхняя граница | Частота | Суммарная частота |
| 49,5 | 59.5 | 5 | 5 |
| 59,5 | 69,5 | 10 | 15 |
| 69,5 | 79,5 | 30 | 45 |
| 79,5 | 89,5 | 40 | 85 |
| 89,5 | 99,5 | 15 | 100 |
Первая метка на оси x равна 44,5. Это представляет собой интервал, простирающийся от 39.от 5 до 49,5. Поскольку наименьший результат теста равен 54,5, этот интервал используется только для того, чтобы график касался оси x . Точка с номером 54,5 представляет собой следующий интервал или первый «настоящий» интервал из таблицы и содержит пять баллов. Это рассуждение применяется для каждого из оставшихся интервалов с точкой 104,5, представляющей интервал от 99,5 до 109,5. Опять же, этот интервал не содержит данных и используется только для того, чтобы график касался оси x . Глядя на график, мы говорим, что это распределение искажено, потому что одна сторона графика не отражает другую сторону.
Точка с номером 54,5 представляет собой следующий интервал или первый «настоящий» интервал из таблицы и содержит пять баллов. Это рассуждение применяется для каждого из оставшихся интервалов с точкой 104,5, представляющей интервал от 99,5 до 109,5. Опять же, этот интервал не содержит данных и используется только для того, чтобы график касался оси x . Глядя на график, мы говорим, что это распределение искажено, потому что одна сторона графика не отражает другую сторону.
Попробуйте
Постройте частотный полигон возрастов президентов США на момент инаугурации, показанный на [ссылка].
| Возраст при инаугурации | Частота |
|---|---|
| 41,5–46,5 | 4 |
| 46,5–51,5 | 11 |
| 51,5–56,5 | 14 |
| 56,5–61,5 | 9 |
| 61,5–66,5 | 4 |
66. 5–71,5 5–71,5 | 2 |
Первая метка на оси x — 39. Это представляет интервал от 36,5 до 41,5. Поскольку нет возрастов меньше 41,5 лет, этот интервал используется только для того, чтобы график касался оси x . Точка с номером 44 представляет собой следующий интервал или первый «реальный» интервал из таблицы и содержит четыре балла. Это рассуждение применяется для каждого из оставшихся интервалов с точкой 74, представляющей интервал от 71.от 5 до 76,5. Опять же, этот интервал не содержит данных и используется только для того, чтобы график касался оси x . Глядя на график, мы говорим, что это распределение искажено, потому что одна сторона графика не отражает другую сторону.
Полигоны частот полезны для сравнения распределений. Это достигается путем наложения полигонов частот, нарисованных для разных наборов данных.
Мы построим наложенный многоугольник частот, сравнивая баллы из [ссылка] с итоговой числовой оценкой учащихся.
| Частотное распределение итоговых результатов тестов по исчислению | |||
|---|---|---|---|
| Нижняя граница | Верхняя граница | Частота | Суммарная частота |
| 49,5 | 59,5 | 5 | 5 |
| 59,5 | 69,5 | 10 | 15 |
| 69,5 | 79,5 | 30 | 45 |
| 79.5 | 89,5 | 40 | 85 |
| 89,5 | 99,5 | 15 | 100 |
| Распределение частот для итоговых оценок по математическому анализу | |||
|---|---|---|---|
| Нижняя граница | Верхняя граница | Частота | Суммарная частота |
| 49,5 | 59,5 | 10 | 10 |
59. 5 5 | 69,5 | 10 | 20 |
| 69,5 | 79,5 | 30 | 50 |
| 79,5 | 89,5 | 45 | 95 |
| 89,5 | 99,5 | 5 | 100 |
Предположим, мы хотим изучить температурный диапазон региона за целый месяц. Каждый день в полдень мы отмечаем температуру и записываем это в журнал.С этими данными можно проводить различные статистические исследования. Мы могли бы найти среднюю или медианную температуру за месяц. Мы могли бы построить гистограмму, отображающую количество дней, в течение которых температура достигает определенного диапазона значений. Однако все эти методы игнорируют часть собранных нами данных.
Одной из характеристик данных, которую мы, возможно, захотим рассмотреть, является время. Поскольку каждая дата связана с показаниями температуры за день, нам не нужно думать о данных как о случайных. Вместо этого мы можем использовать указанное время, чтобы установить хронологический порядок данных. График, который распознает этот порядок и отображает изменение температуры в течение месяца, называется графиком временных рядов.
Вместо этого мы можем использовать указанное время, чтобы установить хронологический порядок данных. График, который распознает этот порядок и отображает изменение температуры в течение месяца, называется графиком временных рядов.
Чтобы построить график временных рядов, мы должны просмотреть обе части нашего парного набора данных. Начнем со стандартной декартовой системы координат. Горизонтальная ось используется для отображения приращений даты или времени, а вертикальная ось используется для отображения значений измеряемой переменной.Делая это, мы делаем так, чтобы каждая точка на графике соответствовала дате и измеренному количеству. Точки на графике обычно соединяются прямыми линиями в том порядке, в котором они встречаются.
Следующие данные показывают годовой индекс потребительских цен за каждый месяц в течение десяти лет. Постройте график временных рядов только для данных годового индекса потребительских цен.
| Год | Январь | фев | март | апр | май | июнь | июль |
|---|---|---|---|---|---|---|---|
| 2003 | 181. 7 7 | 183,1 | 184,2 | 183,8 | 183,5 | 183,7 | 183,9 |
| 2004 | 185,2 | 186,2 | 187,4 | 188,0 | 189,1 | 189,7 | 189,4 |
| 2005 | 190,7 | 191,8 | 193,3 | 194,6 | 194,4 | 194,5 | 195,4 |
| 2006 | 198.3 | 198,7 | 199,8 | 201,5 | 202,5 | 202,9 | 203,5 |
| 2007 | 202.416 | 203.499 | 205.352 | 206.686 | 207,949 | 208.352 | 208.299 |
| 2008 | 211.080 | 211.693 | 213,528 | 214.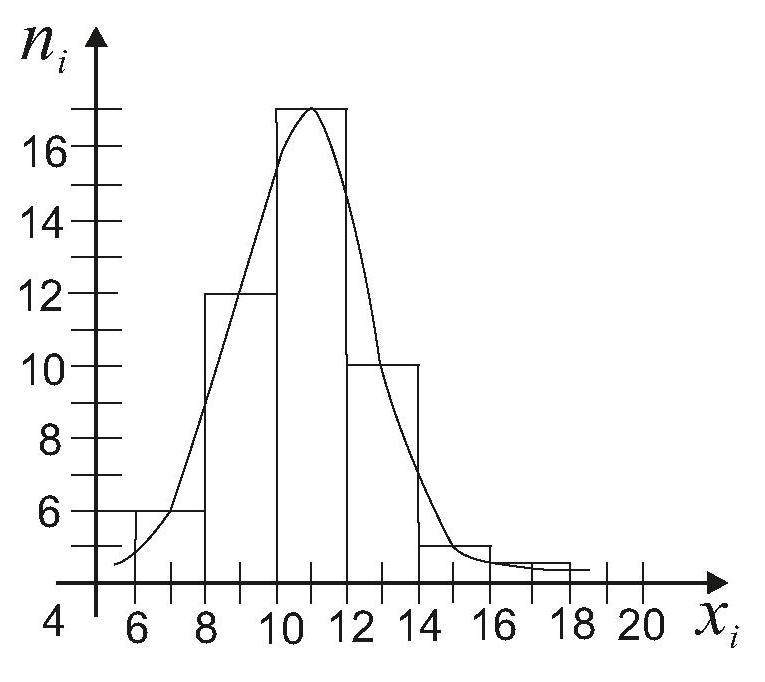 823 823 | 216.632 | 218.815 | 219.964 |
| 2009 | 211.143 | 212.193 | 212.709 | 213.240 | 213.856 | 215.693 | 215.351 |
| 2010 | 216 687 | 216.741 | 217.631 | 218.009 | 218,178 | 217,965 | 218.011 |
| 2011 | 220.223 | 221.309 | 223.467 | 224,906 | 225,964 | 225.722 | 225,922 |
| 2012 | 226,665 | 227,663 | 229,392 | 230.085 | 229.815 | 229.478 | 229.104 |
| Год | авг | сен | окт | ноябрь | декабрь | Годовой |
|---|---|---|---|---|---|---|
| 2003 | 184. 6 6 | 185,2 | 185,0 | 184,5 | 184,3 | 184,0 |
| 2004 | 189,5 | 189,9 | 190,9 | 191,0 | 190,3 | 188,9 |
| 2005 | 196,4 | 198,8 | 199,2 | 197,6 | 196,8 | 195,3 |
| 2006 | 203.9 | 202,9 | 201,8 | 201,5 | 201,8 | 201,6 |
| 2007 | 207,917 | 208.490 | 208,936 | 210.177 | 210.036 | 207,342 |
| 2008 | 219.086 | 218.783 | 216.573 | 212.425 | 210.228 | 215.303 |
| 2009 | 215. 834 834 | 215,969 | 216,177 | 216.330 | 215,949 | 214.537 |
| 2010 | 218.312 | 218.439 | 218.711 | 218.803 | 219,179 | 218.056 |
| 2011 | 226,545 | 226.889 | 226.421 | 226.230 | 225,672 | 224,939 |
| 2012 | 230.379 | 231.407 | 231,317 | 230.221 | 229.601 | 229.594 |
Попробуйте
Следующая таблица является частью набора данных с сайта www.worldbank.org. Используйте таблицу, чтобы построить график временных рядов выбросов CO 2 для США.
| Выбросы CO2 | |||
|---|---|---|---|
| Украина | Соединенное Королевство | США | |
| 2003 | 352 259 | 540 640 | 5 681 664 |
| 2004 | 343 121 | 540 409 | 5 790 761 |
| 2005 | 339 029 | 541 990 | 5 826 394 |
| 2006 | 327 797 | 542 045 | 5 737 615 |
| 2007 | 328 357 | 528 631 | 5 828 697 |
| 2008 | 323 657 | 522 247 | 5 656 839 |
| 2009 | 272 176 | 474 579 | 5 299 563 |
Использование графика временных рядов
Графики временных рядов являются важными инструментами в различных приложениях статистики. При записи значений одной и той же переменной в течение длительного периода времени иногда бывает трудно различить какую-либо тенденцию или закономерность. Однако, когда одни и те же точки данных отображаются графически, некоторые функции выделяются. Графики временных рядов позволяют легко определить тенденции.
При записи значений одной и той же переменной в течение длительного периода времени иногда бывает трудно различить какую-либо тенденцию или закономерность. Однако, когда одни и те же точки данных отображаются графически, некоторые функции выделяются. Графики временных рядов позволяют легко определить тенденции.
Данные о ежегодных убийствах в Детройте, 1961–1973 гг., из книги Ганста и Мейсона «Регрессионный анализ и его применение», Марсель Деккер
«Хронология: Путеводитель по президентам США: информация о месте рождения каждого президента, политической партии, сроке полномочий и многом другом.Scholastic, 2013. Доступно на сайте http://www.scholastic.com/teachers/article/timeline-guide-us-presidents (по состоянию на 3 апреля 2013 г.).
«Президенты». Монстр фактов. Pearson Education, 2007. Доступно на сайте http://www.factmonster.com/ipka/A01
«Статистика продовольственной безопасности». Продовольственная и сельскохозяйственная организация Объединенных Наций. Доступно на сайте http://www.fao.org/economic/ess/ess-fs/en/ (по состоянию на 3 апреля 2013 г.).
Доступно на сайте http://www.fao.org/economic/ess/ess-fs/en/ (по состоянию на 3 апреля 2013 г.).
«Индекс потребительских цен.Министерство труда США: Бюро статистики труда. Доступно в Интернете по адресу http://data.bls.gov/pdq/SurveyOutputServlet (по состоянию на 3 апреля 2013 г.).
«Выбросы CO2 (кт)». The World Bank, 2013. Доступно на сайте http://databank.worldbank.org/data/home.aspx (по состоянию на 3 апреля 2013 г.).
«Данные временного ряда рождений». Главное регистрационное управление Шотландии, 2013 г. Доступно на сайте http://www.gro-scotland.gov.uk/statistics/theme/vital-events/births/time-series.html (по состоянию на 3 апреля 2013 г.).
«Демография: дети в возрасте до 5 лет с недостаточным весом». Индексмунди. Доступно на сайте http://www.indexmundi.com/g/r.aspx?t=50&v=2224&aml=en (по состоянию на 3 апреля 2013 г.).
Ганст, Ричард, Роберт Мейсон. Регрессионный анализ и его применение: подход, ориентированный на данные .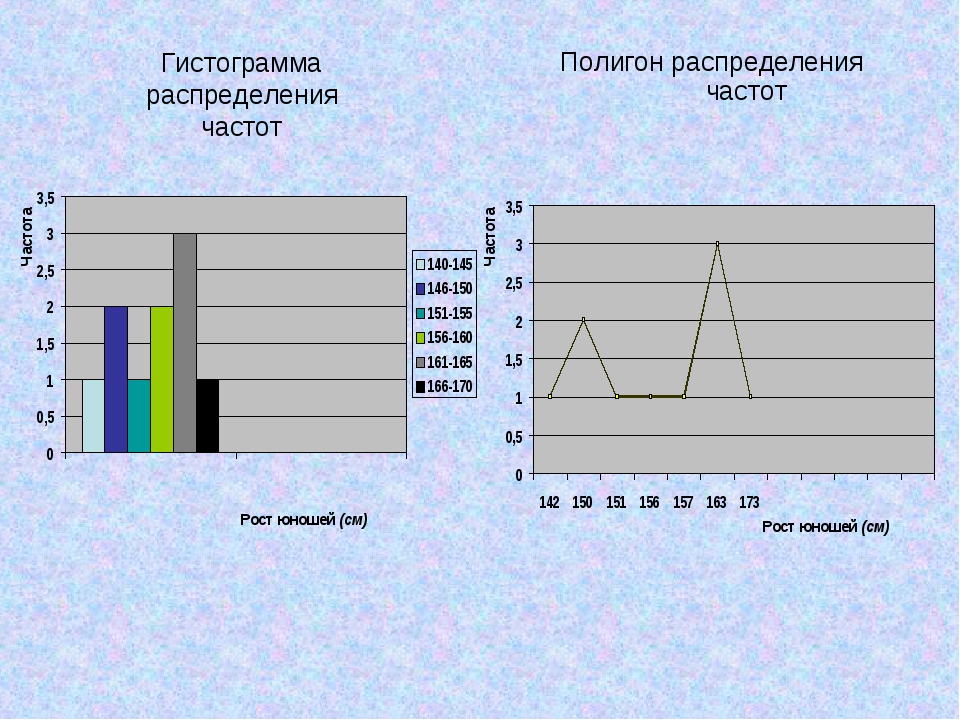 CRC Press: 1980.
CRC Press: 1980.
«Избыточный вес и ожирение: факты ожирения взрослых». Центры по контролю и профилактике заболеваний. Доступно на сайте http://www.cdc.gov/obesity/data/adult.html (по состоянию на 13 сентября 2013 г.).
Гистограмма представляет собой графическую версию частотного распределения. График состоит из полос одинаковой ширины, расположенных рядом друг с другом. Горизонтальная шкала представляет классы значений количественных данных, а вертикальная шкала представляет частоты. Высота столбиков соответствует частотным значениям. Гистограммы обычно используются для больших непрерывных наборов количественных данных. Частотный полигон также можно использовать при графическом отображении больших наборов данных с повторяющимися точками данных.Данные обычно идут по оси х , а частота отображается на оси х . Графики временных рядов могут быть полезны при просмотре больших объемов данных для одной переменной за определенный период времени.
Шестьдесят пять случайно выбранных продавцов автомобилей спросили, сколько машин они обычно продают за одну неделю. Четырнадцать человек ответили, что обычно продают три машины; девятнадцать обычно продают четыре машины; двенадцать обычно продают пять автомобилей; девять обычно продают шесть автомобилей; одиннадцать вообще продают семь машин.Заполнить таблицу.
| Значение данных (количество автомобилей) | Частота | Относительная частота | Суммарная относительная частота |
|---|---|---|---|
Чему соответствует столбец частоты в [ссылка]? Почему?
Чему соответствует столбец относительной частоты в [link]? Почему?
В чем разница между относительной частотой и частотой для каждого значения данных в [ссылка]?
Относительная частота показывает долю точек данных, которые имеют каждое значение. Частота сообщает число точек данных, которые имеют каждое значение.
Частота сообщает число точек данных, которые имеют каждое значение.
В чем разница между кумулятивной относительной частотой и относительной частотой для каждого значения данных?
Чтобы построить гистограмму для данных в [ссылка], определите соответствующие минимальные и максимальные значения x и y и масштабирование. Нарисуйте гистограмму. Обозначьте горизонтальную и вертикальную оси словами. Включите числовое масштабирование.
Ответы будут разными.Показана одна возможная гистограмма:
Построить полигон частот для следующего:
Пульс для женщин Частота 60–69 12 70–79 14 80–89 11 90–99 1 100–109 1 110–119 0 120–129 1 Фактическая скорость в зоне 30 миль в час Частота 42–45 25 46–49 14 50–53 7 54–57 3 58–61 1 Смола (мг) в сигаретах без фильтра Частота 10–13 1 14–17 0 18–21 15 22–25 7 26–29 2
Постройте полигон частот на основе распределения частот для 50 стран с самым высоким рейтингом по глубине голода.
| Глубина голода | Частота |
|---|---|
| 230–259 | 21 |
| 260–289 | 13 |
| 290–319 | 5 |
| 320–349 | 7 |
| 350–379 | 1 |
| 380–409 | 1 |
| 410–439 | 1 |
Найдите среднюю точку для каждого класса.Они будут отображаться на оси x . Значения частоты будут нанесены на график по оси y .
Используйте две таблицы частоты, чтобы сравнить ожидаемую продолжительность жизни мужчин и женщин из 20 случайно выбранных стран. Включите наложенный полигон частот и обсудите формы распределений, центр, разброс и любые выбросы. Какой вывод можно сделать о продолжительности жизни женщин по сравнению с мужчинами?
| Ожидаемая продолжительность жизни при рождении – женщины | Частота |
|---|---|
| 49–55 | 3 |
| 56–62 | 3 |
| 63–69 | 1 |
| 70–76 | 3 |
| 77–83 | 8 |
| 84–90 | 2 |
| Ожидаемая продолжительность жизни при рождении – мужчины | Частота |
|---|---|
| 49–55 | 3 |
| 56–62 | 3 |
| 63–69 | 1 |
| 70–76 | 1 |
| 77–83 | 7 |
| 84–90 | 5 |
Постройте график временных рядов для (а) числа рождений мужского пола, (б) числа рождений женского пола и (в) общего числа рождений.
| Пол/год | 1855 | 1856 | 1857 | 1858 | 1859 | 1860 | 1861 |
| Женский | 45 545 | 49 582 | 50 257 | 50 324 | 51 915 | 51 220 | 52 403 |
| Мужской | 47 804 | 52 239 | 53 158 | 53 694 | 54 628 | 54 409 | 54 606 |
| Итого | 93 349 | 101 821 | 103 415 | 104 018 | 106 543 | 105 629 | 107 009 |
| Пол/Год | 1862 | 1863 | 1864 | 1865 | 1866 | 1867 | 1868 | 1869 |
| Женский | 51 812 | 53 115 | 54 959 | 54 850 | 55 307 | 55 527 | 56 292 | 55 033 |
| Мужской | 55 257 | 56 226 | 57 374 | 58 220 | 58 360 | 58 517 | 59 222 | 58 321 |
| Итого | 107 069 | 109 341 | 112 333 | 113 070 | 113 667 | 114 044 | 115 514 | 113 354 |
| Пол/Год | 1871 | 1870 | 1872 | 1871 | 1872 | 1827 | 1874 | 1875 |
| Женский | 56 099 | 56 431 | 57 472 | 56 099 | 57 472 | 58 233 | 60 109 | 60 146 |
| Мужской | 60 029 | 58 959 | 61 293 | 60 029 | 61 293 | 61 467 | 63 602 | 63 432 |
| Итого | 116 128 | 115 390 | 118 765 | 116 128 | 118 765 | 119 700 | 123 711 | 123 578 |
В следующих наборах данных перечислены штатные полицейские на 100 000 жителей, а также количество убийств на 100 000 жителей города Детройт, штат Мичиган, за период с 1961 по 1973 год.
| Год | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 |
| Полиция | 260,35 | 269,8 | 272.04 | 272,96 | 272,51 | 261,34 | 268,89 |
| Убийства | 8,6 | 8,9 | 8,52 | 8,89 | 13.07 | 14.57 | 21,36 |
| Год | 1968 | 1969 | 1970 | 1971 | 1972 | 1973 |
| Полиция | 295,99 | 319,87 | 341,43 | 356,59 | 376,69 | 390,19 |
| Убийства | 28.03 | 31,49 | 37,39 | 46,26 | 47,24 | 52.33 |
- Постройте график двойного временного ряда, используя общую ось x для обоих наборов данных.

- Какая переменная увеличивалась быстрее всего? Объяснять.
- Повлияло ли увеличение количества полицейских в Детройте на количество убийств? Объяснять.
Предположим, что три книжных издателя заинтересованы в количестве книг в мягкой обложке, которые взрослые покупают в месяц. Каждое издательство провело опрос. В ходе опроса взрослых потребителей спросили, сколько художественных книг в мягкой обложке они купили в предыдущем месяце.Результаты следующие:
| Количество книг | Частота. | Отн. Частота |
|---|---|---|
| 0 | 10 | |
| 1 | 12 | |
| 2 | 16 | |
| 3 | 12 | |
| 4 | 8 | |
| 5 | 6 | |
| 6 | 2 | |
| 8 | 2 |
| Количество книг | Частота. | Отн. Частота |
|---|---|---|
| 0–1 | 20 | |
| 2–3 | 35 | |
| 4–5 | 12 | |
| 6–7 | 2 | |
| 8–9 | 1 |
Зачастую круизные лайнеры проводят все операции на борту, за исключением азартных игр, в безналичном порядке. В конце круиза гости оплачивают один счет, покрывающий все транзакции на борту. Предположим, что 60 одиноких путешественников и 70 пар были опрошены относительно их бортовых счетов за семидневный круиз из Лос-Анджелеса на Мексиканскую Ривьеру. Ниже приводится сводка счетов для каждой группы.
В конце круиза гости оплачивают один счет, покрывающий все транзакции на борту. Предположим, что 60 одиноких путешественников и 70 пар были опрошены относительно их бортовых счетов за семидневный круиз из Лос-Анджелеса на Мексиканскую Ривьеру. Ниже приводится сводка счетов для каждой группы.
| Сумма(💲) | Частота | Отн.Частота |
|---|---|---|
| 51–100 | 5 | |
| 101–150 | 10 | |
| 151–200 | 15 | |
| 201–250 | 15 | |
| 251–300 | 10 | |
| 301–350 | 5 |
- Укажите относительную частоту для каждой группы.
- Построить гистограмму для группы одиночных. Масштабируйте ось x на ширину 💲50. Используйте относительную частоту на оси y .
- Построить гистограмму для группы пар.
 Масштабируйте ось x на ширину 💲50. Используйте относительную частоту на оси y .
Масштабируйте ось x на ширину 💲50. Используйте относительную частоту на оси y . - Сравните два графика:
- Укажите два сходства между графиками.
- Укажите два различия между графиками.
- В целом графики больше похожи или отличаются?
- Постройте новый график для пар вручную.Поскольку каждая пара платит за двух человек, вместо масштабирования оси x на 💲50, масштабируйте ее на 💲100. Используйте относительную частоту на оси y .
- Сравните график для одиночек с новым графиком для пар:
- Укажите два сходства между графиками.
- В целом графики больше похожи или отличаются?
- Как масштабирование графика для пар изменило способ сравнения его с графиком для одиночек?
- Основываясь на графиках, считаете ли вы, что отдельные люди тратят столько же, более или менее, как одинокие, так и в паре? Объясните почему одним-двумя полными предложениями.

| Сумма(💲) | Частота | Относительная частота |
|---|---|---|
| 51–100 | 5 | 0,08 |
| 101–150 | 10 | 0,17 |
| 151–200 | 15 | 0,25 |
| 201–250 | 15 | 0,25 |
| 251–300 | 10 | 0.17 |
| 301–350 | 5 | 0,08 |
| Сумма(💲) | Частота | Относительная частота |
|---|---|---|
| 100–150 | 5 | 0,07 |
| 201–250 | 5 | 0,07 |
| 251–300 | 5 | 0,07 |
| 301–350 | 5 | 0.07 |
| 351–400 | 10 | 0,14 |
| 401–450 | 10 | 0,14 |
| 451–500 | 10 | 0,14 |
| 501–550 | 10 | 0,14 |
| 551–600 | 5 | 0,07 |
| 601–650 | 5 | 0,07 |
- Ответы могут отличаться. Возможные ответы включают в себя:
- Оба графика имеют один пик.
- Оба графика используют интервалы классов шириной, равной 💲50.
- Ответы могут отличаться.Возможные ответы включают в себя:
- График пар содержит интервал классов без значений.
- Для отображения данных по парам требуется почти в два раза больше интервалов занятий.

- Ответы могут отличаться. Возможные ответы: Графики больше похожи, чем различны, потому что общие закономерности для графиков одинаковы.
- Оба графика имеют один пик.
- Оба графика отображают 6 интервалов классов.
- Оба графика показывают одинаковую общую картину.
- Ответы могут отличаться. Возможные ответы включают: Хотя ширина интервалов занятий для пар в два раза больше, чем интервалы занятий для одиночек, графики больше похожи, чем различаются.
 Возможные ответы включают: Судя по гистограммам, кажется, что расходы не сильно отличаются от одиноких людей до людей, которые являются частью пары. Общие схемы одинаковые. Диапазон расходов для пар примерно в два раза выше, чем для отдельных лиц.
Возможные ответы включают: Судя по гистограммам, кажется, что расходы не сильно отличаются от одиноких людей до людей, которые являются частью пары. Общие схемы одинаковые. Диапазон расходов для пар примерно в два раза выше, чем для отдельных лиц.Двадцать пять случайно выбранных студентов спросили, сколько фильмов они посмотрели на прошлой неделе.Результаты приведены ниже.
| Количество фильмов | Частота | Относительная частота | Суммарная относительная частота |
|---|---|---|---|
| 0 | 5 | ||
| 1 | 9 | ||
| 2 | 6 | ||
| 3 | 4 | ||
| 4 | 1 |
- Построить гистограмму данных.

- Заполните столбцы таблицы.
Используйте следующую информацию, чтобы ответить на следующие два упражнения: Предположим, сто одиннадцать человек, которые делали покупки в специальном магазине футболок, спросили, сколько у них есть футболок, каждая из которых стоит больше 💲19.
Процент людей, у которых есть не более трех футболок стоимостью более 💲19 каждая, составляет примерно:
- 21
- 59
- 41
- Невозможно определить
Если данные были собраны путем опроса первых 111 человек, вошедших в магазин, то тип выборки:
- кластер
- простой случайный
- многослойный
- удобство
Ниже приведены показатели ожирения за 2010 год, составленные U.США и Вашингтон, округ Колумбия.
 5
5 1
1Постройте столбчатую диаграмму показателей ожирения в вашем штате и в четырех ближайших к вам штатах. Подсказка: пометьте ось x состояниями.
Глоссарий
- Частота
- количество раз, когда значение данных встречается
- Гистограмма
- графическое представление в формате x – y формы распределения данных в наборе данных; x представляют данные, а y представляют частоту или относительную частоту.Граф состоит из смежных прямоугольников.
- Относительная частота
- отношение количества раз, когда значение данных встречается в наборе всех результатов, к количеству всех результатов
Распределение частот
J Pharmacol Pharmacother. январь-март 2011 г.; 2(1): 54–56.
S Manikandan
Помощник редактора, JPP
Помощник редактора, JPP
Адрес для корреспонденции: Manikandan S., Кафедра фармакологии, Медицинский колледж и научно-исследовательский институт Индиры Ганди, Кадиркамам, Пудучерри, Индия. Электронная почта: moc.oohay@100nadnakinamАвторское право © Журнал фармакологии и фармакотерапииЭто статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии, что оригинал работа цитируется правильно.
Эта статья была процитирована другими статьями в PMC.ВВЕДЕНИЕ
Следующим шагом после завершения сбора данных является организация данных в осмысленной форме, чтобы можно было легко увидеть тенденцию, если таковая имеется, возникающая из данных.Одним из распространенных методов организации данных является построение частотного распределения. Частотное распределение представляет собой организованное табличное/графическое представление количества лиц в каждой категории по шкале измерения.[1] Это позволяет исследователю удобно просматривать все данные. Он показывает, являются ли наблюдения высокими или низкими, а также сосредоточены ли они в одной области или разбросаны по всей шкале. Таким образом, частотное распределение представляет собой картину того, как отдельные наблюдения распределяются по шкале измерений.
Частотное распределение представляет собой организованное табличное/графическое представление количества лиц в каждой категории по шкале измерения.[1] Это позволяет исследователю удобно просматривать все данные. Он показывает, являются ли наблюдения высокими или низкими, а также сосредоточены ли они в одной области или разбросаны по всей шкале. Таким образом, частотное распределение представляет собой картину того, как отдельные наблюдения распределяются по шкале измерений.
ОТОБРАЖЕНИЕ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
Таблицы частот
Таблица частот (распределений) показывает различные категории измерений и количество наблюдений в каждой категории. Прежде чем строить таблицу частот, следует иметь представление о диапазоне (минимальные и максимальные значения). Диапазон разделен на произвольные интервалы, называемые «интервалом класса». Если интервалов классов слишком много, то уменьшения громоздкости данных не произойдет, а также станут заметны незначительные отклонения. С другой стороны, если их очень мало, то нельзя определить форму самого распределения. Как правило, достаточно 6–14 интервалов.[2]
С другой стороны, если их очень мало, то нельзя определить форму самого распределения. Как правило, достаточно 6–14 интервалов.[2]
Ширину класса можно определить, разделив диапазон наблюдений на количество классов. Ниже приведены некоторые рекомендации относительно ширины классов:[1]
Рекомендуется иметь одинаковую ширину классов. Неравную ширину классов следует использовать только тогда, когда в данных существуют большие пробелы.
Интервалы классов должны быть взаимоисключающими и непересекающимися.
Следует избегать открытых классов в нижней и верхней части (например, <10, >100).
Таблица частотного распределения частоты пульса в покое у здоровых лиц приведена в . Он также дает кумулятивную и относительную частоту, что облегчает интерпретацию данных.
Таблица 1
Таблица 1
Частота Распределение скорости пульса отдыха у здоровых добровольцев (N = 63)
| Pulse / Min | Частота | Совокупная частота | Относительная кумулятивная частота (%) |
|---|---|---|---|
| 60–64 | 2 | 2 | 3. 17 17 |
| 7 9 | |||
| 70-74 11 | 20 | ||
| 75-79 15 | 35 | 55.56 | |
| 10 | 45 | ||
| 85-89 9 | 54 | ||
| 90-94 6 | 60 | ||
| 95–99 | 3 | 63 | 100 |
Графики распределения частот
График распределения частот представляет собой схематическое изображение информации в таблице частот.
Гистограмма
Гистограмма представляет собой графическое представление интересующей переменной по оси X и количества наблюдений (частоты) по оси Y . Проценты можно использовать, если целью является сравнение двух гистограмм с разным количеством субъектов. Гистограмма используется для отображения частоты, когда данные измеряются на интервальной шкале или шкале отношений. изображает гистограмму, построенную для данных, приведенных в .
Гистограмма частоты пульса в покое у здоровых добровольцев (N = 63)
Гистограмма и гистограмма могут выглядеть одинаково, но между ними есть три важных различия:[3,4]
На гистограмме есть нет промежутка между столбцами, так как переменная непрерывна.На гистограмме между столбцами будет пространство.
Не все столбцы гистограммы должны иметь одинаковую ширину (зависит от интервала класса), тогда как на гистограмме они равны.
Площадь каждого столбца соответствует частоте на гистограмме, тогда как на столбчатой диаграмме это высота [].
Многоугольник частот
Многоугольник частот строится путем соединения всех средних точек вершин столбцов гистограммы прямой линией без отображения столбцов.Многоугольник частот помогает легко сравнивать два распределения частот. Когда общая частота велика, а интервалы классов узки, полигон частот становится гладкой кривой, известной как кривая частот. Полигон частот, иллюстрирующий данные, показан на .
Частотный полигон частоты пульса в покое у здоровых добровольцев (N = 63)
Диаграмма с прямоугольниками и усами
Этот график, впервые описанный Тьюки в 1977 году, также можно использовать для иллюстрации распределения данных.Имеется вертикальный или горизонтальный прямоугольник (прямоугольник), концы которого соответствуют верхнему и нижнему квартилям (75 и 25 процентилей соответственно). Следовательно, средние 50% наблюдений представлены прямоугольником. Длина прямоугольника указывает на изменчивость данных. Линия внутри прямоугольника обозначает медиану (иногда помечается знаком плюс).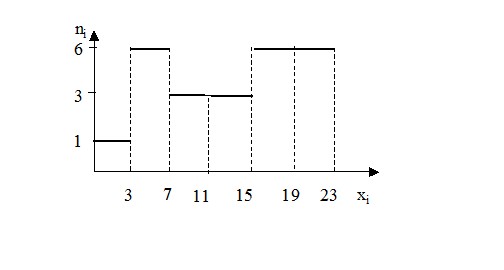 Положение медианы указывает, искажены данные или нет. Если медиана ближе к верхнему квартилю, то они имеют отрицательную асимметрию, а если ближе к нижнему квартилю, то положительную асимметрию.
Положение медианы указывает, искажены данные или нет. Если медиана ближе к верхнему квартилю, то они имеют отрицательную асимметрию, а если ближе к нижнему квартилю, то положительную асимметрию.
Линии за пределами прямоугольника с обеих сторон известны как усы []. Эти усы в 1,5 раза превышают длину прямоугольника, т. е. межквартильный размах (IQR). Конец усов называется внутренним забором, а любое значение за его пределами — выбросом. Если распределение симметрично, то усы имеют одинаковую длину. Если данные разрежены с одной стороны, соответствующий боковой ус будет коротким. Внешнее ограждение (обычно не маркированное) находится на расстоянии, в три раза превышающем IQR, по обе стороны от коробки.Причина наличия внутреннего и внешнего забора в 1,5 и 3 раза больше IQR, соответственно, заключается в том, что 95% наблюдений попадают в 1,5 раза больше IQR, а 99% — в 3 раза больше IQR.
Схематическая диаграмма «прямоугольника и усов»
ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЯ ЧАСТОТ
Существуют четыре важные характеристики частотного распределения. [6] Они следующие:
[6] Они следующие:
Показатели центральной тенденции и местоположения (среднее, медиана, мода)
Показатели дисперсии (диапазон, дисперсия, стандартное отклонение)
Степень симметрии/асимметрии (асимметрия)
Плоскостность или остроконечность (эксцесс).
Подробнее об этом будет рассказано в следующем выпуске.
Сноски
Источник поддержки: Нет
Конфликт интересов: Не объявлено
ССЫЛКИ
1. Gravetter FJ, Wallnau LB. 5-е изд. Бельмонт: Уодсворт – Обучение Томсона; 2000. Статистика для поведенческих наук. [Google Академия]2. Доусон Б., Трапп Р.Г. 4-е изд. Нью-Йорк: Макгроу Хилл; 2004. Базовая и клиническая биостатистика. [Google Академия]3. Сундарам К.Р., Двиведи С.Н., Шринивас В.1-е изд. Нью-Дели: B.I Publications Pvt Ltd; 2010. Принципы и методы медицинской статистики. [Google Академия]4. Swinscow TDV, Кэмпбелл MJ. (индийский) 10-е изд.







 Повторите это действие для каждого компонента, который вы хотите изменить.
Повторите это действие для каждого компонента, который вы хотите изменить. 45
45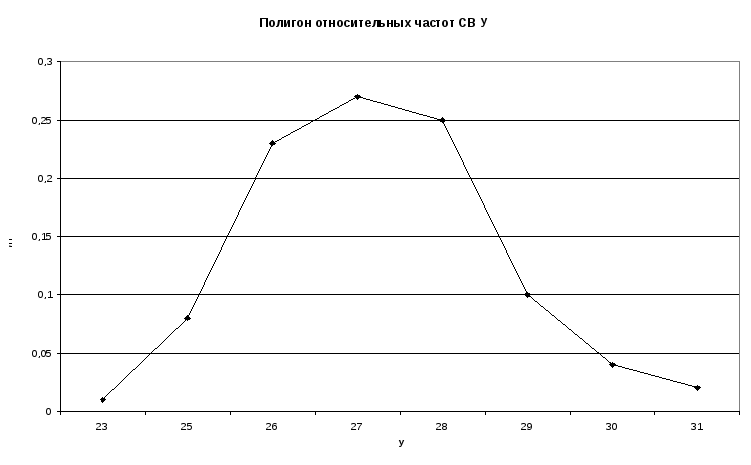 45
45
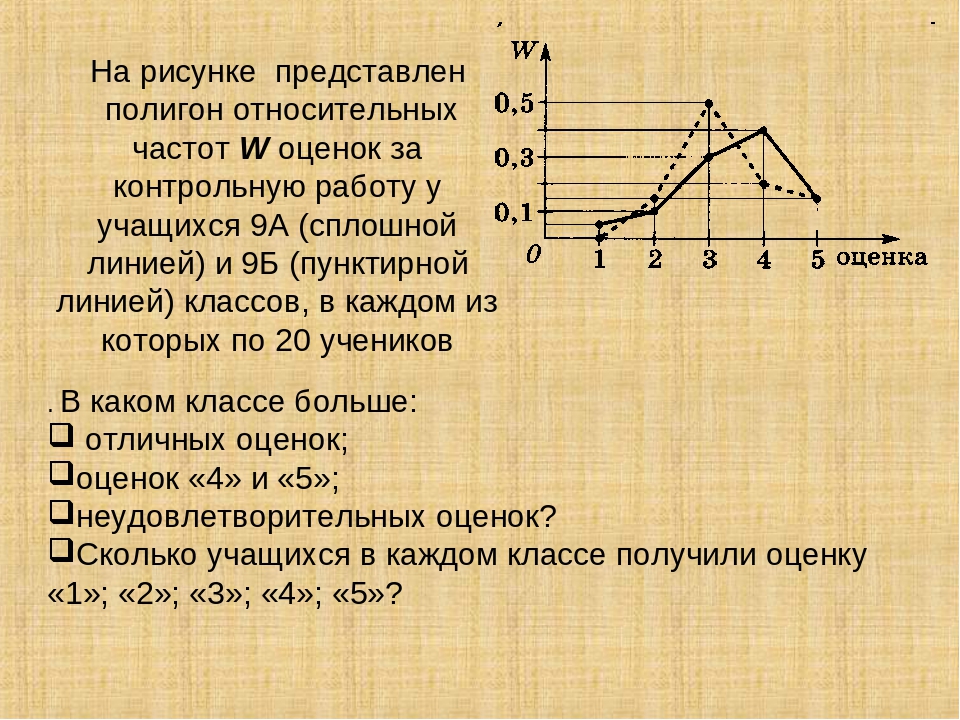 43
43 9)
9) 09
09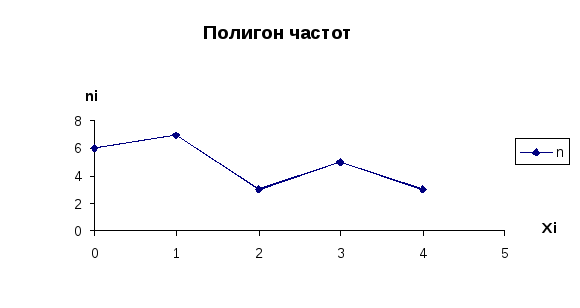 3;
7.2)
3;
7.2)
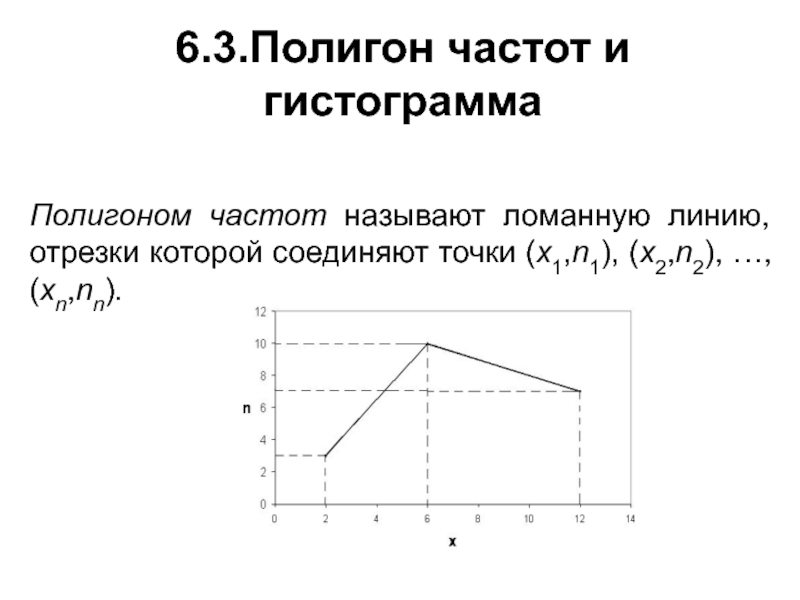 Полигон частот должен выглядеть так, как показано на графике вверху этой статьи.
Полигон частот должен выглядеть так, как показано на графике вверху этой статьи. Ожидаемое значение также указывает
Ожидаемое значение также указывает Доступно на сайте http://www.fao.org/economic/ess/ess-fs/en/ (по состоянию на 3 апреля 2013 г.).
Доступно на сайте http://www.fao.org/economic/ess/ess-fs/en/ (по состоянию на 3 апреля 2013 г.).
 org/contents/30189442-699…
org/contents/30189442-699… 5-60,5
5-60,5

 Масштабируйте ось x на ширину 💲50. Используйте относительную частоту на оси y .
Масштабируйте ось x на ширину 💲50. Используйте относительную частоту на оси y .