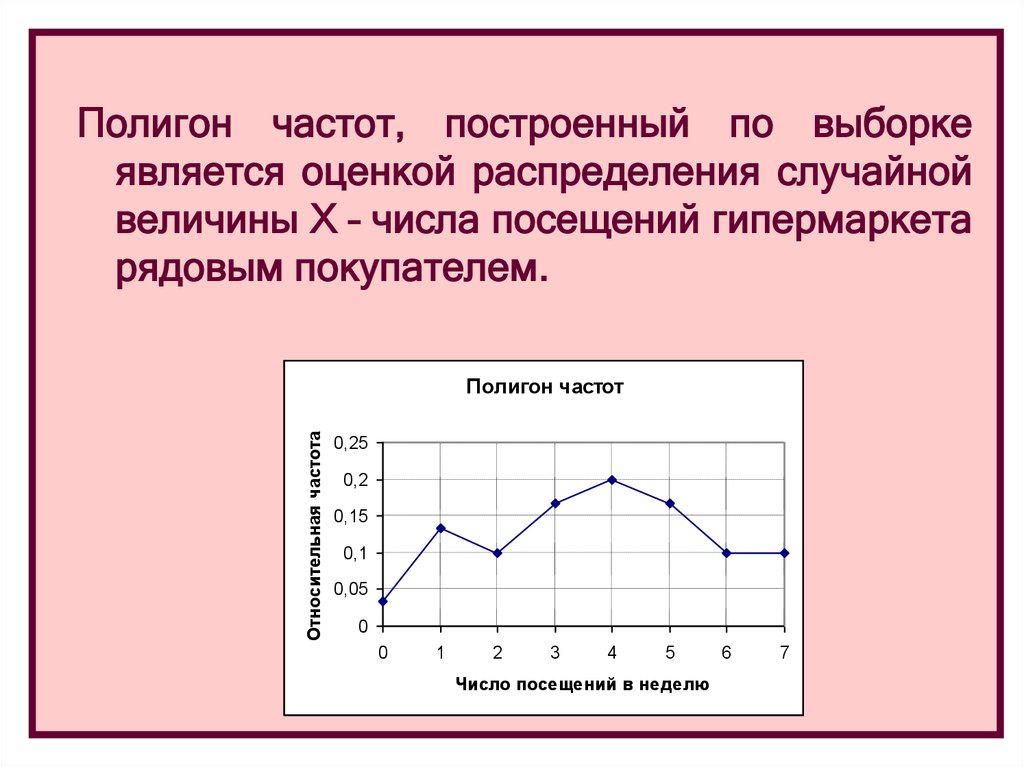
Построить полигон частот онлайн: Группировка статистических данных онлайн
Децили
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9.,
По заданному вариационному ряду найдем децили с помощью калькулятора.
| Группы | x | Кол-во f | x·f | S | (x-x)·f | (x-x)2·f | (x-x)3·f | (x-x)4·f | Частота |
| 0.06 — 0.27 | 0.16 | 2 | 0.33 | 2 | 0.72 | 0.26 | -0.0926 | 0.0333 | 0.1 |
| 0.27 — 0.47 | 0.37 | 7 | 2.59 | 9 | 1. | 0.17 | -0.0255 | 0.0039 | 0.35 |
| 0.47 — 0.68 | 0.58 | 7 | 4.03 | 16 | 0.36 | 0.0184 | 0.0009 | 0 | 0.35 |
| 0.68 — 0.88 | 0.78 | 3 | 2.34 | 19 | 0.77 | 0.2 | 0.0506 | 0.013 | 0.15 |
| 0.88 — 1.09 | 0.99 | 0 | 0 | 19 | 0 | 0 | 0 | 0 | 0 |
| 1.09 — 1.29 | 1.19 | 1 | 1.19 | 20 | 0.67 | 0.44 | 0.3 | 0.2 | 0.05 |
| 20 | 10.47 | 0 | 3.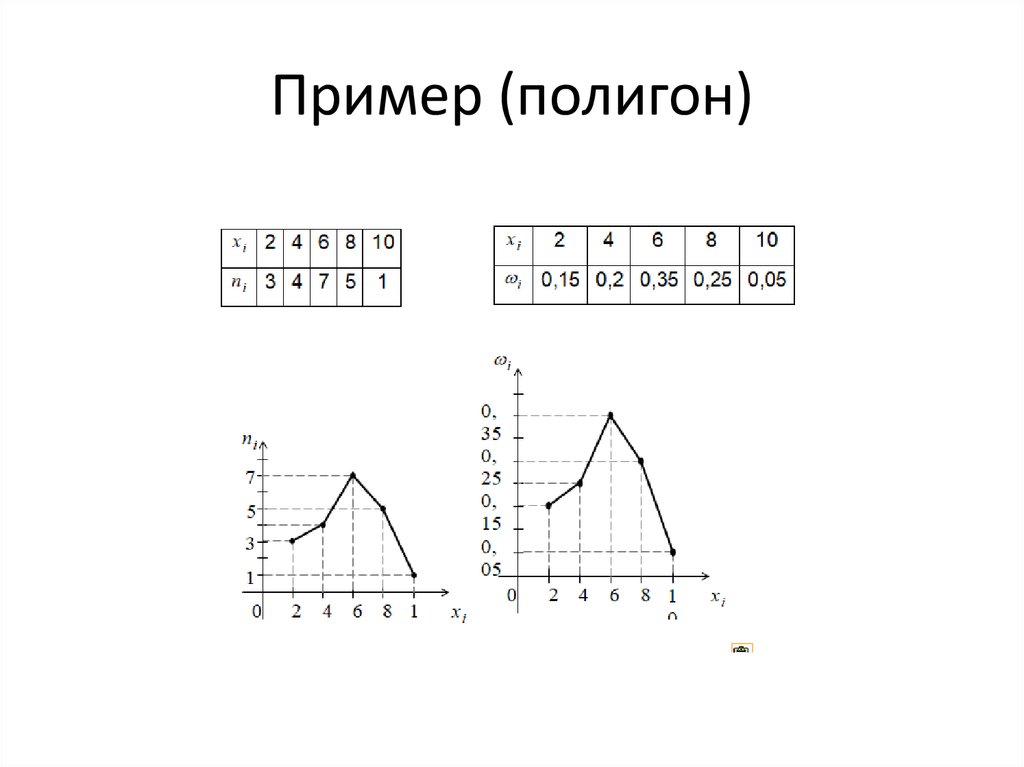 59 59
| 1.08 | 0.23 | 0.25 | 1 |
- Решение
- Видео решение
Для оценки ряда распределения найдем следующие показатели:
Средняя взвешенная
Мода
Выбираем в качестве начала интервала 0.2672, так как именно на этот интервал приходится наибольшее количество
Наиболее часто встречающееся значение ряда – 0.47
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше
Таким образом, 50% единиц совокупности будут меньше по величине 0.5
Квартили
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1 и Q2; 25% — между Q2 и Q3; остальные 25% превосходят Q3
Таким образом, 25% единиц совокупности будут меньше по величине 0.
 36
36
Q2 совпадает с медианой, Q2 = 0.5
Остальные 25% превосходят значение 0.65.
Квартильный коэффициент дифференциации.
k = Q1 / Q3
k = 0.36 / 0.65 = 0.55
Таким образом, 10% единиц совокупности будут меньше по величине 0.27
Остальные 10% превосходят 0.81
Показатели вариации
Размах вариации
R = Xmax — Xmin
R = 1.29 — 0.062 = 1.23
Среднее линейное отклонение
Каждое значение ряда отличается от другого не более, чем на 0.18
Дисперсия
Несмещенная оценка дисперсии.
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 0.52 не более, чем на 0.23
Оценка среднеквадратического отклонения.
Коэффициент вариации
Поскольку v>30% ,но v<70%, то вариация умеренная.
Показатели формы распределения.
Коэффициент осцилляции
Относительное линейное отклонение
Относительный показатель квартильной вариации
Степень асимметрии
Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
Положительная величина указывает на наличие правосторонней асимметрии
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Ex > 0 — островершинное распределение
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего
Поскольку n<=30, то определяем значение tkp по таблице распределения Стьюдента
По таблице Стьюдента находим Tтабл
Ф(tkp) = 1- p = 1- 0. 954 = 0.05
954 = 0.05
Tтабл (n-1;α) = (19;0.05) = 1.729
(0.52 — 0.09;0.52 + 0.09) = (0.43;0.61)
С вероятностью 0.954 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
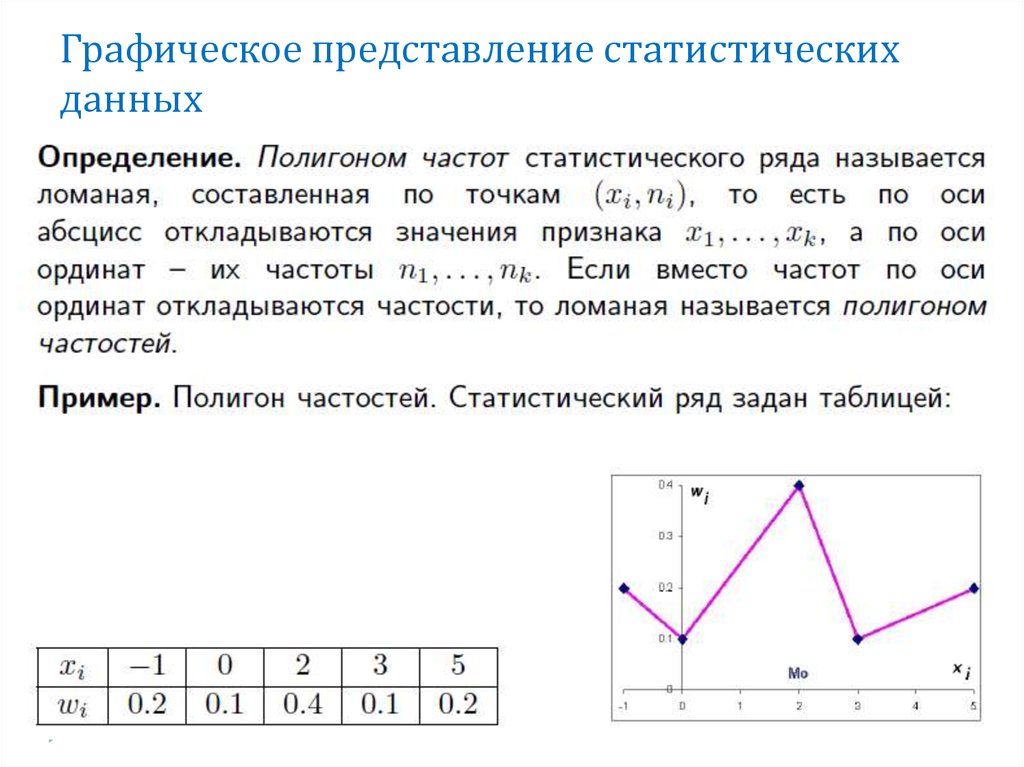
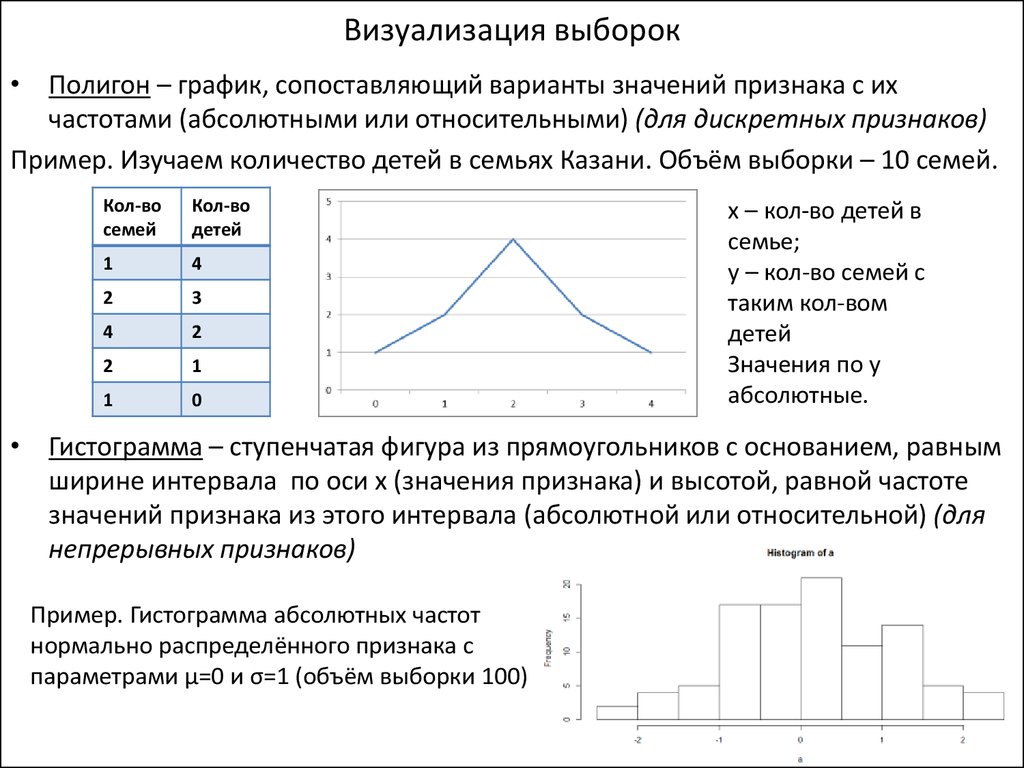
Полигон и гистограмма частот и частостей (относительных частот). Кумулятивная кривая (кумулята). Огива. Теория вероятностей и математическая статистика
Для наглядности строят различные графики статистического распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
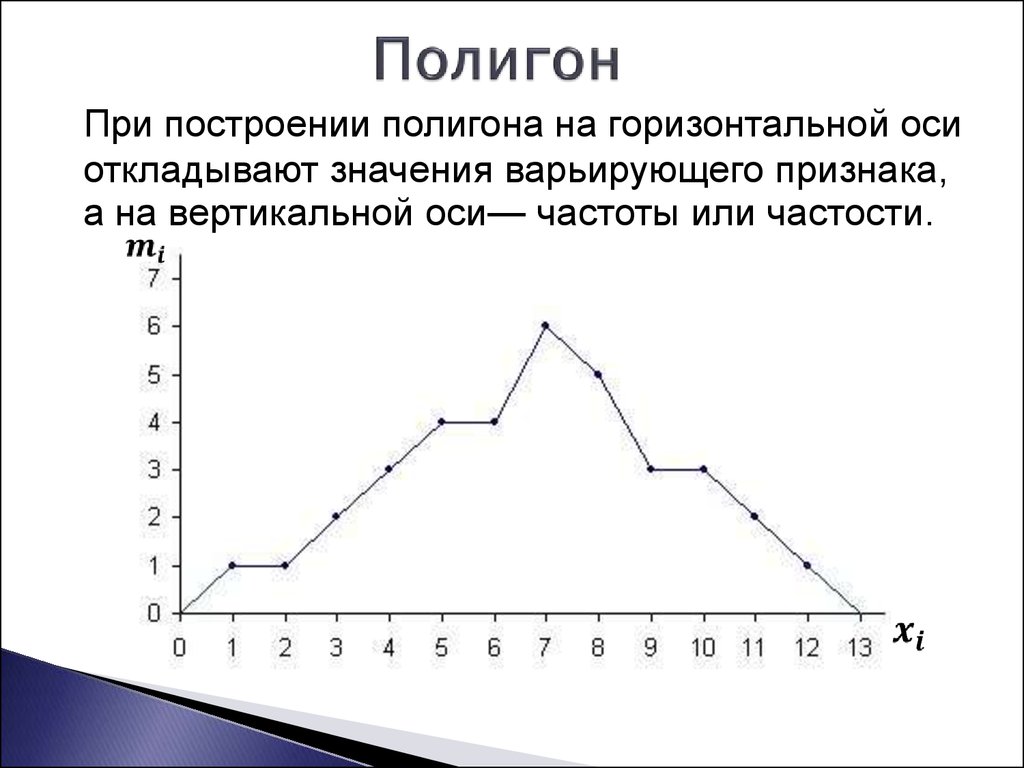
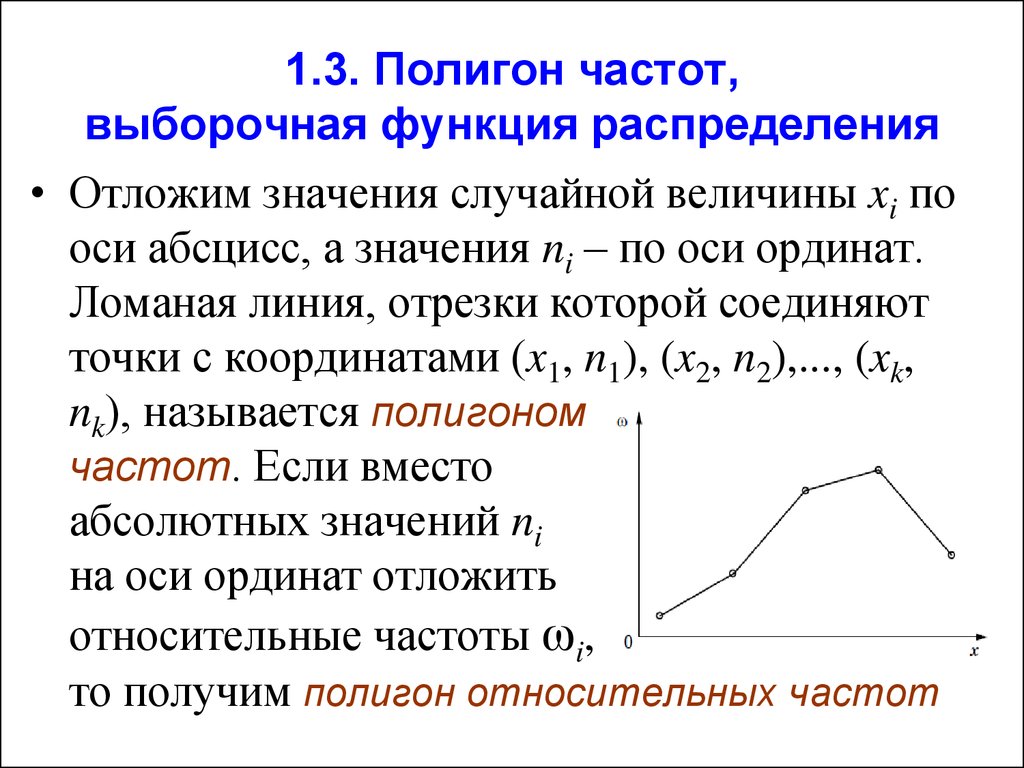
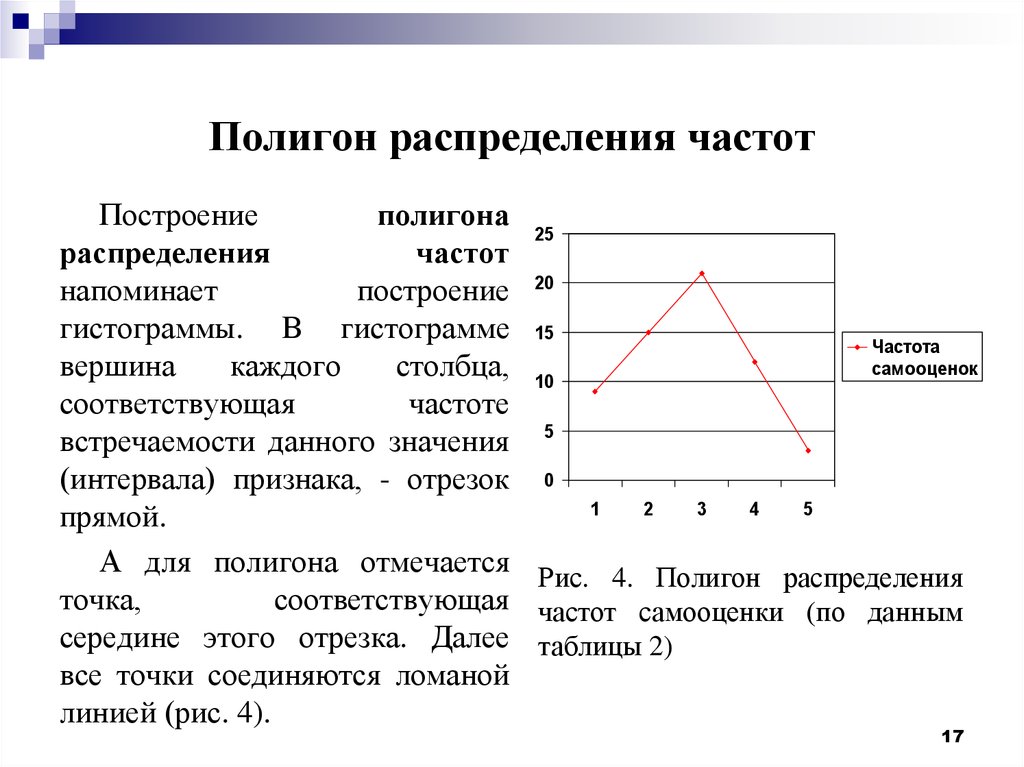
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки . Для построения полигона относительных частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им относительные частоты (частости) . Такие точки соединяют отрезками прямых и получают полигон частот.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
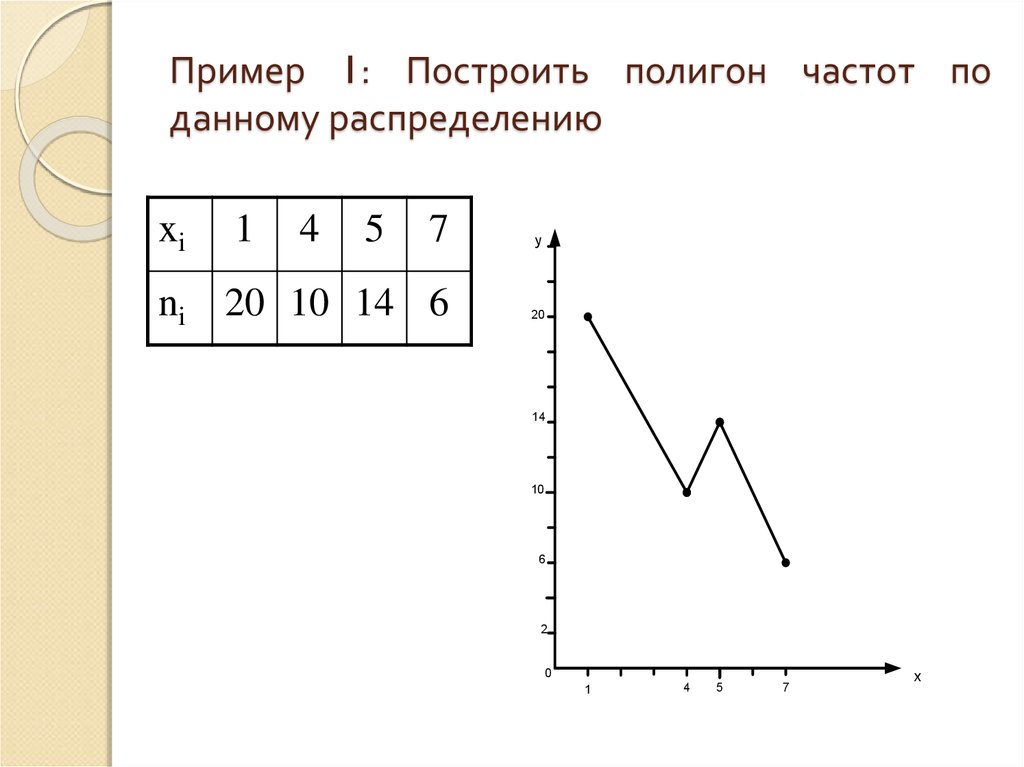
Пример 1
Построить полигон частот и полигон относительных частот (частостей):
| 2 | 7 | 8 | 15 | 16 | 17 | |
| 15 | 35 | 64 | 55 | 10 |
Решение
Вычислим относительные частоты (частости):
| Относительные частоты, | ||
| 2 | 15 |
0. 075 075
|
| 7 | 35 | |
| 8 | 64 | 0.320 |
| 15 | 55 | 0.275 |
| 16 | 21 | 0.105 |
| 17 | 10 | 0.050 |
| Итого | 1.000 |
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
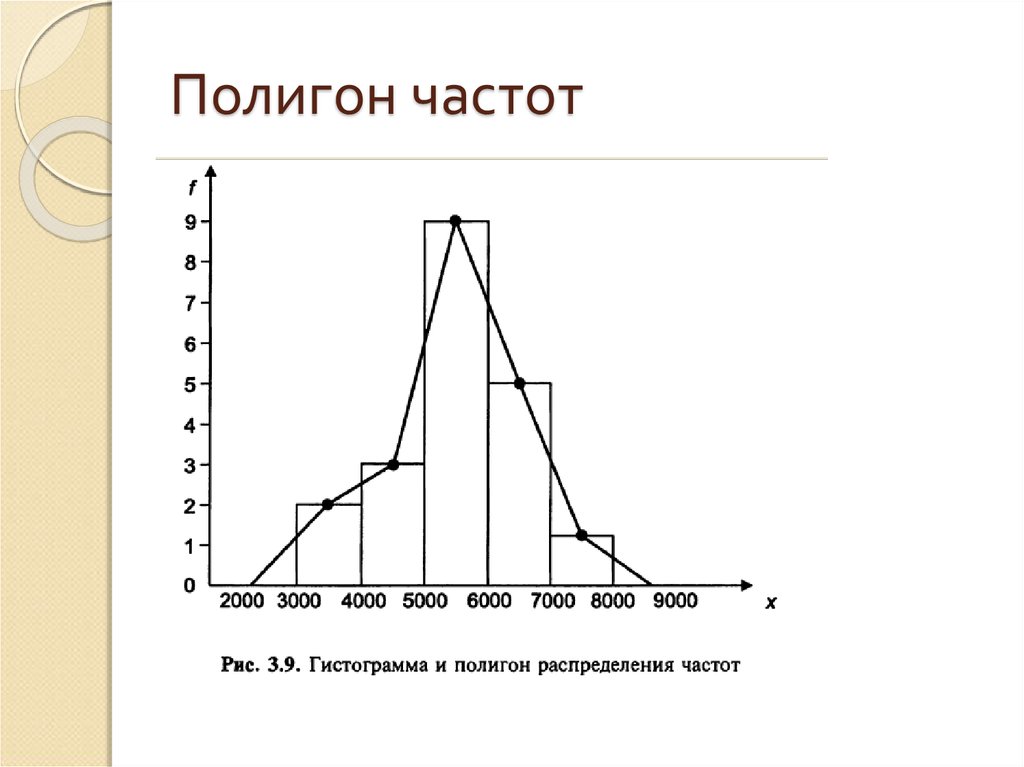
Гистограмма
В случае интервального статистического распределения целесообразно построить гистограмму.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты (в случае равных интервалов) должны быть пропорциональны частотам. При построении гистограммы с неравными интервалами по оси ординат наносят не частоты, а плотность частоты . Это необходимо сделать для устранения влияния величины интервала на распределение и иметь возможность сравнивать частоты.
В случае построения гистограммы относительных частот (гистограммы частостей) высоты в случае равных интегралов должны быть пропорциональны относительной частоте , а в случае неравных интервалов высота равна плотности относительной частоты .
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пример 2
Построить гистограмму частот и относительных частот (частостей)
| 2-5 | 5-8 | 8-11 | 11-14 | 14-17 | 17-20 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим относительные частоты:
| Интервалы, | Относительные частоты, | |
| 2 – 5 | 15 |
0. 075 075
|
| 5 – 8 | 35 | 0.175 |
| 8 – 11 | 64 | 0.320 |
| 11 – 14 | 55 | 0.275 |
| 14 – 17 | 21 | 0.105 |
| 17 – 20 | 10 | 0.050 |
| Итого | 200 | 1.000 |
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
| 2-4 | 4-8 | 8-13 | 13-15 | 15-17 | 17-20 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим плотности частоты:
| Интервалы, | Длина интервала, | Плотность частоты, | |
| 2 – 4 | 15 | 2 |
7. 500 500
|
| 4 – 8 | 35 | 4 | 8.750 |
| 8 – 13 | 64 | 5 | 12.800 |
| 13 – 15 | 55 | 2 | 27.500 |
| 15 – 17 | 21 | 2 | 10.500 |
| 17 – 20 | 10 | 3 |
3. 333 333
|
| Итого | 200 | — | — |
Гистограмма частот
Кроме этой задачи на другой странице сайта есть пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.
Пример 4
Построить кумулятивную кривую:
| 2 | 5 | 8 | 11 | 14 | 17 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим накопленные частоты:
| Накопленные частоты, | ||
| 2 | 15 | 15 |
| 7 | 35 | 50 |
| 8 | 64 | 114 |
| 15 | 55 | 169 |
| 16 | 21 | 190 |
| 17 | 10 | 200 |
| Итого | 200 | — |
Кумулятивная кривая
Редактор полигональных графиков частот — MathCracker.
 com
comРешатели Статистика
Инструкции: Используйте этот редактор графиков полигонов частот, чтобы построить полигон частот на основе выборки, предоставленной в виде сгруппированных данных, с классами и частотами. Пожалуйста, введите эти классы и частоты в форму ниже:
Классы или значения (пример: 3–5, 8 и т. д. По одному в строке)
Частоты
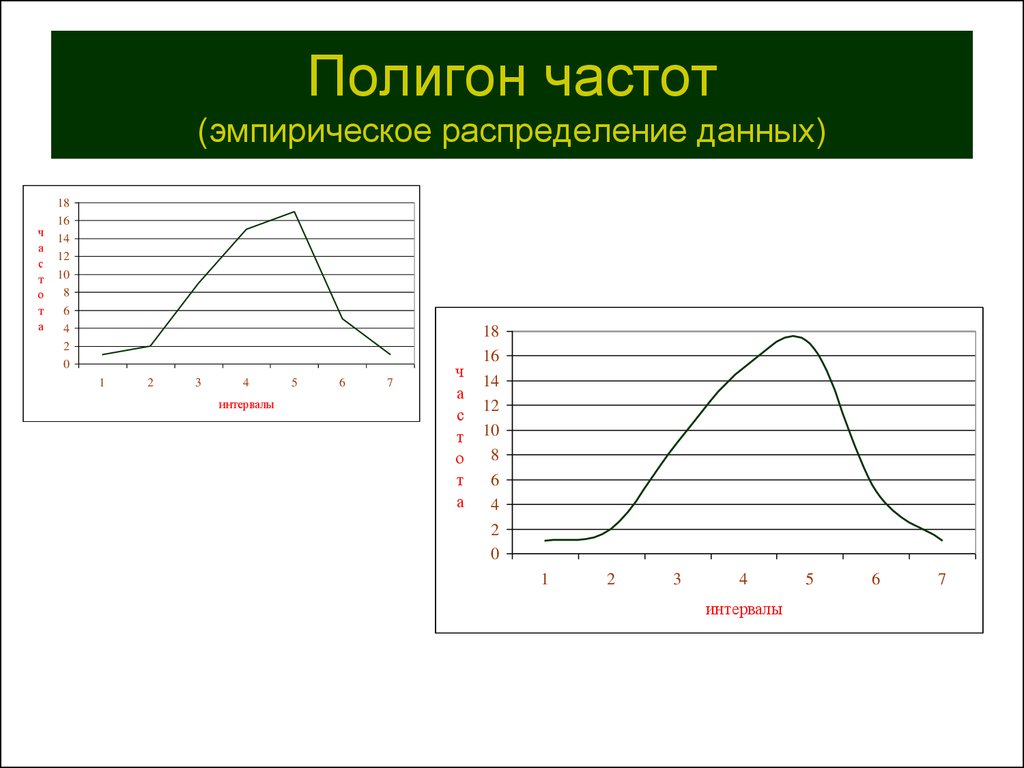
Идея сгруппировать данные в большинстве случаев состоит в том, чтобы обобщить выборку, часто используя показатели центральной тенденции, меры дисперсии и диаграммы.
Одной из диаграмм, описывающих выборку, является полигон частот, который дает вам быстрый снимок распределения значений в выборке.
Графически полигон частот будет выглядеть так:
Как вы на самом деле строите полигон частот?
Частотный многоугольник на самом деле довольно легко построить:
Во-первых, вам нужно иметь частотное распределение данных либо с точки зрения частоты отдельных значений, либо с точки зрения классов.
Во-вторых, вы помещаете классы (или отдельные значения) на ось X, а их частоты — на ось Y и наносите на график все соответствующие точки (X, Y).
В-третьих, вы соединяете эти точки прямыми линиями, начиная с точек слева и направо.
Это именно то, что делает для вас этот генератор полигонов частот, и большинство пакетов статистического программного обеспечения (например, Excel) могут сделать для вас.
Теперь, если вам вместо этого нужно построить полигон кумулятивной частоты, вам понадобится это создатель графиков .
Другие средства создания диаграмм описательной статистики
Создатели диаграмм очень важны во время получения быстрого, но достаточно подходящего описания формы распределения случайной величины, которая является выборкой.
Возможно, вам будет интересно ознакомиться с нашим создатель гистограммы , что, возможно, даст вам более точное представление о форме распределения. Вы также можете использовать это круговая диаграмма или же создатель коробочного сюжета , для соответствующего уровня измерения.
Базовый пакет статистики Описательная статистика Редактор частотных полигонов Графический многоугольник частоты Генератор полигонов частот Создатель графиков Графический инструмент Калькулятор статистики Решатель статистики
Как создать полигон частот в R?
В этой статье мы обсудим, как создать полигон частот на языке программирования R.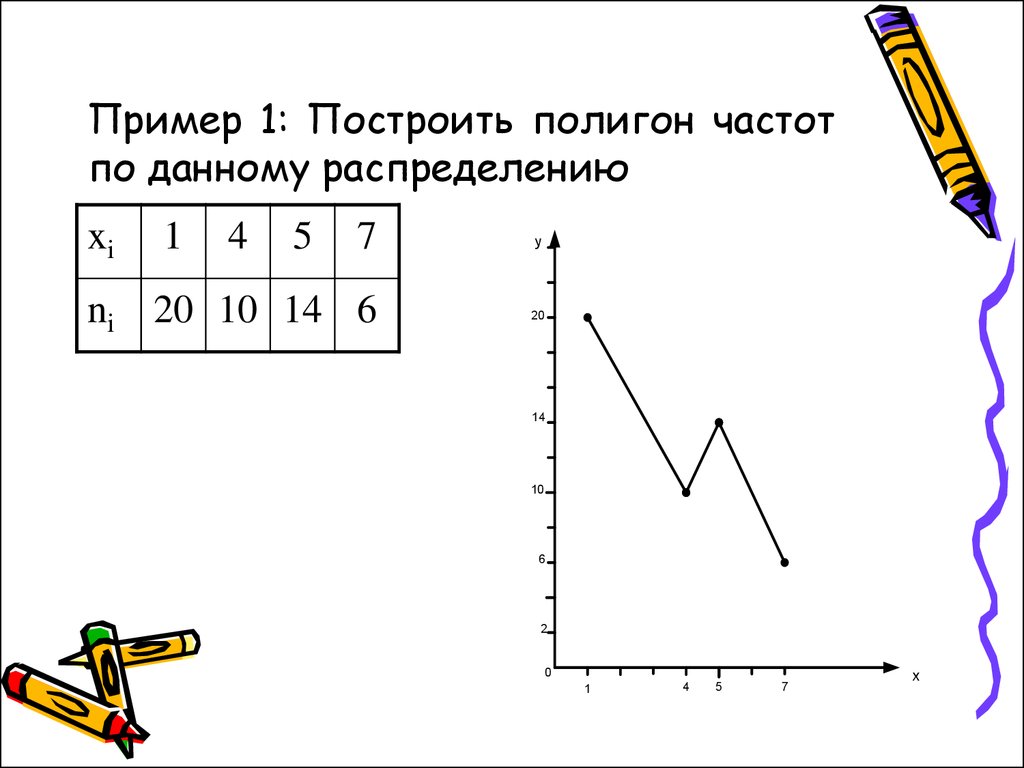
Частотные полигоны представляют собой графики значений во фрейме данных для визуализации формы распределения значений. Это помогает нам сравнивать различные кадры данных и визуализировать кумулятивное частотное распределение кадров данных. Многоугольник частот указывает количество вхождений для каждого отдельного класса во фрейме данных.
Создать полигон частот в Base R:
Чтобы создать базовый полигон частот в языке R, мы сначала создадим линейный график для строящихся переменных. Затем мы используем функцию polygon() для создания многоугольника частот.
Синтаксис: plot( x, y ) polygon( c( xmin, x, xmax ), c( ymin, y, ymax ), col )
где,
- x0 и 6y определяет вектор данных для данных по осям x и y.
- xmin и ymin: определяет минимальный предел осей x и y.
- xmax и ymax: определяет максимальный предел осей x и y.
- col: определяет цвет полигона частот.
Пример:
Здесь базовый полигон частот, созданный в Base R с помощью функции polygon().
R
|
Вывод:
Создать полигон частот с помощью ggplot2 :
Чтобы создать базовый полигон частот на языке R с помощью пакета ggplot2, мы используем функцию geom_freqpoly(). По умолчанию ggplot2 использует 30 бинов для создания полигона частот. Уменьшив количество бинов, можно сделать линии на графике более плавными.
По умолчанию ggplot2 использует 30 бинов для создания полигона частот. Уменьшив количество бинов, можно сделать линии на графике более плавными.
Синтаксис: ggplot( df, aes(value)) + geom_freqpoly( bins )
где,
- df: определяет размер фрейма данных для визуализации.
- значение: определяет имя столбца оси Y.
- бинов: определяет гладкость графика.
Пример:
Здесь базовый полигон частот, созданный с помощью пакета ggplot2.
R
|
Output:
Frequency Polygon с цветом заливки с использованием пакета ggplot2:
Чтобы создать полигон базовой частоты с цветом заливки на языке R с помощью пакета ggplot2, мы используем функцию geom_area(). мы используем параметр fill функции geom_area(), чтобы заполнить полигон частот желаемым цветом.
Синтаксис: ggplot( df, aes(value)) + geom_area(aes(y=..count..), bins, fill )
где
- определяет данные 6df кадр для визуализации.
- значение: определяет имя столбца оси Y.
- бинов: определяет гладкость графика.
- fill: определяет цвет заливки графика:
Пример:
Здесь базовый многоугольник частот, созданный с помощью пакета ggplot2 и окрашенный с помощью функции geom_area().
R
|

 frame
frame