Понятие логарифма и его свойства: Урок 24. логарифмы. свойства логарифмов — Алгебра и начала математического анализа — 10 класс
Урок 24. логарифмы. свойства логарифмов — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок № 24. Логарифм. Свойства логарифмов.
Перечень вопросов, рассматриваемых в теме
1. Определение логарифма.
2. Основное логарифмическое тождество.
3. Свойства логарифмов.
Глоссарий по теме
Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .
Логарифмирование – это действие нахождения логарифма числа.
Основное логарифмическое тождество:
Свойства логарифмов. При , справедливы равенства:
— логарифм произведения: ;
— логарифм частного: ;
— логарифм степени: .
Основная литература:
Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия.
Открытые электронные ресурсы:
http://fipi.ru/
Теоретический материал для самостоятельного изучения
При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение имеет корень 5, т. к. значит , В уравнении число 5 не является степенью 2, значит предыдущий способ решения не подходит. Нам известно, что уравнение имеет единственный корень. Посмотрим это на графике.
Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.
Дадим определение логарифма.
Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .
Т. е. логарифм числа по основанию , есть некоторое число такое, что .
Пример 1.
, т. к. выполнены все условия определения:
выполнены все условия определения:
1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) .
Пример 2.
, т. к. выполнены все условия определения:
1) ; 2) 2 > 0, 2 ≠ 1; 3) .
Это действие называется логарифмированием.
Логарифмирование – это действие нахождения логарифма числа.
Существует краткая запись определения логарифма:
так называемое основное логарифмическое тождество. Его используют при вычислениях.
Пример 3.
(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)
Пример 4.
(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)
Решим несколько задач с использованием определения логарифма.
Задача 1. Вычислить .
Решение. Пусть тогда по определению логарифма Приведем левую и правую части к одному основанию. 27 = 33, 81 = 34, значит . Отсюда следует, что
Задача 2. Вычислить .
Решение. Для вычисления воспользуемся свойствами степеней: 1) , 2) и основным логарифмическим тождеством: .
.
Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.
1. Логарифм произведения.
Логарифм произведения чисел по основанию равен сумме логарифма по основанию и логарифма по основанию .
Пример 5.
2. Логарифм частного.
Логарифм частного чисел по основанию равен разности логарифма по основанию и логарифма по основанию .
Пример 6.
3. Логарифм степени.
Логарифм числа по основанию равен произведению показателя и логарифма по основанию .
Пример 7.
Важно! Свойства выполняются при ,
Примеры и разбор решения заданий тренировочного модуля
№ 1. Вычислите: .
Решение:
Чтобы выполнить это задание нам понадобятся следующие определения и свойства:
- ;
- .
 {k}} b=\frac{1}{k} \cdot \log _{a} b$
{k}} b=\frac{1}{k} \cdot \log _{a} b$8 $\log _{a} b=\frac{1}{\log _{b} a}$
9 $\log _{a} b=\frac{\log _{c} b}{\log _{c} a}$ — переход к новому основанию.
Примеры решения задач
Пример
Задание.
Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:
$\log _{a} \sqrt{a b}=\frac{1}{2} \log _{a}(a b)=\frac{1}{2}\left(\log _{a} a+\log _{a} b\right)=\frac{1}{2}(1+7)=4$
Ответ. $\log _{a} \sqrt{a b}=4$
Больше примеров решенийЧитать дальше: основное логарифмическое тождество.
Слишком сложно?
Формулы и свойства логарифмов не по зубам? Тебе ответит эксперт через 10 минут!
Базовые свойства логарифмов. Алгебра, 11 класс: уроки, тесты, задания.
1. 
Логарифм произведения Сложность: лёгкое
2 2. Логарифм частного Сложность: лёгкое
2 3. 
Формула перехода от одного основания логарифма к другому основанию Сложность: лёгкое
2 4. Сумма логарифмов, логарифм степени Сложность: лёгкое
3 5. 
Основное логарифмическое тождество (логарифм степени) Сложность: среднее
4 6. Свойства логарифмов (степени и произведения) Сложность: среднее
4 7. 
Свойства логарифмов (степени и частного) Сложность: среднее
4 8. Логарифм степени (произведение) Сложность: среднее
3 9. 
Логарифм степени (частное) Сложность: среднее
5 10. Свойства логарифмов (степень основания, основное логарифмическое тождество) Сложность: среднее
7 11. 
Свойства логарифмов Сложность: сложное
7 12. Свойства логарифмической функции Сложность: среднее
2 13. 
Формула перехода к новому основанию (метод подстановки) Сложность: сложное
7 14. Логарифм произведения (тригонометрическое выражение) Сложность: сложное
7 15. 
Логарифм произведения Сложность: сложное
5 Понятие логарифма. Свойства логарифма — презентация онлайн
1. Понятие логарифма. Свойства логарифма
Урок 35-362. Изобретение логарифмов, сократив работу астронома, продлило ему жизнь.
Для чего были придуманы
логарифмы?
П.С. Лаплас
Изобретение
логарифмов,
сократив работу
астронома,
продлило ему
жизнь.3. Цели урока
•Ввести понятие «логарифм числа».
•Рассмотреть свойства логарифмов.
• Познакомиться с историей
возникновения логарифмов.
У
y=16
y=2x
16
y=10
8
y=4
4
log210
1
0
2
4
Х
Термин «логарифм» возник из
сочетания греческих слов λόγος (logos) отношение, соотношение и ἀριθμός
(arithmos) — число.
«отношение чисел».
log21=0, log22=1, log24=2, log28=3
1,2,4,8…-геометрическая
прогрессия,
0,1,2,3…-арифметическая
прогрессия.6. Найдите :
Log28= 3
Log232= 5
Log24= 2
Log216= 4
Log981= 2
Log33= 1
Log12144= 2 Log327= 3
Log464= 3
Log5125= 3
Log31= 0
Log525= 2
Log381= 4
Log636= 2
Log66= 1
Log749= 2
Log10100= 2
Log101= 07. Определение логарифма
23=8
log28=3
Логарифмом числа 8 по основанию 2 называется
показатель степени, в которую нужно
возвести число 2, чтобы получить число 8
ax=b
a >0
a≠1
b>0
logab=x
a >0
a≠1
b>08.
 Определение логарифма Логарифмом числа b по основанию a называется
Определение логарифма Логарифмом числа b по основанию a называется
показатель степени, в которую нужно
возвести число a, чтобы получить число b
( а>0, a 1, b>0)
Основное логарифмическое тождество
a
logab
=b9. Свойства, следующие из определения
• logaa=1
• loga1=0
c
logaa =c10. Найдите ошибку:
Log11=1
Log416=4 Log2(-8)=3
Log(-12)144=2
1Log749=2
5Log 5=1
2
2
5
7Log 49=2
7
1Log 49=1
2
7
9Log (-9)=-1
9
Log40=411. Прологарифмируйте :
Вариант 1
Вариант 2
Log28= 3
Log232= 5
Log216= 4
Log981= 2
Lоg10100= 2
Lоg101000= 3
4Log 64= 64
5Log 25= 25
Log31= 0
Log61= 0
4
5
Десятичным называется
логарифм, основание которого
равно 10. Обозначается lg b, т.е.
lg b=log10 b.
Натуральным называется
логарифм, основание которого
равно e. Обозначается ln b, т. е.
е.
ln b=loge b.
Десятичный
логарифм
Натуральный
логарифм
log10 → lg
loge → ln
е ≈
2,718281828…
Примеры:
ln e=1,
ln1=0,
ln e2=2.
Примеры:
lg10=1,
lg1=0,
lg0,01=-2.14. Логарифмические таблицы
Титульный
лист книги
Дж. Непера
«Описание
удивительной
таблицы
логарифмов».
Издание 1620 г.17. Логарифмические палочки
Гунтер – изобретатель
логарифмической линейки
Через десяток лет после
появления логарифмов
Непера английский
ученый Гунтер изобрел
очень популярный прежде
счетный прибор –
логарифмическую линейку.
Без логарифмической линейки не были бы
построены ни первые компьютеры, ни
микрокалькуляторы.
У инженера и астронома не было
инструмента полезнее, чем
логарифмическая линейка.
1
m
a
m
a
1
log 3
81
1
1
log 2 , log 3
,
8
27
1
, log 3
,
27
n
a a
m
log 8 5 64 , log 3 7 27 ,
log 3 7 27 ,
log 8 2, log 32 2,
log 32 2,
m
n
1
n
, log 3
4
a
m
a
1
,
27
1
1
log 5 4
, log 3 4
,
125
27
m
n26.
 Итог урока Что называют логарифмом
Итог урока Что называют логарифмом
положительного числа b по основанию a
(a>0, a≠1)?
• Существует ли логарифм нуля;
логарифм отрицательного числа?
Домашнее задание.
Если со всеми предложенными заданиями Вы
справились без ошибок, то Ваше домашнее
задание: п.37, № 489, № 490, № № 495(b,в),
№496(b,в,г).
Если при выполнении предложенных заданий Вы
испытывали затруднения и не смогли всё выполнить правильно, то Ваше домашнее задание: п.37, № 476, № 483(b,в), № 488, № 495(b,в).
« СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ
ИЛИ ЧАС, В КОТОРЫЙ ТЫ НЕ УСВОИЛ
НИЧЕГО НОВОГО И НИЧЕГО НЕ ПРИБАВИЛ К СВОЕМУ ОБРАЗОВАНИЮ.»
Я. А. КОМЕНСКИЙ.Понятие логарифма. Свойства логарифма. Десятичные и натуральные логарифмы
1. Понятие логарифма. Свойства логарифма. Десятичные и натуральные логарифмы.
2. Основные вопросы:
1. Понятие логарифма. Свойства
логарифма.
2. Формула перехода к другому
основанию.
3. Десятичные и натуральные
логарифмы.
3. Немного истории
Потому-то, словно пена
Опадают наши рифмы
И величие степенно
Отступает в логарифмы.
Борис Слуцкий
Первый изобретатель
логарифмов —
шотландский барон Джон
Непер (1550—1617)4. Решите уравнение.
1)
Мы искали
х показатель степени,
Решить
а надо
в, где
а 0основание
и а 1, b0,5 ,0
0,5х =32,уравнение
в который
возвести
х = — 5.
чтобы получить 32.
значит, найти показательстепени,
2)
в который надоМы
возвести
основание
a,
искали показатель
степени,
в который надо возвести основание
чтобы получить
число b
чтобы получить 27.
1
,
3
3)
Показатель
степени – это и есть логарифм
4х+1+4х = 320 , Мы искали показатель степени,
условиях).
4х(4+1) (при
= 320 ,определенных
в который надо возвести
основание 4,
4х = 64 ,
чтобы получить 64.
х = 3.
Слово ЛОГАРИФМ
происходит от греческих слов
— число и отношение
• Первые таблицы логарифмов назывались
• «Описание удивительной таблицы
логарифмов»
(1614 г.) и
• «Устройство удивительной таблицы
логарифмов»
(1619 г.)
56. Определение логарифма
Логарифмом числа b>0 по основанию
a>0, a ≠ 1 , называется показатель степени,
в которую надо возвести число a, чтобы
получить число b.
Логарифм числа b по основанию a
обозначается
logab7. ПРИМЕРЫ
1) log232, здесь b = 32, a = 2, c = 5.
log232 = 5 , т. к. 25 = 32 .
2) log50,04 ,
здесь b = 0,04, a = 5, c = — 2.
log50,04 = — 2, т. к. 5-2 = 1/25 = 0,04 .
3) Найти х, такое, что log8х = 1/3.
По определению логарифма
х = 81/3 = 2.
c
a
= b logab = c
Откуда получаем основное
логарифмическое тождество
(b > 0, a > 0, a 1)
a
loga b
b9. ПРИМЕРЫ
1) 0,5
2)
5
5
2log5 3
log5 3
log0,5 6
6 .
(( 5 ) )
3.
2 log5 310. Свойства логарифма
1. Логарифм единицы
log
1
0
a
2. Логарифм основания
log a 1
a11. Свойства логарифма
3. Логарифм произведения равен
сумме логарифмов множителей:
log xy log x log y
a
a
a12. Свойства логарифма
4. Логарифм частного равен
логарифмов делимого без логарифма
делителя:
x
log
log x log y
a y
a
a13. Свойства логарифма
5.1. Логарифм степени равен
произведению показателя степени на
логарифм ее основания:
5.1) log x
a
p
p log a x.14. Свойства логарифма
5.2. При возведении основания в
некоторую (не нулевую) степень логарифм
делится на этот показатель степени:
1
5.2) log p b log a b.
a
p15. Свойства логарифма
6. Логарифм корня равен отношению
логарифма подкоренного выражения и
показателя корня:
log
b
m
a
log а b
m16.
 Свойства логарифма 7. Переход от одного основания к
Свойства логарифма 7. Переход от одного основания к
другому
log b
c
log b
a
log a
c17. Следствия
1
1) log b
a
log a
b
3) log
2) log
b
log
a
am
a
n
b
b
n
log a b.
m
Свойства логарифмов: ПРИМЕРЫ
• 1. Вычислить: log612 + log63
Решение:
log612 +log63 = log6(12*3) = log636 = log662 = 2
Ответ: 2.
• 2. Вычислить: log5250 – log52.
Решение:
log5250 – log52 = log5(250/2) = log5125 = 3
Ответ: 3.
• 3. Вычислить: 27 log3 2
Решение:
3 log3 2
log3 8
log3 2
=
3
3
8
27
Ответ: 8.
1819. Натуральный и десятичный логарифмы.
Десятичным называется логарифм,
основание которого равно 10.
Обозначается lg b, т.е. lg b=log10 b.
Натуральным называется логарифм,
основание которого равно e.
Обозначается ln b, т.е. ln b=loge b.20. Свойства натуральных логарифмов
Чтобы по известному десятичному логарифму числа х найти
его натуральный логарифм, нужно разделить десятичный
логарифм числа х на десятичный логарифм числа е:
lg x
lg x
ln x
2. 30259 lg x
30259 lg x
lg e 0.43429
Чтобы по известному натуральному логарифму числа х
найти его десятичный логарифм, нужно умножить
натуральный логарифм числа х на десятичный логарифм
числа е:
lg x lg e ln x 0.43429 ln x
Число lg e=0.43429 называется модулем
десятичных логарифмов и обозначается через М.21. Решение упражнений
1) log 5 16 log 2 25
Воспользуемся сначала свойством log a b n n log a b
log 5 2 log 2 5 4 log 5 2 2 log 2 5
4
2
Теперь перейдем к основанию 2
1
8
log 2 5 8
log 2 5
log a b
1
log c a23. 2) Найдите значение выражения
2
3
log5 7
log5 3
9 4
1
log3 4
log c b
log a b
log c a
2 log3 7
3
9 4
log4 3
1
log a b
log c a
3 3
9 4
9 7 9 3 9 (7 3) 9 4 36
2
log3 7
log4 324. 3)Найдите значение выражения , если
Решение:
log a (a b ) log a a log a b
5
2
5
2
1
7
5 2
5 2 12
log b a
2
Ответ: 12
1
log a b
log c aПонятие логарифма
Вопросы занятия:
· ввести понятие логарифма;
· познакомить с основным логарифмическим тождеством;
· рассмотреть некоторые свойства логарифмов.

Материал урока
Давайте рассмотрим простое показательное уравнение и решим его графически.
Легко заметить, что эти графики пересекаются в точке с координатами два, четыре, значит, x = 2 – это единственный корень уравнения.
Рассуждая аналогично, легко записать, что корнем уравнения 2x= 8 будет x = 3.
Теперь давайте попробуем решить уравнение 2x= 6.
По графику видно, что данное уравнение имеет решение, причём единственное. Но точное значение по графику мы определить не можем, единственное что мы можем сказать, это то что корень этого уравнения лежит в промежутке (2; 3).
Для корней такого уравнения был введён специальный символ:
Тогда корнем уравнения 2x = 6 будет
Теперь для любого уравнения вида:
можно записать решение:
Очевидно, что с помощью нового символа можно записать корень любого уравнения вида:
Этот корень равен:
Запишем чёткое определение.

Определение.
Логарифмом положительного числа b по положительному, не равному единице основанию a называют показатель степени, в которую нужно возвести число а, чтобы получить число b.
Обратите внимание, что положительным должно быть только основание логарифма. Само значение логарифма может быть и отрицательным, потому что значение логарифма – это степень, а возводить в отрицательную степень мы умеем.
Например
Из определения логарифма легко вывести следующие формулы:
А теперь давайте вернёмся к первому примеру и постараемся определить, что это за число:
Можно предположить, что это будет иррациональное число. Докажем или опровергнем это предположение.
Допустим, что это рациональное число. Тогда:
Правая часть равенства делится на 3, а левая часть на 3 не делится. Получили, что такое равенство невозможно.
 То есть
невозможно подобрать такую рациональную степень, чтобы при возведении в неё
двойки получилось шесть. Таким образом, пришли к противоречию, то есть
доказали, что это иррациональное число.
То есть
невозможно подобрать такую рациональную степень, чтобы при возведении в неё
двойки получилось шесть. Таким образом, пришли к противоречию, то есть
доказали, что это иррациональное число.Давайте ещё раз посмотрим на определение логарифма.
Поскольку логарифм – это такой показатель степени, в которую нужно возвести основание а, чтобы получить число b, то можно записать:
Это равенство называется основным логарифмическим тождеством.
Например:
Запишем важное правило:
Операцию нахождения логарифма числа называют логарифмированием.
Эта операция является обратной по отношению к возведению в степень с соответствующим основанием:
Рассмотрим несколько примеров.
Пример.
Пример.
Пример.
«Логарифм и его свойства»
«Возьми столько, сколько ты можешь и хочешь,
но не меньше обязательного».
Предмет: Алгебра и начала анализа, урок-усвоение новых знаний
Тема: «Логарифм и его свойства» (1 урок- 45 минут)
Класс: 11
Технологии: ПК, проектор, экран, презентация Power Point
Аннотация: урок является урок является уроком усвоения новых знаний.
Цели урока
· знать и уметь записывать определение логарифма, основного логарифмического тождества, познакомиться и изучить свойства логарифмов.
· Научиться различать свойства по их записи и применять их при решении заданий.
· Закрепить вычислительные навыки.
· Формировать ЗУНы к сдаче ЕГЭ.
Базовые знания:
· определение показательной функции;
· свойства показательной функции;
· определение показательного уравнения, основные методы и приёмы решения показательных уравнений;
Тип урока: сообщение новых знаний.

Методы работы:
· проблемный;
· частично-поисковый.
Виды работ:
· индивидуальная;
· коллективная;
· фронтальная.
Мотивация познавательной деятельности: на занятии необходимо предоставить учащимся возможность проявить сообразительность, смекалку в формировании навыков самостоятельной работы, работы с учебником, навыков самостоятельного добывания знаний.
Время проведения: 45 мин
Оборудование:
· таблица свойств логарифмов;
· текст «Из истории логарифмов»;
· плакаты;
· карточки-задания (кроссворд)
· обучающие карточки;
· набор тестов;
· ПК учителя, мультимедийный проектор;
· Презентация, содержащая материал для повторения и закрепления теоретических знаний, для отработки навыков практического применения теории к решению упражнений, создания проблемной ситуации, для самоконтроля, содержащая сведения из истории логарифмов
План урока1.
 Организационный момент. 1 мин.
Организационный момент. 1 мин.2. Постановка цели. 1 мин.
3. Проверка ранее изученного материала 5 мин (кроссворд)
4. Введение понятия логарифм.
1. Определение логарифма. 5 мин
2. Историческая справка, применение логарифмов. 7 мин
3. Основное логарифмическое тождество. 10 мин
4. Основные свойства логарифмов 10 мин
5. Обобщение и систематизация знаний. 7 мин .
6. Домашнее задание. 1 мин.
7. Применение знаний, умений и навыков. 15 мин.
8. Подведение итогов. 5 мин.
Ход урока:1. Организационный момент. Приветствие.2. Постановка цели.— Ребята, сегодня на уроке вам предстоит проверить умения решать простейшие показательные уравнения, чтобы можно было ввести новое для вас понятие, затем познакомимся со свойствами нового понятия; вы должны научиться различать эти свойства по их записи; научиться применять эти свойства при решении заданий.

Будьте собраны, внимательны и наблюдательны. Успехов!
3. Проверка ранее изученного материала. (слайды 1–2– Назовите новое понятие, с которым мы познакомимся
2. Решение кроссворда учащимися.
1. Как называется функция вида у = kх + в?
2. Как называется функция вида у = а (а больше нуля, и а не равно 1)?
3. В каких единицах измеряется угол?
4. Как называется график функции у = tg x ?
5. Как называется функция вида у = ах+ вх + с (а не равно 0 )?
6. Как называется уравнение, содержащее знак корня?
7. Каким способом нужно решить уравнение sin x = 2 ?
8. Точка х называется точкой ………. функции f, если для всех х из некоторой окрестности х выполняется неравенство f(x) ≤ f(х).
4. Введение понятия логарифм. (слайды 3,4)– Тема нашего урока “Логарифм, его свойства”. Попробуйте найти корень уравнения 2х = 5.
 Ответ данного уравнения мы можем записать с
помощью нового понятия. Прочитайте текст слайда и запишите корень уравнения.
Ответ данного уравнения мы можем записать с
помощью нового понятия. Прочитайте текст слайда и запишите корень уравнения.4.1. Определение логарифма (слайды 5–7) Из предыдущей темы вы помните, что уравнение вида
a= b, (a>0, a1) при b ≤ 0- не имеет решения, при b> 0 имеет единственное решение. Этот корень называется логарифмом b по основанию a и обозначается = Х т.е.
Логарифмом положительного числа b по основанию a, где a>0, a ≠ 1 называется показатель степени х, в которую надо возвести a, чтобы получить число b. Из предыдущей темы вы помните, что уравнение вида
1) log 10 100 = 2, т.к. 102 = 100 (определение логарифма и свойства степени),
2) log 5 53 = 3, т.к. 53 = 53 (…),
3) log 4 = –1, т.к. 4–1 = (…)Историческая справка – (сообщение обучающегося)
4.2. Историческая справка (слайд 8) В течение 16 в.
 резко возрос объем работы, связанный с проведением приближенных
вычислений в ходе решения разных задач, и в первую очередь задач астрономии,
имеющей непосредственное практическое применение (в частности, при определении
положения судов по звездам и по Солнцу). Наибольшие проблемы возникали при
выполнении операций умножения и деления. Попытки частичного упрощения этих
операций путем сведения их к сложению большого успеха не приносили. Поэтому
открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию
их логарифмов стало великим открытием.
резко возрос объем работы, связанный с проведением приближенных
вычислений в ходе решения разных задач, и в первую очередь задач астрономии,
имеющей непосредственное практическое применение (в частности, при определении
положения судов по звездам и по Солнцу). Наибольшие проблемы возникали при
выполнении операций умножения и деления. Попытки частичного упрощения этих
операций путем сведения их к сложению большого успеха не приносили. Поэтому
открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию
их логарифмов стало великим открытием.Слово логарифм происходит от греческого и переводится, как отношение чисел.
Первым изобретателем логарифмов стал Дж.Непер (1594).(слайд №8) Выбор такого названия объясняется тем, что логарифмы возникли при сопоставлении двух чисел, одно из которых является членом арифметической прогрессии, а другое – геометрической.
Логарифмы с основанием е ввел Спейдел (1619 г.) Название более позднего происхождения натуральный (естественный0 объясняется «естественностью» этого логарифма.

Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не ограничились разработкой новой теории. Было создано практическое средство – таблицы логарифмов, — резко повысившие производительность труда вычислителей. Через 9 лет после издания первых таблиц, английским математиком Д. Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений.(вплоть до появления вычислительных машин)
Первые таблицы логарифмов составлены независимо друг от друга шотландским математиком Дж.Непером(1550-1617) и швейцарце И.Бюрги (1552-1632), а первые таблицы десятичных логарифмов составлены по совету Непера английским математиком Г.Бриггсом(1561-1630).Таким образом логарифмы явились одним из величайших открытий в математике.
4.4. Основное логарифмическое тождество (слайды 12-14)=b .
1) (32)log 3 7 = (3log 3 7)2 = 72 = 49 (степень степени, основное логарифмическое тожество, определение степени),
4.5 Основные свойства логарифмов (слайд 21)
2) 7 2 log 7 3 = (7 log 7 3)2 = 32 = 9 (…),
3) 10 3 log 10 5 = (10 log 10 5)3 = 53 = 125 (…),
4) 0,1 2 log 0,1 10 = (0,1 log 0,1 10)2 = 102 = 100 (…).
Вы замечательно справились с примерами. А теперь вычислите следующие задания, записанные на доске:
а) log 153 + log 155 = …,
б) log 1545 – log 153 = …,
в) log 48 =…,
г) 7 = … .А как вы думаете, что мы должны знать, чтобы выполнять действия с логарифмами?
(Свойства логарифмов)Перед вами таблица со свойствами логарифмов. Надо дать название каждому свойству и правильно сформулировать их”.
Слайд 21
5. Обобщение и систематизация знаний.№
Название свойства логарифмов
Свойства логарифмов
1.
Логарифм единицы.
log a1 = 0, a > 0, a 1.

2.
Логарифм основания.
log aa = 1, a > 0, a 1.
3.
Логарифм произведения.
log a(xy) = log ax + log ay, a > 0, a 1, x > 0, y>0.
4.
Логарифм частного.
log a = log ax — log ay,
a > 0, a 1, x > 0, y > 0.5.
Логарифм степени.
log axn = n log ax,
x > 0, a > 0, a 1, nR.6.
Формула перехода к новому основанию
a > 0, a 1, b > 0, b 1, x > 0.

Слайды 22-24
6. Домашнее задание. 7. Подведение итогов. (слайды 20 – 24)Дайте ответы на вопросы
– Сформулируйте определение логарифма и выполните соответствующую запись.
– Какие виды логарифмов существуют? Выполните их запись.
– Запишите основное логарифмическое тождество.– Происхождение слова “логарифм”. Кто изобрел логарифмы, в каком году, краткие сведения о них?
– Кто ввел логарифм с основанием е, который называют натуральным логарифмом?
– Из чего возникла практика использования логарифмов?
– Кто и когда изобрел первую логарифмическую линейку, первые таблицы логарифмов?Свойства логарифма – объяснение и примеры
Прежде чем перейти к свойствам логарифмов, давайте кратко обсудим связь между логарифмами и показателями степени . Логарифм числа определяется как степень или индекс, в который нужно возвести данное основание, чтобы получить число.

При этом a x = M; где a и M больше нуля и a ≠ 1, тогда мы можем символически представить это в логарифмической форме как;
Журнал m = x
примеры:
- 2 -3 = 1 / 8 ⇔ log 2 ( 1 / 8 ) = -3
- 10 -2 = 0.01 ⇔ log 10 01 = -2
- 2 6 = 64 ⇔ log 2 64 = 6
- 3 2 = 9 ⇔ log 3 9 = 2
- 5 4 = 625 ⇔ log 5 625 = 4
- 7 0 = 1 ⇔ log 7 1 = 0
- 3 — 4 = 1/3 4 = 1/81 ⇔ log 3 1/81 = -4
- 10 -2 = 1/100 = 0,01 ⇔ log 10 01 = -2
Свойство произведения логарифмов
- Пусть X = LOG A M и Y = LOG A
- преобразование каждого из эти уравнения к экспоненциальному виду.
- Умножьте экспоненциальные условия (M & N):
- основание общее, поэтому складываем показатели степени:
- Берем бревно с основанием «а» с обеих сторон.

- Применение правила степени логарифма.
- Теперь подставьте значения x и y в полученное выше уравнение.
- log50 + log 2 = log100 = 2
- log 2 (4 x 8) = log 2 (2 2 x 2 3 ) = 5 3
Факторное свойство логарифмов
- Пусть X = LOG A M и Y = LOG A
- преобразовать каждое из этих уравнений к показательной форме.

- Разделите экспоненциальные условия (M & N):
- Поскольку основание общее, поэтому вычтите показатели степени:
- Берем бревно с основанием «а» с обеих сторон.
- Применение правила степени логарифмирования для обеих сторон.
- Теперь подставьте значения x и y в полученное выше уравнение.
Степенное свойство логарифмов
- Перепишите как экспоненциальное уравнение.
- Возьмем степень «n» в обеих частях уравнения.
- 90 по основанию уравнения a.
- LOG A A XN = LOG A M N ⇒ XN Log A A = log a M n ⇒ xn = log a M n
- Теперь подставьте значения x и y в полученное выше уравнение и упростите его.
- Выразите каждый логарифм в экспоненциальной форме, пуская;
- Преобразовать в экспоненциальную форму,
- Подстановка значение х.
- Логарифм 1 по любому конечному ненулевому основанию равен нулю.
- Логарифм любого положительного числа к тому же базу равно 1.
- Логарифмы разбивают произведения на суммы по свойству 1, но логарифм суммы нельзя переписать .
 За
Например, мы ничего не можем сделать с выражением ln(x 2 + 1).
За
Например, мы ничего не можем сделать с выражением ln(x 2 + 1). - log u — log v равен log(u/v) по свойству 2, не равен log u/log v.
- журнал 1
- ln e
- журнал5 (15)
Если основание не указано, предполагается, что оно равно 10.
. Это десятичный логарифм,
Это десятичный логарифм,лог 1=лог10 1=0
Натуральный логарифм по определению имеет основание e ,
ln e=loge e=1
Поскольку у нас 5−1=15,
log5 (15)=−1
- журнал 1/4 4
- журнал2/3 (32)
- log1/4 4=−1 потому что (14)−1=4
- log2/3 (32)=−1 потому что (23)−1=32
- журнал5 625
- 5log5 3
- эльн 5
- log5 625=log5 54=4
- 5log5 3=3
- элн 5=5
- журнал 2 x4
- log5 (x).
Применение свойства степени логарифмов.
log2 x4=4log2 x
Напомним, что квадратный корень можно выразить с помощью рациональных показателей, x=x1/2.
 Сделайте эту замену, а затем примените свойство степени логарифмов.
Сделайте эту замену, а затем примените свойство степени логарифмов.log5 (x)=log5 x1/2=12log5 x
Начните с расширения, используя суммы и коэффициенты, а затем замените на и на b соответствующим логарифмом.
log2 (8x2y)=log2 8+log2 x2+log2 y=log2 8+2log2 x+log2 y=3+2a+b
Разверните, а затем замените на , на b и на , где это необходимо.
log2 (2x4z)=log2 (2×4)−log2 z1/2=log2 2+log2 x4−log2 z1/2=log2 2+4log2 x−12log2 z=1+4a−12b
- Для любого основания b>0 и b≠1 мы можем сказать, что logb 1=0, logb b=1, log1/b b=−1 и что logb (1b)=−1.
- Обратными свойствами логарифма являются logb bx=x и blogb x=x, где x>0.
- Свойство произведения логарифма позволяет нам записать произведение в виде суммы: logb (xy)=logb x+logb y.
- Факторное свойство логарифма позволяет нам записать частное как разность: logb (xy)=logb x−logb y.
- Свойство степени логарифма позволяет нам записывать показатели в виде коэффициентов: logb xn=nlogb x.
- Поскольку натуральный логарифм является логарифмом по основанию e , ln x=loge x, к нему применимы все свойства логарифма.
- Мы можем использовать свойства логарифма для расширения логарифмических выражений, используя суммы, разности и коэффициенты.
 Логарифмическое выражение полностью расширяется, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью расширяется, когда свойства логарифма больше не могут быть применены. - Мы можем использовать свойства логарифма для объединения выражений, содержащих логарифмы, в один логарифм с коэффициентом 1. Это важный навык, который необходимо изучить в этой главе.
пер (1e)
log1/2 (12)
log2 (xy2)
log5 (25x)
log3 (x3yz2)
журнал (xy3z2)
log5 (1x2yz)
журнал4 (116x2z3)
log3 (x2y3z)
журнал (2(x+y)3z2)
журнал (100×3(y+10)3)
log7 (x(y+z)35)
log5 (x3yz23)
журнал (x2y3z25)
log3 (27x2y3z)
log3 (xy3z)
log3 (9x2yz3)
log3 (x3yz2)
log2 5+2log2 x+log2 y
log3 4+3log3 x+12log3 y
3log2 x−2log2 y+12log2 z
4log x-log y-log 2
log3 x−2log3 y+5log3 z
7log x−log y−2log z
2ln x−3ln y−ln z
23log3 x−12(log3 y+log3 z)
15(log7 x+2log7 y)−2log7 (z+1)
−ln 2+2ln (x+y)−ln z
−3ln (x−y)−ln z+ln 5
13(ln x+2ln y)−(3ln 2+ln z)
4log 2+23log x−4log (y+z)
log2 3−2log2 x+12log2 y−4log2 z
2log5 4−log5 x−3log5 y+23log5 z
лог (х+1)+лог (х−1)
log2 (x+2)+log2 (x+1)
ln (x2+2x+1)−ln (x+1)
пер (x2−9)−ln (x+3)
log5 (x3−8)−log5 (x−2)
log3 (x3+1)−log3 (x+1)
log x+log (x+5)−log (x2−25)
log (2x+1)+log (x−3)−log (2×2−5x−3)
3log3 x−log3 y−2log3 z
−2log5 x−log5 y−log5 z
log7 2+12log7 x+12log7 y
2log3 x+13log3 y−log3 z
2+3log x−3log (y+10)
3log5 x−13log5 y−23log5 z
лн (6.
 2)−15≈−13,2
2)−15≈−13,2log2 (x3zy2)
ln (xzy6)
журнал (x7yz2)
log3 (x23yz)
log2 (2xy)
log2 (xy23)
ln ((x+y)22z)
ln (xy238z)
log2 (3yx2z4)
журнал (хх-5)
logb (m+n) ≠ logb m + logb n
logb (mn) ≠ logb m — logb n
Во многих научных исследованиях и исследованиях используется логарифм.

Логарифмы помогают найти значение pH в химии, потому что значение pH может быть небольшим, поэтому мы используем логарифм, чтобы иметь диапазон для его использования для небольших чисел.
Логарифмы широко используются в банковской сфере.
Логарифмы используются для определения периода полураспада радиоактивных материалов.
Используется для обнаружения сейсмических волн.
Он играет очень важную роль в области медицины или техники.
- \({\log _4}16\)
- \({\log _2}16\)
- \({\log _6}216\)
- \(\displaystyle {\log _5}\frac{1}{{125}}\)
- \({\log _{\frac{1}{3}}}81\)
- \({\log _{\frac{3}{2}}}\displaystyle \frac{{27}}{8}\)
- \(\лог 1000\)
- \(\log \displaystyle \frac{1}{{100}}\)
- \(\ln \displaystyle \frac{1}{{\bf{e}}}\)
- \(\ln \sqrt {\bf{e}} \)
- \({\log _{34}}34\)
- \({\log _8}1\)
- Если \({\log _b}x = {\log _b}y\), то \(x = y\).
- \(7 {\ log _ {12}} x + 2 {\ log _ {12}} y \)
- \(3\лог х — 6\лог у\)
- \(5\ln \left( {x + y} \right) — 2\ln y — 8\ln x\)
Логарифмические свойства
Логарифмические свойства и правила полезны, поскольку они позволяют расширять, сокращать или решать логарифмические уравнения.Именно по этим причинам.
В большинстве случаев вам предлагается запомнить правила при решении логарифмических задач, но как эти правила получены.
В этой статье мы рассмотрим свойства и правила логарифмов, выведенных с использованием законов показателей.
Правило произведения гласит, что умножение двух или более логарифмов с общим основанием равно сложению отдельных логарифмов i.е.
Журнал A (MN) = log A M + Log A N
NДоказательство
⇒ A x = M
⇒ A Y = N
A x * A y = Mn
a x + y = MN
log a (a x + y ) = log a (MN)
LOG A M N ⇒ N Журнал A M
(X + Y) LOG A A = LOG A (MN)
(x + y) = log A (MN)
Log M + LOG A N = LOG A (MN)
(MN)
, следовательно, доказано
LOG A (MN) = LOG A M + LOG A N
Примеры:
Это правило гласит, что отношение двух логарифмов с одинаковыми основаниями равно разности логарифмов i.е.
Журнал A (M / N) = LOG A M — LOG A N
Доказательство
⇒ A x = M
⇒ A Y = N
A x / A Y = M / N
a x – y = M/N
log a (a x – y ) = log a (M/N)
LOG A M N ⇒ N Журнал A M
(X — Y) LOG A A = LOG A (M / N)
(x — Y) = log a (M/N)
log a M – log a N = log a (M/N)
Следовательно, доказано N
Согласно степенному свойству логарифма логарифм числа ‘M’ с показателем ‘n’ равен произведению показателя степени на логарифм числа ( без показателя) i.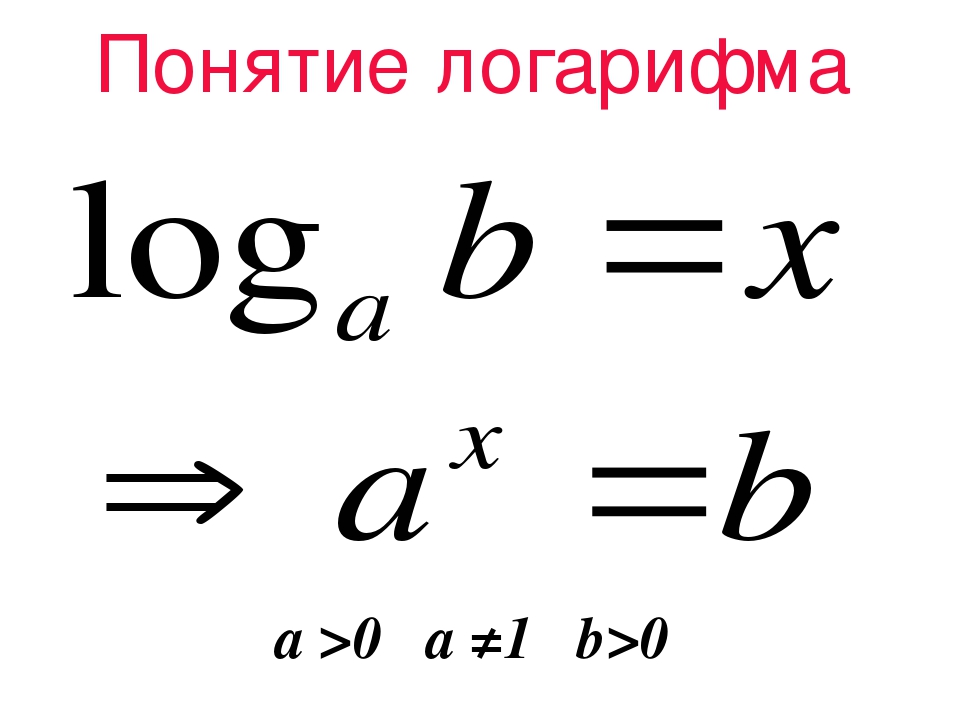 е.
е.
Журнал A M N = N Журнал A M
Доказательство
X = LOG A M
a x = M
(a x ) n = M n
⇒ a xn = M n
LOG A A XN = LOG A M N
Мы знаем,
x = log A M
Итак,
xn = log A M N ⇒ N Log A M = LOG A M N
, доказал
Журнал A M N = N LOG 9007 N = N ПРИМЕРА A M
Примеры:
Log100 3 = 3 log100 = 3 x 2 = 6
Изменение базового свойства logarithms
изменение свойства основания логарифма, мы можем переписать данный логарифм как отношение двух логарифмов с любым новым основанием. Это дано как:
Это дано как:
Журнал A M = LOG B M / log B N
1 илиLOG A M = LOG B M × LOG N B
его доказательство можно сделать, используя свойство один к одному и правило мощности для логарифмов.
Доказательство
Let,
x = log N M
M = N x
Журнал B N x = log B M
x LOG B M
B Mx = log B M / log B N
LOG A M = LOG B M / LOG B N
1 или мы можем написать его как,Журнал A M = LOG B M × LOG A B
Значит, доказано.
Другие свойства логарифмов включают:
Доказательство:
Журнал A 1 = 0⟹ A 0 = 1
Доказательство:
Журнал A a=1 ⟹ a 1 = a
Пример:
log 5 15 = log 15/log 5
Свойства логарифмов
Свойства логарифмовСодержание: Эта страница соответствует § 4.3 (стр. 341) текста.
Предлагаемые проблемы из текста:
р. 345 #3, 7, 9, 11, 13, 25, 27, 33, 35, 45, 49, 53, 91
Смена базы
Свойства логарифмов
Смена базы
В то время как большинство научных калькуляторов имеют кнопки только для десятичного и натурального логарифмов, другие
логарифмы могут быть вычислены с помощью следующей формулы замены основания.
Сменная базовая формула
Пример 1 .
Оценить журнал 5 3. Формула изменения базы позволяет нам оценить это выражение, используя любой другой логарифм, поэтому мы решим эту задачу двумя способами, используя сначала натуральный логарифм, затем десятичный логарифм.
Натуральный логарифм:
десятичный логарифм:
Упражнение 1 :
Из логарифмического тождества 1 следует, что log 2 8 = 3.
(a) Используйте калькулятор и формулу изменения основания с натуральным логарифмом, чтобы проверить, что log 2 8 = 3,
(b) Используйте калькулятор и формулу изменения основания с десятичным логарифмом, чтобы проверить, что log 2 8 = 3,
Ответить
Упражнение 2 :
Из логарифмического тождества 2 следует, что .
Проверьте это, оценив log 4 7, а затем возведя 4 в эту степень.
Ответить
Вернуться к содержанию
Свойства логарифмов
| 1. log a (ув) = log a u + log a v | 1. ln (ув) = ln u + ln v |
| 2. log a (u / v) = log a u — log a v | 2. ln (u/v) = ln u — ln v |
| 3.log a u n = n log a u | 3. лн у н = н пер у |
Свойства слева справедливы для любого основания a.
Свойства справа являются переформулировкой общих свойств натурального логарифма.
Многие логарифмические выражения могут быть переписаны в расширенном или сокращенном виде с использованием трех указанных выше свойств.
Расширение — это разбиение сложного выражения на более простые компоненты. Конденсация — это обратная сторона этого
процесс.
Конденсация — это обратная сторона этого
процесс.
Пример 2 .
Расширение выражения.
переписать с использованием экспоненциальной записи недвижимость 3 имущество 1
Пример 3 .
Расширение выражения.
свойство 2 имущество 1 недвижимость 3
Пример 4 .
Сжатие выражения.
собственность 3 имущество 1 собственность 2
Распространенные ошибки
Упражнение 3 :
(a) Разверните выражение . Ответ
(b) Сократите выражение 3 log x + 2 log y — (1/2) log z. Ответ
Вернуться к содержанию
Свойства логарифма
Логарифмы и их обратные свойства
Вспомним определение логарифма по основанию- b : дано b>0, где b≠1,
y=logb x если и только если x=by
Используйте это определение для преобразования логарифмов в экспоненциальную форму.Делая это, мы можем получить несколько свойств:
LOGB 1 = 0, потому что B0 = 1LoGB B = 1, потому что B1 = Blogb (1b) = — 1, потому что B-1 = 1b
Пример 1
Оценка:
Решение:
Кроме того, рассмотрим дробные основания формы 1/b, где b>1.
log1/b b=−1 потому что (1b)−1=1−1b−1=b1=b
Пример 2
Оценка:
Решение:
Для заданной экспоненциальной функции, определяемой формулой f(x)=bx, где b>0 и b≠1, ее обратным является логарифм по основанию, b , f−1(x)=logb x. А поскольку f(f−1(x))=x и f−1(f(x))=x, мы имеем следующие свойства, обратные логарифму. Учитывая b>0, мы имеем logb bx=x и blogb x=x, когда х>0.:
А поскольку f(f−1(x))=x и f−1(f(x))=x, мы имеем следующие свойства, обратные логарифму. Учитывая b>0, мы имеем logb bx=x и blogb x=x, когда х>0.:
f−1(f(x))=logb bx=xandf(f−1(x))=blogb x=x ,x>0
Поскольку f−1(x)=logb x имеет область определения, состоящую из положительных значений (0,∞), свойство blogb x=x ограничено значениями, где x>0.
Пример 3
Оценка:
Решение:
Применение обратного свойства логарифма.
Таким образом, когда b>0 и b≠1, мы имеем следующие свойства:
logb 1=0 | logb b=1 |
log1/b b=−1 | logb (1b)=−1 |
logb bx=x | блогb x=x, x>0 |
Попробуй! Оценка: log 0. 00001
00001
Ответ: −5
Произведение, частное и степенные свойства логарифмов
В этом разделе развиваются три очень важных свойства логарифма. Эти свойства позволят нам расширить наши возможности для решения многих других уравнений. Начнем с присвоения u и v следующих логарифмов, а затем запишем их в экспоненциальной форме:
logb x=u ⇒ bu=xlogb y=v ⇒ bv=y
Подставьте x=bu и y=bv в логарифм произведения logb (xy) и логарифм частного logb (xy).Затем упростите, используя правила показателей степени и свойства, обратные логарифму.
Логарифм произведения | Логарифм частного |
|---|---|
logb (xy)=logb (bubv)=logb bu+v=u+v=logb x+logb y | logb (xy)=logb (bubv)=logb bu−v=u−v=logb x−logb y |
Это дает нам два важных свойства: свойство произведения логарифмов logb (xy)=logb x+logb y; логарифм произведения равен сумме логарифмов множителей. ,
,
logb (xy)=logb x+logb y
и частное свойство логарифмов logb (xy)=logb x−logb y; логарифм частного равен разности логарифма числителя и логарифма знаменателя.,
logb (xy)=logb x−logb y
На словах логарифм произведения равен сумме логарифмов множителей. Точно так же логарифм частного равен разности логарифма числителя и логарифма знаменателя.
Пример 4
Запишите в виде суммы: log2 (8x).
Решение:
Примените свойство произведения логарифмов, а затем упростите.
log2 (8x)=log2 8+log2 x=log2 23+log2 x=3+log2 x
Ответ: 3+log2 x
Пример 5
Запишите как разницу: log (x10).
Решение:
Примените частное свойство логарифмов, а затем упростите.
log (x10)=log x−log 10=log x−1
Ответ: log x−1
Далее мы начнем с logb x=u и перепишем его в экспоненциальной форме. Возведя обе части в n -ю степень, снова приведите к логарифмическому виду, а затем обратно подставьте.
Возведя обе части в n -ю степень, снова приведите к логарифмическому виду, а затем обратно подставьте.
logb x=u ⇒ bu=x(bu)n=(x )nlogb xn=nu ⇐ bnu=xnlogb xn=nlogb x
Это приводит нас к свойству мощности логарифмов logb xn=nlogb x; логарифм величины, возведенной в степень, равен произведению этой степени на логарифм величины.,
logb xn=nlogb x
Другими словами, логарифм величины, возведенной в степень, равен произведению этой степени на логарифм величины.
Пример 6
Напишите как продукт:
Решение:
Таким образом,
Свойство произведения логарифмов | logb (xy)=logb x+logb y |
Частное свойство логарифмов | logb (xy)=logb x−logb y |
Степенное свойство логарифмов | logb xn=nlogb x |
Мы можем использовать эти свойства для расширения логарифмов, включая произведения, частные и степени, используя суммы, разности и коэффициенты. Логарифмическое выражение полностью расширяется, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью расширяется, когда свойства логарифма больше не могут быть применены.
Внимание! Важно отметить следующее:
log (xy)≠log x⋅log y и log (xy)≠log xlog y
Пример 7
Полностью развернуть: ln (2×3).
Решение:
Напомним, что натуральный логарифм представляет собой основание логарифма e , ln x=loge x.Поэтому применимы все свойства логарифма.
ln (2×3)=ln 2+ln x3 правило произведения для логарифмов=ln 2+3ln x степенное правило для логарифмов
Ответ: ln 2+3ln x
Пример 8
Полное раскрытие: log 10xy23.
Решение:
Начните с перезаписи кубического корня, используя рациональный показатель степени 13, а затем примените свойства логарифма.
log 10xy23=log (10xy2)1/3=13log (10xy2)=13(log 10+log x+log y2)=13(1+log x+2log y)=13+13log x+23log y
Ответ: 13+13log x+23log y
Пример 9
Полностью раскрыть: log2 ( (x+1)25y).
Решение:
Применяя свойство произведения к знаменателю, позаботьтесь о распределении отрицательного значения, полученного в результате применения свойства частного.
log2 ( (x+1)25y)=log2 (x+1)2−log2 (5y)=log2 (x+1)2−(log2 5+log2 y) распределение.=log2 (x+1)2− log2 5−log2 y=2log2 (x+1)−log2 5−log2 y
Ответ: 2log2 (x+1)−log2 5−log2 y
Предупреждение : Не существует правила, позволяющего разложить логарифм суммы или разности.Другими словами,
log (x±y)≠log x±log y
Попробуй! Полностью разверните: ln (5y4x).
Ответ: ln 5+4ln y−12ln x
Пример 10
Учитывая, что log2 x=a, log2 y=b и log2 z=c, напишите следующее в терминах a , b и c :
а. log2 (8x2y)
log2 (8x2y)
б.log2 (2x4z)
Решение:
Далее мы сконденсируем логарифмические выражения. Как мы увидим, важно уметь объединять выражения с участием логарифмов в единый логарифм с коэффициентом 1. Это будет одним из первых шагов при решении логарифмических уравнений.
Пример 11
Запишите в виде одинарного логарифма с коэффициентом 1: 3log3 x−log3 y+2log3 5.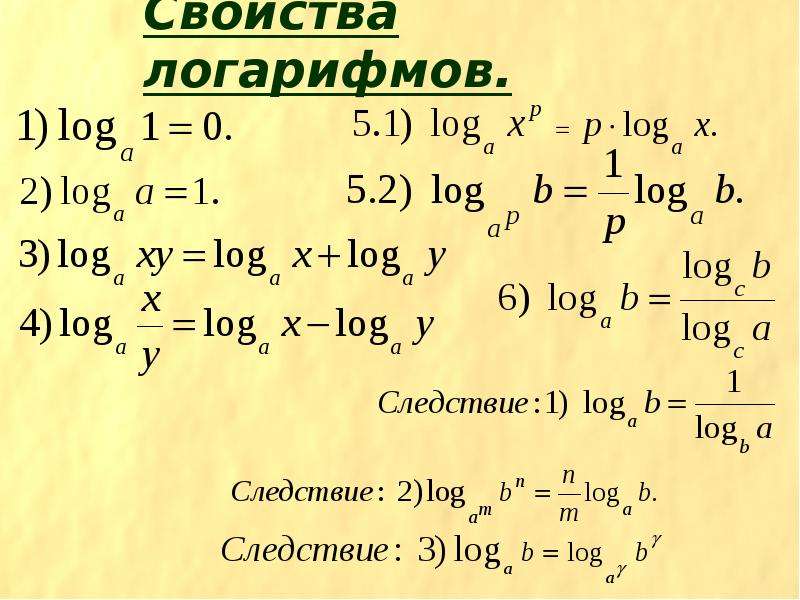
Решение:
Начните с перезаписи всех логарифмических членов с коэффициентом 1. Для этого используйте правило степени. Затем используйте правила произведения и частного для дальнейшего упрощения.
3log3x−log3y+2log35={log3x3−log3y}+log352 частное свойство={log3(x3y)+log325} product свойство=log3(x3y⋅25)=log3(25x3y)Ответ: log3 (25x3y)
Пример 12
Запишите в виде одинарного логарифма с коэффициентом 1: 12ln x−3ln y−ln z.
Решение:
Начните с записи коэффициентов логарифмов как степеней их аргументов, после чего мы дважды применим правило отношения слева направо.
12ln x−3ln y−ln z=ln x1/2−ln y3−ln z=ln (x1/2y3)−ln z=ln (x1/2y3÷z)=ln (x1/2y3⋅1z)=ln (x1/2y3z) или =ln (xy3z)
Ответ: ln (xy3z)
Попробуй! Запишите в виде одинарного логарифма с коэффициентом 1: 3log (x+y)−6log z+2log 5.
Ответ: log (25(x+y)3z6)
Ключевые выводы
Тематические упражнения
Часть A. Логарифмы и их обратные свойства
Оценка:
Найти :
Часть B: Произведение, частное и степенные свойства логарифмов
Полностью раскрыть.
При данных log3 x=a, log3 y=b и log3 z=c запишите следующие логарифмы через a , b и c .
Учитывая logb 2=0.43, logb 3=0,68 и logb 7=1,21, рассчитайте следующее. (Подсказка: разверните, используя суммы, разности и частные множителей 2, 3 и 7.)
Расширьте, используя свойства логарифма, а затем аппроксимируйте с помощью калькулятора до ближайшей десятой.
Запишите в виде одинарного логарифма с коэффициентом 1.
Выразите в виде единичного логарифма и упростите.
ответы
доказательств свойств логарифма — ChiliMath
Свойства или правила логарифмирования выводятся с использованием законов экспоненты. k}} \right) = k \cdot {\log _b}x
k}} \right) = k \cdot {\log _b}x
4) Изменение основного свойства: {\log _a}x = {\Large{{{{{\log }_b}x} \over {{{\log }_b}a}}}}
Верно, что логарифмическое уравнение может быть выражено как показательное уравнение, и наоборот.{\цвет{красный}у}}
По существу это означает, что существует эквивалентность между логарифмическими операторами и экспоненциальными операторами.
Таким образом, при заданном логарифмическом выражении мы можем выразить его как показательное выражение. Таким же образом, если у нас есть экспоненциальное выражение, мы можем преобразовать его в логарифмическое выражение.
Теперь приступим к доказательству четырех (4) свойств или правил логарифмирования.
Доказательство произведения Свойство логарифма
\large{\log _b}\left( {{x \cdot y}} \right) = {\log _b}x + {\log _b}y
Шаг 1: Пусть {\color{red}m} = {\log _b}x и {\color{blue}n} = {\log _b}y.{м + п}}} \справа)}
\large{{\log _b}\left({xy} \right) = m + n}
Шаг 5: Наконец, замените выражения для \color{red}m и \color{blue}{n}, которые мы присвоили на шаге 1. k}} \right) = \left({{{\log }_b}x} \right)k}
k}} \right) = \left({{{\log }_b}x} \right)k}
Нам просто нужно очистить правую часть уравнения, поставив переменную k перед логарифмическим выражением.{\ большой {{\ цвет {красный} k}}}}} \ справа)}
Шаг 4: Теперь примените Степенное правило логарифмирования к правой части экспоненциального уравнения, чтобы уменьшить показатель степени k. Затем найдите k, разделив обе части уравнения на {\log _b}\left( a \right).
\large{{\log _b}\left( x \right) = {\color{red}k} \cdot {\log _b}\left(a \right)}
\Large{{{{{\log }_b}\left( x \right)} \over {{{\log }_b}\left( a \right)}} = {{{\color{red}k } \cdot {{\log }_b}\left( a \right)} \over {{{\log }_b}\left( a \right)}}}
{\ Large {{{{{\ log } _b} \ left (x \ right)} \ over {{{\ log } _b} \ left ( a \ right)}}}} = {\ color {red} к}
Шаг 5: Наш последний шаг — подставить обратно выражение для k = {\log _a}x.Мы установили его на шаге 1.
{\ Large {{{{{\ log } _b} \ left (x \ right)} \ over {{{\ log } _b} \ left ( a \ right)}}}} = {\ color {red} к}
{\ Large {{{{{\ log }_b} \ left (x \ right)} \ over {{{\ log } _b} \ left ( a \ right)}}}} = {\ log _a} x
или
{\log _a}x={\Large{{{{{\log}_b}\left(x\right)} \over{{{\log}_b}\left(a\right)}}}}
Вас также может заинтересовать:
Правила логарифмирования
Значение, определение, типы, свойства, приложения и часто задаваемые вопросы
Логарифм Значение
Логарифм — это слово и понятие, придуманное шотландским математиком Джоном Нейпиром. Логарифм происходит от комбинации двух греческих слов: логос, означающий принцип или мысль, и арифмос, означающий число.
Логарифм происходит от комбинации двух греческих слов: логос, означающий принцип или мысль, и арифмос, означающий число.
Определение логарифма
Логарифм — это степень, в которую нужно возвести число, чтобы получить определенное число. Обозначается логарифмом числа. Пример: лог(х).
Логарифм Примеры для классов 9, 10 и 11;
, если y=ax
, то logay= x
а является основанием.
x — показатель степени.
Где, a> 0, ≠ 1, y ≠ 0
Например: 25 = 32
log232 = 5
Log3 9 = 2 | 32 = 9 |
Log3 81 = 4 | 34 = 81 |
Log5 625 = 4 | 54 = 625 |
Типы логарифмов
Логарифм, основание которого равно 10, называется десятичным логарифмом. По сути, это то, сколько 10 нужно умножить, чтобы получить заданное число. Обозначается как log 10 или log.
По сути, это то, сколько 10 нужно умножить, чтобы получить заданное число. Обозначается как log 10 или log.
Например:
log 100
= log 10²
= 2log 10
= 2
Логарифм, по основанию которого считается e (постоянная Эйлера), называется натуральным логарифмом. Это число e, которое нужно умножить, чтобы получить данное число.
Например:
e= 2,71828
Натуральный логарифм числа, например. 56 обозначается Ln56.
In 56= 4.02535169
Свойства логарифма
1. logb (mn) = n logb m (логарифм мощности)
Пример: log10 (23)= 3log102
2. + logbn (правило произведения)
Пример: log10 (14)= log10 (7*2)= log10 7 + logb 2
3. logb (m/n)= logb m – logb n (правило частного)
Пример : log10 (4/5)= logb 4 – logb 5
4. logb 1= 0
logb 1= 0
5. logb (m) = ln m / ln b (изменение базового правила)
или logb (n) = log10n / log10 b
Например: log10 (7) = ln 7 / ln 10
6.ln(1/x) = -ln (x) (логарифм обратного правила)
Например: . ln(1/5) = -ln (5)
Примечание для класса 9
Применение логарифмов
В эту технологическую эпоху люди всегда находят способы делать что-то все проще и легче. Поэтому люди изобрели калькуляторы и логарифмы, чтобы упростить решение математических уравнений.
Итак, преимущества понимания понятия Логарифм:
Некоторые решенные задачи на логарифм для класса 10
1. Если loga p= q, выразить aq-1 через a и p.
Решение:
loga p= q
ap= q
ap/a = q/a
aq-1 = p/a
2. Решите: (3+log7 x)/(4 – 2 log7x) = 2
Решите: (3+log7 x)/(4 – 2 log7x) = 2
Решение:
3+log x = 8 – 4log7x
5log7x = 5
log7x = 1
x = 71 = 7
3.Решите (log 2x) 2 – log2x2 — 32 = 0. Дан x — целое число.
Решение:
(log2x)2 – log 2×4 — 32 = 0.
⇒ (log 2x)2 – 4log2 x — 32 = 0……(1)
log 2x = y (скажем, )
(i) ⇒ у2 – 4у – 32 = 0
⇒ у2 – 8у + 4у – 32 = 0
⇒ у (у – 8) + 4 (у – 8) = 0
⇒ (у – 8) (y + 4) = 0
⇒ y = 8, -4
⇒ log2x = 8 или log2x = — 4
X=28 = 256.
Так как x целое число, то x = 256 .{n}\] = n log\[_{b}\] a)
⇒ 4 = log\[_{\frac{1}{3}}\] \[\frac{1}{81}\ ] (Поскольку log\[_{b}\] b = 1)
⇒ log\[_{\frac{1}{3}}\] \[\frac{1}{81}\] = 4
Следовательно, логарифмическая форма имеет вид
Алгебра — Логарифмические функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 6-2: Логарифмические функции
В этом разделе нам нужно перейти к функциям логарифмирования.Это может быть сложной функцией для построения графика сразу. Будут некоторые другие обозначения, к которым вы не привыкли, и некоторые свойства могут быть не такими интуитивными. Однако не отчаивайтесь. Как только вы разберетесь с ними, вы обнаружите, что они на самом деле не так уж плохи, и обычно требуется немного поработать с ними, чтобы понять их.
Вот определение функции логарифмирования.
Если \(b\) — любое число такое, что \(b > 0\) и \(b \ne 1\) и \(x > 0\), то
\[y = {\log _b}x\hspace{0.y} = x\) называется экспоненциальной формой .Обратите внимание, что требование \(x > 0\) на самом деле является результатом того факта, что мы также требуем \(b > 0\). Если вы думаете об этом, это будет иметь смысл. Мы возводим положительное число в степень, поэтому результат не может быть ничем иным, как другим положительным числом. Очень важно помнить, что мы не можем логарифмировать ноль или отрицательное число.
Теперь давайте обратимся к используемым здесь обозначениям, так как обычно это самое большое препятствие, которое учащиеся должны преодолеть, прежде чем начать понимать логарифмы.Во-первых, «логарифмическая» часть функции — это просто три буквы, которые используются для обозначения того факта, что мы имеем дело с логарифмом. Они не являются переменными и не означают умножения. Они здесь только для того, чтобы сказать нам, что мы имеем дело с логарифмом.
Они здесь только для того, чтобы сказать нам, что мы имеем дело с логарифмом.
Далее, \(b\), который подстрочный индекс в части «журнала», указывает нам, что такое база, так как это важная часть информации. Кроме того, несмотря на то, как это может выглядеть, в логарифмической форме выше нет возведения в степень.x}\) в такой форме, но это не так. Просто похоже, что это может быть то, что происходит.
Важно соблюдать прямолинейность записи логарифмов, иначе вам будет очень сложно их понять и работать с ними.
Теперь давайте кратко рассмотрим, как мы вычисляем логарифмы.
Пример 1 Оцените каждый из следующих логарифмов. Реальность такова, что прямое вычисление логарифмов может быть очень трудным процессом даже для тех, кто действительно в них разбирается. Обычно гораздо проще сначала преобразовать логарифмическую форму в экспоненциальную. В такой форме мы обычно можем получить ответ довольно быстро.
Обычно гораздо проще сначала преобразовать логарифмическую форму в экспоненциальную. В такой форме мы обычно можем получить ответ довольно быстро.
a \({\log _4}16\) Показать решение
Итак, на самом деле мы просим следующее.
\[{\log _4}16 = ?\]Как было предложено выше, давайте преобразуем это в экспоненциальную форму.
\[{\log _4}16 = ?\hspace{0,25 дюйма} \Rightarrow {\mbox{ }}\hspace{0.4}\), и т. д. , пока не получите 16. В этом случае нам нужен показатель степени 4. Следовательно, значение этого логарифма равно. \[{\log _2}16 = 4\]Перед тем, как перейти к следующей части, обратите внимание, что основа для них является очень важной частью обозначений. Изменение базы изменит ответ, поэтому нам всегда нужно отслеживать базу.
c \({\log _6}216\) Показать решение
Мы сделаем это без каких-либо реальных объяснений, чтобы увидеть, насколько хорошо вы справились с вычислением логарифмов. 3}}} = \frac{{27}}{8}\]
3}}} = \frac{{27}}{8}\]
Надеюсь, теперь у вас есть представление о том, как вычислять логарифмы, и вы начинаете разбираться в обозначениях. Есть еще несколько оценок, которые мы хотим сделать, однако нам нужно ввести некоторые специальные логарифмы, которые встречаются на очень регулярной основе. Это десятичный логарифм и натуральный логарифм . Вот определения и обозначения, которые мы будем использовать для этих двух логарифмов.
\[\begin{align*}& {\mbox{десятичный логарифм:}}\hspace{0.25 дюймов} \ log x = {\ log _ {10}} x \\ & {\ mbox {натуральный логарифм:}} \ hspace {0,25 in} \ ln x = {\ log _ {\ bf {e}}} x \конец{выравнивание*}\] Итак, десятичный логарифм — это просто логарифм по основанию 10, за исключением того, что мы опустили часть обозначения «по основанию 10». Точно так же натуральный логарифм — это просто логарифмическая база \(\bf{e}\) с другим обозначением, где \(\bf{e}\) — то же число, которое мы видели в предыдущем разделе и определяется как \({\bf{e}} = 2,718281828 \ldots\).
Давайте взглянем еще на пару оценок.
Пример 2 Оцените каждый из следующих логарифмов.Чтобы выполнить первые четыре вычисления, нам просто нужно вспомнить, как они обозначаются и какое основание подразумевается этими обозначениями.0} = 1\). Опять же, обратите внимание, что база, которую мы здесь используем, не изменит ответ.
Таким образом, при вычислении логарифмов все, что мы на самом деле спрашиваем, это какой показатель степени мы положили в основание, чтобы получить число в логарифме.
Теперь, прежде чем мы перейдем к некоторым свойствам логарифмов, давайте сначала нарисуем пару быстрых графиков.
Этот пример имеет две точки. Во-первых, он познакомит нас с графиками двух логарифмов, которые мы, скорее всего, увидим в других классах. Кроме того, это даст нам некоторую практику использования нашего калькулятора для оценки этих логарифмов, потому что реальность такова, что именно так нам нужно будет выполнять большинство этих оценок.
Вот таблица значений двух логарифмов.
| \(х\) | \(\лог х\) | \(\пер х\) |
|---|---|---|
| \(\frac{1}{2}\) | -0.3010 | -0,6931 |
| 1 | 0 | 0 |
| 2 | 0,3010 | 0,6931 |
| 3 | 0,4771 | 1,0986 |
| 4 | 0. r}} \right) = r{\log _b}x\) r}} \right) = r{\log _b}x\)Мы ничего не будем делать с последним свойством в этом разделе; это здесь только ради полноты. Мы подробно рассмотрим это свойство в нескольких разделах. Первые два свойства, перечисленные здесь, могут сначала немного сбить с толку, так как с одной стороны у нас есть произведение или частное внутри логарифма, а с другой стороны у нас есть сумма или разность двух логарифмов.Нам просто нужно быть осторожными с этими свойствами и использовать их правильно. Также обратите внимание, что не существует правил разложения логарифма суммы или разности двух членов. Для ясности отметим следующее: \[\ begin{align*}{\log _b}\left( {x + y} \right) & \ne {\log _b}x + {\log _b}y\\ {\log _b}\left( {x — y} \right) & \ne {\ log _b} x — {\ log _b} y \ end {align*} \] Будьте осторожны с ними и не пытайтесь их использовать, поскольку они просто не соответствуют действительности. Теперь, когда мы сделали это, мы можем использовать свойство 7 для каждого из этих отдельных логарифмов, чтобы получить окончательный упрощенный ответ.{\ гидроразрыва {1} {2}}} \] Записанный в этой форме, мы видим, что у всего члена есть одна экспонента, и поэтому мы позаботимся об этом в первую очередь. \[\ln \sqrt {xy} = \frac{1}{2}\ln \left( {xy} \right)\]Теперь займемся товаром. \[\ln \sqrt {xy} = \frac{1}{2}\left( {\ln x + \ln y} \right)\]Обратите внимание на круглые скобки в этом ответе. \(\frac{1}{2}\) умножает исходный логарифм, поэтому также потребуется умножить весь «упрощенный» логарифм.2}} \справа)\] Теперь мы подошли к сути этой проблемы. Второй логарифм настолько упрощен, насколько это возможно. Помните, что мы не можем разбить логарифм суммы или разности, и поэтому его нельзя разбить дальше. Кроме того, мы можем иметь дело с показателями степени только в том случае, если член в целом возводится в степень. Итак, мы можем еще больше упростить первый логарифм, но второй логарифм уже нельзя упростить.2}} \справа)\] Теперь нам нужно обработать несколько примеров, которые идут в другую сторону. Следующий набор примеров, вероятно, более важен, чем предыдущий. Мы будем выполнять такую работу с логарифмом в нескольких разделах. Пример 5 Запишите каждое из следующих чисел в виде одинарного логарифма с коэффициентом 1. Инструкция, требующая коэффициента 1, означает, что когда мы дойдем до конечного логарифма, перед логарифмом не должно стоять никакого числа. Обратите внимание, что в этих примерах будут использоваться свойства 5–7, только мы будем использовать их в обратном порядке. У нас будут выражения, которые выглядят как правая часть свойства, и мы будем использовать свойство, чтобы записать его так, чтобы оно выглядело как левая сторона свойства. a \(7{\log _{12}}x + 2{\log _{12}}y\) Показать решение Первым шагом здесь является избавление от коэффициентов при логарифмах. Это будет использовать свойство 7 в обратном порядке.6}}}} \справа)\] В этом случае мы имеем дело с тремя терминами, и ни одно из свойств не содержит трех терминов. Это не проблема. Давайте сначала позаботимся о коэффициентах и в то же время вычтем знак минус из двух последних членов. Причина этого будет очевидна на следующем шаге. \[5\ln \left( {x + y} \right) — 2\ln y — 8\ln x = \ln {\left({x + y} \right)^5} — \left( {\ ln {y^2} + \ln {x^8}} \right)\]Теперь обратите внимание, что количество в скобках представляет собой сумму двух логарифмов и поэтому может быть объединено в один логарифм с произведением следующим образом: \[5\ln \left( {x + y} \right) — 2\ln y — 8\ln x = \ln {\left({x + y} \right)^5} — \ln \left( {{y^2}{x^8}} \справа)\] Теперь у нас осталось два логарифма, и они представляют собой разность логарифмов, поэтому мы можем записать это как один логарифм с частным. Последняя тема, которую нам необходимо обсудить в этом разделе, — это изменение формулы с основанием . Большинство современных калькуляторов способны вычислять десятичные и натуральные логарифмы. Однако на этом все, так что же нам делать, если нам нужно вычислить еще один логарифм, что не может быть сделано легко, как мы сделали в первом наборе примеров, которые мы рассмотрели? Для этого у нас есть изменение базовой формулы.Вот изменение базовой формулы. \[{\log _a}x = \frac{{{{\log }_b}x}}{{{{\log }_b}a}}\], где мы можем выбрать \(b\) как угодно. Чтобы использовать это, чтобы помочь нам оценить логарифмы, это обычно обычный или натуральный логарифм. Вот изменение формулы основания с использованием как десятичного логарифма, так и натурального логарифма. \[{\log _a}x = \frac{{\log x}}{{\log a}}\hspace{0,25in}{\log _a}x = \frac{{\ln x}}{{\ в а}}\] Давайте посмотрим, как это работает на примере. , и это просто не то, на что кто-то может ответить навскидку. Если бы 7 было 5, или 25, или 125, и т. д. . мы могли бы сделать это, но это не так. Поэтому приходится использовать формулу замены основания. Теперь мы можем использовать любой из них, и мы получим тот же ответ. Итак, давайте используем оба и проверим это. Начнем с десятичного логарифма замены основания. \[{\log _5}7 = \frac{{\log 7}}{{\log 5}} = \frac{{0.845098040014}}{{0,698970004336}} = 1,205512\]Теперь давайте попробуем представить формулу замены основания в виде натурального логарифма. \[{\log _5}7 = \frac{{\ln 7}}{{\ln 5}} = \frac{{1,945 | 906}}{{1,609437

 {k}} b=\frac{1}{k} \cdot \log _{a} b$
{k}} b=\frac{1}{k} \cdot \log _{a} b$







 Определение логарифма Логарифмом числа b по основанию a называется
Определение логарифма Логарифмом числа b по основанию a называется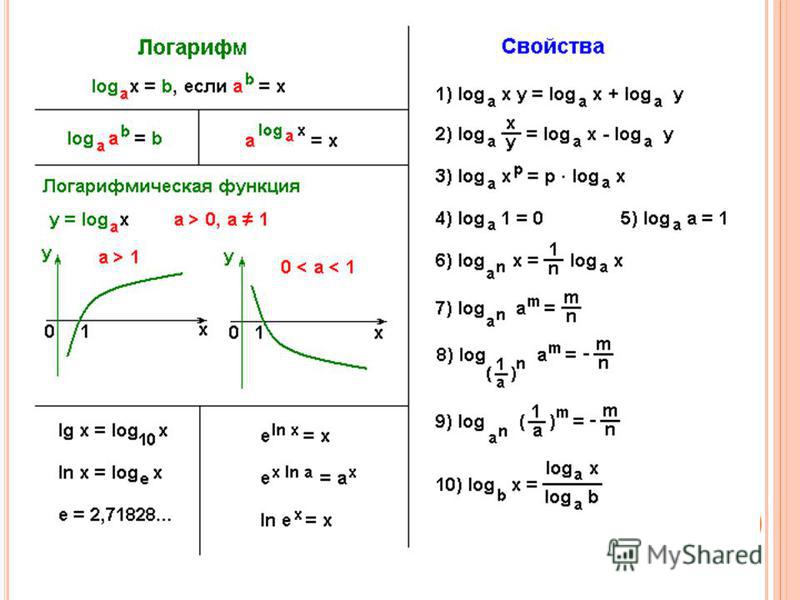 е.
е. Итог урока Что называют логарифмом
Итог урока Что называют логарифмом


 Свойства логарифма 7. Переход от одного основания к
Свойства логарифма 7. Переход от одного основания к 30259 lg x
30259 lg x

 То есть
невозможно подобрать такую рациональную степень, чтобы при возведении в неё
двойки получилось шесть. Таким образом, пришли к противоречию, то есть
доказали, что это иррациональное число.
То есть
невозможно подобрать такую рациональную степень, чтобы при возведении в неё
двойки получилось шесть. Таким образом, пришли к противоречию, то есть
доказали, что это иррациональное число.

 Организационный момент. 1 мин.
Организационный момент. 1 мин.
 Ответ данного уравнения мы можем записать с
помощью нового понятия. Прочитайте текст слайда и запишите корень уравнения.
Ответ данного уравнения мы можем записать с
помощью нового понятия. Прочитайте текст слайда и запишите корень уравнения. резко возрос объем работы, связанный с проведением приближенных
вычислений в ходе решения разных задач, и в первую очередь задач астрономии,
имеющей непосредственное практическое применение (в частности, при определении
положения судов по звездам и по Солнцу). Наибольшие проблемы возникали при
выполнении операций умножения и деления. Попытки частичного упрощения этих
операций путем сведения их к сложению большого успеха не приносили. Поэтому
открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию
их логарифмов стало великим открытием.
резко возрос объем работы, связанный с проведением приближенных
вычислений в ходе решения разных задач, и в первую очередь задач астрономии,
имеющей непосредственное практическое применение (в частности, при определении
положения судов по звездам и по Солнцу). Наибольшие проблемы возникали при
выполнении операций умножения и деления. Попытки частичного упрощения этих
операций путем сведения их к сложению большого успеха не приносили. Поэтому
открытие логарифмов, сводящее умножение и деление чисел к сложению и вычитанию
их логарифмов стало великим открытием.






 Проверьте это, оценив log 4 7, а затем возведя 4 в эту степень.
Проверьте это, оценив log 4 7, а затем возведя 4 в эту степень. За
Например, мы ничего не можем сделать с выражением ln(x 2 + 1).
За
Например, мы ничего не можем сделать с выражением ln(x 2 + 1).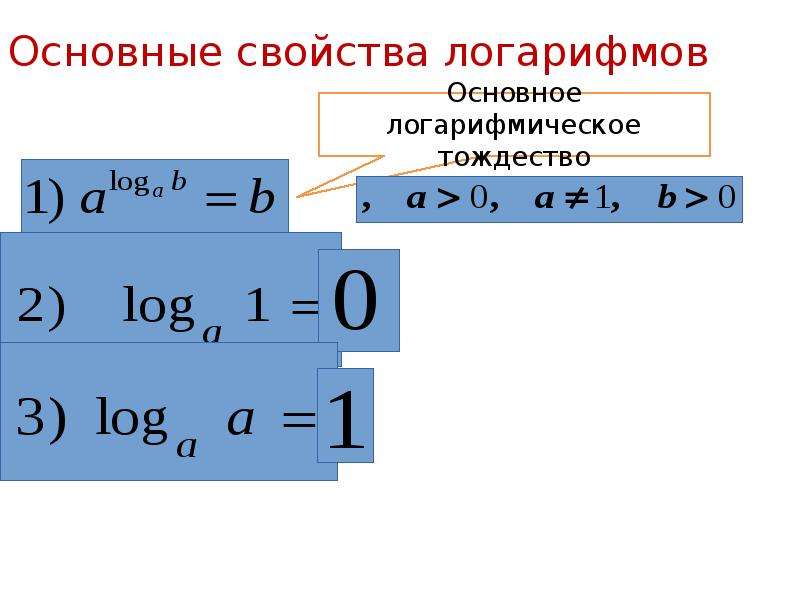 Это десятичный логарифм,
Это десятичный логарифм, Сделайте эту замену, а затем примените свойство степени логарифмов.
Сделайте эту замену, а затем примените свойство степени логарифмов. Логарифмическое выражение полностью расширяется, когда свойства логарифма больше не могут быть применены.
Логарифмическое выражение полностью расширяется, когда свойства логарифма больше не могут быть применены. 2)−15≈−13,2
2)−15≈−13,2
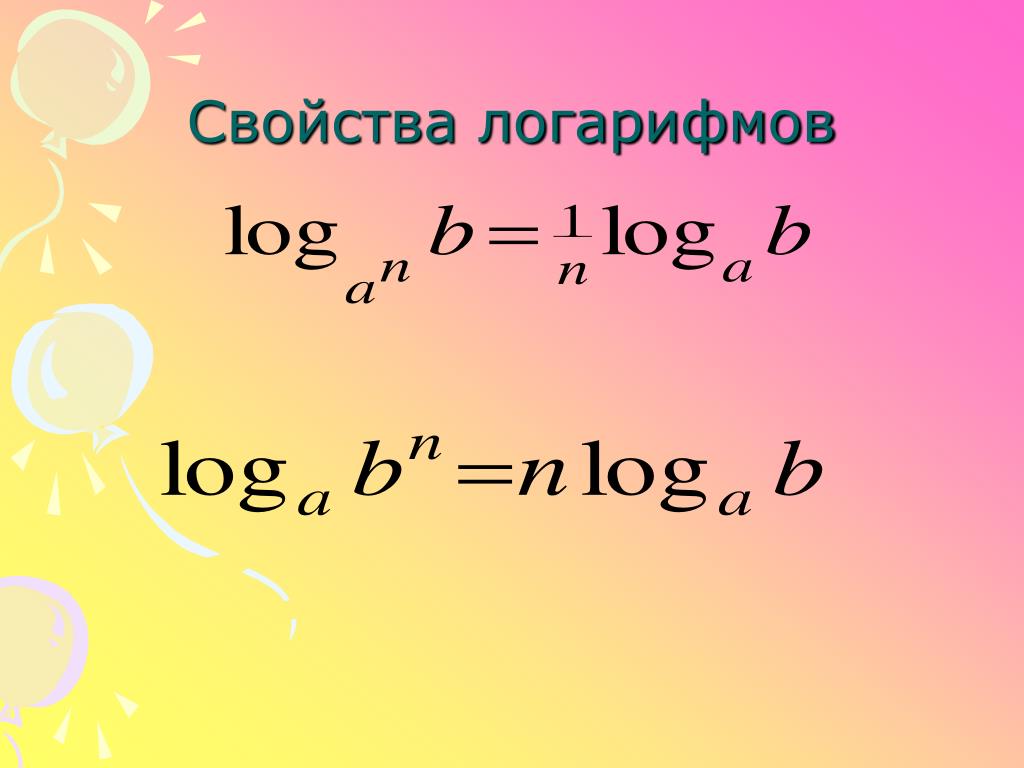 5}} \вправо)\]
5}} \вправо)\] Тот факт, что обе части этого термина возведены в квадрат, не имеет значения. Это должен быть весь член в квадрате, как в первом логарифме.
Тот факт, что обе части этого термина возведены в квадрат, не имеет значения. Это должен быть весь член в квадрате, как в первом логарифме.
 8}}}} \справа)\]
8}}}} \справа)\] ?} = 7\]
?} = 7\]
 Тогда «y» называется логарифмом «x» по основанию «p» и записывается как
Тогда «y» называется логарифмом «x» по основанию «p» и записывается как Экспоненциальная форма – 10 -2 = 0.01
Экспоненциальная форма – 10 -2 = 0.01  е. 4 x 4 x 4 x 4 x 4 = 1024)
е. 4 x 4 x 4 x 4 x 4 = 1024)

 Обозначается как log 10 x просто обозначается как log x
Обозначается как log 10 x просто обозначается как log x 
