Пи на 4 на окружности: Как обозначать числа с пи на числовой окружности?
Как обозначать числа с пи на числовой окружности?
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа \(2π\), \(π\), \(\frac{π}{2}\), \(-\frac{π}{2}\), \(\frac{3π}{2}\)
Как вы знаете из прошлой статьи, радиус числовой окружности равен \(1\). Значит, длина окружности равняется \(2π\) (вычислили по формуле \(l=2πR\)). С учетом этого отметим \(2π\) на числовой окружности. Чтобы отметить это число нужно пройти от \(0\) по числовой окружности расстояние равно \(2π\) в положительном направлении, а так как длина окружности \(2π\), то получается, что мы сделаем полный оборот. То есть, числу \(2π\) и \(0\) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки — это нормально для числовой окружности.
Теперь обозначим на числовой окружности число \(π\). \(π\) – это половина от \(2π\). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от \(0\) в положительном направлении половину окружности.
Отметим точку \(\frac{π}{2}\). \(\frac{π}{2}\) – это половина от \(π\), следовательно чтобы отметить это число, нужно от \(0\) пройти в положительном направлении расстояние равное половине \(π\), то есть четверть окружности.
Обозначим на окружности точки \(-\)\(\frac{π}{2}\). Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.
Нанесем \(-π\). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.
Теперь рассмотрим пример посложнее. Отметим на окружности число \(\frac{3π}{2}\). Для этого дробь \(\frac{3}{2}\) переведем в смешанный вид \(\frac{3}{2}\)\(=1\)\(\frac{1}{2}\), т.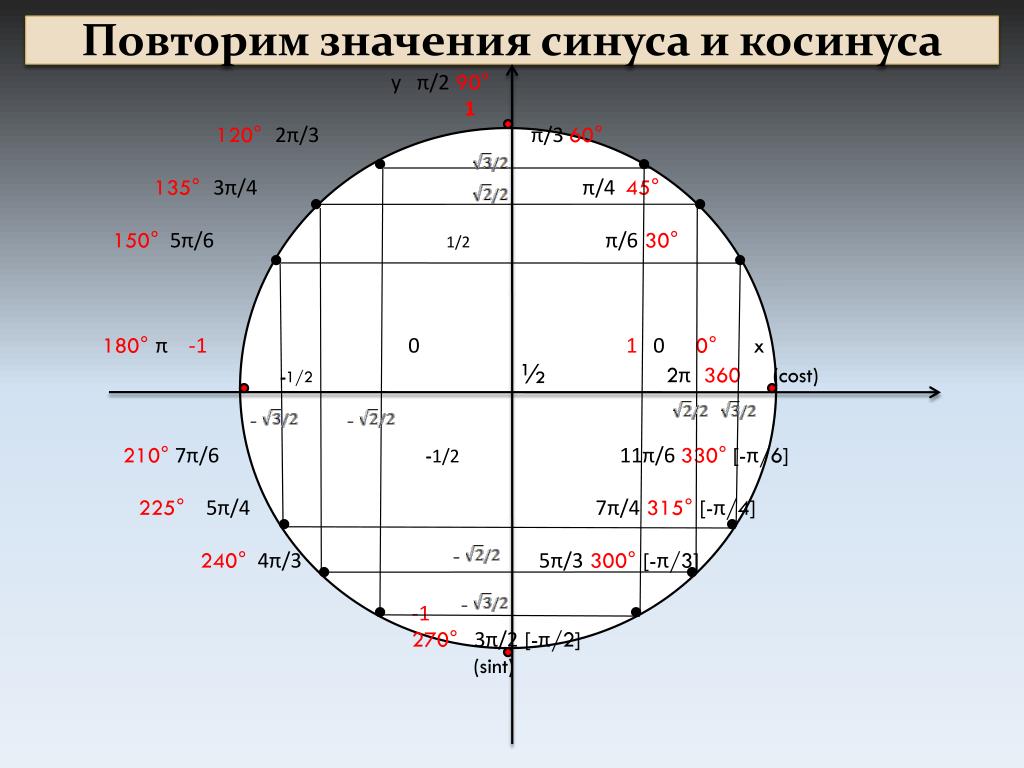 е. \(\frac{3π}{2}\)\(=π+\)\(\frac{π}{2}\). Значит, нужно от \(0\) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
е. \(\frac{3π}{2}\)\(=π+\)\(\frac{π}{2}\). Значит, нужно от \(0\) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
Задание 1. Отметьте на числовой окружности точки \(-2π\),\(-\)\(\frac{3π}{2}\).
Обозначаем числа \(\frac{π}{4}\), \(\frac{π}{3}\), \(\frac{π}{6}\)
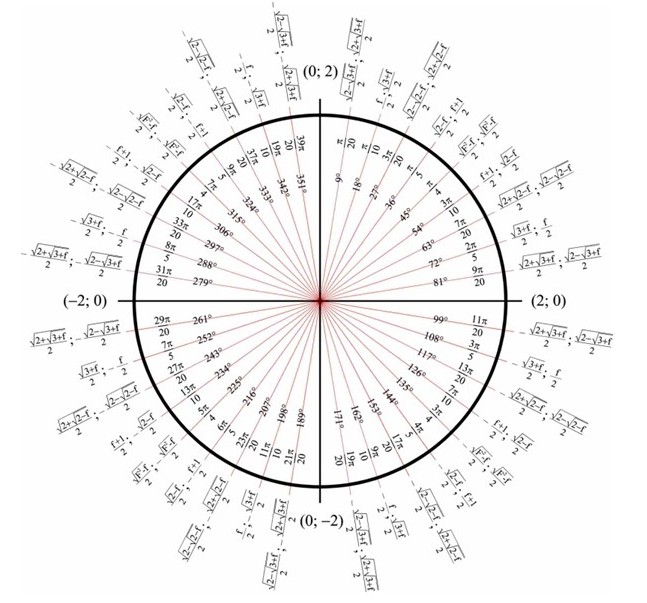
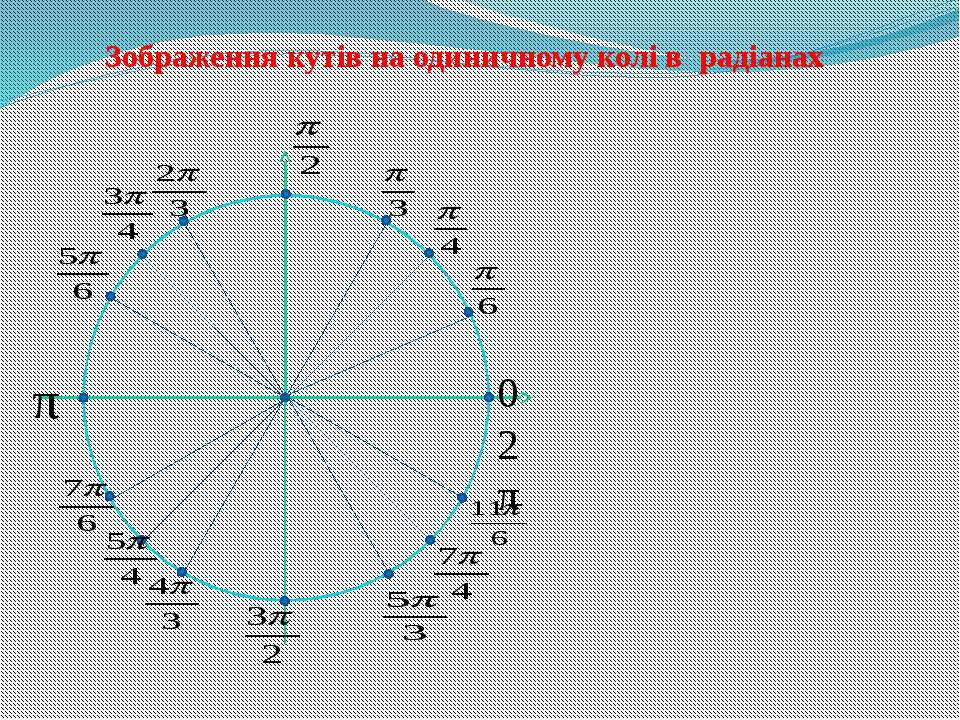
Выше мы нашли значения в точках пересечения числовой окружности с осями \(x\) и \(y\). Теперь определим положение промежуточных точек. Для начала нанесем точки \(\frac{π}{4}\), \(\frac{π}{3}\) и \(\frac{π}{6}\).
\(\frac{π}{4}\) – это треть от \(π\) (иначе говоря,\(\frac{π}{3}\)\(=π:3\)), поэтому расстояние \(\frac{π}{3}\) – это треть от полукруга.
\(\frac{π}{6}\) – это половина \(\frac{π}{3}\) (ведь \(\frac{π}{6}\)\(=\)\(\frac{π}{3}\)\(:2\)) поэтому расстояние \(\frac{π}{6}\) – это половина от расстояния \(\frac{π}{3}\).
Вот так они расположены друг относительно друга:
Замечание: Расположение точек со значением \(0\), \(\frac{π}{2}\),\(π\), \(\frac{3π}{2}\), \(\frac{π}{4}\), \(\frac{π}{3}\), \(\frac{π}{6}\) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа \(\frac{7π}{6}\), \(-\frac{4π}{3}\), \(\frac{7π}{4}\)
Обозначим на окружности точку \(\frac{7π}{6}\), для этого выполним следующие преобразования: \(\frac{7π}{6}\)\(=\)\(\frac{6π + π}{6}\)\(=\)\(\frac{6π}{6}\)\(+\)\(\frac{π}{6}\)\(=π+\)\(\frac{π}{6}\).
Отметим на окружности точку \(-\)\(\frac{4π}{3}\). Преобразовываем: \(-\)\(\frac{4π}{3}\)\(=-\)\(\frac{3π}{3}\)\(-\)\(\frac{π}{3}\)\(=-π-\)\(\frac{π}{3}\). Значит надо от \(0\) пройти в отрицательную сторону расстояние \(π\) и еще \(\frac{π}{3}\).
Нанесем точку \(\frac{7π}{4}\), для этого преобразуем \(\frac{7π}{4}\)\(=\)\(\frac{8π-π}{4}\)\(=\)\(\frac{8π}{4}\)\(-\)\(\frac{π}{4}\)\(=2π-\)\(\frac{π}{4}\). Значит, чтобы поставить точку со значением \(\frac{7π}{4}\), надо от точки со значением \(2π\) пройти в отрицательную сторону расстояние \(\frac{π}{4}\).
Задание 2. Отметьте на числовой окружности точки \(-\)\(\frac{π}{6}\),\(-\)\(\frac{π}{4}\),\(-\)\(\frac{π}{3}\),\(\frac{5π}{4}\),\(-\)\(\frac{7π}{6}\),\(\frac{11π}{6}\), \(\frac{2π}{3}\),\(-\)\(\frac{3π}{4}\).
Обозначаем числа \(10π\), \(-3π\), \(\frac{7π}{2}\) ,\(\frac{16π}{3}\), \(-\frac{21π}{2}\), \(-\frac{29π}{6}\)
Запишем \(10π\) в виде \(5 \cdot 2π\). Вспоминаем, что \(2π\) – это расстояние равное длине окружности, поэтому чтобы отметить точку \(10π\), нужно от нуля пройти расстояние равное \(5\) окружностям. Нетрудно догадаться, что мы окажемся снова в точке \(0\), просто сделаем пять оборотов.
Из этого примера можно сделать вывод:
Числам с разницей в \(2πn\), где \(n∈Z\) (то есть \(n\) — любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше \(2π\) (или меньше \(-2π\)), надо выделить из него целое четное количество \(π\) (\(2π\), \(8π\), \(-10π\)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Еще один вывод:
Точке, которой соответствует \(0\), также соответствуют все четные количества \(π\) (\(±2π\),\(±4π\),\(±6π\)…).
Теперь нанесем на окружность \(-3π\). \(-3π=-π-2π\), значит \(-3π\) и \(–π\) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в \(-2π\)).
Кстати, там же будут находиться все нечетные \(π\).
Точке, которой соответствует \(π\), также соответствуют все нечетные количества \(π\) (\(±π\),\(±3π\),\(±5π\)…).
Сейчас обозначим число \(\frac{7π}{2}\). Как обычно, преобразовываем: \(\frac{7π}{2}\)\(=\)\(\frac{6π}{2}\)\(+\)\(\frac{π}{2}\)\(=3π+\)\(\frac{π}{2}\)\(=2π+π+\)\(\frac{π}{2}\). Два пи – отбрасываем, и получается что, для обозначения числа \(\frac{7π}{2}\) нужно от нуля в положительную сторону пройти расстояние равное \(π+\)\(\frac{π}{2}\) (т.е. половину окружности и еще четверть).
Отметим \(\frac{16π}{3}\). Вновь преобразования: \(\frac{16π}{3}\)\(=\)\(\frac{15π + π}{3}\)\(=\)\(\frac{15π}{3}\)\(+\)\(\frac{π}{3}\)\(=5π+\)\(\frac{π}{3}\)\(=4π+π+\)\(\frac{π}{3}\). Ясно, что от нуля надо пройти расстояние равное \(π+\)\(\frac{π}{3}\) – и мы найдем место точки \(\frac{16π}{3}\).
Нанесем на окружность число \(-\)\(\frac{21π}{2}\).
\(-\)\(\frac{21π}{2}\)\(= -\)\(\frac{20π}{2}\)\(-\)\(\frac{π}{2}\)\(=-10π-\)\(\frac{π}{2}\). Значит, место \(-\)\(\frac{21π}{2}\) совпадает с местом числа \(-\)\(\frac{π}{2}\).
Обозначим \(-\)\(\frac{29π}{6}\).
\(-\)\(\frac{29π}{6}\)\(=-\)\(\frac{30π}{6}\)\(+\)\(\frac{π}{6}\)\(=-5π+\)\(\frac{π}{6}\)\(=-4π-π+\)\(\frac{π}{6}\). Для обозначение \(-\)\(\frac{29π}{6}\), на числовой окружности надо от точки со значением \(–π\) пройти в положительную сторону \(\frac{π}{6}\).
Задание 3. Отметьте на числовой окружности точки \(-8π\),\(-7π\), \(\frac{11π}{4}\),\(-\)\(\frac{7π}{3}\),\(\frac{17π}{6}\),\(-\)\(\frac{20π}{3}\),\(-\)\(\frac{11π}{2}\).
Отметьте на числовой окружности точки \(-8π\),\(-7π\), \(\frac{11π}{4}\),\(-\)\(\frac{7π}{3}\),\(\frac{17π}{6}\),\(-\)\(\frac{20π}{3}\),\(-\)\(\frac{11π}{2}\).
Тригонометрические функции. Числовая окружность. Синус и косинус
Числовая окружность изображена на рис. 37:
Рис. 37
Иначе говоря, это множество точек координатной плоскости, координаты которых удовлетворяют уравнению .
Представим себе, что точка равномерно движется по числовой окружности против часовой стрелки со скоростью 1.
Будем предполагать, что это движение обладает следующими свойствами ( — положение точки в момент времени ):
1. — точка числовой окружности.
2. .
3. .
4. имеет положительные координаты.
6. расстояние между точками и равно расстоянию между точками и .
Примечание. Расстояние между точками и вычисляется по формуле
Определение синуса и косинуса
Определение. Предположим, что точка равномерно движется по числовой окружности так, что выполняются свойства 1–6. Абсцисса точки называется косинусом числа , ордината — синусом числа .
Задачи.
1) Найдите координаты точек .
2) Изобразите на числовой окружности дугу, описываемую движущейся точкой в течение промежутков времени
1. .
2. .
3) Отметьте на числовой окружности положения, которые занимает движущаяся точка в моменты времени
1. , где — целое число.
2. , где — целое число. 2 = 1, \\ x = y. \end {cases}$
2 = 1, \\ x = y. \end {cases}$
Решив данную систему, получаем: $y = x =\frac{\sqrt{2}}{2}$.
Значит, координаты точки M, соответствующей числу $\frac{π}{4}$, будут $M(\frac{π}{4})=M(\frac{\sqrt{2}}{2};\frac{\sqrt{2}}{2})$.
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.
Координаты точек числовой окружности
Рассмотрим примеры
Пример 1.
Найти координату точки числовой окружности: $Р(45\frac{π}{4})$.
Решение:
Т.к. числам $t$ и $t+2π*k$, где k-целое число, соответствует одна и та же точка числовой окружности то:
$45\frac{π}{4} = (10 + \frac{5}{4}) * π = 10π +5\frac{π}{4} = 5\frac{π}{4} + 2π*5$.
Значит, числу $45\frac{π}{4}$ соответствует та же точка числовой окружности, что и числу $\frac{5π}{4}$. Посмотрев значение точки $\frac{5π}{4}$ в таблице, получаем:
$P(\frac{45π}{4})=P(-\frac{\sqrt{2}}{2};-\frac{\sqrt{2}}{2})$.
Пример 2.
Найти координату точки числовой окружности: $Р(-\frac{37π}{3})$.
Решение:
Т.к. числам $t$ и $t+2π*k$, где k-целое число, соответствует одна и та же точка числовой окружности то:
$-\frac{37π}{3} = -(12 + \frac{1}{3})*π = -12π –\frac{π}{3} = -\frac{π}{3} + 2π*(-6)$.
Значит, числу $-\frac{37π}{3}$ соответствует та же точка числовой окружности, что и числу $–\frac{π}{3}$, а числу –$\frac{π}{3}$ соответствует та же точка, что и $\frac{5π}{3}$. Посмотрев значение точки $\frac{5π}{3}$ в таблице, получаем:
$P(-\frac{37π}{3})=P(\frac{{1}}{2};-\frac{\sqrt{3}}{2})$.
Пример 3.
Найти на числовой окружности точки с ординатой $у =\frac{1}{2}$ и записать, каким числам $t$ они соответствуют?
Решение:
Прямая $у =\frac{1}{2}$ пересекает числовую окружность в точках М и Р. Точка М соответствует числу $\frac{π}{6}$ (из данных таблицы). Значит, и любому числу вида: $\frac{π}{6}+2π*k$. Точка Р соответствует числу $\frac{5π}{6}$, а значит, и любому числу вида $\frac{5π}{6} +2 π*k$.
Получили, как часто говорят в таких случаях, две серии значений:
$\frac{π}{6} +2 π*k$ и $\frac{5π}{6} +2π*k$.
Ответ : $t=\frac{π}{6} +2 π*k$ и $t=\frac{5π}{6} +2π*k$.
Пример 4.
Найти на числовой окружности точки с абсциссой $x≥-\frac{\sqrt{2}}{2}$ и записать, каким числам $t$ они соответствуют.
Решение:
Прямая $x =-\frac{\sqrt{2}}{2}$ пересекает числовую окружность в точках М и Р. Неравенству $x≥-\frac{\sqrt{2}}{2}$ соответствуют точки дуги РМ. Точка М соответствует числу $3\frac{π}{4}$ (из данных таблицы). Значит, и любому числу вида $-\frac{3π}{4} +2π*k$. Точка Р соответствует числу $-\frac{3π}{4}$, а значит, и любому числу вида $-\frac{3π}{4} +2π*k$.
Тогда получим $-\frac{3π}{4} +2 π*k ≤t≤\frac{3π}{4} +2πk$.
Ответ : $-\frac{3π}{4} +2 π*k ≤t≤\frac{3π}{4} +2πk$.
Задачи для самостоятельного решения
1) Найти координату точки числовой окружности: $Р(\frac{61π}{6})$.
2) Найти координату точки числовой окружности: $Р(-\frac{52π}{3})$.
3) Найти на числовой окружности точки с ординатой $у = -\frac{1}{2}$ и записать, каким числам $t$ они соответствуют.
4) Найти на числовой окружности точки с ординатой $у ≥ -\frac{1}{2}$ и записать, каким числам $t$ они соответствуют.
5) Найти на числовой окружности точки с абсциссой $x≥-\frac{\sqrt{3}}{2}$ и записать, каким числам $t$ они соответствуют.
Тригонометрические уравнения
Решение простейших тригонометрических уравнений
Градусы и радианы
Знакомство с тригонометрической окружностью
Повороты на тригонометрической окружности
Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».
Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах.
1 радиан = 180/π ≈ 57,3 градусов
Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.
Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!
О графиках синуса, косинуса и тангеса поговорим в другой статье.
А сейчас начем с декартовой (прямоугольной) системы координат.
Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.
На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.
А теперь отметим основные значения градусов и радиан на окружности.
Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.
Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).
А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).
Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).
Главное — направление, куда мы будем смотреть, а не угол!
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!
Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°…
А теперь у тебя есть два пути:
Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.
Попасть в любую точку можно с помощью суммы или разности двух табличных значений.
Сразу попробуем разобрать на примере:
Пример №1. cos(x) = ½
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.
Дело за малым — найти эти углы.
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.
Или запомнить такой прием:
Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).
Например, требуется найти sin(π/2): π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.
cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).
Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).
И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:
Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на …=-225°=135°=495°=…
То же самое и здесь! Разные углы могут отражать одно и то же направление.
Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.
Таким образом, попасть в первое направление 60° можно: …,60°-360°, 60°, 60°+360°,…
И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)
Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же).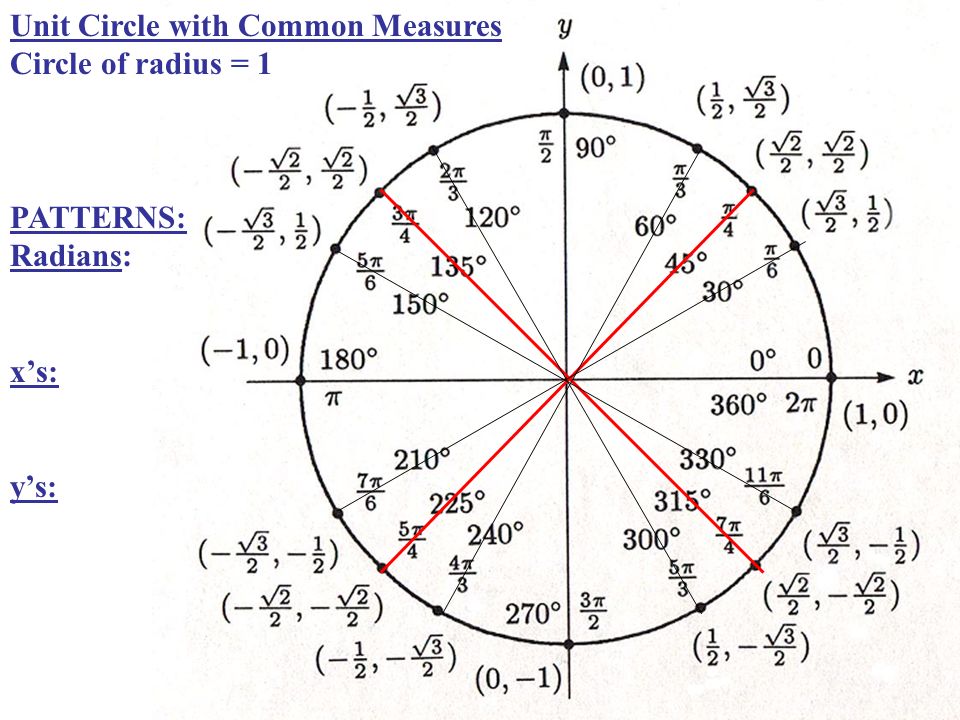 Аналогично x = −60 + 360n.
Аналогично x = −60 + 360n.
Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.
Ответ: x = π/3 + 2πn, x= −π/3 + 2πk, (n, k)∈Ζ.
Пример №2. 2sinx = √2
Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2
1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.
Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.
И еще не забудем добавить +2πn, n∈Ζ.
Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.
Пример №3. tg(x + π/4) = √3
Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.
tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.
1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.
По мнемоническому правилу при тангенсе √3 первое значение — это π/3.
3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.
4) Но мы нашли только y, вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.
Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.
Теперь корни на окружности будут здесь:
Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.
Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).
Ответ можно записать и так: π/12 + πn, n∈Ζ.
Пример №4: −10ctg(x) = 10
Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.
1) Проведем прямую через эту точку и начало координат.
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).
Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π…) так намного меньше шансов запутаться.
Не забываем добавить к каждой точке 2πk.
Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.
Алгоритм решения тригонометрических уравнений (на примере cos(x) = −√3/2):
- Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
- Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
- Точки пересечения с окружностью и будут являться корнями уравнения.
- Значение одной точки (без разницы, как в нее попадете) +2πk.
Будь в курсе новых статеек, видео и легкого математического юмора.
| | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Чиcло пи. π, 2π, 1/π, π/2, π/3, π/4, π/180, (π/180)2, π2, π3, π4 и др.
| |||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.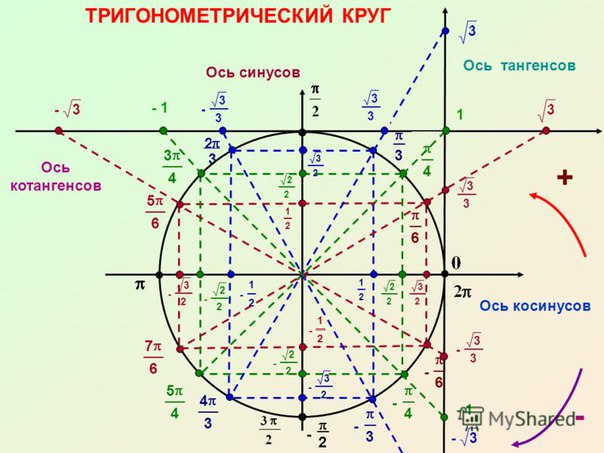 | ||||||||||||||||||||||||||||||
| TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||
Тетрадка в клеточку — Пример
В качестве ответа введите обозначение соответствующей точки из показанных на числовой окружности.
Найдите на числовой окружности точку, которая соответствует заданному числу:
4.Найдите на числовой окружности точку, которая соответствует заданному числу:
5.Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:0
Найдите на числовой окружности точку, которая соответствует заданному числу:π
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:
Найдите на числовой окружности точку, которая соответствует заданному числу:−π
Найдите на числовой окружности точку, которая соответствует заданному числу:−2π
Tau Day | No, really, pi is wrong: The Tau Manifesto by Michael Hartl
Я продолжаю быть удивлённым тем, насколько этот предмет богат, и моё понимание \( \pi \) и \( \tau \) продолжает движение вперёд.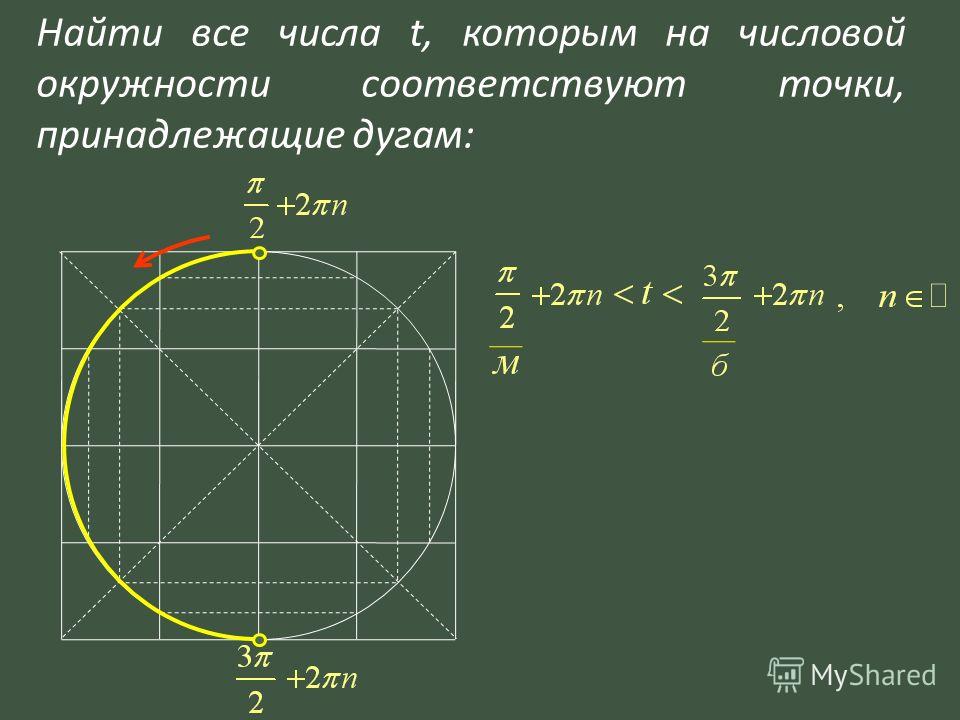 {n-1} \) разные числа. Другими словами, геометрическая важность \( \pi \) это результат математической шутки.
{n-1} \) разные числа. Другими словами, геометрическая важность \( \pi \) это результат математической шутки.
Пи
Нарисуйте круг диаметром (полностью поперек круга) 1
Тогда окружность (полностью по кругу) равна 3,14159265 … число, известное как Pi
Pi (произносится как «пирог») часто пишется с использованием греческого символа π
.Определение π:
Окружность
, разделенная на Диаметр
окружности.
Длина окружности, разделенная на диаметр круга, всегда равна π, независимо от того, насколько большой или малый круг!
Чтобы помочь вам вспомнить, что такое π … просто нарисуйте эту диаграмму.
В поисках Пи себя
Нарисуйте круг или используйте что-нибудь круглое, например тарелку.
Измерьте по краю (окружность ):
Получил 82 см
Измерьте поперек круга (диаметр ):
Получил 26 см
Разделить:
82 см / 26 см = 3.1538 …
Это довольно близко к π. Может, если точнее замерил?
Использование Pi
Мы можем использовать π, чтобы найти окружность, когда мы знаем диаметр
Окружность = π × Диаметр
Пример. Вы ходите по кругу диаметром 100 м. Как далеко вы прошли?
Пройденное расстояние = Окружность
= π × 100 м
= 314,159 … м
= 314 м (с точностью до м)
Также мы можем использовать π, чтобы найти диаметр, когда мы знаем окружность
Диаметр = Окружность / π
Пример: Сэм измерил 94 мм на внешней стороне трубы… каков его диаметр?
Диаметр = Окружность / π
= 94 мм / π
= 29,92 … мм
= 30 мм (с точностью до мм)
Радиус
Радиус составляет половину диаметра, поэтому мы также можем сказать:
Для круга радиусом из 1
Расстояние на полпути вокруг окружности равно π = 3,14159265 . ..
..
цифр
π примерно равно:
3.14159265358979323846…
Цифры продолжаются без единого шаблона.
π было вычислено с точностью до пятидесяти триллионов десятичных знаков, и все еще нет , нет шаблона для цифр
Приближение
Быстрое и простое приближение для π — 22/7
22/7 = 3,1428571 …
Но, как видите, 22/7 — это , не совсем верно . На самом деле π не равно отношению любых двух чисел, что делает его иррациональным числом.
Действительно хорошее приближение, лучше, чем 1 часть из 10 миллионов, составляет:
355/113 = 3,1415929 …
(подумайте о «113355», косой чертой посередине «113/355», затем переверните «355/113»)
Резюме:
| 22/7 | = | 3,14 28571 … |
| 355/113 | = | 3,141592 9 … |
| π | = | 3.14159265 … |
Запоминание цифр
Я обычно помню просто «3,14159», но вы также можете сосчитать буквы:
«Можно мне сегодня большую тару сливочного масла»
3 1 4 1 5 9 2 6 5
до 100 знаков после запятой
Вот π с первыми 100 десятичными знаками:
| 3,14159265358979323846264338327950288 4197169399375105820974944592307816 4062862089986280348253421170679… |
Самостоятельное вычисление числа Пи
Есть много специальных методов, используемых для вычисления π, и вот один из них, который вы можете попробовать сами: он называется серия Нилаканта (в честь индийского математика, жившего в 1444–1544 годах).
Это продолжается вечно и имеет такую схему:
3+ 4 2 × 3 × 4 — 4 4 × 5 × 6 + 4 6 × 7 × 8 — 4 8 × 9 × 10 +.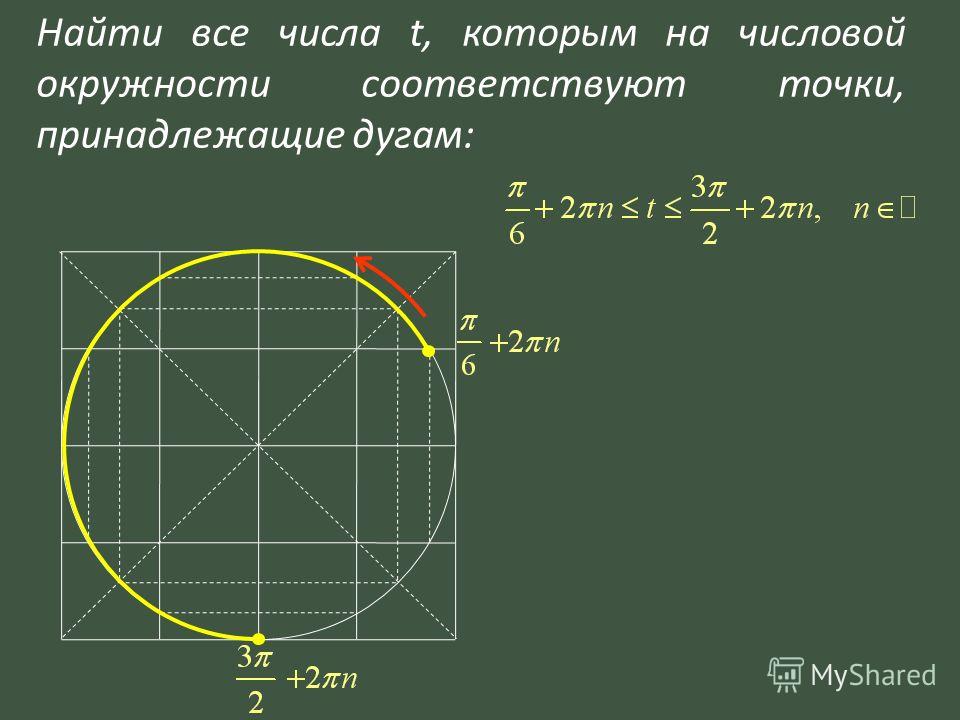 ..
..
(Обратите внимание на узор + и -, а также на узор чисел под линиями.)
Это дает следующие результаты:
| Срок | Результат (до 12 знаков после запятой) |
|---|---|
| 1 | 3 |
| 2 | 3,166666666667 |
| 3 | 3,133333333333 |
| 4 | 3,145238095238 |
| … | … и т. Д.! … |
Возьмите калькулятор (или воспользуйтесь таблицей) и посмотрите, сможете ли вы добиться лучших результатов.
День Пи
ДеньПи отмечается 14 марта. Март — 3-й месяц, поэтому он выглядит как 3/14
.Почему PI не равно 4, математика — это здорово и другие загадки.
На днях я столкнулся с интересной проблемой аппроксимации круга с помощью ограничивающего квадрата, который, кажется, доказывает пи = 4. Парадокс подал интереснейший коллекционер головоломок Сураджит Басу, друг и вдохновитель всей жизни. См. «Сонату для черепахи без сопровождения», чтобы узнать, почему!
Вот оскорбительный парадокс:
Это пример того, как можно ответить на нелогичные вопросы с помощью небольшого расчета.
Ключ состоит в том, чтобы понять, что независимо от того, насколько близко мы аппроксимируем круг, ортогональные линии аппроксимации, образованные инвертированием квадратных углов , на самом деле никогда не будут касательными к окружности.
Обратите внимание, что по мере приближения к 90 градусам горизонтальная линия намного длиннее вертикальной. То же самое и с приближением 0 и 180 — вертикальная линия намного больше горизонтальной составляющей.
Если мы возьмем квадрант круга — скажем, верхний левый квадрант, движущийся против часовой стрелки сверху налево — мы можем представить, что каждая бесконечно малая дуга ( под углом тета) аппроксимируется горизонтальной линией, которая приблизительная длина дуги, умноженная на косинус угла , а вертикальная линия — это та же дуга, умноженная на синус угла.
Вот примерное изображение:
Таким образом, каждая дуга аппроксимируется двумя линиями, а мы просто складываем все приближения. Вот здесь-то и появляются исчисления и ограничения. Для одного квадранта от 0 до 90 градусов вот результат:
Умножьте на четыре, и вы получите 8 * r (или 4 * диаметр).Вуаля!
PI не равно 4, , потому что приблизительная цифра никогда не совпадает с кругом, даже в пределе бесконечного числа приближений.
Из этого следует интересный результат: большинство кругов в цифровом представлении (ч / б) должны иметь яркость (или цветовую плотность) 4 / пи — или примерно на 27% ярче, чем реальный круг того же размера в реальном масштабе времени. Мир.
Кроме того, сглаживание можно сделать более умным способом, чтобы не только сглаживать края, но и уменьшать яркость, чтобы относительная яркость круга была такой же, как физическая реальность — когда разрешение изображения меньше человеческого. разрешение глаза?
Является ли это одной из причин, почему переход Apple на дисплей Retina, где разрешение пикселей лучше, чем разрешение сетчатки, отличает iPhone (а теперь и iPad3) от других?
Больше вопросов, чем ответов.
кругов
| Определение: Круг — это геометрическое место всех точек, равноудаленных от центральной точки. |
Определения, относящиеся к кругам
arc: изогнутая линия, которая является частью окружности круг
аккорд: отрезок линии внутри круга, который касается 2 точки на окружности.
2
Уравнение окружности: (полярные координаты)
для круга с центром (0, 0): r () = радиусдля круга с центром с полярными координатами: (c,) и радиус a :
r 2 — 2cr cos ( -) + с 2 = а 2Уравнение окружности: (параметрические координаты)
для круга с началом (j, k) и радиусом r:
x (t) = r cos (t) + j y (t) = г sin (t) + кЧто такое Пи и как оно возникло?
Вкратце, пи — это греческая буква, обозначающая р или π — это отношение длины окружности любого круга к диаметру этого круга.Независимо от размера круга это отношение всегда будет равно пи. В десятичной форме значение пи составляет примерно 3,14. Но пи — иррациональное число, а это означает, что его десятичная форма не заканчивается (например, 1/4 = 0,25) и не становится повторяющейся (например, 1/6 = 0,166666 …). (Всего с 18 десятичными знаками число пи равно 3,141592653589793238.) Следовательно, полезно иметь сокращенное обозначение отношения длины окружности к диаметру. Согласно « A History of Pi » Петра Бекмана, греческая буква π была впервые использована для этой цели Уильямом Джонсом в 1706 году, вероятно, как сокращение периферии, и стала стандартной математической записью примерно 30 лет спустя.
Проведите небольшой эксперимент: с помощью циркуля нарисуйте круг. Возьмите один кусок веревки и поместите его на вершину круга ровно один раз. Теперь распрямите веревку; его длина называется окружностью круга. Измерьте окружность линейкой. Затем измерьте диаметр круга, то есть длину от любой точки круга прямо через его центр до другой точки на противоположной стороне. (Диаметр в два раза больше радиуса, длины от любой точки круга до его центра.Если вы разделите окружность круга на диаметр, вы получите примерно 3,14 — независимо от того, какой размер круга вы нарисовали! У большего круга будет большая окружность и больший радиус, но соотношение всегда будет тем же.
Если бы вы могли точно измерить и разделить, вы бы получили 3,141592653589793238 … или пи.
Иначе говоря, если вы разрежете несколько кусков веревки, длина которых равна диаметру, вам понадобится чуть больше трех из них, чтобы покрыть окружность круга.
Пи чаще всего используется в некоторых вычислениях, касающихся кругов. Пи не только связывает окружность и диаметр. Удивительно, но он также связывает диаметр или радиус круга с площадью этого круга по формуле: площадь равна пи, умноженному на квадрат радиуса. Кроме того, число пи часто неожиданно появляется во многих математических ситуациях. Например, сумма бесконечного ряда
1 + 1/4 + 1/9 + 1/16 + 1/25 + … + 1 / n2 + … равно π 2 /6
Важность числа Пи была признана не менее 4000 лет назад. A History of Pi отмечает, что к 2000 году до нашей эры «вавилоняне и египтяне (по крайней мере) знали о существовании и значении константы π», признавая, что каждый круг имеет одинаковое отношение длины окружности к диаметру. И вавилоняне, и египтяне имели грубые численные приближения к значению числа пи, а более поздние математики в Древней Греции, особенно Архимед, улучшили эти приближения. К началу 20 века было известно около 500 цифр числа Пи.С развитием вычислений, благодаря компьютерам, мы теперь знаем больше, чем первые шесть миллиардов цифр числа Пи.
Триггерные значения на единичной окружности
Java-игры: Карточки, сопоставление, концентрация и поиск слов.
Вы попрактикуетесь в нахождении триггерных значений углов на единичной окружности.
75 tan pi
82 0
A B sin pi / 6 1/2 cos pi / 6 sq root3 / 2 tan pi / 6 sq 903/3 sin pi / 4 sq root2 / 2 cos pi / 3 1/2 tan pi / 3 sqroot 3 cos pi / 2 sin pi / 2 1 cos 2pi / 3 -1/2 cos 3pi / 4 -sqroot2 / 2 cos 5pi / 6 — / 2 cos pi / 4 sqroot2 / 2 tan pi / 4 1 sin pi / 3 sqroot3 / 2 tan pi / 2 sin 2pi / 3 sqroot3 / 2 tan 2pi / 3 s qroot 3 sin 3pi / 4 sqroot2 / 2 tan 3pi / 4 -1 sin 5 pi / 6 1/2 655 9017 tan 5pi -sqroot3 / 3 sin pi 0 cos pi -1 tan pi 0 sin 7pi / 6 -1 cos 7pi / 6 -sqroot3 / 2 tan 7pi / 6 sqroot 3/3 sin 5pi / 4 -sqroot2 / 2 4 — 9017 cos5 5pi sqroot2 / 2
tan 5pi / 4 1 sin 4pi / 3 -sqroot3 / 2 cos 4pi / 3 -1/2 sqroot 3 sin 3pi / 2 -1 cos 3pi / 2 0 tan 3pi / 2 undefined sin 5pi / 3 -sqroot3 / 2 905pi cos 5pi / 3 1/2 -sqroot3 sin 7pi / 4 -sqroot2 / 2 cos 7pi / 4 sqroot2 / 2 tan 7pi / 4 6 -1/2 cos 11pi / 6 sqroot3 / 2 tan 11pi / 6 -sqroot3 / 3 sin 2pi 0 cos1 tan 2pi 0 sin 0pi 0 cos 0pi 1 074 900 tan 0pi
Тригонометрические функции и единичная окружность
Рад
Радианы — это еще один способ измерения углов, и величина угла может быть преобразована между градусами и радианами.
\ circ} {\ pi}} [/ латекс].
Радианная мера угла — это отношение длины дуги к радиусу круга [латекс] \ displaystyle {\ left (\ theta = \ frac {s} {r} \ right)} [/ latex] . Другими словами, если [latex] s [/ latex] — это длина дуги круга, а [latex] r [/ latex] — это радиус круга, то центральный угол, содержащий эту дугу, измеряется в радианах. Ключевые термины
- дуга : Непрерывная часть окружности круга.
- окружность : длина линии, ограничивающей круг.
- радиан : стандартная единица измерения углов в математике. Мера центрального угла круга, который пересекает дугу, равную по длине радиусу этого круга.
Введение в радианы
Напомним, что деление круга на 360 частей дает измерение в градусах. Это произвольное измерение, и мы можем выбрать другие способы разделить круг.Чтобы найти другую единицу, представьте себе процесс рисования круга. Представьте, что вы остановились до того, как круг завершился. Нарисованная вами часть называется дугой. Дуга может быть частью полного круга, полного круга или более чем полного круга, представленного более чем одним полным оборотом. Длина дуги вокруг всего круга называется окружностью этого круга.
Окружность круга
[латекс] C = 2 \ pi r [/ латекс]
Если мы разделим обе части этого уравнения на [латекс] r [/ латекс], мы получим отношение окружности, которое всегда равно [латексу] 2 \ pi [/ латексу] к радиусу, независимо от длины радиус.Таким образом, длина окружности любого круга равна [латексу] 2 \ пи \ приблизительно в 6,28 [/ латексу] раз больше длины радиуса. Это означает, что если мы возьмем струну такой же длины, как радиус, и будем использовать ее для измерения последовательных длин по окружности, то будет место для шести полных длин струны и чуть больше четверти седьмой, как показано на диаграмме. ниже.
Длина окружности по сравнению с радиусом : длина окружности чуть более чем в 6 раз превышает длину радиуса.
{\ circ}} [/ latex].
Измерение угла в радианах
Длина дуги [латекс] s [/ латекс] — это длина кривой вдоль дуги. Так же, как полная длина окружности всегда имеет постоянное отношение к радиусу, длина дуги, образованная любым заданным углом, также имеет постоянную связь с радиусом, независимо от длины радиуса.
Это отношение, называемое радианной мерой, одинаково независимо от радиуса круга — оно зависит только от угла. Это свойство позволяет нам определять меру любого угла как отношение длины дуги [latex] s [/ latex] к радиусу [latex] r [/ latex].
[латекс] \ displaystyle {\ begin {align} s & = r \ theta \\ \ theta & = \ frac {s} {r} \ end {align}} [/ latex]
Измерительные радианы: (a) под углом 1 радиан; длина дуги равна радиусу [латекс] r [/ латекс]. (b) Угол в 2 радиана имеет длину дуги [латекс] s = 2r [/ латекс]. (c) Полный оборот составляет [латекс] 2 \ pi [/ латекс], или около 6,28 радиана.
Пример
Какова мера данного угла в радианах, если длина его дуги равна [латекс] 4 \ pi [/ латекс], а радиус — [латекс] [/ латекс] 12?
Подставьте значения [latex] s = 4 \ pi [/ latex] и [latex] r = 12 [/ latex] в формулу угла:
[латекс] \ displaystyle {\ begin {align} \ theta & = \ frac {s} {r} \\ & = \ frac {4 \ pi} {12} \\ & = \ frac {\ pi} {3 } \\ & = \ frac {1} {3} \ pi \ end {align}} [/ latex]
Угол имеет размер [latex] \ displaystyle {\ frac {1} {3} \ pi} [/ latex] радиан.
Определение тригонометрических функций на единичной окружности
Определение точек на единичной окружности позволяет применять тригонометрические функции к любому углу.
Цели обучения
Используйте прямоугольные треугольники, нарисованные в единичной окружности, чтобы определить тригонометрические функции для любого угла
Основные выводы
Ключевые моменты
- Координаты [latex] x [/ latex] — и [latex] y [/ latex] в точке единичной окружности, заданной углом [latex] t [/ latex], определяются функциями [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex].
{\ circ} [/ латекс].
- Единичный круг демонстрирует периодичность тригонометрических функций, показывая, что они приводят к повторяющемуся набору значений через равные промежутки времени.
Ключевые термины
- периодичность : качество функции с повторяющимся набором значений через равные промежутки времени.
- единичная окружность : окружность с центром в начале координат и радиусом 1.
- квадрант : четыре четверти координатной плоскости, образованные осями [латекс] х [/ латекс] — и [латекс] у [/ латекс].
Тригонометрические функции и единичная окружность
Мы уже определили тригонометрические функции в терминах прямоугольных треугольников. В этом разделе мы переопределим их в терминах единичной окружности. Напомним, что единичный круг — это круг с центром в начале координат и радиусом 1. Угол [латекс] t [/ латекс] (в радианах) образует дугу длиной [латекс] s [/ латекс].
Оси x- и y- делят координатную плоскость (и единичную окружность, поскольку она центрирована в начале координат) на четыре четверти, называемых квадрантами.Мы помечаем эти квадранты, чтобы имитировать направление движения положительного угла. Четыре квадранта обозначены I, II, III и IV.
Для любого угла [latex] t [/ latex] мы можем обозначить пересечение его стороны и единичного круга его координатами, [latex] (x, y) [/ latex]. Координаты [latex] x [/ latex] и [latex] y [/ latex] будут выходными данными тригонометрических функций [latex] f (t) = \ cos t [/ latex] и [latex] f (t). = \ sin t [/ latex] соответственно. Это означает:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ y & = \ sin t \ end {align}} [/ latex]
Эти координаты показаны на диаграмме единичного круга.
Единичный круг: координаты точки на единичной окружности, центральный угол которой составляет [латекс] t [/ латекс] радиан.
Обратите внимание, что значения [latex] x [/ latex] и [latex] y [/ latex] задаются длинами двух сторон треугольника, окрашенных в красный цвет. Это прямоугольный треугольник, и вы можете видеть, как длины этих двух сторон (и значения [latex] x [/ latex] и [latex] y [/ latex]) задаются тригонометрическими функциями [latex] t [/латекс].
В качестве примера того, как это применимо, рассмотрим диаграмму, показывающую точку с координатами [latex] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] по единичной окружности.
Точка на единичном круге: точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2} \ right)} [/ latex] на единичном круге .
Мы знаем, что для любой точки единичного круга координата [latex] x [/ latex] равна [latex] \ cos t [/ latex], а координата [latex] y [/ latex] — [latex] ] \ sin t [/ латекс]. Применяя это, мы можем определить, что [latex] \ displaystyle {\ cos t = — \ frac {\ sqrt2} {2}} [/ latex] и [latex] \ displaystyle {\ sin t = — \ frac {\ sqrt2} {2}} [/ латекс] для угла [латекс] t [/ латекс] на схеме.
Напомним, что [латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ latex]. Применяя эту формулу, мы можем найти тангенс любого угла, обозначенного единичной окружностью. Для угла [латекс] t [/ латекс], указанного на диаграмме единичного круга, показывающего точку [латекс] \ displaystyle {\ left (- \ frac {\ sqrt2} {2}, \ frac {\ sqrt2} {2 } \ right)} [/ latex], касательная:
[латекс] \ displaystyle {\ begin {align} \ tan t & = \ frac {\ sin t} {\ cos t} \\ & = \ frac {- \ frac {\ sqrt2} {2}} {- \ гидроразрыв {\ sqrt2} {2}} \\ & = 1 \ end {align}} [/ latex]
Ранее мы обсуждали тригонометрические функции применительно к прямоугольным треугольникам.{\ circ} [/ латекс].
Дальнейшее рассмотрение единичной окружности
Координаты определенных точек на единичной окружности и мера каждого угла в радианах и градусах показаны на диаграмме координат единичной окружности.
Эта диаграмма позволяет наблюдать за каждым из этих углов, используя тригонометрические функции.
Координаты единичной окружности : Единичная окружность, показывающая координаты и угловые размеры определенных точек.
Мы можем найти координаты любой точки единичной окружности.Учитывая любой угол [латекс] t [/ латекс], мы можем найти координату [latex] x [/ latex] или [latex] y [/ latex] в этой точке, используя [latex] x = \ text {cos} t [/ latex] и [latex] y = \ text {sin} t [/ latex].
Единичный круг демонстрирует периодичность тригонометрических функций. Периодичность относится к способу, которым тригонометрические функции приводят к повторяющемуся набору значений через равные промежутки времени. Взгляните на [latex] x [/ latex] -значения координат в единичном круге выше для значений [latex] t [/ latex] от [latex] 0 [/ latex] до [latex] 2 {\ pi} [/ latex]:
[латекс] {1, \ frac {\ sqrt {3}} {2}, \ frac {\ sqrt {2}} {2}, \ frac {1} {2}, 0, — \ frac {1} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {\ sqrt {3}} {2}, -1, — \ frac {\ sqrt {3}} {2}, — \ frac {\ sqrt {2}} {2}, — \ frac {1} {2}, 0, \ frac {1} {2}, \ frac {\ sqrt {2}} {2}, \ frac { \ sqrt {3}} {2}, 1} [/ латекс]
Мы можем идентифицировать закономерность в этих числах, которые колеблются между [латекс] -1 [/ латекс] и [латекс] 1 [/ латекс].Обратите внимание, что этот шаблон будет повторяться для более высоких значений [latex] t [/ latex]. Напомним, что эти значения [latex] x [/ latex] соответствуют [latex] \ cos t [/ latex]. Это показатель периодичности функции косинуса.
Пример
Решите [латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)}} [/ latex].
Похоже, это будет сложно решить. Однако обратите внимание, что диаграмма единичного круга показывает координаты в [latex] \ displaystyle {t = \ frac {7 \ pi} {6}} [/ latex].Поскольку координата [latex] y [/ latex] соответствует [latex] \ sin t [/ latex], мы можем идентифицировать, что
[латекс] \ displaystyle {\ sin {\ left (\ frac {7 \ pi} {6} \ right)} = — \ frac {1} {2}} [/ latex]
Специальные уголки
Единичный круг и набор правил можно использовать для вызова значений тригонометрических функций специальных углов.
Цели обучения
Объясните, как свойства синуса, косинуса и тангенса и их знаки в каждом квадранте дают свои значения для каждого из специальных углов.
Основные выводы
Ключевые моменты
- Тригонометрические функции для углов в единичной окружности можно запомнить и вызвать с помощью набора правил.
- Знак тригонометрической функции зависит от квадранта, в который попадает угол, и мнемоническая фраза «Умный класс триггера» используется для определения того, какие функции в каком квадранте положительны.
- Базовые углы в квадранте I используются для определения значения любого угла в квадрантах II, III или IV. Базовый угол образует тот же угол с осью [latex] x [/ latex], что и рассматриваемый угол.
- В единичную окружность включаются только функции синуса и косинуса для особых углов.Однако, поскольку тангенс получается из синуса и косинуса, его можно вычислить для любого из специальных углов.
Ключевые термины
- специальный угол : угол, кратный 30 или 45 градусам; тригонометрические функции легко записываются под этими углами.
Тригонометрические функции специальных углов
Напомним, что определенные углы и их координаты, которые соответствуют [latex] x = \ cos t [/ latex] и [latex] y = \ sin t [/ latex] для данного угла [latex] t [/ latex], можно определить по единичному кругу.{\ circ} \ right)} & = 1 \\ \ end {align}} [/ latex]
Выражения для косинусных функций этих специальных углов также просты.
Обратите внимание, что, хотя только синус и косинус определяются непосредственно единичной окружностью, касательную можно определить как частное, включающее эти два:
[латекс] \ displaystyle {\ tan t = \ frac {\ sin t} {\ cos t}} [/ latex]
Функции касания также имеют простые выражения для каждого из специальных углов.
Мы можем наблюдать эту тенденцию на примере.{\ circ} \ right)}} \\ & = \ frac {\ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \\ & = \ frac {\ sqrt {3 }} {2} \ cdot \ frac {2} {1} \\ & = \ sqrt {3} \ end {align}} [/ latex]
Запоминание тригонометрических функций
Понимание единичной окружности и способность быстро решать тригонометрические функции для определенных углов очень полезно в области математики.
{\ circ} [/ латекс].
Для любого заданного угла в первом квадранте существует угол во втором квадранте с таким же значением синуса. Поскольку значение синуса является координатой [latex] y [/ latex] на единичной окружности, другой угол с таким же синусом будет иметь такое же значение [latex] y [/ latex], но будет иметь противоположное значение [latex] x [/ latex] -значение. Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол.Угол с таким же косинусом будет иметь одно и то же значение [latex] x [/ latex], но будет иметь противоположное значение [latex] y [/ latex]. Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на диаграммах ниже, угол [латекс] \ альфа [/ латекс] имеет то же значение синуса, что и угол [латекс] t [/ латекс]; значения косинуса противоположны. Угол [латекс] \ бета [/ латекс] имеет то же значение косинуса, что и угол [латекс] t [/ латекс]; значения синуса противоположны.
[латекс] \ displaystyle {\ begin {align} \ sin t = \ sin \ alpha \ quad & \ text {and} \ quad \ cos t = — \ cos \ alpha \\ \ sin t = — \ sin \ beta \ quad & \ text {and} \ quad \ cos t = \ cos \ beta \ end {align}} [/ latex]
Контрольные углы: На левом рисунке [латекс] t [/ latex] является контрольным углом для [латекс] \ альфа [/ латекс].{\ circ} [/ latex] или [latex] 0 [/ latex] и [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex] радиан. Для любого угла в квадранте II, III или IV существует опорный угол в квадранте I.
Базовые углы в каждом квадранте: Для любого угла в квадрантах II, III или IV существует опорный угол в квадранте I.
Таким образом, чтобы вызвать любой синус или косинус особого угла, вы должны иметь возможность идентифицировать его угол с осью [latex] x [/ latex], чтобы сравнить его с опорным углом.
{\ circ})} \\ & = \ frac {- \ frac {\ sqrt {2}} {2}} {- \ frac {\ sqrt {2}} {2}} \\ & = — \ frac { \ sqrt {2}} {2} \ cdot — \ frac {2} {\ sqrt {2}} \\ & = 1 \ end {align}} [/ latex]
Синус и косинус как функции
Функции синуса и косинуса можно изобразить, используя значения из единичной окружности, и на обоих графиках можно наблюдать определенные характеристики.
Цели обучения
Опишите характеристики графиков синуса и косинуса
Основные выводы
Ключевые моменты
- И синусоидальную функцию [latex] (y = \ sin x) [/ latex], и косинусную функцию [latex] (y = \ cos x) [/ latex] можно изобразить, нанеся точки, полученные из единичной окружности, с каждая координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] представляет собой соответствующее значение функции под этим углом.
- Синус и косинус — периодические функции с периодом [латекс] 2 \ pi [/ латекс].
- И синус, и косинус имеют домен [latex] (- \ infty, \ infty) [/ latex] и диапазон [latex] [- 1, 1] [/ latex].
- График [latex] y = \ sin x [/ latex] симметричен относительно начала координат, потому что это нечетная функция, в то время как график [latex] y = \ cos x [/ latex] симметричен относительно [latex ] y [/ latex] -axis, потому что это четная функция.
Ключевые термины
- период : интервал, содержащий значения, которые повторяются в функции.
- четная функция : Непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = f (x) [/ latex], с симметрией относительно оси [латекс] y [/ латекс].
- нечетная функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , с симметрией относительно начала координат.
- периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], который повторяется через равные промежутки времени.
Графические функции синуса и косинуса
Напомним, что функции синуса и косинуса связывают значения действительных чисел с координатами [latex] x [/ latex] и [latex] y [/ latex] точки на единичной окружности. Так как же они выглядят на графике на координатной плоскости? Начнем с синусоидальной функции [latex] y = \ sin x [/ latex]. Мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ sin х [/ латекс]:
[латекс] \ displaystyle {(0, 0) \ quad (\ frac {\ pi} {6}, \ frac {1} {2}) \ quad (\ frac {\ pi} {4}, \ frac { \ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {2}, 1 ) \\ (\ frac {2 \ pi} {3}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {3 \ pi} {4}, \ frac {\ sqrt {2} } {2}) \ quad (\ frac {5 \ pi} {6}, \ frac {1} {2}) \ quad (\ pi, 0)} [/ latex]
Построение точек из таблицы и продолжение по оси [latex] x [/ latex] дает форму синусоидальной функции.
График синусоидальной функции: График точек с координатами [latex] x [/ latex], являющимися углами в радианах, и координатами [latex] y [/ latex], являющимися функцией [latex] \ sin x [/ latex] .
Обратите внимание на положительные значения синуса между [latex] 0 [/ latex] и [latex] \ pi [/ latex], которые соответствуют значениям синусоидальной функции в квадрантах I и II на единичной окружности, и синусоидальной значения отрицательны между [латекс] \ пи [/ латекс] и [латекс] 2 \ пи [/ латекс], которые соответствуют значениям синусоидальной функции в квадрантах III и IV на единичной окружности.
Построение значений синусоидальной функции: Точки на кривой [латекс] y = \ sin x [/ latex] соответствуют значениям синусоидальной функции на единичной окружности.
Теперь давайте посмотрим на функцию косинуса, [latex] f (x) = \ sin x [/ latex].
Опять же, мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ cos х [/ латекс]:
[латекс] \ displaystyle {(0, 1) \ quad (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {2}) \ quad (\ frac {\ pi} {4} , \ frac {\ sqrt {2}} {2}) \ quad (\ frac {\ pi} {3}, \ frac {1} {2}) \ quad (\ frac {\ pi} {2}, 0 ) \\ (\ frac {2 \ pi} {3}, — \ frac {1} {2}) \ quad (\ frac {3 \ pi} {4}, — \ frac {\ sqrt {2}} { 2}) \ quad (\ frac {5 \ pi} {6}, — \ frac {\ sqrt {3}} {2}) \ quad (\ pi, -1)} [/ latex]
Как и в случае с функцией синуса, мы можем построить точки для построения графика функции косинуса.
График функции косинуса: Точки на кривой [latex] y = \ cos x [/ latex] соответствуют значениям функции косинуса на единичной окружности.
Поскольку мы можем вычислять синус и косинус любого действительного числа, обе эти функции определены для всех действительных чисел. Если рассматривать значения синуса и косинуса как координаты точек на единичной окружности, становится ясно, что диапазон обеих функций должен быть интервалом [latex] \ left [-1, 1 \ right] [/ latex].
Определение периодических функций
На графиках для функций синуса и косинуса форма графика повторяется после [latex] 2 \ pi [/ latex], что означает, что функции являются периодическими с периодом [latex] 2 \ pi [/ latex].Периодическая функция — это функция с повторяющимся набором значений через равные промежутки времени. В частности, это функция, для которой конкретный сдвиг по горизонтали, [латекс] P [/ латекс], приводит к функции, равной исходной функции:
[латекс] f (x + P) = f (x) [/ латекс]
для всех значений [latex] x [/ latex] в домене [latex] f [/ latex]. Когда это происходит, мы называем наименьший такой горизонтальный сдвиг с [latex] P> 0 [/ latex] периодом функции.
На приведенной ниже диаграмме показаны несколько периодов функций синуса и косинуса.
Периоды функций синуса и косинуса: Функции синуса и косинуса являются периодическими, что означает, что определенный горизонтальный сдвиг, [latex] P [/ latex], приводит к функции, равной исходной функции: [latex] f (x + P) = f (x) [/ латекс].
Четные и нечетные функции
Еще раз взглянув на функции синуса и косинуса в домене с центром на оси [latex] y [/ latex], можно выявить симметрии. Как видно на графике синусоидальной функции, она симметрична относительно начала координат, что указывает на то, что это нечетная функция.На всем протяжении графика любые две точки с противоположными значениями [latex] x [/ latex] также имеют противоположные значения [latex] y [/ latex]. Это характерно для нечетной функции: два входа, которые являются противоположными, имеют выходы, которые также являются противоположными. Другими словами, если [латекс] \ sin (-x) = — \ sin x [/ latex].
Нечетная симметрия синусоидальной функции: Синусоидальная функция нечетная, что означает, что она симметрична относительно начала координат.
График функции косинуса показывает, что он симметричен относительно оси y .Это указывает на то, что это четная функция. Для четных функций любые две точки с противоположными значениями [latex] x [/ latex] имеют одинаковое значение функции. Другими словами, [латекс] \ cos (-x) = \ cos x [/ latex]. Мы можем видеть из графика, что это правда, сравнивая значения [latex] y [/ latex] графика с любыми противоположными значениями [latex] x [/ latex].
Четная симметрия функции косинуса: Функция косинуса четная, что означает, что она симметрична относительно оси [latex] y [/ latex].
Касательная как функция
Характеристики касательной функции можно увидеть на ее графике.
Цели обучения
Опишите характеристики графика касательной функции
Основные выводы
Ключевые моменты
- Функция касательной не определена при любом значении [latex] x [/ latex], где [latex] \ cos x = 0 [/ latex], и ее график имеет вертикальные асимптоты при этих значениях [latex] x [/ latex] .
- Касательная — периодическая функция с периодом [латекс] \ пи [/ латекс].
- График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией.
Ключевые термины
- периодическая функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex] с набором значений, повторяющихся через равные промежутки времени.
- период : интервал, содержащий минимальный набор значений, которые повторяются в периодической функции.
- нечетная функция : непрерывный набор точек [latex] \ left (x, f (x) \ right) [/ latex], в которых [latex] f (-x) = -f (x) [/ latex] , и есть симметрия относительно начала координат.
- вертикальная асимптота : прямая линия, параллельная оси [latex] y [/ latex], к которой кривая приближается произвольно близко, когда кривая уходит в бесконечность.
Построение касательной функции
Касательную функцию можно изобразить, построив точки [latex] \ left (x, f (x) \ right) [/ latex]. Форму функции можно создать, найдя значения тангенса под определенными углами. Однако невозможно найти касательные функции для этих особых углов с единичной окружностью.Мы применяем формулу [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], чтобы определить касательную для каждого значения.
Мы можем проанализировать графическое поведение касательной функции, посмотрев на значения некоторых специальных углов. Рассмотрим точки ниже, для которых координаты [latex] x [/ latex] представляют собой углы в радианах, а координаты [latex] y [/ latex] — [latex] \ tan x [/ latex]:
[латекс] \ displaystyle {(- \ frac {\ pi} {2}, \ text {undefined}) \ quad (- \ frac {\ pi} {3}, — \ sqrt {3}) \ quad (- \ frac {\ pi} {4}, -1) \ quad (- \ frac {\ pi} {6}, — \ frac {\ sqrt {3}} {3}) \ quad (0, 0) \\ (\ frac {\ pi} {6}, \ frac {\ sqrt {3}} {3}) \ quad (\ frac {\ pi} {4}, 1) \ quad (\ frac {\ pi} {3 }, \ sqrt {3}) \ quad (\ frac {\ pi} {2}, \ text {undefined})} [/ latex]
Обратите внимание, что [latex] \ tan x [/ latex] не определено в [latex] \ displaystyle {x = — \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ латекс].
Вышеупомянутые пункты помогут нам нарисовать наш график, но нам нужно определить, как граф ведет себя там, где он не определен. Давайте рассмотрим последние четыре пункта. Мы можем определить, что значения [latex] y [/ latex] увеличиваются по мере того, как [latex] x [/ latex] увеличивается и приближается к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex]. Мы могли бы рассмотреть дополнительные точки между [latex] \ displaystyle {x = 0} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex], и мы увидим, что это держит. Точно так же мы видим, что [latex] y [/ latex] уменьшается по мере приближения [latex] x [/ latex] к [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex], потому что выходные становиться все меньше и меньше.
Напомним, что существует несколько значений [latex] x [/ latex], которые могут дать [latex] \ cos x = 0 [/ latex]. В любой такой точке [latex] \ tan x [/ latex] не определено, потому что [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex]. При значениях, при которых функция касания не определена, на ее графике наблюдаются разрывы. При этих значениях график касательной имеет вертикальные асимптоты.
График функции касательной: функция касательной имеет вертикальные асимптоты в [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ пи} {2}} [/ латекс].
Характеристики графика касательной функции
Как и функции синуса и косинуса, тангенс является периодической функцией. Это означает, что его значения повторяются через равные промежутки времени. Период касательной функции равен [latex] \ pi [/ latex], потому что график повторяется на [latex] x [/ latex] -осных интервалах [latex] k \ pi [/ latex], где [latex] k [/ latex] — это константа. На графике функции касательной на интервале [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex] к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex], мы можем увидеть поведение графика за один полный цикл функции.
Если мы посмотрим на
любой больший интервал, мы увидим, что характеристики графика повторяются.График функции касательной симметричен относительно начала координат и, следовательно, является нечетной функцией. Другими словами, [latex] \ text {tan} (- x) = — \ text {tan} x [/ latex] для любого значения [latex] x [/ latex]. Любые две точки с противоположными значениями [latex] x [/ latex] производят противоположные значения [latex] y [/ latex]. Мы можем видеть, что это правда, рассматривая значения [latex] y [/ latex] графика при любых противоположных значениях [latex] x [/ latex].Рассмотрим [латекс] \ displaystyle {x = \ frac {\ pi} {3}} [/ latex] и [latex] \ displaystyle {x = — \ frac {\ pi} {3}} [/ latex]. Выше мы уже определили, что [латекс] \ displaystyle {\ tan (\ frac {\ pi} {3}) = \ sqrt {3}} [/ latex] и [latex] \ displaystyle {\ tan (- \ frac { \ pi} {3}) = — \ sqrt {3}} [/ latex].
Секанс и тригонометрические функции
Тригонометрические функции имеют обратные величины, которые можно вычислить с помощью единичной окружности.
Цели обучения
Расчет значений тригонометрических функций, обратных синусу, косинусу и тангенсу
Основные выводы
Ключевые моменты
- Секущая функция обратна функции косинуса [latex] \ displaystyle {\ left (\ sec x = \ frac {1} {\ cos x} \ right)} [/ latex].Его можно найти для угла [латекс] t [/ latex], используя координату [latex] x [/ latex] связанной точки на единичной окружности: [latex] \ displaystyle {\ sec t = \ frac { 1} {x}} [/ латекс].
- Функция косеканса является обратной функцией синусоидальной функции [latex] \ displaystyle {\ left (\ csc x = \ frac {1} {\ sin x} \ right)} [/ latex]. Его можно найти для угла [латекс] t [/ latex], используя координату [latex] y [/ latex] связанной точки на единичном круге: [latex] \ displaystyle {\ csc t = \ frac { 1} {y}} [/ латекс].
- Функция котангенса является обратной функцией касательной [латекс] \ displaystyle {\ left (\ cot x = \ frac {1} {\ tan x} = \ frac {\ cos t} {\ sin t} \ right) }[/латекс].
Его можно найти для угла, используя координаты [latex] x [/ latex] и [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ cot t = \ frac {\ cos t} {\ sin t} = \ frac {x} {y}} [/ latex].
Ключевые термины
- секанс : величина, обратная функции косинуса
- косеканс : функция, обратная синусоиде
.- котангенс : величина, обратная касательной функции
Введение в взаимные функции
Мы обсудили три тригонометрические функции: синус, косинус и тангенс.Каждая из этих функций имеет обратную функцию, которая определяется обратной величиной отношения исходной тригонометрической функции. Обратите внимание, что обратные функции отличаются от обратных функций. Обратные функции — это способ работы в обратном направлении или определения угла с учетом тригонометрического отношения; они предполагают работу с теми же соотношениями, что и исходная функция.
Три взаимные функции описаны ниже.
Секант
Секущая функция обратна функции косинуса и обозначается сокращенно как [латекс] \ сек [/ латекс].
Его можно описать как отношение длины гипотенузы к длине соседней стороны в треугольнике.[латекс] \ displaystyle {\ begin {align} \ sec x & = \ frac {1} {\ cos x} \\ \ sec x & = \ frac {\ text {hypotenuse}} {\ text {смежный}} \ end {align}} [/ latex]
Секанс легко вычислить со значениями в единичной окружности. Напомним, что для любой точки круга значение [latex] x [/ latex] дает [latex] \ cos t [/ latex] для соответствующего угла [latex] t [/ latex].Следовательно, секущая функция для этого угла равна
.[латекс] \ displaystyle {\ sec t = \ frac {1} {x}} [/ латекс]
Косеканс
Функция косеканса является обратной функцией синусоиды и обозначается сокращенно как [latex] \ csc [/ latex]. Его можно описать как отношение длины гипотенузы к длине противоположной стороны треугольника.
[латекс] \ displaystyle {\ begin {align} \ csc x & = \ frac {1} {\ sin x} \\ \ csc x & = \ frac {\ text {hypotenuse}} {\ text {напротив}} \ end {align}} [/ latex]
Как и секанс, косеканс может быть вычислен со значениями в единичной окружности.Напомним, что для любой точки круга значение [latex] y [/ latex] дает [latex] \ sin t [/ latex]. Следовательно, функция косеканса для того же угла равна
[латекс] \ Displaystyle {\ csc t = \ frac {1} {y}} [/ латекс]
Котангенс
Функция котангенса обратна функции тангенса и обозначается сокращенно как [latex] \ cot [/ latex]. Его можно описать как отношение длины соседней стороны к длине гипотенузы в треугольнике.
[латекс] \ displaystyle {\ begin {align} \ cot x & = \ frac {1} {\ tan x} \\ \ cot x & = \ frac {\ text {смежный}} {\ text {противоположный}} \ end {align}} [/ latex]
Также обратите внимание, что поскольку [latex] \ displaystyle {\ tan x = \ frac {\ sin x} {\ cos x}} [/ latex], его обратное значение равно
[латекс] \ displaystyle {\ cot x = \ frac {\ cos x} {\ sin x}} [/ латекс]
Котангенс также можно вычислить со значениями в единичной окружности.Применяя координаты [latex] x [/ latex] и [latex] y [/ latex], связанные с углом [latex] t [/ latex], получаем
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ \ cot t & = \ frac {x} {y} \ end {align}} [/ латекс]
Вычисление взаимных функций
Теперь мы распознаем шесть тригонометрических функций, которые можно вычислить, используя значения в единичном круге. Напомним, что мы использовали значения функций синуса и косинуса для вычисления функции тангенса.Мы будем следовать аналогичному процессу для обратных функций, ссылаясь на значения в единичном круге для наших расчетов.
Например, давайте найдем значение [latex] \ sec {\ left (\ frac {\ pi} {3} \ right)} [/ latex].
Применяя [латекс] \ displaystyle {\ sec x = \ frac {1} {\ cos x}} [/ latex], мы можем переписать это как:
[латекс] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)} = \ frac {1} {\ cos {\ left ({\ frac {\ pi} {3}} \ right)}}} [/ латекс]
Из единичного круга мы знаем, что [латекс] \ displaystyle {\ cos {\ left ({\ frac {\ pi} {3}} \ right)} = \ frac {1} {2}} [/ latex] .
Используя это, можно найти значение [latex] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)}} [/ latex]:
[латекс] \ displaystyle {\ begin {align} \ sec {\ left (\ frac {\ pi} {3} \ right)} & = \ frac {1} {\ frac {1} {2}} \\ & = 2 \ end {align}} [/ латекс]
Остальные взаимные функции могут быть решены аналогичным образом.
Пример
Используйте единичный круг для вычисления [латекс] \ sec t [/ latex], [latex] \ cot t [/ latex] и [latex] \ csc t [/ latex] в точке [latex] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex].
Точка на единичном круге: Точка [латекс] \ displaystyle {\ left (- \ frac {\ sqrt {3}} {2}, \ frac {1} {2} \ right)} [/ latex] , показанный в единичном круге.
Поскольку нам известны координаты [latex] (x, y) [/ latex] точки на единичной окружности, обозначенной углом [latex] t [/ latex], мы можем использовать эти координаты для нахождения трех функций.
Напомним, что координата [latex] x [/ latex] дает значение для функции косинуса, а координата [latex] y [/ latex] дает значение для функции синуса.Другими словами:
[латекс] \ displaystyle {\ begin {align} x & = \ cos t \\ & = — \ frac {\ sqrt {3}} {2} \ end {align}} [/ latex]
и
[латекс] \ displaystyle {\ begin {align} y & = \ sin t \\ & = \ frac {1} {2} \ end {align}} [/ latex]
Используя эту информацию, можно вычислить значения обратных функций под углом [латекс] t [/ латекс]:
[латекс] \ displaystyle {\ begin {align} \ sec t & = \ frac {1} {\ cos t} \\ & = \ frac {1} {x} \\ & = \ left (\ frac {1 } {- \ frac {\ sqrt {3}} {2}} \ right) \\ & = — \ frac {2} {\ sqrt {3}} \\ & = \ left (- \ frac {2} { \ sqrt {3}} \ cdot \ frac {\ sqrt {3}} {\ sqrt {3}} \ right) \\ & = — \ frac {2 \ sqrt {3}} {3} \ end {align} } [/ латекс]
[латекс] \ displaystyle {\ begin {align} \ cot t & = \ frac {\ cos t} {\ sin t} \\ & = \ frac {x} {y} \\ & = \ left (\ frac {- \ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} \ right) \\ & = \ left (- \ frac {\ sqrt {3}} {2} \ cdot \ frac {2} {1} \ right) \\ & = — \ sqrt {3} \ end {align}} [/ latex]
[латекс] \ displaystyle {\ begin {align} \ csc t & = \ frac {1} {\ sin t} \\ & = \ frac {1} {y} \\ & = \ left (\ frac {1 } {\ frac {1} {2}} \ right) \\ & = 2 \ end {align}} [/ latex]
Обратные тригонометрические функции
Каждая тригонометрическая функция имеет обратную функцию, которую можно изобразить в виде графика.
{- 1} x = y [/ latex].{-1} [/ латекс]
однозначная функция : функция, которая никогда не сопоставляет отдельные элементы своего домена с одним и тем же элементом своего диапазона. Введение в обратные тригонометрические функции
Обратные тригонометрические функции используются для нахождения углов треугольника, если нам заданы длины сторон. Обратные тригонометрические функции могут использоваться, чтобы определить, какой угол даст определенное значение синуса, косинуса или тангенса.
Чтобы использовать обратные тригонометрические функции, мы должны понимать, что обратная тригонометрическая функция «отменяет» то, что «делает» исходная тригонометрическая функция, как и в случае с любой другой функцией и ее обратной.{-1} (б) = а [/ латекс]. Однако функции синуса, косинуса и тангенса — это , а не взаимно однозначных функций. График каждой функции не прошел бы тест горизонтальной линии. Фактически, никакая периодическая функция не может быть взаимно однозначной, потому что каждый выход в ее диапазоне соответствует по крайней мере одному входу в каждом периоде, а количество периодов бесконечно. Как и в случае с другими функциями, которые не являются взаимно однозначными, нам нужно будет ограничить область определения каждой функции, чтобы получить новую функцию, которая является взаимно однозначной. Мы выбираем домен для каждой функции, который включает число [latex] 0 [/ latex].
Функции синуса и косинуса в ограниченных областях: (a) Функция синуса, показанная в ограниченной области [latex] \ left [- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ справа] [/ латекс]; (b) Функция косинуса, показанная в ограниченной области [latex] \ left [0, \ pi \ right] [/ latex].
График функции синуса ограничен областью [latex] [- \ frac {\ pi} {2}, \ frac {\ pi} {2}] [/ latex] и графиком функции косинуса ограничено [латексом] [0, \ pi] [/ латексом]. График касательной функции ограничен [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Касательная функция в ограниченной области
Функция касательной, показанная в ограниченной области [latex] \ left (- \ frac {\ pi} {2}, \ frac {\ pi} {2} \ right) [/ latex].
Эти варианты выбора ограниченных доменов в некоторой степени произвольны, но они имеют важные полезные характеристики. Каждый домен включает начало координат и некоторые положительные значения, и, что наиболее важно, каждый результат дает взаимно однозначную функцию, которая является обратимой. Традиционный выбор для ограниченной области касательной функции также имеет то полезное свойство, что он простирается от одной вертикальной асимптоты к другой вместо того, чтобы разбиваться на части асимптотой.{-1} x \ quad \ text {имеет домен} \ quad \ left (- \ infty, \ infty \ right) \ quad \ text {и диапазон} \ quad \ left (- \ frac {\ pi} {2} , \ frac {\ pi} {2} \ right)} [/ latex]
Графы обратных тригонометрических функций
Функция синуса и функция обратного синуса (или арксинуса): функция арксинуса является отражением функции синуса относительно линии [latex] y = x [/ latex].
Чтобы найти область определения и диапазон обратных тригонометрических функций, мы меняем область определения и диапазон исходных функций.
Функция косинуса и функция обратного косинуса (или арккосинуса): Функция арккосинуса является отражением функции косинуса относительно линии [латекс] y = x [/ latex].
Каждый график обратной тригонометрической функции является отражением графика исходной функции относительно линии [латекс] y = x [/ latex].
Функция тангенса и функция арктангенса (или арктангенса): Функция арктангенса является отражением функции касательной относительно линии [latex] y = x [/ latex].{-1} х = у [/ латекс].
Расчет Pi с использованием метода Монте-Карло
Расчет Pi с использованием метода Монте-Карло
Расчет числа Pi методом Монте-Карло
Ив Андерссон
Начало: Пи: один расчет
«Метод Монте-Карло» — это метод решения задач с использованием статистики. 2 Тогда число Пи приблизительно равно:
4 * м пи = --- NХотя метод Монте-Карло часто бывает полезен для решения проблем в физике и математике, которые не могут быть решены аналитическими средствами, это довольно медленный метод вычисления числа пи. Для расчета каждого значащая цифра, потребуется примерно в 10 раз больше попыток, чем вычислить предыдущую значащую цифру.
Отличный подарок ко Дню Пи!
Los Boludos
Сделано из оригинальных старинных электронных ламп!
Ева Андерссон (eve @ eveandersson.com)Комментарии
Регарин программа
Привет эвеандр Это суреш здесь, делаю мой магистр по компьютерам в АГУ. Поскольку я аспирант, на самом деле у нас была тема по Монте-Карло (расчет пи). Когда я прошел через ваш сайт, я получил материал по этой теме, я Я хотел бы знать всю процедуру и программный код для того, чтобы четко понять себя. Буду признателен вам и спасибо за рассмотрение моего вышеуказанного запроса.С уважением суреш
— Суреш Бабу Гаджела
Re: Регарин программа
Интересно, ищет ли Суреш что-то подобное.
#! / Usr / bin / env питон случайный импорт импортная математика count_inside = 0 для подсчета в диапазоне (0, 10000): d = math.hypot (random.random (), random.random ()) если d- Ларри Хоскен
еще цифры
Вау, кто-то прислал мне письмо об этом примере. Она написала:
Большое Вам спасибо за это! Но мне хотелось бы порадовать Вашей помощи. Подскажите, пожалуйста, что нужно добавить в эту программу, чтобы получить сопоставление Pi в таком виде 3.******** (то есть в твоей программе там 4 числа после точки, но мне нужно 8 чисел).
Во-первых, бесполезный буквальный ответ: Чтобы указать, что вы хотите просмотреть 8 цифр номера, вы можете использовать форматированную строку. То есть вместо чего-то вроде
печать 4.0 * M / N… можно сказать что-то вроде
печать '% 0.8f'% (4.0 * M / N)Однако, когда вы попробуете это, вы увидите, что это не так полезно: наш результат — целое число, деленное на 10000.Таким образом, последние несколько цифр всегда равны нулю. Это приводит к соблазну использовать более длинный цикл, чтобы получить более точный ответ. Но на моем слабом компьютере использование более длинного цикла приводит к слишком долгому времени работы. И вызывает вопросы о том, насколько хорош мой генератор случайных чисел. А когда переходить на числа произвольной точности? Ой, теперь голова болит.
— Ларри Хоскен
Магические числа
Привет,. Я хотел бы отметить тот факт, что этот метод особенно хорошо работает, когда вы составляете 14 пар случайных чисел.0,5
S = S + y
конец
T = 4 * S / n
печать (T)
— Сциллард Бокрос
Практическая демонстрация
В «Эксплораториуме Сан-Франциско» — возможно, самом крутом детском музее на планете — выставлен большой автомат для подбрасывания фишек для покера, чтобы дети могли вычислить Пи. Во время моего последнего визита туда толпа детей — даже не ботаников (извините, Ева, у меня стереотип …) — все стояли и смотрели это.— Эйдан Меррит
Старый метод
Этот метод был известен как «Метод французского лейтенанта» или «Метод создания камней для литья под давлением в пруду».МАРИО
— МАРИО ГИОИА
Пи — мой путь
Привет, Ева — только что нашла тебя.

 .
. 2
2  Если бы вы могли точно измерить и разделить, вы бы получили 3,141592653589793238 … или пи.
Если бы вы могли точно измерить и разделить, вы бы получили 3,141592653589793238 … или пи.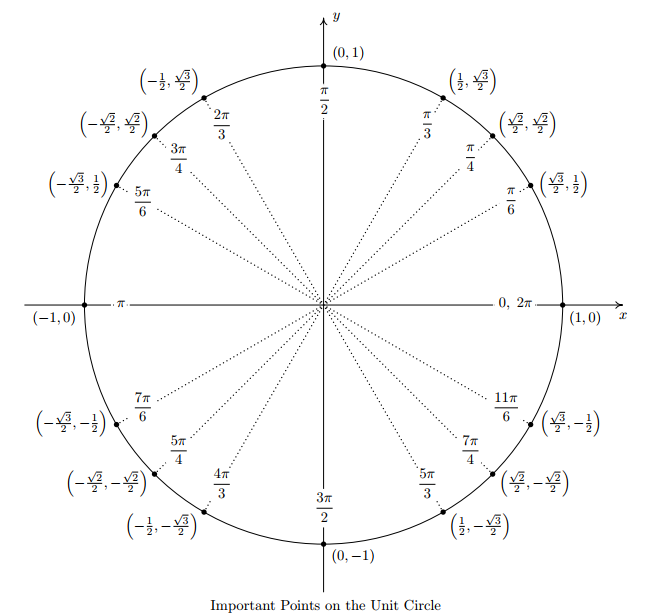 \ circ} {\ pi}} [/ латекс].
\ circ} {\ pi}} [/ латекс].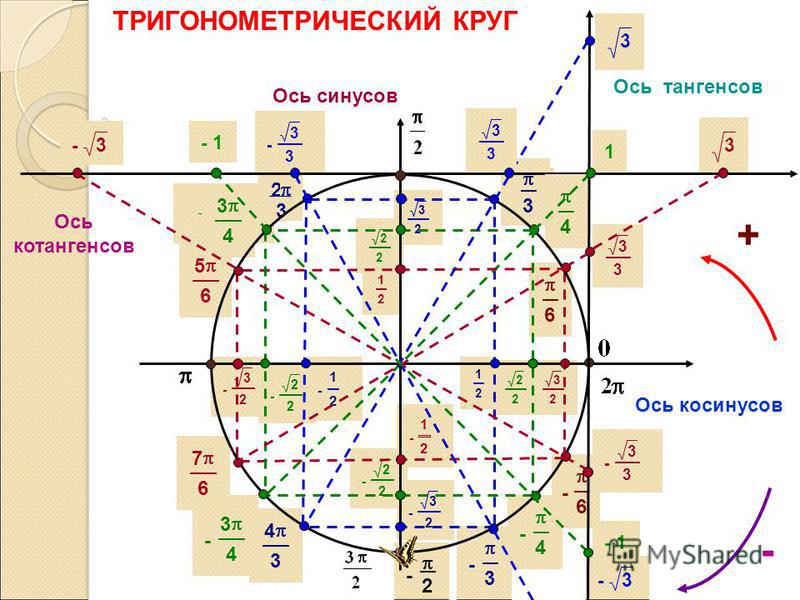 {\ circ}} [/ latex].
{\ circ}} [/ latex]. {\ circ} [/ латекс].
{\ circ} [/ латекс].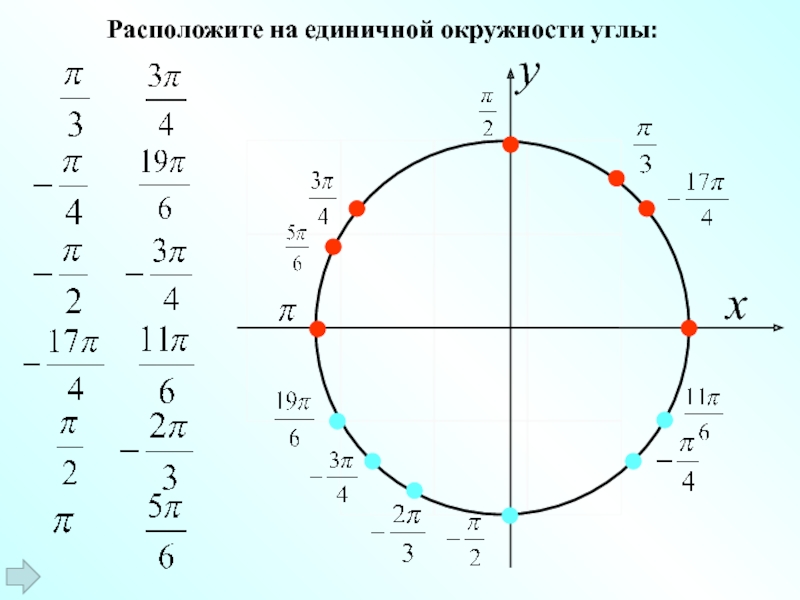
 Эта диаграмма позволяет наблюдать за каждым из этих углов, используя тригонометрические функции.
Эта диаграмма позволяет наблюдать за каждым из этих углов, используя тригонометрические функции.
 {\ circ} [/ латекс].
{\ circ} [/ латекс]. {\ circ})} \\ & = \ frac {- \ frac {\ sqrt {2}} {2}} {- \ frac {\ sqrt {2}} {2}} \\ & = — \ frac { \ sqrt {2}} {2} \ cdot — \ frac {2} {\ sqrt {2}} \\ & = 1 \ end {align}} [/ latex]
{\ circ})} \\ & = \ frac {- \ frac {\ sqrt {2}} {2}} {- \ frac {\ sqrt {2}} {2}} \\ & = — \ frac { \ sqrt {2}} {2} \ cdot — \ frac {2} {\ sqrt {2}} \\ & = 1 \ end {align}} [/ latex]
 Опять же, мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ cos х [/ латекс]:
Опять же, мы можем создать таблицу значений и использовать их для построения графика. Ниже приведены некоторые значения синусоидальной функции на единичном круге, где координата [latex] x [/ latex] представляет собой угол в радианах, а координата [latex] y [/ latex] — [latex] \ cos х [/ латекс]: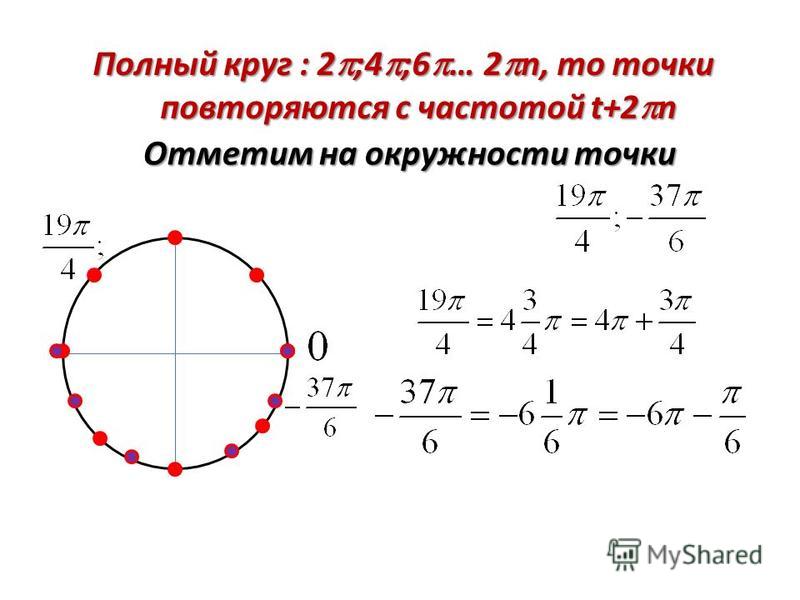 На приведенной ниже диаграмме показаны несколько периодов функций синуса и косинуса.
На приведенной ниже диаграмме показаны несколько периодов функций синуса и косинуса.
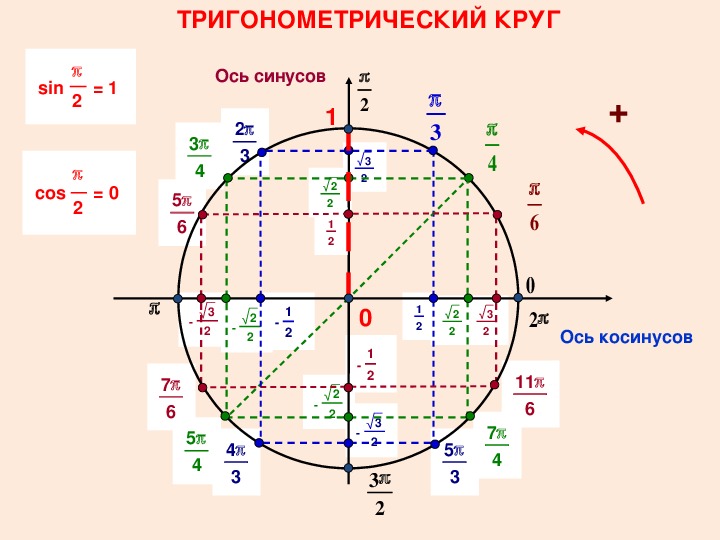 Вышеупомянутые пункты помогут нам нарисовать наш график, но нам нужно определить, как граф ведет себя там, где он не определен. Давайте рассмотрим последние четыре пункта. Мы можем определить, что значения [latex] y [/ latex] увеличиваются по мере того, как [latex] x [/ latex] увеличивается и приближается к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex]. Мы могли бы рассмотреть дополнительные точки между [latex] \ displaystyle {x = 0} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex], и мы увидим, что это держит. Точно так же мы видим, что [latex] y [/ latex] уменьшается по мере приближения [latex] x [/ latex] к [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex], потому что выходные становиться все меньше и меньше.
Вышеупомянутые пункты помогут нам нарисовать наш график, но нам нужно определить, как граф ведет себя там, где он не определен. Давайте рассмотрим последние четыре пункта. Мы можем определить, что значения [latex] y [/ latex] увеличиваются по мере того, как [latex] x [/ latex] увеличивается и приближается к [latex] \ displaystyle {\ frac {\ pi} {2}} [/ latex]. Мы могли бы рассмотреть дополнительные точки между [latex] \ displaystyle {x = 0} [/ latex] и [latex] \ displaystyle {x = \ frac {\ pi} {2}} [/ latex], и мы увидим, что это держит. Точно так же мы видим, что [latex] y [/ latex] уменьшается по мере приближения [latex] x [/ latex] к [latex] \ displaystyle {- \ frac {\ pi} {2}} [/ latex], потому что выходные становиться все меньше и меньше.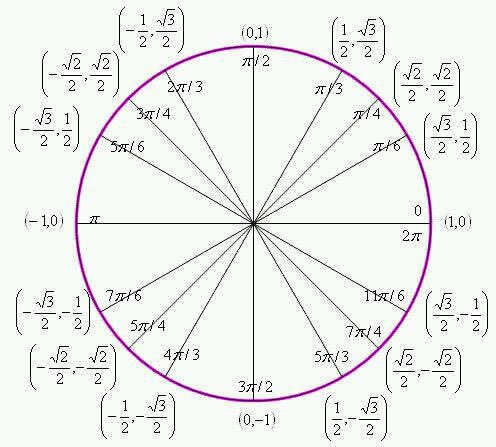 Если мы посмотрим на
Если мы посмотрим на 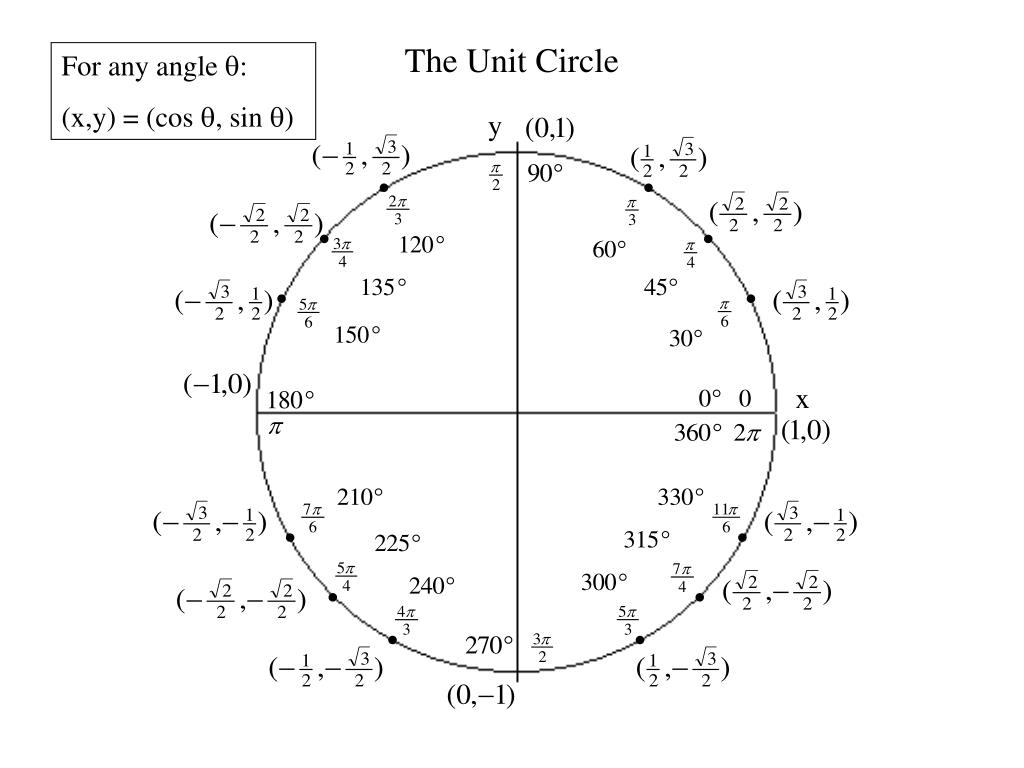 Его можно найти для угла, используя координаты [latex] x [/ latex] и [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ cot t = \ frac {\ cos t} {\ sin t} = \ frac {x} {y}} [/ latex].
Его можно найти для угла, используя координаты [latex] x [/ latex] и [latex] y [/ latex] соответствующей точки на единичной окружности: [latex] \ displaystyle {\ cot t = \ frac {\ cos t} {\ sin t} = \ frac {x} {y}} [/ latex].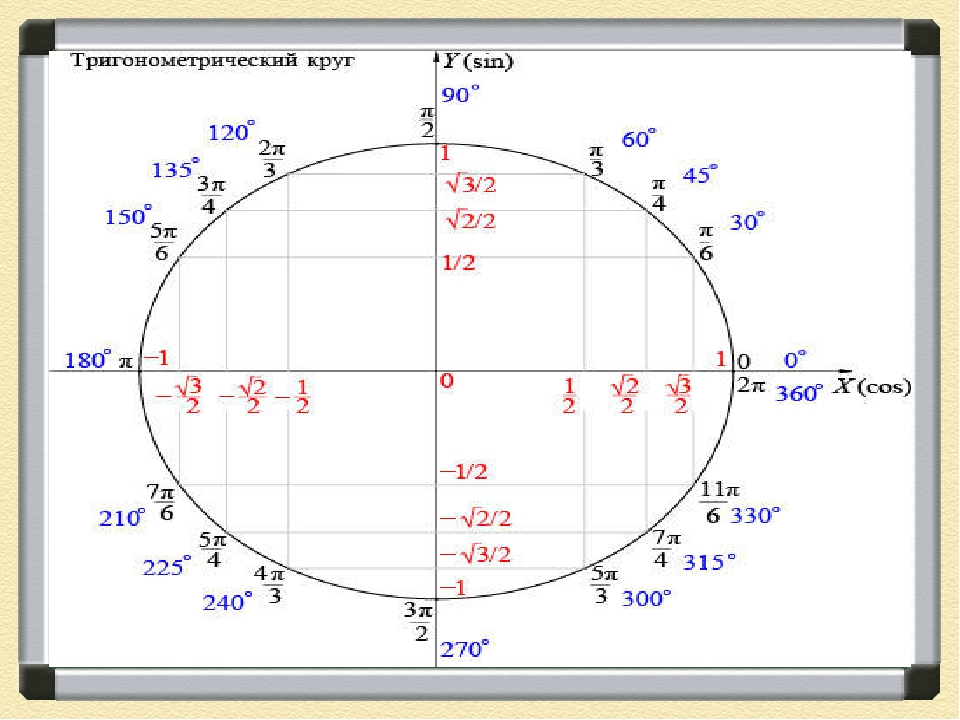
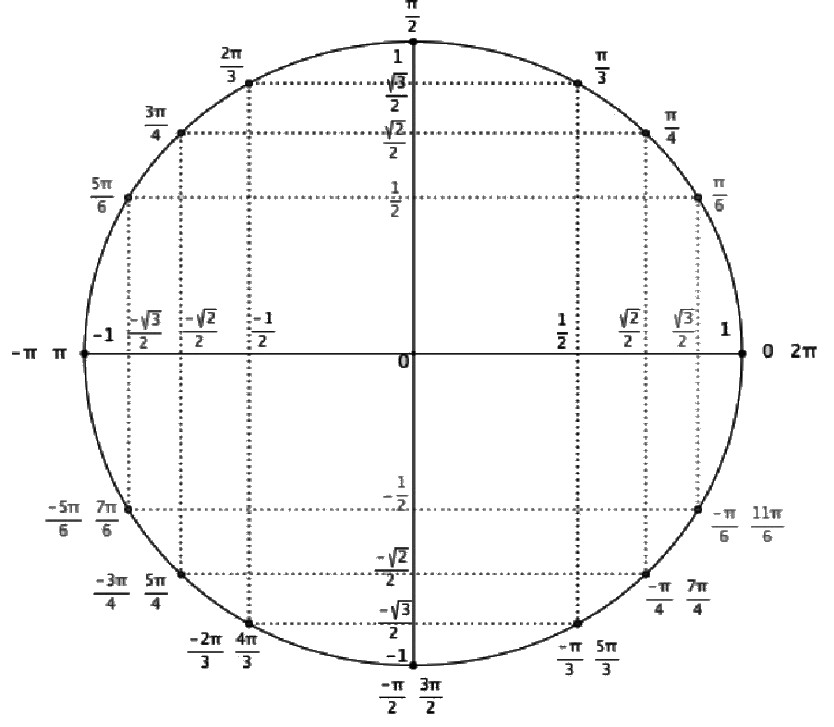 Используя это, можно найти значение [latex] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)}} [/ latex]:
Используя это, можно найти значение [latex] \ displaystyle {\ sec {\ left (\ frac {\ pi} {3} \ right)}} [/ latex]: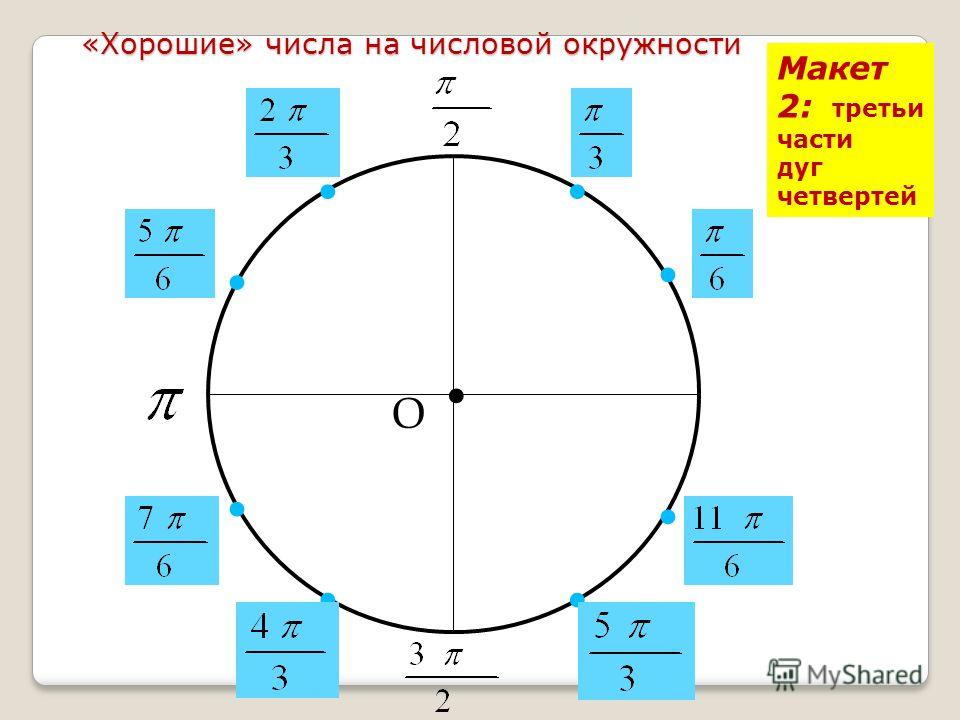 {- 1} x = y [/ latex].{-1} [/ латекс]
{- 1} x = y [/ latex].{-1} [/ латекс]
 2
Тогда число Пи приблизительно равно:
2
Тогда число Пи приблизительно равно:  ******** (то есть в твоей программе там
4 числа после точки, но мне нужно 8 чисел).
******** (то есть в твоей программе там
4 числа после точки, но мне нужно 8 чисел).