Паутинообразная модель рынка одного товара – Тема 1. Паутинообразная модель рынка одного товара

Тема 1. Паутинообразная модель рынка одного товара

Модуль 1	Динамические модели рынка одного товара
Тема 1	Паутинообразная модель рынка одного товара
1.1	Паутинообразная модель рынка одного товара в дискретном анализе
1.2	Паутинообразная модель с параметрами рынка, изменяющими во времени
1.3	Модель рынка одного товара с включением запасов
1.4	Устойчивость рыночного равновесия в концепции Л. Вальраса и А. Маршалла

1. Паутинообразная модель рынка одного товара в дискретном анализе

Простейшие модели экономического равновесия разработаны в 30-50гг. 20-го века.

Рассмотрим рынок одного товара. Сделаем ряд допущений:

— у производителей не возникают трудности с покупкой ресурсов;

— объединим всех покупателей в одну группу и будем рассматривать их как одного покупателя;

— объединим всех продавцов в другую группу и будем рассматривать их как одного продавца;

— допустим, что весь произведенный товар реализуется сразу (единовременно).

Рассмотрим ситуацию на рынке, когда предложение товара постоянно отстает от спроса на один интервал, используя дискретный анализ.

Интервалы времени одинаковы и последовательно принимают значения:

Если (time) – текущий интервал времени, то – предшествующий, апоследующий интервал времени. Такая ситуация нередко наблюдается на рынке нового товара. Функции спроса и предложения на данный товар являются некоторыми функциями от цены:и

Объем товара произведен в предыдущем временном интервале, а реализуется в текущем интервале. Поэтому. Производители руководствуются ценойи производят продукцию в объеме. Данное предложение товара реализуется в следующем временном интервале по новой цене спроса.

Общую схему действия модели можно представить следующим образом:

в начальный интервал времени имеем,

в следующий интервал времени имееми т.д.

Так как известны функции спроса и предложения, то можно определить равновесную цену. Для этого необходимо приравнять функции спроса и предложения: , где(equilibrium) – индекс, означающий равновесное значение величины объема и цены, соответственно ().Если функции спроса и предложения линейны, то, приравнивая их, получим одну точку равновесия и единственное значение равновесной цены и равновесного объема.

Если функции спроса и предложения не линейны, то получим два или более значений равновесной цены и равновесного объема. В таком случае необходимо провести дополнительное исследование и определить, в какую точку равновесия приходит система под влиянием спроса и предложения и факторов их определяющих.

Проиллюстрируем графически паутинообразную модель. Первоначально находимся в точке . В этой точке производители руководствуются ценойи производят продукцию в объемев период времени. Реализуется товар в точкев периодепо цене спроса. В периодепроизводители увеличивают предложение товара до, так как цена товара повысилась, и находятся в точке на кривой предложения с координатами. Продается товар в точке. Поскольку предложение товара возросло, то, чтобы продать весь товар, приходится снизить цену сдо.

В следующий период времени производители руководствуются ценой, производят объем продукциив точке на кривой предложения с координатами. Реализуется эта продукция по ценев точкеи т.д. Рынок приходит в состояние равновесия в точкеС.

Аналитическая интерпретация модели состоит в следующем. Для простоты будем считать, что спрос и предложение являются линейными функциями:

; ,

где – конкретные параметры каждого товара, имеющие экономический смысл. Находим равновесные объем и цену, приравняв функцию спроса и предложения:. Подставим равновесное значение цены в функции спроса и предложения и определим равновесный объем:. Так как в точке равновесия объем спроса равен объему предложения, то справедливо выражение:

. (1.1)

Запишем условие равновесия для любого времени :

(1.2)

Выражение (1.2) справедливо для любой точки. Знак равенства в выражении (1.2) означает, что весь произведенный продукт реализован. Вычтем из уравнения (1.2) уравнение (1.1):

.

Перейдем к следующим обозначениям: характеризует отклонение объема выпуска в любой период времени от равновесного объема выпуска;

представляет отклонение цены спроса в любой момент времени от равновесного значения;- отклонение цены предложения в период времениот равновесного значения.

Тогда действие модели можно представить разностными уравнениями:

(1.3).

Выражение (1.3) аналогично выражению (1.2), но описывает отклонения цены и выпуска в некоторый период времени от их равновесных значений. Из уравнения (1.3) можно выразить значение цены в любой период времени следующим образом:. Обозначим, тогда. Величина, так как наклон кривой спроса для нормальных товаров отрицателен, а наклон кривой предложения – положителен. Так как, то, где- известная величина – цена в начальный период времени, аможно определить из уравнения (1.3), поскольку известны функции спроса и предложения.

Во все периоды времени имеем:

;

;

;

;

………………………………..;

для любого периода имеем:.

Отклонение цены в любой период времени от ее равновесного значения принимает то положительные, то отрицательные значения. Так как начальное отклонение, то- положительная величина. Число- величина отрицательная, так как- наклон кривой предложения,- наклон кривой спроса. Обозначим. Тогда

;

;

;

……………… .

Знак отклонения будет чередоваться: минус, плюс, минус и т.д. Следовательно, ценабудет то меньше, то больше равновесной цены. Общее решение, полученное методом итерации:. Отсюда.

У данной модели есть развитие. Под влиянием неценовых факторов спроса и предложения кривые спроса и предложения перемещаются, и с помощью модели можно проанализировать, как рынок приходит в состояние равновесия до того периода пока не возникает новое возмущение. Например,

в спокойное течение дел на рынке вмешивается резкий рост предложения, если продавцы выбрасывают запасы товара. В новой ситуации в анализе рынка товара следует соединить рассмотренную модель с моделью включения запаса.

studfiles.net

Паутинообразная модель рынка одного товара

1. Паутинообразная модель рынка одного товара в дискретном анализе

Простейшие модели экономического равновесия разработаны в 30-50 гг. ХХ-го века.

Рассмотрим рынок одного товара.

Сделаем ряд допущений:

— у производителей не возникают трудности с покупкой ресурсов;

— объединим всех покупателей в одну группу и будем рассматривать их как одного покупателя;

— объединим всех продавцов в другую группу и будем рассматривать их как одного продавца;

— допустим, что весь произведенный товар реализуется сразу (единовременно).

Рассмотрим ситуацию на рынке, когда предложение товара постоянно отстает от спроса на один интервал, используя дискретный анализ.

Интервалы времени одинаковы и последовательно принимают значения:

Если (time) – текущий интервал времени, то – предшествующий, а последующий интервал времени. Такая ситуация нередко наблюдается на рынке нового товара. Функции спроса и предложения на данный товар являются некоторыми функциями от цены: и

Объем товара произведен в предыдущем временном интервале , а реализуется в текущем интервале . Поэтому . Производители руководствуются ценой и производят продукцию в объеме . Данное предложение товара реализуется в следующем временном интервале по новой цене спроса .

Общую схему действия модели можно представить следующим образом:

в начальный интервал времени имеем ,

в следующий интервал времени имеем и т.д.

Так как известны функции спроса и предложения, то можно определить равновесную цену. Для этого необходимо приравнять функции спроса и предложения: , где (equilibrium) – индекс, означающий равновесное значение величины объема и цены, соответственно (). Если функции спроса и предложения линейны, то, приравнивая их, получим одну точку равновесия и единственное значение равновесной цены и равновесного объема.

Если функции спроса и предложения не линейны, то получим два или более значений равновесной цены и равновесного объема. В таком случае необходимо провести дополнительное исследование и определить, в какую точку равновесия приходит система под влиянием спроса и предложения и факторов их определяющих.

Проиллюстрируем графически паутинообразную модель. Первоначально находимся в точке . В этой точке производители руководствуются ценой и производят продукцию в объеме в период времени . Реализуется товар в точке в периоде по цене спроса . В периоде производители увеличивают предложение товара до , так как цена товара повысилась, и находятся в точке на кривой предложения с координатами . Продается товар в точке . Поскольку предложение товара возросло, то, чтобы продать весь товар, приходится снизить цену с до .

В следующий период времени производители руководствуются ценой , производят объем продукции в точке на кривой предложения с координатами . Реализуется эта продукция по цене в точке и т.д. Рынок приходит в состояние равновесия в точке С.

Аналитическая интерпретация модели состоит в следующем. Для простоты будем считать, что спрос и предложение являются линейными функциями:

; ,

где – конкретные параметры каждого товара, имеющие экономический смысл. Находим равновесные объем и цену, приравняв функцию спроса и предложения: . Подставим равновесное значение цены в функции спроса и предложения и определим равновесный объем: . Так как в точке равновесия объем спроса равен объему предложения, то справедливо выражение:

. (1.1)

Запишем условие равновесия для любого времени :

(1.2)

Выражение (1.2) справедливо для любой точки. Знак равенства в выражении (1.2) означает, что весь произведенный продукт реализован. Вычтем из уравнения (1.2) уравнение (1.1):

.

Перейдем к следующим обозначениям: характеризует отклонение объема выпуска в любой период времени от равновесного объема выпуска; представляет отклонение цены спроса в любой момент времени от равновесного значения; — отклонение цены предложения в период времени от равновесного значения.

Тогда действие модели можно представить разностными уравнениями:

(1.3).

Выражение (1.3) аналогично выражению (1.2), но описывает отклонения цены и выпуска в некоторый период времени от их равновесных значений. Из уравнения (1.3) можно выразить значение цены в любой период времени следующим образом: .

Обозначим , тогда. Величина , так как наклон кривой спроса для нормальных товаров отрицателен , а наклон кривой предложения – положителен . Так как , то

,

где — известная величина – цена в начальный период времени , а можно определить из уравнения (1.3), поскольку известны функции спроса и предложения.

Во все периоды времени имеем:

;

;

;

;

………………………………..;

для любого периода имеем:.

Отклонение цены в любой период времени от ее равновесного значения принимает то положительные, то отрицательные значения. Так как начальное отклонение , то — положительная величина. Число — величина отрицательная, так как — наклон кривой предложения, — наклон кривой спроса. Обозначим . Тогда

;

;

;

……………… .

Знак отклонения будет чередоваться: минус, плюс, минус и т.д. Следовательно, цена будет то меньше, то больше равновесной цены. Общее решение, полученное методом итерации: . Отсюда .

У данной модели есть развитие. Под влиянием неценовых факторов спроса и предложения кривые спроса и предложения перемещаются, и с помощью модели можно проанализировать, как рынок приходит в состояние равновесия до того периода пока не возникает новое возмущение. Например, в спокойное течение дел на рынке вмешивается резкий рост предложения, если продавцы выбрасывают запасы товара.

В новой ситуации в анализе рынка товара следует соединить рассмотренную модель с моделью включения запаса.

studfiles.net

простые динамические модели рынка одного товара

1. Паутинообразная модель рынка одного товара (дискретная и непрерывная модели).

Дискретная модель.

Простейшие модели экономического равновесия разрабатны в 30-50гг. 20-го века.

Рассмотрим рынок одного товара. Сделаем ряд допущений:

— у производителей не возникают трудности с покупкой ресурсов;

— объединим всех покупателей в одну группу и будем рассматривать их как одного покупателя;

— объединим всех продавцов в другую группу и будем рассматривать их как одного продавца;

— допустим, что весь произведенный товар реализуется сразу (единовременно).

Рассмотрим ситуацию на рынке, когда предложение товара постоянно отстает от спроса, в дискретном анализе на один интервал.

Интервалы времени одинаковы и последовательно принимают значения:

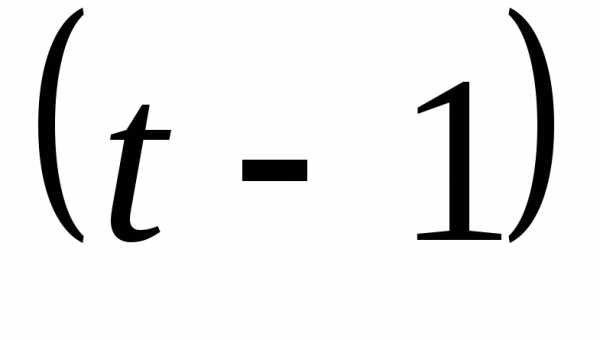Если (time) – текущий интервал времени, то – предшествующий, а 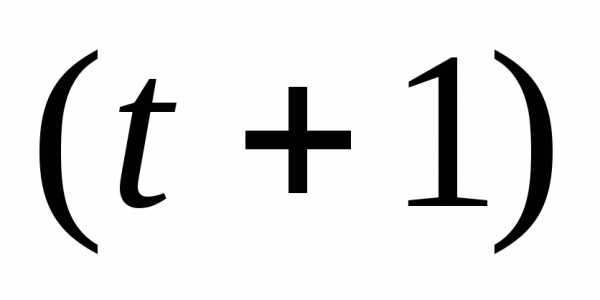последующий интервал времени.

Такая ситуация нередко наблюдается на рынке нового товара. Функции спроса и предложения на данный товар являются некоторыми функциями от цены: 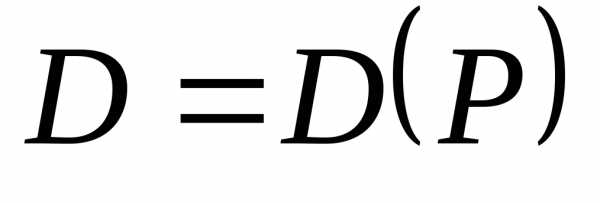и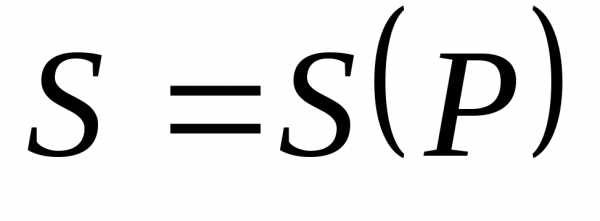

Объем товара произведен в предыдущем временном интервале , а реализуется в текущем интервале .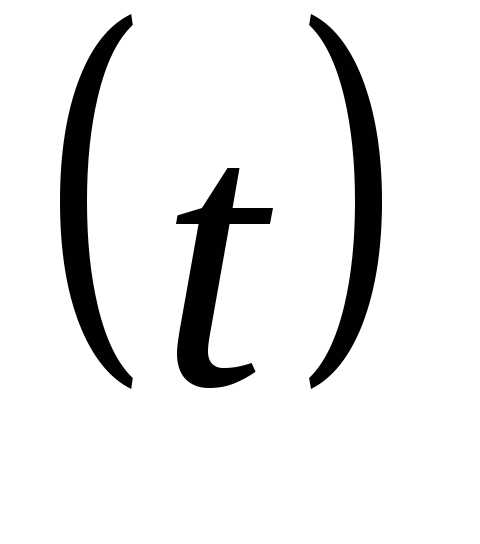

Производители руководствуются ценой и производят продукцию в объеме . Данное предложение товара реализуется в следующем временном интервале по новой цене спроса .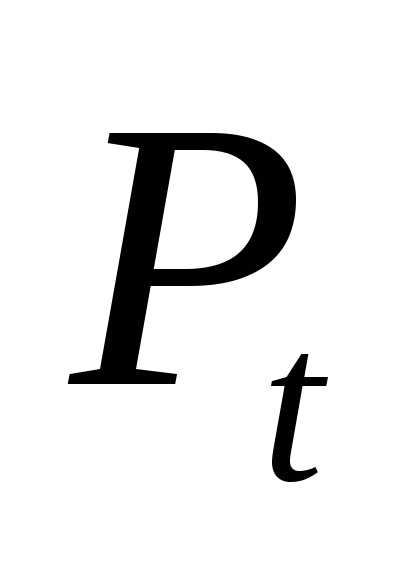

Общую схему действия модели можно представить следующим образом:

в начальный интервал времени 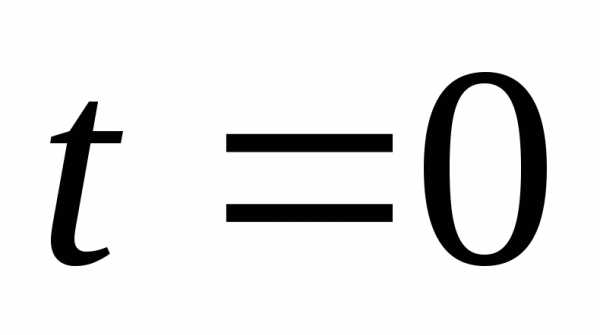имеем ,

в следующий интервал времени 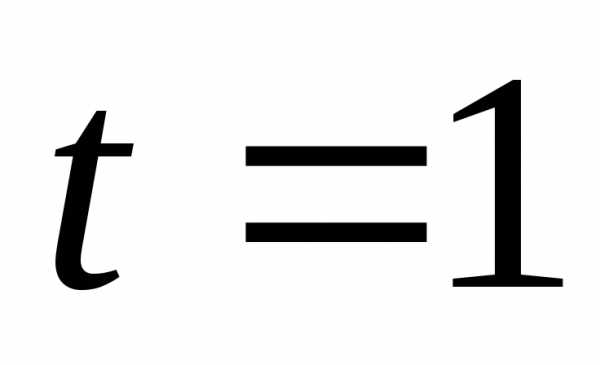имеем и т.д.

Так как известны функции спроса и предложения, то можно определить равновесную цену. Для этого необходимо приравнять функции спроса и предложения:

,

где (equilibrium) — индекс, означающий равновесное значение величины объема и цены, соответственно ().

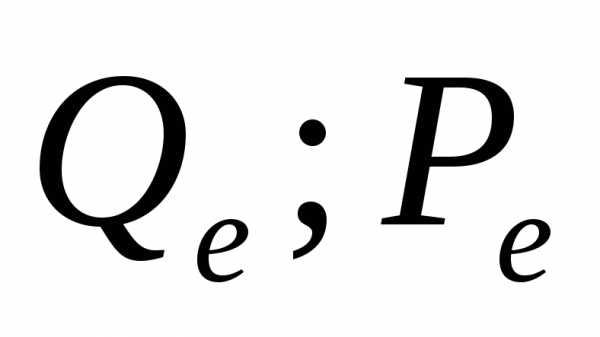Если функции спроса и предложения линейны, то, приравнивая их, получим одну точку равновесия и единственное значением равновесной цены и равновесного объема.

Если функции спроса и предложения не линейны, то получим два или более значений равновесной цены и равновесного объема. В таком случае необходимо провести дополнительное исследование и определить, в какую точку равновесия приходит система под влиянием спроса и предложения и факторов их определяющих.

Проиллюстрируем графически паутинообразную модель. Первоначально находимся в точке . В этой точке производители руководствуются ценой и производят продукцию в объеме в период времени .

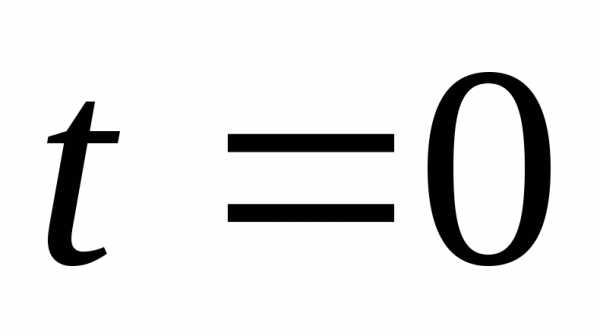Реализуется товар в точке в периоде 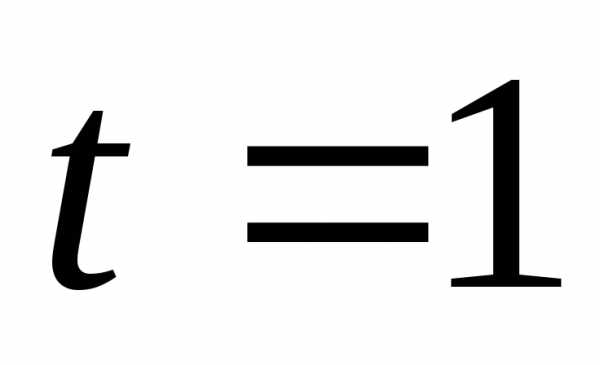по цене спроса 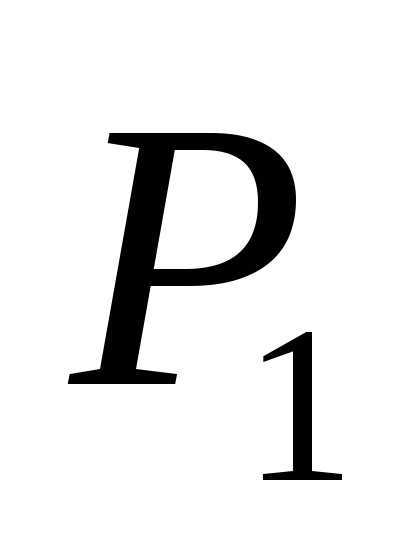. В периоде производители увеличивают предложение товара до , так как выросла цена товара, и находятся в точке на кривой предложения с координатами .

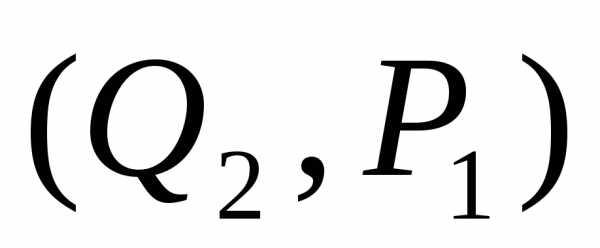Продается товар в точке . Поскольку предложение товара возросло, то, чтобы продать весь товар, приходится снизить цену с 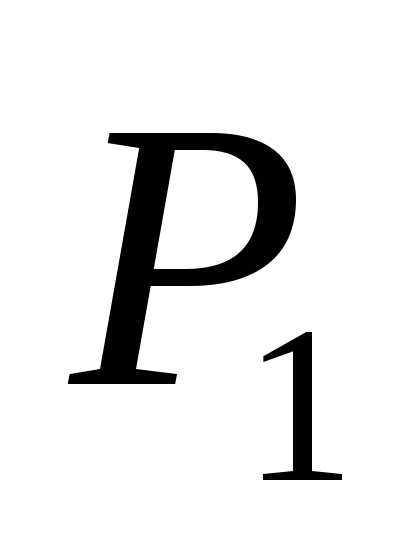до .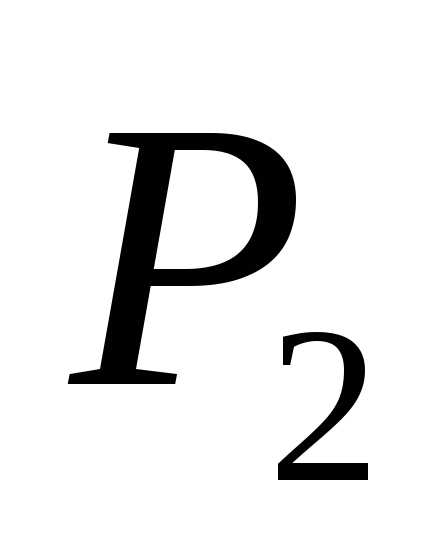

В следующий период времени 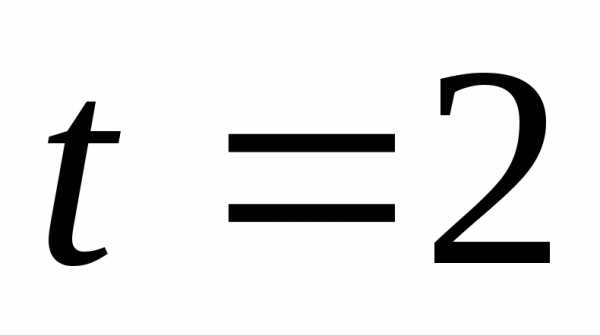производители руководствуются ценой 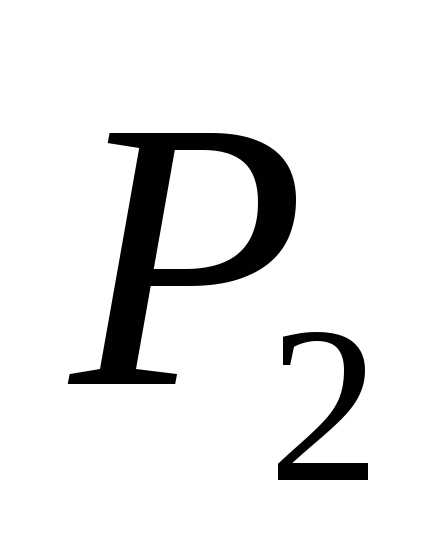, производят объем продукции в точке на кривой предложения с координатами 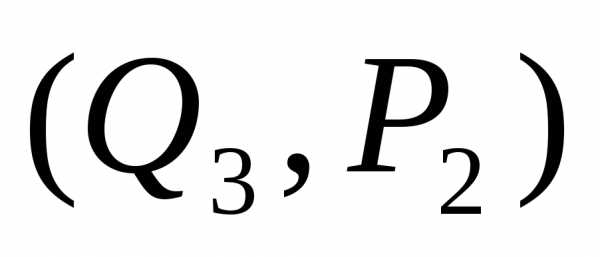. Реализуется эта продукция по цене в точке и т.д. Рынок приходит в состояние равновесия в точке С.

Аналитическая интерпретация модели состоит в следующем:

Для простоты будем считать, что спрос и предложения являются линейными функциями:

; ,

где 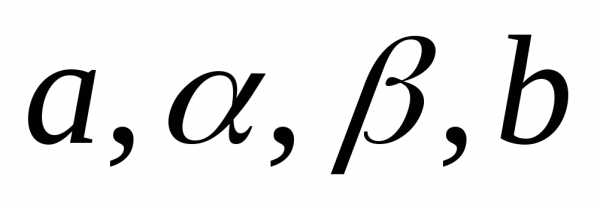– конкретные параметры каждого товара.

Находим равновесные объем и цену, приравняв функцию спроса и предложения: .

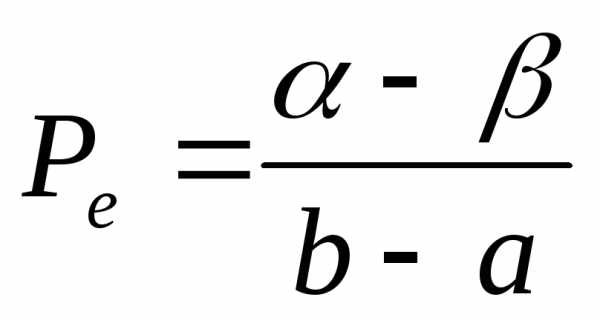Подставим равновесное значение цены в функции спроса и предложения и определим равновесный объем: 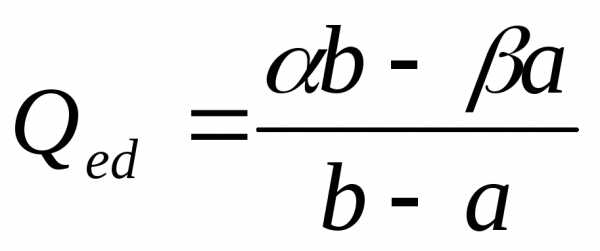. Так как в точке равновесия объем спроса равен объему предложение, то справедливо выражение:

. (1)

Запишем условие равновесия для любого времени :

(2)

Выражение (2) справедливо для любой точки. Подставляя в выражении (2) знак равенства, предполагаем, что весь произведенный продукт реализован.

Вычтем из уравнения (2) уравнение (1):

.

Перейдем к следующим обозначениям:

характеризует отклонение объема выпуска в любой период времени от равновесного объема выпуска;

представляет отклонение цены спроса в любой момент времени от равновесного значения;

— отклонение цены предложения в любой момент времени от равновесного значения.

Тогда действие модели можно представить разностными уравнениями:

(3).

Выражение (3) аналогично выражению (2), но описывает отклонение цены и выпуска в некоторый период времени от их равновесных значений.

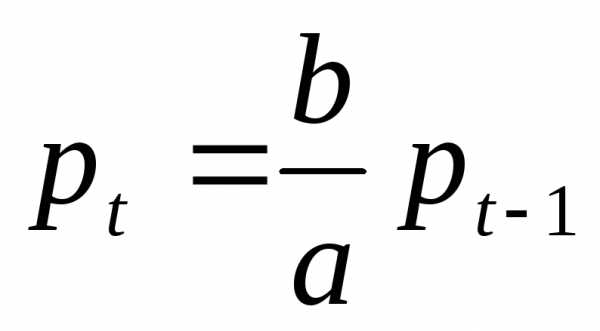Из уравнения (3) можно выразить значение цены в любой период времени следующим образом: . Обозначим 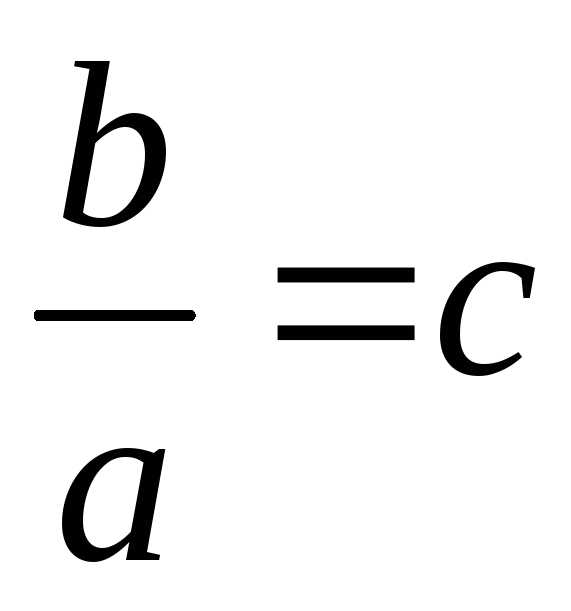, тогда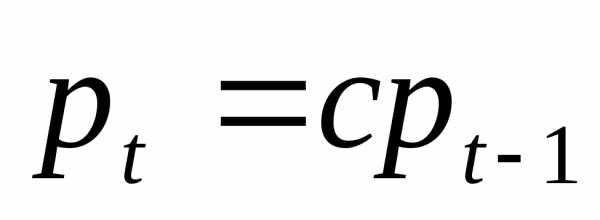. Величина 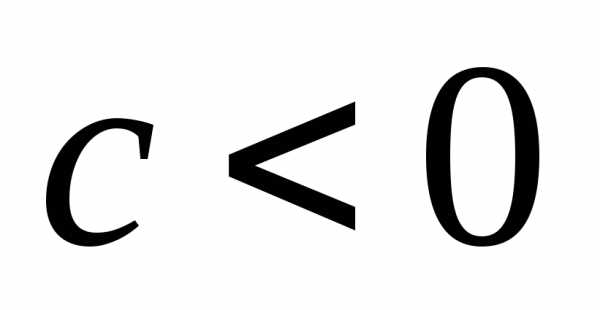, так как наклон кривой спроса для нормальных товаров отрицателен , а наклон кривой предложения – положителен .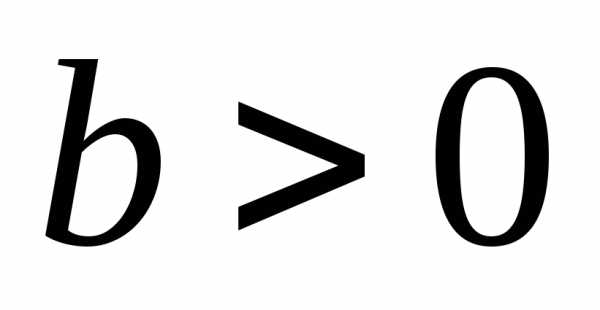

Так как , то , где — известная величина – цена в начальный период времени , а можно определить из уравнения (3), поскольку известны функции спроса и предложения.

Во все периоды времени имеем:

;

;

;

,

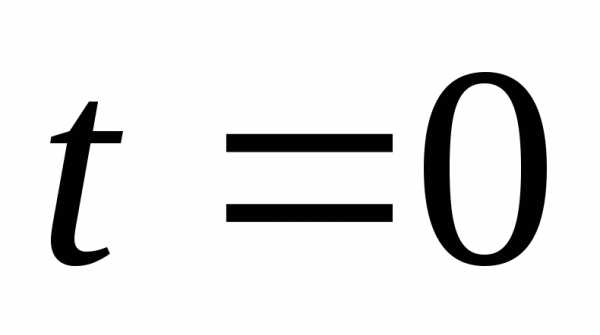
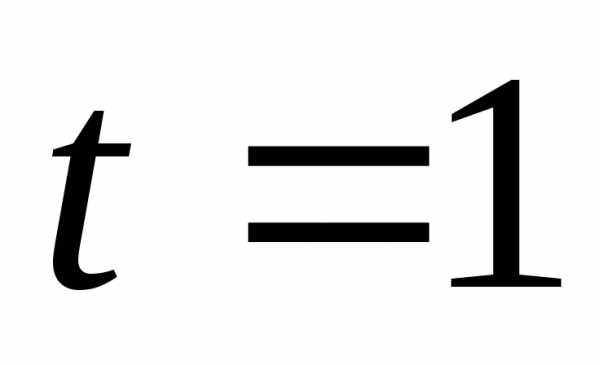
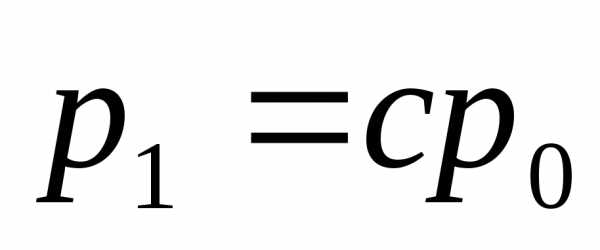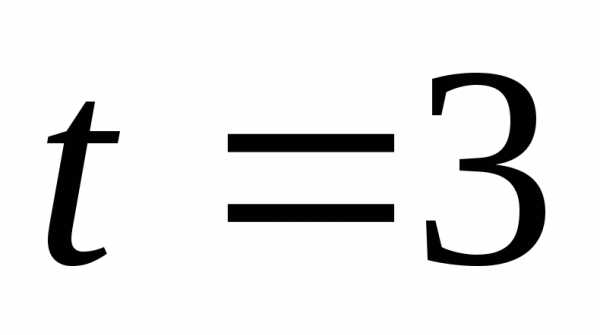
т.е. для любого периода времени имеем . Отсюда

.

Отклонение цены в любой период времени от ее равновесного значения 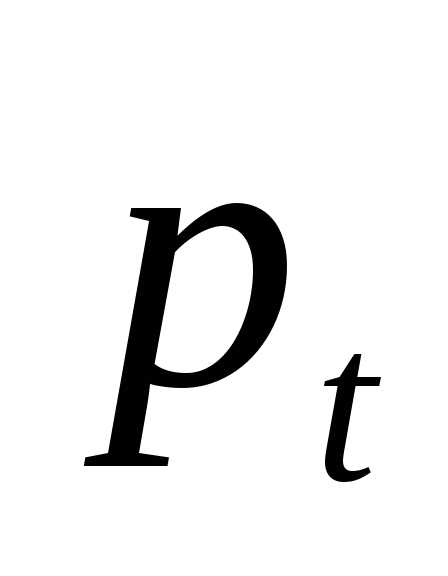принимает то положительные, то отрицательные значения. Так как начальное отклонение , то 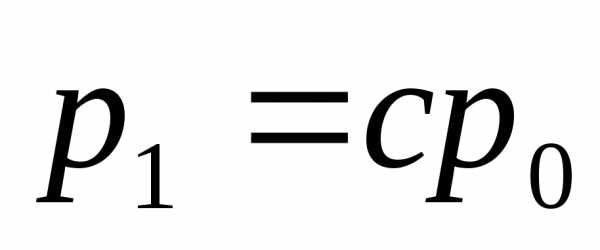— положительная величина.

Число — величина отрицательная, так как 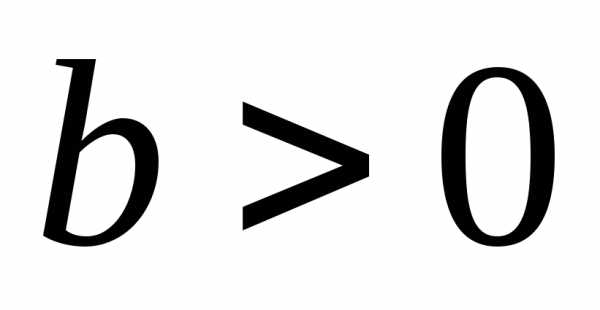— наклон кривой предложения, 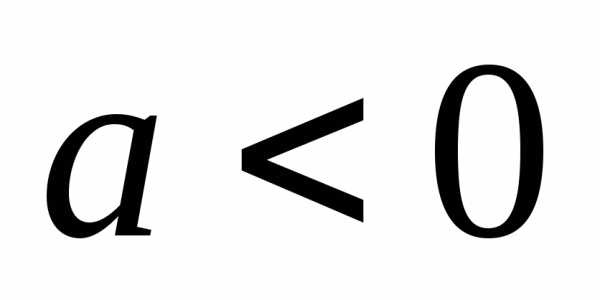— наклон кривой спроса. Обозначим 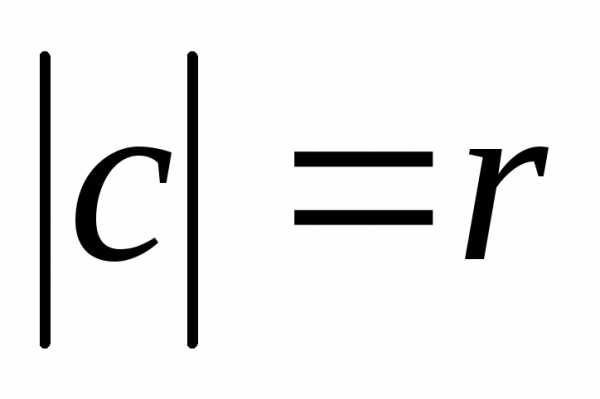. Тогда

;

;

;

….;

, т.е. знак отклонения будет чередоваться: минус, плюс, минус и т.д. Следовательно, будет то меньше, то больше равновесной цены.

У данной модели есть развитие. Под влиянием неценовых факторов спроса и предложения кривые спроса и предложения перемещаются, и с помощью модели можно рассматривать, как рынок приходит в состояние равновесия до того периода пока не возникает новое возмущение.

Например, в спокойное течение дел на рынке вмешивается резкий рост предложения, если продавцы выбрасывают запасы товара. В новой ситуации в анализе рынка товара следует соединить рассмотренную модель с моделью включения запаса.

Непрерывная модель.

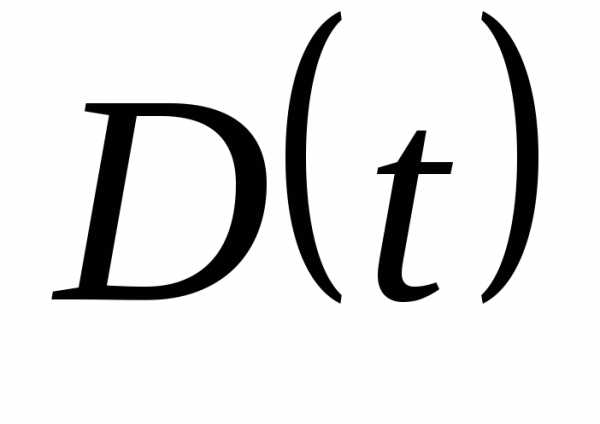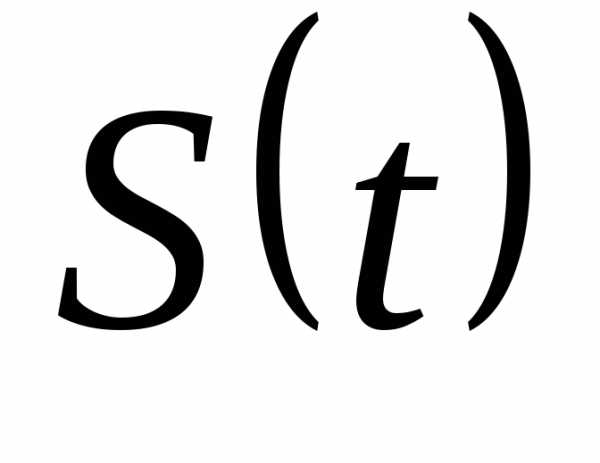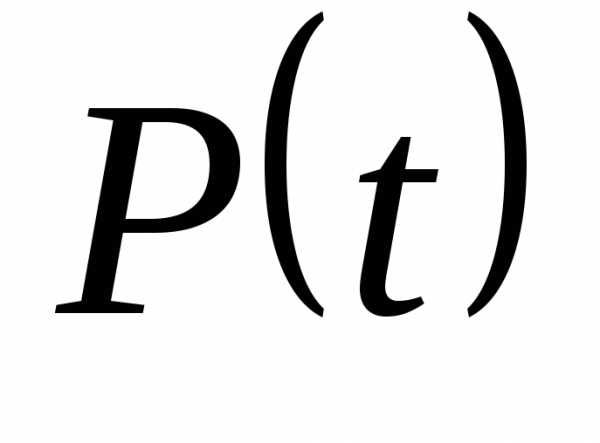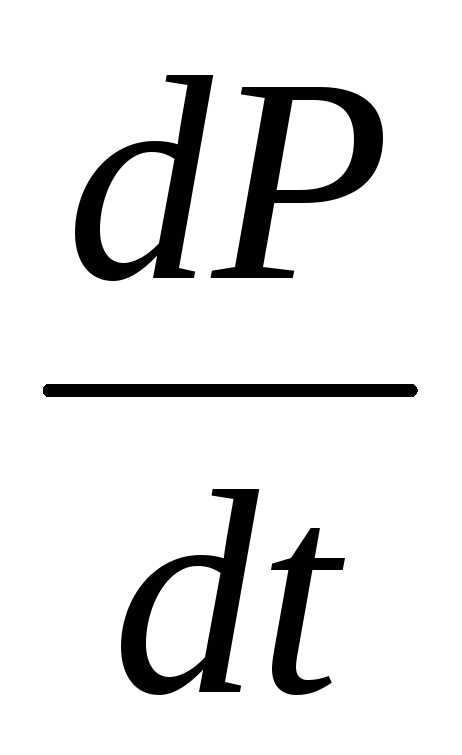В модели время течет непрерывно, , и все параметры являются функциями времени: , , . Поскольку изменение цены происходит на стороне спроса, то спрос зависит от цены и ее изменения , а предложение зависит только от цены. В каждый момент времени спрос поглощает предложение, т.е. .

Используем линейные функции спроса и предложения в следующем виде: ; .

Определим равновесные значения цены и объема, приравняв функции спроса и предложения:

. (1)

Так как в точке равновесия цена задана рынком, то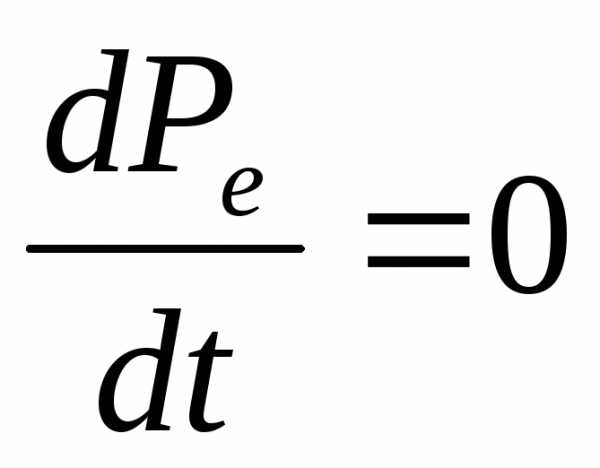

Значения 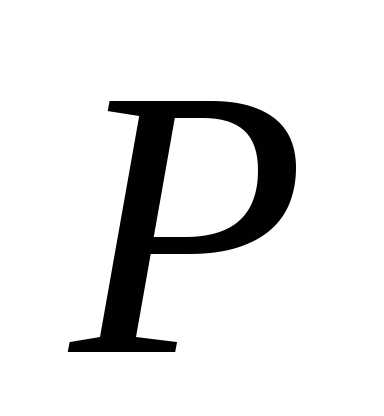и в любой момент времени удовлетворяют равенству:

. (2)

Вычитаем из выражения (2) выражение (1) и получим:

.

Как и в дискретной модели вводим обозначение: . Тогда . В новых обозначениях выражение (2) принимает вид:

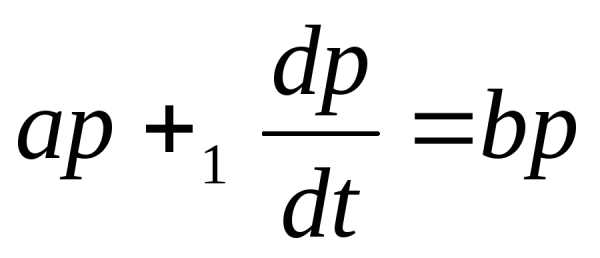(3).

Уравнения (2) и (3) представляют собой дифференциальные уравнения первого порядка. Обозначаем 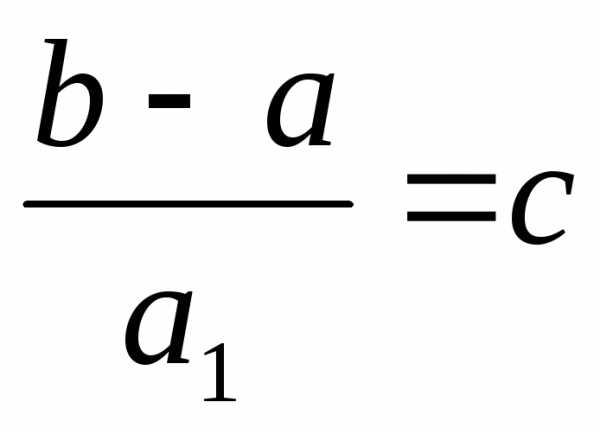, тогда .

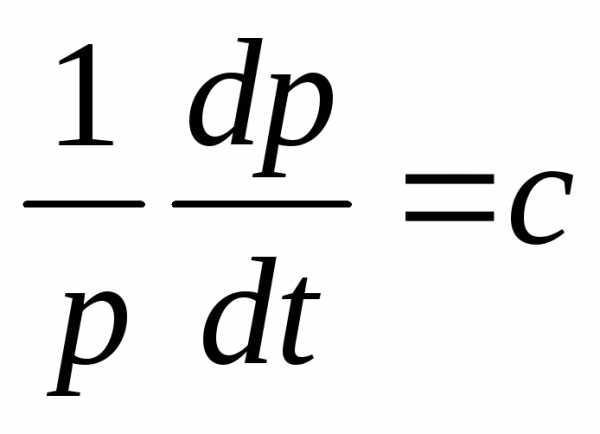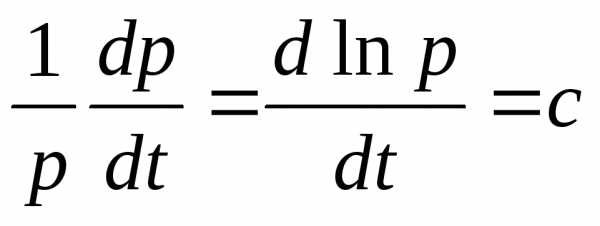— дифференциальное уравнение относительно .

Используя правило логарифмического дифференцирования, получим: . Решение имеет вид: 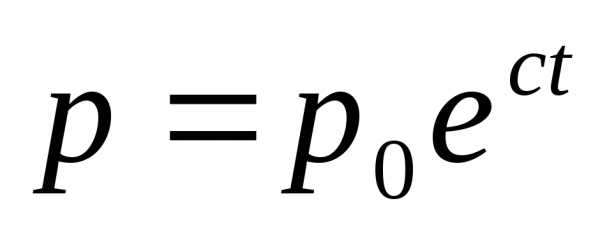, . Следовательно, . Зная цену, и подставив ее в функцию предложения, всегда можно найти объем продукции, который надо произвести.

studfiles.net

Паутинообразная модель

Рыночное равновесие

Каждая экономическая система стремится к стабильному положению, средством выражения которого является рыночное равновесие.

Определение 1

Под рыночным равновесием экономики понимается такое ее состояние, при котором количество товара, пользующегося устойчивым спросом по определенной цене, соответствует количеству товара, предлагаемого по этой же цене к реализации.

Такое количество товара, при котором спрос и предложение достигают равенства, обозначается как равновесный объем, а цена, соответствующая им, как равновесная цена.

В реальности уровень осуществляемые сделки купли-продажи могут иметь диапазон цен, ограниченный верхним и нижним пределом цены. Рыночное равновесие представляет собой обобщенную экономическую модель, характеризующую условную точку равновесия, устраивающего и продавцов, и покупателей. Рыночное равновесие характеризуется оптимальное поведение субъектов на рынке.

Существуют различные модели рыночного равновесия, к числу которых относится и паутинообразная модель.

Понятие паутинообразной модели рыночного равновесия

Определение 2

Под паутинообразной моделью (или теоремой) понимают вид макроэкономической модели, действующей в рамках совершенной конкуренции в виде механизма установления цен на основе соотношения спроса и предложения на товары короткого периода хранения и допускающей что возвращение к состоянию прежнего рыночного равновесия не обязательно.

Паутинообразная модель была названа так в 1934 году английским экономистом венгерско-еврейского происхождения Николасом Калдором в связи с тем, что кривые, отражающие изменение цены, внешне напоминают паутину.

Регулярность повторения циклов производства и цен на сырьевые товары была отмечена еще в 1876 году в работе американского металлургического фабриканта Сэмюэля Беннера «Пророчество Беннера будущих взлетов и падения цен». Впоследствии с ним согласились М. Эзекиель и Г.С. Хаас в работе «Факторы, влияющие на цену свинины» (1926 год) и А. Ханау в статье «Прогноз цен на свинину» (1927 год), сформировавшие свиной бизнес-цикл, ставший основой открытых позднее циклов Китчина.

К исследованию колебаний цен на рынках той продукции, производство которой характеризуется продолжительным периодом времени, но при этом имеет небольшой срок хранения, на которых объем производства находится в зависимости от цены, ожидаемой на момент осуществления сделки, а предложение, в свою очередь, определяет текущую цену, независимо друг от друга, но практически одновременно в 1930 году обратились такие специалисты как:

• голландский экономист Ян Тинберген;
• американский экономист Генри Щульц;
• итальянский экономист Умберто Ричи.

В 1934 году Николас Калдор написал статью «Определение статистического равновесия», в которой в какой-то мере подвел итог проведенным исследованиям и ввел термин «паутинообразная модель».

Основное содержание модели и ее разновидности

В основу содержания паутинообразной модели заложен следующий тезис: колебания спроса и предложения устанавливают цены, которые вне равновесного состояния необязательно обеспечивают возвращение к нему.

На основе установившейся на рынке цены производитель принимает решение об объеме продукции, которую он готов поставить на рынок в будущий период времени. При высокой текущей цене производитель стремиться к увеличению объема производства с тем, чтобы по завершении производственного цикла осуществить поставку товара на рынок.

Рыночная ситуация при этом характеризуется опозданием производителя в пределах производственного цикла, поскольку принятие решения об объемах производства, предполагаемых к поставке в будущем, основывается на текущих ценах.

Однако равновесие, включая и равновесную цену, устанавливается в той точке, где объем предложения совпадает с объемом спроса.

В связи с этим различают следующие виды паутинообразной модели:

• во-первых, модель со сходящейся спиралью, характеризующаяся большей крутизной кривой предложения по сравнению с падающей кривой спроса, что приводит к затуханию колебаний и внутреннему раскручиванию спирали;
• во-вторых, модель с раскручивающейся спиралью, характеризующаяся меньшей крутизной кривой предложения по сравнению с кривой спроса, что обеспечивает раскручивание спирали и увеличение колебаний;
• в-третьих, модель с постоянными колебаниями, характеризующаяся одинаковой крутизной линий спроса и предложения, приводящей к бесконечным повторяющимся колебаниям вокруг равновесного предложения;
• в-четвертых, модель с нелинейными колебаниями, характеризующаяся меньшей крутизной кривой предложения в точке равновесия по сравнению с кривой спроса. Незначительные изменения приводят к раскручиванию колебаний, а значительные изменения обеспечивают затухание колебаний до определенного уровня, где они носят постоянный характер.

В начале ХХ века применение паутинообразной модели получило положительную оценку в отношении ее применения к анализу рынка свинины и кукурузы, а также в 1950-х годах при применении денежной теории и теории экономических циклов, в 1970-х годах на рынках труда врачей, юристов и инженеров.

Недостатки паутинообразной модели

К недостаткам модели некоторые исследователи относят следующие:

• продолжающийся выпуск продукции даже в условиях предвидения производителями будущих потерь;
• недостаток четких определений и отсутствие перехода между краткосрочными и долгосрочными кривыми предложения;
• предсказание моделью более короткого ценового цикла, чем наблюдаемого на практике.

Замечание 1

Ограничение паутинообразной модели заключается в том, что ее применение возможно только по отношению к определенным видам продукции, поскольку она игнорирует определенные факторы, так как климат, изменение спроса потребителей и прочие.

Установление устойчивого равновесия не значит остановку развития производства, в связи с чем устойчивость равновесия достаточно условна.

spravochnick.ru

Паутинообразная модель с параметрами рынка, изменяющими во времени

В модели время течет непрерывно, , и все параметры являются функциями времени:,,. Поскольку изменение цены происходит на стороне спроса, то спрос зависит от ценыи ее изменения, а предложение зависит только от цены. В каждый момент времени спрос поглощает предложение, т.е..

Используем линейные функции спроса и предложения в следующем виде: ;. Определим равновесные значения цены и объема, приравняв функции спроса и предложения:

. (1.4)

Так как в точке равновесия цена задана рынком, то Значенияив любой момент времени удовлетворяют равенству:

. (1.5)

Вычитаем из выражения (1.5) выражение (1.4) и получим:

.

Как и в дискретной модели вводим обозначение: . Тогда. В новых обозначениях выражение (1.5) принимает вид:

(1.6)

Уравнения (1.5) и (1.6) представляют собой дифференциальные уравнения первого порядка. Обозначаем , тогда. Имеем- дифференциальное уравнение относительно. Используя правило логарифмического дифференцирования, получим:. Решение имеет вид:. При,. Следовательно,. Зная начальную цену, и подставив ее в функцию предложения, всегда можно найти объем продукции, который надо произвести.

Устойчивость равновесия. Сдвиг равновесия. На рынке устанавливается равновесие, если спрос на товар равен его предложению. Объем продукта и его цену называют равновесными. Но равновесие устанавливается редко. Если рыночная цена больше равновесной цены, то на рынке образуется излишек товара; если цена меньше равновесной, то спрос превышает предложение и существует дефицит товара. Равновесие является устойчивым, если после его нарушения рынок приходит в состояние равновесия и устанавливаются прежние равновесные цена и объем. Если же после нарушения равновесия устанавливается новое равновесие (в новой точке), изменяется уровень цены и объема спроса-предложения, то такое равновесие является неустойчивым. Рассмотрим три случая устойчивости равновесия на примере паутинообразной модели.

Случай 1. Для нормального товара наклон кривой предложения положителен, наклон кривой спроса – отрицателен: ;. Если наклон кривой спроса больше наклона кривой предложения и,, то при,- бесконечно малая величина и система приходит в состояния равновесия. Равновесие при названных условиях устойчиво. Эта ситуация представлена на рисунке 1.

Случай 2. Если наклоны кривых спроса и предложения равны, хотя и различаются знаками, ;, то. Тогда,

Рис. 2. Равномерные колебания цены и спроса-предложения на рынке одного товара.

система характеризуется равномерными колебаниями цены и объема (рис.2). На рынке такая ситуация встречается крайне редко.

Случай 3. Если наклон кривой предложения в точке равновесия превышает абсолютное значение (значение по модулю) наклона кривой спроса, то,. Тогда привеличинастановится бесконечно большой, имеет место взрывное колебание и неустойчивое равновесие (рис. 3).

Рис. 3. Взрывное колебание.

Воздействие изменяющихся неценовых факторов спроса и предложения приводит к сдвигу равновесия. Возникшее новое равновесие может также описываться одним из трех вышеприведенных случаев.

3. Модель с включением запасов

В паутинообразной модели цена устанавливалась так, чтобы поглотить все предложение. Запасы товаров или отсутствовали или оставались неизменными. Модель можно расширить, учитывая наличие запасов. Можно выстроить следующую последовательность событий. Поставки товара вливаются в общую массу запасов, и фактический спрос удовлетворяется за счет запасов. В анализе появляется еще один субъект экономических отношений – продавцы товара. Таким образом, производители поставляют товар продавцам, имеющим запасы и реализующих товар, и покупатели. Действие модели начинается с продажи товара покупателям и установления цены в соответствии с размером запасов.

Для дискретного случая, если величина запасов в конце интервала составляет, то изменение запасов в течение этого интервала равно. В зависимости от особенностей установления цены, зависящей от величины запасов, можно построить несколько моделей.

Модель 1. В период продавцы устанавливают цену. Она больше цены, если в предшествующий период запасы уменьшились. Цена повышается пропорционально сокращению запасов:.

Модель 2. В период ценаповышается, если в предшествующий период уровень запасов был ниже равновесного объема. Повышение цены пропорционально нехватке товаров до объема. Цена равна.

Модель 3 рассматривается в непрерывном анализе. В каждый момент времени продавцы устанавливают цену так, что скорость возрастания цены пропорциональна скорости уменьшения запасов:

,

где — положительная величина. Используем линейные функции спроса и предложения:. Тогда имеем:или

(1.7)

В точке равновесия , поэтому

(1.8)

откуда находим равновесную цену .

Вычитаем из уравнения (1.7) уравнение (1.8), получим: . Введем обозначение, тогда. Уравнение модели приобретает вид:. Обозначим, тогда. В итоге имеем- дифференциальное уравнение относительно.

Используя правило логарифмического дифференцирования, нахождения производной логарифма сложной функции, получим: . Решение имеет вид:. При,. Следовательно,. Зная начальную цену, и подставив ее в функцию предложения, всегда можно найти объем продукции, который надо произвести.

В случае нормальных товаров ,, и множительпри, стремится, а. Это справедливо для всех значений. Величинаопределяет скорость приспособления цены к изменению запасов. Чем больше, тем быстрееприближается к равновесной цене.

studfiles.net

Паутинообразная модель рынка — Энциклопедия по экономике

В реальной жизни предложение реагирует на цены с некоторым лагом, т.е. сегодняшнее предложение S(t) определяется ценой предыдущего периода P(t— 1), а сегодняшний спрос D(t) определяется ценой текущего периода P(t). Это явилось основой построения паутинообразной модели рынка, главная цель которой заключается в предсказании эффективности  [c.329]
См. также Паутинообразная модель, Рынок, Функция спроса.  [c.22]

О научном исследовании вопросов рыночного равновесия см. в ст. «Равновесие». См. также Аукционер Вальраса, «Нащупывание «, Паутинообразная модель, Рынок.  [c.315]

Паутинообразная модель рынка и ряд  [c.100]

Паутинообразная модель рынка 445  [c.445]

Паутинообразная модель рынка  [c.445]

Классическая теория основывается на предположении о стабильности равновесия, т. е. о способности рынка самостоятельно вернуться в положение равновесия в случае отклонения от него. Всегда ли это так В данном вопросе нам поможет разобраться паутинообразная модель рынка.  [c.321]

Равновесие по Вальрасу Равновесие по Маршаллу Краевое равновесие Паутинообразная модель рынка Частичное равновесие Общее равновесие Эффекты обратной связи  [c.340]

Паутинообразная модель рынка (15)  [c.807]

В связи с тем, что траектории р(0), р(1), р(2),. .. рыночной цены соответствует геометрическая иллюстрация, похожая на паутину, данная динамическая модель и получила название «паутинообразной модели». Биржевой рынок (например, рынок ценных бумаг или иностранной валюты) является удачным примером паутинообразной модели спрос на товар определяется на бирже ее участниками и зависит от текущих котировок, а предложение, как правило, реагирует на цену с некотором лагом. В этом случае, наблюдая текущую динамику биржевых котировок, можно предсказывать их будущие значения на некоторый промежуток времени.  [c.64]

Дефицит товара Конкуренция покупателей Избыток товара (затоваривание) Конкуренция продавцов Статическое равновесие Динамическое равновесие Паутинообразная модель Сходящаяся паутинообразная модель Расходящаяся паутинообразная модель Паутинообразная модель с регулярными колебаниями Налоги и субсидии и рыночное равновесие Максимальная цена (ценовой потолок, верхний предел цены) и рыночное равновесие Теневая экономика («черный рынок») Теневая цена  [c.74]

Если исходить из стандартных предпосылок паутинообразной модели, то наиболее неустойчив рынок, изображаемый графиком  [c.79]

Таким образом, оба подхода (модели) описывают механизм достижения устойчивости равновесия рынка с учетом временных изменений величин спроса, предложения и цен при условии, что кривые спроса и предложения пересекаются и имеют одинаковый угол наклона. Однако существуют и другие аналогичные модели. Так, о характере достижения устойчивого равновесия рынка во временном аспекте дает представление так называемая динамическая паутинообразная модель. Ее суть заключается в установлении степени реакции предложения на изменение цены, приводящей к достижению рыночного равновесия.  [c.191]

Примером паутинообразной модели может служить валютный рынок спрос на валюту определяется на бирже в зависимости от ее текущего курса, а предложение реагирует на цену с некоторым опозданием. Поэтому динамика текущих валютных курсов позволяет прогнозировать цену валюты через некоторый промежуток времени. Паутинообразная модель отражает значение эластичности спроса и предложения для понимания механизма рыночного равновесия, определения закономерностей поведения покупателей и продавцов на различных рынках и в разных экономических системах.  [c.194]

Концептуальная модель любого процесса динамики цен включает взаимодействие трех подсистем, которые можно условно назвать «товаропроизводитель», «потребитель» и «рынок» (рис. 5.3.2). Паутинообразная модель (модель А), в которой спрос отстает от предложения на один период D(Pt+1) = S(Pt), также вписывается в схему рис. 5.3.2. Эта модель — одна из исторически первых динамических моделей рынка, отражающих поведение участников. Она служит хорошей иллюстрацией применения метода моделирования при анализе экономических процессов.  [c.325]

Прозрачность» рынка 313 «Пункт» обслуживания 138, 295 Паутинообразная модель 260 Первая разность 299 Первичная информация 134, 317 Первичная экономическая информация  [c.481]

Перейдем теперь непосредственно к анализу устойчивости рыночного равновесия. Как мы уже знаем, такой анализ требует построения модели, в которой фактор времени был бы учтен явным образом (динамическая модель рынка). Рассмотрим в качестве примера одну из простейших динамических моделей — так называемую «паутинообразную» модель.  [c.140]

Предположим, что предложение пшеницы со стороны ее производителей не зависит от цены пшеницы в данном году. (Сколько пшеницы произведено — столько и предлагается на рынке). Поэтому линии предложения пшеницы со стороны ее производителей вертикальны. В. первом «урожайном» году эта линия занимает положение NS, во втором «неурожайном» году она занимает положение RS2. Напомним, что в разделе 1 настоящей лекции при обсуждении паутинообразной модели так же, как и сейчас, предполагалось, что предложение не зависит от цены текущего периода. Тем не менее, линии предложения имели положительный наклон. Дело в том, что тогда линии предложения характеризовали зависимость объема предложения в данном году от цены предыдущего года, в настоящем же случае линии предложения характеризуют зависимость объема предложения в данном году от цены данного года.  [c.147]

Чтобы продемонстрировать суть противоречия, возникающего при внешнем задании функции ожиданий, Мут обратился к так называемой паутинообразной модели. Он рассматривал рынок одного товара. По предположению, изменение спроса относительно равновесного значения в момент / (/>() есть функция отклонения текущей цены от равновесия (pt), т.е.  [c.591]

ПАУТИНООБРАЗНАЯ МОДЕЛЬ — теоретическое построение, объясняющее траекторию движения рынка к равновесному состоянию при запаздывании реакции спроса или предложения на изменение цен.  [c.280]

Рассмотрим подробнее на рис. 15.За, как в результате затухающих ценовых колебаний устанавливается равновесие. В паутинообразной модели предполагается, что объем спроса ориентируется на фактическую цену товара текущего периода. Объемом предложения текущего периода руководят ценовые ожидания предшествовавшего периода, основанные на предположении, что текущая цена сохранится и в следующем периоде (т. е. объем выпуска текущего периода производители планируют в предыдущем периоде, исходя из цен, сложившихся на тот период). На рис. 15.За производители в текущем периоде to предлагают товар в объеме Q0 по цене Р0, что ниже равновесных параметров рынка. При цене Р0 наблюдается дефицит, который толкает цену товара к повышению и она, превысив равновесный уровень РЕ, устанавливается на уровне Р Именно эта высокая цена и повлияет на решение производителей увеличить выпуск в следующем периоде до уровня Qr Однако в следующем периоде t, объем спроса, ориентирующегося на цену РГ окажется меньше предложения. Избыток товара на рынке собьет цену ниже равновесной до уровня Р2. Но разница между Ре и Р2, как видно из рисунка, меньше, чем между РЕ и РГ Соответственно, в период t2 объем предложения при цене Р2 снизится до 02, что несколько ближе к равновесному, чем объем предложения предыдущего периода. Так, постепенно в результате ценовой и количественной (объемной) подстройки предложение полностью найдет спрос в объеме QE при цене РЕ. На рынке автоматически установится равновесие.  [c.322]

Существуют обучающиеся автоматические системы в технической кибернетике напр., разного рода приборы управления на летательных аппаратах, в технологических агрегатах, обеспечивающие оптимальное протекание процессов. Разработаны также системы распознавания образов, построенные на принципе О. Процессом О. можно назвать поведение участников рынка (напр., в паутинообразной модели, в аукционе и т.д.), когда они меняют свои решения сообразно ситуации, приближаясь к точкеравповесия или инойцели. См. также А даптивыое управление.  [c.234]

ПАУТИНООБРАЗНАЯ МОДЕЛЬ [ obweb model] — одна из простейших динамических моделей, используемых в экономической литературе для демонстрации процесса формирования цен в условиях конкурентного рынка. В модели поставка товара на рынок в определенном году зависит от условий (в том числе цен), сложившихся в прошлом периоде (для сельского хозяйства — в прошлом году). Спрос же определяется ценой текущего периода.  [c.260]

См. также Вебпена парадокс, Дуополия, Конкуренция, Концентрация рынка, Макроэкономическое регулирование, Монопольная власть, Монополистическая конкуренция, Монопсоничес-кая власть, Монопсония, Несовершенство рынка, Олигополия, Паутинообразная модель, Пигу эффект, Предложение, Равновесие, Рынок капиталов. Рыночное равновесие, Спрос.  [c.314]

АНТОН Игорь, ты знаешь английское слово obweb ИГОРЬ Да, это переводится как паутина. Понимаю почему ты спрашиваешь. В экономической теории есть паутинообразная модель, объясняющая, как цена плетет паутину рынка. АНТОН Рассматривается, наверное, как рыночная цена постепенно приводит спрос и предложение к равновесию ИГОРЬ Ты совершенно прав, друг мой. Именно постепенно. Для этого полезно представить, что продавцы наших яблок каждый день принимают решение о том, сколько яблок им нужно  [c.137]

economy-ru.info

Паутинообразная модель. Паутинообразная модель, которая (в отличие от ранее рассмотренных) относится к числу

Паутинообразная модель, которая (в отличие от ранее рассмотренных) относится к числу динамических, т. е. учитывающих фактор времени. Паутинообразная модель рассматривает процесс формирования равновесия в условиях, когда реакция участников сделок на изменяющиеся условия рынка растянута по времени.

Для примера чаще всего берут различные отрасли сельскохозяйственного производства, например, выращивание птицы. Предположим, наш производитель ориентировался на рыночную цену P_t, по которой птицу продавали в данном году. Естественно, он ожидает сохранения сложившихся цен и определяет объем производства птицы (Q_t) в следующем году исходя из этих цен. Предположим, что рынок вышел из состояния равновесия. Спрос на птицу снизился, и по цене P_t потребители уже не станут покупать столько продукции, сколько раньше. Чтобы реализовать произведенное количество производитель вынужден снижать цену до P₁, т. е. до уровня цены спроса на данное количество птицы (рис. 6.9).

Рис. 6.9 Паутинообразная модель

Но такая низкая цена вынудит какую-то часть производителей покинуть данный рынок. Предложение упадет до Q₁, на рынке возникнет дефицит и, как следствие, будет повышение цен до P₂. Это в свою очередь вызовет расширение предложения, но не до исходного уровня Q_t, а до чуть меньших размеров Q₂. В дальнейшем процесс идет по той же схеме и в конечном итоге, описывая круги сужающейся спирали вокруг точки О, производители «нащупывают» равновесную цену.

В описанном варианте отклонение от равновесия с течением времени уменьшается, т. е. система стремится к положению равновесия. Но возможны и иные варианты, представленные на графиках 6.10 (а и б), когда отклонение от равновесия возрастает (рис. 6.10 а) и когда отклонения от равновесия стабильно держатся на одном уровне (рис.6.10 б).

Рис.6.10. Паутинообразная модель с неустойчивым равновесием

Примером паутинообразной модели может служить не только рынок сельскохозяйственной продукции. Эта модель применима почти во всех случаях, когда спрос зависит от текущих цен, а предложение реагирует с некоторым временным отставанием. Явления этого типа можно наблюдать, допустим, на биржевом рынке ценных бумаг и валюты: спрос мгновенно реагирует на текущие котировки, а предложение меняется медленнее.

Но бывают на биржах и взрывные колебания — так называемые биржевые паники, когда за считанные минуты ценные бумаги могут резко обесцениться. Чтобы во время паники отклонения цен от равновесного уровня не зашли слишком далеко, биржи на время прерывают свои операции. В течение перерыва и сторона спроса, и сторона предложения успевают обдумать ситуацию. Разрыв между ними по времени принятия решений исчезает, и на следующий день паника обычно проходит.

Паутинообразная модель применима и к рынку дипломированных экономистов. Их предложение, т. е. выпуск вузами, ориентируется на спрос и соответственно на заработную плату, которая была 5 лет назад. Ведь именно тогда нынешние выпускники поступали на первый курс.

Неравновесие на рынке

Паутинообразная модель, как и все простые модели, значительно упрощает действительную ситуацию. На самом деле выбор объема предложения на будущий год отнюдь не сводится к механической подстройке под ценовые условия, сложившиеся в предыдущем году. Участники рынка пытаются прогнозировать ситуацию, а некоторые из них (в первую очередь фирмы-монополисты) способны и активно на нее воздействовать. Не остаются неизменными и кривые спроса и предложения. Под воздействием неценовых факторов они испытывают постоянные смещения. Словом, паутинообразная модель отражает рыночную реальность не лучше, чем изучаемая в школе принципиальная схема двигателя внутреннего сгорания может помочь при ремонте мотора последней модели «Жигулей».

Однако паутинообразная модель исключительно полезна своим общим подходом к рыночному равновесию, а именно демонстрацией того, что рынок отнюдь не во всех случаях автоматически устанавливает равновесие.

На рис. 6.11 обобщен спектр возможных вариантов динамики цен и объемов предложения (P, Q) с течением времени (Т). Как и в паутинообразной модели, их отклонения от равновесного уровня (Р₀, Q₀) могут либо постепенно затухать, либо увеличиваться, либо держаться на одном уровне. Наконец, еще один, ранее не рассматривавшийся нами вариант показан на графике 6.11 г. Увеличивающаяся амплитуда отклонений от равновесия может завершиться переходом всей системы к новому равновесию (Р₁, Q₁).

Рис. 6.11. Колебания затухающие (а), взрывные (б),
стационарные (в) и переход к новому равновесию (г)

ГЛОССАРИЙ

Неценовые факторы предложения — на объем предложения влияют: технические возможности производителя, цены используемых ресурсов, налоги и дотации, ожидания продавцов, цены на другие товары (взаимозаменяемые и взаимодополняемые), число продавцов и прочие факторы.

Неценовые факторы спроса — на объем спроса влияют: доходы потребителей, цены на другие товары (взаимозаменяемые и взаимодополняемые), вкусы покупателей, размер рынка, ожидания покупателей и другие факторы.

Потребительское ожидание — представление потребителей и фирм о том, что произойдет или какие условия сложатся в будущем.

Потребительское предпочтение — упорядоченная система относительных оценок полезности различных наборов благ.

Предложение — желание и способность продавцов совершать сделки по продаже поставленного на рынок товара.

Равновесная цена — цена, уравновешивающая величины спроса и предложения на рынке в результате действия конкурентных сил.

Равновесный объем производства — количество продукции, предлагаемое по сформировавшейся в рамках всей отрасли равновесной цене.

Рыночное равновесие — ситуация, когда взаимодействие спроса и предложение определяет равновесные значения цен и объемов продукции. Совпадение интересов покупателей и продавцов.

Спрос — желание потенциальных и фактических покупателей приобрести определенные товары и услуги.

Эффект дохода — изменение величины спроса на товар, вызванное изменением реального дохода потребителя в результате изменения цены одного из товаров, входящих в его потребительский набор.

Эффект замещения — изменение величины спроса на товар, вызванное перераспределением структуры потребления (соотношения средств, выделяемых на покупку разных товаров) в результате изменения цены одного из товаров, входящих в потребительский набор.

megaobuchalka.ru