P a b 25 a 7 найдите b: P(a,b)=25, a=7. Найдите b.
Угол между векторами.
Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Пример 1. Найти угол между векторами a = {3; 4} и b = {4; 3}.Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.Найдем модули векторов:
|a| = √32 + 42 = √9 + 16 = √25 = 5|b| = √42 + 32 = √16 + 9 = √25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| |a| · |b| | 5 · 5 | 25 |

Решение: Найдем скалярное произведение векторов:
a·b = 5 · 7 + 1 · 5 = 35 + 5 = 40.Найдем модули векторов:
|a| = √72 + 12 = √49 + 1 = √50 = 5√2|b| = √52 + 52 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| |a| · |b| | 5√2 · 5√2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Пример 3. Найти угол между векторами a = {3; 4; 0} и b = {4; 4; 2}.Найдем модули векторов:
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| |a| · |b| | 5 · 6 | 15 |

Решение: Найдем скалярное произведение векторов:
a·b = 1 · 5 + 0 · 5 + 3 · 0 = 5.Найдем модули векторов:
|a| = √12 + 02 + 32 = √1 + 9 = √10|b| = √52 + 52 + 02 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
cos α = a · b|a| · |b| = 5√10 · 5√2 = 12√5 = √510 = 0.1√5фото, отзывы, адрес, цены – Афиша-Рестораны
Москва, 2-я Брестская, 39, стр. 2
Фактический график ресторана может отличаться от указанного
Обстоятельный английский паб на 2-й Брестской
Добавить
фотографию
Отзывов пока нет.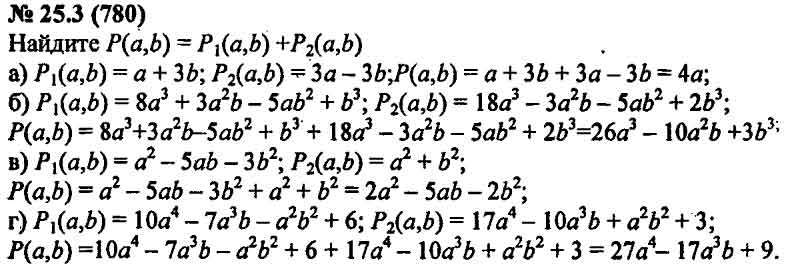 Станьте первым, кто напишет
Станьте первым, кто напишет
Ресторан о себе
- Бар Three Tuns Pub оформлен так, что гости чувствуют себя непринужденно и комфортно. Дизайн интерьера паба выполнен в английском стиле. Английский стиль заведения дарит гостям уют и создаёт ощущение приятной старины. Мы достигли этого с помощью характерного гарнитура (темной деревянной ме…
- Бар Three Tuns Pub оформлен так, что гости чувствуют себя непринужденно и комфортно. Дизайн интерьера паба выполнен в английском стиле. Английский стиль заведения дарит гостям уют и создаёт ощущение приятной старины. Мы достигли этого с помощью характерного гарнитура (темной деревянной мебели), качественных материалов для отделки (кирпича, натурального камня) и приглушенного освещения. Невозможно представить себе паб без большой барной стойки с высокими табуретками. В заведении есть также контактная барная стойка.

Новости и акции
- 26 апреля Авторская колонка
- 13 пабов Москвы, которые надо посетить «before you die»
- По просьбе «Афиши–Рестораны» автор блога PubsMoscow Игорь Самсонович составил топ лучших пабов Москвы — в нем чёртова дюжина заведений, от старинного Sally O’Brien’s до свеженького Dubliner. Пост заканчивается, майские на носу — берите на заметку!
Популярные рестораны
Вас может заинтересовать
Ирландский Паб «THE Hill’s PUB», Russia (8(4722)257172)
что говорят другие: User (27/08/2018 21:44)Сегодня смотрим за игрой⚽️ команд Чемпионата Англии 🏴 «Манчестер Юнайтед» или «Тоттенхэм»? ⠀ Кто победит?🏆 ⠀ ______________
.
 .. The Hills Pub (4722) 25-71-72 ⠀ ▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород
.. The Hills Pub (4722) 25-71-72 ⠀ ▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгородSee More
User (27/08/2018 16:04)
Как говорится, в понедельник день тяжелый😔, но только не в твоём пабе🍀 ⠀ Потому что у нас с понедельника по среду «Турбо Бонус»🔋 ⠀ Вы можете ВЫГОДНО и главное ВКУСНО 😋 провести время в HILLS PUB🍀… ⠀ ______________
The Hills Pub (4722) 25-71-72 ⠀ ▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород
See More
User (26/08/2018 23:18)
Фанаты футбола ⚽️кайфуйте🔥
Сегодня в пабе🍀 два мощнейших противостояния.
Отличный отдых воскресным вечером☺️… ______________
The Hills Pub (4722) 25-71-72 ▪ул. Костюкова, 46 Б
#hillspub #thehillspub #pub #паб #белгород
See More
User (26/08/2018 17:03)
Оторвитесь от экранов мониторов💻, отложите в сторону планшет📱 — рассаживайтесь за игровым 🎲столом и встретьтесь лицом к лицу с реальными героями🤹🏼♂️) ⠀ В твоём пабе🍀 отличный выбор настольных игр и хорошая компания🎁 ⠀ ______________
. .. The Hills Pub (4722) 25-71-72 ▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород
.. The Hills Pub (4722) 25-71-72 ▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород
See More
User (25/08/2018 21:08)
Ваш счастливый номер 13🔥 ⠀ Лагер HOP HOUSE 13 от Guinness только в твоём пабе🍀 ⠀ _____________… ⠀ The Hills Pub
(4722) 25-71-72
▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород.
See More
User (25/08/2018 15:35)
Твой праздник 🍾 запомнится надолго, если ты будешь отмечать 🎉 его в твоём пабе🍀 ⠀ Вкусная кухня, отличные напитки 🍷 и бонусы от паба🍀 в честь твоего праздника🎁 ⠀ ______________… ⠀ The Hills Pub (4722) 25-71-72 ⠀ ▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород
See More
User (24/08/2018 23:09)
Сегодня состоится 🎉интересное противостояние в Российской премьер-лиге⚽️ ⠀ Не пропусти! ⠀ ______________
… The Hills Pub ⠀ (4722) 25-71-72 ⠀ ▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород
See More
User (24/08/2018 17:38)
Сегодня пятница❤️ Мы ее дождались☺️ ⠀ Сегодня в пабе 🍀будет много друзей и отличная музыка 🎶 в исполнении группы «The Big Lebowski”🎸 ⠀. .. Давайте как следует отдохнём в летние выходные😊 ⠀ ______________
.. Давайте как следует отдохнём в летние выходные😊 ⠀ ______________
The Hills Pub ⠀ (4722) 25-71-72 ⠀ ▪ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород
See More
User (23/08/2018 21:59)
Сегодня целых два ✌🏼 супер-матча⚽️ с участием команды из России 🇷🇺
Так что берём светлое 🍺и проводим отличный вечер 🔥в твоем пабе🍀
The Hills Pub … (4722) 25-71-72
▪ул. Костюкова, 46 Б
#hillspub #thehillspub #pub #паб #белгород
See More
User (23/08/2018 18:29)
Ждёте пятницу?🎉 Мы тоже ждем😊
Потому что в твоём пабе🍀 будут THE BIG LEBOWSKI 🎸
… Всем быть обязательно❗️ ________________ The Hills Pub (4722) 25-71-72 ▪️ул. Костюкова, 46 Б
#hillspub #thehillspub #pub #паб #белгород
See More
User (23/08/2018 02:26)
Самое лучшее для ценителей настоящих сигар 🚬в твоём пабе🍀
________________ The Hills Pub (4722) 25-71-72… ▪️ул. Костюкова, 46 Б
#hillspub #thehillspub #pub #паб #белгород
See More
User (22/08/2018 17:39)
Сегодня HILLS PUB🍀 приглашает всех болельщиков и любителей футбола ⚽️отлично провести время ⏰и посмотреть прямую трансляцию Лиги Чемпионов в твоём пабе🍀
Вас ждёт свежее пиво 🍺 и отличные закуски 🍢
________________. .. The Hills Pub (4722) 25-71-72 ▪️ул. Костюкова, 46 Б
.. The Hills Pub (4722) 25-71-72 ▪️ул. Костюкова, 46 Б
#hillspub #thehillspub #pub #паб #белгород #паббелгород
See More
User (21/08/2018 22:04)
Сегодня встречаемся в твоём пабе🍀 и смотрим противостояние Португалии и Греции.
Кто победит сегодня?
________________… The Hills Pub (4722) 25-71-72 ▪️ул. Костюкова, 46 Б
#hillspub #thehillspub #pub #паб #белгород #паббелгород
See More
User (21/08/2018 15:22)
Свежайшие мидии 🍢в сопровождении бокала любимого 🍸напитка — так можно охарактеризовать грядущий вторник в твоём пабе🍀
Остаётся только забронировать столик👨🍳и подключить «Турбо Бонус» для очень ВЫГОДНОЙ скидки😉
________________… The Hills Pub (4722) 25-71-72 ▪️ул. Костюкова, 46 Б
#hillspub #thehillspub #pub #паб #белгород #паббелгород
See More
User (20/08/2018 23:42)
Никита 👨🍳напоминает, что с понедельника по среду действует «Турбо Бонус» 🔋и ты просто не можешь упустить возможность 🍔ПОПРОБОВАТЬ ВСЕ БЛЮДА из нашего меню со скидкой до 40%🔥 ⠀ ________________ The Hills Pub (4722) 25-71-72. .. ▪️ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород #паббелгород
.. ▪️ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород #паббелгород
See More
User (20/08/2018 14:32)
А Вы знали, что способ подачи ▪️Guinness отличается от налива обычного пива🍻 ⠀ Идеальная пинта Guinness наливается в 2❗️ этапа: ⠀ • Бокал необходимо держать под углом 45 градусов;… • Бокал держать под 45 градусов. Затем, после того, как бокал заполнен на ¾, нужно дождаться пока пенная шапка не поднимется; • Чтобы долить в бокал оставшееся пиво, можно придать бокалу вертикальное положение; • Обычно процесс заливания пива Guinness в бокал занимает 119 секунд, а пенка – это неотъемлемый атрибут проведения дегустации. ⠀ ТОЛЬКО в ТВОЁМ ПАБЕ🍀 опытные бармены с удовольствием угостят Вас «Идеальной пинтой Guinness” 🍺 ⠀ ________________ The Hills Pub (4722) 25-71-72 ▪️ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород #паббелгород
See More
User (19/08/2018 23:16)
Знакомство с сигарной 🚬культурой советуют начинать с легких, но ароматных сигар. ⠀ Такие табачные изделия помогут распробовать вкус дыма💨, почувствовать каждую его нотку 🎹и постепенно привыкнуть к крепости. ⠀ ________________… The Hills Pub🍀 ⠀ (4722) 25-71-72 ▪️ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород #паббелгород
⠀ Такие табачные изделия помогут распробовать вкус дыма💨, почувствовать каждую его нотку 🎹и постепенно привыкнуть к крепости. ⠀ ________________… The Hills Pub🍀 ⠀ (4722) 25-71-72 ▪️ул. Костюкова, 46 Б ⠀ #hillspub #thehillspub #pub #паб #белгород #паббелгород
See More
User (19/08/2018 18:05)
В уютной обстановке, в кругу семьи👫, можно отлично провести время ⏰за увлекательной 🎲настольной игрой.
В твоём пабе🍀 широкий выбор игр на любой вкус😊
#hillspub #thehillspub #pub #паб #белгород #паббелгород
User (19/08/2018 00:43)
Виски 🥃 Lagavulin 16 Years Old 🔥не оставит равнодушным никого.
Истинные знатоки советуют употреблять его в чистом виде или с несколькими прохладными каплями 💦воды.
А попробовать его можно в твоём любимом пабе🍀
… #hillspub #thehillspub #pub #паб #белгород #паббелгород #виски
See More
косоугольных треугольников
косоугольных треугольников Наклонный треугольник — это любой треугольник, не являющийся прямоугольным.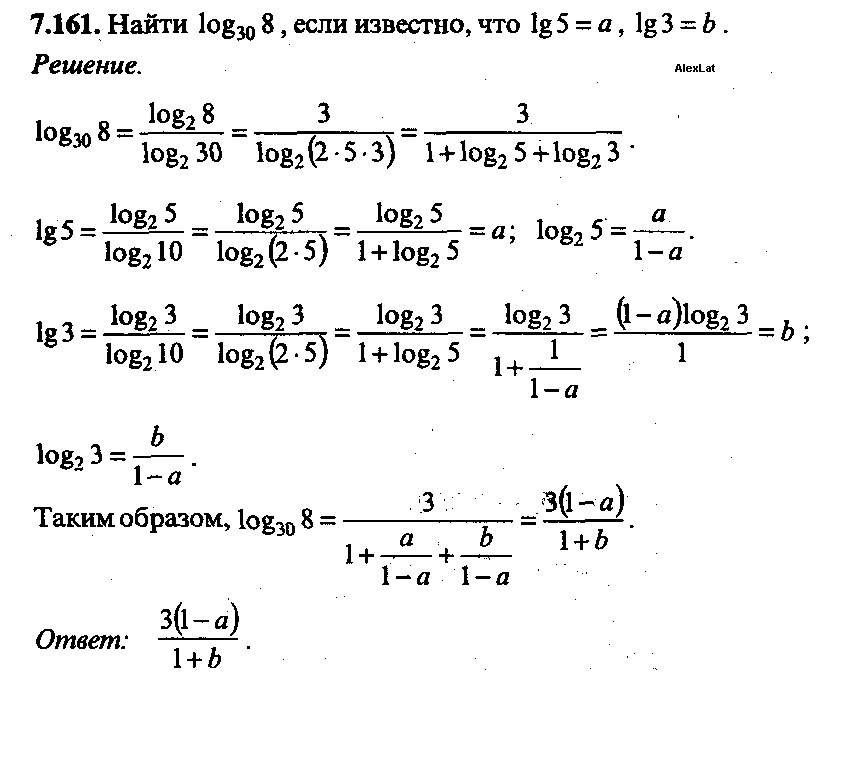 Это может быть остроугольный треугольник (все три угла треугольника меньше прямых) или тупоугольный треугольник (один из трех углов больше прямого). На самом деле, для целей тригонометрии класс «косоугольных треугольников» может с тем же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.
Это может быть остроугольный треугольник (все три угла треугольника меньше прямых) или тупоугольный треугольник (один из трех углов больше прямого). На самом деле, для целей тригонометрии класс «косоугольных треугольников» может с тем же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.
Примем соглашение о обозначении частей косоугольных треугольников, обобщающее правило для прямоугольных треугольников.Пусть углы обозначены А, В, и С, , а противоположные им стороны обозначены а, b, и с, соответственно.
Решение косоугольных треугольников
Тригонометрия косоугольных треугольников не так проста, как прямоугольных треугольников, но есть две теоремы геометрии, которые дают полезные законы тригонометрии. Они называются «законом косинусов» и «законом синусов». Есть и другие «законы», которые использовались раньше, но с момента повсеместного использования калькуляторов этих двух законов достаточно.
Закон косинусов
Это просто сформулированное уравнение:Это похоже на теорему Пифагора, за исключением последнего члена, и если C — прямой угол, последний член исчезает (поскольку косинус 90° равен 0), так что закон косинусов на самом деле является обобщением закона косинусов. Теорема Пифагора.
Обратите внимание, что каждый треугольник дает три уравнения закона косинусов, так как вы можете переставлять буквы по своему усмотрению.Затем две другие версии
Закон косинусов связывает три стороны треугольника с одним из углов. Вы можете использовать его несколькими способами.
Во-первых, если известен один угол и две смежные стороны, то можно определить и противоположную сторону.Например, если угол C = 60°, сторона a = 5, а сторона b = 8, то по закону косинусов c 2 = 25 + 64 – 80 cos 60°.
Во-вторых, если вы знаете все три стороны треугольника, то можете использовать их для нахождения любого угла. Например, если три стороны равны a = 5, b = 6 и c = 7, то закон косинусов гласит: = 12/60 = 0.2, а с помощью калькулятора C = 1,3734 радиана = 78,69°.
Примечание: Если треугольник тупоугольный, то cos C отрицателен. Предположим, что три стороны равны a = 5, b = 6 и c = 10. Тогда закон косинусов гласит: 100 = 25 + 36 – 60 cos /60 = — 0,81667. Как видно из графиков на предыдущей странице, косинус тупого угла отрицателен. Это нормально, и ваш калькулятор правильно вычислит арккосинус.Вы получите
Закон синусов
Закон синусов также представляет собой просто сформулированное уравнение Обратите внимание, что закон синусов гласит, что три отношения равны. Как и закон косинусов, вы можете использовать закон синусов двумя способами.
Как и закон косинусов, вы можете использовать закон синусов двумя способами.
Во-первых, если известны два угла и сторона, противолежащая одному из них, то можно определить сторону, противолежащую другому из них. Например, если угол A = 30°, угол B = 45°, а сторона a = 16, то по закону синусов (sin 30°)/16 = (sin 45°)/ b . Решение для b дает b = 16(sin 45°)/(sin 30°) = 22,6274.
Во-вторых, если вы знаете две стороны и угол, противолежащий одной из них, то вы можете почти определить угол, противолежащий другой из них. Например, если сторона a = 25, сторона b = 15, а угол A = 40°, то по закону синусов (sin 40°)/25 = (sin B )/15. Нахождение sin B дает sin B = 15 (sin 40°)/25 = 0.38567. Теперь арксинус 0,38567 = 22,686°.
Предупреждение: возможно, у вас нет правильного ответа. Есть два угла между 0 и 180 ° с данным синусоидальным; второй является дополнением первого. Таким образом, в данном случае вторым является тупой угол 180 – 22,686 = 157,314°. Эта ситуация неопределенная. Зная две стороны и угол, противолежащий одной из них, не всегда достаточно для определения треугольника. В геометрии не существует детерминистской теоремы о конгруэнтности «бок-бок-угол».
Таким образом, в данном случае вторым является тупой угол 180 – 22,686 = 157,314°. Эта ситуация неопределенная. Зная две стороны и угол, противолежащий одной из них, не всегда достаточно для определения треугольника. В геометрии не существует детерминистской теоремы о конгруэнтности «бок-бок-угол».
Проблемы
553. AB — линия длиной 652 фута на одном берегу ручья, а C — точка на противоположном берегу. A = 53° 18′ и B = 48° 36′. Найдите ширину потока от С до АВ.
557. В треугольнике ABC, a = 700 футов, B = 73° 48′, и C = 37° 21′. Если M является средней точкой BC , найдите длины AM, и углы BAM и MAC.
561. Три окружности радиусов 3, 4 и 5 касаются друг друга снаружи. Найдите углы треугольника, образованного соединением их центров.
563. A и B точки на противоположных берегах реки. На одном берегу линия AC измеряется 650 футов. Угол A = 73° 40′, а C = 52° 38′. Найдите АБ.
На одном берегу линия AC измеряется 650 футов. Угол A = 73° 40′, а C = 52° 38′. Найдите АБ.
570. P и Q две недоступные точки.Чтобы найти расстояние между ними, в произведенном QP берется точка A и измеряется линия AB длиной 1200 футов, образующая угол PAB = 26° 35′. Угол ABP = 48° 12′ и ABQ = 106° 42′. Как долго PQ ?
579. Стороны параллелограмма равны AB = 209,16 и AD = 347,25, а диагональ AC = 351,47. Найдите углы и другую диагональ.
580. В параллелограмме ABCD, диагональ AC = 521,16, затем угол ABC = 110° 48′ 12″, и BAC = 2 2 Найдите длины сторон и другой диагонали.
586. Диагонали параллелограмма равны 374,14 и 427,21, а угол между ними равен 70° 12′ 38″. Найдите стороны.
590. Стороны четырехугольника по порядку равны 763. 83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами равен 53° 13′ 12″. Найдите остальные три угла.
83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами равен 53° 13′ 12″. Найдите остальные три угла.
593. A и B — это две точки на противоположных сторонах водоема, и замеры должны производиться по линии AB в точках на одну четверть, половину и три четверти расстояние от A до B. На берегу измеряется линия AC длиной 1200 футов, а углы BAC = 63° 19′ и ACB = 78° 43′.Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, в соответствующих точках на АВ ?
608. На одной стороне линии потока PA = 586,3 фута, PB = 751,6 фута являются мерами, угол APB равен 167° 36′. Q — точка на противоположной стороне потока. Угол PAQ = 63° 18′ и PBQ = 49° 24′. Найдите PQ.
612. Чтобы найти расстояние между двумя недоступными точками P и Q, линия AB длиной 763,4 фута откладывается так, что AB пересекает PQ 9 отрезки AB и PQ не пересекаются].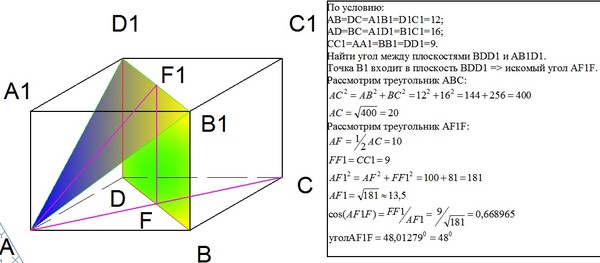 Углы PAB = 98° 47′, QAB = 41° 36′, PBA = 37° 16′ и QBA = 94° 12′. Найдите длину PQ.
Углы PAB = 98° 47′, QAB = 41° 36′, PBA = 37° 16′ и QBA = 94° 12′. Найдите длину PQ.
Советы
553. Вы можете использовать закон синусов, чтобы определить любую из длин AB или BC. Задача состоит в том, чтобы найти расстояние от C до AB. Это означает, что вы опускаете перпендикуляр из точки C на эту линию и определяете ее длину. Вы можете использовать угол A и линию AC , чтобы найти его, или вы можете использовать угол B и линию BC , чтобы найти его.
557. Тот же намек, что и 553.
561. Окружности касаются друг друга, поэтому линия из одного центра в другой есть сумма радиусов одной окружности и другой. У вас есть треугольник со сторонами 7, 8 и 9. Вы можете использовать закон косинусов, чтобы найти углы.
563. Здесь хорошо работает закон синусов.
570. Нарисуйте фигуру. Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов треугольника ABP, , и вы можете найти AQ , используя закон синусов треугольника ABQ.
Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов треугольника ABP, , и вы можете найти AQ , используя закон синусов треугольника ABQ.
579. Вы знаете стороны треугольников ABC и ADC, поэтому можете определить их углы. В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
580. Сначала решите треугольник ABC. Далее в треугольнике ABD вы знаете две стороны и легко можете определить угол BAD.
586. «Включенный угол» — это один из двух углов между двумя диагоналями. Другой прилежащий угол — это дополнение к нему 180° – 70° 12′ 38″. Пусть P будет точкой пересечения двух диагоналей. Это середина каждой диагонали, так что вы знаете расстояние между P и любой вершиной.Примените закон косинусов к двум треугольникам с вершинами P и двум вершинам параллелограмма.
590. Вы знаете стороны четырехугольника ABCD и угол при B. Вы можете решить треугольник ABC. Тогда вы знаете все стороны треугольника ACD, и можете найти его углы.
593. Сначала определите расстояние AB по закону синусов.Тогда для каждого из правильных положений лодки P, известны две стороны и угол между ними треугольника PAC, , так что по закону косинусов можно определить нужный угол.
608. Сначала решите треугольник APB. Тогда у вас будет достаточно информации, чтобы решить треугольник AQB.
612. Есть несколько способов решить эту проблему. Вот один из способов. Определить PA по закону синусов для треугольника PAB, и определить QA по закону синусов для треугольника QAB. Затем используйте закон косинусов для треугольника PAQ.
Ответы
553. 345,43 футов.
557. 490,83 футов.
561. 48° 11′ 24″, 58° 24′ 42″, 73° 23′ 54″.
563. 640 футов 10 дюймов.
570. 651,9 футов.
579. 106° 18′ 46″, 73° 41′ 14″, 452,92.
580. 255,93, 372,11, 369,22.
586. 231,94, 328,93.
590. 125° 6′ 12″, 70° 57′ 54″, 110° 42′ 42″.
593. 23° 27′, 47° 58, 66° 34′.
608. 854,6 фута.
612. 920,76 футов.
Как найти наклон перпендикулярной линии
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
Руководство по телефону Cisco Unified IP Phone 7962G и 7942G и краткий справочник по Cisco Unified Communications Manager 7.1(2) (SCCP и SIP)
%PDF-1.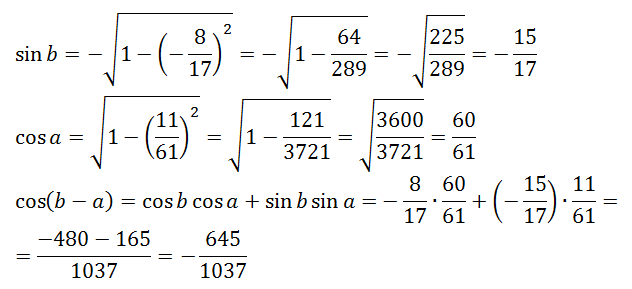 4
%
1 0 объект >поток
application/pdfРуководство по телефонам Cisco Unified IP 7962G и 7942G и краткий справочник по Cisco Unified Communications Manager 7.1(2) (SCCP и SIP) iText 1.4.1 (от lowagie.com) конечный поток
эндообъект
2 0 объект >поток
application/pdfРуководство по телефонам Cisco Unified IP 7962G и 7942G и краткий справочник по Cisco Unified Communications Manager 7.
4
%
1 0 объект >поток
application/pdfРуководство по телефонам Cisco Unified IP 7962G и 7942G и краткий справочник по Cisco Unified Communications Manager 7.1(2) (SCCP и SIP) iText 1.4.1 (от lowagie.com) конечный поток
эндообъект
2 0 объект >поток
application/pdfРуководство по телефонам Cisco Unified IP 7962G и 7942G и краткий справочник по Cisco Unified Communications Manager 7. 1(2) (SCCP и SIP) iText 1.4.1 (от lowagie.com) конечный поток
эндообъект
3 0 объект>
эндообъект
4 0 объект >поток
хв, * ЛКЛ.
1(2) (SCCP и SIP) iText 1.4.1 (от lowagie.com) конечный поток
эндообъект
3 0 объект>
эндообъект
4 0 объект >поток
хв, * ЛКЛ. Q,HHLK,ϳsrqw6TH/r
w3T0TI24R0
Q,HHLK,ϳsrqw6TH/r
w3T0TI24R0
Независимые и взаимоисключающие события – вводная статистика
Независимые и взаимоисключающие события , а не означают одно и то же.
Независимые события
Два события независимы, если верно следующее:
- Р ( А | Б ) = Р ( А )
- Р ( Б | А ) = Р ( Б )
- P ( A И B ) = P ( A ) P ( B )
Два события A и B являются независимыми, если знание того, что одно произошло, не влияет на вероятность возникновения другого. Например, результаты двух ролей честной кости являются независимыми событиями. Исход первого броска не влияет на вероятность исхода второго броска. Чтобы показать, что два события независимы, необходимо показать только одно из вышеперечисленных условий. Если два события НЕ являются независимыми, то мы говорим, что они зависимы .
Например, результаты двух ролей честной кости являются независимыми событиями. Исход первого броска не влияет на вероятность исхода второго броска. Чтобы показать, что два события независимы, необходимо показать только одно из вышеперечисленных условий. Если два события НЕ являются независимыми, то мы говорим, что они зависимы .
Отбор проб может производиться с заменой или без замены .
- С заменой : Если каждый элемент популяции заменяется после его выбора, то этот элемент может быть выбран более одного раза.Когда выборка выполняется с замещением, события считаются независимыми, то есть результат первого выбора не изменит вероятности второго выбора.
- Без замены : При отборе проб без замены каждый член генеральной совокупности может быть выбран только один раз. В этом случае на вероятность второго выбора влияет результат первого выбора. События считаются зависимыми или не независимыми.

Если неизвестно, являются ли A и B независимыми или зависимыми, предполагает, что они зависимы, пока не будет показано обратное .
У вас есть хорошо перетасованная колода из 52 карт. Он состоит из четырех мастей. Масти — трефы, бубны, червы и пики. В каждой масти по 13 карт, состоящих из 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (валет), Q (дама), K (король) этот костюм.
а. Выборка с заменой:
Предположим, вы выбираете три карты с заменой. Первая карта, которую вы выберете из 52 карт, — это Q пик. Вы кладете эту карту обратно, перетасовываете карты и выбираете вторую карту из колоды из 52 карт.Это десятка треф. Вы кладете эту карту обратно, перетасовываете карты и выбираете третью карту из колоды из 52 карт. На этот раз карта снова Q пик. Ваши выборы { Q пик, десятка треф, Q пик}. Вы дважды выбрали Q пик. Вы выбираете каждую карту из колоды из 52 карт.
Ваши выборы { Q пик, десятка треф, Q пик}. Вы дважды выбрали Q пик. Вы выбираете каждую карту из колоды из 52 карт.
б. Выборка без замены:
Допустим, вы выбираете три карты без замены. Первая карта, которую вы выберете из 52 карт, это K червей.Вы откладываете эту карту в сторону и выбираете вторую карту из 51 карты, оставшейся в колоде. Это тройка бубнов. Вы откладываете эту карту в сторону и выбираете третью карту из оставшихся 50 карт в колоде. Третья карта — J пик. Ваши выборы: { K червей, тройка бубен, J пик}. Поскольку вы выбрали карты без замены, вы не можете выбрать одну и ту же карту дважды.
Попробуйте
У вас есть хорошо перетасованная колода из 52 карт.Он состоит из четырех мастей. Масти — трефы, бубны, червы и пики. В каждой масти по 13 карт, состоящих из 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (валет), Q (дама), K (король) этот костюм. Наугад выбираются три карты.
В каждой масти по 13 карт, состоящих из 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (валет), Q (дама), K (король) этот костюм. Наугад выбираются три карты.
- Предположим, вы знаете, что выбраны карты Q пик, K червей и Q пик. Можете ли вы решить, была ли выборка с заменой или без?
- Предположим, вы знаете, что выбраны карты Q пик, K червей и J пик.Можете ли вы решить, была ли выборка с заменой или без?
У вас есть хорошо перетасованная колода из 52 карт. Он состоит из четырех мастей. Масти — трефы, бубны, червы и пики. В каждой масти по 13 карт: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (валет), Q (дама) и K (король). этого костюма. S = пики, H = червы, D = бубны, C = трефы.
этого костюма. S = пики, H = червы, D = бубны, C = трефы.
- Предположим, вы выбираете четыре карты, но не кладете их обратно в колоду.Ваши карты: QS , 1 D , 1 C , QD .
- Предположим, вы выбираете четыре карты и кладете каждую карту обратно перед тем, как взять следующую карту. Ваши карты KH , 7 D , 6 D , KH .
Какой из a. или б. вы пробовали с заменой и какие вы пробовали без замены?
а. Без замены; б. С заменой
Попробуйте
У вас есть хорошо перетасованная колода из 52 карт.Он состоит из четырех мастей. Масти — трефы, бубны, червы и пики.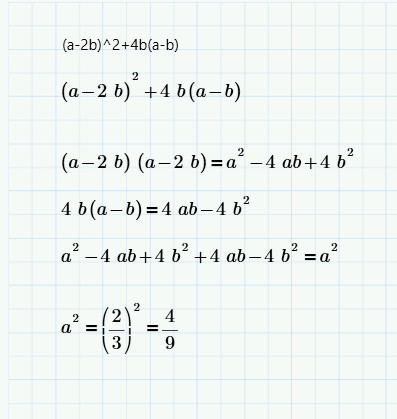 В каждой масти по 13 карт: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (валет), Q (дама) и K (король). этого костюма. S = пики, H = червы, D = бубны, C = трефы. Предположим, вы пробуете четыре карты без замены. Какие из следующих исходов возможны? Ответьте на тот же вопрос для выборки с заменой.
В каждой масти по 13 карт: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, J (валет), Q (дама) и K (король). этого костюма. S = пики, H = червы, D = бубны, C = трефы. Предположим, вы пробуете четыре карты без замены. Какие из следующих исходов возможны? Ответьте на тот же вопрос для выборки с заменой.
- КС , 1 Д , 1 К , КД
- КХ , 7 Д , 6 Д , КХ
- КС , 7 Д , 6 Д , КС
Взаимоисключающие события
A и B являются взаимоисключающими событиями, если они не могут произойти одновременно. Это означает, что A и B не имеют общих исходов и P ( A AND B ) = 0.
Это означает, что A и B не имеют общих исходов и P ( A AND B ) = 0.
Например, предположим, что пространство выборки S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Пусть А = {1, 2, 3, 4, 5}, В = {4, 5, 6, 7, 8} и С = {7, 9}. А И В = {4, 5}. P ( A AND B ) = и не равно нулю. Следовательно, A и B не исключают друг друга. A и C не имеют общих чисел, поэтому P ( A AND C ) = 0. Таким образом, A и C являются взаимоисключающими.
Таким образом, A и C являются взаимоисключающими.
Если неизвестно, являются ли A и B взаимоисключающими, предполагают, что это не так, пока не будет доказано обратное . Следующие примеры иллюстрируют эти определения и термины.
Подбросьте две честные монеты. (Это эксперимент.)
Пример пространства { HH , HT , TH , TT }, где T = хвосты и H = головы.Результатами являются HH , HT , TH и TT . Исходы HT и TH разные. HT означает, что на первой монете выпал орел, а на второй – решка. TH означает, что на первой монете выпала решка, а на второй – орёл.
TH означает, что на первой монете выпала решка, а на второй – орёл.
Попробуйте
Возьмите две карты из стандартной колоды из 52 карт с замещением. Найдите вероятность того, что выпадет хотя бы одна черная карта.
Подбросьте две честные монеты.Найдите вероятности событий.
- Пусть F = событие получения не более одной решки (ноль или одна решка).
- Пусть G = событие получения двух одинаковых граней.
- Пусть H = событие выпадения орла при первом броске, за которым следует орел или решка при втором броске.
- Являются ли F и G взаимоисключающими?
- Пусть J = событие выпадения всех решек. Являются ли J и H взаимоисключающими?
Посмотрите на образец пространства на (рисунок).
- Ноль (0) или одна (1) решка выпадает, когда выпадают результаты HH , TH , HT . Р ( Ф ) =
- Два лица одинаковы, если выпадет HH или TT . Р ( Г ) =
- Выпадение орла при первом подбрасывании, за которым следует орел или решка при втором подбрасывании, происходит, когда выпадает HH или HT . Р ( Н ) =
- F и G разделяют HH , поэтому P ( F AND G ) не равен нулю (0).
 F и G не исключают друг друга.
F и G не исключают друг друга. - Получение всех решек происходит, когда решки выпадают на обеих монетах ( TT ). Результатами H являются HH и HT .
J и H не имеют ничего общего, поэтому P ( J И H ) = 0. J и H исключают друг друга.
Попробуйте
В коробке два шара, один белый и один красный.Выбираем один шарик, кладем его обратно в коробку, и выбираем второй шарик (выборка с заменой). Найдите вероятность следующих событий:
- Пусть F = событие выпадения белого шара дважды.

- Пусть G = событие получения двух шаров разного цвета.
- Пусть H = событие получения белого цвета при первом выборе.
- Являются ли F и G взаимоисключающими?
- Являются ли G и H взаимоисключающими?
Бросьте один правильный шестигранный кубик.Демонстрационное пространство {1, 2, 3, 4, 5, 6}. Пусть событие A = лицо нечетное. Тогда A = {1, 3, 5}. Пусть событие B = лицо четное. Тогда В = {2, 4, 6}.
- Найдите дополнение A , A′ . Дополнение A , A′ равно B , потому что A и B вместе составляют пространство выборки.
 P ( A ) + P ( B ) = P ( A ) + P ( A′ ) = 1.Кроме того, P ( A ) = и P ( B ) =.
P ( A ) + P ( B ) = P ( A ) + P ( A′ ) = 1.Кроме того, P ( A ) = и P ( B ) =. - Пусть событие C = нечетные грани больше двух. Тогда C = {3, 5}. Пусть событие D = все четные грани меньше пяти. Тогда D = {2, 4}. P ( C AND D ) = 0, потому что у вас не может быть одновременно четного и нечетного лица. Следовательно, C и D являются взаимоисключающими событиями.

- Пусть событие E = все грани меньше пяти. E = {1, 2, 3, 4}.
Являются ли события C и E взаимоисключающими? (Ответьте да или нет.) Почему или почему нет?
№ C = {3, 5} и E = {1, 2, 3, 4}. P ( C И E ) = . Чтобы быть взаимоисключающими, P ( C AND E ) должны быть равны нулю.
- Найдите P ( C | A ). Это условная вероятность.Напомним, что событие C — это {3, 5}, а событие A — это {1, 3, 5}.
 Чтобы найти P ( C | A ), найдите вероятность C , используя выборочное пространство A . Вы уменьшили пространство выборки с исходного пространства выборки {1, 2, 3, 4, 5, 6} до {1, 3, 5}. Итак, P ( C | A ) = .
Чтобы найти P ( C | A ), найдите вероятность C , используя выборочное пространство A . Вы уменьшили пространство выборки с исходного пространства выборки {1, 2, 3, 4, 5, 6} до {1, 3, 5}. Итак, P ( C | A ) = .
Попробуйте
Let event A = изучение испанского языка. Пусть событие B = изучение немецкого языка.Затем A И B = изучение испанского и немецкого языков. Предположим, что P ( A ) = 0,4 и P ( B ) = 0,2. P ( A И B ) = 0,08. Являются ли события A и B независимыми? Подсказка: вы должны показать ОДНО из следующего:
Являются ли события A и B независимыми? Подсказка: вы должны показать ОДНО из следующего:
- Р ( А | Б ) = Р ( А )
- Р ( Б | А ) = Р ( Б )
- P ( A И B ) = P ( A ) P ( B )
Р ( А | Б ) =
События независимы, потому что P ( A | B ) = P ( A ).
Пусть событие G = посещение урока математики. Пусть событие H = посещение урока естествознания. Затем G И H = уроки математики и науки. Предположим, что P ( G ) = 0,6, P ( H ) = 0,5 и P ( G И H ) = 0,3. Являются ли G и H независимыми?
Если G и H независимы, то необходимо показать ОДИН из следующего:
- П ( Г | Н ) = П ( Г )
- P ( H | G ) = P ( H )
- P ( G И H ) = P ( G ) P ( H )
ПРИМЕЧАНИЕ
Ваш выбор зависит от имеющейся у вас информации. Вы можете выбрать любой из методов здесь, потому что у вас есть необходимая информация.
Вы можете выбрать любой из методов здесь, потому что у вас есть необходимая информация.
а. Покажите, что P ( G | H ) = P ( G ).
P ( G | H ) = = = 0,6 = P ( G )
б. Показать P ( G И H ) = P ( G ) P ( H ).
P ( G ) P ( H ) = (0.6)(0,5) = 0,3 = P ( G И H )
Поскольку G и H независимы, знание того, что человек посещает урок естествознания, не меняет вероятность того, что он или она посещает урок математики. Если бы эти два события не были независимыми (то есть, они были бы зависимыми), то знание того, что человек посещает урок естествознания, изменило бы вероятность того, что он или она будет заниматься математикой. Для практики покажите, что P ( H | G ) = P ( H ), чтобы показать, что G и H являются независимыми событиями.
Если бы эти два события не были независимыми (то есть, они были бы зависимыми), то знание того, что человек посещает урок естествознания, изменило бы вероятность того, что он или она будет заниматься математикой. Для практики покажите, что P ( H | G ) = P ( H ), чтобы показать, что G и H являются независимыми событиями.
Попробуйте
В мешке шесть красных и четыре зеленых шарика. Красные шарики отмечены цифрами 1, 2, 3, 4, 5 и 6. Зеленые шарики отмечены цифрами 1, 2, 3 и 4.
- R = красный шарик
- G = зеленый мрамор
- O = шарик с нечетным номером
- Образец пространства S = { R 1, R 2, R 3, R 4, R 5, R 6, г 1, г 2, Г 3, Г 4}.

S имеет десять исходов. Что такое P ( G И O )?
Let event C = посещение урока английского языка. Пусть событие D = урок речи.
Предположим P ( C ( C ) = 0,75, P ( D ) = 0,3, P ( C | D ) = 0,75 и P ( C и d и d ) = 0,225.
Обоснуйте свои ответы на следующие вопросы численно.
- Являются ли C и D независимыми?
- Являются ли C и D взаимоисключающими?
- Что такое P ( D | C )?
- Да, потому что P ( C | D ) = P ( C ).

- Нет, потому что P ( C И D ) не равно нулю.
- P ( D | C ) = = = 0.3
Попробуйте
Студент идет в библиотеку. Пусть события B = студент извлекает книгу и D = студент извлекает DVD. Предположим, что P ( B ) = 0,40, P ( D ) = 0,30 и P ( B AND D ) = 0,20.
- Найдите P ( B | D ).
- Найдите P ( D | B ).

- Являются ли B и D независимыми?
- Являются ли B и D взаимоисключающими?
В коробке три красные карты и пять синих карт.Красные карточки отмечены цифрами 1, 2 и 3, а синие карточки отмечены цифрами 1, 2, 3, 4 и 5. Карты хорошо перетасованы. Вы лезете в коробку (вы не можете в нее заглянуть) и берете одну карту.
Let R = взята красная карта, B = взята синяя карта, E = взята карта с четным номером.
Образец пространства S = R = R 2, R 2, R 3, B 1, B 2, B 3, B 4, B 5. S имеет восемь исходов.
S имеет восемь исходов.
- P ( R ) = . Р ( Б ) = . P ( R AND B ) = 0. (Вы не можете взять одну карту одновременно красную и синюю.)
- P ( E ) = . (Есть три карты с четными номерами: R 2, B 2 и B 4.)
- P ( E | B ) = . (Есть пять синих карт: Б 1, Б 2, Б 3, Б 4 и Б 5.Из синих карт две четные карты; В 2 и В 4.
 )
) - P ( B | E ) = . (Есть три карты с четными номерами: R 2, B 2 и B 4. Из четных карт синие; B 2 и B 4.)
- События R и B являются взаимоисключающими, поскольку P ( R И B ) = 0,
- Пусть G = карта с номером больше 3. Г = { В 4, В 5}. P ( G ) = . Пусть H = синяя карта с номерами от одного до четырех включительно. H = { B 1, B 2, B 3, B 4}.
 P ( G | H ) = . (Единственная карта в H , имеющая номер больше трех, это B 4.) Поскольку = , P ( G ) = P ( G | H ), это означает, что G и H независимы.
P ( G | H ) = . (Единственная карта в H , имеющая номер больше трех, это B 4.) Поскольку = , P ( G ) = P ( G | H ), это означает, что G и H независимы.
Попробуйте
На баскетбольной арене,
- 70% болельщиков болеют за хозяев поля.
- 25% болельщиков одеты в синее.
- 20% болельщиков одеты в синее и болеют за команду гостей.
- Среди болельщиков, которые болеют за команду гостей, 67% одеты в синюю форму.
Пусть A будет событием, когда болельщик болеет за команду гостей.
Пусть B будет событием, когда болельщик одет в синее.
Являются ли события поддержки команды гостей и ношения синего независимыми? Являются ли они взаимоисключающими?
В определенном классе колледжа 60% учащихся составляют женщины. Пятьдесят процентов всех учеников в классе носят длинные волосы. Сорок пять процентов студентов — девушки, у них длинные волосы. Среди студенток 75% имеют длинные волосы. Пусть F будет событием, что студентка — женщина. Пусть L будет событием, что у студента длинные волосы. Случайным образом выбирается один ученик.Являются ли события женского пола и длинных волос независимыми?
- В этом примере приведены следующие вероятности:
- Р ( Ф ) = 0,60; П ( Д ) = 0,50
- P ( F И L ) = 0,45
- P ( L | F ) = 0,75
ПРИМЕЧАНИЕ
Ваш выбор зависит от имеющейся у вас информации. В этом примере можно использовать первое или последнее условие в списке.Вы еще не знаете P ( F | L ), поэтому не можете использовать второе условие.
В этом примере можно использовать первое или последнее условие в списке.Вы еще не знаете P ( F | L ), поэтому не можете использовать второе условие.
Решение 1. Проверьте, являются ли P ( F И L ) = P ( F ) P ( L ). Нам дано, что P ( F AND L ) = 0,45, но P ( F ) P ( L ) = (0,60)(0,50) = (0,60)(0,50) События женского пола и длинных волос не являются независимыми, потому что P ( F AND L ) не равно P ( F ) P ( L ).
Решение 2. Проверьте, равно ли P ( L | F ) P ( L ). Нам дано, что P ( L | F ) = 0,75, но P ( L ) = 0,50; они не равны. События женского пола и длинных волос не являются независимыми.
Интерпретация результатов Факты того, что ты женщина и у тебя длинные волосы, не являются независимыми; знание того, что ученица — женщина, изменяет вероятность того, что у ученицы длинные волосы.
Попробуйте
Марк решает, по какой дороге идти на работу. Его выбор: I = Автомагистраль между штатами и F = Пятая улица.
- P ( I ) = 0,44 и P ( F ) = 0,56
- P ( I AND F ) = 0, потому что Марк будет идти на работу только одним маршрутом.

Какова вероятность P ( I ИЛИ F )?
- Бросьте одну честную монету (у монеты две стороны, H и T ).Итоги ________. Подсчитайте результаты. Есть ____ результатов.
- Бросьте один правильный шестигранный кубик (на кубике 1, 2, 3, 4, 5 или 6 точек). Итоги ________________. Подсчитайте результаты. Есть ___ исходов.
- Умножьте два числа исходов. Ответ _______.
- Если вы подбросите одну правильную монету и подбросите одну правильную шестигранную кость, ответ в части c. — количество результатов (размер выборочного пространства). Каковы результаты? (Подсказка: два исхода — H 1 и T 6.)
- Событие A = решка ( H ) на монете, за которой следует четное число (2, 4, 6) на кубике.

А = {_________________}. Найдите P ( A ). - Event B = решка на монете, за которой следует тройка на кубике. Б = {________}. Найдите P ( B ).
- Являются ли A и B взаимоисключающими? (Подсказка: что такое P ( A AND B )? Если P ( A AND B ) = 0, то A и B 9057 равны)
- Являются ли A и B независимыми? (Подсказка: P ( A и B и P ) = P ( A ) P ( B )? Если P ( A и B ) = р.
 ( A ) P ( B ), то A и B независимые. Если нет, то зависимые).
( A ) P ( B ), то A и B независимые. Если нет, то зависимые).
- H и T ; 2
- 1, 2, 3, 4, 5, 6; 6
- 2(6) = 12
- T
- T 1, T 2, T 3, T 4, T 5, T 5, T 6, H 1, H 2, H 3, H 4 , Х 5, Х 6
- А = { Н 2, Н 4, Н 6}; П ( А ) =
- В = { Н 3}; Р ( Б ) =
- Да, потому что P ( A И B ) = 0
- P ( A И B ) = 0.
 P ( A ) P ( B ) = . P ( A AND B ) не равно P ( A ) P ( B ), поэтому A и B и B
P ( A ) P ( B ) = . P ( A AND B ) не равно P ( A ) P ( B ), поэтому A и B и B
Попробуйте
В коробке два шара, один белый и один красный. Выбираем один шарик, кладем его обратно в коробку, и выбираем второй шарик (выборка с заменой). Пусть T — событие выпадения белого шара дважды, F — событие выпадения белого шара первым, S — событие выпадения белого шара во втором розыгрыше.
- Вычислить P ( T ).

- Вычислить P ( T | F ).
- Являются ли T и F независимыми?
- Являются ли F и S взаимоисключающими?
- Являются ли F и S независимыми?
Обзор главы
Два события A и B являются независимыми, если знание того, что одно произошло, не влияет на вероятность возникновения другого.Если два события не являются независимыми, то говорят, что они зависимы.
При выборке с замещением каждый элемент совокупности заменяется после его выбора, так что этот элемент может быть выбран более одного раза, а события считаются независимыми. При выборке без замены каждый член совокупности может быть выбран только один раз, и события не считаются независимыми. Когда события не имеют общих результатов, они исключают друг друга.
Когда события не имеют общих результатов, они исключают друг друга.
выборочных пространств, событий и их вероятностей
Примеры пространств и событий
Бросание обычного шестигранного игрального кубика является известным примером случайного эксперимента , действия, для которого можно перечислить все возможные исходы, но для которого нельзя с уверенностью предсказать фактический исход любого конкретного испытания эксперимента. В такой ситуации мы хотим присвоить каждому результату, такому как выпадение двойки, число, называемое вероятностью исхода, которое указывает, насколько вероятно, что исход произойдет.Точно так же мы хотели бы присвоить вероятность любому событию или совокупности результатов, например выпадению четного числа, которая указывает, насколько вероятно, что событие произойдет, если эксперимент будет выполнен. Этот раздел обеспечивает основу для обсуждения вероятностных проблем с использованием только что упомянутых терминов.
Определение
A случайный эксперимент — это механизм, дающий определенный результат, который невозможно предсказать с уверенностью.Выборочное пространство . Набор всех возможных исходов случайного эксперимента. Число , связанное со случайным экспериментом, представляет собой множество всех возможных исходов. Событие . Любой набор исходов. — это подмножество выборочного пространства.
Определение
Говорят, что событие E происходит в конкретном испытании эксперимента, если наблюдаемый результат является элементом множества E .
Пример 1
Создайте образец пространства для эксперимента, состоящего из подбрасывания одной монеты.
Решение:
Результаты можно обозначить как h для голов и t для решек. Тогда образцом пространства является множество S={h,t}.
Тогда образцом пространства является множество S={h,t}.
Пример 2
Создайте тестовое пространство для эксперимента, состоящего из броска одного игрального кубика.Найдите события, соответствующие фразам «выпало четное число» и «выпало число больше двух».
Решение:
Исходы могут быть помечены в соответствии с количеством точек на верхней грани игральной кости. Тогда образцом пространства является множество S={1,2,3,4,5,6}.
Четными исходами являются 2, 4 и 6, поэтому событием, соответствующим фразе «выпало четное число», является множество {2,4,6}, которое естественно обозначить буквой Е .Пишем E={2,4,6}.
Аналогично, событием, которое соответствует фразе «выпало число больше двух», является множество T={3,4,5,6}, которое мы обозначили T .
Графическое представление выборочного пространства и событий представляет собой диаграмму Венна , как показано на рисунке 3. 1 «Диаграммы Венна для двух выборочных пространств» для примечания 3.6 «Пример 1» и примечания 3.7 «Пример 2». В общем случае выборочное пространство S представлено прямоугольником, исходы — точками внутри прямоугольника, а события — овалами, заключающими исходы, из которых они состоят.
1 «Диаграммы Венна для двух выборочных пространств» для примечания 3.6 «Пример 1» и примечания 3.7 «Пример 2». В общем случае выборочное пространство S представлено прямоугольником, исходы — точками внутри прямоугольника, а события — овалами, заключающими исходы, из которых они состоят.
Рисунок 3.1 Диаграммы Венна для двух выборочных пространств
Пример 3
Случайный эксперимент заключается в подбрасывании двух монет.
- Постройте образец пространства для ситуации, когда монеты неразличимы, например, два новых пенни.
- Постройте пример пространства для ситуации, когда монеты различимы, например, одна копейка, а другая пятицентовая монета.
Решение:
- После того, как монеты подброшены, вы видите либо две решки, которые могут быть помечены как 2h, либо две решки, которые могут быть помечены как 2t, либо разные монеты, которые могут быть помечены как d .
 Таким образом, выборочное пространство равно S={2h,2t,d}.
Таким образом, выборочное пространство равно S={2h,2t,d}. - Поскольку мы можем отличить монеты друг от друга, теперь монеты могут различаться двумя способами: пенни-орел и пятицентовик решка или пенни-решка и пятицентовик решка. Мы можем обозначить каждый результат как пару букв, первая из которых указывает, как приземлился пенни, а вторая — как приземлился пятицентовик.Образцовое пространство тогда S′={hh,ht,th,tt}.
Устройство, которое может быть полезно для определения всех возможных результатов случайного эксперимента, особенно того, который можно рассматривать как протекающий поэтапно, называется древовидной диаграммой . Это описано в следующем примере.
Пример 4
Создайте выборочное пространство, описывающее все семьи с тремя детьми в соответствии с полом детей в соответствии с порядком рождения.
Решение:
Два исхода — «два мальчика, затем девочка», которые мы могли бы обозначить как bbg, и «девочка, затем два мальчика», которые мы могли бы обозначить как gbb. Очевидно, что исходов много, и когда мы пытаемся перечислить их все, может быть трудно быть уверенным, что мы нашли их все, если мы не будем действовать систематически. Древовидная диаграмма, показанная на рис. 3.2 «Древовидная диаграмма для семей с тремя детьми», дает систематический подход.
Очевидно, что исходов много, и когда мы пытаемся перечислить их все, может быть трудно быть уверенным, что мы нашли их все, если мы не будем действовать систематически. Древовидная диаграмма, показанная на рис. 3.2 «Древовидная диаграмма для семей с тремя детьми», дает систематический подход.
Рис. 3.2 Древовидная схема для трехдетных семей
Диаграмма была построена следующим образом. Есть две возможности для первого ребенка, мальчика или девочки, поэтому мы рисуем два отрезка, выходящих из начальной точки, один заканчивается на b для «мальчика», а другой заканчивается на g для «девочки». ” Для каждой из этих двух возможностей для первого ребенка есть две возможности для второго ребенка, «мальчика» или «девочки», поэтому из каждого из b и g мы проводим два отрезка линии, один отрезок оканчивается на b и один в г .Для каждой из четырех конечных точек теперь на диаграмме есть две возможности для третьего ребенка, поэтому мы повторяем процесс еще раз.
Отрезки называются ветвями дерева. Правая конечная точка каждой ветви называется узлом . Крайние правые узлы — это конечных узлов ; каждому соответствует исход, как показано на рисунке.
Из дерева легко прочитать восемь результатов эксперимента, поэтому пространство выборки, читая сверху вниз конечные узлы дерева,
S={bbb,bbg,bgb,bgg,gbb,gbg,ggb,ggg}Вероятность
Определение
Вероятность исхода Число, которое измеряет вероятность исхода. e в пространстве выборок S — это число p между 0 и 1, которое измеряет вероятность того, что e произойдет в одном испытании соответствующего случайного эксперимента. Значение p = 0 соответствует невозможности исхода e , а значение p = 1 соответствует исходу e достоверности.
Определение
Вероятность событияЧисло, измеряющее вероятность события. A — это сумма вероятностей отдельных исходов, из которых она состоит. Обозначается P(A).
Следующая формула выражает содержание определения вероятности события:
Если событие E равно E={e1,e2,…,ek}, то
P(E)=P(e1)+P(e2)+ · · · +P(ek)Рисунок 3.3 «Выборочные пространства и вероятность» графически иллюстрирует определения.
Рисунок 3.3 Пространства выборок и вероятность
Поскольку все пространство выборки S является событием, которое обязательно произойдет, сумма вероятностей всех исходов должна быть равна 1.
В обычном языке вероятности часто выражаются в процентах. Например, мы бы сказали, что вероятность дождя завтра составляет 70%, что означает, что вероятность дождя равна 0,70. Мы будем использовать эту практику здесь, но во всех последующих расчетных формулах мы будем использовать форму 0.70 а не 70%.
Мы будем использовать эту практику здесь, но во всех последующих расчетных формулах мы будем использовать форму 0.70 а не 70%.
Пример 5
Монета называется «уравновешенной» или «справедливой», если вероятность выпадения каждой стороны одинакова. Назначьте вероятность каждому результату в пространстве выборки для эксперимента, состоящего из подбрасывания одной честной монеты.
Решение:
С исходами, помеченными h для орла и t для решки, выборочное пространство представляет собой множество S={h,t}. Поскольку исходы имеют одинаковые вероятности, которые в сумме должны составлять 1, каждому исходу присваивается вероятность 1/2.
Пример 6
Кубик называется «сбалансированным» или «справедливым», если каждая грань с одинаковой вероятностью выпадет сверху. Назначьте вероятность каждому результату в пространстве выборки для эксперимента, состоящего в подбрасывании единственного игрального кубика. Найти вероятности событий E : «выпало четное число» и T : «выпало число больше двух».
Найти вероятности событий E : «выпало четное число» и T : «выпало число больше двух».
Решение:
С исходами, помеченными в соответствии с количеством точек на верхней грани игральной кости, выборочное пространство представляет собой набор S={1,2,3,4,5,6}.Поскольку существует шесть равновероятных исходов, сумма которых должна давать 1, каждому присваивается вероятность 1/6.
Поскольку E={2,4,6}, P(E)=1/6+1/6+1/6=3/6=1/2.
Поскольку T={3,4,5,6}, P(T)=4∕6=2∕3.
Пример 7
Подбрасываются две честные монеты. Найдите вероятность того, что монеты совпадут, т. е. обе решки или решки.
Решение:
В примечании 3.8 «Пример 3» мы построили выборочное пространство S={2h,2t,d} для ситуации, когда монеты идентичны, и выборочное пространство S′={hh,ht,th,tt} для ситуации, когда две монеты можно отличить друг от друга.
Теория вероятностей не говорит нам как присваивать вероятности исходам, а только что делать с ними после их присвоения. В частности, при использовании выборочного пространства S совпадающие монеты представляют собой событие M={2h,2t}, которое имеет вероятность P(2h)+P(2t).Используя выборочное пространство S ‘, сопоставление монет — это событие M ‘= {hh, tt}, которое имеет вероятность P (hh) + P (tt). В физическом мире не должно иметь значения, идентичны монеты или нет, и поэтому мы хотели бы присвоить вероятности исходам так, чтобы числа P(M) и P(M′) были одинаковыми и наилучшим образом соответствовали тому, что мы наблюдайте, когда настоящие физические эксперименты проводятся с монетами, которые кажутся честными. Фактический опыт показывает, что исходы в S’ равновероятны, поэтому мы присваиваем каждой вероятности 1/4, а затем
P(M’)=P(hh)+P(tt)=14+14=12Аналогичным образом, исходя из опыта, подходящим выбором для результатов в S является:
P(2h)=14 P(2t)=14 P(d)=12, которые дают тот же окончательный ответ
Р(М)=Р(2ч)+Р(2т)=14+14=12 Предыдущие три примера иллюстрируют, как вероятности могут быть вычислены простым подсчетом, когда выборочное пространство состоит из конечного числа равновероятных исходов. В некоторых ситуациях отдельные результаты любого выборочного пространства, представляющего эксперимент, неизбежно неодинаково вероятны, и в этом случае вероятности не могут быть вычислены простым подсчетом, а должна использоваться вычислительная формула, данная в определении вероятности события.
В некоторых ситуациях отдельные результаты любого выборочного пространства, представляющего эксперимент, неизбежно неодинаково вероятны, и в этом случае вероятности не могут быть вычислены простым подсчетом, а должна использоваться вычислительная формула, данная в определении вероятности события.
Пример 8
Распределение учащихся местной средней школы по расовому и этническому признаку: 51% белых, 27% черных, 11% латиноамериканцев, 6% азиатов и 5% всех остальных.Учащийся выбирается случайным образом из этой средней школы. (Выбор «случайно» означает, что каждый ученик имеет равные шансы быть выбранным.) Найдите вероятности следующих событий:
- B : студент черный,
- M : студент из меньшинства (то есть не белый),
- N : студент не черный.
Решение:
Эксперимент представляет собой действие по случайному выбору учащегося из числа учащихся старшей школы. Очевидным примерным пространством является S={w,b,h,a,o}. Поскольку 51% учащихся белые и все учащиеся имеют одинаковые шансы быть выбранными, P(w)=0,51, и аналогично для других результатов. Эта информация сведена в следующую таблицу:
Очевидным примерным пространством является S={w,b,h,a,o}. Поскольку 51% учащихся белые и все учащиеся имеют одинаковые шансы быть выбранными, P(w)=0,51, и аналогично для других результатов. Эта информация сведена в следующую таблицу:
- Поскольку B={b}, P(B)=P(b)=0,27.
- Поскольку M={b,h,a,o}, P(M)=P(b)+P(h)+P(a)+P(o)=0,27+0,11+0,06+0,05=0,49
- Поскольку N={w,h,a,o}, P(N)=P(w)+P(h)+P(a)+P(o)=0.51+0,11+0,06+0,05=0,73
Пример 9
Учащийся старшей школы, рассмотренный в Примечании 3.18 «Пример 8», может быть разбит на десять категорий следующим образом: 25% белых мужчин, 26% белых женщин, 12% чернокожих мужчин, 15% чернокожих женщин, 6% латиноамериканских мужчин. , 5% латиноамериканских женщин, 3% азиатских мужчин, 3% азиатских женщин, 1% мужчин из других меньшинств вместе взятых и 4% женщин из других меньшинств вместе взятых. Учащийся выбирается случайным образом из этой средней школы.Найдите вероятности следующих событий:
Учащийся выбирается случайным образом из этой средней школы.Найдите вероятности следующих событий:
- B : студент черный,
- MF: студентка из меньшинства,
- ФН: студентка не черная.
Решение:
Теперь выборочное пространство равно S={wm,bm,hm,am,om,wf,bf,hf,af,of}. Информацию, приведенную в примере, можно обобщить в следующей таблице, называемой двусторонней таблицей непредвиденных обстоятельств :
| Пол | Раса/этническая принадлежность | ||||
|---|---|---|---|---|---|
| Белый | Черный | Латиноамериканец | Азии | Другие | |
| Мужской | 0. 25 25 | 0,12 | 0,06 | 0,03 | 0,01 |
| Женский | 0,26 | 0,15 | 0,05 | 0,03 | 0,04 |
- Поскольку B={bm,bf}, P(B)=P(bm)+P(bf)=0.12+0,15=0,27.
- Поскольку MF={bf,hf,af,of}, P(M)=P(bf)+P(hf)+P(af)+P(of)=0,15+0,05+0,03+0,04=0,27
- Поскольку FN={wf,hf,af,of}, P(FN)=P(wf)+P(hf)+P(af)+P(of)=0,26+0,05+0,03+0,04=0,38
Ключевые выводы
- Выборочное пространство случайного эксперимента представляет собой совокупность всех возможных результатов.

- Событие, связанное со случайным экспериментом, является подмножеством выборочного пространства.
- Вероятность любого исхода — это число от 0 до 1. Вероятности всех исходов в сумме составляют 1.
- Вероятность любого события A равна сумме вероятностей исходов A .
Упражнения
В коробке 10 белых и 10 черных шариков.Создайте образец пространства для эксперимента по случайному извлечению с заменой двух шариков подряд и каждый раз отмечая цвет. (Вытягивание «с возвратом» означает, что первый шарик возвращается до того, как будет вытащен второй шарик.)
В коробке 16 белых и 16 черных шариков. Создайте образец пространства для эксперимента по случайному извлечению с заменой трех шариков подряд и каждый раз отмечая цвет.
 (Вытягивание «с возвратом» означает, что каждый шарик возвращается до того, как будет вытащен следующий шарик.)
(Вытягивание «с возвратом» означает, что каждый шарик возвращается до того, как будет вытащен следующий шарик.)В коробке 8 красных, 8 желтых и 8 зеленых шариков. Создайте образец пространства для эксперимента по случайному извлечению с заменой двух шариков подряд и каждый раз отмечая цвет.
В коробке 6 красных, 6 желтых и 6 зеленых шариков.Создайте образец пространства для эксперимента по случайному извлечению с заменой трех шариков подряд и каждый раз отмечая цвет.
В ситуации упражнения 1 перечислите исходы, включающие каждое из следующих событий.
- Извлечено хотя бы по одному шарику каждого цвета.

- Белый шарик не рисуется.
- Извлечено хотя бы по одному шарику каждого цвета.
В ситуации упражнения 2 перечислите исходы, включающие каждое из следующих событий.
- Извлечено хотя бы по одному шарику каждого цвета.
- Белый шарик не рисуется.
- Нарисовано больше черных, чем белых шариков.
В ситуации упражнения 3 перечислите исходы, включающие каждое из следующих событий.
- Желтый шарик не нарисован.
- Два вытащенных шарика одного цвета.
- Извлечено хотя бы по одному шарику каждого цвета.

В ситуации упражнения 4 перечислите исходы, включающие каждое из следующих событий.
- Желтый шарик не нарисован.
- Три извлеченных шарика одного цвета.
- Извлечено хотя бы по одному шарику каждого цвета.
Предполагая, что все исходы равновероятны, найдите вероятность каждого события в упражнении 5.
Предполагая, что все исходы равновероятны, найдите вероятность каждого события в упражнении 6.
Предполагая, что все исходы равновероятны, найдите вероятность каждого события в упражнении 7.

Предполагая, что все исходы равновероятны, найдите вероятность каждого события в упражнении 8.
Пример пространства S={a,b,c,d,e}.Определите два события как U={a,b,d} и V={b,c,d}. Предположим, что P(a) и P(b) равны 0,2, а P(c) и P(d) равны 0,1.
- Определите, каким должно быть P(e).
- Найти P(U).
- Найти P(V).
Пример пространства S={u,v,w,x}. Определите два события как A={v,w} и B={u,w,x}.Предположим, что P(u)=0,22, P(w)=0,36 и P(x)=0,27.
- Определите, каким должно быть P(v).

- Найти П(А).
- Найдите P(B).
- Определите, каким должно быть P(v).
Пример пространства S={m,n,q,r,s}. Определите два события как U={m,q,s} и V={n,q,r}. Вероятности некоторых исходов приведены в следующей таблице:
Вероятность исхода0.180.160.240.21- Определите, каким должно быть значение P(q).
- Найти P(U).
- Найти P(V).
Пример пространства S={d,e,f,g,h}. Определите два события как M={e,f,g,h} и N={d,g}. Вероятности некоторых исходов приведены в следующей таблице:
ИсходefghВероятность0.220.130.270. 19
19- Определите, какой должна быть P(g).
- Найти P(M).
- Найти P(N).
Базовый
Выборочное пространство, описывающее все трехдетные семьи в соответствии с полом детей в порядке их рождения, было построено в примечании 3.9 «Пример 4». Определите результаты, которые включают каждое из следующих событий в эксперименте случайного выбора семьи из трех детей.
- Как минимум один ребенок — девочка.
- Не более одного ребенка — девочка.
- Все дети девочки.
- Ровно двое детей девочки.
- Первенец — девочка.

Пространство выборки, описывающее три подбрасывания монеты, такое же, как и построенное в Примечании 3.9 «Пример 4», где «мальчик» заменен на «орел», а «девочка» заменен на «решку». Определите исходы каждого из следующих событий в эксперименте по подбрасыванию монеты три раза.
- Монета чаще выпадает орлом, чем решкой.
- Монета выпадает орлом столько же раз, сколько решкой.
- Монета выпадает как минимум дважды.
- При последнем подбрасывании монета выпадает орлом.
Предполагая, что исходы равновероятны, найдите вероятность каждого события в упражнении 17.
Предполагая, что исходы равновероятны, найдите вероятность каждого события в упражнении 18.

Приложения
Следующая двусторонняя таблица непредвиденных обстоятельств дает разбивку населения в конкретном регионе в зависимости от возраста и употребления табака:
Возраст Употребление табака Курильщик Для некурящих До 30 лет 0.05 0,20 старше 30 лет 0,20 0,55 Человек выбран случайным образом.
 Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий.- Курильщик.
- Лицо моложе 30 лет.
- Курильщик моложе 30 лет.
Следующая двусторонняя таблица непредвиденных обстоятельств дает разбивку населения в конкретном регионе в зависимости от партийной принадлежности ( A , B , C или None ) и мнения о выпуске облигаций:
Принадлежность Мнение Сувениры Противостоит Затрудняюсь ответить А 0.  12
120,09 0,07 Б 0,16 0,12 0,14 С 0.04 0,03 0,06 Нет 0,08 0,06 0,03 Человек выбран случайным образом.
 Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий.- Лицо связано с партией B .
- Лицо связано с какой-то партией.
- Лицо выступает за выпуск облигаций.
- Лицо не имеет партийной принадлежности и не определилось с выпуском облигаций.
Следующая двусторонняя таблица непредвиденных обстоятельств дает разбивку населения замужних или ранее состоявших в браке женщин старше детородного возраста в определенной местности в зависимости от возраста вступления в первый брак и количества детей:
Возраст Количество детей 0 1 или 2 3 или больше До 20 лет 0.  02
020,14 0,08 20–29 0,07 0,37 0,11 30 лет и старше 0.10 0,10 0,01 Случайным образом выбрана женщина. Найдите вероятность каждого из следующих событий.
- Женщине было за двадцать, когда она вышла замуж в первый раз.

- В первый брак женщине было 20 лет и больше.
- У женщины не было детей.
- В первом браке женщине было около 20 лет, и у нее было как минимум трое детей.
- Женщине было за двадцать, когда она вышла замуж в первый раз.
Следующая двусторонняя таблица непредвиденных обстоятельств дает разбивку взрослого населения в определенной местности в зависимости от самого высокого уровня образования и от того, регулярно ли человек принимает пищевые добавки:
Образование Использование добавок Принимает Не берет Без диплома об окончании средней школы 0.  04
040,06 Диплом средней школы 0,06 0,44 Степень бакалавра 0,09 0,28 Высшее образование 0.01 0,02 Взрослый выбран случайным образом. Найдите вероятность каждого из следующих событий.
- Человек имеет среднее образование и регулярно принимает пищевые добавки.

- Человек имеет высшее образование и регулярно принимает пищевые добавки.
- Человек регулярно принимает БАДы.
- Человек не принимает БАД регулярно.
- Человек имеет среднее образование и регулярно принимает пищевые добавки.
Дополнительные упражнения
Большие наборы данных 4 и 4А записывают результаты 500 подбрасываний монеты.Найдите относительную частоту каждого исхода 1, 2, 3, 4, 5 и 6. Является ли монета «сбалансированной» или «честной»?
Большие наборы данных 6, 6A и 6B содержат результаты случайного опроса 200 избирателей в каждом из двух регионов, в ходе которых их просили выразить, предпочитают ли они кандидата A на место в Сенате США или какого-либо другого кандидата.

- Найдите вероятность того, что случайно выбранный избиратель из этих 400 отдаст предпочтение кандидату A .
- Найдите вероятность того, что случайно выбранный избиратель из 200 жителей района 1 предпочтет кандидата A (отдельно записанного в большом наборе данных 6A).
- Найдите вероятность того, что случайно выбранный избиратель из 200 жителей района 2 предпочтет кандидата A (отдельно записанного в большом наборе данных 6B).
Упражнения с большими наборами данных
Примечание. Эти наборы данных отсутствуют, но вопросы приведены здесь для справки.
ответов
S={rr,ry,rg,yr,yy,yg,gr,gy,gg}
- {рр,рг,гр,гг}
- {рр, гг,гг}
- ∅
- {bbg, bgb, bgg, gbb, gbg, ggb, ggg}
- {ббб,ббг,бгб,гбб}
- {гггг}
- {бгг, гбг, ггг}
- {гбб, гбг, ггб, ггг}
Относительные частоты от 1 до 6 равны 0.
 16, 0,194, 0,162, 0,164, 0,154 и 0,166. Создается впечатление, что матрица не сбалансирована.
16, 0,194, 0,162, 0,164, 0,154 и 0,166. Создается впечатление, что матрица не сбалансирована.
Решения NCERT для математики класса 9 Глава 6
Страница № 96:
Вопрос 1:
На данном рисунке прямые AB и CD пересекаются в точке O. Если и найти ∠BOE и рефлекс ∠COE.
Ответ:
Видеорешение для линий и углов (Страница: 96 , Q.No.: 1)
Решение NCERT для математики класса 9 — линии и углы 96 , вопрос 1
Страница № 97:
Вопрос 2:
На данном рисунке прямые XY и MN пересекаются в точке О. Если ∠POY = и a : b = 2 : 3, найдите c .
Если ∠POY = и a : b = 2 : 3, найдите c .
Ответ:
Пусть обыкновенное отношение между a и b равно x.
∴ a = 2 x и b = 3 x
XY — прямая, на ней стоят лучи OM и OP.
∴ ∠XOM + ∠MOP + ∠POY = 180º
б + а + ∠POY = 180º
3 х + 2 х + 90º = 180º
5 х = 90º
х = 18º
a = 2 х = 2 х 18 = 36º
b = 3 x= 3 × 18 = 54º
МН — прямая.Рэй ОКС стоит на нем.
∴ b + c = 180º (линейная пара)
54° + с = 180°
с = 180º − 54º = 126º
∴ с = 126º
Видеорешение для линий и углов (Страница: 97 , Q.No.: 2)
Решение NCERT для математики класса 9 — линии и углы 97 , вопрос 2
Страница № 97:
Вопрос 3:
На данном рисунке ∠PQR = ∠PRQ, затем докажите, что ∠PQS = ∠PRT.
Ответ:
На данном рисунке ST — прямая линия, на которой стоит луч QP.
∴ ∠PQS + ∠PQR = 180° (линейная пара)
∠PQR = 180º − ∠PQS (1)
∠PRT + ∠PRQ = 180º (линейная пара)
∠PRQ = 180º − ∠PRT (2)
Дано, что ∠PQR = ∠PRQ.
Приравнивая уравнения (1) и (2), получаем
180° − ∠PQS = 180 − ∠PRT
∠PQS = ∠PRT
Видеорешение для линий и углов (Страница: 97 , Q.№: 3)
Решение NCERT для математики класса 9 — линии и углы 97 , вопрос 3
Страница № 97:
Вопрос 4:
Если на данном рисунке, то доказать, что АОБ является линией.
Ответ:
Можно заметить, что
x + y + z + w = 360º (полный угол)
Дано,
х + у = г + ш
∴ х + у + х + у = 360º
2( х + у ) = 360º
х + у = 180º
Поскольку x и y образуют линейную пару, AOB является линией.
Видеорешение для линий и углов (Страница: 97 , Q.No.: 4)
Решение NCERT для математики класса 9 — линии и углы 97 , вопрос 4
Страница № 97:
Вопрос 5:
На данном рисунке POQ — это строка. Луч OR перпендикулярен прямой PQ. OS — еще один луч, лежащий между лучами OP и OR. Докажите, что
Ответ:
Дано, что OR ⊥ PQ
∴ ∠ПОР = 90º
⇒ ∠POS + ∠SOR = 90º
∠ROS = 90º − ∠POS … (1)
∠QOR = 90º (как ИЛИ ⊥ PQ)
∠QOS — ∠ROS = 90º
∠ROS = ∠QOS − 90º … (2)
Складывая уравнения (1) и (2), получаем
2 ∠ROS = ∠QOS − ∠POS
∠ROS = (∠QOS — ∠POS)
Видеорешение для линий и углов (Страница: 97 , Q.
 №: 5)
№: 5)Решение NCERT по математике для класса 9 — линии и углы 97 , вопрос 5
Страница № 97:
Вопрос 6:
Дано, что ∠XYZ = и XY приводится в точку P. Нарисуйте фигуру по данной информации. Если луч YQ делит пополам ∠ZYP, найти ∠XYQ и отражение ∠QYP.
Ответ:
Дано, что прямая YQ делит пополам ∠PYZ.
Следовательно, ∠QYP = ∠ZYQ
Можно заметить, что PX является линией. На нем стоят лучи YQ и YZ.
∴ ∠XYZ + ∠ZYQ + ∠QYP = 180º
⇒ 64º + 2∠QYP = 180º
⇒ 2∠QYP = 180º − 64º = 116º
⇒ ∠QYP = 58º
Кроме того, ∠ZYQ = ∠QYP = 58º
Рефлекс ∠QYP = 360º − 58º = 302º
∠XYQ = ∠XYZ + ∠ZYQ
= 64° + 58° = 122°
Видеорешение для линий и углов (Страница: 97 , Q.
 №: 6)
№: 6)Решение NCERT по математике для класса 9 — линии и углы 97 , вопрос 6
Страница № 103:
Вопрос 1:
Найдите на данном рисунке значения x и y и покажите, что AB || КОМПАКТ ДИСК.
Ответ:
Можно заметить, что
50º + x = 180º (Линейная пара)
x = 130º … (1)
Кроме того, y = 130º (вертикально противоположные углы)
Так как х и y являются параллельными внутренними углами для прямых AB и CD, а также меры этих углов равны между собой, то прямая AB || КОМПАКТ ДИСК.
Видеорешение для линий и углов (Страница: 103 , Q.No.: 1)
Решение NCERT по математике для класса 9 — линии и углы 103 , вопрос 1
Страница № 104:
Вопрос 2:
На данном рисунке, если AB || компакт-диск, компакт-диск || EF и y :z = 3:7, находим х .
Ответ:
Дано, что AB || CD и CD || ЭФ
∴ АВ || компакт-диск || EF (Прямые, параллельные одной прямой, параллельны друг другу)
Можно заметить, что
x = z (чередование внутренних углов) … (1)
Дано, что y : z = 3: 7
Пусть обыкновенное отношение между y и z равно a .
∴ y = 3 a и z = 7 a
Кроме того, x + y = 180° (совмещенные внутренние углы на одной стороне поперечной)
z + y = 180° [с использованием уравнения (1)]
7 a + 3 a = 180º
10 a = 180º
a = 18º
∴ x = 7 a = 7 × 18º = 126º
Видеорешение для линий и углов (Страница: 104 , Q.
 №: 2)
№: 2)Решение NCERT по математике для класса 9 — линии и углы 104 , вопрос 2
Страница № 104:
Вопрос 3:
На данном рисунке, если AB || CD, EF ⊥ CD и ∠GED = 126º, найти ∠AGE, ∠GEF и ∠FGE.
Ответ:
Дано,
АБ || CD
ЭФ ⊥ CD
∠GED = 126º
⇒ ∠ГЭФ + ∠ФЭД = 126º
⇒ ∠GEF + 90º = 126º
⇒ ∠GEF = 36º
∠AGE и ∠GED — альтернативные внутренние углы.
⇒ ∠ВОЗРАСТ = ∠GED = 126º
Однако ∠AGE + ∠FGE = 180º (линейная пара)
⇒ 126º + ∠FGE = 180º
⇒ ∠FGE = 180º − 126º = 54º
∴ ∠AGE = 126º, ∠GEF = 36º, ∠FGE = 54º
Видеорешение для линий и углов (Страница: 104 , Q.No.: 3)
Решение NCERT по математике для класса 9 — линии и углы 104 , вопрос 3
Страница № 104:
Вопрос 4:
На данном рисунке, если PQ || ST, ∠PQR = 110º и ∠RST = 130º, найти ∠QRS.
[ Подсказка : Проведите прямую, параллельную ST, через точку R.]
Ответ:
Проведем прямую XY, параллельную ST и проходящую через точку R.
∠PQR + ∠QRX = 180° (совмещенные внутренние углы на одной стороне поперечного QR)
⇒ 110º + ∠QRX = 180º
⇒ ∠QRX = 70º
Также
∠RST + ∠SRY = 180° (совмещенные внутренние углы на одной стороне поперечного SR)
130º + ∠SRY = 180º
∠SRY = 50º
XY — прямая.На нем стоят RQ и RS.
∴ ∠QRX + ∠QRS + ∠SRY = 180º
70º + ∠QRS + 50º = 180º
∠QRS = 180º − 120º = 60º
Видеорешение для линий и углов (Страница: 104 , Q.No.: 4)
Решение NCERT по математике для класса 9 — линии и углы 104 , вопрос 4
Страница № 104:
Вопрос 5:
На данном рисунке, если AB || CD, ∠APQ = 50º и ∠PRD = 127º, найти x и y .
Ответ:
∠APR = ∠PRD (альтернативные внутренние углы)
50º + y = 127º
y = 127º − 50º
y = 77º
Кроме того, ∠APQ = ∠PQR (альтернативные внутренние углы)
50º = х
∴ x = 50º и y = 77º
Видеорешение для линий и углов (Страница: 104 , Q.№: 5)
Решение NCERT по математике для класса 9 — линии и углы 104 , вопрос 5
Страница № 104:
Вопрос 6:
На данном рисунке PQ и RS — два зеркала, расположенные параллельно друг другу. Падающий луч AB попадает на зеркало PQ в точке B, отраженный луч движется по пути BC, попадает на зеркало RS в точке C и снова отражается обратно по CD. Докажите, что АВ || КОМПАКТ ДИСК.
Докажите, что АВ || КОМПАКТ ДИСК.
Ответ:
Нарисуем BM ⊥ PQ и CN ⊥ RS.
Как PQ || РС,
Следовательно, БМ || CN
Таким образом, BM и CN — две параллельные прямые, и поперечная прямая BC пересекает их в точках B и C соответственно.
∴∠2 = ∠3 (альтернативные внутренние углы)
Однако ∠1 = ∠2 и ∠3 = ∠4 (по законам отражения)
∴ ∠1 = ∠2 = ∠3 = ∠4
Кроме того, ∠1 + ∠2 = ∠3 + ∠4
∠ABC = ∠DCB
Однако это альтернативные внутренние углы.
∴ АВ || CD
Видеорешение для линий и углов (Страница: 104 , Q.No.: 6)
Решение NCERT по математике для 9 класса — линии и углы 104 , вопрос 6
Страница № 107:
Вопрос 1:
На данном рисунке стороны QP и RQ ΔPQR приводятся к точкам S и T соответственно. Если ∠SPR = 135º и ∠PQT = 110º, найдите ∠PRQ.
Если ∠SPR = 135º и ∠PQT = 110º, найдите ∠PRQ.
Ответ:
Дано,
∠SPR = 135º и ∠PQT = 110º
∠SPR + ∠QPR = 180º (парные линейные углы)
⇒ 135º + ∠QPR = 180º
⇒ ∠QPR = 45º
Кроме того, ∠PQT + ∠PQR = 180º (парные линейные углы)
⇒ 110º + ∠PQR = 180º
⇒ ∠PQR = 70º
Так как сумма всех внутренних углов треугольника равна 180º, то для ΔPQR
∠QPR + ∠PQR + ∠PRQ = 180º
⇒ 45º + 70º + ∠PRQ = 180º
⇒ ∠PRQ = 180º − 115º
⇒ ∠PRQ = 65º
Видеорешение для линий и углов (Страница: 107 , Q.№: 1)
Решение NCERT по математике для класса 9 — линии и углы 107 , вопрос 1
Страница № 107:
Вопрос 2:
На данном рисунке ∠X = 62º, ∠XYZ = 54º. Если YO и ZO являются биссектрисами ∠XYZ и ∠XZY соответственно ΔXYZ, найдите ∠OZY и ∠YOZ.
Если YO и ZO являются биссектрисами ∠XYZ и ∠XZY соответственно ΔXYZ, найдите ∠OZY и ∠YOZ.
Ответ:
Так как сумма всех внутренних углов треугольника равна 180º, то для ΔXYZ
∠X + ∠XYZ + ∠XZY = 180º
62º + 54º + ∠XZY = 180º
∠XZY = 180º — 116º
∠XZY = 64º
∠OZY = = 32º (OZ — биссектриса угла ∠XZY)
Аналогично, ∠OYZ = = 27º
Используя свойство суммы углов для ΔOYZ, получаем
∠OYZ + ∠YOZ + ∠OZY = 180º
27º + ∠YOZ + 32º = 180º
∠YOZ = 180º − 59º
∠YOZ = 121º
Видеорешение для линий и углов (Страница: 107 , Q.№: 2)
Решение NCERT по математике для класса 9 — линии и углы 107 , вопрос 2
Страница № 107:
Вопрос 3:
На данном рисунке, если AB || DE, ∠BAC = 35º и ∠CDE = 53º, найти ∠DCE.
Ответ:
АБ || DE и AE — трансверсаль.
∠BAC = ∠CED (альтернативные внутренние углы)
∴ ∠CED = 35º
В ΔCDE,
∠CDE + ∠CED + ∠DCE = 180º (свойство суммы углов треугольника)
53º + 35º + ∠DCE = 180º
∠DCE = 180º − 88º
∠DCE = 92º
Видеорешение для линий и углов (Страница: 107 , Q.№: 3)
Решение NCERT по математике для класса 9 — линии и углы 107 , вопрос 3
Страница № 107:
Вопрос 4:
Если на данном рисунке прямые PQ и RS пересекаются в точке T, так что ∠PRT = 40º, ∠RPT = 95º и ∠TSQ = 75º, найти ∠SQT.
Ответ:
Используя свойство суммы углов для ΔPRT, мы получаем
∠PRT + ∠RPT + ∠PTR = 180º
40º + 95º + ∠PTR = 180º
∠PTR = 180º − 135º
∠PTR = 45º
∠STQ = ∠PTR = 45º (вертикально противоположные углы)
∠STQ = 45º
Используя свойство суммы углов для ΔSTQ, мы получаем
∠STQ + ∠SQT + ∠QST = 180º
45º + ∠SQT + 75º = 180º
∠SQT = 180º − 120º
∠SQT = 60º
Видеорешение для линий и углов (Страница: 107 , Q.
 №: 4)
№: 4)Решение NCERT по математике для класса 9 — линии и углы 107 , вопрос 4
Страница № 108:
Вопрос 5:
На данном рисунке, если PQ ⊥ PS, PQ || SR, ∠SQR = 28º и ∠QRT = 65º, затем найдите значения x и y .
Ответ:
Дано, что PQ || SR и QR — поперечная линия.
∠PQR = ∠QRT (альтернативные внутренние углы)
х + 28º = 65º
х = 65° − 28°
х = 37º
Используя свойство суммы углов для ΔSPQ, мы получаем
∠SPQ + x + y = 180º
90° + 37° + y = 180°
y = 180º − 127º
y = 53º
x = 37º и y = 53º
Видеорешение для линий и углов (Страница: 108 , Q.
 №: 5)
№: 5)Решение NCERT по математике для класса 9 — линии и углы 108 , вопрос 5
Страница № 108:
Вопрос 6:
На данном рисунке сторона QR ΔPQR приведена в точку S. Если биссектрисы ∠PQR и ∠PRS пересекаются в точке T, то докажите, что ∠QTR=∠QPR.
Ответ:
В ΔQTR ∠TRS — внешний угол.
∠QTR + ∠TQR = ∠TRS
∠QTR = ∠TRS − ∠TQR (1)
Для ΔPQR ∠PRS — внешний угол.
∠QPR + ∠PQR = ∠PRS
∠QPR + 2∠TQR = 2∠TRS (поскольку QT и RT являются биссектрисами угла)
∠QPR = 2(∠TRS — ∠TQR)
∠QPR = 2∠QTR [с помощью уравнения (1)]
∠QTR = ∠QPR
Видеорешение для линий и углов (Страница: 108 , Q.No.: 6)
Решение NCERT по математике для класса 9 — линии и углы 108 , вопрос 6
Посмотреть решения NCERT для всех глав класса 9
Формула A∩B — Вероятность, Примеры
Пересечение B — это множество, содержащее элементы, общие для обоих множеств A и B. Символ, используемый для обозначения пересечения множеств A и B, — это ∩, он пишется как A ∩ B и читается как «пересечение A B». Пересечение двух или более множеств — это множество элементов, общих для каждого множества. A ∩ B можно легко определить, проверив элементы, которые присутствуют как в A, так и в B. Давайте рассмотрим концепцию A ∩ B с помощью некоторых решенных примеров для лучшего понимания.
Символ, используемый для обозначения пересечения множеств A и B, — это ∩, он пишется как A ∩ B и читается как «пересечение A B». Пересечение двух или более множеств — это множество элементов, общих для каждого множества. A ∩ B можно легко определить, проверив элементы, которые присутствуют как в A, так и в B. Давайте рассмотрим концепцию A ∩ B с помощью некоторых решенных примеров для лучшего понимания.
Что такое формула перекрестка B?
A ∩ B — это множество, состоящее из элементов, общих как для A, так и для B.Формула A пересечения B представляет элементы, которые присутствуют как в A, так и в B, и обозначается через A ∩ B. Итак, используя определение пересечения множеств, формула A пересечения B:
A ∩ B = {x : x ∈ A и x ∈ B}
Что такое формула P(A∩B)?
P(A ∩ B) — это вероятность того, что оба независимых события «A» и «B» произойдут вместе. Символ «∩» означает пересечение. Эта формула используется для быстрого прогнозирования результата. Когда события независимы, мы можем использовать правило умножения, которое гласит, что два события A и B независимы, если появление одного события не меняет вероятность другого события. Формула P(A∩B) может быть записана как P(A∩B) = P(A) × P(B). Формула P(A∩B) задается как:
Когда события независимы, мы можем использовать правило умножения, которое гласит, что два события A и B независимы, если появление одного события не меняет вероятность другого события. Формула P(A∩B) может быть записана как P(A∩B) = P(A) × P(B). Формула P(A∩B) задается как:
P(A∩B) Формула
Р(А∩В) = Р(А) × Р(В)
где,
- P(A∩B) = Вероятность того, что оба независимых события «A» и «B» произойдут вместе.
- P(A) = Вероятность события «А»
- P(B) = Вероятность события «B»
Чтобы вычислить P(A∩B) для зависимых событий, мы используем понятие условной вероятности и перепишем формулу как
P(A∩B) = P(A|B)P(B) или P(A∩B) = P(B|A)P(A)
Количество элементов в A∩B
Чтобы определить количество элементов в пересечении A B, воспользуемся формулой объединения A B.Мы знаем, что количество элементов в A U B равно n(A U B) = n(A) + n(B) — n(A ∩ B), где
- n(A U B) = количество элементов в A U B
- n(A) = количество элементов в A
- n(B) = количество элементов в B
- n(A ∩ B) = количество элементов в A ∩ B
Если взять n(A ∩ B) с одной стороны, а все остальные члены с другой, то формула для числа элементов в A ∩ B будет выглядеть так:
n(A∩B) = n(A) + n(B) — n(A U B)
Важные примечания к формуле A Intersection B
- A ∩ B = {x : x ∈ A и x ∈ B}
- А∩В = В∩А
- n(A∩B) = n(A) + n(B) — n(AUB)
- Для независимых событий A и B, P(A∩B) = P(A) × P(B)
- Для зависимых событий A и B: P(A∩B) = P(A|B)P(B) или P(A∩B) = P(B|A)P(A)
Связанные темы по формуле A∩B
Часто задаваемые вопросы по формуле A∩B
Что такое формула A∩B в теории множеств?
Используя определение пересечения множеств, формула пересечения B выглядит следующим образом: A ∩ B = {x: x ∈ A и x ∈ B}
Что такое формула P(A∩B)?
P(A∩B) — вероятность того, что оба независимых события «A» и «B» произойдут вместе, формула P(A∩B) может быть записана как P(A∩B) = P(A) × P(B ),
где,
- P(A∩B) = Вероятность того, что оба независимых события «A» и «B» произойдут вместе.

- P(A) = Вероятность события «А»
- P(B) = Вероятность события «B»
Как найти A ∩ B?
A ∩ B можно определить, рассматривая только те элементы, которые присутствуют как в A, так и в B. A ∩ B состоит только из общих элементов.
Что представляет (A ∩ B) в формуле P(A ∩ B)?
(A ∩ B) в P(A ∩ B) Формула представляет собой пересечение двух событий A и B. Символ ‘∩’ обозначает пересечение.
Как применить формулу P(A ∩ B)?
Мы применяем формулу P(A ∩ B) для вычисления вероятности того, что два независимых события A и B произойдут вместе.Он задается как P(A∩B) = P(A) × P(B), где P(A) — вероятность события «A», а P(B) = вероятность события «B».
Как найти формулу P(A ∩ B) для двух независимых событий?
Мы можем найти вероятность пересечения двух независимых событий как P(A ∩ B) = P(A) × P(B), где P(A) — вероятность события «A», а P( B) = вероятность события «B», а P(A ∩ B) — это вероятность того, что оба независимых события «A» и «B» происходят вместе.



 F и G не исключают друг друга.
F и G не исключают друг друга.
 P ( A ) + P ( B ) = P ( A ) + P ( A′ ) = 1.Кроме того, P ( A ) = и P ( B ) =.
P ( A ) + P ( B ) = P ( A ) + P ( A′ ) = 1.Кроме того, P ( A ) = и P ( B ) =.
 Чтобы найти P ( C | A ), найдите вероятность C , используя выборочное пространство A . Вы уменьшили пространство выборки с исходного пространства выборки {1, 2, 3, 4, 5, 6} до {1, 3, 5}. Итак, P ( C | A ) = .
Чтобы найти P ( C | A ), найдите вероятность C , используя выборочное пространство A . Вы уменьшили пространство выборки с исходного пространства выборки {1, 2, 3, 4, 5, 6} до {1, 3, 5}. Итак, P ( C | A ) = .


 )
) P ( G | H ) = . (Единственная карта в H , имеющая номер больше трех, это B 4.) Поскольку = , P ( G ) = P ( G | H ), это означает, что G и H независимы.
P ( G | H ) = . (Единственная карта в H , имеющая номер больше трех, это B 4.) Поскольку = , P ( G ) = P ( G | H ), это означает, что G и H независимы.

 ( A ) P ( B ), то A и B независимые. Если нет, то зависимые).
( A ) P ( B ), то A и B независимые. Если нет, то зависимые). P ( A ) P ( B ) = . P ( A AND B ) не равно P ( A ) P ( B ), поэтому A и B и B
P ( A ) P ( B ) = . P ( A AND B ) не равно P ( A ) P ( B ), поэтому A и B и B 
 Таким образом, выборочное пространство равно S={2h,2t,d}.
Таким образом, выборочное пространство равно S={2h,2t,d}.
 (Вытягивание «с возвратом» означает, что каждый шарик возвращается до того, как будет вытащен следующий шарик.)
(Вытягивание «с возвратом» означает, что каждый шарик возвращается до того, как будет вытащен следующий шарик.)



 19
19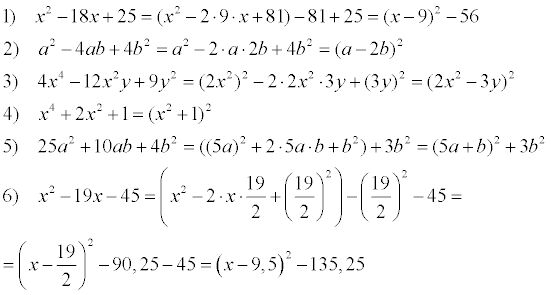

 12
12 Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий. 02
02
 04
04

 16, 0,194, 0,162, 0,164, 0,154 и 0,166. Создается впечатление, что матрица не сбалансирована.
16, 0,194, 0,162, 0,164, 0,154 и 0,166. Создается впечатление, что матрица не сбалансирована.