Определитель матрицы 4х4 формула: Как найти определитель матрицы 2х2, 3х3 и 4х4
Определитель матрицы: алгоритм, примеры вычисления, правила
Определение 1Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.
|А|, ∆, det A — символы, которыми обозначают определитель матрицы.
Способ вычисления определителя выбирают в зависимости от порядка матрицы.
Пример 1Определитель матрицы 2-го порядка вычисляют по формуле:
А=1-231.
Решение:
det A=1-231=1×1-3×(-2)=1+6=7
Определитель матрицы 3-го порядка: правило треугольника
Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:
- правило треугольника;
- правило Саррюса.
Как найти определитель матрицы 3-го порядка по методу треугольника?
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
Пример 2А=13402115-1
det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Разложение матрицы по элементам строки:
det A=ai1×Ai1+ai2×Ai2+…+аin×Аin
Разложение матрицы по элементам столбца:
det A=а1i×А1i+а2i×А2i+…+аni×Аni
ЗамечаниеЕсли раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
Пример 5А=01-132100-24513210
Решение:
- раскладываем по 2-ой строке:
А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310
- раскладываем по 4-му столбцу:
А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321
Свойства определителя
Свойства определителя
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
А=134021005
Решение:
det А=134021005=1×5×2=10
ЗамечаниеОпределитель матрицы, который содержит нулевой столбец, равняется нулю.
теоремы и примеры нахождения определителей
Содержание:
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
$$\left| \begin{array}{ll}{a_{11}} & {a_{12}} \\ {a_{21}} & {a_{22}}\end{array}\right|=a_{11} \cdot a_{22}-a_{12} \cdot a_{21}$$
Пример
Задание. Вычислить определитель второго порядка
$\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$
Вычислить определитель второго порядка
$\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|$
Ответ. $\left| \begin{array}{rr}{11} & {-2} \\ {7} & {5}\end{array}\right|=69$
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
$$\left| \begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$
$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$
Слишком сложно?
Методы вычисления определителей не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Вычислить определитель $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|$ методом треугольников.
Решение. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=3 \cdot 1 \cdot(-2)+4 \cdot(-2) \cdot(-1)+$
$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$
Ответ. $\left| \begin{array}{rrr}{3} & {3} & {-1} \\ {4} & {1} & {3} \\ {1} & {-2} & {-2}\end{array}\right|=54$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$
Пример
Задание. Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$ Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка. Пример Задание. Вычислить определитель $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|$ Решение. {1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$
{1+3} \cdot \left| \begin{array}{cc}{4} & {5} \\ {7} & {8}\end{array}\right|=-3+12-9=0$
$$\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {4-4 \cdot 1} & {5-4 \cdot 2} & {6-4 \cdot 3} \\ {7-7 \cdot 1} & {8-7 \cdot 2} & {9-7 \cdot 3}\end{array}\right|=$$
$$=\left| \begin{array}{rrr}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {-6} & {-12}\end{array}\right|=\left| \begin{array}{ccc}{1} & {2} & {3} \\ {0} & {-3} & {-6} \\ {0} & {2 \cdot(-3)} & {2 \cdot(-6)}\end{array}\right|=0$$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $\left| \begin{array}{lll}{1} & {2} & {3} \\ {4} & {5} & {6} \\ {7} & {8} & {9}\end{array}\right|=0$
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Пример
Задание. Вычислить определитель
$\left| \begin{array}{llll}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|$ , разложив его по элементам какой-то строки или какого-то столбца.
$$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$
Ответ. $\left| \begin{array}{cccc}{9} & {8} & {7} & {6} \\ {5} & {4} & {3} & {2} \\ {1} & {0} & {1} & {2} \\ {3} & {4} & {5} & {6}\end{array}\right|=0$
Замечание
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель $\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_{11}$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
$$\Delta=\left| \begin{array}{rrrr}{-2} & {1} & {3} & {2} \\ {3} & {0} & {-1} & {2} \\ {-5} & {2} & {3} & {0} \\ {4} & {-1} & {2} & {-3}\end{array}\right|=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {2} & {-5} & {3} & {0} \\ {-1} & {4} & {2} & {-3}\end{array}\right|$$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$$\Delta=-\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {3} & {-1} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
И снова, если
диагональный элемент будет равен $\pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {3} & {-1} & {2} \\ {0} & {2} & {5} & {-1}\end{array}\right|$$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$$\Delta=\left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {-10} & {-10} \\ {0} & {0} & {-1} & {-9}\end{array}\right|$$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
$$\Delta=-10 \left| \begin{array}{rrrr}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {-1} & {-9}\end{array}\right|=$$
$$=-10 \cdot \left| \begin{array}{cccc}{1} & {-2} & {3} & {2} \\ {0} & {-1} & {-3} & {-4} \\ {0} & {0} & {1} & {1} \\ {0} & {0} & {0} & {-8}\end{array}\right|=(-10) \cdot 1 \cdot(-1) \cdot 1 \cdot(-8)=-80$$
Ответ. $\Delta=-80$
Теорема Лапласа
Теорема
Пусть $\Delta$ — определитель $n$-го порядка. Выберем в нем произвольные $k$ строк (или столбцов), причем $k \leq n-1$ . Тогда сумма произведений всех миноров $k$-го порядка, которые содержатся в выбранных $k$ строках (столбцах), на их алгебраические дополнения равна определителю.
Пример
Задание. Используя теорему Лапласа, вычислить определитель $\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|$
Решение. {2+4+5} \cdot \left| \begin{array}{ccc}{2} & {3} & {0} \\ {3} & {2} & {1} \\ {1} & {1} & {2}\end{array}\right|=$$
{2+4+5} \cdot \left| \begin{array}{ccc}{2} & {3} & {0} \\ {3} & {2} & {1} \\ {1} & {1} & {2}\end{array}\right|=$$
$$=-23+128+90=195$$
Ответ. $\left| \begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \\ {0} & {1} & {0} & {-1} & {2} \\ {3} & {2} & {1} & {0} & {1} \\ {0} & {4} & {0} & {-5} & {0} \\ {1} & {1} & {2} & {-2} & {1}\end{array}\right|=195$
Читать дальше: обратная матрица.
Линейная алгебра на Python. [Урок 4]. Определитель матрицы
Четвертый урок из цикла “Линейная алгебра на Python“, посвящен понятию определителя матрицы и его свойствам.
Определитель матрицыОпределитель матрицы размера (n-го порядка) является одной из ее численных характеристик. Определитель матрицы A обозначается как |A| или det(A), его также называют детерминантом. Рассмотрим квадратную матрицу 2×2 в общем виде:
Определитель такой матрицы вычисляется следующим образом:
➣ Численный пример
Перед тем, как привести методику расчета определителя в общем виде, введем понятие минора элемента определителя. Минор элемента определителя – это определитель, полученный из данного, путем вычеркивания всех элементов строки и столбца, на пересечении которых стоит данный элемент. Для матрицы 3×3 следующего вида:
Минор M23 будет выглядеть так:
Введем еще одно понятие – алгебраическое дополнение элемента определителя – это минор этого элемента, взятый со знаком плюс или минус:
В общем виде вычислить определитель матрицы можно через разложение определителя по элементам строки или столбца. Суть в том, что определитель равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения. Для матрицы 3×3 это правило будет выполняться следующим образом:
Это правило распространяется на матрицы любой размерности.
➣ Численный пример
➤ Пример на Python
На Python определитель посчитать очень просто. Создадим матрицу A размера 3×3 из приведенного выше численного примера:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
Для вычисления определителя этой матрицы воспользуемся функцией det() из пакета linalg.
>>> np.linalg.det(A) -14.000000000000009
Мы уже говорили про особенность работы Python с числами с плавающей точкой, поэтому можете полученное значение округлить до -14.
Свойства определителя матрицы.
Свойство 1. Определитель матрицы остается неизменным при ее транспонировании:
➤Пример на Python
Для округления чисел будем использовать функцию round().
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(A.T)
[[-4 10 8]
[-1 4 3]
[ 2 -1 1]]
>>> det_A = round(np.linalg.det(A), 3)
>>> det_A_t = round(np.linalg.det(A.T), 3)
>>> print(det_A)
-14.0
>>> print(det_A_t)
-14.0
Свойство 2. Если у матрицы есть строка или столбец, состоящие из нулей, то определитель такой матрицы равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 0 0 0; 8 3 1')
>>> print(A)
[[-4 -1 2]
[ 0 0 0]
[ 8 3 1]]
>>> np.linalg.det(A)
0.0
Свойство 3. При перестановке строк матрицы знак ее определителя меняется на противоположный:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1') >>> print(A) [[-4 -1 2] [10 4 -1] [ 8 3 1]] >>> B = np.matrix('10 4 -1; -4 -1 2; 8 3 1') >>> print(B) [[10 4 -1] [-4 -1 2] [ 8 3 1]] >>> round(np.linalg.det(A), 3) -14.0 >>> round(np.linalg.det(B), 3) 14.0
Свойство 4. Если у матрицы есть две одинаковые строки, то ее определитель равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> np.linalg.det(A)
0.0
Свойство 5. Если все элементы строки или столбца матрицы умножить на какое-то число, то и определитель будет умножен на это число:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> B = A.copy()
>>> B[2, :] = k * B[2, :]
>>> print(B)
[[-4 -1 2]
[10 4 -1]
[16 6 2]]
>>> det_A = round(np.linalg.det(A), 3)
>>> det_B = round(np.linalg.det(B), 3)
>>> det_A * k
-28.0
>>> det_B
-28.0
Свойство 6. Если все элементы строки или столбца можно представить как сумму двух слагаемых, то определитель такой матрицы равен сумме определителей двух соответствующих матриц:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> B = np.matrix('-4 -1 2; 8 3 2; 8 3 1')
>>> C = A.copy()
>>> C[1, :] += B[1, :]
>>> print(C)
[[-4 -1 2]
[ 4 2 4]
[ 8 3 1]]
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 8 3 2]
[ 8 3 1]]
>>> round(np. linalg.det(C), 3)
4.0
>>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3)
4.0
linalg.det(C), 3)
4.0
>>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3)
4.0
Свойство 7. Если к элементам одной строки прибавить элементы другой строки, умноженные на одно и тоже число, то определитель матрицы не изменится:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> k = 2
>>> B = A.copy()
>>> B[1, :] = B[1, :] + k * B[0, :]
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 2 2 3]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
-14.0
Свойство 8. Если строка или столбец матрицы является линейной комбинацией других строк (столбцов), то определитель такой матрицы равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> A[1, :] = A[0, :] + k * A[2, :]
>>> round(np.linalg.det(A), 3)
0.0
Свойство 9. Если матрица содержит пропорциональные строки, то ее определитель равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> A[1, :] = k * A[0, :]
>>> print(A)
[[-4 -1 2]
[-8 -2 4]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
0.0P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Вычисление определителя матрицы в EXCEL. Примеры и описание
Вычислим определитель (детерминант) матрицы с помощью функции МОПРЕД() или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).
Определитель матрицы (det) можно вычислить только для квадратных матриц, т.е. у которых количество строк равно количеству столбцов.
Для вычисления определителя в MS EXCEL есть специальная функция МОПРЕД() . В аргументе функции необходимо указать ссылку на диапазон ячеек (массив), содержащий элементы матрицы (см. файл примера ).
Массив может быть задан не только как интервал ячеек, например A7:B8 , но и как массив констант , например =МОПРЕД({5;4:3;2}) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на именованный диапазон .
Для матриц порядка 2 можно определитель можно вычислить без использования функции МОПРЕД() . Например, для вышеуказанной матрицы выражение =A7*B8-B7*A8 вернет тот же результат.
Для матрицы порядка 3, например размещенной в диапазоне A16:C18 , выражение усложняется =A16*(B17*C18-C17*B18)-B16*(A17*C18-C17*A18)+C16*(A17*B18-B17*A18) (разложение по строке).
В
файле примера
для матрицы 3 х 3 определитель также вычислен через разложение по столбцу и по правилу Саррюса.
Свойства определителя
Теперь о некоторых свойствах определителя (см. файл примера ):
- Определитель транспонированной матрицы равен определителю исходной матрицы
- Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
- Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
- Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет равен определителю исходной матрицы, умноженному на k
- Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
- det(А)=1/det(А -1 ), где А -1 — матрица обратная матрице А (А — квадратная невырожденная матрица).
Вычисление определителя матрицы по определению (до 6 порядка включительно)
СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОПРЕД() .
Как было показано выше для вычисления матриц порядка 2 и 3 существуют достаточно простые формулы и правила. Для вычисления определителя матриц более высокого порядка (без использования функции МОПРЕД() ) придется вспомнить определение:
Определителем квадратной матрицы порядка
n
х
n
является сумма, содержащая
n!
слагаемых (
=ФАКТР(n)
). Каждое слагаемое представляет собой произведение
n
элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы
А
. Перед
k-ым
слагаемым появляется коэффициент
(-1)
, если элементы матрицы
А
в произведении упорядочены по номеру строки, а количество инверсий в
k-ой
перестановке множества номеров столбцов нечетно.
Перед
k-ым
слагаемым появляется коэффициент
(-1)
, если элементы матрицы
А
в произведении упорядочены по номеру строки, а количество инверсий в
k-ой
перестановке множества номеров столбцов нечетно.
где ( α 1 , α 2 ,…, α n ) — перестановка чисел от 1 до n , N( α 1 , α 2 ,…, α n ) — число инверсий в перестановке , суммирование идёт по всем возможным перестановкам порядка n .
Попытаемся разобраться в этом непростом определении на примере матрицы 3х3.
Для матрицы 3 х 3, согласно определения, число слагаемых равно 3!=6, а каждое слагаемое состоит из произведения 3-х элементов матрицы. Ниже приведены все 6 слагаемых, необходимых для вычисления определителя матрицы 3х3:
- а21*а12*а33
- а21*а32*а13
- а11*а32*а23
- а11*а22*а33
- а31*а22*а13
- а31*а12*а23
а21, а12 и т.д. — это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.
Посмотрим на формулу выше (см. определение). Предположим, что второй индекс у каждого элемента матрицы (от 1 до n) соответствует номеру столбца матрицы (хотя это может быть номер строки (это не важно т.к. определители матрицы и ее транспонированной матрицы равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго — 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).
Теперь понятно, почему среди слагаемых нет а11*а22*а13, т. к. согласно определения ( в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы
А ),
а в нашем слагаемом нет элемента из строки 3.
к. согласно определения ( в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы
А ),
а в нашем слагаемом нет элемента из строки 3.
Примечание : Перестановкой из n чисел множества (без повторов) называется любое упорядочивание данного множества, отличающиеся друг от друга лишь порядком входящих в них элементов. Например, дано множество их 3-х чисел: 1, 2, 3. Из этих чисел можно составить 6 разных перестановок: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 1, 2), (3, 2, 1). См. статью Перестановки без повторений: Комбинаторика в MS EXCEL
Число перестановок множества из 3-х чисел =3!=6 (что, конечно, равно числу слагаемых в выражении для расчета определителя, т.к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).
СОВЕТ : Для матрицы 4 порядка существует 4! перестановок, т.е. 26, что соответствует 26 слагаемым, каждое из которых является произведением различных 4-х элементов матрицы. Все 26 перестановок можно найти в статье Перебор всех возможных Перестановок в MS EXCEL .
Теперь, когда разобрались со слагаемыми, определим множитель перед каждым слагаемым (он может быть +1 или -1). Множитель определяется через четность числа инверсий соответствующей перестановки.
Примечание : Об инверсиях перестановок (и четности числа инверсий) можно почитать, например, в статье Перестановки без повторений: Комбинаторика в MS EXCEL
Например, первому слагаемому соответствует перестановка (2, 1, 3), у которой 1 инверсия (нечетное число) и, соответственно, -1 в степени 1 равно -1. Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.д.
Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.д.
Сложив все слагаемые: (-1)*(а21*а12*а33)+(+1)*(а21*а32*а13)+(-1)*(а11*а32*а23)+(+1)*(а11*а22*а33)+(-1)*(а31*а22*а13)+(+1)*(а31*а12*а23) получим значение определителя.
В файле примера на листе 4+, и зменяя порядок матрицы с помощью элемента управления Счетчик , можно вычислить определитель матрицы до 6 порядка включительно.
Следует учитывать, что при вычислении матрицы 6-го порядка в выражении используется уже 720 слагаемых (6!). Для 7-го порядка пришлось бы сделать таблицу для 5040 перестановок и, соответственно, вычислить 5040 слагаемых! Т.е. без использования МОПРЕД() не обойтись (ну, или можно вычислить определитель вручную методом Гаусса).
вычисление матриц
Вы искали вычисление матриц? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление матрицы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление матриц».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычисление матриц,вычисление матрицы,вычисление определителей онлайн,вычисление определителя 4 порядка онлайн,вычисление определителя 4 порядка онлайн с решением,вычисление определителя калькулятор онлайн,вычисление определителя матрицы,вычисление определителя матрицы калькулятор,вычисление определителя матрицы онлайн,вычисление определителя онлайн,вычисление определителя онлайн калькулятор,вычислите определитель 3 порядка,вычислите определитель матрицы онлайн,вычислитель определитель матрицы онлайн,вычислитель определителя онлайн,вычислить матрица,вычислить онлайн определитель 4 порядка,вычислить онлайн определитель второго порядка,вычислить определитель 2 порядка онлайн,вычислить определитель 4 го порядка онлайн,вычислить определитель 4 порядка калькулятор,вычислить определитель 4 порядка калькулятор онлайн,вычислить определитель 4 порядка онлайн,вычислить определитель 4 порядка онлайн калькулятор,вычислить определитель 4 порядка онлайн с подробным решением,вычислить определитель второго порядка онлайн,вычислить определитель второго порядка онлайн с решением,вычислить определитель используя свойства определителя онлайн,вычислить определитель калькулятор,вычислить определитель матрицы 4х4,вычислить определитель матрицы 4х4 онлайн с решением,вычислить определитель матрицы калькулятор,вычислить определитель матрицы калькулятор онлайн,вычислить определитель матрицы онлайн,вычислить определитель матрицы онлайн калькулятор,вычислить определитель матрицы онлайн с решением,вычислить определитель матрицы онлайн с решением подробно,вычислить определитель методом понижения порядка онлайн,вычислить определитель онлайн,вычислить определитель онлайн 4 порядка,вычислить определитель онлайн калькулятор,вычислить определитель онлайн с подробным решением,вычислить определитель онлайн с подробным решением онлайн,вычислить определитель с подробным решением онлайн,вычислить определитель третьего порядка,вычислить определитель четвертого порядка онлайн,вычислить определитель четвертого порядка онлайн с подробным решением,вычислить определитель четвертого порядка онлайн с решением,вычислить определитель четвертого порядка с решением онлайн,вычислить определить,вычислить определить онлайн,вычислить определить онлайн 4 на 4,детерминант матрицы 4 на 4,детерминант матрицы калькулятор,детерминант матрицы онлайн,детерминант матрицы онлайн калькулятор,детерминант онлайн,задачи определитель матрицы,используя свойства определителя вычислить определитель онлайн,как вычислить матрицу,как вычислить определитель 4 порядка онлайн с решением подробно,как вычислить определитель матрицы 4х4,как найти определитель матрицы,как найти определитель матрицы 4х4,как найти определитель матрицы 4х4 онлайн,как найти определитель матрицы 5х5,как посчитать матрицу 4 на 4,калькулятор визначників,калькулятор визначників онлайн,калькулятор вычисления определителя матрицы,калькулятор вычислить определитель,калькулятор вычислить определитель 4 порядка,калькулятор вычислить определитель 4 порядка онлайн,калькулятор вычислить определитель матрицы,калькулятор детерминант матрицы,калькулятор детерминанта матрицы,калькулятор для определителей,калькулятор матриц 4 порядка,калькулятор матриц матричный метод,калькулятор матриц матричным методом,калькулятор матриц онлайн определитель,калькулятор матриц онлайн определитель с решением,калькулятор матриц онлайн с решением определитель,калькулятор матриц определителей,калькулятор матриц определитель,калькулятор матриц определитель онлайн,калькулятор матрица определитель,калькулятор матрицы 4 порядка,калькулятор матрицы вычислить определитель,калькулятор матрицы вычислить определитель матрицы,калькулятор матрицы детерминант,калькулятор матрицы онлайн найти определитель,калькулятор матрицы определитель онлайн калькулятор с подробным решением,калькулятор матричный метод,калькулятор матричный метод онлайн,калькулятор матричный способ,калькулятор найти определитель матрицы,калькулятор онлайн вычисление определителя,калькулятор онлайн вычислить определитель матрицы,калькулятор онлайн вычислить определитель матрицы онлайн с решением,калькулятор онлайн матриц определитель,калькулятор онлайн матрица определитель,калькулятор онлайн матричный метод,калькулятор онлайн метод матричный,калькулятор онлайн найти определитель,калькулятор онлайн найти определитель матрицы,калькулятор онлайн обчислити визначник,калькулятор онлайн определителей,калькулятор онлайн определители,калькулятор онлайн определителя,калькулятор определения,калькулятор определителей,калькулятор определителей 4 порядка,калькулятор определителей матриц,калькулятор определителей матриц онлайн,калькулятор определителей матрицы,калькулятор определителей онлайн,калькулятор определители,калькулятор определители онлайн,калькулятор определитель,калькулятор определитель 4 порядка,калькулятор определитель матриц,калькулятор определитель матриц онлайн,калькулятор определитель матрицы,калькулятор определитель матрицы 4 порядка,калькулятор определитель третьего порядка онлайн с решением,калькулятор определителя,калькулятор определителя 4 порядка,калькулятор определителя 4 порядка онлайн,калькулятор определителя матрицы,калькулятор определителя матрицы онлайн,калькулятор определителя онлайн,калькулятор систем матриц,калькулятор союзной матрицы,линейная алгебра онлайн калькулятор,матрица 3 на 3 онлайн,матрица 4 порядка онлайн,матрица вычисление,матрица вычислить,матрица калькулятор онлайн определитель,матрица калькулятор определитель,матрица метод треугольника онлайн,матрица нахождение определителя,матрица онлайн калькулятор определитель,матрица онлайн определитель,матрица определитель калькулятор,матрица определитель калькулятор онлайн,матрица определитель онлайн,матрица определитель онлайн калькулятор,матрица четвертого порядка онлайн,матрицы onlinemschool,матрицы вычисление,матрицы калькулятор найти определитель матрицы,матрицы онлайн калькулятор найти определитель,матрицы определитель 4 порядка онлайн,матрицы считать,матричный калькулятор матричный способ,матричный калькулятор метод,матричный калькулятор онлайн матричный метод,матричный калькулятор онлайн метод матричный,матричный калькулятор определитель,матричный метод калькулятор,матричный метод калькулятор онлайн с подробным решением,матричный метод онлайн калькулятор с подробным решением,матричный способ калькулятор,матричный способ калькулятор онлайн,матричный способ онлайн калькулятор,метод матричный калькулятор,метод матричный онлайн калькулятор,метод матричный онлайн калькулятор с подробным решением,метод треугольника матрица онлайн,метод треугольника матрицы онлайн,метод элементарных преобразований матрицы онлайн калькулятор,модуль матрицы,найти детерминант матрицы онлайн,найти определитель калькулятор онлайн,найти определитель матрицы 3х3 онлайн,найти определитель матрицы 4х4,найти определитель матрицы 4х4 онлайн,найти определитель матрицы 4х4 онлайн с решением,найти определитель матрицы калькулятор онлайн,найти определитель матрицы онлайн,найти определитель матрицы онлайн 4х4,найти определитель матрицы онлайн калькулятор,найти определитель матрицы онлайн с подробным решением,найти определитель матрицы онлайн с решением,найти определитель матрицы с решением онлайн,найти определитель онлайн,найти определитель онлайн калькулятор,найти определить матрицы,нахождение детерминанта матрицы,нахождение определителя матрица,нахождение определителя матрицы 4 порядка онлайн,нахождение определителя матрицы онлайн,нахождение определителя матрицы онлайн с решением,нахождение определителя онлайн,обчислити визначник калькулятор онлайн,обчислити визначник онлайн калькулятор,онлайн вычисление определителей,онлайн вычисление определителя 4 порядка,онлайн вычисления определителя матрицы,онлайн вычислитель определителя,онлайн вычислить определитель четвертого порядка,онлайн детерминант,онлайн калькулятор визначників,онлайн калькулятор вычисление определителя,онлайн калькулятор вычислить определитель,онлайн калькулятор вычислить определитель 4 порядка,онлайн калькулятор вычислить определитель матрицы,онлайн калькулятор детерминант матрицы,онлайн калькулятор матриц определителей,онлайн калькулятор матриц определитель,онлайн калькулятор матриц определитель с решением,онлайн калькулятор матриц с решением определитель,онлайн калькулятор матрица определитель,онлайн калькулятор матрицы вычислить определитель,онлайн калькулятор матрицы детерминант,онлайн калькулятор матрицы найти определитель,онлайн калькулятор матричный метод,онлайн калькулятор матричный способ,онлайн калькулятор метод матричный,онлайн калькулятор метод саррюса,онлайн калькулятор найти определитель,онлайн калькулятор найти определитель матрицы,онлайн калькулятор обчислити визначник,онлайн калькулятор определение матрицы,онлайн калькулятор определителей,онлайн калькулятор определителей матриц,онлайн калькулятор определители,онлайн калькулятор определитель,онлайн калькулятор определитель 4 порядка,онлайн калькулятор определитель второго порядка,онлайн калькулятор определитель матриц,онлайн калькулятор определитель матрица,онлайн калькулятор определитель матрицы,онлайн калькулятор определитель матрицы 4 порядка,онлайн калькулятор определитель матрицы с подробным решением,онлайн калькулятор определитель матрицы с решением,онлайн калькулятор определителя,онлайн калькулятор определителя 4 порядка,онлайн калькулятор определителя матрицы,онлайн калькулятор присоединенная матрица,онлайн калькулятор решение определителей,онлайн матрица 3 на 3,онлайн определение определителя матрицы,онлайн определители,онлайн определители матриц,онлайн определитель 2 порядка,онлайн определитель 4 порядка,онлайн определитель матрицы 4 порядка,онлайн определитель матрицы 4х4,онлайн определитель матрицы с решением,онлайн определитель четвертого порядка,онлайн определить,онлайн подсчет определителя матрицы,онлайн расчет определителя матрицы,онлайн решение матриц 4 порядка,онлайн решение матриц методом,онлайн решение матрицы 3 на 3,онлайн решение матрицы определитель,онлайн решение определителей,онлайн решение определителей 4 порядка,онлайн решение определители,онлайн решение определитель,онлайн решение определитель матрицы,онлайн решение определителя,онлайн решение определителя 4 порядка,онлайн решить определитель,онлайн решить определитель 4 порядка,онлайн считать определитель,определение матрицы онлайн калькулятор,определение онлайн,определение определителя матрицы онлайн,определители 4 порядка онлайн,определители вычислить,определители калькулятор,определители калькулятор онлайн,определители матриц онлайн,определители онлайн,определители онлайн калькулятор,определители онлайн решение,определители решение онлайн,определитель 2 порядка онлайн,определитель 4 го порядка калькулятор онлайн,определитель 4 го порядка онлайн,определитель 4 порядка калькулятор,определитель 4 порядка калькулятор онлайн,определитель 4 порядка матрицы онлайн,определитель 4 порядка онлайн,определитель 4 порядка онлайн калькулятор,определитель 4 порядка онлайн с решением,определитель 4 порядка онлайн с решением подробно,определитель 4 порядка решить онлайн,определитель 5 порядка онлайн,определитель второго порядка онлайн калькулятор,определитель как считать,определитель калькулятор,определитель калькулятор матриц,определитель калькулятор онлайн,определитель матриц калькулятор,определитель матриц онлайн калькулятор,определитель матрица калькулятор онлайн,определитель матрица онлайн калькулятор,определитель матрицы 3х3 онлайн,определитель матрицы 4 порядка калькулятор,определитель матрицы 4 порядка онлайн,определитель матрицы 4 порядка онлайн калькулятор,определитель матрицы 4х4,определитель матрицы 4х4 найти,определитель матрицы 4х4 онлайн,определитель матрицы 4х4 формула,определитель матрицы 5х5,определитель матрицы калькулятор,определитель матрицы онлайн,определитель матрицы онлайн 4 порядка,определитель матрицы онлайн 4х4,определитель матрицы онлайн калькулятор,определитель матрицы онлайн калькулятор с подробным решением,определитель матрицы онлайн калькулятор с решением,определитель матрицы онлайн по строке,определитель матрицы онлайн решение,определитель матрицы онлайн с буквами,определитель матрицы онлайн с решением,определитель матрицы по строке онлайн,определитель матрицы рассчитать,определитель матрицы рассчитать онлайн,определитель матрицы решение онлайн,определитель матрицы с буквами онлайн,определитель матрицы с решением онлайн,определитель матрицы с решением онлайн калькулятор,определитель матрицы считать онлайн,определитель онлайн,определитель онлайн 2 порядка,определитель онлайн калькулятор,определитель онлайн решение,определитель онлайн решить,определитель посчитать,определитель решение матрицы онлайн,определитель решение онлайн,определитель решить,определитель решить онлайн,определитель считать,определитель считать онлайн,определитель третьего порядка онлайн калькулятор,определитель четвертого порядка калькулятор онлайн,определитель четвертого порядка онлайн,определить вычислить онлайн,определить матрицы калькулятор,определить матрицы онлайн,определить онлайн,определить онлайн матрицы,определить посчитать онлайн,подсчет определителя матрицы онлайн,поиск определителя матрицы онлайн,получить нули в строке матрицы онлайн калькулятор,посчитать детерминант матрицы онлайн,посчитать онлайн определитель,посчитать онлайн определитель 4 порядка,посчитать определитель,посчитать определитель 4 порядка онлайн,посчитать определитель матрицы,посчитать определитель матрицы онлайн,посчитать определитель онлайн,посчитать определить онлайн,приведение матрицы к диагональному виду онлайн,привести к диагональному виду матрицу онлайн,привести матрицу к диагональному виду онлайн,рассчитать определитель матрицы,рассчитать определитель матрицы онлайн,рассчитать определитель онлайн,расчет матрицы,расчет определителя матрицы онлайн,решение матриц 4 порядка онлайн,решение матриц 4х4,решение матриц методом онлайн,решение матриц онлайн 4 порядка,решение матриц онлайн методом,решение матрицы онлайн 3 на 3,решение матрицы онлайн определитель,решение матрицы определитель онлайн,решение онлайн матриц 4 порядка,решение онлайн определитель,решение онлайн определитель матрицы,решение онлайн определителя,решение определителей 4 порядка онлайн,решение определителей онлайн,решение определители онлайн,решение определитель матрицы онлайн,решение определитель онлайн,решение определителя 4 порядка онлайн,решение определителя онлайн,решить онлайн определитель,решить онлайн определитель 4 порядка,решить определитель 4 порядка онлайн,решить определитель онлайн,сделать линейные преобразования найти определитель,считать онлайн определитель,считать онлайн определитель матрицы,считать определитель,считать определитель матрицы онлайн,считать определитель онлайн,теорема лапласа онлайн калькулятор,упростить и вычислить определитель. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычисление матриц. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычисление определителей онлайн).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычисление матриц. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычисление определителей онлайн).
Где можно решить любую задачу по математике, а так же вычисление матриц Онлайн?
Решить задачу вычисление матриц вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Функция МОПРЕД — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование MDETERM в Microsoft Excel.
Описание
Возвращает определитель матрицы (матрица хранится в массиве).
Синтаксис
МОПРЕД(массив)
Аргументы функции МОПРЕД описаны ниже.
Замечания
-
Массив может быть задан как интервал ячеек, например A1:C3, как массив констант, например {1;2;3:4;5;6:7;8;9}, как имя для интервала или массива.

-
Функция МОПРЕД возвращает значение ошибки #ЗНАЧ! в случаях, указанных ниже.
-
Если какая-либо ячейка в массиве пуста или содержит текст.
-
Если количество строк в массиве не равно количеству столбцов.
-
-
Определитель матрицы — это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех строк и трех столбцов, определитель вычисляется следующим образом:
МОПРЕД(A1:C3)
равно A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)
-
Определители матриц обычно используются при решении систем уравнений с несколькими неизвестными.
-
Функция МОПРЕД производит вычисления с точностью примерно 16 значащих цифр, что может в некоторых случаях приводить к незначительным ошибкам. Например, определитель сингулярной матрицы отличается от нуля на 1E-16.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Данные | Данные | Данные | Данные |
|---|---|---|---|
|
1 |
3 |
8 |
5 |
|
1 |
3 |
6 |
1 |
|
1 |
1 |
1 |
0 |
|
7 |
3 |
10 |
2 |
|
Формула |
Описание |
Результат |
|
|
=МОПРЕД(A2:D5) |
Определитель приведенной выше матрицы. |
88 |
|
|
=МОПРЕД({3;6;1:1;1;0:3;10;2}) |
Определитель матрицы, представленной в виде массива констант. |
1 |
|
|
=МОПРЕД({3;6:1;1}) |
Определитель матрицы в массиве констант. |
-3 |
|
|
=МОПРЕД({1;3;8;5:1;3;6;1}) |
Возвращает сообщение об ошибке, так как массив имеет разное количество строк и столбцов. |
#ЗНАЧ! |
Как найти дискриминант матрицы
Страницы работы
Содержание работы
Методические указания для выполнения лабораторных работ по дисциплине
ст. преп. каф. Информатика
Лабораторная работа №5
Обработка матриц. Решение систем линейных уравнений матричным способом.
Цель работы: Получить практические навыки по возможностям обработки матриц в MCAD и решению систем уравнений с использованием матриц.
Задание к лабораторной работе.
1. Загрузить среду MCAD и набрать там пояснения
а) Включить русский шрифт. б) Установить тип шрифта Courier New Cyr. в) В появившемся окне набрать рекомендуемый текст.
a. Лабораторная работа №5 в среде MathCAD
b. Выполнил студент(ка) ФИО, группа, шифр
2. Скопировать задание из таблицы 6 и вставить в среду MathCAD
а) Нажать левую кнопку мыши и выделить вариант задания из таблицы 1. б) Скопировать задание в буфер обмена (Правка->копировать).в) Установить курсор( красный крестик) в нужное место и вставить из буфера (Правка->вставить).
б) Скопировать задание в буфер обмена (Правка->копировать).в) Установить курсор( красный крестик) в нужное место и вставить из буфера (Правка->вставить).
3. Задать данную матрицу.
a) Набрать имя матрицы и установить с панели инструментов знак присваивания :=
b) Открыть панель векторов и матриц (значок есть на панели Математика)
c) Выбрать там шаблон матрицы
d) Указать нужное количество строк и столбцов
e) Заполнить шаблон значениями из своего варианта
4. Для получения матрицы B, умножим матрицу A на число, равное номеру вашего варианта + 1, так для 14 варианта матрицу A надо умножить на 15.
5. Для получения D умножим имеющиеся матрицы между собой.
6. Для нахождения дискриминантов матриц выбираем значок модуля на панели матриц, указываем имя и ставим знак равенства.
7. Для решения системы линейных уравнений необходимо задать матрицу коэффициентов (коэффициенты брать со знаком, если переменной нет в уравнении, значит коэффициент равен 0), вектор-столбец свободных членов
8. Решение будет найдено по формуле:
Таблица 6
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т. е. № варианта) плюс 1.
е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
1. Решить с применением операций над матрицами.
Задача. Дана матрица А:
Получите матрицу В, умножив матрицу А на число, равное вашему варианту (т.е. № варианта) плюс 1.
Получите матрицу D, умножив матрицы А и В друг на друга.
Найти дискриминант матриц A, B, D.
2. Решить систему уравнений матричным способом. Провести проверку правильности решения.
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Определители матриц часто используются в вычислениях, в линейной алгебре и аналитической геометрии. Вне академического мира определители матриц постоянно требуются инженерам и программистам, в особенности тем, кто работает с компьютерной графикой. Если вы уже знаете, как найти определитель матрицы размерностью 2×2, то из инструментов для нахождения определителя матрицы 3×3 вам будут необходимы только сложение, вычитание и умножение.
Определение
Определитель (детерминант) квадратной матрицы A – это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.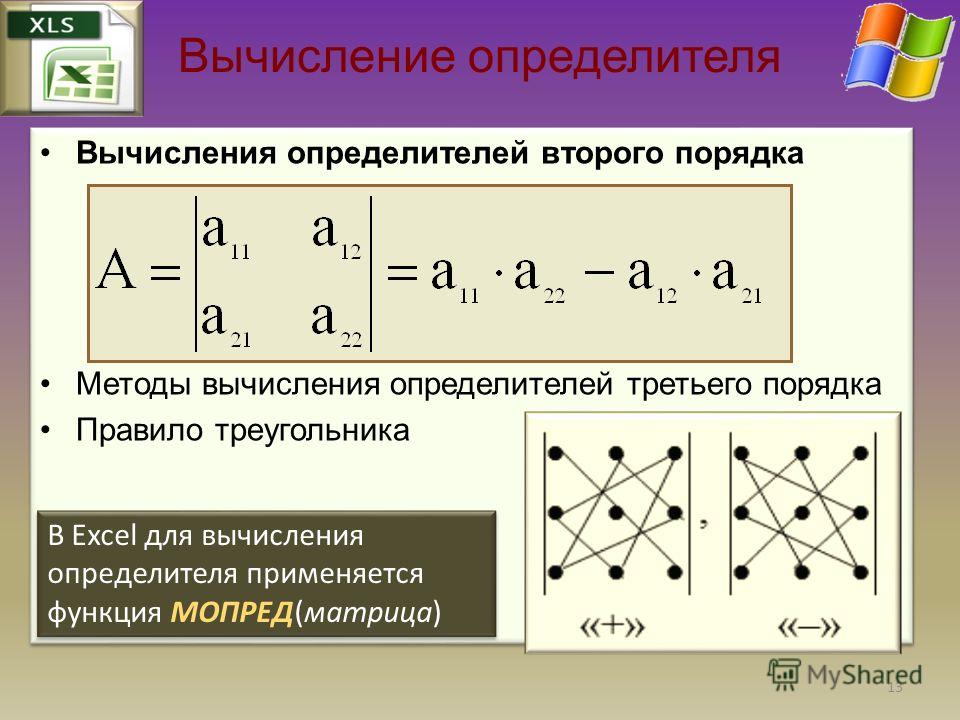
Обозначения
Пусть $ A = egin 1 & 4 & 2 \ 5 & 3 & 7 \ 6 & 2 & 1 end$
$det(A) = left|A
ight| = egin 1 & 4 & 2 \ 5 & 3 & 7 \ 6 & 2 & 1 end$
Свойства определителя
- Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12
$egin 1 & 4 & 2\ 0 & 0 & 0\ 3 & 9 & 5 end= 0$ или $egin1 & 4 & 0\ 4 & 2 & 0\ 3 & 9 & 0 end=0$
Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13
$egin 1 & 4 & 2\ 1 & 4 & 2\ 3 & 9 & 5 end= 0$ или $egin1 & 4 & 1\ 4 & 2 & 4\ 3 & 9 & 3 end=0$
Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
Пример 14
$egin 1 & 4 & 2\ 2 & 8 & 4\ 3 & 9 & 5 end= 0$ (две первые строки пропорциональны)
или
$egin8 & 4 & 7\ 4 & 2 & 3\ 18 & 9 & 8 end=0$ (два первых столбца пропорциональны)
Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15
$egin 1 & 4 & 2\ 7 & 2 & 3\ 8 & 6 & 5 end= 0$ $R_ <1>+R_ <2>=R_<3>$ или
$ egin 9 & 12 & 3\ 1 & 8 & 7\ 5 & 7 & 2 end=0$ $C_<1>+C_<3>=C_<2>$
При вычислении определителя можно выносить общие множители целых строк или столбцов.
Пример 17
$egin 1 & 5\ 3 & 8 end$ $xlongequal+R_<2>> egin1>4 & 13\ 3 & 8 end$
Пример 18
$egin1 & 5\ 3 & 8 end$ $xlongequal+C_<2>> egin1>6 & 5\ 11 & 8 end$
При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент .
Пример 20
$egin 1 & 5\ 3 & 8 end$ $xlongequal<5C_<1>-C_<2>> egin0 & 5\ 7 & 8 end$
Минор матрицы
Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.
Пример 21
$A=egin 1 & 4 & 2 \ 5 & 3 & 7 \ 6 & 2 & 1 end$
Один из миноров матрицы A есть $egin 1 & 2\ 5 & 3 end$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)
Другим минором является $egin 1 & 2 \ 6 & 1 end$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)
Пример 22
$B=egin 2 & 5 & 1 & 3\ 4 & 1 & 7 & 9\ 6 & 8 & 3 & 2\ 7 & 8 & 1 & 4 end$
Один из миноров матрицы B есть $ egin 1 & 7 & 9\ 8 & 3 & 2\ 8 & 1 & 4 end$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)
Другим минором является $egin 1 & 7 \ 8 & 3 end$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Пусть $A= egin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_<1,n>\ a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n>\ a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n>\ . & . & . & . & .& .\ a_ & a_ & a_ & . & . & a_ end$
Можно определить минор $Delta_$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_$ квадратной матрицы A. Такой минор называется дополнительным.
Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_<2,1>$.
Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем
Минор, дополнительный к элементу 2, есть $Delta_ <2,1>= 7$. <7>cdotDelta_<2,5>= -Delta_ <2,5>$ соответствует элементу $a_<2,5>$.
<7>cdotDelta_<2,5>= -Delta_ <2,5>$ соответствует элементу $a_<2,5>$.
Порядок определителя
Порядок определителя матрицы равен числу ее строк и столбцов.
Пример 26
$egin 1 & 4\ 6 & 2\ end$ (матрица имеет 2 строки и 2 столбца, так что порядок определителя равен 2)
Пример 27
$egin 4 & 7 & 9\ 6 & 3 & 2\ 7 & 1 & 4\ end$ (матрица имеет 3 строки и 3 столбца, так что порядок определителя равен 3)
Вычисление определителя матрицы
Определитель матрицы равен сумме произведений элементов любой строки или любого столбца и их алгебраических дополнений.
$left| A
ight| = egin a_ <1,1>& a_ <1,2>& a_ <1,3>& . & . & a_<1,n>\ a_ <2,1>& a_ <2,2>& a_ <2,3>& . & . & a_<2,n>\ a_ <3,1>& a_ <3,2>& a_ <3,3>& . & . & a_<3,n>\ . & . & . & . & .& .\ a_ & a_ & a_ & . & . & a_\ end$
Можно посчитать определитель, например, используя строку i:
Либо же можно посчитать определитель, используя столбец j:
Вычисление определителя матрицы 2×2
Используем строку 1, чтобы вычислить определитель.
Заметим, что $ Delta_<1,1>= a_ <2,2>$ и $ Delta_<1,2>=a_<2,1>$
$ left| A
ight| =a_ <1.1>cdot a_<2,2>- a_ <1.2>cdot a_<2,1>$
$color < egina & b\ c & d end=a cdot d – b cdot c>$
Пример 28
$egin 2 & 5\ 3 & 8 end=2 cdot 8 – 3 cdot 5 = 16 -15 =1$
Пример 29
$egin -4 & 7\ -2 & 9 end=-4 cdot 9 – 7 cdot (-2) = -36 -(-14) =-36 + 14 = – 22$
Вычисление определителя матрицы 3×3
Используем строку 1, чтобы вычислить определитель.
Упростить получение последней формулы можно следующим образом.
Начнем с того, что перепишем первые две строки под определителем как показано ниже. <2>end$
<2>end$
Используя свойства определителей, модифицируем строку 1 так, чтобы два элемента обратились в 0. В этом случае, когда мы используем полученную выше формулу для определителя матрицы 3×3, нет необходимости вычислять алгебраические дополнения этих элементов, поскольку их произведение будет равно 0.
Вычисление определителя матрицы 4×4
Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3.
Но сначала надо использовать свойства определителей:
- Проверим, не выполняется ли одно из условий того, что определитель равен 0.
- Проверим, нельзя ли вынести общий множитель из одной или нескольких строк или столбцов.
- Проверим, не является ли данная матрица матрицей Вандермонде, возможно, такой, в которой некоторые строки или столбцы переставлены.
В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение – это определитель матрицы 3×3, который считается по уже известной формуле.
Пример 33
$egin 1 & 3 & 9 & 2\ 5 & 8 & 4 & 3\ 0 & 0 & 0 & 0\ 2 & 3 & 1 & 8 end$
Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0.
Пример 34
$egin 1 & 3 & 1 & 2\ 5 & 8 & 5 & 3\ 0 & 4 & 0 & 0\ 2 & 3 & 2 & 8 end$
Замечаем, что $C_<1>$ равно $C_<3>$, следовательно, определитель равен 0.
Пример 35
$egin 1 & 3 & 9 & 2\ 5 & 8 & 4 & 3\ 10 & 16 & 18 & 4\ 2 & 3 & 1 & 8 end$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0.<1+4>$
$ = (-10)cdot egin -1 & 1 & 2\ 2 & 3 & 1\ 1 & -1 & -2 end=$ $(-10)cdot((-1)cdot 3cdot (-2) +2 cdot (-1)cdot2 + 1cdot 1cdot 1$ $-(2cdot 3cdot 1 + 1cdot (-1)cdot (-1) + (-2)cdot1cdot2))$ $= -10cdot(6 -4 +1 -6 – 1 + 4) =0$
Определитель квадратной матрицы
6.4 — Определитель квадратной матрицыОпределитель — это действительное число, связанное с каждой квадратной матрицей. Я еще не нашел хорошего Английское определение детерминанта. Все, что я могу найти, определяет это с точки зрения математическая формула или предлагает некоторые из ее использования. Есть даже определение определитель, который определяет его в терминах самого себя.
Определитель квадратной матрицы A обозначается как «det A» или | А |,Теперь последний выглядит как абсолютное значение A, но вам придется применить контекст. Если вертикальные линии проходят вокруг матрица, то есть определитель.
В строке ниже показаны два способа записи определителя.
| 3 | 1 | = | дет | 3 | 1 | ||
| 5 | 2 | 5 | 2 |
Определитель матрицы 2 × 2
Определитель матрицы 2 × 2 находится во многом как операция поворота.Это произведение элементов на главной диагонали за вычетом произведение элементов от главной диагонали.
Свойства детерминантов
- Определитель — действительное число, а не матрица.
- Определитель может быть отрицательным числом.
- Он вообще не связан с абсолютным значением, за исключением того, что они оба используют вертикальные линии.
- Определитель существует только для квадратных матриц (2 × 2, 3 × 3, … n × n). Определитель матрицы 1 × 1 — это единственное значение в определителе.
- Обратная матрица будет существовать, только если определитель не равен нулю.
Расширение с использованием младших и сомножителей
Определение определителя, которое у нас есть до сих пор, относится только к матрице 2 × 2. Есть ярлык для матрица 3 × 3, но я твердо верю, что вам следует изучить способ, который будет работать для всех размеров, а не только для частный случай для матрицы 3 × 3.
Метод называется расширением с использованием миноров и сомножителей. Прежде чем мы сможем использовать их, нам нужно их определить.
Несовершеннолетние
Второстепенным для любого элемента является определитель, который получается, когда строка и столбец что элементы удалены.
Обозначение M ij используется для обозначения минорной части элемента. в строке i и столбце j. Таким образом, M 21 будет означать второстепенное значение для элемента. в строке 2, столбце 1.
Рассмотрим определитель 3 × 3, показанный ниже. Я включил заголовки, чтобы вы можете держать строки и столбцы ровными, но обычно вы не включаете те.Мы собираемся найти нескольких несовершеннолетних.
| С 1 | С 2 | С 3 | |
|---|---|---|---|
| R 1 | 1 | 3 | 2 |
| р 2 | 4 | 1 | 3 |
| R 3 | 2 | 5 | 2 |
Поиск второстепенного для R
2 C 1Младший — это определитель, который остается при удалении строки и столбца. элемента, для которого вы пытаетесь найти второстепенное.Это означает, что мы должны удалить строка 2 и столбец 1, а затем найдите определитель.
| С 2 | С 3 | ||
|---|---|---|---|
| R 1 | 3 | 2 | = 3 (2) — 5 (2) = 6-10 = -4 |
| R 3 | 5 | 2 |
Как видите, второстепенное значение для строки 2 и столбца 1 — M 21 = -4.
Попробуем еще.
Поиск второстепенного для R
3 C 2На этот раз мы удалим строку 3 и столбец 2.
| С 1 | С 3 | ||
|---|---|---|---|
| R 1 | 1 | 2 | = 1 (3) — 4 (2) = 3-8 = -5 |
| р 2 | 4 | 3 |
Таким образом, второстепенное значение для строки 3, столбца 2 — M 32 = -5.
Матрица несовершеннолетних
Когда вы просто пытаетесь найти определитель матрицы, это перебор. Но для него есть одно чрезвычайно полезное приложение, которое даст нам практику. поиск несовершеннолетних.
Матрица миноров — это квадратная матрица, в которой каждый элемент является второстепенным. для номера в этой позиции.
Вот общая матрица миноров для определителя 3 × 3.
| С 1 | С 2 | С 3 | |||
|---|---|---|---|---|---|
| R 1 | М 11 | М 12 | М 13 | ||
| р 2 | М 21 | М 22 | М 23 | ||
| R 3 | M 31 | М 32 | М 33 |
Найдем матрицу миноров для нашего исходного определителя.Здесь определитель.
| С 1 | С 2 | С 3 | |
|---|---|---|---|
| R 1 | 1 | 3 | 2 |
| р 2 | 4 | 1 | 3 |
| R 3 | 2 | 5 | 2 |
Вот работа по поиску каждого несовершеннолетнего в матрице несовершеннолетних.
| С 1 | С 2 | С 3 | |
|---|---|---|---|
| R 1 | = 2-15 = -13 | = 8–6 = 2 | = 20 — 2 = 18 |
| р 2 | = 6-10 = -4 | = 2 — 4 = -2 | = 5-6 = -1 |
| R 3 | = 9 — 2 = 7 | = 3-8 = -5 | = 1–12 = -11 |
И, наконец, матрица миноров.Опять же, метки ставить не нужно для строки и столбцов, но это может вам помочь.
| С 1 | С 2 | С 3 | |||
|---|---|---|---|---|---|
| R 1 | -13 | 2 | 18 | ||
| р 2 | -4 | -2 | -1 | ||
| R 3 | 7 | -5 | -11 |
Кофакторы
Кофактор для любого элемента является второстепенным или противоположным второстепенным, в зависимости от того, где находится элемент в исходном определителе.Если строка и столбец элемента суммируется до четного числа, тогда сомножитель — это так же, как несовершеннолетний. Если сумма строки и столбца элемента получается нечетной число, то сомножитель — это противоположность второстепенному.
Ооо — ты понял? Нечетное меняет знаки, четное — тот же знак. Дежавю. Мы говорим об этом с момента раздела 3.2 о многочленах.
Знаковая диаграмма
Вместо того, чтобы складывать строку и столбец элемента, чтобы проверить, является четным или нечетным, многие люди предпочитают использовать знаковую диаграмму.Знаковая диаграмма — это либо a + или — для каждого элемента в матрице. Первый элемент (строка 1, столбец 1) является всегда а + и чередуется оттуда.
Примечание. Знак «+» не означает «положительный», а «-» — отрицательный. + Означает то же самое знак как несовершеннолетний и — означает противоположность несовершеннолетнему. Подумайте об этом дополнении и вычитание, а не положительное или отрицательное.
Вот знаковая диаграмма для определителя 2 × 2.
Вот знаковая диаграмма для определителя 3 × 3.
| С 1 | С 2 | С 3 | |
|---|---|---|---|
| R 1 | + | – | + |
| р 2 | – | + | – |
| R 3 | + | – | + |
Матрица сомножителей
Опять же, если все, что вы пытаетесь сделать, это найти определитель, вам не нужно проделать такую большую работу.
Матрица сомножителей — это матрица, найденная заменой каждого элемента матрицу ее сомножителем. Это матрица несовершеннолетних с измененными знаками по элементам в позициях -.
| С 1 | С 2 | С 3 | |||
|---|---|---|---|---|---|
| R 1 | -13 | -2 | 18 | ||
| р 2 | 4 | -2 | 1 | ||
| R 3 | 7 | 5 | -11 |
Расширение для поиска определителя
Вот шаги, которые нужно выполнить, чтобы найти определитель.
- Выберите любую строку или столбец в матрице. Неважно, какая строка или какая столбец, который вы используете, ответ будет одинаковым для любой строки. Есть несколько строк или столбцы, которые проще, чем другие, но мы вернемся к этому позже.
- Умножить каждые элемент в этой строке или столбце по его кофактору и добавьте. В результате определитель.
Разложим нашу матрицу по первой строке.
Из диаграммы знаков мы видим, что 1 находится в положительном положении, 3 — в отрицательном положение, а 2 находится в положительном положении.Поставив + или — перед элемент, он заботится о корректировке знака при переходе от второстепенного к кофактору.
| + 1 | 1 | 3 | –3 | 4 | 3 | + 2 | 4 | 1 |
| 5 | 2 | 2 | 2 | 2 | 5 |
= 1 (2-15) — 3 (8-6) + 2 (20-2)
= 1 (-13) — 3 (2) + 2 (18)
= -13-6
+ 36
= 17
Определитель этой матрицы равен 17.
Как я сказал ранее, на самом деле не имеет значения, какую строку или столбец вы используете.
Давайте попробуем еще раз, но на этот раз расширим вторые столбцы. Как усилие для экономии времени миноры для этого столбца (из матрицы миноров) были 2, -2 и -5. Исходные элементы были 3, 1 и 5. 3 и 5 отрицательны. позиции.
Определитель= — 3 (2) + 1 (-2) — 5 (-5) = -6-2 + 25 = 17
Разверните любую строку или любой столбец, вы получите 17.
Но диагонали делать нельзя.Если попробовать по главной диагонали, получится
+ 1 (-13) + 1 (-2) + 2 (-11) = -13-2-22 = -37
Некоторые строки или столбцы лучше других
- Выберите строку или столбец с наибольшим количеством нулей.
Поскольку каждый младший или сомножитель умножается на элемент в матрице, выбор строки или столбца с большим количеством нулей означает, что вы будете умножение на множество нулей. Умножение на ноль совсем не занимает много времени. Фактически, если элемент равен нулю, вы не нужно даже найти несовершеннолетнего или кофактор. - Выберите строку или столбец с наибольшими числами (или переменными) в нем.
Элементы в строке или столбце, по которым вы разворачиваете, не используются для поиска несовершеннолетние. Единственное место, где они умножаются, — это один раз в расширении. Если вы выберете строку или столбец с наименьшие числа, то каждое младшее число будет произведением большего числа.
Если вы выберете строку или столбец, в котором есть переменные, то вы только имеют умножить на переменные один раз, во время раскрытия.
Обратная матрица (пересмотрено)
Давайте на этот раз рассмотрим наш исходный определитель как матрицу.
| 1 | 3 | 2 | ||
| 4 | 1 | 3 | ||
| 2 | 5 | 2 |
Найдите матрицу миноров , как описано выше.
| -13 | 2 | 18 | ||
| -4 | -2 | -1 | ||
| 7 | -5 | -11 |
Превратите его в матрицу сомножителей , изменив знаки на соответствующих элементы на основе знаковой диаграммы.
| -13 | -2 | 18 | ||
| 4 | -2 | 1 | ||
| 7 | 5 | -11 |
Найдите примыкание к , переставив матрицу сомножителей.
Чтобы транспонировать матрицу, вы переключаете строки и столбцы. То есть строки стать столбцами и столбцы становятся строками. Транспонирование матрицы можно найти с помощью TI-82. или калькулятор TI-83, введя имя матрицы и затем выбрав Матрица, Math, а затем вариант 2, буква T с надстрочным индексом, например [A] T .
| -13 | 4 | 7 | ||
| -2 | -2 | 5 | ||
| 18 | 1 | -11 |
Наконец разделите сопряженную матрицу на определитель матрицы.В этой задаче определитель равен 17, поэтому мы разделим каждый элемент на 17. Результирующая матрица — , обратная исходной матрицы.
| -13/17 | 4/17 | 7/17 | ||
| -2/17 | -2/17 | 5/17 | ||
| 18/17 | 1/17 | -11/17 |
Матрица, обратная матрице, находится путем деления сопряженной матрицы матрица по определителю матрицы.Не пытайтесь это сделать на своем калькулятор, поскольку калькулятор не позволяет разделить матрицу на скаляр. Вместо этого вам придется умножить на обратное значение определителя.
Если вы проверите это с помощью своего калькулятора, вы можете убедиться, что на самом деле обратное — это сопряженное, деленное на определитель.
Поскольку обратная величина — это присоединенный элемент, деленный на детерминант, мы можем понять, почему обратное не существует, если определитель равен нулю. Это приведет к делению на ноль, что не определено.
Детерминанты более крупного порядка
Найдем определитель системы 4х4.
| С 1 | С 2 | С 3 | С 4 | |
|---|---|---|---|---|
| R 1 | 3 | 2 | 0 | 1 |
| р 2 | 4 | 0 | 1 | 2 |
| R 3 | 3 | 0 | 2 | 1 |
| R 4 | 9 | 2 | 3 | 1 |
Выберите строку или столбец с наибольшим количеством нулей.В данном случае это второй столбец.
Для каждого элемента исходной матрицы свой минор будет определителем 3 × 3. Придется расширить каждый из них на с использованием трех определителей 2 × 2.
Вот почему мы хотим развернуть второй столбец. Несовершеннолетние умножаются по их элементам, поэтому, если элемент в исходной матрице равен 0, он не действительно имеет значение, что такое несовершеннолетний, и мы можем сэкономить много времени, не имея найти это. Во втором столбце вам не нужно будет искать двух несовершеннолетних. потому что их соответствующий элемент во втором столбце равен нулю.
| — 2 | 4 | 1 | 2 | + 0 | — 0 | + 2 | 3 | 0 | 1 | ||||||
| 3 | 2 | 1 | ? | ? | 4 | 1 | 2 | ||||||||
| 9 | 3 | 1 | 3 | 2 | 1 |
Мы действительно могли бы заполнить эти два средних младших, но поскольку они умножаются на 0, неважно, какие они.Фактически, вы могли бы так же легко пропустить их.
Теперь осталось найти два определителя 3×3.
В первом определителе 3×3, нулей нет, поэтому выберите строку или столбец с наибольшими числами. Что будет столбцом 1, поэтому разверните его по первому столбцу.
Уведомление 4 находится в положительном положении. Таблицы знаков начинаются заново с каждого новый определитель. Положение числа в исходной матрице не имеет значение, только его положение в текущей матрице.
| 4 | 1 | 2 | ||||||||||
| 3 | 2 | 1 | = | + 4 | 2 | 1 | — 3 | 1 | 2 | + 9 | 1 | 2 |
| 9 | 3 | 1 | 3 | 1 | 3 | 1 | 2 | 1 |
= 4 (2-3) — 3 (1-6) + 9 (1-4) = 4 (-1) — 3 (-5) + 9 (-3 ) = -4 + 15 — 27 = -16
Рассмотрим другую матрицу 3 × 3.В этом в строке стоит 0 1 и столбец 2. Любой из них будет хорошим выбором для расширения, но поскольку в строке 1 числа немного больше, мы расширимся по первой строке.
| 3 | 0 | 1 | ||||||||||
| 4 | 1 | 2 | = | + 3 | 1 | 2 | –0 | ? | ? | + 1 | 4 | 1 |
| 3 | 2 | 1 | 2 | 1 | ? | ? | 3 | 2 |
= 3 (1-4) — 0 (не имеет значения) + 1 (8-3) = 3 (-3) + 1 (5) = -9 + 5 = -4
Когда вы идете искать определитель, помните, что были элементы из исходная матрица 4 × 4, умноженная на каждый из этих определителей 3 × 3.Первый — -2, второй — +2.
Определитель = -2 (-16) + 2 (-4) = 32 — 8 = 24
Худший сценарий
Чтобы найти определитель 3×3 без нулей, вам нужно найти три определителя 2×2.
Чтобы найти определитель 4×4 без нулей, вам нужно найти четыре определителя 3×3, каждый из которых затем становится тремя определителями 2×2, что в сумме дает двенадцать определителей 2×2.
Чтобы найти определитель 5×5 без нулей, вам нужно найти пять определителей 4×4, каждый из которых затем становится четырьмя детерминантами 3×3, каждый из которых становится тремя детерминантами 2×2, в сумме шестидесяти определителей 2×2.
Использование калькулятора
После этой последней проблемы вы должны спросить себя, нет ли более простого пути. Ну да, есть, если в определителе нет никаких переменных. Вы можете воспользоваться калькулятором.
Обозначение, которое использует калькулятор TI-82 или TI-83, — это обозначение Det A. Итак, после входа в матрицу в одну из доступных матриц на калькуляторе, введите DET, выбрав Матрица, Математика и выбор варианта 1. Затем введите название матрицы, которую вы используете.
Вам не нужно использовать круглые скобки (если у вас нет TI-83), но вы можете, если ты хочешь найти определитель продукта «det ([A] * [B])» или определитель транспонирования «det ([A] T ) «как в отличие от транспонирования определителя «(det [A]) T» . Кстати, калькулятор не найдет транспонирование определителя, потому что то детерминант — скаляр (действительное число), а калькулятор знает только, как найти транспонирование матрицы. Транспонирование скаляр — это то, что скаляр.
Треугольные матрицы
Вам действительно понравится находить определители этих матриц.
- Верхняя треугольная матрица
- Матрица, в которой все ненулевые элементы находятся либо на главной диагонали, либо над ней. То есть все ненулевые значения находятся в верхнем треугольнике. Все ниже диагонали это ноль.
- Нижняя треугольная матрица
- Матрица, в которой все ненулевые элементы находятся либо на главной диагонали, либо ниже нее.
- То есть все ненулевые значения находятся в нижнем треугольнике. Все выше диагонали равно нулю.
- Диагональная матрица
- Матрица, в которой все ненулевые элементы находятся на главной диагонали. Все выключено главная диагональ — ноль.
Определителем треугольной или диагональной матрицы является произведение элементов по главной диагонали.
Операции с элементарными строками
Было три элементарных операции со строками, которые могли быть выполнены, которые возвращали эквивалентная система.С определителями, поскольку определитель транспонирования такой же, как и у Определитель матрицы, элементарные операции со строками также могут применяться к столбцам.
Выполняя сокращение строк (используя поворот на 1, если хотите), вы можете поместить матрицу в треугольная форма. Как только он приобретет треугольную форму, все, что вам нужно сделать, это умножить на элементы на главной диагонали, и у вас есть определитель.
Давайте рассмотрим каждую из трех элементарных операций со строками.
- Если вы поменяете местами две строки или два столбца в определителе, результирующий определитель будет отличаются только знаком.То есть, если вы меняете местами строки или столбцы, результирующий определитель будет противоположно исходному определителю.
- Если вы умножаете строку или столбец на ненулевую константу, определитель умножается на эту та же ненулевая константа.
- Если вы умножите строку или столбец на ненулевую константу и добавите ее к другой строке или столбцу, при замене этой строки или столбца определитель не изменяется.
Эта последняя операция эквивалентна повороту на единицу!
Предупреждение, если ваша точка поворота — это число, отличное от единицы, то вы умножаете каждую строку, которую вы изменение поворотным элементом.Итак, если вы повернетесь к 3 и измените две строки, то полученный определитель будет в 3 * 3 = 9 раз больше, чем исходный определитель.
Пока вы выбираете единицу, все будет в порядке.
Вам не нужно помещать матрицу в сокращенную форму строки-эшелон или даже форму строки-эшелона. Вы можете в любой момент остановить сокращение и расширить, используя миноры и кофакторы. Что я Предлагаю это стержень там, где он есть, а затем разверните.
Нулевые детерминанты
Определитель матрицы будет равен нулю, если
- Вся строка нулевая.
- Две строки или столбцы равны.
- Строка или столбец является постоянным числом, кратным другой строке или столбцу.
Помните, что матрица обратима и невырождена тогда и только тогда, когда определитель не равен нулю. Итак, если определитель равен нулю, матрица сингулярна и не имеет обратной.
Определитель матрицы — 2×2, 3×3, 4×4 …
Автор Каталин Дэвид
Определение
Определитель квадратной матрицы A — это целое число, полученное с помощью ряда методов, использующих элементы матрицы.
Обозначение
Пусть $ A = \ begin {pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \ end {pmatrix} $
$ det (A) = \ left | A \ right | знак равно \ begin {vmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \ end {vmatrix} $
Свойства определителя
- Если матрица имеет строку или столбец со всеми элементами, равными 0 , то ее определитель равен 0 .
Пример 12
$ \ begin {vmatrix} 1 и 4 и 2 \\ 0 & 0 & 0 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ или же $ \ begin {vmatrix} 1 и 4 и 0 \\ 4 и 2 и 0 \\ 3 и 9 и 0 \ end {vmatrix} = 0 $ - Если матрица имеет две равные строки или два равных столбца , тогда ее определитель равен 0 .
Пример 13
$ \ begin {vmatrix} 1 и 4 и 2 \\ 1 и 4 и 2 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ или же $ \ begin {vmatrix} 1 и 4 и 1 \\ 4 и 2 и 4 \\ 3 и 9 и 3 \ end {vmatrix} = 0 $ - Если матрица имеет две пропорциональные строки или два пропорциональных столбца , тогда ее определитель равен 0 .
Пример 14
$ \ begin {vmatrix} 1 и 4 и 2 \\ 2 и 8 и 4 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ (первые две строки пропорциональны)
или
$ \ begin {vmatrix} 8 и 4 и 7 \\ 4 и 2 и 3 \\ 18 и 9 и 8 \ end {vmatrix} = 0 $ (первые два столбца пропорциональны) - Если строка или столбец является суммой или разностью других строк, соответственно столбцов , то определитель равен 0 .
Пример 15
$ \ begin {vmatrix} 1 и 4 и 2 \\ 7 и 2 и 3 \\ 8 и 6 и 5 \ end {vmatrix} = 0 $ $ R_ {1} + R_ {2} = R_ {3} $ или$ \ begin {vmatrix} 9 и 12 и 3 \\ 1 и 8 и 7 \\ 5 и 7 и 2 \ end {vmatrix} = 0 $ $ C_ {1} + C_ {3} = C_ {2} $
- В определителе мы можем индивидуально выделить целые числа из строк и столбцов.
Пример 16
В определителе
$ \ begin {vmatrix} 3 и 9 и 12 \\ 5 и 1 и 8 \\ 7 и 4 и 2 \ end {vmatrix} $, мы вычитаем 3 из строки 1 $ (R_ {1}) $ и получаем:
$ 3 \ cdot \ begin {vmatrix} 1 и 3 и 4 \\ 5 и 1 и 8 \\ 7 и 4 и 2 \ end {vmatrix} $, затем мы вычитаем 2 из столбца 3 $ (C_ {3}) $:
$ 6 \ cdot \ begin {vmatrix} 1 и 3 и 2 \\ 5 и 1 и 4 \\ 7 и 4 и 1 \ end {vmatrix} $ - В определителе мы можем добавлять или вычитать строки или столбцы из других строк, соответственно столбцов, и значение определителя остается прежним.
Пример 17
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {R_ {1} + R_ {2}} \ begin {vmatrix} 4 и 13 \\ 3 и 8 \ end {vmatrix} $
Пример 18
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {C_ {1} + C_ {2}} \ begin {vmatrix} 6 и 5 \\ 11 и 8 \ end {vmatrix} $ - В определителе мы можем складывать или вычитать несколько строк или столбцов.
Пример 19
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {2R_ {1} + 3R_ {2}} \ begin {vmatrix} 11 и 34 \\ 3 и 8 \ end {vmatrix} $Пример 20
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {5C_ {1} -C_ {2}} \ begin {vmatrix} 0 и 5 \\ 7 и 8 \ end {vmatrix} $ - Определитель матрицы равен определителю ее транспонирования.
- Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.
Минор матрицы
Определитель, полученный путем исключения некоторых строк и столбцов в квадратной матрице, называется минором этой матрицы.
Пример 21
$ A = \ begin {pmatrix}
1 и 4 и 2 \\
5 и 3 и 7 \\
6 и 2 и 1
\ end {pmatrix} $
Одним из миноров матрицы A является $ \ begin {vmatrix} 1 и 4 \\ 5 и 3 \ end {vmatrix} $ (получается путем исключения строки 3 и столбца 3 из матрицы A)
Другой минор — $ \ begin {vmatrix} 1 и 2 \\ 6 и 1 \ end {vmatrix} $ (получается путем исключения строки 2 и столбца 2 из матрицы A)
Пример 22
$ B = \ begin {pmatrix}
2 и 5 и 1 и 3 \\
4 и 1 и 7 и 9 \\
6 и 8 и 3 и 2 \\
7 и 8 и 1 и 4
\ end {pmatrix}
$
Одним из миноров матрицы B является $ \ begin {vmatrix} 1 и 7 и 9 \\ 8 и 3 и 2 \\ 8 и 1 и 4 \ end {vmatrix} $ (получается путем исключения строки 1 и столбца 1 из матрицы B)
Другой несовершеннолетний $ \ begin {vmatrix} 1 и 7 \\ 8 и 3 \ end {vmatrix} $ (получается путем исключения строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Позволять $ A = \ begin {pmatrix} a_ {1,1} и a_ {1,2} и a_ {1,3} &.&. & a_ {1, n} \\ a_ {2,1} и a_ {2,2} и a_ {2,3} &. &. & a_ {2, n} \\ а_ {3,1} и а_ {3,2} и а_ {3,3} &. &. & a_ {3, n} \\ . &. &. &. &. &. \\ a_ {n, 1} и a_ {n, 2} и a_ {n, 3} &. &. & Аня} \ end {pmatrix} $
Мы можем связать минор $ \ Delta_ {i, j} $ (полученный путем исключения строки i и столбца j) с любым элементом $ a_ {i, j} $ матрицы A.
Пример 23
$ A = \ begin {pmatrix}
4 и 7 \\
2 и 9
\ end {pmatrix} $
Нам нужно определить минор, связанный с 2.Поскольку этот элемент находится в строке 2, столбце 1, то 2 — это $ a_ {2,1} $.
Нам нужно удалить строку 2 и столбец 1 из матрицы A, в результате получится
Младший из 2 равен $ \ Delta_ {2,1} = 7 $.
Пример 24
$ B = \ begin {pmatrix}
1 и 4 и 2 \\
5 и 3 и 7 \\
6 и 2 и 1
\ end {pmatrix} $
Мы должны определить младший, связанный с 7. Поскольку этот элемент находится в строке 2, столбце 3, то 7 — это $ a_ {2,3} $.
Мы должны удалить строку 2 и столбец 3 из матрицы B, в результате чего получится
Минор 7 равен $ \ Delta_ {2,3} = \ begin {vmatrix} 1 и 4 \\ 6 и 2 \ end {vmatrix} $
Пример 25
$ C = \ begin {pmatrix}
2 и 5 и 1 и 3 \\
4 и 1 и 7 и 9 \\
6 и 8 и 3 и 2 \\
7 и 8 и 1 и 4
\ end {pmatrix} $
Мы должны определить минор, связанный с 5.Поскольку этот элемент находится в строке 1, столбце 2, то 5 — это $ a_ {1,2} $.
Мы должны удалить строку 1 и столбец 2 из матрицы C, в результате чего получится
Минор из 5 равен $ \ Delta_ {1,2} = \ begin {vmatrix} 4 и 7 и 9 \\ 6 и 3 и 2 \\ 7 и 1 и 4 \\ \ end {vmatrix} $
Кофактор элемента матрицы
Пусть $ A = \ begin {pmatrix} a_ {1,1} и a_ {1,2} и a_ {1,3} &. &. & a_ {1, n} \\ a_ {2,1} и a_ {2,2} и a_ {2,3} &. &.{7} \ cdot \ Delta_ {2,5} = — \ Delta_ {2,5} $ соответствует элементу $ a_ {2.5} $
Порядок определителя
Порядок определителя равен количеству строк и столбцов в нем. {i + 3} \ cdot \ Delta_ {i, 3} +.{3} \ cdot \ Delta_ {1,2} = a_ {1,1} \ cdot \ Delta_ {1,1} -a_ {1.2} \ cdot \ Delta_ {1,2}
долл. СШАОднако $ \ Delta_ {1,1} = a_ {2,2} $ и $ \ Delta_ {1,2} = a_ {2,1} $
$ \ left | A \ right | = a_ {1.1} \ cdot a_ {2,2} — a_ {1.2} \ cdot a_ {2,1} $
$ \ color {красный} { \ begin {vmatrix} а & б \\ CD \ end {vmatrix} = a \ cdot d — b \ cdot c} $
Пример 28
$ \ begin {vmatrix}
2 и 5 \\
3 и 8
\ end {vmatrix} = 2 \ cdot 8 — 3 \ cdot 5 = 16-15 = 1 $
Пример 29
$ \ begin {vmatrix}
-4 & 7 \\
-2 и 9
\ end {vmatrix} = -4 \ cdot 9 — 7 \ cdot (-2) = -36 — (- 14) = -36 + 14 = — 22 $
Вычисление определителя 3×3
Мы используем строку 1 для вычисления определителя.{4} \ cdot \ Delta_ {1,3} = $ $ a_ {1,1} \ cdot \ Delta_ {1,1} -a_ {1.2} \ cdot \ Delta_ {1,2} + a_ {1.3} \ cdot \ Delta_ {1,3} $
$ \ Delta_ {1,1} = \ begin {vmatrix} а_ {2,2} и а_ {2,3} \\ а_ {3,2} и а_ {3,3} \ end {vmatrix} = a_ {2,2} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,2} $
$ \ Delta_ {1,2} = \ begin {vmatrix} а_ {2,1} и а_ {2,3} \\ а_ {3,1} и а_ {3,3} \ end {vmatrix} = a_ {2,1} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,1} $
$ \ Delta_ {1,3} = \ begin {vmatrix} а_ {2,1} и а_ {2,2} \\ а_ {3,1} и а_ {3,2} \ end {vmatrix} = a_ {2,1} \ cdot a_ {3,2} -a_ {2,2} \ cdot a_ {3,1} $
$ \ left | A \ right | = a_ {1,1} \ cdot (a_ {2,2} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,2}) — a_ {1,2} \ cdot ( a_ {2,1} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,1}) + $ $ a_ {1,3} \ cdot (a_ {2,1} \ cdot a_ {3,2} -a_ {2,2} \ cdot a_ {3,1}) = $ $ a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} -a_ {1,1} \ cdot a_ {2,3} \ cdot a_ {3,2} -a_ {1 , 2} \ cdot a_ {2.1} \ cdot a_ {3,3} + a_ {1,2} \ cdot a_ {2,3} \ cdot a_ {3,1} + $ $ a_ {1,3} \ cdot a_ {2,1} \ cdot a_ {3,2} -a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} = $ $ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {1,2} \ cdot a_ {2,3} \ cdot a_ {3, 1} + a_ {1,3} \ cdot a_ {2,1} \ cdot a_ {3,2} -} $ $ \ color {красный} {(a_ {1,1} \ cdot a_ {2,3} \ cdot a_ {3,2} + a_ {1,2} \ cdot a_ {2,1} \ cdot a_ {3 , 3} + a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1})} $
Чтобы быстрее достичь последнего отношения, мы можем использовать следующий метод.
Сначала перепишем первые две строки под определитель следующим образом.
$ \ begin {vmatrix}
\ color {красный} {a_ {1,1}} & a_ {1,2} & a_ {1,3} \\
\ color {red} {a_ {2,1}} & \ color {red} {a_ {2,2}} & a_ {2,3} \\
\ color {red} {a_ {3,1}} & \ color {red} {a_ {3,2}} & \ color {red} {a_ {3,3}}
\ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc}
a_ {1,1} & \ color {красный} {a_ {1,2}} & \ color {красный} {a_ {1,3}} \\
a_ {2,1} & a_ {2,2} & \ color {красный} {a_ {2,3}} \\
\ end {array} $
Мы умножаем элементы на каждой из трех красных диагоналей (главной диагонали и тех, что под ней), и складываем результаты:
$ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {2,1} \ cdot a_ {3,2} \ cdot a_ {1,3} + a_ {3,1} \ cdot a_ {1,2} \ cdot a_ {2 , 3}} $
$ \ begin {vmatrix}
\ color {red} {a_ {1,1}} & \ color {red} {a_ {1,2}} & \ color {blue} {a_ {1,3}} \\
\ color {red} {a_ {2,1}} & \ color {blue} {a_ {2,2}} & \ color {blue} {a_ {2,3}} \\
\ color {blue} {a_ {3,1}} & \ color {blue} {a_ {3,2}} & \ color {blue} {a_ {3,3}}
\ end {vmatrix} $
$ \ hspace {2mm}
\ begin {array} {ccc}
\ color {blue} {a_ {1,1}} & \ color {blue} {a_ {1,2}} & \ color {red} {a_ {1,3}} \\
\ color {blue} {a_ {2,1}} & \ color {red} {a_ {2,2}} & \ color {red} {a_ {2,3}} \\
\ end {array} $
Мы умножаем элементы на каждой из трех синих диагоналей (вторичная диагональ и те, что под ней), и складываем результаты:
$ \ color {blue} {a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} + a_ {2,3} \ cdot a_ {3,2} \ cdot a_ {1, 1} + a_ {3,3} \ cdot a_ {1,2} \ cdot a_ {2,1}} $
Если вычесть два отношения, мы получим формулу определителя:
$ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {2,1} \ cdot a_ {3,2} \ cdot a_ {1, 3} + a_ {3,1} \ cdot a_ {1,2} \ cdot a_ {2,3} -} $ $ \ color {красный} {(a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} + a_ {2,3} \ cdot a_ {3,2} \ cdot a_ {1 , 1} + a_ {3,3} \ cdot a_ {1,2} \ cdot a_ {2,1})} $
Пример 30
$ A = \ begin {pmatrix}
1 и 4 и 3 \\
2 и 1 и 5 \\
3 и 2 и 1 \\
\ end {pmatrix} $
$ \ begin {vmatrix}
1 и 4 и 3 \\
2 и 1 и 5 \\
3 и 2 и 1 \\
\ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc}
1 и 4 и 3 \\
2 и 1 и 5 \\
\ end {array} $
$ = 1 \ cdot1 \ cdot1 + 2 \ cdot2 \ cdot3 + 3 \ cdot4 \ cdot5 — (3 \ cdot1 \ cdot3 + 5 \ cdot2 \ cdot1 + 1 \ cdot4 \ cdot2) = $ 1 $ + 12 + 60 — (9 + 10 + 8) = 73-27 = 46 $
Пример 31
$ A = \ begin {pmatrix}
3 и 5 и 1 \\
1 и 4 и 2 \\
7 и 1 и 9 \\
\ end {pmatrix} $
$ \ begin {vmatrix}
3 и 5 и 1 \\
1 и 4 и 2 \\
7 и 1 и 9 \\
\ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc}
3 и 5 и 1 \\
1 и 4 и 2 \\
\ end {array} $
$ = 3 \ cdot4 \ cdot9 + 1 \ cdot1 \ cdot1 + 7 \ cdot5 \ cdot2 — (1 \ cdot4 \ cdot7 + 2 \ cdot1 \ cdot3 + 9 \ cdot5 \ cdot1) = $ 108 $ + 1 + 70 — (28 + 6 + 45) = 79-79 = 100 $
Есть определители, элементами которых являются буквы. {2 }] $
Пример 32
Вычисляем определитель матрицы Вандермонда.{2}
\ end {vmatrix} = $
$ \ begin {vmatrix} а-с и б-с \\ (a-c) (a + c) и (b-c) (b + c) \ end {vmatrix} = $ $ (a-c) (b-c) \ begin {vmatrix} 1 и 1 \\ а + с и б + с \ end {vmatrix} = $
$ = (a-c) (b-c) [(b + c) — (a + c)] = $ $ (a-c) (b-c) (b + c-a-c) = (a-c) (b-c) (b-a) $
Вычисление определителя 4×4
Для вычисления определителей 4×4 воспользуемся общей формулой.
Перед применением формулы, используя свойства определителей:
- Мы проверяем, выполняется ли какое-либо из условий, при которых значение определителя равно 0.
- Мы проверяем, можем ли мы исключить какую-либо строку или столбец.
- Мы проверяем, является ли определитель матрицей Вандермонда или он имеет те же элементы, но переупорядоченные, в любой строке или столбце.
В любом из этих случаев мы используем соответствующие методы вычисления определителей 3×3. Мы модифицируем строку или столбец, чтобы заполнить их 0, за исключением одного элемента. Определитель будет равен произведению этого элемента и его сомножителя. В этом случае сомножитель — это определитель 3×3, который вычисляется по его специальной формуле.
Пример 33
$ \ begin {vmatrix}
1 и 3 и 9 и 2 \\
5 и 8 и 4 и 3 \\
0 & 0 & 0 & 0 \\
2 и 3 и 1 и 8
\ end {vmatrix} $
Мы замечаем, что все элементы в строке 3 равны 0, поэтому определитель равен 0.
Пример 34
$ \ begin {vmatrix}
1 и 3 и 1 и 2 \\
5 и 8 и 5 и 3 \\
0 & 4 & 0 & 0 \\
2 и 3 и 2 и 8
\ end {vmatrix} $
Мы замечаем, что $ C_ {1} $ и $ C_ {3} $ равны, поэтому определитель равен 0.
Пример 35
$ \ begin {vmatrix}
1 и 3 и 9 и 2 \\
5 и 8 и 4 и 3 \\
10 и 16 и 18 и 4 \\
2 и 3 и 1 и 8
\ end {vmatrix} $
Мы замечаем, что строки 2 и 3 пропорциональны, поэтому определитель равен 0.
Пример 36
$ \ begin {vmatrix}
\ color {красный} {4} & 3 & 2 & 2 \\
0 & 1 & -3 & 3 \\
0 и -1 и 3 и 3 \\
0 и 3 и 1 и 1
\ end {vmatrix} $
Поскольку в столбце 1 есть только один элемент, отличный от 0, мы применяем общую формулу, используя этот столбец. {2 + 2} \ cdot
\ begin {vmatrix}
4 и 2 и 8 \\
1 и 3 и 1 \\
2 и 1 и 7
\ end {vmatrix} = $
$ = 4 \ cdot3 \ cdot7 + 1 \ cdot1 \ cdot8 + 2 \ cdot2 \ cdot1 $ $ — (8 \ cdot3 \ cdot2 + 1 \ cdot1 \ cdot4 + 7 \ cdot2 \ cdot1) = $
84 $ + 8 + 4- 48-4-14 = 30 $
Пример 38
$ \ begin {vmatrix}
1 и -2 и 3 и 2 \\
2 и 3 и 1 и -1 \\
3 и 3 и 3 и 3 \\
-1 и 4 и 2 и 1 \\
\ end {vmatrix} $
Мы можем вынести 3 из строки 3:
$ 3 \ cdot
\ begin {vmatrix}
1 и -2 и 3 и 2 \\
2 и 3 и 1 и -1 \\
1 и 1 и 1 и 1 \\
-1 и 4 и 2 и 1 \\
\ end {vmatrix} $
Поскольку в строке 3 есть только элементы, равные 1, мы можем легко сделать нули.{3 + 4} \ cdot $ $ = (- 1) \ cdot
\ begin {vmatrix}
-1 & -4 & 1 \\
3 и 4 и 2 \\
-2 и 3 и 1 \\
\ end {vmatrix} $
$ = — ((- 1) \ cdot 4 \ cdot 1 +3 \ cdot 3 \ cdot1 + (-2) \ cdot (-4) \ cdot 2 $ $ — (1 \ cdot 4 \ cdot (-2) + 2 \ cdot 3 \ cdot (-1) + 1 \ cdot (-4) \ cdot3)) $ $ = — (- 4 + 9 + 16 + 8 + 6 + 12) = -47 $
Пример 39
$ \ begin {vmatrix}
2 и 5 и 1 и 4 \\
4 и 1 и 6 и 3 \\
5 и 3 и 7 и 2 \\
1 и 0, 2 и 4
\ end {vmatrix} $
В этом примере мы можем использовать последнюю строку (которая содержит 1) и сделать нули в первом столбце.{4 + 1} \ cdot \ begin {vmatrix} 5 & -3 & -4 \\ 1 и -2 и -13 \\ 3 и -3 и -18 \ end {vmatrix} = $ $ (- 1) \ cdot \ begin {vmatrix} 5 & -3 & -4 \\ 1 и -2 и -13 \\ 3 и -3 и -18 \ end {vmatrix} $
Мы вычитаем -1 из столбца 2 и -1 из столбца 3.
$ (-1) \ cdot (-1) \ cdot (-1) \ cdot
\ begin {vmatrix}
5 и 3 и 4 \\
1 и 2 и 13 \\
3 и 3 и 18
\ end {vmatrix} = $
$ (- 1) \ cdot
\ begin {vmatrix}
5 и 3 и 4 \\
1 и 2 и 13 \\
3 и 3 и 18
\ end {vmatrix} = $
$ — [5 \ cdot 2 \ cdot 18 + 1 \ cdot 3 \ cdot 4+ 3 \ cdot 3 \ cdot 13 — (4 \ cdot 2 \ cdot 3 \ cdot + 13 \ cdot 3 \ cdot 5 + 18 \ cdot 3 \ cdot 1)] = $
$ — (180 + 12 + 117-24-195-54) = 36 $
Пример 40
$ \ begin {vmatrix}
4 и 7 и 2 и 3 \\
1 и 3 и 1 и 2 \\
2 и 5 и 3 и 4 \\
1 и 4, 2 и 3
\ end {vmatrix} $
В столбце 3 стоит 1, поэтому мы сделаем нули в строке 2. {1 + 4} $
$ = (-10) \ cdot \ begin {vmatrix} -1 и 1 и 2 \\ 2 и 3 и 1 \\ 1 и -1 и -2 \ end {vmatrix} = $ $ (- 10) \ cdot ((- 1) \ cdot 3 \ cdot (-2) +2 \ cdot (-1) \ cdot2 + 1 \ cdot 1 \ cdot 1 $ $ — (2 \ cdot 3 \ cdot 1 + 1 \ cdot (-1) \ cdot (-1) + (-2) \ cdot1 \ cdot2)) $ $ = -10 \ cdot (6-4 +1-6-1 + 4) = 0 $
Определитель матрицы
Определитель матрицы — это специальное число , которое можно вычислить из квадратной матрицы.
Матрица — это массив чисел:
Матрица
(в ней 2 строки и 2 столбца)
Определитель этой матрицы (расчеты объяснены позже):
3 × 6 — 8 × 4 = 18 — 32 = −14
Для чего это нужно?
Определитель помогает нам найти обратную матрицу, говорит нам о матрице, которая полезна в системах линейных уравнений, исчислении и многом другом.
Символ
Символ для определителя представляет собой две вертикальные линии с каждой стороны.
Пример:
| A | означает определитель матрицы A
(точно такой же символ, что и абсолютное значение.)
Расчет определителя
Прежде всего, матрица должна быть квадратных (т.е. иметь такое же количество строк, как и столбцов). Тогда это просто арифметика. Вот как:
Для матрицы 2 × 2
Для матрицы 2 × 2 (2 строки и 2 столбца):
Определитель:
| A | = ad — bc
«Определитель A равен a, умноженному на d минус b, умноженному на c»
Легко вспомнить, когда вы думаете о кресте:
|
Пример:
| B | = 4 × 8 — 6 × 3
= 32–18
= 14
Для матрицы 3 × 3
Для матрицы 3 × 3 (3 строки и 3 столбца):
Определитель:
| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
«Определитель A равен… etc »
Может показаться сложным, но есть закономерность :
Для определения определителя матрицы 3 × 3 :
- Умножьте a на определитель матрицы 2 × 2 , то есть не в строке или столбце .
- Аналогично для b и для c
- Суммируйте их, но помните минус перед цифрой b
В качестве формулы (вспомните, что вертикальные полосы || означают «определитель») :
«Определитель A равен умноженному на определитель… etc »
Пример:
| C | = 6 × (−2 × 7 — 5 × 8) — 1 × (4 × 7 — 5 × 2) + 1 × (4 × 8 — (−2 × 2))
= 6 × (−54) — 1 × (18) + 1 × (36)
= −306
Для матриц 4 × 4 и выше
Шаблон продолжается для матриц 4 × 4:
- плюс a , умноженное на определитель матрицы, которая равна , а не в строке или столбце ,
- минус b , умноженное на определитель матрицы, которая равна , а не в строке или столбце b ,
- плюс c , умноженное на определитель матрицы, которая равна , а не в строке или столбце c ,
- минус d , умноженное на определитель матрицы, которая равна , а не в строке или столбце d ,
В виде формулы:
Обратите внимание на шаблон + — + — (+ a… −b … + c … −d …). Это важно помнить.
Шаблон продолжается для матриц 5 × 5 и выше. Обычно для таких случаев лучше использовать Матричный калькулятор!
Не единственный путь
Этот метод расчета называется «разложением Лапласа», и мне он нравится, потому что его легко запомнить. Но есть и другие методы (чтобы вы знали).
Сводка
- Для матрицы 2 × 2 определитель равен ad — bc
- Для матрицы 3 × 3 умножьте a на определитель матрицы 2 × 2 , то есть , а не в строке или столбце , аналогично для b и c , но помните, что b имеет отрицательный знак!
- Шаблон продолжается для больших матриц: умножьте a на определитель матрицы , то есть , а не в строке или столбце , продолжайте таким же образом по всей строке, но помните + — + — шаблон. 3 = -1 $
$$ \ begin {pmatrix} 0 & 0 & -4 \\ -5 & 0 & 3 \\ 0 & 0 & -6 \\ \ end {pmatrix}
$о * $$ \ begin {pmatrix} 0 и 3 \\ 0 & -6 \\ \ end {pmatrix} $$ что дает 0 (0-0) = 0
$, очевидно, следующая матрица будет выглядеть так же, как верхний член во втором столбце — ноль, поэтому определитель для этого будет $ 0 $.4 = 1 9000 долларов США. 3
$$ \ begin {pmatrix} 0 и 3 и -4 \\ -5 и -8 и 3 \\ 0 и 5 и -6 \\ \ end {pmatrix}
$для определителя:
0 раз $$ \ begin {pmatrix} -8 & 3 \\ 5 & -6 \\ \ end {pmatrix} $$ что дает $ 0 (48-15) = 0 $
-3 раза $$ \ begin {pmatrix} -5 & 3 \\ 0 & -6 \\ \ end {pmatrix}
$, что дает -3 (30-0) = -90 $
излишне продолжать, потому что после окончательного вычисления для этого второстепенного значения я получаю -100 и в результате получаю det M3 = -190 и получаю определитель нулей для следующего определителя M4.что дает: $ 0 (5) + 0 (-7) + (-90) (2) + (0) (2) $, что дает Det Ax $ = -380. $ В книге указано, что это 20 долларов, и когда я сделал это в калькуляторе, он получил 20, но проблема в том, что и книга, и калькулятор расширяются по строке с наибольшим количеством нулей, но теоретически НЕ ВАЖНО, КАКАЯ строка или столбец, который вы выбрали для расширения, должны получить тот же ответ. Так что это? Мои вычисления неверны или я ошибаюсь в предположении, что вы можете расширить любую строку или столбец? Разве это не важно, только если определитель не равен нулю? или имеет значение точное значение в более сложных случаях?
линейная алгебра — Самый простой способ вычислить определитель этой матрицы 4×4
Как предложено в комментариях, устранение Гаусса обычно является правильным решением, и в этом случае оно также является самым быстрым:
$$ \ det A = \ det \ begin {pmatrix} 2 и 3 и 1 и 0 \\ 4 & -2 & 0 & -3 \\ 8 и -1 и 2 и 1 \\ 1 и 0 и 3 и 4 \\ \ end {pmatrix} знак равно \ det \ begin {pmatrix} 0 и 3 и -5 и -8 \\ 0 & -2 & -12 & -19 \\ 0 & -1 & -22 & -31 \\ 1 и 0 и 3 и 4 \\ \ end {pmatrix} знак равно (-1) ^ {4 + 1} \ cdot 1 \ cdot \ det \ begin {pmatrix} 3 & -5 & -8 \\ -2 и -12 и -19 \\ -1 и -22 и -31 \\ \ end {pmatrix} знак равно — \ det \ begin {pmatrix} 0 & -71 & -101 \\ 0 и 32 и 43 \\ -1 и -22 и -31 \\ \ end {pmatrix} знак равно -1 \ cdot (-1) ^ {3 + 1} \ cdot (-1) \ cdot \ det \ begin {pmatrix} -71 и -101 \\ 32 и 43 \\ \ end {pmatrix} = (-71) \ cdot 43 — (- 101) \ cdot 32 = 179
$( Результат, подтвержденный Wolfram Alpha; я никогда не мог вспомнить формулу 3×3, поэтому не использую ее )
Если вам абсолютно нужна матрица с верхней диагональю, вы можете это сделать, но это всего лишь ограничение обычного алгоритма:
$$ \ det A = \ det \ begin {pmatrix} 2 и 3 и 1 и 0 \\ 4 & -2 & 0 & -3 \\ 8 и -1 и 2 и 1 \\ 1 и 0 и 3 и 4 \\ \ end {pmatrix} знак равно \ det \ begin {pmatrix} 2 и 3 и 1 и 0 \\ 0 & -8 & -2 & -3 \\ 0 & -13 & -2 & 1 \\ 0 & — \ frac12 & \ frac52 & 4 \\ \ end {pmatrix} знак равно \ det \ begin {pmatrix} 2 и 3 и 1 и 0 \\ 0 & -8 & -2 & -3 \\ 0 & 0 &? &? \\ 0 & 0 &? &? \\ \ end {pmatrix} знак равно \ det \ begin {pmatrix} 2 и 3 и 1 и 0 \\ 0 & -8 & -2 & -3 \\ 0 & 0 &? &? \\ 0 & 0 & 0 &? \\ \ end {pmatrix}
$( Мне сейчас лень вычислять $? $, Просто продолжайте процедуру исключения по Гауссу.Тогда определитель будет произведением записей на диагонали. )
Для собственных значений: да, необходимо вычислить характеристический полином.
linear algebra — Определитель матрицы 4×4 Линейная алгебра
— Определитель матрицы 4×4 — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 780 раз
$ \ begingroup $Найдите определители матриц A = $ \ begin {bmatrix} a & 3 & 0 & 5 \\ 0 & b & 0 & 2 \\ 1 & 2 & c & 3 \\ 0 & 0 & 0 & d \ end {bmatrix} $ и B = $ \ begin {bmatrix} x & y & z & t \\ 2 & 1 & 1 & 2 \\ 2 & 3 & 1 & 4 \\ 1 & 3 & 2 & 3 \ end {bmatrix} $.
Я попытался уменьшить матрицу A, сформировав треугольную матрицу, но смог получить что-нибудь конкретное.
Создан 29 ноя.
abcdefabcdef2,17522 золотых знака1313 серебряных знаков2525 бронзовых знаков
$ \ endgroup $ 1 $ \ begingroup $HNT: A: 4-й ряд, затем для второстепенного 3-го столбца.
Создан 29 ноя.
Кола Б.Кола Б.2,11311 золотых знаков99 серебряных знаков2020 бронзовых знаков
$ \ endgroup $ 3 $ \ begingroup $Для первого: $$ \ begin {vmatrix} a & 3 & 0 & 5 \\ 0 & b & 0 & 2 \\ 1 & 2 & c & 3 \\ 0 & 0 & 0 & d \ end {vmatrix} = c \ begin { vmatrix} a & 3 & 5 \\ 0 & b & 2 \\ 0 & 0 & d \ end {vmatrix} = cd \ begin {vmatrix} a & 4 \\ 0 & b \ end {vmatrix} = abcd.
$Для второго:
$$ \ begin {vmatrix} x & y & z & t \\ 2 & 1 & 1 & 2 \\ 2 & 3 & 1 & 4 \\ 1 & 3 & 2 & 3 \ end {vmatrix} = x \ begin {vmatrix} 1 & 1 & 2 \\ 3 & 1 & 4 \\ 3 & 2 & 3 \ end {vmatrix} — y \ begin {vmatrix} 2 & 1 & 2 \\ 2 & 1 & 4 \\ 1 & 2 & 3 \ end {vmatrix} + z \ begin {vmatrix} 2 & 1 & 2 \\ 2 & 3 & 4 \\ 1 & 3 & 3 \ end {vmatrix} — w \ begin {vmatrix} 2 & 1 & 1 \\ 2 & 3 & 1 \\ 1 & 3 & 2 \ end {vmatrix}.
$Создан 30 ноя.
Иво ТерекиИво Терек2,1k1111 золотых знаков7070 серебряных знаков189189 бронзовых знаков
$ \ endgroup $ $ \ begingroup $ПОДСКАЗКА : для B не беспокойтесь о треугольной матрице; вместо этого используйте сомножители в первой строке.Это дает вам чисто численные вычисления, когда попытка сделать что-то треугольное потребует относительно сложной работы с существующими переменными.
Создан 29 ноя.
Дэн УзнанскиDan Uznanski8,78222 золотых знака1717 серебряных знаков3535 бронзовых знаков
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Калькулятор определяющей матрицы 2×2 3×3 4×4 NxN
Поиск инструмента
Определитель матрицы
Инструмент для вычисления определителя матрицы.Определитель квадратной матрицы M — это полезное значение, вычисляемое из ее внутренних элементов и обозначаемое det (M) или | M |.
Результаты
Определитель матрицы — dCode
Метка (и): Матрица
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Рекламные объявления
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор определителя матрицы 2×2
Погрузка…
Рассчитать
(если это сообщение не исчезает, попробуйте обновить страницу)Калькулятор определителя матрицы 3×3
Загрузка …
Рассчитать
(если это сообщение не исчезает, попробуйте обновить страницу)Калькулятор определителя Matrix 4×4
Загрузка …
Рассчитать
(если это сообщение не исчезает, попробуйте обновить страницу)Калькулятор определителя матрицы NxN
Ответы на вопросы (FAQ)
Как вычислить определитель матрицы?
Для квадратной матрицы 2×2 (порядок 2) вычисление выглядит следующим образом:
$$ \ begin {vmatrix} a & b \\ c & d \ end {vmatrix} = ad — bc $$
Пример: $$ \ begin {vmatrix} 1 & 2 \\ 3 & 4 \ end {vmatrix} = 1 \ times 4 — 2 \ times 3 = -2 $$
Для матрицы большего размера, такой как порядок 3 (3×3), вычислите:
$$ \ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix} = a \ begin {vmatrix} e & f \\ h & i \ end {vmatrix} — b \ begin {vmatrix} d & f \\ g & i \ end {vmatrix} + c \ begin {vmatrix} d & e \\ g & h \ end {vmatrix} \\ = aei-afh + bfg-bdi + cdh-ceg $$
Вычисленные подматрицы называются минорами исходной матрицы.
Идея та же для матриц большего размера:
Для порядка 4 определитель матрицы 4×4 :
$$ \ begin {vmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \ end {vmatrix} = a \ begin {vmatrix} f & g & h \\ j & k & l \\ n & o & p \ end {vmatrix} — b \ begin {vmatrix} e & g & h \\ i & k & l \\ m & o & p \ end {vmatrix} + c \ begin {vmatrix} e & f & h \\ i & j & l \\ m & n & p \ end {vmatrix} — d \ begin {vmatrix} e & f & g \\ i & j & k \\ m & n & o \ end {vmatrix} \\ = \\ a (fkp — flo — gjp + gln + hjo — hkn) — b (ekp — elo — gip + glm + hio — hkm) + c (ejp — eln — fip + flm + hin — hjm) — d (ejo — ekn — fio + fkm + gin — gjm) \\ = \\ afkp — aflo — agjp + agln + ahjo — ahkn — bekp + belo + bgip — bglm — bhio + bhkm + cejp — celn — cfip + cflm + chin — chjm — dejo + dekn + dfio — dfkm — dgin + dgjm $$
Как вычислить определитель для неквадратной матрицы?
Определитель неквадратной матрицы не определен, он не существует согласно определению определителя.
По какой формуле вычисляется определитель матрицы порядка n?
Нет другой формулы, кроме приведенного выше объяснения для общего случая матрицы порядка n.
Как вычислить определитель матрицы 1х1?
Для матрицы 1×1 определитель является единственным элементом матрицы.
Пример: $$ | 1 | = 1 $$
Что такое определитель единичной матрицы?
Определитель единичной матрицы равен 1.
Пример: $$ \ begin {vmatrix} 1 & 0 \\ 0 & 1 \ end {vmatrix} = 1 \ times 1 — 0 \ times 0 $$
Пример: $$ \ begin {vmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {vmatrix} = (1 \ times 1 \ times 1) — (1 \ раз 0 \ раз 0) + (0 \ раз 0 \ раз 0) — (0 \ раз 0 \ раз 1) + (0 \ раз 0 \ раз 0) — (0 \ раз 1 \ раз 0) = 1 $ $
Только член, соответствующий умножению диагонали, будет равен 1, а остальные члены будут нулевыми.
Как найти определитель матрицы по ее собственным значениям?
Определитель матрицы является произведением ее собственных значений (включая комплексные значения и потенциальную кратность).
Задайте новый вопросИсходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Определитель матрицы». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любых алгоритмов, апплетов или фрагментов «Определителя матрицы» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любые другие. Определитель функции Матрицы (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанную на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)), и никакая загрузка данных, скрипт, копирование и доступ к API для «Определителя матрицы» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.


 matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> B = np.matrix('10 4 -1; -4 -1 2; 8 3 1')
>>> print(B)
[[10 4 -1]
[-4 -1 2]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
14.0
matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> B = np.matrix('10 4 -1; -4 -1 2; 8 3 1')
>>> print(B)
[[10 4 -1]
[-4 -1 2]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
14.0 linalg.det(C), 3)
4.0
>>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3)
4.0
linalg.det(C), 3)
4.0
>>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3)
4.0
