Определитель 4 порядка формула: Найти определитель матрицы четвертого порядка

Содержание

Найти определитель матрицы четвертого порядка

Основные определения и формула для нахождения определителя матрицы четвертого порядка

Часто в математических и прикладных задачах возникает необходимость использовать матрицы. Дадим определение матрицы.

Определение 1

Матрица — это прямоугольная таблица скаляров (элементов некоторого поля), состоящая из заданного количества столбцов и заданного количества строк.

Выделяют разные матрицы. Нам пригодятся понятие следующих:

если матрица имеет единственный элемент, то она является совпадающей со своим единственным скаляром;
квадратной матрицей называют такую матрицу, у которой количество столбцов совпадает с количеством строк.

Алгебраические операции над матрицами имеют свой алгоритм и порядок, отличающийся от тех же операций над обычными числами. Помимо алгебраических операций, существуют и другие операции над матрицами. Например, операция транспонирования матрицы.

Часто учащиеся сталкиваются с задачами по нахождению определителя матриц разных порядков.

Под матрицами первого, второго, третьего, четвёртого и т.д. порядка понимаются квадратные матрицы. Дадим определение определителю.

Определение 2

Определитель или детерминант матрицы — это определённое число, которое можно поставить в соответствие какой-либо квадратной матрице. Если элементы матрицы действительные числа, то и определитель будет действительным числом. Определитель обозначают $\det A$ или $|A|$.

Определитель первого порядка равен скаляру данной матрицы. Определители второго и третьего порядка высчитываются в определённом порядке, то есть по известным формулам.

Для вычисления определителя больше третьего порядка, необходимо понимание минора матрицы.

Определение 3

Минор матрицы третьего порядка — это определитель второго порядка, полученной из заданной матрицы третьего порядка вычеркиванием $i$-ой строки и $j$-го столбца. Минор обозначают $M$.

Формула для определителя четвёртого порядка:

$|A|=a_{11}M_{11}-a_{12}M_{12}+a_{13}M_{13}-a_{14}M_{14}$.

Пример решения

Решим пример.

Пример 1

$A = \begin{pmatrix}1&0&2&-1\\0&0&1&4\\-3&0&0&2\\6&-3&-1&0\end{pmatrix}.$

$|A| = \begin{vmatrix}1&0&2&-1\\0&0&1&4\\-3&0&0&2\\6&-3&-1&0\end{vmatrix}=1\cdot\begin{vmatrix}0&1&4\\0&0&2\\-3&-1&0\end{vmatrix}-0\cdot\begin{vmatrix}0&1&4\\-3&0&2\\6&-1&0\end{vmatrix}+2\cdot\begin{vmatrix}0&0&4\\-3&0&2\\6&-3&0\end{vmatrix}-(-1)\cdot\begin{vmatrix}0&0&1\\-3&0&0\\6&-3&-1\end{vmatrix}=1\cdot(-3)-0\cdot24+2\cdot36-(-1)\cdot9=78.$

В рамках учебной программы принято использовать однотипные примеры с действительными числами. Зная формулу, очевидно, что все примеры будут аналогичны друг другу.

Теорема Лапласа

Существует также метод нахождения определителя четвертого порядка по теореме Лапласа. Тогда понадобится следующее понятие:

Определение 4

Алгебраическое дополнение элемента $a_{ij}$ матрицы третьего порядка — минор элемента $a_{ij}$, умноженный на $(-1)^{i+j}$.

Теорема 1

Определитель четвертого порядка равен сумме всех четырёх произведений следующего вида: каждый из четырёх элементов какой-либо фиксированной строки (столбца) этой матрицы умножается на его алгебраическое дополнение.

Эта теорема распространяется на матрицы любого порядка.

При ручном решении подобных задач главное помнить о внимательности и сосредоточенности, а также уметь проявлять терпение, когда дело касается большой матрицы или матрицы с большими значениями элементов. На практике в современных условиях для решения подобных задач применяют вычислительные машины.

Как вычислить определитель четвертого порядка

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей, он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

Определитель можно вычислить только для квадратной матрицы (более подробно см. Действия с матрицами)

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения: Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.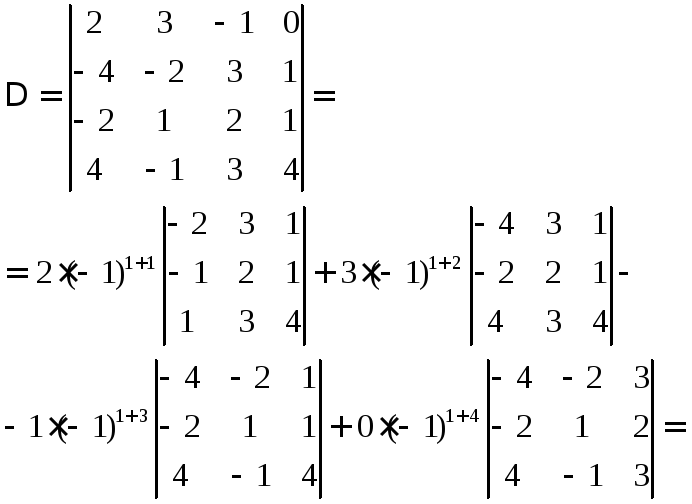

Начнем с определителя «два» на «два»:

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 – нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу.
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель

по первой строке.
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу:

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя.

Автор: Емелин Александр

(Переход на главную страницу)

Профессиональная помощь по любому предмету – Zaochnik.com

Основные определения и формула для нахождения определителя матрицы четвертого порядка

Часто в математических и прикладных задачах возникает необходимость использовать матрицы.

Дадим определение матрицы.

Матрица – это прямоугольная таблица скаляров (элементов некоторого поля), состоящая из заданного количества столбцов и заданного количества строк.

Выделяют разные матрицы. Нам пригодятся понятие следующих:

если матрица имеет единственный элемент, то она является совпадающей со своим единственным скаляром;
квадратной матрицей называют такую матрицу, у которой количество столбцов совпадает с количеством строк.

Часто учащиеся сталкиваются с задачами по нахождению определителя матриц разных порядков. Под матрицами первого, второго, третьего, четвёртого и т.д. порядка понимаются квадратные матрицы. Дадим определение определителю.

Попробуй обратиться за помощью к преподавателям

Определитель или детерминант матрицы – это определённое число, которое можно поставить в соответствие какой-либо квадратной матрице. Если элементы матрицы действительные числа, то и определитель будет действительным числом. Определитель обозначают $det A$ или $|A|$.

Для вычисления определителя больше третьего порядка, необходимо понимание минора матрицы.

Минор матрицы третьего порядка – это определитель второго порядка, полученной из заданной матрицы третьего порядка вычеркиванием $i$-ой строки и $j$-го столбца. Минор обозначают $M$.

Формула для определителя четвёртого порядка:

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Определителем матрицы второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя: ; ; ; detA (детерминант).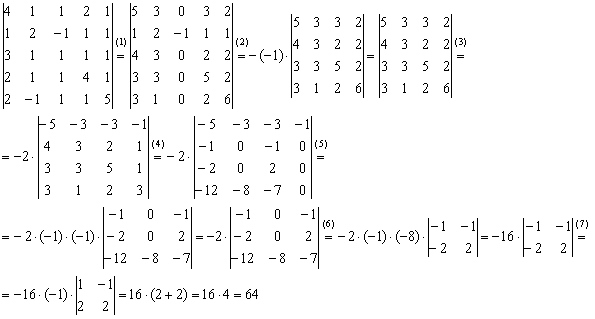

Пример: .

Определителем матрицы третьего порядка называется число или математическое выражение, вычисляемое по следующему правилу

Наиболее простым способом вычисления определителя третьего порядка является дописывание снизу определителя двух первых строк.

В образованной таблице чисел перемножаются элементы, стоящие на главной диагонали и на диагоналях параллельных главной, знак результата произведения не изменяется. Следующим этапом вычислений является аналогичное перемножение элементов, стоящих на побочной диагонали и на параллельных ей. Знаки у результатов произведений меняются на противоположные. Затем складываем полученные шесть слагаемых.

Пример:

Разложение определителя по элементам некоторой строки (столбца).

Минором М_ij элемента а_ij квадратной матрицы А называется определитель, составленный из элементов матрицы А, оставшихся после вычеркивания i-ой строки и j-го столбца.

Например, минором к элементу а₂₁ матрицы третьего порядка будет определитель .

Будем говорить, что элемент а_ij занимает четное место, если i+j (сумма номеров строки и столбца на пересечении которых находится данный элемент) – четное число, нечетное место, если i+j – нечетное число.

Алгебраическим дополнением А_ij элемента а_ij квадратной матрицы А называется выражение (или величина соответствующего минора, взятого со знаком «+», если элемент матрицы занимает четное место, и со знаком «-», если элемент занимает нечетное место).

Пример:

– алгебраическое дополнение элемента а₂₃= 4;

– алгебраическое дополнение элемента а₂₂= 1.

Теорема Лапласа. Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.

Проиллюстрируем на примере определителя третьего порядка. Вычислить определитель третьего порядка разложением по первой строке можно следующим образом

Аналогично можно вычислить определитель третьего порядка, разложив по любой строке или столбцу. Удобно раскладывать определитель по той строке (или столбцу), в которой содержится больше нулей.

Пример:

Таким образом, вычисление определителя 3-го порядка сводится к вычислению 3-х определителей второго порядка. В общем случае можно вычислить определитель квадратной матрицы n-го порядка, сводя его к вычислению n определителей (n-1)-го порядка

Замечание. Не существует простых способов для вычисления определителей более высокого порядка, аналогичных способам вычисления определителей 2-го и 3-го порядка. Поэтому для вычисления определителей выше третьего порядка может использоваться только метод разложения.

Пример. Вычислить определитель четвертого порядка.

Разложим определитель по элементам третьей строки

Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

2. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный.

3. Определитель с двумя одинаковыми строками (столбцами) равен 0.

4. Общий множитель всех элементов некоторой строки (столбца) определителя можно вынести за знак определителя.

5. Определитель не изменится, если к элементам одного из его столбцов (строки) прибавить соответствующие элементы любого другого столбца (строки), умноженные на некоторое число.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10568 – | 7328 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

как считать по столбцу, как вычислить от треугольной матрицы

Определитель матрицы 4 порядка

Определение

Матрица представляет собой прямоугольную таблицу скаляров, то есть элементов некоторого поля, которая состоит из определенного числа столбцов и определенного числа строк.

Существует разные типы матриц. При рассмотрении данной темы важно уточнить понятия некоторых из них:

в том случае, когда матрица обладает единственным элементом, она является совпадающей со своим единственным скаляром;
квадратная матрица представляет собой такую матрицу, которая имеет равное число столбцов и строк.

Алгебраические действия с матрицами характеризуются определенным алгоритмом и порядком. Подобные операции отличаются от манипуляций с простыми числами. Кроме алгебраических действий, над матрицами выполняют и другие операции. К примеру, транспортирование матрицы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В задачах часто встречаются примеры нахождения определителя матриц разных порядков. Матрицы первого, второго, третьего, четвертого и других порядков относят к квадратным матрицам.

Определение

Определитель или детерминант матрицы является определенным числом, которое можно поставить в соответствие некой квадратной матрице.

В том случае, когда элементы матрицы имеют вид действительных чисел, то и определитель является действительным числом. Определитель обозначают detA или |A|. Определитель первого порядка соответствует скаляру рассматриваемой матрицы.

Определители второго и третьего порядка определяются в соответствии со стандартным алгоритмом, то есть с помощью известных формул. Для того чтобы вычислить определитель больше третьего порядка, требуется ознакомиться с понятием минора матрицы (М).

Определение

Минор матрицы третьего порядка является определителем второго порядка, который получен из заданной матрицы третьего порядка путем вычеркивания i-ой степени и j-го столбца.

Примечание

Изучая материалы по теме матричного определителя, можно встретить термин «детерминант». Фактически данные понятия идентичны. Однако детерминант обладает множеством значений в других научных областях, что объясняет использование его русского перевода в математике.

Свойства определителя:

при перестановке местами двух строк или столбцов знак определителя меняется;
при умножении строки или столбца на число, весь определить также умножится на число;
в том случае, когда одну строку сколько угодно раз прибавляют или вычитают из другой, определитель не меняется;
при наличии одинаковых, пропорциональных или заполненных нулями двух строк определителя весь определитель равен нулю;
все перечисленные свойства справедливы в случае столбцов;
транспортирование матрицы не сопровождается изменением определителя;

определитель произведения матриц равен произведению определителей.{N (a_{1},a_{2},…a_{n})}}*a_{1a_{1}}a_{2a_{2}}…a_{na_{n}}\)

Каждое слагаемое является произведением n-элементов, которые взяли по одному из каждой строки и каждого столбца, умноженное на (-1) в степени Np, определяемое, как количество инверсий.

Геометрический смысл понятия заключается в том, что определитель представляет собой объем параллелепипеда, получаемый в том случае, если рассмотреть строки, как вектора, образующие ребра геометрической фигуры.

При этом число строк или столбцов соответствует количеству векторов. Таким образом, в случае матрицы А = (2*2), получается двухмерный параллелограмм, а детерминант является площадью рассматриваемой фигуры. Если А = (3*3), то геометрическая фигура будет иметь вид трехмерного параллелепипеда, а определитель – являться его объемом.

Правильная расстановка индексов в матрице

Определение

Индексы являются координатами элемента в системе.

Каждый элемент обладает парой индексов:

первый – определяет строку;
второй – указывает столбец.

Так как порядок представляет собой число строк или столбцов в квадратной матрице, то он определяется с помощью m-индекса нижней строки или n-индекса крайнего правого столбца. Данный метод используют при очень больших таблицах, когда считать строки или столбы неудобно.

Матрица представляет собой таблицу, заполненную числами. Одной из ее ключевых характеристик является размерность, то есть число строк и столбцов, из которых она состоит. Как правило, говорят, что какая-то матрица A имеет размер $\left[ m\times n \right]$, если в ней имеется m строк и n столбцов. Запись имеет следующий вид:

$A=\left[ m\times n \right]$

или $A=\left( {{a}_{ij}} \right),\quad 1\le i\le m;\quad 1\le j\le n.$

Существуют и другие обозначения для матрицы. В любом случае, при разных $\left[ m\times n \right]$ и ${{a}_{ij}}$ возникает вопрос расстановки индексов. В этом случае целесообразно обратиться к обычной системе координат:

Источник: berdov.com

Данная система имеет начало координат (точка $ O=\left( 0;0 \right)$) оси x и y, а каждая точка на плоскости однозначно определяется по координатам:

$A=\left( 1;2 \right)$

$B=\left( 3;1 \right)$ и так далее.

Следует поставить рассматриваемую систему рядом с матрицей, таким образом, чтобы начало координат совпадало с левым верхним углом, что существенно облегчит задачу определения индексов. Оси должны быть направлены так, чтобы охватить всю систему. При этом необходимо повернуть систему координат. Правильный вариант расположения представлен на рисунке:

Источник: berdov.com

Получается, что любая клетка матрицы обладает однозначными координатами х и у. К примеру, запись ${{a}_{24}}$ означает, что мы обращаемся к элементу с координатами x=2 и y=4. Размеры матрицы также однозначно заданы двумя числами:

Источник: berdov.com

Общая схема вычисления определителей

Определение

Теорема Лапласа о разложении определителя: пусть в матрице размера выбрано k строк или столбцов, причем .{i+j}}\cdot {{M}_{ij}}}\)

Таким образом удалось вывести формулу для разложения определителя по строке. Аналогичный метод можно использовать для того, чтобы разложить определитель по столбцам.

Данное следствие позволяет сделать несколько выводов:

методика подходит для строк и столбцов;
число слагаемых в разложении в любом случае составляет n;
вместо одного определителя $\left[ n\times n \right]$ необходимо вычислить несколько определителей размера на единицу меньше $\left[ \left( n-1 \right)\times \left( n-1 \right) \right].$

Практическое применение алгоритма можно продемонстрировать, решая задачу по нахождению определителя матрицы:

$\left| \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\end{matrix} \right|$

В первую очередь необходимо разложить данный определитель по первой строке:

$\begin{align} \left| A \right|=1\cdot {{\left( -1 \right)}^{1+1}}\cdot \left| \begin{matrix} 5 & 6 \\ 8 & 9 \\\end{matrix} \right|+ & \\ 2\cdot {{\left( -1 \right)}^{1+2}}\cdot \left| \begin{matrix} 4 & 6 \\ 7 & 9 \\\end{matrix} \right|+ & \\ 3\cdot {{\left( -1 \right)}^{1+3}}\cdot \left| \begin{matrix} 4 & 5 \\ 7 & 8 \\\end{matrix} \right|= & \\\end{align}$

Отсюда следует:

$\begin{align} &=1\cdot \left( 45-48 \right)-2\cdot \left( 36-42 \right)+3\cdot \left( 32-35 \right)= \\ &=1\cdot \left( -3 \right)-2\cdot \left( -6 \right)+3\cdot \left( -3 \right)=0.{4+4}}\cdot \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end{matrix} \right| & \\\end{align}$

От пары слагаемых можно избавиться. В результате останется пара определителей 3х3:

$\begin{align} & \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end{matrix} \right|=0+0+1-1-1-0=-1; \\ & \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end{matrix} \right|=0+1+1-0-0-1=1. \\\end{align}$

$\left| \begin{matrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end{matrix} \right|=1\cdot \left( -1 \right)+\left( -1 \right)\cdot 1=-2$

В результате вычислений получен ответ: -2

Метод понижения порядка

Упростить расчеты при вычислении определителей можно, используя их свойства. Например, требуется вычислить определитель:

$\begin{vmatrix}6&3&8&-4\\5&6&4&2\\0&3&4&2\\4&1&-4&6\end{vmatrix}$

Следует вынести из третьего столбца множитель 4:

$\begin{vmatrix}6&3&8&-4\\5&6&4&2\\0&3&4&2\\4&1&-4&6\end{vmatrix}=4\cdot\begin{vmatrix}6&3&2&-4\\5&6&1&2\\0&3&1&2\\4&1&-1&6\end{vmatrix}$

Далее следует вынести из четвертого столбца множитель 2:

$4\cdot\begin{vmatrix}6&3&2&-4\\5&6&1&2\\0&3&1&2\\4&1&-1&6\end{vmatrix}=4\cdot2\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}$

Затем можно прибавить к строке №1 строку №2, умноженную на (-2):

$8\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}$

Следующим шагом будет сложение строки №3 и строки №2, умноженной на (-1):

$8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\4&1&-1&3\end{vmatrix}$

Далее нужно прибавить к четвертой строке вторую, умноженную на 1:

$8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\9&7&0&4\end{vmatrix}$

Можно разложить определитель по третьему столбцу:

$8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\9&7&0&4\end{vmatrix}=8\cdot1\cdot(-1)^{2+3}\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=8\cdot(-1)^{5}\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=-8\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}$

Если прибавить к первой строке третью, умноженную на 1, получим:

$-8\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=-8\begin{vmatrix}5&-2&0\\-5&-3&0\\9&7&4\end{vmatrix}$

Затем необходимо разложить определитель по третьему столбцу и вычислить его:

$-8\begin{vmatrix}5&-2&0\\-5&-3&0\\9&7&4\end{vmatrix}=-8\cdot4\cdot(-1)^{3+3}\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\cdot(-1)^{6}\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}$

Далее следует прибавить к строке №2 строку №1, умноженную на 1:

$-32\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\begin{vmatrix}5&-2\\0&-5\end{vmatrix}$

При разложении определителя по столбцу №1 и замене определителя 1-го порядка единственным его элементом получим:

$-32\begin{vmatrix}5&-2\\0&-5\end{vmatrix}=-32\cdot5\cdot(-1)^{1+1}\cdot(-5)=-32\cdot5\cdot1\cdot(-5)=800$

Приведение к треугольному виду

Методика заключается в приведении определителя к треугольнику. После этого остается вычислить произведение элементов, расположенных на главной диагонали. С помощью данного способа вычислим определитель:

$\begin{vmatrix}4&-2&0&5\\3&2&-2&1\\-2&1&3&-1\\2&3&-6&-3\end{vmatrix}$

В первую очередь следует поменять местами первую и третью строки:

$\begin{vmatrix}4&-2&0&5\\3&2&-2&1\\-2&1&3&-1\\2&3&-6&-3\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\2&3&-6&-3\end{vmatrix}$

Далее первую строку, умноженную на 1, можно прибавить к четвертой:

$-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\2&3&-6&-3\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\0&4&-3&-4\end{vmatrix}$

Затем нужно к строке №3 прибавить строку №1, умноженную на 2:

$-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\0&4&-3&-4\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}$

Следующий шаг – умножение второй строки на 2:

$\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\6&4&-4&2\\0&0&6&3\\0&4&-3&-4\end{vmatrix}$

Сложим вторую и первую строку, умноженную на 3:

$-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\6&4&-4&2\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}$

После умножения строки №4 на 7 получим:

$-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&28&-21&-28\end{vmatrix}$

Затем следует прибавить к четвертой строке вторую строку, умноженную на (-4):

$-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&28&-21&-28\end{vmatrix}=-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&0&-41&-24\end{vmatrix}$

В результате смены мест столбцов №3 и №4 получим:

$-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&0&-41&-24\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&-24&-41\end{vmatrix}$

После того, как третья строка, умноженная на 8, будет прибавлена к четвертой строке, получится вычислить определитель:

$\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&-24&-41\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&0&7\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\cdot(-2)\cdot7\cdot3\cdot7=-21$

4 порядка матрицы

Вы искали 4 порядка матрицы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление определителей 4 порядка, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «4 порядка матрицы».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 4 порядка матрицы,вычисление определителей 4 порядка,вычисление определителя 4 порядка,вычисление определителя 4 порядка сведением его к определителю 2 порядка,вычисление определителя матрицы 4 порядка,вычисление определителя четвертого порядка,вычислите определитель 4 порядка,вычислите определитель четвертого порядка от треугольной матрицы,вычислить определитель 4 го порядка,вычислить определитель 4 порядка,вычислить определитель матрицы 4 на 4,вычислить определитель матрицы 4 порядка с решением,вычислить определитель матрицы четвертого порядка,вычислить определитель четвертого порядка,вычислить определитель четвертого порядка матрицы,как вычислить минор матрицы 4 порядка,как вычислить определитель 4 порядка,как вычислить определитель матрицы 4 на 4,как вычислить определитель матрицы 4 порядка,как вычислить определитель четвертого порядка,как вычислять определители 4 порядка,как искать определитель матрицы 4 порядка,как найти минор 4 порядка,как найти определитель 4 порядка,как найти определитель 4 порядка для чайников,как найти определитель матрицы 4 на 4,как найти определитель матрицы 4 порядка,как найти определитель матрицы четвертого порядка,как найти определитель четвертого порядка,как найти определитель четвертого порядка матрицы,как находить определитель 4 порядка,как находить определитель матрицы 4 порядка,как посчитать определитель 4 порядка,как посчитать определитель матрицы 4 на 4,как решать матрицу 4 порядка,как решать матрицы 4 на 4,как решать матрицы 4 порядка,как решать определители 4 порядка,как решать определители 4 порядка для чайников,как решать определитель 4 порядка,как решить матрицу 4 на 4,как решить определитель 4 порядка примеры,как решить определитель 4 порядка решить,как считать матрицу 4 на 4,как считать определители 4 порядка,как считать определитель 4 на 4,как считать определитель 4 порядка,как считать определитель матрицы 4 на 4,как считать определитель матрицы 4 порядка,матрица 4 порядка,матрица 4 порядка определитель,матрица 4 порядка примеры,матрица определитель 4 порядка,матрица четвертого порядка,матрицы 4 на 4 как решать,матрицы 4 порядка,матрицы 4 порядка как решать,матрицы 4 порядка решение,матрицы вычисление определителя 4 порядка,матрицы вычислить определитель четвертого порядка,матрицы определитель 4 на 4,матрицы определитель четвертого порядка,матрицы четвертого порядка,найти определитель 4 порядка,найти определитель матрицы 4 на 4,найти определитель матрицы 4 порядка,найти определитель четвертого порядка,нахождение определителя матрицы 4 порядка,определители 4 порядка,определители 4 порядка как вычислять,определители 4 порядка как решать,определители 4 порядка примеры,определители четвертого порядка,определители четвертого порядка примеры,определитель 4 го порядка примеры,определитель 4 на 4,определитель 4 на 4 как считать,определитель 4 порядка,определитель 4 порядка как найти,определитель 4 порядка как находить,определитель 4 порядка как решать,определитель 4 порядка как считать,определитель 4 порядка матрица,определитель 4 порядка найти,определитель 4 порядка примеры,определитель 4 порядка примеры решения,определитель матрица 4 порядка,определитель матрицы 4 порядка,определитель матрицы 4 порядка как считать,определитель матрицы четвертого порядка,определитель четвертого порядка,определитель четвертого порядка как вычислить,определитель четвертого порядка как найти,определитель четвертого порядка матрицы,определитель четвертого порядка найти,определитель четвертого порядка формула,решение матриц 4 порядка,решение матрица 4 на 4,решение матрицы 4 на 4,решение матрицы 4 порядка,решение определителей 4 порядка,решение определителя 4 порядка,треугольный определитель 4 порядка,формула определитель четвертого порядка. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 4 порядка матрицы. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычисление определителя 4 порядка).

Где можно решить любую задачу по математике, а так же 4 порядка матрицы Онлайн?

Решить задачу 4 порядка матрицы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Определители квадратных матриц


	Главная > Учебные материалы > Математика: Определители квадратных матриц


	1.Определители квадратных матриц. 2.Свойства определителей.

	1 2 3 4 5 6 7 8 9


	1.Определители квадратных матриц. Как известно из раздела матричной алгебры, матрицы получили широкое распрастранение в экономике. Для того, чтобы как-то характеризовать матрицу, а также решать различные задачи с использованием матриц, в математике введено понятие определитель матрицы. Т.е. определитель матрицы — это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать.
	Для матрицы первого порядка определитель равен элементу а11.
	Для матрицы второго порядка определитель равен разности произведений элементов матрицы, рассчитанный по формуле:
	Для матрицы третьего порядка определитель равен числу, рассчитанному по формуле:
	Определители квадратных матриц можно вычислить и другим способом: с помощью разложения элементов матрицы по строке. Для того, чтобы использовать такой способ, предварительно рассчитывают миноры и алгебраические дополнения. Минором Mij элемента аij называется определитель n-1 порядка, а алгебраическое дополнение это произведение Аij = (-1)^i+j Mij
	Таким образом, определитель третьего порядка можно разложить по элементам первой строки так:
	2.Свойства определителей.
	1. При транспонировании определитель не меняется. 2. Если поменять местами любые две строки (столбца) матрицы, то определитель поменяет знак на противоположный. 3. Для любой матрицы, определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. 4. Определитель равен нулю, если матрица содержит две одинаковые строки (столбца). 5. Определитель равен нулю, если все элементы какой-либо строки (столбца) равны нулю. 6. Если суммировать произведения элементов любой строки (столбца) на алгебраические дополнения элементов любой другой строки (столбца), то определитель равен нулю. 7. Общий множитель любой строки (столбца) можно вынести за знак определителя.



	Пример.




	1 2 3 4 5 6 7 8 9

Как вычислить определитель матрицы 4 порядка. Вычисление определителей

Инструкция

Для вычисления детерминанта (Det A) матрицы размерностью 5х5 проведите элементов по первой строке. Для этого возьмите первый элемент данной строки и вычеркните из матрицы строку и столбец, на пересечении которых он находится. Запишите формулу произведения первого и определителя полученной матрицы 4 порядка: a11*detM1 – это будет первое слагаемое для нахождения Det A. В оставшейся четырехразрядной матрице М1 вам будет позже так же найти определитель (дополнительный минор).

Аналогичным образом, последовательно вычеркивайте столбец и строку, содержащие 2, 3, 4 и 5 элемент первой строки начальной матрицы, и находите для каждого из них соответствующую матрицу 4х4. Запишите произведения этих элементов на дополнительные миноры: a12*detM2, a13*detM3, a14*detM4, a15*detM5.

Найдите определители полученных матриц 4 порядка. Для этого проведите тем же методом понижение размерности. Первый элемент b11 матрицы M1 умножьте на определитель оставшейся матрицы 3х3 (C1). Детерминант же трехмерной матрицы можно легко по формуле: detC1 = c11* c22*c33 + c13* c21*c32 + c12* c23*c31 — c21* c12*c33 — c13* c22*c31 — c11* c32*c23, где cij – элементы полученной матрицы C1.

Далее рассмотрите аналогично второй элемент b12 матрицы М1 и вычислите его с соответствующим дополнительным минором detC2 полученной трехмерной матрицы. Таким же образом найдите произведения для 3 и 4 элемента первой матрицы 4 порядка. После чего определите искомый дополнительный минор матрицы detМ1. Для этого, согласно формуле разложения по строке, : detМ1 = b11*detC1 — b12*detC2 + b13*detC3 — b14*detC4. Вы получили первое слагаемое, необходимое для нахождения Det A.

Вычислите остальные слагаемые определителя матрицы пятого порядка, аналогичным образом понижая размерность каждой матрицы 4 порядка. Окончательная так: Det A = a11*detM1 — a12*detM2 + a13*detM3 — a14*detM4 + a15*detM5.

Инструкция

Самая простая и краткая формулировка этой операции такова: матрицы перемножаются по алгоритму «строка на столбец».

Теперь подробнее об этом правиле, а также о возможных ограничениях и особенностях.

Умножение на единичную матриц переводит исходную матрицы саму в себя (эквивалентно умножению чисел, где один из элементов 1). Аналогично, умножение на нулевую матрицу даёт нулевую матрицу.

Главное условие, накладываемое на участвующие в операции матрицы вытекает из способа выполнения : строк в первой матрице должно быть столько же, сколько столбцов во второй. Нетрудно догадаться, что в противном просто не на что.

Также стоит отметить ещё один важный момент: у умножения матриц нет коммутативности (или «перестановочности»), иначе говоря, А умножить на B не равняется B умножить на А. Запомните это и не путайте с правилом для умножения чисел.

Теперь, собственно сам процесс умножения.

Пусть мы умножаем матрицу А на матрицу B справа.

Берём первую строчку матрицы А и ее i-ый элемент умножаем на i-ый элемент первого столцба матрицы B. Все полученные складываем и записываем на место а11 в итоговую матрицу.

Затем также поступаем с первой строкой матрицы А и 3-им, 4-ым и т.д. столбцами матрицы Б, заполнив, таким образом, первую строчку итоговой матрицы.

Теперь переходим ко второй строке и снова перемножаем её последовательно на все столбцы, начиная с первого. Записываем результат во вторую строку итоговой матрицы.

Затем к 3-ей, 4-ой и т.д.

Повторяем , пока не перемножим все строки в матрице А со всеми столбцами матрицы В.

Матрицы — это эффективный способ представления числовой информации. Решение любой системы линейных уравнений можно записать в виде матрицы (прямоугольника, составленного из чисел). Умение перемножать матрицы — один из самых важных навыков, которым обучают на курсе «Линейной алгебры» в высших учебных заведениях.

Вам понадобится

Инструкция

Для проверки этого условия проще всего воспользоваться следующим алгоритмом — запишите размерность первой матрицы как (a*b). Дальше размерность второй — (c*d). Если b=c — матрицы соразмерны, их можно перемножать.

Дальше произведите само перемножение. Помните — при перемножении двух матриц получается матрица. То есть, задача перемножения сводится к задаче нахождения новой, с размерностью (a*d). На СИ задачи перемножения матрицы выглядит следующим образом:
void matrixmult(int m1[n], int m1_row, int m1_col, int m2[n], int m2_row, int m2_col, int m3[n], int m3_row, int m3_col)
{ for (int i = 0; i for (int j = 0; j m3[i][j]=0;
for (int k = 0; k for (int i = 0; i for (int j = 0; j m3[i][k] += m1[i][j] * m2[j][k];
}

Проще говоря, новой матрицы — это сумма произведений элементов строки первой матрицы на элементы столбца второй матрицы. Если вы элемент третьей матрицы с номером (1;2), то вы должны просто умножить первую строку первой матрицы на второй столбец второй. Для этого считаете начальную сумму равной нулю. Дальше умножаете первый элемент первой строки на первый элемент второго столбца, значение добавляете в сумму. Делаете так: умножаете i-тый элемент первой строки на i-тый элемент второго столбца и добавляете результаты к сумме, пока не кончится строка. Итоговая сумма и будет искомым элементом.

После того, как вы нашли все элементы третьей матрицы, записываете ее. Вы нашли произведение матриц.

Источники:

Главный математический портал России в 2019
как находить произведение матриц в 2019

Определитель (детерминант) матрицы — одно из важнейших понятий линейной алгебры. Определитель матрицы представляет собой многочлен от элементов квадратной матрицы. Чтобы вычислить определитель четвертого порядка, нужно общим правилом вычисления определителя.

Вам понадобится

Инструкция

Квадратная матрица четвертого представляет из себя из четырех строк и четырех столбцов. Ее определитель считается по общей рекурсивной формуле, приведенной на рисунке. M с индексами является дополнительным минором этой матрицы. Минор квадратной матрицы порядка n M с индексом 1 вверху и индексами от 1 до n внизу, — это определитель матрицы, который получается из исходной вычеркиванием первой строки и j1.(1+j))aij, то есть одного из членов перовой строки матрицы, взятого с положительным или знаком, на квадратную третьего порядка (минор квадратной матрицы).

Получившиеся миноры, которые представляют из себя матрицы третьего порядка, можно уже по известной частной формуле, без использования новых миноров. Определители квадратной матрицы третьего порядка можно рассчитать по так называемому «правилу треугольника». Формулу для расчета определителя в этом случае выводить не нужно, а можно запомнить ее геометрическую схему. Эта изображена на приведенном рисунке. В результате |А| = a11*a22*a33+a12*a23*a31+a13*a21*a32-a11*a23*a32-a12*a21*a33-a13*a22*a31.
Следовательно, миноры вычислены и определитель квадратной матрицы четвертого порядка может быть посчитан.

Источники:

как рассчитать определитель

Вам понадобится

Инструкция

Запустите программу Microsoft Office Excel. В меню ввода данных впишите данную вам матрицу для последующего вычисления ее определителя. Выделите одну из незанятых ячеек таблицы, после чего введите следующую формулу: “=МОПРЕД(ak:fg)”. В данном случае ak будет означать координаты, соответствующие левому верхнему углу заданной матрицы, а fg – нижнему правому. Для получения определителя нажмите клавишу Enter. Нужное значение будет отображено в выбранной вами пустой ячейке.

Используйте функционал Excel для вычисления и других значений. В случае если вы не умеете использовать формулы в Microsoft Office Excel, скачайте специальную тематическую литературу, и после прочтения вам будет достаточно легко сориентироваться по данной программе.

Внимательно изучите наименования значений формул в данном программном обеспечении, поскольку при неправильном их вводе у вас могут испортиться сразу все результаты, в особенности это касается тех, кто выполняет сразу несколько одинаковых вычислений по одной одновременно.

Время от времени выполняйте проверку полученных в Microsoft Office Excel результатов вычисления. Это связано с тем, что в системе могли произойти какие-либо изменения со временем, в частности это относится к тем, кто выполняет работу по шаблона. Всегда нелишним будет лишний раз сверить результаты сразу нескольких текущих вычислений.

Также при работе с формулами будьте крайне осторожны и не допускайте появления в вашем компьютере вирусов. Даже в случае если операции с формулами в Microsoft Office Excel понадобится вам единоразово, изучите функционал данной программы в большей степени, поскольку эти навыки помогут вам в дальнейшем лучше понимать автоматизацию учета и применять Excel для выполнения определенных заданий.

Определитель – одно из понятий матричной алгебры. Это квадратная матрица, состоящая из четырех элементов, а чтобы вычислить определитель второго порядка , нужно воспользоваться формулой разложения по первой строке.

Инструкция

Определитель квадратной – это , которое используется в различных расчетах. Он незаменим при нахождении обратной матрицы, миноров, алгебраических дополнений, операции деления , но чаще всего необходимость перехода к определителю возникает при решении систем линейных уравнений.

Матрица второго порядка представляет собой совокупность четырех элементов, расположенных на двух строках и столбцах. Эти числа соответствуют коэффициентам системы уравнений неизвестными, которые применяются при рассмотрении множества прикладных задач, например, экономических.

Переход к компактным матричным вычислениям помогает быстро две вещи: во-первых, имеет ли эта решение, во-вторых, найти его. Достаточным условием решения является

Лекция 6

Матрицы

6.1. Основные понятия

Определение 1. Матрицей называется прямоугольная таблица чисел.

Для обозначения матрицы используются круглые скобки или сдвоенные вертикальные линии:

Числа, составляющие матрицу, называются ее элементами , элементматрицырасположен в ее-й строке и-м столбце.

Числа и(число строк и столбцов матрицы) называются ее порядками.

Говорят также, что — матрица размером
.

Если
, матрицаназываетсяквадратной .

Для краткой записи используется также обозначение
(или
) и далее указывается, в каких пределах изменяютсяи, например,
,
,
. (Запись читается так: матрицас элементами,изменяется отдо,- отдо.)

Среди квадратных матриц отметим диагональные матрицы , у которых все элементы с неравными индексами (
) равны нулю:

Будем говорить, что элементы
расположены на главной диагонали.

Диагональная матрица вида

называется единичной матрицей.

В дальнейшем будут встречаться матрицы вида

и
,

которые называются треугольными матрицами, а также матрицы, состоящие из одного столбца:

и одной строки:

(матрица-столбец и матрица-строка ).

Матрица, все элементы которой равны нулю, называется нулевой.

6.2. Определители порядка n

Пусть дана квадратная матрица порядка :

. (6.1)

Составим всевозможные произведения элементов матрицы, расположенных в разных строках и разных столбцах, т.е. произведения вида

. (6.2)

Число произведений вида (6.2) равно (примем этот факт без доказательства).

Будем считать все эти произведения членами определителя порядка , соответствующего матрице (6.1).

Вторые индексы множителей в (6.2) составляют перестановку первых натуральных чисел
.

Говорят, что числа ив перестановке составляютинверсию , если
, а в перестановкерасположено раньше.

Пример 1. В перестановке шести чисел,
, числаи,и,и,и,исоставляют инверсии.

Перестановка называется четной , если число инверсий в ней четно, инечетной , если число инверсий в ней нечетно.

Пример 2. Перестановка
— нечетная, а перестановка
— четная (инверсий).

Определение 2. Определителем порядка , соответствующим матрице (6.1), называется алгебраическая сумма членов , составленная следующим образом : членами определителя служат всевозможные произведения элементов матрицы , взятых по одному из каждой строки и каждого столбца , причем слагаемое берется со знаком «+», если множество вторых индексов является четной перестановкой чисел
, и со знаком «–», если нечетной.

Обозначать определитель матрицы (6.1) принято так:

Замечание. Определение 2 для
и
приводит к уже знакомым нам определителям 2-го и 3-го порядка:

Транспонированием вокруг главной диагонали матрицыназывается переход к матрице
, для которой строки матрицыявляются столбцами, а столбцы — строками:

Будем говорить, что определитель
получен транспонированием определителя.

Свойства определителя порядка п:

1.
(определитель не меняется при транспонировании вокруг главной диагонали).

2. Если одна из строк определителя состоит из нулей, определитель равен нулю.

3. От перестановки двух строк определитель меняет лишь знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на число , определитель умножится на.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы -й строки определителя представлены в виде суммы
, то определитель равен сумме двух определителей, у которых все строки, кроме-й, такие же, как в исходном определителе, а-я строка в одном определителе состоит из, а в другом — из.

Определение 3. -я строка определителя называется линейной комбинацией остальных его строк , если такие , что, умножая -ю строку на, а затем складывая все строки , кроме -й , получаем -ю строку.

8. Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю.

9. Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число.

Замечание. Мы сформулировали свойства определителя для строк. В силу свойства 1 (
) они справедливы и для столбцов.

Все приведенные свойства были доказаны на практических занятиях для
; для произвольногопримем их без доказательства.

Если в определителе порядкавыбрать элементи вычеркнуть столбец и строку, на пересечении которых расположен, оставшиеся строки и столбцы образуют определитель порядка
, который называетсяминором определителя, соответствующим элементу.

Пример 3. В определителе

минором элемента
является определитель
.

Определение 4. Алгебраическим дополнением элементаопределителяназывается его минор , умноженный на
, где — номер строки , — номер столбца , в которых расположен выбранный элемент .

Пример 4. В определителе

алгебраическое дополнение
.

Теорема 1 (о разложении по строке). Определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения.

Теорема 1 позволяет свести вычисление определителя порядка к вычислениюопределителей порядка
.

Пример 5 . Вычислить определитель четвертого порядка:

Воспользуемся теоремой 1 и разложим определитель по 4-й строке:

Замечание. Можно вначале упростить определитель, воспользовавшись свойством 9, а затем использовать теорему 1. Тогда вычисление определителя порядкасведется к вычислениювсего одного определителя порядка
.

Пример 6. Вычислить

Прибавим первый столбец ко второму и первый столбец, умноженный на (
), к третьему, в результате получим

Теперь применим теорему 1 и разложим по последней строке:

вычисление определителя 4-го порядка свелось к вычислению всего одного определителя 3-го порядка.

вычисление определителя третьего порядка свелось к вычислению всего одного определителя второго порядка.

Пример 7. Вычислить определитель порядка:

Первую строку прибавим ко второй, третьей и т.д. -й строке. Придем к определителю

Получен определитель треугольного вида.

Применим
раз теорему 1 (разложим по первому столбцу) и получим

Замечание. Определитель треугольного вида равен произведению элементов главной диагонали.

6.3. Основные операции над матрицами

Определение 5. Две матрицы
,
,
, и
,
,
, будем называть равными, если
.

Краткая запись:
.

Таким образом, две матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы равны.

Определение 6. Суммой двух матриц
,
,
, и
,
,
, называется такая матрица
,
,
, что
.

Иначе говоря, складывать можно только матрицы одних и тех же порядков, причем сложение осуществляется поэлементно.

Пример 8. Найти сумму матриц

и
.

В соответствии с определением 6 найдем

Правило сложения матриц распространяется на сумму любого конечного числа слагаемых.

Определение 7. Произведением матрицы
,
,
, на вещественное число называется такая матрица
,
,
, для которой
.

Иными словами, чтобы умножить матрицу на число, нужно умножить на это число все ее элементы и оставить полученные произведения на прежних местах.

Пример 9. Найти линейную комбинацию
матриц

и
.

Пользуясь определением 7, получаем

,
,

Свойства операций сложения матриц

и умножения на число:

1. Сложение коммутативно:
.

2. Сложение ассоциативно:.

3. Существует нулевая матрица
, удовлетворяющая условию
для всехА .

4. Для любой матрицы А существует противоположная матрицаВ , удовлетворяющая условию
.

Для любых матриц А иВ и любых действительных чисел
имеют место равенства:

5.
.

6.
.

7.
.

8.
.

Проверим свойство 1. Обозначим
,
. Пусть
,

,
. Имеем

и так как равенство доказано для произвольного элемента, в соответствии с определением 5
. Свойство 1 доказано.

Аналогично доказывается свойство 2.

В качестве матрицы возьмем матрицу порядка
, все элементы которой равны нулю.

Сложив с любой матрицейпо правилу, данному в определении 6, мы матрицуне изменим, и свойство 3 справедливо.

Проверим свойство 4. Пусть
. Положим
. Тогда
, следовательно, свойство 4 справедливо.

Проверку свойств 5 — 8 опустим.

Определение 8. Произведением матрицы
,
,
, на матрицу
,
,
, называется матрица
,
,
, с элементами
.

Краткая запись:
.

Пример 10. Найти произведение матриц

и
.

В соответствии с определением 8 найдем

Пример 11. Перемножить матрицы

и
.

Замечание 1. Число элементов в строке матрицыравно числу элементов в столбце матрицы(число столбцов матрицыравно числу строк матрицы).

Замечание 2. В матрице
строк столько же, сколько в матрице, а столбцов столько же, сколько в.

Замечание 3. Вообще говоря,
(умножение матриц некоммутативно).

Чтобы обосновать замечание 3, достаточно привести хотя бы один пример.

Пример 12. Перемножим в обратном порядке матрицыииз примера 10.

таким образом, в общем случае
.

Отметим, что в частном случае равенство
возможно.

Матрицы и, для которых выполняется равенство
, называютсяперестановочными, иликоммутирующими .

Упражнения.

1. Найти все матрицы, перестановочные с данной:

а)
; б)
.

2. Найти все матрицы второго порядка, квадраты которых равны нулевой матрице.

3. Доказать, что
.

Свойства умножения матриц:

Умножение дистрибутивно.

Пусть имеется квадратная матрица A размером n x n .
Определение. Определителем называется алгебраическая сумма всевозможных произведений элементов, взятых по одному из каждого столбца и каждой строки матрицы A . Если в каждом таком произведении (члене определителя) множители расположены в порядке следования столбцов (т.е. вторые индексы элементов a ij в произведении расположены в порядке возрастания), то со знаком (+) берутся те произведения, у которых перестановка первых индексов чётная, а со знаком (-) – те, у которых она нечетная.
.
Здесь — число инверсий в перестановке индексов i 1 , i 2 , …, i n .

Методы нахождения определителей

Определитель матрицы разложением по строкам и столбцам через миноры.
Определитель методом приведения к треугольному виду (методом Гаусса)

Свойство определителей

При транспонировании матрицы её определитель не меняется.
Если поменять местами две строки или два столбца определителя, то определитель изменит знак, а по абсолютной величине не изменится.
Пусть C = AB где A и B квадратные матрицы. Тогда detC = detA ∙ detB .
Определитель с двумя одинаковыми строками или с двумя одинаковыми столбцами равен 0. Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.
Определитель с двумя пропорциональными строками или столбцами равен 0.
Определитель треугольной матрицы равен произведению диагональных элементов. Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали.
Если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число.
Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
Теорема Якоби: Если к элементам некоторого столбца определителя прибавить соответствующие элементы другого столбца, умноженные на произвольный множитель λ, то величина определителя не изменится.

Таким образом, определитель матрицы остается без изменения, если:

транспонировать матрицу;
прибавить к какой-либо строке другую строку, умноженную на любое число.

Задание 1 . Вычислить определитель, разлагая его по строке или столбцу.
Решение :xml :xls
Пример 1 :xml :xls

Задание 2 . Вычислить определитель двумя способами: а) по правилу «треугольников»; б) разложением по строке.

Решение .
а) Слагаемые, входящие в со знаком «минус», строятся таким же образом относительно побочной диагонали.

= 2 0 0 — 2 4 2 — (-1) 2 0 + (-1) 1 2 + (-2) 2 4 — (-2) 1 0 = -34
б) Запишем матрицу в виде:

Главный определитель:
∆ = 2 (0 0-2 4)-(-1 (2 0-2 1))+(-2 (2 4-0 1)) = -34

Задание 3 . Укажите, чему равен определитель квадратной матрицы A четвертого порядка, если ее ранг r(A)=1.
Ответ: det(A) = 0.

«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи , то решайте их .»
Д. Пойа (1887-1985 г.)

(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

С каждой квадратной матрицей связывают число . Это число называется определителем матрицы. Определитель вычисляется по особым правилам и обозначается |A|, det A , ΔA.

Число строк (столбцов) определителя называется его порядком .

Определитель первого порядка матрицы равен элементу a 11: |A|=a 11

Не путать определитель первого порядка с модулем.

Определитель второго порядка обозначается символом

и равен |A|=a 11 a 22 -a 12 a 21

Определитель 3-го порядка обозначается символом

Для запоминания этой формулы используют схематические правила (правило треугольника или Саррюса )

Правило Саррюса.

Правило треугольника.

Посмотрим на примере, как используются эти правила.

ПРИМЕР:

Правило Саррюса

Допишем к определителю два первых столбца.

Правило треугольника

Такой способ вычисления определителей не подходит для определителей 4-го порядка и выше. Прежде чем указать правило, которое позволяет находить определители любого порядка, рассмотрим понятие алгебраического дополнения элемента матрицы.

Алгебраическим дополнением (А ij ) элемента а ij определителя матрицы А называется число, равное произведению (-1) i+j (в степени номер строки плюс номер столбца этого элемента) на определитель, который получается из данного в результате вычеркивания строки и столбца, где стоит этот элемент.

ПРИМЕР:

Вычислить алгебраическое дополнение А 21 элемента а 21 .

РЕШЕНИЕ:

По определению алгебраического дополнения

Вычисление определителя произвольного порядка. Определитель равен сумме произведений элементов любой его строки (или столбца) на соответствующие алгебраические дополнения.

, разложение определителя 4-го порядка по первой строке выглядит следующим образом:

Второго порядка называется число, равное разности между произведением чисел, образующих главную диагональ, и произведением чисел, стоящих на побочной диагонали, можно встретить следующие обозначения определителя: ; ; ; detA (детерминант).

Пример:
.

Пример:

Разложение определителя по элементам некоторой строки (столбца).

Минором М ij элемента а ij квадратной матрицы А называется определитель, составленный из элементов матрицы А , оставшихся после вычеркивания i- ой строки и j -го столбца.

Например, минором к элементу а 21 матрицы третьего порядка
будет определитель
.

Будем говорить, что элемент а ij занимает четное место, если i+j (сумма номеров строки и столбца на пересечении которых находится данный элемент) — четное число, нечетное место, если i+j — нечетное число.

Алгебраическим дополнением А ij элемента а ij квадратной матрицы А называется выражение (или величина соответствующего минора, взятого со знаком «+», если элемент матрицы занимает четное место, и со знаком «-», если элемент занимает нечетное место).

Пример:

а 23 = 4;

— алгебраическое дополнение элемента а 22 = 1.

Теорема Лапласа . Определитель равен сумме произведений элементов некоторой строки (столбца) на соответствующие им алгебраические дополнения.

Пример :

Таким образом, вычисление определителя 3-го порядка сводится к вычислению 3-х определителей второго порядка. В общем случае можно вычислить определитель квадратной матрицы n -го порядка, сводя его к вычислению n определителей (n-1 )-го порядка

Пример . Вычислить определитель четвертого порядка.

Разложим определитель по элементам третьей строки

Свойства определителей:

1. Определитель не изменится, если его строки заменить столбцами и наоборот.

2. При перестановке двух соседних строк (столбцов) определитель меняет знак на противоположный.

3. Определитель с двумя одинаковыми строками (столбцами) равен 0.

Вычисление определителей 2-го, 3-го и высших порядков

115

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 1

1. Определитель 2-го и 3-го порядков.

Матрицей размера m  n называется совокупность mn чисел, расположенных в виде таблицы из m строк и n столбцов:

Для квадратных матриц существует численная характеристика, которая также имеет и многочисленные другие приложения – определитель.

Для обозначения определителя употребляется запись:

или det A .

Приведем формулы вычисления определителей второго и третьего порядков:

(1.1)

(1.2)

Выражение определителя третьего порядка является достаточно громоздким. Для запоминания формулы существуют два удобных способа. Первый способ вычисления определителя третьего порядка схематично можно изобразить следующим образом:

2. Определитель произвольного порядка.

Пусть А – квадратная матрица с элементами .

Дополнительным минором элемента называется определитель матрицы, полученной изА вычеркиванием той строки и того столбца, на пересечении которых стоит элемент , т.е.i-й строки и j-го столбца.

Алгебраическим дополнением элемента называется произведение:

. (1.3)

Определитель квадратной матрицы А может быть вычислен по формулам:

(1.4а)

(1.4б)

Эти формулы называются формулами разложения определителя по i-й строке и по j-му столбцу, соответственно.

В качестве примера запишем формулу разложения определителя третьего порядка по первой строке:

(1.5)

Заметим, что при использовании формулы разложения определителя по строке (или по столбцу) удобно иметь в этой строке (в этом столбце) много элементов, равных нулю (тогда соответствующие им миноры не надо будет вычислять). Поэтому полезно предварительно так преобразовать определитель, чтобы в одной из строк (или в одном из столбцов) только один элемент остался, отличный от нуля. При этом разрешается производить следующие преобразования:

1) прибавлять к одной из строк (одному из столбцов) другую строку (столбец), умноженную на некоторое число;

2) выносить общий множитель строки (столбца) за знак определителя;

3) при перестановке строк или столбцов необходимо изменить знак определителя на противоположный.

Из формул (1.4а) и (1.4б) разложения определителя по строке или столбцу следует формула для вычисления определителя треугольной матрицы:

. (1.6)

Примеры решения задач

1. Вычислить определитель второго порядка: .

Решение: Используем формулу (1.1): .

2. Вычислить определитель 3-го порядка: .

Решение: Вычисляя определитель разложением по первой строке по формуле (1.5), получим:

3. Вычислить определитель треугольной матрицы

Решение: Из шести слагаемых в формуле (1.2) не равным нулю будет только одно: . Следовательно, определитель равен 6. Тот же самый ответ можно было получить, используя формулу (1.6).

4. Вычислить определитель разложением по какой-нибудь строке или столбцу:

Решение: Удобнее всего вычислять определитель разложением по строке или столбцу, содержащим наибольшее количество нулей. Разложим определитель по 2-й строке (см. формулу (1.4а)):

5. Вычислить определитель 4-го порядка разложением по строке или столбцу:

Решение: Удобнее пользоваться разложением по строке или столбцу, содержащим наибольшее количество нулей. Разложим определитель по первой строке (см. формулу (1.4а)):

6. Вычислить определитель приведением к треугольному виду:

Решение: Прибавляя к каждой строке определителя первую строку, получим:

Здесь мы использовали формулу (1.6).

Определитель матрицы 4×4 — Как вычислить определитель матрицы 4×4?

Введение в определитель матрицы 4×4

Определитель матрицы 4 × 4 — это уникальное число, которое также вычисляется по определенной формуле. Если порядок матриц находится в n x n, то это квадратная матрица. Итак, здесь 4 × 4 — это квадратная матрица с четырьмя строками и четырьмя столбцами. Если A — квадратная матрица, то определитель матрицы A представляется как | A |.

Узнать определитель матрицы 4 × 4? мы будем использовать обычный метод, существует определитель матрицы 4 × 4, формула, которую мы обычно используем для нахождения определителя матрицы 3 × 3.

Определение определителя

Самый простой способ — сформулировать определитель, учитывая верхний ряд элементов и соответствующие миноры. Возьмите первый элемент верхнего ряда и затем умножьте его на второстепенный, а после этого вычтите произведение второго элемента на второстепенное.Продолжайте попеременно складывать и вычитать произведение каждого элемента верхней строки с заданным второстепенным, пока не будут учтены все элементы верхней строки.

Определители также играют очень важную роль в нахождении обратной матрицы, а также для решения систем линейных уравнений. В следующей части мы также предполагаем, что у нас есть квадратная матрица (m равно n). Определитель матрицы A будет подставлен как det (A) или | A |. Сначала будет введен определитель матриц 2 × 2 и 3 × 3, затем будет рассмотрен случай n × n.

Что такое матрица?

Прежде чем изучать операции с матрицей, давайте обсудим, что такое матрица. Матрица может быть определена как прямоугольный массив чисел или символов, которые обычно располагаются в строках и столбцах. Порядок матрицы также можно определить как количество строк и количество. колонн. Записи также являются числами в матрице, и каждое из чисел называется элементом. Множественное число матрицы слов известно как матрицы.

Размер матрицы называется матрицей n на m и записывается как m × n, где n — количество строк, а m — количество столбцов.Например, у нас есть матрица 3 × 2, потому что количество строк здесь равно 3, а количество столбцов здесь равно 2.

[Изображение будет загружено в ближайшее время]

Размеры матрицы также может быть определено как количество строк и столбцов матрицы в указанном порядке. Поскольку приведенная выше матрица A имеет 2 строки и 3 столбца, она известна как матрица 2 × 3.

Ярлык для поиска ранга матрицы

Общее количество линейно независимых векторов в матрице равно общему количеству ненулевых строк в ее строке, присутствующей в матрице эшелона.Итак, чтобы узнать ранг матрицы, мы обычно должны преобразовать матрицу в ее форму эшелона строк, а затем подсчитать общее количество ненулевых строк.

Символ определителя

Символ определителя — две вертикальные линии с обеих сторон.

Пример:

| A | обозначает определитель матрицы A

(тот же символ, что и абсолютное значение)

Для матрицы 2 × 2

Для матрицы 2 × 2 (2 строки, 2 столбца):

A = \ [\ begin {bmatrix} a & b \\ c & d \ end {bmatrix} \]

Определитель записывается как:

| A | = ad — bc

Это очень легко вспомнить, когда вы думаете о кресте:

Синий воспринимается положительно (+ ad),
Красный воспринимается отрицательно (-bc )

Определитель для матрицы 2 × 2

Если A — произвольная матрица A 2 × 2, элементы задаются следующим образом:

A = \ [\ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix} \]

, то определитель a и этой матрицы выставляется следующим образом:

det (A) = lAl = \ [ \ begin {vmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {vmatrix} \] = a \ [_ {11} \] a \ [_ {22} \ ] — a \ [_ {21} \] a \ [_ {12} \]

Для матрицы 3 × 3

Для матрицы 3 × 3 (3 строки, 3 столбца):

A = \ [ \ begin {bmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {bmatrix} \]

Определитель записывается как:

| A | будет равно a (ei — fh) — b (di — fg) + c (dh — eg)

Это может показаться сложным, но есть известный шаблон:

[Изображение будет загружено в ближайшее время]

To определить определитель для матрицы 3 × 3 вот точки:

Умножьте a на определитель матрицы 2 × 2, которая не находится в строке или столбце.
Также для b и также для c
Сложите их, но также помните о минусе перед b

Что касается формулы (помните, что вертикальные полосы || обозначают как « определитель «):

lAl = a. \ [\ begin {vmatrix} e & f \\ h & i \ end {vmatrix} \] — b. \ [\ begin {vmatrix} d & f \\ g & i \ end {vmatrix} \] + c. \ [\ begin {vmatrix} d & e \\ g & h \ end {vmatrix} \]

Как вычислить определитель матрицы 4 × 4?

Прежде чем мы попытаемся найти определитель матрицы 4 × 4, сначала давайте проверим несколько условий, приведенных ниже.

Если присутствует какое-либо условие, где определитель матрицы 4 × 4 может быть равен 0 (например, полная строка или полный столбец равен 0)
Если вычитание любой из строк или столбца возможный.
Если элементы матрицы совпадают, но затем переупорядочены по любому из столбцов или строк.

В любом из трех приведенных выше случаев используются соответствующие методы для вычисления определителей 3 x 3.Мы меняем строку или столбец, чтобы заполнить их 0, за исключением одного элемента. Определитель матрицы 4 × 4 будет эквивалентен произведению этого элемента и его кофактора. В этой ситуации кофактор представляет собой определитель 3 × 3, который оценивается по его конкретной формуле.

Определители матриц высшего порядка

Как мы уже говорили ранее, идея состоит в том, чтобы предположить, что предыдущие свойства, которым удовлетворяет определитель матриц порядка 2, все еще остаются в силе в целом.Другими словами, мы предполагаем:

1.: Любая матрица A и ее транспонирование имеют один и тот же определитель, то есть
2.: Определитель треугольной матрицы — это произведение значений диагонали.
3.: Если мы поменяем местами две строки, определитель новой матрицы будет противоположен старой.
4.: Если мы умножим одну строку на константу, определитель новой матрицы будет определителем старой, умноженной на константу.
5.: Если мы добавим одну строку к другой, умноженную на константу, определитель новой матрицы будет таким же, как и у старой.
6.: У нас есть

В частности, если A обратимый (что происходит тогда и только тогда, когда ), тогда

Итак, посмотрим, как это работает в случае матрицы порядка 4.

Пример. Оценить

У нас есть

Если мы вычтем каждую строку, умноженную на соответствующее число, из первой строки, мы получим

Первый ряд не трогаем и работаем с остальными рядами.Мы меняем вторую местами на третью, чтобы получить

Если мы вычтем каждую строку, умноженную на соответствующее число, из второй строки, мы получим

Используя предыдущие свойства, мы имеем

Если мы умножим третью строку на 13 и прибавим ее к четвертой, мы получим

что равно 3. Складывая все числа вместе, получаем

Эти вычисления кажутся довольно длинными. Позже мы увидим, что общая формула для определителя действительно существует.

Пример. Оценить

В этом примере мы не будем приводить детали элементарных операций. У нас есть

Пример. Оценить

У нас есть

Общая формула для определителя Пусть A — квадратная матрица порядка n. Писать A = ( a _ij), где a _ij — это запись в строке с номером i и столбце с номером j, для а также .Для любых i и j установите A _ij (называемый кофакторами ) как определитель квадратной матрицы порядка (n-1), полученной из A путем удаления строки номер i и номер столбца j, умноженные на (-1) ^{i + j}. У нас есть

для любых фиксированных и , и

для любого фиксированного j . Другими словами, у нас есть два типа формул: по строке (номер i ) или по столбцу (номер j ).Подойдет любая строка или любой столбец. Уловка состоит в том, чтобы использовать строку или столбец с большим количеством нулей.
В частности, у нас по строкам

или же

или же

В качестве упражнения напишите формулы по столбцам.

Пример. Оценить

Мы будем использовать общую формулу по третьей строке. У нас есть

Какой метод оценки детерминанта проще? Ответ зависит от человека, оценивающего детерминант.Некоторым нравятся элементарные операции со строками, а некоторым — общая формула. Главное — получить правильный ответ.

Обратите внимание, что все вышеперечисленные свойства остаются в силе в общем случае. Также вы должны помнить, что понятие определителя существует только для квадратных матриц.

[Геометрия] [Алгебра] [Тригонометрия] [Исчисление] [Дифференциальные уравнения] [Матричная алгебра]

S.O.S MATH: Домашняя страница

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем С.ОПЕРАЦИОННЫЕ СИСТЕМЫ. Математика CyberBoard.

Автор : М.А.Хамси

Определитель матрицы 3×3 (общий и сокращенный метод)

Как мы видели в прошлых уроках, чтобы определить, что является определителем матрицы, нам нужно вернуться к нашему определению матрицы.Помните, что мы узнали, что матрица — это упорядоченный список чисел, заключенный в прямоугольную скобку. Этот список также можно назвать прямоугольным массивом, и он обеспечивает упорядоченный способ отображения «списка» информационных элементов. Если вы хотите более подробно ознакомиться с определением матрицы, вы можете вернуться к нашему уроку по обозначению матриц.

Матрица описывает линейное преобразование или линейную карту, которая является своего рода транскрипцией между двумя типами алгебраических структур, такими как векторные поля.Таким образом, мы можем разрешить системы линейных уравнений, представив линейную систему в виде матрицы. Матричное представление линейной системы создается с использованием всех переменных коэффициентов, найденных в системе, и использования их в качестве элементов для построения прямоугольного массива расширенной матрицы соответствующего размера. В такой матрице результаты каждого уравнения из системы будут помещены справа от вертикальной линии, которая представляет знак равенства.

Зная это, в этом уроке основное внимание будет уделено процессу оценки определителя матрицы 3×3 и двум возможным методам, которые можно использовать.

Какой определитель матрицы

Используя знание того, что матрица представляет собой массив, содержащий информацию о линейном преобразовании, и что этот массив может быть согласован с коэффициентами каждой переменной в системе уравнений, мы можем описать функцию определителя: определитель будет масштабироваться линейное преобразование из матрицы, это позволит нам получить обратную матрицу (если таковая имеется) и поможет в решении систем линейных уравнений, создав условия, при которых мы можем ожидать определенных результатов или характеристик от система (в зависимости от определителя и типа линейной системы, мы можем знать, можем ли мы ожидать уникального решения, более одного решения или вообще ни одного решения для системы).

Но есть условие для получения определителя матрицы: матрица должна быть квадратной матрицей, чтобы ее можно было вычислить. Следовательно, упрощенное определение состоит в том, что определитель — это значение, которое может быть вычислено из квадратной матрицы, чтобы помочь в разрешении систем линейных уравнений, связанных с такой матрицей. Определителя неквадратной матрицы не существует, математически определены только определители квадратных матриц.

Определитель матрицы можно обозначить просто как det A, det (A) или | A |.Это последнее обозначение происходит от обозначения, которое мы непосредственно применяем к матрице, определитель которой мы получаем. Другими словами, мы обычно записываем матрицы и их определители очень похожим образом:

Уравнение 1: Разница между обозначениями матрицы и определителя

Обратите внимание на разницу: матрица записана в прямоугольных скобках, а компоненты определителя матрицы окружены двумя прямыми линиями.

Сегодняшний урок будет сосредоточен на процессе вычисления определителя матрицы 3×3, используя подход свойств определителя матрицы, которые были кратко рассмотрены на прошлых уроках.Помните, что мы рассмотрим эту полную тему на следующем уроке, который называется: свойства детерминантов. Тем не менее, важно помнить об этих свойствах при выполнении расчетов упражнений в последнем разделе этого урока.

Как найти определитель матрицы 3×3

Существует два метода нахождения определителя матрицы 3×3: общий метод и сокращенный метод. Как и звучат названия каждого из них, общий метод — это «формальный» метод, который можно использовать математически, следуя всем правилам и производя некоторые второстепенные вычисления определителя матрицы по пути нахождения окончательного решения.Хотя метод быстрого доступа — это более хитрый трюк, который мы можем использовать для упрощения вычислений, при этом стараясь не забыть числа, порядок, в котором они должны быть умножены, и некоторые перестановки элементов в матрице.

После того, как вы взглянете на оба метода, чтобы найти определитель матрицы 3×3, вы всегда можете выбрать тот, который вам больше всего подходит, и использовать его для своих исследований, но помните, что важно знать оба из них, на случай, если вас когда-нибудь спросят сравнить результаты с ними.

Итак, без дальнейших задержек, давайте определим определитель матрицы 3×3 A, как показано ниже, чтобы мы могли наблюдать, как его можно вычислить обоими методами:

Уравнение 2: Определитель матрицы A

Общий метод
Общий метод получения определителя матрицы 3×3 состоит из разбиения матрицы на вторичные матрицы меньших размеров в процессе, называемом «расширением первой строки». Этот процесс использует элементы из первой строки матрицы 3×3 и использует их как множители в сумме умножений, при которой большая матрица перераспределяется.
Давайте шаг за шагом рассмотрим, как вычислить определитель матрицы 3×3:
1. Сначала вы берете первый элемент первой строки и умножаете его на вторичную матрицу 2×2, которая получается из элементов, оставшихся в матрице 3×3, которые не принадлежат строке или столбцу, к которому принадлежит ваш первый выбранный элемент.
  Взяв в качестве ссылки определитель матрицы 3×3, показанный в уравнении 2, мы строим первую часть результата этой операции, выбирая первый элемент первой строки и столбца (который является константой «a»), а затем умножаем его на матрица, созданная из четырех элементов, которые не принадлежат ни одной строке столбца, в котором находится «a».Умножьте «a» на полученную вторичную матрицу 2×2, и это будет первый член решения.
2. Второй член начинается со второго элемента верхней строки (константа «b»), сопровождаемого отрицательным знаком, который теперь будет умножать вторичную матрицу 2×2, которая снова получается из четырех элементов в матрице, которые не принадлежат в любой столбец строки, в которой находится «b».
3. Повторяем первый шаг, но уже с третьим элементом из верхней строки матрицы.
Итак, определитель матричной формулы 3×3 для общего метода:
Уравнение 3: Уравнение для определителя матрицы 3×3 посредством общего метода
Процесс называется расширением первой строки, потому что, как вы можете видеть в уравнении 3, все элементы из первой строки исходной матрицы 3×3 остаются основными факторами в расширении, для которого необходимо решить. Все матрицы 2×2 в раскрытии — это то, что мы называем «вторичными матрицами», и их можно легко разрешить, используя уравнение, изученное на определителе на уроке по матрице 2×2.
Итак, принимая во внимание формулу для определителя квадратной матрицы размером 2×2, мы видим, что уравнение 3 дает:
Уравнение 4: Уравнение для определителя матрицы 3×3 посредством общего метода (часть 2)
На этом этапе вы, возможно, заметили, что поиск определителя матрицы размером больше 2×2 становится долгим испытанием, но логика процесса остается той же, и поэтому сложность аналогична, единственный ключевой момент — отслеживать операции вы прорабатываете даже больше с матрицами даже большего размера, чем 3×3.
Сокращенный метод
Определитель метода быстрого доступа к матрице 3×3 — это хитрый трюк, который упрощает вычисление определителя большой матрицы путем прямого умножения и добавления (или вычитания) всех элементов в их необходимом виде, без необходимости пройти через матричное расширение первой строки и без необходимости оценивать детерминанты вторичных матриц.
Весь процесс того, как вычислить определитель матрицы 3×3, используя сокращенный метод, можно увидеть в уравнении ниже:
Уравнение 5: Быстрый метод получения определителя матрицы 3×3
Теперь давайте поясним метод быстрого доступа:
При вычислении определителя матрицы размера nxn (в данном случае матрицы 3×3), как показано выше, обратите внимание, что мы сначала переписываем матрицу, сопровождаемую повторением двух ее первых столбцов, теперь записанных снаружи с правой стороны.
Тогда значение определителя будет результатом вычитания между сложением произведений всех умножений вниз-вправо и умножений вниз-влево. Сказано более ясно, в общей сложности будет три полных диагонали, идущих от верхнего левого угла до нижнего правого, и еще один набор из трех полных диагоналей, идущих от верхнего правого угла до нижнего левого угла.
Мы умножим элементы каждой диагонали вместе, а затем сложим их с результатами, полученными на других диагоналях.Есть кое-что, что нужно иметь в виду, все умножения диагоналей, идущие от верхнего левого угла к нижнему правому, имеют внутренний положительный знак, умноженный на них, в то время как все умножения диагоналей, идущие сверху справа налево, имеют внутренний отрицательный знак, умноженный на них. к ним, и поэтому при сложении результатов всех умножений получится вычитание, подобное тому, которое показано в уравнении 5.
Хотя этот метод проще в применении, чем общий метод, его немного сложно объяснить из-за того, что все операции умножения и сложения выполняются одновременно, поэтому мы рекомендуем вам использовать уравнение 5 в качестве руководства и уделять пристальное внимание к видео, где демонстрируются примеры этого метода.
В последнем разделе этого урока мы проработаем набор из трех различных матриц 3×3 и их детерминанты. Мы рекомендуем вам сравнить процессы для обоих методов, чтобы лучше понять их.

Определитель большой матрицы

Процесс вычисления определителя матрицы большей размерности, чем 3×3, следует той же логике, что и то, что мы видели до сих пор. Используя общий метод на матрице A 4×4, где ее первая (верхняя) строка соответствует элементам a, b, c и d, мы вычисляем определитель матрицы следующим образом:

Уравнение 6: Определитель матрицы 4×4

Мы еще раз расширили определитель на его первую строку и получили вторичные матрицы, которые в данном случае являются матрицами 3×3, каждая из которых может быть расширена и разбита на матрицы 2×2.Шаблон в процессе повторяется, вы можете продолжать работать таким образом с еще более крупными квадратными матрицами, и он всегда будет работать, но если вам больше нравится метод ярлыков, то вас ждет удовольствие, поскольку метод работает точно так же как и в случае с матрицами 3×3, он просто увеличивает количество элементов, с которыми вы работаете, но логика и перестановка точно такие же (умножение сверху слева вниз справа имеет положительный знак, умножения от верхнего правого угла до нижнего левого угла имеют внутренний отрицательный знак).

Вы взволнованы, увидев, как сокращенный метод работает с матрицами большего размера? Мы рекомендуем вам попробовать это самостоятельно, чтобы вы могли увидеть весь процесс. Вы всегда можете вернуться и решить ту же матрицу, используя общий метод, и доказать, что ваш результат верен.

Упражнения по вычислению определителя матрицы 3×3

В следующих упражнениях мы решим определитель матрицы 3×3, предоставленной в каждом случае, с помощью соответствующего метода, а в конце мы сравним полученные результаты.

Обратите внимание, что матрицы A, B и C, представленные в обоих разделах упражнений выше, абсолютно одинаковы. Это было сделано специально, чтобы вы могли сравнить результаты обоих методов и посмотреть, как они дают одинаковые значения.

Чтобы завершить этот урок, мы хотели бы порекомендовать вам эту статью о том, как вычислить детерминанты, и другую статью о детерминанте квадратной матрицы, где вы найдете гораздо больше примеров, чем приведенные здесь.

Надеемся, этот урок был интересным и полезным, до встречи в следующем!

Второстепенные и кофакторы: расширение по ряду

Несовершеннолетние и кофакторы: Введение;
Расширение вдоль ряда (стр. 1 из 3)

Нахождение определителя из 22 матрица проста: вы просто выполняете умножение крест-накрест и вычитаете:

Процесс для 33 матрицы, хоть и немного беспорядочные, но все же довольно просты: вы добавляете повторение первого и второго столбцов до конца определителя, умножьте по всем диагоналям, сложите и вычтите в соответствии с правило:

Но для 44-х и более крупные детерминанты, вы должны вернуться к меньшим 22 и 33 детерминанты с помощью вещей, называемых «несовершеннолетними» и «кофакторами».

«Минор» — это определитель квадратной матрицы, образованной удалением одной строки и одной столбец из некоторой большей квадратной матрицы. Так как рядов много и столбцов в исходной матрице, из нее можно сделать много миноров. Эти Несовершеннолетние помечаются в соответствии с удаленной строкой и столбцом. Так что если вы должны были пойти, скажем, на _2,4 запись из какой-то матрицы А и вычеркните строку и столбец, которые проходят через эту запись (т. е. если вы удалите второй строка и четвертый столбец матрицы), определитель новой (и меньшей) матрицы называется «второстепенным M _2,4 «.

матрица A	все зачеркнуть записи, разделяющие строку или столбец с записью a _2,4	младший M _2,4

Как только вы найдете несовершеннолетнего M _i,
j , вы берете индекс имени несовершеннолетнего (« i, j «часть) и сложите два числа i и j .Какой бы результат вы ни получили от этого дополнения, сделайте это значение силой на 1, так что вы получите «+1» или «1», в зависимости от того, я + j четный или странный. Затем умножьте это на младший
M _i,
к . Это дает вы «кофактор» A _i,
к . То есть:

(1) ^{i + j} M _i,
к = А _я,
к

Но вы еще не закончили.Да, есть еще кое-что.

Найти определитель матрицы А , вам нужно выбрать строку или столбец матрицы, найти все кофакторы для этой строки или столбца умножьте каждый сомножитель на его запись в матрице, и затем сложите все полученные значения. Авторские права Элизабет Стапель 2006-2011 Все права защищены

Хорошо, да; это вероятно не имело особого смысла.Вот по-другому:

У вас есть матрица А . Вам нужно найти его определяющий фактор.
Это слишком велико, чтобы найти более простые методы, поэтому вам придется найти его, «расширяя строка или столбец ».
Ваш первый шаг в этом «раскрытие» — это выбор строки или столбца. Скажем ты выбрать третий ряд.
За каждую запись в В третьей строке вы найдете сомножитель этой записи и умножите запись по его кофактору. То есть для _3,1 запись А , вы найдете кофемашину A _3,1, а затем умножьте сомножитель на a _3,1 запись: ( a _3,1) ( A _3,1).Для входа a _3,2, вы найдете кофемашину A _3,2, и умножаем: ( a _3,2) ( A _3,2). И так далее.
Тогда сложите все из этих продуктов: ( a _3,1) ( A _3,1) + ( a _3,2) ( A _3,2) + ( a _3,3) ( A _3,3) +….

Полученная сумма равна значение определителя матрицы A .

(Из-за этого беспорядка никто определяет детерминанты вручную, если этого можно избежать: всего , поэтому требуется много чуткой к ошибкам бездумной ворчливой работы.)

Странный факт: это не так независимо от того, какую строку или столбец вы используете для своего расширения; вы получите одинаковое значение независимо. Но эта гибкость может быть полезной.

Найти определитель следующей матрицы, развернув (a) по первой строке и (b) по третьему столбцу. (c) Сравните результаты каждого расширения.

(а) Расширить по первая строка, мне нужно найти второстепенные, а затем кофакторы первой строки записи: a _1,1, a _1,2, a _1,3, и а _1,4.


M _1,1	M _1,2	M _1,3	M _1,4

M _1,1 = 0	M _1,2 = 0	M _1,3 = 3	M _1,4 = 0
A _1,1 = (1) ^{1 + 1} M _1,1 = (1) ² (0) = 0	A _1,2 = (1) ^{1 + 2} M _1,2 = (1) ³ (0) = 0	A _1,3 = (1) ^{1 + 3} M _1,3 = (1) ⁴ (3) = 3	А _1,4 = (1) ^{1 + 4} M _1,4 = (1) ⁵ (0) = 0

Итак, определитель эта матрица:

дет ( A ) = a _1,1 A _1,1 + a _1,2 A _1,2 + a _1,3 A _1,3 + a _1,4 A _1,4
знак равно 1 (0) + 3 (0) + (2) (3) + 1 (0)
знак равно 6

Теперь мне нужно развернуться вниз колонка…

Вверх | 1 | 2 | 3 | Вернуться к указателю Далее >>

Цитируйте эту статью как:

Стапель, Элизабет. «Минорные и сомножители: введение; расширение по рядку».
Purplemath . Доступно с https://www.purplemath.com / modules / minors.htm .
Дата обращения [Дата] [Месяц] 2016 г.

Как оценивать детерминанты высшего порядка в алгебре — Видео и стенограмма урока

Детерминанты

Мы определяем детерминант как особое число, вычисляемое из квадратной матрицы. Детерминанты важно изучать и уметь вычислять, потому что они предоставляют полезную информацию о матрице и помогают найти обратную матрицу.Они также полезны в высшей математике, например в исчислении.

При работе с определителями у нас есть особый символ для них. Матрицы записываются в квадратных скобках, а определитель матрицы записывается вертикальными полосами, как и те, которые вы используете для абсолютного значения. Итак, определитель матрицы M, [M] выглядит так: D = | M | где M обозначает матрицу M.

Единственными видами матриц, для которых мы можем вычислить определитель, являются квадратные матрицы. Это матрицы с одинаковым количеством строк и столбцов.Да, количество строк и столбцов одинаково для квадратной матрицы. Их называют квадратными, потому что форма матрицы похожа на квадрат. Матрицы 2 x 2, 3 x 3 и 4 x 4 являются квадратными матрицами. Мы можем найти определители для всех этих матриц.

Основным определителем является матрица 2 x 2. Формула для определения определителя такой матрицы следующая:

Здесь происходит то, что мы берем номера нашей верхней строки один за другим.Глядя на первое число в верхней строке, мы визуально отменяем все числа в той же строке и столбце. Остается номер d . Умножаем a на d . Проделаем то же самое для второго числа в верхнем ряду, b . Мы визуально убираем все числа в той же строке и столбце, что и b . Остается c . Затем мы умножаем их вместе. Теперь вычитаем это произведение из первого.

Давайте посмотрим, как это делается, на примере.Начнем с нашей матрицы 2 x 2.

Определитель затем записывается с помощью столбцов абсолютного значения.

Мы написали заглавную букву D для обозначения определителя, а затем у нас есть столбцы абсолютных значений вокруг нашей матрицы, чтобы показать, что мы будем вычислять определитель. Определитель этой матрицы 1 * 4 — 2 * 3. Мы взяли каждое число из верхней строки и умножили его на противоположное число.

На самом деле, когда мы смотрим на первое число в верхней строке, 1, мы мысленно отменяем все числа в той же строке и столбце. У нас остается 4. Это число, на которое мы умножаем нашу единицу. Глядя на второе число в верхнем ряду, 2, мы снова мысленно отменяем все числа, которые находятся в той же строке и столбце. Мысленно сокращаем числа в верхнем ряду и во втором столбце. У нас осталось число 3, поэтому мы умножаем наши 2 на 3.

У нас также есть образец плюса и минуса вдоль верхнего ряда.Наше первое число всегда плюс, потом — минус. Если наша матрица больше, то следующим числом будет плюс, а затем снова отрицательное. Вот почему у нас есть 1 * 4 — 2 * 3. Выполняя этот расчет, мы получаем 4 — 6 для определителя -2.

Определитель матрицы 3×3 — ChiliMath

Стандартная формула для определения определителя матрицы 3 × 3 представляет собой разбиение меньших задач определителя 2 × 2 , с которыми очень легко справиться. Если вам нужно напомнить что-то новое, посмотрите мой другой урок о том, как найти определитель 2 × 2.Предположим, нам дана квадратная матрица A, где,

Определитель матрицы A вычисляется как

Вот ключевые моменты:

Обратите внимание, что элементы верхней строки, а именно a, b и c, служат в качестве скалярных умножителей для соответствующей матрицы 2 на 2.

Скаляр a умножается на матрицу 2 × 2 оставшихся элементов, созданную, когда вертикальные и горизонтальные отрезки линии проходят через a.

Тот же процесс применяется для построения матриц 2 × 2 для скалярных множителей b и c.

Определитель матрицы 3 x 3 (анимированный)

Примеры того, как найти определитель матрицы 3 × 3

Пример 1: Найдите определитель матрицы 3 × 3 ниже.

Приведенная ниже настройка поможет вам найти соответствие между общими элементами формулы и элементами реальной проблемы.

Применяя формулу,

Пример 2: Вычислите определитель матрицы 3 × 3 ниже.

Будьте очень осторожны при замене значений в правильные места в формуле. Распространенные ошибки возникают, когда учащиеся становятся неосторожными на начальном этапе подстановки значений.

Вдобавок убедитесь, что ваша арифметика верна. В противном случае одна ошибка в вычислении приведет к неверному ответу.

С,

наше вычисление определителя становится…

Пример 3: Найдите определитель матрицы 3 × 3 ниже.

Наличие нуля (0) в первой строке должно значительно упростить наши вычисления. Помните, что эти элементы в первой строке действуют как скалярные множители. Следовательно, умножение нуля на что-либо приведет к исчезновению всего выражения.

Вот снова настройка, показывающая соответствующее числовое значение каждой переменной в формуле.

По формуле имеем…

Практика с рабочими листами

Возможно, вас заинтересует:

Детерминанты матрицы 2 × 2

разложений Лапласа для определителя

Используя определение определителя, в примере 5 было получено следующее выражение:

Это уравнение можно переписать следующим образом:

Каждый член справа имеет следующую форму:

В частности, отметим, что

Если A = [ a _ij ] является матрицей n x n , то определитель матрицы ( n — 1) x ( n — 1), которая остается после Строка и столбец, содержащие запись a _ij удалены, называется a _ij второстепенный , обозначается mnr ( a _ij ).Если a _ij minor умножить на (−1) ^{i + j}, то результат будет называться a _ij кофактор , обозначенный cof ( a 136j ). То есть

Используя эту терминологию, приведенное выше уравнение для определителя матрицы 3 x 3 A равно сумме произведений элементов в первой строке и их сомножителей:

Это называется расширением Лапласа по первой строке.Также можно показать, что определитель равен разложению Лапласа на второй строки ,

или третьим рядом ,

Верно даже больше. Определитель также равен разложению Лапласа по первому столбцу

по второму столбцу или по третьему столбцу. Хотя формула разложения Лапласа для определителя была явно проверена только для матрицы 3 x 3 и только для первой строки, можно доказать, что определитель любой матрицы nxn равен разложению Лапласа по любой строке или любому столбцу .

Пример 1 : Вычислить определитель следующей матрицы, используя разложение Лапласа по второму столбцу:

Записи во втором столбце: a ₁₂ = −1, a ₂₂ = 2 и a ₃₂ = 0. Минорные значения этих записей, mnr ( a ₁₂), mnr ( a ₂₂) и mnr ( a ₃₂) вычисляются следующим образом:

Поскольку сомножители во втором столбце записей равны

расширение Лапласа по второму столбцу становится

Обратите внимание, что не было необходимости вычислять младший или сомножитель записи (3, 2) в A , поскольку эта запись была 0.В общем, при вычислении определителя методом разложения Лапласа выбирайте строку или столбец с наибольшим количеством нулей. Минорные элементы этих записей не нужно оценивать, потому что они не будут вносить никакого вклада в определитель.

Фактор (-1) ^{i + j}, который умножает на _ij младший, чтобы дать кофактор _ij , приводит к шахматной схеме знаков; каждый знак дает значение этого коэффициента при вычислении кофактора a _ij от a _ij minor.Например, шаблон шахматной доски для матрицы 3 x 3 выглядит так:

Для матрицы 4 x 4 шахматная доска имеет вид

и так далее.

Пример 2 : Вычислить определитель следующей матрицы:

Сначала найдите строку или столбец с наибольшим количеством нулей. Здесь это третья строка, содержащая два нуля; разложение Лапласа по этой строке будет содержать только два ненулевых члена. Образец шахматной доски, показанный выше для матрицы 4 на 4, подразумевает, что младший элемент записи a ₃₁ = 1 будет умножен на +1, а младший элемент записи a ₃₄ = 2 будет умножен на −1, чтобы получить соответствующие кофакторы:

Теперь каждый из этих кофакторов, которые сами по себе являются определяющими, можно оценить с помощью разложения Лапласа.Раскрывая третий столбец,

Другой сомножитель вычисляется путем раскрытия его первой строки:

Следовательно, оценка det A с помощью разложения Лапласа вдоль третьей строки A дает

Пример 3 : Перекрестное произведение двух 3-векторов, x = x ₁ i + x ₂ j + x ₃ 41 k и и и и y = y ₁ i + y ₂ j + y ₃ k , проще всего вычислить, выполнив разложение Лапласа по первой строке символического определителя

Это расширение дает

Для иллюстрации, перекрестное произведение векторов x = 3 j -3 k и y = −2 i + 2 j — k равно

Пример 4 : Есть ли связь между определителем A ^T и определителем A ?

В случае 2 на 2 легко увидеть, что det ( A ^T) = det A :

В случае 3 на 3 расширение Лапласа по первой строке A дает тот же результат, что и расширение Лапласа по первому столбцу A ^T, подразумевая, что det ( A ^T) = det A :

Начиная с расширения

для определителя нетрудно дать общее доказательство того, что det ( A ^T) = det A .

Пример 5 : Примените результат det ( A ^T) = det A для оценки

при том, что

(где a, e, g, n, o, p и r — скаляры).

Поскольку обмен одной строкой меняет знак определителя (Свойство 2), обмен двумя строками,

оставит определитель без изменений:

Но определитель матрицы равен определителю ее транспонирования, поэтому

Следовательно,

Пример 7 : Учитывая, что числа 1547, 2329, 3893 и 4471 делятся на 17, докажите, что определитель

также делится на 17, не оценивая его.

Из-за результата det ( A ^T) = det A , каждое свойство определителя, которое включает строки A , подразумевает другое свойство определителя, включающее столбцы A . Например, определитель является линейным в каждом столбце , меняет знак, если два столбца меняются местами, не изменяется, если к другому столбцу добавляется кратное одному столбцу , и так далее.

Для начала умножьте первый столбец A на 1000, второй столбец на 100 и третий столбец на 10. Определитель полученной матрицы будет в 1000 · 100 · 10 раз больше, чем определитель A :

Затем добавьте второй, третий и четвертый столбцы этой новой матрицы к ее первому столбцу. Ни одна из этих операций с столбцами не изменяет определитель; таким образом,

Поскольку каждая запись в первом столбце этой последней матрицы делится на 17, каждый член в разложении Лапласа по первому столбцу будет делиться на 17, и, таким образом, сумма этих членов, которая дает определитель, будет делиться на 17.Поскольку 17 делит 10 ⁶ det A , 17 должно делить det A , потому что 17 является простым числом и не делит 10 ⁶.

Пример 7 : Полезная концепция в исчислении более высоких измерений (например, в связи с формулой замены переменных для множественных интегралов) — это концепция якобиана отображения. Пусть x и y заданы как функции независимых переменных u и v :

Якобиан карты ( u, v ) ↦ ( x, y ), величина, обозначенная символом δ ( x, y ) / δ ( u, v ), определяется как следующий определитель:

Для иллюстрации рассмотрим преобразование полярных координат ,

Якобиан этого отображения ( r , θ) ↦ ( x, y ) равен

Тот факт, что якобиан этого преобразования равен r , составляет коэффициент r в известной формуле

, где R ‘- область в плоскости r −θ, отображаемая (*) в область интегрирования R в плоскости x − y .

Якобиан также можно расширить до трех переменных. Например, точку в 3-пространстве можно задать, задав ее сферические координаты — ϕ и θ — которые связаны с обычными прямоугольными координатами — x, y и z — уравнениями

См. Рисунок.

Рисунок 1

Якобиан отображения (ρ, ϕ, θ) ↦ ( x, y, z ) равен

По разложению Лапласа по третьему ряду,

Тот факт, что якобиан этого преобразования равен ρ ² sin ϕ, составляет коэффициент ρ ² sin ϕ в формуле для изменения переменных в тройном интеграле с прямоугольных на сферические координаты:

Расширения Лапласа после сокращения строк .Полезность метода разложения Лапласа для оценки определителя увеличивается, когда ему предшествуют элементарные операции со строками. Если такие операции выполняются с матрицей, количество нулей в данном столбце может быть увеличено, тем самым уменьшая количество ненулевых членов в разложении Лапласа вдоль этого столбца.

Пример 8 : Вычислить определитель матрицы

Следующие операции сокращения строк, поскольку они просто включают добавление числа, кратного одной строке к другой, не изменяют значение определителя:

Теперь, когда определитель этой последней матрицы вычисляется с использованием разложения Лапласа по первому столбцу, остается только один ненулевой член:

Следовательно, det A = −5.

Пример 9 : Вычислить определитель матрицы

Чтобы избежать создания большого количества нецелочисленных записей во время процесса сокращения строки, коэффициент 2 сначала делится из нижней строки. Поскольку умножение строки на скаляр умножает определитель на этот скаляр,

Теперь, поскольку элементарные операции со строками

не изменяют определитель, расширение Лапласа по первому столбцу этой последней матрицы завершает оценку определителя A :

РубрикаРазное

Определитель 4 порядка формула: Найти определитель матрицы четвертого порядка

Найти определитель матрицы четвертого порядка

Основные определения и формула для нахождения определителя матрицы четвертого порядка

Пример решения

Теорема Лапласа

Как вычислить определитель четвертого порядка

Основные определения и формула для нахождения определителя матрицы четвертого порядка

как считать по столбцу, как вычислить от треугольной матрицы

Определитель матрицы 4 порядка

Правильная расстановка индексов в матрице

Общая схема вычисления определителей

Метод понижения порядка

Приведение к треугольному виду

4 порядка матрицы

Где можно решить любую задачу по математике, а так же 4 порядка матрицы Онлайн?

Определители квадратных матриц

1.Определители квадратных матриц.

2.Свойства определителей.

Пример.

Как вычислить определитель матрицы 4 порядка. Вычисление определителей

Методы нахождения определителей

Свойство определителей

Вычисление определителей 2-го, 3-го и высших порядков

1. Определитель 2-го и 3-го порядков.

2. Определитель произвольного порядка.

Примеры решения задач

Определитель матрицы 4×4 — Как вычислить определитель матрицы 4×4?

Введение в определитель матрицы 4×4

Определение определителя

Что такое матрица?

Ярлык для поиска ранга матрицы

Символ определителя

Для матрицы 2 × 2

Определитель для матрицы 2 × 2

Для матрицы 3 × 3

Как вычислить определитель матрицы 4 × 4?

Определители матриц высшего порядка

Определитель матрицы 3×3 (общий и сокращенный метод)

Определитель матрицы 3×3 (общий и сокращенный метод)

Какой определитель матрицы

Как найти определитель матрицы 3×3

Определитель большой матрицы

Упражнения по вычислению определителя матрицы 3×3

Второстепенные и кофакторы: расширение по ряду

Как оценивать детерминанты высшего порядка в алгебре — Видео и стенограмма урока

Детерминанты

Определитель матрицы 3×3 — ChiliMath

Определитель матрицы 3 x 3 (анимированный)

Примеры того, как найти определитель матрицы 3 × 3

разложений Лапласа для определителя

Добавить комментарий Отменить ответ