Окружность для тригонометрии: Тригонометрическая окружность — универсальная шпаргалка по тригонометрии (ЕГЭ — 2021)
Единичная окружность в тригонометрии
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.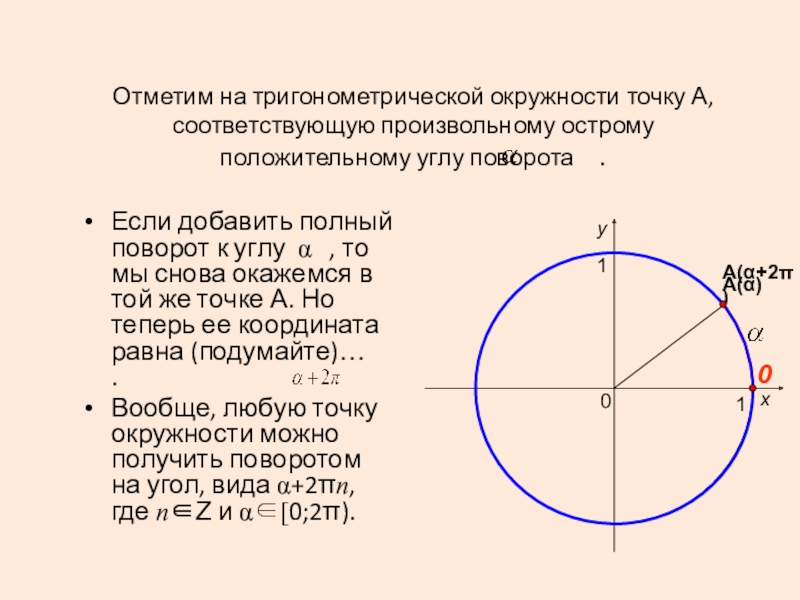
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.

- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. 2 = 1
2 = 1
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Для чего использовать единичную окружность
- определить синус, косинус, тангенс и котангенс угла
- найти значения тригонометрических функций для некоторых значений числового и углового аргумента
- вывести основные формулы тригонометрии
- вывести формулы приведения
- найти области определения и области значений тригонометрических функций
- определить периодичность тригонометрических функций
- определить четность и нечетность тригонометрических функций
- определить промежутки возрастания и убывания тригонометрических функций
- определить промежутки знакопостоянства тригонометрических функций
- применить радианное измерение углов
- найти значения обратных тригонометрических функций
- решить простейшие тригонометрические уравнения

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в современную школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!
| Табличка на двери |
Тригонометрическая окружность. Тригонометрические функции — презентация онлайн
1. Тригонометрическая окружность. Тригонометрические функции
2. Основные вопросы:
• Понятие угла. Градусная и радианныемеры измерения угловых величин.
Изображение вещественных чисел на
единичной окружности.
• Определение и свойства
тригонометрических функций.
• Квадранты единичной окружности.
Знаки тригонометрических функций.
22.11.2018
2
3. Тригонометрия — математическая дисциплина, изучающая зависимость между сторонами и углами треугольника.
22.11.20183
Угол — это часть плоскости,
ограниченная двумя лучами, выходящими из
одной точки, вершины угла.
Угол разбивает плоскость на две части.
Каждая из них называется
углом.
Плоские углы с общими сторонами называются
.
В качестве единицы измерения углов принят
градус —
развернутого угла (прямой).
5
Угол в 10 – это угол,
который опишет
луч, совершив
1/360 часть
полного оборота
вокруг своей
начальной точки
против часовой
стрелки.
6
Теорема 1. Отношение
длины окружности к
ее диаметру не
зависит от
окружности, т.е. одно
и то же для любых
окружностей.
22.11.2018
7
Центральным углом в
окружности
называется плоский
угол с вершиной в ее
центре.
Часть окружности, расположенная внутри
плоского угла, называется дугой окружности,
соответствующей этому центральному углу
Градусной мерой дуги окружности называется градусная мера
соответствующего центрального угла. Развернутому углу
(прямой) соответствует длина полуокружности πR.
22.11.2018
8
Радианной мерой угла
называется
отношение длины
соответствующей
дуги к радиусу
окружности.
22.11.2018
9
22.11.2018
10
Углом в 1 радиан
называется
центральный
угол,
опирающийся на
дугу, равную по
длине радиусу
окружности
22.11.2018
11
1 рад = 180º º
π
1рад ≈57,3º
αрад = 180º º α
π
1 º = π рад
180 º π
α º = π α рад
180 º
12. 1рад ≈57,3º
22.11.201813
Синусом острого угла прямоугольного треугольника
называется отношение
противолежащего катета к гипотенузе
Sin A = BC:AB
Косинусом острого угла
прямоугольного треугольника
называется отношение
прилежащего катета к гипотенузе
Cos A = AC :AB
Тангенсом острого угла
прямоугольного треугольника
называется отношение противолежащего
катета к прилежащему катету
Tg A = BC:AC
14. Синус, косинус и тангенс острого угла прямоугольного треугольника
Определение единичной окружностиАвтоматический показ
Окружность радиуса 1
с центром в начале
координат называют
единичной
окружностью.
Зададим соответствие между
множеством действительных
чисел и точками единичной
окружности следующим
образом:
15. Определение единичной окружности
,Так как длина окружности вычисляется по формуле С 2 R, то
можно получить изображение таких чисел на окружности как:
2 ,
3 , 4 и т.д., учитывая, что R 1 и C 2 .
1. Каждому действительному
числу соответствует
единственная точка окружности.
2.Каждая точка окружности
изображает бесконечное
множество действительных
чисел.
В
С
А
D
3. Точки A, B, C, D назовем
узловыми.
Фактически, мы получили
принципиально новую систему
координат – криволинейную. Но
точка единичной окружности имеет
одну координату. (Почти все
также, как и в прямоугольной
системе координат.)
y
B ( x; y )
o
c
x
y
sin
R
x
cos
R
y
tg
x
x
ctg
y
Координаты
у π/2 90°
120° 2π/3
135° 3π/4
1
150° 5π/6
180° π -1
—
—
1/2
π/6 30°
0
1 0 0°
½
-1/2
210° 7π/6
225° 5π/4
240° 4π/3
π/3 60°
π/4 45°
-1/2
-1
270° 3π/2 [-π/2]
(sint)
2π 360
x
(cost)
11π/6 330° [-π/6]
7π/4 315° [-π/4]
5π/3 300° [-π/3]
19. Координаты
Синусом угла х называет сяординат а т очки, полученной
поворот ом т очки (1; 0)
вокруг начала координат на
угол х (обозначает ся sin x ).
20. Определение синуса и косинуса
Тангенсом угла х называется отношениесинуса угла х к косинусу угла х.
21. Определение тангенса
Кот ангенсом угла х называет ся от ношениекосинуса угла х к синусу угла х.
22. Определение котангенса
y+
o+
—
—
x
y
—
y
СИНУС
—
o
+
+
КОСИНУС
+
+
o
—
x
ТАНГЕНС И
КОТАНГЕНС
x
23. ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Основные тригонометрические тождества1.
24. Основные тригонометрические тождества
22.11.201825
25. Домашнее задание
26
|
Что такое тригонометрическая окружность? | О математике понятно
Итак, друзья, я вас поздравляю! Начальный этап знакомства с тригонометрией благополучно пройден. Подытожим его. Теперь мы с вами:
1. Знаем, что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике.
2. Знаем, как устроена связь между тригонометрическими функциями одного и того же угла и умеем находить полный набор функций, если известна хотя бы одна из них. Кроме того, ещё мы умеем (надеюсь) пользоваться основными тригонометрическими формулами. А чего? Зря, что ли, примеры разбирали?)
Это — самые азы тригонометрии. Без этих элементарных знаний и навыков — дальше никуда. Так что, прошу прогуляться и почитать, пока не поздно. Тем более там всё очень просто и доступно.)
Идём дальше.
Как мы уже с вами знаем, у каждого острого угла в прямоугольном треугольнике имеется свой джентльменский набор тригонометрических функций. Знаем длины катетов и гипотенузу, делим друг на друга и считаем себе. И так для любого острого угла. Всё элементарно.
Вопрос: а если угол сделать тупым? Скажем, вот таким:
Что делать? Развалился наш прямоугольный треугольник. Ни катетов больше нет, ни гипотенузы… А тригонометрические функции тоже ушли в небытие, да?
Если бы древние математики не нашли выход из этой ситуации, то, возможно, вы бы сейчас и не читали этот сайт. Ибо не было бы у нас тогда ни планшетов, ни компьютеров, ни смартфонов, ни многих других полезных штучек…
Так как можно определять любые тригонометрические функции любых углов без прямоугольного треугольника? Что ж, пришла пора взрослеть дальше. Знакомимся!
Тригонометрическая окружность. Единичная окружность. Числовая окружность. Что всё это значит?
Это очень простые понятия. Более того, эти понятия — верный друг и надёжный помощник во всех разделах тригонометрии! От простой работы с углами в градусах или в радианах до тригонометрических уравнений и неравенств. Почему? А потому, что эта штука — своего рода шпаргалка! Причём совершенно законная! Обычно ведь что бывает: за шпоры выгоняют, двойки ставят… А тут нарисовал окружность, угол, функцию — и сразу увидел всё что тебя интересует.
Например, такое простое задание:
Что больше — sin200° или sin(-100°)?
Кто не в теме, тот отдыхает в сторонке. А кто в теме, тот нацарапает что-то типа вот такого наскального рисунка:
и сразу же увидит всю необходимую информацию!
И никто слова не скажет! Даже суровая комиссия в боевой обстановке ЕГЭ. Так зачем же такой шанс упускать, правда?
Чуть позже, в соответствующем уроке, мы разберём эту страшную задачку. И про злые углы типа -100 градусов тоже поговорим.)
А пока начнём. Для начала нарисуем самый обычный привычный нам острый угол. Назовём его, как обычно, «альфа». Вот так:
Угол как угол, пока ничего выдающегося, но… Раз есть угол (пока что острый), то у него должны быть и свои тригонометрические функции! Косинус там или тангенс… А где их взять? Ни гипотенузы, ни катетов больше нет, только угол. Тупик?
Спокойствие! Сейчас всё увидите.)
Для начала нарисуем самые обычные и знакомые нам координатные оси. OX по горизонтали, OY — по вертикали, всё чин-чинарём… Нарисуем и… приколотим горизонтальную сторону угла к положительной полуоси OX. Приколотим покрепче, дабы не оторвать ненароком.) Вершину угла поместим в начало координат, точку О. А вот вторую сторону угла прибивать не будем и оставим подвижной. Зачем? А чтобы угол менять можно было. Хотим побольше, хотим поменьше. Хотим острый, хотим тупой — любой! Раздвижной у нас угол будет. Как угол раствора циркуля, только одна из его ножек будет прибитой.) Конец подвижной стороны обозначим буквой А.
Получим вот такой незамысловатый рисунок:
Итак, угол у нас пристроен, это хорошо. А где же его синус и косинус — спросите вы? Потерпите минутку, торопыги, сейчас всё увидите! Я же только начал.)
Введём теперь координаты x и y конца подвижной стороны угла (точки А) и отметим их на осях. Это будут точки В и С соответственно. Ясное дело, что ОВ и ОС — какие-то числа. Длины отрезков. Или координаты точки А.
ОВ = х
ОС = у
Так вот, оказывается, иксовая координата точки А (отрезок ОВ) будет косинусом угла альфа, а игрековая координата (отрезок ОС) — его синусом!
Смотрим на рисунок:
Стоп-стоп! С какого такого перепугу-то? Ведь мы же чётко зарубили себе на носу из прошлых двух уроков, что синус и косинус — это отношения сторон в прямоугольном треугольнике! Которые от длин этих самых сторон никак не зависят. А у нас тут координаты точки А присутствуют. Которые могут быть любыми!
Всё верно. Любыми. Но! Давайте посмотрим внимательнее на треугольник АВО. Прямоугольный, между прочим.) Ибо координаты точки, они обычно перпендикулярами отмечаются на осях, да… По нашему заклинанию косинус угла альфа — это отношение прилежащего катета к гипотенузе. Или ОВ/ОА. Синус альфа — соответственно ОС/ОА. Причём мы с вами помним, что синус/косинус никак не зависят от длин сторон. А это совсем прекрасно! Почему? А потому, что мы имеем полное право выбирать длины сторон как хотим. Как нам удобно, так и выберем. В частности, мы имеем полное право принять длину гипотенузы ОА за единичку (ОА=1)! Причём единицы измерения нас вообще не волнуют — миллиметр, километр, миля, дюйм… Синус и косинус от этого всё равно не изменятся.)
Почему именно гипотенуза (а не катеты) и именно единичка (а не 2, 10, 157 и т.д)? Потому, что так нам (и древним людям) очень удобно! Именно при таком выборе у нас достигаются максимальные упрощения. Смотрите, что получается:
Вот и все дела.) Косинус — иксовая координата точки А, а синус — игрековая (если гипотенуза ОА — единичка). Да, ненаучно, да нестрого, но зато понятно. И запоминается проще. А запомнить очень важно. Причём, запомнить надёжно!
Запоминаем:
Косинус — по Х, синус — по Y.
Именно в таком порядке. Не путаемся!
Как видите, всё просто. Пока что всё идёт в рамках геометрии восьмого класса. С той лишь разницей, что катеты превратились у нас в координаты х и у точки А, а гипотенуза — та и вовсе превратилась в единичку. Очень удобное число.) Однако… Тема урока называется «Тригонометрическая окружность», не так ли? Пока ни слова про окружность не было!
Всё правильно. Но остались совсем пустяки. Сейчас мы с вами резко повзрослеем и колоссально расширим наши возможности всего одним движением руки! Как? Очень просто. Берём подвижную сторону угла (т.е. ОА) и… проворачиваем её вокруг точки О на полный оборот! Как вы думаете, какую линию при этом опишет точка А? Ну, конечно! Окружность!
Вот так:
Вот и всё. Это и есть тригонометрическая окружность!
Это научное название. А на математическом сленге обычно говорят «тригонометрический круг». Или совсем коротко — просто «круг». Или — «радар» :).
Ну хорошо, окружность начертили. Но почему — тригонометрическая? Окружность как окружность… Вскрою тайну. Любой точке на окружности соответствуют два числа — координаты этой точки по X и координаты этой точки по Y. То есть, А(х; у). А икс и игрек у нас что? Только что разбирались… Да! Косинус и синус угла альфа. То есть, не что иное, как его тригонометрические функции. Вот и весь смысл.
А теперь, вспомнив, что ОА = 1 и что ОА — радиус окружности, можно сообразить, что это же самое понятие — и единичная окружность тоже.
А если вспомнить самый первый урок по тригонометрии (а чуть конкретнее — то, что синус и косинус — просто какие-то числа), то наша с вами тригонометрическая окружность будет ещё и числовой окружностью.
Вот так. Сразу три термина в одном. Очень удобно и практично.
Запоминаем:
Тригонометрическая, единичная и числовая окружности — это всё одно и то же понятие. В рамках тригонометрии.
Так, ну хорошо. Окружность изобразили. Угол у нас крутящийся, меняющийся. А раз крутящийся, то нам уже ничто не запрещает прокрутить подвижную сторону ОА куда угодно. Например, так, чтобы угол альфа стал каким-нибудь тупым!
Хотя бы вот так:
А как увидеть его синус и косинус? Не вопрос! Всё точно так же. Опускаем перпендикуляры из точки А на оси OX и OY и всё видим:
Самые глазастые, возможно, уже заметили, что синус угла альфа у нас положительный (точка С лежит на положительной полуоси OY). А вот косинус альфа — отрицательный! Ибо точка В, иксовая координата точки А (т.е. не что иное, как косинус альфа!), лежит на отрицательной полуоси OХ. Значит, у любого тупого угла синус положительный, а косинус — отрицательный. Чего, кстати, принципиально не бывает в прямоугольном треугольнике: там все тригонометрические функции — синус, косинус, тангенс, котангенс — положительные.
А здесь — пожалуйста! Не зря же мы с вами расширили наши возможности!) Ну а коли так, раз уж мы столкнулись с отрицательным косинусом у тупого угла, то пришла пора разобраться и с такой важной штукой, как знаки синуса/косинуса по четвертям. До кучи и знаки тангенса/котангенса разберём сразу же.
Знаки синуса и косинуса, тангенса и котангенса по четвертям.
Всё проще простого. Для начала напомню, что координатные четверти (или по-другому квадранты) в тригонометрии нумеруются точно так же, как и при работе с обычными задачами на координаты точек — против часовой стрелки.
Вот так:
А что же со знаками синуса/косинуса по четвертям? Тоже всё элементарно, Ватсон.) С первой и второй четвертями мы уже разобрались выше. Незаметно для себя.) С первой четвертью вообще вопросов нет. Там только острые углы, у которых все функции (в том числе и синус с косинусом) — положительные. Со второй четвертью тоже всё ясно: синус положительный, а косинус — отрицательный. Это мы уже выяснили, когда тупой угол рисовали.
Осталось лишь разобраться с третьей и четвёртой четвертями. Как? Точно так же! Не зря же мы с вами тут углы мотать учимся потихоньку.)
Мы же знаем, что ОА — подвижная сторона нашего угла альфа. Вот и продолжим её крутить от положительной полуоси ОХ в нужную нам сторону! В третью четверть. Получим вот такую картинку:
Как видно из рисунка, для любого угла в третьей четверти уже станет отрицательным не только косинус, но и синус тоже:
Для четвёртой четверти тоже ничего хитрого. Крутим и рисуем:
И видим, что синус в четвёртой четверти остаётся по-прежнему отрицательным. А косинус? Да! Косинус снова становится положительным:
Так, по всем четвертям пробежались. Как видите, всё просто. Для лучшего запоминания можно нарисовать знаки синуса/косинуса прямо на нашем круге.
Запоминаются обе картинки достаточно просто и быстро. Особенно если железно помнить наше секретное заклинание: «Косинус — по икс, синус — по игрек.» Кстати, сопоставьте заклинание с картинками! Очень полезно.)
Ну хорошо, с синусом/косинусом всё понятно. А тангенс и котангенс? Тоже никаких проблем. Если, конечно, помнить из второго урока, что тангенс — это синус поделить на косинус:
А котангенс — наоборот.
Вот теперь и прикинем. В первой четверти у нас всё шоколадно. Всё с плюсом — и синус и косинус. А плюс поделить на плюс — что будет? Конечно же, плюс! Во второй четверти знаки синуса и косинуса — разные. Плюс и минус. А это значит, что их отношение (что синуса к косинусу, что наоборот) будет всегда отрицательным. Ибо в борьбе минуса с плюсом всегда выигрывает минус. Так уж повелось в математике.) В третьей четверти как синус, так и косинус имеют знак «минус». А их отношение? Минус на минус — будет… будет… плюс! А в четвёртой четверти знаки синуса/косинуса опять разные. Стало быть, их отношение (тангенс с котангенсом) снова будет с минусом! Вот и все дела.)
Получаем для тангенса/котангенса вот такую картинку:
Запомнить знаки тоже проще простого: плюс-минус-плюс-минус. Простое чередование знаков.)
И вот тут у некоторых назревает закономерный вопрос:
А можно ли увидеть тангенс и котангенс на круге? Синус — по игрек, косинус — по икс. Это понятно.) А тангенс и котангенс???
Ух, какие вы любопытные, оказывается! Все-то секреты вам раскрой сразу же! Да, можно! Можно увидеть тангенс и котангенс на числовой окружности! Любого угла. Только для этого на нашем рисунке необходим ещё один дополнительный взмах пера. Всего один. Какой именно — в спецтеме «Тангенс и котангенс на тригонометрической окружности».
Итак, полдела сделали. Нарисовали угол, с его помощью начертили окружность. Осталась вторая половина дела. А именно — научиться проделывать обратную операцию. По любой произвольной точке на окружности научиться определять сам угол! А вот эта задачка та ещё…
Об этом — в следующей теме: «Как отсчитывать углы на тригонометрической окружности?».
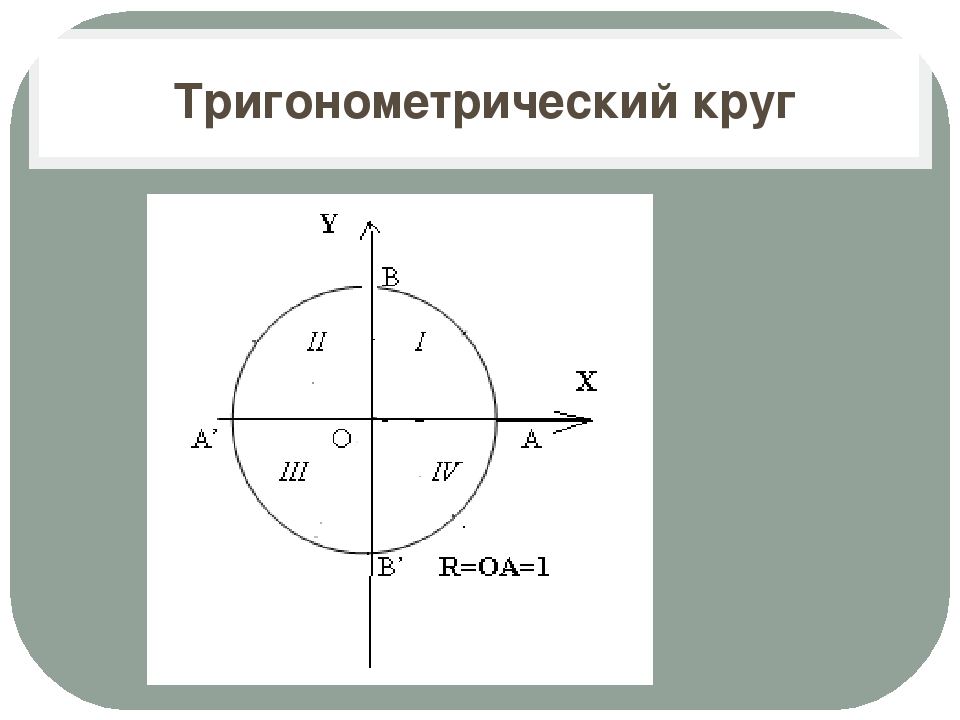
Тригонометрический круг
Тригонометрический круг — это окружность с единичным радиусом и центром в начале осей координат, каждая точка которой образует треугольник с точками:- точка в начале осей координат (точка 0;0)
- точка на окружности (выбрана нами)
- точка на оси X, которая является проекцией выбранной нами точки на эту ось (перпендикуляр к оси X)
Как видно, такой треугольник является прямоугольным, так как из выбранной нами точки на ось абсцисс всегда опускается перпендикуляр. То есть сторона, соединяющая начало координат и выбранную нами точку на тригонометрическом круге ( на приведенном рисунке обозначенную как B, B1. B2, B3) всегда является гипотенузой прямоугольного треугольника, проекция выбранной точки — это катет, а сторона от точки пересечения с осью X образует второй катет.
Угол, который образуется между осью абсцисс (осью X) и гипотенузой треугольника — является углом, для которого и вычисляются значения тригонометрических функций. Этот угол отсчитывается от положительного направления оси абсцисс (оси X) как ноль, далее против часовой стрелки. Таким образом, полный круг составляет 360 градусов или 2π радиан.
Чтобы вычислить значение тригонометрической функции для выбранного угла тригонометрического круга достаточно воспользоваться координатами точки, принадлежащей окружности тригонометрического круга. На приведенном выше рисунке, показано вычисление значения синуса для всех углов.
Например, sin α для треугольника OBC (где координаты точки B равны (x,y) ) ,будет равен: y / √ ( x2 + y2)
Свойства тригонометрического круга
Если последовательно вычислять значения тригонометрических функций для тригонометрического круга, то становится видно, что результат таких вычислений меняет свой знак в зависимости от того, в какой четверти тригонометрического круга выбрана точка. При этом знак тригонометрической функции в пределах одной и той же четверти сохраняется.Знаки тригонометрических функций в координатных четвертях в тригонометрическом круге
Преобразование углов больше 360 градусов или 2π радиан
Как видно из картинок, после того, как значение угла превысит 360 градусов (или 2π радиан), то результат вычисления значения будет тем же самым. То есть, для того, чтобы привести значение к «нормальному» — нужно вычесть из имеющегося значения 360 градусов или 2π радиан и повторять операцию столько раз, пока результат не станет меньше 360 или 2π.
Тригонометрические соотношения в прямоугольном треугольнике | Описание курса | Радианы и градусы. Радiани i градуси
Тригонометрия. Единичная окружность
Цель: научить использовать единичную окружность при решении различных тригонометрических заданий.
В школьном курсе математики возможны различные варианты введения тригонометрических функций. Наиболее удобной и часто используемой является «числовая единичная окружность». Её применение в теме «Тригонометрия» весьма обширно.
Единичная окружность используется для:
– определения синуса, косинуса, тангенса и котангенса угла;
– нахождения значений тригонометрических функций для некоторых значений числового и углового аргумента;
– выведение основных формул тригонометрии;
– выведения формул приведения;
– нахождения области определения и области значений тригонометрических функций;
– определения периодичности тригонометрических функций;
– определения четности и нечетности тригонометрических функций;
– определения промежутков возрастания и убывания тригонометрических функций;
– определения промежутков знакопостоянства тригонометрических функций;
– радианного измерения углов;
– нахождения значений обратных тригонометрических функций;
– решение простейших тригонометрических уравнений;
– решение простейших неравенств и др.
Таким образом, активное осознанное владение учащимися данным видом наглядности дает неоспоримые преимущества для овладения разделом математики «Тригонометрия».
Использование ИКТ на уроках преподавания математики позволяет облегчить овладение числовой единичной окружностью. Конечно, интерактивная доска имеет широчайший диапазон применения, однако не во всех классах она есть. Если же говорить о применении презентаций, то на просторах Интернета и их выбор велик, и каждый педагог может найти наиболее приемлемый вариант для своих уроков.
В чем особенность представляемой мною презентации?
Данная презентация предполагает различные варианты использования и не является наглядностью к конкретному уроку в теме «Тригонометрия». Каждый слайд данной презентации можно использовать обособлено, как на этапе объяснения материала, формирования навыков, так и для рефлексии. При создании данной презентации особое внимание уделялось «читаемости» её с дальнего расстояния, поскольку количество учеников со сниженным зрением постоянно растет. Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.
Данная презентация поможет педагогам познакомить учеников с единичной окружностью в 9 классе на уроках геометрии при изучении темы «Соотношения между сторонами и углами треугольника». И, конечно, она поможет расширить и углубить навык работы с единичной окружностью при решении тригонометрических заданий у учащихся старшего звена обучения на уроках алгебры.
Слайды 3, 4 поясняют построение единичной окружности; принцип определения местоположения точки на единичной окружности в I и II координатных четвертях; переход от геометрических определений функций синус и косинус (в прямоугольном треугольнике) к алгебраическим на единичной окружности.
Слайды 5-8 поясняют, как найти значения тригонометрических функций для основных углов I координатной четверти.
Слайды 9-11 поясняет знаки функций в координатных четвертях; определение промежутков знакопостоянства тригонометрических функций.
Слайд 12 используется для формирования представлений о положительных и отрицательных значениях углов; знакомством с понятием периодичности тригонометрических функций.
Слайды 13, 14 используются при переходе на радианную меру угла.
Слайды 15-18 не анимированы и используются при решении различных тригонометрических заданий, закрепления и проверки результатов усвоения материала.
Содержание:
- Титульный лист.
- Целеполагание.
- Построение единичной окружности. Основные значения углов в градусной мере.
- Определение синуса и косинуса угла на единичной окружности.
- Табличные значения для синуса в порядке возрастания.
- Табличные значения для косинуса в порядке возрастания.
- Табличные значения для тангенса в порядке возрастания.
- Табличные значения для котангенса в порядке возрастания.
- Знаки функции sin α.
- Знаки функции cos α.
- Знаки функций tg α и ctg α.
- Положительные и отрицательные значения углов на единичной окружности.
- Радианная мера угла.
- Положительные и отрицательные значения углов в радианах на единичной окружности.
- Различные варианты единичной окружности для закрепления и проверки результатов усвоения материала.
Тригонометрические функции и унитарный круг — x-engineer.org
Обычный подход в тригонометрии — использовать унитарный круг для представления тригонометрических функций. Чтобы представить унитарный круг, мы используем x-y декартовую систему координат и круг с радиусом , равным 1 . Центр круга находится в начале системы x-y.
Изображение: Тригонометрический круг с четырьмя квадрантами
Унитарный круг разделен на 4 части, названные квадрантами .Первый квадрант (I) образован положительными осями x и y. Если мы нарисуем любой радиус унитарного круга в первом квадранте, угол с положительной осью x может иметь любое значение от 0 до 90 °.
Угол может быть измерен в градусах (°) или радианах . Полный круг имеет угол 360 ° или 2π радиан.
В таблице ниже мы суммируем эквивалент между градусами и радианами для квадрантов унитарной окружности.
| Квадрант I | Квадрант II | Квадрант III | Квадрант IV | |
| Начало | 0 ° (0) | 90 ° (π / 2 ) | 180 ° (π) | 270 ° (3π / 2) |
| Конец | 90 ° (π / 2) | 180 ° (π) | 270 ° (3π / 2) | 360 ° (2π) |
На рисунке ниже мы видим унитарный круг с углами, кратными 30 ° и 45 °.Кроме того, для каждого значения угла градуса у нас есть значение в радианах и x-y координаты точки пересечения между сегментом угла и единичной окружностью.
Изображение: Унитарный круг с углами (градусами и радианами) и координатами x-y
Преобразование между градусами и радианами подробно объясняется в статье Как преобразовывать градусы в радианы и из радиан в градусы.Теперь возьмем любой угол φ в единичной окружности.Угол φ образуется между отрезком AB (длина 1) и осью x. Координаты x-y точки B будут длиной отрезков ABx и ABy (см. Ниже).
Изображение: Унитарный круг для тригонометрических функций
Если мы применим определение тригонометрических функций для угла φ, мы получим:
\ [\ begin {уравнение *} \ begin {split}\ text {sin} (\ varphi) & = \ frac {BB_x} {AB} = \ frac {BB_x} {1} = BB_x & = AB_y \\
\ text {cos} (\ varphi) & = \ frac {AB_x} {AB} = \ frac {AB_x} {1} & = AB_x \\
\ text {tg} (\ varphi) & = \ frac {BB_x} {AB_x} & = \ frac {AB_x} {AB_y} \\
\ text {cosec } (\ varphi) & = \ frac {AB} {BB_x} = \ frac {1} {BB_x} & = \ frac {1} {AB_y} \\
\ text {sec} (\ varphi) & = \ frac {AB} {AB_x} & = \ frac {1} {AB_x} \\
\ text {ctg} (\ varphi) & = \ frac {AB_x} {BB_x} & = \ frac {AB_x} {AB_y}
\ end {split} \ end {формула *} \]
Как вы можете видеть , все тригонометрические функции выражаются только функцией xy, координаты точки B, длины отрезков ABx и ABy.
Таким образом, мы можем найти значения тригонометрических функций для любого заданного угла φ.
В качестве упражнения мы собираемся вычислить и построить значения тригонометрических функций для каждого квадранта. Возьмем 30 ° (квадрант I), 120 ° (квадрант II), 210 ° (квадрант III) и 300 ° (квадрант IV).
| Квадрант I | Квадрант II | Квадрант III | Квадрант IV | |
| Угол (φ) | 30 ° | 120 ° | 210 ° | 300 ° |
| Синус | 0.50 | 0,87 | -0,50 | -0,87 |
| Косинус | 0,87 | -0,50 | -0,87 | 0,50 |
| Касательная | 0,58 | -1,73 | -1,73 | |
| Косеканс | 2,00 | 1,15 | -2,00 | -1,15 |
| Секант | 1,15 | -2.00 | -1,15 | 2,00 |
| Котангенс | 1,73 | -0,58 | 1,73 | -0,58 |
Анализируя значения тригонометрической функции, мы видим, что:
- функция синуса положительна в квадрантах I и II и отрицательна в квадрантах II и IV
- функция косинуса положительна в квадрантах I и IV и отрицательна в квадрантах II и III
- функция тангенса положительна в квадрантах I и III и отрицательна в квадрантах II и IV
- функция косеканса положительна в квадрантах I и II и отрицательна в квадрантах II и IV
- функция секанса положительна в квадрантах I и IV и отрицательна в квадрантах II и III
- функция котангенса положительна в квадрантах I и III и отрицательные в квадрантах II и IV
Имеется графическое представление всех тригонометрических функций ar прямоугольный треугольник внутри единой окружности.Мы также можем визуализировать результат тригонометрических функций как сегменты, соединенные друг с другом.
Изображение: декартово представление тригонометрических функций на единичной окружности
Мы видим, что длины сегментов на самом деле являются значениями, возвращаемыми тригонометрическими функциями . В каждом квадранте мы получаем прямоугольный треугольник, сегменты и высота которого являются результатами тригонометрических функций.
Зная, как представить треугольник для первого квадранта, мы можем вычислить остальные три путем вертикального и горизонтального переворота первого квадранта.
Для любых вопросов или замечаний относительно этого руководства, пожалуйста, используйте форму комментариев ниже.
Не забывайте ставить лайки, делиться и подписываться!
Что такое единичный круг в тригонометрии?
Обновлено 3 ноября 2020 г.
Ли Джонсон
Тригонометрия может показаться довольно абстрактной темой. Такие загадочные термины, как «грех» и «потому что», кажется, просто не соответствуют чему-либо в действительности, и их трудно понять как концепции. Единичный круг существенно помогает в этом, предлагая прямое объяснение того, какие числа вы получаете, когда берете синус, косинус или тангенс угла.Для любого студента, изучающего естественные науки или математику, понимание единичного круга может действительно укрепить ваше понимание тригонометрии и того, как использовать функции.
TL; DR (слишком длинный; не читал)
Радиус единичной окружности равен единице. Представьте себе систему координат xy , начинающуюся в центре этого круга. Углы точек отсчитываются от того места, где x = 1 и y = 0, в правой части круга. Углы увеличиваются при движении против часовой стрелки.
Используя эту структуру, и y для координаты y и x для координаты x точки на окружности:
sin θ = y
cos θ = x
И, следовательно:
tan θ = y / x
What Единичный круг?
«Единичная» окружность имеет радиус 1.Другими словами, расстояние от центра круга до любой части края всегда равно 1. Единица измерения на самом деле не имеет значения, потому что самое важное в единичной окружности — это то, что она делает много уравнений и вычислений. проще.
Он также служит полезной основой для определения углов. Представьте, что центр окружности находится в центре системы координат с горизонтальной осью x и вертикальной осью y .Круг пересекает ось x под углом x = 1, y = 0. Ученые и математики определяют угол от этой точки, двигаясь против часовой стрелки. Таким образом, точка x = 1, y = 0 на окружности находится под углом 0 °.
Определения греха и созвездия с единичным кругом
Обычные определения греха, созвездия и загара, которые даются учащимся, относятся к треугольникам. В них указано:
\ sin θ = \ frac {\ text {напротив}} {\ text {hypotenuse}} \\ \, \\ \ cos θ = \ frac {\ text {смежный}} {\ text {hypotenuse} } \\ \, \\ \ tan θ = \ frac {\ sin θ} {\ cos θ}
«Противоположная» относится к длине стороны треугольника, противоположной углу, «смежная» относится к длине стороны, расположенной рядом с углом, а «гипотенуза» относится к длине диагональной стороны треугольника.
Представьте, что вы создаете треугольник, так что гипотенуза всегда была радиусом единичной окружности, с одним углом на краю круга и одним в его центре. Это означает, что гипотенуза = 1 в приведенных выше уравнениях, поэтому первые две становятся:
\ sin θ = \ frac {\ text {противоположный}} {1} = \ text {противоположный} \\ \, \\ \ cos θ = \ frac {\ text {смежный}} {1} = \ text {смежный} \\
Если вы сделаете рассматриваемый угол равным углу в центре круга, противоположным будет просто y — координата, а смежная — это просто координата x точки на окружности, которая касается треугольника.Другими словами, sin возвращает координату y на единичной окружности (используя координаты, начинающиеся в центре) для заданного угла, а cos возвращает координату x . Вот почему cos (0) = 1 и sin (0) = 0, потому что на данный момент это координаты. Аналогично, cos (90) = 0 и sin (90) = 1, потому что это точка с x = 0 и y = 1. В форме уравнения:
\ sin θ = y \ \ \ cos θ = x
Отрицательные углы также легко понять на основе этого.Отрицательные углы (измеренные по часовой стрелке от начальной точки) имеют ту же координату x , что и соответствующий положительный угол, поэтому:
\ cos -θ = \ cos θ
Однако координата y переключатели, что означает, что
\ sin -θ = — \ sin θ
Определение загара с единичной окружностью
Определение загара, приведенное выше:
\ tan θ = \ frac {\ sin θ } {\ cos θ}
Но с определениями sin и cos единичной окружности, вы можете видеть, что это эквивалентно:
\ tan θ = \ frac {\ text {противоположный}} {\ text {смежный}}
Или, если мыслить в терминах координат:
\ tan θ = \ frac {y} {x}
Это объясняет, почему tan не определен для 90 ° или −270 ° и 270 ° или −90 ° (где x = 0), потому что на ноль нельзя делить.
Графические тригонометрические функции
Графическое изображение sin или cos становится проще, если вы думаете о единичной окружности. Координата x плавно изменяется при перемещении по кругу, начиная с 1 и уменьшаясь до минимума -1 при 180 °, а затем увеличиваясь таким же образом. Функция sin делает то же самое, но сначала увеличивается до максимального значения 1 под углом 90 °, а затем следует той же схеме. Считается, что эти две функции сдвинуты по фазе на 90 ° друг с другом.
Для построения графика загар необходимо разделить y на x , поэтому его сложнее построить, а также есть точки, где он не определен.
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопье: | 780-427-1179 | |
| Adresse de Courriel: | cshelpdesk @ gov.ab.ca | |
Единичный круг — алгебра и тригонометрия
Цели обучения
В этом разделе вы будете:
- Найдите значения функции для синуса и косинуса
- Определите область и диапазон функций синуса и косинуса.
- Найдите опорные углы.
- Используйте исходные углы для оценки тригонометрических функций.
Ищете острые ощущения? Тогда подумайте о поездке на Singapore Flyer, самом высоком колесе обозрения в мире. Колесо обозрения, расположенное в Сингапуре, взлетает на высоту 541 фут — чуть больше десятой мили! Описанное как колесо обозрения, всадники наслаждаются захватывающими видами, путешествуя с земли на вершину и снова вниз по повторяющейся схеме. В этом разделе мы рассмотрим этот тип вращательного движения по окружности.Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат. Затем мы можем обсудить круговое движение в терминах пар координат.
Нахождение синусов и косинусов специальных углов
Мы уже узнали некоторые свойства специальных углов, такие как преобразование радианов в градусы, и нашли их синусы и косинусы, используя прямоугольные треугольники. Мы также можем вычислить синусы и косинусы особых углов, используя тождество Пифагора.
Нахождение синусов и косинусов углов
Затем мы найдем косинус и синус под углом или Сначала мы нарисуем треугольник внутри круга с одной стороной под углом, а другая под углом, как показано на (Рисунок). Если в результате два прямоугольных треугольника объединить в один большой треугольник, обратите внимание, что все три угла этого большего треугольника будут такими, как показано на (Рисунок).
Рисунок 12. Рисунок 13.Поскольку все углы равны, стороны также равны.Вертикальная линия увеличилась, так как все стороны равны, мы также можем сделать вывод, что или с
А поскольку в нашем единичном круге
Используя тождество Пифагора, мы можем найти значение косинуса.
Координаты точки на окружности с радиусом под углом at Радиус единичной окружности, 1, служит гипотенузой прямоугольного треугольника 30-60-90 градусов, как показано на (Рисунок). Угол имеет меру. В какой-то момент мы проводим угол с мерой. Мы знаем, что углы в треугольнике складываются из суммы углов. Теперь у нас есть равносторонний треугольник.Поскольку каждая сторона равностороннего треугольника имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Рисунок 13.Угол составляет 30 °. Угол равен двойному углу, поэтому его размер составляет 60 °. Это серединный перпендикуляр к нему, поэтому он разрезает пополам. Это означает, что это радиус, или Обратите внимание, что это координата x точки, которая находится на пересечении угла 60 ° и единичной окружности. Это дает нам треугольник с гипотенузой 1 и длиной стороны
.Из теоремы Пифагора получаем
Подставляя получаем
Решая для получения
Поскольку конечная сторона находится в квадранте I, где координата y- положительна, мы выбираем положительное значение.
В (60 °) координаты точки на окружности радиуса под углом a, поэтому мы можем найти синус и косинус.
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. (Рисунок) суммирует эти значения.
(рисунок) показывает общие углы в первом квадранте единичной окружности.
Рисунок 14.Использование калькулятора для поиска синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов, мы обращаемся к компьютеру или калькулятору. Будьте внимательны. : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы измерения входного значения. Когда мы вычисляем на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в режиме радиан.
Как записаться
Если задан угол в радианах, воспользуйтесь графическим калькулятором, чтобы найти косинус.
- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Попробуй
Оценить
[show-answer q = ”fs-id2027699 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2027699 ″]
приблизительно 0,866025403
[/ hidden-answer]
Поиск опорных углов
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса.Поскольку значение синуса является координатой y на единичной окружности, другой угол с таким же синусом будет иметь то же значение y , но будет иметь противоположное значение x . Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол. Угол с таким же косинусом будет иметь одинаковое значение x , но будет иметь противоположное значение y .Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на (Рисунок), угол имеет то же значение синуса, что и угол, значения косинуса противоположны. Угол имеет то же значение косинуса, что и угол, значения синуса противоположны.
Рисунок 16.Напомним, что исходный угол угла — это острый угол, образованный конечной стороной угла и горизонтальной осью. Базовый угол — это всегда угол между идиандианами. Как видно из (Рисунок), для любого угла в квадрантах II, III или IV существует опорный угол в квадранте I.
Рисунок 17.Поиск опорного угла
Найдите опорный угол, как показано на (Рисунок).
Рисунок 17. [show-answer q = ”fs-id1710670 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1710670 ″]
Поскольку он находится в третьем квадранте, опорный угол составляет
[/ скрытый-ответ]Попробуй
Найдите опорный угол
[show-answer q = ”fs-id1967998 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1967998 ″]
[/ hidden-answer]
Использование опорных углов
А теперь давайте вернемся к колесу обозрения, представленному в начале этого раздела.Предположим, всадник делает снимок, остановившись на высоте двадцати футов над уровнем земли. Затем всадник совершает поворот на три четверти по кругу. Что такое новый рост райдера? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса под углами, превышающими 90 градусов, или под отрицательным углом. Базовые углы позволяют оценивать тригонометрические функции для углов вне первого квадранта. Их также можно использовать для поиска координат этих углов.Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором находится конечная сторона угла.
Использование опорных углов для поиска координат
Теперь, когда мы узнали, как находить значения косинуса и синуса для особых углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных особых углов единичной окружности. Они показаны на (Рисунок). Найдите время, чтобы узнать координаты всех основных углов в первом квадранте.
Ключевые уравнения
| Косинус | |
| Синус | |
| Пифагорейская идентичность |
Упражнения по разделам
Устный
Опишите единичный круг.
[show-answer q = ”fs-id2077250 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2077250 ″]
Единичный круг — это круг радиуса 1 с центром в начале координат.
[/ hidden-answer]
Что означают координаты x- и y- точек на единичной окружности?
Обсудите разницу между концевым углом и опорным углом.
[show-answer q = ”fs-id1827178 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1827178 ″]
Coterminal углы — это углы, которые имеют одну и ту же конечную сторону. Базовый угол — это размер наименьшего острого угла, образованного конечной стороной угла и горизонтальной осью.
[/ hidden-answer]
Объясните, чем косинус угла во втором квадранте отличается от косинуса его опорного угла в единичной окружности.
Объясните, чем синус угла во втором квадранте отличается от синуса его опорного угла в единичной окружности.
[show-answer q = ”fs-id1801846 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1801846 ″]
Значения синуса равны.
[/ hidden-answer]
Алгебраические
В следующих упражнениях используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором находится определяемая конечная точка.
и
и
[show-answer q = ”fs-id2261414 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2261414 ″]
Я
[/ hidden-answer]
и
и
[show-answer q = ”fs-id2645567 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2645567 ″]
IV
[/ hidden-answer]
Для следующих упражнений найдите точное значение каждой тригонометрической функции.
[show-answer q = ”fs-id2236023 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2236023 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2379850 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2379850 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2084847 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2084847 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2212611 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2212611 ″]
0
[/ hidden-answer]
[show-answer q = ”fs-id2387567 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2387567 ″]
–1
[/ hidden-answer]
[show-answer q = ”fs-id1760509 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1760509 ″]
[/ hidden-answer]
Числовой
Для следующих упражнений укажите исходный угол для данного угла.
[show-answer q = ”fs-id2523531 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2523531 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2227804 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2227804 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2369627 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2369627 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2266093 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2266093 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1535165 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1535165 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2077048 ″] Показать решение [/ show-answer][hidden-answer a = ”fs-id2077048 ″]
[/ hidden-answer]
Для следующих упражнений найдите опорный угол, квадрант конечной стороны, а также синус и косинус каждого угла.Если угол не является одним из углов единичной окружности, воспользуйтесь калькулятором и округлите до трех десятичных знаков.
[show-answer q = ”fs-id2283059 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2283059 ″]
Квадрант IV,
[/ hidden-answer]
[show-answer q = ”fs-id1861830 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1861830 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id2782866 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2782866 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id2516883 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2516883 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id1577224 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1577224 ″]
Квадрант III,
[/ hidden-answer]
[show-answer q = ”fs-id2547413 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2547413 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id2755206 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2755206 ″]
Квадрант II,
[/ hidden-answer]
[show-answer q = ”fs-id2428233 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2428233 ″]
Квадрант IV,
[/ hidden-answer]
Найдите требуемое значение для следующих упражнений.
Ифанди в четвертом квадранте, найдите
Ифанди в первом квадранте, найдите
[show-answer q = ”fs-id2256400 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2256400 ″]
[/ hidden-answer]
Ифанди во втором квадранте, найдите
Ифанди в третьем квадранте, найдите
[show-answer q = ”fs-id2280210 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2280210 ″]
[/ hidden-answer]
Найдите координаты точки на окружности радиуса 15, соответствующей углу
.Найдите координаты точки на окружности радиуса 20, соответствующей углу
. [show-answer q = ”fs-id2800208 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2800208 ″]
[/ hidden-answer]
Найдите координаты точки на окружности радиуса 8, соответствующей углу
.Найдите координаты точки на окружности радиуса 16, соответствующей углу
. [show-answer q = ”fs-id2757988 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2757988 ″]
[/ hidden-answer]
Укажите область определения функций синуса и косинуса.
Укажите диапазон функций синуса и косинуса.
[show-answer q = ”fs-id1347973 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1347973 ″]
[/ hidden-answer]
Технологии
Для следующих упражнений используйте графический калькулятор.
[show-answer q = ”fs-id2428151 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2428151 ″]
-0,1736
[/ hidden-answer]
[show-answer q = ”fs-id2363394 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2363394 ″]
0.9511
[/ hidden-answer]
[show-answer q = ”fs-id17 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id17 ″]
-0,7071
[/ hidden-answer]
[show-answer q = ”fs-id1675635 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1675635 ″]
-0,1392
[/ hidden-answer]
[show-answer q = ”fs-id2497789 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2497789 ″]
−0.7660
[/ hidden-answer]
Расширения
Оцените следующие упражнения.
[show-answer q = ”fs-id2755303 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2755303 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2755134 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2755134 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2631652 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2631652 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2523205 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2523205 ″]
[/ hidden-answer]
[show-answer q = ”fs-id2756010 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2756010 ″]
0
[/ hidden-answer]
Реальные приложения
Для следующих упражнений используйте этот сценарий. Ребенок входит в карусель, которая совершает один оборот за одну минуту.Ребенок входит в точку, то есть в правильном положении на север. Предположим, карусель вращается против часовой стрелки.
Какие координаты ребенка через 45 секунд?
Какие координаты ребенка через 90 секунд?
[show-answer q = ”fs-id2245184 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2245184 ″]
[/ hidden-answer]
Какие координаты ребенка через 125 секунд?
Когда у ребенка будут координаты, если поездка длится 6 минут? (Есть несколько ответов.)
[show-answer q = ”fs-id2755933 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id2755933 ″]
37,5 секунды, 97,5 секунды, 157,5 секунды, 217,5 секунды, 277,5 секунды, 337,5 секунды
[/ hidden-answer]
Когда у ребенка будут координаты, если поездка длится 6 минут?
Глоссарий
- функция косинуса
- значение x точки на единичной окружности, соответствующее заданному углу
- Пифагорейская идентичность
- следствие теоремы Пифагора, утверждающее, что квадрат косинуса заданного угла плюс квадрат синуса этого угла равняется 19 · 1035
- синусоидальная функция
- значение y точки на единичной окружности, соответствующее заданному углу
Единичный круг — тригонометрия
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Тригонометрия — тригонометрия с использованием кругов — треугольник, угол, тригонометрия и функции
Сотни лет тригонометрия считалась полезной только для определения сторон и углов треугольника.Однако, когда математики разработали более общие определения синуса, косинуса и тангенса, тригонометрия стала гораздо более важной в математике и науке. Общие определения тригонометрических функций были разработаны, рассматривая эти значения как точки на единичной окружности.
Единичный круг — это круг, радиус которого равен одной единице, что означает x 2 + y 2 = 1. Если мы считаем, что круг представляет вращение стороны угла, то тригонометрический функции могут быть определены координатами x и y точки вращения.Например, координаты точки P (x, y) можно использовать для определения прямоугольного треугольника с гипотенузой длины r. Тогда тригонометрические функции могут быть представлены следующими уравнениями.
Определив тригонометрические функции как таковые, можно построить график каждой из них, отложив ее значение в зависимости от величины угла, который она представляет.
Поскольку значение для x и y никогда не может быть больше единицы на единичной окружности, диапазон для графиков синуса и косинуса составляет от 1 до -1.Величина угла может быть любым действительным числом, поэтому область графиков представляет собой вещественных чисел . (Углы, превышающие 360 ° или 2π радиан, представляют собой угол с более чем одним оборотом вращения). Графики синуса и косинуса являются периодическими, потому что они повторяют свои значения или имеют период каждые 360 ° или 2π радиан. Они также имеют амплитуду, равную единице, которая определяется как половина разницы между максимальным (1) и минимальным (-1) значениями.
Возможны графики других тригонометрических функций.Из них наиболее важным является график касательной функции. Как и графики синуса и косинуса, функция тангенса является периодической, но имеет период 180 ° или π радиан. Поскольку касательная равна y / x, его диапазон составляет от — ∞ до ∞, а амплитуда — ∞.
Периодичность тригонометрических функций более важна для современной тригонометрии, чем соотношения, которые они представляют. Математики и ученые теперь могут описывать многие типы природных явлений, которые периодически повторяются с помощью тригонометрических функций.Например, время закатов, восходов и комет может быть вычислено благодаря тригонометрическим функциям. Также их можно использовать для описания сезонных изменений температуры, движения волн в океане и даже качества музыкального звука.
Книги
Барнетт, Раймонд А., Майкл Зейглер, Карл Байлин и Стивен Хит. Аналитическая тригонометрия с приложениями. 7 изд. Нью-Йорк: Джон Вили и сыновья, 1998.
Блитцер, Роберт и др. Алгебра и тригонометрия. 2-е изд. Englewood Cliffs, NJ: Prentice Hall, 2003.
.Ларсон, Рон. Исчисление с аналитической геометрией. Бостон: Колледж Хоутон Миффлин, 2002.
Стюарт, Джеймс и др. Тригонометрия Пасифик Гроув, Калифорния: Брукс / Коул, 2003.
Вайсштейн, Эрик В. Краткая энциклопедия математики CRC. Нью-Йорк: CRC Press, 1998.
Что нужно знать о SAT
Вы можете вспомнить, как запомнили единичный круг на уроке математики, или, может быть, вы в настоящее время изучаете его и задаетесь вопросом, увидите ли вы когда-нибудь эту тему за пределами классной комнаты.Будет ли это отображаться на SAT, и как знание (или незнание) этого повлияет на ваш результат? Читай дальше что бы узнать.
Что такое единичный круг?Единичная окружность — это тригонометрическая концепция, которая позволяет математикам расширять синус, косинус и тангенс на градусы за пределы традиционного прямоугольного треугольника. Если вы помните, синус, косинус и тангенс — это отношения сторон треугольника по отношению к обозначенному углу, обычно называемому тета или.
- Синус — это отношение длины противоположного катета прямоугольного треугольника к длине гипотенузы.
- Косинус — это отношение длины соседнего катета прямоугольного треугольника к длине гипотенузы.
- Касательная — это отношение длины противоположной ножки к длине соседней ножки.
Используя эти традиционные определения, мы ограничены описанием углов, которые мы находим в прямоугольных треугольниках, которые составляют от 0 до 90 градусов. В некоторых случаях нам нужно знать эти значения для углов больше 90, и единичный круг делает это возможным.
Окружность единицы названа так потому, что ее радиус равен 1 единице. Его центр находится в начале координат, а все точки вокруг круга находятся на расстоянии 1 единицы от центра. Если мы проведем линию от центра до точки на окружности, длина этой линии будет равна единице (как показано ниже). Затем мы можем добавить линию, чтобы создать прямоугольный треугольник, где высота равна координате y, а длина равна координате x. Эти меры отмечены буквами a и b соответственно.Таким образом, точка на окружности — это (a, b).
Значения a и b зависят от угла; в приведенном выше примере нам нужно найти (или знать) градус от положительной оси x до конечной стороны, отмеченной темно-зеленым цветом. Но мы можем использовать приведенный выше круг, чтобы выяснить общие отношения a и b в любой степени внутри круга.
Используя наши стандартные определения триггеров, приведенные выше, мы можем найти косинус и синус теты. Косинус смежен с гипотенузой, или a / 1.Это сводится к тому, чтобы просто быть. Синус противоположен гипотенузе, или b / 1. Опять же, это сводится к просто b. Точка (a, b) выше может быть переписана как (cos Θ, sin Θ). Фактически, это верно для любой точки единичной окружности, где вы создаете угол с помощью конечной стороны. Теперь мы можем найти синус и косинус для углов, равных 0 или более 90.
Хотя это верно для любого угла единичного круга, большинство учителей математики (и SAT) сосредотачиваются на точках, образованных прямоугольным треугольником 45-45-90 и треугольником 30-60-90 (используя 30 и 60).Поскольку теперь у нас есть мера (30, 45 или 60), мы можем найти косинус и синус для каждого из этих углов в соответствии с единичной окружностью.
Прежде чем мы перейдем к отображению полного единичного круга, давайте поговорим о радианах. Радианы используются для измерения дуги окружности, образованной конечной стороной (отмечена темно-зеленым цветом выше). Окружность единичного круга можно быстро найти, используя стандартную формулу длины окружности, которая равна 2πr. Радиус равен 1, что означает, что длина окружности единичной окружности равна 2π.
Давайте представим, что конечная сторона начинается с положительной оси x справа и вращается вокруг начала координат против часовой стрелки, что не похоже на стрелку часов, а наоборот. Когда он снова достигнет положительной оси x, он завершит поворот на 360 градусов. Таким образом, 360 градусов соответствуют 2π (или всей окружности). Каждая другая точка, соответственно, меньше 2π пропорционально количеству градусов, на которое терминальная сторона переместилась из начального положения справа.
Теперь мы можем использовать соотношение для преобразования градусов в радианы и наоборот. Если нам даны градусы, мы можем умножить их на 2π / 360. Если нам даны радианы, мы можем умножить значение на 360 / 2π.
Вот единичный круг, который вы знаете и любите. Каждый квадрант следует шаблонам, описанным выше.
Нужно ли это знать для SAT?В качестве одного из основных тестов, используемых при поступлении, SAT позволяет проверять все, что рассматривается на уроках математики в старших классах.Следовательно, есть вероятность, что единичный круг появится на экзамене SAT, который вы в конечном итоге пройдете.
Тем не менее, единичный круг не часто тестируется, и многие проблемы, связанные с единичным кругом, могут быть решены другими способами (как и большинство задач на SAT можно решить несколькими способами). По данным Совета колледжей, единичный кружок подпадает под категорию «Дополнительные темы по математике», на которые приходится только 10%, или 6 вопросов, во всем тесте по математике. Это 6 вопросов, разбросанных по разделам с калькулятором и без него.
Дополнительные темы по математике, как правило, отдают предпочтение нескольким другим математическим предметам, прежде чем они дойдут до единичного круга и радианов, например:
- Линии и углы
- Треугольники и другие многоугольники
- Круги (с геометрической точки зрения)
- Площадь и объем
- Координатная геометрия (уравнения прямых и окружностей в координатной плоскости)
- Базовая тригонометрия
- Комплексные числа.
Как вы понимаете, создатели тестов не всегда могут объединить все вышеперечисленные темы и единичный круг в шесть вопросов, хотя эти вопросы иногда требуют решения двух или более тем.Некоторые бесплатные практические тесты College Board не содержат ни одного вопроса, требующего знания единичного круга.
Тем не менее, если вы хотите получить высший балл за SAT Math Test, вы должны чувствовать себя уверенно практически по любой теме, которую SAT может бросить в их тест, включая единичный круг. Вы не должны пренебрегать темой только для того, чтобы обнаружить, как назло, что она появляется в конкретном тесте, который вы проходите.
Если вы не стремитесь к совершенству, но все же стремитесь к хорошему результату, вы можете сосредоточиться на областях математики, которые всегда проверяются на SAT или чаще проверяются.Чтобы узнать больше о темах, тестируемых на SAT Math, ознакомьтесь с нашим сообщением Что такое математический раздел теста SAT?
.





 Вот как она звучит:
Вот как она звучит:


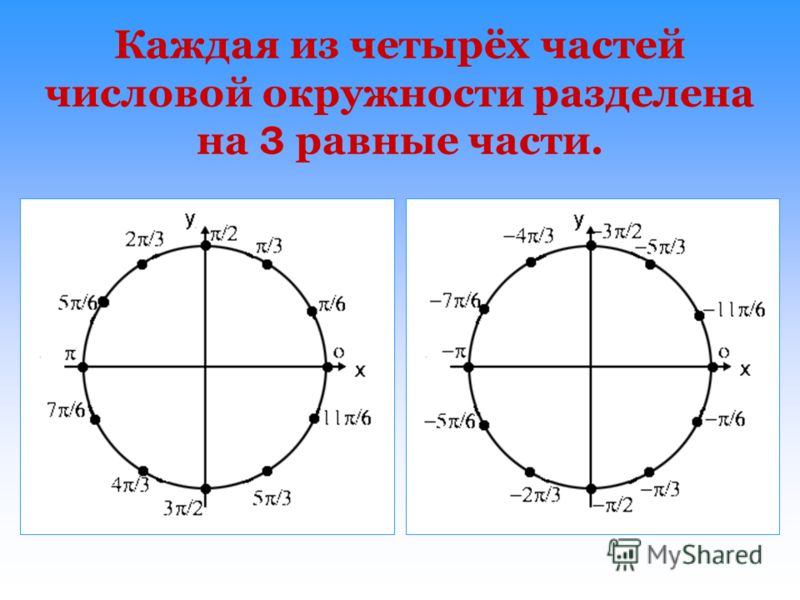
 ..
..
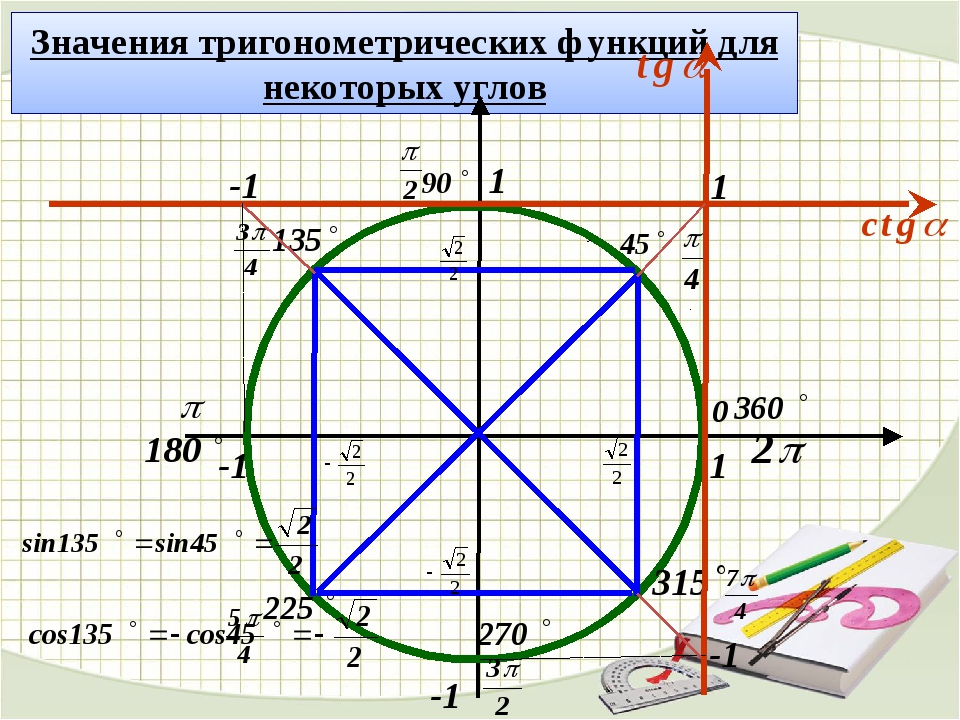
 Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
 И математики нас этому постоянно учат. Вот пример.
И математики нас этому постоянно учат. Вот пример.