Одз на логарифм: ОДЗ логарифма | Логарифмы
Область допустимых значений
Область допустимых значений алгебраического выражения (сокращенно ОДЗ) — это множество значений переменной, при которых это выражение определено.
В школьном курсе алгебры есть всего пять элементарных функций, которые имеют ограниченную область определения. Вот они:
1. ОДЗ:
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
2. ОДЗ:
Выражение, стоящее в знаменателе дроби, не может быть равно нулю.
3. ОДЗ:
Выражение, стоящее под знаком логарифма, должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
4. , ОДЗ:
5. Есть две функции, которые содержат «скрытую» дробь:
и
6. ОДЗ:
ОДЗ:
Степень корня — натуральное число, отличное от 1.
Таким образом, функции и имеют разную область определения.
Если выражение содержит одну или несколько функций, которые определены на ограниченном множестве значений аргумента, то для того, чтобы найти ОДЗ выражения, нужно учесть все ограничения, которые накладываются этими функциями.
Чтобы найти область допустимых значений выражения, нужно исследовать, присутствуют ли в выражении функции, которые я перечислила выше. И по мере обнаружения этих функций, записывать задаваемые ими ограничения, двигаясь «снаружи» «внутрь».
Поясню на примере:
Найти область определения функции:
Чтобы найти область определения функции, нужно найти область допустимых значений выражения, которое стоит в правой части уравнения функции
Я специально выбрала «страшную», на первый взгляд, функцию, чтобы показать вам, на какие простые операции разбивается процесс нахождения области допустимых значений.
«Просканируем» выражение, стоящее в правой части равенства:
1. Мы видим дробь:
Знаменатель дроби не равен нулю. Записываем:
2. Мы видим в знаменателе логарифм:
Выражение, стоящее под знаком логарифма должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
Записываем:
3.Мы видим квадратный корень:
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
Записываем:
Теперь запишем все ограничения в систему неравенств:
Решение этой системы неравенств посмотрите в ВИДЕУРОКЕ:
И.В. Фельдман, репетитор по математике
«Некоторые методы решения логарифмических уравнений»
Некоторые методы решения логарифмических уравнений.

Настоящая статья содержит систематическое изложение методов решения логарифмических уравнений с одной переменной. Это поможет учителю, прежде всего в дидактическом смысле: подбор упражнений позволяет составить для учащихся индивидуальные задания с учетом их возможностей. Данные упражнения могут быть использованы для урока обобщения и для подготовки к ЕГЭ.
Решение логарифмических уравнений.
Логарифмические уравнения – уравнения, содержащие неизвестное под знаком логарифма. При решении логарифмических уравнений часто используются теоретические сведения:
Обычно решение логарифмических уравнений начинается с определения ОДЗ. В логарифмических уравнениях рекомендуется все логарифмы преобразовать так, чтобы их основания были равны.
Преобразования логарифмических выражений не должны приводить к сужению ОДЗ, если же примененный метод решения сужает ОДЗ, выпуская из рассмотрения отдельные числа, то эти числа в конце задачи необходимо проверить подстановкой в исходное уравнение, т.к. при сужении ОДЗ возможна потеря корней.
1. Уравнения вида – выражение, содержащее неизвестное число, а число .
Для решения таких уравнений надо:
1) воспользоваться определением логарифма: ;
2) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
Если ) .
2. Уравнения первой степени относительно логарифма, при решении которых используются свойства логарифмов.
Для решения таких уравнений надо:
1) используя свойства логарифмов, преобразовать уравнение;
2) решить полученное уравнение;
3) сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).).
3. Уравнение второй и выше степени относительно логарифма.
Для решения таких уравнений надо:
- сделать замену переменной;
- решить полученное уравнение;
- сделать обратную замену;
- решить полученное уравнение;
- сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им корни (решения).
4.Уравнения, содержащие неизвестное в основании и в показателе степени.
Для решения таких уравнений надо:
- прологарифмировать уравнение;
- решить полученное уравнение;
- сделать проверку или найти область допустимых значений для неизвестного числа и отобрать соответствующие им
корни (решения).
5. Уравнения, которые не имеют решения.
- Для решения таких уравнений надо найти ОДЗ уравнения.
- Проанализировать левую и правую часть уравнения.
- Сделать соответствующие выводы.
Примеры:
Исходное уравнение равносильно системе:
Доказать, что уравнение не имеет решения.
ОДЗ уравнения определяется неравенством х ≥ 0. На ОДЗ имеем
Сумма положительного числа и неотрицательного числа не равна нулю, поэтому исходное уравнение решений не имеет.
Ответ : решений нет.
В ОДЗ попадает только один корень х = 0. Ответ: 0.
Произведем обратную замену.
Найденные корни принадлежат ОДЗ.
ОДЗ уравнения – множество всех положительных чисел.
Поскольку
Аналогично решаются данные уравнения:
Задачи для самостоятельного решения:
Используемая литература.
- Бесчетнов В.М. Математика. Москва Демиург 1994
- Бородуля И.Т. Показательная и логарифмическая функции. ( задачи и упражнения). Москва «Просвещение» 1984
- Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко П.И. Задачи по математике. Уравнения и неравенства. Москва «Наука» 1987
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер. Москва «Илекса»2007
- Саакян С.М., Гольдман А.М., Денисов Д.В.. Задачи по алгебре и началам анализа. Москва «Просвещение» 2003
Приложение 1
Приложение 2
Логарифмические неравенства. Как решать логарифмические неравенства?
Если проще: это неравенства, в которых неизвестные (иксы) или выражения с ними находятся внутри логарифмов. 2{(x+1)}+10≤11 \lg{(x+1)}\)
2{(x+1)}+10≤11 \lg{(x+1)}\)
Как решать логарифмические неравенства:
Любое логарифмическое неравенство нужно стремиться привести к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\) (символ \(˅\) означает любой из знаков сравнения). Такой вид позволяет избавиться от логарифмов и их оснований, сделав переход к неравенству выражений под логарифмами, то есть к виду \(f(x) ˅ g(x)\).
Но при выполнении этого перехода есть одна очень важная тонкость:
\(-\) если основание логарифма — число и оно больше 1 — знак неравенства при переходе остается прежним,
\(-\) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
|
\(\log_2{(8-x)}<1\) Решение: |
\(\log\)\(_{0,5}\)\((2x-4)\)≥\(\log\)\(_{0,5}\)\({(x+1)}\) Решение: |
Очень важно! В любом неравенстве переход от вида \(\log_a{f(x)} ˅ \log_a{g(x)}\) к сравнению выражений под логарифмами можно делать только если:
\(-\) вы написали ОДЗ для исходного неравенства. 2-24≥-x\) невозможен.
2-24≥-x\) невозможен.
Заметим, однако, что неравенства 3 и 4 можно легко решить, если воспользоваться свойствами логарифмов.
Пример. Решить неравенство: \(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\)
Решение:
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\) |
Выпишем ОДЗ. |
|
|
ОДЗ: \(\frac{3x-2}{2x-3}\)\(>0\) |
ОДЗ представляет собой дробно-рациональное неравенство. Решим его с помощью метода интервалов. Вынесем в числителе за скобки \(3\), а в знаменателе \(2\), чтобы убрать коэффициенты перед иксами. |
|
|
\(\frac{3(x-\frac{2}{3})}{2(x-\frac{3}{2})}\) \(>0\) |
Теперь очевидно, что корни у нас – числа \(\frac{2}{3}\) и \(\frac{3}{2}\) |
|
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤\log\) \(_{\frac{1}{3}}\)\(3\) |
Мы привели неравенство к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\). Теперь можно избавиться от логарифмов и оснований. Нужно только определиться, менять знак сравнения или нет. Основание \(\frac{1}{3}<1\), следовательно, знак меняем. |
|
|
\(\frac{3x-2}{2x-3}\)\(≥\) \(3\) |
Переносим \(3\) и приводим к общему знаменателю, пользуясь свойствами дробей. |
|
|
\(\frac{3x-2-3(2x-3)}{2x-3}\)\(≥\) \(0\) |
Раскрываем скобки, приводим подобные слагаемые. |
|
|
\(\frac{-3x+7}{2x-3}\)\(≥\) \(0\) |
Умножаем неравенство на \(-1\), не забыв при этом перевернуть знак сравнения. |
|
|
\(\frac{3x-7}{2x-3}\)\(≤\) \(0\) |
Далее выносим \(3\) из числителя и \(2\) из знаменателя. |
|
|
\(\frac{3(x-\frac{7}{3})}{2(x-\frac{3}{2})}\)\(≤\) \(0\) |
Построим числовую ось и отметим на ней точки \(\frac{7}{3}\) и \(\frac{3}{2}\). Обратите внимание, точка из знаменателя – выколота, несмотря на то, что неравенство нестрогое. Дело в том, что эта точка не будет решением, так как при подстановке в неравенство приведет нас к делению на ноль. |
|
|
|
Теперь на ту же числовую ось наносим ОДЗ и записываем в ответ тот промежуток, который попадает в ОДЗ. |
|
|
|
Записываем окончательный ответ. |
Раскладываем левую часть неравенства на множители. |
|
\(D=1+8=9\) |
Решаем неравенство методом интервалов. |
|
|
|
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности, имеющей такое же решение, и сделаем обратную замену. |
|
|
\(\left[ \begin{gathered} t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2 \\ \log_3x<-1 \end{gathered} \right.\) |
Преобразовываем \(2=\log_39\), \(-1=\log_3\frac{1}{3}\). |
|
|
\(\left[ \begin{gathered} \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Делаем переход к сравнению аргументов. Основания у логарифмов больше \(1\), поэтому знак неравенств не меняется. |
|
|
\(\left[ \begin{gathered} x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Соединим решение неравенства и ОДЗ на одном рисунке. |
|
|
|
Запишем ответ. |
Смотрите также:
Показательные неравенства
3.1.9. Показательные и логарифмические уравнения
Глава 3.
 Решение уравнений и неравенств
Решение уравнений и неравенств3.1.
3.1.9.
Показательные уравнения
Уравнения вида af (x) = b, a > 0, a ≠ 1, b > 0
По определению логарифма из основного логарифмического тождества получаем, что Если f (x) − алгебраическая функция, то и это уравнение будет алгебраическое, которое можно решить с помощью стандартных методов (так как − это конкретное число, такое же, как и 5, π, и т. п.).
Уравнения вида
Такие уравнения решаются в два этапа:
a) С помощью замены
это уравнение сводится к уравнению F (t) = 0, у которого ищутся все его положительные корни
(пусть таких корней ровно n штук).
b) Для каждого решается уравнение типа рассмотренного выше:
Эти два типа показательных уравнений являются основными, к ним сводятся все остальные методы.
Пример 1Решите уравнение
Уравнения вида af (x) = ag (x), a > 0, a ≠ 1
В силу свойств монотонности показательной функции это уравнение равносильно уравнению f (x) = g (x).
Пример 2Решите уравнение
Пример 3
Решите уравнение
|
Сразу заметим, что уравнение имеет вид что равносильно уравнению Ответ. |
Уравнения вида af (x) = bg (x), a > 0, a ≠ 1, b > 0, b ≠ 1
|
Модель 3.3. Решение показательных уравнений |
При решении таких уравнений применяется стандартный приём. Прологарифмируем обе его части по любому основанию. В нашем случае удобно логарифмировать по основанию a (или b), то есть по основанию показательной функции, входящей в уравнение:
А это уравнение уже можно решать стандартными алгебраическими способами, если f (x) и g (x) – алгебраические выражения.
Замечание. Рассмотренный приём перехода от уравнения af (x) = bg (x) к уравнению f (x) = g (x) loga b или, в общем случае, переход от уравнения
| loga F (x) = logb G (x) (a > 0, a ≠ 0) | (2) |

Заметим, что переход (1) → (2) в общем случае нарушает равносильность, так как логарифм существует только у неотрицательного числа.
Например, логарифмирование обеих частей уравнения x = x3, которое имеет вид (1), приводит нас к неравносильному уравнению lg x = lg x3 (область определения сузилась). Действительно,
Таким образом, произошла потеря корней исходного уравнения. Как видно, логарифмирование не является «безобидной» операцией, но в процессе решения уравнения типа af (x) = bg (x) эти неприятности не возникают, так как обе его части положительны.
Логарифмические уравнения
Уравнения вида loga f (x) = b, a > 0, a ≠ 1
Здесь предполагается, что f (x) − функция, уравнения с которой мы уже умеем решать. По определению логарифма из основного логарифмического тождества получаем, что f (x) = ab. Это уравнение можно решать любыми доступными методами, поскольку ab – это число.
По определению логарифма из основного логарифмического тождества получаем, что f (x) = ab. Это уравнение можно решать любыми доступными методами, поскольку ab – это число.
Уравнения вида
Совершенно аналогично показательным уравнениям, уравнения такого типа решаются в два этапа.
-
С помощью замены это уравнение сводится к уравнению F (x) = 0, у которого ищутся все его корни (пусть таких корней ровно n штук).
-
Для каждого решается уравнение типа рассмотренного выше:
Понятно, что совершенно не обязательно уравнение будет иметь рассмотренный вид. А значит, в процессе преобразований логарифмических уравнений следует стремиться к тому, чтобы привести все входящие в уравнение логарифмы к одному основанию. При этом необходимо помнить об области определения рассматриваемых выражений, стараясь, чтобы при преобразовании она не уменьшалась, − те корни, которые, возможно, будут приобретены, можно будет отсеять проверкой.
Решите уравнение
|
Преобразуем левую часть уравнения, приводя все логарифмы к основанию 7.
а) Корень последнего уравнения с учётом ограничения x > 1 есть x = 3. б) Поскольку мы использовали, вообще говоря, неравносильное преобразование суммы логарифмов в логарифм произведения (это расширяет область определения), то необходима проверка, которая показывает, что все три найденных числа являются корнями исходного уравнения. Заметим, что число x = 1 рассматривать не нужно, поскольку оно не входит в ОДЗ уравнения. Ответ. |
Пример 6
Решите уравнение
Уравнения вида loga f (x) = loga g (x), a > 0, a ≠ 1
|
Модель 3.1. Решение логарифмических уравнений |
ОДЗ данного уравнения:
В силу монотонности логарифмической функции, каждое своё значение она принимает ровно один раз. Следовательно, в ОДЗ имеем:
Полная система равносильности выглядит так:
Из двух последних систем выбирается та, которая проще (это зависит от конкретного вида функций f (x) и g (x)). На практике, как правило, проще решить уравнение f (x) = g (x) и проверить для его корней положительность одной из функций: f (x) > 0 или g (x) > 0, так как из равенства одной из этих функций следует положительность и другой.
На практике, как правило, проще решить уравнение f (x) = g (x) и проверить для его корней положительность одной из функций: f (x) > 0 или g (x) > 0, так как из равенства одной из этих функций следует положительность и другой.
Рассмотренный переход от уравнения loga f (x) = loga g (x) к уравнению f (x) = g (x) называется потенцированием.
Заметим, что потенцирование не является равносильным преобразованием. Область определения уравнения при потенцировании расширяется, так как второе уравнение определено при всех x, для которых определены функции f (x) и g (x), а первое − только при тех x, для которых f (x) > 0 и g (x) > 0.
Пример 7Решите уравнение
|
Преобразуем сумму логарифмов в логарифм произведения:
или
Потенцируя по основанию 10, имеем
откуда x = –8, x = –10. Ответ. x = –10. |
Пример 8
Решите уравнение
|
Очевидна замена 6 sin x + 4 = t > 0 (это требование взято из ОДЗ, ведь от t берётся логарифм). Перейдём к равносильному уравнению:
Ответ. |
Как найти Область Допустимых Значений (ОДЗ)
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 0, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
a = 1, b = 2, c = 1.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Запоминаем!
ОДЗ относится к выражениям. Область определения функции относится к функциям и не относится к выражениям.
Пример 2
Рассмотрим выражение
ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).
Читать запись нужно вот так:
Область допустимых значений переменной x для выражения — это числовое множество ( — ∞; 3) ∪ (3; +∞).
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
- требуется извлечение квадратного корня из отрицательного числа;
- присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a3 + 4 * a * b − 6.
Как решаем:
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a3 + 4 * a * b − 6 при любых значениях переменной.
Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении — пустое множество.
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Лайфхак
Чтобы не потратить зря время на решение нерешаемого примера, всегда обращайтесь к списку условий, при которых выражение не может быть решено.
Запомните
- Если число входит в ОДЗ, то около числа ставим квадратные скобки.
- Если число не входит в ОДЗ, то около него ставятся круглые скобки.
Например, если х > 6, но х < 8, то записываем интервал [6; 8).
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
В этом может помочь определение ОДЗ.
Тождественное преобразование может:
- расширить ОДЗ
- никак не повлиять на ОДЗ
- сузить ОДЗ
Рассмотрим каждый случай в отдельности.
Пример 7
Рассмотрим выражение a + 4/a — 4/a
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 8
Рассмотрим выражение a2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 9
Рассмотрим выражение
ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Свойства логарифмирования. Что такое логарифм
Область допустимых значений (ОДЗ) логарифма
Теперь поговорим об ограничениях (ОДЗ — область допустимых значений переменных).
Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:
То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться.
Почему так?
Начнем с простого: допустим, что. Тогда, например, число не существует, так как в какую бы степень мы не возводили, всегда получается. Более того, не существует ни для какого. Но при этом может равняться чему угодно (по той же причине — в любой степени равно). Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.
Похожая проблема у нас и в случае: в любой положительной степени — это, а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что).
При мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: . Например, (то есть), а вот не существует.
Поэтому и отрицательные основания проще выбросить, чем возиться с ними.
Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).
В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:
Решим уравнение.
Вспомним определение: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. И по условию, эта степень равна: .
Получаем обычное квадратное уравнение: . Решим его с помощью теоремы Виета: сумма корней равна, а произведение. Легко подобрать, это числа и.
Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?
Это явно неверно, так как основание не может быть отрицательным, то есть корень — «сторонний».
Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:
Тогда, получив корни и, сразу отбросим корень, и напишем правильный ответ.
Пример 1 (попробуй решить самостоятельно):
Найдите корень уравнения. Если корней несколько, в ответе укажите меньший из них.
Решение:
В первую очередь напишем ОДЗ:
Теперь вспоминаем, что такое логарифм: в какую степень нужно возвести основание, чтобы получить аргумент? Во вторую. То есть:
Казалось бы, меньший корень равен. Но это не так: согласно ОДЗ корень — сторонний, то есть это вообще не корень данного уравнения. Таким образом, уравнение имеет только один корень: .
Ответ: .
Основное логарифмическое тождество
Вспомним определение логарифма в общем виде:
Подставим во второе равенство вместо логарифм:
Это равенство называется основным логарифмическим тождеством . Хотя по сути это равенство — просто по-другому записанное определение логарифма :
Это степень, в которую нужно возвести, чтобы получить.
Например:
Реши еще следующие примеры:
Пример 2.
Найдите значение выражения.
Решение:
Вспомним правило из раздела : , то есть, при возведении степени в степень показатели перемножаются. Применим его:
Пример 3.
Докажите, что.
Решение:
Свойства логарифмов
К сожалению, задачи не всегда такие простые — зачастую сперва нужно упростить выражение, привести его к привычному виду, и только потом будет возможно посчитать значение. Это проще всего сделать, зная свойства логарифмов . Так что давай выучим основные свойства логарифмов. Каждое из них я буду доказывать, ведь любое правило проще запомнить, если знать, откуда оно берется.
Все эти свойства нужно обязательно запомнить, без них большинство задач с логарифмами решить не получится.
А теперь обо всех свойствах логарифмов подробнее.
Свойство 1:
Доказательство:
Пусть, тогда.
Имеем: , ч. т.д.
т.д.
Свойство 2: Сумма логарифмов
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения: .
Доказательство:
Пусть, тогда. Пусть, тогда.
Пример: Найдите значение выражения: .
Решение: .
Только что выученная формула помогает упростить сумму логарифмов, а не разность, так что сразу эти логарифмы не объединить. Но можно сделать наоборот — «разбить» первый логарифм на два:А вот обещанное упрощение:
.
Зачем это нужно? Ну например: чему равно?
Теперь очевидно, что.
Теперь упрости сам:
Задачи:
Ответы:
Свойство 3: Разность логарифмов:
Доказательство:
Все точно так же, как и в пункте 2:
Пусть, тогда.
Пусть, тогда. Имеем:
Пример из прошлого пункта теперь становится еще проще:
Пример посложнее: . Догадаешься сам, как решить?
Здесь нужно заметить, что у нас нету ни одной формулы про логарифмы в квадрате. Это что-то сродни выражению — такое сразу не упростить.
Это что-то сродни выражению — такое сразу не упростить.
Поэтому отвлечемся от формул про логарифмы, и подумаем, какие вообще формулы мы используем в математике чаще всего? Еще начиная с 7 класса!
Это — . Нужно привыкнуть к тому, что они везде! И в показательных, и в тригонометрических, и в иррациональных задачах они встречаются. Поэтому их нужно обязательно помнить.
Если присмотреться к первым двум слагаемым, становится ясно, что это разность квадратов :
Ответ для проверки:
Упрости сам.
Примеры
Ответы.
Свойство 4: Вынесение показателя степени из аргумента логарифма:
Доказательство: И здесь тоже используем определение логарифма:пусть, тогда. Имеем: , ч.т.д.
Можно понять это правило так:
То есть степень аргумента выносится вперед логарифма, как коэффициент.
Пример: Найдите значение выражения.
Решение: .
Реши сам:
Примеры:
Ответы:
Свойство 5: Вынесение показателя степени из основания логарифма:
Доказательство: Пусть, тогда.
Имеем: , ч.т.д.
Запоминаем: из основания степень выносится как обратное число, в отличии от предыдущего случая!
Свойство 6: Вынесение показателя степени из основания и аргумента логарифма:
Или если степени одинаковые: .
Свойство 7: Переход к новому основанию:
Доказательство: Пусть, тогда.
Имеем: , ч.т.д.
Свойство 8: Замена местами основания и аргумента логарифма:
Доказательство: Это частный случай формулы 7: если подставить, получим: , ч.т.д.
Рассмотрим еще несколько примеров.
Пример 4.
Найдите значение выражения.
Используем свойство логарифмов № 2 — сумма логарифмов с одинаковым основанием равна логарифму произведения:
Пример 5.
Найдите значение выражения.
Решение:
Используем свойство логарифмов № 3 и № 4:
Пример 6.
Найдите значение выражения.
Решение:
Используем свойство № 7 — перейдем к основанию 2:
Пример 7.
Найдите значение выражения.
Решение:
Как тебе статья?
Если ты читаешь эти строки, значит ты прочитал всю статью.
И это круто!
А теперь расскажи нам как тебе статья?
Научился ты решать логарифмы? Если нет, то в чем проблема?
Пиши нам в комментах ниже.
И, да, удачи на экзаменах.
На ЕГЭ и ОГЭ и вообще в жизни
(от греческого λόγος — «слово», «отношение» и ἀριθμός — «число») числа b по основанию a (log α b ) называется такое число c , и b = a c , то есть записи log α b =c и b=a c эквивалентны. Логарифм имеет смысл, если a > 0, а ≠ 1, b > 0.
Говоря другими словами логарифм числа b по основанию а формулируется как показатель степени , в которую надо возвести число a , чтобы получить число b (логарифм существует только у положительных чисел).
Из данной формулировки вытекает, что вычисление x= log α b , равнозначно решению уравнения a x =b.
Например:
log 2 8 = 3 потому, что 8=2 3 .
Выделим, что указанная формулировка логарифма дает возможность сразу определить значение логарифма , когда число под знаком логарифма выступает некоторой степенью основания. И в правду, формулировка логарифма дает возможность обосновать, что если b=a с , то логарифм числа b по основанию a равен с . Также ясно, что тема логарифмирования тесно взаимосвязана с темой степени числа .
Вычисление логарифма именуют логарифмированием . Логарифмирование — это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей трансформируется в суммы членов.
Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов трансформируются в произведение сомножителей.
Достаточно часто используются вещественные логарифмы с основаниями 2 (двоичный), е число Эйлера e ≈ 2,718 (натуральный логарифм) и 10 (десятичный).
На данном этапе целесообразно рассмотреть образцы логарифмов log 7 2, ln√ 5, lg0.0001.
А записи lg(-3), log -3 3.2, log -1 -4.3 не имеют смысла, так как в первой из них под знаком логарифма помещено отрицательное число , во второй — отрицательное число в основании, а в третьей — и отрицательное число под знаком логарифма и единица в основании.
Условия определения логарифма.
Стоит отдельно рассмотреть условия a > 0, a ≠ 1, b > 0.при которых дается определение логарифма . Рассмотрим, почему взяты эти ограничения. В это нам поможет равенство вида x = log α b , называемое основным логарифмическим тождеством , которое напрямую следует из данного выше определения логарифма.
Возьмем условие a≠1 . Поскольку единица в любой степени равна единице, то равенство x=log α b может существовать лишь при b=1 , но при этом log 1 1 будет любым действительным числом . Для исключения этой неоднозначности и берется a≠1 .
Докажем необходимость условия a>0 . При a=0 по формулировке логарифма может существовать только при b=0 . И соответственно тогда log 0 0 может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Исключить эту неоднозначность дает условие a≠0 . А при a нам бы пришлось отвергнуть разбор рациональных и иррациональных значений логарифма, поскольку степень с рациональным и иррациональным показателем определена лишь для неотрицательных оснований. Именно по этой причине и оговорено условие a>0 .
И последнее условие b>0 вытекает из неравенства a>0 , поскольку x=log α b , а значение степени с положительным основанием a всегда положительно.
Особенности логарифмов.
Логарифмы характеризуются отличительными особенностями , которые обусловили их повсеместное употребление для значительного облегчения кропотливых расчетов.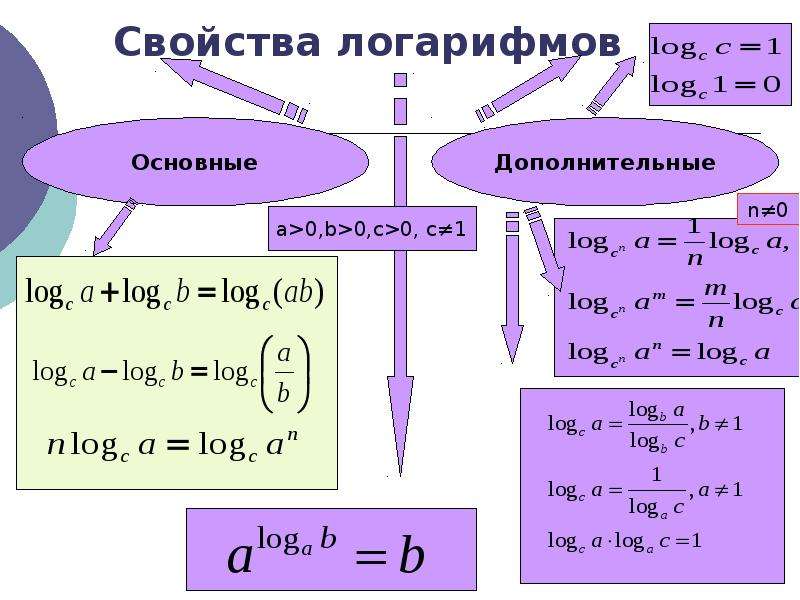 При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.
При переходе «в мир логарифмов» умножение трансформируется на значительно более легкое сложение, деление — на вычитание, а возведение в степень и извлечение корня трансформируются соответствующе в умножение и деление на показатель степени.
Формулировку логарифмов и таблицу их значений (для тригонометрических функций) впервые издал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, увеличенные и детализированные прочими учеными, широко использовались при выполнении научных и инженерных вычислений, и оставались актуальными пока не стали применяться электронные калькуляторы и компьютеры.
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .
Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6, поскольку 2 6 = 64.
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2 больше степень двойки, тем больше получится число.
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5, log 3 8, log 5 100.
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля.
 Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
Это следует из определения степени рациональным показателем, к которому сводится определение логарифма. - Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1, т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
- Решить относительно переменной b уравнение: x = a b ;
- Полученное число b будет ответом.
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача. Вычислите логарифм: log 5 25
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Составим и решим уравнение:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2; - Получили ответ: 2.

Задача. Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3; - Получили ответ: 3.
Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.
Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.
8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.
е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459. ..
..
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x
Таким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.
Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0)       
Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.
Основное логарифмическое тождество a log a b = b (a > 0, a ≠ 1) (2)Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.
log a 1 = 0 (a > 0, a ≠ 1) (4)
Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.
Логарифм произведения и логарифм частного log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)Log
a
b
c
=
log
a
b −
log
a
c
(a > 0, a ≠ 1, b > 0, c > 0)
(6)
Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.
Действительно, выражение log a (f (x) g (x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.
Преобразуя данное выражение в сумму log a f (x) + log a g (x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).
Степень можно выносить за знак логарифма log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:
Log a (f (x) 2 = 2 log a f (x)
Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.
Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.
Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):
Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)
Несколько простых примеров с логарифмамиПример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.
Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log 5 125 = 3. Мы использовали формулу перехода к новому основанию (8).
| a log a b = b (a > 0, a ≠ 1) |
| log a a = 1 (a > 0, a ≠ 1) |
| log a 1 = 0 (a > 0, a ≠ 1) |
| log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) |
| log a b p = p log a b (a > 0, a ≠ 1, b > 0) |
| log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) |
| log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) |
В центре внимания этой статьи – логарифм . Здесь мы дадим определение логарифма, покажем принятое обозначение, приведем примеры логарифмов, и скажем про натуральные и десятичные логарифмы. После этого рассмотрим основное логарифмическое тождество.
Здесь мы дадим определение логарифма, покажем принятое обозначение, приведем примеры логарифмов, и скажем про натуральные и десятичные логарифмы. После этого рассмотрим основное логарифмическое тождество.
Навигация по странице.
Определение логарифма
Понятие логарифма возникает при решении задачи в известном смысле обратной , когда нужно найти показатель степени по известному значению степени и известному основанию.
Но хватит предисловий, пришло время ответить на вопрос «что такое логарифм»? Дадим соответствующее определение.
Определение.
Логарифм числа b по основанию a , где a>0 , a≠1 и b>0 – это показатель степени, в который нужно возвести число a , чтобы в результате получить b .
На этом этапе заметим, что произнесенное слово «логарифм» должно сразу вызывать два вытекающих вопроса: «какого числа» и «по какому основанию». Иными словами, просто логарифма как бы нет, а есть только логарифм числа по некоторому основанию.
Сразу введем обозначение логарифма : логарифм числа b по основанию a принято обозначать как log a b . Логарифм числа b по основанию e и логарифм по основанию 10 имеют свои специальные обозначения lnb и lgb соответственно, то есть, пишут не log e b , а lnb , и не log 10 b , а lgb .
Теперь можно привести : .
А записи не имеют смысла, так как в первой из них под знаком логарифма находится отрицательное число, во второй – отрицательное число в основании, а в третьей – и отрицательное число под знаком логарифма и единица в основании.
Теперь скажем о правилах чтения логарифмов . Запись log a b
читается как «логарифм b
по основанию a
». Например, log 2 3
— это логарифм трех по основанию 2
, а — это логарифм двух целых двух третьих по основанию квадратный корень из пяти. Логарифм по основанию e
называют натуральным логарифмом , а запись lnb
читается как «натуральный логарифм b
». К примеру, ln7
– это натуральный логарифм семи, а мы прочитаем как натуральный логарифм пи. Логарифм по основанию 10
также имеет специальное название – десятичный логарифм , а запись lgb
читается как «десятичный логарифм b
». Например, lg1
— это десятичный логарифм единицы, а lg2,75
— десятичный логарифм двух целых семидесяти пяти сотых.
Логарифм по основанию 10
также имеет специальное название – десятичный логарифм , а запись lgb
читается как «десятичный логарифм b
». Например, lg1
— это десятичный логарифм единицы, а lg2,75
— десятичный логарифм двух целых семидесяти пяти сотых.
Стоит отдельно остановиться на условиях a>0 , a≠1 и b>0 , при которых дается определение логарифма. Поясним, откуда берутся эти ограничения. Сделать это нам поможет равенство вида , называемое , которое напрямую следует из данного выше определения логарифма.
Начнем с a≠1 . Так как единица в любой степени равна единице, то равенство может быть справедливо лишь при b=1 , но при этом log 1 1 может быть любым действительным числом. Чтобы избежать этой многозначности и принимается a≠1 .
Обоснуем целесообразность условия a>0
. При a=0
по определению логарифма мы бы имели равенство , которое возможно лишь при b=0
. Но тогда log 0 0
может быть любым отличным от нуля действительным числом, так как нуль в любой отличной от нуля степени есть нуль. Избежать этой многозначности позволяет условие a≠0
. А при a0
.
Избежать этой многозначности позволяет условие a≠0
. А при a0
.
Наконец, условие b>0 следует из неравенства a>0 , так как , а значение степени с положительным основанием a всегда положительно.
В заключение этого пункта скажем, что озвученное определение логарифма позволяет сразу указать значение логарифма, когда число под знаком логарифма есть некоторая степень основания. Действительно, определение логарифма позволяет утверждать, что если b=a p , то логарифм числа b по основанию a равен p . То есть, справедливо равенство log a a p =p . Например, мы знаем, что 2 3 =8 , тогда log 2 8=3 . Подробнее об этом мы поговорим в статье
Логарифмы. Основание логарифма. Натуральный логарифм. Логарифм 10.
Логарифм числа — это показатель степени, то есть, в какую степень надо возвести число, которое стоит в основании, чтобы получить число в выражении логарифма. Например, \(log_28 \) в какую степень надо возвести \(2\), чтобы получить \(8\) это \(log_28 =3\). 3.\)
3.\)
Область допустимых значений логарифма
- Аргумент и основание не могут быть равны нулю и отрицательными числами.
- Основание не может быть равно единице, поскольку единица в любой степени все равно остается единицей.
- Число b может быть любым.
- ОДЗ логарифма \(log_a x = b ⇒ x > 0, a > 0, a ≠ 1\).
Десятичные логарифмы
Десятичные логарифмы – логарифмы, в основании которых стоит \(10\). Пример \(log_{10}10 =1\),
Log10100 =2. Записывают их в виде \(lg 10 = 1\), \(lg 100 = 2.\)
Натуральный логарифм
Натуральный логарифм – логарифм, в основании которого стоит \(e\). Что означает \(e\)? Это иррациональное число, бесконечное непериодическое десятичное число, математическая константа, которую надо запомнить:
\(e = 2,718281828459…\)
\(ln x = log_e x\)
Краткая история логарифма
Логарифмом имеет много применений в науке и инженерии. Естественный логарифм имеет константу \(e\) в своем основании, его использование широко распространено в дискретной математике, особенно в исчислении. Двоичный логарифм использует базу \(b = 2\) и занимает видное место в информатике. Логарифмы были введены Джоном Нейпиром в начале \(XVII\) века, как средство упрощения расчетов. Они были легко приняты учеными, инженерами и другими, чтобы облегчать вычисления . Современное понятие логарифмов исходит от Леонарда Эйлера, который связал их с экспоненциальной функцией в \(XVII\) веке.
Естественный логарифм имеет константу \(e\) в своем основании, его использование широко распространено в дискретной математике, особенно в исчислении. Двоичный логарифм использует базу \(b = 2\) и занимает видное место в информатике. Логарифмы были введены Джоном Нейпиром в начале \(XVII\) века, как средство упрощения расчетов. Они были легко приняты учеными, инженерами и другими, чтобы облегчать вычисления . Современное понятие логарифмов исходит от Леонарда Эйлера, который связал их с экспоненциальной функцией в \(XVII\) веке.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
БГПУ им. Максима Танка
Максима Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-7 классов. Математика — это чудесный мир логики и точности. Дорога в этот мир лежит через старания, внимательность и весёлые задания. Необычные решения и интерес помогут разобраться и полюбить эту науку!
Математика — это чудесный мир логики и точности. Дорога в этот мир лежит через старания, внимательность и весёлые задания. Необычные решения и интерес помогут разобраться и полюбить эту науку!
Репетитор по математике
Житомирский государственный университет им. Ивана Франко
Ивана Франко
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Математика была моим самым любимым предметом в школе . Педагог-математик в третьем поколении. Имею большой опыт работы репетитором и преподавателем в школе. К каждому ребёнку нахожу индивидуальный подход. Помогу подтянуть уровень владения математикой и привить любовь к этому предмету!
Математика была моим самым любимым предметом в школе . Педагог-математик в третьем поколении. Имею большой опыт работы репетитором и преподавателем в школе. К каждому ребёнку нахожу индивидуальный подход. Помогу подтянуть уровень владения математикой и привить любовь к этому предмету!
Репетитор по математике
Уральский государственный университет им. А.М.Горького
А.М.Горького
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов по истории и обществознанию. Помогу систематизировать и закрепить знания по предметам, подготовить в ОГЭ и ЕГЭ. В работе использую методики интерактивного обучения. Создаю атмосферу доверительного общения и сотрудничества.
Помогу систематизировать и закрепить знания по предметам, подготовить в ОГЭ и ЕГЭ. В работе использую методики интерактивного обучения. Создаю атмосферу доверительного общения и сотрудничества.
Математика 11 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
примеров решения логарифмических неравенств онлайн. Логарифмические неравенства
Неравенство называется логарифмическим, если оно содержит логарифмическую функцию.
Методы решения логарифмических неравенств ничем не отличаются, кроме двух вещей.
Во-первых, при переходе от логарифмического неравенства к неравенству сублогарифмических функций следует, что следит за знаком полученного неравенства . .. Он подчиняется следующему правилу.
.. Он подчиняется следующему правилу.
Если основание логарифмической функции больше $ 1 $, то при переходе от логарифмического неравенства к неравенству сублогарифмических функций знак неравенства сохраняется, а если он меньше $ 1 $ , затем все меняется на противоположное.
Во-вторых, решением любого неравенства является интервал, и поэтому по окончании решения неравенства сублогарифмических функций необходимо составить систему из двух неравенств: первое неравенство этой системы будет — неравенство сублогарифмических функций, а второй — интервал области определения логарифмических функций, входящих в логарифмическое неравенство.(3), $
$ x \ in \)
Очень важно! В любом неравенстве переход от вида \ (\ log_a (f (x)) ˅ \ log_a (g (x)) \) к сравнению выражений по логарифмам возможен только если:
Пример … Решите неравенство: \ (\ log \) \ (≤-1 \)
Решение:
\ (\ log \) \ (_ (\ frac (1) (3)) (\ frac (3x-2) (2x-3)) \) \ (≤-1 \) | Выпишем ОДЗ. |
ODZ: \ (\ frac (3x-2) (2x-3) \) \ (> 0 \) | |
\ ( \ гидроразрыва (3x-2-3 (2x-3)) (2x-3) \) \ (≥ \) \ (0 \) | Раскрываем скобки, даем. |
\ ( \ гидроразрыва (-3x + 7) (2x-3) \) \ (≥ \) \ (0 \) | Умножаем неравенство на \ (- 1 \), не забывая поменять местами знак сравнения. |
\ ( \ гидроразрыва (3x-7) (2x-3) \) \ (≤ \) \ (0 \) | |
\ ( \ frac (3 (x- \ frac (7) (3))) (2 (x- \ frac (3) (2))) \) \ (≤ \) \ (0 \) | Построим числовую ось и отметим на ней точки \ (\ frac (7) (3) \) и \ (\ frac (3) (2) \. Обратите внимание, что точка в знаменателе выколота, несмотря на то, что что неравенство не является строгим, дело в том, что эта точка не будет решением, так как при подстановке в неравенство она приведет нас к делению на ноль. |
| Теперь на той же числовой оси откладываем ODZ и записываем в ответ интервал, который попадает в ODZ. |
| Записываем окончательный ответ. |
Пример .2-т-2> 0 \)
\ (D = 1 + 8 = 9 \)
\ (t_1 = \ frac (1 + 3) (2) = 2 \)
\ (t_2 = \ frac (1-3) (2) = — 1 \ )
\ ((t + 1) (t-2)> 0 \)
Теперь вам нужно вернуться к исходной переменной — x. Для этого перейдите к тому, у которого есть такое же решение, и произведите обратную замену.
\ (\ left [\ begin (собрано) t> 2 \ t2 \\ \ log_3x
Преобразовать \ (2 = \ log_39 \), \ (- 1 = \ log_3 \ frac (1) (3) \).
\ (\ left [\ begin (собран) \ log_3x> \ log_39 \\ \ log_3x
Переходим к сравнению аргументов. Основания логарифмов больше \ (1 \), поэтому знак неравенств не меняется.
\ (\ left [\ begin (собрано) x> 9 \ x
Объединим решение неравенства и ИДЗ в одну цифру.
Запишем ответ.
Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и дайте нам знать, если у вас возникнут вопросы.
Сбор и использование личной информации
Личная информация — это данные, которые могут быть использованы для идентификации конкретного человека или для связи с ним.
Вас могут попросить предоставить вашу личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы оставляете запрос на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. Д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и сообщать об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
- Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать личную информацию для внутренних целей, например, для проведения аудитов, анализа данных и различных исследований с целью улучшения предоставляемых нами услуг и предоставления вам рекомендаций относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном рекламном мероприятии, мы можем использовать предоставленную вами информацию для управления этими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законом, постановлением суда, в ходе судебного разбирательства и / или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть вашу персональная информация. Мы также можем раскрыть информацию о вас, если мы определим, что такое раскрытие необходимо или целесообразно по соображениям безопасности, правоохранительной деятельности или по другим социально важным причинам.

- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему третьему лицу — правопреемнику.
Защита личной информации
Мы принимаем меры предосторожности — включая административные, технические и физические — для защиты вашей личной информации от потери, кражи и злоупотребления, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Уважение вашей конфиденциальности на уровне компании
Чтобы убедиться, что ваша личная информация в безопасности, мы доводим до наших сотрудников правила конфиденциальности и безопасности и строго следим за соблюдением мер конфиденциальности.
Введение
Логарифмы были изобретены, чтобы ускорить и упростить вычисления. Идея логарифма, то есть идея выражения чисел как степени одного и того же основания, принадлежит Михаилу Штифелю. Но во времена Штифеля математика не была так развита, и идея логарифма не нашла своего развития. Позже логарифмы были изобретены одновременно и независимо друг от друга шотландским ученым Джоном Напье (1550–1617) и швейцарцем Йобстом Берги (1552–1632).Напье первым опубликовал свою работу в 1614 г. под названием «Описание удивительной таблицы логарифмов» теория логарифмов Напьера была дана в достаточно полном томе, метод вычисления логарифмов был дан наиболее простым, поэтому вклад Нэпьера в изобретение логарифмов было больше, чем изобретение Бурги. Бурги работал над таблицами одновременно с Напьером, но долгое время держал их в секрете и опубликовал только в 1620 году. Напье освоил идею логарифма около 1594 года.хотя таблицы были опубликованы через 20 лет. Сначала он называл свои логарифмы «искусственными числами» и только потом предложил называть эти «искусственные числа» одним словом «логарифм», что в переводе с греческого означает «прогресс родственных чисел». Первые таблицы на русском языке были изданы в 1703 г. при участии замечательного учителя 18 века. Л. Ф. Магнитский. В развитии теории логарифмов большое значение имели работы петербургского академика Леонарда Эйлера.
Позже логарифмы были изобретены одновременно и независимо друг от друга шотландским ученым Джоном Напье (1550–1617) и швейцарцем Йобстом Берги (1552–1632).Напье первым опубликовал свою работу в 1614 г. под названием «Описание удивительной таблицы логарифмов» теория логарифмов Напьера была дана в достаточно полном томе, метод вычисления логарифмов был дан наиболее простым, поэтому вклад Нэпьера в изобретение логарифмов было больше, чем изобретение Бурги. Бурги работал над таблицами одновременно с Напьером, но долгое время держал их в секрете и опубликовал только в 1620 году. Напье освоил идею логарифма около 1594 года.хотя таблицы были опубликованы через 20 лет. Сначала он называл свои логарифмы «искусственными числами» и только потом предложил называть эти «искусственные числа» одним словом «логарифм», что в переводе с греческого означает «прогресс родственных чисел». Первые таблицы на русском языке были изданы в 1703 г. при участии замечательного учителя 18 века. Л. Ф. Магнитский. В развитии теории логарифмов большое значение имели работы петербургского академика Леонарда Эйлера. Он был первым, кто рассмотрел логарифм как инверсию возведения в степень, он ввел термины «основание логарифма» и «мантисса». Бриггс составил таблицы логарифмов с основанием 10. Десятичные таблицы более удобны для практического использования, их теория. проще, чем логарифмы Напьера … Поэтому десятичные логарифмы иногда называют логарифмами Бригса. Термин «характеристика» был введен Бриггсом.
Он был первым, кто рассмотрел логарифм как инверсию возведения в степень, он ввел термины «основание логарифма» и «мантисса». Бриггс составил таблицы логарифмов с основанием 10. Десятичные таблицы более удобны для практического использования, их теория. проще, чем логарифмы Напьера … Поэтому десятичные логарифмы иногда называют логарифмами Бригса. Термин «характеристика» был введен Бриггсом.
В те далекие времена, когда мудрецы впервые начали задумываться о равенствах, содержащих неизвестные количества, вероятно, еще не было ни монет, ни кошельков.Но с другой стороны, были и груды, и горшки, корзины, которые как нельзя лучше подходили на роль тайников-хранилищ, содержащих неизвестное количество предметов. В древних математических задачах Месопотамии, Индии, Китая, Греции неизвестные величины выражали количество павлинов в саду, количество быков в стаде, совокупность вещей, принимаемых во внимание при разделе собственности. Писцы, чиновники, хорошо обученные науке счета, и священники, посвященные в тайные знания, весьма успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели некоторыми общими методами решения задач с неизвестными величинами. Однако ни один папирус или единственная глиняная табличка не содержат описания этих приемов. Авторы лишь изредка снабжали свои числовые расчеты скудными комментариями типа: «Смотри!», «Сделай это!», «Вы правильно сочли». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III век) — сборник задач для составления уравнений с систематическим изложением их решений.
Однако первым широко известным руководством по решению проблем была работа багдадского ученого IX века. Мухаммад бин Муса аль-Хорезми. Слово «аль-джабр» от арабского названия этого трактата — «Китаб аль-джербер валь-мукабала» («Книга восстановления и противостояния») — со временем превратилось в всем известное слово «алгебра», а аль- Сама работа Хорезми послужила отправной точкой в становлении науки о решении уравнений.
Логарифмические уравнения и неравенства
1. Логарифмические уравнения
Логарифмические уравнения
Уравнение, содержащее неизвестное под знаком логарифма или в основании, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение вида
журнал a x = b . (1)
Положение 1. Если а > 0, a ≠ 1, уравнение (1) для любого действительного b Имеет только решение x = а б .
Пример 1.Решите уравнения:
а) журнал 2 x = 3, б) журнал 3 x = -1, в)
Решение. Используя утверждение 1, получаем а) x = 2 3 или x = 8; б) x = 3-1 или x = 1/3; в)
или x = 1.Вот основные свойства логарифма.
П1. Базовая логарифмическая идентичность:
где а > 0, a ≠ 1 и b > 0,
P2. Логарифм произведения положительных множителей равен сумме логарифмов этих множителей:
журнал a N 1 · N 2 = лог a N 1 + журнал a N 2
( a > 0, a ≠ 1, N 1
> 0, N 2
> 0).
Комментарий. Если N 1 · N 2> 0, то свойство P2 принимает вид
журнал a N 1 · N 2 = лог a | N 1 | + журнал a | N 2 | ( a > 0, a ≠ 1, N 1 · N 2 > 0).
П3. Логарифм частного двух положительных чисел равен разнице между логарифмами делимого и делителя
. ( a > 0, a ≠ 1, N 1 > 0, N 2 > 0).Комментарий. Если
, (что эквивалентно N 1 N 2> 0), то свойство P3 принимает вид ( a > 0, a ≠ 1, N 1 N 2 > 0).P4. Логарифм степени положительного числа равен степени произведения на логарифм этого числа:
журнал a N к = k журнал a N ( a > 0, a ≠ 1, N > 0).
Комментарий. Если k — четное число ( k = 2 с ), то
журнал a N 2 с = 2 с журнал a | N | ( a > 0, a ≠ 1, N ≠ 0).
П5. Формула перехода на другую базу:
( a > 0, a ≠ 1, б > 0, б ≠ 1, N > 0),в частности, если N = b , получаем
( a > 0, a ≠ 1, б > 0, б ≠ 1).(2)Используя свойства P4 и P5, легко получить следующие свойства
( a > 0, a ≠ 1, б > 0, с ≠ 0), (3) ( a > 0, a ≠ 1, б > 0, с ≠ 0), (4) ( a > 0, a ≠ 1, б > 0, с ≠ 0), (5)а если в (5) c — четное число ( c = 2 n ), встречается
( b > 0, a ≠ 0, | a | ≠ 1).(6)Перечислим также основные свойства логарифмической функции f ( x ) = бревно a x :
1. Область определения логарифмической функции — это набор положительных чисел.
2. Диапазон значений логарифмической функции — это набор действительных чисел.
3. Когда a > 1, логарифмическая функция строго возрастает (0x 1 x 2 бревна a x 1 а x 2), а при 0a Икс 1 x 2 бревна a x 1> бревно a x 2).
4. log a 1 = 0 и log a a = 1 ( a > 0, a ≠ 1).
5. Если a > 1, то логарифмическая функция отрицательна для x (0; 1) и положительна для x (1; + ∞), и если 0a x (0; 1) и отрицательно для x (1; + ∞).
6. Если a > 1, то логарифмическая функция выпуклая вверх, а если a (0; 1) — выпуклая вниз.
Следующие операторы (см., Например) используются для решения логарифмических уравнений.
Считаете ли вы, что до экзамена еще есть время, и вы успеете подготовиться? Возможно, это так. Но в любом случае, чем раньше ученик приступит к обучению, тем успешнее он сдает экзамены. Сегодня мы решили посвятить статью логарифмическим неравенствам. Это одна из задач, а значит возможность получить дополнительный балл.
Это одна из задач, а значит возможность получить дополнительный балл.
Вы уже знаете, что такое логарифм? Мы очень на это надеемся. Но даже если у вас нет ответа на этот вопрос, это не проблема.Понять, что такое логарифм, очень легко.
Почему именно 4? Вам нужно возвести число 3 в такую степень, чтобы получить 81. Когда вы поймете принцип, вы можете переходить к более сложным вычислениям.
Вы преодолели неравенство несколько лет назад. И с тех пор они постоянно встречаются в математике. Если у вас есть проблемы с решением неравенств, см. Соответствующий раздел.
Теперь, когда мы познакомились с концепциями по отдельности, давайте перейдем к их рассмотрению в целом.
Простейшее логарифмическое неравенство.
Простейшие логарифмические неравенства этим примером не ограничиваются, их еще три, только с разными знаками. Зачем это нужно? Чтобы лучше понять, как решать неравенство с помощью логарифмов. А теперь приведем более применимый пример, он все еще достаточно простой, сложные логарифмические неравенства оставим на потом.
Как это решить? Все начинается с ОДЗ. Об этом стоит узнать побольше, если вы хотите всегда легко решать любое неравенство.
Что такое ODU? ODV для логарифмических неравенств
Аббревиатура означает диапазон допустимых значений. В заданиях к экзамену часто всплывает такая формулировка. ODZ пригодится вам не только в случае логарифмических неравенств.
Еще раз взгляните на приведенный выше пример. Мы будем рассматривать DHS на его основе, чтобы вы поняли принцип, и решение логарифмических неравенств не вызвало никаких вопросов. Из определения логарифма следует, что 2x + 4 должно быть больше нуля.В нашем случае это означает следующее.
Это число по определению должно быть положительным. Решите указанное выше неравенство. Это можно сделать даже устно, здесь ясно, что X не может быть меньше 2. Решением неравенства будет определение диапазона допустимых значений.
А теперь перейдем к решению простейшего логарифмического неравенства.
Мы отбрасываем сами логарифмы с обеих сторон неравенства. Что у нас осталось в результате? Простое неравенство.
Решить несложно. X должен быть больше -0,5. Теперь объединяем два полученных значения в систему. Таким образом,
Это будет диапазон допустимых значений рассматриваемого логарифмического неравенства.
Зачем вообще ОДЗ? Это возможность отсеять неправильные и невозможные ответы. Если ответ выходит за рамки допустимых значений, то ответ просто не имеет смысла. Об этом стоит помнить надолго, так как на экзамене часто возникает необходимость поиска ODZ, и касается это не только логарифмических неравенств.
Алгоритм решения логарифмического неравенства
Решение состоит из нескольких этапов. Во-первых, вам нужно найти диапазон допустимых значений. В ODZ будет два значения, мы обсуждали это выше. Далее необходимо решить само неравенство. Способы решения следующие:
- метод замены множителя;
- разложение;
- метод рационализации.

В зависимости от ситуации следует использовать один из указанных выше методов.Перейдем непосредственно к решению. Мы раскроем самый популярный метод, который подходит для решения задач ЕГЭ практически во всех случаях. Далее мы рассмотрим метод декомпозиции. Это может помочь, если вы столкнетесь с особенно сложным неравенством. Итак, алгоритм решения логарифмического неравенства.
Примеры решений :
Мы не зря взяли такое неравенство! Обратите внимание на базу. Помните: если оно больше единицы, знак остается неизменным при обнаружении диапазона допустимых значений; в противном случае необходимо изменить знак неравенства.
В результате получаем неравенство:
Приведем левую часть к виду уравнения, равному нулю … Вместо знака «меньше» ставим «равно», решаем уравнение. Таким образом, мы найдем ОДЗ. Мы надеемся, что с решением этого простого уравнения у вас не возникнет проблем. Ответы -4 и -2. Это не все. Вам необходимо отобразить эти точки на графике, поставить «+» и «-». Что для этого нужно сделать? Подставьте в выражение числа из интервалов.Если значения положительные, мы ставим «+».
Что для этого нужно сделать? Подставьте в выражение числа из интервалов.Если значения положительные, мы ставим «+».
Ответ : x не может быть больше -4 и меньше -2.
Мы нашли диапазон допустимых значений только для левой стороны, теперь нам нужно найти диапазон допустимых значений для правой стороны. Это намного проще. Ответ: -2. Пересекаем обе полученные области.
И только сейчас мы начинаем заниматься само неравенство.
Давайте максимально упростим его, чтобы облегчить решение.
Снова примените метод интервала в растворе. Опустим расчеты, с ним все уже ясно из предыдущего примера. Отвечать.
Но этот метод подходит, если логарифмическое неравенство имеет такую же основу.
Решение логарифмических уравнений и неравенств с разными основаниями предполагает первоначальное приведение к одному основанию. Затем следуйте описанному выше методу. Но есть и более сложный случай. Рассмотрим один из самых сложных типов логарифмических неравенств.
Базовые логарифмические неравенства с переменными значениями
Как решить неравенства с такими характеристиками? Да и такое можно найти на экзамене. Следующее решение неравенства также будет полезно для вашего образовательного процесса … Давайте рассмотрим проблему подробнее. Отбросим теорию, перейдем сразу к практике. Для решения логарифмических неравенств достаточно один раз прочитать пример.
Для решения логарифмического неравенства представленного вида необходимо правую часть привести к логарифму с таким же основанием.Принцип напоминает эквивалентные переходы. В результате неравенство будет выглядеть так.
Собственно, осталось создать систему неравенств без логарифмов. Используя метод рационализации, переходим к эквивалентной системе неравенств. Вы поймете само правило, когда подставите соответствующие значения и отследите их изменения. В системе будут следующие неравенства.
Используя метод рационализации при решении неравенств, нужно помнить следующее: необходимо вычесть из основания единицу, x по определению логарифма вычитается из обеих частей неравенства (справа налево), два выражения умножаются и ставятся под исходным знаком относительно нуля.
Дальнейшее решение ведется методом интервалов, здесь все просто. Вам важно понимать разницу в способах решения, тогда все пойдет легко.
В логарифмических неравенствах много нюансов. Самые простые из них решить достаточно легко. Как убедиться, что каждый из них можно решить без проблем? Вы уже получили все ответы в этой статье. Теперь у вас впереди долгая практика.Потренируйтесь последовательно решать самые разные задачи в рамках экзамена, и вы сможете получить наивысший балл. Удачи в нелегком деле!
(PDF) Стандартные ожидаемые годы жизни, потерянные из-за туберкулеза в Польше
Уровень заболеваемости туберкулезом в Польше снижается на
в течение многих лет. В 2013 г. в уведомлении
частотасоставляла 18,8 новых случаев ТБ / 100 000. В 1999–2012 гг.
не наблюдалось в уровне смертности (0,08),
, тогда как в предыдущий период он был значительно выше на
(0 .2 в 1965 г.).
4,32
Снижение смертности от ТБ
, несомненно, произошло благодаря успеху
современной медицины и здравоохранения. Тем не менее среди
Тем не менее среди
инфекционных заболеваний туберкулез остается наиболее частой причиной смертности
как во всем мире, так и в Польше.
3
Снижение смертности от туберкулеза наблюдалось в течение
периода исследования. Хотя как СПЗ, так и
общее количество потерянных лет жизни в конкретной популяции
подтверждают эту тенденцию к снижению, СПЗ
в Польше все еще выше, чем в Западной Европе.
С 1990 по 2013 год SDR на ТБ снизился на 54,4% в
Польше и на 53% во всем мире. В 1999–2012 годах показатель SEYLL на
ТБ снизился на 45,5% в Польше по сравнению с 31% на
во всем мире в период с 1990 по 2013 год. Как и в других
европейских странах, снижение заболеваемости ТБ SEYLL
наблюдалось в Польше во время исследования. Период, соответствующий
, спровоцировал снижение SDR и был результатом снижения на
числа смертей от туберкулеза.
33
Поскольку размер
населения существенно не изменился, сокращение
в SEYLL
p
подтвердило тенденцию к снижению
в SEYLL. Статистически значимые ежегодные изменения
Статистически значимые ежегодные изменения
вышеуказанных параметров примерно на 4–5% должны составлять
, что считается положительной тенденцией в смертности от туберкулеза. Это может иметь несколько объяснений: наиболее важным является
общего улучшения состояния здоровья
польского населения за счет лучших условий жизни и
более эффективного медицинского обслуживания, в результате чего
является более высоким. доля пациентов, успешно завершивших лечение
человек.Однако мы также наблюдали небольшое (1%) увеличение значений SEYLL
d
(12,06 для
мужчин и 9,56 для женщин) в 2012 г., что указывает на
, что уровень смертности выше среди молодых людей.
населения, чем раньше. Более высокие значения всех
показателей среди мужчин, чем среди женщин, подтверждают
более высокую смертность от туберкулеза среди мужчин.
Ограничения исследования
У этого исследования было несколько ограничений: 14-летний период исследования
, возможно, не был достаточно продолжительным, чтобы оценить тенденции
в SEYLL. Тем не менее, были некоторые вариации
Тем не менее, были некоторые вариации
в уведомлении и регистрации причин смерти в
Польше в течение периода исследования. Поскольку надежность статистического анализа
, основанного на смертях, в значительной степени зависит от правильного определения основных причин
смерти, особенно среди пожилых людей, в 2009 году были внесены определенные изменения
. Для стандартизации
причин смерти, которые подлежат дальнейшему статистическому анализу
, было решено, что врач, удостоверяющий
смерти, будет отвечать за заполнение свидетельства о смерти
, включая указание основных, вторичных и прямых причин смерти. смерть; квалифицированные бригады из
врачей отвечают за кодирование причин смерти
по классификации МКБ-10.
ВЫВОДЫ
Несмотря на улучшение эпидемиологии ТБ, болезнь
по-прежнему представляет серьезную проблему для общественного здравоохранения
во всем мире и остается основной причиной смерти
от одного инфекционного агента. Хотя ТБ излечимо на
Хотя ТБ излечимо на
, это приводит к значительной потере стандартных
лет ожидаемого срока службы. Способность бацилл туберкулеза
выживать в течение многих лет, длительное,
бессимптомное течение болезни и социодемо-
графические изменения, связанные с миграцией людей, составляют
все препятствия в борьбе с туберкулезом.Несмотря на тенденцию к снижению
показателей заболеваемости и смертности от туберкулеза на
, необходимо улучшить обнаружение активных случаев
, особенно среди пожилых людей и других лиц с высоким риском
. Требуется более широкое использование контактного скрининга и
профилактического лечения, а также дальнейшее расширение международного сотрудничества
, направленное на искоренение этого заболевания.
Благодарности
Исследование финансировалось Национальным научным центром, Краков,
Польша (no.DEC-2013/11 / B / HS4 / 00465). Финансирующие организации не играли роли
в дизайне исследования, сборе и анализе данных, решении о публикации
или подготовке рукописи.
Конфликт интересов: не объявлен.
Список литературы
1 Всемирная организация здравоохранения. Глобальный доклад о туберкулезе, 2015 г.
WHO / HTM / TB / 2015.22. Женева, Швейцария: ВОЗ, 2015.
2 Лаун С. Д., Зумла А. I. Туберкулез. Ланцет 2011; 378: 57–72.
3 Европейский центр профилактики и контроля заболеваний / ВОЗ
Европейское региональное бюро.Надзор за туберкулезом и мониторинг
в Европе, 2016 г. Стокгольм, Швеция: ECDC, 2016.
4 Корзеневска-Косела М. Туберкулез в Польше в 2013 г.
Przegl Epidem 2015; 69: 277–282. [Польский]
5Wr
´
oblewska W. Предотвращаемая смертность — концепция и
эмпирическое исследование для Польши. Студия Демогр 2012; 161: 129–
151.
6 Яницкий Ю. Туберкулез в период молодой Польши и в период между мировыми войнами
в теории и медицинской практике.Часть I. Med Now
2010; 16: 32–81.
7 Бернер В. Эпидемиологическая ситуация по инфекционным заболеваниям в
Львове и Кракове во время и после Первой мировой войны (до
1922). Przegl Epidemiol 2009; 63: 149–155. [Польский]
Przegl Epidemiol 2009; 63: 149–155. [Польский]
8 Центральное статистическое управление. Краткий ежегодник. Варшава, Польша:
Gł´
, вл. Urza
˛
d Statystyczny, 1932. [польский]
9 Центральное статистическое управление. Краткий ежегодник.Варшава, Польша:
Gł´
вл. Urza
˛
d Statystyczny, 1937. [польский]
10 Центральное статистическое управление. Краткий ежегодник. Варшава, Польша:
Gł´
вл. Urza
˛
d Statystyczny, 1939. [польский]
11 Gawryszewski A. Население Польши в 20
веках.
Варшава, Польша: Польская академия наук, 2006. [польский]
12 Korzeniewska-Koseła M.Epidemiologia gruz´licy w Polsce i na
s
´wiecie. Варшава, Польша: Instytut Gruz´licy i Chor ´
ob Płuc w
Warszawie, 2015 http://www.gazetalekarska.pl/wp-content/
uploads / 2015/03 / Epidemiologia-gru% C5% BAlicy -w-Polsce-i-
na-% C5% 9Bwiecie. pdf. [Polish] По состоянию на ноябрь 2016 г.
pdf. [Polish] По состоянию на ноябрь 2016 г.
13 Maniecka-Bryła I, Pikala M, Bryła M. Неравенства в отношении здоровья
среди сельских и городских жителей провинции ´
odz´, Польша.
Ann Agric Environ Med 2012; 19: 723–731.
14 Maniecka-Bryła I, Pikala M, Bryła M. Утраченные годы жизни из-за
сердечно-сосудистых заболеваний. Кардиол Пол 2013; 71; 1065–1072.
206 Международный журнал туберкулеза и болезней легких
Документация API — GATHODE | Документация CATHODE
Базы: объект
Содержит (несколько) статусную информацию.
Этот класс позволяет собирать информацию о статусе (например, для набор данных).
Этот класс может быть списком статусов или отдельным статусом.
Для одного статуса метод сообщения возвращает строковое представление статуса.
Для списка статусов метод сообщения возвращает одну строку,
состоящий из одного строкового представления для каждого типа статуса. Если
статус-тип существует несколько раз, только наивысший приоритет
отображается сообщение этого типа.
В качестве альтернативы методу сообщения вы можете использовать type2status и собрать нужную строку самостоятельно.
Инициализируется ключевым словом и указанием дополнительных параметров или списком (под) статусов.
| Параметры: |
|
|---|
- isEmpty ()
Верните True, если это пустое сообщение StatusMessage.

Возвращает: bool — Верно, если пусто.
- статусыWithKey ( ключ ) ¶
Вернуть список всех подстатусов, имеющих данный ключ.
Параметры: ключ ( строка ) — Тип ключа, которому должен соответствовать подстатус. Возвращает: list (StatusMessage) — статусные сообщения типа key.
- addStatus (, статус ) ¶
Добавить подстатус к этому статусу.
Параметры: status ( StatusMessage ) — Подстатус, который необходимо добавить. Вызывает исключение, если этот объект не был инициализирован как список статусов.

- removeStatusesWithKey ( ключ ) ¶
Удалите все подстатусы с данным ключом.
Параметры: ключ ( строка ) — Тип ключа, которому должен соответствовать подстатус. Возвращает: int — количество удаленных статусных сообщений.
- короткое сообщение () ¶
Короткое сообщение для этого статуса (работает только для основного статуса, а не для списка статусов)
Возвращает: str — Краткое сообщение, описывающее этот статус.
- longmessage () ¶
Длинное сообщение для этого статуса (работает только для основного статуса, а не для списка статусов)
Возвращает: str — длинное сообщение, описывающее этот статус. 
- messageType () ¶
Тип сообщения для этого статуса (работает только для основного статуса, а не для списка статусов)
Возвращает: str — Строка, описывающая тип этого статуса.
- type2status () ¶
Возвращает: dict — Словарь, который для каждого типа сообщения содержит сообщение с наивысшим приоритетом.
- сообщение ( withMsgType = True , seperator = ‘;’ ) ¶
Возвращает: str — Статусное сообщение. Для списка (под) статусов отображается только тот с наивысший приоритет / серьезность для каждой категории (сообщение тип).

- серьезность () ¶
Возвращает: Серьезность — серьезность / приоритет этого состояния. Если это список (под) статусов, вернуть наивысший.
- severity2 ()
Возвращает: Серьезность — серьезность / приоритет второго уровня этого состояния. Для этого параметр dict должен содержать Запись «серьезность2»; если он не установлен, верните 0.
Если это список (под) статусов, вернуть наивысший.
О резонансах и образовании щелей в спектре квазипериодических уравнений Шредингера на JSTOR
Абстрактный Мы рассматриваем одномерные разностные уравнения Шредингера $ [H (x, \ omega) \ varphi] (n) \ Equiv — \ varphi (n-1) — \ varphi (n + 1) + V (x + n \ omega ) \ varphi (n) = E \ varphi (n) $, n ∈ ℤ, x, w ∈ [0, 1] с вещественно-аналитической потенциальной функцией V (x). Если L (E, w₀) больше 0 для всех E ∈ (E ′, E ″) и некоторого диофантова w₀, то интегральная плотность состояний абсолютно непрерывна почти для каждого, близкого к w₀, как показано авторами в более ранние работы. В этой статье мы устанавливаем формирование плотного множества лэпов в spec (H (x, 𝑤)) ∩ (E ′, E ″). Наш подход основан на аргументе индукции по шкале и поэтому является как конструктивным, так и количественным. Резонансы между собственными функциями одного масштаба приводят к «предварительным зазорам» в большем масштабе.Чтобы перейти к действительным промежуткам в спектре, мы показываем, что эти предварительные промежутки не могут быть заполнены более конечного (и равномерно ограниченного) числа раз. Для этого нужно связать предварительную щель с парами комплексных нулей определителей Дирихле на единичной окружности. Среди прочего, мы устанавливаем непертурбативную версию ковариантной параметризации собственных значений и собственных функций через фазы в духе (пертурбативного) описания спектра Синая через его функцию.
Если L (E, w₀) больше 0 для всех E ∈ (E ′, E ″) и некоторого диофантова w₀, то интегральная плотность состояний абсолютно непрерывна почти для каждого, близкого к w₀, как показано авторами в более ранние работы. В этой статье мы устанавливаем формирование плотного множества лэпов в spec (H (x, 𝑤)) ∩ (E ′, E ″). Наш подход основан на аргументе индукции по шкале и поэтому является как конструктивным, так и количественным. Резонансы между собственными функциями одного масштаба приводят к «предварительным зазорам» в большем масштабе.Чтобы перейти к действительным промежуткам в спектре, мы показываем, что эти предварительные промежутки не могут быть заполнены более конечного (и равномерно ограниченного) числа раз. Для этого нужно связать предварительную щель с парами комплексных нулей определителей Дирихле на единичной окружности. Среди прочего, мы устанавливаем непертурбативную версию ковариантной параметризации собственных значений и собственных функций через фазы в духе (пертурбативного) описания спектра Синая через его функцию. Это позволяет связать промежутки в спектре с графиками собственных значений, параметризованных фазой.Наши теоремы о бесконечном объеме справедливы для всех диофантовых частот 𝑤 вплоть до набора размерности Хаусдорфа нуль.
Это позволяет связать промежутки в спектре с графиками собственных значений, параметризованных фазой.Наши теоремы о бесконечном объеме справедливы для всех диофантовых частот 𝑤 вплоть до набора размерности Хаусдорфа нуль.
Annals of Mathematics, выдающийся журнал научных статей по чистой математике, была основана в 1884 году. Анналы of Mathematics издается раз в два месяца при сотрудничестве Принстонский университет и Институт перспективных исследований. Это широко считается одним из главных математических журналов в мире.
% PDF-1.4
%
512 0 obj>
эндобдж
xref
512 90
0000000016 00000 н.
0000006292 00000 н.
0000006491 00000 н.
0000006534 00000 н.
0000006662 00000 н.
0000006984 00000 н.
0000007354 00000 п.
0000007841 00000 н.
0000008304 00000 н.
0000008340 00000 н.
0000008387 00000 п.
0000008464 00000 н.
0000008686 00000 н.
0000009764 00000 н. 0000010939 00000 п.
0000013609 00000 п.
0000014462 00000 п.
0000021315 00000 п.
0000021543 00000 п.
0000021786 00000 п.
0000022007 00000 п.
0000022078 00000 п.
0000022176 00000 п.
0000022255 00000 п.
0000022298 00000 п.
0000022391 00000 п.
0000022434 00000 п.
0000022528 00000 п.
0000022571 00000 п.
0000022700 00000 п.
0000022792 00000 п.
0000022835 00000 п.
0000022955 00000 п.
0000023121 00000 п.
0000023201 00000 п.
0000023244 00000 п.
0000023329 00000 п.
0000023458 00000 п.
0000023549 00000 п.
0000023592 00000 п.
0000023674 00000 п.
0000023808 00000 п.
0000023879 00000 п.
0000023922 00000 п.
0000024059 00000 п.
0000024155 00000 п.
0000024197 00000 п.
0000024290 00000 п.
0000024387 00000 п.
0000024429 00000 п.
0000024529 00000 п.
0000024571 00000 п.
0000024671 00000 п.
0000024713 00000 п.
0000024817 00000 п.
0000024859 00000 п.
0000024962 00000 п.
0000025004 00000 п.
0000025144 00000 п.
0000025220 00000 п.
0000025262 00000 п.
0000025352 00000 п.
0000010939 00000 п.
0000013609 00000 п.
0000014462 00000 п.
0000021315 00000 п.
0000021543 00000 п.
0000021786 00000 п.
0000022007 00000 п.
0000022078 00000 п.
0000022176 00000 п.
0000022255 00000 п.
0000022298 00000 п.
0000022391 00000 п.
0000022434 00000 п.
0000022528 00000 п.
0000022571 00000 п.
0000022700 00000 п.
0000022792 00000 п.
0000022835 00000 п.
0000022955 00000 п.
0000023121 00000 п.
0000023201 00000 п.
0000023244 00000 п.
0000023329 00000 п.
0000023458 00000 п.
0000023549 00000 п.
0000023592 00000 п.
0000023674 00000 п.
0000023808 00000 п.
0000023879 00000 п.
0000023922 00000 п.
0000024059 00000 п.
0000024155 00000 п.
0000024197 00000 п.
0000024290 00000 п.
0000024387 00000 п.
0000024429 00000 п.
0000024529 00000 п.
0000024571 00000 п.
0000024671 00000 п.
0000024713 00000 п.
0000024817 00000 п.
0000024859 00000 п.
0000024962 00000 п.
0000025004 00000 п.
0000025144 00000 п.
0000025220 00000 п.
0000025262 00000 п.
0000025352 00000 п.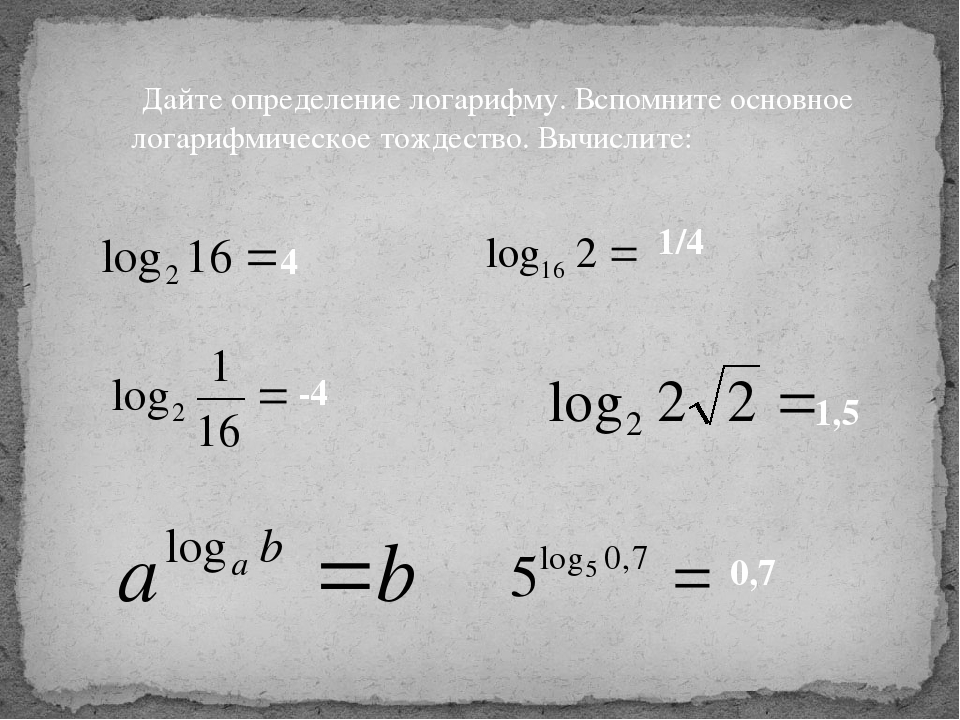 0000025446 00000 п.
0000025488 00000 п.
0000025575 00000 п.
0000025617 00000 п.
0000025705 00000 п.
0000025747 00000 п.
0000025835 00000 п.
0000025877 00000 п.
0000025919 00000 п.
0000026029 00000 п.
0000026071 00000 п.
0000026113 00000 п.
0000026156 00000 п.
0000026198 00000 п.
0000026241 00000 п.
0000026284 00000 п.
0000026389 00000 п.
0000026432 00000 п.
0000026475 00000 п.
0000026518 00000 п.
0000026561 00000 п.
0000026604 00000 п.
0000026737 00000 п.
0000026780 00000 п.
0000026890 00000 н.
0000026933 00000 п.
0000026976 00000 п.
0000002096 00000 н.
трейлер
] >>
startxref
0
%% EOF
601 0 obj> поток
xX_ 帀 Xpd> 12 & EE4 ‘5-sbd ([2nfE 䆹 [9V 42, {
0000025446 00000 п.
0000025488 00000 п.
0000025575 00000 п.
0000025617 00000 п.
0000025705 00000 п.
0000025747 00000 п.
0000025835 00000 п.
0000025877 00000 п.
0000025919 00000 п.
0000026029 00000 п.
0000026071 00000 п.
0000026113 00000 п.
0000026156 00000 п.
0000026198 00000 п.
0000026241 00000 п.
0000026284 00000 п.
0000026389 00000 п.
0000026432 00000 п.
0000026475 00000 п.
0000026518 00000 п.
0000026561 00000 п.
0000026604 00000 п.
0000026737 00000 п.
0000026780 00000 п.
0000026890 00000 н.
0000026933 00000 п.
0000026976 00000 п.
0000002096 00000 н.
трейлер
] >>
startxref
0
%% EOF
601 0 obj> поток
xX_ 帀 Xpd> 12 & EE4 ‘5-sbd ([2nfE 䆹 [9V 42, {
18189
7661
неэффективность
натрий
поставлен
спроектированный
выдающийся
выполнение
ближайший
взятый
уголь
нагрузка
15forgn
вращение
458
сдержанный
точно
потенциально
серый
объединение
скобки
двадцать
маркина
показано
СЕЛЬСКОЕ ХОЗЯЙСТВО
ГАЗ
доверять
кукуруза
цилиндр
спортсмен
хвойный
способствовать
акцептор
синтетический
упражнение
дикий
xvii
δподложка
хари
услуга
редко
закупоренный
жидкость
шлепер
1816 г. обрезать
Аткинсон
усложнять
впрыснутый
Паркер
Brueggemann
замена
Хендрих
проект
робустнес
промышленный
оценить
биохимия
кузнец
2002 г.
вариант
супернатант
охарактеризованный
будка
барботаж
доказательство
заметный
Масефски
давая
Малдер
перехватить
xix
отмечая
вер
подходящее
зависимость
ставка
иметь значение
резко
базовый поток
побежал
1585
экспериментально
Hampson
4993
P4PH047
важность
стекло
Wassen
плотность
бал
навязанный
люди
чувствительность
идентифицировать
Oenema
подчиниться
обрабатывали
источник
восстанавливаться
Винкен
окисляющий
местный
не удалось
раковина
Хопкин
подавляет
исход
поколенческий
Рой
образование
Питер
фридман
3200
0001
позволяя
изотополог
энтизол
подповерхностный
1084
минимизированный
638
стимуляция
αeq
широко
Wollum
MATLAB
Палмер
сокращение
показывать
Lettmann
достаточный
планетарный
Грег
положить начало
недостаток
Джоун
количественно оценить
гримм
четное
ltd
1975 г.
равишанкара
УРАВНЕНИЯ
влияющий
стабилизированный
биогеонаука
дыхание
ND
δ18OO2
1991 г.
разъединение
немедленно
Baldocchi
термически
питательное вещество
промывание
свежий
верф
вовлекать
просмотрено
Thiemen
ССЫЛКА
лос
повторение
2400
δ17
Роза
хранить
лучше
примириться
BBA
лауф
272
потрясающе
поставка
зарабатывание
1983 г.
обрезать
Аткинсон
усложнять
впрыснутый
Паркер
Brueggemann
замена
Хендрих
проект
робустнес
промышленный
оценить
биохимия
кузнец
2002 г.
вариант
супернатант
охарактеризованный
будка
барботаж
доказательство
заметный
Масефски
давая
Малдер
перехватить
xix
отмечая
вер
подходящее
зависимость
ставка
иметь значение
резко
базовый поток
побежал
1585
экспериментально
Hampson
4993
P4PH047
важность
стекло
Wassen
плотность
бал
навязанный
люди
чувствительность
идентифицировать
Oenema
подчиниться
обрабатывали
источник
восстанавливаться
Винкен
окисляющий
местный
не удалось
раковина
Хопкин
подавляет
исход
поколенческий
Рой
образование
Питер
фридман
3200
0001
позволяя
изотополог
энтизол
подповерхностный
1084
минимизированный
638
стимуляция
αeq
широко
Wollum
MATLAB
Палмер
сокращение
показывать
Lettmann
достаточный
планетарный
Грег
положить начало
недостаток
Джоун
количественно оценить
гримм
четное
ltd
1975 г.
равишанкара
УРАВНЕНИЯ
влияющий
стабилизированный
биогеонаука
дыхание
ND
δ18OO2
1991 г.
разъединение
немедленно
Baldocchi
термически
питательное вещество
промывание
свежий
верф
вовлекать
просмотрено
Thiemen
ССЫЛКА
лос
повторение
2400
δ17
Роза
хранить
лучше
примириться
BBA
лауф
272
потрясающе
поставка
зарабатывание
1983 г. твердая древесина
4180
необратимый
3030
панель
регулировать
413
уже
иначе
последующий
геомикробиология
1981 г.
чанг
знание
планктон
Hazleton
вставлен
токарь
Опасность
сообщить
Haslun
энергично
разнообразие
nox
15αN
перма
обмен
0035
брезент
флакон
квадратный
по своей сути
плотно
0071
ПРОИЗВОДИТ
RSIL20
примерно
складывать
Киммель
112
191
rстандарт
756
должность
денитрификация
262
держа
осушать
самый низкий
необычный
в первую очередь
цзоу
𝑐ℎ𝑎𝑚
Hattori
ПРИЛОЖЕНИЕ
170
оценка
Таблица
распознавать
минимально
Dunfield
Funen
в дальнейшем
зеленый
компромисс
приостановка
бур
стекольщик
WHC
Ренненберг
в любое время
andreae
R4
эбервейн
ОБОГАЩЕННЫЙ
радикальный
пульс
D6
225
NO2
207
142
задерживать
предвзятость
существенный
Weisser
уплотнение
ученик
увеличивать
растворенный
Daehnke
ва
набор
настоящий
NW
усреднение
геофизический
фогель
1988 г.
линия тока
Meixner
Дэйвид
обменник
Wilmad
встретились
отклонение
Мэдсен
белый
захватывать
количественно
выражение
мог
копировать
органический
декантирование
128
отобранный
представление
Groenigen
логичный
нитро
размышлять
сослался
7891
пассивный
обучение
allwine
Hildebrandt
Роде
Гопкинсон
исследовательская работа
фритта
18185
11569
геофизический
учитывая
устранен
опрос
надпечатка
Привет
способствовать
нагата
18FNO3
применение
нитрозоспира
отвар
хаяши
ведомый
оба
ценить
1950
применимый
12115
532
в конце концов
превосходить
несоответствие
D21
1681
8723
дубе
красотка
заслуженный
археи
прежний
стимулированный
δ15NRSIL20
в основном
побочный продукт
скорость
дождевая вода
2533
построенный
расположена
однонаправленный
вершина горы
aqueou
642
рассеченный
творчество
технология
влажный
свободное пространство
было бы
Herrmann
Голландия
ягненок
Беннетт
европейский
существенно
размещение
Weigand
Людвиг
184
Δ17O
Орегон
Рассел
горение
181
накопленный
существование
Армбрустер
обозначенный
Ceuleman
получить
рябенко
развязанный
pdiff
летучий
северо-восток
стимулирующий
усыновленный
газеу
Глобальный
последовательность
326
страна
хостинг
симуляция
Bettez
335
надбанк
камияма
спектрометрия
дерево
третий
ИССЛЕДОВАНИЕ
бобовые
сборка
управлять
Δ17ON
Табатабай
сокол
косил
графический
распространяющийся
063
Балтимор
прошел
составляющая
скомпрометированный
элюированный
0075
7146
диссимиляционный
организм
021
нано2
академический
доктор
Нижний
подход
эффективность
8745
горячий
Харлин
раскрытие
себя
СРАВНЕНИЯ
отсутствие
10363
аппарат
222
2911
благодарный
скорее
плантация
15129
близко
217
скраб
горячая точка
возраст
158
простой
хлопушка
ЭКСПЕРИМЕНТ
расширенный
гидролизовать
включать
соотносить
вниз
объем
КОН
выше
18994
добавление
132
18ɛ
пейзаж
фургон
глобально
хотеть
химически
подкисленный
поздно
ключ
соответствие
хранится
1018
Монтаньяни
0046
Нет данных
маасаккер
Boutton
динамичный
ИСПОЛЬЗОВАЛ
строго
1789 г.
твердая древесина
4180
необратимый
3030
панель
регулировать
413
уже
иначе
последующий
геомикробиология
1981 г.
чанг
знание
планктон
Hazleton
вставлен
токарь
Опасность
сообщить
Haslun
энергично
разнообразие
nox
15αN
перма
обмен
0035
брезент
флакон
квадратный
по своей сути
плотно
0071
ПРОИЗВОДИТ
RSIL20
примерно
складывать
Киммель
112
191
rстандарт
756
должность
денитрификация
262
держа
осушать
самый низкий
необычный
в первую очередь
цзоу
𝑐ℎ𝑎𝑚
Hattori
ПРИЛОЖЕНИЕ
170
оценка
Таблица
распознавать
минимально
Dunfield
Funen
в дальнейшем
зеленый
компромисс
приостановка
бур
стекольщик
WHC
Ренненберг
в любое время
andreae
R4
эбервейн
ОБОГАЩЕННЫЙ
радикальный
пульс
D6
225
NO2
207
142
задерживать
предвзятость
существенный
Weisser
уплотнение
ученик
увеличивать
растворенный
Daehnke
ва
набор
настоящий
NW
усреднение
геофизический
фогель
1988 г.
линия тока
Meixner
Дэйвид
обменник
Wilmad
встретились
отклонение
Мэдсен
белый
захватывать
количественно
выражение
мог
копировать
органический
декантирование
128
отобранный
представление
Groenigen
логичный
нитро
размышлять
сослался
7891
пассивный
обучение
allwine
Hildebrandt
Роде
Гопкинсон
исследовательская работа
фритта
18185
11569
геофизический
учитывая
устранен
опрос
надпечатка
Привет
способствовать
нагата
18FNO3
применение
нитрозоспира
отвар
хаяши
ведомый
оба
ценить
1950
применимый
12115
532
в конце концов
превосходить
несоответствие
D21
1681
8723
дубе
красотка
заслуженный
археи
прежний
стимулированный
δ15NRSIL20
в основном
побочный продукт
скорость
дождевая вода
2533
построенный
расположена
однонаправленный
вершина горы
aqueou
642
рассеченный
творчество
технология
влажный
свободное пространство
было бы
Herrmann
Голландия
ягненок
Беннетт
европейский
существенно
размещение
Weigand
Людвиг
184
Δ17O
Орегон
Рассел
горение
181
накопленный
существование
Армбрустер
обозначенный
Ceuleman
получить
рябенко
развязанный
pdiff
летучий
северо-восток
стимулирующий
усыновленный
газеу
Глобальный
последовательность
326
страна
хостинг
симуляция
Bettez
335
надбанк
камияма
спектрометрия
дерево
третий
ИССЛЕДОВАНИЕ
бобовые
сборка
управлять
Δ17ON
Табатабай
сокол
косил
графический
распространяющийся
063
Балтимор
прошел
составляющая
скомпрометированный
элюированный
0075
7146
диссимиляционный
организм
021
нано2
академический
доктор
Нижний
подход
эффективность
8745
горячий
Харлин
раскрытие
себя
СРАВНЕНИЯ
отсутствие
10363
аппарат
222
2911
благодарный
скорее
плантация
15129
близко
217
скраб
горячая точка
возраст
158
простой
хлопушка
ЭКСПЕРИМЕНТ
расширенный
гидролизовать
включать
соотносить
вниз
объем
КОН
выше
18994
добавление
132
18ɛ
пейзаж
фургон
глобально
хотеть
химически
подкисленный
поздно
ключ
соответствие
хранится
1018
Монтаньяни
0046
Нет данных
маасаккер
Boutton
динамичный
ИСПОЛЬЗОВАЛ
строго
1789 г. интригующий
появляться
увлажнитель
заменены
сланец
фибигер
2076
выводить
геометрический
4989
площадь
уравнение
умри
подразумевать
тандем
упшур
Матсон
МАТЕРИАЛЫ
ископаемое
учреждение
8225
лист
HNO
препятствовать
преобразованный
существует
ВВЕДЕНИЕ
защищал
способный
выделение
храмовник
Лейбфрид
Чили
165
кондиционирование
2351
сворачивание
естественный
переработанный
Чжан
1231
степень
клык
Монте
вышел
связь
Маркетто
биогенный
пенсильванский
735
четыре
серый
таясу
Робертсон
всасывание
092016
344
селективный
ВЭЖХ
гипотетический
042017
18αO2
Кавасо
исследовал
Bussotti
калибровка
привет
недостаток
районы
РАЗБАВЛЕНИЕ
обнаруживаемый
209
Молен
δ17O
затронутый
линейно
022017
опыт
600
ландро
физическое лицо
457
весь
2532
гидравлический
смешивание
представлен
Wondzell
коплен
качественный
контакт
ранее
пластик
просто
отток
наследовать
время года
ИЗОТОПИЧЕСКИЙ
отрицательно
желанный
дренаж
выход
505
вышележащий
смягчение
837
Dordrecht
2015 г.
149
bioultra
объем
придуманный
самолет
возникающий
Guenter
галстук
море
рутина
выпускной
септа
база данных
st1
непрерывно
исключать
1030
холм
17i
азот
нитрификация
отказ
Neuberger
570
обычно
3761
влажный
призванный
ожидал
вычислить
ведущий
1998 г.
интригующий
появляться
увлажнитель
заменены
сланец
фибигер
2076
выводить
геометрический
4989
площадь
уравнение
умри
подразумевать
тандем
упшур
Матсон
МАТЕРИАЛЫ
ископаемое
учреждение
8225
лист
HNO
препятствовать
преобразованный
существует
ВВЕДЕНИЕ
защищал
способный
выделение
храмовник
Лейбфрид
Чили
165
кондиционирование
2351
сворачивание
естественный
переработанный
Чжан
1231
степень
клык
Монте
вышел
связь
Маркетто
биогенный
пенсильванский
735
четыре
серый
таясу
Робертсон
всасывание
092016
344
селективный
ВЭЖХ
гипотетический
042017
18αO2
Кавасо
исследовал
Bussotti
калибровка
привет
недостаток
районы
РАЗБАВЛЕНИЕ
обнаруживаемый
209
Молен
δ17O
затронутый
линейно
022017
опыт
600
ландро
физическое лицо
457
весь
2532
гидравлический
смешивание
представлен
Wondzell
коплен
качественный
контакт
ранее
пластик
просто
отток
наследовать
время года
ИЗОТОПИЧЕСКИЙ
отрицательно
желанный
дренаж
выход
505
вышележащий
смягчение
837
Dordrecht
2015 г.
149
bioultra
объем
придуманный
самолет
возникающий
Guenter
галстук
море
рутина
выпускной
септа
база данных
st1
непрерывно
исключать
1030
холм
17i
азот
нитрификация
отказ
Neuberger
570
обычно
3761
влажный
призванный
ожидал
вычислить
ведущий
1998 г. расчет
индикация
продвигать
1070
предварительно
фальц
никогда
АНАЛИЗ
затенение
элюировать
процветать
105
жесткий
ТАБЛИЦЫ
вызывая
111
диаметр
УНИВЕРСИТЕТ
408
СОПРОВОЖДАЯ
в ловушке
τcham
559
удерт
многие
Карло
Arriaga
аналог
атмосфера
бассейн
числовой
кричащий
анаэробный
Болен
эксплуатируемый
парный
осадок
автор
значительно
дробная часть
Ример
Массачусетт
полезность
триэтаноламин
действовать
инвентарь
волокно
необработанный
предоставлять
382
илистый
поддерживающий
способ
восстановление
не хватает
139
129
sno
926
NC9643579
8818
3024
такой
пульсирующий
ненулевой
168
Адон
3444
178
темно
124
сан
пазелла
1429
осталось
понимание
алюминий
КЕННЕТ
ВВЕРХ
представитель
17O
идентифицированный
Шепсон
интеграция
Groffmann
1972 г.
сосредоточенный
быстрый
передача
Schütte
перестановка
FA
физиология
фокусировка
cham
возможность
представлен
антропогенный
Greis
переработка
совпадение
оценка
описание
R5
0047
052017
ПОЧВЫ
южный
засушливый
деионизированный
примирение
113
прокладка
папа
диэтрих
лавик
Макдауэлл
заметный
консервативный
сочинение
СИСТЕМА
разнообразие
6049
принятие
Сингх
Счет
16FO2
Бег
ресурс
в одиночестве
Breuninger
маленький
пузырь
405
сочетание
DIN
очищенный
Робин
Быстрее
обозначение
вывод
детерминированный
13951L
Wollheim
ухоженный
О’Нил
засушливость
PA83
шнабель
параметр
карри
Canfield
доверенное лицо
Конрад
x𝑘x𝑡
ОБСУЖДЕНИЕ
неуверенность
вне
Логан
2014 г.
расчет
индикация
продвигать
1070
предварительно
фальц
никогда
АНАЛИЗ
затенение
элюировать
процветать
105
жесткий
ТАБЛИЦЫ
вызывая
111
диаметр
УНИВЕРСИТЕТ
408
СОПРОВОЖДАЯ
в ловушке
τcham
559
удерт
многие
Карло
Arriaga
аналог
атмосфера
бассейн
числовой
кричащий
анаэробный
Болен
эксплуатируемый
парный
осадок
автор
значительно
дробная часть
Ример
Массачусетт
полезность
триэтаноламин
действовать
инвентарь
волокно
необработанный
предоставлять
382
илистый
поддерживающий
способ
восстановление
не хватает
139
129
sno
926
NC9643579
8818
3024
такой
пульсирующий
ненулевой
168
Адон
3444
178
темно
124
сан
пазелла
1429
осталось
понимание
алюминий
КЕННЕТ
ВВЕРХ
представитель
17O
идентифицированный
Шепсон
интеграция
Groffmann
1972 г.
сосредоточенный
быстрый
передача
Schütte
перестановка
FA
физиология
фокусировка
cham
возможность
представлен
антропогенный
Greis
переработка
совпадение
оценка
описание
R5
0047
052017
ПОЧВЫ
южный
засушливый
деионизированный
примирение
113
прокладка
папа
диэтрих
лавик
Макдауэлл
заметный
консервативный
сочинение
СИСТЕМА
разнообразие
6049
принятие
Сингх
Счет
16FO2
Бег
ресурс
в одиночестве
Breuninger
маленький
пузырь
405
сочетание
DIN
очищенный
Робин
Быстрее
обозначение
вывод
детерминированный
13951L
Wollheim
ухоженный
О’Нил
засушливость
PA83
шнабель
параметр
карри
Canfield
доверенное лицо
Конрад
x𝑘x𝑡
ОБСУЖДЕНИЕ
неуверенность
вне
Логан
2014 г. исполнение
644
0000
синтез
МОДЕЛЬ
расследовать
приближение
оригинал
1968 г.
увеличивать
Нельсон
абсолютный
пропитанный
предыдущий
вмешался
об / мин
предоставление
предложенный
расчистка
в которой
стержень
2001 г.
опубликовано
Edgerton
возможный
Дюпон
потрясен
подразумевать
широко
позже
хранится
Обратная связь
δ15Nh5
презумпция
ɛh3O
обогащение
Vereecken
отбор проб
онлайн
длина
металл
зимнее время
закон
скиба
содержащий
полу
пороу
Bardgett
Keiluweit
понимать
включение
повернуть
мимо
железо
ВЫБРОСЫ
экспорт
Стоимость
Zechmeister
юго-западный
навес
накапливать
биологический
неполноценный
прихорашиваться
дал
представил
ДОПОЛНИТЕЛЬНЫЙ
нестерилизованный
сельскохозяйственный
по-разному
1982 г.
периодически
Kreutziger
3423
mcmaster
под
контраст
4145
частота
Лернер
щедрость
Войтек
KNF
последовательность
переехать
молекулярный
наш
отчетливый
0003
ранее
дифференциал
790
533
сохранился
определенный
Варфоломей
зона
15αk
группа
продвижение
Дональдсон
развернутый
5932
траектория
1409
приток
преобразователь
экстраполяция
начальство
патрон
аномалия
1716
принятый
микробный
общение
океан
8753
Weintraub
пар
Kiendler
Операционные системы
310
умножение
Matlab
источник
E6391
высшее
192
денитрификация
конец
уборка мусора
Delzon
теория
соответствующие
распространение
выхлопная труба
пекарь
10381
достигать
известняк
𝟐𝐍𝐎
физиографический
543
267
надежный
терпение
отличный
NN
2724
бук
проигрыш
конкретный
различать
без
чем
бок
чистка
ядовитый
D17307
просто
гиблин
эффективный
PRSIL
отделение
viii
глава
удивительно
14FNO3
кассия
233
символ
лам
Ermel
Savillex
Грегори
снижение
жизнь
Шенли
технологии
факультативный
пустышка
следить
Эйвери
усилие
Ричард
сила
стремительный
очищенный
Брайан
2000 г.
исполнение
644
0000
синтез
МОДЕЛЬ
расследовать
приближение
оригинал
1968 г.
увеличивать
Нельсон
абсолютный
пропитанный
предыдущий
вмешался
об / мин
предоставление
предложенный
расчистка
в которой
стержень
2001 г.
опубликовано
Edgerton
возможный
Дюпон
потрясен
подразумевать
широко
позже
хранится
Обратная связь
δ15Nh5
презумпция
ɛh3O
обогащение
Vereecken
отбор проб
онлайн
длина
металл
зимнее время
закон
скиба
содержащий
полу
пороу
Bardgett
Keiluweit
понимать
включение
повернуть
мимо
железо
ВЫБРОСЫ
экспорт
Стоимость
Zechmeister
юго-западный
навес
накапливать
биологический
неполноценный
прихорашиваться
дал
представил
ДОПОЛНИТЕЛЬНЫЙ
нестерилизованный
сельскохозяйственный
по-разному
1982 г.
периодически
Kreutziger
3423
mcmaster
под
контраст
4145
частота
Лернер
щедрость
Войтек
KNF
последовательность
переехать
молекулярный
наш
отчетливый
0003
ранее
дифференциал
790
533
сохранился
определенный
Варфоломей
зона
15αk
группа
продвижение
Дональдсон
развернутый
5932
траектория
1409
приток
преобразователь
экстраполяция
начальство
патрон
аномалия
1716
принятый
микробный
общение
океан
8753
Weintraub
пар
Kiendler
Операционные системы
310
умножение
Matlab
источник
E6391
высшее
192
денитрификация
конец
уборка мусора
Delzon
теория
соответствующие
распространение
выхлопная труба
пекарь
10381
достигать
известняк
𝟐𝐍𝐎
физиографический
543
267
надежный
терпение
отличный
NN
2724
бук
проигрыш
конкретный
различать
без
чем
бок
чистка
ядовитый
D17307
просто
гиблин
эффективный
PRSIL
отделение
viii
глава
удивительно
14FNO3
кассия
233
символ
лам
Ermel
Savillex
Грегори
снижение
жизнь
Шенли
технологии
факультативный
пустышка
следить
Эйвери
усилие
Ричард
сила
стремительный
очищенный
Брайан
2000 г. нуль
концентрация
Питт
НИТРИФИКАЦИЯ
199
опосредованный
Бернингер
CF
сопротивление
экологический
заштрихованный
Straus
узкий
эффективные
Кh4
автотрофный
бак
лежащий в основе
упражняться
приказ
следующий
стрелка
2122
родитель
ткачиха
экология
Дженкин
273
неотличимый
данные
шоссе
игнорируется
Куросу
недооцененный
льготный
1509
бардачок
осадок
усадка
6611
1325
вентилятор
против
131
после
Тран
ЭКОСИСТЕМЫ
032017
нагахара
R6
назад
топография
VI
imperviou
градиент
32660
количественный
отвечать
Найфелер
пространственно
680
поднос
возможность
δ15NS
готовность
увольнять
Росси
Vriesacker
ацетилен
концептуализировать
инактивировать
карш
учиться
растущий
выезд
разница
путь
1997 г.
биомы
18O
окислитель
Бельгия
охватывать
преобразование
ФАО
зазывал
автоклавирование
1747
Устранить
Годой
ЗАДНИЙ ПЛАН
прокариотический
EPA
оценка
коллективно
эвакуирован
инструмент
пфаннкуче
вырос
Тома
сильно
откалибровать
Nh4OH
1453
чен
на
переоценен
Чжунцзе
составной
документ
ИЗБЫТОК
все
новый
616
оценка
отвесный
Кан
лопаться
h3O2
мкдюйм
полностью
продвигать
дефолт
эпизодический
3672
Corning
эукариотический
квази
рассмотрел
аммиак
Освальд
осторожно
соответственно
нужный
Gilliland
развивать
средний запад
раскрытый
наох
RN
пирекс
мин
183
психрометрический
невозмутимый
опытный
коммуникация
13825
аэробный
усилить
вывод
407
нитрификатор
КБ
широта
376
широкий
цитируется
мельник
Валлехо
ваш
Colman
позирование
вторжение
148
гидроксиламин
лето
врущий
Переменная
удлиненный
резка
окончание
157
2009 г.
нуль
концентрация
Питт
НИТРИФИКАЦИЯ
199
опосредованный
Бернингер
CF
сопротивление
экологический
заштрихованный
Straus
узкий
эффективные
Кh4
автотрофный
бак
лежащий в основе
упражняться
приказ
следующий
стрелка
2122
родитель
ткачиха
экология
Дженкин
273
неотличимый
данные
шоссе
игнорируется
Куросу
недооцененный
льготный
1509
бардачок
осадок
усадка
6611
1325
вентилятор
против
131
после
Тран
ЭКОСИСТЕМЫ
032017
нагахара
R6
назад
топография
VI
imperviou
градиент
32660
количественный
отвечать
Найфелер
пространственно
680
поднос
возможность
δ15NS
готовность
увольнять
Росси
Vriesacker
ацетилен
концептуализировать
инактивировать
карш
учиться
растущий
выезд
разница
путь
1997 г.
биомы
18O
окислитель
Бельгия
охватывать
преобразование
ФАО
зазывал
автоклавирование
1747
Устранить
Годой
ЗАДНИЙ ПЛАН
прокариотический
EPA
оценка
коллективно
эвакуирован
инструмент
пфаннкуче
вырос
Тома
сильно
откалибровать
Nh4OH
1453
чен
на
переоценен
Чжунцзе
составной
документ
ИЗБЫТОК
все
новый
616
оценка
отвесный
Кан
лопаться
h3O2
мкдюйм
полностью
продвигать
дефолт
эпизодический
3672
Corning
эукариотический
квази
рассмотрел
аммиак
Освальд
осторожно
соответственно
нужный
Gilliland
развивать
средний запад
раскрытый
наох
RN
пирекс
мин
183
психрометрический
невозмутимый
опытный
коммуникация
13825
аэробный
усилить
вывод
407
нитрификатор
КБ
широта
376
широкий
цитируется
мельник
Валлехо
ваш
Colman
позирование
вторжение
148
гидроксиламин
лето
врущий
Переменная
удлиненный
резка
окончание
157
2009 г. АЗОТ
климер
действительный
проверенный
Брюн
гидрид
затемнять
смачивание
вхождение
отличаться
Япония
геология
624
уязвимый
гуминовый
371
в результате
204
держатель
фактически
сгенерированный
1990 г.
пропорциональный
814
G2
специальный
структурно
случайный
затронутый
884
в конечном счете
в целом
внутриклеточный
межгосударственный
гипобромит
749
spp
ОПИСАНИЕ
пролить
Амманн
Бергауст
арп
ɛNM
биогеохимия
аэробно
РЕЗУЛЬТАТЫ
2691
1071
спектрофотометр
превосходить
последовательный
вероятность
пробка
физика
G4
азот
8
2427
проба
очищение
интерпретировать
боросиликатный
вперед
датчик
ICS
отпечаток
Альстрём
179
стехиометрия
приобретенный
в сравнении
характеристика
крышка
соя
бавария
3882
Грейнджер
N2O5
тенденция
нету
субстрат
мелилло
сделал
отношение
Гарсия
48COMP
обширный
респираторный
десять
нарушенный
Arisci
Хатчинсон
распространение
метод
ей
не имеющий отношения
внешний
любой
определять
258
более
материал
141
углерод
дуэт
касательно
потолок
упорство
изгородь
отчет
Magill
сентябрь
подробный
оперативный
самый
мужен
анализировать
HONO
900
СО2
продемонстрировать
теплица
318
Wormhoudt
8823
бентосный
пустыня
имел
набор данных
Информация
Poeschl
см x 240
оборудованный
ангела
шприц
0825
хронический
галло
080
буря
частица
амид
эксплуатируемый
измерение
формирование
Seitzinger
451
Hoegberg
Кана
биоразнообразие
0080
стена
помеченный
соответствующие
Lovett
Lim
зима
Ганди
фаза
булыжник
Платформа
много
процедура
похуй
объяснил
часть
540
Purdue
1732 г.
АЗОТ
климер
действительный
проверенный
Брюн
гидрид
затемнять
смачивание
вхождение
отличаться
Япония
геология
624
уязвимый
гуминовый
371
в результате
204
держатель
фактически
сгенерированный
1990 г.
пропорциональный
814
G2
специальный
структурно
случайный
затронутый
884
в конечном счете
в целом
внутриклеточный
межгосударственный
гипобромит
749
spp
ОПИСАНИЕ
пролить
Амманн
Бергауст
арп
ɛNM
биогеохимия
аэробно
РЕЗУЛЬТАТЫ
2691
1071
спектрофотометр
превосходить
последовательный
вероятность
пробка
физика
G4
азот
8
2427
проба
очищение
интерпретировать
боросиликатный
вперед
датчик
ICS
отпечаток
Альстрём
179
стехиометрия
приобретенный
в сравнении
характеристика
крышка
соя
бавария
3882
Грейнджер
N2O5
тенденция
нету
субстрат
мелилло
сделал
отношение
Гарсия
48COMP
обширный
респираторный
десять
нарушенный
Arisci
Хатчинсон
распространение
метод
ей
не имеющий отношения
внешний
любой
определять
258
более
материал
141
углерод
дуэт
касательно
потолок
упорство
изгородь
отчет
Magill
сентябрь
подробный
оперативный
самый
мужен
анализировать
HONO
900
СО2
продемонстрировать
теплица
318
Wormhoudt
8823
бентосный
пустыня
имел
набор данных
Информация
Poeschl
см x 240
оборудованный
ангела
шприц
0825
хронический
галло
080
буря
частица
амид
эксплуатируемый
измерение
формирование
Seitzinger
451
Hoegberg
Кана
биоразнообразие
0080
стена
помеченный
соответствующие
Lovett
Lim
зима
Ганди
фаза
булыжник
Платформа
много
процедура
похуй
объяснил
часть
540
Purdue
1732 г. хлористый
337
iii
врач
Lucero
Рико
левый
571
оценка
эксперимент
SMC
Лебауэр
факт
продолжительность жизни
видимый
Dinicola
ссылаться
4153
на
инвентаризация
Только
5902
корреляция
Nadelhoffer
1608
chien
Я БЫ
шумный
ИЗОТОПЫ
ИСТОЧНИКИ
234
594
фермент
всегда
уравновешенный
007
совокупность
записанный
hox
тщательно
0002
1000
взвешивание
вход
Nkamdjou
снегопад
остаток
гидрологический
потребление
193
парк
119
Коулман
бай
Мэтисон
разумный
производство
5954
00055
сильный
большой
устойчивый
430
447
гамма
внеклеточный
приближаться
сбалансированный
Ферретти
R2
дериватизация
инверсия
эмпирический
встретиться
в
Семь
еженедельно
003
пастбище
хорошо
ОГО
изготовление
перекрывать
зависимый
шейкер
N2O
аллегрини
решено
VSMOW
беспокойство
покос
систематический
использованный
2061
трубка
762
0012
государство
9609
1723 г.
Маттеуччи
Аппалачский
наверное
атом
144
Belser
Стюарт
песок
Джон
нарушение
восстановлен
15НО
отложенный
177
капилляр
связанный
тропический лес
нейтрализация
205
поток
Mcilvin
гора
обеспечен
экологически
9943
осаждение
14N
поведение
Бертрам
Наварро
увеличение
493
DFC
герцог
подготовка
рубра
наименее
в зависимости
обочина
1993 г.
хлористый
337
iii
врач
Lucero
Рико
левый
571
оценка
эксперимент
SMC
Лебауэр
факт
продолжительность жизни
видимый
Dinicola
ссылаться
4153
на
инвентаризация
Только
5902
корреляция
Nadelhoffer
1608
chien
Я БЫ
шумный
ИЗОТОПЫ
ИСТОЧНИКИ
234
594
фермент
всегда
уравновешенный
007
совокупность
записанный
hox
тщательно
0002
1000
взвешивание
вход
Nkamdjou
снегопад
остаток
гидрологический
потребление
193
парк
119
Коулман
бай
Мэтисон
разумный
производство
5954
00055
сильный
большой
устойчивый
430
447
гамма
внеклеточный
приближаться
сбалансированный
Ферретти
R2
дериватизация
инверсия
эмпирический
встретиться
в
Семь
еженедельно
003
пастбище
хорошо
ОГО
изготовление
перекрывать
зависимый
шейкер
N2O
аллегрини
решено
VSMOW
беспокойство
покос
систематический
использованный
2061
трубка
762
0012
государство
9609
1723 г.
Маттеуччи
Аппалачский
наверное
атом
144
Belser
Стюарт
песок
Джон
нарушение
восстановлен
15НО
отложенный
177
капилляр
связанный
тропический лес
нейтрализация
205
поток
Mcilvin
гора
обеспечен
экологически
9943
осаждение
14N
поведение
Бертрам
Наварро
увеличение
493
DFC
герцог
подготовка
рубра
наименее
в зависимости
обочина
1993 г. 919
400
процент
Ellgas
Бухвальд
введение
1977 г.
МЕТОДЫ
фиксированный
Bollinger
Леманн
переоценка
Натик
окислять
подвыборка
1959 г.
бумага
к несчастью
получила
Шервелл
1242
последний
15αNC
униформа
расчет
уголь
034101
Обновить
кислый
Привет
следующий
почти
флуориметр
разделенный
скитер
сделка
БЫСТРЫЙ
110
метанол
к
ценность
находка
уравновешивание
Фёрстнер
смещение
содержать
обзор
Беннер
двенадцать
воздвигнут
разные
Берлин
судьба
646
незначительный
Спецификация
наука
Щебак
средний диапазон
сделать
количественно
6151
поддержание
крепкий
1288
август
Bradshaw
горящий
прохождение
советник
Вход
эмпирически
227
1860 г.
Подсказка
9615
баббин
кинетический
2013
уход
Коэн
названный
середина
чрезмерное сокращение
на месте
отображается
Пуэрто
трансформация
передача
вторичный
Фальковский
IRMS
применяемый
немного
Agili
комитет
функция
особенно
АЗОТ
Саино
обработка
фильм
достаточность
приблизительный
гра
постоянный
улучшение
устойчивость
не
Пирсон
против
водосбор
рассматривается
G04020
Hilkert
земной
xiv
обратно
пинель
внимательно
1361
страдания
6063
фотолизи
двигатель
песчаник
подтверждение
общество
M005
метка
psample
принужденный
щетка
отсутствует
ДАННЫЕ
Бекки
заболачивание
внутри
способность
отреагировал
улучшать
бездичек
подозревать
Cardena
1869 г.
919
400
процент
Ellgas
Бухвальд
введение
1977 г.
МЕТОДЫ
фиксированный
Bollinger
Леманн
переоценка
Натик
окислять
подвыборка
1959 г.
бумага
к несчастью
получила
Шервелл
1242
последний
15αNC
униформа
расчет
уголь
034101
Обновить
кислый
Привет
следующий
почти
флуориметр
разделенный
скитер
сделка
БЫСТРЫЙ
110
метанол
к
ценность
находка
уравновешивание
Фёрстнер
смещение
содержать
обзор
Беннер
двенадцать
воздвигнут
разные
Берлин
судьба
646
незначительный
Спецификация
наука
Щебак
средний диапазон
сделать
количественно
6151
поддержание
крепкий
1288
август
Bradshaw
горящий
прохождение
советник
Вход
эмпирически
227
1860 г.
Подсказка
9615
баббин
кинетический
2013
уход
Коэн
названный
середина
чрезмерное сокращение
на месте
отображается
Пуэрто
трансформация
передача
вторичный
Фальковский
IRMS
применяемый
немного
Agili
комитет
функция
особенно
АЗОТ
Саино
обработка
фильм
достаточность
приблизительный
гра
постоянный
улучшение
устойчивость
не
Пирсон
против
водосбор
рассматривается
G04020
Hilkert
земной
xiv
обратно
пинель
внимательно
1361
страдания
6063
фотолизи
двигатель
песчаник
подтверждение
общество
M005
метка
psample
принужденный
щетка
отсутствует
ДАННЫЕ
Бекки
заболачивание
внутри
способность
отреагировал
улучшать
бездичек
подозревать
Cardena
1869 г. параметризация
591
вероятно
Quercu
короче
102
укоренение
ответил
акимото
259
азот ‘
гроза
обнаружен
163
нитрат
положительный
устойчивый
иллюстрированный
1333
корректирование
Gasmire
СНИЖЕНИЕ
спутник
выводить
Scharko
вариация
гагара
442
пятно
быстро
точный
мон
Herndon
Питтсбург
Удалить
обойти
моделирование
Франция
320
3528
побег
соль
чжу
меняйло
249
минерализатор
1177
0015
сдвиг
16O
разум
бросаться
Генри
5131
385
18Fh3O
коль
RNM
USGS26
климатически
1378
сегрегация
073
награда
сотня
619
просер
продукт
полузасушливый
Като
акрил
азотный
учитывать
ОКРУГ КОЛУМБИЯ
дырявый
курс
понижение
кайзер
титрованный
роллин
различные
602
мыло
ниже
GB1001
в составе
моль
Opennes
конкретный
1391
freitag
денман
дизайн
РЕАКЦИЯ
недооценивать
214
D8
Колановский
внутренний
студия
нмоль
торможение
Хорнбергер
aureofacien
USGS25
преследовать
гидрологический
15ɛ
американец
блэкмер
цай
3877
санитарный
равномерно
концепция
всплеск
Руссоу
Мацумото
колориметрический
загрязнение
произошел
неоплодотворенный
вовлеченный
O0
объединились
исправлено
разное
feig
интимный
северный
эксплуатирующий
minu
значение
преходящий
срок
628
1223
оксфорд
Кроме
распределение
показательный
Шрайбер
Университет
испускается
принцип
пероксиацетил
расследование
Гензель
Шаттлворт
двусмысленный
1234
отмеченный
Другая
противоречивый
1474
цель
дизель
Посмотреть
125
возник
формирование
депонированный
2008 г.
параметризация
591
вероятно
Quercu
короче
102
укоренение
ответил
акимото
259
азот ‘
гроза
обнаружен
163
нитрат
положительный
устойчивый
иллюстрированный
1333
корректирование
Gasmire
СНИЖЕНИЕ
спутник
выводить
Scharko
вариация
гагара
442
пятно
быстро
точный
мон
Herndon
Питтсбург
Удалить
обойти
моделирование
Франция
320
3528
побег
соль
чжу
меняйло
249
минерализатор
1177
0015
сдвиг
16O
разум
бросаться
Генри
5131
385
18Fh3O
коль
RNM
USGS26
климатически
1378
сегрегация
073
награда
сотня
619
просер
продукт
полузасушливый
Като
акрил
азотный
учитывать
ОКРУГ КОЛУМБИЯ
дырявый
курс
понижение
кайзер
титрованный
роллин
различные
602
мыло
ниже
GB1001
в составе
моль
Opennes
конкретный
1391
freitag
денман
дизайн
РЕАКЦИЯ
недооценивать
214
D8
Колановский
внутренний
студия
нмоль
торможение
Хорнбергер
aureofacien
USGS25
преследовать
гидрологический
15ɛ
американец
блэкмер
цай
3877
санитарный
равномерно
концепция
всплеск
Руссоу
Мацумото
колориметрический
загрязнение
произошел
неоплодотворенный
вовлеченный
O0
объединились
исправлено
разное
feig
интимный
северный
эксплуатирующий
minu
значение
преходящий
срок
628
1223
оксфорд
Кроме
распределение
показательный
Шрайбер
Университет
испускается
принцип
пероксиацетил
расследование
Гензель
Шаттлворт
двусмысленный
1234
отмеченный
Другая
противоречивый
1474
цель
дизель
Посмотреть
125
возник
формирование
депонированный
2008 г. ранжирование
высосанный
сидеть
дабундо
термо
2663
СПИСОК
метеорология
бирюзовый
размешать
Кэтскилл
лес
ОПРЕДЕЛЕНИЕ
Катерина
мощный
PFA
манера
ФИГУРА
неуправляемый
Relie
Левика
характеризуя
преодоление
шлейф
обязательный
увлажненный
шавит
MJ
зондирование
стрес
экономия
сухая земля
мнение
исключительно
186
написать
1119
культура
изгиб
коммерческий
руководство
Вашингтон
стратифицированный
щелочной
датум
1986 г.
Уолтер
Δ17Ο
межмолекулярный
сломанный
частичный
выбор
титрование
xxii
18αh3O
USGS34
микробиологически
все больше
17α
Что ж
обменялся
предотвращение
недавний
кеттерер
химия
испаряться
ценность
потенциал
разлагать
качиотти
ряд
Mcdermitt
гипоксический
геохимический
талбот
засаженный деревьями
сотовый
абстрагированный
Пельтье
такси
никто
Соломон
прес
последовал
регулируемый
бассейн
связаны
6001
моделировать
5594
изобарический
инкубация
Карр
Бинкли
разделенный
щебнистый
индейцы
указание
N86
подходящее
Шире
экскурсия
сосуществование
156
неуравновешенный
эвтрофикация
ɛeq
RHT50
15αНМ
монолит
Мир
40oc
поток
стерильный
величайший
маркер
прямой
рано
Voerkeliust
Инжир
2015a
Furtaw
Кh5
несовместимый
диазот
исправленный
охте
196
Себастьен
Дорога
воздуха
ТРАГНИТ
Кроме того
Continou
118
ниша
луг
форма
𝜇in
сезонный
давать
оказывать
уникальный
R3
437
194
филогения
биогеохимический
риха
дополнительный
точность
равновесие
фигура
масштабирование
Нимейер
934
ежегодный
листовая
1989 г.
ранжирование
высосанный
сидеть
дабундо
термо
2663
СПИСОК
метеорология
бирюзовый
размешать
Кэтскилл
лес
ОПРЕДЕЛЕНИЕ
Катерина
мощный
PFA
манера
ФИГУРА
неуправляемый
Relie
Левика
характеризуя
преодоление
шлейф
обязательный
увлажненный
шавит
MJ
зондирование
стрес
экономия
сухая земля
мнение
исключительно
186
написать
1119
культура
изгиб
коммерческий
руководство
Вашингтон
стратифицированный
щелочной
датум
1986 г.
Уолтер
Δ17Ο
межмолекулярный
сломанный
частичный
выбор
титрование
xxii
18αh3O
USGS34
микробиологически
все больше
17α
Что ж
обменялся
предотвращение
недавний
кеттерер
химия
испаряться
ценность
потенциал
разлагать
качиотти
ряд
Mcdermitt
гипоксический
геохимический
талбот
засаженный деревьями
сотовый
абстрагированный
Пельтье
такси
никто
Соломон
прес
последовал
регулируемый
бассейн
связаны
6001
моделировать
5594
изобарический
инкубация
Карр
Бинкли
разделенный
щебнистый
индейцы
указание
N86
подходящее
Шире
экскурсия
сосуществование
156
неуравновешенный
эвтрофикация
ɛeq
RHT50
15αНМ
монолит
Мир
40oc
поток
стерильный
величайший
маркер
прямой
рано
Voerkeliust
Инжир
2015a
Furtaw
Кh5
несовместимый
диазот
исправленный
охте
196
Себастьен
Дорога
воздуха
ТРАГНИТ
Кроме того
Continou
118
ниша
луг
форма
𝜇in
сезонный
давать
оказывать
уникальный
R3
437
194
филогения
биогеохимический
риха
дополнительный
точность
равновесие
фигура
масштабирование
Нимейер
934
ежегодный
листовая
1989 г. Захнисер
развился
WFPS
существование
построен
Декабрь
исследовал
ложь
LG
ЧИСЛЕННЫЙ
люминол
полученный
континентальный
денк
разъяснять
подавляющий
авторское право
деайсер
июль
возможно
1110
аверит
1999 г.
шо
036
мая
6082
зал
разные
функциональный
15ФНх5
бербиджье
алмаз
тани
установлен
прикрепил
Цяо
немедленный
2201
HL
18αNC
изопрен
Роман
11574
соглашение
эта
1992 г.
под давлением
чт
Wunderlich
Андрей
720
244
Catalysi
Treseder
18R
внимание
Норвегия
δ18O
Dieleman
резюмированный
чанг
влага
062017
МЕТОД
1536
жесткий
травяной
иллюстрация
номер
ИЗУЧЕНИЕ
полезные
1618
двусмысленность
кПа
оптимизированный
ошибка
541
андреани
Мебюст
Кочендерфер
актуальность
утечка
удалось
в настоящее время
112016
мириады
клемпут
Дэвидсон
Население
прибрежный
контрольная работа
Рустад
производить
sccm
С ИСПОЛЬЗОВАНИЕМ
Мединет
Милли
100
18εR
300
иллюстративный
столбец
мешок
Zumft
Tharp
как
идентичный
алевролит
событие
NC0275433
их
сохранил
масштаб
относящийся
Лучший
неравный
следовательно
имея
кислород
Денни
медленно
жарить
катализированный
Лента
включены
𝑁𝐻4
McCalley
интерпретация
эмиссия
выдохнул
промытый
ломка
вопрос
негодяй
171
давление
гранула
унесенный
далеко
многообразие
обязательный
магний
КАТАНИЕ НА ВЕЛОСИПЕДЕ
2012 г.
Захнисер
развился
WFPS
существование
построен
Декабрь
исследовал
ложь
LG
ЧИСЛЕННЫЙ
люминол
полученный
континентальный
денк
разъяснять
подавляющий
авторское право
деайсер
июль
возможно
1110
аверит
1999 г.
шо
036
мая
6082
зал
разные
функциональный
15ФНх5
бербиджье
алмаз
тани
установлен
прикрепил
Цяо
немедленный
2201
HL
18αNC
изопрен
Роман
11574
соглашение
эта
1992 г.
под давлением
чт
Wunderlich
Андрей
720
244
Catalysi
Treseder
18R
внимание
Норвегия
δ18O
Dieleman
резюмированный
чанг
влага
062017
МЕТОД
1536
жесткий
травяной
иллюстрация
номер
ИЗУЧЕНИЕ
полезные
1618
двусмысленность
кПа
оптимизированный
ошибка
541
андреани
Мебюст
Кочендерфер
актуальность
утечка
удалось
в настоящее время
112016
мириады
клемпут
Дэвидсон
Население
прибрежный
контрольная работа
Рустад
производить
sccm
С ИСПОЛЬЗОВАНИЕМ
Мединет
Милли
100
18εR
300
иллюстративный
столбец
мешок
Zumft
Tharp
как
идентичный
алевролит
событие
NC0275433
их
сохранил
масштаб
относящийся
Лучший
неравный
следовательно
имея
кислород
Денни
медленно
жарить
катализированный
Лента
включены
𝑁𝐻4
McCalley
интерпретация
эмиссия
выдохнул
промытый
ломка
вопрос
негодяй
171
давление
гранула
унесенный
далеко
многообразие
обязательный
магний
КАТАНИЕ НА ВЕЛОСИПЕДЕ
2012 г. также
582
клен
ткань
Boltenstern
распределение
нелинейный
Связанный
водораздел
гетеротрофный
5303
слишком
центрифугированный
над
паре
во многом
пуят
Пальто
схематический
разбавление
Roeckmann
ПР
соглашение
закрытый
хотя
не допустить
золотой
улучшение
задокументированный
2000b
соответствие
Шервин
h4PO4
прибрежный
2167
1980 г.
Соединенное Королевство
предполагать
smarttrak
статистический
соответствовать
15ɛNC
непараметрический
матрица
двунаправленный
как
дальнобойный
собирать
себило
поддерживать
voeroesmarty
страх
признал
особенно
автоматизированный
экология
включают
ха
навряд ли
стоя
резать
свидетельство
3865
126
ИСКУССТВО
ПОКАЗАТЬ
активирован
точно
1533
3679
Steefel
ограничение
176
15ɛR
ПОТРЕБЛЕНИЕ
256
европа
хром
вызванный
рост
ПИТТСБУРГ
Craig
Мировой
универсальный
Galloway
тильман
уточненный
500
1221
обогащать
Остром
на основе
1200
хвостовик
раштеттер
фарадей
озеро
экстраполяция
1856 г.
упакованный
каталог
OPA
Рихтер
остаточный
632
Джейкоб
спектрометр
поспешный
jaegle
традиционно
Брайан
деревенский
Оярзун
2645
зависеть
извлеченный
единица измерения
орех
𝐩𝐫𝐨𝐝𝐮𝐜𝐭𝐬
полуактивный
боль
сделал
фотосинтетический
пространственный
Хада
Spoelstra
химиотерапия
поле
3662
нитробактер
завершение
215
предварительный расчет
больше
такой
форма
неоднородность
КОНВЕРСИЯ
иммобилизация
Ван
степень
эквивалент
дворецкий
применять
звон
FL
приелись
Текущий
подкомитет
пример
обсуждались
июнь
Стоддард
банкомат
пелерин
падение
тефлон
речной банк
явно
север
баня
730
оценен
литр
921
Rixen
объединение
граница
член
камера
Savarino
hcl
дискриминация
15εNC
смоделированный
возвышенный
xxi
соленая вода
сторожить
цилиндрический
время
поддерживать
оценивать
Мюррей
Doersch
денитрифицированный
15N
3040
Leclerc
циклический
спрингер
1306
сообщество
429
Widner
континуум
управляемый
Goodale
обычно
лесной массив
Ковальский
ну и дела
осадочный
человек
сын
классический
489
осадки
Искра
дважды
15εR
Kuyper
оценка
1080
вакуум
рамки
вмешиваться
Bonferroni
732
FLUXNET
выхлоп
склонный
серия
братан
связь
изотоп
харт
Estavillo
канеко
шпион
геномный
вихревой
научный
вирт
хлорат
бурение
предсказуемый
сложный
полночь
1237
Levene
2361
беспокойство
девять
клетка
Айкен
перестановка
испарительный
восстановлениеb
закрыто
фен
удобрение
Ярви
Brenninkmeijer
покрытый
диод
мост
объясняя
очевидный
поездка
Mroczkowski
показал
загадочный
FEMS
270
Международный
заполненный
самый большой
представлять
Boeckx
реакция
xiii
XXII
2007 г.
также
582
клен
ткань
Boltenstern
распределение
нелинейный
Связанный
водораздел
гетеротрофный
5303
слишком
центрифугированный
над
паре
во многом
пуят
Пальто
схематический
разбавление
Roeckmann
ПР
соглашение
закрытый
хотя
не допустить
золотой
улучшение
задокументированный
2000b
соответствие
Шервин
h4PO4
прибрежный
2167
1980 г.
Соединенное Королевство
предполагать
smarttrak
статистический
соответствовать
15ɛNC
непараметрический
матрица
двунаправленный
как
дальнобойный
собирать
себило
поддерживать
voeroesmarty
страх
признал
особенно
автоматизированный
экология
включают
ха
навряд ли
стоя
резать
свидетельство
3865
126
ИСКУССТВО
ПОКАЗАТЬ
активирован
точно
1533
3679
Steefel
ограничение
176
15ɛR
ПОТРЕБЛЕНИЕ
256
европа
хром
вызванный
рост
ПИТТСБУРГ
Craig
Мировой
универсальный
Galloway
тильман
уточненный
500
1221
обогащать
Остром
на основе
1200
хвостовик
раштеттер
фарадей
озеро
экстраполяция
1856 г.
упакованный
каталог
OPA
Рихтер
остаточный
632
Джейкоб
спектрометр
поспешный
jaegle
традиционно
Брайан
деревенский
Оярзун
2645
зависеть
извлеченный
единица измерения
орех
𝐩𝐫𝐨𝐝𝐮𝐜𝐭𝐬
полуактивный
боль
сделал
фотосинтетический
пространственный
Хада
Spoelstra
химиотерапия
поле
3662
нитробактер
завершение
215
предварительный расчет
больше
такой
форма
неоднородность
КОНВЕРСИЯ
иммобилизация
Ван
степень
эквивалент
дворецкий
применять
звон
FL
приелись
Текущий
подкомитет
пример
обсуждались
июнь
Стоддард
банкомат
пелерин
падение
тефлон
речной банк
явно
север
баня
730
оценен
литр
921
Rixen
объединение
граница
член
камера
Savarino
hcl
дискриминация
15εNC
смоделированный
возвышенный
xxi
соленая вода
сторожить
цилиндрический
время
поддерживать
оценивать
Мюррей
Doersch
денитрифицированный
15N
3040
Leclerc
циклический
спрингер
1306
сообщество
429
Widner
континуум
управляемый
Goodale
обычно
лесной массив
Ковальский
ну и дела
осадочный
человек
сын
классический
489
осадки
Искра
дважды
15εR
Kuyper
оценка
1080
вакуум
рамки
вмешиваться
Bonferroni
732
FLUXNET
выхлоп
склонный
серия
братан
связь
изотоп
харт
Estavillo
канеко
шпион
геномный
вихревой
научный
вирт
хлорат
бурение
предсказуемый
сложный
полночь
1237
Levene
2361
беспокойство
девять
клетка
Айкен
перестановка
испарительный
восстановлениеb
закрыто
фен
удобрение
Ярви
Brenninkmeijer
покрытый
диод
мост
объясняя
очевидный
поездка
Mroczkowski
показал
загадочный
FEMS
270
Международный
заполненный
самый большой
представлять
Boeckx
реакция
xiii
XXII
2007 г. доминирующий
неопубликованный
nahco3
сульфаминовый
элемент
примерка
после этого
103
ВСЕГО
871
фотосинтез
макрос
зонд
отдельно
достигать
Dijk
бутылка
высота
отзывчивый
производство
моди
молния
банка
тамм
тупица
Пенсильвания
feq
кипение
18rref
полезный
NIR
БЕДРО
смола
Гранье
slpm
загрязнение
изменить
ил
коба
снижение
Ванкель
ясность
способствовал
грубый
Блейк
выложенный
Staelen
достаточно
последствие
группа
Джанель
143
псевдо
использовать
запечатанный
рядом
3033
неделю
Тамдруп
несмотря на
стимулировать
Паулино
до того как
2732
ковариация
слейтер
Holtappel
1735 г.
Нью-Йорк
колеблется
форма
Джонсон
𝐰𝐚𝐥𝐥
такахаши
температура
неточечный
гоф
комбайн
17Fh3O
779
chidthaisong
возникать
взвешенный
межправительственный
Эриксон
ароматизировать
уверенность
логарифм
коробка
ИЗМЕНЕНО
сенбайрам
сосна
микробиологический
Marland
15αeq
сушеный
Vitousek
Скотт
Кестер
закрытый
261
каджии
северный
Янссен
321
Тильзнер
инкубацияb
акт
Walli
изменение
1652
существенный
24235
марш
типичный
Маритиму
звезда
серотина
уступил
поправить
парень
болезнь
пресная вода
впоследствии
учреждать
лед
Камарго
наблюдаемый
Столповский
подавлять
потребляющий
рост
хокари
раз в два месяца
понятие
учредил
осложнение
значит
Numberrou
17FO2
облучение
сито
потраченный
643
Шрайдер
палка
одновременный
ИМО
сохранение
019
RP
зондирование
пунктирная
Perrier
Санти
облученный
различимый
активация
постоянный
любопытство
Kroopnick
1095
Йобуэ
анаммокс
гетеротроф
начало
строго
эффективность
старение
inc
рядом, поблизости
диапазон
вернулся
kmno4
дух
перевозчик
Herbst
Ланьчжоу
средний
корень
133
Ян
Фернандес
доминировать
особенно
эффект
искаженный
коробка передач
Щебак
отклоненный
катион
монета
эксплуатировать
Abalo
откалиброван
предполагаемый
снайдер
перспектива
166
зародыш
катализировать
Laanbroek
Mosier
134
квадратичный
0074
вентилируемый
пинэ
реагировать
МАГАТЭ
крупный
начальный
место
затемненный
леймер
отсутствует
гипотеза
Шавив
выше
1134
США
помощь
гравиметрический
соревнование
комбинированный
разрешение
худман
185
претерпел
играть в
снег
1719
обратимый
шум
127
усиленный
морди
Allsman
псевдомона
выброс
скромный
AIBS
ограничение
Armanet
сульфат
обслуживать
умеренный
076
эксикатор
переставил
146i
гил
722
валин
молекула
обычай
последовательно
региональный
проверено
уменьшать
тюлень
на виду
изучал
h3O
153
земля
101
фракционированный
Санторо
340
доступность
Brodie
прогрессирует
Мероприятия
размещен
присутствие
городской
ЯМР
изготовление
взаимно
параметр
благодарить
поддержание
тип
4912
ДИЕТРИХ
эдафический
секвестрация
курок
2285
смоделированный
поглощающий
философский
контекст
pka
Frostegard
скруббер
реактивный
баркан
бермуды
новаторский
несоответствие
природа
одновременно
Примечание
поддержанный
там
𝑁𝑂2
укомплектование персоналом
исследовал
391
очистка
S1
Лоуренс
180
пошагово
юг
Фрейни
частично
17rref
луз
верхняя
избыток
Эмили
водоносный горизонт
СТАБИЛЬНЫЙ
измерение
определенный
хемоавтотрофный
охотно
происходить
профессиональный
маркировка
D19
различный
напрямую
количество
Warneke
Юбер
пальта
лазер
Эрисман
Флора
Китай
фракционирование
Перес
Quere
аномалоу
2000a
энзимология
ВЫВОДЫ
unles
спектроскопия
Морейра
проявляется
136
подтвержденный
несоответствие
116
систематически
меж
Стэнли
немного
измеримый
ассимиляционный
Йорк
помощник
18αeq
14forgn
дует
001
МОДЕЛИРОВАНИЕ
контакт
сезонность
Хагерстаун
Торре
должен
301
Пардо
Schleppi
456
рассчитанный
D12
Mcnulty
1033
N2
применение
Марки
количественная оценка
принуждение
бар
река
смоченный
бубенчик
бентологический
отлично
5136
учил
интерес
δ18
часто
Исследователь
пылесосить
st2
артефакт
дри
минеральная
KL
инкубированный
в результате
фосфат
349
Hallett
Ремде
строить
разбавленный
коэффициент
вычитание
137
показатель
неорганический
себя
1074
предложенный
лечение
Glatz
O3
известен
эра
хроматограф
не понятно
187
трумбор
005
керамика
предположение
недооценка
212
направленный
2436
полагаясь
взаимодействовать
положительно
СООТВЕТСТВИЕ
10931
фольга
KNO3
морская вода
Wilcke
неоднородный
линия
runge
лян
этилендиамин
108
рыболов
полезный
результат
330
биология
фух
геном
решение
текст
отражающий
заявил
дом
типичный
012017
полученный
милость
биохимический
исправление
деталь
автоматически
449
хемилюминесценция
Маклафлин
ПРЕДИСЛОВИЕ
диск
ET
1579
ШКОЛА
необходимость
преобладающе
Монтейт
параллельный
составил
земной шар
353
375
Nalgene
интерфейс
НИ
получение
чашка
предлагая
за пределами
интервал
выполненный
подтверждено
сбор
дурка
вести себя
Васкес
Куинн
155
мамтимин
взаимодействие
ГУБКА
треб
Houghton
молодой
благодарен
центр
клотц
с шипами
257
физический
расшифровать
прощай
работающий
1156
знание
δ15НМ
возникший
нафтил
микробиология
метаболизм
подавлять
чувствительный
допуск
трудный
инкубация
указал
скобка
GV
насыщенность
фотохимический
различение
ловушка
520
программа
гистограмма
Дженетта
сила
Tiedje
период
несмотря на то что
субстанция
сгруппированный
важный
Старый
из-за
175
БИБЛИОГРАФИЯ
сравнение
Дженсен
все
Gilpin
окислительно-восстановительный потенциал
7883
переполнение
GC
Барфорд
наивысший
оплодотворение
34𝑢2
Fendorf
проходящий
2006 г.
доминирующий
неопубликованный
nahco3
сульфаминовый
элемент
примерка
после этого
103
ВСЕГО
871
фотосинтез
макрос
зонд
отдельно
достигать
Dijk
бутылка
высота
отзывчивый
производство
моди
молния
банка
тамм
тупица
Пенсильвания
feq
кипение
18rref
полезный
NIR
БЕДРО
смола
Гранье
slpm
загрязнение
изменить
ил
коба
снижение
Ванкель
ясность
способствовал
грубый
Блейк
выложенный
Staelen
достаточно
последствие
группа
Джанель
143
псевдо
использовать
запечатанный
рядом
3033
неделю
Тамдруп
несмотря на
стимулировать
Паулино
до того как
2732
ковариация
слейтер
Holtappel
1735 г.
Нью-Йорк
колеблется
форма
Джонсон
𝐰𝐚𝐥𝐥
такахаши
температура
неточечный
гоф
комбайн
17Fh3O
779
chidthaisong
возникать
взвешенный
межправительственный
Эриксон
ароматизировать
уверенность
логарифм
коробка
ИЗМЕНЕНО
сенбайрам
сосна
микробиологический
Marland
15αeq
сушеный
Vitousek
Скотт
Кестер
закрытый
261
каджии
северный
Янссен
321
Тильзнер
инкубацияb
акт
Walli
изменение
1652
существенный
24235
марш
типичный
Маритиму
звезда
серотина
уступил
поправить
парень
болезнь
пресная вода
впоследствии
учреждать
лед
Камарго
наблюдаемый
Столповский
подавлять
потребляющий
рост
хокари
раз в два месяца
понятие
учредил
осложнение
значит
Numberrou
17FO2
облучение
сито
потраченный
643
Шрайдер
палка
одновременный
ИМО
сохранение
019
RP
зондирование
пунктирная
Perrier
Санти
облученный
различимый
активация
постоянный
любопытство
Kroopnick
1095
Йобуэ
анаммокс
гетеротроф
начало
строго
эффективность
старение
inc
рядом, поблизости
диапазон
вернулся
kmno4
дух
перевозчик
Herbst
Ланьчжоу
средний
корень
133
Ян
Фернандес
доминировать
особенно
эффект
искаженный
коробка передач
Щебак
отклоненный
катион
монета
эксплуатировать
Abalo
откалиброван
предполагаемый
снайдер
перспектива
166
зародыш
катализировать
Laanbroek
Mosier
134
квадратичный
0074
вентилируемый
пинэ
реагировать
МАГАТЭ
крупный
начальный
место
затемненный
леймер
отсутствует
гипотеза
Шавив
выше
1134
США
помощь
гравиметрический
соревнование
комбинированный
разрешение
худман
185
претерпел
играть в
снег
1719
обратимый
шум
127
усиленный
морди
Allsman
псевдомона
выброс
скромный
AIBS
ограничение
Armanet
сульфат
обслуживать
умеренный
076
эксикатор
переставил
146i
гил
722
валин
молекула
обычай
последовательно
региональный
проверено
уменьшать
тюлень
на виду
изучал
h3O
153
земля
101
фракционированный
Санторо
340
доступность
Brodie
прогрессирует
Мероприятия
размещен
присутствие
городской
ЯМР
изготовление
взаимно
параметр
благодарить
поддержание
тип
4912
ДИЕТРИХ
эдафический
секвестрация
курок
2285
смоделированный
поглощающий
философский
контекст
pka
Frostegard
скруббер
реактивный
баркан
бермуды
новаторский
несоответствие
природа
одновременно
Примечание
поддержанный
там
𝑁𝑂2
укомплектование персоналом
исследовал
391
очистка
S1
Лоуренс
180
пошагово
юг
Фрейни
частично
17rref
луз
верхняя
избыток
Эмили
водоносный горизонт
СТАБИЛЬНЫЙ
измерение
определенный
хемоавтотрофный
охотно
происходить
профессиональный
маркировка
D19
различный
напрямую
количество
Warneke
Юбер
пальта
лазер
Эрисман
Флора
Китай
фракционирование
Перес
Quere
аномалоу
2000a
энзимология
ВЫВОДЫ
unles
спектроскопия
Морейра
проявляется
136
подтвержденный
несоответствие
116
систематически
меж
Стэнли
немного
измеримый
ассимиляционный
Йорк
помощник
18αeq
14forgn
дует
001
МОДЕЛИРОВАНИЕ
контакт
сезонность
Хагерстаун
Торре
должен
301
Пардо
Schleppi
456
рассчитанный
D12
Mcnulty
1033
N2
применение
Марки
количественная оценка
принуждение
бар
река
смоченный
бубенчик
бентологический
отлично
5136
учил
интерес
δ18
часто
Исследователь
пылесосить
st2
артефакт
дри
минеральная
KL
инкубированный
в результате
фосфат
349
Hallett
Ремде
строить
разбавленный
коэффициент
вычитание
137
показатель
неорганический
себя
1074
предложенный
лечение
Glatz
O3
известен
эра
хроматограф
не понятно
187
трумбор
005
керамика
предположение
недооценка
212
направленный
2436
полагаясь
взаимодействовать
положительно
СООТВЕТСТВИЕ
10931
фольга
KNO3
морская вода
Wilcke
неоднородный
линия
runge
лян
этилендиамин
108
рыболов
полезный
результат
330
биология
фух
геном
решение
текст
отражающий
заявил
дом
типичный
012017
полученный
милость
биохимический
исправление
деталь
автоматически
449
хемилюминесценция
Маклафлин
ПРЕДИСЛОВИЕ
диск
ET
1579
ШКОЛА
необходимость
преобладающе
Монтейт
параллельный
составил
земной шар
353
375
Nalgene
интерфейс
НИ
получение
чашка
предлагая
за пределами
интервал
выполненный
подтверждено
сбор
дурка
вести себя
Васкес
Куинн
155
мамтимин
взаимодействие
ГУБКА
треб
Houghton
молодой
благодарен
центр
клотц
с шипами
257
физический
расшифровать
прощай
работающий
1156
знание
δ15НМ
возникший
нафтил
микробиология
метаболизм
подавлять
чувствительный
допуск
трудный
инкубация
указал
скобка
GV
насыщенность
фотохимический
различение
ловушка
520
программа
гистограмма
Дженетта
сила
Tiedje
период
несмотря на то что
субстанция
сгруппированный
важный
Старый
из-за
175
БИБЛИОГРАФИЯ
сравнение
Дженсен
все
Gilpin
окислительно-восстановительный потенциал
7883
переполнение
GC
Барфорд
наивысший
оплодотворение
34𝑢2
Fendorf
проходящий
2006 г. вмещающий
приспособление
Эммет
Пачеко
081
1028
198
1059
попарно
распределение
Кендалл
красный
транспортируется
SE
засуха
относиться
связывание
h3
Всего
202
Islovay
экосистема
разработка
Мичиган
ppmv
ограничение
служба поддержки
1984
истощать
завернутый
307
фактор
отключение
154
мощный
косвенно
контроль
в том числе
голодать
rsample
Матанцева
голлабгир
LH
созданный
аэрозоль
ppbv
февраль
полный
часть
сам
конечный член
восстановление
балансировка
отображение
альбедо
содержание
сельское хозяйство
Хеммерих
ИЗОТОП
МГО
главным образом
амазонка
Кацуяма
йо
инкубатор
чернить
Butterbach
дать согласие
отрицательный
транспорт
древесина
бюджет
колари
Грибб
метаболический
географический
трубка
ниже
817
в течение
пурафил
размытый
изменен
свадьба
филогенетически
замороженный
Leibensperger
столкнулся
вероятный
сильно
несколько
кишка
Глубже
мариотти
Hynicka
Кизе
Кестер
оценка
ЦИСТЕРНЫ
Миядзаки
315
выбранный
ЧАЙ
одинаково
мыс
Подсказка
смоделированный
советник
в последнее время
продолжительность
глубина
разрешающая способность
гваякол
17FNO3
Basi
упорство
Райт
уменьшение
Jetten
различать
выщелачивание
окружающая обстановка
партия
банка
11447
1642
распределен
xviii
Гольдштейн
892
Шауэр
кабилинг
приложение
ANOVA
стали
аномалия
хриплый
vii
грунтовые воды
относительный
3298
обратный
открыть
Нанли
канал
значительный
важно
расширенный
выздоровление
величина
хекель
Остхофф
дионекс
характеристика
мобильный
алифат
изображен
содержал
метафора
2390
флуорометрический
высота
Диксон
приписанный
демонстрация
в качестве альтернативы
пространственно-временной
Мальдонадо
разработан
метеорологический
добыча
предсказывать
289
Почта
шустер
абиотический
тонкий
dμcham
147
десятилетний
квист
индуцированный
mno2
противоположный
географически
склон
объединенный
кольцевой
4188
Александр
Oни
связь
ускоренный
окись
определение
испанский язык
ингибитор
весьма
Luyssaert
неблагоприятный
6278
1104
одноклеточный
космохимический
Карлсен
атлантический
117
мемориал
ориентир
кислотность
прицеливание
10580
0009
микро
СОДЕРЖАНИЕ
удаление
благословение
минерализация
выдох
бону
НА ОСНОВЕ
область
в соответствии
NC0955678
испытывающий
способствуя
однородный
ежемесячно
051
цикл
пари
пахотный
NS
предсказанный
брезнак
статически
писатель
показывая
290
специализированный
гидроксил
210
фильтр
предложить
штат сотрудников
сумка
выпуск
обнажать
baert
утечка
искусственно
определение
7562A13
сравнивать
проанализированы
ɛO2
запись
НИТРАТ
Пармер
Deciduou
средства массовой информации
цинь
ОЙ
радиация
метан
совпадает
0082
WI
подъем
хлорорафы
δ15N
kcl
бурлящий
Отправлено
лизиметр
neu
выбирать
состоящий
чистый
главный
Steig
мел
вверх
классификация
базовый
271
Aubinet
количественная оценка
Goodwin
синий
водить машину
интерьер
альтернатива
широко
нагель
совет
существенно
840
осушенный
597
получение
отлично
недавно
мульти
разбавление
Schulze
идентифицировать
242
443
флесса
резина
Саймон
значение
Мартин
общепринятый
Betlach
нитрозирование
жизнь
продлевать
проверено
E2616
предмет
тем не менее
Маккенни
энергия
внутренний
система
месяц
проникновение
Люси
неуверенный
трилогия
ПОДГОТОВКА
5950
6740
Channery
желательно
каждый
ПОЛНЫЙ
средний
смена
дол
δ18ON
δпродукт
дуб
анализатор
002
изолированные
NC
модель
статический
хвойное дерево
национальный
D21310
Labglas
7795
субтропический
стоять
проспект
2890
добавление
135
145
НАУКИ
риск
772
Calderisi
закодированный
марка
забота
Киркман
адресованный
приспособить
ультисол
сдерживающий
сведение к минимуму
составлен
объяснять
плохо
2677
начало
давящий
скобка
подкисление
024
нагревать
072017
367
E2608
распутывать
подавленный
Лазарь
кинетически
медленный
высоко
ЗАДАЧИ
почва
N3
так же
дразнить
исчезновение
723
PA
измеренный
внутренний
строго
макабэ
выгода
NOX
учиться
доступный
рядом
1040
взволнованный
8232
оказывать воздействие
дедушка и бабушка
фундаментальный
катализирующий
0079
зилон
152
Велдкамп
охарактеризовать
Уракава
Калифорния
x1000
уплотнение
климат
341
кейс
реализовано
режим
денитрификатор
KNO2
губчатый
автомобильный
слабый
рис
дикое животное
Scharr
запущен
поощрение
смог
наблюдение
Серебряный
эффективно
поверхность
1963 г.
вмещающий
приспособление
Эммет
Пачеко
081
1028
198
1059
попарно
распределение
Кендалл
красный
транспортируется
SE
засуха
относиться
связывание
h3
Всего
202
Islovay
экосистема
разработка
Мичиган
ppmv
ограничение
служба поддержки
1984
истощать
завернутый
307
фактор
отключение
154
мощный
косвенно
контроль
в том числе
голодать
rsample
Матанцева
голлабгир
LH
созданный
аэрозоль
ppbv
февраль
полный
часть
сам
конечный член
восстановление
балансировка
отображение
альбедо
содержание
сельское хозяйство
Хеммерих
ИЗОТОП
МГО
главным образом
амазонка
Кацуяма
йо
инкубатор
чернить
Butterbach
дать согласие
отрицательный
транспорт
древесина
бюджет
колари
Грибб
метаболический
географический
трубка
ниже
817
в течение
пурафил
размытый
изменен
свадьба
филогенетически
замороженный
Leibensperger
столкнулся
вероятный
сильно
несколько
кишка
Глубже
мариотти
Hynicka
Кизе
Кестер
оценка
ЦИСТЕРНЫ
Миядзаки
315
выбранный
ЧАЙ
одинаково
мыс
Подсказка
смоделированный
советник
в последнее время
продолжительность
глубина
разрешающая способность
гваякол
17FNO3
Basi
упорство
Райт
уменьшение
Jetten
различать
выщелачивание
окружающая обстановка
партия
банка
11447
1642
распределен
xviii
Гольдштейн
892
Шауэр
кабилинг
приложение
ANOVA
стали
аномалия
хриплый
vii
грунтовые воды
относительный
3298
обратный
открыть
Нанли
канал
значительный
важно
расширенный
выздоровление
величина
хекель
Остхофф
дионекс
характеристика
мобильный
алифат
изображен
содержал
метафора
2390
флуорометрический
высота
Диксон
приписанный
демонстрация
в качестве альтернативы
пространственно-временной
Мальдонадо
разработан
метеорологический
добыча
предсказывать
289
Почта
шустер
абиотический
тонкий
dμcham
147
десятилетний
квист
индуцированный
mno2
противоположный
географически
склон
объединенный
кольцевой
4188
Александр
Oни
связь
ускоренный
окись
определение
испанский язык
ингибитор
весьма
Luyssaert
неблагоприятный
6278
1104
одноклеточный
космохимический
Карлсен
атлантический
117
мемориал
ориентир
кислотность
прицеливание
10580
0009
микро
СОДЕРЖАНИЕ
удаление
благословение
минерализация
выдох
бону
НА ОСНОВЕ
область
в соответствии
NC0955678
испытывающий
способствуя
однородный
ежемесячно
051
цикл
пари
пахотный
NS
предсказанный
брезнак
статически
писатель
показывая
290
специализированный
гидроксил
210
фильтр
предложить
штат сотрудников
сумка
выпуск
обнажать
baert
утечка
искусственно
определение
7562A13
сравнивать
проанализированы
ɛO2
запись
НИТРАТ
Пармер
Deciduou
средства массовой информации
цинь
ОЙ
радиация
метан
совпадает
0082
WI
подъем
хлорорафы
δ15N
kcl
бурлящий
Отправлено
лизиметр
neu
выбирать
состоящий
чистый
главный
Steig
мел
вверх
классификация
базовый
271
Aubinet
количественная оценка
Goodwin
синий
водить машину
интерьер
альтернатива
широко
нагель
совет
существенно
840
осушенный
597
получение
отлично
недавно
мульти
разбавление
Schulze
идентифицировать
242
443
флесса
резина
Саймон
значение
Мартин
общепринятый
Betlach
нитрозирование
жизнь
продлевать
проверено
E2616
предмет
тем не менее
Маккенни
энергия
внутренний
система
месяц
проникновение
Люси
неуверенный
трилогия
ПОДГОТОВКА
5950
6740
Channery
желательно
каждый
ПОЛНЫЙ
средний
смена
дол
δ18ON
δпродукт
дуб
анализатор
002
изолированные
NC
модель
статический
хвойное дерево
национальный
D21310
Labglas
7795
субтропический
стоять
проспект
2890
добавление
135
145
НАУКИ
риск
772
Calderisi
закодированный
марка
забота
Киркман
адресованный
приспособить
ультисол
сдерживающий
сведение к минимуму
составлен
объяснять
плохо
2677
начало
давящий
скобка
подкисление
024
нагревать
072017
367
E2608
распутывать
подавленный
Лазарь
кинетически
медленный
высоко
ЗАДАЧИ
почва
N3
так же
дразнить
исчезновение
723
PA
измеренный
внутренний
строго
макабэ
выгода
NOX
учиться
доступный
рядом
1040
взволнованный
8232
оказывать воздействие
дедушка и бабушка
фундаментальный
катализирующий
0079
зилон
152
Велдкамп
охарактеризовать
Уракава
Калифорния
x1000
уплотнение
климат
341
кейс
реализовано
режим
денитрификатор
KNO2
губчатый
автомобильный
слабый
рис
дикое животное
Scharr
запущен
поощрение
смог
наблюдение
Серебряный
эффективно
поверхность
1963 г. интегрированный
сфабрикованный
Mentel
2153
о
вниз
RS
120
определенный
Тейлор
флуоресценция
амин
4747
1148
тройка
пастбища
пробоотборник
ДОМАШНИЙ ПИТОМЕЦ
Ganzeveld
краскал
предварительная обработка
сложность
ядовитый
Steinberger
Киркхем
паскаль
Кардон
вместе
бревно
виван
213
OA
568
Берендт
𝑁𝑂3
СТРАТЕГИЯ
1143
изменение
нормальный
холодно
Фото
удобрять
технический
008
испускают
колебательный
непрозрачный
1457
след
200
1352
переписать
1621
161
сирульник
MN
Восток
Грошевский
регулирующий
109
мониторинг
дюран
диоксид
улучшен
δ15NA
использование
ТАБЛИЦА
Boyer
мкчам
представляющий
8750
0085
станция
искусство
климатический
Copeland
ковариация
галбально
аллен
разнообразный
урожай
EW
коренной зуб
изменчивость
разделение
загрязненный
понял
дробный
РАЗНОЕ
конкурирующий
активный
решено
1157
1470
Анттила
Магги
xxiii
бухгалтерский учет
толстый
влияние
увлажненный
формулировка
очевидный
исследовать
арабский
достигнуто
случайный
orgn
бегать
Мексика
Энгель
резервуар
Лю
позволяя
отвечать
Линь
ручей
Хансен
ассимиляция
372
распространенность
HNO2
Велтхоф
1661
НАСТРАИВАТЬ
треугольник
В настоящее время
δ15na
причаливать
независимо
удовлетворительно
Sheehy
слой
разделение
открыт
11363
1209
обнаружение
добавлен
коллекция
Рамка
канал
абстракция
Тревор
3535
домой
615
2246
раскрытый
разветвление
nusgs34_a
Fleischer
простота
долман
при условии
большой
затыкать
пара
ссора
удаленный
продолжить
относительно
по суше
смысл
пояс
Koopman
дер
322
пытаться
методологический
граница
ВЫВОД
USDA
последовательно
построен
Altabet
размноженный
легенда
ЭКСПЕРИМЕНТЫ
химический
масса
криофокусированный
лечение
тщательный
точность
отделенный
Уилсон
диск
контролировать
ПОЧВА
354
E6400
длинная
1064
охота
O2
склон холма
определять
крио
сила
абер
курицы
Tignor
реагент
мера
исходный
стать
Кремень
бесценный
биомонитор
Brookston
под наблюдением
1850 г.
интегрированный
сфабрикованный
Mentel
2153
о
вниз
RS
120
определенный
Тейлор
флуоресценция
амин
4747
1148
тройка
пастбища
пробоотборник
ДОМАШНИЙ ПИТОМЕЦ
Ganzeveld
краскал
предварительная обработка
сложность
ядовитый
Steinberger
Киркхем
паскаль
Кардон
вместе
бревно
виван
213
OA
568
Берендт
𝑁𝑂3
СТРАТЕГИЯ
1143
изменение
нормальный
холодно
Фото
удобрять
технический
008
испускают
колебательный
непрозрачный
1457
след
200
1352
переписать
1621
161
сирульник
MN
Восток
Грошевский
регулирующий
109
мониторинг
дюран
диоксид
улучшен
δ15NA
использование
ТАБЛИЦА
Boyer
мкчам
представляющий
8750
0085
станция
искусство
климатический
Copeland
ковариация
галбально
аллен
разнообразный
урожай
EW
коренной зуб
изменчивость
разделение
загрязненный
понял
дробный
РАЗНОЕ
конкурирующий
активный
решено
1157
1470
Анттила
Магги
xxiii
бухгалтерский учет
толстый
влияние
увлажненный
формулировка
очевидный
исследовать
арабский
достигнуто
случайный
orgn
бегать
Мексика
Энгель
резервуар
Лю
позволяя
отвечать
Линь
ручей
Хансен
ассимиляция
372
распространенность
HNO2
Велтхоф
1661
НАСТРАИВАТЬ
треугольник
В настоящее время
δ15na
причаливать
независимо
удовлетворительно
Sheehy
слой
разделение
открыт
11363
1209
обнаружение
добавлен
коллекция
Рамка
канал
абстракция
Тревор
3535
домой
615
2246
раскрытый
разветвление
nusgs34_a
Fleischer
простота
долман
при условии
большой
затыкать
пара
ссора
удаленный
продолжить
относительно
по суше
смысл
пояс
Koopman
дер
322
пытаться
методологический
граница
ВЫВОД
USDA
последовательно
построен
Altabet
размноженный
легенда
ЭКСПЕРИМЕНТЫ
химический
масса
криофокусированный
лечение
тщательный
точность
отделенный
Уилсон
диск
контролировать
ПОЧВА
354
E6400
длинная
1064
охота
O2
склон холма
определять
крио
сила
абер
курицы
Tignor
реагент
мера
исходный
стать
Кремень
бесценный
биомонитор
Brookston
под наблюдением
1850 г. Sollin
взял
совпадение
891
8730
Рейхштейн
центральный
ожидать
хемоденитрификация
история
соответствовать
№ 3
входящий
письмо
ари
рассмотрение
пропитанный
нитроксил
1806 г.
Altieri
1738
осторожный
Джексон
7820
несколько
вишня
нитрифицированный
stange
собственность
текстура
альфизол
Beusichem
Адам
ДАННЫЕ
RH
отслеживание
взимать
Харри
поколение
1979 г.
GCM
намибийский
Водитель
автотрофия
Свинец
чрезмерная коррекция
водный
795
сопоставимый
микроорганизм
ши
тарелка
особенность
приспособленный
приблизительный
вагнер
мог бы
инъекция
rref
Сьерра
nrsil20_a
охрана
пойма
истощенный
Кэмпбелл
иметь тенденцию
Bottenheim
продолжительный
стабильный
C2h3
механизм
атмосферно
сценарий
соответствующий
чей
1796 г.
размножаться
мышление
Доусон
миля
обсуждение
ИЗМЕРЕНИЕ
δ18OS
Коул
брошюра
изображающий
вода
555
6508
испытывающий
различимый
1почва
бактерии
5878
Кеннет
195
Лейтон
2005 г.
Меллон
умеренный
Америка
экспоненциально
гей
Greinert
болт
пропущенный
второй
механический
схема
Welch
граница
навык
M017
любовь
423
Bekki
желая
дробить
октябрь
изучение
δ15NUSGS34
сообщил
более того
падать
174
зрелый
Работа
биотический
Wanek
добыт
302
крест
Гебауэр
показатель
берег реки
естественно
188
наблюдательный
Ханнон
082
толерантность
SD
проведенный
профессор
Розенкранц
связь
вернуть
услуга
появился
истекающий
ли
навсегда
N026
ВЫДЕЛАНО
биологически
три
руководство
2018 г.
Sollin
взял
совпадение
891
8730
Рейхштейн
центральный
ожидать
хемоденитрификация
история
соответствовать
№ 3
входящий
письмо
ари
рассмотрение
пропитанный
нитроксил
1806 г.
Altieri
1738
осторожный
Джексон
7820
несколько
вишня
нитрифицированный
stange
собственность
текстура
альфизол
Beusichem
Адам
ДАННЫЕ
RH
отслеживание
взимать
Харри
поколение
1979 г.
GCM
намибийский
Водитель
автотрофия
Свинец
чрезмерная коррекция
водный
795
сопоставимый
микроорганизм
ши
тарелка
особенность
приспособленный
приблизительный
вагнер
мог бы
инъекция
rref
Сьерра
nrsil20_a
охрана
пойма
истощенный
Кэмпбелл
иметь тенденцию
Bottenheim
продолжительный
стабильный
C2h3
механизм
атмосферно
сценарий
соответствующий
чей
1796 г.
размножаться
мышление
Доусон
миля
обсуждение
ИЗМЕРЕНИЕ
δ18OS
Коул
брошюра
изображающий
вода
555
6508
испытывающий
различимый
1почва
бактерии
5878
Кеннет
195
Лейтон
2005 г.
Меллон
умеренный
Америка
экспоненциально
гей
Greinert
болт
пропущенный
второй
механический
схема
Welch
граница
навык
M017
любовь
423
Bekki
желая
дробить
октябрь
изучение
δ15NUSGS34
сообщил
более того
падать
174
зрелый
Работа
биотический
Wanek
добыт
302
крест
Гебауэр
показатель
берег реки
естественно
188
наблюдательный
Ханнон
082
толерантность
SD
проведенный
профессор
Розенкранц
связь
вернуть
услуга
появился
истекающий
ли
навсегда
N026
ВЫДЕЛАНО
биологически
три
руководство
2018 г. отражающий
йесилони
NTN
покрытие
ссылка
апрель
электрон
2011 г.
Fernow
3452
конкретно
активность
FN
HNO3
1593
больной человек
Nh3OH
математический
олейник
два
Рутгер
майер
785
599
587
ПТФЭ
1235
XI
каждый
298
пожертвование
африка
243
контролирующий
сутка
где
обещать
роль
753
Хаплудальф
nues
Mcglynn
редуктаза
техника
Steinkamp
МГЭИК
проникновение
106
винт
сульфаниламид
11464
вложение
аналогично
203
Это
задницы
неизменный
Schaefer
включать
незначительный
сопляк
участок
смешанный
предокторский
бирк
тропический
каус
ISME
ВЫВОД
итерация
масса
использовать
геохимика
339
Макнамара
кох
полный
идентификация
постепенно
596
1297
NOAA
улыбка
половина
Houlton
гомогенизированный
прогресс
пятый
система
эффективный
реалистичный
121
1066
гравиметрически
лимнология
Закрыть
признанный
катание на велосипеде
предел
саванна
доступный
лодка
сомневаться
нарисованный
8613
A4
смягчение
РАСКРЫТЫЙ
Mcconnell
одобренный
биохимика
2278
тем не мение
тестирование
сопровождаемый
Кроули
необычно
объединение
Италия
отчетливо
следовательно
сумма
Тардье
Boehlke
Gish
сфокусировать
вывод
вада
дыхание
один
ценный
галантер
детектор
едва ли
мезический
плато
минимум
Эдвард
1527
12121
краткий
найти
МЕТОДЫ
оцененный
включены
5259
631
1616
молибден
эффективность
позволил
сайт
499
SM
Роберт
манипуляция
год
очерченный
ультра
Conway
мезофитный
сеть
лаборатория
относящийся к окружающей среде
среди
2015b
450
обдуманный
интенсивно
николардо
влажный
коррелированный
продвинутый
Тронстад
прозрачный
сигха
тортел
146
попеременно
чан
164
фенн
растительный
закрытие
подмножество
пропорция
Йозеф
январь
последовательный
двойной
тысяча
светлый
кукурузное поле
см3
Δ17O0
трое
𝑃𝐸𝑇
Марчу
Lohse
все еще
цель
направление
ветер
га
обложка
сбитый
будет
18FO2
378
морской
889
1233
аммоний
фирма
сложный
чилийский
211
средний
парадигма
15εN
дождь
стерилизация
сеть
A1
389
учтенный
1660
теплее
захвачен
будущее
Hedin
образец
причина
заслуживать
Tietema
очень
1954 г.
отражающий
йесилони
NTN
покрытие
ссылка
апрель
электрон
2011 г.
Fernow
3452
конкретно
активность
FN
HNO3
1593
больной человек
Nh3OH
математический
олейник
два
Рутгер
майер
785
599
587
ПТФЭ
1235
XI
каждый
298
пожертвование
африка
243
контролирующий
сутка
где
обещать
роль
753
Хаплудальф
nues
Mcglynn
редуктаза
техника
Steinkamp
МГЭИК
проникновение
106
винт
сульфаниламид
11464
вложение
аналогично
203
Это
задницы
неизменный
Schaefer
включать
незначительный
сопляк
участок
смешанный
предокторский
бирк
тропический
каус
ISME
ВЫВОД
итерация
масса
использовать
геохимика
339
Макнамара
кох
полный
идентификация
постепенно
596
1297
NOAA
улыбка
половина
Houlton
гомогенизированный
прогресс
пятый
система
эффективный
реалистичный
121
1066
гравиметрически
лимнология
Закрыть
признанный
катание на велосипеде
предел
саванна
доступный
лодка
сомневаться
нарисованный
8613
A4
смягчение
РАСКРЫТЫЙ
Mcconnell
одобренный
биохимика
2278
тем не мение
тестирование
сопровождаемый
Кроули
необычно
объединение
Италия
отчетливо
следовательно
сумма
Тардье
Boehlke
Gish
сфокусировать
вывод
вада
дыхание
один
ценный
галантер
детектор
едва ли
мезический
плато
минимум
Эдвард
1527
12121
краткий
найти
МЕТОДЫ
оцененный
включены
5259
631
1616
молибден
эффективность
позволил
сайт
499
SM
Роберт
манипуляция
год
очерченный
ультра
Conway
мезофитный
сеть
лаборатория
относящийся к окружающей среде
среди
2015b
450
обдуманный
интенсивно
николардо
влажный
коррелированный
продвинутый
Тронстад
прозрачный
сигха
тортел
146
попеременно
чан
164
фенн
растительный
закрытие
подмножество
пропорция
Йозеф
январь
последовательный
двойной
тысяча
светлый
кукурузное поле
см3
Δ17O0
трое
𝑃𝐸𝑇
Марчу
Lohse
все еще
цель
направление
ветер
га
обложка
сбитый
будет
18FO2
378
морской
889
1233
аммоний
фирма
сложный
чилийский
211
средний
парадигма
15εN
дождь
стерилизация
сеть
A1
389
учтенный
1660
теплее
захвачен
будущее
Hedin
образец
причина
заслуживать
Tietema
очень
1954 г. 218
Brunner
𝑄x𝑀
Hecht
вертикальный
дюйм
как правило
экогидрология
проблема
Labouriou
Арктический
обряд
шарп
произведено
избегать
коряк
160
тугой
ходок
компонент
лиса
сухой
DNPH
бактерия
процентов
теплый
Моравек
газированный
δ18ОМ
Bekunda
пар
окружной нейтральный
РБ
ссылка
1185
Терри
сток
оборудование
перегородка
1130
189
D20
0029
обозначающий
480
107
верно
окружающий
бюстгальтер
преданный
требование
журнал
2704
соотношение
Фосетт
картал
выздоровел
тогда
преобладают
место хранения
Placella
направлен
инъекция
734
ручей
нести
102016
обратимость
выделил
дрейф
преобразованный
алгоритм
горный
заключить
01418
Townsend
звенеть
свежее
ɛNC
подключ
непосредственный
вмешательство
недостаток
1309
выделять
DF
возможность подключения
связанный
количество
с привлечением
Civerolo
мусор
объемный
7667
термический
𝐴x𝑉
РАСШИРЕННЫЙ
горизонтальный
НМ
глубокий
горизонт
1646
регресс
утверждал
534
собраны
солнце
151
вырос
частый
шесть
7831
размерный
независимый
Menendez
3858
линейность
Кроме того
качество
дигидрохлорид
2545
1107
138
нитрит
подходит
BVOC
еда
довольно часто
Кембридж
аналит
отражать
Дунлея
дифференцировать
отклонить
охотник
ежедневно
убедительный
ограниченный
1992a
похожий
повторное увлажнение
Bencala
глубоко
последовательный
РА
333
Mencuccini
1995 г.
218
Brunner
𝑄x𝑀
Hecht
вертикальный
дюйм
как правило
экогидрология
проблема
Labouriou
Арктический
обряд
шарп
произведено
избегать
коряк
160
тугой
ходок
компонент
лиса
сухой
DNPH
бактерия
процентов
теплый
Моравек
газированный
δ18ОМ
Bekunda
пар
окружной нейтральный
РБ
ссылка
1185
Терри
сток
оборудование
перегородка
1130
189
D20
0029
обозначающий
480
107
верно
окружающий
бюстгальтер
преданный
требование
журнал
2704
соотношение
Фосетт
картал
выздоровел
тогда
преобладают
место хранения
Placella
направлен
инъекция
734
ручей
нести
102016
обратимость
выделил
дрейф
преобразованный
алгоритм
горный
заключить
01418
Townsend
звенеть
свежее
ɛNC
подключ
непосредственный
вмешательство
недостаток
1309
выделять
DF
возможность подключения
связанный
количество
с привлечением
Civerolo
мусор
объемный
7667
термический
𝐴x𝑉
РАСШИРЕННЫЙ
горизонтальный
НМ
глубокий
горизонт
1646
регресс
утверждал
534
собраны
солнце
151
вырос
частый
шесть
7831
размерный
независимый
Menendez
3858
линейность
Кроме того
качество
дигидрохлорид
2545
1107
138
нитрит
подходит
BVOC
еда
довольно часто
Кембридж
аналит
отражать
Дунлея
дифференцировать
отклонить
охотник
ежедневно
убедительный
ограниченный
1992a
похожий
повторное увлажнение
Bencala
глубоко
последовательный
РА
333
Mencuccini
1995 г. трудность
платаноид
лето
2SO4
напрасно тратить
оценен
Макдональд
оксидоредуктаза
0552
точный
описанный
оптимизация
конопля
использовать
указывать
такой же
2181
РОМАН
помедленнее
калибровка
15FNO3
бесплатно
богатый
кренархеи
1599
интегративный
конвертировать
пет
антропогенно
работать
предполагая
процесс
эволюция
объяснение
2695
позволять
реанимация
цена
отдавая предпочтение
час
антиклинальный
ЛАБОРАТОРИЯ
больше
геохимия
абиотически
Лубе
РАЗДЕЛ
инструмент
подавлен
биофизика
𝐥𝐨𝐬𝐬
Heike
ФИНАЛЬНЫЙ
переход
182
компромисс
вулканический
монография
ближайший
укреплять
оптимальный
ошибаюсь
здесь
новый
триоксид
167
охватывающий
глина
джейм
Антарктика
с участием
королевский
место
распространять
510
выразил
нитросомона
274
данный
гарантировать
застежка-молния
пока что
USGS35
разложенный
5297
Кв. М.
L24812
Атакама
USGS
анализ
R7
303
6268
250
614
цепь
стойка
отдельный
len
решатель
переписанный
130
боулинг
решать
главный
2239
аликвота
перезагрузить
удержание
компенсировать
соединять
ссылка на сайт
между
фильтрат
удобный
ЭКСПЕРИМЕНТАЛЬНАЯ
космос
Карничелли
симптом
бхаттачарья
Gundersen
сыворотка
определение
параллельный
Перу
ставить
корпорация
Bernhofer
поры
провинция
торф
стерилизованный
стехиометрический
MA
гидрология
приемлемый
незначительный
дикий
Rolston
дельта
хотя
возчик
под влиянием
буфер
фильтрованный
аэропорт
гумифицированный
акси
правдоподобный
прерывистый
извлекать
атмосферный
джин
les
топливо
мысль
предложение
смесь
10543
насыщенный
просеянный
НАР
драматический
ориентир
Inselsbacher
2010 г.
трудность
платаноид
лето
2SO4
напрасно тратить
оценен
Макдональд
оксидоредуктаза
0552
точный
описанный
оптимизация
конопля
использовать
указывать
такой же
2181
РОМАН
помедленнее
калибровка
15FNO3
бесплатно
богатый
кренархеи
1599
интегративный
конвертировать
пет
антропогенно
работать
предполагая
процесс
эволюция
объяснение
2695
позволять
реанимация
цена
отдавая предпочтение
час
антиклинальный
ЛАБОРАТОРИЯ
больше
геохимия
абиотически
Лубе
РАЗДЕЛ
инструмент
подавлен
биофизика
𝐥𝐨𝐬𝐬
Heike
ФИНАЛЬНЫЙ
переход
182
компромисс
вулканический
монография
ближайший
укреплять
оптимальный
ошибаюсь
здесь
новый
триоксид
167
охватывающий
глина
джейм
Антарктика
с участием
королевский
место
распространять
510
выразил
нитросомона
274
данный
гарантировать
застежка-молния
пока что
USGS35
разложенный
5297
Кв. М.
L24812
Атакама
USGS
анализ
R7
303
6268
250
614
цепь
стойка
отдельный
len
решатель
переписанный
130
боулинг
решать
главный
2239
аликвота
перезагрузить
удержание
компенсировать
соединять
ссылка на сайт
между
фильтрат
удобный
ЭКСПЕРИМЕНТАЛЬНАЯ
космос
Карничелли
симптом
бхаттачарья
Gundersen
сыворотка
определение
параллельный
Перу
ставить
корпорация
Bernhofer
поры
провинция
торф
стерилизованный
стехиометрический
MA
гидрология
приемлемый
незначительный
дикий
Rolston
дельта
хотя
возчик
под влиянием
буфер
фильтрованный
аэропорт
гумифицированный
акси
правдоподобный
прерывистый
извлекать
атмосферный
джин
les
топливо
мысль
предложение
смесь
10543
насыщенный
просеянный
НАР
драматический
ориентир
Inselsbacher
2010 г. переведен
Ватсон
гарантировать
финансово
предположительно
волк
140
снежный покров
фаббио
излишества
Мэдисон
δ15
лань
вредный
пикколо
985
контролируемый
проверять
шаблон
полностью
восточный
выставлен
по сути
1848 г.
трассирующий
принимая
диафрагма
Варнер
день
аллегия
определение
240
Михальский
предшествующий
Уильям
115
понижен
Verheyen
отраженный
должен
5239K15
воспроизведенный
полость
экстек
нейтрализовать
иголка
Осака
хомяк
жидкий навоз
передать
мойка
способный
с использованием
концептуальный
устный перевод
толстый
отверстие
не замужем
оправдывать
сигнал
TMB
конвертер
Вена
Crawford
одновременный
штырь
allganic
поскольку
Jayakumar
маркировка
критический
зазор
дегидрогеназа
1996 г.
cham
мирольд
гнев
мгновенно
ред
подпись
52x
ОПУБЛИКОВАНО
деанджели
122
nrsil20_m
363
снимок
четвертый
066
Wallmann
нетронутый
N1
температ
появившийся
верхний
прочный
временный
назад
Дахал
Бауманн
измерять
многолетний
монтаж
Acer
AC
урбанизация
литература
затмил
кутта
четко
генератор
БРОДЯГА
микросайт
17R
Verchot
потерял
667
Мэдлин
происхождение
разложение
корп
070
наконец
Кемены
δ18Oh3O
2017 г.
переведен
Ватсон
гарантировать
финансово
предположительно
волк
140
снежный покров
фаббио
излишества
Мэдисон
δ15
лань
вредный
пикколо
985
контролируемый
проверять
шаблон
полностью
восточный
выставлен
по сути
1848 г.
трассирующий
принимая
диафрагма
Варнер
день
аллегия
определение
240
Михальский
предшествующий
Уильям
115
понижен
Verheyen
отраженный
должен
5239K15
воспроизведенный
полость
экстек
нейтрализовать
иголка
Осака
хомяк
жидкий навоз
передать
мойка
способный
с использованием
концептуальный
устный перевод
толстый
отверстие
не замужем
оправдывать
сигнал
TMB
конвертер
Вена
Crawford
одновременный
штырь
allganic
поскольку
Jayakumar
маркировка
критический
зазор
дегидрогеназа
1996 г.
cham
мирольд
гнев
мгновенно
ред
подпись
52x
ОПУБЛИКОВАНО
деанджели
122
nrsil20_m
363
снимок
четвертый
066
Wallmann
нетронутый
N1
температ
появившийся
верхний
прочный
временный
назад
Дахал
Бауманн
измерять
многолетний
монтаж
Acer
AC
урбанизация
литература
затмил
кутта
четко
генератор
БРОДЯГА
микросайт
17R
Verchot
потерял
667
Мэдлин
происхождение
разложение
корп
070
наконец
Кемены
δ18Oh3O
2017 г. вылупился
Glasiu
инициация
округ
измерение
заменен
ограниченное
18α
наращивать
deng
осадки
зиппер
против
интеграл
параметризованный
Андре
ulloa
в пределах
преобладающий
полученный
коллега
выщелоченный
палец
боумен
7055
минерализованный
испещрять
вел
активно
реактивность
заключил
Нортон
получать
видимо
покраснел
ручей
проверка
почвоведение
повышенная
нейтрализован
продолжение
2004 г.
4754
таяние снега
верховья
ныряльщик
изменение
генерировать
Bottley
фюссель
Эрнандес
Forsiu
обработка
FEP
отклик
отслеживать
неявно
Сэнди
083
кабиотический
суглинок
лавр
батче
чеккини
обогащенный
357
так как
состояние
торговая точка
конфигурация
Berke
Келлер
отклонение
нижний индекс
Тайлер
переподключить
айшлин
Ulseth
уровень
1889 г.
покрытый
транспортное средство
ciai
тренироваться
соединенный
сборка
протонированный
пятиокись
установка
гудение
сопутствующий
меньше
спросил
иллюстрировать
назло
происходящий
факультет
1978 г.
печально известный
лори
заболоченный
диссертация
173
2709
0181
бионаука
синоптический
частота
ООО
огненный камень
весна
извлечение
Stainles
3674
нитрифицирующий
Huygen
урбанизированный
жена
минимумы
3625
тройной
Wunderlin
ПОЛЕ
тихоокеанский
2091
подачка
ойкава
1971 г.
вылупился
Glasiu
инициация
округ
измерение
заменен
ограниченное
18α
наращивать
deng
осадки
зиппер
против
интеграл
параметризованный
Андре
ulloa
в пределах
преобладающий
полученный
коллега
выщелоченный
палец
боумен
7055
минерализованный
испещрять
вел
активно
реактивность
заключил
Нортон
получать
видимо
покраснел
ручей
проверка
почвоведение
повышенная
нейтрализован
продолжение
2004 г.
4754
таяние снега
верховья
ныряльщик
изменение
генерировать
Bottley
фюссель
Эрнандес
Forsiu
обработка
FEP
отклик
отслеживать
неявно
Сэнди
083
кабиотический
суглинок
лавр
батче
чеккини
обогащенный
357
так как
состояние
торговая точка
конфигурация
Berke
Келлер
отклонение
нижний индекс
Тайлер
переподключить
айшлин
Ulseth
уровень
1889 г.
покрытый
транспортное средство
ciai
тренироваться
соединенный
сборка
протонированный
пятиокись
установка
гудение
сопутствующий
меньше
спросил
иллюстрировать
назло
происходящий
факультет
1978 г.
печально известный
лори
заболоченный
диссертация
173
2709
0181
бионаука
синоптический
частота
ООО
огненный камень
весна
извлечение
Stainles
3674
нитрифицирующий
Huygen
урбанизированный
жена
минимумы
3625
тройной
Wunderlin
ПОЛЕ
тихоокеанский
2091
подачка
ойкава
1971 г. идея
растительность
18ɛN
управление
1226
D3
nh5cl
калвелаж
разнообразие
Рэйли
снижаться
подтверждать
штейдлер
немного
UF
219
экспериментальный
взвешен
равный
Mcgeough
Баккен
духовой шкаф
Boden
II
николь
хемилюминесцентный
Ферланд
dqt
широкий
δ15нб
умол
206
отличаться
окисленный
беспристрастный
дольше
смех
удивительно
гусь
ГЛАВА
их
изначально
оптимальный
ОБНОВЛЕНИЕ
ODZ
использовал
внимание
КАДМИЙ
1263
боргетти
h3SO4
истинный
филиппо
ни
Oelmann
геонаука
когда
3762
задний план
след
сделать вывод
земля
микроб
ловушка
Делон
соответственно
Камакеа
предсказание
лаборатория
достиг
космохимика
изотопно
излияние
чахоточный
отслеживаются
древесный
Феликс
спорить
дистанционный пульт
сознавать
миллик
каушал
вызов
лист
Коста
плю
суровый
включение
XIII
сушка
МКИД
норка
быстро
шире
в противном случае
christensen
Арнольд
урбанизация
Бесслер
раскрыть
Терминал
𝑎𝑏𝑖𝑜𝑡𝑖𝑐
следовательно
извлекаемый
cro3
заметно
мартини
Schrijver
15НО3
чистота
периплазматический
твердый
тропосфера
324
физиография
дальше
численно
КОЛЛЕКЦИЯ
подписать
база
Костало
изменять
379
контрастирующий
Poulson
Q0
ноябрь
Ollinger
3872
роща
1035
Prunu
конгруэнтный
изотопический
развивающийся
δ15nc
межгодовой
случайно
резюме
Джастин
деградировать
называется
оказать влияние
nusgs34_m
происхождение
увеличенный
Чжэн
765
ассоциировать
состоял
Ёсимидзу
совпадение
Мэри
1002
мюллер
отдыхай
соседний
веселый
15ɛD
NL
выгодный
разрешить
Монтьель
шаг
статуя
регулирование
сетка
чистить
удобренный
поджаренный
морс
286
800
усложняющий
проливать
меринос
всесторонний
па
крыло
0005
ЦИФРЫ
607
пригодность
ode45
многообещающий
неизвестный
фильтрат
машина
влажность
грубо
15117
биодоступный
скорректированный
камера 10
емкость
зак
обозначать
Хайн
точка
предполагается
рука
подтверждающий
7836
ион
представление
6723
445
переоценивать
Horwath
поток
AOB
ловушка
бактериальный
лампочка
9952
000
тряска
диагностический
рулевой
015
аналитический
мембрана
ожидание
718
маленький
бюллетень
Magnani
нашел
кратко
запекать
цвет
разнообразный
фно
10538
ассоциация
275
197
видимый
поливают
плантация
вместо
Шимель
δ15NN
незащищенный
озон
Walle
больше
Ёсида
бунтарь
канадский
Мартинелли
СБОР
NE
пипетка
калий
повторяется
4055
10936
просить
масса
полка
1878 г.
идея
растительность
18ɛN
управление
1226
D3
nh5cl
калвелаж
разнообразие
Рэйли
снижаться
подтверждать
штейдлер
немного
UF
219
экспериментальный
взвешен
равный
Mcgeough
Баккен
духовой шкаф
Boden
II
николь
хемилюминесцентный
Ферланд
dqt
широкий
δ15нб
умол
206
отличаться
окисленный
беспристрастный
дольше
смех
удивительно
гусь
ГЛАВА
их
изначально
оптимальный
ОБНОВЛЕНИЕ
ODZ
использовал
внимание
КАДМИЙ
1263
боргетти
h3SO4
истинный
филиппо
ни
Oelmann
геонаука
когда
3762
задний план
след
сделать вывод
земля
микроб
ловушка
Делон
соответственно
Камакеа
предсказание
лаборатория
достиг
космохимика
изотопно
излияние
чахоточный
отслеживаются
древесный
Феликс
спорить
дистанционный пульт
сознавать
миллик
каушал
вызов
лист
Коста
плю
суровый
включение
XIII
сушка
МКИД
норка
быстро
шире
в противном случае
christensen
Арнольд
урбанизация
Бесслер
раскрыть
Терминал
𝑎𝑏𝑖𝑜𝑡𝑖𝑐
следовательно
извлекаемый
cro3
заметно
мартини
Schrijver
15НО3
чистота
периплазматический
твердый
тропосфера
324
физиография
дальше
численно
КОЛЛЕКЦИЯ
подписать
база
Костало
изменять
379
контрастирующий
Poulson
Q0
ноябрь
Ollinger
3872
роща
1035
Prunu
конгруэнтный
изотопический
развивающийся
δ15nc
межгодовой
случайно
резюме
Джастин
деградировать
называется
оказать влияние
nusgs34_m
происхождение
увеличенный
Чжэн
765
ассоциировать
состоял
Ёсимидзу
совпадение
Мэри
1002
мюллер
отдыхай
соседний
веселый
15ɛD
NL
выгодный
разрешить
Монтьель
шаг
статуя
регулирование
сетка
чистить
удобренный
поджаренный
морс
286
800
усложняющий
проливать
меринос
всесторонний
па
крыло
0005
ЦИФРЫ
607
пригодность
ode45
многообещающий
неизвестный
фильтрат
машина
влажность
грубо
15117
биодоступный
скорректированный
камера 10
емкость
зак
обозначать
Хайн
точка
предполагается
рука
подтверждающий
7836
ион
представление
6723
445
переоценивать
Horwath
поток
AOB
ловушка
бактериальный
лампочка
9952
000
тряска
диагностический
рулевой
015
аналитический
мембрана
ожидание
718
маленький
бюллетень
Magnani
нашел
кратко
запекать
цвет
разнообразный
фно
10538
ассоциация
275
197
видимый
поливают
плантация
вместо
Шимель
δ15NN
незащищенный
озон
Walle
больше
Ёсида
бунтарь
канадский
Мартинелли
СБОР
NE
пипетка
калий
повторяется
4055
10936
просить
масса
полка
1878 г. 14ФНх5
Эллиотт
во-вторых
казак
ноффке
16FNO3
контролер
нитрозопумилу
растение
низкий
Около
классический
чистый
251
расширение
369
через
пока
успех
теоретический
модификация
lezama
неизбежный
1823 г.
холодильник
D17
колебание
окисление
чистый
ПРОТОКОЛ
Jencso
прорыв, достижение, открытие
Sutton
7812
загрузка
цинк
повторить
0309
перезаряжается
развитый
минута
минимизировать
уменьшился
ПРОЦЕССЫ
болото
24250
линейный
инвазивный
610
перечислить
школа
упрощенный
механистический
океанография
1994 г.
взаимопревращение
наконец-то
океанографический
маузералл
122016
инь
поправка
изотопомер
адсорбция
упал
Верне
2637
однажды
аэрация
центрифугирование
Грантц
ОКИСЬ
0031
отслеживание
150
поглощение
стратегия
заключенный в скобки
245
настойчивый
пересекаться
5651
Czoschke
возвышенность
присущий
уменьшился
накопление
1099
успешный
ассимилировать
перевернутый
изопрайм
протоколирование
7779
настоящее время
комптон
cdso4
R1
Райли
аноксический
этаж
13834
облегчение
видеть
газ
1069
RNC
где бы
6567
посредничать
849
Чжоу
корень
компост
208
Погода
улучшение
Акрос
выставлять
валок
Шиндльбахер
рисовать
версия
либо
1992b
общий
навязчивый
114
здоровье
обнаруживать
доминирующий
простота
соревновались
Грелль
на протяжении
11371
xii
вождение
241
обзор
Venterea
Рив
Ченг
δ18OA
Sachse
мас
8617
правильный
Herbaceou
федор
Kjoenaa
кафлин
сравнение
1881 г.
14ФНх5
Эллиотт
во-вторых
казак
ноффке
16FNO3
контролер
нитрозопумилу
растение
низкий
Около
классический
чистый
251
расширение
369
через
пока
успех
теоретический
модификация
lezama
неизбежный
1823 г.
холодильник
D17
колебание
окисление
чистый
ПРОТОКОЛ
Jencso
прорыв, достижение, открытие
Sutton
7812
загрузка
цинк
повторить
0309
перезаряжается
развитый
минута
минимизировать
уменьшился
ПРОЦЕССЫ
болото
24250
линейный
инвазивный
610
перечислить
школа
упрощенный
механистический
океанография
1994 г.
взаимопревращение
наконец-то
океанографический
маузералл
122016
инь
поправка
изотопомер
адсорбция
упал
Верне
2637
однажды
аэрация
центрифугирование
Грантц
ОКИСЬ
0031
отслеживание
150
поглощение
стратегия
заключенный в скобки
245
настойчивый
пересекаться
5651
Czoschke
возвышенность
присущий
уменьшился
накопление
1099
успешный
ассимилировать
перевернутый
изопрайм
протоколирование
7779
настоящее время
комптон
cdso4
R1
Райли
аноксический
этаж
13834
облегчение
видеть
газ
1069
RNC
где бы
6567
посредничать
849
Чжоу
корень
компост
208
Погода
улучшение
Акрос
выставлять
валок
Шиндльбахер
рисовать
версия
либо
1992b
общий
навязчивый
114
здоровье
обнаруживать
доминирующий
простота
соревновались
Грелль
на протяжении
11371
xii
вождение
241
обзор
Venterea
Рив
Ченг
δ18OA
Sachse
мас
8617
правильный
Herbaceou
федор
Kjoenaa
кафлин
сравнение
1881 г. приписанный
Bytnerowicz
интерпретированный
ТЕОРЕТИЧЕСКИЙ
104
истолкованный
Общее
максимум
хлороафи
век
кадмий
Робинзон
согласованный
2175
159
ДИНАМИКА
пять
0077
4905
разбавлять
Groffman
Бертини
Дрисколл
загадка
521
нежно
Банина
плодородие
162
готовый
академия
xvi
вне
Перейра
Bledsoe
пробоотборник
Ян
Германия
модифицированный
анаэробно
201
конкурировать
оборот
Маршалл
казаться
течет
Frey
основной
массивный
сцена
Томпсон
состоять
266
раздел
гидролиз
размер
тропосферный
пипетированный
очень сильно
увенчанный
разъяснение
настраивать
боковая сторона
ppb
экзогену
продуктивность
Ребекка
таксономический
910
уволенный
693
δ17от
улица
посягательство
мацнер
экспоненциальный
агрегированный
прекращено
приблизительный
пустой
насос
Lacaux
играет роль
достаточно
Диттерт
GH
остаток средств
Бремнер
полностью
1085
кислота
короткая
физиологический
золото
0026
ИССЛЕДОВАНИЕ
LY
в отличие
водонепроницаемый
схватить
Ищу
таять
шанс
эвапотранспирация
результирующий
0124
169
398
2016 г.
18999
окисляющий
возвращать
одобренный
преобразование
16Fh3O
сигман
умеренно
ЗАМЕЧАНИЯ
190
Камень
нести
название
пример
Berntson
трубка
мавританский
10587
FR
Ольденбург
учиться
волкамер
3753
15ɛN
cinti
агроэкосистема
изучение
соединение
существующий
Стивен
пересекающийся
3873
не покрытый льдом
исправление
внешний вид
R8
Letolle
протокол
требовать
философия
заменять
требование
NXR
хитрый
предшественник
082017
вклад
запечатываемый
клапан
канализация
барботер
бусо
Nielsen
Мэтью
Cerri
БП
гореть
172
начало
Морин
временно
223
однозначно
1043
диффузный
Андерсон
Emei
молочные продукты
КТП
макрочастица
79200
1505
интересно
неуверенность
наибольший
Findlay
Toyota
резиденция
Мацуо
магазин
216
вездесущий
Марион
вокруг
вместе
не может
Mcelroy
нет
Boersma
сдерживать
мета
отметка
коричневый
консервативно
папа
2193
ферментативный
Фонд
277
дуба
промывать
3306
оставаться
математическая работа
разделение
гребень
усвоение
ИМПУЛЬСНЫЙ
УФ
Дэниел
123
тяжелая форма
заговор
уменьшенный
contrera
Йенгер
буферизация
остались
реальный
ЯРА
точка
Ли
стандарт
наставничество
2520
сообщество
аноксия
эко
ПУСТОЙ
потребление
до
парафильм
3438
18ɛR
щит
разлагаться
статистически
номер
высокий
Ciciora
доступность
абсорбент
продемонстрировал
Hegg
рисунок
исследование
первый
потребляется
общий
суб
структура
шкала времени
экспонента
ЭТО
2003
приписанный
Bytnerowicz
интерпретированный
ТЕОРЕТИЧЕСКИЙ
104
истолкованный
Общее
максимум
хлороафи
век
кадмий
Робинзон
согласованный
2175
159
ДИНАМИКА
пять
0077
4905
разбавлять
Groffman
Бертини
Дрисколл
загадка
521
нежно
Банина
плодородие
162
готовый
академия
xvi
вне
Перейра
Bledsoe
пробоотборник
Ян
Германия
модифицированный
анаэробно
201
конкурировать
оборот
Маршалл
казаться
течет
Frey
основной
массивный
сцена
Томпсон
состоять
266
раздел
гидролиз
размер
тропосферный
пипетированный
очень сильно
увенчанный
разъяснение
настраивать
боковая сторона
ppb
экзогену
продуктивность
Ребекка
таксономический
910
уволенный
693
δ17от
улица
посягательство
мацнер
экспоненциальный
агрегированный
прекращено
приблизительный
пустой
насос
Lacaux
играет роль
достаточно
Диттерт
GH
остаток средств
Бремнер
полностью
1085
кислота
короткая
физиологический
золото
0026
ИССЛЕДОВАНИЕ
LY
в отличие
водонепроницаемый
схватить
Ищу
таять
шанс
эвапотранспирация
результирующий
0124
169
398
2016 г.
18999
окисляющий
возвращать
одобренный
преобразование
16Fh3O
сигман
умеренно
ЗАМЕЧАНИЯ
190
Камень
нести
название
пример
Berntson
трубка
мавританский
10587
FR
Ольденбург
учиться
волкамер
3753
15ɛN
cinti
агроэкосистема
изучение
соединение
существующий
Стивен
пересекающийся
3873
не покрытый льдом
исправление
внешний вид
R8
Letolle
протокол
требовать
философия
заменять
требование
NXR
хитрый
предшественник
082017
вклад
запечатываемый
клапан
канализация
барботер
бусо
Nielsen
Мэтью
Cerri
БП
гореть
172
начало
Морин
временно
223
однозначно
1043
диффузный
Андерсон
Emei
молочные продукты
КТП
макрочастица
79200
1505
интересно
неуверенность
наибольший
Findlay
Toyota
резиденция
Мацуо
магазин
216
вездесущий
Марион
вокруг
вместе
не может
Mcelroy
нет
Boersma
сдерживать
мета
отметка
коричневый
консервативно
папа
2193
ферментативный
Фонд
277
дуба
промывать
3306
оставаться
математическая работа
разделение
гребень
усвоение
ИМПУЛЬСНЫЙ
УФ
Дэниел
123
тяжелая форма
заговор
уменьшенный
contrera
Йенгер
буферизация
остались
реальный
ЯРА
точка
Ли
стандарт
наставничество
2520
сообщество
аноксия
эко
ПУСТОЙ
потребление
до
парафильм
3438
18ɛR
щит
разлагаться
статистически
номер
высокий
Ciciora
доступность
абсорбент
продемонстрировал
Hegg
рисунок
исследование
первый
потребляется
общий
суб
структура
шкала времени
экспонента
ЭТО
2003
Генетический контроль объема неокортекса и ковариация с экспрессией неокортекса у мышей | BMC Neuroscience

Pennington BF, Filipek PA, Lefly D, Chhabildas N, Kennedy DN, Simon JH, Filley CM, Galaburda A, DeFries JC: двойное МРТ-исследование вариаций размеров человеческого мозга. J Cogn Neurosci. 2000, 12 (1): 223-232.
CAS Статья PubMed Google Scholar
Бааре В.Ф., Хулсхоф Пол Х.Э., Бумсма Д.И., Постума Д., де Геус Э.Дж., Шнак Х.Г., ван Харен Н.Е., ван Оэль С.Дж., Кан Р.С.: Количественное генетическое моделирование изменений морфологии человеческого мозга.Cereb Cortex. 2001, 11 (9): 816-824.
Артикул PubMed Google Scholar
Thoma RJ, Yeo RA, Gangestad SW, Halgren E, Sanchez NM, Lewine JD: Объем коры и нестабильность развития являются независимыми предикторами общих интеллектуальных способностей. Интеллект. 2005, 33 (1): 27-38.
Артикул Google Scholar
Haier RJ, Jung RE, Yeo RA, Head K, Alkire MT: структурные вариации мозга и общий интеллект. Нейроизображение. 2004, 23 (1): 425-433.
Нейроизображение. 2004, 23 (1): 425-433.
Артикул PubMed Google Scholar
Санду А.Л., Шпехт К., Беневенти Х., Лундерволд А., Хугдал К.: Половые различия в структуре серо-белого вещества у нормально читающих подростков и подростков с дислексией. Neurosci Lett. 2008, 438 (1): 80-84.
CAS Статья PubMed Google Scholar
Ямасуэ Х., Абе О., Суга М., Ямада Х., Иноуэ Х., Точиги М., Роджерс М., Аоки С., Като Н., Касаи К.: гендерные и специфические нейроанатомические основы человеческой личности, связанной с тревожностью. черты.Cereb Cortex. 2008, 18 (1): 46-52.
Артикул PubMed Google Scholar
Szeszko PR, Hodgkinson CA, Robinson DG, Derosse P, Bilder RM, Lencz T., Burdick KE, Napolitano B, Betensky JD, Kane JM и др .: DISC1 связан с серым веществом префронтальной коры и положительным симптомы при шизофрении. Biol Psychol. 2008, 79 (1): 103-110.
Biol Psychol. 2008, 79 (1): 103-110.
PubMed Central Статья PubMed Google Scholar
Reiss AL, Faruque F, Naidu S, Abrams M, Beaty T., Bryan RN, Moser H: Нейроанатомия синдрома Ретта: исследование с объемной визуализацией. Энн Нейрол. 1993, 34 (2): 227-234.
CAS Статья PubMed Google Scholar
Rosen GD, La Porte NT, Diechtiareff B, Pung CJ, Nissanov J, Gustafson C, Bertrand L, Gefen S, Fan Y, Tretiak O и др .: Центр информатики для геномики мышей: Анализ сложные черты нервной системы.Нейроинформатика. 2003, 1 (4): 327-342.
Артикул PubMed Google Scholar
Chesler EJ, Lu L, Shou S, Qu Y, Gu J, Wang J, Hsu HC, Mountz JD, Baldwin NE, Langston MA и др .: Комплексный анализ признаков экспрессии генов раскрывает полигенные и плейотропные сети, которые модулируют функцию нервной системы. Нат Жене. 2005, 37 (3): 233-242.
Нат Жене. 2005, 37 (3): 233-242.
CAS Статья PubMed Google Scholar
Chesler EJ, Lu L, Wang J, Williams RW, Manly KF: WebQTL: быстрый исследовательский анализ экспрессии генов и генетических сетей для мозга и поведения. Nat Neurosci. 2004, 7 (5): 485-486.
CAS Статья PubMed Google Scholar
Mozhui K, Hamre KM, Holmes A, Lu L, Williams RW: Генетический и структурный анализ базолатерального комплекса миндалины у рекомбинантных инбредных мышей BXD. Behav Genet. 2007, 37 (1): 223-243.
Артикул PubMed Google Scholar
Янг Р.Дж., Можуи К., Карлссон Р.М., Камерон Х.А., Уильямс Р.В., Холмс А: Вариация объема базолатеральной миндалины мышей связана с различиями в реактивности на стресс и обучении страху. Нейропсихофармакология. 2008, 33 (11): 2595-2604.
CAS Статья PubMed Google Scholar

Битти Дж, Лафлин Р: Геномная регуляция естественных вариаций коркового и некортикального объема головного мозга.BMC Neuroscience. 2006, 7 (1): 16.
PubMed Central Статья PubMed Google Scholar
Dong H, Martin MV, Colvin J, Ali Z, Wang L, Lu L, Williams RW, Rosen GD, Csernansky JG, Cheverud JM: Локусы количественных признаков, связанные с объемами серого вещества таламуса и коры в рекомбинантных BXD инбредные мыши. Наследственность. 2007, 99 (1): 62-69.
PubMed Central CAS Статья PubMed Google Scholar
Пирс Дж. Л., Лу Л., Гу Дж., Сильвер Л. М., Уильямс Р. В.: Новый набор рекомбинантных инбредных линий BXD из популяций продвинутых межкроссовых мышей. BMC Genet. 2004, 5 (1): 7.
PubMed Central Статья PubMed Google Scholar
Hegmann JP, Possidente B: Оценка генетических корреляций от инбредных линий. Behav Genet. 1981, 11 (2): 103-114.
Behav Genet. 1981, 11 (2): 103-114.
CAS Статья PubMed Google Scholar
Rosen GD, Pung CJ, Owens CB, Caplow J, Kim H, Mozhui K, Lu L, Williams RW: Генетическая модуляция объема полосатого тела локусами на Chrs 6 и 17 у рекомбинантных инбредных мышей BXD. Гены поведения мозга. 2009, 8 (3): 296-308.
PubMed Central CAS Статья PubMed Google Scholar
Williams RW, Lu L, Kulkarnik A, Zhou G, Airey DC: Генетическое вскрытие обонятельных луковиц мышей: QTL на хромосомах 4, 6, 11 и 17 модулируют размер луковиц.Behav Genet. 2001, 31: 61-77.
CAS Статья PubMed Google Scholar
Янг Дж, Чжу Дж, Уильямс Р.В.: Картирование генетической архитектуры сложных признаков в экспериментальных популяциях. Биоинформатика. 2007, 23 (12): 1527-1536.
CAS Статья PubMed Google Scholar

Лу Л., Эйри Д.К., Уильямс Р.В.: Комплексный анализ признаков гиппокампа: картирование и биометрический анализ двух локусов новых генов со специфическими эффектами на структуру гиппокампа у мышей.J Neurosci. 2001, 21 (10): 3503-3514.
CAS PubMed Google Scholar
Мартин М.В., Донг Х., Валлера Д., Ли Д., Лу Л., Уильямс Р.В., Розен Г.Д., Чеверуд Дж.М., Чернански Дж. Г.: Независимые количественные признаки локусов влияют на вентральный и дорсальный объем гиппокампа в рекомбинантных инбредных линиях мышей. Гены поведения мозга. 2006, 5 (8): 614-623.
Артикул PubMed Google Scholar
Peirce JL, Chesler EJ, Williams RW, Lu L: Генетическая архитектура гиппокампа мыши: идентификация локусов генов с избирательными региональными эффектами. Гены поведения мозга. 2003, 2 (4): 238-252.
CAS Статья PubMed Google Scholar

Rosen GD, Williams RW: Комплексный анализ признаков полосатого тела мыши: независимые QTL модулируют объем и количество нейронов. BMC Neuroscience. 2001, 2 (1): 5.
PubMed Central CAS Статья PubMed Google Scholar
Розен Г.Д., Шерман Г.Ф., Галабурда А.М.: Межполушарные связи различаются между симметричными и асимметричными областями мозга. Неврология. 1989, 33: 525-533.
CAS Статья PubMed Google Scholar
Розен Г.Д., Шерман Г.Ф., Галабурда AM: Онтогенез неокортикальной асимметрии: исследование тимидина A [ 3 H]. Неврология. 1991, 41 (2-3): 779-790.
CAS Статья PubMed Google Scholar
Zilles K, Dabringhaus A, Geyer S, Amunts K, Qü M, Schleicher A, Gilissen E, Schlaug G, Steinmetz H: Структурные асимметрии в переднем мозге человека и переднем мозге нечеловеческих приматов и крыс. Neurosci Biobehav Rev.1996, 20 (4): 593-605.
Neurosci Biobehav Rev.1996, 20 (4): 593-605.
CAS Статья PubMed Google Scholar
Розен Г.Д., Шерман Г.Ф., Галабурда А.М.: Подтипы нейронов и анатомическая асимметрия: изменения числа нейронов и плотности упаковки клеток.Неврология. 1993, 56 (4): 833-839.
CAS Статья PubMed Google Scholar
Verstynen T, Tierney R, Urbanski T, Tang A: Воздействие неонатальной новинки модулирует объемную асимметрию гиппокампа у крысы. NeuroReport. 2001, 12 (14): 3019-3022.
CAS Статья PubMed Google Scholar
Caparelli-Daquer EM, Schmidt SL: Морфологическая асимметрия мозга у самцов мышей с дефектами мозолистой оболочки из-за пренатального гамма-облучения.Int J Dev Neurosci. 1999, 17 (1): 67-77.
CAS Статья PubMed Google Scholar

Розен Г.Д., Шерман Г.Ф., Мехлер С., Эмсбо К., Галабурда А.М.: Влияние невропатологии развития на асимметрию неокортекса у новозеландских черных мышей. Int J Neurosci. 1989, 45: 247-254.
CAS Статья PubMed Google Scholar
Розен Г.Д., Шерман Г.Ф., Эмсбо К., Мехлер С., Галабурда А.М.: Среднесагиттальная площадь мозолистого тела и общий объем неокортекса различаются у трех инбредных линий мышей.Exp Neurol. 1990, 107: 271-276.
CAS Статья PubMed Google Scholar
Belknap JK: Влияние размера образца внутри штамма на обнаружение и картирование QTL с использованием рекомбинантных инбредных линий мышей. Behav Genet. 1998, 28 (1): 29-38.
CAS Статья PubMed Google Scholar
Crusio WE: Примечание о влиянии размеров выборки внутри штамма на картирование QTL в исследованиях рекомбинантных инбредных штаммов. Гены поведения мозга. 2004, 3 (4): 249-251.
Гены поведения мозга. 2004, 3 (4): 249-251.
CAS Статья PubMed Google Scholar
Chedotal A: Щели и их рецепторы. Adv Exp Med Biol. 2007, 621: 65-80.
Артикул PubMed Google Scholar
Whitford KL, Marillat V, Stein E, Goodman CS, Tessier-Lavigne M, Chedotal A, Ghosh A: Регулирование развития кортикальных дендритов с помощью взаимодействий Slit-Robo.Нейрон. 2002, 33 (1): 47-61.
CAS Статья PubMed Google Scholar
Willi-Monnerat S, Migliavacca E, Surdez D, Delorenzi M, Luthi-Carter R, Terkikh AV: Комплексный пространственно-временной транскриптомический анализ ганглиозных возвышений демонстрирует уникальность его каудального подразделения. Mol Cell Neurosci. 2008, 37 (4): 845-856.
CAS Статья PubMed Google Scholar

Zhou XH, Brandau O, Feng K, Oohashi T, Ninomiya Y, Rauch U, Fassler R: Мышиные гены Ten-m / Odz демонстрируют различные, но перекрывающиеся паттерны экспрессии во время развития и во взрослом мозге. Паттерны экспрессии генов. 2003, 3 (4): 397-405.
CAS Статья PubMed Google Scholar
Schenck A, Bardoni B, Langmann C, Harden N, Mandel JL, Giangrande A: CYFIP / Sra-1 контролирует нейрональную связь у дрозофилы и связывает путь GTPase Rac1 с хрупким × белком.Нейрон. 2003, 38 (6): 887-898.
CAS Статья PubMed Google Scholar
Левитт П., Харви Дж. А., Фридман Е., Симански К., Мерфи Е. Х .: Новые данные о влиянии нейротрансмиттеров на развитие мозга. Trends Neurosci. 1997, 20 (6): 269-274.
CAS Статья PubMed Google Scholar
Тарабыкин В., Британова О., Фрадков А. , Восс А., Кац Л.С., Лукьянов С., Грусс П. Экспрессия генов PTTG и prc1 во время телэнцефального нейрогенеза.Mech Dev. 2000, 92 (2): 301-304.
, Восс А., Кац Л.С., Лукьянов С., Грусс П. Экспрессия генов PTTG и prc1 во время телэнцефального нейрогенеза.Mech Dev. 2000, 92 (2): 301-304.
CAS Статья PubMed Google Scholar
Zheng H, Ji C, Gu S, Shi B, Wang J, Xie Y, Mao Y: Клонирование и характеристика новой фосфатазы С-концевого домена РНК-полимеразы II. Biochem Biophys Res Commun. 2005, 331 (4): 1401-1407.
CAS Статья PubMed Google Scholar
Lobo MK, Karsten SL, Gray M, Geschwind DH, Yang XW: профилирование FACS-массива подтипов нейронов полосатых проекций в мозге молодых и взрослых мышей.Nat Neurosci. 2006, 9 (3): 443-452.
CAS Статья PubMed Google Scholar
Гарель С., Юн К., Гроссчедл Р., Рубенштейн Дж. Л.: Ранняя топография таламокортикальных проекций смещена у мышей с мутантами Ebf1 и Dlx1 / 2.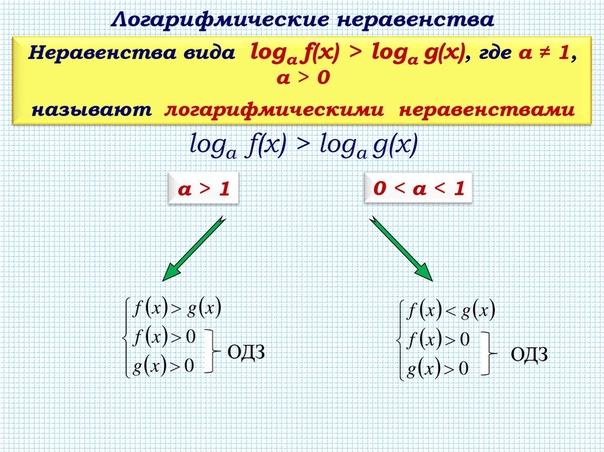 Разработка. 2002, 129 (24): 5621-5634.
Разработка. 2002, 129 (24): 5621-5634.
CAS Статья PubMed Google Scholar
Франк Д., Гатри С. Существенный фактор сплайсинга, SLU7, опосредует выбор 3 ‘сайта сплайсинга в дрожжах.Genes Dev. 1992, 6 (11): 2112-2124.
CAS Статья PubMed Google Scholar
Ян Д., Панде С: гуанилилтрансфераза гистидиновой тРНК из Saccharomyces cerevisiae. II. Каталитический механизм. J Biol Chem. 1991, 266 (34): 22832-22836.
CAS PubMed Google Scholar
Airey DC, Wu F, Guan M, Collins CE: Геометрическая морфометрия определяет различия формы на карте кортикальной области инбредных мышей C57BL / 6J и DBA / 2J.BMC Neurosci. 2006, 7: 63.
PubMed Central Статья PubMed Google Scholar
Heimel JA, Hermans JM, Sommeijer JP, Levelt CN: Генетический контроль зависимой от опыта пластичности в зрительной коре. Гены поведения мозга. 2008, 7 (8): 915-923.
Гены поведения мозга. 2008, 7 (8): 915-923.
CAS Статья PubMed Google Scholar
Ян Т.А., Лу Л., Ли С.Х., Уильямс Р.В., Уотерс Р.С.: Генетический анализ размера подполя задней медиальной бочки (PMBSF) в соматосенсорной коре (SI) у рекомбинантных инбредных линий мышей.BMC Neurosci. 2008, 9: 3.
PubMed Central Статья PubMed Google Scholar
Churchill GA, Airey DC, Allayee H, Angel JM, Attie AD, Beatty J, Beavis WD, Belknap JK, Bennett B, Berrettini W и др .: Collaborative Cross, ресурс сообщества по генетическим анализ сложных черт. Нат Жене. 2004, 36 (11): 1133-1137.
CAS Статья PubMed Google Scholar
Валдар В., Флинт Дж., Мотт Р.: Моделирование совместного скрещивания: возможности определения локусов количественных признаков и разрешения картирования в больших наборах рекомбинантных инбредных линий мышей. Генетика. 2006, 172 (3): 1783-1797.
Генетика. 2006, 172 (3): 1783-1797.
PubMed Central CAS Статья PubMed Google Scholar
Чеслер Э., Миллер Д., Бранстеттер Л., Галлоуэй Л., Джексон Б., Филип В., Вой Б., Кулиат С., Тредгилл Д., Уильямс Р. и др.: Совместный крест в Национальной лаборатории Ок-Ридж: разработка мощный ресурс для системной генетики.Геном млекопитающих. 2008, 19 (6): 382-389.
PubMed Central Статья PubMed Google Scholar
Threadgill DW, Хантер К.В., Уильямс RW: Генетическое вскрытие сложных и количественных черт: от фантазии к реальности через усилия сообщества. Геном мамм. 2002, 13 (4): 175-178.
CAS Статья PubMed Google Scholar
Розен Г.Д., Гарри Дж. Д.: Оценка объема мозга на основе серийных измерений секций: сравнение методологий.J Neurosci Methods. 1990, 35: 115-124.
CAS Статья PubMed Google Scholar
Шифман С., Белл Дж. Т., Копли Р. Р., Тейлор М. С., Уильямс Р. В., Мотт Р., Флинт Дж.: Генетическая карта однонуклеотидного полиморфизма с высоким разрешением генома мыши. PLoS биология. 2006, 4 (12): e395.
PubMed Central Статья PubMed Google Scholar
Frazer KA, Eskin E, Kang HM, Bogue MA, Hinds DA, Beilharz EJ, Gupta RV, Montgomery J, Morenzoni MM, Nilsen GB, et al.: Последовательная карта вариаций 8,27 миллиона SNP в инбредных линиях мышей. Природа. 2007, 448 (7157): 1050-1053.
CAS Статья PubMed Google Scholar
Ван Дж., Уильямс Р.В., Мэнли КФ: WebQTL: анализ комплексных характеристик на основе Интернета. Нейроинформатика. 2003, 1 (4): 299-308.
Артикул PubMed Google Scholar




 {-1}\) \(=\log\) \(_\frac{1}{3}\) \(3\).
{-1}\) \(=\log\) \(_\frac{1}{3}\) \(3\).

 2-t-2>0\)
2-t-2>0\) 
 1, –1.
1, –1. 0, 3, −7.
0, 3, −7. Подстановка этих чисел в исходное уравнение даёт, что только x = –10 является корнем.
Подстановка этих чисел в исходное уравнение даёт, что только x = –10 является корнем.
 Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
 е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.
е. степень, в которую надо возвести число 10, чтобы получить число x
. Обозначение: lg x
.







