Начальное положение точки модуль r 3 0 чему равен: Задачи по физике решаем вместе
Урок 2. равномерное прямолинейное движение материальной точки — Физика — 10 класс
Физика, 10 класс
Урок 2. Равномерное прямолинейное движение материальной точки
Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.
Глоссарий по теме:
Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Траектория — линия, по которой движется точка в пространстве.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.
Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М. : Просвещение, 2016.– С.10-30.
: Просвещение, 2016.– С.10-30.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы по теме урока:
http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni.htm.
Теоретический материал для самостоятельного изучения
Основная задача классической механики — определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. Сформулируем
 Нет абсолютно неподвижных тел.
Нет абсолютно неподвижных тел.Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.
Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.
Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.
Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.
Математически это принято записывать в виде:
Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.
В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:
Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.
Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.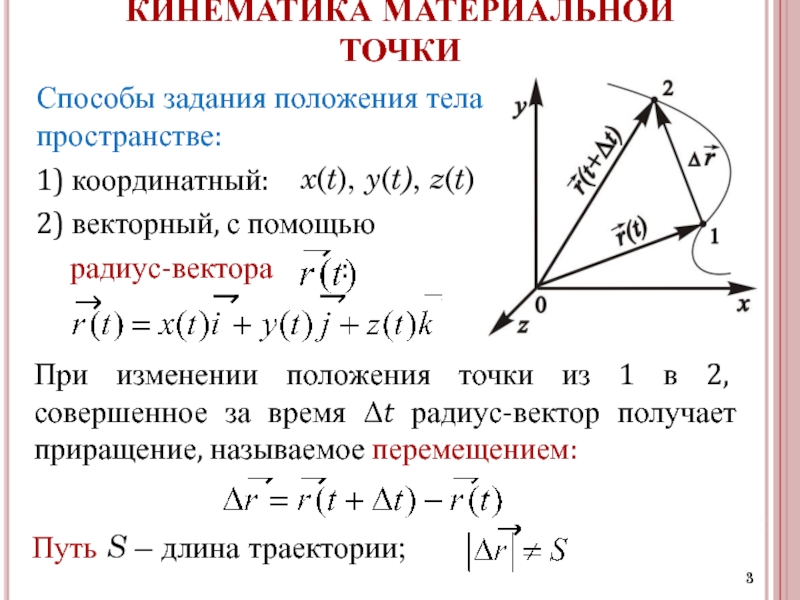
Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют
Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.
Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор задает положение точки в начальный момент времени t0, а радиус-вектор- в момент времени t. Тогда промежуток времени:
,
и перемещение:
.
Подставляя выражение для скорости, получим:
Если начальный момент времени t0 принять равным нулю, то скорость равна:
Выразим отсюда радиус-вектор :
Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме.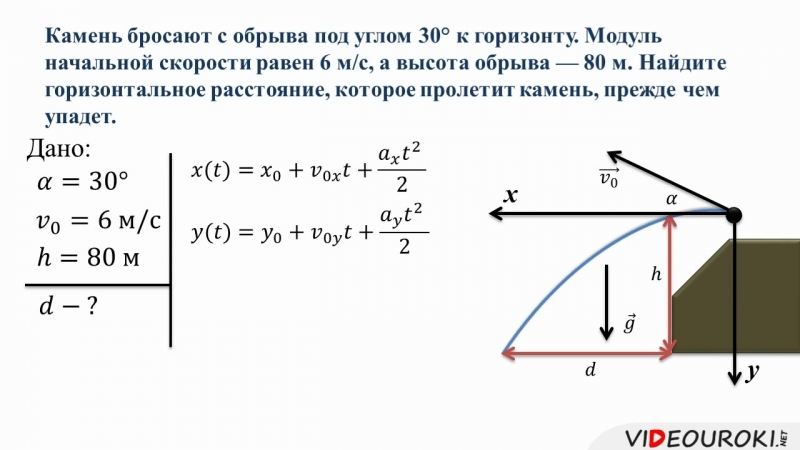 Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
х=х0+vхt.
Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:
Его можно найти, зная модуль скорости
Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.
Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х0+𝞾хt. График движения представляет собой прямую линию:
Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой больше угол наклона первой прямой , т.е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Примеры и разбор решения заданий
1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?
Дано: xо = — 10 м, t = 5 c, ʋ = 2 м/с. Найти s, х.
Решение: координату точки найдем по формуле:
х = х0 + 𝞾х t
Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:
х = — 10 + 2· 5 = 0 (м).
Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.
2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.
Дано:
Найти .
Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:
,
где — искомая величина.
Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины
Ответ: .
Вектор соединяющий начальное положение. Перемещением наз-ся вектор, соединяющий начальную и конечную точки траектории. Основные понятия кинематики
Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.
Если
два тела взаимодействуют друг с другом,
то в результате изменяется скорость
обоих тел, т. е. в процессе взаимодействия
оба тела приобретают ускорения.
Отношение ускорений двух данных тел
оказывается постоянным при любых
воздействиях. В физике принято, что
массы взаимодействующих тел обратно
пропорциональны ускорениям, приобретаемым
телами в результате их взаимодействия.
е. в процессе взаимодействия
оба тела приобретают ускорения.
Отношение ускорений двух данных тел
оказывается постоянным при любых
воздействиях. В физике принято, что
массы взаимодействующих тел обратно
пропорциональны ускорениям, приобретаемым
телами в результате их взаимодействия.
Сила – это количественная мера взаимодействия тел. Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую природу: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной . Векторная сумма всех сил, действующих на тело, называетсяравнодействующей силой .
Для измерения сил необходимо установить эталон силы и способ сравнения других сил с этим эталоном.
В
качестве эталона силы можно взять
пружину, растянутую до некоторой
заданной длины. Модуль силы F 0 ,
с которой эта пружина при фиксированном
растяжении действует на прикрепленное
к ее концу тело, называют эталоном
силы . Способ сравнения других сил с эталоном
состоит в следующем: если тело под
действием измеряемой силы и
эталонной силы остается
в покое (или движется равномерно и
прямолинейно), то силы равны по
модулю F = F 0 (рис. 1.7.3).
Способ сравнения других сил с эталоном
состоит в следующем: если тело под
действием измеряемой силы и
эталонной силы остается
в покое (или движется равномерно и
прямолинейно), то силы равны по
модулю F = F 0 (рис. 1.7.3).
Если измеряемая сила F больше (по модулю) эталонной силы, то можно соединить две эталонные пружины параллельно (рис. 1.7.4). В этом случае измеряемая сила равна 2F 0 . Аналогично могут быть измерены силы 3F 0 , 4F 0 и т. д.
Измерение сил, меньших 2F 0 , может быть выполнено по схеме, показанной на рис. 1.7.5.
Эталонная сила в Международной системе единиц называется ньютон (Н).
Сила в 1 Н сообщает телу массой 1 кг ускорение 1 м/с 2
На
практике нет необходимости все
измеряемые силы сравнивать с эталоном.
Для измерения сил используют пружины,
откалиброванные описанным выше
способом. Такие откалиброванные
пружины называются динамометрами . Сила измеряется по растяжению
динамометра (рис. 1.7.6).
Сила измеряется по растяжению
динамометра (рис. 1.7.6).
Законы
механики Ньютона — три
закона, лежащие в основе т. н. классической
механики. Сформулированы И. Ньютоном
(1687). Первый закон: “Всякое тело
продолжает удерживаться в своём
состоянии покоя или равномерного и
прямолинейного движения, пока и
поскольку оно не понуждается приложенными
силами изменить это состояние”. Второй
закон: “Изменение количества движения
пропорционально приложенной движущей
силе и происходит по направлению той
прямой, по которой эта сила действует”.
Третий закон: “Действию всегда есть
равное и противоположное противодействие,
иначе, взаимодействия двух тел друг
на друга между собой равны и направлены
в противоположные стороны”.
1.1. Зако́н
ине́рции (Первый закон Нью́тона) :
свободное тело, на которое не действуют
силы со стороны других тел, находится
в состоянии покоя или равномерного
прямолинейного движения (понятие
скорости здесь применяется к центру
масс тела в случае непоступательного
движения). Иными словами, телам
свойственна ине́рция (от лат. inertia —
“бездеятельность”, “косность”), то
есть явление сохранения скорости,
если внешние воздействия на них
скомпенсированы.
Системы
отсчёта, в которых выполняется закон
инерции, называются инерциальными
системами отсчёта (ИСО).
Впервые
закон инерции был сформулирован
Галилео Галилеем, который после
множества опытов заключил, что для
движения свободного тела с постоянной
скоростью не нужно какой-либо внешней
причины. До этого общепринятой была
иная точка зрения (восходящая к
Аристотелю): свободное тело находится
в состоянии покоя, а для движения с
постоянной скоростью необходимо
приложение постоянной силы.
Впоследствии
Ньютон сформулировал закон инерции
в качестве первого из трёх своих
знаменитых законов.
Принцип
относительности Галилея: во всех
инерциальных системах отсчета все
физические процессы протекают
одинаково. В системе отсчета, приведенной
в состояние покоя или равномерного
прямолинейного движения относительно
инерциальной системы отсчета (условно
— “покоящейся”) все процессы протекают
точно так же, как и в покоящейся
системе.
Иными словами, телам
свойственна ине́рция (от лат. inertia —
“бездеятельность”, “косность”), то
есть явление сохранения скорости,
если внешние воздействия на них
скомпенсированы.
Системы
отсчёта, в которых выполняется закон
инерции, называются инерциальными
системами отсчёта (ИСО).
Впервые
закон инерции был сформулирован
Галилео Галилеем, который после
множества опытов заключил, что для
движения свободного тела с постоянной
скоростью не нужно какой-либо внешней
причины. До этого общепринятой была
иная точка зрения (восходящая к
Аристотелю): свободное тело находится
в состоянии покоя, а для движения с
постоянной скоростью необходимо
приложение постоянной силы.
Впоследствии
Ньютон сформулировал закон инерции
в качестве первого из трёх своих
знаменитых законов.
Принцип
относительности Галилея: во всех
инерциальных системах отсчета все
физические процессы протекают
одинаково. В системе отсчета, приведенной
в состояние покоя или равномерного
прямолинейного движения относительно
инерциальной системы отсчета (условно
— “покоящейся”) все процессы протекают
точно так же, как и в покоящейся
системе. Следует
отметить что понятие инерциальной
системы отсчета — абстрактная модель
(некий идеальный объект рассматриваемый
вместо реального объекта. Примерами
абстрактной модели служат абсолютно
твердое тело или невесомая нить),
реальные системы отсчета всегда
связаны с каким-либо объектом и
соответствие реально наблюдаемого
движения тел в таких системах с
результатами расчетов будет
неполным. 1.2
Закон движения —
математическая формулировка того,
как движется тело или как происходит
движение более общего вида.
В
классической механике материальной
точки закон движения представляет
собой три зависимости трёх пространственных
координат от времени, либо зависимость
одной векторной величины (радиус-вектора)
от времени, вида.
Закон
движения может быть найден, в зависимости
от задачи, либо из дифференциальных
законов механики, либо из
интегральных. Закон
сохранения энергии —
основной закон природы, заключающийся
в том, что энергия замкнутой системы
сохраняется во времени.
Следует
отметить что понятие инерциальной
системы отсчета — абстрактная модель
(некий идеальный объект рассматриваемый
вместо реального объекта. Примерами
абстрактной модели служат абсолютно
твердое тело или невесомая нить),
реальные системы отсчета всегда
связаны с каким-либо объектом и
соответствие реально наблюдаемого
движения тел в таких системах с
результатами расчетов будет
неполным. 1.2
Закон движения —
математическая формулировка того,
как движется тело или как происходит
движение более общего вида.
В
классической механике материальной
точки закон движения представляет
собой три зависимости трёх пространственных
координат от времени, либо зависимость
одной векторной величины (радиус-вектора)
от времени, вида.
Закон
движения может быть найден, в зависимости
от задачи, либо из дифференциальных
законов механики, либо из
интегральных. Закон
сохранения энергии —
основной закон природы, заключающийся
в том, что энергия замкнутой системы
сохраняется во времени. Другими
словами, энергия не может возникнуть
из ничего и не может в никуда исчезнуть,
она может только переходить из одной
формы в другую.
Закон
сохранения энергии встречается в
различных разделах физики и проявляется
в сохранении различных видов энергии.
Например, в классической механике
закон проявляется в сохранении
механической энергии (суммы потенциальной
и кинетической энергий). В термодинамике
закон сохранения энергии называется
первым началом термодинамики и говорит
о сохранении энергии в сумме с тепловой
энергией.
Поскольку
закон сохранения энергии относится
не к конкретным величинам и явлениям,
а отражает общую, применимую везде и
всегда, закономерность, то правильнее
называть его не законом, а принципом
сохранения энергии.
Частный
случай — Закон сохранения механической
энергии — механическая энергия
консервативной механической системы
сохраняется во времени. Проще говоря,
при отсутствии сил типа трения
(диссипативных сил) механическая
энергия не возникает из ничего и не
может никуда исчезнуть.
Другими
словами, энергия не может возникнуть
из ничего и не может в никуда исчезнуть,
она может только переходить из одной
формы в другую.
Закон
сохранения энергии встречается в
различных разделах физики и проявляется
в сохранении различных видов энергии.
Например, в классической механике
закон проявляется в сохранении
механической энергии (суммы потенциальной
и кинетической энергий). В термодинамике
закон сохранения энергии называется
первым началом термодинамики и говорит
о сохранении энергии в сумме с тепловой
энергией.
Поскольку
закон сохранения энергии относится
не к конкретным величинам и явлениям,
а отражает общую, применимую везде и
всегда, закономерность, то правильнее
называть его не законом, а принципом
сохранения энергии.
Частный
случай — Закон сохранения механической
энергии — механическая энергия
консервативной механической системы
сохраняется во времени. Проще говоря,
при отсутствии сил типа трения
(диссипативных сил) механическая
энергия не возникает из ничего и не
может никуда исчезнуть. Ек1+Еп1=Ек2+Еп2
Закон
сохранения энергии — это интегральный
закон. Это значит, что он складывается
из действия дифференциальных законов
и является свойством их совокупного
действия. Например, иногда говорят,
что невозможность создать вечный
двигатель обусловлена законом
сохранения энергии. Но это не так. На
самом деле, в каждом проекте вечного
двигателя срабатывает один из
дифференциальных законов и именно он
делает двигатель неработоспособным.
Закон сохранения энергии просто
обобщает этот факт.
Согласно
теореме Нётер, закон сохранения
механической энергии является
следствием однородности времени. 1.3.
Зако́н сохране́ния и́мпульса (Зако́н
сохране́ния коли́чества движения 2й
закон Ньютона) утверждает,
что сумма импульсов всех тел (или
частиц) замкнутой системы есть величина
постоянная.
Из
законов Ньютона можно показать, что
при движении в пустом пространстве
импульс сохраняется во времени, а при
наличии взаимодействия скорость его
изменения определяется суммой
приложенных сил.
Ек1+Еп1=Ек2+Еп2
Закон
сохранения энергии — это интегральный
закон. Это значит, что он складывается
из действия дифференциальных законов
и является свойством их совокупного
действия. Например, иногда говорят,
что невозможность создать вечный
двигатель обусловлена законом
сохранения энергии. Но это не так. На
самом деле, в каждом проекте вечного
двигателя срабатывает один из
дифференциальных законов и именно он
делает двигатель неработоспособным.
Закон сохранения энергии просто
обобщает этот факт.
Согласно
теореме Нётер, закон сохранения
механической энергии является
следствием однородности времени. 1.3.
Зако́н сохране́ния и́мпульса (Зако́н
сохране́ния коли́чества движения 2й
закон Ньютона) утверждает,
что сумма импульсов всех тел (или
частиц) замкнутой системы есть величина
постоянная.
Из
законов Ньютона можно показать, что
при движении в пустом пространстве
импульс сохраняется во времени, а при
наличии взаимодействия скорость его
изменения определяется суммой
приложенных сил. В классической
механике закон сохранения импульса
обычно выводится как следствие законов
Ньютона. Однако этот закон сохранения
верен и в случаях, когда ньютоновская
механика неприменима (релятивистская
физика, квантовая механика).
Как
и любой из законов сохранения, закон
сохранения импульса описывает одну
из фундаментальных симметрий, —
однородность пространства Третий
закон Ньютона объясняет,
что происходит с двумя взаимодействующими
телами. Возьмём для примера замкнутую
систему, состоящую из двух тел. Первое
тело может действовать на второе с
некоторой силой F12, а второе — на первое
с силой F21. Как соотносятся силы? Третий
закон Ньютона утверждает: сила действия
равна по модулю и противоположна по
направлению силе противодействия.
Подчеркнём, что эти силы приложены к
разным телам, а потому вовсе не
компенсируются.
Сам
закон:
Тела
действуют друг на друга с силами,
направленными вдоль одной и той же
прямой, равными по модулю и противоположными
по направлению: .
В классической
механике закон сохранения импульса
обычно выводится как следствие законов
Ньютона. Однако этот закон сохранения
верен и в случаях, когда ньютоновская
механика неприменима (релятивистская
физика, квантовая механика).
Как
и любой из законов сохранения, закон
сохранения импульса описывает одну
из фундаментальных симметрий, —
однородность пространства Третий
закон Ньютона объясняет,
что происходит с двумя взаимодействующими
телами. Возьмём для примера замкнутую
систему, состоящую из двух тел. Первое
тело может действовать на второе с
некоторой силой F12, а второе — на первое
с силой F21. Как соотносятся силы? Третий
закон Ньютона утверждает: сила действия
равна по модулю и противоположна по
направлению силе противодействия.
Подчеркнём, что эти силы приложены к
разным телам, а потому вовсе не
компенсируются.
Сам
закон:
Тела
действуют друг на друга с силами,
направленными вдоль одной и той же
прямой, равными по модулю и противоположными
по направлению: .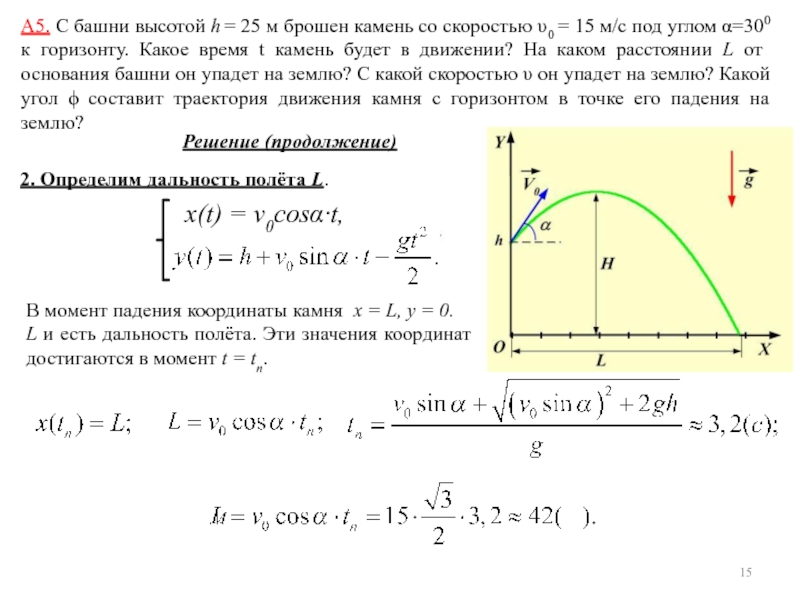 1.4.
Силы инерции Законы
Ньютона, строго говоря, справедливы
только в инерциальных системах отсчета.
Если мы честно запишем уравнение
движения тела в неинерциальной системе
отсчета, то оно будет по виду отличаться
от второго закона Ньютона. Однако
часто, для упрощения рассмотрения,
вводят некую фиктивную “силу инерции”,
и тогда эти уравнения движения
переписываются в виде, очень похожем
на второй закон Ньютона. Математически
здесь всё корректно (правильно), но с
точки зрения физики новую фиктивную
силу нельзя рассматривать как нечто
реальное, как результат некоторого
реального взаимодействия. Ещё раз
подчеркнём: “сила инерции” — это
лишь удобная параметризация того, как
отличаются законы движения в инерциальной
и неинерциальной системах отсчета. 1.5.
Закон вязкости Закон
вязкости (внутреннего трения) Ньютона
— математическое выражение, связывающее
напряжение внутреннего трения τ
(вязкость) и изменение скорости среды
v в пространстве
(скорость
деформации) для текучих тел (жидкостей
и газов):
где
величина η называется коэффициентом
внутреннего трения или динамическим
коэффициентом вязкости (единица СГС
— пуаз).
1.4.
Силы инерции Законы
Ньютона, строго говоря, справедливы
только в инерциальных системах отсчета.
Если мы честно запишем уравнение
движения тела в неинерциальной системе
отсчета, то оно будет по виду отличаться
от второго закона Ньютона. Однако
часто, для упрощения рассмотрения,
вводят некую фиктивную “силу инерции”,
и тогда эти уравнения движения
переписываются в виде, очень похожем
на второй закон Ньютона. Математически
здесь всё корректно (правильно), но с
точки зрения физики новую фиктивную
силу нельзя рассматривать как нечто
реальное, как результат некоторого
реального взаимодействия. Ещё раз
подчеркнём: “сила инерции” — это
лишь удобная параметризация того, как
отличаются законы движения в инерциальной
и неинерциальной системах отсчета. 1.5.
Закон вязкости Закон
вязкости (внутреннего трения) Ньютона
— математическое выражение, связывающее
напряжение внутреннего трения τ
(вязкость) и изменение скорости среды
v в пространстве
(скорость
деформации) для текучих тел (жидкостей
и газов):
где
величина η называется коэффициентом
внутреннего трения или динамическим
коэффициентом вязкости (единица СГС
— пуаз). Кинематическим коэффициентом
вязкости называется величина μ = η / ρ
(единица СГС — Стокс, ρ − плотность
среды).
Закон
Ньютона может быть получен аналитически
приемами физической кинетики, где
вязкость рассматривается обычно
одновременно с теплопроводностью и
соответсвующим законом Фурье для
теплопроводности. В кинетической
теории газов коэффициент внутреннего
трения вычисляется по формуле где
— средняя скорость теплового
движения молекул, λ − средняя длина
свободного пробега.
Кинематическим коэффициентом
вязкости называется величина μ = η / ρ
(единица СГС — Стокс, ρ − плотность
среды).
Закон
Ньютона может быть получен аналитически
приемами физической кинетики, где
вязкость рассматривается обычно
одновременно с теплопроводностью и
соответсвующим законом Фурье для
теплопроводности. В кинетической
теории газов коэффициент внутреннего
трения вычисляется по формуле где
— средняя скорость теплового
движения молекул, λ − средняя длина
свободного пробега.
Проекцию считают положительной если (а х >0) от проекции начала вектора к проекции его конца нужно идти по направлению оси. В противном случае проекция вектора (а х
0) от проекции начала вектора к проекции его конца нужно идти по направлению оси. В противном случае проекция вектора (а х
0) от проекции начала вектора к проекции его конца нужно идти по направлению оси. В противном случае проекция вектора (а х
0) от проекции начала вектора к проекции его конца нужно идти по направлению оси. В противном случае проекция вектора (а х 0) от проекции начала вектора к проекции его конца нужно идти по направлению оси. В противном случае проекция вектора (а х
В противном случае проекция вектора (а х 0) от проекции начала вектора к проекции его конца нужно идти по направлению оси. В противном случае проекция вектора (а х
Путь или перемещение мы оплачиваем при поездке в такси? Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. Найти путь и перемещение мяча. Велосипедист движется по окружности с радиусом 30 м. Чему равны путь и перемещение велосипедиста за половину оборота? За полный оборот?
§ § 2,3 ответить на вопросы в конце параграфа. Упр. 3, стр.15 На рис. показана траектория АВСД движения точки из А в Д. Найти координаты точек начала и конца движения, пройденный путь, перемещение, проекцию перемещения на оси координат. Решить задачу (по желанию):Катер прошел на северо-восток 2 км, а затем в северном направлении еще 1 км. Найти геометрическим построением перемещение (S) и его модуль (S).
Определение 1
Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.
Существуют несколько видов движений и траекторий твердого тела:
- поступательное;
- вращательное, то есть движение по окружности;
- плоское, то есть перемещение по плоскости;
- сферическое, характеризующее движение по поверхности сферы;
- свободное, иначе говоря, произвольное.
Рисунок 1 . Определение точки при помощи координат x = x (t) , y = y (t) , z = z (t) и радиус-вектора r → (t) , r 0 → является радиус-вектором точки в начальный момент времени
Положение материальной точки в пространстве в любой момент времени может быть задано при помощи закона движения, определенный координатным способом, через зависимость координат от времени x = x (t) , y = y (t) , z = z (t) или от времени радиус-вектора r → = r → (t) , проведенного из начала координат к заданной точке. Это показано на рисунке 1 .
Определение 2S → = ∆ r 12 → = r 2 → — r 1 → – направленный отрезок прямой, соединяющий начальную с конечной точкой траектории тела. Значение пройденного пути l равняется длине траектории, пройденной телом за определенный промежуток времени t .
Значение пройденного пути l равняется длине траектории, пройденной телом за определенный промежуток времени t .
Рисунок 2 . Пройденный путь l и вектор перемещения s → при криволинейном движении тела, a и b – начальная и конечная точки пути, принятые в физике
Определение 3
По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Путь – скалярная величина. Считается числом.
Сумма двух последовательных перемещений из точки 1 в точку 2 и из токи 2 в точку 3 является перемещением из точки 1 в точку 3 , как показано на рисунке 3 .
Рисунок 3 . Сумма двух последовательных перемещений ∆ r → 13 = ∆ r → 12 + ∆ r → 23 = r → 2 — r → 1 + r → 3 — r → 2 = r → 3 — r → 1
Когда радиус-вектор материальной точки в определенный момент времени t является r → (t) , в момент t + ∆ t есть r → (t + ∆ t) , тогда ее перемещение ∆ r → за время ∆ t равняется ∆ r → = r → (t + ∆ t) — r → (t) .
Перемещение ∆ r → считается функцией времени t: ∆ r → = ∆ r → (t) .
Пример 1
По условию дан движущийся самолет, представленный на рисунке 4 . Определить вид траектории точки М.
Рисунок 4
Решение
Необходимо рассмотреть систему отсчета I , называемую «Самолет» с траекторией движения точки М виде окружности.
Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.
Пример 2
Дана материальная точка, которая совершает движение из А в В. Значение радиуса окружности R = 1 м. Произвести нахождение S , ∆ r → .
Решение
Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:
Подставляем числовые значения и получаем:
S = 3 , 14 · 1 м = 3 , 14 м.
Перемещением ∆ r → в физике считается вектор, соединяющий начальное положение материальной точки с конечным, то есть А с В.
Подставив числовые значения, вычислим:
∆ r → = 2 R = 2 · 1 = 2 м.
Ответ: S = 3 , 14 м; ∆ r → = 2 м.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Вопрос 1.Радиус-вектор.Вектор перемещения.
— радиус-вектор — это вектор, проведенный от точки отсчета О к рассматриваемой точке М.
— перемещение (или изменение радиус-вектора) – это вектор, соединяющий начало и конец траектории.
радиус-вектор в прямоугольной системе декартовых координат:
Где -называют координатами точки.
Вопрос 2.Скорость перемещения. Средняя и мгновенная скорости.
Скорость перемещения (вектор)-показывает, как изменяется перемещение в единицу времени.
Средняя: Мгновенная:
Мгновенная скорость всегда направлена по касательной к траектории,
а средняя – совпадает с вектором перемещения.
Проекция: Модуль:
Вопрос 3. Путь.Его связь с модулем скорости.
Путь.Его связь с модулем скорости.
S – путь – это длина траектории (скалярная величина, > 0).
S-площадь фигуры, ограниченной кривой v(t) и прямыми t 1 и t 2 .
Вопрос 4.Ускорение.Модуль ускорения.
Ускорение — по смыслу – показывает, как изменяется скорость в единицу времени.
Проекция: Модуль: Среднее значение:
Вопрос 5.Неравномерное движение точки по криволинейной траектории.
Если точка движется по криволинейной траектории, то целесообразно разложить ускорение на составляющие, одна из которых направлена по касательной и называется тангенциальным или касательным ускорением , а другая направлена по нормали к касательной, т.е. по радиусу кривизны, к центру кривизны и называется нормальным ускорением.
Характеризует изменение скорости по направлению, – по величине.
Где r — радиус кривизны.
У точки, движущейся по криволинейной траектории, всегда есть нормальное ускорение, а тангенциальное – только тогда, когда скорость изменяется по величине.
(2, 3)Тема 2. КИНЕМАТИЧНСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ.
Вопрос 1.Получить кинематические уравнения движения r(t) и v(t).
Два дифференциальных и связанных с ними двух интегральных векторных уравнениях:
→ и — кинематические уравнения равнопеременного точки при .
Вопрос 2. Получить кинематические уравнения движения x(t),y(t),v x (t) и v y (t), для брошенного тела.
Вопрос 3. Получить кинемат. уравнения движения x(t),y(t),v x (t) и v y (t), для тела, брошенного под углом.
Вопрос 4. Получить уравнение движения для тела, брошенного под углом.
Тема 3. КИНЕМАТИКА ВРАЩЕНИЯ.
Вопрос 1.Кинематические характеристики вращательного движения.
угловое перемещение — угол поворота радиус-вектора.
угловая скорость — показывает, как изменяется угол поворота радиус-вектора.
угловое ускорение — показывает, как изменяется угловая скорость за единицу времени.
Вопрос 2. Связь между линейными и угловыми характеристиками движения точки
Вопрос 3.Получите кинематическое уравнения w (t) и ф (t).
То кинематические уравнения после интегрирования примут более простой вид: — кин. уравнения равноускор.(+) и равнозамедл.(-) вращательного движения.
(4, 5, 6) Тема 4. КИНЕМАТИКА АТТ.
Вопрос 1.Определение АТТ. Поступательные и вращательные движения АТТ.
АТТ называется тело, деформациями которого можно пренебречь в условиях данной задачи.
Все движения АТТ можно разложить на поступательное и вращательное, относительно некоторой мгновенной оси. Поступательное движение – это движение, при котором прямая, проведенная через любые две точки тела, перемещается параллельно самой себе. При поступательном движении все точки тела совершают одинаковые перемещения.Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
В качестве кинематического уравнения вращательного движения АТТ достаточно знать уравнение j (t) для угла поворота радиус-вектора, проведенного от оси вращения к какой-либо точке тела (если ось неподвижна). Т.е., принципиально кинематические уравнения движения для точки и АТТ не отличаются.
Тема 5. ЗАКОНЫ НЬЮТОНА.
Тема 6. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
Тема 7. РАБОТА. МОЩНОСТЬ. ЭНЕРГИЯ.
Вопрос 7. Законы сохранения применительно к абсолютно упругому удару двух шаров.
Абсолютно упругий удар – это такой удар, при котором сохраняется кинетическая энергия всей системы.
Тема 10. СИЛОВЫЕ ПОЛЯ
Вопрос 3. Сокращение длины.
l 0 – длина стержня в системе, относительно которой он покоится (в нашем случае в К ), l – длина этого отрезка в системе, относительно которой он движется (К¢ ). т.к. и найдем связь между l и l 0 : .
Таким образом, из СТО следует, что размеры движущихся тел должны сокращаться в направлении их движения, но реального сокращения нет, т.к. все ИСО равноправны.
Вопрос 2.Идеальный газ
Простейшей моделью реальных газов является идеальный газ . С ма кро скопической точки зрения – это газ, для которого выполняются газовые законы (pV = const, p/T = const, V/T = const ). С ми кро скопической точки зрения – это газ, для которого можно пренебречь: 1) взаимодействием молекул между собой и 2) собственным объемом молекул газа по сравнению с объемом сосуда, в котором находится газ.
Уравнение, связывающее между собой параметры состояния, называется уравнением состояния газа. Одно из простейших уравнений состояния — это
( ; ; ) уравнение Менделеева – Клапейрона.
(n – концентрация, k – постоянная Больцмана) — уравнение состояния идеального газа в другой форме.
Тема 15. ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ
ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ
Вопрос 1. Основные понятия. Обратимые и необратимые процессы.
Обратимый процесс — это такой процесс перехода системы из состояния А в состояние В , при котором возможен обратный переход от В к А через те же промежуточные состояния и при этом в окружающих телах не происходит никаких изменений. Система называется изолированной , если она не обменивается энергией с окружающей средой. На графике состояния обозначаются точками, а процессы – линиями.
Величины, которые зависят только от состояния системы и не зависят от процессов, посредством которых система пришла в данное состояние, называются функциями состояния . Величины, значения которых в данном состоянии зависят от предшествующих процессов, называются функциями процессов — это теплота Q и работа A ,их изменение обозначают часто как dQ, dA или . (d — греческая буква — дельта)
Работа и теплота – это две формы передачи энергии от одних тел к другим. При совершении работы меняется относительное расположение тел или частей тела. Передача энергии в виде теплоты осуществляется при контакте тел – за счет теплового движения молекул.
При совершении работы меняется относительное расположение тел или частей тела. Передача энергии в виде теплоты осуществляется при контакте тел – за счет теплового движения молекул.
К внутренней энергии относят: 1)кинетическую энергию теплового движения молекул (но не кинетическую энергию всей системы в целом), 2)потенциальную энергию взаимодействия молекул между собой, 3)кинетическую и потенциальную энергию колебательного движения атомов в молекуле, 4)энергию связи электронов с ядром в атоме, 5)энергию взаимодействия протонов и нейтронов внутри ядра атома. Эти энергии по величине очень сильно отличаются друг от друга, например, энергия теплового движения молекул при 300 К ~ 0,04 эВ, энергия связи электрона в атоме ~ 20-50 эВ, а энергия взаимодействия нуклонов в ядре ~10 МэВ. Поэтому эти взаимодействия рассматривают по отдельности.
Внутренняя энергия идеального газа – это кинетическая энергия теплового движения его молекул. Она зависит только от температуры газа. Ее изменение имеет одинаковое выражение для любых процессов в идеальных газах и зависит только от начальной и конечной температур газа. — внутренняя энергия идеального газа.
Ее изменение имеет одинаковое выражение для любых процессов в идеальных газах и зависит только от начальной и конечной температур газа. — внутренняя энергия идеального газа.
Тема 16.
Вопрос 1. Энтропия
II начало термодинамики, как и I начало, является обобщением большого числа опытных фактов и имеет несколько формулировок.
Введем сначала понятие «энтропия», которое играет ключевую роль в термодинамике. Энтропия — S – одна из важнейших термодинамических функций, характеризующая состояние или возможные изменения состояния вещества – это многогранное понятие.
1)Энтропия – это функция состояния . Введение таких величин ценно тем, что при любых процессах изменение функции состояния одинаково, поэтому сложный реальный процесс можно заменить «выдуманными» простыми процессами. Например, реальный процесс перехода системы из состояния А в состояние В (см. рис.) можно заменить на два процесса: изохорический А®С и изобарический С®В.
Энтропия определяется следующим образом.
Для обратимых процессов в идеальных газах можно получить формулы для вычисления энтропии в различных процессах. Выразим dQ из I начала и подставим в выражение для dS .
общее выражение для изменения энтропии в обратимых процессах.
Интегрируя, получим выражения для изменения энтропии в различных изопроцессах в идеальных газах.
Вопрос 2,3,4.изобарический, изохорический, изотермический
Во всех расчетах энтропии имеет значение только разность энтропий конечного и начального состояний системы
2)Энтропия мера рассеяния энергии.
| запишем I начало термодинамики для обратимого изотермического процесса, учитывая, что dQ=T×dS и выразим работуdА | |
| термодинамическая функция называется свободной энергией величина называется связанной энергией | |
Из формул можно сделать вывод, что в работу можно перевести не весь запас внутренней энергии системы U . Часть энергии TS нельзя перевести в работу, она рассеивается в окружающей среде. И эта «связанная» энергия тем больше, чем больше энтропия системы. Следовательно, энтропию можно назвать мерой рассеяния энергии. Часть энергии TS нельзя перевести в работу, она рассеивается в окружающей среде. И эта «связанная» энергия тем больше, чем больше энтропия системы. Следовательно, энтропию можно назвать мерой рассеяния энергии. |
3)Энтропия – мера беспорядка системы
Введем понятие термодинамической вероятности.Пусть мы имеет ящик, разделенный на n отсеков. В ящике по всем отсекам свободно перемещается N молекул. В первом отсеке окажется N 1 молекул, во втором отсеке N 2 молекул,…,
в n -ом отсеке — N n молекул. Число способов w , которыми можно распределить N молекул по n состояниям (отсекам) называется термодинамической вероятностью . Иначе говоря, термодинамическая вероятность показывает, сколькими микро распределениями можно получить данное макро распределение Она вычисляется по формуле:
Для примера вычисления w рассмотрим систему, состоящую из трех молекул 1, 2 и 3, которые свободно перемещаются в ящике с тремя отсеками.
В данном примере N = 3 (три молекулы) и n = 3 (три отсека), молекулы считаются различимыми.
В первом случае макрораспределение – это равномерное распределение молекул по отсекам, оно может осуществиться 6-ью микрораспределениями. Вероятность такого распределение самая большая. Равномерное распределение можно назвать «беспорядком» (по аналогии с разбросанными вещами в комнате) В последнем случае, когда молекулы собираются только в одном отсеке вероятность наименьшая. Проще говоря, из повседневных наблюдений мы знаем, что молекулы воздуха более или менее равномерно распределяются в помещении, и практически совершенно невероятно, чтобы все молекулы собрались в одном углу комнаты. Однако теоретически такая вероятность существует.
Больцман постулировал, что энтропия прямо пропорциональна натуральному логарифму термодинамической вероятности:
Следовательно, энтропию можно назвать мерой беспорядка системы.
Вопрос 6.Теперь мы можем сформулировать II начало термодинамики .
| 1)При любых процессах, происходящих в теплоизолированной системе, энтропия системы не может убывать: |
| Знак «=» относится к обратимым процессам, знак «>» — к необратимым (реальным) процессам. В незамкнутых системах энтропия может меняться любым образом. |
| Иначе говоря, в замкнутых реальных системах возможны только те процессы, при которых энтропия возрастает. Энтропия связана с термодинамической вероятностью, следовательно, ее увеличение в замкнутых системах означает рост «беспорядка» системы, т.е. молекулы стремятся прийти в одинаковое энергетическое состояние и с течением времени все молекулы должны иметь одинаковую энергию. Отсюда был сделан вывод о стремлении нашей Вселенной к тепловой смерти. «Энтропия мира стремится к максимуму» (Клаузиус). Так как законы термодинамики выведены на основе человеческого опыта в масштабах Земли, то вопрос об их применимости в масштабах Вселенной остается открытым |
3) «Невозможно построить вечный двигатель второго рода, т. е. такую периодически действующую машину, действие которой состояло бы только в поднятии груза и охлаждении теплового резервуара» (Томсон, Планк) е. такую периодически действующую машину, действие которой состояло бы только в поднятии груза и охлаждении теплового резервуара» (Томсон, Планк) |
| Обязательно должно быть еще тело, которому «придется» отдать часть теплоты. Просто отнимать тепло от некоторого тела и превращать его в работу невозможно потому, что такой процесс сопровождается уменьшением энтропии нагревателя. Следовательно, нужно еще одно тело – холодильник, энтропия которого будет увеличиваться, чтобы DS = 0 . Т.е. у нагревателя забирается теплота, за счет этого может быть совершена работа, но часть теплоты «теряется», т.е. передается холодильнику. |
Вопрос 7. КРУГОВЫЕ ПРОЦЕССЫ (ЦИКЛЫ)
Круговым процессом или циклом называется такой процесс, при котором система, пройдя ряд состояний, возвращается в исходное состояние. Если процесс осуществляется по часовой стрелке, он называется прямым , против часовой стрелки –обратным . Т.к. внутренняя энергия является функцией состояния, то в круговом процессе
Устройство, в котором затрачивается теплота, а получается работа, называется тепловой машиной . Все тепловые машины работают по прямому циклу, состоящему из различных процессов. Устройство, работающее по обратному циклу, называется холодильной машиной . В холодильной машине затрачивается работа, а в результате от холодного тела отнимается теплота, т.е. происходит дополнительное охлаждение этого тела.
Все тепловые машины работают по прямому циклу, состоящему из различных процессов. Устройство, работающее по обратному циклу, называется холодильной машиной . В холодильной машине затрачивается работа, а в результате от холодного тела отнимается теплота, т.е. происходит дополнительное охлаждение этого тела.
Рассмотрим цикл Карно для идеальной тепловой машины. Предполагается, что рабочее тело – идеальный газ, трение отсутствует. Этот цикл, состоящий из двух изотерм и двух адиабат, реально не осуществим, но он сыграл огромную роль в развитии термодинамики и теплотехники и позволил проанализировать коэффициент полезного действия (КПД) тепловых машин.
Таким образом, за цикл газу было сообщено Q 1 теплоты, холодильнику передано Q 2 теплоты и получена работа А .
Из полученного выражения следует, что: 1) КПД всегда меньше единицы,
2)КПД не зависит от рода рабочего тела, а только от температуры нагревателя и холодильника, 3)чтобы повысить КПД нужно увеличить температуру нагревателя и уменьшить температуру холодильника.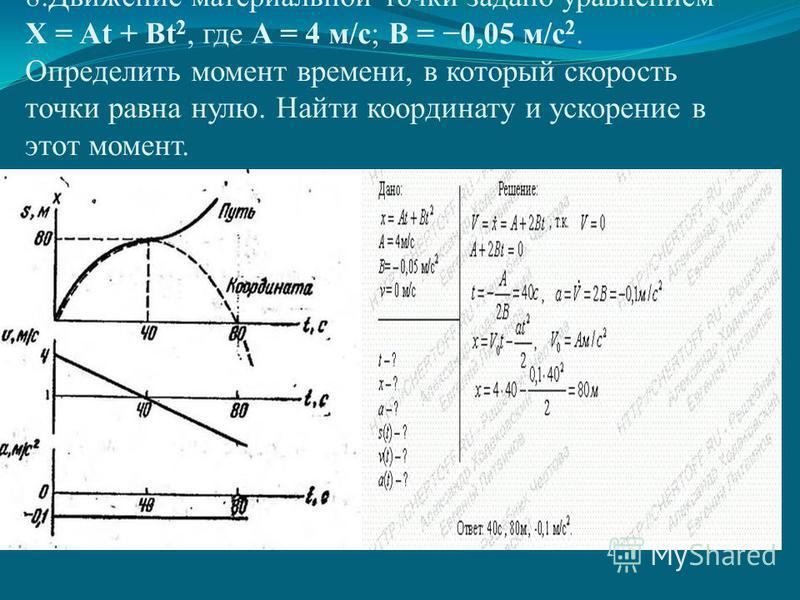 В современных двигателях в качестве нагревателя используются горючие смеси — бензин, керосин, дизельное топливо и др., имеющие определенные температуры горения. Холодильником служит чаще всего окружающая среда. Следовательно, реально увеличить КПД можно только за счет уменьшения трения в различных узлах двигателя и машины.
В современных двигателях в качестве нагревателя используются горючие смеси — бензин, керосин, дизельное топливо и др., имеющие определенные температуры горения. Холодильником служит чаще всего окружающая среда. Следовательно, реально увеличить КПД можно только за счет уменьшения трения в различных узлах двигателя и машины.
Тема 18.Вопрос 1.АГРЕГАТНЫЕ СОСТОЯНИЯ ВЕЩЕСТВА
Молекулы представляют собой сложные системы электрически заряженных частиц. Основная масса молекулы и весь ее положительный заряд сосредоточены в ядрах, их размеры порядка 10 — 15 — 10 — 14 м, а размер самой молекулы, включая электронную оболочку, примерно 10 — 10 м. В целом молекула электрически нейтральна. Электрическое поле ее зарядов в основном сосредоточено внутри молекулы и за ее пределами резко убывает. При взаимодействии двух молекул одновременно проявляются и силы притяжения и силы отталкивания, они по-разному зависят от расстояния между молекулами (см рис.- пунктирные линии). Одновременное действие межмолекулярных сил дает зависимость силы F от расстояния r между молекулами, характерную и для двух молекул, и атомов, и ионов (сплошная кривая). На больших расстояния молекулы практически не взаимодействуют, на очень малых расстояния преобладают силы отталкивания. На расстояниях, равных нескольким диаметрам молекул действуют силы притяжения. Расстояние r o между центрами двух молекул, на котором F=0, — это положение равновесия. Так как сила связана с потенциальной энергией F=-dE пот /dr , то интегрирование даст зависимость потенциальной энергии от r (потенциальная кривая). Равновесное положение соответствует минимуму потенциальной энергии —U min . Для различных молекул вид потенциальной кривой аналогичен, но числовые значения r o и U min различны и определяются природой данных молекул.
На больших расстояния молекулы практически не взаимодействуют, на очень малых расстояния преобладают силы отталкивания. На расстояниях, равных нескольким диаметрам молекул действуют силы притяжения. Расстояние r o между центрами двух молекул, на котором F=0, — это положение равновесия. Так как сила связана с потенциальной энергией F=-dE пот /dr , то интегрирование даст зависимость потенциальной энергии от r (потенциальная кривая). Равновесное положение соответствует минимуму потенциальной энергии —U min . Для различных молекул вид потенциальной кривой аналогичен, но числовые значения r o и U min различны и определяются природой данных молекул.
Кроме потенциальной, молекула обладает еще и кинетической энергией. Минимальная потенциальная энергия у каждого сорта молекул своя, а кинетическая энергия зависит от температуры вещества (Е кин ~ кТ ). В зависимости от соотношения между этими энергиями данное вещество может находиться в том или ином агрегатном состоянии. Например, вода может быть в твердом состоянии (лед), в жидком и в виде пара.
Например, вода может быть в твердом состоянии (лед), в жидком и в виде пара.
У инертных газов U min невелики, поэтому они переходят в жидкое состояние при очень низких температурах. У металлов большие величины U min поэтому они находятся в твердом состоянии вплоть до температуры плавления – это могут быть сотни и тысячи градусов.
Вопрос 3.
Смачивание приводит к тому, что на стенках сосуда жидкость как бы «ползет» по стенке, и ее поверхность искривляется. В широком сосуде это искривление практически незаметно. В узких трубках – капиллярах – этот эффект можно наблюдать визуально. За счет сил поверхностного натяжения создается дополнительное (по сравнению с атмосферным) давление Dр , направленное к центру кривизны поверхности жидкости.
Дополнительное давление вблизи искривленной поверхности жидкости D р приводит к подъему (при смачивании) или опусканию (при несмачивании) жидкости в капиллярах.
При равновесии дополнительное давление равно гидростатическому давлению столбика жидкости. Из формулы Лапласа для капилляра круглого сечения Dp = 2s /R , гидростатическое давление р = r g h . Приравнивая Dр = р , найдем h .
Из формулы Лапласа для капилляра круглого сечения Dp = 2s /R , гидростатическое давление р = r g h . Приравнивая Dр = р , найдем h .
Из формулы видно, что чем меньше радиус капилляра, тем выше подъем (или опускание) жидкости.
Явление капиллярности чрезвычайно распространено в природе и технике. Например, проникновение влаги из почвы в растения осуществляется посредством подъема ее по капиллярным каналам. К капиллярным явлениям относится также такое явление, как движение влаги по стенам помещения, приводящее к сырости. Очень большую роль капиллярность играет при добыче нефти. Размеры пор в породе, содержащей нефть, чрезвычайно малы. Если добываемая нефть окажется несмачивающей по отношению к породе, то она закупорит канальца, и извлечь ее будет очень трудно. Добавляя к жидкости некоторые вещества даже в очень малом количестве, можно существенно изменить ее поверхностное натяжение. Такие вещества называются поверхностно-активными веществами. радиус-вектор в прямоугольной системе декартовых координат:
радиус-вектор в прямоугольной системе декартовых координат:
Где -называют координатами точки.
Открытая Физика. Основные понятия кинематики
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.
Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.
В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Колесо обозрения», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.
Понятие материальной точки играет важную роль в механике.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени радиус-вектора r⟶=r⟶(t) (векторный способ), проведенного из начала координат до данной точки (рис. 1.1.1).
Перемещением тела s⟶=Δr⟶=r⟶-r⟶0 называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.
В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения Δs⟶. При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).
Для характеристики движения вводится понятие средней скорости: υ⟶=Δs⟶Δt=Δr⟶Δt.
В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt: υ⟶=Δs⟶Δt=Δr⟶Δt; (Δt→0).
В математике такой предел называют производной и обозначают dr⟶dt или r→˙(t).
Мгновенная скорость υ⟶ тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.
1.1.3.
При движении тела по криволинейной траектории его скорость υ⟶ изменяется по модулю и направлению. Изменение вектора скорости υ⟶ за некоторый малый промежуток времени Δt можно задать с помощью вектора Δυ⟶ (рис. 1.1.4).
Вектор изменения скорости Δυ⟶=υ⟶2-υ⟶1 за малое время Δt можно разложить на две составляющие: Δυ⟶τ, направленную вдоль вектора υ⟶ (касательная составляющая), и Δυ⟶n, направленную перпендикулярно вектору υ⟶ (нормальная составляющая).
Мгновенным ускорением (или просто ускорением) a⟶ тела называют предел отношения малого изменения скорости Δυ⟶ к малому промежутку времени Δt, в течение которого происходило изменение скорости:
a⟶=Δυ⟶Δt=Δυ⟶τΔt+Δυ⟶nΔt; (Δt→0).
Направление вектора ускорения a⟶ в случае криволинейного движения не совпадает с направлением вектора скорости υ⟶. Составляющие вектора ускорения a⟶ называют касательным (тангенциальным) a⟶τ и нормальным a⟶n ускорениями (рис. 1.1.5).
Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю: aτ=ΔυΔt; (Δt→0).
Вектор a⟶τ направлен по касательной к траектории.
Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент: an=υ2R.
Вектор a→n всегда направлен к центру окружности (см. §1.6).
§1.6).
Из рис. 1.1.5 видно, что модуль полного ускорения равен a=aτ2+an2.
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение s→, скорость υ→ и ускорение a→. Путь l является скалярной величиной. Перемещение s→, скорость υ→ и ускорение a→ – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
Справочник к разделу «Кинематика»
Основные термины и формулы.→ kinematika.docx
→ Тест по теме.
1. Механика – наука об общих законах движения тел.
2. Механическое движение – изменение положения тела в пространстве относительно других с течением времени.
3. Кинематика – это раздел механики, изучающий способы описания движения и связь между величинами, характеризующими эти движения.
4. Тело отсчета – это тело, относительно которого задается положение данного тела или же данной точки.
5. Система отсчета – тело отсчета, связанная с ним система координат, прибор для измерения времени.
6. Радиус – вектор — вектор, проведенный из начала координат в данную точку.
7. Проекцией вектора на координатную ось называется длина отрезка между проекциями начала и конца вектора на данную ось, взятую со знаком «плюс», если направление вектора совпадает с направлением оси и «минус», если направление вектора противоположно направлению оси.
8. Модуль вектора равен корню квадратному из суммы квадратов проекций вектора на координатные оси.
9. Траектория – линия, по которой движется тело.
10. Прямолинейное движение – траектория прямая линия, криволинейное – траектория кривая линия.
11. Перемещение – ВФВ, характеризующая изменение положения тела, равна вектору, соединяющему начальное положение с последующим.
12. Пройденный путь – СФВ, равная длине траектории по которой движется тело.
13. Равномерное движение – тело за равные промежутки времени проходит одинаковые пути, может быть прямолинейным и криволинейным.
14. Скорость ВФВ, характеризующая быстроту изменения положения тела в пространстве, равна: отношению перемещения ко времени, за которое это перемещение совершено; перемещению в единицу времени. Направлена по касательной к траектории.
15. Мгновенная скорость – ВФВ, равная пределу отношения перемещения к промежутку времени в течение которого это перемещение произошло, при условии — промежуток времени стремится к нулю. Направлена по касательной к траектории.
16. Ускорение – ВФВ, характеризующая быстроту изменения скорости, равна: изменению скорости в единицу времени; пределу отношения изменения скорости к промежутку времени в течение которого это изменение произошло, при условии — промежуток времени стремится к нулю.
17. Равномерное движение по окружности – движение с постоянными по модулю скоростью и ускорением, но меняющимися по направлению: скорость направлена по касательной к траектории, проведенной в данной точке, а ускорение перпендикулярно скорости, т.е. по радиусу к центру, центростремительное.
18. Период обращения – СФВ, время, за которое тело делает полный оборот.
19. Частота обращения – СФВ, равная числу оборотов в единицу времени.
20. Поступательное движение – движение твердого тела, при котором любая прямая, проведенная в теле перемещается параллельно себе.
21. Угловая скорость – СФВ, равная углу поворота в единицу времени, отношению угла поворота к промежутку времени, за который этот поворот произошел
22. Модуль перемещения равен площади фигуры под графиком скорости в осях (vx , t)
Автор: Зырянова Ольга Степановна.
Вектор положения— объяснение и примеры
Мы можем использовать вектор положения , чтобы сообщить нам положение одного объекта относительно другого. В частности, вектор положения:
В частности, вектор положения:
«Вектор, который указывает местоположение или положение данной точки относительно произвольной контрольной точки, такой как начало координат».
В этом разделе мы обсудим следующие аспекты векторов положения:
- Что такое вектор положения?
- Как найти вектор положения
Что такое вектор положения?
Часто векторы, которые начинаются в начале координат и заканчиваются в любой произвольной точке, называются векторами положения.Они используются для определения положения точки относительно начала координат.
Направление вектора положения указывает от начала координат к данной точке. В c \ декартовой системе координат, если точка O — начало координат, а Q — некоторая точка (x1, y1), тогда вектор положения, направленный из точки O в точку Q, представлен как OQ . В трехмерном пространстве, если O = (0,0,0) и Q = (x1, y1, z1), то вектор положения r точки Q представлен следующим образом:
r = x1i + y1j + z1k
Предположим, у нас есть два вектора, A и B, с векторами положения a = (2,4) и b = (3, 5) соответственно. Затем мы можем записать координаты векторов A и B как:
Затем мы можем записать координаты векторов A и B как:
A = (2,4), B = (3, 5)
Как найти вектор положения
Перед определяя вектор положения точки, нам сначала нужно определить координаты этой точки. Предположим, у нас есть две точки, M и N, где M = (x1, y1) и N = (x2, y2). Затем мы хотим найти вектор положения из точки M в точку N, вектор MN . Чтобы определить этот вектор положения, мы вычитаем соответствующие компоненты M из N :
MN = (x2-x1, y2-y1)
Формула вектора положения
Используя информацию выше, мы можем обобщить формула, которая будет определять вектор положения между двумя точками, если бы мы знали положение точек в плоскости xy.
Например, рассмотрим точку P, которая имеет координаты (xk, yk) в плоскости xy, и другую точку Q, которая имеет координаты (xk + 1, yk + 1). Формула для определения вектора положения от P до Q:
PQ = ((xk + 1) -xk, (yk + 1) -yk)
Помните, что вектор положения PQ относится к вектору, который начинается в точке P и заканчивается в точке Q. Точно так же, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:
Точно так же, если мы хотим найти вектор положения из точки Q в точку P, мы можем написать:
QP = (xk — (xk + 1), yk — (yk + 1))
Примеры
В этом разделе мы обсудим некоторые примеры задач вектора положения и их пошаговые решения.Это поможет глубже понять векторы позиций.
Пример 1
По двум точкам A = (-4, 6) и B = (5, 12) определите вектор положения AB. Затем , вычисляют величину вектора AB .
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения AB :
AB = (x2-x1, y2-y1)
Где x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Таким образом, просто подставляя значения точек A и B в приведенное выше уравнение, мы можем найти вектор положения AB :
AB = (5 — (- 4), 12-6)
AB = ((5+ 4), 12-6)
AB = (9, 6)
Таким образом, вектор положения AB эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц, чтобы вправо по оси x и на 6 единиц вверх по оси y.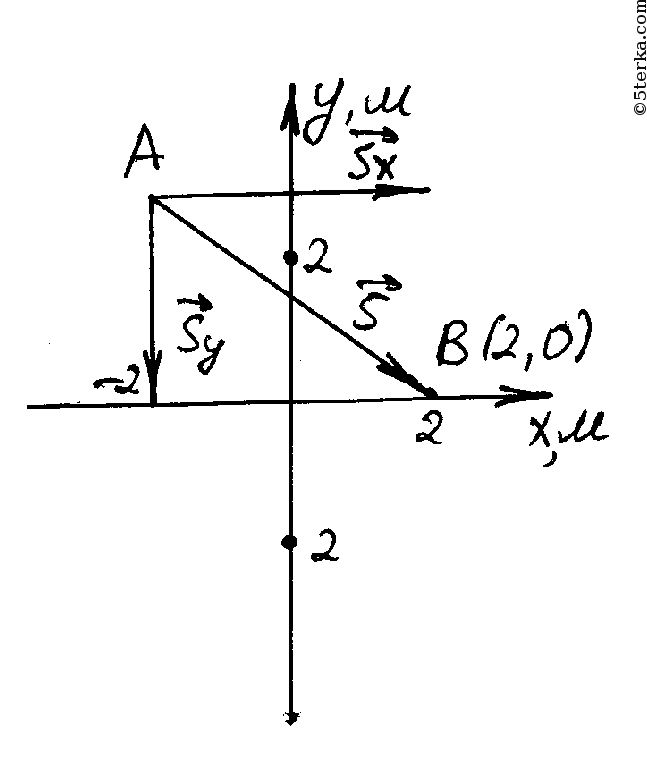 2
2
| AB | = √81 + 36
| AB | = √117
| AB | = 3√13
Пример 2
Учитывая две точки A = (-4, 6) и B = (5, 12), определите вектор положения BA. Затем вычислите величину вектора BA и опишите взаимосвязь между вектором положения AB и вектором положения BA .
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу, чтобы найти вектор положения BA :
BA = (x1-x2, y1-y2)
Где x1, y1 представляют координаты точки A, а x2, y2 представляют координаты точки B.Обратите внимание, что вектор положения BA представляет собой вектор, направленный от точки B к точке A. Он отличается от вектора положения AB, , который направлен от A к B. Таким образом, просто помещая значения точек A и B в приведенном выше уравнении мы можем найти вектор положения BA:
BA = (-4-5), 6-12)
BA = (-9, -6)
Таким образом, вектор положения BA эквивалентен вектору, который начинается в начале координат и направлен в точку на 9 единиц влево по оси x и на 6 единиц вниз по оси y. 2
2
| BA | = √81 + 36
| BA | = √117
| BA | = 3√13
Напомним, что в первом примере мы нашли вектор положения AB для тех же точек, а в этом примере мы определили вектор положения BA. Два вектора положения имеют одинаковую величину. Поскольку они имеют противоположные направления, отношения между ними следующие:
BA = -1 * (9, 6)
BA = -1 * AB
BA = — AB
Таким образом, два вектора положения параллельны друг другу и противоположны друг другу.То есть они отрицания друг друга.
Пример 3
Учитывая, что вектор положения точки, S1, равен OS1 = (2, 3), и что вектор S1S2 = (-3, 6), определить вектор положения точки точка S2, OS2 .
Решение
Сначала мы строим вектор OS1 с его начальной точкой в начале координат (0,0) и конечной точкой в точке (2,3). Мы также строим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x, y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает связь между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в S1 и направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом:
Мы также строим вектор OS2, , который начинается в начале координат и заканчивается в точке S2.Обозначим неизвестное положение S2 произвольными координатными точками (x, y). Поскольку мы знаем вектор положения S1S2 и знаем, что он дает связь между S1 и S2, мы также можем нарисовать S1S2. Это направленный вектор, начальная точка которого находится в S1 и направлен на три единицы влево и на шесть единиц вверх. Из изображения ниже видно, что у нас есть треугольник 0S1S2. Таким образом, теперь мы можем использовать закон треугольника (или правило «голова к хвосту») сложения векторов для определения координат точки S2 следующим образом:
S1S2 = OS1 + OS2
OS2 = S1S2 — OS1
Подставляя данные значения в это уравнение, мы получаем:
OS2 = (-3, 6) — (2, 3)
OS2 = (-3, 6) + ( -2, -3)
OS2 = (-3-2, 6-3)
OS2 = (-5, 3)
Таким образом, OS2 = (- 5, 3) является вектор положения для точки S2.
Пример 4
Учитывая две точки M = (4, m) и Q = (-n, -3), определите вектор положения QM.
Решение
Учитывая две точки в системе координат xy, мы можем использовать следующую формулу для определения вектора положения Q :
QM = (-n-4, -3-m) .
Поскольку нам неизвестны координаты QM или значения n и m, мы не можем упростить уравнение.2
| R | = √100 + 25 + 9
| R | = √100 + 25 + 9
| R | = √134
Пример 6
Учитывая точки c = 5i + 6j + 3k и d = 2i + 5j — 2k в ортогональной системе, определите вектор положения между этими двумя точками, CD.
Решение
Учитывая две точки, мы можем использовать следующую формулу для определения вектора положения CD :
CD = (2-5, 5-5, -2-3)
CD = (-3, 0, -5)
CD = -3i + 0j -5k
Практические вопросы- Пусть u = (-1, 4) и v = (2 , 5).
 Определите вектор положения, представленный UV .
Определите вектор положения, представленный UV . - Пусть u = (-1, 4) и v = (2, 5). Определите вектор положения, представленный VU .
- Пусть v = (3, 5) и VM = (-6, 3). Найдите вектор положения точки m.
- Для данного b = (3,2,5) определите его вектор положения, R. Затем найдите длину вектора
- Пусть вектор AB начинается с a = (1, 2) и заканчивается на Ь = (2, 3). Определите его вектор положения и его длину.
- Пусть вектор OB начинается с o = (0,0) и заканчивается на b = (-2, 6). Определите его вектор положения.
Ответы
- UV = (3,1). Направление UV на 3 единицы вправо по оси x и на 1 единицу вверх.
- VU = (-3, -1). Направление VU — на 3 единицы влево по оси x и на 1 единицу вниз. Два вектора UV и VU, противоположны по направлению.

- Вектор положения точки m может быть задан OM = (-9, -2)
- R = 3i + 2j + 5k — вектор положения, и его длина | R | = √38
- Вектор положения равен AB = (1,1), а его длина равна | AB | = √2
- Вектор положения OB = (-2,6), а его длина равна | OB | = √40
3.2 Исчисление векторно-значных функций — Исчисление Том 3
Цели обучения
- 3.2.1 Напишите выражение для производной векторной функции.
- 3.2.2 Найдите касательный вектор в точке для данного вектора положения.
- 3.2.3 Найдите единичный касательный вектор в точке для данного вектора положения и объясните его значение.
- 3.2.4
Вычислить определенный интеграл векторнозначной функции.

Чтобы изучить исчисление векторных функций, мы идем по тому же пути, что и при изучении действительных функций.Сначала мы определяем производную, затем исследуем приложения производной, а затем переходим к определению интегралов. Однако по пути мы найдем некоторые интересные новые идеи в результате векторной природы этих функций и свойств пространственных кривых.
Производные векторных функций
Теперь, когда мы увидели, что такое вектор-функция и как выйти за ее пределы, следующим шагом будет научиться дифференцировать вектор-функцию. Определение производной векторной функции почти идентично определению вещественной функции одной переменной.Однако, поскольку диапазон векторной функции состоит из векторов, то же самое верно и для диапазона производной векторной функции.
Определение
Производная векторной функции r (t) r (t) равна
. r ′ (t) = limΔt → 0r (t + Δt) −r (t) Δt, r ′ (t) = limΔt → 0r (t + Δt) −r (t) Δt, (3. 5)
5)
при наличии ограничения. Если существует r ′ (t) r ′ (t), то r дифференцируемо при t. Если r ′ (t) r ′ (t) существует для всех t в открытом интервале (a, b), (a, b), то r дифференцируемо на интервале (a, b).(а, б). Чтобы функция была дифференцируемой на отрезке [a, b], [a, b], также должны существовать следующие два предела:
r ′ (a) = lim∆t → 0 + r (a + ∆t) −r (a) ∆tandr ′ (b) = lim∆t → 0 − r (b + ∆t) −r (b) ∆t.r ′ (a) = limΔt → 0 + r (a + Δt) −r (a) Δtandr ′ (b) = limΔt → 0 − r (b + Δt) −r (b) Δt. Многие правила вычисления производных от действительных функций могут быть применены также к вычислению производных от векторных функций. Напомним, что производную функции с действительным знаком можно интерпретировать как наклон касательной или мгновенную скорость изменения функции.Производная векторной функции также может пониматься как мгновенная скорость изменения; например, когда функция представляет положение объекта в данный момент времени, производная представляет его скорость в тот же момент времени.
Теперь продемонстрируем взятие производной векторнозначной функции.
Пример 3,4
Нахождение производной векторной функции
Используйте определение для вычисления производной функции
r (t) = (3t + 4) i + (t2−4t + 3) j.r (t) = (3t + 4) i + (t2−4t + 3) j.Решение
Давайте воспользуемся уравнением 3.5:
r ′ (t) = limΔt → 0r (t + Δt) −r (t) Δt = limΔt → 0 [(3 (t + Δt) +4) i + ((t + Δt) 2−4 (t + Δt) +3) j] — [(3t + 4) i + (t2−4t + 3) j] Δt = limΔt → 0 (3t + 3Δt + 4) i− (3t + 4) i + (t2 + 2tΔt + (Δt) 2 −4t − 4Δt + 3) j− (t2−4t + 3) jΔt = limΔt → 0 (3Δt) i + (2tΔt + (Δt) 2−4Δt) jΔt = limΔt → 0 (3i + (2t + Δt − 4) j) = 3i + (2t − 4) jr ′ (t) = limΔt → 0r (t + Δt) −r (t) Δt = limΔt → 0 [(3 (t + Δt) +4) i + ((t + Δt) 2 −4 (t + Δt) +3) j] — [(3t + 4) i + (t2−4t + 3) j] Δt = limΔt → 0 (3t + 3Δt + 4) i− (3t + 4) i + ( t2 + 2tΔt + (Δt) 2−4t − 4Δt + 3) j− (t2−4t + 3) jΔt = limΔt → 0 (3Δt) i + (2tΔt + (Δt) 2−4Δt) jΔt = limΔt → 0 (3i + (2t + Δt − 4) j) = 3i + (2t − 4) j.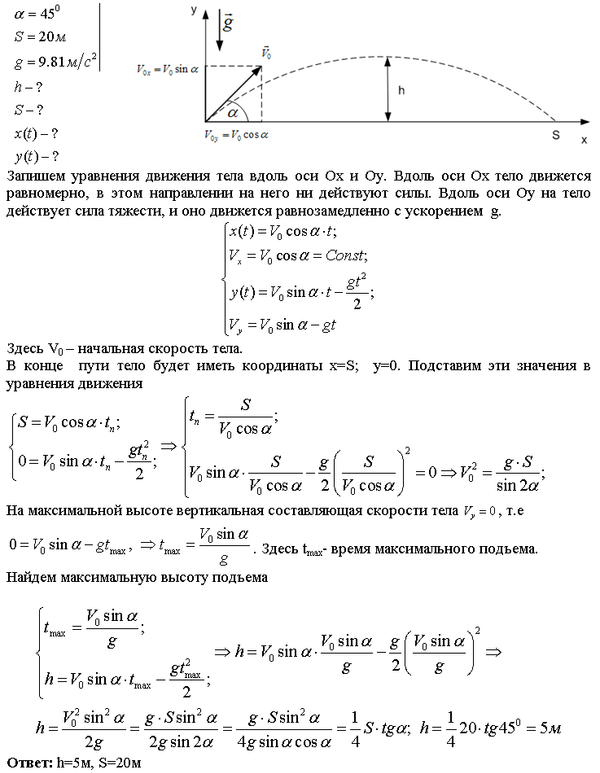
Контрольно-пропускной пункт 3,4
Используйте определение, чтобы вычислить производную функции r (t) = (2t2 + 3) i + (5t − 6) j.r (t) = (2t2 + 3) i + (5t − 6) j.
Обратите внимание, что в вычислениях в примере 3.4 мы также могли получить ответ, сначала вычислив производную каждой компонентной функции, а затем поместив эти производные обратно в векторнозначную функцию. Это всегда верно для вычисления производной векторнозначной функции, будь то в двух или трех измерениях.Сформулируем это в следующей теореме. Доказательство этой теоремы следует непосредственно из определений предела вектор-функции и производной вектор-функции.
Теорема 3,2
Дифференцирование векторных функций.
Пусть f, g, и h — дифференцируемые функции от t.
- Если r (t) = f (t) i + g (t) j, r (t) = f (t) i + g (t) j, то r ′ (t) = f ′ (t) i + g ′ (t) jr ′ (t) = f ′ (t) i + g ′ (t) j.

- Если r (t) = f (t) i + g (t) j + h (t) k, r (t) = f (t) i + g (t) j + h (t) k, то r ′ (T) = f ′ (t) i + g ′ (t) j + h ′ (t) k.r ′ (t) = f ′ (t) i + g ′ (t) j + h ′ (t) k.
Пример 3.5
Вычисление производной векторных функций
Используйте дифференцирование векторных функций для вычисления производной каждой из следующих функций.
- r (t) = (6t + 8) i + (4t2 + 2t − 3) jr (t) = (6t + 8) i + (4t2 + 2t − 3) j
- r (t) = 3costi + 4sintjr (t) = 3costi + 4sintj
- r (t) = etsinti + etcostj − e2tkr (t) = etsinti + etcostj − e2tk
Решение
Мы используем дифференцирование векторных функций и то, что мы знаем о дифференцировании функций одной переменной.
- Первый компонент r (t) = (6t + 8) i + (4t2 + 2t − 3) jr (t) = (6t + 8) i + (4t2 + 2t − 3) j равен f (t) = 6t. + 8. f (t) = 6t + 8. Второй компонент равен g (t) = 4t2 + 2t − 3.
 g (t) = 4t2 + 2t − 3. Имеем f ′ (t) = 6f ′ (t) = 6 и g ′ (t) = 8t + 2, g ′ (t) = 8t + 2, поэтому теорема дает r ′ (t) = 6i + (8t + 2) jr ′ (t) = 6i + (8t + 2) j.
g (t) = 4t2 + 2t − 3. Имеем f ′ (t) = 6f ′ (t) = 6 и g ′ (t) = 8t + 2, g ′ (t) = 8t + 2, поэтому теорема дает r ′ (t) = 6i + (8t + 2) jr ′ (t) = 6i + (8t + 2) j. - Первый компонент — это f (t) = 3costf (t) = 3cost, а второй компонент — это g (t) = 4sint.g (t) = 4sint. Имеем f ′ (t) = — 3sintf ′ (t) = — 3sint и g ′ (t) = 4cost, g ′ (t) = 4cost, поэтому получаем r ′ (t) = — 3sinti + 4costj.r ′ (t) = — 3sinti + 4costj.
- Первый компонент r (t) = etsinti + etcostj − e2tkr (t) = etsinti + etcostj − e2tk равен f (t) = etsint, f (t) = etsint, второй компонент — g (t) = etcost, g (t) = etcost, а третий компонент — h (t) = — e2t.h (t) = — e2t. Имеем f ′ (t) = et (sint + cost), f ′ (t) = et (sint + cost), g ′ (t) = et (cost − sint), g ′ (t) = et (cost −sint) и h ′ (t) = — 2e2t, h ′ (t) = — 2e2t, поэтому теорема дает r ′ (t) = et (sint + cost) i + et (cost − sint) j − 2e2tk .r ′ (t) = et (sint + cost) i + et (cost − sint) j − 2e2tk.
Контрольно-пропускной пункт 3.
 5
5Вычислить производную функции
r (t) = (tlnt) i + (5et) j + (cost − sint) k.r (t) = (tlnt) i + (5et) j + (cost − sint) k.Мы можем распространить на вектор-функции свойства производной, которые мы представили во Введении в производные. В частности, правило множественных констант, правила суммы и разности, правило произведения и правило цепочки распространяются на векторнозначные функции. Однако в случае правила произведения на самом деле существует три расширения: (1) для вещественнозначной функции, умноженной на вектор-функцию, (2) для скалярного произведения двух векторнозначных функций и (3 ) для векторного произведения двух вектор-функций.
Теорема 3.3
Свойства производной векторных функций.
Пусть r и u будут дифференцируемыми векторными функциями от t , пусть f будет дифференцируемой действительной функцией от t, и пусть c будет скаляром.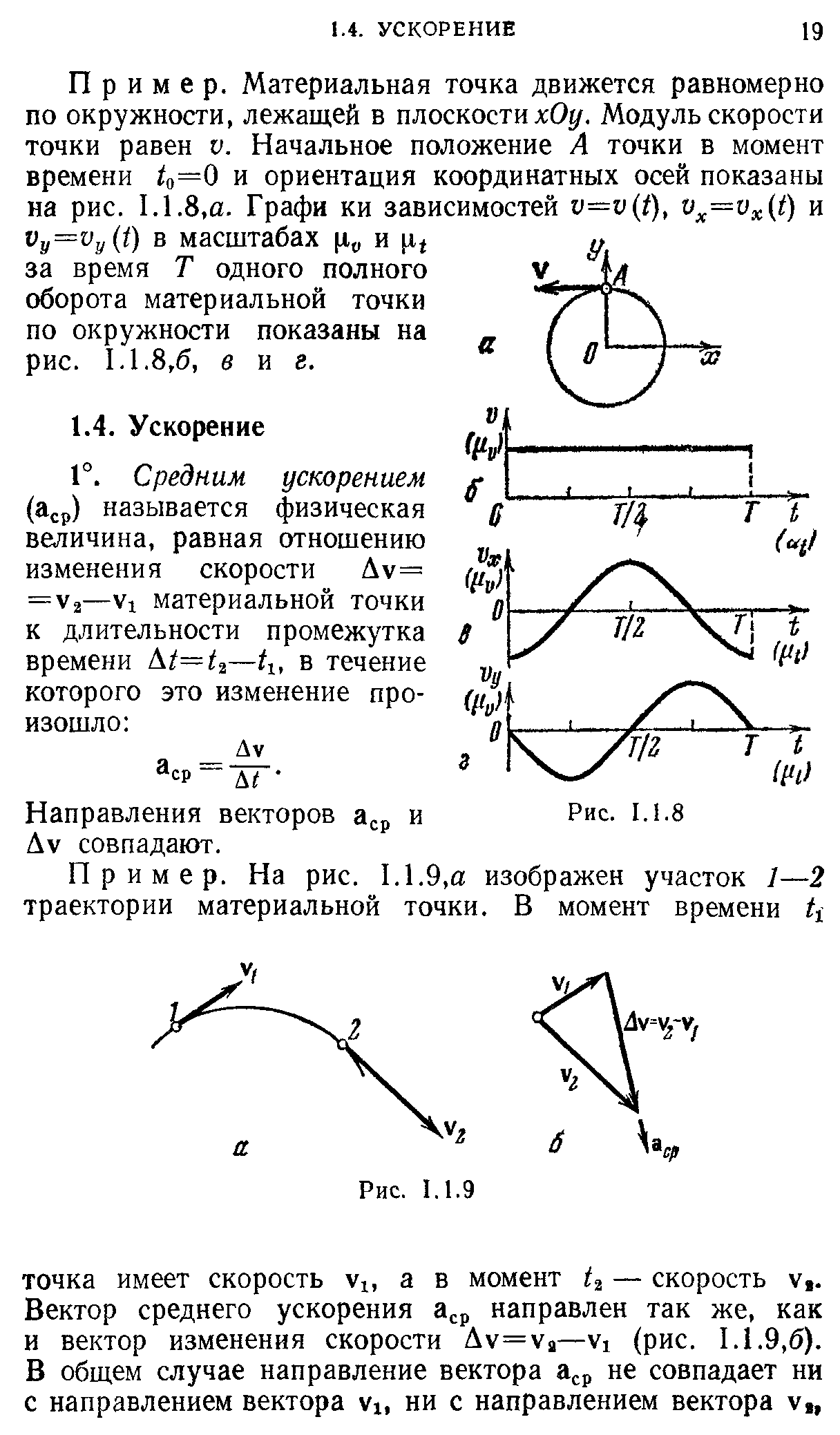
Проба
Доказательства первых двух свойств следуют непосредственно из определения производной векторнозначной функции. Третье свойство может быть получено из первых двух свойств, а также правила произведения из Введение в производные инструменты. Пусть u (t) = g (t) i + h (t) j.u (t) = g (t) i + h (t) j. Тогда
Третье свойство может быть получено из первых двух свойств, а также правила произведения из Введение в производные инструменты. Пусть u (t) = g (t) i + h (t) j.u (t) = g (t) i + h (t) j. Тогда
Для подтверждения собственности iv.пусть r (t) = f1 (t) i + g1 (t) jr (t) = f1 (t) i + g1 (t) j и u (t) = f2 (t) i + g2 (t) ju ( t) = f2 (t) i + g2 (t) j. Тогда
ddt [r (t) · u (t)] = ddt [f1 (t) f2 (t) + g1 (t) g2 (t)] = f1 ′ (t) f2 (t) + f1 (t) f2 ′ (t) + g1 ′ (t) g2 (t) + g1 (t) g2 ′ (t) = f1 ′ (t) f2 (t) + g1 ′ (t) g2 (t) + f1 (t) f2 ′ (t) + g1 (t) g2 ′ (t) = (f1′i + g1′j) · (f2i + g2j) + (f1i + g1j) · (f2′i + g2′j) = r ′ (t ) · U (t) + r (t) · u ′ (t) . ddt [r (t) · u (t)] = ddt [f1 (t) f2 (t) + g1 (t) g2 (t) ] = f1 ′ (t) f2 (t) + f1 (t) f2 ′ (t) + g1 ′ (t) g2 (t) + g1 (t) g2 ′ (t) = f1 ′ (t) f2 (t ) + g1 ′ (t) g2 (t) + f1 (t) f2 ′ (t) + g1 (t) g2 ′ (t) = (f1′i + g1′j) · (f2i + g2j) + (f1i + g1j) · (f2′i + g2′j) = r ′ (t) · u (t) + r (t) · u ′ (t).
ddt [r (t) · u (t)] = ddt [f1 (t) f2 (t) + g1 (t) g2 (t) ] = f1 ′ (t) f2 (t) + f1 (t) f2 ′ (t) + g1 ′ (t) g2 (t) + g1 (t) g2 ′ (t) = f1 ′ (t) f2 (t ) + g1 ′ (t) g2 (t) + f1 (t) f2 ′ (t) + g1 (t) g2 ′ (t) = (f1′i + g1′j) · (f2i + g2j) + (f1i + g1j) · (f2′i + g2′j) = r ′ (t) · u (t) + r (t) · u ′ (t).Доказательство свойства v. Аналогично доказательству свойства iv. Свойство vi. можно доказать с помощью цепного правила. Наконец, свойство vii. следует из свойства iv:
ddt [r (t) · r (t)] = ddt [c] r ′ (t) · r (t) + r (t) · r ′ (t) = 02r (t) · r ′ (t) = 0r (t) · r ′ (t) = 0.ddt [r (t) · r (t)] = ddt [c] r ′ (t) · r (t) + r (t) · r ′ (t ) = 02r (t) · r ′ (t) = 0r (t) · r ′ (t) = 0.□
Теперь несколько примеров использования этих свойств.
Пример 3,6
Использование свойств производных векторных функций
Для векторнозначных функций
r (t) = (6t + 8) i + (4t2 + 2t − 3) j + 5tkr (t) = (6t + 8) i + (4t2 + 2t − 3) j + 5tk.
и
u (t) = (t2−3) i + (2t + 4) j + (t3−3t) k, u (t) = (t2−3) i + (2t + 4) j + (t3−3t) k,вычисляет каждую из следующих производных, используя свойства производной векторнозначных функций.
- ddt [r (t) · u (t)] ddt [r (t) · u (t)]
- ddt [u (t) × u ′ (t)] ddt [u (t) × u ′ (t)]
Решение
- Имеем r ′ (t) = 6i + (8t + 2) j + 5kr ′ (t) = 6i + (8t + 2) j + 5k и u ′ (t) = 2ti + 2j + (3t2−3) ku ′ (t) = 2ti + 2j + (3t2−3) k. Следовательно, согласно собственности iv .:
ddt [r (t) · u (t)] = r ′ (t) · u (t) + r (t) · u ′ (t) = (6i + (8t + 2) j + 5k) · ((t2 −3) i + (2t + 4) j + (t3−3t) k) + ((6t + 8) i + (4t2 + 2t − 3) j + 5tk) · (2ti + 2j + (3t2−3) k) = 6 (t2−3) + (8t + 2) (2t + 4) +5 (t3−3t) + 2t (6t + 8) +2 (4t2 + 2t − 3) + 5t (3t2−3) = 20t3 + 42t2 + 26т − 16.ddt [r (t) · u (t)] = r ′ (t) · u (t) + r (t) · u ′ (t) = (6i + (8t + 2) j + 5k) · ((t2 −3) i + (2t + 4) j + (t3−3t) k) + ((6t + 8) i + (4t2 + 2t − 3) j + 5tk) · (2ti + 2j + (3t2−3) k) = 6 (t2−3) + (8t + 2) (2t + 4) +5 (t3−3t) + 2t (6t + 8) +2 (4t2 + 2t − 3) + 5t (3t2−3) = 20t3 + 42t2 + 26т − 16.
- Во-первых, нам нужно адаптировать свойство v. Для этой задачи:
ddt [u (t) × u ′ (t)] = u ′ (t) × u ′ (t) + u (t) × u ″ (t). ddt [u (t) × u ′ (t)] = u ′ (t) × u ′ (t) + u (t) × u ″ (t).Напомним, что произведение любого вектора на себя равно нулю. Кроме того, u ″ (t) u ″ (t) представляет собой вторую производную от u (t): u (t):
. u ″ (t) = ddt [u ′ (t)] = ddt [2ti + 2j + (3t2−3) k] = 2i + 6tk.u ″ (t) = ddt [u ′ (t)] = ddt [2ti + 2j + (3t2−3) k] = 2i + 6tk.Следовательно,
ddt [u (t) × u ′ (t)] = 0 + ((t2−3) i + (2t + 4) j + (t3−3t) k) × (2i + 6tk) = | ijkt2−32t + 4t3− 3t206t | = 6t (2t + 4) i− (6t (t2−3) −2 (t3−3t)) j − 2 (2t + 4) k = (12t2 + 24t) i + (12t − 4t3) j− ( 4t + 8) k.ddt [u (t) × u ′ (t)] = 0 + ((t2−3) i + (2t + 4) j + (t3−3t) k) × (2i + 6tk) = | ijkt2−32t + 4t3−3t206t | = 6t (2t + 4) i− (6t (t2−3) −2 (t3−3t)) j − 2 (2t + 4) k = (12t2 + 24t) i + (12t −4t3) j− (4t + 8) к.
Контрольно-пропускной пункт 3,6
Для векторных функций r (t) = costi + sintj − e2tkr (t) = costi + sintj − e2tk и u (t) = ti + sintj + costk, u (t) = ti + sintj + costk, вычислить ddt [r (t) · r ′ (t)] ddt [r (t) · r ′ (t)] и ddt [u (t) × r (t)]. ddt [u (t) × r (t)].
ddt [u (t) × r (t)].
Касательные векторы и единичные касательные векторы
Вспомните из введения в производные, что производную в точке можно интерпретировать как наклон касательной к графику в этой точке. В случае векторной функции производная представляет собой касательный вектор к кривой, представленной функцией. Рассмотрим вектор-функцию r (t) = costi + sintj.r (t) = costi + sintj. Производная этой функции равна r ′ (t) = — sinti + costj.r ′ (t) = — sinti + costj.Если подставить значение t = π / 6t = π / 6 в обе функции, мы получим
r (π6) = 32i + 12jandr ′ (π6) = — 12i + 32j.r (π6) = 32i + 12jandr ′ (π6) = — 12i + 32j.График этой функции показан на рисунке 3.5 вместе с векторами r (π6) r (π6) и r ′ (π6) .r ′ (π6).
Фигура 3.5 Касательная в точке вычисляется по производной векторной функции r (t) .r (t). Обратите внимание, что вектор r ′ (π6) r ′ (π6) касается окружности в точке, соответствующей t = π / 6. t = π / 6.Это пример касательного вектора к плоской кривой, определяемой формулой r (t) = costi + sintj.r (t) = costi + sintj.
t = π / 6.Это пример касательного вектора к плоской кривой, определяемой формулой r (t) = costi + sintj.r (t) = costi + sintj.
Определение
Пусть C — кривая, заданная векторной функцией r, , и предположим, что r ′ (t) r ′ (t) существует, когда t = t0.t = t0. Касательный вектор v при t = t0t = t0 — это любой вектор, такой, что когда хвост вектора помещен в точку r (t0) r (t0) на графике, вектор v касается кривой C Вектор r ′ (t0) r ′ (t0) является примером касательного вектора в точке t = t0.т = т0. Кроме того, предположим, что r ′ (t) ≠ 0. r ′ (t) ≠ 0. Главный единичный касательный вектор при t определен как
. T (t) = r ′ (t) ‖r ′ (t) ‖, T (t) = r ′ (t) ‖r ′ (t) ‖,(3,6)
предоставил ‖r ′ (t) ‖ ≠ 0.‖r ′ (t) ‖ ≠ 0.
Единичный касательный вектор — это именно то, на что это похоже: единичный вектор, касательный к кривой. Чтобы вычислить единичный касательный вектор, сначала найдите производную r ′ (t) .r ′ (t). Во-вторых, рассчитайте величину производной. Третий шаг — разделить производную на ее величину.
Чтобы вычислить единичный касательный вектор, сначала найдите производную r ′ (t) .r ′ (t). Во-вторых, рассчитайте величину производной. Третий шаг — разделить производную на ее величину.
Пример 3,7
Нахождение единичного касательного вектора
Найдите единичный касательный вектор для каждой из следующих векторных функций:
- r (t) = costi + sintjr (t) = costi + sintj
- u (t) = (3t2 + 2t) i + (2−4t3) j + (6t + 5) ku (t) = (3t2 + 2t) i + (2−4t3) j + (6t + 5) k
Решение
-
Первый шаг: r ′ (t) = — sinti + costj Второй шаг: ‖r ′ (t) ‖ = (- sint) 2+ (cost) 2 = 1 Третий шаг: T (t) = r ′ (t) ‖r ′ (t) ‖ = −sinti + costj1 = −sinti + costj Первый шаг: r ′ (t) = — sinti + costj Второй шаг: ‖r ′ (t) ‖ = (- sint) 2+ (cost) 2 = 1 Третий шаг: T (t) = r ′ (t) ‖r ′ (t) ‖ = −sinti + costj1 = −sinti + costj -
Первый шаг: u ′ (t) = (6t + 2) i − 12t2j + 6k Второй шаг: ‖u ′ (t) ‖ = (6t + 2) 2 + (- 12t2) 2 + 62 = 144t4 + 36t2 + 24t + 40 = 236t4 + 9t2 + 6t + 10 Третий шаг: T (t) = u ′ (t) ‖u ′ (t) ‖ = (6t + 2) i − 12t2j + 6k236t4 + 9t2 + 6t + 10 = 3t + 136t4 + 9t2 + 6t + 10i − 6t236t4 + 9t2 + 6t + 10j + 336t4 + 9t2 + 6t + 10k Первый шаг: u ′ (t) = (6t + 2) i − 12t2j + 6k Второй шаг: ‖u ′ (t) ‖ = ( 6t + 2) 2 + (- 12t2) 2 + 62 = 144t4 + 36t2 + 24t + 40 = 236t4 + 9t2 + 6t + 10 Третий шаг: T (t) = u ′ (t) ‖u ′ (t) ‖ = ( 6t + 2) i − 12t2j + 6k236t4 + 9t2 + 6t + 10 = 3t + 136t4 + 9t2 + 6t + 10i − 6t236t4 + 9t2 + 6t + 10j + 336t4 + 9t2 + 6t + 10k
Контрольно-пропускной пункт 3.
 7
7Найдите единичный касательный вектор для вектор-функции
r (t) = (t2−3) i + (2t + 1) j + (t − 2) k.r (t) = (t2−3) i + (2t + 1) j + (t − 2) k.Интегралы от векторных функций
Мы ввели первообразные вещественнозначных функций в первообразные и определенные интегралы вещественнозначных функций в Определенном интеграле. Каждое из этих понятий может быть расширено до векторных функций. Кроме того, точно так же, как мы можем вычислить производную векторнозначной функции, дифференцируя составляющие функции по отдельности, мы можем вычислить первообразную таким же образом.Кроме того, основная теорема исчисления применима и к векторным функциям.
Первообразная векторной функции появляется в приложениях. Например, если вектор-функция представляет скорость объекта в момент времени t , то ее первообразная представляет положение. Или, если функция представляет ускорение объекта в данный момент времени, тогда первообразная представляет его скорость.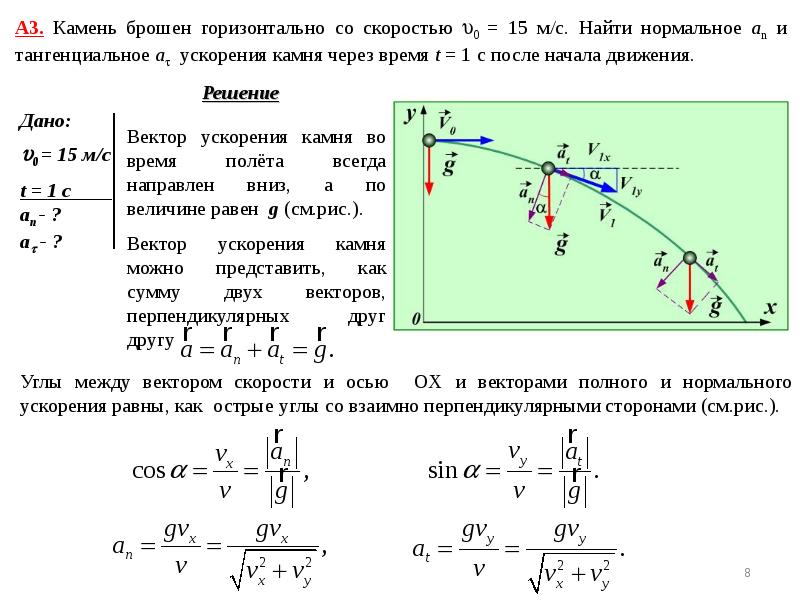
Определение
Пусть f, g, и h — интегрируемые действительные функции на отрезке [a, b].[а, б].
- Неопределенный интеграл векторной функции r (t) = f (t) i + g (t) jr (t) = f (t) i + g (t) j равен
∫ [f (t) i + g (t) j] dt = [∫f (t) dt] i + [∫g (t) dt] j.∫ [f (t) i + g (t) j] dt = [∫f (t) dt] i + [∫g (t) dt] j.(3,7)
Определенный интеграл векторнозначной функции равен
∫ab [f (t) i + g (t) j] dt = [∫abf (t) dt] i + [∫abg (t) dt] j.∫ab [f (t) i + g (t) j ] dt = [abf (t) dt] i + [∫abg (t) dt] j.(3.8)
- Неопределенный интеграл вектор-функции r (t) = f (t) i + g (t) j + h (t) kr (t) = f (t) i + g (t) j + h ( t) k составляет
∫ [f (t) i + g (t) j + h (t) k] dt = [∫f (t) dt] i + [∫g (t) dt] j + [∫h (t) dt] k.∫ [f (t) i + g (t) j + h (t) k] dt = [∫f (t) dt] i + [∫g (t) dt] j + [∫h (t) dt] k.(3.9)
Определенный интеграл векторнозначной функции равен
Ab [f (t) i + g (t) j + h (t) k] dt = [∫abf (t) dt] i + [∫abg (t) dt] j + [∫abh (t) dt] k . ∫ab [f (t) i + g (t) j + h (t) k] dt = [∫abf (t) dt] i + [∫abg (t) dt] j + [∫abh (t) dt] k.
∫ab [f (t) i + g (t) j + h (t) k] dt = [∫abf (t) dt] i + [∫abg (t) dt] j + [∫abh (t) dt] k.(3.10)
Поскольку неопределенный интеграл векторной функции включает неопределенные интегралы компонентных функций, каждый из этих компонентных интегралов содержит константу интегрирования.Все они могут быть разными. Например, в двумерном случае мы можем иметь
∫f (t) dt = F (t) + C1 и g (t) dt = G (t) + C2, ∫f (t) dt = F (t) + C1 и g (t) dt = G (t ) + C2,, где F и G являются первообразными f и g, соответственно. Тогда
∫ [f (t) i + g (t) j] dt = [∫f (t) dt] i + [∫g (t) dt] j = (F (t) + C1) i + (G (t) + C2) j = F (t) i + G (t) j + C1i + C2j = F (t) i + G (t) j + C, ∫ [f (t) i + g (t) j] dt = [∫f (t) dt] i + [∫g (t) dt] j = (F (t) + C1) i + (G (t) + C2) j = F (t) i + G (t) j + C1i + C2j = F (t) i + G (t) j + C, где C = C1i + C2j. С = C1i + C2j. Следовательно, постоянная интегрирования становится постоянным вектором.
С = C1i + C2j. Следовательно, постоянная интегрирования становится постоянным вектором.
Пример 3.8
Интеграция векторных функций
Вычислите каждый из следующих интегралов:
- ∫ [(3t2 + 2t) i + (3t − 6) j + (6t3 + 5t2−4) k] dt∫ [(3t2 + 2t) i + (3t − 6) j + (6t3 + 5t2−4) k] dt
- ∫ [〈t, t2, t3〉 × 〈t3, t2, t〉] dt∫ [〈t, t2, t3〉 × 〈t3, t2, t〉] dt
- ∫0π / 3 [sin2ti + tantj + e − 2tk] dt∫0π / 3 [sin2ti + tantj + e − 2tk] dt
Решение
- Используем первую часть определения интеграла пространственной кривой:
∫ [(3t2 + 2t) i + (3t − 6) j + (6t3 + 5t2−4) k] dt = [∫3t2 + 2tdt] i + [∫3t − 6dt] j + [∫6t3 + 5t2−4dt] k = ( t3 + t2) я + (32t2−6t) j + (32t4 + 53t3−4t) k + C.∫ [(3t2 + 2t) i + (3t − 6) j + (6t3 + 5t2−4) k] dt = [∫3t2 + 2tdt] i + [∫3t − 6dt] j + [∫6t3 + 5t2−4dt] k = ( t3 + t2) я + (32t2−6t) j + (32t4 + 53t3−4t) k + C.
- Сначала вычислите 〈t, t2, t3〉 × 〈t3, t2, t〉: 〈t, t2, t3〉 × 〈t3, t2, t〉:
〈T, t2, t3〉 × 〈t3, t2, t〉 = | ijktt2t3t3t2t | = (t2 (t) −t3 (t2)) i− (t2 − t3 (t3)) j + (t (t2) −t2 ( t3)) k = (t3 − t5) i + (t6 − t2) j + (t3 − t5) k. 〈t, t2, t3〉 × 〈t3, t2, t〉 = | ijktt2t3t3t2t | = (t2 (t) — t3 (t2)) i− (t2 − t3 (t3)) j + (t (t2) −t2 (t3)) k = (t3 − t5) i + (t6 − t2) j + (t3 − t5) k.
Затем подставьте это обратно в интеграл и проинтегрируйте:
∫ [〈t, t2, t3〉 × 〈t3, t2, t〉] dt = ∫ (t3 − t5) i + (t6 − t2) j + (t3 − t5) kdt = (t44 − t66) i + (t77 − t33 ) j + (t44 − t66) к + C.∫ [〈t, t2, t3〉 × 〈t3, t2, t〉] dt = ∫ (t3 − t5) i + (t6 − t2) j + (t3 − t5) kdt = (t44 − t66) i + (t77 − t33 ) j + (t44 − t66) к + C. - Используйте вторую часть определения интеграла пространственной кривой:
∫0π / 3 [sin2ti + tantj + e − 2tk] dt = [∫0π / 3sin2tdt] i + [∫0π / 3tantdt] j + [∫0π / 3e − 2tdt] k = (- 12cos2t) | 0π / 3i− (ln (стоимость)) | 0π / 3j− (12e − 2t) | 0π / 3k = (- 12cos2π3 + 12cos0) i− (ln (cosπ3) −ln (cos0)) j− (12e − 2π / 3−12e − 2 (0)) k = (14 + 12) i — (- ln2) j− (12e − 2π / 3−12) k = 34i + (ln2) j + (12−12e − 2π / 3) k. ∫0π / 3 [sin2ti + tantj + e − 2tk] dt = [∫0π / 3sin2tdt] i + [∫0π / 3tantdt] j + [∫0π / 3e − 2tdt] k = (- 12cos2t) | 0π / 3i− (ln (стоимость)) | 0π / 3j− (12e − 2t) | 0π / 3k = (- 12cos2π3 + 12cos0) i− (ln (cosπ3) −ln (cos0)) j− (12e − 2π / 3−12e − 2 (0)) k = (14 + 12) i — (- ln2) j− (12e − 2π / 3−12) k = 34i + (ln2) j + (12−12e − 2π / 3) k.
∫0π / 3 [sin2ti + tantj + e − 2tk] dt = [∫0π / 3sin2tdt] i + [∫0π / 3tantdt] j + [∫0π / 3e − 2tdt] k = (- 12cos2t) | 0π / 3i− (ln (стоимость)) | 0π / 3j− (12e − 2t) | 0π / 3k = (- 12cos2π3 + 12cos0) i− (ln (cosπ3) −ln (cos0)) j− (12e − 2π / 3−12e − 2 (0)) k = (14 + 12) i — (- ln2) j− (12e − 2π / 3−12) k = 34i + (ln2) j + (12−12e − 2π / 3) k.
Контрольно-пропускной пункт 3.8
Вычислите следующий интеграл:
∫13 [(2t + 4) i + (3t2−4t) j] dt.∫13 [(2t + 4) i + (3t2−4t) j] dt.Раздел 3.2 Упражнения
Вычислить производные векторных функций.
41 год .r (t) = t3i + 3t2j + t36kr (t) = t3i + 3t2j + t36k
42 .r (t) = sin (t) i + cos (t) j + etkr (t) = sin (t) i + cos (t) j + etk
43 год .r (t) = e − ti + sin (3t) j + 10tk.r (t) = e − ti + sin (3t) j + 10tk. Здесь показан эскиз графика.Обратите внимание на изменяющуюся периодичность графика.
44 .r (t) = eti + 2etj + kr (t) = eti + 2etj + k
46 .
r (t) = teti + tln (t) j + sin (3t) kr (t) = teti + tln (t) j + sin (3t) k
47 .r (t) = 1t + 1i + arctan (t) j + lnt3kr (t) = 1t + 1i + arctan (t) j + lnt3k
48 .r (t) = tan (2t) i + sec (2t) j + sin2 (t) kr (t) = tan (2t) i + sec (2t) j + sin2 (t) k
49 .r (t) = 3i + 4sin (3t) j + tcos (t) kr (t) = 3i + 4sin (3t) j + tcos (t) k
50 .r (t) = t2i + te − 2tj − 5e − 4tkr (t) = t2i + te − 2tj − 5e − 4tk
Для следующих задач найдите касательный вектор при указанном значении t .
51 .r (t) = ti + sin (2t) j + cos (3t) k; t = π3r (t) = ti + sin (2t) j + cos (3t) k; t = π3
52 .r (t) = 3t3i + 2t2j + 1tk; t = 1r (t) = 3t3i + 2t2j + 1tk; t = 1
53 .r (t) = 3eti + 2e − 3tj + 4e2tk; r (t) = 3eti + 2e − 3tj + 4e2tk; t = ln (2) t = ln (2)
54 .r (t) = cos (2t) i + 2sintj + t2k; t = π2r (t) = cos (2t) i + 2sintj + t2k; t = π2
Найдите единичный касательный вектор для следующих параметризованных кривых.
r (t) = 6i + cos (3t) j + 3sin (4t) k, r (t) = 6i + cos (3t) j + 3sin (4t) k, 0≤t <2π0≤t <2π.Здесь представлены два вида этой кривой:
56 .r (t) = costi + sintj + sintk, r (t) = costi + sintj + sintk, 0≤t <2π.0≤t <2π.
57 .r (t) = 3cos (4t) i + 3sin (4t) j + 5tk, 1≤t≤2r (t) = 3cos (4t) i + 3sin (4t) j + 5tk, 1≤t≤2
58 .r (t) = ti + 3tj + t2kr (t) = ti + 3tj + t2k.
Пусть r (t) = ti + t2j − t4kr (t) = ti + t2j − t4k и s (t) = sin (t) i + etj + cos (t) ks (t) = sin (t) i + etj + cos (t) k. Вот график функции:
Найдите следующее.
60 .ddt [t2 · s (t)] ddt [t2 · s (t)]
61 .ddt [r (t) · s (t)] ddt [r (t) · s (t)]
62 .Вычислите первую, вторую и третью производные r (t) = 3ti + 6ln (t) j + 5e − 3tk.r (t) = 3ti + 6ln (t) j + 5e − 3tk.
63 .Найдите r ′ (t) · r ″ (t) для r (t) = — 3t5i + 5tj + 2t2k.r ′ (t) · r ″ (t) forr (t) = — 3t5i + 5tj + 2t2k.
64 .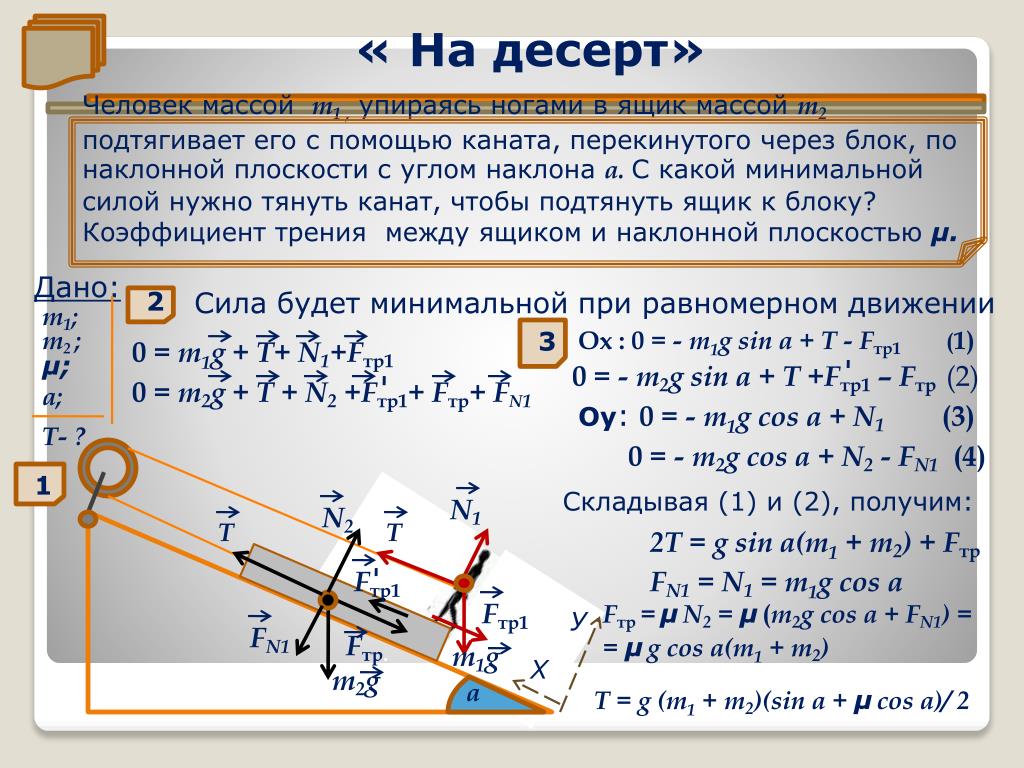
Функция ускорения, начальная скорость и начальное положение частицы равны
a (t) = — 5costi − 5sintj, v (0) = 9i + 2j, и r (0) = 5i.a (t) = — 5costi − 5sintj, v (0) = 9i + 2j и r (0) = 5i.
Найдите v (t) и r (t) .v (t) и r (t).
Вектор положения частицы равен r (t) = 5sec (2t) i − 4tan (t) j + 7t2k.r (t) = 5sec (2t) i − 4tan (t) j + 7t2k.
- Изобразите функцию положения и отобразите вид графика, который иллюстрирует асимптотическое поведение функции.
- Найдите скорость при t приближается, но не равна π / 4π / 4 (если она существует).
Найдите скорость и скорость частицы с помощью функции положения r (t) = (2t − 12t + 1) i + ln (1−4t2) jr (t) = (2t − 12t + 1) i + ln ( 1−4t2) j.Скорость частицы — это величина скорости и обозначается как r ‘(t) ‖.r’ (t) ‖.
Частица движется по круговой траектории радиуса b согласно функции r (t) = bcos (ωt) i + bsin (ωt) j, r (t) = bcos (ωt) i + bsin (ωt) j , где ωω — угловая скорость, dθ / dt. dθ / dt.
dθ / dt.
Найдите функцию скорости и покажите, что v (t) v (t) всегда ортогональна r (t) .r (t).
68 .Покажите, что скорость частицы пропорциональна угловой скорости.
69 .Вычислить ddt [u (t) × u ′ (t)] ddt [u (t) × u ′ (t)], если u (t) = t2i − 2tj + k.u (t) = t2i − 2tj + k.
70 .Найти первообразную r ‘(t) = cos (2t) i − 2sintj + 11 + t2kr’ (t) = cos (2t) i − 2sintj + 11 + t2k, удовлетворяющую начальному условию r (0) = 3i− 2j + kr (0) = 3i − 2j + k.
71 .Оценить ∫03‖ti + t2j‖dt.∫03‖ti + t2j‖dt.
72 .Объект стартует из состояния покоя в точке P (1,2,0) P (1,2,0) и движется с ускорением a (t) = j + 2k, a (t) = j + 2k, где ‖ a (t) ‖‖a (t) ‖ измеряется в футах в секунду в секунду.Найдите местоположение объекта через t = 2t = 2 сек.
73 . Покажите, что если скорость частицы, движущейся по кривой, представленной векторной функцией, постоянна, то функция скорости всегда перпендикулярна функции ускорения.
Для r (t) = ti + 3tj + t2kr (t) = ti + 3tj + t2k и u (t) = 4ti + t2j + t3k, u (t) = 4ti + t2j + t3k, найти ddt (r (t ) × u (t)). Ddt (r (t) × u (t)).
75 .Дано r (t) = 〈t + cost, t − sint〉, r (t) = 〈t + cost, t − sint〉, найти скорость и скорость в любое время.
76 .Найдите вектор скорости для функции r (t) = 〈et, e − t, 0〉 .r (t) = 〈et, e − t, 0〉.
77 .Найдите уравнение касательной к кривой r (t) = 〈et, e − t, 0〉 r (t) = 〈et, e − t, 0〉 при t = 0.t = 0.
78 .Опишите и нарисуйте кривую, представленную векторной функцией r (t) = 〈6t, 6t − t2〉 .r (t) = 〈6t, 6t − t2〉.
79 .Найдите наивысшую точку кривой r (t) = 〈6t, 6t − t2〉 r (t) = 〈6t, 6t − t2〉 и укажите значение функции в этой точке.
Вектор положения частицы равен r (t) = ti + t2j + t3k.r (t) = ti + t2j + t3k. График показан здесь:
80 .Найдите вектор скорости в любой момент.
81 год . Найдите скорость частицы в момент времени t = 2t = 2 сек.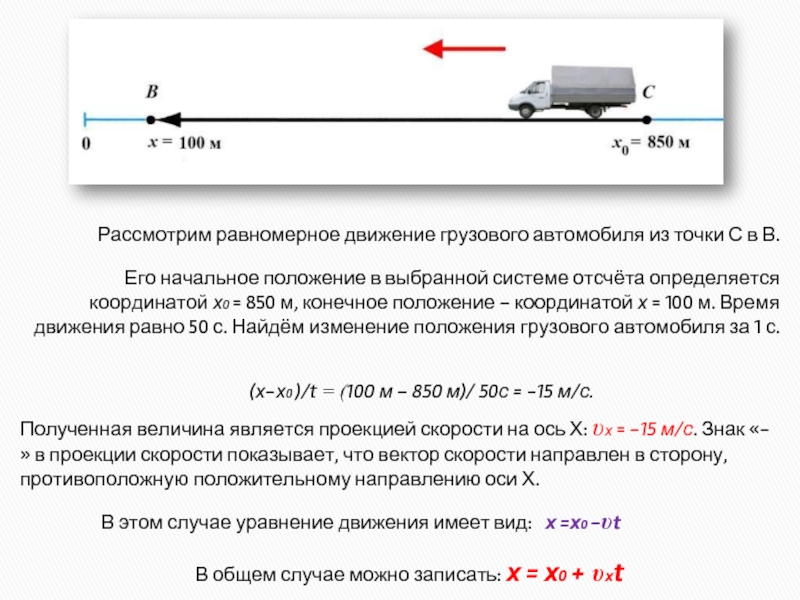
Найдите ускорение в момент времени t = 2t = 2 сек.
Частица движется по спирали с уравнением r (t) = cos (t) i + sin (t) j + tk.r (t) = cos (t) i + sin (t) j + tk . Смотрите график, представленный здесь:
Найдите следующее:
83 .Скорость частицы в любой момент
84 .Скорость частицы в любой момент
85 .Ускорение частицы в любой момент
86 .Найдите единичный касательный вектор спирали.
Частица движется по эллипсу с уравнением r (t) = costi + 2sintj + 0k.r (t) = costi + 2sintj + 0k. Найдите следующее:
88 .Скорость частицы при t = π4t = π4
89 .Ускорение частицы при t = π4t = π4
Для векторной функции r (t) = 〈tant, sect, 0〉 r (t) = 〈tant, sect, 0〉 (график показан здесь) найдите следующее:
93 .Найти минимальную скорость частицы, движущейся по кривой r (t) = 〈t + cost, t − sint〉 r (t) = 〈t + cost, t − sint〉 t∈ [0,2π) .t∈ [0,2π).
Для r (t) = ti + 2sintj + 2costkr (t) = ti + 2sintj + 2costk и u (t) = 1ti + 2sintj + 2costk, u (t) = 1ti + 2sintj + 2costk, найдите следующее:
95 .
ddt (r (t) × u (t)) ddt (r (t) × u (t))
96 .Теперь используйте правило произведения для производной от перекрестного произведения двух векторов и покажите, что этот результат совпадает с ответом на предыдущую задачу.
Найдите единичный касательный вектор T (t) для следующих векторных функций.
97 .r (t) = 〈t, 1t〉. R (t) = 〈t, 1t〉. График показан здесь:
98 .r (t) = 〈tcost, tsint〉 r (t) = 〈tcost, tsint〉
99 .r (t) = 〈t + 1,2t + 1,2t + 2〉 r (t) = 〈t + 1,2t + 1,2t + 2〉
Вычислите следующие интегралы:
100 .∫ (eti + sintj + 12t − 1k) dt∫ (eti + sintj + 12t − 1k) dt
101 .∫01r (t) dt, ∫01r (t) dt, где r (t) = 〈t3,1t + 1, e − t〉 r (t) = 〈t3,1t + 1, e − t〉
Argand Diagram — обзор
4.2 Разложение спектров диэлектрической функции и характеристических спектров потерь электронов на элементарные компоненты
Экспериментальный спектр отражательной способности, а также другие вычисленные на его основе функции собирают все индивидуальные переходы из занятого состояния в незанятое. Для стеклообразных соединений важно решить обратную задачу: имея интегральную кривую, необходимо восстановить вклады элементарных переходов и определить параметры каждого (максимальная энергия E i , ее полуширина H i и высота I i и площадь переходных полос S i и сила осциллятора).Это возможно методом объединенных (комбинированных) диаграмм Аргана ε 2 ( E ) = f 1 ((ε 1 ) ( E )). На основе полученных спектров ε 2 ( E ) и ε 1 ( E ) строится объединенная (совмещенная) ассоциированная диаграмма Аргана. Затем, начиная с наиболее интенсивного максимума ε 2 ( E ), последовательно извлекаются отдельные полосы с последующей оптимизацией разложения.
Для стеклообразных соединений важно решить обратную задачу: имея интегральную кривую, необходимо восстановить вклады элементарных переходов и определить параметры каждого (максимальная энергия E i , ее полуширина H i и высота I i и площадь переходных полос S i и сила осциллятора).Это возможно методом объединенных (комбинированных) диаграмм Аргана ε 2 ( E ) = f 1 ((ε 1 ) ( E )). На основе полученных спектров ε 2 ( E ) и ε 1 ( E ) строится объединенная (совмещенная) ассоциированная диаграмма Аргана. Затем, начиная с наиболее интенсивного максимума ε 2 ( E ), последовательно извлекаются отдельные полосы с последующей оптимизацией разложения.
В спектрах потерь электронов аналогами функций ε 2 и ε 1 являются функции −Im ε −1 и −Re ε −1 .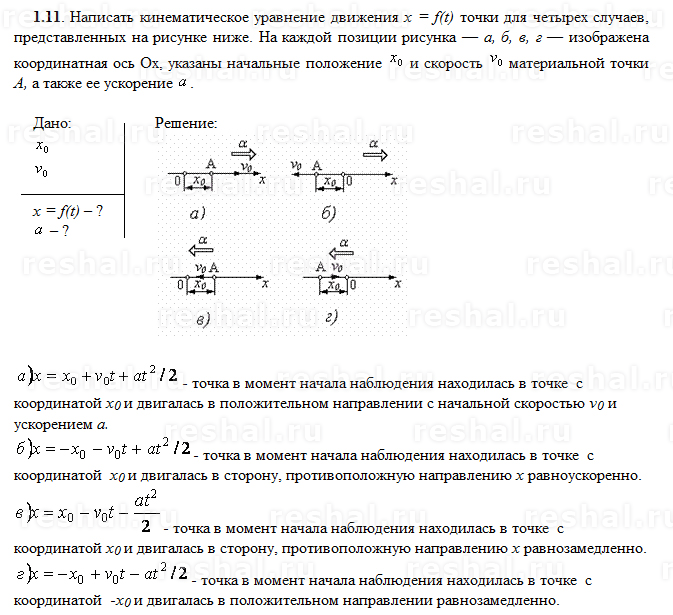 Поэтому расчет спектра элементарных продольных составляющих и определение их параметров выполняется аналогично расчетам поперечных составляющих с использованием метода совмещенных (комбинированных) диаграмм Аргана для −Im ε −1 = f 2 (-Re ε -1 ). Теоретически энергия продольной компоненты всегда несколько больше энергии ее поперечного аналога.Количественные оценки этого сдвига Δ E известны только для свободных экситонов (Соболев, Немошкаленко, 1992).
Поэтому расчет спектра элементарных продольных составляющих и определение их параметров выполняется аналогично расчетам поперечных составляющих с использованием метода совмещенных (комбинированных) диаграмм Аргана для −Im ε −1 = f 2 (-Re ε -1 ). Теоретически энергия продольной компоненты всегда несколько больше энергии ее поперечного аналога.Количественные оценки этого сдвига Δ E известны только для свободных экситонов (Соболев, Немошкаленко, 1992).
Функция потерь электронов зависит от ε1 и ε2: −Im ε − 1 = ε2 (ε22 + ε12) −1. Из анализа этой формулы и спектров потерь некоторых исследованных материалов (Pines, 1966) следует, что интенсивность длинноволновой части в спектре потерь всегда намного ниже (по сравнению с коротковолновой), чем в спектр ε 2 .
Основные расчетные параметры поперечной (1) и продольной (2) составляющих приведены в таблице II.В переходах g-As 2 S 3 обнаружено девять поперечных (№№ 1–9) и восемь продольных (№№ 3–9 и 6 ′) компонент. Малые значения функций потерь в диапазоне E <4 эВ сделали невозможным выделение слабых полос № 1 и 2. Интегральные кривые оптических спектров содержат всего три максимума (ε 2 , R ). со слабой триплетной тонкой структурой наиболее длинноволнового максимума отражательной способности.
Малые значения функций потерь в диапазоне E <4 эВ сделали невозможным выделение слабых полос № 1 и 2. Интегральные кривые оптических спектров содержат всего три максимума (ε 2 , R ). со слабой триплетной тонкой структурой наиболее длинноволнового максимума отражательной способности.
Таблица II. Энергии (эВ) E i максимума, полуширина H i и области S i компонент зоны для двух вариантов (1 и 2) разложения спектров ε 2 и −Im ε −1 и возможные энергии E n оптических переходов (варианты a и b) g-As 2 S 3
| No. | E i | H i | S i | E n | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ε 2 | ε 2 | −Im ε −1 | ε 2 | A | B | ||||||||||||||||||||||||||||
1 47| 2 47 | 2 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | | ||||||||||||||||||||||||
| 1 | 3. 2 2 | 3,2 | — | — | 0,4 | 0,9 | — | — | 0,8 | 6,4 | — | 36 —3,0 | 36 | 3637 3,6— | — | 0,7 | 1,0 | — | — | 2,3 | 2,5 | — | — | — | — | 452 | 4,1 | 4,2 | — | 1,2 | 0,9 | 4,2 | — | 3,8 | 6,8 | 0,1 | — | — | 36 36 910 | 4,6 | 4,9 | — | — | 1,0 | 1,0 | — | — | 3,3 | 0,2 | — | — | — | 36 91025,2 | 4,9 | — | 2,0 | 1,1 | 1,0 | — | 1,8 | 5,6 | 0,2 | — | 5,8 | 72 | 3636 —5,9 | — | 2,0 | 1,1 | 1,0 | — | 1,8 | 5,6 | 0,2 | — | 6,3 | 36 6,4 61136454 | — | — | — | 1,3 | — | — | — | 6,2 | — | — | — | 37374545 | 9 | 7,1 | 6,7 | 2,1 | — | 1,6 | 3,0 | 1,8 | — | 0,4 | 0,5 | 6,9 | — | 45— | 4568 | — | — | — | 1,6 | — | — | — | 7,0 | — | — | — | 36 — 3645 | 8,3 | — | 1,6 | — | 1,2 | — | 0,4 | — | 0,2 | — | — | — |
| 4 | 9,7 | — | 1,6 | 1,0 | 1,6 | — | 5,9 | 0,1 | 0,2 | 7,5 | — | ||||||||||||||||||||||
| 3,0 | 1,3 | 1,1 | — | 4,4 | 3,3 | 0,2 | — | — | — | ||||||||||||||||||||||||
12,0. 3 3 | 11,8 | 11,9 | 1,0 | 1,4 | 1,4 | 2,3 | 0,7 | 2,2 | 0,4 | 0,5 | 11,5 | 12,0 | — | 13,7 | — | 1,6 | — | 1,2 | — | 2,2 | — | 0,2 | — | — | 72|||||||||
| 15.9 | — | — | — | 0,8 | — | — | — | 2,0 | — | — | |||||||||||||||||||||||
| 11 | —373737 | 373737 911 — | 1,8 | — | — | — | 1,6 | — | — | 16,0 | 15,2 | ||||||||||||||||||||||
| 12 | 9119 | — | 1,9 | — | 7,0 | — | 1,4 | — | 12,9 | — | — | ||||||||||||||||||||||
| — | — | 6,3 | — | — | — | 5,5 | — | — | |||||||||||||||||||||||||
| 14 | — | —37 | — | — | 6. 1 1 | — | — | — | 1,6 | — | — | ||||||||||||||||||||||
| 15 | — | — | — | 38.0 | —3737373737 | —— | — | 0,9 | — | — | |||||||||||||||||||||||
Полуширины H и большинства компонент разложения спектров находятся в интервале 1-2 эВ.Это значительно затрудняет выделение слабых длинноволновых полос спектра потерь и определение значений энергии сдвигов Δ E между обоими переходными компонентами. Длинноволновые компоненты (№№ 1–3) в основном в 1.5–2 раза уже остальных. Площади полос S i (и вероятности переходов) поперечных компонент в 10–20 раз больше значений продольных S i (№№.3–5 и 8) и 3–5 раз (№ 6 и 7). Это не только подтверждает теоретические качественные оценки большей интенсивности поперечных компонентов (Pines, 1966; Соболев, Немошкаленко, 1988), но также количественно устанавливает, что поперечные компоненты намного больше по интенсивности, чем продольные для большинства переходных полос.
В приведенном выше обсуждении интерпретации максимумов интегральных спектров оптических функций g-As 2 S 3 значения энергии E n возможных переходов были оценены (Таблица I) на на основе данных РФЭС о плотности оккупированных штатов (Бишоп, Шевчик, 1975; Саланек, Заллен, 1976) и величине E г . Согласно этим оценкам, наиболее интенсивные извлеченные нами компоненты могут быть связаны с переходами в более низкие незанятые состояния из максимумов зон занятых состояний (значения E n в Таблице II). Остальные компоненты обусловлены переходами от максимумов XPS-спектров к более высоким незанятым состояниям и из максимумов более тонкой структуры очень широких полос XPS-спектров, чем было получено в Salaneck и Zallen (1976). Хорошее согласие между нашими оценками, касающимися спектра возможных переходов, и результатами разложения спектра ε 2 на компоненты подтверждает результаты Salaneck и Zallen (1976) о квинтете или более сложной структуре высшей валентной зоны занятых состояния g-As 2 S 3 .
Впервые получены полные наборы спектров основных оптических функций g-As 2 S 3 в диапазоне 0–12 и 0–35 эВ, их интегральные спектры диэлектрической функции и Характерные функции объемных потерь электронов разложены на поперечную и продольную составляющие. Определены основные параметры компонентов и предложена схема их интерпретации в рамках модели переходов от максимумов плотностей занятых состояний к незанятым состояниям.Эти результаты существенно расширяют объем информации об оптических спектрах и электронной структуре g-As 2 S 3 в широком диапазоне энергий фундаментального поглощения. В принципе, они закладывают новую основу для теоретических расчетов электронной структуры стеклообразных материалов.
2.5: Скорость и ускорение — математика LibreTexts
Поскольку векторы скорости и ускорения определены как первая и вторая производные вектора положения, мы можем вернуться к вектору положения путем интегрирования.
Пример \ (\ PageIndex {4} \)
Вы — противник и заметили летящую к вам ракету на позиции
.\ [\ textbf {r} _e = 1000 \ hat {\ textbf {i}} + 500 \ hat {\ textbf {j}} \]
со скоростью
\ [\ textbf {v} _e = -30 \ hat {\ textbf {i}} + 3 \ hat {\ textbf {j}}. \]
Вы можете стрелять противоракетами со скоростью 100 метров в секунду. Под каким углом стрелять, чтобы перехватить ракету. Предположим, что гравитация — единственная сила, действующая на снаряды.
Решение
Вектор ускорения ракеты противника
\ [\ textbf {a} _e (t) = -9,8 \ hat {\ textbf {j}}. \]
Интегрируя, получаем вектор скорости
\ [\ textbf {v} _e (t) = v_1 \ hat {\ textbf {i}} + (v_2-9.8t) \ hat {\ textbf {j}}. \]
Установка \ (t = 0 \) и использование начальной скорости вражеской ракеты дает
\ [\ textbf {v} _e (t) = -30 \ hat {\ textbf {i}} + (3-9. 8t) \ hat {\ textbf {j}}. \]
8t) \ hat {\ textbf {j}}. \]
Теперь проинтегрируйте снова, чтобы найти функцию положения
\ [\ textbf {r} _e (t) = (-30t + r_1) \ hat {\ textbf {i}} + (-4.2 + 3t + 500) \ hat {\ textbf {j}}. \]
Ускорение вашей противоракетной ракеты тоже
\ [\ textbf {a} _y (t) = -9,8 t \ hat {\ textbf {j}}. \]
Интегрируя, получаем вектор скорости
\ [\ textbf {v} _y (t) = v_1 \ hat {\ textbf {i}} + (v_2-9.8t) \ hat {\ textbf {j}}. \]
Поскольку величина нашей скорости равна 100, мы можем сказать, что
\ [\ textbf {v} _y (0) = 100 \ cos q \ hat {\ textbf {i}} + 100 \ sin q \ hat {\ textbf {j}}. \]
Так что
\ [\ textbf {v} _y (t) = 100 \ cos q \ hat {\ textbf {i}} + (100 \ sin q -9.2 + 3т + 500. \]
Первое уравнение дает
\ [t = \ dfrac {1000} {100 \ cos q + 30}. \]
Упрощение второго уравнения и замена дает
\ [\ dfrac {100000 \ sin q} {100 \ cos q + 30} = \ dfrac {3000} {100 \ cos q + 30} + 500. \]
\]
Очистите знаменатели, чтобы получить
\ [100000 \ sin q = 3000 + 50000 \ cos q + 15000. \]
На этом этапе мы используем калькулятор, чтобы найти для \ (q \) значение
.\ [q = 0,62535 \; рад. \]
MathScene — Векторы — Урок 3
MathScene — Векторы — Урок 32008 Расмус Эхф и Джанн Сак |
Урок 3
Векторы в системе координат
Пример 1
В точка A имеет координаты (2, 2), а точка B — координаты (6, 5) (см. диаграмму).Координаты вектора
Мы
можно использовать формулу для расстояния между двумя точками, чтобы найти расстояние
между A и B, то есть длина вектора
(см. Правило Пифагора в уроке 2). Формула выглядит следующим образом:
Подставляя заданные координаты в формулу, получаем:
Мы видим, что числа под квадратным корнем — это просто координаты
вектор. Это, конечно, потому, что длина вектора — это просто
гипотенуза в прямоугольном треугольнике с более короткими сторонами 3 и 4.
Это, конечно, потому, что длина вектора — это просто
гипотенуза в прямоугольном треугольнике с более короткими сторонами 3 и 4.
Формула длины вектора, начинающегося в точке
A = (x 1 , y 1 ) и заканчивается на B = (x 2 ,
y 2 ) равен:
Если координаты вектора равны то у нас есть следующее правило:
Пример 2
Найдите вектор что параллельно и который имеет длину 2 единицы (видеть диаграмму).
Два треугольника на диаграмме похожи, поэтому соответствующие
стороны находятся в одинаковом соотношении.
||
= t ∙ ||. Число t — это соотношение между соответствующими сторонами. Соотношение есть.
Соотношение есть.
Мы можем найти координаты как
следует:
Если векторы и являются параллельно, то существует такое число t, что:
= т ∙ |
Пример 3
Какие из следующих векторов параллельны и .
Если векторов и являются параллельно, то существует такое число t, что = т ∙. Если векторы и являются параллельно существует такое число r, что знак равно г ∙.
Мы можно найти числа t и r, используя координаты x, а затем проверить, чтобы увидеть будут ли найдены те же значения, когда мы используем координаты y.
= т ∙
3 = t ∙ 13 дает t = 3/13 = 2/9
4 = t ∙ 18 также дает t = 4/18 = 2/9
В векторов и соток параллель .
= г ∙
3 = r ∙ 6 дает r =
4 = r ∙ 9 дает r = 4/9
В
векторов и соток
не параллельно (Это означает, что
и
являются
тоже не параллельно).
Вектор на схеме имеет координаты . В вектор начинается в точке (0, 0) и заканчивается в (3, 2), поэтому координаты конечная точка совпадает с координатами самого вектора.Это верно для все векторы, которые начинаются в начале системы координат, то есть в точка (0, 0).
Вектор, начинающийся в точке (0, 0), имеет те же координаты, что и его конечная точка. Этот вектор называется вектором положения для A. |
Каждая точка в системе координат может быть представлена своим вектором положения. Координаты точки и ее вектор положения совпадают.Это может быть очень полезно при просмотре переводов в системе координат.
Пример 4
Треугольник, изображенный на схеме, должен быть переведен на вектор .
Мы используем векторы положения точек вершин (−3, 0),
(2, −2) и (3, 1) и складываем вектор
каждому из них.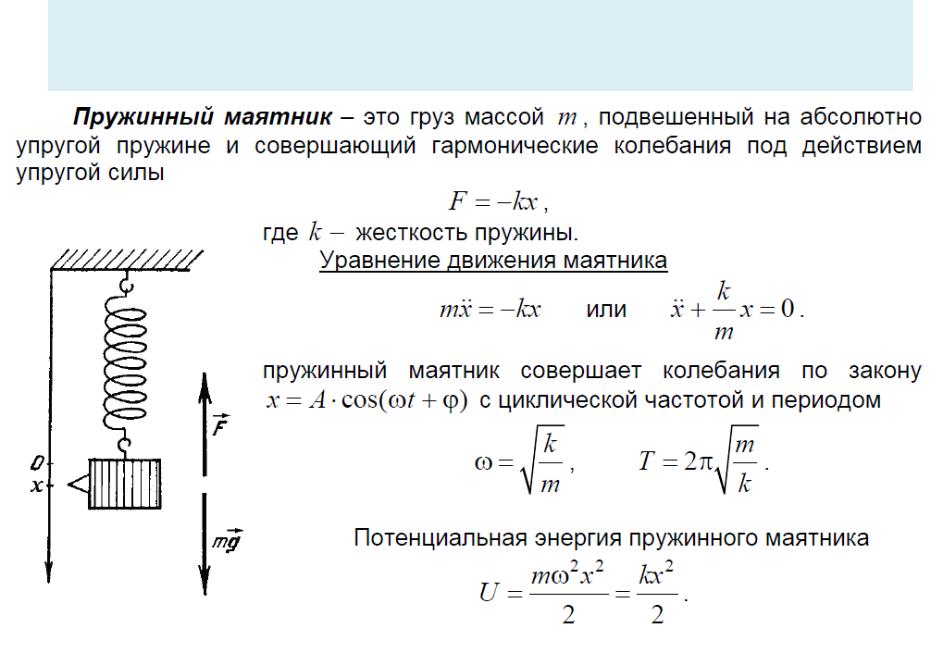
Это дает нам новый вектор положения каждой вершины.Схема ниже показывает перевод.
Пример 5
Теперь мы будем использовать векторы положения, чтобы найти середину отрезка AB, если A = (1, 2) и B = (4, 3).
Как обычно, точка O является началом системы координат. Если M середина AB тогда:
знак равно + ∙
Вектор является вектор положения точки M и, следовательно, имеет те же координаты, что и точка M, которую мы хотим вычислить.Вектор вектор положения A. Чтобы достичь средней точки M, нам нужно добавить половину вектор. Нарисуйте диаграмму, чтобы увидеть это.
Для начала нам нужно найти вектор .
Теперь мы можем найти .
знак равно + ∙
Координаты M такие же, как у вектора положения. или (2, 2) .
Легко найти формулу, по которой мы сможем найти координаты
середина отрезка AB.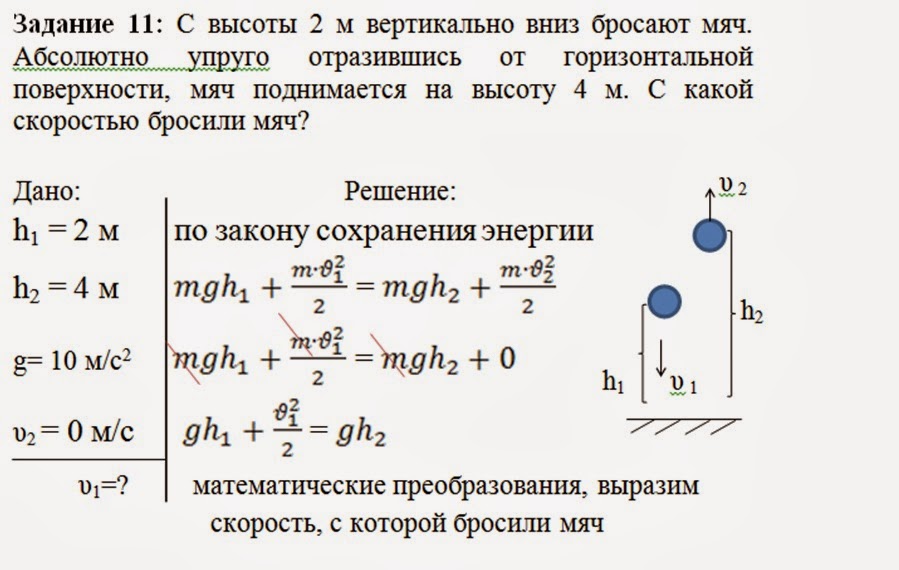
2 = + ∙ + — ∙
Мы видим, что вектор положения середины отрезка представляет собой своего рода
среднее из векторов положения конечных точек. Таким образом, мы можем найти
координаты средней точки путем нахождения среднего значения координат x и y
координаты соответственно.
Это приводит нас к правилу, которое мы называем правилом средней точки.
Середина M отрезка AB задается правилом: .Правило использования координат: . |
Пример 6
Вершины треугольника ABC равны A = (1, 2), B = (4, 3) и C = (3, 0).
Найдите длину прямой от A до середины стороны BC (медиана треугольник ABC).
Начнем с поиска середины BC, используя указанное выше правило.
Назовем среднюю точку M и найдем ее вектор положения
(видеть
диаграмму).
Следовательно, M, середина BC имеет координаты
М = (3, 1).
Далее находим координаты вектора .
Наконец, мы можем найти длину вектора как обязательный.
≈ 2,55
= + ∙
= + ∙ — ∙
= — ∙ — ∙
Когда мы складываем их вместе, гаснет и получаем:
3 = + +
Чтобы найти координаты T, мы берем среднее значение x и y координаты вершин соответственно. |
Таким образом, мы находим точку пересечения T медиан треугольник, найдя своего рода среднее из векторов положения вершины. Таким образом, это правило является расширением правила средней точки.
Пример 7
Найдите точку пересечения T медиан треугольника ABC (
центр) при условии, что A = (1, 2), B = (4, 3) и C = (3, 0) (см.
диаграмму). |
Центр T = (2, 1) .
Попробовать викторину
3
по векторам.
Не забудьте использовать контрольный список, чтобы отслеживать свою работу.
7.Векторы в трехмерном пространстве
Ранее мы видели, как представить двумерные векторы на плоскости x — y .
Теперь мы расширяем идею представления трехмерных векторов с помощью осей x — y — z . (См. «Трехмерную систему координат» для справки по этому поводу).
Пример
Вектор OP имеет начальную точку в начале координат O (0, 0, 0) и конечную точку в P (2, 3, 5). Мы можем нарисовать вектор OP следующим образом:
Величина трехмерного вектора
Ранее мы видели, что расстояние между двумя точками в трехмерном пространстве равно
. 2) = 6.16 \ «единиц» `
2) = 6.16 \ «единиц» `Добавление трехмерных векторов
Ранее мы видели, как складывать двумерные векторы. Теперь мы расширим идею для трехмерных векторов.
Мы просто складываем компоненты i вместе, затем компоненты j и, наконец, компоненты k .
Пример 1
Два якоря удерживают корабль на месте, и их силы, действующие на корабль, представлены векторами A и B следующим образом:
A = 2 i + 5 j — 4 k и B = −2 i — 3 j — 5 k
Если бы мы заменили 2 якоря на 1 якорь, какой вектор представляет этот единственный вектор?
Ответ
Задача просто требует, чтобы мы сложили векторы, чтобы получить единственный результирующий вектор.
A + B
= (2 + −2) i + (5 — 3) j + (−4 — 5) k
= 0 i + 2 j — 9 k
= 2 j — 9 k
Точечное произведение трехмерных векторов
Чтобы найти скалярное произведение (или скалярное произведение) трехмерных векторов, мы просто расширяем идеи скалярного произведения в двух измерениях, с которыми мы встречались ранее.
Пример 2 — Точечное произведение с использованием величины и угла
Найдите скалярное произведение векторов P и Q , учитывая, что угол между двумя векторами составляет 35 ° и
.| P | = 25 ед. с и | Q | = 4 шт.
Ответ
Используя нашу формулу для скалярного произведения:
P • Q = | P | | Q | cos θ
имеем:
P • Q
= | P | | Q | cos θ
= 25 × 4 × cos 35 °
= 81.92
Пример 3 — Точечное произведение, если векторы кратны единичным векторам
Найдите скалярное произведение векторов A и B (они взяты из нашего примера привязки выше):
A = 2 i + 5 j — 4 k и B = −2 i — 3 j — 5 k
Ответ
A • B
= (2 i + 5 j — 4 k ) • (−2 i — 3 j — 5 k )
= (2 × −2) + (5 × −3) + (−4 × −5)
= −4 + −15 + 20
= 1
Направление косинусов
Предположим, у нас есть вектор OA с начальной точкой в начале координат и конечной точкой в A.
Предположим также, что у нас есть единичный вектор в том же направлении, что и OA . (См. Напоминание об единичных векторах).
Пусть наш единичный вектор будет:
u = u 1 i + u 2 j + u 3 k
На графике u — это единичный вектор (черный), указывающий в том же направлении, что и вектор OA , и i , j и k (единичные векторы в x-, y- и z- соответственно) отмечены зеленым.
Теперь мы увеличиваем вектор и и немного меняем ориентацию, как показано ниже:
Теперь, если на диаграмме выше,
α — это угол между u и осью x (темно-красным),
β — угол между u и осью y (зеленым) и
γ — угол между .u и z — ось (розовая),
, то мы можем использовать скалярное произведение и записать:
u 1
= u • i
= 1 × 1 × cos α
= cos α
u 2
= u • j
= 1 × 1 × cos β
= cos β
u 3
= u • k
= 1 × 1 × cos γ
= cos γ
Итак, мы можем записать единичный вектор и как:
u = cos α i + cos β j + cos γ k
Эти 3 косинуса называются направляющими косинусами .
Угол между трехмерными векторами
Ранее мы видели, как найти угол между двумерными векторами. Мы используем ту же формулу для трехмерных векторов:
`theta = arccos ((P * Q) / (| P || Q |))`
Пример 4
Найдите угол между векторами P = 4 i + 0 j + 7 k и Q = -2 i + j + 3 k .
Ответ
Векторы P и Q следующие.Вектор P находится на плоскости x — z (обратите внимание, что значение y для вектора P равно «0»), а Q «отстает» от y — z самолет.
По формуле
`theta = arccos ((P * Q) / (| P || Q |))`
имеем:
P • Q
= (4 i + 0 j + 7 j ) • (−2 i + j + 3 k)
= (4 × −2) + (0 × 1) + (7 × 3)
= 13
А теперь знаменатель:
`| P || Q | = sqrt (4 ^ 2 + (0) ^ 2 + 7 ^ 2)` `xxsqrt ((- 2) ^ 2 + 1 ^ 2 + 3 ^ 2)`
`= sqrt (65) sqrt (14)`
`= 30.
166 \ «единиц» `
Так
θ = arccos (13 ÷ 30,166)
Следовательно, угол между векторами P и Q равен
.θ = 64,47 °
Упражнение
Найдите угол между векторами P = 3 i + 4 j -7 k и Q = -2 i + j + 3 k .
Ответ
По формуле
`theta = arccos ((P * Q) / (| P || Q |))`
сначала находим скалярное произведение:
P • Q
= (3 i + 4 j -7 j ) • (−2 i + j + 3 k)
= (3 × −2) + (4 × 1) + (−7 × 3)
= −23
А теперь знаменатель:
| P | | Q |
= √ (3 2 + 4 2 + (−7) 2 ) × √ ((- 2) 2 + 1 2 + 3 2 )
= 32.
187
Так
θ = arccos (−23 ÷ 32,187)
Следовательно, угол между векторами P и Q равен
.θ = 135,6 °
Приложение
У нас есть куб ABCO PQRS, у которого есть нить по диагонали куба от B до S, а другая по другой диагонали от C до P
Какой угол между двумя струнами?
Ответ
Для удобства предположим, что у нас есть единиц куба (каждая сторона имеет длину 1 единицу), и мы разместим его так, чтобы один угол куба находился в начале координат.
Единичные векторы i , j и k действуют в направлениях x -, y — и z — соответственно. Итак, на нашей диаграмме, поскольку у нас есть единичный куб,
OA = i
OC = j
OS = k
Из диаграммы мы видим, что для перехода от B к S нам нужно пройти −1 единицу в направлении x , −1 единицу в направлении y и вверх на 1 единицу в направлении z . .Поскольку у нас есть единичный куб, мы можем написать:
.Поскольку у нас есть единичный куб, мы можем написать:
БС = −i — j + k
и аналогично:
CP = i — j + k
Скалярное произведение векторов BS и CP :
BS • CP = | BS | | CP | cos θ
, где θ — угол между BS и CP .
Таким образом, угол θ равен
θ = arccos [( BS • CP ) ÷ ( | BS | | CP | )]
Сейчас,
BS • CP
= ( −i — j + k ) • ( i — j + k )
= – 1 + 1 + 1
= 1
и
| BS | | CP |
`= sqrt ((- 1) ^ 2 + (-1) ^ 2 + 1 ^ 2)` `× sqrt (1 ^ 2 + (-1) ^ 2 + 1 ^ 2)`
`= (sqrt3) (sqrt3)`
= 3
Так
`θ = arccos (1/3)`
θ = 70.

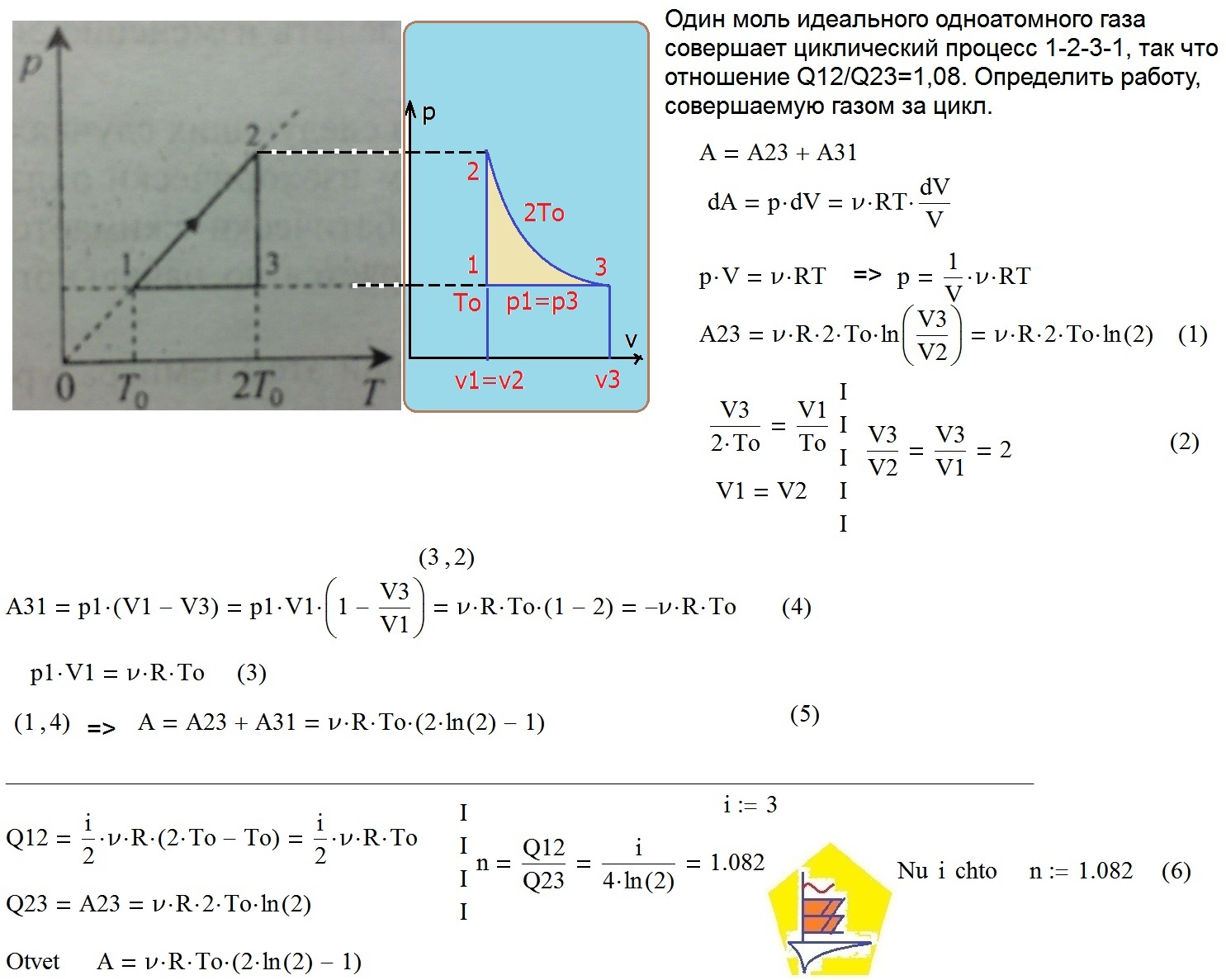 Определите вектор положения, представленный UV .
Определите вектор положения, представленный UV .


 g (t) = 4t2 + 2t − 3. Имеем f ′ (t) = 6f ′ (t) = 6 и g ′ (t) = 8t + 2, g ′ (t) = 8t + 2, поэтому теорема дает r ′ (t) = 6i + (8t + 2) jr ′ (t) = 6i + (8t + 2) j.
g (t) = 4t2 + 2t − 3. Имеем f ′ (t) = 6f ′ (t) = 6 и g ′ (t) = 8t + 2, g ′ (t) = 8t + 2, поэтому теорема дает r ′ (t) = 6i + (8t + 2) jr ′ (t) = 6i + (8t + 2) j.
 ∫ab [f (t) i + g (t) j + h (t) k] dt = [∫abf (t) dt] i + [∫abg (t) dt] j + [∫abh (t) dt] k.
∫ab [f (t) i + g (t) j + h (t) k] dt = [∫abf (t) dt] i + [∫abg (t) dt] j + [∫abh (t) dt] k.
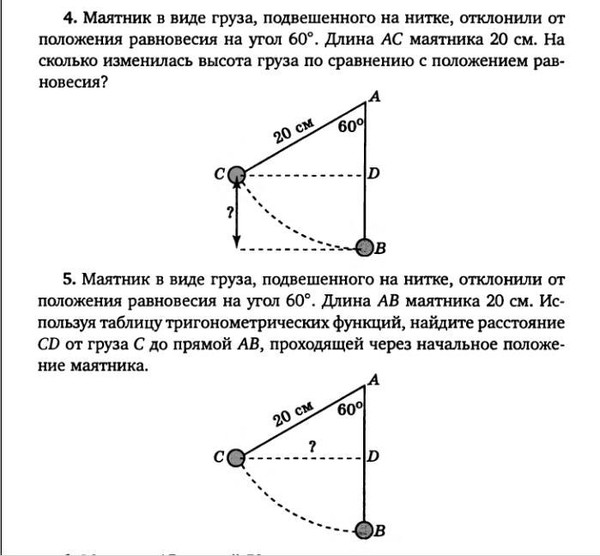 ∫0π / 3 [sin2ti + tantj + e − 2tk] dt = [∫0π / 3sin2tdt] i + [∫0π / 3tantdt] j + [∫0π / 3e − 2tdt] k = (- 12cos2t) | 0π / 3i− (ln (стоимость)) | 0π / 3j− (12e − 2t) | 0π / 3k = (- 12cos2π3 + 12cos0) i− (ln (cosπ3) −ln (cos0)) j− (12e − 2π / 3−12e − 2 (0)) k = (14 + 12) i — (- ln2) j− (12e − 2π / 3−12) k = 34i + (ln2) j + (12−12e − 2π / 3) k.
∫0π / 3 [sin2ti + tantj + e − 2tk] dt = [∫0π / 3sin2tdt] i + [∫0π / 3tantdt] j + [∫0π / 3e − 2tdt] k = (- 12cos2t) | 0π / 3i− (ln (стоимость)) | 0π / 3j− (12e − 2t) | 0π / 3k = (- 12cos2π3 + 12cos0) i− (ln (cosπ3) −ln (cos0)) j− (12e − 2π / 3−12e − 2 (0)) k = (14 + 12) i — (- ln2) j− (12e − 2π / 3−12) k = 34i + (ln2) j + (12−12e − 2π / 3) k.
 u и z — ось (розовая),
u и z — ось (розовая),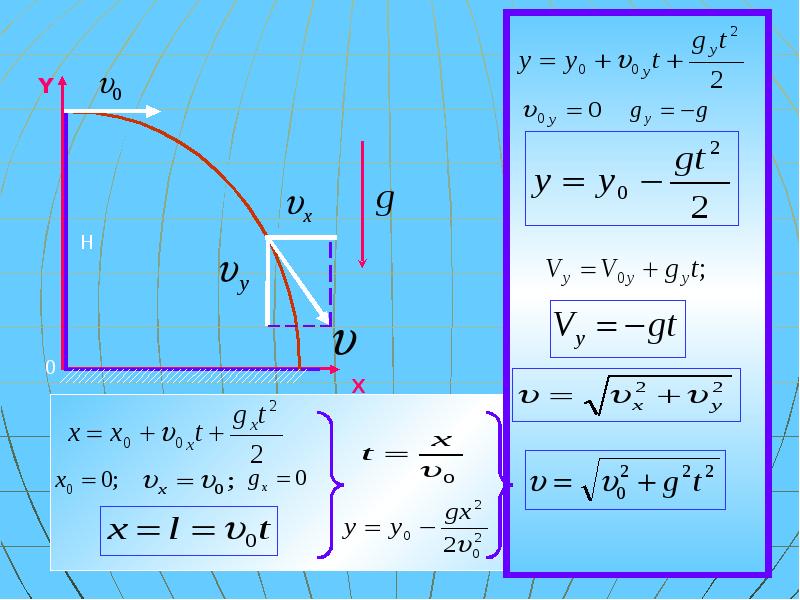 166 \ «единиц» `
166 \ «единиц» `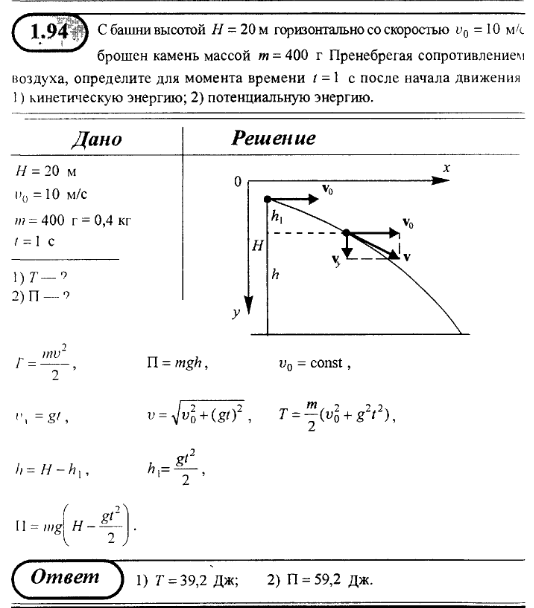 187
187