Мультипликативная модель это: Модель мультипликативная — Энциклопедия по экономике
Модель мультипликативная — Энциклопедия по экономике
Способ абсолютных разниц применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных моделях ( Y = xt-x x x i) и моделях мультипликативно-аддитивного типа Y= (а — Ь)с и Y = = a(b — с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. [c.58]Рассмотрим алгоритм расчета факторов этим способом в моделях мультипликативно-аддитивного вида. Для примера возьмем факторную модель прибыли от реализации продукции [c.58]
Модель мультипликативная — жестко детерминированная факторная модель, в которую факторы входят в виде произведения. [c.535]
Влияние использования материальных ресурсов на величину материальных затрат оценивается с использованием двух-факторных моделей мультипликативная модель изучает влияние материалоемкости по прямым затратам и коэффициента соотношения общих и прямых затрат аддитивная модель — влияние материалоемкости отдельных видов материальных ресурсов на совокупный показатель материалоемкости.
Аддитивная модель. Мультипликативная модель. Автокорреляция. Лаг. [c.23]
Строго говоря, все сезонные модели мультипликативны и имеют лишь один линейный элемент (роп), он и будет аддитивным. [c.28]
В данном случае для преобразования исходной факторной модели, построенной на математических зависимостях, использованы способы удлинения и расширения. В результате получилась более содержательная модель мультипликативно-аддитивно-кратного вида, которая имеет большую познавательную ценность, поскольку учитывает причинно-следственные связи между показателями. Данная модель позволяет исследовать, как влияют на доходность капитала объем продаж, отпускные цены, себестоимость реализованной продукции, внереализационные финансовые результаты, а также скорость обращения капитала. [c.96]
Итак, мы рассмотрели четыре способа выявления сезонной компоненты аддитивную модель, мультипликативную модель, метод экспоненциального сглаживания с тремя параметрами, гармонический анализ Фурье (рис.
П-7). В нашем примере оказалось, что наименьшую ошибку дает мультипликативная модель, т. е. применение индексов сезонности.
[c.439]
Поскольку модель мультипликативная, то применимы следующие способы ее обработки. [c.37]
Методика построения мультипликативных моделей эффективности производства. [c.106]
Вычислительная схема реализации расчетов по модели (2)— (9) на основе мультипликативного алгоритма симплекс. — метода показана на рисунке. [c.100]
Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, атакже от возможностей детализации и формализации показателей в пределах установленных правил. [c.34]
В результате получается конечная мультипликативная модель в виде произведения нового набора факторов. [c.35]
Наиболее универсальным из них является способ цепной подстановки.
Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя. Порядок применения этого способа рассмотрим на примере, приведенном в табл. 4.1.
[c.55]
Как нам уже известно, объем валовой продукции (ВП) зависит от двух основных факторов первого порядка численности рабочих (ЧР) и среднегодовой выработки (ГВ).
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях. Здесь используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов. Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y ab . [c.59]
Мультипликативные модели — модели умножения. Например, объем продукции может быть определен по выражению [c.85]
Для кратной формы связи, при тех же предположениях, что и для мультипликативной модели [c.273]
Корреляционная модель себестоимости добычи нефти и попутного газа по указанным факторам была рассчитана по мультипликативной функции Кобба — Дугласа (41). В результате решения этой модели было составлено сводное уравнение по нефтедобывающей промышленности Украинской ССР [c.90]
Основным недостатком логарифмического метода анализа является то, что он не может быть универсальным , его нельзя применять при анализе любого вида моделей факторных систем.
Если при анализе мультипликативных моделей факторных систем при использовании логарифмического метода достигается получение точных величин влияния факторов (в. случае, когда Az = 0), то при таком же анализе кратных моделей факторных систем получение точных величин влияния факторов не удается.
[c.126]
Формирование рабочих формул интегрального метода для мультипликативных моделей. Применение интегрального метода факторного анализа в детерминированном экономическом анализе наиболее полно решает проблему получения однозначно определяемых величин влияния факторов. [c.134]
Выше было установлено, что любую модель конечной факторной системы можно привести к двум видам — мультипликативной и кратной. Это условие предопределяет то, что исследователь имеет дело с двумя основными видами моделей факторных систем, так как остальные модели — это их разновидности. [c.134]
Для облегчения решения задачи построения подынтегральных выражений в зависимости от вида модели факторной системы (мультипликативные или кратные) предложим матрицы исходных значений для построения подынтегральных выражений элементов структуры факторной системы.
Принцип, заложенный в матрицах, позволяет построить подынтегральные выражения элементов структуры факторной системы для любого набора элементов модели конечной факторной системы. В основном построение подынтегральных выражений элементов структуры факторной системы — процесс индивидуальный, и в случае, когда число элементов структуры измеряется большим количеством, что в экономической практике является редкостью, исходят из конкретно заданных условий.
[c.134]
При формировании рабочих формул расчета влияния факторов в условиях применения ЭВМ пользуются следующими правилами, -отражающими механику работы с матрицами подынтегральные выражения элементов структуры факторной системы для мультипликативных моделей строятся путем произведения полного набора элементов значений, взятых по каждой строке матрицы, отнесенных к определенному элементу структуры факторной системы с последующей расшифровкой [c.134]
Элементы мультипликативной модели [c.135]
В случае отсутствия универсальных вычислительных средств предложим чаще всего встречающийся в экономическом анализе набор формул расчета элементов структуры для мультипликативных (табл.
Набор частных свойств специфичен, как и формы их синтеза. В большинстве случаев отдельные свойства коррелируют, что обусловливает т.н. мультипликативный эффект взаимоусиления (чаще) или взаимовлияния на полезность (качество) изделия. Поэтому приближенный к истине при отсутствии теоретически обоснованной модели является способ выражения интегрального показателя качества функцией вида [c.124]
Алгоритм расчета для мультипликативной четырехфакторнон модели валовой продукции выглядит следующим образом [c.58]
Интегральный метол применяется для измерения влияния факторов в мультипликативных, кратных и кратно-а 1дитии ых моделях. Его использование позволяет получать более точные результаты расчета влияния факторов по сравнению со способами г пной подстановки, абсолютных и относительных разниц, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к последнему фактору, а делится поровну между ними.
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. Как п при интегрировании, здесь результат расчета также не зависит от месторасположения факторов в модели. По сравнению с интегральным методом логарифмирование обеспечивает более высокую точность расчетов. Если при интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В тгом его преимущество, а недостаток — в ограниченности сферы применения. [c.63]
При построении моделей себестоимости добычи нефти и газа по НГДУ Прикарпатья (линейная, полином третьей степени мультипликативная функция Кобба — Дугласа) ни одна из них не выдержала проверки на адекватность (табл. 29). Величины критериев, характеризующих экономико-статистическую достоверность кинетической производственной функции по нефтегазодобывающим управлениям Прикарпатья, приведены в табл.
30.
[c.94]
Построенные многофакторные корреляционные модели по нефте-х добывающей промышленности Украины, нефтегазодобывающим управлениям Прикарпатья, НГДУ Долинанефтегаз вида множественной линейной функции, мультипликативной функции Кобба — Дугласа, кинетической производственной функции позволили сделать количественную оценку влияния различных факторов в их взаимосвязи на динамику себестоимости добычи нефти и попутного газа. Исследована специфика экономико-математического моделирования в нефтедобывающей промышленности, и с этих позиций обосновано использование в качестве функции себестоимости добычи нефти и газа кинетической трансцендентной функции вида [c.111]
Как видно, метод взвешенных конечных разностей учитывает все варианты подстановок. Одновременно при усреднении нельзя получить однозначное количественное значение отдельных факторов. Этот метод весьма трудоемкий и по сравнению с предыдущим методом усложняет вычислительную процедуру, так как приходится перебирать все возможные варианты подстановок.
В своей основе метод взвешенных конечных разностей идентичен (только для двухфактор-ной мультипликативной модели) методу простого прибавления неразложимого остатка при делении этого остатка между факторами поровну. Это подтверждается следующим преобразованием формулы
[c.124]
В более общем виде этот метод был описан еще А. Хума-лом, который писал Такое разделение прироста произведения может быть названо нормальным. Название оправдывается тем, что полученное правило разделения остается в силе при любом числе сомножителей, а именно прирост произведения разделяется между переменными сомножителями пропорционально логарифмам их коэффициентов изменения [69, с. 207]. Действительно, в случае наличия большего числа сомножителей в анализируемой мультипликативной модели факторной системы (например, z = хурт) суммарное приращение результативного показателя Az составит [c.125]
Вид моделей факторной системы /= xyzq (мультипликативная модель). [c.135]
25. Мультипликативная модель временного ряда.
Для выявления структуры временного ряда, т.е. определения количественных значений компонентов, составляющих уровней ряда, чаще всего используют аддитивную или мультипликативную модели временных рядов.
Мультипликативная модель. У=Т*S*E
T-трендовая компонента
S-сезонная компонента
E-случайная компонента
Мультипликативная модель используется в случае, если амплитуда сезонных колебаний увеличивается или уменьшается.
Алгоритм построения модели. Процесс построения модели включает в себя следующие шаги:
Выравнивание уровней исходного ряда методом скользящей средней.
Расчет значений сезонной компоненты S
Устранение сезонной компоненты из исходного уровня ряда и получение выровненных данных без S
Аналитическое выравнивание уровней ряда и расчет значений фактора Т
Расчет полученных значений (Т* S) для каждого уровня ряда
Расчет абсолютных или относительных ошибок модели.
(или 4.Определение тенденции временного ряда и уравнения тренда; 5.Расчет абсолютных или относительных ошибок модели.)
26 Выделение сезонной составляющей
Оценку сезонной компоненты можно найти как частное от деления фактических уровней ряда на центрированные скользящие средние .
Для начала необходимо найти средние за период (квартал, месяц) оценки сезонной компоненты Si . В моделях сезонной компоненты обычно предполагается что сезонные взаимодействия за период взаимопоглощаются .
В мультипликативной модели взаимопоглощаемость сезонных воздействий выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле.
Выравнивание
исходных уровней с помощью скользящей
средней: а) Суммируются уровни ряда последовательно
за каждый период времени за каждые 4
квартала со сдвигом на 1 момент времени
и определяются условные годовые объемы
потребления б) Разделим полученные
суммы на 4, получим скользящие средние.
Полученные выравненные значения не
содержат сезонной компоненты. в) Приводим
эти значения в соответствие с фактическими
моментами времени для чего найдем
среднее значение из 2-х скользящих
средних – центрированные скользящие
средние.
27.Коэффициент корреляции.
Для определения степени линейной связи рассчитывается коэфф-т корреляции.
, -11.
Для определения нелинейной связи определяется индекс корреляции
, 0 1
Коэффициент детерминации: R2=2-для лин. связи. R2=2-для нелин. связи.
Показывает на сколько % изменения показателя у от своего среднего значения зависит от изменения фактора х от своего среднего значения. Чем ближе значение R² к 1, тем точнее модель.
Из всех полученных уравнений регрессии, лучшей является та, у которой коэф-т детерминации больший.
Если
исследуется несколько факторов (больше2)
то в этом случае рассчитывается
множественный коэфф-т
корреляции.
RY,X1,X2..XN-множественный
коэфф-т корреляции.
При анализе влияния нескольких факторов друг на друга определяется корреляционная матрица, которая состоит из всех возможных парных линейных коэфф-тов корреляции.
Корреляционная матрица:
мультипликативная модель — это… Что такое мультипликативная модель?
- мультипликативная модель
- мат. multiplicative model
Большой англо-русский и русско-английский словарь. 2001.
- мультипликативная константа
- мультипликативная неаддитивность
Смотреть что такое «мультипликативная модель» в других словарях:
модель прогноза риска — Концептуальная модель оценки риска, создаваемого радиационным облучением при низких дозах и мощностях дозы на основе эпидемиологических данных, касающихся риска от высоких доз и/или мощностей дозы.
аддитивная модель прогноза риска {additive risk… … Справочник технического переводчикаМодель Солоу — Неоклассическая модель экономического роста Роберта Солоу основывается на производственной функции Кобба Дугласа. Основное отличие модели Солоу от производственной функции заключается в том, что автор вводит технический прогресс как фактор… … Википедия
Ряды динамики — Процесс развития, движения социально экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики, которые представляют собой ряды изменяющихся во времени значений статистического… … Википедия
ГОСТ Р 51086-97: Датчики и преобразователи физических величин электронные. Термины и определения — Терминология ГОСТ Р 51086 97: Датчики и преобразователи физических величин электронные. Термины и определения оригинал документа: 16 абсолютная аддитивная чувствительность электронного датчика [преобразователя физической величины] к влияющей… … Словарь-справочник терминов нормативно-технической документации
группировка — структура логики.
В психологию это понятие ввел в 1937 г. Ж. Пиаже в качестве одного из основных понятий своей концепции интеллекта операциональной. Группировка считается связующим звеном между логическими и психологическими структурами. В… … Большая психологическая энциклопедияМ — Магистраль [turnpike] Мажоритарный акционер (Majority shareholder) Мажоритарная доля собственности (majority interest) Мажоритарный контроль (majority control) … Экономико-математический словарь
относительная — 3.1.24 относительная vmin или Y (relative vmin or Y): Отношение максимальной нагрузки Emax к минимальному поверочному интервалу весоизмерительного датчика vmin. Это отношение характеризует разрешающую способность весоизмерительного датчика, не… … Словарь-справочник терминов нормативно-технической документации
Линейность по параметрам — Линейность по параметрам свойство эконометрических моделей, позволяющее рассматривать их с эконометрической точки зрения (с точки зрения оценки параметров) как линейные модели.
Содержание 1 Определение 2 Линеаризация 3 … ВикипедияРобастное управление — Робастное управление совокупность методов теории управления, целью которых является синтез такого регулятора, который обеспечивал бы хорошее качество управления (к примеру, запасы устойчивости), если объект управления отличается от… … Википедия
Робастная система — Робастное управление совокупность методов теории управления, целью которых является синтез такого регулятора, который обеспечивал бы хорошее качество управления (к примеру, запасы устойчивости), если объект управления отличается от расчётного… … Википедия
Робастный контроллер — Робастное управление совокупность методов теории управления, целью которых является синтез такого регулятора, который обеспечивал бы хорошее качество управления (к примеру, запасы устойчивости), если объект управления отличается от расчётного… … Википедия
аддитивная модель прогноза риска {additive risk… … Справочник технического переводчика
В психологию это понятие ввел в 1937 г. Ж. Пиаже в качестве одного из основных понятий своей концепции интеллекта операциональной. Группировка считается связующим звеном между логическими и психологическими структурами. В… … Большая психологическая энциклопедия
Содержание 1 Определение 2 Линеаризация 3 … Википедия1) Мультипликативная модель:
;
,
для определения влияния фактора «а» подставляем вместо его планового значения фактическое, все остальные факторы остаются неизменными, в результате получается первый условный показатель:
;
для определения влияния фактора «в» в модель первого условного показателя подставляем фактическую величину фактора «в», остальные факторы остаются неизменными, в результате получается второй условный показатель:
;
расчет влияния фактора «а» на величину результативного показателя:
;
расчет влияния фактора «в» на величину результативного показателя:
;
расчет влияния фактора «с» на величину результативного показателя:
;
балансовая увязка влияния факторов на результативный показатель:
;
;
2) Кратная модель:
; ;
первый условный показатель:
;
расчет влияния фактора «а» на величину результативного показателя:
;
расчет влияния фактора «в» на величину результативного показателя:
;
балансовая увязка влияния факторов:
; ;
3) Комбинированная модель:
;
;
первый условный показатель:
;
второй условный показатель:
;
расчет влияний факторов «а», «b», «с» на величину результативного показателя:
; ;;
балансовая увязка влияния факторов:
; .
6. Порядок расчета влияния факторов приемом абсолютных разниц
Способ абсолютных разниц применяется в детерминированном факторном анализе для расчета влияния факторов на результативный показатель в мультипликативных и мультипликативно-аддитивных моделях. Он применяется тогда, когда исходные данные уже содержат абсолютные отклонения по факторным показателям.
Последовательность решения задачи с помощью данного способа:
Построение математической факторной модели.
Деление факторов на количественные и качественные.
Деление количественных показателей на первичные, вторичные и т.д.
Составление факторной модели в таком виде, чтобы на первом месте стоял первичный количественный фактор, на втором – вторичный, на последнем – качественный.
Расчет влияния факторов.
Проверка правильности расчетов путем балансовой увязки и выводы.
Для расчета влияния факторов определяется абсолютная величина прироста исследуемого фактора и умножается на плановую величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Математическое описание способа абсолютных разниц:
1) Мультипликативная модель:
; ;
определение абсолютного отклонения по каждому фактору:
; ;;
расчет влияния каждого фактора на результативный показатель:
;
;
;
балансовая увязка влияния факторов:
; ;
2) Комбинированная модель:
; ;
расчет влияния каждого фактора на результативный показатель:
;
;
;
балансовая увязка влияния факторов:
; .
7. Табличный и графический способы анализа
Графический способ анализа позволяет выразить зависимость между показателями при помощи графиков или диаграмм. Графики представляют собой условное изображение числовых величин в форме линий, плоскостей, столбиков и других геометрических фигур. Числовые значения величин переводят в графическое изображение при помощи масштаба. Графический способ наглядно и доступно отражает взаимосвязь показателей между собой, тенденции и закономерности развития деятельности конкретного предприятия или отрасли в целом. При помощи графиков иллюстрируют взаимосвязь между различными показателями, сравнивают отчетные данные за несколько периодов, а также отчетные данные с плановыми, характеризуют структуру какого-либо явления.
Графики
являются одной из форм оперативного
контроля и управления хозяйственными
процессами. Различают следующие виды
графиков: линейные, круговые, столбиковые,
ленточные, криволинейные диаграммы и
др.
При построении графиков должны соблюдаться выразительность, наглядность, простота.
Однако графики имеют и ряд недостатков по сравнению с таблицами:
не могут включать большое количество данных;
указываются приблизительные данные;
построение осуществляется вручную – это трудоемкий процесс, однако с использованием компьютера эта задача упрощается.
Составление таблиц широко используется в экономическом анализе для подготовки и обработки информации, так как обеспечивает:
уменьшение объема исходных данных в отчетных документах;
систематизацию данных и выявление закономерностей;
наглядность;
уменьшение объема аналитических пояснений.
Таблица
данных – это
система строк и столбцов, в которых в
определенной последовательности и
связи излагаются информационные сведения
об анализируемом явлении или объекте.
В таблице слева находится подлежащее,
справа – сказуемое. В подлежащем
указывается объект, в сказуемом – его
характеристика в количественной форме
в виде системы показателей.
По характеру подлежащего таблицы бывают простые, групповые и комбинационные.
По аналитическому содержанию различают таблицы, отражающие:
характеристику изучаемого объекта;
порядок расчета показателей;
структурные изменения в составе показателей;
взаимосвязь показателей по различным признакам;
результаты расчета влияния факторов на результативный показатель;
методику подсчета резервов;
сводные результаты анализа.
Заголовки
граф таблицы содержат название
показателей, единицы их измерения.
Завершает таблицу итоговая строка.
В таблицах данные принято располагать в следующей последовательности:
– абсолютные, затем относительные показатели;
– исходная информация, затем расчетные показатели;
– факторы, а затем результативный показатель.
По результатам анализа составляют сводные таблицы, в которых систематизируют данные аналитического исследования хозяйственной деятельности предприятия.
8. Порядок расчета влияния факторов способом
относительных разниц
Способ относительных разниц применяется в детерминированном факторном анализе для измерения влияния факторов в мультипликативных моделях. Данный способ применяется тогда, когда исходные данные уже содержат определенные ранее относительные приросты факторных показателей в процентах или коэффициентах.
Последовательность решения задачи с помощью данного способа следующая:
1.
Построение математической факторной
модели.
2. Деление факторов на количественные и качественные.
3. Деление количественных показателей на первичные, вторичные и т.д.
4. Составление факторной модели в таком виде, чтобы на первом месте стоял первичный количественный фактор, на втором – вторичный, на последнем – качественный.
5. Расчет влияния факторов.
6. Проверка правильности расчетов путем балансовой увязки и выводы.
Математическое описание способа относительных разниц:
; ;
для расчета влияния фактора «а» необходимо плановое значение результативного показателя умножить на относительный прирост данного фактора, который рассчитывается делением абсолютного прироста фактора «а» на плановое значение фактора «а»:
;
для расчета влияния фактора «в» необходимо к плановому значению результативного показателя прибавить величину влияния фактора «а» на результативный показатель и полученную сумму умножить на относительный прирост фактора «в»:
;
для расчета влияния фактора «с» необходимо к плановому значению результативного показателя прибавить величину влияния факторов «а» и «в» на результативный показатель и полученную сумму умножить на относительный прирост фактора «с»:
;
балансовая увязка влияния факторов на результативный показатель:
; .
Мультипликативная модель, смешанные и кратные модели, логарифмический способ и способ долевого участия
- Подробности
- Категория: Экономический анализ
Мультипликативная модель представляет собой произведение факторов:
Примером мультипликативной модели является двухфакторная модель объема реализации
N = Ч · В,
где Ч – среднесписочная численность работников; В – выработка на одного работника.
Кратные модели представляют собой отношение факторов и имеют вид
,
где Z – совокупный показатель.
Смешанные модели представляют собой комбинацию перечисленных моделей.
Примером смешанной модели является формула расчета интегрального показателя рентабельности:
,
где R к – рентабельность капитала; Rnp – рентабельность продаж; F e —фондоемкость основных средств; E з – коэффициент закрепления оборотных средств.
Логарифмический способ применим к кратным и мультипликативным моделям. Основан на логарифмировании отклонения отчетного и базисного значений результативного признака, равного отношению соответствующих произведений факторов, так как изменение показателей может быть оценено с помощью как абсолютных, так и относительных показателей.
Способ долевого участия заключается в определении доли каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост совокупного показателя. Он применяется к аддитивным моделям и чаще всего для оценки влияния факторов второго или третьего порядков.
Для примера можно рассмотреть модель зависимости фонда заработной платы от средней заработной платы и численности персонала:
ФЗ = ЗП · Ч,
где ФЗ – фонд заработной платы; ЗП – средняя заработная плата; Ч – среднесписочная численность.
Смотрите также:
Как разложить данные временных рядов на тренды и сезонность
Дата публикации 2017-01-30
Разложение временных рядов включает в себя представление о серии как о комбинации компонентов уровня, тренда, сезонности и шума.
Разложение обеспечивает полезную абстрактную модель для размышления о временных рядах в целом и для лучшего понимания проблем во время анализа и прогнозирования временных рядов.
В этом руководстве вы узнаете, как разложить временные ряды и как автоматически разбивать временные ряды на его компоненты с помощью Python.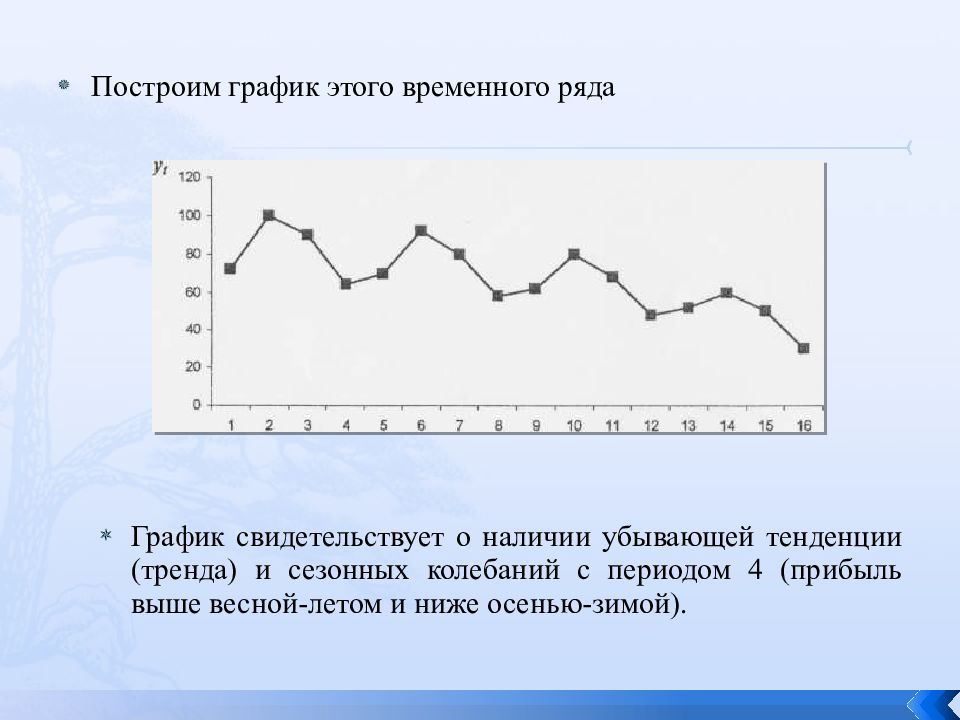
После завершения этого урока вы узнаете:
- Метод анализа временных рядов и как он может помочь с прогнозированием.
- Как автоматически разложить данные временных рядов в Python.
- Как разложить аддитивные и мультипликативные задачи временных рядов и построить результаты.
Давайте начнем.
Компоненты временного ряда
Полезной абстракцией для выбора методов прогнозирования является разбиение временного ряда на систематические и несистематические компоненты.
- систематическая: Компоненты временного ряда, которые имеют последовательность или повторяемость и могут быть описаны и смоделированы.
- Несистематический: Компоненты временного ряда, которые не могут быть смоделированы напрямую.
Считается, что данный временной ряд состоит из трех систематических компонентов, включая уровень, тренд, сезонность, и одного несистематического компонента, называемого шумом.
Эти компоненты определены следующим образом:
- уровень: Среднее значение в серии.
- тенденция: Увеличение или уменьшение значения в серии.
- Сезонность: Повторяющийся краткосрочный цикл в серии.
- Шум: Случайное изменение в ряду.
Объединение компонентов временного ряда
Считается, что серия представляет собой совокупность или комбинацию этих четырех компонентов.
Все серии имеют уровень и шум. Компоненты тренда и сезонности являются необязательными.
Полезно думать о компонентах как о комбинированных или аддитивных, или мультипликативных.
Аддитивная модель
Аддитивная модель предполагает, что компоненты добавляются вместе следующим образом:
y(t) = Level + Trend + Seasonality + NoiseАддитивная модель является линейной, где изменения во времени последовательно вносятся в одну и ту же величину.
Линейный тренд — это прямая линия.
Линейная сезонность имеет одинаковую частоту (ширина циклов) и амплитуду (высота циклов).
Мультипликативная модель
Мультипликативная модель предполагает, что компоненты умножаются вместе следующим образом:
y(t) = Level * Trend * Seasonality * NoiseМультипликативная модель является нелинейной, такой как квадратичная или экспоненциальная. Изменения увеличиваются или уменьшаются со временем.
Нелинейный тренд — это изогнутая линия.
Нелинейная сезонность имеет возрастающую или уменьшающуюся частоту и / или амплитуду во времени.
Разложение как инструмент
Это полезная абстракция.
Декомпозиция в основном используется для анализа временных рядов, а в качестве инструмента анализа она может использоваться для информирования моделей прогнозирования о вашей проблеме.
Он обеспечивает структурированный подход к проблеме прогнозирования временных рядов, как с точки зрения сложности моделирования, так и с точки зрения того, как наилучшим образом охватить каждый из этих компонентов в данной модели.
Каждый из этих компонентов — это то, о чем вам нужно подумать и рассмотреть во время подготовки данных, выбора модели и настройки модели. Вы можете обратиться к нему явно с точки зрения моделирования тренда и вычитания его из ваших данных, или неявно, предоставив достаточно истории для алгоритма, чтобы смоделировать тренд, если он может существовать.
Вы можете или не можете быть в состоянии чисто или идеально разбить ваш конкретный временной ряд как аддитивную или мультипликативную модель.
Проблемы реального мира беспорядочные и шумные. Могут быть аддитивные и мультипликативные компоненты. Может быть тенденция увеличения, сопровождаемая снижением тенденции. Могут быть неповторяющиеся циклы, смешанные с повторяющимися компонентами сезонности.
Тем не менее, эти абстрактные модели предоставляют простую структуру, которую вы можете использовать для анализа ваших данных и изучения способов обдумывания и прогнозирования вашей проблемы.
Автоматическая декомпозиция временных рядов
Есть методы дляавтоматически разлагаетсявременной ряд.
Библиотека statsmodels обеспечивает реализацию простого или классического метода декомпозиции в функции, называемойseasonal_decompose (), Требуется указать, является ли модель аддитивной или мультипликативной.
Оба будут давать результат, и вы должны быть осторожны, чтобы быть критичным при интерпретации результата. Обзор графика временных рядов и некоторая сводная статистика часто могут быть хорошим началом, чтобы понять, выглядит ли ваша проблема временных рядов аддитивной или мультипликативной.
seasonal_decompose ()Функция возвращает объект результата. Объект результата содержит массивы для доступа к четырем частям данных из декомпозиции.
Например, приведенный ниже фрагмент демонстрирует, как разложить ряд на трендовый, сезонный и остаточный компоненты в предположении аддитивной модели.
Объект результата обеспечивает доступ к тренду и сезонным сериям в виде массивов. Он также обеспечивает доступ к остаткам, которые являются временными рядами после тренда, и сезонные компоненты удаляются.
Наконец, оригинальные или наблюдаемые данные также сохраняются.
from statsmodels.tsa.seasonal import seasonal_decompose
series = ...
result = seasonal_decompose(series, model='additive')
print(result.trend)
print(result.seasonal)
print(result.resid)
print(result.observed)Эти четыре временных ряда могут быть построены непосредственно из объекта результата, вызвавсюжет()функция. Например:
from statsmodels.tsa.seasonal import seasonal_decompose
from matplotlib import pyplot
series = ...
result = seasonal_decompose(series, model='additive')
result.plot()
pyplot.show()Давайте посмотрим на некоторые примеры.
Аддитивное разложение
Мы можем создать временной ряд, состоящий из линейно возрастающего тренда от 1 до 99 и некоторого случайного шума, и разложить его как аддитивную модель.
Поскольку временные ряды были придуманы и представлены в виде массива чисел, мы должны указать частоту наблюдений (частота = 1аргумент).
Если предоставляется объект серии Pandas, этот аргумент не требуется.
from random import randrange
from pandas import Series
from matplotlib import pyplot
from statsmodels.tsa.seasonal import seasonal_decompose
series = [i+randrange(10) for i in range(1,100)]
result = seasonal_decompose(series, model='additive', freq=1)
result.plot()
pyplot.show()Выполнение примера создает серию, выполняет декомпозицию и выводит на график 4 результирующих ряда.
Мы можем видеть, что весь ряд был взят в качестве компонента тренда и что не было сезонности.
Мы также можем видеть, что остаточный участок показывает ноль. Это хороший пример, когда наивное или классическое разложение не смогло отделить шум, который мы добавили, от линейного тренда.
Наивный метод декомпозиции является простым, и существуют более продвинутые декомпозиции, такие как сезонная и трендовая декомпозиция с использованиемЛесс или STL разложение,
Осторожность и здоровый скептицизм необходимы при использовании автоматических методов разложения.
Мультипликативное Разложение
Мы можем построить квадратичный временной ряд как квадрат временного шага от 1 до 99, а затем разложить его в предположении мультипликативной модели.
from pandas import Series
from matplotlib import pyplot
from statsmodels.tsa.seasonal import seasonal_decompose
series = [i**2.0 for i in range(1,100)]
result = seasonal_decompose(series, model='multiplicative', freq=1)
result.plot()
pyplot.show()Запустив пример, мы видим, что, как и в аддитивном случае, тренд легко выделяется и полностью характеризует временной ряд.
Экспоненциальные изменения могут быть сделаны линейными путем преобразования данных. В этом случае квадратичный тренд можно сделать линейным, взяв квадратный корень. Экспоненциальный рост сезонности можно сделать линейным, взяв натуральный логарифм.
Опять же, важно рассматривать декомпозицию как потенциально полезный инструмент анализа, но рассмотреть возможность изучения множества различных способов ее применения для вашей задачи, таких как данные после их преобразования или остаточные ошибки модели.
Давайте посмотрим на набор данных реального мира.
Набор данных пассажиров авиакомпании
Набор данных «Пассажиры авиакомпании» описывает общее количество пассажиров авиакомпании за период времени.
Единицы измерения числа пассажиров авиакомпании в тысячах. Имеется 144 ежемесячных наблюдения с 1949 по 1960 год.
Узнайте больше и загрузите набор данных из Data Market,
Загрузите набор данных в текущий рабочий каталог с именем файла «авиакомпания-passengers.csv«.
Во-первых, давайте наметим необработанные наблюдения.
from pandas import Series
from matplotlib import pyplot
series = Series.from_csv('airline-passengers.csv', header=0)
series.plot()
pyplot.show()Рассматривая линейный график, можно предположить, что может быть линейный тренд, но трудно быть уверенным в том, чтобы смотреть в глаза. Существует также сезонность, но амплитуда (высота) циклов, по-видимому, увеличивается, что говорит о мультипликативности.
Мы примем мультипликативную модель.
В приведенном ниже примере декомпозиция данных о пассажирах авиакомпании рассматривается как мультипликативная модель.
from pandas import Series
from matplotlib import pyplot
from statsmodels.tsa.seasonal import seasonal_decompose
series = Series.from_csv('airline-passengers.csv', header=0)
result = seasonal_decompose(series, model='multiplicative')
result.plot()
pyplot.show()Выполнение примера отображает наблюдаемые, трендовые, сезонные и остаточные временные ряды.
Мы видим, что информация о тенденциях и сезонности, извлеченная из ряда, кажется разумной. Остатки также интересны, показывая периоды высокой изменчивости в ранние и поздние годы ряда.
Дальнейшее чтение
В этом разделе перечислены некоторые ресурсы для дальнейшего чтения о декомпозиции временных рядов.
Резюме
В этом уроке вы обнаружили декомпозицию временных рядов и способы декомпозиции данных временных рядов с помощью Python.
В частности, вы узнали:
- Структура разложения временных рядов на уровень, тренд, сезонность и шум.
- Как автоматически декомпозировать набор данных временных рядов с помощью Python.
- Как разложить аддитивную или мультипликативную модель и построить график результатов.
У вас есть вопросы о разложении временных рядов или об этом уроке?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Оригинальная статья
АДДИТИВНО-МУЛЬТИПЛИКАТИВНАЯ МОДЕЛЬ ОЦЕНКИ ИННОВАЦИЙ | Опубликовать статью ВАК, elibrary (НЭБ)
Минакова Т. Е. 1, Минаков В. Ф. 2
1Кандидат технических наук, доцент,
Национальный минерально-сырьевой университет «Горный»,
2доктор технических наук, профессор,
Санкт-Петербургский государственный экономический университет
АДДИТИВНО-МУЛЬТИПЛИКАТИВНАЯ МОДЕЛЬ ОЦЕНКИ ИННОВАЦИЙ
Аннотация
Разработана математическая аддитивно-мультипликативная модель оценки инновационных проектов. Отличается учетом как достоинств проектов, так и допустимости по дискретным показателям. Предназначена для отбора проектов для инвестирования.
Ключевые слова: инновационный проект, оценка, модель.
Minakova T.E., Minakov V.F.
1PhD of technical science, associate professor,
National Mineral Resources University,
2Doctor of technical science, professor,
St. Petersburg State University of economics
ADDITIVE AND MULTIPLICATIVE MODEL OF ASSESSMENT FOR INNOVATION
Abstract
The mathematical additive and multiplicative model of an assessment of innovative projects is developed. Differs the account as advantages of projects, and an admissibility on discrete indicators. It is intended for selection of projects for investment.
Keywords: innovative project, assessment, model.
Практика управления современными предприятиями требует оценки и принятия решений об использовании инноваций [1, 2], изменяющих способы производства, продукцию, ее качество [3-6]. В наибольшей степени это относится к стратегиям развития информационных ресурсов [7].
Анализ используемых в настоящее время методов, моделей, метрик и критериев оценки инновационных проектов [8, 9] позволяет установить, что очень часто допускается необоснованное арифметическое суммирование показателей оценки: аналоговых показателей, например, эффективности, и показателей соответствия проекта его инновационному назначению – дискретных показателей в виде метрики:
,
где – метрика инновационного проекта;
– вес показателя.
Такой подход не позволяет исключить проекты, аналогичные фильтрам Петрика, при попытках его внедрения для очистки радиоактивной воды и последующего использования ее в качестве питьевой. Модель, следовательно, должна даже при наличии большого числа достоинств проекта (отражаемых аналоговыми показателями), исключать возможность его реализации, то есть дискретно нивелировать оценку [10].
В связи с этим предлагается разделение показателей инновационных проектов на два ключевых класса:
– аналоговые (непрерывные) показатели – это класс показателей инновационного проекта позволяющий оценить предпочтительные свойства проекта на каждом из этапов его жизненного цикла, позволяющие получить показатель проекта как сумму его нормированных характеристик, отражающих достоинства;
– дискретные (прерывистые) показатели, независимые от аналогового результата оценки инновационных проектов, например, принимающие нулевое или единичное значение, позволяющие отклонять проекты в случае невозможности их реализации по критерию недопустимости таких проектов для использования.
Если метрики предпочтительных характеристик проектов могут быть отражены аддитивно в интегральном показателе, то возможность или невозможность принятия проекта должна учитываться мультипликативно, отображая тем самым логическую операцию «И». Смысл такой операции и характерен для дискретных булевых величин: отбор инновационного проекта и принятие к реализации предполагает и наличие достоинств проекта, сумма которых учитывается аддитивно, и одновременно требуется реализуемость и допустимость реализации проекта по критически важным показателям.
Следовательно, формализованная математическая интегральная оценка инновационного проекта должна быть выражена аддитивно-мультипликативной моделью:
где Р – интегральная оценка (рейтинговая) инновационного проекта;
– аналоговый показатель;
– критически важные дискретные показатели инновационного проекта,
j – номер дискретного показателя.
Заключение
Аддитивно-мультипликативная модель оценки инноваций позволяет, во-первых, учесть все преимущества инновационного проекта, во-вторых, исключает его применение в случае несоответствия критическим показателям (законность, безопасность для жизни и здоровья потребителей).
Литература
Аддитивная модель и мультипликативная модель
Регрессионный анализ>
Аддитивная модель и мультипликативная модель в регрессии
Аддитивная модель и мультипликативная модель являются обобщениями «обычной» модели линейной регрессии (Hastie & Tibshirani, 1990).
Аддитивная модель представляет собой арифметическую сумму индивидуальных эффектов переменных-предикторов. Для двухфакторного эксперимента (X, Y) аддитивная модель может быть представлена как:
Y = B 0 + B 1 X 1 + B 2 X 2 + ε
Аналогично мультипликативная модель может быть представлена как:
Y = B 0 * B 1 X 1 * B 2 X 2 + ε
Их преимущество в том, что они более гибкие, чем линейные модели, но сохраняют многие из желаемых свойств своих линейных аналогов (Shalizi, 2015).Однако у моделей есть проблемы с выбором модели, переоснащением и мультиколлинеарностью.
Аддитивная и мультипликативная модель во временных рядах
Термины могут также относиться к конкретной модели для данных временных рядов, где модель может быть разложена на четыре различных компонента, связанных в аддитивном смысле. Например, модель может быть представлена так:
y т = T т + S т + C т + R т
В суммировании (сигма) аддитивная модель может быть представлена эквивалентно следующим образом:
Или
Если компоненты связаны вместо умножения, модель является мультипликативной моделью :
y т = T т * S т * C т * R т
Мультипликативная модель обычно считается более точной, чем аддитивная (Fleming & Nellis, 2000).
Список литературы
Флеминг, М. и Неллис, Дж. (2000). Принципы прикладной статистики: комплексный подход с использованием MINITAB и Excel. Thomson Learning.
Хасти, Т. и Тибширани, Р. (1990). Обобщенные аддитивные модели. Чепмен и Холл / CRC
Шализи, К. (2015). Глава 9: Аддитивные модели. Получено 3 августа 2020 г. по адресу: https://www.stat.cmu.edu/~cshalizi/uADA/15/lectures/10.pdf
Tibshirani, R. (2014). Аддитивные модели. Расширенные методы анализа данных (36-402 / 36-608).Получено 3 августа 2020 г. по адресу: https://www.stat.cmu.edu/~ryantibs/advmethods/notes/addmodels.pdf
. ————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Мультипликативная модель— обзор
2 Смертность
Общий коэффициент смертности (CDR) — количество смертей на 1000 человек населения — широко используется в качестве основного показателя уровня смертности (см. Таблицу 2 для отдельных показателей смертности). На это особенно сильно влияет возрастной состав населения из-за большого разброса показателей смертности по возрасту. Повозрастные коэффициенты смертности — количество смертей в определенном возрасте на 1000 человек этого возраста — находятся на следующем уровне детализации, обычно с разбивкой по полу.При наличии информации хорошего качества рассчитываются ставки, специфичные для однолетних возрастных групп, а не для пятилетних возрастных групп. Коэффициенты, зависящие от однолетнего возраста, имеют особое значение для младшей и старшей частей возрастного диапазона, поскольку в этих возрастных диапазонах различия в показателях между соседними однолетними возрастами могут быть значительными. Возраст может быть сгруппирован по-разному, в зависимости от степени детализации, необходимой для анализа, и характера имеющихся данных. Однако даже при использовании пятилетних групп часто выделяются возрастные группы от 0 до 1 и от 1 до 4 из-за относительно высокого уровня смертности младенцев даже в странах с низкой смертностью.
Таблица 2. Выборочные показатели смертности
| Показатель | Определение | Примечания |
|---|---|---|
| Общий коэффициент смертности (CDR) Период | DP × 1000 | D происходящие в течение определенного года / периода. P = человеко-лет, прожитых a в течение года или периода. |
| Возрастной коэффициент смертности Период; когорта | M x = DxPx × 1000 | D x = количество смертей в возрасте x в течение года или периода b . P x = человеко-лет a в возрасте x или в возрастной группе x в течение года или периода b . |
| Коэффициент младенческой смертности (IMR) Период; когорта | D0B | D 0 = смерти младенцев до 12 месяцев в течение года или периода b . B = рождений в течение года или периода b |
| Коэффициент младенческой смертности Период; когорта | D0P0 | P 0 = человеко-лет a в возрасте до одного года в течение года или периода b . |
| Коэффициент материнской смертности (иногда называемый коэффициентом материнской смертности) Период; когорта | DmB | D m = материнская смертность в течение года или периода b . |
| Коэффициент материнской смертности Период; когорта | DmP15-49f | P f 15-49 = количество прожитых женщинами лет a в возрасте 15-49 лет в течение года или периода b (возрастные ограничения могут различаться). |
Измерение смертности до некоторой степени упрощается тем фактом, что смерть наступает в конечном итоге для всех и происходит только один раз. Эти двойные аспекты означают, что общие и повозрастные коэффициенты смертности обязательно относятся к типу 1 (см. «Демографические измерения: общие вопросы и показатели фертильности», ): риск смерти универсален, и, поскольку смерть наступает только один раз в жизни, в настоящее время никто с риском смерти могли испытать это событие ранее. Уровни смертности настолько тесно и систематически связаны с возрастом и, в меньшей степени, с полом, что их специфичность по возрасту и полу подходит для большинства демографических целей.Другие параметры личного времени требуются гораздо реже при определении показателей смертности. Однако коэффициенты смертности также могут зависеть от социального класса, расы / этнической принадлежности, дохода, района проживания (город / село или субнациональный регион), семейного положения и других подобных социально-экономических характеристик. Анализ по таким факторам представляет интерес для изучения социальных и экономических различий в состоянии здоровья, а также для актуарных целей и целей общественного здравоохранения. С такими подспецификациями коэффициенты смертности также могут относиться к типу 2.
Уровень младенческой смертности (IMR) сообщается и публикуется широко, отчасти как демографический показатель, но также как показатель социально-экономического развития.Он определяется как количество смертей младенцев (детей в возрасте до одного года) на 1000 рождений в конкретный год. Таким образом, это не показатель, как обычно указывается, поскольку числитель не является оценкой человеко-лет, подверженных риску события, и будет неточным для этой цели в той мере, в какой рождаемость будет колебаться из года в год. Однако это удобный способ измерения, поскольку он может быть получен путем простого подсчета жизненных событий и не требует оценки численности населения по возрасту. Он имеет правильно заданный аналог в коэффициенте детской смертности , количестве смертей младенцев (в возрасте до одного года) в год на 1000 человеко-лет, живущих в возрасте до одного года.Также различают несколько показателей смертности в течение первого года жизни, как из-за резкого снижения показателей смертности в течение первых 12 месяцев жизни, так и из-за меняющейся роли эндогенных (генетических, внутриутробных, перинатальных) и экзогенных (экологических, внешних). ) причины смерти. В самом раннем послеродовом периоде преобладают эндогенные причины, после чего значение экзогенных факторов возрастает. Уровень перинатальной смертности определяется как число поздних внутриутробных смертей плюс число смертей в течение одной недели после рождения на 1000 общих поздних смертей плода плюс живорождений.Уровень неонатальной смертности определяется как количество смертей в течение одного месяца (28 дней) после рождения на 1000 живорождений, а уровень постнеонатальной смертности — как количество смертей от 28 дней до одного года на 1000 живорождений. живорожденные. Вероятность смерти между рождением и пятым днем рождения широко упоминается в современной демографической литературе как уровень детской смертности , хотя последний более правильно определяется как число смертей детей в возрасте до пяти лет на 1000 человек. -лет в возрастной группе.Определение вероятности (также иногда обозначаемое как риск детской смертности ) стало широко распространенным, поскольку смертность детей в возрасте до пяти лет представляет особый интерес в менее развитых обществах с высокой смертностью, для которых используются косвенные методы (см. Демографические методы: косвенная оценка ). Используется для оценки детской смертности, оценивая вероятность когорты, а не коэффициент. В обществах с высокой смертностью обычно нет хорошей статистики естественного движения населения, и может быть трудно сформулировать точные предположения о среднем количестве лет, прожитых умершими, и, таким образом, получить оценку прожитых человеко-лет.
Материнская смерть — это смерть, которая наступает во время беременности или в течение 42 дней после окончания беременности по причине, связанной с беременностью или состоянием, усугубленным беременностью; термин, таким образом, включает смерти, связанные с абортами. Материнская смертность чаще всего представлена коэффициентом материнской смертности . : число материнских смертей на 100 000 живорождений за период. Многие авторы и во многих источниках ссылаются на этот показатель как на уровень материнской смертности , хотя на самом деле это не соответствует действительности.Строго говоря, коэффициент материнской смертности . — это число материнских смертей на 100 000 женщин репродуктивного возраста за период, и некоторые авторы используют этот термин в этом смысле. Из контекста должно быть ясно, какое определение используется.
Смертность по причинам смерти, примером которых является материнская смертность, является основным способом дезагрегирования показателей смертности, помимо возраста и пола. Международная классификация болезней, которая в настоящее время разрабатывается и время от времени пересматривается Всемирной организацией здравоохранения, представляет собой стандартную схему классификации причин смерти.Показатели смертности по причинам смерти бывают двух видов. Коэффициенты смертности от конкретных причин относятся к числу смертей от определенной причины в течение периода на 100 000 населения и могут также зависеть от возраста и / или пола. Для этой цели обычно используется множитель, превышающий 1000, поскольку количество смертей от одной причины обычно относительно невелико. С другой стороны, коэффициенты смертности от конкретных причин относятся к процентной доле всех смертей, произошедших по определенной причине, в целом или по возрасту и полу, и имеют значение, когда информация о знаменателях населения является неточной или недоступной.Анализ пропорциональной смертности используется, в частности, при изучении профессиональной смертности.
2.1 Стандартизация по возрасту
Из-за значительных различий в уровнях смертности по возрасту (и в возрастной структуре по времени и месту) межнациональные, территориальные или временные сравнения уровня смертности требуют стандартизации показателей смертности по возрасту. . Прямая стандартизация, при которой используется стандартное возрастное распределение, дает напрямую стандартизированный коэффициент смертности . Косвенная стандартизация, при которой выбирается стандартный набор возрастных коэффициентов смертности, дает два показателя: стандартизованный коэффициент смертности (SMR) и косвенно стандартизованный коэффициент смертности .SMR дает индексную цифру, выражающую уровень смертности в индексируемой популяции по сравнению с уровнем смертности в стандартной популяции, обычно установленный на 100: это просто отношение наблюдаемых смертей к ожидаемым в индексной популяции, при этом ожидаемые смерти основаны на стандарте. возрастные показатели населения. Умножение SMR на CDR в стандартной популяции дает косвенно стандартизованный коэффициент смертности в индексной популяции. Прямая стандартизация требует, чтобы возрастные коэффициенты смертности были известны и точно рассчитывались в популяциях, подлежащих стандартизации.Если возрастные коэффициенты неизвестны или подвержены значительным ошибкам, необходимо использовать косвенный метод. Статистическая теория выделяет вариант косвенной стандартизации как оптимальный, когда мультипликативная модель верна для силы смертности.
2.2 Ожидаемая продолжительность жизни и таблицы продолжительности жизни
Ожидаемая продолжительность жизни при рождении , e 0 , может рассматриваться как индикатор «времени» смертности, а также сводка общего уровня смертности в популяции. .Он измеряет время в том смысле, что он представляет собой ожидаемое или среднее количество лет, прожитых человеком или группой лиц на протяжении всей их жизни с заданным набором повозрастных коэффициентов смертности. Поскольку смерть наступает повсеместно и навсегда удаляет человека из населения, любое увеличение показателей смертности в любом возрасте обязательно отражается в сокращении продолжительности жизни, в то время как снижение показателей смертности в любом возрасте обязательно сопровождается увеличением продолжительности жизни. На ожидаемую продолжительность жизни влияет как уровень смертности населения, так и структура смертности по возрасту.В результате две группы населения с одинаковой общей продолжительностью жизни могут различаться по возрастным коэффициентам смертности. Ожидаемая продолжительность жизни рассчитывается по таблице продолжительности жизни (см. Таблица продолжительности жизни ) и поэтому стандартизирована по возрасту. Рассматриваемая таблица дожития может быть основана на возрастных коэффициентах смертности, полученных за календарный период или в когорте рожденных. Если на основе таблицы продолжительности жизни за период, ожидаемая продолжительность жизни и другие функции таблицы смертности являются синтетическими когортными показателями и разделяют недостатки всех синтетических мультипликативных показателей (см. «Демографические измерения: общие вопросы и показатели фертильности», ).
Таблица дожития — это центральный аналитический метод в демографии, имеющий множество различных применений. Однако для этого требуются данные, поскольку для этого требуется информация о возрастных коэффициентах смертности и, следовательно, о распределении смертей по возрасту, а также оценки населения по возрасту. Поскольку подробные данные такого рода часто недоступны для исторического населения и для менее развитых стран, были разработаны наборы модельных таблиц дожития, соответствующие различным уровням и моделям смертности (Coale et al.1983 г., Организация Объединенных Наций 1982 г.). Такие компиляции позволяют делать оценки уровня и / или возрастной структуры смертности на основе информации, которая сама по себе недостаточна для их определения (см. Демографические методы: косвенная оценка ).
5.1 Модели разложения | STAT 510
Основная команда — разложить .
Для аддитивной модели разложить (название серии, тип = «добавка») .
Для мультипликативного разложения разложите (название серии, тип = «multiplicative») .
Важный первый шаг : Предварительно вы должны использовать команду ts для определения сезонного диапазона для ряда.
Для квартальных данных это может быть name of series = ts (name of series, freq = 4) .
Для ежемесячных данных это может быть name of series = ts (name of series, freq = 12) .
Вы можете построить элементы разложения, указав команду разложения в качестве аргумента команды построения графика.
Например,
участок (разложить (заработок, тип = "мультипликативный")) Другой способ построения графика — сохранить результаты разложения в именованном объекте, а затем построить этот объект.Например,
разложить = разложить (заработок, тип = "мультипликативный")
участок (разложить) Чтобы увидеть все элементы сохраненного объекта, просто введите его имя. Например, при вводе декомпозиции будут показаны все элементы декомпозиции в приведенном выше примере.
Когда декомпозиция сохраняется в объекте, у вас также есть доступ к различным элементам декомпозиции. Например, в только что приведенном примере разложить \ $ рисунок содержит значения сезонных эффектов для четырех кварталов.
Вы можете «распечатать» сезонные цифры, просто введя разложить \ $ цифра . Вы можете построить их, используя график (разложить \ $ figure) .
Пример 5-1 Продолжение: Разложение добавок для производства пива
Следующие команды позволили получить график и числовой вывод, который следует для серии производства австралийского пива.
Скачать данные: beerprod.dat
beerprod = scan ("beerprod.dat")
beerprod = ts (beerprod, freq = 4)
decompbeer = разложить (beerprod, type = "добавка")
сюжет (декомпбир)
декомпбир График показывает наблюдаемый ряд, сглаженную линию тренда, сезонную модель и случайную часть ряда.
Примечание!
Сезонный паттерн — это регулярно повторяющийся паттерн.
Вот числовой результат:
| 1 квартал | 2 кв. | 3 квартал | 4 квартал | |
|---|---|---|---|---|
| 1 | 7,896324 | -40.678676 | -24.650735 | 57,433088 |
| 2 | 7,896324 | -40.678676 | -24.650735 | 57,433088 |
| 3 | 7,896324 | -40.678676 | -24.650735 | 57.433088 |
| 4 | 7,896324 | -40.678676 | -24.650735 | 57,433088 |
| 5 | 7,896324 | -40.678676 | -24.650735 | 57,433088 |
| … те же ряды до 18… | ||||
| 1 квартал | 2 кв. | 3 квартал | 4 квартал | |
|---|---|---|---|---|
| 1 | NA | NA | 255.3250 | 254.4125 |
| 2 | 257.4500 | 260.1000 | 262,8375 | 264,6875 |
| 3 | 265.4125 | 264.6500 | 262,4625 | 260.4000 |
| 4 | 261.2625 | 262,9875 | 266,1875 | 269,2375 |
| 5 | 270.5125 | 271,4625 | 272,1750 | 274.0125 |
| 6 | 274,3750 | 277.4500 | 278.9750 | 279.1750 |
| 7 | 282,9000 | 285,2875 | 287,9375 | 290,3875 |
| … и так до 18-го ряда… | ||||
| 1 квартал | 2 кв. | 3 квартал | 4 квартал | |
|---|---|---|---|---|
| 1 | NA | NA | -3.77426471 | -3,44558824 |
| 2 | -3,34632353 | 8.47867647 | -2,08676471 | -1,72058824 |
| 3 | -1,40882353 | 8.82867647 | -0,81176471 | -4,43308824 |
| 4 | 7.75882353 | 4,447 | 8,36 323529 | -12,37058824 |
| 5 | 7,647 | -4,28382353 | 12,87573529 | -20.04558824 |
| 6 | 12.42867647 | -4,17132353 | 2.87573529 | 2,591 |
| 7 | -11,69632353 | 5,147 | 6,51 323529 | -2.12058824 |
| … и так до 18-го ряда… | ||||
| (1) | 7.896324 | -40.678676 | -24.650735 | 57,433088 |
|---|
Использование сезонных значений
Элементы фигуры \ $ — это эффекты для четырех кварталов.
Примечание!
Значения сезонного эффекта повторяются каждый год (строка) в объекте \ $ Season вверху этой страницы.
Сезонные значения используются для сезонной корректировки будущих значений.Предположим, например, что сезонное значение следующего квартала 4 после конца ряда имеет значение 535. Сезонный эффект четвертого квартала составляет 57,433088, или около 57,43. Таким образом, для этого будущего значения «десезонное» или сезонно скорректированное значение = 535 — 57,43 = 477,57.
Как рассчитывались значения тренда
Значения тренда были определены как «центрированные» скользящие средние для диапазона 4 (поскольку в году четыре квартала). Вот как будет рассчитано центрированное скользящее среднее для time = 3.
Усреднение наблюдаемых значений данных при временах от 1 до 4:
\ (\ dfrac {1} {4} (x_1 + x_2 + x_3 + x_4) \)
Усреднение значений от 2 до 5:
\ (\ dfrac {1} {4} (x_2 + x_3 + x_4 + x_5) \)
Затем усредните эти два средних значения:
\ begin {multline} \ dfrac {1} {2} \ left (\ dfrac {1} {4} (x_1 + x_2 + x_3 + x_4) + \ dfrac {1} {4} (x_2 + x_3 + x_4 + x_5) \ right) \\ \ shoveleft {= \ dfrac {1} {8} x_1 + \ dfrac {1} {4} x_2 + \ dfrac {1} {4} x_3 + \ dfrac {1} {4} x_4 + \ dfrac {1} {8} x_5} \ end {multline}
В более общем смысле, более сглаженная центрированная скользящая средняя для времени t (с 4 кварталами) равна
.\ (\ dfrac {1} {8} x_ {t-2} + \ dfrac {1} {4} x_ {t-1} + \ dfrac {1} {4} x_t + \ dfrac {1} {4 } x_ {t + 1} + \ dfrac {1} {8} x_ {t + 2} \)
Ниже приведены первые 8 значений из наблюдаемого ряда.Значение сглаженного тренда для времени 3 в ряду (3 квартал года 1) составляет 255,325, а значение сглаженного тренда для времени 4 составляет 254,4125. Используйте приведенные ниже данные, чтобы проверить эти значения (и ваше понимание процедуры).
| 1 квартал | 2 кв. | 3 квартал | 4 квартал | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 284.{5} \ dfrac {1} {12} x_ {t + j} \ right) + \ dfrac {1} {24} x_ {t + 6} \)Пример 5-1 Продолжение: Мультипликативное разложение для производства пиваСледующие две команды выполнят мультипликативное разложение производственного ряда пива и распечатают сезонные эффекты.
Сезонные (квартальные) эффекты:
Для сезонной корректировки значения разделите наблюдаемое значение ряда на сезонные факторы. Например, если значение будущего квартала 4 равно 535, значение с учетом сезонных колебаний = 535 / 1,1775147 = 454,34677. Сезонная и трендовая декомпозиция LowessСглаживание нижнего предела по существу заменяет значения «локально взвешенной» устойчивой регрессионной оценкой значения.Команда R stl выполняет аддитивную декомпозицию, в которой более низкое сглаживание используется для оценки тенденции и (потенциально) сезонных эффектов. Есть несколько параметров, которые можно настроить, но значение по умолчанию неплохо работает. Для нашего примера производства пива работает следующая команда:
«Периодический» параметр, по сути, заставляет оценивать сезонные эффекты обычным способом, как средние значения без тренда.Альтернативой этому является s.window = некоторое нечетное количество лагов, которое использует процедуры сглаживания по минимуму для оценки сезонных эффектов на основе количества лет = заданному значению s.window . Когда вы это сделаете, сезонные эффекты будут меняться по мере продвижения по серии. Вот фрагмент результата команды Примечание!
Дополнительные сезонные эффекты: 8,06289, -41,58529, -24,68456, 58,20698 . Это не сильно отличается от того, что мы получили от аддитивного разложения.Эти сезонные значения составляли .\ $ фигура (1) 7,896324 -40,678676 -24,650735 57,433088 Команда plot (stl (beerprod, «периодический»)) дала следующий сюжет. Сезонность в Python: аддитивная или мультипликативная модель? | Зигмундо Прейсслер-младший, доктор философииВы начали анализировать свои графики и осознали, что более половины из них менялись с течением времени? Поздравляю, похоже, у вас в руках есть временные ряды 🙂 Работа с временными рядами не так уж и сложна, когда у нас в руках мощные «функции» в Python, такие как Pandas и библиотека Statsmodels. Но послушайте, это же не семиголовое существо. Однако не забудьте убедиться, что это последовательность, взятая в равные последовательные интервалы времени. И если вы используете Pandas, например, для индексации рамки даты по полю даты, а также проверяете, действительно ли тип данных этого поля является датой, а не просто типом объекта, хорошо? Важной характеристикой временного ряда, которую необходимо проанализировать, является сезонность. Это характеристика временного ряда, имеющего поведение по умолчанию в пределах определенного временного интервала.Если этот образец повторяется в течение того же самого интервала времени, тогда мы будем иметь образец с сезонным поведением.
Существует два основных метода анализа сезонности временного ряда: аддитивный и мультипликативный. Синтетически это модель данных, в которой эффекты отдельных факторов дифференцируются и добавляются для моделирования данных. Его можно представить следующим образом: y (t) = Уровень + Тренд + Сезонность + Шум В аддитивной модели поведение является линейным, где изменения во времени постоянно происходят на одну и ту же величину, как линейный тренд.В этой ситуации линейная сезонность имеет одинаковую амплитуду и частоту. В этой ситуации компоненты тренда и сезонности умножаются, а затем добавляются к компоненту ошибки. Он не является линейным, может быть экспоненциальным или квадратичным и представлен изогнутой линией, как показано ниже: y (t) = Уровень * Тренд * Сезонность * Шум В отличие от аддитивной модели, мультипликативная модель имеет возрастающую или убывающую амплитуду. и / или частота с течением времени. Анализ временных рядов: основыЧТО ТАКОЕ ВРЕМЕННЫЙ РЯД? Временной ряд — это совокупность наблюдений за четко определенными элементами данных, полученных в результате повторных измерений с течением времени.Например, измерение стоимости розничных продаж каждый месяц в году будет включать временной ряд. Это связано с тем, что выручка от продаж четко определена и постоянно измеряется через равные промежутки времени. Данные, собираемые нерегулярно или только один раз, не являются временными рядами. Наблюдаемый временной ряд можно разделить на три компонента: тренд (долгосрочное направление), сезонный (систематические, связанные с календарем движения) и нерегулярные (несистематические краткосрочные колебания). ЧТО ТАКОЕ СЕРИИ АКЦИЙ И ПОТОКОВ? Временные ряды можно разделить на два разных типа: запасы и потоки. Серия запасов — это мера определенных атрибутов в определенный момент времени, которую можно рассматривать как «инвентаризацию». Например, Ежемесячное обследование рабочей силы является показателем запаса, поскольку в нем учитывается, был ли человек трудоустроен в отчетную неделю. Ряды потоков — это ряды, которые являются мерой активности за определенный период. Например, обзоры деятельности Розничная торговля, . Производство также является показателем расхода, потому что каждый день производится определенное количество, а затем эти суммы суммируются, чтобы получить общую стоимость производства за данный отчетный период. Основное различие между серией запасов и потоков состоит в том, что ряды потоков могут содержать эффекты, связанные с календарем (эффекты торговых дней). Оба типа рядов по-прежнему можно скорректировать на сезонность, используя один и тот же процесс сезонной корректировки. КАКОВЫ СЕЗОННЫЕ ЭФФЕКТЫ? Сезонный эффект — это систематический и календарный эффект. Некоторые примеры включают резкую эскалацию в большинстве розничных серий, которая происходит примерно в декабре в связи с рождественским периодом, или увеличение потребления воды летом из-за более теплой погоды.К другим сезонным эффектам относятся эффекты торгового дня (количество рабочих или торговых дней в данном месяце меняется от года к году, что влияет на уровень активности в этом месяце) и переходящий праздничный день (время праздников, таких как Пасха, варьируется, поэтому эффекты праздника будут ощущаться в разные периоды каждый год). Сезонная корректировка — это процесс оценки и последующего удаления из временного ряда систематических и связанных с календарем влияний.Наблюдаемые данные необходимо скорректировать с учетом сезонных колебаний, поскольку сезонные эффекты могут скрывать как истинное базовое движение в ряду, так и некоторые несезонные характеристики, которые могут представлять интерес для аналитиков. ПОЧЕМУ МЫ НЕ МОЖЕМ ПРОСТО СРАВНИТЬ ОРИГИНАЛЬНЫЕ ДАННЫЕ ЗА ОДИН ПЕРИОД КАЖДЫЙ ГОД? Сравнение исходных данных за один и тот же период каждого года не устраняет полностью все сезонные эффекты. Некоторые праздники, такие как Пасха и Китайский Новый год, выпадают на разные периоды каждого года, поэтому они будут искажать наблюдения.Кроме того, годовые значения будут смещены любыми изменениями в сезонных моделях, которые происходят с течением времени. Например, рассмотрим сравнение двух последовательных мартовских месяцев, то есть сравните уровень исходных рядов, наблюдаемых в марте для 2000 и 2001 годов. Это сравнение игнорирует трогательный праздничный эффект Пасхи. В большинстве лет Пасха приходится на апрель, но если Пасха выпадает на март, уровень активности может сильно различаться для этого месяца в некоторых сериях. Это искажает первоначальные оценки.Сравнение этих двух месяцев не отразит основную закономерность данных. При сравнении также игнорируются эффекты торгового дня. Если два последовательных месяца марта имеют разный состав торговых дней, это может отражать разные уровни активности в исходных условиях, даже если основной уровень активности не изменился. Таким же образом можно игнорировать любые изменения сезонных моделей. Исходные оценки также содержат влияние нерегулярной составляющей. Если величина нерегулярной составляющей ряда высока по сравнению с величиной составляющей тренда, основное направление ряда может быть искажено. Однако основным недостатком сравнения исходных данных за год является отсутствие точности и временные задержки в определении поворотных точек в серии. Точки поворота возникают, когда направление базового уровня ряда изменяется, например, когда последовательно убывающий ряд начинает неуклонно расти. Если мы сравним данные с разницей в год в исходном ряду, мы можем пропустить поворотные моменты, происходящие в течение года. Например, если исходная оценка марта 2001 г. выше, чем исходная оценка марта 2000 г., сравнивая эти годовые значения, мы можем сделать вывод, что уровень активности увеличился в течение года.Однако до сентября 2000 г. этот ряд мог увеличиваться, а затем начал неуклонно снижаться. Когда во временном ряду преобладает тренд или нерегулярные компоненты, практически невозможно идентифицировать и удалить то, что присутствует небольшая сезонность. Следовательно, сезонная корректировка несезонного ряда нецелесообразна и часто приводит к искусственному сезонному элементу. ЧТО ТАКОЕ СЕЗОННОСТЬ? Сезонный компонент состоит из эффектов, которые достаточно стабильны по времени, направлению и величине.Он возникает из-за систематических влияний, связанных с календарем, таких как:
Он также включает связанные с календарем систематические эффекты, которые нестабильны в их годовом графике или вызваны изменениями календаря от года к году, например:
КАК МЫ ОПРЕДЕЛЯЕМ СЕЗОННОСТЬ? Сезонность во временном ряду можно определить по равномерно разнесенным пикам и впадинам, которые имеют постоянное направление и примерно одинаковую величину каждый год относительно тренда.На следующей диаграмме показан сильно сезонный ряд. Очевидно, что в декабре в Новом Южном Уэльсе наблюдается значительный сезонный рост розничных продаж из-за рождественских покупок. В этом примере величина сезонной составляющей увеличивается со временем, как и тенденция. ЧТО ТАКОЕ НЕРЕГУЛЯРНОЕ? Нерегулярная составляющая (иногда также называемая остатком) — это то, что остается после оценки и удаления сезонных и трендовых составляющих временного ряда.Это результат краткосрочных колебаний в ряду, которые не являются ни систематическими, ни предсказуемыми. В очень нерегулярных рядах эти колебания могут доминировать над движениями, которые маскируют тренд и сезонность. Следующий график представляет собой весьма нерегулярный временной ряд: Тренд ABS определяется как «долгосрочное» движение во временном ряду без связанных с календарем и нерегулярных эффектов и является отражением базового уровня.Это результат таких влияний, как рост населения, инфляция цен и общие экономические изменения. На следующем графике показан ряд, в котором наблюдается очевидная тенденция к росту с течением времени: КАКИЕ МОДЕЛИ ИСПОЛЬЗУЮТСЯ ДЛЯ РАЗЛОЖЕНИЯ НАБЛЮДЕННОГО ВРЕМЕННОГО РЯДА? Модели разложения обычно являются аддитивными или мультипликативными, но также могут принимать другие формы, такие как псевдоаддитивные. Аддитивное разложение В некоторых временных рядах амплитуда как сезонных, так и нерегулярных колебаний не изменяется по мере того, как уровень тренда повышается или понижается.В таких случаях уместна аддитивная модель. В аддитивной модели наблюдаемый временной ряд (O t ) рассматривается как сумма трех независимых компонентов: сезонного S t , тренда T t и нерегулярного То есть Каждый из трех компонентов имеет те же блоки, что и исходная серия. Сезонно скорректированный ряд получается путем оценки и удаления сезонных эффектов из исходного временного ряда.Расчетная сезонная составляющая обозначается как Сезонно скорректированные оценки могут быть выражены следующим образом: В символах, На следующем рисунке показан типичный аддитивный ряд. Базовый уровень ряда колеблется, но величина сезонных всплесков остается примерно стабильной. Рисунок 4: Сектор государственного управления и другие текущие переводы в другие сектора Мультипликативное разложение Во многих временных рядах амплитуда как сезонных, так и нерегулярных колебаний увеличивается по мере повышения уровня тренда.В этой ситуации обычно уместна мультипликативная модель. В мультипликативной модели исходный временной ряд выражается как произведение тренда, сезонной и нерегулярной составляющих. или Сезонно скорректированные данные будут иметь следующий вид: или Согласно этой модели, тренд имеет те же единицы, что и исходный ряд, но сезонные и нерегулярные компоненты являются безразмерными факторами, распределенными около 1. Большинство рядов, проанализированных АБС, демонстрируют характеристики мультипликативной модели.По мере изменения базового уровня ряда изменяется и величина сезонных колебаний. Мультипликативная модель не может использоваться, если исходный временной ряд содержит очень маленькие или нулевые значения. Это потому, что число нельзя разделить на ноль. В этих случаях используется псевдоаддитивная модель, сочетающая элементы как аддитивной, так и мультипликативной моделей.Эта модель предполагает, что сезонные и нерегулярные колебания зависят от уровня тренда, но не зависят друг от друга. Исходные данные могут быть выражены в следующей форме: Псевдоаддитивная модель продолжает соглашение мультипликативной модели, в котором как сезонный фактор S t , так и нерегулярный фактор I t центрированы вокруг единицы. Поэтому нам нужно вычесть единицу из S t и I t , чтобы гарантировать, что члены T t x (S t — 1) и T t x (I t — 1) центрированы. около нуля.Эти термины можно интерпретировать как аддитивные сезонные и аддитивные нерегулярные компоненты соответственно, и поскольку они сосредоточены вокруг нуля, исходные данные O t будут сосредоточены вокруг значений тренда T t . Оценка с учетом сезонных колебаний определяется как: , где и — оценки тенденции и сезонной составляющей. В псевдоаддитивной модели тренд имеет те же единицы, что и исходный ряд, но сезонные и нерегулярные компоненты являются безразмерными факторами, распределенными около 1. Пример ряда, для которого требуется модель псевдоаддитивной декомпозиции, показан ниже. Эта модель используется, поскольку зерновые культуры выращиваются только в определенные месяцы, а урожайность практически равна нулю в течение одного квартала каждого года. Пример: Разложение Шискина Разложение Шискина дает графики исходных рядов, рядов с сезонной корректировкой, рядов трендов, остаточных (нерегулярных) факторов и между месячными (сезонными) и внутримесячными (торговый день) факторами, которые объединяются, чтобы сформировать комбинированные поправочные коэффициенты.Остаточные (нерегулярные) факторы находятся путем деления сезонно скорректированного ряда на ряд тренда. На рисунке 7 показано разложение Шискина для ряда розничных продаж Австралии. Рисунок 7: Разложение Шискина для общего розничного товарооборота Австралии, май 1990 г. — май 2000 г. КАК Я ЗНАЮ КАКУЮ МОДЕЛЬ РАЗЛОЖЕНИЯ ИСПОЛЬЗОВАТЬ? Чтобы выбрать подходящую модель декомпозиции, аналитик временных рядов исследует график исходного ряда и пробует ряд моделей, выбирая ту, которая дает наиболее стабильную сезонную составляющую.Если величина сезонной составляющей относительно постоянна независимо от изменений тренда, подходит аддитивная модель. Если он меняется с изменением тренда, наиболее вероятным кандидатом является мультипликативная модель. Однако если ряд содержит значения, близкие или равные нулю, и величина сезонной составляющей, по-видимому, зависит от уровня тренда, тогда наиболее подходящей является псевдоаддитивная модель. ЧТО ТАКОЕ СЕЗОННАЯ И НЕРЕГУЛЯРНАЯ (SI) КАРТА? После оценки компонента тренда его можно удалить из исходных данных, оставив после себя комбинированные сезонные и нерегулярные компоненты или SI.Сезонная и нерегулярная диаграмма или диаграмма SI графически представляет SI для определенных месяцев или кварталов в диапазоне ряда. Следующий график представляет собой диаграмму SI для месячного ряда с использованием модели мультипликативной декомпозиции. Точки представляют SI, полученные из временного ряда, а сплошная линия показывает сезонную составляющую. Сезонная составляющая рассчитывается путем сглаживания SI для удаления нерегулярных влияний.Графики SI полезны для определения того, вызваны ли краткосрочные движения сезонными или нерегулярными влияниями. На приведенном выше графике видно, что SI колеблются беспорядочно, что указывает на то, что в анализируемом временном ряду преобладает его нерегулярный компонент. Диаграммы SI также используются для определения сезонных перерывов, движущихся графиков праздников и экстремальных значений во временном ряду. CIMA BA1 Примечания: C2c. Аддитивные и мультипликативные моделиSyllabus C2c)Сезонные факторы для аддитивных и мультипликативных моделей. Тренд и сезонные колебанияСезонные колебания возникают в краткосрочной перспективеОчень важно различать тренд и сезонные колебания. Необходимо исключить сезонные колебания, чтобы оставить цифру, указывающую на Тренд . Методы расчета Сезонная вариация:
Аддитивная модельЭто основано на идее, что каждый фактический результат состоит из двух влияний. Временной ряд = Тренд (T) + Сезонная вариация (SV) Аддитивная модель — ступени
ИллюстрацияРассчитайте средние сезонные колебания по следующим данным.
Мультипликативная модельАддитивная модель предполагает, что сезонные колебания не увеличиваются со временем. Это маловероятно — например, быстрорастущие компании будут иметь увеличивающиеся показатели продаж и, следовательно, более высокие сезонные колебания. Этот недостаток аддитивной модели уловлен мультипликативной моделью . Мультипликативная модель обычно считается лучшей, поскольку она предполагает, что сезонные компоненты прогноза составляют постоянную долю продаж. Временной ряд = тренд x сезонная вариация (SV) Мультипликативная модель — шаги
Иллюстрация — Мультипликативная модельПрогнозированиеИллюстрация — Добавочная модельТенденция для пассажиров поездов на станции Паддингтон определяется соотношением: у = 5.2 + 0,24 х y = количество пассажиров в год x = период времени (2010 = 1) Какая тенденция в 2019 году?
Иллюстрация — Мультипликативная модельКомпания использует мультипликативную модель временных рядов. Тренд = 500 + 30 т T1 = Первый квартал 2010 г. Среднее сезонное изменение: 1-й квартал = -20 Каков прогноз продаж на 3 квартал 2012 года? Решение Если T1 = первый квартал 2010 года, то в третьем квартале 2012 года будет 11. T = (500 + (30 x 11)) x 116% = 963 Является ли мой временной ряд аддитивным или мультипликативным?[Эта статья была впервые опубликована на сайте R — Locke Data и любезно предоставлена R-блоггерам].(Вы можете сообщить о проблеме с содержанием на этой странице здесь)Хотите поделиться своим контентом на R-bloggers? щелкните здесь, если у вас есть блог, или здесь, если у вас его нет. Данные временных рядов — важная область анализа, особенно если вы много занимаетесь веб-аналитикой. Чтобы иметь возможность эффективно анализировать временные ряды, это помогает понять взаимосвязь между общей сезонностью активности и лежащей в основе тенденцией. Взаимодействие между трендом и сезонностью обычно классифицируется как аддитивное или мультипликативное.В этом посте рассматривается, как мы можем классифицировать данный временной ряд как один или другой, чтобы облегчить дальнейшую обработку. Аддитивный или мультипликативный?Важно понять, в чем разница между мультипликативным временным рядом и аддитивным, прежде чем мы продолжим. Временной ряд состоит из трех компонентов: То, как эти три компонента взаимодействуют, определяет разницу между мультипликативным и аддитивным временными рядами. В мультипликативном временном ряду компоненты умножаются вместе, чтобы образовать временной ряд. Если у вас есть тенденция к увеличению, амплитуда сезонной активности увеличивается. Все становится еще более преувеличенным.Это обычное дело, когда вы смотрите на веб-трафик. В аддитивном временном ряду компоненты складываются, образуя временной ряд. Если у вас есть восходящий тренд, вы по-прежнему видите пики и впадины примерно одинакового размера на протяжении всего временного ряда. Это часто наблюдается в индексированных временных рядах, где абсолютное значение растет, но изменения остаются относительными.
Для этого есть пакетКогда я впервые начал проводить анализ временных рядов, единственным способом визуализировать, как временной ряд разделяется на различные компоненты, было использование базы R. Примерно в то время, когда я чувствовал боль, кто-то выпустил расширение временных рядов ggplot2! Я буду использовать ggseas, где смогу. Мы будем использовать набор данных sample_ts
Разложение данныхЧтобы определить, является ли временной ряд аддитивным или мультипликативным, временной ряд должен быть разбит на составляющие.
ТрендПервым извлекаемым компонентом является тренд. Есть несколько способов сделать это, и некоторые из самых простых способов включают вычисление скользящего среднего или медианы. sample_ts [, trend: = zoo :: rollmean (Value, 8, fill = NA, align = "right")]
СезонностьСезонность — это циклические закономерности, возникающие в наших временных рядах после удаления тренда из данных. Конечно, способ удаления тренда данных должен быть аддитивным или мультипликативным, в зависимости от типа вашего временного ряда. Поскольку на данный момент мы не знаем тип временного ряда, мы сделаем и то, и другое. sample_ts [, `: =` (detrended_a = Value - тренд, detrended_m = Value / trend)]
Чтобы вычислить сезонность, нам нужно выяснить, каковы типичные значения без тренда в течение цикла. Здесь я рассчитаю среднее значение для наблюдений в Q1, Q2, Q3 и Q4. sample_ts [, `: =` (season_a = mean (detrended_a, na.rm = TRUE),
Season_m = среднее значение (detrended_m, na.rm = ИСТИНА)),
на =. (квартал (TimePeriod))]
ОстатокТеперь, когда у нас есть два компонента, мы можем вычислить остаток в обеих ситуациях и посмотреть, какой из них подходит лучше. sample_ts [, `: =` (остаток_а = detrended_a - сезонный_а,
Остаточная_м = detrended_m / сезонная_м)]
Визуализация декомпозиции Я обработал числа, но вы также можете выполнить визуальное разложение. ggseas дает нам функцию ggsdc (sample_ts, aes (x = TimePeriod, y = Value), method = "разложить",
частота = 4, s.window = 8, type = "add") + geom_line () +
ggtitle ("Добавка") + theme_minimal ()
Оценка соответствияПосле разложения наших данных нам нужно сравнить остатки. Поскольку мы просто пытаемся классифицировать временные ряды, нам не нужно делать ничего особенно сложного — большая часть этого упражнения — создать быструю функцию, которую можно было бы использовать для выполнения начальной классификации в среде пакетной обработки, чтобы проще лучше. Мы собираемся проверить, сохраняется ли степень корреляции между точками данных в остатках.Это коэффициент автокорреляции (ACF), и у него есть функция для его расчета. Поскольку некоторые корреляции могут быть отрицательными, мы выберем тип с наименьшей суммой квадратов значений корреляции. ssacf Собираем все вместеЭто не полностью обобщенная функция (поскольку у нее нет настраиваемых лагов, медианы, сезонности и т. Д.), Но если бы мне пришлось подать заявку на выполнение этого упражнения по нескольким временным рядам из этого набора данных, моя общая функция и использование были бы похожи на : ssacf
ЗаключениеЭто очень простой способ быстро оценить, являются ли несколько временных рядов аддитивными или мультипликативными. Это эффективная отправная точка для условной обработки пакетов временных рядов. Получите GIST кода, использованного в этом блоге, чтобы проработать его самостоятельно. Если у вас есть более простой способ классификации временных рядов, дайте мне знать в комментариях! Сообщение Является ли мой временной ряд аддитивным или мультипликативным? впервые появился на Locke Data. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||