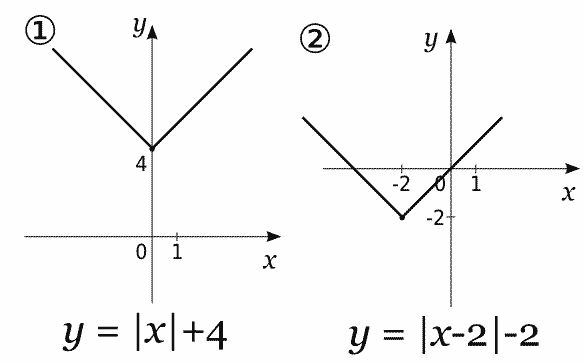Модуль икс равен 5: Уравнения с модулями. Модули
Модуль числа. Простое уравнение с модулем. Корень уравнения с модулем.
Наиболее часто возникают ошибки при решении уранений с модулем. Давайте разберем решение простейших уравнений с модулем. Чтобы решить уранения с модулем, надо знать определение модуля. Модуль обозначает абсолютное значение числа и записывается вертикальными черточками:
\(|a|\) — читается как модуль числа \(a\).
Определение модуля:
Модуль числа \(|-5|\) из определения является расстоянием от \(-5\) до \(0\).
- Если модуль числа равен положительному значению, то уравнение имеет два корня.
- Если модуль числа равен нулю, то уравнение имеет один корень.
- Если модуль равен отрицательному значению, то уравнение не имеет корней.
Пример 1. Решите \(|x|=3\)
Решение:
\(|x|=3\)
\(x = 3\) или \(x = -3\)
Уранение имеет два корня
Ответ: \(x = 3\) или \(x = -3\).
Пример 2. Решите \(|x|=0\)
Решение:
\(|x|=0\)
\(x = 0\)
Уравнение имеет один корень
Ответ: \(x = 0\).
Пример 3. Решите \(|x|=-3\)
Решение:
Модуль не может быть равен отрицательному значению!!!
корней нет
Ответ: корней нет.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
 Максима Танка
Максима ТанкаПроведенных занятий:
Форма обучения:
Дистанционно (Скайп)
 Математика — это чудесный мир логики и точности. Дорога в этот мир лежит через старания, внимательность и весёлые задания. Необычные решения и интерес помогут разобраться и полюбить эту науку! Оставить заявку
Математика — это чудесный мир логики и точности. Дорога в этот мир лежит через старания, внимательность и весёлые задания. Необычные решения и интерес помогут разобраться и полюбить эту науку! Оставить заявкуВятский государственный университет
Проведенных занятий:
Форма обучения:
Репетитор 8-11 классов. Использую индивидуальный подход к каждому ученику. Помогу разобраться в сложных темах и успешно сдать ОГЭ и ЕГЭ. Химия — это интересно. Химия — просто.
Использую индивидуальный подход к каждому ученику. Помогу разобраться в сложных темах и успешно сдать ОГЭ и ЕГЭ. Химия — это интересно. Химия — просто.
Репетитор по математике
Брянский государственный технический университет
Проведенных занятий:
Дистанционно (Скайп)
 Научу Вашего ребенка ПОНИМАТЬ английский язык. Благодаря моему обучению на Мальте, разработал свою методику преподавания.
Со мной английский — это просто!
Научу Вашего ребенка ПОНИМАТЬ английский язык. Благодаря моему обучению на Мальте, разработал свою методику преподавания.
Со мной английский — это просто!
Геометрия с нуля
- — Индивидуальные занятия
- — Бесплатное вводное занятие
Похожие статьи
Записаться на бесплатный урок
Уравнения с модулями. Графический метод
Простыми уравнения с модулями называем уравнения вида
|x|=5; |x-3|=2; ||2x-1|-5|=3; |1-x|=4
в которых переменная входит однократно и линейно.
Решать модульные уравнения можно как с помощью метода раскрытия модулей так и графически. В данной статье большое внимание будет уделено именно графическому методу раскрытия модулей. Для этого постепенно будет раскрыта суть преобразований с модулями. Таким образом удается решить множество тестовых задач в которых требуется найти количество решений уравнения с модулем.
Для наглядности приведем график модуль функции y=|x| ( «галочки»)
Далее представим смещение графика модуль функции по оси Ox, например y=|x-7|. Такая запись означает что функция равна нулю когда дужка равна нулю
x-7=0; –> x=7.
Так что «галочка» переносится вправо на 7.
Если подмодульную функцию умножить на (-1) то график функции не изменится |7-x|=|x-7|.
Если в модуле имеем суммирование |x+5| то смещение графика модуль функции выполняем в сторону отрицательных переменных
Самое интересное в вычислениях происходит когда имеем уравнение вида модуль в модуле
||x|-6|, ||x|+3|
Тогда выполняем перенос графика внутреннего модуля по оси вниз или вверх и симметричное отображение значений, которые идут ниже оси Oх вверх.
Следующая функция это модуль поднят вверх на три.
Далее, если в задании спрашивают «Какое количество корней уравнения ||x|-6|=2?» то необходимо провести лишь линию y=2 и подсчитать количество точек пересечения с графиком модуль функции
Уравнение имеет 4 решения. Лучше решать графически уравнение с модулями на листке в клеточку, есть лучшая привязка к квадратикам. Задача в каждом из случаев сводится к смещению, отображения и параллельному переносу графика модуль функции |x|. Решим несколько примеров чтоб Вы понимали насколько эффективная методика графического раскрытия модулей.
Пример 1. Найти корни уравнения ||x-2|-5|=3.
Решение: Имеем задания типа модуль от модуля. Выполняем построение первого (внутреннего) модуля
Далее параллельно переносим линии вниз на 5, чтобы получить график функции y=|x-2|-5
Следующим шагом отражаем все что находится ниже оси абсцисс. Это и будет искомая модуль функция y=||x-2|-5|. Также выполняем построение прямой у=3
Также выполняем построение прямой у=3
Нетрудно определить по рисунку что решениями уравнения с модулями будут значения
x=-6; x=0;x=4; x=10.
На этом пример выполнен. Далее будет меньше детализации, однако суть алгоритма графического построения Вам будет понятен.
Пример 2. Найти количество корней следующего уравнения с модулем |||x+1|-3|-5|=2.
Решение: Имеем уравнения с двумя вложенными модулями. График первого вложенного модуля получим смещением в отрицательную сторону оси абсцисс модуль функции на единицу. Далее параллельно переносим полученный график вниз на 3 и отразим относительно оси Ox все минусовые y. Полученный график снова опускаем вниз, на этот раз на 5 клеток и симметрично отражаем все что находится ниже оси Ox. Выполняем построение правой стороны уравнения – прямой y=2.
В результате у Вас должен получиться похожий конечный график модуль функции
Из построения видим, что имеем пять точек пересечения прямой с модуль-функцией, а следовательно и 5 корней уравнения. Вот и все решения примера с модулями. Классическое раскрытие модулей для этого примера занимает очень много времени и существует вероятность неправильного решения уравнения. Преимущество графического метода по времени решения видна невооружённым глазом.
Вот и все решения примера с модулями. Классическое раскрытие модулей для этого примера занимает очень много времени и существует вероятность неправильного решения уравнения. Преимущество графического метода по времени решения видна невооружённым глазом.
Пример 3. При каком значении параметра a уравнение с модулем ||x-4|-2|=a-3 имеет три, четыре корня?
Решение: Выполняем построение модулей, которые находятся в левой части уравнения
Из построения видим, если правая сторона уравнения с модулями равна 2 то имеем три точки пересечения. Если от 0 до 2 не учитывая краев – 4 корни уравнения. Отсюда получим уравнение для определеения параметра
a-3=2; – > a=5.
и неровности
a-3>0; a>3;
a-3< 2; a < 5 .
В итоге: уравнение имеет 3 корня когда параметр равен a=5
и 4 корня если параметр принадлежит интервалу a=(3..5).
В подобных примерах надо быть очень внимательными так как часто именно вопрос ставится так, чтобы помочь Вам или наоборот «навредить». Например: «Сколько положительных корней имеет уравнение с модулями?», «Найдите сумму решений уравнения», «Найдите наибольшее целое значение параметра» и тому подобные. Поэтому вдумчиво читайте что от Вас требуют, а уже потом приступайте к вычислениям.
Например: «Сколько положительных корней имеет уравнение с модулями?», «Найдите сумму решений уравнения», «Найдите наибольшее целое значение параметра» и тому подобные. Поэтому вдумчиво читайте что от Вас требуют, а уже потом приступайте к вычислениям.
Похожие материалы:
Модуль
Модулем положительного числа называют само это число; модулем отрицательного числа называют число, ему противоположное; модуль нуля равен нулю.\(|a|=\begin{cases} a, \;\; если \; a>0 \\ 0, \; если\;\; a=0\\ -a,\; если \;\; a<0 \end{cases}\)
Второе название модуля – «абсолютное значение действительного числа».
Фактически модуль делает всё, что находится внутри него положительным. Поэтому чтобы правильно его раскрыть, необходимо сначала выяснить знак выражения внутри него:
— если подмодульное выражение положительно, модуль просто убирается. 4+1\)
4+1\)
Пример. Вычислить значение выражения \(|7-x|-|x+3|\), при \(x>12\).
Решение: При любом \(x\) большем \(12\), первое подмодульное выражение будет отрицательно, а второе – положительно. Соответственно, первый модуль будет раскрываться с минусом, а второй – с плюсом (значит перед ним останется минус, который стоял перед ним до раскрытия):
\(|7-x|-|x+3|=-(7-x)-(x+3)=-7+x-x-3=-10\)
Ответ: \(-10\)
Геометрическое определение модуля
\(|a|\) — это расстояние от \(0\) до числа \(a\) на числовой оси
Пример. Чему равен \(|5|\) и \(|-5|\)?
Представим числовую ось и отметим на ней точки \(5\) и \(-5\). Какое будет расстояние от нуля до этих точек? Очевидно \(5\).
Значит ответ: \(|5|=5\), \(|-5|=5\).
Так как модуль это расстояние, а расстояние не может выражаться отрицательным числом, то он всегда положителен.
Понимать легче второе определение, но практике удобнее использовать первое.
Решение простейших уравнений с модулем
Уравнения вида \(|f|=g\) решается с помощью перехода к совокупности \( \left[ \begin{gathered}f= g\\ f=-g\end{gathered}\right.\) , при условии, что \(g≥0\).
Сначала об условии \(g≥0\). Откуда оно берется? Из определения модуля, ведь модуль всегда неотрицателен (то есть, положителен или равен нулю). Поэтому условие \(g≥0\) обязательно. Иначе уравнение не будет иметь решения.
Теперь о совокупности. Почему уравнение распадается на два? Давайте, к примеру, рассмотрим уравнение \(|x|=3\). Какое число под модулем будет равно \(3\)? Конечно \(3\) и \(-3\), потому что \(|3|=3\), \(|-3|=3\). Корни уравнения \(|x|=3\): \(3\) и \(-3\). Логично? Логично! В общем виде получается, что подмодульное выражение \(f\) должно быть равно \(g\) и \(-g\). Иначе равенство не получится.
Пример.
 Решить уравнение:
Решить уравнение:|
\(|x-1|=3x\) |
Найдем ограничения уравнения. Запишем его немного правее от основного решения |
|
|
\(3x≥0\) |
Когда ограничение записано — можно со спокойной душой решать уравнение. Избавимся от модуля и перейдем к совокупности уравнений |
|
|
\( \left[ \begin{gathered}x-1=3x\\ x-1=-3x\end{gathered}\right.\) |
Перед нами 2 линейных уравнения. Решаем их с помощью известного заклинания: «иксы влево, числа вправо» |
|
|
\( \left[ \begin{gathered}x-3x=1\\ x+3x=1\end{gathered}\right. |
Приведем подобные слагаемые |
|
|
\( \left[ \begin{gathered}-2x=1\\ 4x=1\end{gathered}\right.\) |
|
Поделим первое уравнение на \(-2\), второе на \(4\). |
|
\( \left[ \begin{gathered} x=-\frac{1}{2}\\ x=\frac{1}{4}\end{gathered}\right.\) |
|
Корень \(-\)\(\frac{1}{2}\) – не подходит, т.к. \(x≥0\). Остается корень \(\frac{1}{4}\), его и запишем в ответ |
Ответ: \(\frac{1}{4}\)
Решение простейших неравенств с модулем
Неравенство вида \(|f|< c\) решается с помощью перехода к двойному неравенству \( -c< f< c\) , при условии, что \(c>0\).

Начнем опять с условия. Почему \(c>0\)? Потому что, иначе неравенство не будет иметь решения. Здесь все также как в уравнениях. В самом деле, когда, например, модуль икса меньше \(-7\)? Никогда!
Теперь разберем неравенство \(|x|<3\). Какие иксы нам подойдут? Все от \(-3\) до \(3\). Иначе говоря, икс должен лежать между \(-3\) и \(3\). Это утверждение можно записать вот так \(-3< x <3\) либо системой \(\begin{cases}x<3\\x > -3\end{cases}\). В любом случае ответ будет \(xϵ (-3;3)\).
Неравенство вида \(|f|>c\) решается с помощью перехода к совокупности неравенств \( \left[ \begin{gathered} f>c\\ f< -c\end{gathered}\right.\), при условии, что \(c≥0\).
А здесь почему \(c≥0\)? Потому что иначе решать нечего: если \(c\) отрицательно, то модуль абсолютно любого икса нам подойдет. И значит ответ, икс – любое число.
Теперь о переходе. Рассмотрим неравенство \(|x|>3\). Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).
Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).
|
\(|3x-7|≤8\) |
\(|3x-11|≥11\) |
|
|
\(-8≤3x-7≤8\) \(|+7\) |
\( \left[ \begin{gathered}3x-11≥11\\ 3x-11≤-11\end{gathered}\right.\) |
|
|
\(-1≤3x≤15\) |
\( \left[ \begin{gathered}3x≥22\\ 3x≤0\end{gathered}\right.\) |
|
|
\(-\frac{1}{3}≤x≤5\) |
\( \left[ \begin{gathered}x≥\frac{22}{3}\\ x≤0\end{gathered}\right. |
|
|
Ответ: \([ -\frac{1}{3};5]\) |
Ответ: \( (-\infty;0]\cup [ \frac{22}{3};\infty)\) |
Смотрите также:
Свойства модуля
Решение уравнений с модулем
Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.
Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.
Число -5 имеет знак «-» и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= — f(x), если f(x) < 0
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3<0.
Чтобы решить уравнение , содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля.
Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.
Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.
А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.
Рассмотрим простой пример.
Решим уравнение:
|x-3|=-x2+4x-3
1. Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3<0, т.е. если х<3
2. Мы получили два числовых промежутка: х≥3 и х<3.
Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:
А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:
x-3=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
x2 -3х=0
и решим это уравнение.
Это уравнение имеет корни:
х1=0, х2=3
Внимание! поскольку уравнение x-3=-x2+4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х2=3.
Этому условию удовлетворяет только х2=3.
Б) При x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:
3-x=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х<3!
Раскроем скобки, приведем подобные члены. Получим уравнение:
x2-5х+6=0
х1=2, х2=3
Внимание! поскольку уравнение 3-х=-x2+4x-3 существует только на промежутке x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х1=2.
Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.
Ответ: х=3, х=2
что это такое и как его найти?
Модуль — математическое понятие, которое проходят в шестом классе. Сам по себе числовой модуль не представляет собой ничего сложного, это одна из простейших тем в начальной математике. Но если случайно пропустить изучение нужного параграфа, то можно столкнуться с непониманием темы. Поэтому напомним, что именно называется модулем, как его найти для разных чисел, и что представляет собой это понятие по сути.
Но если случайно пропустить изучение нужного параграфа, то можно столкнуться с непониманием темы. Поэтому напомним, что именно называется модулем, как его найти для разных чисел, и что представляет собой это понятие по сути.
Модуль с точки зрения геометрии
Забегая вперед, попробуем сразу понять, что же представляет собой модуль на практике — так будет легче уловить его смысл. Нарисуем на листе бумаги прямую координат, возьмем нуль за точку отсчета, а по правую и по левую стороны на одинаковом расстоянии поставим некие две точки — например, 5 и -5.
Модулем будет считаться именно фактическое расстояние до нуля от -5 и от 5. Очевидно, что это расстояние будет совершенно одинаковым. Поэтому в обоих случаях модуль будет равняться числу «5» — и неважно, какой знак стоит перед исходным числом, которое мы рассматриваем.
Как найти модуль числа?
Теперь, когда мы визуально представляем, что же такое модуль, будет проще понять формулировку из учебника. Она гласит, что модулем некоего числа является само это число, если оно положительное, число, противоположное исходному числу, если оно отрицательное, и нуль, если модуль мы ищем для нуля.
Это можно сформулировать и иначе — модулем любого числа будет само это число в абсолютном выражении, то есть без учета знака. Записывается модуль так — по обе стороны от нужного числа ставятся вертикальные линии, например, модуль для числа «5» будет равен «5», а записываться он будет, как |5|.
Из всего, что мы рассказали выше, можно вывести несколько строгих правил для модулей.
- Может ли модуль быть отрицательным? Нет! Модуль может быть только положительным. Даже если речь идет об отрицательном числе, например, -7, то его модуль будет равен |7| — числу, противоположному исходному.
- Для нуля модуль всегда будет равен нулю. Верно и другое — нуль может быть модулем исключительно в том случае, если вычисляется он для числа нуль, и ни в каком другом.
- Если нужно найти модуль для выражения типа a*b, то есть модуль произведения, то можно сначала найти модуль а, затем модуль b, и перемножить их друг на друга.
- То же самое касается и деления — если нам нужно разделить y на z и найти модуль получившегося числа, то можно взять модуль y и разделить его на модуль z.
 Результат будет одним и тем же.
Результат будет одним и тем же.
Похожие статьи
Внеклассный урок — Модуль числа
Модуль числаМодулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 5 является 5, модулем числа –5 тоже является 5.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |5|, |х|, |а| и т.д.
Правило:
|а| = а, если а ≥ 0. |а| = –а, если а < 0. |
Пояснение:
|5| = 5
Читается так: модулем числа 5 является 5.
|–5| = –(–5) = 5
Читается так: модулем числа –5 является 5.
|0| = 0
Читается так: модулем нуля является ноль.
Свойства модуля:
1) Модуль числа есть неотрицательное число: |а| ≥ 0 2) Модули противоположных чисел равны: |а| = |–а| 3) Квадрат модуля числа равен квадрату этого числа: |а|2 = a2 4) Модуль произведения чисел равен произведению модулей этих чисел: |а · b| = |а| · |b| 6) Модуль частного чисел равен отношению модулей этих чисел: |а : b| = |а| : |b| 7) Модуль суммы чисел меньше или равен сумме их модулей: |а + b| ≤ |а| + |b| 8) Модуль разности чисел меньше или равен сумме их модулей: |а – b| ≤ |а| + |b| 9) Модуль суммы/разности чисел больше или равен модулю разности их модулей: |а ± b| ≥ ||а| – |b|| 10) Постоянный положительный множитель можно вынести за знак модуля: |m · a| = m · |а|, m >0 11) Степень числа можно вынести за знак модуля: |аk| = |а|k, если аk существует 12) Если |а| = |b|, то a = ± b |
Геометрический смысл модуля.
Модуль числа – это величина расстояния от нуля до этого числа.
Для примера возьмем снова число 5. Расстояние от 0 до 5 такое же, что и от 0 до –5 (рис.1). И когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Впрочем, не совсем верно: расстояние мы измеряем только положительными числами – или неотрицательными числами. Пусть цена деления нашей шкалы составляет 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до –5 тоже 5 см.
На практике часто расстояние отмеряется не только от нуля – точкой отсчета может быть любое число (рис.2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками а и b на числовой прямой.
Пример 1. Решить уравнение |х – 1| = 3.
Решение.
Смысл уравнения в том, что расстояние между точками х и 1 равно 3 (рис.2). Поэтому от точки 1 отсчитываем три деления влево и три деления вправо – и наглядно видим оба значения х:
х1 = –2, х2 = 4.
Можем и вычислить.
│х – 1 = 3
│х – 1 = –3
↕
│х = 3 + 1
│х = –3 + 1
↕
│х = 4
│ х = –2.
Ответ: х1 = –2; х2 = 4.
Пример 2. Найти модуль выражения:
3√5 – 10.
Решение.
Сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 – это довольно сложно. Поступим проще: возведем в корень 3 и 10. Затем сравним величину чисел, составляющих разность:
3 = √9. Следовательно, 3√5 = √9 · √5 = √45
10 = √100.
Мы видим, что первое число меньше второго. Значит, выражение отрицательное, то есть его ответ меньше нуля:
3√5 – 10 < 0.
Но согласно правилу, модулем отрицательного числа является это же число с противоположным знаком. У нас отрицательное выражение. Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:
Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:
–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.
Ответ:
|3√5 – 10| = 10 – 3√5.
Простейшие уравнения с модулем. Тест
Определение. Геометрический смысл
Модуль (или абсолютная величина) числа (обозначается как )— неотрицательное число, определение которого зависит от типа числа
А именно:
Мы будем называть данное правило правилом раскрытия модуля.
Например, так как , попадаем в первую строку (ситуацию).
так как попадаем во вторую ситуацию.
С геометрической точки зрения, – есть расстояние между числом и началом координат.
Решением уравнения, например, являются числа и , потому что расстояние от точки координатной прямой до нуля равно , и расстояние от точки до нуля также равно 6.
|| с геометрической точки зрения означает расстояние между точками и .
Полезные примеры
1) Раскрыть модуль:
Так как больше, чем , то , а значит согласно правилу раскрытия модуля.
2) Раскрыть модуль:
Так как больше нуля при всех значениях , то согласно правилу раскрытия модуля.
3) Раскрыть модуль:
Так как , то , а значит, согласно правилу раскрытия модуля.
Решение уравнений
1) Решить уравнение .
Модуль – всегда неотрицательная величина, поэтому уравнение решений не имеет.
Ответ: { }
2) Решить уравнение: .
Модуль раскрывается таким образом в случае, когда .
Ответ:
3) Решить уравнение:
Согласно геометрическому смыслу модуля левая и правая части равенства представляют из себя одно и то же.
Ответ:
4) Решить уравнение:
Раскрываем модуль согласно правилу раскрытия модуля:
а)
Имеем: ,
Откуда .
Поскольку мы находимся в ситуации , то подходит только корень .
б)
Имеем: ,
Откуда или .
Поскольку мы находимся в ситуации , то ни один корень из найденных в пункте (б) нам не подходит.
Ответ: .
Коротко можно было бы решение оформить так:
5) Решить уравнение:
Раскрываем модуль согласно правилу раскрытия модуля:
a) Первый случай:
Что равносильно .
б) Второй случай:
Что равносильно
Ответ:
6) Решить уравнение:
Можно было бы действовать согласно правилу раскрытия модуля, но проще будет в данном случае рассуждать так:
Внутри модуля может «скрываться» как так и .
Поэтому или
или
Из первого уравнения или , а второе уравнение корней не имеет.
Ответ:
7) Решить уравнение:
Раскрываем модуль согласно правилу раскрытия модуля:
а) Первый случай:
Рассмотрим отдельно первую строку системы:
Рассмотрим уравнение из системы:
или
Разложим на множители левую часть уравнения способом группировки, предварительно разбив среднее слагаемое на два:
Откуда (трехчлен в скобках корней не имеет).
Данный корень удовлетворяет первой строке системы, он пойдет в ответ.
б) Второй случай:
Решение неравенства системы:
Корень удовлетворяет решению неравенства системы.
Собираем решения.
Ответ:
Также, смотрите «Модуль. Простейшие неравенства с модулем» здесь.
Вы можете пройти тест по теме «Модуль. Раскрытие модуля. Простешие уравнения с модулем»
Базовая математика в JavaScript — числа и операторы — Изучение веб-разработки
На этом этапе курса мы обсуждаем математику в JavaScript — как мы можем использовать операторы и другие функции для успешного манипулирования числами для выполнения наших ставок.
| Предварительные требования: | Базовая компьютерная грамотность, базовое понимание HTML и CSS, понимание того, что такое JavaScript. |
|---|---|
| Цель: | Для ознакомления с основами математики в JavaScript. |
Ладно, может и нет. Некоторые из нас любят математику, некоторые из нас ненавидят математику с тех пор, как нам пришлось изучать таблицы умножения и деление в столбик в школе, а некоторые из нас сидят где-то посередине. Но никто из нас не может отрицать, что математика — это фундаментальная часть жизни, без которой мы далеко не продвинемся. Это особенно верно, когда мы учимся программировать JavaScript (или любой другой язык в этом отношении) — так много из того, что мы делаем, зависит от обработки числовых данных, вычисления новых значений и т. Д., Что вы не удивитесь, узнав этот JavaScript имеет полнофункциональный набор доступных математических функций.
В этой статье обсуждаются только основные части, которые вам сейчас необходимо знать.
Типы чисел
В программировании даже простая десятичная система счисления, которую мы все так хорошо знаем, сложнее, чем вы думаете. Мы используем разные термины для описания различных типов десятичных чисел, например:
- Целые числа — числа с плавающей запятой без дроби. Они могут быть как положительными, так и отрицательными, например 10, 400 или -5.
- Числа с плавающей запятой (с плавающей запятой) имеют десятичные и десятичные знаки, например 12.5 и 56.7786543.
- Двойные числа — это особый тип чисел с плавающей запятой, которые имеют большую точность, чем стандартные числа с плавающей запятой (что означает, что они точны до большего числа десятичных знаков).
У нас даже есть разные системы счисления! Десятичное число — это основание 10 (это означает, что в каждом столбце используется 0–9), но у нас также есть такие вещи, как:
- Двоичный — язык нижнего уровня компьютеров; 0 и 1.

- Octal — База 8, использует 0–7 в каждом столбце.
- Шестнадцатеричный — База 16, использует 0–9, а затем a – f в каждом столбце. Возможно, вы уже встречались с этими числами при настройке цветов в CSS.
Прежде чем вы начнете беспокоиться о таянии вашего мозга, остановитесь прямо здесь! Для начала, в этом курсе мы будем придерживаться десятичных чисел; вы редко будете сталкиваться с необходимостью начать думать о других типах, если вообще когда-нибудь.
Вторая хорошая новость заключается в том, что в отличие от некоторых других языков программирования, JavaScript имеет только один тип данных для чисел, как целых, так и десятичных знаков — как вы уже догадались, Number .Это означает, что с какими бы числами вы ни работали в JavaScript, вы обрабатываете их точно так же.
Примечание: На самом деле, в JavaScript есть второй числовой тип, BigInt, который используется для очень и очень больших целых чисел. Но для целей этого курса мы просто будем беспокоиться о значениях
Но для целей этого курса мы просто будем беспокоиться о значениях Number .
Для меня все числа
Давайте быстро поиграем с числами, чтобы заново познакомиться с основным синтаксисом, который нам нужен. Введите перечисленные ниже команды в консоль JavaScript инструментов разработчика.
- Прежде всего, давайте объявим пару переменных и инициализируем их целым числом и числом с плавающей запятой, соответственно, затем снова введем имена переменных, чтобы убедиться, что все в порядке:
const myInt = 5; const myFloat = 6,667; myInt; myFloat; - Числовые значения вводятся без кавычек — попробуйте объявить и инициализировать еще пару переменных, содержащих числа, прежде чем двигаться дальше.
- Теперь давайте проверим, что обе наши исходные переменные имеют один и тот же тип данных.В JavaScript есть оператор
typeof, который делает это. Введите следующие две строки, как показано:
Вы должны получитьtypeof myInt; typeof myFloat;«число», возвращенное в обоих случаях — это значительно упрощает нам задачу, чем если бы разные числа имели разные типы данных, и нам приходилось обращаться с ними по-разному. Фух!
Фух!
Полезные числовые методы
Объект Number , экземпляр которого представляет все стандартные числа, которые вы будете использовать в своем JavaScript, имеет ряд полезных методов, доступных для управления числами.Мы не рассматриваем их подробно в этой статье, потому что мы хотели сохранить ее как простое введение, а пока охватить только самые основные основы; однако, прочитав этот модуль пару раз, стоит перейти на страницы со ссылками на объекты и узнать больше о том, что доступно.
Например, чтобы округлить ваше число до фиксированного числа десятичных знаков, используйте метод toFixed () . Введите в консоль браузера следующие строки:
const lotOfDecimal = 1.766584958675746364;
lotOfDecimal;
const twoDecimalPlaces = lotOfDecimal.toFixed (2);
twoDecimalPlaces;
Преобразование в числовые типы данных
Иногда может получиться число, которое хранится как строковый тип, что затрудняет выполнение вычислений с ним. Чаще всего это происходит, когда данные вводятся в форму ввода, а тип ввода — текст. Есть способ решить эту проблему — передать строковое значение в конструктор
Чаще всего это происходит, когда данные вводятся в форму ввода, а тип ввода — текст. Есть способ решить эту проблему — передать строковое значение в конструктор Number () , чтобы вернуть числовую версию того же значения.
Например, попробуйте ввести в консоль следующие строки:
пусть myNumber = '74';
myNumber + = 3;
Вы получите результат 743, а не 77, потому что myNumber фактически определяется как строка. Вы можете проверить это, набрав следующее:
Исправить расчет можно так:
Арифметические операторы — это основные операторы, которые мы используем для суммирования в JavaScript:
| Оператор | Имя | Назначение | Пример |
|---|---|---|---|
+ | Дополнение | Складывает два числа. | 6 + 9 |
– | Вычитание | Вычитает правое число из левого. | 20-15 |
* | Умножение | Умножает два числа. | 3 * 7 |
/ | Отдел | Делит левое число на правое. | 10/5 |
% | Остаток (иногда называется по модулю) | Возвращает остаток, оставшийся после того, как вы разделили левое число. на количество целых частей, равное правильному числу. | |
** | Показатель | Увеличивает число с основанием до степени степени ,
то есть базовое число , умноженное само на себя, экспонента раза. Впервые он был представлен в EcmaScript 2016. Впервые он был представлен в EcmaScript 2016. | 5 ** 2 (возвращает 25 , что совпадает с 5 * 5 ). |
Примечание: Иногда в арифметических операциях можно встретить числа, называемые операндами.
Примечание: Иногда можно увидеть экспоненты, выраженные с помощью более старого метода Math.pow () , который работает очень похожим образом. Например, в Math.pow (7, 3) , 7 — основание, а 3 — показатель степени, поэтому результат выражения — 343 . Math.pow (7, 3) эквивалентно 7 ** 3 .
Нам, вероятно, не нужно учить вас выполнять основы математики, но мы хотели бы проверить ваше понимание синтаксиса. Попробуйте ввести приведенные ниже примеры в консоль JavaScript инструментов разработчика, чтобы ознакомиться с синтаксисом.
- Сначала попробуйте ввести несколько собственных простых примеров, например
- Вы также можете попробовать объявить и инициализировать некоторые числа внутри переменных и попытаться использовать их в суммах — переменные будут вести себя точно так же, как значения, которые они содержат для целей суммы.Например:
const num1 = 10; const num2 = 50; 9 * число1; num1 ** 3; число2 / число1; - Наконец, в этом разделе попробуйте ввести несколько более сложных выражений, например:
5 + 10 * 3; число2% 9 * число1; число2 + число1 / 8 + 2;
Части этого последнего набора вычислений могут дать не совсем тот результат, которого вы ожидали; раздел ниже может дать ответ, почему.
Приоритет оператора
Давайте посмотрим на последний пример сверху, предполагая, что num2 содержит значение 50, а num1 содержит значение 10 (как первоначально указано выше):
Как человек, вы можете прочитать это как «50 плюс 10 равно 60» , затем «8 плюс 2 равно 10» и, наконец, «60, разделенное на 10, равно 6» .
Но браузер делает «10, разделенное на 8, равно 1,25» , затем «50 плюс 1,25 плюс 2 равняется 53,25» .
Это происходит из-за приоритета операторов . — некоторые операторы применяются раньше других при вычислении результата вычисления (в программировании оно называется выражением ). Приоритет операторов в JavaScript такой же, как и на уроках математики в школе — сначала всегда выполняются умножение и деление, затем сложение и вычитание (вычисление всегда выполняется слева направо).
Если вы хотите переопределить приоритет операторов, вы можете заключить в круглые скобки части, которые должны быть обработаны в первую очередь. Итак, чтобы получить результат 6, мы могли бы сделать это:
Попробуйте и убедитесь.
Иногда вам нужно многократно прибавлять или вычитать единицу к значению числовой переменной или из него. Это удобно сделать с помощью операторов инкремента ( ++ ) и декремента (–). Мы использовали
Мы использовали ++ в нашей игре «Угадай число» еще в нашей первой заставке в статье о JavaScript, когда мы добавили 1 к нашей переменной guessCount , чтобы отслеживать, сколько предположений пользователь оставил после каждого поворота.
Давайте попробуем поиграть с ними на вашей консоли. Для начала обратите внимание, что вы не можете применить их непосредственно к числу, что может показаться странным, но мы присваиваем переменной новое обновленное значение, а не работаем с самим значением. Следующее вернет ошибку:
Итак, вы можете увеличивать только существующую переменную. Попробуйте это:
Ладно, странность номер 2! Когда вы это сделаете, вы увидите, что возвращается значение 4 — это потому, что браузер возвращает текущее значение, , затем увеличивает переменную.Вы можете увидеть, что оно увеличилось, если вы снова вернете значение переменной:
То же самое и с - : попробуйте следующее
пусть num2 = 6;
num2--;
num2;
Примечание: Вы можете заставить браузер делать это наоборот — увеличивать / уменьшать переменную , затем возвращать значение — поместив оператор в начало переменной, а не в конец. Попробуйте еще раз приведенные выше примеры, но на этот раз используйте
Попробуйте еще раз приведенные выше примеры, но на этот раз используйте ++ num1 и --num2 .
Операторы присваивания — это операторы, которые присваивают значение переменной. Мы уже использовали самый простой, = , множество раз — он присваивает переменной слева значение, указанное справа:
пусть x = 3;
пусть y = 4;
х = у;
Но есть и более сложные типы, которые предоставляют полезные ярлыки, чтобы сделать ваш код более аккуратным и эффективным. Наиболее распространенные перечислены ниже:
| Оператор | Имя | Назначение | Пример | Ярлык для |
|---|---|---|---|---|
+ = | Дополнительное задание | Добавляет значение справа к значению переменной слева, затем возвращает новое значение переменной | х + = 4; | х = х + 4; |
- = | Присваивание вычитания | Вычитает значение справа из значения переменной слева, и возвращает новое значение переменной | х - = 3; | х = х - 3; |
* = | Назначение умножения | Умножает значение переменной слева на значение справа, и возвращает новое значение переменной | х * = 3; | х = х * 3; |
/ = | Назначение дивизии | Делит значение переменной слева на значение справа, и возвращает новое значение переменной | х / = 5; | х = х / 5; |
Попробуйте ввести некоторые из приведенных выше примеров в свою консоль, чтобы понять, как они работают. В каждом случае проверьте, сможете ли вы угадать значение, прежде чем вводить вторую строку.
В каждом случае проверьте, сможете ли вы угадать значение, прежде чем вводить вторую строку.
Обратите внимание, что вы вполне можете использовать другие переменные в правой части каждого выражения, например:
пусть x = 3;
пусть y = 4;
х * = у;
В этом упражнении вы будете управлять некоторыми числами и операторами, чтобы изменить размер поля. Коробка рисуется с помощью API браузера, называемого Canvas API. Не нужно беспокоиться о том, как это работает — просто сконцентрируйтесь на математике.Ширина и высота поля (в пикселях) определяются переменными x и y , которым изначально присвоено значение 50.
Открыть в новом окне
В редактируемом поле кода выше есть две строки, отмеченные комментарием, который мы хотели бы, чтобы вы обновили, чтобы поле увеличивалось / уменьшалось до определенных размеров, используя определенные операторы и / или значения в каждом случае. Попробуем следующее:
- Измените строку, которая вычисляет x, чтобы поле оставалось шириной 50 пикселей, но 50 вычислялось с использованием чисел 43 и 7 и арифметического оператора.

- Измените строку, которая вычисляет y, так, чтобы прямоугольник был высотой 75 пикселей, но 75 вычисляется с использованием чисел 25 и 3 и арифметического оператора.
- Измените строку, в которой вычисляется x, чтобы поле было шириной 250 пикселей, но 250 вычисляется с использованием двух чисел и оператора остатка (по модулю).
- Измените строку, которая вычисляет y, так, чтобы прямоугольник был высотой 150 пикселей, но 150 вычисляется с использованием трех чисел и операторов вычитания и деления.
- Измените строку, которая вычисляет x, так, чтобы поле было шириной 200 пикселей, но 200 вычисляется с использованием числа 4 и оператора присваивания.
- Измените строку, которая вычисляет y, так, чтобы поле было высотой 200 пикселей, но 200 вычисляется с использованием чисел 50 и 3, оператора умножения и оператора присваивания сложения.
Не волнуйтесь, если вы полностью испортили код. Вы всегда можете нажать кнопку «Сброс», чтобы все снова заработало. После того, как вы правильно ответили на все вышеперечисленные вопросы, не стесняйтесь еще немного поиграть с кодом или создать свои собственные задачи.
После того, как вы правильно ответили на все вышеперечисленные вопросы, не стесняйтесь еще немного поиграть с кодом или создать свои собственные задачи.
Иногда нам нужно запустить тесты true / false, а затем действовать соответственно в зависимости от результата этого теста — для этого мы используем операторов сравнения .
| Оператор | Имя | Назначение | Пример |
|---|---|---|---|
=== | Строгое равенство | Проверяет идентичность левого и правого значений друг другу | 5 === 2 + 4 |
! == | Строгое неравенство | Проверяет, идентичны ли левое и правое значения друг другу | 5! == 2 + 3 |
< | Менее | Проверяет, меньше ли левое значение правого. | 10 <6 |
> | Больше | Проверяет, больше ли левое значение правого. | 10> 20 |
<= | Меньше или равно | Проверяет, меньше ли левое значение правому или равно ему. | 3 <= 2 |
> = | Больше или равно | Проверяет, больше ли левое значение правому или равно ему. | 5> = 4 |
Примечание: Вы можете увидеть, как некоторые люди используют == и ! = в своих тестах на равенство и неравенство. Это допустимые операторы в JavaScript, но они отличаются от === /! == . В предыдущих версиях проверяется, совпадают ли значения, но не совпадают ли типы данных значений. Последние, строгие версии проверяют равенство как значений, так и их типов данных.Строгие версии, как правило, приводят к меньшему количеству ошибок, поэтому мы рекомендуем вам их использовать.
Последние, строгие версии проверяют равенство как значений, так и их типов данных.Строгие версии, как правило, приводят к меньшему количеству ошибок, поэтому мы рекомендуем вам их использовать.
Если вы попытаетесь ввести некоторые из этих значений в консоль, вы увидите, что все они возвращают истинных / ложных значений - те логические значения, которые мы упоминали в прошлой статье. Они очень полезны, поскольку позволяют нам принимать решения в нашем коде, и используются каждый раз, когда мы хотим сделать какой-то выбор. Например, логические значения могут использоваться для:
- Отображение правильной текстовой метки на кнопке в зависимости от того, включена функция или выключена
- Отображать сообщение о завершении игры, если игра окончена, или сообщение о победе, если игра была выиграна.
- Отображать правильное сезонное приветствие в зависимости от сезона праздников
- Увеличение или уменьшение масштаба карты в зависимости от выбранного уровня масштабирования
Мы рассмотрим, как кодировать такую логику, когда рассмотрим условные операторы в будущей статье. А пока давайте посмотрим на быстрый пример:
А пока давайте посмотрим на быстрый пример:
Машина остановлена.
const btn = document.querySelector ('кнопка');
const txt = document.querySelector ('p');
btn.addEventListener ('щелчок', updateBtn);
function updateBtn () {
if (btn.textContent === 'Запустить машину') {
btn.textContent = 'Остановить машину';
txt.textContent = 'Машина запустилась!';
} еще {
btn.textContent = 'Запустить машину';
текст.textContent = 'Машина остановлена.';
}
}
Открыть в новом окне
Вы можете увидеть, что оператор равенства используется внутри функции updateBtn () . В этом случае мы не проверяем, имеют ли два математических выражения одно и то же значение - мы проверяем, содержит ли текстовое содержимое кнопки определенную строку, - но действует тот же принцип. Если при нажатии кнопки в данный момент отображается надпись «Запустить машину», мы меняем ее метку на «Остановить машину» и обновляем ее соответствующим образом.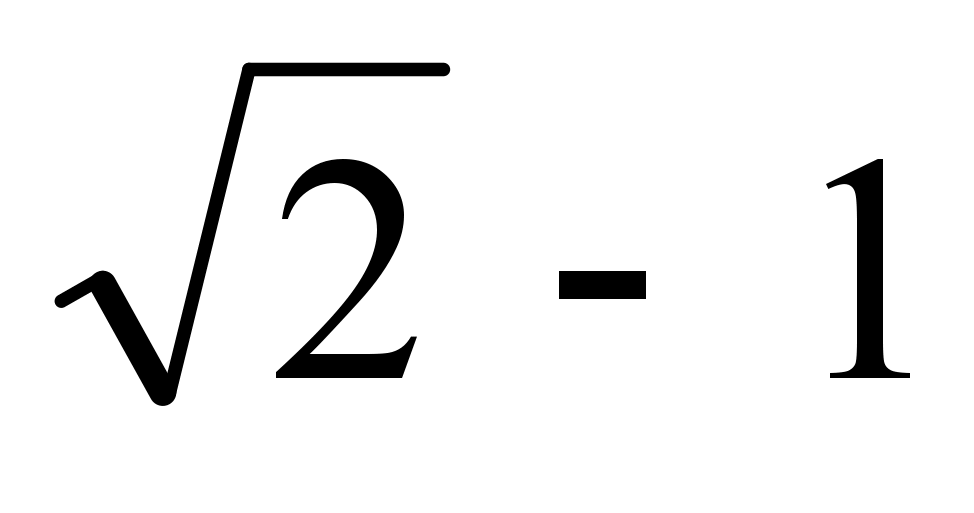 Если при нажатии кнопки в данный момент отображается сообщение «Остановить машину», мы снова переключаем дисплей.
Если при нажатии кнопки в данный момент отображается сообщение «Остановить машину», мы снова переключаем дисплей.
Примечание: Такой элемент управления, который переключается между двумя состояниями, обычно называется переключателем . Он переключает одно состояние на другое - свет включен, свет выключен и т. Д.
Вы дошли до конца этой статьи, но можете ли вы вспомнить самую важную информацию? Вы можете найти дополнительные тесты, чтобы убедиться, что вы сохранили эту информацию, прежде чем двигаться дальше - см. Проверка своих навыков: математика.
В этой статье мы рассмотрели основную информацию, которую вам нужно знать о числах в JavaScript на данный момент. Вы будете видеть числа, используемые снова и снова, на протяжении всего изучения JavaScript, так что сейчас неплохо избавиться от этого. Если вы один из тех людей, которым не нравится математика, вас может утешить тот факт, что эта глава была довольно короткой.
В следующей статье мы исследуем текст и то, как JavaScript позволяет нам манипулировать им.
Примечание: Если вам нравится математика и вы хотите узнать больше о том, как она реализована в JavaScript, вы можете найти более подробную информацию в основном разделе JavaScript MDN.Отличное место для начала - это статьи о числах и датах, а также о выражениях и операторах.
FAQ: Результаты функции mod (x, y)
Примечание. Этот FAQ основан на вопросе и ответах, которые появились на Статалист.Почему функция mod (x, y) иногда дает загадочные результаты? Почему
mod (0.3,0.1) не равно 0?| Заголовок | Результаты функции mod (x, y) | |
| Автор | Николас Дж.Кокс, Даремский университет, Великобритания Thomas J. Steichen |
Мод ( x , y ) функция (см. [FN] functions ) эквивалентна x - y *
этаж (х / у) . Здесь floor () возвращает
наибольшее целое число, не превышающее его аргумент, так что floor (2) = 2, этаж (2. 3) = 2, этаж (−2) = −2, и этаж (−2,3) = −3.Другими словами, это остаток на
разделив x на y. Очевидно, что 0,3 кратно 0,1 и что
результат должен быть 0, но с учетом
3) = 2, этаж (−2) = −2, и этаж (−2,3) = −3.Другими словами, это остаток на
разделив x на y. Очевидно, что 0,3 кратно 0,1 и что
результат должен быть 0, но с учетом
. дисплей мод (0.3,0.1)
Stata показывает 0,1.
Это ошибка? Не совсем, но вряд ли результат будет таким, каким вы хотеть. Это происходит потому, что int (0.3 / 0.1) = 2 для машинной точности и а не 3, как ожидалось из обычной арифметики. Следовательно, 0,1 отображается как остаток или модуль.
Поясним более подробно. Такие числа, как 0,3 и 0,1, нельзя рассматривать как
точные двоичные эквиваленты; см. [U] 13.12 Точность и проблемы
в нем . Чтобы показать это, мы будем использовать% 21.18f в качестве формата отображения, который
позволяет нам видеть базовые значения с почти такой же точностью, что и Stata.
(Stata также предоставляет специальный формат% 21x, который показывает точное значение
в специальном шестнадцатеричном формате, который вы, возможно, захотите изучить. Этот формат
был впервые доступен в конце цикла разработки Stata 6.0. См. Также [U] 12.2 Числа и [U] 12.5.1 Числовые форматы .)
Этот формат
был впервые доступен в конце цикла разработки Stata 6.0. См. Также [U] 12.2 Числа и [U] 12.5.1 Числовые форматы .)
. di% 21.18f .3
0,299999999999999990
. di% 21.18f .1
0,100000000000000010
Здесь мы используем практически каждый бит, чтобы получить ближайшую машинную десятичную дробь. приближение мы можем к истинным десятичным дробям 0,3 и 0,1. Ясно, что ни номер представлен именно в автомате.
Если мы сравним
.di% 21.18f .3 / .1
2,999999999999999600
с участием
. di% 21.18f 3
3.000000000000000000
также ясно, что в машинной десятичной системе число 3 не равно 0,3 / 0,1. Этот
происходит потому, что 3 можно точно представить, а 0,3 / 0,1 - это просто
smidgen меньше из-за аппроксимации, необходимой для представления 0,3 и 0,1.
Ясно, что целая часть 0,3 / 0,1 = 2,999999999999999600 равна 2, причем
следствие, что mod (0. 3,0.1) отображается как 0,1 (точнее, это
0,099999999999999978 в машинной десятичной системе, но отображение Stata по умолчанию
формат округляет до 0,1).
3,0.1) отображается как 0,1 (точнее, это
0,099999999999999978 в машинной десятичной системе, но отображение Stata по умолчанию
формат округляет до 0,1).
Пользователи могут получить лучшие результаты, используя float () и round () , но возможно, лучший совет - предостережение: лучше не пробовать точность работать с дробными аргументами в mod () . Тебе может быть лучше посоветовал поработать над эквивалентной задачей, используя целые числа.
Если вам нужны более подробные сведения, введите точность поиска в Stata, чтобы определить различные ресурсы.Сообщения в блоге Уильяма Гулда: особенно рекомендуется.
Функция абсолютного значения, функция модуля
| x | всегда положительный, независимо от того, начали ли мы с + x или -x.
| г | всегда положительный, независимо от того, начали ли мы с + y или -y.
Сложив или вычтя их без абсолютных значений, вы получите один из четырех возможных результатов:
(+ x) + (+ y) или (+ x) + (-y) или (-x) + (+ y) или (-x) + (-y)
Поскольку оба имеют одинаковый знак (xy> 0), это первое утверждение всегда верно, оно верно даже для x> y во втором утверждении. Но второе утверждение, | x | - | y | = | x - y | тогда xy <0 кажется ложным.
Но второе утверждение, | x | - | y | = | x - y | тогда xy <0 кажется ложным.
Сначала займемся сложением ... Мы будем использовать x = 3 и y = 10 для наших примеров:
Оба отрицательные: -3 + (-10) = -13.
Оба положительных: 3 + 10 = 13.
Итак, пока оба числа имеют одинаковый знак (именно это означает xy> 0), ответ будет ± 13. Как только вы поместите это в абсолютное значение, оба результата будут положительными 13 и | x | + | y | = | x + y |
Значение | -3 | + | -10 | = 3 + 10 = 13 (индивидуальные значения абс) и
| (-3) + (-10) | = | -13 | = 13 (объединить в один абс) (13 = 13, так что работает)
| x | + | y | = | х + у | если оба числа имеют одинаковый знак (xy> 0)
Здесь оба числа положительные:
| 3 | + | 10 | = 3 + 10 = 13 и | 3 + 10 | = | 13 | = 13 (13 = 13 так работает)
С другой стороны, если одно положительное, а другое отрицательное, вы, по сути, вычитаете.
Например, -3 + 10 = 7 или 3 + (-10) = -7
С разными знаками вы получите +7 или -7 в зависимости от порядка вычитания. Если вы поместите любой из этих результатов в абсолютное значение, вы получите ПОЛОЖИТЕЛЬНЫЙ 7.
Все четыре случая с вычитанием, когда x Оба положительных: | 3 | - | 10 | = 3 - 10 = -7 и вместе внутри | 3-10 | = | -7 | = 7 (-7 ≠ 7 так не получится!) Оба отрицательных: | -3 | - | -10 | = 3 - 10 = -7 и вместе внутри | -3 - (-10) | = | 7 | = 7 (-7 ≠ 7 так не получится!) Разные знаки (xy <0): Положения "3" и "10": | -3 | - | 10 | = 3 - 10 = -7 и вместе внутри | -3 - 10 | = | -13 | = 13 (-7 ≠ 13 так не получится!) Положения "10" и "3": | 3 | - | -10 | = 3 - 10 = -7 и вместе внутри | 3 - (-10) | = | 3 + 10 | = 13 (-7 ≠ 13 так не получится!) Второй, | x | - | y | = | x - y | when xy <0 не работает ни в одном из четырех случаев, пока x (примечание: | x | - | y | может дать отрицательный результат (когда | x | <| y |), а | x - y | всегда будет положительным) Но, если мы потребуем, чтобы x> y, так что теперь x = 10 и y = 3, мы имеем это: Обе позиции: | 10 | - | 3 | = 10 - 3 = 7 и | 10 - 3 | = | 7 | = 7 (7 = 7 так работает) Оба нег: | -10 | - | -3 | = 10 - 3 = 7 и | -10 - (-3) | = | -10 + 3 | = | -7 | = 7 (7 = 7 так работает) Положения "10" и "3": | -10 | - | 3 | = 10 - 3 = 7 и | -10 - (+3) | = | -13 | = 13 (7 ≠ 13, так что НЕ РАБОТАЕТ!) Положения «10» и отрицательные «3»: | 10 | - | - = 3 | = 10 - 3 = 7 и | 10 - (-3) | = | 10 + 3 | = | 13 | = 13 (7 ≠ 13, так что НЕ РАБОТАЕТ!) Таким образом, вторая формулировка исходной задачи, вероятно, должна сказать xy> 0 AND x> y. Я нашел это в Интернете - истинное утверждение: | x-y |> | x | - | y | для xy <0. Это НЕРАВЕНСТВО верно, УРАВНЕНИЕ во второй строке неверно. Числа чрезвычайно распространены в программировании. Они используются для представления таких вещей, как размер экрана, географическое положение, деньги и очки, количество времени, которое проходит в видео, положение игровых аватаров и цвета посредством присвоения числовых кодов. Умение эффективно выполнять математические операции в программировании - важный навык, который нужно развивать, потому что вам придется часто работать с числами. Хотя понимание математики на высоком уровне, безусловно, может помочь вам стать лучшим программистом, это не является обязательным условием. Если у вас нет математического образования, попробуйте рассматривать математику как инструмент для достижения того, чего вы хотите достичь, и как способ улучшить свое логическое мышление. Мы будем работать с двумя наиболее часто используемыми числовыми типами данных Python, целыми числами и с плавающей запятой : В этом руководстве будут рассмотрены операторы, которые можно использовать с числовыми типами данных в Python. У вас должен быть установлен Python 3 и настроена среда программирования на вашем компьютере или сервере. Если у вас не настроена среда программирования, вы можете обратиться к руководствам по установке и настройке для локальной среды программирования или среды программирования на вашем сервере, соответствующей вашей операционной системе (Ubuntu, CentOS, Debian и т. Д.)) Оператор - это символ или функция, обозначающая операцию. Например, в математике знак «плюс» или «+» - это оператор, обозначающий сложение. В Python мы увидим некоторые знакомые операторы, перенесенные из математики, но другие операторы, которые мы будем использовать, специфичны для компьютерного программирования. Вот краткая справочная таблица математических операторов в Python. В этом руководстве мы рассмотрим все следующие операции. Мы также рассмотрим составные операторы присваивания, включая В Python операторы сложения и вычитания работают аналогично математике. Фактически, вы можете использовать язык программирования Python в качестве калькулятора. Информация: Чтобы следовать примеру кода в этом руководстве, откройте интерактивную оболочку Python в своей локальной системе, выполнив команду Давайте рассмотрим несколько примеров, начиная с целых чисел: Выход Вместо того, чтобы передавать целые числа непосредственно в оператор Выход Поскольку целые числа могут быть как положительными, так и отрицательными (а также 0), мы можем сложить отрицательное число с положительным числом: Выход Сложение будет вести себя аналогично с числами с плавающей запятой: Выход Поскольку мы сложили вместе два числа с плавающей запятой, Python вернул значение с плавающей запятой с десятичным разрядом. Синтаксис вычитания такой же, как и для сложения, за исключением того, что вы измените свой оператор со знака плюс ( Выход Здесь мы вычли целое число из числа с плавающей запятой.Python вернет число с плавающей запятой, если хотя бы одно из чисел, участвующих в уравнении, является числом с плавающей запятой. Унарное математическое выражение состоит только из одного компонента или элемента, а в Python знаки плюс и минус могут использоваться как один элемент в паре со значением, чтобы вернуть идентичность значения ( Знак плюс, хотя и не используется обычно, указывает на идентичность значения.Мы можем использовать знак плюса с положительными значениями: Выход Когда мы используем знак плюса с отрицательным значением, он также возвращает идентичность этого значения, и в этом случае это будет отрицательное значение: Выход При отрицательном значении знак «плюс» возвращает то же отрицательное значение. Знак минус также меняет знак значения.Итак, когда мы передаем положительное значение, мы обнаруживаем, что знак минус перед значением возвращает отрицательное значение: Выход В качестве альтернативы, когда мы используем унарный оператор знака минус с отрицательным значением, будет возвращено положительное значение: Выход Унарные арифметические операции, обозначенные знаком плюс и минус, возвращают либо идентичность значения в случае Как сложение и вычитание, умножение и деление будут очень похожи на то, как они действуют в математике. Знак, который мы будем использовать в Python для умножения, - Вот пример умножения в Python с двумя значениями с плавающей запятой: Выход Когда вы делите в Python 3, ваше частное всегда будет возвращаться как число с плавающей запятой, даже если вы используете два целых числа: Выход Это одно из основных различий между Python 2 и Python 3. Подход Python 3 дает дробный ответ, поэтому при использовании Python 2 В Python 3 вы можете использовать Оператор Давайте посмотрим на модуль в действии: Выход Чтобы разбить это, 85, деленное на 15, возвращает частное 5 с остатком 10. Если мы используем два числа с плавающей запятой по модулю, для остатка будет возвращено значение с плавающей запятой: Выход В случае деления 36,0 на 6,0 остатка нет, поэтому возвращается значение Оператор Давайте посмотрим на пример с переменными: Увеличение числа с плавающей запятой В Python, как и в математике, мы должны помнить, что операторы будут оцениваться в порядке приоритета, а не слева направо или справа налево. Если мы посмотрим на следующее выражение: Мы можем читать его слева направо, но помните, что сначала будет выполнено умножение, поэтому, если мы вызовем Выход Это потому, что Если вместо этого мы хотим добавить значение Выход Один из способов запомнить порядок работы - использовать аббревиатуру PEMDAS : Возможно, вы знакомы с другим сокращением порядка операций, например BEDMAS или BODMAS .Какую бы аббревиатуру вы ни выбрали, постарайтесь помнить ее при выполнении математических операций в Python, чтобы получить ожидаемые результаты. Самый распространенный оператор присваивания - тот, который вы уже использовали: знак равенства При программировании обычно используются составные операторы присваивания, которые выполняют операцию над значением переменной, а затем присваивают полученное новое значение этой переменной. Эти составные операторы объединяют арифметический оператор с оператором Выход Сначала мы устанавливаем переменную Операторы составного присваивания часто используются в случае для циклов , которые вы будете использовать, если хотите повторить процесс несколько раз: Выход С помощью цикла for мы смогли автоматизировать процесс оператора Python имеет составной оператор присваивания для каждого из арифметических операторов, обсуждаемых в этом руководстве: Операторы составного присваивания могут быть полезны, когда что-то нужно постепенно увеличивать или уменьшать, или когда вам нужно автоматизировать определенные процессы в вашей программе. В этом руководстве описаны многие операторы, которые вы будете использовать с целочисленными и числовыми типами данных с плавающей запятой. Если вы хотите продолжить читать о числах в Python, вы можете перейти к встроенным функциям Python 3 для работы с числами. Чтобы узнать больше о других типах данных, взгляните на Общие сведения о типах данных в Python 3 и узнайте о том, как преобразовывать типы данных, прочитав Как преобразовывать типы данных в Python 3. Похоже, вы используете устройство с "узкой" шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). В этом разделе мы собираемся найти область между двумя кривыми.На самом деле есть два случая, которые мы собираемся рассмотреть. В первом случае мы хотим определить область между \ (y = f \ left (x \ right) \) и \ (y = g \ left (x \ right) \) на интервале \ (\ left [{ яркий]\). Мы также будем предполагать, что \ (f \ left (x \ right) \ ge g \ left (x \ right) \). Взгляните на следующий рисунок, чтобы понять, на что мы изначально будем смотреть. В разделе «Формулы площади и объема» главы «Дополнительно» мы вывели следующую формулу для площади в данном случае. Прежде всего, что мы подразумеваем под «замкнутой территорией». Это означает, что интересующая нас область должна иметь одну из двух кривых на каждой границе области. Итак, вот график двух функций с заштрихованной областью. Обратите внимание, что мы не берем какую-либо часть области справа от точки пересечения этих двух графиков. В этой области нет границы с правой стороны, поэтому она не является частью замкнутой области.2} \) является верхней функцией, и они будут правильными для подавляющего большинства \ (x \) 's. Однако в данном случае это младшая из двух функций. Пределы интегрирования для этого будут точками пересечения двух кривых. В этом случае довольно легко увидеть, что они будут пересекаться в точках \ (x = 0 \) и \ (x = 1 \), так что это пределы интегрирования. Итак, интеграл, который нам потребуется вычислить, чтобы найти площадь, равен Прежде чем перейти к следующему примеру, следует отметить несколько важных моментов. Во-первых, почти во всех этих задачах граф требуется. Часто ограничивающая область, которая дает пределы интегрирования, трудно определить без графика. Кроме того, без графика часто бывает трудно определить, какая из функций является верхней, а какая нижней функцией.Это особенно верно в случаях, подобных последнему примеру, где ответ на этот вопрос фактически зависел от диапазона значений \ (x \), которые мы использовали. Наконец, в отличие от площади под кривой, которую мы рассматривали в предыдущей главе, площадь между двумя кривыми всегда будет положительной. Если мы получим отрицательное число или ноль, мы можем быть уверены, что где-то допустили ошибку, и нам нужно будет вернуться и найти ее. Также обратите внимание, что иногда вместо того, чтобы говорить регион, заключенный в, мы говорим регион, ограниченный. В этом случае последние две части информации, \ (x = 2 \) и ось \ (y \), сообщают нам правую и левую границы области. Также напомним, что ось \ (y \) задается линией \ (x = 0 \). Вот график с заштрихованной областью. Здесь, в отличие от первого примера, две кривые не пересекаются. Вместо этого мы полагаемся на две вертикальные линии, чтобы ограничить левую и правую стороны области, как мы отметили выше Вот интеграл, который даст площадь.2} + 10 \) и \ (y = 4x + 16 \).
Показать решение В этом случае точки пересечения (которые нам в конечном итоге понадобятся) будет нелегко идентифицировать по графику, поэтому давайте продолжим и получим их сейчас. Обратите внимание, что для большинства этих проблем вы не сможете точно определить точки пересечения на графике, и вам придется определять их вручную. Итак, похоже, что две кривые пересекутся в точках \ (x = - 1 \) и \ (x = 3 \).Если они нам нужны, мы можем получить значения \ (y \), соответствующие каждому из них, вставив значения обратно в любое из уравнений. Мы предоставим вам проверить, что координаты двух точек пересечения на графике равны \ (\ left ({- 1,12} \ right) \) и \ (\ left ({3,28} \ right) ) \). Также обратите внимание: если вы не умеете строить графики, знание точек пересечения может помочь хотя бы в начале построения графика. Вот график региона. С помощью графика мы теперь можем определить верхнюю и нижнюю функцию, и теперь мы можем найти замкнутую область.2} + 10 \), \ (y = 4x + 16 \), \ (x = - 2 \) и \ (x = 5 \).
Показать решение Итак, функции, используемые в этой задаче, идентичны функциям из первой задачи. Вот график этого региона. Хорошо, у нас тут небольшая проблема.Наша формула требует, чтобы одна функция всегда была верхней функцией, а другая функция всегда была нижней функцией, а здесь этого явно нет. Однако на самом деле проблема не в этом, как может показаться на первый взгляд. Есть три области, в которых одна функция всегда является верхней функцией, а другая всегда является нижней функцией. Итак, все, что нам нужно сделать, это найти площадь каждой из трех областей, что мы можем сделать, а затем сложить их все. Вот площадь.5 \\ & = \ frac {{14}} {3} + \ frac {{64}} {3} + \ frac {{64}} {3} \\ & = \ frac {{142}} {3 } \ end {align *} \]
Пример 5 Определите площадь области, заключенной в \ (y = \ sin x \), \ (y = \ cos x \), \ (x = \ frac {\ pi} {2} \) и \ ( у \) - ось. Итак, похоже, что две кривые пересекутся в точках \ (y = - 2 \) и \ (y = 4 \), или, если нам нужны полные координаты, они будут: \ (\ left ({- 1, - 2 } \ right) \) и \ (\ left ({5,4} \ right) \). Вот эскиз двух кривых. Если мы не будем осторожны, у нас возникнет серьезная проблема. До сих пор мы использовали верхнюю функцию и нижнюю функцию. Для этого обратите внимание, что на самом деле есть две части региона, которые будут выполнять разные нижние функции. В диапазоне \ (\ left [{- 3, - 1} \ right] \) парабола фактически является одновременно верхней и нижней функцией. Чтобы использовать формулу, которую мы использовали до сих пор, нам нужно решить параболу для \ (y \).Это дает, , где «+» означает верхнюю часть параболы, а «-» - нижнюю часть. , и в нашем случае у нас есть одна функция, которая всегда слева, а другая всегда справа. Так что в данном случае это определенно правильный путь. Обратите внимание, что нам нужно будет переписать уравнение линии, поскольку оно должно быть в форме \ (x = f \ left (y \ right) \), но это достаточно легко сделать.4 \\ & = 18 \ end {align *} \] Это то же самое, что мы получили, используя первую формулу, и это было определенно проще, чем первый метод. Итак, в этом последнем примере мы видели случай, когда мы могли использовать любую формулу для определения площади. Однако второе было определенно легче. Студенты часто приходят в класс по математике с мыслью, что единственный простой способ работать с функциями - использовать их в форме \ (y = f \ left (x \ right) \). Функция модуля дает величину числа независимо от его знака. Ее также называют функцией абсолютного значения. В математике модуль действительного числа x задается функцией модуля , обозначаемой | x |. Это дает неотрицательное значение x. Модуль или абсолютное значение числа также рассматривается как расстояние числа от начала координат или нуля. В этой статье мы узнаем об определении функции модуля, вычислении модуля для чисел, переменных и многочленов, а также решенных примерах и вопросах функции модуля.
Как делать математику в Python 3 с операторами
Введение
-1 , 0 , 1 ,…).
9.0 или -2.25 ). Предварительные требования
Операторы

Эксплуатация Что возвращает х + у Сумма x и y х - у Разница между x и y -х Изменен знак x + х Идентичность x х * у Произведение x и y х / у Частное x и y х // у Коэффициент от разделения этажей x и y х% у Остаток от x / y х ** у x до y power + = и * = , которые объединяют арифметический оператор с оператором = .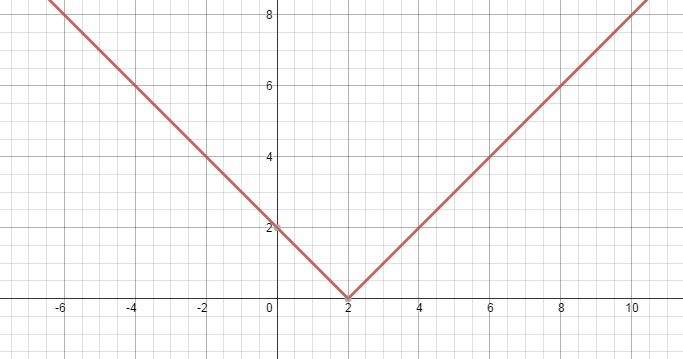
Сложение и вычитание
python3 . Затем вы можете копировать, вставлять или редактировать примеры, добавляя их после приглашения >>> .
печать (1 + 5)
print , мы можем инициализировать переменные для обозначения целочисленных значений:
а = 88
б = 103
печать (a + b)
с = -36
d = 25
печать (c + d)
е = 5.  5
f = 2,5
печать (e + f)
5
f = 2,5
печать (e + f)
+ ) на знак минус (–):
г = 75,67
в = 32
печать (г - ч)
Унарные арифметические операции
+ ) или изменить знак значения.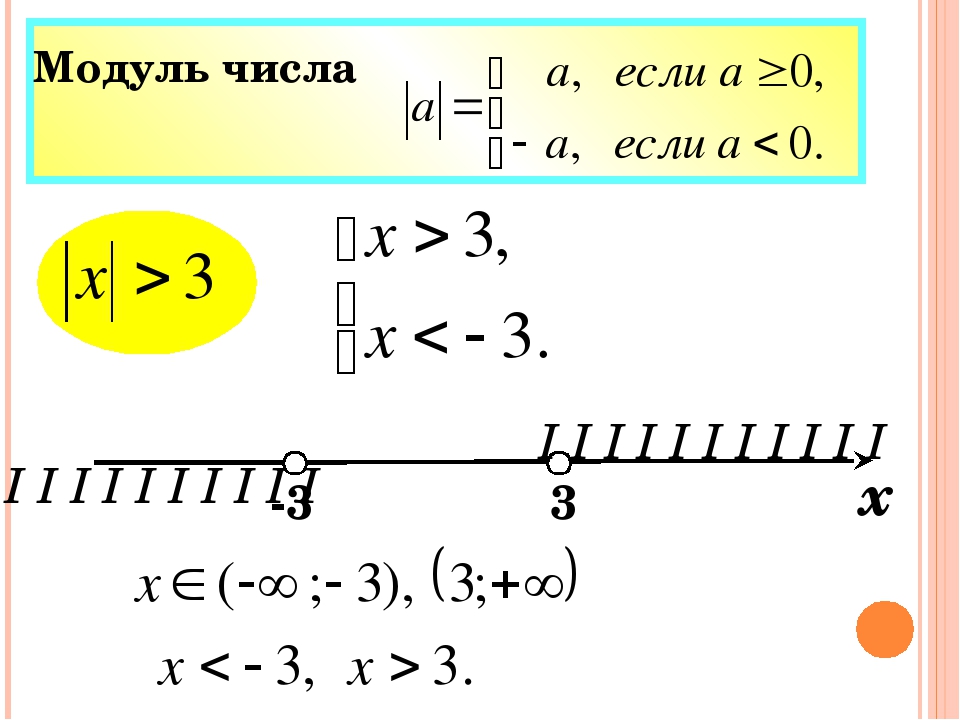 (
( - ).
я = 3,3
печать (+ я)
Дж = -19
печать (+ j)
я = 3,3
печать (-i)
Дж = -19
печать (-j)
+ i , либо знак, противоположный значению, как в случае -i .
Умножение и деление
* , а знак, который мы будем использовать для деления, - /.
к = 100,1
l = 10,1
печать (к * л)
м = 80
п = 5
печать (м / п)
/ для деления 11 на 2 будет возвращено частное 5,5 . В Python 2 частное, возвращаемое для выражения
В Python 2 частное, возвращаемое для выражения 11/2 , составляет 5 ./ выполняет деление этажа , где для частного x возвращаемое число является наибольшим целым числом, меньшим или равным x .Если вы запустите приведенный выше пример print (80/5) с Python 2 вместо Python 3, на выходе вы получите 16 без десятичного разряда. // для выполнения разделения этажа. Выражение 100 // 40 вернет значение 2 . Разделение этажей полезно, когда вам нужно, чтобы частное было целым. по модулю
% представляет собой операцию по модулю, которая возвращает остаток, а не частное после деления.Это полезно, например, для поиска чисел, кратных одному и тому же числу.
o = 85
р = 15
печать (o% p)
 Здесь возвращается значение
Здесь возвращается значение 10 , потому что оператор по модулю возвращает остаток выражения деления.
q = 36.0
г = 6,0
печать (o% p)
0,0 . Мощность
** в Python используется для возведения числа слева в степень правой степени. То есть в выражении 5 ** 3 5 возводится в 3-ю степень. В математике мы часто видим это выражение в виде 5³, а на самом деле 5 умножается само на себя в 3 раза.В Python мы получили бы тот же результат 125 , запустив либо 5 ** 3 , либо 5 * 5 * 5 .
с = 52,25
t = 7
печать (дерьмо)
1063173305051.  292
292
52,25 до степени 7 с помощью оператора ** приводит к возврату большого значения с плавающей запятой. Приоритет оператора
и = 10 + 10 * 5
print (u) , мы получим следующее значение:
10 * 5 оценивается как 50 , а затем мы добавляем 10 , чтобы вернуть 60 в качестве окончательного результата. 10 к 10 , а затем умножить эту сумму на 5 , мы можем использовать круглые скобки, как в математике:
и = (10 + 10) * 5
печать (u)
Заказать Письмо Стенды для 1 п. 
P аренте 2 E E xponent 3 м M повторение 4 Д D ivision 5 А A ddition 6 ю. S убирание Операторы присваивания
= . Оператор присваивания
Оператор присваивания = присваивает значение справа переменной слева. Например, v = 23 присваивает значение целого числа 23 переменной v . = , поэтому для сложения мы объединим + с = , чтобы получить составной оператор + = . Давайте посмотрим, как это выглядит:
Вт = 5
ш + = 1
печать (ш)
w равной значению 5 , затем мы использовали составной оператор присваивания + = , чтобы добавить правое число к значению левой переменной , а затем присвоить результат Вт .
для x в диапазоне (0, 7):
х * = 2
печать (х)
* = , который умножил переменную w на число 2 , а затем присвоил результат переменной w для следующей итерации для цикла.
y + = 1 # сложить и присвоить значение
y - = 1 # вычесть, затем присвоить значение
y * = 2 # умножить и присвоить значение
y / = 3 # разделить, затем присвоить значение
y // = 5 # разделить этаж, затем присвоить значение
y ** = 2 # увеличить до степени, затем присвоить значение
y% = 3 # вернуть остаток, затем присвоить значение

Заключение
Исчисление I - площадь между кривыми
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Раздел 6-2: Площадь между кривыми
 2} \) и \ (y = \ sqrt x \).Показать решение
2} \) и \ (y = \ sqrt x \).Показать решение 2} \, dx}} \\ & = \ left.1 \\ & = \ frac {1} {3} \ end {align *} \]
2} \, dx}} \\ & = \ left.1 \\ & = \ frac {1} {3} \ end {align *} \] 2}}} \), \ (y = x + 1 \), \ (x = 2 \) и ось \ (y \) -.
Показать решение
2}}} \), \ (y = x + 1 \), \ (x = 2 \) и ось \ (y \) -.
Показать решение 2} - 4x - 6 & = 0 \\ 2 \ left ({x + 1} \ right) \ left ({x - 3} \ right) & = 0 \ end {align *} \]
2} - 4x - 6 & = 0 \\ 2 \ left ({x + 1} \ right) \ left ({x - 3} \ right) & = 0 \ end {align *} \] Разница в том, что мы расширили ограниченную область за пределы точек пересечения. Поскольку это те же функции, которые мы использовали в предыдущем примере, мы не будем беспокоиться о повторном поиске точек пересечения.
Разница в том, что мы расширили ограниченную область за пределы точек пересечения. Поскольку это те же функции, которые мы использовали в предыдущем примере, мы не будем беспокоиться о повторном поиске точек пересечения. 2} - 2y - 8 \\ 0 & = \ left ({y - 4} \ right) \ left ({y + 2} \ right) \ end {align *} \]
2} - 2y - 8 \\ 0 & = \ left ({y - 4} \ right) \ left ({y + 2} \ right) \ end {align *} \] {{\, 5}} {{- x + 1 \, dx}} \\ & = \ left.{{\, d}} {{\ left (\ begin {array} {c} {\ mbox {right}} \\ {\ mbox {function}} \ end {array} \ right) - \ left (\ begin {array} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5in} c \ le y \ le d \ ]
{{\, 5}} {{- x + 1 \, dx}} \\ & = \ left.{{\, d}} {{\ left (\ begin {array} {c} {\ mbox {right}} \\ {\ mbox {function}} \ end {array} \ right) - \ left (\ begin {array} {c} {\ mbox {left}} \\ {\ mbox {function}} \ end {array} \ right) \, dy}}, \ hspace {0,5in} c \ le y \ le d \ ] 2} + 4y + 6 \, dy} } \\ & = \ left.3 = \ frac {{64}} {3} \ end {align *} \] Функция модуля упругости
2} + 4y + 6 \, dy} } \\ & = \ left.3 = \ frac {{64}} {3} \ end {align *} \] Функция модуля упругости - формула, график, свойства, примеры
Что такое функция модуля?
Функция модуля, которую также называют абсолютным значением функции, дает величину или абсолютное значение числа независимо от того, положительное или отрицательное число. Он всегда дает неотрицательное значение любого числа или переменной. Функция модуля обозначается как y = | x | или f (x) = | x |, где f: R → R и x ∈ R.
Функция модуля обозначается как y = | x | или f (x) = | x |, где f: R → R и x ∈ R.
| x | - модуль x, где x - действительное число. Если x неотрицательно, тогда f (x) будет иметь то же значение x. Если x отрицательно, тогда f (x) будет величиной x, то есть f (x) = -x, если x отрицательно. Подведем итог приведенной ниже формуле функции модуля.
Формула функции модуля упругости
Значение функции модуля всегда неотрицательно. Если f (x) является модульной функцией, то мы имеем:
- Если x положительный, то f (x) = x
- Если x = 0, то f (x) = 0
- Если x <0, то f (x) = -x
Это означает, что если значение x больше или равно 0, то функция модуля принимает фактическое значение, но если x меньше 0, функция принимает минус фактического значения «x».
Область и диапазон функции модуля
Мы можем применить функцию модуля к любому действительному числу. Диапазон функции модуля - это набор неотрицательных действительных чисел, который обозначается как (0, ∞), а область определения функции модуля - R (где R относится к набору всех положительных действительных чисел). Следовательно, область значений функции модуля - R , а диапазон - (0, ∞).
Следовательно, область значений функции модуля - R , а диапазон - (0, ∞).
Применение функции модуля
Теперь, когда мы знаем формулу функции модуля, давайте рассмотрим несколько примеров, чтобы понять ее применение.Шаги для расчета функции модуля приведены ниже:
Пример: Рассмотрим функцию модуля f (x) = | x |.
- Если x = - 3, то y = f (x) = f (−3) = - (- 3) = 3, здесь x меньше 0.
- Если x = 4, то y = f (x) = f (4) = 4, здесь x больше 0
- Если x = 0, то y = f (x) = f (0) = 0, здесь x равно 0
Подводя итог, можно сказать, что модуль отрицательного числа и положительного числа - это одно и то же число.
График функции модуля
Теперь давайте посмотрим, как построить график для функции модуля.Давайте рассмотрим x как переменную, принимающую значения от -5 до 5. При вычислении модуля для положительных значений «x» линия на графике будет «y = x», а для отрицательных значений «x», линия на графике имеет вид y = -x.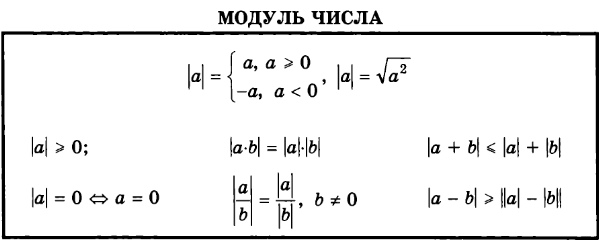
| х | f (x) = | x | |
|---|---|
| -5 | 5 |
| -4 | 4 |
| -3 | 3 |
| -2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
Свойства функции модуля
Теперь, когда у нас есть формула для функции модуля и график функции модуля, давайте теперь исследуем свойства функции модуля:
Производная и интеграл функции упругости
Поскольку мы знаем, что функция модуля f (x) = | x | равно x, если x> 0, и -x, если x <0, поэтому производная функции модуля равна 1, если x> 0, и -1, если x <0.Производная функции модуля не определена для x = 0.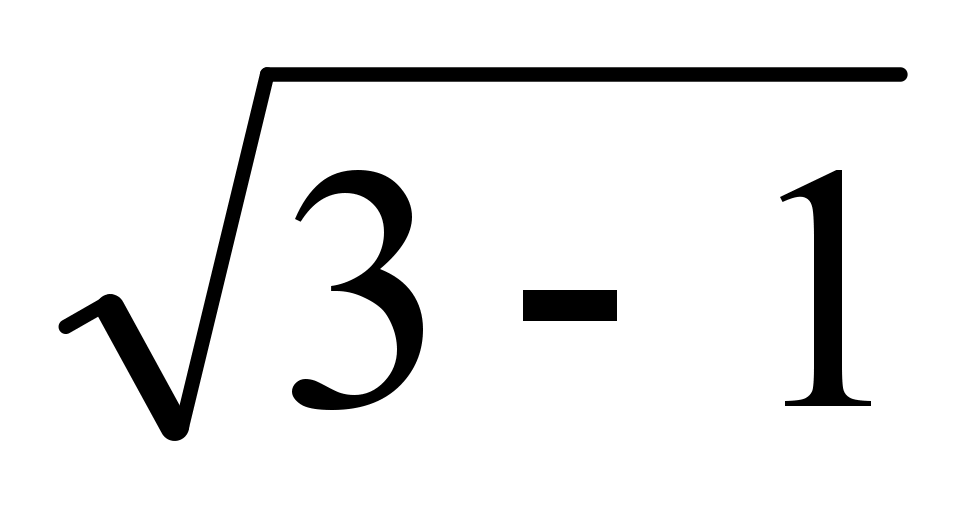 Следовательно, производная функции модуля может быть записана как d (| x |) / dx = x / | x | , для всех значений x и x, не равных 0.
Следовательно, производная функции модуля может быть записана как d (| x |) / dx = x / | x | , для всех значений x и x, не равных 0.
Используя формулу функции модуля и формулы интегрирования, интеграл функции модуля равен (1/2) x 2 + C, если x ≥ 0, а его интеграл равен - (1/2) x 2 + C, если x <0. Следовательно, интегрирование функции модуля может быть выполнено следующим образом:
- ∫ | x | dx = (1/2) x 2 + C, если x ≥ 0
- ∫ | x | dx = - (1/2) x 2 + C, если x <0
Важные примечания к функции модуля
- Функция модуля также называется функцией абсолютного значения и представляет собой абсолютное значение числа.Обозначается он | x |.
- Область модульных функций - это набор всех действительных чисел.
- Диапазон функций модуля - это набор всех действительных чисел, больших или равных 0.
- Вершина графа модулей y = | x | равно (0,0).

Тема, связанная с функцией модуля
Часто задаваемые вопросы о модульной функции
Что такое функция модуля?
Функция модуля, которую также называют абсолютным значением функции, дает величину или абсолютное значение числа независимо от того, положительное или отрицательное число.Функция модуля обозначается как y = | x | или f (x) = | x |, где f: R → R и x ∈ R.
Каковы область и диапазон функции модуля?
Область определения функции модуля - это R (где R относится к набору всех положительных действительных чисел), а диапазон функции модуля - это набор неотрицательных действительных чисел, который обозначается как (0, ∞).
Что такое интеграция функции модуля?
Интеграция функции модуля может быть обозначена как:
- ∫ | x | dx = (1/2) x 2 + C, если x ≥ 0
- ∫ | x | dx = - (1/2) x 2 + C, если x <0
Как отличить функцию модуля упругости?
Поскольку мы знаем, что функция модуля f (x) = | x | равно x, если x> 0, и -x, если x <0, поэтому производная функции модуля равна 1, если x> 0, и -1, если x <0. Производная функции модуля не определена для x = 0. Следовательно, производная функции модуля равна x / | x |, x не равна 0.
Производная функции модуля не определена для x = 0. Следовательно, производная функции модуля равна x / | x |, x не равна 0.
Всегда ли функция модуля положительна?
Модуль положительного числа положительный. Модуль отрицательного числа получается игнорированием знака минус. Таким образом, функция модуля всегда имеет положительные ненулевые значения.
Почему функция модуля упругости не дифференцируема?
Функция модуля | x | не дифференцируема в точке x = 0, поскольку график Mod (x) имеет острую точку в точке x = 0.Кроме того, левый предел и правый предел не равны при x = 0.
Как решить задачи функции модуля?
ПроблемыModulus Functions могут быть решены путем применения модуля к неотрицательному числу, а отрицательное число всегда приводит к одному и тому же числу.
Как вы изобразите функцию модуля упругости?
Взяв отрицательные значения, такие как (-1, -2, -3), и положительные значения, такие как (1,2,3) в соответствии с заданным уравнением модуля, мы можем нарисовать график функции модуля.
3.2: Производная как функция
Цели обучения
- Определите производную функцию заданной функции.
- Постройте производную функцию от графика заданной функции.
- Укажите связь между производными финансовыми инструментами и непрерывностью.
- Опишите три условия, когда функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке.Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Производные функции
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная.Мы можем формально определить производную функцию следующим образом.
Определение: производная функция
Пусть \ (f \) - функция. Производная функция , обозначаемая \ (f '\), является функцией, область определения которой состоит из таких значений \ (x \), что существует следующий предел:
\ [f '(x) = \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h}. \ label {derdef} \]
Функция \ (f (x) \) называется дифференцируемой в точке \ (a \), если существует \ (f '(a) \). В более общем смысле, функция называется дифференцируемой на \ (S \), если она дифференцируема в каждой точке открытого множества \ (S \), а дифференцируемая функция - это функция, в которой \ (f '( x) \) существует в своем домене.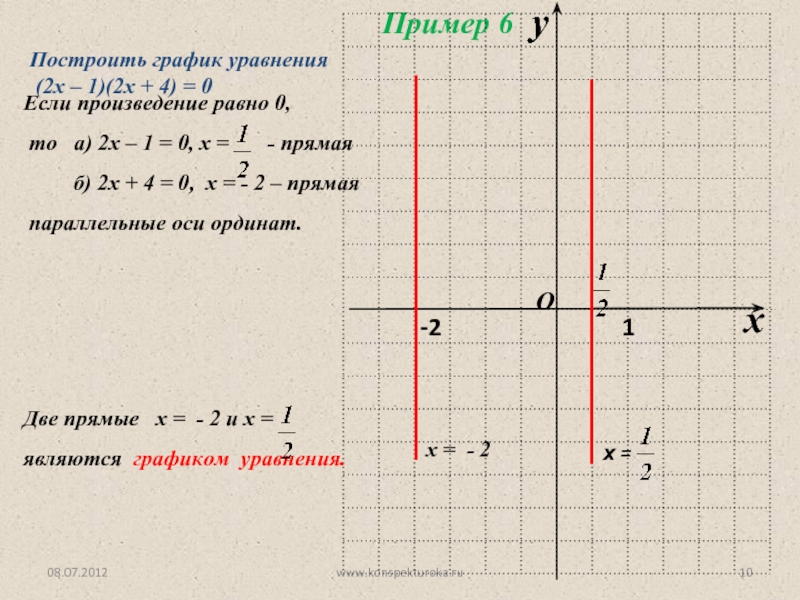
В следующих нескольких примерах мы используем уравнение \ ref {derdef}, чтобы найти производную функции.
Пример \ (\ PageIndex {1} \): поиск производной функции квадратного корня
Найдите производную от \ (f (x) = \ sqrt {x} \).
Решение
Начните непосредственно с определения производной функции.
Заменить \ (f (x + h) = \ sqrt {x + h} \) и \ (f (x) = \ sqrt {x} \) в \ (f '(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \).
| \ (е '(x) = \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} - \ sqrt {x}} {h} \) | ||
| \ (= \ displaystyle \ lim_ {h → 0} \ frac {\ sqrt {x + h} - \ sqrt {x}} {h} ⋅ \ frac {\ sqrt {x + h} + \ sqrt { x}} {\ sqrt {x + h} + \ sqrt {x}} \) | Умножьте числитель и знаменатель на \ (\ sqrt {x + h} + \ sqrt {x} \) без распределения в знаменателе. | |
| \ (= \ Displaystyle \ lim_ {h → 0} \ frac {h} {h \ left (\ sqrt {x + h} + \ sqrt {x} \ right)} \) | Умножьте числители и упростите.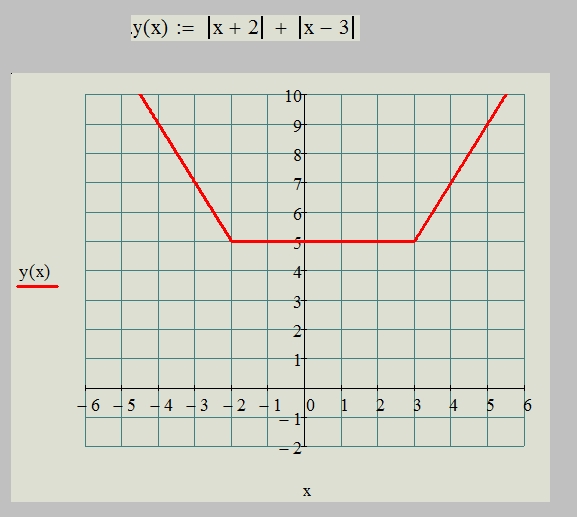 2 \).2−2x \ справа) = 2x − 2 \). Таким образом, для функции \ (y = f (x) \) каждое из следующих обозначений представляет производную от \ (f (x) \): 2 \).2−2x \ справа) = 2x − 2 \). Таким образом, для функции \ (y = f (x) \) каждое из следующих обозначений представляет производную от \ (f (x) \):\ (f '(x), \ quad \ dfrac {dy} {dx}, \ quad y', \ quad \ dfrac {d} {dx} \ big (f (x) \ big) \). Вместо \ (f '(a) \) мы также можем использовать \ (\ dfrac {dy} {dx} \ Big | _ {x = a} \). Нотация \ (\ dfrac {dy} {dx} \) (называемая нотацией Лейбница) довольно распространена в технике и физике. Чтобы лучше понять это обозначение, напомним, что производная функции в точке - это предел наклона секущих линий, когда секущие линии приближаются к касательной.Наклоны этих секущих часто выражаются в виде \ (\ dfrac {Δy} {Δx} \), где \ (Δy \) - разность значений \ (y \), соответствующая разнице в \ (x \) значения, которые выражаются как \ (Δx \) (Рисунок \ (\ PageIndex {1} \)). Таким образом, производная, которую можно представить как мгновенную скорость изменения \ (y \) по отношению к \ (x \), выражается как \ (\ Displaystyle \ frac {dy} {dx} = \ lim_ {Δx → 0} \ frac {Δy} {Δx} \). Построение графика производнойМы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку \ (f '(x) \) дает скорость изменения функции \ (f (x) \) (или наклон касательной линия к \ (f (x) \)). В примере \ (\ PageIndex {1} \) мы обнаружили, что для \ (f (x) = \ sqrt {x} \), \ (f '(x) = \ frac {1} {2 \ sqrt { Икс}}\).Если мы построим график этих функций на тех же осях, как на рисунке \ (\ PageIndex {2} \), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями. Во-первых, мы замечаем, что \ (f (x) \) увеличивается по всей своей области, что означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем \ (f '(x)> 0 \) для всех значений x в его области определения. Пример \ (\ PageIndex {3} \): эскиз производной с использованием функции Используйте следующий график \ (f (x) \), чтобы нарисовать график \ (f '(x) \).2−4 \). На каком интервале находится график \ (f '(x) \) над осью \ (x \)?
Производные финансовые инструменты и непрерывностьТеперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков. Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью.Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке. Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин. Дифференцируемость предполагает непрерывность Пусть \ (f (x) \) - функция и \ (a \) находится в ее области определения. Если \ (f (x) \) дифференцируема в \ (a \), то \ (f \) непрерывна в \ (a \). Проба Если \ (f (x) \) дифференцируемо в \ (a \), то \ (f '(a) \) существует и, если мы положим \ (h = x - a \), то \ (x = a + h \), и поскольку \ (h = xa \ to 0 \), мы можем видеть, что \ (x \ to a \). Затем \ [f '(a) = \ lim_ {h \ to 0} \ frac {f (a + h) -f (a)} {h} \ nonumber \] можно переписать как \ (F '(a) = \ displaystyle \ lim_ {x → a} \ frac {f (x) −f (a)} {x − a} \). Мы хотим показать, что \ (f (x) \) непрерывно в \ (a \), показав, что \ (\ displaystyle \ lim_ {x → a} f (x) = f (a). \) Таким образом, \ (\ begin {align *} \ displaystyle \ lim_ {x → a} f (x) & = \ lim_ {x → a} \; \ big (f (x) −f (a) + f (a) \ big) \\ [4pt] Следовательно, поскольку \ (f (a) \) определено и \ (\ displaystyle \ lim_ {x → a} f (x) = f (a) \), мы заключаем, что \ (f \) непрерывно в \ (а \). □ Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию \ (f (x) = | x | \).2}} = + ∞ \). Таким образом, \ (f '(0) \) не существует. Быстрый взгляд на график \ (f (x) = \ sqrt [3] {x} \) проясняет ситуацию. Функция имеет вертикальную касательную в точке \ (0 \) (рисунок \ (\ PageIndex {5} \)). Рисунок \ (\ PageIndex {5} \): функция \ (f (x) = \ sqrt [3] {x} \) имеет вертикальную касательную в точке \ (x = 0 \). Он непрерывен в \ (0 \), но не дифференцируем в \ (0 \).Функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) также имеет производную, которая демонстрирует интересное поведение в \ (0 \). Мы видим, что \ (е '(0) = \ displaystyle \ lim_ {x → 0} \ frac {x \ sin \ left (1 / x \ right) −0} {x − 0} = \ lim_ {x → 0} \ sin \ left (\ frac {1} {x} \ right) \). Этот предел не существует, в основном потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю (Рисунок \ (\ PageIndex {6} \)). Рисунок \ (\ PageIndex {6} \): функция \ (f (x) = \ begin {cases} x \ sin \ left (\ frac {1} {x} \ right), & & \ text {if} x ≠ 0 \\ 0, & & \ text {if} x = 0 \ end {ases} \) не дифференцируем в \ (0 \).Итого:
| Упростим числитель. |
| \ (= \ Displaystyle \ lim_ {h → 0} (4x + h − 3) \) | Выносим за скобки \ (h \) в числителе и сокращаем, добавляя \ (h \) в знаменатель. | |
| \ (= 4x − 3 \) | Возьми предел. |
Затем найдите \ (f '' (x) \), взяв производную от \ (f '(x) = 4x − 3. \)
| \ (f '' (x) = \ displaystyle \ lim_ {h → 0} \ frac {f '(x + h) −f' (x)} {h} \) | Используйте \ (f '(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) с \ (f' (x) \) в место \ (f (x).3 \), найти \ (a (t). \)
Ключевые понятия
Ключевые уравнения\ (е '(x) = \ displaystyle \ lim_ {h → 0} \ frac {f (x + h) −f (x)} {h} \) Глоссарий
Авторы и указание авторства
|

 \)
\) \)
\)
 Результат будет одним и тем же.
Результат будет одним и тем же.
 Фух!
Фух!
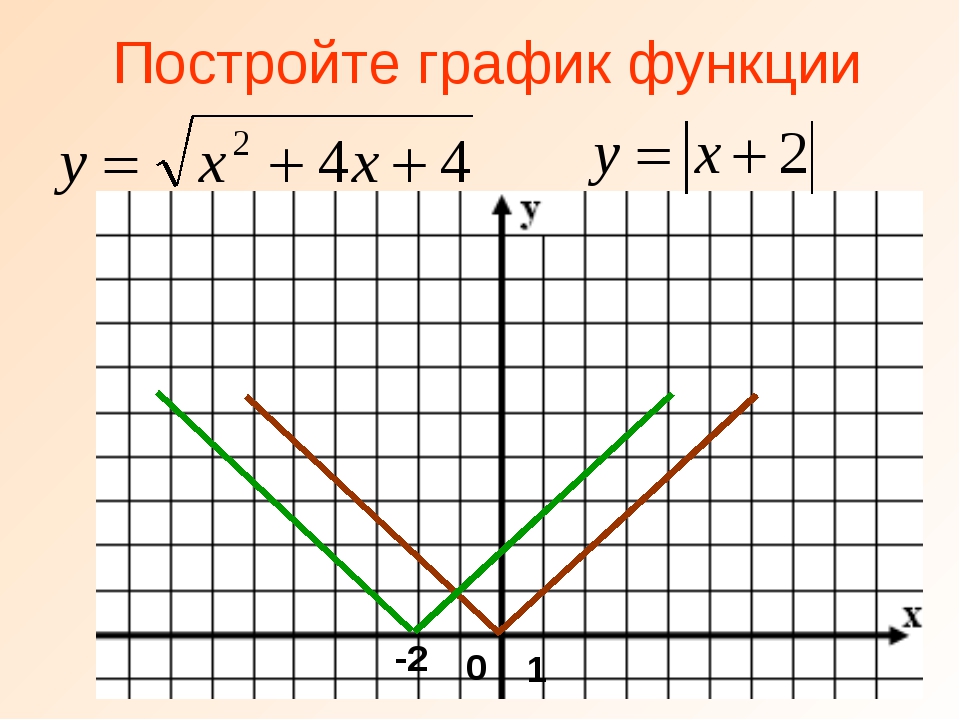

 Кроме того, по мере увеличения \ (x \) наклон касательных к \ (f (x) \) уменьшается, и мы ожидаем увидеть соответствующее уменьшение \ (f '(x) \).2−2x, \; f '(x) = 2x − 2 \). Графики этих функций показаны на рисунке \ (\ PageIndex {3} \). Обратите внимание, что \ (f (x) \) убывает при \ (x <1 \). Для тех же значений \ (x \), \ (f '(x) <0 \). Для значений \ (x> 1 \), \ (f (x) \) увеличивается и \ (f '(x)> 0 \). Кроме того, \ (f (x) \) имеет горизонтальную касательную в точках \ (x = 1 \) и \ (f '(1) = 0 \).
Кроме того, по мере увеличения \ (x \) наклон касательных к \ (f (x) \) уменьшается, и мы ожидаем увидеть соответствующее уменьшение \ (f '(x) \).2−2x, \; f '(x) = 2x − 2 \). Графики этих функций показаны на рисунке \ (\ PageIndex {3} \). Обратите внимание, что \ (f (x) \) убывает при \ (x <1 \). Для тех же значений \ (x \), \ (f '(x) <0 \). Для значений \ (x> 1 \), \ (f (x) \) увеличивается и \ (f '(x)> 0 \). Кроме того, \ (f (x) \) имеет горизонтальную касательную в точках \ (x = 1 \) и \ (f '(1) = 0 \).




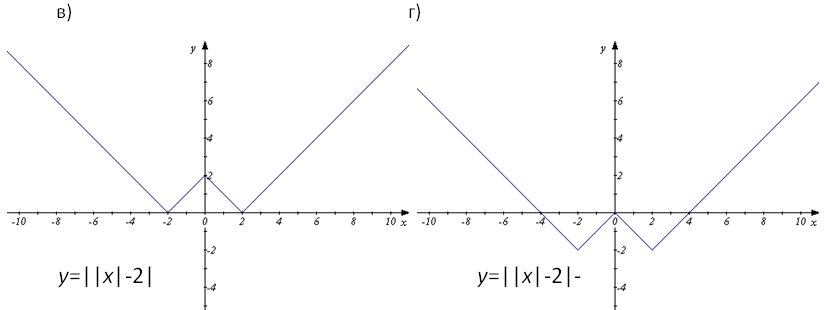 2 + bx + (10b − 5) −5} {x + 10} & & \ text {Substitute} c = 10b − 5.2, & & \ text {if} x≥3 \ end {cases} \) как непрерывные, так и дифференцируемые в точке \ (3 \).
2 + bx + (10b − 5) −5} {x + 10} & & \ text {Substitute} c = 10b − 5.2, & & \ text {if} x≥3 \ end {cases} \) как непрерывные, так и дифференцируемые в точке \ (3 \). n}.2−3h} {h} \)
n}.2−3h} {h} \) {\ text {th}} \).
{\ text {th}} \).