Модуль числа 6 класс правило: Модуль числа — урок. Математика, 6 класс.
Урок 17. противоположные числа. модуль числа — Математика — 6 класс
Математика
6 класс
Урок № 17
Противоположные числа. Модуль числа
Перечень рассматриваемых вопросов:
- Понятие противоположного числа.
- Понятие модуля числа.
- Решение различных заданий по теме «Противоположные числа. Модуль числа».
Тезаурус
Числа, которые отличаются только знаком, называются противоположными.
Модулем положительного числа называют само это число.
Модулем отрицательного числа называют противоположное ему (положительное) число.
Модулем числа 0 является число 0.
Основная литература
- Никольский С. М. Математика. 6 класс: Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н.Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты.

- Шарыгин И.Ф. Задачи на смекалку: 5-6 кл. // И.Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Считается, что если перед целым числом поставить знак «+», то это не изменяет самого числа.
Например,
число 7 можно записать как + 7
число – 7 можно записать как + (– 7)
7 = + 7
– 7 = + (– 7)
Поэтому ряд целых чисел можно записывать в виде:
…, – 6, – 5, – 4, – 3, – 2, – 1, 0, + 1, + 2, + 3, + 4, + 5, + 6, …
Числа, которые отличаются только знаком, называются противоположными.
Например, противоположные числа:
– 7 и + 7
– 53 и 53
Модуль или абсолютная величина числа.
Разбор заданий тренировочного модуля
№ 1. Единичный выбор.
Ответ: + 107.
№2. Ввод с клавиатуры пропущенных элементов в текст.
«Модуль числа и его свойство» (6 класс)
Урок математики в 6 В классе
Тема: «Модуль числа и его свойства»
Тип урока: урок постановки учебной задачи
Формы работы: индивидуальная, фронтальная, парная, групповая.
Методы обучения
Оборудование: компьютер, мультимедийный проектор.
Цели урока:
Познавательные: сформулировать свойства модуля, научиться применять его на практике.
Метапредметные, в том числе:
Регулятивные: поставить учебную задачу на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно; определить последовательность действий для решения поставленной задачи; откорректировать результат с учетом оценки самим обучающимся, учителем, товарищами; осознать качество и уровень усвоения материала.
Коммуникативные: научиться инициативному сотрудничеству в поиске решения поставленной задачи; научиться с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации.
Ход урока
Мотивация.
Актуализация опорных знаний.
Задания для устной работы:
Дайте определение координатной прямой?
Какой знак имеют числа, расположенные на координатной прямой правее нуля? Левее нуля?
Как называются числа, отличающиеся только знаком?
Назовите пары противоположных чисел: 3, 1 ½, 6, -2, 0, 2, -7, -9, 5, -3, -1,5
a, b, c
– k, – p.
– (– a), a – 2, – (b + 1)
На прямой отмечены точки N(-6), D(-4), M(-1), E(2), L(4), A(6). Назовите координаты точек, отмеченных на прямой
Какие из данных точек имеют противоположные координаты?
Найдите значение выражения –(-(-(-x))), -(-(-a)), -(-(-(-(-b))))
Найдите значение выражения –(-k), если –k=-3,5; 6,8; 0; -1/4.

Каким будет число –с, если с-отрицательное, положительное, равно нулю.
Задание на определение темы урока, постановка целей.
Постановка учебной задачи.
На координатной прямой отметьте точки А(6), В(-3) С(5), Е(2) М(-8)
Ответьте на поставленные вопросы:
На каком расстоянии от начала координат расположена точка -3, -8, 5, 6?
Каким числом выражается расстояние от 0 до положительного числа?
Каким числом выражается расстояние от 0 до отрицательного числа?
Равно ли расстояние от 0 до положительного числа самому числу?
Равно ли расстояние от 0 до отрицательного числа самому числу?
Как связано расстояние от 0 до отрицательного числа с самим числом?
Следующие утверждения верны:
Модуль числа 6 равен 6,
модуль числа -3 равен 3,
модуль числа 0 равен 0.
Дайте свои предположения понятия модуль.
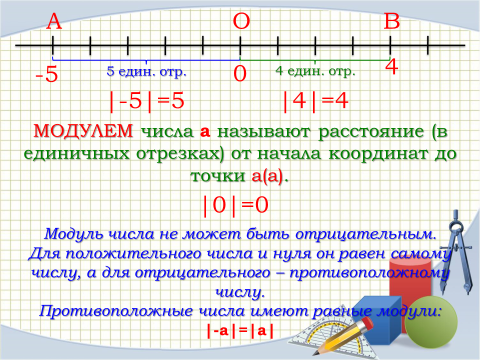
Модулем числа а называется расстояние от точки А(а) на прямой, до начала координат.
Записывается это так: |6|=6, |-3|=3, |0|=0
Найдите модули чисел 81, -1,3, 0, 5,2, -52
Найдите значение модуля |-1,5|, |-5|, |0,5|, |1/3|, |-3,85|, |а|
Решение проблемы.
Для выполнения следующего задания разделимся на 5 групп по 6 человек. Каждой группе необходимо найти модуль числа а, используя те знания, которые у вас есть и сформулировать правило нахождения модуля числа.
|а|=………
Группы выполняют задания.
(Заслушать каждую группу ,сформулировать одно общее правило и записать его в тетрадь)
Первичное закрепление.

Как называются эти числа?
Найдите модуль каждого из чисел.
|2|=2 и |-2|=2
|36|=36 и |-36|=36
|-15|=15 и |15|=15
Сравните эти модули.
Какой вывод можно сделать?
|-а|=|a|
Ребята самостоятельно выполняют задание № 952 с последующей взаимопроверкой.
Запишите все числа, имеющие модуль: а)26; б) 5,7; в) 3¼; г) 0.
Выполнение задания №м953, на слайде разобраны буквы а), б)
Далее выполняют самостоятельно № 953(в-е) с последующей взаимопроверкой.
6,4; -5,8; 3,9; -7,1; 0
7,3; -4,5; 5,9; -8,1; 0
Постановка домашнего задания.
 п.28, учить правило раскрытия знака модуля, выполнить № 953(ж-м), 967, 968, 970, 972.
п.28, учить правило раскрытия знака модуля, выполнить № 953(ж-м), 967, 968, 970, 972.Какие цели мы сегодня ставили на уроке, на все ли поставленные вопросы мы ответили?
Какое определение модуля мы с вами дали?
Каким числом не может быть модуль числа?
Чему равен модуль положительного числа?
Чему равен модуль отрицательного числа?
Чему равен модуль 0?
Заполните, пожалуйста, оценочные карточки по сегодняшнему уроку.
Оценочный лист
| Оценочный лист
|
Оценочный лист
| Оценочный лист
|
Оценочный лист
| Оценочный лист
|
Оценочный лист
| Оценочный лист
|
Оценочный лист
| Оценочный лист
|
Оценочный лист
| Оценочный лист
|
Модуль числа. 6 класс — презентация онлайн
1. Тема урока : «Модуль числа»
2. Знаете ли вы, …
1.Что такое координатная прямая?2.Что называют координатой точки на
прямой?
3.Какие числа называются
противоположными?
4.Как обозначается число, противоположное
числу а?
5.Какие числа называют целыми?
Устный счёт:
1.Даны числа: -9; 12; 3/5; -4,6; 9; 6,08;
-3/5; 0,001; 123; -12; 0.

• Назовите отрицательные,
положительные, натуральные,
дробные, целые числа.
• Назовите числа, противоположные
данным числам.
2.Каким числом будет число –а, если:
• а – отрицательное;
• а = 0;
• а – положительное число.
Запишите число
противоположное данному:
7
–
4
–(–
5)
–
–7
4
5
-3
+(–
6)
-6
–(–
2)
+
2
-9
–
(+9)
–(–(–
-8
5. Упражнения
1. На координатной прямой отмеченыточки М (-7), К(6), В(-6), С(-0,5),
Д(0,5) Какие из них имеют
противоположные координаты?
6. Упражнения
2.Найти расстояние от М(-7) и К(6)до начала отсчета на координатной
прямой.
7. Упражнения
4.Найдите числа, если накоординатной прямой они находятся
на расстоянии:
а) 6 единиц от числа 0,
б) на 10 единиц от числа -4
Из истории математики
Модуль
Модуль числа
числа аа
обозначают
обозначают |а|.

|а|.
Этот
Этот термин
термин
«модуль»
«модуль»
ввел
ввел вв 1806году
1806году
французский
французский
математик
математик Жорж
Жорж Аргон.
Аргон.
9. Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а)
0А(а)
а единиц
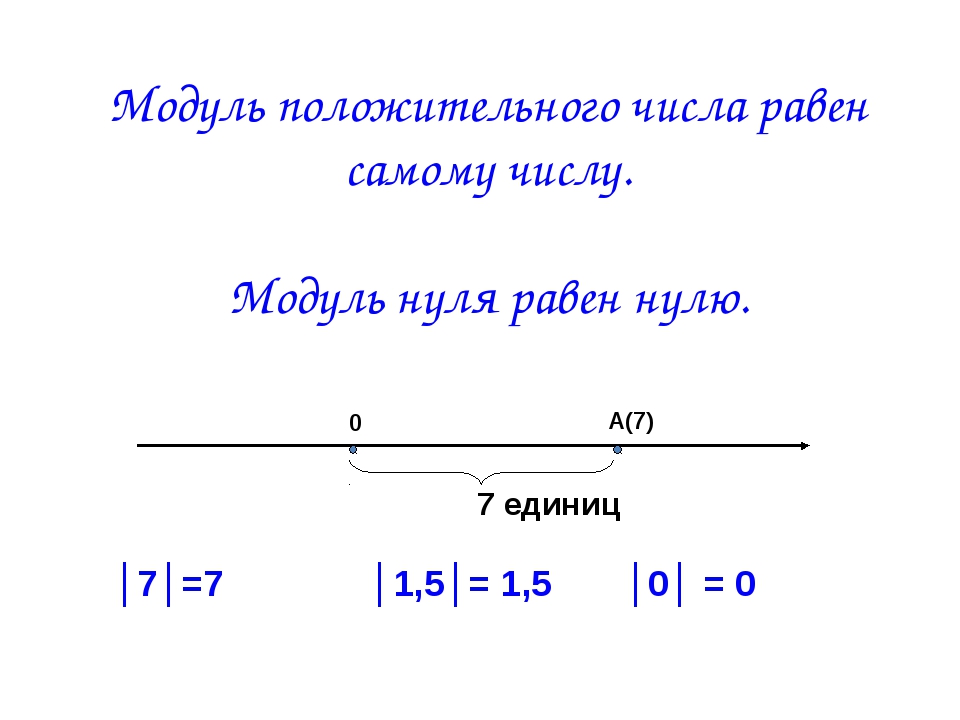
10. Модуль положительного числа равен самому числу. Модуль нуля равен нулю.
А(7)0
7 единиц
│7│=7
│1,5│= 1,5
│0│ = 0
11. Модуль отрицательного числа равен противоположному числу.
0А(- 7)
7 единиц
│- 7│= 7
│- 1,5│ = 1,5
12. Противоположные числа имеют равные модули.
│5│ = 5│
│
-5
5 единиц
│- 5│ = 5
0
5
5 единиц
Модуль не может быть
отрицательным числом!
13. Прикольно!
Представь, что модуль –это баня, а знак «минус»
— грязь.
Оказываясь под знаком
модуля, отрицательное
число «моется» и
выходит без знака
«минус» — чистым.

В бане могут «мыться»
(т.е. стоять под знаком
модуля) как
положительные, так и
отрицательные числа.
14. Найдите модуль каждого из чисел:
12• │12│=
7,08
• │7,08│=
6,32
• │- 6,32│=
0
• │0│=
72
• │ -72│=
15. Найдите значение выражения
│- 8│+│- 2│=
│- 5│-│ 2│= 10
│- 8│∙│ — 3│= 3
│- 27│:│-9│= 24
3
16. Решение уравнений
│х — а│ — расстояние от а до хРешите уравнение.
│х │ = 4
х
-4
Ответ.
0
4
Х=-4 и х=4
17. Примеры решений уравнений.
│Х- 2│ = 52
-3
-5
Ответ.
Х=-3 и Х=7
7
5
18. Решите уравнения
│х│ = 25
│х — 12│ = 6
│х — 3│ = 0
│х│ = — 7,5
х = 25 и х = 25
х = 18 и х = 6
х = 3 и х = -3
Корней нет
19. Поняли?
А теперь…20. Самостоятельная работа
Вариант 1Найдите модуль числа:
— 23; 0,34; — 2/3; 2 3/4.
Запишите числа, модуль которых равен:
4; 0, 23; 3/7; 3 1/4.
Вариант 2
Найдите модуль числа:
52; — 1, 24; — 4 2/3; 3/4.
Запишите числа, модуль которых равен:
9; 0,56; 2 5/7; 1/8.
21. Проверка
Вариант 11. |- 23|=23; |0,34|= 0,34; |2/3|= 2/3; |23/4|=23/4.
2. 4 =|-4|=|4|; 0,23=|-0, 23|=|0,23|;
3/7 = |- 3/7|=|3/7|; 3 1/4 = |-3 1/4|=| 3 1/4 |
Вариант 2
1. |52 | = 52; | -1,24| = 1, 24; |- 4 2/3| = 4 2/3;
|3/4 | = 3/4
2. 9 = | -9 | = | 9 |;
0,56 = |- 0, 56 | = | 0,56 |;
2 5/7 = | -2 5/7 | = | 2 5/7 |; 1/8 = | -1/8 | = | 1/8 |
СПАСИБО ЗА
ВНИМАНИЕ!!!
Модуль числа
Технологическая карта урока
Предмет: математика Класс: 6
Учитель: Больбух В.В.
ГБОУ СОШ № 29 имени М.Т.Калашникова, Г.Севастополь
Учебник (УМК): Никольский С.М., М., Просвещение, 2014
Тема урока: Модуль числа
Цель: Ввести понятие модуль числа.
Задачи:
— Образовательные: Повторить основные понятие по теме «Противоположные числа».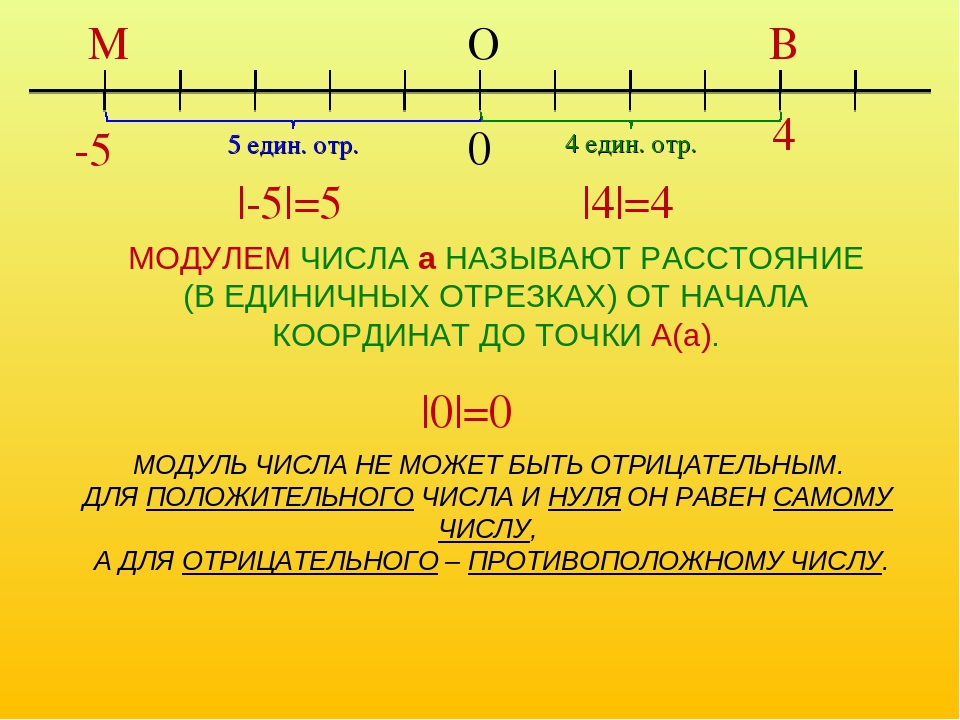 Закрепить новое понятие в ходе решения упражнений.
Закрепить новое понятие в ходе решения упражнений.
— Развивающие: Совершенствование устной речи учащихся по отработке понятийного аппарата
— Воспитательные: формирование у учащихся внимания и навыков контроля и самоконтроля
Тип урока: урок изучения нового материала
Оборудование: интерактивная доска, проектор, ноутбук, индивидуальные карточки, таблица «Модуль числа», электронное приложение к УМК, электронное приложение «Наглядная математика» 6 класс.
Учащиеся владеют
• регулятивными УУД: — формулировать вопросы по теме на основе опорных (ключевых и вопросительных) слов,
• познавательными УУД: -выделять и структурировать информацию, существенную для решения проблемы под руководством учителя,
• личностные УУД: -осуществлять рефлексию своего отношения к содержанию темы по заданному алгоритму.
У учащихся недостаточно сформированы: • коммуникативные УУД: — эффективно сотрудничать, осуществляя взаимопомощь и взаимоконтроль.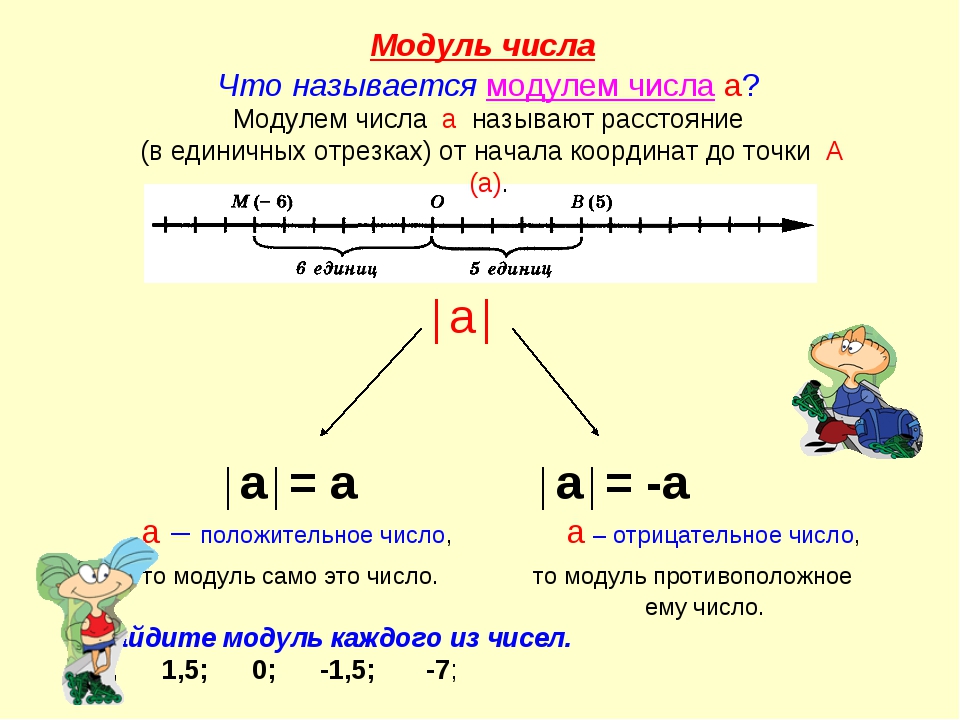
Цели урока как планируемые результаты обучения, планируемый уровень достижения целей:
Вид планируемых учебных действий | Учебные действия | Планируемый уровень достижения результатов обучения |
Предметные | вводят и определяют понятия «модуль», | 1-2 уровень — понимание, адекватное употребление в речи, выборочно — воспроизведение |
знакомятся со свойствами модуля; отрабатывают умение находить модуль и применять свойства модуля. | 1-2 уровень — понимание, адекватное употребление в речи, выборочно — воспроизведение | |
Регулятивные | • самостоятельно ставят новые учебные задачи путем задавания вопросов о неизвестном | 2 уровень — самостоятельное действие учащихся по заданному алгоритму |
• планируют собственную деятельность, определяют средства для ее осуществления | 2 уровень— совместное с учителем действие учащихся на основе знания видов источников информации и способов работы с ними | |
Познавательные | •извлекают необходимую информацию из прослушанного и прочитанного материала | 2 уровень — самостоятельное выполнение действий в условиях взаимопомощи и взаимоконтроля |
•структурируют информации в виде записи выводов и определений | 2 уровень — совместные действия учащихся в условиях взаимопомощи и взаимоконтроля | |
Коммуникативные | • эффективно сотрудничать и способствовать продуктивной кооперации | 1 уровень — выполнение действий по алгоритму под управлением учителя |
Личностные | умение правильно излагать свои мысли, понимать смысл поставленной задачи, личностная саморегуляция в процессе взаимоконтроля | 2 уровень — самостоятельное выполнение действий с опорой на известный алгоритм |
Ход урока
Этапы урока | Деятельность | |
учителя | учащихся | |
Организационный этап | Учитель приветствует учащихся, проверяет их готовность к уроку. «Я сегодня быстро встал, В школу рано прибежал. Очень я хочу учиться, Не лениться, а трудиться» | 1.Учащиеся готовы к началу работы. Настраиваются на успех. |
Этап актуализация знаний. | Учитель: Новые знания нам будет очень трудно осваивать без умения быстро и верно считать, поэтому, как всегда, начнем урок с устных заданий: 1. Дан ряд чисел: — 256; 3000; 4 ; -7 ; 0 ; — 19; -1000. — Дать определение положительного числа и выбрать их. — Дать определение отрицательного числа и выбрать их. — Есть ли среда этих чисел противоположные? Дать определение. — К каким числам относится число 0? — Что такое координатная прямая? — Где на координатной прямой расположены положительные числа? Отрицательные? 2. 3. Между какими целыми числами лежит число На каждом уроке вы, ребята, приобретаете новые знания, которые когда-то открыли великие математики. Знания, полученные сегодня, помогут вам в дальнейшем при изучении многих тем не только в курсе математики, но и при изучении нового курса, который называется алгебра. Чтобы узнать тему урока, решите ребус. — Исходя из названия темы, давайте сформулируем цель нашего урока. Модуль числа — Для того чтобы достичь цели урока, какие задачи нам надо поставить? — Где можно узнать информацию по данной теме? | 1. Учащиеся внимательно слушают учителя и отвечают на вопросы: 2. Называют все целые числа, удовлетворяющие условию задания. 3. Называют числа, между которыми лежит число -6целых одна третья. 4. Учащиеся решают ребус и называют тему урока. 5. Учащиеся формулируют цели урока: узнать, что такое модуль; изучить свойства модуля; изучить материал учебника по этой теме; внимательно слушать учителя; делать необходимые записи в тетрадях. 7. Называют источники информации: учебник, учитель. |
Этап изучение нового материала | Построим координатную прямую; что нужно, чтобы такая прямая существовала? (начало отсчета, положительное направление, единичный отрезок). Задание 1. Отметим на координатной прямой точки А(5), В(2), С(-6), К(-5). Найдем расстояние от начала отсчета до каждой из точки. 9. Модуль числа 1 На электронной доске проектируется таблица с интерактивной моделью Или учитель показывает на таблице, или на доске Для такого расстояния придумано специальное название — модуль. Модулем числа a называют расстояние (в единичных отрезках) от начала координат до точки А(a), изображающей число a. Пишут: |-5|=5; |3|=3, |-7|=7, |-5|=5. Читают: «Модуль числа 3 равен 3. Задание 2. Найдите модули чисел 3; ; 8. , Числа 3; ; 8 — какие? А их модули? Сделайте вывод. (Модуль положительного числа равен самому этому числу, т.е. если a — положительное, то |a|=а). Задание 3. Найдите модули чисел -2; -3; -4 Числа -2; -3; — какие? А их модули? Сделайте вывод. (Модуль отрицательного числа равен числу ему противоположному, т.е. если a — отрицательное, то |a|= — а). А чему равен модуль нуля? |0|=0. (Модуль нуля равен нулю.) Числа 4 и -4; 3 и -3; 2 и -2; 1 и -1 — какие? (противоположные) А модули каждой пары чисел? (равные) Сделайте вывод. (Модули противоположных чисел равны. Модуль любого числа есть число неотрицательное). | 1. Отвечают на вопрос — что нужно, чтобы такая прямая существовала 2. Строят координатную прямую и отмечают на ней точки. 3. Находят расстояние от начала отсчета до каждой точки. Запись учащихся: А(5), ОА=5 В(3), ОВ=3 С(-3), ОС=3 К(-5), ОК=5 Проговариваем: -Точка А с координатой 5, отрезок ОА равен 5 единичным отрезкам 4. 5. Выполняют задание. Делают вывод. Записывают вывод в тетрадь. 6. Выполняют задание. Делают вывод. Записывают вывод в тетрадь. 7. Выполняют задание. Делают вывод. Записывают вывод в тетрадь. |
Этап первичное осмысление и закрепление знаний | Выполните задание и сделайте взаимопроверку. | — Учащиеся выполняют работу на индивидуальных карточках, после выполнения проводят взаимопроверку с соседом по столу На доске слайд с ответами |
Физпауза | Ветер дует нам в лицо, Закачалось деревцо, Ветерок все тише-тише, Деревцо все выше-выше. | Выполняют упражнение стоя, изображая ветер, дерево, становятся на носочки и приседают. |
Этап закрепление изученного материала | Стр. 48 учебника, найдите и прочитайте правило Читайте внимательно, что нового еще вы узнали? (модуль – это абсолютная величина) Устно № 217 Стр 49 посередине Электронное приложение к учебнику УМК Никольского Вычисли модуль и расшифруй число КОТС | Анализируют текст учебника, выделяют неизвестное. 1. Осмысливают и приступают применять новый способ решения на практике. 2. Делают записи в тетрадь. После выполнения задания сверяют с доской. Один из учеников решает у доски с комментарием. 3.Решают самостоятельно, сверяют с доской. |
Этап подведение итогов. Домашнее задание. | -Наш урок подходит к концу, сначала запишем домашнее задание, затем подведем итоги. — На доске: Домашнее задание: п. 2.2, выучить правила. № 218, №222, № 223. — А теперь подведем итоги: Что мы хотели узнать? Что мы узнали? На все ли вопросы мы получили ответы? — Давайте еще раз вспомним определение модуля, свойства модуля Слайд рефлексия «Сегодня на уроке я узнал…» — Итог урока каждый из вас подведет с помощью телеграммы; то есть в виде одного краткого предложения, которое выразит ваше отношение к уроку. Если останется время закончить одно из предложений письменно. Всем спасибо! | 1. Ребята записывают домашнее задание в дневниках. 2. Просматривают домашнее задание, задают вопросы 3. Проводят самоанализ, отвечают на вопросы; вспоминают правила; определение модуля, свойства модуля. 4. В конце своей работы каждый ученик пишет телеграмму. По желанию зачитывают на весь класс |
Уравнения и примеры с отрицательными числами и модул…
Все рациональные числа, которые мы можем себе представить, можно разделить на положительные и отрицательные. Изучается данная тема в 5-6 классах. Начиная с этих классов, учащиеся решают примеры, уравнения и задачи, в которых могут быть как положительные, так и отрицательные числа.
Решение примеров с отрицательными числами без ошибок — очень важный математический навык. То же самое касается и решения уравнений с отрицательными числами. В этом контексте в школьном курсе рассматривается и понятие модуля числа.
Давайте сегодня разберем эти вопросы.
Чтобы отличить положительное число от отрицательного, перед отрицательным числом ставят знак минус.
Например:
«5» – положительное число
«-5» — отрицательное число Если рассматривать числа на координатной прямой, то все числа, находящиеся слева от нуля, будут называться отрицательными, а числа, находящиеся справа от нуля – будут, соответственно, положительными.
Правила сложения, вычитания, умножения и деления отрицательных чисел имеют свои особенности.
Например, если нам необходимо выполнить действие:
«7 + 5»
Т.е. сложить два положительных числа, мы механически складываем их величины и получаем результат:
7 + 5 = 12
Если даже у нас будет длинный и трудоемкий пример, принцип его решения будет точно такой же, если числа положительные, то мы механически складываем их:
7 + 5 + 21 + 17 + 19 + 25 = 94
Операция вычитания может быть уже не такой простой.
Если выражение:
7 – 5 = 2
Мы вычисляем легко, то выражение:
5 – 7 = — 2
Это уже серьезная проверка наших знаний в области отрицательных чисел. Здесь важно в ответе правильно поставить знаки «плюс» и «минус».
Здесь важно в ответе правильно поставить знаки «плюс» и «минус».
Здесь перед числом «7» стоит знак «минус». Получается из меньшего числа «5» нужно вычесть большее число «7».
Как не запутаться?
Есть несколько способов. Один из которых вот какой:
Необходимо вспомнить понятие модуля числа.
Модуль числа – это число, записанное в вертикальных скобках:
|5| или |-7|
Когда мы выводим число из модуля, мы оставляем только его значение, а минус убираем:
|5| = 5
|-7| = 7
Записываем наше выражение для модулей этих чисел:
|5| – |7|
Такая запись позволяет нам определить, какое число большее «по модулю», т.е. по своему абсолютному значению, без учета знака «минус» перед числом и стоит правее на числовой оси.
В нашем случае, это число «7».
Поэтому мы из большего «по модулю» числа вычитаем меньшее «по модулю» число и в ответе ставим тот знак (плюс или минус), который стоял в выражении перед большим «по модулю» числом:
|5| – |7| = — |7 — 5| = — |2| = -2
Второй способ вот какой:
Запишем:
5 + (– 7)
Представим каждое слагаемое как выражение двух чисел, с умножением на «-1», получим:
5 = — 1 · (- 5)
— 7 = — 1 · 7
Теперь сложим эти выражения, как в нашем примере, получим:
5 + (– 7) = (- 1 · (- 5)) + (- 1 · 7)
Вынесем за скобки «-1»:
-1·(- 5 + 7) = -1·(7 – 5) = -1· 2 = — 2
Когда мы выносим за скобку «-1», мы получаем возможность вычитать из большего числа меньшее, что гораздо удобнее.
Теперь мы знаем, как решать примеры с отрицательными числами.
Умножение на «-1» помогает нам вспомнить правила умножения и деления, в выражениях с положительными и отрицательными числами. Вот эти правила:
«Если умножать «минус» на «плюс», то получается в ответе «минус».»
«А если умножать «минус» на «минус», то получается в ответе «плюс».»
Проиллюстрируем все возможные варианты применения этих правил:
5 · 7 = 35
5 · (– 7) = — 35
(- 5) · 7 = — 35
(- 5) · (– 7) = 35
Возьмем более сложный случай, вычислим:
7 · (- 5) · 21 · (- 17)
Чтобы было проще, выполним вычисления по действиям:
1) 7 · (- 5) = — 35
2) 21 · (- 17) = — 357
3) (- 35) · (-357) = 12495
Таким образом:
7· (- 5) · 21 · (- 17) = 12495
Теперь рассмотрим, как решать уравнения с отрицательными числами и переменными.
Возьмем пример с уравнением:
3 + 4(5 – х) = 15
Сначала раскроем скобки:
3 + 4 · 5 + 4 · (- х) = 15
Обязательно обращаем внимание на минусы, стоящие перед числами и переменной «х», помним о приведенном выше правиле, получаем:
3 + 20 – 4х = 15
Приведем подобные (3 + 20 = 23) и запишем:
23 – 4х = 15
Переносим слагаемое без переменной «х» из левой части в правую, меняя при этом перед ним знак на противоположный
— 4х = 15 – 23
После приведения подобных в правой части уравнения (15 – 23 = — 8), получим:
— 4х = — 8
Деление отрицательных чисел проводим по тем же правилам, что и умножение:
х = — 8 : (- 4)
«Минус» делим на «минус», получаем «плюс»:
х = 2
Давайте теперь разберем примеры с модулем числа.
Напомню, что, когда мы выводим число из модуля, мы оставляем только его значение, а минус убираем.
Например:
|5| + |-7| = 5 + 7 = 12
|5| — |-7| = 5 — 7 = — 2
|5| · |-7| = 5 · 7 = 35
|-35| : |-7| = 35 : 7 = 5
Как видите, в примерах, где числа стоят под знаком модуля, необходимо следовать правилу:
«Сначала раскрываем скобки модуля, а потом проводим операции сложения, вычитания, умножения или деления».
Конечно, существуют и более сложные примеры с отрицательными числами и модулями. Чтобы познакомиться с правилами их решения, а также вспомнить все, что необходимо, связанное с модулями — следите за нашими уроками или обратитесь к репетитору на нашем сайте.
Ответы на вопросы к §11.2 учебника «Математика» 6 класс Дорофеев, Шарыгин
Ответы к параграфу 11.2 Сравнение рациональных чисел. Модуль числа
Вопросы к параграфу
1. Расскажите, как с помощью координатной прямой можно сравнить два числа. Покажите схематически, как расположены относительно друг друга числа 4,7 и −2,5, и сравните их.
Решение
Из двух чисел меньше то, которому соответствует точка координатной прямой, расположенная левее, и больше то, которому соответствует точка, расположенная правее.
−2,5 < 4,7
2. Какое число больше: положительное или ноль? отрицательное или ноль? положительное или отрицательно? Приведите примеры.
Решение
Любое положительное число больше нуля, например:
2 > 0;
15,2 > 0.
Любое отрицательное число меньше нуля, например:
−18 < 0;
$-\frac12<0$.
Любое отрицательное число меньше любого положительного числа, например:
−18 < 2;
$-\frac12<15,2$.
3. Покажите с помощью координатной прямой, как сравнить числа −3,5 и −8. Сформулируйте правило сравнения двух отрицательных чисел.
Решение
|−8| = 8;
|−3,5| = 3,5;
8 > 3,5, значит:
−8 < −3,5.
Из двух отрицательных чисел меньше то, у которого модуль больше.
4. Как найти модуль положительного числа, отрицательного числа? Приведите примеры. Чему равен модуль числа 0?
Решение
Модуль положительного числа равен самому числу, например:
|5| = 5;
|2,8| = 2,8.Модуль отрицательного числа равен числу, ему противоположному, например:
|−5| = 5;
|−2,8| = 2,8.Модуль нуля равен нулю.
5. Назовите числа, модуль которых равен 3, и изобразите эти числа на координатной прямой.
Решение
|3| = 3;
|−3| = 3.
Рождение советской ПРО. Как СССР копировал микросхемы
Упрощенно говоря, существуют две больших категории транзисторов: исторически первые серийные – биполярные транзисторы (bipolar junction transistor, BJT) и исторически первые концептуально – полевые транзисторы (field-effect transistor, FET), причем логические элементы, собранные на них, в обоих случаях можно реализовать как в дискретном виде, так и в виде интегральных схем.

Для биполярных транзисторов существовало две основных технологии изготовления: примитивная точечная (point-contact transistor), не имевшая практического применения, и технология транзисторов на pn-переходах (junction transistor).
В свою очередь, переходные транзисторы насчитывали три основных технологических поколения (в зависимости от того, как формировался переход): транзисторы с выращенным переходом (grown-junction transistor, оригинальная работа Шокли, 1948 г.), транзисторы со сплавным переходом (alloy-junction transistor, RCA и General Electric, 1951 г., развитие получили в технологии MAT/MADT от Philco и PADT от Philips) и самые совершенные, транзисторы с переходом, полученным диффузией (diffused-base transistor от Bell Labs, 1954 г., более продвинутые mesa transistor от Texas Instruments, 1957 г., и, наконец, планарные транзисторы от Fairchild Semiconductor, 1959 г.).
В качестве экзотических вариантов существовали также транзисторы с поверхностным барьером (surface-barrier transistor, Philco, 1953 г. ), именно на них были созданы компьютеры MIT Lincoln Laboratory TX0 и TX2, Philco Transac S-1000 и Philco 2000 Model 212, Ferranti-Canada DATAR, Burroughs AN/GSQ-33, Sperry Rand AN/USQ-17 и UNIVAC LARC!
), именно на них были созданы компьютеры MIT Lincoln Laboratory TX0 и TX2, Philco Transac S-1000 и Philco 2000 Model 212, Ferranti-Canada DATAR, Burroughs AN/GSQ-33, Sperry Rand AN/USQ-17 и UNIVAC LARC!
Также были известны транзисторы с дрейфующим полем (drift-field transistor, German Postal Service Central Bureau of Telecommunications Technology, 1953 г.), они использовались в IBM 1620 (1959 г.) под названием Saturated Drift Transistor Resistor Logic (SDTRL).
Для производства микросхем подходили (в теории) три варианта переходных транзисторов – сплавные, меза и планарные.
На практике, конечно же, со сплавными ничего не вышло (остались только бумажные идеи Джеффри Даммера, Бернарда Оливера и Харвика Джонсона, 1953 г.), с меза-транзисторами получилась убогая гибридная TI 502 от Джека Килби, и более желающих экспериментировать не нашлось, а планарный процесс, наоборот, пошел отлично.
Первыми планарными микросхемами стали Fairchild Micrologic (те самые, что использовались в Apollo Guidance Computer и малоизвестных AC Spark Plug MAGIC и Martin MARTAC 420) и Texas Instruments SN51x (использовались в компьютерах NASA Interplanetary Monitoring Probe и ракетах Minuteman II), обе появились в 1961 году.
В целом Fairchild неплохо заработали на программе Apollo – для всех компьютеров суммарно NASA закупило более 200 000 микросхем по $20–30 каждая.
В результате как планарные биполярные транзисторы, так и микросхемы на них использовали для производства компьютеров все 1960-е годы (а микросхемы – и все 1970-е).
Например, великий CDC 6600 был собран в 1964 году на 400 000 кремниевых биполярных транзисторах Fairchild 2N709, изготовленных по наиболее совершенной эпитаксиальной планарной технологии и рассчитанных на сверхвысокую частоту в 10 МГц.
Краткая история логики
Как же организовывали логические ячейки в это время?
Для того, чтобы собрать компьютер, необходимы две вещи.
Во-первых, нужно так или иначе собрать саму логическую схему на ключах, которыми можно управлять.
Во-вторых (и это не менее важно!), нужно усилить сигнал одной ячейки настолько, чтобы она, в свою очередь, могла управлять переключением других, так собираются сложные арифметико-логические цепи.
В исторически первом типе логики – резисторно-транзисторной (resistor-transistor logic, RTL), в качестве усилителя использовался тот же самый единственный транзистор, что служил ключом, более никаких полупроводниковых элементов в схеме не было.
RTL-ячейка выглядит максимально примитивным с точки зрения электротехники образом, например, вот классическая реализация элемента NOR.
Таблица, показывающая как работает NOR-ячейка, и два возможных варианта ее реализации – самый примитивный, двухвходовый 2-NOR, и трехвходовый 3-NOR. Raytheon Apollo Guidance Computer был собран на 4 100 таких 3-NOR микросхем производства Fairchild Semiconductor. Вторая версия, уже для пилотируемых полетов, была усовершенствована до 2 800 микросхем, каждая из которых объединяла два 3-NOR.
AGC – самый известный в мире компьютер, собранный на RTL-логике. Справа – Маргарет Гамильтон (Margaret Hamilton), одна из разработчиц программного обеспечения миссии Apollo (https://wehackthemoon.com, https://www. theatlantic.com).
theatlantic.com).
Естественно, с помощью RTL можно (и нужно!) реализовать и прочие конструкции, например, триггеры.
Первый транзисторный компьютер MIT TX0 был собран в 1956 году на дискретных транзисторах по схеме RTL.
В СССР RTL легла в основу первых осокинских микросхем, о которых мы уже писали – Р12-2 (102, 103, 116, 117) и ГИС «Тропа-1» (201).
RTL была дешевой и простой, но имела кучу недостатков: высокая мощность, что приводило к повышенному нагреву, нечеткий уровень сигналов, низкая скорость, низкая помехоустойчивость и главное – низкая нагрузочная способность выходов.
Большей скоростью обладал вариант RCTL (resistor-capacitor-transistor logic), но он был еще менее помехоустойчивым.
Несмотря на появление более продвинутых серий, RTL использовалась и выпускалась года до 1964.
Одной из самых популярных была серия Fairchild MWuL и чуть более быстрая uL. Эти две группы, дополняющие друг друга по характеристикам, насчитывали около 20 типов ИС и выпускались года три в больших количествах.
В СССР их осилили клонировать в районе 1966 года, а выпускали разные варианты чудовищно допотопной RTL до середины 1980-х, если не далее.
Разработка происходила по классике, со всем подобающим, как было принято в СССР испокон веков (пишет про 111-ю серию известный коллекционер и историк электроники):
Очень редкая бескорпусная РТЛ-логика, одна из первых отечественных логических серий (тема «Микроватт»), разработанная в КБ-2 Ф. Г. Староса. Первоначально она выпускалась под доГОСТовским названием ТИС. История её развития не лишена странных моментов и белых пятен. Предположительно, изначально Старосом в середине 60-х были разработаны 1ЛБ111–1ЛБ113 с разбраковкой по входному/выходному току и времени распространения.Затем (ориентировочно в самом начале 70-х) появляются 1ЛБ111–1ЛБ113, которые бракуются практически по тем же параметрам, но в абсолютном выражении имеют заметно лучшие характеристики. К примеру, время распространения было 600/650 нс, а стало 100/400 нс. Они нашли применение, к примеру, в гибридных микросхемах 207 серии – вероятно, при замене базового логического элемента, собранного на дискретных транзисторах.

Но достаточно быстро, к 1973 году, выпуск быстродействующего варианта был прекращен, также сошли со сцены и 1ЛБ112+1ЛБ113.
Ситуация вернулась к первоначальной. Что означает этот второй авантюрный вариант, теперь довольно трудно установить, но, возможно, разработчиков было двое. Тогда в этой истории появляется хоть какой-то смысл. Видимо, разработчика более быстродействующего варианта к 1973 году загнобили, что согласуется с историей КБ Староса.
Вишенкой на торте в каталоге 1976 года вновь откуда-то появляется 1ЛБ113…
Отметим крайне важный для дальнейших рассуждений момент.
Тип логики – это понятие, применяемое к схемотехнике логического элемента, а не конкретной его имплементации!
RTL можно реализовать как на дискретных элементах, так и в варианте микросхемы. На самом деле, можно даже заменить транзистор лампой и получить resistor-coupled vacuum tube logic – такую использовал первый прототип электронного компьютера в мире – машина Атанасова-Берри (Atanasoff-Berry Computer, 1927–1942 гг. ). В варианте микросхем RTL можно встретить в самых первых чипах – Fairchild Micrologic, а варианте RCTL – в TI SN51x.
). В варианте микросхем RTL можно встретить в самых первых чипах – Fairchild Micrologic, а варианте RCTL – в TI SN51x.
Знаменитая космическая серия RTLC TI SN51x. Сами микросхемы, их внутренне устройство и блок управления Minuteman II с компьютером Autonetics D-37D Missile Guidance System Computer на них (https://minutemanmissile.com/, http://ummr.altervista.org, https://www.petritzfoundation.org)
Нагрузочная способность критична для создания сложных схем – какой там получится компьютер, если наша транзисторная ячейка способна раскачать максимум 2–3 соседа, даже сумматор толковый не соберешь. Довольно быстро возникла идея – использовать транзистор в качестве усилителя сигнала, а логику реализовать на диодах.
Так появился куда более продвинутый вариант логики – диодно-транзисторный (diode–transistor logic, DTL). Бонусом DTL становится высокая нагрузочная способность, хотя скорость по-прежнему оставляет желать лучшего.
Именно DTL являлась основой 90 % машин второго поколения, например, IBM 1401 (чуть модифицированная фирменная версия complemented transistor diode logic – CTDL, упакованная в SMS-карты) и кучи других. Вариантов схемотехнической реализации DTL было едва ли меньше, чем самих машин.
Вариантов схемотехнической реализации DTL было едва ли меньше, чем самих машин.
Элементарная DTL NAND-ячейка и логический блок от БЭСМ-6 на извращенной модификации ECL для сравнения (https://1500py470.livejournal.com).
Естественно, можно обойтись и без транзисторов, тогда получится diode vacuum tube logic (чрезвычайно популярное решение в начале 1950-х, практически все машины, которые принято называть ламповыми, по факту имели логические цепи на диодах, а лампы ничего не вычисляли, просто усиливали сигнал, хрестоматийный пример – М1 Брука).
Еще одним экзотическим по нынешним меркам вариантом является чисто диодная логика (diode-resistor logic, DRL). Изобретенная тогда же, когда появились первые промышленные диоды, она широко использовалась в малых машинах начала 1950-х, например, калькуляторе IBM 608 и БЦВМ Autonetics D-17B от знаменитой ракеты Minuteman I.
До изобретения планарного процесса транзисторы считались неподходящими для критичных военных применений из-за потенциальной ненадежности, поэтому американцы использовали DRL в своих первых ракетах.
Советский ответ Minuteman I использовал ламповый компьютер, и ракета Р-7 (в том числе и из-за большей величины всех прочих компонентов) получилась чудовищно огромной по сравнению с американской: у янки примерно 29 тонн и 16,3х1,68 метра против невероятных 280 тонн и 34х10,3 метра. Даже монструозный LGM-25C Titan II имел размер 31,4х3,05 метра и массу 154 тонны, вообще, советские МБР всегда были куда больше американских, из-за отсталости технологий.
В результате, например, в качестве ответа компактной Ohio class SSBN пришлось разрабатывать хтоническую 941 «Акула» – в лодку, размером с «Огайо», советские ракеты бы просто не поместились.
Кроме компьютеров, DRL десятки лет использовалась во всевозможной заводской автоматике.
Классика DRL – ячейка AND-OR, одна плата от Autonetics D-17B и сам компьютер в сборе (https://minutemanmissile.com, http://www.bitsavers.org)
Транзисторная логика тоже нашла свое воплощение в ИС, начав с чипов Signetics SE100 1962 года.

Чуть позже DTL-версии микросхем были выпущены всеми основными игроками на рынке, включая Fairchild 930 Series, Westinghouse и Texas Instruments, разработавшую на низ БЦВМ D-37C Minuteman II Guidance Computer в том же 1962 году.
В Союзе DTL-микросхемы выпускались в огромных количествах: серии 104, 109, 121, 128, 146, 156, 205, 215, 217, 218, 221, 240 и 511.
Подготовка к производству DTL тоже не обошлась без советских приключений.
Вспоминает Юрий Замотайлов, с. н. с. кафедры ядерной физики ВГУ:
В 1962 году отдел № 8 (начальник отдела Хорошков Ю.В.) выпросили у главного инженера Колесникова В. Г. очень большие деньги для завода того времени для закупки электронной пушки. Цель-то была благородной – делать на ней по невероятно простой (а, следовательно, дешевой) технологии диоды – аналоги нужных для страны Д226. Технология, действительно, несложная: окисление пластин, напыление алюминия, выстрел электронным лучом, скрайбирование и сборка.
Не хочу оправдываться в неудаче, но для общего представления скажу, что вакуумная камера кубической формы, примерно 3 м3, защищенная 5 тоннами свинца от вторичных рентгеновских лучей, была куплена у НИИАТ в Москве.
Знаменита она была тем, что с нее выступал после полета в космос Валерий Быковский. Так что для загрузки в нее деталей операторами она была оснащена лестницей высотой около трех метров. По паспортным данным пучок электронов мог быть сфокусирован до диаметра 100 мкм.
Двухлетняя наладка специалистами НИИАТ и нами дала пучок с минимальным диаметром около миллиметра. Достаточно сказать, что настройка и управление пучком осуществлялась с помощью 148 трансформаторов типа ЛАТР-2.
Короче, пушку пришлось передать в Политехнический институт.
Вы представляете наше душевное состояние?
В отделе некоторые просто перестали здороваться. Хорошков Ю.В., проходя мимо, смотрел сквозь нас.
Интересно, почему же Зеленоград постоянно закупал на Западе оборудование?
Может, по причине того, что советские установки годились только как реквизит фильмов про доктора Франкенштейна?
В итоге на диоды все забили и решили собирать сразу микросхемы (если удастся достать западные степперы).
Начали клонировать DTL.
Но какую же делать схему?
Честно говоря, схемотехники из нас никудышные. В одном из журналов нашли схему ДТЛ с девятью компонентами. Добавив к ней на вход диод, мы и получили ту самую ТС-1.
<…>
Приехав в очередной раз к нам, Шокин А. И., как всегда в сопровождении в то время первого секретаря обкома КПСС С. Д. Хитрова, вечером, в узком кругу, ознакомился с ходом работ. Затем был затронут вопрос о предъявлении к сдаче НИР «Титан» Госкомиссии…
Никогда не забуду слова Шокина: «Мужики! 31 декабря, хоть под самые 24 часа, ко мне домой, но привезите действующую схему». Хитров С.Д. сидит и говорит: «И мне одну!» Меня даже передернуло. Думаю: «Но вам-то зачем?! Дай бог, чтобы получилась одна, доказывающая, что технология принципиально разработана».
Тем не менее фраза Хитрова имела свое действие.
После некоторой паузы министр сказал: «Действительно, один образец как-то не звучит». И, извините, после получасовой торговли договорились, что Госкомиссии будет предъявлено 10 образцов. Мы долго вспоминали Хитрова и забыли лишь после сдачи темы Госкомиссии.
Мы долго вспоминали Хитрова и забыли лишь после сдачи темы Госкомиссии.
Никогда не забуду день, когда, наконец, первый кристалл (целиком!!!) зафурыкал.
Это была большая радость для коллектива, описать которую уже, простите, я не смогу.
Произошло это в середине ноября. Оставалось 1,5 месяца, а надо было сделать еще 9 штук!
И хотя за счет сверхинтенсивной работы партию пластин из 15–20 штук мы прогоняли за 4–5 суток, и партии запускались ежедневно, как это часто бывает в жизни, наступила настоящая полоса неудач. Почти в течение месяца не было ни одного целого кристалла.
Слава Богу, где-то в середине декабря из двух-трех партий Аракчеева И. А. набрала 7 кристаллов и собрала их в корпуса. Честно говоря (теперь в этом можно признаться), Госкомиссии так и было предъявлено 10 колодок для измерения, в которых в восьми были схемы, а в двух пустые корпуса. Но Госкомиссия замерами двух схем удовлетворилась.
<…>
Надо отдать должное Колесникову В. Г. в понимании наших проблем.
Он прекрасно знал, что на том оборудовании, на котором в основном выполнялась часть НИР, выполнить ОКР, организовать серийное производство не могло быть и речи. Еще месяцев за 6 до окончания НИР мы краем уха узнали, что заместитель главного инженера Лаврентьев К. А. уехал в Японию, правда, с какой целью мы не очень-то были осведомлены…
Через пару недель после этого мы накинулись распаковывать печи, привезенные Лаврентьевым из Японии. Это были знаменитые СДО-2, в прямом смысле спасшие нас. Мы их получили как раз в тупиковое время.
Таким образом, Колесников В. Г. заранее выпросил валюту и договорился о поставке оборудования (вместе с печами было получено некоторое оборудование по фотошаблонам и фотолитографии).
<…>
Мы взяли в лабораторию сверх лимита Чернышова А. И. из аспирантуры ВГУ, причем старшим инженером. Я, зная его еще раньше, никакой группы ему не дал (да и он не просил), а поручил поработать с контактами. Месяца два – два с половиной, как мы тогда говорили, никакой отдачи.
И вот однажды он подозвал меня, говорит: «Смотри!»
Проверили кристалл, на входе у двух диодов нет контакта, сама схема, естественно, не функционирует. Затем кладет пластину на самодельную плоскую печку, разогревает ее до 470 градусов и выдерживает 15 минут. После этого на этой пластине мы находим две функционирующие схемы, на другой (аналогичной) – 3 и т. д.
Так был найден режим для вжигания алюминия.
Ведь до этого вжигали алюминий при температуре 300 градусов, пользуясь секретными сообщениями, полученными через 1-й отдел, оказавшимися дезинформационными…
Невольно возникла мысль, какие схемы мы предъявили Госкомиссии? Случайно получившиеся?!
Различные варианты стандартных карт (как правило, 1 карта = 1–2 элемента типа NAND или NOR) от транзисторнных машин 1960–1970 гг., представляют все варианты дискретной логики – DTL, TTL, ECL (фото предоставлено коллекционером http://ummr.altervista.org) /size]
Так в муках рождалась советская микроэлектроника.

На чем собирали «Эльбрус-1»
Наконец, царь-логика, ставшая золотым стандартом до эпохи микропроцессоров, это, конечно, транзисторно-транзисторная (transistor-transistor logic, TTL).
Как явствует из названия, транзисторы здесь используются для выполнения как логических операций, так и усиления сигнала. Реализация TTL требует заменить диоды многоэмиттерным (обычно 2–8 эмиттеров) транзистором.
TTL была изобретена в 1961 году Джеймсом Бьюи (James L. Buie) из компании TRW, который сходу осознал, что она как нельзя лучше подходит для интегральных схем, только появляющихся в те годы. Конечно, TTL можно реализовать и дискретно, но, в отличие от DTL, ее слава пришла вместе с возвышением ИС.
Уже в 1963 году Sylvania выпустила первый комплект микросхем Universal High-Level Logic family (SUHL, использовалась в ракете AIM-54 Phoenix для истребителя Grumman F-14 Tomcat), построенных по транзисторно-транзисторной схеме. Буквально сразу же за Sylvania фирма Transitron выпустила клон их семейства с названием HLTTL, но главное событие было впереди.
В 1964 году Texas Instruments выпускает серию SN5400 для военных, а в 1966 году – вариант SN7400 в пластиковом корпусе для гражданского применения (недолго выпускалась средняя между ними по живучести серия SN8400 для индустриального применения).
Нельзя сказать, что 54/74 обладала какими-то невероятными параметрами, но она была удачно подобрана по элементам и самое главное – имела невероятную рекламу.
Вообще, TI была своеобразным Intel 1960-х – главным законодателем мод на рынке ИС (в основном благодаря невероятно тормознутой политике их основного конкурента Fairchild и чудовищным патентным войнам, а не особому таланту разработчиков).
В результате буквально через пару лет серию 7400 лицензировали десятки фирм – Motorola, AMD, Harris, Fairchild, Intel, Intersil, Signetics, Mullard, Siemens, SGS-Thomson, Rifa, National Semiconductor, и спёр весь Соцблок – СССР, ГДР, Польша, Чехословакия, Венгрия, Румыния и даже КНР, и она стала таким же эталоном, как в 1980-е архитектура x86.
Единственной фирмой, которая не поддалась пропаганде TI, стала, конечно, IBM, корпорация-государство, которая все делала сама.
В результате до середины 1990-х они изготавливали абсолютно оригинальные TTL-чипы собственной, ни с чем не совместимой разработки, и применяли их в IBM System/38, IBM 4300 и IBM 3081.
Типовой MST-модуль (Monolithic Systems Technology) от IBM S/370 и его содержимое (https://habr.com)
Интересно и то, что 7400 серия фактически была не совсем честной TTL-логикой.
Начиная с продвинутой серии 74S (Schottky TTL) 1969 года и далее в 74LS (Low-power Schottky), 74AS (Advanced-Schottky), 74ALS (Advanced-Schottky Low-power) и 74F (Fast Schottky), вышедших в 1985 году, микросхемы вовсе не содержат многоэмиттерного транзистора – вместо него на входах стоят диоды Шоттки.
В результате технически это самая настоящая DTL(S), носящая название TTL, чисто чтобы не путать потребителя и не мешать бизнесу.
TTL и TTL(S) были лишены практически всех недостатков предыдущих семейств – они работали достаточно быстро, были недороги, надежны, мало грелись и имели высокую нагрузочную способность. Микросхемы TTL в зависимости от типа содержали от десятков до тысяч транзисторов и представляли собой элементы от самого примитивного логического вентиля до продвинутого BSP военного назначения.
Микросхемы TTL в зависимости от типа содержали от десятков до тысяч транзисторов и представляли собой элементы от самого примитивного логического вентиля до продвинутого BSP военного назначения.
Элементарная NAND-ячейка TTL-логики
Kenbak-1, предок всех ПК, использовал TTL для своего процессора в 1971 году.
Легендарный терминал Datapoint 2200 1970 года также работал на них (причем позже этот набор послужил прототипом архитектуры Intel 8080). Рабочие станции Xerox Alto 1973 года и Star 1981 года тоже имели процессоры, собранные из дискретных TTL-микросхем, правда, уже масштаба bit-slice процессора.
Практически все компьютеры до середины 1990-х годов в том или ином виде использовали TTL-чипы в некритичных для производительности моментах, как части разнообразных контроллеров шин, например.
Кроме того, до появления FPGA-матриц TTL-чипы активно применяли для прототипирования микропроцессоров (круче всех тут оказался как раз «Эльбрус» – перед тем как выпустить нормальную его версию, ИТМиВТ, по сути, прототипировал на TTL целую машину, которую даже впарил отдельно).
Первый ПК в мире, малыш Kenbak-1, созданный Джоном Блакенбакером (John V. Blankenbaker) в 1971 году. Было выпущено около 40 компьютеров. Сейчас уцелевшие экземпляры стоят около 500 000 долларов. Xerox Alto 1973 года – первая в мире рабочая станция с графической ОС, мышью, WYSIWYG-редакторами и ООП в качестве стандартного средства программирования. Фактически от современного ПК Alto не отличается вообще ничем, кроме производительности. Процессор собран на 4-х TI SN74181, образующих 16-битный BSP (https://t-lcarchive.org, https://3dnews.ru, https://habr.com)
Изначально TI выпустили классическую 74-ю серию и вариант повышенного быстродействия 74H с типовой задержкой всего 6 нс.
Нагрузочная способность равнялась 10 – отличный результат, позволяющий собирать довольно сложные схемы.
Корпус был самым простым – DIP14, в серию входило 8 самых простых (типа NAND) микросхем. Чуть позже номенклатура была расширена (как и типы корпусов, добавились на 16 и 24 вывода) и появился маломощный вариант – 74L, заторможённый до 30 нс на такт.
Первая серия с диодами Шоттки, 74S, вышла в 1971 году, ее скорость возросла почти до уровня советских ECL – 3 нс. В середине 1970-х появилась маломощная 74LS (при той же скорости, что обычная, 74-я мощность уменьшена в 5 раз).
В 1979 году Fairchild решает вставить свои 5 копеек и создает серию 74F по фирменной технологии Isoplanar-II (глубокое селективное окисление, обеспечивающее боковую изоляцию элементов вместо pn-переходов), которую они использовали для всего вообще.
Это позволило взять вожделенный барьер в 2 нс и при этом резко снизить мощность (кстати, для советских TTL-клонов все задержки смело можно множить на 2–3).
Texas Instruments провозились до 1982 года, когда, наконец, осилили серии 74ALS и 74AS практически тех же параметров. 74AS была даже чуть быстрее версии от Fairchild, но грелась в два раза больше и успеха не снискала, а вот 74ALS пользовалась огромной популярностью.
Наконец, лебединой песней TTL стала созданная фирмой Fairchild в 1989 году серия 74Fr, которая была в 1,5 раза быстрее 74F и грелась аналогично в 1,5 раза больше, поэтому была довольно быстро снята с производства.
74ALS же штамповали аж до 2019 года и использовали в куче мелкой автоматики и электроники. Существовала и версия SNJ54 – радиационно-стойкая для космического применения.
Золотая бессмертная классика – 16-битный процессор на TTL-рассыпухе TI SN74xx. Именно так выглядели процессоры 90 % машин в 1965–1975 гг. Конкретно эти платы представляют собой EAU (Extended Arithmetic Unit) модель 8413 (выпущена в 1974 г.) для миникомпьютеров Data General NOVA (примерный аналог по классу DEC PDP-11) и их же семейства Eclipse (S200, S230, C300, C330). Процессор (который сейчас бы назвали FPU) собран как BSP на чипах 74181. Он был совместим также с машинами General Electric Medical Systems, разработанными на основе Data General (http://ummr.altervista.org).
В Союзе к 1967–1968 годам TTL-чипов еще не было.
Именно поэтому в том числе и ЕС ЭВМ, и М10 Карцева, и 5Э53 Юдицкого разрабатывали под самое мощное, что было доступно – разнообразные ГИС. БЭСМ-6 и 5Э92б были вообще транзисторными, как и все гражданские машины. Даже прототип возимой ЭВМ 5Э65 (идеи которого позаимствовал Бурцев для 5Э21 позже), выпущенная в количестве трех штук, с 1969 по 1970 год тоже была транзисторной.
Даже прототип возимой ЭВМ 5Э65 (идеи которого позаимствовал Бурцев для 5Э21 позже), выпущенная в количестве трех штук, с 1969 по 1970 год тоже была транзисторной.
Однако, как мы помним, в 1967–1968 гг. было принято решение о разработке комплекса С-300, и в то же время ИТМиВТ заказывает клонирование серии TI 54/74.
Параллельно Минрадиопром перетягивает на себя все разработки, связанные с ПРО, и примерно в то же время у Бурцева рождается концепция «Эльбруса».
В результате принимается решение начать архитектурные изыскания в области сразу 2-х машин – для возимой ПВО (5Э26) и для стационарной ПРО («Эльбрус»). Параллельно планируется вести разработку долгожданных TTL-чипов, изучать возможности производства ECL-чипов и создавать два компьютера.
Как мы знаем, на практике все пошло не так, как задумано, и куда более примитивную 5Э26 закончили только через 8 лет разработки, а куда как боле навороченный «Эльбрус» выпустили серийно в TTL-версии только к середине 1980-х (а ECL-вариант к началу 1990-х), угробив на проект 20 лет.
На развитие советской TTL значительно повлиял и второй, после ИТМиВТ, серьезный игрок, возникший к 1969 году – НИЦЭВТ, разрабатывавший серию ЕС (а о его огромной роли в разработке советских ECL мы поговорим в следующей части).
Мало кто в курсе, но в золотые 1959–1960 годы не только русские ездили к американцам, но и американцы к нам!
В частности, в 1960 году на International conference on semiconductor physics в Прагу приезжал знаменитый инженер и изобретатель из Texas Instruments, директор по исследованиям приборов под руководством Гордона Тила, доктор Петриц (Richard L. Petritz), один из отцов SN51x.
Из Чехословакии он отправился в Москву, где осматривал советские лаборатории, делился своим опытом и обсуждал физику полупроводников.
Таким образом (с учетом Староса и Берга) практически вся советская микроэлектроника была основана при деятельном и довольно дружелюбном участии американцев.
К 1969 году была закончена разработка знаменитой серии 133 – клона SN5400 в планарном исполнении для военных (ОКР «Логика-2»).
С этого момента постепенно была скопирована вся линейка микросхем от TI:
Именно на этой серии и был создан «Эльбрус-1».
Как и многие в 1990-е, Бурцев внезапно узнал, что основатели Зеленограда Старос и Берг были американцами и, подобно Малашевичу, испытал такой шок, что не преминул вылить на покойных коллег неплохой ушат:
Бессмысленно анализировать талантливо сфабрикованную ложь создателей телепрограммы, в корне исказивших представление об истинных основателях отечественной микроэлектроники и вычислительной техники на ее основе.
Со Старосом и Бергом я был хорошо знаком и достаточно подробно изучал результаты их деятельности в Советском Союзе…
Наверное, это правда, что Старос и Берг, будучи студентами, передавали советской стороне закрытые данные США в области радиолокации. Но что они тем самым оказали нам большую помощь в развитии РЛС – по меньшей мере, преувеличение.
<…>
Облик микроэлектронных устройств по Старосу-Бергу выглядел так: в общий плохо герметизированный корпус помещались кристаллы, извлеченные из корпусных точечных транзисторов.
Естественно, по пути такой микроэлектроники мы пойти не могли.
Тем более, что мы хорошо знали, как работают точечные транзисторы в составе феррито-транзисторной логики, так как использовали их в этих элементах вычислительной техники начиная с 1956 года.
Подтверждение правильности нашего отказа от предлагаемой Старосом микроэлектроники не заставило себя ждать.
В один прекрасный день 1966 года меня вызвал директор нашего института академик Сергей Алексеевич Лебедев и говорит: «Тебя просил срочно приехать Валерий Дмитриевич. Калмыков. Зачем – не сказал, только хитро улыбнулся.
В министерстве Валерий Дмитриевич рассказал: «На днях у Староса был Хрущев. Ему показали ЭВМ под названием УМНХ – машина управления народным хозяйством.
Хрущев рекомендовал использовать УМНХ в управлении народным хозяйством.
После приезда Хрущева был созван обком партии, на котором поставили вопрос о том, нужна ли такая машина в районах. Все секретари заявили, что им такая машина очень нужна.
А делать-то эту ЭВМ кому?
Мне. Я же сомневаюсь в ее необходимости и в том, что УМНХ вообще работает.
Поэтому мы включаем тебя в комиссию по приемке этой машины, но имей в виду, положение трудное – если вы примете машину, придется ее делать, а я этого не хочу, не примете – может быть скандал».
К счастью, все обошлось хорошо.
Приехав в Ленинград и приступив к работе в комиссии, я прежде всего написал маленькие тесты.
Извлеченные из корпуса кристаллы транзисторов, помещенные в общий корпус машины, не работали. Мы, конечно, не могли написать отрицательный акт, и мудрый наш председатель генерал В. Ф. Балашов перенес испытания на шесть месяцев…
Испытания переносили еще много раз, так и не завершив работу комиссии, а про машину УМНХ все забыли…
Однако сами Старос и Берг, а в особенности их коллектив, произвели на нас хорошее впечатление, мы подружились с ними, поделились своим опытом разработки надежных систем.
<…>
Мы, конечно, не могли не спросить своих коллег, работающих в этой лаборатории, что же они показали Хрущеву и как убедили его, что машина УМ-НХ может чем-то управлять? Под большим секретом нам ответили: «Мы показали ему на осциллографе фигуру Лессажу и дали приемник, который вставляется в ухо». Такие приемники подарили и нам, но работали они не более недели.
Такие приемники подарили и нам, но работали они не более недели.
Не надо удивляться и возмущаться – примеры потемкинских деревень и нового платья короля можно встретить, к сожалению, и сегодня, причем в более грубой форме и на достаточно высоком уровне.
И Старос, и Берг были инициативными людьми – изобретателями, но, к сожалению, изобретателями в той области, где место только научно-техническим исследованиям. От изобретателей здесь пользы никакой, одно раздражение.
Поэтому назвать их основателями микроэлектроники Советского Союза никак нельзя, даже если Н. С. Хрущев и назначил Староса главным конструктором Зеленограда.
Еще более ложно утверждение, что они сыграли какую-то положительную роль в развитии вычислительной техники в СССР.
Отношение к этому интервью емко выразил известный бывший разработчик и эксперт по советским чипам:
При всём уважении к академику, несёт он дикую дичь. Ну, по крайней мере, про разработки Староса. Какие точечные транзисторы? Какие, к матери, «извлеченные из корпусных»? Он, видимо, что-то недопонял из старосовских микротранзисторов, потом у себя в голове нарисовал какую-то общую картину, вообще не имеющую отношения к действительности. ..
..
Вообще, здесь можно комментировать каждое предложение, начиная с «по пути такой микроэлектроники мы пойти не могли», а все советские ГИС, на которых собирали все, что можно, за 5 лет до Староса, пардон, это тогда что, это другое?
Не говоря уже, что с чудовищно криво корпусированной ECL, изготовленной мозолистыми руками честных советских людей, а не всякими пришельцами Старосами, 10 лет спустя столкнулся и Бурцев, наплакавшись вволю и задержав «Эльбрус-2» тем самым на несколько лет.
Особенно радует глаз пассаж про «такие приемники подарили и нам, но работали они не более недели. Не надо удивляться и возмущаться – примеры потемкинских деревень и нового платья короля можно встретить, к сожалению, и сегодня».
Эти самые приемники просто волшебные. Если мы хотим доказать ничтожество Староса – они отвратительны. Если мы хотим доказать величие советской сверхнауки – они восхитительны!
До середины семидесятых годов этот микроприемник можно было купить в магазинах СССР и Франции. Этот приемник произвел мировую сенсацию на съезде радиоинженеров в США. О нем писали в газетах: «как СССР смог нас обогнать?». Примечательно, что даже Хрущев брал их с собой за границу как сувениры, дарил Гамалю Насеру и даже самой королеве Елизавете.
Этот приемник произвел мировую сенсацию на съезде радиоинженеров в США. О нем писали в газетах: «как СССР смог нас обогнать?». Примечательно, что даже Хрущев брал их с собой за границу как сувениры, дарил Гамалю Насеру и даже самой королеве Елизавете.
В общем, американец Старос сделал шедевральный бесполезный мусор, превзошедшую американцев потемкинскую деревню.
Чтобы спокойно удерживать в голове эти взаимоисключающие параграфы и не тронуться рассудком, нужно иметь развитый навык двоемыслия, как мы уже описывали, невероятно прокачанный у отечественных академиков еще с 1930-х годов.
Из цитаты также забавно всесилие Калмыкова.
Хрущев подписал постановление об изготовлении УМ-1НХ, однако министру сам черт не брат, вызывает к себе Бурцева и говорит: не нравится мне Старос, завали-ка ты его. Бурцев – это не честный и принципиальный Лукин, которого за нежелание подставить Кисунько выперли из МРП, Бурцев все понимает и через это становится главным по программе ЭВМ для ПРО.
Ну и вообще вся суть отечественных министерств: машина изготовлена?
Да.
Все секретари обкомов за?
Да.
Хрущев за?
Да.
Все бумаги на выпуск подписаны?
Да.
Думаете, машину выпустили?
А шиш, Калмыков, как Баба-яга, против, ему лень возиться.
В этой истории радует одно, через 20 лет карма настигла и Бурцева, и точно так же всеми оплеванный за провал «Эльбруса» он был изгнан из ИТМиВТ, а позже Бабаян дожал его, ликвидировав и ВЦКП РАН и выгнав его на мороз второй раз, да еще и украв всю славу отца советского Burroughs.
Не будем забывать, что «Эльбрусом-1» применение советской TTL не исчерпывалось.
Второе ее важнейшее применение – это ЕС ЭВМ, конкретно – младшие и средние модели Ряда-1 и модифицированного Ряда-1.
О качестве их отлично высказался генеральный конструктор ЕС Пржиялковский:
Нужно отметить, что уже в начале производства машин ЕС ЭВМ выявились существенные проблемы, сопровождавшие отечественную ВТ все дальнейшие годы.
Во-первых, микроэлектронная база, на которой строилась ЕС ЭВМ, создавалась параллельно с машинами. Поскольку цикл разработки ЭВМ составлял минимум три года, то к моменту первой поставки машины потребителю она устаревала по своей элементной базе. До начала 80-х годов отечественные микросхемы неуклонно повышали степень своей интеграции. Так, ЭВМ ЕС-1020 использовала всего восемь типов микросхем серии 155, а к моменту начала ее производства появились еще два десятка типов, причем уже средней степени интеграции.
Во-вторых, химическая промышленность не смогла (а может не хотела?) стабильно выпускать для микросхем с корпусами ДИП пластмассу, обеспечивающую герметичность корпуса. В результате этого микросхемы имели крайне низкую надежность, особенно в условиях принудительной вентиляции шкафов ЭВМ.
<…>
Среди этих машин резко выделяются по технико-экономическим характеристикам модели ЕС-1032.
При единой архитектуре причиной таких великолепных для того времени показателей являлась только технологическая база. Есть смысл несколько остановиться на этом случае, учитывая те серьезные дебаты, которые проходили в высших органах управления СССР (ВПК, ГКНТ, ГОСПЛАН, МРП) при появлении в 1974 г. польской ЭВМ ЕС-1032.
Есть смысл несколько остановиться на этом случае, учитывая те серьезные дебаты, которые проходили в высших органах управления СССР (ВПК, ГКНТ, ГОСПЛАН, МРП) при появлении в 1974 г. польской ЭВМ ЕС-1032.
Процессор этой модели вместе с ОЗУ и каналами располагался в одном шкафу, тогда как отечественные модели ЕС-1022 и ЕС-1033 – в трех. Разработка ее велась на Вроцлавских заводах вне планов СГК ЕС ЭВМ. Когда она была закончена, встал вопрос о принятии ее в ЕС ЭВМ и присвоении ей соответствующего шифра.
При изучении документации на машину выяснилось, что при ее создании нарушены основополагающие документы и стандарты ЕС ЭВМ.
Главным нарушением было использование полной серии микросхем SN74 компании Texas Instrument. Советский аналог этой серии – серия 155 («Логика-2») имела вдвое худшие временные характеристики и в ней отсутствовали схемы повышенной интеграции. Под давлением высших органов страны (в первую очередь ВПК и МО) документами ЕС ЭВМ использование иностранных комплектующих изделий, не имеющих отечественных аналогов, запрещалось категорически.
Аналогичная ситуация была и с блоками питания.
Нарушением руководящих материалов ЕС ЭВМ было использование сдвоенных ТЭЗов размером 280х150 мм.
Все это, а также применение многослойной печатной платы ТЭЗа и использование полупроводникового ЗУ вместо ферритового (в СССР еще не было серийного производства микросхем для ОЗУ) привело к многократному увеличению степени интеграции сменного элемента замены, а следовательно, уменьшению габаритов и снижению потребляемой мощности.
По понятным причинам найти фото плат «Эльбрус-1» не представляется возможным. Примерно представление о микроэлектронике их уровня можно получить из этой картинки. Это космические часы с корабля «Союз», изготовленные в 1984 году на микросхемах 134ЛА8. Они попали в музей в Маунтин-Вью в Калифорнии и были там изучены Кеном Шириффом (Ken Shirriff). Часы, таймер и будильник содержат более 100 ИС, это немного шокирует. Микросхема реализует 4И-НЕ, далее показан распотрошенный чип, его логическая схема, снимок кристалла и участок, отвечающий за 1 транзистор (https://habr. com).
com).
Как мы и говорили – чудовищное воплощение советской TTL (особенно в гражданском варианте) было именно тем, что подкосило Ряд-1 и навсегда оставило у многих впечатление, что выпуск клона IBM был страшнейшей ошибкой.
Сами-то машины были отличными (IBM мусора не сделает, эту архитектуру со страшной силой копировал весь мир, от немцев до японцев), наши разработчики тоже в целом постарались неплохо.
А вот Зеленограду до качественного изготовления чипов, даже на целиком купленных западных линиях, всю его историю было как пешком до Луны. Именно из-за чудовищного качества первых микросхем 155-й серии большинство машин ЕС Ряд-1 вообще не работали или же постоянно и жестоко глючили.
Досадно то, что к концу 1980-х Ряд-1 составлял более 25 % всего объема ЕС ЭВМ, в результате как минимум 1/4 несчастных пользователей по всему Союзу была готова разбить эти чертовы машины кувалдой, в чем не была виновата ни фирма IBM, ни НИЦЭВТ.
Все претензии по справедливости нужно было отправлять в Зеленоград, к Малашевичу, чиновнику МЭП, прославившемуся своими мемуарами, в которых одна история удивительнее другой:
…с момента появления первых ИС прошло всего лишь около 20 лет, а результаты были получены фантастические…
Согласимся, результаты действительно были фантастические, вот только не в позитивном смысле.

В 1972 году ЦРУ подготовило ряд отчетов о состоянии советской микроэлектроники и рассекретило их в 1999 году.
Вот один из них:
…лабораторный анализ доступных образцов, проведенный в США, выявил, что их дизайн довольно примитивен, а качество – в основном низкое.
Образцы явно уступают аналогам, производимым в США.
Даже изделия выпуска 1971 г. с заводской маркировкой, судя по всему, представляют собой прототипы… ничего не известно о наличии серийно выпускаемого в СССР гражданского оборудования, в котором использовались бы интегральные схемы, и нет никаких признаков их использования в оборудовании военного назначения. Если СССР производит микросхемы в промышленных масштабах, то не ясно, где они собираются их использовать или используют.
И если Союз создал масштабную и жизнеспособную индустрию микросхем, то озадачивает также его интерес к крупным закупкам оборудования и технологий у Запада для производства этих изделий…
СССР слишком поздно получил планарную кремниевую технологию и, из-за постоянных сложностей с производством исходного кремниевого материала в достаточном количестве, производство микросхем в Союзе все же началось совсем недавно и в очень небольших объемах…
В 1971 году в СССР планарные и планарно-эпитаксиальные транзисторы составляют всего 1/10 от общего числа типов транзисторов, доступных в советских каталогах.
<…>
Технологии производства отстают на 5–10 лет от используемых в США. На заводе широко используется западное оборудование. Некоторые изделия в финальной стадии тестирования, по-видимому, содержат товарный знак основного американского производителя интегральных микросхем, хотя у агента не было возможности исследовать эти образцы вблизи, чтобы подтвердить данное подозрение.
<…>
Даже ограниченные возможности по выпуску интегральных схем, которые сейчас есть у СССР, в значительной степени являются результатом успеха Советов в приобретении критически важного оборудования из США, Западной Европы и Японии. В то же время, неудача в приобретении ноу-хау, необходимых для развертывания, эксплуатации и поддержки этого оборудования, замедлила усилия по производству микросхем.
В 1999 году ЦРУ рассекретило очередной доклад USSR seeks to build advanced Semiconductor Industry with embargoed western machinery.
Вот что можно почерпнуть из этого интересного документа:
В настоящее время в СССР производство полупроводников составляет менее 2 % от объема, производимого в США, и еще больше отстает от современного состояния.
Большинство военных электронных систем Советов все еще основаны на устаревших технологиях транзисторов или электронных ламп, а выпуск современных компьютеров третьего поколения для обработки данных значительно отстает от намеченных планов.
С 1973 года Москва приобрела оборудования и средств, предназначенных для производства полупроводников, на общую сумму в 40 миллионов долларов…
Власти США, контролирующие экспорт, получили информацию о закупках Советов и задержали поставку определенных элементов, играющих важную роль для автоматической обработки и систем контроля состояния производственной среды. СССР пока еще не получил технологию производства, позволяющую эффективно использовать приобретенное оборудование…
Был предпринят ряд попыток приобрести полные технологические линии производства интегральных схем (ИС), или даже заводы по производству ИС вне легальных каналов, но мы уверены, что они были неуспешными.
В общем, Советы не получили, и даже не пытались получить доступ к соответствующему ноу-хау…
Спорадические закупки западного оборудования для заполнения критических разрывов в производственном процессе, вероятно, позволили СССР запустить производство ИС несколько раньше, чем это было бы возможно в другом случае.
Однако мы убеждены в том, что общее влияние такого подхода на производственные возможности Советов было невелико.
Это связано с нехваткой изготовленного в СССР оборудования и устаревшей технологией производства, а также с почти полным отсутствием контроля качества продукции и состояния производственной среды на советских предприятиях.
К 1973 году, после почти четырех лет производственного опыта, Советы могли производить только относительно простые биполярные малые ИС (с невысокой степенью интеграции), имеющие низкое качество, и выпускаемые в небольших объемах.
До 1973 года Советы выпускали в основном простые типы полупроводников (транзисторы и диоды) на основе германия.
Переход к кремниевой технологии и к производству более современных типов полупроводниковых устройств, включая и интегральные схемы, основанные на кремнии, происходил медленно. Так, СССР в 1972 году выпускал только 10 миллионов ИС, что составляло менее двух процентов от производства США (составляющего более 700 миллионов единиц).
По нашему мнению, Советы смогли достичь даже такого невысокого уровня производства лишь за счет использования больших трудовых ресурсов, применяя неэффективные методы проб и ошибок и используя похищенные или тайно приобретенные западные разработки полупроводниковых устройств.
Советы ощущали отсутствие прогресса в разработке и производстве ИС, и в 1973 году, похоже, решили прибегнуть к крупномасштабной помощи Запада.
В 1973–1974 годах Советы начали искать нелегальные каналы для получения заметных объемов оборудования, включая и наиболее современного из доступного в то время оборудования…
Наконец, СССР сейчас может иметь серийное производство собственных тестовых устройств.
Однако эта технология сегодня устарела и, если только Советы не обновили ее или не использовали более развитые технологии, то она может оказаться неадекватной для современного производства полупроводников высокой плотности.
Этот доклад интересно сочетается со словами Малашевича:
«Тогда в мире было три страны, которые делали, скажем, фотолитографическое оборудование: США, Япония и Советский Союз. Это самое прецизионное оборудование среди всех технических устройств: уровень технологии в микроэлектронике зависит от уровня фотолитографии… Надо помнить, что при всех проблемах, которые испытывала наша страна, только в Советском Союзе была единственная в мире самодостаточная электроника. В которой все было свое и которая сама выпускала всю номенклатуру электронных изделий от радиоламп до СБИС. И обладала собственным материаловедением, собственным машиностроением – все было свое.
Это самое прецизионное оборудование среди всех технических устройств: уровень технологии в микроэлектронике зависит от уровня фотолитографии… Надо помнить, что при всех проблемах, которые испытывала наша страна, только в Советском Союзе была единственная в мире самодостаточная электроника. В которой все было свое и которая сама выпускала всю номенклатуру электронных изделий от радиоламп до СБИС. И обладала собственным материаловедением, собственным машиностроением – все было свое.
Сравнение часов «Союза» и «Шаттла»
При этом уровень военно-космической электроники с архитектурной точки зрения в СССР не отличался от американской, отставание было в уровне интеграции и технологиях.
Пишет Кен Ширрифф:
Для сравнения часов «Союза» с современной им американской космической электроникой 1980-х, я взял плату от компьютера AP-101S космического «Шаттла». На фото ниже показана схема от часов «Союза» (слева) и компьютера «Шаттла» (справа). Хотя компьютер «Шаттла» более продвинут с точки зрения технологий, разница между ними не такая большая, как я ожидал.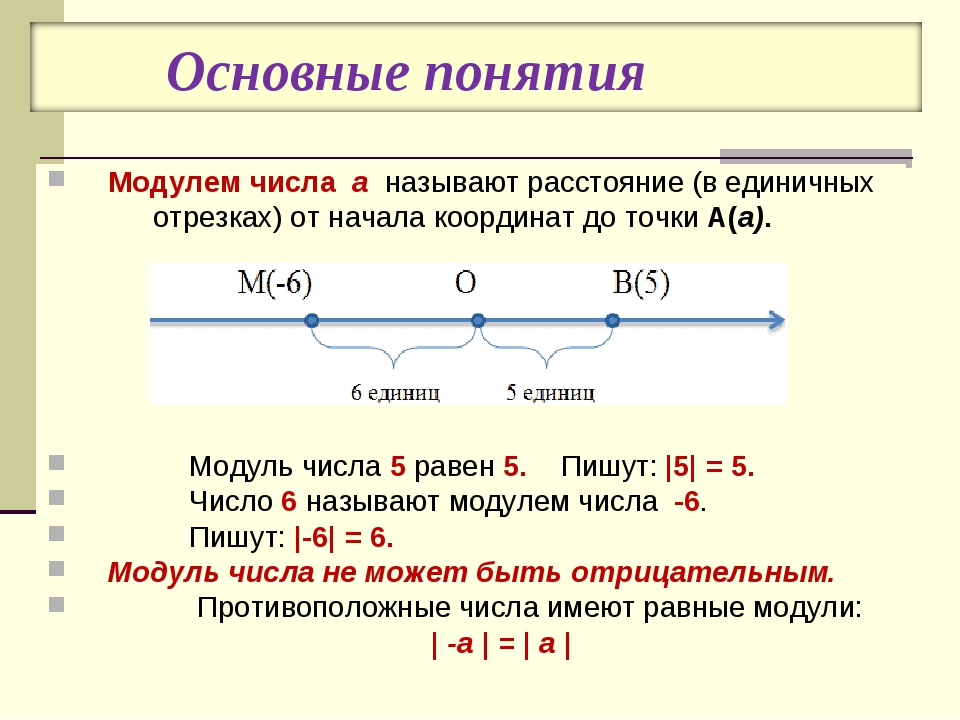
Обе системы сделаны на основе ТТЛ-чипов, хотя чипы у «Шаттла» из более быстрого поколения. Многие чипы у «Шаттла» чуть более сложные; обратите внимание на чипы с 20 контактами вверху.
Большой белый чип куда как более сложный – это чип коррекции ошибок памяти AMD Am2960.
Печатная плата «Шаттла» более продвинутая, у неё больше двух слоёв, из-за чего чипы можно располагать на 50 % плотнее.
В то время считалось, что СССР отстаёт от Запада в ИС-технологиях на 8–9 лет; это совпадает с тем, что видно на основе сравнения двух плат.
Однако что меня удивило, так это схожесть компьютера «Шаттла» и часов «Союза».
Я ожидал, что в компьютере «Шаттла» будут использоваться микропроцессоры 1980-х годов, и он будет опережать часы «Союза» на целое поколение, но оказалось, что обе системы используют технологию ТТЛ, и во многих случаях у чипов оказывается почти одинаковая функциональность.
К примеру, на обеих платах используются чипы, реализующие по 4 NAND-вентиля (поищите слева чип 134ΛБ1A, а справа – 54F00).
Пришествие CMOS
Для общего развития упомянем и историю полевых транзисторов (field-effect transistor, FET).
Как концепция, он появился даже раньше, в работах Лилиенфельда (Julius Edgar Lilienfeld) 1920-х годов и, собственно, его и пытались изготовить Бардин, Браттейн и Шокли, не безуспешно, получив в итоге биполярный транзистор.
Мучения с полевыми транзисторами продлились с 1945 (Heinrich Johann Welker, прототип JFET – junction FET) до 1953 года (патент George F. Dacey и Ian Munro Ross на промышленный, но дорогостоящий и ненадежный способ изготовления JFET).
Технология все равно была настолько сырой и неудачной, что к середине 1950-х большинство исследователей отказались вообще возиться с полевыми транзисторами, а те, что производились – изготавливались малыми тиражами для специальных применений (например, GE Technitron, тонкоплёночный полевой транзистор на сульфиде кадмия 1959 года от RCA, или работы 1960 года от Crystalonics).
Прорыв произошел только в 1959 году, когда американский инженер египетского происхождения Мохаммед Аталла (Mohamed M. Atalla) открыл пассивацию поверхности кремниевых пластин, сделавшую возможным массовое технологичное производство кремниевых ИС.
Atalla) открыл пассивацию поверхности кремниевых пластин, сделавшую возможным массовое технологичное производство кремниевых ИС.
Вместе с еще одним американским иностранцем, корейцем Дионом Кангом (Dawon Kahng), Аталла разработал концепцию формирования металл-оксидных структур для производства FET – так родился новый тип транзистора, metal-oxide-semiconductor FET (MOSFET), представленный в двух вариантах: pMOS (МОП p-типа) и nMOS (МОП n-типа).
Изначально технология не заинтересовала двух серьезных игроков на рынке – лабораторию Bell и TI (те продолжали колупать неудачный JFET, даже выпустив в 1962 году планарную версию на pn-переходе), но оставшиеся: RCA, General Microelectronics, IBM и Fairchild, немедленно продолжили изыскания.
В том же 1962 году RCA изготовил первый прототип MOS-микросхемы на 16 транзисторах (Steve R. Hofstein и Fred P. Heiman), а год спустя инженеры Fairchild Чин-Тан Са (Chih-Tang Sah) и General Microelectronics Фрэнк Уонлес (Frank Marion Wanlass) разработали, наконец, совершенную технологию – комплиментарный металл-оксидный полупроводник, КМОП (complementary metal-oxide-semiconductor, CMOS), по праву занявший место в списке величайших изобретений в истории.
В 1964 году появились первые серийные MOS-транзисторы от RCA и Fairchild, и в том же году General Microelectronics выпустила первую серийную MOS-микросхему, а CMOS-чипы появились в 1968 году в компании Fairchild.
Первым коммерческим применением MOS-микросхем стал заказ NASA на ИС для программы Interplanetary Monitoring Platform, выполненный GM. CMOS стал первым типом логики, получившим исключительно интегральное воплощение, она имела массу преимуществ перед TTL: высочайшая масштабируемость и феноменальная плотность упаковки (позволившая без проблем разрабатывать микросхемы большой и сверхбольшой интеграции), дешевизна, невысокая потребляемая мощность и колоссальный потенциал для различных улучшений.
Дополнительным бонусом стало то, что CMOS требовала на несколько этапов меньше при фотолитографии, что не только снижало стоимость, но и упрощало оборудование и значительно уменьшало вероятность ошибок изготовления.
Единственной проблемой ранних CMOS-чипов стала скорость работы – низкая по сравнению с рассыпухой на TTL и тем более ECL.
В результате все 1970-е годы CMOS активно применялись там, где не требовались экстремальные скорости – в микросхемах ОЗУ и разнообразных микроконтроллерах.
В 1968 году вышла знаменитая серия логики RCA 4000, ставшая для CMOS тем же, чем SN54/74 для TTL. Тогда же RCA создала первую микросхему SRAM на 288 бит. В том же году выходцы из Fairchild инженеры Fairchild Нойс (Robert Norton Noyce), Мур (Gordon Earle Moore) и Гроув (Andrew Stephen Grove) основали Intel, а менеджер Джереми Сандерс (Walter Jeremiah Sanders III) основал AMD.
Изначально инвесторы смотрели на Сандерса косо, так как он был в первую очередь управленцем, а не изобретателем, как Нойс и Мур, однако, эта парочка поспособствовала и созданию AMD, вложив в компанию свои деньги.
Смысл был в том, чтобы начать зарабатывать на военных заказах – в тендерах должны были участвовать минимум две компании, так что Intel не видели вреда в том, чтобы вырастить себе конкурента. План в целом сработал, AMD прославилась множеством оригинальных разработок.
В русских источниках их часто, не разбираясь в теме, называют обычными копиркиными, однако клонировали они только 8080 и x86 (параллельно выпуская и кучу своих архитектур), а все прочее разрабатывали самостоятельно и весьма неплохо, в 1990–2000 гг. уже Intel пришлось догонять AMD.
В начале 1970-х годов CMOS не была самой распространенной технологией, использовалась pMOS, обладавшая тогда куда большим быстродействием, pMOS-чипами были почти все иконические американские микросхемы тех лет.
В 1969 году Intel запустили свою первую и последнюю TTLS-линейку (Intel 3101 SRAM на 64 бита; 3301 ROM; 3105 регистр; серия чипов 300x BSP-процессор), но дальше настало господство pMOS.
Intel 1101 (SRAM на 256 бит), знаменитые процессоры Intel 4004 и Intel 8008, National Semiconductor IMP-16, PACE и SC/MP, микроконтроллер TI TMS1000, Rockwell International PPS-4 и PPS-8 – все это pMOS-чипы.
К 1972 году технология nMOS тоже догнала свою родственницу, Intel 2102 (1 кбит SRAM) был изготовлен на ней. Поскольку подвижность электронов в канале n-типа примерно в три раза превышает подвижность дырок в канале p-типа, nMOS-логика позволяет увеличить скорость переключения.
Поскольку подвижность электронов в канале n-типа примерно в три раза превышает подвижность дырок в канале p-типа, nMOS-логика позволяет увеличить скорость переключения.
По этой причине nMOS быстро начала вытеснять pMOS, и через 10 лет почти все западные микропроцессоры были уже nMOS-чипами. pMOS была дешевле и обеспечивала лучший уровень интеграции, а nMOS – быстрее.
И тут внезапно на рынок ворвались японцы.
Японский ренессанс потихоньку набирал обороты с конца оккупации, и к исходу 1960-х они были готовы побороться за рынок. Решено было начать с дешевой и простой электроники, часов, калькуляторов и т. п., а для них CMOS была идеальным вариантом, максимально дешевая и с минимальным энергопотреблением, а на скорость в часах было наплевать.
В 1969 году Toshiba разработала C2MOS (Clocked CMOS) – технологию с более низким энергопотреблением и более высокой скоростью работы, и применила ее в чипах для карманного калькулятора Elsi Mini LED компании Sharp, выпущенного в 1972 году.
В том же году Suwa Seikosha (сейчас Seiko Epson) начала разработку микросхемы CMOS для своих кварцевых часов Seiko 38SQW, вышедших в 1971 году. Идею переняли даже консервативные швейцарцы, в 1970 году под влиянием японцев Hamilton Watch Company впервые осквернила традиции швейцарского механического мастерства, выпустив электронные часы Hamilton Pulsar Wrist Computer.
Вообще, благодаря сверхмалому по сравнению с TTL энергопотреблению и высокой интеграции, все 1970-е CMOS активно продвигалась на рынке портативных устройств.
На Западе в это время все колупали MOS-технологию, только в 1975 году вышли первые CMOS-процессоры Intersil 6100 и RCA CDP 1801 (самое знаменитое использование – миссия к Юпитеру, Galileo, 1989 год, выбран из-за низкого энергопотребления).
CMOS изначально был в 10 раз тормознутее, например, Intel 5101 (1 кб SRAM, 1974, CMOS) имел время доступа 800 нс, а Intel 2147 (4 кб SRAM, 1976, технология depletion-load nMOS) уже 55–70 нс. Только в 1978 году.
Тосиаки Масухара (Toshiaki Masuhara) из Hitachi создал технологию twin-well Hi-CMOS, чип памяти на которой (HM6147, аналог Intel 2147) был таким же быстрым, но потреблял в 8 раз меньше энергии.
Техпроцессы конца 1970-х лежали в диапазоне 3 мкм, в 1983 году Intel представила 1,5 мкм (Intel 80386), а в 1985–1988 годах ирано-американский инженер Биджан Давари (Bijan Davari) из IBM разработал прототип 250 нм чипа, но серийные устройства были пока куда толще, хотя даже 1 мкм уже хватило для достижения скорости, наконец, превосходящей все прочие виды архитектур ИС.
С середины 1980-х доля CMOS стала расти экспоненциально, и к 2000 году 99,9 % всех выпускаемых в мире микросхем созданы по тем или иным вариантам CMOS-технологии.
Все, что вы хотели знать о CMOS, но боялись спросить. FinFET (fin field-effect transistor) – одна из самых совершенных реализаций CMOS. Два MOSFET на тестовой пластинке, взгляд через микроскоп. Наглядное различие между nMOS и pMOS. Классический вентиль NAND – его схема и физическое воплощение в кремнии (рисунки и фото https://en. wikipedia.org)
wikipedia.org)
Fujitsu освоила 700 нм в 1987 году, затем Hitachi, Mitsubishi Electric, NEC и Toshiba в 1989 году выпустили 500 нм.
Японцы продолжали доминировать в разработке техпроцессов все ранние 1990-е, в 1993 году Sony создала 350 нм, а Hitachi и NEC – наконец, серийные 250 нм.
Американцы в этом плане отставали, например, версии Intel 80486 (выпускавшегося с 1989 по 2007) имели техпроцесс последовательно 1 000, 800 и 600 нм, Pentium 800–250 нм. Hitachi представила 160 нм процесс в 1995 году, в 1996 году Mitsubishi ответила 150 нм, а затем в битву ворвались корейцы, и в 1999 году Samsung Electronics выкатила 140 нм.
Только в 2000 году их, наконец, превзошли американские компании, когда Гуртедж Сингх Сандху (Gurtej Singh Sandhu) и Транг Доан (Trung T. Doan) из Micron Technology изобрели 90 нм техпроцесс. Pentium IV выпускался по техпроцессу 180–65 нм, азиаты не сдавались, в 2002 Toshiba и Sony разработали 65 нм, а затем в высшую лигу добавилась тайванская TSMC с 45 нм в 2004 году.
Разработки Сандху и Доана позволили Micron Technology достичь 30 нм, а с High-κ/metal gate FinFET началась эпоха менее 20 нм.
СССР, к сожалению, никакими прорывами в CMOS-логике похвастать уже не смог и ограничился копированием MOS-чипов 1970-х годов.
Отметим, что термин CMOS описывает не собственно логику работы схемы, а ее техпроцесс (и тем отличается от всех прочих, упомянутых здесь). При этом в рамках CMOS возможны самые разные решения, например, Pass transistor logic (PTL), на которой собирался знаменитый процессор Zilog Z80 (1976) и многие другие чипы.
Были и более экзотические варианты, например, Cascode voltage switch logic (CVSL), а в аналоговых чипах часто применяется Bipolar CMOS (BiCMOS). В 1976 году Texas Instruments выпустила микропроцессор SBP0400, основанный вообще на интегрально-инжекционной логике (integrated injection logic, I2L) – максимально извращенном варианте RTL.
В I2L используют особые «транзисторы» с объединенной базой и общим эмиттером, не способные в нормальном состоянии проводить ток и подключенные к электродам-инжекторам, фактически из этих инжекторов логика и собирается.
Благодаря такому I2L имеет отличный уровень интеграции, превосходящий уровень MOS 1970-х годов, но все портит ее тормознутость, разогнаться более чем до 50 МГц такая схема не сможет.
В итоге I2L-процессоры остались курьезом середины 1970-х, но в СССР успели на всякий случай содрать и их, как микропроцессорные наборы серий К582 и К584.
В конце 1970-х в моду вошла микропроцессорная реализация популярных архитектур мейнфреймов. TI создали TMS9900, DEC – LSI-11, а Data General – mN601 MicroNova.
Возник интересный вопрос – а что случится, если сторонняя компания разработает собственный процессор, полностью совместимый по системе команд?
Ранние патентные войны Intel и AMD привели к тому, что Верховный суд постановил, что сама система команд не может являться объектом патентования, будучи общедоступной по определению, защищена лишь ее конкретная реализация.
Опираясь на это, Fairchild (не решившись обижать реально сильных игроков типа IBM или DEC) взяла и выпустила клон Data General – процессор F9440 MICROFLAME по фирменной технологии I3L (Isoplanar Integrated Injection Logic, усовершенствованный вариант I2L), нагло рекламируя его как полноценную замену мейнфрейму DG Nova 2.
Сказать, что Data General была в ярости – это еще слишком мягко, но по закону они ничего не могли сделать. Чтобы обеспечить контроль над своими клиентами, DG хитро добавила в лицензионное соглашение раздел о том, что программа может работать только на оборудовании Data General, даже если она могла работать на Fairchild F9440 (или любом другом процессоре), и это уже стало бы нарушением копирайта.
В 1978 году Fairchild подала встречный иск, утверждая, что такая лицензия является антиконкурентной, и потребовала 10 миллионов долларов в качестве возмещения ущерба. Чтобы было еще веселее, они выпустили F9445, MICROFLAME II, совместимый с Nova 3, и в рекламе утверждали, что он в 10 раз быстрее.
Однако тут Fairchild сама себе подложила свинью, поскольку разработка настолько сложной топологии задержала все прочие производства и поставила компанию на грань банкротства, тем более что процессор еще и вышел с опозданием. Вдобавок DG заявила, что архитектуру Nova 3 невозможно было воспроизвести без промышленного шпионажа, и вкатила еще один иск.
В 1979 году Fairchild была поглощена нефтяной компанией Schlumberger Limited (Exxon в ответ купила Zilog в 1980 году). Производство F9445 наконец-то началось в первой половине 1981 году. В целом его архитектура похожа на предыдущий, а инструкции Nova 3 эмулируются микрокодом. Включение микрокода позволило использовать чип, не только чтобы подразнить Data General.
В 1980 году ВВС США опубликовали знаменитый стандарт MIL-STD-1750A на 16-разрядную архитектуру набора команд для всего, что летает: от истребителей до спутников. Он определяет только систему команд, но не ее физическое воплощение, в результате множество фирм подключилось к изготовлению разнообразных военных и космических процессоров, соответствующих этой ISA.
Так появились процессоры Signetics, Honeywell, Performance Semiconductor, Bendix, Fairchild, McDonnell Douglas и иных экзотических производителей.
Fairchild разработала для F9445 прошивку, реализующую MIL-STD-1750A, к 1985 году, и так родился F9450. Даже предыдущая версия вышла очень горячей, в новой же пришлось применить не имеющий аналогов корпус из оксида бериллия BeO, имеющего теплопроводность выше, чем у любого неметалла (исключая алмаз), да и выше, чем многие металлы. Процессор получился очень оригинальным и использовался в военных целях до середины 1990-х.
Даже предыдущая версия вышла очень горячей, в новой же пришлось применить не имеющий аналогов корпус из оксида бериллия BeO, имеющего теплопроводность выше, чем у любого неметалла (исключая алмаз), да и выше, чем многие металлы. Процессор получился очень оригинальным и использовался в военных целях до середины 1990-х.
Судебное побоище между Data General и Fairchild продолжалось до 1986 года, в итоге истощенная компания предпочла не продолжать дело и даже выплатить Fairchild отступные в размере 52,5 миллиона долларов. Что забавно, к этому моменту оригинальные Nova 2 и Nova 3 уже не производились.
Судебные иски разорили обе компании, в 1987 году Schlumberger перепродал Fairchild корпорации National Semiconductor, а та прикрыла всю линейку F94xx.
Так закончилась последняя попытка использовать для микропроцессоров что-то, существенно отличное от CMOS.
Британская фирма Ferranti в 1971 году лицензировала у Fairchild чрезвычайно оригинальный процесс диффузной изоляции коллектора (collector-diffusion-isolation, CDI), который они разработали для TTL чипов, но забросили, переключившись на I3L и MOS. В начале 1970-х Министерство обороны Великобритании выдало им заказ на разработку военного микропроцессора на данной технологии.
В начале 1970-х Министерство обороны Великобритании выдало им заказ на разработку военного микропроцессора на данной технологии.
К 1976 году был готов F100-L – отличный 8 МГц 16-битный процессор на примерно 1 500 вентилей, оригинальной системы команд. Он стал первым микропроцессором, созданным в Европе, и оспаривает честь быть первым 16-битным в мире у Texas Instruments TMS9900, вышедшем в том же году. Однако TI использовала nMOS процесс, в результате ее чип получилось утолкать только в громоздкий заказной корпус DIP64, а Ferranti без проблем влез в стандартный с 40 ножками.
Архитектура получилась очень удачной, хотя, увы, она стала не только первым оригинальным европейским чипом, но и последним (если не считать модификации F200-L 1984 года).
Некоторые из процессоров экзотических архитектур, упомянутые в статье. Фото из коллекции автора.
Конец Ferranti был анекдотичен и печален.
К середине 1980-х они зарабатывали отличные деньги на военных заказах в Европе и решили выйти на североамериканский рынок.
Для этого они приобрели компанию International Signal and Control, с 1970-х производящую военное оборудование по заказу Правительства США, в частности ракеты AGM-45 Shrike и RIM-7 Sea Sparrow.
У читателей, возможно, уже возник вопрос – а как это вообще так вышло, что янки продали британцам аж целого своего военного подрядчика?
Они бы еще Raytheon СССР продали!
Только вот подарочек оказался гнилым внутри.
На самом деле, несмотря на прекрасную отчетность, ISC практически ничего не производила и не разрабатывала, а по заказу АНБ и ЦРУ все 1970-е продавала в ЮАР (находящуюся официально под жесточайшими санкциями ООН за плохое отношение к неграм) новейшее американское оружие, средства РЭБ, связи и прочее.
В обмен на это ЮАР позволила церэушникам тайно построить станцию прослушки на мысе Доброй Надежды для слежения за советскими подводными лодками. Однако вышло так, что ЮАР решила поделиться американскими игрушками с Саддамом, и ЦРУ это сильно не понравилось.
Как бы так красиво свернуть весь бизнес и не спалиться, чтобы не отвечать на неприятные вопросы в ООН?
Выход нашли быстро – в 1988 сбагрили ISC британцам.
Те сначала очень обрадовались, а потом закопались поглубже и ахнули.
Оказалось, что никакого легального бизнеса, да и вообще производства, у ISC и в помине нет, все что есть – это бумаги о «произведенных» невероятных технологиях, нужные для отмывания оружейных денег.
Итогом стал невероятный скандал, тяжесть которого легла в основном на нового хозяина.
Основатель ISC Джеймс Гэрин (James Guerin) и 18 его партнеров, которых тащили в федеральную тюрьму на много-много лет, по дороге орали, что они не виноваты, и все было по согласию с АНБ и ЦРУ, но кто же поверит мошенникам?
В 1994 году Бобби Инмэн (Bobby Ray Inman), министр обороны при Клинтоне и член совета директоров ISC, тихонько ушел в отставку, и дело было окончательно замято.
Инмэн вообще был очень интересным человеком – при Рейгане был сначала директором АНБ, потом замдиректора ЦРУ, а параллельно – CEO в Microelectronics and Computer Technology Corporation, один из официальных попечителей Калтеха и член совета директоров Dell, AT&T, Massey Energy и той самой ISC.
В итоге немного заигравшиеся в шпионов американцы получили во время войны в заливе по башке своей же кассетной бомбой Mk 20 Rockeye II, которую по чертежам, переданным в ЮАР, для иракцев собрала чилийская Cardoen Industries, а Ferranti, опозоренная и разоренная, была в 1993 году поглощена Siemens-Plessley.
Советская CMOS связана на 90 % с микропроцессорами – клонами Intel, и к «Эльбрусу» не относится, поэтому мы ее опустим.
В следующей серии нас ждет горячая эмиттерно-связная логика, базовые матричные кристаллы и разработка «Эльбрус-2».
Модульная арифметика (CS 2800, весна 2016 г.)
- определения конгруэнтности
- классы эквивалентности
- определение операций (+, * и т. д.)
Конгруэнция мод м
Обозначение: a | b читается как « a делит b ». По определению, a | b , если существует некоторое число c , такое что c a = b .

Определение: для целого числа m два целых числа a и b конгруэнтны по модулю m , если m |( a − ).Мы пишем a ≡ b ( m o d m ). Я также иногда говорю эквивалент по модулю м .
Примечание: мы используем этот символ «мод» двумя разными способами. Первый был определен в предыдущей лекции: a m o d b обозначает остаток от деления a на b . «Mod m» в a ≡ b ( m o d m ) — это примечание на стороне уравнения, указывающее, что мы имеем в виду, когда говорим «≡ 007 903» 900
Факт: эти два использования «мод» довольно связаны: A ≡ B ( млн. O D M ) Если и только если A M O d м = b м o d м .

Модульные числа (классы эквивалентности по модулю m)
Определение: если A , м ∈ Z , затем [ A ] 4 M 7 M M Класс эквивалентности A MOD M ) — это набор все целые числа, конгруэнтные a , mod m .
Часто m будет понятно из контекста, и в этом случае я его опускаю и просто пишу [ a ].
Пример: Если мы работаем с модом 5, то [2]=[7]=[12]=[−3]=[−8]. Все они дают в остатке 2 при делении на 5.
Примечание: A ≡ B ( м O D M ) Если и только если [ A ] = [ B ] (доказательство простого)
Z m множество всех классов эквивалентности целых чисел по модулю m .
Пример: Z 5 = {[0],[1],[2],[3],[4]}.
 [5] находится в Z 5 , но я не указал его, потому что [5] совпадает с [0].
[5] находится в Z 5 , но я не указал его, потому что [5] совпадает с [0].Вообще, Z м = {[0],[1],…,[ м − 1]}. Другие классы эквивалентности уже содержатся в этом списке. Например, [ м ]=[0], [ м + 1]=[1] и так далее.
, если x 14 M и N и N ∈ , затем N называется представитель из x .
Операции над классами эквивалентности
Мы можем заставить классы эквивалентности вести себя как числа, соответствующим образом определив операции над ними. Нам просто нужно убедиться, что операции, которые мы определяем, имеют смысл.
Дополнение
Мы можем определить сложение следующим образом: если x , y ∈ Z m , то для вычисления x + 6 y:
- выбрать представителей a из x и b из y
- x + y тогда [ a + b ].

Другими словами, [ a ]+[ b ] определяется как [ a + b ]. Пример (все еще работает мод 5): [2]+[6]=[8].
Мы должны проверить, что это определение имеет смысл. Существует свобода выбора различных представителей; мы должны гарантировать, что получим тот же результат, если сделаем другой выбор. Другими словами, мы должны убедиться, что добавление правильно определено .
Пример (все еще мод 5): Вместо записи [2]+[6] мы могли бы написать [7]+[11] и получить [18] вместо [8].Но поскольку 8 ≡ 18, [18] и [8] — один и тот же класс эквивалентности.
Теорема: (Рабочий мод м ) Если A ≡ A ‘и B ≡ B ‘ Тогда A + B ≡ A ‘+ B ‘. Другими словами, если [ a ] = [ a ′] и [ b ] = [ b ′], то [ a + b ] = [ 1 +
5 a ′]. Доказательство: Поскольку ≡ ′, по определению м | а − а ′. Расширяя определение «делит», это означает, что a − a ′ = c m для некоторых c . Точно так же b − b ′ = d m для некоторых d . Добавляя их вместе, у нас есть ( A — A ‘) + ( B — B ‘) = C M + D M . Перестановка выходов ( a + b )−( a ′+ b ′) = ( c + d m ) .Другими словами, м | ( A + B ) — ( A ‘+ B ‘), или A + B ≡ A ‘+ B ‘. Это означает, что [ a + b ] = [ a ‘+ b ‘], что и требовалось.
Расширяя определение «делит», это означает, что a − a ′ = c m для некоторых c . Точно так же b − b ′ = d m для некоторых d . Добавляя их вместе, у нас есть ( A — A ‘) + ( B — B ‘) = C M + D M . Перестановка выходов ( a + b )−( a ′+ b ′) = ( c + d m ) .Другими словами, м | ( A + B ) — ( A ‘+ B ‘), или A + B ≡ A ‘+ B ‘. Это означает, что [ a + b ] = [ a ‘+ b ‘], что и требовалось.
Обозначение
В определении сложения было много слов. Мы можем использовать нотацию определения функции, чтобы сделать его более кратким. Сложение — это функция, которая принимает пару классов эквивалентности и дает класс эквивалентности:
.
+: Z M × Z M → Z M
Задается по правилу [ a ]+[ b ]=[ a + b ].Использование обозначения функции:
+ : ([ a ],[ b ]) → [ a + b ]
Очень важно : Всякий раз, определяя функции в классах эквивалентности таким образом, вы должны проверять правильность определения функции (как мы сделали для добавления). Всегда проверяйте, что выбор разных представителей дает одинаковый ответ.
Умножение, другие операции
Мы можем определить умножение:
*: Z M × Z 157 × M → Z M M M дается *: ([ A ], [ B ]) → [ а б ].
Пример (все еще мод 5): [3][4]=[12].
Доказательство того, что * корректно определено, оставлено на будущее.
Я призываю вас подумать о других операциях и о том, хорошо ли они определены.
Развлечение с модульной арифметикой – BetterExplained
Недавно один читатель предложил мне написать о модульной арифметике (она же «вычитание остатка»). Я не особо задумывался об этом, но понял, что модуль чрезвычайно мощный: он должен быть в нашем умственном наборе инструментов рядом со сложением и умножением.
Вместо того, чтобы бить вас формулами по лицу, давайте рассмотрим идею, которую мы ненавязчиво вынашивали годами. Есть хорошая статья о модульной арифметике, которая вдохновила меня на этот пост.
Нечетный, четный и тричетный
Вскоре после открытия целых чисел (1, 2, 3, 4, 5…) мы поняли, что они делятся на две группы:
- Четное: делится на 2 (0, 2, 4, 6..)
- Нечетное: не делится на 2 (1, 3, 5, 7…)
Почему это различие важно? Это начало абстракции — мы замечаем свойств числа (например, четность или нечетность), а не только само число («37»).
Это огромно — это позволяет нам исследовать математику на более глубоком уровне и находить отношения между типами чисел, а не конкретными. Например, мы можем создать такие правила:
.- Четный x Четный = Четный
- Нечетное x Нечетное = Нечетное
- Чет х Нечет = Чет
Эти правила являются общими — они работают на уровне свойства. (Интуитивно у меня есть химическая аналогия, что «четность» — это молекула, которую имеют некоторые числа, и ее нельзя удалить путем умножения.)
Но четное/нечетное — очень специфическое свойство: деление на 2. А как насчет числа 3? Как насчет этого:
- «Три» означает, что число делится на 3 (0, 3, 6, 9…)
- «Тродд» означает, что вы , а не делитесь на 3 (1, 2, 4, 5, 7, 8…)
Странно, но работает. Вы заметите несколько вещей: есть два типа throdd. Такое число, как «4», на 1 меньше, чем тричетырнадцать (остаток 1), а число 5 — на два (остаток 2).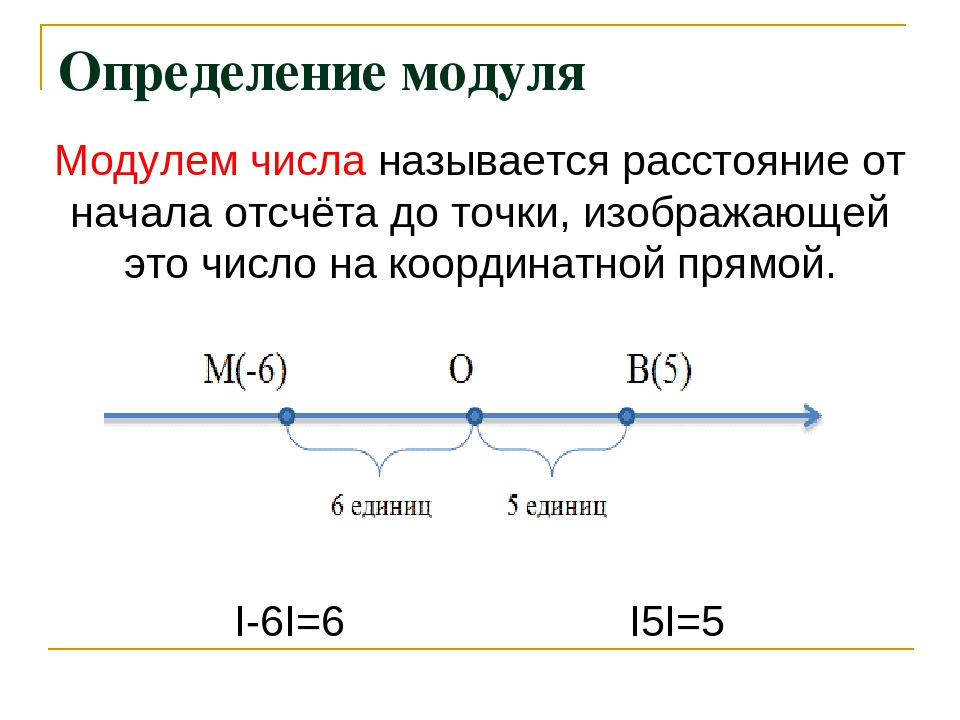
Быть «три» — это еще одно свойство числа.Возможно, это не так полезно сразу, как чет/нечет, но оно есть: мы можем создавать правила, такие как «три семь х тривен = тривен» и так далее.
Но это сводит с ума. Мы не можем все время составлять новые слова.
Введите модуль
Операция по модулю (сокращенно «mod» или «%» во многих языках программирования) — это остаток при делении. Например, «5 mod 3 = 2», что означает, что 2 — это остаток при делении 5 на 3.
Преобразовывая повседневные термины в математические, «четное число» — это число, у которого «0 по модулю 2», то есть оно имеет остаток 0 при делении на 2.Нечетное число — «1 по модулю 2» (с остатком 1).
Почему это круто? Итак, наши правила «чет/нечет» становятся такими:
.- Четный x Четный = 0 x 0 = 0 [четный]
- Нечетное x Нечетное = 1 x 1 = 1 [нечетное]
- Четный x Нечетный = 0 x 1 = 0 [четный]
Круто, да? Довольно легко разобраться — мы преобразовали «свойства» в настоящие уравнения и нашли несколько новых фактов.
Сколько будет четное x четное x нечетное x нечетное? Ну, это 0 x 0 x 1 x 1 = 0. На самом деле, вы можете видеть, что если где-нибудь умножить на четное, то весь результат будет равен нулю… Я имею в виду даже :).
Математика часов
Коварная особенность модульной математики заключается в том, что мы уже использовали ее для измерения времени — иногда называемую «арифметикой часов».
Например: сейчас 7:00 (утра/вечера не имеет значения). Где будет часовая стрелка через 7 часов?
грн. 7 + 7 = 14, но мы не можем показать «14:00» на часах. Значит, должно быть 2. Рассуждаем интуитивно и в математических терминах:
.- (7 + 7) по модулю 12 = (14) по модулю 12 = 2 по модулю 12 [2 — это остаток от деления 14 на 12]
Уравнение «14 mod 12 = 2 mod 12» означает, что «14 часов» и «2 часа» выглядят одинаково на 12-часовых часах.Они конгруэнтны , обозначены тройным знаком равенства: 14 ≡ 2 по модулю 12.
Другой пример: сейчас 8:00. Где будет большая рука через 25 часов?
Вместо того, чтобы прибавлять 25 к 8, вы можете понять, что 25 часов — это просто «1 день + 1 час». Таким образом, часы переведутся на 1 час вперед, в 9:00.
- (8 + 25) мод 12 ≡ (8) мод 12 + (25) мод 12 ≡ (8) мод 12 + (1) мод 12 ≡ 9 мод 12
Вы интуитивно преобразовали 25 в 1 и добавили это к 8.
Забавное свойство: математика просто работает
Используя в качестве аналогии часы, мы можем выяснить, «просто работают» ли правила модульной арифметики (работают).
Сложение/вычитание
Допустим, два времени на наших часах выглядят одинаково («2:00» и «14:00»). Если мы добавим к ним одинаковые «x» часов, что произойдет?
Ну меняют на столько же на часах! 2:00 + 5 часов ≡ 14:00 + 5 часов — оба будут показывать 7:00.
Почему? Ну, нас никогда не волновали лишние «12:00», которые таскал с собой 14-й. Мы можем просто добавить 5 к остатку 2, который есть у обоих, и они продвинутся одинаково. Для всех конгруэнтных чисел (2 и 14) сложение и вычитание дают одинаковый результат.
Для всех конгруэнтных чисел (2 и 14) сложение и вычитание дают одинаковый результат.
Умножение
Труднее понять, остается ли умножение прежним. Если 14 ≡ 2 (mod 12), можем ли мы умножить обе части и получить тот же результат?
Посмотрим — что получится, если умножить на 3?
Ну, 2 часа * 3 ≡ 6 часов. Но что такое «14:00» * 3?
Помните, 14 = 12 + 2. Итак, мы можем сказать
.- 14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3) mod 12
Первую часть (12 * 3) можно игнорировать! «12-часовое переполнение», которое носит с собой 14, просто повторяется несколько раз.Но кого это волнует? Мы все равно игнорируем переполнение.
При умножении важен только остаток, который равен 2 часам для 14:00 и 2:00. Интуитивно я вижу, что умножение не меняет отношения с модульной математикой (вы можете умножить обе части модульного отношения и получить тот же результат). Смотрите ссылку выше для более строгих доказательств — это мои интуитивные карандашные линии.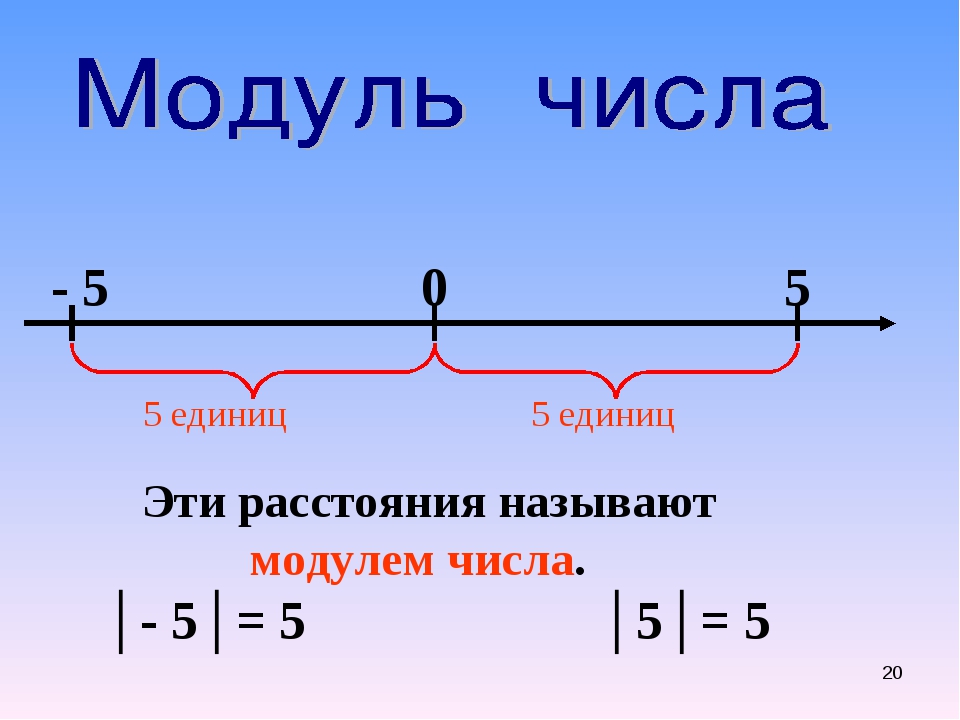
Использование модульной арифметики
Теперь самое интересное — чем полезна модульная арифметика?
Простые расчеты времени
Мы делаем это интуитивно, но лучше дать ему имя.Ваш рейс прибывает в 15:00. Задержка на 14 часов. В какое время он приземлится?
Итак, 14 ≡ 2 mod 12. Поэтому я думаю об этом как о «2 часах и переключении утра/после полудня», поэтому я знаю, что это будет «3 + 2 = 5 утра».
Это немного сложнее, чем простой оператор по модулю, но принцип тот же.
Размещение элементов в случайных группах
Предположим, у вас есть люди, купившие билеты в кино, с номером подтверждения. Вы хотите разделить их на 2 группы.
Что ты делаешь? «Шансы здесь, четы там». Вам не нужно знать, сколько билетов было выдано (первая половина, вторая половина), каждый может определить свою группу мгновенно (без обращения в центральный орган), и схема работает по мере того, как все больше людей покупают билеты.
Нужно 3 группы? Разделите на 3 и возьмите остаток (он же мод 3). У вас будут группы «0», «1» и «2».
В программировании по модулю можно помещать элементы в хеш-таблицу: если в вашей таблице N записей, преобразуйте ключ элемента в число, выполните mod N и поместите элемент в это ведро (возможно, сохраняя связанный список там).По мере увеличения размера вашей хэш-таблицы вы можете пересчитать модуль для ключей.
Выбор случайного предмета
Я использую модуль в реальной жизни. Действительно. У нас есть 4 человека, играющих в игру, и нужно выбрать кого-то, кто пойдет первым. Сыграй в мини-игру мод N! Дайте людям номера 0, 1, 2 и 3.
Теперь все идут «раз, два, три, стрелять!» и высовывает случайное количество пальцев. Сложите их и разделите на 4 — тот, кто точно наберет остаток, ходит первым.(Например: если сумма пальцев равна 11, тот, у кого было «3», ходит первым, так как 11 по модулю 4 = 3).
Это быстро и работает.
Запуск задач в цикле
Предположим, задачи должны выполняться по определенному расписанию:
- Задача A выполняется 3 раза в час
- Задача B выполняется 6 раз в час
- Задача C выполняется 1 раз в час
Как вы храните эту информацию и составляете расписание? В одну сторону:
- Таймер, работающий каждую минуту (отслеживайте минуты как «n»)
- 3x/час означает один раз каждые 60/3 = 20 минут.Таким образом, задача A запускается всякий раз, когда «n % 20 == 0»
- Задача B запускается всякий раз, когда «n % 10 == 0»
- Задача C запускается всякий раз, когда «n % 60 == 0»
О, вам нужна задача C1, которая выполняется 1 раз в час, но не в то же время, что и задача C? Конечно, запустите его, когда «n mod 60 == 1» (по-прежнему один раз в час, но не так, как C1).
Мысленно я вижу цикл, который хочу «побить» через разные промежутки времени, поэтому вставляю мод. Удобно то, что хиты могут перекрываться независимо друг от друга. В этом отношении это немного похоже на XOR (каждое XOR может быть многоуровневым — но это уже другая статья!).
Удобно то, что хиты могут перекрываться независимо друг от друга. В этом отношении это немного похоже на XOR (каждое XOR может быть многоуровневым — но это уже другая статья!).
Точно так же при программировании вы можете распечатать каждый сотый элемент журнала, выполнив: if (n % 100 == 0){ print… }.
Это очень гибкий и простой способ запуска элементов по расписанию. На самом деле, это способ ответить на проверку вменяемости FizzBuzz. Если в вашем batbelt нет операции по модулю, вопрос становится намного сложнее.
Нахождение свойств чисел
Предположим, я сказал вам следующее:
Что вы можете сделать вывод быстро? Что ж, «а» должно быть четным, поскольку оно равно чему-то, что включает умножение на 2.
Если бы я также сказал вам:
Ты бы отказался. Не потому, что вы «знаете», что два продукта разные, а потому, что один явно четный, а другой нечетный. Есть проблема: a не может быть одним и тем же числом в обоих случаях, поскольку свойства не совпадают с .
Такие вещи, как «четный», «три» и «mod n», являются более общими свойствами, чем отдельные числа, и мы можем проверить их согласованность. Таким образом, мы можем использовать модуль, чтобы выяснить, согласуются ли числа, не зная, что они собой представляют!
Если я скажу вам это:
Можно ли решить эти уравнения с целыми числами? Посмотрим:
- 3a + 5b = 8… давайте «mod 3 it»: 0 + 2b ≡ 2 mod 3 или b ≡ 1 mod 3
- 3a + b = 2… давайте «mod 3 it»: 0 + b ≡ 2 mod 3), или b ≡ 2 mod 3
Противоречие, молодцы! Б не может быть одновременно «1 по модулю 3» и «2 по модулю 3» — это так же абсурдно, как быть четным и нечетным одновременно!
Но есть одна загвоздка: числа типа «1.5” не четные и не нечетные — это не целые числа! Модульные свойства применяются к целым числам, поэтому мы можем сказать, что b не может быть целым числом .
Потому что на самом деле мы можем решить это уравнение:
- (3а + 5б) – (3а +б) = 8 – 2
- 4b = 6
- б = 1,5
- 3а + 1,5 = 2, поэтому 3а = 0,5 и а = 1/6
Не соблазняйтесь силой модуля! Знайте его пределы: это относится к целым числам.
Криптография
Игра с числами имеет очень важное применение в криптографии.Это слишком много, чтобы охватить здесь, но модуль используется в обмене ключами Диффи-Хеллмана — используется при настройке SSL-соединений для шифрования веб-трафика.
Простой английский
Компьютерщики любят использовать технические слова в обычном контексте. Вы можете услышать «X такое же, как Y по модулю Z», что примерно означает «Игнорируя Z, X и Y одинаковы».
Например:
- b и B идентичны, капитализация по модулю
- iTouch и iPad идентичны по модулю размера 😉
Вперёд и выше
Странно думать о «полезности» оператора по модулю — это все равно, что кто-то спрашивает, почему экспоненты полезны.В повседневной жизни не очень, но это инструмент для понимания закономерностей в мире и создания своих.
В общем, я вижу несколько общих вариантов использования:
- Редуктор диапазона: возьмите ввод, мод N, и у вас будет число от 0 до N-1.

- Назначение группы: возьмите ввод, мод N, и вы пометите его как группу от 0 до N-1. Эта группа может быть согласована любым количеством сторон — например, разные серверы, которые знают N = 20, могут договориться о том, к какой группе принадлежит ID=57.
- Вывод свойств: обрабатывать числа в соответствии со свойствами (четные, тричетные и т. д.) и разрабатывать принципы, полученные на уровне свойств
Я уверен, что я пропустил еще десятки применений — не стесняйтесь комментировать ниже.Удачной математики!
Другие сообщения из этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: визуальное руководство
- Quick Insight: интуитивное значение подразделения
- Краткий обзор: вычитание отрицательных чисел
- Удивительные закономерности в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (избегая проблемы с оградой)
- Причудливое введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция для золотого сечения
- Различные интерпретации числа ноль
модульная арифметика | Britannica
модульная арифметика , иногда называемая модульная арифметика или часовая арифметика , в самой элементарной форме, арифметика, выполняемая со счетом, который сбрасывается на ноль каждый раз, когда определенное целое число N больше единицы , известный как модуль (mod), был достигнут. Примерами являются цифровые часы в 24-часовой системе, которые сбрасываются на 0 в полночь ( N = 24), и круговой транспортир, размеченный на 360 градусов ( N = 360). Модульная арифметика важна в теории чисел, где она является основным инструментом решения диофантовых уравнений (особенно тех, которые ограничены целочисленными решениями). Обобщения предмета привели к важным попыткам 19-го века доказать последнюю теорему Ферма и развитию важных частей современной алгебры.
Примерами являются цифровые часы в 24-часовой системе, которые сбрасываются на 0 в полночь ( N = 24), и круговой транспортир, размеченный на 360 градусов ( N = 360). Модульная арифметика важна в теории чисел, где она является основным инструментом решения диофантовых уравнений (особенно тех, которые ограничены целочисленными решениями). Обобщения предмета привели к важным попыткам 19-го века доказать последнюю теорему Ферма и развитию важных частей современной алгебры.
В модульной арифметике (с модулем N ) единственными числами являются 0, 1, 2, …, N — 1, и они известны как остатки по модулю N . Остатки складываются путем взятия обычной арифметической суммы, а затем вычитания модуля из суммы столько раз, сколько необходимо, чтобы уменьшить сумму до числа M между 0 и N — 1 включительно. M называется суммой чисел по модулю N . Используя обозначения, введенные немецким математиком Карлом Фридрихом Гауссом в 1801 году, можно написать, например, 2 + 4 + 3 + 7 ≡ 6 (mod 10), где символ ≡ читается как «конгруэнтно».
Примеры использования модульной арифметики встречаются в древнекитайской, индийской и исламской культурах. В частности, они встречаются в календарных и астрономических задачах, поскольку они связаны с циклами (рукотворными или естественными), но модульная арифметика встречается и в чисто математических задачах. Пример из китайской книги 3-го века нашей эры « Sunzi suanjing » (« Mathematical Manual » Сунь Цзы) спрашивает
. У нас есть несколько вещей, но мы не знаем точно, сколько их.Если мы посчитаем их тремя, у нас останется два. Если мы посчитаем пятерками, у нас останется три. Если считать по семеркам, останется два. Сколько вещей есть?
Это эквивалентно запросу решения одновременных сравнений X ≡ 2 (mod 3), X ≡ 3 (mod 5) и X ≡ 2 (mod 7), одно решение которых равно 23. Общее решение таких задач стало известно как китайская теорема об остатках.
Швейцарский математик Леонард Эйлер впервые применил современный подход к конгруэнтности примерно в 1750 году, когда он явно ввел идею конгруэнтности по модулю числа N и показал, что эта концепция разбивает целые числа на N классов конгруэнтности или классов вычетов. Два целых числа принадлежат к одному и тому же классу конгруэнтности по модулю N , если их разность делится на N . Например, если N равно 5, то −6 и 4 являются членами одного и того же класса конгруэнтности {…, −6, −1, 4, 9, …}. Поскольку каждый класс конгруэнтности может быть представлен любым из своих членов, этот конкретный класс можно назвать, например, «классом конгруэнтности -6 по модулю 5» или «классом конгруэнтности 4 по модулю 5».
Два целых числа принадлежат к одному и тому же классу конгруэнтности по модулю N , если их разность делится на N . Например, если N равно 5, то −6 и 4 являются членами одного и того же класса конгруэнтности {…, −6, −1, 4, 9, …}. Поскольку каждый класс конгруэнтности может быть представлен любым из своих членов, этот конкретный класс можно назвать, например, «классом конгруэнтности -6 по модулю 5» или «классом конгруэнтности 4 по модулю 5».
В системе Эйлера любые N чисел, которые дают разные остатки при делении на N , могут представлять классы конгруэнтности по модулю N .Таким образом, одной возможной системой арифметики по модулю 5 будет −2, −1, 0, 1, 2. Добавление классов конгруэнтности по модулю N определяется путем выбора любого элемента из каждого класса, добавления элементов вместе, а затем взятия класс сравнения по модулю N , которому сумма принадлежит как ответ. Эйлер аналогичным образом определил вычитание и умножение классов вычетов. Например, чтобы умножить -3 на 4 (mod 5), сначала умножьте -3 × 4 = -12; поскольку −12 ≡ 3 (mod 5), решение равно −3 × 4 ≡ 3 (mod 5).Эйлер показал, что можно получить один и тот же результат с любыми двумя элементами из соответствующих классов конгруэнтности.
Например, чтобы умножить -3 на 4 (mod 5), сначала умножьте -3 × 4 = -12; поскольку −12 ≡ 3 (mod 5), решение равно −3 × 4 ≡ 3 (mod 5).Эйлер показал, что можно получить один и тот же результат с любыми двумя элементами из соответствующих классов конгруэнтности.
Обратите внимание, что когда модуль N не является простым, деление не всегда возможно. Например, 1 ÷ 2 ≡ 3 (мод. 5), так как 2 × 3 ≡ 1 (мод. 5). Однако уравнение 1 ÷ 2 ≡ X (мод. 4) не имеет решения, поскольку не существует X , такого что 2 × X ≡ 1 (мод. 4). Когда модуль N не является простым, можно разделить класс, представленный r , на класс, представленный s , тогда и только тогда, когда s и N взаимно просты (то есть, если их единственный общий множитель — число 1).Например, 7 ÷ 4 ≡ 4 (мод. 9), поскольку 4 × 4 ≡ 7 (мод. 9) — в этом случае 7 и 9 взаимно просты.
Модульное деление с помощью мультипликативного обратного знаменатель
Модульное деление с помощью обратного мультипликативного знаменательNext: Инвертирование модульно-арифметических функций Вверх: Содержание Предыдущий: Модульное умножение
Модульное деление сложнее. Мы исходим из того, что деление
должно быть противоположно умножению.Мы видели это в моде
7 арифметика, 5 умножить на 6 дает 2. Отсюда следует, что 2 разделить на 6
должно дать 5. Это действительно так.
Мы исходим из того, что деление
должно быть противоположно умножению.Мы видели это в моде
7 арифметика, 5 умножить на 6 дает 2. Отсюда следует, что 2 разделить на 6
должно дать 5. Это действительно так.
Однако это не всегда будет работать. По модулю 15, на что 10 разделить 5? Ну, можно было бы подумать, что ответ будет 2. С другой стороны, поскольку в приведенном выше примере 5 умножить на 5 равно 10, возможно, ответ будет 5. Опять же, в другом примере выше, 8 умножить на 5 равно 10, можно сказать ответ 8.
Вместо того, чтобы допускать несколько ответов, мы бы сказали в этом случае, что нет ответа.Это аналогично делению на ноль в обычном арифметика.
Концепция мультипликативного обратного поможет нам получить ответ
когда он есть, и поможет нам предсказать, когда его нет
отвечать. Мультипликативным обратным числом b является число c .
так что b умножить на c равно 1. В обычной арифметике
мультипликативное обратное число b является обратной величиной b , а именно 1/ b .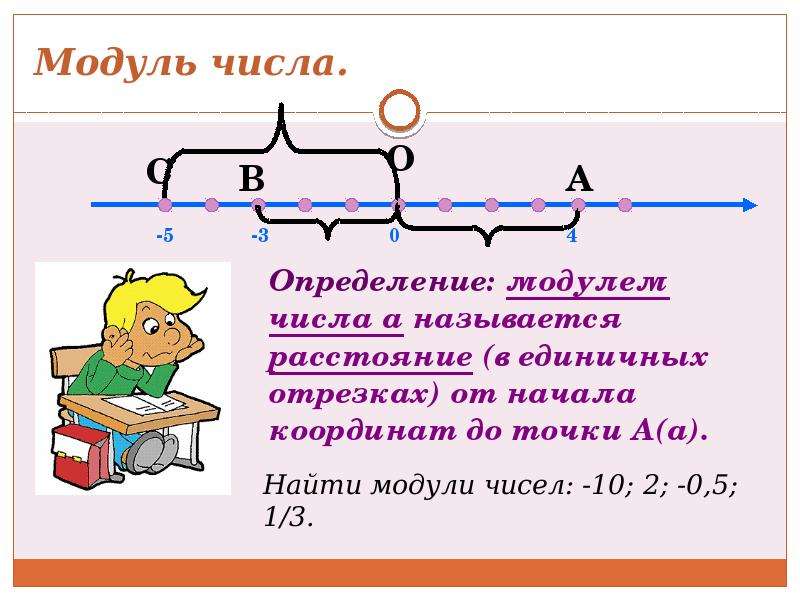 Например, предположим, что мы работаем с модулем 7.
мультипликативное число, обратное 3, равно 5, потому что 3 умножить на 5 равно 1. (Для
по той же причине мультипликативное значение, обратное 5, равно 3.) Мы можем найти
мультипликативные инверсии путем построения таблицы умножения. Вот
таблица умножения по модулю 7.
Например, предположим, что мы работаем с модулем 7.
мультипликативное число, обратное 3, равно 5, потому что 3 умножить на 5 равно 1. (Для
по той же причине мультипликативное значение, обратное 5, равно 3.) Мы можем найти
мультипликативные инверсии путем построения таблицы умножения. Вот
таблица умножения по модулю 7.
Глядя на таблицу, мы видим, что мультипликативная величина, обратная 1, равна 1, мультипликативное обратное 2 равно 4 (и наоборот), мультипликативное значение, обратное 3, равно 5 (и наоборот), и мультипликативное обратное 6 равно 6.Обратите внимание, что 0 не имеет мультипликативное обратное. Это соответствует факту в обычном арифметика, что 1 разделить на 0, не имеет ответа.
Теперь мы знаем, как делить 1 на разные числа по модулю 7: а именно,
1, деленная на b , является мультипликативной инверсией b . Как мы
разделить другие числа? Для целей этого класса ответ таков:
чтобы разделить a на b , просто разделите 1 на b , а затем умножьте
результат от до . Например, разделим 5 на 4 (по модулю 7). Сейчас 1
разделить на 4 равно 2, потому что 2 умножить на 4 равно 1. Следовательно, мы умножаем 5
на 2, получая 3. В Mathese,
Например, разделим 5 на 4 (по модулю 7). Сейчас 1
разделить на 4 равно 2, потому что 2 умножить на 4 равно 1. Следовательно, мы умножаем 5
на 2, получая 3. В Mathese,
следовательно
следовательно
Это сработало? Должны ли мы принять это? Ну, умножь с обеих сторон на 4. С левой стороны получаем 5. С правой стороны получаем получить, что действительно соответствует 5.
Ниже приведены дополнительные примеры мода 7. Проверьте результат, умножив обе части по знаменателю.
Для некоторых модулей некоторые числа не имеют мультипликативных
инверсии. Например, по модулю 15 число 12 не имеет
мультипликативное обратное. Нет числа, которое при умножении на
12 дает результат, конгруэнтный по модулю 15 и 1. Если вы построите
mod 15 таблица умножения, вы найдете множество других стандартных
имена (в частности, 0, 3, 5, 6, 9 и 10) не имеют
мультипликативные инверсии. Это явление исследуется в следующем
раздел.
Обратите внимание, однако, что все еще бывают случаи, когда по модулю 15 деление на 12 имеет смысл. Например, поскольку , это имеет смысл определить как 9. Теория чисел рассчитать такие дроби немного сложнее, чем Теория чисел рассматривается в этом классе, поэтому мы не будем просить вас вычислять такие подразделения.
Next: Инвертирование модульно-арифметических функций Вверх: Содержание Предыдущий: Модульное умножение Лиза Экштейн
Пн, 21 октября, 22:56:24 по восточному поясному времени 1996
Академический календарь | Столичный университет, Колумбус, Огайо,
КАМПУС БЕКСЛИ: летняя сессия | СЕМИНАРИЯ: A-TERM | B-термин
Академический календарь летней сессии
| Летняя сессия | 2022 |
|---|---|
| Начало полного семестра бакалавриата | 9 мая |
| Начало сеанса MBA/MSN I | 9 мая |
| Начало первой летней сессии бакалавриата* | 16 мая |
| Полный срок MAED и начало сессии I | 23 мая |
| Первая сессия Летнего научного института | 23 мая |
| День памяти — без классов | 30 мая |
| Первая сессия Летнего научного института | 17 июня |
| Начало сеанса MMME I | 20 июня |
| Начало второй сессии Летнего научного института | 21 июня |
| Завершение сеанса MBA/MSN I | 24 июня |
| Начало сеанса MBA/MSN II | 27 июня |
| Окончание первой летней сессии бакалавриата* | 1 июля |
| Завершение сессии I MAED | 1 июля |
| День Независимости — без класса | 4 июля |
| Начало II летней сессии бакалавриата* | 5 июля |
| Начало второй сессии MAED | 5 июля |
| Завершение сеанса MMME I | 8 июля |
| Вторая сессия Летнего научного института заканчивается | 18 июля |
| Начало сессии MMME II | 11 июля |
| MMME Session II Ends | 29 июля |
| MBA/MSN/MAED Сессия II Окончание | 12 августа |
| Летняя сессия бакалавриата II, полный семестр и окончание полного семестра MAED* | 19 августа |
* Даты начала и окончания различаются для некоторых отделений бакалавриата. | |
Троицкий лютеранский майский семестр
| Майский семестр | 2022 |
|---|---|
| Начало занятий | 25 апреля |
| Май Срок окончания | 13 мая |
| Приют Кэпстоун | 19 — 20 мая |
| Репетиция открытия | 20 мая |
| Начало | 21 мая |
| Опубликованные оценки за весенний семестр | 27 мая |
Троицкая лютеранская семинария, летний семестр A
| Летний семестр A | 2022 |
|---|---|
| Начало летнего семестра А | 6 июня |
| Неделя интенсивного обучения (первокурсники) | 13–17 июня |
| Летний семестр А заканчивается | 24 июня |
| Летняя оценка A | 8 июля |
Летний семестр B
Троицкой лютеранской семинарии| Летний семестр B | 2022 |
|---|---|
| Начало летнего греческого | 25 июля |
| Летний греческий конец | 12 августа |
| Выставлены оценки B за летний семестр | 26 августа |
Введение в теорию чисел
Раздел 5.
 2 Введение в теорию чисел
2 Введение в теорию чиселМы использовали натуральные числа для решения задач. Это был правильный набор чисел для работы в дискретной математике, потому что мы всегда имели дело с целым рядом вещей. Натуральные числа были инструментом. Давайте на минутку осмотрим этот инструмент. Какие математические открытия мы можем сделать о самих натуральных числах?
Это главный вопрос теории чисел: огромного, древнего, сложного и, главное, прекрасного раздела математики.Исторически теория чисел была известна как королева математики и в значительной степени была ветвью чистой математики, изучаемой сама по себе, а не как средство для понимания приложений реального мира. Однако это изменилось в последние годы, когда были обнаружены приложения теории чисел. Вероятно, наиболее известным примером этого является криптография RSA, один из методов, используемых для шифрования данных в Интернете. Это возможно благодаря теории чисел.
Какие вопросы относятся к области теории чисел? Вот мотивирующий пример. Напомним, в нашем исследовании индукции мы спросили:
Напомним, в нашем исследовании индукции мы спросили:
Какая сумма почтовых расходов может быть произведена с использованием только 5-центовых и 8-центовых марок?
Мы смогли доказать, что можно заработать любую сумму, превышающую 27 центов. Вам может быть интересно, что произойдет, если мы изменим номинал марок. Что, если бы вместо этого у нас были марки номиналом 4 и 9 центов? Будет ли существовать некоторая сумма, после которой все суммы будут возможны? Ну, опять же, мы могли бы заменить две марки по 4 цента на марку по 9 центов или три марки по 9 центов на семь марок по 4 цента.В каждом случае мы можем создать еще один цент почтовых расходов. Использование этого в качестве индуктивного случая позволило бы нам доказать, что может быть произведена любая сумма почтовых расходов, превышающая 23 цента.
Что, если бы у нас были марки по 2 и 4 цента. Здесь он выглядит менее перспективным. Если мы возьмем некоторое количество марок по 2 цента и некоторое количество марок по 4 цента, что мы можем сказать об их сумме? Может ли это когда-нибудь быть странным? Не похоже.
Почему работают 5 и 8, 4 и 9 работают, а 2 и 4 не работают? Что не так с этими цифрами? Если бы я дал вам пару цифр, вы бы сразу сказали, будут они работать или нет? Мы ответим на эти и другие вопросы, предварительно изучив некоторые более простые свойства самих чисел.
Подраздел Делимость
Натуральные числа легко складывать и умножать. Если мы расширим наше внимание на все целые числа, то вычитание также будет легким (нам нужны отрицательные числа, чтобы мы могли вычесть любое число из любого другого числа, даже большее из меньшего). Разделение — это первая операция, которая представляет собой вызов. Если бы мы хотели расширить наш набор чисел, чтобы было возможно любое деление (возможно, исключая деление на 0), нам нужно было бы взглянуть на рациональные числа (набор всех чисел, которые можно записать в виде дробей).Это было бы слишком далеко, поэтому мы откажемся от этого варианта.
На самом деле хорошо, что не каждое число можно разделить на другие числа. Это помогает нам понять структуру натуральных чисел и открывает двери для многих интересных вопросов и приложений.
Это помогает нам понять структуру натуральных чисел и открывает двери для многих интересных вопросов и приложений.
Если заданы числа \(a\) и \(b\text{,}\), возможно, что \(a \div b\) дает целое число. В этом случае мы говорим, что \(b\) делит \(a\text{,}\) в символах, мы пишем \(b \mid a\text{.}\) Если это верно, то \(b\) является делителем или множителем \(a\text{,}\) и \(a\) кратно \(b\text{.}\) In Другими словами, если \(b \mid a\text{,}\), то \(a = bk\) для некоторого целого числа \(k\) (это означает, что \(a\) является некоторым кратным \(b\ )).
Отношение делимости.
Для заданных целых чисел \(m\) и \(n\text{,}\) мы говорим «\(m\) делит \(n\)» и пишем
\begin{уравнение*} м \ середина п \end{уравнение*}
при условии, что \(n \div m\) является целым числом. Таким образом, следующие утверждения означают одно и то же:
- \(\displaystyle m \mid n\)
- \(n = mk\) для некоторого целого числа \(k\)
- \(m\) является множителем (или делителем) \(n\)
- \(n\) кратно \(m\text{.
 }\)
}\)
Обратите внимание, что \(m \mid n\) — это оператор. Это либо правда, либо ложь. С другой стороны, \(n \div m\) или \(n/m\) — это некоторое число. Если мы хотим утверждать, что \(n/m\) не является целым числом, поэтому \(m\) не делится на \(n\text{,}\), то мы можем написать \(m \nmid n\text{ .}\)
Пример 5.2.1.
Решите, является ли каждое из приведенных ниже утверждений верным или ложным.
- \(\displaystyle 4 \середина 20\)
- \(\displaystyle 20\середина 4\)
- \(\displaystyle 0 \середина 5\)
- \(\displaystyle 5\середина 0\)
- \(\displaystyle 7\середина 7\)
- \(\displaystyle 1\середина 37\)
- \(\displaystyle -3 \середина 12\)
- \(\displaystyle 8\середина 12\)
- \(\displaystyle 1642\середина 136299\)
Верно.4 «входит» в 20 пять раз без остатка. Другими словами, \(20 \div 4 = 5\text{,}\) целое число. Мы могли бы также обосновать это, сказав, что \(20\) кратно 4: \(20 = 4\cdot 5\text{.
 }\)
}\)Ложь. Хотя 20 кратно 4, неверно, что \(4\) кратно 20.
Ложь. \(5 \div 0\) даже не определено, не говоря уже о целом числе.
Верно. На самом деле \(x \mid 0\) верно для всех \(x\text{.}\) Это потому, что 0 кратно каждому числу: \(0 = x\cdot 0\text{.}\)
Верно. На самом деле, \(x \mid x\) верно для всех \(x\text{.}\)
Верно. 1 делит каждое число (кроме 0).
Верно. Отрицательные числа прекрасно подходят для отношения делимости. Здесь \(12 = -3 \cdot 4\text{.}\) Также верно, что \(3 \mid -12\) и что \(-3 \mid -12\text{.}\)
Ложь. И 8, и 12 делятся на 4, но это не означает, что \(12\) делится на \(8\text{.}\)
Ложь.Увидеть ниже.
Этот последний пример поднимает вопрос: как можно решить, является ли \(m \mid n\text{?}\) Конечно, если бы у вас был надежный калькулятор, вы могли бы запросить у него значение \(n \div m \text{. }\) Если он выдает что-либо, кроме целого числа, вы знаете, что \(m \nmid n\text{.}\) Это немного похоже на мошенничество: у нас нет деления, поэтому мы должны действительно использовать деление для проверки делимости?
}\) Если он выдает что-либо, кроме целого числа, вы знаете, что \(m \nmid n\text{.}\) Это немного похоже на мошенничество: у нас нет деления, поэтому мы должны действительно использовать деление для проверки делимости?
Хотя мы и не умеем делить, мы знаем, как умножать.Мы могли бы попробовать умножать \(m\) на все большие и большие числа, пока не приблизимся к \(n\text{.}\) Насколько близко? Ну, мы хотим быть уверены, что если мы умножим \(m\) на следующее большее целое число, мы превысим \(n\text{.}\)
.Например, давайте попробуем решить, следует ли \(1642 \mid 136299\text{.}\) начать поиск кратных 1642:
\begin{уравнение*} 1642 \cdot 2 = 3284 \qquad 1642 \cdot 3 = 4926 \qquad 1642\cdot 4 = 6568 \qquad \cdots\text{.} \end{уравнение*}
Все они значительно меньше 136299.Я полагаю, мы можем немного забежать вперед:
\begin{уравнение*} 1642 \cdot 50 = 82100 \qquad 1642 \cdot 80 = 131360 \qquad 1642 \cdot 85 = 139570\text{.} \end{уравнение*}
А, так что нам нужно искать где-то между 80 и 85. Попробуйте 83:
Попробуйте 83:
\begin{уравнение*} 1642 \cdot 83 = 136286\текст{.} \end{уравнение*}
Это лучшее, что мы можем сделать? Как далеко мы от желаемого 136299? Если мы вычтем, мы получим \(136299 — 136286 = 13\text{.}\) Итак, мы знаем, что не можем увеличить число до 84, это будет слишком много.Другими словами, мы обнаружили, что
\begin{уравнение*} 136299 = 83 \cdot 1642 + 13\текст{.} \end{уравнение*}
Поскольку \(13 \lt 1642\text{,}\) теперь мы можем с уверенностью сказать, что \(1642 \nmid 136299\text{.}\)
Оказывается, описанный выше процесс можно повторить для любой пары чисел. Мы всегда можем записать число \(a\) как некоторое кратное числу \(b\) плюс некоторый остаток. Мы знаем это, потому что знаем о делении с остатком из начальной школы.Это просто способ сказать это с помощью умножения. Из-за процедурного характера, который можно использовать для нахождения остатка, этот факт обычно называют алгоритмом деления :
.
Алгоритм деления.
Для любых двух целых чисел \(a\) и \(b\text{,}\) всегда можно найти целое число \(q\), такое что
\begin{уравнение*} а = qb + г \end{уравнение*}
, где \(r\) — целое число, удовлетворяющее \(0 \le r \lt |b|\)
Идея состоит в том, что мы всегда можем взять достаточно большое число, кратное \(b\), так что остаток \( г\) как можно меньше.Мы допускаем возможность \(r = 0\text{,}\), и в этом случае мы имеем \(b \mid a\text{.}\)
Классы остатка подраздела
Алгоритм деления говорит нам, что есть только \(b\) возможных остатков при делении на \(b\text{.}\) Если мы зафиксируем этот делитель, мы сможем сгруппировать целые числа по остатку. Каждая группа называется классом остатков по модулю \(b\) (или иногда классом остатков ).
Пример 5.2.2.
Описать остальные классы по модулю \(5\text{.}\)
Решение Мы хотим классифицировать числа по тому, какой будет их остаток при делении на \(5\text{. }\) Из алгоритма деления мы знаем, что будет ровно 5 классов остатка, потому что есть только 5 вариантов того, что \( r\) может быть (\(0 \le r \lt 5\)).
}\) Из алгоритма деления мы знаем, что будет ровно 5 классов остатка, потому что есть только 5 вариантов того, что \( r\) может быть (\(0 \le r \lt 5\)).
Сначала рассмотрим \(r = 0\text{.}\) Здесь мы ищем все числа, делящиеся на \(5\), поскольку \(a = 5q+0\text{.}\) Другими словами, кратны 5. Получаем бесконечное множество
\begin{уравнение*} \{\ldots, -15, -10, -5, 0, 5, 10, 15, 20, \ldots\}\text{.} \end{уравнение*}
Обратите внимание, что мы также включаем отрицательные целые числа.
Теперь рассмотрим \(r = 1\text{.}\) Какие целые числа при делении на 5 дают в остатке 1? Ну, конечно, 1 подходит, как и 6 и 11. Минусы? Здесь мы должны быть осторожны: \(-6\) НЕ имеет остатка 1. Мы можем написать \(-6 = -2\cdot 5 + 4\) или \(-6 = -1 \cdot 5 — 1\text {,}\), но только один из них является «правильным» экземпляром алгоритма деления: \(r = 4\), так как нам нужно, чтобы \(r\) было неотрицательным. Таким образом, чтобы получить \(r = 1\text{,}\), мы должны иметь \(-4\text{,}\) или \(-9\text{,}\) и т. д.Таким образом мы получаем остаток класса
д.Таким образом мы получаем остаток класса
\begin{уравнение*} \{\ldots, -14, -9, -4, 1, 6, 11, 16, 21, \ldots\}\text{.} \end{уравнение*}
Осталось еще три. Остальные классы для \(2\text{,}\) \(3\text{,}\) и \(4\) соответственно
\begin{уравнение*} \{\ldots, -13, -8, -3, 2, 7, 12, 17, 22,\ldots\} \end{уравнение*}
\begin{уравнение*} \{\ldots, -12, -7, -2, 3, 8, 13, 18, 23, \ldots\} \end{уравнение*}
\begin{уравнение*} \{\ldots, -11, -6, -1, 4, 9, 14, 19, 24, \ldots\}\text{.} \end{уравнение*}
Обратите внимание, что в приведенном выше примере каждое целое число находится ровно в одном классе остатка. Технический способ сказать это состоит в том, что остаточные классы по модулю \(b\) образуют разделов целых чисел. 1 Наиболее важным фактом о разбиениях является то, что можно определить отношение эквивалентности из разбиения: это отношение между парами чисел, которое действует во всех важных отношениях подобно отношению «равно».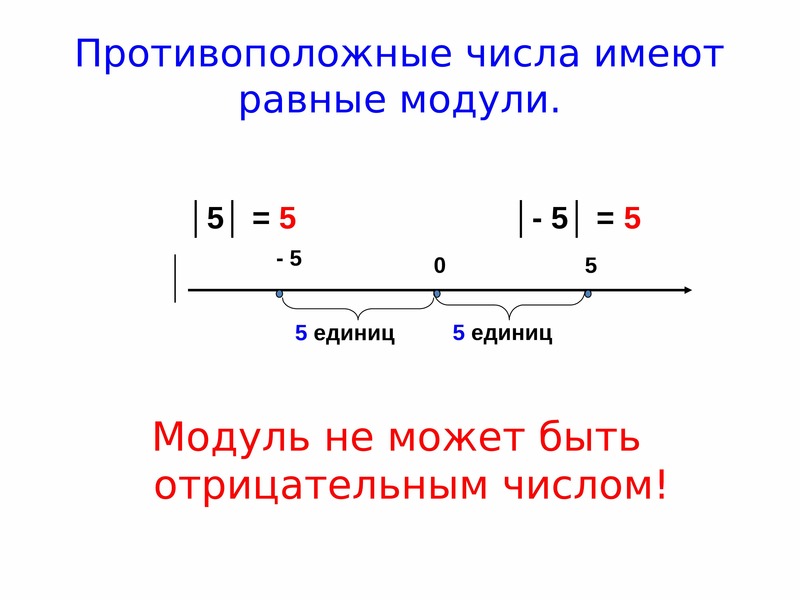 2
2
Можно разработать математическую теорию разбиений, доказать утверждения обо всех разбиениях вообще, а затем применить эти наблюдения к нашему случаю.
Опять же, существует математическая теория отношений эквивалентности, которая применима во многих других случаях, чем тот, который мы здесь рассматриваем.
Если оставить в стороне весь забавный технический язык, идея очень проста. Если два числа принадлежат к одному и тому же классу остатка, то в некотором смысле они одинаковы.То есть это одни и те же с точностью до деления на \(b\) . В случае, когда \(b = 5\) выше, числа \(8\) и \(23\text{,}\) хотя и не являются одним и тем же числом, но при делении на 5 одинаковы, потому что оба есть остаток \(3\text{.}\)
Делитель имеет значение: \(8\) и \(23\) совпадают до деления на \(5\text{,}\), но не до деления на \(7\text{,} \) так как \(8\) имеет остаток 1 при делении на 7, а 23 имеет остаток 2.
Имея все это в виду, давайте введем некоторые обозначения. Мы хотим сказать, что \(8\) и 23 в основном одинаковы, хотя и не равны. Было бы неправильно говорить \(8 = 23\text{.}\) Вместо этого мы пишем \(8 \equiv 23\text{.}\) Но это не всегда верно. Это работает, если мы думаем о делении на 5, поэтому нам нужно как-то это обозначить. На самом деле мы напишем это:
Мы хотим сказать, что \(8\) и 23 в основном одинаковы, хотя и не равны. Было бы неправильно говорить \(8 = 23\text{.}\) Вместо этого мы пишем \(8 \equiv 23\text{.}\) Но это не всегда верно. Это работает, если мы думаем о делении на 5, поэтому нам нужно как-то это обозначить. На самом деле мы напишем это:
\begin{уравнение*} 8 \экв 23 \pmod{5} \end{уравнение*}
, который читается как «8 сравнимо с 23 по модулю 5» (или просто «по модулю 5»). Конечно, тогда мы могли бы заметить, что
\begin{уравнение*} 8 \не\эквивалент 23 \pmod{7}\text{.} \end{уравнение*}
Сравнение по модулю \(n\).
Мы говорим, что \(a\) сравнимо с \(b\) по модулю \(n\) , и пишем
\begin{уравнение*} а \ экв б \ pmod {n} \end{уравнение*}
при условии, что \(a\) и \(b\) имеют одинаковый остаток при делении на \(n\text{.}\) Другими словами, при условии, что \(a\) и \(b\) принадлежат одному и тому же класс остатка по модулю \(n\text{.}\)
Во многих книгах конгруэнтность по модулю \(n\) определяется несколько иначе. Говорят, что \(a \equiv b \pmod{n}\) тогда и только тогда, когда \(n \mid a-b\text{.}\) Другими словами, два числа конгруэнтны по модулю \(n\text{,}\), если их разность кратна \(n\text{.}\). Итак, какое определение является правильным? Оказывается, это не имеет значения: они эквивалентны.
Говорят, что \(a \equiv b \pmod{n}\) тогда и только тогда, когда \(n \mid a-b\text{.}\) Другими словами, два числа конгруэнтны по модулю \(n\text{,}\), если их разность кратна \(n\text{.}\). Итак, какое определение является правильным? Оказывается, это не имеет значения: они эквивалентны.
Чтобы понять почему, рассмотрим два числа \(a\) и \(b\), которые конгруэнтны по модулю \(n\text{.}\). Тогда \(a\) и \(b\) имеют одинаковый остаток, когда делим на \(n\text{.}\) У нас есть
\begin{уравнение*} a = q_1 n + r \qquad\qquad b = q_2 n + r\text{.} \end{уравнение*}
Здесь два \(r\) действительно одинаковы.Рассмотрим, что мы получим, если возьмем разницу между \(a\) и \(b\text{:}\)
.\begin{уравнение*} a-b = q_1n + r — (q_2n + r) = q_1n — q_2 n = (q_1-q_2)n\text{.} \end{уравнение*}
Таким образом, \(a-b\) кратно \(n\text{,}\) или, что то же самое, \(n \mid a-b\text{.}\)
С другой стороны, если мы сначала предположим, что \(n \mid ab\text{,}\), поэтому \(ab = kn\text{,}\), то рассмотрим, что произойдет, если мы разделим каждый член на \(n \text{.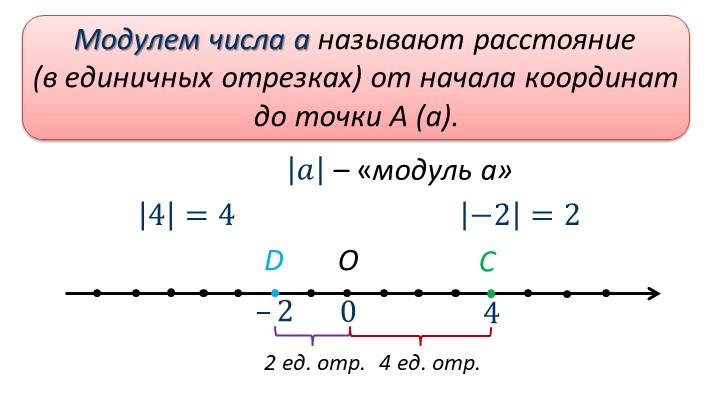 }\) Деление \(a\) на \(n\) оставит некоторый остаток, как и деление \(b\) на \(n\text{.}\) Однако при делении \(kn\) на \(n\) останется 0 остатка. Таким образом, остатки в левой части должны сокращаться. То есть остатки должны быть одинаковыми.
}\) Деление \(a\) на \(n\) оставит некоторый остаток, как и деление \(b\) на \(n\text{.}\) Однако при делении \(kn\) на \(n\) останется 0 остатка. Таким образом, остатки в левой части должны сокращаться. То есть остатки должны быть одинаковыми.
Таким образом имеем:
Конгруэнтность и делимость.
Для любых целых чисел \(a\text{,}\) \(b\text{,}\) и \(n\text{,}\) мы имеем
\begin{уравнение*} a \equiv b \pmod{n} \qquad \text{ тогда и только тогда, когда } \qquad n \mid a-b\text{.} \end{уравнение*}
Также будет полезно переключаться между сравнениями и регулярными уравнениями.Вышеприведенный факт помогает в этом. Мы знаем, что \(a \equiv b \pmod{n}\) тогда и только тогда, когда \(n \mid ab\text{,}\) тогда и только тогда, когда \(ab = kn\) для некоторого целого числа \(k \text{.}\) Переставляя это уравнение, мы получаем \(a = b + kn\text{.}\) Другими словами, если \(a\) и \(b\) конгруэнтны по модулю \(n\ text{,}\), то \(a\) является \(b\) больше, чем некоторое число, кратное \(n\text{. }\). Это согласуется с нашим более ранним наблюдением, что все числа в конкретном остаточном классе являются такая же сумма больше, чем кратно \(n\text{.}\)
}\). Это согласуется с нашим более ранним наблюдением, что все числа в конкретном остаточном классе являются такая же сумма больше, чем кратно \(n\text{.}\)
Конгруэнтность и равенство.
Для любых целых чисел \(a\text{,}\) \(b\text{,}\) и \(n\text{,}\) мы имеем
\begin{уравнение*} a \equiv b \pmod{n} \qquad \text{ тогда и только тогда, когда } \qquad a = b + kn \mbox{ для некоторого целого числа } k \text{.} \end{уравнение*}
Подраздел Свойства конгруэнтности
Ранее мы говорили, что конгруэнтность по модулю \(n\) ведет себя во многих важных отношениях так же, как и равенство. В частности, мы могли бы доказать, что конгруэнтность по модулю \(n\) является отношением эквивалентности , что потребовало бы проверки следующих трех фактов:
Конгруэнтность по модулю \(n\) является отношением эквивалентности.
Для любых целых чисел \(a\text{,}\) \(b\text{,}\) и \(c\text{,}\) и любого положительного целого числа \(n\text{,}\) следующее удержание:
- \(a \equiv a \pmod{n}\text{.
 }\)
}\) Если \(a \equiv b \pmod{n}\), то \(b \equiv a \pmod{n}\text{.}\)
Если \(a \equiv b \pmod{n}\) и \(b \equiv c \pmod{n}\text{,}\), то \(a \equiv c \pmod{n}\text{ .}\)
Другими словами, конгруэнция по модулю \(n\) рефлексивна, симметрична и транзитивна, как и отношение эквивалентности.
Вы должны уделить минутку, чтобы убедиться, что каждое из приведенных выше свойств на самом деле соответствует конгруэнтности. Попробуйте объяснить каждое из них, используя определение остатка и делимости.
Теперь рассмотрим, как конгруэнтность ведет себя при выполнении основных арифметических операций. Мы уже знаем, что если вычесть два конгруэнтных числа, результат будет равен 0 (будет кратен \(n\)). Что, если мы добавим что-то, сравнимое с 1, с чем-то, сравнимым с 2? Получим ли мы что-то, сравнимое с 3?
Сравнение и арифметика.
Предположим, что \(a \equiv b \pmod{n}\) и \(c \equiv d \pmod{n}\text{.}\) Тогда верно следующее:
- \(a+c \equiv b+d \pmod{n}\text{.
 }\)
}\) - \(a-c \equiv b-d \pmod{n}\text{.}\)
- \(ac \equiv bd \pmod{n}\text{.}\)
Приведенные выше факты могут быть написаны немного странно, но идея проста. Если у нас есть истинное соответствие и мы добавляем одно и то же к обеим сторонам, результат все равно будет истинным соответствием. Это звучит так, как будто мы говорим:
Если \(a \equiv b \pmod{n}\), то \(a+c \equiv b+c \pmod{n}\text{.}\)
Конечно, это тоже верно, это частный случай, когда \(c = d\text{.}\) Но то, что мы имеем, работает в более общем случае. Думайте о конгруэнтности как о «в основном равном». Если у нас есть два числа, которые в основном равны, и мы добавляем в основном одно и то же к обеим частям, результат будет в основном равен.
Это кажется разумным. Это правда? Докажем первый факт:
Доказательство.
Предположим, \(a \equiv b \pmod{n}\) и \(c \equiv d \pmod{n}\text{.}\) Это означает \(a = b + kn\) и \(c = d + jn\) для целых чисел \(k\) и \(j\text{. }\) Добавьте эти уравнения:
}\) Добавьте эти уравнения:
\begin{уравнение*} a+c = b+d + kn + jn\text{.} \end{уравнение*}
Но \(kn + jn = (k+j)n\text{,}\), которое просто кратно \(n\text{.}\), поэтому \(a+c = b+d + (j +k)n\text{,}\) или, другими словами, \(a+c \equiv b+d \pmod{n}\)
Аналогично доказываются два других факта.
Одним из важных следствий этих фактов о сравнениях является то, что мы можем заменить любое число в сравнении любым другим числом, с которым оно сравнимо.Вот несколько примеров, чтобы увидеть, как (и почему) это работает:
Пример 5.2.3.
Найдите остаток от деления \(3491\) на \(9\text{.}\)
РешениеМожно было бы разделить в большую сторону, но есть и другой способ. Мы хотим найти \(x\) такой, что \(x \equiv 3491 \pmod{9}\text{.}\) Теперь \(3491 = 3000 + 400 + 90 + 1\text{.}\) Конечно \(90 \equiv 0 \pmod 9\text{,}\), поэтому мы можем заменить 90 в сумме на 0. Почему это нормально? На самом деле мы вычитаем «одно и то же» с обеих сторон:
.
\begin{уравнение*} \begin{align}x \amp \equiv 3000 + 400 + 90 + 1 \pmod 9 \\ — ~~ 0 \ампер\экв 90 \pmod 9 \\ х \амп\экв 3000 + 400 + 0 + 1\pmod 9.\end{выровнено} \end{уравнение*}
Далее обратите внимание, что \(400 = 4 \cdot 100\text{,}\) и \(100 \эквив 1 \pmod 9\) (начиная с \(9 \mid 99\)). Таким образом, мы фактически можем заменить 400 просто 4. Опять же, мы апеллируем к нашему утверждению, что мы можем заменить конгруэнтные элементы, но на самом деле мы апеллируем к свойству 3 арифметики конгруэнтности: мы знаем \(100 \экв 1 \pmod{9}\text{,}\) поэтому, если мы умножим обе части на \(4\text{,}\), мы получим \(400 \equiv 4 \pmod 9\text{.}\)
Точно так же мы можем заменить 3000 на 3, поскольку \(1000 = 1 + 999 \эквив 1 \pmod 9\text{.}\) Таким образом, наша исходная конгруэнтность становится
.\begin{уравнение*} х \экв 3 + 4 + 0 + 1 \pmod 9 \end{уравнение*}
\begin{уравнение*} х \ экв 8 \ pmod 9 \ текст {.} \end{уравнение*}
Следовательно, \(3491\) при делении на 9 дает в остатке 8.
Приведенный выше пример должен убедить вас в том, что известный тест на делимость 9 верен: сумма цифр числа делится на 9 тогда и только тогда, когда исходное число делится на 9. Фактически, теперь мы знаем нечто большее : любое число конгруэнтно сумме своих цифр по модулю 9.p \pmod n\text{.}\) Это просто применение свойства 3 несколько раз.
До сих пор мы видели, как складывать, вычитать и умножать с помощью сравнений. Что насчет деления? Есть причина, по которой мы ждали, чтобы обсудить это. Оказывается, мы не можем просто разделить. Другими словами, даже если \(ad \equiv bd \pmod n\text{,}\) мы не знаем, что \(a \equiv b \pmod n\text{.}\) Рассмотрим, например:
\begin{уравнение*} 18 \экв 42 \pmod 8\текст{.} \end{уравнение*}
Это правда.Теперь \(18\) и \(42\) делятся на 6. Однако
\begin{уравнение*} 3 \не\эквивалент 7 \pmod 8\текст{.} \end{уравнение*}
Хотя это не работает, обратите внимание, что \(3 \equiv 7 \pmod 4\text{.}\) Мы не можем разделить \(8\) на 6, но мы можем разделить 8 на наибольший общий делитель \( 8\) и \(6\text{. }\) Это всегда будет происходить?
}\) Это всегда будет происходить?
Предположим, что \(ad \equiv bd \pmod n\text{.}\) Другими словами, мы имеем \(ad = bd + kn\) для некоторого целого числа \(k\text{.}\) Конечно \( ad\) делится на \(d\text{,}\), как и \(bd\text{.}\) Таким образом, \(kn\) также должно делиться на \(d\text{.}\) Теперь, если \(n\) и \(d\) не имеют общих делителей (кроме 1), то мы должны есть \(d \mid k\text{.}\) Но вообще, если мы попытаемся разделить \(kn\) на \(d\text{,}\), мы не знаем, что получим целое число кратно \(n\text{.}\) Некоторые из \(n\) также могут быть разделены. Чтобы быть в безопасности, давайте разделим столько \(n\), сколько сможем. Возьмите наибольший множитель как \(d\), так и \(n\text{,}\) и сократите его из \(n\text{.}\). Остальные множители \(d\) придут из \(k\text{,}\) без проблем.
Мы будем называть наибольший делитель как \(d\), так и \(n\) \(\gcd(d,n)\text{,}\) для наибольшего общего делителя . В приведенном выше примере \(\gcd(6,8) = 2\), так как наибольший общий делитель 6 и 8 равен 2.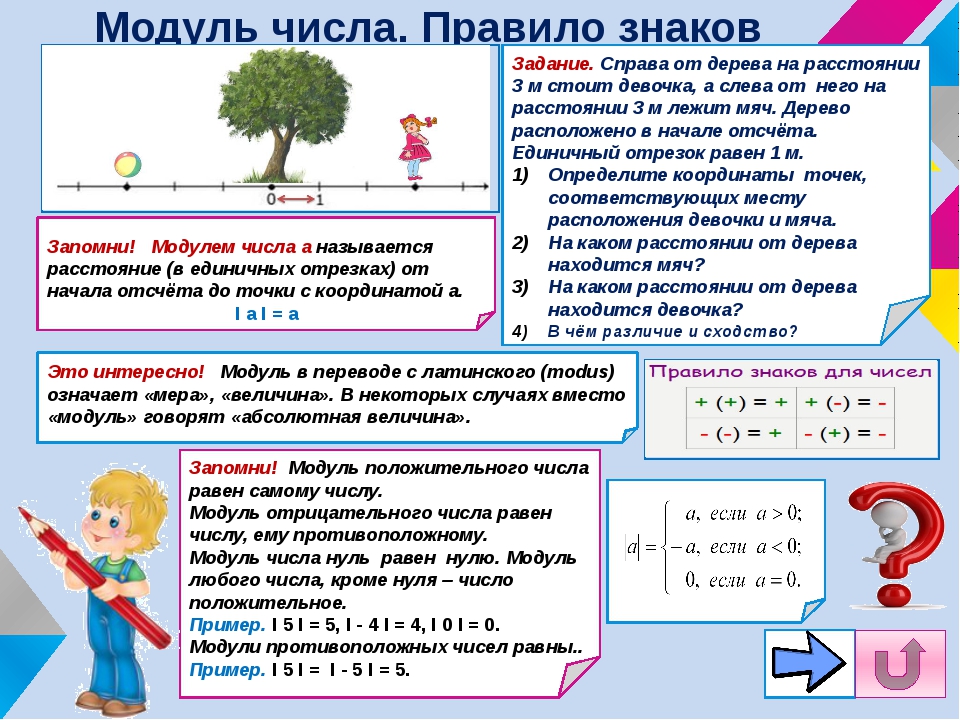
Схождение и деление.
Предположим, \(ad \equiv bd \pmod n\text{.}\) Тогда \(a \equiv b \pmod{\frac{n}{\gcd(d,n)}}\text{.}\)
Если \(d\) и \(n\) не имеют общих делителей, то \(\gcd(d,n) = 1\text{,}\) поэтому \(a \equiv b \pmod n\text{. }\)
Пример 5.2.5.
Упростите следующие сравнения с помощью деления: (a) \(24 \equiv 39 \pmod 5\) и (b) \(24 \equiv 39 \pmod{15}\text{.}\)
Решение(a) И \(24\), и \(39\) делятся на \(3\text{,}\), а \(3\) и \(5\) не имеют общих делителей, поэтому мы получаем
\begin{уравнение*} 8 \экв 13 \pmod 5\текст{.} \end{уравнение*}
(b) Опять же, мы можем разделить на 3. Однако, делая это вслепую, мы получаем \(8 \equiv 13 \pmod{15}\), что уже неверно. Вместо этого мы также должны разделить модуль 15 на наибольший общий делитель \(3\) и \(15\text{,}\), который равен \(3\text{.}\) Снова получаем
\begin{уравнение*} 8 \экв 13 \pmod 5\текст{.} \end{уравнение*}
Подраздел Решение сравнений
Теперь, когда у нас есть некоторые алгебраические правила для управления отношениями конгруэнтности, мы можем попытаться найти неизвестное в конгруэнтности. Например, существует ли значение \(x\), удовлетворяющее
Например, существует ли значение \(x\), удовлетворяющее
\begin{уравнение*} 3x + 2 \экв 4 \pmod{5}\text{,} \end{уравнение*}
и если да, то что это?
В этом примере, поскольку модуль мал, мы могли бы просто попробовать все возможные значения для \(x\text{.}\) На самом деле нужно рассмотреть только 5, так как любое целое число, удовлетворяющее конгруэнтности, может быть заменено любым другим целым числом, сравнимым по модулю 5. Здесь, когда \(x = 4\), мы получаем \(3x + 2 = 14\), которое действительно сравнимо с 4 по модулю 5. Это означает, что \(x = 9\) и \(x = 14\) и \(x = 19\) и т. д. также будут решением, потому что, как мы Как мы видели выше, замена любого числа в конгруэнтности конгруэнтным числом не меняет истинности конгруэнтности.
Итак, в этом примере просто вычислите \(3x + 2\) для значений \(x \in \{0,1,2,3,4\}\text{.}\) Это дает 2, 5, 8, 11 и 14 соответственно, для которых только 14 сравнимо с 4.
Давайте также посмотрим, как вы могли бы решить это, используя наши правила алгебры сравнений. Такой подход был бы намного проще, чем тактика проб и ошибок, если бы модуль был больше. Во-первых, мы знаем, что можем вычесть 2 из обеих частей:
Такой подход был бы намного проще, чем тактика проб и ошибок, если бы модуль был больше. Во-первых, мы знаем, что можем вычесть 2 из обеих частей:
\begin{уравнение*} 3x \экв 2 \pmod{5}\текст{.} \end{уравнение*}
Затем, чтобы разделить обе стороны на 3, мы сначала добавляем 0 к обеим частям. Конечно, в правой части мы хотим, чтобы 0 равнялся 10 (да, \(10\) действительно равно 0, поскольку они конгруэнтны по модулю 5).Это дает
\begin{уравнение*} 3x \эквив 12 \pmod{5}\текст{.} \end{уравнение*}
Теперь разделите обе части на 3. Поскольку \(\gcd(3,5) = 1\text{,}\) нам не нужно менять модуль:
\begin{уравнение*} х \ эквив 4 \ pmod {5} \ text {.} \end{уравнение*}
Обратите внимание, что это на самом деле дает общее решение : не только \(x = 4\text{,}\), но и \(x\) может быть любым числом, сравнимым с 4. Мы можем оставить это так , или напишите «\(x = 4 + 5k\) для любого целого числа \(k\text{.}\)”
Пример 5.2.6.
Решите следующие сравнения для \(x\text{.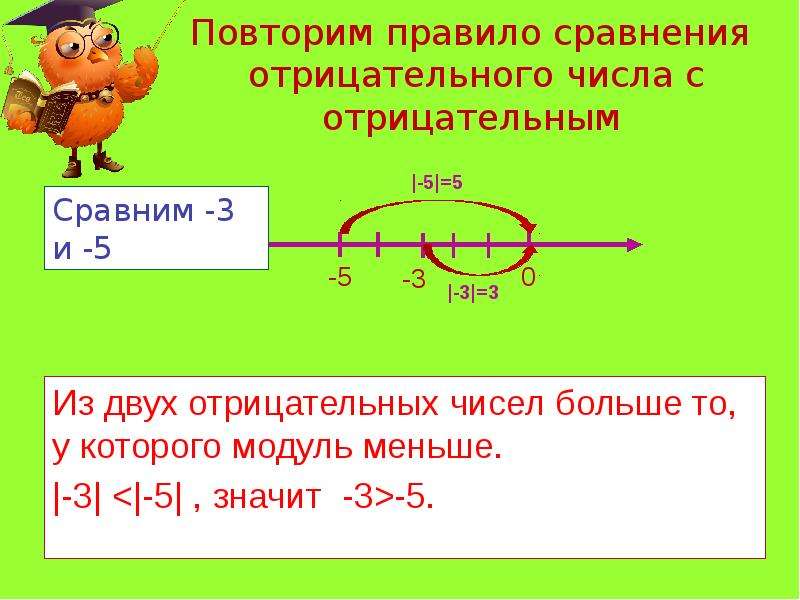 }\)
}\)
- \(7x \экв 12 \pmod{13}\текст{.}\)
- \(84x — 38 \экв 79 \pmod{15}\text{.}\)
- \(20x \экв 23 \pmod{14}\text{.}\)
Все, что нам нужно сделать здесь, это разделить обе части на 7. Мы многократно прибавляем 13 к правой части, пока не получим число, кратное 7 (добавление 13 равносильно добавлению 0, так что это допустимо). Получаем \(25\text{,}\) \(38\text{,}\) \(51\text{,}\) \(64\text{,}\) \(77\) — понял .Итак имеем:
\begin{уравнение*} \begin{align}7x \amp\equiv 12 \pmod{13} \\ 7x \amp \equiv 77 \pmod{13} \\ х \amp \equiv 11 \pmod{13}. \end{выровнено} \end{уравнение*}
Здесь, поскольку у нас есть числа, превышающие модуль, мы можем уменьшить их до применения какой-либо алгебры. Имеем \(84 \equiv 9\text{,}\) \(38 \equiv 8\) и \(79 \equiv 4\text{.}\) Таким образом,
\begin{уравнение*} \begin{align}84x — 38 \amp\equiv 79 \pmod{15} \\ 9x — 8 \ампер\экв 4 \pmod{15} \\ 9x \amp \equiv 12 \pmod{15} \\ 9x \amp \equiv 72 \pmod{15}.
 \end{выровнено}
\end{уравнение*}
\end{выровнено}
\end{уравнение*}Мы получили 72, добавив \(0 \equiv 60 \pmod{15}\) к обеим сторонам сравнения. Теперь разделите обе части на 9. Однако, поскольку \(\gcd(9, 15) = 3\text{,}\), мы также должны разделить модуль на 3:
\begin{уравнение*} х \ эквив 8 \ pmod 5 \ текст {.} \end{уравнение*}
Таким образом, решения — это те значения, которые конгруэнтны 8 или, что то же самое, 3 по модулю 5. Это означает, что в некотором смысле существует 3 решения по модулю 15: 3, 8 и 13. Мы можем записать решение:
\begin{уравнение*} х \экв 3 \pmod{15}; ~~ x \экв 8 \pmod{15}; ~~x \equiv 13 \pmod{15}\text{.} \end{уравнение*}
Сначала уменьшите по модулю 14:
\begin{уравнение*} 20x \экв 23 \pmod{14} \end{уравнение*}
\begin{уравнение*} 6x \эквив 9 \pmod{14}\текст{.} \end{уравнение*}
Теперь мы можем разделить обе части на 3 или попытаться увеличить 9 на кратное 14, чтобы получить кратное 6. Если мы разделим на 3, мы получим
.
\begin{уравнение*} 2x \эквив 3 \pmod{14}\текст{.} \end{уравнение*}
Теперь попробуйте сложить числа, кратные 14, к 3, в надежде получить число, которое можно разделить на 2.Так не пойдет! Каждый раз, когда мы прибавляем 14 к правой части, результат все равно будет нечетным. Мы никогда не получим четное число, поэтому мы никогда не сможем разделить на 2. Таким образом, у сравнения нет решений.
Последнее сравнение выше иллюстрирует то, как сравнения могут не иметь решений. Мы могли бы увидеть это сразу на самом деле. Посмотрите на исходное соответствие:
\begin{уравнение*} 20x \экв 23 \pmod{14}\текст{.} \end{уравнение*}
Если мы запишем это как уравнение, мы получим
\begin{уравнение*} 20x = 23 + 14k\текст{,} \end{уравнение*}
или эквивалентно \(20x — 14k = 23\text{.}\) Легко видеть, что решения этого уравнения в целых числах не будет. Левая часть всегда будет четной, а правая – нечетной. Аналогичная проблема возникла бы, если бы правая часть делилась на любым числом , которым не делилась левая часть.
Итак, в целом, учитывая соответствие
\begin{уравнение*} топор \ эквив б \ pmod {n} \ text {,} \end{уравнение*}
если \(a\) и \(n\) делятся на число, на которое \(b\) не делится, то решений не будет.На самом деле нам действительно нужно проверить только один делитель \(a\) и \(n\text{:}\) наибольшего общего делителя. Таким образом, более компактный способ сказать это:
Сравнений без решений.
Если \(\gcd(a,n) \nmid b\text{,}\), то \(ax \equiv b \pmod{n}\) не имеет решений.
Подраздел Решение линейных диофантовых уравнений
Дискретная математика имеет дело с целым числом вещей. Поэтому, когда мы хотим решить уравнения, мы обычно ищем целых решений.2\text{.}\) Целочисленные решения этого уравнения называются пифагорейскими тройками . В общем, решение диофантовых уравнений сложно (на самом деле, не существует доказуемого общего алгоритма для определения того, имеет ли диофантово уравнение решение, результат, известный как теорема Матиясевича).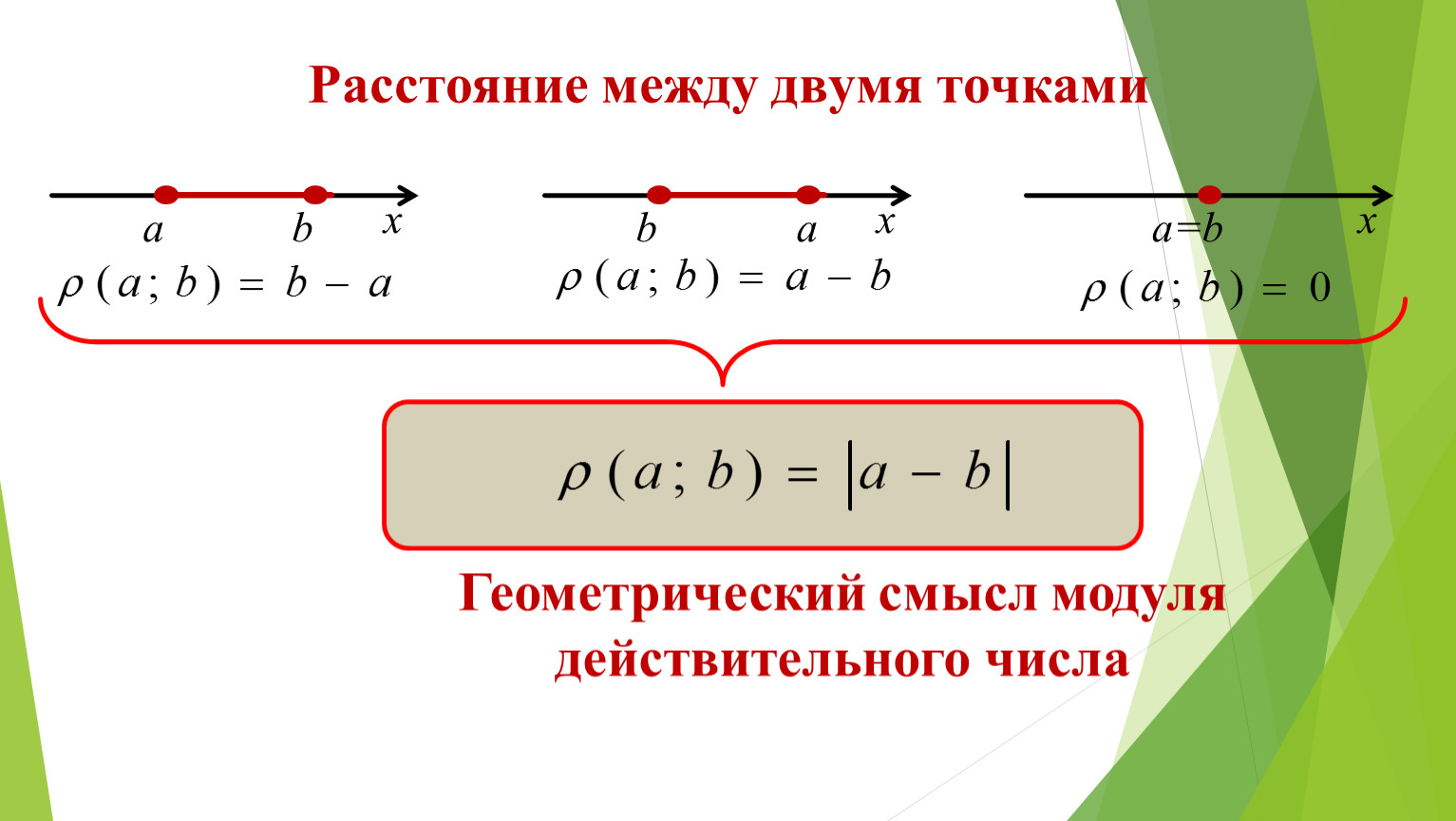 Мы ограничим наше внимание линейными диофантовыми уравнениями, с которыми значительно легче работать.
Мы ограничим наше внимание линейными диофантовыми уравнениями, с которыми значительно легче работать.
Диофантовы уравнения.
Уравнение с двумя или более переменными называется диофантовым уравнением , если интерес представляют только целые числа. линейное диофантово уравнение принимает вид \(a_1x_1 + a_2x_x + \cdots + a_nx_n = b\) для констант \(a_1,\ldots, а_н, б\текст{.}\)
Решение диофантова уравнения — это решение уравнения, состоящее только из целых чисел.
У нас есть инструменты, необходимые для решения линейных диофантовых уравнений. Рассмотрим в качестве основного примера уравнение
\begin{уравнение*} 51x + 87y = 123\text{.} \end{уравнение*}
Общая стратегия состоит в том, чтобы преобразовать уравнение в сравнение, а затем решить это сравнение. 4 Давайте рассмотрим этот конкретный пример, чтобы увидеть, как это может работать.
Конечно, это не единственный путь.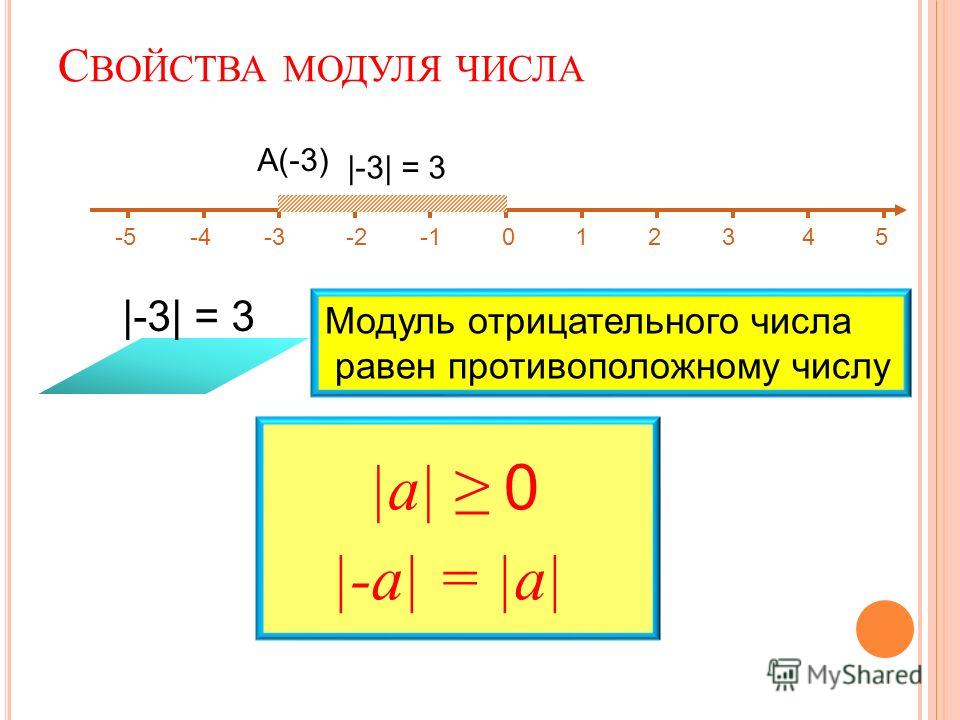 Более распространенным методом было бы применение алгоритма Евклида . Наш способ может быть немного быстрее и представлен здесь в первую очередь для разнообразия.
Более распространенным методом было бы применение алгоритма Евклида . Наш способ может быть немного быстрее и представлен здесь в первую очередь для разнообразия.
Во-первых, проверьте, не существует ли решений, потому что делитель \(51\) и \(87\) не является делителем \(123\text{.}\) Действительно, нам просто нужно проверить, \( \gcd(51, 87) \mid 123\text{.}\) Этот наибольший общий делитель равен 3, и да \(3 \mid 123\text{.}\) В этот момент мы могли бы также вынести этот наибольший общий делитель. Поэтому вместо этого мы решим:
\begin{уравнение*} 17x + 29y = 41\text{.} \end{уравнение*}
Теперь заметьте, что если будут решения, то для этих значений \(x\) и \(y\text{,}\) две части уравнения должны иметь одинаковый остаток, независимо от того, на что делим. В частности, если мы разделим обе части на 17, мы должны получить тот же остаток.Таким образом, мы можем смело писать
\begin{уравнение*} 17x + 29y \экв 41 \pmod{17}\text{.} \end{уравнение*}
Мы выбираем 17, потому что \(17x\) будет иметь остаток 0. Это позволит нам свести конгруэнтность только к одной переменной. Мы могли бы также перейти к конгруэнтности по модулю 29, хотя обычно есть веская причина выбрать меньший вариант, так как это позволит нам уменьшить другой коэффициент. В нашем случае мы уменьшаем сравнение следующим образом:
Это позволит нам свести конгруэнтность только к одной переменной. Мы могли бы также перейти к конгруэнтности по модулю 29, хотя обычно есть веская причина выбрать меньший вариант, так как это позволит нам уменьшить другой коэффициент. В нашем случае мы уменьшаем сравнение следующим образом:
\begin{уравнение*} \begin{align}17x + 29y \amp\equiv 41 \pmod{17} \\ 0x + 12y \amp \equiv 7 \pmod{17} \\ 12 лет \amp \equiv 24 \pmod{17} \\ y \amp \equiv 2 \pmod{17}.\end{выровнено} \end{уравнение*}
Теперь мы знаем, что \(y = 2 + 17k\) будет работать для любого целого числа \(k\text{.}\). Если мы не ошиблись, мы сможем снова вставить это в наш исходное диофантово уравнение для нахождения \(x\text{:}\)
\begin{уравнение*} \begin{align}17x + 29(2 + 17k) \amp = 41\\ 17x \amp = -17 — 29\cdot 17k\\ х \амп = -1-29k. \end{выровнено} \end{уравнение*}
Теперь мы нашли все решения диофантова уравнения. Для каждого \(k\text{,}\) \(x = -1-29k\) и \(y = 2 + 17k\) будет удовлетворяться уравнению. Мы могли бы проверить это для нескольких случаев. Если \(k = 0\text{,}\), то решение равно \((-1,2)\text{,}\) и да, \(-17 + 2\cdot 29 = 41\text{.} \) Если \(k = 3\text{,}\), то решение равно \((-88, 53)\text{.}\) Если \(k = -2\text{,}\), мы получаем \ ((57, -32)\текст{.}\)
Мы могли бы проверить это для нескольких случаев. Если \(k = 0\text{,}\), то решение равно \((-1,2)\text{,}\) и да, \(-17 + 2\cdot 29 = 41\text{.} \) Если \(k = 3\text{,}\), то решение равно \((-88, 53)\text{.}\) Если \(k = -2\text{,}\), мы получаем \ ((57, -32)\текст{.}\)
Подводя итог этому процессу, чтобы решить \(ax + by = c\text{,}\) мы,
Разделите обе части уравнения на \(\gcd(a,b)\) (если это не оставляет правую часть целым числом, решений нет). Предположим, что \(ax + by = c\) уже приведено таким образом.
Выберите меньшее из \(a\) и \(b\) (здесь предположим, что это \(b\)) и преобразуйте в сравнение по модулю \(b\text{:}\)
\begin{уравнение*} ax + by \equiv c \pmod{b}\text{.} \end{уравнение*}
Это приведет к совпадению с одной переменной, \(x\text{:}\)
\begin{уравнение*} топор \equiv c \pmod{b}\text{.} \end{уравнение*}
Решите сравнение, как мы это делали в предыдущем разделе. Запишите решение в виде уравнения, например,
.
\begin{уравнение*} х = п + кб\текст{.} \end{уравнение*}
Подставьте это в исходное диофантово уравнение и найдите \(y\text{.}\)
Если мы хотим знать решения в определенном диапазоне (например, \(0 \le x, y \le 20\)), выбирайте разные значения \(k\), пока не получите все требуемые решения.
Вот еще пример:
Пример 5.2.7.
Как можно заработать 6,37 доллара, используя только 5-центовые и 8-центовые марки? Какое наименьшее и наибольшее количество марок вы могли бы использовать?
РешениеВо-первых, нам нужно диофантово уравнение.Мы будем работать в цифрах центов. Пусть \(x\) будет количеством \(5\)-центовых марок, а \(y\) будет количеством 8-центовых марок. У нас есть:
\begin{уравнение*} 5x + 8y = 637\текст{.} \end{уравнение*}
Преобразовать в сравнение и решить:
\begin{уравнение*}
\begin{align}8y \amp\equiv 637 \pmod{5}\\
3y \amp \equiv 2 \pmod 5\\
3y \amp \equiv 12 \pmod 5\\
y \amp \equiv 4 \pmod 5. \end{выровнено}
\end{уравнение*}
\end{выровнено}
\end{уравнение*}
Таким образом, \(y = 4 + 5k\text{.}\) Тогда \(5x + 8(4+5k) = 637\text{,}\) так что \(x = 121 — 8k\text{.}\)
Здесь говорится, что один из способов заработать 6,37 доллара — взять 121 5-центовую марку и 4 8-центовые марки. Чтобы найти наименьшее и наибольшее количество штампов, попробуйте разные значения \(k\text{.}\)
.| \(к\) | \((х,у)\) | Марки |
| -1 | (129, -1) | невозможно |
| 0 | (121, 4) | 125 |
| 1 | (113, 9) | 122 |
| 2 | (105, 13) | 119 |
| \(\вдоц\) | \(\вдоц\) | \(\вдоц\) |
Это неудивительно.Наличие наибольшего количества марок означает, что у нас есть как можно больше 5-центовых марок, а для получения наименьшего количества марок потребуется иметь наименьшее количество 5-центовых марок. Чтобы минимизировать количество 5-центовых марок, мы хотим выбрать \(k\) так, чтобы \(121-8k\) было как можно меньше (но все же положительно). Когда \(k = 15\text{,}\) мы имеем \(x = 1\) и \(y = 79\text{.}\)
Чтобы минимизировать количество 5-центовых марок, мы хотим выбрать \(k\) так, чтобы \(121-8k\) было как можно меньше (но все же положительно). Когда \(k = 15\text{,}\) мы имеем \(x = 1\) и \(y = 79\text{.}\)
Таким образом, чтобы заработать 6,37 доллара, вы можете использовать всего 80 марок (1 марка по 5 центов и 79 марок по 8 центов) или целых 125 марок (121 марка по 5 центов и 4 марки по 8 центов).
Используя этот метод, если вы можете решать линейные сравнения с одной переменной, вы можете решать линейные диофантовы уравнения с двумя переменными. Однако бывают случаи, когда решение линейной конгруэнтности требует много работы. Например, предположим, что вам нужно решить
\begin{уравнение*} 13x \экв 6 \pmod{51}\текст{.} \end{уравнение*}
Вы могли бы продолжать прибавлять 51 к правой части, пока не получите число, кратное 13: вы получите 57, 108, 159, 210, 261, 312, и 312 — первое из них, которое делится на 13.Это работает, но на самом деле слишком много работы.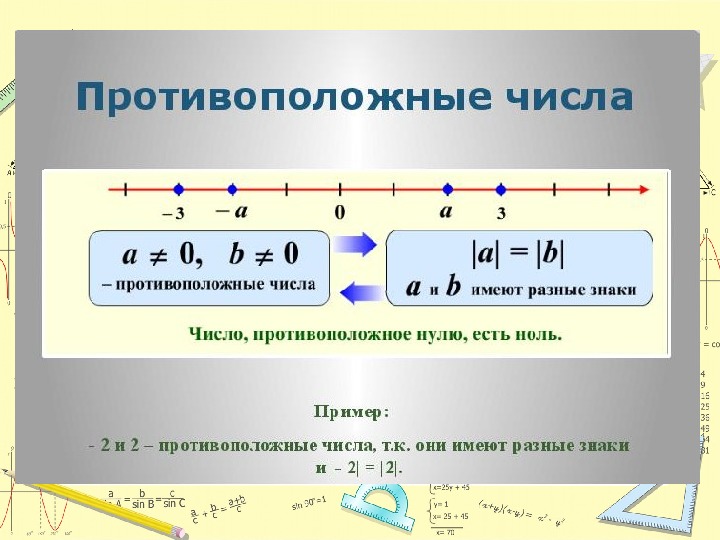 Вместо этого мы могли бы преобразовать обратно в диофантово уравнение:
Вместо этого мы могли бы преобразовать обратно в диофантово уравнение:
\begin{уравнение*} 13x = 6 + 51k\text{.} \end{уравнение*}
Теперь решите это , как в этом разделе. Запишите это как сравнение по модулю 13:
\begin{уравнение*} \begin{align}0 \amp \equiv 6 + 51k \pmod{13}\\ -12k \amp \equiv 6 \pmod{13}\\ 2k \amp \equiv -1 \pmod{13}\\ 2k \amp \equiv 12 \pmod{13}\\ k \amp \equiv 6 \pmod{13}. \end{выровнено} \end{уравнение*}
, поэтому \(k = 6 + 13j\text{.}\) Теперь вернитесь и вычислите \(x\text{:}\)
\begin{уравнение*} \begin{align}13x \amp = 6 + 51(6+13j)\\ х \амп = 24 + 51j. \end{выровнено} \end{уравнение*}
Конечно, вы можете переключаться между сравнениями и диофантовыми уравнениями сколько угодно раз. Если бы вы использовали эту технику только , вы, по сути, воспроизвели бы алгоритм Евклида, более стандартный способ решения диофантовых уравнений.
Упражнения Упражнения
1.

Предположим, что \(a\text{,}\) \(b\text{,}\) и \(c\) являются целыми числами. Докажите, что если \(a \mid b\text{,}\), то \(a \mid bc\text{.}\)
РешениеДоказательство.
Предположим, что \(a \mid b\text{.}\) Тогда \(b\) кратно \(a\text{,}\) или, другими словами, \(b = ak\) для некоторого \ (k\text{.}\) Но тогда \(bc = akc\text{,}\) и поскольку \(kc\) является целым числом, это говорит о том, что \(bc\) кратно \(a\text {.}\) Другими словами, \(a \mid bc\text{.}\)
2.
Предположим, что \(a\text{,}\) \(b\text{,}\) и \(c\) являются целыми числами.Докажите, что если \(a \mid b\) и \(a \mid c\), то \(a \mid b+c\) и \(a \mid b-c\text{.}\)
3.
Выписать оставшиеся классы для \(n = 4\text{.}\)
Решение\(\{\ldots, -8, -4, 0, 4, 8, 12, \ldots\}\text{,}\) \(\{\ldots, -7, -3, 1, 5, 9, 13, \ldots\}\text{,}\)
\(\{\ldots, -6, -2, 2, 6, 10, 14, \ldots\}\text{,}\) и \(\{\ldots, -5, -1, 3, 7 , 11, 15, \ldots\}\text{. }\)
}\)
4.
Какое наибольшее \(n\) такое, что \(16\) и \(25\) находятся в одном и том же остаточном классе по модулю \(n\text{?}\) Выпишите остаточный класс, которому они оба принадлежат, и приведите пример числа больше 100 в этом классе.
5.
Пусть \(a\text{,}\) \(b\text{,}\) \(c\text{,}\) и \(n\) — целые числа. Докажите, что если \(a \equiv b \pmod{n}\) и \(c \equiv d \pmod{n}\text{,}\), то \(ac \equiv bd \pmod{n}\text{ .}\)
РешениеДоказательство.
Предположим, что \(a \equiv b \pmod n\) и \(c \equiv d \pmod n\text{.}\) Это означает \(a = b + kn\) и \(c = d + jn\ ) для некоторых целых чисел \(k\) и \(j\text{.}\) Рассмотрим \(ac\text{.}\) Имеем:
\begin{уравнение*} a-c = b+kn — (d+jn) = b-d + (k-j)n\text{.2 \экв 2 \pmod 4\текст{.}\) Решение
Для всех из них просто подставьте все целые числа от 0 до модуля, чтобы увидеть, какие из них работают.
Нет решений.
- \(x = 2\text{,}\) \(x = 5\text{,}\) \(x = 8\text{.
 }\)
}\) Нет решений.
9.
Определите, какие из следующих сравнений имеют решения, и найдите любые решения (от 0 до модуля) методом проб и ошибок.
- \(4x \эквив 5 \pmod 7\текст{.2 \эквив 2 \pmod 7\текст{.}\)
10.
Решите следующее сравнение \(5x + 8 \equiv 11 \pmod{22}\text{.}\) То есть опишите общее решение.
Решение\(x = 5+22k\) для \(k \in \Z\text{.}\)
11.
Решите сравнение: \(6x \equiv 4 \pmod{10}\text{.}\)
12.
Решите сравнение: \(4x \equiv 24 \pmod{30}\text{.}\)
Решение\(x = 6 + 15k\) для \(k \in \Z\text{.}\)
13.
Решите сравнение: \(341x \equiv 2941 \pmod{9}\text{.}\)
ПодсказкаСначала уменьшите каждое число по модулю 9, что можно сделать, сложив цифры чисел.
14.
Я думаю о числе. Если вы умножите мое число на 7, прибавите 5 и разделите результат на 11, у вас останется остаток 2. Какой остаток вы получите, если разделите мое исходное число на 11?
Решение. Мы должны решить \(7x + 5 \equiv 2 \pmod{11}\text{.}\) Это дает \(x \equiv 9 \pmod{11}\text{.}\) В общем, \( x = 9 + 11k\text{,}\), но при делении любого такого \(x\) на 11 в остатке будет 9.
Мы должны решить \(7x + 5 \equiv 2 \pmod{11}\text{.}\) Это дает \(x \equiv 9 \pmod{11}\text{.}\) В общем, \( x = 9 + 11k\text{,}\), но при делении любого такого \(x\) на 11 в остатке будет 9.
15.
Решите следующее линейное диофантово уравнение, используя модульную арифметику (опишите общие решения).
\begin{уравнение*} 6x + 10y = 32\text{.} \end{уравнение*}
РешениеРазделить на 2: \(3x + 5y = 16\text{.}\) Преобразовать в сравнение по модулю 3: \(5y \equiv 16 \pmod 3\text{,}\), которое сводится к \( 2y \equiv 1 \pmod 3\text{.}\) Итак, \(y \equiv 2 \pmod 3\) или \(y = 2 + 3k\text{.}\) Вставьте это обратно в \(3x + 5y = 16\) и найдите \(x\text{,}\), чтобы получить \(x = 2-5k\text{.}\) Таким образом, общее решение: \(x = 2-5k\) и \(y = 2+3k\) для \(k \in \Z\text{.}\)
16.
Решите следующее линейное диофантово уравнение, используя модульную арифметику (опишите общие решения).
\begin{уравнение*} 17x + 8y = 31\text{.} \end{уравнение*}
17.

Решите следующее линейное диофантово уравнение, используя модульную арифметику (опишите общие решения).
\begin{уравнение*} 35x + 47y = 1\текст{.} \end{уравнение*}
18.
У вас есть 13 унций. бутылка и 20 унций. бутылка, с помощью которой вы хотите измерить ровно 2 унции. Однако у вас ограниченный запас воды. Если какая-либо вода попадает в любую из бутылок, а затем выливается, она исчезает навсегда. С каким наименьшим количеством воды вы можете начать и при этом выполнить задание?
ПодсказкаРешите диофантово уравнение \(13x + 20 y = 2\) (почему?). Затем рассмотрим, какое значение \(k\) (параметр в решении) является оптимальным.
Модульная арифметика: правила и свойства — видео и расшифровка урока
Сложение в модульной арифметике
С модульной математикой можно выполнять многие из тех же операций, что и с обычной математикой.Вот некоторые правила сложения в модульной арифметике:
На основании этих правил мы можем либо сложить числа вместе, либо найти сумму по модулю n . В качестве альтернативы мы можем сначала найти каждое из чисел по модулю n , а затем сложить их вместе. Попробуем работать с модулем 8.
В качестве альтернативы мы можем сначала найти каждое из чисел по модулю n , а затем сложить их вместе. Попробуем работать с модулем 8.
Что такое (4 + 7 + 6 + 8) по модулю 8?
- Сложите числа в скобках: 4 + 7 + 6 + 8 = 25
- Чтобы найти 25mod8, выполните деление: 25 / 8 = 3 с остатком 1
- Следовательно, (4 + 7 + 6 + 8)mod8 конгруэнтно 25mod8, которое конгруэнтно 1mod8
Вычитание в модульной арифметике
Для выполнения вычитания в модульной арифметике можно использовать следующие правила:
Опять же, у нас есть два варианта.Сначала мы можем вычесть числа и найти модуль n . Или мы можем сначала найти каждое из чисел по модулю n , а затем выполнить вычитание. В этом примере давайте работать с модулем 5.
Что такое (104 — 53)mod5?
- Вычтем числа в скобках: 104 — 53 = 51.
 Здесь (104 — 53)mod5 сравнимо с 51mod5.
Здесь (104 — 53)mod5 сравнимо с 51mod5. - Выполните деление: 51 / 5 = 10 с остатком 1. Итак, (104 — 53)mod5 сравнимо с 1mod5.
- В качестве альтернативы мы могли бы сначала найти 104mod5 и 53mod5 или 4mod5 и 3mod5 соответственно, а затем вычесть: 4mod5 — 3mod5 конгруэнтно 1mod5.
При вычитании вы можете получить отрицательное число. Например, предположим, сейчас 4:00 или PM, и мы хотим знать, сколько времени было 11 часов назад, или (4 — 11)mod12 = -7mod12. Чтобы узнать, насколько результат соответствует модулю 12, мы прибавляем кратные 12, пока не получим число от 0 до 11. -7 + 12 = 5
Здесь -7mod12 сравнимо с 5mod12, что означает, что оно было 5. :00AM или PM 11 часов назад. В общем, когда вы получаете отрицательное число и работаете с модулем n , добавляйте кратные n к отрицательному числу, пока не получите число от 0 до n — 1.
Умножение в модульной арифметике
Мы можем использовать следующие правила для выполнения умножения в модульной арифметике:
Здесь мы можем выполнить умножение, а затем найти это число по модулю n . Или мы можем сначала найти каждое число по модулю n , а затем умножить их. Давайте работать по модулю 18.
Или мы можем сначала найти каждое число по модулю n , а затем умножить их. Давайте работать по модулю 18.
Что такое (14 * 20)mod18?
- Умножьте числа в скобках: 14*20 = 280mod18
- Выполните деление: 280/18 = 15 с остатком 10.Таким образом, (14*20)mod18 соответствует 10mod18 .
- Мы также можем сначала найти 14mod18 и 20mod18 или 14mod18 и 2mod18 соответственно, а затем умножить результаты. Здесь (14mod18) * (2mod18) конгруэнтно 28mod18. Когда мы делим 28 на 18, мы получаем 1 с остатком 10; Итак, (14 * 20)mod18 конгруэнтно 10mod18.
Резюме урока
Модульная арифметика также называется арифметикой часов, потому что правила аналогичны традиционному способу определения времени.В модульной арифметике у нас есть модуль , который является целым числом или целым числом, с которого мы начинаем.
При сложении, вычитании или умножении по модулю n мы можем сделать одно из двух:
- Мы можем сначала выполнить операцию, а затем найти это число по модулю n , разделив его на n и определение остатка
- Мы также можем найти каждое число по модулю n по отдельности, а затем выполнить операцию над этими числами
В любом случае, мы получим тот же ответ.

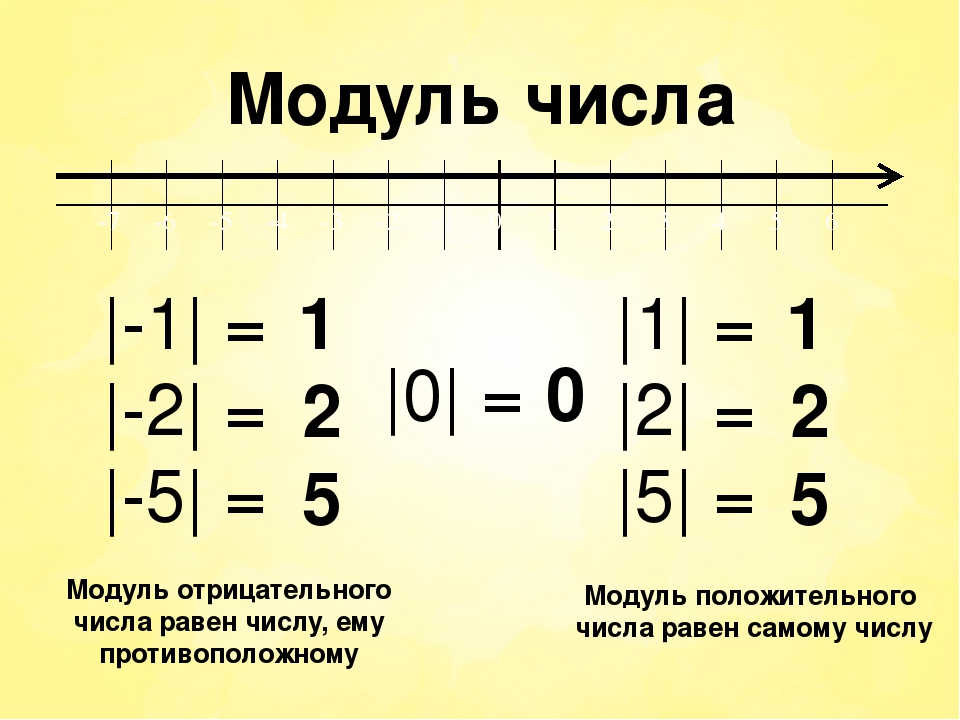


 п.28, учить правило раскрытия знака модуля, выполнить № 953(ж-м), 967, 968, 970, 972.
п.28, учить правило раскрытия знака модуля, выполнить № 953(ж-м), 967, 968, 970, 972. .
.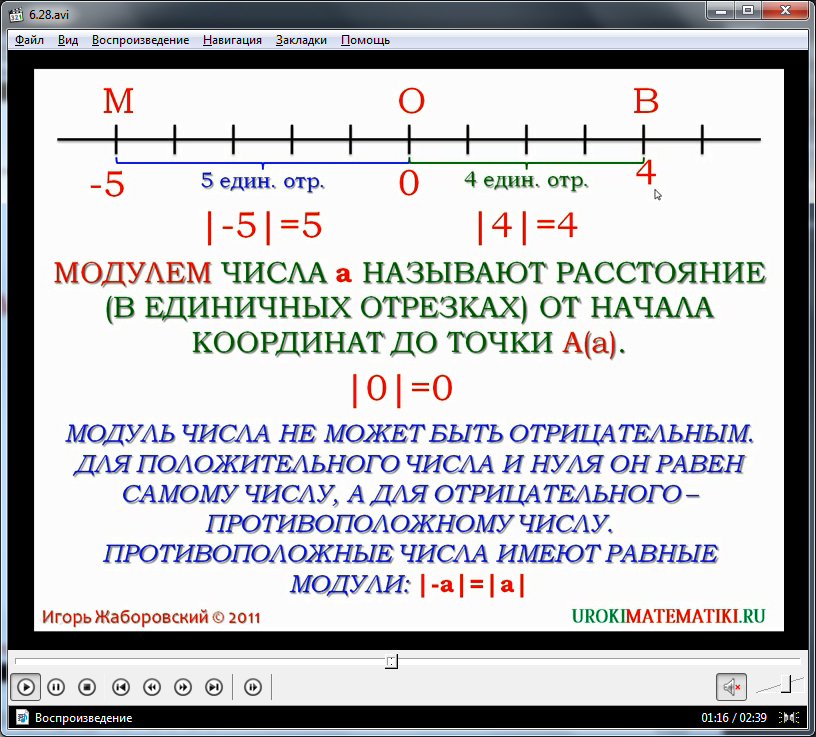 .
. .
. .
. .
. .
.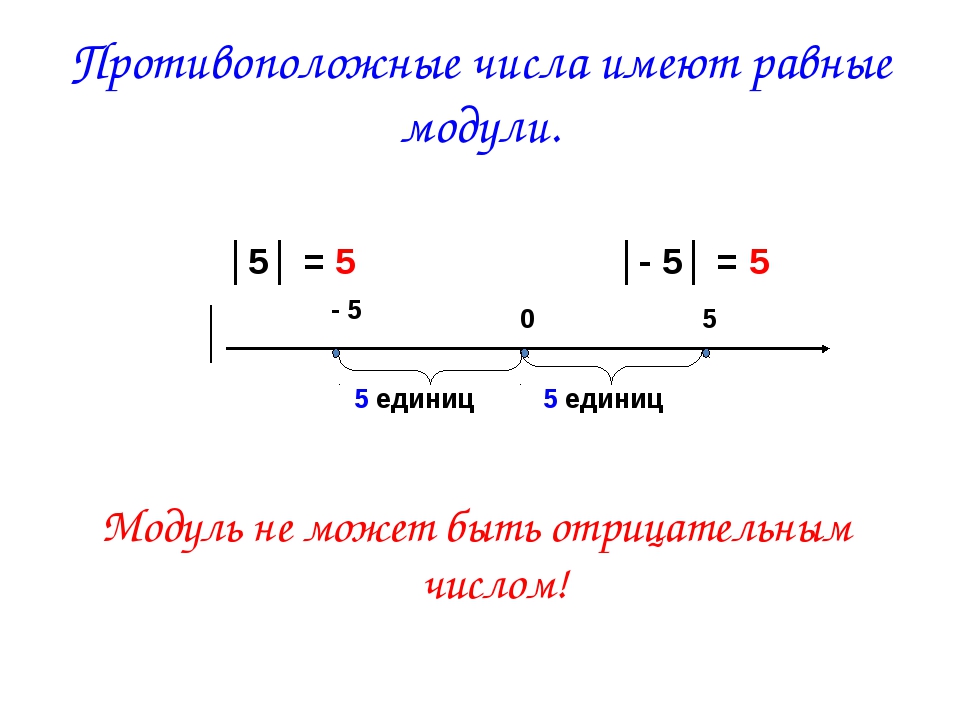 И обращает внимание учащихся на доску, на которой написаны следующие слова:
И обращает внимание учащихся на доску, на которой написаны следующие слова: Назовите все целые числа, которые лежат между числами -2 и 3.
Назовите все целые числа, которые лежат между числами -2 и 3.
 Модуль числа -7 равен 7 и т.д. «.
Модуль числа -7 равен 7 и т.д. «. Записывают в тетрадь определение модуля.
Записывают в тетрадь определение модуля.


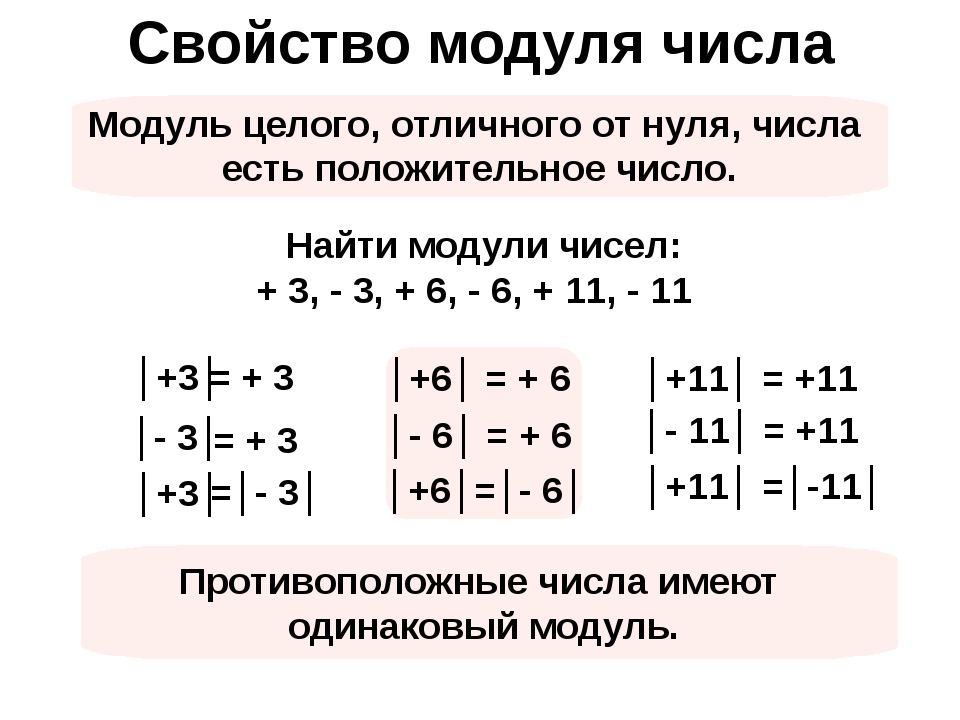

 [5] находится в Z 5 , но я не указал его, потому что [5] совпадает с [0].
[5] находится в Z 5 , но я не указал его, потому что [5] совпадает с [0].
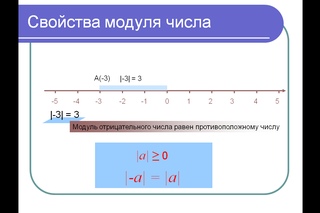
 }\)
}\) }\)
}\) }\)
}\) }\)
}\) \end{выровнено}
\end{уравнение*}
\end{выровнено}
\end{уравнение*}

 }\)
}\) Здесь (104 — 53)mod5 сравнимо с 51mod5.
Здесь (104 — 53)mod5 сравнимо с 51mod5.