Множества в математике это – Множество — Википедия
что это такое, виды математических множеств
Что такое множество в математике? Математическое множество — это несколько отдельных элементов, рассматриваемых, как единое целое. Если обозначить такой элемент буквой a, а само множество — буквой А, то запись будет выглядеть следующим образом:
a ∈ A.
проговаривается эта запись так: a принадлежит А, или А содержит а, или а — элемент А.
Для перечисления элементов множества используются фигурные скобки — {}. То есть, например, множество, в котором а ∈ А, b ∈ A и c ∈ A, будет записываться в таком виде:
{a, b, c}.
Виды множеств.
Пустые множества.
Пустое множество – это то множество, которое вообще не содержит никаких элементов. Обозначается оно цифрой 0 или специальным значком ∅.
Примером пустого множества может служить любое нелогичное понятие
Равные множества.
Равные множества – это два или более множеств, состоящих из равных наборов элементов. Приведём пример. Скажем, все члены Вашей семьи находятся на кухне. Таким образом, Множество «Члены семьи на кухне» будет равно множеству «Члены семьи в квартире».
Если два множества — А и B — состоят из одинакового набора элементов, то они будут равны, то есть А = B. Элементы множеств могут перечисляться в любой последовательности, на результат это никак не влияет. Множество {a, b, c} можно с тем же успехом записать, как {a, c, b}, или {с, b, a}, или {b, c, a}.
Подмножества и надмножества.
Если множества А и B состоят из одинаковых элементов {a, b, c}, то А будет считаться подмножеством B, а B — надмножеством А. Записывается это следующим образом:
A ⊆ B, B ⊇ A.
Бывает так, что множество В содержит в себе каждый из элементов множества А, но в то же время в нем присутствуют и другие элементы, множеству А не принадлежащие. В этом случае множество В становится
Иначе говоря, если А ⊆ В, но при этом А ≠ В, то А ⊂ В, В ⊃ А.
Похожие статьи
infoogle.ru
Список литературы:
Дискретная математика
Яблонский С.В. — Введение в дискретную математику
Белоусов А.И. — Дискретная математика
Капитонова Ю.В. и др. – Лекции по дискретной математике
Судоплатов С.В., Овчинникова Е.В. — Элементы дискретной математики
Хаггарти Р. Дискретная математика для программистов
Зайцева С.С. Дискретная математика
К разделам дискретной математики обычно относятся: теория множеств, комбинаторика, общая алгебра, теория графов, математическая логика, теория алгоритмов, теория автоматов, теория кодирования и т.д.
1. Множества. Операции над множествами.
1.1. Множество. Способы задания множеств.
Дискретная математика изучает в основном конечные множества и операции на них.
В 1872 г. Георг Кантор, создатель теории множеств, дал следующие определения для множества:
Множество – это объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью.
Множество – это определенная совокупность объектов. Эти объекты называются элементами множества.
Множества обозначаются прописными буквами латинского алфавита: A, B, X, Y, A1, A2, …, элементы множеств – строчными буквами: a, b, x, y, a1, a2, … .
Числовые множества:
N — множество всех натуральных чисел;
N0 — множество неотрицательных целых чисел
Z -множество целых чисел;
Q — множество рациональных чисел;
I — множество иррациональных чисел;
R — множество действительных чисел;
C — множество комплексных чисел;
Символ обозначает принадлежность.
Запись  означает, что элемент x принадлежит множеству A.
означает, что элемент x принадлежит множеству A.
Если
элемент x не принадлежит множеству A,
то пишут 
Множества бывают:
конечные; частный случай – единичное (одноэлементное) множество, например, множество преподавателей в этой аудитории, или множество десятичных цифр;
бесконечные; пример – множество натуральных чисел;
пустое (Ø).
Пустым множеством называют множество, не содержащее ни одного элемента.
Способы задания (описания) множеств:
1) Множество A определяется непосредственным перечислением всех своих элементов
Перечислением можно задавать только конечные множества.
2) Множество A определяется как совокупность тех и только тех элементов из некоторого основного множества T, которые обладают общим свойством P(x). В этом случае используется обозначение , т.е. элементы множества задается
Характеристическим предикатом можно задать как конечные, так и бесконечные множества.
3) Множество A можно задать порождающей процедурой (рекурсивное задание, задание алгоритмом). Используется обозначение .
Порождающая процедура – это процедура, которая в процессе работы порождает некоторые объекты, являющиеся элементами определенного множества.
Пример .. – множество натуральных чисел от 1 до 4. Множество задано
Пример .. M=C, C++, Java, C# – множество языков программирования, имеющих С-подобный синтексис. Задано перечислением.
Пример .. Множество A из примера 1.1. можно задать характеристическим предикатом .
Пример .. Зададим рекурсивно множество X алгоритмом:
1) 3X;
2) если
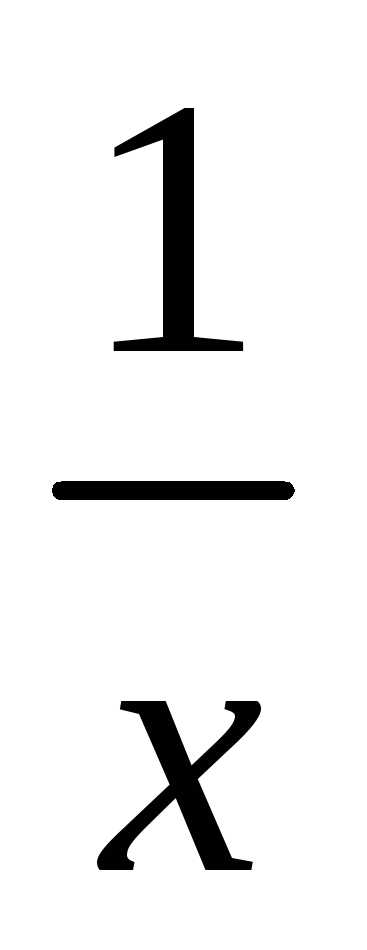 и (1x)
принадлежат X;
и (1x)
принадлежат X;3) других элементов в X нет.
Заметим, что это множество – конечное, и его можно было задать выписыванием его элементов
.
Частным случаем рекурсивного задания множества является способ задания, основанный на процедуре, называемой математической индукцией. Рассмотрим его на примере задания множества натуральных чисел.
Пример .. Множество N задается следующими правилами:
1) задается базис индукции (исходный элемент):
1N;
2) указывается индуктивный переход:
если nN, то (n+1)N;
3) устанавливается правило замыкания:
других элементов, кроме построенных правилами 1 и 2, в N нет.
Задача: Определить различными способами множество М2n-1 всех нечетных чисел, не превышающих 10.
1.2. Подмножество. Равенство множеств.
Универсум. Булеан.
Определение 1.1. Множество A называется подмножеством множества B (обозначается AB), если каждый элемент A есть элемент B, т.е. если xA, то xB.
Символ обозначает отношение включение между множествами.
Пример .. Пусть  и
.
Тогда BA.
и
.
Тогда BA.
Но .
В частности, каждое множество есть подмножество самого себя, т.е. AA.
Определение 1.2. Пусть A и B – некоторые множества. Говорят, что A равно B, и пишут A=B, если для любого x имеем: xA тогда и только тогда, когда xB.
Иначе говоря, A=B тогда и только тогда, когда AB и BA.
Если AB и AB, то это записывается AB, и говорят, что A есть собственное подмножество B. Пустое множество есть подмножество любого данного множества A, т.е. A.
Таким образом, доказательство равенства двух множеств A и B состоит из двух этапов:
1) Доказать, что A есть подмножество B.
2) Доказать, что B есть подмножество A.
Определение 1.3. Универсальное множество U (или универсум) есть множество, обладающее таким свойством, что все рассматриваемые множества являются его подмножествами.
В теории чисел универсальное множество обычно совпадает с множеством всех целых или натуральных чисел. В математическом анализе универсальное множество может быть множество всех действительных чисел или множество всех точек n-мерного пространства.
Следует отметить, что универсальное множество U, хотя, и названо универсальным, однозначно не определено, если точно не указана область рассмотрения (предметная область). Конечно, любое множество, содержащее U, может быть использовано как универсальное множество.
По определению, каждое множество есть подмножество универсального множества.
Пример .. Так, для множества за универсум можно взять множество натуральных чисел, т.е. U=N.
Определение 1.4. Булеаном множества A (обозначается (A)) называется множество, состоящее из всех подмножеств множества A.
Пример .. Пусть 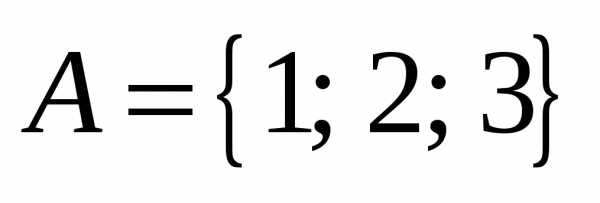 .
.
Следовательно, булеан множества A есть множество (A)=.
Множество A из примера 1.8. содержит три элемента, а булеан (A) состоит из 23=8 элементов. В общем случае, если множество A содержит n элементов, множество (A) включает 2n элементов, т.к. A имеет 2n подмножеств.
По этой причине (A) часто обозначают через 2A.
studfiles.net
Мощность множества — Википедия
Материал из Википедии — свободной энциклопедии
Мо́щность мно́жества, кардина́льное число́ мно́жества (лат. cardinalis ← cardo «главное обстоятельство; основа; сердце») — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.
В основе этого понятия лежат естественные представления о сравнении множеств:
- Любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность, равномощны).
- Обратно: равномощные множества должны допускать такое взаимно-однозначное соответствие.
- Часть множества не превосходит полного множества по мощности (то есть по количеству элементов).
До построения теории мощности множеств множества различались по признакам: пустое/непустое и конечное/бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить.
Мощность множеств позволяет сравнивать бесконечные множества. Например, счётные множества являются самыми «маленькими» бесконечными множествами.
Мощность множества A{\displaystyle A} обозначается через |A|{\displaystyle |A|}. Иногда встречаются обозначения A¯¯{\displaystyle {\overline {\overline {A}}}}, #A{\displaystyle \#A} и card(A){\displaystyle \mathrm {card} (A)}.
ru.wikipedia.org
Теория множеств — Википедия
Материал из Википедии — свободной энциклопедии
Тео́рия мно́жеств — раздел математики, в котором изучаются общие свойства множеств — совокупностей элементов произвольной природы, обладающих каким-либо общим свойством. Создана во второй половине XIX века Георгом Кантором при значительном участии Рихарда Дедекинда, привнесла в математику новое понимание природы бесконечности, была обнаружена глубокая связь теории с формальной логикой, однако уже в конце XIX — начале XX века теория столкнулась со значительными сложностями в виде возникающих парадоксов[⇨], поэтому изначальная форма теории известна как наивная теория множеств[⇨]. В XX веке теория получила существенное методологическое развитие, были созданы несколько вариантов аксиоматической теории множеств[⇨], обеспечивающие универсальный математический инструментарий, в связи с вопросами измеримости множеств тщательно разработана дескриптивная теория множеств[⇨].
Теория множеств стала основой многих разделов математики — общей топологии, общей алгебры, функционального анализа и оказала существенное влияние на современное понимание предмета математики[1]. В первой половине XX века теоретико-множественный подход был привнесён и во многие традиционные разделы математики, в связи с чем стал широко использоваться в преподавании математики, в том числе в школах. Однако использование теории множеств для логически безупречного построения математических теорий осложняется тем, что она сама нуждается в обосновании своих методов рассуждения. Более того, все логические трудности, связанные с обоснованием математического учения о бесконечности, при переходе на точку зрения общей теории множеств приобретают лишь бо́льшую остроту[2].
Начиная со второй половины XX века представление о значении теории и её влияние на развитие математики заметно снизились за счёт осознания возможности получения достаточно общих результатов во многих областях математики и без явного использования её аппарата, в частности, с использованием теоретико-категорного инструментария (средствами которого в теории топосов обобщены практически все варианты теории множеств). Тем не менее, нотация теории множеств стала общепринятой во всех разделах математики вне зависимости от использования теоретико-множественного подхода. На идейной основе теории множеств в конце XX века создано несколько обобщений[⇨], в том числе теория нечётких множеств, теория мультимножеств (используемые в основном в приложениях), теория полумножеств[en] (развиваемая в основ
ru.wikipedia.org
Множество | Математика | FANDOM powered by Wikia
Шаблон:Значения Мно́жество — одно из ключевых понятий математики, в частности, теории множеств и логики.
Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть несводимое к другим понятиям, а значит, и не имеющее определения; для его объяснения используются описательные формулировки, характеризующие множество как совокупность различных элементов, мыслимую как единое целое[1][2]. Также возможно косвенное определение через аксиомы теории множеств. Множество может быть пустым и непустым, упорядоченным и неупорядоченным, конечным и бесконечным, бесконечное множество может быть счётным или несчётным. Более того, как в наивной, так и в аксиоматической теориях множеств любой объект обычно считается множеством.
История понятия
Основы теории конечных и бесконечных множеств были заложены Бернардом Больцано, который сформулировал некоторые из её принципов.
С 1872 года по 1897 год (главным образом в 1872—1884 годы) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств, включая теорию точечных множеств и теорию трансфинитных чисел (кардинальных и порядковых). В этих работах он не только ввёл основные понятия теории множеств, но и обогатил математику рассуждениями нового типа, которые применил для доказательства теорем теории множеств, в частности впервые к бесконечным множествам. Поэтому общепризнано, что теорию множеств создал Георг Кантор. В частности определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты назвал элементами множества. Множество объектов, обладающих свойством $ A(x) $, обозначил $ \{x\mid A(x)\} $. Если некоторое множество $ Y=\{x\mid A(x)\} $, то $ A(x) $ назвал характеристическим свойством множества $ Y $.
Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.
Так как теория множеств фактически используется как основание и язык всех современных математических теорий в 1908 году теория множеств была аксиоматизирована независимо Бертраном Расселом и Эрнстом Цермело. В дальнейшем многие исследователи пересматривали и изменяли обе системы, в основном сохранив их характер. До сих пор они всё ещё известны как теория типов Рассела и теория множеств Цермело. Впоследствии теорию множеств Кантора стало принято называть наивной теорией множеств, а вновь построенную — аксиоматической теорией множеств.
В практике, сложившейся с середины XX века множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).
Элемент множества
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если $ a $ — элемент множества $ A $, то записывают $ a \in A $ («$ a $ принадлежит $ A $»). Если $ a $ не является элементом множества $ A $, то записывают $ a \notin A $ («$ a $ не принадлежит $ A $»). В отличие от мультимножества каждый элемент множества уникален, и во множестве не может быть двух идентичных элементов. Иначе говоря, добавление к множеству элементов, идентичных уже принадлежащим множеству, не меняет его:
- $ \{6, 11\} = \{11, 6\} = \{11, 11, 6, 11, 6\} $.
Некоторые виды множеств и сходных объектов
Специальные множества
Сходные объекты
math.wikia.org
Множества: понятие, определение, примеры
Людям постоянно приходится иметь дело с различными совокупностями предметов, что повлекло за собой возникновение понятия числа, а затем и понятия множества, которое является одним из основных простейших математических понятий и не поддается точному определению. Нижеследующие замечания имеют своей целью пояснить, что такое множество, но не претендуют на то, чтобы служить его определением.
Множеством называется собрание, совокупность, коллекция вещей, объединенных по какому-либо признаку или по какому-либо правилу. Понятие множества возникает путем абстракции. Рассматривая какую-либо совокупность предметов как множество, отвлекаются от всех связей и соотношений между различными предметами, составляющими множества, но сохраняют за предметами их индивидуальные черты. Таким образом, множество, состоящее из пяти монет, и множество, состоящее из пяти яблок, — это разные множества. С другой стороны, множество из пяти монет, расположенных по кругу, и множество из тех же монет, положенных одна на другую, — это одно и то же множество.
Приведем несколько примеров множеств. Можно говорить о множестве песчинок, составляющих кучу песка, о множестве всех планет нашей солнечной системы, о множестве всех людей, находящихся в данный момент в каком-либо доме, о множестве всех страниц этой книги. В математике тоже постоянно встречаются различные множества, например множество всех корней заданного уравнения, множество всех натуральных чисел, множество всех точек на прямой и т. д.
Математическая дисциплина, изучающая общие свойства множеств, т. е. свойства множеств, не зависящие от природы составляющих их предметов, называется теорией множеств. Эта дисциплина начала бурно развиваться в конце XIX и начале XX в. Основатель научной теории множеств — немецкий математик Г. Кантор.
Работы Кантора по теории множеств выросли из рассмотрения вопросов сходимости тригонометрических рядов. Это весьма обычное явление: очень часто рассмотрение конкретных математических задач ведет к построению весьма абстрактных и общих теорий. Значение таких абстрактных построений определяется тем, что они оказываются связанными не только с той конкретной задачей, из которой они выросли, но имеют приложения и в ряде других вопросов. В частности, именно так обстоит дело и с теорией множеств. Идеи и понятия теории множеств проникли буквально во все разделы математики и существенно изменили ее лицо. Поэтому нельзя получить правильного представления о современной математике, не познакомившись с элементами теории множеств. Особенно большое значение имеет теория множеств для теории функций действительного переменного.
Множество считается заданным, если относительно любого предмета можно сказать, принадлежит он множеству или не принадлежит. Иными словами, множество вполне определяется заданием всех принадлежащих ему предметов. Если множество \(M\) состоит из предметов \(a,\,b,\,c,\,\ldots\) и только из этих предметов, то пишут
\(M=\{a,\,b,\,c,\,\ldots\}\)
Предметы, составляющие какое-либо множество, принято называть его элементами. Тот факт, что предмет т является элементом множества \(M\) , записывается в виде
\(\Large{m\in M}\)
и читается: » \(m\) принадлежит \(M\) «, или » \(m\) есть элемент \(M\) «. Если же предмет \(m\) не принадлежит множеству \(M\) , то пишут: \(m\notin M\) . Каждый предмет может служить лишь одним элементом заданного множества; иными словами, все элементы (одного и того же множества отличны
друг от друга.
Элементы множества \(M\) могут сами быть множествами, однако, во избежание противоречий, приходится требовать, чтобы само множество \(M\) не было одним из своих собственных элементов: \(M\notin M\) .
Множество, не содержащее ни одного элемента, называется пустым множеством. Например, множество всех действительных корней уравнения
\(x^2+1=0\)
есть пустое множество. Пустое множество в дальнейшем будем обозначать через \(\varnothing\) .
Если для двух множеств \(M\) и \(N\) каждый элемент \(x\) множества \(M\) является также элементом множества \(N\) , то говорят, что \(M\) входит в \(\) , что \(M\) есть часть \(N\) , что \(M\) есть подмножество \(M\) или что \(M\) содержится в \(N\) ; это записывается в виде
\(M\subseteq N\) или \(N\supseteq M\)
Например, множество \(M=\{1,2\}\) есть часть множества \(N=\{1,2,3\}\) .
Ясно, что всегда \(M\subseteq M\) . Удобно считать, что пустое множество есть часть любого множества.
Два множества равны, если они состоят из одних и тех же элементов. Например, множество корней уравнения \(x^2-3x+2=0\) и множество \(M=\{1,2\}\) между собою равны.
Определим правила действий над множествами.
Объединение или сумма множеств
Пусть имеются множества \(M,N,P,\ldots\) . Объединением или суммой этих множеств называется множество \(X\) , состоящее из всех элементов, принадлежащих хотя бы одному из «слагаемых»
\(X=M+N+P+\ldots\) или \(X=M\cup N\cup P\cup\ldots\)
При этом, даже если элемент \(x\) принадлежит нескольким слагаемым, то он входит в сумму \(M\) лишь один раз. Ясно, что
\(M+M=M\cup M=M\)
и если \(M\subseteq N\) , то
\(M+N=M\cup N=N\)
Пересечение множеств
Пересечением или общей частью множеств \(M,N,P,\ldots\) . называется множество \(Y\) , состоящее из всех тех элементов, которые принадлежат одновременно всем множествам \(M,N,P,\ldots\) .
Ясно, что \(M\cdot M=M\) , и если \(M\subseteq N\) , то \(M\cdot N=M\) .
Если пересечение множеств \(M\) и \(N\) пусто: \(M\cdot N=\varnothing\) , то говорят, что эти множества не пересекаются.
Для обозначения операции суммы и пересечения множеств употребляют также знаки \(\textstyle{\sum}\) и \(\textstyle{\prod}\) . Таким образом,
\(E=\sum E_i\) есть сумма множеств \(E_i\) , a \(F=\prod E_i\) — их пересечение.
Читателю рекомендуется доказать, что сумма и пересечение множеств связаны обычным распределительным законом
\(M(N+P)=MN+MP,\)
а также законом
\(M+NP=(M+N)(M+P).\)
Разность множеств
Разностью двух множеств \(M\) и \(N\) называется множество \(Z\) всех тех элементов из \(Z\) , которые не принадлежат \(N\) :
\(Z=M-N\) или \(Z=M\setminus N\) .
Если \(N\subseteq M\) , то разность \(Z=M\setminus N=M-N\) называют также дополнением к множеству \(N\) относительно \(M\) .
Нетрудно показать, что всегда
\(M(N-P)=MN-MP\) и \((M-N)+MN=M.\)
Таким образом, правила действий над множествами значительно отличаются от обычных правил арифметики.
Конечные и бесконечные множества
Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно.
Рассмотрим два каких-либо множества \(M\) и \(N\) и поставим вопрос о том, одинаково или нет количество элементов в этих множествах.
Если множество \(M\) конечно, то количество его элементов характеризуется некоторым натуральным числом — числом его элементов. В этом случае для сравнения количества элементов множеств \(M\) и \(N\) достаточно сосчитать число элементов в \(M\) , число элементов в \(N\) и сравнить полученные числа. Естественно также считать, что если одно из множеств \(M\) и \(N\) конечно, а другое бесконечно, то бесконечное множество содержит больше элементов, чем конечное.
Однако, если оба множества \(M\) и \(N\) бесконечны, то путь простого счета элементов ничего не дает. Поэтому сразу возникают такие вопросы: все ли бесконечные множества имеют одинаковое количество элементов, или же существуют бесконечные множества с большим и меньшим количеством элементов? Если верно второе, то каким способом можно сравнивать между собой количество элементов в бесконечных множествах? Этими вопросами мы теперь и займемся.
Взаимно однозначное соответствие множеств
Пусть снова \(M\) и \(N\) — два конечных множества. Как узнать, какое из этих множеств содержит больше элементов, не считая числа элементов в каждом множестве? Для этого будем составлять пары, объединяя в пару один элемент из \(M\) и один элемент из \(N\) . Тогда, если какому-нибудь элементу из \(M\) не найдется парного к нему элемента из \(N\) , то в \(M\) больше элементов, чем в \(N\) . Поясним это рассуждение примером.
Пусть в зале находится некоторое число людей и некоторое число стульев. Чтобы узнать, чего больше, достаточно попросить людей занять места. Если кто-нибудь остался без места, значит, людей больше, а если, скажем, все сидят и заняты все места, то людей столько же, сколько стульев. Описанный способ сравнения количества элементов во множествах имеет то преимущество перед непосредственным счетом элементов, что он без особых изменений применяется не только к конечным, но и к бесконечным множествам.
Рассмотрим множество всех натуральных чисел
\(M=\{1,\,2,\,3,\,4,\,\ldots\}\)
и множество всех четных чисел
\(N=\{2,\,4,\,6,\,8,\,\ldots\}\)
Какое множество содержит больше элементов? На первый взгляд кажется, что первое. Однако мы можем образовать из элементов этих множеств пары, как указано ниже.
Таблица 1
\({\color{blue}\begin{array}{c|c|c|c|c|c} {\color{black}M} &{\color{black}1} &{\color{black}2} &{\color{black}3} &{\color{black}4} &{\color{black}\cdots}\\\hline {\color{black}N} &{\color{black}2} &{\color{black}4} &{\color{black}6} &{\color{black}8} &{\color{black}\cdots} \end{array}}\)
Ни один элемент \(M\) и ни один элемент \(N\) не остается без пары. Правда, мы могли бы также образовать пары и так:
Таблица 2
\({\color{blue}\begin{array}{c|c|c|c|c|c|c} {\color{black}M}&{\color{black}1}&{\color{black}2}&{\color{black}3}&{\color{black}4}&{\color{black}5}&{\color{black}\cdots}\\\hline {\color{black}N}&{\color{black}-}&{\color{black}2}&{\color{black}-}&{\color{black}4}&{\color{black}-}&{\color{black}\cdots} \end{array}}\)
Тогда многие элементы из \(M\) остаются без пар. С другой стороны, мы могли бы составить пары и так:
Таблица 3
\({\color{blue}\begin{array}{c|c|c|c|c|c|c|c|c} {\color{black}M}&{\color{black}-}&{\color{black}1}&{\color{black}-}&{\color{black}2}&{\color{black}-}&{\color{black}3}&{\color{black}-}&{\color{black}\cdots}\\\hline {\color{black}N}&{\color{black}2}&{\color{black}4}&{\color{black}6}&{\color{black}8}&{\color{black}10}&{\color{black}12}&{\color{black}14}&{\color{black}\cdots} \end{array}}\)
Теперь многие элементы из \(M\) остаются без пар.
Таким образом, если множества \(A\) и \(B\) бесконечны, то различным способам образования пар соответствуют разные результаты. Если существует такой способ образования пар, при котором у каждого элемента \(A\) и каждого элемента \(B\) имеется парный к нему элемент, то говорят, что между множествами \(A\) и \(B\) можно установить взаимно однозначное соответствие. Например, между рассмотренными выше множествами \(M\) и \(N\) можно установить взаимно однозначное соответствие, как
это видно из табл. 1.
Если между множествами \(A\) и \(B\) можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из \(A\) всегда остаются без пар, то говорят, что множество \(A\) содержит больше элементов, чем \(B\) , или что множество \(A\) имеет большую мощность, чем \(B\) .
Таким образом, мы получили ответ на один из поставленных выше вопросов: как сравнивать между собой количество элементов в бесконечных множествах. Однако это нисколько не приблизило нас к ответу на другой вопрос: существуют ли вообще бесконечные множества. имеющие различные мощности? Чтобы получить ответ на этот вопрос, исследуем некоторые простейшие типы бесконечных множеств.
Счетные множества. Если можно установить взаимно однозначное соответствие между элементами множества \(A\) и элементами множества всех натуральных чисел
\(Z=\{1,\,2,\,3,\,\ldots\},\)
то говорят, что множество \(A\) счетно. Иными словами, множество \(A\) счетно, если все его элементы можно занумеровать посредством натуральных чисел, т. е. записать в виде последовательности
\(a_1,~a_2,~\ldots,~a_n,~\ldots\)
Таблица 1 показывает, что множество всех четных чисел счетно (верхнее число рассматривается теперь как номер соответствующего нижнего числа).
Счетные множества это, так сказать, самые маленькие из бесконечных множеств: во всяком бесконечном множестве содержится счетное подмножество.
Если два непустых конечных множества не пересекаются, то их сумма содержит больше элементов, чем каждое из слагаемых. Для бесконечных множеств это правило может и не выполняться. В самом деле, пусть \(G\) есть множество всех четных чисел, \(H\) — множество всех нечетных чисел и \(Z\) — множество всех натуральных чисел. Как показывает таблица 4, множества \(G\) и \(H\) счетны. Однако множество \(Z=G+H\) вновь счетно.
Таблица 4
\({\color{blue}\begin{array}{c|c|c|c|c|c} {\color{black}G}&{\color{black}2}&{\color{black}4}&{\color{black}6}&{\color{black}8}&{\color{black}\cdots}\\\hline {\color{black}H}&{\color{black}1}&{\color{black}3}&{\color{black}5}&{\color{black}7}&{\color{black}\cdots}\\\hline {\color{black}Z}&{\color{black}1}&{\color{black}2}&{\color{black}3}&{\color{black}4}&{\color{black}\cdots} \end{array}}\)
Нарушение правила «целое больше части» для бесконечных множеств показывает, что свойства бесконечных множеств качественно отличны от свойств конечных множеств. Переход от конечного к бесконечному сопровождается в полном согласии с известным положением диалектики — качественным изменением свойств.
Докажем, что множество всех рациональных чисел счетно. Для этого расположим все рациональные числа в такую таблицу:
Таблица 5
\(\)
Здесь в первой строке помещены все натуральные числа в порядке их возрастания, во второй строке 0 и целые отрицательные числа в порядке их убывания, в третьей строке — положительные несократимые дроби со знаменателем 2 в порядке их возрастания, в четвертой строке — отрицательные несократимые дроби со знаменателем 2 в порядке их убывания и т. д. Ясно, что каждое рациональное число один и только один раз находится в этой таблице. Перенумеруем теперь
все числа этой таблицы в том порядке, как это указано стрелками. Тогда все рациональные числа разместятся в порядке одной последовательности:
Номер места, занимаемого
рациональным числом 1 2 3 4 5 6 7 8 9 . . .
Рациональное число 1. 2, О, 3, — 1, 4 —2 _
Этим установлено взаимно однозначное соответствие между всеми рациональными числами и всеми натуральными числами. Поэтому множество всех рациональных чисел счетно.
Множества мощности континуума
Если можно установить взаимно однозначное соответствие между элементами множества \(M\) и точками отрезка \(0\leqslant x\leqslant1\) , то говорят, что множество \(M\) имеет мощность континуума. В частности, согласно этому определению, само множество точек отрезка \(0\leqslant x\leqslant1\) имеет мощность континуума.
Из рис. 1 видно, что множество точек любого отрезка \(AB\) имеет мощность континуума. Здесь взаимно однозначное соответствие устанавливается геометрически, посредством проектирования.
Нетрудно показать, что множества точек любого интервала \(x\in[a,b]\) и всей числовой прямой \(x\in[-\infty,+\infty]\) — имеют мощность континуума.
Значительно более интересен такой факт: множество точек квадрата \(0\leqslant x\leqslant1,\) \(0\leqslant y\leqslant1\) имеет мощность континуума. Таким образом, грубо говоря, в квадрате «столько же» точек, сколько и в отрезке.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
calcsbox.com
Множество (математика) — это… Что такое Множество (математика)?
Мно́жество — один из ключевых объектов математики, в частности, теории множеств. «Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли» (Г. Кантор). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением (ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики).
В математической логике и дискретной математике часто употребляемый синоним множества — алфавит.
Теории
Существует два основных подхода к понятию множества — наивная и аксиоматическая теория множеств.
«Наивная теория множеств»
Дать определение какому-нибудь понятию — это значит описать это понятие через понятия, определённые ранее. Если число определений в теории конечно, то первое определение должно быть основано на понятиях, которые являются аксиоматическими, то есть изначально неопределёнными. Множество — как раз одно из таких аксиоматических понятий. В рамках наивной теории множеств множеством считается любой чётко определённый набор объектов (элементов множества). Вольное использование наивной теории множеств приводит к некоторым парадоксам, возникающим из-за того, что интуитивное понятие «чётко определённый» на самом деле само не определено чётко. Так как теория множеств, фактически, используется как основание и язык всех современных математических теорий, становится очевидной необходимость её строгой аксиоматизации.
Наивная теория множеств была создана Кантором в конце XIX века.
История определения
До XIX века считалось, что точного определения множества нет. Множеством считалось любое скопление предметов.
В конце XIX века Георг Кантор определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством». Эти объекты называются элементами множества. Множество объектов, обладающих свойством A(x), обозначается . Если некое множество , то A(x) называется характеристическим свойством множества Y.
Эта концепция привела к парадоксам, в частности, к парадоксу Рассела.
После этого теория множеств была аксиоматизирована.
Аксиоматическая теория множеств
На сегодняшний день множество определяется как модель, удовлетворяющая аксиомам ZFC (аксиомы Цермело — Френкеля с аксиомой выбора). При таком подходе в некоторых математических теориях возникают совокупности объектов, которые не являются множествами. Такие совокупности называются классами (различных порядков).
Элемент множества
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают большими буквами латинского алфавита, его элементы — маленькими. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а∉А(а не принадлежит А).
Некоторые виды множеств
По иерархии:
- Множество множеств
- Подмножество
- Надмножество
По ограничению:
Литература
- Столл Р. Р. Множества. Логика. Аксиоматические теории. — М.: Просвещение, 1968. — 232 с.
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
