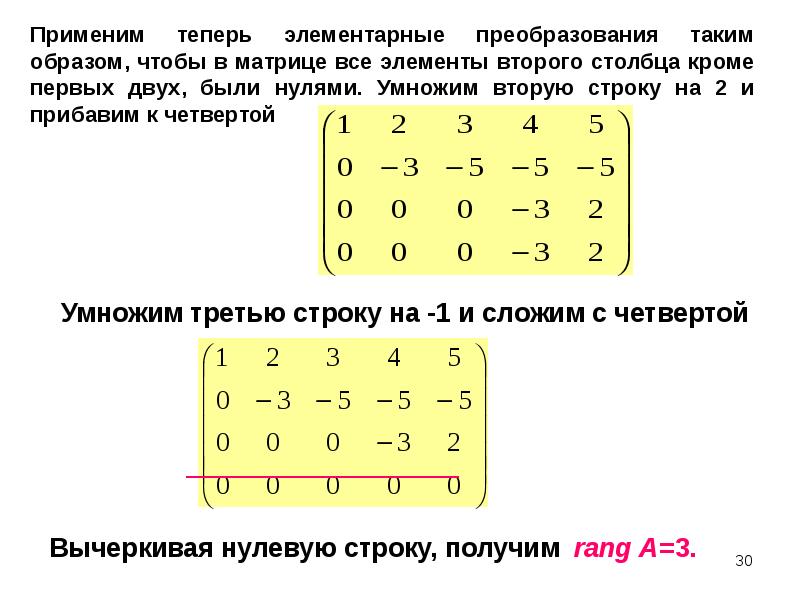
Матрицы сложение строк: Сложение строк матрицы. Решение матриц

умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.

Сложение матриц:

Вычитание и сложение матриц сводится к соответствующим операциям над их элементами. Операция сложения матриц вводится только для матриц одинакового размера, т. е. для матриц, у которых число строк и столбцов соответственно равно. Суммой матриц А и В, называется матрица С, элементы которой равны сумме соответствующих элементов. С = А + В c_ij = a_ij + b_ij Аналогично определяется разность матриц.

Умножение матрицы на число:

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

Произведением матрицы А на число k называется матрица В, такая что

b_ij = k × a_ij. В = k × A b_ij = k × a_ij. Матрица   — А = (-1) × А   называется противоположной матрице А.

Свойства сложения матриц и умножения матрицы на число:

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А — А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; , где А, В и С — матрицы, α и β — числа.

Умножение матриц (Произведение матриц):

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы. Произведением матрицы А_m×n на матрицу В_n×p, называется матрица С_m×p такая, что с_ik = a_i1 × b_1k + a_i2 × b_2k + . .. + a_in × b_nk, т. е. находиться сумма произведений элементов i — ой строки матрицы А на соответствующие элементы j — ого столбца

матрицы В. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А × Е = Е × А = А, где А квадратная матрица, Е — единичная матрица того же размера.

Свойства умножения матриц:

Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких — либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой

матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка. А × Е = Е × А = А

Умножение матриц обладает следующими свойствами: 1. А × (В × С) = (А × В) × С; 2. А × (В + С) = АВ + АС; 3. (А + В) × С = АС + ВС; 4. α × (АВ) = (αА) × В; 5. А × 0 = 0; 0 × А = 0; 6. (АВ)^Т = В^ТА^Т; 7. (АВС)^Т = С^ТВ^ТА^Т; 8. (А + В)^Т = А^Т + В^Т;

2. Определители 2-го и 3-го порядков. Свойства определителей.

Определителем матрицы

второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:

Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.

Знаки, с которыми члены

определителя матрицы входят в формулу нахождения определителя матрицы третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.

Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6

Свойства определителей матриц

Свойства определителей матриц:

Свойство № 1:

Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|^Т

Следствие:

Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2:

При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3:

Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4:

Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4:

Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой

определитель матрицы равен нулю.

Свойство № 5:

Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6:

Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:

Свойство № 7:

Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Пример применения свойств для вычисления определителя матрицы:

Матрицы

	Главная > Учебные материалы > Математика:  Матрицы
	1. Матрицы.    2.Виды матриц.    3.Операции над матрицами.
	1 2 3 4 5 6 7 8 9
	1. Матрицы.    Раздел математики, занимающийся изучением матриц, называется матричной алгеброй. Так как многие экономические явления и процессы можно записать в простой табличной форме, то данный раздел математики имеет важное значение в экономике.
	Матрица представляет собой прямоугольную таблицу чисел размера m x n , содержащую m строк и n столбцов. Числа матрицы называются элементами матрицы. Матрицы обозначаются заглавными буквами, например, А, В, С. Элементы матрицы обозначаются строчными буквами с двойной индексацией: аij , где i – номер строки, j – номер столбца.    Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. aij =bij для любых i = 1,2,3, …, m, j = 1,2,3, … n.
	2.Виды матриц.    Матрица, состоящая из одной строки, называется матрицей строкой. Матрица, состоящая из одного столбца – матрицей столбцом.    Если число строк матрицы равно числу столбцов и равно n, то такая матрица называется квадратной n –го порядка,    Элементы матрицы aij, у которой номер столбца равен номеру строки (i=j) , называются диагональными и образуют главную диагональ матрицы.    Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.    Матрица, у которой все элементы равны нулю, называется нулевой.
	3.Операции над матрицами.    Над матрицами можно производить следующие операции.
	1.Умножение матрицы на число. Произведением матрицы А на число ƛ называется матрица В = ƛА, элементы которой bij = ƛ aij для i= 1,2,3, … m; j = 1,2,3, … n.    2.Сложение матриц. Если матрицы А и В имеют одинаковый размер m x n, то суммой двух матриц называется матрица С = А + В, элементы которой сij = aij + bij для i= 1,2,3, … m; j = 1,2,3, … n.    3.Вычитание матриц. Разность двух матриц одинакового размера определяется через сложение матриц: А-В = А+ (-1)*В.    4.Умножение матриц. Произведение матрицы А на матрицу В существует, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц А и В называется такая матрица С, каждый элемент которой cij равен сумме произведений элементов i – й строки матрицы А на соответствующие элементы j – го столбца матрицы В:
	Примеры:
	1 2 3 4 5 6 7 8 9

Основные сведения о матрицах

В этом разделе мы даем основные сведения о матрицах, необходимые для понимания статистики и анализа данных.

Матрицей размера m x n (читается m на n) называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

Числа, составляющие матрицу, называются элементами матрицы.

Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,….

Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: a_ij, где i — номер строки, j — номер столбца.

Например, матрица:

В сокращенной записи обозначаем A=(a_ij); i=1,2,…m; j=1,2,…,n

Приведем пример матрицы 2 на 2: 

Вы видите, что a₁₁ = 1, a₁₂ = 0, a₂₁ = 2, a₂₂=5

Наряду с круглыми скобками используются и другие обозначения матрицы: 

Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, a_ij = b_ij для любых i=1,2,…m; j=1,2,…n

Виды матриц

Матрица, состоящая из одной строки, называется матрицей (вектором) — строкой, а из одного столбца — матрицей (вектором)- столбцом:

A=(a₁₁,a₁₂,…,a_1n) — матрица — строка

B=

Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.

Например, 

Элементы матрицы a_ij, у которых номер столбца равен номеру строки образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a₁₁, a₂₂,…,a_nn.

Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Операции над матрицами

Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые — специфические.

1. Умножение матрицы на число. Произведение матрицы А на число  называется матрица B=A, элементы которой b_ij=a_ij для i=1,2,…m; j=1,2,…n

Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.

В частности, произведение матрицы А на число 0 есть нулевая матрица.

2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой c_ij=a_ij+b_{ijдля i=1,2,…m; j=1,2,…n (т. е. матрицы складываются поэлементно).}

3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B.

4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A_m∙B _kназывается такая матрица C_m, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

i=1,2,…,m; j=1,2,…,n

Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):

A+B=B+A

(A+B)+C=A+(B+C)

λ (A+B)= λA+ λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ (AB)=( λA)B=A(λB)

A(BC)=(AB)C

Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:

a)      Если АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.

b)      Если АВ и ВА существуют, то они могут быть матрицами разных размеров.

5. Транспонирование матрицы — переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А’ называется транспонированной относительно матрицы А:

Из определения следует, что если матрица А имеет размер m, то транспонированная матрица А’ имеет размер n

В литературе встречаются и другие обозначения транспонированной матрицы, например, А^Т

Связанные определения:
Вырожденная матрица
Обобщенная обратная матрица
Обратная матрица
Плохо обусловленная матрица
Псевдообратная матрица
Эрмитова матрица
Эрмитово-сопряженная матрица

В начало

Содержание портала

Матрицы, основные операции с матрицами

Определение матрицы

Матрицей размера называется набор чисел, записанных в таблицу из строк и столбцов:

   

Матрицу часто окружают обычными скобками:

   

Эти две записи матриц эквиваленты.

Числа, из которых составлена матрица, называются элементами матрицы. Если количество строк матрицы равно количеству её столбцов, то матрица называется квадратной, а число её строк (столбцов) — порядком матрицы.

Матрицы, не являющиеся квадратными, называют прямоугольными.

Говорят, что две матрицы равны, если они имеют одинаковые размеры и все их элементы, стоящие на одинаковых позициях, равны. Пусть, например,

   

Тогда матрицы и равны, если для любого и для любого .

Сложение матриц

Для матриц с одинаковым количеством строк и столбцов вводится понятие суммы.

Пусть

   

Суммой матриц и называется матрица

   

То есть матрица является суммой матриц и , если каждый элемент матрицы равен сумме элементов матриц и , стоящих на тех же местах.

Умножение матрицы на число

Произведением матрицы на число (обозначается ) называется матрица , все элементы которой равны соответствующим элементам матрицы , умноженным на . То есть

   

Нулевой называется матрица, все элементы которой равны 0.

Матрица называется противоположной матрице . Разностью матриц и называется сумма .

Пример. Найти сумму и разность матриц

   

Решение. Сумма матриц

   

Разность матриц

   

Транспонирование матриц

Рассмотрим матрицу

   

состоящую из строк и столбцов. Матрица , все столбцы которой равны соответствующим строкам матрицы , называется транспонированной по отношению к и обозначается :

   

Пример. Транспонировать матрицу

   

Решение.

   

Функции для работы с матрицами в Excel

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

Формулы массива

Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).

Порядок применения формулы массива:

1. Выделить диапазон, где должен появиться результат действия формулы.
2. Ввести формулу (как и положено, со знака «=»).
3. Нажать сочетание кнопок Ctrl + Shift + Ввод.

В строке формул отобразится формула массива в фигурных скобках.

Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.



Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+h3). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

Условие задачи:

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:h21). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Матриц сложение — Энциклопедия по машиностроению XXL

Как и в случае матриц, сложению поворотов в случае их активного представления отвечает произведение кватернионов составляющих поворотов в обратном порядке. При этом все кватернионы заданы в исходном базисе к (/ = 1, 2, 3).  [c.46]

В кинематике механизмов операции сложения матриц и умножения их на скаляр находят применение в действиях над матрицами-столбцами.  [c.631]

При сложении двух матриц одинакового размера получается матрица того же размера, каждый элемент которой равеи сумме соответствующих элементов слагаемых матриц.  [c.104]

Над матрицами можно выполнять действия транспонирования, сложения, умножения. Матрица А, транспонированная по отношению к матрице А, образуется из матрицы А заменой каждой ее строки на столбец того же номера. Например, при транспонировании матрицы  [c.50]

Множество J n всех л-мерных векторов называют линейным алгебраическим пространством, если в нем определены операции сложения и умножения на скаляр точно так же, как для матриц. Число я называется размерностью пространства Rn- Рассмотрим помимо вектора а другой п-мерный вектор  [c.19]

Матрица [/(], называемая глобальной матрицей жесткости или просто матрицей жесткости системы, получается сложением локальных матриц жесткости [Л ] по следующему правилу сначала к нулевой матрице размерности NxN добавляется матрица, в левом верхнем углу которой стоит локальная матрица жесткости 1-го элемента, к получившейся матрице добавляется матрица размера /V х /V, ненулевые элементы которой расположены на пересечении 2-го и 3-го столбцов и 2-й и 3-й строк и равны соответствующим элементам локальной матрицы жесткости для 2-го элемента и т. д. на -м шаге добавляется матрица, ненулевые элементы которой расположены на пересечении к и к- строк и к н k- — столбцов и равны соответствующим элементам локальной матрицы жесткости k-ro элемента.  [c.134]

При вычислении матрицы плотности мы будем предполагать, что рассеянные волны имеют беспорядочные фазы и при сложении в среднем дают нуль. Если и г и г лежат слева от слоя, то  [c.718]

Все остальные неизвестные определяются лишь путем умножения и сложения матриц. Весь процесс вычислений при этом легко программируется с использованием стандартных программ сложения, умножения и обращения матриц.  [c.97]

Непосредственным перемножением и сложением матриц (71.29) нетрудно убедиться, что они удовлетворяют соотношениям (71.28), понимая, что в их правой части стоит единичная матрица. Например, для имеем  [c.387]

Описанная процедура лежит в основе алгоритма формирования глобальной матрицы и глобального вектор-столбца. Как было уже отмечено выше, она реализуется путем последовательного перебора элементов следующим образом. Берется первый элемент, анализируется его строка в индексной матрице и устанавливается, в какие три уравнения этот элемент дает вклад . Далее рассчитываются его локальная матрица и вектор-столбец. При этом расчете используется информация о наличии у данного элемента граничных сторон, содержащаяся в четвертом столбце индексной матрицы. Пусть локальным номерам 1, 2, 3 соответствуют фактические номера i, j, k. Тогда первая строка локальной матрицы и первый коэффициент локального вектор-столбца участвуют в формировании i-й строки глобальной матрицы и i-ro коэффициента глобального вектор-столбца. Производится сложение найденных локальных коэффициентов с имеющимися значениями глобальных коэффициентов дц, Gij, Затем аналогичная процедура повторяется для второй и третьей строк локальной матрицы и второго и третьего коэффициентов локального столбца. Они участвуют в формировании строк глобальной матрицы и коэффициентов глобального столбца с номерами / и к, которые соответствуют локальным номерам 2 и 3.  [c.144]

Сложение и вычитание матриц. Две матрицы можно сложить (вычесть). Для этого необходимо, чтобы порядки матриц были одинаковы, и тогда сложить (вычесть) соответствующие элементы матриц.  [c.179]

Нетрудно убедиться, что выполнение операций дифференцирование вектора [X], умножение матрицы [К] на вектор [Р] и сложение с вектором [F] —приводит к системе уравнений вида (1). Однако матричная форма записи более компактна й упрощает действия по преобразованию системы уравнений.  [c.181]

Полное изображение типа С образуется при перемещении преобразователя в направлении, перпендикулярном к направлению электронного сканирования. При этом сигналы коорди-, нат строки вырабатываются датчиками координат, как в системе с ручным (механическим) сканированием. Более простое решение этой задачи может быть получено с применением двумерного электронного сканирования. Пьезоэлементы двумерной матрицы (например, с числом элементов 8X8) возбуждаются с задержками, обеспечивающими сложение амплитуд акустических импульсов лишь на определенных направлениях в объекте контроля. Аналогично в тракте приема принятые пьезоэлементами сигналы предварительно задерживаются так, что суммирование амплитуд соответствует направлению излучения.  [c.271]

Матрица называется единичной матрицей. Удобство записывать совокупности значений каких-либо величин в таком виде заключается в том, что над матрицами можно производить соответствующие действия (сложение, умножение, см., например, р]).  [c.93]

Бесконечно малые повороты. Целесообразно попытаться установить соответствие между векторами и конечными поворотами, описываемыми ортогональными матрицами. Вектор, который мы поставим в соответствие некоторому повороту, должен, конечно, иметь определенное направление —направление оси вращения и определенную величину, например равную углу поворота. Мы сейчас увидим, что успешно осуществить такое соответствие оказывается невозможным. Предположим, что А и В будут двумя такими векторами , связанными с преобразованиями А и В. Тогда, поскольку это векторы, они должны обладать свойством коммутативности при сложении, т. е. для них должно выполняться равенство  [c.142]

Но сложение двух вращений, т. е. последовательное выполнение одного из них за другим, описывается, как мы знаем, произведением матриц АВ, и это умножение не коммутативно, т. е. АВ =ВА. Следовательно, векторы Л и Д не будут обладать коммутативностью сложения и поэтому их нельзя будет считать в  [c.142]

Мы имеем здесь иллюстрацию сложения вращений согласно формуле (9.13), ибо, транспонируя элементы в (11.1)—(11.3), можно получить матрицы М, М2, Mg и непосредственно убедиться, что матрица М (11.5) представима в виде  [c.47]

В алгебре матриц определяются следующие действия над матрицами а) сложение матриц б) умножение матрицы на число в) умножение матриц. Указанные действия позволяют вычислить соответственно сумму матриц, произведение матрицы на число, произведение матриц и, как следствие, разность матриц.  [c.41]

После построения /-й строки матрицы F выполняется циклический сдвиг элементов матрицы-строки R на один влево или вправо для формирования направлений штриховки, соответствующих углам 45 и 135°. Завершив формирование матрицы F, с помощью логического сложения получим матрицу содержащую описание заштрихованной области сечения  [c.123]

Логическое сложение матриц реализуется путем попарного логического сложения одноименных элементов исходных матриц  [c.123]

Сложение и вычитание матриц. Эти операции имеют смысл лишь при их одинаковой структуре (одинаковом количестве строк и одинаковом количестве столбцов) слагаемых или вычитаемых матриц. Суммой (или разностью) двух (т х п) матриц А =— а,-/ и В = ( fe(jj называется (т х п) матрица С = с у (г = 1, 2,. . ., т, / = 1, 2,. . ., п), элементы которой равны сумме (или разности) соответствующих элементов слагаемых (вычитаемых) матриц, т. е.  [c.22]

Сложение (а следовательно, и вычитание) матриц ассоциативно и коммутативно, т. е.  [c.22]

Операции сложения и вычитания матриц применяются при переносе систем координат в процессе решения задач анализа механизмов (см. гл. 17, п. 34).  [c.22]

Если учесть, что для перемножения двух матриц п-то порядка необходимо осуществить л умножений и п — 1) сложений, то для перемножения двух матриц 4-го порядка нужно произвести 64 умножения и 48 сложений или всего 112 вычислительных действий, а для матриц 3-го порядка соответственно 27 + 18 = = 45 действий.  [c.188]

В нижней траверзе пресса имеется проём для пропуска через пресс балки или двух швеллеров, сложенных стенками нижний стол, на котором устанавливается инструмент, состоит из двух частей. Подушки с матрицами для пробивания отверстий в полках устанавливаются на концах консольных выступов стола.  [c.483]

Рассмотрим, как влияет учет дисперсий на результаты расчета. Формально учет дисперсий выражается в сложении матрицы [а] [а] с диагональной матрицей [ )], имеющей положительные члены. Это способствует улучшению обусловленности матрицы [а] [а], что особенно важно в случаях, когда последняя плохо  [c.58]

Сложение матриц. Суммой матриц  [c.95]

DN — присвоение значений единицы диагональным элементам двумерного массива А+В — сложение матриц А и В  [c.163]

Необходимость применения динамического метода существенно усложняет решение неконсервативных задач устойчивости. Здесь требуется весьма эффективный метод определения частот собственных колебаний. Среди других методов в этом отношении вьщеляется МГЭ. Он позволяет получать точный спектр частот (устраняет недостаток МКЭ), а в трансцендентном частотном уравнении отсутствуют точки разрыва 2-го рода (устраняет недостаток метода перемещений). Дополнительными положительными факторами являются простая логика формирования динамической матрицы устойчивости, отсутствие операций умножения, обращения и сложения матриц, хорошая устойчивость численных операций при вычислении определителя и т.п.  [c.196]

Кватернионное сложение поворотов. Как и в случае матриц, сложению поворотов отвечает произведение кватернионов, при этом активная и пассивная точки зрения на преобразования имеют существенные отличия.  [c.46]

Сложение. Матрицы А п В могут быть сложены, если они имеют оди-накоиое число строк и столбцов.  [c.631]

Таком образом, для выполнения алгоритма (55) требуются два прямых и одно обратное преобразование Ф/рье, а также прямое умножение матрицы на матрицу. Если в качестве дижретного преобразования Фурье использовать алгоритм БПФ, число опера дай сложения составит 2N og2 , а число операций умножения -.  [c.63]

Показано, что в случае произвольных распределений наработок и времени восстановления в матрицу Гб) вводятся ооответствувщие вероятности переходов, а вместо сложения интенсивностей осуществляется умножение вероятностей независимых событий.  [c.15]

Сложение двух матриц не является такой важной операцией, как их умножение, однако оно встречается достаточно часто. Под суммойА + В понимается такая матрица С, элементы которой получаются посредством сложения соответствующих элементов А и В. Таким образом, можно написать  [c.119]

Может показаться, что скорость, большую скорости света с, можно получить с помощью двух последовательных преобразований Лоренца. Пусть, например, вторая система движется относительно первой со скоростью Vi > с/2, а третья система движется относительно второй со скоростью 02, также большей, чем с/2 (в том же направлении). Можно подумать, что скорость третьей системы относительно первой будет тогда больше чем с. Однако это не так, ибо эта скорость не равна просто V -f Ua-Чтобы убедиться в этом, достаточно найти преобразование Ло-)енца, описывающее переход от первой системы к третьей. 1еремножая для этого матрицы рассматриваемых преобразований, мы найдем полное преобразование и увидим, что оно соответствует скорости из, определяемой так называемым законом Эйнштейна для сложения скоростей. Согласно этому закону  [c.217]

Описание механических свойств композитных материалов, которые могут обладать весьма высокой прочностью (особенно статической и ударной), можно производить двумя путями. В первом случае композитные материалы рассматриваются как квазиодно-родные (гомогенные), обладающие в случае объемного дисперсного армирования изотропией деформационных и прочностных свойств, а в случае армирования волокнами, плоскими сетками или тканями — определенного типа анизотропией. Обычно применяют модели ортотропного или трансверсально-изотропного тела. При таком подходе речь идет о механических характеристиках, осред-ненных в достаточно больших объемах, содержащих много однотипных армирующих элементов. Другой, несравненно более сложный, но и более информативный путь состоит в раздельном рассмотрении механических свойств каждой фазы с последующим теоретическим прогнозированием свойств всего композита в целом. При этом приходится рассматривать фактически еще одну дополнительную фазу зоны сопряжения основных фаз, например, матрицы с армирующими волокнами. Механизм повреждений, развивающихся на границах фаз, обычно весьма сложен и определяется помимо свойств основных компонентов гетерогенной системы еще рядом дополнительных факторов, таких как адгезия фаз, технологические и температурные местные напряжения, обычно возникающие вблизи границ, наличие дефектов и др. Границы фаз как зоны концентраций напряжений играют особенно важную роль в развитии много- и малоцикловых усталостных повреждений композитов.  [c.37]

При необходимости подчеркнуть состав множеств D я Z далее будут использоваться и такие обозначения a D, Z] = a[, 2,…,d Z] = a D , 2,…,Z]== = a d I, 2, z] и T. П. С их помощью можно удобно записывать отдельные составные части (подматрицы) матрицы или новые матрицы, образованные на основе a[D, Z], Например, а , 2, k—l, k+l, d z] = a[D/ k), Z]—матрица, полученная из a[D,Z] в результате вычеркивания й-й строки, а d D — k, Z ], где Z — множество четных чисел (Z zZ)—матрица, в которой к тому же еще вычеркнуты все столбцы с нечетными номерами. В частности, a[k, Z] — k-я строка матрицы a[D, Z], а a[D, /] — ее /-Й столбец. Запись a[D 1, 2 + 3 + 5, 4] обозначает матрицу, в которой второй, третий и пятый столбцы сложены поэлементно и полученный суммарный столбец помещен на второе место. Пусть Zi сг Z и Z2 с= Z— подмножества множества Z, причем Z, 0 2=0 Z/», Z — обозначения столбцов, полученных как результат сложения столбцов с номерами из множеств Zi и Z2. Тогда матрица а[0] Zt, Z —(Z1UZ2), Zt  [c.88]

Таким образом, на всех стадиях определения скоростей и моментов используется один и тот же алгоритм, позволяющий легко автоматизировать весь процесс вычисления. Его основной недостаток состоит в том, как уже отмечалось выше, что он производит много лишних действий, связанных с умножением и сложением нулей при вычислении определителей ред-козаполненных матриц. Применение направленных графов и соответствующего математического аппарата [2, 21] дает возможность избавиться от этого недостатка и тем са.мым значительно сократить машинное время решения задачи.  [c.98]

Порядок матриц при транспонировании в общем случае изменяется. Сложение и вычитание матрии  [c.18]

К матрицам одного и того же порядка применимы операции сложения и вычитания. Результатом сложения (вычитания) двух матрии А и В порядка n m является новая матрица С того же порядка, каждый элемент которой jj = ajj bjj, где i — номер строки, j — номер столбца. Пусть,  [c.18]

Число критических сил по МКЭ равно степени кинематической неопределимости стержневой системы, а при формировании векового уравнения используются операции сложения, умножения и траспонирования матриц.  [c.179]

---

Изучаем матрицы в питоне и массивы NumPy в Python

Матрица — это двухмерная структура данных, в которой числа расположены в виде строк и столбцов. Например:

Эта матрица является матрицей три на четыре, потому что она состоит из 3 строк и 4 столбцов.

Python не имеет встроенного типа данных для матриц. Но можно рассматривать список как матрицу. Например:

A = [[1, 4, 5], 
    [-5, 8, 9]]

Этот список является матрицей на 2 строки и 3 столбца.

Обязательно ознакомьтесь с документацией по спискам Python, прежде чем продолжить читать эту статью.

Давайте посмотрим, как работать с вложенным списком.

A = [[1, 4, 5, 12], 
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]]

print("A =", A) 
print("A[1] =", A[1])      # вторая строка
print("A[1][2] =", A[1][2])   # третий элемент второй строки
print("A[0][-1] =", A[0][-1])   # последний элемент первой строки

column = [];        # пустой список
for row in A:
  column.append(row[2])   

print("3rd column =", column)

Когда мы запустим эту программу, результат будет следующий:

A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]
A [1] = [-5, 8, 9, 0]
A [1] [2] = 9
A [0] [- 1] = 12
3-й столбец = [5, 9, 11]

Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач. Но в Python есть более эффективный способ работы с матрицами – NumPy .

NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,

• Ознакомьтесь: Как установить NumPy Python?
• Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.

После установки NumPy можно импортировать и использовать его.

NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:

import numpy as np
a = np.array([1, 2, 3])
print(a)               # Вывод: [1, 2, 3]
print(type(a))         # Вывод: <class 'numpy.ndarray'>

Как видите, класс массива NumPy называется ndarray.

Существует несколько способов создания массивов NumPy.

import numpy as np

A = np.array([[1, 2, 3], [3, 4, 5]])
print(A)

A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой
print(A)

A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел
print(A)

Когда вы запустите эту программу, результат будет следующий:

[[1 2 3]
 [3 4 5]]

[[1.1 2. 3.]
 [3. 4. 5.]]

[[1. + 0.j 2. + 0.j 3. + 0.j]
 [3. + 0.j 4. + 0.j 5. + 0.j]]

import numpy as np

zeors_array = np.zeros( (2, 3) )
print(zeors_array)

'''
 Вывод:
 [[0. 0. 0.]
  [0. 0. 0.]]
'''

ones_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype
print(ones_array)      # Вывод: [[1 1 1 1 1]]

Здесь мы указали dtype — 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2^-31 до 2^-31-1.

import numpy as np

A = np.arange(4)
print('A =', A)

B = np.arange(12).reshape(2, 6)
print('B =', B)

''' 
Вывод:
A = [0 1 2 3]
B = [[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]
'''

Узнайте больше о других способах создания массива NumPy .

Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы. Рассмотрим, как выполнить ту же задачу, используя массив NumPy.

Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.

import numpy as np

A = np.array([[2, 4], [5, -6]])
B = np.array([[9, -3], [3, 6]])
C = A + B      # сложение соответствующих элементов
print(C)

''' 
Вывод:
[[11  1]
 [ 8  0]]
 '''

Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .

Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.

import numpy as np

A = np.array([[3, 6, 7], [5, -3, 0]])
B = np.array([[1, 1], [2, 1], [3, -3]])
C = a.dot(B)
print(C)

''' 
Вывод:
[[ 36 -12]
 [ -1   2]]
'''

Мы используем numpy.transpose для вычисления транспонирования матрицы.

import numpy as np

A = np.array([[1, 1], [2, 1], [3, -3]])
print(A.transpose())

''' 
Вывод:
[[ 1  2  3]
 [ 1  1 -3]]
'''

Как видите, NumPy значительно упростил нашу задачу.

Также можно получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.

import numpy as np
A = np.array([2, 4, 6, 8, 10])

print("A[0] =", A[0])     # Первый элемент     
print("A[2] =", A[2])     # Третий элемент     
print("A[-1] =", A[-1])   # Последний элемент     

Когда вы запустите эту программу, результат будет следующий:

A [0] = 2
A [2] = 6
A [-1] = 10

Теперь выясним, как получить доступ к элементам двухмерного массива (который в основном представляет собой матрицу).

import numpy as np

A = np.array([[1, 4, 5, 12],
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])

#  Первый элемент первой строки
print("A[0][0] =", A[0][0])  

# Третий элемент второй строки
print("A[1][2] =", A[1][2])

# Последний элемент последней строки
print("A[-1][-1] =", A[-1][-1])     

Когда мы запустим эту программу, результат будет следующий:

A [0] [0] = 1
A [1] [2] = 9
A [-1] [- 1] = 19

import numpy as np

A = np.array([[1, 4, 5, 12], 
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])

print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)

Когда мы запустим эту программу, результат будет следующий:

A [0] = [1, 4, 5, 12]
A [2] = [-6, 7, 11, 19]
A [-1] = [-6, 7, 11, 19]

import numpy as np

A = np.array([[1, 4, 5, 12], 
    [-5, 8, 9, 0],
    [-6, 7, 11, 19]])

print("A[:,0] =",A[:,0]) # Первый столбец
print("A[:,3] =", A[:,3]) # Четвертый столбец
print("A[:,-1] =", A[:,-1]) # Последний столбец (четвертый столбец в данном случае)

Когда мы запустим эту программу, результат будет следующий:

A [:, 0] = [1 -5 -6]
A [:, 3] = [12 0 19]
A [:, - 1] = [12 0 19]

Если вы не знаете, как работает приведенный выше код, прочтите раздел «Разделение матрицы».

Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:

import numpy as np
letters = np.array([1, 3, 5, 7, 9, 7, 5])

# с 3-го по 5-ый элементы
print(letters[2:5])        # Вывод: [5, 7, 9]

# с 1-го по 4-ый элементы
print(letters[:-5])        # Вывод: [1, 3]   

# с 6-го до последнего элемента
print(letters[5:])         # Вывод:[7, 5]

# с 1-го до последнего элемента
print(letters[:])          # Вывод:[1, 3, 5, 7, 9, 7, 5]

# список в обратном порядке
print(letters[::-1])          # Вывод:[5, 7, 9, 7, 5, 3, 1]

Теперь посмотрим, как разделить матрицу.

import numpy as np

A = np.array([[1, 4, 5, 12, 14], 
    [-5, 8, 9, 0, 17],
    [-6, 7, 11, 19, 21]])

print(A[:2, :4])  # две строки, четыре столбца

''' Вывод:
[[ 1  4  5 12]
 [-5  8  9  0]]
'''


print(A[:1,])  # первая строка, все столбцы

''' Вывод:
[[ 1  4  5 12 14]]
'''

print(A[:,2])  # все строки, второй столбец

''' Вывод:
[ 5  9 11]
'''

print(A[:, 2:5])  # все строки, с третьего по пятый столбец
''' Вывод:
[[ 5 12 14]
 [ 9  0 17]
 [11 19 21]]
'''

Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.

Данная публикация является переводом статьи «Python Matrices and NumPy Arrays» , подготовленная редакцией проекта.

Операции со строками матрицы

Матрица Операции со строками (стр. 1 из 2)

---

«Операции» математик для «процедур». Четыре основных операции «над числами — сложение, вычитание, умножение, и деление. Для матриц есть три основные операции со строками; что есть три процедуры, которые вы можете проделать со строками матрицы.

---

Первая операция переключение строк. Например, учитывая матрицу:

… вы можете переключать ряды вокруг, чтобы поместить матрицу в более удобное расположение строк, например:

Переключение строк часто обозначено стрелками, например:

При переключении рядов, будьте осторожны, чтобы правильно скопировать записи.

---

Вторая операция умножение строк. Например, учитывая следующую матрицу:

… вы можете умножить первый ряд на 1 получить положительное лидерство значение в первой строке:

Умножение этой строки часто обозначается стрелкой с указанием умножения вверху из него, вот так:

«1 R ₁ » указывает на фактическую операцию.»1″ говорит, что мы умножили на отрицательный; « R ₁ » говорит, что мы работали с первым рядом. Обратите внимание, что второй и третьи строки были скопированы без изменений во вторую матрицу. Умножение применяется только к первой строке, поэтому записи для двух других строк были просто унесены без изменений.

Умножить можно на что угодно тебе нравится. Например, чтобы получить ведущую 1 в третьей строке предыдущей матрицы можно умножить третью строку на отрицательную половину:

Поскольку вы не делали что-либо с первой и второй строками, эти записи были просто скопированы без изменений в новую матрицу.

Вы можете сделать больше одного умножение строк за один шаг, чтобы вы могли выполнить два вышеуказанные шаги всего за один шаг, например:

Это хорошая идея использовать какую-либо форму записи (например, стрелки и нижние индексы выше), чтобы вы может отслеживать вашу работу. Матрицы очень беспорядочные, особенно если вы выполняя их вручную, а заметки могут упростить проверку вашей работы позже.Это также произведет впечатление на вашего учителя.

---

Операция последней строки это добавление строк. Сложение строк аналогично методу «сложения». для решения системы линейных уравнений. Предположим, у вас есть следующая система уравнений:

Вы можете приступить к решению эта система, добавляя столбцы, чтобы получить 4 y = 4:

Можно сделать нечто подобное с матрицами.Например, учитывая следующую матрицу:

… можно «уменьшить» (добавьте больше нулей в начале) во вторую строку, добавив первую строку к это (общая цель с матрицами на этом этапе — получить «1» или «0» а затем «1» в начале каждой строки матрицы). Когда вы сокращали два уравнения линейной системы, добавив, вы нарисовали полосу «равно» поперек снизу и добавлен.Когда вы используете сложение в матрице, вы нужно захватить бумагу для заметок, потому что вы не хотите пытаться работать внутри матрицы. Итак, добавьте две строки на бумагу для заметок:

Царапины не сдавай это!

Это ваша новая секунда строка; вы напишете его вместо старой второй строки.Результат будет выглядят так:

В данном случае « R ₁ + R ₂ » на стрелке означает «Я добавил строку один ко второй строке, и это результат Я получил «. Поскольку первая строка на самом деле не изменилась, а поскольку мы не делать что-нибудь с третьей строкой, эти строки копируются в новую матрицу без изменений.

Верх | 1 | 2 | Возвращаться к указателю Вперед >>

Цитируйте эту статью как:

Стапель, Елизавета.«Матричные операции со строками». Пурпурная Математика . Имеется в наличии из https://www.purplemath.com/modules/mtrxrows.htm . Доступ [Дата] [Месяц] 2016 г.

Операции со строками матрицы

Над строками таблицы используются 3 основные операции. матрица когда вы используете матрицу для решить систему линейных уравнений . Обычно цель состоит в том, чтобы левая часть матрицы выглядела как единичная матрица .

Три операции:

• Переключение строк
• Умножение строки на число
• Добавление строк

Переключение строк

Вы можете переключать строки матрицы, чтобы получить новую матрицу.

[ 2 3 — 2 6 0 0 3 — 6 1 0 2 — 3 ] → [ 1 0 2 — 3 2 3 — 2 6 0 0 3 — 6 ]

В показанном выше примере мы перемещаем строку 1 грести 2 , Строка 2 грести 3 , и строка 3 грести 1 .(Причина в том, чтобы получить 1 в верхнем левом углу.)

Умножение строки на число

Любую строку можно умножить на число. (Это означает умножение каждой записи в строке на одно и то же число.)

[ 1 0 2 — 3 2 3 — 2 6 0 0 3 — 6 ] → р 3 : 1 3 р 3 [ 1 0 2 — 3 2 3 — 2 6 0 0 1 — 2 ]

В этом примере мы умножили строку 3 матрицы на 1 3 .(Это дает нам 1 нам нужно в строке 3 , Столбец 3 .)

Добавление строк

Вы также можете сложить две строки и заменить строку результатом.

Например, в матрицу, приведенную в последнем примере, мы можем добавить строки 2 а также 3 вместе, запись за записью:

[ 2 3 — 2 6 ] + [ 0 0 1 — 2 ] _ [ 2 3 — 1 4 ]

Затем мы заменяем Row 2 с результатом.

[ 1 0 2 — 3 2 3 — 2 6 0 0 1 — 2 ] → р 2 : р 2 + р 3 [ 1 0 2 — 3 2 3 — 1 4 0 0 1 — 2 ]

Добавление нескольких строк

Мы сказали, что было всего три операции, и они есть.Но, используя две последние операции в комбинации, мы можем добавить несколько строк к другим строкам, чтобы ускорить процесс.

Сделайте резервную копию шага, так что у нас есть матрица:

[ 1 0 2 — 3 2 3 — 2 6 0 0 1 — 2 ]

Теперь вместо простого добавления строки 2 + Ряд 3 , Добавить ряд 2 + ( 2 × Строка 3 ) :

[ 2 3 — 2 6 ] + [ 0 0 2 — 4 ] _ [ 2 3 0 2 ]

Затем замените Row 2 с результатом.

[ 1 0 2 — 3 2 3 — 2 6 0 0 1 — 2 ] → р 2 : р 2 + 2 р 3 [ 1 0 2 — 3 2 3 0 2 0 0 1 — 2 ]

Таким образом, мы получаем 0 в строке 2 , Столбец 3 .

Мы можем сделать это снова, чтобы получить 0 в строке 2 , Столбец 1 . Здесь мы умножаем Row 1 от — 2 , добавьте строку 2 и замените Row 2 с результатом.

[ 1 0 2 — 3 2 3 0 2 0 0 1 — 2 ] → р 2 : — 2 р 1 + р 2 [ 1 0 2 — 3 0 3 — 4 8 0 0 1 — 2 ]

Мы покажем еще несколько шагов, чтобы получить 3 × 3 единичная матрица слева (и таким образом решить систему).

Следующим шагом будет добавление Строка 2 + ( 4 × Строка 3 ) чтобы получить 0 в строке 2 , Столбец 3 .

[ 1 0 2 — 3 0 3 — 4 8 0 0 1 — 2 ] → р 2 : р 2 + 4 р 3 [ 1 0 2 — 3 0 3 0 0 0 0 1 — 2 ]

Далее нам понадобится ноль в строке 1 , Столбец 3 .

[ 1 0 2 — 3 0 3 0 0 0 0 1 — 2 ] → р 1 : р 1 — 2 р 3 [ 1 0 0 1 0 3 0 0 0 0 1 — 2 ]

Последний шаг — это просто применение второй операции, умножение строки на число.

[ 1 0 0 1 0 3 0 0 0 0 1 — 2 ] → 1 3 р 3 [ 1 0 0 1 0 1 0 0 0 0 1 — 2 ]

Теперь у нас есть решение в виде упорядоченной тройки ( 1 , 0 , — 2 ) .

Важная заметка: Если уравнения, представленные исходной матрицей, представляют собой идентичные или параллельные линии, вы не сможете получить единичную матрицу, используя эти операции со строками. В этом случае решения либо не существует, либо существует бесконечно много решений системы.

Элементарных матричных операций

Элементарные матричные операции играют важную роль во многих матричных приложения алгебры, такие как найти обратную матрицу а также решение одновременных линейных уравнений.

Элементарные операции

Существует три вида операций с элементарной матрицей.

1. Поменяйте местами две строки (или столбцы).
2. Умножьте каждый элемент в строке (или столбце) на ненулевое число.
3. Умножьте строку (или столбец) на ненулевое число и добавьте результат в другую строку (или столбец).

Когда эти операции выполняются со строками, они вызываются операции элементарной строки ; и когда они исполняются на столбцы, они называются элементарными операциями столбца .

Обозначение элементарных операций

Во многих ссылках вы встретите компактные обозначения для описания элементарные операции. Это обозначение показано ниже.

Описание работы	Обозначение
Рядовые операции
1. Поменяйте местами ряды i и j	R i <--> R j
2.Умножить строку i на s , где s ≠ 0	SR i -> R i
3. Добавьте с раз в строку i в строку j	SR i + R j -> R j
Операции со столбцами
1. Поменяйте местами столбцы i и j	С i <--> С j
2.Умножьте столбец и на с , где с ≠ 0	SC i -> C i
3. Добавьте с раз в столбец i в столбец j	SC i + C j -> C j

Элементарные операторы

Каждый тип элементарной операции может выполняться умножением матриц, с использованием квадратных матриц, называемых элементарных оператора .

Например, предположим, что вы хотите поменять местами строки 1 и 2 матрицы А . Для этого вы можете предварительно умножить A по E для производства B , как показано ниже.

R 1 <--> R 2 =
	E		А

R 1 <--> R 2 =

0 + 2 0 + 4 0 + 6 0 + 1 0 + 3 0 + 5

R 1 <--> R 2 =

= В

Здесь E — элементарный оператор.Он действует на A для создания желаемых перестановок рядов в В . Что мы хотели бы знать, конечно, это как найти E . Читать дальше.

Как выполнять элементарные операции со строками

Для выполнения операции элементарной строки на A , матрица r x c , возьмите следующую шаги.

1. Чтобы найти E , оператор элементарной строки , примените операцию к r x r единичная матрица.
2. Чтобы выполнить операцию элементарной строки, предварительно умножьте A по E .

Мы проиллюстрируем этот процесс ниже для каждого из трех типов элементарных строковые операции.

• Поменять местами два ряда . Предположим, мы хотим поменять местами вторая и третья строки A , матрица 3 x 2. К создаем оператор элементарной строки E , меняем местами вторая и третья строки единичной матрицы Я ₃ .

  Затем поменять местами второй и третий ряды из А , мы умножаем A на E , как показано ниже.

  R 2 <--> R 3 =
  	E		А

  
  

  R 2 <--> R 3 =	1 * 0 + 0 * 2 + 0 * 4 1 * 1 + 0 * 3 + 0 * 5 0 * 0 + 0 * 2 + 1 * 4 0 * 1 + 0 * 3 + 1 * 5 0 * 0 + 1 * 2 + 0 * 4 0 * 1 + 1 * 3 + 0 * 5

  
  

• Умножьте строку на число .Предположим, мы хотим умножьте каждый элемент во второй строке Matrix A на 7. Предположим, что A — это матрица 2 x 3. К создаем элементарный оператор строки E , умножаем каждый элемент во второй строке единичной матрицы I ₂ по 7.

  Затем, чтобы умножить каждый элемент в второй ряд А по 7, умножаем A на E .

  7R 2 -> R 2 =
  	E		А

  
  

  7R 2 -> R 2 =

  1 * 0 + 0 * 3 1 * 1 + 0 * 4 1 * 2 + 0 * 5 0 * 0 + 7 * 3 0 * 1 + 7 * 4 0 * 2 + 7 * 5

  
  
  

• Умножьте строку и добавьте ее к другой строке .Предположим, что A — это матрица 2 x 2. Предположим, мы хотим умножьте каждый элемент в первой строке A на 3; и мы хотим добавить этот результат во вторую строку А . За это Операция по созданию оператора элементарной строки представляет собой двухэтапный процесс. Сначала умножаем каждый элемент в первой строке единичной матрицы I ₂ на 3. Затем мы складываем результат это умножение на вторую строку I ₂ произвести E .

  ..

  	⇒		⇒
  I 2				E

  Затем, чтобы умножить каждый элемент в первую строку A на 3 и прибавьте этот результат к второй ряд, умножаем A на E .

  3R 1 + R 2 -> R 2 =
  	E		А

  
  

  3R 1 + R 2 -> R 2 =

  1 * 0 + 0 * 2 1 * 1 + 0 * 3 3 * 0 + 1 * 2 3 * 1 + 1 * 3

  
  

  3R 1 + R 2 -> R 2 =

Как выполнять операции с элементарными столбцами

Чтобы выполнить элементарную операцию столбца на A , матрица r x c , возьмите следующую шаги.

1. Чтобы найти E , оператор элементарного столбца , применить операцию к c x c единичная матрица.
2. Чтобы выполнить элементарную операцию столбца, умножьте A по E .

Давайте рассмотрим элементарную операцию столбца, чтобы проиллюстрировать процесс. Например, предположим, что мы хотим поменять местами первый и второй столбцы A , матрица 3 x 2.К создаем элементарный оператор столбца E , меняем местами первый и второй столбцы единичной матрицы Я ₂ .

Затем, чтобы поменять местами первую и вторую колонки из А , умножаем A на E , как показано ниже.

С 1 <--> С 2 =
	А		E

C 1 <--> C 2 =

0 * 0 + 1 * 1 0 * 1 + 1 * 0 2 * 0 + 3 * 1 2 * 1 + 3 * 0 4 * 0 + 5 * 1 4 * 1 + 5 * 0

Обратите внимание, что процесс выполнения операции элементарного столбца на r x c матрица очень похожа на процесс выполнения простейшая строчная операция.Основные отличия:

• Для работы на матрице r x c A , оператор строки E создается из r x r единичная матрица; тогда как оператор столбца E создается из c x c единичная матрица.
• Чтобы выполнить операцию со строками, A — это , предварительно умноженное на на E ; тогда как для выполнения операции со столбцом A равно после умножения по E .

Проверьте свое понимание

Задача 1

Предположим, что A — это матрица 4 x 3. Предположим, вы хотите умножаем каждый элемент во втором столбце матрицы A на 9. Найдите оператор элементарного столбца E .

Решение

Чтобы найти оператор элементарного столбца E , мы умножаем каждый элемент во втором столбце единичной матрицы I ₃ на 9.

Как выполнять операции со строками матрицы — математический класс [видео 2021 года]

Переключение

Операция первой строки — переключение . Это операция, когда вы переключаете или меняете местами две строки. В этой матрице мы можем поменять местами первую и третью строки так, чтобы 1 переместилась наверх.

Цель переключения — получить более организованную матрицу. Что я сделал здесь, так это переместил строку с ведущей единицей в первую строку так, чтобы наша первая строка начиналась с единицы и нулей под ней.Наша матрица теперь начинается с 1 в первой строке, 0 во второй строке и 0 в третьей строке.

Мы можем использовать стрелки между нашей исходной матрицей и новой матрицей, чтобы показать, как мы поменяли местами строки. Для нашей матрицы мы можем поместить стрелку от третьей строки в исходной матрице к первой строке в новой матрице, чтобы показать, что мы поменяли первую строку на третью.

Умножение

Наша следующая операция — умножение . Когда мы используем эту операцию, мы умножаем одну строку на определенное число.Цель умножения — получить более организованную матрицу. Когда мы умножаем одну строку на определенное число, мы обязательно умножаем каждую цифру нашей строки на это число. Например, в этой матрице мы можем умножить второе уравнение на 1/5, чтобы изменить первое ненулевое число на 1.

Чтобы показать, что вы сделали, вы можете написать небольшое обозначение между начальной матрицей и конечной матрицей. Для того, что мы сделали, мы можем нарисовать стрелку от второй строки к новой второй строке и написать (1/5) R sub 2, чтобы показать, что мы умножили вторую строку на 1/5.

Добавление

Третья и последняя операция — сложение . Это когда мы складываем две строки вместе. Цель сложения двух строк — упростить нашу матрицу. Мы используем сложение, когда можем изменить конкретное число на 0. Например, в этой матрице мы можем добавить третью строку ко второй строке, чтобы изменить первое число во второй строке на 0.

Чтобы помочь нам отслеживать все наши изменения, мы отмечаем эту операцию, рисуя стрелку от начала второй строки до новой второй строки и пишем поверх стрелки R sub 2 + R sub 3, чтобы мы знали что мы добавили строку два к строке три.

Следует отметить, что когда мы добавляем две строки, мы можем выбрать, какую строку заменить. Если мы добавляем вторую и третью строки, мы можем заменить вторую или третью строку новой строкой. Мы выбираем тот, который даст нам более простую матрицу.

Собираем все вместе

Мы рассмотрели все три операции по отдельности. Объединим их сейчас. Да, мы можем объединить наши операции, чтобы помочь нам лучше организовать и упростить наши матрицы. Наиболее распространенная комбинация — это умножение определенной строки на число, а затем добавление его к другой строке для образования новой строки.Например, в этой матрице мы можем сначала умножить нашу первую строку на -2, а затем добавить ее к третьей строке так, чтобы первое число в третьей строке стало 0.

Чтобы отметить эту операцию, мы можем нарисовать стрелку от начала третьей строки к новой третьей строке и написать поверх нее -2R sub 1 + R sub 3, чтобы сообщить нам, что мы умножили первую строку на -2. а затем добавил его в третью строку. Обратите внимание, поскольку мы комбинируем наши операции, мы оставили первую строку такой же, хотя и умножили ее на -2.Это нормально.

Резюме урока

Давайте рассмотрим то, что мы узнали. Мы узнали, что матрица представляет собой массив чисел, упорядоченных по строкам и столбцам. Матрица 3 x 2 будет иметь три строки и два столбца. Матрицы имеют только три строковые операции. Первый — это переключение, при котором две строки меняются местами. Второй — умножение, при котором одна строка умножается на число. Третий — сложение, которое складывает две строки вместе.

Для каждой выполняемой операции рекомендуется записывать, что вы делали между матрицами, рисуя стрелку и делая небольшие пометки поверх стрелки.Цель всех этих комбинированных операций — лучше организовать и упростить вашу матрицу.

Вы также можете комбинировать операции, чтобы упростить матрицу. Наиболее распространенная комбинация — это умножение одной строки на число, а затем добавление ее к другой строке.

Результаты обучения

По завершении этого урока вы сможете:

• Описать матрицу
• Изменить матрицу путем сложения, умножения и переключения или комбинации трех
• Правильно обозначить модификацию на матрице

Матрицы

Матрица — это массив чисел:

Матрица
(в ней 2 строки и 3 столбца)

Речь идет об одной матрице , или нескольких матрицах .

Мы можем многое с ними сделать …

Добавление

Чтобы сложить две матрицы: сложите числа в соответствующих позициях:

Это расчеты:

3 + 4 = 7	8 + 0 = 8
4 + 1 = 5	6−9 = −3

Две матрицы должны быть одинакового размера, т.е. строки должны совпадать по размеру, а столбцы должны совпадать по размеру.

Пример: матрица с 3 строками и 5 столбцами может быть добавлена ​​к другой матрице из 3 строк и 5 столбцов .

Но не удалось добавить в матрицу с 3 строки и 4 столбца (столбцы не совпадают по размеру)

отрицательный

Негатив матрицы тоже прост:

Это расчеты:

— (2) = — 2	— (- 4) = + 4
— (7) = — 7	— (10) = — 10

Вычитание

Чтобы вычесть две матрицы: вычтите числа в совпадающих позициях:

Это расчеты:

3-4 = -1	8−0 = 8
4−1 = 3	6 — (- 9) = 15

Примечание: вычитание фактически определяется как сложение отрицательной матрицы: A + (−B)

Умножить на константу

Мы можем умножить матрицу на константу (значение 2 в данном случае) :

Это расчеты:

2 × 4 = 8	2 × 0 = 0
2 × 1 = 2	2 × −9 = −18

Мы называем константу скаляром , поэтому официально это называется «скалярное умножение».

Умножение на другую матрицу

Чтобы перемножить две матрицы вместе немного сложнее … прочтите Умножение матриц, чтобы узнать, как.

Разделение

А что с делением? Ну, мы не делим матрицы на , мы делаем это так:

A / B = A × (1 / B) = A × B ^-1

, где B ^-1 означает «обратное» B.

Итак, мы не делим, вместо этого мы умножаем на обратное .

И есть особые способы найти обратное, подробнее см. Обратный к матрице.

Транспонирование

Чтобы «транспонировать» матрицу, поменяйте местами строки и столбцы.

Мы ставим букву «Т» в верхнем правом углу, чтобы обозначить транспонирование:

Обозначение

Матрица обычно обозначается заглавной буквой (например, A или B)

Каждая запись (или «элемент») обозначается строчной буквой с «нижним индексом» строки , столбец :

Строки и столбцы Итак, какая строка, а какая колонка? Ряды идут слева направо Колонны идут вверх-вниз Чтобы помнить, что строки идут перед столбцами, используйте слово «дуга» : а р, в

Пример:

B =

Вот несколько примеров записей:

b _1,1 = 6 (запись в строке 1, столбце 1 — 6)

b _1,3 = 24 (запись в строке 1, столбце 3 — 24)

b _2,3 = 8 (запись в строке 2, столбце 3 — 8)

Часть 2: Операции с матрицами.Матрица A порядка 3 × 3 может быть… | Авниш | Линейная алгебра

Матрица A порядка 3 × 3 может быть представлена ​​как

Здесь элемент в строке 1 и столбце 1 обозначен как a11 , элемент в строке 2 и столбце 1 как a21 и т. Д. .

Чтобы матрицы были равны

1. Порядок матриц должен быть одинаковым
2. Все элементы должны быть одинаковыми

Матрицы будут равны, только если они имеют одинаковый порядок и все элементы одинаковы (здесь 81 не равно 18 )

Для сложения двух матриц элементы, соответствующие одной строке и столбцу, складываются вместе, как в примере ниже, добавляются матрица A порядка 3 × 2 и матрица B того же порядка.

Две матрицы, A и B, добавляются для создания матрицы C

Элемент a11 из матрицы A и элемент b11 из матрицы B будут добавлены так, что c11 матрицы C будет произведено.

Обратите внимание, что A и B имеют одинаковый порядок. Итак, для добавления матриц порядок всех матриц (добавляемых) должен быть одинаковым. Кроме того, итоговая матрица будет того же порядка, что и ее составляющие.

Матрица C имеет порядок 3 × 2, такой же, как у матриц A и B.

Вычитание матрицы аналогично сложению матрицы. В приведенном ниже примере

матрица D — матрица E = матрица F

Вычитание матрицы E из DMatrix F — это матрица разностей E из D

. Здесь скаляр — это величина, которая не является матрицей или просто константа (скаляры будут даны более точное определение в будущей статье о векторах).

Когда мы умножаем 2 (скалярно) на матрицу G , результирующая матрица H просто умножается на 2 на каждый элемент матрицы G .

2 × матрица G — это матрица H

Деление на скаляр очень похоже на умножение на скаляр, поскольку деление матрицы J на 3 (скаляр) аналогично умножению матрицы J на 1/3.

As, J / 3 = (1/3) × J = K

Деление матрицы J на ​​3 дает матрицу K

Умножение матриц поначалу довольно сложно понять, потому что, в отличие от сложения и вычитания, умножение не выполняется путем умножения соответствующих элементов той же строки и столбца.

Один из способов умножения матрицы описан на примере ниже (а еще два способа будут описаны в следующих статьях, а именно).Матрица

U и матрица M будут умножены для получения матрицы N

Для нахождения элементов матрицы N

1. Элемент в строке 1 и столбце 1 матрицы U будет умножен на элемент в строке 1 и столбце 1 матрицы M ( u11 × m11 ).
2. Элемент в строке 1 и столбце 2 матрицы U будет умножен на элемент в строке 2 и столбце 1 матрицы M ( u12 × m21 ).
3. Сложение обоих вычисленных выше произведений даст элемент в строке 1 и столбце 1 матрицы N ( n11 = u11 × m11 + u12 × m21 ).

Подставляем значениями из матрицы U и матрицы M .

n11 = 1 × 3 + 6 × 1 = 9

Итак, строка 1 матрицы U и столбец 1 матрицы M дали элемент в первой строке и первом столбце матрицы N ( n11 ).

Применение аналогичных операций к строке 1 матрицы U и столбцу 2 матрицы M даст элемент в первой строке и втором столбце матрицы N ( n12 ).Дальнейшие вычисления для элементов матрицы N производятся ниже.

Вычисление матрицы N Матрица произведения U и M

Аналогичные операции можно применить, выбрав столбец 1 из матрицы U и строку 1 из матрицы M , так что

n11 = u11 × m11 + u21 × m12 + u31 × m13

, и результирующая матрица будет такой же, как матрица N .

Итак, умножение матриц может быть выполнено либо путем умножения и добавления элементов строк первой матрицы ( U ) и столбцов второй матрицы ( M ) или столбцов первой матрицы ( U ) и строк второй матрицы. матрица ( M ), и результат будет таким же.

Обратите внимание, что матрица N имеет порядок 3 × 3, матрица U имеет порядок 3 × 2, а матрица M имеет порядок 2 × 3. Следовательно, порядок результирующей матрицы в результате умножения равен (количество строк первой матрицы) × (количество столбцов второй матрицы).

Также, если количество столбцов первой матрицы не равно количеству строк второй матрицы, умножение невозможно (потому что не будет достаточного количества элементов для применения операций).

Условия для выполнения матричного умножения

Матричное умножение не коммутативно

Произведение матрицы U и матрицы M не будет равно произведению матрицы M и матрицы U .

матрица U × матрица M ≠ матрица M × матрица U

Умножение матрицы M на матрицу U дает матрицу N * (N звездочка) Как мы уже можем сделать вывод, что N * имеет порядок 2 × 2 , не то же самое, что порядок N (= U × M) Матрица N * не равна матрице N

Следовательно, умножение матриц не коммутативно.

Матричное деление возможно, но оно не похоже на скалярное деление, рассмотренное выше.

Деление матрицы B на матрицу A (B / A) , также может быть записано как B × A⁻¹ .

Здесь A⁻¹ — это матрица, обратная A (обратные будут рассмотрены позже).

A⁻¹ — это просто матрица, которая при умножении на матрицу A дает I (матрица идентичности, также будет обсуждаться в следующих статьях).Так же, как 2 × 2⁻¹ = 1.

Операции с элементарной строкой

Марко Табога, доктор философии

Элементарные операции со строками — это простые операции, которые позволяют преобразовать систему линейных уравнений в эквивалент систему, то есть в новую систему уравнений, имеющую те же решения как исходная система.

Есть три элементарных операции:

• умножение уравнения на ненулевую константу;

• добавление кратного одного уравнения к другому уравнению;

• меняя местами два уравнения.

В этой лекции мы покажем, как эти три операции могут быть выполнены с помощью с помощью матрица представление линейной системы, и мы покажем, что они порождают к эквивалентным системам.

Обозначение

Как и в предыдущих лекциях, система линейные уравнения в неизвестные записываются в матричной форме как где это матрица коэффициентов, это вектор неизвестных и это вектор констант.

Строки системы — это уравнения, где это -го ряд (содержит коэффициенты при -го уравнение) и это -го вход .

Умножение уравнения на ненулевую константу

Первая элементарная операция, которую мы рассматриваем, — это умножение одного уравнение константой .

Если -го уравнение умножается, то мы подставляем уравнение с то уравнение

Исходная матрица коэффициентов и вектор константы что новая система является

Такого же результата можно добиться следующим образом:

1. взять единичная матрица ;

2. умножить -го ряд от и обозначим полученную преобразованную матрицу через :

3. предварительно умножьте обе части матричной формы системы на :

Это легко проверить что

В лекции о Эквивалент систем, мы доказали, что если обратима, то новый система эквивалентна исходной.Но матрица выше обратимо (полный ранг), потому что его строки линейно независимы (ни один из них не может быть записан как линейная комбинация другие).

Таким образом, умножение уравнения на ненулевую константу дает эквивалент система.

Добавление одного уравнения к другому, кратное одному

Вторая рассматриваемая нами операция элементарной строки — это сложение кратного одного уравнения в другое уравнение.

Предположим, мы хотим добавить раз -го уравнение -го уравнение. Затем подставляем уравнение с то уравнение

Исходная матрица коэффициентов и вектор константы стать таким что новая система является

Такого же результата можно добиться следующим образом:

1. взять единичная матрица ;

2. Добавлять раз -го ряд к -го ряд , и обозначим полученную преобразованную матрицу через :

3. предварительно умножьте обе части матричного уравнения на :

Как и раньше, у нас есть это и новая система эквивалентна исходной, потому что обратима (ни одна из его строк не может быть записана как линейная комбинация другие).

Другими словами, мы получаем эквивалентную систему, добавляя кратное одной строки в другой ряд.

Замена двух уравнений местами

Третья операция с элементарной строкой, которую мы рассматриваем, — это замена двух уравнения.

Мы переключаем -го уравнение с участием то -го уравнение

Исходная матрица коэффициентов и вектор константы что новая система является

Тот же результат можно получить следующим образом:

1. взять единичная матрица ;

2. переключить -го ряд с -го строка ( в исходной матрице), а новую матрицу обозначим :

3. предварительно умножьте обе стороны системы на :

Что касается предыдущих элементарных операций, мы имеем это и новая система эквивалентна исходной, потому что обратима (строки такие же , но в другом порядке; они образуют стандартная основа пространства векторы).

Подводя итог, мы получаем эквивалентную систему, меняя местами две строки (две уравнения) системы.

Решенные упражнения

Ниже вы можете найти несколько упражнений с объясненными решениями.

Упражнение 1

Предполагать является система уравнения в неизвестные. Что такое матрица что позволяет заменить второе уравнение четвертым (когда система предварительно умножается на )?

Решение

Матрица получается перестановкой строк единичная матрица:

Упражнение 2

Предположим, у нас есть система уравнения в неизвестные.Что такое матрица что позволяет умножить второе уравнение на ?

Решение

Матрица получается умножением на второй ряд единичная матрица:

Упражнение 3

Предположим, у нас есть система уравнения в неизвестные.