Матрица совместная: определение, основные понятия и виды, матричная форма записи систем уравнений

%d0%a1%d0%be%d0%b2%d0%bc%d0%b5%d1%81%d1%82%d0%bd%d0%b0%d1%8f+%d1%81%d0%b8%d1%81%d1%82%d0%b5%d0%bc%d0%b0+%d1%83%d1%80%d0%b0%d0%b2%d0%bd%d0%b5%d0%bd%d0%b8%d0%b9 — со всех языков на все языки

Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАканАлтайскийАрагонскийАрабскийАстурийскийАймараАзербайджанскийБашкирскийБагобоБелорусскийБолгарскийТибетскийБурятскийКаталанскийЧеченскийШорскийЧерокиШайенскогоКриЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийВаллийскийДатскийНемецкийДолганскийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГэльскийГуараниКлингонскийЭльзасскийИвритХиндиХорватскийВерхнелужицкийГаитянскийВенгерскийАрмянскийИндонезийскийИнупиакИнгушскийИсландскийИтальянскийЯпонскийГрузинскийКарачаевскийЧеркесскийКазахскийКхмерскийКорейскийКумыкскийКурдскийКомиКиргизскийЛатинскийЛюксембургскийСефардскийЛингалаЛитовскийЛатышскийМаньчжурскийМикенскийМокшанскийМаориМарийскийМакедонскийКомиМонгольскийМалайскийМайяЭрзянскийНидерландскийНорвежскийНауатльОрокскийНогайскийОсетинскийОсманскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПортугальскийКечуаКвеньяРумынский, МолдавскийАрумынскийРусскийСанскритСеверносаамскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиШумерскийСилезскийТофаларскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийТувинскийТвиУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВьетнамскийВепсскийВарайскийЮпийскийИдишЙорубаКитайский

 

Все языкиАбхазскийАдыгейскийАфрикаансАйнский языкАлтайскийАрабскийАварскийАймараАзербайджанскийБашкирскийБелорусскийБолгарскийКаталанскийЧеченскийЧаморроШорскийЧерокиЧешскийКрымскотатарскийЦерковнославянский (Старославянский)ЧувашскийДатскийНемецкийГреческийАнглийскийЭсперантоИспанскийЭстонскийБаскскийЭвенкийскийПерсидскийФинскийФарерскийФранцузскийИрландскийГалисийскийКлингонскийЭльзасскийИвритХиндиХорватскийГаитянскийВенгерскийАрмянскийИндонезийскийИнгушскийИсландскийИтальянскийИжорскийЯпонскийЛожбанГрузинскийКарачаевскийКазахскийКхмерскийКорейскийКумыкскийКурдскийЛатинскийЛингалаЛитовскийЛатышскийМокшанскийМаориМарийскийМакедонскийМонгольскийМалайскийМальтийскийМайяЭрзянскийНидерландскийНорвежскийОсетинскийПенджабскийПалиПольскийПапьяментоДревнерусский языкПуштуПортугальскийКечуаКвеньяРумынский, МолдавскийРусскийЯкутскийСловацкийСловенскийАлбанскийСербскийШведскийСуахилиТамильскийТаджикскийТайскийТуркменскийТагальскийТурецкийТатарскийУдмурдскийУйгурскийУкраинскийУрдуУрумскийУзбекскийВодскийВьетнамскийВепсскийИдишЙорубаКитайский

Матрица плотности

Н.

В. Никитин

Матрица плотности

Часть 1. КВАНТОВАЯ МЕХАНИКА ЧИСТЫХ СОСТОЯНИЙ

Постулаты квантовой механики (для чистых состояний)
Теорема о невозможности клонирования произвольного чистого состояния
Первооткрыватели «No-cloning theorem»
Совместное клонирование ортогональных состояний
Теорема о невозможности уничтожения копии произвольного чистого состояния
Люди, доказавшие «No-deleting theorem»
Правила суперотбора

Часть 2. МАТРИЦА ПЛОТНОСТИ: ОСНОВНЫЕ СВОЙСТВА

Смешанные состояния
Матрица плотности чистого состояния
Как строить матрицу плотности чистого состояния |ψ>?

Матрица плотности смешанного состояния
Примеры матриц плотности
«Отцы» матрицы плотности
Неоднозначность разложения матрицы плотности смешанного состояния на чистые
Нерелятивистская матрица плотности спина s = 1/2
Теорема Глизона (1957 г.)
Количественное сравнение квантовых состояний
Как найти F₁(_А, _В)?
Как найти D_Tr{_А, _В)?
Пример вычисления F₁(_А, _В) и D_Tr{_А, _В)
Пример вычисления остальных степеней совпадения и метрик
Матрица плотности составной системы
Запутанные состояния
Квантовое происхождение вероятностей W _ℓ
Клонирование помогает запутанности?
Матрица плотности и постулаты квантовой механики
Факторизация матрицы плотности
Разложение Шмидта
Число Шмидта и запутанные состояния
Разложение Шмидта для трех и более подсистем
Состояния Белла (the Bell states)
Необходимое условие сепарабельности А. Переса
А.Перес и клан Городецких
Состояние Вернера и критерий сепарабельности Переса
Редукционное условие сепарабельности
Состояние Вернера и редукционный критерий

Часть 3. ФОРМУЛА ФОН НЕЙМАНА И ЕЕ СЛЕДСТВИЯ

Условная матрица плотности и формула фон Неймана
Редукция матрицы плотности и парадокс друга Вигнера

Проекционный постулат М.Борна и проекционный постулат Дирака — фон Неймана
Постулат о среднем значении операторов
Модель измерения по фон Нейману
Локальность нерелятивистской квантовой механики на макроскопическом уровне и теорема Эберхарда
Суперпозиция или смесь!
Альтернатива принципу суперпозиции

Часть 4. ЭВОЛЮЦИЯ КВАНТОВОЙ СИСТЕМЫ ВО ВРЕМЕНИ

Эволюция матрицы плотности во времени. Квантовое уравнение Лиувилля (уравнение фон Неймана)
Решение квантового уравнения Лиувилля
Важный частный случай
Уравнение Блоха
Обобщенная формула фон Неймана
Квантовый парадокс Зенона
Производная оператора по времени для смешанных состояний
Квантовое уравнение Лиувилля в координатном представлении

Матрица плотности свободной частицы

Часть 5.

ОПИСАНИЕ ОТКРЫТЫХ КВАНТОВЫХ СИСТЕМ

Распад нестабильной микросистемы
Квантовое уравнение Лиувилля для открытых систем
Эволюция матрицы плотности открытых квантовых систем. Общий подход
Операторы Крауса и представление Крауса для матрицы плотности открытой квантовой системы
Уравнение Линдблада
Как работает уравнением Линдблада. Простой пример
Уравнением Линдблада для наблюдаемых в представлении Гейзенберга
Релаксационное уравнение для частицы в термостате

Часть 6. ОСНОВЫ КЛАССИЧЕСКОЙ ТЕОРИИ ИНФОРМАЦИИ

Классическая энтропия. Биты и наты
Энтропия и информация
Декогеренция и парадокс кота Шредингера
Граница между мирами
Ограничения на величину шенноновской энтропии

Двоичная энтропия
Неравенство Йенсена и вогнутость энтропии Шеннона
Классическая относительная энтропия и неравенство Гиббса
Классическая совместная энтропия и субаддитивность
Условная вероятность и теорема Байеса
Классическая условная энтропия
Доказательство субаддитивности
Классическая взаимная информация
Наглядная связь между различными энтропиями и взаимной информацией
Сильная субаддитивность

Часть 7.

ОСНОВЫ КВАНТОВОЙ ТЕОРИИ ИНФОРМАЦИИ

Квантовая энтропия (энтропия фон Неймана)
Ограничения на величину энтропии фон Неймана
Энтропия чистого состояния
Гипотеза о скрытых параметрах
Тример вычисления энтропии смешанного состояния
Сравнение квантовой и классической энтропии

Квантовая относительная энтропия и неравенство Клейна
Квантовая совместная энтропия и субаддитивность
Свойство субаддитивности для состояния Вернера
Субаддитивность и второе начало термодинамики
Квантовая взаимная информация
Неравенство треугольника (неравенство Араки-Либа)
Вогнутость квантовой энтропии
Теорема о невозможности клонирования произвольного смешанного состояния

Часть 8. НЕРАВЕНСТВА БЕЛЛА И КОРРЕЛЯЦИИ В КВАНТОВОЙ ТЕОРИИ

Одновременная измеримость и неизмеримость
Понятие об элементах физической реальности
Неравенств Белла. Историческая справка
Неравенств Белла. Основная идея

Простой вывод CHSH-неравенства
Вывод CHSH-неравенства из условия неотрицательности совместных вероятностей
Граница Цирельсона
Запутанные состояния вступают в игру
А теперь — пресловутая нелокальность!
CHSH-неравенство и сепарабельные состояния
Носки профессора Бертлмана, запутанность и CHSH-неравенство

Видео лекций

Матрица плотности.

Вводный курс

Обратная связь с автором
    Мне очень хотелось сделать интересный и современный курс, который
бы показал студентам красоту и глубину квантовой теории. Удалось это или нет, судить слушателям и читателям (почти уверен, что курс будет гулять «по интернетам»). Очевидно, что написать столько текста и не сделать ни одной ошибки в формулах или опечатки в словах абсолютно невозможно. Поэтому у меня просьба, если кто найдет ошибку, опечатку или, упаси боже, «дырку» в доказательстве какого-либо утверждения, свяжитесь пожалуйста с автором по e-mail и сообщите ему о своей находке. Вознаграждение не предлагаю. 🙂

    Если у кого-то возникнут пожелания, какие еще интересные вопросы можно было бы включить в курс, я с удовольствием рассмотрю эти предложения (но не обещаю, что приму).
e-mail для связи [email protected], в теме письма просьба указать «Обсуждение лекций по матрице плотности», чтобы мне было легче находить соответствующие сообщения.

    P.S. Работы, опровергающие квантовую физику и теорию относительности, не рассматриваю. Дискуссии на эти темы не веду.

---

 

Системы линейных уравнений (Лекция №14)

Системой m линейных уравнений с n неизвестными называется система вида

где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a

ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы , которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:

1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, . Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, , если бы решение существовало, то x₁ + x₂ равнялось бы одновременно нулю и единице.

Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.

Рассмотрим способы нахождения решений системы.

МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:

Рассмотрим матрицу системы и матрицы столбцы неизвестных и свободных членов

Найдем произведение

т. е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

или короче A∙X=B.

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.

Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A^-1, обратную матрице A: . Поскольку A^-1A = E и E∙X = X, то получаем решение матричного уравнения в виде X = A^-1B.

Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A^-1B.

Примеры. Решить системы уравнений.

1. Найдем матрицу обратную матрице A.

   ,

   Таким образом, x = 3, y = – 1.

2. Итак, х₁=4,х₂=3,х₃=5.

3. Решите матричное уравнение: XA+B=C, где

   Выразим искомую матрицу X из заданного уравнения.

   Найдем матрицу А^-1.

   Проверка:

4. Решите матричное уравнение AX+B=C, где

   Из уравнения получаем .

   Следовательно,

ПРАВИЛО КРАМЕРА

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

Определитель третьего порядка, соответствующий матрице системы, т. е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

Сложим эти уравнения:

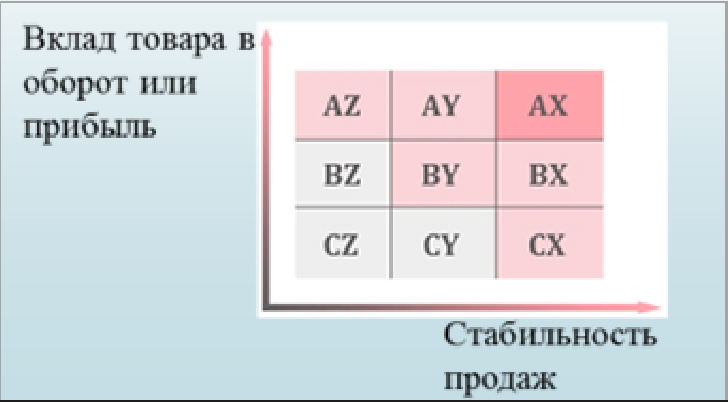
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

Аналогично можно показать, что и .

Наконец несложно заметить, что

Таким образом, получаем равенство: .

Следовательно, .

Аналогично выводятся равенства и , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

1. Итак, х=1, у=2, z=3.

2. Решите систему уравнений при различных значениях параметра p:

   Система имеет единственное решение, если Δ ≠ 0.

   . Поэтому .

   1. При
   2. При p = 30 получаем систему уравнений которая не имеет решений.
   3. При p = –30 система принимает вид и, следовательно, имеет бесконечное множество решений x=y, yÎR.

МЕТОД ГАУССА

Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.

Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

.

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x₁. Для этого второе уравнение разделим на а₂₁ и умножим на –а₁₁, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а₃₁ и умножим на –а₁₁, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x₂.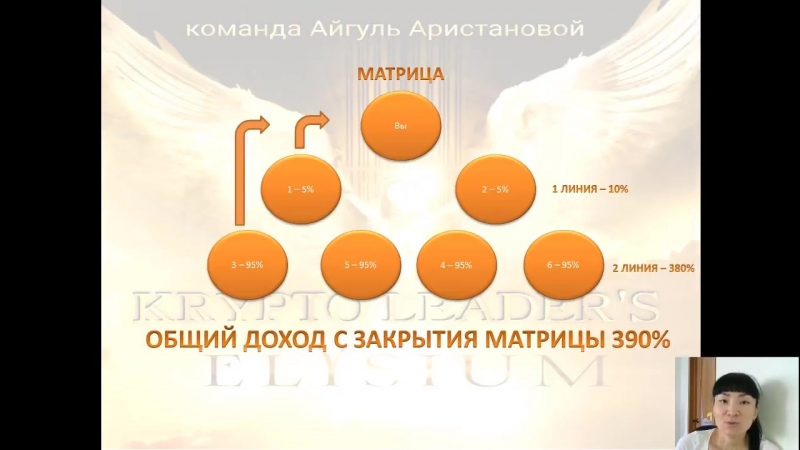 Для этого третье уравнение разделим на , умножим на и сложим со вторым. Тогда будем иметь систему уравнений:

Отсюда из последнего уравнения легко найти x₃, затем из 2-го уравнения x₂ и, наконец, из 1-го – x₁.

При использовании метода Гаусса уравнения при необходимости можно менять местами.

Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.

К элементарным преобразованиям матрицы относятся следующие преобразования:

1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.

Примеры: Решить системы уравнений методом Гаусса.

1. Вернувшись к системе уравнений, будем иметь

2. Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

   Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.

3. Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.

   Вернемся к системе уравнений.

   Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.

Таким образом, система имеет бесконечное множество решений.

Enterprise Virtual Matrix — Barco

О Enterprise Virtual Matrix

Barco Enterprise Virtual Matrix (EVM) представляет собой централизованно управляемую распределенную систему на основе IP-сети, которая позволяет подключать видео, звук, клавиатуру и мышь к входу источника сигнала и одному или нескольким целевым выходам (включая проекторы, мониторы, дисплеи и аудиосистемы). Качество подключений через Barco EVM не отличается от прямого проводного подключения. В результате пользователь не замечает разницы между подключением через EVM устройств на расстоянии в несколько километров и прямым проводным подключением длиной несколько метров. И поскольку система EVM была разработана для работы с конфиденциальной информацией, на разных уровнях системы интегрированы меры безопасности, защищающие необработанные данные от любых потенциальных угроз.

Виртуальная коммутация без потерь

EVM обеспечивает подключение AVoIP 100% без сжатия и функции KVM, давая людям возможность сотрудничать, находясь на расстоянии нескольких километров друг от друга. Для 2D- и 3D-содержимого гарантируется максимальный уровень качества изображения и скорость взаимодействия. Для поддержки очень высоких разрешений в декодере ENA-340 системы EVM имеется функция синхронизированной блокировки кадров между несколькими видеовыходами DP1.2 декодера. Таким образом, можно легко поддерживать настройки, которые требуют сквозной синхронизации между несколькими подключениями DP1. 2 — многодисплейная настройка, содержимое с очень высоким разрешением или настройка видеостены.

Царство гибкости

Сочетание масштабируемости одного порта и структуры лицензий на функциональные возможности гарантирует, что для любых конкретных потребностей бизнеса можно построить любую систему. И если со временем потребности изменятся, систему можно легко адаптировать — в любое время и на любом уровне, — вместо дорогостоящей полной замены. Каждое действие при изменении конфигурации, настройке или обновлении происходит централизованно с помощью единого интерфейса пользователя на основе браузера. Это упрощает эксплуатацию и сопровождение системы и снижает общую стоимость владения.

Как мы построили системы рекомендаций для книг за час Часть 2

Дата публикации Sep 20, 2017

впоследний постмы увидели, как мы можем использовать простые корреляционные методы для определения степени сходства между пользователями книг на основе их рейтинговых записей. В этом посте мы покажем, как вы можете использовать те же самые метрики подобия, чтобы давать рекомендации читателям.

kNN — это алгоритм машинного обучения, позволяющий находить кластеры похожих пользователей на основе общих рейтингов книг и делать прогнозы, используя средний рейтинг топ-k ближайших соседей. Например, мы сначала представляем рейтинги в матрице, причем матрица имеет одну строку для каждого элемента (книги) и один столбец для каждого пользователя, например, так:

Затем мы находим элемент k, который имеет наиболее похожие векторы взаимодействия с пользователем. В этом случае Ближайшие соседи элемента id 5 = [7, 4, 8,…]. Теперь давайте внедрим kNN в нашу систему рекомендации книг.

Данные

Мы используем те же данные о книгах, что и в прошлый раз: они состоят из трех таблиц: рейтинги, информация о книгах и информация о пользователях. Я скачал эти три таблицы изВот,

Информация о рейтинге

Информация о пользователе

Информация о книге

Чтобы обеспечить статистическую значимость, мы будем только смотреть на популярные книги

Чтобы узнать, какие книги популярны, нам нужно объединить данные книг с данными рейтинга.

Затем мы группируем по названиям книг и создаем новый столбец для общего подсчета рейтинга.

Теперь мы объединяем данные рейтинга с данными общего рейтинга, что дает нам именно то, что нам нужно, чтобы отфильтровать менее известные книги.

Давайте посмотрим на статистику общего количества рейтинга:

Средняя книга была оценена только один раз. Давайте посмотрим на верхнюю часть дистрибутива:

Около 1% книг получили 50 и более оценок. Поскольку в наших данных так много книг, мы ограничим их верхним 1%, и это даст нам 2713 уникальных книг.

Фильтр для пользователей только в США и Канаде

Чтобы повысить скорость вычислений, а не сталкиваться с проблемой «MemoryError», я ограничу наши пользовательские данные данными в США и Канаде. А затем объедините данные пользователя с данными рейтинга и данными общего рейтинга.

Внедрение КНН

Мы преобразовываем нашу таблицу в 2D-матрицу и заполняем пропущенные значения нулями (так как мы будем вычислять расстояния между векторами рейтинга). Затем мы преобразуем значения (рейтинги) матрицы данных в скудную разреженную матрицу для более эффективных вычислений.

Нахождение ближайших соседей

Мы используем неконтролируемые алгоритмы сsklearn.neighbors.Алгоритм, который мы используем для вычисления ближайших соседей, является «грубым», и мы указываем «metric = cosine», чтобы алгоритм вычислял косинусное сходство между векторами рейтинга. Наконец, мы подходим к модели.

Протестируйте нашу модель и дайте несколько рекомендаций:

На этом этапе алгоритм kNN измеряет расстояние для определения «близости» экземпляров. Затем он классифицирует экземпляр, находя ближайших соседей, и выбирает самый популярный класс среди соседей.

Отлично! Книги серии Green Mile определенно следует рекомендовать, одну за другой.

Источник:ohAI

Матричная факторизация — это просто математический инструмент для игры с матрицами. Методы матричной факторизации обычно более эффективны, потому что они позволяют пользователям обнаруживать скрытые (скрытые) особенности, лежащие в основе взаимодействия между пользователями и предметами (книгами).

Мы используем разложение по сингулярным числам (SVD) — одну из моделей матричной факторизации для выявления скрытых факторов.

Как и в случае с kNN, мы преобразуем нашу таблицу рейтинга пользователей в США и Канаде в двумерную матрицу (здесь она называется служебной матрицей) и заполняем пропущенные значения нулями.

Затем мы транспонируем эту служебную матрицу, чтобы bookTitles стали строками, а userID — столбцами. После использования TruncatedSVD для его декомпозиции мы встраиваем его в модель для уменьшения размерности. Это сжатие произошло в столбцах датафрейма, поскольку мы должны сохранить названия книг. Мы выбираемn_components = 12только для 12 скрытых переменных, и вы можете видеть, что размеры наших данных были значительно уменьшены с 40017 X 2442 до 2442 X 12.

Мы рассчитываем коэффициент корреляции Пирсона R для каждой пары книг в нашей окончательной матрице. Чтобы сравнить это с результатами kNN, мы выбираем ту же книгу «Зеленая миля: руки Коффи (серия Зеленая миля)», чтобы найти книги с высокими коэффициентами корреляции (между 0,9 и 1,0).

Вот оно!

Не слишком потрепанный! Наша система может превзойти Amazon, как вы думаете? Посмотрите на снимок экрана с заголовком!

Ссылка:музыкальные рекомендации

Оригинальная статья

как развить партнёрство в компании?

В 1630-х гг. Голландию охватила «эпидемия тюльпаномании»: завезённый в Европу из Персии цветок вызвал восторг у знати и быстро адаптировался к климату, так что на растение небывалыми темпами начал расти спрос, а садовники активно занялись селекцией новых сортов.

 

Эпидемия возникла из-за агрессивной спекуляции на стоимости луковиц тюльпанов, торговля которыми якобы обещала немыслимые богатства. Задокументирована сделка¹, когда луковицу сорта Semper Augustus продали за 1000 гульденов – около 10 кг серебра или 856 грамм золота. 

 

Причиной первого в истории биржевого пузыря советский психолог и психиатр В. М. Бехтерев ² назвал «стеническое» (то есть активное) воздействие заинтересованных лидеров мнений на внушаемые массы. Это одно из первых убедительных доказательств, что влияние неформальных лидеров ключевым образом отражается на финансовом результате предприятия.

 

Сегодня недооценивать лидеров команд опасно для конкурентоспособности бизнеса, и руководители это осознают. Как показывает исследование Deloitte Insights (2020)³ , в котором приняли участие 9 000 CEO и HRD из 119 стран мира, вопросы лидерства и развития гибкости для командной работы будут главными HR-трендами в ближайшие 1,5 года, поскольку компании считают лидеров команд своим главным активом.

 

Изучением лидерства занимаются во многих странах, но наибольшей популярностью тема лидерства пользуется в Соединённых Штатах, где существует по меньшей мере 30 специальных исследовательских центров. Один из них – Институт Матрицы Лидерства, основанный в 1990 году году американским организационным консультантом и коучем Аминой Нолан.

 

Матрица лидерства – это метод формирования команды как взаимосвязанной живой системы, построенной на лидерах, горизонтальных связях и внутреннем партнёрстве сотрудников. В его основой лежит сотрудничество, которое в конечном итоге помогает трансформировать команду и добиться роста результатов компании.

 

Может ли матрица лидерства помочь HR-специалисту повысить эффективность команд? Ищем ответ – в новом материале Yva.ai.

 

Развитие концепции лидерства

 

История изучения феномена лидерства насчитывает более 2500 тысяч лет: ещё в Древнем Китае лидерство как особое качество правителей интересовало Конфуция, Лао Цзы, Гуаня Чжуна и др. Основатель даосизма Лао Цзы считал: «Лучшим лидером является тот, о существовании которого люди едва догадываются»⁴.

 

В Античную эпоху понимание лидерства было представлено в основном с точки зрения политики и государственного управления. Одним из первых мыслителей, целенаправленно изучавших явление лидерства, считается Платон.

 

Согласно идеям Платона, люди от природы рождаются разными, и высшая справедливость «состоит в том, чтобы каждый человек занимался делом, к которому у него есть природная склонность»⁵. Это представление, а также идея, что лидерство требует от человека жертвования личными интересами, легло в основу парадигмы лидеров, представленной в трактате «Государство»: 

 

• тип философа (мудреца),
• тип военачальника,
• тип делового человека.

 

Другой античный философ – Аристотель – искал совокупность черт, которые лучше всего определят идеального лидера, и пришёл к выводу, что для формирования доверия последователей лидер обязательно должен обладать тремя качествами:

 

• рассудительностью,
• добротой,
• желанием помогать людям.

 

В эпоху Средневековья идея лидерства человека отходит на второй план, уступая место лидерству церкви и Бога, но в эпоху Возрождения и Новое время интерес к влиянию человека на других вновь возрос и потребовал новых подходов. Так, своего рода концепцию лидерства предложили итальянский мыслитель Никколо Макиавелли в трактате «Государь», английский философ Томас Гоббс – в работах «О гражданине», «Левиафан» и мн. др.

 

Расцвет изучение лидерства начался в XIX веке, тогда появилось много масштабных работ Г. Спенсера, Т. Карлейля, Ф. Гультона, А. Жоли, С. Сигеле, Г. Тарда, Г. Лебона. Исследования этого периода объединяет внимание социологов и философов к взаимоотношениям героя и толпы и инструментам влияния лидера. Например, по мнению Габриэля Тарда, главное, чем должен обладать лидер, чтобы воздействовать на окружающих, – это обаяние⁶.

 

В годы Первой мировой войны исторические события подтолкнули исследование лидерства от описанию к измерениям. Военные психологи разрабатывали личностные тесты для оценки военнослужащих, в том числе использовался подход сравнения личностных качеств лидера и последователя.

 

В 1930-е годы появилась теория черт, заложенная работой Гордона Олпорта «Личность: психологическая интеграция», основная идея которой состояла в соответствии паттернов поведения человека определённым личностным качествам. Этот подход привел исследователей к выводу, что большинство успешных лидеров имеют четыре выраженные черты: 

 

• высокий интеллект, 
• эмоциональную зрелость и широту интересов, 
• внутреннюю мотивацию и стремление к новым достижениям, 
• честность.

 

 

В 40-е годы исследование лидерства снова ушло в военную плоскость (работы К. Берда, В. Иена Кинза, Р. Стогдилла), но в тот же период проводились масштабные исследования, например, в Университете Огайо, в ходе которых выяснилось, что главными параметрами лидерского поведения являются уважение и внимание к людям, а также способность назначать роли себе и своим сотрудникам. Авторы ситуационной теории лидерства К. Бланшар и П. Херси⁷ назвали эти факторы иначе:

 

• ориентация на задачу,
• ориентация на отношения.

 

В 1950-е годы возникла функциональная теория, где лидер рассматривался как функция группы, т. е. акцент сместился с личностных качеств на поведение в ситуации и восприятие лидера окружающими в её контексте. Во второй половине XX века в исследовании лидерства преобладали 3 ключевых подхода: ситуационный, личностный и интеракционный. 

 

Среди российских ученых, изучавших проблему лидерства в XX веке, выделяются работы А. Ф. Лазурского и В. М. Бехтерева, которые разрабатывали «проблему героя и толпы». В частности, А. Ф. Лазурский создал классификацию личностей, а В. М. Бехтерев изучил механизмы влияния личности на группу людей (толпу) и выявил два ключевых способа воздействия: внушение и убеждение.

 

Для современных исследований лидерства характерно рассмотрение феномена с точки зрения совместной групповой деятельности и решения конкретных задач, в том числе задач бизнеса. При этом ключевым отличием лидера становится не наличие / отсутствие особых черт, а некий измеримый уровень влияния, который может накапливаться со временем – социальный капитал.

 

 

Таковой является теория лидерства Ицхака Адизеса и его PAEL-код ролей менеджера, теория ситуационного лидерства Фреда Фидлера, управленческая решётка Роберта Блейка и Джейн Мутон и мн. др.

 

В последние большой резонанс вызывает нейробиологический подход к изучению лидерства, а также исследования в области коллективного и – шире – социального интеллекта (в частности, книга Алекса Пентленда «Социальная физика»).

 

Широким интересом пользуются гибкие методики оценки лидеров и формирования нелинейной командной структуры в компании. К числу таких методик относится матрица лидерства.

 

Матрица лидерства как метод оценки руководителей

 

Матрица лидерства – метод, включающий коммуникативные и лидерские практики, которые позволяют группе в любом контексте функционировать как сложная, адаптивная система, или матричная лидерская сеть.

 

Преимуществом такой команды автор метода Амина Нолан⁸ считает её способность учиться на взаимодействии со средой, внедрять инновации, развиваться и расти. Основными функциями⁹ матрицы лидерства являются:

 

• налаживание кросс-функционального взаимодействия между сотрудниками,
• объединение команды и реализация потенциала каждого сотрудника,
• превращение конфликтных ситуаций из проблемы в ресурс для развития,
• обеспечение спокойной и оперативной реакции на любые изменения рынка,
• повышение скорости принятия управленческих решений,
• обеспечение клиентам сервиса, основанного на заботе и мн. др.

 

Это возможно за счёт того, что матрица рассматривает организацию или команду как сеть партнёрств, которые создают систему взаимозависимого, разделяемого лидерства.

 

 

Каковы основные принципы матрицы лидерства как метода? 

 

• Установление связей в группе. Для успешной коммуникации группы создаём основания, которые будут вовлекать и затрагивать каждого члена команды.

 

• Создание «основы здоровья». Устанавливаем неформальные контакты: это ключ к гибкости и устойчивости команды.

 

• Осознание появления целого. Переход от парадигмы «я» к парадигме «мы». Отслеживаем сигналы группы, приветствуем различия мнений и не пытаемся подвести всех под стандарт.

 

• Формирование культуры обратной связи. Обратную связь стоит рассматривать как инвестицию в совместную работу. Используем её для исследования стилей коммуникации и лидерства.

 

• Распределение ролей. Помогаем сотрудникам освободиться от «аллергии на ответственность» и страха наказания, расширяем поведенческий «арсенал» в качестве лидера и члена группы.

 

Как овладеть методикой матрицы лидерства

 

Комплексное внедрение матриц лидерства в компанию требует ресурсов и системного подхода. Например, в России этим занимается Санкт-Петербургский Институт коучинга. Но кое-что можно реализовать самостоятельно – в качестве пилота построения матричной лидерской сети в вашей компании. Специалисты Международного института MMI, Inc¹⁰. поделились несколькими советами по овладению управлением матрицами лидерства в компании.

 

Совет #1 Определите роли и отношения в матрице

 

Матричная организация работает в двух измерениях: вертикальном и горизонтальном. Лидеры берут на себя несколько ролей в обоих измерениях.

 

Вертикальные роли более привычны – руководитель (коуч) / подчинённый. Бывают моменты, когда непосредственные подчинённые находятся в разных местах и часто поддерживают других лидеров помимо прямого руководителя.

 

Ответственность лидера в роли коуча заключается в том, чтобы обеспечить успех всех подчинённых, помогая им справляться с обязанностями, которые не входят их обычный пул задач, но с которыми они могут справиться – если это необходимо для достижения результата компании.

 

Горизонтальные роли создают и поставляют продукты и услуги клиентам. К ним относятся внутренний поставщик / заказчик, руководитель группы (проекта, продукта или управленческой команды), член команды, заинтересованная сторона и спонсор. 

 

Ответственность в этих ролях заключается в достижении организационных, командных и индивидуальных результатов при построении отношений.

 

Чтобы матрица работала успешно, горизонтальное измерение должно быть основным, потому что работа по доставке продуктов и услуг внешним и внутренним клиентам происходит именно там. Следовательно, необходимо найти людей, у которых больше горизонтальных связей, чем у других: скорее всего, основу матричной сети создадут именно они.

 

 

Совет #2 Внедряйте культуру поведения уполномоченных людей

 

В компаниях у сотрудников нередко можно наблюдать поведение, продиктованное неким «спровоцированным» состоянием. Кто-то пытается взять всё под полный контроль. Кто-то ведёт себя, как хулиган. Кто-то чувствует себя слишком ведомым и ведёт себя, как жертва. Всё это состояния без власти, полномочий и ответственности.

 

А лидеры – люди без аллергии на ответственность. Если вы хотите сформировать вовлечённую команду лидеров, нужно научить сотрудников действовать из уполномоченного, «взрослого» состояния. Быть уполномоченным означает, что лидер сам выбирает, как думать и действовать при взаимодействии с другими.

 

Лидер предпочитает не реагировать на триггеры и не принимать всё близко к сердцу. Кроме того, он распознаёт, когда другие действуют в беспомощном состоянии, и помогает им выйти из него. По методологии лидерства Yva.ai такое поведение часто соответствует обладателям навыков и качеств Интегратора.

 

 

Совет #3 Развивайте партнёрские отношения в команде

 

Выполнение нескольких ролей в матричной организации приводит к множественным отношениям. В горизонтальном измерении отношения не основаны на должностных инструкциях, и, например, у менеджера по продажам нет полномочий требовать что-либо от бухгалтера и наоборот. 

 

Но если возникает проблема с оплатой и скорость решения вопроса повлияет на клиентский опыт, решать её горизонтальным путём – быстрее, чем вертикальным. А сделать это можно только в том случае, если у двух сотрудников разных функций настроены партнёрские отношения.

 

Когда в компании существует культура партнёрства, обратиться друг к другу за помощью могут даже незнакомые друг с другом сотрудники. Основой партнёрских отношений в горизонтальном измерении является не конкуренция, а сотрудничество и достижение общих целей.

 

Важно понимать, что если в компании имеет место политическая конкуренция между подразделениями, то развитию матричной лидерской сети это будет мешать.

 

Совет #4 Примените совместный подход к руководству

 

Лидерство в матрице требует развития у сотрудников способности руководить без административных полномочий – то есть перехода от директивного подхода к совместному лидерству и наделению сотрудников полномочиями: правом принимать решения, ошибаться в определённых пределах, но при необходимости за эти пределы выходить.

 

Поскольку консервативные полномочия здесь отсутствуют, нужно сформировать приверженность членов команды общей цели. Лучший способ для этого – создать условия, при которых все сотрудники будут участвовать в генерации результата.

 

Действующие лидеры выступают в качестве фасилитаторов, используя коллаборацию и инструменты тимбилдинга для достижения командного результата. Они не создают планов, не принимают решений и не решают проблемы сами: они просят участников команды внести свой вклад. Это поможет развить навыки совместного планирования и решения проблем на горизонтальном уровне.

 

Ценность создания матричных лидерских сетей для бизнеса

 

Наградой за усилия по созданию матричной структуры лидерства в компании послужит рост приверженности команды общему делу, более творческие решения и более смелые, результативные действия без неусыпного контроля прямого руководителя.

 

При системной реализации матрицы лидерства позволяет построить живую компанию, принципы которой описал Ари де Гиус в книге «Живая компания. Рост научение и долгожительство в деловой среде». 

 

Такие организации развиваются как живое существо: власть рассредоточена, в ней есть сдержки и противовесы, а лидеры понимают, что они – лишь одно поколение из многих. Вместо KPI здесь ценности и цели, вместо менеджеров – самоуправление и коучинг, а главный принцип – «всё в мире делается людьми и для людей».

 

Хотите узнать, как найти скрытых, невыявленных лидеров вашей компании, чей потенциал не раскрыт или раскрыт не полностью? Исследуйте ваши возможности и возможности ваших сотрудников. Узнайте больше интересных и полезных фактов о лидерстве в бесплатном мастер-классе Давида Яна «5 стилей лидерства для долгосрочного успеха компании». Подключайтесь!

 

 

1. Голландская тюльпаномания: подлинная история первого биржевого пузыря // Д. Пенькова. «Открытие». 2018.
2. Внушение и его роль в общественной жизни // В. М. Бехтерев. СПб: Издание К. Л. Риккера. 1908.
3. Международные тенденции в сфере управления персоналом – 2020 // Deloitte Insights. 2020.
4. Политическое лидерство в трудах китайских философов // О. Ф. Лейченко. «Концепт». 2014.
5. Эволюция философский идей и концепций лидерства // С. А. Сергеева. «Армия и общество». 2013.
6. История изучения лидерства в мировой психолого-педагогической науке // Л. В. Ануфриенко. Полоцкий государственный университет. 2012.
7. Матрица лидерства // Автор24. 2020.
8. Matrix Leadership Institute Consulting. 2020.
9. Амина Нолан и Филипп Гузенюк. Подходы в матрице лидерства // Видеотренинг. 2016.
10. Master the Matrix: 4 Tips to Help You Lead Matrix Teams Successfully // Cathy Cassidy. International Matrix Management Institute
11. Живая компания. Рост научение и долгожительство в деловой среде // Ари де Гиус. Манн, Иванов и Фербер, 2013.

Мастер-класс: «Эмпатия и совместный дизайн»

11 сентября 2019 года участники собрались на семинар в FabLab Западного Рурского университета прикладных наук в Ботропе. «Эмпатия и совместный дизайн: более эффективные системы помощи за счет использования дизайнерского мышления и цифрового производства». 

Был большой интерес к разработке новых стратегий для инклюзивного дизайна и концепций дизайна через сочувствие и к получению или углублению первоначального опыта в области методов цифрового производства. Бизнес-процессы были проанализированы с целью разработки первоначальных подходов к оцифровке процессов или продуктовых идей.

Целью этого семинара было собрать людей вместе, чтобы способствовать обмену опытом в области аддитивных систем. Широкий круг участников и описание индивидуальных потребностей ясно дали понять, какую важную роль следует отводить индивидуальным системам помощи в профессиональной и частной среде.

Индивидуальные системы помощи сегодня становятся все более доступными благодаря возможностям цифровых технологий, в том числе для малых и средних компаний. Однако это также создает новые проблемы для применения технологии в различных областях, таких как инженерия, архитектура, мода и дизайн.

Системы должны, например, упростить работу сотрудников или улучшить пользовательский опыт их продуктов для клиентов, независимо от того, являются ли они людьми с ограниченными возможностями или без них.  

В FabLab после части теоретического дизайн-мышления все участники имели возможность быстро реализовать свои первые идеи с помощью инструментов цифрового прототипирования. На четырех станциях были разработаны новые вспомогательные системы и изготовлены прототипы с помощью 3D-принтеров, 3D-сканеров, лазерных резаков и вязальных машин.

В этом фильме вы можете увидеть впечатления от рабочего дня:

Фильм для семинара «Эмпатия и совместный дизайн: более эффективные системы помощи за счет использования дизайнерского мышления и цифрового производства»

Сочувствие, творческая уверенность в себе и использование новых технологий создают новые вещи.

С помощью персонализированной компьютерной мыши и открывалки для бутылок, разработанных, чтобы облегчить людям с ограниченными физическими возможностями выполнение этой задачи, стало ясно, что улучшать продукты можно только с пониманием проблемы. Изготовленный проводящий и интерактивный материал, который можно использовать в одежде, а также датчик освещенности, встроенный в шкаф, доказывают разнообразие встроенных систем.

В конце семинара стало ясно, что сочувствие, творческая уверенность в себе и использование новых технологий создают вещи, которые революционизируют мир труда и делают возможным стремление к самостоятельной и легкой жизни, с физическими недостатками или без них.

Das Проект Эмшер-Липпе⁴ способствует оцифровке малых и средних компаний в регионе. Основное внимание уделяется инновационным решениям, с помощью которых вы можете использовать потенциал оцифровки для своей компании и своих сотрудников (с ограниченными возможностями и без). Советы по инновациям из матрицы предлагает с помощью различных семинаров первое знакомство с методами цифрового производства и инноваций и делает их осязаемыми в FabLab.

Joint Matrix — Витамины и минералы / Уход за суставами / Рыбий жир / Хорошее самочувствие

Формула максимальной совместной топливной поддержки

Saturn’s Joint Matrix — это лучшая пищевая добавка для суставов в форме одной таблетки! Эта усовершенствованная формула обеспечивает ваше тело новейшими ингредиентами. Эта специальная формула состоит из основы, содержащей несколько питательных веществ.

Факты о дополнении:

Размер порции: 2 порции таблеток

порций в упаковке: 50

глюкозамина сульфат	1000 мг
новозеландский зеленый липидный морской мидий	250 мг
L-гистидин	10 мг
MSM (метилсульфонил)
Витамин A (ацетат)	100iu
Витамин C (аскорбиновая кислота)	1 мг
Витамин E (d-альфа ацетат)	1iu
B-1 (тиамин)	1 мг
B-2 (рибофлавин)	1 мг
Ниацинамид	1 мг
Витамин B-6 (пиридоксин HCl)	1 мг
B-12	10 мкг
Марганец (аспартат)	320 мкг
Цинк (оксид)	200 мкг
Seleniu m (аминокислотный хелат)	20 мкг
Медь (глюконат)	100 мкг
Хром (хлорид)	20 мкг
Поддерживающая матрица для остеосинтеза: хондроитинсульфат, порошок люцерны, L-гистидин Аминокислотный хелат, экстракт юкки, порошок когтя дьявола, цетилмиристолеат.	139 мг

Рекомендуемое применение: 2 таблетки от 1 до 3 раз в день, желательно во время еды или по указанию врача.

Другие ингредиенты: Растительная стеариновая кислота, карбонат кальция, микрокристаллическая целлюлоза, кроскармеллоза натрия, гидроксипропилметилцеллюлоза, растительный стеарат магния и диоксид кремния.

• Maximum Joint Fuel Formula
• Glucosamine & Chondroitin Powerhouse
• Комплекс Osteo-Max для максимальной поддержки

Эти заявления не были оценены Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов.Этот продукт не предназначен для диагностики, лечения или предотвращения каких-либо заболеваний.

Квартира $ 6.95 Доставка

Только ограниченное время

В течение ограниченного времени Saturn предлагает фиксированную стоимость доставки в размере 6,95 долларов США для всех заказов, отправленных в континентальной части США.

Joint Matrix — совместная опора

Дополнительные факты Размер порции: 2 таблетки Количество на порцию % Дневная стоимость

Витамин A (в виде ретинилацетата) 30 мкг 3% Витамин C (в виде аскорбиновой кислоты) 1 мг 2% Витамин E (в виде токоферилацетата d-альфа ) 0.67 мг 4% Тиамин (в виде тиамина HCl) 1 мг 83% Рибофлавин 1 мг 77% Ниацин (в виде ниацинамида) 1 мг 6% Витамин B-6 (в виде пиридоксина HCl) 1 мг 59% Витамин B-12 (в виде цианокобаламина) 10 мкг 417% Цинк (в виде хелата аминокислоты цинка) 0.2 мг 2% Селен (в виде хелата аминокислоты селена) 20 мкг 36% Медь (в виде хелата аминокислоты меди) 0,1 мг 11% Марганец (в виде сульфата марганца) 0,32 мг 14% Хром (в виде хелата аминокислоты хрома) 20 мкг 57% Глюкозамина сульфат 1000 мг * Хондроитинсульфат 100 мг * Новозеландская зеленогубая морская мидия 250 мг * МСМ (метилсульфонил) 800 мг * L-гистидин 10 мг * Бор (в виде хелата аминокислоты бора) 1 мг * Порошок листьев люцерны 25 мг * Экстракт корня юкки (29% сапонинов) 1 мг * Порошок корня дьявольского когтя 1 мг * Цетилмиристолеат 1 мг * * Суточная доза не определена

Другие ингредиенты: растительная стеариновая кислота, карбонат кальция, микрокристаллическая целлюлоза, кроскармеллоза натрия, гидроксипропилметилцеллюлоза, растительный стеарат магния и диоксид кремния.

ПРЕДУПРЕЖДЕНИЕ О АЛЛЕРГЕНАХ: СОДЕРЖИТ РАКУСОВЫЕ РЫБКИ (КРЕВЕТКИ И КРАБЫ) И СОЮ.

Формула без ГМО!

ХРАНИТЬ В НЕДОСТУПНОМ ДЛЯ ДЕТЕЙ МЕСТЕ.НЕ ИСПОЛЬЗУЙТЕ, ЕСЛИ УПЛОТНЕНИЕ БЕЗОПАСНОСТИ ПОВРЕЖДЕНО ИЛИ ОТСУТСТВУЕТ. ХРАНИТЬ В ПРОХЛАДНОМ СУХОМ МЕСТЕ.

ПРЕДЛАГАЕМЫЙ ПРИМЕНЕНИЕ: по 2 таблетки от 1 до 3 раз в день, желательно во время еды или по назначению врача.

ВНИМАНИЕ: Не превышайте рекомендованную дозу.Этот продукт не предназначен для беременных или кормящих матерей или детей в возрасте до 18 лет. Если у вас есть известное заболевание или у вас есть вопросы о целесообразности приема этого продукта, проконсультируйтесь с врачом перед использованием этой или любой другой пищевой добавки. Этот продукт производится и упаковывается на предприятии, которое также может перерабатывать молоко, сою, пшеницу, яйца, арахис, древесные орехи, рыбу и ракообразных.

Эти утверждения не проверялись Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов.Этот продукт не предназначен для диагностики, лечения или предотвращения каких-либо заболеваний.

Формулы могут быть изменены. Пожалуйста, свяжитесь с Vitalabs для получения последних формул.

Canine Matrix Joint Flex Органическая добавка для передвижения грибов для собак — Only Natural Pet

ORGANIC MOBILITY FLEX ДЛЯ СОБАК

Сустав

Canine Matrix изготовлен из сертифицированного USDA органического грибного порошка, который содержит множество витаминов и минералов, а также натуральный глюкозамин, который помогает поддерживать подвижность вашего питомца и снимает воспаление суставов.

Клеточные стенки грибов, естественный источник глюкозамина, находятся в каждом мешочке. Наряду с биотином, витамином D и L-эрготионеином, все это из запатентованной смеси 100% сертифицированной органической биомассы мицелия грибов, выращенной на органическом овсе. Содержит гриб рейши, экстракты которого, как известно, полезны для печени и сердца, иммунной системы, артериального давления, регуляции уровня сахара в крови и аллергии.

Страна происхождения: США

Производитель: Матрица собак

Состав

Содержит запатентованную смесь сертифицированной 100% органической биомассы мицелия грибов, выращенной на органическом овсе: Pleurotus eryngll (King Trumpet), Cordyceps militaris, Antrodia camphorata, Agaricus blazei, Maitake (Grifola frondosa) и Ganoderma lucidum (Lionderma lucidum) Грива).

Рекомендации по кормлению

Инструкция по применению:

Посыпайте грибными добавками сырые, сухие или влажные корма. При кормлении сухими гранулами рекомендуется смочить небольшим количеством воды, но это не обязательно. Отлично подходит и для наших кошачьих друзей!

Дневная дозировка по весу:

Половина чайной ложки на 25 фунтов в день.Мы настоятельно рекомендуем двойную дозу в первые 3 недели использования, продолжать двойную дозу при острых состояниях.

Произошла ошибка при настройке вашего пользовательского файла cookie

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:

• В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
• Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
• Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файлах cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.

Матрица SAFER: новая методология подсчета очков

% PDF-1.7 % 1 0 obj > эндобдж 9 0 объект > эндобдж 2 0 obj > эндобдж 3 0 obj > поток 2016-04-20T09: 27: 36-05: 002016-04-29T08: 34: 16-05: 002016-04-29T08: 34: 16-05: 00 Adobe InDesign CC 2015 (Windows) uuid: 6ba55f34-2b84-4a39 -b652-09970b178d9cxmp.сделал: 6EAC62028FD3E211AE43C4A7B9F13F78xmp.id: b98abfd4-4cc1-984b-a391-cb28f4d79de9proof: pdfxmp.iid: 586206d0-05ac-e347-a2d3-c5eb36f6d839xmp.did: 586206d0-05ac-e347-a2d3-c5eb36f6d839xmp.did: 6EAC62028FD3E211AE43C4A7B9F13F78default

convertedfrom применение / х -indesign в приложение / pdfAdobe InDesign CC 2015 (Windows) / 2016-04-20T09: 27: 36-05: 00

application / pdf

Матрица SAFER: новая методология подсчета очков

Матрица SAFER: новая методология подсчета очков

ВСЕ акк и сертификат

16 мая

Библиотека Adobe PDF 15.0 ЛожьБЕЗОПАСНАЯ матрица: новая методология подсчета очков ВСЕ акк и сертификат 16 мая конечный поток эндобдж 4 0 объект > эндобдж 5 0 obj > эндобдж 6 0 obj > эндобдж 7 0 объект > эндобдж 8 0 объект > эндобдж 10 0 obj > эндобдж 11 0 объект 5152 эндобдж 12 0 объект > эндобдж 13 0 объект > эндобдж 14 0 объект > эндобдж 15 0 объект > эндобдж 16 0 объект > эндобдж 17 0 объект > эндобдж 18 0 объект > эндобдж 19 0 объект > эндобдж 20 0 объект > эндобдж 21 0 объект > поток HWn} * BD *

Жидкий матрикс для суставов — NutriChem

Этот продукт доступен только по рекомендации врача.

• Обеспечивает одну из наиболее полных смесей хорошо изученных питательных веществ для уменьшения симптомов остеоартрита, защиты суставов от дальнейшего повреждения и снижения потребности в рецептурных или безрецептурных обезболивающих
• Содержит смесь сульфата глюкозамина, хондроитинсульфата, гиалуроновой кислоты, метилсульфонилметана (МСМ) и гидролизованного коллагена для общего улучшения выработки суставного хряща и синовиальной жидкости в суставах
• Boswellia serrata, zingiber officinale, harpagophytum procumbens и withania somnifera поставляются в виде высокоэффективных экстрактов, обеспечивающих терапевтическое количество активных ингредиентов и обладающих мощным противовоспалительным действием
• Куркумин представляет собой тщательно стандартизированный и хорошо изученный комплекс uC3 Clear, обеспечивающий минимальное содержание куркуминоидов 95%.
• Добавлен витамин С для поддержки здорового производства коллагена и цинка в форме полного глицинат-хелата (запатентованная доставка TRAACS) для оптимального усвоения
• Доставка жидких продуктов и натуральный ароматизатор зеленого яблока

Лекарственные ингредиенты: каждая столовая ложка (15 мл) содержит:

Коллаген гидролизованный (бычий)	1800 мг
Сульфат глюкозамина	1500 мг
Метилсульфонилметан (МСМ)	750 мг
Экстракт имбиря (корневище, zingiber officinale) 8: 1	100 мг
Экстракт Ашваганды (все растение) 5: 1	200 мг
Экстракт дьявольского когтя (корневой клубень, harpagophytum procumbens) 4: 1	500 мг
uC3 Clear ™ (куркумин, куркума длинная)	50 мг
Экстракт босвеллии (смола, boswellia serrata) 10: 1	100 мг
Гиалуроновая кислота (гиалуронат натрия)	50 мг
Цинк (хелат бисглицината цинка TRAACS®)	15 мг
Витамин С (аскорбиновая кислота)	30 мг

Немедицинские ингредиенты: Очищенная вода, сорбит, глицерин, ксилит, натуральный ароматизатор зеленого яблока, DL-яблочная кислота, сорбат калия, ксантановая камедь, экстракт плодов монаха, экстракт цитрусовых, повидон К-30, солодка экстракт корня.

Взрослые: Принимайте по 1 столовой ложке (15 мл) в день или по указанию врача. Перед употреблением взболтать. После открытия хранить в холодильнике.

Продолжительность использования: Используйте минимум 1 месяц, чтобы увидеть положительный эффект.

Предупреждения: Не использовать, если защитная пломба сломана. Проконсультируйтесь с врачом по поводу использования этого продукта, особенно если симптомы не исчезают или ухудшаются; и перед использованием, если вы беременны, кормите грудью или принимаете лекарства, включая антиагреганты или антикоагулянты, или имеете какое-либо заболевание, включая камни в желчном пузыре, непроходимость желчных протоков, аллергию на моллюсков, язву желудка или избыток желудочной кислоты.Не рекомендуется употребление с алкоголем, другими лекарствами или натуральными продуктами для здоровья с седативными свойствами.

Известные побочные реакции: Известно, что имеет место гиперчувствительность (например, аллергия), и некоторые люди могут испытывать легкие желудочно-кишечные расстройства, такие как диарея, боли в животе, изжога, тошнота и рвота; в этом случае прекратите использование.

Глютен, соя, ГМО и молочные продукты.

Matrix 5 H / A (Pellet) — Добавки для конского сустава | MVP

Всесторонняя совместная поддержка!

Обеспечивает (на порцию 2 унции): 10 000 мг глюкозамина; 125 мг гиалуроновой кислоты; 2,500 мг хондроитинсульфата; 10000 мг МСМ; 1600 мг Ester-C®; 2500 мг юкки; плюс цинк, марганец и витамин Е.

• Продвинутая формула
• Со вкусом яблока
• Концентрированный

# НИЖЕ РЕЙТИНГА

Всесторонняя совместная поддержка!

# ЭТИКЕТКА / НАПРАВЛЕНИЯ

# ИНЖЕНЕРНЫЙ ГЛОССАРИЙ

Глюкозамин является строительным блоком хондроитинсульфата, особого типа полисульфид гликозаминогликана (ГАГ), небольшой, но сложной молекулы, которая играет важную роль в производстве и защите суставов.Глюкозамин играет множество ролей в совместном функционировании и здоровье. Он помогает увеличить производство новых ГАГ и, следовательно, нового хряща, также было показано, что он помогает ингибировать свободные радикалы и ферменты, которые разрушают хрящ.

Гиалуроновая кислота (HA) помогает поддерживать здоровье хрящей и суставной жидкости. Гиалуроновая кислота делает суставную жидкость «липкой», потому что, как известно, она защищает клетки сустава. ГК особенно полезна в периоды сильного стресса суставов.

MSM: (метилсульфонилметан) Помогает организму вырабатывать собственные внутренние антиоксиданты, которые помогают поддерживать естественный воспалительный ответ, обеспечивая защиту от окислительного стресса.Это отличный источник серы, которая играет важную роль в поддержании здоровья коллагена, хрящей, копыт, волос и суставной жидкости.

Хондроитинсульфат работает синергетически с глюкозамином при производстве нового хряща и подавляет действие различных ферментов, разрушающих хрящ. Это также помогает поддерживать естественную воспалительную реакцию, обеспечивая общее здоровье и комфорт суставов.

Юкка — растение, произрастающее в Северной и Центральной Америке, используемое древними и современными цивилизациями для устранения дискомфорта опорно-двигательного аппарата.Активные ингредиенты, выделенные из юкки, обладают антиоксидантными свойствами, помогая поддерживать естественную воспалительную реакцию.

Ester-C® (аскорбат кальция) — уникальный запатентованный комплекс аскорбата, связанный с карбонатом кальция. Ester-C® естественным образом обрабатывается в очищенной воде без использования спиртовых или ацетоновых растворителей. Это делает Ester-C® более доступной, легко усваиваемой формой витамина C. Витамин C является антиоксидантом, который помогает защитить ткани тела, а также играет важную роль в производстве соединительных тканей, таких как сухожилия и связки.У Ester-C® метаболическая активность в 4 раза выше, чем у стандартного витамина C (аскорбиновая кислота).

Цинк (Zn) — это микроминерал, участвующий в более чем 100 ферментных системах, от поддержки образования соединительной ткани и антиоксидантов до углеводного обмена и функции иммунной системы. Он наиболее известен своей ролью в поддержании здоровья кожи и копыт.

Марганец — это микроминерал, который способствует образованию, росту и размножению костей. Он также поддерживает метаболизм углеводов и жиров.Следует рассмотреть возможность приема добавок, потому что не все диеты обеспечивают одинаковый уровень марганца. Он играет важную роль как в молодых растущих, так и в активных лошадях.

Витамин E считается наиболее важным антиоксидантом и тесно взаимодействует с селеном, защищая организм от окислительного стресса, вызванного физическими упражнениями и болезнями. В больших количествах содержится на свежих пастбищах, уровни начинают снижаться в момент, когда пастбища вырезают для сена. Вот почему любая лошадь, у которой нет доступа к траве, независимо от ее уровня активности или здоровья, может быть кандидатом на добавку витамина Е.Лошади не очень эффективно накапливают витамин Е, и его дефицит может ускориться, если в рационе не хватает селена.

Медь (Cu) — это микроминерал, который способствует образованию нормальных соединительных тканей, включая сухожилия, связки, хрящи и кости. Как компонент многих ферментных систем, он также участвует в обеспечении доступа организма к железу для крови, в производстве пигментов кожи и шерсти, в правильной передаче нервных сигналов и в восстановлении антиоксидантов.

#FAQS

Требуется ли ударная доза?

MVP: Matrix 5 H / A не требует нагрузочной дозы.

Будет ли это хорошей добавкой для начинающих тренировок молодой лошади, чтобы помочь с будущими проблемами суставов и профилактикой?

MVP: Matrix 5 H / A обычно подходит для лошадей, выполняющих умеренную и тяжелую работу, и может быть отличным дополнением к программе управления вашей лошадью, поскольку эта добавка обеспечивает поддержку для поддержания здоровья суставов.