Матрицы разложение по строке и столбцу – Разложение определителя по строке (столбцу).

Теорема Лапласа — Википедия

О теореме из теории вероятностей см. статью Локальная теорема Муавра — Лапласа.

Теоре́ма Лапла́са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают формулирование этой теоремы в 1772 году^[1], хотя частный случай этой теоремы о разложении определителя по строке (столбцу) был известен ещё Лейбницу.

Содержание

• 1 Формулировка
• 2 Разложение определителя по строке (столбцу) (Следствие 1)
• 3 Следствие 2 (фальшивое разложение определителя)
• 4 Примечания
• 5 Литература

Для начала, введём несколько определений.

Пусть A=(aij){\displaystyle A=(a_{ij})} — матрица размера n×n{\displaystyle n\times n}, и пусть выбраны любые k{\displaystyle k} строк матрицы A{\displaystyle A} с номерами i1<i2<…<ik{\displaystyle i_{1}<i_{2}<\ldots <i_{k}} и любые k{\displaystyle k} столбцов с номерами j1<j2<…<jk{\displaystyle j_{1}<j_{2}<\ldots <j_{k}}.

ru.wikipedia.org

Разложить определитель по строке или столбцу

Для того что бы вычислить определитель матрицы четвертого порядка или выше можно разложить определитель по строке или столбцу или применить метод Гаусса и привести определитель к треугольному виду. Рассмотрим разложение определителя по строке или столбцу.

Определитель матрицы равен сумме умноженных элементов строки определителя на их алгебраические дополнения:

— разложение по i-той строке.

Определитель матрицы равен сумме умноженных элементов столбца определителя на их алгебраические дополнения:

— разложение по j-той строке.

Для облегчения разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример

Найдем определитель матрицы четвертого порядка.

Будем раскладывать этот определитель за столбцом №3. Сделаем некоторые преобразования, что бы облегчить дальнейшие расчеты.

Сделаем ноль вместо элемента a₄₃=9. Для этого из строки №4 вычтем от соответствующие элементы строки №1 умноженные на 3.
Результат записываем в строке №4 все остальные строки переписываем без изменений.

Вот мы и сделали нолями все элементы, кроме a₁₃ = 3 в столбце № 3. Теперь можно преступить и к дальнейшему разложению определителя за этим столбцом.

Видим, что только слагаемое №1 не превращается в ноль, все остальные слагаемые будут нолями, так как они умножаются на ноль.

Значит, далее нам надо разложить, только один определитель:

Будем раскладывать этот определитель за строкой №1. Сделаем некоторые преобразования, что бы облегчить дальнейшие расчеты.

Видим, что в этой строке есть два одинаковых числа, поэтому вычтем из столбца №3 столбец №2, и результат запишем в столбце №3, от этого величина определителя не изменится.

Далее нам надо сделать ноль вместо элемента a₁₂=4. Для этого мы элементы столбца

№2 умножим на 3 и вычтем от него соответствующие элементы столбца №1 умноженные на 4. Результат записываем в столбце №2 все остальные столбцы переписываем без изменений.

Но при этом надо не забывать, что если мы умножаем столбец №2 на 3, то и весь определитель увеличится в 3. А что бы он не изменился, значит надо его поделить на 3.

Сократим числитель и знаменатель дроби на 3.

Вот мы и сделали нолями все элементы, кроме a₁₁ = 3 в строке № 1

. Теперь можно преступить и к дальнейшему разложению определителя за этой строкой.

Видим, что у нас остался один определитель второго порядка.

Найдем определитель по формуле: a₁₁×a₂₂ — a₂₁×a₁₂.

det(A)=3·(-14)·(-13)-(-6)·(-2)=510

www.mozgan.ru

Алгебра

Часть I

1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ. Определения определителя и его основные свойства. Теорема о разложении определителя по элементам строки (столбца). Критерий обратимости матрицы

   .

Определителем или детерминантом n-го порядка называется число, записываемое в виде

и вычисляемое по данным числам (действительным или комплексным) – элементам определителя – по следующему закону:

,

распространенная на всевозможные различные перестановки из чисел . Число 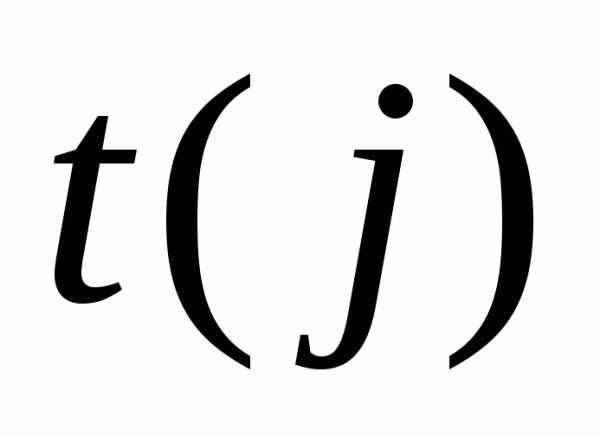равно числу транспозиций, которые нужно сделать, чтобы перейти от основной перестановки к перестановке n-го порядка . Произведение называется членом определителя.

Теорема (разложение определителя по строке или столбцу).

Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки

d = a_{i 1} A_{i 1} + a_{i 2} A_{i 2} +… + a_{i n} A_{i n} (i = )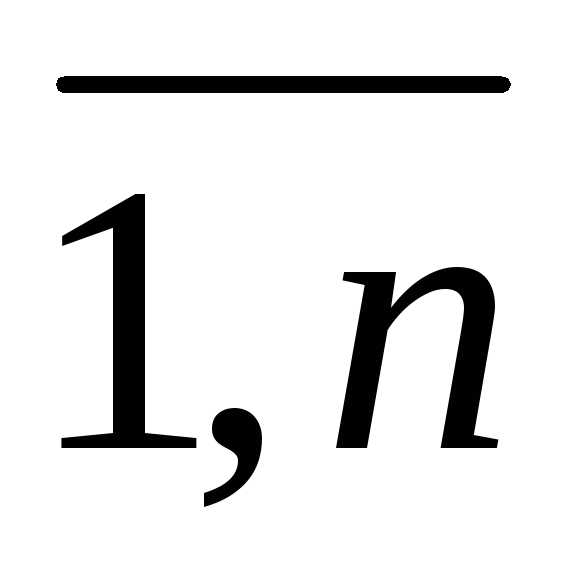

или j- го столбца

d = a_{1 j} A_{1 j} + a_{2 j} A_{2 j} +… + a_nj A_nj (j = ).

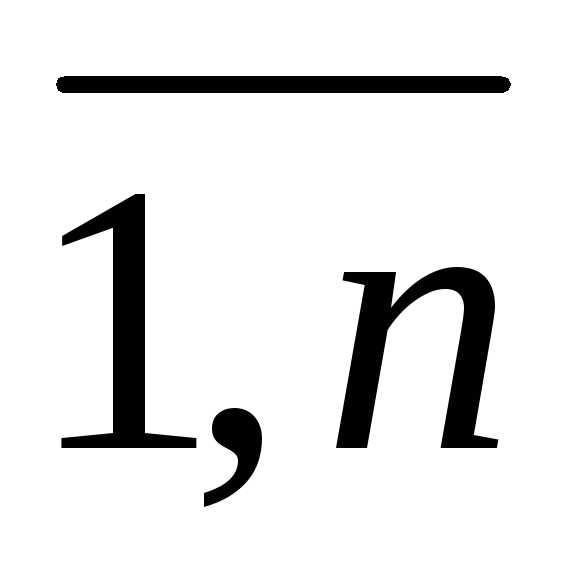В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.

Доказательство.

Убедимся в справедливости теоремы на примере разложения определителя 3-го порядка, например, по 1-й строке. По теореме это разложение будет иметь вид: == а₁₁А₁₁ + а₁₂А₁₂ + а₁₃А₁₃ = {с учетом определения A_ij получим}= =а₁₁(1)²М₁₁ + а₁₂(1)³М₁₂ + а₁₃(1)⁴М₁₃ = а₁₁  а₁₂

+ а₁₃ = а₁₁(а₂₂а₃₃  а₂₃а₃₂)  а₁₂(а₂₁а₃₃  а₂₃а₃₁) + а₁₃(а₂₁а₃₂  а₂₂а₃₁) = =а₁₁а₂₂а₃₃ + а₁₂а₂₃а₃₁ + а₁₃а₂₁а₃₂  а₁₃а₂₂а₃₁  а₁₂а₂₁а₃₃  а₁₁а₂₃а₃₂ = {по правилу треугольников} =

= . Аналогичный результат получается при разложении определителя по любой строке (столбцу). Fin.

Следствие. Если в i–й строке (j-м столбце) определителя  есть только один ненулевой элемент а_ij  0, то результатом разложения определителя по этой строке (столбцу) будет выражение  = а_ijА_ij.

Определители n-го порядка удовлетворяют свойствам:

1) При транспонировании определителя его значение не меняется, (то есть значение определителя не меняется при замене его строк столбцами с теми же номерами).

Доказательство:

 =

= = a₁₁a₂₂  а₁₂а₂₁

NB. Следовательно, строки и столбцы определителя равноправны, поэтому его свойства можно формулировать и доказывать либо для строк, либо для столбцов.

2) При взаимной перестановке любых двух строк (столбцов) определителя его знак меняется на противоположный.

Доказательство:

 == a₁₁a₂₂ а₁₂а₂₁ = (а₁₂а₂₁  a₁₁a₂₂) = 

3) Определитель с двумя одинаковыми строками (столбцами) равен нулю.

Доказательство. Пусть определитель  имеет две одинаковые строки. Если поменять их местами, то, с одной стороны, величина определителя не изменится, так как строки одинаковы, а с другой стороны определитель должен поменять свой знак на противоположный по свойству 2. Таким образом, имеем:  =    = 0.

4) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.

Доказательство:

== a₁₁a₂₂ а₁₂а₂₁ = (a₁₁a₂₂ а₁₂а₂₁) =  .

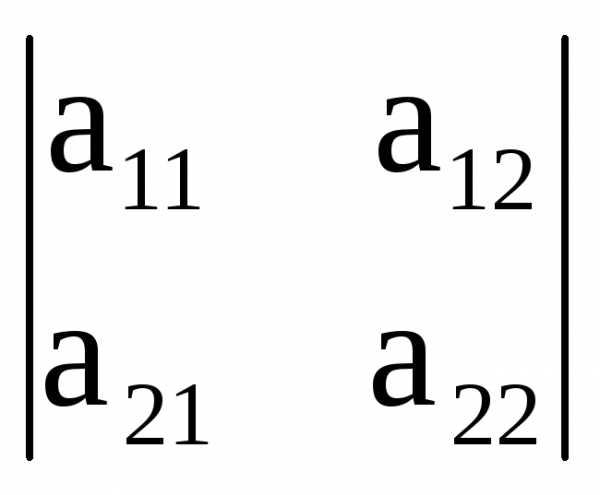Следствие:  = = .

NB. Правило умножения определителя на число. Чтобы умножить определитель на число, надо все элементы какой-то одной его строки (столбца) умножить на это число.

5) Определитель с нулевой строкой (столбцом) равен нулю.

Доказательство. По свойству 4 вынесем общий множитель  = 0 элементов нулевой строки (столбца) за знак определителя. Получим 0 = 0.

6) Определитель с двумя и более пропорциональными строками (столбцами) равен нулю.

Доказательство. Если вынести за знак определителя коэффициент пропорциональности двух строк (столбцов) ≠0, то получится определитель с двумя одинаковыми строками (столбцами), равный нулю по свойству 3.

7) Если каждый элемент какой-либо строки (столбца) определителя представить в

виде суммы k слагаемых, то такой определитель равен сумме k определителей, у которых элементы этой строки (столбца) заменены соответствующими слагаемыми, а все остальные элементы такие же как у исходного определителя.

Доказательство:

== (а₁₁ + b₁₁)а₂₂  (а₁₂ + b₁₂)а₂₁ = (а₁₁а₂₂  а₁₂а₂₁) + (b₁₁а₂₂  b₁₂а₂₁) = = + .

Опр. n-ая строка определителя называется линейной комбинацией его остальных (n1) строк, если ее можно представить в виде суммы произведений этих строк на соответствующие числа ₁, ₂, …, _n1. Например, в определителе

3–я строка является линейной комбинацией первых двух строк.

NB. Линейная комбинация называется тривиальной, если в ней _i = 0. В противном случае линейная комбинация называется нетривиальной (if _i  0).

8 а) Если одна строка (столбец) определителя является линейной комбинацией других его строк (столбцов), то такой определитель равен нулю.

Доказательство:  =

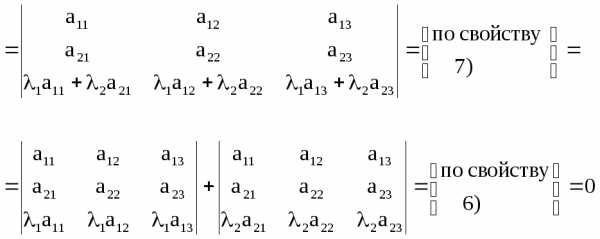8 б) Величина определителя не изменится, если к элементам любой его строки (столбца) прибавить соответствующие элементы любой другой строки (столбца) определителя, умноженные на одно и то же число.

Доказательство:

Пусть =  {к 1-й строке прибавим 2-ю строку, умноженную на число } 

=.

9) Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов любой другой строки (столбца) определителя равна нулю, то есть 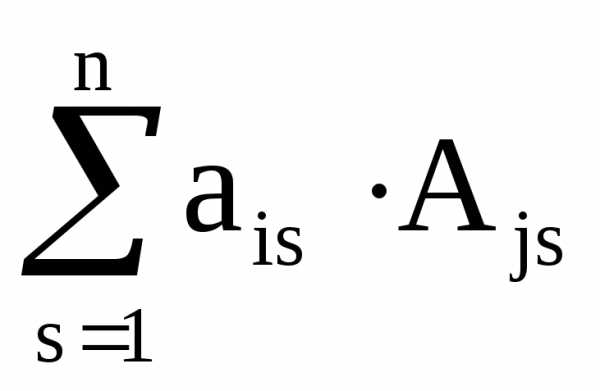= 0 (if i ≠ j).Например, пусть

 =  0

Тогда а₁₁А₂₁ + а₁₂А₂₂ + а₁₃А₂₃ = 0, так как выполнено умножение элементов 1-ой строки определителя на алгебраические дополнения соответствующих элементов 2-ой строки.

Доказательство:

а₁₁А₂₁ + а₁₂А₂₂ + а₁₃А₂₃ = а₁₁(1)²⁺¹ + а₁₂(1)²⁺² + а₁₃(1)²⁺³ =

={это есть разложение по 1-й строке определителя (1)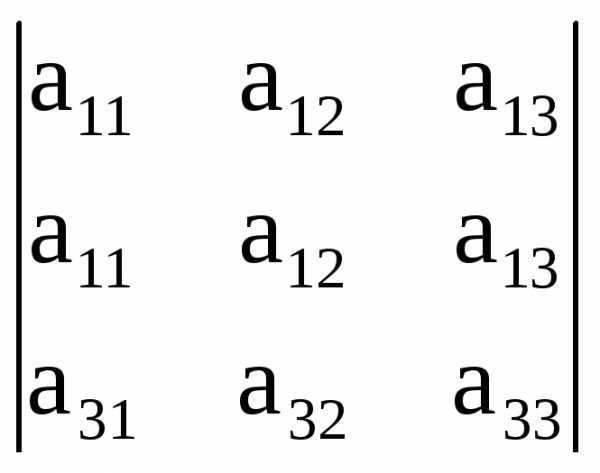 = 0}= 0.

Если определитель 0, то по свойству 8 б) в нем всегда можно «обнулить» i-ю строку (j-й столбец) до единственного ненулевого элемента и разложить определитель по этой строке (столбцу). Применяя эту операцию нужное число раз, всегда можно из определителя n-го порядка получить определитель 2-го порядка.

Обратная матрица

Опр. Матрица называется присоединенной (союзной) к квадратной матрице А, если она состоит из алгебраических дополнений элементов транспонированной матрицы А^т. Чтобы получить присоединенную матрицу , следует транспонировать матрицу А, а затем все ее элементы заменить их алгебраическими дополнениями, то есть

= (3.1)

Опр. Квадратная матрица А называется вырожденной (особенной), если ее определитель |A|=0, и невырожденной, если ее определитель |A|0.

Опр. Квадратная матрица А^1 называется обратной (инверсной) к квадратной матрице А, если выполняется условие

А^1А = АА^1= Е (3.2)

NB. Обратная матрица А^1 возможна только для невырожденной матрицы А.

Теорема.

Для любой невырожденной квадратной матрицы А существует единственная обратная матрица А^1, которая находится по формуле

А^1 = 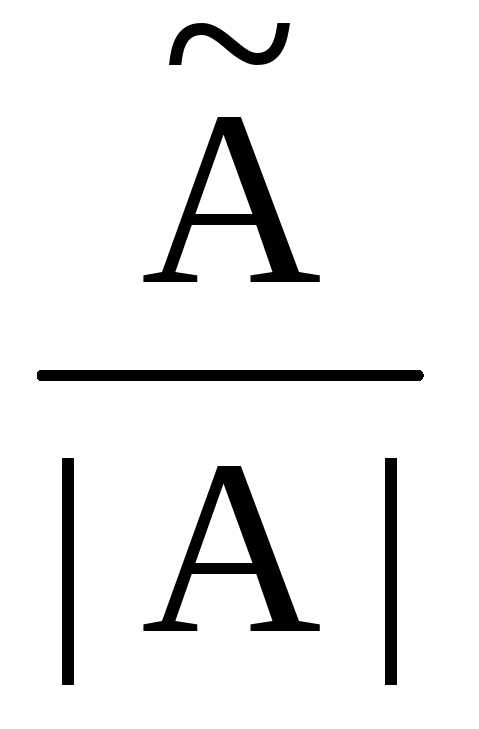(3.3)

Доказательство.

1) Из определения А^1А = АА^1 следует, что А и А^—1 это квадратные матрицы одного порядка.

Пусть матрица А – невырожденная, то есть |A|0. Тогда, по правилу умножения матриц, по теореме Лапласа и по свойству 9 определителей, получим

А =  = =

= |A|= |A|E

Следовательно, А = |A|E. Аналогично доказывается, чтоА = |A|E.

Из А= |A|E  А^1А₌ А^—1×|A|E  Е₌ А^1|A|  ₌ А^1|A|  А^1 = .

2) Докажем единственность обратной матрицы. Предположим, что для матрицы А существует еще одна обратная матрица В. Тогда, согласно определению произведение АВ=Е. Обе части последнего равенства умножим слева на обратную матрицу А^1 и получим: А^1АВ = А^1Е  ЕВ = А^1Е  В = А^1. Fin.

studfiles.net

Разложение определителя по строке или столбцу online…

Последнее время я получал много комментариев на сайте и писем с вопросами: «Как найти определитель четвёртого, пятого порядка?» или что-то подобное. И практически всех этих людей я отправлял посмотреть мои видео-уроки, в которых я подробно об этом рассказываю. Но потом решил упростить вашу работу и сделать online-программу, которая подробно рассказывала бы, как это сделать для любого определителя.

То есть теперь в дополнения к видео-урокам в которых я подробно всё рассказываю на конкретных примерах, вы можете открыть онлайн программку для разложения определителя по строке или столбце. И она всё шаг за шагом вам объяснит, конкретно в вашем случае, с вашим определителем. Этим методом можно решить определитель любого порядка, он раскладывает определителя на произведения элементов строки (или столбца) на их алгебраические дополнения.

Вам просто надо указать размерность определителя, потом в соответствующие ячейки внести все числа и нажать кнопку «Вычислить». Через несколько секунд перед вами будет подробнейшее решение этого определителя. Я постарался расписать там всё до мельчайших деталей, поэтому если вы всё подробно прочитаете и осмыслите, то вам сразу станет понятен весь процесс , и вы сможете самостоятельно решать такие упражнения, а результат сверять с результатом программы. И если они будут не совпадать, то сможете даже посмотреть, на каком этапе сделали ошибку.

Также хотел бы вам порекомендовать освежить в памяти все свойства определителей, которые используются при их преобразовании. Хотя программа указывает, на что надо обратить внимание при решении, но лучше, если это будет у вас в голове, а не в компьютере или тетрадке.

Данная программа пока корректно работает для целых чисел, если ваш определитель состоит из дробей, то лучше использовать эту программу. Но, думаю, в будущем я дополню её, и она будет нормально работать и для дробей.

P.S. Если программа вам понравилась, то не забудьте ею поделится со своими друзьями в социальных сетях, внизу каждой страницы есть специальные кнопки для этого ;)!

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com