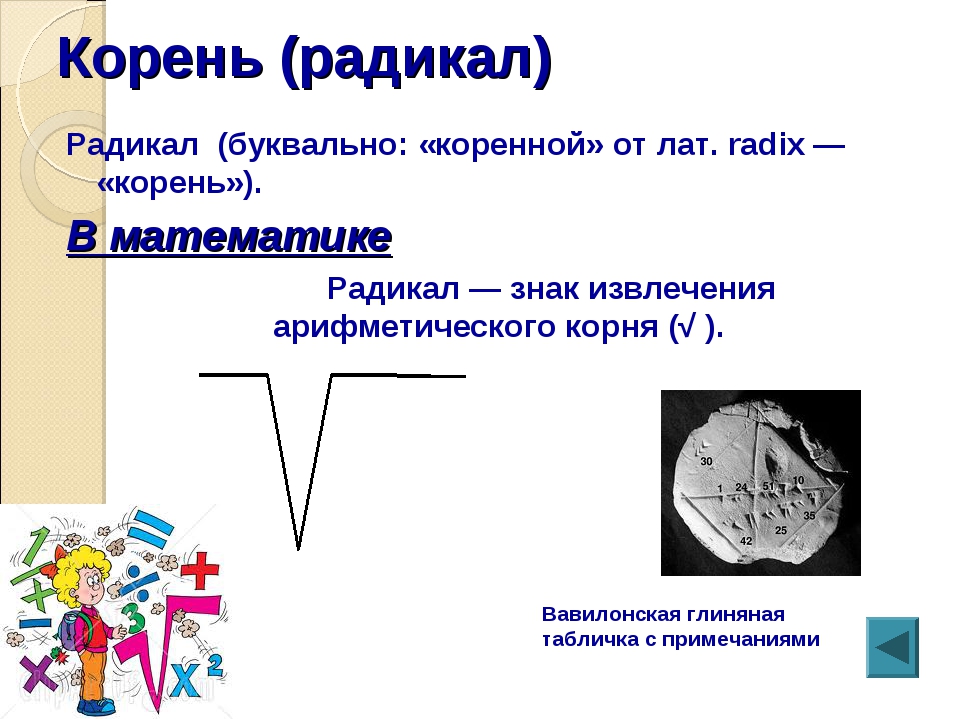
Математический корень что такое: Арифметический квадратный корень (8 класс)
5 копеек = 50 копеек
$$5\text{ копеек} = \sqrt{25\text{ копеек}} = \sqrt{\frac 1 4\text{ рубля}} = \frac 1 2\text{ рубля} = 50\text{ копеек}$$
Свойства корней
$\sqrt{a}$ существует только при $a \ge 0 $
$\sqrt[2k]{a}$ существует только при $a \ge 0, ~ k \in \mathbb{N}; $
$\sqrt[2k+1]{a}$ существует при любых значениях $a$
Для нечетных степеней:
Для четных степеней:
Учебники:
алгебра 7 класс
алгебра 10 класс — Корни. Степень с дробным показателем
День квадратного корня
День квадратного корня — праздник, отмечаемый девять раз в столетие: в день, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года (например, 2 февраля 2004 года: 02-02-04). Впервые этот праздник отмечался 9 сентября 1981 года (09-09-81). Главным блюдом на «праздничном столе» обычно являются вареные кубики из
Главным блюдом на «праздничном столе» обычно являются вареные кубики из
Праздник отмечается всегда в одни и те же дни:
1 января хх01 года 2 февраля хх04 года 3 марта хх09 года 4 апреля хх16 года 5 мая хх25 года 6 июня хх36 года 7 июля хх49 года 8 августа хх64 года 9 сентября хх81 года
Когда будет ближайший день квадратного корня? Кстати, День сурка отмечается 2 февраля.
Квадратный корень
Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня!
Как извлечь (или посчитать) корень квадратный из 4? Нужно просто сообразить: какое число в квадрате даст нам 4? Да конечно же 2: $$ \sqrt4=2 $$
А сколько будет квадратный корень из 9? из 1? из нуля?
Сам значок называется красивым словом «радикал».
Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.
Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да…
Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.
Из каких чисел можно извлекать квадратные корни? Да почти из любых.
Попробуем вычислить вот такой корень: $$ \sqrt{-4} = ? $$ Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.
Что, не подбирается? 2² даёт +4. (-2)² даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу. Поступите в институт — сами узнаете.
Такая же история будет с любым отрицательным числом.
Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла! Это запретная операция. Такая же запретная, как и деление на ноль.
Квадратные корни из отрицательных чисел извлечь нельзя!
Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно: $$ \sqrt2 = 1{,}4142135 \dots $$
Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называют иррациональными. Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют: $ \sqrt2$.
Кстати, именно поэтому выражения с корнями называют иррациональными. Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют: $ \sqrt2$.
Конечно, если корень из числа извлекается ровно, вы обязаны это сделать. Ответ задания в виде, например $ x = \sqrt{16}$ никто не оценит… Надо корень посчитать и написать $х = 4$.
А вот $ x = \sqrt{11}$ вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения: $$ \sqrt{2} = 1{,}4\\ \sqrt{3} = 1{,}7$$
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Арифметический квадратный корень
Для начала опять извлечём квадратный корень их четырёх. Какое число даст в квадрате 4? Два.
Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ $\sqrt4=2$ правильный, а ответ $\sqrt4=-2$ грубейшая ошибка. Вот так.
Так в чём же дело?
Действительно, (-2)² = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.
Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат.
Но если вы решаете какое-нибудь квадратное уравнение, то всегда получается два ответа (с плюсом и минусом) потому, что это — решение уравнения.
См. также Свойства квадратных корней
Доказательство иррациональности некоторых квадратных корней
http://janka-x.livejournal.com/159823.html
статья Л.
2$ оканчиваются нулем. Это единственная общая цифра наборов (2) и (3). Но в этом случае каждое из чисел m и n должно делиться на 5, а это противоречит несократимости дроби $m/n$.
Мы пришли к противоречию. Следовательно, наше допущение неверно, и число $\sqrt2$ — иррациональное.
Аналогично и легко доказывается иррациональность, к примеру, $\sqrt3$ или $\sqrt7$.
Ноль в степени ноль
Ноль в любой степени = 0.
Любое число в нулевой степени = 1.
Ноль в степени ноль?
Это как в известном парадоксе: если снаряд, способный пробить любую броню, столкнётся с бронёй, которую не способен пробить ни один снаряд, что получится?
см также Zero to the power of zero — Wikipedia
Как возводить в иррациональную степень
Как возводить в иррациональную степень | Ботай со мной #017 | Борис Трушин + — YouTube
Объясняет почему ввели степени с целым отрицательным показателем.
Далее захотелось обобщить на нецелые числа.
x = -1$ На множестве целых чисел есть единственное решение -1. На множестве вещественных чисел решений нет, так операция возведения в степень определена только для положительных оснований.
mat/algebra/radical.txt · Последние изменения: 2019/06/04 01:16 — kc
Определение квадратный корень общее значение и понятие. Что это такое квадратный корень
Прежде чем полностью перейти к анализу смысла, мы должны установить, что этимологическое происхождение математического термина «квадратный корень» встречается на латыни, а точнее в объединении двух слов:
основание и квадрат, которое можно перевести как «из четыре. « В области математики корнем называется определенное значение, которое необходимо умножить на себя (либо на одну, либо на несколько возможностей), чтобы получить определенное число. Когда делается ссылка на квадратный корень из числа, идентифицируется число, которое при умножении на один раз приводит к получению первого числа .
Чтобы привести конкретный случай в качестве примера:
квадратный корень из 16 равен 4, так как 4 на 4 равняется 16 . Другими словами, мы можем сказать, что, если мы умножим 4 на себя (4 × 4), мы получим число 16, что равносильно тому, чтобы сказать, что 4 в квадрате приводит к 16. Квадратный корень из 9, с другой стороны, равен 3 . Объяснение операции идентично предыдущему примеру: 3 × 3 = 9, то есть 3 в квадрате или 3, умноженные на себя, позволяют нам получить число 9. Вопрос «какое число умножено на себя, приводит к 9 ? » ( « Какое число для возведения во вторую степень приводит к 9? » Или « Что такое квадратный корень из 9? »
) Дает нам ответ № 3. Среди наиболее значимых свойств, которые определяют квадратный корень, мы должны заявить, что мы находим тот факт, что он превращает рациональные числа в алгебраические.
Также нельзя не учитывать тот факт, что квадратный корень может быть выполнен по-другому, исходя из «объектов», которые он использует для разработки.
Таким образом, например, это может быть сделано с комплексными числами, с кватернионными числами (расширение действительных чисел) или даже с матрицами.
Вопрос о так называемых квадратных корнях был проанализирован во время пифагорейской фазы, после обнаружения, что квадратный корень из двух не был рациональным (потому что не было никакого коэффициента, чтобы выразить это). Расширив определение квадратного корня, математики начали предлагать существование мнимых чисел и комплексных чисел .
Однако, есть гораздо более старые документы, которые показывают нам, как наши предки также использовали вышеупомянутые математические операции, которые теперь занимают нас. В этом смысле необходимо подчеркнуть, что египтяне прибегали к тем же самым, и, таким образом, это можно проверить в известном папирусе Ахмеса, датированном 1650 годом до нашей эры, который был реализован во времена правления Апофиса I.
Копией документа девятнадцатого века до нашей эры является этот цитируемый папирус, также известный как Papiro Rhind, который состоит из ряда задач математического типа, где в дополнение к вышеупомянутым корням есть вычисления площадей, дробей, тригонометрии, правил трех, уравнения линейного типа, прогрессии и четные распределения пропорционального класса.
Символ, который используется для обозначения корня, был создан Кристофом Рудольфом в 1525 году из буквы r, хотя с расширением его удара, чтобы стилизовать его. Сегодня этот символ позволяет обозначать латинское слово radix, откуда происходит корень термина.
термины / Арифметический и алгебраический корни / Математика
По определению, арифметическим корнем n-й степени из неотрицательного числа а называется неотрицательное число в, n-я степень которого равна а. Что касается алгебраического корня, то здесь понятие шире, поскольку нет требования неотрицательности: алгебраическим корнем n-й степени из числа а называется число в, n-я степень которого равна а. Вроде все ясно. А вопрос такой: а в каких случаях какой корень используется? Скажем попалось уравнение с корнями — так какой именно корень имеется в виду? Как это узнать?
Перенесено из ответа.
При извлечении алгебраического корня слева и справа получаются четыре возможных варианта, из которых различных только два — икс равен плюс-минус единице. Теперь такой вопрос — скорее, качественный. При решении уравнения икс в квадрате равен единице можно использовать как арифметический, так и алгебраический корни. Решение при этом получается одно и то же: икс равен плюс-минус единице. Но почему так получается? Ведь при использовании арифметического корня мы просто отбрасываем минус единицу при извлечении корня из единицы. Формально я понимаю, почему все же решение получается полное — потому что при извлечении корня из икса в квадрате получаем модуль икса, оттуда минус и вылезает. Но это формально. А как КАЧЕСТВЕННО объяснить тот факт, что мы не теряем решение, хотя сначала чем-то там пренебрегаем?
Дополнение DocentI. Комментарии растянулись в огромную змею, поэтому пишу здесь.
При использовании арифметического корня мы ничего не отбрасываем. В уравнении $%x^2=1$% x — это число.
n = a$% поступают так: выбирают из них один (который нам больше нравится, обозначим его за $%s_0$%), а остальные выражают через него. Как выбирают? Если можно — берут положительный корень (его называют арифметическим). Если нет положительного — действительный (отрицательный). Если нет и действительного, никакой и не выбирают (в «школьной» математике говорят, что корня нет).
Как выражают остальные решения через выбранное? По заранее доказанным правилам. Для четного n — берем $%s_0$% и $%-s_0$%. Если n нечетно — только $%s_0$%. В случае комплексных корней правила сложнее.
Почему получаем правильное решение? Потому что эта задача решена математиками, описанные выше правила доказаны и внесены в школьную программу.
Квадратный корень из минус единицы: самая важная математическая фантазия в истории | Математика не для всех
Подписывайтесь на канал в Яндекс. Дзен или на канал в телеграм «Математика не для всех», чтобы не пропустить интересующие Вас материалы.
Также есть группы в VK, Одноклассниках и Facebook : всё для математического просвещения!
Итак, квадратный корень из минус единицы. В прошлый раз мы встретились с ним в статье про особенности возведения в степень различных чисел, а также в материале про самые распространенные школьные заблуждения в математике. Кратко напомню, о чём идет речь. Поехали!
Рассмотрим квадратное уравнениеВ школе такие уравнения всегда «расстраивали», ведь решения они «как бы» не имели. Однако с изучением высшей математики становилось ясно, что квадратное уравнение ОБЯЗАНО иметь корни!
Основное ограничение состояло в том, что невозможно было заставить себя работать с «запрещенной» операцией извлечения квадратного корня из отрицательного числа.Леонард Эйлер обошел эти ограничения и впервые ввел обозначение √(-1) , как i — мнимой единицы.
Первая строчка двусмысленна! Поэтому стоит отказаться от её употребленияОднако, утверждать, что √(-1) = i, как многие привыкли, не стоит, потому что:
Первая строчка двусмысленна! Поэтому стоит отказаться от её употребления
Теперь поговорим, как показать мнимую единицу на плоскости и о её значимости.
Источник: https://vk.vkfaces.com/845123/v845123434/1152ae/n_r1myCeEx8.jpgИсточник: https://vk.vkfaces.com/845123/v845123434/1152ae/n_r1myCeEx8.jpg
Небольшое отступление
В рамках цикла про числа, которые нас окружают, я уже написал четыре статьи:
Я не дошёл до главной конструкции — комплексных чисел. Так что пока не вышел этот материал, поверьте на слово, что все вышеперечисленные числа являются комплексными. Иными словами, 0 , 1, 1/2 , √2, i, 3+i, число Пи, число Эйлера, да вообще практически всё, что можно назвать числами в привычном нам виде, называется комплексным числом.
Главное отличие — в той самой «мнимой единице».
Вещественное число — это частный случай комплексного, например 3 = 3+0i, а, например, 3i = 0 + 3i — называется чисто мнимым числом.Таким образом, имеем следующее:
Источник: https://ds02.infourok.ru/uploads/ex/02d9/00006480-60284357/img3.jpgИсточник: https://ds02.infourok.ru/uploads/ex/02d9/00006480-60284357/img3.jpg
На плоскости комплексные числа с ненулевой мнимой частью показываются очень легко. По вертикальной оси откладывается мнимая часть, а по горизонтальной — действительная.
Im Z- imaginary — воображаемый, мнимый. Re Z — Real — действительное, вещественноеIm Z- imaginary — воображаемый, мнимый. Re Z — Real — действительное, вещественное
Например, число z = 2+3i, имеет действительную часть, равную +2 и мнимую равную +3. Строится всё элементарно. Одинокая мнимая единица наносится на плоскость из соображений i=0+1i.

Каждое комплексное число характеризуется модулем и аргументом.
Красным цветом обозначен модуль комплексного числа, желтым его аргумент. Иначе говоря, модуль — это длина от центра координат до точки, а аргумент — это угол поворота.Красным цветом обозначен модуль комплексного числа, желтым его аргумент. Иначе говоря, модуль — это длина от центра координат до точки, а аргумент — это угол поворота.
Комплексные числа — это наиважнейшая математическая абстракция, которая вышла далеко за пределы «чистой математики». Без мнимой единицы и комплексных чисел немыслимо существование электроники, систем радиосвязи, теории относительности, квантовой механики, теории упругости и многих других дисциплин.
Я полностью уверен, что важнее «фантазии», чем мнимая единица, в математике не существовало и навряд ли будет существовать! А как считаете Вы?**************************************************************************
Путеводитель по каналу «Математика не для всех» — здесь собрано больше 100 статей на самые разнообразные темы: как для новичков, так и для более начитанных математиков! Например, почитайте про математическое программирование жизни!Спасибо! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием.
ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM.
**************************************************************************
Вычисление целочисленного квадратного корня / Хабр
Возникла нужда проверить, является ли целое число квадратом, и если да, то вычислить корень. Причем хочется сделать это в целочисленной арифметике. Понятно, что можно реализовать метод Ньютона в целых числах, но он требует деления на каждом шаге. А нельзя ли по другому? Найти квадратный корень по модулю степени двойки, и проверить, а не будет ли он обычным квадратным корнем.
Можно ограничиться нечетными числами: для четного числа, если количество нулевых младших разрядов нечетно, то корня нет, а если четно, то можно сдвинуть число вправо, посчитать корень от нечетного, и сдвинуть обратно влево на половину от первоначального количества нулевых бит.
Для нечетного N и 2k, k > 3, если N ≡ 1 mod 8, то есть 4 разных корня по модулю 2k, а иначе корней нет.
Нам нужен наименьший из этих четырех корней x. При этом другие три корня это 2k — x, 2k-1 + x и 2k — 2k-1 — x
Хочется что-то подобное вычислению обратного по модулю 2k — удваивая количество верных бит за итерацию.
Пусть у нас уже есть корень x0 из N по модулю 2k: N — x02 = 2ka
И мы хотим найти x1 = x0 + 2k-1y, такое чтобы в N — x12 было больше младших нулевых бит.
N — (x0 + 2k-1y)2 = 2ka — 2kx0 * y — 22k-2y2
Поделим на 2k: a — x0 * y — 2k-2y2
И приравняем к 0 по модулю 2k-2: y = a * x0-1 mod 2k-2
Получилии x1 = x0 + 2k-1a * (x0-1 mod 2k-2)
И окончательно x1 = x0 + (N — x02)/2 * (x0-1 mod 2k-2)Из k бит на следующей итерации получится 2(k-1) бит.
Параллельно считаем на каждой итерации обратное к корню.
Тестовый код:
uint8_t sqr16(uint16_t n) { if (n % 8 != 1) return 0; uint16_t sqr = (n + 1) / 2; //4 bit uint16_t inv = 2 - sqr; sqr += inv * (n-sqr*sqr)/2; //6 bit inv *= 2 - sqr * inv; sqr += inv * (n-sqr*sqr)/2; //10 bit //inv *= 2 - sqr * inv; if (sqr & 256) sqr = 0u - sqr; sqr = (uint8_t)sqr; // lowest root if (n == sqr*sqr) return sqr; return 0; }Добавив пару итераций, получим корень из uint_64
О знаке квадратного корня. Историческая справка репетитора по математике
Ззнак квадратного корня знаком всем. Его используют школьники и студенты, преподаватели и репетиторы по математике, доктора наук и академики. Однако не все знают, что современная форма и появилась не сразу. Эволюция знака радикала длилась почти пять веков, начиная с в далекого XIII в., когда итальянские и некоторые европейские математики впервые называли квадратный корень латинским словом Radix (корень) или сокращенно R.
В XV в. Н.Шюке писал вместо . Современный знак корня произошел от обозначения, применяемого немецкими математиками XV-XVI вв., называвшие алгебру — наукой «Косс», а математиков -алгебраистов «коссистами». (Математики XII-XV вв. писали все свои труды исключительно на латинском языке. Они называли неизвестное — res (вещь). Итальянские математики перевели слово res как cosa. Последний термин заимствовали немцы, от которых и появилось коссисты и косс.)
В XV в. некоторые немецкие коссисты для обозначения квадратного корня пользовались точкой перед выражением или числом. В скорописи эти точки заменялись черточками, а позже они перешли в символ
Один такой знак означал обычный квадратный корень. Если нужно было обозначить корень четвертой степени, то применялся сдвоенный знак знак Для обозначения кубического корня использовали утроенный знакКомментарий репетитора по математике: остается только гадать, как именно обозначался корень восьмой степени.
Если брать аналогию с четвертой степенью, то этот знак должен был отождествлять трехкратное извлечение квадратного корня, то есть для этого нужно было поставить три квадратика. Однако, это обозначение занято кубическим корнем.
Скорее всего, в последствии от таких обозначений как раз и образовался знак V, близкий по записи к знакомому школьникам современному знаку, но без верхней черты. Впервые этот знак был замечен в немецкой алгебре «Красивый и быстрый счет при помощи искусных правил алгебры»:
Автором этого труда был преподаватель математики из Вены, уроженец Чехии Криштоф Рудольф. Книга пользовалась большим успехом и постоянно переиздавалась на протяжении всего XVI в. и после аж до 1615г. Знаком корня, предложенного Криштофом пользовались А.Жирар, С.Стевин (он писал показатель корня справа от знака радикала в кружке: V (2) или V (3).
В 1626г. нидерландский математик А.Жирар видоизменил знак корня Рудольфа и ввел совсем близкое к современному обозначение Такая форма записи начала вытеснять прежний знак R.
Однако некоторое время знак корня писали разрывая верхнюю черту, а именно так: .
И только в 1637 году Рене Декарт соединил горизонтальную черту с галочкой, применив новое обозначение в своей книге «геометрия».
Но и здесь не было точной копии современной формы. Запись Декарта несколько отличалась от той, к который мы с вами привыкли одной деталью. У него было записано: , где буква С, поставленная сразу после радикала, указывала на запись кубического корня. В современном виде это выражение выглядело бы так: .
Самое близкое к современному написанию радикала применял Ньютон в своей «Универсальной арифметике» (1685 г.) Впервые запись корня, полностью совпадающая с сегодняшней, встречается в книге французского математика Ролля «Руководство алгебры», вышедшей в 1690 г. Только через некоторое время после ее написания математики планеты принята, наконец, единую и окончательная форма записи квадратного корня:
Колпаков А.Н. Профессиональный репетитор по математике.
Метки: Алгебра
Как быстро извлекать квадратные корни
Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень. Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:
- Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
- Существует алгоритм, с помощью которого эти корни считаются почти устно.
Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней.
Итак, алгоритм:
- Ограничить искомый корень сверху и снизу числами, кратными 10.
Таким образом, мы сократим диапазон поиска до 10 чисел;
- Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
- Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.
Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.
Ограничение корней
В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:
102 = 100;
202 = 400;
302 = 900;
402 = 1600;
…
902 = 8100;
1002 = 10 000.Получим ряд чисел:
100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.
Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:
[Подпись к рисунку]То же самое — с любым другим числом, из которого можно найти квадратный корень.
[Подпись к рисунку]Например, 3364:
Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.
Отсев заведомо лишних чисел
Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.
Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:
Последняя цифра квадрата зависит только от последней цифры исходного числа.
Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.
Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:
Эта таблица — еще один шаг на пути к вычислению корня.
Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
22 = 4;
82 = 64 → 4.Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:
[Подпись к рисунку]Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:
[Подпись к рисунку]Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!
Финальные вычисления
Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.
Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58.
Возведем их в квадрат:
522 = (50 +2)2 = 2500 + 2 · 50 · 2 + 4 = 2704;
582 = (60 − 2)2 = 3600 − 2 · 60 · 2 + 4 = 3364.Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный 🙂
Примеры вычисления корней
Теория — это, конечно, хорошо. Но давайте проверим ее на практике.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]Для начала выясним, между какими числами лежит число 576:
400 < 576 < 900
202 < 576 < 302Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:
24; 26.
Осталось возвести каждое число в квадрат и сравнить с исходным:
242 = (20 + 4)2 = 576
Отлично! Первый же квадрат оказался равен исходному числу.
Значит, это и есть корень.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]Здесь и далее я буду писать только основные шаги. Итак, ограничиваем число:
900 < 1369 < 1600;
302 < 1369 < 402;Смотрим на последнюю цифру:
1369 → 9;
33; 37.Возводим в квадрат:
332 = (30 + 3)2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
372 = (40 − 3)2 = 1600 − 2 · 40 · 3 + 9 = 1369.Вот и ответ: 37.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]Ограничиваем число:
2500 < 2704 < 3600;
502 < 2704 < 602;Смотрим на последнюю цифру:
2704 → 4;
52; 58.Возводим в квадрат:
522 = (50 + 2)2 = 2500 + 2 · 50 · 2 + 4 = 2704;
Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.
Задача. Вычислите квадратный корень:
[Подпись к рисунку]Ограничиваем число:
3600 < 4225 < 4900;
602 < 4225 < 702;Смотрим на последнюю цифру:
4225 → 5;
65.Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:
652 = (60 + 5)2 = 3600 + 2 · 60 · 5 + 25 = 4225;
Все правильно. Записываем ответ.
Заключение
Многие спрашивают: зачем вообще считать такие корни? Не лучше ли взять калькулятор и не парить себе мозг?
Увы, не лучше. Давайте разберемся в причинах. Их две:
- На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
- Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут.
А при виде дробей у них вообще начинается истерика.
В общем, учитесь считать. И все будет хорошо. Удачи!
Смотрите также:
- Выделение полного квадрата
- Преобразование выражений с корнем — часть 1
- Знаки тригонометрических функций
- Задача B1 — время, числа и проценты
- Как решать задачу 18: графический подход
- Задача B2 про комиссию в терминале
Математика 1010 онлайн — Корни и радикалы
Математика 1010 онлайн — Корни и радикалыКафедра математики — Колледж науки — Университет Юты
Корни и радикалы
Корни и радикалы заслуживают отдельной главы и домашнего задания, потому что они часто встречаются в приложениях.
Пусть будет натуральное число , и пусть настоящий номер .
-й корень из это число, которое удовлетворяет Номер обозначается
Например, так как , и поскольку .
Символ называется радикальным символом , и выражение, включающее его, называется радикалом (выражением) .
Если тогда это квадратный корень из и число обычно опускается. Например,
Если , то это кубический корень из .Например, кубический корень из есть , и что из есть .
Если четно и положительно, то их два -th корни из , каждый из которых является отрицательным из другого. Например, поскольку есть два квадратных корня из . В в этом случае по соглашению символ означает положительный -й корень , и он называется основным (-м) корнем из .
Если отрицательно и нечетно, то есть только один -й корень, и он тоже отрицательный. Например,
На данном этапе мы не знаем -го корня, если он четный. и является отрицательным.Это приводит к теме комплексные числа, которые мы рассмотрим позже в курсе.
Радикалы — это всего лишь частные случаи сил , и вы может упростить ваше мышление, если помнить об этом факте:
Из этого наблюдения и свойств полномочия, которые
Решение радикальных уравнений
Уравнение с радикалами называется радикальным уравнением (естественно). Чтобы решить эту проблему, вы просто примените наш общий принцип:
Чтобы решить уравнение, выясните, что вас беспокоит, а затем сделайте то же самое. вещь по обе стороны уравнения, чтобы избавиться от него.
Чтобы избавиться от радикала, вы берете его в силу, которая изменит рациональный показатель натурального числа. Это сработает, если радикал находится на одной стороне уравнения сам по себе.
Давайте рассмотрим несколько простых примеров :
Предполагать
Мы поступаем следующим образом:Вот немного более сложная задача:
Мы получаемНаш последний пример показывает, как избавиться от более чем одного радикала:
Чтобы избавиться от квадратных корней, мы изолируем их и возводим в квадрат один за другим.
время:
В каждом случае мы проверяем наш ответ, подставляя его в исходный уравнение.Например, в последнем уравнении получаем:
Далее в курсе мы рассмотрим более сложные случаи радикальные уравнения.
Числовые значения
Все радикалы в приведенных выше примерах были натуральными числами. Это происходит только благодаря разумному выбору примеров. Часто корни встречающиеся в приложениях иррациональные числа с десятичными расширениями, которые никогда не повторяются и не заканчиваются. В следующей таблице приведены приблизительные значения несколько конкретных радикалов.
Некоторые радикалы (приблизительно)
Операции с квадратными корнями
Операции с квадратными корнями
Вы можете выполнять ряд различных операций с квадратными корнями. Некоторые из этих операций включают один подкоренный знак, в то время как другие могут включать много подкоренных знаков.
Следует внимательно изучить правила, регулирующие эти операции.
Под одним подкоренным знаком
Вы можете выполнять операции под одним подкоренным знаком .
Пример 1
Выполните указанную операцию.
Когда радикальные значения одинаковы
Вы можете прибавлять или вычитать квадратные корни сами по себе, только если значения под радикалом равны. Затем просто добавьте или вычтите коэффициенты (числа перед подкоренным знаком) и сохраните исходное число в подкоренном знаке.
Пример 2
Выполните указанную операцию.
Обратите внимание, что коэффициент 1 понимается в .
Когда радикальные значения отличаются
Вы не можете складывать или вычитать разные квадратные корни.
Пример 3
Сложение и вычитание квадратных корней после упрощения
Иногда после упрощения квадратного корня(ов) становится возможным сложение или вычитание.Всегда упрощайте, если это возможно.
Пример 4
Упростить и добавить.
Их нельзя добавить, пока они не будут упрощены.
Теперь, поскольку оба знака корня одинаковы,
Попробуйте упростить каждое из них.
Теперь, поскольку оба знака корня одинаковы,
Произведения неотрицательных корней
Помните, что при умножении корней знак умножения может опускаться.Всегда упрощайте ответ, когда это возможно.
Пример 5
Умножить.
Если каждая переменная неотрицательна,
Если каждая переменная неотрицательна,
Если каждая переменная неотрицательна,
Частные неотрицательных корней
Для всех положительных чисел
В следующих примерах предполагается, что все переменные положительны.
Пример 6
Разделить. Оставить все дроби с рациональными знаменателями.
Обратите внимание, что знаменатель этой дроби в части (d) иррационален. Чтобы рационализировать знаменатель этой дроби, умножьте его на 1 в виде
.Пример 7
Разделить. Оставить все дроби с рациональными знаменателями.
Первое упрощение:
или
Примечание: Чтобы оставить в знаменателе рациональный член, необходимо умножить и числитель, и знаменатель на , сопряженное знаменателя. Сопряжение двучлена содержит те же члены, но с обратным знаком. Таким образом, ( x + y ) и ( x – y ) сопряжены.
Пример 8
Разделить. Оставить дробь с рациональным знаменателем.
Экспоненты и корни: определение и примеры — видео и расшифровка урока
Показатель степени решения
Помните, что 53? Мы сказали, что это 5 * 5 * 5. Итак, 53 = 125.
Экспоненты заставляют числа взрываться очень быстро. Если у нас есть 124, мы хотим умножить четыре 12 вместе, или 12 * 12 * 12 * 12.
Первые 12 * 12 = 144
144 * 12 = 1,728
1,728 * 12 = 20,736
3 . 20 736.
Что произойдет, если основное число отрицательное, например -32? Мы делаем то же самое, но нам нужно включить отрицательный знак. Так что это -3 * -3, что положительно 9.
Если бы у нас было -33, это было бы -3 * -3 * -3. Отрицательное, умноженное на отрицательное, становится положительным. Но тогда положительный раз отрицательный отрицательный. Итак, -33 = -27.
До сих пор мы рассматривали только выражения с положительными показателями. Что делать, если показатель степени отрицательный? Вот один: 4-2. Что это просит нас сделать? Если положительный показатель степени означает умножение, то отрицательный показатель степени означает противоположность умножения, то есть деление.
Действительно, у нас просто не может быть отрицательного показателя степени. Чтобы сделать его положительным, подставим это же выражение (без знака минус) в качестве знаменателя дроби:
Есть еще одна ситуация с показателем степени: 20. Как мы можем перемножить ноль двоек вместе? Мы не можем. Но каждый раз, когда вы видите 0 в качестве показателя степени, знайте, что ответ равен 1. Итак, 20 = 1. Почему это так? Это называется правилом нулевого показателя. Это немного сложно объяснить, поэтому просто имейте в виду, что выражения с 0 для показателя степени равны 1.
Решение корней
Теперь, когда мы рассмотрели показатели степени, давайте поговорим о корнях. Начнем с простого:
Это называется корнем из 4 или квадратным корнем из 4. Чтобы упростить это, нам просто нужно найти, какое число умножить на 4. Мы знаем, что 2 * 2 = 4, поэтому квадратный корень из 4 равен 2.
Конечно, -2 * -2 = 4 тоже верно, но при использовании подкоренного символа мы придерживаемся положительного результата.
Вот еще один:
Какой квадратный корень из 81? Мы могли бы попробовать несколько чисел, чтобы узнать:
- 7 * 7 = 49
- 8 * 8 = 64
- 9 * 9 = 81
Вот оно! Квадратный корень из 81 равен 9.
Помните этот?
Это кубический корень из 27. На этот раз нам нужно число, равное 27 при трехкратном умножении. Вы можете снова использовать метод проб и ошибок: 2 * 2 * 2 = 8. Это слишком мало. 4 * 4 * 4 = 64. Это слишком много. 3 * 3 * 3 = 27. Вот именно! Таким образом, кубический корень из 27 равен 3.
Резюме урока
Показатель степени говорит нам, сколько числа будет умножено само на себя.Итак, если у нас есть 83, мы хотим умножить три восьмерки, или 8 * 8 * 8.
Корень в основном противоположен. Мы пытаемся найти число, которое мы умножаем само на себя определенное количество раз, чтобы получить число под знаком радикала.
Где вам нужна математика, квадратные корни или алгебра?
You are here: Главная → Статьи → Где нужны квадратные корниУчащиеся часто задаются вопросом, понадобятся ли им математические навыки в реальной жизни. Они, вероятно, осознают необходимость простой математики, такой как сложение, умножение, дроби и проценты, но в средней школе некоторые ученики начинают задаваться вопросом, зачем вообще изучать определенные понятия, такие как квадратные корни или целые числа.Потом, в 8-м или 9-м классе, при сдаче алгебры, многие подростки начинают задавать извечный вопрос: « Где мне когда-нибудь понадобится алгебра? »
Ответ: вам нужна алгебра в любой профессии, требующей высшего образования , например, информатика, электроника, инженерия, медицина (врачи), торговля, коммерческие аналитики, ВСЕ ученые, и т.
д. . Короче говоря, если кто-то даже подумывает о высшем образовании, он должен изучать алгебру. Вам также понадобится алгебра, чтобы сдать тест SAT или GED.
Изучение алгебры также способствует развитию логического мышления и навыков решения задач . Алгебра может повысить ваш интеллект! (Вообще-то, изучение любой математической темы — даже элементарной математики — может сделать это, если она преподносится и преподается так, чтобы развивать мышление человека.)
Вы можете признаться своему ученику (учащимся), что многие математические понятия, изучаемые в средней школе по алгебре, математическому анализу и т. д., , а не необходимы для каждой профессии.Понятия геометрии очень полезны, хотя почти для всех. Никогда не знаешь, построишь ли ты дом или сарай!
Однако решение НЕ изучать алгебру представляет собой большую проблему, потому что большинство подростков в средней школе не уверены, что они собираются делать во взрослой жизни. В таком случае им лучше изучать алгебру и изучать всю математику, которую они могут , чтобы их не остановили в карьере из-за того, что они ее не изучили.
Было много студентов, которые были горько разочарованы, когда после школы они не могли (по крайней мере, не сразу) пойти в интересующую их область обучения из-за отсутствия математических навыков.
И даже если студенты думают, что они знают, кем они хотят быть, сколько раз молодые люди меняли свое мнение? Даже мы, взрослые, не всегда знаем, какая работа или перемены в карьере нас ждут. В прошлом вы вполне могли рассчитывать на то, что станете домохозяйкой (девочка) или продолжите занятие отца (мальчик). В современном мире это не так. У молодежи больше свободы выбора, но обратная сторона этого в том, что им нужно много учиться, чтобы получить хорошее образование.Поскольку они не знают всего о своем будущем, гораздо лучше учиться, даже математике.
Чтобы еще больше помочь учащимся увидеть, как математика и алгебра используются в реальном мире, ознакомьтесь с бесплатными образцами рабочих листов из рабочих тетрадей Make It Real Learning. Эти книги сосредоточены на ответах на вопрос: «Когда я когда-нибудь буду это использовать?» и использовать РЕАЛЬНЫЕ данные в задачах.
Пример: где вам нужны квадратные корни?
Допустим, ваши ученики задаются вопросом: «Зачем мне знать, как вычислять квадратный корень из числа? Действительно ли квадратные корни нужны в реальной жизни вне уроков математики?»
Вот одна идея, которая демонстрирует важное применение квадратных корней в реальной жизни и в то же время позволяет учащимся задуматься о том, где нужна математика.Эта идея лучше всего сработает после того, как вы уже изучили понятие квадратных корней, но еще не коснулись теоремы Пифагора.
- Нарисуйте квадрат на доске или бумаге и проведите в него одну диагональ . Сделайте стороны квадрата равными, скажем, 5 единицам. Затем сделайте изображение прямоугольным треугольником, стерев две стороны квадрата. Затем спросите учащихся , как найти длину наибольшей стороны треугольника.
Студенты, вероятно, не смогут найти длину, если они еще не изучили теорему Пифагора — но это часть «игры».Вы когда-нибудь видели рекламу, в которой вы не могли бы сказать, что они рекламируют? Затем, через несколько недель, реклама изменится и покажет, о чем она.
Это делает вас любопытным.
Итак, дайте им подумать несколько минут (сначала не говорите им ответ). Надеюсь, это вызовет их интерес. Вскоре вы, вероятно, все равно будете изучать теорему Пифагора, так как в учебной программе она часто следует квадратным корням.
- Тогда переходите к вопросу: В каких профессиях или ситуациях вам нужно было бы найти самую длинную сторону прямоугольного треугольника , если вы знаете две другие стороны? Это может вовлечь их!
Ответ: в любой работе, связанной с треугольниками.Например, он нужен плотникам, инженерам, архитекторам, строителям, обмерщикам и разметчикам земли, художникам и дизайнерам.
Однажды я наблюдал за строителями, которые измеряли и отмечали на земле, где будет стоять здание. У них были отмечены стороны, и у них была рулетка для измерения диагоналей, и они спросили МЕНЯ, какой должна быть мера, потому что они не могли точно вспомнить, как это сделать. Эта диагональная проверка должна убедиться, что здание действительно будет прямоугольником, а не трапецией или какой-либо другой формой.
Теперь, помимо этого простого примера, учащихся должны понять ПОНЯТИЕ квадратного корня, чтобы понять других математических понятий . Изучение математики похоже на строительство блочной стены или здания: вам нужны блоки в нижней части, чтобы вы могли строить на них, и если вы оставите отверстия, вы не сможете строить на них.
Понятие квадратного корня является предпосылкой и связано со многими другими математическими понятиями:
- квадратный корень → уравнения 2-й степени → функции и графики
- квадратный корень → теорема Пифагора → тригонометрия
- квадратный корень → дробные показатели степени → функции и графики
- квадратный корень → иррациональные числа → действительные числа
См. также:
Онлайн-ресурсы по математике в реальной жизни — существует множество веб-сайтов, посвященных этому!
Где в быту нужны экспоненты?
Комментарии
Я всегда ненавидел математику, но никогда не думал, что она помешает мне получить высшее образование.Мне было так трудно пройти, что я просто бросил. Я еще не закончил…
Вам нужна математика, чтобы закончить среднюю школу и поступить в колледж.Эм
Какие математические навыки вам нужны, чтобы быть строителем?
Дэвид КуцЯ чувствую, что строителям, прежде всего, нужно хорошо знать свою геометрию, а также все, что касается измерения, площади и объема.
Тогда вам, вероятно, понадобится хорошее понимание процентов и соотношений. Может быть, вы смешиваете бетон, и вам нужен цемент, песок и вода в определенном соотношении.
И потом, строитель, вероятно, должен уметь много считать в уме и быстро вычислять приблизительные сметы для различных размеров, объемов, площадей, количества материалов и цен, а также уметь делать точные расчеты.
Почему медсестры изучают математику?
Райзел МагсалайИм необходимо хорошо разбираться в метрической системе (миллилитры, миллиграммы, килограммы и т.д.). Они должны знать, как рассчитать необходимое количество лекарства.
Например, если нужно дать 5 мг лекарства на 10 кг массы тела, то сколько потребуется этому больному? Или, скажем, 200 мг лекарства в виде таблетки эквивалентны определенному количеству того же лекарства в жидкой форме; потом посчитай сколько надо. Им особенно необходимо хорошо понимать десятичные числа и пропорции.
Я строитель мостов (плотник) в Сан-Диего, Калифорния, и хотел бы, чтобы я уделял больше внимания математике, когда я ходил в школу.Теперь каждый день — это небольшая математическая задача. Поэтому, чтобы сохранить свое конкурентное преимущество в этой высокооборотной отрасли, я решил освежить свои математические навыки.Адриан Чавира
Какая математика вам нужна, если вы врач? Это так же, как в уходе?
спасибо
ЭндиВрачам необходимо хорошее понимание химии, чтобы понимать работу человеческого организма и то, как действуют лекарства, а для этого им нужно хорошо знать математику. Врачам также необходимо логическое мышление и способность понимать научные тексты и рассуждения, и для этого также необходимы хорошие математические навыки.

В общем, будущие врачи должны изучать все возможные математические курсы в средней школе: алгебру, геометрию, тригонометрию, исчисление, статистику.
В каких работах используется теорема Пифагора?Несса
Разного рода инженерам, архитекторам, геодезистам, плотникам и другим специалистам по строительству, машинистам и т.д. нужна Теорема Пифагора. По сути, если вам нужны треугольники при проектировании чего-либо, вам нужна теорема Пифагора.
Вы будете удивлены уровнем математических знаний, необходимых для некоторых «ручных» работ.Я преподаю техническую математику в местном колледже, и студенты постоянно говорят мне, что они используют понятия тригонометрии и алгебры, которые мы изучаем в классе. Одна из самых приятных вещей, которые когда-либо говорил мне студент, это: «Я делаю это (имеется в виду триггер) на уроке механической обработки, но потом я прихожу сюда и учусь понимать это». Когда я преподавал техническую математику II, я был удивлен сложностью курса.
Электротехники делают много триггеров, векторов, комплексных чисел. Техническая математическая последовательность не является «легкой».Никогда не говорите ученику, что ему не понадобится математика в этой профессии. Вы просто не знаете.
Знак квадратного корня (создайте символ корня на клавиатуре)
Квадратный корень √ — это математический текстовый символ (о его значении мы поговорим позже), который люди писали со времен, когда была разработана кодировка ASCII. И вы можете набрать его прямо с клавиатуры. Я покажу вам, как это сделать, используя различные методы в зависимости от вашей операционной системы и вкусов.
Математика ≠ ≤ ≥ ∫ ½ 6 Σ √ π Математика корня
Квадратный корень из некоторого числа «А» — это число «Х», такое, что «Х», умноженный на себя, будет «А».
Каждое положительное число «A» имеет два квадратных корня: положительный и отрицательный ±√a. Хотя главный квадратный корень положительного числа является лишь одним из двух его квадратных корней, обозначение «квадратный корень» часто используется для обозначения главного квадратного корня.Для положительного «A» главный квадратный корень также может быть записан в виде экспоненты, как A 1/2 .
Но корней больше, чем просто квадратных корней! Можно сказать, что N-й корень числа «X» — это число «R», которое при возведении в степень «N» равно «X» и обозначается как Rⁿ = X. Также в случае, если эти корни имеют степень пары (2, 4, 6…), они будут иметь 2 решения, положительное и отрицательное. А те, у которых непарная мощность (1, 3, 5…) будет иметь только одно положительное решение.
Я приведу вам несколько примеров использования клиренса.
Квадратный корень из 9 равен ±3 (обозначается как ±√9 = 3), потому что (±3) 2 = 9 (3·3 = 9)
Корень пятой степени из 34 равен 2,024397... (обозначается как ⁵√34 = 2,024397…), потому что 2,024397 5 = 34
Как ввести символ квадратного корня
Выберите свою систему, чтобы узнать.
ОкнаСостояния сдвига
Настройте раскладку клавиатуры в Windows, чтобы вы могли вводить все дополнительные символы так же просто, как и любой другой текст.Настройка занимает около 5-10 минут, но вы будете печатать как босс. С помощью этой техники вы можете назначить математический символ квадратного корня √ и любые другие текстовые символы на клавиатуре.
Карта символов
CharMap позволяет вам просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере. Вы можете ввести символ квадратного корня, используя его.
МакЭмодзи на iOS (iPhone, iPad и iPod touch)
Простой и красивый способ узнать, как добавить виртуальную клавиатуру для символов Emoji, видимых в виде маленьких картинок.Сама клавиатура предустановлена на вашем устройстве iOS, поэтому вам не нужно ничего скачивать или покупать.
Средство просмотра клавиатуры
Палитра персонажей
Палитра символов позволяет просматривать и использовать все символы и символы, включая знак квадратного корня, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.
линуксС клавиатуры
Карта персонажей
Карта символов позволяет просматривать и использовать все символы и символы, доступные во всех шрифтах (некоторые примеры шрифтов: «Arial», «Times New Roman», «Webdings»), установленных на вашем компьютере.Это также может помочь вам найти коды Unicode для ввода символов с клавиатуры.
HTML-кодНиже приведен список объектов HTML и JavaScript для символа квадратного корня. В Javascript вы должны писать как = «этот символ \u2669», если вы хотите включить специальный символ в строку.
Понимание логарифмов и корней | Бретт Берри | Math Hacks
Бревна и корни — нет, я не про деревья. Я говорю о математическом роде.Бьюсь об заклад, вы думаете,
«Корни, хорошо. Но логарифмы? Разве это не тема алгебры 2?!»
Да, это так! Но кто сказал, что мы не можем научиться этому прямо сейчас? Зачем откладывать на потом то, что можно узнать сегодня? Carpe diem , я прав? Но сначала давайте сделаем краткий обзор. Помните эту диаграмму показателей из второго урока?
Число, которое мы умножаем само на себя, называется основанием . Количество раз, которое мы умножаем на себя, называется степенью или степенью .
Вот несколько примеров показателей степени, чтобы освежить вашу память.
Нам нужно найти операцию, которая возвращает основание из решения экспоненциального уравнения. Вот тут-то и появляются корни.
Предположим, что вместо того, чтобы находить квадрат 9, что равно 81, мы хотим выяснить, какое число, умноженное само на себя, равно 81.
из 81?
Это равно 9, потому что девять в квадрате — это восемьдесят один.
Мы можем извлечь квадратный корень из любого неотрицательного числа , но только квадратные числа дают целые числа. Так что сначала ознакомьтесь с ними. Вот несколько для начала:
Теперь немного терминологии.
Индекс корня необязательный для квадратных корней. Квадратные корни часто записывают:
Индекс необходим только для того, чтобы различать более высокие индексированные корни, такие как кубические корни, четвертые корни, пятые корни и т. д.
Кубические корни просят вас найти число, которое при умножении само на себя три раза по дает подкоренное число, например:
Корни четвертой степени просят вас найти число, которое при умножении на себя четыре раза по дает подкоренное число.
Корни пятой степени просят вас найти число, которое при умножении на себя пять раз дает подкоренное число.
Опять же, вы можете взять любой корень любого неотрицательного числа (а в некоторых случаях и отрицательных чисел), но для многих чисел вам понадобится калькулятор, так как ответы иррациональны. Приведенные выше примеры — это «хорошие дела», которые часто встречаются!
Что, если бы мы захотели найти показатель степени в показательном уравнении? Другими словами, мы хотим изменить возведение в степень.Например, как решить эту проблему?
Поскольку мы запомнили общие степени и корни, мы легко идентифицируем решение как 2, поскольку 6 в степени 2 равно 36. приведенное выше выражение с использованием логарифмической записи , или log для краткости.
Прочтите: « логарифм, основание шесть, из тридцати шести равно 2 ».Терминология:
Другой способ взглянуть на это — спросить:
« Сколько шестерок нужно перемножить, чтобы получить 36? ”
Логарифм определяет количество повторных умножений.
Все просто. Вот еще несколько примеров.
Спасибо за прочтение!
❤ ОСТАВАЙТЕСЬ НА СВЯЗИ ❤
Будьте в курсе всех новостей Math Hacks!
Инстаграм | Фейсбук | Twitter
Таблица квадратов и квадратных корней
Что такое квадратные корни и зачем они нам?
Квадратный корень числа — это число, которое при умножении само на себя дает желаемое значение. Так, например, квадратный корень из 49 равен 7 (7×7=49).Сам процесс умножения числа на называется возведением в квадрат .
Числа, квадратные корни которых являются целыми числами (точнее, целыми положительными числами), называются совершенными квадратными числами. Числа с десятичными знаками не являются идеальными квадратными корнями.
Все положительные числа имеют положительное число в качестве квадратного корня, называемое главным, и отрицательное число. Все эти числа известны как действительные числа.
Все отрицательные числа будут иметь комплексное число в качестве квадратного корня.
Комплексное число – это число, умноженное на , т.е. i — это «мнимый» квадратный корень из -1. Оно называется воображаемым, но для математиков оно существует.
Как извлекать квадратные корни?
Уравнение квадратного корня записывается с использованием подкоренного знака или подкоренного символа (?). Число, из которого мы хотим получить корень, находится после или под хвостом радикала (например, ?3, если мы хотим найти квадратный корень из 3). Число после корня называется подкоренным.На калькуляторе вместо радикала вы можете увидеть «sqrt».
Для чего мы используем квадратные корни?
Возможно, это сложно представить, но квадратные корни — одни из самых полезных чисел. Функции квадратного корня очень важны для физических уравнений всех видов. Они также ценны для статистики; статистики постоянно используют квадратные корни при анализе корреляции между различными точками данных.
Список идеальных квадратов
Используйте эту таблицу, чтобы найти квадраты и квадратные корни чисел от 1 до 100 .
Вы также можете использовать эту таблицу для оценки квадратных корней из больших чисел.
- Например, если вы хотите найти квадратный корень из 2000 , просматривайте средний столбец , пока не найдете число, ближайшее к 2000. Число в среднем столбце, ближайшее к 2000, равно . 2025 .
- Теперь посмотрите на число слева от 2025 , чтобы найти его квадратный корень. Квадратный корень из 2025 равен 45 .
- Следовательно, приблизительный квадратный корень из 2000 равен 45 .
Чтобы получить более точное число, вам придется использовать калькулятор (44,721 — более точный квадратный корень из 2000).
Готовитесь к длительной учебной сессии? Возможно, вы заинтересованы в нашем списке лучших стульев стола 2020.
6 квадратный root 1 1 1. 000
2 4 1.414 3 9 1,732 4 16 2,000 5 25 2,236 6 36 2,449 7 49 49 2.646 8 64 64 2,828 3000 9 81 3000 10 100 3. 162
11 121 3,317 12 144 3,464 13 169 3,606 14 196 3,742 15 225 225 3.873 16 256 4000 17 289 4. 123
4.123 18 324 4.243 19 361 4,359 20 400 4,472 21 441 4,583 22 484 4,690 23 529 529 4.796 576 576 4899 4899 25 625 50033336 26 676 5. 099
27 729 5,196 28 784 5,292 29 841 5,385 30 900 5,477 31 961 961 5.568 32 9 1 024 5,024 5.657 33 1089 5,089 5. 745
34 5156 5.831 35 +1225 5,916 36 1296 6,000 37 1 369 6,083 38 тысячу четыреста сорок четыре +6,164 39 1,521 6.245 9039 6.24540 1 600 6325 6. 325
41 1 681 603 60334 42 6.764 6.481 43 тысяча восемьсот сорок-девять +6,557 44 +1936 6,633 45 2,025 6,708 46 2116 6,782 47 2,209 6036 48 2404 2428 6,928 6. 928
9034 9034 49 2401 7014 9036 50 7.071 51 2601 7,141 52 2704 7,211 53 2809 7,280 54 2916 7,348 55 3 025 7.416 7.416 56 3,136 7. 483
7.483 57 3,249 7.550 58 3364 7.616 59 3481 7,681 60 3600 7,746 61 3721 7,810 62 3844 7,874 63 3 969 7937 7937 64 4 096 4 096 9096 65 4225 8. 062
8.062 66 4 356 8.124 67 4489 8,185 68 4624 8,246 69 4761 8,307 70 4900 8,367 71 5 041 803336 8.426 9039 9272 5,484 5,485 8036 73 5 329 5,344 9. 544
74 5476 8.602 75 5625 8,660 76 5776 8,718 77 5929 8,775 78 6084 8,832 79 6,241 803336 80339 80 6 400 8,444 8. 944
89444 81 6 561 9.000 903482 9.055 83 6889 9,110 84 7056 9,165 85 7225 9,220 86 7396 9,274 7 87 7 569 9.327 9039 9.3279036 88 7,644 7. 381
9.381 9.381 9039 9.3819 921 7 921 9.434 9.434
9036 9100 9.487 91 8281 9,539 92 8464 9,592 93 8649 9,644 94 8836 9,695 95 9 025 9. 747
96 9 216 9,216 9216 9216 9.798 97 97 9 409 9,849 9.84998 9 604 9.899 999 9039 99 99 9 9.950 99 6 9,801 9.950 9.950 9 10 000 10 000 10.000 Примечание: Квадратные корни в этой таблице округляются до ближайшей тысячи.

 2$ оканчиваются нулем. Это единственная общая цифра наборов (2) и (3). Но в этом случае каждое из чисел m и n должно делиться на 5, а это противоречит несократимости дроби $m/n$.
2$ оканчиваются нулем. Это единственная общая цифра наборов (2) и (3). Но в этом случае каждое из чисел m и n должно делиться на 5, а это противоречит несократимости дроби $m/n$. x = -1$ На множестве целых чисел есть единственное решение -1. На множестве вещественных чисел решений нет, так операция возведения в степень определена только для положительных оснований.
x = -1$ На множестве целых чисел есть единственное решение -1. На множестве вещественных чисел решений нет, так операция возведения в степень определена только для положительных оснований.
 Таким образом, например, это может быть сделано с комплексными числами, с кватернионными числами (расширение действительных чисел) или даже с матрицами.
Таким образом, например, это может быть сделано с комплексными числами, с кватернионными числами (расширение действительных чисел) или даже с матрицами.
 При извлечении алгебраического корня слева и справа получаются четыре возможных варианта, из которых различных только два — икс равен плюс-минус единице. Теперь такой вопрос — скорее, качественный. При решении уравнения икс в квадрате равен единице можно использовать как арифметический, так и алгебраический корни. Решение при этом получается одно и то же: икс равен плюс-минус единице. Но почему так получается? Ведь при использовании арифметического корня мы просто отбрасываем минус единицу при извлечении корня из единицы. Формально я понимаю, почему все же решение получается полное — потому что при извлечении корня из икса в квадрате получаем модуль икса, оттуда минус и вылезает. Но это формально. А как КАЧЕСТВЕННО объяснить тот факт, что мы не теряем решение, хотя сначала чем-то там пренебрегаем?
При извлечении алгебраического корня слева и справа получаются четыре возможных варианта, из которых различных только два — икс равен плюс-минус единице. Теперь такой вопрос — скорее, качественный. При решении уравнения икс в квадрате равен единице можно использовать как арифметический, так и алгебраический корни. Решение при этом получается одно и то же: икс равен плюс-минус единице. Но почему так получается? Ведь при использовании арифметического корня мы просто отбрасываем минус единицу при извлечении корня из единицы. Формально я понимаю, почему все же решение получается полное — потому что при извлечении корня из икса в квадрате получаем модуль икса, оттуда минус и вылезает. Но это формально. А как КАЧЕСТВЕННО объяснить тот факт, что мы не теряем решение, хотя сначала чем-то там пренебрегаем? n = a$% поступают так: выбирают из них один (который нам больше нравится, обозначим его за $%s_0$%), а остальные выражают через него. Как выбирают? Если можно — берут положительный корень (его называют арифметическим). Если нет положительного — действительный (отрицательный). Если нет и действительного, никакой и не выбирают (в «школьной» математике говорят, что корня нет).
n = a$% поступают так: выбирают из них один (который нам больше нравится, обозначим его за $%s_0$%), а остальные выражают через него. Как выбирают? Если можно — берут положительный корень (его называют арифметическим). Если нет положительного — действительный (отрицательный). Если нет и действительного, никакой и не выбирают (в «школьной» математике говорят, что корня нет). Также есть группы в VK, Одноклассниках и Facebook : всё для математического просвещения!
Также есть группы в VK, Одноклассниках и Facebook : всё для математического просвещения! Однако, утверждать, что √(-1) = i, как многие привыкли, не стоит, потому что:
Однако, утверждать, что √(-1) = i, как многие привыкли, не стоит, потому что: Главное отличие — в той самой «мнимой единице».
Главное отличие — в той самой «мнимой единице».
 ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM.
ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM. Нам нужен наименьший из этих четырех корней x. При этом другие три корня это 2k — x, 2k-1 + x и 2k — 2k-1 — x
Нам нужен наименьший из этих четырех корней x. При этом другие три корня это 2k — x, 2k-1 + x и 2k — 2k-1 — x Параллельно считаем на каждой итерации обратное к корню.
Параллельно считаем на каждой итерации обратное к корню.
 Если брать аналогию с четвертой степенью, то этот знак должен был отождествлять трехкратное извлечение квадратного корня, то есть для этого нужно было поставить три квадратика. Однако, это обозначение занято кубическим корнем.
Если брать аналогию с четвертой степенью, то этот знак должен был отождествлять трехкратное извлечение квадратного корня, то есть для этого нужно было поставить три квадратика. Однако, это обозначение занято кубическим корнем. Однако некоторое время знак корня писали разрывая верхнюю черту, а именно так: .
Однако некоторое время знак корня писали разрывая верхнюю черту, а именно так: .
 Таким образом, мы сократим диапазон поиска до 10 чисел;
Таким образом, мы сократим диапазон поиска до 10 чисел; Например, 3364:
Например, 3364: Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:
Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например: Возведем их в квадрат:
Возведем их в квадрат: Значит, это и есть корень.
Значит, это и есть корень.
 А при виде дробей у них вообще начинается истерика.
А при виде дробей у них вообще начинается истерика. -й корень из это число, которое удовлетворяет
Номер обозначается
-й корень из это число, которое удовлетворяет
Номер обозначается
 время:
время: Следует внимательно изучить правила, регулирующие эти операции.
Следует внимательно изучить правила, регулирующие эти операции.



 Конечно, -2 * -2 = 4 тоже верно, но при использовании подкоренного символа мы придерживаемся положительного результата.
Конечно, -2 * -2 = 4 тоже верно, но при использовании подкоренного символа мы придерживаемся положительного результата. Корень в основном противоположен. Мы пытаемся найти число, которое мы умножаем само на себя определенное количество раз, чтобы получить число под знаком радикала.
Корень в основном противоположен. Мы пытаемся найти число, которое мы умножаем само на себя определенное количество раз, чтобы получить число под знаком радикала. д. . Короче говоря, если кто-то даже подумывает о высшем образовании, он должен изучать алгебру. Вам также понадобится алгебра, чтобы сдать тест SAT или GED.
д. . Короче говоря, если кто-то даже подумывает о высшем образовании, он должен изучать алгебру. Вам также понадобится алгебра, чтобы сдать тест SAT или GED. Было много студентов, которые были горько разочарованы, когда после школы они не могли (по крайней мере, не сразу) пойти в интересующую их область обучения из-за отсутствия математических навыков.
Было много студентов, которые были горько разочарованы, когда после школы они не могли (по крайней мере, не сразу) пойти в интересующую их область обучения из-за отсутствия математических навыков.

 Мне было так трудно пройти, что я просто бросил. Я еще не закончил…
Мне было так трудно пройти, что я просто бросил. Я еще не закончил…  Например, если нужно дать 5 мг лекарства на 10 кг массы тела, то сколько потребуется этому больному? Или, скажем, 200 мг лекарства в виде таблетки эквивалентны определенному количеству того же лекарства в жидкой форме; потом посчитай сколько надо. Им особенно необходимо хорошо понимать десятичные числа и пропорции.
Например, если нужно дать 5 мг лекарства на 10 кг массы тела, то сколько потребуется этому больному? Или, скажем, 200 мг лекарства в виде таблетки эквивалентны определенному количеству того же лекарства в жидкой форме; потом посчитай сколько надо. Им особенно необходимо хорошо понимать десятичные числа и пропорции. 
 Электротехники делают много триггеров, векторов, комплексных чисел. Техническая математическая последовательность не является «легкой».Никогда не говорите ученику, что ему не понадобится математика в этой профессии. Вы просто не знаете.
Электротехники делают много триггеров, векторов, комплексных чисел. Техническая математическая последовательность не является «легкой».Никогда не говорите ученику, что ему не понадобится математика в этой профессии. Вы просто не знаете. Каждое положительное число «A» имеет два квадратных корня: положительный и отрицательный ±√a. Хотя главный квадратный корень положительного числа является лишь одним из двух его квадратных корней, обозначение «квадратный корень» часто используется для обозначения главного квадратного корня.Для положительного «A» главный квадратный корень также может быть записан в виде экспоненты, как A 1/2 .
Каждое положительное число «A» имеет два квадратных корня: положительный и отрицательный ±√a. Хотя главный квадратный корень положительного числа является лишь одним из двух его квадратных корней, обозначение «квадратный корень» часто используется для обозначения главного квадратного корня.Для положительного «A» главный квадратный корень также может быть записан в виде экспоненты, как A 1/2 . .. (обозначается как ⁵√34 = 2,024397…), потому что 2,024397 5 = 34
.. (обозначается как ⁵√34 = 2,024397…), потому что 2,024397 5 = 34 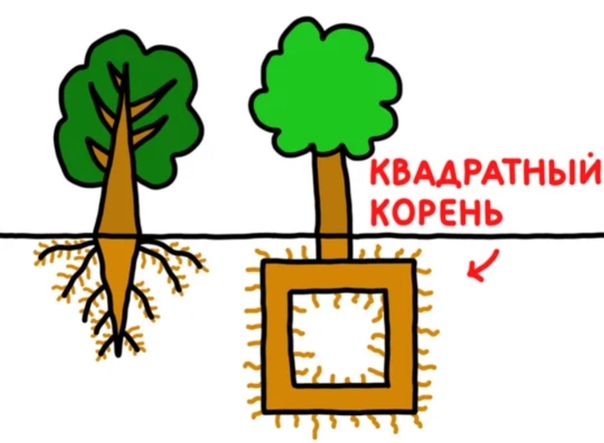 Сама клавиатура предустановлена на вашем устройстве iOS, поэтому вам не нужно ничего скачивать или покупать.
Сама клавиатура предустановлена на вашем устройстве iOS, поэтому вам не нужно ничего скачивать или покупать.
 из 81?
из 81? 
 Все просто. Вот еще несколько примеров.
Все просто. Вот еще несколько примеров. Комплексное число – это число, умноженное на , т.е. i — это «мнимый» квадратный корень из -1. Оно называется воображаемым, но для математиков оно существует.
Комплексное число – это число, умноженное на , т.е. i — это «мнимый» квадратный корень из -1. Оно называется воображаемым, но для математиков оно существует.
 000
000 162
162 123
123 099
099 745
745 325
325 928
928 483
483 062
062 544
544 944
944 381
381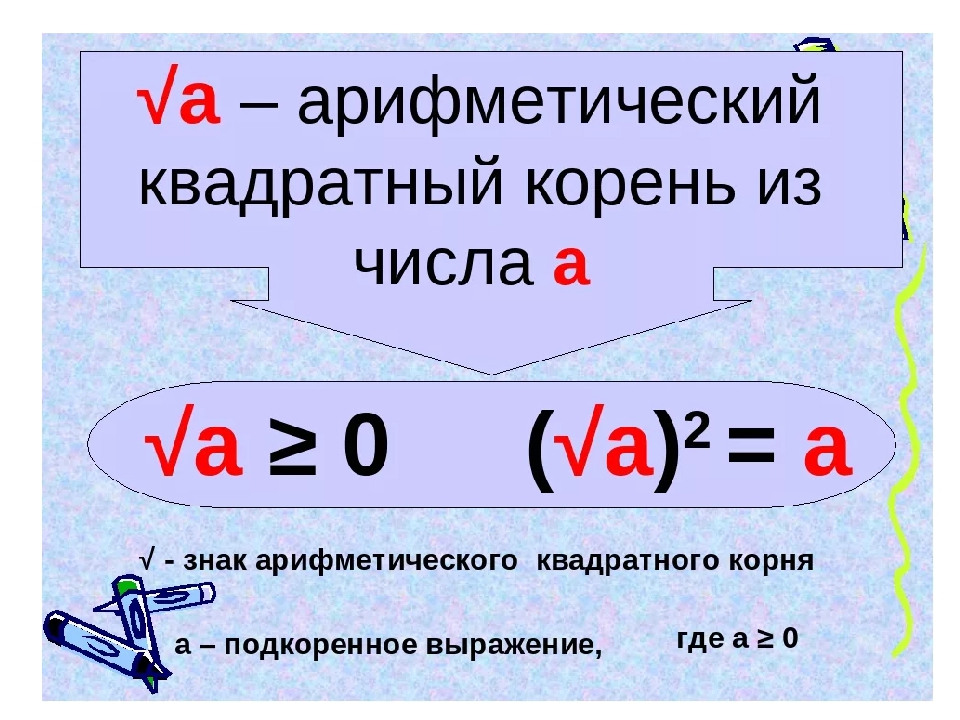 747
747