Математические модели: Математические модели — урок. Информатика, 6 класс.
Урок 10. математические модели. стохастические модели — Информатика — 11 класс
Информатика, 11 класс. Урок № 10.
Тема — Математические модели. Стохастические модели
Цели и задачи урока:
- Сформировать представление о понятии математической модели, познакомиться с моделированием и его этапами.
- Сформировать умение строить модели для прикладных задач (в математике и биологии).
- Научиться пользоваться математическим моделированием для решения биологической задачи «Жертва-хищник».
На уроке вы узнаете:
- Основные этапы математического моделирования.
- Отличие между детерминированными и стохастическими моделями.
- Как решаются методами математического моделирования биологические задачи на численность хищников и травоядных.
Важную роль в изучении закономерностей объективного мира играет математическое моделирование. Наряду с теорией и практикой математическое моделирование является одним из методов познания.
Одним из основоположников математического моделирования в России был академик Александр Андреевич Самарский. Согласно его высказыванию математическое моделирование состоит в замене исходного объекта его образом — математической моделью. И дальнейшее изучение этой модели с помощью реализуемых на компьютере вычислительных алгоритмов. Достоинствами такого метода является:
— Дешевизна процесса, по сравнению с экспериментальными исследованиями.
— Исследование различных вариантов.
— Анализ вклада различных факторов и влияния различных условий.
— Возможность исследовать объекты вообще не доступные для экспериментального наблюдения, например, черные дыры.
Основным инструментом математического моделирования является проведение вычислительного эксперимента (как теоремы и доказательства в теории, наблюдения и измерения в практике).
Проведение вычислительного эксперимента требует четкого плана действия. Можно выделить три этапа вычислительного эксперимента: 1) модель, 2) алгоритм, 3) программа.
На первом этапе формируется некий теоретический эквивалент — модель. Модель может быть как функциональной, то есть в ней описаны уравнения всех процессов явления, так и вариационной, то есть известен отклик системы на некоторые входные данные.
Модель может быть детерминированной, то есть модель описана ясными соотношениями, а может быть стохастической, когда явление описывается вероятностными функциями.
Модель может быть прямая, это когда уравнения заданы и надо найти их решения, а может быть обратная, заключающаяся в том, что надо найти по решению характеристики этой системы.
При любом моделировании существует иерархия моделей. То есть ряд моделей, учитывающих с большей или с меньшей подробностью процессы. Особенно это важно в многофакторных задачах. Например, экологические задачи, где можно учитывать очень много процессов. Но не стоит думать, что если модель учитывает наибольшее количество факторов, то это лучше. Ничего подобного, так как увеличение количества факторов ведет к усложнению модели, а значит решение ее может занимать не оправданно большой объем вычислений.
Вторым этапом математического моделирования является разработка алгоритма, который должен удовлетворять трем принципам:
- Проверка адекватности модели.
- Экономичности по времени решения.
- Адаптивности, то есть применимости к этой модели и вычислительным средствам.
Третий этап состоит в создании программы по алгоритму, которая в свою очередь должна быть экономичной и адаптивной.
Давайте рассмотрим этапы математического моделирования на примере биологической задачи «Жертва-хищник». Рассмотрим математическую модель совместного существования двух биологических видов (популяций) типа «хищник — жертва».
Пусть два биологических вида совместно обитают в изолированной среде. Среда стационарна и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов, который будем называть жертвой. Другой вид — хищник также находится в стационарных условиях, но питается лишь особями первого вида.
Это могут быть: зайцы и волки, львы и зебры, щуки и караси, микробы и антитела, лиса и курица, кошки и мыши, и другие.
Обозначим через N0 начальную численность, а через Ni — численность в i -й год с момента наблюдения.
Так как количество умерших и родившихся животных пропорционально численности, то годовой прирост можно найти как:
kр*Ni–kc*Ni, где kри kc — коэффициенты рождаемости и смертности, определяемые экспериментально. Тогда в i+1 год количество животных можно выразить через Ni:
Ni+1=Ni+kp·Ni–kc·Ni=(1+K)·N
Если K=0 (рождаемость равна смертности), K>0 (количество животных увеличивается),
K<0 (животные вымирают).
Эта модель называется моделью Мальтуса.
Однако такая модель адекватна только при небольших интервалах наблюдения. Поэтому введем максимальную численность популяции L и построим модель таким образом, чтобы в момент, когда численность приближалась к L, коэффициент прироста уменьшался, а значит рост замедляется:
Поэтому введем максимальную численность популяции L и построим модель таким образом, чтобы в момент, когда численность приближалась к L, коэффициент прироста уменьшался, а значит рост замедляется:
, где k — начальный коэффициент (при нулевой численности).
Очень часто животные разводятся искусственно, например, в рыбоводческих хозяйствах или на зверофермах. Тогда в эту модель можно ввести понятие допустимый отлов (R):
Давайте рассмотрим, взаимодействие двух видов: «хищник» и «жертва».
Пусть встреча хищника и жертвы пропорциональна произведению их численностей NiZi. В результате каждый год будет гибнуть bNNiZi жертв, а хищников появляться bZNiZi. Коэффициенты bN и bZ находятся экспериментально.
Тогда численность популяций будет находиться из системы:
Попробуйте самостоятельно получить графики зависимостей численности жертв и хищник для L=100, N 8, bN=0.01 и bZ=0.012, k=0,5. Для этого:
8, bN=0.01 и bZ=0.012, k=0,5. Для этого:
- Откройте Excel.
- В столбце введите значения i от 0 до 30.
- В ячейку C2 и D2 введите начальное значение численности жертвы и хищника соответственно.
- В ячейку В2 введите формулу для нахождения коэффициента прироста и скопируйте ее до строки 32.
- В ячейку С3 введите формулу зависимости численности жертвы и скопируйте ее до строки 32.
- В ячейку D3 введите формулу зависимости численности хищника и скопируйте ее до строки 32.
- Начертите точечный график зависимостей столбцов C и D от A.
Как видно из графика в течении 20 лет происходит «переходный период», когда их численность довольно сильно меняется. Далее наступает равновесие — количество каждого вида остается постоянным. Таким образом в природе соблюдается равновесие.
* Более подробно о математическом моделировании в биологии вы можете посмотреть в учебнике К. Ю. Поляков, Е. А. Еремин. Информатика, 11 класс, ч.1, М: БИНОМ, 2016.
Информатика, 11 класс, ч.1, М: БИНОМ, 2016.
Математические модели в биологии
Профессор Биологического факультета МГУ Галина Юрьевна Ризниченко
Добро пожаловать на мой сайт, посвящённый математическому моделированию в биологии.
Я — доктор физико-математических наук, профессор Биологического факультета Московского государственного университета имени М. В. Ломоносова, где читаю курс лекций «Математические модели в биологии» и межфакультетский учебный курс «Модели нелинейного мира».
Математические модели в биологии
Математические и компьютерные методы занимают важное место в современных биологических исследованиях. Без них было бы невозможным выполнение таких глобальных проектов, как геном человека, расшифровка пространственной структуры сложных биомакромолекул, дистанционная диагностика, компьютерное моделирование новых эффективных лекарств («драг-дизайн»), планирование мероприятий по предотвращению распространения эпидемий, анализ экологических последствий работы промышленных объектов, биотехнологические производства и многое другое.
Многие ученые высказывали мысль о том, что область знаний становится наукой только тогда, когда выражает свои законы в виде математических соотношений. В соответствии с этим самая «научная» наука — физика — наука о фундаментальных законах природы, математика для нее — естественный язык. В биологии, для которой предметом изучения являются индивидуальные живые системы, дело обстоит сложнее. Только в XX веке появились экспериментальные биохимия, биофизика, молекулярная биология, микробиология, вирусология, которые изучают воспроизводимые
В связи с индивидуальностью биологических явлений говорят именно о математических моделях в биологии (а не просто о математическом языке). Слово модель здесь подчеркивает то обстоятельство, что речь идет об абстракции, идеализации, математическом описании скорее не самой живой системы, а некоторых качественных характеристик протекающих в ней процессов. При этом удается сделать и количественные предсказания, иногда в виде статистических закономерностей. В отдельных случаях, например, в биотехнологии, математические модели, как в технике, используются для выработки оптимальных режимов производства.
При этом удается сделать и количественные предсказания, иногда в виде статистических закономерностей. В отдельных случаях, например, в биотехнологии, математические модели, как в технике, используются для выработки оптимальных режимов производства.
В основу сайта положен учебный курс «Математические модели в биологии», читаемый автором для студентов второго курса Биологического факультета Московского государственного университета имени М. В. Ломоносова.
профессор МГУ имени М. В. Ломоносова,
доктор физико-математических наук
Галина Юрьевна Ризниченко
Математические модели в междисциплинарных исследованиях
О профессии
Областью профессиональной деятельности магистра по направлению «Прикладная математика и информатика» является научно-исследовательская работа с акцентом на междисциплинарные исследования: построение математических моделей и исследование их аналитическими методами, разработка алгоритмов, методов, программного обеспечения, создание, поддержка и администрирование информационно-коммуникационных систем, а также работа в общеобразовательных организациях, профессиональных образовательных организациях и организациях дополнительного образования. Успешность профессиональной деятельности в этих областях основана на элегантности и универсальности математических моделей, мощи современных компьютерных систем и эффективности новейших информационных технологий.
Успешность профессиональной деятельности в этих областях основана на элегантности и универсальности математических моделей, мощи современных компьютерных систем и эффективности новейших информационных технологий.
Выпускники востребованы во всех организациях и структурах, где используются компьютерные технологии. Они могут заниматься исследовательской деятельностью, способны решать актуальные задачи фундаментальной и прикладной математики, совершенствовать и реализовывать новые математические методы решения прикладных задач, разрабатывать математические модели и проводить их анализ при решении задач в области профессиональной деятельности, комбинировать и адаптировать существующие информационно-коммуникационные технологии для решения задач в области профессиональной деятельности с учетом требований информационной безопасности.
Учебный процесс
Программа магистратуры ставит перед собой цель сформировать у будущих специалистов современные знания в сфере решения теоретических и прикладных задач, воспитать в студентах склонность к исследовательской деятельности. Обязательная часть программы включает в себя фундаментальную подготовку по математическим дисциплинам, изучение современных математических методов и активную научно-исследовательскую работу.
Обязательная часть программы включает в себя фундаментальную подготовку по математическим дисциплинам, изучение современных математических методов и активную научно-исследовательскую работу.
В ходе обучения по программе студенты изучают следующие дисциплины:
Первый год обучения:
Базовая часть:
«Иностранный язык в профессиональной деятельности магистра»;
«История и методология математики и информатики»;
«Компьютерные технологии в науке и образовании»;
«Прикладные задачи математического моделирования»;
«Научное программирование»;
«Непрерывные математические модели»;
«Технологии вычислительного эксперимента».
Вариативная часть:
«Нелокальные краевые задачи»;
«Высокопроизводительные вычислительные процессы в задачах математической физики»;
«Нелинейные задачи математической физики»;
«Нейронные сети»;
«Математические модели в экономике и экологии».
Блок дисциплин по выбору:
Модуль по выбору 1:
«Математические модели теории упругости»;
«Системы управления с последействием»;
«Нелокальные задачи математической физики»;
«Дополнительные главы теории игр и экономическое моделирование».
Модуль по выбору 2:
«Математические модели сплошных сред»;
«Функционально-дифференциальные уравнения»;
«Дополнительные главы вычислительных методов»;
«Аналитико-численные методы для задач гидродинамики».
Второй год обучения:
Базовая часть:
«Иностранный язык в профессиональной деятельности магистра»;
«Дополнительные главы математического моделирования»;
«Нейронные сети»;
Блок дисциплин по выбору:
Модуль по выбору 1:
«Нелокальные задачи математической физики»;
«Дополнительные главы теории игр и экономическое моделирование».
Модуль по выбору 2:
«Функционально-дифференциальные уравнения»;
«Дополнительные главы вычислительных методов»;
«Аналитико-численные методы для задач гидродинамики».
Значительное время отводится научно-исследовательской деятельности студента, работе в команде исследователей подготовке выпускной работы. Весь учебный процесс и научные исследования проводятся в мультимедийных аудиториях и научно-учебных лабораториях и центрах Математического института имени академика С. М. Никольского, а также в компьютерных классах, оснащенных современным оборудованием и программным обеспечением для проведения вычислительных экспериментов.
М. Никольского, а также в компьютерных классах, оснащенных современным оборудованием и программным обеспечением для проведения вычислительных экспериментов.
Практика
Предусмотренная учебным планом научно-исследовательская работа и практики проводятся на базе Научного центра нелинейных задач математической физики Математического института имени академика С.М. Никольского.
Для магистров ежегодно проводятся мастер-классы ведущих экспертов и представителей работодателей реальных секторов экономики, российских и зарубежных ученых из ведущих вузов и научных центров. Действует общемосковский научный семинар по дифференциальным и функционально-дифференциальным уравнениям, в котором принимают участие крупные российские и зарубежные математики, преподаватели, студенты, аспиранты и докторанты. Математический институт им. С.М. Никольского тесно сотрудничает с МГУ им. М.В. Ломоносова, Математическим институтом им. В.А. Стеклова РАН, Вычислительным центром РАН им. А.А. Дородницына, Московским авиационным институтом.
Карьера
Полученные знания и практические навыки позволяют выпускникам работать в научных и исследовательских центрах. Выпускники востребованы в авиационной и космической отрасли, а благодаря педагогической подготовке также в сфере образования. Кроме того, многие из них работают в финансовой сфере: в банках, крупнейших страховых компаниях, инвестиционных и пенсионных фондах.
Примеры профессий:
— научный сотрудник в научно-исследовательском институте;
— программист, системный администратор в ИТ-предприятиях и подразделениях коммерческих организаций;
— финансовый аналитик и прикладной программист в финансовых подразделениях государственных и коммерческих организаций;
— преподаватель в высшем учебном заведении.
Имеется возможность продолжения обучения в аспирантуре по направлениям:
— 01.06.01 «Математика и механика»;
— 09.06.01 «Информатика и вычислительная техника».
Математические модели в инвестиционных банках
На лекциях и семинарах сотрудники ТехЦентра рассмотрят математические модели, активно используемые ведущими мировыми инвестиционными банками для решения практических задач. Необходимое условие конкурентоспособности в инвестиционно-банковской сфере — знание и использование классических и современных методов математического моделирования.
Необходимое условие конкурентоспособности в инвестиционно-банковской сфере — знание и использование классических и современных методов математического моделирования.
Методы тесно связаны с классическими разделами математических знаний, такими как :
· теория оптимизации
· математическая статистика
· теория вероятностей
Задачи и методы их решения, рассматриваемые в рамках данного курса, проиллюстрированы практическими численными примерами. Примеры решения задач реализованы в виде ноутбуков на языке Python.
Обзор актуальных прикладных задач в инвестиционно-банковской деятельности проводится на основе опыта одного из ведущих глобальных инвестиционных банков – Deutsche Bank AG.
Программа:
Введение.История создания и развития инвестиционных банков. Роль инвестиционных банков в современной мировой экономике.
Расчет честной цены биржевых и внебиржевых инструментов.Отличия биржевой и внебиржевой торговли. Брокеры и дилеры. Валютный рынок: споты, форварды, фьючерсы, свопы. Честная цена финансового инструмента и ее расчет. Примеры и практические задания.
Брокеры и дилеры. Валютный рынок: споты, форварды, фьючерсы, свопы. Честная цена финансового инструмента и ее расчет. Примеры и практические задания.
Построение кривых доходности. Постановка задачи восстановления кривой доходности из наблюдаемых на рынке инструментов. Метод Bootstrap, его преимущества и недостатки. Модификации метода Bootstrap. Примеры и практические задания.
Математические модели опционов.Бизнес-мотивация для опционов. Подход к построению математических моделей. Геометрическое броуновское движение. Модель ценообразования опционов Блэка-Шоулза-Мертона. Обзор вычислительных методов, применяемых для расчетов опционов. Применение метода Монте-Карло, биномиальная модель оценивания опционов. Понятие ожидаемой волатильности и необходимость его моделирования. Поверхности волатильности. Примеры и практические задания.
Оценки рисков.Сложные виды опционов, используемые на практике. Примеры и практические задания.
Математические модели кредитного риска. Кредитный риск контрагента. Модель банкротства контрагента. Рынок кредитных инструментов, свопы на банкротство контрагента. Примеры и практические задания.
Кредитный риск контрагента. Модель банкротства контрагента. Рынок кредитных инструментов, свопы на банкротство контрагента. Примеры и практические задания.
Рыночный риск. Интегральные меры риска: ValueatRisk(VaR) иExpectedShortfall(ES). Методы оценки VaRи ES. Исторические симуляции. Метод моментов и метод Монте-Карло.
По средам 16:40-19:30 ауд. R205
Математическое моделирование и вычислительная математика
April 10, 2017 9:16am
Математик Александр Шапеев о методах оптимизации, численном оценивании неопределенностей и быстрых алгоритмах решения
Что такое моделирование? Моделирование — это создание модели, то есть отражения реальности, более простого, чем реальность. Либо это упрощение другой, более сложной модели: моделью человека может быть рисунок человека, может быть манекен, может быть мышь. Разные модели в разных случаях могут быть более или менее полезны. Например, если дизайнер сделал новый пиджак и хочет понять, хорош он или плох, он использует манекен в качестве модели человека. Если биолог проверяет новое лекарство, то он использует мышь как первую модель человека. Это примеры нематематических моделей. Интересующей нас математической моделью будет либо трехмерная геометрия человека, если речь идет о дизайне одежды, либо дифференциальные уравнения, которые будут описывать эволюцию концентрации лекарства в организме человека или мыши.
Если биолог проверяет новое лекарство, то он использует мышь как первую модель человека. Это примеры нематематических моделей. Интересующей нас математической моделью будет либо трехмерная геометрия человека, если речь идет о дизайне одежды, либо дифференциальные уравнения, которые будут описывать эволюцию концентрации лекарства в организме человека или мыши.
С моей точки зрения, человеком, внесшим наибольший вклад в математическое моделирование, был сэр Исаак Ньютон. Он предложил первые модели, которые используются до сих пор и которые похожи на математические модели, используемые сейчас в науке. Например, известные законы движения, когда Ньютон сказал, что, моделируя любое тело как точку, имеющую массу, мы можем посчитать ускорение, если мы знаем силу, которая действует на эту точку. Зная ускорение, мы знаем скорость; зная скорость, мы можем посчитать траекторию. Это были математические модели, очень похожие на те, которые мы используем сейчас. В молекулярном моделировании мы решаем те же самые уравнения Ньютона, которые были придуманы почти 400 лет назад. Также Ньютон придумал математический аппарат, дифференциальные уравнения и описание всех этих явлений гладкими функциями.
Это были математические модели, очень похожие на те, которые мы используем сейчас. В молекулярном моделировании мы решаем те же самые уравнения Ньютона, которые были придуманы почти 400 лет назад. Также Ньютон придумал математический аппарат, дифференциальные уравнения и описание всех этих явлений гладкими функциями.
Давайте рассмотрим пример моделирования упругого материала ― возьмем линейку. Если мы можем сделать модель линейки, мы надавливаем на нее, и тогда линейка будет отклоняться, мы можем предсказывать форму отклонения этой линейки. Линейка описывается обычной функцией отклонения ее от вертикального положения. При этом, если подумать, модель дифференциального уравнения есть упрощение реальности, хотя первокурсники, возможно, со мной не согласятся. Но если мы рассмотрим пластиковую линейку, то она состоит из органических полимеров ― цепочек углерода, водорода, связанных между собой ковалентными связями, и это очень сложно описать. Зато очень просто описать линейку как непрерывную функцию. При этом линейку из любого материала мы можем описывать теми же самыми уравнениями. В линейке из стали металлические связи, ее структура совершенно другая, но описывается она теми же уравнениями упругости.
При этом линейку из любого материала мы можем описывать теми же самыми уравнениями. В линейке из стали металлические связи, ее структура совершенно другая, но описывается она теми же уравнениями упругости.
После того как мы написали уравнения, мы написали модель, и на этом наша задача математического моделирования выполнена. Если это простые уравнения, мы их можем решить и точно сказать, что формой линейки будет либо парабола, либо полином третьей степени. Но когда это более сложная система (мост), на нем случайным образом расположены машины, мы уже не можем точно написать формулу, какая у этого моста будет упругая деформация. Но мы все равно хотим предсказать, упадет мост или нет, и это делали еще за 100 лет до возникновения компьютеров. Это делали средствами математического анализа, то есть выписывались уравнения, мы их не могли решить, но доказывали свойства про решение этого уравнения ― например, что напряжения в мосте будут меньше пороговых значений.
Пятьдесят лет назад, когда появились первые вычислительные машины, правила игры поменялись. Теперь уравнения, эти математические модели мы можем решать на компьютере, и это дает нам огромные преимущества. Мы можем очень быстро решать для какого-то дизайна моста, какие в нем будут напряжения, и делать выводы о том, хороший это дизайн или плохой.
Теперь уравнения, эти математические модели мы можем решать на компьютере, и это дает нам огромные преимущества. Мы можем очень быстро решать для какого-то дизайна моста, какие в нем будут напряжения, и делать выводы о том, хороший это дизайн или плохой.
Вернемся к простой модели линейки. Если в математической модели она описывается непрерывной функцией, то в компьютере — системой точек и отрезков между ними. При этом точки оказывают сопротивление изгибам отрезков, за счет чего моделируется упругое сопротивление материала. Когда мы дискретизировали модель, перешли к модели дискретных точек, мы, с одной стороны, несколько усложнили модель. Но с другой стороны, теперь эти точки мы можем представить на компьютере. Если у нас линейку представляют 9 точек, то дифференциальные уравнения становятся системой линейных уравнений 9 на 9, которую мы можем легко решить на компьютере. На современных компьютерах мы можем легко решать системы с миллионом или даже миллиардом неизвестных. Это меняет правила игры в том смысле, что мы теперь проводим не натурные эксперименты моста, а делаем дизайн моста на компьютере, проводим численный эксперимент, дальше смотрим, какие у нас напряжения, и пытаемся что-то оптимизировать.
Я упомянул три элемента математического моделирования в вычислительной математике, которые сейчас идут рука об руку: собственно математическое моделирование — построение модели, дискретизация и линейная алгебра, которая позволяет решать дискретные системы уравнений. Четвертая часть — это оптимизация. Методы оптимизации позволяют нам полностью доверить компьютеру, вместо того чтобы руками исправлять дизайн моста, доводить мост до нужных параметров и потом пытаться минимизировать его стоимость. Мы начинаем с того, что делаем дизайн моста, и компьютер нам выдает уже оптимальное решение по напряжениям в мосте и его стоимости.
Про вычислительный эксперимент, который я сейчас описал, говорят, что он стал ни много ни мало третьим способом познания мира. Если первыми двумя были теория и эксперимент, которые еще восходят как минимум к древним грекам, то теперь появилось численное моделирование, которое не является, строго говоря, ни тем ни другим. Теория дает нам математическую модель, и мы как будто делаем эксперимент на компьютере. У нас есть ошибки, погрешности, как и в численных экспериментах, есть знания о том, как этот численный эксперимент провести. Те данные, которые мы получаем, лежат между тем и другим, но ни тем ни другим не являются.
У нас есть ошибки, погрешности, как и в численных экспериментах, есть знания о том, как этот численный эксперимент провести. Те данные, которые мы получаем, лежат между тем и другим, но ни тем ни другим не являются.
Численное моделирование становится все более важной частью современных технологий производства. Особенно это касается нового технологического уклада, в котором изделия проектируются за несколько часов на компьютере, а не на бумаге и чертежах, после этого эти изделия можно распечатать на 3D-принтере и тут же отвезти заказчику или проверить, как они работают. Простые изделия вроде украшений или элементов интерьера уже могут разрабатываться дизайнером, который находится в своем доме на курорте Краснодарского края. Утром, пока вода еще не согрелась, он делает дизайн предмета интерьера, на который получил заказ, и отправляет в соответствующий город, в Воронеж, молодым ребятам, которые напечатают его ночью в гараже на 3D-принтере, и уже утром заказчик получит изделие.
Вычислительные методы при этом играют следующую роль: тест на прочность или другие тесты можно провести прямо на компьютере у дизайнера автоматически. Для этого не нужно будет изготавливать изделие и его тестировать, и работа идет в этом направлении. Даже с такими сложными изделиями, как машины, вагоны, все равно нужно проводить натурные эксперименты, но сейчас тенденция идет к тому, чтобы большую часть экспериментов по тестированию и сертифицированию проводить на компьютере. Это сокращает время тестирования и производства данных изделий.
Для этого не нужно будет изготавливать изделие и его тестировать, и работа идет в этом направлении. Даже с такими сложными изделиями, как машины, вагоны, все равно нужно проводить натурные эксперименты, но сейчас тенденция идет к тому, чтобы большую часть экспериментов по тестированию и сертифицированию проводить на компьютере. Это сокращает время тестирования и производства данных изделий.
Задачи, о которых я рассказывал, например проектирование изделий, были в области вычислительной науки, а стали вычислительными технологиями ― вполне стандартной вещью, которой пользуются инженеры. Акцент в научных разработках сместился в соседнюю область. Например, сейчас активно разрабатываются вычислительные методы для uncertainty quantification, численное оценивание неопределенностей. Это направление о том, что даже если все технологические процессы выдержаны, то изделия, которые получаются, все равно разные, и нужно оценивать то, как эти разные изделия повлияют на работу системы в целом, чтобы быть уверенными, что система даже с изделиями, которые чуть-чуть разные и являются элементами этой системы, работает так, как надо.
Еще одно направление ― это многомасштабное моделирование, и оно заключается в том, что кроме моделирования изделия в целом мы моделируем его микроструктуру. Опять вернемся к линейке. Если мы точно знаем, из какого полимера она состоит, как волокна этого полимера друг на друга зацеплены, то мы можем узнать упругие свойства этой линейки. В отношении линейки это нам не очень интересно, но для современных композитных материалов это очень важно уметь рассчитывать. В современных производственных технологиях стирается разница между материалом и изделием, у нас уже умеют печатать на 3D-принтере изделия из композитных материалов. Композитный материал — это армирующие волокна, матрица. Если мы посмотрим в микроскоп или даже в увеличительное стекло на материал, то мы увидим там много неоднородностей. Если мы хотим это моделировать классическими способами, то для каждого нового такого материала нужно проводить эксперимент, чтобы узнать, какие параметры нужно вставлять в модель. Но с многомасштабным моделированием мы можем моделировать и рассчитывать эту микроструктуру, после чего сразу рассчитывать поведение изделия в целом. Таким образом, для этих новых материалов нам необязательно проводить много экспериментов.
Таким образом, для этих новых материалов нам необязательно проводить много экспериментов.
Еще одно направление ― это быстрые солверы, или быстрые алгоритмы решения. В качестве примера можно привести приложение персонализированной медицины. Когда компания Siemens изготавливает аппарат для МРТ головного мозга, она в своем дата-центре рассчитывает его параметры и вместе с этим аппаратом поставляет софт, которым он пользуется, для того чтобы обработать данные МРТ. Софт делается для среднего человека, и он не совсем оптимален. Сейчас существуют подходы, которые, я думаю, появятся через 3–5 лет, когда катушки, которые создают магнитное поле, будут подстраиваться под пациента. Это, например, может сокращать время исследования с 45 минут до 10, что очень здорово. Но для этого нужно рассчитывать, как система с подвинутыми катушками влияет на головной мозг в данном случае. Если у нас будут более быстрые алгоритмы, то мы можем это рассчитывать прямо на ходу. И может быть, даже мы сможем дойти до такого состояния, когда мы можем очень точно составлять карту головного мозга отдельного человека и проводить диагностику его способностей просто по магнитно-резонансной томографии.
Александр Шапеев
PhD in Mathematics, доцент Центра по научным и инженерным вычислительным технологиям для задач с большими массивами данных Сколковского института науки и технологий (Сколтех)
Источник: postnauka.ru
Математические модели красноярских ученых предскажут, как не допустить кризис
К реализуемому в Красноярске проекту «Развитие динамических математических моделей прогноза критических социально-экономических ситуаций и создание эффективных численных методов решения таких моделей» в качестве ведущих ученых будут привлечены профессора Шухуа Чжан из Тяньцзиньского университета финансов и экономики (Китай) и Александр Лапин из Казанского федерального университета. Исследование будет выполняться в Международной лаборатории математического моделирования, которая была создана ранее в Федеральном исследовательском центре «Красноярский научный центр СО РАН» совместно с Сибирским федеральным университетом и Тяньцзиньским университетом финансов и экономики. Проект Российского научного фонда активизирует ее деятельность, которая также поддерживается китайской стороной.
Проект Российского научного фонда активизирует ее деятельность, которая также поддерживается китайской стороной.
Руководитель проекта, член-корреспондент РАН, доктор физико-математических наук, руководитель научного направления «математическое моделирование» ФИЦ КНЦ СО РАН и научный руководитель Научно-образовательного комплекса в области экономики и управления СФУ Владимир Шайдуров рассказал о его основных задачах и потенциальных практических приложениях.
В чем основная цель проекта?
Мы планируем развивать применяемые в международной практике сложные математические модели для оптимизации расходов и доходов экономической деятельности, достижения заданных социально-экономических целей, прогноза критических ситуаций для экономики отдельных регионов и отраслей.
Сейчас во всем мире и в нашей стране сложилась критическая социально-экономическая ситуация. Как модели, развитием которых вы планируете заниматься, могут помочь преодолевать подобные случаи?
В настоящий момент эти динамические модели, например, могли бы помочь оценить эффективность разных стратегий региональной борьбы с коронавирусом от полной изоляции населения (с замедлением региональной экономики) до осознанных и поддержанных профилактических мер (с активной региональной экономикой) в зависимости от имеющегося состояния и условий. Конечно, такие модели требуют настройки на региональные условия и социальные реакции. Это очевидно из сравнения хода эпидемий коронавируса в разных странах.
Конечно, такие модели требуют настройки на региональные условия и социальные реакции. Это очевидно из сравнения хода эпидемий коронавируса в разных странах.
Необходимо пояснить, что подходы успешного математического моделирования подобных задач пришли из статистической физики, сохранив название «игр среднего поля». «Игра» огромного числа физических частиц, на первый взгляд, состоит в их хаотическом взаимодействии между собой и с электрическим или магнитным полем. Но после предельного перехода, который делают на основании теории вероятности, можно описать эту сложную среду с помощью дифференциальных уравнений с небольшим числом заданных или настраиваемых параметров.
Аналогичный предельный переход делается в социально-экономической сфере для большого числа агентов, покупателей, предприятий и пользователей, мотивируемых личной и коллективной выгодой. Ясно, что настраиваемые параметры и элементы получаемых дифференциальных задач различны для физических и социально-экономических задач. Но такой подход уже используется для принятия решений в экономике, финансах и страховании, хотя настройка этих моделей путем анализа больших данных еще развивается.
Но такой подход уже используется для принятия решений в экономике, финансах и страховании, хотя настройка этих моделей путем анализа больших данных еще развивается.
Если немного пофантазировать, каким будет будущее в плане прогноза и управления критическими социально-экономическими ситуациями? Какова будет роль науки в вопросах принятия решений?
В ходе штатного, не кризисного, социально-экономического состояния математические модели будут давать все более точные результаты, предоставляющие разные варианты для принятия решений. Такие модели будут полезны и для оценки приближения кризисных ситуаций, когда назревает исчерпание кого-либо лимитирующего ресурса, включая недостаток финансовых или организационных средств.
В будущем наука будет играть ту же роль, что и сейчас: это глаза и память для принятия решений. Роль глаз в том, чтобы видеть глубже ‒ лучше понимать причины складывающейся ситуации и дальше ‒ прогнозировать долгосрочные последствия принимаемых решений. А функция науки как памяти в том, чтобы накапливать знания об аналогичных ситуациях и использовать их для принятия решений в будущем.
А функция науки как памяти в том, чтобы накапливать знания об аналогичных ситуациях и использовать их для принятия решений в будущем.
Примеры математической модели управляющей компании
Примеры математической модели управляющей компании
- Страницы / Pages
- 98-108
Аннотация
Рассмотрены две математические модели предприятия сферы жилищно-коммунального хозяйства на примере управляющей компании. Первая модель построена на основе балансовых уравнений предприятия, учтены и систематизированы доходы и расходы управляющей компании. Вторая — представлена в виде задачи оптимального управления. Элементом оптимизации стала дисконтированная прибыль предприятия, а элементом управления — затраты на модернизацию жилого фонда. Обе модели использовались для исследования экономического функционирования управляющих компаний
Список литературы
1. Бабина В. В. Проблемы развития рынка жилищно-коммунальных услуг // Известия Санкт-Петербургского университета экономики и финансов. 2011. Вып. 1.
Бабина В. В. Проблемы развития рынка жилищно-коммунальных услуг // Известия Санкт-Петербургского университета экономики и финансов. 2011. Вып. 1.
2. Евсеева С. А. Проблема несогласованности интересов субъектов хозяйствования в системе менеджмента организаций ЖКХ // Проблемы современной экономики. 2012. № 4.
3. Акифьева Л. В. Зарубежный опыт управления жилищно-коммунальным комплексом // Вестник НГИЭИ. 2012. Т. 1, Вып. 1.
4. Сыропятова С. Б. Зарубежный опыт управления ЖКХ // Вестник Волжского университета им. В. Н. Татищева. 2012. Вып. 21.
5. Волгин Л. Н. Оптимальное дискретное управление динамическими системами. М., 1986.
6. Евтушенко Ю. Г. Методы решения экстремальных задач и их применение в системах оптимизации. М., 1982.
7. Цирлин А. М. Математические модели и оптимальные процессы в макросистемах. М., 2006.
8. Егорова Н. Е., Митрофонова И. Н., Шеин А. М., Королева Н. В. Имитационная модель предприятия ЖКХ как инструмент анализа тарифно-ценового механизма // Аудит и финансовый анализ. 2007. № 6.
2007. № 6.
9. Панжар М. И. Экономико-математическое моделирование жилищно-коммунального комплекса // Экономика строительства и городского хозяйства. Донбасская национальная академия строительства и архитектуры. 2006. Т. 2, № 4. С. 207—213.
10. Петрушевский Ю. Л. Задачи моделирования ценового механизма в жилищно-коммунальном хозяйстве // Экономика промышленности. Институт экономики промышленности НАН Украины. 2012. Т. 57—58, № 1/2. С. 165—169.
11. Хомякова Т. С., Гурлеев В. Г. Разработка организационно-математического моделирования при оценке экономического состояния и деятельности предприятий жилищно-коммунального хозяйства // Аудит и финансовый анализ. 2012. № 2.
12. Вишнева Е. В. Программа оптимизации распределения платежей за ЖКУ : свидетельство о государственной регистрации программы для ЭВМ № 2012615285 от 13.06.2012 г.
13. Вишнева Е. В. Программа анализа затрат предприятия ЖКХ : свидетель¬ство о государственной регистрации программы для ЭВМ № 2013615002 от 27. 05.2013 г.
05.2013 г.
14. Вишнева Е. В., Олиферчик А. А., Толстель О. В., Черных С. В. Некоторые применения генетических алгоритмов // Гибридные и синергетические интеллектуальные системы: теория и практика : матер. 1-го международного симпозиума. Калининград. Ч. 2. С. 384—395.
15. Алексеев В. М., Тихомиров В. М., Фомин С. В. Оптимальное управление. М., 1979.
16. Милютин А. А., Илютович А. Е., Осмоловский Н. П., Чуканов С. В. Оптимальное управление в линейных системах. М., 1993.
17. Понтрягин Л. С., Болтянским В. Г., Гамкрелидзе Р. В., Мищенко Е. Ф. Мате¬матическая теория оптимальных процессов. М., 1969.
18. Chiang A. C. Elements of dynamic optimization. N. Y. ; L. ; P. ; Tokyo ; Toronto : McGraw-Hill Inc., 1992.
19. IZabczyk J., Da Prato G., Jakubczyk B., et. al. Mathematical Control Theory // Trieste: The Abdus Salam International Centre for Theoretical Physics, 2002.
20. Sontag E. D. Mathematical Control Theory. N. Y., 1998.
Математические модели
Математику можно использовать для «моделирования» или представления того, как устроен реальный мир.
Пример: сколько места внутри этой картонной коробки?
Мы знаем три измерения:
- л (длина),
- ш (ширина) и
- ч (высота),
и формула объема прямоугольного параллелепипеда:
Объем = л × ш × ч
Итак, у нас есть (очень простая) математическая модель пространства в этом ящике.
Точно?
Модель не такая, как настоящая.
В нашем примере мы не учли толщину картона и многие другие вещи из «реального мира».
Но, надеюсь, достаточно хорош, чтобы быть полезным .
Если мы платим за объем отправляемой коробки, мы можем сделать несколько измерений и узнать, сколько платить. Это также может быть полезно, когда мы решаем, какую коробку купить, когда нам нужно упаковать вещи. Так что модель полезная! |
Но, возможно, нам нужно больше точности, нам может понадобиться отправлять сотни коробок каждый день, и толщина картона имеет значение. Итак, давайте посмотрим, сможем ли мы улучшить модель :
.Картон имеет толщину «t» и мы измеряем снаружи коробки. Сколько места внутри?
Внутренние размеры необходимо уменьшить на толщину каждой стороны:
- Внутренняя длина л-2т
- Внутренняя ширина w-2t ,
- Внутренняя высота h-2t
и теперь формула:
Внутренний объем = (л-2т) × (вес-2т) × (ч-2т)
Теперь у нас есть лучшая модель .Все еще не идеально (учитывали ли мы потраченное впустую пространство, потому что мы не могли аккуратно упаковать вещи и т. д.), но лучше.
д.), но лучше.
Таким образом, модель не является реальностью, но должна быть достаточно хороша, чтобы быть полезной.
Игра с моделью
Теперь у нас есть модель, мы можем использовать ее по-разному:
Пример: Ваша компания использует коробки размером 200x300x400 мм, толщина картона 5 мм.
Кто-то предлагает использовать картон толщиной 4 мм… насколько это лучше?
Сравним два тома:
- Текущий объем = (200-2×5) × (300-2×5) × (400-2×5) = 21 489 000 мм 3
- Новый объем = (200-2×4) × (300-2×4) × (400-2×4) = 21 977 088 мм 3
Это изменение:
(21 977 088-21 489 000)/21 489 000 ≈ 2% больше объема
Итак, модель полезная .Это дает нам понять, что мы получим на 2% больше места внутри коробки (при тех же внешних размерах).
Но есть еще вещи «реального мира», о которых нужно подумать, например, «достаточно ли он силен?»
Мыслить ясно
Чтобы построить математическую модель, нам также нужно ясно мыслить о фактах!
Пример: на нашей улице собак вдвое больше, чем кошек.
 Как мы запишем это в виде уравнения?
Как мы запишем это в виде уравнения?- Пусть D = количество собак
- Пусть C = количество кошек
Сейчас … в том, что: 2D = C
или должно быть: D = 2C
Подумайте хорошенько!
Правильный ответ: D = 2C
( 2D = C — распространенная ошибка, так как вопрос пишется «дважды… собаки… кошки»)
Вот еще один:
Пример: Вы руководитель восьмичасовых сменных рабочих. Недавно они сократили время перерыва на 10 минут, но общая производительность не улучшилась.
На первый взгляд моделировать нечего, так как изменений в производстве не было.
Но подождите… они работают на 10 минут больше, но производят то же количество, так что производительность в час должна была снизиться!
Допустим, они работали 7 часов (420 минут):
Изменение производительности в час = 410/420 = 0,976. ..
..
Сокращение более чем на 2%
Но что еще хуже: на первые несколько часов смены не влияет более короткое время перерыва, так что в конце смены оно может быть сокращено на 4 или 5%.
Вы могли бы порекомендовать:
- просмотр производительности за каждый час смены
- пробовать разное время перерыва, чтобы посмотреть, как оно повлияет на производительность
Большой пример: самый экономичный размер
Хорошо, давайте попробуем построить и использовать математическую модель для решения реального вопроса.
Ваша компания собирается делать свои коробки!
Было решено, что коробка должна содержать 0.02м 3 (0,02 м3, что равно 20 л) гаек и болтов.
Коробка должна иметь квадратное основание и двойную толщину сверху и снизу.
Картон стоит $0,30 за квадратный метр.
Вы сами выбираете наиболее экономичный размер.
Шаг первый: Нарисуйте эскиз!
Это помогает набросать то, что мы пытаемся решить!
| Основание квадратное, поэтому мы будем использовать букву «w» для обеих длин |
Коробка имеет 4 стороны, двойные верх и низ. Коробку можно вырезать так (но это, вероятно, сложнее): |
Шаг второй: Составьте формулы.
Игнорирование толщины для этой модели:
Объем = w × w × h = w 2 ч
А нам говорят, что объем должен быть 0.02м 3 :
ш 2 ч = 0,02
Области:
Площадь четырех сторон = 4 × ширина × в = 4wh
Площадь двойных вершин и оснований = 4 × w × w = 4w 2
Всего необходимо картона:
Площадь картона = 4wh + 4w 2
Шаг третий: создайте единую формулу стоимости
Нам нужна единая формула стоимости:
Стоимость = 0 долларов США. 30 × Площадь картона
30 × Площадь картона
= 0,30 долл. США × (4 Вт·ч + 4 Вт 2 )
И это стоимость, когда мы знаем ширину и высоту .
С этим может быть сложно работать… функция с двумя переменными.
Но мы можем сделать проще! Потому что ширина и высота уже связаны с объемом:
Объем = w 2 ч = 0,02
… который можно переставить на…
ч = 0.02/в 2
… и это можно ввести в формулу стоимости …
Стоимость = 0,30 долл. США × (4w× 0,02/w 2 + 4w 2 )
А сейчас стоимость напрямую связана с шириной только .
С небольшим упрощением получаем:
Стоимость = 0,30 долл. США × (0,08/w+ 4w 2 )
Шаг четвертый: Постройте и найдите минимальную стоимость
Что заговорить? Ну, формула имеет смысл только для ширины больше нуля, и я также обнаружил, что для ширины больше 0. 5 стоимость становится все больше и больше.
5 стоимость становится все больше и больше.
Итак, вот график этой формулы стоимости для ширины от 0,0 м до 0,55 м :
Участок y= 0,3(0,08/x+4x 2 )
x ширина, y стоимость
Просто на глаз вижу, что стоимость достигает минимума примерно на (0,22, 0,17) . Другими словами:
- при ширине около 0,22 м (значение x),
- минимальная стоимость около $0.17 за коробку (значение Y).
На самом деле, глядя на график, ширина может быть где угодно между 0,20 и 0,24 без существенного влияния на минимальную стоимость.
Шаг пятый: рекомендации
Теперь, используя эту математическую модель, вы можете рекомендовать:
- Ширина = 0,22 м
- Высота = 0,02/ш 2 = 0,02/0,22 2 = 0,413 м
- Стоимость = 0 долларов США.
 30 × (0,08/w+ 4w 2 ) = 0,30 USD × (0,08/0,22+ 4×0,22 2 ) = 0,167 USD
30 × (0,08/w+ 4w 2 ) = 0,30 USD × (0,08/0,22+ 4×0,22 2 ) = 0,167 USD
Или около 16,7 цента за коробку
Но подойдет любая ширина от 0,20 м до 0,24 м.
Вы также можете предложить улучшения для этой модели:
- Включая стоимость клея/скоб и сборки
- Учитывайте отходы при вырезании коробки из картона.
- Подходит ли эта коробка для упаковки, транспортировки и хранения?
- Любые другие идеи!
Предсказание будущего
Математические модели также можно использовать для прогнозирования поведения в будущем.
Пример. Компания по производству мороженого отслеживает, сколько мороженого продается в разные дни.
Сравнивая это с погодой в каждый день, они могут построить математическую модель продаж по сравнению с погодой .
Затем они могут прогнозировать будущие продажи на основе прогноза погоды и решать, сколько мороженого им нужно приготовить … заранее!
Компьютерное моделирование
Математические модели могут быть очень сложными, поэтому математические правила часто записываются в компьютерные программы для создания компьютерной модели.
Поиграйте с простой компьютерной моделью отражения внутри эллипса
или с анимацией одиночного маятника или двойного маятника.
Более сложные примеры включают:
- Прогноз погоды
- Экономические модели (прогнозирование процентных ставок, безработицы и т. д.)
- Общественное здравоохранение против инфекционных заболеваний
- Модели поведения больших конструкций под нагрузкой (мосты, небоскребы и т. д.)
- Многие другие …
Если вы станете экспертом в любой из них, у вас будет работа на всю жизнь!
Математическая модель – обзор
Определите, предполагая линейную, взаимосвязь между следующими переменными:
- (a)
Груз L поднимаемый машиной для приложенного усилия 9043.

E в N 9.5 11,8 14,1 16,3 18,5 л в N 10 15 20 25 30 - (б)
сопротивление R провода разной длины L того же провода.
2.1 4.3 6.3 8.3 10.5 0.5 1.0 1.0 1.5 2.0 2.5
Определите, в какой форме переменные в следующих уравнениях должны принимать при наличии, чтобы дать прямые графики и какие значения градиента и перехвата будет иметь.
- (a)
Период колебаний T маятника связан с длиной L маятника уравнением:
- (b)
Расстояние с , пройденное равномерно ускоряющимся объектом за время t , определяется уравнением:
s=ut+12at2
, где u и- (в)
Э.д.с. e , генерируемое термопарой при температуре θ, определяется уравнением;
e=aθ+bθ2
, где a и b — константы.- (d)
Сопротивление R резистора при температуре h определяется уравнением:
- (f)
Давление p газа и его объем V связаны уравнением:
pV=k
, где k – постоянная.- (г)
Прогиб y свободного конца кантилевера под действием собственного веса w на единицу длины связан с его длиной L уравнением:
y=wL84
где w , E и I — константы.

Измерено сопротивление R лампы при ряде напряжений В и получены следующие данные. Покажите, что закон связи сопротивления с напряжением имеет вид R = ( a / V ) + b и определите значения a и b .
| R в Q. | 70 | 62 | 59 | 56 | 55 |
| V в V | 60 | 100 | 140 | 200 | 240 |
Сопротивление R проводов из определенного материала измерено для диапазона диаметров проводов d и получены следующие результаты.Покажите, что отношение имеет вид R = ( a / d 2 ) + b и определите значения a и b .
| R в Q. | 0,25 | 0,16 | 0,10 | 0,06 | 0,04 |
| д в мм | 0,80 | 1,00 | 1,25 | 1,60 | 2,00 |
Объем V газа измерен при ряде давлений p и получены следующие результаты. Покажите, что отношение имеет вид V = ap b и определите значения a и b .
Покажите, что отношение имеет вид V = ap b и определите значения a и b .
| V в м 3 | 13,3 | 11,4 | 10,0 | 8,9 | 8,0 |
| р в l0 5 Па | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 |
При адиабатическом сжатии газа давление p и температура T измеряются следующим образом.Покажите, что соотношение имеет вид T = a ρ b и определите значения a и b .
| р в 10 5 Па | 1,2 | 1,5 | 1,8 | 2,1 | 2,4 |
| Т в K | 526 | 560 | 589 | 615 | 639 |
Стоимость C в час работы станка зависит от количества изделий n производимых в час. Были получены следующие данные, и ожидается, что они будут соответствовать соотношению вида C = an 3 + b . Покажите, что это так, и определите значения a и b .
Были получены следующие данные, и ожидается, что они будут соответствовать соотношению вида C = an 3 + b . Покажите, что это так, и определите значения a и b .
| С в £ | 31 | 38 | 67 | 94 | 155 |
| н | 10 | 20 | 30 | 40 | 50 |
Ниже приведены рекомендуемые тормозные пути s для автомобилей, движущихся с разной скоростью v .Отношение между s и v имеет вид s = av 2 + bv . Докажите, что это так, и определите значения a и b .
| 5 | 15 | 30 | 50 | 70045 |
| 5 | 10 | 15 | 20 | 25 |

Светимость I лампы зависит от приложенного к ней напряжения В . Соотношение между I и V имеет форму I = aV b . Используйте следующие результаты, чтобы показать, что это так, и определите значения a и b .
| I в канделах | 3,6 | 6,4 | 10.0 | 14.4 | 14.4 | 19.6 | |
| 60 | 80 | 100 | 120 | 140 | 140 |
от лаборатории, считают, что закон, связывающий напряжение v на катушке индуктивности и время t , определяется соотношением является экспоненциальной функцией.Из лабораторных тестов наблюдаемых результатов были:
9004. 4 4 | 9004.8 | 171.6 | 32.49 | 14.1 | 6.12 |
| 10 | 20 | 30 | 50 | 60 | 70 |
Математическая модель – обзор
1.04.2.2.3 Математические формулировки
Математические модели разработаны для интеграции механизмов, участвующих в отложении частиц в легких. Способность этих моделей предсказывать закономерности осаждения частиц зависит от точности описания физических явлений, включенных в модели. Математические модели могут быть чисто эмпирическими или аналитическими.
Различные математические модели отложения частиц в легких были предложены для людей и экспериментальных животных.Первая математическая обработка регионального отложения частиц у людей была сделана с использованием упрощенной модели девяти поколений. Впоследствии были предложены различные усовершенствования и другие математические модели. Эти модели носят компартментальный характер (т. е. модели рассматривают легкое как ряд «коробок», а не как непрерывную структуру) и имеют определенные недостатки, такие как отсутствие точной оценки механизмов потерь и исключение влияния приливного воздуха. смешиваясь с легочным воздухом.Были предложены динамические модели осаждения частиц, в которых многие поколения дыхательных путей рассматриваются как воронкообразная камера. Площадь поперечного сечения камеры зависит от глубины дыхательных путей, измеренной от начала трахеи до интересующей анатомической области. Концентрация вдыхаемых частиц в легочном воздухе в зависимости от глубины дыхательных путей и времени в течение дыхательного цикла описывается уравнением конвекции-диффузии (массовым балансом частиц) с коэффициентом потерь, учитывающим отложение частиц на стенках дыхательных путей.Кроме того, уравнение конвекции-диффузии было решено для каждого дыхательного пути легкого, чтобы рассчитать изменения дозы в результате асимметричной геометрии легкого (RIVM 2002).
Впоследствии были предложены различные усовершенствования и другие математические модели. Эти модели носят компартментальный характер (т. е. модели рассматривают легкое как ряд «коробок», а не как непрерывную структуру) и имеют определенные недостатки, такие как отсутствие точной оценки механизмов потерь и исключение влияния приливного воздуха. смешиваясь с легочным воздухом.Были предложены динамические модели осаждения частиц, в которых многие поколения дыхательных путей рассматриваются как воронкообразная камера. Площадь поперечного сечения камеры зависит от глубины дыхательных путей, измеренной от начала трахеи до интересующей анатомической области. Концентрация вдыхаемых частиц в легочном воздухе в зависимости от глубины дыхательных путей и времени в течение дыхательного цикла описывается уравнением конвекции-диффузии (массовым балансом частиц) с коэффициентом потерь, учитывающим отложение частиц на стенках дыхательных путей.Кроме того, уравнение конвекции-диффузии было решено для каждого дыхательного пути легкого, чтобы рассчитать изменения дозы в результате асимметричной геометрии легкого (RIVM 2002).
Уравнение конвекции-диффузии часто решается напрямую без учета переноса за счет продольной диффузии (т. е. диффузии в направлении потока), поскольку перенос за счет продольной диффузии пренебрежимо мал по сравнению с переносом за счет конвекции. Напротив, аксиальная диффузия (т. е. диффузия, перпендикулярная потоку) может способствовать транспорту наночастиц в легких, тем самым влияя на отложение частиц (Asgharian and Price, 2007).Следовательно, осевая диффузия и дисперсия частиц должны быть включены в модели осаждения наночастиц.
Термин поглощения или потери в математических моделях осаждения частиц в легких учитывает потерю частиц различными механизмами. Предполагается, что эти механизмы потерь независимы, а чистые или комбинированные потери рассчитываются путем наложения потерь по каждому отдельному механизму. Были предложены различные модели потерь по одному механизму. Наиболее широко используются выражения для диффузионных потерь, столкновений с перехватом, седиментации и электростатических сил. Некоторые недавние модели включают взаимодействие различных механизмов. Потери частиц на стенках дыхательных путей и в бифуркациях также были рассчитаны численно с одновременным рассмотрением всех механизмов потерь. Численные расчеты успешно сравнивались с экспериментальными результатами. Однако в этих численных расчетах отсутствует решение в закрытой форме для доли потерь частиц, которое можно было бы включить в модели отложений в легких.
Некоторые недавние модели включают взаимодействие различных механизмов. Потери частиц на стенках дыхательных путей и в бифуркациях также были рассчитаны численно с одновременным рассмотрением всех механизмов потерь. Численные расчеты успешно сравнивались с экспериментальными результатами. Однако в этих численных расчетах отсутствует решение в закрытой форме для доли потерь частиц, которое можно было бы включить в модели отложений в легких.
Эмпирические модели осаждения частиц также были предложены в основном для целей прогнозирования.Рудольф и его коллеги смоделировали легкое как серию из двух фильтров, представляющих трахеобронхиальную и альвеолярную области. Модель в основном основана на экспериментальных данных, полученных для широкого диапазона размеров частиц. Эта модель была принята Международной комиссией по радиологической защите для прогнозирования осаждения частиц, включающая теоретический компонент для масштабирования размера дыхательных путей с учетом различий по полу и возрасту. Асгарян и его коллеги также разработали эмпирическую модель отложения частиц в альвеолярной области на основе опубликованных данных Шлезингера, которую можно распространить на другие области легких.Поскольку эмпирические модели не учитывают структуру дыхательных путей и параметры дыхания и используют очень мало отсеков, их использование весьма ограничено, несмотря на их простоту.
Асгарян и его коллеги также разработали эмпирическую модель отложения частиц в альвеолярной области на основе опубликованных данных Шлезингера, которую можно распространить на другие области легких.Поскольку эмпирические модели не учитывают структуру дыхательных путей и параметры дыхания и используют очень мало отсеков, их использование весьма ограничено, несмотря на их простоту.
Все модели отложений требуют экспериментальной проверки. По этой причине математические модели были также разработаны для экспериментальных животных, для которых доступно множество экспериментальных данных. Математические модели отложения частиц у крыс, хомяков и морских свинок были разработаны несколькими исследователями по аналогии с человеческими моделями (RIVM 2002).Менаш и его коллеги предложили эмпирическую модель, которая также включает вдыхаемость частиц для прогнозирования осаждения в различных областях дыхательных путей. Включение вдыхаемости важно, потому что не все взвешенные в воздухе частицы вдыхаются. Для самых крупных аэрозольных частиц вероятность вдыхания достаточно мала.
Для самых крупных аэрозольных частиц вероятность вдыхания достаточно мала.
Модели полного осаждения объединяют все пять механизмов потерь для прогнозирования потерь частиц в различных областях дыхательных путей. Рисунок 10 является примером результатов таких расчетов.Назальное отложение важно для очень мелких частиц, где осаждение происходит путем диффузии, и для крупных частиц, где осаждение происходит в основном путем удара. Нос является эффективным фильтром для очень крупных и очень мелких частиц. Скорость потока в трахеобронхиальной области высока, поэтому крупные частицы оседают в областях вблизи бифуркаций из-за импакции. В альвеолярной области поток воздуха существенно уменьшился из-за увеличения числа дыхательных путей, поэтому мелкие частицы удаляются из воздуха путем диффузии, а более крупные — путем оседания.Пики на кривых депонирования трахеобронхиальной и легочной областей возникают из-за относительно низкой фильтрации в предшествующих областях.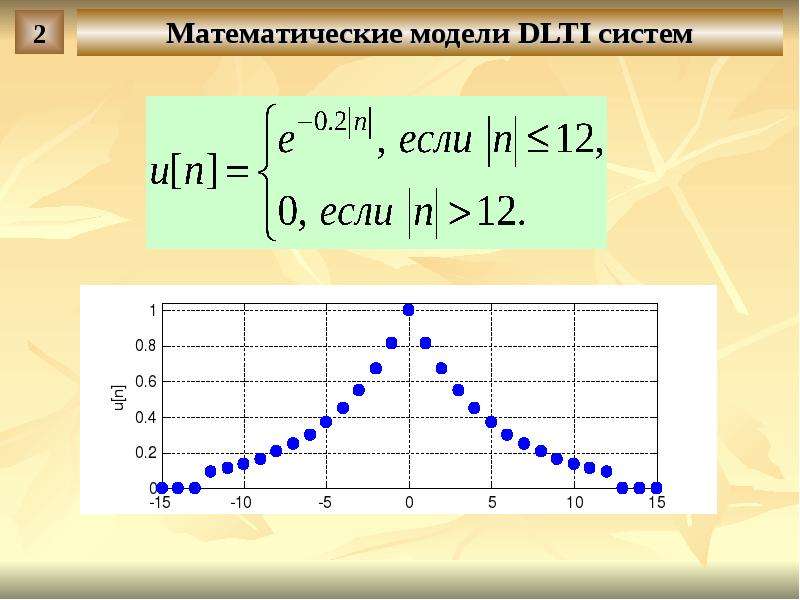 Например, по мере снижения эффективности осаждения более мелких частиц в носовой области эти частицы попадают в трахеобронхиальную область, где они оседают, увеличивая эффективность осаждения в этой области, что приводит к пику на кривой осаждения.
Например, по мере снижения эффективности осаждения более мелких частиц в носовой области эти частицы попадают в трахеобронхиальную область, где они оседают, увеличивая эффективность осаждения в этой области, что приводит к пику на кривой осаждения.
Рисунок 10. Схематическое изображение фракционного осаждения частиц в трех областях дыхательных путей человека в зависимости от размера вдыхаемой частицы и интересующей области дыхательных путей.
Математические модели и методы в прикладных науках
Самые популярные статьи 2021
Бесплатно для чтения: Войдите в свою существующую учетную запись или зарегистрируйте для получения бесплатной учетной записи, чтобы пользоваться этим.
Многомасштабная модель вирусной пандемии: неоднородные интерактивные объекты в глобально связанном мире
Никола Белломо, Ричард Бингхэм, Марк А. Дж. Чапелан, Джованни Дози, Гвидо Форни, Дамиан А. Кнопофф, Джон Ловенгруб, Рейдун Тварок и Мария Энрика Вирджиллито
Анализ стабильности для метода виртуальных элементов
Лоренсу Бейран да Вейга, Карло Ловадина и Алессандро Руссо
Аналитическая основа для метода глобальной оптимизации на основе консенсуса
Хосе А. Каррильо, Янг-Пил Чой, Клаудия Тотцек и Оливер Це
Каррильо, Янг-Пил Чой, Клаудия Тотцек и Оливер Це
Математическое моделирование инвазии рака: множественная роль TGF-пути в пролиферации опухоли и клеточной адгезии
Vasiliki Bitsouni, Mark A.J. Chaplain and Raluca Eftimie
Что такое жизнь? Перспективы математической кинетической теории активных частиц
Никола Белломо, Дилетта Бурини, Джованни Дози, Ливио Джибелли, Дамиан Кнопофф, Нисрин Утада, Пьетро Терна и Мария Энрика Вирджиллито
Подход с использованием множителя Лагранжа к задачам одностороннего вдавливания: корректность и применение к линеаризованной вязкоупругости с необратимой определяющей реакцией
Хиромичи Итоу, Виктор А.Ковтуненко и Кумбаконам Р. Раджагопал
Подход кинетической теории для моделирования гетерогенности и пластичности опухоли и макрофагов при прогрессировании рака
R. Eftimie and L. Gibelli
Статистические решения уравнений Эйлера для несжимаемой жидкости
С. Ланталер, С. Мишра и К. Парес-Пулидо
Ланталер, С. Мишра и К. Парес-Пулидо
Задача о трещинах в контексте неявно заданной квазилинейной вязкоупругости
Хиромичи Итоу, Виктор А.Ковтуненко и Кумбаконам Р. Раджагопал
Нематическое выравнивание самодвижущихся частиц: от частиц к макроскопической динамике
Пьер Дегон и Сара Мерино-Асейтуно
Математические модели
Математические модели — это точное описание проблемы, процесса или технологии в математической форме. Эти модели созданы для того, чтобы больше узнать о технологии, системе или методе. Модели объясняют, почему система или процесс работают именно так, а также помогают изучать эффекты и прогнозировать результаты.Математические модели необходимы ученым и инженерам, потому что они позволяют нам изучать явления, которые невозможно увидеть или измерить. Модели также создаются социологами, экономистами, бизнес-аналитиками и статистиками.
Примеры математических моделей:
• Количество тепла, выделяемое топливным элементом
• Количество топлива, необходимое для топливного элемента
• Количество электроэнергии, вырабатываемой топливным элементом, батареей или солнечным элементом
• Количество ветра, необходимое для производства определенного количества энергии с помощью ветряной башни
• Расход жидкости через проточный канал топливного элемента
• Результаты броска костей
• Погодные условия, такие как тропические штормы и ураганы
• Устойчивость американских горок
• Результаты фондового рынка
Шаги, необходимые для создания математической модели, сопоставимы с этапами, используемыми для научного метода. Это включает в себя наблюдение, исследование, построение модели и прогнозирование результата.
Это включает в себя наблюдение, исследование, построение модели и прогнозирование результата.
Фаза наблюдения включает наблюдение и измерение того, что происходит в реальном мире. Это может состоять из сбора эмпирических данных или количественных измерений. Если мы хотим предсказать количество тепла, которое генерирует топливный элемент , этап наблюдения может включать измерение температуры различных частей топливного элемента (таких как МЭУ , биполярные пластины , концевые пластины ). и температура окружающей среды).Мы можем заметить, что МЭУ нагревается, что влияет на другие измеряемые температуры. Исходя из этого наблюдения, мы можем выбрать гипотезу. На данный момент мы можем не понимать, почему MEA нагревается.
Этап исследования состоит из проведения исследований через Интернет, книги, научные статьи и публикации. Если мы все еще работаем над прогнозированием количества тепла, выделяемого топливным элементом, мы можем провести исследование и выяснить, что существуют уравнения, включающие температуру слоя катализатора МЭБ.
Фаза моделирования включает создание или ввод необходимых уравнений в программное обеспечение, такое как Excel, MATLAB, Mathematica, SASS или другое программное обеспечение. Многие уравнения часто включаются в модель, чтобы предсказать результат. Эмпирические модели создаются с использованием данных, собранных на этапе наблюдения, для создания одного или нескольких уравнений с использованием регрессии или аналогичной методологии. В нашем примере прогнозирования тепла мы можем использовать уравнения поляризации для создания нашей модели.
На этапе прогнозирования используется модель, предназначенная для прогнозирования того, что произойдет в эксперименте, который еще предстоит провести, или в ожидаемом наборе событий в реальном мире.В нашем примере с прогнозированием тепла мы будем использовать нашу модель для прогнозирования температуры топливного элемента и окружающей среды через определенное время (например, при непрерывной работе в течение 72 часов).
Большинство ученых и инженеров проводят эксперименты, а не создают модели, а это означает, что они собирают наблюдения и преобразуют эти наблюдения в математическую модель. Экспериментатор разрабатывает исследование, проводит эксперименты, а затем записывает и анализирует результаты. Напротив, разработчик математического моделирования будет использовать некоторые аспекты реальной проблемы в качестве входных данных в свою числовую систему, но они придумывают свои уравнения из исследований или других исследований.
Экспериментатор разрабатывает исследование, проводит эксперименты, а затем записывает и анализирует результаты. Напротив, разработчик математического моделирования будет использовать некоторые аспекты реальной проблемы в качестве входных данных в свою числовую систему, но они придумывают свои уравнения из исследований или других исследований.
Инженеры часто используют модели различной сложности для правильного проектирования оборудования, устройств и процессов. Например, каждое транспортное средство, самолет или здание является результатом предсказания на основе модели, которое:
• Автомобиль будет работать в соответствии с проектом
.
• Здание будет стоять
• Самолет будет летать
Прогнозирование в инженерном проектировании предполагает, что ресурсы можно инвестировать с уверенностью, потому что прогнозируемый результат будет правильным.В зависимости от конструкции и модели это может также сократить месяцы или годы экспериментального времени. Эксперименты часто адекватно измеряют и анализируют только определенный процент переменных. Кроме того, при исследовании новых технологий важность отдельных переменных может быть неизвестна или не поддается измерению. Чтобы математическая модель была полной, она должна включать все критические переменные.
Кроме того, при исследовании новых технологий важность отдельных переменных может быть неизвестна или не поддается измерению. Чтобы математическая модель была полной, она должна включать все критические переменные.
Шаги по созданию математической модели
Когда вы думаете о создании математической модели, у вас уже есть некоторые наблюдения о реальном мире.Вы должны быть в состоянии легко определить потребность в модели:
• Вы не можете видеть происходящие явления напрямую
• Количество экспериментов было бы слишком дорогостоящим или трудоемким
• Вы не уверены в том, что происходит
Когда вы будете готовы создать математическую модель, некоторые вопросы и мысли, которые могут быть вам полезны, перечислены ниже:
1) Что мы ищем? Как мы должны смотреть на эту модель? Определите основные принципы.Начните с наблюдений за реальным миром и соберите информацию, относящуюся к математической модели.
2) Что мы хотим знать? Необходимо создать список вопросов, на которые нужно ответить. После того, как вы определились с масштабом проблемы, следует определить все соответствующие данные. Вопросы «Что мы знаем?» или «какая информация доступна, чтобы помочь решить нашу проблему?»
После того, как вы определились с масштабом проблемы, следует определить все соответствующие данные. Вопросы «Что мы знаем?» или «какая информация доступна, чтобы помочь решить нашу проблему?»
3) Что мы знаем из экспериментов и литературы? Проведите тщательный поиск литературы.Возможно, кто-то уже создал математическую модель процесса или проблемы, которую вы пытаетесь решить.
4) Как нам посмотреть на его модель? Нарисуйте схемы того, что вы хотите смоделировать. Это поможет прояснить входные и выходные данные вашей модели и начнет определять масштаб проблемы.
5) Какие предположения мы можем сделать, чтобы исключить переменные? Создайте список допущений, чтобы уточнить объем модели.
6) Что предскажет наша модель? Начните с упрощенной модели, а затем усложняйте ее по мере необходимости.Определите и составьте уравнения, которые будут использоваться, и полученные ответы. Если вы строите эмпирическую модель, создайте уравнения на основе полученных данных.
7) Что такое входные и выходные переменные? Создайте список входных и выходных переменных. Определите каждую константу и определите переменные, которые вам нужно решить.
8) Результаты действительны? Проверьте свою модель с помощью данных, которые вы не использовали для создания модели. Определите тесты, которые могут проверить модель.
9) Постоянно тестируйте свою модель и обновляйте уравнения на основе новых данных и информации.
Если есть хорошее согласие между наблюдениями и предсказаниями модели, то математическая система действительно отражает существенные аспекты реального сценария. Однако некоторые математические предсказания могут не согласовываться с наблюдаемыми событиями. Это часто бывает, когда вы создаете новую модель или собрали недостаточно данных. В этом случае модель следует модифицировать для повышения ее точности.Неверные прогнозы могут помочь вам переосмыслить предположения математической модели. Неверные предположения пересмотренной модели приведут к более сложной и точной версии модели. Цель состоит не в том, чтобы создать наиболее точную модель вашей проблемы или процесса, а в том, чтобы модель предсказывала реальный результат.
Цель состоит не в том, чтобы создать наиболее точную модель вашей проблемы или процесса, а в том, чтобы модель предсказывала реальный результат.
Классификация математических моделей
Есть много способов создать одну и ту же математическую модель! Вопреки тому, что может подумать большинство начинающих моделистов, не существует «правильного» пути.Существует две основные классификации моделей — эмпирические и неэмпирические:
1) Эмпирические модели создаются на основе фактических данных и прошлых экспериментов.
2) Неэмпирические модели используют уравнения, основанные на существующих соотношениях в литературе. Модели могут также включать новые уравнения, полученные лицом, проводящим математическое моделирование.
Математические модели часто представляют собой динамические системы, но они также могут быть статистическими или логическими по своей природе:
1) Динамические или статические: В динамических моделях используется реалистичный подход, поскольку они учитывают время или пространство. Обычно это достигается с помощью дифференциальных уравнений (DE) или дифференциальных уравнений в частных производных (PDE). Статические модели часто имеют только одно положение относительно времени или пространства.
Обычно это достигается с помощью дифференциальных уравнений (DE) или дифференциальных уравнений в частных производных (PDE). Статические модели часто имеют только одно положение относительно времени или пространства.
2) Детерминированная или вероятностная: Детерминированная модель — это модель, в которой модель может предсказывать каждое состояние. Эти модели работают одинаково для определенного набора условий. В вероятностной модели случайность должна учитываться распределением вероятностей.
3) Эмпирический: Эта модель основана на экспериментальных результатах.Данные подвергаются статистическому анализу, а затем на их основе разрабатываются эмпирические уравнения.
Если ваша модель точна, ее можно запускать с различными входными данными и условиями для прогнозирования результатов. Надежная математическая модель может заменить эксперименты. Если были собраны важные данные, их можно проанализировать на наличие закономерностей для создания моделей. Процесс построения моделей заставляет ученого или инженера внимательно рассматривать все аспекты проблемы и переоценивать наши убеждения. Этот процесс помогает улучшить наше понимание проблемы, которую необходимо решить. Это более тщательный подход, чем просто сбор данных. Ученые, которые не строят модели, иногда обнаруживают, что после получения значительного количества данных они собрали неверные данные.
Этот процесс помогает улучшить наше понимание проблемы, которую необходимо решить. Это более тщательный подход, чем просто сбор данных. Ученые, которые не строят модели, иногда обнаруживают, что после получения значительного количества данных они собрали неверные данные.
Заключение
Это может показаться пугающим для новичка в математическом моделировании, но я бы рекомендовал начинать как можно проще. Это может включать использование уравнений из учебников или предыдущих занятий, которые вы посещали, чтобы получить ответ, который кажется вам разумным.Это упрощает создание модели, а сложность может быть встроена в модель по мере необходимости. Опытные разработчики моделей могут начать с большей сложности, потому что они понимают, как правильно закодировать модель и вписать ее в существующую модель.
Автор: Доктор Коллин Шпигель Доктор Коллин Шпигель — консультант по математическому моделированию и техническому письму (президент SEMSCIO) и профессор, имеющий докторскую степень. и степень магистра инженерных наук. Она имеет семнадцатилетний опыт работы в области инженерии, статистики, науки о данных, исследований и написания технических текстов для многих компаний в качестве консультанта, сотрудника и независимого владельца бизнеса.Она является автором книг « Проектирование и создание топливных элементов » (McGraw-Hill, 2007 г.) и «Моделирование и моделирование топливных элементов PEM с использованием MATLAB» (Elsevier Science, 2008 г.). Ранее она владела компанией Clean Fuel Cell Energy, LLC, организацией по производству топливных элементов, которая обслуживала ученых, инженеров и профессоров по всему миру.
и степень магистра инженерных наук. Она имеет семнадцатилетний опыт работы в области инженерии, статистики, науки о данных, исследований и написания технических текстов для многих компаний в качестве консультанта, сотрудника и независимого владельца бизнеса.Она является автором книг « Проектирование и создание топливных элементов » (McGraw-Hill, 2007 г.) и «Моделирование и моделирование топливных элементов PEM с использованием MATLAB» (Elsevier Science, 2008 г.). Ранее она владела компанией Clean Fuel Cell Energy, LLC, организацией по производству топливных элементов, которая обслуживала ученых, инженеров и профессоров по всему миру.
Математические модели и экспериментальный анализ поведения
J Exp Anal Behav. 2006 март; 85(2): 275–291.
Государственный университет Южного Коннектикута
Корреспонденцию следует направлять Джеймсу Э.Мазур, кафедра психологии, Университет штата Южный Коннектикут, Нью-Хейвен, Коннектикут 06515, e-mail: ude.tcnrehtuos@1jruzam Поступила в редакцию 21 июля 2005 г. ; Принято 3 октября 2005 г.
; Принято 3 октября 2005 г.
Abstract
Использование математических моделей в экспериментальном анализе поведения с годами увеличилось, и они предлагают несколько преимуществ. Математические модели требуют от теоретиков точности и недвусмысленности, часто допуская сравнения конкурирующих теорий, которые кажутся похожими на словах.Иногда разные математические модели могут одинаково точно прогнозировать большой объем данных. В таких случаях важно найти и исследовать ситуации, для которых конкурирующие модели делают разные прогнозы, потому что, если две модели не являются фактически математически эквивалентными, они основаны на разных предположениях о психологических процессах, лежащих в основе наблюдаемого поведения. Математические модели, разработанные в фундаментальных поведенческих исследованиях, использовались для прогнозирования и контроля поведения в прикладных условиях, и они направляли исследования в других областях психологии.Хорошая математическая модель может обеспечить общую основу для понимания того, что в противном случае могло бы показаться разнообразным и не связанным между собой поведенческими явлениями. Поскольку психологи различаются по своим количественным навыкам и по своей терпимости к математическим уравнениям, для тех, кто разрабатывает математические модели поведения, важно найти способы (такие как словесные аналогии, графические изображения или конкретные примеры) сообщить ключевые предпосылки своих моделей. неспециалистам.
Поскольку психологи различаются по своим количественным навыкам и по своей терпимости к математическим уравнениям, для тех, кто разрабатывает математические модели поведения, важно найти способы (такие как словесные аналогии, графические изображения или конкретные примеры) сообщить ключевые предпосылки своих моделей. неспециалистам.
Ключевые слова: математические модели, уравнения, поведение, подкрепление
С годами исследователи, изучающие основные поведенческие процессы, все больше полагаются в своей работе на математические модели.Создание Общества количественного анализа поведения (SQAB) в 1978 г. и его последующий рост — лишь один из признаков роста интереса к математическому моделированию поведения. Еще одним показателем является количество статей в журнале Journal of the Experimental Analysis of Behavior ( JEAB ), в которых используются математические модели. Для отдельных лет, разделенных 10-летними интервалами, показан процент статей JEAB , в которых представлено хотя бы одно уравнение для описания связи между независимой переменной и зависимой переменной (исключая статьи, в которых проверялись следствия математических моделей, но не явным образом представить уравнения). В этом критерии есть некоторая условность, но нарастающая тенденция к математическому анализу очевидна.
В этом критерии есть некоторая условность, но нарастающая тенденция к математическому анализу очевидна.
Для отдельных лет с 10-летними интервалами процент статей в JEAB , которые включали хотя бы одно уравнение для описания связи между независимой переменной и зависимой переменной.
Некоторых поведенческих аналитиков, начавших свою карьеру, когда математическое моделирование еще не было так распространено в этой области, или тех, кто не использует математические модели в своей работе, эта тенденция может обескураживать.Для некоторых вид уравнения или двух в статье JEAB может быть достаточной причиной, чтобы пропустить статью и перейти к следующей. Им может казаться, что статья с математическими уравнениями выше их понимания или, что еще хуже, не имеет отношения к их интересам. В конце концов, разве экспериментальный анализ поведения не должен касаться поведения , а не математических уравнений и символов?
Неудачи в общении между теми, кто использует математические модели, и теми, кто не использует их в своей работе, характерны не только для психологии. По мере того как в середине девятнадцатого века физическая наука становилась все более количественной, некоторые очень компетентные ученые чувствовали, что их оставили позади. За время своей очень продуктивной карьеры британский физик Майкл Фарадей провел около пятнадцати тысяч экспериментов с электромагнитными полями, но так и не смог понять красивых уравнений теории поля, которые Джеймс Клерк Максвелл вывел из собственных исследований Фарадея. Фарадей спросил Максвелла, может ли он использовать словесные описания или другие средства, чтобы сделать свои уравнения понятными для нематематиков, и Максвелл искренне постарался сделать это.По словам Тимоти Ферриса (1988):
По мере того как в середине девятнадцатого века физическая наука становилась все более количественной, некоторые очень компетентные ученые чувствовали, что их оставили позади. За время своей очень продуктивной карьеры британский физик Майкл Фарадей провел около пятнадцати тысяч экспериментов с электромагнитными полями, но так и не смог понять красивых уравнений теории поля, которые Джеймс Клерк Максвелл вывел из собственных исследований Фарадея. Фарадей спросил Максвелла, может ли он использовать словесные описания или другие средства, чтобы сделать свои уравнения понятными для нематематиков, и Максвелл искренне постарался сделать это.По словам Тимоти Ферриса (1988):
Максвелл услужливо перевел некоторые из своих объяснений теории поля в формулировки механических зубчатых колес и звездочек, которые мог понять Фарадей, но его теория полетела только тогда, когда ее разобрали до голых уравнений. Уравнения Максвелла с фугообразным балансом и силой продемонстрировали, что электричество и магнетизм являются аспектами единой силы, электромагнетизма, и что сам свет является разновидностью этой силы.
Таким образом были объединены то, что было отдельными исследованиями электричества, магнетизма и оптики.(стр. 187)
Неясно, смогут ли когда-нибудь математические модели в психологии достичь широты и мощи уравнений Максвелла; поведение живых организмов очень сложно, и на него влияет множество различных факторов. Тем не менее математические модели могут выполнять несколько полезных функций при экспериментальном анализе поведения. В психологии математические модели предназначены для более точного описания основных поведенческих процессов, чем это можно сделать с помощью простых словесных описаний.Иногда трудно вывести однозначные предсказания из теорий, выраженных словами, но последствия конкурирующих теорий (и различия между ними) часто становятся ясными, когда теории представлены в математической форме. Критические тесты, которые сравнивают количественные прогнозы двух или более разных моделей, могут указать, какие гипотезы о поведенческом процессе жизнеспособны, а какие нет. Исследования, которые проверяют количественные предсказания математических моделей, могут выявить недостатки в современных теориях и привлечь наше внимание к факторам, влияющим на поведение, которые в противном случае могли бы остаться незамеченными.Кроме того, так же, как уравнения Максвелла объединили различные области физики, хорошая математическая модель в психологии может использовать базовый набор принципов для объяснения разнообразного поведения. Наконец, математические модели могут служить руководством для специалистов в смежных областях, таких как поведенческий терапевт, пытающийся предсказать и контролировать поведение в прикладных условиях, или нейробиолог, стремящийся понять биологические основы поведенческого феномена.
Исследования, которые проверяют количественные предсказания математических моделей, могут выявить недостатки в современных теориях и привлечь наше внимание к факторам, влияющим на поведение, которые в противном случае могли бы остаться незамеченными.Кроме того, так же, как уравнения Максвелла объединили различные области физики, хорошая математическая модель в психологии может использовать базовый набор принципов для объяснения разнообразного поведения. Наконец, математические модели могут служить руководством для специалистов в смежных областях, таких как поведенческий терапевт, пытающийся предсказать и контролировать поведение в прикладных условиях, или нейробиолог, стремящийся понять биологические основы поведенческого феномена.
Одна из целей этой статьи — продемонстрировать ценность математических моделей в экспериментальном анализе поведения на нескольких конкретных примерах.Вторая цель состоит в том, чтобы способствовать лучшему общению между теми психологами, которые используют математические модели в своих исследованиях, и теми, кто этого не делает, о чем свидетельствует общение между экспериментатором Фарадеем и математиком Максвеллом.
Лучше, чем просто слова
В некоторых случаях две теории, которые, по-видимому, делают схожие предсказания, когда они сформулированы словами, легче сравнивать и оценивать, когда они представлены в математической форме. Например, две разные теории наказания — отрицательный закон следствия (т.g., Rachlin & Herrnstein, 1969) и теории избегания наказания (например, Dinsmoor, 1954, 1977). Негативный закон эффекта — это просто точка зрения, согласно которой подкрепление и наказание оказывают противоположное влияние на поведение: подкрепление усиливает поведение, а наказание ослабляет его. Теория избегания наказания использует другой подход. Согласно этой теории, когда за реакцией следует наказание, реакция ассоциируется со страхом, который является аверсивным стимулом. Как только это обусловливание произошло, страх будет усиливаться всякий раз, когда животное начинает реагировать, и животное может избавиться от этого страха, выполнив вместо этого какую-то другую реакцию.Поэтому альтернативные реакции подкрепляются уменьшением страха, и их частота увеличивается.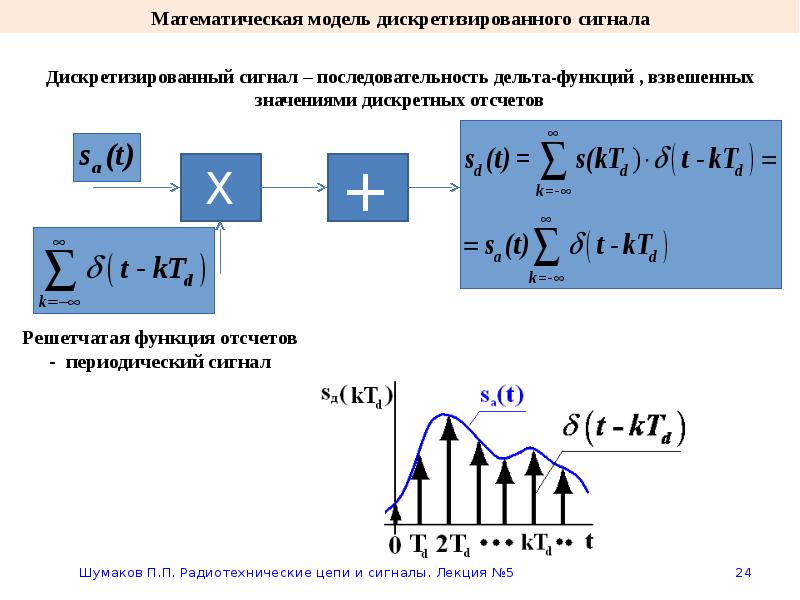 Следовательно, согласно теории избегания, последствия наказания являются косвенными: причина уменьшения наказуемого поведения заключается в том, что уровень подкрепления альтернативного поведения увеличился.
Следовательно, согласно теории избегания, последствия наказания являются косвенными: причина уменьшения наказуемого поведения заключается в том, что уровень подкрепления альтернативного поведения увеличился.
При таком описании предсказания этих двух теорий трудно различить. Хотя они делают свои прогнозы по разным причинам, обе теории, по-видимому, предсказывают один и тот же общий результат: наказание приведет к уменьшению наказуемого поведения.Однако, как только они переведены в математическую форму, становится легче увидеть различные предсказания двух теорий. Делюти (1976) и де Вилье (1977, 1980) разработали две различные количественные модели наказания, которые можно рассматривать как математические версии теории уклонения от наказания и отрицательного закона следствия соответственно. Обе модели начинаются с закона соответствия Херрнштейна (1961), но затем развиваются в разных направлениях.
В простейшей форме закон согласования можно записать следующим образом:
1
, где B 1 и B 2 2 2 — это темпы ответа на графики арматуры 1 и 2, а R 1 и R 2 являются ставками армирования по этим двум графикам. Это уравнение часто применялось к ситуациям выбора, в которых двумя альтернативами являются режимы пищевого подкрепления с переменным интервалом (VI). Представьте, что голубь отвечает на две клавиши, где Ключ 1 дает 75 подкреплений в час, а Ключ 2 дает 25 подкреплений в час, поэтому уравнение 1 предсказывает, что 75% своих ответов голубь будет давать на Ключ 1. Теперь предположим, что в дополнение к производя пищу, ответы на обе клавиши начинают наносить каратели (электрические удары) со скоростью 20 ударов в час на каждую клавишу.Как можно расширить уравнение 1, чтобы справиться с этой ситуацией?
Это уравнение часто применялось к ситуациям выбора, в которых двумя альтернативами являются режимы пищевого подкрепления с переменным интервалом (VI). Представьте, что голубь отвечает на две клавиши, где Ключ 1 дает 75 подкреплений в час, а Ключ 2 дает 25 подкреплений в час, поэтому уравнение 1 предсказывает, что 75% своих ответов голубь будет давать на Ключ 1. Теперь предположим, что в дополнение к производя пищу, ответы на обе клавиши начинают наносить каратели (электрические удары) со скоростью 20 ударов в час на каждую клавишу.Как можно расширить уравнение 1, чтобы справиться с этой ситуацией?
Согласно де Вилье (1977), если наказание противоположно подкреплению, как утверждает отрицательный закон следствия, то наказания, доставляемые каждой альтернативой, должны быть вычтены из подкреплений, доставляемых этой альтернативой:
2
где P 1 и P 2 — ставки наказания по двум ключам.
Напротив, Делюти (Deluty, 1976) придерживался мнения, что наказание за одну реакцию увеличивает подкрепление других реакций, как это предлагается теорией избегания наказания. Следовательно, в его уравнении наказания для одной альтернативы добавляются к подкреплениям для другой альтернативы:
Следовательно, в его уравнении наказания для одной альтернативы добавляются к подкреплениям для другой альтернативы:
3
Чтобы не усложнять этот пример, одному разряду присваивается тот же вес, что и одной доставке еды, но обе модели могут легко дать еду и разряд разного веса, умножив P 1 и P 2 на некоторая константа, отличная от 1. Использование такой константы не изменит представленных здесь общих выводов. В этом примере с R 1 = 75, R 2 = 25 и P 1 = P 2 = 20, уравнение 2 прогнозирует, что процент ответов на ключевой 1 должен увеличиться с 75% до 92% при добавлении ударов к обеим клавишам.И наоборот, уравнение 3 предсказывает, что процент ответов по Ключу 1 должен уменьшиться до 68% при добавлении шоков. В эксперименте с голубями де Вилльерс (1980) обнаружил, что предпочтение клавиши, дающей больше подкрепления, увеличивается, когда к обеим клавишам с одинаковой частотой добавляются разряды. Таким образом, этот результат говорит в пользу предсказаний уравнения 2 по сравнению с предсказаниями уравнения 3.
Таким образом, этот результат говорит в пользу предсказаний уравнения 2 по сравнению с предсказаниями уравнения 3.
Должно быть ясно, что проблема здесь более фундаментальна, чем просто использование знака плюс или минус в уравнении.Эти две модели основаны на двух совершенно разных концепциях воздействия наказания на поведение. Экспериментальные данные свидетельствуют о том, что наказание оказывает свое влияние, ослабляя целевое поведение, как это предусматривает негативный закон воздействия, а не усиливая альтернативное поведение, как предполагает теория избегания. Этот пример иллюстрирует, как две психологические теории, которые, казалось бы, делают схожие предсказания, когда они формулируются в устной форме, на самом деле могут делать совершенно разные предсказания, когда они представлены в математической форме.
Больше, чем подбор кривой
Рассмотрим вопрос о том, какое уравнение лучше всего описывает, как сила подкрепления уменьшается с увеличением задержки. Одно из распространенных предположений (например, Hull, 1943; Killeen, 1994) состоит в том, что градиент задержки подкрепления может быть описан экспоненциальным уравнением:
Одно из распространенных предположений (например, Hull, 1943; Killeen, 1994) состоит в том, что градиент задержки подкрепления может быть описан экспоненциальным уравнением:
4
где V — значение или сила подкрепления подкрепления, доставленного после задержки D секунд, A — значение подкрепления, если бы оно было доставлено немедленно, e — основа натуральный логарифм, а K — параметр, определяющий, насколько быстро V убывает с увеличением задержки.Другое предложение состоит в том, что градиент задержки подкрепления лучше всего описывается гиперболической функцией (например, Мазур, 1987):
5
Эти два разных уравнения описывают кривые затухания, которые имеют довольно похожие формы. показаны данные по 1 голубю в эксперименте, в котором животные выбирали между 45 с воздействия графиков с переменным временем (VT) и однократным предъявлением отсроченного подкрепления (Mazur, 2000a). Задержка была скорректирована в ходе испытаний, чтобы получить точки безразличия, показанные на графике, который изображает уменьшение значения одиночного подкрепления по мере увеличения его задержки. Кривые показывают наиболее подходящие предсказания уравнений 4 и 5 с K , рассматриваемыми как свободный параметр, и оба уравнения учитывают 99% изменчивости данных.
Кривые показывают наиболее подходящие предсказания уравнений 4 и 5 с K , рассматриваемыми как свободный параметр, и оба уравнения учитывают 99% изменчивости данных.
Для обоих уравнений K рассматривалось как свободный параметр.
Кто-то может возразить, что оба уравнения очень хорошо описывают данные и что решение о том, какое из них использовать, является просто вопросом предпочтения.Хотя это может быть верно для этого единственного набора данных, было бы неправильно делать вывод, что разница между уравнениями 4 и 5 несущественна. Эти два уравнения делают совершенно разные прогнозы того, как люди будут выбирать между двумя подкреплениями, которые подаются в разное время (как в так называемой ситуации выбора самоконтроля, в которой человек должен выбирать между небольшим, более непосредственным подкреплением и более крупным подкреплением). , но более отсроченное подкрепление). Экономисты обычно отдают предпочтение экспоненциальному уравнению в качестве временной функции дисконтирования, потому что оно кажется более «рациональным»: все подкрепления сбрасываются на один и тот же процент с течением времени, независимо от их размера или времени их предоставления.Однако, как отмечал Эйнсли (Ainslie, 1975), если параметр дисконтирования K одинаков для обоих подкреплений, экспоненциальное уравнение не допускает инверсии предпочтений в ситуации выбора самоконтроля: человек, который предпочитает больше, больше отложенное подкрепление теперь должно сохранять это предпочтение с течением времени. Напротив, гиперболическое уравнение действительно предсказывает смену предпочтений (например, когда человек на диете клянется, что не будет второй порции за ужином, но затем меняет свое мнение во время еды и съедает больше, чем должен).
, но более отсроченное подкрепление). Экономисты обычно отдают предпочтение экспоненциальному уравнению в качестве временной функции дисконтирования, потому что оно кажется более «рациональным»: все подкрепления сбрасываются на один и тот же процент с течением времени, независимо от их размера или времени их предоставления.Однако, как отмечал Эйнсли (Ainslie, 1975), если параметр дисконтирования K одинаков для обоих подкреплений, экспоненциальное уравнение не допускает инверсии предпочтений в ситуации выбора самоконтроля: человек, который предпочитает больше, больше отложенное подкрепление теперь должно сохранять это предпочтение с течением времени. Напротив, гиперболическое уравнение действительно предсказывает смену предпочтений (например, когда человек на диете клянется, что не будет второй порции за ужином, но затем меняет свое мнение во время еды и съедает больше, чем должен).
Ситуация на самом деле более сложная, потому что, как указали Грин и Майерсон (1993), экспоненциальное уравнение может предсказать смену предпочтений, если параметр затухания K больше для меньшего подкрепления, чем для большего подкрепления. Когда участников-людей просят сделать выбор между гипотетическими денежными подкреплениями разного размера и с разной задержкой, оценки K действительно уменьшаются с увеличением количества подкрепления (например, Green, Fristoe, & Myerson, 1994; Green, Myerson, & McFadden, 1997). ), поэтому изменение предпочтений в этих ситуациях не обязательно противоречит экспоненциальному уравнению.Чтобы предоставить более убедительные доказательства гиперболического уравнения, нужно показать, что изменение предпочтений происходит даже тогда, когда оценки K этого не делают. Исследования с нечеловеческими субъектами предоставили некоторые доказательства этого типа. В то время как реверсия предпочтений достоверно обнаруживается у животных (например, Green, Fisher, Perlow, & Sherman, 1981), исследования на крысах и голубях не обнаружили доказательств того, что значения K уменьшаются при увеличении количества подкрепления (Grace, 1999; Green , Myerson, Holt, Slevin, & Estle, 2004; Ong & White, 2004; Richards, Mitchell, de Wit, & Seiden, 1997).
Когда участников-людей просят сделать выбор между гипотетическими денежными подкреплениями разного размера и с разной задержкой, оценки K действительно уменьшаются с увеличением количества подкрепления (например, Green, Fristoe, & Myerson, 1994; Green, Myerson, & McFadden, 1997). ), поэтому изменение предпочтений в этих ситуациях не обязательно противоречит экспоненциальному уравнению.Чтобы предоставить более убедительные доказательства гиперболического уравнения, нужно показать, что изменение предпочтений происходит даже тогда, когда оценки K этого не делают. Исследования с нечеловеческими субъектами предоставили некоторые доказательства этого типа. В то время как реверсия предпочтений достоверно обнаруживается у животных (например, Green, Fisher, Perlow, & Sherman, 1981), исследования на крысах и голубях не обнаружили доказательств того, что значения K уменьшаются при увеличении количества подкрепления (Grace, 1999; Green , Myerson, Holt, Slevin, & Estle, 2004; Ong & White, 2004; Richards, Mitchell, de Wit, & Seiden, 1997). Имеются и другие свидетельства в пользу гиперболического уравнения, такие как формы функций безразличия, которые получаются, когда животные выбирают между различными комбинациями величины задержки (Mazur, 1987). Суть в том, что, хотя два уравнения могут давать сходные предсказания для некоторых ситуаций (например, теоретические кривые в ), они могут давать совершенно разные предсказания для других ситуаций, и эти различия могут иметь важное теоретическое и практическое значение.
Имеются и другие свидетельства в пользу гиперболического уравнения, такие как формы функций безразличия, которые получаются, когда животные выбирают между различными комбинациями величины задержки (Mazur, 1987). Суть в том, что, хотя два уравнения могут давать сходные предсказания для некоторых ситуаций (например, теоретические кривые в ), они могут давать совершенно разные предсказания для других ситуаций, и эти различия могут иметь важное теоретическое и практическое значение.
Не просто мудрить
Конкурирующие математические модели не всегда дают столь явно отличающиеся предсказания, как предсказания уравнений гиперболического и экспоненциального распада.Иногда предсказания двух или более различных математических моделей довольно схожи для широкого круга экспериментов, и модели кажутся примерно одинаковыми по своей точности предсказания. В этих случаях кажется справедливым спросить, если мы заинтересованы в предсказании поведения и если обе модели одинаково хорошо предсказывают поведение, какая разница, какую из них мы используем?
Мое сравнение трех моделей производительности параллельных цепей (Mazur, 2001) иллюстрирует такую ситуацию. В этом анализе я сравнил прогностическую точность теории уменьшения задержки Фантино (DRT; Squires & Fantino, 1971), модели контекстуального выбора Грейс (CCM; Grace, 1994) и моей гиперболической модели добавленной стоимости (HVA).Чтобы сравнение между моделями было справедливым, я предоставил каждой модели одинаковое количество свободных параметров (от двух до четырех свободных параметров, в зависимости от набора данных), чтобы учесть такие факторы, как систематическая ошибка ответа и индивидуальные различия в чувствительности к различным схемам подкрепления. . Я использовал стандартные методы подгонки кривой, чтобы получить количественные прогнозы на основе этих трех моделей для результатов 19 опубликованных экспериментов с графиками параллельных цепей, которые включали в общей сложности 92 различных набора данных, большинство из которых были получены от отдельных субъектов.Для этих наборов данных на CCM приходилось в среднем 90,8 % дисперсии, на HVA — 89,6 %, а на DRT — 83,0 %.
В этом анализе я сравнил прогностическую точность теории уменьшения задержки Фантино (DRT; Squires & Fantino, 1971), модели контекстуального выбора Грейс (CCM; Grace, 1994) и моей гиперболической модели добавленной стоимости (HVA).Чтобы сравнение между моделями было справедливым, я предоставил каждой модели одинаковое количество свободных параметров (от двух до четырех свободных параметров, в зависимости от набора данных), чтобы учесть такие факторы, как систематическая ошибка ответа и индивидуальные различия в чувствительности к различным схемам подкрепления. . Я использовал стандартные методы подгонки кривой, чтобы получить количественные прогнозы на основе этих трех моделей для результатов 19 опубликованных экспериментов с графиками параллельных цепей, которые включали в общей сложности 92 различных набора данных, большинство из которых были получены от отдельных субъектов.Для этих наборов данных на CCM приходилось в среднем 90,8 % дисперсии, на HVA — 89,6 %, а на DRT — 83,0 %.
Таким образом, при одинаковом количестве свободных параметров две модели давали одинаковые проценты дисперсии, и третья не сильно отставала. Небольшие различия в точности моделей легко могли быть вызваны случайными изменениями данных или произвольными решениями о том, как именно свободные параметры добавлялись к различным моделям. Кажется справедливым спросить: почему важно знать, какая из этих моделей лучше? Если кто-то заинтересован в прогнозировании производительности расписаний с параллельными цепями, кажется, что все три модели достаточно успешны.(Ричард Хернстайн однажды сказал мне: «Если закон соответствия объясняет 90 % дисперсии, для меня этого достаточно. Я не жадный».)
Небольшие различия в точности моделей легко могли быть вызваны случайными изменениями данных или произвольными решениями о том, как именно свободные параметры добавлялись к различным моделям. Кажется справедливым спросить: почему важно знать, какая из этих моделей лучше? Если кто-то заинтересован в прогнозировании производительности расписаний с параллельными цепями, кажется, что все три модели достаточно успешны.(Ричард Хернстайн однажды сказал мне: «Если закон соответствия объясняет 90 % дисперсии, для меня этого достаточно. Я не жадный».)
Ответ на этот вопрос таков: хотя эти три модели часто делают очень похожие прогнозы, они основаны на разных предположениях о психологических процессах, которые вызывают такое поведение. Чтобы показать это, я сначала приведу пример типичного расписания параллельных цепей, а затем представлю уравнения для каждой из трех моделей.
отображает расписание параллельных цепочек. Эта процедура обычно включает два расписания, которые работают во время так называемых начальных звеньев, каждое из которых иногда приводит к своему собственному конечному звену. Каждое конечное звено — это еще один график подкрепления, ведущий к еде. В данном примере при начальных ссылках клавиши ответов белые, и действуют два одинаковых расписания ВИ 60-х годов. Ответы на левую клавишу иногда приводят к тому, что клавиша становится зеленой, а затем еда доставляется по расписанию с фиксированным интервалом (FI) в 10 секунд.Ответы на правую клавишу иногда приводят к тому, что эта клавиша становится красной, а затем еда доставляется по расписанию FI 20-s. После каждой доставки еды клавиши становятся белыми, и первоначальные ссылки снова действуют. Таким образом, процедура параллельных цепочек чередуется между периодом выбора (начальные звенья) и периодом последствий (конечные звенья, в течение которых невозможно переключиться на другую альтернативу).
Каждое конечное звено — это еще один график подкрепления, ведущий к еде. В данном примере при начальных ссылках клавиши ответов белые, и действуют два одинаковых расписания ВИ 60-х годов. Ответы на левую клавишу иногда приводят к тому, что клавиша становится зеленой, а затем еда доставляется по расписанию с фиксированным интервалом (FI) в 10 секунд.Ответы на правую клавишу иногда приводят к тому, что эта клавиша становится красной, а затем еда доставляется по расписанию FI 20-s. После каждой доставки еды клавиши становятся белыми, и первоначальные ссылки снова действуют. Таким образом, процедура параллельных цепочек чередуется между периодом выбора (начальные звенья) и периодом последствий (конечные звенья, в течение которых невозможно переключиться на другую альтернативу).
Типичное расписание параллельных цепей с одинаковыми расписаниями VI 60-х в качестве начальных звеньев и двумя разными расписаниями FI в качестве конечных звеньев.
Обычной мерой предпочтения является доля ответов субъекта в исходных ссылках. Неудивительно, что в этом случае голубь даст больше ответов на левую клавишу, чем на правую, потому что левая клавиша ведет к терминальному звену с более коротким расписанием FI. Однако хорошо известно, что расписания в начальных звеньях, а не только в конечных звеньях, влияют на предпочтения. Если продолжительность двух идентичных графиков начального звена укорачивается, графики конечного звена оказывают большее влияние на предпочтения, и пропорции ответов становятся более экстремальными (Fantino, 1969).Это называется эффектом начальной ссылки . Например, если бы расписания начальной связи в были уменьшены до расписаний VI 30-s, процент ответов на левую клавишу увеличился бы.
Неудивительно, что в этом случае голубь даст больше ответов на левую клавишу, чем на правую, потому что левая клавиша ведет к терминальному звену с более коротким расписанием FI. Однако хорошо известно, что расписания в начальных звеньях, а не только в конечных звеньях, влияют на предпочтения. Если продолжительность двух идентичных графиков начального звена укорачивается, графики конечного звена оказывают большее влияние на предпочтения, и пропорции ответов становятся более экстремальными (Fantino, 1969).Это называется эффектом начальной ссылки . Например, если бы расписания начальной связи в были уменьшены до расписаний VI 30-s, процент ответов на левую клавишу увеличился бы.
Чтобы дать краткое объяснение того, как CCM, DRT и HVA делают прогнозы для графиков параллельных цепочек, уравнения для этих моделей будут представлены в их самых основных формах, без свободных параметров, которые использовались в сравнениях подбора кривой. (Мазур, 2001). Это позволит избежать ненужной сложности и поможет сосредоточиться на принципиальных различиях между моделями.
При рассмотрении математических моделей поведения полезно различать описательные уравнения и теоретические уравнения. Описательное уравнение просто обеспечивает в математической форме удобный способ суммировать отношения между независимой переменной и зависимыми переменными, не давая никакой теоретической основы для использования этого конкретного уравнения. Напротив, теоретическое уравнение выводится из основных принципов или предположений о психологических процессах, которые вызывают рассматриваемое поведение, и форма уравнения отражает эти предположения.CCM, DRT и HVA можно считать теоретическими уравнениями, поскольку они основаны на нескольких основных предположениях о психологических процессах, управляющих поведением выбора. Как будет видно, некоторые из этих предположений являются общими для всех трех моделей, в то время как другие предположения различаются для каждой модели.
Без свободных параметров CCM Грейс (1994) можно записать следующим образом:
6
6
B B B 1 и B 2 2 — это показатели ответов на начальных ссылках одновременных цепей, R I 1 и R I 2 – коэффициенты усиления в начальных звеньях (т. r t 1 и r t 2 — нормы армирования в двух концевых звеньях (нормы на которые терминальные звенья доставляют еду). Таким образом, согласно CCM, ответы выбора в расписаниях параллельных цепочек зависят как от расписаний в начальных звеньях, так и от расписаний в конечных звеньях. Отличительной чертой КМС является соотношение Т t /Т i . T t — средняя продолжительность оконечного соединения, а T i — средняя продолжительность начального соединения. Поскольку соотношение T t / T i используется в качестве показателя степени усиления терминальных звеньев, CCM утверждает, что различия в терминальных звеньях будут иметь большее влияние на предпочтение, когда они длинные по сравнению с конечными звеньями. размеры начальных ссылок, а конечные ссылки будут меньше влиять на предпочтения, если они относительно короткие.
r t 1 и r t 2 — нормы армирования в двух концевых звеньях (нормы на которые терминальные звенья доставляют еду). Таким образом, согласно CCM, ответы выбора в расписаниях параллельных цепочек зависят как от расписаний в начальных звеньях, так и от расписаний в конечных звеньях. Отличительной чертой КМС является соотношение Т t /Т i . T t — средняя продолжительность оконечного соединения, а T i — средняя продолжительность начального соединения. Поскольку соотношение T t / T i используется в качестве показателя степени усиления терминальных звеньев, CCM утверждает, что различия в терминальных звеньях будут иметь большее влияние на предпочтение, когда они длинные по сравнению с конечными звеньями. размеры начальных ссылок, а конечные ссылки будут меньше влиять на предпочтения, если они относительно короткие. Таким образом, в описанном выше примере, когда графики начального звена укорачиваются с VI 60 с до VI 30 с, T t / T i увеличивается, и уравнение 6 предсказывает более сильное предпочтение зеленого цвета. терминальная ссылка.
Таким образом, в описанном выше примере, когда графики начального звена укорачиваются с VI 60 с до VI 30 с, T t / T i увеличивается, и уравнение 6 предсказывает более сильное предпочтение зеленого цвета. терминальная ссылка.
Разрабатывая МКК, Грейс (1994) начала с основного предположения закона соответствия Херрнстайна (1961) о том, что относительная скорость поведения пропорциональна относительной скорости подкрепления (уравнение 1). Закон сопоставления был разработан для учета выбора в простых одновременных расписаниях, которые не имеют терминальных связей.CCM был разработан, чтобы распространить структуру закона сопоставления на расписания параллельных цепей. Грейс предположил, что графики конечных звеньев представляют собой условные подкрепления, значения которых зависят от скорости их подкрепления (90 435 r 90 586 t 90 587 90 436 90 586 1 90 587 и 90 435 r 90 586 t 90 587 90 436 90 586 2 90 587). Грейс также руководствовалась предыдущей работой Баума и Рахлина (1969), которые предположили, что, когда подкрепления различаются по двум или более разным параметрам (например, по скорости, задержке, количеству, качеству), эти разные факторы можно мультипликативно комбинировать для получения меры. общей стоимости подкрепления.Грейс предположил, что аналогичным образом коэффициенты усиления начальных звеньев ( r i 1 и r i 2 ) можно умножить на коэффициенты усиления конечных звеньев (
общей стоимости подкрепления.Грейс предположил, что аналогичным образом коэффициенты усиления начальных звеньев ( r i 1 и r i 2 ) можно умножить на коэффициенты усиления конечных звеньев (
 Конечным результатом этого набора предположений стал CCM. Обратите внимание, что уравнение 6 сводится к простому закону согласования, если T t = 0, то есть когда нет конечной связи.
Конечным результатом этого набора предположений стал CCM. Обратите внимание, что уравнение 6 сводится к простому закону согласования, если T t = 0, то есть когда нет конечной связи.DRT также использует принцип сопоставления в качестве основного предположения, и он также сводится к закону сопоставления Herrnstein (1961), если нет оконечных звеньев. Версия DRT Сквайрса и Фантино (1971) может быть записана следующим образом:
7
Как уже объяснялось, R 1 и R 2 — это скорости подкрепления, но в графике параллельных цепей они являются общими скоростями, включая время как в начальном, так и в конечном звеньях. . T total — среднее общее время до первичного подкрепления от начала начальных звеньев. T t 1 и T t 2 — среднее время до первичного армирования от начала двух конечных звеньев (т. е. средняя продолжительность двух конечных звеньев). Фундаментальное допущение DRT состоит в том, что условное подкрепляющее значение конечной связи определяется величиной уменьшения задержки , которая происходит при вводе каждой конечной связи, по сравнению со средним временем до еды от начала начальных связей.Например, в , T total составляет 45 с (поскольку средняя продолжительность начального соединения составляет 30 с, а средняя продолжительность конечного соединения составляет 15 с), T t 1 равно 10 с, и T t 2 равно 20. Таким образом, начало зеленой клавиши представляет уменьшение задержки на 35 с, но начало красной клавиши представляет сокращение задержки только на 25 с, поэтому DRT прогнозирует предпочтение зеленой альтернативе.
Фундаментальное допущение DRT состоит в том, что условное подкрепляющее значение конечной связи определяется величиной уменьшения задержки , которая происходит при вводе каждой конечной связи, по сравнению со средним временем до еды от начала начальных связей.Например, в , T total составляет 45 с (поскольку средняя продолжительность начального соединения составляет 30 с, а средняя продолжительность конечного соединения составляет 15 с), T t 1 равно 10 с, и T t 2 равно 20. Таким образом, начало зеленой клавиши представляет уменьшение задержки на 35 с, но начало красной клавиши представляет сокращение задержки только на 25 с, поэтому DRT прогнозирует предпочтение зеленой альтернативе.
Помимо предположения о решающей роли сокращения задержки, DRT отличается от CCM своим предположением о том, что поведение выбора также является функцией общей скорости подкрепления ( R 1 и R 2 ), по сравнению с Предположение CCM о том, что это функция коэффициентов усиления начального звена ( r i 1 и r i 2 ). Сквайрс и Фантино (1971) не объяснили, почему они выбрали этот подход, но следствие уравнения 7 состоит в том, что общие уровни первичного подкрепления мультипликативно комбинируются с условными подкрепляющими значениями конечных звеньев для определения поведения выбора. Эта разница между использованием в DRT общих коэффициентов подкрепления и использованием в CCM коэффициентов подкрепления начального звена может показаться тонкой, но для определенных ситуаций выбора она приводит к очень разным прогнозам, которые можно проверить с помощью подходящего плана исследования.
Сквайрс и Фантино (1971) не объяснили, почему они выбрали этот подход, но следствие уравнения 7 состоит в том, что общие уровни первичного подкрепления мультипликативно комбинируются с условными подкрепляющими значениями конечных звеньев для определения поведения выбора. Эта разница между использованием в DRT общих коэффициентов подкрепления и использованием в CCM коэффициентов подкрепления начального звена может показаться тонкой, но для определенных ситуаций выбора она приводит к очень разным прогнозам, которые можно проверить с помощью подходящего плана исследования.
HVA был построен на трех фундаментальных предположениях. Во-первых, подобно CCM и DRT, HVA принимает принцип сопоставления в качестве базового допущения, и он также сводится к закону сопоставления, если нет оконечных звеньев. Во-вторых, HVA построен на предположении, что ценность подкрепления снижается с увеличением задержки в соответствии с гиперболической функцией (как в уравнении 5). После удаления свободных параметров HVA становится:
8
Два крайних левых выражения в уравнении идентичны CCM. Крайнее правое выражение в скобках включает V t 1 и V t 2 , значения двух конечных звеньев, и V i , 9043 значения всех звеньев. из этих значений рассчитываются с использованием вариации гиперболической функции (уравнение 5), которая применяется к случаям, когда задержки до подкрепления являются переменными (Мазур, 1984). В уравнении 8 значение начальных звеньев вычитается из значения каждого конечного звена, потому что третье допущение HVA состоит в том, что выбор зависит от увеличения ценности условного подкрепления (т.т. е. добавленная стоимость), которая возникает, когда начальное звено заканчивается и начинается конечное звено. Для примера в , V i значение начальных ссылок будет низким, поскольку они связаны с длительной задержкой еды. V t 2 , значение красной клеммы немного выше, потому что красная клавиша сигнализирует о более короткой (20 с) задержке до еды.
Крайнее правое выражение в скобках включает V t 1 и V t 2 , значения двух конечных звеньев, и V i , 9043 значения всех звеньев. из этих значений рассчитываются с использованием вариации гиперболической функции (уравнение 5), которая применяется к случаям, когда задержки до подкрепления являются переменными (Мазур, 1984). В уравнении 8 значение начальных звеньев вычитается из значения каждого конечного звена, потому что третье допущение HVA состоит в том, что выбор зависит от увеличения ценности условного подкрепления (т.т. е. добавленная стоимость), которая возникает, когда начальное звено заканчивается и начинается конечное звено. Для примера в , V i значение начальных ссылок будет низким, поскольку они связаны с длительной задержкой еды. V t 2 , значение красной клеммы немного выше, потому что красная клавиша сигнализирует о более короткой (20 с) задержке до еды. V t 1 , значение зеленой терминальной линии, является самым высоким, потому что зеленая клавиша сигнализирует о 10-секундной задержке питания.Таким образом, добавленная стоимость увеличивается, когда начинается левое конечное звено, и, таким образом, HVA предсказывает предпочтение зеленой альтернативы. Когда нет задержек на оконечном звене, как в простых одновременных схемах VI, и объемы подкрепления A одинаковы для обеих альтернатив, 2 оба равны A . В этом случае самое правое выражение в скобках в уравнении 8 становится равным 1.0, а HVA сводится к закону согласования.
V t 1 , значение зеленой терминальной линии, является самым высоким, потому что зеленая клавиша сигнализирует о 10-секундной задержке питания.Таким образом, добавленная стоимость увеличивается, когда начинается левое конечное звено, и, таким образом, HVA предсказывает предпочтение зеленой альтернативы. Когда нет задержек на оконечном звене, как в простых одновременных схемах VI, и объемы подкрепления A одинаковы для обеих альтернатив, 2 оба равны A . В этом случае самое правое выражение в скобках в уравнении 8 становится равным 1.0, а HVA сводится к закону согласования.
CCM, DRT и HVA предсказывают предпочтение для более короткого конечного звена и эффекта начального звена, а также другие результаты графиков параллельных цепочек, и все они сводятся к основному закону соответствия, когда нет конечных звеньев. Это не должно вызывать удивления, потому что математические модели ограничены эмпирическими результатами, и ни одна модель, не учитывающая эти хорошо известные поведенческие явления, не будет восприниматься всерьез. Однако, как показало предыдущее обсуждение, эти три модели основаны на разных предположениях о природе поведения выбора (предположениях, которые могут быть поняты тем, кто не интересуется уравнениями). Для CCM ключевым фактором является контекст , в котором делается выбор (или, точнее, продолжительность периода выбора). Если период выбора велик по сравнению с продолжительностью оконечных соединений, то различия между расписаниями оконечных соединений относительно мало повлияют на предпочтения.Ключевым фактором для DRT является уменьшение задержки : предпочтение зависит от уменьшения времени до подкрепления, о котором сигнализирует начало терминальной связи. Для HVA ключевым фактором является значение (значение условного подкрепления, связанного с каждым графиком), и предпочтение зависит от увеличения значения, о котором сигнализирует начало терминальной связи.
Однако, как показало предыдущее обсуждение, эти три модели основаны на разных предположениях о природе поведения выбора (предположениях, которые могут быть поняты тем, кто не интересуется уравнениями). Для CCM ключевым фактором является контекст , в котором делается выбор (или, точнее, продолжительность периода выбора). Если период выбора велик по сравнению с продолжительностью оконечных соединений, то различия между расписаниями оконечных соединений относительно мало повлияют на предпочтения.Ключевым фактором для DRT является уменьшение задержки : предпочтение зависит от уменьшения времени до подкрепления, о котором сигнализирует начало терминальной связи. Для HVA ключевым фактором является значение (значение условного подкрепления, связанного с каждым графиком), и предпочтение зависит от увеличения значения, о котором сигнализирует начало терминальной связи.
Если бы не было способа провести различие между этими различными предположениями, спорить о них было бы бессмысленно. Однако, когда предположения переводятся в математическую нотацию, различия между ними легче различить, и становится возможным найти случаи, для которых модели дают совершенно разные прогнозы. Например, Савастано и Фантино (1996) показали, что если два терминальных звена удлиняются на одинаковую величину, CCM и DRT предсказывают незначительные изменения предпочтения или их отсутствие, тогда как HVA предсказывает менее экстремальное предпочтение при более длинных терминальных звеньях. Мазур (2000b) показал, что если к типичному двухальтернативному графику параллельных цепей добавляется третья альтернатива, то бывают случаи, когда и DRT, и HVA предсказывают рост предпочтения той из двух исходных альтернатив, которая ранее была предпочтительнее, тогда как CCM прогнозирует отсутствие изменений или снижение предпочтений.Невин и Грейс (2000) отметили, что по мере того, как начальные связи становятся очень длинными, как CCM, так и DRT предсказывают, что реакция выбора должна приближаться к безразличию (одинаковые ответы для двух альтернатив), тогда как HVA предсказывает сохранение предпочтения более короткой конечной связи (приближаясь к асимптоте В t 1 / В t 2 ).
Однако, когда предположения переводятся в математическую нотацию, различия между ними легче различить, и становится возможным найти случаи, для которых модели дают совершенно разные прогнозы. Например, Савастано и Фантино (1996) показали, что если два терминальных звена удлиняются на одинаковую величину, CCM и DRT предсказывают незначительные изменения предпочтения или их отсутствие, тогда как HVA предсказывает менее экстремальное предпочтение при более длинных терминальных звеньях. Мазур (2000b) показал, что если к типичному двухальтернативному графику параллельных цепей добавляется третья альтернатива, то бывают случаи, когда и DRT, и HVA предсказывают рост предпочтения той из двух исходных альтернатив, которая ранее была предпочтительнее, тогда как CCM прогнозирует отсутствие изменений или снижение предпочтений.Невин и Грейс (2000) отметили, что по мере того, как начальные связи становятся очень длинными, как CCM, так и DRT предсказывают, что реакция выбора должна приближаться к безразличию (одинаковые ответы для двух альтернатив), тогда как HVA предсказывает сохранение предпочтения более короткой конечной связи (приближаясь к асимптоте В t 1 / В t 2 ).
Я не буду оценивать эксперименты, предназначенные для проверки этих предсказаний, потому что целью этой статьи не является отстаивание какой-либо конкретной математической модели, и в любом случае потребуется более двух или трех экспериментов, чтобы окончательно определить, какие предсказания модели поддерживаются, а какие нет.Дело в том, что математическая форма этих моделей приводит к однозначным предсказаниям, которые можно строго проверить и сопоставить, чтобы их различные гипотезы о детерминантах поведения выбора можно было подвергнуть эмпирической проверке.
За пределами оперантной лаборатории
Как только в лабораторных исследованиях получены убедительные доказательства существования математического принципа, его часто можно использовать для прогнозирования или управления поведением в прикладных условиях. Закон соответствия Хернштейна (уравнение 1) — хороший пример математического принципа, который использовался психологами во многих реальных условиях.Несколько примеров помогут показать, насколько широко применяется этот принцип выбора.
Закон соответствия можно рассматривать как принцип относительности подкрепления. В нем говорится, что мы не можем предсказать, какое поведение вызовет подкрепление, не зная, какие подкрепления одновременно доступны для других действий. Например, если R 1 остается постоянным при каком-то конкретном значении (например, 40 подкреплений в час), B 1 (поведение, вызывающее это подкрепление) будет больше, если R 2 (скорость подкрепления альтернативного поведения) ниже, чем если бы она была высокой.Bulow и Meller (1998) использовали этот принцип для прогнозирования уровня сексуальной активности и использования противозачаточных средств девочками-подростками. Они пришли к выводу, что, согласно закону соответствия, рискованное сексуальное поведение будет более распространено среди девочек-подростков, для которых альтернативные источники подкрепления были относительно скудными. Они использовали график исследования подросткового подкрепления (Holmes, Heckel, Chestnut, Harris, & Cautela, 1987), чтобы определить, какие занятия каждая девочка находила особенно приятными и как часто она могла заниматься этими видами деятельности. Это обеспечило меру уровня подкрепления, которое было доступно для несексуального поведения для каждой девочки. Бьюлоу и Меллер обнаружили, что девочки с меньшим количеством альтернативных источников подкрепления, как правило, вступали в более рискованную сексуальную активность и что закон соответствия хорошо предсказал уровни сексуальной активности для отдельных девочек в разных возрастных, этнических и социально-экономических группах. . Применяя аналогичные рассуждения, Коррейя, Саймонс, Кэри и Борсари (1998) использовали закон соответствия для прогнозирования употребления наркотиков среди студентов колледжей путем измерения уровней подкрепления студентов за действия без наркотиков.
Это обеспечило меру уровня подкрепления, которое было доступно для несексуального поведения для каждой девочки. Бьюлоу и Меллер обнаружили, что девочки с меньшим количеством альтернативных источников подкрепления, как правило, вступали в более рискованную сексуальную активность и что закон соответствия хорошо предсказал уровни сексуальной активности для отдельных девочек в разных возрастных, этнических и социально-экономических группах. . Применяя аналогичные рассуждения, Коррейя, Саймонс, Кэри и Борсари (1998) использовали закон соответствия для прогнозирования употребления наркотиков среди студентов колледжей путем измерения уровней подкрепления студентов за действия без наркотиков.
Закон соответствия также применялся к поведению учащихся в учебных заведениях. Мы можем думать, что ученики в классе имеют выбор между выполнением своей академической работы и другими, неакадемическими видами поведения. Мартенс и Хоук (1989) наблюдали за поведением девочки с умственной отсталостью в классе, а также за поведением учителя и помощника учителя. Они записывали поведение девочки во время выполнения задания и разрушительное поведение, а также поощрения (например, инструкции, похвалу или другие формы внимания), предоставленные учителем и помощником.Они обнаружили, что закон соответствия дает хорошее описание взаимосвязи между уровнем выполнения задания и разрушительного поведения и уровнем поощрения, полученного девочкой за эти два типа поведения. Сделав еще один шаг вперед, Мартенс, Лохнер и Келли (1992) использовали различные графики ВИ для улучшения адекватного академического поведения у третье- и четвертоклассников, которые тратили чрезмерное количество времени на поведение, не связанное с заданием, и они обнаружили, что показатели — поведение при задании зависело от скорости подкрепления, как и предсказывал закон соответствия.В ряде других исследований закон соответствия применялся к поведению в классе (например, Billington & DiTommaso, 2003; Mace, McCurdy, & Quigley, 1990; Skinner, Robinson, Johns, Logan, & Belfiore, 1996).
Они записывали поведение девочки во время выполнения задания и разрушительное поведение, а также поощрения (например, инструкции, похвалу или другие формы внимания), предоставленные учителем и помощником.Они обнаружили, что закон соответствия дает хорошее описание взаимосвязи между уровнем выполнения задания и разрушительного поведения и уровнем поощрения, полученного девочкой за эти два типа поведения. Сделав еще один шаг вперед, Мартенс, Лохнер и Келли (1992) использовали различные графики ВИ для улучшения адекватного академического поведения у третье- и четвертоклассников, которые тратили чрезмерное количество времени на поведение, не связанное с заданием, и они обнаружили, что показатели — поведение при задании зависело от скорости подкрепления, как и предсказывал закон соответствия.В ряде других исследований закон соответствия применялся к поведению в классе (например, Billington & DiTommaso, 2003; Mace, McCurdy, & Quigley, 1990; Skinner, Robinson, Johns, Logan, & Belfiore, 1996).
Математические модели поведения, разработанные в ходе оперантных исследований, также могут использоваться исследователями в других областях науки, таких как неврология и психофармакология. Например, Kheramin et al. (2002) использовали уравнение гиперболического затухания для отложенных подкреплений (уравнение 5) для оценки влияния поражений головного мозга на выбор крысами самоконтроля (выбор между меньшим, более немедленным подкреплением и более крупным, более отсроченным подкреплением).У людей были получены данные о том, что повреждение орбитальной области префронтальной коры (OPFC) приводит к повышенной склонности к импульсивному выбору (т.е. к выбору меньшего, более непосредственного подкрепления). Как повреждения в OPFC повлияют на выбор крысами самоконтроля? Чтобы ответить на этот вопрос, Kheramin et al. давали крысам с поражениями OPFC и контрольным крысам ряд вариантов между небольшим количеством и большим количеством раствора сахарозы, каждое из которых доставлялось с задержкой. Задержки для малых и больших подкреплений варьировались в ходе испытаний, чтобы исследователи могли оценить набор точек безразличия — пар комбинаций задержки и количества, которые крысы выбирали примерно одинаково часто.Например, из одной серии вариантов экспериментаторы могли обнаружить, что небольшое поощрение, выдаваемое после 1-секундной задержки, было примерно в равной степени предпочтительнее, чем большое подкрепление, выдаваемое после 4-секундной задержки. Из другой серии вариантов они могли бы обнаружить, что небольшое поощрение, доставленное после 5-секундной задержки, было примерно в равной степени предпочтительнее более крупного поощрения, доставленного после 10-секундной задержки. Их исследование было разработано для получения пяти таких точек безразличия как у крыс с поражениями OPFC, так и у контрольных крыс.
Задержки для малых и больших подкреплений варьировались в ходе испытаний, чтобы исследователи могли оценить набор точек безразличия — пар комбинаций задержки и количества, которые крысы выбирали примерно одинаково часто.Например, из одной серии вариантов экспериментаторы могли обнаружить, что небольшое поощрение, выдаваемое после 1-секундной задержки, было примерно в равной степени предпочтительнее, чем большое подкрепление, выдаваемое после 4-секундной задержки. Из другой серии вариантов они могли бы обнаружить, что небольшое поощрение, доставленное после 5-секундной задержки, было примерно в равной степени предпочтительнее более крупного поощрения, доставленного после 10-секундной задержки. Их исследование было разработано для получения пяти таких точек безразличия как у крыс с поражениями OPFC, так и у контрольных крыс.
Основываясь на предыдущих исследованиях с аналогичными процедурами, Kheramin et al. (2002) ожидали, что если задержки для небольших подкреплений отложить по оси x , а задержки для столь же предпочтительных больших подкреплений отложить по оси y , результат должен быть линейной функцией, такой как гипотетическая примеры проиллюстрированы в . Мазур (1987) показал, что модель гиперболического распада (уравнение 5) предсказывает, что эта функция безразличия будет иметь наклон больше единицы и точку пересечения y больше нуля.Но как именно функции безразличия у крыс с поражениями OFPC будут отличаться от функций контрольных крыс? Основываясь на прогнозах, полученных из уравнения 5, Керамин и его коллеги рассмотрели три возможности, как показано на трех панелях. (Выводы для всех этих прогнозов показаны в Приложении.) Предположим, что K , параметр степени дисконтирования в уравнении 5, больше для крыс с поражениями OFPC, что означает, что для этих крыс ценность подкрепления снижается больше. быстро по мере увеличения его задержки.Из уравнения 5 следует, что увеличение K приведет к уменьшению точки пересечения y функции безразличия, но не изменит наклон, как на левой панели . Вторая возможность состоит в том, что повреждения OPFC могут изменить чувствительность крыс к различиям в размерах двух подкрепляющих средств, что представлено параметром A в уравнении 5.
Мазур (1987) показал, что модель гиперболического распада (уравнение 5) предсказывает, что эта функция безразличия будет иметь наклон больше единицы и точку пересечения y больше нуля.Но как именно функции безразличия у крыс с поражениями OFPC будут отличаться от функций контрольных крыс? Основываясь на прогнозах, полученных из уравнения 5, Керамин и его коллеги рассмотрели три возможности, как показано на трех панелях. (Выводы для всех этих прогнозов показаны в Приложении.) Предположим, что K , параметр степени дисконтирования в уравнении 5, больше для крыс с поражениями OFPC, что означает, что для этих крыс ценность подкрепления снижается больше. быстро по мере увеличения его задержки.Из уравнения 5 следует, что увеличение K приведет к уменьшению точки пересечения y функции безразличия, но не изменит наклон, как на левой панели . Вторая возможность состоит в том, что повреждения OPFC могут изменить чувствительность крыс к различиям в размерах двух подкрепляющих средств, что представлено параметром A в уравнении 5. Например, центральная панель показывает предсказания уравнения 5, если Повреждения OPFC повышают чувствительность крысы к различиям в количестве подкрепления — функции безразличия должны иметь более крутые наклоны и более крупные точки пересечения и .Третья возможность заключается в том, что поражения OPFC могут изменить как чувствительность крысы к задержке, так и ее чувствительность к количеству подкрепления. Например, правая панель показывает предсказания уравнения 5 для случая, когда чувствительность к задержке и чувствительность к количеству увеличиваются в результате повреждений OPFC. В этом примере наклон более крутой для крыс с поражениями OPFC, но точка пересечения y практически не изменилась, поскольку влияние увеличения K (которое должно уменьшить точку пересечения y ) и увеличения чувствительности к сумма (которая должна увеличить точку пересечения и ), как правило, нейтрализуют друг друга.
Например, центральная панель показывает предсказания уравнения 5, если Повреждения OPFC повышают чувствительность крысы к различиям в количестве подкрепления — функции безразличия должны иметь более крутые наклоны и более крупные точки пересечения и .Третья возможность заключается в том, что поражения OPFC могут изменить как чувствительность крысы к задержке, так и ее чувствительность к количеству подкрепления. Например, правая панель показывает предсказания уравнения 5 для случая, когда чувствительность к задержке и чувствительность к количеству увеличиваются в результате повреждений OPFC. В этом примере наклон более крутой для крыс с поражениями OPFC, но точка пересечения y практически не изменилась, поскольку влияние увеличения K (которое должно уменьшить точку пересечения y ) и увеличения чувствительности к сумма (которая должна увеличить точку пересечения и ), как правило, нейтрализуют друг друга.

Это разные прогнозы, полученные на основе модели гиперболического распада (уравнение 5), в зависимости от того, вызывают ли поражения увеличение K (левая панель), увеличение чувствительности к количеству подкрепления (центральная панель) или и то, и другое ( правая панель).
В своем эксперименте Kheramin et al. (2002) получили функции безразличия, очень похожие на функции на правой панели.Подумайте, как трудно было бы интерпретировать эту закономерность результатов без подходящего математического анализа. Различия между крысами с поражением OPFC и контрольными крысами кажутся непоследовательными: крысы с поражением OPFC были похожи на контрольных крыс с короткими задержками, но они были менее импульсивными, чем контрольные крысы с более длительными задержками. Почему это должно произойти? Математический анализ, представленный уравнением 5, предлагает объяснение этой модели результатов: он предполагает, что поражения OPFC повышают как чувствительность к задержке, так и чувствительность к количеству подкрепления, и это то, что Kheramin et al. заключил. Этот математический анализ также предлагает конкретные способы проверки этой гипотезы в будущих исследованиях. Например, если количество подкрепления остается одинаковым, модель предсказывает, что крысы с повреждениями OPFC должны демонстрировать большую склонность избегать длительных задержек, чем контрольные крысы (прогноз, который может показаться нелогичным в свете данных Khermin et al., где OPFC -поврежденные крысы обычно принимали более длительные задержки, чем контрольные крысы). И наоборот, если альтернативы различаются по количеству, но не по задержке, тогда крысы с поражениями OPFC должны демонстрировать более сильную тенденцию выбирать большее количество, чем контрольные крысы.
заключил. Этот математический анализ также предлагает конкретные способы проверки этой гипотезы в будущих исследованиях. Например, если количество подкрепления остается одинаковым, модель предсказывает, что крысы с повреждениями OPFC должны демонстрировать большую склонность избегать длительных задержек, чем контрольные крысы (прогноз, который может показаться нелогичным в свете данных Khermin et al., где OPFC -поврежденные крысы обычно принимали более длительные задержки, чем контрольные крысы). И наоборот, если альтернативы различаются по количеству, но не по задержке, тогда крысы с поражениями OPFC должны демонстрировать более сильную тенденцию выбирать большее количество, чем контрольные крысы.
Математические модели иногда могут подсказать исследователям, какие закономерности искать на клеточном уровне. Когда Платт и Глимчер (1999) изучали нейронный контроль саккадических движений глаз обезьян по направлению к зрительным целям, исследование закона соответствия (уравнение 1) побудило их изучить, как нервная активность в определенной области задней теменной коры может быть изменена. зависит от вероятности того, что подкрепление (фруктовый сок) будет доставлено после движения глаз.Они обнаружили, что уровни активности отдельных нейронов в этой области мозга были прямо пропорциональны вероятности того, что за движением глаза к цели последует подкрепление. В другом эксперименте они обнаружили, что уровни активности этих нейронов также были пропорциональны размеру подкрепления (количество сока, которое будет доставлено позже, после того, как был сделан ответ). Платт и Глимчер пришли к выводу, что отдельные нейроны теменной коры кодируют потенциальные значения подкреплений, которые могут следовать за различными возможными движениями глаз, и что эта информация в конечном итоге влияет на выбор обезьян (поскольку на поведенческом уровне выбор обезьянами различных возможных движений). движения глаз соответствовали закону соответствия).Они заявили: «В нашем эксперименте по свободному выбору как обезьяны, так и задние теменные нейроны вели себя так, как будто они знали о преимуществах, связанных с различными действиями» (стр.
зависит от вероятности того, что подкрепление (фруктовый сок) будет доставлено после движения глаз.Они обнаружили, что уровни активности отдельных нейронов в этой области мозга были прямо пропорциональны вероятности того, что за движением глаза к цели последует подкрепление. В другом эксперименте они обнаружили, что уровни активности этих нейронов также были пропорциональны размеру подкрепления (количество сока, которое будет доставлено позже, после того, как был сделан ответ). Платт и Глимчер пришли к выводу, что отдельные нейроны теменной коры кодируют потенциальные значения подкреплений, которые могут следовать за различными возможными движениями глаз, и что эта информация в конечном итоге влияет на выбор обезьян (поскольку на поведенческом уровне выбор обезьянами различных возможных движений). движения глаз соответствовали закону соответствия).Они заявили: «В нашем эксперименте по свободному выбору как обезьяны, так и задние теменные нейроны вели себя так, как будто они знали о преимуществах, связанных с различными действиями» (стр. 238). Еще неизвестно, будут ли дополнительные исследования поддерживать эту интерпретацию, но это дразнящий вывод, поскольку он предлагает прямую параллель между ценностью подкрепления, измеренной в поведенческих исследованиях, и активностью отдельных нейронов. Это яркий пример исследования механизмов мозга, стимулированного математической моделью, полученной из фундаментальных поведенческих исследований.
238). Еще неизвестно, будут ли дополнительные исследования поддерживать эту интерпретацию, но это дразнящий вывод, поскольку он предлагает прямую параллель между ценностью подкрепления, измеренной в поведенческих исследованиях, и активностью отдельных нейронов. Это яркий пример исследования механизмов мозга, стимулированного математической моделью, полученной из фундаментальных поведенческих исследований.
Объединение разнообразных явлений
В лучшем случае математические модели могут обеспечить общую основу для описания разнообразных поведенческих явлений. В течение многих лет Питер Киллин (1975, 1994; Killeen, Hall, Reilly, & Kettle, 2002) разработал и всесторонне протестировал набор математических принципов подкрепления (MPR), которые предназначены для описания взаимосвязи между подкреплением и и оперантное поведение. В основе MPR лежат три концепции: активация, временное ограничение и связь, каждая из которых представлена параметром в модели.Параметр активации представляет собой количество секунд реакции, активируемой каждым стимулом (например, каждой доставкой пищи), параметр временного ограничения представляет собой количество времени, необходимое для завершения одной реакции, а параметр связи основан на памяти животного о недавних событиях. . Грубо говоря, параметр связи измеряет силу связи между реакцией и подкреплением.
. Грубо говоря, параметр связи измеряет силу связи между реакцией и подкреплением.
Начав с этих основных понятий, Киллин (1994) использовал серию уравнений для получения прогнозов поведения при различных режимах подкрепления и сравнил эти прогнозы с данными множества различных экспериментов.Например, он показал, что для графиков отношений MPR правильно предсказывает, что частота ответов должна сначала увеличиваться до максимума, а затем уменьшаться по мере увеличения размера отношения. Для графиков VI он правильно предсказывает криволинейное увеличение скорости реакции с увеличением скорости подкрепления (см. Ресурсы). Для графиков FI он правильно предсказывает увеличение, а затем снижение скорости реакции с увеличением скорости подкрепления.
Применение математических принципов подкрепления Киллина (MPR) к множеству различных поведенческих явлений. Теоретические кривые на каждой панели показывают наиболее подходящие прогнозы МФР. Слева: общая скорость реакции голубей, паузы после подкрепления (PRP) и скорость реакции при беге по графикам FR разного размера (из Bizo & Killeen, 1997, наряду с некоторыми данными из предыдущего исследования Felton & Lyon, 1966). Верхний правый график: скорость реакции голубей на графики VI с разной скоростью подкрепления при разных уровнях лишения пищи (из Killeen, 1994, с использованием данных Heyman & Monaghan, 1987).Нижняя правая панель: уровни активности голубей в 60-секундных интервалах между презентациями пищи после приема различных лекарств (из Killeen, 1975).
Верхний правый график: скорость реакции голубей на графики VI с разной скоростью подкрепления при разных уровнях лишения пищи (из Killeen, 1994, с использованием данных Heyman & Monaghan, 1987).Нижняя правая панель: уровни активности голубей в 60-секундных интервалах между презентациями пищи после приема различных лекарств (из Killeen, 1975).
Способность одной модели успешно предсказывать скорость реакции на эти различные графики подкрепления — немалое достижение, потому что разные графики определяют очень разные функции обратной связи между поведением и подкреплением. Однако MPR может сделать гораздо больше. Разумным манипулированием параметрами модели можно объяснить эффекты множества различных экспериментальных манипуляций, таких как изменение количества силы, необходимой для отклика (Heyman & Monaghan, 1987), топография отклика (McSweeney, 1978) уровень депривации (Snyderman, 1983) и поражения гипоталамуса (Kelsey & Allison, 1976).Кроме того, Бизо и Киллин (1997) показали, что MPR можно использовать для прогнозирования не только общей скорости ответа, но и тонкой структуры ответа на соотношения и интервалы. Например, они показали, что модель может предсказывать продолжительность пауз после подкрепления и частоту бегущей реакции (частоту реакции, исключая паузу после подкрепления) для графиков FR разного размера (см. левые панели).
Например, они показали, что модель может предсказывать продолжительность пауз после подкрепления и частоту бегущей реакции (частоту реакции, исключая паузу после подкрепления) для графиков FR разного размера (см. левые панели).
MPR также применялся к целому ряду других результатов. В своей ранней работе по параметру активации Киллин (1975) продемонстрировал, как его уравнения прекрасно предсказывали увеличение и уменьшение общего уровня активности разных видов между отдельными презентациями пищи.Например, нижняя правая панель показывает уровни активности голубей под действием различных препаратов, когда они получали еду каждые 60 с. Уровни активности голубей (измеряемые датчиками движения на полу испытательной камеры) сначала увеличивались, а затем снижались по мере прохождения 60-секундного интервала, и модель Киллина очень хорошо описывала модели активности. Помимо прогнозирования стабильной производительности при различных схемах подкрепления, MPR применялся к динамическим характеристикам оперантного реагирования. То есть он использовался для прогнозирования оперантной реакции в периоды приобретения, например, когда животное изучает новую реакцию или когда оно адаптируется к новому режиму подкрепления (например, Killeen, 1994; Killeen & Bizo, 1998).
То есть он использовался для прогнозирования оперантной реакции в периоды приобретения, например, когда животное изучает новую реакцию или когда оно адаптируется к новому режиму подкрепления (например, Killeen, 1994; Killeen & Bizo, 1998).
MPR Киллина представляет собой хороший пример математической модели, которая может объяснить широкий спектр результатов, включая как тонкую структуру реагирования на графики подкрепления, так и общую частоту ответов, усвоение и устойчивую производительность, влияние подкреплений на общее состояние. активность и так далее.Без такой модели у нас могло бы возникнуть интуитивное ощущение, что эти различные аспекты оперантного поведения связаны: кажется разумным предположить, что принципы, которые могут предсказать тонкую структуру оперантной реакции, должны быть в состоянии давать предсказания об общей частоте ответов, и что те же самые переменные, которые влияют на поведение во время приобретения, должны продолжать действовать после того, как поведение стабилизируется. Однако в отсутствие модели, которая делает количественные прогнозы, такие утверждения, как «одни и те же принципы поощрения управляют как приобретением, так и долгосрочной эффективностью», не более чем махание рукой.Только когда теория делает конкретные количественные прогнозы и когда эти прогнозы проверяются на реальных данных, мы можем иметь реальную уверенность в таком общем утверждении. Как показывают примеры в этой статье, одно из самых больших преимуществ использования математических моделей заключается в том, что они генерируют точные и проверяемые прогнозы.
Однако в отсутствие модели, которая делает количественные прогнозы, такие утверждения, как «одни и те же принципы поощрения управляют как приобретением, так и долгосрочной эффективностью», не более чем махание рукой.Только когда теория делает конкретные количественные прогнозы и когда эти прогнозы проверяются на реальных данных, мы можем иметь реальную уверенность в таком общем утверждении. Как показывают примеры в этой статье, одно из самых больших преимуществ использования математических моделей заключается в том, что они генерируют точные и проверяемые прогнозы.
Выводы
Цель этой статьи состояла в том, чтобы продемонстрировать некоторые преимущества математических моделей в экспериментальном анализе поведения.Математические модели предлагают психологам ряд преимуществ:
Преобразование вербальной гипотезы в математическую модель заставляет теоретика быть точным и недвусмысленным, и это может указывать на способы проверки конкурирующих теорий, которые звучат так, как будто они делают аналогичные предсказания, когда они формулируются словами (как при сравнении отрицательного закона следствия и теории уклонения от наказания).

Даже когда формы двух математических функций очень похожи (например, гиперболическая и экспоненциальная функции задержки подкрепления в ), эти функции могут делать совершенно разные предсказания поведения с глубокими теоретическими и прикладными последствиями.В этом примере гиперболическая функция предсказывает, что люди часто будут демонстрировать изменение предпочтений в ситуациях выбора самоконтроля с течением времени, в то время как экспоненциальное уравнение не предсказывает никаких изменений предпочтений (если не делать дополнительных предположений об изменении значений параметров, предположений, которые затем можно проверить). чтобы увидеть, применимы ли они на самом деле).
В некоторых случаях конкурирующие математические модели могут одинаково хорошо учитывать большие наборы данных. Но если они на самом деле не эквивалентны математически, разные математические модели основаны на разных предположениях о психологических процессах, лежащих в основе наблюдаемого поведения.
 Например, CCM, DRT и HVA могут учитывать широкий спектр результатов от расписаний параллельных цепочек, но они предполагают разные принципы выбора поведения (зависимость от контекста, уменьшение задержек и добавление ценности). Если мы хотим понять детерминанты выбора, важно знать, какое из этих трех предположений наиболее полезно.
Например, CCM, DRT и HVA могут учитывать широкий спектр результатов от расписаний параллельных цепочек, но они предполагают разные принципы выбора поведения (зависимость от контекста, уменьшение задержек и добавление ценности). Если мы хотим понять детерминанты выбора, важно знать, какое из этих трех предположений наиболее полезно.Математические модели поведения, разработанные в ходе фундаментальных поведенческих исследований, могут использоваться для прогнозирования или управления поведением в прикладных условиях.Эти модели использовались в неврологии и психофармакологии, чтобы помочь исследователям определить функции различных структур мозга и оценить поведенческие эффекты различных лекарств.
Математическая модель может обеспечить общую структуру, объединяющую различные поведенческие явления. MPR Киллина (1994) был представлен как пример математической модели, которая применялась к широкому кругу поведенческих феноменов, но ни в коем случае не единственная.
 Другие примеры включают модель классического обусловливания Рескорла-Вагнера (Rescorla & Wagner, 1972), теорию скалярного ожидания времени Гиббона (1977) и теорию поведенческого импульса Невина (1992), и это лишь некоторые из них.
Другие примеры включают модель классического обусловливания Рескорла-Вагнера (Rescorla & Wagner, 1972), теорию скалярного ожидания времени Гиббона (1977) и теорию поведенческого импульса Невина (1992), и это лишь некоторые из них.
Хотя некоторые из этих моделей относительно просты (например, модели, представляющие отрицательный закон следствия и теорию уклонения от наказания), для других уравнения довольно сложны, как и выводы, которые позволяют применять их к конкретным примерами, и не каждый способен им следовать. Это один из недостатков математического моделирования, но его стоимость с лихвой компенсируется преимуществами. Математическая точность этих теорий позволяет их тщательно проверять, и при проверке этих теорий могут быть продемонстрированы их сильные стороны и выявлены их слабости.Например, модель Рескорла-Вагнера является важной вехой в области классического обусловливания и стимулировала множество исследований. Однако у модели Рескорла-Вагнера есть некоторые хорошо задокументированные ограничения, которые побудили к разработке альтернативных моделей (например, Hall & Pearce, 1983; Mackintosh, 1975; Miller & Schachtman, 1985; Wagner, 1981). Благодаря эмпирической и теоретической работе, которая была стимулирована моделью Рескорла-Вагнера, мы теперь гораздо лучше понимаем богатство и сложность классической обусловленности, чем до того, как эта модель была введена.
Благодаря эмпирической и теоретической работе, которая была стимулирована моделью Рескорла-Вагнера, мы теперь гораздо лучше понимаем богатство и сложность классической обусловленности, чем до того, как эта модель была введена.
В комментарии о некоторых конкурирующих математических моделях времени Киллин (1999) писал: «Если вы думаете, что модели отражают истину или что существует лучшая модель времени, то у вас проблемы. Не существует лучшей модели, не больше, чем лучшей модели автомобиля или лучшей модели купальника, хотя у каждого из нас могут быть свои любимчики. Все зависит от того, что вы хотите сделать с моделью» (стр. 275). Те, кому не нравится изучать математические модели, могут принять это утверждение (от выдающегося специалиста по математическому моделированию) как предлог избегать их.Зачем тратить время и усилия на понимание современных математических моделей поведения, когда нет лучшей модели и когда все они имеют свои слабости и ограничения? Киллин решает эту проблему, утверждая, что «любое понимание включает в себя модели — ссылки на системы, которые существуют в другой области, чем изучаемая вещь. Свободные модели делают расплывчатые ссылки на неоднозначные и случайные причины. Более строгие модели более тщательно подходят к определениям и избегают необоснованных сущностей. Модели явлений не являются причинами явлений; это описания гипотетических структур или функций, которые помогают объяснить, предсказать и контролировать» (стр.276).
Свободные модели делают расплывчатые ссылки на неоднозначные и случайные причины. Более строгие модели более тщательно подходят к определениям и избегают необоснованных сущностей. Модели явлений не являются причинами явлений; это описания гипотетических структур или функций, которые помогают объяснить, предсказать и контролировать» (стр.276).
В этой статье я утверждал, что математические модели часто являются «более точными моделями», чем словесные описания принципов поведения, и что они необходимы для дальнейшего прогресса в экспериментальном анализе поведения. Математические модели могут делать точные и важные утверждения о поведенческих процессах, которые важны для всех, кто заинтересован в объяснении, прогнозировании или контроле поведения в лаборатории или в прикладных условиях. Общение между теми исследователями поведения, которые регулярно используют математические модели, и теми, кто этого не делает, должно быть улицей с двусторонним движением.Те, кто не увлекается математикой, тем не менее могут извлечь пользу из теоретических достижений, являющихся результатом разработки и проверки математических моделей поведения. А те, кто специализируется на математических моделях, могут попытаться найти нематематические способы (такие, как словесные описания, аналогии, диаграммы или конкретные примеры) для передачи существенных идей, содержащихся в математических обозначениях, как можно более широкой аудитории.
А те, кто специализируется на математических моделях, могут попытаться найти нематематические способы (такие, как словесные описания, аналогии, диаграммы или конкретные примеры) для передачи существенных идей, содержащихся в математических обозначениях, как можно более широкой аудитории.
Эти альтернативные способы выражения математических понятий часто могут быть очень полезными.Например, научные писатели нашли много оригинальных способов объяснить теорию относительности Эйнштейна широкому кругу читателей, используя мысленные эксперименты, диаграммы, анимацию, аналогии и другие приемы. В результате, хотя я никогда не изучал математические уравнения общей теории относительности, я чувствую, что у меня есть базовое понимание теории и того, что она говорит о времени, пространстве, материи, энергии, гравитации, скорости света и скоро. Если возможно объяснить широкой аудитории понятия, столь далекие от повседневного опыта, как движение со скоростью, близкой к скорости света, или преобразование материи в энергию, то, безусловно, должно быть возможно объяснить математическую модель поведения тому, кто с математикой не дружит. Даже несмотря на то, что нематематический перевод может потерять часть точности математической модели, он все же может передать существенный момент (например, из закона соответствия, идею относительности эффектов подкрепления, или из скалярной теории ожиданий, насколько точность в временная дискриминация зависит от длительности стимула). Если ценность математической модели зависит от того, как она используется, то те, кто разрабатывает математические модели в психологии, должны стремиться содействовать их использованию не только другими специалистами, но и всеми, кто интересуется объяснением, предсказанием и контролем поведения. .
Даже несмотря на то, что нематематический перевод может потерять часть точности математической модели, он все же может передать существенный момент (например, из закона соответствия, идею относительности эффектов подкрепления, или из скалярной теории ожиданий, насколько точность в временная дискриминация зависит от длительности стимула). Если ценность математической модели зависит от того, как она используется, то те, кто разрабатывает математические модели в психологии, должны стремиться содействовать их использованию не только другими специалистами, но и всеми, кто интересуется объяснением, предсказанием и контролем поведения. .
Благодарности
Подготовка этой рукописи была поддержана грантом MH 38357 от Национального института психического здоровья.
Приложение
Гиперболическая модель (уравнение 5) делает конкретные прогнозы относительно того, как должны измениться формы функций безразличия в результате изменений K или чувствительности к количеству подкрепления. Предположим, что животному предоставляется ряд вариантов выбора между меньшим, более немедленным подкреплением и более крупным, более отсроченным подкреплением.Мы можем начать с предположения, что в точке безразличия (где животное одинаково часто выбирает две альтернативы) V S = V L , где S относится к меньшему подкреплению, а L к большему подкреплению. Из уравнения 5 следует, что A L /(1 + KD L ) = A S /(1 + KD S ).
Предположим, что животному предоставляется ряд вариантов выбора между меньшим, более немедленным подкреплением и более крупным, более отсроченным подкреплением.Мы можем начать с предположения, что в точке безразличия (где животное одинаково часто выбирает две альтернативы) V S = V L , где S относится к меньшему подкреплению, а L к большему подкреплению. Из уравнения 5 следует, что A L /(1 + KD L ) = A S /(1 + KD S ).
Чтобы получить предсказания модели, показанные на , в которой D L (по оси y ) построен как функция D S (по оси x ), мы можем решить Это уравнение для D L , что дает D L = ( A L / A S ) D S + ( A L / А S -1)/ К . Это линейное уравнение с наклоном A L / A / A S и Y Перехват ( A L / A S -1) / K .
Это линейное уравнение с наклоном A L / A / A S и Y Перехват ( A L / A S -1) / K .
В :
рассматриваются три различных возможных последствия некоторых процедурных манипуляций (например, повреждения мозга):
уменьшение точки пересечения и , но без изменения наклона, как показано на левой панели .
Если манипуляция вызовет повышение чувствительности к различиям в количествах подкрепления, это приведет к увеличению отношения чувствительны к различиям в размерах двух подкрепляющих элементов). Поскольку отношение появляется в выражениях как для наклона, так и для точки пересечения y , модель предсказывает, что результатом будет увеличение как наклона, так и точки пересечения y , как показано на центральной панели .
Если манипуляция вызывает увеличение как K , так и чувствительности к количеству, то уравнение предсказывает увеличение наклона (по той же причине, что и в предыдущем случае).
 Тем не менее, он также предсказывает, что влияние изменений в K и чувствительности к количеству будет, как правило, оказывать компенсирующее влияние на точку пересечения y , поскольку увеличение K должно вызывать уменьшение точки пересечения y , но увеличение A L / A S должно привести к увеличению точки пересечения y .Эта возможность изображена на правой панели рисунка.
Тем не менее, он также предсказывает, что влияние изменений в K и чувствительности к количеству будет, как правило, оказывать компенсирующее влияние на точку пересечения y , поскольку увеличение K должно вызывать уменьшение точки пересечения y , но увеличение A L / A S должно привести к увеличению точки пересечения y .Эта возможность изображена на правой панели рисунка.Поскольку функции безразличия, полученные Kheramin et al. (2002) были очень похожи на правую панель, эти исследователи пришли к выводу, что повреждения OPFC вызывают увеличение как K , так и чувствительности к количеству подкрепления.
Ссылки
- Эйнсли Г.В. Видное вознаграждение: поведенческая теория импульсивности и импульсивного контроля. Психологический вестник. 1975; 82: 463–496.[PubMed] [Google Scholar]
- Baum W.M. О двух видах отклонения от закона соответствия: смещении и несоответствии.
 Журнал экспериментального анализа поведения. 1974; 22: 231–242. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Журнал экспериментального анализа поведения. 1974; 22: 231–242. [Бесплатная статья PMC] [PubMed] [Google Scholar] - Baum WM, Rachlin H. Выбор как распределение времени. Журнал экспериментального анализа поведения. 1969; 12: 861–874. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Биллингтон Э.Дж., ДиТоммазо Н.М. Демонстрации и применение закона соответствия в образовании.Журнал поведенческого образования. 2003; 12:91–104. [Google Scholar]
- Бизо Л. А., Киллин П. Р. Модели эффективности графика соотношения. Журнал экспериментальной психологии: процессы поведения животных. 1997; 23: 351–367. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Bulow PJ, Meller PJ Прогнозирование сексуальной активности девочек-подростков и использования противозачаточных средств: применение закона соответствия. Журнал общественной психологии. 1998; 26: 581–596. [Google Scholar]
- Коррейя С.Дж., Саймонс Дж., Кэри К.Б, Борсари Б.Е. Прогнозирование употребления наркотиков: применение поведенческих теорий выбора.
 Аддиктивное поведение. 1998; 23:705–710. [PubMed] [Google Scholar]
Аддиктивное поведение. 1998; 23:705–710. [PubMed] [Google Scholar] - Делюти М.З. Выбор и скорость наказания в параллельных графиках. Журнал экспериментального анализа поведения. 1976; 25: 75–80. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- de Villiers P.A. Выбор параллельных графиков и количественная формулировка закона эффекта. В: Honig WK, Staddon JER, редакторы. Справочник по оперантному поведению.Энглвуд Клиффс, Нью-Джерси: Прентис-Холл; 1977. С. 233–287. [Google Scholar]
- де Вильерс П.А. К количественной теории наказания. Журнал экспериментального анализа поведения. 1980; 33:15–25. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Dinsmoor J.A. Наказание: I. Гипотеза избегания. Психологический обзор. 1954; 61: 34–46. [PubMed] [Google Scholar]
- Dinsmoor J.A. Бегство, избегание, наказание: где мы находимся? Журнал экспериментального анализа поведения.1977; 28: 83–95. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Фантино Э.
 Выбор и скорость подкрепления. Журнал экспериментального анализа поведения. 1969; 12: 723–730. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Выбор и скорость подкрепления. Журнал экспериментального анализа поведения. 1969; 12: 723–730. [Бесплатная статья PMC] [PubMed] [Google Scholar] - Felton M, Lyon D.O. Постподкрепляющая пауза. Журнал экспериментального анализа поведения. 1966; 9: 131–134. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Феррис Т. Взросление в Млечном Пути. Нью-Йорк: якорные книги; 1988. [Google Scholar]
- Гиббон Дж.Теория скалярного ожидания и закон Вебера в хронометраже животных. Психологический обзор. 1977; 84: 279–325. [Google Scholar]
- Грейс Р. Контекстная модель выбора параллельных цепочек. Журнал экспериментального анализа поведения. 1994; 61: 113–129. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Грейс Р.К. Закон сопоставления и зависящее от количества экспоненциальное дисконтирование как учет выбора самоконтроля. Журнал экспериментального анализа поведения. 1999; 71: 27–44. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Green L, Fisher E.
 Б., Перлоу С., Шерман Л. Изменение предпочтений и самоконтроль: выбор как функция суммы вознаграждения и задержки. Письма с анализом поведения. 1981; 1: 43–51. [Google Scholar]
Б., Перлоу С., Шерман Л. Изменение предпочтений и самоконтроль: выбор как функция суммы вознаграждения и задержки. Письма с анализом поведения. 1981; 1: 43–51. [Google Scholar] - Грин Л., Фристоу Н., Майерсон Дж. Дисконтирование во времени и изменение предпочтений при выборе между отсроченными результатами. Психономический бюллетень и обзор. 1994; 1: 383–389. [PubMed] [Google Scholar]
- Грин Л., Майерсон Дж. Альтернативные схемы анализа самоконтроля. Поведение и философия. 1993; 21:37–47. [Google Scholar]
- Грин Л., Майерсон Дж., Холт Д.Д., Слевин Дж.Р., Эстле С.Дж. Дисконтирование отсроченных пищевых вознаграждений у голубей и крыс: есть ли эффект масштаба? Журнал экспериментального анализа поведения. 2004; 81: 39–50. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Грин Л., Майерсон Дж., Макфадден Э. Скорость временного дисконтирования уменьшается с размером вознаграждения. Память и познание. 1997; 25: 715–723. [PubMed] [Google Scholar]
- Холл Г.
 , Пирс Дж. М. Изменения ассоциативности стимулов во время приобретения: последствия для теорий приобретения.В: Commons ML, Herrnstein RJ, Wagner AR, редакторы. Количественный анализ поведения: Vol. 3: Приобретение. Кембридж, Массачусетс: Баллинджер; 1983. стр. 221–239. [Google Scholar]
, Пирс Дж. М. Изменения ассоциативности стимулов во время приобретения: последствия для теорий приобретения.В: Commons ML, Herrnstein RJ, Wagner AR, редакторы. Количественный анализ поведения: Vol. 3: Приобретение. Кембридж, Массачусетс: Баллинджер; 1983. стр. 221–239. [Google Scholar] - Herrnstein R.J. Относительная и абсолютная сила реакции в зависимости от частоты подкрепления. Журнал экспериментального анализа поведения. 1961; 4: 267–272. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Heyman G.M., Monaghan M.M. Влияние изменений в требовании ответа и лишении на параметры уравнения закона согласования: новые данные и обзор.Журнал экспериментальной психологии: процессы поведения животных. 1987; 13: 384–394. [Google Scholar]
- Холмс Г. Р., Хекель Р. В., Честнат Э., Харрис Н., Каутела Дж. Факторный анализ графика опроса подростков (ARSS) с участием первокурсников колледжа. Журнал клинической психологии. 1987; 43: 386–390. [PubMed] [Google Scholar]
- Hull C.
 L. Принципы поведения. Нью-Йорк: Appleton-Century-Crofts; 1943. [Google Scholar]
L. Принципы поведения. Нью-Йорк: Appleton-Century-Crofts; 1943. [Google Scholar] - Келси Дж. Э., Эллисон Дж. Нажатие рычага с фиксированным передаточным числом крысами VMH: Work vs.доступность сахарозного вознаграждения. Физиология и поведение. 1976; 17: 749–754. [PubMed] [Google Scholar]
- Kheramin S, Body S, Mobini S, Ho M.-Y, Velazquez-Martinez DN, Bradshaw CM, Szabadi E, Deakin JFW, Anderson IM Эффекты индуцированных хинолиновой кислотой поражений орбитальной префронтальная кора на межвременном выборе: количественный анализ. Психофармакология. 2002; 165:9–17. [PubMed] [Google Scholar]
- Киллин П. Р. О временном контроле поведения. Психологический обзор.1975; 82: 89–115. [Google Scholar]
- Киллин П. Р. Математические принципы подкрепления. Поведенческие и мозговые науки. 1994; 17:105–172. [Google Scholar]
- Киллин П. Р. Моделирование моделирование. Журнал экспериментального анализа поведения. 1999; 71: 275–280. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Killeen PR, Bizo LA Механика подкрепления.
 Психономический бюллетень и обзор. 1998; 5: 221–238. [Google Scholar]
Психономический бюллетень и обзор. 1998; 5: 221–238. [Google Scholar] - Киллин П.Р., Холл С.С., Рейли М.П, Кеттл Л.С. Молекулярный анализ основных компонентов силы реакции. Журнал экспериментального анализа поведения. 2002; 78: 127–160. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Mace F.C., McCurdy B., Quigley E.A. Побочный эффект вознаграждения, предсказанный теорией соответствия. Журнал прикладного анализа поведения. 1990; 23:197–205. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Mackintosh NJ Теория внимания: вариации связываемости стимулов с подкреплением.Психологический обзор. 1975; 82: 276–298. [Google Scholar]
- Мартенс Б.К., Хоук Дж.Л. Применение закона эффекта Хернштейна к деструктивному поведению умственно отсталой девочки-подростка. Журнал экспериментального анализа поведения. 1989; 51: 17–27. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Martens B.K., Lochner D.G., Kelly S.Q. Влияние подкрепления с переменным интервалом на академическую вовлеченность: демонстрация теории соответствия.
 Журнал прикладного анализа поведения.1992; 25: 143–151. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Журнал прикладного анализа поведения.1992; 25: 143–151. [Бесплатная статья PMC] [PubMed] [Google Scholar] - Мазур Дж. Э. Тесты правила эквивалентности для фиксированной и переменной задержки подкрепления. Журнал экспериментальной психологии: процессы поведения животных. 1984; 10: 426–436. [Google Scholar]
- Мазур Дж. Э. Процедура корректировки для изучения отсроченного подкрепления. В: Commons ML, Mazur JE, Nevin JA, Rachlin H, editors. Количественный анализ поведения: Vol. 5. Влияние задержки и промежуточных событий на ценность подкрепления.Хиллсдейл, Нью-Джерси: Эрлбаум; 1987. С. 55–73. [Google Scholar]
- Мазур Дж. Э. Компромиссы между задержкой, скоростью и количеством подкрепления. Поведенческие процессы. 2000а; 49:1–10. [PubMed] [Google Scholar]
- Мазур Дж. Э. Графики параллельной цепочки с двумя и тремя альтернативами: тест трех моделей. Журнал экспериментальной психологии: процессы поведения животных. 2000b; 26: 286–293. [PubMed] [Google Scholar]
- Мазур Дж.
 Э. Гиперболическая добавленная стоимость и общие модели выбора животных.Психологический обзор. 2001; 108: 96–112. [PubMed] [Google Scholar]
Э. Гиперболическая добавленная стоимость и общие модели выбора животных.Психологический обзор. 2001; 108: 96–112. [PubMed] [Google Scholar] - McSweeney F.K. Прогнозирование одновременного нажатия педали на нажатие педали, реагирующего на простое выполнение графика. Обучение и поведение животных. 1978; 6: 444–450. [Google Scholar]
- Миллер Р.Р., Шахтман Т.Р. Несколько ролей контекста во время поиска. В: Balsam PD, Tomie A, редакторы. Контекст и обучение. Хиллсдейл, Нью-Джерси: Эрлбаум; 1985. [Google Scholar]
- Невин Дж.А. Интегративная модель для изучения поведенческого импульса.Журнал экспериментального анализа поведения. 1992; 57: 301–316. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Nevin J.A., Grace R.A. Поведенческий импульс и закон эффекта. Поведенческие и мозговые науки. 2000; 23:73–130. [PubMed] [Google Scholar]
- Онг Э.Л., Уайт К.Г. Временное дисконтирование в зависимости от суммы? Поведенческие процессы. 2004; 66: 201–212. [PubMed] [Google Scholar]
- Платт М.
 Л., Глимчер П.В. Нейронные корреляты переменных решения в теменной коре.Природа. 1999; 400: 233–238. [PubMed] [Google Scholar]
Л., Глимчер П.В. Нейронные корреляты переменных решения в теменной коре.Природа. 1999; 400: 233–238. [PubMed] [Google Scholar] - Rachlin H, Herrnstein R.J. Возвращение к гедонизму: об отрицательном законе эффекта. В: Кэмпбелл Б.А., Черч Р.М., редакторы. Наказание и агрессивное поведение. Нью-Йорк: Appleton-Century-Crofts; 1969. [Google Scholar]
- Рескорла Р.А., Вагнер А.Р. Теория павловской обусловленности: различия в эффективности подкрепления и отсутствия подкрепления. В: Black AH, Prokasy WF, редакторы. Классическое обусловливание II: текущие исследования и теория.Нью-Йорк: Appleton-Century-Crofts; 1972. С. 64–99. [Google Scholar]
- Ричардс Дж. Б., Митчелл С. Х., де Вит Х., Сейден Л. С. Определение дисконтных функций у крыс с помощью процедуры корректировки. Журнал экспериментального анализа поведения. 1997; 67: 353–366. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Савастано Х.И., Фантино Э. Различия в задержке, а не в соотношениях, выбор управления в параллельных цепочках.
 Журнал экспериментального анализа поведения. 1996; 66: 97–116. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Журнал экспериментального анализа поведения. 1996; 66: 97–116. [Бесплатная статья PMC] [PubMed] [Google Scholar] - Skinner C.H, Робинсон С. Л., Джонс Г. А., Логан П., Белфиоре П. Дж. Применение закона соответствия Херрнстайна, чтобы повлиять на выбор студентов для выполнения сложных академических задач. Журнал экспериментального образования. 1996; 65: 5–17. [Google Scholar]
- Снайдерман М. Масса тела и сила реакции. Письма с анализом поведения. 1983; 3: 255–265. [Google Scholar]
- Сквайрс Н., Фантино Э. Модель выбора в простых параллельных расписаниях и расписаниях параллельных цепочек. Журнал экспериментального анализа поведения. 1971; 15: 27–38.[Бесплатная статья PMC] [PubMed] [Google Scholar]
- Wagner A.R. СОП: модель автоматической обработки памяти в поведении животных. В: Spear NE, Miller RR, редакторы. Обработка информации у животных: механизмы памяти. Хиллсдейл, Нью-Джерси: Эрлбаум; 1981. [Google Scholar]
Зачем использовать математические и статистические модели
Математические модели
Есть несколько ситуаций, в которых математические модели могут быть очень эффективно использованы во вводном обучении.
- Математические модели могут помочь учащимся понять и изучить значение уравнений или функциональных взаимосвязей.
- Программное обеспечение для математического моделирования, такое как Excel, Stella II или интерактивные программы типа JAVA/Macromedia, позволяют относительно легко создать учебную среду, в которой учащиеся-первокурсники могут интерактивно участвовать в управляемом опросе, очных и практических занятиях .
- После разработки концептуальной модели физической системы естественно разработать математическую модель, которая позволит количественно оценить поведение системы.
- Количественные результаты математических моделей можно легко сравнить с данными наблюдений, чтобы определить сильные и слабые стороны модели.
- Математические модели являются важным компонентом окончательной «полной модели» системы, которая фактически представляет собой набор концептуальных, физических, математических, визуализационных и, возможно, статистических подмоделей.

Статистические модели
Надежная статистическая база очень важна в науке.Но степень, в которой статистические идеи подходят для вводного курса, зависит от конкретных целей курса и степени или институциональной структуры. Здесь мы приводим несколько примеров, показывающих, почему и когда статистические модели полезны.
Прогнозы NOAA PMEL для зимних климатических изменений Эль-Ниньо на основе статистического анализа данных.Можно использовать статистические модели или базовую статистику:
- Для характеристики числовых данных, чтобы помочь кратко описать измерения и помочь в разработке концептуальных моделей системы или процесса;
- Для помощи в оценке неопределенностей в данных наблюдений и неопределенностей в расчетах на основе данных наблюдений;
- Чтобы охарактеризовать числовые выходные данные математических моделей, чтобы помочь понять поведение модели и оценить способность модели имитировать важные функции естественной системы (проверка модели).
 Возврат этой информации в процесс разработки модели повысит производительность модели;
Возврат этой информации в процесс разработки модели повысит производительность модели; - Для оценки вероятностного будущего поведения системы на основе прошлой статистической информации используется модель статистического прогнозирования . Этот метод часто используется в прогнозировании климата. Утверждение типа «Южная Калифорния будет влажной этой зимой из-за сильного Эль-Ниньо» основано на модели статистического прогнозирования.
- Экстраполяция или интерполяция данных на основе линейной подгонки (или какой-либо другой математической подгонки) также являются хорошими примерами моделей статистического прогнозирования.
- Для оценки входных параметров более сложных математических моделей.
- Для получения частотных спектров наблюдений и выходных данных модели.



 30 × (0,08/w+ 4w 2 ) = 0,30 USD × (0,08/0,22+ 4×0,22 2 ) = 0,167
30 × (0,08/w+ 4w 2 ) = 0,30 USD × (0,08/0,22+ 4×0,22 2 ) = 0,167
 Таким образом были объединены то, что было отдельными исследованиями электричества, магнетизма и оптики.(стр. 187)
Таким образом были объединены то, что было отдельными исследованиями электричества, магнетизма и оптики.(стр. 187)
 Например, CCM, DRT и HVA могут учитывать широкий спектр результатов от расписаний параллельных цепочек, но они предполагают разные принципы выбора поведения (зависимость от контекста, уменьшение задержек и добавление ценности). Если мы хотим понять детерминанты выбора, важно знать, какое из этих трех предположений наиболее полезно.
Например, CCM, DRT и HVA могут учитывать широкий спектр результатов от расписаний параллельных цепочек, но они предполагают разные принципы выбора поведения (зависимость от контекста, уменьшение задержек и добавление ценности). Если мы хотим понять детерминанты выбора, важно знать, какое из этих трех предположений наиболее полезно.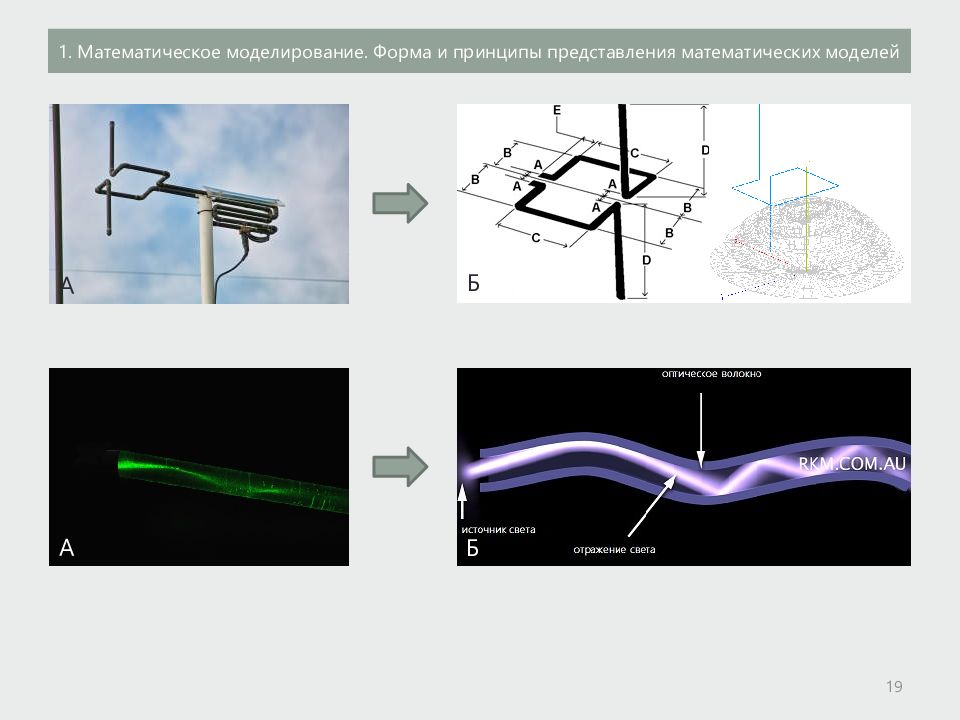 Другие примеры включают модель классического обусловливания Рескорла-Вагнера (Rescorla & Wagner, 1972), теорию скалярного ожидания времени Гиббона (1977) и теорию поведенческого импульса Невина (1992), и это лишь некоторые из них.
Другие примеры включают модель классического обусловливания Рескорла-Вагнера (Rescorla & Wagner, 1972), теорию скалярного ожидания времени Гиббона (1977) и теорию поведенческого импульса Невина (1992), и это лишь некоторые из них. Тем не менее, он также предсказывает, что влияние изменений в K и чувствительности к количеству будет, как правило, оказывать компенсирующее влияние на точку пересечения y , поскольку увеличение K должно вызывать уменьшение точки пересечения y , но увеличение A L / A S должно привести к увеличению точки пересечения y .Эта возможность изображена на правой панели рисунка.
Тем не менее, он также предсказывает, что влияние изменений в K и чувствительности к количеству будет, как правило, оказывать компенсирующее влияние на точку пересечения y , поскольку увеличение K должно вызывать уменьшение точки пересечения y , но увеличение A L / A S должно привести к увеличению точки пересечения y .Эта возможность изображена на правой панели рисунка. Журнал экспериментального анализа поведения. 1974; 22: 231–242. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Журнал экспериментального анализа поведения. 1974; 22: 231–242. [Бесплатная статья PMC] [PubMed] [Google Scholar]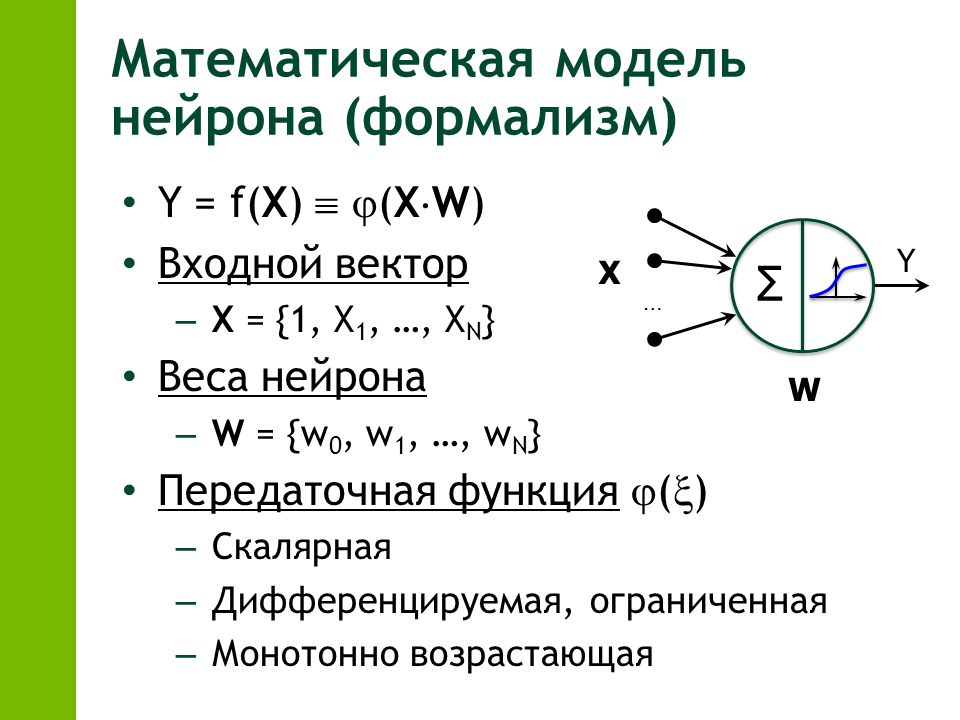 Аддиктивное поведение. 1998; 23:705–710. [PubMed] [Google Scholar]
Аддиктивное поведение. 1998; 23:705–710. [PubMed] [Google Scholar] Выбор и скорость подкрепления. Журнал экспериментального анализа поведения. 1969; 12: 723–730. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Выбор и скорость подкрепления. Журнал экспериментального анализа поведения. 1969; 12: 723–730. [Бесплатная статья PMC] [PubMed] [Google Scholar] Б., Перлоу С., Шерман Л. Изменение предпочтений и самоконтроль: выбор как функция суммы вознаграждения и задержки. Письма с анализом поведения. 1981; 1: 43–51. [Google Scholar]
Б., Перлоу С., Шерман Л. Изменение предпочтений и самоконтроль: выбор как функция суммы вознаграждения и задержки. Письма с анализом поведения. 1981; 1: 43–51. [Google Scholar] , Пирс Дж. М. Изменения ассоциативности стимулов во время приобретения: последствия для теорий приобретения.В: Commons ML, Herrnstein RJ, Wagner AR, редакторы. Количественный анализ поведения: Vol. 3: Приобретение. Кембридж, Массачусетс: Баллинджер; 1983. стр. 221–239. [Google Scholar]
, Пирс Дж. М. Изменения ассоциативности стимулов во время приобретения: последствия для теорий приобретения.В: Commons ML, Herrnstein RJ, Wagner AR, редакторы. Количественный анализ поведения: Vol. 3: Приобретение. Кембридж, Массачусетс: Баллинджер; 1983. стр. 221–239. [Google Scholar] L. Принципы поведения. Нью-Йорк: Appleton-Century-Crofts; 1943. [Google Scholar]
L. Принципы поведения. Нью-Йорк: Appleton-Century-Crofts; 1943. [Google Scholar] Психономический бюллетень и обзор. 1998; 5: 221–238. [Google Scholar]
Психономический бюллетень и обзор. 1998; 5: 221–238. [Google Scholar] Журнал прикладного анализа поведения.1992; 25: 143–151. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Журнал прикладного анализа поведения.1992; 25: 143–151. [Бесплатная статья PMC] [PubMed] [Google Scholar] Э. Гиперболическая добавленная стоимость и общие модели выбора животных.Психологический обзор. 2001; 108: 96–112. [PubMed] [Google Scholar]
Э. Гиперболическая добавленная стоимость и общие модели выбора животных.Психологический обзор. 2001; 108: 96–112. [PubMed] [Google Scholar] Л., Глимчер П.В. Нейронные корреляты переменных решения в теменной коре.Природа. 1999; 400: 233–238. [PubMed] [Google Scholar]
Л., Глимчер П.В. Нейронные корреляты переменных решения в теменной коре.Природа. 1999; 400: 233–238. [PubMed] [Google Scholar] Журнал экспериментального анализа поведения. 1996; 66: 97–116. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Журнал экспериментального анализа поведения. 1996; 66: 97–116. [Бесплатная статья PMC] [PubMed] [Google Scholar]
 Возврат этой информации в процесс разработки модели повысит производительность модели;
Возврат этой информации в процесс разработки модели повысит производительность модели;