Линия косинуса на окружности: Тригонометрическая окружность — универсальная шпаргалка по тригонометрии (ЕГЭ — 2021)
Линия синусов на окружности. Тригонометрическая окружность
{ -∞Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Прежде чем перейти к этому разделу, напомним определения синуса и косинуса, изложенные в учебнике геометрии 7-9 классов.
Синус острого угла t прямоугольного треугольника равен отношению противолежащего катета к гипотенузе (рис.1):
Косинус острого угла t прямоугольного треугольника равен отношению прилежащего катета к гипотенузе (рис.1):
Эти определения относятся к прямоугольному треугольнику и являются частными случаями тех определений, которые представлены в данном разделе.
Поместим тот же прямоугольный треугольник в числовую окружность (рис.2).
Мы видим, что катет b равен определенной величине y на оси Y (оси ординат), катет а равен определенной величине x на оси X (оси абсцисс).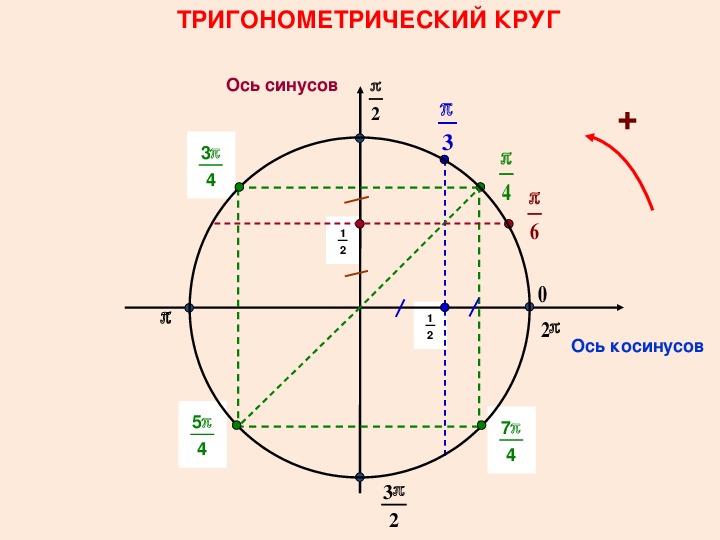
Таким образом, наши формулы обретают иной вид.
Так как b = y , a = x , c = R, то:
y x
sin t = — , cos t = —.
R R
Кстати, тогда иной вид обретают, естественно, и формулы тангенса и котангенса.
Так как tg t = b/a, ctg t = a/b, то, верны и другие уравнения:
tg t = y /x ,
ctg = x /y .
Но вернемся к синусу и косинусу. Мы имеем дело с числовой окружностью, в которой радиус равен 1. Значит, получается:
y
sin t = — = y ,
1
x
cos t = — = x .
1
Так мы приходим к третьему, более простому виду тригонометрических формул.
Эти формулы применимы не только к острому, но и к любому другому углу (тупому или развернутому).
Определения и формулы cos t, sin t, tg t, ctg t.
Из формул тангенса и котангенса следует еще одна формула:
Уравнения числовой окружности.
Знаки синуса, косинуса, тангенса и котангенса в четвертях окружности:
1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть | |
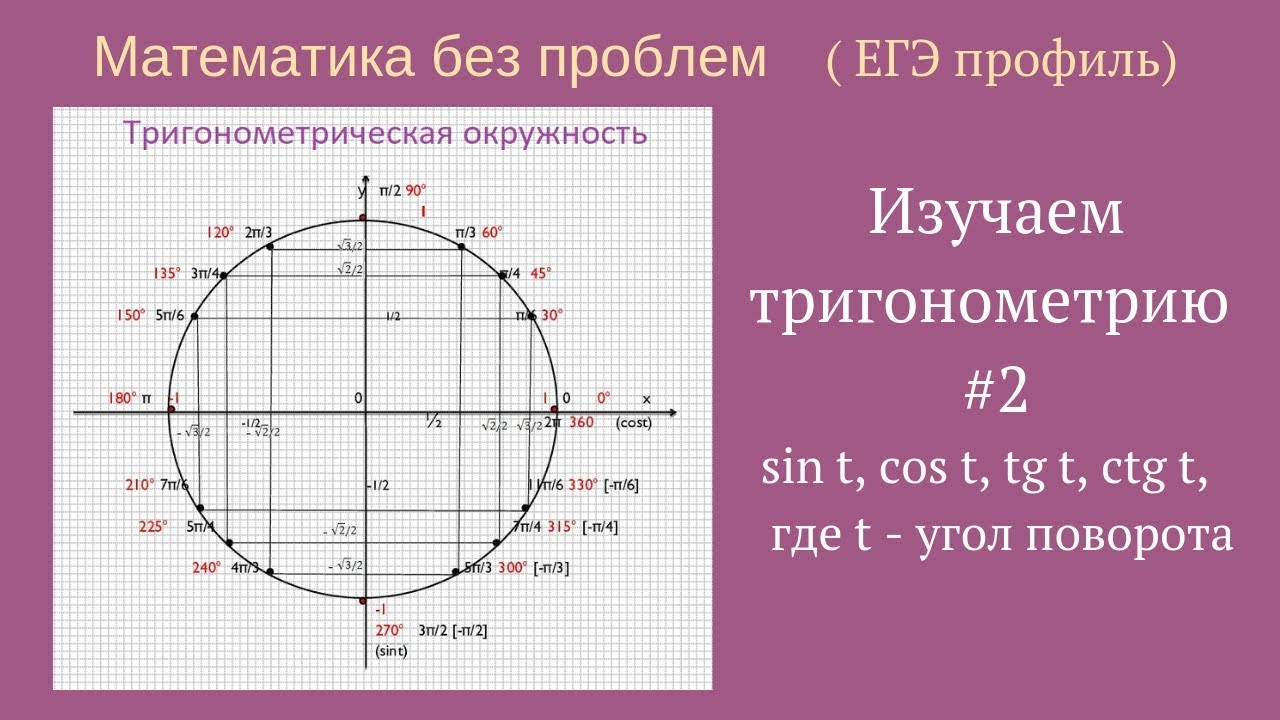
Косинус и синус основных точек числовой окружности:
Как запомнить значения косинусов и синусов основных точек числовой окружности.
Прежде всего надо знать, что в каждой паре чисел значения косинуса стоят первыми, значения синуса – вторыми.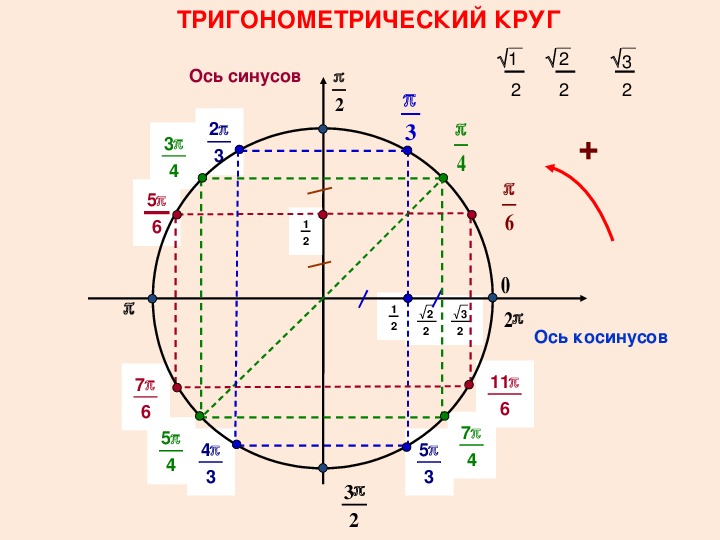
1) Обратите внимание: при всем множестве точек числовой окружности мы имеем дело лишь с пятью числами (в модуле):
1 √2 √3
0; -; —; —; 1.
2 2 2
Сделайте для себя это «открытие» — и вы снимете психологический страх перед обилием чисел: их на самом деле всего-то пять.
2) Начнем с целых чисел 0 и 1. Они находятся только на осях координат.
Не надо учить наизусть, где, к примеру, косинус в модуле имеет единицу, а где 0.
На концах оси косинусов (оси
На концах оси синусов (оси у ) синусы равны модулю 1 , а косинусы равны 0.
Теперь о знаках. Ноль знака не имеет. Что касается 1 – тут просто надо вспомнить самую простую вещь: из курса 7 класса вы знаете, что на оси х справа от центра координатной плоскости – положительные числа, слева – отрицательные; на оси у вверх от центра идут положительные числа, вниз – отрицательные.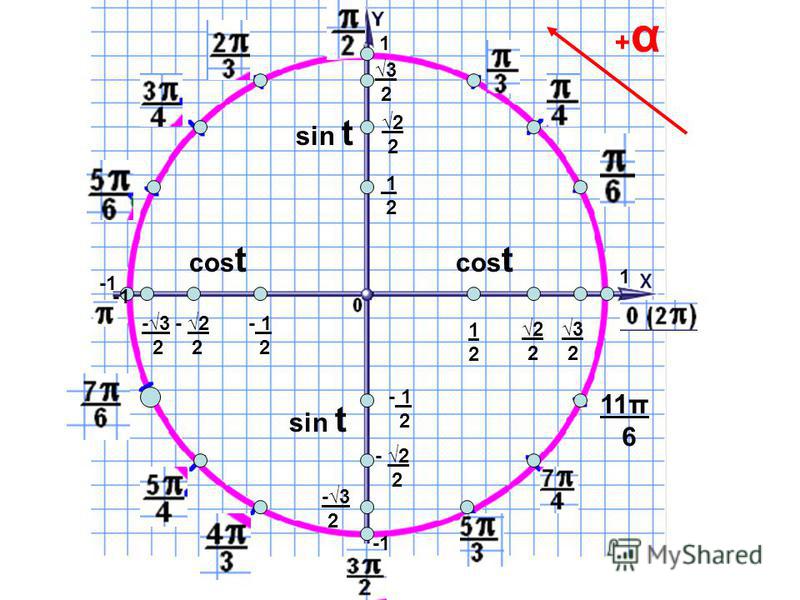 И тогда вы не ошибетесь со знаком 1.
И тогда вы не ошибетесь со знаком 1.
3) Теперь перейдем к дробным значениям.
Во всех знаменателях дробей – одно и то же число 2. Уже не ошибемся, что писать в знаменателе.
В серединах четвертей косинус и синус имеют абсолютно одинаковое значение по модулю: √2/2. В каком случае они со знаком плюс или минус – см.таблицу выше. Но вряд ли вам нужна такая таблица: вы знаете это из того же курса 7 класса.
Все ближайшие к оси х точки имеют абсолютно одинаковые по модулю значения косинуса и синуса: (√3/2; 1/2).
Значения всех ближайших к оси у точек тоже абсолютно идентичны по модулю – причем в них те же числа, только они «поменялись» местами: (1/2; √3/2).
Теперь о знаках – тут свое интересное чередование (хотя со знаками, полагаем, вы должны легко разобраться и так).
Если в первой четверти значения и косинуса, и синуса со знаком плюс, то в диаметрально противоположной (третьей) они со знаком минус.
Если во второй четверти со знаком минус только косинусы, то в диаметрально противоположной (четвертой) – только синусы.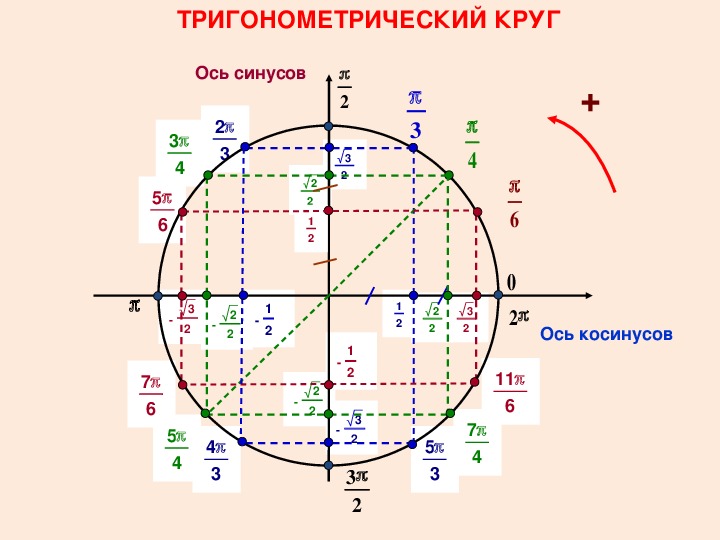
Осталось только напомнить, что в каждом сочетании значений косинуса и синуса первое число – это значение косинуса, второе число – значение синуса.
Обратите внимание еще на одну закономерность: синус и косинус всех диаметрально противоположных точек окружности абсолютно равны по модулю. Возьмем, к примеру, противоположные точки π/3 и 4π/3:
cos π/3 = 1/2, sin π/3 = √3/2
cos 4π/3 = -1/2, sin 4π/3 = -√3/2
Различаются значения косинусов и синусов двух противоположных точек только по знаку. Но и здесь есть своя закономерность: синусы и косинусы диаметрально противоположных точек всегда имеют противоположные знаки.
Важно знать :
Значения косинусов и синусов точек числовой окружности последовательно возрастают или убывают в строго определенном порядке: от самого малого значения до самого большого и наоборот (см. раздел «Возрастание и убывание тригонометрических функций» — впрочем, в этом легко убедиться, лишь просто посмотрев на числовую окружность выше).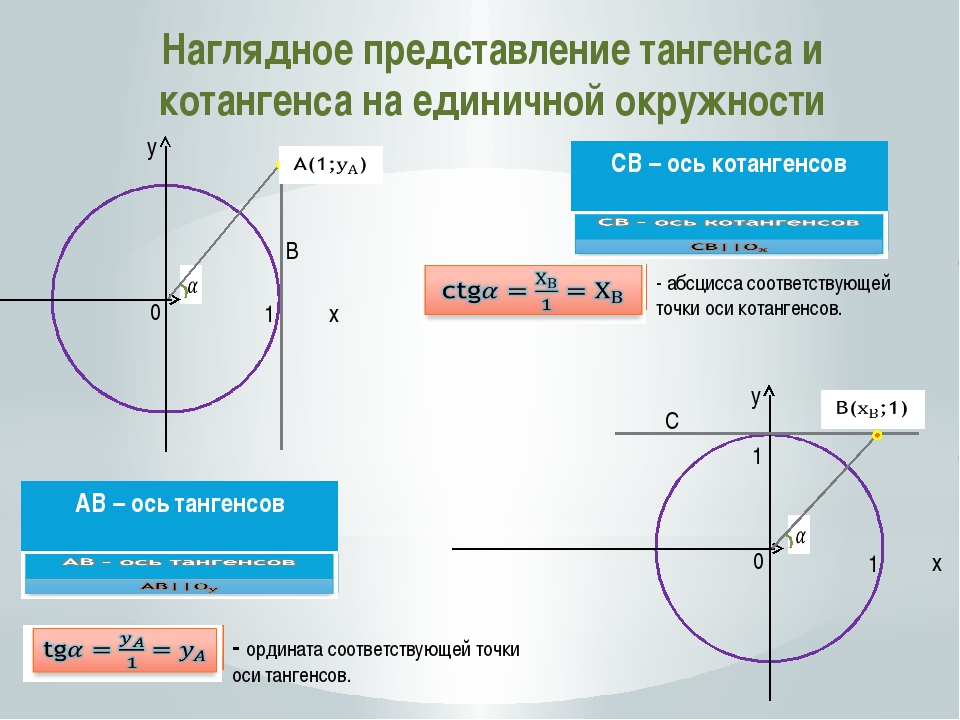
В порядке убывания получается такое чередование значений:
√3 √2 1 1 √2 √3
1; —; —; -; 0; – -; – —; – —; –1
2 2 2 2 2 2
Возрастают они строго в обратном порядке.
Поняв эту простую закономерность, вы научитесь довольно легко определять значения синуса и косинуса.
Тангенс и котангенс основных точек числовой окружности.
Зная косинус и синус точек числовой окружности, легко можно вычислить их тангенс и котангенс. Делим синус на косинус — получаем тангенс. Делим косинус на синус — получаем котангенс. Результаты этого деления — на рисунке.
ПРИМЕЧАНИЕ : В некоторых таблицах значения тангенса и котангенса, равные модулю √3/3, указаны как 1/√3. Ошибки тут нет, так как это равнозначные числа. Если числитель и знаменатель числа 1/√3 умножить на √3, то получим √3/3.
Как запомнить значение тангенсов и котангенсов основных точек числовой окружности.
Здесь такие же закономерности, что и с синусами и косинусами. И чисел тут всего четыре (в модуле): 0, √3/3, 1, √3.
И чисел тут всего четыре (в модуле): 0, √3/3, 1, √3.
На концах осей координат – прочерки и нули. Прочерки означают, что в данных точках тангенс или котангенс не имеют смысла.
Как запомнить, где прочерки, а где нули? Поможет правило.
Тангенс – это отношение синуса к косинусу. На концах оси
Котангенс – это отношение косинуса к синусу. На концах оси косинусов (ось х ) котангенс не существует.
В остальных точках идет чередование всего лишь трех чисел: 1, √3 и √3/3 со знаками плюс или минус. Как с ними разобраться? Запомните (а лучше представьте) три обстоятельства:
1) тангенсы и котангенсы всех середин четвертей имеют в модуле 1.
2) тангенсы и котангенсы ближайших к оси х точек имеют в модуле √3/3; √3.
3) тангенсы и котангенсы ближайших к оси у точек имеют в модуле √3; √3/3.
Не ошибитесь со знаками – и вы большой знаток.
Нелишне будет запомнить, как возрастают и убывают тангенс и котангенс на числовой окружности (см.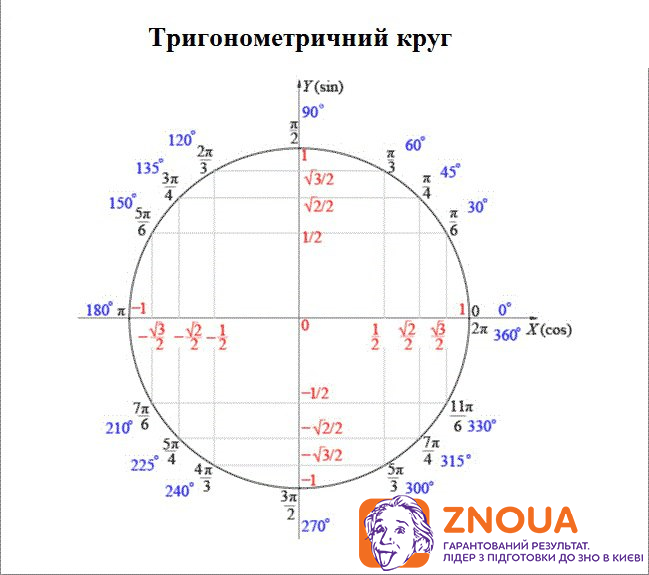
Тригонометрические свойства чисел числовой окружности.
Представим, что определенная точка М имеет значение t.
Свойство 1 :
| | | |
Пояснение . Пусть t = –60º и t = –210º.
cos –60º равен 1/2. Но cos 60º тоже равен 1/2. То есть косинусы –60º и 60º равны как по модулю, так и по знаку: cos –60º = cos 60º.
cos –210º равен –√3/2. Но cos 210º тоже равен –√3/2. То есть: cos –210º = cos 210º.
cos (– t) = cos t.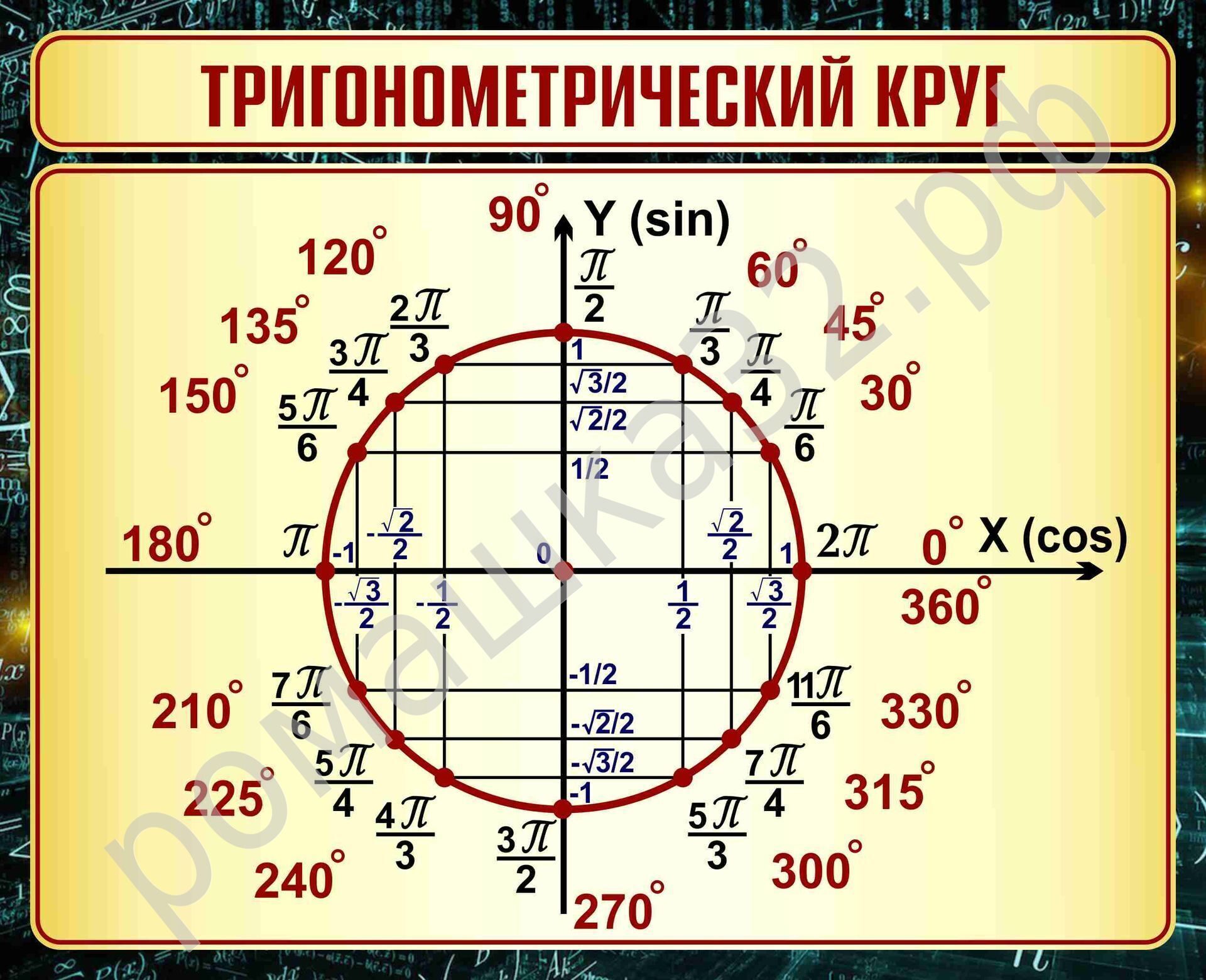
sin –60º равен –√3/2. А sin 60º равен √3/2. То есть sin –60º и sin 60º равны по модулю, но противоположны по знаку.
sin –210º равен 1/2. А sin 210º равен –1/2. То есть sin –210º и sin 210º равны по модулю, но противоположны по знаку.
Таким образом, мы доказали, что sin (– t) = – sin t.
Посмотрите, что происходит с тангенсами и котангенсами этих углов – и вы сами легко докажете себе верность двух других тождеств, приведенных в таблице.
Вывод: косинус – четная функция, синус, тангенс и котангенс – нечетные функции.
Свойство 2: Так как t = t + 2πk , то:
| |
Пояснение
: t и t + 2πk – это одна и та же точка на числовой окружности. Просто в случае с 2πk мы совершаем определенное количество полных оборотов по окружности, прежде чем приходим к точке t.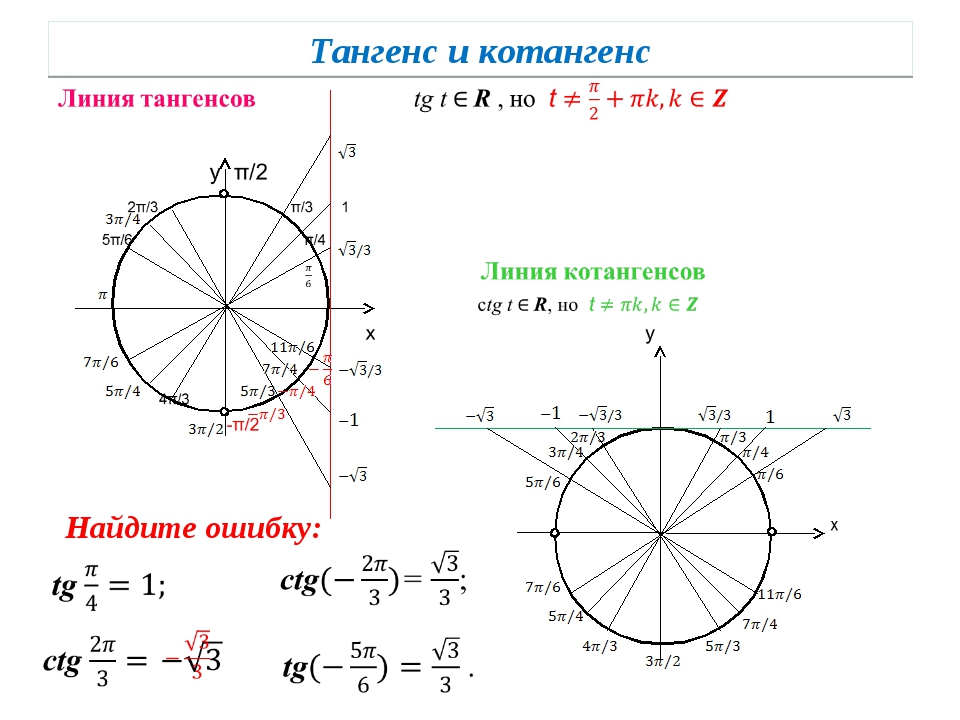 Значит, и равенства, изложенные в этой таблице, очевидны.
Значит, и равенства, изложенные в этой таблице, очевидны.
Свойство 3: Если две точки окружности находятся друг против друга относительно центра О, то их синусы и косинусы равны по модулю, но противоположны по знаку, а их тангенсы и котангенсы одинаковы как по модулю, так и по знаку.
| | | |
Пояснение
: Пусть точка М находится в первой четверти. Она имеет положительное значение синуса и косинуса. Проведем от этой точки диаметр – то есть отрезок, проходящий через центр оси координат и заканчивающийся в точке окружности напротив. Обозначим эту точку буквой N. Как видите, дуга MN равна половине окружности.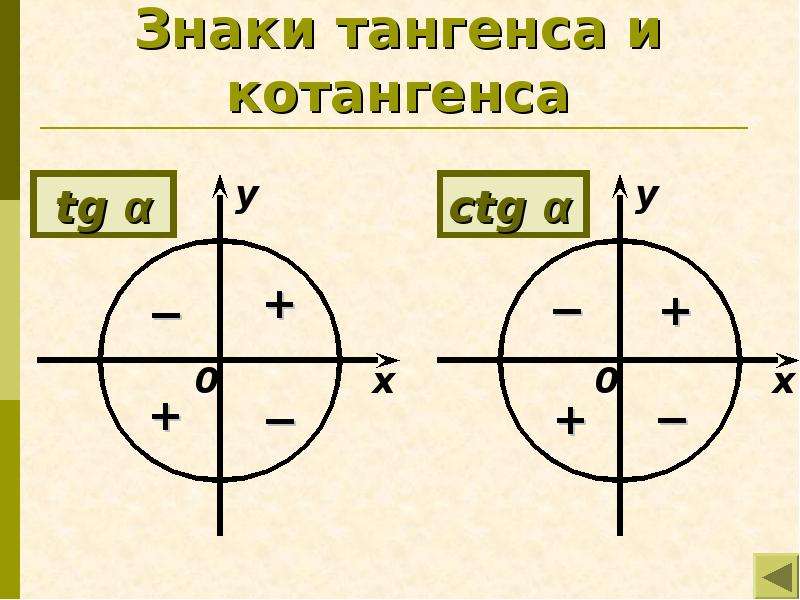 Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).
Вы уже знаете, что половина окружности – это величина, равная π. Значит, точка N находится на расстоянии π от точки М. Говоря иначе, если к точке М прибавить расстояние π, то мы получим точку N, находящуюся напротив. Она находится в третьей четверти. Проверьте, и увидите: косинус и синус точки N – со знаком «минус» (x и y имеют отрицательные значения).
Тангенс и котангенс точки М имеют положительное значение. А тангенс и котангенс точки N? Ответ простой: ведь тангенс и котангенс – это отношение синуса и косинуса. В нашем примере синус и косинус точки N – со знаком «минус». Значит:
–sin t
tg (t + π) = —- = tg t
–cos t
–cos t
ctg (t + π) = —- = ctg t
–sin t
Мы доказали, что тангенс и котангенс диаметрально противоположных точек окружности имеют не только одинаковое значение, но и одинаковый знак.
Свойство 4: Если две точки окружности находятся в соседних четвертях, а расстояние между точками равно одной четверти окружности, то синус одной точки равен косинусу другой с тем же знаком, а косинус одной точки равен синусу второй с противоположным знаком.
π | π |
Позволяют установить ряд характерных результатов – свойств синуса, косинуса, тангенса и котангенса . В этой статье мы рассмотрим три основных свойства. Первое из них указывает знаки синуса, косинуса, тангенса и котангенса угла α в зависимости от того, углом какой координатной четверти является α . Дальше мы рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α при изменении этого угла на целое число оборотов. Третье свойство выражает зависимость между значениями синуса, косинуса, тангенса и котангенса противоположных углов α и −α .
Если же Вас интересуют свойства функций синуса, косинуса, тангенса и котангенса, то их можно изучить в соответствующем разделе статьи .
Навигация по странице.
Знаки синуса, косинуса, тангенса и котангенса по четвертям
Ниже в этом пункте будет встречаться фраза «угол I , II , III и IV координатной четверти». Объясним, что же это за углы.
Возьмем единичную окружность , отметим на ней начальную точку А(1, 0) , и повернем ее вокруг точки O на угол α , при этом будем считать, что мы попадем в точку A 1 (x, y) .
Говорят, что угол α является углом I , II , III , IV координатной четверти , если точка А 1 лежит в I , II , III , IV четверти соответственно; если же угол α таков, что точка A 1 лежит на любой из координатных прямых Ox или Oy , то этот угол не принадлежит ни одной из четырех четвертей.
Для наглядности приведем графическую иллюстрацию. На чертежах ниже изображены углы поворота 30 , −210 , 585 и −45 градусов, которые являются углами I , II , III и IV координатных четвертей соответственно.
Углы 0, ±90, ±180, ±270, ±360, …
градусов не принадлежат ни одной из координатных четвертей.
Теперь разберемся, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, углом какой четверти является α .
Для синуса и косинуса это сделать просто.
По определению синус угла α — это ордината точки А 1 . Очевидно, что в I и II координатных четвертях она положительна, а в III и IV четвертях – отрицательна. Таким образом, синус угла α имеет знак плюс в I и II четвертях, а знак минус – в III и VI четвертях.
В свою очередь косинус угла α — это абсцисса точки A 1 . В I и IV четвертях она положительна, а во II и III четвертях – отрицательна. Следовательно, значения косинуса угла α в I и IV четвертях положительны, а во II и III четвертях – отрицательны.
Чтобы определить знаки по четвертям тангенса и котангенса нужно вспомнить их определения: тангенс – это отношение ординаты точки A 1
к абсциссе, а котангенс – отношение абсциссы точки A 1
к ординате. Тогда из правил деления чисел с одинаковыми и разными знаками следует, что тангенс и котангенс имеют знак плюс, когда знаки абсциссы и ординаты точки A 1
одинаковые, и имеют знак минус – когда знаки абсциссы и ординаты точки A 1
различны. Следовательно, тангенс и котангенс угла имеют знак +
в I
и III
координатных четвертях, и знак минус – во II
и IV
четвертях.
Следовательно, тангенс и котангенс угла имеют знак +
в I
и III
координатных четвертях, и знак минус – во II
и IV
четвертях.
Действительно, например, в первой четверти и абсцисса x , и ордината y точки A 1 положительны, тогда и частное x/y , и частное y/x – положительно, следовательно, тангенс и котангенс имеют знаки + . А во второй четверти абсцисса x – отрицательна, а ордината y – положительна, поэтому и x/y , и y/x – отрицательны, откуда тангенс и котангенс имеют знак минус.
Переходим к следующему свойству синуса, косинуса, тангенса и котангенса.
Свойство периодичности
Сейчас мы разберем, пожалуй, самое очевидное свойство синуса, косинуса, тангенса и котангенса угла. Оно состоит в следующем: при изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса этого угла не изменяются.
Это и понятно: при изменении угла на целое число оборотов мы из начальной точки А
всегда будем попадать в точку А 1
на единичной окружности, следовательно, значения синуса, косинуса, тангенса и котангенса остаются неизменными, так как неизменны координаты точки A 1
.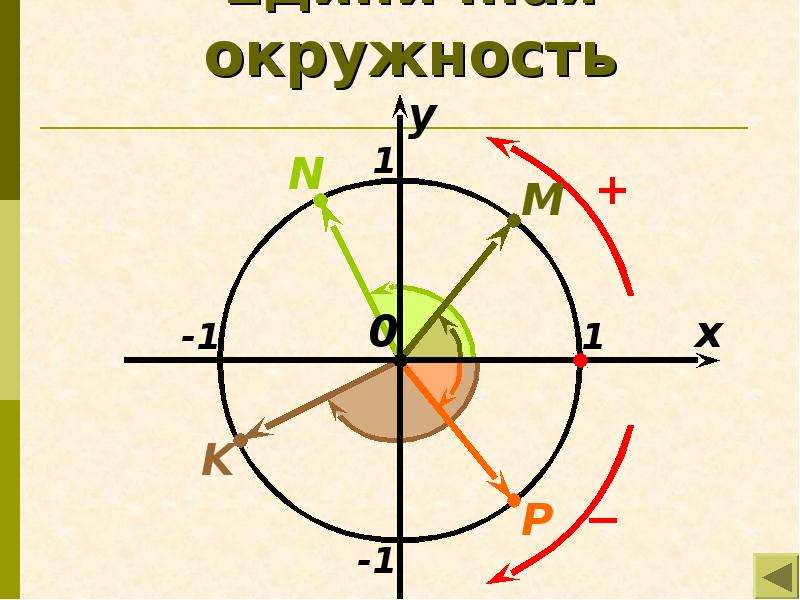
С помощью формул рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать так: sin(α+2·π·z)=sinα , cos(α+2·π·z)=cosα , tg(α+2·π·z)=tgα , ctg(α+2·π·z)=ctgα , где α — угол поворота в радианах, z – любое , абсолютная величина которого указывает количество полных оборотов, на которые изменяется угол α , а знак числа z указывает направление поворота.
Если же угол поворота α задан в градусах, то указанные формулы перепишутся в виде sin(α+360°·z)=sinα , cos(α+360°·z)=cosα , tg(α+360°·z)=tgα , ctg(α+360°·z)=ctgα .
Приведем примеры использования этого свойства. Например, , так как , а . Вот еще пример: или .
Это свойство вместе с формулами приведения очень часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов.
Рассмотренное свойство синуса, косинуса, тангенса и котангенса иногда называют свойством периодичности.
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Пусть А 1
– точка, полученная в результате поворота начальной точки А(1, 0)
вокруг точки O
на угол α
, а точка А 2
– это результат поворота точки А
на угол −α
, противоположный углу α
.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов базируется на достаточно очевидном факте: упомянутые выше точки А 1
и А 2
либо совпадают (при ), либо располагаются симметрично относительно оси Ox
. То есть, если точка A 1
имеет координаты (x, y)
, то точка А 2
будет иметь координаты (x, −y)
. Отсюда по определениям синуса, косинуса, тангенса и котангенса записываем равенства и .
Сопоставляя их, приходим к соотношениям между синусами, косинусами, тангенсами и котангенсами противоположных углов α
и −α
вида .
Это и есть рассматриваемое свойство в виде формул.
Приведем примеры использования этого свойства. Например, справедливы равенства и .
Остается лишь заметить, что свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Понятия синуса, косинуса, тангенса и котангенса являются основными категориями тригонометрии — раздела математики, и неразрывно связаны с определением угла. Владение этой математической наукой требует запоминания и понимания формул и теорем, а также развитого пространственного мышления.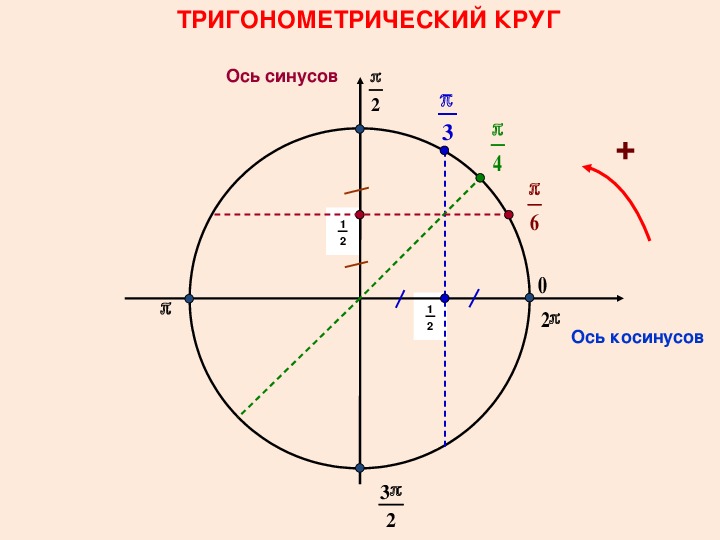 Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности. Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Именно поэтому у школьников и студентов тригонометрические вычисления нередко вызывают трудности. Чтобы побороть их, следует подробнее познакомиться с тригонометрическими функциями и формулами.
Понятия в тригонометрии
Чтобы разобраться в базовых понятиях тригонометрии, следует сначала определиться с тем, что такое прямоугольный треугольник и угол в окружности, и почему именно с ними связаны все основные тригонометрические вычисления. Треугольник, в котором один из углов имеет величину 90 градусов, является прямоугольным. Исторически эта фигура часто использовалась людьми в архитектуре, навигации, искусстве, астрономии. Соответственно, изучая и анализируя свойства этой фигуры, люди пришли к вычислению соответствующих соотношений её параметров.
Основные категории, связанные с прямоугольными треугольниками — гипотенуза и катеты. Гипотенуза — сторона треугольника, лежащая против прямого угла. Катеты, соответственно, это остальные две стороны. Сумма углов любых треугольников всегда равна 180 градусам.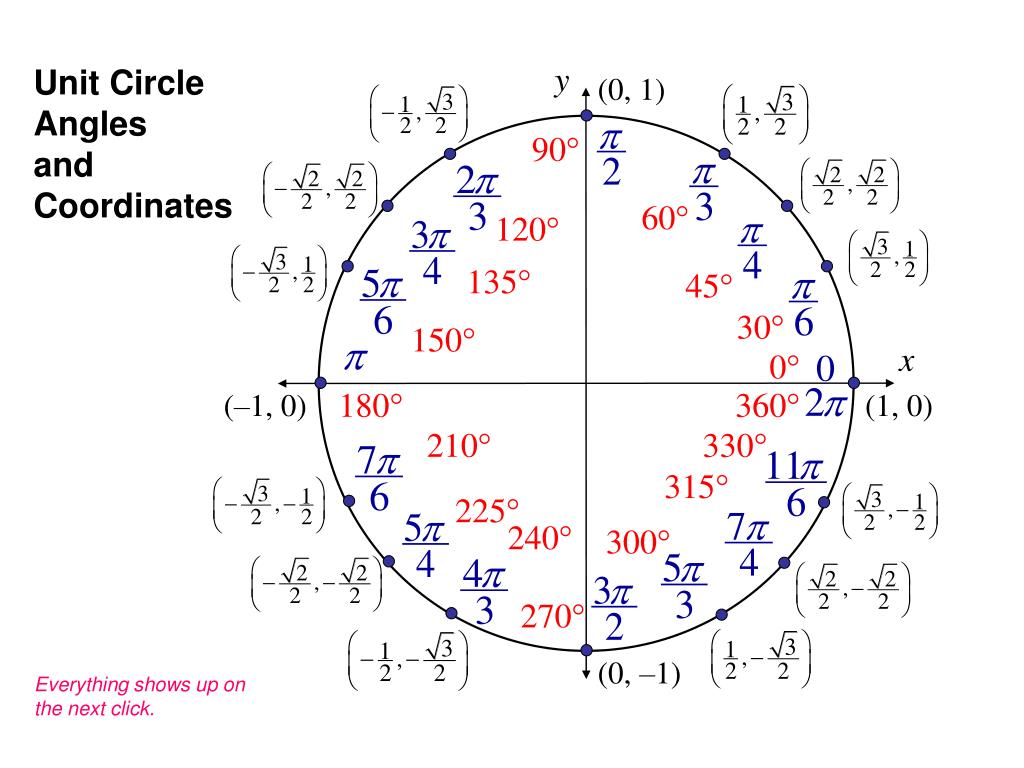
Сферическая тригонометрия — раздел тригонометрии, который не изучается в школе, однако в прикладных науках типа астрономии и геодезии, учёные пользуются именно им. Особенность треугольника в сферической тригонометрии в том, что он всегда имеет сумму углов более 180 градусов.
Углы треугольника
В прямоугольном треугольнике синусом угла является отношение катета, противолежащего искомому углу, к гипотенузе треугольника. Соответственно, косинус — это отношение прилежащего катета и гипотенузы. Оба эти значения всегда имеют величину меньше единицы, так как гипотенуза всегда длиннее катета.
Тангенс угла — величина, равная отношению противолежащего катета к прилежащему катету искомого угла, или же синуса к косинусу. Котангенс, в свою очередь, это отношение прилежащего катета искомого угла к противолежащему кактету. Котангенс угла можно также получить, разделив единицу на значение тангенса.
Единичная окружность
Единичная окружность в геометрии — окружность, радиус которой равен единице.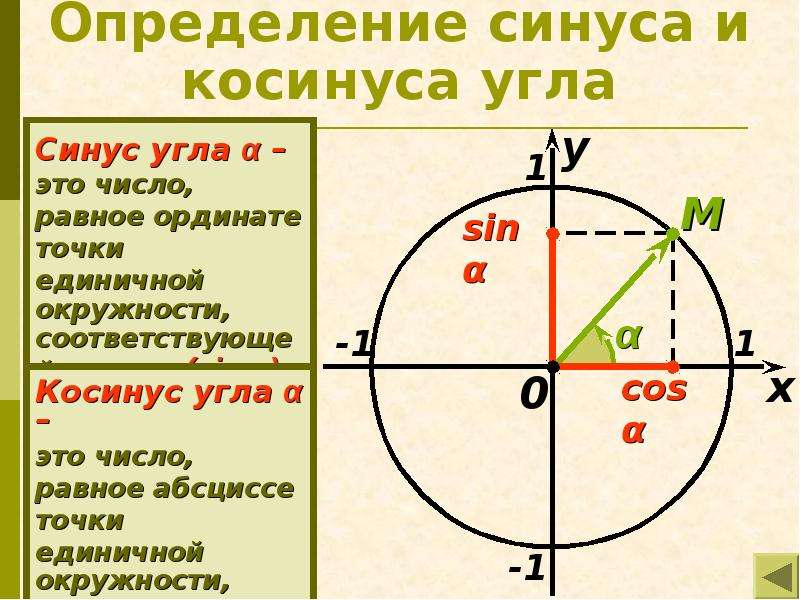 Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс). Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG.
Такая окружность строится в декартовой системе координат, при этом центр окружности совпадает с точкой начала координат, а начальное положение вектора радиуса определено по положительному направлению оси Х (оси абсцисс). Каждая точка окружности имеет две координаты: ХХ и YY, то есть координаты абсцисс и ординат. Выбрав на окружности любую точку в плоскости ХХ, и опустив с неё перпендикуляр на ось абсцисс, получаем прямоугольный треугольник, образованный радиусом до выбранной точки (обозначим её буквой С), перпендикуляром, проведённым до оси Х (точка пересечения обозначается буквой G), а отрезком оси абсцисс между началом координат (точка обозначена буквой А) и точкой пересечения G. Полученный треугольник АСG — прямоугольный треугольник, вписанный в окружность, где AG — гипотенуза, а АС и GC — катеты. Угол между радиусом окружности АС и отрезком оси абсцисс с обозначением AG, определим как α (альфа). Так, cos α = AG/AC. Учитывая, что АС — это радиус единичной окружности, и он равен единице, получится, что cos α=AG.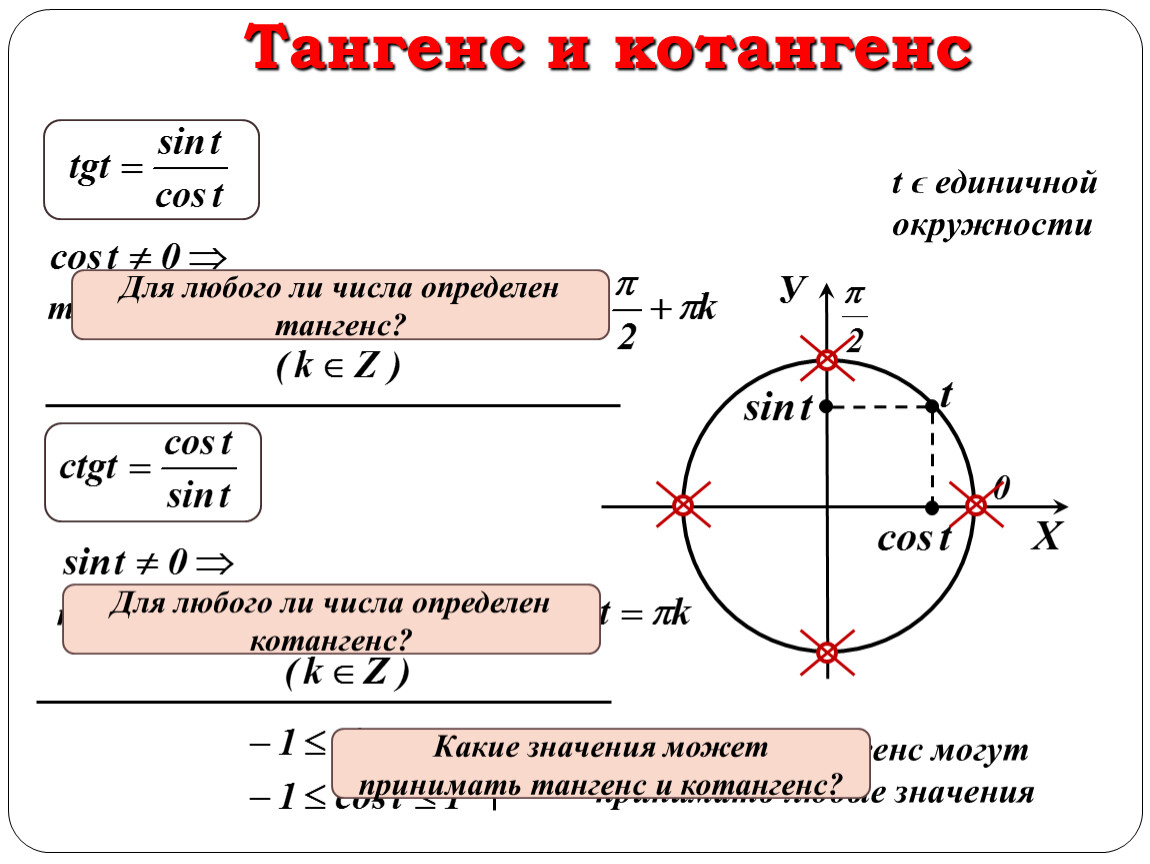 Аналогично, sin α=CG.
Аналогично, sin α=CG.
Кроме того, зная эти данные, можно определить координату точки С на окружности, так как cos α=AG, а sin α=CG, значит, точка С имеет заданные координаты (cos α;sin α). Зная, что тангенс равен отношению синуса к косинусу, можно определить, что tg α = y/х, а ctg α = х/y. Рассматривая углы в отрицательной системе координат, можно рассчитать, что значения синуса и косинуса некоторых углов могут быть отрицательными.
Вычисления и основные формулы
Значения тригонометрических функций
Рассмотрев сущность тригонометрических функций через единичную окружность, можно вывести значения этих функций для некоторых углов. Значения перечислены в таблице ниже.
Простейшие тригонометрические тождества
Уравнения, в которых под знаком тригонометрической функции присутствует неизвестное значение, называются тригонометрическими. Тождества со значением sin х = α, k — любое целое число:
- sin х = 0, х = πk.
- 2. sin х = 1, х = π/2 + 2πk.
 k * arcsin α + πk.
k * arcsin α + πk.
Тождества со значением cos х = а, где k — любое целое число:
- cos х = 0, х = π/2 + πk.
- cos х = 1, х = 2πk.
- cos х = -1, х = π + 2πk.
- cos х = а, |a| > 1, нет решений.
- cos х = а, |a| ≦ 1, х = ±arccos α + 2πk.
Тождества со значением tg х = а, где k — любое целое число:
- tg х = 0, х = π/2 + πk.
- tg х = а, х = arctg α + πk.
Тождества со значением ctg х = а, где k — любое целое число:
- ctg х = 0, х = π/2 + πk.
- ctg х = а, х = arcctg α + πk.
Формулы приведения
Эта категория постоянных формул обозначает методы, с помощью которых можно перейти от тригонометрических функций вида к функциям аргумента, то есть привести синус, косинус, тангенс и котангенс угла любого значения к соответствующим показателям угла интервала от 0 до 90 градусов для большего удобства вычислений.
Формулы приведения функций для синуса угла выглядят таким образом:
- sin(900 — α) = α;
- sin(900 + α) = cos α;
- sin(1800 — α) = sin α;
- sin(1800 + α) = -sin α;
- sin(2700 — α) = -cos α;
- sin(2700 + α) = -cos α;
- sin(3600 — α) = -sin α;
- sin(3600 + α) = sin α.

Для косинуса угла:
- cos(900 — α) = sin α;
- cos(900 + α) = -sin α;
- cos(1800 — α) = -cos α;
- cos(1800 + α) = -cos α;
- cos(2700 — α) = -sin α;
- cos(2700 + α) = sin α;
- cos(3600 — α) = cos α;
- cos(3600 + α) = cos α.
Использование вышеуказанных формул возможно при соблюдении двух правил. Во-первых, если угол можно представить как значение (π/2 ± a) или (3π/2 ± a), значение функции меняется:
- с sin на cos;
- с cos на sin;
- с tg на ctg;
- с ctg на tg.
Значение функции остаётся неизменным, если угол может быть представлен как (π ± a) или (2π ± a).
Во-вторых, знак приведенной функции не изменяется: если он изначально был положительным, таким и остаётся. Аналогично с отрицательными функциями.
Формулы сложения
Эти формулы выражают величины синуса, косинуса, тангенса и котангенса суммы и разности двух углов поворота через их тригонометрические функции.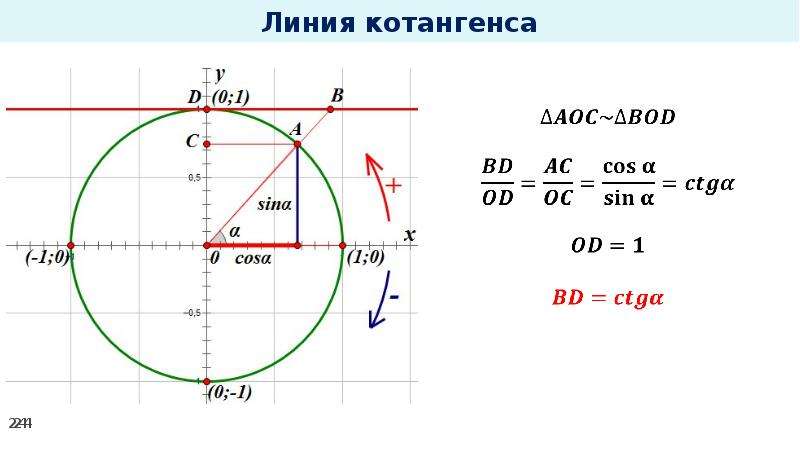 2 x/2) / (2tgx/2), при этом х = π + 2πn.
2 x/2) / (2tgx/2), при этом х = π + 2πn.
Частные случаи
Частные случаи простейших тригонометрических уравнений приведены ниже (k — любое целое число).
Частные для синуса:
| Значение sin x | Значение x |
|---|---|
| 0 | πk |
| 1 | π/2 + 2πk |
| -1 | -π/2 + 2πk |
| 1/2 | π/6 + 2πk или 5π/6 + 2πk |
| -1/2 | -π/6 + 2πk или -5π/6 + 2πk |
| √2/2 | π/4 + 2πk или 3π/4 + 2πk |
| -√2/2 | -π/4 + 2πk или -3π/4 + 2πk |
| √3/2 | π/3 + 2πk или 2π/3 + 2πk |
| -√3/2 | -π/3 + 2πk или -2π/3 + 2πk |
Частные для косинуса:
| Значение cos x | Значение х |
|---|---|
| 0 | π/2 + 2πk |
| 1 | 2πk |
| -1 | 2 + 2πk |
| 1/2 | ±π/3 + 2πk |
| -1/2 | ±2π/3 + 2πk |
| √2/2 | ±π/4 + 2πk |
| -√2/2 | ±3π/4 + 2πk |
| √3/2 | ±π/6 + 2πk |
| -√3/2 | ±5π/6 + 2πk |
Частные для тангенса:
| Значение tg x | Значение х |
|---|---|
| 0 | πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3/3 | π/6 + πk |
| -√3/3 | -π/6 + πk |
| √3 | π/3 + πk |
| -√3 | -π/3 + πk |
Частные для котангенса:
| Значение ctg x | Значение x |
|---|---|
| 0 | π/2 + πk |
| 1 | π/4 + πk |
| -1 | -π/4 + πk |
| √3 | π/6 + πk |
| -√3 | -π/3 + πk |
| √3/3 | π/3 + πk |
| -√3/3 | -π/3 + πk |
Теоремы
Теорема синусов
Существует два варианта теоремы — простой и расширенный.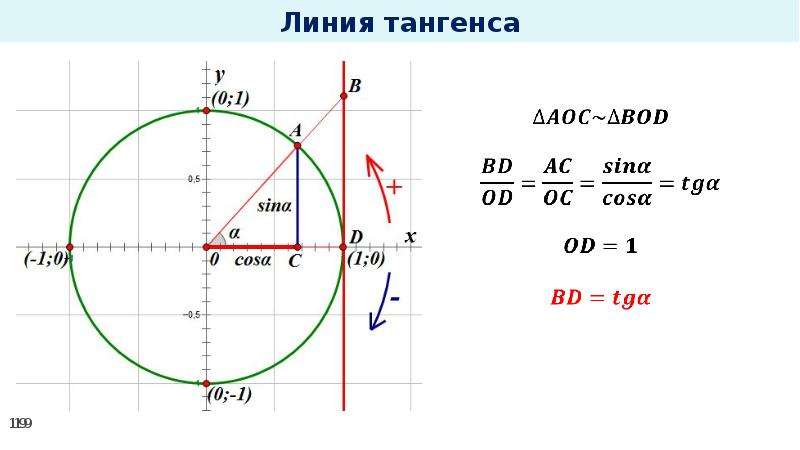 2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
2 — 2*b*c*cos α. В формуле a, b, c — стороны треугольника, и α — угол, противолежащий стороне а.
Теорема тангенсов
Формула выражает связь между тангенсами двух углов, и длиной сторон, им противолежащих. Стороны обозначены как a, b, c, а соответствующие противолежащие углы — α, β, γ. Формула теоремы тангенсов: (a — b) / (a+b) = tg((α — β)/2) / tg((α + β)/2).
Теорема котангенсов
Связывает радиус вписанной в треугольник окружности с длиной его сторон. Если a, b, c — стороны треугольника, и А, В, С, соответственно, противолежащие им углы, r — радиус вписанной окружности, и p — полупериметр треугольника, справедливы такие тождества:
- ctg A/2 = (p-a)/r;
- ctg B/2 = (p-b)/r;
- ctg C/2 = (p-c)/r.
Прикладное применение
Тригонометрия — не только теоретическая наука, связанная с математическими формулами. Её свойствами, теоремами и правилами пользуются на практике разные отрасли человеческой деятельности — астрономия, воздушная и морская навигация, теория музыки, геодезия, химия, акустика, оптика, электроника, архитектура, экономика, машиностроение, измерительные работы, компьютерная графика, картография, океанография, и многие другие.
Синус, косинус, тангенс и котангенс — основные понятия тригонометрии, с помощью которых математически можно выразить соотношения между углами и длинами сторон в треугольнике, и найти искомые величины через тождества, теоремы и правила.
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
- Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Синус и косинус. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти синусы и косинусы угла, представленных как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Синус и косинус − теория, примеры и решения
Пусть задана прямоугольная система координат xOy и пусть на ней нарисована окружность радиусом 1 и с центром в начале координат. Рассмотрим единичный вектор лежащий на оси Ox. Положительным направлением поворота вектора относительно центра координат O принята считать поворот против часовой стрелки, а отрицательным направлнением − по часовой стрелке. Пусть некоторый вектор, совпадающий с вектором , совершивший поворот в положительном направлении совпадает с вектором (Рис.1).
Точку B назовем точкой, соответствующей углу α. Рассмотрим координаты x, y точки B. Абсцис x точки B называют косинусом угла α и обозначают cosα, а ординат y точки B называют синусом угла α и обозначают sinα. Таким образом
Так как мы рассматриваем окружность с радиусом R=1, то
а любая точка на кружности удовлетворяет следующему равенству:
Подставляя (1) и (2) в (3), получим:
На рисунках Рис.2 и Рис.3 представлены некоторые углы единичной окружности в радианах и в градусах. Как преобразовать градусы в радианы и наоборот посмотрите на странице радианы и градусы онлайн.
Как видно из рисунков, оси OX и OY разделяют плоскость на 4 части. Эти части принято пронуменровать римскими числами I, II, III, IV. Каждая часть называется четвертью. На рисунке Рис.2 в каждой четверти окружность разделена на две части, а в Рис.3 − на три.
Пример 1. Найти синус и косинус угла, равного 45°(или радиан)( Рис.4).
Имеем прямоугольный треугольник OxB. Так как угол BOx=45°, то угол OBx=45°. Следовательно треугольник OBx равнобедренный, т.е.
Подставляя (5) в (3), получим:
То есть (учитывая (1) и (2))
В радианных мерах (6) примет следующий вид:
Пример 2. Найти синус и косинус угла, равного 60°(или радиан)( Рис.5).
Имеем прямоугольный треугольник OxB. Так как угол BOx=60°, то угол OBx=30°. Как известно из геометрии, катет, напротив угла 30° равен половине гипотенузы. Т.е.
Подставляя (8) в (3), получим:
В первой четверти x>0, y>0. Тогда, учитывая (1) и (2), решением будет:
или
Пример 3. Найти синус и косинус угла, равного 120°(или радиан)( Рис.6).
Имеем прямоугольный треугольник OxB. Так как угол BOx=120°, то ∠yOB=∠OBx=30°. Как известно из геометрии, катет, напротив угла 30° равен половине гипотенузы. Т.е.
Подставляя (9) в (3), получим:
Во второй четверти x<0, y>0. Тогда, учитывая (1) и (2), решением будет:
или
С помощью вышеизложенных соображений можно построить таблицу синусов и косинусов некоторых углов.
Таблица 1.
Рассмотрим свойства синуса и косинуса.
Свойство 1. Для любого числа α справедливы равенства:
Доказательство. Пусть числу α соответствует точка P на окружности (Рис. 7). Тогда числу −α соответствует точка Q, симметричная точке P относительно оси абсцисс. Эти точки имеют одну и ту же абсциссу, следовательно . Такие точки имеют равные по модулю, но противоположные по знаку ординаты. Следовательно .
Свойство 2. Для любого числа α выполнены равенства (в радианах):
или (в градусах)
где k∈Z (k любое целое число).
Поскольку числам α и α+2πk в радианах соответствует одна и та же точка на числовой окружности, то справедливы равенства (12) и (13). Так как числам α и α+360k в градусах соответствует одна и та же точка на числовой окружности, то выполнены равенства (14) и (15).
Свойство 3. Для любого значения α выполнены равенства (в радианах):
или (в градусах):
Например (в радианах):
или (в градусах):
Доказательство. Пусть числу α соответствует точка P на окружности. Тогда числу α+π (или α+180°) соответствует точка Q, симметричной точке P относительно начала координат (Рис. 8). Абсциссы этих точек равны по модулю но имеют противоположные знаки. Ординаты этих точек равны по модулю и имеют противоположные знаки. А это значит, что выполнены равенства (16),(17),(18),(19).
График функции синус (
y=sin x)Для построения графика функции синус, поставим в соответствие любому числу α, ординату соответствующей точки на единичной окружности (Рис.9).
Пусть точка M движется по окружности в положительном направлении (против часовой стрелки) начиная с точки A. вектор радиус точки M движется по окружности, начиная от точки A.
Вектор радиус точки M с осью OX имеет угол α. Увеличивая этот угол от нуля до π/2 ордината точки M увеличивается от 0 до 1. Далее, увеличивая этот угол от π/2 до π, ордината точки M уменьшается на от 1 до 0. Построим график функции синус на отрезке [0,π]. Так как привычнее запись функции в виде y=sin x, то вместо sin α мы будем использовать sin x, а y− это значение функции соответствующей точке x.
В декартовой прямоугольной системе координат, на оси OX отметим точки (можно взять π≈3 и тогда этим точкам будут соответствовать числа 0, 0.5, 1, 1.5, 2, 2.5, 3). Далее, используя таблицу 1, запишем соответствующие значения y.
Построим график:
Равенство (10) показывает, что функция синус симметрична относительно начала координат (т.е. нечетна). Тогда добавив построенной линии, линию, симметричную относительно начала коордиинат, получим:
Равентство (12)((14)) показывает, что синус периодичная функция с периодом 2π( 360°). Это означает, что функция в диапазоне [−π;π] повторяется начиная с π направо и с −π влево:
Область определения функции синус (−∞;+∞). Область значений: [−1;1].
График функции косинус (
y=cos x)Для построения графика функции косинус, поставим в соответствие любому числу α, абсциссу соответствующей точки на единичной окружности (Рис.13).
Пусть точка M движется по окружности в положительном направлении (против часовой стрелки) начиная с точки A.
Вектор радиус точки M с осью OX имеет угол α. Увеличивая этот угол от нуля до π/2 абсцисс точки M уменьшается от 1 до 0. Далее, увеличивая этот угол от π/2 до π, абсцисс точки M увеличивается от 0 до 1. Построим график функции косинус на отрезке [0,π]. Так как привычнее запись функции в виде y=cos x, то вместо cos α мы будем использовать cos x, а y− это значение функции соответствующей точке x.
В декартовой прямоугольной системе координат, на оси OX отметим точки (можно взять π≈3 и тогда этим точкам будут соответствовать числа 0, 0.5, 1, 1.5, 2, 2.5, 3). Далее, используя таблицу 1, запишем соответствующие значения y.
Построим график:
Равенство (11) показывает, что функция синус симметрична относительно оси ординат (т.е. четна). Тогда добавив построенной линии, линию, симметричную относительно оси ординат, получим:
Равентство (13)((15)) показывает, что косинус периодичная функция с периодом 2π( 360°). Это означает, что функция в диапазоне [−π;π] повторяется начиная с π направо и с −π влево:
Область определения функции косинус (−∞;+∞). Область значений: [−1;1].
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Определение 1Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Пример 1При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Пример 2Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Пример 3Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Пример 4Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Определение 2Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α, cos α, tg α, ctg α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 5Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Определение 3Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Определение 4Тангенс по известному косинусу tg2α+1=1cos2α .
Определение 5Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Определение 6Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Пример 6Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Пример 7Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Пример 8Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Запоминание через понимание. Визуализация синуса
Запоминание через понимание
Смотрим определение синуса в учебнике геометрии. «Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе».
Дает ли это определение понимание синуса? Нет, не дает. Определение не полное. Потому что оно рассматривает только частный случай треугольника — прямоугольный треугольник.
Смотрим определение синуса в учебнике алгебры. «Ордината точки Р, полученной при повороте точки Р (1;0) вокруг начала координат на угол а-радиан, называется синусом числа а, а абсцисса этой точки — косинусом».
Это определение вообще из области математической абстракции, так как вводит отрицательные значения синуса и косинуса. И с пониманием синуса по этому определению ещё больше сложностей.
Есть простой тест на понимание синуса и косинуса. Попросите школьника нарисовать линию косинуса для произвольного треугольника (не прямоугольного). Если он этого сделать не может — он не понимает, что такое синус и косинус.
Иллюстрация 1. Тест на понимание. Где линия косинуса?
(Предполагается описанная окружность с единичным диаметром)
Итак, школьные учебники не дают информации для понимания понятий «синус» и «косинус». Основное понятие тригонометрии (и элементарное понятие) «засекретили», спрятали в частных случаях и в математических абстракциях.
При возникновении проблем с пониманием сейчас можно обратиться к поисковым системам и найти в них недостающую информацию. Чтобы визуализировать синус и косинус, нужно вернуться к истокам тригонометрии, понять, откуда эти понятия появились, и для каких целей.
Изначально синус не связан с треугольником. Синус появился из окружности и вписанного в окружность угла.
В окружности с единичным диаметром синус — это хорда, на которую опирается вписанный угол. А косинус — это перпендикулярная хорде-синусу хорда. На иллюстрации видно, что для любого вписанного угла в окружности имеется две линии синуса и две линии косинуса, которые образуют прямоугольник.
Вот эту иллюстрацию и следует использовать для запоминания понятий «синус» и «косинус». По этой иллюстрации можно дать определение синусу своими словами.
Иллюстрация 2. В окружности с единичным диаметром линии синуса и косинуса (для вписанного угла)
образуют прямоугольник.
На картинке виден частный случай — прямоугольный треугольник,
в котором линия косинуса совпадает с катетом.
Связан ли синус (длина хорды) с противолежащим углом? Ведь мы привыкли говорить «синус угла». Связь длины хорды с углом очень не простая… Скорее, можно говорить о табличном соответствии длины хорды и величины вписанного в окружность угла.
Синус напрямую связан с другим элементом в окружности — с её диаметром. Если мы рассмотрим окружность с произвольным диаметром и вписанный в эту окружность произвольный треугольник (не прямоугольный), то синус получается путем деления стороны треугольника на диаметр этой окружности. То есть, синус — это коэффициент пропорциональности стороны вписанного в окружность треугольника. Понятие «синус» напрямую связано со стороной треугольника. Но традиции есть традции — принято говорить «синус угла».
Как получаются синусы сторон треугольника видно на иллюстрации ниже. Мы можем вычислить синусы всех сторон (или синусы всех углов, как принято говорить), измерив точной линейкой стороны треугольника и диаметр описанной окружности, и разделив каждую сторону на диаметр. Величины углов нам для этого не нужны.
Иллюстрация 3. Опишем вокруг треугольника окружность
и точно измерим стороны треугольника и диаметр окружности
В результате мы получим пропорционально уменьшенный треугольник, вписанный в окружность с единичным диаметром, стороны которого и будут синусами сторон исходного треугольника.
Иллюстрация 4. Стороны треугольника стали синусами,
когда мы уменьшили окружность до единичного диаметра
Усвоив понятие синуса, визуализировав его у себя в воображении, поняв, откуда оно появилось, можно переходить к частным случаям синуса и косинуса, изложенным в учебниках. Легко заметить, что в прямоугольном треугольнике одна из сторон (гипотенуза) одновременно является и диаметром описанной окружности. Теперь становится более понятным определение из учебника геометрии, по которому синус угла — это отношение катета к гипотенузе (т.е., к диаметру окружности). На иллюстрации 2 видно, что косинус совпадает со стороной треугольника только в прямоугольном треугольнике. В любом другом треугольнике линия косинуса находится вне треугольника. В учебнике алгебры, где синус рассматриваются как проекция точки окружности на ось координат, переходят на половины углов и полухорды, и с единичного диаметра на единичный радиус. Для чего? Чтобы ввести отрицательные значения тригонометрических функций.
На иллюстрации 3 и 4 видна теорема синусов. Теорема синусов является очевидной и не нуждается в доказательстве. Если синусы сторон (углов) изначально получены нами путем деления каждой стороны треугольника на диаметр описанной окружности, то отношение любой стороны треугольника к синусу стороны (синусу угла) будет одной и той же величиной, равной диаметру окружности. Это и есть теорема синусов.
a/sinA = b/sinB = c/sinC = d
(sin A — коэффициент пропорциональности стороны «a»)
————————————————-
А как же все таки угол связан со своим синусом?
Ведь для решения задач удобно находить синус угла по значению самого угла. Сейчас это не проблема. На любом калькуляторе вы можете набрать sin (вставить угол) и получить результат с заданной точностью.
Изменение значения синуса при равномерном изменении величины угла визуально похоже на перемещение с равноускоренным движением (представьте падающий на землю шарик и его ускорение в каждую секунду). И очень приблизительные значения синуса (по углу) можно вычислить по формуле перемещения с равноускоренным движением. Но четкой функциональной зависимости значения синуса от величины угла нет. С заданной точностью синус вычисляется по формуле:
В.Козаренко
Дата размещения материала на сайте: 17 марта 2011 года
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Диаметр окружности — отрезок, соединяющий две любые точки расположенные на линии окружности и проходящий через её центр. Диаметр, в два раза больше радиуса
r — радиус окружности
D — диаметр окружности
π ≈ 3.14
Формула длины окружности через радиус или диаметр, (L):
Калькулятор для расчета длины окружности через радиус
Калькулятор для расчета длины окружности через диаметр
S — площадь круга
O — центр круга
π ≈ 3.14
Формула длины окружности через площадь, (L):
Калькулятор для расчета длины окружности через
площадь
Формулы для окружности и круга:
r— радиус окружности
α— угол AOB, в градусах
π ≈ 3.14
Формула длины дуги (L):
Калькулятор для расчета длины дуги окружности :
Формулы для окружности и круга:
a, b, c, — стороны треугольника
Формула периметра треугольника через его стороны (P):
Калькулятор — вычислить, найти периметр разностороннего треугольника
b — длина прямоугольника
a — ширина прямоугольника
Формула периметра прямоугольника, (P):
Калькулятор — вычислить, найти периметр прямоугольника
a, b, c,d — стороны трапеции
Формула периметра трапеции, (P):
Калькулятор — вычислить, найти периметр трапеции
a — сторона ромба
Формула периметра ромба (P):
Калькулятор — вычислить, найти периметр ромба
h — сторона квадрата
Формула периметра квадрата, (P):
Калькулятор — вычислить, найти периметр квадрата
Точка С делит отрезок АВ пополам.
Углы ACD и DCB— прямые, (90°).
m— хорда AD=DB
M— хорда AB
Формула Гюйгенса, длина дуги ADB, (L):
* Погрешность для углов меньше 60°, составляет менее 0,5%
Калькулятор — вычислить, найти длину дуги по формуле Гюйгенса
Формулы для окружности и круга:
Тригонометрический круг со всеми значениями, числовая окружность синус косинус тангенс котангенс, как пользоваться тригонометрическим кругом
Тригонометрический круг один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.
Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.
Тригонометрическая окружность
Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.
Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.
Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Построение единичной окружности
Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.
Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.
Сделать перевод этих показателей просто полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Перевод углов из градусов в радианы
Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.
Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:
1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956
В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:
1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.
Косинус, синус, тангенс, котангенс на тригонометрической окружности
Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.
Заключение
В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.
Синус, косинус угла треугольника
Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе. Косинус угла равен отношению прилежащего катета к гипотенузе.
Если у нас есть треугольник \(ABC\), рисунок выше, для которого \(С\)- прямой угол, то сторонами \(BC\) и \(AC\) будут катеты, а сторона \(AB\) — гипотенуза. Следовательно, по определению, синус угла \(ABC\) равен отношению катета \(АС\) к гипотенузе: синус угла \(ABC=\frac{AC}{AB}\) и синус угла \(BAC=\frac{BC}{AB}\).2\) \(9+16=25\) \(AB=5\) откуда синус равен:
\(sin ∠ BAC = \frac{3}{5}\)
Пример 2. Вычислим синус угла \(ABC\) по углу\( BAC \) 30° градусов в прямоугольном треугольнике \(ACB\).
Самое главное помнить, что сумма всех углов в треугольнике равна 180 °.Найдем угол \(ABC\):
\(180\)° \(-30\)° \(-90\)°\(=60\)°.
\(sin\) \(60\)° возьмем из табличного значения: \(\frac{ \sqrt{3}} { 2}\)
Табличные значения \(sin\) и \(cos\):
Чтобы лучше понимать значения табличные значения синуса и косинуса представим их на координатной окружности: где ось ординат \((y)\) линия синуса, ось абсцисс \((x)\) – линия косинуса. Если вы забыли значения синуса и косинуса \(90\) и \(180\) можно нарисовать рисунок и посмотреть значения, не забывая, что на первом месте стоит \(x\), на втором \(y\) \((x,y)\);
Теорема синусов:
Теорема косинусов:
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
5.2: Единичный круг — функции синуса и косинуса
Мы уже узнали некоторые свойства специальных углов, такие как преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы особых углов, используя Пифагорова идентичность и наши знания о треугольниках.
Нахождение синусов и косинусов углов 45 °
Сначала мы рассмотрим углы \ (45 ° \) или \ (\ dfrac {π} {4} \), как показано на рисунке \ (\ PageIndex {9} \). Треугольник \ (45 ° –45 ° –90 ° \) является равнобедренным треугольником, поэтому координаты \ (x \) и \ (y \) соответствующей точки на окружности совпадают.Поскольку значения x- и \ (y \) одинаковы, значения синуса и косинуса также будут равны.
Рисунок \ (\ PageIndex {9} \)В \ (t = \ frac {π} {4} \), что составляет 45 градусов, радиус единичной окружности делит пополам первый квадратный угол . Это означает, что радиус лежит вдоль прямой \ (y = x \). Единичный круг имеет радиус, равный 1. Итак, прямоугольный треугольник, образованный под линией \ (y = x \), имеет стороны \ (x \) и \ (y \) (с \ (y = x), \) и радиус = 1. См. рисунок \ (\ PageIndex {10} \).2 & = \ dfrac {1} {2} \\ x & = ± \ dfrac {1} {\ sqrt {2}} \ end {align *} \]
В квадранте I, \ (x = \ dfrac {1} {\ sqrt {2}} \).
При \ (t = \ dfrac {π} {4} \) или 45 градусах,
\ [\ begin {align *} (x, y) & = (x, x) = (\ dfrac {1} {\ sqrt {2}}, \ dfrac {1} {\ sqrt {2}}) \ » \ x & = \ dfrac {1} {\ sqrt {2}}, \; y = \ dfrac {1} {\ sqrt {2}} \\ \ cos t & = \ dfrac {1} {\ sqrt {2}}, \; \ sin t = \ dfrac {1} {\ sqrt {2}} \ end {align *} \]
Если мы затем рационализируем знаменатели, мы получим
\ [\ begin {align *} \ cos t & = \ dfrac {1} {\ sqrt {2}} \ dfrac {\ sqrt {2}} {\ sqrt {2}} \\ & = \ dfrac {\ sqrt {2}} {2} \\ \ sin t & = \ dfrac {1} {\ sqrt {2}} \ dfrac {\ sqrt {2}} {\ sqrt {2}} \\ & = \ dfrac { \ sqrt {2}} {2} \ end {align *} \]
Следовательно, координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (45 ° \) равны \ (\ left (\ dfrac {\ sqrt {2 }} {2}, \ dfrac {\ sqrt {2}} {2} \ right) \).
Нахождение синусов и косинусов углов 30 ° и 60 °
Затем мы найдем косинус и синус под углом \ (30 °, \) или \ (\ tfrac {π} {6} \). Сначала мы нарисуем треугольник внутри круга, одна сторона которого расположена под углом \ (30 °, \), а другая — под углом \ (- 30 °, \), как показано на рисунке \ (\ PageIndex {11} \ ). Если полученные два прямоугольных треугольника объединить в один большой треугольник, обратите внимание, что все три угла этого большего треугольника будут равны \ (60 °, \), как показано на рисунке \ (\ PageIndex {12} \).
Рисунок \ (\ PageIndex {11} \) Рисунок \ (\ PageIndex {12} \)Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину \ (2y \), и поскольку все стороны равны, мы также можем заключить, что \ (r = 2y \) или \ (y = \ frac {1} {2} r \). Поскольку \ (\ sin t = y \),
\ [\ sin \ left (\ frac {π} {6} \ right) = \ dfrac {1} {2} \ nonumber \]
А поскольку \ (r = 1 \) в нашем единичном круге ,
\ [\ begin {align *} \ sin \ left (\ frac {π} {6} \ right) & = \ dfrac {1} {2} (1) \\ & = \ dfrac {1} {2} \ end {align *} \]
Используя тождество Пифагора, мы можем найти значение косинуса.2 \ left (\ frac {π} {6} \ right) & = \ dfrac {3} {4} && \ text {Используйте свойство квадратного корня.} \\
\ cos \ left (\ frac {π} { 6} \ right) & = \ pm \ sqrt {\ dfrac {3} {4}} = \ dfrac {\ sqrt {3}} {2} && \ text {Поскольку \ (y \) положительное значение, выберите положительный корень. } \\
\ end {align} \)
Координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (30 ° \): \ (\ left (\ dfrac {\ sqrt {3}} {2}, \ dfrac {1} {2} \ right) \). В точке \ (t = \ dfrac {π} {3} \) (60 °) радиус единичной окружности, 1, служит гипотенузой прямоугольного треугольника 30-60-90 градусов, \ (BAD, \) как показано на рисунке \ (\ PageIndex {13} \).Угол \ (A \) имеет меру 60 °. 60 °. В точке \ (B, \) проведем угол \ (ABC \) с мерой \ (60 ° \). Мы знаем, что сумма углов в треугольнике равна \ (180 ° \), поэтому мера угла \ (C \) также равна \ (60 ° \). Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника \ (ABC \) имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Рисунок \ (\ PageIndex {13} \)Угол \ (ABD \) равен 30 °. Итак, если двойной, угол \ (ABC \) равен 60 °.2 & = \ dfrac {3} {4} \\ y & = ± \ dfrac {\ sqrt {3}} {2} \ end {align *} \]
Поскольку \ (t = \ dfrac {π} {3} \) имеет конечную сторону в квадранте I, где \ (y \) — координата положительна, мы выбираем \ (y = \ dfrac {\ sqrt {3}} {2} \) положительное значение.
В \ (t = \ dfrac {π} {3} \) (60 °) координаты \ ((x, y) \) точки на окружности радиуса \ (1 \) под углом \ (60 ° \) равны \ (\ left (\ dfrac {1} {2}, \ dfrac {\ sqrt {3}} {2} \ right) \), поэтому мы можем найти синус и косинус.
\ ((x, y) = \ left (\ dfrac {1} {2}, \ dfrac {\ sqrt {3}} {2} \ right) \)
\ (x = \ dfrac {1} {2}, \; y = \ dfrac {\ sqrt {3}} {2} \)
\ (\ cos t = \ dfrac {1} {2}, \; \ sin t = \ dfrac {\ sqrt {3}} {2} \)
Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности.Таблица \ (\ PageIndex {1} \) суммирует эти значения.
| Угол | 0 | \ (\ dfrac {π} {6} \) или 30 | \ (\ dfrac {π} {4} \) или 45 ° | \ (\ dfrac {π} {3} \) или 60 ° | \ (\ dfrac {π} {2} \) или 90 ° |
|---|---|---|---|---|---|
| Косинус | 1 | \ (\ dfrac {\ sqrt {3}} {2} \) | \ (\ dfrac {\ sqrt {2}} {2} \) | \ (\ dfrac {1} {2} \) | 0 |
| Синус | 0 | \ (\ dfrac {1} {2} \) | \ (\ dfrac {\ sqrt {2}} {2} \) | \ (\ dfrac {\ sqrt {3}} {2} \) | 1 |
На рисунке \ (\ PageIndex {14} \) показаны общие углы в первом квадранте единичной окружности.
Рисунок \ (\ PageIndex {14} \)Использование калькулятора для поиска синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов , мы обращаемся к компьютеру или калькулятору. Будьте внимательны. : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы для входного значения. Когда мы вычисляем \ (\ cos (30) \) на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в режиме радиан.
Как сделать: если задан угол в радианах, с помощью графического калькулятора найдите косинус
.- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Пример \ (\ PageIndex {4} \): использование графического калькулятора для поиска синуса и косинуса
Оцените \ (\ cos \ left (\ dfrac {5π} {3} \ right) \) с помощью графического калькулятора или компьютера.
Решение
Введите следующие нажатия клавиш:
\ (\ mathrm {COS (5 × π ÷ 3) \; ENTER} \)
\ [\ cos \ left (\ dfrac {5π} {3} \ right) = 0,5 \ nonumber \]
Анализ
Мы можем найти косинус или синус угла в градусах прямо на калькуляторе в градусном режиме. Для калькуляторов или программного обеспечения, которые используют только режим радиан, мы можем найти знак \ (20 ° \), например, включив коэффициент преобразования в радианы как часть входных данных:
\ [\ mathrm {SIN (20 × π ÷ 180) \; ENTER} \ nonumber \]
Попробовать \ (\ PageIndex {4} \)
Вычислить \ (\ sin \ left (\ dfrac {π} {3} \ right) \).
- Ответ
приблизительно 0,866025403
Линейные значения тригонометрических функций. Темы по тригонометрии
Темы | Дом
17
Полный период греха θ
Полный период cos θ
Период tan θ
Прогнозы
ЗНАЧЕНИЕ ЛИНИИ тригонометрической функции — это прямая линия, длина которой представляет собой значение функции.Поскольку при изменении центрального угла значение линии становится своего рода «графиком» функции во время этого изменения. Это лучший способ для ученика визуализировать и запомнить значения каждой функции, в частности синуса, косинуса и тангенса.
Строка значений
Пусть A будет центром единичной окружности радиуса AD, AB.
Из точки B опустите перпендикуляр BC на AD.
Радиус прорисовки AF перпендикулярно DA; нарисуйте DE, FG касательную к окружности; то есть нарисуйте их под прямым углом к радиусам; (Теорема 13)
и продолжаем AB, чтобы встретить эти касательные в точках E, G соответственно.
Тогда, поскольку AG — прямая линия, пересекающая параллельные прямые FG, AD, чередующиеся углы FGA, GAD равны. (Теорема 8)
Следовательно, треугольники ACB, ADE, GFA равноугольные и, следовательно, подобны. (Теорема 15)
Линейные значения функций угла θ теперь выглядят следующим образом; чтобы избежать прокрутки, цифра ниже такая же:
| грех θ | = | CB BA | = | CB 1 | = CB. |
| cos θ | = | AC BA | = | переменного тока 1 | = АС. |
| tan θ | = | DE AD | = | DE 1 | = DE. |
| csc θ | = | AG FA | = | AG 1 | = АГ. |
| сек θ | = | AE DA | = | AE 1 | = АЕ. |
| детская кроватка θ | = | FG FA | = | FG 1 | = FG. |
Теперь мы понимаем, почему функция касательной (DE) называется так: на самом деле это касательная.Секущая функция (AE) является секансом. Он разрезает круг; от латинского secare , чтобы сократить.
Полный период греха θ
Теперь ученик должен попытаться визуализировать, что происходит с CB, линейным значением sin θ, когда AB совершает полный оборот вокруг единичной окружности.
При θ = 0 ° точка B совпадает с D, так что CB обращается в нуль. sin 0 ° = 0.
По мере увеличения θ в первом квадранте CB также увеличивается, пока не достигнет своего максимального значения при 90 °.CB совпадает там с единичным радиусом AF, так что CB = AF = sin 90 ° = 1.
Когда θ, угол DAB, входит во второй квадрант (рис. 2), CB начинает уменьшаться в значении. При 180 ° B совпадает с K, а CB снова обращается в нуль. sin 180 ° = 0,
В третьем квадранте (рис. 3) CB увеличивается, но синус в этом квадранте алгебраически отрицателен. При 270 ° CB совпадает с AL. sin 270 ° имеет свой алгебраический минимум: sin 270 ° = −1.
Наконец, в четвертом квадранте (рис.4) CB уменьшается до тех пор, пока B снова не совпадет с D. sin 360 ° = sin 0 ° = 0.
После прохождения одного полного цикла sin θ прошел все возможные значения. Мы говорим, что sin θ завершил один период. Принято использовать радиан и говорить, что период sin θ равен 2π.
Это означает, что каждые 2π радиан sin θ возвращается к тому же значению строки CB.
Для любого угла θ sin (θ + 2π) = sin θ.
Мы еще вернемся к этому в следующей теме.
Более того, мы видим, что sin θ — линейное значение CB — никогда не имеет значения больше 1: при 90 ° или меньше -1: при 270 °.
−1 ≤ sin θ ≤ 1.
Полный период cos θ
Линейное значение cos θ равно переменному току. Когда линия AB вращается, C перемещается вперед-назад по диаметру KD. При 0 ° AC совпадает с единичным радиусом AD, так что cos 0 ° = 1.
При θ = 90 ° C совпадает с A, так что AC обращается в нуль.cos 90 ° = 0,
При θ = 180 ° C достигает K. AC = AK = cos 180 ° = -1.
При θ = 270 ° C возвращается к A. cos 270 ° = 0.
Наконец, при θ = 360 ° AC снова совпадает с радиусом AD. cos 360 ° = 1.
Период cos θ также равен 2π.
cos θ (AC) также имеет максимальное значение 1: при 0 ° и минимум -1: при 180 °.
−1 ≤ cos θ ≤ 1.
Период tan θ
Значения tan θ, как и значения всех тригонометрических функций, регулярно повторяются.Значения tan θ повторяются каждые π единиц (в радианах). Итак, мы говорим, что tan θ имеет период π.
Так как θ принимает значения от −π / 2 до π / 2, линейное значение DE tan θ проходит через все действительные числа от −∞ до ∞.
График тригонометрической функции, по сути, представляет собой ее линейное значение, построенное как координата y в зависимости от радианного угла x . См. Следующую тему: Графики тригонометрических функций.
Прогнозы
Прямая CD называется вертикальной проекцией прямой AB. (Прямые BD, AC нарисованы перпендикулярно CD. Как будто на AB светит свет, а CD — это тень.)
EF называется горизонтальной проекцией AB.
Теперь, если AB — это единичный радиус, то BC — линейное значение sin θ — это
вертикальная проекция радиуса.А AC — значение линии cos θ — это горизонтальная проекция.
Таким образом, в единичном круге sin θ является вертикальной проекцией радиуса. cos θ — горизонтальная проекция.
Следующая тема: Графики тригонометрических функций
Темы | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
5.2 Единичный круг: функции синуса и косинуса — предварительное вычисление
Цели обучения
В этом разделе вы:
- Найдите значения функции для синуса и косинуса 30 ° или (π6), 45 ° или (π4) 30 ° или (π6), 45 ° или (π4) и 60 ° или (π3) .60 ° или (π3) ).
- Определите область и диапазон функций синуса и косинуса.
- Используйте исходные углы для оценки тригонометрических функций.
Рис. 1 Singapore Flyer — самое высокое колесо обозрения в мире.(кредит: «Vibin JK» / Flickr)
Ищете острые ощущения? Тогда подумайте о поездке на Singapore Flyer, самом высоком колесе обозрения в мире. Колесо обозрения, расположенное в Сингапуре, взлетает на высоту 541 фут — чуть больше десятой мили! Описанное как колесо обозрения, всадники наслаждаются захватывающими видами, путешествуя с земли на вершину и снова вниз по повторяющейся схеме. В этом разделе мы рассмотрим этот тип вращательного движения по окружности. Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат.Затем мы можем обсудить круговое движение в терминах пар координат.
Поиск значений функции для синуса и косинуса
Чтобы определить наши тригонометрические функции, мы начнем с рисования единичного круга, круга с центром в начале координат и радиусом 1, как показано на рисунке 2. Угол (в радианах), который пересекает tt, образует дугу длины s.s. Используя формулу s = rt, s = rt и зная, что r = 1, r = 1, мы видим, что для единичной окружности s = t.s = t.
Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемых квадрантами.Мы помечаем эти квадранты, чтобы имитировать направление, в котором будет разворачиваться положительный угол. Четыре квадранта обозначены I, II, III и IV.
Для любого угла t, t мы можем обозначить пересечение конечной стороны и единичной окружности ее координатами (x, y). (X, y). Координаты xx и yy будут выходными данными тригонометрических функций f (t) = cost f (t) = cost и f (t) = sint, f (t) = sint соответственно. Это означает, что x = costx = cost и y = sint.y = sint.
Рисунок 2 Единичная окружность с центральным углом tt радианыUnit Circle
Единичный круг имеет центр в точке (0,0) (0,0) и радиус 11.В единичном круге длина перехваченной дуги равна радианам центрального угла t.t.
Пусть (x, y) (x, y) будет конечной точкой единичной окружности дуги длины дуги s.s. Координаты (x, y) (x, y) этой точки можно описать как функции угла.
Определение функций синуса и косинуса
Теперь, когда у нас есть помеченная единичная окружность, мы можем узнать, как координаты (x, y) (x, y) соотносятся с длиной и углом дуги. Функция синуса связывает действительное число tt с координатой y точки, где соответствующий угол пересекает единичную окружность.Точнее, синус угла tt равен значению y конечной точки на единичной окружности дуги длиной t.t. На рисунке 2 синус равен y.y. Как и все функции, синусоидальная функция имеет вход и выход. Его вход — мера угла; его выход — координата y соответствующей точки на единичной окружности.
Функция косинуса угла tt равна значению x конечной точки единичной окружности дуги длины t.т. На рисунке 3 косинус равен x.x.
Рисунок 3
Поскольку понятно, что синус и косинус являются функциями, нам не всегда нужно записывать их в скобках: sintsint — это то же самое, что sin (t) sin (t) и costcost. совпадает с cos (t) .cos (t). Аналогичным образом, cos2tcos2t — это обычно используемое сокращенное обозначение для (cos (t)) 2. (cos (t)) 2. Имейте в виду, что многие калькуляторы и компьютеры не распознают сокращенную запись. В случае сомнений используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.
Функции синуса и косинуса
Если tt — действительное число и точка (x, y) (x, y) на единичной окружности соответствует углу t, t, то
Как к
Дана точка P (x, y) (x, y) на единичной окружности, соответствующая углу t, t, найдите синус и косинус.
- Синус tt равен y -координате точки P: sint = y.P: sint = y.
- Косинус tt равен x -координате точки P: стоимость = x.P: стоимость = x.
Пример 1
Поиск значений функции для синуса и косинуса
Точка PP — это точка на единичной окружности, соответствующая углу t, t, как показано на рисунке 4. Найдите cos (t) cos (t) и sin (t) .sin (t).
Рисунок 4
Решение
Мы знаем, что costcost — это координата x соответствующей точки на единичной окружности, а sintsint — это координата y соответствующей точки на единичной окружности.Так:
x = стоимость = 12y = синт = 32x = стоимость = 12y = синт = 32Попробуй # 1
Определенный угол tt соответствует точке на единичной окружности в точке (−22,22) (- 22,22), как показано на рисунке 5. Найдите costcost и sint.sint.
Рисунок 5
Нахождение синусов и косинусов углов на оси
Для квадрантных углов соответствующая точка единичной окружности попадает на ось x- или y .В этом случае мы можем легко вычислить косинус и синус из значений xx и y.y.
Пример 2
Расчет синусов и косинусов по оси
Найдите cos (90 °) cos (90 °) и sin (90 °) .sin (90 °).
Решение
Перемещение на 90 ° 90 ° против часовой стрелки вокруг единичной окружности от положительной оси x приводит нас к вершине круга, где координаты (x, y) (x, y) равны (0, 1), как показано на рисунке 6.
Рисунок 6
Используя наши определения косинуса и синуса,
x = стоимость = cos (90 °) = 0y = sint = sin (90 °) = 1x = стоимость = cos (90 °) = 0y = sint = sin (90 °) = 1Косинус 90 ° равен 0; синус 90 ° равен 1.
Попробуй # 2
Найдите косинус и синус угла π.π.
Идентичность Пифагора
Теперь, когда мы можем определить синус и косинус, мы узнаем, как они соотносятся друг с другом и с единичной окружностью. Напомним, что уравнение единичной окружности: x2 + y2 = 1.x2 + y2 = 1. Поскольку x = costx = cost и y = sint, y = sint, мы можем заменить xx и yy, чтобы получить cos2t + sin2t = 1. cos2t + sin2t = 1. Это уравнение, cos2t + sin2t = 1, cos2t + sin2t = 1, известно как Пифагорейская идентичность .См. Рисунок 7.
Рисунок 7
Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам необходимо дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем, в каком квадранте находится угол, мы можем легко выбрать правильное решение.
Пифагорейская идентичность
Пифагорейская идентичность утверждает, что для любого действительного числа t, t,
cos2t + sin2t = 1 cos2t + sin2t = 1Как к
Зная синус некоторого угла tt и его положение в квадранте, найдите косинус t.т.
- Подставьте известное значение sin (t) sin (t) в тождество Пифагора.
- Решите относительно cos (t) .cos (t).
- Выберите решение с соответствующим знаком для значений x в квадранте, где находится tt.
Пример 3
Нахождение косинуса из синуса или синуса из косинуса
Если sin (t) = 37sin (t) = 37 и tt находится во втором квадранте, найдите cos (t) .cos (t).
Решение
Если мы опустим вертикальную линию из точки на единичной окружности, соответствующей t, t, мы создадим прямоугольный треугольник, из которого мы увидим, что тождество Пифагора — это просто один из случаев теоремы Пифагора.См. Рисунок 8.
Рисунок 8
Подстановка известного значения синуса в пифагорейскую идентичность,
cos2 (t) + sin2 (t) = 1cos2 (t) + 949 = 1cos2 (t) = 4049cos (t) = ± 4049 = ± 407 = ± 2107cos2 (t) + sin2 (t) = 1cos2 (t) +949 = 1cos2 (t) = 4049cos (t) = ± 4049 = ± 407 = ± 2107Поскольку угол находится во втором квадранте, мы знаем, что значение x- является отрицательным действительным числом, поэтому косинус также отрицательный. Так cos (t) = — 2107 cos (t) = — 2107
Попробуй # 3
Если cos (t) = 2425cos (t) = 2425 и tt находится в четвертом квадранте, найдите sin (t).грех (т).
Нахождение синусов и косинусов специальных углов
Мы уже узнали некоторые свойства специальных углов, такие как преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы особых углов, используя тождество Пифагора и наши знания о треугольниках.
Нахождение синусов и косинусов углов 45 °
Сначала мы рассмотрим углы 45 ° 45 ° или π4, π4, как показано на рисунке 9. Треугольник 45 ° –45 ° –90 ° 45 ° –45 ° –90 ° является равнобедренным треугольником, поэтому координаты x- и y соответствующей точки на окружности совпадают.Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны.
Рисунок 9
При t = π4t = π4, что составляет 45 градусов, радиус единичной окружности делит пополам угол первого квадранта. Это означает, что радиус лежит вдоль линии y = x.y = x. Единичный круг имеет радиус, равный 1. Итак, прямоугольный треугольник, образованный ниже линии y = xy = x, имеет стороны xx и y (y = x), y (y = x) и радиус = 1. См. Рисунок 10.
Рисунок 10
Из теоремы Пифагора получаем
Подставляя y = x, y = x, получаем
Комбинируя одинаковые термины, получаем
И решая относительно x, x, получаем
х2 = 12 х = ± 12 х2 = 12 х = ± 12В квадранте I x = 12.х = 12.
При t = π4t = π4 или 45 градусов,
(x, y) = (x, x) = (12,12) x = 12, y = 12cost = 12, sint = 12 (x, y) = (x, x) = (12,12) x = 12 , y = 12cost = 12, sint = 12Если мы затем рационализируем знаменатели, мы получим
cost = 1222 = 22sint = 1222 = 22cost = 1222 = 22sint = 1222 = 22Следовательно, координаты (x, y) (x, y) точки на окружности радиуса 11 под углом 45 ° 45 ° равны (22,22). (22,22).
Нахождение синусов и косинусов под углом 30 ° и 60 °
Далее мы найдем косинус и синус под углом 30 °, 30 ° или π6π6.Сначала мы нарисуем треугольник внутри круга, одна сторона которого расположена под углом 30 °, 30 °, а другая — под углом -30 °, -30 °, как показано на рисунке 11. Если в результате два прямоугольных треугольника имеют вид объединенные в один большой треугольник, обратите внимание, что все три угла этого большего треугольника будут составлять 60 °, 60 °, как показано на рисунке 12.
Рисунок 11
Рисунок 12
Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину 2y, 2y, и поскольку все стороны равны, мы также можем сделать вывод, что r = 2yr = 2y или y = 12r.у = 12р. Поскольку sint = ysint = y,
А так как r = 1r = 1 в нашем единичном круге
sin (π6) = 12 (1) = 12 sin (π6) = 12 (1) = 12Используя тождество Пифагора, мы можем найти значение косинуса.
cos2π6 + sin2 (π6) = 1cos2 (π6) + (12) 2 = 1cos2 (π6) = 34 Используйте свойство квадратного корня. cos (π6) = ± 3 ± 4 = 32 Поскольку y положительно, выберите положительный корень. cos2π6 + sin2 (π6) = 1cos2 (π6) + (12) 2 = 1cos2 (π6) = 34 Используйте свойство квадратного корня. cos (π6) = ± 3 ± 4 = 32 Поскольку y положительно, выбираем положительный корень.Координаты (x, y) (x, y) точки на окружности радиуса 11 под углом 30 ° 30 °: (32,12). (32,12). При t = π3t = π3 (60 °), радиус единичной окружности, 1, служит гипотенузой прямоугольного треугольника 30-60-90 градусов, BAD, BAD, как показано на рисунке 13. Угол AA имеет размер 60 ° 0,60 °. В точке B, B мы проводим угол ABCABC размером 60 ° 0,60 °. Мы знаем, что сумма углов в треугольнике равна 180 °, 180 °, поэтому угол CC также составляет 60 ° 0,60 °. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника ABCABC имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичного круга, все стороны должны иметь длину 1.
Рисунок 13
Угол ABDABD составляет 30 °. Таким образом, в двойном случае угол ABCABC равен 60 °. BDBD — это серединный перпендикуляр к AC, AC, поэтому он разрезает ACAC пополам. Это означает, что ADAD равен 1212 радиусу, или 12,12. Обратите внимание, что ADAD — это координата x точки B, B, которая находится на пересечении угла 60 ° и единичной окружности. Это дает нам треугольник BADBAD с гипотенузой 1 и стороной xx длиной 12,12.
Из теоремы Пифагора получаем
Подставляя x = 12, x = 12, получаем
Решая y, y, получаем
14 + y2 = 1 y2 = 1−14 y2 = 34 y = ± 3214 + y2 = 1 y2 = 1−14 y2 = 34 y = ± 32Поскольку t = π3t = π3 имеет конечную сторону в квадранте I, где координата y- положительна, мы выбираем y = 32, y = 32, положительное значение.
При t = π3t = π3 (60 °) координаты (x, y) (x, y) для точки на окружности радиуса 11 под углом 60 ° 60 ° равны (12,32), (12 , 32), поэтому мы можем найти синус и косинус.
(x, y) = (12,32) x = 12, y = 32cost = 12, sint = 32 (x, y) = (12,32) x = 12, y = 32cost = 12, sint = 32ср. теперь нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. В таблице 1 приведены эти значения.
| Угол | 0 | π6, π6 или 30 | π4, π4 или 45 ° | π3, π3 или 60 ° | π2, π2 или 90 ° |
| Косинус | 1 | 3232 | 2222 | 1212 | 0 |
| Синус | 0 | 1212 | 2222 | 3232 | 1 |
Таблица 1
На рисунке 14 показаны общие углы в первом квадранте единичной окружности.
Рисунок 14
Использование калькулятора для определения синуса и косинуса
Чтобы найти косинус и синус углов, отличных от специальных углов, мы обращаемся к компьютеру или калькулятору. Будьте внимательны. : Большинство калькуляторов можно установить в режим «градус» или «радиан», который сообщает калькулятору единицы для входного значения. Когда мы вычисляем cos (30) cos (30) на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или косинус 30 радиан, если калькулятор находится в режиме радиан.
Как записаться
Для угла в радианах воспользуйтесь графическим калькулятором, чтобы найти косинус.
- Если калькулятор имеет режим градусов и режим радиан, установите его в режим радиан.
- Нажмите кнопку COS.
- Введите значение угла в радианах и нажмите клавишу в скобках «)».
- Нажмите ENTER.
Пример 4
Использование графического калькулятора для поиска синуса и косинуса
Вычислите cos (5π3) cos (5π3) с помощью графического калькулятора или компьютера.
Решение
Введите следующие нажатия клавиш:
COS (5 × π ÷ 3) (5 × π ÷ 3) ВВОД
cos (5π3) = 0,5cos (5π3) = 0,5Анализ
Мы можем найти косинус или синус угла в градусах прямо на калькуляторе в градусном режиме. Для калькуляторов или программного обеспечения, которые используют только режим радиан, мы можем найти синус 20 °, 20 °, например, включив коэффициент преобразования в радианы как часть входных данных:
SIN (20 × π ÷ 180) (20 × π ÷ 180) ВВОД
Попробуй # 4
Вычислить грех (π3).грех (π3).
Определение области и диапазона функций синуса и косинуса
Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области и диапазоны. Каковы области определения функций синуса и косинуса? То есть, какие наименьшие и наибольшие числа могут быть входами функций? Поскольку углы меньше 0 и углы больше 2π2π могут по-прежнему отображаться на единичной окружности и иметь реальные значения x, y, x, y и r, r, не существует нижнего или верхнего предела для углов, которые могут быть входными. к функциям синуса и косинуса.Входными данными для функций синуса и косинуса является поворот от положительной оси x , и это может быть любое действительное число.
Каковы диапазоны функций синуса и косинуса? Каковы наименьшие и наибольшие возможные значения их производительности? Мы можем увидеть ответы, исследуя единичный круг, как показано на рисунке 15. Границы координаты x равны [−1,1]. [- 1,1]. Границы координаты y также равны [−1,1]. [- 1,1]. Следовательно, диапазон функций синуса и косинуса равен [-1,1].[-1,1].
Рисунок 15
Поиск опорных углов
Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с тем же значением синуса. Поскольку значение синуса представляет собой координату y на единичной окружности, другой угол с таким же синусом будет иметь такое же значение y , но будет иметь противоположное значение x .Следовательно, его значение косинуса будет противоположным значению косинуса первого угла.
Аналогично, в четвертом квадранте будет угол с таким же косинусом, что и исходный угол. Угол с таким же косинусом будет иметь то же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположным значению синуса исходного угла.
Как показано на рисунке 16, угол αα имеет то же значение синуса, что и угол t; t; значения косинуса противоположны.Угол ββ имеет то же значение косинуса, что и угол t; t; значения синуса противоположны.
sin (t) = sin (α) и cos (t) = — cos (α) sin (t) = — sin (β) и cos (t) = cos (β) sin (t) = sin (α) и cos (t ) = — cos (α) sin (t) = — sin (β) и cos (t) = cos (β)Рисунок 16
Напомним, что исходный угол угла — это острый угол t, t, образованный конечной стороной угла tt и горизонтальной осью. Базовый угол — это всегда угол между 00 и 90 °, 90 ° или 00 и π2π2 радиан. Как видно из рисунка 17, для любого угла в квадрантах II, III или IV существует опорный угол в квадранте I.
Рисунок 17
Как это сделать
Дан угол между 00 и 2π, 2π, найдите его опорный угол.
- Угол в первом квадранте является его собственным опорным углом.
- Для угла во втором или третьем квадранте опорный угол равен | π − t || π − t | или | 180 ° −t |. | 180 ° −t |.
- Для угла в четвертом квадранте опорный угол равен 2π − t2π − t или 360 ° −t 360 ° −t.
- Если угол меньше 00 или больше 2π, 2π, добавьте или вычтите 2π2π столько раз, сколько необходимо, чтобы найти эквивалентный угол между 00 и 2π.2π.
Пример 5
Поиск опорного угла
Найдите опорный угол 225 ° 225 °, как показано на рисунке 18.
Рисунок 18
Решение
Поскольку 225 ° 225 ° находится в третьем квадранте, исходный угол составляет
| (180 ° −225 °) | = | −45 ° | = 45 ° | (180 ° −225 °) | = | −45 ° | = 45 °Попробуй # 5
Найдите опорный угол 5π3.5π3.
Использование опорных углов
А теперь давайте вернемся к колесу обозрения, представленному в начале этого раздела.Предположим, всадник делает снимок, остановившись на высоте двадцати футов над уровнем земли. Затем всадник совершает поворот на три четверти по кругу. Что такое новый рост райдера? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса под углами, превышающими 90 градусов, или под отрицательным углом. Базовые углы позволяют оценивать тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения координат (x, y) (x, y) для этих углов.Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором находится конечная сторона угла.
Использование опорных углов для вычисления тригонометрических функций
Мы можем найти косинус и синус любого угла в любом квадранте, если мы знаем косинус или синус его опорного угла. Абсолютные значения косинуса и синуса угла такие же, как и у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака значений x в этом квадранте.Синус будет положительным или отрицательным в зависимости от знака значений y в этом квадранте.
Использование опорных углов для нахождения косинуса и синуса
Углы имеют косинусы и синусы с тем же абсолютным значением, что и косинусы и синусы их опорных углов. Знак (положительный или отрицательный) можно определить по квадранту угла.
Как к
Для заданного угла в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.
- Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
- Определите значения косинуса и синуса опорного угла.
- Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.
- Присвойте синусу тот же знак, что и значениям y в квадранте исходного угла.
Пример 6
Использование опорных углов для нахождения синуса и косинуса
- ⓐ Используя опорный угол, найдите точное значение cos (150 °) cos (150 °) и sin (150 °).грех (150 °).
- ⓑ Используя опорный угол, найдите cos5π4cos5π4 и sin5π4.sin5π4.
Решение
- ⓐ 150 ° находится во втором квадранте. Угол, который он образует с осью x , составляет 180 ° — 150 ° = 30 °, поэтому опорный угол составляет 30 °.
Это говорит нам, что 150 ° имеет те же значения синуса и косинуса, что и 30 °, за исключением знака. Мы знаем, что
cos (30 °) = 32andsin (30 °) = 12. cos (30 °) = 32andsin (30 °) = 12.Поскольку 150 ° находится во втором квадранте, координата x точки на окружности отрицательна, поэтому значение косинуса отрицательное. Координата y положительна, поэтому значение синуса положительно.
cos (150 °) = — 32andsin (150 °) = 12 cos (150 °) = — 32andsin (150 °) = 12 - ⓑ 5π45π4 находится в третьем квадранте. Его опорный угол равен 5π4 − π = π4,5π4 − π = π4. Косинус и синус числа π4π4 равны 22,22. В третьем квадранте и xx, и yy отрицательны, поэтому: cos5π4 = −22andsin5π4 = −22cos5π4 = −22andsin5π4 = −22
Попробуй # 6
- ⓐ Используйте опорный угол 315 ° 315 °, чтобы найти cos (315 °) cos (315 °) и sin (315 °).грех (315 °).
- ⓑ Используйте опорный угол −π6 − π6, чтобы найти cos (−π6) cos (−π6) и sin (−π6) .sin (−π6).
Использование опорных углов для поиска координат
Теперь, когда мы узнали, как находить значения косинуса и синуса для особых углов в первом квадранте, мы можем использовать симметрию и опорные углы, чтобы заполнить значения косинуса и синуса для остальных особых углов единичной окружности. Они показаны на рисунке 19. Найдите время, чтобы узнать координаты (x, y) (x, y) всех основных углов в первом квадранте.
Рисунок 19 Специальные углы и координаты соответствующих точек на единичной окружности
Помимо изучения значений специальных углов, мы можем использовать опорные углы, чтобы найти координаты (x, y) (x, y) любой точки на устройстве. круг, используя то, что мы знаем об углах отсчета вместе с идентификаторами
Сначала мы находим опорный угол, соответствующий данному углу. Затем мы берем значения синуса и косинуса опорного угла и даем им знаки, соответствующие значениям квадранта y и x .
Как записаться
Зная угол точки на окружности и радиус окружности, найдите координаты (x, y) (x, y) точки.
- Найдите опорный угол, измерив наименьший угол к оси x .
- Найдите косинус и синус опорного угла.
- Определите соответствующие знаки для xx и yy в данном квадранте.
Пример 7
Использование единичного круга для поиска координат
Найдите координаты точки на единичной окружности под углом 7π6.7π6.
Решение
Мы знаем, что угол 7π67π6 находится в третьем квадранте.
Во-первых, давайте найдем опорный угол, измерив угол к оси x . Чтобы найти опорный угол для угла, конечная сторона которого находится в квадранте III, мы находим разность угла и π.π.
7π6 − π = π67π6 − π = π6Далее мы найдем косинус и синус опорного угла:
cos (π6) = 32sin (π6) = 12 cos (π6) = 32sin (π6) = 12Мы должны определить соответствующие знаки для x и y в данном квадранте.Поскольку наш исходный угол находится в третьем квадранте, где и xx, и yy отрицательны, косинус и синус отрицательны.
cos (7π6) = — 32sin (7π6) = — 12cos (7π6) = — 32sin (7π6) = — 12Теперь мы можем вычислить координаты (x, y) (x, y), используя тождества x = cosθx = cosθ и y = sinθ.y = sinθ.
Координаты точки: (−32, −12) (- 32, −12) на единичной окружности.
Попробуй # 7
Найдите координаты точки на единичной окружности под углом 5π3.5π3.
5.2 Упражнения по разделам
Устные
1.Опишите единичный круг.
2.Что означают координаты x- и y- точек на единичной окружности?
3.Обсудите разницу между котерминальным углом и опорным углом.
4.Объясните, чем косинус угла во втором квадранте отличается от косинуса его опорного угла в единичной окружности.
5.Объясните, чем синус угла во втором квадранте отличается от синуса его опорного угла в единичной окружности.
Алгебраические
В следующих упражнениях используйте заданный знак функций синуса и косинуса, чтобы найти квадрант, в котором находится конечная точка, определяемая tt.
6.sin (t) <0 sin (t) <0 и cos (t) <0cos (t) <0
7.sin (t)> 0 sin (t)> 0 и cos (t)> 0 cos (t)> 0
8.грех (t)> 0 sin (t)> 0 а также cos (t) <0 cos (t) <0
9.sin (t) <0 sin (t) <0 и cos (t)> 0 cos (t)> 0
Для следующих упражнений найдите точное значение каждой тригонометрической функции.
Числовой
Для следующих упражнений укажите исходный угол для данного угла.
Для следующих упражнений найдите опорный угол, квадрант конечной стороны, а также синус и косинус каждого угла. Если угол не является одним из особых углов единичной окружности, воспользуйтесь калькулятором и округлите до трех десятичных знаков.
Найдите требуемое значение для следующих упражнений.
50.Если cos (t) = 17cos (t) = 17 и tt находится в 4 -м квадранте , найдите sin (t) .sin (t).
51.Если cos (t) = 29cos (t) = 29 и tt находится в 1-м квадранте , найдите sin (t) .sin (t).
52.Если sin (t) = 38sin (t) = 38 и tt находится в квадранте 2 и , найдите cos (t) .cos (t).
53.Если sin (t) = — 14sin (t) = — 14 и tt находится в квадранте 3 rd , найдите cos (t).Стоимость).
54.Найдите координаты точки на окружности радиуса 15, соответствующей углу 220 ° .220 °.
55.Найдите координаты точки на окружности с радиусом 20, соответствующей углу 120 ° .120 °.
56.Найдите координаты точки на окружности радиуса 8, соответствующей углу 7π4,7π4.
57.Найдите координаты точки на окружности радиуса 16, соответствующей углу 5π9.5π9.
58.Укажите область определения функций синуса и косинуса.
59.Укажите диапазон функций синуса и косинуса.
Графический
Для следующих упражнений используйте заданную точку на единичном круге, чтобы найти значение синуса и косинуса t .t.
60. 62. 64. 66. 68. 70. 72. 74. 76. 78.Технологии
Для следующих упражнений используйте графический калькулятор.
Расширения
Оцените следующие упражнения.
90.sin (11π3) cos (−5π6) sin (11π3) cos (−5π6)
91.sin (3π4) cos (5π3) sin (3π4) cos (5π3)
92.sin (−4π3) cos (π2) sin (−4π3) cos (π2)
93.sin (−9π4) cos (−π6) sin (−9π4) cos (−π6)
94.sin (π6) cos (−π3) sin (π6) cos (−π3)
95.sin (7π4) cos (−2π3) sin (7π4) cos (−2π3)
96.cos (5π6) cos (2π3) cos (5π6) cos (2π3)
97.cos (−π3) cos (π4) cos (−π3) cos (π4)
98.грех (-5π4) грех (11π6) грех (-5π4) грех (11π6)
99.грех (π) грех (π6) грех (π) грех (π6)
Реальные приложения
Для следующих упражнений используйте этот сценарий. Ребенок входит в карусель, которая совершает один оборот за одну минуту. Ребенок входит в точку (0,1), (0,1), то есть на правильном северном положении.Предположим, карусель вращается против часовой стрелки.
100.Какие координаты ребенка через 45 секунд?
101.Какие координаты ребенка через 90 секунд?
102.Какие координаты ребенка через 125 секунд?
103.Когда у ребенка будут координаты (0.707, –0.707) (0.707, –0.707), если поездка длится 6 минут? (Есть несколько ответов.)
104.Когда у ребенка будут координаты (−0.866, −0,5) (- 0,866, −0,5) если поездка длилась 6 минут?
касательных и уклонов
касательных и уклоновОпределение касательной
Синус и косинус — не единственные тригонометрические функции, используемые в тригонометрии. Многие другие использовались на протяжении веков, такие как гавайские травы и спреды. Самый полезный из них — касательная. В терминах диаграммы единичной окружности касательная — это длина вертикальной линии ED , касательной к окружности от точки касания E до точки D , где эта касательная линия пересекает луч AD , образующий угол.| Если ваш браузер поддерживает Java, вы можете перетащить точку B , чтобы увидеть, как изменяются синус, косинус и тангенс при изменении угла. (Дополнительные сведения об управлении фигурой см. В разделе «Об апплете».) |
Касательная через синус и косинус
Поскольку два треугольника ADE и ABC похожи, мы имеем ED / AE = CB / AC.Но ED = tan A, AE = 1, CB = sin A, и AC = cos AB. Таким образом, мы вывели фундаментальное тождество
Касательные и прямоугольные треугольники
Так же, как синус и косинус могут быть найдены как отношения сторон прямоугольных треугольников, так и касательная.Мы будем использовать три отношения, которые у нас уже есть. Во-первых, tan A = sin A / cos A. Второй, sin A = a / c. В-третьих, cos A = b / c. Разделив a / c на b / c и исключив появившиеся c , мы приходим к выводу, что tan A = a / b. Это означает, что касательная — это противоположная сторона, деленная на соседнюю сторону:
Уклоны линий
Одна из причин, по которой касательные так важны, заключается в том, что они дают наклон прямых линий. Рассмотрим прямую линию, проведенную в координатной плоскости x-y .Точка B — это место, где линия пересекает ось y . Мы можем позволить координатам B быть (0, b ), так что b, , называемый пересечением y , указывает, насколько далеко от оси x лежит B . (Это обозначение противоречит обозначениям сторон треугольника a, b, и c, , поэтому не будем сейчас обозначать стороны.)
Вы можете видеть, что точка 1 справа от начала координат помечена 1, а ее координаты, конечно же, равны (1,0).Пусть C будет точкой, в которой эта вертикальная линия пересекает горизонтальную линию через B. Тогда C имеет координаты (1, b ).
Точка A — это место, где вертикальная линия выше 1 обрезает исходную линию. Пусть м обозначает расстояние, на которое A находится выше C. Тогда A имеет координаты (1, b + m ). Это значение м называется уклоном линии.Если вы переместите вправо на одну единицу в любом месте линии, то вы переместитесь на м вверх и на единицы.
Теперь рассмотрим угол CBA. Назовем его углом наклона . Касательная CA / BC = м /1 = м. Следовательно, уклон — это тангенс угла наклона.
Углы возвышения и понижения
Термин «угол возвышения» относится к углу над горизонтом относительно наблюдателя.Если вы находитесь в точке A, и AH — горизонтальная линия, то угол подъема до точки B над горизонтом равен BAH. Аналогично, «угол падения» до точки C ниже горизонта — это угол CAH.
Касательные часто используются для решения задач, связанных с углами возвышения и депрессии.
Снова общие углы
Мы можем расширить нашу таблицу синусов и косинусов общих углов до касательных.Вам не нужно запоминать всю эту информацию, если вы можете просто запомнить соотношение сторон треугольника 45 ° -45 ° -90 ° и треугольника 30 ° -60 ° -90 °. Отношения — это значения триггерных функций.Обратите внимание, что тангенс прямого угла обозначается как бесконечность. Это потому, что по мере того, как угол увеличивается до 90 °, касательная увеличивается неограниченно. Возможно, лучше будет сказать, что касательная к 90 ° не определена, поскольку, используя определение окружности, луч, выходящий из начала координат под углом 90 °, никогда не пересекает касательную линию.
| Угол | Градусы | Радианы | косинус | синус | тангенс | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 90 ° | π /2 | 9025 60 ° | π /3 | 1/2 | √3 / 2 | √3 | |||||||||||||||
| 45 ° | π /4 | √2 / 2 | 2 | 1 | |||||||||||||||||
| 30 ° | π /6 | √3 / 2 | 1/2 | 1 / √3 | |||||||||||||||||
| 0 ° | 0 ° | 0 | 0 |
Упражнения
29. В прямоугольном треугольнике a = 30 ярдов и загар A = 2. Найдите b и c.
49. cos t = 2 tan t. Найдите значение sin t.
Примечание. В следующих задачах под расстоянием понимается горизонтальное расстояние, если не указано иное; высота объекта означает его высоту над горизонтальной плоскостью через точку наблюдения. Высота глаза наблюдателя не должна приниматься во внимание, если специально не указано иное.В задачах, связанных с тенью от объекта, предполагается, что тень падает в горизонтальной плоскости через основание объекта, если не указано иное.
151. Угол подъема дерева на расстоянии 250 футов составляет 16 ° 13 ‘. Найдите высоту.
152. Найдите высоту шпиля вдали 321 фут, угол подъема 35 ° 16 ‘.
153. С корабля угол подъема вершины маяка на высоте 200 футов над водой составляет 2 ° 20 ‘.Найдите расстояние.
154. С вершины маяка на высоте 165 футов над водой угол падения корабля составляет 3 ° 50 ‘. Найдите расстояние.
159. Найдите высоту башни на расстоянии 186 футов, угол подъема 40 ° 44 ‘.
160. С одной стороны ручья шест высотой 50 футов имеет с противоположной точки угол возвышения 5 ° 33 ‘. Найдите ширину ручья.
164. От одного холма вершина другого на 128 футов выше имеет угол подъема 2 ° 40 ‘. Найдите расстояние.
165. От одного холма до вершины другого расстояние 6290 футов имеет угол возвышения 4 ° 9 ‘. Найдите, насколько высота второго холма превышает высоту первого.
189. Фронтальный конец крыши имеет размер 40 футов в диаметре у основания и 26 футов от основания до конька. Под каким углом наклоняются стропила?
Подсказки
Общий совет для всех этих упражнений — сначала нарисовать фигуру.29. Так как вы знаете a и tan A, вы можете найти b. Затем вы можете определить c по теореме Пифагора, или с помощью синусов, или с помощью косинусов.
49. Вам понадобится два удостоверения личности. Во-первых, tan t = sin t / cos t. Во-вторых, тождество Пифагора, sin 2 t + cos 2 t = 1. Затем вам придется решить квадратное уравнение.
151. Помните, что тангенс угла в прямоугольном треугольнике — это противоположная сторона, деленная на соседнюю сторону. Вы знаете прилегающую сторону (расстояние до дерева) и угол (угол возвышения), поэтому вы можете использовать касательные для определения высоты дерева.
152. Вы знаете угол (опять же, угол возвышения) и прилегающую сторону (расстояние до шпиля), поэтому используйте касательные, чтобы найти противоположную сторону.
153. Используя угол и противоположную сторону, используйте касательную, чтобы найти прилегающую сторону.
154. Тот же намек, что и в 153.
159. Тот же намек, что и в 152.
160. Тот же намек, что и в 153.
164. Тот же намек, что и в 153.
165. Тот же намек, что и в 152.
189. Фронтонный конец крыши представляет собой равнобедренный треугольник.Если провести перпендикулярную линию с гребня, вы получите два равных прямоугольных треугольника. Вам известны две ножки треугольников, поэтому угол наклона стропил можно определить с помощью арктангенса.
Ответы
29. b = a / tan A = 30/2 = 15 ярдов. c = 33,5 ярда.
49. Так как cos t = 2 tan t, , следовательно, cos t = 2 sin t / cos t, so cos 2 t = 2 sin t, и, по пифагорейской идее 1 — sin 2 t = 2 sin t. Это дает вам квадратное уравнение sin 2 t + 2 sin t — 1 = 0. Решение: sin t = –1 ± √2. Из этих двух решений единственно возможным является sin t = √2 — 1.
151. Высота = 250 желто-коричневых 16 ° 13 ‘= 72,7’ = 72’9 дюймов.
152. Высота = 321 желто-коричневый 35 ° 16 ‘= 227 футов.
153. Расстояние = 200 / tan 2 ° 20 ‘= 4908 футов, почти миля.
154. Расстояние = 165 / тангенс угла 3 ° 50 ‘= 2462 фута, почти полмили.
159. Высота = 186 желтовато-коричневый 40 ° 44 ‘= 160 футов.
160. Расстояние = 50 / тангенс угла 5 ° 33 ‘= 515 футов.
164. Расстояние = 128 / tan 2 ° 40 ‘, около 2750 футов, чуть больше полумили.
165. Высота = 6290 желто-коричневый 4 ° 9 ‘= 456,4 фута.
189. tan A = 26/20, поэтому A = 52 °.
Вся элементарная математика — Учебное пособие — Тригонометрия
Единичный круг. Подсчет углов в единичной окружности.Отрицательные и положительные углы. Четверти единичного круга.
Линии синуса и косинуса. Синус. Косинус. Знаки синуса и
косинус в разных четвертях единичной окружности. Касательная
и котангенс линий. Касательная. Котангенс. Признаки
тангенс и котангенс в разных частях единицы
круг.Секанс и косеканс.
Для построения всей тригонометрии, законы которой действительны для любых углов (не только для острых углов, но также для тупых, положительных и отрицательных углов), необходимо Необходимо рассмотреть так называемую единичную окружность , то есть окружность с радиусом, равным 1 (рис.3).
Нарисуем два диаметра: горизонтальный AA и вертикальный BB. Считаем углы от точки А (начальная точка). Отрицательные углы отсчитываются по часовой стрелке, положительный в противоположном направлении.Подвижный радиус OC образует угол с неподвижный радиус OA. Его можно разместить в 1-м квартале (COA), во 2-м квартале (DOA), в 3-м квартале (EOA) или в 4 квартал (FOA). Рассматривая OA и OB как положительные направления, а OA и OB как отрицательные, определяем тригонометрические функции углов следующим образом.
Линия синуса угла (рис.4) — это вертикальный диаметр единичной окружности, косинус линия угла — горизонтальный диаметр единичной окружности. синус угла (Рис.4) — отрезок OB синусоиды, то есть проекция подвижного радиуса ОК к синусоиде; косинус угла — отрезок OA линии косинуса, который — проекция подвижного радиуса OK на косинусную линию.
Знаки синуса и косинуса в разных четвертях единичной окружности показаны на Рис.5 и Рис.6.
Касательная линия (рис.7) — это касательная, проведенная к единичной окружности через точку A горизонтального диаметра .
Линия котангенса (рис.8) — это касательная, проведенная к единичной окружности через точку B вертикального диаметра .
Касательная — это сегмент касательной линии между точкой касания A и точкой пересечения (D, E и т. Д., Фиг.7) касательной и радиусной линией.
Котангенс — это сегмент линии котангенса между точкой B касания и точкой пересечения (P, Q и т. Д., Фиг.8) котангенса и радиуса.
Знаки тангенса и котангенса в разных четвертях единичной окружности см. На рис.9.
Секанс и косеканс определяются как значения, обратные косинусу и синусу соответственно.
3 совета эксперта по использованию единичной окружности
Если вы изучаете тригонометрическую систему или математику — или готовитесь к этому — вам нужно будет познакомиться с единичным кругом. Единичная окружность — это , важный инструмент, используемый для нахождения синуса, косинуса и тангенса угла. Но как это работает? И какую информацию нужно знать, чтобы ею пользоваться?
В этой статье мы объясним, что такое единичный круг и почему вы должны его знать. Мы также даем вам три совета, которые помогут вам запомнить, как использовать единичный круг.
Изображение функции: Gustavb / Wikimedia
Единичный круг: базовое введение
Единичный круг — это круг с радиусом 1. Это означает, что для любой прямой линии, проведенной от центральной точки круга до любой точки на краю круга, длина этой линии всегда будет равна 1.(Это также означает, что диаметр круга будет равен 2, поскольку диаметр равен удвоенной длине радиуса.)
Как правило, центральная точка единичной окружности находится там, где пересекаются оси x и y, или в координатах (0, 0):
Единичная окружность, или триггерная окружность, как ее еще называют, полезно знать, потому что позволяет нам легко вычислять косинус, синус и тангенс любого угла от 0 ° до 360 ° (или от 0 до 2π радиан). 2 $ (где a и b — это длины сторон треугольника, а c — длина гипотенузы).2θ = 1 $$
Имейте в виду, что эти значения могут быть отрицательными в зависимости от сформированного угла и в какой квадрант попадают координаты x и y (более подробно я объясню это позже).
Вот обзор всех основных углов в градусах и радианах на единичной окружности:
Единичный круг — градусы
Круг единиц — Радианы
А что, если треугольник не образовался? Давайте посмотрим на , что происходит, когда угол равен 0 °, образуя горизонтальную прямую линию вдоль оси x:
В этой строке координата x равна 1, а координата y равна 0.Мы знаем, что косинус равен координате x, а синус равен координате y, , поэтому мы можем записать это:
Что если угол равен 90 ° и образует идеально вертикальную линию вдоль оси y?
Здесь мы видим, что координата x равна 0, а координата y равна 1. Это дает нам следующие значения для синуса и косинуса:
- $ \ cos90 ° = 0 $
- $ \ sin90 ° = 1 $
Этот слоган определенно подходит, если вы не любитель математики.
Почему вы должны знать единичный круг
Как указано выше, единичная окружность полезна, потому что позволяет нам легко найти синус, косинус или тангенс любого градуса или радиана. Особенно полезно знать круговую диаграмму единиц, если вам нужно решить определенные триггерные значения для домашнего задания по математике или если вы готовитесь к изучению математического анализа.
Но как именно знание единичного круга может помочь вам? Допустим, вам задали следующую задачу на тесте по математике, и разрешено ли , использовать калькулятор для ее решения:
$$ \ sin30 ° $$
С чего начать? Давайте еще раз взглянем на диаграмму единичного круга — на этот раз со всеми большими углами (как в градусах, так и в радианах) и их соответствующими координатами:
Джим.belk / Викимедиа
Не расстраивайтесь! Помните, все, что вам нужно, это $ \ sin30 ° $. Глядя на этот график, мы видим, что , координата y равна $ 1/2 $ при 30 °. И поскольку координата y равна синусу, наш ответ будет следующим:
$$ \ sin30 ° = 1/2 $$
Но что, если вы столкнетесь с проблемой, в которой вместо градусов используются радианы? Процесс ее решения остается прежним. Скажем, например, у вас возникла проблема, которая выглядит так:
$$ \ cos {{3π} / 4} $$
Опять же, используя диаграмму выше, мы можем видеть, что координата x (или косинус) для $ {3π} / 4 $ (который равен 135 °) составляет $ — {√2} / 2 $.Вот как бы тогда выглядел наш ответ на эту проблему:
$$ \ cos ({3π} / 4) = — {√2} / 2 $$
Все это довольно просто, если у вас есть приведенная выше круговая диаграмма единиц для использования в качестве справочной информации. Но в большинстве случаев (если не всегда) это не так, и вы должны будете отвечать на такие математические вопросы, используя только свой мозг.
Так как же можно запомнить единичный круг? Читайте наши главные советы!
Как запомнить единичный круг: 3 основных совета
В этом разделе мы даем вам несколько основных советов по запоминанию триггерного круга, чтобы вы могли легко использовать его для решения любой математической задачи, которая в нем требует.
Я бы не рекомендовал практиковать единичный круг с клейкими лентами, но, эй, это только начало.
# 1: запоминать общие углы и координаты
Чтобы эффективно использовать единичный круг, вам нужно запомнить наиболее распространенные углы (как в градусах, так и в радианах), а также их соответствующие координаты x и y.
Диаграмма выше представляет собой полезную диаграмму единичного круга, на которую стоит обратить внимание, поскольку она включает все основные углы в градусах и радианах в дополнение к их соответствующим координатным точкам по осям x и y.
Вот диаграмма, содержащая ту же информацию в виде таблицы:
Угол (градусы) | Угол (радианы) | Координаты точки на окружности |
0 ° / 360 ° | 0 / 2π | (1, 0) |
30 ° | $ π / 6 $ | долл. США ({√3} / 2, 1/2) долл. США |
45 ° | $ π / 4 $ | долл. США ({√2} / 2, {√2} / 2) долл. США |
60 ° | $ π / 3 $ | долл. США (1/2, {√3} / 2) долл. США |
90 ° | $ π / 2 $ | (0, 1) |
120 ° | $ {2π} / 3 $ | $ (- 1/2, {√3} / 2) $ |
135 ° | $ {3π} / 4 $ | долл. США (- {√2} / 2, {√2} / 2) долл. США |
150 ° | $ {5π} / 6 $ | $ (- {√3} / 2, 1/2) $ |
180 ° | π | (-1, 0) |
210 ° | {7} долл. США / 6 долл. США долл. США | $ (- {√3} / 2, -1/2) $ |
225 ° | $ {5π} / 4 $ | $ (- {√2} / 2, — {√2} / 2) $ |
240 ° | $ {4π} / 3 $ | $ (- 1/2, — {√3} / 2) $ |
270 ° | $ {3π} / 2 $ | (0, -1) |
300 ° | $ {5π} / 3 $ | долл. США (1/2, — {√3} / 2) долл. США |
315 ° | $ {7π} / 4 $ | долл. США ({√2} / 2, — {√2} / 2) долл. США |
330 ° | $ {11π} / 6 $ | долл. США ({√3} / 2, -1/2) долл. США |
Теперь, хотя вы можете попытаться запомнить все эти координаты и углы, это — много вещей, которые нужно запомнить.
К счастью, есть прием, который поможет вам запомнить самые важные части единичного круга.
Посмотрите на координаты выше, и вы заметите четкую закономерность: все точки (за исключением точек под 0 °, 90 °, 270 ° и 360 °) чередуются только между тремя значениями (положительными или отрицательными):
- $ 1/2
- $ {√2} / 2 $
- $ {√3} / 2 $
Каждому значению соответствует короткая, средняя или длинная линия для косинуса и синуса:
Вот что означают эти длины:
- Короткая горизонтальная или вертикальная линия = 1/2 доллара США
- Средняя горизонтальная или вертикальная линия = $ {√2} / 2 $
- Длинная горизонтальная или вертикальная линия = $ {√3} / 2 $
Например, если вы пытаетесь решить $ \ cos {π / 3} $, вы должны сразу знать, что этот угол (равный 60 °) указывает на короткую горизонтальную линию на единичной окружности. Следовательно, его соответствующая координата x должна равняться $ 1/2 $ (положительное значение, поскольку $ π / 3 $ создает точку в первом квадранте системы координат).
Наконец, хотя полезно запомнить все углы в таблице выше, обратите внимание, что , безусловно, самые важные углы, которые следует запомнить, следующие:
- 30 ° / $ π / 6 $
- 45 ° / $ π / 4 $
- 60 ° / $ π / 3 $
Относитесь к негативам и позитивам, как к кабелям, которые потенциально могут убить вас при неправильном подключении.
# 2: Узнай, что есть отрицательного и что положительного
Очень важно уметь различать положительные и отрицательные координаты x и y, чтобы вы могли найти правильное значение для триггерной проблемы. Напоминаем, что w , будет ли координата на единичной окружности положительной или отрицательной, зависит от , в какой квадрант (I, II, III или IV) попадает точка:
Вот диаграмма, показывающая, будет ли координата положительной или отрицательной в зависимости от квадранта, в котором находится конкретный угол (в градусах или радианах):
Квадрант | Координата X (косинус) | Координата Y (синус) |
Я | + | + |
II | – | + |
III | – | – |
IV | + | – |
Например, на тесте по математике вам задали следующую задачу:
.$$ \ cos210 ° $$
Еще до того, как вы попытаетесь ее решить, вы должны уметь распознать, что ответом будет отрицательное число , поскольку угол 210 ° попадает в квадрант III (где x-координаты всегда отрицательны).
Теперь, используя уловку, которую мы узнали в подсказке 1, вы можете выяснить, что угол 210 ° создает длинной горизонтальной линии. Следовательно, наш ответ таков:
$$ \ cos210 ° = — {√3} / 2 $$
# 3: Умейте находить касательную
Наконец, важно знать, как использовать всю эту информацию о триггерной окружности, синусе и косинусе, чтобы иметь возможность найти тангенс угла.
В триггере, чтобы найти тангенс угла θ (в градусах или радианах), вы просто делите синус на косинус:
$$ \ tanθ = {\ sinθ} / {\ cosθ} $$
Например, вы пытаетесь решить эту проблему:
$$ \ tan300 ° $$
Первый шаг — составить уравнение в терминах синуса и косинуса:
$$ \ tan300 ° = {\ sin300 °} / {\ cos300 °} $$
Теперь, чтобы найти касательную, нам нужно найти синус и косинус 300 °.Вы должны быстро распознать, что угол 300 ° попадает в четвертый квадрант, а это означает, что косинус или координата x будет положительным, а синус или координата y — отрицательным.
Вы также должны сразу знать, что угол 300 ° создает короткую горизонтальную линию и длинную вертикальную линию. Следовательно, косинус (горизонтальная линия) будет равен $ 1/2 $, а синус (вертикальная линия) будет равен $ — {√3} / 2 $ (отрицательное значение y, поскольку эта точка находится в квадранте IV ).
Теперь, чтобы найти касательную, все, что вам нужно сделать, это подключить и решить:
$$ \ tan300 ° = {- {√3} / 2} / {1/2} $$
$$ \ tan300 ° = -√3 $$
Пришло время мурлыкать математические навыки!
Набор вопросов для практики Unit Circle
Теперь, когда вы знаете, как выглядит единичный круг и как его использовать, давайте проверим, что вы узнали, с помощью нескольких практических задач.
вопросов
- $ \ sin45 ° $
- $ \ cos240 ° $
- $ \ cos {5π} / 3 $
- $ \ tan {2π} / 3 $
ответов
- $ {√2} / 2 долл. США
- $ -1 / 2 $
- $ 1/2
- $ -√3 $
Ответ объяснения
# 1: $ \ sin45 ° $
При этой проблеме есть два элемента информации, которые вы должны сразу определить:
- Ответ будет положительным, , поскольку угол 45 ° находится в квадранте I, а синус угла равен координате y
- Угол 45 ° образует вертикальную линию средней длины (для синуса)
Поскольку 45 ° означает положительную линию средней длины, правильный ответ: $ {√2} / 2 $.
Если вы не знаете, как это понять, нарисуйте диаграмму, которая поможет вам определить, будет ли длина линии короткой, средней или длинной.
# 2: $ \ cos240 ° $
Как и в задаче № 1 выше, есть две части информации, которую вы должны быстро понять при решении этой проблемы:
- Ответ будет отрицательным, , поскольку угол 240 ° находится в квадранте III, а косинус угла равен координате x
- Угол 240 ° образует короткую горизонтальную линию (для косинуса)
Поскольку 240 ° обозначает короткую отрицательную линию, правильный ответ: $ -1 / 2 $.
# 3: $ \ cos {5π} / 3 $
В отличие от задач, описанных выше, в этой задаче вместо градусов используется радиан . Хотя это может сделать проблему более сложной для решения, на самом деле здесь используются те же основные шаги, что и для двух других задач.
Во-первых, вы должны понять, что угол $ {5π} / 3 $ находится в квадранте IV, поэтому координата x или косинус будет положительным числом. Вы также должны уметь сказать, что $ {5π} / 3 $ создает короткую горизонтальную линию.
Это дает вам достаточно информации, чтобы определить, что ответ составляет $ 1/2 $.
# 4: $ \ tan {2π} / 3 $
В этой задаче используется тангенс вместо синуса или косинуса, а это значит, что с нашей стороны потребуется немного больше математических вычислений. Прежде всего, вспомните основную формулу для поиска тангенса:
$$ \ tan θ = {\ sin θ} / {\ cos θ} $$
Теперь давайте возьмем полученную степень — $ {2π} / 3 $ — и подставим ее в это уравнение:
$$ \ tan {2π} / 3 = {\ sin {2π} / 3} / {\ cos {2π} / 3} $$
Теперь вы должны быть в состоянии решить для синуса и косинуса отдельно, используя то, что вы запомнили о единичной окружности.Поскольку угол $ {2π} / 3 $ находится в квадранте II, координата x (или косинус) будет отрицательной, а координата y (или синусом) будет положительной.
Затем вы сможете определить на основе одного только угла, что горизонтальная линия — это короткая линия, , а вертикальная линия — это длинная линия. Это означает, что косинус равен $ -1 / 2 $, а синус равен $ {√3} / 2 $.
Теперь, когда мы вычислили эти значения, все, что нам нужно сделать, это вставить их в наше исходное уравнение и найти тангенс:
$$ \ tan {2π} / 3 = {{√3} / 2} / {- 1/2} $$
$$ \ tan {2π} / 3 = -√3 $$
Что дальше?
Если вы скоро будете сдавать SAT или ACT, вам нужно будет знать некоторые триггеры, чтобы вы могли преуспеть в разделе математики. Взгляните на наши экспертные руководства по тестированию SAT и ACT, чтобы вы могли точно узнать, что вам нужно знать в день теста!
Помимо запоминания единичного круга, неплохо научиться вставлять числа и ответы. Прочтите наши руководства, чтобы узнать все об этих двух полезных стратегиях, которые вы можете использовать в любом тесте по математике, включая SAT и ACT!
Файл: Circle cos sin.gif — Wikimedia Commons
Английский: У нас есть единичный круг (с радиусом = 1) зеленого цвета, расположенный в начале координат в правом нижнем углу.В середине этого круга желтым цветом представлен угол тета (θ). Этот угол представляет собой величину вращения против часовой стрелки по кругу, начиная справа по оси x, как показано. Точная копия этого небольшого угла показана вверху справа как наглядная иллюстрация определения θ.
Под этим углом, начиная с начала координат, радиально наружу проводится (тусклая) зеленая линия. Эта линия пересекает единичный круг в одной точке, которая представляет собой зеленую точку, вращающуюся с постоянной скоростью при изменении угла θ, также с постоянной скоростью.
Вертикальное положение этой точки проецируется прямо (вдоль слабой красной линии) на график слева от круга. Это приводит к красной точке. Координата Y этой красной точки (такая же, как координата Y зеленой точки) является значением синусоидальной функции, вычисленной под углом θ, то есть:
- Y координата зеленой точки = sin θ
При изменении угла θ красная точка перемещается вверх и вниз, отслеживая красный график. Это график синусоидальной функции.Слабые вертикальные линии, проходящие слева, отмечают каждый квадрант по окружности, то есть под каждым углом 90 ° или π / 2 радиан. Обратите внимание, как синусоида переходит от 1 к нулю, к -1, а затем обратно к нулю, именно на этих линиях. Это отражает тот факт, что sin (0) = 0, sin (π / 2) = 1, sin (π) = 0 и sin (3π / 2) -1.
Аналогичный процесс выполняется с координатой x зеленой точки. Однако, поскольку координата x отклонена от обычного соглашения для построения графиков (где y = f (x), с вертикальным y и x горизонтальным), была выполнена операция «untilt», чтобы повторить процесс снова в том же ориентация, а не вертикальная.

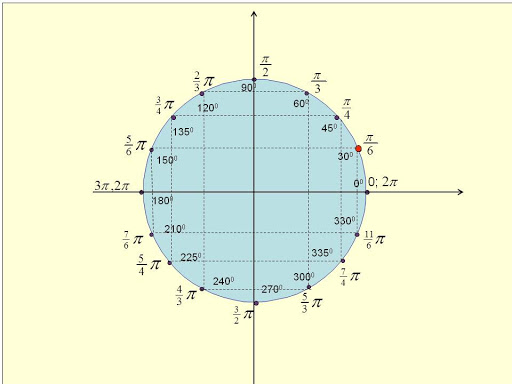 k * arcsin α + πk.
k * arcsin α + πk.