Линейное программирование в экономике: Линейное программирование в экономике

Линейное программирование — Энциклопедия по экономике

При решении описанной задачи могут быть применены методы линейного программирования. В этом случае задача модифицируется в виде  [c.193]
Кроме балансового в плановой работе используются и другие методы экономического анализа и синтеза, прямого счета, расчета по факторам, экстраполяции и итерации, экономико-математические методы (линейного программирования, динамического программирования, матричный и др.), метод экономико-математического моделирования.  [c.72]

Модели оптимизации экономики имеют целью добиться наибольшей результативности (эффективности) использования имеющегося потенциала и ресурсов. Любая экономико-математическая модель — это воспроизведение связей между экономическими явлениями и процессами. Критерии оптимального плана могут быть разными, поэтому в общей форме подразумевается оптимальное сочетание цели и средств социалистического производства за счет интенсивного использования всех имеющихся возможностей. Целевая функция и ограничения выражаются в математическом виде, и решение их методами линейного программирования позволяет найти оптимальный вариант.  [c.73]

В условиях серийного производства при изготовлении на одном оборудовании нескольких видов продукции число машино-смен, нужное для изготовления каждого вида, не равно общему возможному числу смен в месяц. Поэтому возникает необходимость решить вопрос об отборе номенклатуры продукции, закрепляемой за данным оборудованием, и определить, какую продукцию, в какие дни и смены следует изготовлять. Для этого могут быть использованы методы линейного программирования, а также целочисленное программирование.  [c.199]

Известны следующие методы линейное программирование, динамическое программирование, теория игр и массового обслуживания, матричный метод затраты — выпуск и др. Наибольшее распространение получили методы линейного программирования. Задачи, решаемые с помощью этих методов, носят экстремальный характер. Результатом решения является определение максимума или минимума какой-то целевой функции, в качестве которой может приниматься прибыль, выработка товарной продукции, себестоимость и др.

Выбор целевой функции зависит от пели задачи. В связи с переходом на новые условия планирования для предприятия в целом более целесообразна постановка задачи на максимум прибыли (П). Математически такая задача формулируется следующим образом  [c.127]

С помощью методов линейного программирования определяют оптимальную производственную программу, оптимальные варианты смешения (компаундирования) товарных нефтепродуктов, оптимальную технологическую схему, наилучший вариант использования сырья и др. В нефтепереработке наибольшее распространение получило определение методами линейного программирования оптимальной производственной программы.  [c.127]

Для большей сбалансированности всех разделов плана используют также матричные модели затраты — выпуск по форме, аналогичной межотраслевому балансу. Хотя матричная модель не включает всех разделов плана, она позволяет достигнуть четкой сбалансированности его основных разделов. Оптимального варианта такая модель не дает, поэтому использовать ее. можно в сочетании с моделью линейного программирования оптимального варианта производственной программы.  [c.128]

Для оптимизации производственной программы разработан ряд статических экономико-математических моделей, основанных на методах линейного программирования и с достаточной точностью описывающих возможности нефтеперерабатывающего предприятия. Критериями оптимальности служат максимум прибыли, минимум затрат, максимум выработки товарной про-  [c.162]

Возможности увеличения прибыл т и рентабельности производства еще больше возрастают npi. использовании методов линейного программирования для разработки производственной программы предприятия. В этом случае имеется возможность увеличить прибыль предприятия не только в результате более рационального смешения отдельных компонентов при приготовлении товарных нефтепродуктов, но и в результате снижения себестоимости целевой продукции при выборе оптимальных вариантов работы технологических установок.  [c.296]

Рациональное размещение новых предприятий и производств существенно влияет на повышение эффективности производства.

Выбор оптимального варианта осуществляют с учетом экономических, социальных и экологических факторов с применением экономико-математических методов, основанных на нахождении минимума приведенных затрат на выпуск продукции вновь строящихся предприятий. Для выбора оптимального варианта размещения предприятий широко используют модели транспортной задачи, решаемой методами линейного программирования.  [c.328]

МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ применяют для определения оптимального способа распределения дефицитных ресурсов при наличии конкурирующих потребностей. Согласно опросу журналом Форчун вице-президентов по производству из 500 фирм, модели линейного программирования и управления запасами пользуются в промышленности наибольшей популярностью. Линейное программирование обычно используют специалисты штабных подразделений для разрешения производственных трудностей. Некоторые типичные применения этого метода в управлении производством перечислены в табл. 8.1.  [c.232]

Нижеследующий пример иллюстрирует простую ситуацию, в которой для принятия решения следует воспользоваться моделью линейного программирования. Управляющий производством должен решить, сколько галлонов краски каждого из трех ее типов следует производить, чтобы получить наивысшую прибыль. На решение налагается несколько ограничений  [c.232]

Задача проиллюстрирована рис. 8.3. С помощью модели линейного программирования управляющий может определить, какое количество краски каждого типа производить при известных запасах реагентов и имеющемся резерве времени работы оборудования, а также с учетом вклада в прибыль краски каждого типа. Не имея такой модели, крайне сложно принять оптимальное решение даже в сравнительно простой ситуации.  [c.232]

Имитация используется в ситуациях, слишком сложных для математических методов типа линейного программирования. Это может быть связано с чрезмерно  [c.232]

Т а б л 3i ц а 8.1. Типичные варианты применения линейного программирования в управлении производством  [c.233]

Рис. 8.3. Модель линейного программирования (линейное программирование применяется для решения задач с несколькими переменными, как например, задачи об ассортименте красок в тексте).

Теория игр — это метод, используемый для оценки влияния какого-либо действия на конкурентов. Моделями теории очередей можно пользоваться в соответствии со спросом на них. Модели управления запасами помогают руководителю синхронизировать размещение заказов на ресурсы и оптимизировать их объемы, а также определять оптимальное для склада количество готовой продукции. Модели линейного программирования позволяют установить оптимальный способ распределения дефицитных ресурсов между конкурирующими потребностями в них. Имитационное моделирование — это использование устройства, которое имитирует реальный мир. В экономическом анализе используется ряд методов для определения экономического положения организации или осуществимости действия с экономической точки зрения.  [c.244]

А. С. Астахов, восходящая в то время звезда экономики горной промышленности, в своих ранних работах (1966, 1968, 1973) применил методы линейного программирования в горной промышленности и вплотную подошел к парадоксу дисконтирования, но пропустил его открытие.  [c.62]

В ряде случаев проникнуть в изучаемые хозяйственные явления и процессы известными традиционными способами невозможно, необходимы иные приемы анализа. Поэтому в настоящее время при анализе сложных производственно-хозяйствен ных явлений все более широко применяются математические методы. Наибольшее распространение получили такие из них, как линейное программирование, математическая статистика, теория вероятности, экономическая кибернетика и др.  [c.19]

Линейное программирование используется при анализе напряженности плановых заданий, рациональной организации пе-  [c.19]

Преимущество линейного программирования состоит в том, что оно позволяет использовать при анализе деятельности пред приятия различные сочетания математического обеспечения, что позволяет найти наиболее оптимальный вариант для раскрытия изучаемого объекта, не прибегая при этом к нескольким приемам изучения.  [c.20]

Итак, для нахождения оптимальной производственной программы необходимо такое решение системы многих уравнений с многими неизвестными, при котором критерий (целевая функция) достигает оптимума. Система уравнений и неравенств (24.1) — (24.5), (24.7) обладает следующим свойством она линейна относительно неизвестных. Это означает, что неизвестные входят в уравнения, неравенства и критерий лишь в первой степени и что отсутствуют произведения неизвестных. Методом решения подобных задач, которые носят название задач линейного программирования, служит так называемый симплекс-метод. Симплекс-метод изложен в целом ряде книг. Ограничимся лишь его технико-экономической интерпретацией.  [c.413]

Существует хотя бы два допустимых плана. В этом случае, как доказывается в теории линейного программирования, существует бесчисленное множество допустимых планов. Это означает, что все требования внешней среды, все плановые лимиты вышестоящих организаций могут быть выполнены, причем существует возможность рационального использования внутренних производственных ресурсов, например возможность выбора режимов эксплуатации отдельных установок. Именно в данном случае удается оптимизировать работу предприятия за счет выбора рациональных (с точки зрения всего предприятия) режимов эксплуатации отдельных установок, выбора рационального распределения входных и промежуточных материальных потоков.  [c.414]

На предприятиях химической и нефтехимической промышленности, которые отличаются своими специфическими особенностями, оптимизация текущих планов (производственной программы) может быть достигнута в подавляющем большинстве случаев в рамках ЭММ линейного программирования. При этом подразумевается, что решение задачи оптимизации производственной программы предприятия осуществляется на основе информации о его производственных возможностях (набор вариантов).  [c.421]

Рассматриваемая задача решается с помощью экономико-математических методов, в частности, линейного программирования. Целевая функция задачи выглядит при этом следующим образом  [c.17]

Наиболее распространенным методом решения важных практических задач планирования и управления является линейное программирование. С помощью симплекс-метода решаются задачи планирования производственной программы предприятия, объединения, способствующие получению максимального эффекта при ограниченных материальных и трудовых ресурсах. Распределительный метод линейного программирования позволяет выбрать оптимальные варианты планов транспортных перевозок решать задачи по оптимизации планов загрузки оборудования и др.  [c.78]

Рассмотрим постановку задачи определения оптимальной производственной программы отрасли методами линейного программирования.  [c.96]

Математическая модель задачи оптимального компаундирования представляет собой частный случай общей задачи линейного программирования о смесях. При построении математической модели процесса необходимо учитывать те же условия и ограничения, которыми руководствуются при объемных расчетах компаундирования, например подчиненность компонентов правилу аддитивности, приемистость их к ГЭС, технические условия на нефтепродукты согласно ГОСТ, ресурс каждого компонента и др.  [c.134]

Линейная алгебра лежит в основе методов линейного программирования. С помощью этих методов могут быть решены следующие задачи рассчитана производственная мощность предприятия, цехов, участков разработаны производственные задания цехам, участкам и др.  [c.153]

Задачи линейного программирования направлены на нахождение способа эффективного использования или распределения ограниченных ресурсов для достижения поставленных целей. Условия задачи записывают в виде системы линейных уравнений или неравенств (системы ограничений), а результат в виде целевой функции, являющейся суммой произведений найденных значений переменных на присваиваемые им показатели эффективности. Искомыми неизвестными величинами могут быть, например, различные виды оборудования. Коэффициенты при неизвестных в системе ограничений являются заданными постоянными числами и выражают удельные затраты. Коэффициенты при неизвестных в целевой функции — также постоянные величины. Они могут представлять собой себестоимость, цену оборудования, материалов, степень загрузки оборудования и т. п. Свободные члены в ограничениях — это величины тех или иных ресурсов, которые нужно распределить оптимальным образом (запасы материалов, фонды времени работы оборудования).  [c. 153]

После того, как задача сформулирована в терминах линейного программирования, решение ее состоит в применении того или иного расчетного алгоритма. Наиболее распространенными методами решения задач линейного программирования являются симплексный (или метод последовательного улучшения плана), распределительный и индексный. Существует также ряд приближенных методов решения, разработанных для отдельных видов задач (пример решения задачи методом линейного программирования дан ниже).  [c.153]

Применение методов линейного программирования при планировании эксплуатационных затрат на строительство скважин. В этом случае целевая функция задачи имеет следующий вид  [c.156]

Наиболее распространены методы линейного программирования. Результат их решения (как было сказано) — определение максимума или минимума какой-то целевой функции, в качестве которой принимается прибыль, затраты на производство, выработка продукции и др. Выбор целевой функции зависит от цели задачи. В современных условиях более целесообразна постановка задачи на максимум прибыли (П). Математически такая задача формулируется следующим образом  [c.18]

С помощью линейного программирования в основном определяется его производственная программа.  [c.18]

Применение метода линейного программирования для выбора вариантов смешения компонентов в товарные бензины значительно ускоряет все расчеты и дает возможность получить наиболее рентабельный план производства, предусмотрев увеличение выпуска бензинов с повышенной октановой характеристикой. Это, в свою очередь, дает возможность  [c.73]

С помощью метода линейного программирования решают задачи производственного планирования составление оптимальной программы выпуска продукции при заданных ресурсах- оптимальной загрузки оборудования и др.  [c.146]

Транспортную задачу линейного программирования успешно применяют для планирования перевозок. Другая разновидность ее позволяет выбрать наилучшее местоположение для вновь создаваемых предприятий.  [c.146]

В строительств в настоящее время чаще всего применяют простейшие модели оптимального планирования — так называемые модели линейного программирования, которые имеют глубоко разработанные и широко проверенные на практике методы решения. В целом линейное программирование объединяет теорию и методы решения определенного класса задач, в которых требуется найти совокупность переменных, удовлетворяющих линейным ограничениям, и максимизирующую (минимизирующую) линейную целевую функцию этих переменных.  [c.24]

Характерным и наиболее распространенным примером задачи линейного программирования является известная транспортная 24  [c.24]

Одним из наиболее известных методов является система Аккорд (автоматизация контроля и координации оптимальных режимов деятельности). Оптимизация рабочей силы в этой системе выполняется по программе Дельта . Идея алгоритма этой программы сводится к использованию метода линейного программирования на сети. Можно отметить достаточную строгость применяемого в этом методе математического аппарата. Недостаток этого метода заключается в том, что оптимизация проводится без учета механизации работ (путем добавления или изменения одних рабочих).  [c.47]

Зависимость отдельных составляющих целевой функции от числа пунктов разгрузки, включенных в какой-либо вариант внешнего транспортного обеспечения и условно рассматриваемых как непрерывные функции в области целочисленных величин числа пунктов разгрузки пгв, представлена на рис. 27. Как видно из рисунка, с увеличением числа пунктов разгрузки возрастают суммарные затраты на их организацию и уменьшаются транспортные расходы по доставке труб к месту работ. Следовательно, целевая функция как сумма указанных составляющих имеет экстремум при некотором значении числа пунктов разгрузки. Учитывая нелинейную зависимость функционала и его отдельных составляющих от числа вводимых пунктов разгрузки и искомых переменных, для решения поставленной задачи не могут быть применены классические методы математического программирования (например,. линейного). Как известно из курса высшей математики, математическое программирование — область математики, разрабатывающая теорию и методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Само название программирование взято из линейного программирования, где оно обычно обозначает распределение наилучшим образом ограниченных ресурсов для достижения поставленных целей. Следовательно, термин программирование здесь можно заменить термином планирование .  [c.145]

Оптимизация режима работы отдельных технологических установок еще не обеспечивает получения адекватного эффекта в целом по заводу. Ведь все технологические установки связаны единой технологической цепочкой. Поэтому оптимизация работы отдельных технологических установок лишь первый этап работы по повышению эффективности использования средств труда. Вторым этапом этой работы является составление оптимальной производственной программы завода с применением методов линейного программирования. В этом случае  [c.108]

В настоящее время с использованием линейного программирования разрабатываются математические модели оптимальной производственной программы, оптимальной загрузки оборудования, оптимального смешения нефтепродуктов, производительности труда. Это оптимальное решение применяют в качестве модели. Путем сравнения фактических результатов с показателями модели определяют отклонения и их причины с целью разработки мероприятий по приближению к оптимальной модели.  [c.26]

Нефтеперерабатывающая и нефтехимическая промышленность относится к числу отраслей, где математические методы стали использоваться значительно раньше, чем в других отраслях. Основу этих методов составило линейное программирование. ЦЭМИ АН СССР совместно с отраслевыми институтами разработали следующие модели  [c.156]

Ограничивающими условиями служат производительности участков сети и объемы добычи газа. Задача решается на ЭВМ методами линейного программирования. В результате расчета на печать выдаются объемы транспортировки газа по участкам газотранспортной сети, уточненный объем поступления газа из газодобывающих районов, а также возможные объемы недопо-дачи газа потребителям (с указанием узлов, где возможна недо-подача). После выдачи на печать весь этот массив данных (состоящий из номеров переменных и соответствующих численных значений) запоминается в памяти ЭВМ и используется на втором этапе расчета для формирования плана транспорта газа по объединениям Министерства. При формировании плана транспорта газа используется также информация о составе газотранспортного объединения. Эта информация содержит перечень участков газопроводов, принадлежащих данному объединению. В особую группу выделены участки, по которым осуществляется поступление газа данному объединению, а также передача соседним объединениям. Для каждого участка, включенного в такую группу, указывают наименование и код объединения, поставляющего или получающего газ.  [c.191]

Применение метода линейного программирования для выбо-р вариантов смешения компонентов в товарные бензины позволяет значительно ускорить расчеты и выбрать оптимальный план производства, предусмотрев увеличение выпуска бензинов с повышенной октановой характеристикой. Это в свою очередь дает возможность при неизменной себестоимости производства бензиновых компонентов увеличить шработку чистой и товарной продукции в стоимостном выражении, снизить затраты па  [c.294]

Линейное программирование | это… Что такое Линейное программирование?

Линейное программирование [linear programming] — область математического программирования, посвященная теории и методам решения экстремальных задач, характеризующихся линейной зависимостью между переменными.

В самом общем виде задачу Л.п. можно записать так. Даны ограничения типа

или в так называемой канонической форме, к которой можно привести все три указанных случая

Требуется найти неотрицательные числа x_j (j = 1, 2, …, n), которые минимизируют (или максимизируют) линейную форму

Неотрицательность искомых чисел записывается так:

Таким образом, здесь представлена общая задача математического программирования с теми оговорками, что как ограничения, так и целевая функция — линейные, а искомые переменные — неотрицательны. Обозначения можно трактовать следующим образом: b_i — количество ресурса вида i; m   — количество видов этих ресурсов; a_ij   — норма расхода ресурса вида i на единицу продукции вида j; x_j — количество продукции вида j, причем таких видов — n; c_j   — доход (или другой выигрыш) от единицы этой продукции, а в случае задачи на минимум — затраты на единицу продукции; нумерация ресурсов разделена на три части: от 1 до m₁, от m₁ + 1 до m₂ и от m₂ + 1 до m в зависимости от того, какие ставятся ограничения на расходование этих ресурсов; в первом случае — «не больше», во втором — «столько же», в третьем — «не меньше»; Z — в случае максимизации, например, объем продукции или дохода, в случае же минимизации — себестоимость, расход сырья и т. п. Добавим еще одно обозначение, оно появится несколько ниже; v_i — оптимальная оценка i-го ресурса.

Слово «программирование» объясняется здесь тем, что неизвестные переменные, которые отыскиваются в процессе решения задачи, обычно в совокупности определяют программу (план) работы некоторого экономического объекта. Слово, «линейное» отражает факт линейной зависимости между переменными. При этом, как указано, задача обязательно имеет экстремальный характер, т.е. состоит в отыскании экстремума (максимума или минимума) целевой функции.

Следует с самого начала предупредить: предпосылка линейности, когда в реальной экономике подавляющее большинство зависимостей носит более сложный нелинейный характер, есть огрубление, упрощение действительности. В некоторых случаях оно достаточно реалистично, в других же выводы, получаемые с помощью решения задач Л.п. оказываются весьма несовершенными.

Рассмотрим две задачи Л.п. — на максимум и на минимум — на упрощенных примерах. Предположим, требуется разработать план производства двух видов продукции (объем первого — x₁; второго — x₂) с наиболее выгодным использованием трех видов ресурсов (наилучшим в смысле максимума общей прибыли от реализации плана). Условия задачи можно записать в виде таблицы (матрицы):

 

Вид продукции

Норма затратна единицу продукции

Прибыль на единицу продукции

Исходя из норм, зафиксированных в таблице, запишем неравенства (ограничения):

a₁₁x₁ + a₁₂x₂≤ b_i

a₂₁x₁ + a₂₂x₂≤  b₂

a₃₁x₁ + a₃₂x₂≤  b₃

Это означает, что общий расход каждого из трех видов ресурсов не может быть больше его наличия. Поскольку выпуск продукции не может быть отрицательным, добавим еще два ограничения:

x₁≥ 0,  x₂≥ 0.

Требуется найти такие значения x₁ и x₂, при которых общая сумма прибыли, т.е. величина c₁x₁ + c₂ x₂ будет наибольшей, или короче:

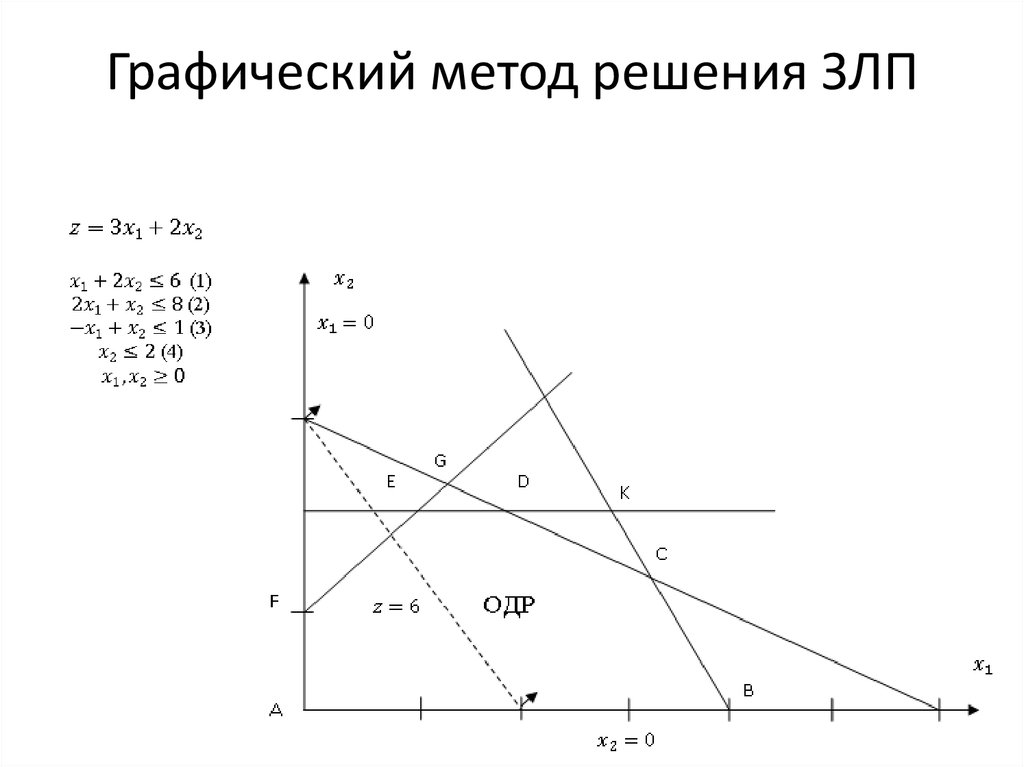
Удобно показать условия задачи на графике (рис. Л.2).

 Рис. Л.2  Линейное программирование, I (штриховкой окантована область допустимых решений)

Любая точка здесь, обозначаемая координатами x₁ и x₂, составляет вариант искомого плана. Очевидно, что, например, все точки, находящиеся в области, ограниченной осями координат и прямой AA, удовлетворяют тому условию, что не может быть израсходовано первого ресурса больше, чем его у нас имеется в наличии (в случае, если точка находится на самой прямой, ресурс используется полностью). Если то же рассуждение отнести к остальным ограничениям, то станет ясно, что всем условиям задачи удовлетворяет любая точка, находящаяся в пределах области, края которой заштрихованы, — она называется областью допустимых решений (или областью допустимых значений, допустимым множеством).

Остается найти ту из них, которая даст наибольшую прибыль, т.е. максимум целевой функции. Выбрав произвольно прямую   c₁x₁ + c₂x₂ = П    и обозначив ее MM, находим на чертеже все точки (варианты планов), где прибыль одинакова при любом сочетании x₁ и x₂ (см. Линия уровня). Перемещая эту линию параллельно ее исходному положению, найдем точку, которая в наибольшей мере удалена от начала координат, однако не вышла за пределы области допустимых значений. (Перемещая линию уровня еще дальше, уже выходим из нее и, следовательно, нарушаем ограничения задачи). Точка M₀ и будет искомым оптимальным планом. Она находится в одной из вершин многоугольника. Может быть и такой случай, когда линия уровня совпадает с одной из прямых, ограничивающих область допустимых значений, тогда оптимальным будет любой план, находящийся на соответствующем отрезке.

Координаты точки M₀ (т.е. оптимальный план) можно найти, решая совместно уравнения тех прямых, на пересечении которых она находится.

Противоположна изложенной другая задача Л.п.: поиск минимума функции при заданных ограничениях. Такая задача возникает, например, когда требуется найти наиболее дешевую смесь некоторых продуктов, содержащих необходимые компоненты (см. Задача о диете). При этом известно содержание каждого компонента в единице исходного продукта — a_ij, ее себестоимость — c_j  ; задается потребность в искомых компонентах —  b_i.

Эти данные можно записать в таблице (матрице), сходной с той, которая приведена выше, а затем построить уравнения как ограничений, так и целевой функции. Предыдущая задача решалась графически. Рассуждая аналогично, можно построить график (рис. Л.3), каждая точка которого — вариант искомого плана: сочетания разных количеств продуктов x₁ и x₂.

Рис.Л.3   Линейное программирование, II

Область допустимых решений здесь ничем сверху не ограничена: нужное количество заданных компонентов тем легче получить, чем больше исходных продуктов. Но требуется найти наиболее выгодное их сочетание. Пунктирные линии, как и в предыдущем примере, — линии уровня. Здесь они соединяют планы, при которых себестоимость смесей исходных продуктов одинакова. Линия, соответствующая наименьшему ее значению при заданных требованиях, — линия MM. Искомый оптимальный план — в точке M₀.

Приведенные крайне упрощенные примеры демонстрируют основные особенности задачи Л.п. Реальные задачи, насчитывающие много переменных, нельзя изобразить на плоскости — для их геометрической интерпретации используются абстрактные многомерные пространства. При этом допустимое решение задачи — точка в n-мерном пространстве, множество всех допустимых решений — выпуклое множество в этом пространстве (выпуклый многогранник).

Задачи Л.п., в которых нормативы (или коэффициенты), объемы ресурсов («константы ограничений«) или коэффициенты целевой функции содержат случайные элементы, называются задачами линейного стохастического программирования; когда же одна или несколько независимых переменных могут принимать только целочисленные значения, то перед нами задача линейного целочисленного программирования. В экономике широко применяются линейно-программные методы решения задач размещения производства (см. Транспортная задача), расчета рационов для скота (см. Задача диеты), наилучшего использования материалов (см. Задача о раскрое), распределения ресурсов по работам, которые надо выполнять (см. Распределительная задача) и т. д.

Разработан целый ряд вычислительных приемов, позволяющих решать на ЭВМ задачи линейного программирования, насчитывающие сотни и тысячи переменных, неравенств и уравнений. Среди них наибольшее распространение приобрели методы последовательного улучшения допустимого решения (см. Симплексный метод, Базисное решение), а также декомпозиционные методы решения крупноразмерных задач, методы динамического программирования и др. Сама разработка и исследование таких методов — развитая область вычислительной математики.

Один из видов решения имеет особое значение для экономической интерпретации задачи Л.п. Он связан с тем, что каждой прямой задаче Л.п. соответствует другая, симметричная ей двойственная задача (подробнее см. также Двойственность в линейном программировании). Если в качестве прямой принять задачу максимизации выпуска продукции (или объема реализации, прибыли и т.д.), то двойственная задача заключается, наоборот, в нахождении таких оценок ресурсов, которые минимизируют затраты. В случае оптимального решения ее целевая функция — сумма произведений оценки (цены) v_i каждого ресурса на его количество b_i— то есть  равна целевой функции прямой задачи. Эта цена называется объективно обусловленной, или оптимальной оценкой, или разрешающим множителем. Основополагающий принцип Л.п. состоит в том, что в оптимальном плане и при оптимальных оценках всех ресурсов затраты и результаты равны.

Оценки двойственной задачи обладают замечательными свойствами: они показывают, насколько возрастет (или уменьшится) целевая функция прямой задачи при увеличении (или уменьшении) запаса соответствующего вида ресурсов на единицу. В частности, чем больше в нашем распоряжении данного ресурса по сравнению с потребностью в нем, тем ниже будет оценка, и наоборот. Не решая прямую задачу, по оценкам ресурсов, полученных в двойственной задаче, можно найти оптимальный план: в него войдут все технологические способы, которые оправдывают затраты, исчисленные в этих оценках (см. Объективно обусловленные (оптимальные) оценки).

Первооткрыватель Л.п. — советский ученый, академик, лауреат Ленинской, Государственной и Нобелевской премий Л.В.Канторович. В 1939 г. он решил математически несколько задач: о наилучшей загрузке машин, о раскрое материалов с наименьшими расходами, о распределении грузов по нескольким видам транспорта и др., при этом разработав универсальный метод решения этих задач, а также различные алгоритмы, реализующие его. Л.В.Канторович впервые точно сформулировал такие важные и теперь широко принятые экономико-математические понятия, как оптимальность плана, оптимальное распределение ресурсов, объективно обусловленные (оптимальные) оценки, указав многочисленные области экономики, где могут быть применены экономико-математические методы принятия оптимальных решений. Позднее, в 40—50-х годах, многое сделали в этой области американские ученые — экономист Т.Купманс и математик Дж. Данциг. Последнему принадлежит термин «линейное программирование».

См. также: Ассортиментные задачи, Базисное решение, Блочное программирование, Булево линейное программирование, Ведущий столбец, Ведущая строка, Вершина допустимого многогранника, Вырожденная задача, Гомори способ, Граничная точка, Двойственная задача, Двойственность в линейном программировании, Дифференциальные ренты, Дополняющая нежесткость, Жесткость и нежесткость ограничений ЛП, Задача диеты, Задача о назначениях, Задача о раскрое, Задачи размещения, Исходные уравнения, Куна — Таккера условия, Множители Лагранжа, Область допустимых решений, Опорная прямая, Распределительные задачи, Седловая точка, Симплексная таблица, Симплексный метод, Транспортная задача.

Экономико-математический словарь: Словарь современной экономической науки. — М.: Дело. Л. И. Лопатников. 2003.

Линейное программирование (поясняется диаграммами)

ОБЪЯВЛЕНИЯ:

I. Общие примечания:

Линейное программирование — это недавно разработанный метод предоставления конкретных численных решений задач, которые раньше можно было решить только в нечетких качественных терминах с использованием аппарата общей теории фирмы.

Таким образом, линейное программирование помогло преодолеть разрыв между абстрактной экономической теорией и принятием управленческих решений на практике.

ОБЪЯВЛЕНИЯ:

Использование линейного программирования быстро расширяется из-за использования компьютеров, которые могут быстро решать сложные задачи, связанные с оптимальным использованием многих ресурсов, предоставляемых фирме в любой конкретный момент времени, и, таким образом, налагают ограничения на выбор фирмы. Линейное программирование можно рассматривать как операционный метод для работы с экономическими отношениями, которые включают разрывы. Это особый подход в рамках общей экономической теории.

Основные сходства и различия между традиционным экономическим анализом и линейным программированием можно обозначить следующим образом. Оба подхода показывают, как экономические агенты (потребители или производители) достигают оптимального выбора, как они планируют или программируют, чтобы достичь максимальной полезности, максимальной прибыли, минимальных затрат и т. д. Ни экономическая теория, ни линейное программирование ничего не говорят о реализации оптимальный план или решение.

Они просто находят оптимальное решение в любой конкретной ситуации. В этом смысле оба подхода представляют собой методы ex ante, направленные на то, чтобы помочь экономическим единицам найти решение, которое достигает их цели (максимизация полезности, максимизация прибыли, минимизация затрат) с учетом их ресурсов (дохода или факторов производства) в любой конкретный момент времени.

Однако в экономической теории оптимальное решение обычно изображается в качественных абстрактных терминах, диаграммах или общих математических символах, тогда как линейное программирование дает конкретные численные решения конкретных оптимизационных задач.

ОБЪЯВЛЕНИЯ:

Еще одно различие между экономическим анализом и линейным программированием заключается в том, что отношения экономической теории обычно нелинейны и изображаются кривыми (а не прямыми линиями), в то время как в линейном программировании все отношения между вовлеченными переменными предполагаются линейными.

Недавно были разработаны методы нелинейного программирования, но их изложение связано с сложной математикой и здесь не будет предприниматься попыток. Мы проиллюстрируем использование линейного программирования на простом примере фирмы, которая имеет заданное количество трех факторов производства, с помощью которых она может производить два товара, x и y. Задача фирмы, учитывая ее ресурсы, состоит в том, чтобы выбрать оптимальную номенклатуру товаров, максимизирующую прибыль фирмы.

II. Постановка задачи линейного программирования:

Предположим, что фирма имеет следующие количества факторов производства

ОБЪЯВЛЕНИЯ:

L = 400 единиц труда (часов)

К = 300 единиц капитала (машино-часов)

S = 1000 единиц земли (квадратный фут)

Фирма может производить либо товар x, либо товар y, используя следующие доступные процессы (виды деятельности)

Другими словами, для производства одной единицы товара x требуется 4 часа труда, 1 машинный час и 2 квадратных фута земли. Точно так же производство одной единицы у требует 1 часа труда, 1 машинного часа и 5 квадратных футов земли. Товар x дает единичную прибыль в размере 2 фунтов стерлингов, а товар y дает единичную прибыль в размере 1,5 фунта стерлингов. Цель фирмы состоит в том, чтобы выбрать оптимальный набор продуктов, то есть такой набор, который максимизирует ее общую прибыль.

Функция общей прибыли может быть записана следующим образом:

Z = 2X + 1 Y

где Z = общая прибыль

ОБЪЯВЛЕНИЯ:

X = количество товара x (или уровень деятельности A ₁ )

Y = количество товара y (или уровень деятельности A ₂ )

2 и 1 — удельная прибыль двух товаров. Функция общей прибыли называется целевой функцией, потому что она выражает цель фирмы, которой в нашем конкретном примере является максимизация прибыли. В общем случае целевая функция — это функция, которая представляет цели экономического агента.

Фирма, стремясь максимизировать свою целевую функцию, сталкивается с рядом ограничений. Мы различаем две группы ограничений: технические (или функциональные) ограничения и ограничения неотрицательности. Технические ограничения устанавливаются состоянием технологии и наличием факторов производства.

ОБЪЯВЛЕНИЯ:

Технических ограничений столько же, сколько факторов производства. Они выражают тот факт, что количества факторов, которые будут поглощены при производстве товаров, не могут превышать наличных количеств этих факторов. Таким образом, технологические ограничения принимают форму неравенств.

В нашем примере три технических ограничения:

4X + 1 Y < 400

1x + 1Y < 300

ОБЪЯВЛЕНИЯ:

2X + 5Y < 1000

, где X и Y — уровни товаров x и y (уровни использования видов деятельности A ₁ и A ₂ ), а целые числа в левой части — технические коэффициенты производства, т. е. фактор затраты, необходимые для производства одной единицы продукции x и y. Цифры справа — это ресурсы, которыми располагает фирма. Эти ограничения неравенства утверждают, что уровни X и Y в оптимальной номенклатуре продуктов не должны требовать больше, чем доступное количество трех ресурсов.

Ограничения неотрицательности выражают необходимость того, что уровни производства товаров не могут быть отрицательными, поскольку отрицательные количества не имеют смысла в экономике. Уровень производства любого товара может быть нулевым или положительным

х > 0

г > 0

Учитывая приведенную выше информацию, задачу линейного программирования можно формально сформулировать следующим образом:

ОБЪЯВЛЕНИЯ:

Обратите внимание, что все ограничения имеют форму неравенств. Таким образом, система не может быть решена обычными методами решения одновременных уравнений. Техника линейного программирования была разработана для решения задач, связанных с неравенствами. Его основной подход заключается в итерации, оптимальное решение определяется путем изучения набора возможных альтернативных решений и постепенного исключения неоптимальных решений, пока не будет достигнуто оптимальное.

III. Определение оптимального решения:

Оптимальное решение находится по точке касания границы области допустимых решений с максимально возможной кривой изопрофита. Оптимальным решением будет точка на границе области всех допустимых решений, поскольку любая точка внутри этой области лежит на нижней линии изопрофита. Ясно, что оптимальное решение зависит от наклона линий изоприбыли, то есть от отношения удельной прибыли двух товаров. В нашем примере оптимальным решением является точка G на рис. 20.7.

В этот момент ассортимент продукции составляет 178 единиц у и 56 единиц х, а максимальная прибыль составляет 290 фунтов стерлингов, что можно проверить с помощью функции прибыли

ОБЪЯВЛЕНИЯ:

Z = 2X + 1Y = 2(56) + 1(178) = 290

Если наклон линии изопрофита равен наклону любой из граничных линий, определяющих область допустимых решений, то единственного оптимального решения задачи линейного программирования не существует. Например, если π _x /π _y = l _x /l _y (= наклон кривой AB, которая является границей для фактора «труд», все точки на отрезке GB будут оптимальными решениями.

Аналогично, если π _x /π _y — s _x /s _y (= наклон EF, который является границей для фактора «земля»), все точки на отрезке EG производства- границей возможностей будут оптимальные решения. Из приведенного выше обсуждения должно быть очевидно, что единственное оптимальное решение существует, если наклон линии, представляющей целевую функцию, имеет значение, лежащее в диапазоне, заданном наклонами граничных линий, которые обозначают технические ограничения задачи линейного программирования.

Мы можем обобщить приведенную выше процедуру определения оптимального решения следующим образом:

Шаг 1:

Запишите технические неравенства в виде равенств и решите их относительно Y

ОБЪЯВЛЕНИЯ:

л ₁ х + / л ₂ у = л

к ₁ Х + к ₂ Y = К

с ₁ Х + с ₂ Y =S

Решая эти уравнения относительно Y, получаем уравнения трех граничных линий:

Уравнение границы L равно

Наклон границы L равен

ОБЪЯВЛЕНИЯ:

∂Y/∂X = – л ₁ / л ₂

Мы можем нарисовать границу L, присвоив X различные значения и нанеся полученные точки на график. (Дано значение L.)

Уравнение границы K равно

Наклон границы K равен

∂Y/∂X = – k ₁ / к ₂

Мы можем нарисовать границу K, присвоив X различные значения (при заданном значении K) и нанеся полученные точки на график.

Уравнение границы S равно

Наклон границы S равен

∂Y/∂X = – с ₁ / с ₂

Мы можем нарисовать границу S, присвоив X различные значения (задав количество S) и нанеся полученные точки на график.

Шаг 2:

Определить область допустимых решений. Это область во всех границах, установленных техническими ограничениями. Только части областей ниже отдельных граничных линий, которые совпадают при объединении различных графиков (шага 1), удовлетворяют всем ограничениям.

Шаг 3:

Определите строки изопрофита, решив уравнение прибыли для Y

Набор линий изопрофита можно нарисовать, присвоив Z и X разные значения.

Шаг 4:

Определите оптимальное решение, сравнив наклон линии изопрофита с наклонами граничных линий, определяющих область допустимых решений. Поскольку все линии имеют отрицательный наклон, мы можем игнорировать их знаки при сравнении. В нашем примере только две граничные линии определяют область допустимых решений. (Фактор К не ограничивает выбор фирмы при наличии других факторов L и S.)

Наклоны граничных линий равны, мы заключаем, что существует единственное решение, и что это оптимальное решение определяется пересечением двух граничных линий, которые определяют область допустимых решений.

IV. Симплексный метод:

Когда переменных, значения которых должны быть определены методом линейного программирования, больше двух, графическое решение затруднено или невозможно, потому что нужны многомерные диаграммы. Можно использовать следующий итерационный метод достижения оптимального решения, называемый симплекс-методом.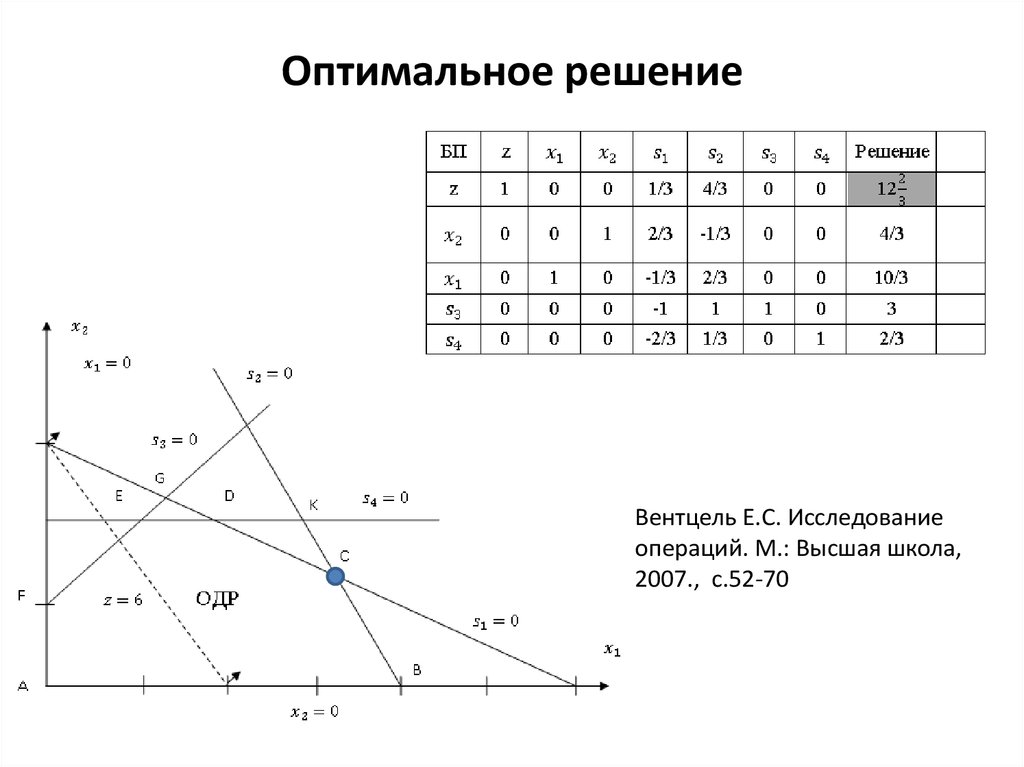

Проиллюстрируем симплекс-метод на следующем примере.

Предположим, что фирма может производить пять товаров, x ₁ , х ₂ , …, х ₅ , с тремя факторами производства Ф ₁ , Ф ₂ , Ф ₃ .

Доступное количество факторов:

F ₁ = 100 единиц труда

F ₂ = 80 единиц капитала

F ₃ = 150 единиц земли

Известные методы производства (процессы или виды деятельности) для каждого продукта

Фирма хочет выбрать такое сочетание продуктов, которое максимизирует общую прибыль z. Обозначим уровни производства пяти товаров прописной буквой X с соответствующим нижним индексом.

С приведенной выше информацией мы можем формально сформулировать задачу линейного программирования следующим образом:

Подставляя техническую информацию нашего примера мы:

Чтобы преодолеть трудности, создаваемые неравенствами в ограничениях, мы преобразуем технические ограничения в равенства, вводя в каждое из них переменную, называемую «переменной запаса», которая будет показывать неиспользованные единицы соответствующего фактора производства. Ясно, что резервных переменных будет столько же, сколько факторов производства. Предполагается, что неиспользованные факторы имеют нулевую рентабельность (ни прибыль, ни убыток).

С введением резервных переменных ограничения становятся:

а. Итерационная процедура

Итерация I:

Мы начинаем с любого возможного решения, находим его прибыльность и рассматриваем, дает ли оно максимальную прибыль по сравнению с другими возможными решениями. Уровни выпуска и неиспользованных факторов в любом решении образуют основу. Самый простой способ начать итерации — начать с базиса, который показывает нулевое производство, то есть он включает в себя три резервных вида деятельности со значениями, равными доступным количествам трех факторов производства, поскольку при отсутствии производства все факторы не используются. . Таким образом, начальное решение (основа I) является источником, где все уровни выпуска равны нулю 9. 0003

X ₁ = X ₂ = X ₃ = X ₄ = X ₅ = 0

и все входы не заняты, так что

S ₁ = F ₁ = 100

5 ₂ = F ₂ = 80

5 ₃ = F ₃ = 150

Это приемлемое решение, поскольку все ограничения соблюдены. Ясно, что это не оптимально, так как прибыль равна нулю, если нет производства

.

Z = 2(0) + 2(0) + 3(0) + 4(0) + 6(0) 4 0(S ₁ ) + 0(S ₂ ) + 0(S ₃ ) = 0

Прежде чем перейти к поиску лучшего возможного решения, мы представим первое решение (Основание I) в виде таблицы (таблица 20.1).

В первой колонке мы показываем действия, включенные в рассматриваемое решение (базис), и уровни их использования. База I включает резервные работы S ₁ , S ₂ , S ₃ , а уровни их использования равны неиспользованным факторам производства, 100 единицам f ₁ , 80 единицам f ₂ и 150 единицам f ₃ .

В столбцы пяти производственных видов деятельности мы вносим затраты трех факторов производства, которые требуются для производства одной единицы соответствующих товаров.

В столбцах резервных видов деятельности мы вставляем единицу для соответствующего фактора производства и ноль для всех остальных факторов.

В последнюю строку таблицы вставляем общую прибыль (Z) Основы и удельную прибыль деятельности с отрицательным знаком. Эта строка (которую мы назовем «строкой прибыльности») имеет решающее значение в итерационной процедуре симплекс-метода, потому что она показывает, какое действие является наиболее прибыльным, и его следует ввести в следующей итерации. Когда все элементы в этой строке становятся положительными или нулевыми, мы останавливаем итерации.

Положительные элементы в «строке рентабельности» говорят о том, что введение соответствующих видов деятельности в Базис приведет к уменьшению общей прибыли. Нулевые элементы в «строке рентабельности» (в столбцах производственной деятельности A _1, … , A ₅ ) означают, что существуют другие оптимальные решения, дающие такую ​​же общую прибыль. Таким образом, когда элементы «строки рентабельности» (столбцов производственной деятельности) либо положительны, либо равны нулю, мы (обычно) останавливаем итерации, поскольку достигнуто оптимальное решение.

Итерация II:

Мы должны найти входящую активность и исходящую активность, то есть ту деятельность, которую мы должны ввести в Основу и ту, которая будет заменена.

В качестве входящей деятельности выбираем деятельность с наибольшей удельной прибылью, то есть деятельность с наибольшим отрицательным элементом в «строке прибыльности». В нашем примере наиболее прибыльным видом деятельности является A ₅ .

Исходящая активность находится путем деления каждого уровня активности в первом базисе (F ₁ , F ₂ и F ₃ в нашем примере) на соответствующий входной коэффициент входящей активности и выбора замены активность старого Базиса, для которого коэффициент наименьший. В нашем примере их 9.0003

Наименьшее отношение равно F ₂ /k ₅ , поэтому исходящая активность равна S ₂ . Новая База будет включать операции S ₁ , A ₅ и S ₃ . Мы замещаем незадействованную деятельность, отношение которой наименьшее, потому что соответствующий ресурс будет исчерпан первым, когда мы расширим производство товара х ₅ (произведенного входящей деятельностью).

Наш следующий шаг — найти элементы новой таблицы итераций.

В этом процессе участвуют следующие этапы:

1. Мы определяем опорный элемент, который является элементом на пересечении входящей и исходящей деятельности. В нашем примере опорным элементом является 2, на пересечении A ₅ и S ₂ .

2. Находим элементы сводной строки, т. е. той строки, которую будет занимать входящая активность, занимающая место исходящей активности. Элементы сводной строки находятся путем деления элементов исходной строки (исходящей активности) на опорный элемент (2 в нашем примере). Элементами сводной строки являются элементы входящей активности (A ₅ ) в новой таблице итераций.

В нашем примере элементы сводной строки:

3. Любой другой элемент во второй итерационной таблице b _i находится путем вычитания из соответствующего исходного элемента a (в первой итерационной таблице) произведения элемента сводной строки, который находится в том же столбце, что и , умноженный на элемент входящей активности, который находится в той же строке, что и _i .

Расчеты показаны в таблице 20.2. Важнейшими данными, необходимыми на этом этапе, являются элементы сводной строки (b ₁₀ , b _{1 1} …, b ₁₈ ) и элементы столбца исходящей деятельности (a ₆ = 2, а ₁₅ = 2, а ₂₄ = 2).

Элементы первой и третьей строк второй итерационной таблицы:

4. Общая прибыль нового решения (Z _ll ) определяется путем умножения уровней деятельности в этой основе на их удельную прибыль

Z _II = π ₆ (S ₁ ) + π ₅ (/A ₅ ) + π ₈ (S ₃ ) (0) = (0) = (6) + (70)(0) = 240

5. Элементы «строки прибыльности» оцениваются так же, как и другие элементы второй итерационной таблицы. То есть из исходных «элементов доходности» вычитаем произведение элемента сводной строки (находящегося в том же столбце, что и π _i.I ) умножить на «элемент рентабельности» входящей деятельности

Мы завершили вычисление элементов второй итерации. Результаты представлены в таблице 20.3.

S ₁ = 20 А ₅ = 40 S ₃ = 70

Ясно, что второе Базисное решение лучше исходного, так как дает общую прибыль в 240 денежных единиц. Однако до тех пор, пока в последней строке итерационной таблицы появляются отрицательные элементы, мы можем дополнительно улучшить наше решение (увеличить прибыль), введя в основу деятельность, имеющую наибольший отрицательный «элемент прибыльности».

В нашем примере деятельность a ₂ , которая производит товар x ₂ , будет входящей деятельностью в новом решении (основа III). Исходящая активность определяется так же, как и в предыдущей итерации. То есть мы делим резервные работы в Базисе II на соответствующие элементы в столбце входящей активности (A ₂ ) и отбрасываем активность с наименьшим соотношением. В нашем примере у нас есть

_20/2 = 10 и _70/1 = 70

Поскольку (20/2) < (70/1), исходящая активность на этой итерации равна 5,. (таблица 20.4.)

Перед тем, как мы приступим к вычислениям третьей итерации, полезно указать значение симплексного критерия. Этот критерий служит для определения того, было ли достигнуто оптимальное решение или можно ли добиться дальнейшего улучшения за счет дополнительных итераций.

Критерий симплекса можно резюмировать в следующих положениях:

Если один или несколько элементов в «строке прибыльности» отрицательные, возможно дальнейшее улучшение решения, и итерации должны продолжаться, если только все элементы входящей активности не положительны или равны нулю. В этом случае мы делаем вывод, что задача не имеет решения или она сформулирована некорректно.

Если все элементы в «строке рентабельности» положительны или равны нулю, Базис в этой таблице является оптимальным решением, и дальнейшие итерации (обычно) не требуются. Включение в Базу деятельности с положительными «элементами рентабельности» снижает общую прибыль фирмы, и, следовательно, такую ​​деятельность не следует рассматривать как средство улучшения решения.

Если некоторые виды производственной деятельности имеют нулевые «элементы прибыльности» в итоговой таблице, существует более одного оптимального решения. Если мы введем в базу деятельность с нулевой «прибыльностью», это не повлияет на общую прибыль.

Итерация III:

Последняя строка второй таблицы итераций содержит отрицательные элементы, поэтому решение можно улучшить. Входящая деятельность — это деятельность с наибольшим отрицательным «элементом рентабельности» (A ₂ в нашем примере), а исходящая активность S ₁ имеет наименьшее отношение (S ₁ /2 = уровень S ₁ в Базисе II, деленный на соответствующий элемент столбца входящей Мероприятия).

Определив входящие и исходящие действия, повторяем вычисления второй итерации:

1. Поворотным элементом является 2, определяемый пересечением входящей и исходящей деятельности.

2. Элементы «осевого ряда» определяются делением элементов исходящей деятельности на опорный элемент. Их

_20/2 = 10, _0/2 = 0, _2/2 = 1, _0/2 = 0, _{1/2, 0/2} = 0, 190 2 , _-1/2 , _0/2 = 0

3. Остальные элементы (c _i ) третьей итерационной таблицы находятся вычитанием из соответствующих элементов второй итерационной таблицы (b _i ) произведение элемента «осевой строки» (который находится в том же столбце, что и b _i ), умноженного на элемент входящей активности (который находится в той же строке, что и b _i ).

Значения элементов третьей итерации:

4. Общая прибыль Базиса III определяется путем сложения произведений уровней деятельности, включенных в этот базис, умноженных на их соответствующую удельную прибыль (как указано в целевой функции)

Z _III = (10) (2) + (40) (6) + (60) (0) = 260

Это больше, чем прибыль предыдущего решения (Z _II = 240).

5. Элементы «строки рентабельности» третьей итерации рассчитываются так же, как и во второй итерации

Итак, мы завершили вычисления элементов третьего Базиса. Результаты представлены в таблице 20.5.

Используя положения симплекс-критерия, замечаем следующее. Все элементы в последней строке («строке прибыльности») либо положительны, либо равны нулю. Это означает, что эта таблица содержит оптимальное решение.

Деятельность этой Базы:

A ₂ = 10 единиц товара x ₂

А ₅ — 40 единиц товара х ₅

S ₃ = 60 единиц неиспользованного фактора F ₃

Суммарная прибыль от этого оптимального решения составляет 260 денежных единиц. Учитывая, что в последней строке (и в столбцах производственной деятельности) стоят нули, мы делаем вывод, что приведенное выше решение не единственно. То есть есть другие оптимальные решения (к которым относится производственная деятельность с нулевыми «элементами рентабельности»). Эти альтернативные оптимальные решения, конечно, дают одинаковую общую прибыль. Поскольку мы нашли оптимальное решение, мы не будем продолжать дальнейшие итерации. Однако бывают случаи, когда может оказаться полезным определение дополнительных оптимальных решений.

V. Двойная проблема и теневые цены:

Основная задача, для решения которой используется метод линейного программирования, называется основной задачей. Каждой основной проблеме соответствует двойная проблема, которая дает дополнительную информацию лицу, принимающему решение. Природа двойственной проблемы зависит от основной проблемы. Если основная задача — задача максимизации, то двойственная к ней — задача минимизации. Точно так же, если основная задача — это задача минимизации, ее двойственная — задача максимизации.

Подробное рассмотрение двойственной проблемы выходит за рамки этой книги. Здесь мы сконцентрируемся на двойной проблеме нашего предыдущего примера максимизации прибыли. Двойная проблема в этом случае заключается в минимизации затрат, и из ее решения мы получаем теневые цены на факторы производства, используемые фирмой.

Двойственная задача может быть решена независимо от основной по процедуре, аналогичной описанной выше. Однако значения, полученные из решения двойственного, также получаются как побочный продукт последней итерации первичного, что дает оптимальное решение.

В нашем примере теневыми ценами трех факторов производства являются элементы, появляющиеся в последних трех ячейках «строки прибыльности» таблицы 20.5.) Если оптимальное решение содержит временную активность, показывающую, что некоторое количество соответствующего фактора остается безработных этот фактор имеет теневую цену, равную нулю.

Если факторы используются полностью, их теневые цены положительны. В нашем примере теневые цены факторного труда (F ₁ ) и факторного капитала (F ₂ ), которые полностью используются в оптимальном решении, отображаются как положительные и равны 1 и 2 денежным единицам соответственно. Скрытая цена факторной земли (F ₃ ) равна нулю, потому что этот фактор не используется полностью в оптимальном решении.

Скрытые цены факторов представляют собой вмененные издержки или альтернативные издержки факторов для конкретной фирмы. Как таковые, они являются важными индикаторами расширения фирмы. Они показывают, какие факторы являются узкими местами для дальнейшего расширения фирмы, поскольку эти факторы будут проявляться с положительной теневой ценой (альтернативной стоимостью) в оптимальном решении.

Кроме того, теневые цены на ресурсы можно сравнить с их рыночными ценами и помочь предпринимателю решить, выгодно ли нанимать дополнительные единицы этих факторов. Скрытая цена фактора показывает, насколько увеличится прибыль фирмы, если фирма будет использовать дополнительную единицу этого фактора.

В нашем примере мы видим, что если бы фирма наняла дополнительную единицу труда, ее прибыль увеличилась бы на 1 денежную единицу. Точно так же, если бы фирма использовала дополнительную единицу капитала, ее прибыль увеличилась бы на 2 денежные единицы. Но чтобы нанять дополнительные единицы L и/или k, фирме пришлось бы заплатить их рыночную цену (заработную плату или ренту с капитала).

Таким образом, если теневая цена фактора выше его рыночной цены, фирме будет выгоднее увеличить использование этого фактора, поскольку чистая прибыль фирмы увеличится. Очевидно, что теневые цены, значения которых оцениваются методом линейного программирования, имеют большое практическое значение для фирмы.

Факторы ценообразования производства и распределения доходов

Факторы ценообразования на совершенно конкурентных рынках (с диаграммой)

линейное программирование | Определение и факты

Ключевые люди:

Джордж Данциг Василий Леонтьев Леонид Витальевич Канторович Тьяллинг К. Купманс

Похожие темы:

симплексный метод возможное решение набор ограничений крайняя точка резервная переменная

Просмотреть весь связанный контент →

линейное программирование , метод математического моделирования, при котором линейная функция максимизируется или минимизируется при различных ограничениях. Этот метод был полезен для принятия количественных решений в бизнес-планировании, в промышленной инженерии и, в меньшей степени, в социальных и физических науках.

Решение задачи линейного программирования сводится к нахождению оптимального значения (наибольшего или наименьшего, в зависимости от задачи) линейного выражения (называемого целевой функцией) с учетом набора ограничений, выраженных в виде неравенств:

Дополнительная информация по этой теме

оптимизация: линейное программирование

Хотя линейное программирование широко используется в настоящее время для решения повседневных задач принятия решений, до 1947 года оно было сравнительно неизвестно…

a , b и c являются константами, определяемыми возможностями, потребностями, затратами, прибылью и другими требованиями и ограничениями задачи. Основное предположение при применении этого метода состоит в том, что различные отношения между спросом и доступностью являются линейными; то есть ни один из x _i возводится в степень, отличную от 1. Чтобы получить решение этой задачи, необходимо найти решение системы линейных неравенств (то есть множество n значения переменных x _i , что одновременно удовлетворяет всем неравенствам). Затем целевая функция оценивается путем подстановки значений x _i в уравнение, которое определяет ф .

Впервые серьезные попытки применения метода линейного программирования были предприняты в конце 1930-х годов советским математиком Леонидом Канторовичем и американским экономистом Василием Леонтьевым в области производственных графиков и экономики соответственно, но их работа игнорировалась на протяжении десятилетий. Во время Второй мировой войны линейное программирование широко использовалось для управления транспортировкой, планированием и распределением ресурсов с учетом определенных ограничений, таких как стоимость и доступность. Эти заявления во многом способствовали признанию приемлемости этого метода, который получил дальнейшее развитие в 1919 г.