Квадратное уравнение линейное – Линейные и квадратные уравнения
Линейные и квадратные уравнения
Определение
Уравнение (с одной переменной) — это некоторое равенство двух выражений, содержащее неизвестную (переменную). \[f(x)=g(x) \qquad \qquad (1)\]Пусть для определенности все дальнейшие уравнения содержат переменную, обозначенную буквой \(x\).
Замечание
Заметим, что \(x\) — это просто некоторое число, значение которого неизвестно.
Определение
Областью определения (или областью допустимых значений, сокращенно ОДЗ) любого уравнения вида \((1)\) будем называть множество значений переменной \(x\), при которых определены (то есть не теряют смысла) функции \(f(x)\) и \(g(x)\).
Пример
Уравнение \(\dfrac {10}{x-1}=5\) определено при всех значениях переменной \(x\), кроме \(x=1\), потому что в этом случае знаменатель дроби в левой части равенства обращается в ноль. Значит, ОДЗ уравнения \(x\in (-\infty;1)\cup(1;+\infty)\).
Определение
Корнем уравнения называется то числовое значение \(x\), при котором уравнение обращается в верное равенство.
Иногда корни уравнения называют решением этого уравнения.
Например, корнем уравнения из предыдущего примера является число \(x=3\), потому как тогда уравнение принимает вид \(\dfrac{10}{3-1}=5\) или, что то же самое, \(5=5\), что является верным равенством.
Замечание
1) Заметим, что уравнение может как иметь корни, так и не иметь корней. Например, уравнение \(\dfrac 1x=0\) ни при каких значениях \(x\) не может быть верным, потому что дробь равна нулю, когда ее числитель равен нулю, а знаменатель при этом не теряет смысла. У нашей дроби числитель \(1\ne 0\).
2) Фраза “решить уравнение” означает найти все корни данного уравнения или доказать, что корней нет.
Определение
Два уравнения равносильны (или эквивалентны), если они имеют одинаковые решения.
Например, уравнения \(x=3\) и \(3x=6+x\) эквивалентны, т.к. оба имеют единственное решение \(x=3\).
Эквивалентность уравнений обозначается так: \(x=3 \quad \Leftrightarrow \quad 3x=6+x\).
Свойства уравнений
1. В любом уравнении можно переносить слагаемые из одной части равенства в другую, при этом меняя их знак на противоположный. При этом полученное уравнение равносильно исходному.
2. В любом уравнении можно правую и левую части умножать или делить на одно и то же число, не равное нулю. При этом полученное уравнение равносильно исходному.
Например, уравнение \(0,5x=-2\) равносильно уравнению \(x=-4\), которое получено из исходного путем умножения обеих частей на \(2\).
3. В любом уравнении можно к правой и левой частям прибавлять одно и то же число. При этом полученное уравнение равносильно исходному.
Например, уравнение \(x+2=5x^2\) после прибавления к обеим частям \(-2\) примет вид \(x=5x^2-2\).
\[{\Large{\text{Линейные уравнения}}}\] Линейное уравнение – это уравнение вида \[ax + b = 0\qquad \qquad (2)\] где \(a\ne 0,b\) – числа, или уравнение, к нему сводящееся.
ОДЗ линейного уравнения \((2)\) — все \(x \in\mathbb{R}\).
Линейное уравнение \(ax+b=0\) преобразуется в \(ax=-b\) и всегда имеет единственное решение \(x=-\dfrac ba\).
Например, \(2x-4=0\) имеет корень \(x=2\).
Замечание: при переносе слагаемых из одной части равенства в другую знак слагаемого меняется на противоположный. Например, выражение \(x-5=8\) преобразуется в выражение \(x=8+5\).
Знак, стоящий перед слагаемым – это и есть его знак, то есть в выражении \(x-5\) два слагаемых: \(x\) и \(-5\). Если перед слагаемым не стоит никакого знака, то подразумевается, что перед ним стоит знак “\(+\)”.
\[{\Large{\text{Квадратные уравнения}}}\] Квадратное уравнение – это уравнение вида \[ax^2+bx+c=0 \qquad \qquad (3)\] где \(a, b, c\) – числа, причем \(a\ne 0\), или уравнение, к нему сводящееся.
Число \(a\) называется старшим (первым) коэффициентом, число \(b\) – вторым коэффициентом, число \(c\) – свободным членом.
Замечание
1) Заметим, что если \(a=0\), то уравнение \((3)\) становится линейным; именно поэтому в определении \(a\ne 0\).
2) Выражение \(ax^2+bx+c\) называется квадратичным (квадратным) трехчленом.
ВАЖНО! Обращаем ваше внимание на то, что, например, в квадратном трехчлене \(7-x^2+2x\) коэффициент \(a=-1\), \(b=2\) и \(c=7\)! Так как \(7-x^2+2x=-x^2+2x+7\), а по определению \(a\) – коэффициент перед \(x^2\), \(b\) – коэффициент перед \(x\), \(c\) – свободный член.
Определение
Дискриминантом квадратного уравнения \((3)\) называется выражение \(D=b^2-4ac\).
Корни квадратного уравнения
1) Если дискриминант квадратного уравнения больше нуля (\(D>0\)), то оно имеет два различных корня \[x_1=\dfrac{-b-\sqrt D}{2a} \qquad \text{и} \qquad x_2=\dfrac{-b+\sqrt D}{2a}\]
2) Если дискриминант квадратного уравнения равен нулю (\(D=0\)), то оно имеет два совпадающих корня (часто говорят, что оно имеет один корень) \[x=-\dfrac b{2a}\]
3) Если дискриминант квадратного уравнения меньше нуля (\(D<0\)), то оно не имеет корней.
Пример:
Решите уравнение \[3x^2 — 33x + 90 = 0.\]
Решение.
Найдём дискриминант данного уравнения: \[D = 33^2 — 4\cdot 3\cdot 90 = 9\] Следовательно, уравнение имеет два различных корня, равных \[x_1=\dfrac{33 + 3}{6} = 6 \qquad \text{и} \qquad x_2=\dfrac{33 —
3}{6} = 5\]
Теорема Виета
Пусть квадратное уравнение \(ax^2 + bx + c = 0\), \(a\neq 0\), имеет два корня \(x_1\) и \(x_2\) (возможно, совпадающих), то есть \(D\geqslant 0\). Тогда их сумма равна \[x_1+x_2=-\dfrac{b}{a}\] а их произведение равно \[x_1\cdot x_2=\dfrac{c}{a}\]
Доказательство
Сумма корней этого уравнения равна \[\dfrac{-b + \sqrt{D}}{2a} + \dfrac{-b — \sqrt{D}}{2a} = -\dfrac{2b}{2a} = -\dfrac{b}{a}\] Произведение корней этого уравнения равно \[\dfrac{-b + \sqrt{D}}{2a} \cdot \dfrac{-b — \sqrt{D}}{2a} = \dfrac{(-b + \sqrt{D})(-b — \sqrt{D})}{4a^2} = \dfrac{b^2 — D}{4a^2} = \dfrac{4ac}{4a^2} = \dfrac{c}{a}\]
Определение
Квадратное уравнение называется приведенным, если старший коэффициент \(a=1\).
Любое квадратное уравнение можно сделать приведенным: для этого необходимо разделить уравнение на \(a\).
Следствие
Для приведенного квадратного уравнения \(x^2+px+q=0\) теорема Виета выглядит следующим образом: \[x_1+x_2=-p, \qquad \qquad x_1\cdot x_2=q\]
Теорема: разложение на множители квадратного трехчлена
Пусть уравнение \(ax^2 + bx + c = 0\), \(a\neq 0\), имеет два корня (возможно, совпадающих), то есть \(D\geqslant 0\). Тогда при любом значении \(x\) выполнено \[ax^2 + bx + c = a(x — x_1)(x — x_2),\] где \(x_1\) и \(x_2\) – корни уравнения \(ax^2 + bx + c = 0\) (возможно, совпадающие).
Доказательство
Сделаем преобразования: \[\begin{aligned} &a(x-x_1)(x-x_2)=a\left(x — \dfrac{-b + \sqrt{D}}{2a}\right)\left(x — \dfrac{-b — \sqrt{D}}{2a}\right) =a\left(x^2 — x\left(\dfrac{-b + \sqrt{D}}{2a} + \dfrac{-b — \sqrt{D}}{2a}\right) + \dfrac{b^2 — D}{4a^2}\right)=\\[2ex] &=a\left(x^2-x\cdot \left(-\dfrac ba\right)+\dfrac{b^2-(b^2-4ac)}{4a^2}\right) =a(x^2+\dfrac ba x+\dfrac ca)=ax^2+bx+c \end{aligned}\]
Пример
Разложить на множители квадратный трехчлен \(3x^2-2x-1\).
Решение.
Рассмотрим уравнение \(3x^2-2x-1=0\) и найдем его корни.
\(D=(-2)^2-4\cdot 3\cdot (-1)=16\), значит
\[x_1=\dfrac{2-4}{2\cdot 3}=-\dfrac 13 \qquad \qquad x_2=\dfrac{2+4}{2\cdot 3} =1\]
Таким образом, \(3x^2-2x-1=3(x-1)(x+\frac13)=(x-1)(3x+1)\).
\[{\Large{\text{Простейшие кубические уравнения}}}\] \(\bullet\) Кубический корень из числа \(a\) – это такое число \(b\), которое при возведении в куб равно \(a\): \[\sqrt[3] a=b\quad \text{то же самое, что }\quad a=b^3\] \(\bullet\) Таблица кубов чисел от 1 до 10: \[\begin{array}{|ll|}
\hline
1^3=1 & \quad6^3=216 \\
2^3=8 & \quad7^3=343\\
3^3=27 & \quad8^3=512\\
4^3=64 & \quad9^3=729\\
5^3=125 & \quad10^3=1000\\
\hline \end{array}\] \(\bullet\) Простейшие кубические уравнения – уравнения, сводящиеся к виду \[x^3=a\] Для любого числа \(a\) такие уравнения имеют единственный корень \[x=\sqrt[3]a\] Пример:
1) решением уравнения \(x^3=-8\) является \(x=\sqrt[3]{-8}=-2\).
2) решением уравнения \(x^3=64\) является \(x=4\).
shkolkovo.net
4.2. Линейные уравнения
Определение
4.4. Линейное уравнение – это уравнение вида
,
где
 ,
,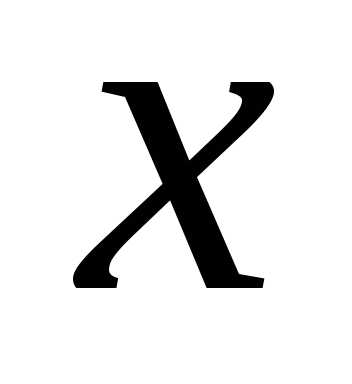 — переменная.
— переменная.
Число корней
линейного уравнения зависит от значений  и
и .
При
.
При линейное уравнение имеет единственное
решение
линейное уравнение имеет единственное
решение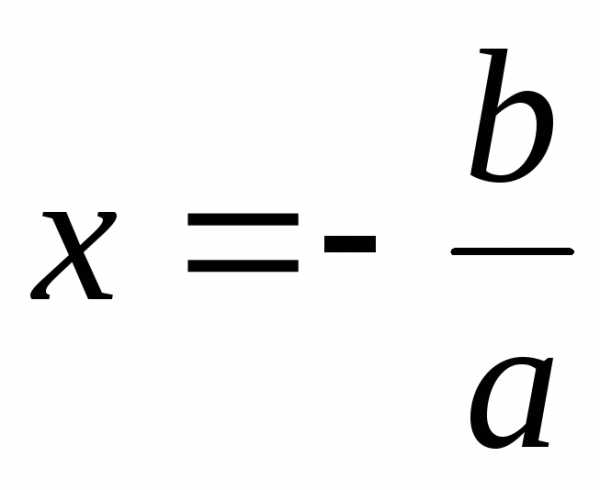 ;
при
;
при ,
, — не имеет решений; при
— не имеет решений; при ,
, — принимает види имеет бесконечное множество решений:
— принимает види имеет бесконечное множество решений: .
.
Пример 4.1. Решить уравнение
Решение. Умножим обе части уравнения на НОК(2; 4; 3)=12:
,
 (единственное
решение).
(единственное
решение).
Ответ: 62.
Пример 4.2. Решить уравнение: .
Решение. .
Не существует таких 
 ,
которые удовлетворяют последнему
уравнению, значит, исходное уравнение
решений не имеет.
,
которые удовлетворяют последнему
уравнению, значит, исходное уравнение
решений не имеет.
Ответ: нет решений.
Пример 4.3. Решить уравнение .
Решение. .
Любое 

удовлетворяет последнему уравнению, а значит и исходному. Таким образом, уравнение имеет бесконечно много решений.
Ответ: 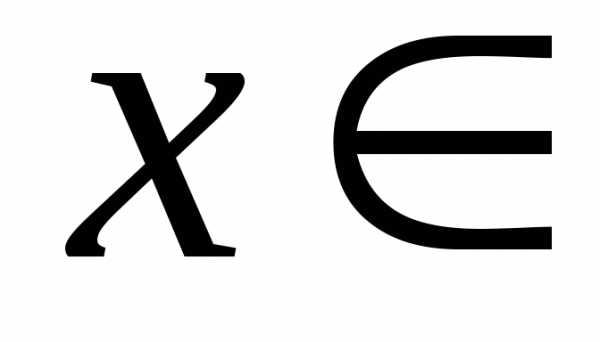
 .
.
4.3. Квадратные уравнения и уравнения, сводящиеся к ним
Определение
4.5. Квадратным уравнением называется
уравнение вида
,
где и
и
 ,
, – переменная, при этом
– переменная, при этом  (при
(при 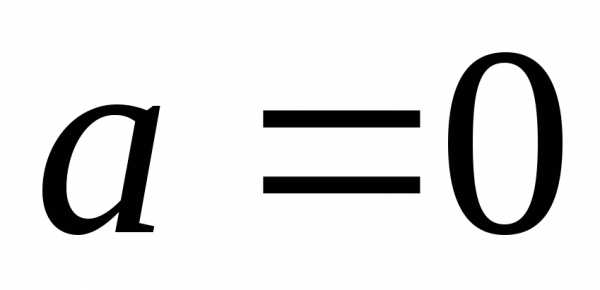 уравнение превращается в линейное.)
уравнение превращается в линейное.)
Если  или
или ,
а также в случае одновременного равенства
нулю этих коэффициентов квадратное
уравнение называютнеполным и решают стандартными способами
разложения на множители.
,
а также в случае одновременного равенства
нулю этих коэффициентов квадратное
уравнение называютнеполным и решают стандартными способами
разложения на множители.
Пример 4.4. Решить уравнение .
Решение. Данное
уравнение является неполным (

Ответ: 0; 2.
Пример 4.5. Решить уравнение .
Решение. ( ): .
): .
Ответ: 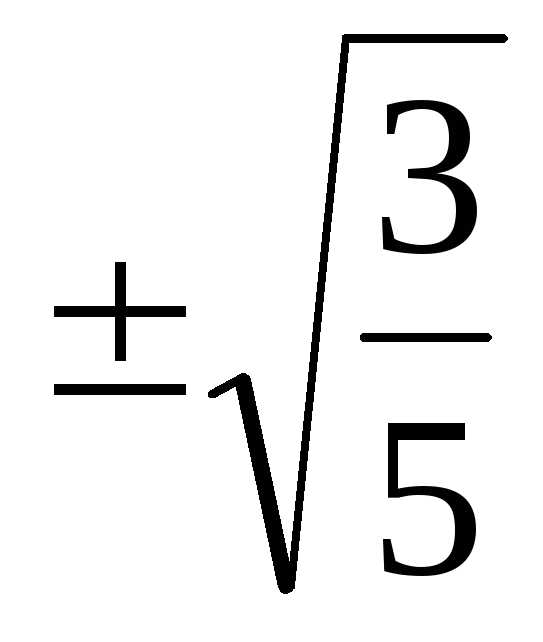 .
.
Для решения полного квадратного уравнения используют обычную формулу корней квадратного уравнения:
 ,
где
–дискриминант квадратного уравнения.
,
где
–дискриминант квадратного уравнения.
Возможны три различных случая:
1. если  ,
то уравнение имеетдва
различных действительных корня
,
то уравнение имеетдва
различных действительных корня
 ,
,  ;
;
2. если  ,
то уравнение имеетдва
одинаковых действительных корня
,
то уравнение имеетдва
одинаковых действительных корня

3. если 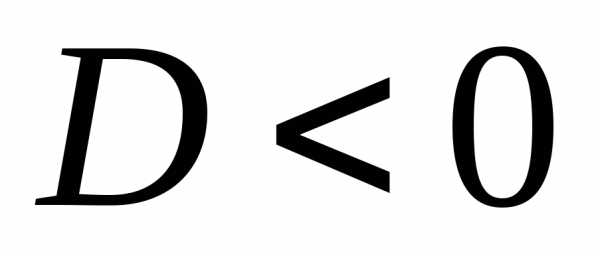 ,
то уравнениене
имеет действительных корней.
,
то уравнениене
имеет действительных корней.
Пример 4.6. Решить уравнение .
Решение. Данное
уравнение является полным, здесь  ,
, ,
,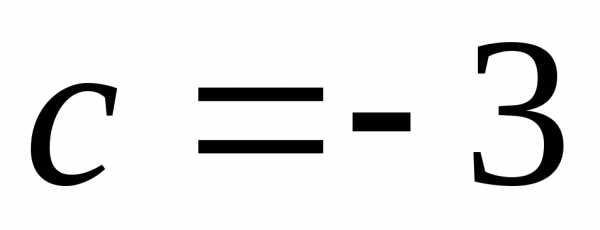 ,,
тогда получаем два различных действительных
корня:
,,
тогда получаем два различных действительных
корня:
; .
Ответ: 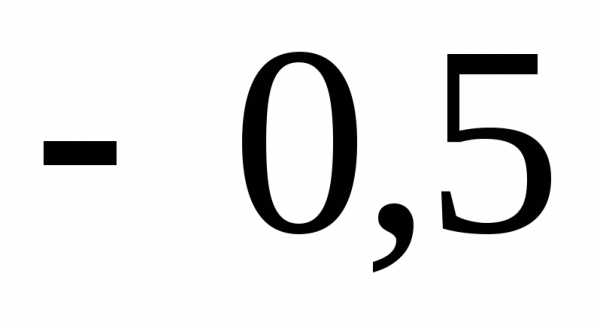
 .
. Определение
4.6. Уравнение
вида
,
где называетсяприведенным
квадратным уравнением.
называетсяприведенным
квадратным уравнением.
Замечание 4.3. Для
решения приведенного квадратного
уравнения, часто используют теорему
Виета:  ,.
,.
Пример 4.7. Решить уравнение: .
Решение.
 ,,
откуда очевидно
,,
откуда очевидно ,
,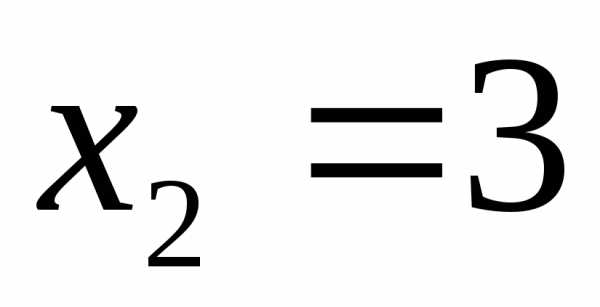 .
.Ответ: 2; 3.
Разложение квадратного трехчлена на множители
Если дискриминант
квадратного трехчлена положителен, то трехчлен можно представить
в виде
,
где ,
, – корни уравнения .
Если дискриминант трехчлена равен нулю, то трехчлен можно представить
в виде
– корни уравнения .
Если дискриминант трехчлена равен нулю, то трехчлен можно представить
в виде 
 – корень уравнения .
– корень уравнения .Рассмотрим далее примеры, в которых используется решение квадратных уравнений.
Пример 4.8. Решить уравнение .
Решение. Область
определения данного уравнения – все
числа, за исключением нуля, то есть  .
Умножим обе части уравнения на
.
Умножим обе части уравнения на и сгруппируем члены:
и сгруппируем члены:
.
Ответ: .
Пример 4.9. Решить уравнение .
Решение. Разложим
числитель и знаменатель дроби, стоящей
в правой части исходного уравнения, на
множители. Для этого найдем корни
уравнений
и.
Корни первого из них ;
; .
Следовательно,.
Корни второго –
.
Следовательно,.
Корни второго – ;
;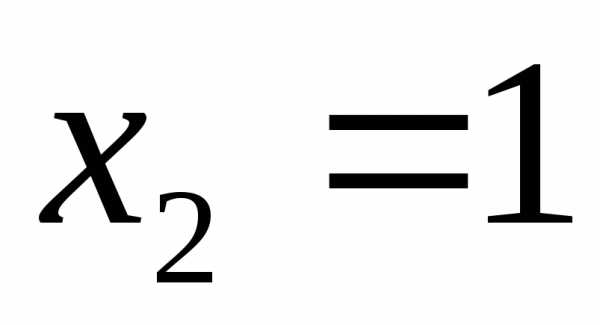 ,
тогда
,
тогда
.
Применяя формулы сокращенного умножения, раскладываем на множители знаменатель дроби, стоящей в правой части:
.
Подставим все полученные выражения в исходное уравнение, тогда получим:
.
В область определения
данного уравнения, а значит, и исходного,
не входят  и
и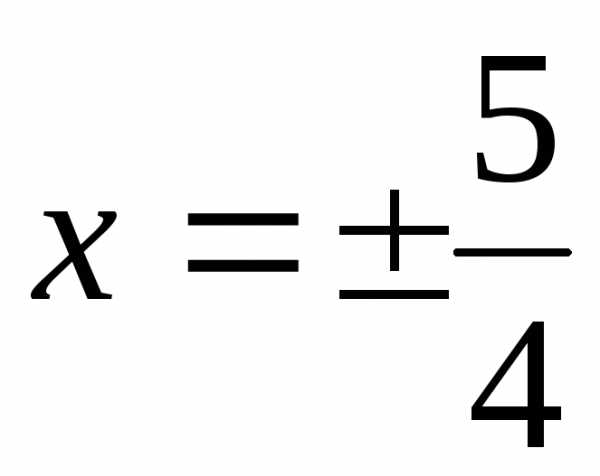 .
Левую часть уравнения сокращаем на
.
Левую часть уравнения сокращаем на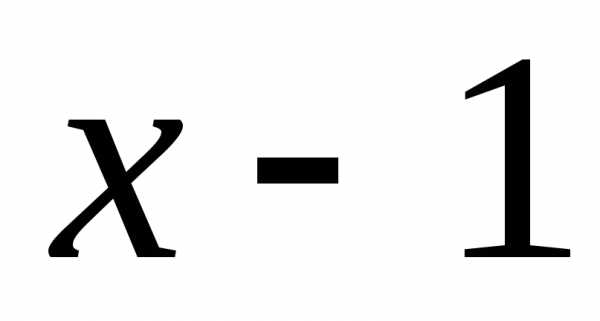 ,
а правую на
,
а правую на ,
тогда получим:
,
тогда получим:

Так как знаменатели дробей равны, то и числители равны, следовательно,
.
Ответ:  .
.
studfiles.net
Линейные и квадратные уравнения. | Социальная сеть работников образования
проверочный тест по теме: «Решение линейных уравнений» Вариант 1.
- -6х – 4 = -9х + 11
1) 3 2) 12 3) 5 4) 1
- 6 – 5х = 2х +5
1) 8 2) 7 3) 4)
- 10(х – 9) = 7
1) 9,7 2) 0,87 3) 4) -0,97
- 5(2х + 4) = 6х – 10 Ответ: ______
- 7(-3 + х) – 2х = -6 Ответ: ______
- 2(х — 3) — 5 = 4х Ответ: ______
- -5 (7 – х) + 2х = -7 Ответ: ______
- Ответ: ______
- Ответ: ______
- 9 + 3(1 – 2х) = 6х – 4 Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: ______
14) 3 – 3(х + 2) = 5 — 5х Ответ: ______
15) 1 + 8х +3(5 – х) = -4х – 2 Ответ: ______
16) -10х – 6(-1 + 6х) = -6х – 4 Ответ: ______
Проверочный тест по теме: «Решение линейных уравнений» Вариант 2.
- 10х + 4 = 7х + 19
1) 1 2) -5 3) 12 4) 5
- 9 – 6х = 8х + 7
1) 2) 3) 1 4) — 5
- 5(х + 2) = 1
1) 1,8 2) 3) -4 4) -1,8
- 7(2х + 3) = 12х + 11 Ответ: ______
- 7(-4 + х) + 3х = 4 Ответ: ______
- 2(х + 7) – 9 = -2х Ответ: ______
- -3 (5 – х) = 11 + 2х Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: ______
- Ответ: _____
- -3 + 4( х – 1) = 5 – 2х Ответ: _____
- 2х – 3 + 2(х — 1) = 3х – 11 Ответ: _____
- 9х – 7(-10 — 3х) = х — 17 Ответ: ______
Ответы к проверочному тесту по теме: «Решение линейных уравнений».
Вариант 1.
1) 3
2)
3) 1
4) – 7, 5
5) 3
6) – 5,5
7) 4
8) – 0,6
9) — 7
10) 1,75
11) – 1,5
12)
13) 7
14) 4
15) – 2
16) 0,25
Ответы к проверочному тесту по теме: «Решение линейных уравнений».
Вариант 2.
1) 4
2) 2
3) 4
4) – 5
5) 3,2
6) – 1,25
7) 26
8) – 3
9) 1,8
10) 3
11) 2
12)
13)
14) 2
15) – 6
16) – 3
Проверочный тест по теме: «Решение квадратных уравнений»
Вариант 1.
1) Решите уравнение: х2 + 4х = 0
1) 0; 4 2) 4 3) 0; -4 4) 1; -4
2) Решите уравнение: 1 – 9у2= 0
Ответ: ________
3) Решите уравнение: –у2 + 3 = 0
Ответ: ________
4) Решите уравнение: х2 – 7х + 12 = 0
1) -3; 4 2) -3; -4 3) 3; -4 4) 3; 4
5) Найдите наименьший корень уравнения:
у2 + 8у + 15 = 0
Ответ: _______
6) Решите уравнение: 2х2 – 7х + 5 = 0
Ответ: _______
7) Найдите сумму корней уравнения:
х2 – 13х + 40 = 0
Ответ: ________
8) Найдите наибольший корень уравнения:
х2 = -15х – 56
Ответ: ________
9) Найдите произведение корней уравнения:
х2 + 16х = — 63
Ответ: ________
10) Соотнесите квадратные уравнения и их корни:
а) х2 + 3х -4 = 0 б) х2 – 9 = 0 в) х2 — 10х + 25 =0
1) х1=-3, х2 = 3 2) х = 5
3) х1=-4, х2= 1 4) нет корней
Ответ:
11) Найдите корни уравнения: 4х +1= — 4х2
Ответ: ________
12) Решите уравнение:
Ответ: ________
13) Решите уравнение: 5(х – 2) = (3х +2)(х – 2)
Ответ: ________
14) Решите уравнение:
Ответ: ________
Проверочный тест по теме: «Решение квадратных уравнений»
Вариант 2.
1) Решите уравнение: 3х2 — х = 0
1) — 2) 0; 3 3) 0; 1 4)
2) Решите уравнение: 1 – 16у2= 0
Ответ: ____
3) Решите уравнение: –у2 + 8 = 0
Ответ:_______
4) Решите уравнение: х2 — 8х + 15 = 0
1) 3; 5 2) -3; -5 3) -3; 5 4) 3; -5
5) Найдите наибольший корень уравнения:
2х2 + 3х + 1 = 0
Ответ: ________
6)Решите уравнение: 4х2 — 7х + 3 = 0
Ответ: ________
7) Найдите сумму корней уравнения:
х2 – 17х + 42 =0
Ответ: ________
8) Найдите наименьший корень уравнения:
х2 = 7х + 18
Ответ: ________
9) Найдите произведение корней уравнения:
х2 + 9х = — 14
Ответ: ________
10) Соотнесите квадратные уравнения и их корни:
а) х2 — х — 2 = 0 б) х2 – х = 0 в) х2 + 25 =0
1) х1=-1, х2 = 1 2) х1 = 0, х2 = 1
3) х1=-1, х2= 2 4) нет корней
Ответ:
11) Найдите корни уравнения: 1 +4у = 5у2
Ответ: ________
12) Решите уравнение:
Ответ: ________
13) Решите уравнение: (х + 3)2 – 16 = (1 – 2х)2
Ответ: ________
14) Решите уравнение:
Ответ: ________
Ответы к проверочному тесту по теме: «Решение квадратных уравнений».
Вариант 1.
1) 3
2)
3)
4) 4
5) -5
6) 1; 2,5
7) 13
8) -7
9) 63
10)
11) -0,5
12) -0,75; 2,5
13) 1; 2
14) -4,8; 2
Ответы к проверочному тесту по теме: «Решение квадратных уравнений».
Вариант 2.
1) 4
2) -0,25; 0,25
3)
4) 1
5) -0,5
6) 0,75; 1
7) 17
8) -2
9) 14
10)
11) -0,2; 1
12) -0,25;
13)
14) -0,8; 3
nsportal.ru
Линейное и квадратное уравнения, система уравнений
На этой странице дано решение примеров Begin38 — Begin40 из задачника Абрамяна, в которых рассматриваются решение простейших уравнений и систем: линейное, квадратное и система линейных уравнений с двумя неизвестными.
Begin38. Решить линейное уравнение A·x + B = 0, заданное своими коэффициентами A и B (коэффициент A не равен 0).
В программе нет проверки на вводимость, и если вы введете число A=0, то в 10 строке произойдет деление на 0. Поэтому нужно вводить не равное 0 число А.
Код Pascal
|
Begin39. Найти корни квадратного уравнения A·x2 + B·x + C = 0, заданного своими коэффициентами A, B, C (коэффициент A не равен 0), если известно, что дискриминант уравнения положителен. Вывести вначале меньший, а затем больший из найденных корней. Корни квадратного уравнения находятся по формуле
x1,2 = (−B ± D1/2)/(2·A),
где D — дискриминант, равный B2 − 4·A·C.Как и в предыдущей программе, здесь нет проверки на то, чтобы А был не равным 0, и то, чтобы дискриминант был положительным. В противном случае или выдаст ошибку, или корни будут равные. К тому же, если A < 0, то первый корень (в формуле D со знаком минус) будет большим, а не меньшим.
Код Pascal
|
Второй вариант решения задачи Begin39 выходит за рамки раздела Begin задачника Абрамяна, поскольку использует условный оператор и циклы с постусловием. Но его следует привести, так как этот способ учитывает проверку в случае неправильного ввода. Также сравните это решение с задачей Proc17.
Код Pascal
|
Begin40. Найти решение системы линейных уравнений вида
A1·x + B1·y = C1,A2·x + B2·y = C2,
заданной своими коэффициентами A1, B1, C1, A2, B2, C2, если известно, что данная система имеет единственное решение. Воспользоваться формуламиx = (C1·B2 − C2·B1)/D, y = (A1·C2 − A2·C1)/D,
где D = A1·B2 − A2·B1.Код Pascal
|
progmatem.ru
Корень квадратного уравнения Википедия
Квадра́тное уравне́ние — алгебраическое уравнение общего вида
- ax2+bx+c=0,{\displaystyle ax^{2}+bx+c=0,}
где x{\displaystyle x} — неизвестное, a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c} — коэффициенты, причём a≠0.{\displaystyle \quad a\neq 0.}
Выражение ax2+bx+c{\displaystyle ax^{2}+bx+c} называют квадратным трёхчленом[1].
Корень — это значение переменной x{\displaystyle x}, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное числовое равенство.
Элементы квадратного уравнения имеют собственные названия[1]:
- a{\displaystyle a} называют первым или старшим коэффициентом,
- b{\displaystyle b} называют вторым, средним или коэффициентом при x{\displaystyle x},
- c{\displaystyle c} называют свободным членом.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент a{\displaystyle a}:
- x2+px+q=0,p=ba,q=ca.{\displaystyle x^{2}+px+q=0,\quad p={\frac {b}{a}},\quad q={\frac {c}{a}}.}
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
ru-wiki.ru
Определение квадратного уравнения | Как успешно обучать математике
Квадратным уравнением называется уравнение вида где – переменная, и — некоторые числа, причём
Я вполне допускаю мысль о том, что не всё сразу понятно в этом определении. Не беспокойтесь! Сейчас во всём разберёмся!
Числа и называются коэффициентами квадратного уравнения:
– первый или старший коэффициент;
– второй коэффициент;
– свободный член. Число не называют третий коэффициент. Для него существует специальное название «свободный член». Почему «свободный член»? Потому что он «свободен» от переменной .
Обратите внимание на то, что число стоит перед , число стоит перед , а число это просто какое-то число, явно не связанное с .
Ограничение для старшего коэффициента
В определении квадратного уравнения есть очень важное ограничение для старшего коэффициента . Ограничение заключается в такой записи . Эта запись говорит о том, что число может принимать любые значения, кроме нуля!
Попробуем разобраться, почему необходимо это ограничение. А что будет, если не учитывать это ограничение? Что тогда произойдёт с уравнением? Давайте снимем ограничение . Ну, не нравится нам это ограничение!
Предположим, что . Что же мы получим в этом случае?
А вот что! Подставим в уравнение вместо число , получим: . Так как , то уравнение примет вид: .
Но, позвольте! Уравнение такого вида является линейным или его ещё можно назвать уравнением первой степени. Ничего общего с квадратным уравнением оно не имеет! А мы-то ведём речь о квадратном уравнении!
Итак, делаем очень важный вывод ограничение крайне необходимо! Потому что если мы не будем его учитывать, то вместо квадратного уравнения получим линейное.
Таким образом, в квадратном уравнении старший коэффициент в ни в коем случае не может быть равным нулю! Никогда!!! Так как иначе квадратное уравнение превратится в линейное.
Повторим ещё раз определение квадратного уравнения.
«Квадратным уравнением называется уравнение вида , где –переменная, и – некоторые числа, причём, .
Я надеюсь, теперь всем понятен смысл этого определения, включая ограничение!
А вот с числами и всё гораздо проще! Числа и запросто могут быть равными нулю! В этом случае получается неполное квадратное уравнение. Об этом мы говорили в предыдущей статье.
vebuchitel.ru
Что такое линейное уравнение | Алгебра
Что такое линейное уравнение? Что называется корнем линейного уравнения? Сколько корней имеет линейное уравнение? Что значить решить линейное уравнение?
В курсе алгебры 7 класса линейное уравнение определяется следующим образом.
Определение.
Линейное уравнение с одной переменной — это уравнение вида ax=b, где a и b — числа, x — переменная.
Корнем линейного уравнения называется значение переменной, при котором уравнение обращается в верное числовое равенство.
Например, корень уравнения 5x=40 равен 8, так как при x=8 это уравнение превращается в верное числовое равенство:
5∙8=40
40=40.
Количество корней линейного уравнения зависит от значения a (коэффициента перед x).
При a≠0 линейное уравнение имеет единственное решение.
Чтобы найти x, обе части уравнения нужно разделить на число, стоящее перед иксом:
Любое число можно разделить на 2, 5 и числа, которые могут быть представлены в виде произведения только двоек и пятёрок ( например, любое число можно разделить на 10, так как 10=2∙5; на 40, так как 40=2∙2∙2∙5).
В остальных случаях ответ записывают в виде обыкновенной дроби (если дробь неправильная, следует выделить из нее целую часть).
При a=0, b≠0 линейное уравнение
не имеет решений.
При любом значении x левая часть уравнения равна нулю, а правая — отлична от нуля. То есть нет ни одного значения x, при котором уравнение обратилось бы в верное числовое равенство.
При a=0, b=0 линейное уравнение
имеет бесконечное множество решений.
При любом значении x левая часть уравнения 0x=0 обращается в нуль, в правой части также стоит нуль. Значит, любое число является корнем этого уравнения, то есть, при любом значении x это уравнение обращается в верное числовое равенство.
Возможные решения линейных уравнений можно изобразить в виде схемы.
Решить линейное уравнение — значит, найти корень (корни) уравнения, либо убедиться, что уравнение не имеет корней.
Решение многих уравнений сводится к решению линейных уравнений.
www.algebraclass.ru
