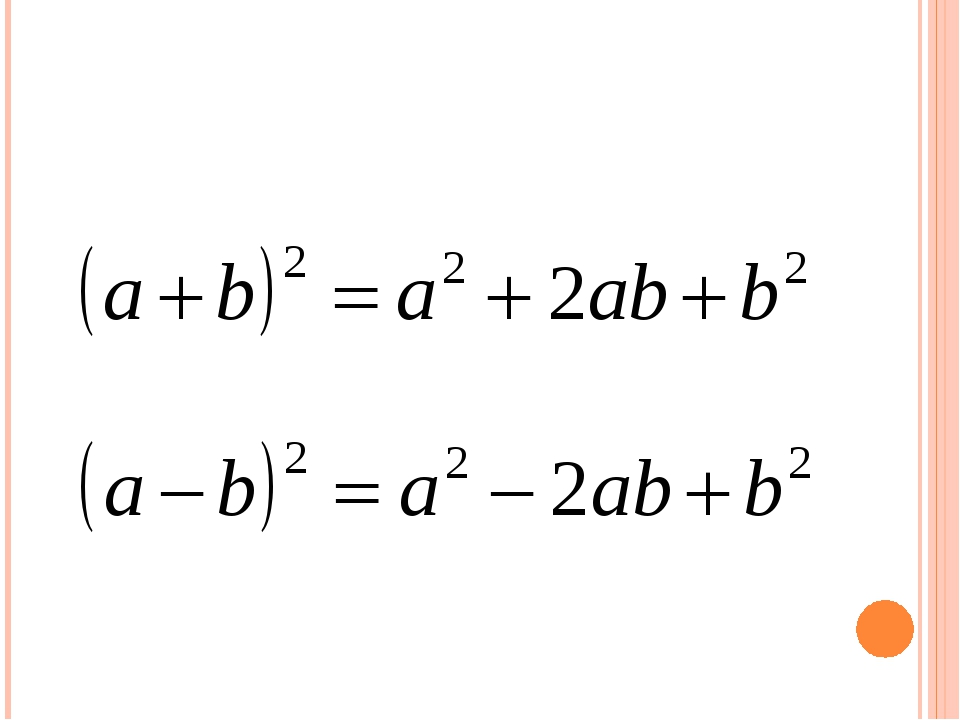Квадратная формула: Формула квадратного уравнения для вычислений

Способы решения квадратных уравнений. Алгебра, 8 класс: уроки, тесты, задания.

1.	Дискриминант квадратного уравнения Сложность: лёгкое	1
2.	Число корней квадратного уравнения Сложность: лёгкое	1
3.	Полное квадратное уравнение (a = 1; b > 0) Сложность: лёгкое	2
4.	Полное квадратное уравнение (а не равно 1) Сложность: среднее	2
5.	Квадратное уравнение, введение новой переменной Сложность: среднее	3
6.	Квадратное уравнение, равенство произведения 0 Сложность: среднее	1
7.	Задача на составление квадратного уравнения Сложность: сложное	4
8.	Сокращение алгебраической дроби, разложение на множители квадратного трёхчлена Сложность: сложное	4
9.	Сокращение алгебраической дроби, формула разности кубов Сложность: сложное	4
10.	Разложение на множители квадратного трёхчлена, отрицательные корни Сложность: сложное	2

Квадратные уравнения: приведённые уравнения, формулы корней

Квадратное уравнение или уравнение второй степени с одним неизвестным — это уравнение, которое после преобразований может быть приведено к следующему виду:

ax² + bx + c = 0  — квадратное уравнение,

где  x  — это неизвестное, а  a,  b  и  c  — коэффициенты уравнения. В квадратных уравнениях  a  называется первым коэффициентом  (a ≠ 0),  b  называется вторым коэффициентом, а  c  называется известным или свободным членом.

Уравнение:

ax² + bx + c = 0

называется полным квадратным уравнением. Если один из коэффициентов 

b  или  c  равен нулю, или нулю равны оба эти коэффициента, то уравнение представляют в виде неполного квадратного уравнения.

Приведённое квадратное уравнение

Полное квадратное уравнение можно привести к более удобному виду, разделив все его члены на  a,  то есть на первый коэффициент:

Затем можно избавиться от дробных коэффициентов, обозначив их буквами  p  и  q:

если	b	= p,  а	c	= q,
	a		a

то получится   x² + px + q = 0.

Уравнение  x² + px + q = 0  называется приведённым квадратным уравнением. Следовательно, любое квадратное уравнение, в котором первый коэффициент равен 1, можно назвать приведённым.

Например, уравнение:

x² + 10x — 5 = 0

является приведённым, а уравнение:

-3x² + 9x — 12 = 0

можно заменить приведённым уравнением, разделив все его члены на  -3:

x² — 3x + 4 = 0.

Решение квадратных уравнений

Чтобы решить квадратное уравнение, надо привести его к одному из следующих видов:

ax² + bx + c = 0;

ax² + 2kx + c = 0;

x² + px + q = 0.

Для каждого вида уравнения есть своя формула нахождения корней:

Вид уравнения	Формула корней
ax2 + bx + c = 0
ax2 + 2kx + c = 0
x2 + px + q = 0	или если коэффициент  p  нечётный

Обратите внимание на уравнение:

ax² + 2kx + c = 0

это преобразованное уравнение  ax² + bx + c = 0,  в котором коэффициент  b  — четный, что позволяет его заменить на вид  2k.   Поэтому формулу нахождения корней для этого уравнения можно упростить, подставив в неё  2k  вместо  b:

Пример 1. Решить уравнение:

3x² + 7x + 2 = 0.

Так как в уравнении второй коэффициент не является чётным числом, а первый коэффициент не равен единице, то искать корни будем по самой первой формуле, называемой общей формулой нахождения корней квадратного уравнения. Сначала определим, чему равны коэффициенты:

a = 3,  b = 7,  c = 2.

Теперь, для нахождения корней уравнения, просто подставим значения коэффициентов в формулу:

x1 =	-2	= —	1	,   x2 =	-12	= -2
	6		3		6

Пример 2:

x² — 4x — 60 = 0.

Определим, чему равны коэффициенты:

a = 1,  b = -4,  c = -60.

Так как в уравнении второй коэффициент — чётное число, то будем использовать формулу для квадратных уравнений с чётным вторым коэффициентом:

x₁ = 2 + 8 = 10,   x₂ = 2 — 8 = -6

Ответ:  10,  -6.

Пример 3.

y² + 11y = y — 25.

Приведём уравнение к общему виду:

y² + 11y = y — 25;

y² + 11y — y + 25 = 0;

y² + 10y + 25 = 0.

Определим, чему равны коэффициенты:

a = 1,  p = 10,  q = 25.

Так как первый коэффициент равен  1,  то будем искать корни по формуле для приведённых уравнений с чётным вторым коэффициентом:

Ответ:  -5.

Пример 4.

x² — 7x + 6 = 0.

Определим, чему равны коэффициенты:

a = 1,  p = -7,  q = 6.

Так как первый коэффициент равен  1,  то будем искать корни по формуле для приведённых уравнений с нечётным вторым коэффициентом:

x₁ = (7 + 5) : 2 = 6,

x₂ = (7 — 5) : 2 = 1.

Ответ:  6,  1.

Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Решение уравнений и неравенств. Системы уравнений. Формулы. Методы.  / / Квадратные уравнения. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. ( Дискриминат на 4 и на 1). Теорема Виета. 3 способа. Поделиться:    Квадратное уравнение. Решение квадратных уравнений. Дискриминант. Формула дискриминанта. Теорема Виета.     Версия для печати. Квадратным уравнением называется уравнение вида:                  , где x — переменная, a,b,c — постоянные (числовые) коэффициенты. В общем случае решение квадратных уравнений сводится к нахождению дискриминанта Формула дискриминанта: . О корнях квадратного уравнения можно судить по знаку дискриминанта (D) : D>0 — уравнение имеет 2 различных вещественных корня D=0 — уравнение имеет 2 совпадающих вещественных корня D<0 — уравнение имеет 2 мнимых корня (для непродвинутых пользователей — корней не имеет) В общем случае корни уравнения равны:                  . Очевидно, в случае с нулевым дискриминантом, оба корня равны                  . Если коэффициент при х четный, то имеет смысл вычислять не дискриминант, а четверть дискриминанта:                  В таком случае корни уравнения вычисляются по формуле:                  Теорема Виета о корнях квадратного уранения. Приведенным квадратным уравнением называется уравнение вида                 , то есть квадратное уравнение с единичным коэффициентом при старшем члене. В этом случае целесообразно применять теорему Виета, которая позволяет получить относительно корней уравнения следующую систему уравнений:                  . Следует заметить, что любое квадратное уравнение может стать приведенным, если его поделить на коэффициент при старшем члене, то есть при х2 Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax² + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k² − ac, а корни по формулам и .

Примеры

Решим квадратное уравнение x² + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.

Любое четное число n можно представить в виде произведения числа 2 и числа k, то есть 2k.

n = 2k

Например, число 10 можно представить как 2 × 5.

10 = 2 × 5

В этом произведении k = 5.

---

Число 12 можно представить как 2 × 6.

12 = 2 × 6

В этом произведении k = 6.

---

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7.

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.

В уравнении x² + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = 3² − 1 × (−16) = 9 + 16 = 25

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x² + 6x − 16 = 0 являются числа 2 и −8.

В отличие от стандартной формулы для вычисления дискриминанта (D=b² − 4ac), в формуле D₁ = k² − ac не нужно выполнять умножение числа 4 на ac.

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

---

Пример 2. Решить квадратное уравнение 5x² − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−3)² − 5 × 1 = 9 − 5 = 4

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

---

Пример 3. Решить квадратное уравнение x² − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D₁ = k² − ac

D₁ = k² − ac = (−5)² − 1 × (−24) = 25 + 24 = 49

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

---

Пример 5. Решить квадратное уравнение

Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k. Получается, что

Найдём дискриминант по формуле D₁ = k² − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .

Вычислим второй корень уравнения:

---

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax² + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

b = 2k

Заменим в уравнении ax² + bx + c = 0 коэффициент b на выражение 2k

ax² + 2kx + c = 0

Теперь вычислим дискриминант по ранее известной формуле:

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac

Вынесем в получившемся выражении за скобки общий множитель 4

D = b² − 4ac = (2k)² − 4ac = 4k² − 4ac = 4(k² − ac)

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k² − ac.

В выражении 4(k² − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k² − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k² − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

D₁ = k² − ac

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax² + bx + c = 0 коэффициент b заменён на выражение 2k. Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k. Также на забываем, что D у нас равно выражению 4(k² − ac)

Но ранее было сказано, что выражение k² − ac обозначается через D₁. Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Задания для самостоятельного решения

Задание 1. Решить уравнение:

Решение:

Ответ: 1; 0,6

Задание 2. Решить уравнение:

Решение:

Ответ:

Задание 3. Решить уравнение:

Решение:

Ответ: 1; −1,4

Задание 4. Решить уравнение:

Решение:

Ответ:

Задание 5. Решить уравнение:

Решение:

Ответ:

Задание 6. Решить уравнение:

Решение:

Ответ:

Задание 7. Решить уравнение:

Решение:

Ответ:

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Формула корней квадратного уравнения

Мы с вами уже знаем, что Квадратным уравнением называется уравнение вида , где  – переменная, ,  и  – некоторые числа, причем .

В алгебре, геометрии, физике и др. науках очень часто решение задачи сводится к нахождению корней квадратных уравнений. Поэтому очень важно научиться решать квадратные уравнения.

Решить уравнение:

Мы с вами решили это уравнение методом выделения полного квадрата, т. е. применили формулу квадрата разности.

Решить уравнение:

Мы снова нашли корни уравнения методом выделения полного квадрата. Но этот метод частенько приводит к громоздким преобразованиям. Поэтому древние  математики вывели формулу корней квадратного уравнения, которую можно применять при решении любого квадратного уравнения.

Можно получить эти формулы, решая квадратное уравнение в общем виде методом выделения полного квадрата.

Итак, рассмотрим квадратное уравнение общего вида , где .

Мы с вами определили, что знак дроби, записанной в правой части уравнения зависит от знака дискриминанта. Поэтому при решении этого уравнения возможны три случая.

Первый случай:

Вывод: уравнение , при , имеет два различных корня. Которые находят по формулам:

Обычно эти формулы объединяют в одну, записывая её следующим образом:

Второй случай:

Вывод: уравнение , при ,имеет единственный корень. Который вычисляется по формуле:

Третий случай:

Вывод: уравнение , при ,не имеет корней.

Таким образом: в зависимости от значения дискриминанта квадратное уравнение , может иметь:

1. Два различных корня:  . При .

2. Один корень: . При .

3. Не имеет корней. При .

Запишем алгоритм решения квадратных уравнений.

Задание: решить уравнения.

Обратите внимание, второй коэффициент в начальном уравнении чётный. Есть формула корней квадратного уравнения с чётным вторым коэффициентом. С помощью неё удобнее вычислять корни. Давайте выведем её.

Давайте найдём корни последнего уравнения по новой формуле.

Итоги:

Выражение  называется дискриминантом квадратного уравнения.

При решении квадратного уравнения возможны три случая в зависимости от знака дискриминанта:

1)                Если , то уравнение имеет два различных корня, которые вычисляются по формуле: .

2)                Если , то уравнение имеет единственный корень, который вычисляется по формуле .

3)                Если , то уравнение не имеет корней.

Решение квадратных уравнений: формула корней, дискриминант, график

Квадратное уравнение – это математическое уравнение, которое в общем виде выглядит так:

ax² + bx + c = 0

Это многочлен второго порядка с 3 коэффициентами:

• a – старший (первый) коэф., не должен быть равен 0;
• b – средний (второй) коэф.;
• c – свободный элемент.

Решением квадратного уравнения является нахождение двух чисел (его корней) – x₁ и x_2.

Формула для вычисления корней

Для нахождения корней квадратного уравнения используется формула:

Выражение внутри квадратного корня называется дискриминантом и обозначается буквой D (или Δ):

D = b² – 4ac

Таким образом, формула для вычисления корней может быть представлена разными способами:

1. Если D>0, у уравнения есть 2 корня:

2. Если D=0, уравнение имеет всего один корень:

3. Если D<0, вещественных корней нет, но есть комплексные:

Решений квадратных уравнений

Пример 1

3x²+5x+2 = 0

Решение:

a = 3, b = 5, c = 2

x₁ = (-5 + 1)/6 = -4/6 = -2/3
x₂ = (-5 – 1)/6  = -6/6 = -1

Пример 2

3x²-6x+3 = 0

Решение:

a = 3, b = -6, c = 3

x₁ = x₂ = 1

Пример 3

x²+2x+5 = 0

Решение:

a = 1, b = 2, c = 5

В данном случае нет вещественных корней, а решением являются комплексные числа:

x₁ = -1 + 2i
x₂ = -1 – 2i

График квадратичной функции

Графиком квадратичной функции является парабола.

f(x) = ax² + bx + c

• Корни квадратного уравнения – это точки пересечения параболы с осью абцисс (X).
• Если корень один – парабола касается оси в одной точке, не пересекая ее.
• При отсутствии вещественных корней (наличии комплексных), график с осю X не соприкасается.

Дискриминант. Теорема Виета

Дискриминант, как и квадратные уравнения начинают изучать в курсе алгебры в 8 классе. Решить квадратное уравнение можно через дискриминант и с помощью теоремы Виета. Методика изучения квадратных уравнений, как и формулы дискриминанта достаточно неудачно прививается школьникам, как и многое в настоящем образовании. Поэтому проходят школьные годы, обучение в 9-11 классе заменяет «высшее образование» и все снова ищут — «Как решить квадратное уравнение?», «Как найти корни уравнения?», «Как найти дискриминант?» и …

Формула дискриминанта

Дискриминант D квадратного уравнения a*x^2+bx+c=0 равен D=b^2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 — уравнение имеет 1 корень (2 совпадающих корня):
D<0 – не имеет действительных корней (в школьной теории). В ВУЗах изучают комплексные числа и уже на множестве комплексных чисел уравнение с отрицательным дискриминантом имеет два комплексных корня.
Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра..

Общая формула для нахождения корней квадратного уравнения:

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни




До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться,

что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0),

или парабола ветвями вниз (a<0).

Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox.
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D<0) – график параболы принадлежит плоскости над осью абсцисс (ветки параболы вверх), или график полностью под осью абсцисс (ветки параболы опущены вниз).

Неполные квадратные уравнения

Если в квадратном уравнении коэффициент при свободном члене или переменной равны нулю то такие уравнения называют неполными. Корни уравнений находим по упрощенной формуле
График функций всегда симметричен относительно начала координат. Стоит отметить, что уравнение имеет действительные корни только тогда, когда в уравнении чередуются знаки при коэффициентах «+, -» или «-, +».
Неполное квадратное уравнение вида
одним из корней всегда имеет точку x=0.
В таком контексте решения квадратных уравнений становится нужным, а при построении графиков парабол, еще и визуально интересным времяпрепровождением, особенно если речь идет о школьном занятии по анализу графика функций, или изучении темы парабол. Поэтому в 8, 9 классе рекомендуем эти две темы в алгебре сочетать.
Если материал помог Вам в обучении, просьба поделиться с друзьями ссылкой на статью!

Формулы площади

( пи = = 3,141592 …)

Площадь Формулы

Примечание: «ab» означает «а» умножить на «б». «a

² » означает «квадрат», что то же самое, что «а» умножить на «а».

Будьте осторожны !! Количество единиц. Используйте то же самое единиц для всех измерений. Примеры

квадрат = a ²

прямоугольник = ab

параллелограмм = bh

трапеция = h / 2 (b ₁ + b ₂ )

круг pi r ²

эллипс = pi r ₁ r ₂

треугольник =

, равная половине длины основания, умноженной на высоту треугольник

равносторонний треугольник =

треугольник с учетом SAS (две стороны и противоположный угол)
= (1/2) a b sin C

треугольник с учетом a, b, c = [s (s-a) (s-b) (s-c)] когда s = (a + b + c) / 2 (формула Герона)

правильный многоугольник = (1/2) n sin (360 ° / n) S ²
когда n = количество сторон и S = ​​длина от центра до угла

Квартир

Площадь измеряется в «квадратных» единицах.Площадь фигуры количество квадратов, необходимых для его полного покрытия, как плитки на пол.

Площадь квадрата = сторона, умноженная на сторону. Поскольку каждая сторона квадрата — это то же самое, это может быть просто длина одной стороны в квадрате.

Если у квадрата одна сторона 4 дюйма, площадь будет 4 дюйма, умноженная на 4 дюйма или 16 квадратных дюймов. (Квадратные дюймы также можно записать в ² .)

Обязательно используйте одни и те же единицы для всех измерений. Нельзя умножить футы на дюймы, квадрат не получается. измерение.

Площадь прямоугольника — это длина сбоку. раз больше ширины. Если ширина 4 дюйма, а длина 6 футов, что это площадь?

НЕ ПРАВИЛЬНО …. 4 раза 6 = 24

ПРАВИЛЬНО …. 4 дюйма равны 1/3 фута. Площадь 1/3 фута умножить на 6 футов = 2 квадратных фута.(или 2 кв. фута, или 2 фута ² ).

Площадь круга, треугольника, квадрата, прямоугольника, параллелограмма, трапеции, эллипса и сектора

Площадь — это размер поверхности!
Узнайте больше о площади или воспользуйтесь калькулятором площади.

Пример: Какова площадь этого прямоугольника?

Формула:

Площадь = Ш × В
Ш = Ширина
В = Высота

Мы знаем w = 5 и h = 3 , поэтому:

Площадь = 5 × 3 = 15

Пример: Какова площадь этого круга?

Радиус = r = 3

Площадь		= π × r 2
		= π × 3 2
		= π × (3 × 3)
		= 3.14159 … × 9
		= 28,27 (до 2 знаков после запятой)

Пример: Какова площадь этого треугольника?

Высота = h = 12

База = b = 20

Площадь = ½ × b × h = ½ × 20 × 12 = 120

Более сложный пример:

Пример: Сэм косит траву по цене 0,10 доллара за квадратный метр

Сколько зарабатывает Сэм, обрабатывая эту область:

Разобьем область на две части:

Часть А представляет собой квадрат:

Площадь A = a ² = 20 м × 20 м = 400 м ²

Часть B представляет собой треугольник.При взгляде сбоку он имеет основание 20 м и высоту 14 м.

Площадь B = ½b × h = ½ × 20 м × 14 м = 140 м ²

Итак, общая площадь:

Площадь = Площадь A + Площадь B = 400 м ² + 140 м ² = 540 м ²

Сэм зарабатывает 0,10 доллара за квадратный метр

Сэм зарабатывает = 0,10 доллара × 540 млн ² = 54

долларов

Площадь кв. Калькулятор

Если вы забыли, как найти площадь квадрата, вы попали в нужное место — этот простой калькулятор площади квадрата — ответ на ваши проблемы.Если вы хотите найти площадь, зная сторону квадрата, или вам нужно вычислить сторону от заданной площади, этот инструмент поможет вам. Прочтите и освежите свою память, чтобы узнать, какова площадь квадрата, и выучить формулу калькулятора. Если вам также нужно рассчитать площадь и диагональ квадрата, воспользуйтесь этим калькулятором квадратов.

Как найти площадь квадрата — формулы

Площадь квадрата равна длине его сторон:

• area = a * a = a² , где a — сторона квадрата

Существуют и другие формулы.В зависимости от того, какой параметр задан, вы можете использовать следующие уравнения:

• площадь = d² / 2 , если известна диагональ
• площадь = периметр² / 16 , если задан периметр
• площадь = 2 * R² зная радиус окружности R
• площадь = 4 * r² по внутреннему радиусу r

Какова площадь квадрата?

Площадь квадрата — это количество квадратных единиц, необходимое для полного заполнения квадрата.Чтобы понять это определение, давайте посмотрим на это изображение шахматной доски:

Доска прямоугольной формы, сторона разделена на восемь частей, всего 64 квадрата. Предположим, что один маленький квадрат имеет длину стороны, равную 1 дюйму. Под площадью такого квадрата можно понимать количество краски, необходимое для покрытия поверхности. Итак, из формулы площади квадрата мы знаем, что площадь = a² = 1 дюйм², и это наша единица площади в случае шахматной доски (количество краски).Тогда площадь шахматной доски 2×2 равна 4 квадратам — так что это 4 кв. М, и нам нужно использовать в 4 раза больше «краски». Полная площадь шахматной доски равна 84 дюйм²: 8 дюймов * 8 дюймов по формуле, или это всего лишь 64 маленьких квадратов с площадью 1 дюйм², поэтому нам нужно в 64 раза больше «краски», чем для одного отдельного квадрата.

Как пользоваться калькулятором площади

Давайте попробуем вычислить площадь квадрата!

1. Найти данное значение .В нашем примере предположим, что мы знаем сторону и хотим вычислить площадь.
2. Введите его в соответствующее поле . Введите значение, например 11 дюймов в коробку со стороны .
3. Область появляется! Это 121 кв. Дюйм. Если вас интересует, сколько это квадратных футов, измените единицу измерения, щелкнув ее название.

Формула квадрата — все формулы квадрата, вывод и решенные примеры

Плоская геометрия или двухмерная геометрия имеют дело с плоскими фигурами, которые можно нарисовать на листе бумаги, такими как линии, кривые, многоугольники, четырехугольники и т. Д.

Плоский объект, который имеет только длину и ширину, имеет двумерную форму. Стороны этой фигуры составляют прямые или изогнутые линии. Кроме того, эти фигуры могут иметь любое количество сторон. Двумерная замкнутая фигура, ограниченная тремя или более чем тремя прямыми линиями, называется многоугольником. Треугольники, квадрат, прямоугольник, пятиугольник, шестиугольник — вот некоторые примеры многоугольников.

Например, треугольники и квадраты являются многоугольниками.

В этой статье давайте изучим квадрат и всю формулу квадрата.

Введение в квадрат

Квадрат — это четырехугольник, все четыре стороны которого равны, а углы равны. Все четыре угла являются прямыми углами, то есть равными 900. Вы также можете рассматривать квадрат как частный случай прямоугольника, когда вы обнаружите, что две соседние стороны имеют одинаковую длину.

(изображение будет загружено в ближайшее время)

Основные свойства квадрата

1. Все четыре стороны имеют одинаковую длину, т. Е. Равны.

2. Противоположные стороны квадрата параллельны.

3. Все четыре угла квадрата — прямые, то есть углы равны 900.

4. Сумма углов квадрата равна 360 градусам.

5. Диагональ квадрата одинаковой длины.

6. Каждая диагональ квадрата делит его на две равные симметричные области

7. Диагонали квадрата пересекают его прямые углы и делят друг друга на половину.

8. Точка пересечения диагоналей называется центром квадрата, а также центром описанной окружности и описанной окружности

9. Каждая диагональ делит угол квадрата пополам, что означает, что они являются биссектрисами углов. площади.

10. Обе диагонали делят квадрат на четыре равных треугольника, причем эти треугольники равнобедренные и прямоугольные.

Вывод формулы квадрата

Площадь квадрата

Площадь — это измерение пространства, занимаемого любыми двухмерными геометрическими фигурами. Площадь любой формы зависит от ее размеров. У разных форм разные области. Например, площадь квадрата отличается от площади прямоугольника.Площадь фигуры рассчитывается в квадратных единицах (квадратных единицах).

(изображение будет загружено в ближайшее время)

Давайте рассмотрим квадрат, у которого длины сторон равны s единицам, а диагональ — единицам d соответственно. Мы знаем, что площадь квадрата — это область, заключенная в его границах. А квадрат — это особый случай прямоугольника, две смежные стороны которого равны по длине. Следовательно, площадь может быть выражена как —

Площадь прямоугольника = Длина × Ширина

Формула площади квадрата = Длина × Ширина

Формула площади квадрата = s × s = s²

Периметр квадрата

Периметр квадрата — это общая длина его границы.Граница квадрата представляет собой сумму длин всех сторон. Периметр фигуры зависит от длины фигуры. Следовательно, периметр выражается как —

Периметр квадрата = Сумма длин четырех сторон

Периметр квадрата = (s + s + s + s) единиц = 4 xs

Диагональ квадрата

Диагональ многоугольника — это линия, соединяющая вершину с несмежной вершиной.

Следовательно, чтобы вычислить длину диагонали квадрата, воспользуемся теоремой Пифагора.Диагональ квадрата делит квадрат на два прямоугольных треугольника. Теперь две соседние стороны квадрата равны по длине. А прямоугольный треугольник работает как равнобедренный треугольник, каждая из сторон которого имеет длину «s».

Таким образом, мы можем применить теорему Пифагора к этим треугольникам, которые имеют основание и перпендикуляр единиц s и гипотенузу единиц d. Итак, согласно формуле мы имеем:

Следовательно, диагональ квадрата формула = s √2

Решенные примеры

Пример 1:

Если длина стороны квадрата равна 9 см.Вычислите площадь квадрата и общую длину его границы.

Решение:

Учитывая, что длина стороны квадрата s = 9 см

У нас есть формула площади как A = s2

= (9) 2

= 81 см2

Общая длина его границы равна Периметр квадрата

У нас периметр = 4s

= 4 x 9

= 36см.

Следовательно, площадь квадрата составляет 81 см2, а общая длина его границы — 36 см.

Пример 2:

Найдите длину диагонали квадрата со стороной 10 см?

Решение:

Как указано,

s = 10 см

Диагональ квадратной формулы:

\ [d = a \ sqrt {2} \]

с заменой значений,

\ [d = 10 \ times \ sqrt {2} \]

i.е. d = 10 × 1,4142

т.е. d = 14,142 см

Следовательно, диагональ будет 14,142 см.

Время проведения теста

1. Вычислите площадь квадрата, длина стороны которого равна 13 см.

2. Найдите длину диагонали квадрата, стороны которого равны 7 см.

Площадь квадрата — веб-формулы

Квадрат — это правильный многоугольник с четырьмя сторонами. У него четыре прямых угла и параллельные стороны. Чтобы вычислить площадь квадрата, умножьте основание на себя, что может быть выражено как сторона × сторона.Если квадрат имеет основание длиной 8 дюймов, его площадь будет 8 × 8 = 64 квадратных дюйма.

Площадь квадрата определяется по:

А = а ²

где a = длина стороны

Периметр квадрата = 4а
Диагональ квадрата = (a) (sqrt (2)) или 1,414 (a)

Пример 1: Найдите площадь квадрата со стороной 15 м.

Решение :

Площадь квадрата = a ² = 15 ² = 225 м ²

Пример 2: Вычислите площадь квадрата, длина стороны которого составляет 35 см.

Решение :

Площадь квадрата определяется как a × a.

Площадь = 35 × 35

Площадь = 1225 см

Пример 3: Какова площадь квадратного поля, если его периметр равен 32 ярду?

Решение :

Периметр квадратного поля = 32 ярда, а поскольку периметр квадрата равен P = 4s, где s — длина стороны.Мы можем легко определить длину, выделив s из приведенной выше формулы:

с = P / 4 = 32/4 = 8 ярдов

Площадь квадратного поля = s × s

Подставляем значение s, получаем:

Площадь = 8 × 8 = 64 ярда ²

Следовательно, площадь квадратного поля составляет 64 ярда ² .

Пример 4: Сторона квадратного парка составляет 200 м.Сколько будет стоить его озеленение при цене 0,5 доллара за кв. М?
Решение :

Что нам нужно сделать, это найти площадь парка, а затем умножить площадь на стоимость за м ² .

Площадь квадратного парка = сторона × сторона

A = с²

Заменить значения и упростить.
А = 200 × 200
A = 40 000 м ²

Площадь озеленения = площадь парка = 40 000 кв. М.

Стоимость посадки травы = площадь посадки травы × ставка за квадратный метр.

Подставим значения получим:
Стоимость = 40 000 x 0,5 = 20 000 долларов США.

Следовательно, стоимость посадки травы составляет 20 000 долларов США.

Пример 5: Квадратный газон окружен дорожкой шириной 2 м. Если площадь дорожки 160 кв.м, найдите площадь газона.

Решение :

Дано: Квадратный газон окружен дорожкой шириной 2 м; площадь дорожки 160 кв.м.
Найти: Площадь газона.
(Подсказка: лужайка окружена дорожкой, т. Е. Дорожка находится на внешнем крае газона. Чтобы найти площадь лужайки, вычтите площадь дорожек из общей площади)
Пусть сторона лужайки будет y, тогда у нас будет:

Внешняя сторона, включая путь = сторона лужайки + ширина дорожки с обеих сторон.
= у + (2 + 2)
= y + 4

Общая площадь, включая путь = (y + 4) × (y + 4).
= y² + 8y + 16 (i).
И площадь газона = (сторона) ² = y × y = y² (ii).

Так как площадь пути задана (160 м ² ), имеем:
Площадь дорожки = Общая площадь, включая дорожку — площадь лужайки.
А = (i) — (ii).
Подставим заданные значения в следующее уравнение, и, выделив y, мы можем определить длину стороны газона:
160 = (y² + 8y + 16) — y²
160 = y² + 8y + 16 — y²
160 = y² — y² + 8y + 16
160 = 8лет + 16
160–16 = 8 лет
144 = 8лет
18 = у
Сторона газона = 18 м

Площадь газона = сторона × сторона

А = с²
А = 18 × 18
A = 324 м ²

Отсюда площадь газона = 324 м ² .2 в камеру.

Нажмите Enter, чтобы увидеть результат.

Совет: Вы также можете щелкнуть другую ячейку, чтобы увидеть результат в квадрате.

Возвести число в квадрат в другую ячейку

Выполните следующие действия:

1. Щелкните внутри ячейки и введите число, которое нужно возвести в квадрат.2 в ячейку B1.

2. Нажмите Enter, чтобы увидеть результат.

Нужна дополнительная помощь?

Вы всегда можете спросить эксперта в сообществе специалистов по Excel или получить поддержку в сообществе Answers.

См. Также

Перемещение или копирование ячеек, строк или столбцов

Завершение квадрата и квадратичной формулы

Результаты обучения

• Заполните квадрат, чтобы решить квадратное уравнение.
• Используйте формулу корней квадратного уравнения, чтобы решить квадратное уравнение.
• Используйте дискриминант, чтобы определить количество и тип решений квадратного уравнения.

Не все квадратные уравнения можно разложить на множители или решить в их исходной форме с использованием свойства квадратного корня. В этих случаях мы можем использовать другие методы для решения квадратного уравнения .

Завершение квадрата

Один метод известен как — завершение квадрата .{2} -6x = 13 [/ латекс].

Показать решение

[латекс] x = 3 \ pm \ sqrt {22} [/ латекс]

Использование квадратичной формулы

Четвертый метод решения квадратного уравнения заключается в использовании квадратной формулы , формулы, которая решает все квадратные уравнения. Хотя квадратная формула работает с любым квадратным уравнением в стандартной форме, легко сделать ошибку при подстановке значений в формулу. Будьте внимательны при замене и используйте круглые скобки при вставке отрицательного числа.{2} — \ left (4 \ right) \ cdot \ left (1 \ right) \ cdot \ left (2 \ right)}} {2 \ cdot 1} \ hfill \\\ hfill & = \ frac {-1 \ pm \ sqrt {1–8}} {2} \ hfill \\ \ hfill & = \ frac {-1 \ pm \ sqrt {-7}} {2} \ hfill \\\ hfill & = \ frac {-1 \ pm я \ sqrt {7}} {2} \ hfill \ end {array} [/ latex]

Решение уравнения: [latex] x = \ frac {-1} {2} + \ frac {i \ sqrt {7}} {2} [/ latex] и [latex] x = \ frac {-1 } {2} — \ frac {i \ sqrt {7}} {2} [/ latex].