Квадрат cos: Квадрат синуса, косинуса, тангенса, котангенса (альфа)
Тригонометрические тождества и преобразования
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:
Простейшие тригонометрические тождества
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.
Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.
Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.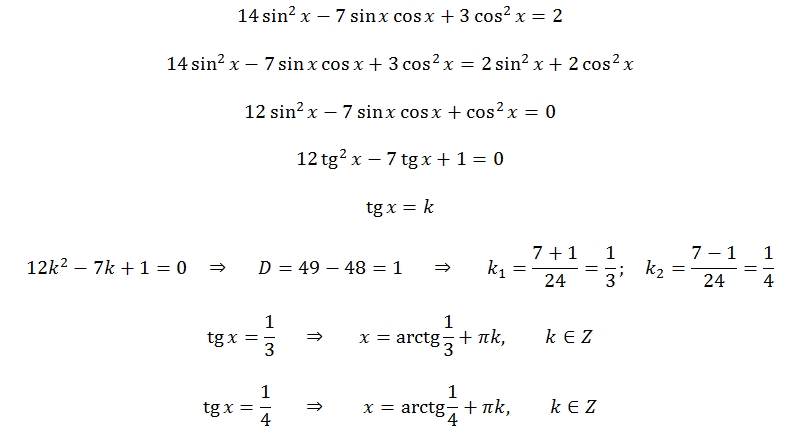
В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
См. также Полный список формул приведения тригонометрических функций.
| Угол |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 — α π/2- α |
180 — α π- α |
270 — α 3π/2- α |
360 — α 2π- α |
| sin | cos α | -sin α | -cos α | cos α | sin α | -cos α | -sin α |
| cos | -sin α | -cos α | sin α | sin α | -cos α | -sin α | cos α |
| tg | -ctg α | tg α | -ctg α | ctg α | -tg α | ctg α | -tg α |
| ctg | -tg α | ctg α | -tg α | tg α | -ctg α | tg α | -ctg α |
Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120) | Описание курса | Пояснение (доказательство) простейших тригонометрических тождеств
Основные формулы тригонометрии.
 — Тригонометрия.
— Тригонометрия.Теорема синусов[править | править вики-текст]
Стороны треугольника пропорциональны синусам противолежащих углов. Для произвольного треугольника
где — радиус окружности, описанной вокруг треугольника.
Теорема косинусов[править | править вики-текст]
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Для плоского треугольника со сторонами и углом , противолежащим стороне ,
или:
Теорема тангенсов[править | править вики-текст]
Формула Эйлера[править | править вики-текст]
Формула Эйлера утверждает, что для любого действительного числа выполнено следующее равенство:
где — основание натурального логарифма, — мнимая единица. Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:
Вышеуказанные уравнения могут быть получены путем сложения или вычитания формул Эйлера:
с последующим решением относительно синуса или косинуса. 3
3
 3
3 2.*(theta)
2.*(theta) он возвращает мне эту ошибку;
Ошибка с использованием греха. Недостаточно входных аргументов.
Я в замешательстве, что мне нужно изменить?
matlab trigonometryПоделиться Источник Nikolaj 28 марта 2013 в 09:27
2 ответа
- MATLAB sin() против sind()
Я заметил, что MATLAB имеет функции sin() и sind() . Я узнал, что sin() принимает угол в радианах, а sind() принимает угол в градусах. Единственная разница, которую я знаю, это то, что sind(180) дает 0, а sin(pi) -нет: >> sin(pi) ans = 1.2246e-016 >> sind(180) ans = 0 Что меня…
- создание изображения в matlab из 9 маленьких белых кругов в большом черном квадрате
Я хочу создать изображение в Matlab большого черного прямоугольника с 9 маленькими кругами, расположенными в виде массива 3×3, выровненного по центру прямоугольника, то есть центральный круг будет иметь свою среднюю точку в центре квадрата.
 2 sin(k*pi*x)$ Я…
2 sin(k*pi*x)$ Я…
Быстрая аппроксимация для sin/cos в MATLABЯ пытаюсь создать быстрое приближение sin и cos в MATLAB, которое является текущим узким местом в моей программе. Существует ли более быстрый метод, чем встроенная процедура? Узкое место: на каждой…
Построение графика sin (x)/(x) в MatlabУ меня возникли проблемы с правильным построением графика sin(x)/(x). В частности, когда x = 0, возвращает NaN в Matlab. Однако при применении правила L’hôpital фактическое значение равно y = 1. мой…
Правила ввода математических выражений
Ввод чисел:
Целые числа вводятся обычным способом, например: 4; 18; 56
Для ввода отрицательного числа необходимо поставить знак минус: -19; -45; -90
Рациональные числа вводятся с использованием символа /, например: 3/4;-5/3;5/(-19)
Вещественные числа вводятся с использованием точки в качестве разделителя целой и дробной частей: 4. 5;-0.4
5;-0.4
Ввод переменных и констант:
Переменные и константы вводятся латинскими буквами, например: x; y; z; a; b.
Константы π и e вводятся как pi и e — соответственно.
Символ бесконечности ∞ вводится двумя маленькими латинскими буквами oo или словом inf.
Соответственно, плюс бесконечность задается как +oo, и минус бесконечность как -oo.Сумма и разность:
Сумма и разность задаются при помощи знаков + и — соответственно, например: 3+a; x+y; 5-4+t; a-b+4; ВНИМАНИЕ! Никаких пробелов между операндами быть не должно, например ввод: x + a — неправильный, правильно вводить так: x+a — без пробелов.
 (1/n)
(1/n)
| Что ввели | Что получится |
|---|---|
| x^4 | x4 |
| (5-2*x)^(1/3) | 52×13 |
| (5/2+x)^4/2 | 52×42 |
| sin(3*x+4)^5 | sin53x4 |
| 1/sqrt(3*x^2+2) | 13×22 |
| (sqrt(x)-2*(x^3)+6)/x | x2x36x |
| e^(3*x)*cos(x)^2 | e3xcos2x |
| ((ln(x-7))^5)/(x-7) | ln5x7x7 |
| 1/(arcsin(x)^2*sqrt(1-x^2)) | 1arcsin2x1x2 |
| 2*x*arccos(3*x^2) | 2xarccos3x2 |
| (5+(x/3)^3)/(8*(x+y)^(1/2)) | 5x338xy |
Теорема Косинусов и Синусов треугольника.
 Формулы и примеры
Формулы и примерыФормулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула Теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.
Из формулы следует: a2 = c2 — b2
К полученному выражению прибавим и отнимем квадрат второго катета:
Но так как b = c * cos α, то
Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. |
Формула теоремы косинусов:
a2 = b2 + c2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
BC2 = (x2 — x1)2 + (y2 — y1)2
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
cos2α + sin2α = 1 — основное тригонометрическое тождество.
b2(cos2α + sin2α) — 2bc cos α + c2 = b2 + c2 — 2bc cos α
Что и требовалось доказать.
Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:
- Когда b2 + c2 — a2 > 0, угол α будет острым.
- Когда b2 + c2 — a2 = 0, угол α будет прямым.
- Когда b2 + c2 — a2 < 0, угол α будет тупым.
Запоминаем
Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b * cos α,
- DB = c – b * cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 — (b * cos α)2
- h2 = a2 — (c – b * cos α)2
Приравниваем правые части уравнений:
- b2 — (b * cos α)2 = a2 — (c — b * cos α)2
либо
- a2 = b2 + c2 — 2bc * cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b2 = a2 + c2 — 2ac * cos β;
- c2 = a2 + b2 — 2ab * cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 — 2bc cos α
b2 = c2 + a2 — 2ca cos β
c2 = a2 + b2 — 2ab cos γ
Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника.
Описание формулы косинуса угла из теоремы косинусов
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Аналогично:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B: - Из треугольника СМВ по теореме косинусов найдём СМ:
Ответ: СМ = √33.
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.
Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.
- Если c2 < a2 + b2, то ∠C — острый.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в онлайн-школу Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.
Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок математики вместе с ребенком и попробуйте сами!
Функция косинус-квадрат — исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел до действительных чисел. Информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференциации и интеграции, представлена в статье.
Посмотреть полный список конкретных функций в этой вики
Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т.Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах.Так, например, угол измеряется как.
Определение
Эта функция, обозначенная, определяется как комбинация функции квадрата и функции косинуса. Явно это карта:
Для краткости запишем как.
Ключевые данные
| Арт. | Значение |
|---|---|
| Домен по умолчанию | все действительные числа, т. Е. Все из. |
| диапазон | , г.е.,. |
| период | , т.е. |
| локальные максимальные значения и точки достижения | Все локальные максимальные значения равны 1 и достигаются при целых кратных. |
| локальные минимальные значения и точки достижения | Все локальные минимальные значения равны 0 и достигаются при нечетных целых кратных. |
| точек перегиба (обе координаты) | нечетных кратных, со значением в каждой точке |
| производная | я. е., отрицательная функция синусоиды двойного угла. е., отрицательная функция синусоиды двойного угла. |
| вторая производная | |
| Высшие производные | раз выражение, которое равно или, в зависимости от остатка от mod 4. |
| первообразное | |
| среднее значение за период | |
| выражение как синусоидальная функция плюс постоянная функция | |
| важные симметрии | even function В общем, имеет зеркальную симметрию относительно всех вертикальных линий, целое число. Также имеет симметрию на пол-оборота относительно всех точек формы, то есть всех точек перегиба. |
| описание интервала на основе увеличения / уменьшения и вогнутости вверх / вниз | Для каждого целого числа интервал от до делится на четыре части: : убывающая и вогнутая вниз : убывающая и вогнутая вверх : увеличивающаяся и вогнутая вверх : увеличивающаяся и вогнутая вниз.  |
Тригонометрические тождества. Темы по тригонометрии.
Темы | Дом
20
Взаимные идентичности
Тангенс и котангенс
Пифагорейские тождества
Формулы сумм и разностей
Формулы двойного угла
Формулы полууглов
Произведений суммой
Суммы по продуктам
ИДЕНТИЧНОСТЬ — ЭТО РАВЕНСТВО, которое истинно для любого значения переменной.(Уравнение — это равенство, которое верно только для определенных значений переменной.)
В алгебре, например, у нас есть это тождество:
( x + 5) ( x — 5) = x 2 — 25.
Значение идентичности состоит в том, что при вычислении мы можем заменить любой член другим. Мы используем идентичность, чтобы придать выражению более удобную форму. В исчислении и во всех его приложениях центральное значение имеют тригонометрические тождества.
На этой странице мы представим основные идентичности. У студента не будет лучшего способа практиковать алгебру, чем доказывать их. Ссылки на доказательства приведены ниже.
Взаимные идентичности
| sin θ | = | 1 csc θ | csc θ | = | 1 sin θ | |
| cos θ | = | 1 сек θ | сек θ | = | 1 cos θ | |
| tan θ | = | 1 детская кроватка θ | детская кроватка θ | = | 1 тангенс угла θ | |
Проба
Опять же, при вычислении мы можем заменить любой член идентичности другим.Итак, если мы видим «sin θ», то можем, если захотим, заменить
| это с « | » 1 csc θ | «; и симметрично, если мы увидим» | 1 csc θ | «, |
, тогда мы можем заменить его на «sin θ».
Проблема 1. Что означает утверждение, что csc θ является обратной величиной
sin θ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Это означает, что их продукт 1.
sin θ csc θ = 1.
Урок 5 алгебры.
Проблема 2. Оценить
tan 30 ° csc 30 ° cot 30 °.
| желто-коричневый 30 ° csc 30 ° cot 30 ° | = | tan 30 ° cot 30 ° csc 30 ° |
| = | 1 · csc 30 ° | |
| = | 2. | |
Тема 4.
Тангенс и котангенс
| тангенс угла θ = | sin θ cos θ | детская кроватка θ = | cos θ sin θ |
Проба
Пример 1. Покажите: tan θ cos θ = sin θ.
Покажите: tan θ cos θ = sin θ.
Решение: Проблема означает, что мы должны написать левую часть, а затем показать с помощью подстановок и алгебры, что мы можем преобразовать ее, чтобы она выглядела как правая часть.
Начинаем:
Мы подошли к правой стороне.
Пифагорейские тождества
| а) | sin 2 θ + cos 2 θ | = | 1. |
| б) | 1 + загар 2 θ | = | сек 2 θ |
| в) | 1 + детская кроватка 2 θ | = | csc 2 θ |
| a ‘) | sin 2 θ | = | 1 — cos 2 θ. |
| cos 2 θ | = | 1 — грех 2 θ. | |
Они называются тождествами Пифагора, потому что, как мы увидим в их доказательстве, они являются тригонометрической версией теоремы Пифагора.
Два идентификатора, помеченные как ‘) — «а-простое число» — просто разные версии а).Первый показывает, как мы можем выразить sin θ через cos θ; второй показывает, как мы можем выразить cos θ через sin θ.
Примечание: sin 2 θ — «синус-квадрат тета» — означает (sin θ) 2 .
Задача 3. Треугольник 3-4-5 прямоугольный.
а) Почему?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Он удовлетворяет теореме Пифагора.
б) Оцените следующее:
| sin 2 θ | = | 16 25 | cos 2 θ | = | 9 25 | sin 2 θ + cos 2 θ | = | 1. |
Пример 2. Показать:
Это то, что мы хотели показать.
Формулы сумм и разностей
| sin (α + β) | = | sin α cos β + cos α sin β |
| sin (α — β) | = | sin α cos β — cos α sin β |
| cos (α + β) | = | cos α cos β — sin α sin β |
| cos (α — β) | = | cos α cos β + sin α sin β |
Примечание: В формулах синуса + или — слева также + или — справа.Но в формулах косинуса + слева становится — справа; и наоборот.
Поскольку эти тождества доказываются непосредственно из геометрии, от студента обычно не требуется усваивать доказательство. Однако все последующие тождества основаны на этих формулах суммы и разности. Студент обязательно должен их знать.
Вот доказательство формул суммы.
Пример 3. Оценить sin 15 °.
Оценить sin 15 °.
| Решение. | sin 15 ° | |||
| Формулы | ||||
| Темы 4 и 5 | ||||
Пример 4.Доказательство:
Это то, что мы хотели доказать.
Формулы двойного угла
Проба
Существует три версии cos 2α. Первый — с точки зрения обоих cos α и sin α. Второй — только по cos α. Третий — только с точки зрения sin α
| Пример 5. Показать: sin 2α |
Это то, что мы хотели доказать.
| Пример 6. Показать: |
| Решение. | грех x |
— согласно предыдущему тождеству с α =.
Формулы полууглов
Следующие ниже формулы половинного угла являются инверсией формул двойного угла, потому что α составляет половину от 2α.
Знак плюс или минус зависит от квадранта. Под корнем косинус имеет знак +; синус, знак -.
Проба
| Пример 7. Вычислить cos | . π 8 | . |
| Пример 8. Вывести идентификатор для tan | . α 2 | . |
при делении числителя и знаменателя на cos α.
Произведений суммой
| а) | sin α cos β | = | ½ [грех (α + β) + грех (α — β)] | |
| б) | cos α sin β | = | ½ [sin (α + β) — sin (α — β)] | |
| в) | cos α cos β | = | ½ [cos (α + β) + cos (α — β)] | |
| г) | sin α sin β | = | −½ [cos (α + β) — cos (α — β)] | |
Проба
Суммы по продуктам
| д) | sin A + sin B | = | 2 sin ½ ( A + B ) cos ½ ( A — B ) |
| е) | sin A — sin B | = | 2 sin ½ ( A — B ) cos ½ ( A + B ) |
| г) | cos A + cos B | = | 2 cos ½ ( A + B ) cos ½ ( A — B ) |
| ч) | cos A — cos B | = | −2 sin ½ ( A + B ) sin ½ ( A — B ) |
В доказательствах ученик увидит, что тождества с e) по h) являются инверсиями соответственно от a) до d), которые доказываются в первую очередь. Тождество f) используется для доказательства одной из основных теорем исчисления, а именно о производной sin x .
Тождество f) используется для доказательства одной из основных теорем исчисления, а именно о производной sin x .
Учащийся не должен пытаться запомнить эти личности. Достаточно попрактиковаться в их доказательствах — и увидеть, что они исходят из формул суммы и разности.
Темы | Дом
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.2 (y) $? — Обмен математическим стеком
Сеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 3к раз
$ \ begingroup $ Для 4. 2 (x)) = \? $
2 (x)) = \? $
Создан 20 дек.
ронноронно6,0471919 серебряных знаков4747 бронзовых знаков
$ \ endgroup $ 3 $ \ begingroup $На первый вопрос отвечает ronno.Что касается вашего второго вопроса, вы можете увидеть, что это правда, просто упростив правую часть каждого уравнения.
Создан 20 дек.
математика1,977 11 золотой знак 99 серебряных знаков253253 бронзовых знака
$ \ endgroup $ $ \ begingroup $ Если кто-то принимает эти три личности:
$$
\ грех ^ 2 \ тета + \ соз ^ 2 \ тета = 1
$$
$$
\ грех (х + у) = \ грех х \ соз у + \ соз х \ грех у
$$
$$
\ соз (х + у) = \ соз х \ соз у — \ грех х \ грех у
$$
Затем следует большой класс других личностей, включая те, что указаны в вашем вопросе.
Теперь, почему человек должен принять три вышеупомянутых личности? Я не знаю их исторических доказательств, хотя первое обычно приписывают пифагору. Способ доказательства этих тождеств зависит от того, как $ \ textbf {определяет} $ концепции $ \ sin $ и $ \ cos $.
Я предпочитаю определение бесконечных рядов, и методы, которые я бы использовал для доказательства этих тождеств, основаны на идеях анализа (включая исчисление) и использовании комплексных чисел.Это определенно не тот способ, которым эти идентичности были исторически доказаны, но я считаю, что это более фундаментальный способ их понимания.
Создан 20 дек.
R RR R1,9499 серебряных знаков1515 бронзовых знаков
$ \ endgroup $ 1Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками тригонометрия или задайте свой вопрос.
 Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.2 $ то же самое? — Обмен математическим стеком
Сеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 2k раз
$ \ begingroup $ Являются ли $ \ cos ^ 2 \ theta $ и $ \ cos \ theta ^ 2 $ одинаковыми?
Я имею в виду, будь то $ \ sin, \ cos, \ tan, \ cot, \ sec, \ csc $. Они такие же? Пожалуйста, помогите математику здесь.
Они такие же? Пожалуйста, помогите математику здесь.
9,51822 золотых знака2323 серебряных знака4545 бронзовых знаков
Создан 24 фев.
$ \ endgroup $ 2 $ \ begingroup $Нет, они не такие.2) $.
Создан 24 фев.
Онил90Онил902,7358 серебряных знаков2525 бронзовых знаков
$ \ endgroup $ 3 $ \ begingroup $ Первое обозначение используется для обозначения
$$ \ cos ^ 2 \ theta = \ left (\ cos \ theta \ right) ^ 2 $$
Ваше второе обозначение обычно читается как
$$ \ cos \ theta ^ 2 = \ cos \ left (\ theta ^ 2 \ right) $$
хотя иногда для ясности предпочтительнее использовать обозначения в правой части.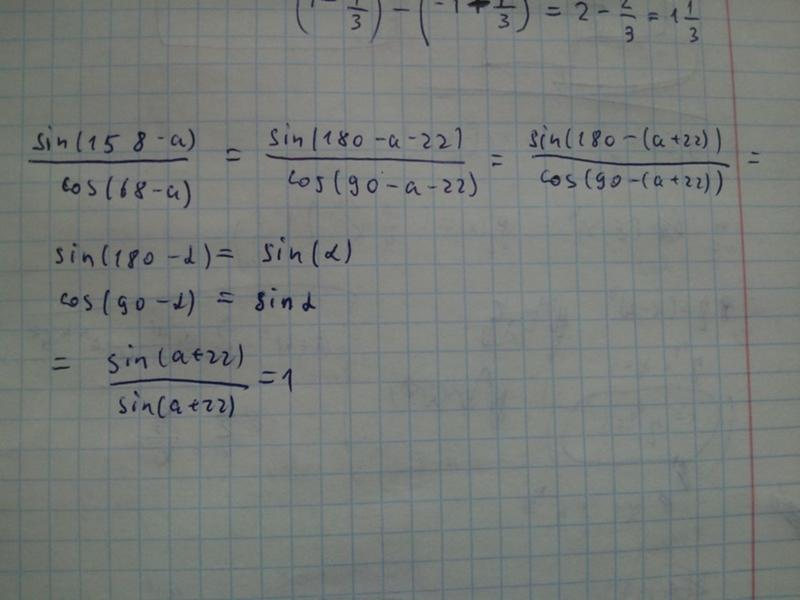 2) $
2) $
Создан 24 фев.
StackTDStackTD26.9k2727 серебряных знаков5757 бронзовых знаков
$ \ endgroup $ 6 $ \ begingroup $Это вопрос синтаксиса.{2}) $.
Следует быть очень осторожным.
Создан 24 фев.
Нг Чунг Так Нг Чунг Так16.9k33 золотых знака1616 серебряных знаков3737 бронзовых знаков
$ \ endgroup $Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками тригонометрия или задайте свой вопрос.
 Mathematics Stack Exchange лучше всего работает с включенным JavaScript
Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Понимание пифагорейской идентичности | StudyPug
Что такое пифагорейские тождества?
Тождество в математике — это всегда верное уравнение. Все пифагорейские тождества включают число 1, и его пифагорейские аспекты можно ясно увидеть при доказательстве теорем о единичной окружности.
Все пифагорейские тождества включают число 1, и его пифагорейские аспекты можно ясно увидеть при доказательстве теорем о единичной окружности.
Пифагорейские тождества
В этом вопросе мы собираемся исследовать пифагорейские тождества. Вы можете обратиться к приведенному ниже списку формул, когда имеете дело с 3 пифагорейскими тождествами.
список пифагорейских тождествДавайте исследуем пифагорейские тождества. В первом из этих трех состояний синус в квадрате плюс косинус в квадрате равняется единице.2 \ тета = 1cos2θ + sin2θ = 1
С чего начать? Вы помните свойства единичного круга? Мы рассмотрели единичный круг в предыдущем разделе. Вкратце, единичный круг — это просто круг с радиусом в одну единицу, то есть радиус должен быть равен единице.
получить пифагорейскую идентичность, используя единичный кругСм. Изображение выше. Мы обозначим точку на окружности в X, Y. Здесь координата X равна X, а координата Y — Y.
С этого момента проведем перпендикулярную линию к оси X. Мы сосредоточимся на этом треугольнике.
Мы сосредоточимся на этом треугольнике.
На этом изображении найдите момент, чтобы вспомнить, что? средства. На самом деле это опорный угол, верно? Это один из самых важных углов в тригонометрии.
Что означает опорный угол, если координата X равна X? Это означает, что длина сегмента X равна X. Аналогичным образом, если координата Y равна Y, это означает, что длина вертикального сегмента треугольника будет Y.
Давайте продемонстрируем это на реальных цифрах, чтобы проиллюстрировать эту концепцию.
иллюстрация взаимосвязи между координатой и длиной отрезков треугольникаВ приведенном выше примере есть точка 3,5. Если мы рисуем треугольник, тройка обозначает координату X. Это означает, что длина этого сегмента равна 3. Теперь, если координата Y равна 5, что это значит? Длина вертикального отрезка треугольника должна составлять пять.
Возвращаясь к предыдущей иллюстрации единичного круга, давайте сосредоточимся на прямоугольном треугольнике и применим теорему Пифагора. Что такое теорема Пифагора? Пифагор говорит нам, что X в квадрате плюс Y в квадрате равняется квадрату гипотенузы. Гипотенуза в данном случае равна единице, поскольку мы используем единичную окружность. Итак, здесь X в квадрате плюс Y в квадрате равняется одному квадрату.
Что такое теорема Пифагора? Пифагор говорит нам, что X в квадрате плюс Y в квадрате равняется квадрату гипотенузы. Гипотенуза в данном случае равна единице, поскольку мы используем единичную окружность. Итак, здесь X в квадрате плюс Y в квадрате равняется одному квадрату.
Одна из замечательных особенностей единичного круга заключается в том, что его координата X также может быть представлена в терминах угла тета. Координата X может быть представлена как косинус-тета, а ее координата Y может быть представлена как синус-тета. Имейте в виду, что это только для единичного круга.2 \ тета = 1 cos2θ + sin2θ = 1
Ответ становится очевидным благодаря использованию единичного круга. Один квадрат — это всего лишь один. Координата X также может быть представлена как тета-косинус. Координата Y может быть представлена как синус-тета. И вуаля! Мы сделали. Используя единичную окружность, мы успешно доказали, что возведенный в квадрат косинус плюс квадрат синуса равняется единице, решая одно из трех тождеств Пифагора.
| За последние несколько страниц вы видели довольно много тригонометрических отождествлений.Для справки удобно иметь их краткое изложение. Эти тождества в основном относятся к одному углу, обозначенному θ , но есть некоторые, которые включают два угла, и для них два угла обозначены α и β . | |
Более важные идентичности.Необязательно знать все личности с головы до ног. Но это вам следует. | |
| Определение отношений для тангенса, котангенса, секанса и косеканса в терминах синуса и косинуса. | |
| Формула Пифагора для синусов и косинусов. Это, наверное, самая важная триггерная идентичность. | |
Идентификаторы, выражающие триггерные функции в терминах их дополнений. В этом нет ничего особенного. Каждая из шести триггерных функций равна своей совместной функции, оцениваемой под дополнительным углом. Каждая из шести триггерных функций равна своей совместной функции, оцениваемой под дополнительным углом. | |
| Периодичность триггерных функций. Синус, косинус, секанс и косеканс имеют период 2 π , а тангенс и котангенс имеют период π . | |
| Тождества для отрицательных углов. Синус, тангенс, котангенс и косеканс являются нечетными функциями, а косинус и секанс — четными функциями. | |
| Тождества Птолемея, формулы суммы и разности для синуса и косинуса. | |
| Формулы двойного угла для синуса и косинуса. Обратите внимание, что существует три формы формулы двойного угла для косинуса. Вам нужно знать только одно, но уметь вывести два других из формулы Пифагора. | |
Менее важные идентичности.Вы должны знать, что эти личности есть, но они не так важны, как упомянутые выше. Все они могут быть получены из вышеперечисленных, но иногда для этого требуется немного поработать. Все они могут быть получены из вышеперечисленных, но иногда для этого требуется немного поработать. | |
| Формула Пифагора для касательных и секущих. Есть еще один для котангенсов и косекансов, но поскольку котангенсы и косекансы нужны редко, в нем нет необходимости. | |
| Идентификаторы, выражающие триггерные функции в терминах их дополнений. | |
| Формулы суммы, разности и двойного угла для тангенса. | |
| Формулы половинных углов. Для синуса и косинуса берут положительный или отрицательный квадратный корень в зависимости от квадранта угла θ /2. Например, если θ /2 — острый угол, тогда будет использоваться положительный корень. | |
Действительно непонятные личности.Они здесь как раз для извращенности. Нет, не совсем. У них есть несколько приложений, но обычно это узкие приложения, и о них также можно забыть, пока они не понадобятся. | |
| Идентификаторы продукта-суммы. Эта группа идентичностей позволяет вам преобразовать сумму или разность синусов или косинусов в произведение синусов и косинусов. | |
| Идентификационные данные продукта. Кроме того: как ни странно, эти идентификаторы продуктов использовались до того, как были изобретены логарифмы для выполнения умножения. Вот как можно использовать второй.Если вы хотите умножить x на y, используйте таблицу, чтобы найти угол α , косинус которого равен x , и угол β , косинус которого равен y . Найдите косинусы суммы α + β . а разность α — β . Усредните эти два косинуса. Вы получаете товар xy ! Три просмотра таблиц и вычисление суммы, разницы и среднего, а не одно умножение. Тихо Браге (1546–1601), среди прочих, использовал этот алгоритм, известный как простафаэрез . | |
Формулы тройного угла.
| |

 2 sin(k*pi*x)$ Я…
2 sin(k*pi*x)$ Я… 5;-0.4
5;-0.4
 (1/n)
(1/n)

 Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах.Так, например, угол измеряется как.
Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах.Так, например, угол измеряется как.