Квадрат a квадрат b квадрат: § Формулы сокращённого умножения. Разность квадратов. Квадрат суммы. Куб суммы. Разность кубов и другие формулы
7.3.1. Примеры для закрепления формул сокращенного умножения.
Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 5.4k. Опубликовано
1) Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a+b)2 = a2+2ab+b2
a) (x + 2y)2 = x2 + 2 ·x·2y + (2y)2 = x2 + 4xy + 4y2
б) (2k + 3n)2 = (2k)2 + 2·2k·3n + (3n)2 = 4k2 + 12kn + 9n2
2) Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)2 = a2-2ab+b2
а) (2a – c)
б) (3a – 5b)2 = (3a)2-2·3a·5b + (5b)2 = 9a2 – 30ab + 25b2
3) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
a2–b2 = (a–b)(a+b)
a) 9x2 – 16y2 = (3x)2 – (4y)2 = (3x – 4y)(3x + 4y)
б) (6k – 5n)( 6k + 5n) = (6k)2 – (5n)2 = 36k2 – 25n2
4) Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a+b)3 = a3+3a2b+3ab2+b3
a) (m + 2n)3 = m3 + 3·m2·2n + 3·m·(2n)2 + (2n)3 = m3 + 6m2n + 12mn2 + 8n3
б) (3x + 2y)3 = (3x)3 + 3·(3x)2·2y + 3·3x·(2y)2 + (2y)3 = 27x3 + 54x2y + 36xy2 + 8y3
5) Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a-b)3 = a3-3a2b+3ab2-b3
а) (2x – y)3 = (2x)3-3·(2x)2·y + 3·2x·y2 – y3 = 8x3 – 12x2y + 6xy2 – y3
б) (x – 3n)3 = x3-3·x2·3n + 3·x·(3n)2 – (3n)3 = x3 – 9x2
6) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a3+b3 = (a+b)(a2–ab+b2)
a) 125 + 8x3 = 53 + (2x)3 = (5 + 2x)(52 — 5·2x + (2x)2) = (5 + 2x)(25 – 10x + 4x2)
б) (1 + 3m)(1 – 3m + 9m2) = 13 + (3m)3 = 1 + 27m3
7) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
a3-b3 = (a-b)(a2+ab+b2)
а) 64с3 – 8 = (4с)3 – 23 = (4с – 2)((4с)2 + 4с·2 + 22) = (4с – 2)(16с2 + 8с + 4)
б) (3a – 5b)(9a2 + 15ab + 25b2) = (3a)3 – (5b)3 = 27a3 – 125b3
Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.Урок алгебры в 7-м классе для дистанционного обучения детей с ограниченными возможностями «Формулы сокращенного умножения»
Цель: научиться применять формулы сокращенного умножения при решении примеров, повторить материал.
План:
- Ключевые слова.
- Доказательство формулы суммы кубов.
- Примеры.
- Повторение.
- Примеры с объяснением
- Домашнее задание.
Ключевые слова: квадрат суммы, квадрат
разности, куб суммы, куб разности, разность
квадратов, сумма кубов, разность кубов.
Квадрат суммы
двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй (a+b)2=a2+2ab+ b2Квадрат разности двух величин равен квадрату первой минус удвоенное произведение первой на вторую плюс квадрат второй.
Произведение суммы двух величин на их разность равно разности их квадратов. (a+b)(a-b)=a2-b2
Куб суммы двух величин равен кубу первой плюс утроенное произведение квадрата первой на вторую плюс утроенное произведение первой на квадрат второй плюс куб второй. (a+b)3=a3+3a2b+3ab2+b3
Куб разности двух величин равен кубу первой
минус утроенное произведение квадрата первой на
вторую плюс утроенное произведение первой на
квадрат второй минус куб второй.
Произведение суммы двух величин на неполный квадрат разности равно сумме их кубов. ( a+b)(a2-ab+b2)=a3+b3
Произведение разности двух величин на неполный квадрат суммы равно разности их кубов. (a-b)(a2+ab+b2)=a3- b3
Очень часто приведение многочлена к стандартному виду можно осуществить путём применения формул сокращённого умножения . Все они доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Формулы сокращённого умножения нужно знать наизусть.
Пример. Докажите формулу a 3 + b 3 = ( a + b )( a 2 – ab + b 2 ).
Решение. Имеем ( a + b )( a 2 –
ab + b 2 ) = a 3 – a 2
b + ab 2 + ba 2 – ab 2
– b 3. Приводя подобные слагаемые, мы
видим, что ( a + b )( a 2 – ab +
b
Приводя подобные слагаемые, мы
видим, что ( a + b )( a 2 – ab +
b
Пример. Упростите выражение (2 x 3 – 5 z )(2 x 3 + 5 z ).
Решение. Воспользуемся формулой разности квадратов, получим: (2 x 3 – 5 z )(2 x 3 + 5 z ) = (2 x 3 ) 2 – (5 z ) 2 = 4 x 6 – 25 z 2.
Ответ. 4 x 6 – 25 z 2.
Разложить многочлен на множители значит представить его в виде произведения более простых многочленов.
Немного теории.
Существует несколько способов разложения:
Вынесение общего множителя за скобки
Алгоритм отыскания общего множителя нескольких одночленов
Найти наибольший общий делитель коэффициентов
всех одночленов, входящих в многочлен, — он и
будет общим числовым множителем (разумеется, это
относится только к случаю целочисленных
коэффициентов).
Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.
Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.
Найти наибольший общий делитель коэффициентов
всех одночленов, входящих в многочлен, — он и
будет общим числовым множителем (разумеется, это
относится только к случаю целочисленных
коэффициентов).
Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.
Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, — он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.
Способ группировки
Алгоритм разложение многочлена на множители способом группировки
- Сгруппировать его члены так, чтобы слагаемые в
каждой группе имели общий множитель.

- Вынести в каждой группе общий множитель в виде одночлена за скобки.
- Вынести в каждой новой группе общий множитель (в виде многочлена) за скобки
Разложение многочлена на множители с помощью комбинации различных приемов
В математике не так часто бывает, чтобы при решении примера применялся только один прием, чаще встречаются комбинированные примеры, где сначала используется один прием, затем другой и т.д. Чтобы успешно решать такие примеры, мало знать сами приемы, надо еще уметь выработать план их последовательного применения. Иными словами, здесь нужны не только знания, но и опыт. Вот такие комбинированные примеры мы и рассмотрим.
Пример 1
Разложить на множители многочлен 36a6b3-96a4b4+64a2b5
Сначала займемся вынесением общего множителя
за скобки. Рассмотрим коэффициенты 36, 96, 64. Все
они делятся на 4.
НОД(36,96,64)=4. Во все члены многочлена входит переменная a (соответственно a6, a4, a2), поэтому за скобки можно вынести a2. Во все члены многочлена входит переменная b (соответственно b3, b4, b5) – за скобки можно вынести b3.
Итак, за скобки вынесем 4a2b3.
36a6b3-96a4b4+64a2b5=4a2b3(9a4-24a2b+16b2).
2) Рассмотрим трехчлен в скобках: 9a4-24a2b+16b2. Выясним, не является ли он полным квадратом. Имеем:
9a4 — 24a2b + 16b2 = (3a2)2 — 2·3a2·4b + (4b)2.
Все условия полного квадрата соблюдены, следовательно,
9a4 — 24a2b + 16b2 = (3a2-4b)2.
3) Комбинируя два приема (вынесение общего множителя за скобки и использование формул сокращенного умножения), получаем окончательный результат:
36a6b3-96a4b4+64a2b5=
4a2b3(3a2-4b)2.
Пример 1
Разложить на множители многочлен 36a6b3-96a4b4+64a2b5
Решение (краткая запись)
36a6b3-96a4b4+64a2b5=4a2b3(9a4-24a2b+16b2) =4a2b3 (3a2-4b)2
Комбинируем два приема:
- вынесение общего множителя за скобки;
- использование формул сокращенного умножения.
Пример 2
Разложить на множители многочлен a2 — с2 + b2 + 2ab
Решение:
Комбинируем два приема:
- группировку;
- использование формул сокращенного умножения
Пример 3
Разложить на множители многочлен y3 – 3y2 + 6y – 8
Попробуйте его решить
Комбинируйте три приема:
- группировку;
- формулы сокращенного умножения;
- вынесение общего множителя за скобки.

Решение:
y3 – 3y2 + 6y – 8=(y3-8)-(3y2-6y) = (y-2)(y2+2y+4)-3y(y-2) = (y-2)(y2+2y+4-3y)=(y-2)(y2-y+4).
Комбинирование различных приемов
Порядок применения различных методов при разложении многочлена на множители
Попробовать разложить многочлен на множители по формулам сокращенного умножения.
“Вынести общий множитель за скобку (если он есть).
Увидеть” и попробовать выделить полный квадрат.
Попытаться применить способ группировки (если предыдущие способы не привели к цели).
За страницами учебника алгебры
Квадратное уравнение – это уравнение вида: ax2+bx+c=0 (где a=0)
Многочлен вида: ax2+bx+с – квадратный трёхчлен.
Коэффициенты: a, b, с (где с – свободный член)
Задание 1. Разложить на множители x2+5x-6,
используя метод предварительного
преобразования.
Разложить на множители x2+5x-6,
используя метод предварительного
преобразования.
Внимание! Делители свободного члена.
Задание 2.
Разложить на множители x3+2x2-5x-6, используя метод предварительного преобразования.
Внимание! Делители свободного члена.
Пример 4
Разложить на множители n3+3n2+2n
Сначала воспользуемся тем, что n можно вынести за скобки: n(n2+3n+2). Теперь к трехчлену n2+3n+2 применим способ группировки, предварительно представив 3n в виде 2n+n. Получим:
n2+3n+2=n2+2n+n+2=(n2+2n)+(n+2)=n(n+2)+(n+2)=(n+2)(n+1).
Окончательно получаем:
n2+3n+2=n(n+1)(n+2).
Задание: самостоятельно попробуйте сделать краткую запись примера
Метод выделения полного квадрата
Пример разложить на множители квадратный трехчлен х2-6x+5
Первый способ.
Используем предварительное преобразование, обращая внимание на свободный член +5. Делители 5: +1,-1,+5,-5.
Представим –6x=–x+(-5x), а затем применим способ группировки:
x2-6x+5=x2-5x+5=(x2-x)+(-5x+5)=x(x-1)-5(x-1)=(x-1)(x-5).
Второй способ.
Применим метод выделения полного квадрата, для этого обратим внимание на удвоенное произведение 6х=2*х*3.
Значит полный квадрат будет справедлив для двух выражений х и 3.
x2-6x+5=(x2-2·x·3+32)-32+5 = (x2-6x+9)-9+5 = (x2-6x+9)-4 = (x-3)2-22=(x-3-2)(x-3+2) = (x-5)(x-1)
ОСНОВНЫЕ РЕЗУЛЬТАТЫ
Мы научились использовать комбинацию различных приемов при разложение многочлена на множители. Попытались выработать план применения на практике.
При разложении многочлена на множители мы использовали следующие способы:
- вынесение общего множителя за скобки;
- группировка, в том числе с использованием предварительного преобразования;
- использование формул сокращенного умножения;
- выделение полного квадрата;
- комбинирование различных приемов.

Домашнее задание. № 645, 654, 648(в,г).
Главная
ГлавнаяНовинки плит
ЛДСП 2750-1830-16мм белый кристалл — N
Подробнее >арт.товара: 41088
ЛДСП 2800-2070-16мм дуб санта-фе винтаж h2330 ST10
Подробнее >арт.товара: 38432
ЛДСП 2800-2070-16мм дуб уайт-ривер песочно-бежевый h2312 ST10
Подробнее >арт.товара: 38446
ЛДСП 2800-2070-16мм камень пьетра гриджиа черный F206 ST9
Подробнее >арт. товара: 38449
товара: 38449
ЛДСП 2800-2070-16мм дуб лоренцо бежево-серый h4146 ST19
Подробнее >арт.товара: 38451
ЛДСП 2800-2070-16мм металлик файнлайн коричневый h4192 ST19
Подробнее >арт.товара: 38452
ЛДСП 2800-2070-16мм дуб галифакс олово h4176 ST37
Подробнее >арт.товара: 38459
ЛДСП 2800-2070-16мм дуб галифакс глазурованный черный h4178 ST37
Подробнее >арт.товара: 38460
ЛДСП 2800-2070-16мм серая галька U201 ST19
Подробнее >арт.товара: 38429
ЛДСП 2800-2070-16мм черный графит U961 ST19
Подробнее >арт. товара: 38436
товара: 38436
ЛДСП 2800-2070-16мм текстиль бежевый F416 ST10
Подробнее >арт.товара: 38437
Металлик файнлайн коричневый h4192 ST19
Подробнее >арт.товара:
Дуб галифакс глазурованный черный h4178 ST37
Подробнее >арт.товара:
Дуб уайт-ривер серо-коричневый h2313 ST10
Подробнее >арт.товара:
Дуб уайт-ривер песочно-бежевый h2312 ST10
Подробнее >арт.товара:
Камень пьетра гриджиа чёрный F206 ST9
Подробнее >арт.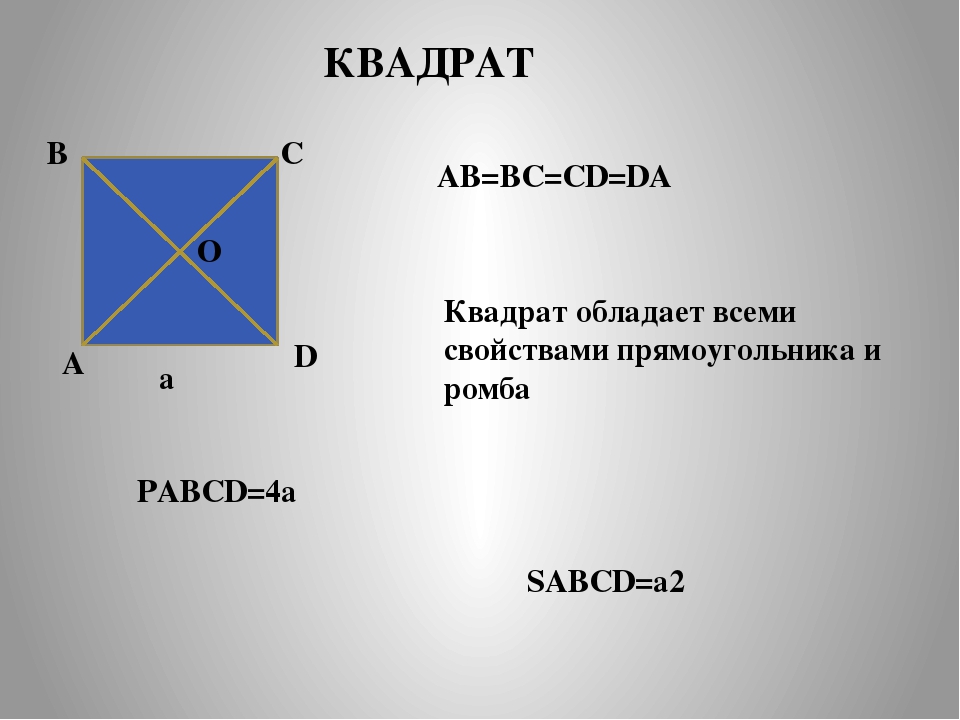 товара:
товара:
Лиственница горная коричневая термо h4408 ST38
Подробнее >арт.товара:
Дуб шерман коньяк коричневый h2344 ST32
Подробнее >арт.товара:
Металлик файнлайн антрацит h4190 ST19
Подробнее >арт.товара:
Робиния брэнсон натуральная коричневая h2251 ST19
Подробнее >арт.товара:
Робиния брэнсон трюфель коричневый h2253 ST19
Подробнее >арт.товара:
Новинки Фурнитуры
Мойка Модель 30, Круглая D475мм, Хлопок Мрамор
Подробнее >арт. товара: 38833
товара: 38833
Мойка Модель 10, Овал малый 575х440х215мм, Бежевый Мрамор
Подробнее >арт.товара: 38844
Мойка Модель 8, Квадратная 425х500х195мм, Песочный Мрамор
Подробнее >арт.товара: 38940
Мойка Модель 161, Прямоугольная 750х505х218мм, Черный Мрамор
Подробнее >арт.товара: 38839
Мойка Модель 150, Прямоугольная Малая 575х470х218мм, Терракот Мрамор
Подробнее >арт.товара: 39845
Мойка BLANCO LEGRA 45 S Шампань (522205)
Подробнее >арт.товара: 40000
Мойка FLORENTINA КОМБИ 650 Антрацит, 650х480х235мм 21. 390.B0650.302
390.B0650.302
арт.товара: 40268
Мойка Модель 9, Квадратная 570х505х200мм, Темно-Серый Мрамор
Подробнее >арт.товара: 40595
Мойка Premial PR 6045 (600х450х230мм, толщ.3мм), Сталь шлифованная
Подробнее >арт.товара: 37182
Мойка Круглая D490, Premial PL 4949, (490*390*180мм, толщ.0,8мм), ДЕКОР
Подробнее >арт.товара: 37536
Мойка Овал Premial PL 7750-D (770х500*180мм, толщ.0,8мм) ДЕКОР
Подробнее >арт.товара: 37537
Мойка Premial PL 6745-Е, (670×450х180мм, толщ. 0,8мм) , Матовая
0,8мм) , Матовая
арт.товара: 37688
Мойка Premial PL 6745-P, (670×450х180мм, толщ.0,8мм) , Глянец
Подробнее >арт.товара: 37689
Мойка Угловая Premial PL 9550C-P, (950×500х180мм, толщ.0,8мм) , Глянец
Подробнее >арт.товара: 38097
Мойка Premial 4848, (480×480х150мм, толщ.0,6мм) , Матовая
Подробнее >арт.товара: 38219
Мойка «Юкинокс» 780х480мм Левая Матовая Гранд GRM780.480 -GT6K 2L (с сифоном S701)
Подробнее >арт.товара: 41235
Корзина сетчатая 485х485х200мм ХРОМ (523)
Подробнее >арт. товара: 37986
товара: 37986
Корзина для белья с доводчиком, полного выдв., графит WG-KOSZ80-60
Подробнее >арт.товара: 36678
Корзина для белья с доводчиком, полного выдв., графит WG-KOSZ90-60
Подробнее >арт.товара: 36679
Корзина с органайзером с доводчиком, полного выдв., графит WG-PRZEG60-60
Подробнее >арт.товара: 36680
Корзина с органайзером с доводчиком, полного выдв., графит WG-PRZEG80-60
Подробнее >арт.товара: 36681
Корзина с органайзером с доводчиком, полного выдв., графит WG-PRZEG90-60
Подробнее >арт.товара: 36682
Крепление для прямоугольной штанги с заглушкой, графит WG-RDRP-60
Подробнее >арт.товара: 37779
Полка для обуви с доводчиком, полного выдв., графит WG-POBUW60-60
Подробнее >арт.товара: 36851
Подвеска каркаса УСИЛЕННАЯ 807.XL CAMAR, Левая L, 807.XL.Z1.IN.SX
Подробнее >арт.товара: 37550
Посудосушитель LOFT 800мм, Черный
Подробнее >арт.товара: 38218
Посудосушитель PANDORA SU07/600 БОЯРД
Подробнее >арт.товара: 41355
Посудосушитель LORA SU06/900 БОЯРД
Подробнее >арт.товара: 41883
Полка для специй и полотенец B-PLANUM, Тефлон, 349*163*118мм SRK221/TFL БОЯРД
Подробнее >арт.товара: 37208
Полка прямая B-PLANUM, Шампань, 21*350*130мм SRK121/CHMP БОЯРД
Подробнее >арт.товара: 37205
Рейлинг B-PLANUM 800мм, Шампань, SRC200/CHMP БОЯРД
Подробнее >арт.товара: 37201
Рейлинг B-PLANUM 800мм, Тефлон, SRC200/TFL БОЯРД
Подробнее >арт.товара: 37202
Крючок для рейлинга B-PLANUM, Шампань, SRh221/CHMP БОЯРД
Подробнее >арт.товара: 37203
Полка для специй 2-х ур. B-PLANUM, Шампань, 329*118*402мм SRK222/CHMP БОЯРД
Подробнее >арт.товара: 37213
Полка для ножей B-PLANUM, Тефлон, 395*89*181мм SRK521/TFL БОЯРД
Подробнее >арт.товара: 37216
Полка для планшета B-PLANUM, Шампань, 144*69*86мм SRK522/CHMP БОЯРД
Подробнее >арт.товара: 37217
Полка для крышек B-PLANUM, Тефлон, 305*313*50мм SRK523/TFL БОЯРД
Подробнее >арт.товара: 37220
ПЛАНКА AL-38 R-9мм торцевая универс. ХРОМ
Подробнее >арт.товара: 40776
Cargo 900мм Посудосушитель CARMA KRS05/1/3/900 с довод. и крепл. к фас. БОЯРД (уп.-1шт.)
Подробнее >арт.товара: 34476
Cargo mini 150мм FLORA KR05/1/3/150/L с доводчиком, боковое крепление БОЯРД (уп.-1шт.)
Подробнее >арт.товара: 34939
Cargo mini 300мм QUADRA KR28/2/3/300 с доводчиком, донное крепление БОЯРД (уп.-1шт.)
Подробнее >арт.товара: 34928
Cargo mini 350мм Корзина для бытовой химии с поддоном с дов. 450х280х360 LS1/350D/D
Подробнее >арт.товара: 33353
Cargo mini 300мм Квадро 3 + направл. Хеттих, бок.крепл., с крепл. к фасаду
Подробнее >арт.товара: 33042
Cargo mini 150мм Квадро 1 + направл. Хеттих, бок.крепл. Левая, с крепл. к фасаду ЧЕРНЫЙ
Подробнее >арт.товара: 36131
Cargo 600мм Посудосушитель выкатной Квадро, хром
Подробнее >арт.товара: 35714
Cargo 600мм Корзина выкатная Квадро, хром
Подробнее >арт.товара: 35719
Винный шкаф Tandem Starax, шир. 400мм (260х470х640) с довод. S-2181
Подробнее >арт.товара: 37229
Пенал М300 с дов. STELLA ESTETICA KR27/3/2/300/1970-2270 БОЯРД
Подробнее >арт.товара: 37977
Cargo 600мм Посудосушитель CARMA KRS05/1/3/600/GRPH с довод. и крепл. к фас., ГРАФИТ БОЯРД (уп-1шт.)
Подробнее >арт.товара: 41776
Cargo mini 150мм Bellissimo KR08/1/3/150/R/GRPH с доводчиком, ПРАВАЯ, ГРАФИТ БОЯРД (уп.-20шт.)
Подробнее >арт.товара: 41968
Распродажи фурнитуры
Мойка КВАДРАТ шоколад 460*510*190мм.
Подробнее >арт.товара: 33698
Мойка ОВАЛ Светло-Серая 765*495*200мм GRANIT
Подробнее >арт.товара: 34987
Мойка Кватро Серая 595*505*200мм GRANIT
Подробнее >арт.товара: 32263
Мойка Кватро Светло-Серая 595*505*200мм GRANIT
Подробнее >арт.товара: 34516
Мойка круглая серый D=510мм, глубина 200мм GRANIT
Подробнее >арт.товара: 26080
Мойка СКАТ Песок 975*505*200мм GRANIT
Подробнее >арт.товара: 34947
Мойка КВАДРАТ Серая 460*510*190мм. GRANIT
Подробнее >арт.товара: 33254
Мойка ОВАЛ Сахара 765*495*200мм GRANIT
Подробнее >арт.товара: 34946
Мойка ОВАЛ Песок 765*495*200мм GRANIT
Подробнее >арт.товара: 34941
Мойка ТЕХНО-780 Серая 780*500*180мм GRANIT
Подробнее >арт.товара: 34924
Мойка ЦЕНТРО Серая 645*505*200мм GRANIT
Подробнее >арт.товара: 34909
Мойка Круглая песок № 1 D=510мм, глубина 200мм GRANIT
Подробнее >арт.товара: 25970
Мойка BLANCORONDOVAL 45 S Шампань (515766)
Подробнее >арт.товара: 25571
Мойка FRANKE ROG 611С 3.5″, белый 114.0192.552
Подробнее >арт.товара: 30730
Мойка Кватро шоколад 595*505*200мм GRANIT
Подробнее >арт.товара: 32058
Мойка Blanco ZIA 9 E аллюметаллик (514757)
Подробнее >арт.товара: 31216
Мойка круглая Сахара D=510мм, глубина 200мм GRANIT
Подробнее >арт.товара: 33128
Мойка КВАДРАТ Песок 460*510*190мм. GRANIT
Подробнее >арт.товара: 33253
Мойка круглая светло-серый D=510мм, глубина 200мм GRANIT
Подробнее >арт.товара: 27448
Мойка круглая шоколад D=510мм, глубина 200мм GRANIT
Подробнее >арт.товара: 31965
Мойка ТЕХНО-780 Шоколад 780*500*180мм GRANIT
Подробнее >арт.товара: 34850
Мойка ОПТИМА Сахара 690*510*200мм GRANIT
Подробнее >арт.товара: 34848
Мойка МЕТРА Шоколад 755х495х180мм GRANIT
Подробнее >арт.товара: 35016
Мойка МЕТРА Черная 755х495х180мм GRANIT
Подробнее >арт.товара: 35072
Мойка СКАТ Светло-Серая 975*505*200мм GRANIT
Подробнее >арт.товара: 35073
Мойка ТЕХНО-755 Сахара 755*500*180мм GRANIT
Подробнее >арт.товара: 35164
Мойка МЕТРА Светло-серая 755х495х180мм GRANIT
Подробнее >арт.товара: 35115
Мойка ОВАЛ Шоколад 765*495*200мм GRANIT
Подробнее >арт.товара: 35033
Мойка ТЕХНО-755 Песок 755*500*180мм GRANIT
Подробнее >арт.товара: 35330
Мойка ЦЕНТРО Светло серая 645*505*200мм GRANIT
Подробнее >арт.товара: 35123
Мойка МЕТРА Песок 755х495х180мм GRANIT
Подробнее >арт.товара: 35519
Мойка ТЕХНО-755 Серая 755*500*180мм GRANIT
Подробнее >арт.товара: 35672
Мойка FRANKE ROG 610-41 3 1/2″, включая стоп-вентиль, сахара арт. 114.0175.358
Подробнее >арт.товара: 29607
Мойка МЕТРА Терракот 755х495х180мм GRANIT
Подробнее >арт.товара: 39305
Мойка круглая Терракот D=510мм, глубина 200мм GRANIT
Подробнее >арт.товара: 39243
Мойка ОВАЛ Терракот 765*495*200мм GRANIT
Подробнее >арт.товара: 39306
Мойка ТЕХНО-755 Терракот 755*500*180мм GRANIT
Подробнее >арт.товара: 39307
Мойка ТЕХНО-780 Терракот 780*500*180мм GRANIT
Подробнее >арт.товара: 39244
Мойка КВАДРАТ Терракот 460*510*190мм. GRANIT
Подробнее >арт.товара: 39254
Мойка Кватро Терракот 595*505*200мм GRANIT
Подробнее >арт.товара: 39304
Набор для мойки арт.112.0061.113: выпуск 3 1/2″, 6 креплений, уплотнит. лента
Подробнее >арт.товара: 28859
Набор для мойки арт.112.0006.332: выпуск 3 1/2″, 8 крепл., уплотнит.лента,шумопогл. резинка,пробка
Подробнее >арт.товара: 28860
Набор для мойки арт.112.0017.718: выпуск 3 1/2″, 10 креплений, уплотнит. лента,шумопогл. резинка
Подробнее >арт.товара: 28864
Набор для мойки арт.112.0006.351: выпуск 3 1/2″, 5 креплений, уплотнит. лента,
Подробнее >арт.товара: 28865
Набор для монтажа мойки арт.112.0198.026: выпуск 3 1/2″,крепл.,уплотн.лента,шум. рез.
Подробнее >арт.товара: 28866
Набор для монтажа мойки арт.112.0198.025: выпуск 3 1/2″крепл.,упл.лента,шум.рез.
Подробнее >арт.товара: 28869
Набор для мойки арт. 112.0198.021, Вентиль 3.5″ + комплект для монтажа
Подробнее >арт.товара: 30043
Смеситель CREMA GT Светло-серый (GERDAMIX)*
Подробнее >арт.товара: 35084
Смеситель CASTANO GT Светло-серый (GERDAMIX)*
Подробнее >арт.товара: 35676
Смеситель DORADO GT Шоколад (GERDAMIX)
Подробнее >арт.товара: 35745
Корзина боковая 3-х ярусная стекло W-BOCZS03-10 белая, с доводчиком, полн.выдв.
Подробнее >арт.товара: 30938
Корзина для белья W-KOSZD90-10 белая, с доводчиком, полн.выдв.
Подробнее >арт.товара: 30942
Корзина для белья ратанг W-KOSZR90-10 белая, с доводчиком, полн.выдв.
Подробнее >арт.товара: 30945
Корзина для белья стекло W-KOSZS80-10 белая, с доводчиком, полн.выдв.
Подробнее >арт.товара: 31007
Ящик Starax для белья выдвижной 700 мм (650-680х520х160) с доводчиком S6226 071542
Подробнее >арт.товара: 30854
Корзина сетчатая ХРОМ 160х500х550 Grandis GW-5055
Подробнее >арт.товара: 33544
Посудосушитель TONICA SU05/900 БОЯРД
Подробнее >арт.товара: 36518
Посудосушитель TONICA SU05/700 БОЯРД
Подробнее >арт.товара: 36517
Разделитель для вкладыша Большой PCD02/GR, серый БОЯРД
Подробнее >арт.товара: 33794
Продольный рейлинг для B-Box SBR06/GR/350 Серый БОЯРД
Подробнее >арт.товара: 34324
Продольный рейлинг для B-Box SBR06/W/500 Белый БОЯРД
Подробнее >арт.товара: 34061
Ящик B-BOX Графит SB04GRPH.1/500 БОЯРД
Подробнее >арт.товара: 34063
Продольный рейлинг для B-Box SBR06/GR/500 Серый БОЯРД
Подробнее >арт.товара: 33808
Продольный рейлинг для B-Box SBR06/W/450 Белый БОЯРД
Подробнее >арт.товара: 33809
Продольный рейлинг для B-Box SBR06/GR/450 Серый БОЯРД
Подробнее >арт.товара: 33807
Держатель продольного рейлинга B-Box SBh30/GRPH Графит БОЯРД
Подробнее >арт.товара: 33802
Держатель продольного рейлинга B-Box SBh30/W Белый БОЯРД
Подробнее >арт.товара: 33803
Держатель передней стенки B-Box SBh43/GR Серый БОЯРД
Подробнее >арт.товара: 33804
Продольный прямоугольный рейлинг для B-Box SBR05/GRPH/450 Графит БОЯРД
Подробнее >арт.товара: 33805
Держатель продольного рейлинга B-Box SBh30/GR Серый БОЯРД
Подробнее >арт.товара: 33801
Продольный рейлинг для B-Box SBR06/W/300 Белый БОЯРД
Подробнее >арт.товара: 34698
Продольный рейлинг для B-Box SBR06/W/350 Белый БОЯРД
Подробнее >арт.товара: 34697
Продольный рейлинг для B-Box SBR06/W/400 Белый БОЯРД
Подробнее >арт.товара: 34696
Продольный рейлинг для B-Box SBR06/GR/300 Серый БОЯРД
Подробнее >арт.товара: 34695
Ящик B-BOX Графит SB04GRPH.1/350 БОЯРД
Подробнее >арт.товара: 34694
Продольный прямоугольный рейлинг для B-Box SBR05/W/450 Белый БОЯРД
Подробнее >арт.товара: 34822
Продольный прямоугольный рейлинг для B-Box SBR05/GR/350 Серый БОЯРД
Подробнее >арт.товара: 36200
Продольный прямоугольный рейлинг для B-Box SBR05/W/400 Белый БОЯРД
Подробнее >арт.товара: 36201
Продольный прямоугольный рейлинг для B-Box SBR05/W/350 Белый БОЯРД
Подробнее >арт.товара: 36202
Продольный рейлинг для B-Box SBR06/GRPH/450 Графит БОЯРД
Подробнее >арт.товара: 36203
Продольный рейлинг для B-Box SBR06/GRPH/350 Графит БОЯРД
Подробнее >арт.товара: 36204
Продольный рейлинг для B-Box SBR06/GRPH/500 Графит БОЯРД
Подробнее >арт.товара: 36205
Высокий держатель передней стенки B-Box SBh44/W Белый
Подробнее >арт.товара: 36849
Передняя стенка ящика SWIMBOX PRO SBW04/GRPH/1200 Графит
Подробнее >арт.товара: 34937
Прямоугольный рейлинг наполнения SWIMBOX PRO SBR07/W/1200 Белый
Подробнее >арт.товара: 34936
Прямоугольный рейлинг наполнения SWIMBOX PRO SBR07/GRPH/1200 Графит
Подробнее >арт.товара: 34935
Держатель передней стенки внутреннего ящика SWIMBOX PRO SBH50/GRPH Графит
Подробнее >арт.товара: 34931
Держатель передней стенки высокого внутреннего ящика SWIMBOX PRO SBH51/GRPH Графит
Подробнее >арт.товара: 34933
Держатель передней стенки высокого внутреннего ящика SWIMBOX PRO SBH51/W Белый
Подробнее >арт.товара: 34934
Ящик SWIMBOX PRO SB11W.1/500, выс. стенки 110мм. Белый, Боярд
Подробнее >арт.товара: 34271
Ящик SWIMBOX PRO SB12GRPH.1/500, выс. стенки 142мм. Графит, Боярд
Подробнее >арт.товара: 34272
Ящик SWIMBOX PRO SB12W.1/450, выс. стенки 142мм. Белый, Боярд
Подробнее >арт.товара: 34055
Ящик SWIMBOX PRO SB13W.1/450, выс. стенки 192мм. Белый, Боярд
Подробнее >арт.товара: 34056
Распродажа плит
ЛДСП 2800-2070-38мм дуб довер бежевый шампань h2348 ST3
Подробнее >арт.товара: 10435
ЛДСП 2800-2070-10мм дуб гладстоун сепия h4342 ST28
Подробнее >арт.товара: 13295
ЛДСП 2800-2070-16мм сосна гаванна черная h4081 ST22
Подробнее >арт.товара: 14956
Столешница-127 -(60) Белый узор 3000-600-60мм
Подробнее >арт.товара: 10027
Кромка-142 Алюминиевая рябь 3000-32мм
Подробнее >арт.товара: 1064
Кромка-142 Алюминиевая рябь 3000-50мм
Подробнее >арт.товара: 1195
Кромка-45 Лесные ветви 3000-32мм Б/К
Подробнее >арт.товара: 10131
Кромка-402 Бриллиант фантазийный 3000-32мм
Подробнее >арт.товара: 11507
Мебель.щит-121 Ольха миндальная 3000-600
Подробнее >арт.товара: 92
Мебель.щит-142 Алюминиевая рябь 3000-600
Подробнее >арт.товара: 1062
Мебель.щит-122 вишня италия 4100-650-8мм
Подробнее >арт.товара: 9544
Столешница-h4090 R9 Дрифтвуд 3000-600-38мм
Подробнее >арт.товара: 9935
Мебельный щит-F328 Изодора антрацит 3000-600-4
Подробнее >арт.товара: 9976
Мебельный щит-F238 Террано черный 3000-600-4
Подробнее >арт.товара: 10046
Кромка меламин-F328 Изодора антрацит 3000-42мм
Подробнее >арт.товара: 9985
Кромка меламин-F131 Трани светло-серый 3000-42мм
Подробнее >арт.товара: 10081
Кромка меламин-h2476 Сосна Авола Шампань 3000-32мм Б/К
Подробнее >арт.товара: 10097
Кромка меламин-F161 Артик серо-голубой 3000-32мм Б/К
Подробнее >арт.товара: 10100
Кромка меламин-F328 Изодора антрацит 3000-32мм Б/К
Подробнее >арт.товара: 10103
Кромка меламин-F238 Террано черный 3000-32мм Б/К
Подробнее >арт.товара: 10105
Кромка меламин-F147 Валентино серый 3000-32мм Б/К
Подробнее >арт.товара: 10109
Кромка меламин-F238 Террано черный 3000-42мм
Подробнее >арт.товара: 10119
Кромка меламин-F142 Эрамоза черный 3000-42мм
Подробнее >арт.товара: 12621
Кромка меламин-h2478 Сосна Авола трюфель 3000-32мм Б/К
Подробнее >арт.товара: 12625
Столешница -2906 Ардезия 3000-600-26мм
Подробнее >арт.товара: 10959
Проф.планка — 130/10бук 13бавария (2,8м.)
Подробнее >арт.товара: 650
Проф.планка — 130/4бук 13бавария (2,8м.)
Подробнее >арт.товара: 657
Проф.планка — 82/10вишня 68оксфорд
Подробнее >арт.товара: 743
Проф.планка — 82/4вишня 68оксфорд (2,8мм.)
Подробнее >арт.товара: 744
Проф.планка — 82/4вишня 91академия (2,8мм.)
Подробнее >арт.товара: 799
Проф.планка — 31/4вишня 91академия (2,8м.)
Подробнее >арт.товара: 824
Проф.планка — 31/8бук 13бавария (2,8м.)
Подробнее >арт.товара: 826
Проф.планка — 31/8вишня 68оксфорд (2,8м.)
Подробнее >арт.товара: 827
Проф.планка — 31/8вишня 91академия (2,8м.)
Подробнее >арт.товара: 828
Проф.планка — 82/8вишня 91академия
Подробнее >арт.товара: 887
Проф.планка — 130/10алюминий (2,8м.)
Подробнее >арт.товара: 945
Проф.планка — 435/4вишня 91академия
Подробнее >арт.товара: 1662
Проф.рейка — 347вишня 91академия
Подробнее >арт.товара: 1666
Проф.планка — 593/8груша с патиной (2,8мм.)
Подробнее >арт.товара: 4397
Проф.рейка — 12бук 13бавария (2,8м.)
Подробнее >арт.товара: 7951
Проф.планка — 31/4орех Ночь Севилья (2,8м.)
Подробнее >арт.товара: 9620
Проф.планка — 31/8орех Ночь Севилья (2,8м.)
Подробнее >арт.товара: 9622
Проф.планка — 43бук 13бавария (2,71м.)
Подробнее >арт.товара: 9806
Проф.планка — 331вишня 91академия
Подробнее >арт.товара: 1485
Проф.планка — 435/4бук 13бавария (2,44м.)
Подробнее >арт.товара: 8620
Проф.планка — 130/10ясень шимо темный (2,8м.)
Подробнее >арт.товара: 12700
Проф.планка — 31/8бук 13бавария (2,75м.)
Подробнее >арт.товара: 12856
закрыть
В связи с перебоями в поставке плитных материалов и комплектующих информацию об их наличии необходимо уточнять дополнительно.
Надеемся на ваше понимание!«Квадрат»
Челябинск, ул. Шарова 77
(351) 734-97-98 (многоканальный)
Пн — Пт: 09.00 — 17.30
Сб: 09.00 — 14.00
Вс: выходной
«Галерея Квадрат»
(выставочный центр)
Челябинск, ул. Свободы 91 корпус 1
+ 7 (919) 314-49-34
Пн — Сб: 10.00 — 19.00
Вс: 10.00 — 16.00
Copyright © «Квадрат» 2021
Кабельная бирка REXANT «№134 (Б.квадрат)» 50 штук 07-6234-1 — цена, отзывы, характеристики, фото
Кабельная бирка REXANT «№134 (Б.квадрат)» 50 штук 07-6234-1 предназначается для маркировки силовых кабелей до 1 кВ. Крепление к кабелю осуществляется при помощи кабельных хомутов.
Длина каждой стороны — 55 мм. Размер отверстия под стяжку 11 мм х 3.5 мм. Диапазон рабочих температур составляет от -40 до +105 градусов.
Для маркировки возможно использование фломастеров 09-3995 или набора маркеров 09-3997 (приобретаются отдельно).
- Форма квадрат
- Количество в упаковке, шт 50
- Материал полипропилен
- Тип кабельная бирка
- Цвет белый
- Габариты, мм 55х55
Параметры упакованного товара
Единица товара: Штука
Вес, кг: 0,12
Длина, мм: 125
Ширина, мм: 200
Высота, мм: 50
Произведено
- Китай — родина бренда
- Китай — страна производства*
- Информация о производителе
Указанная информация не является публичной офертой
На данный момент для этого товара нет расходных материаловСервис от ВсеИнструменты.ру
Мы предлагаем уникальный сервис по обмену, возврату и ремонту товара!
Вернем вам деньги, если данный товар вышел из строя в течение 6 месяцев с момента покупки.
Обратиться по обмену, возврату или сдать инструмент в ремонт вы можете в любом магазине или ПВЗ ВсеИнструменты.ру.Гарантия производителя
Гарантия производителя 12 месяцевГарантийный ремонт
Здесь вы найдете адреса расположенных в вашем городе лицензированных сервисных центров.
| Лицензированные сервисные центры | Адрес | Контакты |
|---|---|---|
СЦ «СДС-Группа» МСК | ул. Фабричная, д. 6, стр. 1 | +7 (495) 225-25-20 |
Квадрат и его свойства, диагонали квадрата, площадь квадрат, теорема
Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.
Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.
Перечислим свойства квадрата:
- Все углы квадрата — прямые, все стороны квадрата — равны.
- Диагонали квадрата равны и пересекаются под прямым углом.
- Диагонали квадрата делят его углы пополам.
Площадь квадрата, очевидно, равна квадрату его стороны: .
Диагональ квадрата равна произведению его стороны на , то есть
.
Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.
1. Найдите сторону квадрата, диагональ которого равна .
Мы знаем, что . Тогда .
2. Найдите радиус окружности, описанной около квадрата со стороной, равной .
Очевидно, радиус окружности равен половине диагонали квадрата.
Ответ: .
3. Найдите сторону квадрата, описанного около окружности радиуса .
Диаметр окружности равен стороне квадрата.
Ответ: .
4. Найдите радиус окружности, вписанной в квадрат , считая стороны квадратных клеток равными .
Чуть более сложная задача. Нарисуйте окружность, вписанную в данный квадрат, то есть касающуюся всех его сторон. Вы увидите, что диаметр этой окружности равен стороне квадрата.
Ответ: .
5. Найдите радиус окружности, вписанной в четырехугольник . В ответе укажите
.
Считаем стороны клеток равными единице. Четырехугольник — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.
Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, . Она равна . Тогда радиус вписанной окружности равен . В ответ запишем .
Ответ: .
Python, корреляция и регрессия: часть 2 / Хабр
Предыдущий пост см. здесь.
Регрессия
Хотя, возможно, и полезно знать, что две переменные коррелируют, мы не можем использовать лишь одну эту информацию для предсказания веса олимпийских пловцов при наличии данных об их росте или наоборот. При установлении корреляции мы измерили силу и знак связи, но не наклон, т.е. угловой коэффициент. Для генерирования предсказания необходимо знать ожидаемый темп изменения одной переменной при заданном единичном изменении в другой.
Мы хотели бы вывести уравнение, связывающее конкретную величину одной переменной, так называемой независимой переменной, с ожидаемым значением другой, зависимой переменной. Например, если наше линейное уравнение предсказывает вес при заданном росте, то рост является нашей независимой переменной, а вес — зависимой.
Описываемые этими уравнениями линии называются линиями регрессии. Этот Термин был введен британским эрудитом 19-ого века сэром Фрэнсисом Гэлтоном. Он и его студент Карл Пирсон, который вывел коэффициент корреляции, в 19-ом веке разработали большое количество методов, применяемых для изучения линейных связей, которые коллективно стали известны как методы регрессионного анализа.
Вспомним, что из корреляции не следует причинная обусловленность, причем термины «зависимый» и «независимый» не означают никакой неявной причинной обусловленности. Они представляют собой всего лишь имена для входных и выходных математических значений. Классическим примером является крайне положительная корреляция между числом отправленных на тушение пожара пожарных машин и нанесенным пожаром ущербом. Безусловно, отправка пожарных машин на тушение пожара сама по себе не наносит ущерб. Никто не будет советовать сократить число машин, отправляемых на тушение пожара, как способ уменьшения ущерба. В подобных ситуациях мы должны искать дополнительную переменную, которая была бы связана с другими переменными причинной связью и объясняла корреляцию между ними. В данном примере это может быть размер пожара. Такие скрытые причины называются спутывающими переменными, потому что они искажают нашу возможность определять связь между зависимыми переменными.
Линейные уравнения
Две переменные, которые мы можем обозначить как x и y, могут быть связаны друг с другом строго или нестрого. Самая простая связь между независимой переменной x и зависимой переменной y является прямолинейной, которая выражается следующей формулой:
Здесь значения параметров a и b определяют соответственно точную высоту и крутизну прямой. Параметр a называется пересечением с вертикальной осью или константой, а b — градиентом, наклоном линии или угловым коэффициентом. Например, в соотнесенности между температурными шкалами по Цельсию и по Фаренгейту a = 32 и b = 1.8. Подставив в наше уравнение значения a и b, получим:
Для вычисления 10°С по Фаренгейту мы вместо x подставляем 10:
Таким образом, наше уравнение сообщает, что 10°С равно 50°F, и это действительно так. Используя Python и возможности визуализации pandas, мы можем легко написать функцию, которая переводит градусы из Цельсия в градусы Фаренгейта и выводит результат на график:
'''Функция перевода из градусов Цельсия в градусы Фаренгейта'''
celsius_to_fahrenheit = lambda x: 32 + (x * 1.8)
def ex_3_11():
'''График линейной зависимости температурных шкал'''
df = pd.DataFrame({'C':s, 'F':s.map(celsius_to_fahrenheit)})
df.plot('C', 'F', legend=False, grid=True)
plt.xlabel('Градусы Цельсия')
plt.ylabel('Градусы Фаренгейта')
plt.show()Этот пример сгенерирует следующий ниже линейный график:
Обратите внимание, как синяя линия пересекает 0 на шкале Цельсия при величине 32 на шкале Фаренгейта. Пересечение a — это значение y, при котором значение x равно 0.
Наклон линии с неким угловым коэффициентом определяется параметром b; в этом уравнении его значение близко к 2. Как видно, диапазон шкалы Фаренгейта почти вдвое шире диапазона шкалы Цельсия. Другими словами, прямая устремляется вверх по вертикали почти вдвое быстрее, чем по горизонтали.
Остатки
К сожалению, немногие связи столь же чистые, как перевод между градусами Цельсия и Фаренгейта. Прямолинейное уравнение редко позволяет нам определять y строго в терминах x. Как правило, будет иметься ошибка, и, таким образом, уравнение примет следующий вид:
Здесь, ε — это ошибка или остаточный член, обозначающий расхождение между значением, вычисленным параметрами a и b для данного значения x и фактическим значением y. Если предсказанное значение y — это ŷ, то ошибка — это разность между обоими:
Такая ошибка называется остатком. Остаток может возникать из-за случайных факторов, таких как погрешность измерения, либо неслучайных факторов, которые неизвестны. Например, если мы пытаемся предсказать вес как функцию роста, то неизвестные факторы могут состоять из диеты, уровня физической подготовки и типа телосложения (либо просто эффекта округления до самого близкого килограмма).
Если для a и b мы выберем неидеальные параметры, то остаток для каждого x будет больше, чем нужно. Из этого следует, что параметры, которые мы бы хотели найти, должны минимизировать остатки во всех значениях x и y.
Обычные наименьшие квадраты
Для того, чтобы оптимизировать параметры линейной модели, мы бы хотели создать функцию стоимости, так называемую функцией потери, которая количественно выражает то, насколько близко наши предсказания укладывается в данные. Мы не можем просто взять и просуммировать положительные и отрицательные остатки, потому что даже самые большие остатки обнулят друг друга, если их знаки противоположны.
Прежде, чем вычислить сумму, мы можем возвести значения в квадрат, чтобы положительные и отрицательные остатки учитывались в стоимости. Возведение в квадрат также создает эффект наложения большего штрафа на большие ошибки, чем на меньшие ошибки, но не настолько много, чтобы самый большой остаток всегда доминировал.
Выражаясь в терминах задачи оптимизации, мы стремимся выявить коэффициенты, которые минимизируют сумму квадратов остатков. Этот метод называется обычными наименьшими квадратами, от англ. Ordinary Least Squares (OLS), и формула для вычисления наклона линии регрессии по указанному методу выглядит так:
Хотя она выглядит сложнее предыдущих уравнений, на самом деле, эта формула представляет собой всего лишь сумму квадратов остатков, деленную на сумму квадратов отклонений от среднего значения. В данном уравнении используется несколько членов из других уравнений, которые уже рассматривались, и мы можем его упростить, приведя к следующему виду:
Пересечение (a) — это член, позволяющий прямой с заданным наклоном проходить через среднее значение X и Y:
Значения a и b — это коэффициенты, получаемые в результате оценки методом обычных наименьших квадратов.
Наклон и пересечение
Мы уже рассматривали функции covariance, variance и mean, которые нужны для вычисления наклона прямой и точки пересечения для данных роста и веса пловцов. Поэтому вычисление наклона и пересечения имеют тривиальный вид:
def slope(xs, ys):
'''Вычисление наклона линии (углового коэффициента)'''
return xs.cov(ys) / xs.var()
def intercept(xs, ys):
'''Вычисление точки пересечения (с осью Y)'''
return ys.mean() - (xs.mean() * slope(xs, ys))
def ex_3_12():
'''Вычисление пересечения и наклона (углового коэффициента)
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см']
y = df['Вес'].apply(np.log)
a = intercept(X, y)
b = slope(X, y)
print('Пересечение: %f, наклон: %f' % (a,b))Пересечение: 1.691033, наклон: 0.014296В результате будет получен наклон приблизительно 0.0143 и пересечение приблизительно 1.6910.
Интерпретация
Величина пересечения — это значение зависимой переменной (логарифмический вес), когда независимая переменная (рост) равна нулю. Для получения этого значения в килограммах мы можем воспользоваться функцией np.exp, обратной для функции np.log. Наша модель дает основания предполагать, что вероятнее всего вес олимпийского пловца с нулевым ростом будет 5.42 кг. Разумеется, такое предположение лишено всякого смысла, к тому же экстраполяция за пределы границ тренировочных данных является не самым разумным решением.
Величина наклона показывает, насколько y изменяется для каждой единицы изменения в x. Модель исходит из того, что каждый дополнительный сантиметр роста прибавляет в среднем 1.014 кг. веса олимпийских пловцов. Поскольку наша модель основывается на данных о всех олимпийских пловцах, она представляет собой усредненный эффект от увеличения в росте на единицу без учета любого другого фактора, такого как возраст, пол или тип телосложения.
Визуализация
Результат линейного уравнения можно визуализировать при помощи имплементированной ранее функции regression_line и простой функции от x, которая вычисляет ŷ на основе коэффициентов a и b.
'''Функция линии регрессии'''
regression_line = lambda a, b: lambda x: a + (b * x) # вызовы fn(a,b)(x)
def ex_3_13():
'''Визуализация линейного уравнения
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=7)
s = pd.Series(range(150,210))
df = pd.DataFrame( {0:s, 1:s.map(regression_line(a, b))} )
df.plot(0, 1, legend=False, grid=True, ax=ax)
plt.xlabel('Рост, см.')
plt.ylabel('Логарифмический вес')
plt.show()Функция regression_line возвращает функцию от x, которая вычисляет a + bx.
Указанная функция может также использоваться для вычисления каждого остатка, показывая степень, с которой наша оценка ŷ отклоняется от каждого измеренного значения y.
def residuals(a, b, xs, ys):
'''Вычисление остатков'''
estimate = regression_line(a, b) # частичное применение
return pd.Series( map(lambda x, y: y - estimate(x), xs, ys) )
constantly = lambda x: 0
def ex_3_14():
'''Построение графика остатков на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
y = residuals(a, b, X, y)
ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=12)
s = pd.Series(range(150,210))
df = pd.DataFrame( {0:s, 1:s.map(constantly)} )
df.plot(0, 1, legend=False, grid=True, ax=ax)
plt.xlabel('Рост, см.')
plt.ylabel('Остатки')
plt.show()График остатков — это график, который показывает остатки на оси Y и независимую переменную на оси X. Если точки на графике остатков разбросаны произвольно по обе стороны от горизонтальной оси, то линейная модель хорошо подогнана к нашим данным:
За исключением нескольких выбросов на левой стороне графика, график остатков, по-видимому, показывает, что линейная модель хорошо подогнана к данным. Построение графика остатков имеет важное значение для получения подтверждения, что линейная модель применима. В линейной модели используются некоторые допущения относительно данных, которые при их нарушении делают не валидными модели, которые вы строите.
Допущения
Первостепенное допущение линейной регрессии состоит в том, что, безусловно, существует линейная зависимость между зависимой и независимой переменной. Кроме того, остатки не должны коррелировать друг с другом либо с независимой переменной. Другими словами, мы ожидаем, что ошибки будут иметь нулевое среднее и постоянную дисперсию по отношению к зависимой и независимой переменной. График остатков позволяет быстро устанавливать, является ли это действительно так.
Левая сторона нашего графика имеет более крупные значения остатков, чем правая сторона. Это соответствует большей дисперсии веса среди более низкорослых спортсменов. Когда дисперсия одной переменной изменяется относительно другой, говорят, что переменные гетероскедастичны, т.е. их дисперсия неоднородна. Этот факт представляет в регрессионном анализе проблему, потому что делает не валидным допущение в том, что модельные ошибки не коррелируют и нормально распределены, и что их дисперсии не варьируются вместе с моделируемыми эффектами.
Гетероскедастичность остатков здесь довольно мала и особо не должна повлиять на качество нашей модели. Если дисперсия на левой стороне графика была бы более выраженной, то она привела бы к неправильной оценке дисперсии методом наименьших квадратов, что в свою очередь повлияло бы на выводы, которые мы делаем, основываясь на стандартной ошибке.
Качество подгонки и R-квадрат
Хотя из графика остатков видно, что линейная модель хорошо вписывается в данные, т.е. хорошо к ним подогнана, было бы желательно количественно измерить качество этой подгонки. Коэффициент детерминации R2, или R-квадрат, варьируется в интервале между 0 и 1 и обозначает объяснительную мощность линейной регрессионной модели. Он вычисляет объясненную долю изменчивости в зависимой переменной.
Обычно, чем ближе R2 к 1, тем лучше линия регрессии подогнана к точкам данных и больше изменчивости в Y объясняется независимой переменной X. R2 можно вычислить с помощью следующей ниже формулы:
Здесь var(ε) — это дисперсия остатков и var(Y) — дисперсия в Y. В целях понимания смысла этой формулы допустим, что вы пытаетесь угадать чей-то вес. Если вам больше ничего неизвестно об испытуемых, то наилучшей стратегией будет угадывать среднее значение весовых данных внутри популяции в целом. Таким путем средневзвешенная квадратичная ошибка вашей догадки в сравнении с истинным весом будет var(Y), т.е. дисперсией данных веса в популяции.
Но если бы я сообщил вам их рост, то в соответствии с регрессионной моделью вы бы предположили, что a + bx. В этом случае вашей средневзвешенной квадратичной ошибкой было бы или дисперсия остатков модели.
Компонент формулы var(ε)/var(Y) — это соотношение средневзвешенной квадратичной ошибки с объяснительной переменной и без нее, т. е. доля изменчивости, оставленная моделью без объяснения. Дополнение R2 до единицы — это доля изменчивости, объясненная моделью.
Как и в случае с r, низкий R2 не означает, что две переменные не коррелированы. Просто может оказаться, что их связь не является линейной.
Значение R2 описывает качество подгонки линии регрессии к данным. Оптимально подогнанная линия — это линия, которая минимизирует значение R2. По мере удаления либо приближения от своих оптимальных значений R2 всегда будет расти.
Левый график показывает дисперсию модели, которая всегда угадывает среднее значение для , правый же показывает меньшие по размеру квадраты, связанные с остатками, которые остались необъясненными моделью f. С чисто геометрической точки зрения можно увидеть, как модель объяснила большинство дисперсии в y. Приведенный ниже пример вычисляет R2 путем деления дисперсии остатков на дисперсию значений y:
def r_squared(a, b, xs, ys):
'''Рассчитать коэффициент детерминации (R-квадрат)'''
r_var = residuals(a, b, xs, ys).var()
y_var = ys.var()
return 1 - (r_var / y_var)
def ex_3_15():
'''Рассчитать коэффициент R-квадрат
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
return r_squared(a, b, X, y)0.75268223613272323В результате получим значение 0.753. Другими словами, более 75% дисперсии веса пловцов, выступавших на Олимпийских играх 2012 г., можно объяснить ростом.
В случае простой регрессионной модели (с одной независимой переменной), связь между коэффициентом детерминации R2 и коэффициентом корреляции r является прямолинейной:
Коэффициент корреляции r может означать, что половина изменчивости в переменной Y объясняется переменной X, но фактически R2 составит 0.52, т.е. 0.25.
Множественная линейная регрессия
Пока что в этой серии постов мы видели, как строится линия регрессии с одной независимой переменной. Однако, нередко желательно построить модель с несколькими независимыми переменными. Такая модель называется множественной линейной регрессией.
Каждой независимой переменной потребуется свой собственный коэффициент. Вместо того, чтобы для каждой из них пытаться подобрать букву в алфавите, зададим новую переменную β (бета), которая будет содержать все наши коэффициенты:
Такая модель эквивалентна двухфакторной линейно-регрессионной модели, где β1 = a и β2 = b при условии, что x1 всегда гарантированно равен 1, вследствие чего β1 — это всегда константная составляющая, которая представляет наше пересечение, при этом x1 называется (постоянным) смещением уравнения регрессии, или членом смещения.
Обобщив линейное уравнение в терминах β, его легко расширить на столько коэффициентов, насколько нам нужно:
Каждое значение от x1 до xn соответствует независимой переменной, которая могла бы объяснить значение y. Каждое значение от β1 до βn соответствует коэффициенту, который устанавливает относительный вклад независимой переменной.
Простая линейная регрессия преследовала цель объяснить вес исключительно с точки зрения роста, однако объяснить вес людей помогает много других факторов: их возраст, пол, питание, тип телосложения. Мы располагаем сведениями о возрасте олимпийских пловцов, поэтому мы смогли бы построить модель, которая учитывает и эти дополнительные данные.
До настоящего момента мы предоставляли независимую переменную в виде одной последовательности значений, однако при наличии двух и более параметров нам нужно предоставлять несколько значений для каждого x. Мы можем воспользоваться функциональностью библиотеки pandas, чтобы выбрать два и более столбцов и управлять каждым как списком, но есть способ получше: матрицы.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Темой следующего поста, поста №3, будут матричные операции, нормальное уравнение и коллинеарность.
Теорема Пифагора
Теорема Пифагора была названа в честь известного греческого математика Пифагора. Это важная формула, которая утверждает следующее: a 2 + b 2 = c 2
Рисунок выше помогает нам понять, почему формула работает. Вы сделали следующее важное наблюдение? Рисунок ниже может помочь!
Обратите внимание, что в красном квадрате есть 2 треугольника, а в синем квадрате также есть 2 треугольника. В черном квадрате есть 4 одинаковых треугольника.
Следовательно, площадь красного квадрата + площадь синего квадрата = площадь черного квадрата
Пусть a = длина стороны красного квадрата
Пусть b = длина стороны синего квадрата
Пусть c = длина стороны черного квадрата
Следовательно, a 2 + b 2 = c 2
Вообще говоря, в любом прямоугольном треугольнике пусть c будет длиной самой длинной стороны (называемой гипотенузой), а a и b — длинами двух других сторон (называемых катетами).Теорема утверждает, что длина гипотенузы в квадрате равна длине стороны a в квадрате плюс длина стороны b в квадрате. В виде уравнения c 2 = a 2 + b 2Таким образом, учитывая две стороны, третью сторону можно найти с помощью формулы.
Мы проиллюстрируем это примерами, но прежде чем продолжить, вы должны знать, как найти квадратный корень из числа и как решить уравнения с помощью вычитания
Упражнение № 1
Пусть a = 3 и b = 4.Найдите c или самую длинную сторону
c 2 = a 2 + b 2
c 2 = 3 2 + 4 2
c 2 = 9 + 16
c 2 = 25
c = √25
Знак (√) означает квадратный корень
c = 5
Упражнение № 2
Пусть c = 10 и a = 8. Найдите b, или другая нога.
c 2 = a 2 + b 2
10 2 = 8 2 + b 2
100 = 64 + b 2
100 — 64 = 64 — 64 + b 2 (минус 64 с обеих сторон для изоляции b 2 )
36 = 0 + b 2
36 = b 2
b = √36 = 6
Упражнение № 3
Пусть c = 13 и b = 5.Найдите
c 2 = a 2 + b 2
13 2 = a 2 + 5 2
169 = a 2 + 25
169-25 = a 2 + 25-25
144 = a 2 + 0
144 = a 2
a = √144 = 12
Пройдите тест по теореме Пифагора ниже, чтобы увидеть, насколько хорошо вы усвоили этот урок.
| Купить исчерпывающую электронную книгу геометрических формул.Все геометрические формулы объясняются хорошо подобранными текстовыми задачами, так что вы можете освоить геометрию. |
Формы гистограмм
19 мая, 21 05:48
Узнайте о различных формах гистограмм. Три наиболее распространенных из этих форм: наклонная, симметричная и однородная.
Подробнее
Квадрат двучлена.Трехчлены полного квадрата
18
Трехчлены полного квадратаКвадратные числа
Квадрат двучлена
Геометрическая алгебра
2-й уровень
( a + b ) ³
Квадрат трехчлена
Завершение квадрата
ДАВАЙТЕ НАЧНЕМ, изучая квадратные числа.Это числа
1 · 1 2 · 2 3 · 3
и так далее. Ниже приведены первые десять квадратных чисел и их корни.
| Квадратные числа | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| Квадратный корень | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 — квадрат единицы.4 — это квадрат 2. 9 — это квадрат 3. И так далее.
Квадратный корень из 1 равен 1. Квадратный корень из 4 равен 2. Квадратный корень из 9 равен 3. И так далее.
В таблице умножения квадратные числа лежат по диагонали.
Квадрат двучлена
( a + b ) 2
Квадрат бинома встречается так часто, что ученик должен сразу же написать окончательный результат.Получится очень специфический трехчлен. Чтобы убедиться в этом, возведем в квадрат ( a + b ):
( a + b ) 2 = ( a + b ) ( a + b ) = a 2 + 2 ab + b
.
Для внешних и внутренних будет
ab + ba = 2 ab .
Порядок факторов не имеет значения.
Квадрат любого бинома дает следующий трехчлен:
1. Квадрат первого члена двучлена: a 2
2. Двойное произведение двух членов: 2 ab
3. Квадрат второго члена: b 2
Квадрат каждого бинома имеет такую форму: a 2 + 2 ab + b 2 .
Признать это — значит знать существенное произведение в «таблице умножения» алгебры.
(См. Урок 8 по арифметике: как мысленно возвести в квадрат число, особенно квадрат 24, который является «биномом» 20 + 4.)
Пример 1. Возвести двучлен в квадрат ( x + 6).
Решение . ( x + 6) 2 = x 2 + 12 x + 36
x 2 — квадрат x .
12 x вдвое больше произведения x на 6. ( x · 6 = 6 x . В два раза больше, чем 12 x .)
36 — это квадрат 6.
x 2 + 12 x + 36 называется трехчленом полного квадрата, который является квадратом бинома.
Пример 2. Возвести двучлен в квадрат (3 x — 4).
Решение .(3 x -4) 2 = 9 x 2 -24 x + 16
9 x 2 — это квадрат 3 x .
−24 x — удвоенное произведение 3 x · −4. (3 x · −4 = −12 x . В два раза больше −24 x .)
16 — это квадрат −4.
Примечание: Если двучлен имеет знак минус, то знак минус появляется только в среднем члене трехчлена.Следовательно, используя двойной знак ± («плюс или минус»), мы можем сформулировать правило следующим образом:
( a ± b ) 2 = a 2 ± 2 ab + b 2
Это означает: если двучлен a + b , то средний член будет +2 ab ; но если двучлен a — b , то средний член будет −2 ab
Квадрат + b или — b , конечно, всегда положительный.Это всегда + b 2 .
Пример 3. (5 x 3 -1) 2 = 25 x 6 -10 x 3 + 1
25 x 6 — квадрат 5 x 3 . (Урок 13: Показатели.)
−10 x 3 — это удвоенное произведение 5 x 3 и −1. (5 x 3 умножить на −1 = −5 x 3 .Дважды, что равно −10 x 3 .)
1 — квадрат −1.
Учащийся должен четко понимать, что ( a + b ) 2 равно , а не a 2 + b 2 , не более чем ( a + b ) 3 равно a 3 + b 3 .
Показатель не может быть «распределен» по сумме.
(См. Тему 25 книги Precalculus: The binomial теорема.)
Пример 4. Является ли это трехчленом полного квадрата: x 2 + 14 x + 49?
Ответ . Да. Это квадрат ( x + 7).
x 2 — квадрат x . 49 — это квадрат 7. А 14 x — удвоенное произведение x · 7.
Другими словами, x 2 + 14 x + 49 может быть разложено на как
x 2 + 14 x + 49 = ( x + 7) 2
Примечание: Если бы коэффициент x был любым числом, кроме 14, это не было бы трехчленом в виде полного квадрата.
Пример 5 Это трехчлен полного квадрата: x 2 + 50 x + 100?
Ответ .Нет это не так. Хотя x 2 — это квадрат x , а 100 — квадрат 10, 50 x не является двойным произведением x · ; 10. (Их произведение дважды равно 20 x .)
Пример 6 Является ли это трехчленом полного квадрата: x 8 -16 x 4 + 64?
Ответ . Да. Это идеальный квадрат x 4 -8.
Задача 1. Какие числа являются квадратными числами?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
1, 4, 9, 16, 25, 36, 49, 64 и т. Д.
Это числа 1 2 , 2 2 , 3 2 и так далее.
Проблема 2.
а) Сформулируйте на словах правило возведения бинома в квадрат.
Квадрат первого члена.
Двойное произведение двух членов.
Квадрат второго члена.
б) Запишите только трехчленное произведение: ( x + 8) 2 = x 2 + 16 x + 64
c) Запишите только трехчленное произведение: ( r + s ) 2 = r 2 + 2 rs + s 2
Проблема 3.Напишите только трехчленное произведение.
| а) | ( x + 1) 2 = x 2 + 2 x + 1 | б) ( x — 1) 2 = | x 2 -2 x + 1 | |
| в) | ( x + 2) 2 = x 2 + 4 x + 4 | г) ( x — 3) 2 = | x 2 -6 x + 9 | |
| e) | ( x + 4) 2 = x 2 + 8 x + 16 | f) ( x — 5) 2 = | x 2 -10 x + 25 | |
| г) | ( x + 6) 2 = x 2 + 12 x + 36 | h) ( x — y ) 2 = | x 2 -2 xy + y 2 | |
Проблема 4.Напишите только трехчленное произведение.
| а) | (2 x + 1) 2 = 4 x 2 + 4 x + 1 | б) (3 x — 2) 2 = | 9 x 2 -12 x + 4 | |
| в) | (4 x + 3) 2 = 16 x 2 + 24 x + 9 | г) (5 x — 2) 2 = | 25 x 2 -20 x + 4 | |
| e) | ( x 3 + 1) 2 = x 6 + 2 x 3 + 1 | f) ( x 4 — 3) 2 = | x 8 -6 x 4 + 9 | |
| г) | ( x n + 1) 2 = x 2 n + 2 x n + 1 | h) ( x n -4) 2 = | x 2 n -8 x n + 16 | |
Проблема 5.Фактор: p 2 + 2 pq + q 2 .
p 2 + 2 pq + q 2 = ( p + q ) 2
Левая часть представляет собой трехчлен полного квадрата.
Задача 6. Если возможно, разложите на множители полный квадрат трехчлена.
| а) | x 2 -4 x + 4 = ( x -2) 2 | б) | x 2 + 6 x + 9 = ( x + 3) 2 | |
| в) | x 2 -18 x + 36 Невозможно. | г) | x 2 -12 x + 36 = ( x -6) 2 | |
| e) | x 2 — 3 x + 9 Невозможно. | е) | x 2 + 10 x + 25 = ( x + 5) 2 | |
Проблема 7.Если возможно, множите на множители полный квадрат трехчлена.
а) 25 x 2 + 30 x + 9 = (5 x + 3) 2
б) 4 x 2 — 28 x + 49 = (2 x -7) 2
c) 25 x 2 -10 x + 4 Невозможно.
г) 25 x 2 -20 x + 4 = (5 x -2) 2
e) 1 — 16 лет + 64 года 2 = (1 — 8 y ) 2
f) 16 m 2 -40 mn + 25 n 2 = (4 m -5 n ) 2
г) x 4 + 2 x 2 y 2 + y 4 = ( x 2 + y 2 ) 2
h) 4 x 6 -10 x 3 y 4 + 25 y 8 Невозможно.
i) x 12 + 8 x 6 + 16 = ( x 6 + 4) 2
j) x 2 n + 8 x n + 16 = ( x n + 4) 2
Геометрическая алгебра
Вот квадрат со стороной a + b .
Состоит из
квадрат со стороной a ,
квадрат со стороной b ,
и два прямоугольника ab .
То есть
( a + b ) 2 = a 2 + 2 ab + b 2 .
2-й уровень
Следующий урок: Разница двух квадратов
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Тригонометрия
ТригонометрияТеорема Пифагора
| Тригонометрия — теорема Пифагора — Содержание |
Тригонометрия — это анализ уникальных геометрических свойства прямоугольного треугольника с использованием пифагорова Теорема.Он был известен еще в древности вавилонянами и был описан в теории древнегреческого математика Пифагора. Тригонометрический функции и тригонометрические законы основаны о доказательстве теоремы Пифагора. Теорема утверждает, что если у прямоугольного треугольника две стороны равны и b, и гипотенуза, равная c, затем квадрат плюс b в квадрате равно c в квадрате. Гипотенуза прямоугольного треугольника сторона, противоположная прямому углу.Есть шесть тригонометрических функций синус, косинус, касательная, косеканс, секанс и котангенс, которые исследуйте отношения двух сторон прямоугольного треугольника. Последние три являются взаимными из первых трех. Чтобы определить, что это верно для любого прямоугольного треугольника означает математическое доказательство теоремы Пифагора используя базовую геометрию. Это математическое соотношение относительно геометрии прямоугольных треугольников дает метод решения треугольник.
| Тригонометрия — Пифагора Теорема — Примеры |
Теорема Пифагора:
В любом прямоугольном треугольнике со сторонами a а b и гипотенуза c,
, тогда a + b = c
или c равно квадрату корень из величины a в квадрате плюс b в квадрате.Пример теоремы Пифагора:
Если прямоугольный треугольник имеет стороны a = 3 и b = 4 и гипотенуза c = 5,
, затем 3 + 4 = 5 и 9 + 16 = 25.
Интерактивная говорящая глава книги по математике
B Square Pizza разносит пироги в стиле Детройта в Чикаго
Представляем B Square Pizza, пиццерию в стиле Детройта в северных пригородах Чикаго, предлагающую бесконтактную доставку и самовывоз с нашей кухни прямо на ваш диван. Благодаря успеху B Square в Уилинге, ресторан теперь работает только с доставкой в центре Чикаго!
Разместите заказ с доставкой в B Square Pizza в Северном пригороде.
Чтобы разместить заказ на вынос пиццы B Square в северных пригородах, позвоните по телефону 224-676-0312.
Разместите заказ с доставкой в B Square Pizza — Чикаго.
Идея появилась, когда шеф-повар из Мичигана Майкл Браунелл (Saranello’s) и шеф-повар / партнер Микаэль Боннер (Saranello’s, Di Pescara, The Ivy Room и Petterino’s) создали идеальную корочку, легкую и воздушную. в комплекте с хрустящими подрумяненными краями.Поверьте, это та пицца в стиле Детройта, которую так ждал Чикаго!
Посмотреть меню из B Square Pizza.
Пиццы квадратной формы выпекаются на сковороде, их можно заказать в размерах 12 и 16 дюймов. Фирменные пироги:
Специальное блюдо Майка Би с колбасой, пепперони, грибами, красным луком, оливками и маринованным перцем
Mama B Square с говяжьими фрикадельками, перцем пепперони
Томат классический с итальянскими помидорами, свежей моцареллой, базиликом, оливковым маслом первого холодного отжима
Гриб с бритыми грибами кремини, сыром робиола, трюфельным маслом и белым соусом
TripleЗеленый со свежим чесноком, шпинатом, капустой, рукколой и красным соусом
В дополнение к детройтским пирогам предлагаются пиццы на тонком тесте и без глютена.
Это не просто пицца… это еще не все! В дополнение к более чем десяти фирменным пирогам, B Square Pizza предлагает свежие салаты, хрустящие куриные крылышки из экологически чистого цыпленка, сырно-чесночный хлеб, выпечку и домашнее негабаритное печенье с шоколадной стружкой и Michigan Cherry Hand Pies на десерт.
Ручные пироги доступны только на Северном берегу.Пицца B Square Pizza — Nothern Suburbs находится по адресу 601 N. Milwaukee Ave., Wheeling, IL.Часы работы: понедельник — четверг с 15:00 до 20:00, пятница с 15:00 до 21:00, суббота с 11:00 до 21:00, воскресенье с 11:00 до 8:00: 00 вечера. Чтобы получить дополнительную информацию и сделать заказ онлайн, посетите bsquarepizzadelivery.com или подпишитесь на Facebook, Instagram и Twitter. Чтобы разместить заказ на вынос, позвоните по телефону 224-676-0312.
B Square Pizza — Чикаго доставка только семь дней в неделю с 16:00 до 21:00, доставка на 5 миль от 620 N. State Street в центре Чикаго. Для получения дополнительной информации и просмотра меню посетите bsquarepizzadelivery.com или подпишитесь на Facebook, Instagram и Twitter. Чтобы разместить заказ на доставку, нажмите здесь. Чтобы подтвердить радиус доставки B Square, напишите по адресу [email protected].
Завершение площади
Заполнение Квадрата — это метод, используемый для решения квадратное уровненеие изменив форму уравнения так, чтобы левая часть идеальный квадрат трехчлен .
Решать а Икс 2 + б Икс + c знак равно 0 заполнив квадрат:
1.Преобразуйте уравнение так, чтобы постоянный член,
c
, один на правой стороне.
2. Если
а
, старший коэффициент (коэффициент
Икс
2
срок), не равно
1
, разделите обе стороны на
а
.
3. Добавьте квадрат половины коэффициента Икс -срок, ( б 2 а ) 2 к обеим сторонам уравнения.
4. Разложите левую часть на множители квадрата двучлена.
5. Возьмите квадратный корень с обеих сторон. (Помнить: ( Икс + q ) 2 знак равно р эквивалентно Икс + q знак равно ± р .)
6. Решите для Икс .
Пример 1:
Решать Икс 2 — 6 Икс — 3 знак равно 0 заполнив квадратик.
Икс 2 — 6 Икс знак равно 3 Икс 2 — 6 Икс + ( — 3 ) 2 знак равно 3 + 9 ( Икс — 3 ) 2 знак равно 12 Икс — 3 знак равно ± 12 знак равно ± 2 3 Икс знак равно 3 ± 2 3
Пример 2:
Решать: 7 Икс 2 — 8 Икс + 3 знак равно 0
7 Икс 2 — 8 Икс знак равно — 3 Икс 2 — 8 7 Икс знак равно — 3 7 Икс 2 — 8 7 Икс + ( — 4 7 ) 2 знак равно — 3 7 + 16 49 ( Икс — 4 7 ) 2 знак равно — 5 49 Икс — 4 7 знак равно ± 5 7 я Икс знак равно 4 7 ± 5 7 я ( Икс — 3 ) 2 знак равно 12 Икс — 3 знак равно ± 12 знак равно ± 2 3 Икс знак равно 3 ± 2 3
Купить крепления, аксессуары и инструменты для стрельбы B-Square
B-SQUARE — это длинный список новинок в отрасли, многие из которых до сих пор не имеют себе равных. B Square Технологии обработки, знания в области машиностроения и инженерные разработки дают компании огромное преимущество перед конкурентами. Большинство монтажных систем BSQUARE представляют собой неразрушающие, не требующие изготовления оружия крепления, которые не требуют ни опыта оружейника, ни сверления и нарезания резьбы на огнестрельном оружии. Эта уникальная концепция дизайна позволяет любому, кто использует систему крепления B-SQUARE и аксессуары для прицелов B-SQUARE, в любой момент вернуть свое огнестрельное оружие в исходное состояние.Эти потрясающие крепления для прицелов позволяют правильно установить прицел!
Компания B-Square уже более 50 лет производит полную линейку высококачественных креплений для оптических прицелов, принадлежностей для оптических прицелов и инструментов для серьезных стрелков. Известная во всем мире своим разнообразным выбором и уникальным дизайном, традиция B-Square продолжается, ежегодно представляя новые продукты. Удовлетворение потребностей гарантировано, и любому стрелку обещана идеальная подгонка оружия, независимо от выбора огнестрельного оружия.Любите ли вы пинк, охоту или серьезно относитесь к аксессуарам для правоохранительных органов, B-Square устанавливает стандарт точности, когда дело доходит до идеального крепления для ваших нужд.
Целью BSQUARE всегда было разработать лучшие аксессуары для огнестрельного оружия для промышленности и предложить крепления для оптических прицелов и аксессуары для оптических прицелов по разумной цене. B-SQUARE стремится стать вашим поставщиком монтажных систем. Самое главное, B-SQUARE будет стоять за любым продуктом, созданным или разработанным нами, и отвечать вашим потребностям с высочайшим приоритетом.Обслуживание клиентов — это фундамент, на котором была построена компания.
B-SQUARE в настоящее время предлагает системы крепления BSquare и аксессуары для оптических прицелов B-Square для более чем 300 видов огнестрельного и пневматического оружия, производимых по всему миру.
B-квадрат Lab
B-square Lab разрабатывает и использует блокчейн для удовлетворения индивидуальных потребностей клиентов.
Использование Square-BaaS значительно сокращает затраты и время на разработку блокчейна.
Обеспечение целостности и отслеживаемости «сертифицированных халяль» продуктов посредством цифровой сертификации. Блокчейн записывает транзакцию для каждого этапа халяльной комплексной проверки и результата заводской комплексной проверки, а клиенты используют QR-код для сканирования и проверки информации.
Служба сертификации и депонирования оригинальных документов: с помощью решения блокчейн исходный документ, авторские права, договор и связанные записи хранятся в сети блокчейн.Уникальные хеш-значения и юридическая аутентичность сохраненных записей генерируются в режиме онлайн. Записи и документы запрашиваются в режиме онлайн для проверки и предотвращения подделки доказательств. Эта услуга «как услуга» особенно полезна для МСП (малых и средних предприятий) по разумной цене.
Служба сертификации медицинских данных: эта служба позволяет безопасно создавать резервные копии и управлять исходными медицинскими данными пациентов, а также хранить присущие им цифровые отпечатки пальцев в блокчейне для сертификации.Square-BaaS специализируется на сборе нетронутых медицинских данных и особенно полезен для компаний, занимающихся цифровым здравоохранением и оборудованием.
Служба защиты авторских прав: придерживаясь концепции «блокчейн +», компания B-square Lab активно работала в области авторского права и запустила комплексное решение для блокчейн в областях защиты авторских прав, интеграции средств массовой информации и интеллектуальной собственности. и другие направления деятельности.
Служба цифровых баллов лояльности: интегрированная платформа, построенная в нижней части лицензированной цепочки B-square Lab, управляет баллами с помощью технологии шифрования блокчейн, позволяя пользователям генерировать отдачу от своего поведения в цифровой жизни в отношении общения, развлечений, покупок, путешествий. , так далее.позволяя серьезно относиться к ценности, создаваемой этими действиями, и капитализировать цифровое поведение пользователя.
Служба дробного владения: служба использует блокчейн для разделения, торговли и проверки дорогостоящей собственности, такой как искусство и недвижимость.
Служба финансирования цепочки поставок: эта служба объединяет финансовую систему цепочки поставок и блокчейн, создает надежную информационную сетевую экосистему между многими предприятиями и финансовыми учреждениями в цепочке поставок, делится различными типами информации, сокращая время сбора данных, проверки и т. Д. оценка и т. д., переходит в доверительное управление и решает проблему высоких финансовых затрат для малого и среднего бизнеса.
Служба децентрализованного идентификатора (DID): основанная на системах блокчейна, децентрализованный идентификатор (DID) имеет такие функции, как независимый контроль, распределенное доверие и защита конфиденциальности.



