Круг тригонометрический отрицательный: Как запомнить тригонометрический круг?
Тригонометрический круг (окружность)
ОПРЕДЕЛЕНИЕТригонометрический круг (окружность) – круг радиуса один (единичная окружность), с центром в начале координат (рисунок 1).
За нулевое положение радиуса, принимается его положение на положительном направлении оси Ox. Угол поворота радиуса отсчитывается от положительного направления оси Ox: с плюсом – против часовой стрелки, с минусом – по часовой стрелке. Полный круг – это . Каждому углу от до соответствует точка на единичной окружности.
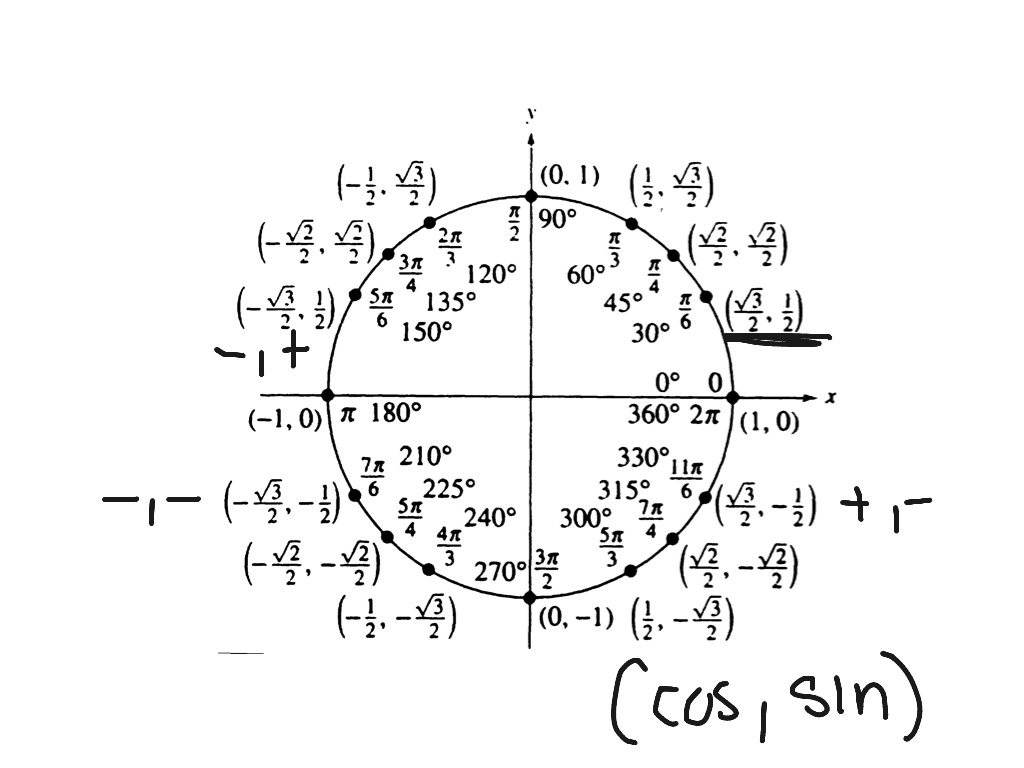
Синусом угла есть ордината точки , а косинусом угла есть абсцисса точки .
Рис. 1
Примеры решения задач
ПРИМЕР 1| Задание | Используя единичную окружность, определить синус и косинус угла . |
| Решение | Отложим на единичной окружности угол равный (рис. 1), ему будет соответствовать точка A окружности. Найдем синус заданного угла. Для нахождения косинуса заданного угла, найдем проекцию точки A на ось Ox. Ею будет точка , тогда абсцисса точка A равна и, соответственно, . |
| Ответ |
Единицы измерения углов
Углы обычно измеряются либо в градусах, либо в радианах. Перевести градусы в радианы просто: 360 градусов (полный круг) соответствует радиан.
ПРИМЕР 2| Задание | Перевести:
1) угол в градусы; 2) угол в радианы. |
| Решение | 1) Для того чтобы перевести угол из радиан в градусы, умножим данный угол на . Получим
2) Для того чтобы перевести заданный угол из градусов в радианы, умножим его на . Получим
|
| Ответ |
На единичной окружности также можно находить углы, которые больше 360 градусов. Поскольку, значения синуса и косинуса на тригонометрическом круге повторяются каждые .
Поскольку, значения синуса и косинуса на тригонометрическом круге повторяются каждые .
| Задание | Найти с помощью единичной окружности синус угла . |
| Решение | Представим данный угол следующим образом
Таким образом, необходимо сделать два полных обхода окружности, а затем остановиться в точке соответствующей углу в (рис. 1). Синусу соответствует ордината этой точки, то есть . |
| Ответ |
Тригонометрические функции
Тригонометрические уравнения и их решение
Косинус 45 градусов
Основное тригонометрическое тождество
Обратные тригонометрические функции
Синус угла
Числовая окружность, тригонометрический круг и единичная окружность
Любая окружность, которую мы соотносим с действительными числами будет  Но на практике (для удобства) используют единичную окружность, т.е. окружность с радиусом = 1 и центром в начале координат.
Но на практике (для удобства) используют единичную окружность, т.е. окружность с радиусом = 1 и центром в начале координат.
Ну, и поскольку у каждой точки окружности есть координаты на осях Х и Y, которые являются косинусом и синусом угла β, соответственно круг является тригонометрическим, т.е. связанным с этими самыми функциями из тригонометрии.
Большой плюс, что на тригонометрическом круге можно увидеть разные углы (а не только, как в треугольнике). Ведь неважно, где мы поставим точку на круге, мы всегда сможем определить для нее косинус и синус по абсциссе и ординате даже по самому простому и схематичному рисунку.
Важно только помнить, что угол всегда рисуется от оси OX (называется углом поворота) и получается такая схема, где положительные углы всегда отображаются против часовой стрелки, а отрицательные — по часовой.
Вместе с положительными углами движется и отсчет четвертей круга:
0° до 90° — I четверть,
90° до 180° — II четверть,
180° до 270° — III четверть,
270° до 360° — IV четверть
Еще лайфхаки с градусами и кругами
Соответственно, если точно помнить, что целый круг — это 360°, то 50° будет в том же месте, где и -310° (проверьте;)
Если нужны углы более 360°, то делим их на 360, отбрасываем целые части и рисуем обычный угол.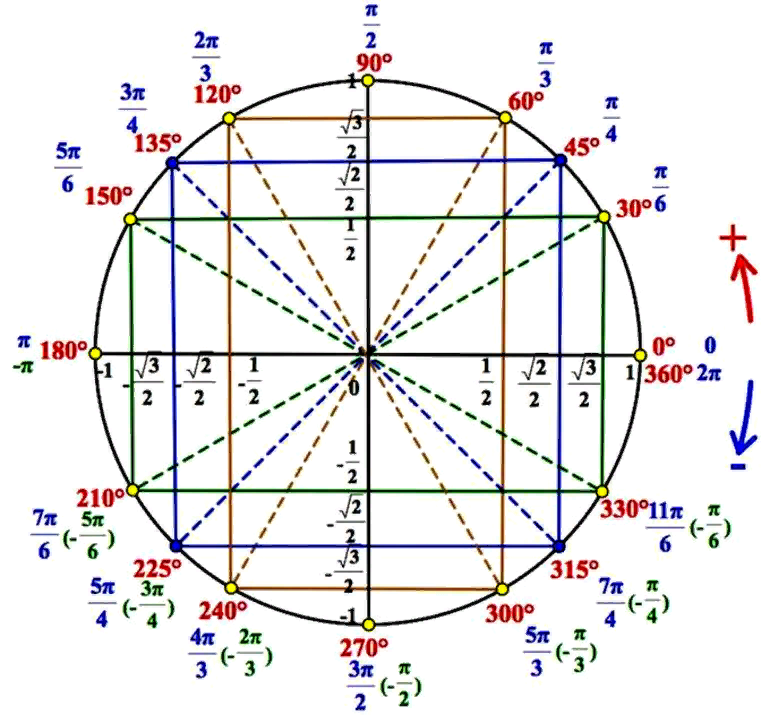
Добавить интересную новость
Тригонометрия. Тригонометрический круг. Единичная окружность. Числовая окружность. Что это такое? Тригонометрическая окружность со всеми
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.

- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.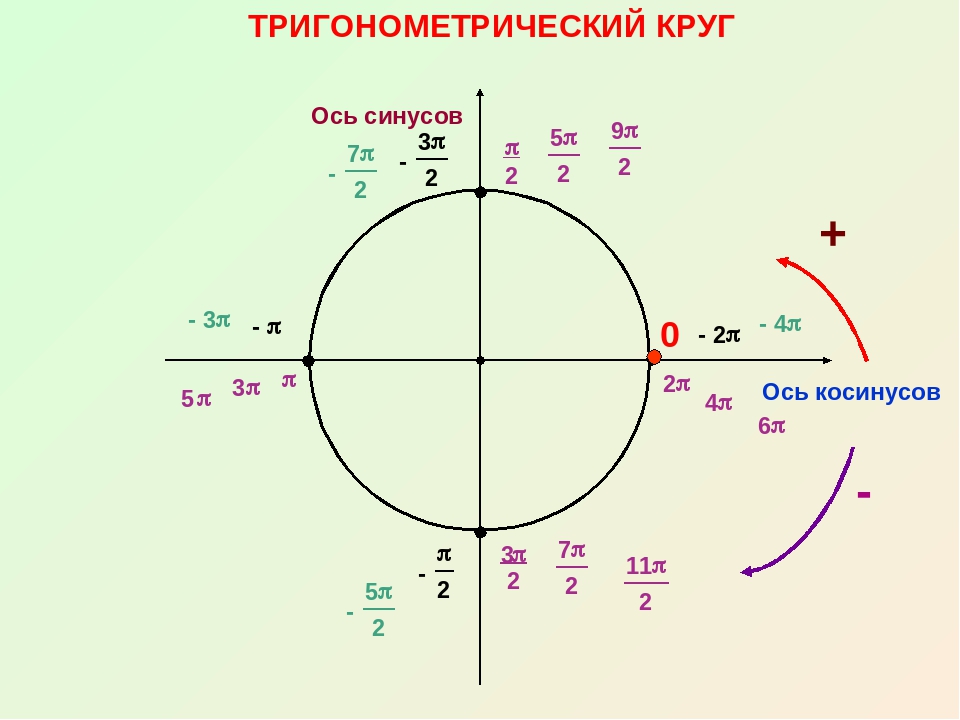
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Назад Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель: научить использовать единичную окружность при решении различных тригонометрических заданий.
В школьном курсе математики возможны различные варианты введения тригонометрических функций. Наиболее удобной и часто используемой является «числовая единичная окружность». Её применение в теме «Тригонометрия» весьма обширно.
Единичная окружность используется для:
– определения синуса, косинуса, тангенса и котангенса угла;
– нахождения значений тригонометрических функций для некоторых значений числового и углового аргумента;
– выведение основных формул тригонометрии;
– выведения формул приведения;
– нахождения области определения и области значений тригонометрических функций;
– определения периодичности тригонометрических функций;
– определения четности и нечетности тригонометрических функций;
– определения промежутков возрастания и убывания тригонометрических функций;
– определения промежутков знакопостоянства тригонометрических функций;
– радианного измерения углов;
– нахождения значений обратных тригонометрических функций;
– решение простейших неравенств и др.
Таким образом, активное осознанное владение учащимися данным видом наглядности дает неоспоримые преимущества для овладения разделом математики «Тригонометрия».
Использование ИКТ на уроках преподавания математики позволяет облегчить овладение числовой единичной окружностью. Конечно, интерактивная доска имеет широчайший диапазон применения, однако не во всех классах она есть. Если же говорить о применении презентаций, то на просторах Интернета и их выбор велик, и каждый педагог может найти наиболее приемлемый вариант для своих уроков.
В чем особенность представляемой мною презентации?
Данная презентация предполагает различные варианты использования и не является наглядностью к конкретному уроку в теме «Тригонометрия». Каждый слайд данной презентации можно использовать обособлено, как на этапе объяснения материала, формирования навыков, так и для рефлексии. При создании данной презентации особое внимание уделялось «читаемости» её с дальнего расстояния, поскольку количество учеников со сниженным зрением постоянно растет. Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.
Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.
Данная презентация поможет педагогам познакомить учеников с единичной окружностью в 9 классе на уроках геометрии при изучении темы «Соотношения между сторонами и углами треугольника». И, конечно, она поможет расширить и углубить навык работы с единичной окружностью при решении тригонометрических заданий у учащихся старшего звена обучения на уроках алгебры.
Слайды 3, 4 поясняют построение единичной окружности; принцип определения местоположения точки на единичной окружности в I и II координатных четвертях; переход от геометрических определений функций синус и косинус (в прямоугольном треугольнике) к алгебраическим на единичной окружности.
Слайды 5-8 поясняют, как найти значения тригонометрических функций для основных углов I координатной четверти.
Слайды 9-11 поясняет знаки функций в координатных четвертях; определение промежутков знакопостоянства тригонометрических функций.
Слайд 12 используется для формирования представлений о положительных и отрицательных значениях углов; знакомством с понятием периодичности тригонометрических функций.
Слайды 13, 14 используются при переходе на радианную меру угла.
Слайды 15-18 не анимированы и используются при решении различных тригонометрических заданий, закрепления и проверки результатов усвоения материала.
- Титульный лист.
- Целеполагание.
- Построение единичной окружности. Основные значения углов в градусной мере.
- Определение синуса и косинуса угла на единичной окружности.
- Табличные значения для синуса в порядке возрастания.
- Табличные значения для косинуса в порядке возрастания.

- Табличные значения для тангенса в порядке возрастания.
- Табличные значения для котангенса в порядке возрастания.
- Знаки функции sin α.
- Знаки функции cos α.
- Знаки функций tg α и ctg α.
- Положительные и отрицательные значения углов на единичной окружности.
- Радианная мера угла.
- Положительные и отрицательные значения углов в радианах на единичной окружности.
- Различные варианты единичной окружности для закрепления и проверки результатов усвоения материала.
Тригонометрический круг. Единичная окружность. Числовая окружность. Что это такое?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются учащимся народом. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии.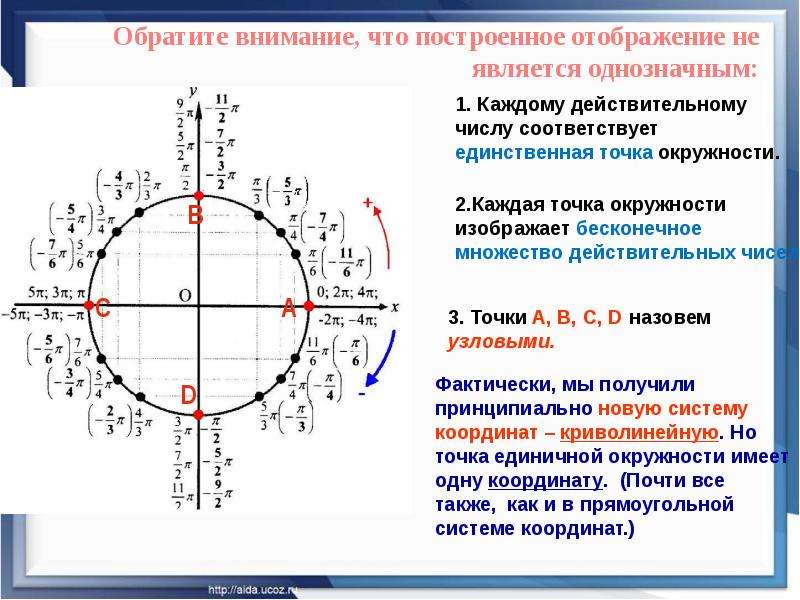 Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.
Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.
Для успешной работы с тригонометрическим кругом нужно знать всего три вещи.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.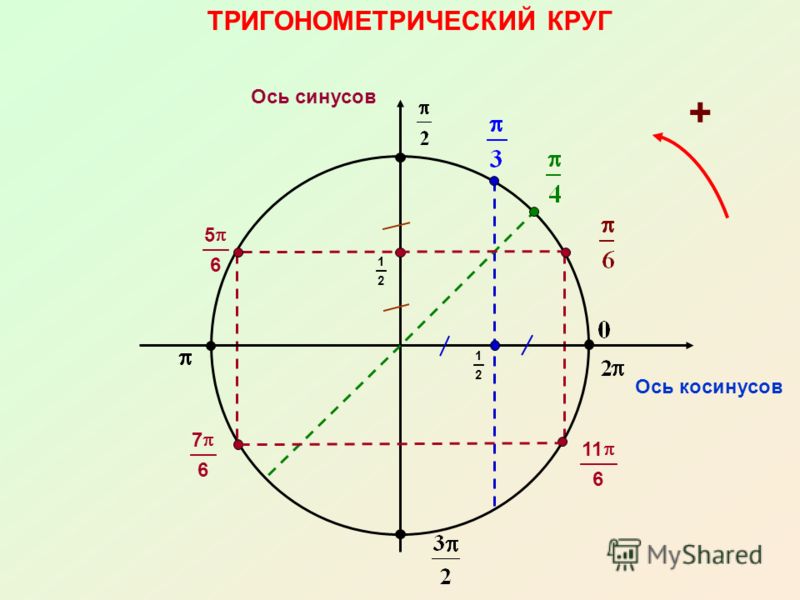
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.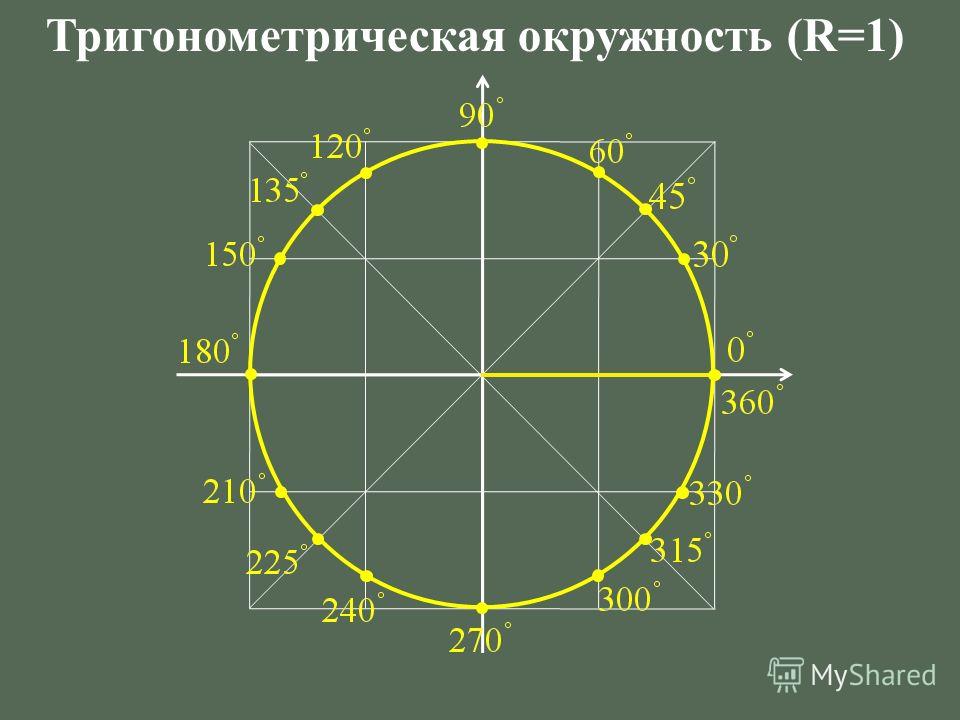
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений.
Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.
Вспомним определения косинуса и синуса.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол .
Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)
Используем эти определения для решения простейших тригонометрических уравнений.
1. Решим уравнение
Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .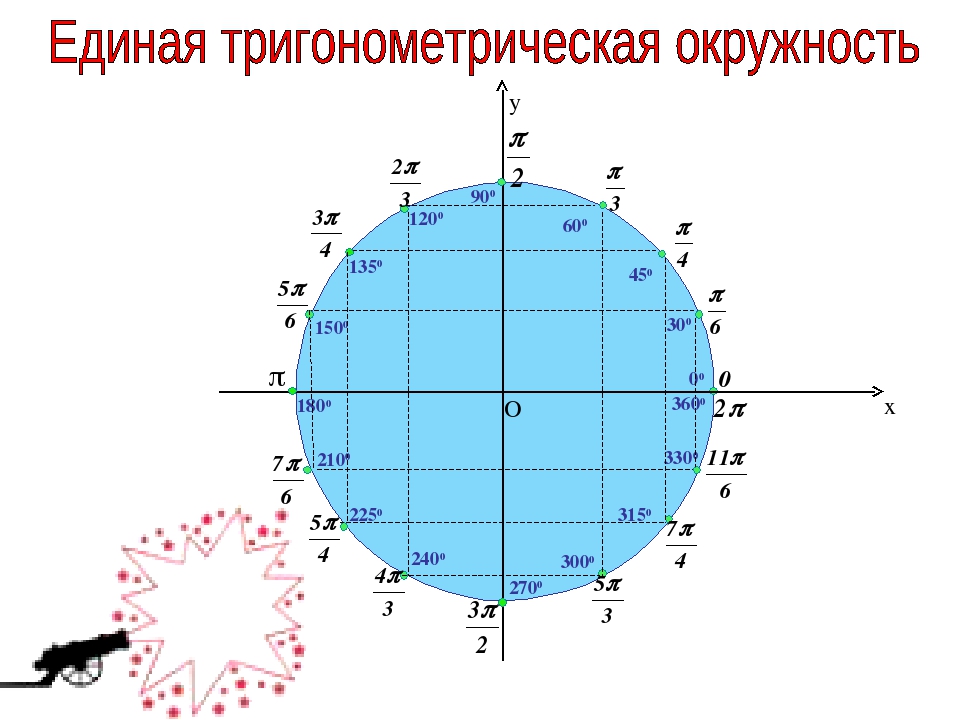
Отметим на оси ординат точку с ординатой :
Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие ординату. Эти точки соответствуют углам поворота на и радиан:
Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой (или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.
То есть первая серия решений исходного уравнения имеет вид:
, , — множество целых чисел (1)
Аналогично, вторая серия решений имеет вид:
, где , . (2)
(2)
Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .
Эти две серии решений можно объединить в одну запись:
Если мы в этой записи возьмем ( то есть четное ), то мы получим первую серию решений.
Если мы в этой записи возьмем ( то есть нечетное ), то мы получим вторую серию решений.
2. Теперь давайте решим уравнение
Так как — это абсцисса точки единичной окружности, полученной поворотом на угол , отметим на оси точку с абсциссой :
Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие абсциссу . Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:
Запишем две серии решений:
,
,
(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .
Объедим эти две серии в одну запись:
3. Решим уравнение
Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY
Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):
Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :
Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии радиан друг от друга, то мы можем записать решение таким образом:
,
4. Решим уравнение
Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .
Отметим на линии котангенсов точку с абсциссой -1:
Соединим эту точку с началом координат прямой и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:
Поскольку эти точки отстоят друг от друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:
В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.
Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:
ОСОБЫЕ РЕШЕНИЯ:
1
Отметим на окружности точки, ордината которых равна 0:
2.
Отметим на окружности единственную точку, ордината которой равна 1:
3.
Отметим на окружности единственную точку, ордината которой равна -1:
Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:
4.
Отметим на окружности точки, абсцисса которых равна 0:
5.
Отметим на окружности единственную точку, абсцисса которой равна 1:
6.
Отметим на окружности единственную точку, абсцисса которой равна -1:
И чуть более сложные примеры:
1.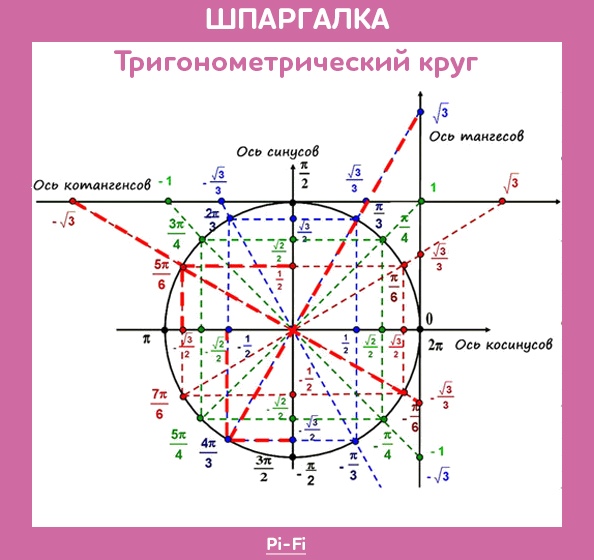
Синус равен единице, если аргумент равен
Аргумент у нашего синуса равен , поэтому получим:
. Разделим обе части равенства на 3:
Ответ:
2.
Косинус равен нулю, если аргумент косинуса равен
Аргумент у нашего косинуса равен , поэтому получим:
Выразим , для этого сначала перенесем вправо с противоположным знаком:
Упростим правую часть:
Разделим обе части на -2:
Заметим, что перед слагаемым знак не меняется, поскольку k может принимать любые целые значения.
Ответ:
И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»
На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и Задание 13»
Могут ли градусы быть отрицательными. Отрицательный угол. Сбор и использование персональной информации
В тригонометрии важным понятием является угол поворота . Ниже мы последовательно будем давать представление о повороте, и вводить все сопутствующие понятия. Начнем с общего представления о повороте, скажем о полном обороте. Далее перейдем к понятию угла поворота и рассмотрим его основные характеристики, такие как направление и величина поворота. Наконец, дадим определение поворота фигуры вокруг точки. Всю теорию по тексту будем снабжать поясняющими примерами и графическими иллюстрациями.
Навигация по странице.
Что называют поворотом точки вокруг точки?
Сразу отметим, что наряду с фразой «поворот вокруг точки» будем также использовать словосочетания «поворот около точки» и «поворот относительно точки», что обозначает одно и то же.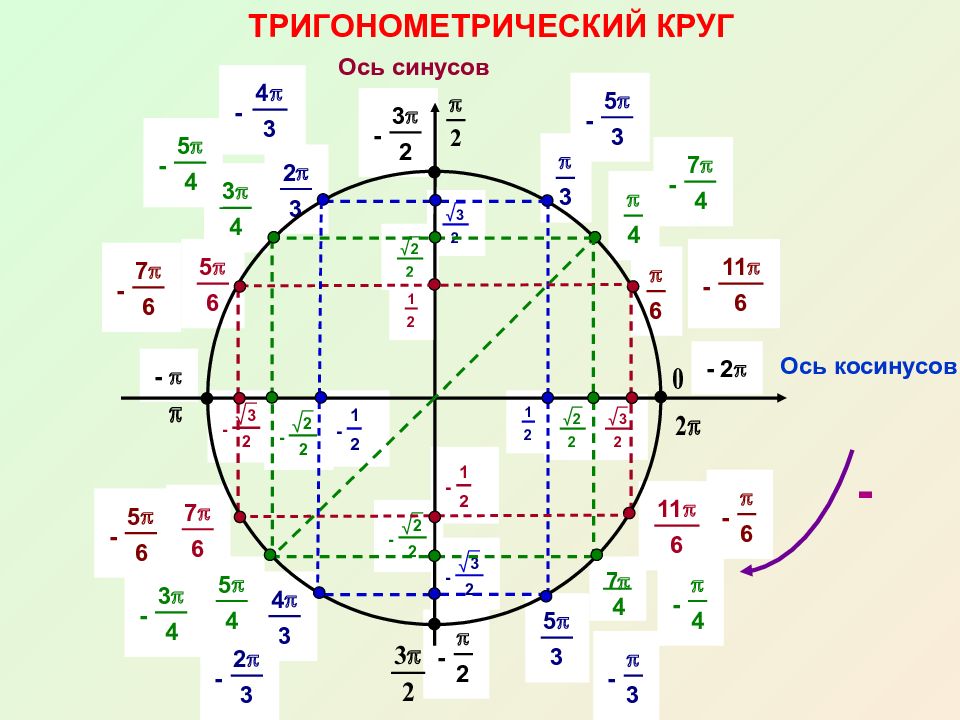
Введем понятие поворота точки вокруг точки .
Сначала дадим определение центра поворота.
Определение.
Точку, относительно которой осуществляется поворот, называют центром поворота .
Теперь скажем, что получается в результате поворота точки.
В результате поворота некоторой точки A относительно центра поворота O получается точка A 1 (которая в случае некоторого количества может совпадать с A ), причем точка A 1 лежит на окружности с центром в точке O радиуса OA . Иными словами, при повороте относительно точки O точка A переходит в точку A 1 , лежащую на окружности с центром в точке O радиуса OA .
Считают, что точка O при повороте вокруг самой себя переходит в саму себя. То есть, в результате поворота вокруг центра поворота O точка O переходит в саму себя.
Также стоит отметить, что поворот точки А
вокруг точки O
стоит рассматривать как перемещение в результате движения точки А
по окружности с центром в точке O
радиуса OA
.
Для наглядности приведем иллюстрации поворота точки А вокруг точки O , на рисунках, расположенных ниже, перемещение точки А в точку А 1 покажем при помощи стрелки.
Полный оборот
Можно выполнить такой поворот точки A относительно центра поворота O , что точка А , пройдя все точки окружности, окажется на прежнем месте. При этом говорят, что точка А совершила вокруг точки O .
Дадим графическую иллюстрацию полного оборота.
Если же не останавливаться на одном обороте, а продолжать движение точки по окружности, то можно выполнить два, три и так далее полных оборотов. На чертеже ниже справа показано, как могут быть произведены два полных оборота, а слева — три оборота.
Понятие угла поворота
Из введенного в первом пункте понятия поворота точки понятно, что существует бесконечное множество вариантов поворота точки А
вокруг точки O
. Действительно, любую точку окружности с центром в точке O
радиуса OA
можно рассматривать как точку A 1
, полученную в результате поворота точки А
. Поэтому, чтобы отличать один поворот от другого, вводится понятие угла поворота .
Поэтому, чтобы отличать один поворот от другого, вводится понятие угла поворота .
Одной из характеристик угла поворота является направление поворота . По направлению поворота судят о том, как осуществляется поворот точки – по часовой стрелке или против часовой стрелки.
Другой характеристикой угла поворота является его величина . Углы поворота измеряются в тех же единицах, что и : наиболее распространены градусы и радианы. Здесь стоит заметить, что угол поворота может выражаться в градусах любым действительным числом из промежутка от минус бесконечности до плюс бесконечности, в отличие от угла в геометрии, величина которого в градусах положительна и не превосходит 180 .
Для обозначения углов поворота обычно используются строчные буквы греческого алфавита: и т.д. Для обозначения большого количества углов поворота часто применяют одну букву с нижними индексами, к примеру, .
Теперь поговорим о характеристиках угла поворота подробнее и по порядку.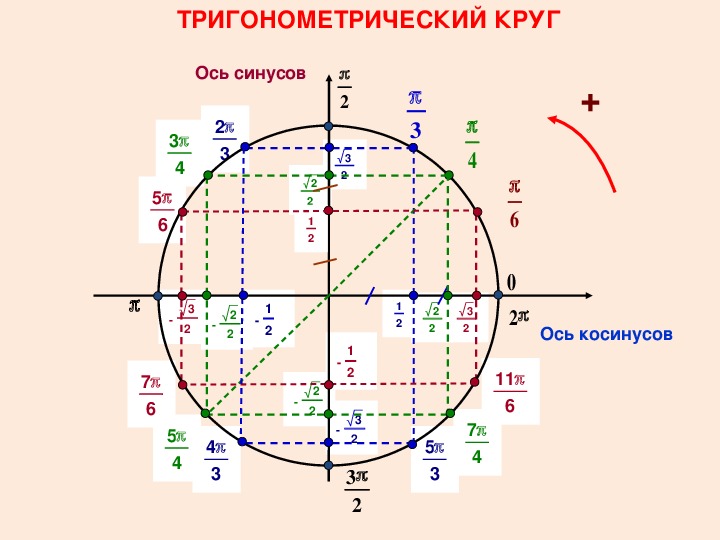
Направление поворота
Пусть на окружности с центром в точке O отмечены точки A и A 1 . В точку А 1 можно попасть из точки A , выполнив поворот вокруг центра O либо по часовой стрелке, либо — против часовой стрелки. Эти повороты логично считать различными.
Проиллюстрируем повороты в положительном и отрицательном направлении. На чертеже ниже слева показан поворот в положительном направлении, а справа – в отрицательном.
Величина угла поворота, угол произвольной величины
Угол поворота точки, отличной от центра поворота, полностью определяется указанием его величины, с другой стороны, по величине угла поворота можно судить о том, как этот поворот был осуществлен.
Как мы уже упоминали выше, величина угла поворота в градусах выражается числом от −∞ до +∞ . При этом знак плюс соответствует повороту по часовой стрелке, а знак минус – повороту против часовой стрелки.
Теперь осталось установить соответствие между величиной угла поворота и тем, какому повороту она соответствует.
Начнем с угла поворота, равного нулю градусам. Этому углу поворота отвечает перемещение точки А в себя. Другими словами, при повороте на 0 градусов вокруг точки O точка А остается на месте.
Переходим к повороту точки А вокруг точки O , при котором поворот происходит в пределах половины оборота. Будем считать, что точка А переходит в точку А 1 . В этом случае абсолютная величина угла AOA 1 в градусах не превосходит 180 . Если поворот происходил в положительном направлении, то величина угла поворота считается равной величине угла AOA 1 , а если поворот происходил в отрицательном направлении, то его величина считается равной величине угла АОА 1 со знаком минус. Для примера приведем рисунок, показывающий углы поворота в 30 , 180 и −150 градусов.
Углы поворота большие 180
градусов и меньшие −180
градусов определяются на основе следующего достаточно очевидного свойства последовательных поворотов : несколько последовательных поворотов точки A
вокруг центра O
равносильны одному повороту, величина которого равна сумме величин этих поворотов.
Приведем пример, иллюстрирующий данное свойство. Выполним поворот точки А относительно точки O на 45 градусов, а затем еще повернем эту точку на 60 градусов, после чего повернем эту точку на −35 градусов. Обозначим промежуточные точки при этих поворотах как A 1 , A 2 и A 3 . В эту же точку А 3 мы могли попасть, выполнив один поворот точки A на угол 45+60+(−35)=70 градусов.
Итак, углы поворота, большие 180 градусов, мы будем представлять как несколько последовательных поворотов на углы, сумма величин которых дает величину исходного угла поворота. Например, угол поворота 279 градусов соответствует последовательным поворотам на 180 и 99 градусов, или на 90 , 90 , 90 и 9 градусов, или на 180 , 180 и −81 градус, или на 279 последовательных поворотов по 1 градусу.
Аналогично определяются и углы поворота, меньшие −180
градусов. К примеру, угол поворота −520
градусов можно интерпретировать как последовательные повороты точки на −180
, −180
и −160
градусов.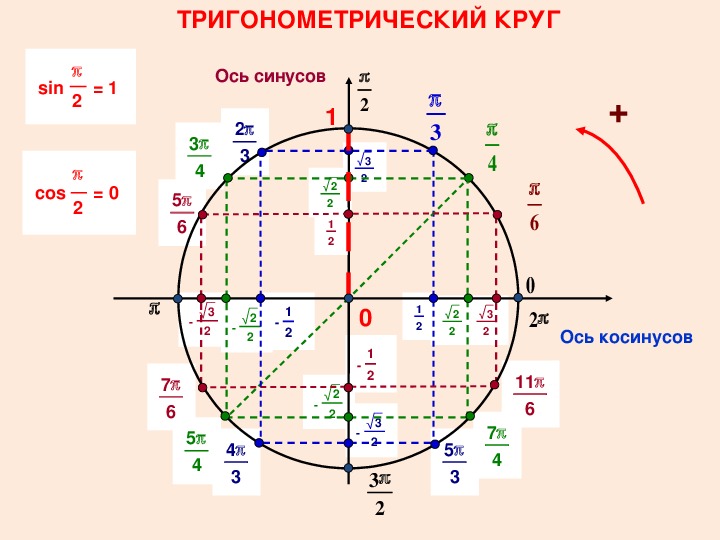
Подведем итог . Мы определили угол поворота, величина которого в градусах выражается некоторым действительным числом из промежутка от −∞ до +∞ . В тригонометрии мы будем работать именно с углами поворота, хотя слово «поворот» часто опускают, и говорят просто «угол». Таким образом, в тригонометрии мы будем работать с углами произвольной величины, под которыми будем понимать углы поворота.
В заключение этого пункта отметим, что полный оборот в положительном направлении соответствует углу поворота в 360
градусов (или 2·π
радианов), а в отрицательном – углу поворота в −360
градусов (или −2·π
рад). При этом удобно большие углы поворота представлять как некоторое количество полных оборотов и еще один поворот на угол величиной от −180
до 180
градусов. Для примера возьмем угол поворота 1 340
градусов. Несложно 1 340
представить как 360·4+(−100)
. То есть, исходному углу поворота отвечают 4
полных оборота в положительном направлении и последующий поворот на −100
градусов.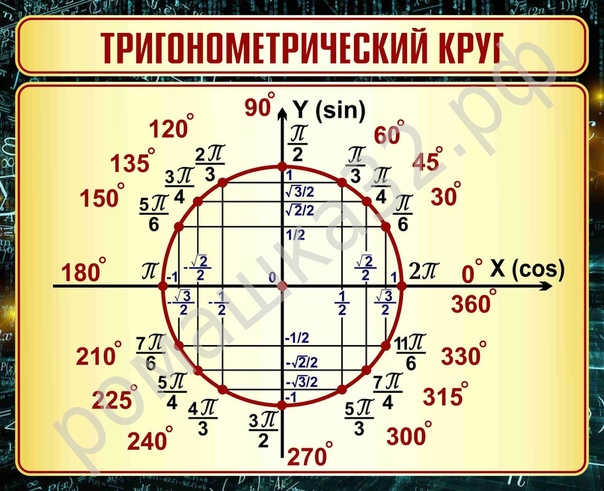 Другой пример: угол поворота −745
градусов можно интерпретировать как два оборота против часовой стрелки и последующий поворот на −25
градусов, так как −745=(−360)·2+(−25)
.
Другой пример: угол поворота −745
градусов можно интерпретировать как два оборота против часовой стрелки и последующий поворот на −25
градусов, так как −745=(−360)·2+(−25)
.
Поворот фигуры вокруг точки на угол
Понятие поворота точки легко расширяется на поворот любой фигуры вокруг точки на угол (речь идет о таком повороте, что и точка, относительно которой осуществляется поворот, и фигура, которую поворачивают, лежат в одной плоскости).
Под поворотом фигуры будем понимать поворот всех точек фигуры вокруг заданной точки на данный угол.
В качестве примера приведем иллюстрацию следующему действию: выполним поворот отрезка AB на угол относительно точки O , это отрезок при повороте перейдет в отрезок A 1 B 1 .
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- isbn 5-09-002727-7
- Башмаков М.
 И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4. - Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции.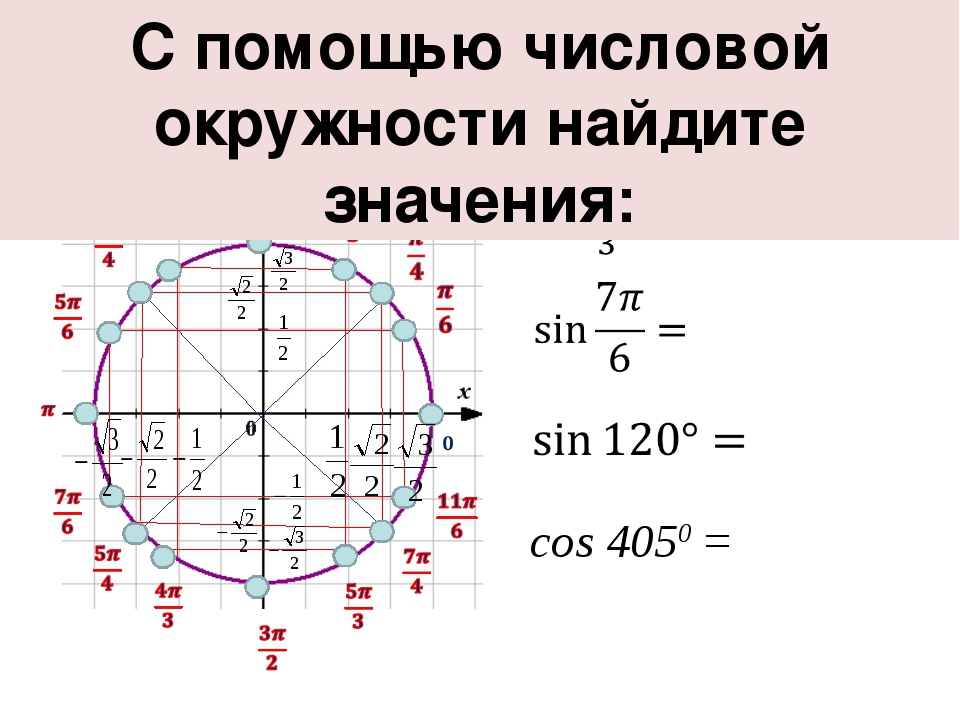 Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Угол: ° π rad =
Преобразовать в: радианы градусы 0 — 360° 0 — 2π положительное отрицательное Вычислять
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.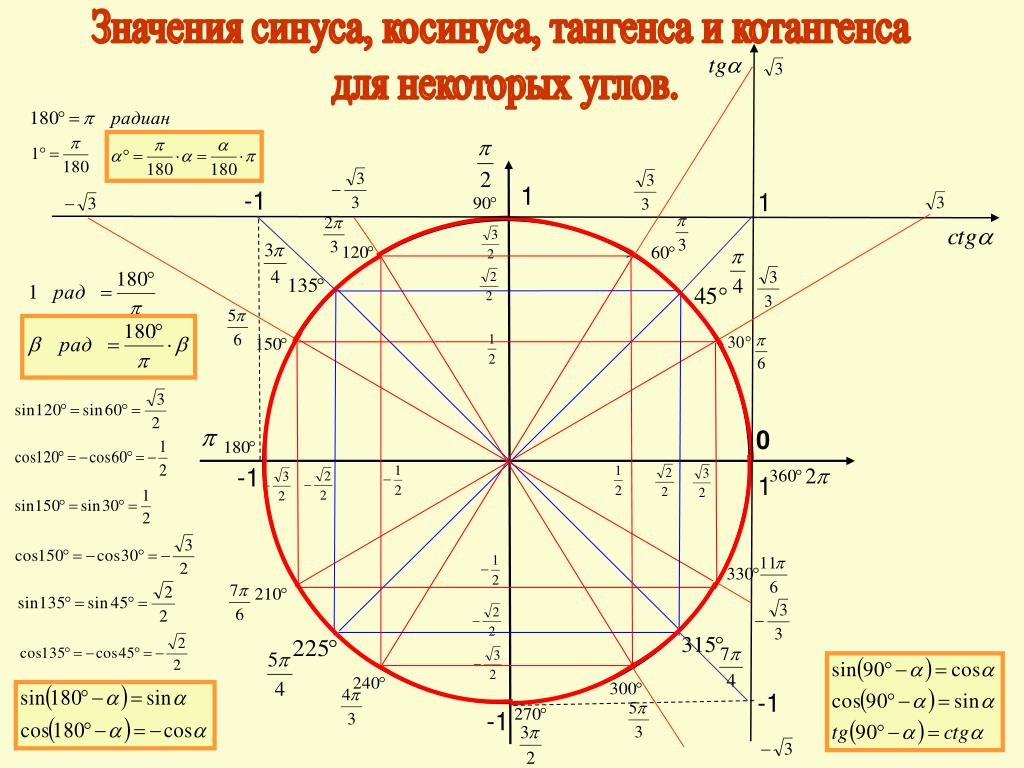
Эти новые области называют углами .
На картинке видны 4 разных угла, образованных пересечением прямых AB и CD
Обычно углы измеряются в градусах, что обозначается как °.
Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°).
Таким образом, градус — это $\frac{1}{360}$ круга.
Углы больше 360 градусов
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.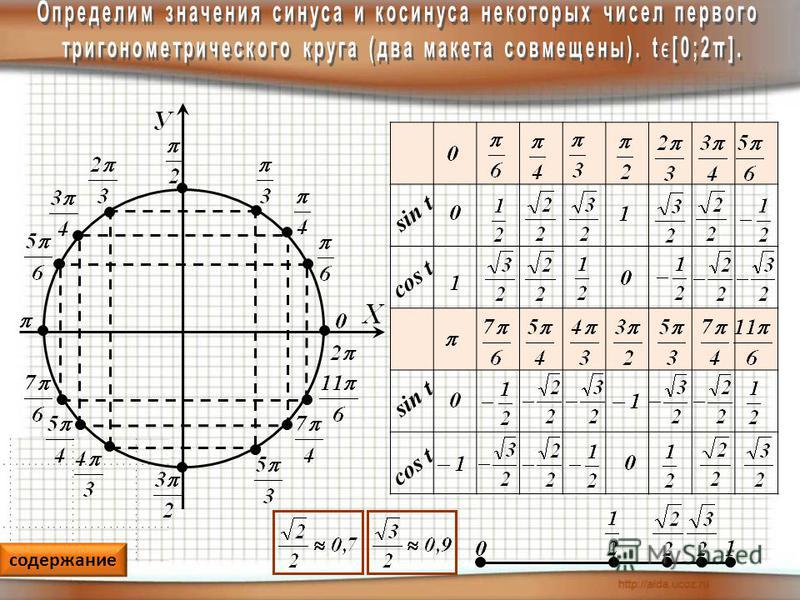 {\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
{\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
Объект описал $2\frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.
Пример 3
1. Найти соответствующий положительный угол
Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°
Радиан
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга.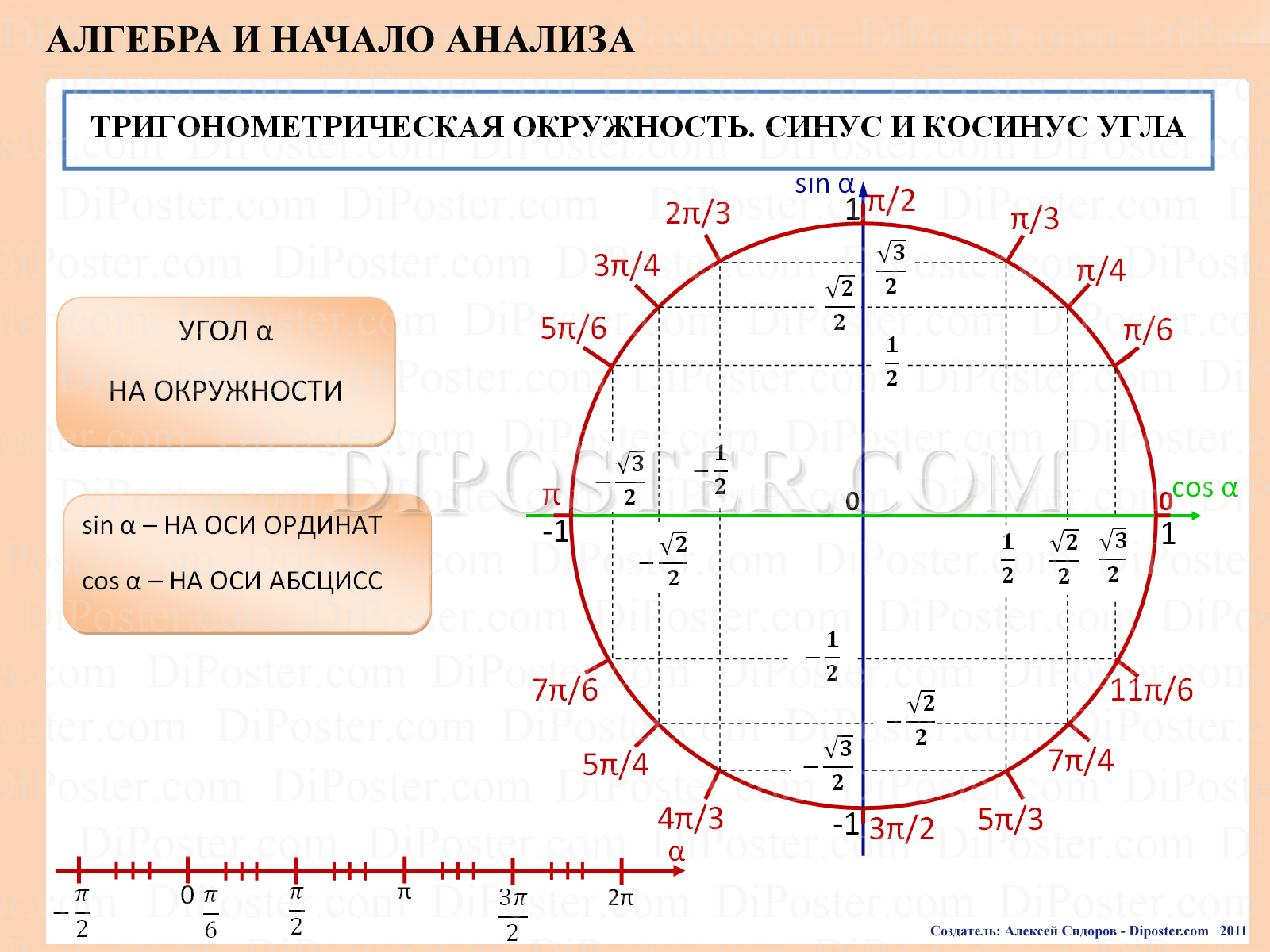 {\circ}$
{\circ}$
c) 1 рад = 57.3°
$2.4 = \frac{2.4 \times 57.3}{1} = 137.52$
Отрицаетльные углы и углы больше, чем $2\pi$ радиан
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.
Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.
Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$
Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.
Пример 6
1. Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$
Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.
b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки
c) $\frac{7}{2}\pi=3.5\pi=2\pi+1.5\pi$, $1.5\pi$ равно три четверти цикла $(\frac{1.5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки
Пара различных лучей Оа и Оb, выходящих из одной точки О, называется углом и обозначается символом (а, b). Точка О называется вершиной угла, а лучи Оа u Оb — сторонами угла. Если А и В — две точки лучей Оа и Оb, то (а, b) обозначается также символом АОВ (рис. 1.1).
Угол (а, Ь) называют развернутым, если лучи Оа и Ob, выходящие из одной точки, лежат на одной прямой и не совпадают (т. е. противоположно направлены).
Рис.1.1
Два угла считаются равными, если один угол можно наложить на другой так, чтобы стороны углов совпадали. Биссектрисой угла называется луч с началом в вершине угла, делящий угол на два равных угла.
Говорят, что луч ОС, исходящий из вершины угла АОВ, лежит между его сторонами, если он пересекает отрезок АВ (рис. 1.2). Говорят, что точка С лежит между сторонами угла, если через эту точку можно провести луч с началом в вершине угла, лежащий между сторонами угла. Множество всех точек плоскости, лежащих между сторонами угла, образует внутреннюю область угла (рис. 1.3). Множество точек плоскости, не принадлежащих внутренней области и сторонам угла, образует внешнюю область угла.
1.2). Говорят, что точка С лежит между сторонами угла, если через эту точку можно провести луч с началом в вершине угла, лежащий между сторонами угла. Множество всех точек плоскости, лежащих между сторонами угла, образует внутреннюю область угла (рис. 1.3). Множество точек плоскости, не принадлежащих внутренней области и сторонам угла, образует внешнюю область угла.
Угол (а, b) считают больше угла (c, d), если угол (с, d) можно наложить на угол (а, b) так, что после совмещения одной пары сторон вторая сторона угла (с, d) будет лежать между сторонами угла (а, b). На рис. 1.4 АОВ больше АОС.
Пусть луч с лежит между сторонами угла (а, b) (рис. 1.5). Пары лучей а, с и с, b образуют два угла. Об угле (а, b) говорят, что он является суммой двух углов (а, с) и (с, b), и пишут: (а, b) = (а, с) + (с, b).
Рис.1.3
Обычно в геометрии имеют дело с углами, меньшими развернутого. Однако в результате сложения двух углов может получиться угол, больший развернутого. В этом случае ту часть плоскости, которая считается внутренней областью угла, отмечают дугой.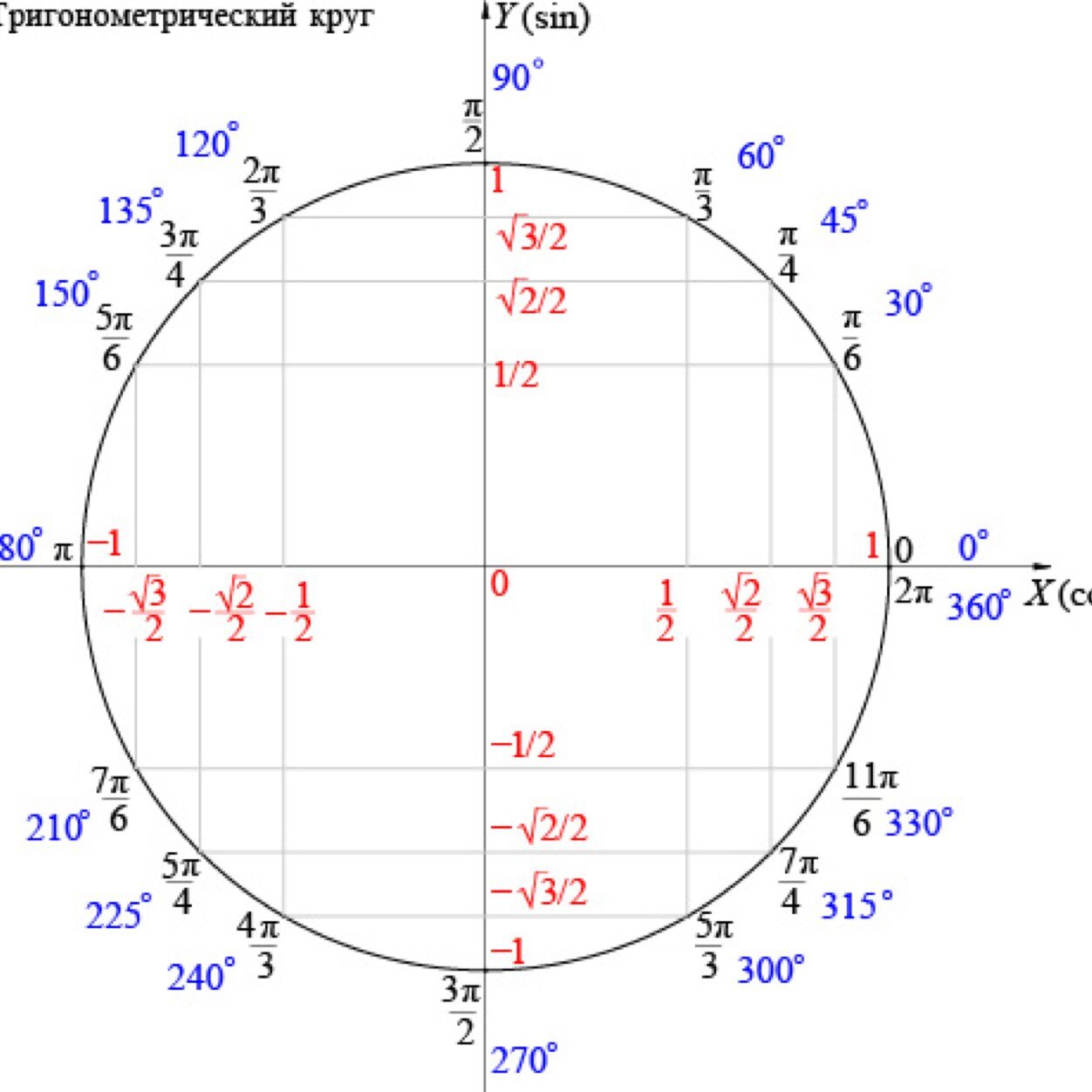 На рис. 1.6 внутренняя часть угла АОВ, полученного в результате сложения углов АОС и СОВ и большего развернутого, отмечена дугой.
На рис. 1.6 внутренняя часть угла АОВ, полученного в результате сложения углов АОС и СОВ и большего развернутого, отмечена дугой.
Рис.1.5
Существуют также углы большие 360°. Такие углы образуются, например, вращением пропеллера самолета, вращением барабана, на который наматывается канат, и т. д.
В дальнейшем при рассмотрении каждого угла условимся считать одну из сторон этого угла его начальной стороной, а другую — конечной стороной.
Любой угол, например угол АОВ (рис. 1.7), можно получить в результате вращения подвижного луча вокруг вершины О от начальной стороны угла (ОА) до его конечной стороны (ОВ). Мы будем измерять этот угол, учитывая полное количество оборотов, сделанных при этом вокруг точки О, а также и направление, в котором происходило вращение.
Положительные и отрицательные углы.
Пусть мы имеем угол, образованный лучами ОА и ОВ (рис.1.8). Подвижный луч, вращаясь вокруг точки О от своего начального положения (ОА), может занять конечное положение (ОВ) при двух различных направлениях вращения. Эти направления показаны на рисунке 1.8 соответствующими стрелками.
Эти направления показаны на рисунке 1.8 соответствующими стрелками.
Рис.1.7
Подобно тому, как на числовой оси одно из двух направлений считается положительным, а другое отрицательным, различают и два различных направления вращения подвижного луча. Условились считать положительным направлением вращения то направление, которое противоположно направлению вращения часовой стрелки. Направление вращения, совпадающее с направлением вращения часовой стрелки, считается отрицательным.
В соответствии с этими определениями углы также подразделяются на положительные и отрицательные.
Положительным углом называется угол, образованный вращением подвижного луча вокруг начальной точки в положительном направлении.
На рисунке 1.9 даны некоторые положительные углы. (Направление вращения подвижного луча показано на чертежах стрелками.)
Отрицательным углом называется угол, образованный вращением подвижного луча вокруг начальной точки в отрицательном направлении.
На рисунке 1.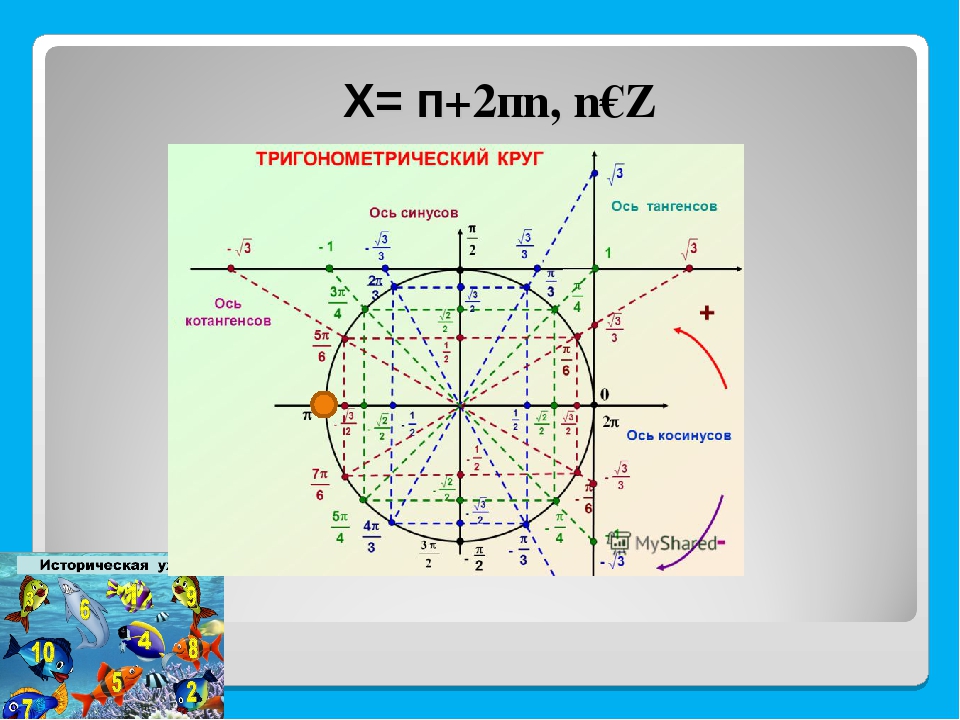 10 изображены некоторые отрицательные углы. (Направление вращения подвижного луча показано на чертежах стрелками.)
10 изображены некоторые отрицательные углы. (Направление вращения подвижного луча показано на чертежах стрелками.)
Но два совпадающих луча могут также образовать и углы +360°п и -360°п (п = 0,1,2,3,…). Обозначим через б наименьший возможный неотрицательный угол поворота, переводящий луч ОА в положение ОВ. Если теперь луч ОВ совершит дополнительно полный оборот вокруг точки О, то получим другую величину угла, а именно: АВО = б + 360°.
Измерение углов дугами окружности. Единицы измерения дуг и углов
В ряде случаев оказывается удобным измерять углы при помощи дуг окружности. Возможность такого измерения основа на известном предложении планиметрии о том, что в одном круге (или в равных кругах) центральные углы и соответствующие им дуги находятся в прямой пропорциональной зависимости.
Пусть некоторая дуга данной окружности принята за единицу измерения дуг. Соответствующий этой дуге центральный угол примем за единицу измерения углов. При таком условии любая дуга окружности и соответствующий этой дуге центральный угол будут содержать одно и то же число единиц измерения.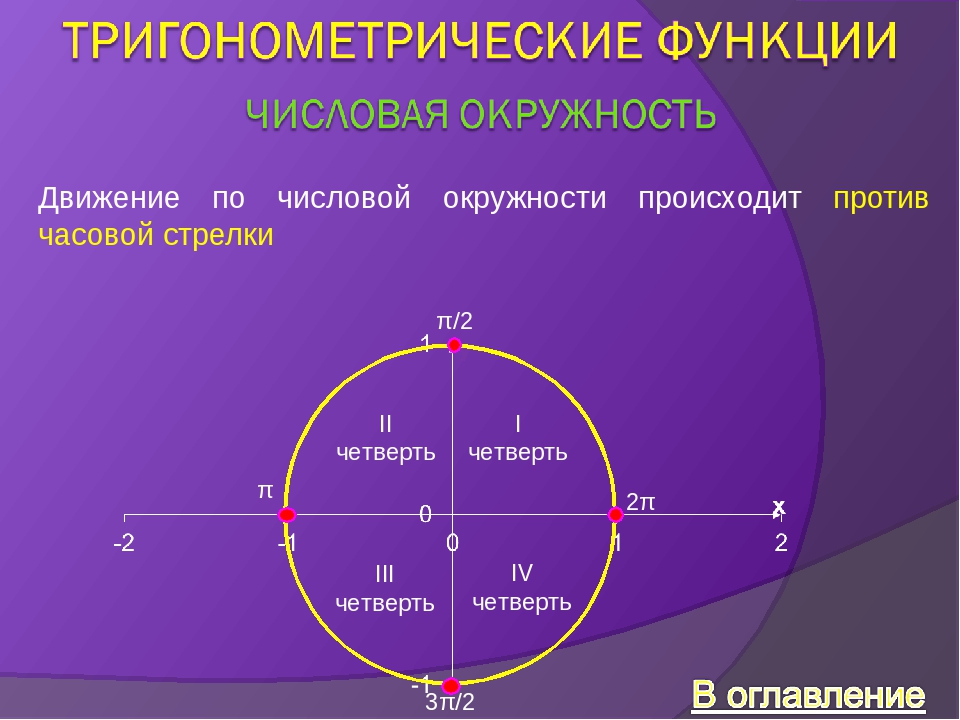 Поэтому, измеряя дуги окружности, можно определять и величину соответствующих этим дугам центральных углов.
Поэтому, измеряя дуги окружности, можно определять и величину соответствующих этим дугам центральных углов.
Рассмотрим две наиболее распространенные системы измерения дуг и углов.
Градусная мера измерения углов
При градусном измерении углов в качестве основной единицы измерения углов (эталонного угла, с которым сравниваются различные углы) берется угол в один градус (обозначается 1?). Угол в один градус — это угол, равный 1/180 части развернутого угла. Угол, равный 1/60 части угла в 1°, — это угол в одну минуту (обозначается 1″). Угол, равный 1/60 части угла в одну минуту,— это угол в одну секунду (обозначается 1″).
Радианная мера измерения углов
Наряду с градусной мерой измерения углов в геометрии и тригонометрии употребляется и другая мера измерения углов, называемая радианной. Рассмотрим окружность радиуса R с центром О. Проведем два радиуса О А и ОВ так, чтобы длина дуги АВ была равна радиусу окружности (рис. 1.12). Получившийся при этом центральный угол АОВ будет углом в один радиан. Угол в 1 радиан принимается за единицу измерения радианной меры измерения углов. При радианном измерении углов развернутый угол равен р радиан.
Угол в 1 радиан принимается за единицу измерения радианной меры измерения углов. При радианном измерении углов развернутый угол равен р радиан.
Градусная и радианная единицы измерения углов связаны равенствами:
1 радиан =180?/р57° 17″ 45″; 1?=р/180 радиана0,017453радиана;
1″=р/180*60 радиана0,000291 радиана;
1″»=р/180*60*60 радиана0,000005 радиана.
Градусную (или радианную) меру угла также называют величиной угла. Величину угла АОВ иногда обозначают /
Классификация углов
Угол, равный 90°, или в радианной мере р/2, называется прямым углом; его часто обозначают буквой d. Угол, меньший 90°, называется острым; угол, больший 90°, но меньший 180°, называется тупым.
Два угла, имеющие одну общую сторону и в сумме составляющие 180°, называются смежными углами. Два угла, имеющие одну общую сторону и в сумме составляющие 90°, называются дополнительными углами.
В прошлом уроке мы с вами успешно освоили (или повторили – кому как) ключевые понятия всей тригонометрии.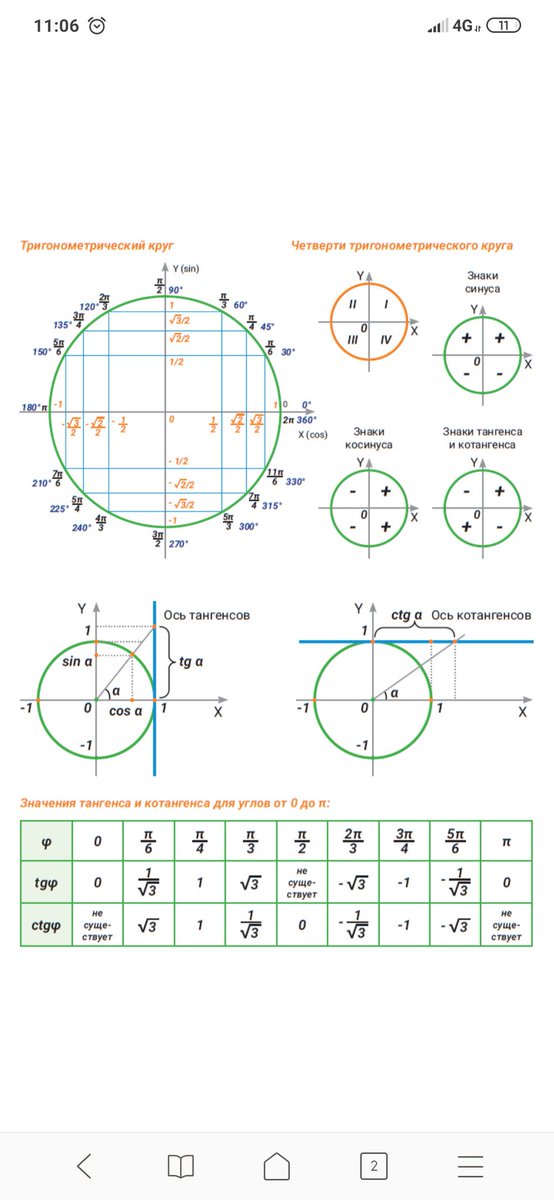 Это тригонометрический круг , угол на круге , синус и косинус этого угла , а также освоили знаки тригонометрических функций по четвертям . Освоили подробно. На пальцах, можно сказать.
Это тригонометрический круг , угол на круге , синус и косинус этого угла , а также освоили знаки тригонометрических функций по четвертям . Освоили подробно. На пальцах, можно сказать.
Но этого пока мало. Для успешного практического применения всех этих простых понятий нам необходим ещё один полезный навык. А именно – правильная работа с углами в тригонометрии. Без этого умения в тригонометрии – никак. Даже в самых примитивных примерах. Почему? Да потому, что угол – ключевая действующая фигура во всей тригонометрии! Нет, не тригонометрические функции, не синус с косинусом, не тангенс с котангенсом а именно сам угол . Нет угла – нету и тригонометрических функций, да…
Как правильно работать с углами на круге? Для этого нам надо железно усвоить два пункта.
1) Как отсчитываются углы на круге?
2) В чём они считаются (измеряются)?
Ответ на первый вопрос – и есть тема сегодняшнего урока.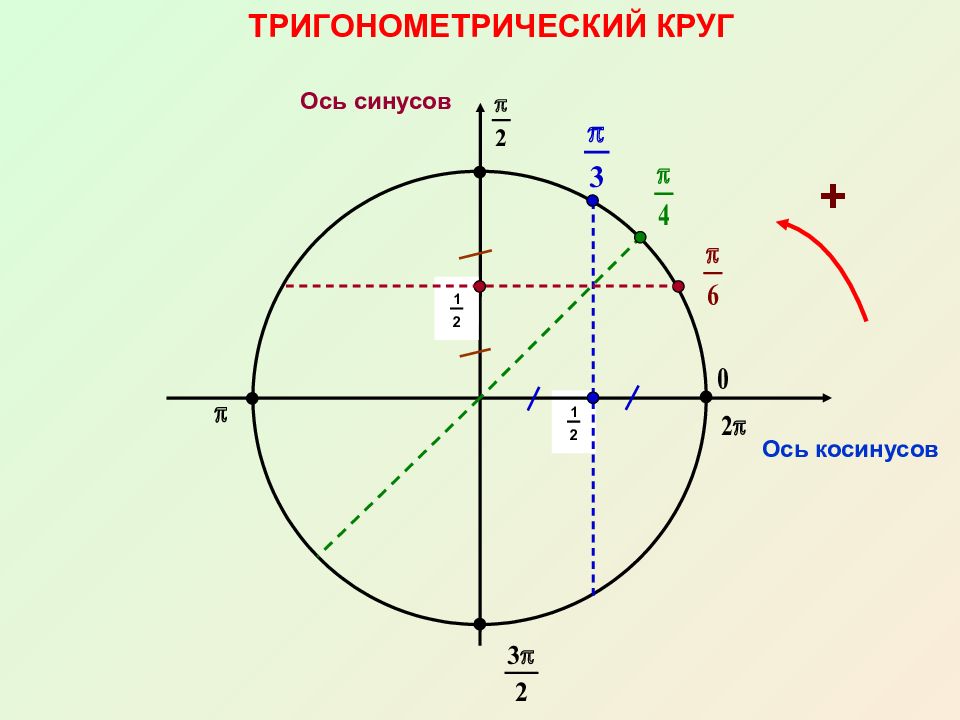 С первым вопросом мы детально разберёмся прямо здесь и сейчас. Ответ на второй вопрос здесь не дам. Ибо достаточно развёрнутый он. Как и сам второй вопрос очень скользкий, да.) Вдаваться в подробности пока не буду. Это – тема следующего отдельного урока.
С первым вопросом мы детально разберёмся прямо здесь и сейчас. Ответ на второй вопрос здесь не дам. Ибо достаточно развёрнутый он. Как и сам второй вопрос очень скользкий, да.) Вдаваться в подробности пока не буду. Это – тема следующего отдельного урока.
Приступим?
Как отсчитываются углы на круге? Положительные и отрицательные углы.
У прочитавших название параграфа, возможно, уже волосы встали дыбом. Как так?! Отрицательные углы? Разве такое вообще возможно?
К отрицательным числам мы с вами уже попривыкли. На числовой оси их изображать умеем: справа от нуля положительные, слева от нуля отрицательные. Да и на градусник за окном поглядываем периодически. Особенно зимой, в мороз.) И денежки на телефоне в «минус» (т.е. долг ) иногда уходят. Это всё знакомо.
А что же с углами? Оказывается, отрицательные углы в математике тоже бывают! Всё зависит от того, как отсчитывать этот самый угол… нет, не на числовой прямой, а на числовой окружности! То бишь, на круге.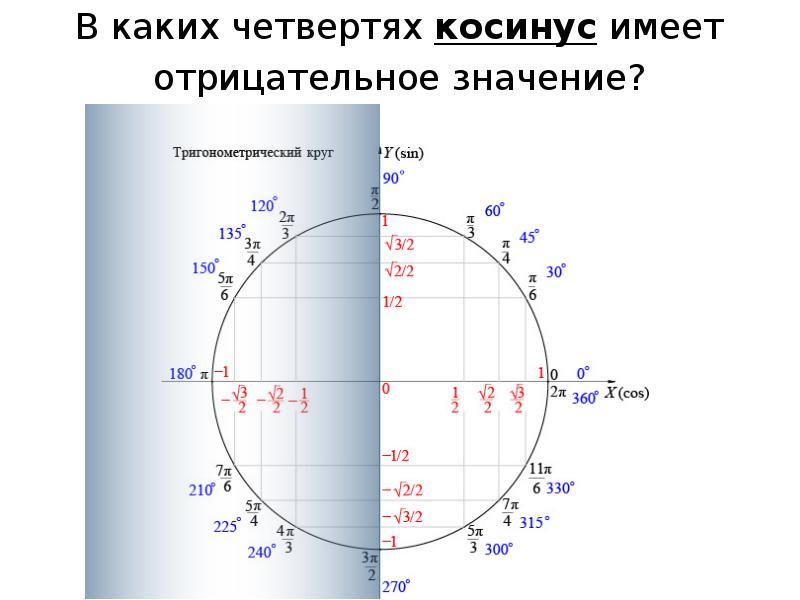 Круг – вот он, аналог числовой прямой в тригонометрии!
Круг – вот он, аналог числовой прямой в тригонометрии!
Итак, как же отсчитываются углы на круге? Ничего не поделать, придётся нам для начала этот самый круг нарисовать.
Я нарисую вот такую красивую картинку:
Она очень похожа на картинки из прошлого урока. Есть оси, есть окружность, есть угол. Но есть и новая информация.
Также я добавил циферки 0°, 90°, 180°, 270° и 360° на осях. Вот это уже поинтереснее.) Что это за циферки? Правильно! Это значения углов, отсчитанные от нашей неподвижной стороны, которые попадают на координатные оси. Вспоминаем, что неподвижная сторона угла у нас всегда крепко-накрепко привязана к положительной полуоси ОХ. И любой угол в тригонометрии отсчитывается именно от этой полуоси. Это базовое начало отсчёта углов надо держать в голове железно. А оси – они же под прямым углом пересекаются, верно? Вот и прибавляем по 90° в каждой четверти.
И ещё добавлена красная стрелочка. С плюсом. Красная – это специально, чтобы в глаза бросалась.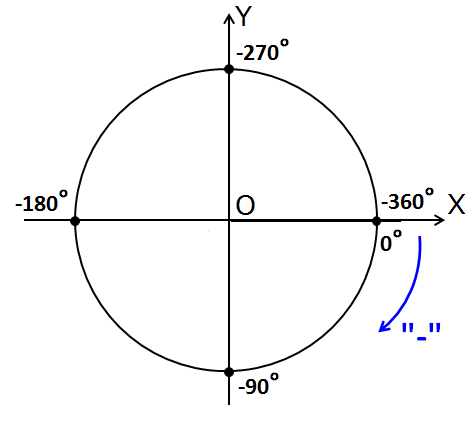 И в память хорошенько врезалась. Ибо это надо запомнить надёжно.) Что же означает эта стрелочка?
И в память хорошенько врезалась. Ибо это надо запомнить надёжно.) Что же означает эта стрелочка?
Так вот оказывается, если наш угол мы будем крутить по стрелочке с плюсом (против часовой стрелки, по ходу нумерации четвертей), то угол будет считаться положительным! В качестве примера на рисунке показан угол +45°. Кстати, обратите внимание, что осевые углы 0°, 90°, 180°, 270° и 360° также отмотаны именно в плюс! По красной стрелочке.
А теперь посмотрим на другую картинку:
Здесь почти всё то же самое. Только углы на осях пронумерованы в обратную сторону. По часовой стрелке. И имеют знак «минус».) Ещё нарисована синяя стрелочка. Также с минусом. Эта стрелочка – направление отрицательного отсчёта углов на круге. Она нам показывает, что, если мы будем откладывать наш угол по ходу часовой стрелки , то угол будет считаться отрицательным. Для примера я показал угол -45°.
Кстати, прошу заметить, что нумерация четвертей никогда не меняется! Неважно, в плюс или в минус мы мотаем углы.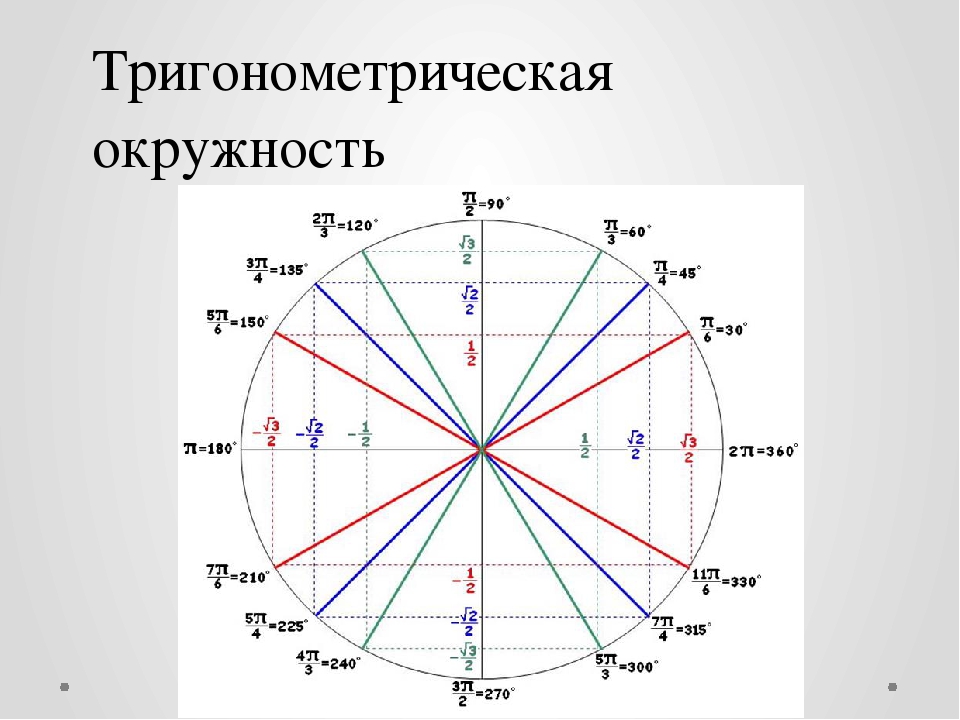 Всегда строго против часовой стрелки.)
Всегда строго против часовой стрелки.)
Запоминаем:
1. Начало отсчёта углов – от положительной полуоси ОХ. По часам – «минус», против часов – «плюс».
2. Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.
Кстати говоря, подписывать углы на осях 0°, 90°, 180°, 270°, 360°, каждый раз рисуя круг – вовсе не обязаловка. Это чисто для понимания сути сделано. Но эти циферки обязательно должны присутствовать в вашей голове при решении любой задачи по тригонометрии. Почему? Да потому, что эти элементарные знания дают ответы на очень многие другие вопросы во всей тригонометрии! Самый главный вопрос – в какую четверть попадает интересующий нас угол? Хотите верьте, хотите нет, но правильный ответ на этот вопрос решает львиную долю всех остальных проблем с тригонометрией. Этим важным занятием (распределением углов по четвертям) мы займёмся в этом же уроке, но чуть позже.
Величины углов, лежащих на осях координат (0°, 90°, 180°, 270° и 360°), надо запомнить! Запомнить накрепко, до автоматизма.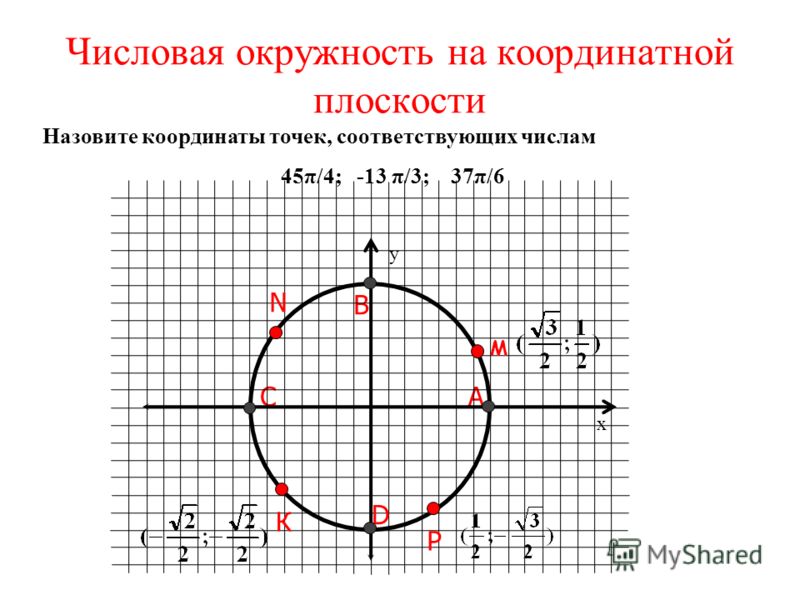 Причём как в плюс, так и в минус.
Причём как в плюс, так и в минус.
А вот с этого момента начинаются первые сюрпризы. И вместе с ними и каверзные вопросы в мой адрес, да…) А что будет, если отрицательный угол на круге совпадёт с положительным? Выходит, что одну и ту же точку на круге можно обозначить как положительным углом, так и отрицательным???
Совершенно верно! Так и есть.) Например, положительный угол +270° занимает на круге то же самое положение , что и отрицательный угол -90°. Или, например, положительный угол +45° на круге займёт то же самое положение , что и отрицательный угол -315°.
Смотрим на очередной рисунок и всё видим:
Точно так же положительный угол +150° попадёт туда же, куда и отрицательный угол -210°, положительный угол +230° – туда же, куда и отрицательный угол -130°. И так далее…
И что теперь делать? Как именно считать углы, если можно и так и сяк? Как правильно?
Ответ: по-всякому правильно! Ни одно из двух направлений отсчёта углов математика не запрещает. А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа «определите наибольший отрицательный угол» и т.п.), то работаем с наиболее удобными нам углами.
А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа «определите наибольший отрицательный угол» и т.п.), то работаем с наиболее удобными нам углами.
Конечно, например, в таких крутых темах, как тригонометрические уравнения и неравенства направление исчисления углов может колоссально влиять на ответ. И в соответствующих темах мы эти подводные камни рассмотрим.
Запоминаем:
Любую точку на круге можно обозначить как положительным, так и отрицательным углом. Любым! Каким хотим.
А теперь призадумаемся вот над чем. Мы выяснили, что угол 45° в точности совпадает с углом -315°? Как же я узнал про эти самые 315
°
? Не догадываетесь? Да! Через полный оборот.) В 360°. У нас есть угол 45°. Сколько не хватает до полного оборота? Отнимаем 45
°
от 360 °
– вот и получаем 315
°
. Мотаем в отрицательную сторону – и получаем угол -315°. Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.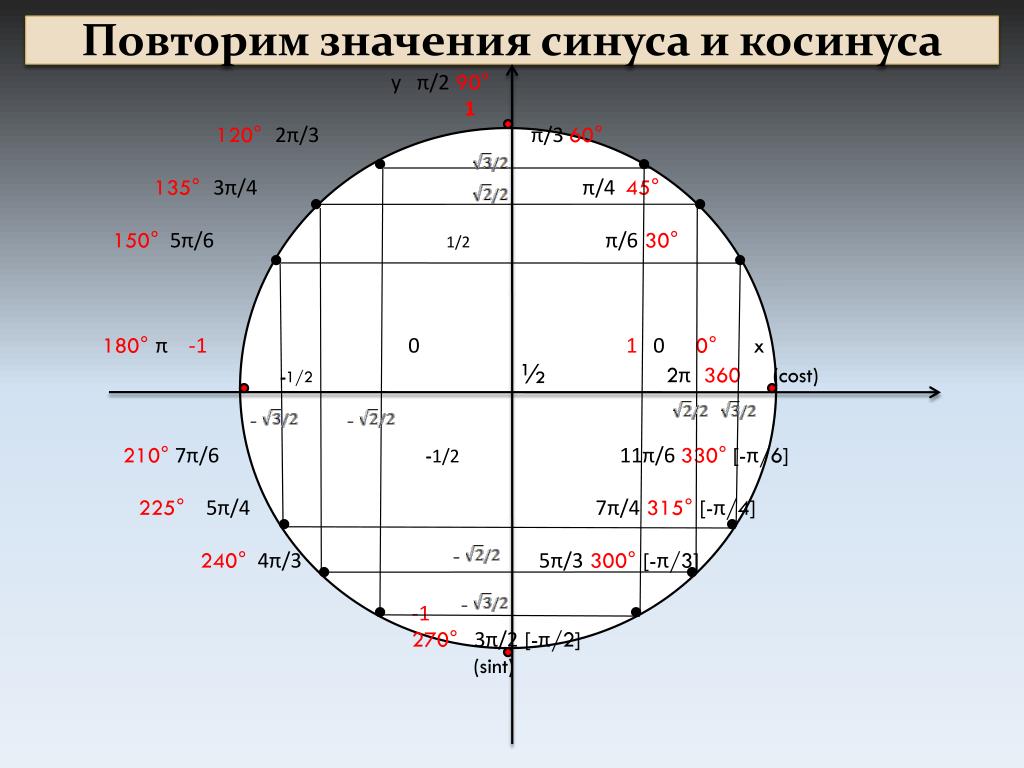
И так надо поступать всегда при переводе положительных углов в отрицательные (и наоборот) – рисуем круг, отмечаем примерно заданный угол, считаем, сколько градусов не хватает до полного оборота, и мотаем получившуюся разность в противоположную сторону. И всё.)
Чем ещё интересны углы, занимающие на круге одно и то же положение, как вы думаете? А тем, что у таких углов совершенно одинаковые синус, косинус, тангенс и котангенс! Всегда!
Например:
Sin45° = sin(-315°)
Cos120° = cos(-240°)
Tg249° = tg(-111°)
Ctg333° = ctg(-27°)
А вот это уже крайне важно! Зачем? Да всё за тем же!) Для упрощения выражений. Ибо упрощение выражений – ключевая процедура успешного решения любых заданий по математике. И по тригонометрии в том числе.
Итак, с общим правилом отсчёта углов на круге разобрались. Ну а коли мы тут заикнулись про полные обороты, про четверти, то пора бы уже покрутить и порисовать эти самые углы.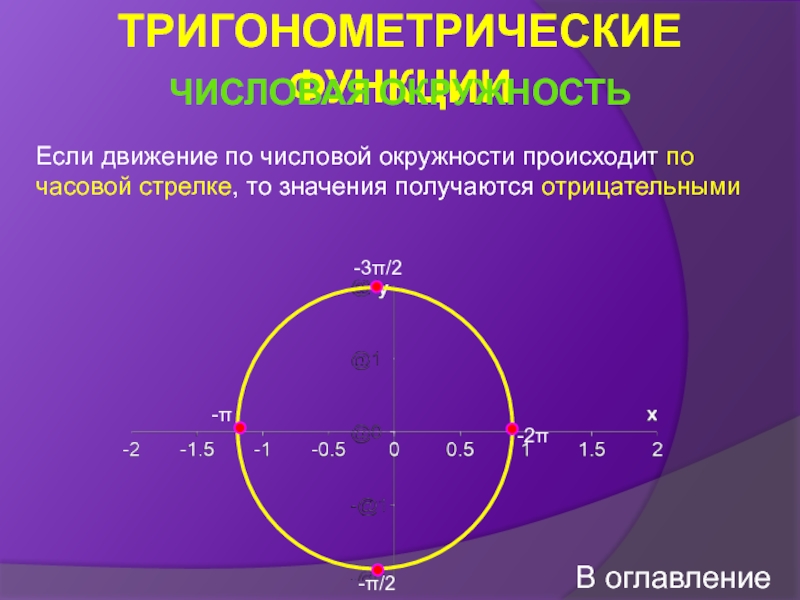 Порисуем?)
Порисуем?)
Начнём пока с положительных углов. Они попроще в рисовании будут.
Рисуем углы в пределах одного оборота (между 0° и 360°).
Нарисуем, например, угол 60°. Тут всё просто, никаких заморочек. Рисуем координатные оси, круг. Можно прямо от руки, безо всякого циркуля и линейки. Рисуем схематично : у нас не черчение с вами. Никаких ГОСТов соблюдать не надо, не накажут.)
Можно (для себя) отметить значения углов на осях и указать стрелочку в направлении против часов. Ведь мы же в плюс откладывать собираемся?) Можно этого и не делать, но в голове держать всяко надо.
И теперь проводим вторую (подвижную) сторону угла. В какой четверти? В первой, разумеется! Ибо 60 градусов – это строго между 0° и 90°. Вот и рисуем в первой четверти. Под углом примерно 60 градусов к неподвижной стороне. Как отсчитать примерно 60 градусов без транспортира? Легко! 60° – это две трети от прямого угла! Делим мысленно первую чертвертинку круга на три части, забираем себе две трети.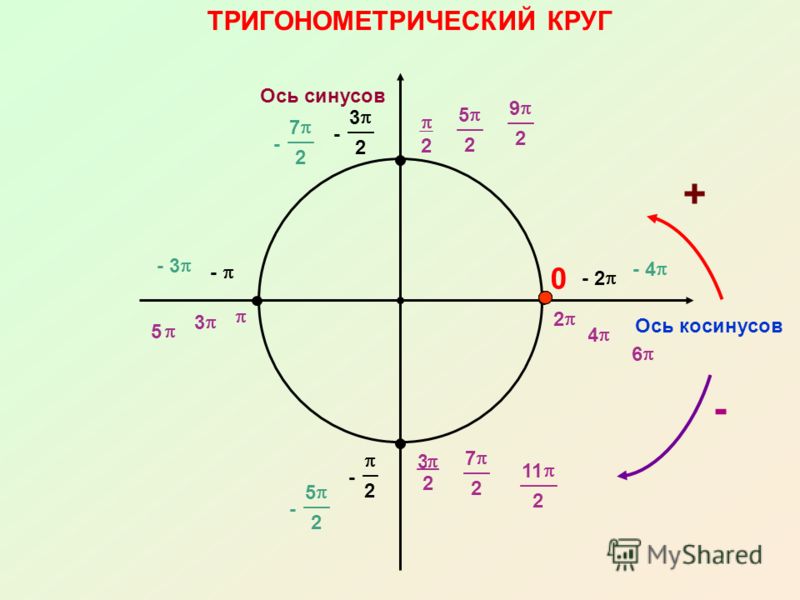 И рисуем… Сколько у нас там по факту получится (если приложить транспортир и померить) – 55 градусов или же 64 – неважно! Важно, что всё равно где-то около 60° .
И рисуем… Сколько у нас там по факту получится (если приложить транспортир и померить) – 55 градусов или же 64 – неважно! Важно, что всё равно где-то около 60° .
Получаем картинку:
Вот и всё. И инструментов не понадобилось. Развиваем глазомер! В задачах по геометрии пригодится.) Этот неказистый рисунок бывает незаменим, когда надо нацарапать круг и угол на скорую руку, не особо задумываясь о красоте. Но при этом нацарапать правильно , без ошибок, со всей необходимой информацией. Например, как вспомогательное средство при решении тригонометрических уравнений и неравенств.
Нарисуем теперь угол, например, 265°. Прикидываем, где он может располагаться? Ну, ясное дело, что не в первой четверти и даже не во второй: они на 90 и на 180 градусов оканчиваются. Можно сообразить, что 265° — это 180° плюс ещё 85°. То есть, к отрицательной полуоси ОХ (там, где 180°) надо добавить примерно 85°. Или, что ещё проще, догадаться, что 265° не дотягивает до отрицательной полуоси OY (там, где 270°) каких-то несчастных 5°. Одним словом, в третьей четверти будет этот угол. Очень близко к отрицательной полуоси OY, к 270 градусам, но всё-таки в третьей!
Одним словом, в третьей четверти будет этот угол. Очень близко к отрицательной полуоси OY, к 270 градусам, но всё-таки в третьей!
Рисуем:
Повторюсь, абсолютная точность здесь не требуется. Пускай в реальности этот угол получился, скажем 263 градуса. Но на самый главный вопрос (какая четверть?) мы ответили безошибочно. Почему этот вопрос самый главный? Да потому, что любая работа с углом в тригонометрии (неважно, будем мы рисовать этот угол или не будем) начинается с ответа именно на этот вопрос! Всегда. Если этот вопрос проигнорировать или пробовать на него ответить мысленно, то ошибки почти неизбежны, да… Оно вам надо?
Запоминаем:
Любая работа с углом (в том числе и рисование этого самого угла на круге) всегда начинается с определения четверти, в которую попадает этот угол.
Теперь, я надеюсь, вы уже безошибочно изобразите углы, например, 182°, 88°, 280°. В правильных четвертях. В третьей, первой и четвёртой, если что…)
Четвёртая четверть заканчивается углом 360°. Это один полный оборот. Ясен перец, что этот угол занимает на круге то же самое положение, что и 0° (т.е. начало отсчёта). Но углы на этом не заканчиваются, да…
Это один полный оборот. Ясен перец, что этот угол занимает на круге то же самое положение, что и 0° (т.е. начало отсчёта). Но углы на этом не заканчиваются, да…
Что делать с углами, большими 360°?
«А такие разве бывают?» – спросите вы. Бывают, ещё как! Бывает, например, угол 444°. А бывает, скажем, угол 1000°. Всякие углы бывают.) Просто визуально такие экзотические углы воспринимаются чуть сложнее, чем привычные нам углы в пределах одного оборота. Но рисовать и просчитывать такие углы тоже надо уметь, да.
Для правильного рисования таких углов на круге необходимо всё то же самое – выяснить, в какую четверть попадает интересующий нас угол. Здесь умение безошибочно определять четверть куда более важно, чем для углов от 0° до 360°! Сама процедура определения четверти усложняется всего одним шагом. Каким, скоро увидите.
Итак, например, нам надо выяснить, в какую четверть попадает угол 444°. Начинаем крутить. Куда? В плюс, разумеется! Угол-то нам дали положительный! +444°.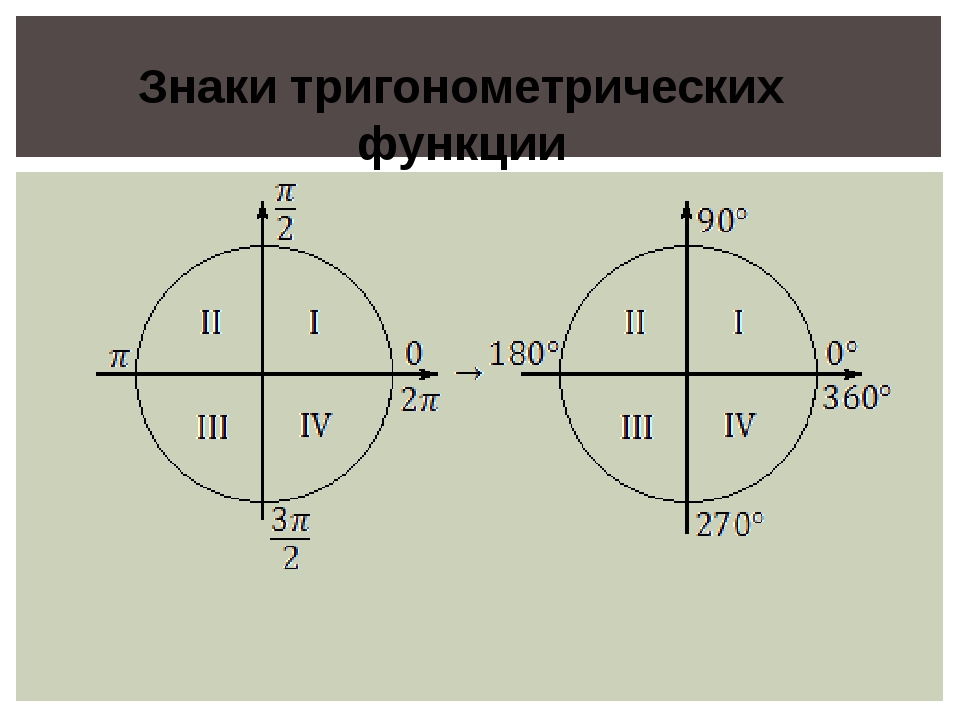 Крутим, крутим… Крутанули на один оборот – дошли до 360°.
Крутим, крутим… Крутанули на один оборот – дошли до 360°.
Сколько там осталось до 444°? Считаем оставшийся хвостик:
444°-360° = 84°.
Итак, 444° — это один полный оборот (360°) плюс ещё 84°. Очевидно, это первая четверть. Итак, угол 444° попадает в первую четверть. Полдела сделано.
Осталось теперь изобразить этот угол. Как? Очень просто! Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.
Вот так:
Здесь я уж не стал загромождать рисунок – подписывать четверти, рисовать углы на осях. Это всё добро уже давно в голове быть должно.)
Зато я «улиткой» или спиралькой показал, как именно складывается угол 444° из углов 360° и 84°. Пунктирная красная линия – это один полный оборот. К которому дополнительно прикручиваются 84° (сплошная линия). Кстати, обратите внимание, что, если этот самый полный оборот отбросить, то это никак не повлияет на положение нашего угла!
А вот это важно! Положение угла 444° полностью совпадает с положением угла 84°. Никаких чудес нет, так уж получается.)
Никаких чудес нет, так уж получается.)
А можно ли отбросить не один полный оборот, а два или больше?
А почему – нет? Если угол здоровенный, то не просто можно, а даже нужно! Угол-то не изменится! Точнее, сам-то угол по величине, конечно же, изменится. А вот его положение на круге – никак нет!) На то они и полные обороты, что сколько экземпляров ни добавляй, сколько ни убавляй, всё равно будешь в одну и ту же точку попадать. Приятно, правда?
Запоминаем:
Если к углу прибавить (отнять) любое целое число полных оборотов, положение исходного угла на круге НЕ изменится!
Например:
В какую четверть попадает угол 1000°?
Никаких проблем! Считаем, сколько полных оборотов сидит в тысяче градусов. Один оборот — это 360°, ещё один – уже 720°, третий — 1080°… Стоп! Перебор! Значит, в угле 1000° сидит два полных оборота. Выбрасываем их из 1000° и считаем остаток:
1000° — 2 ·360° = 280°
Значит, положение угла 1000° на круге то же самое , что и у угла 280°.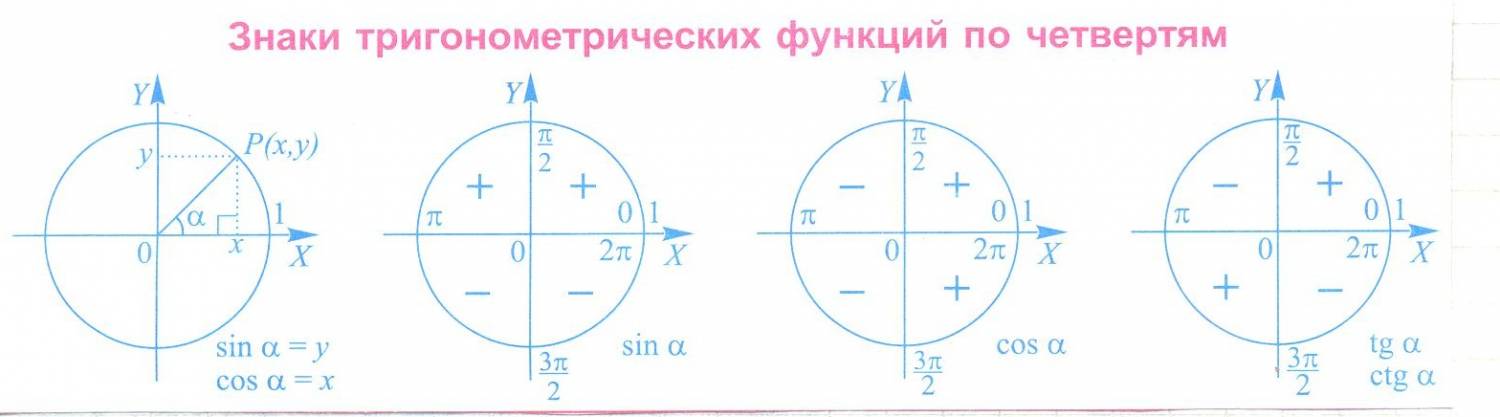 С которым работать уже гораздо приятнее.) И куда же попадает этот угол? В четвёртую четверть он попадает: 270° (отрицательная полуось OY) плюс ещё десяточка.
С которым работать уже гораздо приятнее.) И куда же попадает этот угол? В четвёртую четверть он попадает: 270° (отрицательная полуось OY) плюс ещё десяточка.
Рисуем:
Здесь я уже не рисовал пунктирной спиралькой два полных оборота: уж больно длинная она получается. Просто нарисовал оставшийся хвостик от нуля , отбросив все лишние обороты. Как будто бы их и не было вовсе.)
И ещё раз. По-хорошему, углы 444° и 84°, а также 1000° и 280° – разные. Но для синуса, косинуса, тангенса и котангенса эти углы – одинаковые!
Как вы видите, для того чтобы работать с углами, большими 360°, надо определить, сколько полных оборотов сидит в заданном большом угле. Это и есть тот самый дополнительный шаг, который обязательно надо предварительно проделывать при работе с такими углами. Ничего сложного, правда?
Отбрасывание полных оборотов, конечно, занятие приятное.) Но на практике при работе с совсем уж кошмарными углами случаются и затруднения.
Например:
В какую четверть попадает угол 31240° ?
И что же, будем много-много раз прибавлять по 360 градусов? Можно, если не горит особо. Но мы же не только складывать можем.) Ещё и делить умеем!
Вот и поделим наш большущий угол на 360 градусов!
Этим действием мы как раз и узнаем, сколько полных оборотов запрятано в наших 31240 градусах. Можно уголком поделить, можно (шепну на ушко:)) на калькуляторе.)
Получим 31240:360 = 86,777777….
То, что число получилось дробным – не страшно. Нас же только целые обороты интересуют! Стало быть, до конца делить и не надо.)
Итак, в нашем лохматом угле сидит аж 86 полных оборотов. Ужас…
В градусах это будет 86·360° = 30960°
Вот так. Именно столько градусов можно безболезненно выкинуть из заданного угла 31240°. Останется:
31240° — 30960° = 280°
Всё! Положение угла 31240° полностью идентифицировано! Там же, где и 280°. Т.е. четвёртая четверть. ) Кажется, мы уже изображали этот угол ранее? Когда угол 1000° рисовали?) Там мы тоже на 280 градусов вышли. Совпадение.)
) Кажется, мы уже изображали этот угол ранее? Когда угол 1000° рисовали?) Там мы тоже на 280 градусов вышли. Совпадение.)
Итак, мораль сей басни такова:
Если нам задан страшный здоровенный угол, то:
1. Определяем, сколько полных оборотов сидит в этом угле. Для этого делим исходный угол на 360 и отбрасываем дробную часть.
2. Считаем, сколько градусов в полученном количестве оборотов. Для этого умножаем число оборотов на 360.
3. Отнимаем эти обороты от исходного угла и работаем с привычным углом в пределах от 0° до 360°.
Как работать с отрицательными углами?
Не вопрос! Точно так же, как и с положительными, только с одним единственным отличием. Каким? Да! Крутить углы надо в обратную сторону , в минус! По ходу часовой стрелки.)
Нарисуем, например, угол -200°. Сначала всё как обычно для положительных углов – оси, круг. Ещё синюю стрелочку с минусом изобразим да углы на осях по-другому подпишем.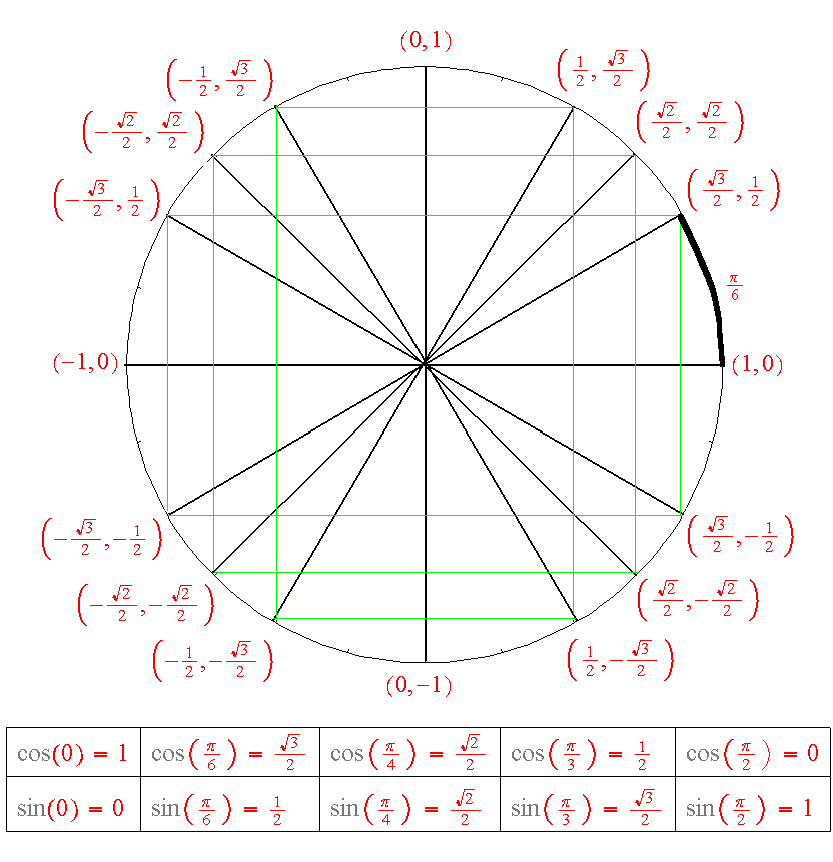 Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.
Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.
Картинка станет вот такой:
При работе с отрицательными углами часто возникает чувство лёгкого недоумения. Как так?! Получается, что одна и та же ось – это одновременно, скажем, и +90° и -270°? Неее, что-то тут нечисто…
Да всё чисто и прозрачно! Мы ведь же уже в курсе, что любую точку на круге можно обозвать как положительным углом, так и отрицательным! Совершенно любую. В том числе и на какой-то из координатных осей. В нашем случае нам нужно отрицательное исчисление углов. Вот и отщёлкиваем в минус все углы.)
Теперь нарисовать правильно угол -200° никакого труда не составляет. Это -180° и минус ещё 20°. Начинаем мотать от нуля в минус: четвёртую четверть пролетаем, третью тоже мимо, доходим до -180°. Куда мотать оставшуюся двадцатку? Да всё туда же! По часам. ) Итого угол -200° попадает во вторую четверть.
) Итого угол -200° попадает во вторую четверть.
Теперь вы понимаете, насколько важно железно помнить углы на осях координат?
Углы на осях координат (0°, 90°, 180°, 270°, 360°) надо помнить именно для того, чтобы безошибочно определять четверть, куда попадает угол!
А если угол большой, с несколькими полными оборотами? Ничего страшного! Какая разница, куда эти самые полные обороты крутить – в плюс или в минус? Точка-то на круге не изменит своего положения!
Например:
В какую четверть попадает угол -2000°?
Всё то же самое! Для начала считаем, сколько полных оборотов сидит в этом злом угле. Чтобы не косячить в знаках, оставим минус пока в покое и просто поделим 2000 на 360. Получим 5 с хвостиком. Хвостик нас пока не волнует, его чуть позже сосчитаем, когда рисовать угол будем. Считаем пять полных оборотов в градусах:
5·360° = 1800°
Воот. Именно столько лишних градусов можно смело выкинуть из нашего угла без ущерба для здоровья.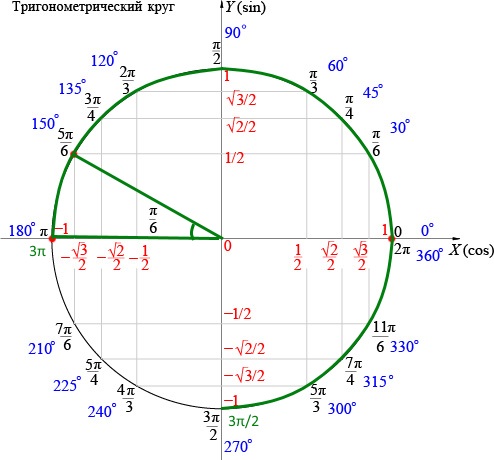
Считаем оставшийся хвостик:
2000° – 1800° = 200°
А вот теперь можно и про минус вспомнить.) Куда будем мотать хвостик 200°? В минус, конечно же! Нам же отрицательный угол задан.)
2000° = -1800° — 200°
Вот и рисуем угол -200°, только уже без лишних оборотов. Только что его рисовали, но, так уж и быть, накалякаю ещё разок. От руки.
Ясен перец, что и заданный угол -2000°, так же как и -200°, попадает во вторую четверть.
Итак, мотаем себе на кру… пардон… на ус:
Если задан очень большой отрицательный угол, то первая часть работы с ним (поиск числа полных оборотов и их отбрасывание) та же самая, что и при работе с положительным углом. Знак «минус» на данном этапе решения не играет никакой роли. Учитывается знак лишь в самом конце, при работе с углом, оставшимся после удаления полных оборотов.
Как видите, рисовать отрицательные углы на круге ничуть не сложнее, чем положительные.
Всё то же самое, только в другую сторону! По часам!
А вот теперь — самое интересное! Мы рассмотрели положительные углы, отрицательные углы, большие углы, маленькие — полный ассортимент. Также мы выяснили, что любую точку на круге можно обозвать положительным и отрицательным углом, отбрасывали полные обороты… Нету никаких мыслей? Должно отложиться…
Также мы выяснили, что любую точку на круге можно обозвать положительным и отрицательным углом, отбрасывали полные обороты… Нету никаких мыслей? Должно отложиться…
Да! Какую точку на круге ни возьми, ей будет соответствовать бесконечное множество углов! Больших и не очень, положительных и отрицательных — всяких! И разница между этими углами будет составлять целое число полных оборотов. Всегда! Так уж тригонометрический круг устроен, да…) Именно поэтому обратная задача — найти угол по известным синусу/косинусу/тангенсу/котангенсу — решается неоднозначно . И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки , тригонометрические уравнения и неравенства ) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)
1. В какую четверть попадает угол -345°?
2. В какую четверть попадает угол 666°?
3.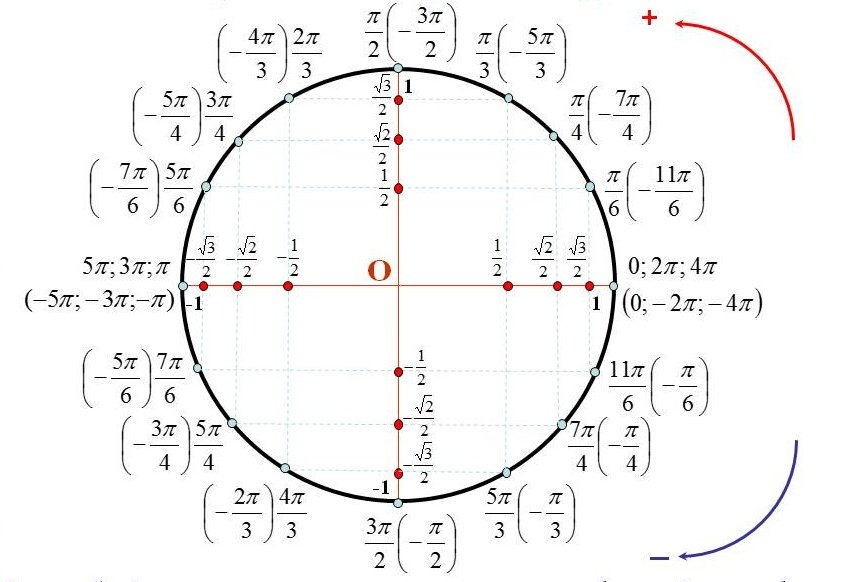 В какую четверть попадает угол 5555°?
В какую четверть попадает угол 5555°?
4. В какую четверть попадает угол -3700°?
5. Какой знак имеет cos 999°?
6. Какой знак имеет ctg 999°?
И это получилось? Прекрасно! Есть проблемы? Тогда вам .
Ответы:
1. 1
2. 4
3. 2
4. 3
5. «+»
6. «-»
В этот раз ответы выданы по порядку в нарушение традиций. Ибо четвертей всего четыре, а знаков так и вовсе два. Особо не разбежишься…)
В следующем уроке мы с вами поговорим про радианы, про загадочное число «пи», научимся легко и просто переводить радианы в градусы и обратно. И с удивлением обнаружим, что даже этих простых знаний и навыков нам будет уже вполне достаточно для успешного решения многих нетривиальных задачек по тригонометрии!
Тригонометрическая окружность со всеми. Тригонометрический круг
Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, :
Мы же здесь будем все подробно разбирать шаг за шагом.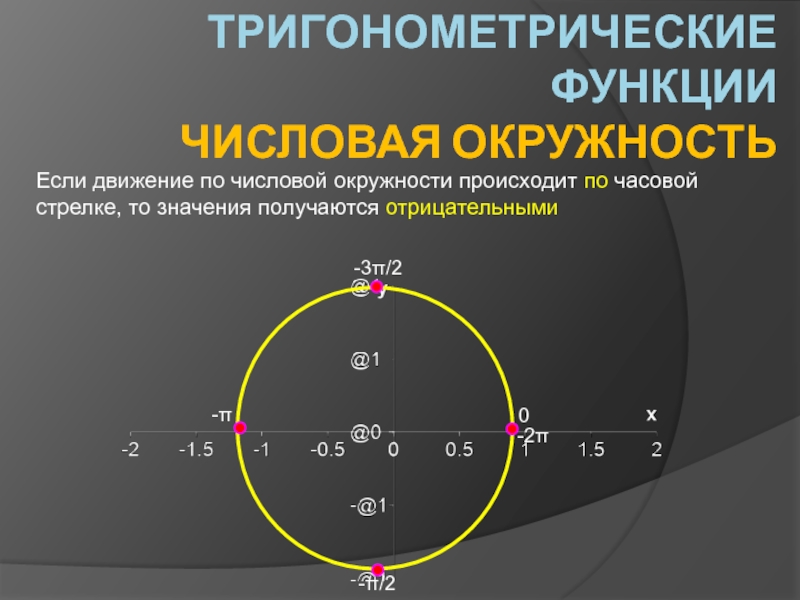
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций , – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, 300 градусов, или -45.
Никак?.. можно, конечно, подключить формулы приведения … А глядя на тригонометрический круг, легко можно ответить на такие вопросы.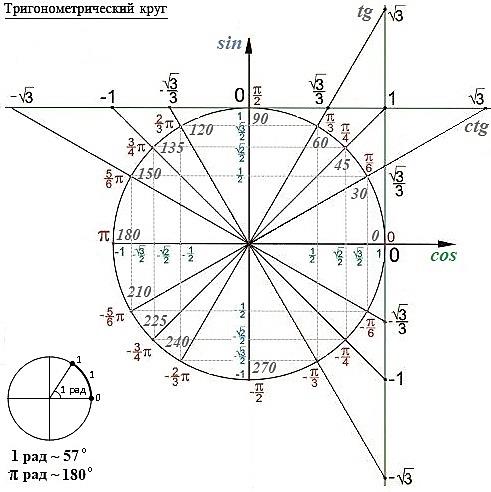 И вы скоро будете знать как!
И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.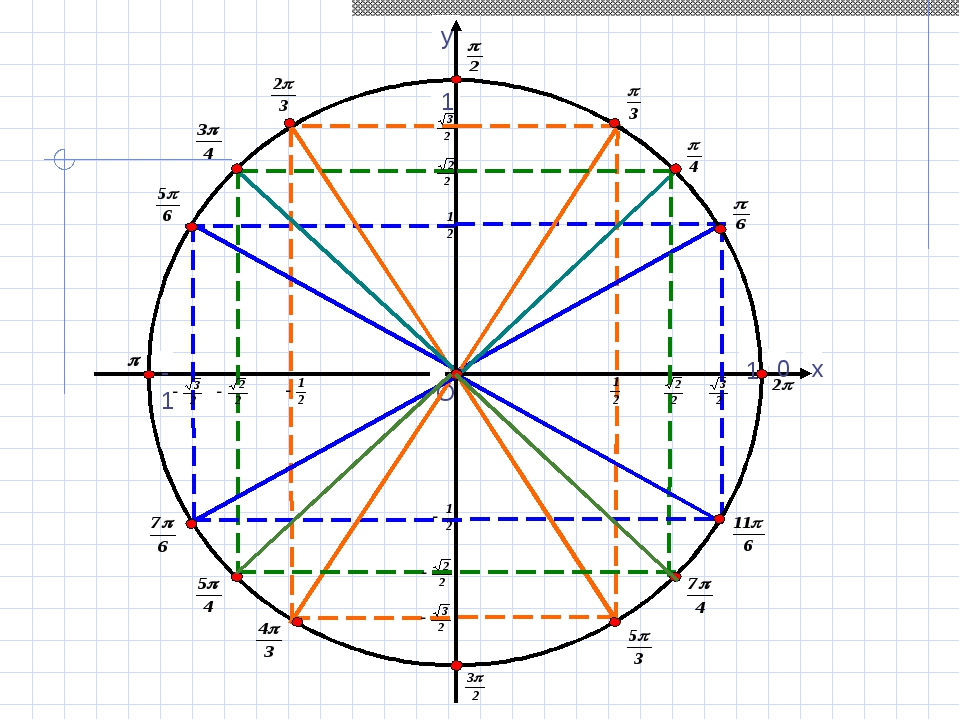
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип , который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ , без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в .
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс.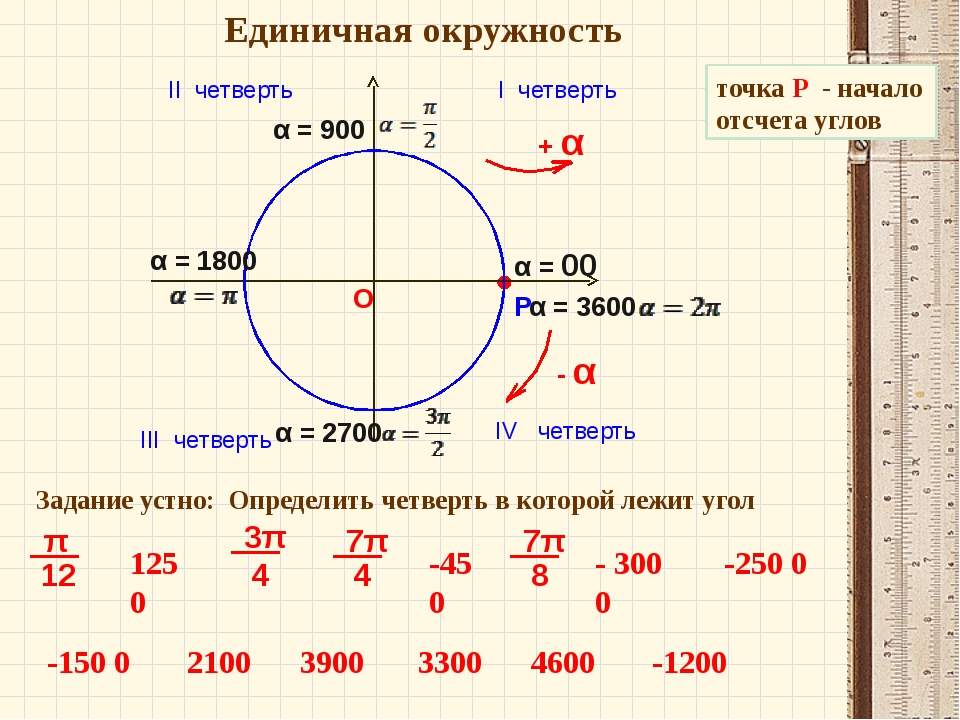 Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.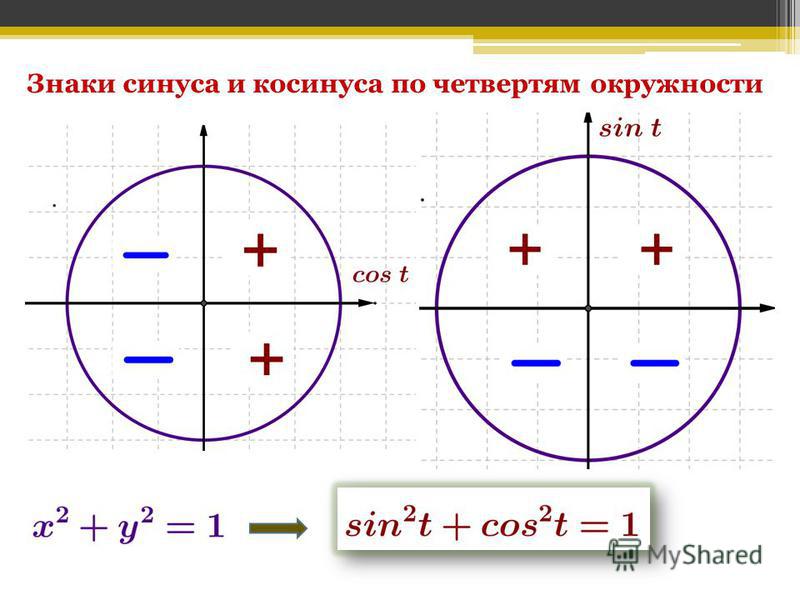
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции. Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Тригонометрический круг. Единичная окружность. Числовая окружность. Что это такое?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются учащимся народом. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.
Для успешной работы с тригонометрическим кругом нужно знать всего три вещи.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Радиан, Углы больше 360 градусов, Положительные и отрицательные углы
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.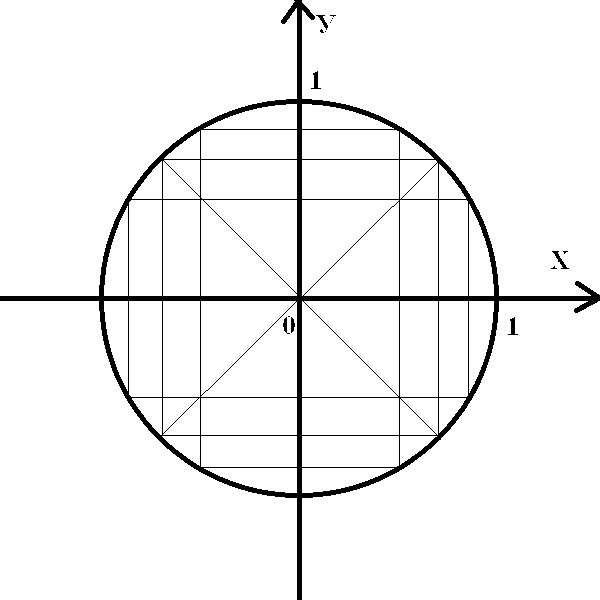
На картинке видны 4 разных угла, образованных пересечением прямых AB и CD
Обычно углы измеряются в градусах, что обозначается как °.
Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°).
Таким образом, градус — это $\frac{1}{360}$ круга.
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.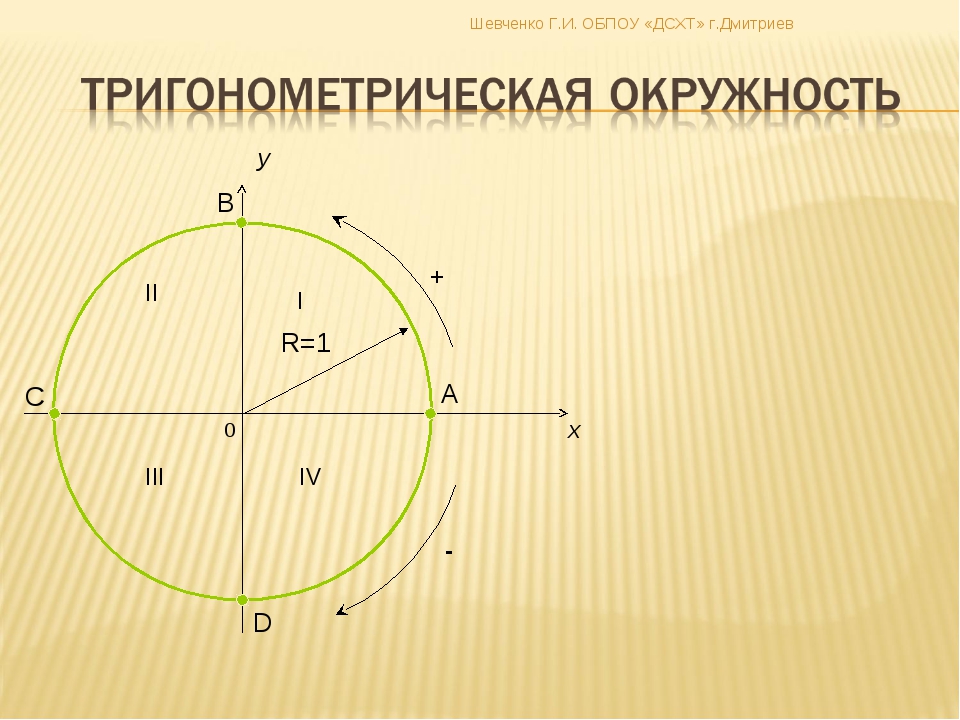 {\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
{\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
Объект описал $2\frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.
Пример 3
1.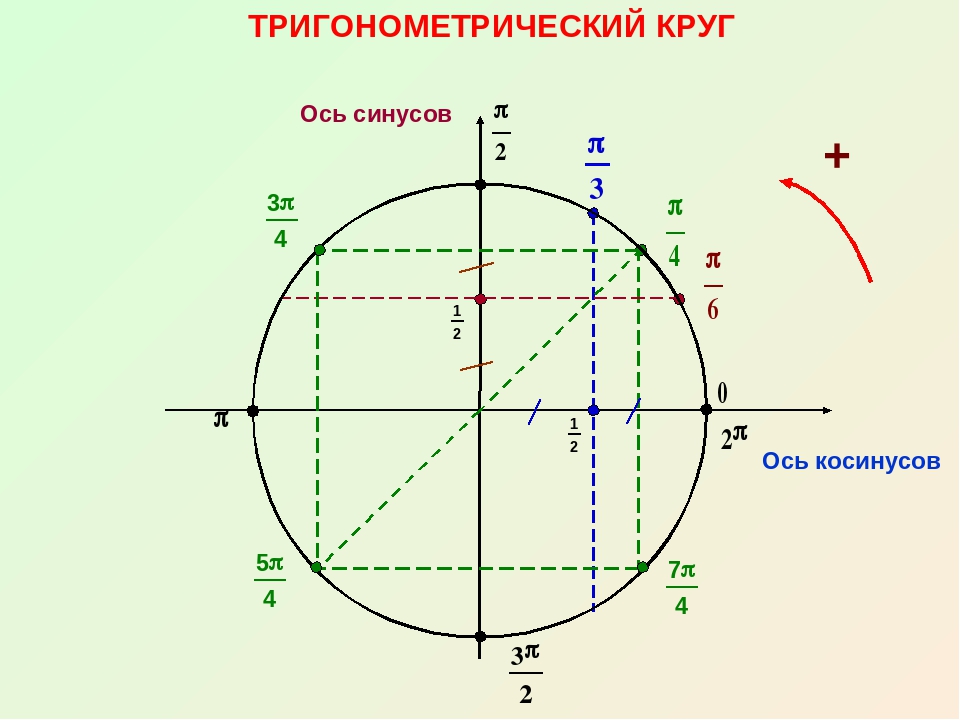 Найти соответствующий положительный угол
Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга.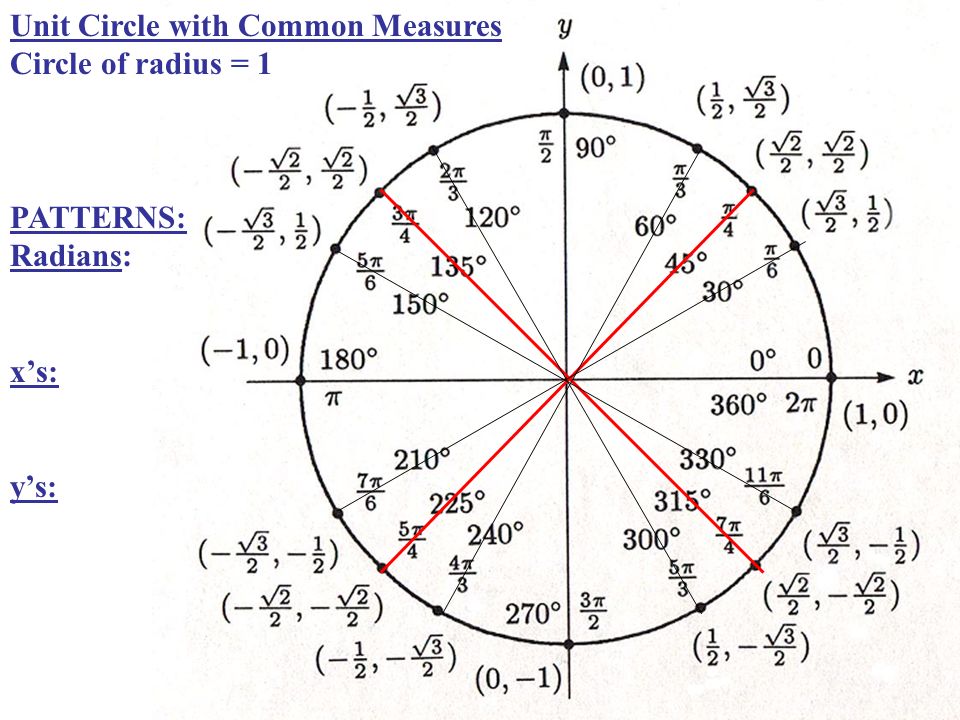 {\circ}$
{\circ}$
c) 1 рад = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$
Отрицаетльные углы и углы больше, чем $2\pi$ радиан
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.
Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.
Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$
Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.
Пример 6
1.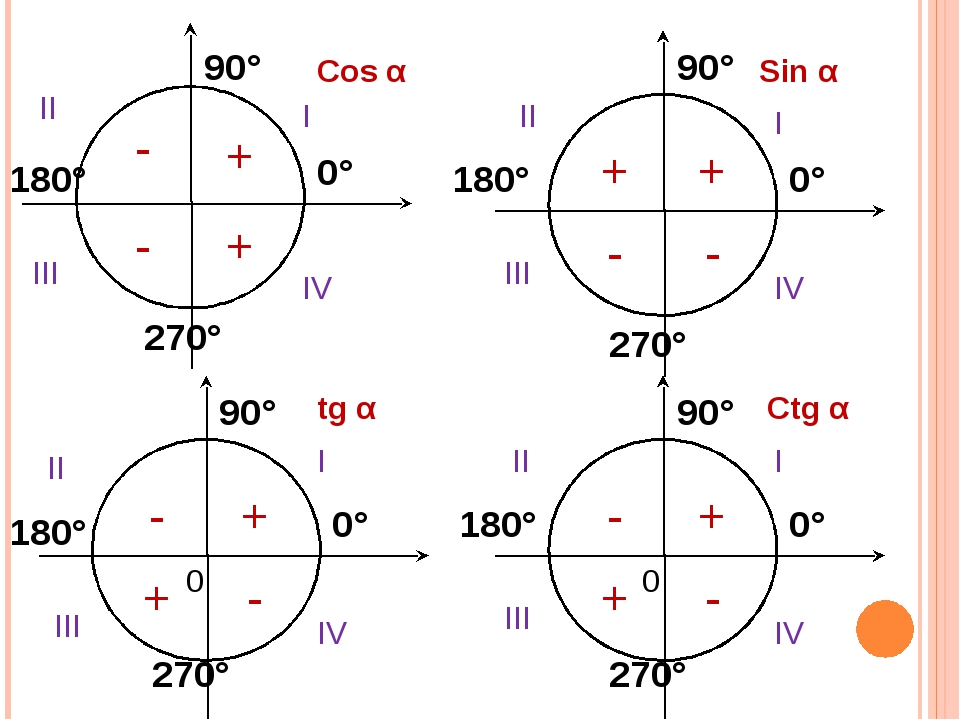 Найти количество кругов пройденных объектом при данных углах
Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$
Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.
b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки
c) $\frac{7}{2}\pi=3,5\pi=2\pi+1,5\pi$, $1,5\pi$ равно три четверти цикла $(\frac{1,5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки
Единичный круг — Разделы по тригонометрии
Темы | Дом
15
Определения
Знаки в каждом квадранте
Квадрантные углы
Единица окружности
АНАЛИТИЧЕСКАЯ ТРИГОНОМЕТРИЯ является расширением тригонометрии прямоугольного треугольника. Действие происходит на плоскости x — y .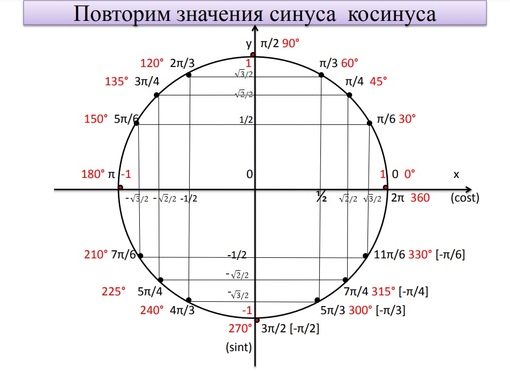 Поскольку тригонометрия фактически используется в вычислениях и физике, речь не идет о решении треугольников.Оно становится математическим описанием вещей, которые вращаются или вибрируют, таких как свет, звук, траектории планет вокруг солнца или спутников вокруг земли. Поэтому необходимо иметь углы любой величины и распространять на них значения тригонометрических функций. Мы делаем это сейчас.
Поскольку тригонометрия фактически используется в вычислениях и физике, речь не идет о решении треугольников.Оно становится математическим описанием вещей, которые вращаются или вибрируют, таких как свет, звук, траектории планет вокруг солнца или спутников вокруг земли. Поэтому необходимо иметь углы любой величины и распространять на них значения тригонометрических функций. Мы делаем это сейчас.
Пусть радиус длиной r образует угол θ в стандартном положении, и пусть его конечная точка имеет координаты ( x , y ).Возникает вопрос: как мы теперь определим шесть тригонометрических функций θ?
Мы возьмем пример с первого квадранта. В этом квадранте
радиус r закончится в точке ( x , y ). Эти координаты определяют прямоугольный треугольник. Далее следуют определения прямоугольного треугольника (тема 2) шести тригонометрических функций.
| sin θ | = | у р | csc θ | = | р у | |
| cos θ | = | x р | сек θ | = | р х | |
| тан θ | = | г х | детская кроватка θ | = | х у | |
Согласно теореме Пифагора,
Таким образом, мы распространяем смысл тригонометрических функций на углы, которые оканчиваются в любом квадранте. Это с точки зрения координат ( x , y ) конечной точки на расстоянии r от начала координат.
Это с точки зрения координат ( x , y ) конечной точки на расстоянии r от начала координат.
Но прежде чем мы приведем пример, подумайте над этим вопросом:
Будет ли функция θ зависеть от длины r ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала ответь на вопрос сам!
Нет, не будет.Функции определяются как отношений сторон, а не их длин.
Предположим, что AB и AC — два разных радиуса. Но треугольники ABD, ACE подобны. (Теорема 15) Пропорционально,
ДБ : ВА = ЕС : СА
sin θ — напротив гипотенузы — не зависит от длины радиуса. И аналогично для остальных функций. Поэтому мы можем выбрать любой радиус, какой пожелаем. Обычно мы берем r = 1.Как мы увидим, это называется единичным кругом.
Тригонометрические функции на самом деле зависят только от угла θ — и именно поэтому мы говорим, что они являются функциями θ.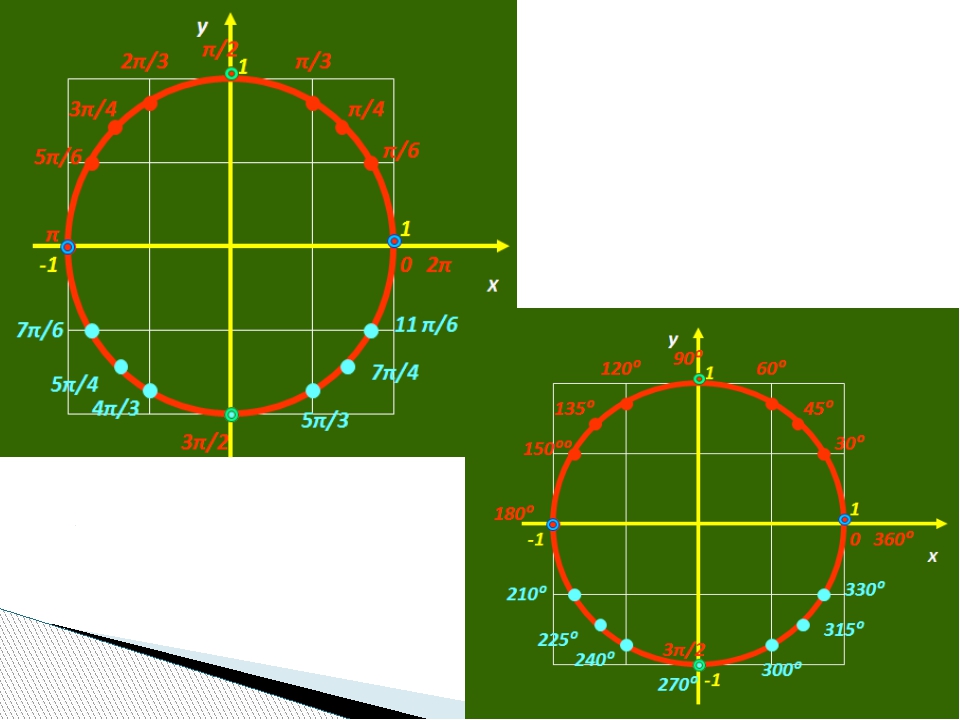
Пример 1. Прямая, вставленная в начало координат, заканчивается в точке (3, 2), поскольку она образует угол θ в стандартном положении. Оцените все шесть функций θ.
Ответить . x = 3, y = 2. Следовательно, согласно определениям:
| sin θ | = | у р | = | 2 | csc θ | = | р у | = | 2 | |
| cos θ | = | x р | = | 3 | сек θ | = | р х | = | 3 | |
| тан θ | = | г х | = | 2 3 | детская кроватка θ | = | х у | = | 3 2 | |
Проблема 1. Прямая из начала координат заметает угол θ и заканчивается в точке (3, −4). Оцените шесть функций θ.
Прямая из начала координат заметает угол θ и заканчивается в точке (3, −4). Оцените шесть функций θ.
х = 3, у = -4. Следовательно,
| sin θ | = − | 4 5 | csc θ | = − | 5 4 | |
| cos θ | = | 3 5 | сек θ | = | 5 3 | |
| тан θ | = − | 4 3 | детская кроватка θ | = − | 3 4 | |
Проблема 2.Знаки в каждом квадранте.
а) Алгебраический знак sin θ всегда будет знаком какой
а) координаты? y , потому что sin θ = y / r , а r всегда положительно.
а) Следовательно, в каких квадрантах sin θ — y — будет положительным? I и II.
а) В каких квадрантах sin θ будет отрицательным? III и IV.
b) Алгебраический знак cos θ всегда будет знаком какой
b) координаты? x , потому что cos θ = x / r , и снова r всегда равно
положительный.
а) Следовательно, в каких квадрантах cos θ — x — будет положительным? I и IV.
а) В каких квадрантах cos θ будет отрицательным? II и III.
c) В каких квадрантах алгебраический знак тангенса θ ( y / x ) будет положительным?
I и III. x и y будут иметь одинаковые знаки.
d) В каких квадрантах алгебраический знак тангенса θ будет отрицательным?
II и IV. x и y будут иметь противоположные знаки.
д) csc θ будет иметь тот же знак, что и какая другая функция?
sin θ, потому что они обратны.
е) сек θ будет иметь тот же знак, что и какая другая функция?
cos θ
g) cot θ будет иметь тот же знак, что и какая другая функция?
желтовато-коричневый θ
Квадрантные углы
Квадрантальный угол — это угол, который заканчивается на оси x или y .
Проблема 3.
а) Каковы квадрантные углы в градусах?
0°, 90°, 180°, 270°; и котерминальные с ними углы.
b) Каковы квадрантные углы в радианах?
| 0, | № 2 | , π, | 3π 2 | ; и котерминальные с ними углы. |
c) Когда угол заканчивается на оси x , каково значение
c) y -координата? 0. На оси x y = 0,
d) Когда угол заканчивается на оси y , каково значение
c) x -координата? 0.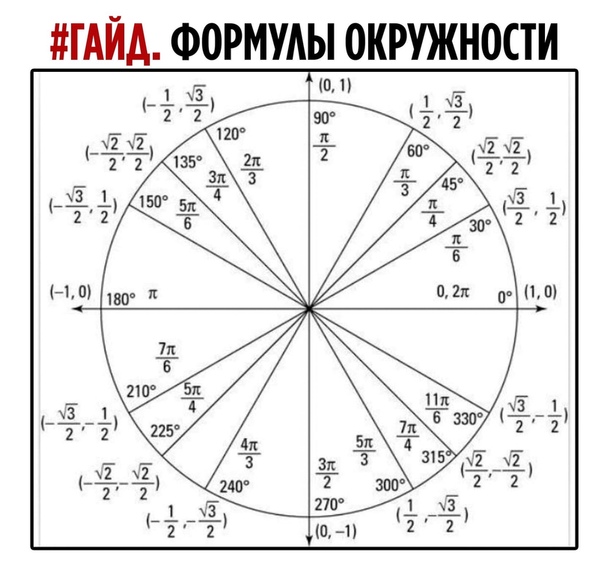 На оси y x = 0,
На оси y x = 0,
Итак, арифметический факт состоит в том, что не существует числа со знаменателем 0.
Следовательно, если тригонометрическая функция имеет знаменатель — x или y — равный 0, функция не будет существовать в этом квадрантном угле.
Например,
Везде, где x = 0, тангенс θ не будет существовать. Где х = 0? Когда угол заканчивается на оси y .
| tan θ не будет существовать при θ = | № 2 | и θ = | 3π 2 | или по адресу – | № 2 | , то есть |
котерминал.
Эти значения θ будут особенностями тангенса θ. (Тема 18 предварительного исчисления.)
Задача 4. Для каких квадрантных углов не существуют следующие функции?
| а) детская кроватка θ | детская кроватка θ = | х у | . Следовательно, всякий раз, когда y = 0, то есть на Следовательно, всякий раз, когда y = 0, то есть на |
ось x — кроватка θ не будет существовать.cot θ не будет существовать при θ = 0 и θ = π.
б) сек θ
| с θ = | р х | . Следовательно, сек θ не будет существовать там, где x = 0, |
| , который находится на оси y . сек θ не будет существовать при θ = | № 2 |
в) sin θ
| sin θ = | у р | .Но r никогда не равно 0. Нет угла, для которого |
sin θ не существует.
Единица окружности
Тригонометрические функции являются функциями только угла θ. Поэтому мы можем выбрать любой радиус, какой пожелаем, и самым простым является круг радиуса 1, единичный круг.
На единичном круге функции имеют особенно простую форму. Например,
| sin θ | = | г 1 | = y . |
| потому что θ | = | х 1 | = x . |
Значение sin θ равно координате y конечной точки единичного радиуса Значение cos θ равно x -координате
Что касается квадрантных углов, единичный круг иллюстрирует следующее:
Если функция существует в квадрантном угле,
она может иметь только значения 0, 1 или −1.
Рассмотрим sin θ для каждого квадрантного угла. Мы только что видели, что значение sin θ равно y -координата:
sin θ = y .
Следовательно, в каждом квадрантном угле значение sin θ — от y — равно 0, 1 или −1.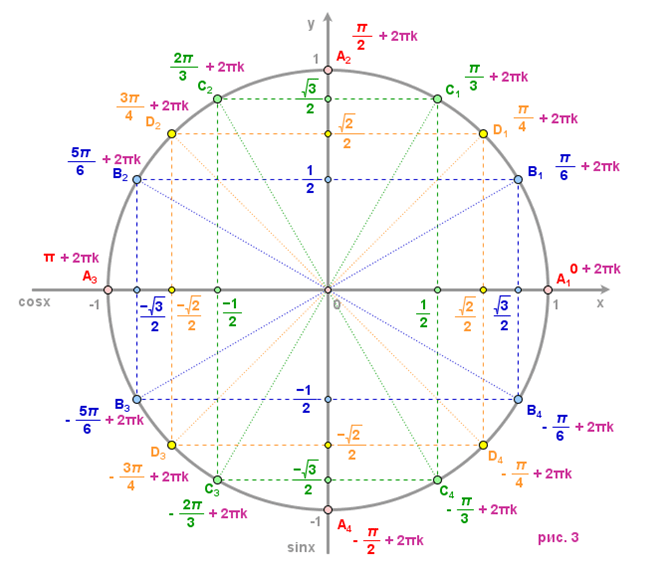
| При θ = 0, | sin θ = 0, | |
| При θ = | № 2 | , sin θ = 1. |
| При θ = π, | sin θ = 0, | |
| При θ = | 3π 2 | , sin θ = −1. |
Чтобы оценить функцию в квадрантном угле, учащийся должен начертить единичный круг.
Проблема 5. Оцените следующее. Нет таблиц
а) cos 0°
, потому что 0° = 1.cos θ равен x -координате.
б) cos 90° = 0 в) cos 180° = −1
г) cos 270° = 0
д) тангенс 0°
тангенс 0° = 0. тангенс θ равен y / x = 0/1 = 0,
е) тангенс 90° 1/0 не существует.
ж) тангенс 180° = 0
ч) tan 270° не существует.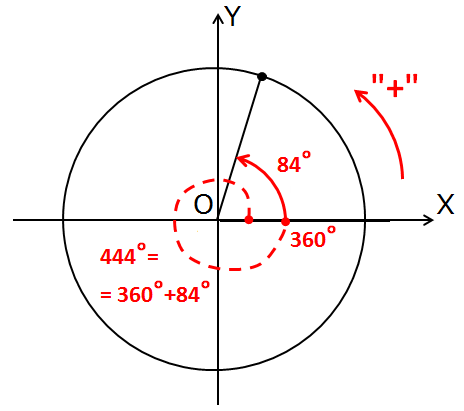
Проблема 6. Оцените следующее — если оно существует. Нет столов.
| б) грех | № 2 | = 1 | в) грех | № | = 0 | г) cos | № | = −1 |
| д) детская кроватка 0 | = x / y .Не существует. | е) детская кроватка | № 2 | = 0 |
| г) загар | № 2 | Не существует. | з) сек 0 | = 1/ х = 1 |
| i) csc (− | № 2 | ) | = −1 | к) sin 2π | = 0 |
| л) sin 3π | = 0 | м) sin 4π | = 0 |
| м) sin (−π) | = 0 | п) cos 2π | = 1 |
| о) cos 3π | = −1 | р) cos 4π | = 1 |
| q) cos 5π | = −1 |
Проблема 7. Объясните, почему мы можем написать следующее, где n может быть любым целым числом:
Объясните, почему мы можем написать следующее, где n может быть любым целым числом:
cos n π = (−1) n
(−1) n = ±1, в соответствии с тем, что n четно или нечетно. Если n четно (или 0), то cos n π сотерминально 0 радианам, и (−1) n = 1. котерминальна π радианам, и (−1) n = −1.
См. единичный круг.
Следующая тема: Тригонометрические функции любого угла
Темы | Дом
Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
2.3.8: Тригонометрические функции отрицательных углов
Углы, измеренные вращением по часовой стрелке от положительной оси \(x\). {\circ}\).{\circ}\)
{\circ}\).{\circ}\)
Чтобы просмотреть ответы на вопросы, откройте этот PDF-файл и найдите раздел 1.19.
Словарь
| Срок | Определение |
|---|---|
| Отрицательный угол | Отрицательный угол — это угол, измеренный при вращении по часовой стрелке (а не против часовой стрелки) от положительной оси \(x\). |
Круговые функции
График уравнения x 2 + y 2 = 1 представляет собой окружность в прямоугольной системе координат.Этот график называется единичной окружностью , имеет центр в начале координат и радиус 1 единицу. Тригонометрические функции определяются таким образом, что их доменов представляют собой наборы углов , а их диапазоны представляют собой наборы действительных чисел.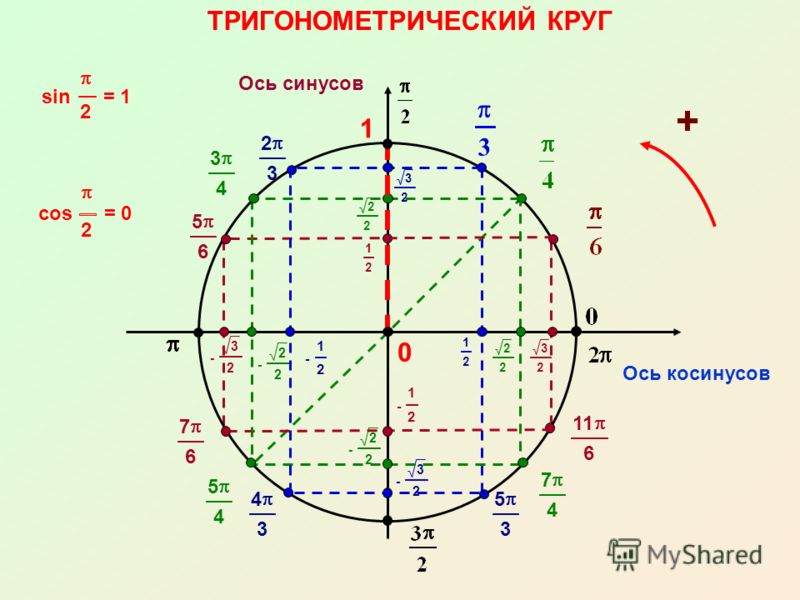 Круговые функции определены таким образом, что их областей определения представляют собой наборы чисел , которые соответствуют мерам (в радианах) углов аналогичных тригонометрических функций. Диапазоны этих круговых функций, как и их аналогичные тригонометрические функции, представляют собой наборы действительных чисел.Эти функции называются круговыми, потому что радианные меры углов определяются длинами дуг окружностей. В частности, тригонометрические функции, определенные с помощью единичного круга, ведут непосредственно к этим круговым функциям.
Круговые функции определены таким образом, что их областей определения представляют собой наборы чисел , которые соответствуют мерам (в радианах) углов аналогичных тригонометрических функций. Диапазоны этих круговых функций, как и их аналогичные тригонометрические функции, представляют собой наборы действительных чисел.Эти функции называются круговыми, потому что радианные меры углов определяются длинами дуг окружностей. В частности, тригонометрические функции, определенные с помощью единичного круга, ведут непосредственно к этим круговым функциям.
Начните с единичного круга x 2 + y 2 = 1, показанного на рисунке . Точка A (1,0) расположена на пересечении единичной окружности и оси x . Пусть q — любое действительное число.Начните с точки A и измерьте | q | единиц по единичной окружности против часовой стрелки, если q > 0, и по часовой стрелке, если q < 0, заканчивая точкой P ( x, y ). Задайте синус и косинус q как координаты точки P . Другие круговые функции (тангенс, котангенс, секанс и косеканс) могут быть определены через синус и косинус.
Задайте синус и косинус q как координаты точки P . Другие круговые функции (тангенс, котангенс, секанс и косеканс) могут быть определены через синус и косинус.
Рисунок 1
Sin q и cos q существуют для каждого действительного числа q , потому что (cos q , sin q ) являются координатами точки P , расположенной на единичной окружности, что соответствует дуге длины | д |. Поскольку эта длина дуги может быть положительной (против часовой стрелки) или отрицательной (по часовой стрелке), домен каждой из этих круговых функций представляет собой набор действительных чисел. Диапазон более ограничен.Косинус и синус — это абсцисса и ордината точки, которая движется по единичной окружности, и они варьируются от −1 до 1. Следовательно, диапазон каждой из этих функций представляет собой набор действительных чисел z , таких что −1 ⩽ z ⩽ 1 (см.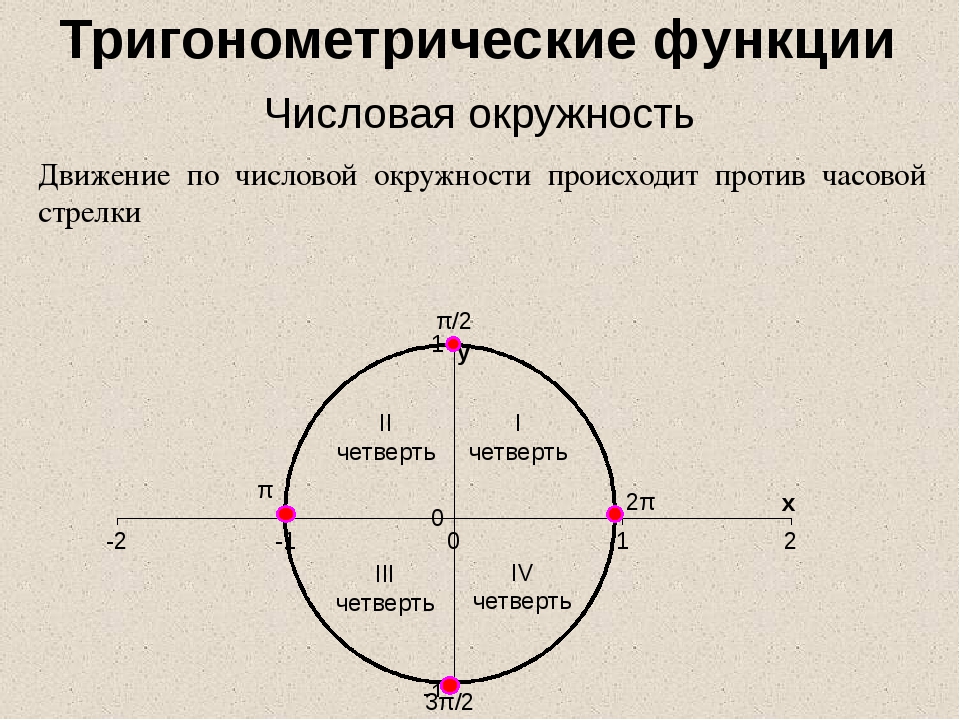 рис. 2).
рис. 2).
Рисунок 2
Диапазон значений триггерных функций.
Пример 1: Какие значения x в области синусоидальной функции между −2π и 2π имеют значение диапазона, равное 1 (рис. 3 )?
Рисунок 3
Чертеж для примера 1.
Значение диапазона sin x равно 1, если точка P имеет координаты (0, 1). Это происходит, когда x = π/2 и x = −3π/2.
Пример 2: Какие значения x в области функции косинуса между −2π и 2π имеют значение диапазона −1 (рис. 4 )?
Рисунок 4
Чертеж для примера 2.
Значение диапазона cos x равно −1, когда точка P (cos x , sin x ) имеет координаты (−1, 0).Это происходит, когда x = π и x = −π.
Пример 3: Точка P находится на единичной окружности. Длина дуги от точки А (1,0) до точки Р составляет q единиц. Каковы значения шести круговых функций q ?
Значения синуса и косинуса следуют из определений и являются координатами точки P . Остальные четыре функции получены с использованием синуса и косинуса.
Знак каждой из шести круговых функций (см. Таблицу 1) зависит от длины дуги q . Обратите внимание, что четыре интервала для q непосредственно соответствуют четырем квадрантам для тригонометрических функций.
Тождества с отрицательными углами в тригонометрии — видео и расшифровка урока
Тождества с отрицательным углом
Тождества с отрицательным углом — это тригонометрические тождества, которые показывают отношения между тригонометрическими функциями, когда мы берем тригонометрическую функцию отрицательного угла. Эти тождества следующие:
Эти тождества следующие:
- sin(- x ) = -sin( x )
- cos(- х ) = cos( х )
- загар (- х ) = -загар ( х )
- csc(- х ) = -csc( х )
- сек(- х ) = сек( х )
- детская кроватка (- x ) = — детская кроватка ( x )
Хорошая новость заключается в том, что эти тождества с отрицательными углами довольно легко запомнить.Вы можете видеть, что функция косинуса и функция секанса — единственные в списке, которые не меняют знак. Для всех остальных тригонометрических функций в списке отрицательный угол изменит знак функции. Довольно просто, правда?
Итак, теперь, когда мы знаем эти личности, мы можем увидеть, что случилось с вами и вашим коллегой. Обратите внимание на тождество с отрицательным углом, включающее функцию косинуса. У нас есть cos(- x ) = cos( x ). Это говорит нам, что cos(-30) = cos(30).Ах-ха! Неудивительно, что вы и ваш коллега пришли к одному и тому же результату. Вам нужно будет решить, какой угол использовать при соединении балок, используя какие-то другие критерии.
Вам нужно будет решить, какой угол использовать при соединении балок, используя какие-то другие критерии.
Мы видим, что использование тождеств с отрицательным углом может происходить в окружающем нас мире. Давайте рассмотрим еще несколько примеров, чтобы лучше ознакомиться с этими тождествами.
Пример 1
На этот раз предположим, что вы занимаетесь скрапбукингом и хотите, чтобы фотография определенным образом помещалась на странице.Вы собираетесь создать угол x из фотографии и плотной бумаги, такой, что sec( x ) = 2. Вы обнаружите, что когда вы работаете с углом, который имеет меру 60 градусов, у вас есть:
Вы пробуете этот ракурс, и он выглядит не совсем правильным, поэтому вы хотите знать, есть ли другой ракурс, который удовлетворит вашим критериям. Введите тождества с отрицательным углом! Согласно тождествам с отрицательным углом, мы имеем, что sec(- x ) = sec( x ).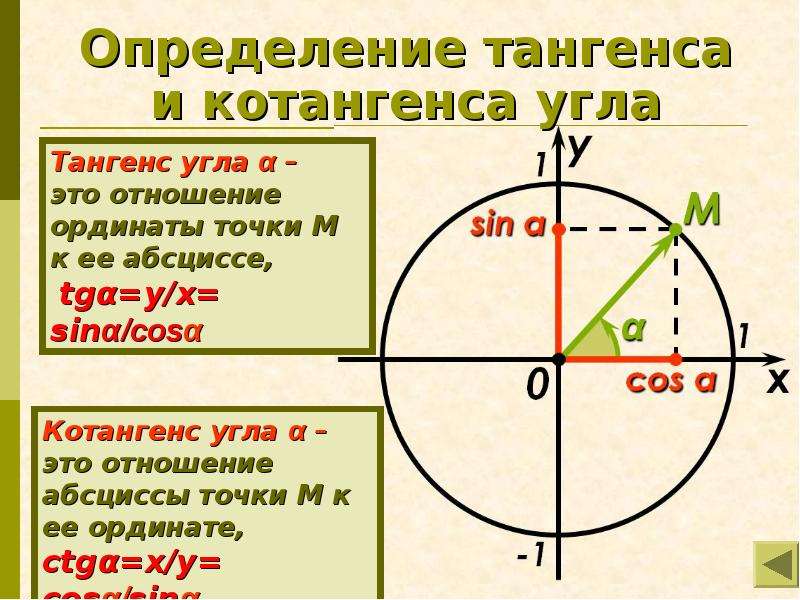 Следовательно, должно быть так, что sec(-60) = sec(60) = 2. Вы вздыхаете с облегчением и пытаетесь использовать угол с мерой -60 градусов. Это выглядит идеально!
Следовательно, должно быть так, что sec(-60) = sec(60) = 2. Вы вздыхаете с облегчением и пытаетесь использовать угол с мерой -60 градусов. Это выглядит идеально!
Пример 2
Рассмотрим еще один пример. Скажем, вы сидите на уроке тригонометрии, и инструктор говорит вам значение sin(45).
Исходя из этого, ваш инструктор хочет, чтобы вы нашли значение греха (-45). У меня отличные новости! Мы можем использовать наши отрицательные угловые тождества, чтобы найти это.Тождество с отрицательным углом, включающее функцию синуса, дает, что sin(- x ) = -sin( x ). Нам дано, что sin(45) = √2 / 2. Следовательно, -sin(45) = -√2 / 2.
2/2 и sin(- x ) = -sin( x ), должно быть так, что sin(-45) = -√2/2. между различными вариациями тригонометрических функций.Тождества отрицательных углов дают связь между тригонометрическими функциями, когда мы берем тригонометрическую функцию отрицательного угла.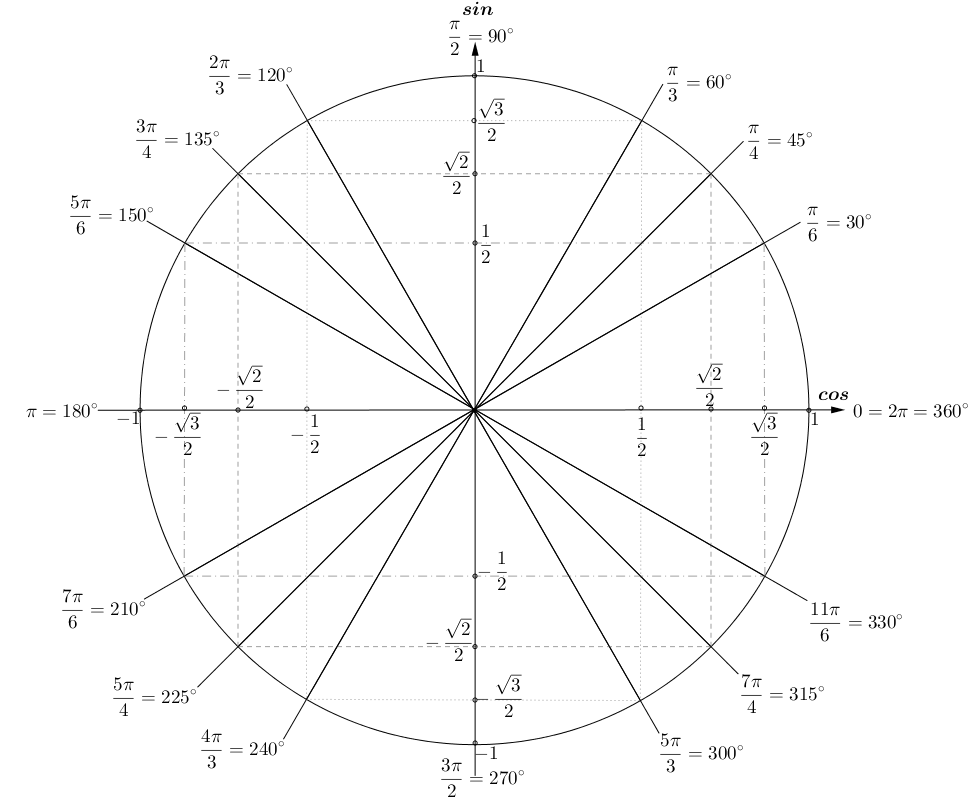 Эти отрицательные угловые тождества заключаются в следующем.
Эти отрицательные угловые тождества заключаются в следующем.
- sin(- x ) = -sin( x )
- cos(- х ) = cos( х )
- загар (- х ) = -загар ( х )
- csc(- х ) = -csc( х )
- сек(- х ) = сек( х )
- детская кроватка (- x ) = — детская кроватка ( x )
Мы можем использовать эти тождества во многих различных областях, таких как тригонометрия, строительство, строительство, астрономия и физика.По мере того, как вы продвигаетесь вперед в изучении тригонометрии, вы обнаружите, что эти тождества бесценны.
Тригонометрия: Введение в круг единиц — II
В этом видео мы расширим ваши знания о круге триггеров. Смотрите, впитывайте, а затем будьте готовы к вопросам на следующем тесте.
Теперь мы можем продолжить обсуждение тригонометрии единичного круга. Итак, в предыдущем видео мы обсудили базовые определения знака и косигна элементарных триггерных функций из единичного круга.И просто краткое напоминание здесь, что мы сделали, конечно. Мы помещаем нашу розетку в треугольник внутри единичного круга так, чтобы гипотенуза единичного круга была радиусом, и, конечно же, радиус единичного круга равен 1.
Итак, в предыдущем видео мы обсудили базовые определения знака и косигна элементарных триггерных функций из единичного круга.И просто краткое напоминание здесь, что мы сделали, конечно. Мы помещаем нашу розетку в треугольник внутри единичного круга так, чтобы гипотенуза единичного круга была радиусом, и, конечно же, радиус единичного круга равен 1.
Это означает, что соседняя сторона равна x, а противоположная сторона равна y. И мы можем определить косинус как синус. Косинус тета равен x, а синус тета равен y.
Другими словами, синус и косинус определяются в терминах. Если у нас есть радиус под углом тета, где этот радиус пересекает единичную окружность? И что координаты этой точки x, y, где радиус равен единичной окружности, дают определение синуса и косинуса.
Определение окружности базового блока
Итак, это основное определение синуса и косинуса в виде единичной окружности. В прошлом видео мы говорили о том, как найти значения синуса и косинуса просто на осях. От положительной и отрицательной оси x и положительной и отрицательной оси y. В этом видео мы можем поговорить о попадании в квадранты. Когда мы начинаем смотреть на наклонные углы, которые не лежат на оси.
От положительной и отрицательной оси x и положительной и отрицательной оси y. В этом видео мы можем поговорить о попадании в квадранты. Когда мы начинаем смотреть на наклонные углы, которые не лежат на оси.
Итак, сначала поговорим о квадрантах. Квадрант тета сообщает нам положительный или отрицательный знак синуса и косинуса именно потому, что мы знаем положительные и отрицательные знаки x и y в разных квадрантах.Давайте подумаем об этом. В первом квадранте x и y оба положительны. Итак, это означает, что sin и cos оба здесь положительны.
В этом есть смысл. Все выходы являются выходами первого квадранта, все они положительные. Теперь, когда мы перейдем ко второму квадранту. Во втором квадранте помните, что y по-прежнему положителен, но теперь косинус отрицателен. Итак, это означает, что синус положителен, а косинус отрицателен во втором квадранте. Когда мы переходим в третий квадрант, и у, и х отрицательны, поэтому и синус, и косинус отрицательны.
Когда мы перейдем к четвертому квадранту, то теперь у нас будет отрицательное значение y, но положительное значение x. А значит, знак отрицательный, а косинус положительный. Очень легко определить положительные или отрицательные знаки этих двух функций в другом квадранте только из квадранта. Сам квадрант дает нам действительно важную информацию.
А значит, знак отрицательный, а косинус положительный. Очень легко определить положительные или отрицательные знаки этих двух функций в другом квадранте только из квадранта. Сам квадрант дает нам действительно важную информацию.
Мы также можем посмотреть на тангенс так, чтобы тангенс был синусоидально косинусным, то есть у более х. Так что это будет положительно везде, где у и х имеют один и тот же знак.Ну, y и x оба положительны в первом квадранте. И они оба отрицательны в третьем квадранте.
Таким образом, положительное значение над положительным является положительным, но отрицательное значение над отрицательным также является положительным. Итак, тангенс положителен, когда синус и косинус имеют один и тот же знак, либо они оба положительны, либо оба отрицательны. И это происходит в первом и третьем квадранте.
В двух других квадрантах x и y имеют противоположные знаки. Один положительный, другой отрицательный. Таким образом, у вас есть отрицательный результат над положительным или положительный над отрицательным, что дает отрицательную дробь.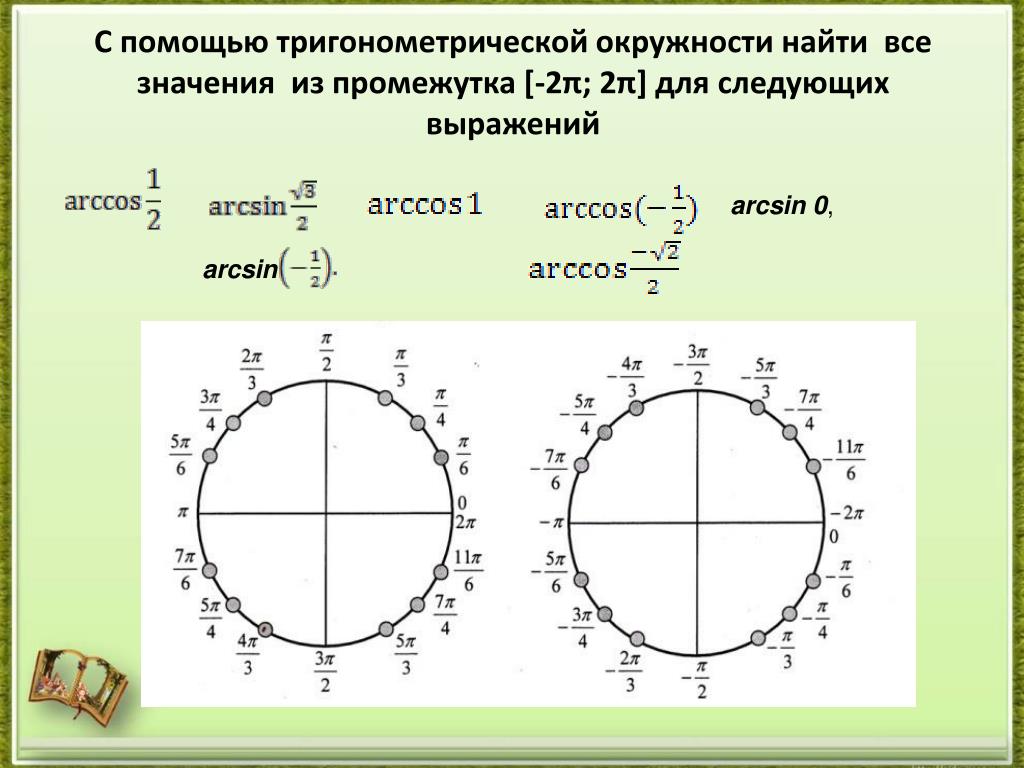 Итак, тангенс отрицателен, когда синус и косинус имеют противоположные знаки во второй и четвертой четвертях. Обратите внимание, что синус, косинус и тангенс, все три положительны в первом квадранте.
Итак, тангенс отрицателен, когда синус и косинус имеют противоположные знаки во второй и четвертой четвертях. Обратите внимание, что синус, косинус и тангенс, все три положительны в первом квадранте.
Это единственный квадрант, в котором все три положительны, а затем и каждый другой квадрант. Два из них отрицательные и только один из них положительный. И поэтому, когда мы идем вокруг, все наши положительные грехи положительны, тангенс положителен, косинус положителен. Некоторым нравится помнить, что, как и все студенты, берут математику.
Если это поможет вам запомнить это, это здорово. Теперь, как это поможет нам? Что ж, теперь мы на пути к выяснению значений синуса, косинуса и тангенса для углов, которые не лежат на оси, углы, которые находятся в квадрантах. И очень важно понимать, что мы получаем информацию о позитиве или негативе исключительно из квадрантов.
Итак, теперь предположим, что нам нужны значения sin 150 градусов и косинуса 150 градусов. Это квадрант двух углов.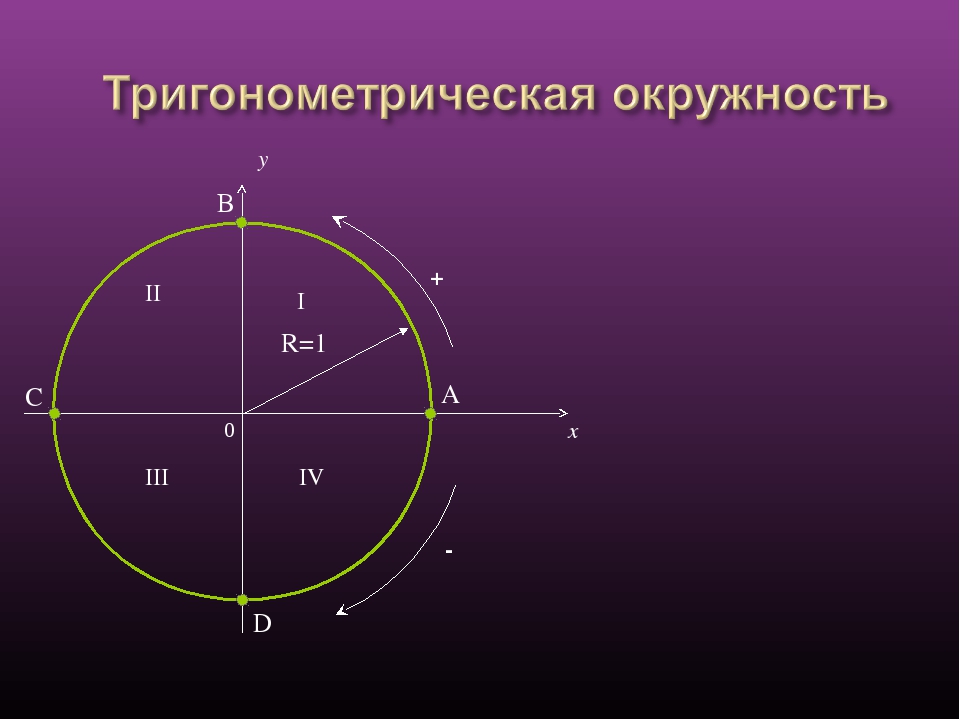 Итак, давайте сначала подумаем о том, что мы знаем.Из квадранта мы сразу знаем, что мы, конечно же, во втором квадранте, Y положительное, X отрицательное. Это означает, что синус меньше 50° будет положительным, а косинус отрицательным.
Итак, давайте сначала подумаем о том, что мы знаем.Из квадранта мы сразу знаем, что мы, конечно же, во втором квадранте, Y положительное, X отрицательное. Это означает, что синус меньше 50° будет положительным, а косинус отрицательным.
У нас легко есть положительные и отрицательные синусы, теперь нам нужно получить числовые значения. Итак, давайте поговорим об этом. Обратите внимание, что 150° равно 180 минус 30. Это означает, что один из способов получить угол в 150 градусов — это развернуться на полные 180, а затем вернуться на 30. Давайте подумаем об этом.Это означает, что мы можем нарисовать маленький треугольник в Q2.
И мы видим, что мы получаем этот маленький треугольник в QII с углом 30 градусов. Это конгруэнтно первому квадранту треугольника с углом 30 градусов. Это означает, что длины этих сторон будут точно такими же, как длины сторон угла в 30 градусов. И, конечно же, длины сторон определяют значения греха и косинуса.
Значит, по крайней мере абсолютное значение sin будет одинаковым для 150 и 30.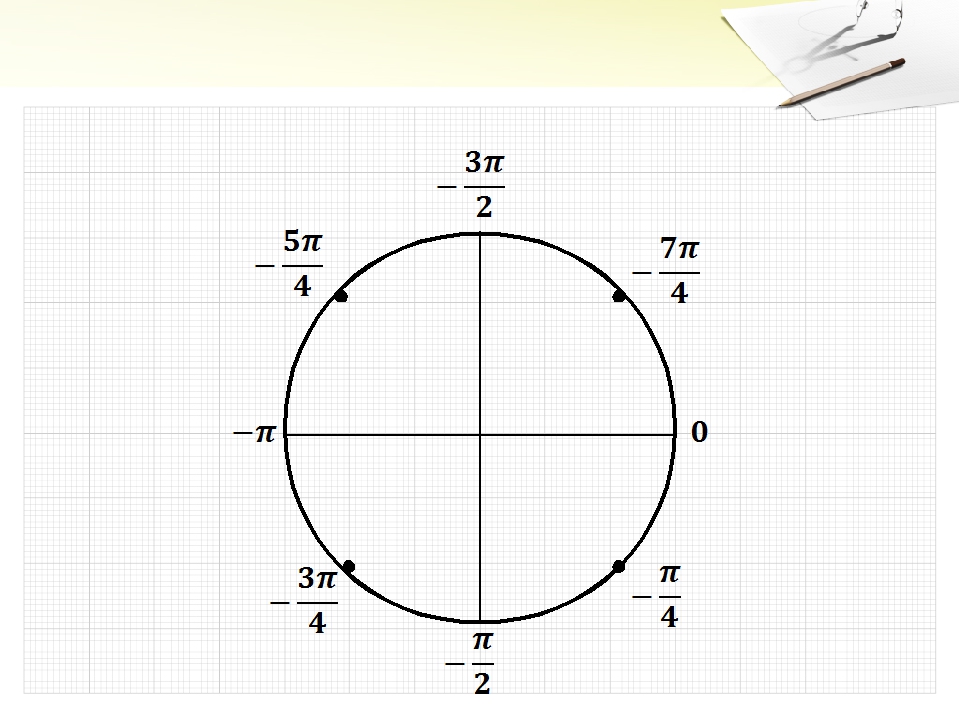 Абсолютное значение косинуса будет одинаковым для 150 и 30. Итак, каковы значения синуса и косинуса 30 градусов? Ну, мы говорили об этом немного пару видео назад. Итак, вы, возможно, помните, что мы выяснили, что sin(30°) = 1/2, cos(30°) = корень 3/2.
Абсолютное значение косинуса будет одинаковым для 150 и 30. Итак, каковы значения синуса и косинуса 30 градусов? Ну, мы говорили об этом немного пару видео назад. Итак, вы, возможно, помните, что мы выяснили, что sin(30°) = 1/2, cos(30°) = корень 3/2.
Ну, теперь мы золотые, потому что синус синуса и косинус 150 градусов будут иметь одинаковые абсолютные значения. Итак, теперь мы знаем абсолютные значения, все, что нам нужно знать, это положительные и отрицательные знаки. Но мы уже выяснили это, мы получаем это из квадрантов.Итак, синус по-прежнему будет положительным, а косинус отрицательным во втором квадранте, и это сразу нам говорит. Просто возьмите эти абсолютные значения и отрегулируйте положительные и отрицательные знаки.
Итак, синус 150 градусов будет половиной косинуса 150 градусов, это будет отрицательный корень 3 из 2. Вот как мы находим эти значения.
Опорные углы
Чтобы решить эту проблему, мы использовали опорный угол. Это действительно важная идея. Это одна из важнейших идей тригонометрии.Идея опорного угла для любого угла больше 90 градусов.
Это одна из важнейших идей тригонометрии.Идея опорного угла для любого угла больше 90 градусов.
Итак, мы переходим во второй квадрант, третий квадрант и четвертый квадрант. Что мы хотим сделать, так это представить себе сегмент. Это идет от того места, где эта точка заканчивается, опущенная на ось x. Вы будете рисовать либо по положительной, либо по отрицательной оси X, и вы сделаете маленький треугольник, и в этом маленьком треугольнике будет острый угол. Этот острый угол является опорным углом.
И получается, что треугольник, который вы делаете, всегда будет конгруэнтным треугольнику, который вы получили бы в первом квадранте с опорным углом.Таким образом, все значения триггерной функции в любом квадранте будут равны, они будут иметь то же абсолютное значение, что и те же триггерные функции опорного угла. Конечно, эталонный угол будет иметь положительные результаты. Таким образом, единственное, что вам нужно выяснить, это то, что их синус или косинус должен быть отрицательным в другом квадранте.
И опять же, мы можем понять это из самого квадранта. Таким образом, любая триггерная функция любого большого угла имеет то же абсолютное значение, что и триггерная функция опорного угла.А затем мы просто находим положительный или отрицательный результат в квадранте, и все готово. Таким образом, мы получаем положительный или отрицательный результат из квадранта. Мы получаем числовое значение из эталонной настройки.
Итак, давайте остановимся на 30 градусах и подумаем о том, что будет иметь эталонный угол 30 градусов. Мы уже сделали это во втором квадранте. А в третьем квадранте? Таким образом, во втором квадранте это угол 150 градусов, который имеет референс 30. В третьем квадранте мы должны пройти весь путь до 180 градусов, а затем мы должны пройти еще 30 градусов, так что будет 210 градусов.
Итак, 210 градусов имеют опорный угол 30. Таким образом, у него точно такие же абсолютные значения, как у синуса и косинуса 30 градусов, но теперь оба они должны быть отрицательными. Теперь мы могли бы сказать, что синус 210 градусов равен отрицательной половине. Косинус 210 градусов — это отрицательный корень 3 из 2. Итак, мы снова используем те же абсолютные значения. И просто поставив знак минус перед ними обоими, а теперь давайте перейдем к QIV.
Теперь мы могли бы сказать, что синус 210 градусов равен отрицательной половине. Косинус 210 градусов — это отрицательный корень 3 из 2. Итак, мы снова используем те же абсолютные значения. И просто поставив знак минус перед ними обоими, а теперь давайте перейдем к QIV.
Что ж, в QIV мы должны полностью развернуться на 360 градусов, а затем вернуться на 30 градусов, чтобы получить 330 градусов.Итак, это угол в QIV, который имеет опорный угол 30 градусов. Итак, опять же, абсолютно то же значение, что и у синуса 30 градусов и косинуса 30 градусов. В QIV мы знаем, что x положителен, а y отрицателен.
Таким образом, синус отрицательный, а косинус положительный. Те же значения с отрицательным синусом sin(330°) = 1/2, cos(330°) = положительный корень 3/2. Итак, обратите внимание, что мы можем повторно использовать значения SOHCATOA в первом квадранте. Мы можем перерабатывать их в каждом квадранте, просто меняя местами положительные и отрицательные знаки.В этом прелесть опорного угла.
Контрольный угол: мощный инструмент
Таким образом, тест, как правило, не требует от нас прямого вычисления синуса и косинуса для таких углов, как этот. Тем не менее, знание и понимание опорного угла является чрезвычайно мощным инструментом решения проблем. И снова я помещу здесь еще одну рекламу. Если вы переходите к исчислению, вам придется делать подобные оценки, как только вы начнете исчисление.
Так что это действительно важная идея, которую нужно понять, если вы думаете о том, чтобы заняться исчислением позже.
Практическая задача
Вот учебная задача, похожая на тест учебная задача. Поставьте видео на паузу, а потом поговорим об этом. Хорошо. Если тангенс у, некоторый угол у, равен 2 корня из 2, и мы знаем, что у находится между 180 и 270 градусами. Другими словами, это угол третьего квадранта, который из следующих значений является значением косинуса?
И поэтому я просто укажу здесь третий квадрант, мы знаем, что и x, и y отрицательны, поэтому мы сразу знаем, что косинус будет отрицательным. И на самом деле все пять вариантов ответа отрицательные, поэтому нам все равно придется выбрать отрицательный. Давайте подумаем, как найти это числовое значение. Итак, мы собираемся использовать опорный угол.
И на самом деле все пять вариантов ответа отрицательные, поэтому нам все равно придется выбрать отрицательный. Давайте подумаем, как найти это числовое значение. Итак, мы собираемся использовать опорный угол.
Давайте просто предположим, что мы построили остроугольный треугольник, где угол имеет тангенс из двух корней из двух. Итак, мы позволим R быть опорным углом Y. Итак, R и Y, их два, R — острый угол, Y — угол третьего квадранта, но R — опорный угол Y. И мы знаем что если тангенс равен двум больше двух, мы можем просто сделать противоположное равным двум больше двух, а прилежащее равным единице.
На самом деле это треугольник, который не помещается внутри единичного круга, он немного больше. Это не имеет значения, коэффициенты останутся прежними. Итак, нам нужно найти d. И поэтому мы можем сделать это только с помощью теоремы Пифагора. Итак, обычная теорема Пифагора: d в квадрате = 1 в квадрате + (2 корень 2) в квадрате.
Ну, это 1 в квадрате, а затем 2 корень 2, это 2 в квадрате, что в 4 раза больше корня из двух в квадрате, что равно двум, и, таким образом, четыре корня из двух, что равно восьми, а затем восемь плюс один равно девяти, так что это d в квадрате.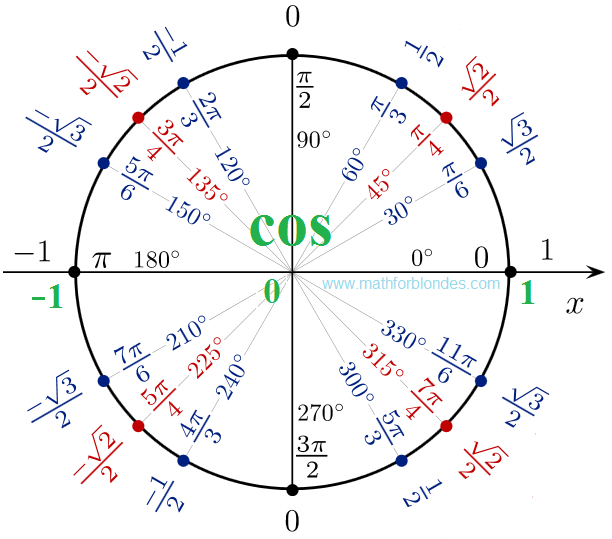 D в квадрате должен быть положительным, потому что это длина, то есть квадратный корень из девяти, что равно трем, так что теперь мы знаем d. Итак, теперь внутри этого маленького эталонного треугольника мы можем найти косинус.
D в квадрате должен быть положительным, потому что это длина, то есть квадратный корень из девяти, что равно трем, так что теперь мы знаем d. Итак, теперь внутри этого маленького эталонного треугольника мы можем найти косинус.
Косинус(R) равен одной трети. Ну, теперь мы золотые. Мы знаем, что косинус (Y) будет иметь точно такое же абсолютное значение, и нам просто нужно скорректировать положительный знак на отрицательный. И поэтому, конечно, снова в третьем квадранте нам нужно что-то негативное. Итак, мы берем это же абсолютное значение и делаем его отрицательным, поэтому косинус y будет равен -1/3.
Итак, мы возвращаемся к нашим ответам и выбираем -1/3.
Резюме
Таким образом, мы можем определить положительный или отрицательный знак по квадранту угла. Для любого угла больше 90 градусов мы знаем, что синус и косинус этого угла будут иметь те же абсолютные значения, что и синус опорного угла и косинус опорного угла.
Итак, мы смогли вычислить маленькую SOHCATOA опорного угла. И вы могли бы понять это либо из свойств специальных треугольников, возможно, вам придется использовать теорему Пифагора, как мы использовали в практической задаче.Но мы можем выяснить все в этом остроугольном треугольнике, а затем мы можем скорректировать положительные или отрицательные знаки из квадранта.
И вы могли бы понять это либо из свойств специальных треугольников, возможно, вам придется использовать теорему Пифагора, как мы использовали в практической задаче.Но мы можем выяснить все в этом остроугольном треугольнике, а затем мы можем скорректировать положительные или отрицательные знаки из квадранта.
Майк работал экспертом по GMAT в Magoosh, помогая создавать сотни видеоуроков и практических вопросов, чтобы помочь учащимся GMAT добиться успеха.Он также был признан «участником месяца» более двух лет в GMAT Club. Майк имеет A.B. по физике (окончание с отличием ) и степень МТС. в религиях мира, оба из Гарварда. Помимо стандартного тестирования, Майк имеет более чем 20-летний опыт преподавания как в частных, так и в государственных средних школах, специализируясь на математике и физике.
 В свободное время Майк любит разбивать настольные мячи на орбите, и, несмотря на то, что у него нет явных дефектов черепа, он настаивает на том, чтобы болеть за нью-йоркский Метс.Узнайте больше о GMAT из видеороликов Майка на Youtube и ресурсов, таких как What is a Good GMAT Score? и диагностический тест GMAT.
В свободное время Майк любит разбивать настольные мячи на орбите, и, несмотря на то, что у него нет явных дефектов черепа, он настаивает на том, чтобы болеть за нью-йоркский Метс.Узнайте больше о GMAT из видеороликов Майка на Youtube и ресурсов, таких как What is a Good GMAT Score? и диагностический тест GMAT.Просмотреть все сообщения
Вся элементарная математика — Учебное пособие — Тригонометрия
Единичный круг.Подсчет углов единичной окружности.Отрицательные и положительные углы. Четверти единичного круга.
Линии синусов и косинусов. Синус. Косинус. Знаки синуса и
косинус в разных четвертях единичной окружности. Тангенс
и котангенсы. Тангенс. Котангенс. Знаки
тангенс и котангенс в разных четвертях единицы
круг.
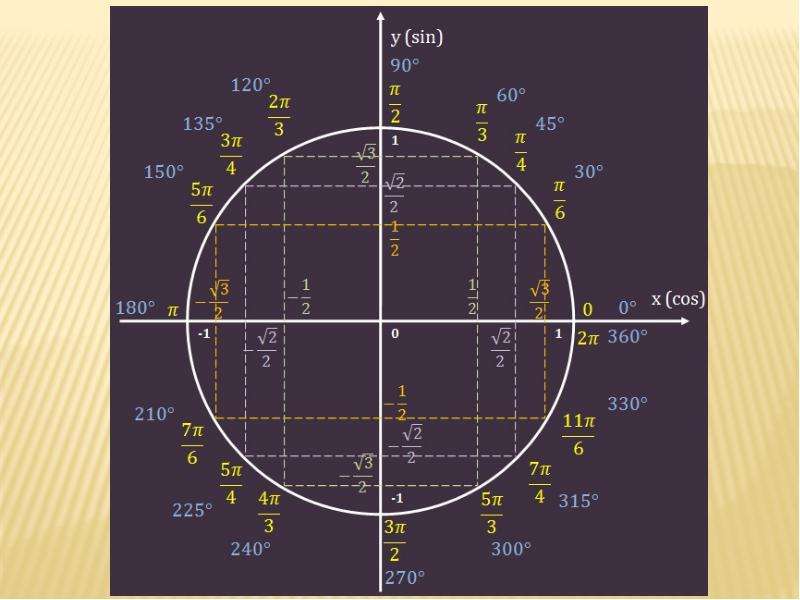 Секанс и косеканс.
Секанс и косеканс. Построить всю тригонометрию, законы которой справедливы для любых углов (не только для острых, но и для тупых, положительных и отрицательных углов), необходимо необходимо рассмотреть так называемую единичную окружность , то есть окружность с радиусом, равным 1 (рис.3).
Проведем два диаметра: горизонтальный АА и вертикальный ВВ. Считаем углы от точки А (начальной точки). Отрицательные углы отсчитываются по часовой стрелке, положительный в противоположном направлении. Подвижный радиус ОС образует угол с неподвижный радиус OA. Его можно разместить в 1-й четверти (COA), во 2-й четверти (DOA), в 3-й четверти (EOA) или в 4-я четверть (ФОА). Считая ОА и ОВ положительными направлениями, а ОА и ОВ отрицательными, мы определяем тригонометрические функции углов следующим образом.
синусоида угла ( рис.4 ) есть вертикаль диаметр единичной окружности, косинус линия угла — горизонталь диаметр единичной окружности. A синус угла
( Рис.4 ) – отрезок OB синусоиды, то есть проекция подвижного радиуса
нормально к синусоиде; косинус угла — отрезок ОА косинуса, т.е.
есть проекция подвижного радиуса ОК на косинус.
A синус угла
( Рис.4 ) – отрезок OB синусоиды, то есть проекция подвижного радиуса
нормально к синусоиде; косинус угла — отрезок ОА косинуса, т.е.
есть проекция подвижного радиуса ОК на косинус.
Знаки синуса и косинуса в разных четвертях единичной окружности показаны на рис.5 и рис.6.
Касательная (рис. 7) является касательной, проведенной к единичной окружности через точку A горизонтального диаметра .
Котангенс (рис.8) является касательной, проведенной к единичной окружности через точку B вертикального диаметра .
Касательная — это отрезок касательной между точкой касания A и точкой пересечения (D, E и т. д.)., рис.7 ) касательной и радиусной линии.
Котангенс представляет собой отрезок линии котангенса между точкой касания B и точкой пересечения ( P, Q и т. д., рис.8 ) линии котангенса и линии радиуса.
Знаки тангенса и котангенса в разных четвертях единичной окружности см. на рис.9.
на рис.9.
Секанс и косеканс определяются как обратные величины косинуса и синуса соответственно.
%PDF-1.3 % 8 0 объект > эндообъект внешняя ссылка 8 79 0000000016 00000 н 0000001924 00000 н 0000002076 00000 н 0000002105 00000 н 0000002183 00000 н 0000002582 00000 н 0000002819 00000 н 0000002848 00000 н 0000003034 00000 н 0000003196 00000 н 0000003285 00000 н 0000003937 00000 н 0000004133 00000 н 0000004542 00000 н 0000004722 00000 н 0000004744 00000 н 0000010847 00000 н 0000010869 00000 н 0000016796 00000 н 0000016818 00000 н 0000022809 00000 н 0000022831 00000 н 0000028850 00000 н 0000028872 00000 н 0000035280 00000 н 0000035302 00000 н 0000035499 00000 н 0000035802 00000 н 0000035993 00000 н 0000036103 00000 н 0000036211 00000 н 0000036532 00000 н 0000036939 00000 н 0000037379 00000 н 0000037569 00000 н 0000037960 00000 н 0000038160 00000 н 0000039418 00000 н 0000039624 00000 н 0000039779 00000 н 0000045905 00000 н 0000045927 00000 н 0000052042 00000 н 0000052065 00000 н 0000062851 00000 н 0000166043 00000 н 0000166184 00000 н 0000166325 00000 н 0000166472 00000 н 0000166619 00000 н 0000166763 00000 н 0000166907 00000 н 0000167054 00000 н 0000167201 00000 н 0000167345 00000 н 0000167489 00000 н 0000167632 00000 н 0000167775 00000 н 0000168491 00000 н 0000168638 00000 н 0000168778 00000 н 0000168918 00000 н 0000169059 00000 н 0000169202 00000 н 0000169349 00000 н 0000169491 00000 н 0000169633 00000 н 0000169775 00000 н 0000169915 00000 н 0000170056 00000 н 0000170198 00000 н 0000170345 00000 н 0000170488 00000 н 0000170630 00000 н 0000170777 00000 н 0000170923 00000 н 0000171069 00000 н 0000002260 00000 н 0000002561 00000 н трейлер ] >> startxref 0 %%EOF 9 0 объект > эндообъект 10 0 объект [ 11 0 Р ] эндообъект 11 0 объект > /Ф 17 0 Р >> эндообъект 12 0 объект > эндообъект 85 0 объект > ручей Hb«e`4@b D80Ip`alfCaG»m r,)A^XX0\aaPt 4o_Kd&/0_`|A_}/oʀ**0>
.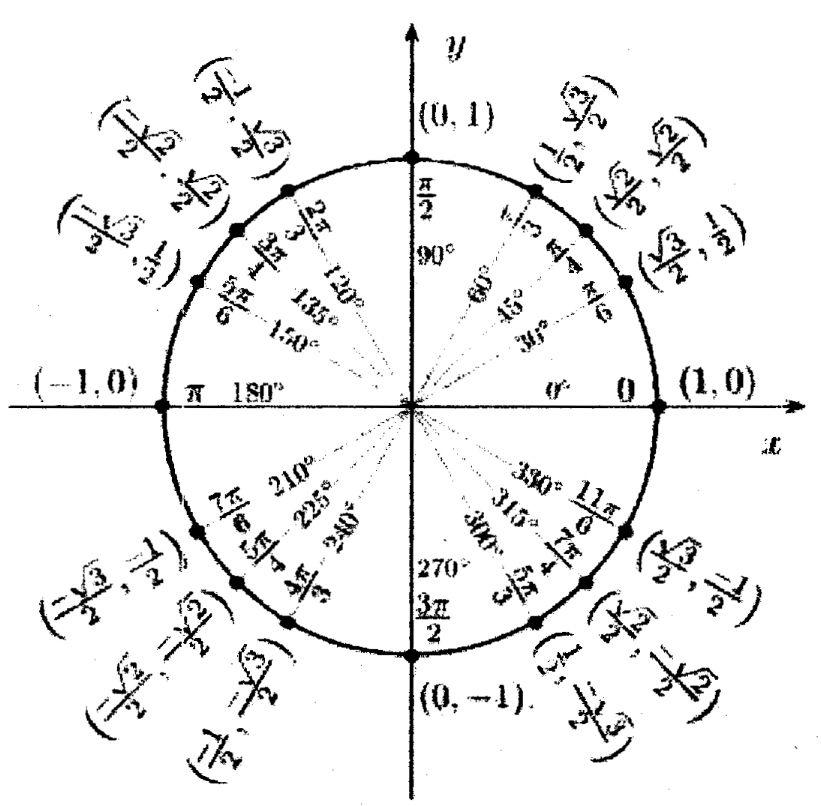

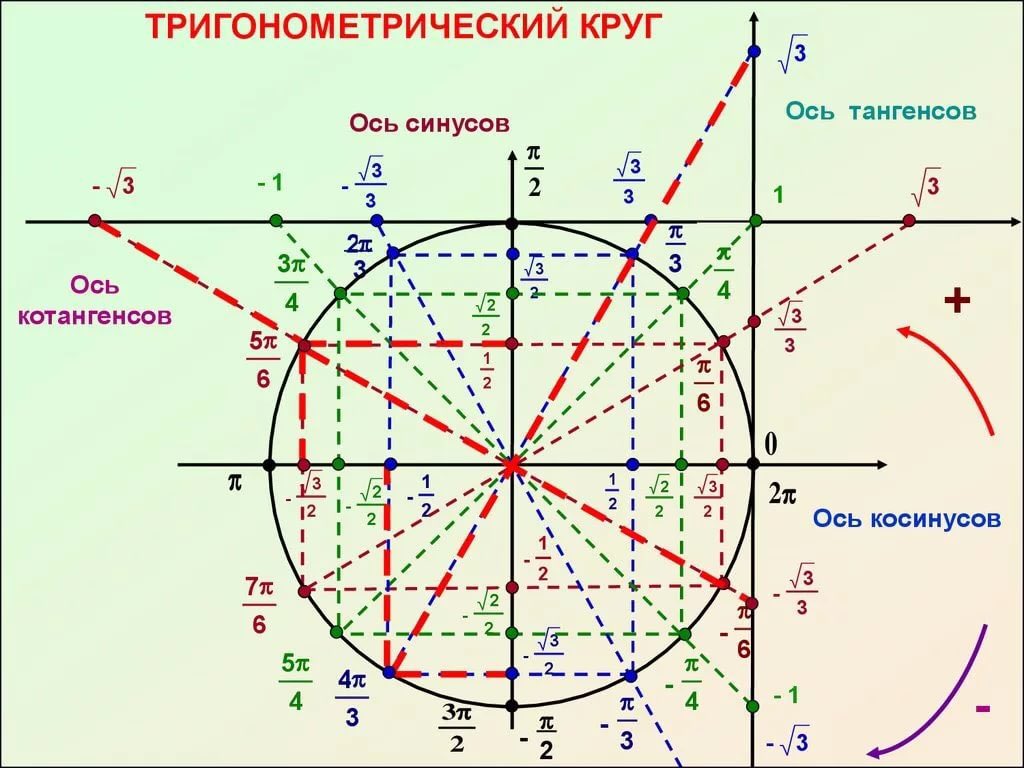
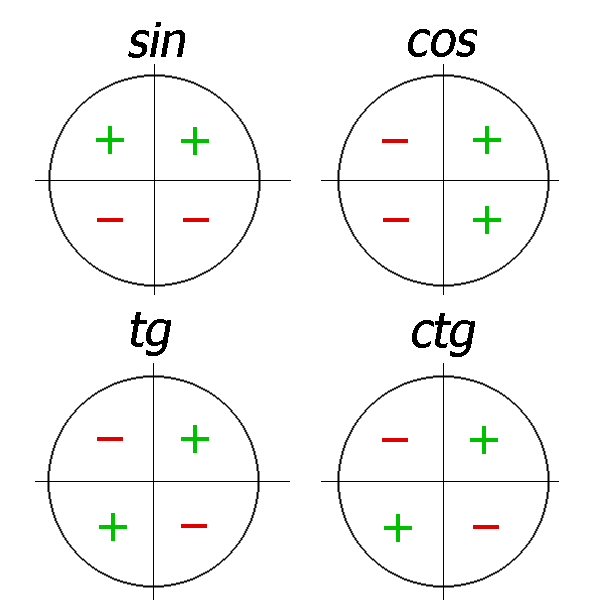
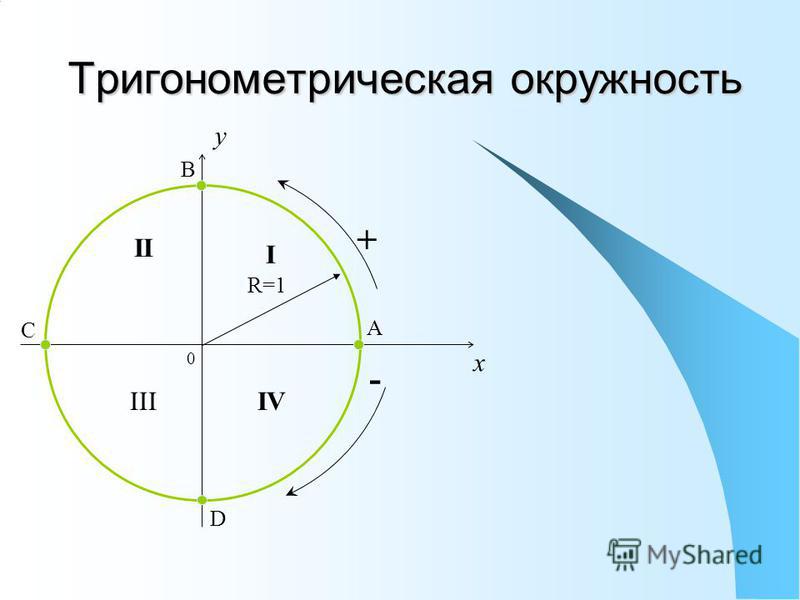
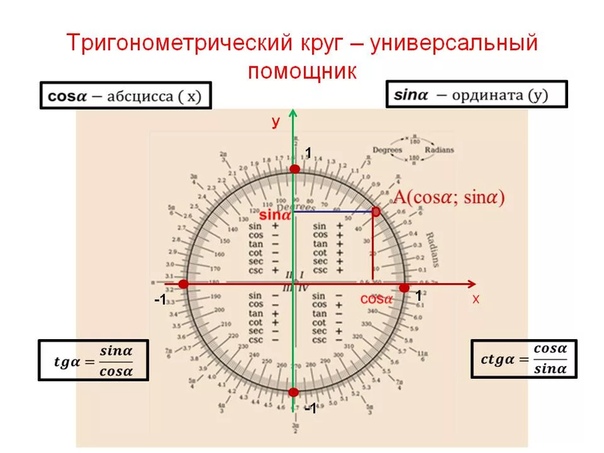
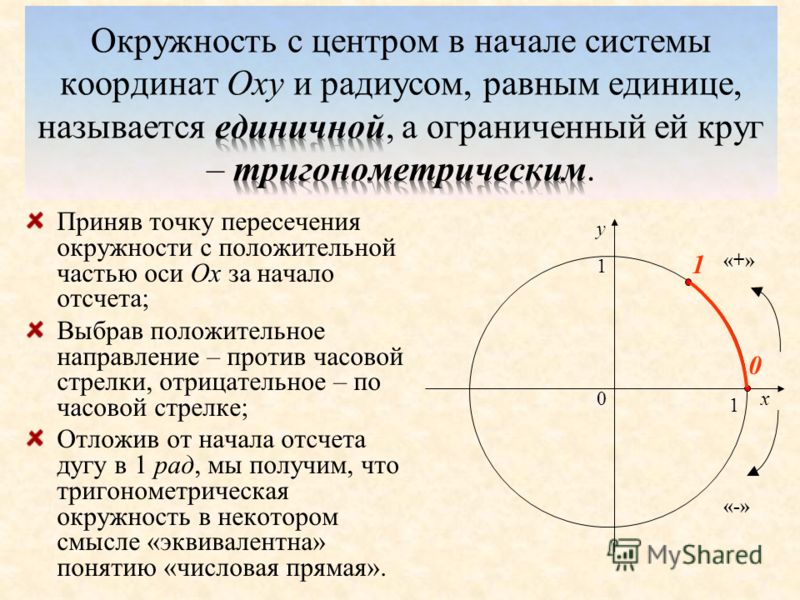 И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.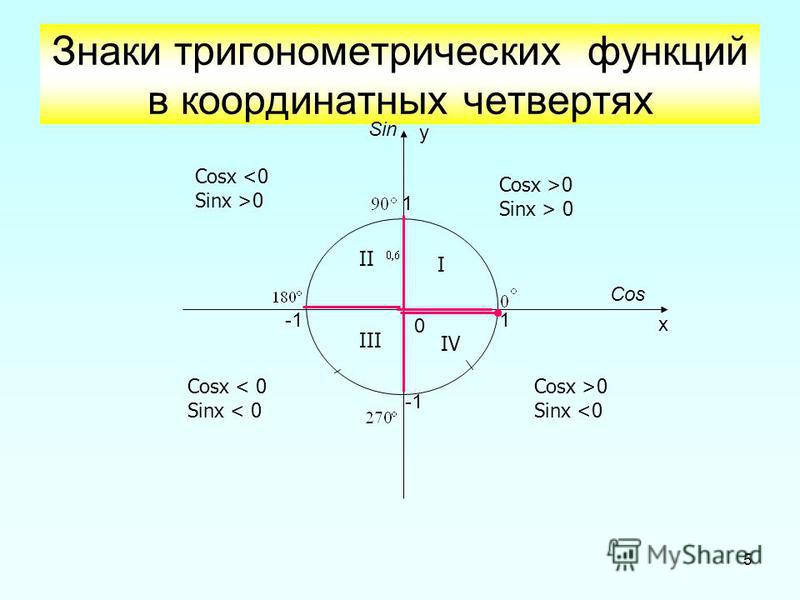
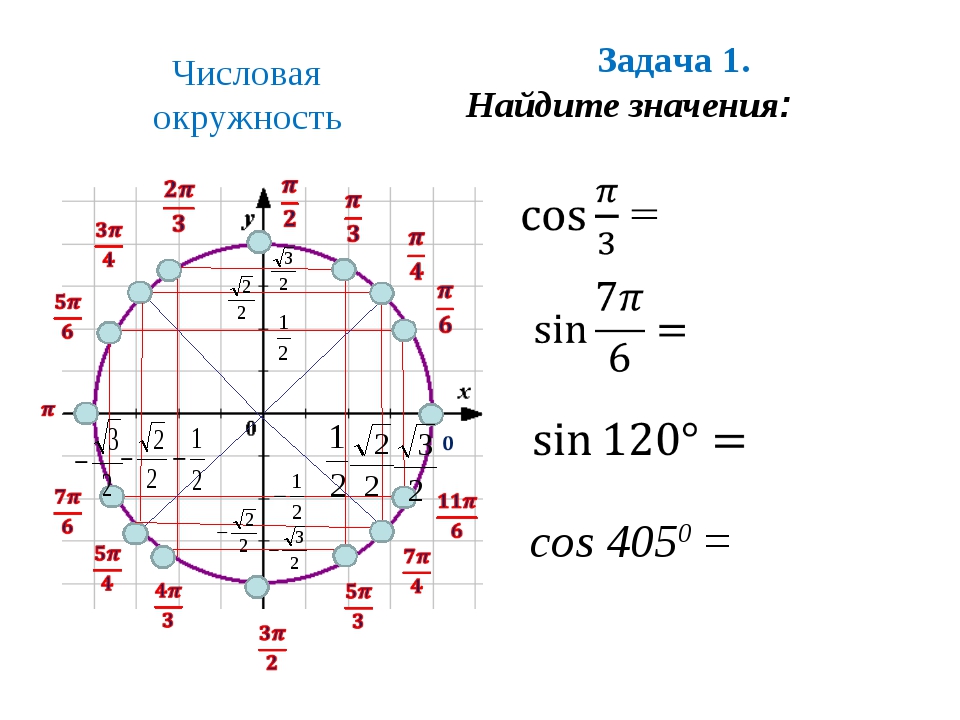


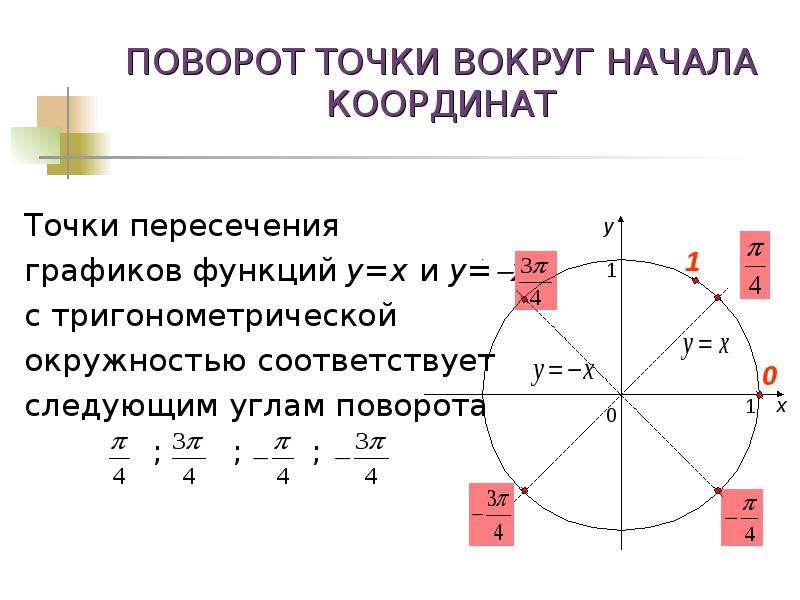
 В свободное время Майк любит разбивать настольные мячи на орбите, и, несмотря на то, что у него нет явных дефектов черепа, он настаивает на том, чтобы болеть за нью-йоркский Метс.Узнайте больше о GMAT из видеороликов Майка на Youtube и ресурсов, таких как What is a Good GMAT Score? и диагностический тест GMAT.
В свободное время Майк любит разбивать настольные мячи на орбите, и, несмотря на то, что у него нет явных дефектов черепа, он настаивает на том, чтобы болеть за нью-йоркский Метс.Узнайте больше о GMAT из видеороликов Майка на Youtube и ресурсов, таких как What is a Good GMAT Score? и диагностический тест GMAT.