Косинус равен 2: Таблица косинусов. Косинусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов углов.
Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Версия для печати.cos(0°)=cos(360°)=1; точная, но чуть более сложная таблица ( с точностью до 1″) здесь.
|
Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций Доп. Инфо:
|
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x относительно x | |
| 11 | Вычислим интеграл | интеграл x^2 относительно x | |
| 12 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x относительно x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x относительно x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 41 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 50 | Вычислим интеграл | интеграл 1 относительно x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x относительно x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) относительно x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) относительно x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 от 0 до 10 относительно x | |
| 84 | Вычислим интеграл | интеграл от ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 относительно x | |
| 91 | Вычислим интеграл | интеграл x^2e^x относительно x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) относительно x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
ACOS (функция ACOS) — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции ACOS в Microsoft Excel.
Описание
Возвращает арккосинус числа. Арккосинус числа — это угол, косинус которого равен числу. Угол определяется в радианах в интервале от 0 до «пи».
Синтаксис
ACOS(число)
Аргументы функции ACOS описаны ниже.
Замечания
Если нужно преобразовать результат из радиан в градусы, умножьте его на 180/ПИ() или используйте функцию ГРАДУСЫ.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Формула | Описание | Результат |
|---|---|---|
|
=ACOS(-0,5) |
Арккосинус числа -0,5 в радианах, 2*ПИ/3 (2,094395) |
2,094395102 |
|
=ACOS(-0,5)*180/ПИ() |
Арккосинус -0,5 в градусах |
120 |
|
=ГРАДУСЫ(ACOS(-0,5)) |
Арккосинус -0,5 в градусах |
120 |
Таблица косинусов, полная таблица косинусов для студентов
Содержание:
Таблица косинусов — наровне с таблицей синусов изучается в самом начале тригонометрии (И вместе с таблицей синусов является основным материалом тригонометрии). Без понимания данного материала и без знания хотя бы части таблицы косинусов будет очень сложно изучать тригонометрию и применять тригонометричекие формулы. Даже в университетском курсе часто используется тригонометрия, при решении интегралов и производных. Пользуйте таблицей косинусов на здоровье.
Таблица косинусов 0° — 180°
|
|
|
Таблица косинусов 180° — 360°
|
|
|
На нашем сайте в основном автоматические находятся программы для решения задач по математике, но также мы собрали много теоретического материала по математике и в частности по тригонометрии. Здесь Вы можете найти таблицы тригонометрических функций: таблицу косинусов, таблицу синусов, таблицу котангенсов и таблицу тангенсов. Также для улучшения понимания материала по тригонометрии мы добавили тригонометрические формулы, чтобы вызывало меньше затруднений решение тригонометрических задач по математике. Пользуйтесь нашим сайтом и таблицей косинусов на здоровье.
Слишком сложно?
Таблица косинусов, таблица значений косинусов не по зубам? Тебе ответит эксперт через 10 минут!
Таблица косинусов — 2mb.ru
Таблица косинусов является одной из основных таблиц, которые используются в геометрии.
В ней представлены косинусы углов от 0 до 360 градусов. Таблица позволяет решать математические задачи, в которых необходимо использовать тригонометрические данные без применения расчетов и калькулятора.
Таблица косинусов 0° – 180°.
|
|
|
Таблица косинусов 180° – 360°.
|
|
|
Таблица косинусов
Таблица косинусовГлавная > к >
Таблица косинусов для основных углов: 0°, 90°, 180°, 270°, 360°.
| Угол х (в градусах) |
0° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|
| Угол х (в радианах) |
0 | ||||
| cos x | 1 | 0 | -1 | 0 | 1 |
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) |
0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) |
0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) |
√2/2 (0,7071) |
1/2 (0,5) |
0 | -1/2 (-0,5) |
-√2/2 (-0,7071) |
-√3/2 (-0,8660) |
-1 | -√3/2 (-0,8660) |
-√2/2 (-0,7071) |
-1/2 (-0,5) |
0 | 1/2 (0,5) |
√2/2 (0,7071) |
√3/2 (0,8660) |
1 |
Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°.
Таблица косинусов — это посчитанные значения косинусов от 0° до 360°.
Если не под рукой калькулятора — таблица косинусов может пригодиться.
Для того, чтобы узнать чему равен косинус от нужного Вам угла достаточно найти его в таблице:
| cos 1° | = 0,9998 | cos 91° | = -0,0175 | cos 181° | = -0,9998 | cos 271° | = 0,0175 |
|---|---|---|---|---|---|---|---|
| cos 2° | = 0,9994 | cos 92° | = -0,0349 | cos 182° | = -0,9994 | cos 272° | = 0,0349 |
| cos 3° | = 0,9986 | cos 93° | = -0,0523 | cos 183° | = -0,9986 | cos 273° | = 0,0523 |
| cos 4° | = 0,9976 | cos 94° | = -0,0698 | cos 184° | = -0,9976 | cos 274° | = 0,0698 |
| cos 5° | = 0,9962 | cos 95° | = -0,0872 | cos 185° | = -0,9962 | cos 275° | = 0,0872 |
| cos 6° | = 0,9945 | cos 96° | = -0,1045 | cos 186° | = -0,9945 | cos 276° | = 0,1045 |
| cos 7° | = 0,9925 | cos 97° | = -0,1219 | cos 187° | = -0,9925 | cos 277° | = 0,1219 |
| cos 8° | = 0,9903 | cos 98° | = -0,1392 | cos 188° | = -0,9903 | cos 278° | = 0,1392 |
| cos 9° | = 0,9877 | cos 99° | = -0,1564 | cos 189° | = -0,9877 | cos 279° | = 0,1564 |
| cos 10° | = 0,9848 | cos 100° | = -0,1736 | cos 190° | = -0,9848 | cos 280° | = 0,1736 |
| cos 11° | = 0,9816 | cos 101° | = -0,1908 | cos 191° | = -0,9816 | cos 281° | = 0,1908 |
| cos 12° | = 0,9781 | cos 102° | = -0,2079 | cos 192° | = -0,9781 | cos 282° | = 0,2079 |
| cos 13° | = 0,9744 | cos 103° | = -0,225 | cos 193° | = -0,9744 | cos 283° | = 0,225 |
| cos 14° | = 0,9703 | cos 104° | = -0,2419 | cos 194° | = -0,9703 | cos 284° | = 0,2419 |
| cos 15° | = 0,9659 | cos 105° | = -0,2588 | cos 195° | = -0,9659 | cos 285° | = 0,2588 |
| cos 16° | = 0,9613 | cos 106° | = -0,2756 | cos 196° | = -0,9613 | cos 286° | = 0,2756 |
| cos 17° | = 0,9563 | cos 107° | = -0,2924 | cos 197° | = -0,9563 | cos 287° | = 0,2924 |
| cos 18° | = 0,9511 | cos 108° | = -0,309 | cos 198° | = -0,9511 | cos 288° | = 0,309 |
| cos 19° | = 0,9455 | cos 109° | = -0,3256 | cos 199° | = -0,9455 | cos 289° | = 0,3256 |
| cos 20° | = 0,9397 | cos 110° | = -0,342 | cos 200° | = -0,9397 | cos 290° | = 0,342 |
| cos 21° | = 0,9336 | cos 111° | = -0,3584 | cos 201° | = -0,9336 | cos 291° | = 0,3584 |
| cos 22° | = 0,9272 | cos 112° | = -0,3746 | cos 202° | = -0,9272 | cos 292° | = 0,3746 |
| cos 23° | = 0,9205 | cos 113° | = -0,3907 | cos 203° | = -0,9205 | cos 293° | = 0,3907 |
| cos 24° | = 0,9135 | cos 114° | = -0,4067 | cos 204° | = -0,9135 | cos 294° | = 0,4067 |
| cos 25° | = 0,9063 | cos 115° | = -0,4226 | cos 205° | = -0,9063 | cos 295° | = 0,4226 |
| cos 26° | = 0,8988 | cos 116° | = -0,4384 | cos 206° | = -0,8988 | cos 296° | = 0,4384 |
| cos 27° | = 0,891 | cos 117° | = -0,454 | cos 207° | = -0,891 | cos 297° | = 0,454 |
| cos 28° | = 0,8829 | cos 118° | = -0,4695 | cos 208° | = -0,8829 | cos 298° | = 0,4695 |
| cos 29° | = 0,8746 | cos 119° | = -0,4848 | cos 209° | = -0,8746 | cos 299° | = 0,4848 |
| cos 30° | = 0,866 | cos 120° | = -0,5 | cos 210° | = -0,866 | cos 300° | = 0,5 |
| cos 31° | = 0,8572 | cos 121° | = -0,515 | cos 211° | = -0,8572 | cos 301° | = 0,515 |
| cos 32° | = 0,848 | cos 122° | = -0,5299 | cos 212° | = -0,848 | cos 302° | = 0,5299 |
| cos 33° | = 0,8387 | cos 123° | = -0,5446 | cos 213° | = -0,8387 | cos 303° | = 0,5446 |
| cos 34° | = 0,829 | cos 124° | = -0,5592 | cos 214° | = -0,829 | cos 304° | = 0,5592 |
| cos 35° | = 0,8192 | cos 125° | = -0,5736 | cos 215° | = -0,8192 | cos 305° | = 0,5736 |
| cos 36° | = 0,809 | cos 126° | = -0,5878 | cos 216° | = -0,809 | cos 306° | = 0,5878 |
| cos 37° | = 0,7986 | cos 127° | = -0,6018 | cos 217° | = -0,7986 | cos 307° | = 0,6018 |
| cos 38° | = 0,788 | cos 128° | = -0,6157 | cos 218° | = -0,788 | cos 308° | = 0,6157 |
| cos 39° | = 0,7771 | cos 129° | = -0,6293 | cos 219° | = -0,7771 | cos 309° | = 0,6293 |
| cos 40° | = 0,766 | cos 130° | = -0,6428 | cos 220° | = -0,766 | cos 310° | = 0,6428 |
| cos 41° | = 0,7547 | cos 131° | = -0,6561 | cos 221° | = -0,7547 | cos 311° | = 0,6561 |
| cos 42° | = 0,7431 | cos 132° | = -0,6691 | cos 222° | = -0,7431 | cos 312° | = 0,6691 |
| cos 43° | = 0,7314 | cos 133° | = -0,682 | cos 223° | = -0,7314 | cos 313° | = 0,682 |
| cos 44° | = 0,7193 | cos 134° | = -0,6947 | cos 224° | = -0,7193 | cos 314° | = 0,6947 |
| cos 45° | = 0,7071 | cos 135° | = -0,7071 | cos 225° | = -0,7071 | cos 315° | = 0,7071 |
| cos 46° | = 0,6947 | cos 136° | = -0,7193 | cos 226° | = -0,6947 | cos 316° | = 0,7193 |
| cos 47° | = 0,682 | cos 137° | = -0,7314 | cos 227° | = -0,682 | cos 317° | = 0,7314 |
| cos 48° | = 0,6691 | cos 138° | = -0,7431 | cos 228° | = -0,6691 | cos 318° | = 0,7431 |
| cos 49° | = 0,6561 | cos 139° | = -0,7547 | cos 229° | = -0,6561 | cos 319° | = 0,7547 |
| cos 50° | = 0,6428 | cos 140° | = -0,766 | cos 230° | = -0,6428 | cos 320° | = 0,766 |
| cos 51° | = 0,6293 | cos 141° | = -0,7771 | cos 231° | = -0,6293 | cos 321° | = 0,7771 |
| cos 52° | = 0,6157 | cos 142° | = -0,788 | cos 232° | = -0,6157 | cos 322° | = 0,788 |
| cos 53° | = 0,6018 | cos 143° | = -0,7986 | cos 233° | = -0,6018 | cos 323° | = 0,7986 |
| cos 54° | = 0,5878 | cos 144° | = -0,809 | cos 234° | = -0,5878 | cos 324° | = 0,809 |
| cos 55° | = 0,5736 | cos 145° | = -0,8192 | cos 235° | = -0,5736 | cos 325° | = 0,8192 |
| cos 56° | = 0,5592 | cos 146° | = -0,829 | cos 236° | = -0,5592 | cos 326° | = 0,829 |
| cos 57° | = 0,5446 | cos 147° | = -0,8387 | cos 237° | = -0,5446 | cos 327° | = 0,8387 |
| cos 58° | = 0,5299 | cos 148° | = -0,848 | cos 238° | = -0,5299 | cos 328° | = 0,848 |
| cos 59° | = 0,515 | cos 149° | = -0,8572 | cos 239° | = -0,515 | cos 329° | = 0,8572 |
| cos 60° | = 0,5 | cos 150° | = -0,866 | cos 240° | = -0,5 | cos 330° | = 0,866 |
| cos 61° | = 0,4848 | cos 151° | = -0,8746 | cos 241° | = -0,4848 | cos 331° | = 0,8746 |
| cos 62° | = 0,4695 | cos 152° | = -0,8829 | cos 242° | = -0,4695 | cos 332° | = 0,8829 |
| cos 63° | = 0,454 | cos 153° | = -0,891 | cos 243° | = -0,454 | cos 333° | = 0,891 |
| cos 64° | = 0,4384 | cos 154° | = -0,8988 | cos 244° | = -0,4384 | cos 334° | = 0,8988 |
| cos 65° | = 0,4226 | cos 155° | = -0,9063 | cos 245° | = -0,4226 | cos 335° | = 0,9063 |
| cos 66° | = 0,4067 | cos 156° | = -0,9135 | cos 246° | = -0,4067 | cos 336° | = 0,9135 |
| cos 67° | = 0,3907 | cos 157° | = -0,9205 | cos 247° | = -0,3907 | cos 337° | = 0,9205 |
| cos 68° | = 0,3746 | cos 158° | = -0,9272 | cos 248° | = -0,3746 | cos 338° | = 0,9272 |
| cos 69° | = 0,3584 | cos 159° | = -0,9336 | cos 249° | = -0,3584 | cos 339° | = 0,9336 |
| cos 70° | = 0,342 | cos 160° | = -0,9397 | cos 250° | = -0,342 | cos 340° | = 0,9397 |
| cos 71° | = 0,3256 | cos 161° | = -0,9455 | cos 251° | = -0,3256 | cos 341° | = 0,9455 |
| cos 72° | = 0,309 | cos 162° | = -0,9511 | cos 252° | = -0,309 | cos 342° | = 0,9511 |
| cos 73° | = 0,2924 | cos 163° | = -0,9563 | cos 253° | = -0,2924 | cos 343° | = 0,9563 |
| cos 74° | = 0,2756 | cos 164° | = -0,9613 | cos 254° | = -0,2756 | cos 344° | = 0,9613 |
| cos 75° | = 0,2588 | cos 165° | = -0,9659 | cos 255° | = -0,2588 | cos 345° | = 0,9659 |
| cos 76° | = 0,2419 | cos 166° | = -0,9703 | cos 256° | = -0,2419 | cos 346° | = 0,9703 |
| cos 77° | = 0,225 | cos 167° | = -0,9744 | cos 257° | = -0,225 | cos 347° | = 0,9744 |
| cos 78° | = 0,2079 | cos 168° | = -0,9781 | cos 258° | = -0,2079 | cos 348° | = 0,9781 |
| cos 79° | = 0,1908 | cos 169° | = -0,9816 | cos 259° | = -0,1908 | cos 349° | = 0,9816 |
| cos 80° | = 0,1736 | cos 170° | = -0,9848 | cos 260° | = -0,1736 | cos 350° | = 0,9848 |
| cos 81° | = 0,1564 | cos 171° | = -0,9877 | cos 261° | = -0,1564 | cos 351° | = 0,9877 |
| cos 82° | = 0,1392 | cos 172° | = -0,9903 | cos 262° | = -0,1392 | cos 352° | = 0,9903 |
| cos 83° | = 0,1219 | cos 173° | = -0,9925 | cos 263° | = -0,1219 | cos 353° | = 0,9925 |
| cos 84° | = 0,1045 | cos 174° | = -0,9945 | cos 264° | = -0,1045 | cos 354° | = 0,9945 |
| cos 85° | = 0,0872 | cos 175° | = -0,9962 | cos 265° | = -0,0872 | cos 355° | = 0,9962 |
| cos 86° | = 0,0698 | cos 176° | = -0,9976 | cos 266° | = -0,0698 | cos 356° | = 0,9976 |
| cos 87° | = 0,0523 | cos 177° | = -0,9986 | cos 267° | = -0,0523 | cos 357° | = 0,9986 |
| cos 88° | = 0,0349 | cos 178° | = -0,9994 | cos 268° | = -0,0349 | cos 358° | = 0,9994 |
| cos 89° | = 0,0175 | cos 179° | = -0,9998 | cos 269° | = -0,0175 | cos 359° | = 0,9998 |
| cos 90° | = 0 | cos 180° | = -1 | cos 270° | = -0 | cos 360° | = 1 |
Теорема косинусов — Тригонометрия
Формулировка теоремы косинусов:Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними.
Доказательство теоремы косинусов:
Рассмотрим треугольник ABC.
Из вершины C на сторону AB опустим высоту CD.
Исходя из того, что треугольник ADC является прямоугольным, то
величину стороны AD можно найти из соотношения тригонометрических
функций :
AD / AC = cos α
AD = AC
cos α
AD = b cos α
Длину стороны BD найдем как разность AB и AD:
BD = AB — AD
BD = c − b cosα
Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
CD2 + BD2 = BC2
CD2 + AD2 = AC2
откуда
CD2 = BC2 — BD2
CD2 = AC2 —
AD2
Поскольку левые части уравнений равны, то приравняем правые части уравнений:
BC2 — BD2 =
AC2 —
AD2
a2 — ( c − b cos α )2 = b2 — ( b cos α )2
a2 = ( c − b cos α )2 + b2 — ( b cos α )2
a2 = b2 + c 2 — 2bc cos α + ( b cos α )2 — ( b cos α )2
a2 = b2 + c 2 — 2bc cos α
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
косинусов
Затем рассмотрим углы 30 ° и 60 °. В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения сторон равны 1: √3: 2. Отсюда следует, что sin 30 ° = cos 60 ° = 1/2, и sin 60 ° = cos 30 ° = √3 / 2.
Эти результаты занесены в эту таблицу.
| Угол | Градус | Радианы | косинус | синус |
|---|---|---|---|---|
| 90 ° | π /2 | 0 | 1 | |
| 60 ° | π /3 | 1/2 | √3 / 2 | |
| 45 ° | π /4 | √2 / 2 | √2 / 2 | |
| 30 ° | π /6 | √3 / 2 | 1/2 | |
| 0 ° | 0 | 1 | 0 |
Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой.30. b = 2,25 метра и cos A = 0,15. Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. b = 6,4, c = 7,8. Найдите A, и a.
36. A = 23 ° 15 ‘, c = 12.15. Найдите a, и b.
Подсказки
30. Косинус A связывает b с гипотенузой c, , так что вы можете сначала вычислить c. Как только вы узнаете b и c, , вы сможете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух сторон, которых вы не знаете, а именно a / c. Тем не менее, это дает вам уравнение, с которым можно работать: 1/3 = a / c. Тогда c = 3 a. Из теоремы Пифагора тогда следует, что a 2 + 144 = 9 a 2 . Вы можете решить это последнее уравнение для a , а затем найти c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
Ответы
30. c = b / cos A = 2,25 / 0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a составляет 4,24 ‘или 4’3 дюйма.
c = 3 a , что равно 12.73 ‘или 12’9 «.
35. cos A = b / c = 6,4 / 7,8 = 0,82. Следовательно, A = 34,86 ° = 34 ° 52 ‘, или около 35 °.
a 2 = 7,8 2 — 6,4 2 = 19,9, поэтому a составляет около 4,5.
36. a = c sin A = 12,15 sin 23 ° 15 ‘= 4,796.
b = c cos A = 12,15 cos 23 ° 15 ‘= 11.17.
Другие формы формулы двойного угла косинуса — Концепция
Формула двойного угла косинуса: cos (2theta) = cos2 (theta) — sin2 (theta). Комбинируя эту формулу с тождеством Пифагора, cos2 (theta) + sin2 (theta) = 1, появляются две другие формы: cos (2theta) = 2cos2 (theta) -1 и cos (2theta) = 1-2sin2 (theta). Их можно использовать для нахождения формул уменьшения мощности, которые уменьшают триггерную функцию второй или более высокой степени до первой степени.Эти формулы очень полезны в математическом анализе.
Я хочу поговорить о других формах тождеств двойного угла косинуса. Во-первых, давайте вспомним пифагорейскую идентичность и две другие ее формы. Косинус в квадрате плюс синус в квадрате, равный 1, также может быть записан как косинус в квадрате, тета равен 1 минус синус в квадрате, тета или синус в квадрате, тета равен 1 минус косинус в квадрате, тета. Теперь исходная формула двойного угла косинуса такова: косинус 2 тэта равен косинусу в квадрате тета минус синус в квадрате тета, но я могу использовать свои пифагоровы тождества, чтобы переписать это, так что другой формой будет косинус ой косинус 2 тета равен альфа косинус тета I ‘ Я заменим его на 1 минус синус в квадрате тета минус синус тета синус в квадрате тета, и это 1 минус 2 синус в квадрате тета, так что это вторая форма, косинус 2 тета равен 1 минус 2 синус в квадрате тета, но мы также можем сделать косинус 2 тета равным и начав отсюда я могу заменить синус в квадрате на 1 минус косинус, поэтому я получаю косинус в квадрате тета минус 1 минус синус в квадрате тета и минус распределяется, я получаю минус 1, извините, это должен быть косинус, поехали, наш минус 1 распределяет мы получаем минус 1 и минус минус плюс косинус в квадрате тета, поэтому косинус в квадрате тета минус 1 плюс косинус в квадрате тета равен 2, косинус в квадрате тета минус 1, они очень похожи.Косинус 2 тета равен 1 минус 2, синус в квадрате тета, косинус 2 тета равен 2 косинусу в квадрате минус 1.
Для того, чтобы запомнить, какой из них является, помните, что исходная формула двойного угла косинуса косинус — это тот, что положительный синус — это тот, который отрицателен, поэтому в других формах синус все еще отрицательный, а косинус все еще положительный.
Закон косинусов
Для любого треугольника:
a , b и c — боковые стороны. C — угол противоположной стороны c |
Закон косинусов (также называемый правилом косинусов ) гласит:
c 2 = a 2 + b 2 — 2ab cos (C)
Это помогает нам решать несколько треугольников. Посмотрим, как им пользоваться.
Пример: Какова длина стороны «c» …?
Мы знаем угол C = 37º, а стороны a = 8 и b = 11
Закон косинусов говорит: c 2 = a 2 + b 2 — 2ab cos (C)
Введите известные нам значения: c 2 = 8 2 + 11 2 — 2 × 8 × 11 × cos (37º)
Сделайте некоторые вычисления: c 2 = 64 + 121 — 176 × 0.798…
Дополнительные вычисления: c 2 = 44,44 …
Извлеките квадратный корень: c = √44,44 = 6,67 с точностью до 2 знаков после запятой
Ответ: c = 6,67
Как помнить
Как можно запомнить формулу?
Что ж, полезно знать, что это теорема Пифагора с кое-чем дополнительным, чтобы она работала для всех треугольников:
Теорема Пифагора:
(только для прямоугольных треугольников) a 2 + b 2 = c 2
Закон косинусов:
(для всех треугольников) a 2 + b 2 — 2ab cos (C) = c 2
Итак, чтобы запомнить:
- думаю « abc »: a 2 + b 2 = c 2 ,
- , затем 2 nd « abc «: 2ab cos ( C ),
- и сложите их вместе: a 2 + b 2 — 2ab cos (C) = c 2
Когда использовать
Закон косинусов полезно найти:
- третья сторона треугольника, когда мы знаем две стороны и угол между ними (как в примере выше)
- углы треугольника, когда мы знаем все три стороны (как в следующем примере)
Пример: что такое угол «C»…?
Сторона длины «8» противоположна углу C , поэтому это сторона c . Две другие стороны — a и b .
Теперь давайте поместим то, что мы знаем, в Закон косинусов :
Начать с: c 2 = a 2 + b 2 — 2ab cos (C)
Вставьте a, b и c: 8 2 = 9 2 + 5 2 — 2 × 9 × 5 × cos (C)
Вычислить: 64 = 81 + 25 -90 × cos (C)
Теперь мы используем наши навыки алгебры, чтобы переставить и решить:
Вычтем 25 с обеих сторон: 39 = 81 -90 × cos (C)
Вычтем 81 из обеих частей: −42 = −90 × cos (C)
Поменять местами стороны: −90 × cos (C) = −42
Разделим обе части на −90: cos (C) = 42/90
Обратный косинус: C = cos −1 (42/90)
Калькулятор: C = 62.2 ° (с точностью до 1 знака после запятой)
В других формах
Более простая версия для углов
Мы только что видели, как найти угол, когда мы знаем три стороны. Потребовалось довольно много шагов, поэтому проще использовать «прямую» формулу (которая представляет собой просто перестановку формулы c 2 = a 2 + b 2 — 2ab cos (C) формулы). Может быть в любой из этих форм:
cos (Кл) = a 2 + b 2 — c 2 2ab
cos (А) = б 2 + с 2 — а 2 2bc
cos (B) = c 2 + a 2 — b 2 2ca
Пример: найти угол «C» по закону косинусов (угловая версия)
В этом треугольнике мы знаем три стороны:
Используйте Закон косинусов (угловая версия), чтобы найти угол C :
cos C = (a 2 + b 2 — c 2 ) / 2ab
= (8 2 + 6 2 -7 2 ) / 2 × 8 × 6
= (64 + 36 — 49) / 96
= 51/96
= 0.53125
C = cos −1 (0,53125)
= 57,9 ° с точностью до одного десятичного знака
Версии для a, b и c
Кроме того, мы можем переписать формулу c 2 = a 2 + b 2 — 2ab cos (C) в форму 2 = и b 2 =.
Вот все три:
a 2 = b 2 + c 2 — 2bc cos (A)
b 2 = a 2 + c 2 — 2ac cos (B)
c 2 = a 2 + b 2 — 2ab cos (C)
Но проще запомнить форму « c 2 =» и при необходимости изменить буквы!
Как в этом примере:
Пример: найти расстояние «z»
Буквы разные! Но это не имеет значения.Мы можем легко заменить x на a, y на b и z на c
Начать с: c 2 = a 2 + b 2 — 2ab cos (C)
x для a, y для b и z для cz 2 = x 2 + y 2 — 2xy cos (Z)
Введите известные нам значения: z 2 = 9,4 2 + 6,5 2 — 2 × 9,4 × 6,5 × cos (131º)
Вычислить: z 2 = 88,36 + 42,25 — 122,2 × (-0,656 …)
z 2 = 130,61 + 80.17 …
z 2 = 210,78 …
z = √210,78 … = 14,5 с точностью до 1 десятичного знака.
Ответ: z = 14,5
Вы заметили, что cos (131º) отрицателен, и это меняет последний знак в вычислении на + (плюс)? Косинус тупого угла всегда отрицателен (см. Единичный круг).
Шесть функций (Триггер без слез, часть 2)
Шесть функций (Триггер без слез, часть 2)Триггер без слез Часть 2:
Авторские права 19972020 Стэн Браун, BrownMath.com
Резюме: Каждая из шести триггерных функций просто одна сторона прямоугольного треугольника разделена на другую сторону . Или, если вы нарисуете треугольник в единичной окружности , каждая функция — длина одного отрезка линии. простой способ запомнить все шесть определений: запомнить определения синуса и косинуса а затем запомните остальные четыре как комбинации синуса и косинуса , не как самостоятельные функции.
Два основных: синус и косинус
Картинка стоит тысячи слов (вот почему требуется тысяча слов). раз дольше скачивать).Триггерные функции — это не что иное, как длины различных сторон прямоугольного треугольника в различных соотношениях . Так как сторон три, то 3 × 2 = 6 разные способы сделать соотношение (дробь) сторон. Это почему есть шесть триггерных функций, не больше и не меньше .
Из этих шести функций тройка, косинус и касательно львиная доля работы. (Остальные изучаются, потому что их можно использовать для упростите некоторые выражения.) Ну начнем с синуса и косинуса, потому что они действительно основные а остальные зависят от них.
Вот один из обычных способов показать прямоугольный треугольник. Ключевым моментом является то, что строчные буквы а , б , в стороны, противоположные углам, отмеченным соответствующими заглавные буквы A , B , C . В большинстве книг используется это соглашение: строчная буква для стороны, противоположной углу верхнего регистра .
Два основных определения отмечены на схеме. Вы должны сохранить их в памяти .Фактически, они должны стать второй натурой для вы, чтобы вы их узнавали, как бы ни повернулся треугольник вокруг. Всегда, всегда синус угла равен противоположному сторона, деленная на гипотенузу (opp / hyp на диаграмме). Косинус равен равна смежной стороне, деленной на гипотенузу (adj / hyp).
(1) Запомнить:
синус = (противоположная сторона) / гипотенуза
косинус = (смежная сторона) / гипотенуза
Какой синус у B на диаграмме? Помните opp / hyp: противоположное сторона b , а гипотенуза c , поэтому sin B = b / c .А как насчет косинуса B ? Помните прил / гип: прилегающая сторона a , поэтому cos B = a / c .
Вы заметили, что синус одного угла является косинусом другого? Так как A + B + C = 180 для любого треугольник, а C — 90 в этом треугольнике, A + B должны равно 90. Следовательно A = 90 — B и B = 90 — A .Когда два угла складываются 90, каждый угол — это со дополнением другого, а синус каждого угла составляет co, синус другого угла. Это идентификаторы совместных функций :
(2) sin A = cos (90 — A ) или cos (π / 2 — A )
cos A = sin (90 — A ) или sin (π / 2 — A )
Выражения для длин сторон
Определения синуса и косинуса можно немного изменить, чтобы позвольте вам записать длины сторон через гипотенуза и углы.Например, когда вы знаете что b / c = cos A , вы можно умножить на c и получаем b = c × cos A . Вы можете написать еще выражение для длины b , которое использует синус вместо косинуса? Помните, что противоположность гипотенузы равна синусу, поэтому b / c = sin B . Умножить через c , и у вас есть b = c × sin B .
Вы видите, как записать два выражения для длины стороны а ? Пожалуйста, работайте с определениями и убедитесь, что a = c × sin A = c × cos B .
Пример: Дан прямоугольный треугольник с углом A = 52 и гипотенуза c = 150 м. Какая длина стороны b ? Подсказка: нарисуйте картинку и обозначьте A , c , и b .
Решение: Картинки всегда хорошие. Ты не нужно зацикливаться на том, чтобы получить точную картину, но, по крайней мере, сделать это близко. Это поможет вам понять, когда ваш ответ невозможен, так что вы знаете, что совершили ошибку. В моем маленьком эскизе я установил чтобы сделать угол A чуть больше 45, но на мой взгляд похоже немного меньше. Это нормально.
Вы можете заметить, что я пометил сторону как , хотя мы не нужно это для проблемы. Я сделал это, поэтому у меня не было подумать, с какой стороны было б .Всегда помни правило что сторона с данной буквой противоположна углу с этим письмо. (И, условно, мы всегда ставим C справа угол, так что c гипотенуза.)
Когда у вас есть изображение, решить проблему довольно просто. простой. Вы хотите что-то, связанное с A , это прилегающая сторона и гипотенуза; это должен быть косинус.
cos A = b / c
б = c × cos A = 150 × cos 52 = около 92.35 м.
Пример: Оттяжка закреплена в земле. и прикреплен к вершине 45-футового флагштока. Если он встречается с землей под углом 63, какова длина растяжки?
Решение: Предположительно флагшток вертикальный, поэтому это прямоугольный треугольник с A = 63, a = 45 футов, и гипотенуза c неизвестный. Какая функция задействует противоположную сторону и гипотенузу? Это должен быть синус. Ты знаешь что
sin A = a / c
Следовательно,
c = a / sin A = 45 / sin 63 = около 50.5 футов
Вам может быть интересно, как найти стороны или углы треугольников. когда нет прямого угла. Ну что ж, под темой Решение треугольников.
Синус и косинус в единичной окружности
Часто всплывает один важный особый случай. Предположим, что гипотенуза c = 1; тогда мы называем треугольник a прямоугольный треугольник . Из приведенных выше абзацев видно, что если c = 1, то a = sin A и b = cos A .Другими словами, в прямоугольный треугольник с противоположной стороной будет равен синусу, а соседняя сторона будет равна косинусу угла.
Треугольник часто рисуют в единичном круге , круге радиус 1, как показано справа. Угол A находится в центре окружности, а на соседней стороне лежит по оси x. Если вы сделаете это, гипотенуза будет радиусом, равным 1. Координаты ( x , y ) внешнего конца гипотенузы — ноги треугольника x и y : ( x , y ) = (cos A , sin A ). Единичный круг — ваш друг : он может помочь вам визуализировать участки триггерных тождеств.
Другие четыре: касательная, котангенс, секанс, косеканс
Остальные четыре функции не имеют реальной самостоятельной жизни; Они просто комбинации первых двух . Вы могли бы сделать все тригонометрия, не зная ничего больше, чем синусы и косинусы. Но зная что-то в остальных четырех, особенно касательное, часто может спасти вас шаги в вычислении, и ваш учитель будет ожидать, что вы знаете о них к экзаменам.
Мне легче запомнить (извините!) Определение касательной через синус и косинус:
(3) Запомнить:
tan A = (sin A ) / (cos A )
Вы будете использовать функцию тангенса (tan) намного больше чем последние три функции. (Я доберусь до них через минуту.)
Есть альтернативный способ запомнить значение касательной . Помните из схемы что sin A = напротив / гипотенуза и cos A = смежный / гипотенуза.Подставьте их в уравнение 3, определение функция загара, и у вас загар A = (противоположный / гипотенуза) / (смежный / гипотенуза) или
(4) касательная = (противоположная сторона) / (смежная сторона)
Обратите внимание, что это , а не помечены как запомнить: вам не нужно запомнить, потому что это вытекает непосредственно из определения уравнение 3, и фактически эти два утверждения эквивалент. Я решил представить их в таком порядке, чтобы минимизировать беспорядок opp, adj и hyp среди sin, cos и загар.Однако, если хотите, можете запомнить уравнение 4, а затем вывести эквивалентное тождество уравнение 3, когда вам это нужно.
Пример: Оттяжка закреплена в земле и прикреплена на вершину 45-футового флагштока. Как далеко якорь от базы флагштока, если провод встречается с землей в угол 63?
Решение: Это вариант предыдущий пример. Этот время, вы хотите знать сторону, прилегающую к углу A , а не гипотенуза.Как и раньше, предположим, что флагшток вертикальный, поэтому это прямоугольный треугольник с A = 63, a = 45 футов, и прилегающая сторона b неизвестный. Какая функция задействует соседнюю сторону и противоположную сторону? Это касательная. Вы знаете, что
загар A = a / b
Следовательно,
b = a / tan A = 45 / tan 63 = около 22,9 футов
Итак, я сказал, что вы можете выполнить все триггеры только с синусами и косинусы.Как это сработает для этой проблемы? Ну синус и косинус обеим нужна гипотенуза, так что у вас будет
sin A = a / c ⇒ c = a / sin A и
cos A = b / c ⇒ c = b / cos A . Следовательно,
b / cos A = a / sin A
b = a × cos A / sin A = 45 × cos 63 / sin 63 = около 22.9 футов
В конце концов, вы попали в то же место, но путь был дольше. Таким образом, хотя это и не обязательно, касательная может облегчить вашу работу.
Остальные три триггера функции котангенс, секанс и косеканс являются определяется в терминах первых трех . Они используются реже, но упрощают некоторые проблемы в исчисление. В практических задачах, не связанных с исчислением, они вам практически никогда не понадобятся.
(5) Запомнить:
Детская кроватка A = 1 / (желтовато-коричневый A )
сек A = 1 / (cos A )
csc A = 1 / (sin A )
Угадайте что! Это последняя триггерная идентификация, которую вам нужно запомнить.
(Вы, вероятно, обнаружите, что в конечном итоге запомните некоторые другие личности, даже не намереваясь, просто потому, что вы их используете часто. Но уравнение 5 делает последние, что вам придется сесть и запомнить только их собственн.)
К сожалению, определения в уравнении 5 не являются самая легкая вещь в мире для запоминания. Равняется ли секанс на 1? синус или 1 над косинусом? Вот два полезных совета : Каждое из этих определений имеет совместную функцию с одной и только с одной стороны. уравнения, поэтому у вас не возникнет соблазна подумать, что sec A равно 1 / sin A .А секанс и косеканс идут вместе, как синус и косинус, поэтому у вас не возникнет соблазна подумать, что детская кроватка A равно 1 / sin A .
За альтернативный подход к запоминанию выше идентификаторов, вам может понравиться:
Вы можете сразу заметить важную связь между касательной и котангенс. Каждый является совместной функцией другого, как синус и косинус:
(6) желто-коричневый A = детская кроватка (90 — A ) или детская кроватка (π / 2 — A )
Детская кроватка A = желто-коричневый (90 — A ) или коричневый (π / 2 — A )
Если вы хотите это доказать, это легко определения и уравнение 2:
Детская кроватка A = 1 / tan A
Примените определение загара:
Детская кроватка A = 1 / (sin A / cos A )
Упростим дробь:
Детская кроватка A = cos A / sin A
Применить уравнение 2:
детская кроватка A = sin (90 — A ) / cos (90 — A )
Наконец, признайте, что эта дробь соответствует определению функция загара, уравнение 3:
Детская кроватка A = коричневый (90 — A )
Касательная и co тангенс — это такие же функции, как синус и co синус.Выполняя такую же замену, вы можете показать, что секанс и Секущие co также являются совместными функциями:
(7) с A = csc (90 — A ) или csc (π / 2 — A )
csc A = сек (90 — A ) или сек (π / 2 — A )
Шесть функций в одном изображении
Вы видели ранее, как синус и косинус угла — стороны треугольника в единичной окружности. Оказывается что все шесть функций могут быть изображены таким образом геометрически.
единичный круг (радиус = AB = 1)
sin θ = BC;
cos θ = AC;
загар θ = ED
csc θ = AG;
сек θ = AE;
детская кроватка θ = FG
Изображение предоставлено TheMathPage
На рисунке справа треугольник ABC имеет угол θ при центр единичной окружности (AB = радиус = 1). Ты уже знайте, что BC = sin θ и AC = cos θ .
А как насчет загара θ ? Ну, так как DE касается единицы круг, вы можете догадаться, что его длина составляет загар θ , и вы бы верно.Треугольники ABC и AED похожи, поэтому
ED / AD = BC / AC
ED / 1 = sin θ / cos θ
ED = загар θ
Больше информации исходит от той же пары одинаковых треугольников:
AE / AB = AD / AC
AE / 1 = 1 / cos θ
AE = сек θ
Длины для детской кроватки θ и csc θ придут. из другого треугольника, GAF.Этот треугольник также похож на треугольник AED. (Почему? FG перпендикулярно FA, а FA перпендикулярно ОБЪЯВЛЕНИЕ; следовательно, FG и AD параллельны. В начале геометрии вы узнал, что когда параллельные линии разрезаются третьей линией, соответствующие углы, обозначенные как θ в диаграммы равны. Таким образом, FG касается единицы окружности, а значит, углы G и θ равны. )
Используя аналогичные треугольники GAF и AED,
FG / FA = AD / ED
FG / 1 = 1 / tan θ
FG = детская кроватка θ
В этом есть смысл: FG касается единичной окружности и является тангенс дополнения угла θ , а именно угла GAF.Следовательно, FG — котангенс исходного угла θ (или угла GAD).
Наконец, снова используя ту же пару похожих треугольников, вы также можно сказать, что
AG / FA = AE / ED
AG / 1 = сек θ / tan θ
AG = (1 / cos θ ) / (sin θ / cos θ )
AG = 1 / sin θ
AG = csc θ
Эта диаграмма прекрасно передает геометрическое значение всех шести триггерных функций, когда угол θ проведен в центре единичный круг:
sin θ = BC; cos θ = переменный ток; tan θ = ED
csc θ = AG; сек θ = AE; детская кроватка θ = FG
Практические задачи
Чтобы извлечь максимальную пользу из этих проблем, поработайте над ними. без предварительного просмотра решений.Вернитесь к главе текст, если вам нужно освежить память.
Рекомендация : Работайте на бумаге труднее обмануть себя, действительно ли ты полностью разобраться в проблеме.
Вы найдете полный решения для всех проблем. Не просто проверяй свой ответы, но проверьте и свой метод.
1 Найдите все шесть функций угла 30. Найдите синус, косинус, и тангенс 60. 2 Найдите sin A , sin B , tan A и tan B .3 A ≈ 53,13. Найдите примерную площадь треугольник. Подсказка: площадь треугольника равна основание × высота /2.BTW: Зачем называть это синусом?
Очевидно, почему название тангенс имеет смысл: тангенс угла — это длина отрезка, касательного к единичной окружности. А как же синус функция? Как он получил свое название?
Посмотрите на изображение еще раз, и обратите внимание, что sin θ = BC — половина хорды круга.Индуистский математик Арьябхата старший (около 475550) использовал слово jya или jiva для этого полуаккорда. В арабском переводе это слово осталось без изменений, но в арабской системе письма джива было написано так же, как арабское слово джайб, означает грудь, складку или залив. Латинское слово, обозначающее грудь, залив или кривую. синус, или синус на английском языке, и начинается с Gherardo из Кремона (ок. 11141187), ставшая общепринятым термином.
Эдмунд Гюнтер (15811626), кажется, был первым опубликовать сокращения sin и tan для sin и касательная.
Мой источник этой истории — Эли Маорс Тригонометрический Наслаждения (1998, Princeton University Press), стр. 3536. Я настоятельно рекомендую вам обратиться к книге для более полного отчета.
Что нового
- 27 сентября 2017 г. : откорректировать 29,2 футов до 22,9 футов, здесь и здесь, спасибо Райану МакПарлану.
- 29 октября 2016 г. :
- (промежуточные изменения подавлены)
- 19 февраля 1997 г. : Новый документ.
следующий: 3 / Специальные уголки
Косинус
Косинус, записываемый как cos (θ), является одной из шести основных тригонометрических функций.
Определения косинусов
Существует два основных способа обсуждения тригонометрических функций: в терминах прямоугольных треугольников и в терминах единичной окружности. Чаще всего вводят определение тригонометрических функций в виде прямоугольного треугольника, за которым следуют их определения в терминах единичной окружности.
Определение прямоугольного треугольника
Для прямоугольного треугольника с острым углом θ значение синуса этого угла определяется как отношение длины соседней стороны к длине гипотенузы.
Стороны прямоугольного треугольника обозначаются следующим образом:
- Соседний: сторона рядом с θ, которая не является гипотенузой
- Справа: сторона, противоположная θ.
- Гипотенуза: самая длинная сторона треугольника, противоположная прямому углу.
Пример:
Найдите cos (θ) для прямоугольного треугольника ниже.
Мы также можем использовать функцию косинуса при решении реальных задач, связанных с прямоугольными треугольниками.
Пример:
Самолет пролетает над человеком. Человек регистрирует угол возвышения 25 °, когда расстояние по прямой (гипотенуза треугольника) между человеком и самолетом составляет 14 миль. Какое расстояние по горизонтали между самолетом и человеком?
Учитывая информацию выше, мы можем сформировать прямоугольный треугольник, в котором x — это расстояние по горизонтали между человеком и плоскостью, расстояние по прямой между человеком и плоскостью — это гипотенуза, а расстояние по вертикали между конечными концами x, а гипотенуза образует прямой угол треугольника.Затем мы можем найти горизонтальное расстояние x, используя функцию косинуса:
x = 14 × cos (25 °) ≈ 12,69
Горизонтальное расстояние между человеком и самолетом составляет около 12,69 миль.
Определение единичной окружности
Тригонометрические функции также могут быть определены как значения координат на единичной окружности. Единичный круг — это круг радиуса 1 с центром в начале координат. Определение тригонометрических функций в прямоугольном треугольнике допускает углы от 0 ° до 90 ° (0 и в радианах).Использование определений единичного круга позволяет нам расширить область определения тригонометрических функций на все действительные числа. См. Рисунок ниже.
Учитывая точку (x, y) на окружности единичной окружности, мы можем сформировать прямоугольный треугольник, как показано на рисунке. В таком треугольнике гипотенуза — это радиус единичного круга, или 1. θ — это угол, образованный между начальной стороной угла вдоль оси x и конечной стороной угла, образованной вращением луча по часовой стрелке или против часовой стрелки.Конечная сторона угла — это гипотенуза прямоугольного треугольника и радиус единичной окружности. Следовательно, он всегда имеет длину 1. Таким образом, мы можем использовать определение косинуса в прямоугольном треугольнике, чтобы определить, что
означает, что значение x любой точки на окружности единичной окружности равно cos (θ).
В отличие от определений тригонометрических функций, основанных на прямоугольных треугольниках, это определение работает для любого угла, а не только для острых углов прямоугольных треугольников, если он находится в пределах области cos domain (θ).Область определения функции косинуса — (-∞, ∞), а диапазон функции косинуса — [-1, 1].
Значения функции косинуса
Существует множество методов, которые можно использовать для определения значения косинуса, например, обращение к таблице косинусов, использование калькулятора и аппроксимация с использованием ряда косинусов Тейлора. В большинстве практических случаев нет необходимости вычислять значение косинуса вручную, и вам будет предоставлена таблица, калькулятор или другие справочные материалы.
Калькулятор косинусов
Ниже приведен калькулятор, позволяющий определить значение косинуса угла или угол по значению косинуса.
Часто используемые уголки
Хотя мы можем найти cos (θ) для любого угла, есть некоторые углы, которые чаще используются в тригонометрии. Ниже приведены 16 часто используемых углов в радианах и градусах, а также координаты их соответствующих точек на единичной окружности.
Приведенный выше рисунок служит справочным материалом для быстрого определения косинусов (значение x) и синусов (значение y) углов, которые обычно используются в тригонометрии. Как видно из рисунка, косинус имеет значение 0 при 90 ° и значение 1 при 0 °.Синус следует противоположному шаблону; это потому, что синус и косинус являются совместными функциями (описаны позже). Другие часто используемые углы — 30 ° (), 45 ° (), 60 ° () и их соответствующие кратные. Значения косинуса и синуса этих углов стоит запомнить в контексте тригонометрии, поскольку они очень часто используются.
Один из методов, который может помочь запомнить эти значения, — это выразить все значения cos (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° и до 90 °, cos (0 °) = 1 =.Последующие значения cos (30 °), cos (45 °), cos (60 °) и cos (90 °) следуют шаблону, так что, используя значение cos (0 °) в качестве эталона, найти значения косинуса для последующих углов, мы просто уменьшаем число под знаком корня в числителе на 1, как показано ниже:
С 90 ° до 180 ° вместо этого мы увеличиваем число под корнем на 1, но также должны учитывать квадрант, в котором находится угол. Косинус отрицателен в квадрантах II и III, поэтому значения будут равными, но отрицательными. .В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений. Аналогичный метод запоминания можно использовать и для синуса. При необходимости обратитесь к странице синуса.
Знание значений косинуса и синуса для углов в первом квадранте позволяет нам определить их значения для соответствующих углов в остальных квадрантах в координатной плоскости с помощью опорных углов.
Опорный угол
Базовый угол — это острый угол (<90 °), который можно использовать для обозначения угла любой меры.Любой угол в координатной плоскости имеет опорный угол от 0 ° до 90 °. Это всегда наименьший угол (относительно оси x), который может быть получен с конечной стороны угла. На рисунке ниже показан угол θ и его опорный угол θ '.
Поскольку θ ‘является опорным углом θ, cos both (θ) и cos (θ’) имеют одинаковое значение. Например, 30 ° — это опорный угол 150 °, и если мы обратимся к единичному кругу, мы увидим, что косинусы обоих имеют величину, хотя и имеют разные знаки.Поскольку все углы имеют опорный угол, нам действительно нужно знать только значения cos (θ) (а также значения других тригонометрических функций) в квадранте I. Все другие соответствующие углы будут иметь значения той же величины, и мы просто нужно обратить внимание на их знаки, основанные на квадранте, в котором находится конечная сторона угла. Ниже приведена таблица, показывающая знаки косинуса, синуса и тангенса в каждом квадранте.
| Косинус | Синус | Касательная | |
| Квадрант I | + | + | + |
| Квадрант II | — | + | — |
| Квадрант III | — | — | + |
| Квадрант IV | + | — | — |
После определения опорного угла мы можем определить значение тригонометрических функций в любом из других квадрантов, применив соответствующий знак их значения для опорного угла.Чтобы найти опорный угол заданного угла θ, можно использовать следующие шаги:
- Вычтите 360 ° или 2π из угла столько раз, сколько необходимо (угол должен быть от 0 ° до 360 ° или от 0 до 2π). Если полученный угол составляет от 0 ° до 90 °, это опорный угол.
- Определите, в каком квадранте лежит конечная сторона угла (начальная сторона угла расположена вдоль положительной оси x)
- В зависимости от того, в каком квадранте находится конечная сторона угла, используйте уравнения в таблице ниже, чтобы найти опорный угол.В квадранте I θ ‘= θ.
| Квадрант II | Квадрант III | Квадрант IV |
|---|---|---|
| θ ‘= 180 ° — θ | θ ‘= θ — 180 ° | θ ‘= 360 ° — θ |
Пример:
Найдите cos (120 °).
- θ уже находится между 0 ° и 360 °
- 120 ° лежит во II квадранте
- 180 ° — 120 ° = 60 °, поэтому исходный угол составляет 60 °
.120 ° находится в квадранте II, а косинус отрицателен во втором квадранте, поэтому:
Пример:
Найдите cos (1050 °).
- 1050 ° — 360 ° = 690 ° — 360 ° = 330 °
- 330 ° лежит в квадранте IV
- 360 ° — 330 ° = 30 °, поэтому исходный угол равен 30 °
. 330 ° находится в квадранте IV, а косинус положительный в квадранте IV, поэтому:
Свойства функции косинуса
Ниже приводится ряд свойств функции косинуса, которые может быть полезно знать при работе с тригонометрическими функциями.
Косинус является совместной функцией синуса
Кофункция — это функция, в которой f (A) = g (B) при условии, что A и B являются дополнительными углами. В контексте косинуса и синуса
cos (θ) = sin (90 ° — θ)
sin (θ) = cos (90 ° — θ)
Пример:
cos (30 °) = sin (90 ° — 30 °) = sin (60 °)
Ссылаясь на единичный круг, показанный выше, мы можем подставить значения для cos (30 °) и sin (60 °) и увидеть, что:
Косинус — четная функция
Четная функция — это функция, в которой f (x) = f (-x), что означает, что отражение графика по оси Y даст тот же график.Таким образом,
cos (θ) = cos (-θ)
Пример:
cos (60 °) = cos (-60 °)
cos (60 °) = cos (300 °)
Обращаясь к единичной окружности, мы видим, что cos (60 °) = и cos (-60 °) эквивалентен cos (300 °), который также равен. Это только один пример, но это свойство верно для всех θ.
Косинус — периодическая функция
Периодическая функция — это функция f, в которой существует некоторое положительное значение p, такое что
е (х + р) = е (х)
для всех x в области f, p — наименьшее положительное число, для которого f является периодическим, и называется периодом f.
Тригонометрические функции обычно используются для моделирования периодических явлений из-за их периодичности; независимо от того, с какой точки мы начинаем на единичной окружности, если мы пройдем расстояние 2π (360 °) по единичной окружности от этой точки, мы вернемся к нашей начальной точке. Если мы посмотрим на функцию косинуса, мы обнаружим, что она повторяется каждые 2π, поэтому 2π — это период функции косинуса. Мы можем записать это как:
cos (θ + 2π) = cos (θ)
Чтобы учесть несколько полных оборотов, это также можно записать как
cos (θ + 2πn) = cos (θ)
, где n — целое число.
На рисунке ниже показан пример этой периодичности.
Синим цветом мы это видим. . Если мы прибавим 2π к, мы получим угол, показанный красным,. Как видно из рисунка, несмотря на разную степень вращения в обоих углах, их конечные стороны совершенно одинаковы, что означает, что. Мы могли бы добавить еще 2π и все равно увидеть, что оно имеет то же значение косинуса, что и. Такова природа периодических функций. называются концевыми углами; это углы с одинаковой начальной и конечной сторонами, но с разными поворотами.
Примеры:
1.
2.
График функции косинуса
График косинуса является периодическим, что означает, что он повторяется бесконечно и имеет область значений -∞ Если бесконечно повторять эту часть y = cos inde (x) слева и справа, то получится полный график косинуса.Ниже приведен график, показывающий четыре периода функции косинуса в интервале [-4π, 4π]. На этом графике мы видим, что y = cos (x) демонстрирует симметрию оси y; отражение графика косинуса по оси y дает тот же график. Это подтверждает, что косинус является четной функцией, поскольку cos (x) = cos (-x). Общий вид функции косинуса: y = A · cos (B (x — C)) + D где A, B, C и D — константы.Чтобы иметь возможность изобразить уравнение косинуса в общем виде, нам нужно сначала понять, как каждая из констант влияет на исходный график y = cos (x), как показано выше. Чтобы применить все, что написано ниже, уравнение должно иметь форму, указанную выше; будьте осторожны со знаками. A — амплитуда функции; высота от центра графика до максимума или минимума. В y = cos (x) центром является ось x, а амплитуда равна 1, или A = 1, поэтому самая высокая и самая низкая точки, которых достигает график, равны 1 и -1, диапазон cos (x) . По сравнению с y = cos (x), показанным ниже фиолетовым цветом, функция y = 2 cos (x) (красный) имеет амплитуду, которая в два раза больше, чем у исходного графика косинуса. B — используется для определения периода функции; период функции — это расстояние от пика до пика (или любой точки на графике до следующей совпадающей точки) и может быть найден как. В y = cos (x) период равен 2π. Мы можем подтвердить это, посмотрев на пики на графике косинусов. При x = 0 y = cos (x) имеет пик.Первый раз на функции появляется еще один пик при x = & plusmn2π, подтверждая, что период косинуса равен 2π. По сравнению с y = cos (x), показанным ниже фиолетовым цветом, который имеет период 2π, y = cos (2x) (красный) имеет период
. Это означает, что график повторяется каждое π, а не каждые 2π. C — фазовый сдвиг функции; фазовый сдвиг определяет, как функция сдвигается по горизонтали. Если C отрицательно, функция сдвигается влево. Если C положительно, функция сдвигается вправо.Остерегайтесь знака; если у нас есть уравнение, то C нет, потому что это уравнение в стандартной форме. Таким образом, мы бы сместили единицы графика влево. На рисунке ниже показано y = cos (x) (фиолетовый) и (красный). Используя один из пиков графика косинуса в качестве ориентира, мы можем увидеть, что пик в точке (0,1) был смещен влево от своего исходного положения и теперь находится в точке (, 1). D — вертикальный сдвиг функции; если D положительный, график сдвигается вверх на D единиц, а если он отрицательный, график сдвигается вниз. По сравнению с y = cos (x), показанным ниже фиолетовым цветом, с центром на оси x (y = 0), y = cos (x) +5 (красный) с центром на линии y = 5 (синий). Объединив все приведенные выше примеры, на рисунке ниже показан график (красный) по сравнению с графиком y = cos (x) (фиолетовый). См. Также синус, тангенс, единичную окружность, тригонометрические функции, тригонометрию. М.Борн Для угла θ в прямоугольном треугольнике, как показано, мы назовем стороны как: Мы, , определяем три тригонометрических отношения синус θ , косинус θ и тангенс θ следующим образом (мы обычно записываем их в сокращенной форме sin θ cos θ и tan θ ): `sin theta = текст (напротив) / текст (гипотенуза)` cos \ theta = text (смежный) / text (гипотенуза) `tan theta = text (напротив) / text (смежный)` Чтобы запомнить это, многие люди используют SOH CAH TOA, то есть: S дюйм θ = O pposite / H ypotenuse, C os θ = A djacent / H ypotenuse и T и θ = O pposite / A djacent Часто бывает полезно использовать обратные отношения, в зависимости от проблемы.(На простом английском языке, величина, обратная дроби, находится путем переворачивания дроби.) «косеканс» \ θ` является обратной величиной «синуса» \ θ`, «секущая» \ θ` является обратной величиной «косинус» \ θ`, а «Котангенс» \ θ` является обратной величиной «касательной» \ θ` Обычно мы записываем их в краткой форме как `csc \ θ`,` sec \ θ` и `cot \ θ` . (В некоторых учебниках « csc » пишется как « cosec ». Это то же самое.) `csc \ theta = text (гипотенуза) / текст (напротив)` sec \ theta = text (гипотенуза) / текст (рядом) `cot \ theta = text (смежный) / text (напротив)` Важное примечание: Существует большая разница между csc θ и sin -1 θ . Итак, на вашем калькуляторе не используйте кнопку sin -1 , чтобы найти csc θ . Мы познакомимся с идеей sin -1 θ в следующем разделе, Значения тригонометрических функций. Для угла в стандартном положении мы определяем тригонометрические отношения в виде x , y и r : `sin theta = y / r« cos theta = x / r` `tan theta = y / x` Обратите внимание, что мы все еще определяем sin θ as «opp» / «hyp» `; cos θ как «adj» / «hyp» `, и tan θ as «opp» / «adj» `, , но мы используем конкретные значения x -, y — и r , определяемые точкой ( x , y ), через которую проходит терминальная сторона.2) ` Неудивительно, что обратные отношения определяются аналогичным образом в терминах значений x -, y — и r — следующим образом: `csc \ theta = r / y« sec \ theta = r / x` `детская кроватка \ theta = x / y` Мы увидим несколько примеров нахождения точных значений в следующем разделе «Значения тригонометрических функций». В прошлой статье мы увидели, как правило синуса помогает нам вычислить недостающий угол или недостающую сторону, когда известны две стороны и один угол или когда известны два угла и одна сторона. Но что вы будете делать, когда вам даны только три стороны треугольника и вам нужно найти все углы? В 15 -м веке эта проблема была решена, когда персидский математик Джамшид аль-Каши представил закон косинусов в форме, пригодной для триангуляции. Во Франции она до сих пор известна как Теорема д’Аль-Каши . В этой статье вы узнаете о: Закон косинусов также называется правилом косинусов , — это формула, которая связывает длины трех сторон треугольника с косинусом. Правило косинуса полезно двумя способами: Рассмотрим наклонный треугольник ABC, показанный ниже. Наклонный треугольник — это не прямоугольный треугольник. Помните, что длина сторон обозначена строчными буквами, а углы — заглавными. Также обратите внимание, что для каждого угла длина противоположной стороны обозначается одной и той же буквой. Закон косинусов гласит, что: ⇒ (a) 2 = [b 2 + c 2 — 2bc] cos ( A ) ⇒ (b) 2 = [a 2 + c 2 — 2ac] cos ( B ) ⇒ (c) 2 = [a 2 + b 2 — 2bc] cos ( C ) Вы заметили, что уравнение c 2 = a 2 + b 2 — 2bc cos ( C ) похоже на теорему Пифагора, за исключением последних членов, ”- 2bc cos ( C ).По этой причине мы можем сказать, что теорема Пифагора является частным случаем правила синуса. Правило косинусов можно доказать, рассматривая случай прямоугольного треугольника. В этом случае проведем перпендикулярную линию от точки A до точки O на стороне BC. Пусть сторона AM будет h. В прямоугольном треугольнике ABM косинус угла B определяется как: Cos ( B ) = Соседний / Гипотенуза = BM / BA Cos ( B ) = BM / c BM = c cos ( B ) Учитывая, что BC = a, следовательно, MC рассчитывается как: MC = a — BM = a — c cos ( B ) ……………………………………………… (i) В треугольнике ABM , синус угла B определяется выражением; Синус B = Противоположность / Гипотенуза = h / c h = c синус B …………………………………………………… (ii) Применяя теорему Пифагора в прямоугольный треугольник AMC , имеем, AC 2 = AM 2 + MC 2 ……………………………………………… (iii) Подставьте уравнение (i) и (ii) в уравнение (iii). b 2 = (c синус B) 2 + ( a — c Cos B ) 2 b 2 = c 2 синус 2 B + a 2 — 2ac Cos B + c 2 Cos 2 C Преобразование приведенного выше уравнения: b 2 = c 2 Синус 2 B + c 2 Cos 2 C + a 2 — 2ac Cos B Факторинг. b 2 = c 2 (синус 2 B + Cos 2 C ) + a 2 — 2ac Cos B Но из тригонометрических тождеств мы знаем, что , sin 2 θ + cos 2 θ = 1 Следовательно, b 2 = c 2 + a 2 — 2ac Cos B Следовательно, косинус закон доказан. Если вам нужно найти длины сторон треугольника, мы воспользуемся правилом косинуса в форме; ⇒ (a) 2 = [b 2 + c 2 — 2bc] cos ( A ) ⇒ (b) 2 = [a 2 + c 2 — 2ac] cos ( B ) ⇒ (c) 2 = [a 2 + b 2 — 2bc] cos ( C ) И если нам нужно найти размер угла , воспользуемся правилом косинуса формы; ⇒ cos A = (b 2 + c 2 — a 2 ) / 2bc ⇒ cos B = (a 2 + c 2 — b 2 ) / 2ac ⇒ cos C = (a 2 + b 2 — c 2 ) / 2ab Давайте теперь проверим наше понимание правила косинуса, попробовав несколько примеров задач. Пример 1 Вычислите длину стороны AC треугольника, показанного ниже. Решение Поскольку мы хотим вычислить длину, мы будем использовать правило косинуса в форме; ⇒ (b) 2 = [a 2 + c 2 — 2ac] cos ( B ) Путем подстановки получаем, b 2 = 4 2 + 3 2 — 2 x 3 x 4 cos ( 50 ) b 2 = 16 + 9 — 24cos50 = 25 — 24cos 50 b 2 = 9.575 Определите квадратный корень из обеих частей, чтобы получить b = √9,575 = 3,094. Следовательно, длина АС = 3,094 см. Пример 2 Вычислите все три угла треугольника, показанного ниже. Решение Поскольку все три стороны треугольника заданы, нам нужно найти размеры трех углов A, B и C. Здесь мы будем использовать правило косинуса в форма; ⇒ Cos (A ) = [b 2 + c 2 — a 2 ] / 2bc ⇒ Cos (B) = [a 2 + c 2 — b 2 ] / 2ac ⇒ Cos ( C) = [a 2 + b 2 — c 2 ] / 2ab Решите для угла A: Cos A = (7 2 + 5 2 -10 2 ) / 2 x 7 x 5 Cos A = (49 + 25-100) / 70 Cos A = -26/70 Cos A = — 0 .3714. Теперь определите cos, обратный — 0,3714. A = Cos -1 — 0,3714. A = 111,8 ° Решить для угла B: Путем подстановки, cos B = (10 2 + 5 2 -7 2 ) / 2 x 10 x 7 Упростить . Cos B = (100 + 25 — 49) / 140 Cos B = 76/140 Определите cos, обратный 76/140 B = 57,12 ° Решите для угла C: Путем замены, cos C = (10 2 + 7 2 -5 2 ) / 2 x 10 x 7 Cos C = (100 + 49-25) / 140 Cos C = 124 / 140 Определите cos, обратный 124/140. C = 27,7 ° Следовательно, три угла треугольника равны; А = 111,8 °, В = 57,12 ° и С = 27,7 °. Уравнение общего косинуса
2. Синус, косинус, тангенс и обратные отношения
Взаимные тригонометрические отношения
Тригонометрические функции на плоскости
x-y Правило косинуса — объяснение и примеры
Что такое закон косинусов?
Формула закона косинусов
Доказательство закона косинусов
Как использовать правило косинуса?

 9998
9998 9781
9781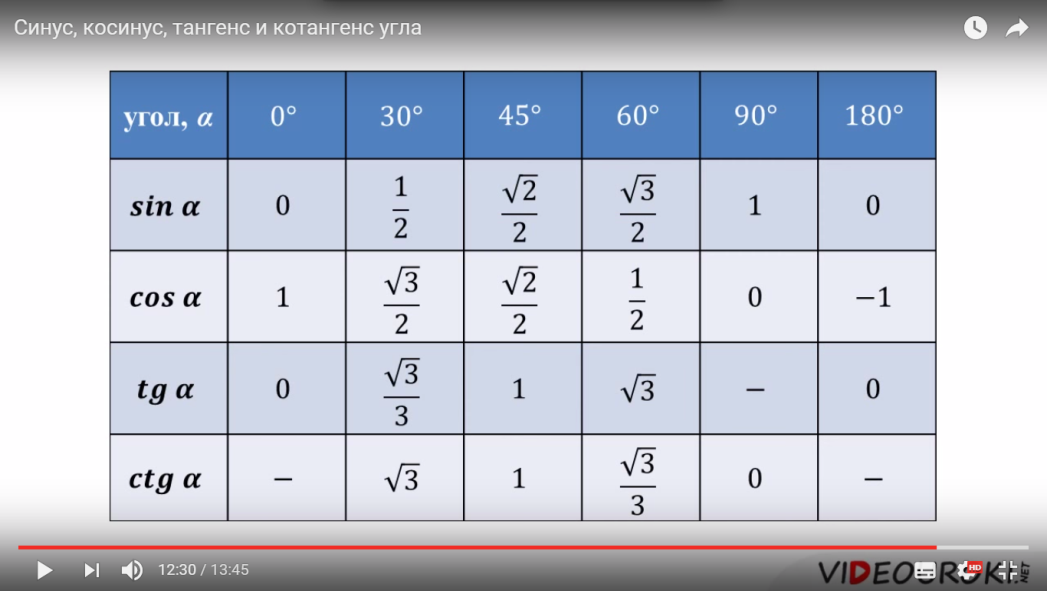 9205
9205 829
829 7071
7071 5592
5592 3907
3907 2079
2079 0175
0175 1219
1219 2924
2924 454
454 6018
6018 7314
7314 8387
8387 9205
9205 9744
9744 9986
9986 9962
9962