Корень степени n его свойства – формулировки, доказательства, примеры, свойства корней n й степени

§1 Корень n-степени и его свойства

1.	Произведение иррациональных чисел	1 вид — рецептивный	лёгкое	1 Б.	Действия с корнями. Свойства корней.
2.	Действия с иррациональными числами	2 вид — интерпретация	лёгкое	1 Б.	Свойства корней. Знание результат дейсвий с иррациональными числами.
3.	Деление иррациональных чисел	1 вид — рецептивный	лёгкое	2 Б.	Действия с корнями. Свойства корней.
4.	Корень степени n	2 вид — интерпретация	лёгкое	1 Б.	Вычисление корня степени n из отрицательного и положительного числа.
5.	Вычисление корня степени n	2 вид — интерпретация	лёгкое	1 Б.	Вычисление корня степени n из целого числа.
6.	Подкоренное число и показатель степени	1 вид — рецептивный	лёгкое	2 Б.	Определение подкоренного числа и показателя степени
7.	Корень n-й степени (десятичные дроби)	1 вид — рецептивный	лёгкое	1 Б.	Вычисление корня n-й степени
8.	Корень n-й степени (обыкновенные дроби)	1 вид — рецептивный	лёгкое	2 Б.	Вычисление корня n-й степени
9.	Корень из произведения, десятичные дроби и целые числа	1 вид — рецептивный	лёгкое	2 Б.	Вычисление корня степени n из произведения
10.	Корень из произведения, целые числа и обыкновенные дроби	1 вид — рецептивный	лёгкое	3 Б.	Вычисление корня степени n из произведения
11.	Корень из частного, обыкновенные дроби	1 вид — рецептивный	лёгкое	2 Б.	Вычисление корня степени n из дроби
12.	Корень из произведения	2 вид — интерпретация	лёгкое	4 Б.	Вычисление корня степени n из произведения
13.	Корень из корня	1 вид — рецептивный	лёгкое	1 Б.	Преобразование корня степени n из корня степени n к корню
14.	Извлечение корня из степени	2 вид — интерпретация	лёгкое	3 Б.	Применение свойства «извлечение корня из корня»
15.	Показатели корня	2 вид — интерпретация	лёгкое	2 Б.	Приведение к одному показателю корня
16.	Корни с разными показателями	2 вид — интерпретация	лёгкое	2 Б.	Приведение к одному показателю корня
17.	Корень из корня степени	1 вид — рецептивный	лёгкое	1 Б.	Преобразование к корню степени n
18.	Корень n-й степени (целые числа)	2 вид — интерпретация	среднее	3 Б.	Вычисление разности произведений целых чисел и корней n-й степени
19.	Сравнение иррациональных чисел	2 вид — интерпретация	среднее	2 Б.	Расположение чисел в порядке убывания (возрастания)
20.	Уравнение (степень)	2 вид — интерпретация	среднее	2 Б.	Решение уравнения
21.	Корень n-й степени (целые числа и десятичные дроби)	2 вид — интерпретация	среднее	3 Б.	Вычисление разности произведений корней n-й степени и целых чисел
22.	Область определения функции корня n-й степени, чётная и нечётная степени	2 вид — интерпретация	сложное	5 Б.	Нахождение области определения функции
23.	Область определения функции корня n-й степени (нечётная степень)	2 вид — интерпретация	среднее	3 Б.	Нахождение области определения функции корня n-й степени
24.	Область определения функции корня n-й степени (четная степень)	2 вид — интерпретация	среднее	3 Б.	Нахождение области определения функции корня n-й степени
25.	Область определения функции, противоположный квадратный трёхчлен (чётная степень)	2 вид — интерпретация	среднее	10 Б.	Решение квадратного неравенста, применение теоремы Виета для нахождения области определения функции n-го корня
26.	Возрастание функции корня n-й степени	2 вид — интерпретация	среднее	3 Б.	Определение промежутков возрастания, построение графика функции корня n-й степени
27.	Область значений функции корня n-й степени	2 вид — интерпретация	среднее	3 Б.	Найти область значений, построить график функции корня n-й степени
28.	Решение уравнения графически (нечётная степень)	2 вид — интерпретация	среднее	5 Б.	Решение уравнения графически. Нахождение точек пересечения двух графиков функций, одним из которых является график функции корня n-й степени
29.	Возрастание функции корня n-й степени вида y=f(x+m) или y=f(x)+b (чётная степень)	2 вид — интерпретация	среднее	3 Б.	Определение промежутков возрастания, построение графика функции корня n-й степени вида y=f(x)+b и y=f(x+m) схематически
30.	Область значений функции вида y=f(x+m) или y=f(x)+b (нечётная степень)	2 вид — интерпретация	среднее	3 Б.	Найти область значений, построить график функции корня n-й степени вида y=f(x)+b или y=f(x+m) схематически
31.	Область определения функции корня n-й степени, дробь (чётная степень)	2 вид — интерпретация	среднее	3 Б.	Нахождение области определения функции корня n-й степени, приведение неравенства к линейному
32.	Область определения функции, квадратный трёхчлен (чётная степень)	2 вид — интерпретация	среднее	5 Б.	Решение квадратного неравенства, нахождение корней квадратного трехчлена через дискриминант
33.	Корень из произведения степеней, корень в степени (целые числа)	2 вид — интерпретация	среднее	3 Б.	Упрощение выражения
34.	Корень из дроби	2 вид — интерпретация	среднее	5 Б.	Применение свойств: корень из дроби, корень из произведения
35.	Произведение корней	2 вид — интерпретация	среднее	4 Б.	Применение свойства
36.	Частное корней	2 вид — интерпретация	среднее	3 Б.	Применение свойства
37.	Произведение корня из произведения степеней и корня из степени	2 вид — интерпретация	среднее	5 Б.	Вычисление значения проризведения
38.	Корень из частного степеней	2 вид — интерпретация	среднее	3 Б.	Вычисление корня степени n из дроби
39.	Корень из степени	2 вид — интерпретация	среднее	4 Б.	Применение свойства корень в степени
40.	Сравнение корней	2 вид — интерпретация	среднее	3 Б.	Сравнение корней с разными показателями
41.	Произведение корней с разными показателями	2 вид — интерпретация	среднее	3 Б.	Преобразование произведения корней к корню степени n
42.	Частное корней с разными показателями	2 вид — интерпретация	среднее	3 Б.	Преобразование частного корней к корню степени n
43.	Произведение корней с разными показателями из произведений степеней	2 вид — интерпретация	среднее	6 Б.	Преобразование произведения корней из произведений степеней к корню степени n
44.	Степень произведения (число и корень)	2 вид — интерпретация	среднее	6 Б.	Возведение в степень произведения
45.	Степень произведения (одночлен и корень)	2 вид — интерпретация	среднее	4 Б.	Возведение в степень произведения
46.	Корень из произведения степеней (десятичные дроби)	2 вид — интерпретация	среднее	4 Б.	Вычисление значения выражения
47.	Возведение в степень произведения (переменная и корень)	2 вид — интерпретация	среднее	6 Б.	Возведение в степень произведения
48.	Возведение в степень произведения (степень и корень)	2 вид — интерпретация	среднее	3 Б.	Возведение в степень произведения
49.	Произведение корней из произведений степеней	2 вид — интерпретация	среднее	6 Б.	Преобразование произведения корней из произведений к корню степени n
50.	Вычиcление выражения	2 вид — интерпретация	среднее	3 Б.	Свойства корней. Формула сокращенного умножения. Определение иррациональных чисел.
51.	Уравнение n-ой степени	2 вид — интерпретация	среднее	2 Б.	Решение уравнения n-ой степени.
52.	Область определения функции, сумма корней (чётная степень)	2 вид — интерпретация	сложное	7 Б.	Решение системы квадратных неравенств, применение теоремы Виета для нахождения области определения функции n-го корня
53.	Область определения функции, дробь (нечётная степень)	2 вид — интерпретация	сложное	3 Б.	Нахождение области определения функции, метод интервалов.
54.	Область определения функции корня n-й степени, сумма корней	2 вид — интерпретация	сложное	5 Б.	Нахождение области определения функции корня n-й степени (чётная и нечётная степени)

www.yaklass.ru

Корень n-ой степени и его свойства

Корень п -й степени и его свойства

Определение корня п -й степени

Арифметическим корнем п -й степени из неотрицательного числа а называется такое неотрицательное число b , п -я степень которого равна а .

Если п – нечетное число, то выражение имеет смысл при любом а .

Если п – четное число, то выражение имеет смысл лишь при .

Примеры

Свойства арифметического корня

• Корень из произведения неотрицательных множителей равен произведению корней этих множителей.

• Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.

3. Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не измениться.

4.

Практическое задание

Самостоятельная работа

Домашняя работа

• Решите уравнение:

videouroki.net

Основные свойства корней — Мегаобучалка

Корень n-й степени, его свойства.

Арифметическим корнем n-й степени из числа а называют неотрицательное число , n-я степень которого равна а.

Обозначается арифметический корень n-й степени из числа а

,

где n- показатель корня,

а- подкоренное выражение.

Знак называют еще радикалом.

Арифметический корень второй степени называется корнем квадратным и обозначается √, арифметический корень третьей степени называется кубическим корнем о обозначается

Например :

а) и 2≥0;

б) и 3≥0;

в)

Из определения арифметического корня n-й степени следует, что при четом n подкоренное выражение должно быть больше или равно нулю, а значит и значение такого корня тоже неотрицательно, например: арифметический корень 4-й степени из числа -81 не существует, так как ни одно число в четвертой степени не даст -81 ( при возведении в четную степень значение выражения всегда неотрицательно).

При нечетном показателе корня подкоренное выражение может быть отрицательным, и тогда минус может быть вынесен за знак коня.

Например:

 

Уравнение хⁿ=а.

Уравнение хⁿ=а при нечетном n имеет единственное решение х= .

Например : х³=-125;

х= ;

х=- ;

х=-5.

Для наглядности сделаем проверку:

(-5)³=-125;

-125=-125- верно.

Ответ : х=-5.

Уравнение хⁿ=а при четном n имеет и положительном а имеет два корня

х=± .

Например:

х⁴=16;

х₁= ; х₂=- ;

х₁=2; х₂=-2.

Можно убедиться при проверке, что 2⁴=16 и (-2)⁴=16.

Ответ : ±2.

Иногда нужно применить такое свойство арифметического корня n-й степени:

|х|, если n четно;

х, если n нечетно.

х, если х≥0;

Вспомним, что |х|= -х, если х<0.

Например :

.

Так как <0, следовательно

.

Основные свойства корней.

Для арифметического корня n-й степени, как и для квадратного корня, существуют операции внесения множителя под знак корня и вынесение множителя из-под знака корня.

Например :

2 .

Из примера видно, что для внесения множителя под знак корня n-й степени его нужно

возвести в n-ю степень. Нужно помнить, что под знак с четным показателем мы имеем право внести только положительный множитель, например:

Аналогично производится вынесение множителя из-под знака корня , например:

а)

б)

в)

 

формулой n-го члена ап: a_n= a₁+ d · (n — 1)

формулой n-го члена гп:

Функции y=kx (где k — любое натуральное число). Прямая пропорциональность, график прямая.
Свойства:
область определения — R
область значений — R
нечетная
при к >0 функция возрастает, при к <0 –убывает

 

 

Корень квадратного уравнения (формула)

Корни уравнения ax2 + bx + c = 0 (a ¹ 0) находят по формуле . Выражение D = b2 – 4ac называют дискриминантом квадратного уравнения. Квадратное уравнение имеет действительные корни (или корень) тогда и только тогда, когда его дискриминант неотрицателен. Если , можно применить формулу .

если просто уравнений, а не систем, то алгоритм прост: 1. неизвестные влево, сложить коэфициенты; числа вправо, также сложить (с учетом знака конечно) 2. разделить правую часть на коэфициент при неизвестном 2прим. если коеф.=0 и справа 0 — любое число есть решение уравнения если коеф.=0 а справа не 0 — уравнение решения не имеет

 

 

megaobuchalka.ru

Тема урока » Корень n-ой степени из действительного числа и его свойства»

Тема: Корень n-ой степени из действительного числа и его свойства

Цель урока: рассмотреть свойства корня n-ой степени из действительного числа

Задачи урока: решение примеров по данной теме

Ход урока:

I этап: Организационный момент, приветствие, проверка домашнего задания

II этап: Новая тема:

Корнем —ной степени, где– натуральное число и   , из числа  называют такое число  , -я степень которого равна  . Записывают:   или   . Тогда, если   , то   . Число  называют подкоренным выражением, а число  – показателем корня. 

Неотрицательный корень -ной степени из неотрицательного числа  называют арифметическим корнем -ной степени из числа  . Например:   ,   . Если показатель корня четное число, то подкоренное выражение не может быть отрицательным числом, так как четная степень и положительного и отрицательного числа есть число положительное.  Если показатель корня равен числу  , то имеем корень второй степени или квадратный корень из неотрицательного числа , который принято обозначать   или  . Например:   ;   . Если показатель корня нечетное число, то подкоренное выражение может быть положительным числом, отрицательным числом и числом  .  Если показатель корня равен числу  , то имеем корень третьей степени или кубический корень из числа , который принято обозначать   . Например:  ;  

Свойства корней:

 ; (1.16)  ; (1.17)  ; (1.18)
 ; (1.19)  . (1.20)

При четном значении  свойства 1.16 и 1.17 справедливы, если значения  и  неотрицательные, а свойство 1.18 справедливо, если к тому же  . Свойства 1.19 и 1.20 справедливы при любых значениях  и  . 

Например:   ;   ;   ;   ;   .

Внесение множителя под знак корня

Если показатель корня нечетное число, то для любого числа  и натурального числа  справедливо равенство:

  . (1.21) Если   , то  . 

Например,   .

Вынесение множителя из-под знака корня 

Если показатель корня нечетное число, то справедливо равенство:

 . (1.22)

Если показатель корня четное число, то справедливо равенство:

 . (1.23)

Например:   ;   .

Сравнение выражений, содержащих корни

1. Если   , то   . Например,   .

2. Если   и   , то   . Например,   .

3. Если   и  , то   . Например,   .

4. Чтобы сравнить числа   и   , необходимо представить их в виде корня одной и той же степени.

5. Чтобы сравнить числа  и   необходимо или извлечь корень -ой степени из  или представить число  в виде   . 

Степень с действительным показателем 

Степени с действительным показателем обладают всеми свойствами степеней с целым показателем. При этом следует помнить, что: 

а) степень числа с натуральным показателем имеет смысл для любого основания, так как эта степень определяется с помощью операции умножения;

б) степень с целым отрицательным показателем имеет смысл для любого основания, кроме основания  , так как эта степень определяется с помощью операций умножения и деления; 

в) степень с рациональным показателем определяется с помощью операции извлечения корня, которая всегда выполнима, если основание степени положительное число и не всегда выполнима, если основание степени отрицательное число; 

г) степень с любым действительным показателем всегда определена, если ее основание – положительное число. 

Среднее арифметическое и среднее геометрическое 

Чтобы найти среднее арифметическое нескольких чисел необходимо сумму этих чисел разделить на их количество. 

Например, среднее арифметическое чисел ,  и  равно   .

Чтобы найти среднее геометрическое двух положительных чисел, необходимо извлечь корень второй степени из произведения этих чисел. Чтобы найти среднее геометрическое  положительных чисел, необходимо извлечь корень степени  из произведения этих чисел. Например, среднее геометрическое чисел , ,  и  равно   .

III этап: подведение итогов

IV этап: домашнее задание ?

infourok.ru

Корень n-ой степени и его свойства

Корень n- ой степени и его свойства

І. Понятие корня n- ой степени

Определение 1 . Корнем n — ой степени из неотрицательного числа а ( n = 2,3,4,5,…) называют такое неотрицательное число, при возведении в степень n которого получается число а

Терминология

Замечания:

Определение 2.

• Корнем нечетной степени n из отрицательного числа а ( n =3,5,7,…) называется такое отрицательное число, при возведении которого в степень n получается число а
• Корнем нечетной степени n из отрицательного числа а ( n =3,5,7,…) называется такое отрицательное число, при возведении которого в степень n получается число а
• Корнем нечетной степени n из отрицательного числа а ( n =3,5,7,…) называется такое отрицательное число, при возведении которого в степень n получается число а
• Корнем нечетной степени n из отрицательного числа а ( n =3,5,7,…) называется такое отрицательное число, при возведении которого в степень n получается число а
• Корнем нечетной степени n из отрицательного числа а ( n =3,5,7,…) называется такое отрицательное число, при возведении которого в степень n получается число а

Заме ч ание:

четной неотрицательного нечетной любого

ІІІ. Свойства корня n- ой степени

Замечание:

Все рассмотренные свойства распространяются на случай корней нечетных степеней.

Если же a

videouroki.net

Корень n-ой степени и его свойства І. Понятие

Описание презентации Корень n-ой степени и его свойства І. Понятие по слайдам

Корень n-ой степени и его свойства І. Понятие корня n- ой степени ІІ. Функции ІІІ. Свойства корня n- ой степени ІV. Преобразования иррациональных выражений

І. Понятие корня n-ой степени Определение 1. Корнем n -ой степени из неотрицательного числа а ( n= 2, 3, 4, 5, …) называют такое неотрицательное число, при возведении в степень n которого получается число а

Терминология √ — радикал n -показатель корня а — подкоренное число (выражение)

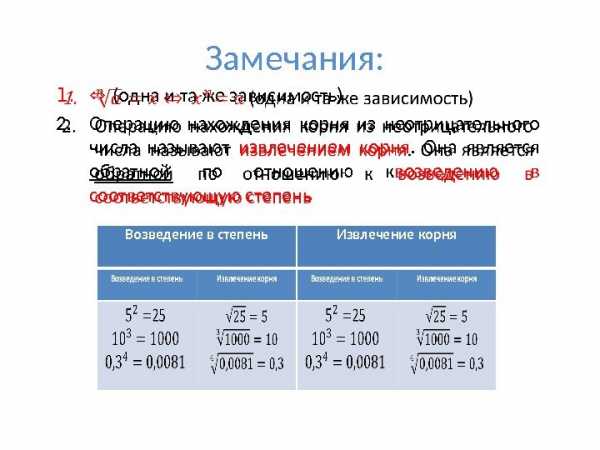Замечания: 1. ⇔ (одна и та же зависимость) 2. Операцию нахождения корня из неотрицательного числа называют извлечением корня. Она является обратной по отношению к возведению в соответствующую степень Возведение в степень Извлечение корня 25 Возведение в степень Извлечение корня

Определение 2. Корнем нечетной степени n из отрицательного числа а (n=3, 5, 7, …) называется такое отрицательное число, при возведении которого в степень n получается число а

Замечание: Корень четной степени имеет смысл только для неотрицательного подкоренного числа; корень нечетной степени имеет смысл для любого подкоренного числа

– степенное уравнение Если

ІІ. Функции • Свойства функции • Если n — четное Если n — нечетное 1. Ни четная, ни нечетная 2. Возрастает на 3. Не ограничена сверху. Ограничена снизу 4. Непрерывна на 5. Выпукла вверх на 6. Дифференцируема на 1. Нечетная 2. Возрастает на 3. Не является ограниченной 4. Непрерывна на 5. Выпукла вверх на , выпукла вниз на 6. Дифференцируема на Если n — четное Если n — нечетное

График функции

present5.com

Корень n-й степени и его свойства.

¦Пример 1. ¦

¦ Решим неравенство х6>20 ¦

¦ Это неравенство равносильно неравенству х6-20>0. Так как функция ¦

¦f(x)=х6-20 непрерывна, можно воспользоваться методом интервалов. ¦

¦ 6|\\ 6|\ ¦

¦ Уравнение х6-20=0 имеет два корня : ? 20 и — ? 20 . Эти числа разби- ¦

¦вают числовую прямую на три промежутка. Решение данного неравенства — ¦

¦ 6|\\ 6|\\ ¦

¦объединение двух из них : (-4; -? 20 ) (? 20 ;4) ¦

¦ ¦

¦Пример 2. 3|\ 5|\ ¦

¦ Сравним числа ? 2 и ? 3 ¦

¦ 3|\ 5|\ ¦

¦ Представим ? 2 и ? 3 в виде корней с одним и тем же показателем: ¦

¦ ¦

¦ 3|\ 15|\ 15|\ 5|\ 15|\ 15|\ ¦

¦ ? 2 = ? 25 = ?32 а ? 3 = ? 33 = ? 27 из неравенства ¦

¦ 15|\ 15|\ 3|\ 5|\ ¦

¦ 32 > 27 следует, что ?32 и ? 27 ,и значит, ? 2 > ? 3 ¦

+————————————————————————-+

¦ Иррациональные уравнения. ¦

¦ ¦

¦ Пример 1. |\\\ ¦

¦ Решим уравнение ? x2 — 5 = 2 ¦

¦ Возведем в квадрат обе части уравнения и получим х2 — 5 = 4, отсюда ¦

¦следует, что х2=9 х=3 или -3. ¦

¦ Проверим, что полученные части являются решениями уравнения. ¦

¦Действительно, при подстановке их в данное уравнение получаются верные ¦

¦равенства |\\ |\\\ ¦

¦ ? 32-5 = 2 и ? (-3)2-5 = 2 ¦

¦ ¦

¦ Пример 2. |\ ¦

¦ Решим уравнение ? х = х — 2 ¦

¦ Возведя в квадрат обе части уравнения, получим х = х2 — 4х + 4 ¦

¦После преобразований приходим к квадратному уравнению х2 — 5х + 4 = 0 ¦

¦корни которого х=1 и х=4. Проверим являются ли найденные числа реше- ¦

¦ниями данного уравнения. При подстановке в него числа 4 получаем вер- ¦

¦ное равенство ?4 = 4-2 т.е. 4 — решение данного уравнения. При подста- ¦

¦новке же числа 1 получаем в правой части -1, а в левой 1. Следователь- ¦

¦но, 1 не является решением уравнения ; говорят, что это посторонний ¦

¦корень, полученный в результате принятого способа решения . ¦

¦ О Т В Е Т : Х=4 ¦

+————————————————————————-+

¦ Степень с рациональным показателем. ¦

¦ Пример 1. ¦

¦ 3|\ 4|\\ 4|\ ¦

¦Найдем значение выражения 81/3 = ? 8 = 2 ; 813/4 = ? 813 = (?81)3= 33= ¦

¦=27 ¦

¦ ¦

¦ Пример 2. ¦

¦ Сравним числа 2300 и 3200 . Запишем эти числа в виде степени с ра- ¦

¦циональным показателем : ¦

¦ 2300 = (23)100 = 8100 ; 3200 = (32)100 = 9100 ¦

¦ Так как 8<9 получаем : ¦

¦ 8100 < 9100 т.е. 2300 < 3200 . ¦

¦ ¦

L—————————————————————————

studyport.ru