Корень пример: Корень — определение понятия, примеры в русском языке

Свойства арифметического квадратного корня. Квадратный корень из степени. Преобразование выражений, содержащих

Свойства арифметического квадратного корня. Квадратный корень из степени.

Арифметический квадратный корень обладает рядом свойств.

ab=ab (a,b≥0). Если a и b – неотрицательные числа, то корень из их произведения равен произведению корней.

Доказательство: воспользуемся определением квадратного корня.

(ab)2=ab

(ab)2=ab

Функция y=x2 при х≥0 принимает свои значения ровно один раз.

Следовательно, ab=ab, так как равны их квадраты.

Примеры:

36·25=36∙25=6∙5=30

8·50=8∙2∙25=16∙25=4∙5=20

Рассмотрим обобщение первого свойства: abc=abc при a,b,c≥0.

Корень из произведения неотрицательных множителей равен произведению корней этих множителей.

Примеры:

81·4·16=81416=9∙2∙4=72

0,01·8·50=0,01∙8∙2∙25=0,011625=0,1∙4∙5=2

ab=ab (a>0, b≥0). Если а – неотрицательное число, а b – положительное число, то корень из их отношения равен отношению корней.

Доказательство: воспользуемся определением квадратного корня.

ab2=ab

ab2=(a)2(b)2=ab

Функция y=x2 при х≥0 принимает свои значения ровно один раз.

Следовательно, ab=ab, так как равны их квадраты.

Примеры:

49=49=23

1916=2516=2516=54=114

 

a2n=anпри a≥0, n∈N

Доказательство: воспользуемся определением квадратного корня.

(a2n)2=a2n

(an)2=a2n

Функция y=x2 при х≥0 принимает свои значения ровно один раз.

Следовательно, a2n=an, так как равны их квадраты.

Примеры:

36=32∙3=33=27

x8=x2∙4=x4 при x≥0

Рассмотренные свойства широко используются в различных задачах.

Разберем пример:

132-122=(13-12)(13+12)=1∙25=5

Конечно, в данном примере можно было просто вычислить квадраты указанных чисел, а затем посчитать их разность. Однако подсчёт «в лоб» станет слишком трудным для больших чисел.

Рассмотрим одну из самых распространённых и грубейших ошибок, которую часто допускают при работе с квадратными корнями.

Утверждение а±b=a±b – НЕВЕРНО!

В качестве подтверждения рассмотрим следующий пример: 9+16=25=5, а 9+16=3+4=7. Как видим, применение неправильной формулы приводит к неправильным результатам.

 

Как найти корень из числа. Извлечение корней: способы, примеры, решения

Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.

Ниже мы по очереди рассмотрим основные способы извлечения корней.

Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.

Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.

Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.

Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.

Приступим.

Использование таблицы квадратов, таблицы кубов и т.д.

В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т.д. Что же представляют собой эти таблицы?

Таблица квадратов целых чисел от 0 до 99 включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0 до 99 . Для примера выберем строку 8 десятков и столбец 3 единицы, этим мы зафиксировали число 83 . Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0 до 99 . На пересечении выбранной нами строки 8 десятков и столбца 3 единицы находится ячейка с числом 6 889 , которое является квадратом числа 83 .

Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.

Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т.д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.

Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.

В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .

Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.

Разложение подкоренного числа на простые множители

Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем

: после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.

Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .

Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.

Разберемся с этим при решении примеров.

Пример.

Извлеките квадратный корень из 144 .

Решение.

Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .

Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.

Разложим 144 на простые множители:

То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .

Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .

Ответ:

Для закрепления материала рассмотрим решения еще двух примеров.

Пример.

Вычислите значение корня .

Решение.

Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .

Ответ:

Пример.

Является ли значение корня целым числом?

Решение.

Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.

Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.

Ответ:

Нет.

Извлечение корней из дробных чисел

Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби

: корень из дроби равен частному от деления корня из числителя на корень из знаменателя.

Разберем пример извлечения корня из дроби.

Пример.

Чему равен квадратный корень из обыкновенной дроби 25/169 .

Решение.

По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5 , а квадратный корень из знаменателя равен 13 . Тогда . На этом извлечение корня из обыкновенной дроби 25/169 завершено.

Ответ:

Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.

Пример.

Извлеките кубический корень из десятичной дроби 474,552 .

Решение.

Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .

Ответ:

.

Извлечение корня из отрицательного числа

Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a и нечетного показателя корня 2·n−1 справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.

Рассмотрим решение примера.

Пример.

Найдите значение корня .

Решение.

Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .

Приведем краткую запись решения: .

Ответ:

.

Порязрядное нахождение значения корня

В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n -ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.

На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.

Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.

Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2 , на втором – 2,2 , на третьем – 2,23 , и так далее 2,236067977… . Опишем, как происходит нахождение значений разрядов.

Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .

Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.

Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9 , вычисляя соответственно 0 2 , 1 2 , …, 9 2 до того момента, пока не получим значение, большее подкоренного числа 5 . Все эти вычисления удобно представлять в виде таблицы:

Так значение разряда единиц равно 2 (так как 2 2 5 ). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9 , сравнивая полученные значения с подкоренным числом 5 :

Так как 2,2 2 5 , то значение разряда десятых равно 2 . Можно переходить к нахождению значения разряда сотых:

Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .

Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.

Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =02 151,186 , таким образом, старшим разрядом является разряд десятков.

Определим его значение.

Так как 10 3 2 151,186 , то значение разряда десятков равно 1 . Переходим к единицам.

Таким образом, значение разряда единиц равно 2 . Переходим к десятым.

Так как даже 12,9 3 меньше подкоренного числа 2 151,186 , то значение разряда десятых равно 9 . Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.

На этом этапе найдено значение корня с точностью до сотых: .

В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.

Список литературы.

• Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
• Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
• Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).

Формулы корней. Свойства квадратных корней.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень. ..»
И для тех, кто «очень даже…»)

В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.

Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…

Начнём с самой простой. Вот она:

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Для вычисления квадратного корня без калькулятора существует несколько методов.

Как найти корень из числа – 1 способ

• Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
• Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.

• Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя. Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
• Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
• В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
• Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
• Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
  √5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18.
• Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.

Как найти корень из числа – 2 способ

• Другой способ заключается в делении в столбик. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
• В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
• Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
• При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.

На первый взгляд может показаться, что процедура разложения квадратного корня на множители сложная и неприступная. Но это не так. В этой статье мы расскажем вам, как подступиться к квадратному корню и множителям, а также легко и просто разложить квадратный корень, воспользовавшись двумя проверенными методами.

Yandex.RTB R-A-339285-1

Разложение корня на множители

Для начала определим цель процедуры разложения квадратного корня на множители. Цель — упростить квадратный корень и записать его в удобном для вычислений виде.

Определение 1

Разложение квадратного корня на множители — нахождение двух или нескольких чисел, которые, при условии перемножения их друг на друга, дадут число равное исходному. Например: 4×4 = 16.

Если вы найдете множители, то сможете легко упростить выражение с квадратным корнем или вовсе его упразднить:

Пример 1

Разделите подкоренное число на 2, если оно четное.

Подкоренное число всегда следует делить на простые числа, поскольку любое значение простого числа можно разложить на простые множители. Если у вас нечетное число, то попробуйте разделить его на 3. Не делится на 3? Делите дальше на 5, 7, 9 и т.д.

Запишите выражение в виде корня произведения двух чисел.

Например, можно упростить таким способом 98: = 98 ÷ 2 = 49 . Из этого следует, что 2 × 49 = 98 , поэтому можно переписать задачу следующим образом: 98 = (2 × 49) .

Продолжите раскладывать числа, пока под корнем не останется произведение двух одинаковых чисел и других чисел.

Возьмем наш пример (2 × 49) :

Поскольку 2 уже и так максимально упрощено, необходимо упростить 49 . Ищем простое число, на которое можно разделить 49 . Очевидно, что ни 3 , ни 5 не подходят. Остается 7: 49 ÷ 7 = 7 , поэтому 7 × 7 = 49 .

Записываем пример в следующем виде: (2 × 49) = (2 × 7 × 7) .

Упростите выражение с квадратным корнем.

Поскольку в скобках у нас произведение 2 и двух одинаковых чисел (7) , то мы можем вынести за знак корня число 7 .

Пример 2

(2 × 7 × 7) = (2) × (7 × 7) = (2) × 7 = 7 (2) .

В тот момент, когда под корнем оказалось два одинаковых числа, останавливайтесь с разложением чисел на множители. Конечно, если вы использовали все возможности по максимуму.

Запомните: существуют корни, которые можно упрощать многократно.

В таком случае, числа, которые мы выносим из-под корня, и числа, которые стоят перед ним, перемножаются.

Пример 3

180 = (2 × 90) 180 = (2 × 2 × 45) 180 = 2 45

но 45 можно разложить на множители и еще раз упростить корень.

180 = 2 (3 × 15) 180 = 2 (3 × 3 × 5) 180 = 2 × 3 5 180 = 6 5

Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.

Если после разложения подкоренного выражения на произведение простых чисел, у вас не получилось получить два одинаковых числа, то такой корень упростить нельзя.

Пример 4

70 = 35 × 2 , поэтому 70 = (35 × 2)

35 = 7 × 5 , поэтому (35 × 2) = (7 × 5 × 2)

Как видим, все три множителя — простые числа, которые нельзя разложить на множители. Среди них нет одинаковых чисел, поэтому не представляется возможным вынести целое число из-под корня. Упростить 70 нельзя.

Полный квадрат

Запомните несколько квадратов простых чисел.

Квадрат числа получается, если умножить его на самого себя, т.е. при возведении в квадрат. Если вы запомните десяток квадратов простых чисел, то это очень упростить вам жизнь в дальнейшем упрощении корней.

Пример 5

1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81 10 2 = 100

В случае если под знаком корня квадратного корня находится полный квадрат, то стоит убрать знак корня и записать квадратный корень данного полного квадрата.

Сложно? Нет:

Пример 6

1 = 1 4 = 2 9 = 3 16 = 4 25 = 5 36 = 6 49 = 7 64 = 8 81 = 9 100 = 10

Попробуйте разложить число под знаком корня на произведения полного квадрата и другого числа.

Если вы видите, что подкоренное выражение раскладывается на произведение полного квадрата и какого-либо числа, то, запомнив несколько примеров, вы существенно сэкономите время и нервы:

Пример 7

50 = (25 × 2) = 5 2 . Если подкоренное число оканчивается на 25, 50 или 75, вы всегда можете разложить его на произведение 25 и какого-то числа.

1700 = (100 × 17) = 10 17 . Если подкоренное число оканчивается на 00, вы всегда можете разложить его на произведение 100 и какого-то числа.

72 = (9 × 8) = 3 8 . Если сумма цифр подкоренного числа равна 9, вы всегда можете разложить его на произведение 9 и какого-то числа.

Попробуйте разложить подкоренное число на произведение нескольких полных квадратов: вынесите их из-под знака корня и перемножьте.

Пример 8

72 = (9 × 8) 72 = (9 × 4 × 2) 72 = 9 × 4 × 2 72 = 3 × 2 × 2 72 = 6 2

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Цель упрощения квадратного корня – это переписать его в такой форме, которую проще использовать в вычислениях. Разложение числа на множители – это нахождение двух или нескольких чисел, которые при перемножении дадут исходное число, например, 3 х 3 = 9. Найдя множители, вы сможете упростить квадратный корень или вообще избавиться от него. Например, √9 = √(3×3) = 3.

Если подкоренное число четное, разделите его на 2. Если подкоренное число нечетное, попробуйте разделить его на 3 (если число на 3 не делится, делите его на 5, 7 и так далее по списку простых чисел). Делите подкоренное число исключительно на простые числа, так как любое число можно разложить на простые множители. Например, вам не нужно делить подкоренное число на 4, так как 4 делится на 2, а вы уже разделили подкоренное число на 2.

Перепишите задачу как корень из произведения двух чисел. Например, упростим √98: 98 ÷ 2 = 49, поэтому 98 = 2 x 49. Перепишите задачу так: √98 = √(2 x 49).

Продолжите разложение чисел до тех пор, пока под корнем не останется произведение двух одинаковых чисел и других чисел. Это имеет смысл, если задуматься о смысле квадратного корня: √(2 х 2) равен числу, которое, будучи умноженным само на себя, будет равно 2 х 2. Очевидно, что это число 2! Повторите описанные выше действия для нашего примера: √(2 х 49).

• 2 уже максимально упрощено, так как это простое число (см. список простых чисел выше). Поэтому разложите на множители число 49.
• 49 на 2, 3, 5 не делится. Поэтому переходите к следующему простому числу – 7.
• 49 ÷ 7 = 7, поэтому 49 = 7 x 7.
• Перепишите задачу так: √(2 x 49) = √(2 x 7 x 7).

Упростите квадратный корень. Так как под корнем находится произведение 2 и двух одинаковых чисел (7), вы можете вынести такое число за знак корня. В нашем примере: √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).

• Как только под корнем вы получили два одинаковых числа, вы можете остановиться с разложением чисел на множители (если их все еще можно разложить). Например, √(16) = √(4 х 4) = 4. Если вы продолжите разложение чисел на множители, вы получите тот же ответ, но проделаете больше вычислений: √(16) = √(4 х 4) = √(2 х 2 х 2 х 2) = √(2 х 2) √(2 х 2) = 2 х 2 = 4.

Некоторые корни можно упрощать многократно. В этом случае числа, выносимые из-под знака корня, и числа, стоящие перед корнем, перемножаются. Например:

• √180 = √(2 x 90)
• √180 = √(2 x 2 x 45)
• √180 = 2√45, но 45 можно разложить на множители и еще раз упростить корень.
• √180 = 2√(3 x 15)
• √180 = 2√(3 x 3 x 5)
• √180 = (2)(3√5)
• √180 = 6√5

Если вы не можете получить два одинаковых числа под знаком корня, то такой корень упростить нельзя. Если вы разложили подкоренное выражение на произведение простых множителей, и среди них нет двух одинаковых чисел, то такой корень упростить нельзя. Например, попробуем упростить √70:

• 70 = 35 x 2, поэтому √70 = √(35 x 2)
• 35 = 7 x 5, поэтому √(35 x 2) = √(7 x 5 x 2)
• Все три множителя являются простыми, поэтому их больше нельзя разложить на множители. Все три множителя разные, поэтому вы не сможете вынести целое число из-под знака корня. Следовательно, √70 упростить нельзя.

Слова с корнем и окончанием примеры 10 слов

Для того, чтобы определить слова, имеющие корень и окончание, и привести их примеры, необходимо для начала определить для каждого, что такое корень и окончание.

Что такое корень слова?

Корнем слова называют часть слова, которая часто является неизменяемой для всех видов родственных слов, а также которая отражает основное значение. Слова с одним и тем же неизменяемым корнем называют однокоренными. Например, фронт, фронтальный, прифронтовой, фронту и др.

В одном слове могут встречаться два и более корня, такие слова называются сложными. Например, газонокосилка (первый корень – газон, второй – кос (от слова косить)), хлебобулочный (первый корень – хлеб, второй – булоч.).

Что такое окончание слова?

Окончанием называют изменяемую часть слова, которая служит для образования новых форм слов, а также служит для логической связи в предложениях и словосочетаниях. Окончание придает слову значение числа, рода, лица и падежа. Слово не всегда имеет окончание (примеры слов без окончания). Встречаются случаи, когда окончание у слова есть, но его нельзя ни увидеть, ни услышать по звуку, такое окончание называется нулевым. Для того, чтобы определить сколько в слове букв и звуков ознакомьтесь с отдельной статьёй.

Слово в некоторых случаях может иметь два окончания, бывает, также что окончание стоит не в самом конце слова. В этих случаях чтобы определить в слове окончание придется воспользоваться фонетической транскрипцией. От суффиксов, которые также образуют слово, окончание отличается характером (который оно придает слову) грамматического значения. Только те слова могут иметь окончание, которые склоняются (по падежам) или изменяются (по родам, числам). Склоняются слова прилагательные, глаголы, причастия, существительные, числительные, местоимения.

Чтобы сформировать окончание, необходимо изменить слово по числу: груз (ед. ч.), грузы (мн. ч.). Изменить по падежу: карусель (именительный падеж), каруселью (творительный падеж). По роду: бегал (муж. род), бегала (жен. род).

Слова, образованные с помощью окончания и корня

Теперь мы знаем, что такое корень и окончание и можем привести примеры слов, где оно образовано только этими двумя частями слова.

1. Гвозди – в этом слове корнем, а также основой является «Гвозд», «и» – окончание.
2. Липа – корень слова «Лип», окончание «а».
3. Корова – корнем слова является «Коров», окончание «а».
4. Хвосту – в слове корень «Хвост», окончание «у».
5. Деньги – корень слова «Деньг», окончание слова «и».
6. Сладости – в слове корнем является часть «Сладост», «и» — окончание.
7. Враги – корень слова «Враг» (может изменяться – вражеский (корень – «враж»)), окончание – «и».
8. Звезда – в слове корень «Звезд», «а» — является окончанием.
9. Книга – в этом слове изменяемый корень «Книг» (во мн. ч. – книжки), окончание – «а».
10. Флейта – корень слова «Флейт», окончание – «а».

Сервисы для разбора слова на корень, окончание и другие части

В Интернете вы можете найти специальные сервисы, которые позволят вам разобрать любое литературное слово по частям в один клик. Один из таких сервисов – Morphemeonline.ru. Это удобный сайт, который позволяет не только разобрать слова по составу (инструкция по ссылке), но также имеет описание всех частей и правил, которые относятся к частям слова. В правой части экрана вы можете с ними ознакомиться.

Для того, чтобы разобрать слово на корень и окончание:

1. Зайдите на главную страницу сайта.
2. В правой части, над базой знаний «По составу» находится окно, в которое необходимо вписать свое слово для разбора.

3. И в левой части вы получите разбор слова на все части, которое оно содержит. А также над разбором вы сможете увидеть графическое обозначение частей слова.

2.1.5. Корни многочлена

Данный многочлен имеет целые коэффициенты. Если целое число является корнем этого многочлена, то оно является делителем числа 16. Таким образом, если у данного многочлена есть целые корни, то это могут быть только числа ±1; ±2; ±4; ±8; ±16. Непосредственной проверкой убеждаемся, что число 2 является корнем этого многочлена, то есть x³ – 5x² – 2x + 16 = (x – 2)Q(x), где Q(x) − многочлен второй степени. Следовательно, многочлен разлагается на множители, один из которых (x – 2).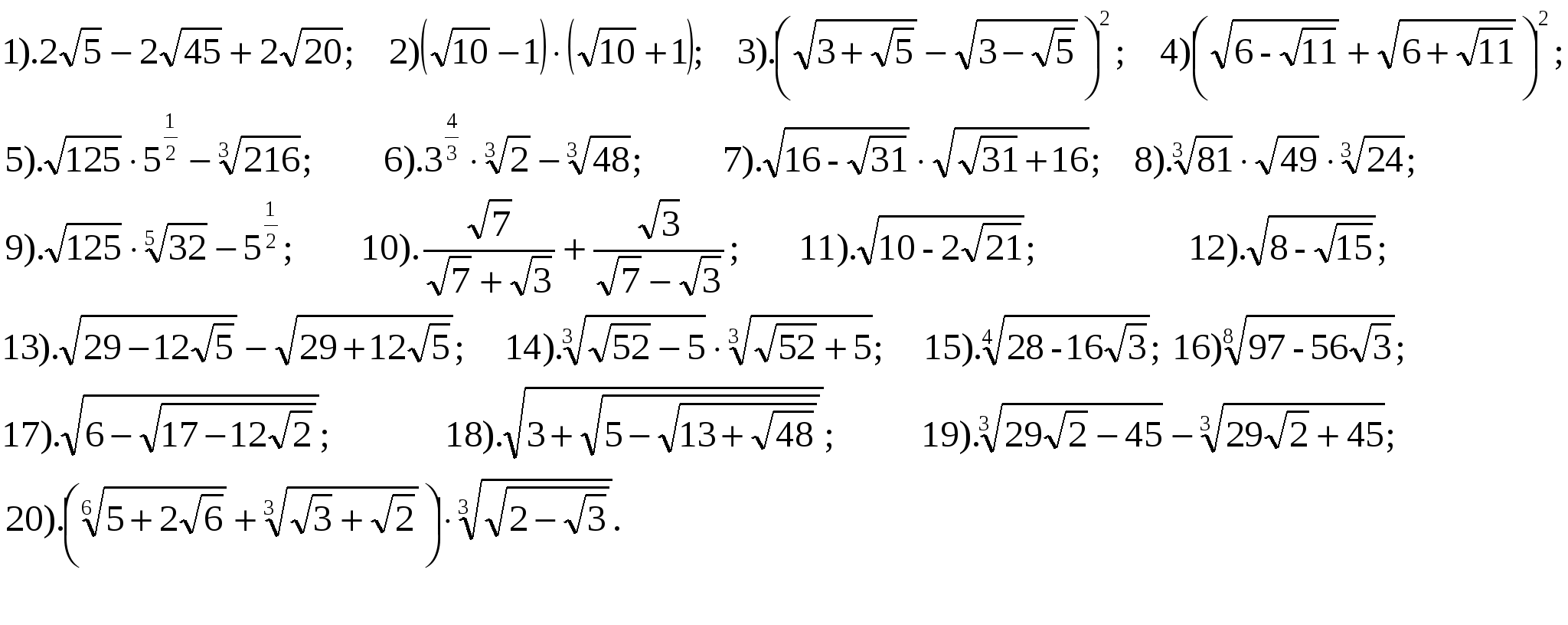 Для поиска вида многочлена Q(x) воспользуемся так называемой схемой Горнера. Основным преимуществом этого метода является компактность записи и возможность быстрого деления многочлена на двучлен. По сути, схема Горнера является другой формой записи метода группировки, хотя, в отличие от последнего, является совершенно ненаглядной. Ответ (разложение на множители) тут получается сам собой, и мы не видим самого процесса его получения. Мы не будем заниматься строгим обоснованием схемы Горнера, а лишь покажем, как она работает.

	1	−5	−2	16
2	1	−3	−8	0

В прямоугольную таблицу 2 × (n + 2) , где n − степень многочлена, (см. рис.) в верхнюю строчку выписываются подряд коэффициенты многочлена (левый верхний угол при этом оставляют свободным). В нижний левый угол записывают число − корень многочлена (или число x₀, если мы хотим разделить на двучлен (x – x₀)), в нашем примере это число 2. Далее вся нижняя строчка таблицы заполняется по следующему правилу.

Во вторую клетку нижней строки «сносится» число из клетки над ней, то есть 1. Затем поступают так. Корень уравнения (число 2) умножают на последнее написанное число (1) и складывают результат с числом, которое стоит в верхнем ряду над следующей свободной клеткой, в нашем примере имеем:

2 ∙ 1 + (–5) = –3.

Результат записывается в свободную клетку под тем числом, с которым только что производилось сложение, то есть под −5.

Далее корень 2 умножается на последнюю написанную цифру, то есть на −3, и складывается с числом, которое стоит в верхнем ряду над следующей свободной клеткой, то есть −2; имеем:

2 ∙ (–3) + (–2) = –8.

Результат пишем в свободную клетку под −2. Далее поступаем аналогично:
В последней клетке (правый нижний угол), если нигде не совершено ошибки и 2 − действительно корень данного многочлена, должен получиться нуль. Это признак правильного решения. В общем случае в этой клетке оказывается остаток от деления исходного многочлена на (x – 2) (в нашем примере). У нас получился 0, следовательно, 2 − действительно корень этого многочлена.

Полученные числа 1, −3, −8 являются коэффициентами многочлена, который получается при делении исходного многочлена на x – 2. Значит, результат деления:

1 · x2 + (–3)x + (–8) = x2 – 3x – 8.

Степень многочлена, полученного в результате деления, всегда на 1 меньше, чем степень исходного. Итак:

x3 – 5x2 – 2x + 16 = (x – 2)(x2 – 3x – 8).

Корни многочлена второй степени ищутся легко уже описанным выше способом (по формуле корней) и равны: и Окончательно:

Ответ. 

Найти корень уравнения пример | Геометрия

Найти корень уравнения пример | Геометрия — просто!

Добрый день!

Сегодня мы разберём примеры задания 5 ЕГЭ — найти корень уравнения.
В этом задании собраны разнообразные уравнения — линейные, квадратные, иррациональные, показательные, логарифмические, тригонометрические.
Каждое из них решается по своей методике
и по своим правилам.
Решим некоторые из них.

Задание 1. найти корень уравнения √(2х + 31) = 9

Решение: чтобы найти корень данного уравнения,
обе части его возводим в степень 2.
При этом, обязательным условием должна быть
неотрицательность правой части уравнения.
У нас справа стоит число 9, значит можно возвести
правую и левую часть в квадрат.
2х + 31 = 81
2х = 81 — 31
2х = 50
х = 25.
Ответ: корень уравнения х = 25.

Задание 2. найти корень уравнения √(4х + 5) = 5

Решение: закрепим изученное ещё одним примером.
4х + 5 = 25
4х = 25 — 5
4х = 20
х = 5.
Ответ: корень уравнения х = 5.

Задание 3. Найти корень уравнения log

₆ (8 – x) = log₃₆ 9
Решение: Число 36 можно представить,  как 6², а 9 как 3².
Перепишем наше уравнение:
log₆ (8 – x) = log₆² 3²
По свойству логарифма степени выносим перед логарифмом:
log₆ (8 – x) = 2/2log₆ 3
log₆ (8 – x) = log₆ 3
Логарифмы равны, основания тоже равны,
значит равны и выражения, стоящие под знаком логарифма.
8 – x = 3
8 – х >0  О.Д.З.
х <8
х = 5
Ответ: корень уравнения х = 5

Задание 4.

Найти корень уравнения  log₄ (х + 7) = 2
Решение: здесь мы просто воспользуемся свойством логарифма:
log₄ (х + 7) = 2
х + 7 = 4²
х = 16 — 7
х = 9
Ответ: корень уравнения х = 9.

Задание 5.  Найти  корень уравнения  (х+11)² = 44х

Решение: В левой части уравнения квадрат суммы двух чисел.
Раскрываем скобки:
х² + 22х + 121 = 44х  Переносим 44х влево с противоположным знаком.
х² — 22х + 121 = 0    А это, в свою очередь, квадрат разности двух чисел.
(х-11)² = 0.
Корень у этого уравнения один и он равен 11.
Ответ: корень уравнения 11.

Задание 6. Найдите корень уравнения:   3

^5+3х = 9^2х
Решение:  В левой части показательного уравнения в основании стоит 3,
а в правой — 9.
9 можно представить, как 3².
Значит, правую часть уравнения можно представить как   (3²)^2х
При возведении степени в степень,  показатели степеней перемножаются.
Получим    (3²)^2х = 3^4х
А теперь можно решить уравнение.
3^5+3х = 9^2х
3^5+3х = 3^4х
Поскольку степени равны, основания тоже равны,
значит, равны показатели степеней.
5+3х = 4х
5 = 4х — 3х
х=5
Ответ: корень уравнения 5.

На сегодня всё.

Успехов и до новых задач!

 

Вам так же будет интересно:

Оставить комментарий

Квадратный корень, урок по алгебре для 8 класса, арифметический квадратный корень

Дата публикации: 09 апреля 2017.

Квадратный корень, обозначение

Ребята, мы переходим к изучению одного из ключевых понятий в алгебре 8 класса. Корень квадратный, что же это такое?
Давайте графически решим уравнение $x^2=4$. 2}$.
Корень квадратный (и вообще корень любой степени) важная операция в математике, и ввод такой операции не прихоть, а реальная необходимость.

Задачи для самостоятельного решения

1. Вычислите:
а) $\sqrt{64}$.
б) $\sqrt{4}$.
в) $\sqrt{-9}$.
г) $\sqrt{\frac{36}{81}}$.
2. Вычислите: $\sqrt{4225}$.

Слово «корень» в примерах предложений

 2281789 У нас нет  корня  пива. СК 1
1994371 Том сказал мне, что он часто пьет пиво  root , но он не только никогда не пил елового пива, он даже никогда о нем не слышал. СК 1
3118275 Я  рутирую  для вас. Гибридный
1994362 Вам нравится пиво  root ? Спамстер
1730751 За кого ты  болеешь за ? Гайбраш88
2953812 Мы все  болели за Тома . СК
18505 Деньги — это  корень  всех зол.оркрист
1056333 Чему равен квадратный  корень  из 100? Мофли
661273 Я всегда  root  для аутсайдера. даринмекс
46161 Подтяните растение за корни   . СК
992006 Бедность есть  корень  всех зол.  СК
3157883 Том обычно пьет диетическое  корневое  пиво. СК
2985595 Доберёмся до  корня  дела. острозубый
35861 Морковь и репа съедобные  корнеплоды  . СМ
2619472 Куб  корень  из двадцати семи равен трем. оркрист
864505 Безденежье —  корень  всех зол.Крис
521016 Корни  дерева  уходят глубоко в землю. даринмекс
2985605 Трудно  искоренить  определенные предубеждения. острозубый
274279  корень  цветка слаб, как пальчик младенца. СК
2619471 Квадрат  корня  из ста сорока четырех равен двенадцати. оркрист
625174 Корневая  система дерева  простирается на тридцать метров. даринмекс
376881 Часть этого убеждения  коренится  в моем собственном опыте. саиб
1112680 Учитель спросил его: "Что такое квадратный  корень  из 256?" Алексмарсело
1112686 Ученик ответил: «Корень  в квадрате  из 256 равен шестнадцати.Алексмарсело
1602299 Свинья фыркнула, пока  копалась вокруг  в поисках трюфелей. человек600
322003 В школе мы узнали, что квадрат  корня  из девяти равен трем.  СК
1101266  Пиво Root  считается классическим американским безалкогольным газированным напитком. СК
954283 Некоторые люди говорят, что человеческая природа  корень  для неудачника. СК
323856  Корень  проблемы - отсутствие связи между отделами. корвард
3219557 Коренная   причина проблем Мэри — это то, как с ней обращались в детстве.Патгфишер


 

корень | математика | Britannica

root , в математике решение уравнения, обычно выражаемое числом или алгебраической формулой.

В IX веке арабские писатели обычно называли один из равных множителей числа jadhr («корень»), а их средневековые европейские переводчики использовали латинское слово radix (от которого происходит прилагательное radix ). . Если a — положительное действительное число, а n — положительное целое число, то существует уникальное положительное действительное число x такое, что x ⁿ  =  a . Это число — (основной) n -й корень из a — записывается как ⁿ Квадратный корень из √ a или a ^{1/ n} . Целое число n называется индексом корня. Для n  = 2 корень называется квадратным корнем и записывается Квадратный корень из √ a . Корень ³ Квадратный корень из √ из называется кубическим корнем из из . Если a отрицательное, а n нечетное, единственный отрицательный корень n -й из a называется главным.Например, главный кубический корень из –27 равен –3.

Викторина Британника

Числа и математика

A-B-C, 1-2-3… Если вы считаете, что подсчет чисел похож на чтение алфавита, проверьте, насколько свободно вы владеете языком математики в этом тесте.

Если целое число (целое положительное) имеет рациональный корень n -й степени — i.т. е. такую, которую можно записать в виде обыкновенной дроби, — тогда этот корень должен быть целым числом. Таким образом, 5 не имеет рационального квадратного корня, потому что 2 ² меньше 5, а 3 ² больше 5. Ровно n комплексных чисел удовлетворяют уравнению x ⁿ  = 1, и они назвал комплекс н -й корнями единства. Если правильный многоугольник из n сторон вписан в единичную окружность с центром в начале координат так, что одна вершина лежит на положительной половине оси x , радиусы вершин являются векторами, представляющими комплекс n н -й корни единства.Если корень, вектор которого образует наименьший положительный угол с положительным направлением оси x , обозначить греческой буквой омега, ω, то ω, ω ² , ω ³ , …, ω _ⁿ  = 1 составляют все n -й корней из единицы. Например, ω = — ¹ / 2 + ^{квадратный корни of√ -3} / ₂ , ω ² = — ¹ / ₂ — ^{квадратный корень из√ -3} / ₂ и ω ³  = 1 — кубические корни из единицы.Любой корень, обозначаемый греческой буквой эпсилон, ε, обладающий тем свойством, что ε, ε ² , …, ε ⁿ  = 1 дает все n -е корни из единицы, называется примитивным. Очевидно, задача нахождения n -го корня из единицы эквивалентна задаче вписания правильного многоугольника с n сторонами в окружность. Для каждого целого числа n можно определить n -й корень из единицы в терминах рациональных чисел с помощью рациональных операций и радикалов; но их можно построить с помощью линейки и циркуля (т.т. е., определяемые в терминах обычных арифметических операций и квадратных корней), только если n является произведением различных простых чисел вида 2 ^h + 1, или 2 ^k , умноженных на такое продукта или имеет вид 2 ^к . Если a комплексное число, отличное от 0, уравнение x ⁿ  =  a имеет ровно n корней, и все n -го корня a из этих корней на n -й корней из единицы.

Термин , корень , был перенесен из уравнения x ⁿ  =  a во все полиномиальные уравнения. Таким образом, решение уравнения F ( x ) = A ₀ N + A 1 1 x ^{N — 1} + … + A N — 1 N — 1 x + N _{N 6 = 0, с A 0 ≠ 0, называется корнем уравнения.Если коэффициенты лежат в комплексном поле, уравнение n -й степени имеет ровно n (не обязательно различных) комплексных корней. Если коэффициенты вещественные, а n нечетное, то корень вещественный. Но уравнение не всегда имеет корень в поле коэффициентов. Таким образом, x ²  − 5 = 0 не имеет рационального корня, хотя его коэффициенты (1 и –5) являются рациональными числами.}

В более общем смысле термин корень может применяться к любому числу, которое удовлетворяет любому заданному уравнению, будь то полиномиальное уравнение или нет.Таким образом, π является корнем уравнения x  sin ( x ) = 0.

Самый быстрый словарь в мире | Vocabulary.com

корень слова форма слова после удаления всех аффиксов

письменное слово письменная форма слова

корневая гниль Болезнь, характеризующаяся загниванием корней; вызванные различными грибами

Редфорд Американский актер и режиссер, сыгравший вместе с Полом Ньюманом в нескольких фильмах (1936 г. р.)

палаш меч с широким лезвием и двумя режущими кромками

доброе слово то, что рекомендует (или выражает одобрение) человека или вещь как достойного или желательного

зубатка североамериканская трава с острыми чешуйчатыми или зубчатыми корнями

root для поддержки или присоединения к

хорда гибкая стержнеобразная структура, образующая опорную ось тела у низших хордовых и низших позвоночных, а также у зародышей высших позвоночных

ругательство оскорбительное или неприличное слово или фраза

54″>

корневой волос тонкий волосовидный отросток эпидермальной клетки сразу за кончиком; поглощает питательные вещества из почвы

рутбир газированный напиток, содержащий экстракты кореньев и трав

пустырник горький трава Старого Света, произрастающая на живых изгородях и опушках лесов, с зубчатыми листьями и белыми или бледно-розовыми цветками

подножка узкая платформа, на которой можно стоять или упираться ногами

корнеплоды, выращенные для расширения корней: e.г. свекла

абсолютно неподвижен

укоренившиеся со спутанными или плотно спутанными корнями

54″>

переформулировать одно и то же сообщение другими словами

получить известие узнать или узнать

120 корневых слов, префиксов и суффиксов Список в формате PDF

корпус

ped	футов	педаль, пешеходная, шагомер
фобия	страх	клаустрофобия, гидрофобия, арахнофобия
тел.	звук	телефон, саксофон, микрофон
фото	свет	фотон, фотография, фотосинтез
физ	; природа	врач, физик, телосложение
плекс	деталей; ед.	комплекс, кинозал, дуплекс
поли	много	полигон, политеизм, полиграф
порт	нести	аэропорт, транспорт, импорт
поз.	поставить; место	позиция, составление, депозит
пост	после	апостериор, постскриптум, отложить
до	до	предварительная игра, предварительный просмотр, предоплата
псих	ум	психология, экстрасенс, психиатр
четырехъядерный	четыре	четверной, квадрантный, квадратичный
по	снова	восстановить, возместить, обновить
ретро	задняя часть; назад	ретроспективный, ретроактивный, ретроградный
разрыв	перерыв	прерывать, прерывать, извергать
прицел	вид; см.	перископ, зрительная труба, микроскоп
сценарий/письмо	написать	набросать, прописать, рукопись
раздел	вырезать	сечение, рассечение, пересечение
полуфабрикат	половина	полукруг, полуфинал, точка с запятой
чувств/отправлено	чувствовать	сентиментальный, чувствительный, согласие
социальный	человек	социология, социальная, ассистент
соль	один	соло, одинокий, пустынный
спец.	см.	осмотр, зрелище, зритель
спираль	дышать	сговариваться, вдохновлять, дышать
структура	сборка	строительство, структура, инструкция
суб	под	метро, ​​подводная лодка, подзаголовок
супер	окончено; больше	начальник, надзиратель, наложение
синхрон/символ	с; вместе	симпатия, синоним, симптом
технический	ремесло; навык	техника, технология, техник
теле	далеко	телевизор, телефон, телескоп
земля/земля	земель; земля	местность, терраса, территория
те/тео	год	теология, монотеизм, политеизм
терм	тепло	термометр, термос, гипотермия
ция	действие; состояние бытия	заражение, добавление, праздник
тракт	тяга; тянуть	притягивать, вычитать, сжимать
транс	в поперечнике; через	преобразование, транзакция, перевод
три	три	штатив, трехколесный, тройной
и	не	несчастный, нездоровый, опасный
универсальный	один	одноколесный велосипед, единый, объединенный
вакуум	пустой	вакуум, вакуум, вакуум
или	как	предотвратить, место проведения, изобрести
верт/верс	очередь	разговор, интроверт, обратный
видео/видео	см.	видимое, видео, телевидение
зоопарк	животное	зоология, смотритель зоопарка, зоопарк

Квадратный корень – формула, примеры

Квадратный корень числа — это операция, обратная возведению числа в квадрат.Квадрат числа — это значение степени 2 числа, а квадратный корень числа — это число, которое нам нужно умножить само на себя, чтобы получить исходное число. Если «а» — это квадратный корень из «b», это означает, что a×a=b. Квадрат любого числа всегда является положительным числом, поэтому каждое число имеет два квадратных корня, одно положительное значение и одно отрицательное значение. Например, и 2, и -2 являются квадратными корнями из 4. Но в большинстве случаев вы обнаружите, что только положительное значение записывается как квадратный корень.

Что такое квадратный корень?

Квадратный корень числа — это число, которое умножается само на себя, чтобы получить произведение. Мы узнали о показателях. Квадраты и квадратные корни являются специальными показателями. Рассмотрим число 9. Когда 3 умножается само на себя, получается 9 как произведение. Когда показатель степени равен 2, он называется квадратом. Когда показатель степени равен 1/2, он называется квадратным корнем. Например, √(n × n) = √n ² = n, где n — целое положительное число.

Определение квадратного корня

Квадратный корень числа равен степени 1/2 этого числа. Другими словами, это число, которое мы умножаем само на себя, чтобы получить исходное число. Он представлен с помощью символа «√». Символ квадратного корня называется радикалом, тогда как число под символом квадратного корня называется радикалом, который используется для представления квадратного корня любого натурального числа.

Методы нахождения квадратного корня из чисел

Очень легко найти квадратный корень из числа, являющегося полным квадратом.Совершенные квадраты — это те положительные числа, которые можно записать как произведение числа самого на себя. другими словами, совершенные квадраты — это числа, равные степени 2 любого целого числа. Мы можем использовать четыре метода, чтобы найти квадратный корень из чисел , и эти методы следующие:

• Повторное вычитание квадратного корня
• Извлечение квадратного корня методом простой факторизации
• Квадратный корень по методу оценки
• Извлечение квадратного корня методом деления в длину

Обратите внимание, что первые три метода удобно использовать для идеальных квадратов, а четвертый метод, т.е.Метод длинного деления можно использовать для любого числа, независимо от того, является ли оно полным квадратом или нет.

Метод многократного вычитания квадратного корня

Это очень простой метод. Мы будем вычитать последовательные нечетные числа из числа, для которого мы находим квадратный корень, пока не достигнем 0. Количество раз, которое мы вычитаем, является квадратным корнем данного числа. Этот метод работает только для совершенных квадратных чисел. Найдем квадратный корень из 16, используя этот метод.

• 16 — 1 = 15
• 15 — 3 =12
• 12 — 5 = 7
• 7- 7 = 0

Вы можете заметить, что мы вычли 4 раза.Таким образом, √16 = 4

Извлечение квадратного корня методом простой факторизации

Разложение любого числа на простые множители означает представление этого числа как произведения простых чисел. Чтобы найти квадратный корень заданного числа с помощью метода простой факторизации, мы следуем шагам, указанным ниже:

• Шаг 1: Разделите заданное число на его простые множители.
• Шаг 2: Сформируйте пары одинаковых множителей так, чтобы оба множителя в каждой паре были равны.
• Шаг 3: Возьмите один множитель из пары.
• Шаг 4: Найдите произведение множителей, полученных путем взятия одного множителя из каждой пары.
• Шаг 5: Это произведение равно квадратному корню из заданного числа.

Найдем квадратный корень из 144 этим методом.

Этот метод работает, когда заданное число является числом в идеальном квадрате.

Квадратный корень по методу оценки

Оценка и аппроксимация относятся к разумному предположению фактического значения, чтобы сделать расчеты более простыми и реалистичными.Этот метод помогает в оценке и аппроксимации квадратного корня из заданного числа. Воспользуемся этим методом, чтобы найти √15. Найдите числа с совершенным квадратом, ближайшие к 15. 9 и 16 — это числа с совершенным квадратом, ближайшие к 15. Мы знаем, что √16 = 4 и √9 = 3. Отсюда следует, что √15 лежит между 3 и 4. Теперь нам нужно посмотрим, ближе ли √15 к 3 или 4. Рассмотрим 3,5 и 4. 3,5 ² = 12,25 и 4 ² = 16. Таким образом, √15 лежит между 3,5 и 4 и ближе к 4.

Найдем квадраты числа 3.8 и 3. 9. 3,8 ² = 14,44 и 3,9 ² = 15,21. Это означает, что √15 находится между 3,8 и 3,9. Мы можем повторить процесс и проверить между 3,85 и 3,9. Мы можем заметить, что √15 = 3,872.

Это очень долгий и трудоемкий процесс.

Извлечение квадратного корня методом деления в длину

Длинное деление — это метод деления больших чисел на шаги или части, разбивающий задачу деления на последовательность более простых шагов. С помощью этого метода мы можем найти точный квадратный корень из любого заданного числа.Давайте разберемся с процессом нахождения квадратного корня методом деления в длину на примере. Найдем квадратный корень из 180.

• Шаг 1: Поместите черту над каждой парой цифр числа, начиная с разряда единицы (крайняя правая сторона). У нас будет две пары, т.е. 1 и 80
• Шаг 2: Мы делим крайнее левое число на наибольшее число, квадрат которого меньше или равен числу в самой левой паре.

Шаг 3: Опустите число под следующей чертой справа от остатка.Прибавьте к делителю последнюю цифру частного. Справа от полученной суммы найдите подходящее число, которое вместе с результатом суммы образует новый делитель для нового делимого, переносимого вниз.

Шаг 4: Новое число в частном будет иметь то же число, которое было выбрано в делителе. Условие то же — либо меньше, либо равно дивиденду.

Шаг 5: Теперь мы продолжим этот процесс дальше, используя десятичную точку и добавляя нули попарно к остатку.

Шаг 6: Полученное частное будет квадратным корнем числа.

Таблица квадратного корня

Таблица квадратных корней содержит числа и их квадратные корни. Также полезно находить квадраты чисел. Вот список квадратных корней совершенных квадратных чисел и некоторых несовершенных квадратных чисел от 1 до 10.

Номер	Квадратный корень
1	1
2	1.414
3	1,732
4	2
5	2,236
6	2,449
7	2,646
8	2.828
9	3
10	3,162

Квадратные корни чисел, которые не являются полными квадратами, являются частью иррациональных чисел.

Формула квадратного корня

Квадратный корень есть не что иное, как показатель степени 1/2. Формула квадратного корня используется для нахождения квадратного корня из числа.Мы знаем формулу экспоненты: \(\sqrt[\text{n}]{x}\) = x ^1/n . Когда n=2, мы называем это квадратным корнем. Мы можем использовать любой из вышеперечисленных методов для нахождения квадратного корня, например разложение на простые множители, длинное деление и так далее. 9 ^1/2 = √9 = √(3×3) = 3. Итак, формула для записи квадратного корня числа: √x= x ^1/2 .

Как упростить квадратный корень?

Чтобы упростить квадратный корень, нам нужно найти простую факторизацию данного числа.Если фактор нельзя сгруппировать, сохраните его под символом квадратного корня. Правило упрощения квадратного корня: √xy = √(x × y), где x и y — положительные целые числа. Например: √12 = \(\sqrt{2 \times 2\times3}\) = 2√3

Для дробей также действует аналогичное правило: √x/√y = √(x/y). Например: √50/√10 = √(50/10)= √5

Квадратный корень из отрицательного числа

Квадратный корень из отрицательного числа не может быть действительным числом, так как квадрат является либо положительным числом, либо нулем.Но у комплексных чисел есть решения квадратного корня из отрицательного числа. Главный квадратный корень -x равен: √(-x)= i√x. Здесь i — квадратный корень из -1.

Например: возьмем квадратное число, например 16. Теперь давайте посмотрим на квадратный корень из -16. Настоящего квадратного корня из -16 не существует. √(-16)= √16 × √(-1) = 4i (как √(-1)= i), где i представлено как квадратный корень из -1. Итак, 4i — это квадратный корень из -16.

Квадрат числа

Любое число, возведенное в степень два (y ² ), называется квадратом основания.Итак, 5 ² называется квадратом числа 5, а 8 ² — квадратом числа 8. Мы можем легко найти квадрат числа, умножив основание два раза. Например, 5 в квадрате — это 5×5=25, а 8 в квадрате — это 8×8=64. Когда мы находим квадрат целого числа, полученное число является одним из совершенных квадратов. Некоторые из наших идеальных квадратов: 4, 9, 16, 25, 36, 49, 64 и так далее. Квадрат числа, независимо от того, положительное оно или отрицательное, всегда является положительным числом.

Как найти квадрат числа?

Квадрат числа можно найти, умножив число само на себя. Для однозначных чисел мы можем использовать таблицы умножения, чтобы найти квадрат, а в случае двух или более двузначных чисел мы выполняем умножение числа само по себе, чтобы получить ответ. Например, 9×9=81, где 81 — это квадрат 9. Аналогично, 3×3 = 9, где 9 — это квадрат 3.

Связанные статьи

Ниже приведен список тем, которые тесно связаны с квадратными корнями.

Квадратный корень из чисел

Часто задаваемые вопросы о квадратном корне

Что такое квадратный корень в математике?

Квадратный корень — это число, которое нам нужно умножить само на себя, чтобы получить исходное число. Например, 2 — это квадратный корень из 4, так как 2 × 2 = 4.

☛ Чек:

Как найти квадратный корень из числа?

Квадратный корень из числа можно найти любым из четырех способов, приведенных ниже:

• Метод повторного вычитания
• Метод простой факторизации
• Метод оценки и приближения
• Метод длинного деления.

Как найти квадратный корень из десятичного числа?

Квадратный корень из десятичного числа можно найти с помощью метода оценки или метода деления в большую сторону. В случае десятичных чисел мы делаем пары целых частей числа и дробных частей отдельно. И затем, мы выполняем процесс деления в длинную точно так же, как и любое другое целое число.

Может ли квадратный корень быть отрицательным?

Квадратный корень числа может быть отрицательным. Фактически, все совершенные квадраты, такие как 4, 9, 25, 36 и т. д., имеют два квадратных корня, одно положительное значение и одно отрицательное значение. Квадратные корни из 4 равны -2 и 2. Точно так же квадратные корни из 9 равны 3 и -3.

Что вы называете символом квадратного корня?

Символ, используемый для обозначения квадратного корня, называется подкоренным знаком ‘√ ‘. Термин, написанный внутри подкоренного знака, называется подкоренным.

Что такое формула для вычисления квадратного корня числа?

Квадратный корень из любого числа можно выразить по формуле: √y = y ^½ .

Что такое квадрат и квадратный корень числа?

Квадрат и квадратный корень числа являются обратной операцией друг друга.Если возвести в квадрат число z как (z×z) z ² , то квадратный корень из z ² , т. е. √z равен числу z.

Какой метод используется для нахождения квадратного корня из неполных квадратных чисел?

В математике несовершенным или несовершенным квадратным числом считается число, представленное в десятичной форме. Квадратный корень из несовершенного квадратного числа можно вычислить, используя метод деления в длинную сторону.

Как упростить квадратный корень на калькуляторе?

Чтобы найти значение квадратного корня любого числа, нам просто нужно сначала вставить символ квадратного корня √x в калькулятор и ввести число x.

☛ Чек:

Как умножить два значения квадратного корня?

Допустим, у нас есть два числа a и b. Сначала найдем квадратный корень из чисел a и b. Затем, найдя квадратный корень, мы умножим значение квадратного корня вместе. Поясним это на практической иллюстрации.
Квадратный корень из 4 равен 2, а квадратный корень из 16 равен 4. Теперь мы умножим значение квадратного корня из 4 и 16, т. е. 2 × 4 = 8.

Каковы применения формулы квадратного корня?

Существуют различные применения формулы квадратного корня

• Формула квадратного корня в основном используется в алгебре и геометрии.Помогает найти корни квадратного уравнения.
• Мы можем легко вычислить площадь, объем и другие измерения, используя формулу квадратного корня.
• Широко используется инженерами.

Что такое символ квадратного корня?

Символ квадратного корня также называется радикалом, который обозначается как ‘√ ‘, а число внутри символа называется подкоренной.

квадратных корней — объяснение и примеры

В математике квадратный корень из числа x таков, что число y является квадратом x, упрощенно записывается как y ²  = x.

Например, 5 и -5 являются квадратными корнями из 25, потому что:

5 x 5 = 25 и -5 x -5 = 25.

Квадратный корень из числа x обозначается знаком корня √x или x ^1/2 . Например, квадратный корень из 16 представлен как: √16 = 4. Число, квадратный корень которого вычисляется, называется подкоренным числом. В этом выражении √16 = 4 число 16 является подкоренным числом.

Что такое квадратный корень?

Квадратный корень — это операция, обратная возведению числа в квадрат.Другими словами, квадратный корень — это операция, которая отменяет показатель степени 2.

Свойства

• Совершенное квадратное число имеет совершенный квадратный корень.
• Четное совершенное число имеет четный квадратный корень.
• Нечетное совершенное число имеет нечетный квадратный корень.
• Квадратный корень из отрицательного числа не определен.
• Только числа, заканчивающиеся четным числом нулей, имеют квадратный корень.

 

Как найти квадратный корень из чисел?

Есть несколько способов найти квадрат чисел.Мы увидим несколько здесь.

Повторное вычитание

Этот метод включает в себя успешное и многократное вычитание из числа нечетных чисел, таких как 1, 3, 5 и 7, до тех пор, пока не будет достигнут ноль. Квадрат числа равен количеству или частоте вычитания числа

Предположим, нам нужно вычислить квадрат совершенного числа, такого как 25, операция выполняется так:

—15 = 16 9 — 7 9 — 9

25 — 1	= 24	= 24
24 -3	= 21	= 21
21 -5	= 16	= 9	9 — 9	= 0

Вы можете заметить, что частота вычитания равна 5, поэтому квадратный корень из 25 равен 5.

Факторизация простых чисел

В этом методе число с полным квадратом разлагается на множители путем последовательного деления. Простые множители группируются в пары, и вычисляется произведение каждого числа. Таким образом, произведение равно квадратному корню из числа. Чтобы найти квадрат совершенного числа, такого как: 144, выполните следующее:

• 144 = 2 × 2 × 2 × 2 × 3 × 3.
• Соедините простые множители.
• Выбор одного числа из каждой пары.
• 2 × 2 × 3 = 12.
• Таким образом, √144 = 12.

Метод деления

Метод деления является подходящим методом вычисления квадрата большого числа. Ниже приведены необходимые шаги:

• Над каждой парой цифр, начиная с правой стороны, ставится черта.
• Разделите число в левом конце на число, квадрат которого меньше или эквивалентен числам под левым концом.
• Возьмите это число как делитель и частное. Точно так же возьмите крайнее левое число в качестве делимого
• Разделите, чтобы получить результат
• Опустите следующее число с чертой справа от остатка
• Умножьте делитель на 2.
• Справа от этого нового делителя найдите подходящее делимое. Этот процесс повторяется до тех пор, пока мы не получим ноль в качестве остатка. Следовательно, квадрат числа равен частному.

Квадратный корень из 225 вычисляется как

• Начинайте деление с крайней левой стороны.
• В данном случае 1 — это наше число, квадрат которого меньше 2.
• Присвоение 1 в качестве делителя и частного и умножение на 2 дает:
• Выполните шаги, чтобы получить 15 в качестве частного.

Анализ первопричин: определение, примеры и методы

Как провести эффективный анализ основных причин: приемы и методы

Существует большое количество методов и стратегий, которые мы можем использовать для анализа первопричин, и это ни в коем случае не исчерпывающий список. Ниже мы рассмотрим некоторые из наиболее распространенных и широко полезных методов.

5 почему

Одним из наиболее распространенных методов анализа первопричин является подход «5 почему». Мы также можем думать об этом как о раздражающем подходе малыша. За каждым ответом на вопрос ПОЧЕМУ следует дополнительный, более глубокий вопрос «Хорошо, но ПОЧЕМУ?» вопрос. Дети удивительно эффективны в анализе первопричин. Здравый смысл подсказывает, что около пяти вопросов «ПОЧЕМУ?» могут привести нас к большинству основных причин, но нам может понадобиться от двух до 50 «ПОЧЕМУ?». Пример: Давайте вернемся к нашему примеру с сотрясением мозга в футболе. Во-первых, наш игрок представит проблему: почему у меня такая сильная головная боль? Это наше первое ПОЧЕМУ.Первый ответ: Потому что я не могу видеть прямо. Второе почему: Почему ты не видишь прямо? Второй ответ: Потому что я ударился головой о землю. Третье почему: Почему твоя голова ударилась о землю? Третий ответ: меня повалили на землю и сильно ударили головой. В-четвертых, почему: Почему так больно ударяться о землю? Четвертый ответ: Потому что я был без шлема. Пятое почему: Почему ты был без шлема? Пятый ответ: потому что у нас не хватило шлемов в раздевалке.Ага. После этих пяти вопросов мы обнаруживаем, что основной причиной сотрясения мозга, скорее всего, было отсутствие шлемов. В будущем мы могли бы снизить риск такого типа сотрясения мозга, убедившись, что у каждого футболиста есть шлем. (Конечно, шлемы не защищают нас от сотрясений мозга. Будьте в безопасности!) «5 почему» помогают избежать предположений. Находя подробные ответы на дополнительные вопросы, ответы с каждым разом становятся все более четкими и краткими. В идеале последнее ПОЧЕМУ приведет к неудачному процессу, который затем можно будет исправить.

Анализ изменений/анализ событий

Еще один полезный метод анализа первопричин — тщательный анализ изменений, приведших к событию. Этот метод особенно удобен, когда существует большое количество потенциальных причин. Вместо того, чтобы смотреть на конкретный день или час, когда что-то пошло не так, мы смотрим на более длительный период времени и получаем исторический контекст. 1. Во-первых, мы бы перечислили все возможные причины, приведшие к событию. Это должно быть каждый раз, когда происходило изменение к лучшему или худшему или к доброкачественному. Пример: Допустим, событие, которое мы собираемся проанализировать, представляет собой необычайно успешный день распродаж в Нью-Йорке, и мы хотели узнать, почему оно было таким замечательным, чтобы попытаться воспроизвести его. Во-первых, мы бы перечислили каждую точку контакта с каждым из основных клиентов, каждое событие, каждое возможно значимое изменение. 2. Во-вторых, мы бы классифицировали каждое изменение или событие по степени нашего влияния на него. Мы можем классифицировать как внутренние/внешние, собственные/не принадлежащие или что-то подобное. Пример: В нашем замечательном примере с днем ​​продаж мы начали бы сортировать такие вещи, как «Представитель отдела продаж представил новую презентацию о социальном влиянии» (внутреннее) и другие события, такие как «Последний день квартала» (внешнее) или « Первый день весны» (Внешний). 3. В-третьих, мы переходили от события к событию и решали, было ли это событие несвязанным фактором, коррелирующим фактором, способствующим фактором или вероятной первопричиной. Именно здесь происходит основная часть анализа, и именно здесь можно использовать другие методы, такие как «5 почему». Пример: В ходе нашего анализа мы обнаруживаем, что наша модная новая презентация по продажам была на самом деле несвязанным фактором, но тот факт, что это был конец квартала, определенно способствовал этому. Тем не менее, один фактор был определен как наиболее вероятная основная причина: руководитель отдела продаж в этом районе переехал в новую квартиру с более короткими поездками на работу, а это означает, что она начала появляться на встречах с клиентами на 10 минут раньше в течение последней недели квартала. 4. В-четвертых, мы смотрим, как мы можем воспроизвести или устранить первопричину. Пример: Хотя не все могут переехать в новую квартиру, наша организация решила, что если торговые представители появятся на встречах с клиентами на 10 минут раньше в последнюю неделю квартала, они смогут повторить этот успех основной причины.

Причина и следствие Диаграмма Fishbone

Еще один распространенный метод — создание диаграммы «рыбья кость», также называемой диаграммой Исикавы, для визуального сопоставления причин и следствий. Это может помочь определить возможные причины проблемы, побуждая нас следовать категорическим разветвленным путям к потенциальным причинам, пока мы не окажемся на правильном пути.Это похоже на 5 Почему, но гораздо более наглядно. Обычно мы начинаем с проблемы в середине диаграммы (позвоночник рыбьего скелета), затем проводим мозговой штурм по нескольким категориям причин, которые затем помещаем в ответвления от основной линии (реберные кости рыбьего скелета). . Категории очень широкие и могут включать такие вещи, как «Люди» или «Окружающая среда». После группировки категорий мы разбиваем их на более мелкие части. Например, в разделе «Люди» мы можем рассмотреть потенциальные первопричинные факторы, такие как «руководство», «укомплектование кадрами» или «обучение».По мере того, как мы углубляемся в потенциальные причины и подпричины, подвергая сомнению каждую ветвь, мы приближаемся к источникам проблемы. Мы можем использовать этот метод, удаляя несвязанные категории и определяя коррелирующие факторы и вероятные первопричины. Для простоты внимательно рассмотрите категории, прежде чем создавать диаграмму. Общие категории для рассмотрения в диаграмме Fishbone:

• Машина (оборудование, технология)
• Метод (процесс)
• Материал (включая сырье, расходные материалы и информацию)
• Человек/умственная сила (физическая или умственная работа)
• Измерение (осмотр)
• Миссия (цель, ожидание)
• Управление / власть денег (лидерство)
• Техническое обслуживание
• Товар (или услуга)
• Цена
• Продвижение (маркетинг)
• Процесс (системы)
• Люди (персонал)
• Вещественные доказательства
• Производительность
• Окружение (место, окружающая среда)
• Поставщики
• Навыки

Советы по эффективному анализу первопричин

Задавайте вопросы, чтобы уточнить информацию и приблизить нас к ответам. Чем больше мы сможем детализировать и изучить каждую потенциальную причину, тем больше вероятность, что мы найдем основную причину. Как только мы поверим, что определили первопричину проблемы (а не просто еще один симптом), мы можем задать еще больше вопросов: почему мы уверены, что это первопричина, а не это? Как мы можем исправить эту основную причину, чтобы предотвратить повторение проблемы? Используйте простые вопросы, такие как «почему?» «как?» и «что это здесь значит?» проложить путь к пониманию.

Работайте в команде и смотрите свежим взглядом

Будь то просто партнер или целая команда коллег, любые дополнительные глаза помогут нам быстрее найти решения, а также послужат проверкой от предвзятости.Получение информации от других также предложит дополнительные точки зрения, помогая нам бросить вызов нашим предположениям.

План будущего анализа основных причин

Когда мы проводим анализ первопричин, важно знать о самом процессе. Записывать. Задавайте вопросы о самом процессе анализа. Узнайте, подходит ли определенный метод или метод лучше всего для ваших конкретных бизнес-потребностей и сред.

Не забывайте также проводить анализ основных причин успеха

Анализ первопричин — отличный инструмент для выяснения того, где что-то пошло не так.Обычно мы используем RCA как способ диагностики проблем, но он может быть столь же эффективным для поиска основной причины успеха. Если мы находим причину успеха, сверхдостижения или преждевременного дедлайна, редко бывает плохой идеей выяснить основную причину того, почему дела идут хорошо. Такой анализ может помочь расставить приоритеты и упреждающе защитить ключевые факторы, и мы сможем перевести успех в одной области бизнеса на успех в другой области.

.