Корень математический: Задачи по школьной математике. Квадратный корень
Арифметический корень в математике с примерами решения и образцами выполнения
Если а есть положительное рациональное число, представляющее собой точный квадрат, то арифметический квадратный корень из него есть положительное рациональное число. Например:
Если положительное рациональное число Q не представляет собой точного квадрата, то арифметический квадратный корень из него есть положительное иррациональное число. Например:
суть числа иррациональные.
Сказанное относительно арифметического квадратного корня распространяется соответствующим образом на кубические корни и на корни любой степени. Например:
Корни суть числа иррациональные.
Действительные корни нечетных степеней из отрицательного числа суть числа отрицательные. Например:
Действительных корней четной степени из отрицательных чисел не существует.
Например, не существует такого действительного числа q, чтобы равенство
было справедливым.
В самом деле, будет положительным числом и тогда, когда q положительно, и тогда, когда q отрицательно.
Поэтому т. е. символ не представляет собой никакого действительного числа.
Арифметические корни из степенейОчевидно, что
Правило. Если подкоренное выражение представляет степень положительного числа а и при этом показатель этой степени делится на показатель корня, то арифметический корень будет равен степени, основанием которой служит а, а показателем — частное от деления показателя степени, стоящей под корнем, на показатель корня.
Действительно,
Примеры:
О выражении
Если а > 0, то
Если же а < 0, то
Во всех случаях
Например,
О выражении
Из определения следует, что
Действительно, пусть
Тогда
Подставляя вместо q равное ему выражение получим
что и требовалось доказать.
Примеры:
Основное свойство арифметического корня
Вспомогательные предложенияОпределение:
Если М и N два различных действительных числа, то М> N, если разность М— N есть число положительное.
Предложение 1-е.
Если А > В и m>0, то Am>Вm.
Доказательство:
Разность Am — Вm можно записать в виде
По условию А — В > 0 и m > 0, следовательно, разность Am — Вm есть число положительное, а это и значит, что Am > Вm
Предложение 2-е.
Если а > b и с > d и при этом все числа а, b, с, d положительные, то
Доказательство:
Из того, что а > b и с > 0 следует ас > bc. Из того, что
Из того, что
с > d и b > О следует bc > bd. Из того, что ас>bс и bc>bd следует, что ac>bd, что и требовалось доказать.
Предложение 3-е.
Если х > у и при этом числа х, у
Доказательство:
Из того, что х > у и х>0 следует
Из того, что х > у и у > 0 следует
Из того, что и следует
Продолжая аналогичные рассуждения, получим:
что и требовалось доказать.
Предложение 4-е.
Если и числа х и у положительные, то х = у.
Доказательство. Предположим, что х> у, тогда что противоречит условию. Предположим, что у > х, тогда что также противоречит условию. Значит, не может быть, чтобы числа х к  Как раз это и требовалось доказать.
Как раз это и требовалось доказать.
Примечание:
Из равенства не всегда следует равенство х = у. Например, равенство является верным, хотя числа+ 5 и — 5 не равны друг другу.
Формулировка основного свойства арифметического корняАрифметическое значение корня не изменится, если показатель корня умножить на натуральное число, а подкоренное выражение возвысить в степень этого же натурального числа, т. е.
(q и р — натуральные числа и Q 0).
Доказательство:
Очевидно, что (см. стр. 270). Также очевидно, что
Две величины, порознь равные третьей, равны между собой. Поэтому
Но так как числа — положительны, то
что и требовалось доказать.
Примеры:
Основное свойство арифметического корня позволяет нам сокращать показатель корня в тех случаях, когда это возможно.
Примеры:
Основное свойство арифметического корня позволяет нам приводить к общему показателю корни, имеющие разные показатели.
Примеры:
Корни можно заменить соответственно следующими корнями
Корни можно заменить соответственно корнями
Корни можно заменить соответственно корнями
Корни можно заменить соответственно корнями
Чтобы определить, какое из двух чисел, например, или больше, приведем эти корни к общему показателю:
Ясно, что
Действия над арифметическими корнями
УмножениеПроизведение корней, имеющих одинаковые показатели, равно корню с тем же показателем из произведения подкоренных выражений перемножаемых корней, т. е.
(n — число натуральное, а и b — числа положительные).
Доказательство:
Очевидно, что
Tакже очевидно, что
Две величины, порознь равные третьей, равны между собой. Поэтому
Поэтому
Но так как числа положительные, то
что и требовалось доказать.
Совершенно аналогичным путем можно доказать правила для других действий.
Другие действия(Правило деления корней, имеющих одинаковые показатели.)
(Правило возведения корня в степень.)
(Правило извлечения корня из корня.)
Учащемуся предлагается самостоятельно сформулировать и доказать каждое из трех последних правил.
Примечание:
Обратим внимание на то, что равенство
справедливо лишь при условии, что а > 0. (При не будет действительным числом.)
Примеры:
Правило. Чтобы перемножить или разделить корни, имеющие разные показатели, необходимо привести эти корни предварительно к общему показателю.
Примеры:
Запишем равенство в обратном порядке:
Отсюда правило: корень из произведения равен произведению корней из сомножителей.
Пример:
Аналогично
Пример:
Некоторые важные преобразования
Вывод множителей из-под знака корняПусть а и b — положительные числа. Тогда
Рассмотрим выражение
Пусть при делении числа m на n получается в частном k, а в остатке r. Тогда и мы получим
Пусть a — отрицательное число, а b — положительное. Тогда
Итак, если подкоренное выражение разлагается на такие множители, что из некоторых можно извлечь точный корень, то такие множители по извлечении из них корня могут быть выведены из-под знака корня в качестве множителей.
Пусть а и b — положительные числа. Тогда
Пусть а — отрицательное число, а b — положительное. Тогда
Тогда
Пусть а и b — положительные числа. Тогда
Устранение иррациональности в знаменателе дробиУстранить иррациональность в знаменателе дроби — это значит преобразовать дробь, знаменатель которой содержит корни, к новой дроби, знаменатель которой корней не содержит.
а) Случай, когда знаменатель есть корень.
б) Случай, когда знаменатель есть сумма или разность, содержащая квадратные корни.
в) Случай, когда знаменатель есть сумма или разность, содержащая кубические корни.
Устранение иррациональности в числителе дробиУстранить иррациональность в числителе дроби — это значит преобразовать дробь, числитель которой содержит корни, к новой дроби, числитель которой корней не содержат.
Эта операция производится аналогично тому, как и операции, указанные в предыдущем пункте. Например:
Нормальный вид корня
Корень считается приведенным к нормальному виду, если:
1) возможные множители вынесены за знак корня;
2) подкоренное выражение приведено к целому виду;
3) показатель корня и показатель степени подкоренного выражения сделаны взаимно простыми.
Примеры:
Подобные корни и их приведение
Корни называются подобными, если после приведения их к нормальному виду окажутся одинаковыми как их подкоренные выражения, так и показатели корней.
Примеры:
Корни — подобны.
Действительно,
Корни — подобны. Действительно,
Корни подобны. Действительно,
Приведение подобных корнейПримеры:
При извлечении корня из суммы нельзя производить извлечение корней из слагаемых, т. е. нельзя писать
е. нельзя писать
Например:
Отсюда видно, что
Преобразование сложного корня
Выражения вида
называются сложными корнями.
Теорема:
Если а > 0, b > 0 и то верны формулы
Докажем справедливость первой формулы. Очевидно, что
С другой стороны,
Две величины, порознь равные третьей, равны между собой. Поэтому
Основания этих квадратов положительны, а поэтому
что и требовалось доказать.
Совершенно так же доказывается и вторая формула.
Доказанные формулы представляют особый интерес в том случае, когда разность представляет собой точный квадрат. В этом случае сложный корень представляется в виде суммы или разности двух несложных корней. Например:
Замечание:
Корни иногда называют радикалами.
есть радикал n-й степени. Символ eсть знак радикала n-й степени.
Символ eсть знак радикала n-й степени.
Корнем n-й степени из числа а называется всякое число х, n-я степень которого равна а.
Правило нахождения всех значений корня n-й степени из любого числа изложено в гл. «Комплексные числа».
В настоящей главе мы изучали лишь арифметические значения корней.
О возможности нахождения арифметического корня с любой степенью точности
Мы покажем сейчас, что элементарным способом можно находить значение любого арифметического корня с любой степенью точности. Сущность этого способа раскроем на примере хотя бы
Пусть требуется найти Сначала среди чисел 1,0; 1,1; 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 2,0 найдем два таких рядом стоящих числа, чтобы куб левого был меньше 2, а куб правого — больше 2.
Очевидно, что Поэтому
Далее Значит,
Наконец, Значит,
Теперь можно сказать, что 1,2 будет приближенным значением с недостатком, а 1,3 с избытком, с точностью до .
Чтобы получить приближенные значения с точностью до , надо испытать числа
Этот процесс можно продолжить как угодно далеко и таким путем получить значение с любой степенью точности.
Изложенный элементарный способ имеет принципиальное значение, но не практическое. Практически пользоваться этим способом крайне неудобно, так как он слишком громоздок. Принципиальное же значение этого способа заключается в том, что он убеждает нас в возможности отыскания значений любого арифметического корня с любой степенью точности.
Для практического же вычисления значений любых арифметических корней существуют другие более удобные способы. Один из этих способов мы встретим в главе «Логарифмы».
Для нахождения приближенных значений часто встречающихся величин можно пользоваться готовыми таблицами. Пример подобной таблицы приведен ниже.
Таблица квадратов, кубов, корней квадратных, корней кубических и обратных величин
Такого рода таблицы, значительно более полные и с более высокой степенью точности, даны, например, в книге Барлоу: «Таблицы квадратов, кубов, корней квадратных, корней кубических и обратных величин».
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Корень (в математике) — «Энциклопедия»
КОРЕНЬ в математике,
1) степени n из числа а, число х такое, что хn = а. Действие нахождения корня называется извлечением корня. В области действительных чисел существует ровно один корень нечётной степени из любого действительного числа, причём корень из положительного числа положителен, а из отрицательного отрицателен. Корень чётной степени из положительного числа имеет два значения, равные по абсолютной величине и противоположные по знаку. Корень чётной степени из отрицательного числа в области действительных чисел не существует, потому что чётная степень любого действительного числа положительна. Положительный корень степени n из положительного числа а называется арифметическим корнем и обозначается n√а (√а при n = 2). Второй, отрицательный корень, существующий при чётном n, обозначается n√а. Если же рассматриваются оба значения корня, то перед знаком радикала ставится двойной знак, например √4= +2. В этом случае говорят об алгебраических значениях корня. Существует ровно один арифметический корень данной степени из данного положительного числа.
Действие нахождения корня называется извлечением корня. В области действительных чисел существует ровно один корень нечётной степени из любого действительного числа, причём корень из положительного числа положителен, а из отрицательного отрицателен. Корень чётной степени из положительного числа имеет два значения, равные по абсолютной величине и противоположные по знаку. Корень чётной степени из отрицательного числа в области действительных чисел не существует, потому что чётная степень любого действительного числа положительна. Положительный корень степени n из положительного числа а называется арифметическим корнем и обозначается n√а (√а при n = 2). Второй, отрицательный корень, существующий при чётном n, обозначается n√а. Если же рассматриваются оба значения корня, то перед знаком радикала ставится двойной знак, например √4= +2. В этом случае говорят об алгебраических значениях корня. Существует ровно один арифметический корень данной степени из данного положительного числа. Для числа 0 существует ровно один корень любой степени и он равен 0.
Для числа 0 существует ровно один корень любой степени и он равен 0.
Реклама
В области комплексных чисел при а≠0 существует n различных корней степени n. Например, значениями 3√8 являются числа 2, -1 + i√3, -1 — i√3, где i — мнимая единица. Корень степени n из единицы, т. е. решение уравнения хn = 1, можно записать в виде
Формулу для корней n-й степени из любого комплексного числа z = r (cos φ + i sin φ), r > 0, 0 ≤ φ < 2π, смотри в статье Комплексное число. Все эти корни находятся на комплексной плоскости в вершинах правильного n-угольника с центром в точке нуль, одна из вершин которого находится в точке n√r(cos(φ/n) + i sin(φ/n)).
К нахождению корней математиков древности приводили различные геометрические задачи. Среди вавилонских клинописных текстов (2-е тысячелетие до нашей эры) имеются описания приближённого нахождения корня и таблицы квадратных корней, а в египетских папирусах встречается и особый знак для извлечения корня.![]() Древнегреческие математики установили несоизмеримость стороны квадрата с его диагональю (равной а√2, если а — его сторона), что позднее привело к открытию иррациональных чисел. Индийский учёный Ариабхата (5 век нашей эры) описал правила для извлечения квадратных и кубических корней. Омар Хайям, арабский учёный аль-Каши (15 век), немецкий математик М. Штифель (16 век) извлекали корни высших степеней, исходя из формулы для (а + b)n. Л. Эйлер дал сохранившие своё значение до наших дней приближённые способы извлечения корней. Квадратные корни из отрицательных чисел, встречавшиеся у Дж. Кардано и итальянского математика Р. Бомбелли в 16 веке, привели к открытию комплексных чисел. Об истории знака для корня смотри в статье Математические знаки.
Древнегреческие математики установили несоизмеримость стороны квадрата с его диагональю (равной а√2, если а — его сторона), что позднее привело к открытию иррациональных чисел. Индийский учёный Ариабхата (5 век нашей эры) описал правила для извлечения квадратных и кубических корней. Омар Хайям, арабский учёный аль-Каши (15 век), немецкий математик М. Штифель (16 век) извлекали корни высших степеней, исходя из формулы для (а + b)n. Л. Эйлер дал сохранившие своё значение до наших дней приближённые способы извлечения корней. Квадратные корни из отрицательных чисел, встречавшиеся у Дж. Кардано и итальянского математика Р. Бомбелли в 16 веке, привели к открытию комплексных чисел. Об истории знака для корня смотри в статье Математические знаки.
2) Корни алгебраического уравнения
a0xn + а1xn-1 + … +аn = 0
— число с, которое при подстановке его вместо х обращает левую часть уравнения в нуль. Корень этого уравнения называется также корнем многочлена
fn(x) = а0хn + а1xn-1 + . n \sqrt{a}\)
n \sqrt{a}\)
Термин » корень » иногда называют «радикалом» — это тоже самое.
Извлечение корня — это арифметическая операция, обратная возведению в степень.
Степенью \(n\) числа \(a\) называют произведение \(n\) множителей, каждый из которых равен \(a\).
Если в радикальном выражении нет показателя, то показатель принимается равным \(2\), то есть пишут \( \sqrt{a} \), т.е. опускают показатель корня — и такое выражение называют квадратным корнем.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Российская таможенная академия
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 8-11 классов по обществознанию. Моя основная задача — помочь школьнику с комфортом подготовиться к сдаче выпускных экзаменов на максимальный для ученика балл. В своей деятельности использую собственные наработки, только современные и актуальные материалы. Мои выпускники являются студентами/выпускниками СПбГУ, ВШЭ, МГИМО, РГПУ им. А.И. Герцена, ВУМО, РАНХиГС, РТА и др.
Моя основная задача — помочь школьнику с комфортом подготовиться к сдаче выпускных экзаменов на максимальный для ученика балл. В своей деятельности использую собственные наработки, только современные и актуальные материалы. Мои выпускники являются студентами/выпускниками СПбГУ, ВШЭ, МГИМО, РГПУ им. А.И. Герцена, ВУМО, РАНХиГС, РТА и др.
Репетитор по математике
Татарский государственный гуманитарно-педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор английского языка 5,6 классов. На уроках использую интерактивный метод обучения. Большое внимание уделяю развитию коммуникативных навыков, но грамматику не надо забывать! Изучать иностранный язык — это изучать культуру другого народа. Это сложно, но интересно.
На уроках использую интерактивный метод обучения. Большое внимание уделяю развитию коммуникативных навыков, но грамматику не надо забывать! Изучать иностранный язык — это изучать культуру другого народа. Это сложно, но интересно.
Репетитор по математике
Пермский государственный гуманитарно-педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике.
Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике.
Математика 10 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Курсы ОГЭ
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Квадратные корниS-KUZ ‹ Сергей Кузнецов — репетитор по математике
Что такое квадратный корень?Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня) в математике обозначается вот таким значком:
Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня) в математике обозначается вот таким значком:
Сам значок называется красивым словом «радикал«.
Как извлечь корень? Это лучше рассмотреть на примерах.
Как извлечь (или посчитать — это всё едино) корень квадратный из 4? Нужно просто сообразить: какое число в квадрате даст нам 4? Да конечно же 2! Значит:
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:
А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:
Уловили, что такое квадратный корень? Тогда считаем примеры:
Ответы (в беспорядке): 6; 1; 4; 9; 5.
Решили? Действительно, уж куда проще-то?!
Но… Что делает человек, когда видит какое-нибудь задание с корнями?
Тосковать начинает человек… Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень…
Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах…
Пунктик первый. Корни надо узнавать в лицо!
Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…
В этом и есть сложность извлечения корней.
Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.
Приходится подбирать ответ и проверять его на попадание возведением в квадрат.Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да…
Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём тудаи обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.
И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…
Итак, что такое квадратный корень и как извлекать корни — думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.
Теперь выясним ИЗ ЧЕГО можно их извлекать.
Пунктик второй. Корень, я тебя не знаю!
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзяих извлекать.
Попробуем вычислить вот такой корень:
Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.
Что, не подбирается? 22 даёт +4. (-2)2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.
Такая же история будет с любым отрицательным числом. Отсюда вывод:
Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно!Или, другими словами:
Квадратные корни из отрицательных чисел извлечь нельзя!Зато из всех остальных — можно. Например, вполне можно вычислить
Например, вполне можно вычислить
или
На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!
Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:
или
и т.д…
Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:
Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называютиррациональными. Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:
Если при решении примера у вас получилось что-то неизвлекаемое, типа:
то так и оставляем. Это и будет ответ.
Это и будет ответ.
Нужно чётко понимать, что под значками
, , ……
и так далее, скрываются просто числа! Неровные, лохматые, иррациональные, но числа!
Конечно, если корень из числа извлекается ровно, вы обязаны это сделать. Ответ задания в виде, например
никто не оценит… Надо корень посчитать и написать
х = 4.
А вот
вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения:
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Идём дальше.
Пунктик третий. Самый хитрый.
Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!
Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!
Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…
Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ
Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ
правильный, а ответ
грубейшая ошибка. Вот так.
Так в чём же дело?
Действительно, (-2)2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.
Но! В школьном курсе математики принято считать за квадратные корни
только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: арифметический квадратный корень из числа а — это неотрицательное число, квадрат которого равен а. Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические. Хотя особо об этом не упоминается.Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.
Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.
Уравнение простое, пишем ответ (как учили):
Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух ответов:
и
Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда неотрицательное! А здесь один из ответов — отрицательный! Непорядок. Это первая ( но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:
Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня. Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения. Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
Если вы
просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:Потому, что это —
арифметический квадратный корень.Но если вы решаете какое-нибудь квадратное уравнение, типа:
то
всегда получается два ответа (с плюсом и минусом):Потому, что это — решение уравнения.
Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)
Формулы корней. Свойства квадратных корней.
В предыдущем уроке мы разобрались, что такое квадратный корень. Пришла пора разобраться, какие существуют формулы для корней, каковы свойства корней, и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Напоминаю: а и b — неотрицательные числа! Иначе формула смысла не имеет…
Это свойство корней, как видите простое, короткое и безобидное. Но с помощью этой формулы корней можно делать массу полезных вещей! Разберём на примерах все эти полезные вещи.
Полезная вещь первая. Эта формула позволяет нам умножать корни.
Как умножать корни?
Да очень просто. Прямо по формуле. Например:
Казалось бы, умножили, и что? Много ли радости?! Согласен, немного… А вот как вам такой пример?
Из множителей корни ровно не извлекаются. А из результата — отлично! Уже лучше, правда? На всякий случай сообщу, что множителей может быть сколько угодно. Формула умножения корней всё равно работает. Например:
А из результата — отлично! Уже лучше, правда? На всякий случай сообщу, что множителей может быть сколько угодно. Формула умножения корней всё равно работает. Например:
Так, с умножением всё ясно, зачем нужно это свойство корней — тоже понятно.
Полезная вещь вторая. Внесение числа под знак корня.
Как внести число под корень?
Предположим, что у нас есть вот такое выражение:
Можно ли спрятать двойку внутрь корня? Легко! Если из двойки сделать корень, сработает формула умножения корней. А как из двойки корень сделать? Да тоже не вопрос! Двойка — это корень квадратный из четырёх!
Вот и пишем:
Корень, между прочим, можно сделать из любого неотрицательного числа! Это будет корень квадратный из квадрата этого числа. 3 — корень из 9. 8 — корень из 64. 11 — корень из 121. Ну, и так далее.
Конечно, расписывать так подробно нужды нет. Разве что, для начала… Достаточно сообразить, что любое неотрицательное число, умноженное на корень, можно внести под корень. Но — не забывайте! — под корнем это число станет квадратом самого себя. Это действие — внесение числа под корень — можно ещё назвать умножением числа на корень. В общем виде можно записать:
Но — не забывайте! — под корнем это число станет квадратом самого себя. Это действие — внесение числа под корень — можно ещё назвать умножением числа на корень. В общем виде можно записать:
Процедура простая, как видите. А зачем она нужна?
Как и любое преобразование, эта процедура расширяет наши возможности. Возможности превратить жестокое и неудобное выражение в мягкое и пушистое). Вот вам простенький пример:
Как видите, свойство корней, позволяющее вносить множитель под знак корня, вполне годится для упрощения.
Кроме того, внесение множителя под корень позволяет легко и просто сравнивать значения различных корней. Безо всякого их вычисления и калькулятора! Третья полезная вещь.
Как сравнивать корни?
Это умение очень важно в солидных заданиях, при раскрытии модулей и прочих крутых вещах.
Сравните вот эти выражения. Какое из них больше? Без калькулятора! С калькулятором каждый… э-э-э… короче, каждый справится!)
Так сразу и не скажешь… А если внести числа под знак корня?
и
Запомним (вдруг, не знали?): если число под знаком корня больше, то и сам корень — больше! Отсюда сразу правильный ответ, безо всяких сложных вычислений и расчётов:
и, следовательно:
Здорово, да? Но и это ещё не всё! Вспомним, что все формулы работают как слева направо, так и справа налево. Мы пока формулу умножения корней слева направо употребляли. Давайте запустим это свойство корней наоборот, справа налево. Вот так:
Мы пока формулу умножения корней слева направо употребляли. Давайте запустим это свойство корней наоборот, справа налево. Вот так:
И какая разница? Разве это что-то даёт!? Конечно! Сейчас сами увидите.
Предположим, нам нужно извлечь (без калькулятора!) корень квадратный из числа 6561. Кое-кто на этом этапе и падёт в неравной борьбе с задачей… Но мы упорные, мы не сдаёмся! Полезная вещь четвёртая.
Как извлекать корни из больших чисел?
Вспоминаем формулу извлечения корней из произведения. Ту, что я чуть выше написал. Но где у нас произведение!? У нас огромное число 6561 и всё… Да, произведения здесь нет. Но если нам надо — мы егосделаем! Разложим это число на множители. Имеем право.
Для начала сообразим, на что делится это число ровно? Что, не знаете!? Признаки делимости забыли!? Зря.На 3 и на 9 делится это число. Потому, что сумма цифр (6+5+6+1=18) делится на эти числа. Это один из признаков делимости. На три нам делить ни к чему (сейчас поймёте, почему), а вот на 9 поделим. Хотя бы и уголком. Получим 729. Вот мы и нашли два множителя! Первый — девятка (это мы сами выбрали), а второй — 729 (такой уж получился). Уже можно записать:
Хотя бы и уголком. Получим 729. Вот мы и нашли два множителя! Первый — девятка (это мы сами выбрали), а второй — 729 (такой уж получился). Уже можно записать:
Улавливаете идею? С числом 729 поступим аналогично. Оно тоже делится на 3 и 9. На 3 опять не делим, делим на 9. Получаем 81. А это число мы знаем! Записываем:
Всё получилось легко и элегантно! Корень пришлось по кусочкам извлекать, ну и ладно. Так можно поступать с любыми большими числами. Раскладывать их на множители, и — вперёд!
Кстати, а почему на 3 делить не надо было, догадались? Да потому, что корень из трёх ровно не извлекается! Имеет смысл раскладывать на такие множители, чтобы хотя бы из одного корень хорошо извлекался. Это 4, 9, 16 ну, и так далее. Делите своё громадное число на эти числа поочерёдно, глядишь, и повезёт!
Но не обязательно. Может и не повезти. Скажем, число 432 при разложении на множители и использовании формулы корней для произведения даст такой результат:
Ну и ладно. Всё равно мы упростили выражение. В математике принято оставлять под корнем самое маленькое число из возможных. В процессе решения все зависит от примера (может и без упрощения всё посокращается), а вот в ответе надо дать результат, который уже дальнейшему упрощению не поддаётся.
Всё равно мы упростили выражение. В математике принято оставлять под корнем самое маленькое число из возможных. В процессе решения все зависит от примера (может и без упрощения всё посокращается), а вот в ответе надо дать результат, который уже дальнейшему упрощению не поддаётся.
Кстати, знаете, что мы с вами сейчас с корнем из 432 сделали?
Мы вынесли множители из-под знака корня! Вот так называется эта операция. А то попадётся задание — «вынести множитель из-под знака корня» а мужики-то и не знают…) Вот вам ещё одно применение свойства корней. Полезная вещь пятая.
Как вынести множитель из-под корня?
Легко. Разложить подкоренное выражение на множители и извлечь корни, которые извлекаются. Смотрим:
Ничего сверхъестественного. Важно правильно выбрать множители. Здесь мы разложили 72 как 36·2. И всё получилось удачно. А могли разложить иначе: 72 = 6·12. И что!? Ни из 6, ни из 12 корень не извлекается… Что делать?!
Ничего страшного. Или поискать другие варианты разложения, или продолжать раскладывать всё до упора! Вот так:
Или поискать другие варианты разложения, или продолжать раскладывать всё до упора! Вот так:
Как видим, всё получилось. Это, кстати, не самый быстрый, но самый надёжный способ. Раскладывать число на самые маленькие множители, а затем собирать в кучки одинаковые. Способ успешно применяется и при перемножении неудобных корней. Например, надо вычислить:
Перемножать всё — сумасшедшее число получится! И как потом из него корень извлекать?! Опять на множители раскладывать? Не, лишняя работа нам ни к чему. Сразу раскладываем на множители и собираем одинаковые по кучкам:
Вот и всё. Конечно, раскладывать до упора не обязательно. Всё определяется вашими личными способностями. Довели пример до состояния, когда вам всё ясно, значит, можно уже считать. Главное — не ошибаться. Не человек для математики, а математика для человека!)
Применим знания к практике? Начнём с простенького:
1. Вычислить:
2. Вычислить (без калькулятора!):
Вычислить (без калькулятора!):
3. Вычислить:
Слегка усложним:
4. Вычислить:
Чуть ближе к ГИА:
5. Выполнить действия:
Ну и, самое крутое, прямо как в ГИА:
6. Укажите наибольшее из следующих чисел:
Ответы для заданий 1 — 4, в беспорядке: 2; 1; 9, 96.
Ответы на задания 5 — 6 здесь не дам). В этих примерах главное не ответ, а принцип решения. Если знаете как делать подобные задания, ответ сам получится. Если не знаете, ответ особого смысла не имеет).
Подведём итоги.
Обратите внимание. Всего одно свойство корней, одна небольшая формула умножения корней — и какие разнообразные возможности для практического применения!
Формула умножения корней позволяет:
— умножать корни,
— вносить число под корень,
— сравнивать корни,
— извлекать корни из больших чисел,
— выносить множитель из-под корня.
И все эти возможности вытекают из одной небольшого свойства корней. Мощное свойство, но… одно. Это — как табурет на одной ножке…) Сидеть можно, но с изрядными усилиями.
В нашем арсенале есть ещё два свойства корней. Одно — простое, второе — не очень. Но разобраться с ними можно и нужно. Оба этих свойства — в следующем уроке. Там же — примеры для тренировки. Там же описана одна тупая, но очень популярная ошибка в корнях, после которой люди бьют себя по голове и страшно ругаются…
Как делить корни?
Продолжаем развлечение? В предыдущих уроках мы осознали, что такое квадратный корень. И разобрались как умножать корни. Формулу умножения корней мы разобрали по винтикам. Очень уж она полезная в решении примеров! Осталось ещё две. Переходим к следующей формуле. Это будет деление корней.
Формула столь же проста, как и умножение. Вот она:
Напоминаю: здесь а — неотрицательное число (больше или равно нулю), b — положительное (больше нуля)! Иначе формула смысла не имеет… Об этих тонкостях мы ниже поговорим.
У формулы деления корней возможности не так обширны, как у умножения. Что можно делать прямо по формуле? Очевидно, делить корни.
Элементарно. Вот вам примерчик:
В этом примере деление корней помогло нам получить хороший ответ. Бывают более хитрые преобразования. Например:
Здесь мы превратили двойку в корень квадратный из четырёх. Исключительно для того, чтобы формулуделения корней в дело употребить. Как видите, ничего здесь сложного нет.
Рассмотрим формулу деления корней в обратном направлении. Справа налево. Вот так:
Какие возможности раскрывает нам такая запись? Ничего нового, думаете? Ошибаетесь! Забавно, но простая запись формулы в другом направлении частенько высвечивает дополнительные возможности!
В нашем случае такая формулировка деления корней здорово помогает извлекать корни из дробей! Например, пусть нам надо извлечь квадратный корень из дроби 25/144. Спокойно пишем себе:
Спокойно пишем себе:
Вот и все дела! От работы с дробью целиком, мы переходим к работе отдельно с числителем, отдельно со знаменателем. Что гораздо проще. А если дробь десятичная? Не вопрос! Если сразу корень не можете извлечь — переводите десятичную дробь в обыкновенную, и — вперёд! По формуле деления корней. Например:
Бывает ещё круче, когда корень из смешанного числа надо извлечь! Как поступаем? Правильно! Переводим смешанное число в неправильную дробь — и по знакомой формуле деления корней! К примеру, вот так:
Что, забыли, как переводить дроби? Срочно прокрутите страницу выше и вспоминайте. А то ни дробь преобразовать, ни сократить её… И зачем вам тогда квадратные корни?
Надеюсь, что деление корней проблем не составляет. Простая и безобидная формула, простое употребление. Теперь в нашем арсенале уже две формулы. Умножение и деление корней. Табурет на двух ножках. Сидеть можно, но… некомфортно.)
Займёмся последним свойством квадратных корней. Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. Или корень в квадрате. Или корень из степени. Корень в степени. Всяко называют. Но суть одна. Это возведение в степень подкоренного выражения или самого корня.
Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. Или корень в квадрате. Или корень из степени. Корень в степени. Всяко называют. Но суть одна. Это возведение в степень подкоренного выражения или самого корня.
Можно ли корень возвести в квадрат? А почему нет? Умножить корень сам на себя — да все дела! И не только в квадрат можно. В любую степень. А извлечь корень из квадрата? Да тоже не проблема! Мы же умеем корень из произведения извлекать. Так что можно извлечь корень не только из квадрата, но и из любой степени.
Но именно эти действия вызывают массу проблем… С этим надо разобраться основательно. Что мы сейчас и сделаем. Начнём с безобидного действия. С корня в квадрате.
Как возвести корень в квадрат?
Так как посчитать корень в квадрате? Очень просто. Прямо по смыслу корня. Что такое корень квадратный из двух, например? Это число, которое при возведении в квадрат должно дать двойку. Так вот, если мы число, которое при возведении в квадрат должно дать двойку, возведём-таки в этот самый квадрат? Что получим? Двойку, конечно! Т.е. подкоренное выражение. Или, в общем виде:
Что такое корень квадратный из двух, например? Это число, которое при возведении в квадрат должно дать двойку. Так вот, если мы число, которое при возведении в квадрат должно дать двойку, возведём-таки в этот самый квадрат? Что получим? Двойку, конечно! Т.е. подкоренное выражение. Или, в общем виде:
Вот и всё! Никаких подводных камней, всё строго по формуле! Возведение в квадрат корня квадратного из любого выражения даст нам это самое выражение. Понятно, что а — число неотрицательное. Иначе формула смысла не имеет.
А если корень не в квадрате, а в другой степени? Не вопрос! Если, конечно, знаете действия со степенями… По правилам этих действий сами приведём исходное выражение к корням в квадрате и всё посчитаем. Например, вот так (расписываю подробно):
Как видим, корень исчезает, Степень результата в два раза меньше исходной степени.
Если степень нечётная — разложим исходное выражение на множители, и все дела:
Так поступаем с любой степенью корня из любого выражения, и всё у нас посчитается, упростится и получится. Корень в квадрате — штука бесхитростная. Разберёмся теперь с корнем из квадрата.
Корень в квадрате — штука бесхитростная. Разберёмся теперь с корнем из квадрата.
Как извлечь корень из квадрата?
Пусть у нас есть хорошее число 2. Возведём его в квадрат.
22 = 4
Кто бы спорил? А теперь давайте обратно, извлечём из результата квадратный корень:
Опять всё чудесно, правда? С чего начали, к тому и вернулись! Стало быть, можно записать:
Оно и естественно, правда? Возведение в квадрат компенсируется обратной операцией — извлечением квадратного корня. В общем виде формула выглядит вот так:
Стоп! Внимание! Во всех учебниках, справочниках и пособиях рядом с такой формулой всегда пишут:»где а — больше, либо равно нулю». В этих словах, которые многие просто пропускают, и кроются главные сложности корней. Потому, что в примерах а частенько бывает отрицательным! Пока и мы будем считать, что а — неотрицательное. Для простоты.Продолжаем. Корень из квадрата извлекается просто. А если у нас подкоренное выражение не в квадрате, а в другой степени? Допустим, в четвёртой? Да нет проблем. Приведём нашу степень к квадрату. Вот так:
Корень из квадрата извлекается просто. А если у нас подкоренное выражение не в квадрате, а в другой степени? Допустим, в четвёртой? Да нет проблем. Приведём нашу степень к квадрату. Вот так:
24=(22)2
Для таких преобразований надо опять-таки знать действия со степенями, но тут уж ничего не поделаешь…
Теперь по формуле корня из квадрата:
Вот и всё. Корень из любой чётной степени даст в результате подкоренное выражение в степени, в два раза меньше исходной. Корень из 310 ? Легко! Это будет 35. Корень из 518 ? Запросто! Это будет 59. Ну, и так далее.
А если степень нечётная? Подумаешь! Раскладываем подкоренное выражение на множители — и вперёд! Используем вынесение множителя из-под корня. Например:
Всё просто. Но до сего момента мы работали только с неотрицательными числами и выражениями. Как только в игру вступают отрицательные величины, простота куда-то пропадает начисто… Вернём эту простоту и ясное понимание.
Вот тут и будет мрачный заяц. Для лучшего запоминания.) Концентрируем внимание и собираем весь интеллект в кулак!)
Итак, откуда в корнях могут появиться отрицательные числа и выражения?
Пунктик первый. Отрицательные значения даны прямо в задании. Вспоминаем пример корня из квадрата двойки:
Здесь всё понятно и просто.
А теперь попробуем вычислить:
Берём, и просто считаем, безо всяких формул:
(-2)
2 = 4Извлекаем корень из четырёх и получаем 2. Так как арифметический квадратный корень (а в школе мы работаем только с такими!) —
всегда число неотрицательное! То есть:А если бы мы использовали формулу:
получили бы не два, а
минус два! Что является ошибкой.Не работает эта формула для отрицательных значений.
Для того, чтобы формула корня из квадрата работала для
всех значений а, она записывается вот так:Это и есть последнее, третье свойство корней. Корень из квадрата. Третья ножка для табурета.)
Корень из квадрата. Третья ножка для табурета.)
Здесь появляется страшный значок для старшеклассников. Модуль. Если вы пока не сильны в раскрытии модулей, не волнуйтесь. Здесь он означает лишь то, что при любом знаке а, результат извлечения корня из квадрата будет всегда неотрицательный. Формула стала полноценной. Модуль просто отсекает минусы:
Пунктик второй. Отрицательные значения спрятаны в буквах и дополнительных условиях. Например, требуется упростить выражение:
где х<0.
Казалось бы, ответ прост. Получится просто х. Но зачем тогда дополнительная информация?! Приходится соображать. Если х<0, это отрицательное число. Минус два, или минус тридцать, там… Но корень квадратный отрицательным быть не может! Это будет точно х, но он должен быть с плюсом! Где взять плюс? А мы его сделаем! Если перед заведомо отрицательным числом, поставить минус, это число станет, число станет… положительным! И верное решение выглядит так.
Собственно, это и есть главная трудность в работе с корнями. В отличие от более простых разделов математики, здесь правильный ответ частенько не вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.)
И как справляться со всем разнообразием заданий с корнями? А есть ещё иррациональные уравнения и неравенства, где эти пунктики играют главную роль…
Спокойно! Вникайте и запоминайте.
Главный практический совет по работе с квадратными корнями.
В любом задании с квадратными корнями
лично контролируйте знаки подкоренного выражения и результата извлечения корня.Прикидывайте, и оценивайте ситуацию, исходя из внешнего вида примера и
всех дополнительных условий задания. Если под знаком корня — минус, дальше можно не решать. Выражение не имеет смысла. Что нам делать нечего, бессмысленные выражения решать?!Если под корнем всё нормально, плюс, а в результате извлечения получается заведомый минус — сделайте из него плюс! Этого требуют правила действий с квадратными корнями.

Ну вот, основные тонкости корней мы разобрали. Теперь об одной ошибке, рассказать про которую я обещал в предыдущем уроке. Эта ошибка ничего общего с тонкостями не имеет! Это абсолютно тупой косяк, о котором и говорить-то неловко. Но надо. Слишком часто он встречается…
Обратите внимание! Все свойства корней связаны с умножением-делением. И ни одного — со сложением-вычитанием! На сложение-вычитание корней — не существует специальных формул!Однако народ складывает… И не самый трудный народ… Поэтому громко напоминаю:
или:
Хотя одинаковые корни можно, конечно, складывать-вычитать. Как приводить подобные с буквами. Например:
или:
Но эти действия к специфическим свойствам корней не имеют никакого отношения.
А теперь попрактикуемся в корнях. От примитивных заданий до продвинутых. Все ответы даны в беспорядке.
Вычислить:
Ответы: 1, 9, 2.
Примитив? Тогда решаем дальше.
Упростить:
Ответы: 3а4 b, -4а4 b5 , 3а.
Получилось? Неплохо. А как вам эти примерчики?
Вычислить (все буквы — неотрицательные):
Ответы (в беспорядке): выражение не имеет смысла; 5; 4; 1; -3; 0,5
Всё нормально!? Отлично. Корни — не ваша проблема.
Материал позаимствован с замечательного сайта: http://egesdam.ru/page260.php . Спасибо автору за понятное изложение материала!Квадратный корень из 2
Квадратный корень из 2: Диалог о числе и последовательности . Дэвид Флэннери. 2006, xii, 260 стр., 31 иллюстрация, 25 долларов, твердый переплет, ISBN 0-387-20220-X. Нью-Йорк: Copernicus Books (Springer), www.springer.com.
В первые годы преподавания математики в старшей школе я порекомендовал « Как решить задачу » от Полии особенно умному старшекласснику. Через шесть недель она вернула книгу и пачку бумаг с решениями всех задач.Она продолжила аспирантуру по математике, получив докторскую степень. в Боулдере, штат Колорадо, и с тех пор с удовольствием занимается математикой и преподаванием математики. Книга Дэвида Флэннери «. Квадратный корень из 2 » — это книга, которую можно порекомендовать особо способным старшеклассникам, а не игнорировать новичков в колледже. Начиная со страницы 1 и заканчивая ее заключением, это мастерский диалог в порядке Сократа и мальчика-раба. Оба диалога начинаются с одной и той же задачи — поиска квадрата, который в два раза больше другого, хотя цели у них разные.Там, где Сократ (или действительно Платон?) стремился установить существование врожденных идей, Фланнери стремится пробудить в своем ученике холодную страсть к математике. Давайте рассмотрим, что происходит в пяти главах.
Через шесть недель она вернула книгу и пачку бумаг с решениями всех задач.Она продолжила аспирантуру по математике, получив докторскую степень. в Боулдере, штат Колорадо, и с тех пор с удовольствием занимается математикой и преподаванием математики. Книга Дэвида Флэннери «. Квадратный корень из 2 » — это книга, которую можно порекомендовать особо способным старшеклассникам, а не игнорировать новичков в колледже. Начиная со страницы 1 и заканчивая ее заключением, это мастерский диалог в порядке Сократа и мальчика-раба. Оба диалога начинаются с одной и той же задачи — поиска квадрата, который в два раза больше другого, хотя цели у них разные.Там, где Сократ (или действительно Платон?) стремился установить существование врожденных идей, Фланнери стремится пробудить в своем ученике холодную страсть к математике. Давайте рассмотрим, что происходит в пяти главах.
В то время как задача создания квадрата, площадь которого в два раза больше, чем у другого, проста, найти его меру не так просто. Если сторона меньшего квадрата равна 1, то сторона его двойника называется √2, квадратным корнем из двух. Но что это? Прийти к пониманию этой меры и есть цель диалога.Учитель предлагает отведения, которые ученик изучает и использует для рисования проекций. Учащийся быстро понимает, что то, что может быть построено геометрически, невозможно передать числами. Нет квадратного числа, которое в два раза больше другого. Тем не менее введение алгебры дает m 2 = 2 n 2 . Исследование колонн чисел м в операции, которая занимает м 2 до 2 N 2 N 2 , приводит к соотношению м 2 = 2 N 2 ± 1.Отсюда ученик находит путь к м / n = √2 и начинает изучение м / n . Получается последовательность 1/1, 3/2, 7/5, 17/12, 41/29 . . ., каждый последующий член последовательности ближе к значению √2. При внимательном изучении членов последовательности учащийся обнаруживает (и позже доказывает) первую из нескольких провокационных формул.
Если сторона меньшего квадрата равна 1, то сторона его двойника называется √2, квадратным корнем из двух. Но что это? Прийти к пониманию этой меры и есть цель диалога.Учитель предлагает отведения, которые ученик изучает и использует для рисования проекций. Учащийся быстро понимает, что то, что может быть построено геометрически, невозможно передать числами. Нет квадратного числа, которое в два раза больше другого. Тем не менее введение алгебры дает m 2 = 2 n 2 . Исследование колонн чисел м в операции, которая занимает м 2 до 2 N 2 N 2 , приводит к соотношению м 2 = 2 N 2 ± 1.Отсюда ученик находит путь к м / n = √2 и начинает изучение м / n . Получается последовательность 1/1, 3/2, 7/5, 17/12, 41/29 . . ., каждый последующий член последовательности ближе к значению √2. При внимательном изучении членов последовательности учащийся обнаруживает (и позже доказывает) первую из нескольких провокационных формул. Затем, и я пропускаю здесь много «хороших вещей», Фланнери и его ученик находят более мощные формулы для максимально близкого приближения к десятичному представлению значения √2.Осторожно, ученика подводят к доказательству каждого шага прогресса. Фланнери цитирует четверостишие, доказывающее иррациональность √2 , как введение в завершение студентом четырехкратного заряда, возникающего из √2. Цветочная композиция из натуральных чисел √ n , n завершает приятное чтение. Не следует упускать из виду хорошую историю в истории, как возможности для прогресса в диалоге. Вклад древних индусов и греков (Гиппаса из Метапонта, Евклида, Героя Александрийского и Паппа), Кристоффа Рудольфа, Джона Пелла, Бертрана Рассела, Г.Признаны Х. Харди и Рамануджан с адекватным указанием современных писателей в ссылках.
Затем, и я пропускаю здесь много «хороших вещей», Фланнери и его ученик находят более мощные формулы для максимально близкого приближения к десятичному представлению значения √2.Осторожно, ученика подводят к доказательству каждого шага прогресса. Фланнери цитирует четверостишие, доказывающее иррациональность √2 , как введение в завершение студентом четырехкратного заряда, возникающего из √2. Цветочная композиция из натуральных чисел √ n , n завершает приятное чтение. Не следует упускать из виду хорошую историю в истории, как возможности для прогресса в диалоге. Вклад древних индусов и греков (Гиппаса из Метапонта, Евклида, Героя Александрийского и Паппа), Кристоффа Рудольфа, Джона Пелла, Бертрана Рассела, Г.Признаны Х. Харди и Рамануджан с адекватным указанием современных писателей в ссылках.
Фланнери создал увлекательный диалог из истории и теории, который предлагает учащимся проникнуть в мыслительный ум работающего математика. Он также изложил ряд виньеток, которые находчивый учитель мог бы превратить в упражнения для открытия.
Барнабас Хьюз OFM, почетный профессор Калифорнийского государственного университета, Нортридж
См. также обзор MAA Дуга Энсли и Джона Энсли.
math — Математические функции — Документация Python 3.10.2
Этот модуль обеспечивает доступ к математическим функциям, определенным языком C стандарт.
Эти функции нельзя использовать с комплексными числами; использовать функции программы
то же имя из модуля cmath , если вам требуется поддержка сложных
числа. Различие между функциями, поддерживающими комплексные числа, и
те, которые не делаются, поскольку большинство пользователей не хотят учиться так много
математика, необходимая для понимания комплексных чисел.Получение исключения
вместо сложного результата позволяет раньше обнаружить неожиданный комплекс
число, используемое в качестве параметра, чтобы программист мог определить, как и почему оно
был создан в первую очередь.
Этот модуль обеспечивает следующие функции. За исключением случаев, когда явно
в противном случае все возвращаемые значения являются числами с плавающей запятой.
За исключением случаев, когда явно
в противном случае все возвращаемые значения являются числами с плавающей запятой.
Теоретико-числовые функции и функции представления
-
мат.потолок( x ) Возвращает максимальное значение x , наименьшее целое число, большее или равное x .Если x не является числом с плавающей запятой, делегируется
x.__ceil__(), который должен возвращатьИнтегральное значение.
-
мат.гребень( n , k ) Вернуть количество способов выбора k элементов из n элементов без повторения и без порядка.
Вычисляется как
n! / (k! * (n - k)!), когдаk <= nи оценивает к нулю, когдаk > n.Также называется биномиальным коэффициентом, поскольку он эквивалентен коэффициенту k-го члена полиномиального разложения выражение
(1 + x) ** n.
Вызывает
TypeError, если какой-либо из аргументов не является целым числом. ВыдаетValueError, если любой из аргументов отрицательный.
-
мат.копия( x , y ) Возвращает число с плавающей запятой с величиной (абсолютным значением) x , но со знаком и .На платформах, поддерживающих нули со знаком,
copysign(1.0, -0.0)возвращает -1.0 .
-
мат.фабрики( x ) Возвращает абсолютное значение x .
-
мат.факториал( x ) Возвращает факториал x в виде целого числа. Выдает
ValueError, если x не является целым или отрицательно.Устарело, начиная с версии 3.9: прием чисел с плавающей запятой с целыми значениями (например,
5.) устарел. 0
0
-
мат.этаж( x ) Возвращает пол размером x , наибольшее целое число меньше или равное x . Если x не является числом с плавающей запятой, делегируется
x.__floor__(), который должен возвращатьИнтегральное значение.
-
мат.fmod( x , и ) Возврат
fmod(x, y), как определено библиотекой платформы C. Обратите внимание, что Выражение Pythonx % yможет не возвращать тот же результат. Цель С стандартом является то, чтоfmod(x, y)точно (математически; до бесконечности точность), равныйx - n*yдля некоторого целого числа n такого, что результат имеет тот же знак, что и у x , и звездная величина меньшеабс(у).Pythonx % yвместо этого возвращает результат со знаком y и может быть неточно вычислимым для аргументов с плавающей запятой. Например,
Например, fmod(-1e-100, 1e100)равно-1e-100, но результатом Python-1e-100 % 1e100является1e100-1e-100, что не может быть представлено в точности как число с плавающей запятой и округляется до удивительного1e100. За по этой причине функцияfmod()обычно предпочтительнее при работе с числа с плавающей запятой, в то время как Pythonx % yпредпочтительнее при работе с целыми числами.
-
мат.частота( x ) Вернуть мантиссу и показатель степени x в виде пары
(m, e). м поплавок а e — целое число, такое чтоx == m * 2**eточно. Если x равно нулю, возвращает(0.0, 0), иначе0.5 <= абс(м) < 1. Используется для «выбора обособленно» внутреннее представление поплавка переносимым способом.
-
мат.
fsum( повторяемый ) Возвращает точную сумму значений с плавающей запятой в итерируемом объекте. Избегает потеря точности из-за отслеживания нескольких промежуточных частичных сумм:
>>> сумма([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) 0,9999999999999999 >>> fsum([.1, .1, .1, .1, .1, .1, .1, .1, .1, .1]) 1,0
Точность алгоритма зависит от арифметических гарантий IEEE-754 и типичный случай, когда режим округления является получетным.На некоторых не-Windows сборки, базовая библиотека C использует добавление расширенной точности и может время от времени округлять промежуточную сумму дважды, что приводит к тому, что она оказывается ошибочной. младший значащий бит.
Для дальнейшего обсуждения и двух альтернативных подходов см. кулинарную книгу ASPN. рецепты точного суммирования с плавающей запятой.
-
мат.НОД( *целые числа ) Возвращает наибольший общий делитель указанных целочисленных аргументов.
 Если какой-либо из аргументов отличен от нуля, то возвращаемое значение является наибольшим.
положительное целое число, являющееся делителем всех аргументов. Если все аргументы
равны нулю, то возвращаемое значение равно
Если какой-либо из аргументов отличен от нуля, то возвращаемое значение является наибольшим.
положительное целое число, являющееся делителем всех аргументов. Если все аргументы
равны нулю, то возвращаемое значение равно 0.gcd()без аргументов возвращает0.Изменено в версии 3.9: Добавлена поддержка произвольного количества аргументов. Раньше только два аргументы были поддержаны.
-
мат.isclose( a , b , * , rel_tol=1e-09 , abs_tol=0.0 ) Вернуть
Истина, если значения a и b близки друг к другу иЛожьиначе.Считаются ли два значения близкими, определяется в соответствии с заданы абсолютные и относительные допуски.
rel_tol — относительный допуск — максимально допустимая разница между a и b относительно большего абсолютного значения a или b .
 Например, чтобы установить допуск 5%, введите
Например, чтобы установить допуск 5%, введите rel_tol=0.05. По умолчанию допуск равен1e-09, что гарантирует, что два значения совпадают примерно с точностью до 9 знаков после запятой. rel_tol должен быть больше нуля.abs_tol — минимальный абсолютный допуск — полезно для сравнения вблизи нуль. abs_tol должен быть не меньше нуля.
Если ошибок нет, результат будет таким:
абс(а-б) <= макс(отн_допуск * макс(абс(а), абс(б)), абс_доп).Специальные значения IEEE 754
NaN,infи-infбудут обрабатывается в соответствии с правилами IEEE. В частности,NaNне считается близко к любому другому значению, включаяNaN.infи-infтолько считают близкими себе.См. также
PEP 485 — Функция проверки приблизительного равенства
-
мат.
бесконечность( x ) Возврат
True, если x не является ни бесконечностью, ни NaN, иЛожьиначе.(Обратите внимание, что0.0считается конечным числом .)
-
мат.isinf( x ) Возврат
True, если x является положительной или отрицательной бесконечностью, иЛожьиначе.
-
мат.Иснан( х ) Возврат
True, если x является NaN (не числом), иFalseв противном случае.
-
мат.квт( n ) Возвращает целый квадратный корень из неотрицательного целого числа n . Это пол точного квадратного корня из n или, что то же самое, наибольшее целое число a такое, что a ² ≤ n .

Для некоторых приложений может быть удобнее использовать наименьшее целое число. a так, что n ≤ a ², или, другими словами, потолок точный квадратный корень из n .Для положительных n это можно вычислить с помощью
а = 1 + iqrt(n - 1).
-
мат.lcm( *целые числа ) Возвращает наименьшее общее кратное указанных целочисленных аргументов. Если все аргументы отличны от нуля, то возвращаемое значение является наименьшим. положительное целое число, кратное всем аргументам. Если какой-либо из аргументов равно нулю, то возвращаемое значение равно
0.lcm()без аргументов возвращает1.
-
мат.ldexp( x , и ) Возврат
x * (2**i). Это по существу обратная функцияфрэксп().
-
мат.модф( х ) Возвращает дробную и целую части x . Оба результата несут знак размером x и являются поплавками.
-
мат.следующий за( x , y ) Возвращает следующее значение с плавающей запятой после x по направлению к y .
Если x равно y , вернуть y .
Примеры:
math.nextafter(x, math.inf)идет вверх: к положительной бесконечности.math.nextafter(x, -math.inf)идет вниз: к минус бесконечности.мат.nextafter(x, 0.0)приближается к нулю.math.nextafter(x, math.copysign(math.inf, x))уходит от нуля.
См. также
math.ulp().
-
мат.
пермь( n , k = Нет ) Вернуть количество способов выбора k элементов из n элементов без повторений и по порядку.
Вычисляется как
n! / (н - к)!, когдаk <= nи оценивает к нулю, когдаk > n.Если k не указано или имеет значение None, то k по умолчанию равно n и функция возвращает
n!.Вызывает
TypeError, если какой-либо из аргументов не является целым числом. ВыдаетValueError, если любой из аргументов отрицательный.
-
мат.продукт( повторяемый , * , начало=1 ) Вычислить произведение всех элементов входных данных iterable .По умолчанию начальное значение для продукта равно
1.Если итерируемый объект пуст, вернуть начальное значение.
 Эта функция
предназначен специально для использования с числовыми значениями и может отклонять
нечисловые типы.
Эта функция
предназначен специально для использования с числовыми значениями и может отклонять
нечисловые типы.
-
мат.остаток( x , y ) Возвращает остаток x в стиле IEEE 754 относительно y . За конечное x и конечное ненулевое y , это разница
x - n*y, гдеn— ближайшее целое число к точному значению частногоx / у.Еслиx / yнаходится точно посередине между двумя последовательными целыми числами, ближайшее четное целое число используется дляn. Остатокr = остаток(х, y), таким образом, всегда удовлетворяетabs(r) <= 0,5 * abs(y).Особые случаи соответствуют IEEE 754: в частности,
остаток(х, math.inf)x для любых конечных x иостатка(x, 0)иостаток(math.inf, x)повышениеValueErrorдля любого не-NaN x . Если результат операции остатка равен нулю, этот ноль будет иметь
тот же знак, что и x .
Если результат операции остатка равен нулю, этот ноль будет иметь
тот же знак, что и x .На платформах, использующих двоичные числа с плавающей запятой IEEE 754, результат этого операция всегда точно представима: ошибка округления не вносится.
-
мат.ствол( x ) Возвращает
Действительное значениеx , усеченное доИнтеграл(обычно целое число). делегатых.__trunc__().
-
мат.пульпа( x ) Возвращает значение младшего бита числа с плавающей запятой x :
Если x является NaN (не числом), вернуть x .
Если x отрицательно, вернуть
ulp(-x).Если x является положительной бесконечностью, вернуть x .
Если x равно нулю, вернуть наименьшее положительное денормализованное представимое число с плавающей запятой (меньше минимального положительного нормализованное с плавающей запятой,
сис.). float_info.min
float_info.min Если x равно наибольшему положительному представимому вещественному числу, вернуть значение младшего значащего бита x , так что первый float меньше x равно
x - ulp(x).В противном случае ( x — положительное конечное число) вернуть значение наименьшего значащий бит x , так что первое число с плавающей запятой больше x
x + ulp(x).
ULP расшифровывается как «Единица на последнем месте».
См. также
math.nextafter()иsys.float_info.epsilon.
Обратите внимание, что frexp() и modf() имеют разные шаблоны вызова/возврата
чем их эквиваленты C: они принимают один аргумент и возвращают пару
значения, а не возвращать их второе возвращаемое значение через «выходной
параметр» (в Python такого нет).
Для функций ceil() , floor() и modf() обратите внимание, что все числа с плавающей запятой достаточно большой величины являются точными целыми числами. Типы с плавающей запятой в Python обычно имеют точность не более 53 бит (такая же, как у
платформа C двойного типа), и в этом случае любой поплавок x с
Типы с плавающей запятой в Python обычно имеют точность не более 53 бит (такая же, как у
платформа C двойного типа), и в этом случае любой поплавок x с абс(х) >= 2**52 обязательно не имеет дробных битов.
Степенные и логарифмические функции
-
мат.exp( x ) Возврат e в степени x , где e = 2,718281… основание натуральных логарифмов. Обычно это более точно, чем математика
.е ** хилиpow(math.e, x).
-
мат.expm1( x ) Возврат e в степени x минус 1. Здесь e - основание натурального числа логарифмы. Для маленьких поплавков x вычитание в
exp(x) - 1может привести к значительной потере точности;expm1()Функция предоставляет способ вычислить это количество с полной точностью:>>> из математического импорта exp, expm1 >>> exp(1e-5) - 1 # дает результат с точностью до 11 знаков 1.
 0000050000069649e-05
>>> expm1(1e-5) # результат с точностью до полной точности
1.0000050000166668e-05
0000050000069649e-05
>>> expm1(1e-5) # результат с точностью до полной точности
1.0000050000166668e-05
-
мат.журнал( x [, база ]) С одним аргументом вернуть натуральный логарифм x (по основанию e ).
С двумя аргументами вернуть логарифм x к заданному основанию , рассчитывается как
log(x)/log(base).
-
мат.log1p( x ) Возвращает натуральный логарифм числа 1+x (по основанию e ). То Результат рассчитывается с точностью до x , близких к нулю.
-
мат.журнал2( x ) Возвращает логарифм по основанию 2 x . Обычно это точнее, чем
лог(х, 2).См. также
int.bit_length()возвращает количество бит, необходимое для представления целое число в двоичном формате, за исключением знака и ведущих нулей.
-
мат.журнал10( x ) Возвращает логарифм по основанию 10 числа x . Обычно это более точно чем
log(x, 10).
-
мат.pow( x , y ) Возврат
xв степениy. Исключительные случаи следуют Приложение «F» стандарта C99, насколько это возможно. Особенно,мощность(1.0, x)иpow(x, 0.0)всегда возвращать1.0, даже когдаxравно нулю или NaN. Если обаxиyконечны,xотрицательно, аyне является целым числом, тогдаpow(x, y)не определено и вызываетValueError.В отличие от встроенного оператора
**,math.pow()преобразует оба его аргументы типаfloat. Используйте**или встроенныйpow()функция для вычисления точных целочисленных степеней.
-
мат.кв( x ) Возвращает квадратный корень из x .
Тригонометрические функции
-
мат.акос( х ) Возвращает арккосинус x в радианах. Результат находится между
0ипи.
-
мат.как( x ) Возвращает арксинус x в радианах.Результат находится между
-pi/2ипи/2.
-
мат.атан( х ) Возвращает арктангенс x в радианах. Результат находится между
-pi/2ипи/2.
-
мат.атан2( г , х ) Возврат
atan(y/x), в радианах. Результат находится между
Результат находится между -piиpi.Вектор на плоскости от начала координат до точки(x, y)составляет этот угол с положительной осью X. Сутьatan2()в том, что знаки обоих входные данные ему известны, поэтому он может вычислить правильный квадрант для угла. Например,atan(1)иatan2(1, 1)оба равныpi/4, ноatan2(-1, -1)равно-3*pi/4.
-
мат.потому что( х ) Возвращает косинус x радиан.
-
мат.дист( р , к ) Возвращает евклидово расстояние между двумя точками p и q , каждая задан как последовательность (или итерируемая) координат. Две точки должны иметь одинаковую размерность.
Примерно эквивалентно:
sqrt(sum((px - qx) ** 2.
 0 для px, qx в zip(p, q)))
0 для px, qx в zip(p, q)))
-
мат.гипот( *координаты ) Вернуть евклидову норму,
sqrt(sum(x**2 for x в координатах)).Это длина вектора от начала до точки дается по координатам.Для двумерной точки
(x, y)это эквивалентно вычислению гипотенуза прямоугольного треугольника по теореме Пифагора,кв.(х*х + у*у).Изменено в версии 3.8: Добавлена поддержка n-мерных точек. Раньше только два размерный случай был поддержан.
Изменено в версии 3.10: Повышена точность алгоритма, поэтому максимальная ошибка до 1 ulp (единица на последнем месте).Как правило, результат почти всегда правильно округляется с точностью до 1/2 пульпы.
-
мат.грех( х ) Возвращает синус x радиан.
-
мат.желтовато-коричневый( x ) Возвращает тангенс x радиан.

Угловое преобразование
-
мат.градусов( x ) Преобразование угла x из радианов в градусы.
-
мат.радиан( x ) Преобразование угла x из градусов в радианы.
Гиперболические функции
Гиперболические функции аналоги тригонометрических функций, основанные на гиперболах вместо кругов.
-
мат.акош( х ) Возвращает гиперболический арккосинус x .
-
мат. Возврат обратного гиперболического синуса x .
-
мат.атанх( х ) Возвращает гиперболический арктангенс x .
-
мат.
cosh( x ) Возвращает гиперболический косинус x .
-
мат. Возвращает гиперболический синус x .
-
мат.танх( x ) Возвращает гиперболический тангенс x .
Специальные функции
-
мат. Вернуть функцию ошибки в х .
Функцию
erf()можно использовать для вычисления традиционных статистических данных. функции, такие как кумулятивное стандартное нормальное распределение:по определению фи(х): «Накопленная функция распределения для стандартного нормального распределения» вернуться (1.0 + erf(x / sqrt(2.0))) / 2.0
-
мат.erfc( x ) Возвращает дополнительную функцию ошибки с разрешением x .
 Дополнительная ошибка
функция определяется как
Дополнительная ошибка
функция определяется как 1.0 - erf(x). Он используется для больших значений x , где вычитание от одного приведет к потере значимости.
-
мат.гамма( x ) Вернуть функцию гаммы в х .
-
мат.гамма( x ) Возвращает натуральный логарифм абсолютного значения гаммы работает при разрешении x .
Константы
-
мат.Пи Математическая константа π = 3,141592…, с доступной точностью.
-
мат.и Математическая константа e = 2.718281…, с доступной точностью.
-
мат.тау Математическая константа τ = 6,283185…, с доступной точностью.
 Тау — постоянная окружности, равная 2 π , отношение длины окружности к
его радиус. Чтобы узнать больше о Тау, посмотрите видео Ви Харта «Пи есть (все еще)».
Неправильно, и начать праздновать
Тау день, съев в два раза больше пирога!
Тау — постоянная окружности, равная 2 π , отношение длины окружности к
его радиус. Чтобы узнать больше о Тау, посмотрите видео Ви Харта «Пи есть (все еще)».
Неправильно, и начать праздновать
Тау день, съев в два раза больше пирога!
-
мат.инф Положительная бесконечность с плавающей запятой.(Для отрицательной бесконечности используйте
-math.inf.) Эквивалентен выводуfloat('inf').
-
мат.нан Значение с плавающей запятой «не число» (NaN). Эквивалентно выходу
поплавок('нан').
Сведения о реализации CPython: Модуль math состоит в основном из тонких оболочек вокруг платформы C
Функции математических библиотек. Поведение в исключительных случаях следует Приложению F
стандарт C99, где это уместно.Текущая реализация повысит ValueError для недопустимых операций, таких как sqrt(-1. или  0)
0) log(0.0) (где Приложение F C99 рекомендует сигнализировать о недопустимой операции или делении на ноль),
и OverflowError для результатов, которые переполняются (например, ехр(1000.0) ). NaN не будет возвращен ни одной из функций
выше, если только один или несколько входных аргументов не были NaN; в этом случае,
большинство функций вернут NaN, но (опять же, следуя приложению F C99)
есть некоторые исключения из этого правила, например pow(float('nan'), 0.0) или гипот(с плавающей запятой('нан'), с плавающей запятой('инф')) .
Обратите внимание, что Python не пытается отличить сигнальные значения NaN от тихие NaN, и поведение для сигнализации NaN остается неопределенным. Типичное поведение — рассматривать все NaN так, как если бы они были тихими.
См. также
- Модуль
cmath Комплексные числовые версии многих из этих функций.
2.
 2 - 4(1)с
\конец{выравнивание*}
2 - 4(1)с
\конец{выравнивание*}Возможные парные значения \((b;c)\): \((1;1),~(1;2),~(1;3),~(2;1),~(2;2),~(2;3),~(3;1), ~(3;2),~(3;3)\).Соответствующие значения \(\Delta\): \((\Delta < 0),~(\Delta < 0),~(\Delta < 0),~(\Delta = 0),~(\Delta < 0),~(\Delta < 0),~(\Delta >0),~(\Delta > 0),~(\Delta < 0)\)
\(\Delta ≥ 0\) (и, следовательно, корни действительны) для \((b;c) = (2;1),~(3;1),~(3;2)\)
математических корней
математических корней Магазин не будет работать корректно в случае, если куки отключены.
Похоже, в вашем браузере отключен JavaScript. Для наилучшего взаимодействия с нашим сайтом обязательно включите Javascript в своем браузере.
- Домой
- Плакат «Математические корни»
Красочный плакат указывает путь к математическому успеху; позитивный настрой, математические способности в уме, понимание математической лексики и символов, вычислительные навыки, применение формул, решение проблем, хорошие привычки в учебе и работе.
Красочный плакат указывает путь к математическому успеху: позитивный настрой, развитие и использование математических навыков в уме, понимание математической лексики и символов, развитие сильных вычислительных навыков, понимание и использование формул, проверка ответов на правильность и обоснованность, использование методов решения задач , а также принятие хороших привычек в учебе и работе. 17" х 22".
17" х 22".
- Математические корни Плакаты
- Читает «Чем сильнее математические корни, тем выше дерево успеха»
- Отличное дополнение к классу!
- Размер 17 x 22 дюйма
| Страна производитель | США |
|---|---|
| Цвет | Зеленый |
| Материал | бумага |
| Размеры продукта | 17" Ш x 22" Т |
| Безопасность | Нет опасности удушья |
| УПК | 727638022685 |
об обновлениях и акциях
×
Степени и корни: другие корни в математике
Как вы знаете, если вы просматриваете эту серию математических видео по порядку — в последнем видео мы рассмотрели квадратные корни. Теперь в этом видео мы рассмотрим другие корни в математике — например, кубические корни и т. д.
Теперь в этом видео мы рассмотрим другие корни в математике — например, кубические корни и т. д.
В этом уроке мы поговорим о других корнях. Кубические корни, корни четвертой степени и тому подобное. Точно так же, как квадратный корень более или менее «отменяет действие возведения в квадрат». Конечно, мы узнали, что это не совсем так, есть корни более высокого порядка, которые аналогичным образом уничтожают другие силы. Например, кубические корни отменяют действие кубирования чего-либо.
Кубические корни, корни четвертой степени и тому подобное. Точно так же, как квадратный корень более или менее «отменяет действие возведения в квадрат». Конечно, мы узнали, что это не совсем так, есть корни более высокого порядка, которые аналогичным образом уничтожают другие силы. Например, кубические корни отменяют действие кубирования чего-либо.
Так же, как мы можем возвести что-то в третью степень, мы можем найти, какое число, возведенное в третью степень, будет соответствовать определенному результату.Прежде всего, поговорим об обозначениях. Квадратный корень из k, радикал k, обозначает квадратный корень из k. Обозначения для всех остальных корней аналогичны, мы используем тот же подкоренной символ. Но для всех остальных корней мы ставим небольшое число перед корнем, чтобы обозначить порядок корня.
Другими словами, берем ли мы кубический корень, корень четвертой степени, корень пятой степени и т. д. Итак, для кубического корня мы должны поставить небольшую цифру 3 перед знаком радикала, и это будет обозначать кубический корень из k. Мы также должны думать о положительных и отрицательных числах, потому что положительные и отрицательные числа здесь довольно сложны. Помните, что, прежде всего, мы возводим в квадрат.
Мы также должны думать о положительных и отрицательных числах, потому что положительные и отрицательные числа здесь довольно сложны. Помните, что, прежде всего, мы возводим в квадрат.
Положительный в квадрате положительный, отрицательный в квадрате тоже положительный, понятно? Так что это верно для возведения в квадрат. Поэтому верно, что если у нас есть x2 = положительное, то это имеет два решения, одно положительное и одно отрицательное. Например, х в квадрате равно 9, это может быть плюс 3 или минус 3. Напротив, х2 = отрицательное не имеет возможного решения, х в квадрате равно отрицательному 9, не существует действительного числа, удовлетворяющего этому уравнению.
Другие корни в математике: кубические корни
Положительные и отрицательные корни для кубов немного отличаются. Помните, что если мы возьмем в куб положительное, то получим положительное, а если возьмем в куб отрицательное, то получим отрицательное. Следовательно, x3 = положительное имеет одно положительное решение, а x3 = отрицательное имеет одно отрицательное решение. Таким образом, вы не получаете проблему двойных корней в одном случае и никакого решения в другом случае, как мы получили для возведения в квадрат.
Таким образом, вы не получаете проблему двойных корней в одном случае и никакого решения в другом случае, как мы получили для возведения в квадрат.
С квадратными корнями мы можем найти квадратный корень только из положительных чисел.Конечно, мы могли бы также найти квадратный корень из 0, но мы не можем извлечь квадратный корень из минуса, ясно? Таким образом, почти по той же причине, как мы не можем возвести что-то в квадрат и получить отрицательное значение, мы не можем извлечь квадратный корень из отрицательного значения. Но для кубических корней правила совсем другие.
Мы можем извлечь кубический корень из любого числа на числовой прямой, положительного, нулевого или отрицательного. Итак, мы можем возвести каждое число в отрицательной строке в третью степень и найти из него кубический корень.Например, кубический корень из 8 равен 2, кубический корень из 0 равен 0, а кубический корень из -8 равен -2.
Итак, в отличие от квадратного корня, кубический корень может иметь отрицательный результат.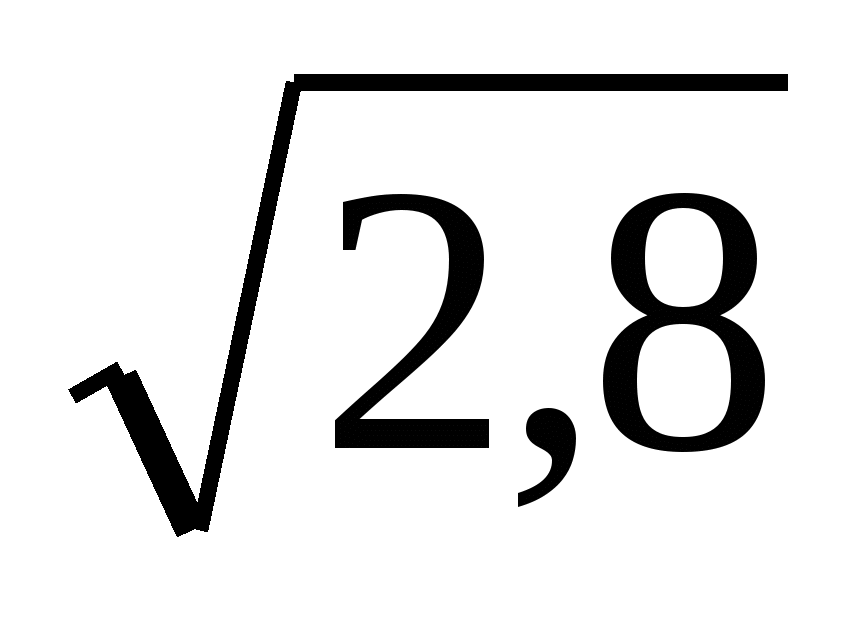 Когда мы вкладываем негатив, мы получаем негатив. Для быстрых вычислений полезно запомнить кубы до 10. Конечно, первые шесть очень важно запомнить, и действительно, если вы знаете все 10, это сэкономит время. И пару вещей отмечу.
Когда мы вкладываем негатив, мы получаем негатив. Для быстрых вычислений полезно запомнить кубы до 10. Конечно, первые шесть очень важно запомнить, и действительно, если вы знаете все 10, это сэкономит время. И пару вещей отмечу.
Обратите внимание, что 8 в кубе, конечно же, будет 2 в 9-м.Обратите внимание, что 4 в кубе — это 2 в квадрате в кубе. Так что это будет 2 к 6-му. Это также будет 2 в 3-м квадрате или 8 в квадрате. И, конечно, 8 в квадрате тоже 64. Итак, здесь есть некоторые закономерности, которые мы можем наблюдать, применяя наши законы показателей.
Таким образом, если мы запоминаем эти кубы автоматически, мы запоминаем кучу кубических корней. А так может быть очень удобно. Кубические корни относительно редко встречаются в тестах. Корни более высокого порядка, четвертый корень, пятый корень, шестой корень встречаются еще реже.Так что это не очень вероятные темы, поэтому сразу предупрежу.
Общие закономерности корней в математике
Но скажу несколько слов в общем обо всех корнях. Так что это верно для всех возможных корней в математике: квадратного корня, кубического корня и т. д. Здесь мы поговорим обо всех закономерностях.
Так что это верно для всех возможных корней в математике: квадратного корня, кубического корня и т. д. Здесь мы поговорим обо всех закономерностях.
Во-первых, корень квадратный из а, корень 4-й степени из а, корень 6-й степени из а и т. д. — они называются четными корнями . Поэтому, когда у нас там записано четное число, это четный корень.
Изображение от dizain
И, конечно, с квадратным корнем подразумевается два, так что это тоже четный корень. Кубический корень, корень 5-й степени, корень 7-й степени называются нечетными корнями. Итак, мы отличаем все четные корни от всех нечетных. И причина, по которой мы это делаем, заключается в том, что те же положительные и отрицательные явления, о которых мы говорили с квадратами и кубами, распространяются на все четные и нечетные числа.
Как и в случае с квадратными корнями, мы можем взять любой четный корень из положительного числа, что приведет к положительному результату.Но мы не можем извлечь четный корень из отрицательного числа. Мы пытались взять четный корень из отрицательного числа, он не определен. Оно ничему не равно на числовой прямой. Напротив, как и в случае с кубическими корнями, любой нечетный корень из положительного числа положителен. И любой нечетный корень отрицательного является отрицательным.
Мы пытались взять четный корень из отрицательного числа, он не определен. Оно ничему не равно на числовой прямой. Напротив, как и в случае с кубическими корнями, любой нечетный корень из положительного числа положителен. И любой нечетный корень отрицательного является отрицательным.
Таким образом, это следует той же схеме плюс-минус. Для других свойств я буду использовать обозначение с буквой n перед знаком радикала. Итак, у нас есть корень n-й степени из a. И здесь я говорю об общем корне.Конечно, подразумевается, что n — целое число, большее или равное 2. Для всех корней мы можем взять корень n-й степени из 0, и он будет равен 0. А корень n-й степени из 1 равен 1, так что это верно для всех корней. значения н.
Дополнительные общие черты для всех корней в математике
Все корни сохраняют порядок неравенства. Итак, если у нас есть три числа подряд — если они положительные числа — мы берем из них корни. Пока это один и тот же корень, который мы извлекаем из каждого числа, они остаются в том же порядке неравенства.
Например, предположим, что нам нужно вычислить корень 4-й степени из 50. Ну, мы хотели бы найти его между двумя четвертыми степенями.
Итак, мы знаем, что 2 в 4-м равно 16, 3 в 4-м равно 81. Итак, поскольку 50 находится между 16 и 81, мы можем извлечь из них корень 4-го порядка. И мы видим, что 4-й корень из 50 должен быть десятичным числом где-то между 2 и 3. Тест не предполагает, что вы сделаете что-то более причудливое с поиском 4-го корня из 50, но до тех пор, пока вы можете выяснить, какой между двумя целыми числами, это нормально.
Сравните размер корней разных порядков
Мы также можем сравнить размеры корней разных порядков. Таким образом, для числа больше 1 — чем выше корень, тем меньше фактическое число. Таким образом, корень n-го порядка является корнем более высокого порядка, чем корень m-го порядка. И корень mth меньше. Итак, давайте подумаем об этом, предположим, что мы извлекаем разные корни из 19. Ну, конечно, квадратный корень из 19 должен быть меньше, чем 19.
Теперь кубический корень из 19 должен быть еще меньше, потому что он занимает всего два квадратного корня.Если мы умножим два квадратных корня вместе, мы получим 19. Мы должны умножить три кубических корня вместе, чтобы получить 19. И тогда мы можем расширить эту логику. Ну, 4-й корень должен быть еще меньше, потому что мне нужно умножить четыре из них, чтобы получить 19. Я должен умножить пять из них или шесть из них и так далее.
Наблюдение за появлением закономерностей
Итак, это означает, что по мере того, как мы получаем корни все более и более высокого порядка, все эти числа становятся меньше. Но они всегда больше 1. Теперь, даже если мы не можем понять, что такое десятичные дроби, должно быть верно, что корень 30-й степени из 19 меньше, чем корень 20-й степени из 19.Другими словами, мы должны быть в состоянии сделать это сравнение, даже если мы не можем определить точные значения этих десятичных знаков.
Изображение New Africa
Теперь, когда мы попадаем в область между 0 и 1, все становится немного иначе.
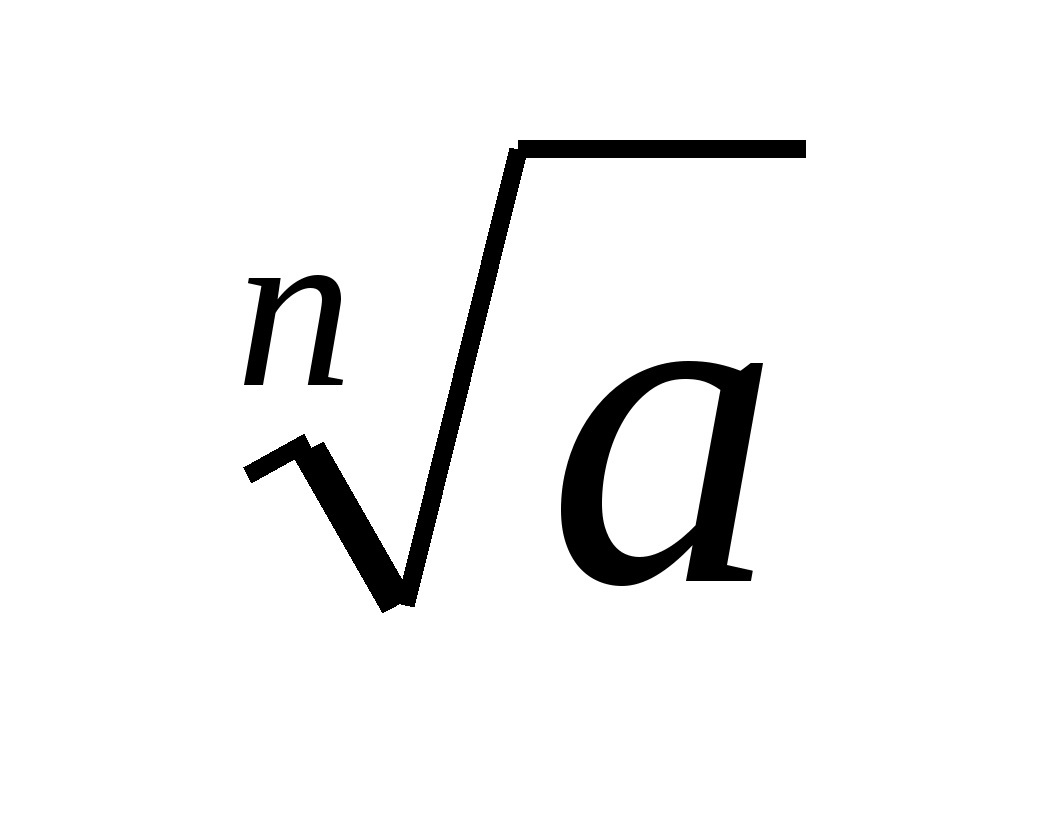 И вы, возможно, помните, здесь все было по-другому. Прежде всего, если мы возьмем корень, корни больше, чем b, если предположить, что b — это дробь между 0 и 1. И чем выше порядок корня, тем выше он становится.
И вы, возможно, помните, здесь все было по-другому. Прежде всего, если мы возьмем корень, корни больше, чем b, если предположить, что b — это дробь между 0 и 1. И чем выше порядок корня, тем выше он становится.Итак, n — корень более высокого порядка, он выше. Корень n-й степени b больше, чем корень m-й степени b. Итак, предположим, что мы берем разные корни, скажем, из двух пятых. Ну, две пятых меньше, чем квадратный корень из двух пятых. Это будет меньше, чем кубический корень, который меньше корня в четвертой степени, и так далее.
Продолжаем эту схему. Оказывается, все эти корни остаются меньше 1. Таким образом, они становятся все больше, больше и больше, но никогда не становятся больше 1. И эта закономерность продолжается со всеми корнями более высокого порядка.Таким образом, даже если бы нам пришлось сравнить два очень высоких корня, мы могли бы сказать, например, что мы знаем, что корень в 50-й степени из двух пятых должен быть больше, чем корень в две пятых, но он должен быть меньше, чем корень в 75-й степени из две пятых.
И 75-й корень из двух пятых по-прежнему должен быть меньше 1. Таким образом, мы должны быть в состоянии выяснить, где эти четыре члена попадают в неравенство, даже если мы можем вычислить точные десятичные значения этих корней. Подводя итог, можно сказать, что чем выше порядок корня, тем ближе результат к 1.То есть, если числа больше 1, извлечение корней более высокого порядка делает их все меньше и меньше, приближая их к 1.
Извлечение корней из чисел от 0 до 1 делает их больше, и они приближаются все ближе и ближе к 1. Итак, это это закономерность, все приближается к 1. И одна из причин этого, конечно же, в том, что мы можем взять любой корень из 1 и он будет равен 1. Эти свойства редко проверяются, и только на самых сложных задачах теста .
Итак, еще раз, это не то, что вы будете видеть каждый раз, когда садитесь за тест.Это очень редкие проблемы.
Резюме
Таким образом, в отличие от квадратных корней, мы можем извлекать кубические корни как из положительных, так и из отрицательных значений, это отличная идея. На самом деле мы можем взять любой четный корень из положительных, но не из отрицательных, но мы можем взять любой нечетный корень из любого числа на числовой прямой.
На самом деле мы можем взять любой четный корень из положительных, но не из отрицательных, но мы можем взять любой нечетный корень из любого числа на числовой прямой.
Это тоже отличная идея. Любой корень из 1 равен 1, а любой корень из 0 равен 0. Все корни сохраняют порядок неравенств, предполагая, что все числа положительные.И чем выше порядок корня, тем ближе результат к 1. Итак, опять же, числа больше 1, когда мы извлекаем корни, становятся меньше и приближаются к 1.
Когда мы извлекаем корни из чисел, находящихся между 0 и 1, они становятся больше и приближаются к 1.
Майк работал экспертом по GMAT в Magoosh, помогая создавать сотни видео уроков и практические вопросы, чтобы помочь студентам GMAT добиться успеха. Он также был признан «участником месяца» более двух лет в GMAT Club.Майк имеет A.B. по физике (окончание с отличием ) и степень МТС. в религиях мира, оба из Гарварда. Помимо стандартного тестирования, Майк имеет более чем 20-летний опыт преподавания как в частных, так и в государственных средних школах, специализируясь на математике и физике.
 В свободное время Майк любит разбивать настольные мячи на орбите, и, несмотря на то, что у него нет явных дефектов черепа, он настаивает на том, чтобы болеть за нью-йоркский Метс. Узнайте больше о GMAT из видеороликов Майка на Youtube и ресурсов, таких как What is a Good GMAT Score? и диагностический тест GMAT.
В свободное время Майк любит разбивать настольные мячи на орбите, и, несмотря на то, что у него нет явных дефектов черепа, он настаивает на том, чтобы болеть за нью-йоркский Метс. Узнайте больше о GMAT из видеороликов Майка на Youtube и ресурсов, таких как What is a Good GMAT Score? и диагностический тест GMAT.Просмотреть все сообщения
Вставка и вычисление простых математических уравнений в OneNote
Вам не нужен калькулятор, чтобы найти ответы на простые математические задачи. Вы можете записывать математические уравнения во время встречи, конференции или занятия, а OneNote мгновенно вычисляет для вас результаты.
Введите уравнение, которое вы хотите рассчитать. Например, введите 95+83+416 , чтобы вычислить сумму чисел 95, 83 и 416, или SQRT(15) , чтобы вычислить квадратный корень из 15.
После уравнения, не вводя пробел, введите знак равенства (=) и нажмите клавишу ПРОБЕЛ.
 Ответ появится после знака равенства.
Ответ появится после знака равенства.Советы:
Не используйте пробелы в уравнении. Введите числа, операторы и функции как одну непрерывную строку текста.
Коды функций не чувствительны к регистру.Например, SQRT(3)=, sqrt(3)= или Sqrt(3)= будет вычислять один и тот же ответ.
Чтобы создать новую строку после ответа, нажмите Enter (вместо пробела) после знака равенства.
Если вы хотите, чтобы в ваших заметках был только ответ, после того, как он будет рассчитан, вы можете удалить предшествующее ему уравнение. Ответ останется в ваших заметках.
Примеры простых расчетов
Ниже приведены несколько примеров математических выражений, которые может вычислять OneNote.
Среднемесячный объем продаж продукта. Например, если общий годовой доход составляет 215 000 долларов США, введите 215 000 долларов США/12= и нажмите клавишу ПРОБЕЛ.
Общая стоимость ежемесячных платежей. Например, введите 48*129,99 долларов США=, а затем нажмите пробел, чтобы рассчитать стоимость 48 ежемесячных платежей по 129,99 долларов США за платеж.
Синус угла в 30 градусов. Например, введите sin(30)= и нажмите клавишу ПРОБЕЛ.
Более полные математические уравнения. Например, введите (6+7) / (4*sqrt(3))=, а затем нажмите клавишу ПРОБЕЛ, чтобы вычислить ответ на (6+7), разделенный на (4 умноженный на квадратный корень из 3).
Поддерживаемые арифметические операторы
В уравнениях можно использовать следующие операторы.
Оператор | Значение | Пример |
+ (плюс) | Дополнение | 3+3 |
- (знак минус) | Вычитание | 3-1 |
* (звездочка) | Умножение | 3*3 |
X (верхний или нижний регистр) | Умножение | 3х3 |
/ (косая черта) | Отдел | 3/3 |
% (знак процента) | Процент | 20% |
^ (вставка) | Возведение в степень | 3^2 |
! (восклицательный знак) | Расчет факториала | 5! |
Поддерживаемые математические и тригонометрические функции
Вы можете использовать математические и тригонометрические функции из следующей таблицы для своих уравнений.
Примечание. Чтобы вычислить функцию, введите ее код (например, SQRT для квадратного корня) и сразу после него укажите число, угол или переменные в скобках, как показано в столбце «Синтаксис».
Функция | Описание | Синтаксис |
АБС | Возвращает абсолютное значение числа | АБС (номер) |
ACOS | Возвращает арккосинус числа | ACOS(номер) |
ASIN | Возвращает арксинус числа | ASIN(номер) |
АТАН | Возвращает арктангенс числа | АТАН(номер) |
COS | Возвращает косинус числа | COS(номер) |
ДЭГ | Преобразует угол (в радианах) в градусы | град(угол) |
ЛН | Возвращает натуральный логарифм числа | ЛН(номер) |
ЛОГ | Возвращает натуральный логарифм числа | Журнал(номер) |
ЛОГ2 | Возвращает логарифм числа по основанию 2. | LOG2(номер) |
ЛОГ10 | Возвращает логарифм числа по основанию 10. | LOG10(номер) |
МОД | Возвращает остаток от операции деления | (число)MOD (число) |
ИП | Возвращает значение π как константу | ИП |
PHI | Возвращает значение Φ (золотое сечение) | PHI |
ПЛТ | Расчет платежа по кредиту на основе постоянной процентной ставки, постоянного количества платежей и текущей стоимости общей суммы | PMT(ставка;nper;pv) |
РАД | Преобразует угол (в градусах) в радианы | РАД(угол) |
СИН | Возвращает синус заданного угла | SIN(угол) |
КВАРТИРА | Возвращает положительный квадратный корень | SQRT(номер) |
ТАН | Возвращает тангенс числа | ТАН(номер) |
Какие математические понятия вы применяли при извлечении квадратных корней? Объясните, как вы их применили?
С К.
математические понятия или принцип
Кеннет С. ответил • 22.06.17
Экспертная помощь по алгебре/тригонометрии/(пред)исчислению для гарантии успеха в 2018 году
Представленный вопрос включает в себя: Объясните, как вы их применили?Я бы исправил это предложение следующим образом: Объясните, как вы их применили?
Чтобы получить квадратный корень из числа (кроме уже совершенного квадрата, такого как √121 = 11), обычно используется калькулятор.Больше не учат скучному и сложному методу извлечения квадратного корня вручную.
Чтобы извлечь квадратный корень из большого составного числа, нужно научиться переписывать число в его уникальной простой факторизации.
Пример: рассмотрим √6048. начните с получения 3(2016) = 3(3)(672) = 3 2 • 4•168 = 3 2 • 4 2 • 42=3 2 • 2 4 • 2•3 •7
Примечание: числа делятся на 3, если сумма их цифр кратна 3Извлечение квадратного корня из каждого множителя дает √6048 = 3(2 2 )√(2•3•7) = 12√ 42
Другой метод основан на десятичных логарифмах:
log 6048 = 3.781611782
половина этого логарифма равна 1,8891
101,8891 = = 77,76888838
проверка: √6048 = 77,76888838 (последняя работа была выполнена на Casio fx-350ES05 Plus) 9000ES05 Plus
Все еще ищете помощи? Получите правильный ответ, быстро.
ИЛИ
Найдите онлайн-репетитора сейчас Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ – — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° − ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ е ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А А Â Ã Ä Å Æ Ç Э Э Ê Ë Я Я Я Я Ð С Ò О Ô Õ О Ø О Ш Ù Ú Û О Ý Ÿ Þ а а â г ä å æ ç э э э ë я я я я ð с ò о ô х ö ø œ ш ù ú û ü ý þ ÿ А В Г Δ Е Ζ Η Θ я Κ Λ М N Ξ О Π Р Σ Т Υ Φ Χ Ψ Ом α β γ дельта ε ζ η θ я κ λ мю ν ξ о π р ς о т υ ф х ψ ю ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊ .



 0
0 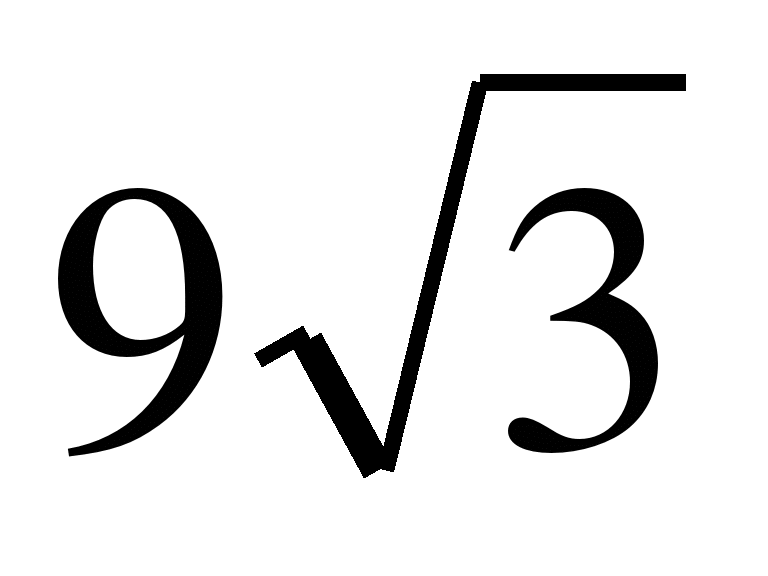
 Если какой-либо из аргументов отличен от нуля, то возвращаемое значение является наибольшим.
положительное целое число, являющееся делителем всех аргументов. Если все аргументы
равны нулю, то возвращаемое значение равно
Если какой-либо из аргументов отличен от нуля, то возвращаемое значение является наибольшим.
положительное целое число, являющееся делителем всех аргументов. Если все аргументы
равны нулю, то возвращаемое значение равно  Например, чтобы установить допуск 5%, введите
Например, чтобы установить допуск 5%, введите 



 Эта функция
предназначен специально для использования с числовыми значениями и может отклонять
нечисловые типы.
Эта функция
предназначен специально для использования с числовыми значениями и может отклонять
нечисловые типы. Если результат операции остатка равен нулю, этот ноль будет иметь
тот же знак, что и x .
Если результат операции остатка равен нулю, этот ноль будет иметь
тот же знак, что и x . float_info.min
float_info.min  0000050000069649e-05
>>> expm1(1e-5) # результат с точностью до полной точности
1.0000050000166668e-05
0000050000069649e-05
>>> expm1(1e-5) # результат с точностью до полной точности
1.0000050000166668e-05
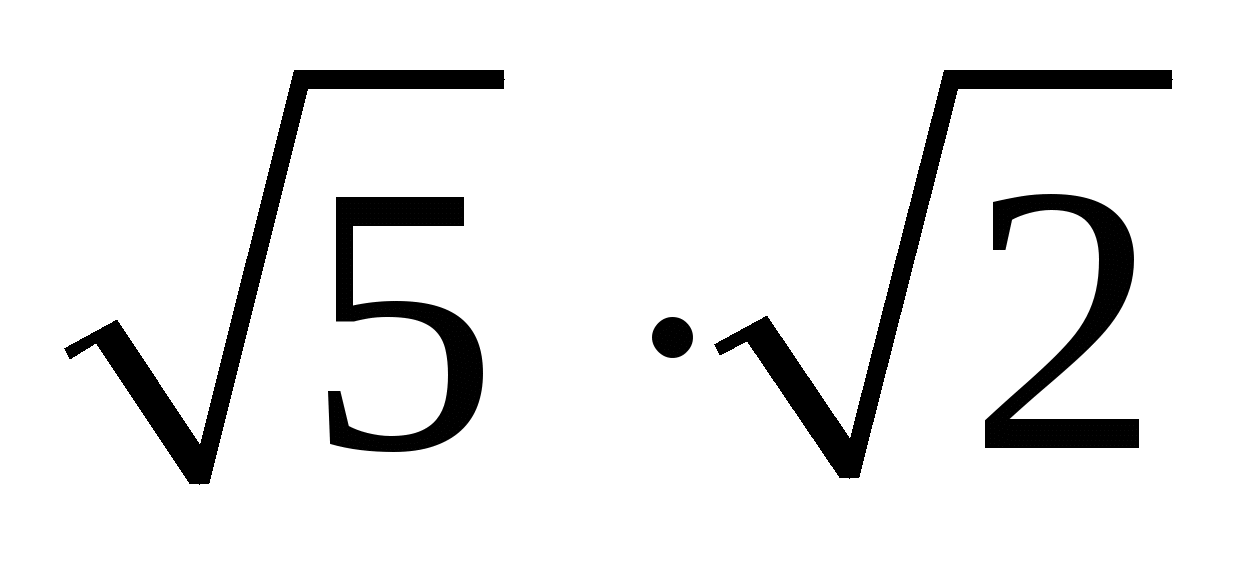
 Результат находится между
Результат находится между  0 для px, qx в zip(p, q)))
0 для px, qx в zip(p, q)))


 Дополнительная ошибка
функция определяется как
Дополнительная ошибка
функция определяется как  Тау — постоянная окружности, равная 2 π , отношение длины окружности к
его радиус. Чтобы узнать больше о Тау, посмотрите видео Ви Харта «Пи есть (все еще)».
Неправильно, и начать праздновать
Тау день, съев в два раза больше пирога!
Тау — постоянная окружности, равная 2 π , отношение длины окружности к
его радиус. Чтобы узнать больше о Тау, посмотрите видео Ви Харта «Пи есть (все еще)».
Неправильно, и начать праздновать
Тау день, съев в два раза больше пирога! Ответ появится после знака равенства.
Ответ появится после знака равенства.