Корень квадратный корень кубический: Кубический корень — урок. Алгебра, 8 класс.
Кубический корень. Извлечение кубического корня
- Главная
- Калькуляторы
- Математика
- Арифметика
- Кубический корень. Извлечение кубического корня
Кубический корень из a, обозначающийся как 3√a или как a1/3 — решение уравнения x3 = a (обычно подразумеваются вещественные решения).
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел.
Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.
Алгоритм извлечения кубического корня
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше.

- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a2× x+30× a × x2+x3 такое число x, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
КОРЕНЬ КУБИЧЕСКИЙ — это.
 .. Что такое КОРЕНЬ КУБИЧЕСКИЙ?
.. Что такое КОРЕНЬ КУБИЧЕСКИЙ?- КОРЕНЬ КУБИЧЕСКИЙ
КОРЕНЬ КУБИЧЕСКИЙ (обозначение 3Ц), число, которое необходимо дважды умножить на само себя для получения заданного числа. Например, кубический корень из 64 равняется 4, поскольку 4x4x4 = 64. В этом случае записывают:
Научно-технический энциклопедический словарь.
- КОРЕНЬ КВАДРАТНЫЙ
- КОРИ
Смотреть что такое «КОРЕНЬ КУБИЧЕСКИЙ» в других словарях:
КОРЕНЬ — КОРЕНЬ, корня, мн. корни, корней, м. 1. Вросшая в землю часть растения, через к рую оно всасывает соки из почвы.
 Бурей выворотило деревья с корнями. Дуб глубоко пустил корни в землю. || Древесина или вещество этой части растения. Лакричный корень … Толковый словарь Ушакова
Бурей выворотило деревья с корнями. Дуб глубоко пустил корни в землю. || Древесина или вещество этой части растения. Лакричный корень … Толковый словарь УшаковаКОРЕНЬ КВАДРАТНЫЙ — КОРЕНЬ КВАДРАТНЫЙ, число, обозначаемое как х, которое при умножении на само себя дает число х. Квадратный КОРЕНЬ из 4 равен 2, следовательно Ц4 = 2; Ц2 = 1,4142 (с точностью до четырех разрядов десятичной дроби). Отрицательные числа имеют… … Научно-технический энциклопедический словарь
корень — сущ., м., употр. сравн. часто Морфология: (нет) чего? корня, чему? корню, (вижу) что? корень, чем? корнем, о чём? о корне и на корню; мн. что? корни, (нет) чего? корней, чему? корням, (вижу) что? корни, чем? корнями, о чём? о корнях 1. Корень это … Толковый словарь Дмитриева
Корень n-й степени — Арифметический корень n й степени (n > 0) из неотрицательного числа есть единственное неотрицательное решение уравнения .
 Обозначается символом (или просто при ) … Википедия
Обозначается символом (или просто при ) … ВикипедияКУБИЧЕСКИЙ — (от слова куб). 1) имеющий вид куба. 2) мера, имеющая форму куба, т. е. правильного шестигранника. 3) корень, всякая величина, которая, будучи помножена три раза сама на себя, дает данную величину. Словарь иностранных слов, вошедших в состав… … Словарь иностранных слов русского языка
кубический — КУБИЧЕСКИЙ, КУБИЧНЫЙ ая, ое. cubique adj. <, лат. cubicus. 1. Имеющий форму куба. шестигранника. Сл. 18. Большая голова кубической фигуры. С. Меран 20. Горница имела совершенно кубический вид. ТВЭО 50 14. 2. Связанный с объемом, измерением… … Исторический словарь галлицизмов русского языка
КОРЕНЬ — муж. корешек, шечек, коренек ·умалит. корнишка презрительное, корнища увеличительное, подземная часть всякого растения. У деревьев различают становой и боковые корни, а при них корешки и мелкие мочки. вбирающие влагу. Корень бывает: луковичный,… … Толковый словарь Даля
КУБИЧЕСКИЙ — КУБИЧЕСКИЙ, кубическая, кубическое.

кубический корень — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN third root … Справочник технического переводчика
КОРЕНЬ ЧИСЛА — (root of number) Число х, чье значение в степени r равно у. Если у=хr, то х – корень r – степени от у. Например, в уравнении у=х2, х является квадратным корнем из у, и записывается следующим образом: x=√ y=y1/2; если z=x3, то х – кубический… … Экономический словарь
Существование единственного значения кубического корня из числа
Покажем теперь, что из числа a можно извлечь только один кубический корень.
Рассмотрим три разных варианта значений, которые может принимать подкоренное выражение:
Пусть:
Тогда рассмотрим кубический корень из нуля:
Чтобы определить этот корень воспользуемся определением, т. е. найдем такое число, которое при возведении в третью степень даст подкоренное выражение – нуль:
е. найдем такое число, которое при возведении в третью степень даст подкоренное выражение – нуль:
Очевидно, что это число нуль. следовательно, можем заключить, что при извлечении кубического корня, получаем только одно значение, равное нулю.
Теперь рассмотрим положительные значения подкоренного выражения и покажем, что кубический корень из положительного выражения не может быть ни отрицательным числом, ни нулем.
Пусть b – кубический корень из числа a:
Тогда из определения кубического корня:
Так как:
То:
Данное неравенство возможно только при b>0, так как только положительное число в нечетной степени является положительным числом.
Следовательно, кубический корень из положительного числа
Теперь предположим, что помимо числа b существует еще один кубический корень из числа a, и обозначим его буквой c. Причем c является положительным числом, так как мы рассматриваем положительные значения подкоренного выражения, и мы доказали, что кубический корень из положительного числа является положительным числом.
Причем c является положительным числом, так как мы рассматриваем положительные значения подкоренного выражения, и мы доказали, что кубический корень из положительного числа является положительным числом.
Тогда по определению кубического корня:
И:
Вычтем из первого равенства второе:
Воспользуемся формулой разности кубов:
Значит:
Произведение равно нулю, если хотя бы один из множителей равен нулю:
Из первого равенства имеем:
Второе равенство не верно, так как по условию c>0, b>0, а значит:
Следовательно, мы показали, что для положительного подкоренного выражения значение кубического корня – единственное и положительное.
Рассмотрим отрицательные подкоренные выражения:
Рассуждения будут аналогичны рассуждениям для положительных выражений под знаком корня.
Так как:
То:
Данное неравенство возможно только при b<0, так как только отрицательное число в нечетной степени является отрицательным числом.
Следовательно, кубический корень из отрицательного числа a является отрицательным числом.
Теперь предположим, что помимо числа b существует еще один кубический корень из числа a, и обозначим его буквой c. Причем c является отрицательным числом, так как мы рассматриваем отрицательные значения подкоренного выражения, и мы доказали, что кубический корень из отрицательного числа является отрицательным числом.
Тогда по определению кубического корня:
И:
Вычтем из первого равенства второе:
Воспользуемся формулой разности кубов:
Значит:
Произведение равно нулю, если хотя бы один из множителей равен нулю:
Из первого равенства имеем:
Рассмотрим второе равенство:
Так как по условию c<0, b<0, а произведение двух отрицательных чисел – число положительное:
Следовательно:
Итак, мы показали, что для отрицательного подкоренного выражения значение кубического корня – единственное и отрицательное.
Свойство корня третьей степени доказано.
Другие свойства кубического корня можно посмотреть в главе: Свойства корней.
Корень из числа: определения, примеры
Квадратный корень, арифметический квадратный корень
Чтобы понять определение корня из числа, и квадратного корня в частности, нужно иметь представление о степени с натуральным показателем. В этом пункте мы часто будем сталкиваться со второй степенью числа — квадратом числа.
Начнем с определения квадратного корня.
Определение
Квадратный корень из числа a — это число, квадрат которого равен a.
Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (52=5·5=25, (−0,3)2=(−0,3)·(−0,3)=0,09, (0,3)2=0,3·0,3=0,09 и 02=0·0=0). Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.
Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.
Следует отметить, что не для любого числа a существует действительное число, квадрат которого равен a. А именно, для любого отрицательного числа a не существует ни одного действительного числа b, квадрат которого равнялся бы a. В самом деле, равенство a=b2 невозможно для любого отрицательного a, так как b2 – неотрицательное число при любом b. Таким образом, на множестве действительных чисел не существует квадратного корня из отрицательного числа. Иными словами, на множестве действительных чисел квадратный корень из отрицательного числа не определяется и не имеет смысла.
Отсюда вытекает логичный вопрос: «А для любого ли неотрицательного a существует квадратный корень из a»? Ответ – да. Обоснованием этого факта можно считать конструктивный способ, используемый для нахождения значения квадратного корня.
Тогда встает следующий логичный вопрос: «Каково число всех квадратных корней из данного неотрицательного числа a – один, два, три, или еще больше»? Вот ответ на него: если a равно нулю, то единственным квадратным корнем из нуля является нуль; если же a – некоторое положительное число, то количество квадратных корней из числа a равно двум, причем корни являются противоположными числами. Обоснуем это.
Начнем со случая a=0. Сначала покажем, что нуль действительно является квадратным корнем из нуля. Это следует из очевидного равенства 02=0·0=0 и определения квадратного корня.
Теперь докажем, что 0 – единственный квадратный корень из нуля. Воспользуемся методом от противного. Предположим, что существует некоторое число b, отличное от нуля, которое является квадратным корнем из нуля. Тогда должно выполняться условие b2=0, что невозможно, так как при любом отличном от нуля b значение выражения b2 является положительным. Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.
Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.
Переходим к случаям, когда a – положительное число. Выше мы сказали, что всегда существует квадратный корень из любого неотрицательного числа, пусть квадратным корнем из a является число b. Допустим, что существует число c, которое тоже является квадратным корнем из a. Тогда по определению квадратного корня справедливы равенства b2=a и c2=a, из них следует, что b2−c2=a−a=0, но так как b2−c2=(b−c)·(b+c), то (b−c)·(b+c)=0. Полученное равенство в силу свойств действий с действительными числами возможно лишь тогда, когда b−c=0 или b+c=0. Таким образом, числа b и c равны или противоположны.
Если же предположить, что существует число d, являющееся еще одним квадратным корнем из числа a, то рассуждениями, аналогичными уже приведенным, доказывается, что d равно числу b или числу c. Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.
Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.
Для удобства работы с квадратными корнями отрицательный корень «отделяется» от положительного. С этой целью вводится определение арифметического квадратного корня.
Определение
Арифметический квадратный корень из неотрицательного числа a – это неотрицательное число, квадрат которого равен a.
Для арифметического квадратного корня из числа a принято обозначение . Знак называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.
Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня – подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.
Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.
При чтении слово «арифметический» часто опускается, например, запись читают как «квадратный корень из семи целых двадцати девяти сотых». Слово «арифметический» произносят лишь тогда, когда хотят особо подчеркнуть, что речь идет именно о положительном квадратном корне из числа.
В свете введенного обозначения из определения арифметического квадратного корня следует, что и для любого неотрицательного числа a.
Квадратные корни из положительного числа a с помощью знака арифметического квадратного корня записываются как и . Например, квадратные корни из числа 13 есть и . Арифметический квадратный корень из нуля равен нулю, то есть, . Для отрицательных чисел a записи мы не будем придавать смысла вплоть до изучения комплексных чисел. Например, лишены смысла выражения и .
На базе определения квадратного корня доказываются свойства квадратных корней, которые часто применяются на практике.
Нахождение квадратных корней заслуживает детального изучения, этой теме посвящена отдельная статья извлечение квадратных корней.
В заключение этого пункта заметим, что квадратные корни из числа a являются решениями квадратного уравнения вида x2=a относительно переменной x.
К началу страницы
Кубический корень в Excel — Офис Ассист
Извлечение корня из числа является довольно распространенным математическим действием. Оно применяется и для различных расчетов в таблицах. В Microsoft Excel есть несколько способов посчитать данное значение. Давайте подробно рассмотрим различные варианты осуществления подобных расчетов в этой программе.
Содержание
Способы извлечения
Существуют два основных способа расчета данного показателя. Один из них подходит исключительно для вычисления квадратного корня, а второй можно использовать для расчета величины любой степени.
Способ 1: применение функции
Для того, чтобы извлечь квадратный корень используется функция, которая так и называется КОРЕНЬ. Её синтаксис выглядит следующим образом:
=КОРЕНЬ(число)
Для того, чтобы воспользоваться данным вариантом, достаточно записать в ячейку или в строку функций программы это выражение, заменив слово «число» на конкретную цифру или на адрес ячейки, где она расположена.
Для выполнения расчета и вывода результата на экран жмем кнопку ENTER.
Кроме того, можно применить данную формулу через мастер функций.
- Кликаем по ячейке на листе, куда будет выводиться результат вычислений. Переходим по кнопке «Вставить функцию», размещенную около строки функций.
- В открывшемся списке выбираем пункт «КОРЕНЬ». Кликаем по кнопку «OK».
- Открывается окно аргументов. В единственном поле данного окна нужно ввести либо конкретную величину, из которой будет происходить извлечение, либо координаты ячейки, где она расположена.
 1/n
1/nn — это степень возведения.
Таким образом, этот вариант является намного универсальнее, чем использование первого способа.
Как видим, несмотря на то, что в Excel нет специализированной функции для извлечения кубического корня, данное вычисление можно провести, используя возведение в дробную степень, а именно — 1/3. Для извлечения квадратного корня можно воспользоваться специальной функцией, но существует также возможность сделать это путем возведения числа в степень. На этот раз нужно будет возвести в степень 1/2. Пользователь сам должен определить, какой способ вычислений для него удобнее.
Корень 3 степени из 0.25. Кубический корень (извлечение без калькулятора)
Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем.
 Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.Шаги
Часть 1
Извлечение кубического корня на простом примереЗапишите задачу. Извлечение кубического корня вручную похоже на деление в столбик, но с некоторыми нюансами. Сначала запишите задачу в определенной форме.
- Запишите число, из которого нужно извлечь кубический корень. Число разбейте на группы по три цифры, причем отсчет начните с десятичной запятой. Например, нужно извлечь кубический корень из 10. Напишите это число так: 10, 000 000. Дополнительные нули призваны повысить точность результата.
- Возле и над числом нарисуйте знак корня. Представьте, что это горизонтальная и вертикальная линии, которые вы рисуете при делении в столбик.
 2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.
2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.
Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток).
Подумайте, является ли полученный ответ достаточно точным. Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1.
- Чтобы проверить точность ответа, возведите его в куб: 2,1*2,1*2,1 = 9,261.
- Если вы считаете, что ответ достаточно точный, вычисления можно не продолжать; в противном случае проделайте еще одно вычитание.
Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше.
 {3}=729}
, то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.
{3}=729}
, то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа.
- В нашем примере число 600 находится между числами 512 и 729. Например, к первому найденному числу (8) припишите цифру 5. Получится число 8,5.
- В нашем примере: 8 , 5 ∗ 8 , 5 ∗ 8 , 5 = 614 , 1. {\displaystyle 8,5*8,5*8,5=614,1.}
Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число.
 {3}=614,1}
. Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.
{3}=614,1}
. Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа.
- В нашем примере 8 , 44 ∗ 8 , 44 ∗ 8 , 44 = 601 , 2 {\displaystyle 8,44*8,44*8,44=601,2} . Это чуть больше исходного числа, поэтому оцените другое (меньшее) число, например, 8,43: 8 , 43 ∗ 8 , 43 ∗ 8 , 43 = 599 , 07 {\displaystyle 8,43*8,43*8,43=599,07} . Таким образом, значение кубического корня из 600 лежит между 8,43 и 8,44.
Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее.
 {3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.
{3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.
При решении некоторых технических задач бывает нужно посчитать корень третьей степени . Иногда это число еще называют кубическим корнем. Корнем третьей степени из данного числа называют такое число, куб (третья степень) которого равняется данному. То есть если y – корень третьей степени числа x, то должно выполняться условие: y?=x (икс равно игрек куб).
Вам понадобится
- калькулятор или компьютер
Инструкция
- Чтобы посчитать корень третьей степени , воспользуйтесь калькулятором. Желательно, чтобы это был не обычный калькулятор, а калькулятор, используемый для инженерных расчетов. Однако даже на таком калькуляторе вы не найдете специальную кнопку для извлечения корня третьей степени . Поэтому используйте функцию для возведения числа в степень. Извлечению корня третьей степени соответствует возведение в степень 1/3 (одна треть).
 y.
y. - Если корень третьей степени приходится считать систематически, то воспользуйтесь программой MS Excel. Чтобы посчитать корень третьей степени в «Екселе», введите в любую клетку знак «=», а затем, выберите значок «fx» — вставка функции. В появившемся окошке в списке «Выберите функцию» выберите строку «СТЕПЕНЬ». Нажмите кнопку «Ок». Во вновь появившемся окошке введите в строку «Число» значение числа, из которого нужно извлечь корень. В строку «Степень» введите число «1/3» и нажмите «Ок». В клетке таблицы появится искомое значение кубического корня из исходного числа.
Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.
Математическое обозначение
«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина.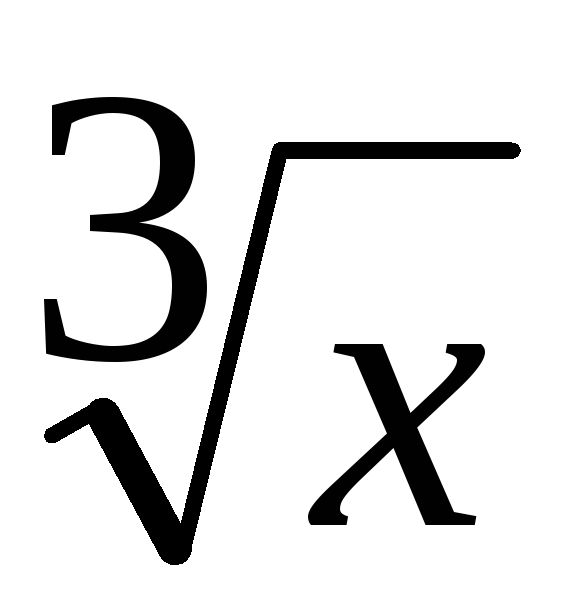 С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
Квадратный корень
Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…
Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.
Кубический корень
Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…
Для остальных чисел кубические корни являются иррациональными числами. В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
Корень n-ной степени
Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Рассмотрим пример
Диагональ квадрата
Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из и в конечном итоге принимает вид:
d = a × sqrt(2).
Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.
Заключение
Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.
Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».
В-третьих, для них справедливы все действия со степенями.
- Их можно перемножать. Тогда показатели степеней складываются.

- Корни можно разделить. Степени нужно будет вычесть.
- И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя.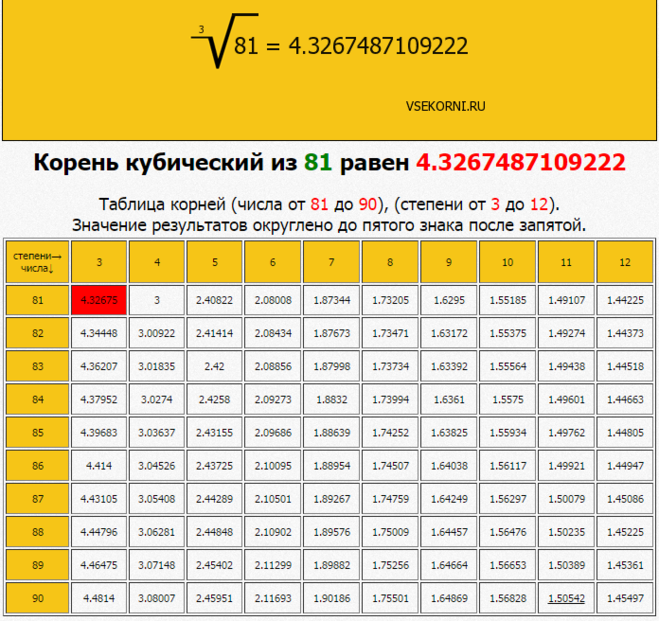 Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
- Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой.
 Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать. - Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
- Выполнить вычитание.
- К остатку приписать первую группу цифр после запятой.
- В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
- Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
- Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.
Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
- 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
- После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
- а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3
- Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
- Вычитание дает 1176, а над корнем появилось число 4.
- Приписать к остатку три нуля.
- а = 24. Тогда 172800 х + 720 х 2 + х 3
- х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
- Снова приписать нули.
- а = 246. Неравенство получается таким: 18154800х + 7380х 2 + х 3
- х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.
Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.
Необычный способ извлечения кубического корня
Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.
К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.
Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.
Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.
Размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.
Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т. д.
д.
Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.
Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице .
Извлечение квадратного корня
Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.
Пример решения квадратных корней в калькуляторе:
Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.
Квадратный корень из отрицательного числа:
Корень третьей степени
Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).
Она вставляет в строке ввода запись sqrt3(x).
Корень 3 степени:
Корень степени n
Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).
Корень 4 степени:
Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n. В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.
Корень 5 степени с приблизительным результатом:
Корень из дроби
Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.
Квадратный корень из дроби:
Корень из корня
В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Пример, как извлечь корень из корня:
Степень в корне
Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.
Квадратный корень из степени:
Все функции нашего бесплатного калькулятора собраны в одном разделе.
Решение корней в онлайн калькуляторе was last modified: Март 3rd, 2016 by Admin
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Калькулятор кубического корня
Использование калькулятора
Воспользуйтесь этим калькулятором, чтобы найти кубический корень из положительных или отрицательных чисел. Учитывая число x , кубический корень x — это число на , такое что a 3 = x . Если x положительный , будет положительным, если x отрицательно будет отрицательным.Кубические корни — это особая форма нашего общего
Калькулятор радикалов.
Учитывая число x , кубический корень x — это число на , такое что a 3 = x . Если x положительный , будет положительным, если x отрицательно будет отрицательным.Кубические корни — это особая форма нашего общего
Калькулятор радикалов.
Пример кубических корней:
- Третий корень 64, или 64, радикал 3, или кубический корень из 64 записывается как \ (\ sqrt [3] {64} = 4 \).
- Третий корень из -64, или -64, радикал 3, или кубический корень из -64 записывается как \ (\ sqrt [3] {- 64} = -4 \).
- Кубический корень из 8 записывается как \ (\ sqrt [3] {8} = 2 \).
- Кубический корень из 10 записывается как \ (\ sqrt [3] {10} = 2.{\ frac {1} {3}} \). Распространенное определение кубического корня отрицательного числа таково:
(-x) 1/3 = — (x 1/3 ) . [1] Например:
[1] Например:- Кубический корень -27 записывается как \ (\ sqrt [3] {- 27} = -3 \).
- Кубический корень -8 записывается как \ (\ sqrt [3] {- 8} = -2 \).
- Кубический корень из -64 записывается как \ (\ sqrt [3] {- 64} = -4 \).
Кубические корни (для целочисленных результатов от 1 до 10)
- Кубический корень из 1 1
- Кубический корень из 8 равен 2
- Кубический корень из 27 равен 3
- Кубический корень из 64 составляет 4
- Кубический корень из 125 составляет 5
- Кубический корень из 216 равен 6
- Кубический корень из 343 равен 7
- Кубический корень из 512 равен 8
- Кубический корень из 729 составляет 9
- Кубический корень из 1000 составляет 10
Для вычисления дробных показателей используйте наш калькулятор для Дробные экспоненты.

Список литературы
[1] Вайсштейн, Эрик В. «Кубический корень». От MathWorld — Интернет-ресурс по Wolfram. Кубический корень
Математика — это забавные кубические корни
Калькулятор квадрата, куба, квадратного корня и кубического корня
Калькулятор квадрата, куба, квадратного корня и кубического корня
Квадрат, куб, квадратный корень и кубический корень для чисел с диапазоном 0-100
Число
xКвадратный
x 2Куб
x 3Квадратный корень
x 1/2Кубический корень
x 1/31 1 1 901 1.000 1.000 2 4 8 1.  414
4141.260 3 9 27 1.732 1.442 2.000 1,587 5 25 125 2,236 1,710 6 36 216 2.449 1,817 7 49 343 2,646 1,913 8 64 512 2,812 9030 2,812 3.000 2.080 10 100 1000 3.162 2.154 11 121 1331 3.317 2,224 12 144 1728 3,464 2,289 13 169 2197 9012 9012 9012 2197 9012 9012 27301 3,742 2,410 15 225 3375 3,873 2,466 16 256 4096 4.  000
0002,520 17 289 4913 4,123 2,571 18 324 5832 4,243 1910 9030 4,359 2,668 20 400 8000 4,472 2,714 21 441 9261 4.583 2,759 22 484 10648 4,690 2,802 23 529 12167 9030529 12167 9030 9030 9030 4,796 9030 12167 90104,796 9030 4,899 2,884 25 625 15625 5,000 2,924 26 676 17576 17576 17576 099 2.962 27 729 19683 5.196 3.  000
00028 784 21952 784 21952 9030 9030 9030 5,385 3,072 30 900 27000 5,477 3,107 31 961 29791 5.568 3,141 32 1024 32768 5,657 3,175 33 1089 35937 5,831 3,240 35 1225 42875 5,916 3,271 36 1296 46656 000 3,302 37 1369 50653 6,083 3,332 38 1444 54872
90301444 903054872 6,164 901 9030 6,245 3,391 40 1600 64000 6,325 3,420 41 1681 68921 6.  403
4033,448 42 1764 74088 6,481 3,476 43 43 1849 79507 9030 79507 6,557 9001 9030 6,633 3,530 45 2025 6,708 3,557 46 2116 97336 6. 30 97336 782 3.583 47 2209 103823 6.856 3.609 48 2304 110592 9012 9012 7.000 3.659 50 2500 125000 7.071 3.684 51 2601 132651 7. 30 141 3,708 52 2704 140608 7,211 3,733 53 2809 148877 148877
307,348 3,780 55 3025 166375 7,416 3,803 56 3136 175616 175616 483 3,826 57 3249 185193 7,550 3,849 58 3364 195112 9012 7,681 3,893 60 3600 216000 7,746 3,915 61 3721 226981 8103,936 62 3844 238328 7,874 3,958 63 3969 2500129 9012 9012 3969 250047 9030 9030 8.  000
0004.000 65 4225 274625 8.062 4.021 66 4356 287496 8. 30 124 4,041 67 4489 300763 8,185 4,062 68 4624 314432 8,246 314432 8,246 8,307 4,102 70 4900 343000 8,367 4,121 71 5041 357911 4264,141 72 5184 373248 8,485 4,160 73 5329 389012 5329 389012 8,544 8,602 4,198 75 5625 421875 8,660 4,217 76 5776 4312976 8. 718 30
304,236 77 5929 456533 8.775 4,254 78 6084 474552 9012 7912 9030 4,29 9030 4,29 8,888 4,291 80 6400 512000 8,944 4,309 81 6561 531441 9 531441 9 0004,327 82 6724 551368 9,055 4,344 83 6889 571787 9012 9,110 9,110 9030 9,165 4,380 85 7225 614125 9,220 4,397 86 7396 636056 2744,414 87 7569 658503 9,327 4,431 88 7744 681472 9012 9012 9030 9 9030 9 9,434 4,465 90 8100 729000 9,487 4,481 91 8281 123571 5394,498 92 8464 778688 9,592 4,514 93 8649 8043512 9,612 9012 9030 9,695 4,547 95 9025 857375 9,747 4,563 96 9216 884736 9.  798
7984,579 97 9409 9,849 4,595 98 9604 941192 9604 9301 9,950 4,626 100 10000 1000000 10.000 4,642 Загрузите и распечатайте квадрат, куб, квадратный корень
и кубический корень диаграммы
3D-модельИспользуйте расширение Engineering ToolBox Sketchup — для добавления кубических линий в модели Sketchup.
Квадратный корень и кубический корень
Квадратный корень и кубический корень Символ
Квадратный корень
Квадратный корень из числа x — это то число, которое при умножении на само дает число x. Число x представляет собой полный квадрат.
Например, 22 = 4, или квадратный корень из 4 равен 2
32 = 9, или квадратный корень из 9 равен 3
42 = 16, или квадратный корень из 16 равен 4
.
 квадратный корень равен \ [\ sqrt {} \]
квадратный корень равен \ [\ sqrt {} \]Следовательно, квадратный корень из 4 представляется как \ [\ sqrt {4} \] = 2.
И квадратный корень из 9 представляется как \ [\ sqrt {9} \] = 3 и так далее.
Кубический корень
Кубический корень числа а — это то число, которое при трехкратном умножении на само себя дает само число «а».
Например, 23 = 8, или кубический корень из 8 равен 2
33 = 27, или кубический корень из 27 равен 3
43 = 64, или кубический корень из 64 равен 4
. кубический корень равен 1/3 или ∛
Таким образом, кубический корень из 8 представлен как \ [\ sqrt [3] {8} \] = 2, а корень из 27 — как \ [\ sqrt [3] {27} \] = 3
и т. Д.
Свойства квадратного корня:
Если единичная цифра числа — 2, 3, 7 и 8, то его квадратный корень не является натуральным числом.

Если число заканчивается нечетным числом нулей, то его квадратный корень не является натуральным числом.
Квадратный корень четного числа является четным, а нечетного — нечетным.
Отрицательные числа не имеют квадратного корня в наборе действительных чисел.
Свойства корня куба
Корень куба всех нечетных чисел является нечетным числом.Например: \ [\ sqrt [3] {27} \] = 3, \ [\ sqrt [3] {125} \] = 5.
Кубический корень всех четных натуральных чисел четный. Например: \ [\ sqrt [3] {8} \] = 2, \ [\ sqrt [3] {64} \] = 4.
Кубический корень отрицательного целого числа всегда дает отрицательный результат.
Методы нахождения квадратного корня и кубического корня:
Во-первых, квадратный корень из пяти чисел и кубический корень легко запомнить.
 Но когда нам нужно найти квадратный корень и кубический корень из больших чисел, мы можем использовать следующие методы, чтобы найти его.Это
Но когда нам нужно найти квадратный корень и кубический корень из больших чисел, мы можем использовать следующие методы, чтобы найти его.ЭтоМетод факторизации простых чисел
Метод длинного деления
Этот метод поможет вам найти квадратные корни и кубический корень из заданного числа, но если квадратный корень и кубический корень из первых 10 чисел запоминаются, это поможет вам быстрее решить ваши проблемы. Вот формат таблицы квадратного корня и кубического корня, который поможет вам запомнить эти квадратные корни и кубические корни.
Квадратный корень и кубический корень от 1 до 15
Список квадратного корня и список кубического корня от 1 до 15 помогут вам решить самые трудоемкие длинные уравнения в кратчайшие сроки.Эта таблица квадратного корня и кубического корня будет полезна вам на каждом этапе.
Квадратный корень и кубический корень Таблица
Квадратный корень числа
Число
Кубический корень числа
\ [\ sqrt {4} \] 2
\ [\ sqrt [3] {8} \]
2
\ [\ sqrt {9} \]
3
\ [\ sqrt [3] {27} \]
3
\ [\ sqrt {16} \]
4
\ [\ sqrt [3] {64} \] 4
\ [\ sqrt {25} \]
5
\ [\ sqrt [3] {135 } \]
5
\ [\ sqrt {36} \]
6
\ [\ sqrt [3] {216} \]
6
\ [\ sqrt {49} \]
7
\ [\ sqrt [3] { 343} \]
7
\ [\ sqrt {64} \]
8
\ [\ sqrt [3] {512} \]
8
\ [\ sqrt {81} \]
9
\ [\ sqrt [3] {729} \]
9
\ [\ \ sqrt {100} \]
10
\ [\ sqrt [3] {1000} \]
10
\ [\ sqrt {121} \]
11
\ [\ sqrt [3] {1331} \]
11
\ [\ sqrt {144} \]
12
\ [\ sqrt [3] {1728} \]
12
\ [\ sqrt {169} \]
13
\ [\ sqrt [3] {2197} \]
13
\ [\ sqrt {196} \] 14
\ [\ sqrt [3] {2744} \]
14
\ [\ sqrt {225} \]
15
\ [\ sqrt [3] {3375} \]
15
Воспользуйтесь этим списком квадратного корня и списком кубического корня и найдите квадратный корень ниже и пример кубического корня.

Решенные примеры
Пример квадратного корня и кубического корня
Пример 1: Найти кубический корень из 2744
Решение:
Методом простой факторизации
Шаг 1. Сначала мы берем простые множители данного числа
2744 = 2 x 7 x 2 x 2 x 7 x 7
Шаг 2: Сформируйте группы из трех одинаковых множителей
= 2 x 2 x 2 x 7 x 7 x 7
Шаг 3: Выньте по одному множителю из каждой группы и размножаться.
= 23 x 73
= 143
Следовательно, \ [\ sqrt [3] {2744} \] = 14
Пример 2: Найдите кубический корень из 1728 методом длинного деления
Решение:
2
1728
2
864
2
2
12 9
2
108
2
54
3
27
3
3
1
Сейчас,
913 44 \ [\ sqrt [3] {1728} \] = \ [\ sqrt [3] {2X2X2X2X2X2X3X3} \]= 2 x 2 x 3
= 12
Quiz
Еще немного квадратного корня и кубического корня примеры для решения.

Оцените квадратный корень из 666
Найдите значение \ [\ sqrt {256} \]
Используя разложение на простые множители, найдите значение \ [\ sqrt [3] {1331} \ ]
Используя метод деления в столбик, найдите значение \ [\ sqrt [3] {729} \]
корней с более высоким индексом | Purplemath
Purplemath
Операции с кубическими корнями, корнями четвертой степени и другими корнями с более высоким индексом работают аналогично квадратным корням, хотя в некоторых случаях нам нужно немного расширить наше мышление.Я объясню по ходу дела.
Упрощение терминов с более высоким индексомНа предыдущих страницах мы упростили квадратные корни, исключив из радикала любой множитель, встречающийся в наборах по два.
 Для второго корня нам понадобилась вторая копия.
Для второго корня нам понадобилась вторая копия.Для корней с более высоким индексом рассуждения те же. Если у нас есть кубический корень, мы можем исключить любой фактор, встречающийся в наборах по три; из корня четвертой степени мы вычитаем любой фактор, который встречается в наборах по четыре; из корня пятой степени мы исключаем любой фактор, встречающийся в наборах по пять штук; и так далее.Например:
MathHelp.com
Упростить
Раньше я мог извлечь из квадратного корня все, что у меня было две копии.
 Таким же образом теперь я могу извлечь из корня четвертой степени все, что у меня есть четыре копии. Поскольку 16 = 2 4 , то:
Таким же образом теперь я могу извлечь из корня четвертой степени все, что у меня есть четыре копии. Поскольку 16 = 2 4 , то:Упростите кубический корень:
Я беру кубический корень. Затем я могу вывести из радикала любой фактор, который встречается трижды.Поскольку 8 = 2 3 , то этот радикал полностью упростится.
Упростите кубический корень:
Мой первый шаг — полностью учесть это:
54 = 2 · 27 = 2 · (3 · 3 · 3)
У меня есть три копии 3, поэтому я могу вытащить 3 из корня куба, оставив 2 внутри.

Упростить:
Снова начну с факторинга:
48 = 3 · 16 = 3 · 2 · 2 · 2 · 2
У меня есть четыре копии фактора 2, но это кубический корень, поэтому я могу извлечь 2 только для трех из этих копий.3 и четвертая 2 останутся внутри радикала.
Упростить:
Я знаю, что 27 = 3 3 , поэтому кубический корень упростится до целого числа. Потом закончу умножением.
Упростить:
Мне дали переменные внутри этого радикала, но процесс работает так же, как всегда.
 Я беру пятый корень, поэтому могу вытащить из радикала все, для чего у меня есть пять копий.
Я беру пятый корень, поэтому могу вытащить из радикала все, для чего у меня есть пять копий.32 — это 2 5 , так что это произойдет вне корня. x 10 = ( x 2 ) 5 , поэтому выйдет x 2 . y 6 = ( y 5 ) ( y 1 ), поэтому я смогу вытащить y , оставив последние y внутри корня.И z 7 = ( z 5 ) ( z 2 ), поэтому я смогу вытащить z , оставив z 2 внутри.
Моя работа выглядит так:
Примечание. Когда вы упрощаете радикальные выражения с помощью переменных, если радикал является корнем с четным индексом (например, квадратный корень или корень четвертой степени), они, вероятно, укажут, что вы должны «предполагать, что все переменные неотрицательны.
 «(или» положительный «).Это сделано для того, чтобы вам не приходилось учитывать, нужны ли столбцы абсолютных значений для вашего ответа. Если вы не уверены, о чем я говорю, проверьте здесь.
«(или» положительный «).Это сделано для того, чтобы вам не приходилось учитывать, нужны ли столбцы абсолютных значений для вашего ответа. Если вы не уверены, о чем я говорю, проверьте здесь.
Умножение корней с более высоким индексомУпростите выражение кубического корня:
Это умножение работает так же, как умножение квадратных корней, в том смысле, что произведение двух одинаковых корней с более высоким индексом может быть преобразовано в корень с более высоким индексом произведения.Затем я упрощаю как обычно.
Упростите продукт:
В данном случае они дали мне продукт четвертого корня. Я могу превратить продукт радикалов в радикал продукта.
 Тогда я могу упростить.
Тогда я могу упростить.
Добавление корней с более высоким индексомУпростить:
Термины в этом выражении являются кубическими корнями, но я могу объединить их, только если они кубические корни одного и того же значения.Прямо сейчас это не так. Поэтому я сначала упрощу радикалы, а затем посмотрю, смогу ли я пойти дальше.
Замечу, что 8 = 2 3 и 64 = 4 3 , так что я действительно смогу полностью упростить радикалы.
Упростить:
Я вообще не могу упростить второй радикал.Но я могу упростить первый радикал, потому что 81 = 3 4 = (3 3 ) (3).
 Итак, я получу сумму двух корней третьих из трех, которые я могу объединить.
Итак, я получу сумму двух корней третьих из трех, которые я могу объединить.
Разделение корней с более высоким индексомУпростите кубический корень:
Знаменатель — это куб, равный 27 = 3 3 , поэтому я легко могу упростить и прийти к «рационализированному» знаменателю:
Упростите кубический корень:
Это похоже на предыдущее упражнение, но здесь куб (то есть 27) находится в числителе.Я не могу упростить это выражение должным образом, потому что я не могу упростить радикал в знаменателе до целых чисел:
Чтобы рационализировать знаменатель, содержащий квадратный корень, мне потребовались две копии любых множителей внутри радикала.
 Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.У меня есть одна копия множителя 5 в знаменателе.Я умножу сверху и снизу на кубический корень из 25, что даст дополнительные две копии 5, которые мне нужны, чтобы рационализировать знаменатель.
Это последнее выражение, возможно, ненамного «проще», чем исходное выражение. В этом контексте «упростить» означало «рационализировать знаменатель». Часто «правильный» ответ будет не намного, если вообще, «проще», чем тот, с которого вы начали.
Упростить:
Так как 72 = 8 × 9 = (2 × 2 × 2) × (3 × 3), у меня есть только три двойки и две тройки. Другими словами, при нынешней дроби мне не хватит каких-либо факторов знаменателя, чтобы избавиться от радикала.

Чтобы извлечь что-либо из корня четвертой степени, мне нужно по четыре копии каждого фактора.Для радикала этого знаменателя мне понадобятся еще две тройки и еще одна 2. Итак, я умножу верхнюю и нижнюю часть на корень четвертой степени из 3 · 3 · 2 = 18.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в работе с выражениями с более высоким индексом. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/radicals6.htm
восточноазиатских математиков | Britannica
Текстовые источники
Книги, написанные в Китае с I века до нашей эры по VII век нашей эры, а затем в XIII веке, легли в основу развития математики в Восточной Азии.
 К ним относятся большинство последующих математических работ. Ссылки, найденные в сохранившихся математических сочинениях этого периода, а также ссылки, сделанные в библиографиях, составленных для династических летописей, указывают на то, что в текстовой записи есть много пробелов. Самые старые из дошедших до нас работ, вероятно, сохранились, потому что они стали официальными книгами, преподаваемыми в контексте китайской системы гражданских экзаменов.
К ним относятся большинство последующих математических работ. Ссылки, найденные в сохранившихся математических сочинениях этого периода, а также ссылки, сделанные в библиографиях, составленных для династических летописей, указывают на то, что в текстовой записи есть много пробелов. Самые старые из дошедших до нас работ, вероятно, сохранились, потому что они стали официальными книгами, преподаваемыми в контексте китайской системы гражданских экзаменов.Самая важная работа в истории математики на китайском языке — Jiuzhang suanshu ( Девять глав по математическому искусству ), которая содержит арифметические, алгебраические и геометрические алгоритмы, связанные с проблемами, некоторые из которых вызывают обязанности гражданской администрации: обследование полей (площадей), взимание налогов в соответствии с различными видами зерна (соотношениями), определение заработной платы государственных служащих в соответствии с их положением в иерархии (неравное распределение), измерение запланированных земляных работ для определения потребностей в рабочей силе и зернохранилищ для определения вместимости (объемов) хранения, взимания справедливых налогов (проблемы сочетания различных пропорций) и т.
 д.Этот сборник I века до н. Э. (Специалисты расходятся во мнениях относительно точной даты его завершения) был восстановлен на основе двух основных источников. Самый старый из сохранившихся экземпляров, который также является старейшей из когда-либо напечатанных книг по математике, датируется 1213 годом. Однако сохранились только первые пять глав. Полная книга, известная сегодня как Девять глав , является результатом филологической работы 18-го века, основанной как на прежнем источнике, так и на исчерпывающих цитатах из китайской энциклопедии 15-го века, Yongle dadian , составленной при императоре Юнлэ (1402 г.) –24).В любом случае, как Евклид Elements , Девять глав собрал и систематизировал многие математические достижения (включая арифметические, геометрические и алгебраические алгоритмы) предыдущих периодов. И, как Elements на Западе, Девять глав сыграли выдающуюся роль в развитии математики в Восточной Азии. Большинство математиков ссылались на нее, и большинство предметов, над которыми они работали, проистекали из нее.
д.Этот сборник I века до н. Э. (Специалисты расходятся во мнениях относительно точной даты его завершения) был восстановлен на основе двух основных источников. Самый старый из сохранившихся экземпляров, который также является старейшей из когда-либо напечатанных книг по математике, датируется 1213 годом. Однако сохранились только первые пять глав. Полная книга, известная сегодня как Девять глав , является результатом филологической работы 18-го века, основанной как на прежнем источнике, так и на исчерпывающих цитатах из китайской энциклопедии 15-го века, Yongle dadian , составленной при императоре Юнлэ (1402 г.) –24).В любом случае, как Евклид Elements , Девять глав собрал и систематизировал многие математические достижения (включая арифметические, геометрические и алгебраические алгоритмы) предыдущих периодов. И, как Elements на Западе, Девять глав сыграли выдающуюся роль в развитии математики в Восточной Азии. Большинство математиков ссылались на нее, и большинство предметов, над которыми они работали, проистекали из нее. Его формат, принятый большинством последующих авторов, состоит из задач, для которых дается числовой ответ и общая процедура решения.Как и в случае с любой канонической работой, многие ученые написали комментарии к Девять глав , добавив объяснения и доказательства, переписав процедуры и предложив новые. Самый важный из сохранившихся комментариев, приписываемый Лю Хуэю (III век), содержит самые ранние китайские математические доказательства в современном понимании.
Его формат, принятый большинством последующих авторов, состоит из задач, для которых дается числовой ответ и общая процедура решения.Как и в случае с любой канонической работой, многие ученые написали комментарии к Девять глав , добавив объяснения и доказательства, переписав процедуры и предложив новые. Самый важный из сохранившихся комментариев, приписываемый Лю Хуэю (III век), содержит самые ранние китайские математические доказательства в современном понимании.В течение 7-го века, некоторые другие книги были собраны вместе с Девять глав и ханьским астрономическим трактатом Zhoubi («Гномон Чжоу») группой под руководством имперского математика и астронома Ли Чуньфэн.Этот сборник, известный как Shibu suanjing («Десять классиков математики»), стал пособием для чиновников, прошедших обучение в недавно созданном офисе математики. Хотя некоторые люди продолжали получать официальную математическую подготовку после этого, никаких успехов в математике нельзя было зафиксировать до 11 века.
 В то время (1084 г.) были отредактированы и напечатаны «Десять классиков», что, по-видимому, было связано с возобновлением деятельности в математике в XI и XII веках.Об этой деятельности известно только из более поздних цитат, но она, вероятно, открыла путь к крупным достижениям во второй половине 13 века. В то время Китай был разделен на Север и Юг, и достижения математиков в обоих регионах известны: на юге — Цинь Цзюшао и Ян Хуэй, а на севере — Ли Е и Чжу Шицзе. Математические исследования на Севере и Юге, кажется, развивались независимо, но они свидетельствуют об общей основе.
В то время (1084 г.) были отредактированы и напечатаны «Десять классиков», что, по-видимому, было связано с возобновлением деятельности в математике в XI и XII веках.Об этой деятельности известно только из более поздних цитат, но она, вероятно, открыла путь к крупным достижениям во второй половине 13 века. В то время Китай был разделен на Север и Юг, и достижения математиков в обоих регионах известны: на юге — Цинь Цзюшао и Ян Хуэй, а на севере — Ли Е и Чжу Шицзе. Математические исследования на Севере и Юге, кажется, развивались независимо, но они свидетельствуют об общей основе.В то время как некоторые основные труды 13-го века записаны в Yongle dadian , математические знания быстро ухудшились, о чем свидетельствуют комментарии к этим книгам, написанные к концу 15-го века, которые показывают, что их больше не понимали.К 17 веку было доступно несколько древнекитайских математических работ. После этого, когда китайские ученые узнали о европейских достижениях, они начали искать такие работы по всей стране и стремились их интерпретировать.
 Конец 18 века ознаменовался большим движением редактирования вновь открытых текстов. Эти критические издания сегодня являются основными источниками по истории китайской математики. Открытие новых источников сейчас происходит редко, хотя в 20 веке математическая книга была найдена в могиле, запечатанной до конца 2 века до нашей эры, что на несколько веков отодвинуло назад самый ранний известный источник по этому вопросу.Не исключено, что археология обнаружит новые открытия и спровоцирует революцию, сопоставимую с той, что произошла в историографии Китая в целом.
Конец 18 века ознаменовался большим движением редактирования вновь открытых текстов. Эти критические издания сегодня являются основными источниками по истории китайской математики. Открытие новых источников сейчас происходит редко, хотя в 20 веке математическая книга была найдена в могиле, запечатанной до конца 2 века до нашей эры, что на несколько веков отодвинуло назад самый ранний известный источник по этому вопросу.Не исключено, что археология обнаружит новые открытия и спровоцирует революцию, сопоставимую с той, что произошла в историографии Китая в целом.Квадратный корень и кубический корень — Степень и корни — KS3 Maths Revision
Квадратный корень
Противоположность возведения числа в квадрат называется нахождением квадратного корня .
2 = 4 \ times 4 = 16 \)).2 = 10 \ раз 10 = 100 \)).- Вопрос
Что такое квадратный корень из \ ({4} \)?
- Показать ответ
\ (2 \ times 2 = 4 \), поэтому \ ({2} \) является квадратным корнем из \ ({4} \).
Символ \ (\ sqrt {} \) означает квадратный корень, поэтому:
\ (\ sqrt {36} \) означает «квадратный корень из \ ({36} \)».
\ [\ sqrt {36} = 6 \]
0.0.0.1:0.1.0.$0.$1.$12″> \ (\ sqrt {81} \) означает «квадратный корень из \ ({81} \)».\ [\ sqrt {81} = 9 \]
Вы также найдете квадратный корень на вашем калькуляторе.{3} \ sqrt {} \) означает кубический корень, поэтому:
\ (\ sqrt [3] {125} \) означает «кубический корень из \ ({125} \).
\ [\ sqrt [3] {125} = 5 \]
\ (\ sqrt [3] {64} \) означает «кубический корень из \ ({64} \).
\ [\ sqrt [3] {64} = 4 \]
Простые приемы для поиска квадратного и кубического корня
Найти квадратный или кубический корень из числа — непростая задача. Когда вы сдаете экзамен с ограниченным сроком, например CAT, CMAT, CET, NMAT и т.
 Д., Это может истощить ваше драгоценное время. Это хуже, когда нахождение квадратного или кубического корня является лишь частью более серьезной проблемы, как в задачах интерпретации данных или сложного процента в Quantitative Aptitude.
Д., Это может истощить ваше драгоценное время. Это хуже, когда нахождение квадратного или кубического корня является лишь частью более серьезной проблемы, как в задачах интерпретации данных или сложного процента в Quantitative Aptitude.
Итак, если ваша ментальная математика немного слаба, давайте научимся быстро и легко находить квадратный корень или кубический корень из числа. Этот трюк наверняка сэкономит вам как минимум 40 секунд вычислений на каждый вопрос. Сначала вам будет сложно, но со временем вы сможете найти квадратный или кубический корень из любого числа. Тогда приступим.Поиск квадратного корня:
103 2 = 10609
Шаг 1. Добавьте число к разряду единиц:
103 + 3 = 106
Шаг 2. Возведите в квадрат однозначное число (если результат — однозначный, поставьте перед ним 0):
3 2 = 09
Шаг 3. Поместите результат из шага 2 рядом с результатом из шага 1: 1060997 2 = 9409
Шаг 1.
 Вычтем число из 100: 100-97 = 3
Вычтем число из 100: 100-97 = 3Шаг 2. Вычтите число (из Шага 1) из исходного числа: 97-3 = 94
Шаг 3. Возвести в квадрат результат из шага 1 (если результат представляет собой одну цифру, поставьте перед ним 0): 3 2 = 09
Шаг 4. Поместите результат из шага 3 рядом с результатом из шага 2: 9409
48 2 = 2304
Шаг 1. Вычтем число из 50: 50-48 = 2
Шаг 2. Вычтите результат (из Шага 1) из 25: 25-2 = 23
Шаг 3. Возвести в квадрат результат, полученный на шаге 1, если результат представляет собой одну цифру, поставьте перед ним 0): 2 2 = 04
Шаг 4. Поместите результат из шага 3 рядом с результатом из шага 2: 2304
53 2 = 2809
Шаг 1. Добавьте 25 к разряду единиц: 25 + 3 = 28
Шаг 2.
 Возвести в квадрат однозначное число (если результат — однозначный, поставьте перед ним 0): 3 2 = 09
Возвести в квадрат однозначное число (если результат — однозначный, поставьте перед ним 0): 3 2 = 09Шаг 3. Поместите результат из шага 2 рядом с результатом из шага 1: 2809
Поиск корня куба:
- УКАЗАНИЕ ЦИФР ЕДИНИЦ
Сначала нам нужно запомнить кубы от 1 до 10 и единицы измерения этих кубов. На рисунке ниже показаны единицы измерения кубиков (справа) чисел от 1 до 10 (слева).
1 = 1
2 = 8
3 = 7
4 = 4
5 = 5
6 = 6
7 = 3
8 = 2
9 = 9
10 = 0
Теперь, со ссылкой на вышесказанное, мы можем однозначно сказать, что:
Всякий раз, когда единичная цифра числа равна 9, единичная цифра куба этого числа также будет 9. Точно так же, если единичная цифра числа равна 9, единичная цифра кубического корня этого числа также будет 9. Аналогично, если единичная цифра числа равна 2, единичная цифра куба этого числа будет 8, и наоборот, если единичная цифра числа равна 8, единичной цифрой корня куба этого числа будет 2.
 Точно так же это будет применяться и к разрядам единиц других чисел.
Точно так же это будет применяться и к разрядам единиц других чисел.- ПОЛУЧЕНИЕ КУБИЧЕСКОГО КОРНЯ ИЗ ОСТАВШИХСЯ ЦИФРОВ
Давайте посмотрим на это на примере. Обратите внимание, что этот метод работает только в том случае, если указанное число представляет собой идеальный куб.
Найдите кубический корень из 474552.
Цифра единицы 474552 равна 2. Таким образом, мы можем сказать, что цифра единицы его кубического корня будет 8.
Теперь мы находим кубический корень из 447552, вычисляя оставшиеся цифры.
Рассмотрим оставшиеся цифры, оставив последние 3 цифры.т.е. 474.
Так как 474 находится между кубами 7 и 8.
Значит, десятичная цифра кубического корня определенно будет 7
, то есть кубический корень из 474552 будет 78.
Возьмем другой пример.
Найдите кубический корень из 250047.
Так как единичная цифра числа равна 7, то единичная цифра в корне куба будет 3.



 Бурей выворотило деревья с корнями. Дуб глубоко пустил корни в землю. || Древесина или вещество этой части растения. Лакричный корень … Толковый словарь Ушакова
Бурей выворотило деревья с корнями. Дуб глубоко пустил корни в землю. || Древесина или вещество этой части растения. Лакричный корень … Толковый словарь Ушакова Обозначается символом (или просто при ) … Википедия
Обозначается символом (или просто при ) … Википедия
 1/n
1/n Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе. 2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.
2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты. {3}=729}
, то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.
{3}=729}
, то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа. {3}=614,1}
. Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.
{3}=614,1}
. Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44. {3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.
{3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1. y.
y.
 Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.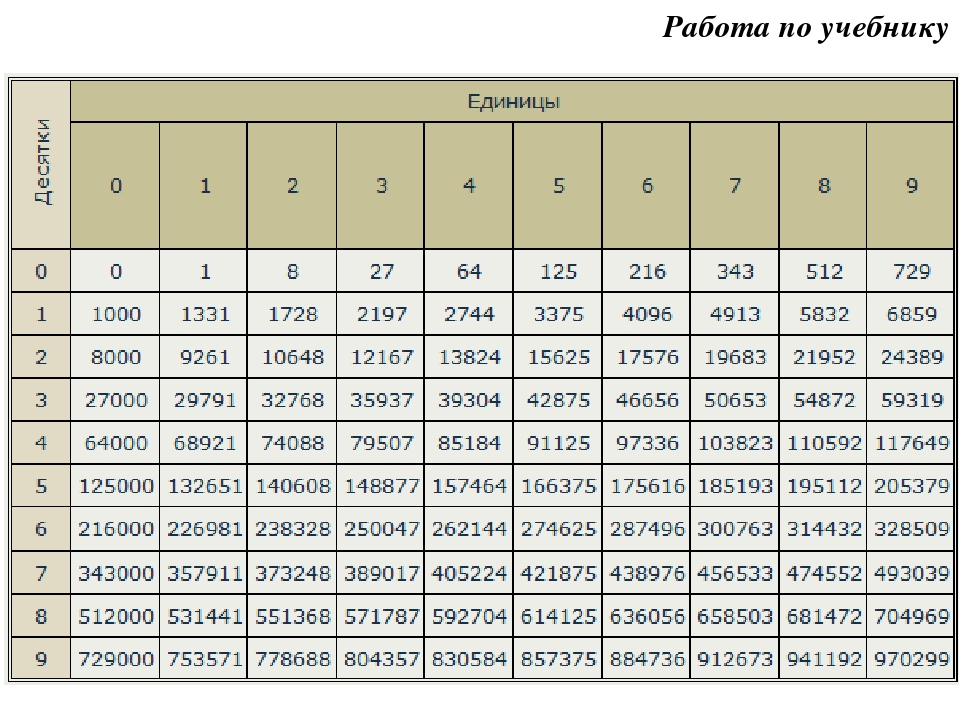 Таблица степеней от 1 до 100. Таблица корней от 1 до 1000000.
Таблица степеней от 1 до 100. Таблица корней от 1 до 1000000. [1] Например:
[1] Например:
 414
414 000
000 000
000 403
403 000
000 30
30 798
798 квадратный корень равен \ [\ sqrt {} \]
квадратный корень равен \ [\ sqrt {} \]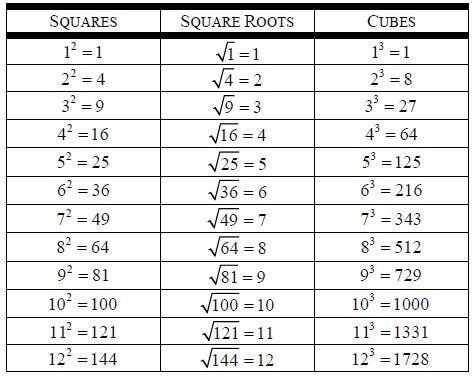
 Но когда нам нужно найти квадратный корень и кубический корень из больших чисел, мы можем использовать следующие методы, чтобы найти его.Это
Но когда нам нужно найти квадратный корень и кубический корень из больших чисел, мы можем использовать следующие методы, чтобы найти его.Это
 Для второго корня нам понадобилась вторая копия.
Для второго корня нам понадобилась вторая копия. Таким же образом теперь я могу извлечь из корня четвертой степени все, что у меня есть четыре копии. Поскольку 16 = 2 4 , то:
Таким же образом теперь я могу извлечь из корня четвертой степени все, что у меня есть четыре копии. Поскольку 16 = 2 4 , то:
 Я беру пятый корень, поэтому могу вытащить из радикала все, для чего у меня есть пять копий.
Я беру пятый корень, поэтому могу вытащить из радикала все, для чего у меня есть пять копий. «(или» положительный «).Это сделано для того, чтобы вам не приходилось учитывать, нужны ли столбцы абсолютных значений для вашего ответа. Если вы не уверены, о чем я говорю, проверьте здесь.
«(или» положительный «).Это сделано для того, чтобы вам не приходилось учитывать, нужны ли столбцы абсолютных значений для вашего ответа. Если вы не уверены, о чем я говорю, проверьте здесь. Тогда я могу упростить.
Тогда я могу упростить. Итак, я получу сумму двух корней третьих из трех, которые я могу объединить.
Итак, я получу сумму двух корней третьих из трех, которые я могу объединить. Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
 К ним относятся большинство последующих математических работ. Ссылки, найденные в сохранившихся математических сочинениях этого периода, а также ссылки, сделанные в библиографиях, составленных для династических летописей, указывают на то, что в текстовой записи есть много пробелов. Самые старые из дошедших до нас работ, вероятно, сохранились, потому что они стали официальными книгами, преподаваемыми в контексте китайской системы гражданских экзаменов.
К ним относятся большинство последующих математических работ. Ссылки, найденные в сохранившихся математических сочинениях этого периода, а также ссылки, сделанные в библиографиях, составленных для династических летописей, указывают на то, что в текстовой записи есть много пробелов. Самые старые из дошедших до нас работ, вероятно, сохранились, потому что они стали официальными книгами, преподаваемыми в контексте китайской системы гражданских экзаменов. д.Этот сборник I века до н. Э. (Специалисты расходятся во мнениях относительно точной даты его завершения) был восстановлен на основе двух основных источников. Самый старый из сохранившихся экземпляров, который также является старейшей из когда-либо напечатанных книг по математике, датируется 1213 годом. Однако сохранились только первые пять глав. Полная книга, известная сегодня как Девять глав , является результатом филологической работы 18-го века, основанной как на прежнем источнике, так и на исчерпывающих цитатах из китайской энциклопедии 15-го века, Yongle dadian , составленной при императоре Юнлэ (1402 г.) –24).В любом случае, как Евклид Elements , Девять глав собрал и систематизировал многие математические достижения (включая арифметические, геометрические и алгебраические алгоритмы) предыдущих периодов. И, как Elements на Западе, Девять глав сыграли выдающуюся роль в развитии математики в Восточной Азии. Большинство математиков ссылались на нее, и большинство предметов, над которыми они работали, проистекали из нее.
д.Этот сборник I века до н. Э. (Специалисты расходятся во мнениях относительно точной даты его завершения) был восстановлен на основе двух основных источников. Самый старый из сохранившихся экземпляров, который также является старейшей из когда-либо напечатанных книг по математике, датируется 1213 годом. Однако сохранились только первые пять глав. Полная книга, известная сегодня как Девять глав , является результатом филологической работы 18-го века, основанной как на прежнем источнике, так и на исчерпывающих цитатах из китайской энциклопедии 15-го века, Yongle dadian , составленной при императоре Юнлэ (1402 г.) –24).В любом случае, как Евклид Elements , Девять глав собрал и систематизировал многие математические достижения (включая арифметические, геометрические и алгебраические алгоритмы) предыдущих периодов. И, как Elements на Западе, Девять глав сыграли выдающуюся роль в развитии математики в Восточной Азии. Большинство математиков ссылались на нее, и большинство предметов, над которыми они работали, проистекали из нее. Его формат, принятый большинством последующих авторов, состоит из задач, для которых дается числовой ответ и общая процедура решения.Как и в случае с любой канонической работой, многие ученые написали комментарии к Девять глав , добавив объяснения и доказательства, переписав процедуры и предложив новые. Самый важный из сохранившихся комментариев, приписываемый Лю Хуэю (III век), содержит самые ранние китайские математические доказательства в современном понимании.
Его формат, принятый большинством последующих авторов, состоит из задач, для которых дается числовой ответ и общая процедура решения.Как и в случае с любой канонической работой, многие ученые написали комментарии к Девять глав , добавив объяснения и доказательства, переписав процедуры и предложив новые. Самый важный из сохранившихся комментариев, приписываемый Лю Хуэю (III век), содержит самые ранние китайские математические доказательства в современном понимании. В то время (1084 г.) были отредактированы и напечатаны «Десять классиков», что, по-видимому, было связано с возобновлением деятельности в математике в XI и XII веках.Об этой деятельности известно только из более поздних цитат, но она, вероятно, открыла путь к крупным достижениям во второй половине 13 века. В то время Китай был разделен на Север и Юг, и достижения математиков в обоих регионах известны: на юге — Цинь Цзюшао и Ян Хуэй, а на севере — Ли Е и Чжу Шицзе. Математические исследования на Севере и Юге, кажется, развивались независимо, но они свидетельствуют об общей основе.
В то время (1084 г.) были отредактированы и напечатаны «Десять классиков», что, по-видимому, было связано с возобновлением деятельности в математике в XI и XII веках.Об этой деятельности известно только из более поздних цитат, но она, вероятно, открыла путь к крупным достижениям во второй половине 13 века. В то время Китай был разделен на Север и Юг, и достижения математиков в обоих регионах известны: на юге — Цинь Цзюшао и Ян Хуэй, а на севере — Ли Е и Чжу Шицзе. Математические исследования на Севере и Юге, кажется, развивались независимо, но они свидетельствуют об общей основе. Конец 18 века ознаменовался большим движением редактирования вновь открытых текстов. Эти критические издания сегодня являются основными источниками по истории китайской математики. Открытие новых источников сейчас происходит редко, хотя в 20 веке математическая книга была найдена в могиле, запечатанной до конца 2 века до нашей эры, что на несколько веков отодвинуло назад самый ранний известный источник по этому вопросу.Не исключено, что археология обнаружит новые открытия и спровоцирует революцию, сопоставимую с той, что произошла в историографии Китая в целом.
Конец 18 века ознаменовался большим движением редактирования вновь открытых текстов. Эти критические издания сегодня являются основными источниками по истории китайской математики. Открытие новых источников сейчас происходит редко, хотя в 20 веке математическая книга была найдена в могиле, запечатанной до конца 2 века до нашей эры, что на несколько веков отодвинуло назад самый ранний известный источник по этому вопросу.Не исключено, что археология обнаружит новые открытия и спровоцирует революцию, сопоставимую с той, что произошла в историографии Китая в целом. Д., Это может истощить ваше драгоценное время. Это хуже, когда нахождение квадратного или кубического корня является лишь частью более серьезной проблемы, как в задачах интерпретации данных или сложного процента в Quantitative Aptitude.
Д., Это может истощить ваше драгоценное время. Это хуже, когда нахождение квадратного или кубического корня является лишь частью более серьезной проблемы, как в задачах интерпретации данных или сложного процента в Quantitative Aptitude. Вычтем число из 100: 100-97 = 3
Вычтем число из 100: 100-97 = 3 Возвести в квадрат однозначное число (если результат — однозначный, поставьте перед ним 0): 3 2 = 09
Возвести в квадрат однозначное число (если результат — однозначный, поставьте перед ним 0): 3 2 = 09 Точно так же это будет применяться и к разрядам единиц других чисел.
Точно так же это будет применяться и к разрядам единиц других чисел.