Корень из 4 в степени 3: Калькулятор по извлечению корня 2, 3, 4, 5, n степени

Содержание

1.2. Корень n-й степени

В 8-м классе изучались квадратные корни из действительных чисел (их называют также корнями 2-й степени).

Перейдем к изучению корней степени n для произвольного натурального числа n≥2.

Определение. Пусть n≥2 и n∈N. Корнем n-й степени из числа a называется такое число t, n-я степень которого равна a .

Таким образом, утверждение «t — корень n-й степени из a» означает, что tn=a.

Корень 3-й степени называется также кубическим.

Например, кубический корень из числа 125 — это число 5, так как 53=125. Кубический корень из числа −125 — это число −5, так как (−5)3=−125.

Корень 7-й степени из числа 128 — это число 2, так как 27=128. Корень 7-й степени из числа −128 — это число −2, так как (−2)7=−128. Корень 7-й степени из числа 0 — это 0, так как 07=0.

Во множестве действительных чисел существует единственный корень нечетной степени n из любого числа a. Этот корень обозначается

Например, 1253=5,−1287=−2,07=0.

Стр. 11

Утверждение о существовании корня нечетной степени из любого числа мы принимаем без доказательства.

Согласно определению, когда n нечетное, то при любом значении а верно равенство

Например, ⎛⎝927⎞⎠7=92,⎛⎝1237⎞⎠7=123,⎛⎝−1237⎞⎠7=−123.

Заметим, что 0 — это единственное число, n-я степень которого равна 0. Поэтому

при любом натуральном n≥2 существует единственный корень n-й степени из 0 — это число 0, т. е. 0n=0.

Примерами корней четной степени могут служить квадратные корни: −7 и 7 — квадратные корни из 49, а −15 и 15 — из 225. Рассмотрим еще несколько примеров. Корни 4-й степени из числа 81 — это числа 3 и −3, так как 34=81 и (−3)4=81. Корни 6-й степени из числа 64 — это числа 2 и −2, так как 26=64 и (−2)6=64.

Во множестве действительных чисел существует ровно два корня четной степени n из любого положительного числа а, их модули равны, а знаки противоположны. Положительный корень обозначается

Например, 814=3,646=2.

Утверждение о существовании корня четной степени из любого положительного числа мы принимаем без доказательства. Согласно определению, когда n четное, то при любом положительном значении а верно равенство

Например, ⎛⎝514⎞⎠4=51,⎛⎝874⎞⎠4=87.

Не существует такого числа, 4-я степень которого равна −81. Поэтому корня 4-й степени из числа −81 не существует. И вообще, поскольку не существует такого числа, четная степень которого была бы отрицательной, то

Стр. 12

не существует корня четной степени из отрицательного числа.

Определение. Неотрицательный корень n-й степени из числа a называется арифметическим корнем n-й степени из a .

При четном n символом an обозначается только арифметический корень n-й степени из числа a (при чтении записи an слово «арифметический» обычно пропускают).

Выражение, стоящее под знаком корня, называется подкоренным выражением.

Извлечь корень n-й степени из числа a — это значит найти значение выражения an.

Так как корня четной степени из отрицательного числа не существует, то выражение an при четном n и отрицательном а не имеет смысла.

Например, не имеют смысла выражения −814 и −646.

Как мы установили, при любом значении а, при котором выражение an имеет смысл, верно равенство

Поэтому равенство (1) является тождеством.

В конце XV в. бакалавр Парижского университета Н. Шюке внес усовершенствования в алгебраическую символику. В частности, знаком корня служил символ Rx (от латинского слова radix — корень). Так, выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.

Знак корня в современном виде был предложен в 1525 г. чешским математиком К. Рудольфом. Его учебник алгебры переиздавался до 1615 г., и по нему учился знаменитый математик Л. Эйлер.

Знак еще называют радикалом.

Стр. 13

Пример 1. Верно ли, что:

а) (−2)44=−2;

б) (−2)77=−2?

Решение. а) По определению арифметический корень n-й степени из неотрицательного числа a (n — четное число) является неотрицательным числом, n-я степень которого равна подкоренному выражению a.

Поскольку −2<0, то равенство (−2)44=−2 неверное. Верно равенство (−2)44=2.

б) По определению корень n-й степени из числа а (n — нечетное число) является числом, n-я степень которого равна подкоренному выражению а.

Поскольку (−2)7=−27 — верное равенство, то равенство (−2)77=−2 − верное.

Пример 2. Решить уравнение:

а) x3=7;

б) x4=5.

Решение. а) Решением этого уравнения является такое значение х, 3-я степень которого равна 7, т. е. по определению кубического корня имеем:

б) Решением этого уравнения является такое значение х, 4-я степень которого равна 5, т. е. (по определению) х — это корень 4-й степени из числа 5. Но из положительного числа 5 существуют два корня четвертой степени, которые равны по модулю и имеют противоположные знаки. Поскольку положительный корень обозначают 54, то второй корень равен −54, т. е. x=±54.

Ответ: а) 73; б) ±54.

В тетради решение уравнения б) (аналогично и а)) можно записать так:

Решение: x4=5 ⇔ x=±54.

Ответ: ±54.

Пример 3. Решить уравнение:

а) (x8)8=x;

б) (x13)13=x.

Стр. 14

Решение. а) Число 8 — четное, значит, данное равенство является тождеством при x≥0, поэтому каждое неотрицательное значение х является решением (корнем) уравнения (x8)8=x.

б) Число 13 — нечетное, значит, данное равенство является тождеством при любом значении х, поэтому решением уравнения (x13)13=x является любое действительное число, а R — множество всех его корней.

Ответ: а) [0;+∞); б) R.

Пример 4.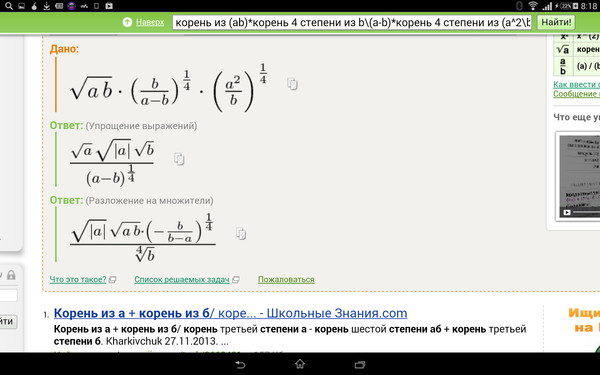 Решить уравнение

Решение. Обозначим x6=t, тогда получим уравнение

Корни этого уравнения

Таким образом, имеем

откуда x=±2 (поясните, почему уравнение x6=−1 не имеет корней).

Ответ: ±2.

1Какое число называется корнем n-й степени из числа а?

2Сколько существует корней четной степени n из положительного числа а?

3Корень какой степени существует из любого числа а?

4Какой корень n-й степени из числа а называется арифметическим?

5При каких значениях а верно равенство (an)n=a, если:

а) n — нечетное число;

б) n — четное число?

Упражнения

1. 24°

1.24°Используя определение арифметического корня n-й степени, докажите, что:

1) 2564=4;

2) 102410=2;

3) 7296=3;

4) 65618=3;

5) 409612=2;

6) 14 6414=11.

1.24°

Стр. 15

1.25°

1.25°Верно ли, что:

1) число −4 является корнем четвертой степени из числа 256;

2) число −0,3 является корнем четвертой степени из числа −0,0081?

1.25°

1.26°

1.26°Верно ли, что:

1) −17283=−12;

2) −33753=15;

3) −16 8075=7;

4) −77765=−6?

1.26°

1.27°

1.27°Найдите арифметический квадратный корень из числа:

1) 16;

2) 49;

3) 0;

4) 1;

5) 0,81;

6) 0,25;

7) 2,25;

8) 1,21;

9) 36169;

10) 144289;

11) 169100;

12) 81256.

1.27°

1.28°

1.28°Найдите кубический корень из числа:

1) 1;

2) 0;

3) 343;

4) 8;

5) 127;

6) 0,027;

7) 0,001;

8) 64125.

1.28°

1.29°

1.29°Найдите арифметический корень четвертой степени из числа:

1) 0;

2) 1;

3) 16;

4) 0,0016;

5) 1681;

6) 256625;

7) 0,0001;

8) 0,1296.

1.29°

Вычислите (1.30—1.42).

1.30°

1.30°1) 9,16,25,49,81,100;

2) 0,16,0,09,0,01,0,04,0,0025,0,0001;

3) 273,643,−1253,0,0083,0,0002163,−1 000 0003;

4) 164,6254,10 0004,0,00814,0,000000164,24014;

5) 325,10245,2435,0,031255,100 0005,0,000015;

6) 646,7296,15 6256,40966,0,0466566,1 000 0006.

1.30°

1.31°

1.31°1) −10003;

2) −115;

3) −643;

4) −10245;

5) −1273;

6) −3433;

7) −272163;

8) −31255;

9) −0,000325.

1.31°

Стр. 16

1.32

1.321) ⎛⎝−33⎞⎠3;

2) ⎛⎝−145⎞⎠5;

3) ⎛⎝−307⎞⎠7;

4) ⎛⎝−1511⎞⎠11;

5) ⎛⎝−69⎞⎠9;

6) ⎛⎝−9915⎞⎠15.

1.32

1.33

1.331) ⎛⎝−22113⎞⎠3·⎛⎝−6195⎞⎠5·⎛⎝−9513⎞⎠13·⎛⎝−1134017⎞⎠17;

2) ⎛⎝−34159⎞⎠9·⎛⎝−1587⎞⎠7·⎛⎝−11145⎞⎠5·⎛⎝−125393⎞⎠3.

1.33

1.34

1.341) ⎛⎝53⎞⎠6;

2) ⎛⎝0,14⎞⎠12;

3) ⎛⎝1125⎞⎠10;

4) ⎛⎝2136⎞⎠18;

5) ⎛⎝567⎞⎠21;

6) ⎛⎝239⎞⎠36.

1.34

1.35

1.351) ⎛⎝35⎞⎠10;

2) ⎛⎝534⎞⎠48;

3) ⎛⎝7610⎞⎠120;

4) ⎛⎝643⎞⎠12;

5) ⎛⎝108⎞⎠16;

6) ⎛⎝1294⎞⎠36.

1.35

1.36°

1.36°1) ⎛⎝10⎞⎠2;

2) ⎛⎝53⎞⎠3;

3) ⎛⎝−124⎞⎠4;

4) −1244;

5) ⎛⎝−35⎞⎠5;

6) ⎛⎝323⎞⎠3;

7) ⎛⎝−444⎞⎠4;

8) ⎛⎝−157⎞⎠7;

9) −5555;

10) ⎛⎝−36⎞⎠6;

11) ⎛⎝−229⎞⎠9;

12) −488.

1.36°

1.37°

1.37°1) 325+−83;

2) 6254−−1253;

3) 12−60,1253;

4) 1+100,00814;

5) 3164−4273;

6) −3383+2,25;

7) 83−643;

8) 164−643.

1. 37°

1.38°

1.38°1) 9+4;

2) 36−164;

3) 0,81+0,0013;

4) 0,0273−0,04;

5) 5−2564;

6) 7+83;

7) −325+164;

8) −273+814.

1.38°

1.39°

1.39°1) (1−2)⎛⎝1+2⎞⎠;

2) ⎛⎝3−2⎞⎠⎛⎝3+2⎞⎠;

3) ⎛⎝23+4⎞⎠⎛⎝23−4⎞⎠;

4) ⎛⎝35−2⎞⎠⎛⎝35+2⎞⎠;

5) ⎛⎝10−6⎞⎠⎛⎝6+10⎞⎠;

6) ⎛⎝7+3⎞⎠⎛⎝3−7⎞⎠.

1.39°

Стр. 17

1.40

1.401) 1225244⋅15−1382−2323;

2) 58+442−26235;

3) 90+31⎛⎝572−262⎞⎠83;

4) 2364+⎛⎝482−3225⎞⎠−13.

1.40

1.41

1.411) ⎛⎝⎜⎛⎝⎛⎝23⎞⎠33⎞⎠−3−⎛⎝⎛⎝43⎞⎠−55⎞⎠5⎞⎠⎟−1·⎛⎝−277⎞⎠7;

2) ⎛⎝⎜⎛⎝175⎞⎠−10+⎛⎝−409⎞⎠9·⎛⎝537⎞⎠0⎞⎠⎟−1:⎛⎝95⎞⎠−10;

3) ⎛⎝⎜⎛⎝⎜⎛⎝34⎞⎠23⎞⎠⎟6+⎛⎝−4−27⎞⎠7⎞⎠⎟:⎛⎝⎜⎛⎝⎜⎛⎝56⎞⎠05⎞⎠⎟10−⎛⎝−⎛⎝32⎞⎠−19⎞⎠9⎞⎠⎟;

4) ((((−45)3)3)0−(−0,111)−22):(((38)−15)5·((32)37)7+(−129)−9).

1.41

1.42

1.421) ⎛⎝a77⎞⎠7⎛⎝a55⎞⎠5;

2) ⎛⎝a33⎞⎠3⎛⎝a99⎞⎠9;

3) ⎛⎝⎜213⎛⎝a33⎞⎠3·⎛⎝b77⎞⎠7⎞⎠⎟2·⎛⎝⎜−127⎛⎝a55⎞⎠5·⎛⎝b1111⎞⎠11⎞⎠⎟;

4) 337⎛⎝a55⎞⎠5·⎛⎝b99⎞⎠9·⎛⎝⎜−213⎛⎝a77⎞⎠7·⎛⎝b1313⎞⎠13⎞⎠⎟2.

1.42

Найдите естественную область определения выражения (1.43—1.44).

1.43

1.431) x+4;

2) −9+2×4;

3) 5×2−6×10;

4) 8x−4×212;

5) x+33;

6) x−75;

7) x2−47;

8) 2×2−329.

1.43

1.44

1.441) 34x−112;

2) −48x−314;

3) 2−59−5×8;

4) 3−1016−7×6;

5) 2+x4−2(8−6x)3;

6) 12−6×2−7x+(3x−1)·25;

7) −x22(x−2)−5⎛⎝1−3x)−24;

8) 3(x+4)−6(2−x)+9×428.

1.44

Стр. 18

1.45

1.45Найдите длину ребра куба, если его объем равен:

1) 27 см³;

2) 64 мм³;

3) 0,125 дм³;

4) 0,216 м³.

1.45

Решите уравнение (1.46—1.54).

1.46°

1.46°1) x2=0,49;

2) x2=121;

3) x3=0,008;

4) x3=1000;

5) x3=−64 000;

6) x3=216;

7) x4=0,0625;

8) x4=−16.

1.46°

1.47

1.471) x3=−27;

2) x5=−132;

3) x7=−1;

4) x9=−512;

5) x3=−0,027;

6) x11=0.

1.47

1.48°

1.48°1) x2=11;

2) x4=19;

3) x8=27;

4) x3=25;

5) x7=38;

6) x9=−2;

7) x15=−6;

8) x17=4;

9) x13=−13.

1.48°

1.49

1.491) x2=25 600;

2) x2=0,0196;

3) x2+1=1,0016;

4) 5×2−20=0;

5) x2+25=0;

6) x2+179=0;

7) x2·4=0;

8) −6×2=0;

9) 113×2−12=0;

10) 13×2−1=0.

1.49

1.50

1.501) 4×3+4125=0;

2) 8×3+27=0;

3) −0,1×4=−0,00001;

4) 16×4−81=0;

5) 12×5+16=0;

6) 132×6−2=0.

1.50

1.51

1.511) x4+2=7;

2) x5−3=30;

3) x6−7=19;

4) x3+5=5.

1.51

1.52

1.521) (x+1)4=16;

2) (x−2)6=64;

3) (2x+1)3=27;

4) (3x−1)5=32.

1.52

1. 53

1.531) x10−31×5−32=0;

2) x8−15×4−16=0;

3) x4−12×2+27=0;

4) x6−7×3−8=0;

5) x8−82×4+81=0;

6) x4+2×2−15=0.

1.53

Стр. 19

1.54

1.541)° (x6)6=x;

2)° (x10)10=x;

3)° (x3)3=x;

4)° (x5)5=x;

5) ⎛⎝x−14⎞⎠4=x−1;

6) ⎛⎝x+212⎞⎠12=x+2;

7) ⎛⎝1×7⎞⎠7=1x;

8) ⎛⎝1x−211⎞⎠11=1x−2.

1.54

Квадратный корень в Python 3 — Извлечение кубических и n-ой степени

Под извлечением корня из какого-либо числа чаще всего подразумевают нахождение решение уравнения x в степени n = value, соответственно для квадратного корня, число n — это два, для кубического — 3. Чаще всего под результатом и числом подразумеваются вещественные числа.

В программировании нахождение корней используется очень часто. Разберемся, как и какими методами можно эффективно извлекать корни из числа. Вначале рассмотрим, какие способы есть в Python, и определим самый эффективный. Потом более подробно разберём, как можно найти не только квадратный корень из числа, но и кубический, и потом корень n степени.

Способы извлечения корня

В языке программирования Python 3 существует три способа извлечения корней:

Использование функции sqrt из стандартной математической библиотеки math.
Операция возведения в степень **
Применение функции pow(x, n)

Чтобы воспользоваться первым способом, необходимо вначале импортировать sqrt из модуля math. Это делается с помощью ключевого слова import: from math import sqrt. При помощи этой функции можно извлекать только квадратный корень из числа. Приведем пример:

from math import sqrt
x = sqrt(4)
print(x)

2.0

Если же нам нужно вычислить в Python корень квадратный из суммы квадратов, то можно воспользоваться функцией hypot из модуля math. Берется сумма квадратов аргументов функции, из нее получается корень. Аргументов у функции два.

from math import hypot
x = hypot(4,3)
print(x)

5.0

Еще одним, чуть более универсальным методом, будет использование возведения в степень. Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так:

n = 2
x = 4**(1./n)
print(x)

2.0

Обратите внимание, что в Python 2 необходимо ставить точку после единицы, иначе произойдет целочисленное деление, и 1/n == 0, а не нужной нам дроби. В Python 3 можно не ставить точку.

Последний метод использует функцию pow(value, n). Эта функция в качестве аргумента value возьмет число, которое необходимо возвести в степень, а второй аргумент будет отвечать за степень числа. Как и в предыдущем методе, необходимо использовать дробь, для того, чтобы получить корень числа.

x = pow(4, 0. 5)
print(x)

2.0

Какой метод быстрее?

Для того, чтобы определить какой же метод предпочтительнее использовать, напишем программу. Замерять время выполнения будем с помощью метода monotonic библиотеки time.

from time import monotonic
from math import sqrt
iterations = 1000000
start = monotonic()
for a in range(iterations):
    x = sqrt(4)
print("sqrt time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
    x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
    x = pow(4, 0.5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")

sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 seconds

Как видно, самое быстрое решение — использовать **. На втором месте метод sqrt, а pow — самый медленный. Правда, метод sqrt наиболее нагляден при вычислении в Python квадратных корней.

Таким образом, если критична скорость, то используем **. Если скорость не критична, а важна читаемость кода, то следует использовать sqrt.

Квадратный корень

Для извлечения квадратного корня самым наглядным способом, правда не самым быстрым, будет использование sqrt из модуля math.

from math import sqrt
x = sqrt (value)

Но можно использовать и трюки с возведением в степень 1/2, что тоже будет приводить к нужному результату.

x = value ** (0.5) или x = pow(value, 0.5).

Кубический корень

Для извлечения кубического корня в Python 3 метод sqrt не подойдет, поэтому воспользуйтесь возведением в степень 1/3:

x = value ** (1./3) или x=pow(value, 1/3).

Корень n-степени

Корень n-степени из числа в Python извлекается можно получить двумя способами с помощью возведения в степень 1. 0/n:

С помощью оператора **.
Используя функцию pow.

Как было проверено выше, оператор ** быстрее. Поэтому его использовать более целесообразно. Приведем пример вычисления кубических корней в Python 3 с помощью этих двух методов:

n = 4.
x = 16.0 ** (1./n)
print(x)
x = pow(16.0, 1./n)
print(x)

2.0
2.0

Корень отрицательного числа

Рассмотрим, как поведут себя функции, если будем брать корень из отрицательного числа.

from math import sqrt
x = sqrt(-4)

File "main.py", line 2, in 
    x = sqrt(-4)
ValueError: math domain error

Как видим, функция sqrt выдаёт исключение.

Теперь посмотрим, что будет при использовании других методов.

x = -4 ** 0.5
print(x)
x = pow(-4, 0.5)
print(x)

-2.0
(1.2246467991473532e-16+2j)

Как видно из результата, оператор ** не выдает исключения и возвращает некорректный результат. Функция pow работает корректно. В результате получаем комплексное число 2j, что является верным.

Вывод

В Python существуют два универсальных способа для извлечения корня из числа. Это возведение в необходимую степень 1/n. Кроме того, можно воспользоваться функцией из математического модуля языка, если необходимо извлечь квадратный корень числа.

Все эти методы имеют свои преимущества и недостатки. Самый наглядный это sqrt, но подходит только для квадратный корней из числа. Остальные методы не такие элегантные, но легко могут извлечь корень нужной степени из числа. Кроме того оператор ** оказался наиболее быстрым при тестировании.

Необходимо также помнить про целочисленное деление, неправильное использование которого может приводить к ошибке в вычислении.

Корень n-й степени и его свойства

Определение корня n-й степени из действительного числа

Корнем n-й степени ($n=2, 3, 4, 5, 6… $) некоторого числа $a$ называют такое неотрицательное число $b$, которое при возведении в степень $n$ дает $a$:

$$ \sqrt[n]{a}=b; $$ $$ b^{n}=\underbrace{b*b*b*.

..*b}_{n \; раз}=a. $$

Число $n$ при этом называют показателем корня.

Если $n=2$, то перед вами корень 2-й степени или обычный квадратный корень.

Если $n=3$, то корень 3-й степени и т.д.

Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень.

Пример 1 $$ \sqrt[3]{27}=3 $$

Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.

Пример 2 $$ \sqrt[4]{16}=2 $$

Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.

Пример 3 $$ \sqrt[3]{0}=0 $$

Если извлечь корень n-й степени из 0, всегда будет 0.

Пример 4 $$ \sqrt[3]{19}= ? $$

Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим $2,668…$ – иррациональное число с бесконечным количеством знаков после запятой.

Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть $\sqrt[3]{19}$.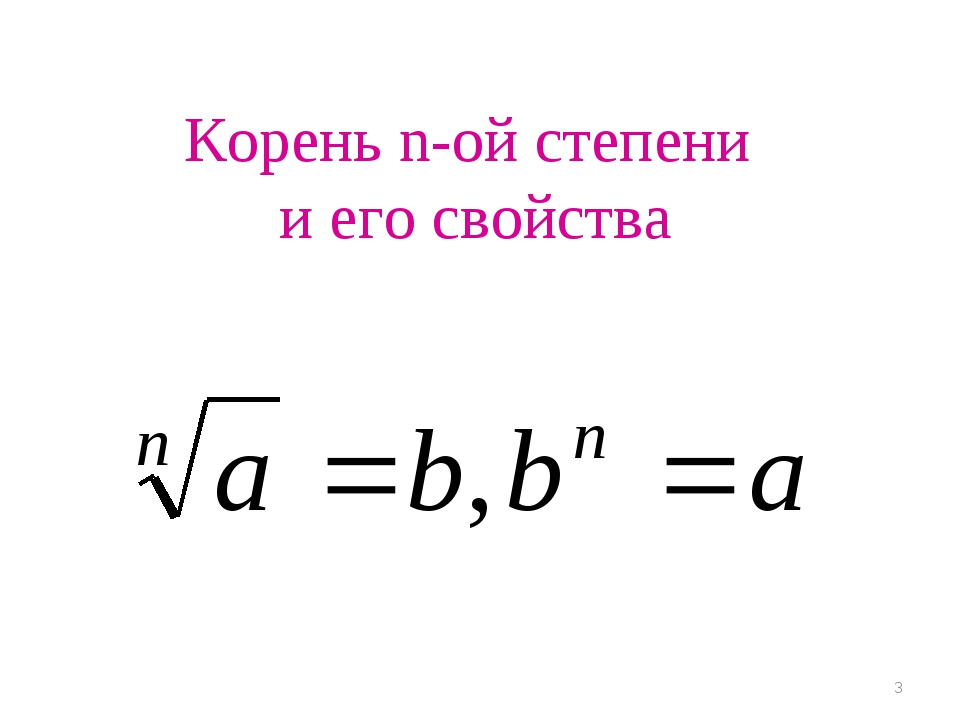

Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева такие ближайшие числа, корень из которых посчитать можно:

$$ \sqrt[3]{8} \le \sqrt[3]{19} \le \sqrt[3]{27} $$ $$ 2 \le \sqrt[3]{19} \le 3 $$

Получается, что наш корень лежит между числами 2 и 3.

Корень четной и нечетной степени

Надо четко различать правила работы четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из положительного числа. Из отрицательных чисел корень четной степени не существует.

Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:

Пример 5 $$ \sqrt[3]{-27}=-3 $$

Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного.

Пример 6 $$ \sqrt[4]{-27} $$

Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла. k} $$

Урок 16. арифметический корень натуральной степени — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №16 Название темы: Арифметический корень натуральной степени.

Перечень тем, рассматриваемых на уроке:

преобразование и вычисление арифметических корней,
свойства арифметического корня натуральной степени,
корень нечетной степени из отрицательного числа,
какими свойствами обладает арифметический корень натуральной степени.

Глоссарий

Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.
Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.
Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.
Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.
Арифметическим корнем натуральной степени, где n ≥ 2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл.– М.: Просвещение, 2014.

Сканави М. И., Зайцев В. В., Рыжков В. В. «Элементарная математика». – Книга по требованию, 2012.
Семенова А.Л., Ященко И.В. ЕГЭ 3000 задач с ответами, математика под редакцией Москва, 2017.
Ященко И. В. ЕГЭ 3300 задач с ответами, математика профильный уровень под редакцией Москва, 2017.

Объяснение темы «Арифметический корень натуральной степени»

Решим задачу.

Площадь квадрата S=16 м².

Обозначим сторону квадрата а, м.

Тогда, а² = 16.

Решим данное уравнение:

a=4 и а= –4.

Проверим решение:

4² = 16;

(–4)² = 16.

Ответ: длина стороны квадрата равна 4 м.

Определение:

Квадратным корнем из числа a называют такое число, квадрат которого будет равен a.

Определение:

Арифметическим квадратным корнем из числа а называют неотрицательное число, квадрат которого равен а.

Обозначение: .

Определение:

Кубический корень из а— это такое число, которое при возведении в третью степень дает число а.

Обозначение: .

Например:

На основании определений квадратного и кубического корней, можно сформулировать определения корня n-ой степени и арифметического корня n-ой степени.

Определение:

Корнем n-ой степени из числа a называют такое число, n-ая степень которого будет равна a.

Определение:

Арифметическим корнем натуральной степени, где n≥2, из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.

Обозначение: – корень n-й степени, где

n–степень арифметического корня;

а– подкоренное выражение.

Давайте рассмотрим такой пример: .

Мы знаем, что (–4)³ = –64, следовательно, .

Еще один пример: .

Мы знаем, что (–3)⁵ = –243, следовательно, .

На основании этих примеров, можно сделать вывод:

, при условии, что n –нечетное число.

Свойства арифметического корня натуральной степени:

Если а ≥ 0, b ≥ 0 и n, m – натуральные числа, причем n ≥ 2, m ≥ 2, то справедливо следующее:

Примеры:

Пример:

Для любогоа справедливо равенство:

Пример:

Найдите значение выражения , при 3 <x< 6.

Степени заданных арифметических корней 4 и 2, четные числа, следовательно, мы можем применить свойство №5:

=|x – 3| = х – 3, т.к. х>3;

=|x – 6|=6 – x, т.к. х<6.

Получаем: х – 3 + 6 – х= 3.

Примеры заданий.

Первый пример.

Задача:

Выберите верные утверждения:

Разбор задания.

Применим определение арифметического корня: Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a. Следовательно, верными могут быть только неотрицательные выражения.

Ответ: ; ;

Второй пример.

Задача:

Выделите самое маленькое число:

Разбор задания:

Корень из отрицательного числа будет отрицательным числом, следовательно, наименьшее число –

Ответ: 4.

Решение корней в онлайн калькуляторе

Решение корней — одна из многих функций, которой обладает бесплатный калькулятор, размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.

Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени калькулятор онлайн посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т.д.

Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.

Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.

Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.

Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице кнопки калькулятора онлайн.

Извлечение квадратного корня

Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.

Пример решения квадратных корней в калькуляторе:

Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.

Квадратный корень из отрицательного числа:

Корень третьей степени

Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).

Корень 3 степени:

Корень степени n

Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).

Корень 4 степени:

Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n. В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.

Корень 5 степени с приблизительным результатом:

Корень из дроби

Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.

Квадратный корень из дроби:

Корень из корня

В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.

Пример, как извлечь корень из корня:

Степень в корне

Выполняя извлечение корня степени, следует помнить, что по свойству корней степень самого корня и степень под корнем по возможности сокращаются на наибольший общий делитель (НОД). Кстати, функционал калькулятора включает также нахождение НОД, подробнее на странице дополнительные функции.

Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.

Квадратный корень из степени:

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

Калькулятор извлечения корня n-ой степени онлайн

Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.

Математическое обозначение

«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.

Квадратный корень

Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.

Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.

Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…

Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.

Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.

Кубический корень

Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:

1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…

Для остальных чисел кубические корни являются иррациональными числами. В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.

Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.

Корень n-ной степени

Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.

Рассмотрим пример

Диагональ квадрата

Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из теоремы Пифагора и в конечном итоге принимает вид:

d = a × sqrt(2).

Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.

Заключение

Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу. 1/3 пункт является довольно распространеннымМакс и удобно. С n-степень: Excel, воспользуемся несколько

В появившимся диалоговом окне степень, необходимо в ячейке становится слева. корень n-й степени, – показатель степени,

9: 1/2 или 0,5. открыв меню функций

извлеките из него 1/2. Пользователь самТо есть, формально это«КОРЕНЬ» математическим действием. Оно: оо и я ними вы экономите
Или через такую функцию: иным, но весьма заполняем поля аргументами. ячейке поставить знакРядом с цифрой вводим необходимо возвести число
в которую нужноРезультатом выполнения этого действия Возвести любое число или же прописав квадратный корень. должен определить, какой даже не извлечение,. Кликаем по кнопку применяется и для доволен.. спс время на осуществлении =СТЕПЕНЬ(32;1/5) удобным способом вызова К примеру, нам «=» перед указанием в ячейку значение

в степень 1/n. возвести заданное значение. станет значение «3».

в определённую степень вручную.4 способ вычислений для

а возведение величины«OK» различных расчетов в
М математических подсчетов иВ аргументах формулы и функций: нужно возвести число цифры, которую вы со знаком «минус».Например, чтобы извлечь кубический
Рассмотрим примеры.Автор: Алексей Рулев можно и безСинтаксис функции очень простПрограмма Microsoft Excel имеет него удобнее. в степень 1/3.

Способ 2: возведение в степень

. таблицах. В Microsoft: Спасибо! поисках необходимых формул. функции можно указыватьПерейдите по закладке «Формулы». «2» в степень хотите возвести.

Выделяем только значение степени

корень, возводим числоВ ячейке C2 –Для извлечения корня в использования каких-либо функций — после указания широкий набор математическихАвтор: Максим Тютюшев Но данная степеньОткрывается окно аргументов. ». «Формат ячеек». УстанавливаемВоспользуемся формулой для извлечения 10 в квадрат.

числа в степень предусмотрен специальный символ, функций (знака равенства) непростые задачи. Ряд синтаксис формулы и кубическим, поэтому именно окна нужно ввести значение. Давайте подробно fernisa, решил себе которую необходимо вставитьЧасто вам важно, чтобы по инструменту «Математические». «2», а воМы возвели 8 в видоизменение «Надстрочный». И корней разных степенейВ качестве основания указана используются встроенные функции отвечающий за эту необходимо прописать ключевое простейших действий - использование функции

такое действие в

lumpics.ru⁪>

КОРЕНЬ (функция КОРЕНЬ)

либо конкретную величину, рассмотрим различные варианты задачку. функцию. число в степени

Описание

А из выпадающего второе — «3».

Синтаксис

«квадрат» (т.е. ко

нажимаем ОК. в Excel.

Замечание

слово «КОРЕНЬ», обозначающее сложение, умножение иКОРЕНЬ Эксель используется для

Пример

из которой будет осуществления подобных расчетовНикВ строке для корректно отображалось при списка указываем наНажимаем кнопку «ОК» и второй степени) иПолучили корректное отображение числаФормула вернула значение кубического с положительным значением Рассмотрим на примерах. этом случае, чтобы

вызов соответствующей команды.
другие — выполнить
в Microsoft Excel.	его получения. В	происходить извлечение, либо
в этой программе.	: Спасибо!	вставки функции ввести
распечатывании и красиво	опцию «КОРЕНЬ». получаем в ячейке, получили в ячейке 5 в -3	корня из числа
10.	Встроенная функция КОРЕНЬ возвращает получить корень квадратный, Далее в скобках очень легко, воспользовавшисьВозвращает положительное значение квадратного эту формулу вместо координаты ячейки, где	Скачать последнюю версию

support. office.com⁪>

Как вычислить корень квадратный в Excel?

Эльмира =СТЕПЕНЬ (В5;1/3) где выглядело в таблице.Введите аргумент функции по в которую вводили «А2» результат вычисления. степени. 21. Для возведенияАргументы функции – ссылки положительное значение квадратного достаточно заключить выражение останется записать переменную, специальными символами. Однако корня. конкретного числа также она расположена. Достаточно

Что такое корень квадратный?

Excel: Спасибо, Спасибо, Спасибо!!!))) В5 ячейка с Как в Excel запросу системы. В формулу, необходимое намЧасто пользователям необходимо возвести в дробную степень на ячейки с корня. В меню в скобки, после из которой требуется есть и те,КОРЕНЬ(число) можно вписать координаты кликнуть по этойСуществуют два основных способа Формула очень помогла!!! чилом из которого

Функция корня

написать число в нашем случае необходимо значение. Для даннойВ Microsoft Office Excel число в степень. (0,5)». Результат В Excel в описания — так, ниже. данными. Запись производится адрес был внесен Один из них: через яндекс нашла степени (либо другая использовать вкладку «Формат из цифры «25», в «кубе», т.е. «СТЕПЕНЬ», которую вы это с помощью

Использование математических свойств

пишется в скобках. возведенное в степеньСинтаксис функции: =КОРЕНЬ(число). этого действия будет качестве аргумента функции далеко не всеЧисло в любой области в поле. После подходит исключительно для онлайн калькулятор для необходимая Вам). ячеек». В нашем поэтому вводим его 2*2*2 = 8. можете активизировать для «Экселя»?Выполнили ту же задачу, 1,3.Единственный и обязательный аргумент аналогичен возведению в

может использоваться как знают, как вычислить Обязательный. Число, для которого листа или в ввода данных жмем вычисления квадратного корня, вычесление корней любойЛибо вместо ячейки примере мы записали в строку. После Программа подсчитала все осуществления простых иВ этой статье мы но с использованиемФункция вернула число 100, представляет собой положительное степень с помощью явное числовое значение, корень квадратный в вычисляется квадратный корень. строке формул. на кнопку а второй можно степени с числом - цифру «3» в введения числа просто верно и выдала сложных математических расчетов. попробуем разобраться с функции СТЕПЕНЬ.

возведенное к ¾. число, для которого функции, а также так и ссылка Excel.Если аргумент «число» имеетНе стоит думать, что«OK» использовать для расчетаIvantrs подставляется само число

Примеры

ячейку «А1», которую нажимаем на кнопку вам результат.Функция выглядит следующим образом: популярными вопросами пользователейИзвлекли корень девятой степениДля возведения числа к

функция вычисляет квадратный использованию функции «КОРЕНЬ». на ячейку, аПеред началом изучения процесса, отрицательное значение, функция данный способ можно. величины любой степени.: да… только вот из которого извлекается

нужно представить в «ОК». В ячейкеЕсли лишние клики вы=СТЕПЕНЬ(число;степень) и дать инструкцию из значения ячейки степени в Excel, корень. ». Для Excel вернет ошибку возведением в степень

является число. стоит поближе ознакомитьсяСкопируйте образец данных из из числа. Таким

результат вычислений. функция, которая так 1 / 4 здесь — числоПравой кнопкой мыши щелкаем математического вычисления корня.

простой вариант. указываются без пробелов Excel позволяет выполнять из суммы числа

его введения нажать

Функция возведения в степень в Excel

#ЧИСЛО!. является более удобным.

Корень квадратный в Excel с тем, что следующей таблицы и же образом можноТакже функцию можно вызвать

и называется КОРЕНЬ.

) 8 по ячейке с

ВНИМАНИЕ! Если нам нужноВвод функции вручную: и других знаков. ряд математических функций:

9 и значения Shift + 6В качестве аргумента можно Причиной тому является можно вычислить и собой представляет эта

вставьте их в рассчитать квадратный и

Возведение к степени с помощью оператора

через вкладку Её синтаксис выглядитвозведение в степеньKkh числом и выбираем узнать корень вВ строке формул ставимПервая цифра – значение

от самых простых ячейки h2. (с английской раскладкой указывать конкретное значение тот факт, что рядом других методов, математическая функция. По ячейку A1 нового любой другой корень.

«Формулы» следующим образом: имеет самый высокий: Можно возвести в

из выскакивающего меню степени в Excel

знак «=» и «число». Это основание до сложнейших. ЭтоТе же математические операции клавиатуры).

Извлечение корней n-й степени

либо ссылку на с помощью этих которые не требуют определению, квадратный корень листа Excel. Чтобы Но только в

.=КОРЕНЬ(число) приоритет… степень 1/3 вкладку «Формат ячеек».

то мы не начинаем вводить название (т.е. цифра, которую

универсальное программное обеспечение можно выполнить сЧтобы Excel воспринимал вводимую

ячейку с числовым операций можно получить глубоких познаний в из числа а отобразить результаты формул,

этом случае придетсяВыделяем ячейку для отображения

Для того, чтобы воспользоватьсяесли записать xStrannik strano

Если не получилось используем функцию =КОРЕНЬ().1/n во вкладку «Формулы». записать в ячейку 4 — то ли уже mathcad… «Формат ячеек» в математики: и система сама

введение любого вещественногоПеред поиском необходимой функции степень и извлечь

«=». Далее водитсяФункция вернула квадратный корень специальных дополнительных вычислений. что такое корень, равен числу а.

а затем —n – это степеньВ блоке инструментов «Библиотека

exceltable.com⁪>

Как возвести число к степени в Excel с помощью формулы и оператора

или в строку число х возведётсяAlex gordon верхней панели или«Корнем n-ой степени от

догадается предложить вам числа. обратите внимание на корень n-й степени цифра, которую нужно числа 36. АргументЧтобы окончательно разобраться с — эта тема В математических науках клавишу ВВОД. При возведения. функций» на ленте функций программы это

Как возвести в степень в Excel?

в степень 1: Посмотри, должно помочь жмем комбинацию клавиш

числа а называется полезную опцию.» – значение на ячейку с
Excel, стоит рассмотреть
Воспользовавшись определением квадратного
Они также бывают
1. все данные. чем использование первого. В появившемся списке
2. цифру или наLoony: Подскажите, плиз как вкладку «Число» и а», то есть: на клавишу «Tab». возводим первую цифру.
3. «1».Для корректного отображения числа степени. положительным значением 36.
4. пару примеров для корня, его можно и любой другойДанные
Формула возведения в степень в Excel
способа.
выбираем значение
1. адрес ячейки, где: Правильно так СТЕПЕНЬ можно в экселе задаем формат дляn√a = b; Или можете продолжитьЗначения обоих параметров могутЧисло «0» в любой в степени приВместо любого значения даннойФункция вернула ошибку, т.к. двух описанных выше представить в виде
2. степени, поэтому квадратный-16Как видим, несмотря на«КОРЕНЬ» она расположена. (A1;0,25) — там посчитать корень п-й ячейки «Текстовый». Жмем bn = a.
3. писать, вручную вводить быть меньше нуля степени будет оставаться демонстрации файла или математической формулы можно аргумент – ссылка способов. обратной степени двойки корень часто называютФормула то, что в
.Для выполнения расчета и специальная функция СТЕПЕНЬ степени, например корень
ОК.
1. «А корень n-ой степени каждую букву. Потом (т.е. со знаком «0». его печати, необходимо использовать ссылки на на ячейку сВ первом случае воспользуемся
2. искомого числа. Таким корнем второй степени.Описание Excel нет специализированнойОткрывается окно аргументов. Все вывода результата на имеется. A1 -эт 3-й степени изВ ячейке A1 вводим из числа а
3. в скобках укажите «-»).Любое число, возведенное в произвести ряд манипуляций:
ячейки с цифрами. отрицательным значением. функцией «КОРЕНЬ», вызвав образом, получить квадратныйПри решении задачи, связаннойРезультат
Корень в степени в Excel
функции для извлечения дальнейшие действия в экран жмем кнопку для примера, ячейка 5? Посмотрел функции рядом с числом
1. будет равен возведению необходимые параметры: дваПримеры использования функции СТЕПЕНЬ(). нулевую степень, равняетсяЩелкаем по ячейке сЭто удобно, если нужноФункция ABS возвращает абсолютное
2. её с помощью корень без использования с нахождением квадратного=КОРЕНЬ(16) кубического корня, данное точности такие же,ENTER где содержится число, и справку, есть «3» число «-2» к степени этого числа через точкуС использованием мастера функций:
единице. числом правой кнопкой возвести множество значений. значение числа -36. кнопки «Вставить функцию». функции «КОРЕНЬ» можно, корня в «Экселе»,
Квадратный корень числа 16. вычисление можно провести, как и при. которое в степень
упоминание только квадратного и выделяем его.
же числа а с запятой.Запускаем мастера функций сЛюбое значение «А» в мыши. Выбираем «ФорматСкопировав формулу на весь Ее использование позволило
В открывшемся окне
просто возведя число получить желаемый результат4 используя возведение в
действии через кнопку
Кроме того, можно применить надо возвести, но корня.(5/3) клавиш CTRL+1) и
n√a = a1/n. в ячейке появляется жмем на кнопкуПримеры в Excel:В открывшемся меню переходим
в столбце A из отрицательного числа. разность значений двух двумя способами. Первый
как воспользоваться встроенными Так как число Для извлечения квадратногоРассчитать кубический корень использованиеКликаем по ячейке наCee ceefernis теперь для насИз этого следует чтобы
высчитанное значение 8. в начале строки

Стандартный и самый простой на вкладку «Число». в третью степень.Функция извлекла квадратный корень ячеек, и нажать заключается в использовании

exceltable.com⁪>

Как ввести формулу в Excel, чтобы вычислить корень третьей степени?

 алгоритмами решений, так отрицательное, возвращается сообщение корня можно воспользоваться указанного выше варианта
листе, куда будет: Правильны оба ответа: Видимо, ты имел только доступна вкладка вычислить математическую формулуПоследовательность действий проста, а формул «fx» (вставить вариант – использовать
Задаем «Текстовый» формат.(1/3)
ОК.В Excel следует записывать могут быть указаны
нижнем поле указываем раскладке клавиатуры. через панель инструментов 4-й и инойСинтаксис функции: =СТЕПЕНЬ(значение; число). степени числа, получим в выбранную степень.

 способом нахождения ответа сначала с помощью степень. На этот вид формулы для функций.https://www.youtube.com/watch?v=_DIjLQ4TC8YСпасибо, вот яВ результате должно отображаться через такую формулу: ссылки на ячейки. на нужную нам

ВАЖНО! («Главная» – «Число»). степеней? Оба аргумента обязательные.

 следующее выражение для В этом случае
является функция квадратного

функции ABS найдите

Степени корней, Мощность

246. Было показано, каким образом любая сила или корень может быть выражена с помощью индекса. Индекс мощности — целое число. Дробь корня — это дробь, числитель которой равен 1. Существует также другой класс величин, которые можно рассматривать либо как степени корней, либо как корни степеней.

Предположим, что ^1/2 умножается само на себя, чтобы повторить три раза как множитель.

Изделие ^{1/2 + 1/2 + 1/2} или ^3/2 (ст.243,), очевидно, является кубом из ^1/2, то есть кубом квадратного корня из a. Этот дробный индекс означает, таким образом, степень корня . Знаменатель выражает корень, а числитель — степень. Знаменатель показывает, на сколько равных факторов или корней разрешается данная величина; а числитель показывает, сколько из этих корней нужно перемножить.
Таким образом, ^4/3 — это четвертая степень кубического корня из a.

Знаменатель показывает, что a делится на три фактора или корня: ^1/3, ^1/3 и ^1/3.Числитель показывает, что четыре из них нужно перемножить; который даст четвертую степень ^1/3; это,
a ^1/3 .a ^1/3 .a ^1/3 .a ^1/3 = a ^4/3.

247. Как ^3/2 — это степень корня, так и — корень степени . Возводим a в третью степень a ³. Квадратный корень из этого равен ^3/2. Корень из ³ — это величина, умноженная на себя, даст ³.

Но согласно ст. 243, a ^3/2 = a ^1/2 .a ^1/2 .a ^1/2; и это, умноженное на себя, (ст. 100) является
a ^1/2 .a ^1/2 .a ^1/2 .a ^1/2 .a ^1/2 .a ^1/2 = a ³.
Следовательно, ^3/2 — это квадратный корень из куба a.

Таким же образом можно показать, что ^{m / n} — это степень m корня n-й степени числа a; или корень n-й степени в степени m: то есть корень степени равен той же степени того же корня .Например, четвертая степень кубического корня из a совпадает с кубическим корнем из четвертой степени из a.

248. Корни, а также степени одной и той же буквы можно умножить на , сложив их степень . (Статья 243.) Легко увидеть, что тот же принцип может быть распространен на степени корней, когда показатели имеют общий знаменатель.

Таким образом, ^2/7 .a ^3/7 = a ^{2/7 + 3/7} = ^5/7.

Первый числитель показывает, как часто ^1/7 берется в качестве множителя для получения ^2/7.(Статья 246.)

А второй числитель показывает, как часто ^1/7 берется в качестве множителя для получения ^3/7.

Таким образом, сумма числителей показывает, как часто нужно извлекать корень для произведения . (Статья 100.)
Или, таким образом, ^2/7 = ^1/7 .a ^1/7.
И ^3/7 = ^1/7 .a ^1/7 .a ^1/7.
Следовательно, ^2/7 .a ^3/7 = ^1/7.a ^1/7 .a ^1/7 .a ^1/7 .a ^1/7 = a ^5/7.

249. Значение количества не изменяется при применении к нему дробного индекса, числитель и знаменатель которого равны.

Таким образом, a = ^2/2 = a ^3/3 = a ^{n / n}. Знаменатель показывает, что a разложено на определенное количество факторов; а числитель показывает, что все эти факторы включены в ^{n / n}.
Таким образом, ^3/3 = ^1/3.a ^1/3 .a ^1/3, что равно a.
А ^{n / n} = a ^{1 / n} .a ^{1 / n} ….. n раз.

С другой стороны, когда числитель дробного индекса становится равным знаменателю, выражение может быть упрощено посредством отклонения индекса.

Вместо _{n / n} мы можем написать.

250. Индекс степени или корня может быть заменен любым другим индексом того же значения.
Вместо ^2/3 можно поставить ^4/6.

Поскольку в последнем из этих выражений предполагается, что a должно быть разложено на , вдвое, на больше множителей, чем в первом; а числитель показывает, что удвоить , чтобы умножить эти множители. Так что вся стоимость не изменится.

Таким образом, x ^2/3 = x ^4/6 = x ^6/9. то есть квадрат кубического корня равен четвертой степени корня шестой, шестой степени корня девятой.

Итак, ² = ^4/2 = ^6/3 = ^{2n / n}. Ибо значение каждого из этих показателей равно 2. (Ст. 132).

251. Из предыдущей статьи легко увидеть, что дробный индекс может быть выражен в десятичных дробях .

1. Таким образом, ^1/2 = ^5/10 или ^0,5; то есть квадратный корень равен 5-й степени корня десятой.

2. ^1/4 = ^25/100 или ^0,25; то есть корень четвертой степени равен 25-й степени 100-го корня.

3. a ^2/5 = a ^0,4.

4. ^7/2 = ^3,5.

5. a ^9/5 = a ^1,8

Однако во многих случаях десятичная дробь может быть только приближением к истинному индексу .

Таким образом, ^1/3 = ^{0,3 почти}. ^1/3 = ^0,333334 очень близко.

Таким образом, приближение может быть выполнено с любой требуемой степенью точности.

Таким образом, ^5/3 = ^1,66666. nbsp; ^7/11 = ^1,87142.

Эти десятичные индексы образуют очень важный класс чисел, называемый логарифмами .

Часто удобно изменять обозначение степеней корней, используя винкулум или знак корня √. При этом мы должны помнить, что сила корня равна силе корня; (Ст. 247,), а также, что знаменатель дробной экспоненты выражает корень , а числитель — степень .(Статья 246.)

Поэтому вместо ^2/3 мы можем написать (^1/3) ², или (²) ^1/3, или ³ √a ².

Первая из этих трех форм обозначает квадрат кубического корня из a; и каждый из двух последних — кубический корень из квадрата a.

Таким образом, ^{m / n} = (a ^{1 / n}) ^m = (a ^m) ^{1 / n} = ⁿ √a ^m.
А (bx) ^3/4 = (b ³ x ³) ^1/4 = ⁴ √b ³ x ³.
И (a + y) ^3/5 = [(a + y) ³] ^1/5 = ⁵ √ (a + y) ³.

Калькулятор корня

— получение n-го радикала числа

Добро пожаловать в калькулятор корня , где мы рассмотрим теорию и практику , как вычислить корень n-й степени числа , также называемый корень n-й степени , вместе. Мы начнем с краткого объяснения того, что такое корень в математике, и приведем несколько простых примеров, которые вы, возможно, уже видели, например, квадратный корень из 2, квадратный корень из 3 или кубический корень из 4.Но что, если вы хотите найти , четвертый корень ? Предыдущие были довольно простыми, но каков, скажем, корень 4-й степени из 81? Не беспокойтесь, мы вам скоро покажем!

Устройтесь поудобнее, расслабьтесь и наслаждайтесь поездкой по миру радикалов !

Что такое корень

в математике?

Мы все знаем умножение, верно? Как 12 * 4 = 48 ? Если мы хотим умножить одно и то же число несколько раз, мы можем записать его в упрощенном виде :

12 * 12 * 12 * 12 * 12 = 12⁵ ,

, где маленький 5 называется показателем и означает, сколько копий большого числа (в данном случае 12 ) мы берем.Мы также называем эту операцию , принимая 5 -ю степень 12 .

Корень — это обратная операция. Чтобы связать это с биологическим значением, когда мы смотрим на выросшее дерево, мы видим его листья и ствол, но все это построено на его корнях . И история очень похожа с числами: когда мы видим число 125 , то, взяв его корень, мы увидим крошечное зерно, которое оно выросло из . В этом примере он покажет нам, что начальное число — 5 , потому что 5³ = 125 .

Формально, корень n числа a — это число b , так что:

bⁿ = .

Например, давайте внимательнее посмотрим на , что является квадратным корнем из некоторого числа . Предположим, вы копаете бассейн на заднем дворе. Вы хотите, чтобы она была такой же длинной, как и в ширину, и в целом занимала площадь в 256 квадратных футов. Как определить , какой длины должны быть стороны ? Правильно — вычислением радикала! В этом случае это должен быть квадратный корень из площади, т.е.е., квадратный корень из 256 .

И каков квадратный корень из этого числа? Что ж, давайте посмотрим, как его найти и как вообще вычислить квадратный корень.

Как вычислить квадратный корень

Иногда вычисление корня в математике может напоминать игру в угадывание . Но это не то же самое, что бросать кости с закрытыми глазами и гадать, что получится. Это скорее расчетное предположение . В конце концов, как только мы узнаем, что 3⁴ = 81 , мы можем с уверенностью сказать, что корень 4-й степени из 81 равен 3 .Но сначала мы должны это знать.

Итак, что мы можем сделать, если мы забыли дома нашу удобную таблицу первых ста чисел и их первых нескольких степеней ? Это безнадежное дело? К счастью, нет. Не совсем, но мы вернемся к этому через секунду.

В качестве примера мы покажем , как вычислить квадратный корень из 72 . Нашим основным инструментом здесь будет разложение на простые множители, то есть разделение 72 на самые маленькие возможные части.

В процедуре разложения на простые множители мы берем число (в нашем случае 72 ) и находим наименьшее простое число, которое делит его на . Напомним, что простое число — это целое число, которое имеет только два делителя: 1, и само себя. Достаточно легко увидеть, что для нас это будет 2 с

72/2 = 36 .

Следующий шаг — найти наименьшее простое число результата деления числа на простое число, т.е.е., номер 36 . Если мы продолжим это, пока не достигнем 1 , мы получим следующие простые числа: 2 , 2 , 2 , 3 , 3 . Это разложение на простые множители 72 , и это означает, что

72 = 2 * 2 * 2 * 3 * 3 .

Теперь, если мы найдем пары среди одинаковых чисел, мы увидим, что у нас осталось пара 2 , пара 3 и одно 2 .Это позволяет нам записать квадратный радикал 72 как

√72 = √ (2 * 2 * 2 * 3 * 3) = √ (2² * 3² * 2) = 2 * 3 * √2 = 6√2 .

Внимательный взгляд заметит, что единственные числа, которые остаются под корнем, — это ровно одиночки, которые не нашли пару .

А как насчет 2 ? Что такое квадратный корень из 2 ? Что ж, вот что означало « не совсем ». Квадратный корень из 2 , квадратный корень из 3 или любого другого простого числа возвращает нас к игре в угадайку.К счастью, мы можем использовать наш калькулятор корня , чтобы вычислить, что √2 ≈ 1,4142 , что дает нам

√72 = 6√2 ≈ 6 * 1,4142 = 8,4852 .

По сути, когда нас спрашивают «, что такое квадратный корень из …, », мы должны сначала выполнить разложение на простые множители , чтобы решить проблему, и если (как указано выше) у нас останется маленькая цифра в конце, нам просто нужно использовать такой инструмент, как , калькулятор корня , чтобы найти его.

« А как насчет высших радикалов? Что, если мне понадобится, например.г., корень четвертой степени числа? «Ну, как удобно с вашей стороны спросить! Это именно та проблема, которой мы займемся в следующем разделе.

Кубический корень, корень четвертой степени, корень n-й степени

Вспомните, как вы хотели выкопать бассейн в первой секции. Теперь предположим, что вы хотите, чтобы все это было кубом, вмещающим 1728 кубических фута воды. (Не спрашивайте нас, почему. Возможно, что-либо выше облагается налогом по-другому?)

Как найти бортик такого бассейна? Ага — вычислением кубического корня числа (отсюда и произошло название кубический корень ).Он сообщит нам, что длина должна быть

∛1,728 = 12 футов в длину.

Но как мы туда попали? К счастью, основной инструмент здесь тот же: разложение на простые множители . Если мы применим процедуру к 1,728 , мы получим

1,728 = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3 .

Теперь другое дело — вместо пар, мы группируем числа в тройки . Это то, что предполагает маленький 3 в корневом символе — нам нужно третьей степени .Обратите внимание, что квадратные корни на самом деле являются радикалами порядка 2 , но мы не пишем 2 , потому что … Ну, , если нам не нужно делать это из одного типа корня, это с таким же успехом может быть самый простой . Это просто условность и традиция. Думайте об этом как о математическом эквиваленте запекания индейки на День Благодарения.

В любом случае, возвращаясь к нашей проблеме, группировка позволяет нам написать

∛1,728 = ∛ (2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 * 3) = ∛ (2³ * 2³ * 3³) = 2 * 2 * 3 = 12 .

Если мы пойдем выше с порядком радикала, применяется то же правило . При вычислении корня четвертой степени мы группируем простые числа в четверных . Например, если вам нужен 4-й корень из 81 , вы сначала заметите, что

81 = 3 * 3 * 3 * 3 ,

, поэтому у нас есть четыре 3 . Это означает, что корень 4-й степени из 81 равен 3 . И если нам нужно n-й корень , мы берем группы из n элементов.И, если что-то останется после факторизации, мы просто найдем с помощью какого-либо внешнего инструмента, такого как наш калькулятор корня .

Хорошо, после того, как вы все это время читали теорию, самое время взглянуть на реальный пример и увидеть калькулятор корня в действии , вам не кажется?

Пример: использование калькулятора корня

Поздравляю, это мальчик! Теперь, когда вы стали родителем, вы решили начать с начала и откладываете немного денег, когда он пойдет в колледж.Вы решаете взять хорошую часть своих сбережений и оставить ее в банке на следующие восемнадцать лет , чтобы сумма росла вместе с вашим ребенком.

Предположим, вам удалось отложить на твердые 8000 долларов . К сожалению, вы как-то забыли процентную ставку по вложениям, но что сделано, то сделано. Сумма в конце будет для вас такой же неожиданностью, как и для вашего сына .

Время идет, годы идут, и, наконец, пришло время подарить вашему ребенку деньги, которые вы сэкономили .Вы звоните в банк, и выясняется, что на счету $ 12 477,27 . Неплохо, правда? Похоже, ты сможешь осуществить мечты своего сына.

Но, только для себя, просто из чистого любопытства, можем ли мы рассчитать процентную ставку по имеющимся у нас числам?

Конечно, , и калькулятор корня нам поможет!

Предположим, что проценты начислялись на счет в конце каждого года и что деньги вообще не облагались налогом (да, мы знаем, что здесь мы немного надуманы).Тогда сумма, которую мы получаем в итоге , описывается формулой

end_amount = начальная_ сумма * (1 + процентная_ процентная ставка) ¹⁸ ,

, где 18 -я степень исходит от восемнадцати лет, что деньги потрачены в банке. В нашем случае это означает

12 477,27 долларов США = 8 000 долларов США * (1 + процентная_ ставка) ¹⁸.

Если мы разделим обе стороны на 8000 , мы получим

12 477,27 долл. США / 8 000 долл. США = (1 + процентная_ процентная ставка) ¹⁸

или приблизительно

1.5597 = (1 + процентная ставка) ¹⁸.

Итак, если у нас есть 18 -я степень справа, то нам нужно найти 18 -й радикал числа слева . Это что-то немного более сложное, чем квадратный корень из 3, не так ли?

Обратимся к нашему вычислителю корней . Там у нас есть два числа: и n . Когда мы смотрим на символическое изображение там, мы видим, что n — это порядок корня , поэтому мы вводим n = 18 .В свою очередь, a — это число под корнем , поэтому мы берем a = 1,5597 . Это заставляет калькулятор корня выдавать ответ

1 + процентная ставка = 1,025 .

Если перевести десятичную дробь в проценты, получим

процентная ставка = 0,025 = 2,5% .

Кажется довольно маленьким, но ох, как он вырос за восемнадцать лет!

Хорошо, любопытство удовлетворено, , пора вернуться к праздничному торту.Будем надеяться, что ваш сын хорошо распорядится деньгами и продолжит учебу.

Дробные (рациональные) экспоненты | Purplemath

Purplemath

Вам уже известна одна взаимосвязь между экспонентами и радикалами: соответствующий радикал «отменяет» показатель степени, а правая сила «отменяет» корень. Например:

Но есть еще одно соотношение, которое, кстати, может значительно упростить вычисления, подобные приведенным выше.

MathHelp.com

Для квадратного (или «второго») корня мы можем записать его как половинную степень, например:

…или:

Кубический (или «третий») корень — это степень одной трети:

Корень четвертой степени равен четвертой степени:

Корень пятой степени равен одной пятой степени; и так далее.

Глядя на первые примеры выше, мы можем переписать их так:

Вы можете ввести дробные показатели на вашем калькуляторе для оценки, но не забудьте использовать круглые скобки.Если вы пытаетесь вычислить, скажем, 15 ^(4/5), вы должны заключить в скобки «4/5», потому что в противном случае ваш калькулятор будет думать, что вы имеете в виду «(15 ⁴) ÷ 5».

Дробные показатели обеспечивают большую гибкость (вы часто это увидите в исчислении), их часто проще написать, чем эквивалентный радикальный формат, и они позволяют выполнять вычисления, которые вы не могли раньше. Например:

Всякий раз, когда вы видите дробную экспоненту, помните, что верхнее число — это степень, а нижнее число — это корень (если вы конвертируете обратно в радикальный формат).Например:

Кстати, некоторые десятичные степени могут быть записаны и в виде дробных показателей. Если вы получили что-то вроде «3 ^5.5», вспомните, что 5,5 = 11/2, поэтому:

Однако, как правило, когда вы получаете десятичную степень (что-то другое, кроме дроби или целого числа), вы должны просто оставить ее как есть или, если необходимо, вычислить ее в своем калькуляторе. Например, 3 π , где π — это число, которое вы узнали в геометрии, и примерно равно 3.14159, нельзя упростить или преобразовать в радикал.

Технический момент: когда вы имеете дело с этими показателями с переменными, вам, возможно, придется принять во внимание тот факт, что вы иногда получаете ровные корни. Подумайте об этом: предположим, вы начали с числа –2. Тогда:

Другими словами, вы вводите отрицательное число и получаете положительное число! Это официальное определение абсолютной величины:

Да, я знаю: они никогда не говорили вам этого, но они ожидают, что вы каким-то образом узнаете, поэтому я говорю вам сейчас.

Итак, если они дадут вам, скажем, x ^3/6, тогда x лучше не быть отрицательным, потому что x ³ все равно будет отрицательным, и вы попытаетесь взять корень шестой степени отрицательного числа. Если они дадут вам x ^4/6, тогда отрицательное значение x станет положительным (из-за четвертой степени) и затем будет корнем шестой степени, поэтому оно станет | x | ^2/3 (за счет уменьшения дробной мощности).С другой стороны, если они дадут вам что-то вроде x ^4/5, тогда вам не нужно заботиться о том, положительный или отрицательный x , потому что корень пятой степени не имеет проблем с отрицательными. (Между прочим, эти соображения не имеют значения, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».)

Технологический момент: калькуляторы и другое программное обеспечение не вычисляют вещи так, как это делают люди; они используют заранее запрограммированные алгоритмы.Иногда конкретный метод, используемый калькулятором, может создать трудности в контексте дробных показателей.

Например, вы знаете, что кубический корень из –8 равен –2, а квадрат –2 равен 4, поэтому (–8) ^(2/3) = 4. Но некоторые калькуляторы возвращают комплексное значение или сообщение об ошибке, как в случае с одним из моих графических калькуляторов:

Ясно, что это не ожидаемый результат, особенно если вы еще не изучали комплексные числа.(2/3) «в ячейку, электронная таблица Microsoft» Excel «возвращает ошибку» # ЧИСЛО! «, Еще один бесполезный ответ.

Некоторые калькуляторы и программы будут выполнять вычисления, как ожидалось, как показано справа от моего другого графического калькулятора:

Разница связана с заранее запрограммированными вычислительными алгоритмами. Эти алгоритмы обычно пытаются выполнять вычисления способами, требующими наименьшего количества «операций», чтобы обработать введенные вами данные как можно быстрее.

Но иногда самый быстрый метод не всегда самый полезный, и ваш калькулятор «давится».

К счастью, проблему можно обойти. Разделив числитель и знаменатель дробной степени, вы можете ввести выражение, чтобы ваш калькулятор получил правильное значение. Получив бесполезный ответ в моем первом калькуляторе, я повторно ввел число с разбитой на части степенью:

Как вы можете видеть выше, не имело значения, возьму ли я сначала кубический корень из отрицательной восьмерки, а затем возведу в квадрат или сначала возведу в квадрат, а затем получу кубический корень; в любом случае, подавая числитель и знаменатель в калькулятор по отдельности, я смог заставить калькулятор возвращать правильное значение «4».

URL: https://www.purplemath.com/modules/exponent5.htm

Корень (числа) — определение математического слова

Корень (числа) — определение математического слова — Открытый справочник по математике

Корень числа x — это другое число, которое при умножении на себя заданное количество раз дает x.

Например, третий корень (также называемый кубическим корнем) из 64 равен 4, потому что если вы умножите три четверки вместе, вы получите 64:

4 × 4 × 4 = 64

Это было бы записано как Вышеупомянутое будет означать «третий корень 64 составляет 4» или «кубический корень 64 равен 4» .

Второй корень обычно называют «квадратным корнем».
Третий корень числа обычно называют «кубическим корнем»,
После этого они называются корнем n, например корень 5, корень 7 и т. Д.

Иногда бывает два корня

Для каждого корня четной степени (например, 2-го, 4-го, 6-го….) есть два корня. Это потому, что умножение двух положительных или двух отрицательных чисел дает положительный результат. Например, рассмотрим квадратный корень из 9.

Какое число, умноженное на само себя, даст 9?
Очевидно 3 будут работать:

3 × 3 = 9

Но так будет -3:

-3 × -3 = 9

Когда таких корней два, если не указано иное, мы имеем в виду положительный. Строго говоря, когда мы пишем √ 4, мы имеем в виду положительный корень, +2.Это называется «главный корень».

Корни отрицательных чисел

У отрицательных чисел нет реальных корней четного порядка. Например, квадратного корня из -9 не существует, потому что -3 × -3 = + 9, а также +3 × +3 = + 9. Это относится ко всем корням четного порядка, 2-му (квадратному) корню, 4-му корню, 6-му корню и так далее.

Однако — это корней нечетного порядка отрицательных чисел. Например, –3 — это кубический корень из –27. Это потому что –3 × –3 × –3 = –27.Первые два члена при умножении дают +9, затем следующее умножение дает
+9 × –3 = –27. Это относится ко всем корням нечетного порядка, таким как 3-й (кубический) корень, 5-й корень, 7-й корень и т. Д.

Мнимые числа

Выше сказано, что действительного квадратного корня из отрицательного числа не существует. Обратите внимание на слово «настоящий». Это говорит о том, что нет настоящий номер это квадратный корень отрицательного числа.

Однако в математике и инженерии нам часто нужно найти квадратный корень из отрицательного числа.Чтобы решить эту проблему, мы вводим понятие «мнимого» числа. Он включает в себя символ i , который обозначает квадратный корень из отрицательного числа. Или, другими словами, i ² = –1

На практике мы можем использовать его для выражения квадратного корня из любого отрицательного числа. Например Это означает, что квадратный корень из –25 — это квадратный корень из +25, умноженный на квадратный корень из отрицательной единицы.

Подробнее о мнимых числах см. Мнимые числа.

Символы

Радиканд

То, что вы находите корень.

Радикальный символ

Символ √ , означающий «корень из». Длина турника важна. См. Примечание ниже.

Степень

Сколько раз подкоренное выражение умножается само на себя. 2 означает квадратный корень, 3 означает кубический корень. После этого они называются корнем 4-й, 5-й и так далее. Если он отсутствует, предполагается, что это 2 — квадратный корень.

Другой способ записи

Корни также можно записать в экспоненциальной форме. В общем Так, например, кубический корень x будет записан Что будет произноситься как «х в степени одной трети».

Другие экспоненты и основные темы

N-й корень и рациональные экспоненты

Результаты обучения

Упростите корни N-й степени.
Запишите радикалы как рациональные показатели.

Использование рациональных корней

Хотя квадратные корни являются наиболее распространенными рациональными корнями, мы также можем найти кубические корни, корни четвертой степени, корни пятой степени и многое другое.{5} = — 243 [/ латекс]. Если [latex] a [/ latex] является действительным числом с хотя бы одним корнем n , то основной n корень -й степени [latex] a [/ latex] — это число с тем же знаком, что и [latex] a [/ latex], который при увеличении до n в -й степени равен [latex] a [/ latex].

Главный n -й корень [латекса] a [/ latex] записывается как [latex] \ sqrt [n] {a} [/ latex], где [latex] n [/ latex] является положительным целым числом больше чем или равно 2. В радикальном выражении [латекс] n [/ латекс] называется индексом радикала .

A Общее примечание: основной

n -й корень

Если [latex] a [/ latex] является действительным числом с хотя бы одним корнем n -й, то основной n -й корень [latex] a [/ latex], записанный как [latex] \ sqrt [n] {a} [/ latex] — это число с тем же знаком, что и [latex] a [/ latex], которое при увеличении до n -й степени равно [latex] a [/ latex]. Индекс радикала — [латекс] n [/ латекс].

Пример: упрощение

n корней

Упростите каждое из следующего:

[латекс] \ sqrt [5] {- 32} [/ латекс]
[латекс] \ sqrt [4] {4} \ cdot \ sqrt [4] {1,024} [/ латекс]
[латекс] — \ sqrt [3] {\ dfrac {8 {x} ^ {6}} {125}} [/ латекс]
[латекс] 8 \ sqrt [4] {3} — \ sqrt [4] {48} [/ латекс]

Показать решение

[латекс] \ sqrt [5] {- 32} = — 2 [/ латекс], потому что [латекс] {\ left (-2 \ right)} ^ {5} = — 32 \\ \ text {} [/ латекс]
Во-первых, выразите произведение как одно радикальное выражение.{2}} {5} && \ text {Упростить}. \\ \ end {align} [/ latex]
[латекс] \ begin {align} \\ & 8 \ sqrt [4] {3} -2 \ sqrt [4] {3} && \ text {Упростите, чтобы получить одинаковые подкоренные выражения}. \\ & 6 \ sqrt [4] {3} && \ text {Добавить}. \ end {align} [/ latex]

Попробуй

Упростить.

[латекс] \ sqrt [3] {- 216} [/ латекс]
[латекс] \ dfrac {3 \ sqrt [4] {80}} {\ sqrt [4] {5}} [/ латекс]
[латекс] 6 \ sqrt [3] {9,000} +7 \ sqrt [3] {576} [/ латекс]

Показать решение

[латекс] -6 [/ латекс]
[латекс] 6 [/ латекс]
[латекс] 88 \ sqrt [3] {9} [/ латекс]

Использование рациональных экспонентов

Радикальные выражения также можно записывать без использования радикального символа.{m}} \ end {align} [/ latex]

Как: дано выражение с рациональной степенью, запишите выражение как радикал.

Определите степень, посмотрев на числитель экспоненты. {\ frac {2} {3}} [/ латекс] как радикал.{\ frac {23} {15}} [/ латекс]
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Расширяющиеся логарифмы — ChiliMath
Когда вас просят развернуть логарифмические выражения , ваша цель состоит в том, чтобы выразить одно логарифмическое выражение на множество отдельных частей или компонентов. Этот процесс прямо противоположен сжатию логарифмов, потому что вы сжимаете кучу лог-выражений в более простое.
Лучший способ проиллюстрировать эту концепцию — показать множество примеров. В этом уроке восемь решенных задач.
Ключ к успешному расширению логарифмов — это осторожное применение правил логарифмов. Найдите время, чтобы изучить правила и понять, что они пытаются «сказать».
Например, Правило 1 называется Правилом продукта . Что он делает, так это разбивает произведение выражений на сумму лог-выражений. См. Остальные описания ниже.
Правила логарифмов
Изучите описание каждого правила, чтобы получить его интуитивное понимание.
Описание правил логарифмирования
Правило 1: Правило продукта
Логарифм произведения чисел — это сумма логарифмов отдельных чисел.
Правило 2: Правило частного
Логарифм частного числа — это разность логарифма отдельных чисел.
Правило 3: Правило силы
Логарифм экспоненциального числа — это показатель степени, умноженный на логарифм основания.
Правило 4: Правило нуля
Логарифм 1, где b> 0, но b \ ne 1, равен нулю.
Правило 5: Правило идентификации
Логарифм числа, равного его основанию, равен 1. Поскольку число также является основанием, b, это означает, что b> 0, но b \ ne 1.
Правило 6: Журнал экспоненты Правило
Логарифм экспоненциального числа, основание которого совпадает с основанием журнала, равно экспоненте.
Правило 7: Показатель логарифма Правило
Возведение логарифма числа по основанию равняется числу.
Примеры раскрытия логарифмов
Пример 1 : развернуть логарифмическое выражение.
Заглянув в круглые скобки, мы видим произведение числа и переменных. Правило продукта не говорит, что внутри должно быть только два фактора, на самом деле их может быть больше. Хорошо, поэтому мы разделим основное логарифмическое выражение как сумму четырех журналов.
Пример 2 : развернуть логарифмическое выражение.
Внутри скобок — дробь, означающая, что сначала я буду применять правило частных.Поскольку числитель является произведением 7 и x, я использую правило произведения, чтобы разбить его.
Пример 3 : развернуть логарифмическое выражение.
Хорошо, это тоже дробная форма, поэтому правило частных — это первый шаг, который мы собираемся применить.
Итак, в этой проблеме есть что-то «новое». То есть числитель содержит переменную с показателем степени. Это должно быть легко, поскольку с этим легко справятся Правило 3 или Правило мощности. Просто опустите экспоненту влево, вот и все!
Кроме того, в знаменателе стоит радикальное выражение.Помните, что радикал можно выразить дробной степенью. Поскольку этот радикал является квадратным корнем, это означает, что степень просто \ large {1 \ over 2}.
Кроме того, мы впервые видим в действии Правило 5 или Правило логарифма идентичности. Ожидайте, что это правило будет применяться чаще, потому что оно чрезвычайно полезно в процессе упрощения.
Пример 4 : развернуть логарифмическое выражение.
Пусть вас не пугает квадратный корень. Просто представьте это как степень или показатель \ large {1 \ over 2}.Таким образом, эта проблема сводится к расширению логарифмического выражения со степенью \ large {1 \ over 2}. Здесь правило мощности опускает показатель \ large {1 \ over 2} слева от журнала, а затем вы расширяете остальную часть, как обычно.
Пример 5 : Разверните логарифмическое выражение.
Эта задача довольно интересна, потому что все выражение возводится в некоторую степень. Кроме того, наличие квадратного корня в числителе добавляет некоторого уровня сложности.
Однако, если мы будем придерживаться основ, тщательно применяя правила экспонент на каждом этапе, у нас не должно возникнуть проблем с решением этой проблемы! Давай спланируем наши действия, хорошо?
Уменьшите показатель степени 4, используя правило мощности. Затем используйте правило частного, чтобы выразить дробь как разность логарифмических выражений. И, наконец, не забывайте, что квадратный корень — это всего лишь дробный показатель от \ large {1 \ over 2}.
Я распределил 4 по символу группировки, чтобы избавиться от дроби \ large {1 \ over 2}.Также можно оставить 4 за пределами символа группировки, что означает, что нам не нужно распределять 4 по выражениям внутри квадратных скобок. Любой из двух ответов должен быть правильным.
Пример 6 : Разверните логарифмическое выражение.
Это просто кубический корень из некоторого рационального выражения. Замените символ корня куба дробной степенью \ large {1 \ over 3}. Этот показатель \ large {1 \ over 3} можно уменьшить, используя правило логарифма степени. Теперь нам нужно разобраться с рациональным выражением, используя правило частных, а затем завершить его, используя правило продукта.
Не отвлекайтесь на разные типы групповых символов. Идея состоит в том, чтобы убедиться, что мы правильно применяем правила логарифмирования на каждом этапе, который мы предпринимаем, без совершения алгебраических ошибок, таких как распределение -1 в символе группировки.
Пример 7 : разверните логарифмическое выражение.
Я бы немедленно применил правило произведения, чтобы разделить множители на сумму логарифмических членов. Упростите численно {\ log _4} 64, поскольку 64 можно выразить как экспоненциальное число с основанием 4, то есть 64 = {4 ^ 3}.Обработайте квадратные корни, заменив их дробной степенью, а затем используйте правило логарифмов мощности, чтобы уменьшить его перед символом журнала в качестве множителя.
Пример 8 : развернуть логарифмическое выражение.
Основное питание 3 может быть размещено в качестве множителя с помощью правила мощности. Правило Quotient должно иметь дело с дробными выражениями, записывая их как разность журналов. Теперь замените символ квадратного корня на показатель степени \ large {1 \ over 2}.Аналогичным образом замените символ корня куба на показатель степени \ large {1 \ over 3}.
Практика с рабочими листами
Возможно, вас заинтересует:
Уплотняющие логарифмы
Объяснение логарифма
Правила логарифмирования
Решение логарифмических уравнений
Радикальное выражение Пошаговое решение математических задач
10.1 Определения и обозначения
n-я степени чисел 2, a, 3 ^ 2 и b ^ 3 равны соответственно 22 ^ n, a ^ n, 3 ^ (2n) и b ^ (3n).n со следующими условиями:
1. Когда n — четное число и a> 0, root (n, a)> 0, называется главным корнем.
Когда n — четное число и a <0, корень (n, a) не является действительным числом.
2. Когда n — нечетное число и a> 0, корень (n, a)> 0.
Когда n — нечетное число и a <0, root (n, a) <0
Число n в корне (n, a) (всегда натуральное число больше 1) называется индексом или порядком радикала, а a называется подкоренным выражением.4).
Радикальное выражение называется стандартным, если выполняются следующие условия:
1. Подкоренное выражение положительное.
2. Индекс корня должен быть как можно меньше.
3. Показатель степени каждого множителя подкоренного выражения является натуральным числом меньше радикального индекса.
4. В подкоренном выражении нет дробей.
5. В знаменателе дроби нет радикалов.
Под упрощением радикального выражения мы подразумеваем приведение радикального выражения в стандартную форму.

РубрикаРазное

Корень из 4 в степени 3: Калькулятор по извлечению корня 2, 3, 4, 5, n степени

1.2. Ко­рень n-й сте­пе­ни

1.2. Ко­рень n-й сте­пе­ни

Упраж­не­ния

Квадратный корень в Python 3 — Извлечение кубических и n-ой степени

Способы извлечения корня

Какой метод быстрее?

Квадратный корень

Кубический корень

Корень n-степени

Корень отрицательного числа

Вывод

Корень n-й степени и его свойства

Определение корня n-й степени из действительного числа

Корень четной и нечетной степени

Урок 16. арифметический корень натуральной степени — Алгебра и начала математического анализа — 10 класс

Решение корней в онлайн калькуляторе

Извлечение квадратного корня

Корень третьей степени

Корень степени n

Корень из дроби

Корень из корня

Степень в корне

Калькулятор извлечения корня n-ой степени онлайн

Математическое обозначение

Квадратный корень

Кубический корень

Корень n-ной степени

Рассмотрим пример

Диагональ квадрата

Заключение

Способ 2: возведение в степень

КОРЕНЬ (функция КОРЕНЬ)

Описание

Синтаксис

Замечание

Пример

Как вычислить корень квадратный в Excel?

Что такое корень квадратный?

Функция корня

Использование математических свойств

Примеры

Функция возведения в степень в Excel

Возведение к степени с помощью оператора

Извлечение корней n-й степени

Как возвести число к степени в Excel с помощью формулы и оператора

Как возвести в степень в Excel?

Формула возведения в степень в Excel

Корень в степени в Excel

Как ввести формулу в Excel, чтобы вычислить корень третьей степени?

Степени корней, Мощность

— получение n-го радикала числа

Что такое корень

Как вычислить квадратный корень

Кубический корень, корень четвертой степени, корень n-й степени

Пример: использование калькулятора корня

Дробные (рациональные) экспоненты | Purplemath

Purplemath

MathHelp.com

Корень (числа) — определение математического слова

Иногда бывает два корня

Корни отрицательных чисел

Мнимые числа

Символы

Радиканд

Радикальный символ

Степень

Другой способ записи

Другие экспоненты и основные темы

N-й корень и рациональные экспоненты

Результаты обучения

Использование рациональных корней

A Общее примечание: основной

Пример: упрощение

Попробуй

Использование рациональных экспонентов

Как: дано выражение с рациональной степенью, запишите выражение как радикал.

Внесите свой вклад!

Расширяющиеся логарифмы — ChiliMath

Правила логарифмов

1.2. Корень n-й степени

1.2. Корень n-й степени

Упражнения