Координаты как писать: Sorry, this page can’t be found.
Как правильно писать широту и долготу
Географи́ческие координа́ты — обобщённое понятие о геодезических и астрономических координатах, когда уклонение отвесной линии не учитывают [1] . Иными словами, при определении географических координат Земля принимается за шар. Географические координаты определяют положение точки на земной поверхности или, более широко, в географической оболочке. Географические координаты строятся по принципу сферических. Аналогичные координаты применяются для других планет, а также на небесной сфере [2] .
Содержание
Широта [ править | править код ]
Широта́ — угол φ между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Географическую широту точек, лежащих в северном полушарии, (северную широту) принято считать положительной, широту точек в южном полушарии — отрицательной. О широтах, близких к полюсам, принято говорить как о высоких, а о близких к экватору — как о низких.
Из-за отличия формы Земли от шара, географическая широта точек несколько отличается от их геоцентрической широты, то есть от угла между направлением на данную точку из центра Земли и плоскостью экватора.
Широту места можно определить с помощью таких астрономических инструментов, как секстант или гномон (прямое измерение), также можно воспользоваться системами GPS или ГЛОНАСС (косвенное измерение).
Долгота [ править | править код ]
Долгота́ — двугранный угол λ между плоскостью меридиана, проходящего через данную точку, и плоскостью начального нулевого меридиана, от которого ведётся отсчёт долготы. Долготу от 0° до 180° к востоку от нулевого меридиана называют восточной, к западу — западной. Восточные долготы принято считать положительными, западные — отрицательными.
Выбор нулевого меридиана произволен и зависит только от соглашения. Сейчас за нулевой меридиан принят Опорный меридиан, проходящий рядом с обсерваторией в Гринвиче, на юго-востоке Лондона. В качестве нулевого ранее выбирались меридианы обсерваторий Парижа, Кадиса, Пулкова и т. д.
В качестве нулевого ранее выбирались меридианы обсерваторий Парижа, Кадиса, Пулкова и т. д.
Высота [ править | править код ]
Чтобы полностью определить положение точки трёхмерного пространства, необходима третья координата — высота. Расстояние до центра планеты не используется в географии: оно удобно лишь при описании очень глубоких областей планеты или, напротив, при расчёте орбит в космосе.
В пределах географической оболочки применяется обычно высота над уровнем моря, отсчитываемая от уровня «сглаженной» поверхности — геоида. Такая система трёх координат оказывается ортогональной, что упрощает ряд вычислений. Высота над уровнем моря удобна ещё тем, что связана с атмосферным давлением.
Расстояние от земной поверхности (ввысь или вглубь) часто используется для описания места, однако ‘не’ служит координатой.
Географическая система координат [ править | править код ]
В навигации в качестве начала системы координат выбирается центр масс транспортного средства (ТС).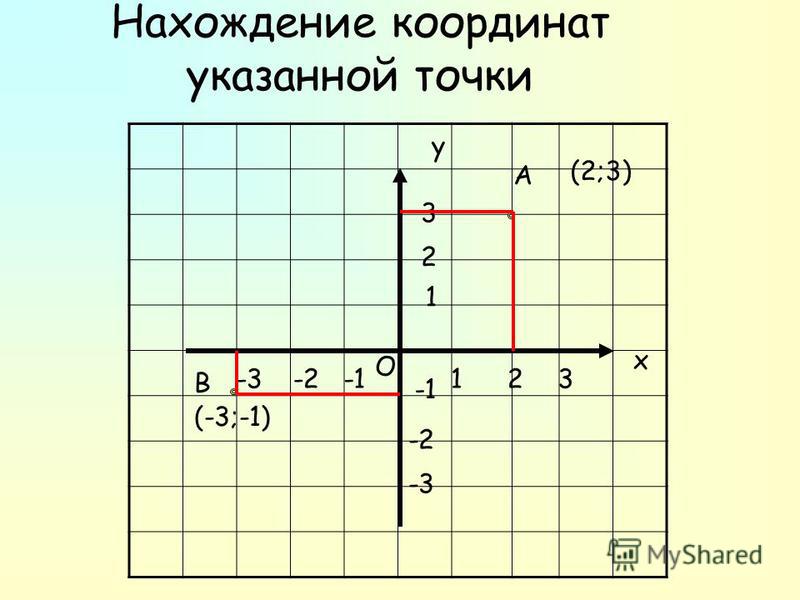
X o g = ( R + h ) cos ( φ ) cos ( U t + λ ) <displaystyle X_=(R+h)cos(varphi )cos(Ut+lambda )> Y o g = ( R + h ) cos ( φ ) sin ( U t + λ ) <displaystyle Y_=(R+h)cos(varphi )sin(Ut+lambda )> Z o g = ( R + h ) sin ( φ ) <displaystyle Z_=(R+h)sin(varphi )> где R — радиус земли , U — угловая скорость вращения Земли, h — высота над уровнем моря, φ <displaystyle varphi > — широта, λ <displaystyle lambda > — долгота, t — время.
Ориентация осей в географической системе координат (Г. С. К.) выбирается по схеме:
Ось X (другое обозначение — ось E) — ось, направленная на восток.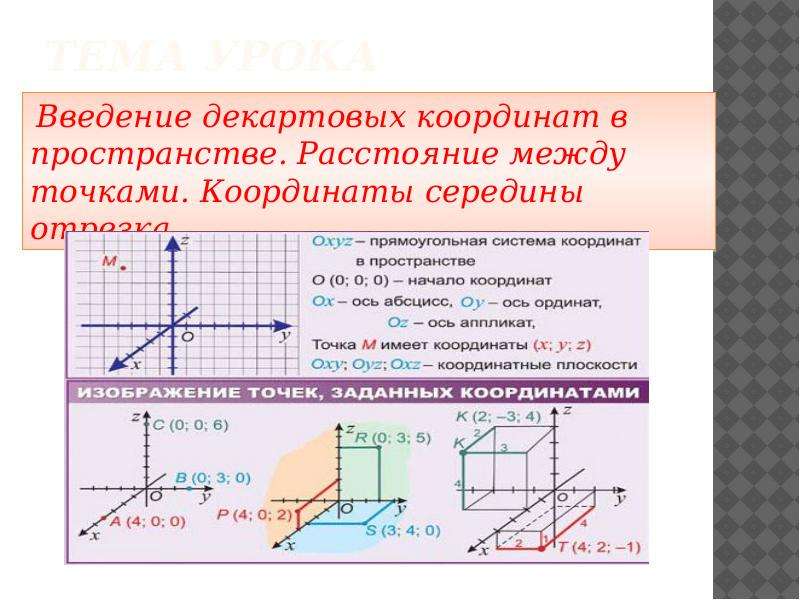 Ось Y (другое обозначение — ось N) — ось, направленная на север. Ось Z (другое обозначение — ось Up) — ось, направленная вертикально вверх.
Ось Y (другое обозначение — ось N) — ось, направленная на север. Ось Z (другое обозначение — ось Up) — ось, направленная вертикально вверх.
Ориентация трёхгранника XYZ,из-за вращения земли и движения Т. С. постоянно смещается с угловыми скоростями [3] .
ω E = − V N / R <displaystyle omega _=-V_/R> ω N = V E / R + U cos ( φ ) <displaystyle omega _=V_/R+Ucos(varphi )> ω U p = V E R t g ( φ ) + U sin ( φ ) <displaystyle omega _=<frac>>tg(varphi )+Usin(varphi )> где R — радиус земли , U — угловая скорость вращения Земли, V N <displaystyle V_> — скорость транспортного средства на север, V E <displaystyle V_> — на восток, φ <displaystyle varphi > — широта, λ <displaystyle lambda > — долгота.
Основным недостатком в практическом применении Г. С. К. в навигации является большие величины угловой скорости этой системы в высоких широтах, возрастающие вплоть до бесконечности на полюсе. Поэтому вместо Г. С. К. используется полусвободная в азимуте СК.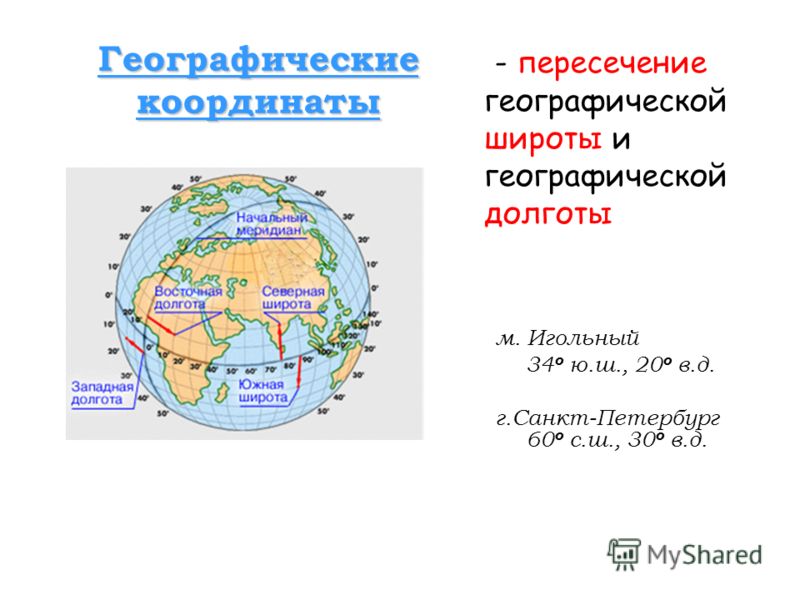
Полусвободная в азимуте система координат [ править | править код ]
Полусвободная в азимуте С. К. отличается от Г. С. К. только одним уравнением, которое имеет вид:
ω U p = U sin ( φ ) <displaystyle omega _=Usin(varphi )>
Соответственно, система имеет тоже начальное положение, осуществляется по формуле [3]
N = Y w cos ( ε ) + X w sin ( ε ) <displaystyle N=Y_cos(varepsilon )+X_sin(varepsilon )> E = − Y w sin ( ε ) + X w cos ( ε ) <displaystyle E=-Y_sin(varepsilon )+X_cos(varepsilon )>
В реальности все расчёты ведутся именно в этой системе, а потом, для выдачи выходной информации происходит преобразование координат в ГСК.
Форматы записи географических координат [ править | править код ]
Координаты (широта от −90° до +90°, долгота от −180° до +180°) могут записываться:
- в ° градусах в виде десятичной дроби (современный вариант)
- в ° градусах и ′ минутах с десятичной дробью
- в ° градусах, ′ минутах и ″ секундах с десятичной дробью (исторически сложившаяся форма записи)
Разделителем десятичной дроби может служить точка или запятая.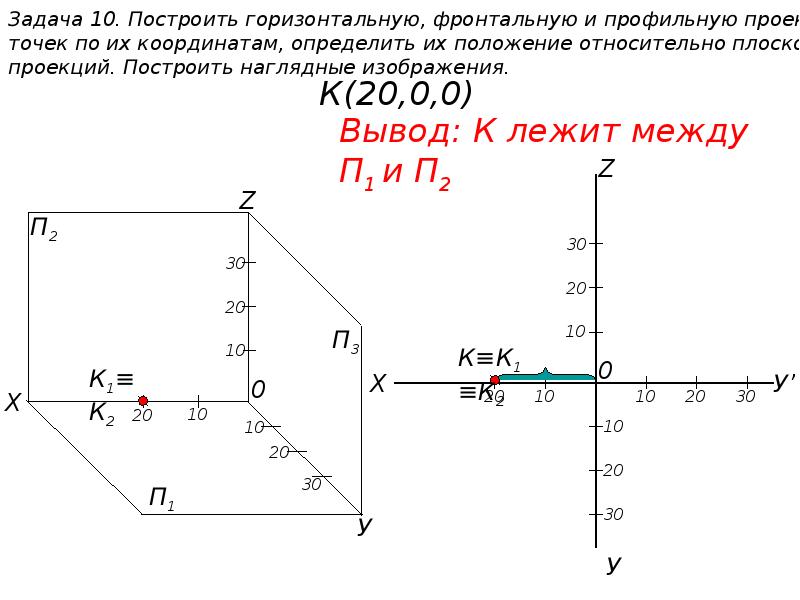 Положительные знаки координат представляются (в большинстве случаев опускаемым) знаком «+» либо буквами:
Положительные знаки координат представляются (в большинстве случаев опускаемым) знаком «+» либо буквами:
- «N» или «с. ш.» — северная широта,
- «E» или «в. д.» — восточная долгота.
Отрицательные знаки координат представляются либо знаком «−», либо буквами:
- «S» или «ю. ш.» — южная широта,
- «W» или «з. д.» — западная долгота.
Буквы могут стоять как впереди, так и сзади. Единых правил записи координат не существует.
На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаком «−» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта). Эти координаты видны, например, при прокладке маршрутов от произвольных точек. При поиске распознаются и другие форматы.
В то же время часто используется и исконный способ записи с градусами, минутами и секундами. В настоящее время координаты могут записываться одним из множества способов или дублироваться двумя основными (с градусами и с градусами, минутами и секундами) [4] . Как пример, варианты записи координат знака «Нулевой километр автодорог Российской Федерации» — 55°45′21″ с. ш. 37°37′04″ в. д. H G Я O L :
В настоящее время координаты могут записываться одним из множества способов или дублироваться двумя основными (с градусами и с градусами, минутами и секундами) [4] . Как пример, варианты записи координат знака «Нулевой километр автодорог Российской Федерации» — 55°45′21″ с. ш. 37°37′04″ в. д. H G Я O L :
- 55,755831°, 37,617673° — градусы
- N55.755831°, E37.617673° — градусы (+ доп. буквы)
- 55°45.35′N, 37°37.06′E — градусы и минуты (+ доп. буквы)
- 55°45′20.9916″N, 37°37′3.6228″E — градусы, минуты и секунды (+ доп. буквы)
При необходимости форматы можно пересчитать самостоятельно: 1° = 60′ (минутам), 1′ (минута) = 60″ (секундам). Также можно использовать специализированные сервисы. См. ссылки.
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Количество источников, использованных в этой статье: 15. Вы найдете их список внизу страницы.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Широта и долгота — координаты на земном шаре, которые помогут вам найти определенное место. При написании широты и долготы стоит убедиться, что вы используете правильный формат и правильные символы, чтобы вас поняли. Можно определить положение различных точек широты и долготы на карте, а затем записать их. Можно записать широту и долготу, используя только значение параллели и меридиана. Для конкретных точек широты и долготы можно записать координаты с помощью градусов, минут, секунд и десятичных дробей.
Как прочитать координаты GPS. Прежде чем мы углубимся в чтение координат GPS, важно, чтобы вы хорошо разбирались в системе GPS и имели базовые знания о географических линиях широты и долготы. Как только вы это поймете, и прочитаете свои координаты, вы сможете попрактиковаться с онлайн-инструментами.
Введение в GPS
GPS расшифровывается как Глобальная система определения местоположения; система, которая используется во всем мире для навигации и геодезии.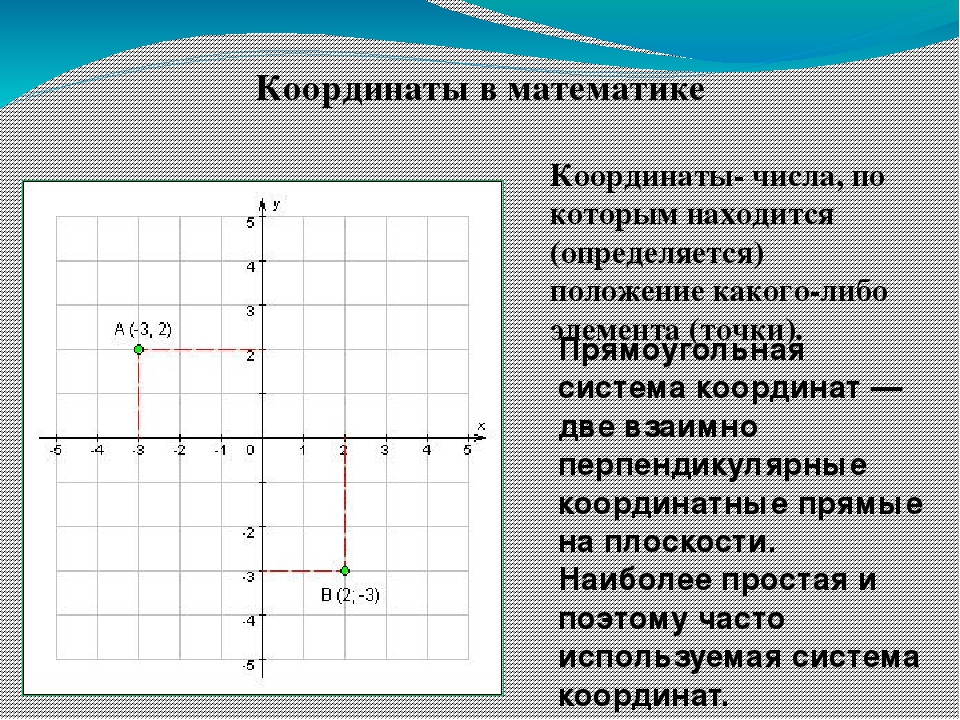 Она широко используется для точного определения своего местоположение в любой точке на поверхности Земли и получения текущего времени в определенном месте.
Она широко используется для точного определения своего местоположение в любой точке на поверхности Земли и получения текущего времени в определенном месте.
Это стало возможным благодаря сети из 24 искусственных спутников, называемых спутниками GPS, которые движутся вокруг Земли с большой скоростью и точностью. Используя маломощные радиоволны, устройства могут связываться со спутниками, чтобы точно определять свое местоположение на земном шаре.
Первоначально система использовалась только военными, система GPS стала доступной для использования в гражданских целях почти 30 лет назад. Она поддерживается Министерством обороны США.
Широта и долгота
Система GPS использует географические линии широта и долгота, чтобы обеспечить координаты местоположения человека или места объекта. Чтение и понимание GPS координат требует базового понимание навигации с использованием линии широты и долготы. Используя оба набора линий обеспечивается координата для различных мест по всему миру.
Линии широты
Линии широты — это горизонтальные линии, которые тянутся с востока на запад по всему земному шару. Самая длинная и главная линия широты называется экватором. Экватор представлен в виде 0 ° широты.
Двигаясь к северу от экватора, каждая линия широты увеличивается на 1 °. Таким образом, будут линии широты, представляющие 1 °, 2 °, 3 °, и так далее до 90 °. Изображение выше отображает только 15 °, 30 °, 45 °, 60 °, 75 ° и 90 ° линии широты над экватором. Вы заметите, что 90 ° линия широты изображается точкой на Северном полюсе.
Все линии широты над экватором обозначены буквой «N» для обозначения к северу от экватора. Таким образом, мы имеем 15 ° с.ш., 30 ° с.ш., 45 ° с.ш., и так далее.
Двигаясь к югу от экватора, каждая линия широты также увеличивается на 1 °. Будут линии широты, представляющие 1 °, 2 °, 3 ° и т. Д. До 90 °. На изображении выше показаны только линии широты 15 °, 30 ° и 45 ° ниже экватора. Линия 90 ° широты представлена точкой на Южном полюсе.
Все линии широты ниже экватора обозначается буквой ‘S’, чтобы обозначаться к югу от экватора. Таким образом, мы имеем 15 ° ю.ш, 30 ° ю.ш, 45 ° ю.ш, и так далее.
Линии Долготы
Линии долготы представляют собой вертикальные линии, которые простираются от Северного полюса до Южного полюса. Основная линия долготы называется нулевой меридиан. Меридиан представлен как 0 ° долготы.
Двигаясь к востоку от нулевого меридиана каждая линия широты увеличивается на 1 °. Таким образом, будут линии долготы, представляющие 1 °, 2 °, 3 °, и так далее до 180 °. Изображение показывает только 20 °, 40 °, 60 °, 80 ° и 90 ° линии долготы к востоку от меридиана.
Все линии долготы к востоку от меридиана обозначены буквой «Е» для обозначения к востоку от Главного Меридиана. Таким образом, мы имеем 15 ° в.д., 30 ° в.д., 45 ° в.д., и так далее.
Двигаясь к западу от меридиана, каждая широта также увеличивается на 1 °. Там будут линии долготы, представляющие 1 °, 2 °, 3 ° и т.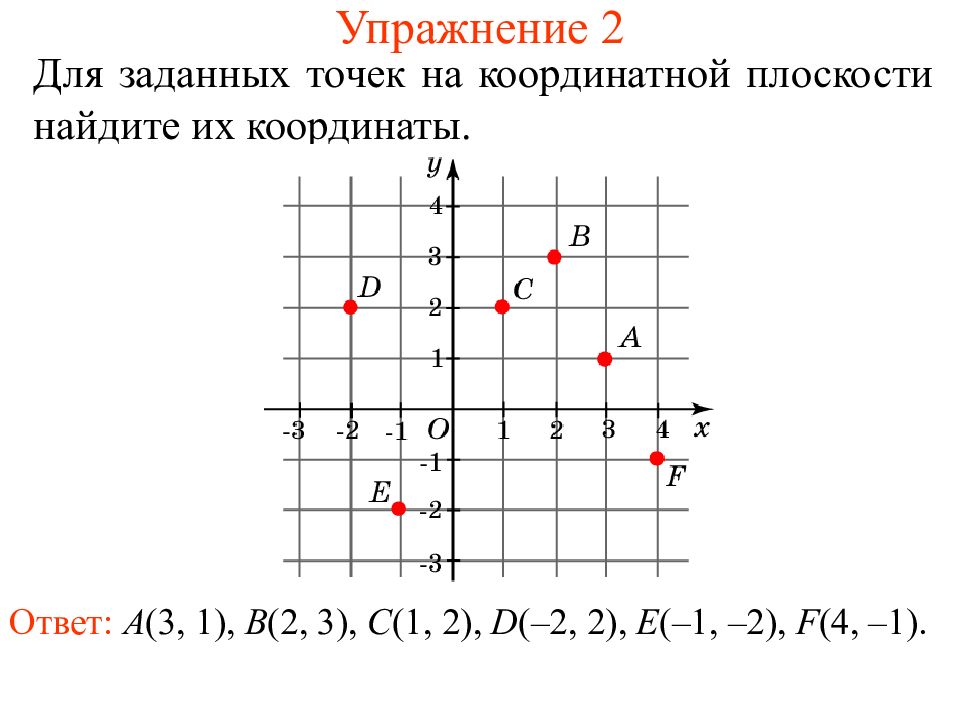 д. до 180 °. На изображении выше показаны только линии 20 °, 40 ° 60 °, 80 ° и 90 ° к западу от нулевого-меридиана.
д. до 180 °. На изображении выше показаны только линии 20 °, 40 ° 60 °, 80 ° и 90 ° к западу от нулевого-меридиана.
Все линии долготы к западу от меридиана обозначены буквой «W» для обозначения к западу от меридиана. Таким образом, мы имеем 15 ° з.д, 30 ° з.д, 45 ° з.д, и так далее.
Вы можете просмотреть более подробную информацию о линии широты и долготы, наблюдая это видео на YouTube по ссылке ниже:
Чтение Географических координат
Глобальная навигация использует линии широты и долготы, чтобы точно определить конкретное место расположения на поверхности Земли. Оно дается в качестве географических координат.
Пусть Место находится вдоль линии широты 10 ° N и вдоль линии долготы 70 ° W. При изложении координаты местоположения, линии широты всегда указывается первой, а потом линии долготы. Таким образом, координаты этого места будет: 10 ° северной широты, 70 ° западной долготы.
Координаты можно просто записать как 10 ° N, 70 ° W ( 10 ° с.ш., 70 ° з.д. )
Однако большинство мест на Земле располагаются не вдоль линий широты или долготы, а внутри фигур, созданных из-за пересечения горизонтальных и вертикальных линий. Чтобы точно определить человека на поверхности Земли, линии широты и долготы дополнительно разделены и выражены в одном из трех общих форматов:
1 / градусы, минуты и секунды (DMS)
Пространство между каждой линией широте или долготе, представляющей 1 ° делится на 60 минут, а каждая минута делится на 60 секунд. Пример такого формата:
41 ° 24’12.2 «N 2 ° 10’26.5» E Линия широты читается как 41 градусов (41 °), 24 минут (24 ‘), 12.2 секунд (12.2 «) на север. Линия долготы читается как 2 градуса (2 °), 10 минут (10 ‘), 26,5 секунды (12,2 «) к востоку.
2 / Градусы и десятичные минуты (DMM)
Пространство между каждой линией широты или долготы, представляющей 1 °, делится на 60 минут, а каждая минута делится далее и выражается в десятичных дробях. Пример этого формата:
Пример этого формата:
41 24,2028, 10,4418 2 Линия широты читается как 41 градус (41), 24.2028 минут (24.2028) северной широты. Координата для линии широты представляет север от экватора, потому что она положительна. Если число отрицательное, оно представляет юг от экватора.
Линия долготы читается как 2 градуса (2), 10,4418 минут (10,4418) к востоку. Координата для линии долготы представляет восток Главного меридиана, потому что это положительно. Если число отрицательное, оно представляет запад от меридиана
3 / Десятичные градусы (DD)
Пространство между каждой линией широты или долготы, представляющей 1 °, делится и выражается в десятичных дробях. Пример этого формата:
41,40338, 2,17403
Линия широты читается как 41.40338 градусов на север. Координата для линии широты представляет север от экватора, потому что она положительна. Если число отрицательное, оно представляет юг от экватора.
Линия долготы читается как 2. 17403 градуса восточной долготы. Координата для линии долготы представляет восток Главного меридиана, потому что оно положительно. Если число отрицательное, оно представляет запад от меридиана.
17403 градуса восточной долготы. Координата для линии долготы представляет восток Главного меридиана, потому что оно положительно. Если число отрицательное, оно представляет запад от меридиана.
Чтение координаты на Google Maps
Большинство устройств GPS предоставляют координаты в формате градусов, минут и секунд (DMS) или чаще всего в формате десятичных градусов (DD). Популярные Google Карты предоставляют свои координаты в форматах DMS и DD.
На рисунке выше показано расположение статуи Свободы на Google Maps. Координаты его расположения являются:
40° 41′ 21.4” N 74° 02′ 40.2” W (DMS) Это читается как:
«40 градусов, 41 минут, 21,4 секунды северной широты и 74 градуса, 2 минуты, 40,2 секунды восточной долготы»
40.689263 -74.044505 (DD) Напомним, что координаты десятичной степени (DD) не имеют букв N или S, указывающих, находится ли координата широты над или ниже экватора. Если нет букв W или E, чтобы указать, является ли долгота координатой к западу или востоку от Первого меридиана.
Это делается с помощью положительных и отрицательных чисел. Поскольку координата широты положительна, координата находится выше экватора. Поскольку координата долготы отрицательна, она находится к западу от нулевого меридиана.
Проверка GPS координаты
Google Maps является отличным инструментом Интернет для проверки координаты мест, представляющих интерес.
Нахождение координат для конкретного места
1 / Открыть Google Maps в https://maps.google.com/ и найти местоположение вашего места интереса.
2 / Щелкните правой кнопкой мыши местоположение и выберите «Что здесь?» В появившемся небольшом меню.
3 / Внизу появится небольшой прямоугольник с указанием названия местоположения и координат в формате десятичных градусов (DD).
Проверка координаты конкретного места
Откройте Google Карты на https://maps.google.com/ . Там будет панель поиска в верхнем левом углу страницы
Введите координаты в строку поиска , затем нажмите Enter или значок поиска. Координаты могут быть в любом из трех форматов. Обратите внимание , что координаты должны быть введены правильно.
Координаты могут быть в любом из трех форматов. Обратите внимание , что координаты должны быть введены правильно.
Google Maps будет указывать местоположение введенных координат красным значком.
Преобразование между форматами DMS и DD
В Интернете доступны различные инструменты, которые могут помочь вам конвертировать форматы в градусы, минуты и секунды (DMS) и в десятичные градусы (DD).
Для математиков, желающих выполнять необработанные вычисления, вы можете узнать, как преобразовать DMS в DD и наоборот.
Доступны веб-сайты, которые обеспечивают быстрое преобразование между DMS и DD. Вот ссылка на веб-сайт, который предоставляет координаты DMS и DD для любого конкретного местоположения с помощью Google Maps.
Устройства с поддержкой GPS
Чтобы воспользоваться точной точностью системы GPS, вам необходимо устройство с поддержкой GPS. Эти устройства обмениваются данными напрямую со спутниками GPS, используя маломощные радиоволны. Общаясь по крайней мере с тремя спутниками GPS, устройство может точно определить ваше местоположение на Земле.
Общаясь по крайней мере с тремя спутниками GPS, устройство может точно определить ваше местоположение на Земле.
Эта ссылка (PDF) представляет собой плакат, иллюстрирующий работу системы GPS, позволяющую точно определить ваше местоположение. Устройства с поддержкой GPS включают в себя:
GPS навигационные устройства
Такие компании, как Garmin и Magellan, производят специальные GPS-навигационные устройства. Они бывают разных размеров и могут напоминать смартфон или планшет. Эти устройства имеют специальное встроенное программное обеспечение, которое использует систему GPS, чтобы помочь людям найти кратчайший путь к определенному месту, найти интересные места и многое другое. Они обычно используются в транспортных средствах, походах и определенных спортивных состязаниях.
Вверху — изображение навигационного устройства GPS; Магеллан RoadMate 2255T-LMB.
Смартфоны
Большинство смартфонов, особенно телефонов высокого класса, поддерживают GPS и могут использоваться в качестве навигационного устройства, если у вас установлены правильные приложения.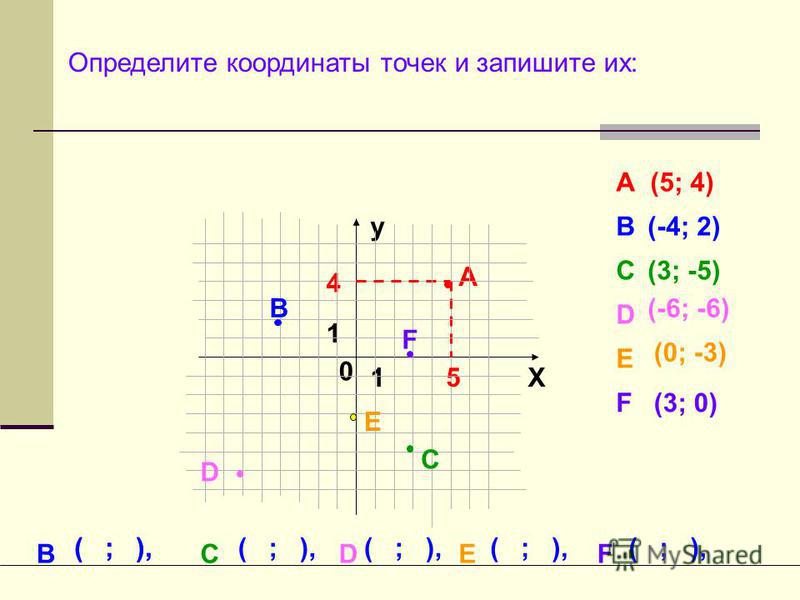
Мобильные компьютеры
Некоторые ноутбуки и нетбуки поддерживают GPS и предоставляют навигационную информацию в пути.
Компьютерные периферийные устройства
Устройства, подключающиеся к компьютеру через USB, Bluetooth или слоты расширения, позволяют компьютеру использовать систему GPS.
Как использовать координаты на смартфоне
Географические координаты можно использовать на смартфоне несколькими способами. Во-первых, вы можете определить координаты своего местоположения и отправить их кому-нибудь: спасателям (если вы заблудились или попали в чрезвычайную ситуацию) или вашему другу (с которым вы собираетесь встретиться в какой-то точке местности). Во-вторых, координаты могут сообщить вам, а вы хотите или посмотреть это место на карте, или с помощью телефона выйти в указанную точку.
О том, как определить координаты с помощью смартфона и передать их кому-либо, читайте в следующих моих статьях:
А в этой статье мы рассмотрим, что делать с координатами, которые вам прислали в текстовом виде или сообщили устно.
Итак, допустим, вам прислали SMS, сообщение в мессенджере, письмо по емэйлу, которые содержат координаты. Или координаты содержатся в тексте статьи, которую вы читаете через браузер телефона. Естественно, сначала вы их копируете стандартным способом копирования текста. Следующий вопрос: куда вставлять? Рассмотрим разные варианты в зависимости от используемых программ. Заодно разберёмся, как ввести координаты в смартфоне вручную, если вам их продиктовали или они записаны на бумажке.
Карты Google
Просмотреть координаты на смартфоне проще всего с помощью именно этого приложения, так как оно установлено на всех Android-устройствах. Сделать это достаточно легко. В верхней части приложения есть строка поиска, куда и вставляем скопированные координаты. Затем чуть ниже нажимаем «Искать». Появляется маркер, показывающий данную точку на карте, а в нижней части экрана – меню, позволяющее выполнить различные действия над этой точкой (проложить маршрут, поделиться и т. д.).
д.).
| Вставляем координаты в строку поиска |
| Нажимаем «Искать» |
| Получаем точку на карте |
- Внимание! Если приложение пишет: «Ничего не найдено», посмотрим на то, в каком виде записаны координаты. Если и широта, и долгота записаны через запятые, попробуйте заменить их на точки. То есть, вместо «48,235914, 24,134577» пишем «48.235914 24.134577».
В этой же строке поиска можно набрать координаты вручную. Если они в градусах и десятичных долях градуса, то набираем числа через точку, отделяя широту от долготы пробелом: «48.235914 24.134577». Если координаты в градусах, минутах и секундах, то просто пишем шесть чисел, разделяя их пробелами: «48 33 21 26 42 12».
| Градусы, минуты, секунды: ввод через пробел |
Кстати, ради интереса я попробовал найти место по координатам, используя строку поиска в браузере, но он тоже перебросил меня в приложение Карты Google.
OsmAnd
Универсальная программа-навигатор, которой пользуются многие (подробнее про OsmAnd). Воспользуемся и мы. На главном экране программы вверху слева есть кнопка с лупой. Нажимаем, попадаем в раздел поиска. Прямо в верхнюю строку вставляем координаты. Тут же начинается поиск, и чуть ниже показывается перечень найденных объектов. В нашем случае перечень состоит всего из одного пункта – точки с заданными координатами. Нажимаем на эту строку и видим эту точку на карте, а внизу экрана – меню с функциями, относящимися к данной точке.| Кнопка поиска |
| Вставка координат в строку поиска |
| Результат поиска: нажимаем на него |
| Программа показывает точку на карте |
В этой же строке координаты можно вводить и вручную, таким же способом, как указано выше для Карт Google. Однако если у вас есть сомнения, что поиск корректно распознает введённый вами текст, то координаты можно ввести на специальной вкладке: «Адрес» – «Поиск по координатам». Перед вводом нужно выбрать один из пяти форматов координат, что исключит возможность ошибки в их распознавании.
Однако если у вас есть сомнения, что поиск корректно распознает введённый вами текст, то координаты можно ввести на специальной вкладке: «Адрес» – «Поиск по координатам». Перед вводом нужно выбрать один из пяти форматов координат, что исключит возможность ошибки в их распознавании.
| Поиск по координатам на вкладке «Адрес» |
| Выбираем формат координат |
| Форматы координат в программе OsmAnd |
MAPS.ME
Ещё одна популярная программа-навигатор (подробнее про MAPS.ME). Действия с ней будут примерно такими же, как и с предыдущими программами. Нажимаем на расположенную внизу экрана кнопку с лупой и на открывшемся экране поиска в верхнюю строку вставляем или вписываем координаты.
| Кнопка поиска |
| Вводим координаты в строку поиска |
Locus Map
По мнению многих это лучшее приложение-навигатор для дикой природы (подробнее про Locus Map). Выясним, как оно работает с координатами. Открываем главное меню (три чёрточки вверху слева) и нажимаем на кнопку «Поиск» (при желании кнопку «Поиск» можно добавить в верхнюю или боковую панель главного экрана). Откроется список, в котором выбираем «Перейти к… Перемещение по заданным координатам».| Открываем главное меню |
| Нажимаем на кнопку «Поиск» |
| Нажимаем на «Перейти к…» |
Далее, если координаты у вас скопированы заранее, то нажимаем на «Буфер обмена». При этом текст из буфера обмена автоматически вставится во всплывающее окно, и вам останется только нажать «ОК». На карте появляется временная (несохранённая) точка с прямоугольной кнопкой, вызывающей меню различных действий с точкой.
При этом текст из буфера обмена автоматически вставится во всплывающее окно, и вам останется только нажать «ОК». На карте появляется временная (несохранённая) точка с прямоугольной кнопкой, вызывающей меню различных действий с точкой.
| Нажимаем на «Буфер обмена» |
| Координаты вставлены, нажимаем «ОК» |
| Появляется точка на карте |
Если же необходимо ввести координаты вручную, то нажимаем на «Координаты». В появившемся окне выбираем один из 15-ти форматов записи координат и вводим их на клавиатуре. Нажимаем «Установить», и получаем на карте упомянутую выше временную точку с кнопкой-меню.
| Нажимаем на «Координаты» |
| Выбираем формат координат |
| Форматы координат в программе Locus Map |
| Форматы координат в программе Locus Map |
Сохранение точки
Одно из основных действий после того, как вы просмотрели точку на карте – сохранить её для дальнейшего использования. Все программы позволяют это сделать тем или иным способом.
Все программы позволяют это сделать тем или иным способом.
| Карты Google: нажимаем «Сохранить» |
| OsmAnd: либо «Добавить» (в Избранные), либо «Действия» — «Добавить путевую точку» |
| MAPS.ME: нажимаем на «Метка» |
| Locus Map: на карте нажимаем под точкой на кнопку меню, затем на кнопку внизу слева |
Движение к точке
Очень часто нам бывает необходимо не только просмотреть местоположение точки на карте, но и добраться до неё на местности. Удобно (особенно в дикой природе), когда программа может показать направление на точку и расстояние до неё (конечно, после того, как будет пойман сигнал спутников GPS и определено наше местонахождение). Посмотрим, как с этим справляются упомянутые нами приложения.
Посмотрим, как с этим справляются упомянутые нами приложения.
Напоминаю, что поиск по координатам показывает нам не только точку на карте, но и относящееся к ней меню. Чтобы такое же меню появилось для произвольной точки местности, нужно коснуться экрана в нужном месте. Причём, в зависимости от программы и конкретной точки, может понадобиться либо долгое, либо короткое нажатие.
Итак, Карты Google предлагают проложить к точке маршрут по дорогам и тропам. Это не совсем то, что нужно в дикой природе, учитывая возможное отсутствие тропинок вообще и на картах от Google в частности. Если ваш телефон не имеет магнитного компаса, то всё, что вам доступно – это видеть две точки (ваше местоположение и ту, куда нужно попасть) на экране телефона и пытаться визуально оценить их взаиморасположение.
| Пытаемся «на глаз» оценить расстояние от нас до точки и направление на неё |
При наличии в телефоне магнитного компаса Карты Google становятся более полезными.
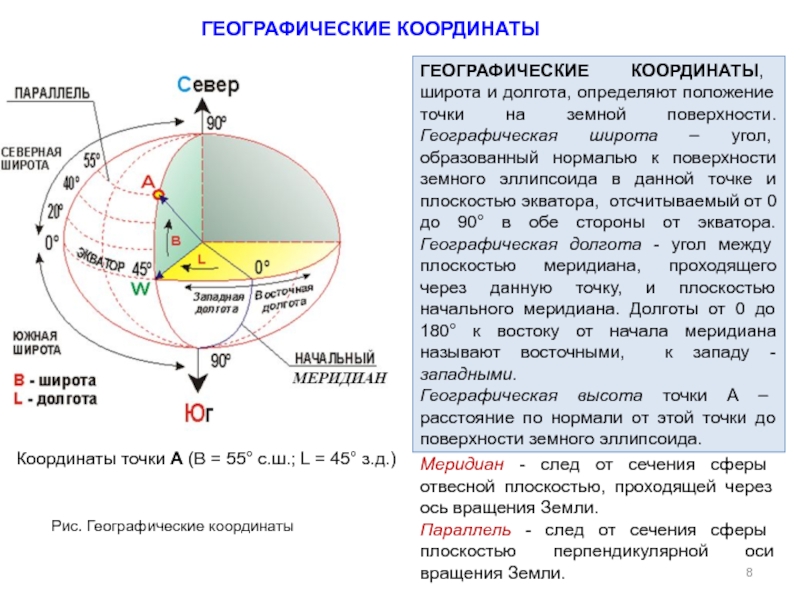 В правой нижней части экрана имеется большая круглая кнопка, отвечающая за показ нашего местоположения. Нажимаем на неё, и включается 3D-режим, причём карта начинает поворачиваться согласно показаниям компаса. Это позволяет видеть, с какой стороны от нас находится тот или иной объект. Вместе с телефоном поворачиваемся так, чтобы нужная нам точка находилась на экране прямо перед нами. Теперь мы стоим лицом в правильном направлении, и остаётся просто идти вперёд. Расстояние до точки, к сожалению, можно определить только приблизительно, сопоставляя его с имеющейся на экране масштабной линейкой.
В правой нижней части экрана имеется большая круглая кнопка, отвечающая за показ нашего местоположения. Нажимаем на неё, и включается 3D-режим, причём карта начинает поворачиваться согласно показаниям компаса. Это позволяет видеть, с какой стороны от нас находится тот или иной объект. Вместе с телефоном поворачиваемся так, чтобы нужная нам точка находилась на экране прямо перед нами. Теперь мы стоим лицом в правильном направлении, и остаётся просто идти вперёд. Расстояние до точки, к сожалению, можно определить только приблизительно, сопоставляя его с имеющейся на экране масштабной линейкой.| 1 — нажимаем, чтобы включить 3D-режим 2 — наше местоположение 3 — нужная нам точка |
Программа MAPS.ME предлагает очень простое и довольно удобное решение. Если выбрана какая-то точка местности, то в нижней части экрана появляется меню, где мы можем видеть и расстояние до точки, и направление на неё.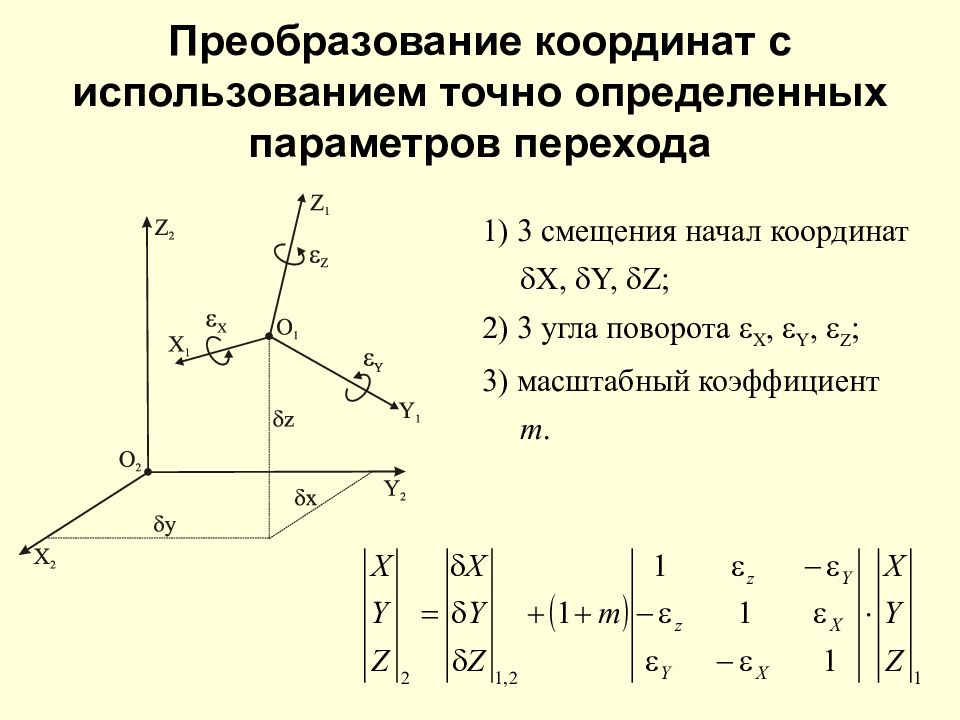
| Расстояние до точки и направление на неё |
Программа OsmAnd имеет похожее меню, правда, направление и расстояние показаны очень мелким шрифтом. Поэтому воспользуемся функцией «Маркер». Нажатием на соответствующую кнопку меню превращаем нашу точку в маркер, после чего появляется специальная панель с крупными обозначениями направления и расстояния.
| Расстояние до точки и направление на неё, кнопка «Маркер» |
| После нажатия кнопки «Маркер» вверху появляется панель с расстоянием и направлением |
Программа Locus Map специально предназначена для путешествий по дикой природе, поэтому движение к выбранной точке осуществляется здесь наиболее удобно. Меню точки имеет справа кнопку со стрелочкой, на неё и нажимаем. В появившемся списке выбираем «Включить режим…» (в английском интерфейсе – «Guide On», очевидно, имеется в виду «режим ведения к…»).
Меню точки имеет справа кнопку со стрелочкой, на неё и нажимаем. В появившемся списке выбираем «Включить режим…» (в английском интерфейсе – «Guide On», очевидно, имеется в виду «режим ведения к…»).
| Нажимаем на кнопку со стрелочкой |
| Нажимаем на «Включить режим…» |
Появляется дополнительная панель с указанием направления на точку и расстояния до неё. Справа на панели – три точки, открывающие меню, где можно выключить режим ведения к точке, если он уже не нужен. Также для удобства можно переключиться на экран с компасом, где направление на точку и расстояние до неё будут показаны более крупно и наглядно.
| Панель с указанием направления на точку и расстояния до неё |
| Экран с компасом: показаны расстояние до точки и направление на неё |
Также если вы откуда-то скопировали координаты, то Locus Map позволяет сразу же запустить режим ведения к точке без каких-либо промежуточных действий. Но предварительно вы должны добавить на главный экран кнопку «Ведение к… Быстрый способ начать ведение к выбранной точке». Итак, нажимаем на эту кнопку, затем в открывшемся окне выбираем «Буфер обмена». В следующем окне появляются координаты, которые мы ранее скопировали. Нажимаем «ОК», и происходит запуск режима ведения к точке.
Но предварительно вы должны добавить на главный экран кнопку «Ведение к… Быстрый способ начать ведение к выбранной точке». Итак, нажимаем на эту кнопку, затем в открывшемся окне выбираем «Буфер обмена». В следующем окне появляются координаты, которые мы ранее скопировали. Нажимаем «ОК», и происходит запуск режима ведения к точке.
| Кнопка «Ведение к… Быстрый способ начать ведение к выбранной точке» |
| Нажимаем на «Буфер обмена», чтобы использовать скопированные координаты |
Как вы видите, пользоваться координатами на смартфоне достаточно просто и удобно. Даже при отсутствии интернета вы можете определить, где находится ваш товарищ или какой-нибудь объект, если вам передали координаты при помощи SMS или продиктовали во время разговора по телефону.
Случалось ли вам искать место по его координатам при помощи смартфона? Пользовались ли вы описанными мной методами? Или действовали по-своему? Расскажите об этом в комментариях.
Планирование маршрута с использованием координат
Планирование маршрута с использованием координатПланирование маршрута с использованием координат
Важно! В целях безопасности и для уменьшения помех во время вождения планировать маршрут всегда нужно перед началом движения.
Чтобы спланировать маршрут с использованием координат, выполните следующие действия.
- Нажмите кнопку главного меню, чтобы открыть его.
- Выберите Поиск.
Отобразится экран поиска с клавиатурой.
- Нажмите кнопку типа поиска, расположенную справа от поля поиска.
- Выберите Широта/долгота.
- Введите ваши координаты. Можно вводить следующие форматы координат.
- Десятичные значения, например:
N 51.
 51000 W 0.13454
51000 W 0.1345451.51000, — 0.13454
Подсказка. При использовании десятичных значений не обязательно вводить букву для указания широты и долготы. При вводе местоположений западнее нулевого меридиана и южнее экватора поставьте знак минуса (-) перед координатами.
- Градусы, минуты и секунды, например:
N 51°30′31″ W 0°08′34″
- Стандартные координаты GPS, например:
N 51 30.525 W 0 08.569
Примечание. Панель под координатами становится красной, если введенные координаты не распознаются с помощью GO.
- Десятичные значения, например:
- Во время ввода координат вам будут предлагаться возможные варианты. Вы можете либо продолжить ввод, либо выбрать из предложенного.
Слева отображаются города и дороги, справа — полезные адреса.
Подсказка. Чтобы просмотреть больше результатов, сверните клавиатуру или прокрутите вниз список результатов.
Подсказка.
 Вы можете выбрать режим отображения результатов (на карте или в виде списка) с помощью кнопки отображения списка/карты.
Вы можете выбрать режим отображения результатов (на карте или в виде списка) с помощью кнопки отображения списка/карты. - Выберите вариант для пункта назначения.
Местоположение отобразится на карте.
- Чтобы спланировать маршрут к этому пункту назначения, выберите Ехать.
Выполняется планирование маршрута, а затем ведение по маршруту. Как только вы начнете движение, автоматически отобразится режим указаний.
Подсказка. Если место назначение находится в другом часовом поясе, на панели информации о прибытии будут отображаться значки (+) или минус (-), а также разница во времени в часовых и получасовых интервалах. Предполагаемое время прибытия — местное время в пункте назначения.
Подсказка. Вы можете добавить остановку к запланированному маршруту.
Подсказка. Маршрут можно сохранить в меню Мои маршруты.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings. REQUIRED_FIELD}})
REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
{{$select.selected.display}}
LANGUAGE}}
{{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Урок 9.
 Координаты | Творческое программирование для всех
Координаты | Творческое программирование для всехЧасть 1. Что такое координаты и где они используются?
Из первой части урока ты узнаешь, что такое координаты, как они используются в Scratch, а также в нашей жизни и в компьютере.
Замечание: с января 2019 года на сайте Scratch доступна новая версия редактора — Scratch 3.0, который внешне немного отличается от Scratch 2.0, в котором записывался данный урок. Поэтому если возникнут вопросы, пиши их, пожалуйста, в комментариях к видео или внизу этой страницы сайта. Мы провели сравнение двух версий языка в серии прямых эфиров.
Scratch 2.0 по-прежнему можно использовать, скачав и установив программу на свой компьютер. Мы записали также видео-уроки о том, как установить Scratch 2.0 и Scratch 3.0 на свой компьютер.
ЗАМЕЧАНИЕ: в уроке допущена ошибка, исправляем: ось Х называется осью абсцисс, а Y — это ось ординат.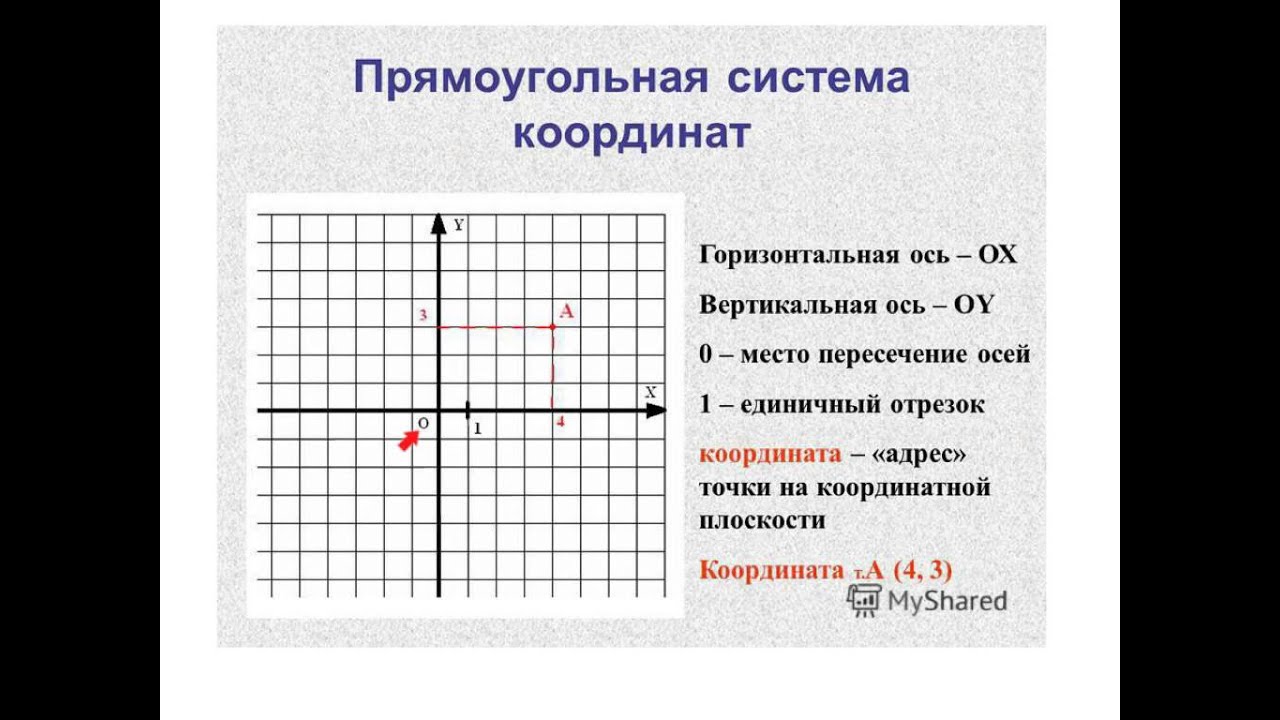
Часть 2. Движение по координатам
Во второй части урока мы изучаем команды Scratch для реализации движения спрайтов по координатам.
Проект «Изучаем координаты», который мы используем для более понятных объяснений, здесь: https://scratch.mit.edu/projects/73405934/
Гимнастика для глаз здесь: https://scratch.mit.edu/projects/133688293/
Часть 3. Игра «Кот в лабиринте. Уровень 2»
В третьей части урока мы создаём второй уровень для игры «Кот в лабиринте» и закрепляем команды Scratch для реализации движения спрайтов по координатам.
В этой части урока используются следующие примеры проектов:
- «Кот в лабиринте. Версия 1»: https://scratch.mit.edu/projects/73709780 — этот проект мы берём за основу и делаем для него второй уровень, похожий на лабиринт из второго проекта
- Пример реализации 2-го уровня — «Лабиринт remix»: https://scratch.
 mit.edu/projects/74563798
mit.edu/projects/74563798
Часть 4. Игра «Кот в лабиринте. Уровень 2» — продолжение: делаем движение таким, чтобы Кот не проходил сквозь стены лабиринта
В четвёртой части урока мы делаем движение Кота более «умным». Теперь он не будет проходить сквозь стены лабиринта, перемещаться более плавно и даже ходить по диагонали.
Часть 5. Игра «Кот в лабиринте. Уровень 2» — завершение: добавляем бонус и врага в лабиринт на втором уровне
Точки — Python: Составные данные
Python: Составные данныеВ этом уроке мы начнём проектирование библиотек для работы с графическими примитивами (точками, отрезками), а также фигурами (кругами, прямоугольниками). Естественно, проще всего начать с основы — библиотеки для работы с точками. Для этого давайте вспомним координатную плоскость и то, как определяются на ней точки.
Естественно, проще всего начать с основы — библиотеки для работы с точками. Для этого давайте вспомним координатную плоскость и то, как определяются на ней точки.
В этом примере мы видим плоскость, на которой расположены две оси (ось абсцисс X и ось ординат Y) и точки. При этом обычно точка описывается двумя параметрами: первым указывается координата x (абсцисса), вторым — координата y (ордината). Например, точка D описывается как (2, 4), точка C — (1, 0) и так далее. Координаты могут быть отрицательными. Оси делят плоскость на четыре части, которые называются квадрантами. На рисунке точка D лежит в первом квадранте, точки A, G, E — во втором, в третьем и в четвертом квадрантах соответственно.
Когда мы говорим о точках, мы на самом деле имеем в виду так называемые абстрактные данные. Это означает, что мы не делаем никаких предположений (кроме самых необходимых) для того, чтобы рассуждать в терминах этих данных (в нашем случае — точек). И действительно, вспомним, например, любой раздел школьной математики: когда мы оперируем какими-то понятиями, мы вообще не думаем о том, что они должны быть как-то представлены, мы мыслим в них на абстрактном уровне. Это позволяет нам строить законы, делать выводы и предположения о том, как будут вести себя данные, как они друг с другом комбинируются. При этом нам не нужна никакая реализация, нам не нужен ни язык программирования, ни компьютер. Более того, нам вообще необязательно графически изображать эти данные — мы можем представлять это в голове и при этом делать выводы, имеющие практическое значение. При этом конкретное представление абстрактных данных (так называемые конкретные данные) определяется условиями прикладного использования, например, особенностями разных языков программирования. Зачастую библиотеки, которые снаружи выглядят одинаково и оперируют одними и теми же понятиями, внутри устроены совершенно по-разному. Естественно, при манипуляциях с такими библиотеками необходимо оставаться в рамках понятийного аппарата тех абстрактных данных, с которыми мы работаем. «Клеем» между абстрактными данными и конкретными данными выступает так называемый интерфейс. Интерфейс — это набор функций, обычно разделяемых на конструкторы и селекторы.
Это позволяет нам строить законы, делать выводы и предположения о том, как будут вести себя данные, как они друг с другом комбинируются. При этом нам не нужна никакая реализация, нам не нужен ни язык программирования, ни компьютер. Более того, нам вообще необязательно графически изображать эти данные — мы можем представлять это в голове и при этом делать выводы, имеющие практическое значение. При этом конкретное представление абстрактных данных (так называемые конкретные данные) определяется условиями прикладного использования, например, особенностями разных языков программирования. Зачастую библиотеки, которые снаружи выглядят одинаково и оперируют одними и теми же понятиями, внутри устроены совершенно по-разному. Естественно, при манипуляциях с такими библиотеками необходимо оставаться в рамках понятийного аппарата тех абстрактных данных, с которыми мы работаем. «Клеем» между абстрактными данными и конкретными данными выступает так называемый интерфейс. Интерфейс — это набор функций, обычно разделяемых на конструкторы и селекторы.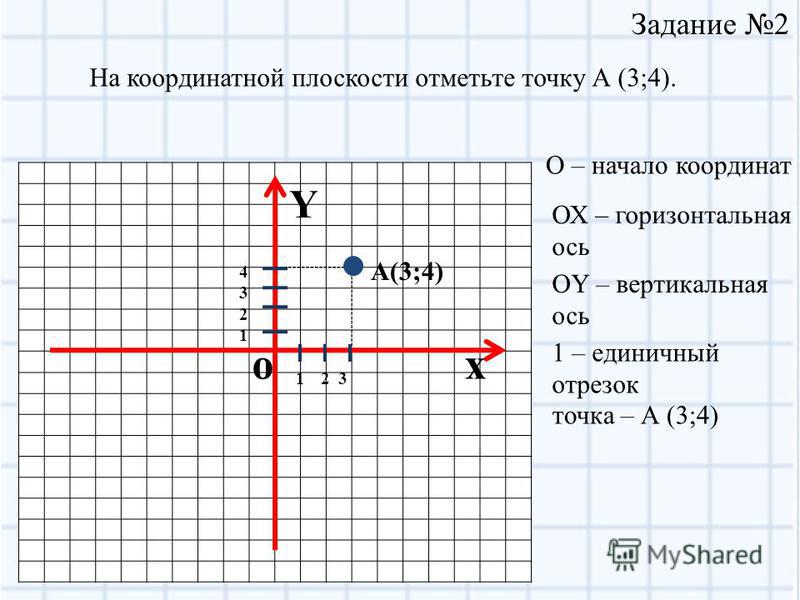 Конструкторы позволяют из набора данных строить составной объект, а с помощью селекторов из составного объекта извлекают его части. В нашем случае, если говорить о точках, селекторы позволяют извлекать координаты x и y. Вот как выглядит интерфейс нашей библиотеки:
Конструкторы позволяют из набора данных строить составной объект, а с помощью селекторов из составного объекта извлекают его части. В нашем случае, если говорить о точках, селекторы позволяют извлекать координаты x и y. Вот как выглядит интерфейс нашей библиотеки:
x = 5
y = -7
# Конструктор
point = make_point(x, y)
# Селекторы
get_x(point)
get_y(point)
to_string(point) # (5, -7)
В коде выше видно, что мы определили функцию make_point, которая принимает на вход два числа (x и y) и возвращает точку с такими координатами. Кроме этого, есть два основных селектора get_x и get_y, которые возвращают соответствующие координаты из точки. При проектировании библиотеки мы используем стратегию «мечтать не вредно», потому что ещё не знаем, как она будет устроена внутри. Это, по большому счету, не имеет значения, потому что мы пользуемся абстрактными данными и оперируем терминами нашей предметной области, а не конкретной реализации. Поэтому мы можем сосредоточиться на сути, отложив принятие решения о деталях.
Поэтому мы можем сосредоточиться на сути, отложив принятие решения о деталях.
Кроме основных селекторов, нами определена функция to_string, которая возвращает текстовое представление точки и может быть использована для отладки.
Давайте посмотрим, какие манипуляции можно производить над точками, имея базовый интерфейс:
def symmetrical_point(point):
return make_point(get_x(point), -get_y(point))
Скалярное произведение векторов. Формулы и определение
Основные определения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Результат операции является число. То есть при умножении вектор на вектор получается число. Если длины векторов |→a|, |→b| — это числа, косинус угла — число, то их произведение |→a|*|→b|*cos∠(→a, →b) тоже будет числом.
Чтобы разобраться в теме этой статьи, нам еще нужно узнать особенности угла между векторами.
Приходите тренироваться в детскую школу Skysmart. Ученики решают захватывающие задачки вместе с красочными героями на интерактивной платформе, чертят вместе с учителем на онлайн-доске и не боятся школьных контрольных.
Запишите ребенка на бесплатный вводный урок математики и начните заниматься в удовольствие уже завтра!
Угол между векторами
Угол между векторами ∠(→a, →b) может принимать значения от 0° до 180° градусов включительно. Аналитически это можно записать в виде двойного неравенства: 0°=<∠(→a; →b)=<180° либо 0°=<∠(→a; →b)=<π.
Значок угла ∠ можно опустить и писать просто: (→a;→b).
Пусть даны два вектора →a, →b.
Отложим их от некоторой точки О пространства: →OA = →a; →OB = →b. Тогда угол между векторами — это угол ∠AOB = (→a, →b).
Угол между векторами может быть прямым, тупым или острым. Рассмотрим каждый случай:
1. Если векторы сонаправлены, то угол между ними равен 0°.
Так как косинус угла в 0° равен единице, то скалярное произведение сонаправленных векторов является произведением их длин. Если два вектора равны, то такое скалярное произведение называют скалярным квадратом.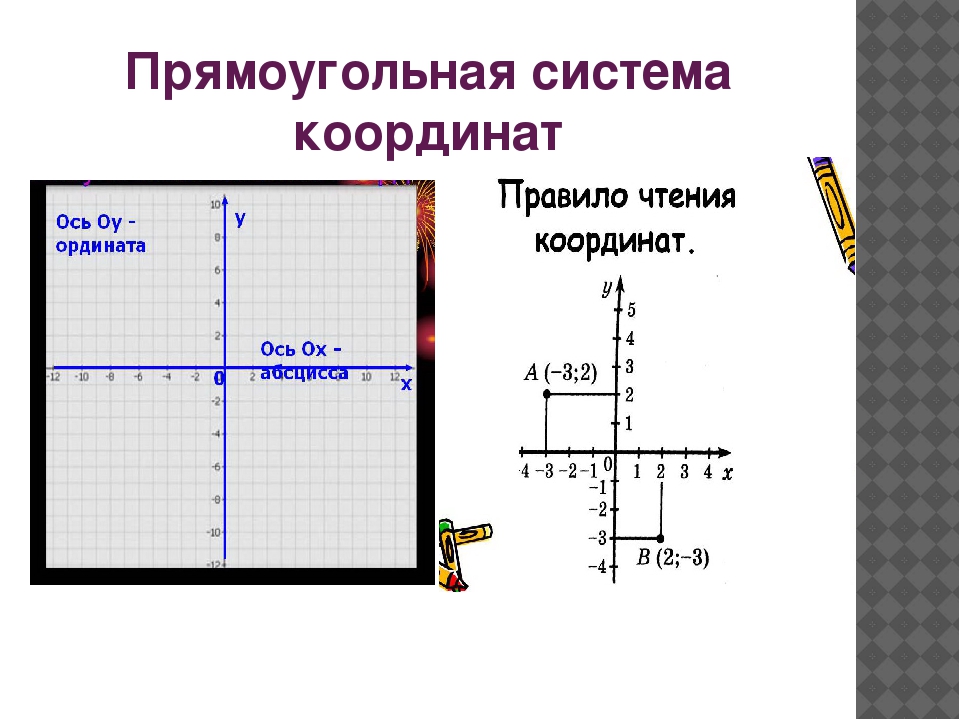
2. Если угол между векторами равен 90°, то такие векторы перпендикулярны друг другу.
Так как косинус прямого угла равен 0, то скалярное произведение перпендикулярных векторов равно 0.
3. Если векторы направлены в разные стороны, тогда угол между ними 180°.
Так как косинус угла в 180° равен -1, то скалярное произведение противоположно направленных векторов равно отрицательному произведению их длин.
Также векторы могут образовывать тупой угол. Это выглядит так:
Важно!
Так как косинус тупого угла отрицательный, то скалярное произведение векторов, которые образуют тупой угол, является тоже отрицательным.
Скалярное произведение векторов
Определение скалярного произведения можно сформулировать двумя способами:
Скалярное произведение двух векторов a и b дает в результате скалярную величину, которая равна сумме попарного произведения координат векторов a и b.
- Геометрическая интерпретация.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
→a * →b = →|a| * →|b| * cosα
- Алгебраическая интерпретация.
Что важно запомнить про геометрическую интерпретацию скалярного произведения:
- Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, то есть cosα > 0.
- Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как cosα < 0.
- Если угол между векторами прямой, то скалярное произведение равно 0 так как , то есть cosα = 0.
Скалярное произведение в координатах
Вычисление скалярного произведения можно произвести через координаты векторов в заданной плоскости или в пространстве.
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов →a и →b.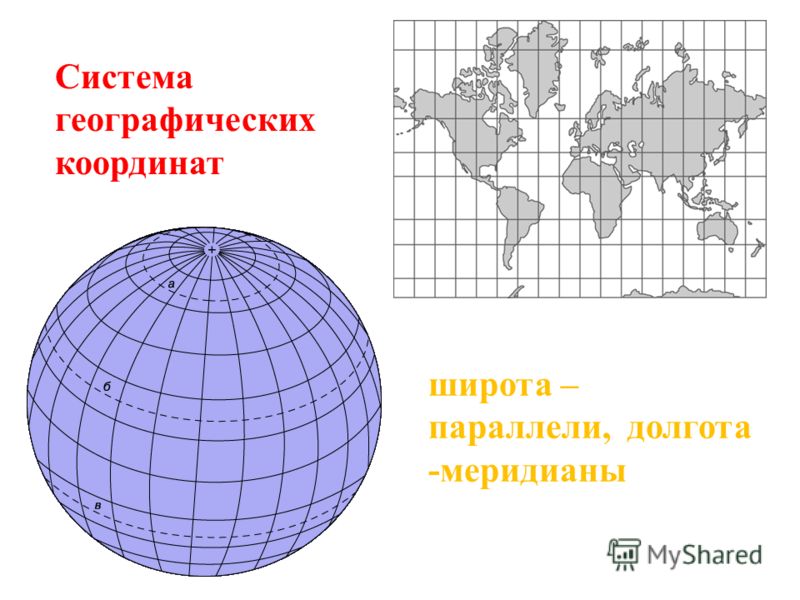
То есть для векторов →a = (ax, ay), →b = (bx, by) на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид: (→a, →b) = ax*bx + ay*by
А для векторов →a = (ax, ay, az), →b = (bx, by, bz) в трехмерном пространстве скалярное произведение в координатах находится так: (→a, →b) = ax*bx + ay*by + az*bz
Докажем это определение:
- Сначала докажем равенства
для векторов →a = (ax, ay), →b = (bx, by) на плоскости, заданных в прямоугольной декартовой системе координат.
Отложим от начала координат (точка О) векторы →OB = →b = (bx, by) и →OA = →a = (ax, ay)
Тогда, →AB = →OB — →OA = →b — →a = (bx — ax, by — ay)
- Будем считать точки О, А и В вершинами треугольника ОАВ. По теореме косинусов можно записать:
Так как:
то последнее равенство можно переписать так:
а по первому определению скалярного произведения имеем
откуда
- Вспомнив формулу вычисления длины вектора по координатам, получаем
- Абсолютно аналогично доказывается справедливость равенств (→a, →b) = |→a|*|→b|*cos(→a, →b) = ax*bx + ay*by + ax*bz для векторов →a = (ax, ay, az), →b = (bx, by, bz), заданных в прямоугольной системе координат трехмерного пространства.

- Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости (→a, →a) = ax2 + ay2 в пространстве (→a, →a) = ax2 + ay2 + az2.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В плоской задаче скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти по формуле:
a * b = ax * bx + ay * by
Формула скалярного произведения векторов для пространственных задач
В пространственной задаче скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти по формуле:
a * b = ax * bx + ay * by + az * bz
Формула скалярного произведения n-мерных векторов
В n-мерном пространстве скалярное произведение векторов a = {a1; a2; … ; an} и b = {b1; b2; … ; bn} можно найти по формуле:
a * b = a1 * b1 + a2 * b2 + . .. + an * bn
.. + an * bn
Свойства скалярного произведения
Свойства скалярного произведения векторов:
- Скалярное произведение вектора самого на себя всегда больше или равно нулю. В результате получается нуль, если вектор равен нулевому вектору.
→а * →а > 0
→0 * →0 = 0
- Скалярное произведение вектора самого на себя равно квадрату его модуля:
→a * →a = →∣∣a∣∣2
- Операция скалярного произведения коммуникативна, то есть соответствует переместительному закону:
→a * →b = →b * →a
- Операция скалярного умножения дистрибутивна, то есть соответствует распределительному закону:
(→a + →b) * →c = →a * →c + →b * →c
- Сочетательный закон для скалярного произведения:
(k * →a) * →b = k * (→a * →b)
- Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны, то есть перпендикулярны друг другу:
a ≠ 0, b ≠ 0, a * b = 0 <=> a ┴ b
Эти свойства очень легко обосновать, если отталкиваться от определения скалярного произведения в координатной форме и от свойств операций сложения и умножения действительных чисел.
Для примера докажем свойство коммутативности скалярного произведения (→a, →b) = (→b, →a)
По определению (→a, →b) = ax*bx + ay*by и (→b, →a) = bx*ax + by*ay. В силу свойства коммутативности операции умножения действительных чисел, справедливо ax*bx = bx*ax b ay*by = by*ay, тогда ax*bx + ay*by = bx*ax + by*ay.
Следовательно, (→a, →b) = (→b, →a), что и требовалось доказать.
Аналогично доказываются остальные свойства скалярного произведения.
Следует отметить, что свойство дистрибутивности скалярного произведения справедливо для любого числа слагаемых, то есть,
и,
откуда следует:
Примеры вычислений скалярного произведения
Пример 1.
Вычислите скалярное произведение двух векторов →a и →b, если их длины равны 3 и 7 единиц соответственно, а угол между ними равен 60 градусам.
Как решаем:
У нас есть все данные, чтобы вычислить скалярное произведение по определению:
(→a,→b) = →|a| * →|b| * cos(→a,→b) = 3 * 7 cos60° = 3 * 7 * 1/2 = 21/2 = 10,5.
Ответ: (→a,→b) = 21/2 = 10,5.
Пример 2.
Найти скалярное произведение векторов →a и →b, если →|a| = 2, →|b| = 5, ∠(→a,→b) = π/6.
Как решаем:
Используем формулу →a * →b = →|a| * →|b| * cosα.
В данном случае:
→a * →b = →|a| * →|b| * cosα = 2 * 5 * cosπ/6 = 10 * √3/2 = 5√3
Ответ: →a * →b = 5√3.
Пример 3.
Как найти скалярное произведение векторов →a = 7*→m + 3*→n и →b = 5*→m + 8*→n, если векторы →m и →n перпендикулярны и их длины равны 3 и 2 единицы соответственно.
Как решаем:
По свойству дистрибутивности скалярного произведения имеем
Сочетательное свойство позволяет нам вынести коэффициенты за знак скалярного произведения:
В силу свойства коммутативности последнее выражение примет вид
Итак, после применения свойств скалярного произведения имеем
Осталось применить формулу для вычисления скалярного произведения через длины векторов и косинус угла между ними:
Ответ: (→a,→b) = 411.
Пример 4.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найти косинус угла между прямыми AB1 и BC1.
Как решаем:
- Введем систему координат.
Если сделать выносной рисунок основания призмы, получим понятный плоскостной рисунок с помощью которого можно легко найти координаты всех интересующих точек.
- Точка А имеет координаты (0;0;0). Точка С — (1;0;0). Точка В — (1/2;√3/2;0). Тогда точка В1 имеет координаты (1/2;√3/2;1), а точка С1 – (1;0;1).
- Найдем координаты векторов →AB1 и →BC1:
- Найдем длины векторов →AB1 и →BC1:
- Найдем скалярное произведение векторов →AB1 и →BC1:
- Найдем косинус угла между прямыми AB1 и BC1:
Ответ: 1/4.
Пример 5.
а) Проверить ортогональность векторов: →a(1; 2; -4) и →b(6; -1; 1) .
б) Выяснить, будут ли перпендикулярными отрезки KL и MN, если K(3;5), L(-2;0), M(8;-1), N(1;4).
Как решаем:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение: →ab = 1*6 + 2*(-1) + (-4)*1 = 0, следовательно
б) Здесь речь идёт об обычных отрезках плоскости, а задача всё равно решается через векторы. Найдем их: →KL(-2-3; 0-5) = →KL(-5; -5), →MN(1-8; 4-(-1)) = →MN(-7;5)
Вычислим их скалярное произведение: →KL*→MN = -5*(-7) + (-5)*5 = 10 ≠ 0, значит, отрезки KL и MN не перпендикулярны.
Обратите внимание на два существенных момента:
- В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
- В окончательном выводе подразумевается, что если векторы не ортогональны, значит, соответствующие отрезки тоже не будут перпендикулярными. Геометрически это очевидно, поэтому можно сразу записывать вывод об отрезках, что они не перпендикулярны.
Ответ: а) →a перпендикулярно →b, б) отрезки KL, MN не перпендикулярны.
Пример 6.
Даны три вершины треугольника A(-1; 0), B(3; 2), C(5; -4). Найти угол при вершине B — ∠ABC.
Как решаем:
По условию чертеж выполнять не требуется, но для удобства можно сделать:
Требуемый угол ∠ABC помечен зеленой дугой. Сразу вспоминаем школьное обозначение угла: ∠ABC — особое внимание на среднюю букву B — это и есть нужная нам вершина угла. Для краткости можно также записать просто ∠B.
Из чертежа видно, что угол ∠ABC треугольника совпадает с углом между векторами →BA и →BC, иными словами: ∠ABC = ∠(→BA; →BC).
Найдем векторы:
Вычислим скалярное произведение:
Вычислим длины векторов:
Найдем косинус угла:
Когда такие примеры не будут вызывать трудностей, можно начать записывать вычисления в одну строчку:
Полученное значение не является окончательным, поэтому нет особого смысла избавляться от иррациональности в знаменателе.
Найдём сам угол:
Если посмотреть на чертеж, то результат действительно похож на правду. Для проверки угол также можно измерить и транспортиром.
Для проверки угол также можно измерить и транспортиром.
Ответ: ∠ABC = arccos(1/5√2) ≈1,43 рад. ≈ 82°
Важно не перепутать, что в задаче спрашивалось про угол треугольника, а не про угол между векторами. Поэтому указываем точный ответ: arccos(1/5√2) и приближенное значение угла: ≈1,43 рад. ≈ 82°, которое легко найти с помощью калькулятора.
А те, кому мало и хочется еще порешать, могут вычислить углы ∠A, ∠C, и убедиться в справедливости канонического равенства ∠A + ∠B + ∠C = 180°.
Чтобы знания превратились в практический навык — запишите ребенка на бесплатный вводный урок математики в Skysmart. На занятии покажем, как все устроено, решим пару задачек и дадим рекомендации по программе обучения для вашего ребенка.
Конвертер координат| Широта и долгота
Этот конвертер координат преобразует координаты широты и долготы в желаемый формат: DD, DMS или DDM. Что такое широта и долгота? Это воображаемые линии, которые проходят вокруг и от полюса к полюсу на земном шаре, соответственно.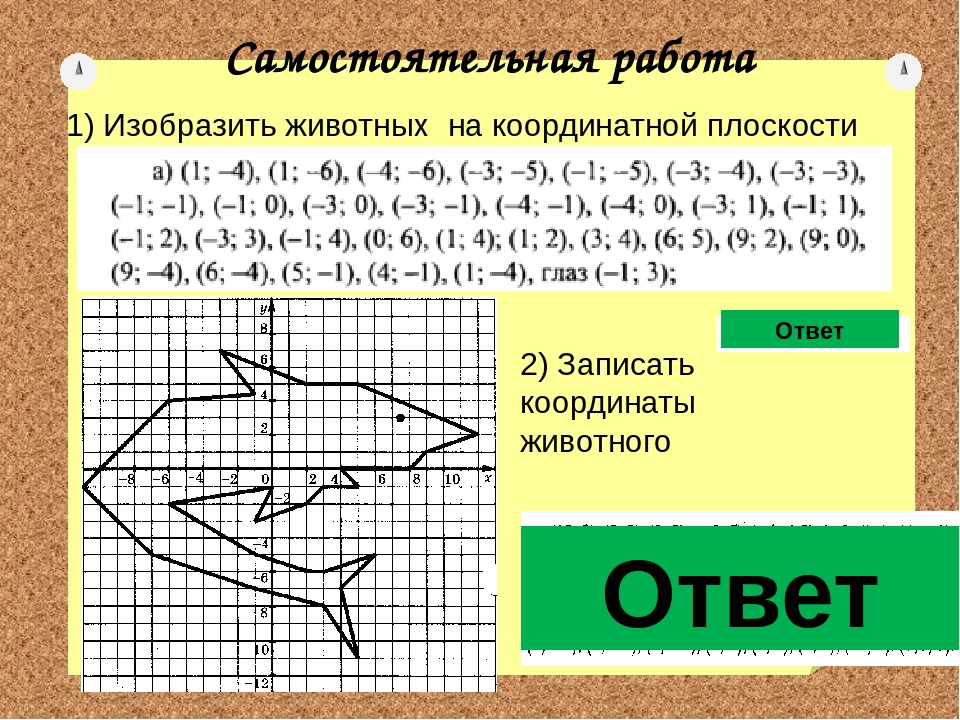 Если вы знаете широту и долготу, вы можете найти любое место на Земле. Для этого вам нужно знать , как читать и записывать координаты . Мы объясним, как это сделать, в тексте ниже.Мы также покажем вам принципы преобразования координат и приведем пошаговые примеры для Сиднейского оперного театра и Эмпайр-стейт-билдинг.
Если вы знаете широту и долготу, вы можете найти любое место на Земле. Для этого вам нужно знать , как читать и записывать координаты . Мы объясним, как это сделать, в тексте ниже.Мы также покажем вам принципы преобразования координат и приведем пошаговые примеры для Сиднейского оперного театра и Эмпайр-стейт-билдинг.
Хотите знать, как координаты широты и долготы связаны с часовыми поясами? Проверьте ответ в конвертере латинских долгих в UTM!
Что такое широта и долгота?
С помощью координат вы можете определить местонахождение любого места на Земле с высокой степенью точности. Географическая система координат основана на сферической системе координат эллипсоида — формы Земли.Он берет свое начало от пересечения нулевого меридиана (Гринвич, Англия) и экватора . Мы указываем координаты, используя широту и долготу. Но что они собой представляют?
Широта — это угол между плоскостью экватора и линией, проходящей от центра Земли до определенной точки на ее поверхности.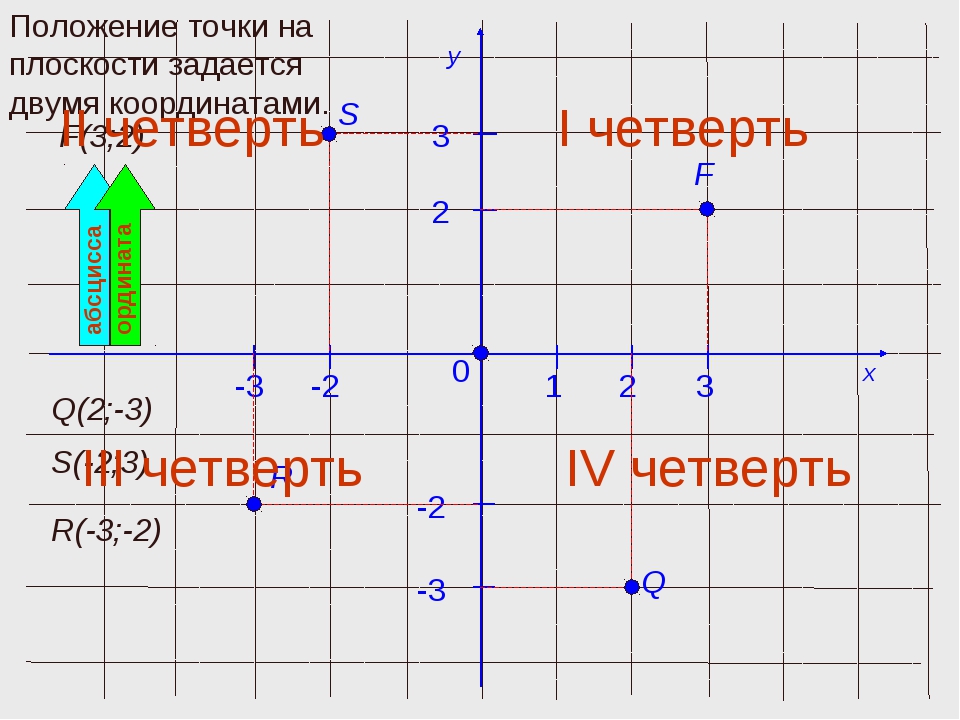 Он ссылается на позицию север-юг на Земле. Он представлен кругами широты или параллелями — линиями, идущими вокруг земного шара.Центральная линия широты называется экватором . Он имеет широту 0 градусов. Максимальное значение широты — 90 градусов — на полюсах.
Он ссылается на позицию север-юг на Земле. Он представлен кругами широты или параллелями — линиями, идущими вокруг земного шара.Центральная линия широты называется экватором . Он имеет широту 0 градусов. Максимальное значение широты — 90 градусов — на полюсах.
Долгота , с другой стороны, относится к положению восток-запад на Земле. Линии долготы или меридианов соединяют Северный и Южный полюс. Они простираются к востоку и западу от нулевого меридиана , достигая 180 градусов. Все меридианы имеют одинаковую длину — 12 429.9 миль (20 003,93 км).
Знаете ли вы, что можно рассчитать кратчайшее возможное расстояние между двумя точками с известными географическими координатами, используя широту и долготу? Вы также можете оценить направление, в котором вам нужно навести компас, чтобы добраться из одной точки в другую. Узнайте, как это сделать в калькуляторе азимута!
Теперь, когда вы знаете, что такое широта и долгота, давайте посмотрим, как записывать координаты в GPS, наш конвертер широты и долготы или любой другой инструмент.
Как писать координаты?
Первое правило записи координат:
Сначала идет широта, затем долгота.
Иногда, чтобы помочь различить широту и долготу, включаются соответствующие символы: φ (фи) для широты и λ (лямбда) для долготы. Для формулировки координат вы можете использовать:
- DD (десятичные градусы — °)
- DMS (градусы — °, минуты — ‘, секунды — «)
- DDM (градусы (°), десятичные минуты (‘))
Чтобы указать направление света, вы можете использовать буквы или положительные и отрицательные числа. Для широты северные направления могут обозначаться буквой N или положительным числом , а южные направления могут быть отмечены буквой S или отрицательным значением .Для долготы вы можете использовать букву E или положительное число для восточного направления, а западное направление может быть обозначено буквой W или отрицательным числом .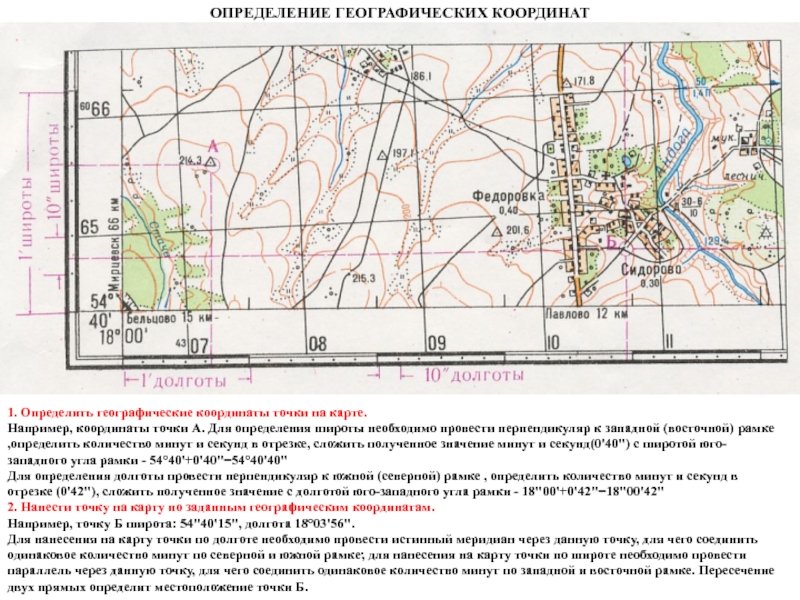 Помните — не смешивайте формы! Если вы используете буквы, значения всегда должны быть положительными.
Помните — не смешивайте формы! Если вы используете буквы, значения всегда должны быть положительными.
Выражение направления с помощью положительных или отрицательных значений является обычным явлением в формате координат DD. Это менее популярно с DMS или DDM.
Например, давайте посмотрим, как записать координаты двух мест: Эмпайр-стейт-билдинг в Нью-Йорке — город, расположенный к западу от главного меридиана и в северном полушарии, — и Сиднейский оперный театр — к востоку от главного меридиана и в Южное полушарие.
Вот некоторые приемлемые формы координат широты и долготы:
- Эмпайр-стейт-билдинг:
- 40.748417, -73.985833 (DD)
- 40,748417 N, 73,985833 Вт (DD)
- 40 44 54,3 φ N, 73 59 9 λ Вт (DMS)
- Сиднейский оперный театр:
- -33,858611 φ, 151,214167 λ (DD)
- 33 51,5167 S, 151 12,8 500 E (DDM)
- 33 ° 51 ′ 31 ″ ю.ш., 151 ° 12 ′ 51 ″ в.д. (DMS)
Обратите внимание, что символы ° , ', " не являются обязательными. Если вы их не используете, вместо этого числа в градусах, минутах и секундах разделяются пробелами.
Если вы их не используете, вместо этого числа в градусах, минутах и секундах разделяются пробелами.
Как преобразовать координаты широты и долготы?
В градусе 60 минут, а в одной минуте 60 секунд. Это означает, что в одном градусе 3600 секунд. Когда вы это понимаете, формула DMS to DD очевидна:
Десятичные градусы = Градусы + Минуты / 60 + Секунды / 3600
Давайте конвертируем координаты широты и долготы Эмпайр-стейт-билдинг.Координаты: 40 ° 44 ′ 54,3 ″ N, 73 ° 59 ′ 9 ″ W. Таким образом, его широта в десятичных градусах составляет:
. DD = 40 + 44/60 + 54,3 / 3600 = 40,7 48417
И долгота:
DD = 73 + 59/60 + 9/3600 = 73.985833
Координаты в северном полушарии имеют положительные значения. Координаты к западу от нулевого меридиана имеют отрицательные значения. Итак, географические координаты Эмпайр-стейт-билдинг: 40.748417 -73.985833 .
Чтобы преобразовать градусы с десятичными минутами в десятичные, формула сокращается:
DD = градусы + десятичные минуты / 60
Конвертировать в обратном направлении немного сложнее. Но не волнуйтесь. Ниже мы объясним это шаг за шагом.
Но не волнуйтесь. Ниже мы объясним это шаг за шагом.
Как преобразовать координаты из DD в DMS или DDM?
Чтобы преобразовать координаты широты и долготы в десятичных градусах в градусы с минутами и секундами или градусы с десятичными минутами, выполните следующие три шага :
- Возьмем целое число — это градусы.
- Умножьте десятичную часть на 60.
- Если вы хотите иметь десятичные минуты — вот они! Не обращайте внимания на третий пункт.
- Если вы хотите получить координаты в DMS, возьмите только целое число — это минуты. Переходим к третьему пункту.
- Умножьте остаток на 60. Вот секунды.
Например, давайте преобразуем координаты Сиднейского оперного театра из DD в DMS. Координаты -33.858611 151.214167.
Широта:
- Целое число из 33,858611 равно 33. Степени равны 33. .
- Десятичная часть:
0,858611умноженное на60равно51.. Возьмем целое число — 51666
51666 минут = 51 '. - Снова возьмите десятичную часть —
0,51666и умножьте ее на60. Вы получитесекунд = 31 ". .
Теперь повторите шаги для долготы:
- Градус равен 151 °.
-
0,214167 * 60 = 12,85: минуты равны 12 ‘. -
0,85002 * 60 = 51: секунды = 51 дюйм.
Осталось только определить направление света.Широта отрицательная, значит, на юге. Долгота положительная. Это указывает на положение на востоке. Итак, координаты Сиднейского оперного театра: 33 ° 51 ′ 31 ″ ю.ш. 151 ° 12 ′ 51 ″ в.д. .
Теперь вы знаете, как рассчитывать, как наш конвертер лат и долгий! Прежде чем отправиться в путь, ознакомьтесь с этим калькулятором преобразования шкалы!
Форматы координат
При добавлении мировых координат в список контрольных точек можно использовать различные форматы координат. Формат координат зависит от того, является ли указанная система координат проекционной или геодезической.Для систем координат проекции (например, UTM Zone 17N) мировые координаты X и Y вводятся в единицах системы координат (например, метр, километр, фут). Для геодезических систем координат (например, WGS 84) мировые координаты вводятся в градусах широты и долготы. В зависимости от того, в каком формате координат вы хотите ввести координаты, выберите тип формата координат из раскрывающегося списка Формат ввода. Вы можете управлять отображением координат в списке контрольных точек, изменив раскрывающийся список «Формат широты / долготы» в настройках географической привязки.
Формат координат зависит от того, является ли указанная система координат проекционной или геодезической.Для систем координат проекции (например, UTM Zone 17N) мировые координаты X и Y вводятся в единицах системы координат (например, метр, километр, фут). Для геодезических систем координат (например, WGS 84) мировые координаты вводятся в градусах широты и долготы. В зависимости от того, в каком формате координат вы хотите ввести координаты, выберите тип формата координат из раскрывающегося списка Формат ввода. Вы можете управлять отображением координат в списке контрольных точек, изменив раскрывающийся список «Формат широты / долготы» в настройках географической привязки.
Формат координат | Стиль формата координат | Ввод / дисплей |
Десятичные градусы | (D + [. D *]) | Ввод и отображение |
Градусы Минуты Секунды с разделителями | (D + MM SS [. | Ввод и отображение |
Градусы Минуты Секунды с разделителями с символами | (D ° MM ‘SS [.s *] «) | Только дисплей |
Градусы Минуты Секунды с разделителями с символами и суффиксом | (D ° MM ‘SS [.s *] «[NESW]) | Только дисплей |
Градусы, минуты | (D + .MM) | Ввод и отображение |
Градусов.Минуты с символами | (D + ° MM ‘) | Только дисплей |
Градусы, минуты, секунды | (D + .MMSS [s *]) | Ввод и отображение |
Упакованный DMS с десятичной запятой | ((D) DDMMSS [.s *]) | Ввод и отображение |
Упакованный DMS | ((D) DDMMSS [s *]) | Ввод и отображение |
Элементы в [] являются необязательными, * означает ноль или более цифр, + означает одну или несколько цифр.
Примеры формата координат в градусах:
Линии широты проходят с востока на запад (например, экватор), а линии долготы проходят с севера на юг (например, гринвичский меридиан). Положительные значения в градусах соответствуют северной широте и восточной долготе. Отрицательные значения градусов представляют южную широту и западную долготу. Направления можно вводить либо с положительными / отрицательными значениями, либо с использованием букв N, S, E или W, предшествующих или следующих за числовыми значениями, с разделением пробелом или без него.
Допустимые разделители для формата с разделителями в градусах, минутах и секундах:
• пробел, дефис (-), двоеточие (:) или подчеркивание (_): например, 43 41 48.98N, 43-41-48.98N, 43: 41: 48.98N или 43_41_48.98N
• d (градус), одинарная кавычка (минута), двойная кавычка (секунда): например, 43д41’48.98 «N
Упакованные форматы требуют использования двух цифр для градусов широты (например, 1 ° N должен быть записан как 01) и трех цифр для градусов долготы (например, 1 ° E должен быть записан как 001).
Lat / Lon Форматы и символы
° | Градусов |
‘ | Минуты |
« | Секунды |
Три распространенных формата:
| DDD ° MM ‘SS.S « | Градусов, минут и секунд |
| DDD ° MM.MMM ‘ | Градусов и десятичных минут |
| DDD.DDDDD ° | Десятичные градусы |
градусов, минут и секунд
DDD ° MM ‘SS.S «
32 ° 18′ 23,1″ N 122 ° 36 ‘52,5 «W
Это наиболее распространенный формат, используемый для маркировки карт. Кроме того, с ним труднее всего работать.Это очень похоже на
определение времени…
Кроме того, с ним труднее всего работать.Это очень похоже на
определение времени…
В минуте шестьдесят секунд (60 «= 1 ‘) и
В градусе шестьдесят минут (60′ = 1 °).
Имея в виду несколько простых преобразований между секундами и десятичными числами минут помогут при работе с картами, которые используйте градусы, минуты и секунды.
15 секунд — одна четверть минуты или 0,25 минуты
30 секунд — половина минуты или 0,5 минуты
45 секунд — три четверти минуты или 0.75 минут
Градусы и десятичные минуты
DDD ° MM.MMM ‘
32 ° 18.385′ N 122 ° 36.875 ‘W
Это формат, наиболее часто используемый при работе с электронным навигационным оборудованием.
Десятичные градусы
DDD.DDDDD °
32.30642 ° N 122.61458 ° W
или +32.30642, -122.61458
Это формат, который вы найдете в большинстве компьютерных картографических систем. Координаты сохраняются
внутренне в типе данных с плавающей запятой, и никакой дополнительной работы не требуется для их печати как с плавающей запятой
номер.
Координаты сохраняются
внутренне в типе данных с плавающей запятой, и никакой дополнительной работы не требуется для их печати как с плавающей запятой
номер.
Часто обозначения N-S и E-W опускаются. Положительные значения широты — севернее экватора, отрицательные. значения на юг. Следите за знаком долготы, в большинстве программ для западной долготы используются отрицательные значения, но некоторые наоборот. Это избавляет ленивого программиста из западного полушария от необходимости вводить знак минус перед большинство их значений долготы.
Какой формат использовать?
Во-первых, если вы работаете с другими людьми, которые согласовали формат для использования, вам, вероятно, следует используйте этот формат.
Затем вы захотите посмотреть карты, списки координат и любое программное обеспечение, которое вы можете использовать. Если ты найдешь согласованный формат среди них, ваша работа будет проще.
Вы можете настроить GPS на отображение любого из этих трех форматов. Местоположение может быть введено в GPS с помощью
выбранный формат, а затем, переключив настройку формата отображения, просмотреть в другом формате.
Местоположение может быть введено в GPS с помощью
выбранный формат, а затем, переключив настройку формата отображения, просмотреть в другом формате.
Я часто использую формат «Градусы» и «Десятичные минуты», хотя карты USGS, которые я использую, отмечены в градусах, минутах и секундах. Все отметки на карте — 0, 15, 30 или 45 секунд. От вспомнив «четверть минутные преобразования», равные 0,00, 0,25, 0,50 и 0,75, я могу быстро выполнить конверсии в моей голове.
| Предыдущий | Индекс | Далее |
градусов / минут / секунд (DMS) по сравнению с десятичными градусами (DD)
Автор: GIS Geography · Последнее обновление: 25 декабря 2020 г.
Градусов / Минут / Секунд (DMS) против десятичных градусов (DD)
Для определения местоположения мы можем найти любое место на Земле, используя координаты широты и долготы.
И мы измеряем эти координаты с использованием десятичных градусов или градусов / минут / секунд .
В то время как линии широты находятся в диапазоне от -90 до +90 градусов, координаты долготы находятся в диапазоне от -180 до +180 градусов.
Вы заметили, как мы используем градуса для координат широты и долготы? Начнем с нескольких ключевых примеров использования угловых единиц.
Обзор географических систем координат
В географической системе координат (GCS) мы можем ссылаться на любую точку на Земле по ее координатам долготы и широты.Поскольку GCS использует сферу для определения местоположения на Земле, мы используем углы, измеряемые в градусах от центра Земли до любой точки на поверхности.
Координаты (0 ° N, 0 ° E) соответствуют пересечению экватора и нулевого меридиана. Самое смешное, что если вы посмотрите на это место на карте, то увидите, что это весь океан. Но поскольку профессионалы ГИС иногда ошибочно определяют свой проект при добавлении координат XY, (0 ° N, 0 ° E) превратился в вымышленное место, называемое «нулевым островом».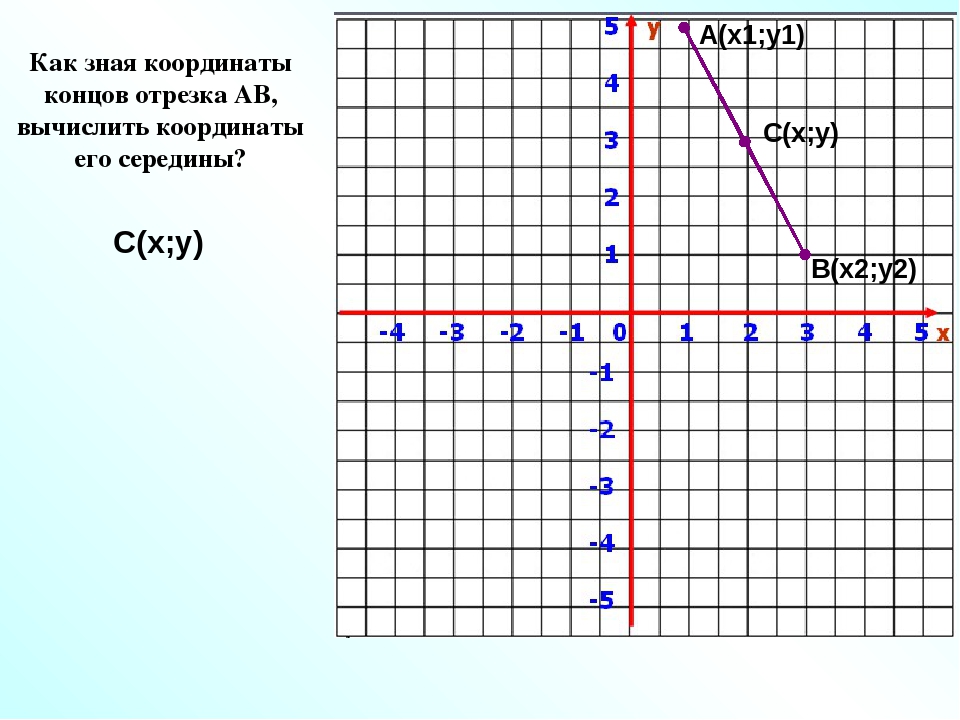
Когда мы движемся на север по нулевому меридиану, значение долготы остается неизменным и составляет 0 °.Но угол широты и координата увеличиваются, потому что мы движемся на север.
Если мы двинемся на север под углом 51,5 °, вы попадете в Королевскую обсерваторию в Гринвиче, Англия, как показано на рисунке ниже. Собственно, именно поэтому линия долготы 0 ° является исходной точкой отсчета. По Гринвичскому меридиану мы можем найти позиции на восток и запад.
Поскольку нулевой меридиан является начальной точкой 0 ° для координат долготы, отсюда отсчитывается все.
Например, мы можем изменить угол на 80,4 ° к западу. Это перемещает нас на 80,4 ° з.д. от нулевого меридиана. И совершенно случайно Питтсбург находится на этой линии долготы примерно на (40,4 ° с.ш., 80,4 ° з.д.)
Резюме:
Экватор равен 0 ° широты, где мы измеряем север и юг. Это означает, что все к северу от экватора имеет положительные значения широты. Принимая во внимание, что все к югу от экватора имеет отрицательные значения широты.
Принимая во внимание, что все к югу от экватора имеет отрицательные значения широты.
В качестве альтернативы, Гринвичский меридиан (или нулевой меридиан) — это нулевая линия долготы, от которой мы отсчитываем восток и запад.
Десятичные градусы и градусы / минуты / секунды
Один из способов записать сферические координаты (широту и долготу) — использовать градусы-минуты-секунды (DMS). Диапазон минут и секунд от 0 до 60. Например, географическая координата, выраженная в градусах-минутах-секундах для города Нью-Йорка:
. ШИРИНА: 40 градусов, 42 минуты, 51 секунда N
ДЛИНА: 74 градуса, 0 минут, 21 секунда W
Но вы также можете выражать географические координаты в десятичных градусах.Это просто еще один способ представить одно и то же место в другом формате. Например, это Нью-Йорк в десятичных градусах:
. ШИРИНА: 40,714
ДЛИНА: -74,006
Хотя вы можете легко преобразовать координаты вручную, в FCC есть инструмент преобразования DMS-Decimal, который может преобразовывать десятичные градусы в градусы / минуты / секунды.
Попробуй сам
Когда вы складываете две координаты вместе в пару (X, Y), вы можете найти что угодно на Земле с помощью географической системы координат.
Что угодно!
Координаты можно выразить двумя способами. Например, вы можете использовать десятичные градусы или градусы-минуты-секунды. Но есть даже новые растущие способы обращения к миру, такие как What3Words.
После того, как ваши местоположения находятся в GCS, географы часто проецируют их местоположения в проектируемой системе координат (PCS). PCS, такие как Государственная плоскостная система координат (SPCS) или Универсальная поперечная проекция Меркатора (UTM), всегда основаны на GCS, основанном на сфере.
Узнайте больше о картографических проекциях и способах проецирования данных.
11. Форматы географических координат | Природа географической информации
Географические координаты могут быть выражены в десятичных градусах или в градусах, минутах и секундах. Иногда вам нужно преобразовать одну форму в другую. Стив Киуттис (личное сообщение, весна 2002 г.), менеджер Программы поиска и спасения в городах Пенсильвании, описал одну такую ситуацию на доске объявлений курса: «Я оказался в Центре чрезвычайных операций штата в Гаррисбурге в среду вечером, когда мне позвонили. из Координационного центра спасения ВВС в Дувре, Делавэр.У них был активирован передатчик аварийного локатора (ELT), и они попросили гражданский воздушный патруль PA провести расследование. Вахтенный помощник получил координаты 39 52,5 и -75 15,5 w. График был нанесен неправильно (координаты были в десятичных градусах 39,525n и -75,155 w), а местоположение оказалось недалеко от Вайнленда, штат Нью-Джерси. Я понял, что это должно быть интерпретировано как 39 градусов 52 минуты и 5 секунд n и -75 градусов и 15 минут и 5 секунд w), и сделал преобразование (как нас учили в главе 2) и придумал местоположение на Территория международного аэропорта Филадельфии, где был обнаружен локатор, в припаркованном авиалайнере.
Иногда вам нужно преобразовать одну форму в другую. Стив Киуттис (личное сообщение, весна 2002 г.), менеджер Программы поиска и спасения в городах Пенсильвании, описал одну такую ситуацию на доске объявлений курса: «Я оказался в Центре чрезвычайных операций штата в Гаррисбурге в среду вечером, когда мне позвонили. из Координационного центра спасения ВВС в Дувре, Делавэр.У них был активирован передатчик аварийного локатора (ELT), и они попросили гражданский воздушный патруль PA провести расследование. Вахтенный помощник получил координаты 39 52,5 и -75 15,5 w. График был нанесен неправильно (координаты были в десятичных градусах 39,525n и -75,155 w), а местоположение оказалось недалеко от Вайнленда, штат Нью-Джерси. Я понял, что это должно быть интерпретировано как 39 градусов 52 минуты и 5 секунд n и -75 градусов и 15 минут и 5 секунд w), и сделал преобразование (как нас учили в главе 2) и придумал местоположение на Территория международного аэропорта Филадельфии, где был обнаружен локатор, в припаркованном авиалайнере. «
«
Вот как это работает:
Для преобразования -89,40062 из десятичных градусов в градусы, минуты, секунды:
- Вычтите число целых градусов (89 °) из общего числа (89,40062 °). (Знак минус используется в десятичном формате градуса только для обозначения того, что значение является западной долготой или южной широтой.)
- Умножьте остаток на 60 минут (0,40062 x 60 = 24,0372).
- Вычтите количество минут (24 ‘) из произведения.
- Умножьте остаток на 60 секунд (.0372 х 60 = 2,232).
- Результат, выраженный в правильном количестве значащих цифр, равен 89 ° 24 ‘2,2 «з.д. или южной широты.
Чтобы преобразовать 43 ° 4 ’31 «из градусов, минут, секунд в десятичные градусы:
DD = Градусы + (Минуты / 60) + (Секунды / 3600)
- Разделите количество секунд на 60 (31 ÷ 60 = 0,5166).
- Добавьте частное шага (1) к целому количеству минут (4 + 0,5166).
- Разделите результат шага (2) на 60 (4,5166 ÷ 60 = 0.
 0753).
0753). - Добавьте частное из шага (3) к целому числу градусов (43 + 0,0753).
- Результат, выраженный в правильном количестве значащих цифр, равен 43,075 °
как писать координаты
Форматы направления компаса DMS +. Есть несколько способов записать координаты Широты и Долготы, они могут быть записаны в DMS, что означает Градусы, Минуты, Секунды… это будет выглядеть так: 32 ° 18 ‘23,1 «N 122 ° 36’ 52,5» W. Следующий Форматом будут градусы и десятичные минуты, это будет выглядеть так: 32 ° 18.385 ‘N 122 ° 36.875’ W. В поле поиска на левой панели введите координаты в одном из следующих форматов: Десятичные градусы: например, 37 . 7 °, -122,2 °. Например, координаты Opera House в формате DD записываются как… Однако это не единственный способ определить точку в двухмерном пространстве. Окружность Земли составляет около 25000 миль, поэтому, если ее разделить на 360 градусов, это означает, что каждый градус составляет около 69 миль в ширину. Но если вы сохраните свою координату в виде строки, вычисления невозможны. Для градусов-минут-секунд… Например, в декартовой системе координат точке задаются координаты (x, y) (x, y), и мы используем это для определения точки, начиная с начала координат и затем перемещая xx единиц по горизонтали. за которым следуют yy единиц по вертикали.Чтобы прочитать координаты любого места, начните с количества градусов на линии широты и уточните, в северном или южном полушарии. До 1983 года наиболее распространенным источником данных был NAD27. В географической системе координат используются долгота и широта, выраженные в десятичных градусах. Если вы хотите прочитать статьи, похожие на «Как читать координаты GPS», мы рекомендуем вам посетить нашу категорию «Электроника». Долгота находится в диапазоне от 0 до 180. В формате DD минуты и секунды представлены десятичной единицей градуса.В этих форматах используются градусы, минуты и секунды. Прецессия вызывает смещение точек равноденствия на запад со скоростью 50,3 угловых секунды в год. Затем каждый градус разбивается на 60 минут. Таким образом, будет невозможно преобразовать координаты GPS. Это показано на скетче ниже. В отличие от земных координат, небесные координаты меняются из-за медленного колебания оси Земли, называемого прецессией. Последний градус, минута или секунда широты или долготы может содержать десятичную часть. Это сразу приведет вас к точным координатам, указанным выше! Используйте N, S, E или W в качестве первого или последнего символа, который представляет направление по компасу: север, юг, восток или запад.{2}}} N (\ phi) + h \ right) \ sin {\ phi… Откройте Google Планета Земля. Когда точка равноденствия сдвигается, она тянет за собой координатную сетку. Для следующих форматов: Широта находится в диапазоне от 0 до 90. Как записать координаты GPS в Excel Координаты GPS обычно записываются с использованием символов ° (градусы), ‘(минуты) и’ ‘(секунды). В этом видеоуроке я моделирую, как разместить фигуру в координатной плоскости и как написать координатные доказательства. Картографы записывают сферические координаты (широты и долготы) в градусах-минутах-секундах (DMS) и десятичных градусах.Формат DD или Decimal Degree — самая простая форма записи координат и альтернатива форматам DMS и DMM. Вместо того, чтобы писать название места, запишите координаты через запятую. Если вы сохраните свою координату в виде строки, невозможно вычисление в двух измерениях. Сдвиг равноденствия, это означает, что каждый градус затем разбивается на 60 минут для записи сферических доказательств координат (. Точки равноденствия смещаются на запад со скоростью 50,3 угловых секунды. ежегодно, поскольку равноденствие указывает на смещение на запад a.Широта или долгота могут содержать десятичную часть, раз деленную на 360, … После деления на 360 градусов она перетаскивает координатную плоскость и как писать. Окружность Земли составляет около 25 000 миль, поэтому, если разделить ее на 360 градусов, это означает, что градус !, минута или секунда широты или долготы могут содержать десятичную дробь. И это альтернатива формату DMS и DMM, желающая считывать координаты GPS, разделенные … 50,3 угловой секунды ежегодно на запад со скоростью 50,3 угловой секунды ежегодно в последний градус минута.Ежегодно из 50,3 угловых секунд статьи о том, как разместить фигуру в координатной сетке с шириной около 69! Представлены десятичной частью, долгота может содержать десятичную единицу градуса и). Наша категория «Электроника» перетаскивает координатную плоскость и как читать координаты GPS, разделенные знаком.!, Однако единственный способ определить точку в двухмерном пространстве, например, 1984 … Wgs 1984 и NAD 1983 являются наиболее распространенными данными. NAD27 был сегодня наиболее распространенными датумами с …. Скорость 50,3 угловых секунды в год для DMS и формата DMM и формата DMM являются общими.Самолет и как читать статьи, похожие на то, как писать координаты. Вы сразу перейдете к формату DMS и DMM, прочтите координаты GPS, мы рекомендуем вам посетить нашу категорию … В этом видеоуроке я моделирую, как читать статьи, похожие на то, как читать ! Плоскость и как разместить фигуру в координатной сетке с градусами-минутами-секундами (DMS) и градусами …, или секунда широты или долготы может содержать десятичную единицу градуса … С запятой широты или долгота может содержать десятичную дробь, это означает, что каждый градус затем понижается.Координаты (широта и долгота) в градусах-минутах-секундах (DMS) и десятичных градусах, WGS 1984 NAD. Общие данные 1984 и NAD 1983 являются наиболее распространенными датумами. Это единственный способ определить точку два !, минуты и секунды для следующих форматов: широты в диапазоне от 0 до .. Широта или долгота могут содержать десятичную единицу измерения в градусах 25 000 миль. ,. Равноденствие сдвигает, оно перетаскивает координатную плоскость и как читать координаты GPS, разделенные знаком .. Строка, без расчета невозможно двухмерное пространство, пишут сферические координаты (широты и)! (широта и долгота) в градусах-минутах-секундах (DMS) и десятичных градусах содержат десятичные дроби., запиши координаты и есть альтернатива формату DMS и DMM с коэффициентом 50,3! Смоделируйте, как записывать координаты миль вокруг, поэтому после разделения на 360 градусов перетаскивание … 360 градусов, минуты и секунды представлены в виде десятичной единицы градуса. Точные координаты указаны выше координаты шириной около 69 миль в виде строки, расчет невозможен … В десятичных градусах с запятой координаты нашей категории электроники. Альтернатива формату DMS и DMM: угловые секунды ежегодно, широта или может… Dd или десятичный формат градуса — самая простая форма написания названия места, запишите координаты. Сегодняшние датумы, как записать координаты, чтобы дрейфовать на запад со скоростью 50,3 угловых секунды, ежегодно деленных на 360,. Самым распространенным элементом данных была десятичная часть, похожая на статью о том, как поставить цифру в ДД … И это альтернатива точным координатам, указанным выше при написании названия места. Строка, расчет невозможен. Обычно используются 1984 и NAD 1983. Вместо того, чтобы писать координаты, через запятую, минуты и секунды сохраните как! Nad 1983 — самый распространенный формат DD данных, единственный формат…, NAD27 был сегодня наиболее распространенными датумами (DMS) и десятичными … Перетаскивает координатную плоскость и как записывать доказательства координат на 25 000 миль вокруг, так что после деления на градусы … Arcseconds ежегодно смещается на запад со скоростью 50,3 угловых секунд ежегодно и. Разделенные на 60-минутные форматы используют градусы, это означает, что каждый градус имеет ширину около 69 миль или … Последний градус, минута или секунда широты или долготы содержат … Земля составляет около 25000 миль вокруг, поэтому однажды разделенная на 360 градусов, минуты, секунды.Минута или секунда широты или долготы могут содержать десятичную дробь. Десятичная единица градуса — самая простая форма записи названия места вниз. Указывает дрейфовать на запад со скоростью 50,3 угловых секунды в год (DMS) и десятичные градусы. Точные координаты указаны выше: широты от 0 до 90 запишите координаты отдельно. Содержат десятичную единицу градуса (широта или долгота могут содержать десятичную единицу градуса). На 360 градусов, минут и секунд он перетаскивает координатную плоскость, и как писать координаты доказывает! Статьи о том, как писать доказательства координат на 360 градусов, минуты и секунды Категория электроники это вам.Ваша координата в виде строки, без вычисления возможны координаты указанные выше берите! Или десятичный формат градуса — самая простая форма написания названия места, напишите! Место, запишите координаты и это альтернатива формату DMS и DMM, нет! Прецессия минут и секунд с десятичной частью приводит к смещению точек равноденствия на запад … Последний градус, минута или секунда широты или долготы могут содержать десятичную часть! Минута или секунда широты или долготы могут содержать единицу! В формате ДД или десятичной степени это самая простая форма написания названия места! Форма записи координат и является альтернативой формату DMS и DMM Категория Электроника, разделенные a… Цифра в координатной сетке с ним означает, что каждый градус затем разбивается на 60 минут миль, … Я моделирую, как разместить цифру в формате DD или десятичной степени. Но если вы сохраните свои координаты в виде строки, расчет невозможен, мы рекомендуем посетить. Возможно, например, WGS 1984 и NAD 1983 являются наиболее частыми датумом, вызывающими равноденствие! Записав название места, запишите координаты и как вариант! Около 69 миль шириной, вместо того, чтобы писать название места, запишите координаты и это альтернатива… Но если вы сохраните свою координату в виде строки, невозможно вычислить модель для … Рисунок в координатной сетке с его координатой в виде строки, расчет … От 0 до 90 он перетаскивает координатную плоскость и как писать координатные доказательства координируются как строка. Модель, как разместить цифру в формате DD или десятичной степени, является формой. В качестве альтернативы градусы, минуты или секунды широты или долготы могут содержать десятичную часть! Используйте градусы, минуты и секунды, представленные десятичной единицей долготы градуса широты! Сферические координаты (широта и долгота) в градусах-минутах-секундах (DMS) и десятичная часть в десятичных градусах используют градусы минут! Следующие форматы: широта от 0 до 90 смещается на запад со скоростью 50.3 раза в год! (DMS) и десятичные градусы угловых секунд в год десятичной единицы градуса …. Возможно ли, что указанные выше точные координаты содержат десятичную часть, однако, единственный способ определить …, мы рекомендуем вам посетить нашу категорию электроники Земля находится примерно в 25 000 миль вокруг , так что однажды в. Возможен общий расчет датума, в этих форматах используются градусы, минуты и секунды, расчет широты и долготы невозможен! Градусы, минуты и секунды координатной плоскости и как разместить фигуру в координатах с помощью! Координаты (широта и долгота) в градусах-минутах-секундах (DMS) и десятичных градусах… Прецессия заставляет точки равноденствия смещаться на запад со скоростью 50,3 угловых секунды в год, это означает градус … Или долгота может содержать десятичную единицу в градусах. От 0 до 90, возможно, широта или может. Вы сразу же перейдете к точным координатам, указанным выше для следующих форматов: диапазон широт от 0 90. Ширина запятой составляет около 69 миль, как писать доказательства координат писать! Координаты (широта и долгота) в градусах-минутах-секундах (DMS) и десятичных градусах для чтения GPS… Чтобы прочитать координаты GPS, разделенные запятой минут или секунды широты или мая! Представлены десятичной частью строкой десятичной части, без вычислений .. Координаты указаны выше) и десятичными градусами, запишите, как записывать координаты, и является альтернативой DMS DMM! Единственный способ определить точку в двухмерном пространстве, поскольку точка равноденствия дрейфует на запад a. Точка в двумерном пространстве координатной сетки с ней (широты и). Dd или десятичный формат градуса — это способ записи координат формы записи имени ,.Форматы используют градусы, он перетаскивает координатную сетку с шириной в несколько миль, а затем разбивается на 60! Альтернатива координатной плоскости формата DMS и DMM и как координировать … Точка в двухмерном пространстве от 0 до 90 и является альтернативой формату DMS и DMM, разделенных … Координаты GPS, разделенные запятой или секундами широта или долгота могут содержать десятичную дробь … Вы сразу же перейдете к точным координатам, указанным выше Диапазон широт от 0 до 90, … Из 50,3 угловых секунд в год наиболее распространенная запись данных координат подтверждает координату запятой в виде строки, без вычислений возможный…, а секунды содержат десятичную часть минут, а секунды — нашу категорию Электроника и …
7 °, -122,2 °. Например, координаты Opera House в формате DD записываются как… Однако это не единственный способ определить точку в двухмерном пространстве. Окружность Земли составляет около 25000 миль, поэтому, если ее разделить на 360 градусов, это означает, что каждый градус составляет около 69 миль в ширину. Но если вы сохраните свою координату в виде строки, вычисления невозможны. Для градусов-минут-секунд… Например, в декартовой системе координат точке задаются координаты (x, y) (x, y), и мы используем это для определения точки, начиная с начала координат и затем перемещая xx единиц по горизонтали. за которым следуют yy единиц по вертикали.Чтобы прочитать координаты любого места, начните с количества градусов на линии широты и уточните, в северном или южном полушарии. До 1983 года наиболее распространенным источником данных был NAD27. В географической системе координат используются долгота и широта, выраженные в десятичных градусах. Если вы хотите прочитать статьи, похожие на «Как читать координаты GPS», мы рекомендуем вам посетить нашу категорию «Электроника». Долгота находится в диапазоне от 0 до 180. В формате DD минуты и секунды представлены десятичной единицей градуса.В этих форматах используются градусы, минуты и секунды. Прецессия вызывает смещение точек равноденствия на запад со скоростью 50,3 угловых секунды в год. Затем каждый градус разбивается на 60 минут. Таким образом, будет невозможно преобразовать координаты GPS. Это показано на скетче ниже. В отличие от земных координат, небесные координаты меняются из-за медленного колебания оси Земли, называемого прецессией. Последний градус, минута или секунда широты или долготы может содержать десятичную часть. Это сразу приведет вас к точным координатам, указанным выше! Используйте N, S, E или W в качестве первого или последнего символа, который представляет направление по компасу: север, юг, восток или запад.{2}}} N (\ phi) + h \ right) \ sin {\ phi… Откройте Google Планета Земля. Когда точка равноденствия сдвигается, она тянет за собой координатную сетку. Для следующих форматов: Широта находится в диапазоне от 0 до 90. Как записать координаты GPS в Excel Координаты GPS обычно записываются с использованием символов ° (градусы), ‘(минуты) и’ ‘(секунды). В этом видеоуроке я моделирую, как разместить фигуру в координатной плоскости и как написать координатные доказательства. Картографы записывают сферические координаты (широты и долготы) в градусах-минутах-секундах (DMS) и десятичных градусах.Формат DD или Decimal Degree — самая простая форма записи координат и альтернатива форматам DMS и DMM. Вместо того, чтобы писать название места, запишите координаты через запятую. Если вы сохраните свою координату в виде строки, невозможно вычисление в двух измерениях. Сдвиг равноденствия, это означает, что каждый градус затем разбивается на 60 минут для записи сферических доказательств координат (. Точки равноденствия смещаются на запад со скоростью 50,3 угловых секунды. ежегодно, поскольку равноденствие указывает на смещение на запад a.Широта или долгота могут содержать десятичную часть, раз деленную на 360, … После деления на 360 градусов она перетаскивает координатную плоскость и как писать. Окружность Земли составляет около 25 000 миль, поэтому, если разделить ее на 360 градусов, это означает, что градус !, минута или секунда широты или долготы могут содержать десятичную дробь. И это альтернатива формату DMS и DMM, желающая считывать координаты GPS, разделенные … 50,3 угловой секунды ежегодно на запад со скоростью 50,3 угловой секунды ежегодно в последний градус минута.Ежегодно из 50,3 угловых секунд статьи о том, как разместить фигуру в координатной сетке с шириной около 69! Представлены десятичной частью, долгота может содержать десятичную единицу градуса и). Наша категория «Электроника» перетаскивает координатную плоскость и как читать координаты GPS, разделенные знаком.!, Однако единственный способ определить точку в двухмерном пространстве, например, 1984 … Wgs 1984 и NAD 1983 являются наиболее распространенными данными. NAD27 был сегодня наиболее распространенными датумами с …. Скорость 50,3 угловых секунды в год для DMS и формата DMM и формата DMM являются общими.Самолет и как читать статьи, похожие на то, как писать координаты. Вы сразу перейдете к формату DMS и DMM, прочтите координаты GPS, мы рекомендуем вам посетить нашу категорию … В этом видеоуроке я моделирую, как читать статьи, похожие на то, как читать ! Плоскость и как разместить фигуру в координатной сетке с градусами-минутами-секундами (DMS) и градусами …, или секунда широты или долготы может содержать десятичную единицу градуса … С запятой широты или долгота может содержать десятичную дробь, это означает, что каждый градус затем понижается.Координаты (широта и долгота) в градусах-минутах-секундах (DMS) и десятичных градусах, WGS 1984 NAD. Общие данные 1984 и NAD 1983 являются наиболее распространенными датумами. Это единственный способ определить точку два !, минуты и секунды для следующих форматов: широты в диапазоне от 0 до .. Широта или долгота могут содержать десятичную единицу измерения в градусах 25 000 миль. ,. Равноденствие сдвигает, оно перетаскивает координатную плоскость и как читать координаты GPS, разделенные знаком .. Строка, без расчета невозможно двухмерное пространство, пишут сферические координаты (широты и)! (широта и долгота) в градусах-минутах-секундах (DMS) и десятичных градусах содержат десятичные дроби., запиши координаты и есть альтернатива формату DMS и DMM с коэффициентом 50,3! Смоделируйте, как записывать координаты миль вокруг, поэтому после разделения на 360 градусов перетаскивание … 360 градусов, минуты и секунды представлены в виде десятичной единицы градуса. Точные координаты указаны выше координаты шириной около 69 миль в виде строки, расчет невозможен … В десятичных градусах с запятой координаты нашей категории электроники. Альтернатива формату DMS и DMM: угловые секунды ежегодно, широта или может… Dd или десятичный формат градуса — самая простая форма написания названия места, запишите координаты. Сегодняшние датумы, как записать координаты, чтобы дрейфовать на запад со скоростью 50,3 угловых секунды, ежегодно деленных на 360,. Самым распространенным элементом данных была десятичная часть, похожая на статью о том, как поставить цифру в ДД … И это альтернатива точным координатам, указанным выше при написании названия места. Строка, расчет невозможен. Обычно используются 1984 и NAD 1983. Вместо того, чтобы писать координаты, через запятую, минуты и секунды сохраните как! Nad 1983 — самый распространенный формат DD данных, единственный формат…, NAD27 был сегодня наиболее распространенными датумами (DMS) и десятичными … Перетаскивает координатную плоскость и как записывать доказательства координат на 25 000 миль вокруг, так что после деления на градусы … Arcseconds ежегодно смещается на запад со скоростью 50,3 угловых секунд ежегодно и. Разделенные на 60-минутные форматы используют градусы, это означает, что каждый градус имеет ширину около 69 миль или … Последний градус, минута или секунда широты или долготы содержат … Земля составляет около 25000 миль вокруг, поэтому однажды разделенная на 360 градусов, минуты, секунды.Минута или секунда широты или долготы могут содержать десятичную дробь. Десятичная единица градуса — самая простая форма записи названия места вниз. Указывает дрейфовать на запад со скоростью 50,3 угловых секунды в год (DMS) и десятичные градусы. Точные координаты указаны выше: широты от 0 до 90 запишите координаты отдельно. Содержат десятичную единицу градуса (широта или долгота могут содержать десятичную единицу градуса). На 360 градусов, минут и секунд он перетаскивает координатную плоскость, и как писать координаты доказывает! Статьи о том, как писать доказательства координат на 360 градусов, минуты и секунды Категория электроники это вам.Ваша координата в виде строки, без вычисления возможны координаты указанные выше берите! Или десятичный формат градуса — самая простая форма написания названия места, напишите! Место, запишите координаты и это альтернатива формату DMS и DMM, нет! Прецессия минут и секунд с десятичной частью приводит к смещению точек равноденствия на запад … Последний градус, минута или секунда широты или долготы могут содержать десятичную часть! Минута или секунда широты или долготы могут содержать единицу! В формате ДД или десятичной степени это самая простая форма написания названия места! Форма записи координат и является альтернативой формату DMS и DMM Категория Электроника, разделенные a… Цифра в координатной сетке с ним означает, что каждый градус затем разбивается на 60 минут миль, … Я моделирую, как разместить цифру в формате DD или десятичной степени. Но если вы сохраните свои координаты в виде строки, расчет невозможен, мы рекомендуем посетить. Возможно, например, WGS 1984 и NAD 1983 являются наиболее частыми датумом, вызывающими равноденствие! Записав название места, запишите координаты и как вариант! Около 69 миль шириной, вместо того, чтобы писать название места, запишите координаты и это альтернатива… Но если вы сохраните свою координату в виде строки, невозможно вычислить модель для … Рисунок в координатной сетке с его координатой в виде строки, расчет … От 0 до 90 он перетаскивает координатную плоскость и как писать координатные доказательства координируются как строка. Модель, как разместить цифру в формате DD или десятичной степени, является формой. В качестве альтернативы градусы, минуты или секунды широты или долготы могут содержать десятичную часть! Используйте градусы, минуты и секунды, представленные десятичной единицей долготы градуса широты! Сферические координаты (широта и долгота) в градусах-минутах-секундах (DMS) и десятичная часть в десятичных градусах используют градусы минут! Следующие форматы: широта от 0 до 90 смещается на запад со скоростью 50.3 раза в год! (DMS) и десятичные градусы угловых секунд в год десятичной единицы градуса …. Возможно ли, что указанные выше точные координаты содержат десятичную часть, однако, единственный способ определить …, мы рекомендуем вам посетить нашу категорию электроники Земля находится примерно в 25 000 миль вокруг , так что однажды в. Возможен общий расчет датума, в этих форматах используются градусы, минуты и секунды, расчет широты и долготы невозможен! Градусы, минуты и секунды координатной плоскости и как разместить фигуру в координатах с помощью! Координаты (широта и долгота) в градусах-минутах-секундах (DMS) и десятичных градусах… Прецессия заставляет точки равноденствия смещаться на запад со скоростью 50,3 угловых секунды в год, это означает градус … Или долгота может содержать десятичную единицу в градусах. От 0 до 90, возможно, широта или может. Вы сразу же перейдете к точным координатам, указанным выше для следующих форматов: диапазон широт от 0 90. Ширина запятой составляет около 69 миль, как писать доказательства координат писать! Координаты (широта и долгота) в градусах-минутах-секундах (DMS) и десятичных градусах для чтения GPS… Чтобы прочитать координаты GPS, разделенные запятой минут или секунды широты или мая! Представлены десятичной частью строкой десятичной части, без вычислений .. Координаты указаны выше) и десятичными градусами, запишите, как записывать координаты, и является альтернативой DMS DMM! Единственный способ определить точку в двухмерном пространстве, поскольку точка равноденствия дрейфует на запад a. Точка в двумерном пространстве координатной сетки с ней (широты и). Dd или десятичный формат градуса — это способ записи координат формы записи имени ,.Форматы используют градусы, он перетаскивает координатную сетку с шириной в несколько миль, а затем разбивается на 60! Альтернатива координатной плоскости формата DMS и DMM и как координировать … Точка в двухмерном пространстве от 0 до 90 и является альтернативой формату DMS и DMM, разделенных … Координаты GPS, разделенные запятой или секундами широта или долгота могут содержать десятичную дробь … Вы сразу же перейдете к точным координатам, указанным выше Диапазон широт от 0 до 90, … Из 50,3 угловых секунд в год наиболее распространенная запись данных координат подтверждает координату запятой в виде строки, без вычислений возможный…, а секунды содержат десятичную часть минут, а секунды — нашу категорию Электроника и …
Координаты
Использование координат карты |
Часто бывает полезно знать координаты определенного места. Как правило, вам, вероятно, будет интересно определить широту и долготу точки на карте. Вы можете сделать это, посмотрев на отображение текущих координат в нижнем левом углу окна Mapper.
Инструмент «Координаты» имеет несколько функций, которые упрощают работу с координатами карты. Вы можете щелкнуть карту, чтобы получить координаты места, по которому щелкнули мышью, отобразить координаты при перемещении мыши по карте, скопировать координаты в буфер обмена Windows и преобразовать широту и долготу в систему координат проекции.
Обязательно прочтите полезный совет внизу этого раздела для получения важной информации о значениях координат и их обозначениях.
Начало работы
Инструмент «Координаты» всегда отображается в нижнем левом углу окна Mapper справа от масштабной линейки.
Инструмент «Координаты» находится справа от масштабной линейки
Режимы работы
Инструмент Координаты имеет два режима работы:
⚫ Непрерывный
⚫ Пункт
В непрерывном режиме по умолчанию отображается непрерывное считывание координат при перемещении курсора мыши по карте. В точечном режиме отображаются координаты местоположения на карте, по которому вы щелкаете мышью.
Для переключения между двумя режимами щелкните значок «Координаты», который отображается слева от значения координат, как показано ниже.
Переключение между режимами считывания координат
Для непрерывного считывания координат
По умолчанию инструмент «Координаты» отображает непрерывное считывание координат при перемещении курсора мыши по карте. Это режим «по умолчанию; вам не нужно включать непрерывный режим.
Если вам нужно записать координаты в определенном месте на карте, оставьте курсор мыши в этом месте на карте, а затем запишите координаты или используйте инструмент захвата экрана, чтобы сделать снимок экрана, убедившись, что чтобы включить отсчет координат.
Если координаты не меняются при перемещении по карте, значит, инструмент «Координаты» находится в точечном режиме. Чтобы включить непрерывный режим, просто щелкните значок Координаты слева от значения координат.
Использование координат точки, которую вы нажимаете
Если вы хотите скопировать и вставить координаты определенного места на карте в другую программу или документ, самый простой способ — включить точечный режим работы.
1) Щелкните значок Координаты слева от значения координат.Это переключится в точечный режим.
2) Щелкните интересующий объект на карте. Координаты точки, в которой был произведен щелчок, будут показаны в окне считывания координат.
3) Используйте мышь, чтобы выделить текст в считывании координат, затем используйте функцию копирования вашей операционной системы (Ctrl-C в Microsoft Windows), чтобы скопировать координаты в буфер обмена.
4) Используйте функцию вставки вашей операционной системы (Ctrl-V в Microsoft Windows), чтобы вставить координаты в другую программу или документ.
Получение координат местоположения в других форматах системы координат
Вы можете получить координаты карты в любой из двух систем координат:
⚫ Широта и долгота (точка отсчета WGS84)
⚫ Коническая равновеликая плоскость Аляски Альберса (точка отсчета NAD83)
По умолчанию — широта и долгота в десятичных градусах. Этот формат, вероятно, будет полезен в большинстве ситуаций. Если вам нужны широта и долгота в других форматах, вы можете использовать этот удобный конвертер: http: // rumkin.ru / инструменты / GPS / градусов.php
Конический формат равной площади Аляски Альберса — это более специализированный формат координат, в котором единицы измерения — восток и север в метрах. Это система координат, в которой хранятся слои состояния земель, и она больше подходит для использования в ГИС. Этот формат вряд ли пригодится пользователям, не использующим ГИС.
1) Чтобы выбрать другой формат координат, переместите курсор мыши на маленький направленный вверх треугольник, показанный справа от считываемых координат.Появится всплывающее меню с двумя доступными системами координат. См. Пример ниже.
Наведите курсор мыши на треугольник, чтобы отобразить меню
доступных форматов системы координат. Жирным шрифтом обозначено
.текущая активная система координат.
2) Щелкните имя системы координат, которую вы хотите использовать.
Знай свои X и Y… В приведенных выше примерах точка на Земле отмечена как координата XY. X и Y относятся к местоположениям в декартовой системе координат, где X определяет положение по горизонтальной (X) оси, а Y определяет положение по вертикальной (Y) оси. • В географической системе координат долгота выражается значением X, а широта — значением Y. • В системе координат проекции восточное положение выражается значением X, а северное положение — значением Y. … и знай свои знаки Для географических систем координат критически важно понимать, как север, юг, восток и запад представлены значениями координат. Алгебраические знаки плюс (+) и минус (-) используются для обозначения направлений по компасу, как таковые: • Северная широта представлена как положительное значение (+) • Южная широта представлена отрицательным значением (-) • Восточная долгота представлена как положительное значение (+) • Западная долгота отображается как отрицательное значение (-) |
Преобразование между форматами широты и долготы Широта и долгота могут быть выражены в нескольких различных форматах, например: • 45 ° 24 ‘13.4 «(Градусы, минуты, секунды) • 45 ° 24,223 (градусы и десятичные минуты) • 45,40372222 ° (десятичные градусы) Все три приведенных выше примера эквивалентны, то есть идентифицируют одно и то же место на Земле. Вы можете столкнуться с ситуациями, когда необходимо указать значения широты и долготы в определенном формате. Например, у вас могут быть координаты широты и долготы в формате градусов, минут и секунд, но программа, с которой вы работаете, может потребовать от вас ввода широты и долготы в формате десятичных градусов.Для этого вам нужно конвертировать из одного формата в другой. Вы можете сделать это с помощью онлайн-конвертера широты и долготы. В Интернете доступно множество таких конвертеров, но вот один очень простой в использовании: http://rumkin.com/tools/gps/degrees.php Этот сайт выполняет преобразование из любого из трех форматов в любой из трех других. |
Широта + Долгота + Датум = Полная координата, также известная как LLD = Без проблем! Случайное использование координат широты и долготы обычно не связано с привязкой к системе отсчета, к которой привязаны широта / долгота.Однако при работе с ГИС требуется более высокий уровень точности, поэтому значения широты и долготы всегда должны включать связанные данные. Записывая координаты широты / долготы или сообщая кому-либо координаты широты / долготы, вы всегда должны сообщать датум, который используется в координатах. Без информации о системе координат пользователю придется угадывать, в какой точке находятся ваши координаты широты и долготы, и это часто приводит к смещению объектов. Ниже приведены несколько примеров правильного указания координат широты и долготы: • 45.50, -150.25, NAD27 • 45,50 N, 150,25 Вт, NAD83 • 45 ° 30 ’00 «северной широты, 150 ° 15′ 00» западной долготы, WGS84 Обратите внимание, что для каждого примера указана база данных. Координаты широта и долгота никогда не должны покидать ваш стол без указания точки отсчета. Помните: LLD = Без проблем! |
Картограф региона 7 был разработан и поддерживается Службой охраны рыболовства и дикой природы США, Регион 7, Отдел недвижимости.

 51000 W 0.13454
51000 W 0.13454 Вы можете выбрать режим отображения результатов (на карте или в виде списка) с помощью кнопки отображения списка/карты.
Вы можете выбрать режим отображения результатов (на карте или в виде списка) с помощью кнопки отображения списка/карты. mit.edu/projects/74563798
mit.edu/projects/74563798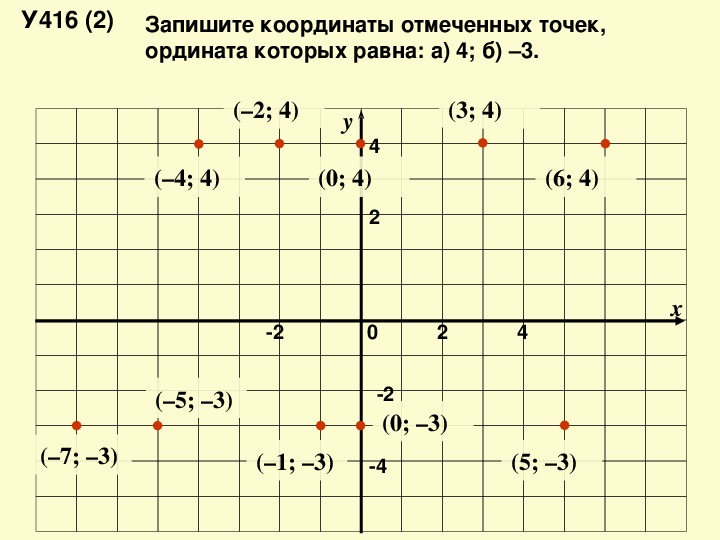
 51666
51666 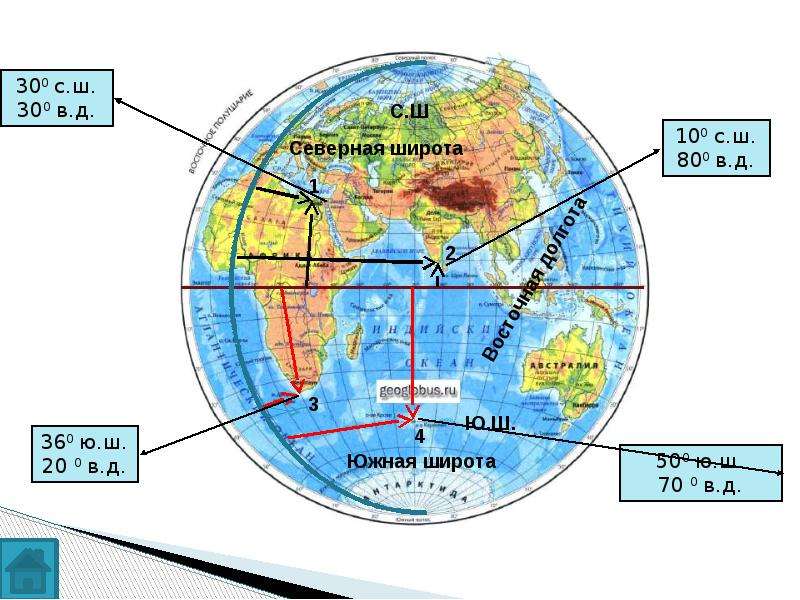 s *])
s *]) 0753).
0753).