Компоненты уравнений: Урок 3. решение уравнений с неизвестным уменьшаемым. решение уравнений с неизвестным вычитаемым — Математика — 3 класс
Урок 3. решение уравнений с неизвестным уменьшаемым. решение уравнений с неизвестным вычитаемым — Математика — 3 класс
Математика, 3 класс
Урок № 3.Решение уравнений с неизвестным уменьшаемым.
Решение уравнений с неизвестным вычитаемым
Перечень вопросов, рассматриваемых в теме:
— Что такое уравнение?
— Как найти неизвестное уменьшаемое?
— Как найти неизвестное вычитаемое?
Глоссарий по теме:
Уравнение – равенство с неизвестным.
Уменьшаемое – компонент вычитания. Число, из которого производят вычитание.
Вычитаемое – компонент вычитания. Число, с помощью которого вычитают.
Разность – результат вычитания.
Основная и дополнительная литература по теме урока:
- Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 8-9.
- Моро М. И.
 , Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 7.
, Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 7. - М. И. Моро, С. И. Волкова. Для тех, кто любит математику 3 класс. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 4-6.
Теоретический материал для самостоятельного изучения
Рассмотрим группы уравнений. Чем они отличаются?
В первой группе записана сумма чисел. Неизвестный компонент в уравнениях – слагаемое.
Вспомним: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. В первом уравнение х = 29; во втором – х = 23.
Во второй группе уравнений записана разность чисел. Компоненты вычитания: уменьшаемое, вычитаемое. Результат вычитания – разность. Неизвестным в уравнениях может быть уменьшаемое или вычитаемое.
Рассмотрим рисунок и составим равенства
8 — 6 = 2 2 + 6 = 8 8 — 2 = 6
Вывод: если к разности прибавить вычитаемое, то получим уменьшаемое.
Это правило позволит решать уравнения, в которых неизвестное число – уменьшаемое.
Вывод: если из уменьшаемого вычесть разность, то получим вычитаемое.
Это правило позволит решать уравнения, в которых неизвестное число – вычитаемое.
При решении любого уравнения обязательно пользуемся алгоритмом решения уравнения.
Алгоритм:
- Прочитать уравнение и определить компоненты действий;
- Определить неизвестный компонент;
- Вспомнить правило для его нахождения;
- Применить это правило;
- Выполнить вычисления;
- Записать ответ;
- Выполнить проверку правильности решения.
Применим знания в решении уравнений.
Х – 36 = 40
В уравнение неизвестно уменьшаемое. Вспоминаем правило: чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое. Применяем правило и вычисляем.
Х = 40 + 36
Х = 76
Необходимо выполнить проверку.
76 – 36 = 40
Производим вычисления в левой части равенства.
40 = 40
Уравнение решено верно.
Решим следующее уравнение.
82 – х = 5
В уравнение неизвестно вычитаемое. Вспоминаем правило для его нахождения: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Применяем правило и производим вычисление.
Х = 82 – 5
Х = 77
Выполняем проверку.
82 – 77 = 5
5 = 5
Выполним тренировочные задания.
1. Выберите значения х, которые получатся при решении уравнения:
Х — 28 = 40
Х = 16;
Х = 68;
Х = 12.
Правильный ответ:
Х = 68.
2. Образуйте пары: компоненты вычитания – их названия. Соедините линиями.
Правильный ответ:
Общие сведения об уравнениях
Уравнения — одна из сложных тем для усвоения, но при этом они являются достаточно мощным инструментом для решения большинства задач.
С помощью уравнений описываются различные процессы, протекающие в природе. Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
Уравнения широко применяются в других науках: в экономике, физике, биологии и химии.
В данном уроке мы попробуем понять суть простейших уравнений, научимся выражать неизвестные и решим несколько уравнений. По мере усвоения новых материалов, уравнения будут усложняться, поэтому понять основы очень важно.
Что такое уравнение?
Уравнение — это равенство, содержащее в себе переменную, значение которой требуется найти. Это значение должно быть таким, чтобы при его подстановке в исходное уравнение получалось верное числовое равенство.
Например выражение 3 + 2 = 5 является равенством. При вычислении левой части получается верное числовое равенство 5 = 5.
А вот равенство 3 + x = 5 является уравнением, поскольку содержит в себе переменную x, значение которой можно найти. Значение должно быть таким, чтобы при подстановке этого значения в исходное уравнение, получилось верное числовое равенство.
Другими словами, мы должны найти такое значение, при котором знак равенства оправдал бы свое местоположение — левая часть должна быть равна правой части.
Уравнение 3 + x = 5 является элементарным. Значение переменной x равно числу 2. При любом другом значении равенство соблюдáться не будет
Говорят, что число 2 является корнем или решением уравнения 3 + x = 5
Корень или решение уравнения — это значение переменной, при котором уравнение обращается в верное числовое равенство.
Корней может быть несколько или не быть совсем. Решить уравнение означает найти его корни или доказать, что корней нет.
Переменную, входящую в уравнение, иначе называют неизвестным. Вы вправе называть как вам удобнее. Это синонимы.
Примечание. Словосочетание «решить уравнение» говорит самó за себя. Решить уравнение означает «уравнять» равенство — сделать его сбалансированным, чтобы левая часть равнялась правой части.
Выразить одно через другое
Изучение уравнений по традиции начинается с того, чтобы научиться выражать одно число, входящее в равенство, через ряд других. Давайте не будем нарушать эту традицию и поступим также.
Давайте не будем нарушать эту традицию и поступим также.
8 + 2
Данное выражение является суммой чисел 8 и 2. Значение данного выражения равно 10
8 + 2 = 10
Получили равенство. Теперь можно выразить любое число из этого равенства через другие числа, входящие в это же равенство. К примеру, выразим число 2.
Чтобы выразить число 2, нужно задать вопрос: «что нужно сделать с числами 10 и 8, чтобы получить число 2». Понятно, что для получения числа 2, нужно из числа 10 вычесть число 8.
Так и делаем. Записываем число 2 и через знак равенства говорим, что для получения этого числа 2 мы из числа 10 вычли число 8:
2 = 10 − 8
Мы выразили число 2 из равенства 8 + 2 = 10. Как видно из примера, ничего сложного в этом нет.
При решении уравнений, в частности при выражении одного числа через другие, знак равенства удобно заменять на слово «есть». Делать это нужно мысленно, а не в самом выражении.
Так, выражая число 2 из равенства 8 + 2 = 10 мы получили равенство 2 = 10 − 8. Данное равенство можно прочесть так:
2 есть 10 − 8
То есть знак = заменен на слово «есть». Более того, равенство 2 = 10 − 8 можно перевести с математического языка на полноценный человеческий язык. Тогда его можно будет прочитать следующим образом:
Число 2
или
Число 2 есть разница между числом 10 и числом 8.
Но мы ограничимся лишь заменой знака равенства на слово «есть», и то будем делать это не всегда. Элементарные выражения можно понимать и без перевода математического языка на язык человеческий.
Вернём получившееся равенство 2 = 10 − 8 в первоначальное состояние:
8 + 2 = 10
Выразим в этот раз число 8. Что нужно сделать с остальными числами, чтобы получить число 8? Верно, нужно из числа 10 вычесть число 2
8 = 10 − 2
Вернем получившееся равенство 8 = 10 − 2 в первоначальное состояние:
8 + 2 = 10
В этот раз выразим число 10.
10 = 8 + 2
Пример 2. Рассмотрим равенство 8 − 2 = 6
Выразим из этого равенства число 8. Чтобы выразить число 8 остальные два числа нужно сложить:
8 = 6 + 2
Вернем получившееся равенство 8 = 6 + 2 в первоначальное состояние:
8 − 2 = 6
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно из 8 вычесть 6
2 = 8 − 6
Пример 3. Рассмотрим равенство 3 × 2 = 6
Выразим число 3. Чтобы выразить число 3, нужно 6 разделить 2
Вернем получившееся равенство в первоначальное состояние:
3 × 2 = 6
Выразим из этого равенства число 2. Чтобы выразить число 2, нужно 6 разделить 3
Пример 4. Рассмотрим равенство
Выразим из этого равенства число 15. Чтобы выразить число 15, нужно перемножить числа 3 и 5
15 = 3 × 5
Вернем получившееся равенство 15 = 3 × 5 в первоначальное состояние:
Выразим из этого равенства число 5. Чтобы выразить число 5, нужно 15 разделить 3
Чтобы выразить число 5, нужно 15 разделить 3
Правила нахождения неизвестных
Рассмотрим несколько правил нахождения неизвестных. Возможно, они вам знакомы, но не мешает повторить их ещё раз. В дальнейшем их можно будет забыть, поскольку мы научимся решать уравнения, не применяя эти правила.
Вернемся к первому примеру, который мы рассматривали в предыдущей теме, где в равенстве 8 + 2 = 10 требовалось выразить число 2.
В равенстве 8 + 2 = 10 числа 8 и 2 являются слагаемыми, а число 10 — суммой.
Чтобы выразить число 2, мы поступили следующим образом:
2 = 10 − 8
То есть из суммы 10 вычли слагаемое 8.
Теперь представим, что в равенстве 8 + 2 = 10 вместо числа 2 располагается переменная x
8 + x = 10
В этом случае равенство 8 + 2 = 10 превращается в уравнение 8 + x = 10, а переменная x берет на себя роль так называемого неизвестного слагаемого
Наша задача найти это неизвестное слагаемое, то есть решить уравнение 8 + x = 10. Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Для нахождения неизвестного слагаемого предусмотрено следующее правило:
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Что мы в принципе и сделали, когда выражали двойку в равенстве 8 + 2 = 10. Чтобы выразить слагаемое 2, мы из суммы 10 вычли другое слагаемое 8
2 = 10 − 8
А сейчас, чтобы найти неизвестное слагаемое x, мы должны из суммы 10 вычесть известное слагаемое 8:
x = 10 − 8
Если вычислить правую часть получившегося равенства, то можно узнать чему равна переменная x
x = 2
Мы решили уравнение. Значение переменной x равно 2. Для проверки значение переменной x отправляют в исходное уравнение 8 + x = 10 и подставляют вместо x. Так желательно поступать с любым решённым уравнением, поскольку нельзя быть точно уверенным, что уравнение решено правильно:
В результате получается верное числовое равенство. Значит уравнение решено правильно.
Значит уравнение решено правильно.
Это же правило действовало бы в случае, если неизвестным слагаемым было бы первое число 8.
x + 2 = 10
В этом уравнении x — это неизвестное слагаемое, 2 — известное слагаемое, 10 — сумма. Чтобы найти неизвестное слагаемое x, нужно из суммы 10 вычесть известное слагаемое 2
x = 10 − 2
x = 8
Вернемся ко второму примеру из предыдущей темы, где в равенстве 8 − 2 = 6 требовалось выразить число 8.
В равенстве 8 − 2 = 6 число 8 это уменьшаемое, число 2 — вычитаемое, число 6 — разность
Чтобы выразить число 8, мы поступили следующим образом:
8 = 6 + 2
То есть сложили разность 6 и вычитаемое 2.
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 8 располагается переменная x
x − 2 = 6
В этом случае переменная x берет на себя роль так называемого неизвестного уменьшаемого
Для нахождения неизвестного уменьшаемого предусмотрено следующее правило:
Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое.
Что мы и сделали, когда выражали число 8 в равенстве 8 − 2 = 6. Чтобы выразить уменьшаемое 8, мы к разности 6 прибавили вычитаемое 2.
А сейчас, чтобы найти неизвестное уменьшаемое x, мы должны к разности 6 прибавить вычитаемое 2
x = 6 + 2
Если вычислить правую часть, то можно узнать чему равна переменная x
x = 8
Теперь представим, что в равенстве 8 − 2 = 6 вместо числа 2 располагается переменная x
8 − x = 6
В этом случае переменная x берет на себя роль неизвестного вычитаемого
Для нахождения неизвестного вычитаемого предусмотрено следующее правило:
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Что мы и сделали, когда выражали число 2 в равенстве 8 − 2 = 6. Чтобы выразить число 2, мы из уменьшаемого 8 вычли разность 6.
А сейчас, чтобы найти неизвестное вычитаемое x, нужно опять же из уменьшаемого 8 вычесть разность 6
x = 8 − 6
Вычисляем правую часть и находим значение x
x = 2
Вернемся к третьему примеру из предыдущей темы, где в равенстве 3 × 2 = 6 мы пробовали выразить число 3.
В равенстве 3 × 2 = 6 число 3 — это множимое, число 2 — множитель, число 6 — произведение
Чтобы выразить число 3 мы поступили следующим образом:
То есть разделили произведение 6 на множитель 2.
Теперь представим, что в равенстве 3 × 2 = 6 вместо числа 3 располагается переменная x
x × 2 = 6
В этом случае переменная x берет на себя роль неизвестного множимого.
Для нахождения неизвестного множимого предусмотрено следующее правило:
Чтобы найти неизвестное множимое, нужно произведение разделить на множитель.
Что мы и сделали, когда выражали число 3 из равенства 3 × 2 = 6. Произведение 6 мы разделили на множитель 2.
А сейчас для нахождения неизвестного множимого x, нужно произведение 6 разделить на множитель 2.
Вычисление правой части позволяет нам найти значение переменной x
x = 3
Это же правило применимо в случае, если переменная x располагается вместо множителя, а не множимого. Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x.
Представим, что в равенстве 3 × 2 = 6 вместо числа 2 располагается переменная x.
В этом случае переменная x берет на себя роль неизвестного множителя. Для нахождения неизвестного множителя предусмотрено такое же, что и для нахождения неизвестного множимого, а именно деление произведения на известный множитель:
Чтобы найти неизвестный множитель, нужно произведение разделить на множимое.
Что мы и сделали, когда выражали число 2 из равенства 3 × 2 = 6. Тогда для получения числа 2 мы разделили произведение 6 на множимое 3.
А сейчас для нахождения неизвестного множителя x мы разделили произведение 6 на множимое 3.
Вычисление правой части равенства позволяет узнать чему равно x
x = 2
Множимое и множитель вместе называют сомножителями. Поскольку правила нахождения множимого и множителя совпадают, мы можем сформулировать общее правило нахождения неизвестного сомножителя:
Чтобы найти неизвестный сомножитель, нужно произведение разделить на известный сомножитель.
Например, решим уравнение 9 × x = 18. Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 18 разделить на известный сомножитель 9
Отсюда .
Решим уравнение x × 3 = 27. Переменная x является неизвестным сомножителем. Чтобы найти этот неизвестный сомножитель, нужно произведение 27 разделить на известный сомножитель 3
Отсюда .
Вернемся к четвертому примеру из предыдущей темы, где в равенстве требовалось выразить число 15. В этом равенстве число 15 — это делимое, число 5 — делитель, число 3 — частное.
Чтобы выразить число 15 мы поступили следующим образом:
15 = 3 × 5
То есть умножили частное 3 на делитель 5.
Теперь представим, что в равенстве вместо числа 15 располагается переменная x
В этом случае переменная x берет на себя роль неизвестного делимого.
Для нахождения неизвестного делимого предусмотрено следующее правило:
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
Что мы и сделали, когда выражали число 15 из равенства . Чтобы выразить число 15, мы умножили частное 3 на делитель 5.
А сейчас, чтобы найти неизвестное делимое x, нужно частное 3 умножить на делитель 5
x = 3 × 5
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x.
x = 15
Теперь представим, что в равенстве вместо числа 5 располагается переменная x.
В этом случае переменная x берет на себя роль неизвестного делителя.
Для нахождения неизвестного делителя предусмотрено следующее правило:
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
Что мы и сделали, когда выражали число 5 из равенства . Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
Чтобы выразить число 5, мы разделили делимое 15 на частное 3.
А сейчас, чтобы найти неизвестный делитель x, нужно делимое 15 разделить на частное 3
Вычислим правую часть получившегося равенства. Так мы узнаем чему равна переменная x.
x = 5
Итак, для нахождения неизвестных мы изучили следующие правила:
- Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое;
- Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое;
- Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность;
- Чтобы найти неизвестное множимое, нужно произведение разделить на множитель;
- Чтобы найти неизвестный множитель, нужно произведение разделить на множимое;
- Чтобы найти неизвестное делимое, нужно частное умножить на делитель;
- Чтобы найти неизвестный делитель, нужно делимое разделить на частное.

Компоненты
Компонентами мы будем называть числа и переменные, входящие в равенство
Так, компонентами сложения являются слагаемые и сумма
Компонентами вычитания являются уменьшаемое, вычитаемое и разность
Компонентами умножения являются множимое, множитель и произведение
Компонентами деления являются делимое, делитель и частное
В зависимости от того, с какими компонентами мы будем иметь дело, будут применяться соответствующие правила нахождения неизвестных. Эти правила мы изучили в предыдущей теме. При решении уравнений желательно знать эти правило наизусть.
Пример 1. Найти корень уравнения 45 + x = 60
45 — слагаемое, x — неизвестное слагаемое, 60 — сумма. Имеем дело с компонентами сложения. Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
Вспоминаем, что для нахождения неизвестного слагаемого, нужно из суммы вычесть известное слагаемое:
x = 60 − 45
Вычислим правую часть, получим значение x равное 15
x = 15
Значит корень уравнения 45 + x = 60 равен 15.
Чаще всего неизвестное слагаемое необходимо привести к виду при котором его можно было бы выразить.
Пример 2. Решить уравнение
Здесь в отличие от предыдущего примера, неизвестное слагаемое нельзя выразить сразу, поскольку оно содержит коэффициент 2. Наша задача привести это уравнение к виду при котором можно было бы выразить x
В данном примере мы имеем дело с компонентами сложения — слагаемыми и суммой. 2x — это первое слагаемое, 4 — второе слагаемое, 8 — сумма.
При этом слагаемое 2x содержит переменную x. После нахождения значения переменной x слагаемое 2x примет другой вид. Поэтому слагаемое 2x можно полностью принять за неизвестное слагаемое:
Теперь применяем правило нахождения неизвестного слагаемого. Вычитаем из суммы известное слагаемое:
Вычитаем из суммы известное слагаемое:
Вычислим правую часть получившегося уравнения:
Мы получили новое уравнение . Теперь мы имеем дело с компонентами умножения: множимым, множителем и произведением. 2 — множимое, x — множитель, 4 — произведение
При этом переменная x является не просто множителем, а неизвестным множителем
Чтобы найти этот неизвестный множитель, нужно произведение разделить на множимое:
Вычислим правую часть, получим значение переменной x
Для проверки найденный корень отправим в исходное уравнение и подставим вместо x
Получили верное числовое равенство. Значит уравнение решено правильно.
Пример 3. Решить уравнение 3x + 9x + 16x = 56
Cразу выразить неизвестное x нельзя. Сначала нужно привести данное уравнение к виду при котором его можно было бы выразить.
Приведем подобные слагаемые в левой части данного уравнения:
Имеем дело с компонентами умножения. 28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
28 — множимое, x — множитель, 56 — произведение. При этом x является неизвестным множителем. Чтобы найти неизвестный множитель, нужно произведение разделить на множимое:
Отсюда x равен 2
Равносильные уравнения
В предыдущем примере при решении уравнения 3x + 9x + 16x = 56, мы привели подобные слагаемые в левой части уравнения. В результате получили новое уравнение 28x = 56. Старое уравнение 3x + 9x + 16x = 56 и получившееся новое уравнение 28x = 56 называют равносильными уравнениями, поскольку их корни совпадают.
Уравнения называют равносильными, если их корни совпадают.
Проверим это. Для уравнения 3x + 9x + 16x = 56 мы нашли корень равный 2. Подставим этот корень сначала в уравнение 3x + 9x + 16x = 56, а затем в уравнение 28x = 56, которое получилось в результате приведения подобных слагаемых в левой части предыдущего уравнения. Мы должны получить верные числовые равенства
Мы должны получить верные числовые равенства
Согласно порядку действий, в первую очередь выполняется умножение:
Подставим корень 2 во второе уравнение 28x = 56
Видим, что у обоих уравнений корни совпадают. Значит уравнения 3x + 9x + 16x = 56 и 28x = 56 действительно являются равносильными.
Для решения уравнения 3x + 9x + 16x = 56 мы воспользовались одним из тождественных преобразований — приведением подобных слагаемых. Правильное тождественное преобразование уравнения позволило нам получить равносильное уравнение 28x = 56, которое проще решать.
Из тождественных преобразований на данный момент мы умеем только сокращать дроби, приводить подобные слагаемые, выносить общий множитель за скобки, а также раскрывать скобки. Существуют и другие преобразования, которые следует знать. Но для общего представления о тождественных преобразованиях уравнений, изученных нами тем вполне хватает.
Рассмотрим некоторые преобразования, которые позволяют получить равносильное уравнение
Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.
и аналогично:
Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.
Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.
Пример 1. Решить уравнение
Вычтем из обеих частей уравнения число 10
Приведем подобные слагаемые в обеих частях:
Получили уравнение 5x = 10. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 10 разделить на известный сомножитель 5.
Отсюда .
Вернемся к исходному уравнению и подставим вместо x найденное значение 2
Получили верное числовое равенство. Значит уравнение решено правильно.
Значит уравнение решено правильно.
Решая уравнение мы вычли из обеих частей уравнения число 10. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 2
Пример 2. Решить уравнение 4(x + 3) = 16
Раскроем скобки в левой части равенства:
Вычтем из обеих частей уравнения число 12
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 4x, а в правой части число 4
Получили уравнение 4x = 4. Имеем дело с компонентами умножения. Чтобы найти неизвестный сомножитель x, нужно произведение 4 разделить на известный сомножитель 4
Отсюда
Вернемся к исходному уравнению 4(x + 3) = 16 и подставим вместо x найденное значение 1
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение 4(x + 3) = 16 мы вычли из обеих частей уравнения число 12. В результате получили равносильное уравнение 4x = 4. Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
В результате получили равносильное уравнение 4x = 4. Корень этого уравнения, как и уравнения 4(x + 3) = 16 так же равен 1
Пример 3. Решить уравнение
Раскроем скобки в левой части равенства:
Прибавим к обеим частям уравнения число 8
Приведем подобные слагаемые в обеих частях уравнения:
В левой части останется 2x, а в правой части число 9
В получившемся уравнении 2x = 9 выразим неизвестное слагаемое x
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 4,5
Получили верное числовое равенство. Значит уравнение решено правильно.
Решая уравнение мы прибавили к обеим частям уравнения число 8. В результате получили равносильное уравнение . Корень этого уравнения, как и уравнения так же равен 4,5
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.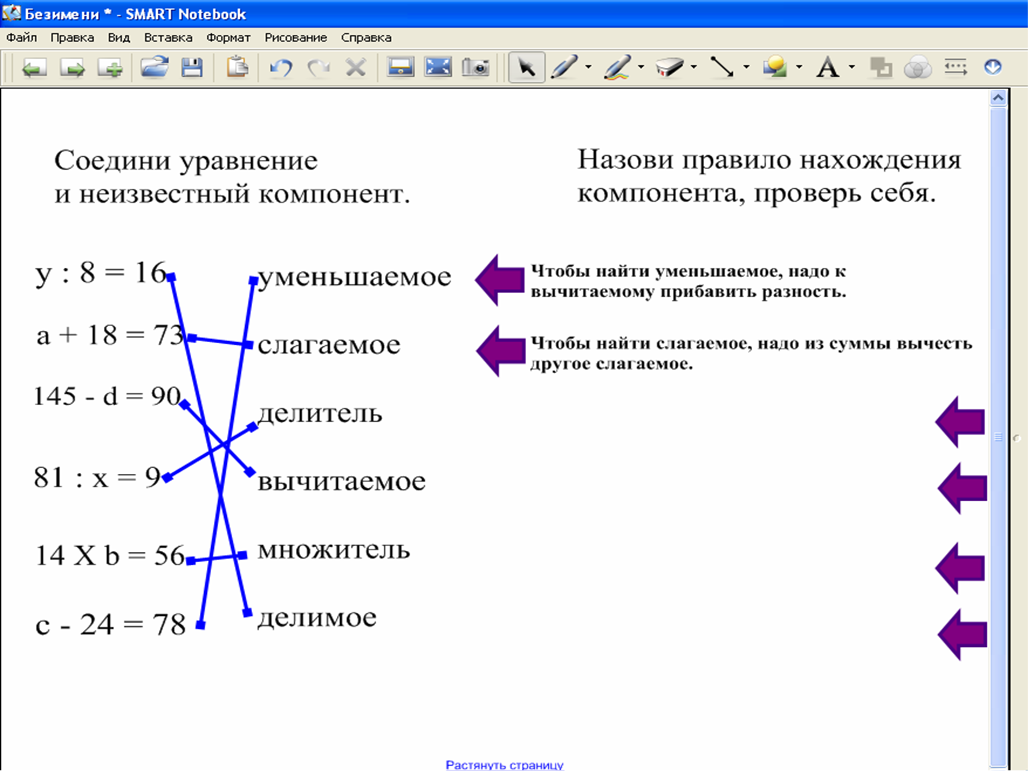
То есть корень уравнения не изменится, если мы перенесем слагаемое из одной части уравнения в другую, изменив его знак. Это свойство является одним из важных и одним из часто используемых при решении уравнений.
Рассмотрим следующее уравнение:
Корень данного уравнения равен 2. Подставим вместо x этот корень и проверим получается ли верное числовое равенство
Получается верное равенство. Значит число 2 действительно является корнем уравнения .
Теперь попробуем поэкспериментировать со слагаемыми этого уравнения, перенося их из одной части в другую, изменяя знаки.
Например, слагаемое 3x располагается в левой части равенства. Перенесём его в правую часть, изменив знак на противоположный:
Получилось уравнение 12 = 9x − 3x. Приведем подобные слагаемые в правой части данного уравнения:
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Найдём этот известный сомножитель:
Отсюда x = 2. Как видим, корень уравнения не изменился. Значит уравнения 12 + 3x = 9x и 12 = 9x − 3x являются равносильными.
На самом деле данное преобразование является упрощенным методом предыдущего преобразования, где к обеим частям уравнения прибавлялось (или вычиталось) одно и то же число.
Мы сказали, что в уравнении 12 + 3x = 9x слагаемое 3x было перенесено в правую часть, изменив знак. В реальности же происходило следующее: из обеих частей уравнения вычли слагаемое 3x
Затем в левой части были приведены подобные слагаемые и получено уравнение 12 = 9x − 3x. Затем опять были приведены подобные слагаемые, но уже в правой части, и получено уравнение 12 = 6x.
Но так называемый «перенос» более удобен для подобных уравнений, поэтому он и получил такое широкое распространение. Решая уравнения, мы часто будем пользоваться именно этим преобразованием.
Равносильными также являются уравнения 12 + 3x = 9x и 3x − 9x = −12. В этот раз в уравнении 12 + 3x = 9x слагаемое 12 было перенесено в правую часть, а слагаемое 9x в левую. Не следует забывать, что знаки этих слагаемых были изменены во время переноса
Следующее правило, которое позволяет получить равносильное уравнение, выглядит следующим образом:
Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному.
Другими словами, корни уравнения не изменятся, если обе его части умножить или разделить на одно и то же число. Это действие часто применяется тогда, когда нужно решить уравнение содержащее дробные выражения.
Сначала рассмотрим примеры, в которых обе части уравнения будут умножаться на одно и то же число.
Пример 1. Решить уравнение
При решении уравнений, содержащих дробные выражения, сначала принято упростить это уравнение.
В данном случае мы имеем дело именно с таким уравнением. В целях упрощения данного уравнения обе его части можно умножить на 8:
Мы помним, что для умножения дроби на число, нужно числитель данной дроби умножить на это число. У нас имеются две дроби и каждая из них умножается на число 8. Наша задача умножить числители дробей на это число 8
Теперь происходит самое интересное. В числителях и знаменателях обеих дробей содержится множитель 8, который можно сократить на 8. Это позволит нам избавиться от дробного выражения:
В результате останется простейшее уравнение
Ну и нетрудно догадаться, что корень этого уравнения равен 4
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получается верное числовое равенство. Значит уравнение решено правильно.
При решении данного уравнения мы умножили обе его части на 8. В результате получили уравнение . Корень этого уравнения, как и уравнения равен 4. Значит эти уравнения равносильны.
Значит эти уравнения равносильны.
Множитель на который умножаются обе части уравнения принято записывать перед частью уравнения, а не после неё. Так, решая уравнение , мы умножили обе части на множитель 8 и получили следующую запись:
От этого корень уравнения не изменился, но если бы мы сделали это находясь в школе, то нам сделали бы замечание, поскольку в алгебре множитель принято записывать перед тем выражением, с которым он перемножается. Поэтому умножение обеих частей уравнения на множитель 8 желательно переписать следующим образом:
Пример 2. Решить уравнение
Умнóжим обе части уравнения на 15
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5
Перепишем то, что у нас осталось:
Раскроем скобки в правой части уравнения:
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях, получим
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 5
Получается верное числовое равенство. Значит уравнение решено правильно. При решении данного уравнения мы умножили обе го части на 15. Далее выполняя тождественные преобразования, мы получили уравнение 10 = 2x. Корень этого уравнения, как и уравнения равен 5. Значит эти уравнения равносильны.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на 3
В левой части можно сократить две тройки, а правая часть будет равна 18
Останется простейшее уравнение . Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:
Отсюда
Вернемся к исходному уравнению и подставим вместо x найденное значение 9
Получается верное числовое равенство. Значит уравнение решено правильно.
Значит уравнение решено правильно.
Пример 4. Решить уравнение
Умнóжим обе части уравнения на 6
В левой части уравнения раскроем скобки. В правой части множитель 6 можно поднять в числитель:
Сократим в обеих частях уравнениях то, что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки в обеих частях уравнения:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное x, сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой:
Приведем подобные слагаемые в обеих частях:
Теперь найдем значение переменной x. Для этого разделим произведение 28 на известный сомножитель 7
Отсюда x = 4.
Вернемся к исходному уравнению и подставим вместо x найденное значение 4
Получилось верное числовое равенство. Значит уравнение решено правильно.
Пример 5. Решить уравнение
Раскроем скобки в обеих частях уравнения там, где это можно:
Умнóжим обе части уравнения на 15
Раскроем скобки в обеих частях уравнения:
Сократим в обеих частях уравнения, то что можно сократить:
Перепишем то, что у нас осталось:
Раскроем скобки там, где это можно:
Воспользуемся переносом слагаемых. Слагаемые, содержащие неизвестное, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Не забываем, что во время переноса, слагаемые меняют свои знаки на противоположные:
Приведем подобные слагаемые в обеих частях уравнения:
Найдём значение x
В получившемся ответе можно выделить целую часть:
Вернемся к исходному уравнению и подставим вместо x найденное значение
Получается довольно громоздкое выражение. Воспользуемся переменными. Левую часть равенства занесем в переменную A, а правую часть равенства в переменную B
Левую часть равенства занесем в переменную A, а правую часть равенства в переменную B
Наша задача состоит в том, чтобы убедиться равна ли левая часть правой. Другими словами, доказать равенство A = B
Найдем значение выражения, находящегося в переменной А.
Значение переменной А равно . Теперь найдем значение переменной B. То есть значение правой части нашего равенства. Если и оно равно , то уравнение будет решено верно
Видим, что значение переменной B, как и значение переменной A равно . Это значит, что левая часть равна правой части. Отсюда делаем вывод, что уравнение решено правильно.
Теперь попробуем не умножать обе части уравнения на одно и то же число, а делить.
Рассмотрим уравнение 30x + 14x + 14 = 70x − 40x + 42. Решим его обычным методом: слагаемые, содержащие неизвестные, сгруппируем в левой части уравнения, а слагаемые, свободные от неизвестных — в правой. Далее выполняя известные тождественные преобразования, найдем значение x
Далее выполняя известные тождественные преобразования, найдем значение x
Подставим найденное значение 2 вместо x в исходное уравнение:
Теперь попробуем разделить все слагаемые уравнения 30x + 14x + 14 = 70x − 40x + 42 на какое-нибудь число. Замечаем, что все слагаемые этого уравнения имеют общий множитель 2. На него и разделим каждое слагаемое:
Выполним сокращение в каждом слагаемом:
Перепишем то, что у нас осталось:
Решим это уравнение, пользуясь известными тождественными преобразованиями:
Получили корень 2. Значит уравнения 15x + 7x + 7 = 35x − 20x + 21 и 30x + 14x + 14 = 70x − 40x + 42 равносильны.
Деление обеих частей уравнения на одно и то же число позволяет освобождать неизвестное от коэффициента. В предыдущем примере когда мы получили уравнение 7x = 14, нам потребовалось разделить произведение 14 на известный сомножитель 7. Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Но если бы мы в левой части освободили неизвестное от коэффициента 7, корень нашелся бы сразу. Для этого достаточно было разделить обе части на 7
Этим методом мы тоже будем пользоваться часто.
Умножение на минус единицу
Если обе части уравнения умножить на минус единицу, то получится уравнение равносильное данному.
Это правило следует из того, что от умножения (или деления) обеих частей уравнения на одно и то же число, корень данного уравнения не меняется. А значит корень не поменяется если обе его части умножить на −1.
Данное правило позволяет поменять знаки всех компонентов, входящих в уравнение. Для чего это нужно? Опять же, чтобы получить равносильное уравнение, которое проще решать.
Рассмотрим уравнение . Чему равен корень этого уравнения?
Прибавим к обеим частям уравнения число 5
Приведем подобные слагаемые:
А теперь вспомним про коэффициент буквенного выражения. Что же представляет собой левая часть уравнения . Это есть произведение минус единицы и переменной x
Это есть произведение минус единицы и переменной x
То есть минус, стоящий перед переменной x, относится не к самой переменной x, а к единице, которую мы не видим, поскольку коэффициент 1 принято не записывать. Это означает, что уравнение на самом деле выглядит следующим образом:
Имеем дело с компонентами умножения. Чтобы найти х, нужно произведение −5 разделить на известный сомножитель −1.
или разделить обе части уравнения на −1, что еще проще
Итак, корень уравнения равен 5. Для проверки подставим его в исходное уравнение. Не забываем, что в исходном уравнении минус стоящий перед переменной x относится к невидимой единице
Получилось верное числовое равенство. Значит уравнение решено верно.
Теперь попробуем умножить обе части уравнения на минус единицу:
После раскрытия скобок в левой части образуется выражение , а правая часть будет равна 10
Корень этого уравнения, как и уравнения равен 5
Значит уравнения и равносильны.
Пример 2. Решить уравнение
В данном уравнении все компоненты являются отрицательными. С положительными компонентами работать удобнее, чем с отрицательными, поэтому поменяем знаки всех компонентов, входящих в уравнение . Для этого умнóжим обе части данного уравнения на −1.
Понятно, что от умножения на −1 любое число поменяет свой знак на противоположный. Поэтому саму процедуру умножения на −1 и раскрытие скобок подробно не расписывают, а сразу записывают компоненты уравнения с противоположными знаками.
Так, умножение уравнения на −1 можно записать подробно следующим образом:
либо можно просто поменять знаки всех компонентов:
Получится то же самое, но разница будет в том, что мы сэкономим себе время.
Итак, умножив обе части уравнения на −1, мы получили уравнение . Решим данное уравнение. Из обеих частей вычтем число 4 и разделим обе части на 3
Когда корень найден, переменную обычно записывают в левой части, а её значение в правой, что мы и сделали.
Пример 3. Решить уравнение
Умнóжим обе части уравнения на −1. Тогда все компоненты поменяют свои знаки на противоположные:
Из обеих частей получившегося уравнения вычтем 2x и приведем подобные слагаемые:
Прибавим к обеим частям уравнения единицу и приведем подобные слагаемые:
Приравнивание к нулю
Недавно мы узнали, что если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
А что будет если перенести из одной части в другую не одно слагаемое, а все слагаемые? Верно, в той части откуда забрали все слагаемые останется ноль. Иными словами, не останется ничего.
В качестве примера рассмотрим уравнение . Решим данное уравнение, как обычно — слагаемые, содержащие неизвестные сгруппируем в одной части, а числовые слагаемые, свободные от неизвестных оставим в другой. Далее выполняя известные тождественные преобразования, найдем значение переменной x
Теперь попробуем решить это же уравнение, приравняв все его компоненты к нулю. Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Для этого перенесем все слагаемые из правой части в левую, изменив знаки:
Приведем подобные слагаемые в левой части:
Прибавим к обеим частям 77, и разделим обе части на 7
Альтернатива правилам нахождения неизвестных
Очевидно, что зная о тождественных преобразованиях уравнений, можно не заучивать наизусть правила нахождения неизвестных.
К примеру, для нахождения неизвестного в уравнении мы произведение 10 делили на известный сомножитель 2
Но если в уравнении обе части разделить на 2 корень найдется сразу. В левой части уравнения в числителе множитель 2 и в знаменателе множитель 2 сократятся на 2. А правая часть будет равна 5
Уравнения вида мы решали выражая неизвестное слагаемое:
Но можно воспользоваться тождественными преобразованиями, которые мы сегодня изучили. В уравнении слагаемое 4 можно перенести в правую часть, изменив знак:
Далее разделить обе части на 2
В левой части уравнения сократятся две двойки. Правая часть будет равна 2. Отсюда .
Правая часть будет равна 2. Отсюда .
Либо можно было из обеих частей уравнения вычесть 4. Тогда получилось бы следующее:
В случае с уравнениями вида удобнее делить произведение на известный сомножитель. Сравним оба решения:
Первое решение намного короче и аккуратнее. Второе решение можно значительно укоротить, если выполнить деление в уме.
Тем не менее, необходимо знать оба метода, и только затем использовать тот, который больше нравится.
Когда корней несколько
Уравнение может иметь несколько корней. Например уравнение x(x + 9) = 0 имеет два корня: 0 и −9.
В уравнении x(x + 9) = 0 нужно было найти такое значение x при котором левая часть была бы равна нулю. В левой части этого уравнения содержатся выражения x и (x + 9), которые являются сомножителями. Из законов умножения мы знаем, что произведение равно нулю, если хотя бы один из сомножителей равен нулю (или первый сомножитель или второй).
То есть в уравнении x(x + 9) = 0 равенство будет достигаться, если x будет равен нулю или (x + 9) будет равно нулю.
x = 0 или x + 9 = 0
Приравняв к нулю оба этих выражения, мы сможем найти корни уравнения x(x + 9) = 0. Первый корень, как видно из примера, нашелся сразу. Для нахождения второго корня нужно решить элементарное уравнение x + 9 = 0. Несложно догадаться, что корень этого уравнения равен −9. Проверка показывает, что корень верный:
−9 + 9 = 0
Пример 2. Решить уравнение
Данное уравнение имеет два корня: 1 и 2. Левая часть уравнения является произведение выражений (x − 1) и (x − 2). А произведение равно нулю, если хотя бы один из сомножителей равен нулю (или сомножитель (x − 1) или сомножитель (x − 2)).
Найдем такое x при котором выражения (x − 1) или (x − 2) обращаются в нули:
Подставляем по-очереди найденные значения в исходное уравнение и убеждаемся, что при этих значениях левая часть равняется нулю:
Когда корней бесконечно много
Уравнение может иметь бесконечно много корней. То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
То есть подставив в такое уравнение любое число, мы получим верное числовое равенство.
Пример 1. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения и привести подобные слагаемые, то получится равенство 14 = 14. Это равенство будет получаться при любом x
Пример 2. Решить уравнение
Корнем данного уравнения является любое число. Если раскрыть скобки в левой части уравнения, то получится равенство 10x + 12 = 10x + 12. Это равенство будет получаться при любом x
Когда корней нет
Случается и так, что уравнение вовсе не имеет решений, то есть не имеет корней. Например уравнение не имеет корней, поскольку при любом значении x, левая часть уравнения не будет равна правой части. Например, пусть . Тогда уравнение примет следующий вид
Пусть
Пример 2. Решить уравнение
Решить уравнение
Раскроем скобки в левой части равенства:
Приведем подобные слагаемые:
Видим, что левая часть не равна правой части. И так будет при любом значении y. Например, пусть y = 3.
Буквенные уравнения
Уравнение может содержать не только числа с переменными, но и буквы.
Например, формула нахождения скорости является буквенным уравнением:
Данное уравнение описывает скорость движения тела при равноускоренном движении.
Полезным навыком является умение выразить любой компонент, входящий в буквенное уравнение. Например, чтобы из уравнения определить расстояние, нужно выразить переменную s.
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении левую и правую часть поменяем местами:
У нас получилась формула нахождения расстояния, которую мы изучали ранее.
Попробуем из уравнения определить время. Для этого нужно выразить переменную t.
Умнóжим обе части уравнения на t
В правой части переменные t сократим на t и перепишем то, что у нас осталось:
В получившемся уравнении v × t = s обе части разделим на v
В левой части переменные v сократим на v и перепишем то, что у нас осталось:
У нас получилась формула определения времени, которую мы изучали ранее.
Предположим, что скорость поезда равна 50 км/ч
v = 50 км/ч
А расстояние равно 100 км
s = 100 км
Тогда буквенное уравнение примет следующий вид
Из этого уравнения можно найти время. Для этого нужно суметь выразить переменную t. Можно воспользоваться правилом нахождения неизвестного делителя, разделив делимое на частное и таким образом определить значение переменной t
либо можно воспользоваться тождественными преобразованиями. Сначала умножить обе части уравнения на t
Сначала умножить обе части уравнения на t
Затем разделить обе части на 50
Пример 2. Дано буквенное уравнение . Выразите из данного уравнения x
Вычтем из обеих частей уравнения a
Разделим обе части уравнения на b
Теперь, если нам попадется уравнение вида a + bx = c, то у нас будет готовое решение. Достаточно будет подставить в него нужные значения. Те значения, которые будут подставляться вместо букв a, b, c принято называть параметрами. А уравнения вида a + bx = c называют уравнением с параметрами. В зависимости от параметров, корень будет меняться.
Решим уравнение 2 + 4x = 10. Оно похоже на буквенное уравнение a + bx = c. Вместо того, чтобы выполнять тождественные преобразования, мы можем воспользоваться готовым решением. Сравним оба решения:
Видим, что второе решение намного проще и короче.
Для готового решения необходимо сделать небольшое замечание. Параметр b не должен быть равным нулю (b ≠ 0), поскольку деление на ноль на допускается.
Пример 3. Дано буквенное уравнение . Выразите из данного уравнения x
Раскроем скобки в обеих частях уравнения
Воспользуемся переносом слагаемых. Параметры, содержащие переменную x, сгруппируем в левой части уравнения, а параметры свободные от этой переменной — в правой.
В левой части вынесем за скобки множитель x
Разделим обе части на выражение a − b
В левой части числитель и знаменатель можно сократить на a − b. Так окончательно выразится переменная x
Теперь, если нам попадется уравнение вида a(x − c) = b(x + d), то у нас будет готовое решение. Достаточно будет подставить в него нужные значения.
Допустим нам дано уравнение 4(x − 3) = 2(x + 4). Оно похоже на уравнение a(x − c) = b(x + d). Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Оно похоже на уравнение a(x − c) = b(x + d). Решим его двумя способами: при помощи тождественных преобразований и при помощи готового решения:
Для удобства вытащим из уравнения 4(x − 3) = 2(x + 4) значения параметров a, b, c, d. Это позволит нам не ошибиться при подстановке:
Как и в прошлом примере знаменатель здесь не должен быть равным нулю (a − b ≠ 0). Если нам встретится уравнение вида a(x − c) = b(x + d) в котором параметры a и b будут одинаковыми, мы сможем не решая его сказать, что у данного уравнения корней нет, поскольку разность одинаковых чисел равна нулю.
Например, уравнение 2(x − 3) = 2(x + 4) является уравнением вида a(x − c) = b(x + d). В уравнении 2(x − 3) = 2(x + 4) параметры a и b одинаковые. Если мы начнём его решать, то придем к тому, что левая часть не будет равна правой части:
Пример 4. Дано буквенное уравнение . Выразите из данного уравнения x
Дано буквенное уравнение . Выразите из данного уравнения x
Приведем левую часть уравнения к общему знаменателю:
Умнóжим обе части на a
В левой части x вынесем за скобки
Разделим обе части на выражение (1 − a)
Линейные уравнения с одним неизвестным
Рассмотренные в данном уроке уравнения называют линейными уравнениями первой степени с одним неизвестным.
Если уравнение дано в первой степени, не содержит деления на неизвестное, а также не содержит корней из неизвестного, то его можно назвать линейным. Мы еще не изучали степени и корни, поэтому чтобы не усложнять себе жизнь, слово «линейный» будем понимать как «простой».
Большинство уравнений, решенных в данном уроке, в конечном итоге сводились к простейшему уравнению, в котором нужно было произведение разделить на известный сомножитель. Таковым к примеру является уравнение 2(x + 3) = 16. Давайте решим его.
Давайте решим его.
Раскроем скобки в левой части уравнения, получим 2x + 6 = 16. Перенесем слагаемое 6 в правую часть, изменив знак. Тогда получим 2x = 16 − 6. Вычислим правую часть, получим 2x = 10. Чтобы найти x, разделим произведение 10 на известный сомножитель 2. Отсюда x = 5.
Уравнение 2(x + 3) = 16 является линейным. Оно свелось к уравнению 2x = 10, для нахождения корня которого потребовалось разделить произведение на известный сомножитель. Такое простейшее уравнение называют линейным уравнением первой степени с одним неизвестным в каноническом виде. Слово «канонический» является синонимом слов «простейший» или «нормальный».
Линейное уравнение первой степени с одним неизвестным в каноническом виде называют уравнение вида ax = b.
Полученное нами уравнение 2x = 10 является линейным уравнением первой степени с одним неизвестным в каноническом виде. У этого уравнения первая степень, одно неизвестное, оно не содержит деления на неизвестное и не содержит корней из неизвестного, и представлено оно в каноническом виде, то есть в простейшем виде при котором легко можно определить значение x. Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Вместо параметров a и b в нашем уравнении содержатся числа 2 и 10. Но подобное уравнение может содержать и другие числа: положительные, отрицательные или равные нулю.
Если в линейном уравнении a = 0 и b = 0, то уравнение имеет бесконечно много корней. Действительно, если a равно нулю и b равно нулю, то линейное уравнение ax = b примет вид 0x = 0. При любом значении x левая часть будет равна правой части.
Если в линейном уравнении a = 0 и b ≠ 0, то уравнение корней не имеет. Действительно, если a равно нулю и b равно какому-нибудь числу, не равному нулю, скажем числу 5, то уравнение ax = b примет вид 0x = 5. Левая часть будет равна нулю, а правая часть пяти. А ноль не равен пяти.
Если в линейном уравнении a ≠ 0, и b равно любому числу, то уравнение имеет один корень. Он определяется делением параметра b на параметр a
Действительно, если a равно какому-нибудь числу, не равному нулю, скажем числу 3, и b равно какому-нибудь числу, скажем числу 6, то уравнение примет вид .
Отсюда .
Существует и другая форма записи линейного уравнения первой степени с одним неизвестным. Выглядит она следующим образом: ax − b = 0. Это то же самое уравнение, что и ax = b, но параметр b перенесен в левую часть с противоположным знаком. Такие уравнение мы тоже решали в данном уроке. Например, уравнение 7x − 77 = 0. Уравнение вида ax − b = 0 называют линейным уравнением первой степени с одним неизвестным в общем виде.
В будущем после изучения рациональных выражений, мы рассмотрим такие понятия, как посторонние корни и потеря корней. А пока рассмотренного в данном уроке будет достаточным.
Задания для самостоятельного решения
Задание 1. Используя метод переноса слагаемого, решите следующее уравнение:
Задание 2. Используя метод прибавления (или вычитания) числа к обеим частям, решите следующее уравнение:
Задание 3. Решите уравнение:
Задание 4. Решите уравнение:
Задание 5. Решите уравнение:
Решите уравнение:
Задание 6. Решите уравнение:
Задание 7. Решите уравнение:
Задание 8. Решите уравнение:
Задание 9. Решите уравнение:
Задание 10. Решите уравнение:
Задание 11. Решите уравнение:
Задание 12. Решите уравнение:
Задание 13. Решите уравнение:
Задание 14. Решите уравнение:
Задание 15. Решите уравнение:
Задание 16. Решите уравнение:
Задание 17. Решите уравнение:
Задание 18. Решите уравнение:
Задание 19. Решите уравнение:
Задание 20. Решите уравнение:
Задание 21. Решите уравнение:
Задание 22. Решите уравнение:
Задание 23. Решите уравнение:
Задание 24. Решите уравнение:
Задание 25. Решите уравнение:
Задание 26. Решите уравнение:
Задание 27. Решите уравнение:
Задание 28. Решите уравнение:
Решите уравнение:
Задание 29. Решите уравнение:
Задание 30. Решите уравнение:
Задание 31. Решите уравнение:
Задание 32. В следующем буквенном уравнении выразите переменную x:
Задание 33. В следующем буквенном уравнении выразите переменную x:
Задание 34. В следующем буквенном уравнении выразите переменную x:
Задание 35. В следующем буквенном уравнении выразите переменную x:
Задание 36. В следующем буквенном уравнении выразите переменную y:
Задание 37. В следующем буквенном уравнении выразите переменную z:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Памятка для обучающегося «Правила нахождения компонентов при решении уравнений», 5 класс
ПРАВИЛА НАХОЖДЕНИЯ КОМПОНЕНТОВ | ПРАВИЛА НАХОЖДЕНИЯ КОМПОНЕНТОВ | ||
Компоненты при сложении: I слагаемое, II слагаемое. Результат сложения: Сумма. I сл + II сл = Сум I сл = Сум – II сл II сл = Сум – I сл | Компоненты при вычитании: Уменьшаемое, вычитаемое. Результат вычитания: Разность. Ум – Выч = Разн Ум = Разн + Вычит Вычит = Ум – Разн | Компоненты при сложении: I слагаемое, II слагаемое. Результат сложения: Сумма. I сл + II сл = Сум I сл = Сум – II сл II сл = Сум – I сл | Компоненты при вычитании: Уменьшаемое, вычитаемое. Результат вычитания: Разность. Ум – Выч = Разн Ум = Разн + Вычит Вычит = Ум – Разн |
Сложение показывает сумму всех слагаемых | Вычитание показывает на сколько уменьшаемое больше вычитаемого | Сложение показывает сумму всех слагаемых | Вычитание показывает на сколько уменьшаемое больше вычитаемого |
Компоненты при умножении: I множитель, II множитель. Результат умножения: Произведение. I мн · II мн = Произвед I мн = Произвед : II мн II мн = Произвед : I мн | Компоненты при делении: Делимое, делитель Результат деления: Частное . Делим : делит = Частное Делим = Част · делит делит = Делим : Част | Компоненты при умножении: I множитель, II множитель. Результат умножения: Произведение. I мн · II мн = Произвед I мн = Произвед : II мн II мн = Произвед : I мн | Компоненты при делении: Делимое, делитель Результат деления: Частное . Делим : делит = Частное Делим = Част · делит делит = Делим : Част |
Умножение показывает сумму нескольких одинаковых слагаемых | Деление показывает во сколько раз делимое больше делителя | Умножение показывает сумму нескольких одинаковых слагаемых | Деление показывает во сколько раз делимое больше делителя |
Компоненты при сложении:
I слагаемое, II слагаемое.
Результат сложения: Сумма.
I сл + II сл = Сум
I сл = Сум – II сл
II сл = Сум – I сл
Компоненты при вычитании:
Уменьшаемое, вычитаемое.
Результат вычитания: Разность.
Ум – Выч = Разн
Ум = Разн + Вычит
Вычит = Ум – Разн
Компоненты при сложении:
I слагаемое, II слагаемое.
Результат сложения: Сумма.
I сл + II сл = Сум
I сл = Сум – II сл
II сл = Сум – I сл
Компоненты при вычитании:
Уменьшаемое, вычитаемое.
Результат вычитания: Разность.
Ум – Выч = Разн
Ум = Разн + Вычит
Вычит = Ум – Разн
Сложение показывает сумму всех слагаемых
Вычитание показывает на сколько уменьшаемое больше вычитаемого
Сложение показывает сумму всех слагаемых
Вычитание показывает на сколько уменьшаемое больше вычитаемого
Компоненты при умножении:
I множитель, II множитель.
Результат умножения: Произведение.
I мн · II мн = Произвед
I мн = Произвед : II мн
II мн = Произвед : I мн
Компоненты при делении:
Делимое, делитель
Результат деления: Частное .
Делим : делит = Частное
Делим = Част · делит
делит = Делим : Част
Компоненты при умножении:
I множитель, II множитель.
Результат умножения: Произведение.
I мн · II мн = Произвед
I мн = Произвед : II мн
II мн = Произвед : I мн
Компоненты при делении:
Делимое, делитель
Результат деления: Частное .
Делим : делит = Частное
Делим = Част · делит
делит = Делим : Част
Умножение показывает сумму нескольких одинаковых слагаемых
Деление показывает во сколько раз делимое больше делителя
Умножение показывает сумму нескольких одинаковых слагаемых
Деление показывает во сколько раз делимое больше делителя
Раздел Повторение курса математики 5 класса | Школа: | ||||
Дата: | ФИО учителя: | ||||
Класс: 6 | Количество присутствующих: | отсутствующих: | |||
Тема урока | Уравнения. | ||||
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 5.2.2.1 решать уравнения на основе правил нахождения неизвестных компонентов арифметических действий; 5.2.2.2 использовать приёмы проверки правильности решения уравнений | ||||
Цели урока | Учащиеся: · повторят правила нахождения неизвестных при решении элементарных уравнений; · будут объяснять ход решения уравнения; ·
использовать уравнения при решении текстовых задач. | ||||
Критерии оценивания | Учащийся: · правильно называет компоненты арифметических действий; · знает, что такое уравнение: находить корень уравнения, делает проверку правильности решения; · при решении текстовых задач правильно составляет математическую модель задачи и по нему уравнение; | ||||
Языковые цели
| Учащиеся: При обсуждении и изложении решения текстовых задач и примеров правильно составляют уравнения. Лексика и терминология, специфичная для предмета: уравнение, решить уравнение, корень уравнения. Полезные выражения для диалогов и письма: Уравнением называют равенство… Чтобы найти корень уравнения …. Для нахождения корня уравнения … | ||||
Привитие ценностей | Самостоятельность,
трудолюбие, внимательность, ответственность. | ||||
Межпредметные связи | Разделы математики, естественные науки, в практической деятельности. | ||||
Предварительные знания | Понятие уравнения, компоненты арифметически х действий, порядок выполнения арифметических действий. | ||||
Ход урока | |||||
Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы | |||
Начало урока 0-10 мин | Организационный момент: · концентрация внимания учащихся; · совместно определить тему и цели урока/ЦО в процессе повторения темы «Уравнения» и устных упражнений; ·
определить
«зону ближайшего развития» учащихся, ожидания к концу урока. Повторение материала с целью актуализации знаний. Вопросы к классу: Как найти неизвестное слагаемое, уменьшаемое, вычитаемое, множитель, делимое, делитель? или ; или ; или ; или . Желательно, чтобы ученик при ответе приводил пример к правилу и решение примера. Устный опрос: 1. Какое равенство называют уравнением? 2. Что значит решить уравнение? 3. Что называют корнем уравнения? 4. Сколько корней имеет уравнение? (приведите примеры). 5. Всегда ли уравнение имеет корень? 6. Как сделать проверку правильности решения уравнения? Предложить ученикам устные упражнения. Приложение 1. Задание можно организовать по рядам, по группам. Каждой группе предложить 1 столбец и предложить соревнование: Кто быстрее? Решите уравнения на скорость. | Презентация Приложение 1 | |||
Середина урока 11 -16 мин
| Индивидуальная
работа. Деятельность учащихся направлена формирование знаний и развитие навыков, относящихся к целям урока, используя свойства вычитания суммы из числа или вычитания числа из суммы. Приложение 2 |
Презентация
Приложение 2 | |||
Середина урока 16 — 25 мин
| Коллективная работа. Решение текстовых задач с помощью уравнения. Вначале деятельности начинаем с примера с геометрическим рисунком. По рисунку составить и решить уравнение, если известен периметр треугольника, а стороны даны буквенными выражениями. Совместно с учащимися составить алгоритм (схему) решения текстовой задачи с помощью уравнения. При решении задачи, проведи анализ условия, результаты оформи в виде таблицы, схемы, рисунка или краткой записи. 1. 2. Составь буквенное и числовое выражения по условию задачи. 3. Составь уравнение. 4. Реши уравнение. 5. Ответь на вопрос задачи. Разобрать образец: Задача. Сумма двух чисел равна 76, а разность их 12. Найди эти числа. Решение: 1) Пусть — первое число, — второе число. 2) Составим буквенное и числовое выражения по условию задачи. Сумма их: , что составляет 76. 3) Составим уравнение: . 4) Решим уравнение: . . 5) Ответим на вопрос задачи: 32 — 1 число, — 2 число. Проверка: ; Ответ: 1 число — 32, 2 число — 44. Заготовьте иллюстрации или, при наличии компьютеров, презентацию, чтобы визуально закрепить алгоритм (схему) решения текстовой задачи с помощью уравнения. Для закрепления решить самостоятельно в
парах задачи из Приложения 3. | Приложение 3 | |||
Середина урока 26 — 36 | Групповая работа. Деление на группы произвольное. Закрепление понимания алгоритма решения составных уравнений. Можно группы сделать разноуровневые. Работая в группах, разобрать данный алгоритм и образец решения. Каждый член группы решает не менее 2 уравнений из первого задания. 2 задание решают коллективно. Алгоритм 1. Определи порядок действий. 2. Выдели последнее. 3. Рассмотри выражение, находящееся справа и слева от последнего действия и определи вид простейшего уравнения, один из компонентов которого выражение, содержащее переменную х. Обозначь его за Х. 4. Реши новое уравнение. 5. Корень уравнения не найден? Решай, начиная вновь с пункта 1. Пример решения уравнения: 20 : (33 — 4x) + 47 = 51 Решить
уравнения из Приложения 4. Обменятся решениями между группами для оценки. | Приложение 4 | |||
Конец урока 37-40 мин | Рефлексия. Оценить работу учащихся на каждом этапе урока Ответить на вопросы: Что узнал? Чему научился? Что осталось непонятным? Над чем надо поработать? |
| |||
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности
| |||
Дифференциация
выражена в подборе заданий, в ожидаемом результате от конкретного ученика, в
оказании индивидуальной поддержки учащемуся, в подборе учебного материала и
ресурсов с учетом индивидуальных способностей учащихся. | Предусмотрена самопроверка по ключу, в ходе которой ученики оценивают умение применять формулы. В ходе коллективной деятельности при решении задач устно оценивается вычислительные навыки учащихся. | Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу. При использовании ИКТ применять правила ТБ. Следить за осанкой учащихся. | |||
Компонент уравнение материального баланса — Справочник химика 21
Обозначим весовые количества фракций через, а концентрацию компонентов в них — где верхний индекс обозначает номер фракции, а нижний — компонент. Уравнение материального баланса стадии разделения по компоненту будет [c.157] Графики могут строиться либо на основе массовых или мольных долей, либо на основе любой другой постоянной единицы концентрации каждого из компонентов. Уравнения материального баланса и принципы равновесия применимы в любом случае, т. е. результаты расчета не зависят от использованных единиц концентрации. При этом следует отметить, что кривые, полученные построением на основе различных единиц концентрации, не будут идентичными. [c.452]
Уравнения материального баланса и принципы равновесия применимы в любом случае, т. е. результаты расчета не зависят от использованных единиц концентрации. При этом следует отметить, что кривые, полученные построением на основе различных единиц концентрации, не будут идентичными. [c.452]
Способ представления состава нефтяных смесей влияет на фор-му записи исходной системы уравнений математического описания процесса и на особенности расчета процесса ректификации. При интегральном методе представления непрерывной смеси все расчетные уравнения сохраняют свой вид, как и для дискретных смесей, если в них заменить концентрации компонентов дифференциальными функциями распределения состава смеси. Например, уравнения материального баланса и фазового равновесия при ректификации непрерывной смеси в простой колонне принимают следующий вид [c.87]
Из уравнения материального баланса по компоненту А [c. 485]
485]
Уравнение материального баланса процесса однократной перегонки многокомпонентной системы по общему числу молей потоков сырья, дистиллята и остатка сохраняет, очевидно, вид уравнения (11.1), а материальный баланс по произвольному -тому компоненту системы представится выражением [c.72]
Производительность. 4. Концентрации компонентов на входе и выходе из аппарата. Требуется определить 1. Физические параметры смеси. 2. Расход поглотителя или веса чистых компонентов (уравнения материального баланса). 3. Движущую силу процесса. [c.113]
Исходя из соображения, что общее число кмолей компонентов системы до и после процесса остается неизменным, а меняется лишь их распределение между фазами, можно составить уравнение материального баланса по числу кмолей низкокипящего компонента (НКК) [c.65]
Графически представленная связь между степенью отгона и температурой процесса однократной перегонки под заданным внешним давлением называется кривой однократной перегонки. Как показано выше, ее уравнение для бинарной системы получается путем совместного решения уравнений материального баланса, написанных для каждого компонента, и уравнения парожидкостного равновесия. [c.68]
Как показано выше, ее уравнение для бинарной системы получается путем совместного решения уравнений материального баланса, написанных для каждого компонента, и уравнения парожидкостного равновесия. [c.68]
Пусть в перегонном кубе к некоторому текущему моменту времени число молей кипящей жидкости равно g, ее состав х, а концентрация равновесной паровой фазы у. При бесконечно малом выкипании кубовой жидкости в паровую фазу перейдет у ду кмолей низкокипящего компонента (НКК). Материальный баланс этого элементарного процесса по НКК представится уравнением [c.69]
Совместное решение этого уравнения с уравнениями материального баланса по общему количеству потоков и по количеству содержащего в них компонента позволяет получить связь между составами и тепловыми параметрами сырья п продуктов разделения [c.281]
При обычно используемом на практике противоточном движении фаз газ входит в колонну снизу и удаляется из нее сверху.
 В общем случае газовая смесь содержит растворимый и нерастворимый (инертный) компоненты. Пусть число молей нерастворимого газа, проходящее за единицу времени через единицу поперечного сечения колонны, будет С, а соответствующий объем жидкости Ь. При прохождении газа через всю колонну он теряет молей растворимого компонента (на Смолей нерастворимого газа), которые приобретаются жидкостью. По мере увеличения расстояния Я от верха колонны к ее низу количество абсорбируемого компонента, приходящееся на О молей нерастворимого газа и одновременно на объем жидкости Ь, возрастает вследствие переноса этого компонента из газовой в жидкую фазу на этом участке. Ясно, что для самого низа колонны g = gg. Эти соображения являются основой для составления уравнения материального баланса, связывающего составы жидкости и газа в произвольной точке колонны. [c.182]
В общем случае газовая смесь содержит растворимый и нерастворимый (инертный) компоненты. Пусть число молей нерастворимого газа, проходящее за единицу времени через единицу поперечного сечения колонны, будет С, а соответствующий объем жидкости Ь. При прохождении газа через всю колонну он теряет молей растворимого компонента (на Смолей нерастворимого газа), которые приобретаются жидкостью. По мере увеличения расстояния Я от верха колонны к ее низу количество абсорбируемого компонента, приходящееся на О молей нерастворимого газа и одновременно на объем жидкости Ь, возрастает вследствие переноса этого компонента из газовой в жидкую фазу на этом участке. Ясно, что для самого низа колонны g = gg. Эти соображения являются основой для составления уравнения материального баланса, связывающего составы жидкости и газа в произвольной точке колонны. [c.182] Решая уравнение материального баланса колонны по произвольному -тому компоненту относительно его содержания в дистилляте, можно получить [c. 361]
361]
Исключая одну из концевых концентраций г-того компонента, например хщ, с помощью уравнения материального баланса [c.386]
Из уравнений материального баланса укрепляющей секции для общего числа кмолей и числа кмолей данного -того компонента [c.407]
Из уравнений материального баланса произвольного объема отгонной секции, составленных по общему числу кмолей потоков п по числам кмолей отдельных компонентов [c.407]
Исходя из соображения, что веса компонентов системы до и после испарения остаются неизменными, меняется же их распределение между фазами, можно составить уравнение материального баланса рассматриваемого процесса [c.42]
Итак, уравнение материального баланса по молям целевого компонента для первой тарелки (рис. 25, б) [c.80]
Пусть к концу частичного однократного испарения начальной смеси при температуре I весовая доля отгона равна е. В момент достижения равновесия вес паров будет равен 1е и вес жидкого остатка Ц1—е). Из уравнения материального баланса по компоненту да, играющему роль низкокипящего компонента, можно вывести соотношение, выражающее весовую долю отгона е в функции составов равновесных фаз и начального состава системы [c.44]
В момент достижения равновесия вес паров будет равен 1е и вес жидкого остатка Ц1—е). Из уравнения материального баланса по компоненту да, играющему роль низкокипящего компонента, можно вывести соотношение, выражающее весовую долю отгона е в функции составов равновесных фаз и начального состава системы [c.44]
Так, уравнения материального баланса для какого-нибудь объема второй колонны по общему весу потоков и по весу содержащегося в них компонента W представятся соотношениями [c.75]
Для потоков паров и флегмы в первой питательной секции колонны, куда подается поток сырья I, можно написать следующие уравнения материального баланса по общему их весу и по весу содержащегося в них компонента [c.95]
Для определения соотношения, связывающего составы х иу и теплосодержания и д встречных потоков флегмы и паров в каком-нибудь текущем сечении средней секции изучаемой колонны, составляю ся для ее объема, заключенного между каким-либо сечением этой секции и верхом или низом колонны, уравнения материального баланса общего веса потоков и веса содержащегося в них компонента [c. 123]
123]
Таким образом (4.28) представляет собой уравнение материального баланса для абсорбера с п теоретическими тарелками и связывает начальную и конечную концентрации целевого компонента в газовой фазе с технологическими параметрами процесса и числом теоретических тарелок. [c.81]
Уравнение материального баланса по целевому компоненту можно записать следующим образом [c.95]
Рассмотрим постановку оптимальной задачи для каскада реакторов идеального смешения, в котором проводится с/ожная химическая реакция, не изменяющая общего числа молей реагирующей смеси. Математическое описание каскада аппаратов с таг ой реакцией представляет собой систему уравнений материальных балансов для всех (или только ключевых)компонентов смеси,записандых для всех реакторов каскада [c.156]
По уравнению материального баланса определяется количество поглощаемого компонента, кг/ч [c.96]
Уравнения материального баланса используют для расчета полей концентраций компонентов, уравнение баланса тепловой энергии — для расчета поля температуры, уравнение баланса кинетической энергии — для расчета поля давления. Для большинства промышленных аппаратов изменение давления не сказывается существенно на результатах процесса, и уравнение баланса кинетической энергии можно записать в виде [c.98]
Для большинства промышленных аппаратов изменение давления не сказывается существенно на результатах процесса, и уравнение баланса кинетической энергии можно записать в виде [c.98]
Для вывода уравнения рабочей линии укрепляющей секции запишем уравнение материального баланса по легколетучему компоненту для части колонны выше сечения а—а (см. рис. 35) [c.108]
Если Со — концентрация -го компонента на входе в аппарат, С ь = С,о+АС1 — на выходе из аппарата, С — на входе в элементарный слой, — на выходе из элементарного слоя, то получим следующие уравнения материальных балансов. [c.100]
Уравнение материального баланса для одного компонента смеси будем называть проектным уравнением реактора. В общем случае баланс исходного вещества А можно представить следующим образом [c.292]
В соответствии с диффузионной моделью концентрация трассера или целевого компонента при отсутствии источников и стоков описывается нестационарным уравнением материального баланса [c. 148]
148]
Подставляя в уравнения материального баланса (VIII.8), написанные по компонентам / и к, найденную зависимость (VIII.21), можно рассчитать содержание компонента к в дистилляте [c.360]
При расчете колонн обычно известны и а, а содерн анием низкокипящего компонента в ректификате и остатке т. е. четкостью ректификации, задаются. Следовательно, уравнение материального баланса (228) дает возможность онределить количество ректификата [c.212]
Вывод основных расчетных выражений, используемых для определения количеств и составов равновесных фаз процесса однократной перегонки углеводородных систем в присутствпп водяного пара, ведется обычным путем — совместным решением уравнения материального баланса (11.52) и обобщенного уравнения парожидкостного равновесия (11.54). Если решить эти два уравнения относительно или у. и просуммировать полученные выражения по всем п углеводородным компонентам системы, можно получить [c. 88]
88]
Пусть над единицей площади тарелки через слой флегмы высотой 2 барботируют пузырьки пара, обогащающиеся НКК за счет его диффузии из жидкой фазы. При установившемся состоянии в условиях, когда переносимый из одной фазы в другую компонент не накапливается вблизи межфазовой поверхности контакта, количество вещества, покидающего одну фазу, должно равняться Т0Л1У К0о1ичеству, которое поступает в другую. На этом основании уравнение материального баланса массообмена на элементарной высоте с1г слоя флегмы представится следующими эквивалентными выражениями (рис. 111.39) [c.210]
Как будет показано далее, в отличие от случая разделения бинарной системы, для сложной колонны нельзя назначать заранее полный состав обоих ее продуктов. Обычно наперед назначаются концентрации двух компонентов — одного в дистилляте, другого в остатке, или же относительные извлечения этих компонентов из заданного сырья, а необходимое сочетание концентраций лсех остальных компонентов дистиллята и остатка, отвечающее выбранным условиям разделения, определяется методом последовательных приближений, чаще всего путем совместного решения уравнений материального баланса и парожидкостного равновесия. [c.344]
[c.344]
Чпсло независимых уравнении материального баланса ( 11.29) и для иерво1о и д.ия второго классов фракционировки равно (га — 1). Что же касается уравнений ( 11.28), то, поскольку их нельзя написать по компоненту, одна из концевых котщон-траций которого равна пулю, общее чпсло этих независимых уравнений будет равно [(га — 1) — г, где 2 — число нулевых [c.317]
Из уравнений материального баланса произвольного объема отгонной секцин, составленных по общему числу молей потоков и но числам молей отдельных компонентов [c.399]
В остальных столбцах табл. VII.20 по обычным уравнениям материального баланса нитательпой секции последовательно рассчитаны для всех у т С-компонентов системы значения g ,x и далее соответствуго- [c.414]
Обращаясь к основному уравнению массопередачи М — = КАгуРх, отметим, что М — количество передаваемого из фазы в фазу вещества, зависящее от требуемой степени извлечения целевых компонентов и количества сырьевого потока, — рассчитывается из уравнения материального баланса —поверхность контакта фаз — связана с размерами, конструктивными особенностями и гидродинамикой массообменного аппарата К, Аср — коэффициент массопередачи и средняя движущая сила — определяются кинетикой процесса, природой и составом контактирующих фаз они отражают конкретные условия массообменного процесса и характеризуют его специфику. [c.55]
[c.55]
Запишем уравнение материального баланса не Для всего абсорбера, а для его части от низа абсорбера до некоторого сечения АВ. Будем считать, что в сечении АВ газовая фзза имеет относительную концентрацию целевого компонента у, а жидкая —X. [c.73]
Уравнение материального баланса, характеризующее изменение концентрации -го компонента в реакторе полного смешения за время й% составляется аналогично уравнению (П.1), но с той разницей, что для рассматриваемого случая удобно вместо произведения Widx ввести приращение С . Тогда это уравнение после некоторых преобразований приводится к виду [c.21]
Нахождение неизвестных компонентов в равенствах
Конспект урока«Нахождение неизвестного числа в равенствах с помощью правил нахождения неизвестных компонентов действий».
Цели урока:
- обучать познавательным УУД: умение ставить учебную задачу и добиваться её выполнения, развивать мыслительные операции анализа, синтеза, сравнения, формулировать речевое высказывание в устной форме; формировать умение комментировать выполняемые операции; отрабатывать устные и письменные вычислительные навыки.

- развивать навыки коммуникативного общения: использовать различные диалогические приёмы, соблюдать культуру поведения в учебном диалоге;
- формировать личностные УУД: ответственность за свою деятельность; эмоционально-положительное восприятие учения; уверенность в себе; развивать межличностные отношения в процессе совместной деятельности(работа в парах).
- развивать регулятивные УУД: планировать свою работу, сохранять заданную цель, контролировать свою деятельность по результату.
Тип урока: комбинированный.
Используемые технологии: технология деятельностного метода, информационно-коммуникационные, здоровьесберегающие.
Оборудование: учебник «математика» В.Н. Рудницкой, листы с заданиями для групповой работы, памятки «выучи наизусть» с правилами нахождения компонентов действий, памятки «компоненты действий», модели правил.
Ход урока
1. Мотивация к учебной деятельности
Мотивация к учебной деятельности
Цели: создать мотивацию к деятельности на уроке посредством создания математических образов. Определить содержательные рамки урока: решения уравнений на нахождение компонентов арифметических действий.
Ребята, покажите с каким настроением вы пришли на урок?
— Учебник на столе у вас?
Будьте внимательны,
А ручки и тетрадки?
Послушны, наблюдательны,
Тогда урок начнём сейчас,
Чтобы математику знать,
Раз всё у вас в порядке.
Нужно серьёзно всё изучать!
2. Актуализация знаний и умений.
Цель: воспроизвести знания, умения и навыки, достаточные для построения нового способа действия.
Ребята, какие математические действия вы знаете?
Как называются компоненты математических действий?
Перед вами различные математические записи.
750:50 =15
523 + 452 = 975
408+ К = 1340
1900 – у = 855
35 х 100 = 3500
168 : а = 42
— Что записано на доске? (равенства)
— На какие группы можно разделить эти равенства? (числовые и буквенные)
— Как мы называем буквенные равенства? (Уравнение)
Что такое уравнение?
— Предположите, какая тема сегодняшнего урока? (Тема урока: «Решение уравнений»).
— Что значит решить уравнение? ?(Найти неизвестный компонент, при котором получается верное равенство.)
— Мы умеем решать уравнения и находить неизвестные компоненты? ( да)
— А зачем тогда мы будем сегодня решать уравнения? ( чтобы повторить, совершенствовать навыки счёта, вспомнить как находятся компоненты…). А новое мы с вами будем узнавать, решая уравнения?
— Еще 3-4 тысячи лет до нашей эры египтяне умели решать простейшие уравнения, вид которых не был похож на современные. Затем греки унаследовали знания египтян, и пошли дальше. А в Средней Азии в древнем городе Хорезм, трудился великий ученый эпохи IX века – Мухаммад аль Хорезми. Он первый ввёл понятие уравнения.
Правильно вы, ребята, сказали, что решить уравнение, значит найти неизвестный компонент, при котором получается верное равенство.
3. Выявление причин затруднения и постановка цели деятельности.
Цели: выявить и зафиксировать место и причину затруднения; согласовать цель и тему урока.
А какие компоненты мы с вами умеем находить? Правила назовите.
Какие компоненты ещё можно находить в равенствах?
Посмотрите на уравнения. Мы можем сейчас решить эти уравнения? (нет). Почему? ( Мы не умеем находить эти компоненты)
— Какую цель мы поставим перед собой? Чтобы вы хотели узнать сегодня на уроке? ( Научиться решать другие уравнения. Находить компоненты: делитель, множитель, слагаемое, вычитаемое.)
Что для этого нам нужно? Какими быть на уроке? (внимательными, трудолюбивыми,…)
4. Построение проекта выхода из затруднения
Цели: организовать построение детьми нового способа проговаривания, устраняющего причину затруднения; зафиксировать новый способ действий в речи и знаково.
– Чтобы правильно решить уравнение, давайте составим алгоритм (программу действий) решения уравнений.
– Перед вами этапы решения уравнения. Согласны ли вы с данным алгоритмом? Почему? Восстановите последовательность.
1. Выполняю проверку.
2. Нахожу неизвестный компонент по правилу.
3. Вспоминаю правило нахождения неизвестного компонента.
4. Определяю неизвестный компонент.
5. Записываю ответ.
6. Читаю уравнение.
Получаем алгоритм решения уравнений:
1. Читаю уравнение.
2. Определяю неизвестный компонент.
3. Вспоминаю правило нахождения неизвестного компонента.
4. Нахожу неизвестный компонент по правилу.
5. Записываю ответ.
6. Выполняю проверку.
5. Первичное закрепление во внешней речи. Цель: cоздать условия для фиксации изученного способа действий во внешней речи.
— Проговорим ещё раз каждый пункт составленного алгоритма.
6. Открытие нового знания.
Цель: научиться находить неизвестные компоненты действий, решение уравнения с применением алгоритма.
Решите уравнения с пошаговой записью по алгоритму (задание по вариантам)
Решим уравнение. К доске пойдёт…
К доске пойдёт…
198 – х = 39 ( решают и записывают по алгоритму)
Что нужно было найти? (вычитаемое) сделайте вывод, как найти вычитаемое? ( чтобы найти вычитаемое, надо из уменьшаемого вычесть разность)
Работа в группах: 1 группа – нахождение неизвестного 2го слагаемого 94+х=126
2 группа – нахождение неизвестного 2 го множителя 32 х Х = 192
3 группа – нахождение неизвестного делителя. 384: а = 96
7. Первичное закрепление.
Цель: cоздать условия для фиксации изученного способа действий во внешней речи. Решить уравнения, найти неизвестные компоненты: А – 18 = 40, 35: S = 7, 150 х D =450,Н+ 98 = 100, Ех 4 = 400, 500: С = 10.
8. Самостоятельная работа с самопроверкой по эталону.
Цели: Повторение компонентов действий. Организовать повторение записи предложения в виде выражения.
— Ребята, можете теперь решить уравнения, которые на доске? ( самостоятельно решают уравнения).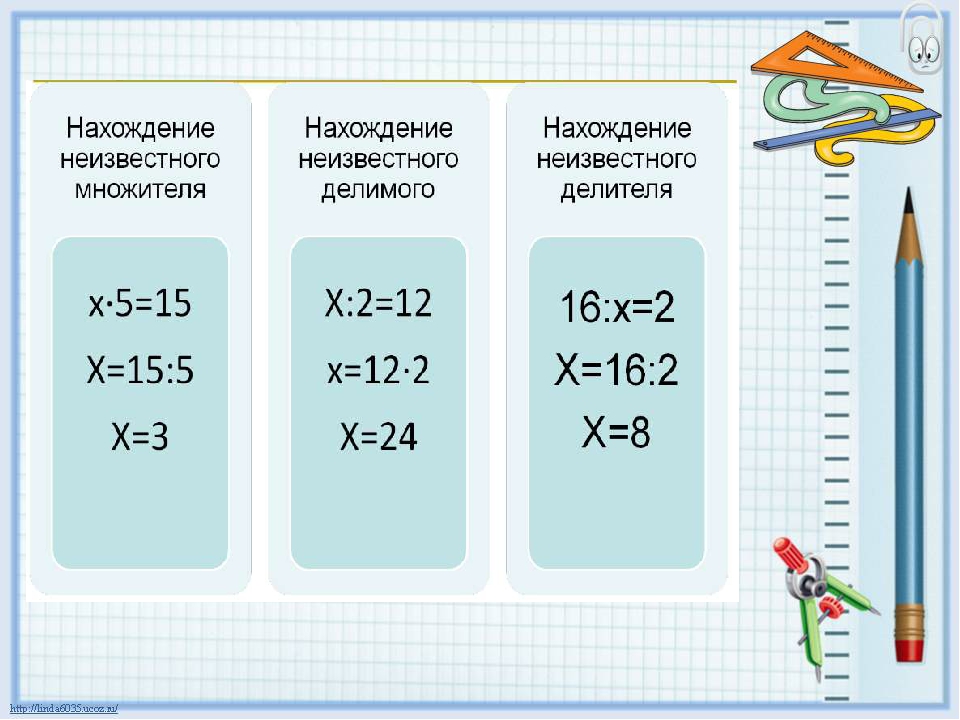 1 группа – 1 уравнение, 2 группа – 2 уравнение, 3 группа – 3 уравнение. Самопроверка по эталону.
1 группа – 1 уравнение, 2 группа – 2 уравнение, 3 группа – 3 уравнение. Самопроверка по эталону.
9. Рефлексия учебной деятельности (домашнее задание)
Цели: зафиксировать в речи новый способ действий, изученный на уроке; зафиксировать затруднения, которые остались, и способ их преодоления; оценить собственную деятельность на уроке.
— Чему вы учились сегодня на уроке? (Мы учились решать уравнения)
— Что значит решить уравнение?(Найти неизвестный компонент, при котором получается верное равенство).
— Что интересного узнали?
— Какую цель мы ставили на сегодняшний урок? Достигли ли мы поставленной цели урока?
— Домашнее задание: выучить правила ( раздаются памятки с правилами)
Рефлексия светофор: зелёный кружок – мне сегодня с урока всё понятно и я молодец!
Жёлтый кружок – мне не всё понятно, но я старался!
Красный кружок – мне нужно быть внимательнее на уроке!
— Я благодарю всех вас за работу на уроке и желаю, чтобы вы всегда правильно решали уравнения. Всем отличного настроения. Урок окончен.
Всем отличного настроения. Урок окончен.
Презентация «КОМПОНЕНТЫ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ» — математика, презентации
библиотека
материалов
Содержание слайдов
Номер слайда 1
Основные понятия Компоненты арифметических действий и нахождение неизвестных компонентов — при сложении — при вычитании — при умножении — при делении Контрольные вопросы Проверь себя!
Номер слайда 2
Уравнение – равенство, содержащее неизвестное число. Корень уравнения – найденное значение неизвестного числа. Решить уравнение – значит найти все его корни.
Корень уравнения – найденное значение неизвестного числа. Решить уравнение – значит найти все его корни.
Номер слайда 3
слагаемое, слагаемое, сумма. Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. X +55 = 95 X = 95 – 55 X = 40
Номер слайда 4
При вычитании: уменьшаемое, вычитаемое, разность Чтобы найти неизвестное уменьшаемое, надо сложить вычитаемое и разность. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность. Y – 67 = 33 Y = 67 +33 Y=100. 86 –Z = 36 Z = 86 – 36 Z =50.
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность. Y – 67 = 33 Y = 67 +33 Y=100. 86 –Z = 36 Z = 86 – 36 Z =50.
Номер слайда 5
При умножении: множитель, множитель, произведение. Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель. 9 * m =108 m =108 : 9 m =12. C * 3 =183 C =183 : 3 C = 61.
Номер слайда 6
При делении: делимое, делитель, частное. Чтобы найти неизвестное делимое, надо частное умножить на делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное. X : 12 = 5
X = 5*12
X =60.
64 : y = 14
y = 64 : 14
y = 4.
Чтобы найти неизвестное делимое, надо частное умножить на делитель. Чтобы найти неизвестный делитель, надо делимое разделить на частное. X : 12 = 5
X = 5*12
X =60.
64 : y = 14
y = 64 : 14
y = 4.
Номер слайда 7
Что такое уравнение? Что значит решить уравнение? Что такое корень уравнения? Как найти компоненты при сложении? Как найти компоненты при вычитании? Как найти компоненты при умножении? Как найти компоненты при делении?
Номер слайда 8
Реши уравнение X +256 = 905 638 + z = 806 Y –2901 = 468 6703 – c = 303 X * 45 = 945 80 : y =16 Y: 23 = 23 ( 91 – 3 z ) : 4 = 16 75 🙁 69 – 4 x ) = 15
Номер слайда 9
Математика — Элементы уравнения
Уравнение — это математическое выражение со знаком равенства.
Другие возможные элементы уравнения:
- номера
- переменных
- бинарные операторы (+, -, * или ÷)
- унарные операторы (+ или -)
- кронштейны
- степеней (x y )
- функций (sin (), log () и т. Д.)
Они объясняются ниже:
Номера
Существуют разные типы номеров, например:
- Z — Целые числа — целые числа:… -3, -2, -1, 0, 1, 2, 3 … положительные, нулевые и отрицательные.
- — Реальный
числа — числа, которые являются непрерывными, например, когда мы представляем точки вдоль линии — на этом сайте я иногда буду использовать термин «скалярный» для обозначения «действительных» чисел, хотя строго этот термин следует использовать при масштабировании вектора — в компьютерных программах действительные числа имеют конечную длину и могут иметь десятичную точку и / или показатель степени. Это позволяет нам аппроксимировать большинство действительных чисел, но это только приближение.

- Q — Рациональный числа — целые числа и дроби, где числитель и знаменатель являются целыми числами.
- Радикальные целые числа — целые числа плюс любая комбинация сложения, вычитания, умножения, деления и извлечения корня.
- Q alg — Корень полинома Z — Комплексное число состоит не только из радикальных целых чисел, но и закрывается суммой, разностью, произведением, частным и корнем n th .
- Числа по модулю n
- C — Комплексные числа — числа с действительной и мнимой частями.
- H — Кватернион — Комплексное число, элементы которого являются комплексными числами.
- O — Octonion — Кватернион, элементами которого являются комплексные числа.
- Векторы — одномерные массивы чисел.
- Матрицы — двумерные массивы чисел.
и эти номера можно закодировать по-разному:
- двоичный
- восьмеричное
- десятичное
- шестнадцатеричный
Если не указано иное, мы обычно предполагаем, что числа являются десятичными.
Переменные
Иногда уравнение содержит число, но мы еще не знаем его значения, или мы можем применить уравнение к диапазону значений.
Пример первого — использование x как неизвестного, например
х + 1 = 3
Примером второго может быть уравнение прямой:
у = 2 * х + 3
Обычно мы используем:
x, y, z для неизвестных.
a, b, c для значений, которые еще не указаны.
Бинарные операторы
Операторы:
- + добавить
- — вычесть
- * умножить (было x, но для компьютеров необходимо изменить, чтобы отличать его от 24-й буквы алфавита)
- ÷ или / делить
возьмите два числа по бокам и замените их одним числом.
Дополнение
На следующем графике высота дана как a + b, это дает плоскую плоскость под 45 ° как к a, так и к b:
как был создан этот график
Конечно, плоскость бесконечна во всех направлениях, но здесь мы показали только часть плоскости.
Умножение
На следующем графике высота дана как a * b, это дает поверхность, состоящую из прямых линий в направлениях a или b (билинейные). Если мы возьмем направление под 45 ° как к a, так и к b, то мы получим параболу.
как был создан этот график
Унарные операторы
Операторы:
применяется к номеру справа. «-» инвертирует число (вычитает из 0) «+» означает, что число справа положительное (по умолчанию).
Кронштейны
Когда мы смешиваем + и *, то ответ, который мы получаем, зависит от порядка, в котором мы их применяем.
Например,
2 + 1 * 3
Чтобы прояснить это, мы можем заключить в скобки операцию, которая будет применяться первой:
(2 + 1) * 3 = 9
2 + (1 * 3) = 5
Если мы не укажем, что имеет приоритет, используя скобки, то по умолчанию * и ÷ имеют приоритет над + и -. Итак,
2 + 1 * 3 = 5
Функции
Функция берет одно число и использует его для генерации другого числа. Например, функция sin () принимает угол в качестве входных данных и возвращает соотношение противоположности и гипотенузы в прямоугольном треугольнике.
Например, функция sin () принимает угол в качестве входных данных и возвращает соотношение противоположности и гипотенузы в прямоугольном треугольнике.
Алгебра — Определения
Это может помочь вам сначала прочитать Введение в алгебру
Что такое уравнение
Уравнение говорит, что две вещи равны. У него будет знак равенства «=», например:
.Это уравнение говорит: то, что слева (x + 2), равно тому, что справа (6)
Таким образом, уравнение похоже на оператор : «, это равно , что »
Части уравнения
Так люди могут говорить об уравнениях, есть названий для разных частей (лучше, чем сказать «вот эта штука»!)
Здесь мы есть уравнение, в котором 4x — 7 равно 5, и все его части:
A Переменная — это символ числа, которое мы еще не знаем.Обычно это буква типа x или y.
Число называется константой .
Коэффициент — это число, используемое для умножения переменной ( 4x означает 4 умножить на x , поэтому 4 — коэффициент)
Переменные сами по себе (без номера рядом с ними) на самом деле имеют коэффициент 1 ( x на самом деле 1x )
Иногда коэффициент представляет собой букву типа a или b вместо числа:
Пример: ax
2 + bx + c- x — переменная
- a и b — коэффициенты
- c — постоянная
Оператор — это символ (например, +, × и т. Д.), Который показывает операцию (т. Е. Мы хотим что-то сделать со значениями).
Д.), Который показывает операцию (т. Е. Мы хотим что-то сделать со значениями).
A Член — это либо одно число, либо переменная, либо числа и переменные, умноженные вместе.
Выражение — это группа терминов (термины разделены знаками + или -)
Итак, теперь мы можем сказать такие вещи, как «это выражение имеет только два члена», или «второй член является константой», или даже «вы уверены, что коэффициент действительно равен 4?»
Экспоненты
Показатель степени (например, 2 в x 2 ) говорит , сколько раз использовать значение при умножении.
Примеры:
8 2 = 8 × 8 = 64
y 3 = y × y × y
y 2 z = y × y × z
Показатели упрощают запись и использование множества умножений
Пример: y 4 z 2 проще, чем y × y × y × y × z × z
Полином
Пример полинома: 3x 2 + x — 2
Многочлен может иметь констант , переменных и показателей 0,1,2,3 ,. ..
..
Но в нем никогда не бывает деления на переменную.
Мономиальное, Биномиальное, Трехчленное
Есть специальные имена для многочленов с 1, 2 или 3 членами:
Понятия «Нравится»
подобных терминов — это терминов , переменные которых (и их показатели, такие как 2 в x 2 ) совпадают.
Другими словами, термины, которые «похожи» друг на друга. (Примечание: коэффициенты могут быть разными)
Пример:
Все ли похожи на термины , потому что все переменные xy 2
компонентных уравнений — MATLAB и Simulink
Определение уравнений компонентов
Цель раздела уравнений — установить математические отношения между переменными, параметрами, входами, выходами, временем и производными по времени каждого из этих элементов компонента.
Простая алгебраическая система
В этом примере показана реализация простой алгебраической системы.
Использовать время моделирования в уравнениях
В этом примере показано, как получить доступ к глобальному времени моделирования из уравнения раздел.
Использование условных выражений в уравнениях
Вы можете указать условные уравнения с помощью операторов if .
Использование промежуточных членов в уравнениях
Учебники часто определяют определенные члены уравнения в отдельных уравнениях, а затем заменяют эти промежуточные уравнения в основное.
Использование таблиц поиска в уравнениях
Вы можете использовать функцию tablelookup в уравнениях раздел файла Simscape ™ для интерполяции входных значений на основе набора точек данных в одномерной, двухмерной или трехмерной таблице.
Программирование ошибок и предупреждений во время выполнения
Используйте конструкцию assert для реализации сообщений об ошибках и предупреждениях времени выполнения для настраиваемого блока.
Исходные уравнения
Укажите дополнительные уравнения, которые будут выполняться только во время инициализации модели.
Функции Simscape
Используйте функции Simscape для повторного использования выражений в уравнениях и объявлениях элементов несколько компонентов.
Импорт символьных математических формул Toolbox
Пример использования программного обеспечения Symbolic Math Toolbox ™ для решения физических уравнений сгенерируйте код в соответствующем формате для раздела уравнений языка Simscape и включить сгенерированный код в раздел уравнения файла компонента.
Как писать уравнения и формулы — Видео и стенограмма урока
Элементы уравнения
Уравнение всегда можно отличить по знаку равенства (=). Уравнения могут иметь констант , которые являются известными значениями, а также переменных , которые являются неизвестными значениями, обычно выражаемыми буквами.
Уравнения могут иметь констант , которые являются известными значениями, а также переменных , которые являются неизвестными значениями, обычно выражаемыми буквами.
Вот несколько простых примеров уравнений:
5 + 6 = 11
x + 4 = 15
Взгляните на простое уравнение, которое может присваивать значение переменной:
x = 5
Уравнениям вообще не обязательно должны быть числа.Например, вы можете обнаружить, что две переменные равны друг другу. Каждый раз, когда вы видите знак равенства, вы знаете, что смотрите на уравнение. В этом разница между уравнением и выражением , которое представляет собой математическую связь между переменными и / или числами, но без установки выражения, равного чему-то другому, например этому:
5 c + 2
Мы можем преобразовать выражение в уравнение, установив его равным чему-то вроде этого:
x + 5 = 10
Вопрос, на который вы пытаетесь ответить, заключается в том, какое значение плюс 5 равно 10. Ответ, конечно же, 5.
Ответ, конечно же, 5.
Формулы как специальные уравнения
Формула имеет более одной переменной и использует эти несколько переменных для выражения важной взаимосвязи. Например, d = rt — это формула для решения задач «пройденное расстояние». Обратите внимание: когда переменные склеены без знака операции между ними, это означает их умножение. Итак, в формуле d = rt скорость ( r ) и пройденное время ( t ) умножаются вместе, чтобы получить общее пройденное расстояние ( d ).
Уравнение и компоненты формул
В алгебре уравнения и формулы состоят из членов , которые представляют собой группы переменных и чисел, связанных умножением и делением. Затем члены связываются знаком равенства и операциями сложения и вычитания.
Обычно такой член, как -9 xy , может иметь следующее:
- Коэффициент , который представляет собой число, которое умножается на оставшуюся часть члена .
- Одна или несколько переменных, умноженные вместе
- Показатели , которые представляют собой количество раз, которое переменная умножается сама на себя

В 5 x ² 5 умножается на оставшуюся часть члена.Показатель степени 2 означает, что на самом деле получается два числа x , которые умножаются вместе. Этот термин означает 5 раз x раз x .
Каждая сторона уравнения или формулы будет иметь один или несколько членов, связанных сложением или вычитанием. Две стороны уравнения или формулы будут равны (имеют одинаковое значение), например:
5 x ² = 2 x — 3
Word Проблема Уравнения
Проблема слов — это математическая задача, представленная в формате рассказа вместо письменного уравнения.Один из шагов в решении проблемы со словами — написать уравнение или формулу, подходящую для ситуации.
Например:
У Мэри на столе было 5 конфет. Вошла Марсия и добавила еще. Когда Мэри пересчитала все кусочки, на столе оказалось 11 конфет. Сколько конфет Марсия добавила к 5, что лежала на столе у Мэри?
Когда Мэри пересчитала все кусочки, на столе оказалось 11 конфет. Сколько конфет Марсия добавила к 5, что лежала на столе у Мэри?
На самом деле нет такой формулы, как d = rt для этой ситуации, но мы можем довольно легко написать уравнение для нее.Пройдя через то, что мы знаем из проблемы, мы можем:
- Записать 5 для оригинальных леденцов Мэри: 5
- Поставьте знак плюс (‘+’) рядом с 5, так как Марсия вошла и добавила несколько: 5 +
- Поместите переменную с другой стороны от «+», чтобы представить неизвестное количество конфет, которое добавила Марсия: 5 + x
- Поставьте знак равенства, чтобы показать, что всего конфет: 5 + x =
- Запишите общее количество конфет, указанное в задаче: 5 + x = 11
Вот и все! Вы написали уравнение для задачи со словом!
Резюме урока
Давайте уделим несколько минут тому, чтобы повторить, что мы узнали об уравнениях и формулах и о том, как их решать. Во-первых, уравнение — это способ сказать, что одна вещь равна или имеет то же значение, что и другая. Формула — это специальное уравнение, которое выражает важную взаимосвязь между переменными, выражающими часто используемые идеи, такие как скорость, температура и т. Д. Мы также узнали, что выражение представляет собой взаимосвязь между значениями и / или переменными, не имеющими знака равенства. ; в то время как переменные (или заполнители для значений, которые мы не знаем) могут быть помещены рядом в формуле или уравнении, чтобы показать умножение этих переменных.Словесную проблему можно перевести в уравнение или формулу, присвоив правильный символ или число каждому значению, неизвестному и взаимосвязанному в словесной задаче, и записав это в виде простого математического утверждения.
Во-первых, уравнение — это способ сказать, что одна вещь равна или имеет то же значение, что и другая. Формула — это специальное уравнение, которое выражает важную взаимосвязь между переменными, выражающими часто используемые идеи, такие как скорость, температура и т. Д. Мы также узнали, что выражение представляет собой взаимосвязь между значениями и / или переменными, не имеющими знака равенства. ; в то время как переменные (или заполнители для значений, которые мы не знаем) могут быть помещены рядом в формуле или уравнении, чтобы показать умножение этих переменных.Словесную проблему можно перевести в уравнение или формулу, присвоив правильный символ или число каждому значению, неизвестному и взаимосвязанному в словесной задаче, и записав это в виде простого математического утверждения.
компонентов вектора
В двумерной системе координат любая
вектор
можно разбить на
Икс
-компонент и
у
-компонент.
v → знак равно 〈 v Икс , v у 〉
Например, на рисунке ниже вектор v → разбит на две составляющие, v Икс и v у .Пусть угол между вектором и его Икс -компонент быть θ .
Вектор и его компоненты образуют прямоугольный треугольник, как показано ниже.
Компоненты на приведенном выше рисунке можно быстро прочитать. Вектор в компонентной форме имеет вид v → знак равно 〈 4 , 5 〉 .
В тригонометрические соотношения установить связь между величина вектора и компоненты вектора.
потому что θ знак равно Прилегающая сторона Гипотенуза знак равно v Икс v
грех θ знак равно Обратная сторона Гипотенуза знак равно v у v
v Икс знак равно v потому что θ
v у знак равно v грех θ
С помощью Теорема Пифагора в прямоугольном треугольнике с длинами v Икс и v у :
| v | знак равно v Икс 2 + v у 2
Здесь указанные числа представляют собой величины векторов.
Дело 1: По заданным компонентам вектора найдите величину и направление вектора.
В этом случае используйте следующие формулы.
Величина вектора равна | v | знак равно v Икс 2 + v у 2 .
Чтобы найти направление вектора, решите загар θ знак равно v у v Икс за θ .
Случай 2: Зная величину и направление вектора, найдите компоненты вектора.
В этом случае используйте следующие формулы.
v Икс знак равно v потому что θ
v у знак равно v грех θ
Пример:
Величина вектора
F
→
является
10
единиц и направление вектора
60
°
с горизонтальным. Найдите компоненты вектора.
Найдите компоненты вектора.
F Икс знак равно F потому что 60 ° знак равно 10 ⋅ 1 2 знак равно 5
F у знак равно F грех 60 ° знак равно 10 ⋅ 3 2 знак равно 5 3
Итак, вектор
F
→
является
〈
5
,
5
3
〉
.
частей выражения: термины, факторы и коэффициенты — видео и стенограмма урока
Термины, факторы и коэффициенты
Как мы уже говорили, математическое выражение содержит числа, переменные, символы и операторы, связанные сложением, вычитанием, умножением и делением. Сначала рассмотрим части выражения, связанные со сложением и вычитанием. Эти части называются терминами .
Рассмотрим наш пример 3 x 2 + 7 x . Мы видим, что 3 x 2 и 7 x соединены сложением. Следовательно, в этом математическом выражении мы называем 3 x 2 и 7 x членами.
Теперь давайте поговорим о факторах в математическом выражении. В математическом выражении множителей являются частями выражения, которые связаны умножением.Например, рассмотрим математические выражения 5 x y и ( x -2) ( x + 5). В первом выражении мы видим, что умножаем 5 на x на y , поэтому мы бы назвали коэффициенты 5, x и y математического выражения. Точно так же в выражении ( x -2) ( x + 5) мы умножаем ( x -2) и ( x + 5), поэтому мы вызываем ( x -2) и ( x + 5) множителей выражения.
В первом выражении мы видим, что умножаем 5 на x на y , поэтому мы бы назвали коэффициенты 5, x и y математического выражения. Точно так же в выражении ( x -2) ( x + 5) мы умножаем ( x -2) и ( x + 5), поэтому мы вызываем ( x -2) и ( x + 5) множителей выражения.
Пока все хорошо, правда? Рассмотрим еще одну часть математического выражения. Коэффициенты. Коэффициент — это число, которое умножается на переменную в математическом выражении. Чтобы проиллюстрировать это, рассмотрим условия нашего начального примера:
3 x 2 + 7 x . В каждом из членов 3 x 2 и 7 x , x является переменной, и в обоих терминах мы умножаем число на переменную.В первом члене 3 x 2, 3 умножается на переменную, поэтому 3 — это коэффициент. Во втором члене 7 x , 7 умножается на переменную, поэтому 7 — это коэффициент.
Мы видим, что члены, множители и коэффициенты составляют математические выражения. Каждая из этих частей выражения имеет свою метку и функцию. Чем больше мы работаем с математическими выражениями, тем больше мы знакомы с этими частями, поэтому давайте взглянем на несколько примеров, чтобы действительно реализовать эту концепцию (предназначенная для бейсбольной игры).
Примеры
Предположим, вы бросаете мяч в воздух, и высоту мяча от земли можно смоделировать с помощью математического выражения -16 x 2 + 20 x + 6.
Мы хотим идентифицировать члены и коэффициенты в этом выражении. Сначала мы рассматриваем члены выражений или части выражения, которые связаны сложением или вычитанием.
Мы видим, что части выражения, связанные сложением или вычитанием, равны -16 x 2, 20 x и 6. Следовательно, это термины выражения.
Следовательно, это термины выражения.
Теперь давайте рассмотрим коэффициенты или числа, которые умножаются на переменную в каждом из членов. В первом члене -16 x 2, -16 умножается на переменную x , поэтому -16 является коэффициентом. Во втором члене 20 x , 20 умножается на переменную x , поэтому 20 — это коэффициент. В последнем члене 6 нет переменной, поэтому 6 не называется коэффициентом. На самом деле, когда у нас есть термин, который представляет собой просто число, подобное этому, мы называем это число константой , поэтому 6 в этом выражении является константой.
Как оказалось, мы можем фактически разложить математическое выражение на множители -16 x 2 + 20 x + 6, чтобы получить (8 x + 2) (- 2 x + 3). Когда мы пишем выражение в его факторизованной форме, у нас появляется новое математическое выражение, в котором есть два фактора. Можете ли вы определить факторы?
Можете ли вы определить факторы?
Если вы сказали, что коэффициенты равны 8 x + 2 и -2 x + 3, то вы правы! В выражении (8 x + 2) (- 2 x + 3) мы умножаем 8 x + 2 и -2 x + 3 вместе, поэтому эти два выражения являются множителями.
Краткое содержание урока
Математическое выражение — это выражение, которое содержит числа, переменные, символы и операторы, связанные со сложением, вычитанием, умножением и делением. Каждое математическое выражение состоит из разных частей. Три из этих частей — это члены, факторы и коэффициенты. члены математического выражения являются частями выражения, связанными со сложением или вычитанием.Коэффициенты в математическом выражении являются частями выражения, связанными с умножением. Наконец, коэффициенты в математическом выражении — это числа, умноженные на переменную.
Мы используем все эти разные части для создания математических выражений. Это очень полезно, потому что все эти части собраны вместе, чтобы представить явления реального мира в математическом выражении. Здорово, что теперь мы знакомы с каждой из этих частей целого!
Векторные компоненты
Математика и естественные науки были изобретены людьми для описания и понять мир вокруг нас.Мы наблюдаем, что есть некоторые количества и процессы в наш мир, который зависит от направления , в котором они происходят, и есть некоторые количества, которые не зависят по направлению. Математики и ученые называют количество которое зависит от направления , векторная величина . Количество которая не зависит от направления, называется скалярной величиной . А векторная величина имеет две характеристики: величина и направление . Когда сравнение две векторные величины одного типа, необходимо сравнить обе величина и направление.
На этом слайде мы описываем математическую концепцию, уникальную для векторов;
вектор компонентов . Компоненты вектора позволяют нам разбить единичную векторную величину
на две (или более) скалярные величины, с которыми мы имеем больше
математический опыт.
Компоненты вектора используются в векторной алгебре для
добавлять,
вычесть и умножить векторы.
Компоненты вектора позволяют нам разбить единичную векторную величину
на две (или более) скалярные величины, с которыми мы имеем больше
математический опыт.
Компоненты вектора используются в векторной алгебре для
добавлять,
вычесть и умножить векторы.
На рисунках векторы обычно обозначаются стрелкой. Длина стрелки указывает величину вектора и кончик стрелки указывает направление.Вектор помечены алфавитным букву с чертой сверху, чтобы отличить ее от скаляра. Обозначим величину вектора символом | a | . Направление будет измеряться под углом фи относительно координаты ось х . Ось координат y перпендикулярна х . Примечание: Оси координат x и y сами по себе векторы! У них есть величина и направление.Сначала ты сталкиваются с осями координат, когда вы учитесь строить графики. Так что у тебя есть какое-то время использовал векторы, даже не подозревая об этом!
Если мы построим пунктирную линию из кончика вектора , то получим идущий параллельно оси x, он пересекает ось y в том месте, где мы
этикетка ау . Аналогично линия от кончика вектора
параллельно оси Y разрезает ось X на и ось . С помощью
синус и косинус
отношения из
тригонометрия:
Аналогично линия от кончика вектора
параллельно оси Y разрезает ось X на и ось . С помощью
синус и косинус
отношения из
тригонометрия:
ay = | a | * грех (фи)
ax = | a | * cos (фи)
Звоним топор x-компонент из a и ay Y-компонент из а .Компонентные уравнения представляют собой скалярных уравнений; | а | и тригонометрический функции просто скаляры. Любая алгебра, связанная с эти величины будут скалярной алгеброй, а не векторной алгеброй. По сути, мы заменили единичную векторную величину на . с двумя скалярными величинами ax и ay .
Присмотревшись очень внимательно к этим двум уравнениям, мы замечаем, что они полностью определить вектор количества a ; они указывают как величина, так и направление a .2)
Зачем идти на все эти хлопоты? Потому что в аэрокосмической отрасли мы часто имеем дело
с силами и
силы — векторы.

 , Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 7.
, Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 7.


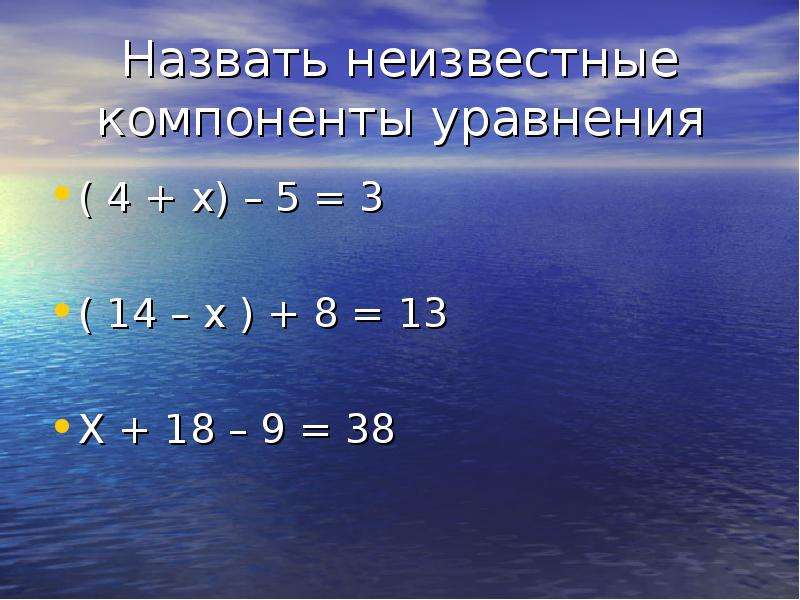 Повтор 5 класса. Уравнения. Поурочный план.Вариант 2
Повтор 5 класса. Уравнения. Поурочный план.Вариант 2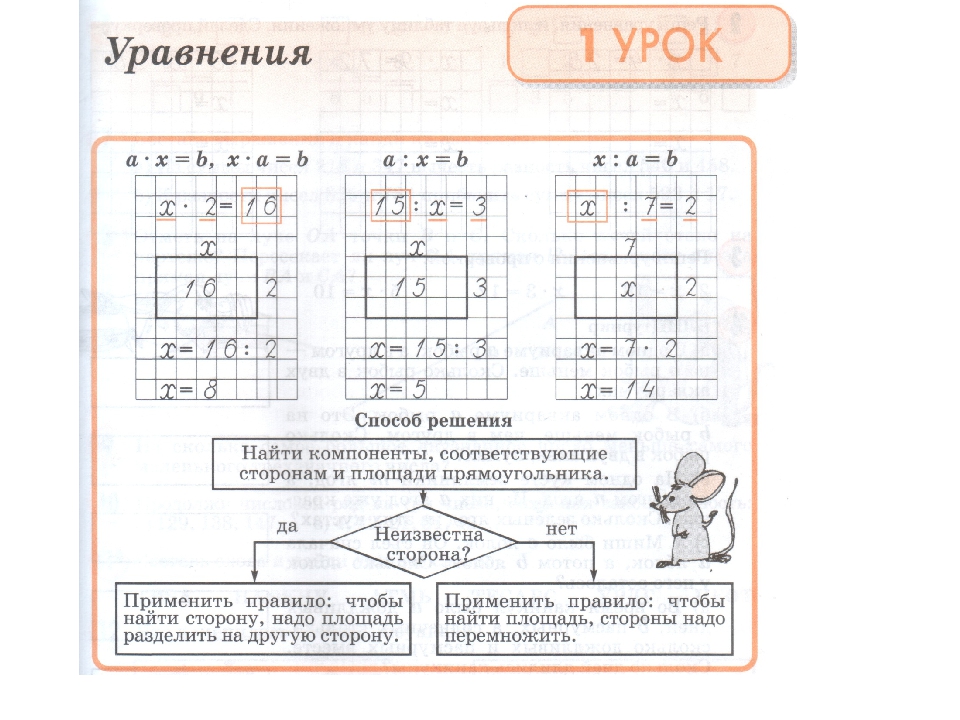
 Привитие ценностей
осуществляется посредством самостоятельного решения заданий, применение
знаний и обсуждения друг с другом.
Привитие ценностей
осуществляется посредством самостоятельного решения заданий, применение
знаний и обсуждения друг с другом.
 Решение уравнений, используя свойства вычитания.
Решение уравнений, используя свойства вычитания. Обозначь неизвестную величину.
Обозначь неизвестную величину.
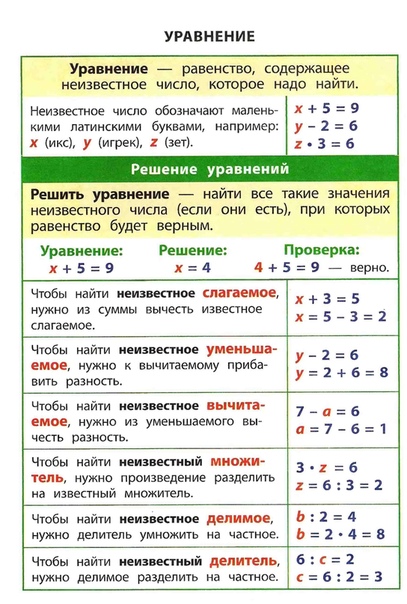 Учитель проходит по рядам, слушает, при
необходимости корректирует решения, оказывает помощь слабоуспевающим. По
истечению времени попросить учеников озвучить некоторые решения. Обратить
внимание на соответствие поставленной цели.
Учитель проходит по рядам, слушает, при
необходимости корректирует решения, оказывает помощь слабоуспевающим. По
истечению времени попросить учеников озвучить некоторые решения. Обратить
внимание на соответствие поставленной цели. Более способным
учащимся предлагаются задания более высокого уровня.
Более способным
учащимся предлагаются задания более высокого уровня.
