Коефіцієнт еластичності: Формула коэффициента эластичности и примеры
Блог: Цінова еластичність | Datawiz.io
Antonina Kelman10 березня 2016 р. 16:09
Кожен рітейлер колись задумувався про те, як зміниться попит на товар, якщо змінити його ціну. Це ж може привести не тільки до збільшення прибутку, а і до значних фінансових втрат. Очевидно, що ціна має надзвичайно важливу роль для покупця. Вони реагують на ціну, формують своє відношення до товару, визначаючи доцільність його придбання.
Згідно простого закону, товар з низькою ціною буде мати більший попит. Але різноманітні товари реагують на зміну ціни по-різному. А саме на це, перш за все, мають звертати увагу рітейлери. Чи будуть купувати товар, якщо його ціна збільшиться? Чи збільшиться попит, якщо ціна на товар зменшиться? Чи збільшиться прибуток при зміні ціни?
Для отримання відповіді на ці запитання використовують поняття цінової еластичності. Цінова еластичність допомагає виявити, як саме впливає зміна ціни на попит. З часом, цінову еластичність почали використовувати не тільки в наукових роботах, але і на практиці.
Як же виявити цінову еластичність товару? Власник магазину вирішив зменшити ціну одного товару на 2%. Через деякий час він побачив, що попит на цей товар збільшився на 6%. Таким чином, зменшивши ціну на товар він збільшив попит на нього. Використовуючи формулу:
E = (ΔQ/Qd)/(ΔP/P)
ΔQ/Qd – відносна зміна попиту,
ΔP/P- відносна зміна ціни, ми отримуємо E — коефіцієнт еластичності. В даному випадку він рівний 3.
Цей коефіцієнт означає, що попит
Але бувають випадки, коли коефіцієнт еластичності буде менше 1. Це означає, що попит нееластичний. Тобто, зміна ціни не призвела до зміни попиту. Покупці не сильно реагують на зміну ціни товару. В таких випадках при підвищенні ціни, товар і дальше будуть купувати.
Покупці не сильно реагують на зміну ціни товару. В таких випадках при підвищенні ціни, товар і дальше будуть купувати.
Варто пам’ятати, що не все так просто. На цінову еластичність впливає багато факторів. Наприклад, чим більше замінників даного товару, тим більш
Також варто сказати, що попит на предмети розкоші зазвичай еластичні, а на предмети першої необхідності — нееластичні. При збільшенні ціни на предмети першої необхідності (хліб, молоко, рибу і т. д.) покупці незначно скоротять покупки цих товарів. Як би не піднялась ціна на хліб, він незамінний в нашому раціоні. Тому попит на нього майже не зміниться. В той же час при рості ціни на предмети розкоші, споживачі можуть відмовитись від нього зовсім або ж перенести покупку на пізніший період.
Також варто враховувати привички та вподобання клієнтів. Хтось звик купувати продукцію одного виробника, комусь ця продукція подобається, а для когось це уже просто звичка. Якщо ціна на цю продукцію збільшиться, то попит на неї не впаде. Тобто попит буде нееластичним. Але пам’ятайте, що при збереженні токаї ситуації споживач може змінити свої вподобання на покупки більш дешевого товару.
Інколи при підвищенні ціни на товар, всупереч до всіх законів логіки, попит на нього може зростати. Такі тенденції ми багато раз спостерігали. Наприклад, при підвищенні цін на товари життєвого значення, люди з невисоким рівнем доходу збільшують попит на них. Це відбувається через побоювання ще більшого подорожчання.
Чи наприклад, при підвищенні цін на предмети розкоші. Деякі люди, схильні до демонстративного споживання, купують їх у великих кількостях. І не дивлячись на ріст цін попит на них буде зростати.
Цінова еластичність демонструє як покупець реагує на зміни ціни товару. Знаючи це, рітейлери можуть визначити оптимальну ціну на товар, не втративши свого покупця. І що найголовніше рітейлери збільшать свої доходи.
І що найголовніше рітейлери збільшать свої доходи.
(PDF) ДЕТЕРМІНАНТИ СПОЖИВЧОЇ ПОВЕДІНКИ: ЕЛАСТИЧНІСТЬ ПОПИТУ DETERMINANTS OF CONSUMER BEHAVIOR: ELASTICITY OF DEMAND
— слабкий і помірний зв’язок між ціною і обсягом попиту;
— зростання тісноти взаємозв’язку між ціною і попитом при використанні замість даних базового ряду,
показників обсягу продажів очищених від сезонної компоненти. Тому надалі в аналізі еластичності будуть
використані саме показники попиту очищені від сезонної компоненти.
Відсутність кореляції між фактичними даними продажів і динамікою цін на дизельне паливо, газ не
дозволило охарактеризувати цінову еластичність на основі середнього коефіцієнта еластичності. Зіставлення
цін на товари-субститути газ/бензин показало, що періодам зростання попиту на газ (понад 10%) відповідають
або передують періоди зростання ціни на бензин з одночасним зниженням ціни на газ (рис.1). Зіставлення
тривалості і амплітуди цінових коливань дозволило сформулювати гіпотезу про залежність піків зростання
попиту на газ від цінової політики на товари-субститути, що виражається в одночасному впливі на попит
ефектів цінової і перехресної еластичності.
Для перевірки гіпотези використано базисні темпи приросту, що характеризують амплітуду коливання
цін і попиту. Базисні темпи приросту розраховано по відношенню до значень ряду, що характеризують піки
зростання (зниження) і відображають зміну напрямку динаміки показника. На основі отриманих відносних
відхилень розраховано точкові коефіцієнти цінової еластичності по сформованій вибірці, до якої увійшли
періоди зростання попиту на газ за умови зниження ціни газу (табл.4).
Таблиця 4
Обчислення точкових коефіцієнтів цінової еластичності газу по сформованій вибірці
Період
Ціна газу
Попит на газ
Відносні відхилення Еd
ціни попиту
без лагу в реакції
попиту
лаг в реакції попиту —
1 міс
при збереженні
реакції попиту
протягом кількох
місяців
*
до
періоду
динаміка ціни за
кілька місяців
(до піків росту)
до попереднього
періоду
динаміка попиту
за кілька місяців
(до піків росту)
Лютий 2017 12,13 59,58 -0,03 0,05 -1,77
Березень 2017 11,58 62,29 -0,05 0,05 -1,00
-1,62
Квітень 2017 11,32 64,51 -0,02 -0,09 0,04 0,14 -1,63
-1,47
Липень 2017 11,49 61,41 -0,01 0,03 -2,77
Січень 2018 12,72 69,18 0,00 -0,14 0,17 0,25 -2,88
-1,71
Квітень 2018 12,69 66,05 -0,05 0,10 -2,25
Травень 2018 12,50 68,31 -0,02 -0,06 0,03 0,14 -2,26
-2,34
Липень 2018 13,26 66,05 0,02 -0,02 -1,32
Серпень 2018 13,28 65,70 0,00 -0,01 -3,02
Січень 2019 14,54 80,68 -0,11 0,22 -2,10
Квітень 2019 11,27 74,67 0,06 -0,07 -1,32
Серпень 2019 12,87 81,46 -0,05 0,08 -1,64
Вересень 2019 11,58 87,59 -0,10 -0,14 0,08 0,16 -1,61
-1,10
Жовтень2019 11,97 82,97 0,03 -0,05 -1,56
Грудень 2019 11,60 86,18 -0,01 0,04 -3,51
-2,44
Примітки. Реакція попиту при збереженні динаміки цін зберігається до3-4місяців.
Реакція попиту при збереженні динаміки цін зберігається до3-4місяців.
Врахування впливу фактора цінової еластичності дозволило зменшити відхилення прогнозованих
даних від фактичних при перевірці моделі тренду. Для деяких періодів, де за результатами обчислення
точкового коефіцієнта еластичності попит характеризується як жорсткий, корегування тренду на Кзміни попиту
також наближує теоретичне значення тренду до фактичного ряду, що пояснюємо пролонгованим впливом
цінової еластичності з попередніх періодів.
Пряма еластичність попиту за ціною
Розглянемо для початку поняття еластичності попиту за ціною, що визначається відповідним коефіцієнтом.
Цінова еластичність запитуваної кількості блага, або, інакше кажучи, пряма еластичність попиту за ціною(г \ — грецька літера «ця»), визначається як процентна зміна обсягу попиту, поділене на процентну зміну ціни, причому обсяг попиту є залежною змінною величиною.
Зобразимо в це формалізованому вигляді:
AQ / Q ^ P AQ
АР / Р Q АР (ЗЛ)
де Д — символ (грецька буква «дельта»), що позначає зміна;
AQ — зміна попиту;
АР — зміна ціни.
Існує два методи обчислення коефіцієнта еластичності: 1) визначення дугового і +2) точкової еластичності.
Дугова еластичність. Почнемо з розгляду дугової еластичності.
Дугового еластичністю називається еластичність між двома точками лінії попиту або пропозиції.
Дугову еластичність можна виміряти як мінімум чотирма способами.
1. Рух від верхньої точки (А) на нижній (В). Якщо ми хочемо виміряти коефіцієнт дугової еластичності, рухаючись від точки А до точки В, то отримаємо:
4 (значення Q в точці В) — 3 (значення Q в точці A) (i QB) — 3 (QA)
__________3 (значення Q в точці А) ___________ 3 (Q4)
4 (значення Р в точці В) — 5 (значення Р в точці А) ЦРВ) — 5 (РА)
5 (значеніеРвточкеЛ) 5 (РЛ)
2. Рух від нижньої точки (У) на верхній (А).Якщо ми вимірюємо дугову
еластичність, рухаючись у протилежному напрямку: від точки В до точки А
то коефіцієнт еластичності вийде іншим:
71 =
3 (QA) — A () QB _j.
4 QB)_ 4
5 (РА)-ЦРВ) 1_
А (РВ)4
1.
Тим самим ми прийшли до такого висновку: коефіцієнт еластичності попиту змінює своє значення в залежності від напрямку руху відліку. Для того аби уникнути цього незручності, можна обраховувати дугову еластичність, наприклад, відносячи різниця до найменшої (чи найбільшою) величиною.
де О — менша зростання кількості; Р — величина менша ціни.
mm
Вважаючи таким чином, отримаємо таке значення коефіцієнту еластичності:
4 (QB) — 3 (QA)
4 (РВ) — 5 (РА) _j_ +3
4 (РВ) 4
Отже, ми отримали три різні відповіді на одне питання. Всі три еластичності значення мають знак мінус (негативні).
Еластичність попиту за ціною, як правило, є величиною негативною.
Знак мінус засвідчує про негативний нахил кривої попиту, і його можна не приймати до уваги.У випадку, коли крива попиту являє собою виключення із закону попиту та має позитивний нахил, коефіцієнт цінової еластичності буде позитивною, що слід підкреслити особливо. 3-4 5 + 4_ 9 Л_3 + 45-4 «7»
3-4 5 + 4_ 9 Л_3 + 45-4 «7»
Остання формула демонструє відмінний від трьох попередніх показник дугової еластичності, або еластичність між двома точками.
Отже, всіма перерахованими вище способами ми вимірювали дугову ела стічность.Всі чотири представлених способу вимірювання дугової еластичності мають право на життя, але всі дають різні результати. Щоб уникнути цієї плутанину, економісти домовилися обчислювати дугову еластичність методом центральної точки, т. тобто способом четвертим.
Точкова еластичність. Тепер розглянемо поняття точкової еластичності (або еластичності в точці).
Точкова еластичність характеризують відносна зміна обсягу попиту при нескінченно малій зміні ціни.
Вислів точкової еластичності має вигляд:
DQ _ / Q _ dQР_
Л_ dP / P dp ~ Q (32)
Формула точкової еластичності (3.2) відрізняється від дугової еластичності формули (3. 1) тем, що має справу з нескінченно малими величинами. Якщо пряма попиту задана функцією Q = а — Ьр, то нахил цієї прямої дорівнює Ь = dQ / dP.
1) тем, що має справу з нескінченно малими величинами. Якщо пряма попиту задана функцією Q = а — Ьр, то нахил цієї прямої дорівнює Ь = dQ / dP.
На підставі цієї формули можна зробити надзвичайно важливий висновок: коефіцієнт еластичності для цієї прямої лінії попиту різний в різних її точках. Це неважко довести графічним спосіб.
Як виміряти крапкову еластичність її точок?
Нахил прямої лінії ABC виражається відношенням dQ / dP; це можна висловити ставленням DC / BD. Друга частина формули (3.2) буде виглядати так:
Р BD Q ~ 0 D
Тоді формула еластичності (3.1) приймає вигляд: Ц = DC BD DC BD 0 D ~ OD
Таким чином, ми дійшли дуже важливого висновку: еластичність в точці прямої лінії попиту дорівнює або відношенню довжин відрізків, що проекція даного пункту відсікає на осях, або стосовно відрізків самої лінії. У такий спосіб:
якщо (Ш = DC, то ц = 1;
якщо (Ш>DC, то ц> 1;
якщо (Ш то ц
Зрозуміло, що еластичність у точці А прямує до нескінченності (°°), а в точці С дорівнює нулю (0), а в точці В ми маємо одиничну еластичність.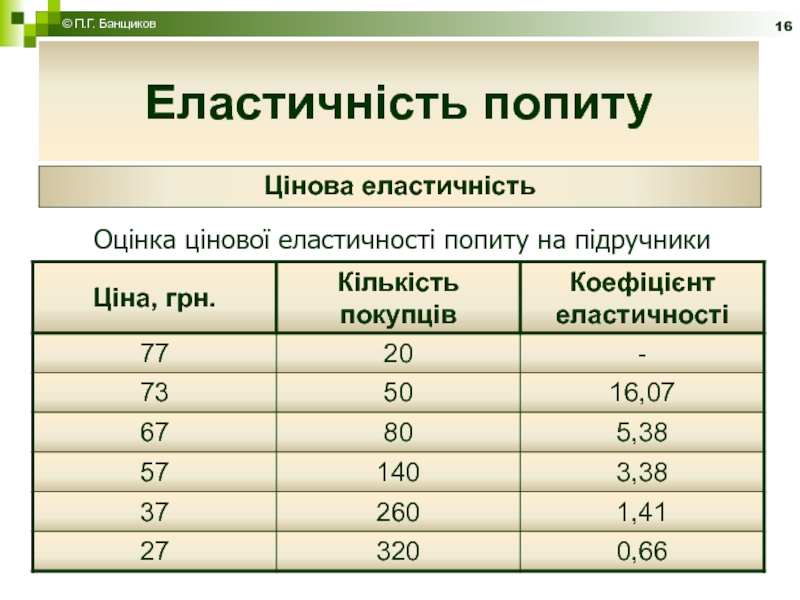 На відрізку АВ лінія попиту еластичний, а на відрізку нд нееластичні.
На відрізку АВ лінія попиту еластичний, а на відрізку нд нееластичні.
Природно, що можна зобразити і криву лінію попиту. В такому разі слід провести дотичну до тієї точки кривої, де ми бажаємо виміряти коефіцієнт цінової точкової еластичності, і цю дотичну продовжити до перетину з осями координат.
Не слід ототожнювати нахил лінії з еластичність.
Ми знаємо, що формула еластичності складається з двох співмножників: (AQ / AP) і (Р / 0. Перший з цих співмножників постійний, так як він визначає нахил лінії.Та зате другий співмножники (Р / 0 змінюється в залежності від положе вання точки на лінії. Тому всі похилі прямі змінюють свою еластичність попиту від точки до точки і судити тільки по нахилу прямої лінії про її еластичності не слід.
Усі прямі похилі лінії попиту з негативним нахилом мають різну еластичність в різних точках. Тільки у рівнобедрений гіперболи коефіцієнт еластичності дорівнює одиниці в будь-якій її точке. 1
1
Якщо зміна ціни не викликає ніякої зміни попиту, то ми маємо справу з нульовою еластичністю попиту: р \ — 0.
Навпаки, якщо будь-яка нескінченно мала зміна ціни викликає нескінченне збільшення попиту, то в наявності попит з нескінченною еластичністю: г \ = ° о.
Вертикальне пряма попиту має нульовий еластичністю, а горизонтальна — нескінченної за величиною еластичністю.
Як знайти коефіцієнт еластичності |ЯкПросто
Еластичність попиту або пропозиції є важливою характеристикою, яка дає точну кількісну оцінку впливу певних факторів на обсяги продажів. Щоб визначити ступінь чутливості ринку до подібних дій, потрібно знайти коефіцієнт еластичності.
Інструкція
- Різні товари на ринку продаються по-різному, і цьому є безліч причин, які в кінцевому підсумку зводяться до певного співвідношення між попитом і пропозицією. Це співвідношення є базовим законом ринку і залежить від багатьох факторів: ціна самого товару, його аналога, який може віддати перевагу споживач, рівень доходів потенційного покупця і т.

- В загальному вигляді еластичність — це зміна деякої функції внаслідок зміни її аргументу. Іншими словами, математично цю характеристику можна представити у вигляді дробу: відносини відносного приросту функції до приросту незалежної змінної.
- Коефіцієнт еластичності показує ступінь збільшення або зменшення обсягу попиту / пропозиції при зміні деякого фактора на 1%. Таким чином, можна заздалегідь розрахувати реакцію споживача і виробити потрібну стратегію, наприклад, провести стимулюючу рекламну акцію, організувати знижки деяким категоріям покупців на обмежений час і т.д.
- Щоб знайти коефіцієнт еластичності, можна скористатися двома методами: обчислення по дузі і в точці. Вибір способу залежить від того, якими вихідними даними ви маєте в своєму розпорядженні. Наприклад, дугова еластичність передбачає розрахунок між двома конкретними точками на графіку (кривій) попиту або пропозиції. При цьому необхідно знати ціни та обсяги продукції на початку і кінці вийшла дуги.

- Якщо всі зазначені дані у вас є, то скористайтеся такою формулою:
Ke = (Q2 — Q1) / ((Q2 + Q1) / 2): (P2 — P1) / ((P2 + P1) / 2), де:
Ke — коефіцієнт еластичності;
Q1 і Q2 — обсяги продукції в першій і другій точці дуги;
- Точкову еластичність легко визначити, якщо вам відомий тільки початковий рівень цін і функція попиту (пропозиції) при цій величині. Для розрахунку знайдіть її похідну і помножте на співвідношення між аргументом і функцією:
Ke = Q ‘(P) • P / Q (P), де:
Р — ціна;
Q (P) — функція попиту / пропозиції по даній ціні;
Q ‘(P) — її перша похідна.
ЕЛАСТИЧНІСТЬ ПОПИТУ НА КРЕДИТ – АНАЛІЗ ТЕНДЕНЦІЙ — Секція_3_2014_11_25 — 2014_11_25_Lviv — Архів / Archive — SOPHUS
УДК 336.77.067.21/22
Чікіта Ірина
к.е.н., доцент
Львівська комерційна академія
м. Львів
Львів
ЕЛАСТИЧНІСТЬ ПОПИТУ НА КРЕДИТ – АНАЛІЗ ТЕНДЕНЦІЙ
Анотація
У статті висвітлені результати аналізу цінової еластичності попиту на кредит з боку різних економічних агентів у довгому і короткому періодах. Зокрема, досліджено вплив нецінових факторів на формування попиту на кредит усіх суб’єктів економіки.
Ключові слова: еластичність попиту, кредит, депозит, парадокс Гіффена, аналіз.
В сьогоднішніх умовах стимулювання економічного зростання залишається чи не найважливішим завданням для виходу вітчизняної економіки з кризи. Серед факторів, які негативно впливають на зростання ВВП з боку фінансової системи зарубіжні економісти називають збільшення банківської маржі як різниці між процентними ставками за кредитами і депозитами [1, 2, 3].
Дослідження банківської маржі в Україні показали [4], що протягом 2005-2012 вона перебувала у діапазоні від 5% до 8% у національній валюті, і це значно вище від рівня, який спостерігається у економіках розвинутих країн. При цьому, процентні ставки за кредит збільшуються саме в ті періоди, коли економічне зростання сповільнюється.
При цьому, процентні ставки за кредит збільшуються саме в ті періоди, коли економічне зростання сповільнюється.
З метою вивчення можливості зниження відсоткових ставок без втрати банківською системою доходів було здійснено аналіз цінової еластичності попиту на кредит з боку різних економічних агентів у довгому і короткому періодах. Проведений аналіз показав, що в короткому періоді (помісячно) попит на кредити переважно еластичний, в окремі місяці значення еластичності прямує до безмежності, а в довгому періоді (по роках) попит еластичний в періоди економічного розвитку (2006-2007, 2011 рр.) та нееластичний у період спаду (2008-2009, 2012 рр.) [4].
Одночасно було виявлено, що в багатьох часових проміжках значення еластичності було додатнім, тобто обсяги кредитування зростали при зростанні процентної ставки. В економічній теорії додатне значення показника еластичності пояснюється парадоксом Гіффена. Його суть полягає в тому, що при зростанні ціни на деякі товари, їх споживання збільшується за рахунок економії на інших товарах, що зумовлено переважанням ефекту доходу над ефектом заміщення.
Ще одне пояснення парадоксу Гіффена – інфляційні очікування економічних агентів, що змушує їх збільшувати попит на товар в очікуванні його подорожчання.
Прийнято вважати, що товаром Гіффена є переважно товари першої необхідності, зокрема продукти харчування, (наприклад, картопля), а кредит до таких товарів не відноситься. Однак здійснені розрахунки [4] однозначно демонструють, що додатне значення еластичності попиту на кредит з боку нефінансових корпорацій є непоодиноким явищем, а з боку домогосподарств взагалі переважає. З цього робимо висновок про високий вплив нецінових факторів на формування попиту на кредит усіх суб’єктів економіки.
Для вивчення дії таких нецінових чинників нами проведено оцінку чутливості попиту на кредит до змін у доході суб’єктів господарської діяльності (без банків та бюджетних установ) і населення на основі статистичних даних у довгому періоді (рік) (табл1).
Інтерпретація показника чутливості попиту від доходу пов’язана з поділом благ на товари вищої споживчої цінності (нормальні товари) та нижчої споживчої цінності, а також предмети розкоші та предмети першої необхідності. Для товарів нижчої споживчої цінності показник еластичності від доходу є від’ємним, що пов’язане з відмовою від них з ростом доходу. Якщо коефіцієнт еластичності є меншим за 1, товар вважається першої необхідності. Його частка у витратах споживача зменшується зі зростанням доходу, а попит загалом зростає зі зменшенням доходів. У свою чергу, попит на товари розкоші зі збільшенням доходів підвищується, коефіцієнт еластичності за доходом відповідно є більшим за 1.
Таблиця 1
Еластичність попиту на кредит за доходом суб’єктів господарювання та населення за 2006 — 2013 роки
Період | Еластичність попиту на кредит за доходом | |
суб’єктів господарювання | населення | |
2006 | 1,3 | 3,6 |
2007 | 1,7 | 1,9 |
2008 | 0,7 | 0,2 |
2009 | 2,4 | -20,3 |
2010 | 1,6 | 1,1 |
2011 | 0,8 | 3,7 |
2012 | 0,8 | 0,4 |
2013 | -4,3 | 5,3 |
Джерело: розраховано за даними: http://www. ukrstat.gov.ua/
ukrstat.gov.ua/
З наведених розрахунків еластичності попиту на кредит за доходом видно, що для суб’єктів господарювання він є меншим за 1 у період 2008 р. та 2011-2012 рр., а у 2013 взагалі має від’ємне значення. Таким чином, простежується зв’язок між загальною макроекономічною ситуацією та попитом на кредит з боку підприємств: кризові явища, скорочення обсягів виробництва і рестрикційна грошово-кредитна політика зумовлюють таке неоднозначне явище, як перетворення кредиту на ”товар першої необхідності“, а згодом, на ”товар нижчої споживчої якості“. Для населення, ставки кредитування для якого традиційно вищі, зміни мають дещо іншу амплітуду: у найбільш критичний період – 2009 р., – величезне від’ємне значення еластичності за доходом, а у 2009 та 2012 рр. – кредит є ”товаром першої необхідності“.
Зауважимо, що результати розрахунків не можуть вважатися цілковито об’єктивними внаслідок значного тіньового обороту в нашій державі, що не дозволяє встановити обсяги фактичних доходів економічних агентів із достатньоюточністю. Крім того, еластичність за доходом варіюється залежно від груп споживачів, що в умовах сучасного стану подання статистичної інформації врахувати неможливо. Разом з тим, наведені дані не суперечать попередньо виявленим тенденціям, що дозволяє опиратися на них у здійсненому дослідженні.
Крім того, еластичність за доходом варіюється залежно від груп споживачів, що в умовах сучасного стану подання статистичної інформації врахувати неможливо. Разом з тим, наведені дані не суперечать попередньо виявленим тенденціям, що дозволяє опиратися на них у здійсненому дослідженні.
Висновок, який можна зробити з результатів аналізу полягає, на наш погляд, у констатації недостатньої монетизації економіки і потреби у збільшенні фінансового забезпечення економічних агентів, зокрема, через кредитний канал. Це підтверджується зростанням попиту на кредит при збільшенні процентних ставок та еластичністю за доходом, меншою за 1 практично у ті ж самі часові періоди. Також значним є фактор негативних очікувань, який формує поведінку суб’єктів ринку та приводить до зростання потреби в кредитуванні. Крім того, позиціонування кредиту як товару Гіффена означає відсутність у економічних агентів альтернативних до кредиту джерел фінансового забезпечення (товарів-субститутів у термінології економічної теорії).
Все це дозволяє зробити припущення про доцільність розширення кредитування суб’єктів господарської діяльності та необхідність змін у грошово-кредитній політиці держави для стимулювання економічного зростання.
Список використаних джерел
- Koivu T. Do efficient banking sectors accelerate economic growth in transition countries? / Tuuli Koivu // BOFIT Discussion Paper. – 2002. – N 14. : [Електронний ресурс]. – Режим доступу : http://129.3.20.41/eps/mac/papers/0212/0212013.pdf.
- Financial Development and Economic Growth: Evidence from Ten New EU Members / Guglielmo Maria Caporale, Christophe Rault, Robert Sova and Anamaria Sova // Working Paper No. 09-37. — October 2009 : [Електронний ресурс]. – Режим доступу : http://www.brunel.ac.uk/__data/assets/pdf_file/0014/82130/0937.pdf
- Djalilov К. Piesse J Financial Development and Growth in Transition Countries: A study of Central Asia/ Khurshid Djalilov Jenifer Piesse //Research papers.
 Bournemouth University Business School. – October 2011 : [Електронний ресурс]. – Режим доступу : http://business.bournemouth.ac.uk/downloads/ Djalilov_and_ Piesse.pdf
Bournemouth University Business School. – October 2011 : [Електронний ресурс]. – Режим доступу : http://business.bournemouth.ac.uk/downloads/ Djalilov_and_ Piesse.pdf - Чікіта І. Б. Еластичність попиту на кредити як фактор підвищення впливу банківської системи на економічне зростання / І. Б. Чікіта // Вісник Національного банку України. – 2013. — № 8. – С. 52-56
Коэффициент эластичности – обзор
11.2.2. НЕПРЯМЫЕ МЕТОДЫ ДЛЯ ОПРЕДЕЛЕНИЯ FCC
Методы, описанные в этом разделе, характеризуются как косвенные, поскольку упругости сначала определяются экспериментально, а затем определяются коэффициенты контроля потока с использованием теорем МСА. В основе этого подхода лежат два основных допущения: (1) метаболическая система описана адекватно, , т. е. , все реакции и соответствующие регуляторные взаимодействия включены в описание системы, и (2) система находится в стационарном состоянии и начальное состояние. концентрации субстрата и конечного продукта фиксируются на постоянном уровне. Чтобы убедиться в выполнении этих предположений, целесообразно проверить результаты непосредственным определением хотя бы одного из управляющих коэффициентов системы. В своем анализе глюконеогенеза в клетках печени крыс Groen, et al. , (1986) определили все коэффициенты эластичности (см. также пример 11.2) и использовали теоремы МСА для расчета FCC этого пути. Для проверки результатов они также определили коэффициент отклика пути по отношению к пирувату, субстрату.Поскольку была также определена эластичность первой реакции (пируваткарбоксилаза) по отношению к пирувату, FCC первой стадии можно было рассчитать, используя определение коэффициента отклика [уравнение. (11.12)].
Чтобы убедиться в выполнении этих предположений, целесообразно проверить результаты непосредственным определением хотя бы одного из управляющих коэффициентов системы. В своем анализе глюконеогенеза в клетках печени крыс Groen, et al. , (1986) определили все коэффициенты эластичности (см. также пример 11.2) и использовали теоремы МСА для расчета FCC этого пути. Для проверки результатов они также определили коэффициент отклика пути по отношению к пирувату, субстрату.Поскольку была также определена эластичность первой реакции (пируваткарбоксилаза) по отношению к пирувату, FCC первой стадии можно было рассчитать, используя определение коэффициента отклика [уравнение. (11.12)].
Для определения коэффициентов эластичности можно применять ряд различных подходов. Далее приводится краткое описание наиболее распространенных.
Двойная модуляция
Чтобы проиллюстрировать этот метод, рассмотрим гексозоизомеразную реакцию пути ЭМИ:
(11.31) ⋯ → Глюкоза — 6 — фосфат ⟶gpructose — 6-фасфат → ⋯
Скорость реакции изомеразы зависит только от концентраций показанных соединений, IE , V GPI = F ( c G6P , c F6P ). В стационарном состоянии скорость этой реакции равна потоку Дж через путь ЭМИ и, следовательно,
В стационарном состоянии скорость этой реакции равна потоку Дж через путь ЭМИ и, следовательно,
(11,32)dJ=∂vGPI∂CG6PdcG6P+∂vF6P∂cF6P
Масштабирование этого уравнения с учетом стационарного потока и перегруппировки результат дает:
(11.33)d ln J =ɛG6PGP1d ln cG6P+ɛF6PGPId ln cF6P
В контрольном эксперименте можно измерить концентрации двух метаболитов и установившийся поток. Затем можно ввести возмущение, например, . , путем изменения концентрации внеклеточной глюкозы, чтобы получить новый набор стационарных измерений концентрации потока и метаболитов. 4 Путем аппроксимации дифференциалов в уравнении. (11.33) по разностям, этот эксперимент с возмущением дает уравнение, связывающее измерения потока и концентрации с двумя коэффициентами упругости.Если ввести второе возмущение, дополнительный набор данных для стационарного потока и концентраций метаболитов может дать второе уравнение, из которого можно рассчитать два коэффициента эластичности.
Этот подход, называемый двойной модуляцией, был впервые описан Касером и Бернсом (1979). Очевидно, что два возмущения должны быть спланированы так, чтобы получить два линейно независимых уравнения , т. е. , при этом должно выполняться следующее неравенство:34)d ln cG6P1d ln cF6P1≠d ln cG6P2d ln cF6P2
Надстрочные индексы в уравнении (11.34) относятся к измерениям, полученным после соответствующего возмущения. Если разница между двумя членами уравнения. (11.34) мало, оба уравнения плохо подходят для расчета упругости, и решение становится очень чувствительным к экспериментальной ошибке. На самом деле, во многих путях может быть экспериментально трудно получить линейно независимый набор измерений, который удовлетворяет уравнению. (11.34). Чтобы повысить вероятность того, что такие измерения действительно независимы, предполагается, что модуляция выполняется как выше, так и ниже исследуемого пути (Fell, 1992). Еще одним недостатком этого подхода является то, что он требует небольших изменений, чтобы удовлетворительно аппроксимировать дифференциалы конечными разностями, и такие изменения, вероятно, будут определяться непропорциональными экспериментальными ошибками. Отмечено, что для большинства ферментативных реакций помимо реагента и продукта реакции существуют и другие эффекторы, э.г. , кофакторы и ингибиторы. Это означает, что скорость реакции является функцией более чем двух переменных, использованных в предыдущем примере. Поскольку для описания влияния каждой из этих переменных требуется разная эластичность, становится необходимым провести более двух экспериментов с возмущениями, которые приведут к линейно независимым уравнениям.
Отмечено, что для большинства ферментативных реакций помимо реагента и продукта реакции существуют и другие эффекторы, э.г. , кофакторы и ингибиторы. Это означает, что скорость реакции является функцией более чем двух переменных, использованных в предыдущем примере. Поскольку для описания влияния каждой из этих переменных требуется разная эластичность, становится необходимым провести более двух экспериментов с возмущениями, которые приведут к линейно независимым уравнениям.
Одиночная модуляция
Если известен один из коэффициентов эластичности для последовательности реакций, подобной той, что в уравнении (11.31), другой коэффициент упругости можно определить из одного эксперимента по модуляции.Преимущество этого подхода состоит в том, что можно применять несколько модуляций одного типа, но разной величины, а также можно использовать графический метод для определения дифференциальных членов в уравнении. (11.33). Гроен, и др. (1986) использовали этот метод для определения коэффициента эластичности пируваткиназы по отношению к фосфоенолпирувату и коэффициента эластичности пируваткарбоксилазы по отношению к цитоплазматическому оксалоацетату (см. также пример 11.2). Этот подход, очевидно, более надежен, чем метод двойной модуляции, но он по-прежнему основан на хорошей оценке дифференциальных членов в уравнении.(11.33) и, конечно же, знание одного коэффициента эластичности.
также пример 11.2). Этот подход, очевидно, более надежен, чем метод двойной модуляции, но он по-прежнему основан на хорошей оценке дифференциальных членов в уравнении.(11.33) и, конечно же, знание одного коэффициента эластичности.
Подход сверху вниз
Во многих ситуациях подробная информация, предоставляемая всеми FCC, на самом деле не нужна, тогда как более важно определить группу реакций, в которых находится большая часть контроля потока. Это может помочь сосредоточиться на соответствующих частях метаболизма. Кроме того, повторяя эту процедуру, можно локализовать управление потоком на все более мелких группах реакций. Группировка реакций — мощная концепция в анализе управления потоками метаболических путей, и она подробно обсуждается в главе 13.Основная идея исходит из нисходящего подхода к MCA, предложенного Брандом, Брауном и сотрудниками, согласно которому изучаемый путь делится на сегменты (или группы) только с одним общим метаболитом (Браун, и др. ). , 1990a; Hafner, et al. , 1990):
). , 1990a; Hafner, et al. , 1990):
(11,35)S⟶Группа 1×⟶Группа 2P
В разветвленном пути общий промежуточный продукт X, очевидно, является метаболитом точки ветвления, тогда как для линейного пути X будет одним из метаболитов K линейного пути (см. ниже).Групповые коэффициенты контроля потока могут быть введены, чтобы обеспечить меру степени контроля потока, осуществляемого реакциями в группе. Легко показать, что коэффициенты управления потоком для каждой из двух групп в уравнении (11.35) равна сумме FCC для отдельных ступеней в группах (Браун, и др. , 1990a) и что коэффициенты контроля группового потока подчиняются теореме суммирования,
(11.36)CGroup 1J+CGroup 2J=1
В дополнение к группе ККК может быть введен набор коэффициентов эластичности по отношению к промежуточному метаболиту для описания влияния этого метаболита на скорость реакций в группе (см. также главу 13):
(11 .37)ɛXGroup i=CXvGroup i∂vGroup i∂cX i ∈ { 1,2 }
По аналогии с теоремой связности, групповые коэффициенты эластичности и групповые коэффициенты контроля потока связаны соотношением
JGro1+1Group1X4) (1CGroup1Gro11) CGroup 2J ɛXGroup 2=0
Аналогичные теоремы справедливы для коэффициентов контроля групповой концентрации (Brown, et al. , 1990a).
, 1990a).
Когда траектория сегментирована, можно определить общие коэффициенты эластичности, e.г. , с помощью экспериментов с двойной модуляцией, или, если известен один из коэффициентов эластичности, другой можно определить с помощью экспериментов с одиночной модуляцией. Из ур. 11.36 и (11.38), затем можно рассчитать групповые FCC, чтобы обеспечить меру контроля потока, находящегося в каждом из двух сегментов пути. Поскольку путь, в принципе, может быть сегментирован в любом произвольном положении, можно постепенно сузить группу индивидуальных реакций с наибольшей группой FCC. Предпосылкой для применения метода двойной (или одиночной) модуляции является, однако, отсутствие эффекторов, отличных от промежуточного звена пути X, иными словами, не допускаются никакие перекрестные помехи между реакционными группами, кроме тех, которые происходят через промежуточный метаболит X.Это может быть серьезным недостатком, поскольку существует много ситуаций, когда взаимодействия между двумя группами могут происходить иначе, чем через общий метаболит X. Представлен метод оценки силы таких взаимодействий и степени, в которой они влияют на определение FCC на основе измерений потока. в главе 13. Нисходящий подход был применен Брандом, Брауном и сотрудниками при анализе окислительного фосфорилирования (см. пример 11.3), и он также полезен для анализа сложных реакционных сетей, как показано в главе 13, где подход описан более подробно.
Представлен метод оценки силы таких взаимодействий и степени, в которой они влияют на определение FCC на основе измерений потока. в главе 13. Нисходящий подход был применен Брандом, Брауном и сотрудниками при анализе окислительного фосфорилирования (см. пример 11.3), и он также полезен для анализа сложных реакционных сетей, как показано в главе 13, где подход описан более подробно.
Расчет коэффициентов эластичности на основе кинетических моделей
Если доступна действующая математическая модель скорости ферментативной реакции, ее эластичность по отношению к эффекторам и субстратам можно легко рассчитать, используя определение коэффициента эластичности. Для целей контрольного анализа не требуется, чтобы кинетическое выражение было механистически основано, если оно правильно описывает кинетический эффект различных эффекторов. Этот подход является прямым и очень надежным, но он поднимает фундаментальный вопрос: правильно ли кинетика фермента in vitro описывает функцию фермента in vivo . К счастью, значения v max компенсируются при расчете коэффициентов эластичности, и проблема сводится к определению сродства (или K m ). Также важно учитывать все возможные эффекторы в этих исследованиях. Кроме того, поскольку малые коэффициенты эластичности обычно связаны с большими коэффициентами контроля, эффекторы с низкими коэффициентами эластичности являются наиболее важными для контроля потока, тогда как в большинстве исследований кинетики ферментов in-vitro наблюдается тенденция фокусироваться на эффекторах с большими значениями. эластичности.Еще одно предостережение при использовании кинетических данных in vitro заключается в том, что большинство исследований кинетики ферментов основано на измерениях начальной скорости, когда продукт реакции отсутствует. Очевидно, что эта экспериментальная ситуация не является репрезентативной для условий in-vivo.
К счастью, значения v max компенсируются при расчете коэффициентов эластичности, и проблема сводится к определению сродства (или K m ). Также важно учитывать все возможные эффекторы в этих исследованиях. Кроме того, поскольку малые коэффициенты эластичности обычно связаны с большими коэффициентами контроля, эффекторы с низкими коэффициентами эластичности являются наиболее важными для контроля потока, тогда как в большинстве исследований кинетики ферментов in-vitro наблюдается тенденция фокусироваться на эффекторах с большими значениями. эластичности.Еще одно предостережение при использовании кинетических данных in vitro заключается в том, что большинство исследований кинетики ферментов основано на измерениях начальной скорости, когда продукт реакции отсутствует. Очевидно, что эта экспериментальная ситуация не является репрезентативной для условий in-vivo.
Существует множество примеров определения эластичности по кинетическим моделям. В своем анализе глюконеогенеза в клетках печени крыс Groen, et al. , (1986) определили некоторые коэффициенты эластичности, используя этот подход (см. Пример 11.2), а при анализе гликолиза у S. cerevisiae, Galazzo and Bailey (1990) определили коэффициенты групповой эластичности для всех ключевых стадий и использовали их для расчета FCC пути от глюкозы до этанола в взвешенных и иммобилизованных клетки. Эта тема более подробно рассматривается в главах 12 и 13.
В своем анализе глюконеогенеза в клетках печени крыс Groen, et al. , (1986) определили некоторые коэффициенты эластичности, используя этот подход (см. Пример 11.2), а при анализе гликолиза у S. cerevisiae, Galazzo and Bailey (1990) определили коэффициенты групповой эластичности для всех ключевых стадий и использовали их для расчета FCC пути от глюкозы до этанола в взвешенных и иммобилизованных клетки. Эта тема более подробно рассматривается в главах 12 и 13.
Коэффициент упругости – обзор
10.2.1 Основные уравнения упругости неоднородных материалов в плоскости
Основные уравнения неоднородных материалов имеют ту же форму, что и уравнения для однородных твердых тел, за исключением что свойства материала являются функциями пространственного положения.В плоской упругости неоднородных материалов закон Гука с коэффициентами упругости, зависящими от пространственного положения, можно записать как
(10.23)σxx=λ*(x,y)(exx+eyy)+2µ(x,y)exxσyy=λ* (x,y)(exx+eyy)+2µ(x,y)eyyσxy=2µ(x,y)exy
, где λ ( x , y ) и µ ( x , y ) — это пространственные постоянные позиции, зависящие от позиции, которые связаны с модулем Young E ( x , y ) и соотношение Poasson ν ( x , y ) на
Λ (x,y)=E(x,y)ν(x,y)[1+ν(x,y)][1−2ν(x,y)],µ(x,y)=E(x, y)2[1+ν(x,y)]
и λ *( x , y ) определяется выражением
уравнения(10. 23) можно выразить следующим образом:
23) можно выразить следующим образом:
(10.24)exx=12µ(x,y)[σxxλ*(x,y)2(λ*(x,y)+µ(x,y))(σxx+ σyy)]eyy=12µ(x,y)[σyyλ*(x,y)2(λ*(x,y)+µ(x,y))(σxx+σyy)]exy=12µ(x,y) σxy
При сплошном анализе градуированных композитов упругие свойства можно рассчитать на основе микромеханической модели (например, модели Мори-Танака, разработанной Венгом [10-3]), или можно предположить, что они следуют некоторым элементарным функциям, которые в соответствии с микромеханическим анализом. Часто используются экспоненциально изменяющийся модуль Юнга и постоянный коэффициент Пуассона, что приводит к постоянным коэффициентам, уравнениям в частных производных для полей перемещений.
В дополнение к основному закону, уравнения равновесия,
(10.25)∂σxx∂x+∂σxy∂y=0∂σxy∂x+∂σyy∂y=0
и соотношения деформации-перемещения,
( 10.26)exx=∂ux∂x,eyy=∂uy∂y, exy=12∂ux∂y+∂uy∂x
также должно выполняться.
Путем устранения напряжений и деформаций в уравнениях. (10.23), (10. 25) и (10.26), мы можем получить следующие основные уравнения для перемещений u x и u y :
25) и (10.26), мы можем получить следующие основные уравнения для перемещений u x и u y :
(10.27)(λ∗+µ)∂∂x∂ux∂x+∂uy∂y+µ∇2ux+∂λ∗∂x∂ux∂x+∂uy∂y+2∂µ∂x∂ux∂x+∂µ∂y ∂ux∂y+∂uy∂x=0,(λ∗+µ)∂∂y∂ux∂x+∂uy∂y+µ∇2uy+∂λ∗∂y∂ux∂x+∂uy∂y+2∂µ∂ y∂uy∂y+∂µ∂x∂ux∂y+∂uy∂x=0
, где ∇ 2 — оператор Лапласа. Для неоднородного материала с экспоненциально изменяющимся модулем и постоянным коэффициентом Пуассона, т.е. β и γ — материальные константы, определяющие уравнения (10.27) для перемещений, приведенных к
(10,29)(κ+1)∂2ux∂x2+(κ−1)∂2ux∂y2+2∂uy∂x∂y+β(κ+1)∂ux∂x+ γ(κ−1)∂ux∂y+γ(κ−1)∂uy∂x+β(3−κ)∂uy∂y=0,(κ−1)∂2uy∂x2+(κ+1)∂ 2uy∂y2+2∂ux∂x∂y+γ(3−κ)∂ux∂x+β(κ−1)∂ux∂y+β(κ−1)∂uy∂x+γ(κ+1 ) ∂uy∂y = 0
, где , где κ = 3 — 4 ν 0 для плоской штаммы и κ = (3 — ν 0 ) / (1 + ν 0 ) для плоского напряжения. Уравнения в уравнении (10. Уравнение (10.27) используется в методе смещения для плоской упругости неоднородных материалов. В равной степени может быть принят метод функции напряжения. В этом случае напряжения выражаются через функцию напряжений Эйри ϕ следующим образом: Уравнения равновесия (10.25) удовлетворяются при этих напряжениях. Использование закона Гука Ур. (10.24) и соотношение деформация-перемещение (10.24). (10.26) дает основное уравнение функции напряжения Эйри для обычных неоднородных материалов в условиях плоского напряжения: (10.31)1E∇2∇2ϕ+2∂∂x1E∂∇2ϕ∂x+∂∂y1E∂∇2ϕ∂y+∇21E∇2ϕ−∂2∂y21+νE∂2ϕ∂x2−∂2∂x21+νE∂2ϕ∂ y2+2∂2∂x∂y1+νE∂2ϕ∂x∂y=0 Для плоской деформации E и ν в этом уравнении следует заменить на E /(1 − ν 2 ) и ν /(1 − ν ) соответственно. (10.32)∇2∇2ϕ−2β∂∂x+γ∂∂y∇2ϕ+β2−ν0γ2∂2ϕ∂x2+2(1+ν0)βγ∂2ϕ∂x∂y+γ2−ν0β2∂2ϕ∂y2=0 Как мы видели, коэффициент уравнения, оцененный с помощью регрессионного анализа МНК, дает оценку наклона прямой линии, которая, как предполагается, является отношением между зависимой переменной и, по крайней мере, одной независимой переменной. Из исчисления наклон линии является первой производной и говорит нам о величине воздействия изменения переменной на одну единицу на значение переменной, измеренное в единицах переменной.Как мы видели в случае с фиктивными переменными, это может проявляться как параллельный сдвиг оцениваемой линии или даже изменение наклона линии через интерактивную переменную. Здесь мы хотим исследовать концепцию эластичности и то, как мы можем использовать регрессионный анализ для оценки различных эластичностей, которые интересуют экономистов. Понятие эластичности заимствовано из техники и физики, где оно используется для измерения реакции материала на силу, обычно физическую силу, такую как растягивающая/вытягивающая сила.Именно отсюда мы получаем термин «эластичная» лента. В экономике речь идет о некоторой рыночной силе, такой как изменение цены или дохода. Эластичность измеряется как процентное изменение/реакция как в технических приложениях, так и в экономике. Ценность измерения в процентах заключается в том, что единицы измерения не играют роли в значении измерения и, таким образом, позволяют проводить прямое сравнение эластичностей. Например, если цена на бензин увеличилась, скажем, на 50 центов по сравнению с начальной ценой в 3 евро.00 и привело к снижению ежемесячного потребления для потребителя с 50 галлонов до 48 галлонов, мы рассчитываем эластичность как 0,25. Ценовая эластичность – это процентное изменение количества товара в результате некоторого процентного изменения цены. 16-процентное увеличение цены вызвало только 4-процентное снижение спроса: 16-процентное изменение цены → 4-процентное изменение количества или 0,04/0,16 = 0,25. Хотя это обсуждение касалось изменений цен, любая из независимых переменных в уравнении спроса будет иметь соответствующую эластичность. Таким образом, существует эластичность дохода, которая измеряет чувствительность спроса к изменениям в доходе: не очень чувствительна к спросу на продукты питания, но очень чувствительна к яхтам. А теперь представьте спрос на очень дорогой товар. Опять же, мера эластичности выражается в процентах, поэтому эластичность можно непосредственно сравнить с эластичностью бензина: эластичность 0,25 для бензина дает ту же информацию, что и эластичность 0,25 для автомобиля стоимостью 25 000 фунтов стерлингов.Потребитель считает, что оба товара имеют мало заменителей и, следовательно, имеют неэластичные кривые спроса, эластичность которых меньше единицы. Математические формулы для различных эластичностей: Где η — греческая строчная буква eta, используемая для обозначения эластичности. ∆ читается как «изменение». Где Y используется как символ дохода. Где P2 — цена товара-заменителя. При ближайшем рассмотрении ценовой эластичности мы можем записать формулу как: Где расчетный коэффициент для цены в регрессии МНК. Первая форма уравнения демонстрирует принцип измерения эластичности в процентах. Конечно, обычные коэффициенты наименьших квадратов обеспечивают оценку влияния единичного изменения независимой переменной X на зависимую переменную, измеряемую в единицах Y. Однако эти коэффициенты не являются эластичностями и показаны вторым способом. записать формулу эластичности как производную от расчетной функции спроса, которая представляет собой просто наклон линии регрессии.Умножение времени наклона дает эластичность, измеряемую в процентах. Вдоль прямолинейной кривой спроса изменение в процентах, то есть эластичность, непрерывно изменяется по мере изменения масштаба, в то время как наклон, расчетный коэффициент регрессии, остается постоянным. Возвращаясь к спросу на бензин. Изменение цены с 3,00 до 3,50 евро означало увеличение цены на 16 процентов. Если бы начальная цена составляла 5,00 фунтов стерлингов, то то же самое повышение на 50 центов было бы только 10-процентным увеличением, создающим другую эластичность. Чтобы дать осмысленную оценку эластичности спроса, принято оценивать эластичность в точке средних значений. Помните, что все линии регрессии МНК проходят через точку среднего. В этот момент находится наибольший вес данных, используемых для оценки коэффициента.Формула для оценки эластичности после оценки кривой спроса МНК выглядит следующим образом: Где и — средние значения этих данных, используемых для оценки , ценового коэффициента. Тот же метод можно использовать для оценки других эластичностей функции спроса, используя соответствующие средние значения других переменных; например, доход и цена товаров-заменителей. Обычные оценки методом наименьших квадратов обычно предполагают, что взаимосвязь совокупности между переменными является линейной, поэтому имеет вид, представленный в уравнении регрессии. Подводя итог, можно выделить четыре случая: Случай 1: Обычный случай наименьших квадратов начинается с линейной модели, разработанной выше: , где коэффициент независимой переменной представляет собой наклон прямой линии и, таким образом, измеряет влияние единичного изменения X на Y, измеряемое в единицах Y. Случай 2: Основное оценочное уравнение: Уравнение оценивается путем преобразования значений Y в логарифмы и использования методов МНК для оценки коэффициента переменной X, b. Умножение на 100 для преобразования в проценты и перестановка членов дает: — это процентное изменение Y в результате изменения единицы X. Случай 3: В этом случае возникает вопрос: «Какова единица изменения Y в результате процентного изменения X?» Какова потеря дохода в долларах в результате пятипроцентного увеличения цены или каково общее влияние на долларовую стоимость пятипроцентного увеличения затрат на рабочую силу? Расчетное уравнение для этого случая будет: Здесь расчетный дифференциал оценочного уравнения равен: Разделите на 100, чтобы получить проценты, а перестановка членов даст: Следовательно, это увеличение Y, измеренное в единицах от увеличения X на один процент. Случай 4. Это случай эластичности, когда и зависимая, и независимая переменные преобразуются в логарифмические значения перед оценкой МНК. Это известно как логарифмический случай или двойной логарифмический случай, и он дает нам прямые оценки эластичности независимых переменных. Расчетное уравнение: Дифференциация у нас: таким образом: и наше определение эластичности. Мы пришли к выводу, что мы можем напрямую оценить эластичность переменной посредством двойного логарифмического преобразования данных. Расчетный коэффициент является эластичностью. Обычно используется двойное логарифмическое преобразование всех переменных при оценке функций спроса, чтобы получить оценки всех различных эластичностей кривой спроса. Почему в линейной регрессии нам нужен диапазон независимой (X) переменной? Точность оценки переменной Y зависит от исследуемого диапазона независимой (X) переменной.Если мы исследуем очень небольшой диапазон переменной X, мы не сможем много использовать регрессию. Также не рекомендуется экстраполяция. Предположим, вы собрали следующую информацию, где X — диаметр ствола дерева, а Y — высота дерева. Уравнение регрессии: Как вы оцениваете среднюю высоту всех деревьев с диаметром ствола 7 дюймов? Производители химикатов, используемых в ошейниках от блох, заявляют, что при стандартных условиях испытаний каждая дополнительная единица химиката приведет к сокращению численности блох на 5 (т. Предположим, что тест был проведен и результаты с компьютера включают: Перехват = 60 Наклон = −4 Стандартная ошибка коэффициента регрессии = 1,0 степени свободы для ошибки = 2000 95% доверительный интервал для наклона −2,04, −5,96 Соответствует ли это доказательство утверждению о том, что количество блох уменьшается со скоростью 5 блох на единицу химического вещества? Как мы видели, коэффициент уравнения, оцененный с помощью регрессионного анализа МНК, дает оценку наклона прямой линии, которая, как предполагается, является отношением между зависимой переменной и, по крайней мере, одной независимой переменной.Из исчисления наклон линии является первой производной и говорит нам о величине влияния изменения переменной XX на одну единицу на значение переменной YY, измеренное в единицах переменной YY. Понятие эластичности заимствовано из техники и физики, где оно используется для измерения реакции материала на силу, обычно физическую силу, такую как растягивающая/вытягивающая сила. Именно отсюда мы получаем термин «эластичная» лента. В экономике речь идет о некоторой рыночной силе, такой как изменение цены или дохода. Эластичность измеряется как процентное изменение/реакция как в технических приложениях, так и в экономике. Ценность измерения в процентах заключается в том, что единицы измерения не играют роли в значении измерения и, таким образом, позволяют проводить прямое сравнение эластичностей.Например, если цена бензина увеличилась, скажем, на 50 центов по сравнению с начальной ценой в 3 доллара, что вызвало снижение ежемесячного потребления потребителем с 50 галлонов до 48 галлонов, мы рассчитываем, что эластичность составит 0,25. Хотя это обсуждение касалось изменений цен, любая из независимых переменных в уравнении спроса будет иметь соответствующую эластичность. Таким образом, существует эластичность дохода, которая измеряет чувствительность спроса к изменениям в доходе: не очень чувствительна к спросу на продукты питания, но очень чувствительна к яхтам. Если уравнение спроса содержит термин для товаров-заменителей, скажем, шоколадных батончиков в уравнении спроса на печенье, то можно измерить реакцию спроса на печенье на изменения цен на шоколадные батончики.Это называется перекрестной ценовой эластичностью спроса, и с точки зрения маркетинга ее можно рассматривать как лояльность к бренду. Насколько реагирует спрос на Coca-Cola на изменение цен на Pepsi? А теперь представьте спрос на очень дорогой товар. Опять же, мера эластичности выражается в процентах, поэтому эластичность можно напрямую сравнить с эластичностью бензина: эластичность 0,25 для бензина дает ту же информацию, что и эластичность 0,25 для автомобиля стоимостью 25 000 долларов. Математические формулы для различных эластичностей: Где η — строчная греческая буква eta используется для обозначения эластичности. ∆ читается как «изменение». Где Y используется как символ дохода. Где P2 — цена товара-заменителя. При ближайшем рассмотрении ценовой эластичности мы можем записать формулу в виде: Где bb — оценочный коэффициент для цены в регрессии МНК. Первая форма уравнения демонстрирует принцип измерения эластичности в процентах. Конечно, обычные коэффициенты наименьших квадратов обеспечивают оценку влияния единичного изменения независимой переменной X на зависимую переменную, измеряемую в единицах Y. Вдоль прямолинейной кривой спроса процентное изменение, то есть эластичность, постоянно изменяется по мере изменения масштаба, в то время как наклон, расчетный коэффициент регрессии, остается постоянным.Возвращаясь к спросу на бензин. Изменение цены с 3,00 до 3,50 долларов означало увеличение цены на 16 процентов. Если бы начальная цена составляла 5 долларов, то то же увеличение на 50 центов было бы всего лишь 10-процентным увеличением, создающим другую эластичность. Каждая прямолинейная кривая спроса имеет диапазон эластичности, начиная с верхнего левого угла, высокие цены, с большими числами эластичности, эластичный спрос и уменьшающийся по мере спуска по кривой спроса неэластичный спрос. Чтобы дать осмысленную оценку эластичности спроса, принято оценивать эластичность в точке средних.Помните, что все линии регрессии МНК проходят через точку среднего. В этот момент находится наибольший вес данных, используемых для оценки коэффициента. Формула для оценки эластичности после оценки кривой спроса МНК принимает следующий вид: этих данных используется для оценки bb, ценового коэффициента. Тот же метод можно использовать для оценки других эластичностей функции спроса, используя соответствующие средние значения других переменных; например, доход и цена товаров-заменителей. Обычные оценки методом наименьших квадратов обычно предполагают, что взаимосвязь совокупности между переменными является линейной, поэтому имеет форму, представленную в уравнении регрессии. В этой форме интерпретация коэффициентов описана выше; просто коэффициент дает оценку влияния изменения X на одну единицу на Y, измеренное в единицах Y. Подводя итог, можно выделить четыре случая: Случай 1: Обычный случай наименьших квадратов начинается с линейной модели, разработанной выше: где коэффициент независимой переменной b=dYdXb=dYdX представляет собой наклон прямая линия и, таким образом, измеряет влияние единичного изменения X на Y, измеряемое в единицах Y. Случай 2: Базовое оценочное уравнение: Уравнение оценивается путем преобразования значений Y в логарифмы и использования методов МНК для оценки коэффициента переменной X, b. Это называется полулогарифмической оценкой. Опять же, дифференцирование обеих частей уравнения позволяет нам разработать интерпретацию коэффициента X b: Умножение на 100 для преобразования в проценты и перестановка членов дает: 29) представляют собой дифференциальные уравнения в частных производных с постоянными коэффициентами, которые можно рассматривать аналитически или полуаналитически.
29) представляют собой дифференциальные уравнения в частных производных с постоянными коэффициентами, которые можно рассматривать аналитически или полуаналитически. Снова рассмотрим неоднородный материал с постоянным коэффициентом Пуассона и экспоненциально изменяющимся модулем (уравнение). (10.28). Теперь основное уравнение функции напряжения Эйри Eq. (10.31) сводится к
Снова рассмотрим неоднородный материал с постоянным коэффициентом Пуассона и экспоненциально изменяющимся модулем (уравнение). (10.28). Теперь основное уравнение функции напряжения Эйри Eq. (10.31) сводится к Эластичность и логарифмическое преобразование – вводная бизнес-статистика

 Это называется неэластичным спросом, означающим небольшую реакцию на изменение цены. Это происходит потому, что реальных заменителей бензина практически нет; возможно общественный транспорт, велосипед или пешком.Технически, конечно, процентное изменение спроса в результате повышения цены представляет собой снижение спроса, поэтому ценовая эластичность является отрицательным числом. Однако принято говорить об эластичности как абсолютном значении числа. Некоторые товары имеют много заменителей: груши для яблок для слив, для винограда и т.д. и т.п. Эластичность для таких товаров больше единицы и называется эластичностью по спросу. Здесь небольшое процентное изменение цены вызовет большое процентное изменение величины спроса.Потребитель легко сместит спрос на близкий заменитель.
Это называется неэластичным спросом, означающим небольшую реакцию на изменение цены. Это происходит потому, что реальных заменителей бензина практически нет; возможно общественный транспорт, велосипед или пешком.Технически, конечно, процентное изменение спроса в результате повышения цены представляет собой снижение спроса, поэтому ценовая эластичность является отрицательным числом. Однако принято говорить об эластичности как абсолютном значении числа. Некоторые товары имеют много заменителей: груши для яблок для слив, для винограда и т.д. и т.п. Эластичность для таких товаров больше единицы и называется эластичностью по спросу. Здесь небольшое процентное изменение цены вызовет большое процентное изменение величины спроса.Потребитель легко сместит спрос на близкий заменитель. Если уравнение спроса содержит термин для товаров-заменителей, скажем, шоколадных батончиков в уравнении спроса на печенье, то можно измерить реакцию спроса на печенье на изменения цен на шоколадные батончики.Это называется перекрестной ценовой эластичностью спроса, и с точки зрения маркетинга ее можно рассматривать как лояльность к бренду. Насколько реагирует спрос на Coca-Cola на изменение цен на Pepsi?
Если уравнение спроса содержит термин для товаров-заменителей, скажем, шоколадных батончиков в уравнении спроса на печенье, то можно измерить реакцию спроса на печенье на изменения цен на шоколадные батончики.Это называется перекрестной ценовой эластичностью спроса, и с точки зрения маркетинга ее можно рассматривать как лояльность к бренду. Насколько реагирует спрос на Coca-Cola на изменение цен на Pepsi? *** QuickLaTeX не может скомпилировать формулу:
\text{Ценовая эластичность:}\phantom{\rule{0. 1em}{0ex}}{\text{η}}_{\text{p}}=\frac{\left(\text{%∆Q}\ вправо)}{\влево(\текст{%∆P}\вправо)}
*** Сообщение об ошибке:
Пакет inputenc Ошибка: символ Юникода η (U+03B7)
начальный текст: ...city:}\phantom{\rule{0.1em}{0ex}}{\text{η}
Файл закончился при сканировании с использованием \frac .
Экстренная остановка.
1em}{0ex}}{\text{η}}_{\text{p}}=\frac{\left(\text{%∆Q}\ вправо)}{\влево(\текст{%∆P}\вправо)}
*** Сообщение об ошибке:
Пакет inputenc Ошибка: символ Юникода η (U+03B7)
начальный текст: ...city:}\phantom{\rule{0.1em}{0ex}}{\text{η}
Файл закончился при сканировании с использованием \frac .
Экстренная остановка.
*** QuickLaTeX не может скомпилировать формулу:
\text{Эластичность дохода:}\phantom{\rule{0.1em}{0ex}}{\text{η}}_{\text{Y}}=\frac{\left(\text{%∆Q}\ вправо)}{\влево(\текст{%∆Y}\вправо)}
*** Сообщение об ошибке:
Пакет inputenc Ошибка: символ Юникода η (U+03B7)
начальный текст: ...city:}\phantom{\rule{0.1em}{0ex}}{\text{η}
Файл закончился при сканировании с использованием \frac .
Экстренная остановка.
*** QuickLaTeX не может скомпилировать формулу:
\text{Перекрестная эластичность:}\phantom{\rule{0. 1em}{0ex}}{\text{η}}_{\text{p1}}=\frac{\left(\text{%∆}) {\ text{Q}}_{1}\right)}{\left(\text{%∆}{\text{P}}_{2}\right)}
*** Сообщение об ошибке:
Пакет inputenc Ошибка: символ Юникода η (U+03B7)
начальный текст: ...city:}\phantom{\rule{0.1em}{0ex}}{\text{η}
Файл закончился при сканировании с использованием \frac .Экстренная остановка.
1em}{0ex}}{\text{η}}_{\text{p1}}=\frac{\left(\text{%∆}) {\ text{Q}}_{1}\right)}{\left(\text{%∆}{\text{P}}_{2}\right)}
*** Сообщение об ошибке:
Пакет inputenc Ошибка: символ Юникода η (U+03B7)
начальный текст: ...city:}\phantom{\rule{0.1em}{0ex}}{\text{η}
Файл закончился при сканировании с использованием \frac .Экстренная остановка.
*** QuickLaTeX не может скомпилировать формулу:
{\ text {η}} _ {\ text {p}} = \ frac {\ left (\ text {% ∆Q} \ right)} {\ left (\ text {% ∆P} \ right)} = \ frac{\text{dQ}}{\text{dP}}\left(\frac{\text{P}}{\text{Q}}\right)=\text{b}\left(\frac{\ текст{P}}{\текст{Q}}\справа)
*** Сообщение об ошибке:
Пакет inputenc Ошибка: символ Юникода η (U+03B7)
начальный текст: $ {\ text {η}
Файл закончился при сканировании с использованием \frac .Экстренная остановка.

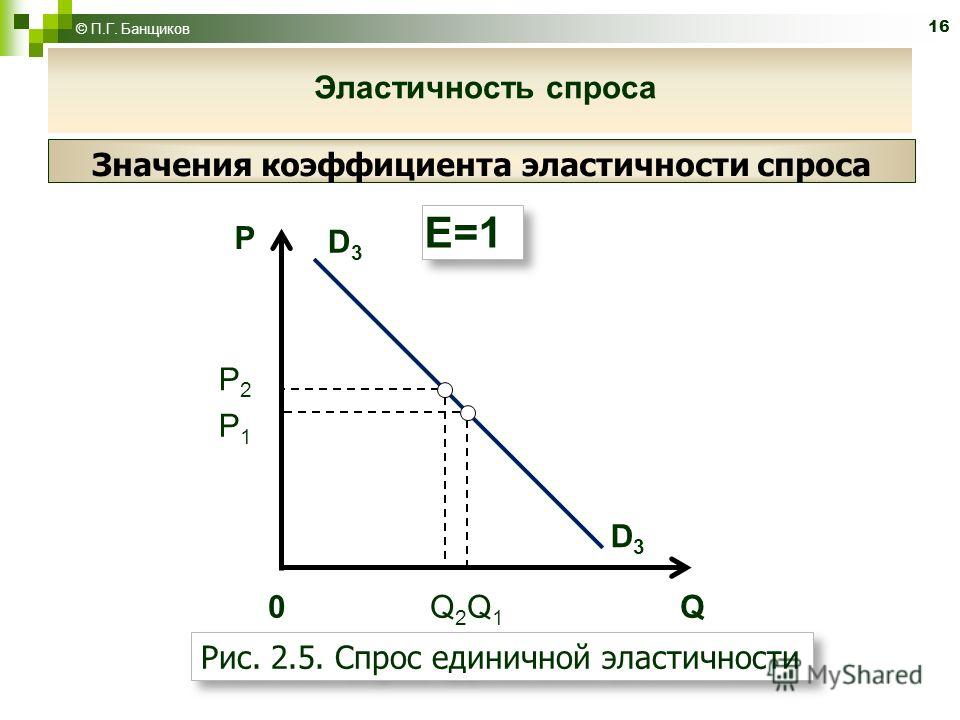 Каждая прямолинейная кривая спроса имеет диапазон эластичности, начиная с верхнего левого угла, высокие цены, с большими числами эластичности, эластичный спрос и уменьшающийся по мере спуска по кривой спроса неэластичный спрос.
Каждая прямолинейная кривая спроса имеет диапазон эластичности, начиная с верхнего левого угла, высокие цены, с большими числами эластичности, эластичный спрос и уменьшающийся по мере спуска по кривой спроса неэластичный спрос. Логарифмическое преобразование данных
 В этой форме интерпретация коэффициентов описана выше; просто коэффициент дает оценку влияния изменения X на одну единицу на Y, измеренное в единицах Y. Не имеет значения, где именно вдоль линии нужно провести измерение, потому что это прямая линия с постоянным наклоном. таким образом, постоянный предполагаемый уровень воздействия на единицу изменения. Однако может случиться так, что аналитик пожелает оценить не простое единичное измеренное влияние на переменную Y, а величину процентного воздействия на Y одной единицы изменения переменной X.Таким случаем может быть то, как единичное изменение опыта, скажем, одного года, влияет не на абсолютную сумму заработной платы рабочего, а на процентное влияние на заработную плату рабочего. В качестве альтернативы может быть задан вопрос об измеряемом в единице измерения воздействии на Y определенного процентного увеличения X. Примером может быть: «На сколько долларов увеличатся продажи, если фирма потратит на X процентов больше на рекламу?» Третья возможность — это рассмотренный выше случай эластичности.
В этой форме интерпретация коэффициентов описана выше; просто коэффициент дает оценку влияния изменения X на одну единицу на Y, измеренное в единицах Y. Не имеет значения, где именно вдоль линии нужно провести измерение, потому что это прямая линия с постоянным наклоном. таким образом, постоянный предполагаемый уровень воздействия на единицу изменения. Однако может случиться так, что аналитик пожелает оценить не простое единичное измеренное влияние на переменную Y, а величину процентного воздействия на Y одной единицы изменения переменной X.Таким случаем может быть то, как единичное изменение опыта, скажем, одного года, влияет не на абсолютную сумму заработной платы рабочего, а на процентное влияние на заработную плату рабочего. В качестве альтернативы может быть задан вопрос об измеряемом в единице измерения воздействии на Y определенного процентного увеличения X. Примером может быть: «На сколько долларов увеличатся продажи, если фирма потратит на X процентов больше на рекламу?» Третья возможность — это рассмотренный выше случай эластичности.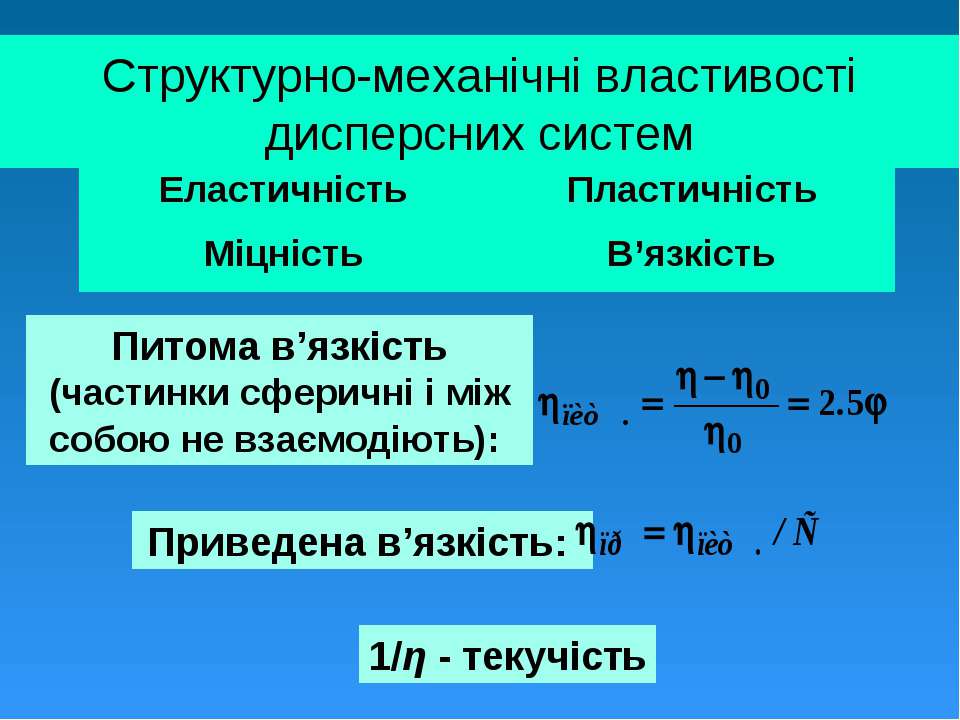 Здесь нас интересует процентное влияние на величину спроса при заданном процентном изменении цены, или дохода, или, возможно, цены замещающего товара.Все три случая можно оценить, преобразовав данные в логарифмы перед запуском регрессии. Полученные коэффициенты затем обеспечат измерение процентного изменения соответствующей переменной.
Здесь нас интересует процентное влияние на величину спроса при заданном процентном изменении цены, или дохода, или, возможно, цены замещающего товара.Все три случая можно оценить, преобразовав данные в логарифмы перед запуском регрессии. Полученные коэффициенты затем обеспечат измерение процентного изменения соответствующей переменной.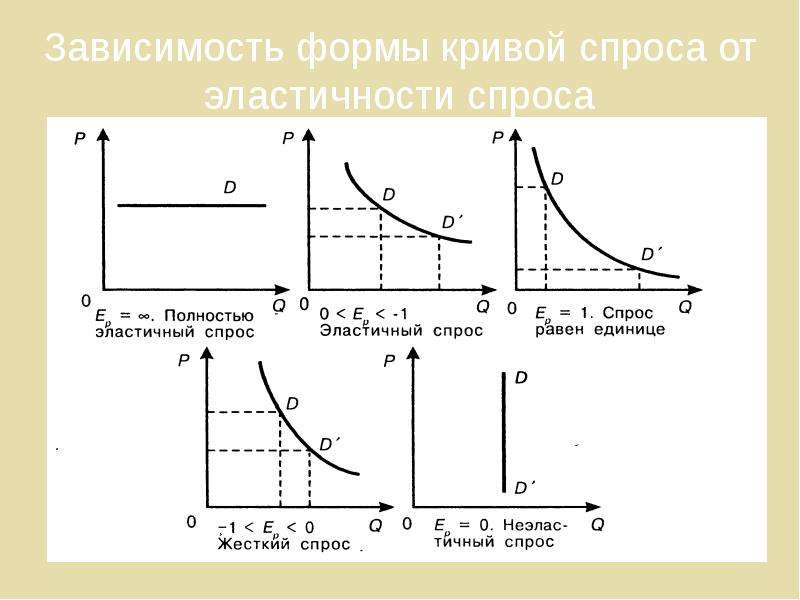 Это называется полулогарифмической оценкой. Опять же, дифференцирование обеих частей уравнения позволяет нам развить интерпретацию коэффициента X b:
Это называется полулогарифмической оценкой. Опять же, дифференцирование обеих частей уравнения позволяет нам развить интерпретацию коэффициента X b: *** QuickLaTeX не может скомпилировать формулу:
100b=\frac{\text{%∆Y}}{\text{Единица измерения ∆X}}
*** Сообщение об ошибке:
Файл закончился при сканировании с использованием \frac .Экстренная остановка.
Таким образом, *** QuickLaTeX не может скомпилировать формулу:
\ frac {b} {100} = \ frac {\ text {d} Y} {100 \ frac {\ text {d} X} {X}} = \ frac {\ text {Единица измерения ∆Y}} {\ text {%∆X}}
*** Сообщение об ошибке:
Файл закончился при сканировании с использованием \frac . Экстренная остановка.
Экстренная остановка.
*** QuickLaTeX не может скомпилировать формулу:
б = \ гидроразрыва {\ текст {% ∆Y}} {\ текст {% ∆ X}}
*** Сообщение об ошибке:
Файл закончился при сканировании с использованием \frac .Экстренная остановка.

Х Д 4 8 2 4 8 18 6 22 10 30 6 8  е. где и , :
е. где и , : 13.5 Интерпретация коэффициентов регрессии: эластичность и логарифмическое преобразование — вводная бизнес-статистика
 Как мы видели в случае с фиктивными переменными, это может проявляться как параллельный сдвиг оцениваемой линии или даже изменение наклона линии через интерактивную переменную. Здесь мы хотим исследовать концепцию эластичности и то, как мы можем использовать регрессионный анализ для оценки различных эластичностей, которые интересуют экономистов.
Как мы видели в случае с фиктивными переменными, это может проявляться как параллельный сдвиг оцениваемой линии или даже изменение наклона линии через интерактивную переменную. Здесь мы хотим исследовать концепцию эластичности и то, как мы можем использовать регрессионный анализ для оценки различных эластичностей, которые интересуют экономистов. Ценовая эластичность – это процентное изменение количества товара в результате некоторого процентного изменения цены. 16-процентное увеличение цены вызвало только 4-процентное снижение спроса: 16-процентное изменение цены → 4-процентное изменение количества или 0,04/0,16 = 0,25. Это называется неэластичным спросом, означающим небольшую реакцию на изменение цены.Это происходит потому, что реальных заменителей бензина практически нет; возможно общественный транспорт, велосипед или пешком. Технически, конечно, процентное изменение спроса в результате повышения цены представляет собой снижение спроса, поэтому ценовая эластичность является отрицательным числом. Однако принято говорить об эластичности как абсолютном значении числа. Некоторые товары имеют много заменителей: груши для яблок для слив, для винограда и т.д. и т.п. Эластичность для таких товаров больше единицы и называется эластичностью по спросу.Здесь небольшое процентное изменение цены вызовет большое процентное изменение величины спроса.
Ценовая эластичность – это процентное изменение количества товара в результате некоторого процентного изменения цены. 16-процентное увеличение цены вызвало только 4-процентное снижение спроса: 16-процентное изменение цены → 4-процентное изменение количества или 0,04/0,16 = 0,25. Это называется неэластичным спросом, означающим небольшую реакцию на изменение цены.Это происходит потому, что реальных заменителей бензина практически нет; возможно общественный транспорт, велосипед или пешком. Технически, конечно, процентное изменение спроса в результате повышения цены представляет собой снижение спроса, поэтому ценовая эластичность является отрицательным числом. Однако принято говорить об эластичности как абсолютном значении числа. Некоторые товары имеют много заменителей: груши для яблок для слив, для винограда и т.д. и т.п. Эластичность для таких товаров больше единицы и называется эластичностью по спросу.Здесь небольшое процентное изменение цены вызовет большое процентное изменение величины спроса.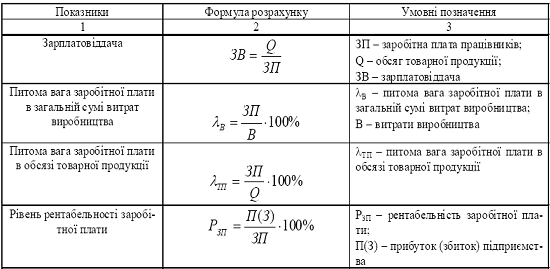 Потребитель легко сместит спрос на близкий заменитель.
Потребитель легко сместит спрос на близкий заменитель. Потребитель считает, что оба товара имеют мало заменителей и, следовательно, имеют неэластичные кривые спроса, эластичность которых меньше единицы.
Потребитель считает, что оба товара имеют мало заменителей и, следовательно, имеют неэластичные кривые спроса, эластичность которых меньше единицы. Эти коэффициенты, однако, не являются коэффициентами эластичности и показаны во втором способе написания формулы эластичности как (dQdP)(dQdP), производная оценочной функции спроса, которая представляет собой просто наклон линии регрессии. Умножение времени наклона PQPQ дает эластичность, измеряемую в процентах.
Эти коэффициенты, однако, не являются коэффициентами эластичности и показаны во втором способе написания формулы эластичности как (dQdP)(dQdP), производная оценочной функции спроса, которая представляет собой просто наклон линии регрессии. Умножение времени наклона PQPQ дает эластичность, измеряемую в процентах.
Логарифмическое преобразование данных
 Не имеет значения, где именно вдоль линии нужно провести измерение, потому что это прямая линия с постоянным наклоном. таким образом, постоянный предполагаемый уровень воздействия на единицу изменения.Однако может случиться так, что аналитик пожелает оценить не простое единичное измеренное влияние на переменную Y, а величину процентного воздействия на Y одной единицы изменения переменной X. Таким случаем может быть то, как единичное изменение опыта, скажем, одного года, влияет не на абсолютную сумму заработной платы рабочего, а на процентное влияние на заработную плату рабочего. В качестве альтернативы может быть задан вопрос об измеряемом в единице измерения воздействии на Y определенного процентного увеличения X. Примером может быть: «На сколько долларов увеличатся продажи, если фирма потратит на X процентов больше на рекламу?» Третья возможность — это рассмотренный выше случай эластичности.Здесь нас интересует процентное влияние на величину спроса при заданном процентном изменении цены, или дохода, или, возможно, цены замещающего товара.
Не имеет значения, где именно вдоль линии нужно провести измерение, потому что это прямая линия с постоянным наклоном. таким образом, постоянный предполагаемый уровень воздействия на единицу изменения.Однако может случиться так, что аналитик пожелает оценить не простое единичное измеренное влияние на переменную Y, а величину процентного воздействия на Y одной единицы изменения переменной X. Таким случаем может быть то, как единичное изменение опыта, скажем, одного года, влияет не на абсолютную сумму заработной платы рабочего, а на процентное влияние на заработную плату рабочего. В качестве альтернативы может быть задан вопрос об измеряемом в единице измерения воздействии на Y определенного процентного увеличения X. Примером может быть: «На сколько долларов увеличатся продажи, если фирма потратит на X процентов больше на рекламу?» Третья возможность — это рассмотренный выше случай эластичности.Здесь нас интересует процентное влияние на величину спроса при заданном процентном изменении цены, или дохода, или, возможно, цены замещающего товара. Все три случая можно оценить, преобразовав данные в логарифмы перед запуском регрессии. Полученные коэффициенты затем обеспечат измерение процентного изменения соответствующей переменной.
Все три случая можно оценить, преобразовав данные в логарифмы перед запуском регрессии. Полученные коэффициенты затем обеспечат измерение процентного изменения соответствующей переменной.
Случай 3: В этом случае возникает вопрос: «Какова единица изменения Y в результате процентного изменения X?» Какова потеря дохода в долларах в результате пятипроцентного увеличения цены или каково общее влияние на долларовую стоимость пятипроцентного увеличения затрат на рабочую силу? Расчетное уравнение для этого случая будет следующим:
Здесь расчетный дифференциал расчетного уравнения:
Разделите на 100, чтобы получить проценты, и перестановка членов дает:
Y%∆XСледовательно, b100b100 — это увеличение Y, измеренное в единицах от увеличения X на один процент.
Случай 4. Это случай эластичности, когда и зависимая, и независимая переменные преобразуются в логарифмические до оценки МНК. Это известно как логарифмический случай или двойной логарифмический случай, и он дает нам прямые оценки эластичности независимых переменных. Расчетное уравнение:
Дифференцируя, мы имеем:
d(logY)=bd(logX)d(logY)=bd(logX)d(logX)=b1XdXd(logX)=b1XdXтаким образом:
1YdY=b1XdXORdYY=bdXXORb =dYdX(XY)1YdY=b1XdXORdYY=bdXXORb=dYdX(XY) и b=%∆Y%∆Xb=%∆Y%∆X наше определение эластичности. Мы пришли к выводу, что мы можем напрямую оценить эластичность переменной посредством двойного логарифмического преобразования данных. Расчетный коэффициент является эластичностью. Обычно используется двойное логарифмическое преобразование всех переменных при оценке функций спроса, чтобы получить оценки всех различных эластичностей кривой спроса.
Мы пришли к выводу, что мы можем напрямую оценить эластичность переменной посредством двойного логарифмического преобразования данных. Расчетный коэффициент является эластичностью. Обычно используется двойное логарифмическое преобразование всех переменных при оценке функций спроса, чтобы получить оценки всех различных эластичностей кривой спроса.
Что такое перекрестная эластичность спроса? Определение перекрестной эластичности спроса, перекрестной эластичности спроса Значение
Определение: Мера реакции спроса на товар на изменение цены на родственный товар называется перекрестной ценовой эластичностью спроса.Он всегда измеряется в процентах.
Описание: Поскольку поведение потребления взаимосвязано, изменение цены на родственный товар приводит к изменению спроса на другой товар. Сопутствующие товары бывают двух видов: заменители и дополнительные товары. В случае, если два товара не связаны между собой, коэффициент перекрестной эластичности равен нулю.
В случае, если два товара являются заменителями друг друга, как чай и кофе, перекрестная ценовая эластичность будет положительной, т.е.е. если цена на кофе увеличивается, спрос на чай увеличивается. С другой стороны, если товары дополняют друг друга по своей природе, например, перо и чернила, то перекрестная эластичность будет отрицательной, т. е. спрос на чернила уменьшится, если цены на перо вырастут, или наоборот.
Посмотрите видео, чтобы узнать больше о перекрестной эластичности спроса.
macromedia.com/go/getflashplayer» quality=»high» src=»http://timesofindia.indiatimes.com/configspace/ads/timesChannelWrapper.swf» type=»application/x-shockwave-flash» wmode=»transparent»/>
. Предположим, что по мере роста цены на индейку
от 35 до 40 центов за фунт, спрос на курятину увеличивается.
от 250 тонн до 275 тонн. Предположим, что в расчете на душу населения
доход увеличивается с 15 000 до 16 000 долларов в зависимости от количества спроса на индейку. Согласно закону спроса, когда цена на товар растет, потребители покупают его меньше, и наоборот. Эластичность спроса определяется как процентное изменение объема спроса, деленное на процентное изменение цены. Если увеличение цены на 10 % приводит к падению спроса на 20 %, то коэффициент эластичности будет равен 20/10 = 2,0.Или, если 15-процентное повышение цены приводит к 10-процентному снижению объема спроса, тогда коэффициент эластичности будет равен 15/10 = 0,67. Если коэффициент больше единицы, спрос считается эластичным. Если меньше единицы, то спрос неэластичен. Коэффициент — это индекс, он не измеряет цену или количество. Эластичность спроса определяется рядом факторов. Если продукт является предметом первой необходимости, например фармацевтическое лекарство, спрос, вероятно, будет неэластичным. Когда потребители имеют неэластичный спрос на продукт, они будут продолжать покупать, даже когда цена растет. Спрос на сигареты, например, остается высоким, несмотря на значительное повышение цен. (Вот почему правительство облагает их налогом, а люди продолжают курить.) С другой стороны, планировщики отпусков обнаружат, что спрос на дорогие отпуска более эластичен, поскольку покупатели будут отговариваться от них, когда цены вырастут. Упражнение. Коэффициенты эластичности
Это
Упражнение включает ряд задач, которые требуют от вас вычисления
коэффициенты эластичности с использованием формул дуговой эластичности.Вы должны тогда
интерпретировать значение расчетной эластичности. Вопросов:
1.
Предположим, что когда цена за
фунт индейки растет
с 35 центов до 40 центов, объем спроса на индейку снижается с
со 180 млн тонн до 160 млн тонн. 2.

Формула дуги для креста
эластичность спроса по цене равна: 3.
Дуговая формула дохода
эластичность спроса это:  увеличивается с 250 тонн до 255 тонн.
увеличивается с 250 тонн до 255 тонн. 4.
На курином рынке
увеличение спроса сдвинет кривую спроса вверх вдоль кривой предложения.  Следовательно, кривая долгосрочного предложения была бы совершенно
горизонтальный.Какова ценовая эластичность предложения при данном
долларовая стоимость?
Следовательно, кривая долгосрочного предложения была бы совершенно
горизонтальный.Какова ценовая эластичность предложения при данном
долларовая стоимость? Ссылки по теме
Как рассчитать эластичность спроса по продажам и цене | Малый бизнес
 Концепция эластичности измеряет, насколько меньше потребители будут покупать при повышении цены. Это важно для каждого владельца малого бизнеса, который должен знать, как изменения цен повлияют на его продажи.
Концепция эластичности измеряет, насколько меньше потребители будут покупать при повышении цены. Это важно для каждого владельца малого бизнеса, который должен знать, как изменения цен повлияют на его продажи. Как измеряется эластичность
Что определяет эластичность
 Спрос на ювелирные изделия будет более эластичным. Если цена товара мала по сравнению с доходом покупателей, спрос будет неэластичным. Вот почему во многих магазинах у кассы так много недорогих безделушек. Наличие заменителей сделает спрос более эластичным. Например, если цена на свинину вырастет, покупатели будут покупать меньше свинины и больше курятины. Наконец, время определяет эластичность. Если человек едет по пустынному участку автострады и замечает, что стрелка указателя уровня топлива приближается к нулю, его спрос на бензин становится неэластичным.
Спрос на ювелирные изделия будет более эластичным. Если цена товара мала по сравнению с доходом покупателей, спрос будет неэластичным. Вот почему во многих магазинах у кассы так много недорогих безделушек. Наличие заменителей сделает спрос более эластичным. Например, если цена на свинину вырастет, покупатели будут покупать меньше свинины и больше курятины. Наконец, время определяет эластичность. Если человек едет по пустынному участку автострады и замечает, что стрелка указателя уровня топлива приближается к нулю, его спрос на бензин становится неэластичным. Значение эластичности



 Bournemouth University Business School. – October 2011 : [Електронний ресурс]. – Режим доступу : http://business.bournemouth.ac.uk/downloads/ Djalilov_and_ Piesse.pdf
Bournemouth University Business School. – October 2011 : [Електронний ресурс]. – Режим доступу : http://business.bournemouth.ac.uk/downloads/ Djalilov_and_ Piesse.pdf